Задачи на сплавы и смеси как решать – Задачи на смеси и сплавы. Учебник по ЕГЭ и ГИА - Управленческое образование

Содержание

Задачи на сплавы и смеси с решениями. на Сёзнайке.ру

Задача №1.

Сплав меди и цинка весом 20кг содержит 30% меди. Добавили 22кг цинка. Сколько нужно добавить меди, чтобы в сплаве стало 60% цинка.

Решение:

I способ:

30% 70%

20кг = 6кг + 36кг

Добавили цинка — +22кг

42кг = 6кг + 36кг

100% = 40% + 60%

36кг составляет 60%.

36:0.6=60кг – новый сплав.

60(кг) = 6(кг) + 36(кг) + x(кг)

x=18 (кг).

II способ:

Очень удобно в задачах на сплавы, смеси, концентрации составлять таблицу по условию задачи (жирным шрифтом), а затем заполнять пустые клетки, руководствуясь законом сохранения массы(объема) и формулами расчета «Процент от числа»

Для начала нужно определить количество объектов, которые участвуют в условии задачи ( в нашем случае их 4), затем занести в таблицу все, что говорится о каждом объекте. По вопросу задачу вводится переменная ( в нашем случае это x кг меди)

Объекты	I	добавили цинка	добавили меди	получили сплав
масса (кг)	20	22	x	20+22+x
% меди	30		100
% цинка		100
масса меди (кг)				60
масса цинка (кг)

Теперь начинаем заполнение пустых клеток:

Объекты	I	добавили цинка	добавили меди	получили сплав
масса (кг)	20	22	x	20+22+x=42+x
% меди	30	0	100	100-60=40
% цинка	100-30=70	100	0	60
масса меди (кг)	(20*30)/100	0	x	(42+x)40/100=(2030)/100+0+x
масса цинка (кг)	(20*70)/100	100	0

Нам, в принципе, достаточно заполнения четырех строк, чтобы составить уравнение.

Обратим внимание на «желтую» клетку- эта клетка является ключом составления уравнения задачи, т.к. мы ее можем заполнить по формуле «40 % от числа 42+x», а также по закону сохранения массы: (20*30)/100+0+x.

Следовательно, имеем уравнение:

Ответ: 18.

Задача №2.

Имеется сплав серебра с медью. Вычислите массу сплава и процентное содержание серебра в нем, зная, что сплавив его с 3кг чистого серебра, получается сплав, содержащий 90% серебра, а сплавив его с 2кг чистого серебра, получается сплав, содержащий 86% серебра.

Решение:

Xкг – масса исходного сплава

(X+3)кг – масса первого сплава

(X+2)кг – масса второго сплава

(X+3)*0.9(кг) – содержание серебра в первом сплаве

(X+2)*0.86(кг) – масса серебра во втором сплаве

(X+3)*0.9-(X+2)*0.86=1

X=0.5

Табличный способ:

По первому предложению составляем таблицу

Объект	I	II	Смесь
m кг	x	3	3+x
% серебра	p	100	90
m_{серебра} кг	x*p/100	3*100/100	(3+x)90/100=xp/100+3*100/100

По второму предложению составляем таблицу

Объект	I	II	Смесь
m кг	x	2	2+x
% серебра	p	100	86
m_{серебра} кг	x*p/100	2*100/100	(2+x)86/100=xp/100+2*100/100

В результате в «желтых» клетках имеем уравнения для системы:

Тогда 0,5p=15, p=30

Ответ: 0,5 кг; 30 % серебра.

Задача №3.

Из 50т руды получают 20т металла, который содержит 12% примесей. Сколько процентов примесей содержит руда?

Решение:

1) Сколько примесей содержится в металле?

20*0.12=2.4(т)

2) 50т = 20т + 3т = (17.6 + 2.4) +30= 17.6+ (2.4 + 30)

металл примеси примеси чистый примеси

металл

3) 50т – 100%

32.4т – x%

50/32,4=100/x ; x=64.8

Табличный способ:

Объект	I	II	Получили
m тн	50	50-20=30	20
% примесей	p	100	12
m_{примесей} тн	50*p/100	30	2012/100=50p/100-30

12*20=50p-3000

50p=3240

p=64.8

Ответ: 64.8%.

Задача №4.

Сплав меди и цинка весом 60 кг содержит 40% меди. Сколько нужно добавить цинка, чтобы в сплаве его концентрация достигла 80%.

Решение:

Табличный способ:

Объект	I	II	Получили
m кг	60	x	60+x
% цинка	100-40=60	100	80
m_цинка кг	60*60/100	x	(60+x)80/100=6060/100+x

Имеем:

(60+x)*0.8=36+x

48+0.8x=36+x

x=60 кг цинка нужно добавить.

Задача №5.

К 15 литрам 10%-ого раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?

Решение:

1) Пусть добавили Xл 5%-ного раствора соли.

(15+X)л – столько стало нового раствора

(15+X)*0.08л – столько в нем содержится соли

2) В 15 литрах 10%-ного раствора содержится

15*0.1=1.5(л) соли

3) В Xл 5%-ного раствора содержится 0.05Xл соли

X=10.

Добавили 10л 5%-ного раствора соли.

Табличный способ:

Объект	I	II	Получили
m л	15	x	15+x
% соли	10	5	8
m_соли л	15*10/100	x*5/100	(15+x)8/100=1510/100+5x/100

Имеем:

8(15+x)=150+5x

3x=30

x=10

Ответ: 10л

Задача №6.

В лаборатории есть раствор соли 4-х различных концентраций. Если смешать I, II, III растворы в весовом отношении 3:2:1, то получится 15%-ный раствор. II, III, IV растворы в равной пропорции дают при смешивании 24%-ный раствор, и , наконец, раствор составленный из равных частей I и III растворов, имеет концентрацию 10%. Какая концентрация будет при смешении II и IV растворов в пропорции 2:1?

Решение:

1) Пусть в 1кг I р-ра – Xкг соли

II р-ра – Yкг соли

III р-ра – Zкг соли

IV р-ра – tкг соли

2) В условии говорится, что если мы смешаем 3кг I раствора, 2кг II раствора и 1кг III раствора, то в получившихся 6кг р-ра будет 6*0.15=0.9кг соли. Но в 3-х кг I р-ра имеется (3X)кг соли, в 2кг II р-ра ее (2Y)кг и в одном кг III р-ра – Zкг. Отсюда получается первое уравнение 3x+2y+Z=0.9

3) Рассуждая аналогично, получим, что

Y + Z + t = 0.72

X + Z = 0.2,

Т.е. получим систему:

Из этой системы нам нужно вычленить 2y + t.

2y+t=0,5(3x+2y+Z)+(y+Z+t)-1,5(x+Z)=0,5^.0,9+0,72-1,5^.0,2=0,87

Значит, если смешать 2кг второго раствора и 1кг четвертого, то в получившихся 3кг смеси будет 0.87кг соли, что составляет 29%, что и требовалось найти.

3кг – 100%

0.87кг – x%

3/0,87=100/x;

x = 29%.

Ответ: 29%

Задача №7.

Даны два сплава. Первый весит 4кг и содержит 70% серебра. Второй весит 3кг и содержит 90% серебра. Сколько кг второго сплава надо сплавить со всем первым сплавом, чтобы получить r%-ный сплав серебра? При каких r задача имеет решение?

Решение:

В первом сплаве – 2.8кг серебра. Пусть надо взять x(кг) второго сплава, чтобы сплавив его со всем первым сплавом, получить такой сплав, как требуется. Весь сплав будет весить (x+4)кг. Серебра в нем будет (2.8+0.9x)кг.

По условию ( 2,8+0,9x)/(x+4)=r/100

(x+4)кг – 100%

2.8+0.9x – r%, откуда x=(4r-280)/(90-r). Задача имеет решение тогда и только тогда, когда 0?x?3 (только в таких пределах можно что-либо взять из куска весом в 3кг), т.е. 0?(4r-280)/(90-r)?3 , откуда 70?r?80 .

Ответ: x=(4r-280)/(90-r), задача имеет решение при 70?r?80.

www.seznaika.ru

Задачи на смеси и сплавы

Задачи на смеси и сплавы легко решить, если правильно оформить условие. Такие задачи проще решать с помощью системы уравнений. Рассмотрим решение задач на смеси и сплавы на примерах.

Начнем с задачи на смеси.

1) Сколько граммов 4-процентного и сколько граммов 10-процентного растворов соли нужно взять, чтобы получить 180 граммов 6-процентного раствора?

Решение:

Пусть x граммов 4-процентного и y граммов 10-процентногорастворов соли нужно взять.

	4%	10%	6%
Раствор	x	y	180
Соль	0,04x	0,1y	0,06·180=10,8

Составим и решим систему уравнений:

Для удобства умножим почленно второе уравнение на 100

Первое уравнение умножим почленно на -10:

Сложив почленно первое и второе уравнение, получим

Отсюда x=120. Подставив в уравнение x+y=180 найденное значение x=120, находим y=60.

Значит, 120 граммов 4-процентного и 60 граммов 10-процентного растворов нужно взять.

Ответ: 120 г, 60 г.

Следующая — задача на сплавы.

2) Сколько килограммов 25-процентного и сколько килограммов 50-процентного сплавов меди нужно взять, чтобы получить 20 килограммов 40-процентного сплава?

Решение:

Пусть x килограммов 25-процентного и y килограммов 50-процентного сплавов меди нужно взять.

	25%	50%	40%
Сплав	x	y	20
Медь	0,25x	0,5y	0,4·20=8

Составим и решим систему уравнений:

Умножим второе уравнение на -4:

Сложив почленно первое и второе уравнение, имеем:

Подставив в первое уравнение найденное значение y=12, находим

Значит, 8 кг 25-процентного и 12 кг 50-процентного сплавов надо взять.

Ответ: 8 кг и 12 кг.

И еще одна задача на смеси и сплавы.

3) В первом бидоне — молоко, жирность которого составляет 3%, во втором — сливки жирностью 18%. Сколько надо взять молока и сколько сливок, чтобы получить 10 литров молока жирностью 6%?

Решение:

Пусть x литров молока жирностью 3% и y литров сливок жирностью 18% надо взять.

	3%	18%	6%
Молоко или сливки	x	y	10
Жир	0,03x	0,18y	0,06·10=0,6

Составим и решим систему уравнений:

Умножим второе уравнение системы на 100:

Затем второе уравнение разделим почленно на -3:

Сложим почленно первое и второе уравнение:

Подставим в первое уравнение системы:

Значит, 8 литров молока жирностью 3% и 2 литра сливок жирностью 18% надо взять.

Ответ: 2 л и 8 л.

www.uznateshe.ru

Решение задач на сплавы, смеси, работу, движение, проценты с использованием таблиц

Разделы: Математика

Цель: научить учащихся, используя таблицу, быстро решать “трудные” задачи.

При решении многих задач можно использовать таблицу, которая мобилизует, упрощает, помогает решению задач. Для начала введем стандартную таблицу.3 на 3 (Три линии по горизонтали и три по вертикали)

Схема таблицы:

Данная таблица приемлема при решении задач на движение, на работу, на сплавы, растворы и проценты. При решении многих задач в столбцах рекомендую детям следующее обозначение (См. презентацию):

Рассмотрим задачи.

1. Имеется руда из двух пластов с содержанием меди (1 вещество) в 6% и 11%.Сколько надо взять “бедной” руды, чтобы получить при смешивании с “богатой” (2 вещество), 20 тонн с содержанием меди 8% (1+2 вещество)?

Возможны наводящие вопросы:

Если первое вещество 6%, то второе сколько %?
Первое обозначаем Х т, а общий вес 20 т, то второго сколько т?
Медь первого куска и второго составляет медь сплава.

Заполним таблицу:

	1-ое вещество (медь)	2-ое вещество	Вес (т)
1.	6%	94%	х
2.	11%	89%	20-х
1. + 2.	8%	92%	20

Составим уравнение с использованием 1-го или 2-го столбца и обязательно 3-го. Получаем линейное уравнение. Решение не вызывает трудности.

1столбец и 3 столбец	или	2столбец и 3 столбец
6х+11(20-х)=8*20		94х+89(20-х)=92*20
х=12

Ответ 12т

2.Раствор 18% соли (1 вещество) массой 2 кг разбавили стаканом воды (2 вещество)0,25 кг. Какой концентрации раствор (1+2 вещество) в процентах в результате был получен?

Возможны наводящие вопросы:

Добавляем чистую воду, тогда сколько % соли?

	1 в-во (соль)	2 в-во (вода)	вес
1	18%	82%	2 кг
2	0%	100%	0,25 кг
1+2	х%	(100-х)%	2,25 кг

1столбец и 3 столбец 2столбец и 3 столбец.

18*2=х*2,25 или 82*2+100*0,25=2,25(100-х)

х=16

Ответ 16%

3.Цену товара первоначально снизили на 20%, затем еще на 15%. На сколько процентов всего снижена цена?

При решении задач на проценты меняется точка отсчета, “стало” из первой строки переходит в “было” второй строки т.д. (См. презентацию)

	Было	Изменение	Стало
1	х	-20%	х-0,2х=0,8х
2	0,8х	-15%	0,8х(1-0.15)=0,68х
	0,68х

Составляем уравнение, отвечая на вопрос задачи:

х-0,68х=0,32х 32%

Ответ 32%

4.Цену на автомобиль подняли сначала на 45%, а затем ещё на 20%,и после перерасчета повысили на 10%. На сколько процентов всего повысилась цена?

	Было	Изменение	Стало
1	х	+45%	х+0,45х=1,45х
2	1,45х	+20%	1,45х(1+0,2)=1,74х
3	1,74х	+10%	1,74х(1+0,1)=1,914х

Составляем уравнение, отвечая на вопрос задачи:

1,914х-1=0,914х 91,4%

Ответ:91,4%

5.Два комбайна убирали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?

	v	t	A
1	1\х	х	1
2	1\(х-6)	х-6	1
1+2	1\4	4	1

1\х+1\(х-6)=1\4

4(х-6)+4х=х(х-6)

х=12

Ответ:12 дней

6.Один завод может выполнить некоторый заказ на 4 дня быстрее, чем другой. За какое время может выполнить этот заказ каждый завод, если известно, что при совместной работе за 24 дня они выполнили заказ, в пять раз больший?

	v	t	A
1.	1\х	х	1
2.	1\(х+4)	х+4	2
1.+2.	5\24	24	5

1\х+1\(х+4)=5\24

5х²-28х-96=0

х=8, 8 дней и 12 дней.

Ответ: 8 дней; 12 дней.

7.Две бригады работниц пропололи по 280 грядок каждая, причем первая бригада, пропалывая в день на 30 грядок меньше, чем вторая работала на 3 дня больше. Сколько дней работала каждая бригада?

	v	t	Vраб
1	х	280\х	280
2	х+30	280\(х+30)	280
		t₁-3=t₂

280\х-3=280\(х+30)

x=40 (грядок), 7 дней и 4 дня.

Ответ: 7 дней, 4 дня.

8.Свежие грибы содержат по массе 90% воды сухие-12% воды. Сколько получиться сухих грибов из 22 кг свежих?

Что происходит с водой? (испаряется)

Какой компонент не меняется? (Вещество)

	Воды	Вещество	Вес
Сухое	12%	88%	х
Свежее	90%	10%	22 кг
		Одинаково

На основании этого составим уравнение:

0,88х=0,1*22

х=2,5

Ответ: 2,5 кг.

Примеры задач для самостоятельного решения:

В результате очистки сырья количество примесей в нём уменьшилось от 20% в исходном сырье до 5% в очищенном. Сколько надо взять исходного сырья, чтобы получить 160 кг очищенного?
Имеется лом стали двух сортов с содержанием никеля 5% и 40%.Сколько нужно взять металла каждого сорта, чтобы получить 140 тонн стали с содержанием никеля 30%?
Цену на столовый сервиз повысили сначала на 25%, а потом ещё на 20%. Во сколько раз увеличилась цена сервиза?
Морская вода содержит 5% (по весу) соли: Сколько кг пресной воды надо добавить к 40 кг морской воды, чтобы концентрация соли в последней стала 2%?
Применить этот метод можно к разным типам задач. Научившись решать не трудные задачи постепенно возможно и усложнение текста. Главное экономия времени. Рассматривая Кимы ЕГЭ задачи такого содержания очень популярны.

Литература:

Система тренировочных задач и упражнений по математике. Симонов А.Я. Бакаев Д.С. Эпельман А.Г. и др.
Задания для проведения письменного экзамена по математике в 9 классе. Под ред. Звавич Л.И., и под ред. Л.В.Кузнецовой.
ДВГТУ центр довузовской подготовки Математика (задачи на сплавы, растворы, на проценты) г. Владивосток 1998 г.

Презентация

19.02.2010

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Различные способы решения задач на смеси, сплавы , растворы

Различные способы решения задач на смеси, сплавы, растворы

Вайланд Анна Павловна, учитель математики МАОУ «Средняя общеобразовательная школа №3»

Балаково – 201 5 2

Проблема и гипотеза

Рассматривая учебники по математике разных авторов, я увидела несколько совершенно разных по типу задач на растворы, а решения одних и тех же задач в одних учебниках были совершенно другими, нежели в других. Поэтому выдвинула свою гипотезу:
Гипотеза: все задачи на растворы, сплавы и смеси делятся на несколько типов, а каждый из типов имеет конкретный способ решения.

Цели и задачи

Систематизировать задачи на растворы, смеси и сплавы;
Найти единый алгоритм решения этих задач;
Научиться решать задачи по заданной теме.

ЕГЭ и межпредметная связь

Созданный мною проект содержит материал по теме «Проценты» из курса математики, который может помочь также и при решении заданий на проценты не только в тестах ЕГЭ по математике за курс основной и средней школы, а так же при изучении химии, биологии, физики и других предметов.

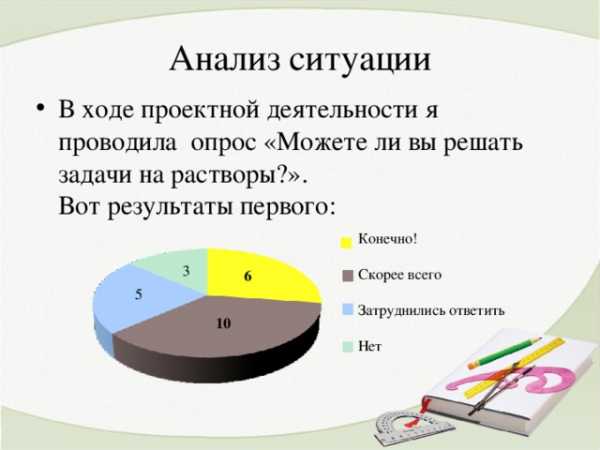
Анализ ситуации

В ходе проектной деятельности я проводила опрос «Можете ли вы решать задачи на растворы?». Вот результаты первого:

Конечно!

Скорее всего

Затруднились ответить

Нет

Введение

Для решения задач на концентрации нужно уметь рассуждать и решать задачи на дроби и проценты, на составление уравнений и их систем. Эти задачи решаются арифметически, применением линейного уравнения и их систем, и другие способы.

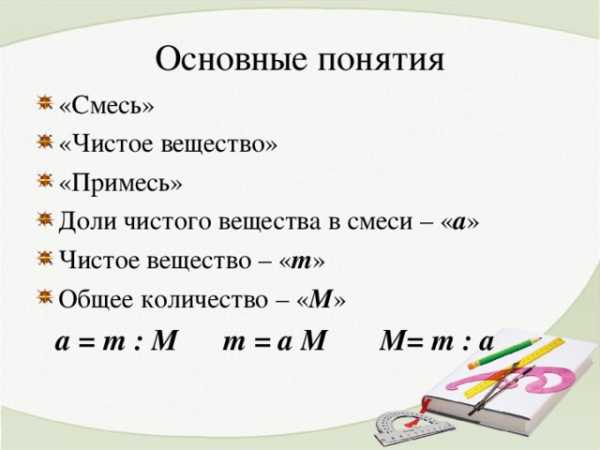
Основные понятия

«Чистое вещество»

«Примесь»
Доли чистого вещества в смеси – « a »
Чистое вещество – « m »
Общее количество – « М »

a = m : M m = a M M = m : a

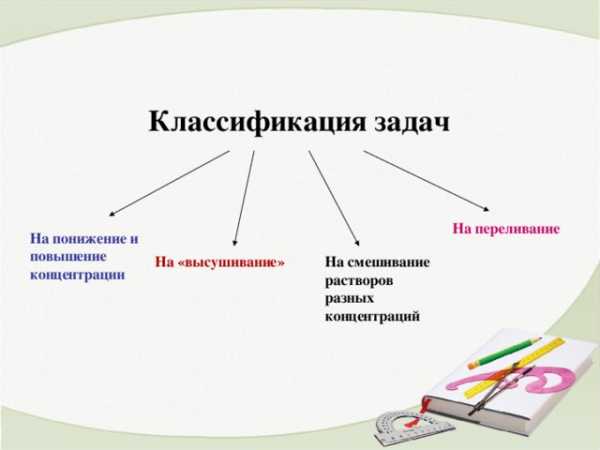
Классификация задач

На переливание

На понижение и повышение концентрации

На «высушивание»

На смешивание растворов разных концентраций

Задачи на понижение и повышение концентрации

Задача №1: сироп содержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15% ?

Задача №2: сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?

Решение задачи №1

II . Правило «креста»

18 15

0 3

I . Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.

Значит, 40 кг – 15 частей тогда, чтобы получить 15% р-р нужно добавить 3 части воды

40:15 · 3=8 кг.

Ответ: 8 кг

Составим и решим уравнение:

0,15(40+х)=0,18*40

х =8

Ответ: 8 кг.

Было

18%=0,18

М(кг)

Стало

т (кг)

15%=0,15

0,18*40

40+ х

0,15(40+ х )

Задачи на высушивание

Задача №3:

Пчелы перерабатывают цветочный нектар в мёд, освобождая его от воды. Нектар содержит 84% воды, а полученный мёд — 20%. Сколько кг нектара нужно переработать пчелам для получения 1 кг мёда?

Решение задачи №3

При решении таких задач надо разделять вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи

1. Арифметический

1) 100-20=80% — составляет основное вещество от полученного мёда.

2) 1*0,8=0,8 кг – масса основное вещество в 1 кг.

3) 100-84 = 16% — составляет основное вещество от собранного нектара.

4) 0,8:0,16 = 5 кг нектара.

Ответ: 5 кг нектара нужно переработать пчелам для получения 1 кг мёда.

2. Правило «креста»

84 80

100

20 16

Значит, 1 кг составляет 16 частей, тогда 80 частей:

1 : 16 * 80 = 5 кг.

Ответ: 5 кг

Задачи, которые решаются с помощью систем линейных уравнений.

Задача №4

Имеется 2 раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200г второго раствора, то получится 50%-ный раствор. Если же слить вместе 300г первого раствора и 200 г второго, то получится 42%-ный раствор. Найти концентрацию второго раствора.

Решение задачи №4

Пусть процентное содержание соли в первом и втором растворах p% и q% соответственно, тогда по условиям задачи можно составить два уравнения:

100 p/100 + 200 q/100=50*(100+200)/100

300 p/100 + 200 q/100=42*(300+200)/100.

Упростив эти уравнения и решив систему, получим p=30 и q=60.

Следовательно, концентрация второго раствора равна 60%

Ответ. 60%

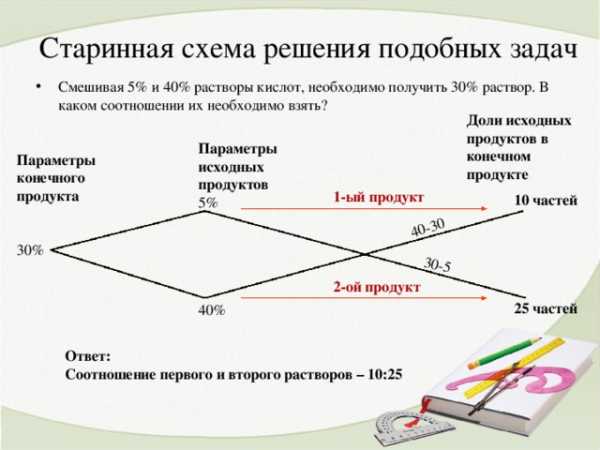
40-30

30-5

Старинная схема решения подобных задач

Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?

Доли исходных продуктов в

конечном продукте

Параметры

исходных

продуктов

40%

Параметры

конечного

продукта

30%

1-ый продукт

2-ой продукт

10 частей

25 частей

Ответ:

Соотношение первого и второго растворов – 10:25

Задачи на переливание

При решении этих задач выполняются следующие допущения: «закон сохранения масс» и «закон сохранения объёмов», как для всей смеси, так и для каждого её компонента. При этом плотности растворов изменяются не значительно и примерно равны плотности воды.

Теперь покажу, как графические иллюстрации к условию задач помогают найти правильный путь к ответу на вопрос задачи

Задача №5

Сначала приготовили 25%-ый водный раствор поваренной соли. Затем одну треть воды выпарили. Найти концентрацию получившегося раствора.

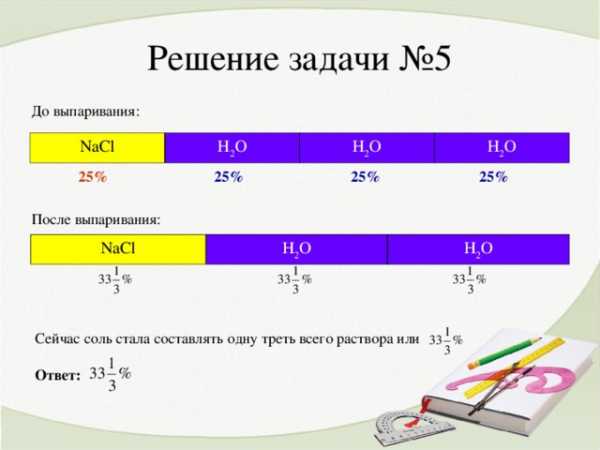
Решение задачи №5

До выпаривания:

NaCl

Н 2 О

25% 25% 25% 25%

После выпаривания:

NaCl

Н 2 О

Сейчас соль стала составлять одну треть всего раствора или

Ответ:

Задача №6

Имеется два сплава золота и серебра. В одном количество этих металлов находится в отношении 1:9, а в другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы как 1:4?

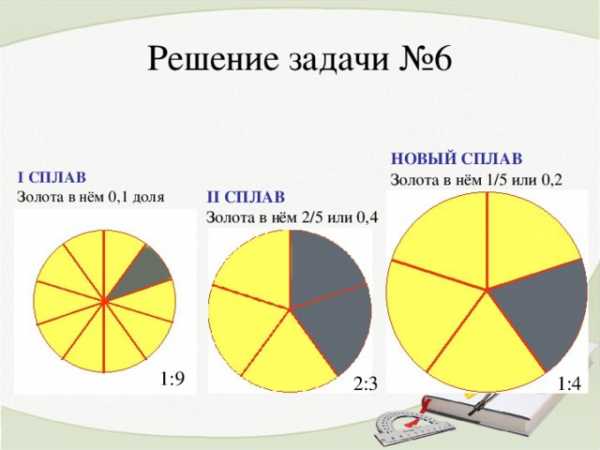
Решение задачи №6

НОВЫЙ СПЛАВ

Золота в нём 1/5 или 0,2

I СПЛАВ

Золота в нём 0,1 доля

II СПЛАВ

Золота в нём 2 / 5 или 0,4

1:9

2:3

1:4

Внесём данные в таблицу:

Имеется два сплава золота и серебра. В одном количество этих металлов находится в отношении 1:9, а в другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы как 1:4?

Название

элементов

Первый сплав

золото

серебро

Масса каждого элемента в сплаве

Второй сплав

золото

серебро

Общая масса сплава

0,1х кг

Новый сплав

X кг

Массовая доля элемента

0,4(15-х) кг

золото

серебро

(15- X) кг

0,1

0,2*15=3 кг

0,4

15 кг

0,2

Решение

0,1х + 0,4(15-х) =3

X =10

m (I сплава) =10 (кг)

m (II сплава) =15 – 10 =5 (кг) Ответ: 10 кг, 5 кг.

Вывод

При решении задач следует руководствоваться тем, что при соединении (разъединении) смесей с одним и тем же чистым веществом количества чистого вещества и общие количества смесей складываются (вычитаются). Складывать и вычитать доли и процентные содержания нельзя .

Вывод

В ходе проектной деятельности я разделила задачи на растворы и смеси по типам и нашла единый алгоритм решения для каждого из типов, следовательно, моя гипотеза подтвердилась .

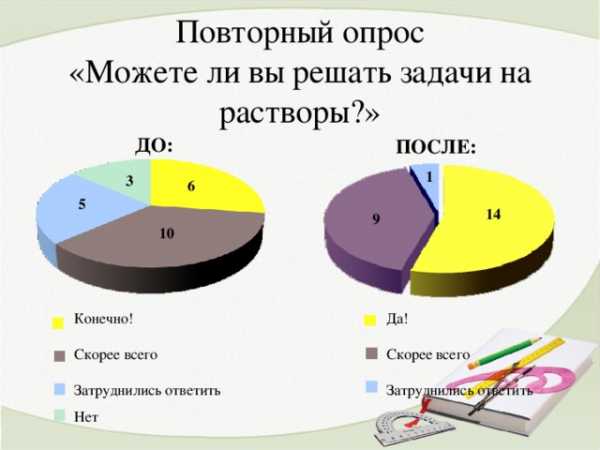
Повторный опрос «Можете ли вы решать задачи на растворы?»

ДО:

ПОСЛЕ:

Да!

Скорее всего

Затруднились ответить

Конечно!

Скорее всего

Затруднились ответить

Нет

Рефлексия

Как видно из результатов опросов, проектная деятельность помогла мне лучше понять сущность процентных задач на растворы и смеси и научила правильно оценивать свои силы.

Список литературы

М.В. Лурье и др. Задачи на составление уравнений, изд-во «Наука», М., 1976 г.
Н.А. Терёшин Прикладная направленность школьного курса математики, «Просвещение», М., 1990 г.
А.В. Шевкин Школьные математические олимпиады, изд-во «Русское слово», 2002г.
О. Городнова Статья «Учимся решать задачи на «смеси и сплавы», г-та «Математика» №36 за 2004 г.

Интернет-ресурсы

1. Открытый банк заданий ЕГЭ по математике

http://www.mathege.ru

2. Шабон оформления презентации

http://www.pedsovet.su

kopilkaurokov.ru

Задачи «на смеси и сплавы» с решениями.

Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты.

Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:

концентрацией данного вещества в смеси (сплаве) называется величина c=m/M;
процентным содержанием данного вещества называется величина с?100%;

Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c?M.

Задачи на смеси (сплавы) можно разделить на два вида:

Задаются, например, две смеси (сплава) с массами m₁ и m₂ и с концентрациями в них некоторого вещества, равными соответственно с₁ и с₂. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c₁m₁+c₂m₂, а концентрация c=(c₁m₁+c₂m₂)/(m₁+m₂).
Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.

При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.

Задача №1.

Из сосуда ёмкостью 54 литра, наполненного кислотой, вылили несколько литров и доли сосуд водой. Потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 литра чистой кислоты. Сколько кислоты вылили в первый раз?

Решение.

Пусть x литров кислоты вылили в первый раз. Тогда в сосуде осталось (54-x) литров. Долив сосуд водой, получим 54 литра смеси, в которой растворилось (54-х) литров кислоты. Значит в одном литре смеси содержится (54-x)/54литров кислоты. Всего за два раза вылили 54-24=30 литров кислоты. В результате получили уравнение: x+x(54-x)/54=30

Решив это уравнение, найдём два корня: х=90 и х=18. Ясно, что значение 90 не удовлетворяет условию задачи.

Ответ: в первый раз было вылито 18 литров воды.

При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве).

Задача №2.

В каких пропорциях нужно смешать раствор 50%-й и 70%-й кислоты, чтобы получить раствор 65%-й кислоты?

Решение.

1 способ

Пусть х г – масса 50%-й кислоты, y г – масса 70%-й кислоты, 0,5х г – масса чистой кислоты в первом растворе, (x+y)г – масса смеси, 0,65(x+y)г — масса чистой кислоты в смеси. Составим уравнение (рис. 6а):

0,5x+0,7y=0,65(x+y)

Получаем соотношение 1:3.

Ответ: 1:3.

Существует и другой способ решения этой задачи. Он называется арифметическим (или старинным) способом.

2 способ

Обоснуем старинный способ решения задач «на смеси».

Пусть требуется смешать растворы а%-й и b%-й кислот, чтобы получить

с%-й раствор.

Пусть х г – масса а%-го раствора, y г – масса b%-го раствора, ax/100 г – масса чистой кислоты в первом растворе, а by/100 г – масса чистой кислоты во втором растворе, c(x+y)/100 г – масса чистой кислоты в смеси.

ax/100+by/100=c(x+y)/100

при упрощении которого станет ясно, что x:y=(b-c):(c-a).

Задача №3.

Имеется два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите, сколько килограммов олова содержится в получившемся новом сплаве.

Решение.

Пусть х кг – количество олова в новом сплаве. Так как новый сплав весит 400 кг и в нём находится 30 % цинка, то он содержит 400*30/100=120 кг, а во втором сплаве (120-y) кг цинка. По условию задачи процентное содержание цинка в двух сплавах равно, следовательно, можно составить уравнение: 100y/150=100(120-y)/250

Из этого уравнения находим, что у=45. Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет 150*40/100=60 кг, а во втором сплаве олова будет (х-60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет 250*26/100=65 кг. Во втором сплаве олова содержится (х-60) кг, цинка 120-45=75 (кг), меди 65 кг и, так как весь сплав весит 250 кг, то имеем:

х-60+75+65=250, откуда х=170 кг

Ответ: 170 кг.

Задача №4.

В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?

Решение.

Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в рудеапишем массу руды, массу железа, концентрацию () руде?

нем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20) до и после удаления примесей.

	Масса руды, кг	Масса железа, кг	Концентрация (доля железа в руде)
Руда	500	х	x/500
Руда после удаления примесей	500-200=300	х-0,125?200=x-25	(x-25)/300

Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна x/500%.

Так как масса железа в 200 кг примесей равна 0,125?200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна (x-25)/300.

По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:

(x-25)/300-1/5=x/500,

5(x-25)-300=3x

x=212,5

Найдём, что х=212,5 кг – масса железа в руде.

Найдём остаток железа в руде после удаления примесей:

212,5-25=187,5 (кг)

Ответ: 187,5 кг.

Мы решили вторую задачу путём составления таблицы, помогающей зрительно воспринимать задачу.

Вывод: задачи «на смеси и сплавы» решаются множеством способов, но в них всегда присутствует концентрация (доля содержания одного вещества в другом), и они всегда решаются путём составления уравнений.

iumka.ru

Решение задач на «сплавы», «смеси», «растворы»

Разделы: Математика

Задачи, связанные с понятием “концентрация” и “процентное содержание”, являются традиционно трудными для обучающихся. В них речь идет о сплавах, растворах и смесях, которые получаются при сплавлении или смешивании различных веществ. При решении таких задач принимаются некоторые допущения. Первое: если смешиваются два раствора, объем которых х и у, то получившаяся смесь будет иметь объем х + у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.

В смесях и растворах содержится некоторый объем чистого вещества. Отношение объема чистого вещества к объему всего раствора называется объемной концентрацией. (Содержание чистого вещества в единице объема). Концентрация, выраженная в процентах, называется процентным содержанием. При решении таких задач удобно пользоваться таблицей, которая помогает понять задачу и по которой легче составить уравнение или систему. В работе приведены решения нескольких задач, а также предложены задачи для самостоятельного решения. Для удобства к задачам прилагаются ответы.

1. Некоторый сплав состоит из двух металлов, входящих в отношении 1 : 2, а другой содержит те же металлы в отношении 2 : 3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий те же металлы в отношении 17 : 27?

Решение: Пусть взято х частей первого сплава и у частей второго. В х частях первого сплава содержится частей первого металла и частей второго. В y частях второго сплава содержится частей первого металла и частей второго.

Составим таблицу:

	В частях	1 металл	2 металл
1 сплав	х частей	частей	частей
2 сплав	у частей	частей	частей
3 сплав	44 части	17 частей	27 частей

Из таблицы видно, что можно получить три уравнения. 1) х + у = 44 , 2)

3) . Решив систему из двух уравнений, получим ответ.

Ответ: 9 частей первого сплава и 35 частей второго сплава.

2. Имеется два слитка, представляющие собой сплавы цинка с медью. Масса первого слитка 2 кг, масса второго – 3 кг. Эти два слитка сплавили вместе с 5 кг сплава цинка с медью, в котором цинка было 45 %, и получили сплав цинка с медью, в котором цинка стало 50%. Если бы процентное содержание цинка в первом слитке было бы равно процентному содержанию цинка во втором, а процентное содержание цинка во втором такое же как в первом, то сплавив эти два слитка с 5 кг сплава, в котором содержится 60% цинка, мы бы получили сплав, в котором цинка содержится 55%. Найдите процентное содержание цинка в первом и втором слитках.

Решение: Составим по условию задачи следующую таблицу

		1 случай		2 случай
	масса	Zn (%)	Zn (кг)	Zn (%)	Zn (кг)
1 сплав	2кг	х %	0,02 х кг	у %	0,02 у кг
2 сплав	3кг	у %	0,03 у кг	х %	0,03 х кг
3 сплав	5кг	45%	2,25 кг	60%	3 кг
4 сплав	10кг	50%	5 кг	55%	5,5 кг

По таблице составим систему уравнений
прибавим к первому уравнению второе, получим

Ответ: 40% и 65%.

Имеется два разных сплава меди со свинцом. Если взять 1 кг первого сплава и 1 кг второго сплава и переплавить их, то получится сплав с содержанием 65% меди. Известно, что если взять кусок № 1 и кусок № 2 первого и второго сплавов соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится сплав с содержанием 60% меди. Какова масса меди, содержащаяся в сплаве, получающемся при совместной переплавке куска первого сплава, равного по массе куску № 2, и куска второго сплава, равного по массе куску № 1?

Решение: Составим по условию задачи следующую таблицу

		1случай		2 случай		3 случай
	масса	Cu (%)	Cu (кг)	масса	Cu (кг)	масса	Cu (кг)
1 сплав	1 кг	n%	0,01n кг	х кг	0,01n кг	у кг	0,01n у кг
2 сплав	1 кг	m%	0,01m кг	у кг	0,01m у кг	х кг	0,01m х кг
3 сплав	2 кг	65%	1,3 кг	7 кг	60% или 4,2 кг

По данным таблицы составим систему уравнений , найти надо значение выражения 0,01n у + 0,01m х. Представим его в виде 0,01(n у + m х). Решим систему уравнений.

. Умножим первое уравнение на третье и вычтем второе.

Ответ: 4,9 кг.

4. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с 5/6 второго, то в получившемся слитке окажется столько золота, сколько было бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?

Решение: Пусть в первом слитке содержится х кг золота и 2х кг меди. Тогда масса всего слитка 3х кг. Пусть во втором слитке содержится 2у кг золота и 3у кг меди. Тогда масса всего слитка 5у кг. Составим таблицу:

По данным таблицы составим систему уравнений

Ответ: 1,2 кг и 2,4 кг.

5. Имеется три слитка: первый слиток – сплав меди с никелем, второй – никель с цинком, третий цинка с медью. Если сплавить первый кусок со вторым, то процент меди в получившемся слитке будет в два раза меньше, чем он был в первом слитке. Если сплавить второй слиток с третьим, то процент никеля в получившемся слитке будет в три раза меньше, чем он был во втором слитке. Какой процент цинка будет содержать слиток, получившийся при сплаве всех трех слитков, если во втором слитке было 6% цинка, а в третьем – 11%?

Решение: Заметим, что во втором слитке нет меди, а если его сплавить с первым, в котором есть медь, то процент меди в новом сплаве будет в 2 раза меньше, чем он был в первом слитке, значит масса первого слитка равна массе второго. Пусть их масса будет х.

Если сплавить второй слиток, в котором есть никель, с третьим слитком, в котором никеля нет, то процент никеля в новом сплаве будет в 3 раза меньше, чем он был во втором слитке. Значит второй слиток по массе в 2 раза больше второго. Значит его масса будет 2х. Занесем данные в таблицу:

	Масса слитка	Zn (%)	Zn (масса)
1 слиток	х	нет	нет
2 слиток	х	6%	0,06х
3 слиток	2х	11%	0,22х
4 слиток	4х	y %	0,28х

Ответ: 7%

6. В сосуде находится определенное количество смеси воды с кислотой. Чтобы уменьшить концентрацию кислоты на 34% (было p%, а стало p-34%) в сосуд надо долить 3 л воды, а чтобы уменьшить её на 17%, надо долить 1 л воды. Какова концентрация кислоты в сосуде?

Решение: Составим по условию задачи следующую таблицу:

Кол-во смеси	Кислота в %	Кислота в литрах
y л	х%	0,01xy
(y + 3) л	(x – 34) %	0,01(y + 3)(x – 34)
(y +1) л	(x – 17) %	0,01(y + 1)(x – 17)

Если к раствору кислоты добавить чистую воду, то изменится концентрация кислоты, а количество кислоты не меняется. На этом основании составим систему уравнений:

Ответ: 68%.

7. Имеется три слитка золота массой 2 кг, 3 кг и 5 кг с различным процентным содержанием золота. Каждый слиток разделен на три куска и из 9 получившихся кусков получили три слитка массой 2 кг, 3 кг и 5 кг, но уже с равным процентным содержанием золота. На какие части следует разделить каждый слиток, чтобы гарантировать равное процентное содержание золота в получившихся слитках независимо от его содержания в исходных слитках.

Решение: Процентное содержание золота в новых получившихся слитках 2 кг, 3 кг и 5 кг будет равно процентному содержанию золота в слитке, который получится если просто сплавить исходные слитки массой 2 кг, 3 кг и 5 кг в десятикилограммовый кусок. Тогда золото входит в каждый новый слиток в отношении 2 : 3 : 5 . Значит нужно Каждый исходный слиток разделить на части пропорциональные этим числам. Всего частей 10. Получим 2 : 10 * 2 = 0,4; 2 : 10 * 3 = 0,6; 2 : 10 * 5 = 1 и т.д. Представим этот результат в виде таблицы.

	Масса слитка	1часть	2часть	3часть
1 слиток	2 кг	0,4 кг	0,6 кг	1 кг
2 слиток	3 кг	0,6 кг	0,9 кг	1,5 кг
3 слиток	5 кг	1 кг	1,5 кг	2,5 кг

Задачи для самостоятельного решения

8. Из трех кусков сплавов меди и никеля с соотношением по массе этих металлов 2 : 1, 3 : 1, 5 : 1 получили новый сплав. Его масса оказалась равной 12 кг, а соотношение меди и никеля в нем составило 4:1. Найти массу каждого исходного куска, если первый весил вдвое больше второго.
Ответ: 1,92 кг, 0,96 кг, 9,12 кг.

9. Из трех кусков сплавов серебра и меди с соотношением масс этих металлов 3:2, 2:3, 1:4 получили новый сплав. Его масса оказалась равной 22 кг, а соотношение серебра и меди в нем составило 1:1. Найти массу каждого исходного куска, если второй весил вдвое больше третьего. Ответ: 13,75 кг, 5,5 кг, 2,75 кг.

10. Из трех кусков сплавов олова и свинца с соотношением масс этих металлов 4 : 1, 1 : 1, 1 : 4 получили новый сплав. Его масса оказалась равной 24 кг, а соотношение олова и свинца в нем составило 2 : 3. Найти массу каждого исходного куска, если первый весил вдвое больше второго.
Ответ: 6,4 кг, 3,2 кг, 14,4 кг.

11. Из трех кусков сплавов золота и серебра с соотношением масс этих металлов 1 : 1, 1 : 5, 5 : 1 получили новый сплав. Его масса оказалась равной 24 кг, а соотношение золота и серебра в нем составило 2 : 1. Найти массу каждого исходного куска, если третий кусок весил втрое больше первого.

12. Имеются два сплава, в одном из которых содержится 20%, в другом 30% олова. Сколько нужно взять первого и второго сплава, чтобы получить 10 кг нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.

13. Имеются два сплава, в одном из которых содержится 40%, а во втором 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра?

14. Имеются два сплава, в одном из которых содержится 10%, а в другом – 20% меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.

15. Имеются два сплава, в одном из которых содержится 30%, а в другом – 50% золота. Сколько кг второго сплава нужно добавить к 10 кг первого, чтобы получить сплав, содержащий 42% золота?
Ответ: 15 кг.

16. Из молока, жирность которого 5%, делают творог, жирностью 0,5%. Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.

17. При смешивании растворов, содержащих 25% и 60% кислоты, получился раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны растворы?
Ответ: 3 : 2.

18. Добытая руда содержит 21% меди, а обогащенная – 45%. Известно, что в процессе обогащения 60% добытой руды идет в отходы. Определить процентное содержание меди в отходах.
Ответ: 5%.

19. В 100 граммов 20%-ного раствора соли добавили 300 граммов ее 10%-ного раствора. Определить концентрацию полученного раствора.
Ответ: 12,5%.

20. Какое количество воды надо добавить к 100 граммам 70%-ной уксусной эссенции, чтобы получить 5% раствор уксуса?
Ответ: 1300 гр.

21. Процентное содержание соли в растворе сначала снизилось на 20%, а затем повысилась на 20%. На сколько процентов изменилось первоначальное содержание соли?
Ответ: на 4%.

22. Морская вода содержит 5% соли. Сколько килограммов пресной воды надо добавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2%.
Ответ: 60 кг.

23. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра составляет веса меди. Сколько килограммов серебра в данном сплаве?
Ответ: 0,25 кг.

24. Имеется лом стали двух сортов с содержанием никеля 5% и 40% . Сколько нужно взять каждого из этих сортов металлолома, чтобы получить 140т стали с содержанием никеля 30%.
Ответ: 40 т и 100 т.

25. Кусок сплава меди с оловом весом 2 кг содержит 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40% меди?
Ответ: 1,5 кг.

26. Сколько чистого спирта надо прибавить к 735 г 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор?
Ответ: 441 г.

27. Сплав из меди и цинка весом в 24 кг при погружении в воду потерял в своем весе Определить количество меди и цинка в этом сплаве, если известно, что медь теряет в воде своего веса, а цинк своего веса.
Ответ: 17 кг и 7 кг.

28. Имеются два сплава золота и серебра. В одном количество этих металлов находится в отношении 2 : 3, а в другом в отношении 3 : 7. Сколько нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро были бы в отношении 5 : 11?
Ответ: 1 кг, 7 кг.

29. Одна бочка содержит смесь спирта с водой в отношении 2 : 3, а другая в отношении 3 : 7. По сколько ведер надо взять из каждой бочки, чтобы составить 12 ведер смеси, в которой спирт и вода были бы в отношении 3 : 5?
Ответ: 9 ведер из первой и 3 ведра из второй.

30. Два раствора, из которых первый содержал 800 г безводной серной кислоты, а второй 600 г безводной серной кислоты, соединили вместе и получили 10 кг нового раствора серной кислоты. Определить вес первого и второго растворов, вошедших в смесь, если известно, что процент содержания безводной серной кислоты в первом растворе на 10% больше, чем процент содержания безводной серной кислоты во втором.
Ответ: 4 кг и 6 кг.

31. Имелось два разных сплава меди. Процент содержания меди в первом сплаве был на 40 меньше, чем процент содержания меди во втором сплаве. После того как их сплавили вместе, получили сплав, содержащий 36% меди. Определить процентное содержание меди в первом и втором сплавах, если известно, содержание меди в первом сплаве было 6 кг, а во втором 12 кг.
Ответ: 20% и 60%.

32. 36 г цинка в воде весят 31 г, а 23 г свинца в воде весят 21 г. Сплав цинка и свинца массой 292 г в воде весит 261 г. Сколько цинка и сколько свинца содержится в сплаве?
Ответ: 108 г цинка и 184 г свинца.

33. В двух одинаковых сосудах, объемом по 30 л каждый, содержится всего 30 л кислоты. Первый сосуд доливают доверху водой и полученной смесью дополняют второй сосуд, затем из второго сосуда отливают в первый 12 литров смеси. Сколько кислоты было первоначально в первом сосуде, если во втором сосуде после переливаний оказалось на 2 л меньше кислоты, чем в первом?
Ответ: 20 литров.

34. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с 5/6 второго, то в получившемся слитке окажется столько золота, сколько было бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?
Ответ: 1,2 кг и 2,4 кг.

35. Имеется два сосуда. В одном содержится три литра 100%-ной серной кислоты, а в другом два литра воды. Из первого сосуда во второй перелили один стакан кислоты, а затем из второго в первый – один стакан смеси. Эту операцию повторили еще два раза. В результате во втором сосуде образовалась 42%-ная кислота. Сколько серной кислоты в процентах содержится теперь в первом сосуде?
Ответ: 72%.

36. Имеется два куска металла массой 1 кг и 2 кг. Из этих кусков сделали два других: первый массой 0,5 кг, содержащий 40% меди, а второй массой 2,5 кг, содержащий 88% меди. Каково процентное содержание меди в исходных кусках?
Ответ: 40% и 100%.

37. Из колбы в пробирку отлили раствора соли. Раствор в пробирке выпаривали, пока процентное содержание соли в нем не увеличилось в два раза. Получившийся раствор вернули в колбу, что увеличило процентное содержание соли в находившемся в колбе растворе на 2 %. Какое процентное содержание соли было в растворе первоначально?
Ответ: 10%.

Литература:

Шарыгин И.Ф. “Математика для поступающих в ВУЗы”. Москва, Дрофа, 2000 г.
Сканави М.И. “2500 задач по математике для поступающих в ВУЗы”. Москва, Оникс, 2003 г.
Черкасов О., Якушев А. “Математика”. Москва, Айрис, 2000 г.
Белоносов В.С., Фокин М.В. “Задачи вступительных экзаменов по математике.” Новосибирск, издательство НГУ, 1995 г.

27.04.2010

xn--i1abbnckbmcl9fb.xn--p1ai

Задачи «на смеси и сплавы» с решениями.

Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:

концентрацией данного вещества в смеси (сплаве) называется величина c=m/M;
процентным содержанием данного вещества называется величина с?100%;

Задачи на смеси (сплавы) можно разделить на два вида:

Задаются, например, две смеси (сплава) с массами m₁ и m₂ и с концентрациями в них некоторого вещества, равными соответственно с₁ и с₂. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c₁m₁+c₂m₂, а концентрация c=(c₁m₁+c₂m₂)/(m₁+m₂).
Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.

Задача №1.

Решение.

Решив это уравнение, найдём два корня: х=90 и х=18. Ясно, что значение 90 не удовлетворяет условию задачи.

Ответ: в первый раз было вылито 18 литров воды.

Задача №2.

В каких пропорциях нужно смешать раствор 50%-й и 70%-й кислоты, чтобы получить раствор 65%-й кислоты?

Решение.

1 способ

0,5x+0,7y=0,65(x+y)

Получаем соотношение 1:3.

Ответ: 1:3.

Существует и другой способ решения этой задачи. Он называется арифметическим (или старинным) способом.

2 способ

Обоснуем старинный способ решения задач «на смеси».

Пусть требуется смешать растворы а%-й и b%-й кислот, чтобы получить

с%-й раствор.

ax/100+by/100=c(x+y)/100

при упрощении которого станет ясно, что x:y=(b-c):(c-a).

Задача №3.

Решение.

х-60+75+65=250, откуда х=170 кг

Ответ: 170 кг.

Задача №4.

Решение.

нем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20) до и после удаления примесей.

	Масса руды, кг	Масса железа, кг	Концентрация (доля железа в руде)
Руда	500	х	x/500
Руда после удаления примесей	500-200=300	х-0,125?200=x-25	(x-25)/300

Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна x/500%.

По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:

(x-25)/300-1/5=x/500,

5(x-25)-300=3x

x=212,5

Найдём, что х=212,5 кг – масса железа в руде.

Найдём остаток железа в руде после удаления примесей:

212,5-25=187,5 (кг)

Ответ: 187,5 кг.

Мы решили вторую задачу путём составления таблицы, помогающей зрительно воспринимать задачу.

lib.repetitors.eu

Задачи на сплавы и смеси как решать – Задачи на смеси и сплавы. Учебник по ЕГЭ и ГИА

Задачи на сплавы и смеси с решениями. на Сёзнайке.ру

Задачи на смеси и сплавы

Решение задач на сплавы, смеси, работу, движение, проценты с использованием таблиц

Различные способы решения задач на смеси, сплавы , растворы

Задачи «на смеси и сплавы» с решениями.

Решение задач на «сплавы», «смеси», «растворы»

Задачи «на смеси и сплавы» с решениями.

Author: alexxlab

Добавить комментарий Отменить ответ

Рубрики