Один из подходов к изучению тригонометрии в 10-м классе
Разделы: Математика
Еще в 1905 г. русские читатели могли прочесть в книге Уильяма Джеймса “Психология” его рассуждения о том, “почему зубрение представляет такой дурной способ учения?”
“Знания, приобретенные путем простого зубрения, почти неизбежно забываются совершенно бесследно. Наоборот, умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергший обсуждению, образует такую систему, вступает в такую связь с остальными сторонами нашего интеллекта, легко возобновляется в памяти массою внешних поводов, что остается надолго прочным приобретением”.
С тех пор прошло более 100 лет, а слова эти поразительно остаются злободневными. В этом каждодневно убеждаешься, занимаясь со школьниками. Массовые пробелы в знаниях настолько велики, что можно утверждать: школьный курс математики в дидактическом и психологическом отношениях – не система, а некое устройство, поощряющее кратковременную память и нисколько не заботиться о памяти долговременной.
Знать школьный курс математики – значит владеть материалом каждого из направлений математики, быть в состоянии актуализировать любое из них в любое время. Чтобы достичь этого, нужно систематически обращаться каждому из них, что порой не всегда возможно из-за сильной загруженности на уроке.
Есть другой путь долговременного запоминания фактов и формул – это опорные сигналы.
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
Самый большой объем изучаемого материала по тригонометрии приходится на долю 10 класса. Большую часть этого материала из тригонометрии можно изучить и запомнить на тригонометрическом круге (окружность единичного радиуса с центром в начале прямоугольной системы координат). Приложение1.ppt
Это следующие понятия тригонометрии:
- определения синуса, косинуса, тангенса и котангенса угла;
- радианное измерение углов;
- область определения и область значений тригонометрических функций
- значения тригонометрических функций для некоторых значений числового и углового аргумента;
- периодичность тригонометрических функций;
- четность и нечетность тригонометрических функций;
- возрастание и убывание тригонометрических функций;
- формулы приведения;
- значения обратных тригонометрических функций;
- решение простейших тригонометрических уравнений;
- решение простейших неравенств;
- основные формулы тригонометрии.
Рассмотрим изучение этих понятий на тригонометрическом круге.
1) Определение синуса, косинуса, тангенса и котангенса.
После введения понятия тригонометрического круга (окружность единичного радиуса с центром в начале координат), начального радиуса (радиус окружности по направлению оси Ох), угла поворота, учащиеся самостоятельно получают определения для синуса, косинуса, тангенса и котангенса на тригонометрическом круге, используя определения из курса геометрии, то есть, рассматривая прямоугольный треугольник с гипотенузой, равной 1.
Косинусом угла называется абсцисса точки на окружности при повороте начального радиуса на данный угол.
Синусом угла называется ордината точки на окружности при повороте начального радиуса на данный угол.
2) Радианное измерение углов на тригонометрическом круге.
После введения радианной меры угла (1 радиан – это центральный угол, которому соответствует длина дуги, равная длине радиуса окружности), учащиеся делают вывод, что радианное измерение угла – это числовое значение угла поворота на окружности, равное длине соответствующей дуги при повороте начального радиуса на заданный угол. .
Тригонометрический круг разделен на 12 равных частей диаметрами окружности. Зная, что угол радианам, можно определить радианное измерение для углов кратных .
и т.д.
А радианные измерения углов, кратных, получаются аналогично:
3) Область определения и область значений тригонометрических функций.
Будет ли соответствие углов поворота и значений координат точки на окружности функцией?
Каждому углу поворота соответствует единственная точка на окружности, значит данное соответствие – функция.
Получаем функции
На тригонометрическом круге видно, что область определения функций – множество всех действительных чисел, а область значений — .
Введем понятия линий тангенсов и котангенсов на тригонометрическом круге.
1) Пусть Введем вспомогательную прямую, параллельную оси Оу, на которой определяются тангенсы для любого числового аргумента.
2) Аналогично получаем линию котангенсов. Пусть у=1, тогда . Значит, значения котангенса определяются на прямой, параллельной оси Ох.
На тригонометрическом круге без труда можно определить область определения и область значений тригонометрических функций:для тангенса —
для котангенса —
4) Значения тригонометрических функций на тригонометрическом круге.
Катет , противолежащий углу в равен половине гипотенузы, то есть Другой катет по теореме Пифагора:
Значит по определению синуса, косинуса, тангенса, котангенса можно определить значения для углов кратных или радианам. Значения синуса определяются по оси Оу, косинуса по оси Ох, а значения тангенса и котангенса можно определить по дополнительным осям, параллельным осям Оу и Ох соответственно.
Табличные значения синуса и косинуса расположены на соответствующих осях следующим образом:
Табличные значения тангенса и котангенса —
На тригонометрическом круге видно, что значения синуса, косинуса повторяются через каждые радиана, а тангенса и котангенса – через радиан.
6)Четность и нечетность тригонометрических функций.
Это свойство можно получить, сравнивая значения положительных и им противоположных углов поворота тригонометрических функций. Получаем, что
Значит, косинус – четная функция, все остальные функции – нечетные.
7) Возрастание и убывание тригонометрических функций.
По тригонометрическому кругу видно, что функция синус возрастает и убывает
Аналогично рассуждая, получаем промежутки возрастания и убывания функций косинуса, тангенса и котангенса.
8) Формулы приведения.
За угол берем меньшее значение угла на тригонометрическом круге. Все формулы получаются в сравнении значений тригонометрических функций на катетах выделенных прямоугольных треугольников.
Алгоритм применения формул приведения:
1) Определить знак функции при повороте на заданный угол.
При повороте на угол функция сохраняется, при повороте на угол — целое, нечетное число, получается кофункция (
9) Значения обратных тригонометрических функций.
Введем обратные функции для тригонометрических функций, пользуясь определением функции.
Каждому значению синуса, косинуса, тангенса и котангенса на тригонометрическом круге соответствует только одно значение угла поворота. Значит, для функции область определения , область значений — Для функции область определения — , область значений — . Аналогично получаем область определения и область значений обратных функций для косинуса и котангенса.
Алгоритм нахождения значений обратных тригонометрических функций:
1) нахождение на соответствующей оси значения аргумента обратной тригонометрической функции;
2) нахождение угла поворота начального радиуса с учетом области значений обратной тригонометрической функции.
Например:
10) Решение простейших уравнений на тригонометрическом круге.
Чтобы решить уравнение вида , найдем точки на окружности, ординаты которых равны и запишем соответствующие углы с учетом периода функции.
Для уравнения , найдем точки на окружности, абсциссы которых равны и запишем соответствующие углы с учетом периода функции.
Аналогично для уравнений вида Значения определяются на линиях тангенсов и котангенсов и записываются соответствующие углы поворота.
11) Решение неравенств.
Чтобы решить неравенства вида , необходимо найти точки на окружности с ординатой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точки на окружности с абсциссой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точку на линии тангенсов с координатой и прочитать соответствующее неравенство против часовой стрелки с учетом области определения и периода функции.
Аналогично для неравенств с котангенсом.
Необходимо практиковать чтение промежутков на тригонометрическом круге, тогда решения неравенств определяются безошибочно.
12) Основные формулы тригонометрии.
1) Основные тригонометрические тождества.
Очевидны выводы формул которые получаются в прямоугольном треугольнике на тригонометрическом круге.
2) Формулы сложения выводятся с использованием скалярного произведения векторов начального и “конечного” радиусов.
Другие формулы сложения получаются с использованием предыдущей, формул приведения и свойств четности и нечетности тригонометрических функций.
Почти все формулы тригонометрии являются следствиями этих основных формул.
Все понятия и формулы тригонометрии получают сами ученики под четким руководством учителя с помощью тригонометрического круга. В дальнейшем этот “круг” будет служить для них опорным сигналом или внешним фактором для воспроизведения в памяти понятий и формул тригонометрии.
Выводы:
Изучение тригонометрии на тригонометрическом круге способствует:
- выбору оптимального для данного урока стиль общения, организации учебного сотрудничества;
- целевые ориентиры урока становятся личностно значимыми для каждого ученика;
- новой материал опирается на личный опыт действия, мышления, ощущения учащегося;
- урок включает в себя различные формы работы и способы получения и усвоения знаний; присутствуют элементы взаимо- и самообучения; само- и взаимоконтроля;
- имеет место быстрое реагирование на непонимание и ошибку (совместное обсуждение, опоры-подсказки, взаимоконсультации).
18.01.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Изучение тригонометрического материала в школьном курсе математики
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Кафедра МПМ
Изучение тригонометрического материала в школьном курсе математики
Реферат
Исполнитель:
Студентка группы М-42 Головачева А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Лебедева М.Т.
Гомель 2007
Содержание
Введение
1. Методика введения понятий синуса, косинуса и тангенса на геометрическом материале. Основные тригонометрические тождества
2. Методика введения определений тригонометрических функций углов от 0° до 180°
3. Методика изучения тригонометрических функций в курсе алгебры
4. Тождественные преобразования тригонометрических выражений. Тригонометрические уравнения и неравенства и методика обучения решению
Заключение
Литература
Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 00 до 1800 ; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
Первые два этапа реализуются в курсе планиметрии. Геометрический характер определений тригонометрических функций объясняет тот факт, что они составляют единственный вид функций, который начинают изучать не в курсе алгебры, а в курсе геометрии. Для геометрии важен «общефункциональный взгляд» на тригонометрические функции, а их прикладная сторона (решение прямоугольных треугольников, применение некоторых тригонометрических тождеств, теорем cos и sin, решение произвольных треугольников). Поэтому в курсе планиметрии нет термина «тригонометрические функции».
Знакомство с тригонометрическим материалом начинается в курсе геометрии при знакомстве с прямоугольным треугольником. Понятия
, и острых углов треугольника вводится для углов от до , как отношение сторон этого треугольника. Предварительно учащиеся должны усвоить названия сторон прямоугольного треугольника: катеты (стороны прямого угла) и гипотенуза (сторона противолежащая прямому углу). Для этого необходимо предложить учащимся прямоугольные треугольники, разнообразные по расположению вершин прямого угла и предложить назвать стороны треугольника.Назовите катеты в
ABC, APN. Назовите гипотенузы в LKM и EFA. Будут ли гипотенузами следующие отрезки: AB, KL, AP, AN, EF, FA в указанных треугольниках и почему?Следующие выражения «прилежащий» и «противолежащий» отрабатываются на следующем этапе. Для этого необходимо по указанным треугольникам предложить учащимся назвать прилежащие и противолежащие острым углам катеты. Назвать отрезки: KL, PN, EA и попросить учащихся назвать те углы, против которых лежат эти катеты или, которым они прилегают.
Первым вводится понятие
угла и доказывается теорема: » Косинус угла зависит от градусной меры угла и не зависит от расположения и размеров треугольника». Это определение уже » работает» при доказательстве теоремы Пифагора.С остальными понятиями учащиеся знакомятся в пункте » Соотношения между сторонами и углами в прямоугольном треугольнике». sin
, tgФормируется свойство: синус и тангенс угла так же, как и косинус, зависят от величины угла.
Для синуса это доказывается так:
=,так как косинус зависит только от величины угла, то и синус зависит только от величины угла.
Из определений
, и получаем следующие правила:— Катет, противолежащий углу
, равен произведению гипотенузы на синус ;— Катет, прилежащий к углу
, равен произведению гипотенузы на косинус ;— Катет, противолежащий углу
, равен произведению второго катета на тангенс .По этим правилам можно находить неизвестные элементы в прямоугольном треугольнике.
Перечисленные правила могут быть выведены учащимися самостоятельно. Для этого предлагаются вопросы: В прямоугольном треугольнике MNP, LN=
, LM=, гипотенуза MP=m. Найти длины катетов этого треугольника. ( Задача решается по определению).Раньше по программе тригонометрические функции и соотношения между углами и сторонами в прямоугольном треугольнике изучались в курсе 8 класса.
После введения понятий
, и рассматривались решения основных задач, связанных с отысканием длин сторон и величин углов в прямоугольном треугольнике.Задача №1. Дано: a, b. Требуется найти
A, B, c.Задача №2. Дано: a, c. Требуется найти
A, B, b.Задача №3. Дано: a,
A. Требуется найти A, b, c.Задача №4. Дано: a,
B. Требуется найти A, b, c.Задача №5. Дано: a,
A. Требуется найти B, a, b.По действующей программе эти задачи в курсе 8 класса (бывший 7 класс) заменены такой: В прямоугольном треугольнике даны: гипотенуза c и острый угол
. Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.Вводятся основные тригонометрические тождества:
, , , .В частности, основное тригонометрическое тождество выводится из формулировки теоремы Пифагора:
, .Учащиеся знакомятся с некоторыми свойствами функций острого угла: 1) при возрастании острого угла
и возрастают, а — убывает; 2) для любого острого угла : , ; которые формулируются как теоремы. Их доказательство связывается с соотношениями острых углов в прямоугольном треугольнике:mirznanii.com
люди,вот зачем учат в школе тригонометрию?она кому-нибудь вообще в жизни понадобилась…
как говорила моя классная руководительница: «Для общего развития! «)))))))))))
честно, вообще не понятно. Нам ее уже 2года вдалбливают- зачем? —НЕИЗВЕСТНО!!!
Тем, кто связан с электричеством, моделированием в пространстве, программированием. Мне точно не повредила. Учите..
А как же! Она очень нужна.. . для дальнейшей учёбы в техникуме или институте.
аха! ! еще всякие функции.. логарифмы… синусы, косинусы ну нахрен оно вооще нужно!!!! пайдешь же ты в магазин… и там небудет написано Пачка макарон стоит sin(180градусов)…. или ln12…=)) БЕСПОЛЕЗНАЯ ПУСТАЯ ТРАТА ВРЕМЕНИ! кто хочет пусть изучает! её,,,.еще много денег берут в уч заведениях за эту ХЕРЬ! НЕНАВИЖУ МАТЕМШУ! В ОСОБЕННОСТИ ГЕОМЕТРИЮ, НУ КАК МОЖНО БУКВЫ (!) «ABC» ВЫЧИТАТЬ/СЛАЖИВАТЬ/УМНОЖАТЬ XDD ЭТО уже выше идиотизма.. это как к КАПУСТЕ В СУП ПОДСЫПАТЬ ГВОЗДЕЙ!!! ! Предмет для самых тех кому жить нехочется нормально….
Тем, кто избрал жизнь, связанную с наукой и техникой, понадобилась. Тригонометрию изучают в школе не исходя из того, что она когда-то в жизни всем обязательно понадобится, а в первую очередь для того, чтобы развить панорамное (абстрактно-логическое) мышление. Школьники чисто психофизически слишком большие обалдуи, чтобы правильно оценить нужность/ненужность получаемых знаний — поскольку области мозга, ответственные за логику, начинают развиваться не раньше 12 лет. И вообще — как говорил Хайнлайн, узкая специализация — удел насекомых, а человек должен знать и уметь всё.
Все буквы алфавита можно тоже не учить, т. к. в жизни некоторые обходятся короткими словами не из всех букв.
А что там такого сложного в тригонометрии? Самая что ни на есть подходящая наука для развития у школьников пространственного мышления и связи его с математикой. Применяется в пределах школьной программы — в физике, алгебре и геометрии. А вот в жизни — тем более. Подавляющее большинство инженерных задач не решить без тригонометрии. Строительство, архитектура, дороги, коммунальные сети, электричество — всё это окружает тебя. И всего этого бы не было, если бы не тригонометрия! И многое-многое другое. Тригонометрия — великая вещь! Это основа человеческих знаний. И изучение её в школе просто необхдимо! Занимайтесь математикой и в частности, тригонометрией. К чёрту все эти тупые дисциплины вроде основ сексуальной грамотности, риторики и стилистики! Не зря сказано — математика — царица всех наук.
лично мне она не нужна. Да и вообще она и так скучная
В школе, девочка, дают начальные знания по всем областям науки, литературы, живописи потому, что в этом возрасте человек не чень хорошо представляет кем он в будущем станет и чем будет заниматься. Это во-первых. Во-вторых, должна быть у культурного человека элементарная образованность. В- третьи, эта тригонометрия развивает соображалку, которой многим явно не хватает. Конечно отсасывать пиво и становиться в позу «раком» в подворотнях многим из совр. молодняка интереснее, для таких школьная программа вообще не нужна. Тут уже есть такой грамотей — про гвозди — который даже падежи не знает.. . Надеюсь, Вы меня поняли.
да. мне пригодилась
Тригонометрия нужна для общего культурного развития каждого цивилизованного человека, и изучают ее в средней ОБЩЕобразовательной школе. Если Вы себя к таковым относите, то пригодится, если не прямо, то опосредованно. Мне пригодилось, а я филолог.
Странный вопрос. Тригонометрия используется везде, где есть малейшие математические операции, будь то физика или что-то ещё. Она используется просто постоянно. Тригонометрия — это просто. Начертите круг радиуса 1 с центром в центре координат. Проведите радиус и из точки пересечения проведите отрезки к осям х и у под прямыми углами. То что получилось на оси у — это синус, на оси х — косинус. Вот и вся тригонометрия, учить там нечего, все остальное — следствие.
иногда помогает, хоть без этого можно прожить если тебе не нужно высшее образование, ты без этого проживешь. p.s.есть такой сериал у америкосов — NUMB3RS, 4ИСЛА, то есть. Занятная штука, о том какое отношение математика играет в реальной жизни
touch.otvet.mail.ru
Репетитор по математике о работе с тригонометрическим кругом
Задачи по тригонометрии являются неотъемлемой частью любого серьезного экзамена. Редкая подготовка к ЕГЭ по математике обходится без внимания репетитора к этому объемному и сложному разделу. С ним связано наибольшее количество ошибок провалов на ЕГЭ у слабых абитуриентов. Рассмотрим методические особенности изучения тригонометрии и частные приемы, которыми обычно пользуется репетитор по математике. Я собираюсь сделать несколько страничек по этой тематике. В начале поговорим о введении тригонометрического круга.
К сожалению, стандарты ГИА по математике заставили пересмотреть школьные программы, в которые в этом году были внесены существенные изменения. Традиционно изучаемую в 9 классе тригонометрию заменили на статистику и теорию вероятностей. Репетитору математике это только усложнило работу. Конечно, и раньше аттестационный экзамен по алгебре не затрагивал синусы и косинусы, но по крайней мере введение в тригонометрию изучалось. Теперь все изменилось на корню и «старт» приходится брать в 10 классе. Для репетитора это означает совмещение двухгодичной подготовки к ЕГЭ с обучением работе на тригонометрическом круге с нуля. Но делать нечего, приходится адаптироваться к новым стандартам и учебникам. Итак, какие методические приемы предлагает репетитор по математике школьнику в этой теме? Насколько разным может быть подход к введению круга? Как построить работу со слабым учеником?
Изучение тригонометрии начинается с измерения и откладывания углов. И уже на этом этапе репетитор по математике может столкнуться с определенными проблемами. С чем они связаны? Обычно путают расположение углов на круге и не видят его в «раскрытом состоянии». Ни в одном учебнике я еще не встречал того, что говорю своим ученикам. Давайте посмотрим на рисунок круга. Что это такое? В глазах ученика это ограниченная замкнутая линия, на которой репетитор по математике наносит какие-то числа и буквы , объявляя их углами. Около одной и той же точки подписывается сразу несколько различных значений. Что это? Еще и радианы вместо привычных градусов. Путаница возникает страшная. Особенно когда репетитор по математике переходит к решению простейших тригонометрических уравнения (это тема в учебнике Мордковича идет чуть ли сразу за тригонометрическим кругом). Как внести ясность в происходящее?
Методика спирали репетитора по математике
Я всегда «разматываю» тригонометрический круг. Как? Что это за действо? Все очень просто. Объясняю так: «углы, как и длины отрезков, откладываются (изображаются) на бесконечной оси. Только для практической работы с процессом изображения удобнее смотать эту ось петлями, или, говоря другими словами, представить ее в виде спирали». И показываю рисунок: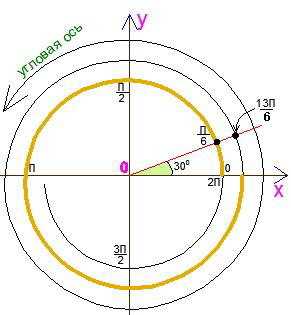
При таком подходе репетитор по математике обеспечивает полную прозрачность действий с углами и ясность в их изображении. Чтобы упростить работу ученика с кругом нужно подать его как ось для углов, которую как веревку намотали на трубу и нарисовали получившейся профиль. Такая методика помогает репетитору по математике снять огромное количество проблем не только на этапе введения самого круга, но и на последующих уроках. особенно в решении уравнений и неравенств, когда приходится записывать целую серию углов, изображающиеся одной и той же точкой или дуги, наложенные друг на друга. Я советую репетитору выделить цветом часть круга, соответствующую одному обороту (на рисунке она показана коричневым цветом) и назвать ее «дорожкой».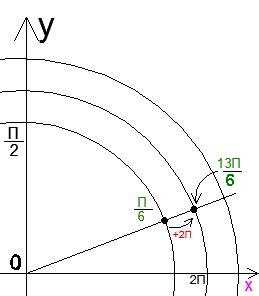 
Сам круг можно еще сравнить с велотреком, по которому движутся велосипедисты от точки старта (в начале отсчета спирали) в положительном или отрицательном направлении. Для перехода с дорожки на дорожку мы прибавляем или отнимаем .
Ученик должен усвоить, что рисунок учебника – картинка затянутой спирали, как будто трубу плотно обмотали веревкой. В таком случае разные отметки (деления) оси (то есть веревки) будут наложены друг на друга и мы увидим что отметки разных углов сливаются в одну точку. Если мы ослабим веревку, то получим спираль, на которой каждый угол изображается отдельно.
В те моменты, когда репетитор по математике чувствует непонимание и путаницу с углами на помощь приходит изображение круга в спиральном виде. Например, решение тригонометрического уравнения можно показать так:
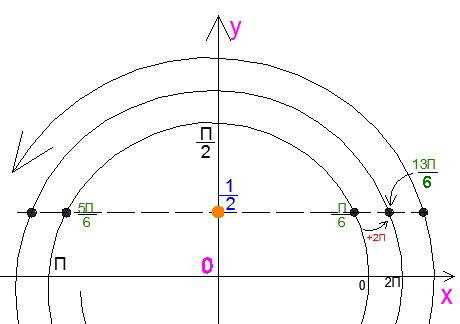
Необходимо сказать, что черные точки (углы) — это и есть решение уравнения. И если мы сожмем спираль (затянем веревку на трубе), то они наложатся друг на друга и превратятся в левую и правую. После этого репетитор может сделать стандартный рисунок. Таким путем преподавателю будет легче объяснить формулы и . а ученик лучше запомнит периодический характер расположения корней.
Александр Николаевич, репетитор по математике Москва, м. Строгино
Метки: Методики для репетиторов, Примеры объяснений, Работа репетитора, Репетиторам по математике
ankolpakov.ru
Ответы@Mail.Ru: Я не понимаю тригонометрию
в 11 классе та же фигня была…. перед экзаменами занимался с репетитором…. ниче вроде сдал…. баллов правда не столько сколько хотелось бы…
а чего там понимать-то? голимые формулы и набор приемов. Только запоминать и решать, решать, решать. Хотите я вас порадую? Век назад гимназисты учили тригонометрию раз в 10 больше, чем сейчас, знали кучи других формул, решали примеры, которые сейчас вряд ли какой действующий математик решит. Просто тогда тригонометрия было необходима для практики, а с появлением компьютеров эти примеры стали не нужны. Кстати, как и так любимое в школе «избавление от иррациональности в знаменателе». Компьютеру посчитать 1/корень из двух не дольше, чем корень из двух / 2.
я вот сама толком не знала тригонометрию. но поступив на физико-математический факультет, мне пришлось подружиться с тригонометрией. как я сделала — взяла маленький блокнотик и писала туда все формулы тригонометрии — от простого к сложному. значения функций я, конечно, написала на первой страничке, чтобы не искать. так я делала в школе. а в универе я просто изготовила маленькие шпоры и таскала их в пенальчике) или внутри тетради по алгебре, геометрии, мат. анализа) вот и все) и признаться — все еще не очень то хорошо знаю эту тригонометрию)) ) учить бессмысленно — если учишь без понимания (
Одно дело не понимать тригонометрию (не понимать, что такое единичная тригонометрическая окружность, почему не существует тангенса пи/2, почему период синуса и косинуса равен 2пи и т. д.) , и совсем другое дело — не уметь решать задачи. Дело в том, что существует ограниченный набор типов задач, чтобы их освоить, необходимо нарешать приличное количество задач на каждый их них. Когда я с очередным учеником (занимаюсь репетиторством по алгебре и геометрии) подхожу к теме «Решение тригонометрических задач», приходит время самых больших домашних заданий — на уроке мы разбираем 1 тип задач на нескольких примерах (за час обычно 5-6 успеваем) , а на дом я даю около 20(!) подобных задач, чтобы «руку набить» и «в голове уложить».
touch.otvet.mail.ru
С какого класса начинается алгебра и геометрия?
С какого класса начинается алгебра и геометрия?
Математика делится на 2 раздела — Алгебра и Геометрия.
В 7 классе этот раздел включает в школу, но по сути и до 7 класса существует и то и то.
Кстати если хотите хорошую логику , то советую вам улучшить знания в Геометрия, геометрия царица всех наук.
Все можно решить с помощью Геометрии.
Алгебра и геометрия начинаются с седьмого класса средней общеобразовательной школы/гимназии/лицея. А до седьмого класса школьники изучают математику. Также семиклассники начинают изучать физику и химию. Алгербу с геометрией нужно изучать тщательно, чтобы успешно сдать ГИА и ЕГЭ в дальнейшем.
Алгебра начинается с пятого класса, а геометрия с седьмого, насколько я помню, до пятого класса математика преподается, по всей видимости те кто отвечал здесь ранее, школу закончили лет двадцать назад)
Математика это придмет который изучают дети с первого по шестой клас , а с седьмого класа она делится на две дисцыплины алгебру и геометрию , в школах с математическим уклоном ети предметы изучают немного раньше .
Такой предмет, как математика в школе присутствует с первого по шестой класс.
А вот с седьмого класса дети изучают уже два предмета:
Современные лицеи, гимназии, спецшколы могут поставить эти предметы в расписание и с первого — шестого класса. В зависимости от их образовательного плана и решения администрации.
Я помню еще из своей школьной жизни, что с первого по седьмой класс ученики изучают математику. Далее эту дисциплину делят на две разные — алгебру и геометрию. Так же в седьмом классе начинают изучать еще и предмет физика, а химию в восьмом.
С седьмого класса начинается алгебра и геометрия, до седьмого класса учат математике. Геометрия и алгебра по сути это и есть математика, просто в седьмом классе ее подразделяют на два класса, на алгебре учат больше считать, а на геометрии рисовать чертижи, высчитывать их длину и так далее.
Алгебра и геометрия это два предмета, которые приходят взамен одному — математики, начиная с 7 класса. С этого времени математический курс изучается по более углубленной программе. Кстати в 7-ом классе также появляется еще и физика.
До шестого включительно обычно идет просто математика. А вот после седьмого класса уже начинается разделение на алгебру и геометрию. Но это все сильно зависит от направленности учебного заведения, степени углубленности программы, по которой идет класс и т.д. Не исключено, что какие-то начала геометрии в математических гимназиях могут давать уже и в начальной школе.
По крайней, когда я учился, математика начала делиться на алгебру и геометрию только в 7 классе. Сейчас, если посмотреть по учебникам, которые выпускаются, то алгебра и геометрия начинается с 7 класса. Хотя я не удивлюсь, что есть какие-то спец лицеи, которые эти предметы начинают изучать раньше.
Алгебра и геометрия в общеобразовательных школах начинаются обычно с седьмого класса.
Алгебра и Геометрия в школьников в общеобразовательных школах начинается с 7 класса . До этого времени общее представление о этих предметах изучается в математике. В спецшколах с углубленным изучением математики эти науки начинают изучать намного раньше.
info-4all.ru
величины и нумерация в начальной школе
В этой статье начинается рубрика «основные содержательные линии в курсе математики начальной школы». Здесь мы разберем, как развивается изучение основных математических понятий с каждым классом начальной школы. Мы рассмотрим такие основные линии, как:
Итак, начнем по порядку.
В первом классе наши дети изучают числа до 100. Чтение, запись и последовательность, а также десятичный состав. Далее во втором классе изучаются уже сотни до тысячи.
Изучается разрядность – единицы, десятки и сотни. Затем в третьем классе изучаются числа до 10000 – чтение, запись, последовательность и разрядный состав.
И наконец, в четвертом классе изучаются числа до 1000000.
Единицы длины начинают изучаться в первом классе с такой величины, как сантиметр. Во втором классе изучаются такие величины, как миллиметр, метр и километр. Изучаются соотношения: 1см = 10мм, 1м = 100см, 1км = 1000м. Дети учатся переводить сантиметры в миллиметры. В третьем классе изучается величина дециметр и соотношения: 1дм = 10см, 1м = 10дм. Переводятся метры в сантиметры, сантиметры в дециметры и обратно. И, наконец, в четвертом классе, дети, продолжая переводить разные величины учатся переводить километры в метры, метры в дециметры, дециметры в миллиметры и обратно.
Единицы площади начинают изучаться со второго класса такими величинами, как квадратный метр, квадратный сантиметр и квадратный километр. В третьем классе используются названия единиц площади в задачах. В четвертом классе дети узнают такие величины, как квадратный дециметр, ар, гектар, квадратный километр. Изучаются соотношения: 1 кв.см = 100 кв.мм, 1 кв.дм = 100 кв.см, 1 кв.м = 100 кв.дм.
Единицы вместимости – в первом классе встречается название литр. Во втором – используются единицы вместимости в задачах, как и в третьем и в четвертом классе.
Единицы времени начинают изучать во втором классе с таких величин, как час и минута. Дети узнают соотношение 1ч = 60 мин. В третьем классе уже изучаются секунды, сутки, неделя, месяц, год и их соотношения: 1мин = 60с, 1сут = 24ч, 1неделя = 7 суткам, 1 год = 365 (366) суткам. А также перевод часов в минуты, минут с секунды, сутки в часы и обратно. В четвертом классе проходят такие величины, как век, тысячелетие и соотношение: 1век = 100годам.
Единицы скорости начинают изучаться с третьего класса с названий: км/ч, км/мин, км/с, м/мин и м/с. В четвертом классе используются названия единиц скорости в задачах.
Единицы массы изучаются с первого класса и начинаются с названия – килограмм. Во втором классе используются названия единиц массы в задачах. В третьем классе уже изучаются величины: тонна, грамм, килограмм и их соотношения: 1кг = 1000г, 1т = 1000кг, а также перевод единиц: килограммы в граммы и обратно. В четвертом классе изучается название центнер и соотношения: 1ц = 100кг, 1т = 10ц, а также перевод килограммов в центнеры, килограммов в тонны, центнеры в тонны и обратно.
В следующих статье этого цикла мы рассмотрим тему “вычислительные навыки” .
<div><img src=”//mc.yandex.ru/watch/12929171″ style=”position:absolute; left:-9999px;” alt=”” /></div>Понравилась статья — поделитесь с друзьями:
Подпишитесь на новости сайта:
Оставляйте пожалуйста комментарии в форме ниже
beginnerschool.ru
