Геометрический сайт
Статьи:
И. Ф. Шарыгин. Избранные статьи djvu. Статьи Игоря Фёдоровича в «Кванте» ссылка.
В. Протасов, В. Тихомиров. Геометрические шедевры Шарыгина (pdf) «Квант», №1, 2006 г.
Классика
Этот раздел предназначен, в первую очередь, школьникам 8-10 классов, которые уверенно справляются с задачами из учебника и решили
узнать чуть больше. И. Ф. Шарыгин. Вокруг биссектрисы «Квант», №8, 1983 г."В этой статье собраны некоторые геометрические факты, прямо или
косвенно связанные с биссектрисой треугольника."
И. Ф. Шарыгин, А. Ягубьянц Окружность девяти точек и прямая Эйлера «Квант» №8, 1981 г. К этой статье рекомендуем такую серию задач.
И. А. Кушнир Золотой ключ Леонарда Эйлера (pdf) «Математика в школах Украины», №13-15, 2012 г.
Рассказывается о приложениях окружности девяти точек для доказательства классических задач. А.Д. Блинков, Ю.А. Блинков. Вневписанная окружность. (pdf) «Квант», №2, 2009 г. В статье излагаются классические факты о вневписанной окружности, обсуждаются задачи, в которых вневписанная окружность возникает
самым неожиданным образом.
Г. Б. Филипповский. Параллелограмм Вариньона решает задачи
Г. Б. Филипповский.О двух параллелограммах в треугольнике. (pdf) «Квант», №4, 2008 г.
Г. Б. Филипповский.Замечательная прямая треугольника. (pdf) «Квант», №4, 2007 г. К статье рекомендуем подборку задач о вписанной окружности.
Конструкции
В.Ю. Протасов. О двух велосипедистах и вешнёвой косточке (pdf) «Квант», №3, 2008 г. "Попробуем подвести некоторые итоги. Две задачи международных олимпиад,
задача о бабочке, два десятка геометрических задач, которые мы сформулировали
в виде упражнений (некоторые из них появлялись на математических олимпиадах,
в Задачнике , и в различных сборниках задач). Список далеко не полный.
И все это выросло из задачи 1, совсем простенькой и неинтересной, которую мы
вначале и решать-то не хотели."
А. Д. Блинков, Ю. А. Блинков. Две окружности в треугольнике, три окружности в треугольнике… (pdf) «Квант», №2, 2012 г.
Г. Б. Филипповский О точке на стороне
и двух параллельных (pdf) «Математика в школах Украины», №4, 2011 г.
А. Полянский. Воробьями по пушкам (pdf) «Квант», №2, 2012 г. Решения упражнений "В этой статье мы пользуясь двумя простыми и элегантными фактами, решим две достаточно сложные задачи."
Теорема Фейербаха и точка Фейербаха
В.Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г. В статье обсуждаются сразу две жемчужины: теорема Тебо и теорема Фейербаха. Оказывается, что одна из теорем является следствием другой!
П.А. Кожевников. Ещё раз о точке Фейербаха. (pdf) Математическое просвещение, Выпуск 15, 2012 г. "В этой заметке предлагается геометрическое доказательство
теоремы Фейербаха, которое дает возможность описать точку Фейербаха
и, в частности, получить отличное от авторского геометрическое решение
задачи 8 из задачного раздела «Математического просвещения», вып. 14,
2010 г."
J.L. Ayme. Красивое доказательство теоремы Фейербаха. (pdf) Очень красивое доказательство теоремы Фейербаха, найдённое не так давно.
Оригинал статьи можно посмотреть на странице автора.
Фольклор. Доказательство теоремы Фейербаха по И. Ф. Шарыгину. (pdf)
Nguyen Minh Ha and Nguyen Pham Dat.Synthetic Proofs of Two Theorems Related to
the Feuerbach Point.(pdf) Forum Geometricorum
Volume 12 (2012) 39–46.
В статье излагаются геометрические доказательства двух замечательных теорем, связанных с точкой Фейербаха.
Кроме цитированной статьи J. Vonk, рекомендуем
заглянуть в статью Куланина Е. Д., в которой теорема Емельянова доказывается с помощью коник. Jan Vonk. The Feuerbach point and reflections of the Euler line. (pdf) Forum Geometricorum, 9 (2009) 47—55. Рассматриваются интересные свойства точки Фейербаха.
Куланин Е.Д., Шихова Н.А. Прямые Эйлера и точки Фейербаха.(pdf) Математическое образование, №2, 2012.
Кожевников П. А.(по статье Д. Гринберга) Обобщение теоремы Фейербаха. (pdf)
Куланин Е. Д. Об описанных окружностях чевианных и педальных треугольников и некоторых кривых, связанных с треугольником. (pdf)
Ежегодник «Математическое просвещение», №9, М., 2005. Доказательство теоремы Фейербаха через коники! В статье указывается целое семейство окружностей, проходящих через точку Фейербаха(например,
окружность, проходящая через основания биссектрис, проходит через точку Фейербаха). Для понимания статьи необходим некоторый опыт работы с
кониками, который можно получить, почитав замечательную книгу А. Акопяна, А. Заславского (pdf).
Построения
А. Д. Блинков Геометрические построения с помощью треугольника-шаблона (pdf) «Квантик», №3-4, 2012 г.
Е. Д. Куланин Еще раз о трисекции угла (pdf) «Математика в школах Украины», №4, 2012 г.
Гомотетия
Рекомендуем такие интересные серии задач на гомотетию:Ортоцентр, середина стороны, точка пересечения касательных и … еще одна точка! (pdf)
Прямая Нагеля (pdf)
Лемма о вписанной окружности
Поворотная гомотетия
Полувписанная окружность, окружности Тебо
А. Гирич Несколько задач о треугольниках и окружностях
текст «Квант», №11, 1990 г.В.Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г. Рекомендуем серию задач про полувписанную окружность:
полувписанная окружность
Изогональное сопряжение
Для первого знакомства с темой рекомендуем книжку В. В. Прасолова.А. В. Акопян, А. А. Заславский Разные взгляды на изогональное сопряжение (pdf) Математическое просвещение, сер. 3, вып. 11, 2007.
Dimitar Belev Some Properties of the Brocard Points of a Cyclic Quadrilateral (pdf), Journal of Classical Geometry, volume 2, 2013
Д. Гринберг Isogonal conjugation with respect to a triangle (zip)
Комбинаторная геометрия
В. Ю. Протасов Теорема Хелли и вокруг неё (pdf) «Квант», №3, 2009 г.
Н. Б. Васильев Формула Пика «Квант», №12, 1974 г. Для дальнейшего знакомства с этим сюжетом рекомендуем книжку Вавилова и Устинова "Многоугольники
на решетках"(pdf).
Н. Б. Васильев Сложение фигур «Квант», №4, 1976 г.
А. Спивак, М. Смуров Покрытие полосками (часть-1) и (часть-2) «Квант», №4-5, 1998 г.
С. Табачников, В. Тиморин Прямая Сильвестра(pdf) «Квант», №5, 2009 г.
Геометрические неравенства
В. Протасов, В. Тихомиров Пространство Lp и замечательные точки треугольника (pdf) «Квант», №2, 2012 г.
Claudi Alsina, Roger B. Nelsen. Геометрическое доказательство неравенства Эрдеша-Морделла.(pdf)
Forum Geometricorum, 7 (2007) 99-102. В статье излагается одно из самых красивых доказательств известного неравенства.
Замечательные кривые
Акопян А. В. Кардиоида. «Квант» №3, 2012 год.
Акопян А. В. Лемниската Бернулли «Квант» №3, 2009 год.
Трисекция. Теорема Морлея
Штейнгарц Л. Снова о теореме Морлея
«Квант» №5, 2009 год.Тоноян Г., Яглом И. Теорема Морлея «Квант» №8, 1978 год.
Е. Д. Куланин Еще раз о трисекции угла (pdf) «Математика в школах Украины», №4, 2012 г.
Алгебра и геометрия
Г. Б. Филипповский Рене Декарт (1596–1650).
Декартова система координат (pdf) «Математика в школах Украины», №35-36, 2011 г.
А.И. Сгибнев. «Геометрия помогает алгебре» (ps, 2M), (ps-zip, 400K), (pdf, 190K)
Тетраэдр
В. Дубровский, В. Матизен. Из геометрии тетраэдра «Квант» №9, 1988 год.
А. Заславский. Описанная и вписанные сферы тетраэдра «Квант» №1, 2004 год.
А. Заславский, Д. Косов. Изогонально сопряжение в тетраэдре и его гранях «Квант» №3, 2004 год.
Миниатюры:
М. Петкова Салфетки «Кванта» и теорема Пифагора (pdf) «Квант» №3, 2012 год.
П. А. Кожевников Задача M2100
Фольклор Задача Ф. Ивлева. (pdf) В заметке решение трудной и красивой задачи разбито на несколько подзадач, что позволяет использовать материал на кружке.
Решения многих задач и различные обобщения можно найти в статье.
Л. А. Емельянов Задача 7.8. (pdf)
www.geometry.ru
Использование теоремы Чевы в школьном курсе геометрии
Разделы: Математика
Введение
В.И. Арнольд в двадцатом столетии говорил: “Математика — это часть физики”. И.Ф. Шарыгин ее продолжил: “А физика — часть геометрии”. Великий французский архитектор Корбюзье как-то воскликнул: “Все вокруг геометрия!”. В начале 21-го столетия мы можем повторить это восклицание. Посмотрите вокруг — всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики. И правда, современная цивилизация — это цивилизация геометрии. Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и ученых.
На самом деле геометрия является очень мощным средством развития личности. Геометрия развивает такие свойства личности, как независимость в суждениях и поведении, способствует творческому развитию и даже имеет отношение к нравственному развитию личности. Иными словами воспитывает творчески думающих и высоконравственных людей. Это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений. Геометрия очень важна для полноценного физиологического (не только интеллектуального) развития ребенка. Уже сам процесс занятий геометрией имеет большое развивающее значение. “
Учитывая всё выше сказанное о необходимости и важности изучения геометрии, хочется рассмотреть вопросы, расширяющие и углубляющие знания и умения учащихся при изучении этого предмета.
На протяжении всего курса планиметрии одной из стержневых фигур является треугольник. Вокруг этой фигуры формируется курс элементарной геометрии. И это не случайно. Несмотря на то, что треугольник едва ли не самая простейшая фигура после отрезка, она имеет много важных и интереснейших свойств. К этим свойствам сводятся свойства других, более сложных фигур. Среди теорем о треугольниках есть и такие, которые люди знают с древнейших времён, например теорема Пифагора. Геометрия треугольника может гордиться теоремами, носящими имена Эйлера, Торричелли, Лейбница. На рубеже XIX-XX веков из-за большого количества работ, посвящённых треугольнику, был образован целый раздел планиметрии “Новая геометрия треугольника”. Многие из этих работ сейчас выглядят малоинтересными, несовершенными, но некоторые теоремы продолжают жить. Одна из таких теорем – теорема Чевы. Эта теорема не входит в обязательную программу школьного курса, несмотря на то, что она может служить отправной точкой при повторении основных свойств треугольников в 9 классе.
Цель данной работы состоит в том, чтобы показать, какую пользу мы можем извлечь из теоремы Чевы в преподавании школьной геометрии.
В частности, с её помощью легко доказываются следующие свойства:
- медианы треугольника пересекаются в одной точке;
- высоты треугольника пересекаются в одной точке;
- биссектрисы внутренних углов треугольника пересекаются в одной точке;
- отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, пересекаются в одной точке.
В конце предлагается ряд простых и не очень простых задач, которые может решить школьник, используя теорему Чевы.
Полностью текст работы вы можете прочитать здесь
Презентация
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Теорема Декарта (геометрия) — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
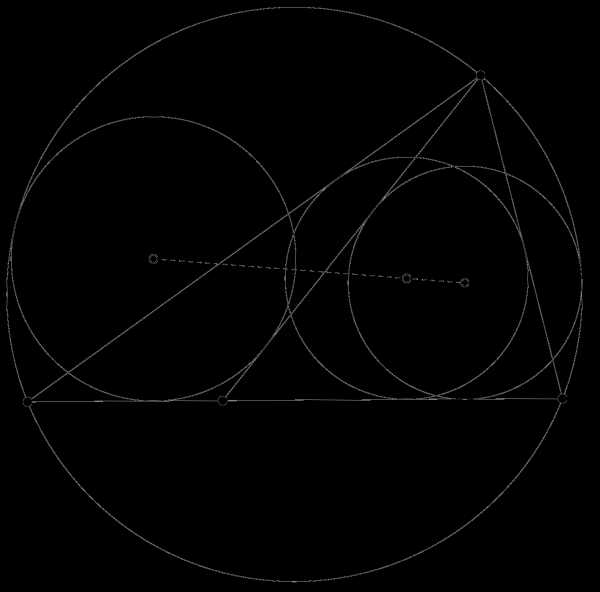
В геометрии теорема Декарта утверждает, что для любых четырёх взаимно касающихся окружностей радиусы окружностей удовлетворяют некоторому квадратному уравнению. Решив это уравнение, можно построить четвёртую окружность, касающуюся остальных трёх заданных окружностей. Теорема названа в честь Рене Декарта, который сформулировал её в 1643 году.
История
Геометрические задачи на касающиеся окружности обсуждались в течение тысячелетий. В древней Греции в III веке до нашей эры Аполлоний Пергский посвятил целую книгу этой теме. К сожалению, книга, носившая название О касаниях, не сохранилась, погибнув при пожаре Александрийской библиотеки.
Рене Декарт обсуждал задачу кратко в 1643 году в письме принцессе Елизавете Богемской. Он пришёл совершенно к тому же решению, что приведено ниже в уравнении (1), и тем самым вписал своё имя в теорему.
Фредерик Содди повторно открыл уравнение в 1936 году. Касающиеся окружности в этой задаче иногда упоминаются как Окружности Содди, возможно потому, что Содди выбрал публикацию своей версии теоремы в виде поэмы, озаглавленной The Kiss Precise (Аккуратный поцелуй), который напечатан в журнале Nature (20 июня 1936). Содди обобщил теорему на сферы. Торольд Госсет обобщил теорему на произвольные размерности.
Определение кривизны
Теорему Декарта проще всего сформулировать в терминах кривизны окружностей. Кривизна окружности определяется как k = ±1/r, где r — её радиус. Чем больше окружность, тем меньше величина её кривизны, и наоборот.
Знак плюс в k = ±1/r ставится, если окружность имеет внешнее касание к другой окружности, как три чёрных окружности на рисунке. Для касающихся окружностей внутренне, как большая красная окружность на рисунке, которая описывает остальные окружности, ставится знак минус.
Если считать, что прямая линия — это вырожденная окружность с нулевой кривизной (а следовательно, с бесконечным радиусом), теорема Декарта применима также и к прямой и двум окружностям, касающимся друг друга попарно. В этом случае теорема даёт радиус третьей окружности, касающейся двух других и прямой.
Если четыре окружности касаются друг друга в шести различных точках и окружности имеют кривизны ki (для i = 1, …, 4), теорема Декарта утверждает[1]:
- <math>(k_1+k_2+k_3+k_4)^2=2\,(k_1^2+k_2^2+k_3^2+k_4^2).</math> (1)
Если пытаться отыскать радиус четвёртой окружности, касающейся трёх касающихся друг друга окружностей, уравнение лучше записать в виде:
- <math> k_4 = k_1 + k_2 + k_3 \pm2 \sqrt{k_1 k_2 + k_2 k_3 + k_3 k_1}. </math> (2)
Знак ± отражает факт, что в общем случае имеется два решения. Если исключить вырожденный случай прямой линии, одно решение положительно, другое же может быть как положительным, так и отрицательным. Если решение отрицательно, оно представляет окружность, описывающую первых три (как показано на рисунке).
Специальные случаи
Если одну из окружностей заменить на прямую линию, то одно из чисел ki, скажем, k3, будет нулевым и выпадает из уравнения (1). Уравнение (2) становится много проще:
- <math>k_4=k_1+k_2\pm2\sqrt{k_1k_2}.</math> (3)
Если две окружности заменить прямыми, касание между двумя окружностями заменяется параллельностью двух прямых. Две другие оставшиеся окружности должны быть равны. В этом случае, с k2 = k3 = 0, уравнение (2) становится тривиальным
- <math>\displaystyle k_4=k_1.</math>
Невозможно заменить три окружности прямыми, поскольку одна окружность и три прямые не могут касаться друг друга попарно. Теорема Декарта неприменима также к случаю, когда все четыре окружности касаются друг друга в одной точке.
Ещё один специальный случай — когда ki являются квадратами,
- <math>(v^2+x^2+y^2+z^2)^2=2\,(v^4+x^4+y^4+z^4) </math>
Эйлер показал, что эквивалентно тройке пифагоровых троек,
- <math>(2vx)^2+(2yz)^2 =\, (v^2+x^2-y^2-z^2)^2 </math>
- <math>(2vy)^2+(2xz)^2 =\, (v^2-x^2+y^2-z^2)^2 </math>
- <math>(2vz)^2+(2xy)^2 =\, (v^2-x^2-y^2+z^2)^2 </math>
и может быть задано параметрическое представление. Если выбрать отрицательный знак кривизны,
- <math>(-v^2+x^2+y^2+z^2)^2=2\,(v^4+x^4+y^4+z^4) </math>
уравнение можно представить в виде хорошо известного параметрического решения[2],
- <math>[v, x, y, z] =\, [2(ab-cd)(ab+cd), (a^2+b^2+c^2+d^2)(a^2-b^2+c^2-d^2), 2(ac-bd)(a^2+c^2), 2(ac-bd)(b^2+d^2)] </math>,
где
- <math>a^4+b^4 =\, c^4+d^4 </math>.
Комплексная теорема Декарта
Для определения окружности полностью нужно знать не только её радиус (или кривизну), но нужно ещё знать и её центр. Соответствующее уравнение лучше всего написать, когда координаты (x, y) представлены в виде комплексного числа z = x + iy. Уравнение тогда выглядит подобно уравнению в теореме Декарта и поэтому называется комплексной теоремой Декарта.
Если даны четыре окружности с кривизнами ki и центрами zi (i = 1…4), вдобавок к равенству (1) выполняется следующее равенство:
- <math>(k_1z_1+k_2z_2+k_3z_3+k_4z_4)^2=2\,(k_1^2z_1^2+k_2^2z_2^2+k_3^2z_3^2+k_4^2z_4^2).</math> (4)
После того, как k4 будет найдено при помощи равенства (2), можно начать вычисление z4 путём изменения уравнения (4) к виду, похожему на (2):
- <math>z_4 = \frac{z_1 k_1 + z_2 k_2 + z_3 k_3 \pm 2 \sqrt{k_1 k_2 z_1 z_2 + k_2 k_3 z_2 z_3 + k_1 k_3 z_1 z_3} }{k_4}.</math>
Снова, в общем случае, имеется два решения для z4, соответствующие двум решениям для k4.
Обобщения
Обобщение для n-мерного пространства иногда упоминается как теорема Содди–Госсе, хотя это сделано уже в 1886 Лахланом (R. Lachlan). В n-мерном евклидовом пространстве максимальное число взаимно касающихся (n – 1)-мерных сфер равно n + 2. Например, в 3-мерном пространстве могут взаимно касаться пять сфер. Кривизны гиперсфер удовлетворяют уравнению
- <math>\left(\sum_{i=1}^{n+2} k_i\right)^2 = n\,\sum_{i=1}^{n+2} k_i^2</math>
и случай ki = 0 соответствует гиперплоскости, точно как в двумерном случае.
Хотя нет 3-мерных аналогов комплексным числам, связь между местоположениями центров можно представить в виде матричных уравнений[3].
Смотрите также
Напишите отзыв о статье «Теорема Декарта (геометрия)»
Примечания
- ↑ Формулу (1) иногда называют теоремой Содди. Он ей посвятил небольшую поэму.
- ↑ [sites.google.com/site/tpiezas/017 A Collection of Algebraic Identities: Sums of Three or More 4th Powers]
- ↑ Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks Beyond the Descartes Circle Theorem // The American Mathematical Monthly. — April 2002. — Т. 109, вып. 4. — С. 338–361.
Ссылки
- [www.cut-the-knot.org/Curriculum/Geometry/Eppstein.shtml Interactive applet demonstrating four mutually tangent circles] at cut-the-knot
- [www.pballew.net/soddy.html The Kiss Precise]
- [www.jwz.org/xscreensaver/screenshots/ XScreenSaver: Screenshots] :: An XScreenSaver display hack visualizes Descartes’ theorem, in hack “Apollonian”.
- [arxiv.org/abs/math/0101066 Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Beyond The Descartes Circle Theorem]
Отрывок, характеризующий Теорема Декарта (геометрия)
Князь Василий исполнил обещание, данное на вечере у Анны Павловны княгине Друбецкой, просившей его о своем единственном сыне Борисе. О нем было доложено государю, и, не в пример другим, он был переведен в гвардию Семеновского полка прапорщиком. Но адъютантом или состоящим при Кутузове Борис так и не был назначен, несмотря на все хлопоты и происки Анны Михайловны. Вскоре после вечера Анны Павловны Анна Михайловна вернулась в Москву, прямо к своим богатым родственникам Ростовым, у которых она стояла в Москве и у которых с детства воспитывался и годами живал ее обожаемый Боренька, только что произведенный в армейские и тотчас же переведенный в гвардейские прапорщики. Гвардия уже вышла из Петербурга 10 го августа, и сын, оставшийся для обмундирования в Москве, должен был догнать ее по дороге в Радзивилов.
У Ростовых были именинницы Натальи, мать и меньшая дочь. С утра, не переставая, подъезжали и отъезжали цуги, подвозившие поздравителей к большому, всей Москве известному дому графини Ростовой на Поварской. Графиня с красивой старшею дочерью и гостями, не перестававшими сменять один другого, сидели в гостиной.
Графиня была женщина с восточным типом худого лица, лет сорока пяти, видимо изнуренная детьми, которых у ней было двенадцать человек. Медлительность ее движений и говора, происходившая от слабости сил, придавала ей значительный вид, внушавший уважение. Княгиня Анна Михайловна Друбецкая, как домашний человек, сидела тут же, помогая в деле принимания и занимания разговором гостей. Молодежь была в задних комнатах, не находя нужным участвовать в приеме визитов. Граф встречал и провожал гостей, приглашая всех к обеду.
«Очень, очень вам благодарен, ma chere или mon cher [моя дорогая или мой дорогой] (ma сherе или mon cher он говорил всем без исключения, без малейших оттенков как выше, так и ниже его стоявшим людям) за себя и за дорогих именинниц. Смотрите же, приезжайте обедать. Вы меня обидите, mon cher. Душевно прошу вас от всего семейства, ma chere». Эти слова с одинаковым выражением на полном веселом и чисто выбритом лице и с одинаково крепким пожатием руки и повторяемыми короткими поклонами говорил он всем без исключения и изменения. Проводив одного гостя, граф возвращался к тому или той, которые еще были в гостиной; придвинув кресла и с видом человека, любящего и умеющего пожить, молодецки расставив ноги и положив на колена руки, он значительно покачивался, предлагал догадки о погоде, советовался о здоровье, иногда на русском, иногда на очень дурном, но самоуверенном французском языке, и снова с видом усталого, но твердого в исполнении обязанности человека шел провожать, оправляя редкие седые волосы на лысине, и опять звал обедать. Иногда, возвращаясь из передней, он заходил через цветочную и официантскую в большую мраморную залу, где накрывали стол на восемьдесят кувертов, и, глядя на официантов, носивших серебро и фарфор, расставлявших столы и развертывавших камчатные скатерти, подзывал к себе Дмитрия Васильевича, дворянина, занимавшегося всеми его делами, и говорил: «Ну, ну, Митенька, смотри, чтоб всё было хорошо. Так, так, – говорил он, с удовольствием оглядывая огромный раздвинутый стол. – Главное – сервировка. То то…» И он уходил, самодовольно вздыхая, опять в гостиную.
– Марья Львовна Карагина с дочерью! – басом доложил огромный графинин выездной лакей, входя в двери гостиной.
Графиня подумала и понюхала из золотой табакерки с портретом мужа.
– Замучили меня эти визиты, – сказала она. – Ну, уж ее последнюю приму. Чопорна очень. Проси, – сказала она лакею грустным голосом, как будто говорила: «ну, уж добивайте!»
Высокая, полная, с гордым видом дама с круглолицей улыбающейся дочкой, шумя платьями, вошли в гостиную.
«Chere comtesse, il y a si longtemps… elle a ete alitee la pauvre enfant… au bal des Razoumowsky… et la comtesse Apraksine… j’ai ete si heureuse…» [Дорогая графиня, как давно… она должна была пролежать в постеле, бедное дитя… на балу у Разумовских… и графиня Апраксина… была так счастлива…] послышались оживленные женские голоса, перебивая один другой и сливаясь с шумом платьев и передвиганием стульев. Начался тот разговор, который затевают ровно настолько, чтобы при первой паузе встать, зашуметь платьями, проговорить: «Je suis bien charmee; la sante de maman… et la comtesse Apraksine» [Я в восхищении; здоровье мамы… и графиня Апраксина] и, опять зашумев платьями, пройти в переднюю, надеть шубу или плащ и уехать. Разговор зашел о главной городской новости того времени – о болезни известного богача и красавца Екатерининского времени старого графа Безухого и о его незаконном сыне Пьере, который так неприлично вел себя на вечере у Анны Павловны Шерер.
– Я очень жалею бедного графа, – проговорила гостья, – здоровье его и так плохо, а теперь это огорченье от сына, это его убьет!
– Что такое? – спросила графиня, как будто не зная, о чем говорит гостья, хотя она раз пятнадцать уже слышала причину огорчения графа Безухого.
– Вот нынешнее воспитание! Еще за границей, – проговорила гостья, – этот молодой человек предоставлен был самому себе, и теперь в Петербурге, говорят, он такие ужасы наделал, что его с полицией выслали оттуда.
– Скажите! – сказала графиня.
– Он дурно выбирал свои знакомства, – вмешалась княгиня Анна Михайловна. – Сын князя Василия, он и один Долохов, они, говорят, Бог знает что делали. И оба пострадали. Долохов разжалован в солдаты, а сын Безухого выслан в Москву. Анатоля Курагина – того отец как то замял. Но выслали таки из Петербурга.
– Да что, бишь, они сделали? – спросила графиня.
– Это совершенные разбойники, особенно Долохов, – говорила гостья. – Он сын Марьи Ивановны Долоховой, такой почтенной дамы, и что же? Можете себе представить: они втроем достали где то медведя, посадили с собой в карету и повезли к актрисам. Прибежала полиция их унимать. Они поймали квартального и привязали его спина со спиной к медведю и пустили медведя в Мойку; медведь плавает, а квартальный на нем.
– Хороша, ma chere, фигура квартального, – закричал граф, помирая со смеху.
– Ах, ужас какой! Чему тут смеяться, граф?
Но дамы невольно смеялись и сами.
– Насилу спасли этого несчастного, – продолжала гостья. – И это сын графа Кирилла Владимировича Безухова так умно забавляется! – прибавила она. – А говорили, что так хорошо воспитан и умен. Вот всё воспитание заграничное куда довело. Надеюсь, что здесь его никто не примет, несмотря на его богатство. Мне хотели его представить. Я решительно отказалась: у меня дочери.
– Отчего вы говорите, что этот молодой человек так богат? – спросила графиня, нагибаясь от девиц, которые тотчас же сделали вид, что не слушают. – Ведь у него только незаконные дети. Кажется… и Пьер незаконный.
Гостья махнула рукой.
– У него их двадцать незаконных, я думаю.
Княгиня Анна Михайловна вмешалась в разговор, видимо, желая выказать свои связи и свое знание всех светских обстоятельств.
wiki-org.ru
Ответы@Mail.Ru: Все теоремы по геометрии.
Через любые две точки Если две прямые имеют общуюможно провести прямую, точку, то они пересекаются.
и притом только одну.
Прямая а и точки А и В.
Прямая а и b пересекаются в точке О.
Две прямые либо имеют только одну общую точку,
либо не имеют общих точек.
Угол.
Угол – это геометрическая фигура, Угол называется развёрнутым, которая состоит из точки и двух лучей, если обе его стороны
исходящих из этой точки. лежат на одной прямой.
Угол с вершиной О и сторонами h и k. Развёрнутый угол с вершиной С
и сторонами p и q.
Развёрнутый угол = 180º; Неразвёрнутый угол < 180º .
Луч, исходящий из вершины угла и Два угла, у которых одна общая
делящий его на два равных угла, сторона общая, а две другие
называется биссектриса угла. являются продолжениями одна
другой, называются смежными.
Два угла, называются вертикальными,
если стороны одного угла являются Сумма смежных углов = 180º.
продолжениями сторон другого.
Две пересекающиеся прямые
Вертикальные углы равны. называются перпендикулярными,
если они образуют 4 прямых угла.
Глава I I.
Треугольники.
Треугольник – геометрическая фигура, РАВС = АВ+ВС+СА.
кот-ая состоит из 3 точек, не лежа-
щих на 1 прямой, соединённых отрезками.
В равных треугольниках против
Треугольник с вершинами А, В, С и соответственно равных сторон
Сторонами а, b, c. лежат равные углы, также против
соответственно равных равных
углов лежат равные стороны.
Теорема: Если 2 стороны и угол Теорема: Из точки, не лежа-
между ними 1-го треугольника щей на прямой, можно провести
соответственно равны 2 сторонам перпендикуляр к этой, и притом
и углу между ними другого только один.
треугольника, то треугольники равны.
Отрезок, соединяющий вершину треуг- Отрезок бисс-сы угла треуг-ка,
ка с серединой противоположной сто- соединяющий вершину треуг-ка
роны, называется медианой треуг-ка. с точкой противоположной сторо- ны, называется бисс-сой треуг-ка.
Перпендикуляр, проведённый из верши-
ны треуг-ка к прямой, содержащей Треуг-к, у кот-го 2 стороны равны,
противоположную сторону, называ- называется равнобедренным.
ется вы
otvet.mail.ru
Теоремы косинусов (сферическая геометрия) — это… Что такое Теоремы косинусов (сферическая геометрия)?
Сферический треугольник.Первая и вторая сферические теоремы косинусов устанавливают соотношения между сторонами и противолежащими им углами сферического треугольника.
Формулировка
Теоремы косинусов для сферического треугольника со сторонами a, b, c и углами A, B, C имеют следующий вид:
Эти две теоремы двойственны по отношению друг к другу, поскольку углы и стороны всякого сферического треугольника дополняются до развёрнутого угла сторонами и углами соответствующего полярного треугольника. Поэтому достаточно доказать одну из них.
Доказательство
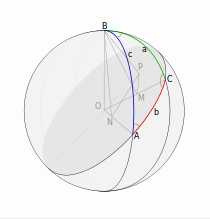Рисунок к доказательству теоремы косинусов с помощью проекций.Доказательство проведём с помощью проекций[1]. На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O. BP — перпендикуляр к плоскости большого круга, проходящего через сторону b, BM — перпендикуляр к OC, BN — перпендикуляр к OA. По утверждению, обратному теореме о трёх перпендикулярах, PM — перпендикуляр к OC, PN — перпендикуляр к OA. Заметим, что угол PMB равен π — C, кроме того, ON = R cos c и OM = R cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON.
- ,
- ,
- ,
- .
Подставляем три последних выражения и указанное выше выражение ON = R cos c в первое выражение и получаем:
- .
Теоремы косинусов для двух других сторон, то есть теорему для cos a и теорему для cos b, получаем аналогично, их также можно получить сразу из формулы для стороны c при помощи круговой перестановки букв:
Сферический треугольник для определения кратчайшего расстояния между точками на Земле.Следствия и применение
Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:
Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек и , разность долгот — , кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии[2]:
Эта формула сразу получается применением теоремы косинусов к стороне AB сферического треугольника PnAB. Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам[3].
Пример 1: определение углового расстояния между двумя светилами на небесной сфере
Определим угловое расстояние (x) между звездой δ Цефея (экваториальные координаты: α1=22ч 29м, δ1=+58° 25′) и галактикой Туманность Андромеды (α2=0ч 43м, δ2=+41° 16′) на небесной сфере. Выражаем α1 в градусах и долях градуса:
Аналогично получаем, что α2=10°,75. Выражаем δ1 в градусах и долях градуса:
Аналогично δ2=41°,27. Применяем теорему косинусов[4]:
Отсюда x=27°,11.
Теорема косинусов в её втором виде (соотношение между тремя углами и стороной) может быть применена для вычисления взаимного наклонения двух орбит при известном наклонении каждой орбиты к какой-то другой плоскости. Например, по этой формуле можно вычислить наклонение орбиты Плутона к орбите Нептуна, используя наклонения их орбит к эклиптике и долготы их восходящих узлов.
Пример 2: определение взаимного наклонения орбит небесных тел
Определим взаимное наклонение (x) орбит Плутона (наклонение орбиты к эклиптике — 17°,14, долгота восходящего узла — 110°,30) и Нептуна (наклонение орбиты к эклиптике — 1°,77, долгота восходящего узла — 131°,79). В соответствующем сферическом треугольнике известны два угла: один равен наклонению орбиты Плутона к эклиптике, другой — дополнению наклонения орбиты Нептуна к эклиптике до 180 градусов. Известна также прилегающая к этим углам сторона, равная разности долгот восходящих узлов Плутона и Нептуна. Осталось применить второй вариант теоремы косинусов — для углов:
Отсюда x≈15°,51.
История
Теорема косинусов для сферического треугольника математиками средневекового Востока в общем виде сформулирована не была, хотя при решении конкретных астрономических задач они иногда пользовались соотношениями, равносильными этой теореме. Эти соотношения, используемые при определении высоты Солнца, встречаются в сочинениях Сабита ибн Корры, ал-Махани, ал-Баттани, Ибн Юниса, ал-Бируни.
Впервые теорему косинусов в явном виде сформулировал в XV веке Региомонтан, назвав её «теоремой Альбатегния» (по латинизированному имени ал-Баттани).
См. также
Примечания
- ↑ Приводится по изданию: Степанов Н.Н. Формулы косинуса стороны // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 24—28. — 154 с.
- ↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы ее задания // Навигация и лоция. — Киев, 2009.
- ↑ Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир, 1988. — С. 44—46. — 168 с. — ISBN 5030009361
- ↑ Lee Kai Ming PHYS 2021 — The Physical Universe. — 2010. — С. 6.
Литература
- Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.
veter.academic.ru
Аксиомы и теоремы геометрии Википедия
Евкли́дова геоме́трия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.).
Основные сведения[ | ]
Элементарная геометрия — геометрия, определяемая в основном группой перемещений (изометрий) и группой подобия. Однако содержание элементарной геометрии не исчерпывается указанными преобразованиями. К элементарной геометрии также относят преобразование инверсии, вопросы сферической геометрии, элементы геометрических построений, теорию измерения геометрических величин и другие вопросы.
Элементарную геометрию часто называют евклидовой геометрией, так как первоначальное и систематическое её изложение, хотя и недостаточно строгое, было в «Началах» Евклида. Первая строгая аксиоматика элементарной геометрии была дана Гильбертом. Элементарная геометрия изучается в средней общеобразовательной школе.
Аксиоматика[ | ]
Задача аксиоматизации элементарной геометрии состоит в построении системы аксиом так, чтобы все утверждения евклидовой геометрии следовали из этих аксиом чисто логическим выводом без наглядности чертежей.
В «Началах» Евклида была дана следующая система аксиом:
- От всякой точки до всякой точки можно провести прямую.
- Ограниченную прямую можно непрерывно продолжать по прямой.
- Из всякого центра всяким радиусом может быть описан круг.
- Все прямые углы равны между собой.
- Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.
Эта система была достаточна для того, чтобы один математик понял другого, но в доказательствах подразумевались и другие утверждения[1]:
- Равные одному и тому же равны между собой
- Eсли к равным прибавляются равные, то и результаты будут равны
- Eсли от равных отнимаются равные, то и остатки будут равны
- Eсли к неравным прибавляются равные, то и целые не будут равны
- Удвоенные одного и того же равны между собой
- Половины одного и того же равны между собой
- Совмещающиеся друг с другом фигуры равны между собой
- Целое больше части
- Две прямые не содержат пространства
Позже была сформулирована теорема Паша, которая не может быть выведена из постулатов Евклида, но неявно считается истинной.
В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Попытки улучшения евклидовой аксиоматики предпринимались до Гильберта Пашем, Шуром[en], Пеано, Веронезе, однако подход Гильберта, при всей его консервативности в выборе понятий, оказался более успешным.
Существуют и другие современные аксиоматики, наиболее известные:
Системы обозначений[ | ]
Существует несколько конкурирующих систем обозначений.
- Точки обычно обозначаются прописными латинскими буквами A,B,C,…{\displaystyle A,B,C,\dots }
ru-wiki.ru
Теорема — геометрия — Большая Энциклопедия Нефти и Газа, статья, страница 3
Теорема — геометрия
Cтраница 3
Абстрактная теория предполагает, что они даны, и не нуждается ни в каких предположениях об их действительном численном значении или о способе их измерения на практике. Целый ряд наиболее важных приложений носит качественный характер и не зависит от численных значений вероятностей событий; общие же выводы теории находят себе многочисленные применения, совершенно так же, как теоремы геометрии служат основой и физических теорий и технических приложений. В тех сравнительно редких случаях, когда требуется знать численное значение вероятностей событий, вычислительные приемы варьируются так же широко, как меняются методы определения расстояний. Когда плотник, землемер, летчик и астроном измеряют расстояния, то в их действиях мало общего. В нашем круге вопросов мы будем, например, рассматривать коэффициент диффузии, определяемый с помощью понятий теории вероятностей. Чтобы найти численное значение этого коэффициента, требуются физические рассмотрения, связывающие явление диффузии с другими теориями; прямое же измерение невозможно. Таблицы продолжительнисти жизни, наоборот, составляются на основании наблюдений. В наиболее важных приложениях определение вероятностей событий или сравнение результатов теории с данными наблюдений требуют применения довольно сложных статистических методов, основанных в свою очередь на тонкой вероятностной теории. Другими словами, хотя наглядный смысл вероятностей событий и ясен, но лишь по мере развития теории мы увидим, как следует применять это понятие. [31]
Египет и Вавилон, познакомившись с др. — вост. ПИФАГОРА ТЕОРЕМА, теорема геометрии, приписываемая Пифагору: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. [32]
На интуитивном уровне эта фраза кажется содержательной — она отвечает нашим представлениям о плоскости. Однако с точки зрения геометрии она лишена смысла, поскольку в аксиомах и теоремах геометрии нет упоминания о каких-либо часовых стрелках. Наша ближайшая задача состоит в том, чтобы придать указанным понятиям ясный геометрический смысл. [33]
В предыдущей главе было доказано, что аксиома параллельности независима от остальных аксиом евклидовой геометрии. Отсюда следует, что, заменив эту аксиому ее отрицанием, мы получим также логически непротиворечивую систему. Геометрия, основанная на этой системе аксиом, называется геометрией Лобачевского. Это позволит теоремы геометрии Лобачевского получать в любой из ее реализаций. [34]
Конечно, этот скачок был достаточно длительным. Есть указания на то, что простейшие теоремы геометрии доказывались уже Филесо. Демокрит дал глубокие для своего времени выводы, содержавшие как бы первый зародыш интегрального исчисления. Открытие несоизмеримых отрезков и последовавшее на ним создание теории отношений несоизмеримых величин было большим достижением греч. Следует различать знание математич. Так, составляющее содержание теоремы Пифагора соотношение между квадратами, построенными на сторонах прямоугольного треугольника, было известно до Пифагора, но соответствующая теорема не была доказана. Помимо понятия о бесконечно продолжаемом ряде целых чисел и неограниченно продолжаемой прямой, возникло также представление о неогранич. Непрерывное, первоначально не подвергавшееся анализу, выступает как неограниченно долимое, содержащее неогранич. При этом, однако, не происходит отказа от существующих теорий; они лишь углубляются и обобщаются. Так, геометрия Лобачевского не опровергает геометрию Эвклида, но обе теории включаются в пек-рую общую систему. Роль каждого из этих факторов различна в каждом конкретном случае. В конечном счете, решающим является влияние др. наук и-гл. [35]
Созданная несколько ранее Ньюэллом н др. программа Логический теоретик, к-рая явилась непосредственным предшественником GPS, использовалась Дж. С помощью этой программы, получившей название SAINT, удавалось брать как неопределенные, так и определенные интегралы, подынтегральные выражения к-рых представляют собой элементарные ф-ции действительных переменных. Большой интерес представляют также работы X. Гелерн-тера в области создания эвристической программы для доказательства теорем геометрии. Его программа моделирует три вычислительные машины ( ВМ): синтаксическую, диаграммную и эвристическую. [36]
Лишь одно препятствие стояло на пути всепроникающего скептицизма Юма — существование общепризнанных истин самой математики. Просто отмахнуться от них Юм не мог, и ему не оставалось ничего другого, как попытаться принизить ценность математических истин. То, что дважды два — четыре, не ново. В действительности дважды два — всего лишь иной способ записать или назвать устно число четыре. Что же касается теорем геометрии, то они представляют собой повторения в более сложной форме аксиом, в которых в свою очередь не больше смысла, чем в утверждении о том, что дважды два — четыре. [37]
Мы воспринимаем, организуем и постигаем опыт в соответствии с теми формами мысли, которые присущи нашему разуму. Опыт попадает в них, словно тесто в форму. Рассудок отпечатывает их на воспринятых чувственных впечатлениях, вынуждая ощущения подстраиваться под априорные формы мысли. Поскольку созерцание пространства присуще разуму, он автоматически постигает некоторые формы пространства. Такие постулаты геометрии, как прямая — кратчайшее расстояние между двумя точками или через любые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну, а также аксиома Евклида о параллельности, которые Кант называл априорными синтетическими суждениями, являются частью оснащения нашего разума. Геометрия как наука занимается изучением логических следствий из этих постулатов. Тот факт, что рассудок воспринимает опыт в понятиях пространственной структуры, предопределяет согласие опыта с исходными аксиомами, постулатами и теоремами геометрии. [38]
Более значительным примером аксиоматического определения является система аксиом геометрии. Рассмат риваемую систему объектов будем разделять на три класса: точки, прямые и плоскости — и будем употреблять для них термины: точка а принадлежит прямой Л, прямая А принадлежит плоскости 51, точка а лежит между точками b и с и другие, выражающие отношения между объектами системы. Вместе с тем, употребляя эти термины, мы не будем вкладывать в них смысла пространственных отношений, а вместо этого выскажем для них некоторую систему аксиом. Это можно сделать по-разному, но существует вполне определенная система аксаом, носящая название системы аксиом геометрии Евклида. Эта система была предложена Гильбертом. В этих аксиомах высказаны все те предпосылки, которые явным или неявным образом употреблялись при доказательстве теорем геометрии Евклида. Таким образом, выводимые из этих теорем следствия адекватно выражают свойства евклидова пространства, интуитивное представление о котором было почерпнуто из непосредственного опыта и существует издавна в умах людей. [39]
Страницы: 1 2 3
www.ngpedia.ru
