Сила тока в электрической цепи – Электрический ток, сила тока, направление электрического тока, напряжение, условие существования тока в проводнике, электрическая цепь, условие существования тока в цепи.

формулы расчета мощности в проводнике

Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.

Электрический ток в проводнике

В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.

От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:

Зависимость силы тока от электрического заряда

Входящие в формулу величины:

• I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
• Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
• Время в секундах.

Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:

I = (qnv)cosαS.

Также используется интегрирование по площади поверхности и сечению проводника.

Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.

Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:                                                                                               

Сила тока участка цепи и цепи с источником тока

Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.

В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.

При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.

Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:

RC = 1/ FC.

Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.

Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:

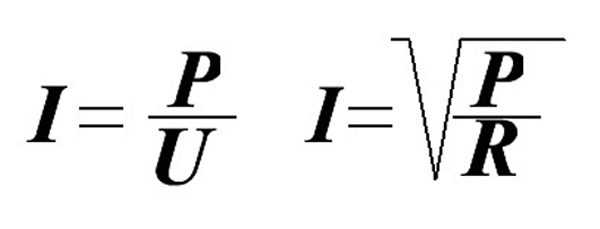
Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.

Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.

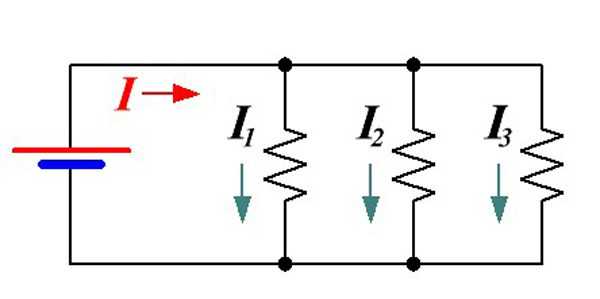
I = I1 + I2 + I3

Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.

Видео

Оцените статью:

elquanta.ru

правила расчета для определения силы тока

На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.

Пример сложных электрических цепей

Пути вычисления электрических схем

Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.

Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.

Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.

Все элементы и устройства подразделяются на три категории:

1. Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
2. Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
3. Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.

Также к основным понятиям электрической схемы относятся:

• Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
• Узел электрической схемы – точка соединения трех и более ветвей схемы;
• Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.

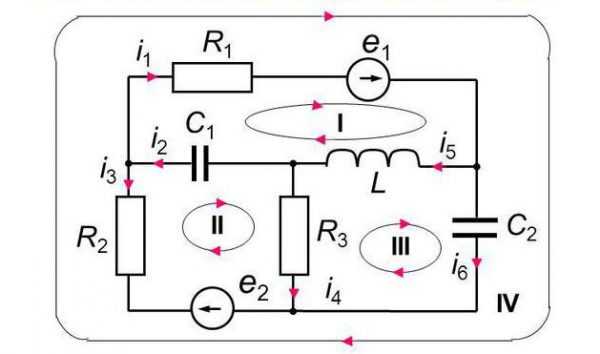
Обозначение ветвей, узлов и контуров на схеме

Метод расчета по законам Ома и Кирхгофа

Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.

Закон Ома для участка цепи

По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:

UR=RI.

Исходя из этой формулы, найти силу тока можно по выражению:

I=UR/R, где:

• UR – напряжение или падение напряжения на резисторе;
• I – ток в резисторе.

Закон Ома для полной цепи

В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:

I=E/Rэ = E/r0+R, где:

• E – ЭДС источника питания;
• rо – внутреннее сопротивление источника питания.

Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.

Первый закон Кирхгофа

Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:

∑mIk=0, где m – число ветвей, подведенных к узлу.

Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».

Второй закон Кирхгофа

Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:

∑nEk=∑mRkIk=∑mUk, где:

• n – число источников ЭДС в контуре;
• m – число элементов с сопротивлением Rk в контуре;
• Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.

Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:

1. Указать относительно положительные направления ЭДС, токов и напряжений;
2. Указать направление обхода контура, описываемого уравнением;
3. Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.

Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи.

Уравнение баланса мощностей имеет вид:

∑EI=∑RI2.

Метод преобразования электрической цепи

Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.

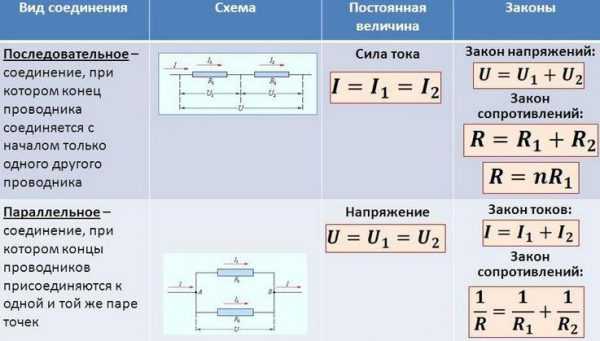
Последовательное и параллельное соединение элементов

Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.

Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду».

По картинке ниже, сопротивления равны:

• R1=R12R31/R12+R31+R23,
• R2=R12R23/R12+R31+R23,
• R3=R31R23/R12+R31+R23.

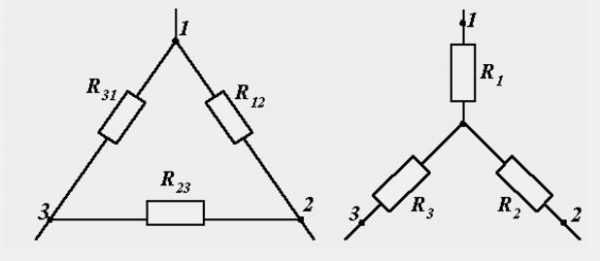
Треугольник и звезда соединений

Дополнительные методы расчета цепей

Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:

1. Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
2. Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
3. Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
4. Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.

Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.

Видео

Оцените статью:

elquanta.ru

Мощность тока в электрических цепях :: SYL.ru

Одним из параметров, характеризующих поведение электронов в электрической цепи, кроме напряжения и тока, выступает мощность. Она является мерой количества работы, которую можно совершить за единицу времени. Работу обычно сравнивают с подъёмом веса. Чем больше вес и высота его подъёма, тем больше работы выполнено. Мощность определяет быстроту совершения единицы работы.

Единицы измерения

Мощность автомобилей исчисляют в лошадиных силах – единице измерения, придуманной изготовителями паровых двигателей с целью измерения работоспособности своих агрегатов в обычном источнике энергии того времени. Мощность автомобиля не говорит, как высоко он может заехать на холм или сколько веса он может перевезти, а только показывает, как быстро он это сделает.

Мощность двигателя зависит от его скорости и вращающего момента выходного вала. Скорость измеряют в оборотах в минуту. Вращающий момент – это момент силы двигателя, который измерялся первоначально в фунт-футах, а сейчас в ньютон-метрах или джоулях.

Тракторный двигатель в 100 л. с. вращается медленно, но с большим крутящим моментом. Мотоциклетный двигатель равной мощности вращается быстро, но с небольшим крутящим моментом. Уравнение расчёта мощности имеет вид:

P = 2π S T / 33000, где S – скорость вращения, об/мин, а T – момент вращения.

Переменными здесь являются момент и скорость. Иначе говоря, мощность прямо пропорциональна ST: P~ST.

Мощность постоянного тока

В электроцепях мощность находится в функциональной зависимости от напряжения и тока. Неудивительно, что она похожа на вышеприведённое уравнение P=IU.

Но тут P не пропорциональна току, умноженному на напряжение, а равняется ему. Исчисляется в ваттах, сокращённо Вт.

Важно знать, что ток и напряжение отдельно мощность не определяют, лишь их совокупность. Напряжение является работой на единицу электрического заряда, а ток – скоростью движения зарядов. Напряжение (эквивалент работы) подобно работе при подъёме веса в противодействие силе гравитации. Ток (эквивалентен скорости) подобен скорости подъёма веса. Их произведение и составляет мощность.

Как тракторный и мотоциклетный моторы, цепь с высоким напряжением и небольшим током способна быть одинаковой мощности с цепью невысокого напряжения и большим током. Напряжение и ток вне взаимосвязи не могут характеризовать мощность электроцепи.

Разомкнутая цепь с напряжением и нулевой силой тока работы не совершает, вне зависимости от высоты напряжения. Ведь, согласно формуле, что угодно, умноженное на 0, даёт 0: P = 0 U = 0. В замкнутой цепи из сверхпроводящего провода с нулевым сопротивлением можно достичь тока при напряжении, равном нулю, что также не приведёт к рассеиванию энергии: P = I 0 = 0.

Лошадиные силы и ватты обозначают одно и то же: количество работы, которую можно совершить за единицу времени. Эти единицы взаимосвязаны соотношением

1 л. с. = 745,7 Вт

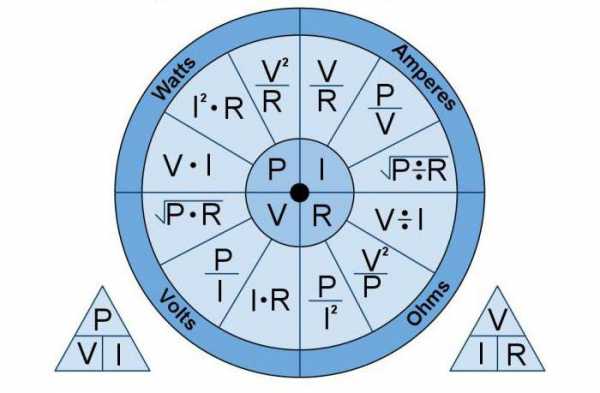
Пример расчёта

Итак, мощность тока электроцепи в ваттах равняется произведению напряжения на ток.

Чтобы определить, например, мощность нагрузки сопротивлением 3 Ом, в цепи с батареей питания напряжением 12 В, необходимо, применив закон Ома, найти ток

I = U/R = 12/3 =4 А

Умножение полученной силы тока на напряжение и даст искомый результат:

P = I U = 4 А 12 В = 48 Вт

Таким образом, лампа потребляет 48 Вт.

Что же произойдёт при увеличении напряжения?

При напряжении 24 В и сопротивлении 3 Ом ток

I= U/R = 24/3 =8 А

При удвоении напряжения удвоилась и сила тока.

P = IU = 8 А 24 В = 192 Вт

Мощность также увеличилась, но больше. Почему? Потому что это функция произведения напряжения на ток, напряжение и ток увеличились в 2 раза, следовательно, мощность возросла в 4 раза. Это можно проверить делением 192 ватт на 48, частное от которого равно 4.

Варианты формулы

Применив алгебру для преобразования формулы, можно взять исходное уравнение и преобразовать его для случаев, когда неизвестен один из параметров.

Если даны напряжение и сопротивление:

P = (U/R) U или P = U²/R

При известной силе тока и сопротивлении:

P = I (I R) или P = I² R

Исторический факт: отношение между рассеиваемой мощностью и силой тока через сопротивление открыл Джеймс Прескотт Джоуль, а не Георг Симон Ом. Оно было опубликовано в 1841 г. в виде уравнения P = I² R и носит название закона Джоуля–Ленца.

Уравнения мощности:

Переменный ток

Закон Ома и Джоуля–Ленца были установлены для постоянного тока, но они справедливы и для мгновенных значений изменяющегося тока и напряжения.

Мгновенное значение P равно произведению мгновенных значений силы тока и напряжения с учётом их смещения по фазе на угол φ:

P(t) = U(t)I(t) = U_m cosωt I_m cos(ωt-φ) = (1/2)U_m I_m cosφ + (1/2) U_m I_m cos(2ωt-φ).

Из уравнения следует, что у мгновенной мощности есть постоянная составляющая, и она совершает колебательные движения вокруг среднего значения с частотой, которая вдвое превышает частоту тока.

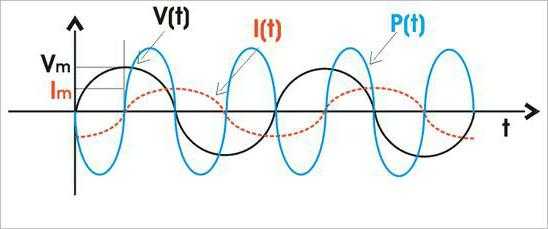
Среднее значение P(t), представляющее практический интерес, равно:

P = (U_mI_m/2) cosφ

С учётом того, что cos φ=R/Z, где Z=(R² + (ωL — 1/ω C)²)^1/2 и U_m/Z = I_m,

P = (R I_m²)/2

Здесь I = I_m 2^-1/2 = 0,707 I_m – эффективное значение силы тока, А.

Аналогично U = U_m2^-1/2 = 0,707 U_m – эффективное напряжение, В.

Средняя мощность через эффективное напряжение и ток определяется

P = U I cos φ, где cos φ – коэффициент мощности.

P в электроцепи переходит в тепловую или другой вид энергии. Наибольшей активной мощности можно достичь при cosφ=1, то есть при отсутствии сдвига фаз. Она носит название полной мощности

S = U I = Z I² = U²/Z

Её размерность совпадает с размерностью P, но с целью отличия S измеряется вольт-амперами, ВА.

Степень интенсивности обмена энергией в электроцепи характеризуется реактивной мощностью

Q = U I sinφ = U I_p = U_p I = X I² = U²/X

Она имеет размерность активной и полной, но с целью различения её выражают вольт-амперами реактивными, ВАр.

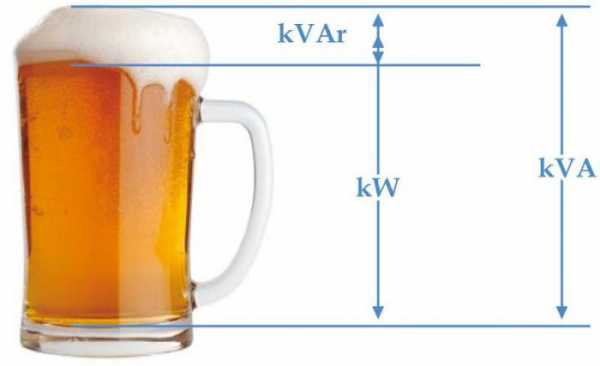
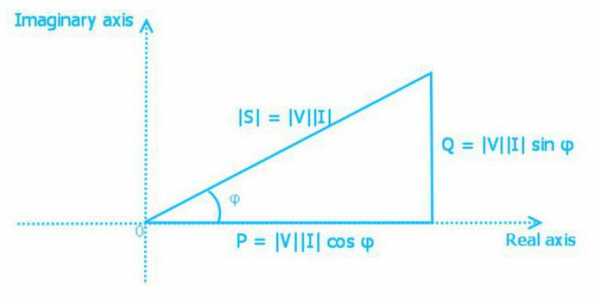
Треугольник мощностей

Мощность активная, реактивная и полная взаимосвязаны выражением

S = (P ²+ Q²)^1/2

Мощность представляют в виде стороны прямоугольного треугольника. Используя законы тригонометрии, можно найти длину одной стороны (количество мощности любого типа) по двум известным сторонам или по длине одной и углу. В таком треугольнике активная мощность является прилежащим катетом, реактивная – противолежащим, а полная мощность – гипотенузой. Угол между катетом активной мощности и гипотенузой равен углу фазы импеданса Z электрической цепи.

Комплексная форма записи этой взаимосвязи следующая:

S = P+jQ = U I cosφ + j U I sinφ= U I e^jφ = U I*, где

S – комплексная мощность;

I* – комплексное сопряжённое значение тока.

Вещественная составляющая комплекса – активная, а мнимая – реактивная.

Мгновенная полная мощность всегда остаётся постоянной величиной.

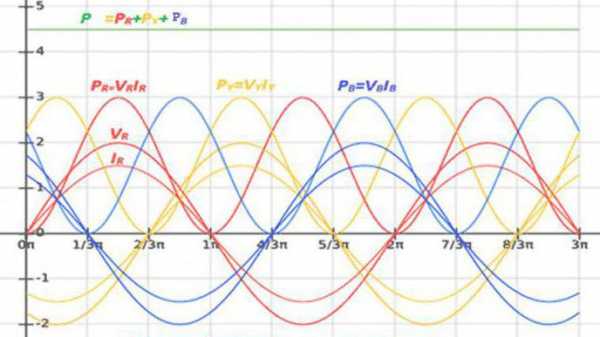
Мощность трёхфазного тока

Нагрузка каждой фазы трёхфазной электроцепи преобразует энергию или обменивается ею с источником питания. Вследствие этого P и Q цепи равняются суммарной мощности всех фаз:

P = P_r+ P_y+ P_b; Q = Q_r+ Q_y+ Q_b – соединение «звезда»;

P = P_ry+ P_yb+ P_br; Q = Q_ry+ Q_yb+ Q_br – соединение «треугольник».

Активные и реактивные мощности каждой фазы определяются, как в однофазной цепи.

Полная мощность трёхфазной цепи:

S = (P²+Q²)^1/2,

что в комплексной форме имеет вид

S = P+jQ = (P_r + P_y + P_b) + j(Q_r + Q_y + Q_b )= S_r + S_y + S_b= U_r I_r + U_y I_y + U_b I_b

Симметричная нагрузка фаз имеет следствием равенство их мощностей. Вот почему мощность тока равна утроенной активной и реактивной мощности фазы:

P = 3P_ф = 3 I_ф U_фcosφ_ф = 3 R_ф I_ф²

Q = 3 Q_ф = 3 I_ф U_ф sinφ_ф = 3 X_ф I_ф²

S = 3 S_ф = 3 I_ф U_ф

I_ф и U_ф здесь можно заменить их линейными значениями, учитывая, что для звезды U_ф=U_л; I_ф=I_л, а для треугольника U_ф=U_л; I_ф=I_л3^-1/2:

P = 3^1/2 I_л U_лcosφ_ф;

Q = 3^{1/2 I_л U_л}sinφ_ф;

S = 3^{1/2 I_л U_л}.

Ток несинусоидальной формы

Определение P в цепи несинусоидального тока аналогично её определению в цепи тока синусоидального, так как за период T средняя мгновенная мощность

P = 1/T∫u i dt

Активная мощность тока определяется суммой P гармонических составляющих, в том числе и постоянной, являющейся гармоникой нулевой частоты.

Реактивная мощность тока подобным образом является результатом сложения Q каждой гармоники.

Q = ∑U_k I_k sinφ_k = ∑ Q_k

Полная мощность определяется произведением эффективного тока и напряжения:

S = I U.

www.syl.ru

Сила тока в электричестве. — МикроПрогер

 

Формула силы тока в электричестве следует из Закона Ома — фундаментального, самого основного закона электричества.

 

I=U/R=[1]A

где I- сила тока (Ампер), U — напряжение (Вольт), R — сопротивление (Ом)

 

 

Если Вам известно напряжение на участке цепи, а также сопротивление проводников, находящимся на этом участке, вы без труда сможете найти силу тока, протекающего через этот участок цепи.

 

Формула Силы тока

 

 

 

Для наглядности, поясним самые важные практические моменты при использовании формулы силы тока и нахождении силы тока при известном напряжении и сопротивлении цепи.

В электрической цепи есть несколько основных составляющих:

• Источник тока
• Потребитель
• Ток I, идущий по цепи от плюса источника к минсу
• Сопротивление R (потребителя, провода, резистора и т.д.)
• Напряжение U, которое создается между плюсом и минусом источника

 

Формула тока электрической цепи связывает напряжение, создаваемое источником, сопротивление и сам ток.

Когда в цепи создается напряжение, по ней начинает бежать ток. Но, встречая на своем пути сопротивление, ток замедляет свое течение и ограничивается(уменьшается).

 

 

Пример

Имеем цепь с источником питания напряжением 20В, есть потребитель — светодиод, который потребляет 18В и ток 20мА. Если встроть в цепь резистор, то при том же напряжении ток, протекающий через светодиод, будет ограничиваться до 19, 15, 2, да скольких угодно мА(милиАмпер).

 

Важный момент

При последовательном подключении ток, протекающий по цепи, одинаков во всех ее участках. При параллельном же соединении, ток распределяется по всем ветвям в зависимости от нагрузки и сопротивлении на каждой из участков цепи. Посмотрите на рисунок ниже:

ток-в-электрической-цепи

Поясним схему и важный момент

Мы нарисовали участок электрической цепи, в которую встроено 4 амперметра(которые мерят силу тока каждый на своем участке — 250мА, 200мА, 50мА, 250мА), а также встроена нагрузка R в виде сопротивления.

Как мы видим, ток, который втекает в цепь и ток, который вытекает из нее, одинаков, не смотря на сопротивление, которое он преодолевает. Да-да, сила тока не превращается в энергию и никуда не пропадает — сколько тока вошло в цепь, столько и вышло.

Сопротивление затрудняет движение тока. Поэтому на нижнем участке цепи амперметр показывает 50 мА, в то время как на верхнем участке 200. Току легче идти по верхнему участку, поэтому большая (но не вся) его часть направляется именно туда.

Если бы Нагрузка R отсутствовала, то ток разделился бы поровну — по 125 мА.

 

Внимание!

Данная схема нарисована для наглядности. На самом деле, если плюс подсоединить к минусу, то произойдет короткое замыкание. Поэтому следует учитывать, что и на верхнем и на нижнем участке стоит повесить по нагрузке, только на нижнем с большим сопротивлением, на верхнем с меньшим.

 

 

В заключение

Итак, мы изучили что представляет из себя формула силы тока. Для большего погружения в тему, рекомендуем прочитать статьи «Что такое электричество» и  «Что такое резистор«. Это не займет у вас много времени, однако поможет понять суть многих вещей, происходящих на участке элементарной электрической цепи.

 

Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)

Автор публикации

не в сети 3 месяца

wandrys

877 Комментарии: 1Публикации: 31Регистрация: 17-03-2016

micro-proger.ru

Формула силы тока

ОПРЕДЕЛЕНИЕ

Сила тока определяется как отношение количества заряда, прошедшего через какую-то поверхность, ко времени прохождения.

   

В формуле – сила тока, – количество заряда, – время.

Единица измерения силы тока – А (ампер).

Обычно под поверхностью, через которую прошёл заряд, понимают сечение проводника. В цепях с постоянным током силу тока находят по закону Ома:

   

Где – напряжение, – сопротивление проводника. Прибор, которой используется для измерения силы тока, называют амперметром.

Примеры решения задач по теме «Сила тока»

ПРИМЕР 1

Задание	Найти силу тока в проводнике, если за 50 сек через него прошёл заряд 43 кКл.
Решение	Напомним, что кКл = Кл. Подставим численные значения в формулу:
Ответ	Сила тока была равна 860 Ампер.

ПРИМЕР 2

Задание	Через сечение проводника за 1 минуту прошёл заряд 10 Кл. Найти сопротивление участка цепи, если напряжение в нём 50 В.
Решение	Найдём силу тока через заряд:     По закону Ома:     Сопоставим формулы:     Подставим числа: (Ом)
Ответ	Сопротивление цепи равно 300 Ом.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

16. Электрический ток. Сила тока. Плотность тока

Электрический ток — направленное движение электрически заряженных частиц под воздействием электрического поля.

Сила тока (I) — скалярная величина, равная отношению заряда (q), прошедшего через поперечное сечение проводника, к промежутку времени (t), в течение которого шёл ток.

I=q/t, где I— сила тока, q — заряд, t — время.

Единица измерения силы тока в системе СИ: [I]=1A (ампер)

17. Источники тока. Эдс источника

Источник тока — это устройство, в котором происходит преобразование какого-либо вида энергии в электрическую энергию.

ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонни­ми силами при перемещении электрического заряда по замкнутой цепи, к этому заряду:

Измеряется в вольтах (В).

Источник ЭДС — двухполюсник, напряжение на зажимах которого не зависит от тока, протекающего через источник и равно его ЭДС. ЭДС источника может быть задана либо постоянным, либо как функция времени, либо как функция от внешнего управляющего воздействия.

18. Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

-закон Ома в интегральной форме R – электрическое сопротивление проводника

Величина, обратная сопротивлению, называется проводимостью. Величина, обратная удельному сопротивлению, называется удельной проводимостью: Единица, обратная Ом, называется Сименсом [См].

— закон Ома в дифференциальной форме.

19. Обобщенный закон Ома

Обобщенный закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока, содержащем резистор и идеальный источник ЭДС (рис.1.2):

;

Формула справедлива для указанных на рис.1.2 положительных направлений падения напряжения на участке цепи (Uab), идеального источника ЭДС (Е) и положительного направления тока (I).

Закон Джоуля-Ленца

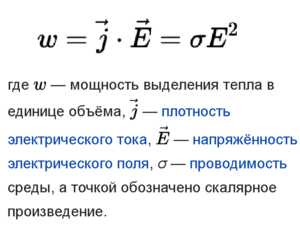
Выражение закона Джоуля — Ленца

Интегральная форма закона

Словесное определение закона Джоуля — Ленца

Если принять, что сила тока и сопротивление проводника не меняется в течение времени, то закон Джоуля — Ленца можно записать в упрощенном виде:

Применив закон Ома и алгебраические преобразования, получаем приведенные ниже эквивалентные формулы:

Эквивалентные выражения теплоты согласно закона Ома

Словесное определение закона Джоуля — Ленца

Если принять, что сила тока и сопротивление проводника не меняется в течение времени, то закон Джоуля — Ленца можно записать в упрощенном виде:

20.Магни́тное по́ле— силовое поле, действующее на движущиесяэлектрические заряды и на тела, обладающиемагнитным моментом, независимо от состояния ихдвижения; магнитная составляющаяэлектромагнитного поля

Магнитное поле может создаваться током заряженных частиц и/илимагнитными моментамиэлектроноватомах (и магнитными моментами другихчастиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции(вектор индукции магнитного поля). С математической точки зрения— векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

Вместе, магнитное и электрическоеполя образуют электромагнитное поле, проявлениями которого являются, в частности свети все другие электромагнитные волны.

Магнитное поле создаётся (порождается) током заряженных частиц или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам)

Графическое изображение магнитных полей

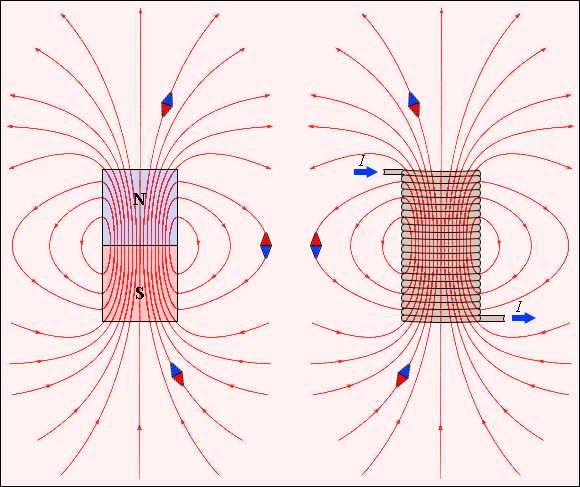
Для графического изображения магнитных полей используются линии магнитной индукции. Линия магнитной индукции –это линия, в каждой точке которой вектор магнитной индукции направлен по касательной к ней.

studfiles.net

Сила тока и напряжение в электрической цепи переменного тока. Сила тока и напряжение в электрической цепи

формулы расчета мощности в проводнике

Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.

Электрический ток в проводнике

В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.

От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:

Зависимость силы тока от электрического заряда

Входящие в формулу величины:

• I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
• Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
• Время в секундах.

Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:

I = (qnv)cosαS.

Также используется интегрирование по площади поверхности и сечению проводника.

Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.

Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:                                                                                               

Сила тока участка цепи и цепи с источником тока

Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.

В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.

При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.

Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:

RC = 1/ FC.

Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.

Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:

Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.

Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.

I = I1 + I2 + I3

Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.

Видео

Оцените статью:

elquanta.ru

Ответы на вопросы «Постоянный электрический ток. § 12. Расчет силы тока и напряжения в электрических цепях»

1. Найдите разность потенциалов на резисторах, сопротивление которых 2 0м и 4 0м, в схеме, изображенной на рисунке 39.[2 В, 8 В]

Дано:

Решение:

Найдем полное сопротивление цепи RП (см. рисунок):

1. Найдите разность потенциалов на резисторах, сопротивление которых 2 0м и 4 0м, в схеме, изображенной на рисунке 39.[2 В, 8 В]

Дано:

Решение:

Найдем полное сопротивление цепи RП (см. рисунок):

в 2 раза больше, чем

следовательно по

пойдет вдвое

меньший ток.

Ответ:

2. В вашем распоряжении три резистора: 3 0м, 5 0м и 6 0м. Какие возможные сопротивления можно получить, комбинируя или используя отдельно эти резисторы? Нарисуйте соОтветствующие схемы соединений. [0,7 Ом; 1,9 Ом; 2,0 Ом; 2,4 Ом; 2,7 Ом; 3 Ом; 3,2 Ом; 3,4 Ом; 5 Ом; 5,7 Ом; 6 Ом; 7 Ом; 7,9 Ом; 8 Ом; 9 Ом; 11 Ом; 14 Ом]

Дано:

Найти: все комбинации

Комбинации из 3-х резисторов:

Комбинации из 2-х резисторов:

Комбинации из 1-ого резистора:

3. Три резистора 40 Ом, 60 Ом и 120 Ом соединены параллельно в группу, которая включена последовательно резисторам сопротивлениями 15 0м и 25 0м. ЭДС источника 240 В. Найдите: 1)силу тока, протекающего через сопротивление 25 0м; 2) разность потенциалов на параллельной группе; 3) напряжение на сопротивлении 15 0м; 4) силу тока через сопротивление 60 Ом; 5) силу тока через сопротивление 40 Ом. [1) 4 А; 2) 80 В; 3) 60 В; 4) 1,34 А; 5) 2 А]

Дано:

Решение:

R1, R2, R3 соединены параллельно, следовательно

Ответ:

4. Найдите заряд на конденсаторе, включенном в электрическую схему, изображенную на рисунке 40. Все величины, указанные на схеме известны. Внутренним сопротивлением источника тока пренебречь.[q = 3CU/4]

Дано:

Решение:

Найдем эквивалентное сопротивление цепи (см. рисунок) без учета конденсатора:

Обозначим напряжение в точке А как

а в точке

Тогда в

точке С напряжение будет таким же, как и в точке А, а в точке D,

IR/2 — сила тока, который идет через верхний резистор.)

Заряд на конденсаторе найдем по формуле

Ответ:

5. Рассчитайте разность потенциалов Uab в электрической схеме, пока

xn—-7sbeb3bupph.xn--p1ai