Самостоятельные работы по теме «Решение тригонометрических уравнений» для 10-х классов физико-математического профиля
Разделы: Математика
Тригонометрические уравнения традиционно входят в число задач, предлагаемых на едином государственном экзамене по математике. Косвенно это обусловлено тем, что не существует единого универсального метода решения тригонометрических уравнений. И решение каждого конкретного уравнения требует хорошего владения навыками тригонометрических преобразований, умения выбрать нужную формулу для упрощения тригонометрического выражения и сведения его к более простому уравнению.
В данном пособии представлены самостоятельные работы для отработки и закрепления навыков решения тригонометрических уравнений.
Самостоятельные работы рассчитаны на учащихся физико-математического классов, однако, могут использоваться и для хорошо успевающих учащихся общеобразовательных учреждений. За каждую из проведенных работ выставляется оценка, что послужит достаточной мотивацией для наиболее полной и качественной домашней проработки пройденного накануне материала, а также для дополнительного повторения и лучшего запоминания формул тригонометрических преобразований, а также методов решения тригонометрических уравнений.
В Приложении 1 приведен математический диктант – задание для проверки усвоения учащимися основных базовых навыков по пройденному материалу. Эту работу полезно использовать и в средней общеобразовательной школе для лучшего запоминания и усвоения основных понятий по данной теме. В Приложении 2 содержится самостоятельная работа, в которой требуется решить уравнения несколько более сложные. Приложение 3 содержит самостоятельную работу, где нужно решить тригонометрические уравнения различными методами. В Приложении 4 содержатся задания, требующие проверки найденных корней на соответствие с ограничениями в исходном уравнении, что является еще более сложной задачей.
Самостоятельные работы составлены в четырех вариантах эквивалентной сложности, которые удобно использовать для промежуточного контроля знаний учащихся, отработки практических навыков решения задач по теме «Решение тригонометрических уравнений».
Представленные в пособии работы позволяют учащимся лучше усвоить пройденный материал по указанной теме, что подтверждено практикой.
Все самостоятельные работы содержат ответы, что позволит значительно сократить время проверки работ преподавателем.
Данное пособие также может быть использовано для организации повторения при подготовке учащихся старших классов к успешной сдаче единого государственного экзамена по математике.
Литература:
- Мордкович А.Г., Денищева Л.О., Звавич Л.И., Корешкова Т.А., Мишустина Т.Н., Рязановский А.Р., Семенов П.В. Алгебра и начала математического анализа 10 класс. Ч. 2. – М.: «Издательство Мнемозина»: ОАО «Московские учебники», 2009.
- Шестаков С.А., Захаров П.И. ЕГЭ 2013. Математика. Задача С1. Уравнения и системы уравнений. – М. : Издательство МЦНМО, 2013.
- Сергеев И.Н., Панферов В.С. ЕГЭ 2013. Математика. Задача С3. Уравнения и неравенства. – М. : Издательство МЦНМО, 2013.
- Ершова А.П., Нелин Е.П. Самостоятельные и контрольные работы по алгебре и началам математического анализа для 10 класса. – М.: Илекса, 2011.
xn--i1abbnckbmcl9fb.xn--p1ai
Урок математики по теме «Решение тригонометрических уравнений»
Разделы: Математика
Цели:
- формирование знаний, умений, навыков решения простейших тригонометрических уравнений и тригонометрических уравнений, приводимых к простейшим тригонометрическим уравнениям с помощью разложения на множители и применения тригонометрических формул;
- развитие умений, навыков применять тригонометрические формулы и алгебраические преобразования для упрощения тригонометрических выражений и решения тригонометрических уравнений;
- воспитывать интерес к предмету, умения делового общения, чувства товарищества.
План урока:
- Организационный момент.
- Актуализация знаний, умений, навыков. (Устный счет)
- Закрепление знаний, умений, навыков решения
простейших тригонометрических уравнений.
(Тест на решение простейших тригонометрических
уравнений с информацией из истории
тригонометрии)
- Работа в группах (учащиеся разного уровня знаний)
- Индивидуальная работа у доски.
- Контроль знаний, умений по решению тригонометрических уравнений.
- Дифференцированная самостоятельная работа с самопроверкой
- Итог урока.
ХОД УРОКА
I. Организационный момент
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». На уроке вы должны быть внимательны, активны, работать с интересом, желанием, чтобы полученные знания переварились и усвоились, ведь они пригодятся вам в дальнейшем.
Сообщается тема и цель урока.
Класс разделен на четыре группы, состоящие из учащихся с различной математической подготовкой. Из числа «сильных» учащихся выбирается в каждой группе консультант, который оценивает работы членов своей группы на каждом этапе урока и заносит результаты в оценочный лист.
Оценочный лист
| Ф.И. учащихся | Домашнее задание |
Решение простейших тригонометрических уравнений | Решение тригонометрических уравнений | Индивидуальная работа | Самостоятельная работа | Итоговая оценка |
На перемене консультанты групп проверяют домашние задание в своей группе и заносят результат проверки в оценочный лист.
II. Актуализация знаний, умений, навыков
Фронтальная устная работа (задания записаны на доске)
Вычислите:
Решить уравнение:
III. Закрепление знаний, умений, навыков
Каждая группа получает тест на отработку умений, навыков решения простейших тригонометрических уравнений. В результате выполнения теста учащиеся узнают имена ученых, которые внесли вклад в развитие тригонометрии. Консультант оценивает работу каждого учащегося своей группы и заносит результаты в оценочный лист.
I группа
Решив эти уравнения, вы узнаете, кто впервые стал обозначать синус и косинус знаками sin и cos
(Иоганн Бернулли)
II группа
Решив эти уравнения, вы узнаете имя и фамилию французского математика, сочинения которого сыграли особую роль в развитии тригонометрии. Этот ученый использовал тригонометрию при решении кубических уравнений.
III группа
Решив эти уравнения, вы узнаете имя и фамилию математика, который разработал теорию тригонометрических функций
(Леонард Эйлер)
IV группа
Решив эти уравнения, вы узнаете имя и фамилию древнегреческого ученого, который вывел формулуsin2x+ cos2x = 1
(Клавдий Птолемей)
IV. Контроль знаний, умений
Группы получают карточки с заданиями: решить уравнения. Группы решают самостоятельно, затем выполняют отчёт о методе решения уравнений на примере уравнений своего задания (у доски).
I группа отчёт у доски б, в, II группа г, а, III группа г, а, IV группа в, б.
Во время работы групп отдельные учащиеся получают индивидуальное задание и работают у доски. Учащиеся сами выбирают уровень задания Б(задания проверяют не только достижение обязательного уровня математической подготовки, но овладение знаниями ,умениями на более высоком уровне) или С (задания рассчитаны на учащихся с хорошей математической подготовкой)
V. Самостоятельная работа по уровням Б и С, ученики сами выбирают уровень.
Выполнение работы учащиеся проверяют по «листу самопроверки» (ответы к каждому уравнению). Консультанты выставляют оценку в оценочный лист.
Уровень Б. Уровень С.
VI. Итог урока
- Какими способами приводили тригонометрические уравнения к простейшим тригонометрическим уравнениям?
- Какие тригонометрические формулы использовали?
- Какие навыки и умения нужны для решения тригонометрических уравнений?
В конце урока консультанты сдают учителю оценочные листы, и он выставляет итоговую оценку за урок в журнале.
Домашнее задание (ученики сами выбирают уровень):
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Самостоятельная работа по теме «Тригонометрические уравнения» (10 класс)
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
sinx = 0;
2tg3x = 0;
2cosx = 1;
2sin(2x – 4π) =;
cos22x = 2;
1 – sin2x = 0;
2cos2x -5cosx – 3 = 0;
3sin2x + 7cosx – 3 = 0;
2tg23x – 3tg3x + 1 = 0;
(1 – cos2x)(сtg(-2x) +
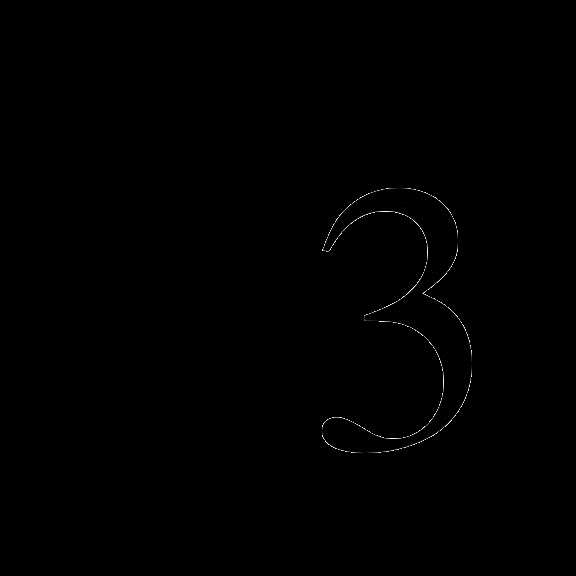 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
cosx = 0;
3ctg2x = 0;
2sinx =
2cos(2x – 4 π) = ;
sin4x = 1;
1 – cos2x = 0;
2 + cos2 x — 3 cos x = 0;
2cos2x + 5sinx – 4 = 0;
tg 2 2x – 9 tg 2x + 8 = 0;
(sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 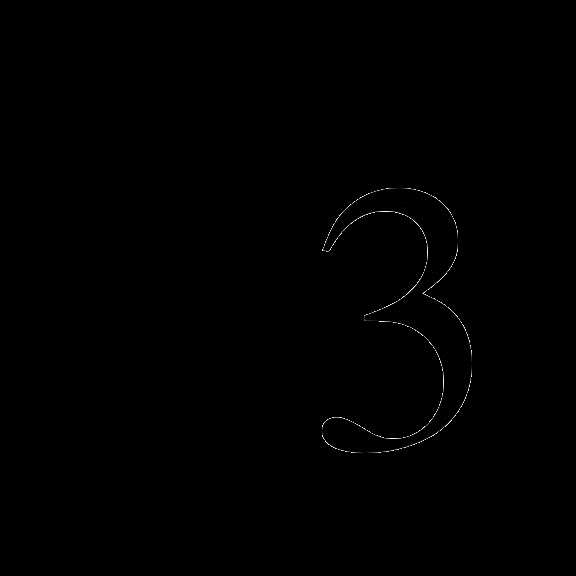 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
3ctg2x = 0;
2sinx =
2cos(2x – 4 π) = ;
sin4x = 1;
1 – cos2x = 0;
2 + cos2 x — 3 cos x = 0;
2cos2x + 5sinx – 4 = 0;
tg 2 2x – 9 tg 2x + 8 = 0;
(sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 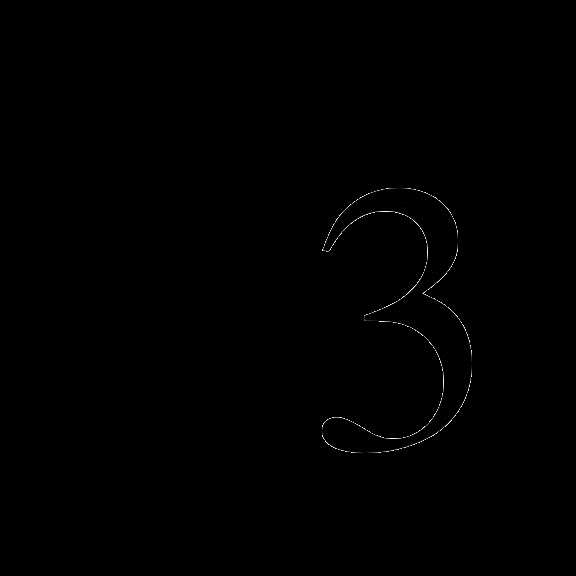 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 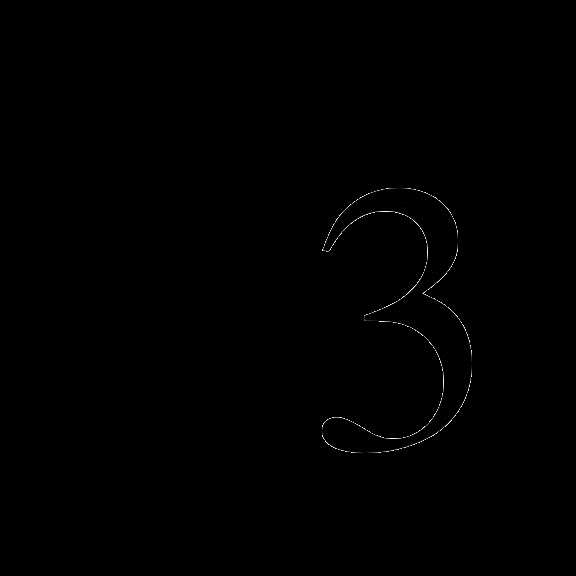 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10.(1 – cos2x)(сtg(-2x) + 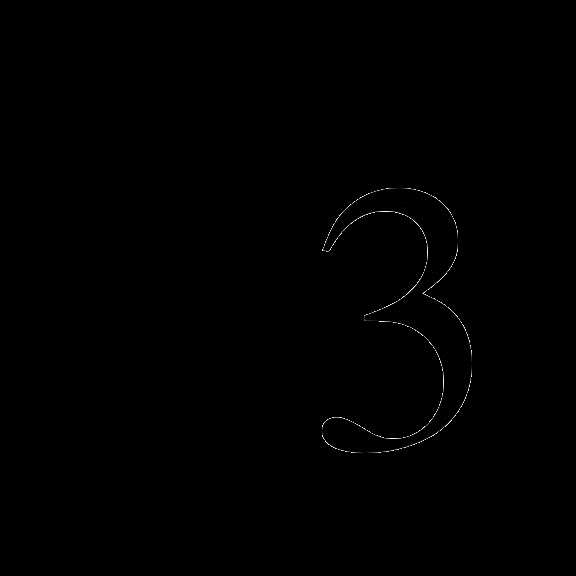 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 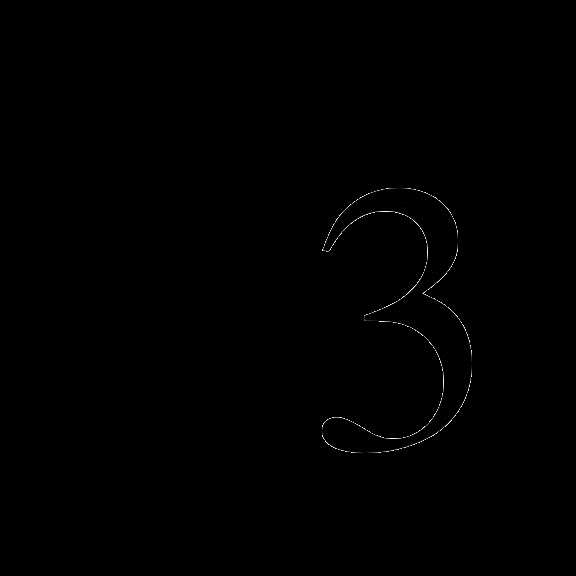 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
infourok.ru
Решение тригонометрических уравнений. 10-й класс
Разделы: Математика
Урок является основополагающим для данной темы. На нем демонстрируются различные способы решения тригонометрических уравнений, а также ведется подготовка к контрольной работе по теме «решения тригонометрических уравнений».
Урок разбит на этапы:
- Постановка целей, мотивировка учащихся.
- Актуализация знаний. Повторение формул тригонометрии.
- Обобщение и систематизация знаний, отработка навыков решений тригонометрических уравнений различными способами, используя на уроке метод критического мышления: Прием «Зигзаг»:
Класс делится на четверки, которые меняются на каждом уроке с тем, чтобы возникали новые комбинации. Затем учащимся предлагается рассчитаться на 1, 2, 3, 4, таким образом, у каждого члена группы появляется свой номер. Весь материал урока делится также на 4 части. Первые номера каждой группы будут отвечать за первую часть, вторые – за вторую часть и так далее. Все первые, вторые, третьи, четвертые номера собираются вместе по однородным группам и выполняют роль экспертных групп: их задача состоит в том, чтобы изучить предложенный учебный материал, обсудить его и объяснить своим партнерам по учению в группах 2-го состава. По завершении работы формируются новые группы, в составе которых есть учащиеся со всеми номерами. - Подведение итогов урока, задание на дом.
Цели урока:
- Образовательные — систематизировать знания учащихся по теме «Решение тригонометрических уравнений». Создать условия для усвоения знаний и умений.
- Развивающие – способствовать формированию умений применять полученные знания в новой ситуации, развивать логическое мышление, математическую речь, умение работать в группах.
- Воспитательная – развивать интерес к математике, познавательную активность, мобильность, коммуникативные навыки.
Ход урока
Повторение.
Изучение темы. «Решение тригонометрических уравнений» мы начали решение простейших тригонометрических уравнений.
Какие это уравнения?
1)cosx = a, где |a| ≤ 1
x = ± arccos a + 2πn, n ∈ Z
2) sin x = a, где |a| ≤ 1
x = (–1)narcsin a + πn, n ∈Z
3) tg x = a, где a ∈ R
x = arctg a + πn, n ∈Z
(Показ слайда №4, 5, приложение)
В решении простейших уравнений использованы такие понятия, как арккосинус, арксинус, арктангенс.
Что называется арккосинусом, арксинусом, арктангенсом числа а?
Арккосинусом числа а ∈ [–1; 1] называется такое число из отрезка [0; π], косинус которого равен а.
Арксинусом числа а ∈ [–1; 1] называют такое число из отрезка ,синус которого равен а.
Арктангенсом числа а ∈ R называют такое число из промежутка , тангенс которого равен а.
(Показ слайда №6, приложение)
Далее при решении более сложных уравнений мы использовали различные способы решений. Какие это способы?
- Решение однородных уравнений.
- Приводимых к квадратному уравнению.
- Метод вспомогательного аргумента.
- Разложение на множители.
- Метод замены переменной.
- Преобразование суммы в произведение и наоборот. И другие способы решений.
(Показ слайда №7 – 9, приложение)
Для осуществления этих решений мы с вами должны повторить изученные ранее тригонометрические формулы и вспомнить, используемые нами рекомендации по решению тригонометрических уравнений.
- Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.
- Если аргументы функции отличаются в 2 раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
- Если аргументы функций отличаются в 4 раза, попробовать привести их к промежуточному двойному аргументу.
- Если есть функции одного аргумента, степени выше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.
- Если сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
- Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать использовать формулы приведения, получить затем случай 5.
- Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента.
- Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла.
Сегодня на уроке мы работаем в группах. 1-красная, 2-зеленая,3-желтая,4-синяя. Каждый участник группы выбирает бейдж с номером. На столе задание, состоящее из четырех уравнений. Учащийся в группе самостоятельно решает уравнения, номер которого соответствует номеру на бейдже. Способ решения вы выбираете сами.
После решения своего уравнения. На следующем этапе работы прошу объединиться в группы по номерам. Так как каждый из вас решал одно и то же уравнение, то сейчас у вас есть возможность выслушать друг друга и найти правильное рациональное решение данного уравнения.
Обсуждение в группах, по мере необходимости консультация учителя. После завершения обсуждения предлагаю вам вернуться в первоначальные группы. Каждый из вас, обсудив решение уравнения, может доступно объяснить решение и ответить на вопросы членов группы.
После обсуждения в группах учитель вызывает к доске любого на выбор ученика из каждой группы и предлагает ему решить уравнение, номер которого не соответствует номеру на его бейдже.
На следующем этапе работы предлагаю вам выполнить самостоятельную работу в виде теста.
Подводя итоги сегодняшнего урока можно сказать, что мы научились решать тригонометрические уравнения различными способами. Обобщили и систематизировали материал по данной теме.
Домашнее задание.
- Решить уравнение тремя различными способами
2 + cos 2x = 4 cos2x - С16 стр.37(дидактический материал)
Список литературы.
- Шестаков С.А., Захаров П.И. ЕГЭ 2010. Математика. Задача С1 — Москва: МЦНМО,2010
- Мордкович А.Г., Семенов П. В. Алгебра и начала анализа профильный уровень 10 класс — Москва: Мнемозина,2007
- Галицкий М.Л., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа 10-11 класс — Москва: Просвещение,1997
- Ершова А.П., Голобородько В. В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 класса — Москва: Илекса , 2005
xn--i1abbnckbmcl9fb.xn--p1ai
Решение тригонометрических уравнений
Решение тригонометрических уравнений
Автор: Петренко Т.Н.
Методическая копилка — Математика
Модульный урок в 10 классе
Тема: «Решение тригонометрических уравнений»
Модульная педагогическая технология конструируется на основе ряда целей. Важнейшая из них – создание комфортного темпа работы для каждого ученика. Каждый ученик получает шанс определить свои возможности в учении и приспособиться к тем уровням изучения материала, которые предложены учителем.
Самым главным отличием технологии является применение принципа планирования совместной деятельности учителя и ученика.
Сначала определяются цели для учащегося, т.е. устанавливается, кто хочет знать не более того, что требуется государственным стандартом, а кто готов заниматься больше, поскольку планирует поступить в институт или просто хочет получить высокую оценку. После того как учащиеся определились со своими целями, учитель выстраивает свое целеполагание, определяя содержание и объем педагогической помощи учащимся.
Исходя из целей проектируется итоговая диагностика. Она создается с учетом уровневой дифференциации, что позволяет учащимся осознанно определять то минимум знаний, который необходим для получения оценки «3».
На основании целеполагания и планируемой итоговой диагностики, отбирается предметное содержание (объяснение и задания из учебника, из дидактических материалов и т. д.).
На основе отобранного содержания выстраивается логика изучения темы (поурочное планирование), определяются время и место промежуточной и итоговой диагностик и учебной коррекции. Для каждого урока определяются микроцели учащихся и приемы обратной связи; создаются опорные конспекты для учащихся и задания к уроку.
В результате описанного процесса учитель создает:
- логическую структуру уроков с промежуточной диагностикой;
- разноуровневые материалы для диагностики знаний учащихся;
- дидактический материал ко всем урокам.
Модульная педагогическая технология помогает осуществлять индивидуальный подход к учащимся, включать каждого в осознанную учебную деятельность, мотивировать ее, формировать навыки самообучения и самоорганизации, обеспечивая тем самым постепенный переход от пассивно воспринимающей позиции ученика к его сотрудничеству с учителем.
Цели изучения этого модуля распределяются по трем уровням: I уровень – самый общий, т.е. знаниями этого уровня должны овладеть все учащиеся, II уровень включает все, что достигнуто на I уровне, но в более сложном виде, а III уровень – все, что достигнуто на I и на II уровнях, но теперь должно применяться в нестандартных ситуациях.
В результате овладения содержанием модуля учащиеся должны уметь:
I уровень — решать простейшие тригонометрические уравнения; решать тригонометрические уравнения по заданному алгоритму;
II уровень — Решать тригонометрические уравнения, самостоятельно выбирая метод решения;
III уровень — применять полученные знания в нестандартной ситуации.
Работа учащихся состоит из нескольких этапов, так называемых учебных элементов. Учебные элементы № 1 – 4 соответствуют I уровню подготовки, № 5 обеспечивает II уровень, № 6 – III уровень подготовки. Каждый учебный элемент содержит или указания учителя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, или ссылки на то, где в учебнике можно найти нужные пояснения, а также список заданий. Индивидуальный оценочный лист приведен ниже.
Оценочный лист учащегося
|
Фамилия |
|||
|
Имя |
|||
|
Учебные элементы |
Количество баллов за основные задания |
Корректирующие задания |
Общее количество баллов за этап |
|
№1 |
|
|
|
|
№2 |
|
|
|
|
№3 |
|
|
|
|
№4 |
|
|
|
|
№5 |
|
|
|
|
№6 |
|
|
|
|
Итоговое количество баллов |
(n) |
||
|
Оценка |
|
||
Прочитав указания учителя, ученик выполняет самостоятельные работы, которые включены в учебный элемент, и проверяет их по эталонам решений. Эталон учитель демонстрирует ученику, когда тот объявляет о завершении самостоятельной работы. Ученик сравнивает свои ответы с эталонными и исправляет ошибки. Если он получил менее указанного в инструкции количества баллов, то должен набрать дополнительные баллы в корректирующих заданиях. Для этого ученик решает задания другого варианта, которые аналогичны тем, где он допустил ошибку. Оценка за весь модуль зависит от суммы n набранных баллов по всем учебным элементам. Если n ³ 32, то ученик получает «5», при 27 £ n £ 31 – оценка «4», при 21£ n £ 26 – оценка «3», при n £ 21 ученик получает «2».
Приведу теперь материалы, предлагаемые ученику в каждом учебном элементе.
Учебный элемент №1
Ц е л ь: Закрепить решение простейших тригонометрических уравнений.
Указания учителя
Вспомните основные правила решения тригонометрических уравнений.
Выполните письменно самостоятельную работу.
Задания самостоятельной работы (на 10 мин)
Решите уравнения (по вариантам по 7 уравнений) Каждое оценивается в 1 балл.
I вариант
cosx=1/2
sinx=-√3/2
tgx=1
cos(x+Π/3)=0
2cosx=1
3tgx=0
sin4x=1
II вариант
sinx=-1/2
cosx=√3/2
ctgx=-1
sin(x-Π/3)=0
4sinx=2
cos4x=0
5tgx=0
Список правильных ответов и критерии оценивания ученик получает от учителя. Учащийся исправляет ошибки и проставляет число заработанных баллов в свой оценочный лист. Если он набрал 6баллов или больше, то переходит к следующему учебному элементу. Если же набрано меньше 6 баллов, то следует прорешать задания другого варианта, аналогичные тем, в которых была допущена ошибка, и поставить набранные баллы в графу «Корректирующие задания».
Учебный элемент №2
Ц е л ь: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.
Указания учителя
Прочитайте внимательно данные ниже пояснения.
Выполните самостоятельные работы.
Метод сведения к квадратному уравнению состоит в том, что, пользуясь изученными формулами ( они собраны в таблицу, которая вывешена в классе), надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x ) или комбинацию функций обозначить через у, получив при этом квадратное уравнение относительно у.
Пример. Решить уравнение 4 – cos2x = 4 sin x.
Р е ш е н и е. Вместо cos2x подставим тождественное ему выражение 1 – sin2x . Тогда исходное уравнение примет вид
4 – (1 –sin2x) = 4 sin x?
3 + sin2x =4 sin x
sin2x – 4 sin x + 3 = 0.
Если положить y = sin x, получим квадратное уравнение y2 – 4y + 3 = 0. Оно имеет корни 1 и 3. Значит, исходное уравнение равносильно совокупности уравнений
sin x = 1 или sin x = 3.
Уравнение sin x = 1 имеет решение
Уравнение sin x = 3 решений не имеет.
О т в е т:
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
tg2 x – 3tg x + 2 = 0 (2 балла),
2cos2 x + 5sin x – 4 =0 (3 балла),
(3 балла).
II вариант
2+ cos2 x — 3 cos x = 0 (2 балла),
4 – 5 cos x – 2 sin2 x = 0 (3 балла),
(3 балла).
Указания учителя
Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, если они есть, поставьте количество баллов в оценочные листы.
Если вы набрали 5 баллов, то переходите к следующему этапу, если же меньше, то решайте задание другого варианта, аналогичное тому, в котором ошиблись.
Учебный элемент №3
Ц е л ь: закрепить навык решения тригонометрических уравнений методом разложения на множители.
Указания учителя
Внимательно прочитайте данные ниже пояснения и выполните задания.
Метод разложения на множители
Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит произведение нескольких множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, исходное уравнение можно представить в виде совокупности более простых уравнений.
К сожалению, нельзя указать единого способа разложения на множители любого выражения. Одними из самых популярных являются способы вынесения за скобки общего множителя, группировки, применения формул сокращенного умножения.
Пример. Решите уравнение 2 sin3 x – cos 2x – sin x = 0 .
Р е ш е н и е. Сначала сгруппируем первый член с третьим, а cos 2x представим в виде cos2 x – sin2 x. Получим
(2sin3 x- sin x) –(cos2 x- sin2 x) = 0
Из выражения, стоящего в первых скобках, вынесем sin x, а в выражении, стоящем во вторых скобках, вместо cos2 x запишем 1 – sin2x. Уравнение примет вид
sin x (2sin2 x – 1) – (1 – 2sin2 x) = 0.
Выполним дальнейшие тождественные преобразования
sin x (2sin2 x – 1)+ (2sin2 x – 1) = 0,
(2sin2 x – 1)×(sin x + 1) = 0.
Отсюда следует, что исходное уравнение равносильно совокупности уравнений
2sin2 x – 1= 0 или sin x + 1= 0
Отсюда . Тогда
или sin x = -1.
О т в е т:
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
sin2 x – sin x = 0 (2 балла),
3cos x + 2sin 2x = 0 (3 балла).
II вариант
ctg2 x – 4ctg x = 0 (2 балла),
5sin 2x – 2sin x = 0 (3 балла).
Указания учителя
Если набрано 5 баллов, то переходите к следующему элементу. Если меньше, то прорешайте соответствующее задание другого варианта.
Учебный элемент №4
Ц е л ь: закрепить навык решения однородных уравнений.
Указания учителя
Прочитайте пояснения и выполните задания.
Однородными называются уравнения вида
a sin x + b cos x = 0,
a sin2 x+ b sin x cos x + c cos2 x = 0
и т. д. Здесь a, b, c – числа.
Покажем сначала, как решать однородное уравнение первой степени, т. е. уравнение вида
a sin x + b cos x = 0.
Пример 1. Решить уравнение 5sin x – 2cos x = 0.
Р е ш е н и е. Поделим обе части уравнения cos x на sin x или. Но предварительно надо доказать, что это выражение никогда не обращается в нуль. Итак, предположим, что cos x = 0. Тогда 5sin x – 2× 0 = 0 Û sin x = 0. Получается, что если sin x = 0, то и cos x = 0, чего быть не может ввиду равенства sin2 x + cos2 x = 1.
Значит, можно поделить уравнение на cos x:
.
Получим уравнение 5tg x – 2 = 0. Отсюда
Аналогично решаются однородные уравнения вида
a sin2 x+ b sin x cos x + c cos2 x = 0.
Их решение начинается с того, что обе части уравнения делят на cos2 x или sin2 x.
Пример 2. 12 sin2x + 3 sin 2x – 2 cos2 x = 2.
Р е ш е н и е. Данное уравнение не является однородным. Но его можно превратить в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin2x+2cos2x.
Приведя подобные члены, получим уравнение
10 sin2 x+ 6 sin x cos x — 4 cos2 x = 0. (*)
Теперь надо доказать, что cos x¹ 0.
Пусть cos x = 0. Подставим это значение косинуса в уравнение (*). Получим 10sin2 x = 0 Û sin x = 0, чего быть не может ввиду равенства sin2 x + cos2 x = 1. Значит, cos x¹ 0. Тогда можно поделить обе части уравнения (*) на cos2 x. Получим 10tg2 x+ 6tg x – 4 = 0 Û tg x = -1 или . Отсюда .
Задания самостоятельной работы (на 10 мин)
Решите уравнения
I вариант
sin x – cos x = 0 (2 балла)
sin2 x – sin 2x = 3cos2 x (3 балла)
II вариант
5sin x + 6cos x = 0 (2 балла)
3sin2 x – 2sin 2x + 5cos2 x = 2 (3 балла)
Указания учителя
Если набрано 5 баллов, то можно переходить к следующему учебному элементу. Если набрано менее 5 баллов, то нужно прорешать тот номер другого варианта, где допущена ошибка.
Учебный элемент №5
Указания учителя
Вы прошли I уровень усвоения материала. Теперь вам самостоятельно придется выбрать метод решения уравнений. Вспомните основные тригонометрические формулы.
Выполните письменно самостоятельную работу.
Задания самостоятельной работы (на 20 мин.)
Решите уравнения
I вариант
cos 2x – 5 sin x – 3 = 0 (1 балл),
sin 2x + cos 2x = 0 (1 балл),
cos2 x – cos 2x = sin x (2 балла).
sin 4x – cos 2x = 0 (2 балла),
(2 балла),
II вариант
cos 2x + 3 sin x = 2 (1 балл),
sin 2x — cos 2x = 0 (1 балл),
6 – 10 cos2 x + 4 cos 2x = sin 2x (2 балла),
cos x cos 2x = 1 (2 балла),
(2 балла).
Указания учителя
Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, если они есть. Проставьте баллы в оценочные листы.
Если набрано 5 баллов или больше, то переходите к следующему учебному элементу, если меньше, то решайте задания другого варианта аналогичные тем, в которых была допущена ошибка.
Учебный элемент №6
Указания учителя
Молодцы! Вы освоили решение уравнений II уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Задания самостоятельной работы
(Они даются в одном варианте и не ограничиваются временными рамками, так как их решают далеко не все учащиеся. А время, отводимое на эту работу, определяется ситуацией на уроке.)
- sin 6x + cos 6x = 1 – 2 sin 3x (2 балла),
- 29 – 36 sin2 (x – 2) – 36 cos (x – 2) = 0 (3 балла),
- (2 балла),
- sin 4x = 2 cos2 x – 1 (2 балла),
- sin x(sin x + cos x) = 1 (3 балла),
- (3 балла).
Указания учителя
В случае затруднений воспользуйтесь подсказками, Данными ниже.
Подсказки
- Воспользуйтесь формулой двойного угла для sin 6x, cos 6x.
- Обозначьте х – 2 = t, решите уравнение, сведя его к квадратному с помощью формулы sin2 t = 1 — cos2 t
- Сгруппируйте первое и третье слагаемые, примените разложение на множители.
- Воспользуйтесь формулой двойного угла для sin 4x, cos 4x, формулой понижения степени 2 cos2 x – 1 = cos 2x.
- Раскройте скобки, примените основное тригонометрическое тождество.
- Приведите дроби к общему знаменателю. А затем используйте основное тригонометрическое тождество sin2 x + cos2 x = 1, сведите уравнение к квадратному.
Указания учителя
Проверьте и оцените свои работы. Исправьте ошибки, если они есть, подсчитайте количество баллов. Проставьте количество баллов в оценочный лист. Оцените свои работы.
Домашнее задание
- Если вы получили оценку «4» или «5», то выполните любое задание из дополнительных глав учебника.
- Если вы получили «3» или»2», то выполните из учебника под редакцией А.Г. Мордковича №№ 18.4; 18.3; 21.24.
www.sud-sosh2.ru
Решение тригонометрических уравнений в 10-м классе
Разделы: Математика
Цели урока:
- Образовательные – обеспечить повторение и систематизацию материала темы. Научить при решении уравнений применять формулы понижения степени. Создать условия контроля усвоения знаний и умений.
- Развивающие – способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
- Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.
Методы обучения: частично – поисковый. Проверка уровня знаний, работа по обобщающей схеме, решение познавательных обобщающих задач, системные обобщения, самопроверка, восприятие нового материала, взаимопроверка.
Формы организации урока: индивидуальная, фронтальная.
Оборудование и источники информации: Экран; мультимедийный проектор; ноутбук. У учащихся на партах листы учета знаний; системно – обобщающая схема; по два подписанных листочка и два бланка для записи ответов.
План урока:
- Оргмомент.
- Проверочная работа по контролю знаний по простейшим тригонометрическим уравнениям.
- Сообщение об истории развития тригонометрии.
- Систематизация теоретического материала.
- Объяснение нового материала
- Обучающая самостоятельная работа.
- Итог урока.
1. Организационный момент. (Презентация. Слайды 1 – 2.)
Французский писатель Анатоль Франс (1844–1924) однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.
Сегодня у нас заключительный урок по теме «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приемы решений тригонометрических уравнений.
Перед нами стоит задача – показать свои знания и умения по решению тригонометрических уравнений.
2. Проверочная работа. (Презентация. Слайды 3, 4, 5.)
Т е м а: «Решение простейших тригонометрических уравнений».
Ц е л ь: контроль знаний и приведение в систему знаний по простейшим тригонометрическим уравнениям.
Работа проводится в двух вариантах. Вопросы проецируются на экран.
Работа окончена, собираются бланки с ответами. Учащиеся отмечают на листочках неправильные шаги и количество правильных ответов, заносят в лист учета знаний.
На экране – слайд 6. (Ответы)
3. Сообщения.
- Развитие тригонометрии. – Презентация. (Выступает подготовленный ученик.)
- История тригонометрических терминов. – Презентация. (Выступает подготовленный ученик.)
4. Систематизация теоретического материала.
- Найти ошибку. (Презентация. Слайд 7)
Цель: повторение понятий арксинус, арккосинус, арктангенс и арккотангенс числа.
- Устные задания на определение вида простейших тригонометрических уравнений. Презентация. Слайды 8 и 9.
Цель: обобщение знаний по видам простейших тригонометрических уравнений.
На слайдах вы видите схемы решений тригонометрических уравнений. Как вы думаете, какая из схем представленной группы является лишней? Что объединяет остальные схемы?
О т в е т ы :
Слайд 8. 5-я схема лишняя, так как эта схема изображает решение уравнения вида sin x = a; 1, 2, 3, 4, 6 – изображают решение уравнений вида cos x = a.
Слайд 9. 1-я схема лишняя, так как она изображает решение уравнения вида cos x = a;
5-я схема лишняя, так как эта схема изображает решение уравнения вида ctg x = a;
2, 3, 4, 6 – изображают решение уравнений вида tg x = a.
Слайды 10, 11. Установить соответствие: Уравнение ↔ Корни.
3. Экспресс-опрос (Презентация. Слайды 12, 13, 14, 15)
Учащимся предлагается определить, решение какого тригонометрического уравнения показано на тригонометрической окружности. Записать его корни
4. Классификация тригонометрических уравнений.
Цель: привести в систему знания по типам и методам решения тригонометрических уравнений.
Слайды 16 – 20 (Презентация). Составление таблицы по методам решения тригонометрических уравнений.
Учащимся предлагается решить уравнения (по вариантам) предварительно определив, что это за уравнение и каким методом оно решается. У доски данную работу выполняет один ученик – решение уравнения одного варианта. Учащиеся, выполняющие работу другого варианта, решают уравнение на листочках.
5. Объяснение нового материала. (Презентация. Слайд 21.)
Цель: Познакомить учащихся с еще одним методом решения тригонометрических уравнений – методом понижения степени уравнений.
Учащимся для рассмотрения новой темы предлагается к решению уравнение:
2sin2 x + cos 4x = 0.
Решение:
6. Самостоятельная работа (обучающего характера).
7. Подведение итогов урока.
8. Домашнее задание.
№ 207 (а, б, в, д), стр. 389 – «Алгебра и начала анализа – 10» Никольский С.М. (2007 г.)
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Открытый урок. Алгебра. 10-й класс. Тема: «Решение простейших тригонометрических уравнений»
Разделы: Математика
Цели:
Оборудование: таблица.
ХОД УРОКА
I. Организационный момент:
1. Приготовление рабочего места. Знакомство с гостями.
2. Сообщение цели урока.
3. Каждый оценит свою работу. (Оценочные листы)
Свойства функции |
Заполнить таблицу |
Частные случаи решения тригонометрических уравнений. |
Решить урав-нения |
Самостоятельная работа |
Оценка учителя |
Итоговая оценка |
|
| Оценка |
II. Домашнее задание:
п.9, №139, 142, творческая работа – прочитать о тригонометрической функции стр.85 (“История тригонометрии”)
III. Актуализация
1. Повторим свойства функции – четность и нечетность. Это нам нужно при решении самостоятельной работы.
arcsin (-) = — arcsin
arccos (-) = – arccos
arctg (-) = — arctg
arcctg (-) = – arcctg
Оценку поставить в оценочный лист.
2. Заполнить таблицу. Эти значения arcsin и arccos нужны при решении тригонометрических уравнений.
— 1 |
— |
— |
— |
0 |
1 |
||||
| arcsin | |||||||||
| arccos |
– Проверьте по таблице. Оцените себя. И я вас оценю.
3. Вспомнить основные формулы решения тригонометрических уравнений, чтобы не допускать ошибок при решении тригонометрических уравнений.
Прослушали эти формулы и зрительно зафиксировали.
Частные случаи решения тригонометрических уравнений.
Заключите, пожалуйста, запись, и будьте внимательны потом, при решении уравнений.
Оценить свою работу.
IV. Решить уравнения
(Проверка домашнего задания). Закрепление. Записать в тетради и на доске с учителем.
— Особое внимание обратить на ход записи решения третьего уравнения. Это подготовка к самостоятельной работе.
Оцените себя.
V. Самостоятельная работа
Это проверка ваших знаний, как вы поняли эту тему.
| I в. 1) cos x= 2) 2cosx — =0 3) 4) 5) |
II в. 1) sin x= 2) 3) 4) 5) |
Проверка решения. Оцените себя.
VI. Итог урока:
— Что вы запомнили на этом уроке?
— Кто не умеет решать?
Последнюю работу проверю и оценки (средний балл) поставлю в журнал.
Спасибо за урок!
Приложение. Решение самостоятельной работы
(Ответы записать на доске)
Поделиться страницей:
xn--i1abbnckbmcl9fb.xn--p1ai
