Решение показательных систем неравенств – Методическая разработка по алгебре (11 класс) по теме: Урок по алгебре «Системы показательных уравнений и неравенств» | скачать бесплатно

Решение системы показательных неравенств. Задание С3

15 Задание (2016) (C3)ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА

Предлагаю вам решить систему показательных неравенств:

,

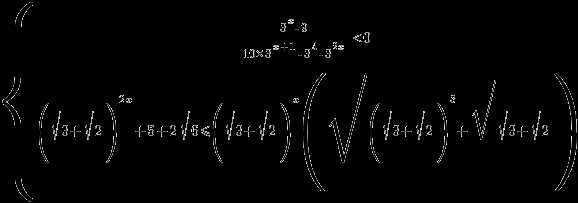а затем сверить свое решение в ВИДЕОУРОКОМ.

Прежде чем приступать к решению, нужно вспомнить теорему Виета для приведенного квадратного уравнения:

Сумма корней приведенного квадратного уравнения  равна свободному члену, а произедение корней равно второму коэффициенту, взятому с противоположным знаком. То есть:

.

Также полезно вспомнить, как выделять полный квадрат в выражении вида .

Для решения второго неравенства нужно представить в виде  квадрата суммы выражение 

Если , то получим систему:

.

Число  можно представить в виде произведения двух множителей двумя способами:

и

Нам надо, чтобы сумма квадратов этих чисел была равна 5. Этому условию удовлетворяет вторая пара: . Тогда получаем:

Теперь попробуйте решить систему самостоятельно, а затем сверьте свое решение с видеоуроком:

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Решение показательных неравенств

3 января 2017

Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое. И что научиться их решать — чуть ли не великое искусство, постичь которое способны лишь Избранные…

Полная брехня! Показательные неравенства — это просто. И решаются они всегда просто. Ну, почти всегда.:)

Сегодня мы разберём эту тему вдоль и поперёк. Этот урок будет очень полезен тем, кто только начинает разбираться в данном разделе школьной математики. Начнём с простых задач и будем двигаться к более сложным вопросам. Никакой жести сегодня не будет, но того, что вы сейчас прочитаете, будет достаточно, чтобы решить большинство неравенств на всяких контрольных и самостоятельных работах. И на этом вашем ЕГЭ тоже.

Как всегда, начнём с определения. Показательное неравенство — это любое неравенство, содержащее в себе показательную функцию. Другими словами, его всегда можно свести к неравенству вида

\[{{a}^{x}} \gt b\]

Где в роли $b$ может быть обычное число, а может быть и что-нибудь пожёстче. Примеры? Да пожалуйста:

\[\begin{align} & {{2}^{x}} \gt 4;\quad {{2}^{x-1}}\le \frac{1}{\sqrt[3]{2}};\quad {{2}^{{{x}^{2}}-7x+14}} \lt 16; \\ & {{0,1}^{1-x}} \lt 0,01;\quad {{2}^{\frac{x}{2}}} \lt {{4}^{\frac{4}{x}}}. \\\end{align}\]

Думаю, смысл понятен: есть показательная функция ${{a}^{x}}$, её с чем-то сравнивают, а затем просят найти $x$. В особо клинических случаях вместо переменной $x$ могут засунуть какую-нибудь функцию $f\left( x \right)$ и тем самым чуть-чуть усложнить неравенство.:)

Конечно, в некоторых случаях неравенство может выглядеть более сурово. Вот, например:

\[{{9}^{x}}+8 \gt {{3}^{x+2}}\]

Или даже вот:

\[5\cdot {{4}^{x}}+2\cdot {{25}^{x}} \gt 7\cdot {{10}^{x}}\]

В целом, сложность таких неравенств может быть самой разной, но в итоге они всё равно сводятся к простой конструкции ${{a}^{x}} \gt b$. А уж с такой конструкцией мы как-нибудь разберёмся (в особо клинических случаях, когда ничего не приходит в голову, нам помогут логарифмы). Поэтому сейчас мы научимя решать такие простые конструкции.

Решение простейших показательных неравенств

Рассмотрим что-нибудь совсем простое. Например, вот это:

\[{{2}^{x}} \gt 4\]

Очевидно, что число справа можно переписать в виде степени двойки: $4={{2}^{2}}$. Таким образом, исходное неравенство перепишется в очень удобной форме:

\[{{2}^{x}} \gt {{2}^{2}}\]

И вот уже руки чешутся «зачеркнуть» двойки, стоящие в основаниях степеней, дабы получить ответ $x \gt 2$. Но перед тем как что там зачёркивать, давайте вспомним степени двойки:

\[{{2}^{1}}=2;\quad {{2}^{2}}=4;\quad {{2}^{3}}=8;\quad {{2}^{4}}=16;…\]

Как видим, чем большее число стоит в показателе степени, тем больше получается число на выходе. «Спасибо, кэп!» — воскликнет кто-нибудь из учеников. Разве бывает по-другому? К сожалению, бывает. Например:

\[{{\left( \frac{1}{2} \right)}^{1}}=\frac{1}{2};\quad {{\left( \frac{1}{2} \right)}^{2}}=\frac{1}{4};\quad {{\left( \frac{1}{2} \right)}^{3}}=\frac{1}{8};…\]

Тут тоже всё логично: чем больше степень, тем больше раз число 0,5 умножается само на себя (т.е. делится пополам). Таким образом, полученная последовательность чисел убывает, а разница между первой и второй последовательностью состоит лишь в основании:

• Если основание степени $a \gt 1$, то по мере роста показателя $n$ число ${{a}^{n}}$ тоже будет расти;
• И наоборот, если $0 \lt a \lt 1$, то по мере роста показателя $n$ число ${{a}^{n}}$ будет убывать.

Суммируя эти факты, мы получаем самое главное утверждение, на котором и основано всё решение показательных неравенств:

Если $a \gt 1$, то неравенство ${{a}^{x}} \gt {{a}^{n}}$ равносильно неравенству $x \gt n$. Если $0 \lt a \lt 1$, то неравенство ${{a}^{x}} \gt {{a}^{n}}$ равносильно неравенству $x \lt n$.

Другими словами, если основание больше единицы, его можно просто убрать — знак неравенства при этом не поменяется. А если основание меньше единицы, то его тоже можно убрать, но при этом придётся поменять и знак неравенства.

Обратите внимание: мы не рассмотрели варианты $a=1$ и $a\le 0$. Потому что в этих случаях возникает неопределённость. Допустим, как решить неравенство вида ${{1}^{x}} \gt 3$? Единица в любой степени снова даст единицу — мы никогда не получим тройку или больше. Т.е. решений нет.

С отрицательными основаниями всё ещё интереснее. Рассмотрим для примера вот такое неравенство:

\[{{\left( -2 \right)}^{x}} \gt 4\]

На первый взгляд, всё просто:

\[4={{2}^{2}}\Rightarrow {{\left( -2 \right)}^{x}} \gt {{2}^{2}}\Rightarrow x \gt 2\]

Правильно? А вот и нет! Достаточно подставить вместо $x$ парочку чётных и парочку нечётных чисел, чтобы убедиться что решение неверно. Взгляните:

\[\begin{align} & x=4\Rightarrow {{\left( -2 \right)}^{4}}=16 \gt 4; \\ & x=5\Rightarrow {{\left( -2 \right)}^{5}}=-32 \lt 4; \\ & x=6\Rightarrow {{\left( -2 \right)}^{6}}=64 \gt 4; \\ & x=7\Rightarrow {{\left( -2 \right)}^{7}}=-128 \lt 4. \\\end{align}\]

Как видите, знаки чередуются. А ведь есть ещё дробные степени и прочая жесть. Как, например, прикажете считать ${{\left( -2 \right)}^{\sqrt{7}}}$ (минус двойка в степени корень из семи)? Да никак!

Поэтому для определённости полагают, что во всех показательных неравенствах (и уравнениях, кстати, тоже) $1\ne a \gt 0$. И тогда всё решается очень просто:

\[{{a}^{x}} \gt {{a}^{n}}\Rightarrow \left[ \begin{align} & x \gt n\quad \left( a \gt 1 \right), \\ & x \lt n\quad \left( 0 \lt a \lt 1 \right). \\\end{align} \right.\]

В общем, ещё раз запомните главное правило: если основание в показательном уравнении больше единицы, его можно просто убрать; а если основание меньше единицы, его тоже можно убрать, но при этом поменяется знак неравенства.

Примеры решения

Итак, рассмотрим несколько простых показательных неравенств:

\[\begin{align} & {{2}^{x-1}}\le \frac{1}{\sqrt[3]{2}}; \\ & {{0,1}^{1-x}} \lt 0,01; \\ & {{2}^{{{x}^{2}}-7x+14}} \lt 16; \\ & {{0,2}^{1+{{x}^{2}}}}\ge \frac{1}{25}. \\\end{align}\]

Первостепенная задача во всех случаях одна и та же: свести неравенств к простейшему виду ${{a}^{x}} \gt {{a}^{n}}$. Именно это мы сейчас и сделаем с каждым неравенством, а заодно повторим свойства степеней и показательной функции. Итак, поехали!

\[{{2}^{x-1}}\le \frac{1}{\sqrt[3]{2}}\]

Что здесь можно сделать? Ну, слева у нас и так стоит показательное выражение — ничего менять не надо. А вот справа стоит какая-то хрень: дробь, да ещё и в знаменателе корень!

Однако вспомним правила работы с дробями и степенями:

\[\begin{align} & \frac{1}{{{a}^{n}}}={{a}^{-n}}; \\ & \sqrt[k]{a}={{a}^{\frac{1}{k}}}. \\\end{align}\]

Что это значит? Во-первых, мы легко можем избавиться от дроби, превратив её в степень с отрицательным показателем. А во-вторых, поскольку в знаменателе стоит корень, было бы неплохо превратить и его в степень — на этот раз с дробным показателем.

Применим эти действия последовательно к правой части неравенства и посмотрим, что получится:

\[\frac{1}{\sqrt[3]{2}}={{\left( \sqrt[3]{2} \right)}^{-1}}={{\left( {{2}^{\frac{1}{3}}} \right)}^{-1}}={{2}^{\frac{1}{3}\cdot \left( -1 \right)}}={{2}^{-\frac{1}{3}}}\]

Не забываем, что при возведении степени в степень показатели этих степеней складываются. И вообще, при работе с показательными уравнениями и неравенствами совершенно необходимо знать хотя бы простейшие правила работы со степенями:

\[\begin{align} & {{a}^{x}}\cdot {{a}^{y}}={{a}^{x+y}}; \\ & \frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}}; \\ & {{\left( {{a}^{x}} \right)}^{y}}={{a}^{x\cdot y}}. \\\end{align}\]

Собственно, последнее правило мы только что и применили. Поэтому наше исходное неравенство перепишется следующим образом:

\[{{2}^{x-1}}\le \frac{1}{\sqrt[3]{2}}\Rightarrow {{2}^{x-1}}\le {{2}^{-\frac{1}{3}}}\]

Теперь избавляемся от двойки в основании. Поскольку 2 > 1, знак неравенства останется прежним:

\[\begin{align} & x-1\le -\frac{1}{3}\Rightarrow x\le 1-\frac{1}{3}=\frac{2}{3}; \\ & x\in \left( -\infty ;\frac{2}{3} \right]. \\\end{align}\]

Вот и всё решение! Основная сложность — вовсе не в показательной функции, а в грамотном преобразовании исходного выражения: нужно аккуратно и максимально быстро привести его к простейшему виду.

Рассмотрим второе неравенство:

\[{{0,1}^{1-x}} \lt 0,01\]

Так, так. Тут нас поджидают десятичные дроби. Как я уже много раз говорил, в любых выражениях со степенями следует избавляться от десятичных дробей — зачастую только так можно увидеть быстрое и простое решение. Вот и мы избавимся:

\[\begin{align} & 0,1=\frac{1}{10};\quad 0,01=\frac{1}{100}={{\left( \frac{1}{10} \right)}^{2}}; \\ & {{0,1}^{1-x}} \lt 0,01\Rightarrow {{\left( \frac{1}{10} \right)}^{1-x}} \lt {{\left( \frac{1}{10} \right)}^{2}}. \\\end{align}\]

Перед нами вновь простейшее неравенство, да ещё и с основанием 1/10, т.е. меньшим единицы. Что ж, убираем основания, попутно меняя знак с «меньше» на «больше», и получаем:

\[\begin{align} & 1-x \gt 2; \\ & -x \gt 2-1; \\ & -x \gt 1; \\& x \lt -1. \\\end{align}\]

Получили окончательный ответ: $x\in \left( -\infty ;-1 \right)$. Обратите внимание: ответом является именно множество, а ни в коем случае не конструкция вида $x \lt -1$. Потому что формально такая конструкция — это вовсе не множество, а неравенство относительно переменной $x$. Да, оно очень простое, но это не ответ!

Важное замечание. Данное неравенство можно было решить и по-другому — путём приведения обеих частей к степени с основанием, большим единицы. Взгляните:

\[\frac{1}{10}={{10}^{-1}}\Rightarrow {{\left( {{10}^{-1}} \right)}^{1-x}} \lt {{\left( {{10}^{-1}} \right)}^{2}}\Rightarrow {{10}^{-1\cdot \left( 1-x \right)}} \lt {{10}^{-1\cdot 2}}\]

После такого преобразования мы вновь получим показательное неравенство, но с основанием 10 > 1. А это значит, что можно просто зачеркнуть десятку — знак неравенства при этом не поменяется. Получим:

\[\begin{align} & -1\cdot \left( 1-x \right) \lt -1\cdot 2; \\ & x-1 \lt -2; \\ & x \lt -2+1=-1; \\ & x \lt -1. \\\end{align}\]

Как видите, ответ получился точь-в-точь такой же. При этом мы избавили себя от необходимости менять знак и вообще помнить какие-то там правила.:)

Идём далее. Рассмотрим чуть более сложное неравенство — в нём в показателе появляется квадратичная функция:

\[{{2}^{{{x}^{2}}-7x+14}} \lt 16\]

Однако пусть вас это не пугает. Чтобы ни находилось в показателях, технология решения самого неравенства остаётся прежней. Поэтому заметим для начала, что 16 = 2⁴. Перепишем исходное неравенство с учётом этого факта:

\[\begin{align} & {{2}^{{{x}^{2}}-7x+14}} \lt {{2}^{4}}; \\ & {{x}^{2}}-7x+14 \lt 4; \\ & {{x}^{2}}-7x+10 \lt 0. \\\end{align}\]

Ура! Мы получили обычное квадратное неравенство! Знак нигде не менялся, поскольку в основании стоит двойка — число, большее единицы.

Далее можно воспользоваться теоремой Виета, либо просто решить уравнение ${{x}^{2}}-7x+10=0$ через дискриминант. В любом случае корни будут ${{x}_{1}}=2$ и ${{x}_{2}}=5$. Отметим их на числовой прямой:

Нули функции на числовой прямой

Расставляем знаки функции $f\left( x \right)={{x}^{2}}-7x+10$ — очевидно, её графиком будет парабола ветвями вверх, поэтому по бокам будут «плюсы». Нас интересует та область, где функция меньше нуля, т.е. $x\in \left( 2;5 \right)$ — это и есть ответ к исходной задаче.

Наконец, рассмотрим ещё одно неравенство:

\[{{0,2}^{1+{{x}^{2}}}}\ge \frac{1}{25}\]

Опять видим показательную функцию с десятичной дробью в основании. Переводим эту дробь в обыкновенную:

\[\begin{align} & 0,2=\frac{2}{10}=\frac{1}{5}={{5}^{-1}}\Rightarrow \\ & \Rightarrow {{0,2}^{1+{{x}^{2}}}}={{\left( {{5}^{-1}} \right)}^{1+{{x}^{2}}}}={{5}^{-1\cdot \left( 1+{{x}^{2}} \right)}}\end{align}\]

В данном случае мы воспользовались приведённым ранее замечанием — свели основание к числу 5 > 1, чтобы упростить себе дальнейшее решение. Точно так же поступим и с правой частью:

\[\frac{1}{25}={{\left( \frac{1}{5} \right)}^{2}}={{\left( {{5}^{-1}} \right)}^{2}}={{5}^{-1\cdot 2}}={{5}^{-2}}\]

Перепишем исходное неравенство с учётом обоих преобразований:

\[{{0,2}^{1+{{x}^{2}}}}\ge \frac{1}{25}\Rightarrow {{5}^{-1\cdot \left( 1+{{x}^{2}} \right)}}\ge {{5}^{-2}}\]

Основания с обеих сторон одинаковы и превосходят единицу. Никаких других слагаемых справа и слева нет, поэтому просто «зачёркиваем» пятёрки и получаем совсем простое выражение:

\[\begin{align} & -1\cdot \left( 1+{{x}^{2}} \right)\ge -2; \\ & -1-{{x}^{2}}\ge -2; \\ & -{{x}^{2}}\ge -2+1; \\ & -{{x}^{2}}\ge -1;\quad \left| \cdot \left( -1 \right) \right. \\ & {{x}^{2}}\le 1. \\\end{align}\]

Вот тут надо быть аккуратнее. Многие ученики любят просто извлечь квадратный корень их обеих частей неравенства и записать что-нибудь в духе $x\le 1\Rightarrow x\in \left( -\infty ;-1 \right]$. Делать этого ни в коем случае нельзя, поскольку корень из точного квадрата — это модуль, а ни в коем случае не исходная переменная:

\[\sqrt{{{x}^{2}}}=\left| x \right|\]

Однако работать с модулями — не самое приятное занятие, правда? Вот и мы не будем работать. А вместо этого просто перенесём все слагаемые влево и решим обычное неравенство методом интервалов:

$\begin{align} & {{x}^{2}}-1\le 0; \\ & \left( x-1 \right)\left( x+1 \right)\le 0 \\ & {{x}_{1}}=1;\quad {{x}_{2}}=-1; \\\end{align}$

Вновь отмечаем полученные точки на числовой прямой и смотрим знаки:

Обратите внимание: точки закрашены

Поскольку мы решали нестрогое неравенство, все точки на графике закрашены. Поэтому ответ будет такой: $x\in \left[ -1;1 \right]$ — не интервал, а именно отрезок.

В целом хотел бы заметить, что ничего сложного в показательных неравенствах нет. Смысл всех преобразований, которые мы сегодня выполняли, сводится к простому алгоритму:

• Найти основание, к которому будем приводить все степени;
• Аккуратно выполнить преобразования, чтобы получилось неравенство вида ${{a}^{x}} \gt {{a}^{n}}$. Разумеется вместо переменных $x$ и $n$ могут стоять гораздо более сложные функции, но смысл от этого не поменяется;
• Зачеркнуть основания степеней. При этом может поменяться знак неравенства, если основание $a \lt 1$.

По сути, это универсальный алгоритм решения всех таких неравенств. А всё, что вам ещё будут рассказывать по этой теме — лишь конкретные приёмы и хитрости, позволяющие упростить и ускорить преобразования. Вот об одном из таких приёмов мы сейчас и поговорим.:)

Метод рационализации

Рассмотрим ещё одну партию неравенств:

\[\begin{align} & {{\text{ }\!\!\pi\!\!\text{ }}^{x+7}} \gt {{\text{ }\!\!\pi\!\!\text{ }}^{{{x}^{2}}-3x+2}}; \\ & {{\left( 2\sqrt{3}-3 \right)}^{{{x}^{2}}-2x}} \lt 1; \\ & {{\left( \frac{1}{3} \right)}^{{{x}^{2}}+2x}} \gt {{\left( \frac{1}{9} \right)}^{16-x}}; \\ & {{\left( 3-2\sqrt{2} \right)}^{3x-{{x}^{2}}}} \lt 1. \\\end{align}\]

Ну и что в них такого особенного? Они же лёгкие. Хотя, стоп! Число π возводится в какую-то степень? Что за бред?

А как возвести в степень число $2\sqrt{3}-3$? Или $3-2\sqrt{2}$? Составители задач, очевидно, перепили «Боярышника» перед тем, как сесть за работу.:)

На самом деле ничего страшного в этих задачах нет. Напомню: показательной функцией называется выражение вида ${{a}^{x}}$, где основание $a$ — это любое положительное число, за исключением единицы. Число π положительно — это мы и так знаем. Числа $2\sqrt{3}-3$ и $3-2\sqrt{2}$ тоже положительны — в этом легко убедиться, если сравнить их с нулём.

Получается, что все эти «устрашающие» неравенства ничем не отличаются решаются от простых, рассмотренных выше? И решаются точно так же? Да, совершенно верно. Однако на их примере я хотел бы рассмотреть один приём, который здорово экономит время на самостоятельных работах и экзаменах. Речь пойдёт о методе рационализации. Итак, внимание:

Всякое показательное неравенство вида ${{a}^{x}} \gt {{a}^{n}}$ равносильно неравенству $\left( x-n \right)\cdot \left( a-1 \right) \gt 0$.

Вот и весь метод.:) А вы думали, что будет какая-нибудь очередная дичь? Ничего подобного! Но этот простой факт, записанный буквально в одну строчку, значительно упростит нам работу. Взгляните:

\[\begin{matrix} {{\text{ }\!\!\pi\!\!\text{ }}^{x+7}} \gt {{\text{ }\!\!\pi\!\!\text{ }}^{{{x}^{2}}-3x+2}} \\ \Downarrow \\ \left( x+7-\left( {{x}^{2}}-3x+2 \right) \right)\cdot \left( \text{ }\!\!\pi\!\!\text{ }-1 \right) \gt 0 \\\end{matrix}\]

Вот и нет больше показательных функций! И не надо помнить: меняется знак или нет. Но возникает новая проблема: что делать с грёбаным множителем \[\left( \text{ }\!\!\pi\!\!\text{ }-1 \right)\]? Мы ведь не знаем, чему равно точное значение числа π. Впрочем, капитан очевидность как бы намекает:

\[\text{ }\!\!\pi\!\!\text{ }\approx 3,14… \gt 3\Rightarrow \text{ }\!\!\pi\!\!\text{ }-1 \gt 3-1=2\]

В общем, точное значение π нас особо-то и не колышет — нам лишь важно понимать, что в любом случае $\text{ }\!\!\pi\!\!\text{ }-1 \gt 2$, т.е. это положительная константа, и мы можем разделить на неё обе части неравенства:

\[\begin{align} & \left( x+7-\left( {{x}^{2}}-3x+2 \right) \right)\cdot \left( \text{ }\!\!\pi\!\!\text{ }-1 \right) \gt 0 \\ & x+7-\left( {{x}^{2}}-3x+2 \right) \gt 0; \\ & x+7-{{x}^{2}}+3x-2 \gt 0; \\ & -{{x}^{2}}+4x+5 \gt 0;\quad \left| \cdot \left( -1 \right) \right. \\ & {{x}^{2}}-4x-5 \lt 0; \\ & \left( x-5 \right)\left( x+1 \right) \lt 0. \\\end{align}\]

Как видите, в определённый момент пришлось разделить на минус единицу — при этом знак неравенства поменялся. В конце я разложил квадратный трёхчлен по теореме Виета — очевидно, что корни равны ${{x}_{1}}=5$ и ${{x}_{2}}=-1$. Дальше всё решается классическим методом интервалов:

Решаем неравенство методом интервалов

Все точки выколоты, поскольку исходное неравенство строгое. Нас интересует область с отрицательными значениями, поэтому ответ: $x\in \left( -1;5 \right)$. Вот и всё решение.:)

Перейдём к следующей задаче:

\[{{\left( 2\sqrt{3}-3 \right)}^{{{x}^{2}}-2x}} \lt 1\]

Тут вообще всё просто, потому что справа стоит единица. А мы помним, что единица — это любое число в нулевой степени. Даже если этим числом является иррациональное выражение, стоящее в основании слева:

\[\begin{align} & {{\left( 2\sqrt{3}-3 \right)}^{{{x}^{2}}-2x}} \lt 1={{\left( 2\sqrt{3}-3 \right)}^{0}}; \\ & {{\left( 2\sqrt{3}-3 \right)}^{{{x}^{2}}-2x}} \lt {{\left( 2\sqrt{3}-3 \right)}^{0}}; \\\end{align}\]

Что ж, выполняем рационализацию:

\[\begin{align} & \left( {{x}^{2}}-2x-0 \right)\cdot \left( 2\sqrt{3}-3-1 \right) \lt 0; \\ & \left( {{x}^{2}}-2x-0 \right)\cdot \left( 2\sqrt{3}-4 \right) \lt 0; \\ & \left( {{x}^{2}}-2x-0 \right)\cdot 2\left( \sqrt{3}-2 \right) \lt 0. \\\end{align}\]

Осталось лишь разобраться со знаками. Множитель $2\left( \sqrt{3}-2 \right)$ не содержит переменной $x$ — это просто константа, и нам необходимо выяснить её знак. Для этого заметим следующее:

\[\begin{matrix} \sqrt{3} \lt \sqrt{4}=2 \\ \Downarrow \\ 2\left( \sqrt{3}-2 \right) \lt 2\cdot \left( 2-2 \right)=0 \\\end{matrix}\]

Получается, что второй множитель — не просто константа, а отрицательная константа! И при делении на неё знак исходного неравенства поменяется на противоположный:

\[\begin{align} & \left( {{x}^{2}}-2x-0 \right)\cdot 2\left( \sqrt{3}-2 \right) \lt 0; \\ & {{x}^{2}}-2x-0 \gt 0; \\ & x\left( x-2 \right) \gt 0. \\\end{align}\]

Теперь всё становится совсем очевидно. Корни квадратного трёхчлена, стоящего справа: ${{x}_{1}}=0$ и ${{x}_{2}}=2$. Отмечаем их на числовой прямой и смотрим знаки функции $f\left( x \right)=x\left( x-2 \right)$:

Случай, когда нас интересуют боковые интервалы

Нас интересуют интервалы, отмеченные знаком «плюс». Осталось лишь записать ответ:

\[x\in \left( -\infty ;0 \right)\bigcup \left( 2;+\infty \right)\]

Переходим к следующему примеру:

\[{{\left( \frac{1}{3} \right)}^{{{x}^{2}}+2x}} \gt {{\left( \frac{1}{9} \right)}^{16-x}}\]

Ну, тут совсем всё очевидно: в основаниях стоят степени одного и того же числа. Поэтому я распишу всё кратко:

\[\begin{matrix} \frac{1}{3}={{3}^{-1}};\quad \frac{1}{9}=\frac{1}{{{3}^{2}}}={{3}^{-2}} \\ \Downarrow \\ {{\left( {{3}^{-1}} \right)}^{{{x}^{2}}+2x}} \gt {{\left( {{3}^{-2}} \right)}^{16-x}} \\\end{matrix}\]

Далее «причёсываем» выражения с обеих частей неравенства и применяем метод рационализации:

\[\begin{align} & {{3}^{-1\cdot \left( {{x}^{2}}+2x \right)}} \gt {{3}^{-2\cdot \left( 16-x \right)}}; \\ & {{3}^{-{{x}^{2}}-2x}} \gt {{3}^{-32+2x}}; \\ & \left( -{{x}^{2}}-2x-\left( -32+2x \right) \right)\cdot \left( 3-1 \right) \gt 0; \\ & -{{x}^{2}}-2x+32-2x \gt 0; \\ & -{{x}^{2}}-4x+32 \gt 0;\quad \left| \cdot \left( -1 \right) \right. \\ & {{x}^{2}}+4x-32 \lt 0; \\ & \left( x+8 \right)\left( x-4 \right) \lt 0. \\\end{align}\]

Как видите, в процессе преобразований пришлось умножать на отрицательное число, поэтому поменялся знак неравенства. В самом конце я вновь применил теорему Виета для разложения на множители квадратного трёхчлена. В итоге ответ будет следующий: $x\in \left( -8;4 \right)$ — желающие могут убедиться в этом, нарисовав числовую прямую, отметив точки и посчитав знаки. А мы тем временем перейдём к последнему неравенству из нашего «комплекта»:

\[{{\left( 3-2\sqrt{2} \right)}^{3x-{{x}^{2}}}} \lt 1\]

Как видим, в основании снова стоит иррациональное число, а справа снова стоит единица. Поэтому перепишем наше показательное неравенство следующим образом:

\[{{\left( 3-2\sqrt{2} \right)}^{3x-{{x}^{2}}}} \lt {{\left( 3-2\sqrt{2} \right)}^{0}}\]

Применяем рационализацию:

\[\begin{align} & \left( 3x-{{x}^{2}}-0 \right)\cdot \left( 3-2\sqrt{2}-1 \right) \lt 0; \\ & \left( 3x-{{x}^{2}}-0 \right)\cdot \left( 2-2\sqrt{2} \right) \lt 0; \\ & \left( 3x-{{x}^{2}}-0 \right)\cdot 2\left( 1-\sqrt{2} \right) \lt 0. \\\end{align}\]

Однако совершенно очевидно, что $1-\sqrt{2} \lt 0$, поскольку $\sqrt{2}\approx 1,4… \gt 1$. Поэтому второй множитель — вновь отрицательная константа, на которую можно разделить обе части неравенства:

\[\begin{matrix} \left( 3x-{{x}^{2}}-0 \right)\cdot 2\left( 1-\sqrt{2} \right) \lt 0 \\ \Downarrow \\\end{matrix}\]

\[\begin{align} & 3x-{{x}^{2}}-0 \gt 0; \\ & 3x-{{x}^{2}} \gt 0;\quad \left| \cdot \left( -1 \right) \right. \\ & {{x}^{2}}-3x \lt 0; \\ & x\left( x-3 \right) \lt 0. \\\end{align}\]

Далее всё просто: находим корни, отмечаем их на числовой прямой, смотрим знаки. Ответ будет следующим: $x\in \left( 0;3 \right)$.

Переход к другому основанию

Отдельной проблемой при решении показательных неравенств является поиск «правильного» основания. К сожалению, далеко не всегда при первом взгляде на задание очевидно, что брать за основание, а что делать степенью этого основания.

Но не переживайте: здесь нет никакой магии и «секретных» технологий. В математике любой навык, который нельзя алгоритмизировать, можно легко выработать с помощью практики. Но для этого придётся решать задачи разного уровня сложности. Например, вот такие:

\[\begin{align} & {{2}^{\frac{x}{2}}} \lt {{4}^{\frac{4}{x}}}; \\ & {{\left( \frac{1}{3} \right)}^{\frac{3}{x}}}\ge {{3}^{2+x}}; \\ & {{\left( 0,16 \right)}^{1+2x}}\cdot {{\left( 6,25 \right)}^{x}}\ge 1; \\ & {{\left( \frac{27}{\sqrt[3]{3}} \right)}^{-x}} \lt {{9}^{4-2x}}\cdot 81. \\\end{align}\]

Сложно? Страшно? Да это же проще, чем цыплёнка об асфальт! Давайте попробуем. Первое неравенство:

\[{{2}^{\frac{x}{2}}} \lt {{4}^{\frac{4}{x}}}\]

Ну, я думают, тут и ежу всё понятно:

\[4={{2}^{2}}\Rightarrow {{4}^{\frac{4}{x}}}={{\left( {{2}^{2}} \right)}^{\frac{4}{x}}}={{2}^{2\cdot \frac{4}{x}}}={{2}^{\frac{8}{x}}}\]

Переписываем исходное неравенство, сводя всё к основанию «два»:

\[{{2}^{\frac{x}{2}}} \lt {{2}^{\frac{8}{x}}}\Rightarrow \left( \frac{x}{2}-\frac{8}{x} \right)\cdot \left( 2-1 \right) \lt 0\]

Да, да, вы всё правильно поняли: я только что применил метод рационализации, описанный выше. Теперь нужно работать аккуратно: у нас получилось дробно-рациональное неравенство (это такое, у которого в знаменателе стоит переменная), поэтому прежде чем что-то приравнивать к нулю, необходимо привести всё к общему знаменателю и избавиться от множителя-константы.

\[\begin{align} & \left( \frac{x}{2}-\frac{8}{x} \right)\cdot \left( 2-1 \right) \lt 0; \\ & \left( \frac{{{x}^{2}}-16}{2x} \right)\cdot 1 \lt 0; \\ & \frac{{{x}^{2}}-16}{2x} \lt 0. \\\end{align}\]

Теперь используем стандартный метод интервалов. Нули числителя: $x=\pm 4$. Знаменатель обращается в ноль только при $x=0$. Итого три точки, которые надо отметить на числовой прямой (все точки выколоты, т.к. знак неравенства строгий). Получим:

Более сложный случай: три корня

Как нетрудно догадаться, штриховкой отмечены те интервалы, на которых выражение слева принимает отрицательные значения. Поэтому в окончательный ответ пойдут сразу два интервала:

\[x\in \left( -\infty ;-4 \right)\bigcup \left( 0;4 \right)\]

Концы интервалов не входят в ответ, поскольку исходное неравенство было строгим. Никаких дополнительных проверок этого ответа не требуется. В этом плане показательные неравенства намного проще логарифмических: никаких ОДЗ, никаких ограничений и т.д.

Переходим к следующей задаче:

\[{{\left( \frac{1}{3} \right)}^{\frac{3}{x}}}\ge {{3}^{2+x}}\]

Здесь тоже никаких проблем, поскольку мы уже знаем, что $\frac{1}{3}={{3}^{-1}}$, поэтому всё неравенство можно переписать так:

\[\begin{align} & {{\left( {{3}^{-1}} \right)}^{\frac{3}{x}}}\ge {{3}^{2+x}}\Rightarrow {{3}^{-\frac{3}{x}}}\ge {{3}^{2+x}}; \\ & \left( -\frac{3}{x}-\left( 2+x \right) \right)\cdot \left( 3-1 \right)\ge 0; \\ & \left( -\frac{3}{x}-2-x \right)\cdot 2\ge 0;\quad \left| :\left( -2 \right) \right. \\ & \frac{3}{x}+2+x\le 0; \\ & \frac{{{x}^{2}}+2x+3}{x}\le 0. \\\end{align}\]

Обратите внимание: в третьей строчке я решил не мелочиться и сразу разделить всё на (−2). Минул ушёл в первую скобку (теперь там везде плюсы), а двойка сократилась с множителем-константой. Именно так и стоит поступать при оформлении реальных выкладок на самостоятельных и контрольных работах — не надо расписывать прям каждое действие и преобразование.

Далее в дело вступает знакомый нам метод интервалов. Нули числителя: а их нет. Потому что дискриминант будет отрицательный. В свою очередь знаменатель обнуляется лишь при $x=0$ — как и в прошлый раз. Ну и понятно, что справа от $x=0$ дробь будет принимать положительные значения, а слева — отрицательные. Поскольку нас интересуют именно отрицательные значения, то окончательный ответ: $x\in \left( -\infty ;0 \right)$.

Идём далее. В следующем задании нас поджидают десятичные дроби:

\[{{\left( 0,16 \right)}^{1+2x}}\cdot {{\left( 6,25 \right)}^{x}}\ge 1\]

А что нужно делать с десятичными дробями в показательных неравенствах? Правильно: избавляться от них, переводя в обыкновенные. Вот и мы переведём:

\[\begin{align} & 0,16=\frac{16}{100}=\frac{4}{25}\Rightarrow {{\left( 0,16 \right)}^{1+2x}}={{\left( \frac{4}{25} \right)}^{1+2x}}; \\ & 6,25=\frac{625}{100}=\frac{25}{4}\Rightarrow {{\left( 6,25 \right)}^{x}}={{\left( \frac{25}{4} \right)}^{x}}. \\\end{align}\]

Ну и что мы получили в основаниях показательных функций? А получили мы два взаимно обратных числа:

\[\frac{25}{4}={{\left( \frac{4}{25} \right)}^{-1}}\Rightarrow {{\left( \frac{25}{4} \right)}^{x}}={{\left( {{\left( \frac{4}{25} \right)}^{-1}} \right)}^{x}}={{\left( \frac{4}{25} \right)}^{-x}}\]

Таким образом исходное неравенство можно переписать так:

\[\begin{align} & {{\left( \frac{4}{25} \right)}^{1+2x}}\cdot {{\left( \frac{4}{25} \right)}^{-x}}\ge 1; \\ & {{\left( \frac{4}{25} \right)}^{1+2x+\left( -x \right)}}\ge {{\left( \frac{4}{25} \right)}^{0}}; \\ & {{\left( \frac{4}{25} \right)}^{x+1}}\ge {{\left( \frac{4}{25} \right)}^{0}}. \\\end{align}\]

Разумеется, при умножении степеней с одинаковым основанием их показатели складываются, что и произошло во второй строчке. Кроме того, мы представили единицу, стоящую справа, тоже в виде степени по основанию 4/25. Осталось лишь выполнить рационализацию:

\[{{\left( \frac{4}{25} \right)}^{x+1}}\ge {{\left( \frac{4}{25} \right)}^{0}}\Rightarrow \left( x+1-0 \right)\cdot \left( \frac{4}{25}-1 \right)\ge 0\]

Заметим, что $\frac{4}{25}-1=\frac{4-25}{25} \lt 0$, т.е. второй множитель является отрицательной константой, и при делении на неё знак неравенства поменяется:

\[\begin{align} & x+1-0\le 0\Rightarrow x\le -1; \\ & x\in \left( -\infty ;-1 \right]. \\\end{align}\]

Наконец, последнее неравенство из текущего «комплекта»:

\[{{\left( \frac{27}{\sqrt[3]{3}} \right)}^{-x}} \lt {{9}^{4-2x}}\cdot 81\]

В принципе, идея решения тут тоже ясна: все показательные функции, входящие в состав неравенства, необходимо свести к основанию «3». Но для этого придётся немного повозиться с корнями и степенями:

\[\begin{align} & \frac{27}{\sqrt[3]{3}}=\frac{{{3}^{3}}}{{{3}^{\frac{1}{3}}}}={{3}^{3-\frac{1}{3}}}={{3}^{\frac{8}{3}}}; \\ & 9={{3}^{2}};\quad 81={{3}^{4}}. \\\end{align}\]

С учётом этих фактов исходное неравенство можно переписать так:

\[\begin{align} & {{\left( {{3}^{\frac{8}{3}}} \right)}^{-x}} \lt {{\left( {{3}^{2}} \right)}^{4-2x}}\cdot {{3}^{4}}; \\ & {{3}^{-\frac{8x}{3}}} \lt {{3}^{8-4x}}\cdot {{3}^{4}}; \\ & {{3}^{-\frac{8x}{3}}} \lt {{3}^{8-4x+4}}; \\ & {{3}^{-\frac{8x}{3}}} \lt {{3}^{4-4x}}. \\\end{align}\]

Обратите внимание на 2-ю и 3-ю строчку выкладок: прежде чем что-то делать с неравенством, обязательно приведите его к тому виду, о котором мы говорили с самого начала урока: ${{a}^{x}} \lt {{a}^{n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.

Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:

\[\begin{align} & -\frac{8x}{3} \lt 4-4x; \\ & 4x-\frac{8x}{3} \lt 4; \\ & \frac{4x}{3} \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end{align}\]

Вот и всё. Окончательный ответ: $x\in \left( -\infty ;3 \right)$.

Выделение устойчивого выражения и замена переменной

В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. Чтобы справиться с ними, необходимо вспомнить правила работы со степенями. В частности — вынесение общих множителей за скобки.

Но самое главное — научиться понимать: что именно можно вынести за скобки. Такое выражение называется устойчивым — его можно обозначить новой переменной и таким образом избавиться от показательной функции. Итак, посмотрим на задачи:

\[\begin{align} & {{5}^{x+2}}+{{5}^{x+1}}\ge 6; \\ & {{3}^{x}}+{{3}^{x+2}}\ge 90; \\ & {{25}^{x+1,5}}-{{5}^{2x+2}} \gt 2500; \\ & {{\left( 0,5 \right)}^{-4x-8}}-{{16}^{x+1,5}} \gt 768. \\\end{align}\]

Начнём с самой первой строчки. Выпишем это неравенство отдельно:

\[{{5}^{x+2}}+{{5}^{x+1}}\ge 6\]

Заметим, что ${{5}^{x+2}}={{5}^{x+1+1}}={{5}^{x+1}}\cdot 5$, поэтому правую часть можно переписать:

\[5\cdot {{5}^{x+1}}+{{5}^{x+1}}\ge 6\]

Заметим, что никаких других показательных функций, кроме ${{5}^{x+1}}$, в неравенстве нет. И вообще, нигде больше не встречается переменная $x$, поэтому введём новую переменную: ${{5}^{x+1}}=t$. Получим следующую конструкцию:

\[\begin{align} & 5t+t\ge 6; \\ & 6t\ge 6; \\ & t\ge 1. \\\end{align}\]

Возвращаемся к исходной переменной ($t={{5}^{x+1}}$ ), а заодно вспоминаем, что 1=5⁰. Имеем:

\[\begin{align} & {{5}^{x+1}}\ge {{5}^{0}}; \\ & x+1\ge 0; \\ & x\ge -1. \\\end{align}\]

Вот и всё решение! Ответ: $x\in \left[ -1;+\infty \right)$. Переходим ко второму неравенству:

\[{{3}^{x}}+{{3}^{x+2}}\ge 90\]

Здесь всё то же самое. Заметим, что ${{3}^{x+2}}={{3}^{x}}\cdot {{3}^{2}}=9\cdot {{3}^{x}}$. Тогда левую часть можно переписать:

\[\begin{align} & {{3}^{x}}+9\cdot {{3}^{x}}\ge 90;\quad \left| {{3}^{x}}=t \right. \\ & t+9t\ge 90; \\ & 10t\ge 90; \\ & t\ge 9\Rightarrow {{3}^{x}}\ge 9\Rightarrow {{3}^{x}}\ge {{3}^{2}}; \\ & x\ge 2\Rightarrow x\in \left[ 2;+\infty \right). \\\end{align}\]

Вот примерно так и нужно оформлять решение на настоящих контрольных и самостоятельных работах.

Что ж, попробуем что-нибудь посложнее. Например, вот такое неравенство:

\[{{25}^{x+1,5}}-{{5}^{2x+2}} \gt 2500\]

В чём тут проблема? Прежде всего, основания показательных функций, стоящих слева, разные: 5 и 25. Однако 25 = 5², поэтому первое слагаемое можно преобразовать:

\[\begin{align} & {{25}^{x+1,5}}={{\left( {{5}^{2}} \right)}^{x+1,5}}={{5}^{2x+3}}; \\ & {{5}^{2x+3}}={{5}^{2x+2+1}}={{5}^{2x+2}}\cdot 5. \\\end{align}\]

Как видите, сначала мы всё привели к одинаковому основанию, а затем заметили, что первое слагаемое легко сводится ко второму — достаточно лишь разложить показатель. Теперь можно смело вводить новую переменную: ${{5}^{2x+2}}=t$, и всё неравенство перепишется так:

\[\begin{align} & 5t-t\ge 2500; \\ & 4t\ge 2500; \\ & t\ge 625={{5}^{4}}; \\ & {{5}^{2x+2}}\ge {{5}^{4}}; \\ & 2x+2\ge 4; \\ & 2x\ge 2; \\ & x\ge 1. \\\end{align}\]

И вновь никаких трудностей! Окончательный ответ: $x\in \left[ 1;+\infty \right)$. Переходим к заключительному неравенству в сегодняшнем уроке:

\[{{\left( 0,5 \right)}^{-4x-8}}-{{16}^{x+1,5}} \gt 768\]

Первое, на что следует обратить внимание — это, конечно, десятичная дробь в основании первой степени. От неё необходимо избавиться, а заодно привести все показательные функции к одному и тому же основанию — числу «2»:

\[\begin{align} & 0,5=\frac{1}{2}={{2}^{-1}}\Rightarrow {{\left( 0,5 \right)}^{-4x-8}}={{\left( {{2}^{-1}} \right)}^{-4x-8}}={{2}^{4x+8}}; \\ & 16={{2}^{4}}\Rightarrow {{16}^{x+1,5}}={{\left( {{2}^{4}} \right)}^{x+1,5}}={{2}^{4x+6}}; \\ & {{2}^{4x+8}}-{{2}^{4x+6}} \gt 768. \\\end{align}\]

Отлично, первый шаг мы сделали — всё привели к одному и тому же основанию. Теперь необходимо выделить устойчивое выражение. Заметим, что ${{2}^{4x+8}}={{2}^{4x+6+2}}={{2}^{4x+6}}\cdot 4$. Если ввести новую переменную ${{2}^{4x+6}}=t$, то исходное неравенство можно переписать так:

\[\begin{align} & 4t-t \gt 768; \\ & 3t \gt 768; \\ & t \gt 256={{2}^{8}}; \\ & {{2}^{4x+6}} \gt {{2}^{8}}; \\ & 4x+6 \gt 8; \\ & 4x \gt 2; \\ & x \gt \frac{1}{2}=0,5. \\\end{align}\]

Естественно, может возникнуть вопрос: каким это образом мы обнаружили, что 256 = 2⁸? К сожалению, тут нужно просто знать степени двойки (а заодно степени тройки и пятёрки). Ну, или делить 256 на 2 (делить можно, поскольку 256 — чётное число) до тех пор, пока не получим результат. Выглядеть это будет примерно так:

\[\begin{align} & 256=128\cdot 2= \\ & =64\cdot 2\cdot 2= \\ & =32\cdot 2\cdot 2\cdot 2= \\ & =16\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =8\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =4\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & ={{2}^{8}}.\end{align}\]

То же самое и с тройкой (числа 9, 27, 81 и 243 являются её степенями), и с семёркой (числа 49 и 343 тоже было бы неплохо запомнить). Ну, и у пятёрки тоже есть «красивые» степени, которые нужно знать:

\[\begin{align} & {{5}^{2}}=25; \\ & {{5}^{3}}=125; \\ & {{5}^{4}}=625; \\ & {{5}^{5}}=3125. \\\end{align}\]

Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.

Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)

Смотрите также:

1. Учимся решать показательные уравнения
2. Различные способы решения показательных уравнений
3. Как сдать ЕГЭ по математике
4. Пробный ЕГЭ 2012. Вариант 12 (без логарифмов)
5. Тригонометрические функции
6. Семинар: ЕГЭ по математике, задачи B3 на площади

www.berdov.com

Решение систем логарифмических и показательных неравенств с репетитором

Автор Сергей

Четверг, Апрель 5, 2012

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.

Для того, чтобы научиться  решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.

1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».

2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.

3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».

Пересечением множеств называется множество, которому принадлежат только те элементы, которые есть у каждого из этих множеств.

Другими словами, если даны два множества и то их пересечением будет являться множество следующего вида:

yourtutor.info

8. Общее повторение курса математики. Подготовка к экзаменам ⋆ Social AstroWay- Развлекательно-информационный портал

На этом уроке мы научимся решать простейшие показательные неравенства, используя свойства монотонности показательной функции, а также рассмотрим основные типы показательных неравенств. Кроме того, мы рассмотрим принципы решения систем показательных уравнений и неравенств.

Подготовка к ЕГЭ по математике

Эксперимент

Урок 2. Показательные неравенства. Системы показательных уравнений и неравенств.

Теория

Конспект урока

На предыдущем уроке мы уже обсуждали важный факт, касающийся показательной функции, а именно то, что она монотонна на всей области определения. То есть, при основании  показательная функция монотонно возрастает (с увеличением переменной увеличиваются и значения функции), а при основании  монотонно убывает (с увеличением переменной значения функции уменьшаются).

Этот факт нам наглядно подтвердили и графики показательной функции для обоих вариантов значения основания.

Это свойство очень помогло нам при решении показательных уравнений, так как из него следовало следующее утверждение: .

Вывод метода решения показательных неравенств

Оказывается, пользуясь этим свойством можно вывести и правило для решения показательных неравенств.

Рассмотрим два случая.

1)                      . В этом случае, как мы уже говорили, показательная функция монотонно возрастает. Поэтому неравенство  будет выполнено для всех  (мы говорили, что значение функции тем больше, чем больше значение переменной, значит, чтобы значение функции было больше, чем , необходимо, чтобы переменная .

2)                      . В этом случае, как мы уже говорили, показательная функция монотонно убывает. Поэтому неравенство  будет выполнено для всех  (мы говорили, что значение функции тем больше, чем меньше значение переменной, значит, чтобы значение функции было больше, чем , необходимо, чтобы переменная .

Общая схема решения показательных неравенств

Таким образом, можно сформулировать общую схему решения показательных неравенств:

1)                      Свести к простейшему показательному неравенству: .

2)                      Решить полученное неравенство по следующему правилу:

То есть, если основание больше 1, то мы сохраняем знак неравенства, а если основание меньше 1, то меняем знак неравенства на противоположный.

Рассмотрим несколько простых примеров.

Пример № 1.

 (знак неравенства не меняется, так как основание 2>1).

Пример № 2.

  (знак неравенства меняется на противоположный, так как основание 0<0,5<1).

 

Стоит отметить, что основные виды показательных неравенств совпадают с основными видами показательных уравнений. Однако решение неравенств, традиционно, несколько сложнее, так как требует, в частности, отслеживания значения основания.

Основные виды показательных неравенств

Основные виды показательных неравенств:

1)   Простейшие ().

2)   Сводящиеся к простейшим с помощью использования свойств степени ().

3)   С вынесением общей степени ().

4)   Сводящиеся к квадратным ().

5)    Однородные ().

Системы показательных уравнений

Системы показательных уравнений можно разделить на несколько типов. 

1)      Самые простые – это системы, в которых оба уравнения сводятся к простейшим. В дальнейшем получается обычная система из двух уравнений с двумя неизвестными, которая решается любым из удобных методов.

Пример такой системы: .

2)      Ещё один важный тип систем показательных уравнений – это системы, которые сводятся к обычным с помощью замены.

Пример такой системы: .

3)      Также существуют системы показательных уравнений, которые решаются различными методами. К ним относятся, к примеру, такие системы: .

Более подробно о решении систем показательных уравнений мы поговорим в практической части урока.

Системы показательных неравенств

Системы показательных неравенств преимущественно решаются стандартным методом.  

Каждое из неравенств решается по отдельности (методы решения показательных неравенств мы подробнее обсудим в практической части урока), а затем находится пересечение полученных множеств решений каждого из неравенств.

Пример системы показательных неравенств: .

На этом уроке мы с вами изучили метод решения простейших показательных неравенств, рассмотрели основные виды показательных неравенств, систем показательных уравнений и неравенств.

В практической части урока мы подробно разберём основные методы решения показательных неравенств, а также систем показательных уравнений и неравенств.

 

Вставка 1. Решение системы неравенств

 

Давайте вспомним – как же решать системы неравенств. Речь пойдёт не о специфических системах (показательных, иррациональных или каких-то других), а о последнем шаге решения таких примеров.

Напомним, что подавляющее большинство таких систем разбиваются на решение нескольких отдельных неравенств. В результате получается несколько различных множеств решений каждого из неравенств. Для получения окончательного ответа необходимо найти пересечение полученных множеств.

Об этой части решения мы и поговорим.

Если у вас есть определённая практика и «набита рука» на решение подобных задач, то найти пересечение числовых множеств можно и «в уме». Однако, если уверенности в правильности выводов нет или множества получаются слишком громоздкими, то лучше воспользоваться проверенным средством – изображением этих множеств на числовой прямой.

 

Давайте вспомним, как это делается, на простых примерах.

 

Пример № 1. Найти решение системы неравенств: .

Решение: изобразим решение каждого из неравенств на числовой прямой. Для этого вспомним основные правила:

1)      Если неравенство строгое (<,>), то соответствующая точка на числовой прямой «выкалывается», а если нестрогое (), то нет.

2)      Если знак неравенства «меньше» или «меньше или равно» (<,), то штрихуется промежуток слева от точки, а если «больше» или «больше или равно» (>,), то – справа.

3)      Решение каждого из неравенств штрихуется по-разному, чтобы впоследствии можно было найти пересечение и выписать окончательный ответ.

Для данной системы неравенств решение будет выглядеть так:

Ответ:

.

 

Пример № 2. Найти решение системы неравенств: .

Решение: изобразим решение каждого из неравенств на числовой прямой.

Для данной системы неравенств решение будет выглядеть так:

Ответ:.

 

Пример № 3. Найти решение системы неравенств: .

Решение: изобразим решение каждого из неравенств на числовой прямой.

Для данной системы неравенств решение будет выглядеть так:

 

Ответ: решений нет.

 

Пример № 4. Найти решение системы: .

Решение: изобразим каждое из множеств на числовой прямой.

Для данной системы пересечение множеств будет следующим:

Ответ:.

 

Полезные ссылки:

1) Алгебра 11 класс: «Показательная функция, ее свойства и простейшие показательные неравенства» 

2) Алгебра 11 класс: «Показательные неравенства» 

3) Алгебра 11 класс: «Показательные неравенства. Более сложные случаи» 

4) Алгебра 11 класс: «Показательно-степенные неравенства» 

Источник Редактор InternetUrok.ru

astroway.info

Основные типы показательных неравенств | Подготовка к ЕГЭ по математике

Сегодня решаем показательные неравенства.

Рассмотрим основные типы  показательных неравенств.

При решении показательных неравенств мы будем использовать следующие переходы:

и

Поясним, первый переход возникает в силу возрастания  показательной функции , второй – в силу убывания функции .

 

Показательные неравенства, сводящиеся к простейшим

Задание 1.

Решить неравенство .

Решение:

Перепишем неравенство следующим образом:

А далее вот так:

Так как – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:

Ответ: .

Задание 2.

Решить неравенство:

Решение:

Перепишем неравенство следующим образом:

Заметим, что  .

В силу того, что основание степени () меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак на ):

Ответ:

 Однородные показательные неравенства 

Задание 3.

Решить неравенство:

Решение:

Вынесем за скобку

Тогда  переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):

Ответ:

Показательные неравенства, сводящиеся к квадратным

Задание 4.

Решить неравенство

Решение:

Разделим обе части неравенства на 3:

Мы видим квадратное неравенство относительно которое будем решать методом интервалов.

Имеем:

или

или 

Ответ:

Задание 5.

Решить неравенство

Решение:

Мы видим квадратное неравенство относительно , которое будем решать методом интервалов.

Находим при помощи дискриминанта корни квадратного трехчлена . Переходим к следующему неравенству:

Получаем: или . Заметьте, нет смысла указывать, что  , так как по определению положительно.

Итак,

Ответ:

Задание 6.

Решить неравенство

Решение:

Разделим обе части неравенства на (можно и на , – как хотите…). Заметим, .

Заметим, что . Аналогично с .

Мы имеем квадратное неравенство относительно

которое будем решать методом интервалов.

Воспользуемся следующим способом превращения суммы в произведение:

где – корни уравнения (в случае неотрицательного дискриминанта квадратного трехчлена).

Заготавливаем шаблончик  и находим корни при помощи дискриминанта, тогда

То есть

Ответ:

Задание 7.

Решить неравенство

Решение:

Перепишем неравенство следующим образом:

Домножим обе части неравенства на   (заметим, ):

Ответ:

Показательные неравенства, сводящиеся к рациональным

Задание 8.

Решить неравенство:  

Решение:

Переносим все в левую сторону неравенства и приводим к общему знаменателю:

Мы можем “отбросить” сумму в силу ее положительности:

Неравенство равносильно следующему:

Ответ:

Неравенства, решаемые графическим методом

Задание 9.

Решить неравенство:

 Решение:

Рассмотрим функции и Обе они определены на . Первая – возрастает, вторая – убывает. Значит, уравнение имеет не более одного решения. Несложно заметить, что является корнем указанного уравнения.

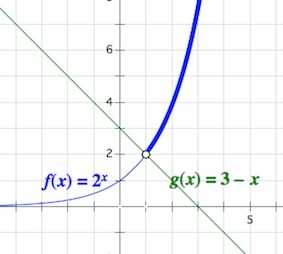
А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения,  мы должны взять те значения , которые отвечают за ту часть графика , что лежит выше графика , то есть .

Ответ:

Для самостоятельной работы:

Решить неравенства:

1.

Ответ: + показать

2.

Ответ: + показать

3.

Ответ: + показать

4.

Ответ: + показать

{-2}

5.

Ответ: + показать

6.

Ответ: + показать

7.

Ответ: + показать

(-1;1]

8.

Ответ: + показать

.

 

 

egemaximum.ru

Решение показательных неравенств

Решение показательных неравенств.

В этой статье, как вы догадались, речь пойдет о решении показательных неравенств. Простейшее показательное неравенство имеет вид:

 V , где  V — один из знаков: <,>,≤, или ≥.

Чтобы решить  показательное неравенство, нам нужно от сравнения степеней перейти к сравнению показателей.

Как мы помним, показательная функция  возрастает при всех действительных значениях , если .  Это значит, что большему значению аргумента соответствует большее значение функции. То есть из неравенства

следует неравенство 

Аналогично, так как показательная функция убывает, если ,  и большему значению аргумента соответствует меньшее значение функции, из  неравенства

следует неравенство 

То есть при решении простейших показательных неравенств прежде чем сравнивать выражения, стоящие в показателе степени, нужно сравнить с единицей основание степеней.

Ещё раз, это важно:

если основание степени больше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства сохраняется

если основание степени больше нуля, но меньше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный.

Все показательные неравенства любого уровня сложности, в конечном итоге, сводятся к решению простейших показательных неравенств.

Рассмотрим несколько примеров.

1. Решим неравенство:

Так как основание степеней , при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный:

Перенесем все влево, и приведем к общему знаменателю:

Корни числителя:

,   

Решим неравенство методом интервалов: нанесем корни числителя и знаменателя на числовую ось и расставим знаки:

Ответ:  ,  ,  

2. Решим неравенство:

Перенесем все слагаемые влево и разложим основания степеней на простые множители:

Если бы это было уравнение, мы решали бы его с помощью замены переменной. Поступим также.

Вообще, показательные неравенства делятся на те же типы, что и показательные уравнения, и решаются теми же способами.

Внимание! Если мы решаем неравенство с помошью замены переменных, то нужно решать  относительно замены до получения простейшего неравенства. Поясню  на этом примере.

Введем замену: , 

Получим систему неравенств:

Отсюда:

То есть 

Запишем двойное неравенство в виде системы:

Вот теперь мы можем вернуться к исходной переменной:

Отсюда: ,  

Ответ: 

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

8. Общее повторение курса математики. Подготовка к экзаменам ⋆ Social AstroWay- Развлекательно-информационный портал

В практической части урока мы разберём различные примеры на решение систем показательных уравнений, основных типов показательных неравенств и их систем..

 

Подготовка к ЕГЭ по математике

Эксперимент

Урок 1. Повторение. Показательная функция. Показательные уравнения

Практика

Простейшие показательные неравенства

Конспект урока

Пример №1. Решить неравенство:

Правило: привести к одинаковому основанию.

Так как основание больше 1, знак неравенства не меняется

Ответ:

 

Пример №2. Решить неравенство:

Так как основание больше 1, знак неравенства не меняется

Ответ:

Пример №3. Решить неравенство:

Так как основание меньше 1, знак неравенства меняется

Ответ:

 

Пример №4. Решить неравенство:

Вспоминаем свойства показательной функции: , значит,  Данное неравенство не имеет решений.

 

Пример №5. Решить неравенство:

По аналогии с предыдущим неравенством:  (а, значит, ) для всех  из области определения, то есть .

Показательные неравенства, которые сводятся к простейшим

Пример №1.

Так как основание меньше 1, знак неравенства меняется

Ответ:

Пример №2. Решите неравенство

Рассмотрим решение данного неравенства двумя способами.

1 способ:

Приведем обе части неравенства к основанию 2:

Так как основание больше 1, знак неравенства не меняется

 

2 способ:

Приведем обе части неравенства к основанию :

Так как основание меньше 1, знак неравенства меняется

Ответ:

 

Пример №3. Решите неравенство

Подсказка: чтобы не ошибиться, лучше приводить обе части неравенства к основанию больше 1, так как в этом случае нет риска забыть о смене знака неравенства.

Вспомним, что:

Поэтому:

Так как основание больше 1, знак неравенства не меняется

Ответ:

 

Пример №4. Решите неравенство

Приведем обе части неравенства к основанию 2:

Так как основание больше 1, знак неравенства не меняется

Ответ:

Показательные неравенства, которые решаются с помощью вынесения общего множителя

С вынесением общей степени

 

Пример №1.  Решите неравенство

Так как основание больше 1, знак неравенства не меняется

Ответ:

Показательное неравенство, которое решается с помощью замены

Сводящиеся к квадратным

Пример №1.  Решите неравенство:

Замена:

Обратная замена:

Ответ:

 

Пример №2. Решите неравенство:

Замена:

Обратная замена:

Ответ:

 

Пример №3. Решите неравенство:

Замена:

 

Обратная замена:

Левое неравенство, как мы помним, выполняется всегда.

Ответ:

Однородные показательные неравенства

Однородные

Пример №1. Решите неравенство:

Замена:

 

Обратная замена:

Ответ:

Системы показательных уравнений

Системы показательных уравнений

Пример №1. Решите систему уравнений:

«Решаем» каждое из уравнений по отдельности, приводя к обычной линейной системе.

1)     

2)     

Получаем систему:

Ответ:

 

Пример №2. Решите систему уравнений:

1)      Перемножим оба уравнения:

2)      Поделим второе уравнение на первое:

Получаем систему:

Ответ:

 

Пример №3. Решите систему уравнений:

Замена:

—

Обратная замена:

Ответ:

 

Пример №4.

Замена:

Рассмотрим решение данной системы двумя способами:

1 способ:

Обратная замена:

2 способ:

Обратная замена:

Ответ:

Системы показательных неравенств

Пример №1.

Правило: решаем каждое из неравенств по отдельности.

1)     

Замена:

Обратная замена:

2)     

3)     

Ответ: решений нет.

Источник Редактор InternetUrok.ru

astroway.info