ДВИ МГУ 18.07.2018 (задания 1-4)
ДВИ МГУ 18.07.2018 (задания 1-4)
1. Какое из чисел и ближе к 2?
Решение. показать
2. Найдите все значения параметра , при которых разность между корнями уравнения максимальна.
Решение. показать
Разность между корнями квадратного уравнения можно понимать как расстояние между ними на числовой прямой.
То есть нам нужно найти, при каком значении параметра расстояние между корнями квадратного уравнения максимально.
Расстояние между корнями квадратного уравнения равно .
Для нашего уравнения
Рассмотрим функцию и исследуем ее на максимум — минимум.
Приравняем производную к нулю и исследуем знаки:
;
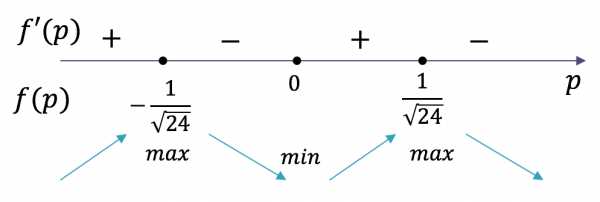
Мы видим, что функция имеет максимум при .
Ответ: .
3. Решите уравнение
Решение. показать
Применим формулу преобразования произведения косинусов в сумму:
Получим:
Отсюда получаем:
или
или
или , .
Ответ:
4. Решите неравенство
Решение. показать
Заметим, что неравенство содержит сопряженные выражения: и .
В этом случае, воспользовавшись формулой разности квадратов, можно одно выражение выразить через другое:
, отсюда
Тогда получим:
Так как , при переходе к сравнению показателей знак неравенства сохраняется. Получаем:
Переносим все слагаемые влево и приводим к общему знаменателю.
Легко проверить, что , отсюда . Умножим обе части неравенства на это выражение, не забыв изменить знак неравенства:
Введем замену:
Получим неравенство относительно переменной :
Корни числителя:
Корень знаменателя: .
Нанесем корни на числовую ось и расставим знаки:
Отсюда или .
Вернемся к исходной переменной:
;
или
Ответ: U
И.В. Фельдман, репетитор по математике
ege-ok.ru
ДВИ МГУ 18.07.2018 (задание 7, стереометрия)
7. Дан прямоугольный параллелепипед с боковыми ребрами . На ребрах нижнего основания отмечены соответсвенно точки , таким образом, что ,, ,. Пусть — центры сфер, описанных около тетраэдров , соответственно. Найдите , если известно, что и .
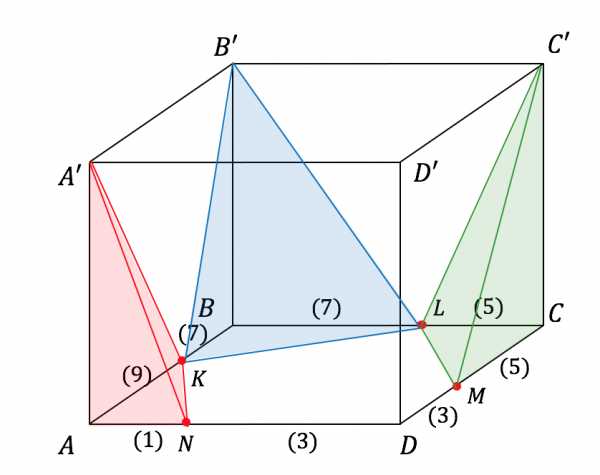
Центр сферы, описанной около тетраэдра равноудален от его вершин. То есть центр сферы лежит на пересечении серединных перпендикулярах к ребрам тетраэдра. Тетраэдры содержат боковые ребра параллелепипеда , серединные перпендикуляры к боковым ребрам параллелепипеда лежат в плоскости, перпендикулярной боковым ребрам. Поэтому центры сфер, описанных около этих тетраэдров лежат в плоскости, которая перпендикулярна боковым ребрам параллелепипеда и проходит через середины этих ребер. То есть в плоскости, параллельной основаниям параллелепипеда.
Кроме того, центр сферы, описанной около тетраэдра, лежит на прямой, которая перпендикулярна грани тетраэдра и проходит через центр окружности, описанной около этой грани.
Рассмотрим тетраэдр . Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы этого треугольника, то есть в середине отрезка . Пусть это точка . Центр сферы, описанной около тетраэдра лежит на прямой, перпендикулярной плоскости , проходящей через точку . И одновременно на серединном перпендикуляре к ребру :
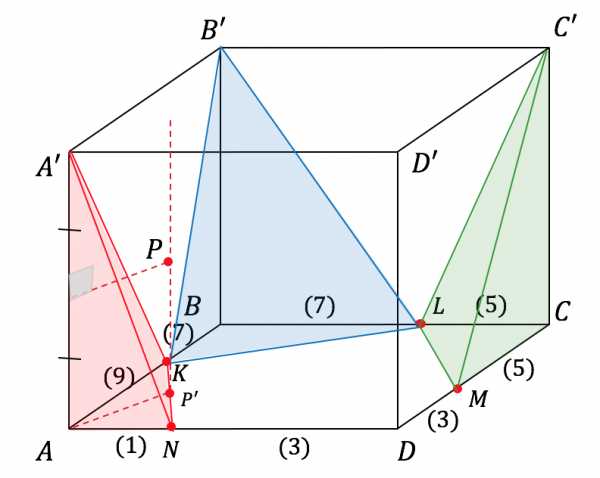
Аналогично построим точки — центры сфер, описанных около тетраэдров :
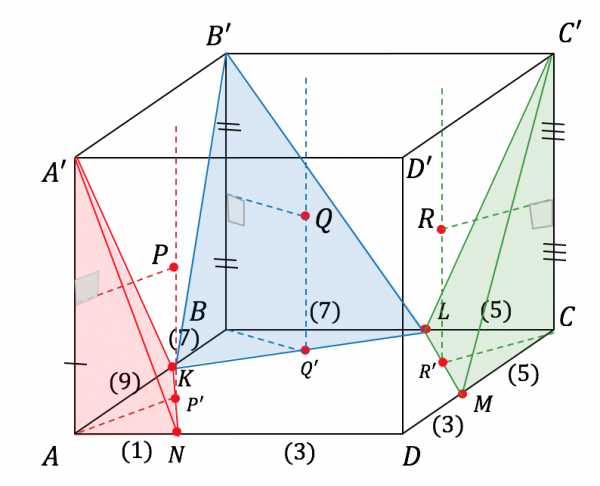
Точки — проекции точек соответственно на плоскость .
Точка — середина отрезка , точка — середина отрезка .Поскольку плоскость, проходящая через точки параллельна плоскости , расстояния между точками равно расстоянию между точками соответственно.
По условию . Пусть , .
Сделаем выносной чертеж:
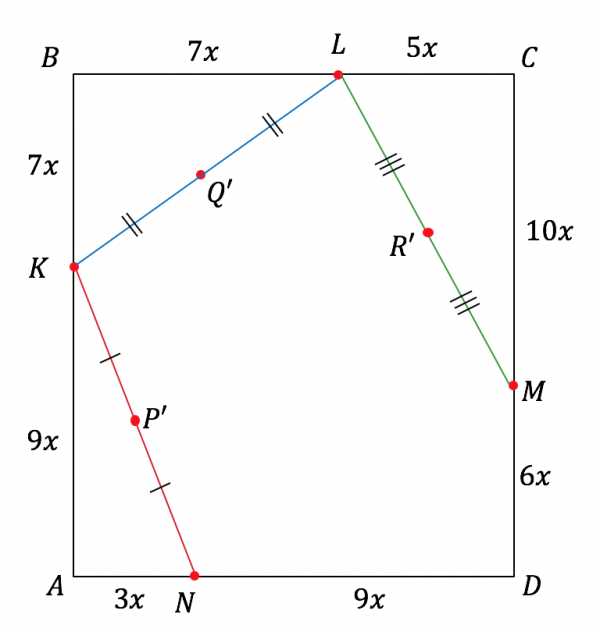
Расстояние между точками и по условию равно 1. Введем систему координат с началом в точке и найдем расстояние между точками и . 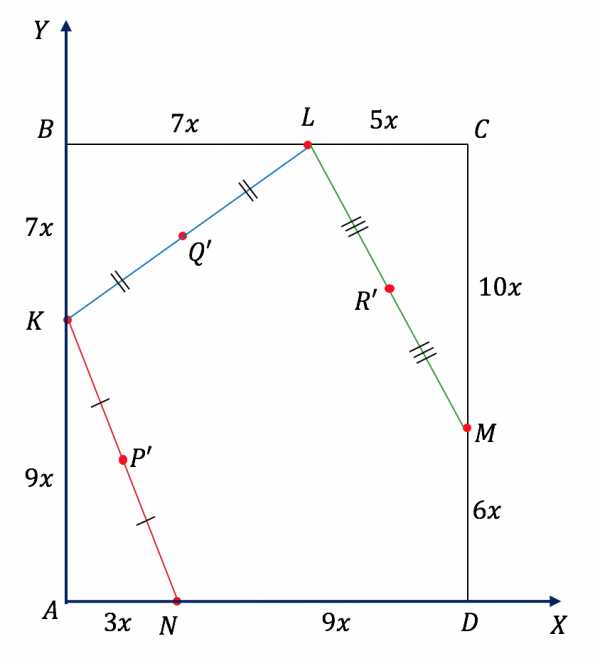
Координаты точек:
; ; .
Координаты векторов:
;
; Отсюда ,
Ответ:
ege-ok.ru
ДВИ МГУ 18.07.2018 (задание 5, планиметрия)
5. Дана трапеция с основаниями и . Пусть — середина отрезка , а — произвольная точка отрезка . Пусть — пересечение отрезков и , а — пересечение отрезков и . Найдите все возможные значения площади треугольника , если известно, что , а площадь треугольника равна .
ege-ok.ru
ДВИ МГУ 18.07.2018 (задание 6, параметры)
ДВИ МГУ 18.07.2018 (задание 6, параметры).
6. Найдите все значения параметра , при которых система
имеет ровно одно решение.
Если у условии задачи требуется найти, при каких значениях параметра система имеет ровно одно решение, то, скорее всего, здесь требуется найти инвариант, то есть некие два выражения, такие, что при замене одного выражения на другое система не изменится.
Преобразуем неравенства системы. В левой части каждого неравенства выделим полный квадрат.
Теперь система принимает такой вид:
Ведем замену переменной:
Тогда
Относительно новых переменных система примет такой вид:
Теперь мы видим, что если в систем заменить на , то система не изменится. Это значит, что если пара является решение системы, то пара также будет ее решением.
Значит, чтобы система имела единственное решение должно выполняться равенство .
Заменим в системе на и получим систему, состоящую из двух одинаковых неравенств:
Теперь найдем, при каких значениях параметра эта система имеет единственное решение. То есть нам надо найти, при каких значениях параметра неравенство имеет единственное решение. Это неравенство имеет единственное решение, если ветви параболы направлены вниз и дискриминант квадратного трехчлена в левой части неравенства равен нулю:
;
Отсюда или . Учитывая условие , остается значение .
Мы нашли это значение параметра исходя из условия, что . Осталось проверить, что при этом значении исходная система имеет единственное решение. Подставим в систему .
Получим:
Разделим оба неравенства на :
Сложим неравенства системы:
Сгруппируем и выделим полный квадрат:
Это неравенство имеет единственное решение, если .
Следовательно, при исходная система имеет единственное решение.
Ответ:
ege-ok.ru
Экзамены для специалистов | Приёмная комиссия мехмата МГУ
С 2008 года при поступлении на мехмат учитываются результаты Единого государственного экзамена (ЕГЭ). Кроме того, поступающие проходят дополнительное вступительное испытание (ДВИ) по математике.
В 2018 году, прием проводится по результатам вступительных испытаний в форме ЕГЭ, подтвержденным свидетельствами о ЕГЭ, выданными в 2014, 2015, 2016, 2017 и 2018 годах. В качестве вступительных экзаменов на оба отделения (математики и механики) принимаются результаты ЕГЭ по следующим предметам:
-
математика,
-
физика,
-
русский язык.
С 2010 года ДВИ проводится только в письменной форме. В 2018 году ДВИ по математике в МГУ проводится централизованно для абитуриентов всех факультетов, которым необходимо сдавать этот экзамен, и засчитывается на все соответствующие специальности, на которые абитуриент подает документы. Дата проведения экзамена – 18 июля 2018 года. Более подробная информация о сроках проведения вступительных испытаний в МГУ имени М.В.Ломоносова для поступающих на обучение по программам подготовки специалиста в 2018 году опубликована на сайте ЦПК.
Консультация по математике состоится 17 июля в 16:00.
В случае, если у Вас не сдан ЕГЭ по какому-либо из необходимых предметов, в МГУ имени М. В. Ломоносова предусмотрены вступительные испытания вместо ЕГЭ для следующих категорий граждан: лица, получившие документ о среднем общем образовании в течение 1 года до дня завершения приема документов и вступительных испытаний включительно, прошедшие государственную итоговую аттестацию по образовательным программам среднего общего образования не в форме ЕГЭ (в том числе лица, прошедшие итоговые аттестационные процедуры в иностранных образовательных организациях) или прошедшие государственную итоговую аттестацию по отдельным общеобразовательным предметам в форме государственного выпускного экзамена и не сдававшие ЕГЭ по соответствующим общеобразовательным предметам.
Экзамены вместо ЕГЭ проводятся в следующие сроки:
11 июля — математика (вместо ЕГЭ)
15 июля — русский язык (вместо ЕГЭ)
16 июля — физика (вместо ЕГЭ)
Наряду с бюджетной формой обучения на механико-математическом факультете существует контрактная форма обучения. Вступительные испытания для поступающих на платной основе проводятся одновременно с основным потоком.
Программу экзамена по математике, а также варианты письменного экзамена прошлых лет вы найдете в разделе Варианты вступительных экзаменов.
pk.math.msu.ru
Дополнительное вступительное испытание (ДВИ) по математике
ДВИ по математике проводится одновременно для ВСЕХ факультетов, где этот экзамен присутствует в списке вступительных испытаний. Этот экзамен проводится по единым заданиям. Работы проверяются в зашифрованном виде и оцениваются по единым критериям. Абитуриент пишет экзамен один раз. Результаты экзамена автоматически засчитываются везде, где абитуриент участвует в конкурсе.
Расписание экзаменов будет опубликовано на сайте Центральной приемной комиссии в июне 2019 г.
Минимальный балл за ДВИ для направления Экономика в 2019 году = 50 баллам, для направления Менеджмент минимальный балл за ДВИ не установлен (достаточно получить положительный балл).
Экзамен письменный, несмотря на то, что в программе есть устная часть.
Программа ДВИ по математике
Структура экзамена (темы, количество заданий) до начала экзамена неизвестна. Критерии оценки работ до публикации результатов неизвестны. Экзамен оценивается в 100-балльной шкале.
Продолжительность экзамена 4 астрономических часа.
Задания прошлых лет можно найти на сайте мехмата или на сайте Центральной приемной комиссии
Что такое «базовый факультет»:
Понятие «базовый факультет» введено для того, чтобы абитуриент знал, какой факультет отвечает за организацию ДВИ для этого абитуриента. Абитуриент может подать документы в МГУ для участия в трех конкурсах, и везде может в качестве экзамена присутствовать ДВИ по математике, поскольку ДВИ по математике является вступительным испытанием на многих факультетах МГУ.
Базовым становится тот факультет, на который абитуриент подал документы в первую очередь. Базовый факультет — это факультет, который отвечает за организацию экзамена для данного абитуриента и проводит для этого абитуриента показ работ, это не обязательно факультет, который абитуриент считает для себя приоритетным.
Правила подачи и рассмотрения апелляций
В целях обеспечения безопасности проведения экзаменов абитуриенты допускаются в аудитории только с ручками, паспортом, пропуском на экзамен, распиской о подаче документов и минеральной водой без газа.
С вещами (сумки, рюкзаки и пр.) абитуриенты в аудиторию не допускаются. все вещи надо оставлять в гардеробе. приносить в аудиторию мобильные телефоны и прочие средства связи, даже в выключенном состоянии, а также шпаргалки и свою бумагу строго запрещено
www.econ.msu.ru
МГУ ДВИ 2017 по математике
Вступительное испытание
по математике в МГУ 2018 года
Июль 2018 г
- Какое из чисел и ближе к ?
- Найдите все значения параметра , при которых разность между корнями уравнения максимальна.
- Решите уравнение
- Решите неравенство
- Дана трапеция с основаниями и . Пусть — середина отрезка , а — произвольная точка отрезка . Пусть — пересечение отрезков и , а — пересечение отрезков и . Найдите все возможные значения площади треугольника , если известно, что , а площадь треугольника равна 4.
- Найдите все значения параметра , при которых система имеет ровно одно решение.
- Дан прямоугольный параллелепипед ABCDA1B1C1D1 с боковыми ребрами AA1, BB1, CC1, DD1. На ребрах AB, BC, CD, DA нижнего основания отмечены соответственно точки K, L, M, N таким образом, что AK:KB = 4:5, BL:LC = 3:1, CM:MD = 7:2, DN:NA = 3:1. Пусть P, Q, R — центры сфер, описанных около тетраэдров AKNA1, BLKB1, CMLC1 соответственно. Найдите PQ, если QR = 1 и AB:BC = 3:2.
- Найдите все пары чисел из промежутка , при которых достигается минимум выражения
Ответы
смотрите еще Вступительные экзамены и МГУ. Дополнительное вступительное испытание 2013
Метки МГУ. Смотреть запись.
www.itmathrepetitor.ru
