Задачи с решениями и ответы к упражнениям
Задачи с решениями и ответы к упражнениям
Страница 103 : 1 » « 187Как связаны ускорение и координата при гармонических колебанияхКак связаны циклическая частота колебаний и период колебанийПочему частота колебаний тела, прикрепленного к пружине, зависит от его массы, а частота колебаний математического маятника от массы не зависитКаковы амплитуды и периоды трех различных гармонических колебаний, графики которых представлены на рисунках 3.8, 3.9Два маятника представляют собой шарики одинакового радиуса, подвешенные на нитях равной длины. Массы шариков различны. Колебания какого из маятников прекратятся быстрее: легкого или тяжелогоПриходилось ли вам наблюдать явление резонанса дома или на улицеДля того чтобы удержать открытую дверь в вестибюле метро, дверь открывается в обе стороны и возвращается в положение равновесия пружинами, нужно приложить к ручке двери силу около 50 Н. Можно ли открыть дверь, приложив к ручке силу 0,005 Н? Трением в петлях двери пренебречь.При каком условии резонансные свойства колебательной системы проявляются отчетливоСколько колебаний совершает математический маятник длиной l = 4,9 м за время t = 5 минВертикально подвешенная пружина растягивается прикрепленным к ней грузом на l=0,8 см. Чему равен период Т свободных колебаний груза? Массой пружины пренебречь.На горизонтальном стержне находится груз, прикрепленный к пружине. Другой конец пружины закреплен. В некоторый момент времени груз смещают от положения равновесия на xm = 10 см и отпускают. Определите координату груза спустя 1/8 периода колебаний. Трение не учитывать.Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Определите отношение кинетической энергии груза к потенциальной энергии системы в момент, когда груз находится в точке, расположенной посредине между крайним положением и положением равновесия.Груз массой 100 г совершает колебания с частотой 2 Гц под действием пружины. Определите жесткость пружины.В Санкт-Петербурге в Исаакиевском соборе висел маятник Фуко, длина которого была равна 98 м. Чему был равен период колебаний маятника?Шарик на пружине сместили на расстояние 1 см от положения равновесия и отпустили. Какой путь пройдет шарик за 2 c, если частота его колебаний v = 5 Гц? Затуханием колебаний можно пренебречь.Тело массой 200 г совершает колебания в горизонтальной плоскости с амплитудой 2 см под действием пружины жесткостью 16 Н/м. Определите циклическую частоту колебаний тела и энергию системы.Автомобиль движется по неровной дороге, на которой расстояние между буграми приблизительно равно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 c. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?Что называют электромагнитными колебаниямиВ чем различие между свободными и вынужденными электромагнитными колебаниямиЧему равна энергия контура в произвольный момент времениПочему при подключении конденсатора к катушке он разряжается постепенноВ чем проявляется аналогия между электромагнитными колебаниями в контуре и колебаниями пружинного маятника?За счет какого явления электрический ток в колебательном контуре не исчезает сразу, когда напряжение на конденсаторе становится равным нулю?В чем различие между свободными и вынужденными электрическими колебаниямиКак изменится период свободных электрических колебаний в контуре, если емкость конденсатора в нем вдвое увеличить или же вдвое уменьшитьКак связаны амплитуды колебаний заряда и тока при разрядке конденсатора через катушкуПри каких условиях в электрической цепи возникают вынужденные электромагнитные колебанияОдинаково ли мгновенное значение силы переменного тока в данный момент времени во всех участках неразветвленной цепиЧему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 ВЧто называют действующими значениями силы тока и напряженияКак связаны между собой действующие значения силы тока и напряжения на конденсаторе в цепи переменного токаВыделяется ли энергия в цепи, содержащей только конденсатор, если активным сопротивлением цепи можно пренебречьВыключатель цепи представляет собой своего рода конденсатор. Почему же выключатель надежно размыкает цепьКак связаны между собой действующие значения силы тока и напряжения на катушке индуктивности, активным сопротивлением которой можно пренебречьПочему ЭДС самоиндукции и напряжение на катушке имеют противоположные знакиfamiredo.ru
Физика. Мякишев, Буховцев, Чаругин. Задача № 23.2
- Физика. Мякишев, Буховцев, Чаругин.
- Механические колебания
- 23.2
Условие задачи 23.2:
Как связаны ускорение и координата при гармонических колебаниях
Решение задачи:
СДЕЛАЙТЕ РЕПОСТ
Решение задачи 23.2
Предыдущая задача:
23.1 Как связаны ускорение и координата при гармонических колебанияхСледующая задача:
23.3 Как связаны ускорение и координата при гармонических колебаниях С другими задачами из решебника по физике Мякишев, Буховцев, Чаругин 11 класс вы можете ознакомиться в соответствующем разделе решебника Физика. Мякишев, Буховцев, Чаругин. studassistent.ru23 Вопрос
Сила Кориолиса равна:
,
где — точечнаямасса,—векторугловой скоростивращающейся системы отсчёта,— вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операциявекторного произведения.
Величина называется кориолисовым ускорением.
24 вопрос
По физической природе
Механические
Электромагнитные(свет,радиоволны, тепловые)
Смешанного типа— комбинации вышеперечисленных
По характеру взаимодействия с окружающей средой
Вынужденные— колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явлениерезонанса: резкое возрастание амплитуды колебаний при совпадениисобственной частотыосциллятораи частоты внешнего воздействия.
Свободные (или собственные)— это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегдазатухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Автоколебания — колебания, при которых система имеет запаспотенциальной энергии, расходующейся на совершение колебаний (пример такой системы —механические часы). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.
Параметрические— колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Случайные— колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
Гармонические колебания— колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х— смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t;
Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное[1]решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой)
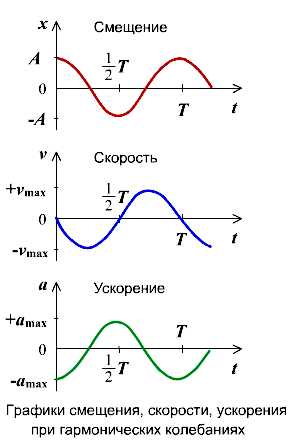
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.
Величина — максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при гармоническом колебании имеем: ,
а для случая нулевой начальной фазы (см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:
—
вторая производная от координаты по времени. Тогда: .
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе).
Величина
— максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,
а для случая нулевой начальной фазы: (см. график).
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
25 вопрос
Гармонические колебания— колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х— смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t;А— амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия;ω— циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;— полная фаза колебаний,— начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное[1]решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой)
26 вопрос
studfiles.net
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ |
||
|
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
|
|
|
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
|
|
|
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. |
||
|
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
|
|
|
Скорость и ускорение при гармонических колебаниях. |
||
|
Согласно определению скорости, скорость – это производная от координаты по времени |
|
|
|
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
|
|
|
Величина — максимальная скорость колебательного движения (амплитуда колебаний скорости). |
|
|
|
Следовательно, для скорости при гармоническом колебании имеем: , а для случая нулевой начальной фазы (см. график). |
||
|
Согласно определению ускорения, ускорение – это производная от скорости по времени: — вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). |
||
|
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы: (см. график). |
||
|
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). |
||
|
Сравним выражения для смещения и ускорения при гармонических колебаниях: и . |
|
|
|
Можно записать: — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
||
|
Часто бывает удобно записывать уравнения для колебаний в виде: , где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения. |
||
www.eduspb.com
Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

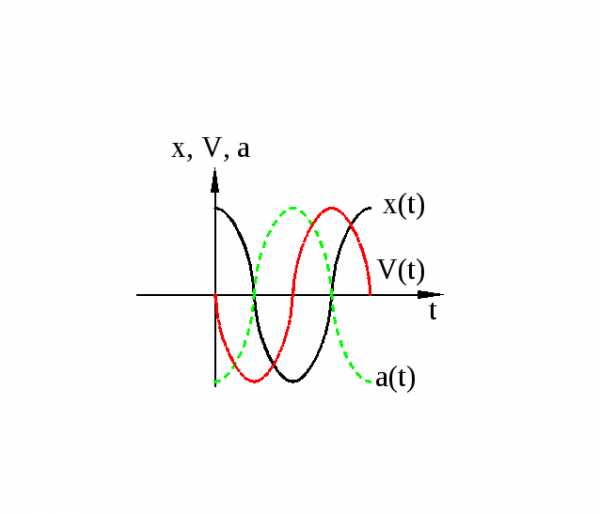
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
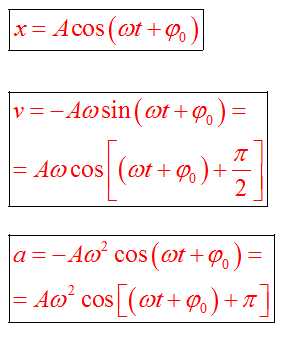
Если колебание описывать по закону синуса
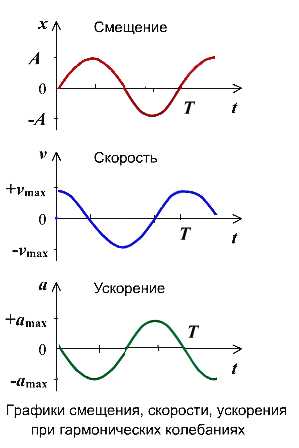
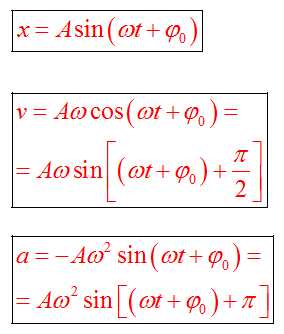
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Находим производную сложной функции.
fizmat.by
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса. Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Математический маятник
|
Колебания математического маятника. | |
|
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити (физическая модель). | |
|
Будем рассматривать движение маятника при условии, что угол отклонения мал, тогда, если измерять угол в радианах, справедливо утверждение: . | |
|
На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную, меняющую ускорение по величине, и нормальную, меняющую ускорение по направлению (центростремительное ускорение, тело движется по дуге). | |
|
Т.к. угол мал, то тангенциальная составляющая равна проекции силы тяжести на касательную к траектории: . Угол в радианах равен отношению длины дуги к радиусу (длине нити), а длина дуги приблизительно равна смещению (x ≈ s): . | |
|
Сравним полученное уравнение с уравнением колебательного движения . Видно, что или- циклическая частота при колебаниях математического маятника. | |
|
Период колебаний или(формула Галилея). |
Формула Галилея |
|
Важнейший вывод: период колебаний математического маятника не зависит от массы тела! |
|
|
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна , а полная механическая энергия равна максимальной потенциальной или кинетической: | |
|
Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: . Т.к. производная от постоянной величины равна нулю, то . Производная суммы равна сумме производных: и . |
|
|
Следовательно: , а значит. | |
|
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). | |
|
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул. |
|
|
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m. Мы знаем, что . Следовательно,. Учитывая, что, получим:. |
|
|
Произведение постоянных величин есть величина постоянная, следовательно: — универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). | |
|
Таким образом, имеем: — уравнение состояния (уравнение Менделеева – Клапейрона). | |
|
Другие формы записи уравнения состояния идеального газа. | |
|
1.Уравнение для 1 моля вещества. Если n=1 моль, то, обозначив объем одного моля Vм, получим: . Для нормальных условий получим: | |
|
2. Запись уравнения через плотность: — плотность зависит от температуры и давления! | |
|
3. Уравнение Клапейрона. Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: |
|
|
Эта запись означает, что для данной массы данного газа справедливо равенство: |
|
|
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: . | |
|
Газовые законы. | |
|
1. Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn; p1=p2=…=pn; T1=T2=…=Tn |
|
|
Доказательство:
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково. |
|
|
2. Закон Дальтона. Давление смеси газов равно сумме парциальных (частных) давлений каждого газа. Доказать: p=p1+p2+…+pn Доказательство: |
|
|
3. Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения. |
|
Уравнение состояния идеального газа. Газовые законы.
Числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения. В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.
При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул): В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы где i — сумма числа поступательных, числа вращательных в удвоенного числа колеба¬тельных степеней свободы молекулы:i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: (1) Внутренняя энергия для произвольной массы m газа. где М — молярная масса, ν — количество вещества.
studfiles.net
Скорость и ускорение при гармоническом колебании.
=
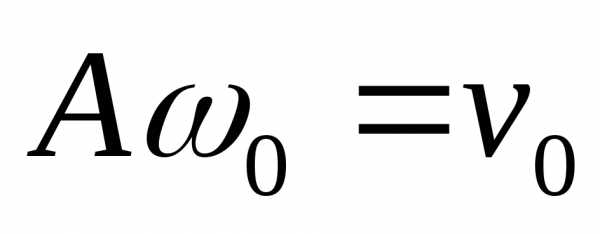 — амплитудное значение скорости
— амплитудное значение скорости
Скорость опережает смещение по фазе на
 .
.
=
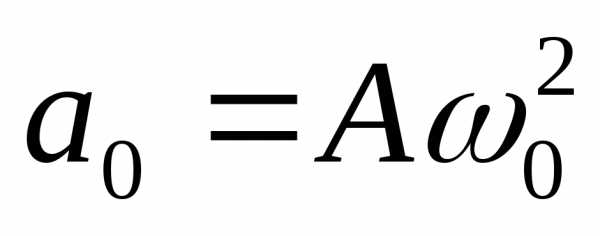
Сдвиг фаз между
 и
и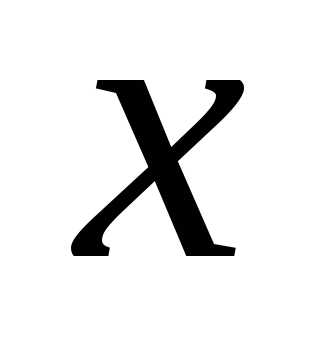 равен
равен ,
они колеблются в противофазах.
,
они колеблются в противофазах.
Сила.
Силы, которые подчиняются закону упругой силы, но по природе своей не являются упругими называются квазиупругими.
Гармонические колебания – это колебания, которые происходят под действием квазиупругой силы, то есть силы, пропорциональной смещению.
-
Энергия гармонического осциллятора.
(кинетическая Энергия, Т + потенциальная энергия, П = полной энергии, Е).
Пусть
.
Тогда
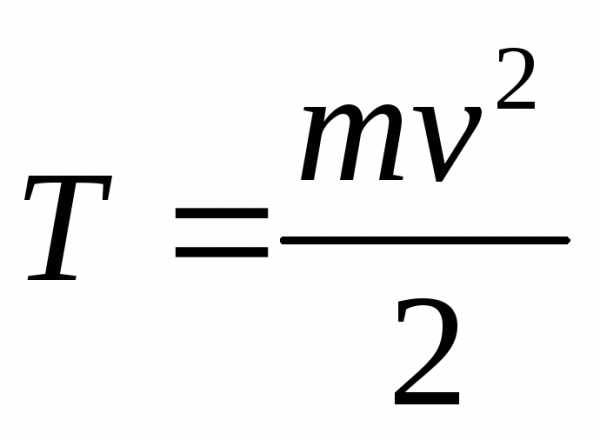 =
=
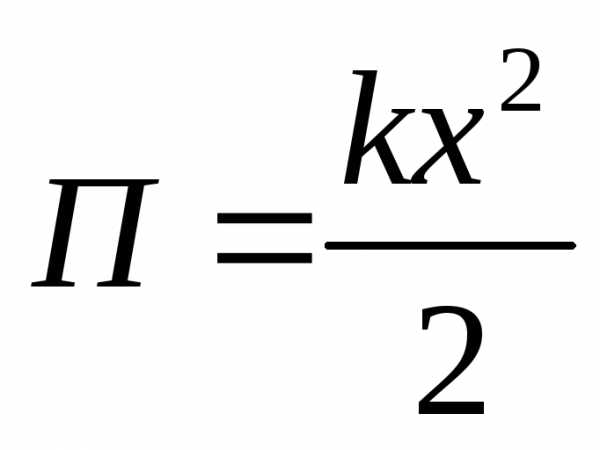 =
=
=+=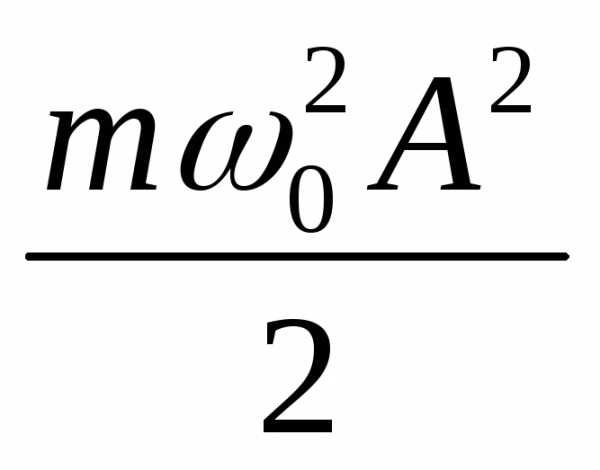 .
.
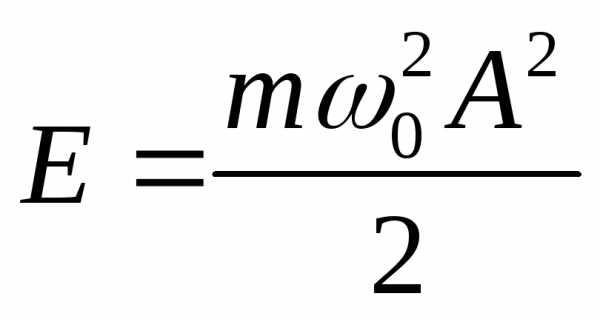
— полная энергия механического осциллятора
не зависит от
 и пропорциональна
и пропорциональна .
Механический осциллятор есть консервативная
система, так как.
.
Механический осциллятор есть консервативная
система, так как.
Выводы:
Кинетическая и потенциальная энергии по отдельности зависят от времени.
Максимальная кинетическая энергия равна максимальной потенциальной энергии и равна полной энергии.
Средняя кинетическая энергия равна средней потенциальной энергии и равна половине полной энергии.
Полная энергия не зависит от времени и пропорциональна квадрату амплитуды.
Лекция 8. Сложение колебаний.
Сложение колебаний – задача сложная и часто пользуются искусственными приемами для ее решения. Представим гармоническое колебание в виде вектора амплитуды.
В момент
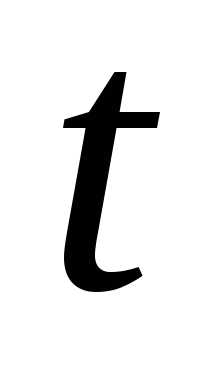 проекция на ось
проекция на ось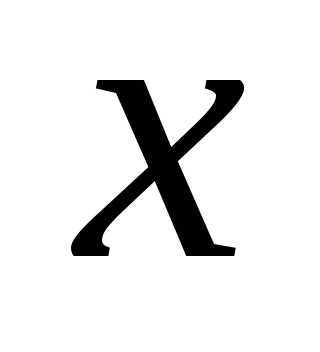 вектора
вектора равна.
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью
равна.
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью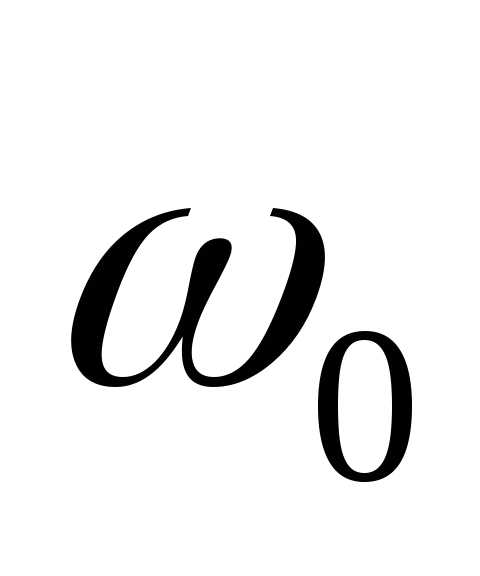 ,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось
,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
-
Сложение гармонических колебаний одного направления и одной частоты.
.
Изобразим их графически:
Векторы
 и
и вращаем с
вращаем с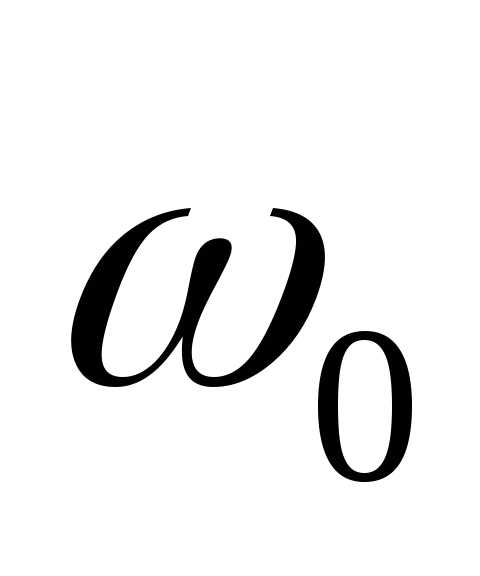 .
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина
.
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина не
меняется. Его проекция совершает
гармонические колебания.
не
меняется. Его проекция совершает
гармонические колебания.
, но.
То есть результирующее колебание гармоническое, имеет ту же частоту, что и слагаемые колебания. Амплитуду находим из начальных условий по формуле
,
-
Биения.
Рассмотрим сложение колебаний одинаковой
амплитуды и близких частот
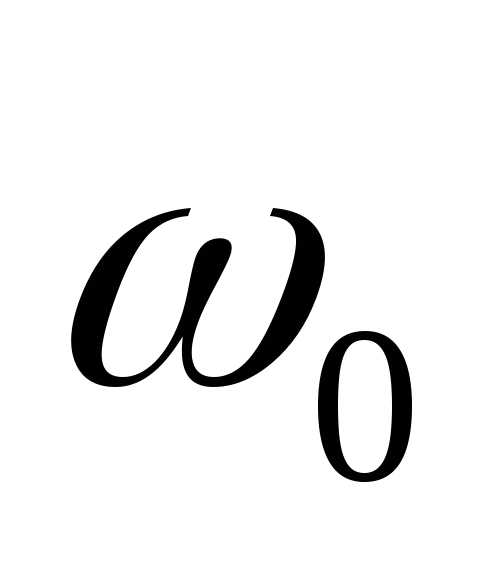 ,
,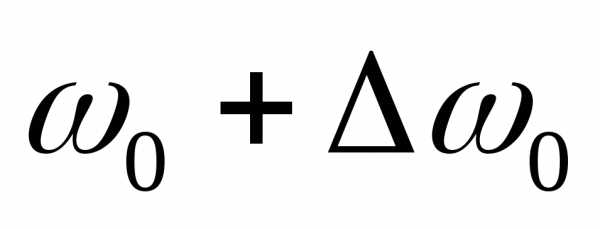 ,.
Решение задачи усложняется.
,.
Решение задачи усложняется.
.
Если изобразить эти колебания с помощью вектора амплитуды, то они вращаются с разными угловыми скоростями, и всегда будет момент, когда . Фазы в этот момент принимают за нуль. Тогда
.
=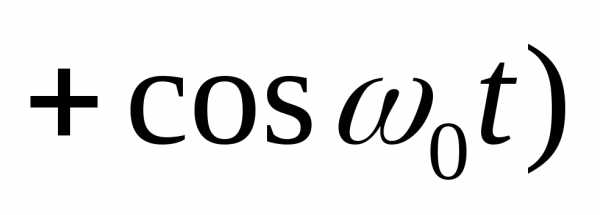 =
=
= .
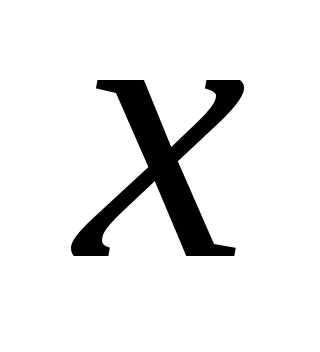 =
=
— уравнение биений. Первый множитель медленно меняется, второй – быстро. Уравнение можно представить в виде
Сравним с уравнением гармонических колебаний
.
Уравнение биений – негармоническое,
но
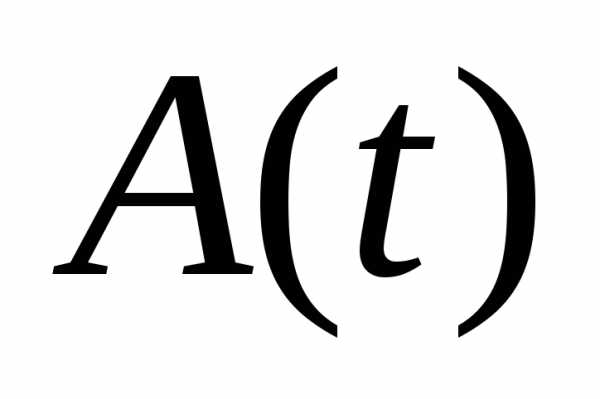 меняется медленно, так как
меняется медленно, так как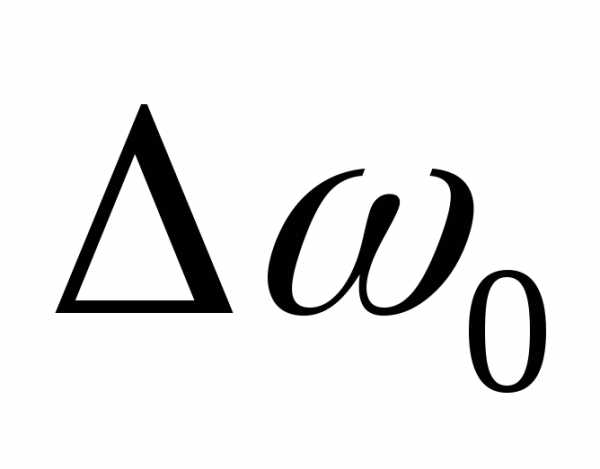 мало.
мало.
.
Поэтому биения – приблизительно
гармонические колебания с медленно
меняющейся амплитудой,
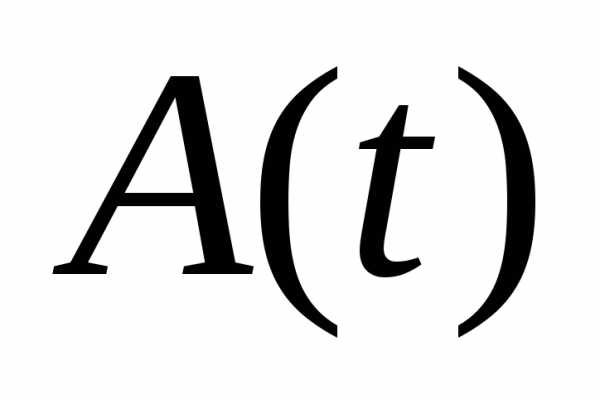 может быть больше и меньше нуля.
может быть больше и меньше нуля.
— амплитуда. Для гармонических колебаний
|
|
— частота биений. |
Амплитуда ограничивает
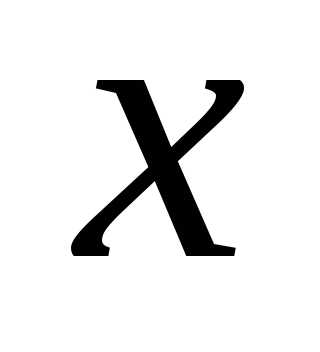 .
(Проводим штрихами симметричную кривую
внизу).Частота.
.
(Проводим штрихами симметричную кривую
внизу).Частота.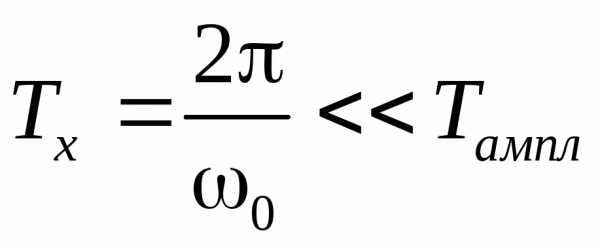 .
Получили биения – усиление и ослабление
колебаний.
.
Получили биения – усиление и ослабление
колебаний.
Метод биений широко применяется на практике. Основан на сравнении искомой частоты с частотой эталона. Метод биений – это один из наиболее точных методов измерения частот, емкостей, индуктивностей. Применяют для настройки музыкальных инструментов.
studfiles.net


 — мало,
— мало,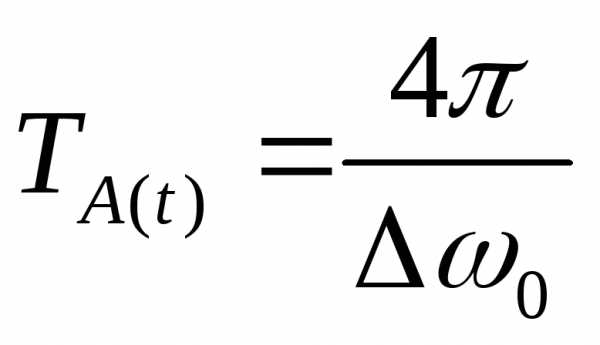 велико.
велико.