Идеальный газ. Уравнение состояния идеального газа. Изопроцессы.
Идеальный газ, уравнение состояния идеального газа, его температура и давление, объем… список параметров и определений, которыми оперируют в соответствующем разделе физики, можно продолжать достаточно долго. Сегодня мы поговорим как раз на эту тему.
Что рассматривается в молекулярной физике?

Основным объектом, который рассматривается в этом разделе, является идеальный газ. Уравнение состояния идеального газа было получено с учетом нормальных условий окружающей среды, и об этом мы поговорим немного позднее. Сейчас давайте подойдем к этой “проблеме” издалека.
Допустим, у нас есть некоторая масса газа. Ее состояние можно определить при помощи трех параметров термодинамического характера. Это, конечно же, давление, объем и температура. Уравнением состояния системы в этом случае будет формула связи между соответствующими параметрами. Она выглядит таким образом: F (p, V, T) = 0.
Вот здесь мы впервые потихоньку подбираемся к появлению такого понятия, как идеальный газ. Им называется газ, в котором взаимодействия между молекулами пренебрежимо малы. Вообще в природе такого не существует. Однако любой сильно разреженный газ близок к нему. От идеального мало чем отличаются азот, кислород и воздух, находящиеся в нормальных условиях. Чтобы записать уравнение состояния идеального газа, мы можем использовать объединенный газовый закон. Получим: pV/T = const.
Связанное понятие № 1: закон Авогадро
Он может рассказать нам о том, что если мы возьмем одинаковое количество молей абсолютно любого случайного газа и поставим их в одинаковые условия, среди которых температура и давление, то газы займут одинаковый объем. В частности, опыт проводился при нормальных условиях. Это означает, что температура была равна 273,15 Кельвинам, давление — одной атмосфере (760 миллиметров ртутного столба или же 101325 Паскалей). При таких параметрах газ занял объем равный 22,4 литра. Следовательно, мы можем говорить о том, что для одного моля любого газа соотношение числовых параметров будет величиной постоянной. Именно поэтому было принято решение этой цифре дать обозначение буквой R и назвать ее универсальной газовой постоянной. Таким образом, она равняется 8,31. Размерность Дж/моль*К.
Идеальный газ. Уравнение состояния идеального газа и манипуляции с ним
Давайте попробуем переписать формулу. Для этого запишем его в таком виде: pV = RT. Далее совершим нехитрое действие, умножим обе части уравнения на произвольное количество молей. Получим pVu = uRT. Примем во внимание тот факт, что произведение молярного объема на количество вещества есть просто объем. Но ведь количество молей одновременно будет равняться частному массы и молярной массы. Именно так выглядит уравнение Менделеева-Клапейрона. Оно дает четкое понятие о том, какую систему образует идеальный газ. Уравнение состояния идеального газа примет вид: pV = mRT/M.
Выведем формулу для давления
Давайте проведем еще некоторые манипуляции с полученными выражениями. Для этого правую часть уравнения Менделеева-Клапейрона умножим и разделим на число Авогадро. Теперь внимательно смотрим на произведение количества вещества на число Авогадро. Это есть не что иное, как общее число молекул в газе. Но в то же время отношение универсальной газовой постоянной к числу Авогадро будет равно постоянной Больцмана. Следовательно, формулы для давления можно записать таким образом: p = NkT/V или p = nkT. Здесь обозначение n это концентрация частиц.
Процессы идеального газа
В молекулярной физике существует такое понятие, как изопроцессы. Это термодинамические процессы, которые имеют место в системе при одном из постоянных параметров. При этом масса вещества также должна оставаться постоянной. Давайте рассмотрим их более конкретно. Итак, законы идеального газа.
Постоянным остается давление
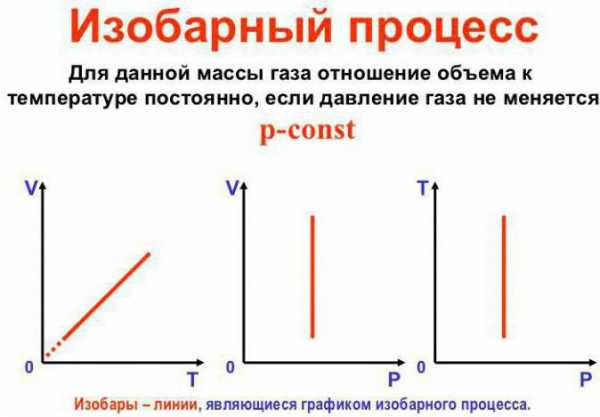
Это закон Гей-Люссака. Выглядит он так: V/T = const. Его можно переписать и по-другому: V = Vo (1+at). Здесь a равняется 1/273,15 К^-1 и носит название «коэффициент объемного расширения». Мы можем подставить температуру как по шкале Цельсия, так и по шкале Кельвина. В последнем случае получим формулу V = Voat.
Постоянным остается объем

Это второй закон Гей-Люссака, более часто называемый законом Шарля. Выглядит он так: p/T = const. Есть и другая формулировка: p = po (1 + at). Преобразования могут быть проведены в соответствии с предыдущим примером. Как можно видеть, законы идеального газа иногда бывают достаточно похожими друг на друга.
Постоянным остается температура

Если температура идеального газа остается величиной постоянной, то мы можем получить закон Бойля-Мариотта. Он может быть записан таким образом: pV = const.
Связанное понятие № 2: парциальное давление
Допустим, у нас имеется сосуд с газами. Это будет смесь. Система находится в состоянии теплового равновесия, а сами газы между собой не реагируют. Здесь N будет обозначать общее количество молекул. N1, N2 и так далее, соответственно, количество молекул в каждом из компонентов имеющейся смеси. Возьмем формулу давления p = nkT = NkT/V. Ее можно раскрыть для конкретного случая. Для двухкомпонентной смеси формула примет вид: p = (N1 + N2) kT/V. Но тогда получится, что общее давление будет суммироваться из частных давлений каждой смеси. А значит, оно будет иметь вид p1 + p2 и так далее. Это и будут парциальные давления.
Для чего это нужно?
Полученная нами формула указывает на то, что давление в системе оказывается со стороны каждой группы молекул. Оно, кстати, не зависит от других. Этим воспользовался Дальтон при формулировании закона, названного впоследствии в его честь: в смеси, где газы не реагируют между собой химически, общее давление будет равно сумме парциальных давлений.
fb.ru
4. Уравнение состояния идеального газа
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
где
— давление,
— молярный объём,
— универсальная газовая постоянная
— абсолютная температура,К.
Так как , где—количество вещества, а , где— масса,—молярная масса, уравнение состояния можно записать:
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта.
— Закон Гей-Люссака.
— закон Шарля (второй закон Гей-Люссака, 1808 г.).А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое. С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объёмводородасоединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
1 Объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
— закон Бойля — Мариотта. Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году. В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где —показатель адиабаты, — внутренняя энергия единицы массы вещества.Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки. С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведениеувеличивается.
5. Основное уравнение молекулярно-кинетической теории идеальных газов
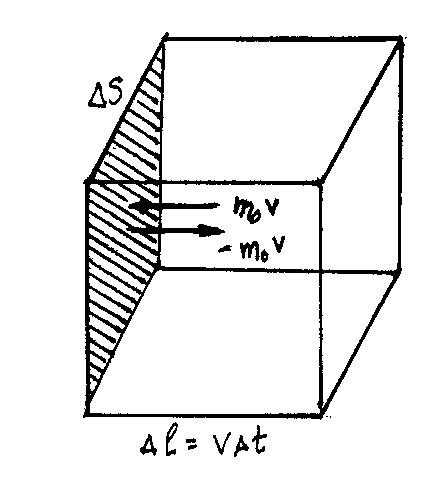
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку DS и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m0v-(-m
0v)=2m0v, где т0 — масса молекулы, v — ее скорость.За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt .Число этих молекул равно nDSvDt (n—концентрация молекул).
Необходимо, однако, учитывать, что реально молекулы движутся к площадке
DS
под разными углами и имеют различные
скорости, причем скорость молекул при
каждом соударении меняется. Для упрощения
расчетов хаотическое движение молекул
заменяют движением вдоль трех взаимно
перпендикулярных направлений, так
что в любой момент времени вдоль каждого
из них движется 1/3 молекул,
причем половина молекул (1/6)
движется вдоль данного направления
в одну сторону, половина — в противоположную.
Тогда число ударов молекул, движущихся
в заданном направлении, о площадку DS
будет
DР = 2m0v•1/6nDSvDt=1/3nm0v2DSDt.
Тогда давление газа, оказываемое им на стенку сосуда,
p=DP/(DtDS)=1/3nm0v2. (3.1)
Если газ в объеме V содержит N молекул,
движущихся со скоростями v1, v2, …, vN, то
целесообразно рассматривать среднюю квадратичную скорость
характеризующую всю совокупность молекул газа.
Уравнение (3.1) с учетом (3.2) примет вид
р = 1/3пт0 <vкв>2. (3.3)
Выражение (3.3) называется основным уравнением молекулярно-кинетической теории идеальных газов. Точный расчет с учетом движения молекул по все-
возможным направлениям дает ту же формулу.
Учитывая, что n = N/V, получим
где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.
Так как масса газа m =Nm0, то уравнение (3.4) можно переписать в виде
pV=1/3m<vкв>2.
Для одного моля газа т = М (М — молярная масса), поэтому
pVm=1/3M<vкв>2,
где Vm — молярный объем. С другой стороны, по уравнению Клапейрона — Менделеева, pVm=RT. Таким образом,
RT=1/3М <vкв>2
Так как М = m0NA, где m0—масса одной молекулы, а NА — постоянная Авогадро, то из уравнения (3.6) следует, что
где k = R/NA—постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
<e0) =E/N = m0 <vкв>)2/2 = 3/2kT(43.8)
(использовали формулы (3.5) и (3.7)) пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при T=0 <e0> =0,,т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (3.8) раскрывает молекулярно-кинетическое толкование температуры.
studfiles.net
2. Идеальный газ. Параметры состояния газа. Уравнение состояния идеального газа.
Простейшим объектом исследования идеальный газ. Идеальным газом называется газ, молекулы которого имеют пренебрежимо малый размер и не взаимодействуют на расстоянии. А при столкновениях взаимодействуют, как абсолютно упругие шары. Идеальный газ – абстракция. Но это понятие полезное, так как упрощает инженерные расчеты тепловых машин и процессов в них происходящих.
Основными параметрами газа, характеризующими
его состояние являются объем,

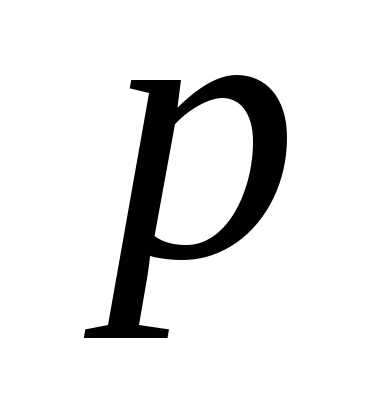 ,
и температура,
,
и температура,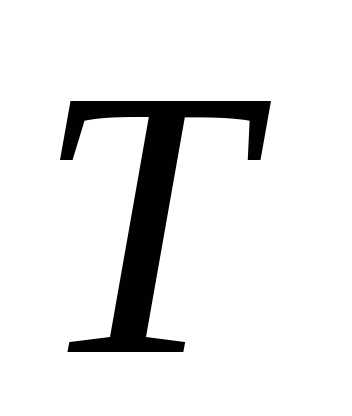 .
. 3. Атомная единица массы (а.Е.М.).
Массы молекул очень малы,
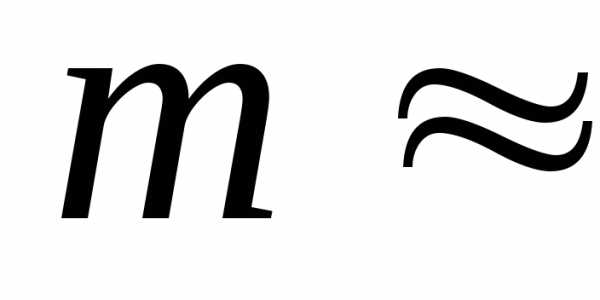 10-27кг. Поэтому для характеристики масс
атомов и молекул применяют величины,
получившие название атомной единицы
массы элемента или молекулы,
10-27кг. Поэтому для характеристики масс
атомов и молекул применяют величины,
получившие название атомной единицы
массы элемента или молекулы,
1а.е.м. = 1,67 10-27кг =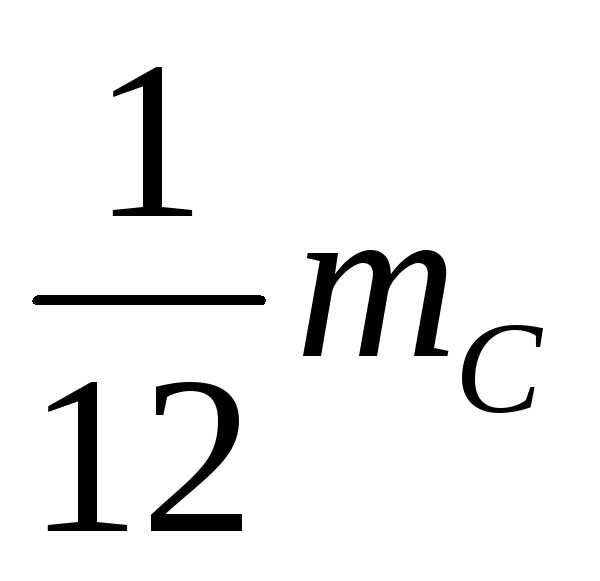 .
.
Массы всех атомов и молекул измеряют в а.е.м.:
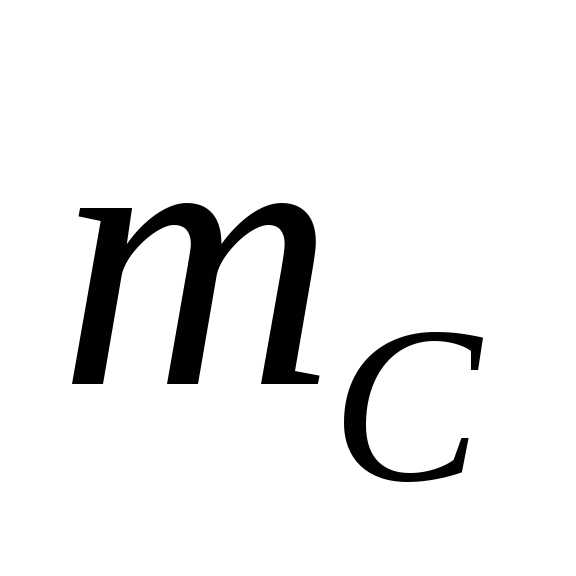 =
12 а.е.м.,
=
12 а.е.м.,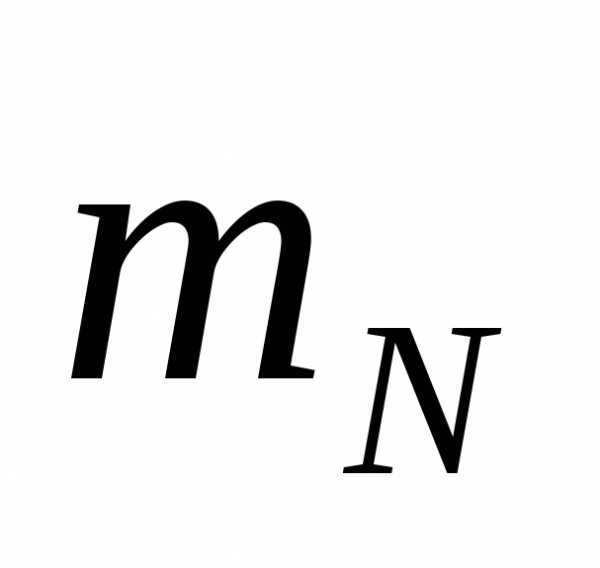 = 14 а.е.м.,
= 14 а.е.м.,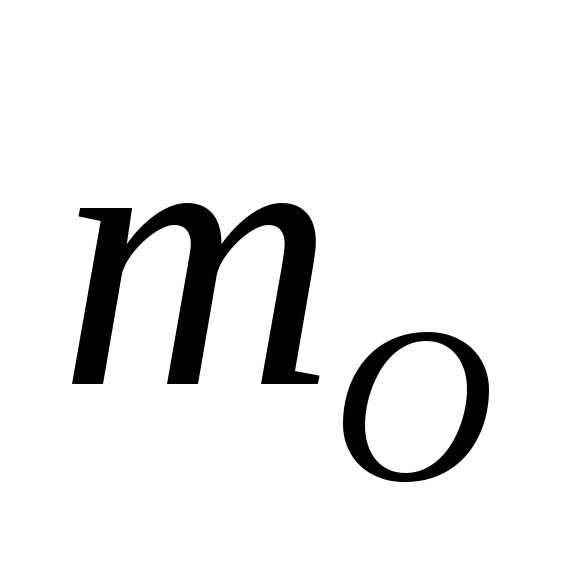 = 16 а.е.м.
= 16 а.е.м.
Относительной молекулярной (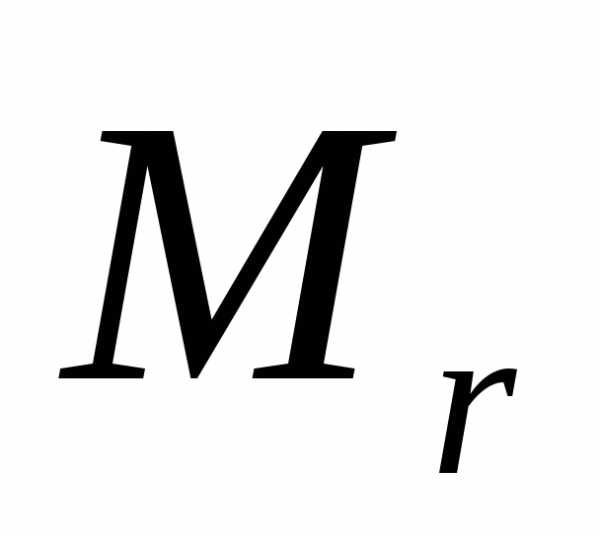
 )
массой называется отношение массы
молекулы или атома к (1/12) массы атома
углерода
)
массой называется отношение массы
молекулы или атома к (1/12) массы атома
углерода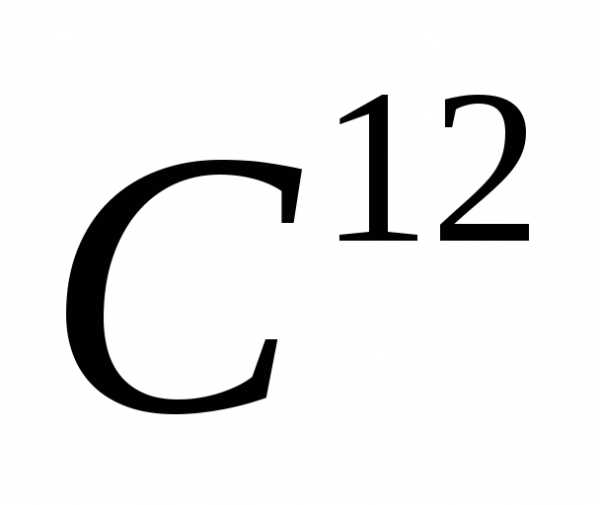 .
.
Как видно из определения
— безразмерные величины. Единица массы,
равная (1/12) массы атома углерода называется атомной единицей массы.
(а.е.м.). Обозначим эту единицу (то есть
а.е.м.), выраженную в килограммах через
называется атомной единицей массы.
(а.е.м.). Обозначим эту единицу (то есть
а.е.м.), выраженную в килограммах через .
Тогда масса атома будет равна
.
Тогда масса атома будет равна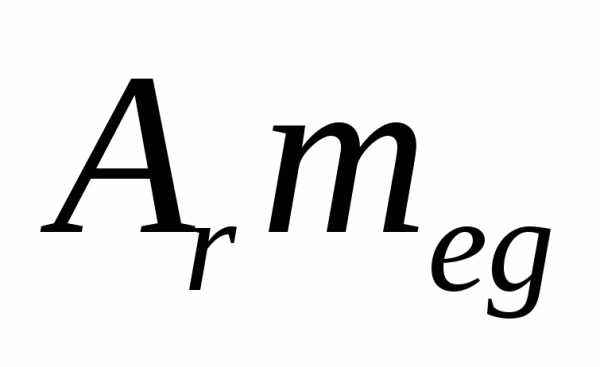 ,
а масса молекулы —
,
а масса молекулы —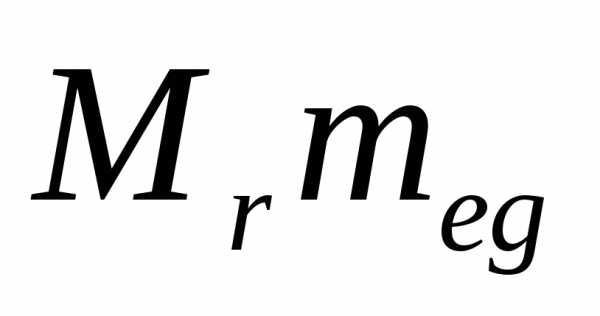 .
.
Количество вещества, которое содержит
число частиц (атомов или молекул), равное
числу атомов в 0,012 кг изотопа

Число частиц, содержащихся в моле
вещества называется числом Авогадро,
 = 6,022 1023моль-1. Массу моля
называют молярной массой,
= 6,022 1023моль-1. Массу моля
называют молярной массой,
(1)
В случае углерода
(кг), (2)
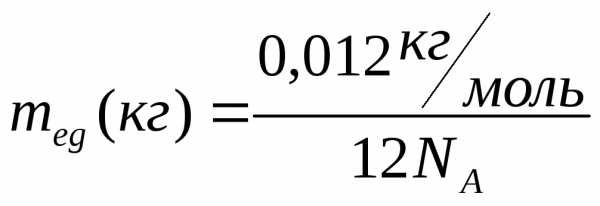 = 1,66 10-27кг.
= 1,66 10-27кг.
Из (2) следует, что
 = 0,001 кг/моль.
(3)
= 0,001 кг/моль.
(3)
Подставляя (3) в (1), имеем
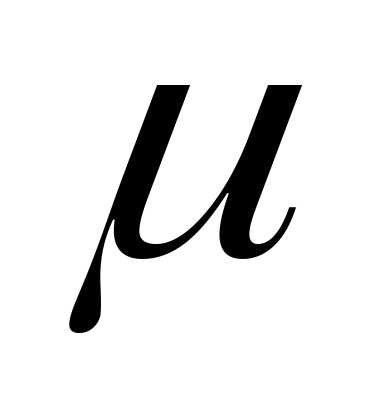 = 0,001
= 0,001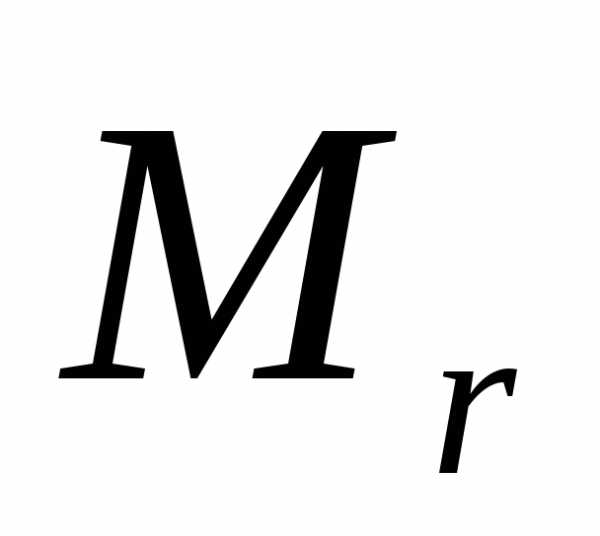 кг/моль
кг/моль
или
 =
= г/моль.
г/моль.
Таким образом, масса моля, выраженная в граммах, численно равна относительной молекулярной массе.
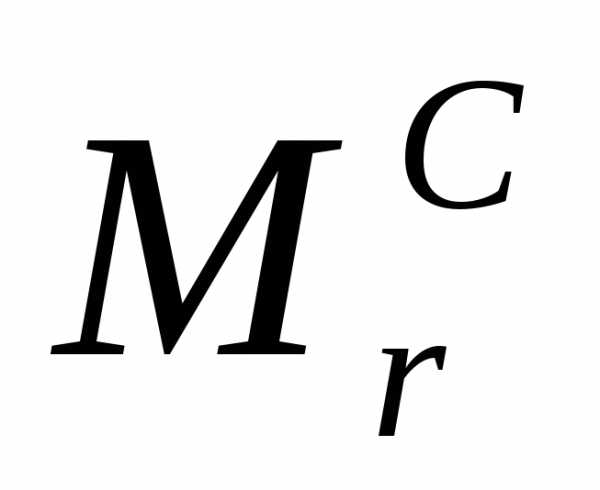 = 12а.е.м.
= 12а.е.м.
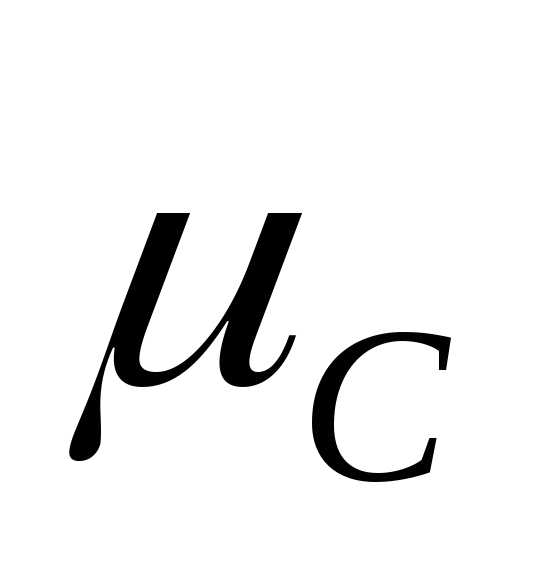 = 12 г/моль,
= 12 г/моль,
 = 16а.е.м.
= 16а.е.м.
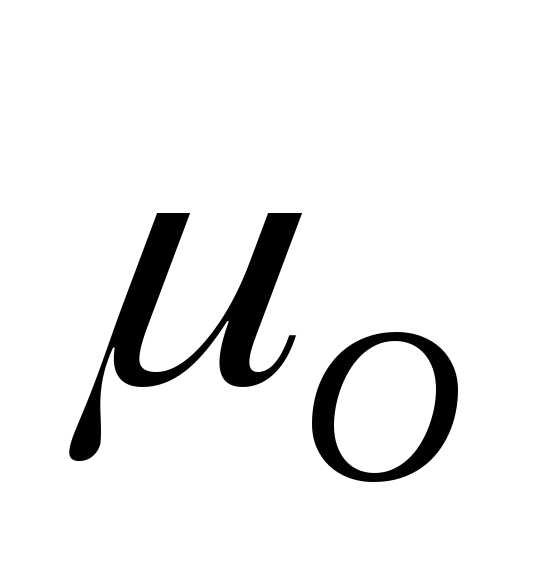 = 16 г/моль,
= 16 г/моль,
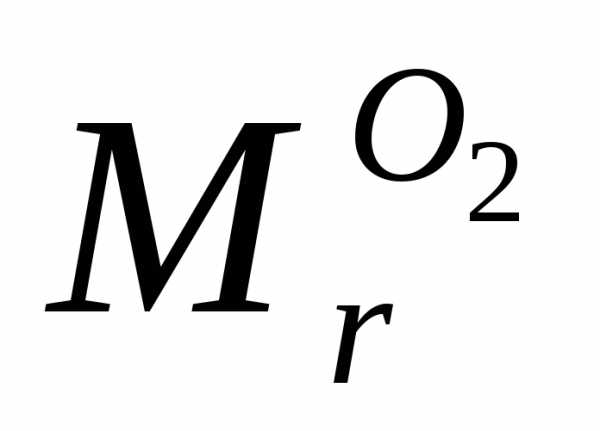 = 32а.е.м.
= 32а.е.м.
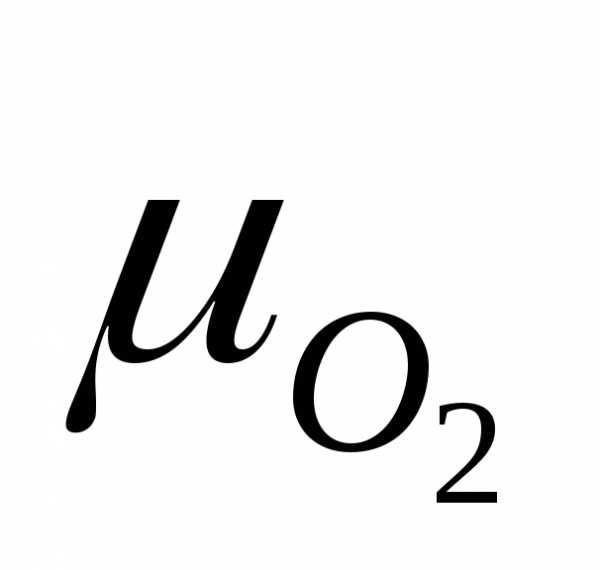 = 32 г/моль.
= 32 г/моль.
4. Свойства идеального газа.
Размеры молекул порядка 1 А =10-10м.
Давление равно силе, действующей
перпендикулярно на единичную площадку,
 .
Давление в СИ измеряется в Па (паскалях).
Па = н/м2, 1 кг/см2= 1 атм = 9,8 104Па, 1 мм рт.ст. = 133 Па.
.
Давление в СИ измеряется в Па (паскалях).
Па = н/м2, 1 кг/см2= 1 атм = 9,8 104Па, 1 мм рт.ст. = 133 Па.
5. Уравнение Менделеева-Клапейрона.
При небольших плотностях газы подчиняются уравнению

— уравнение состояния идеального газа
Менделеева-Клапейрона,
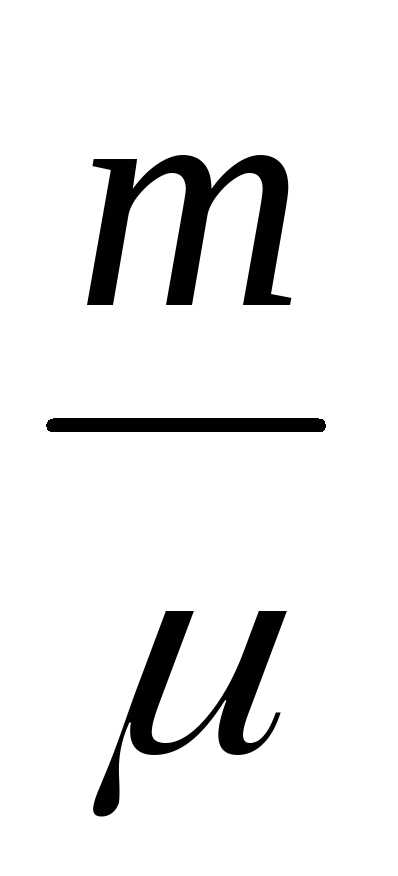 — число молей,
— число молей, = 8,31 Дж/моль К. Можно уравнению придать
другой вид, если ввести величины
= 8,31 Дж/моль К. Можно уравнению придать
другой вид, если ввести величины
= 1,38 10-23Дж/К:
.
Если
 — концентрация частиц, то
— концентрация частиц, то
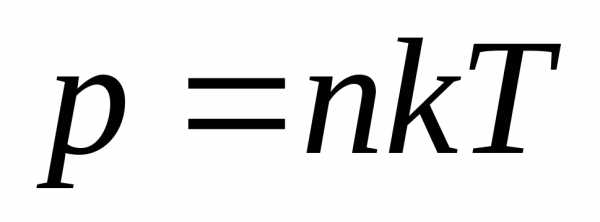 .
.
Если
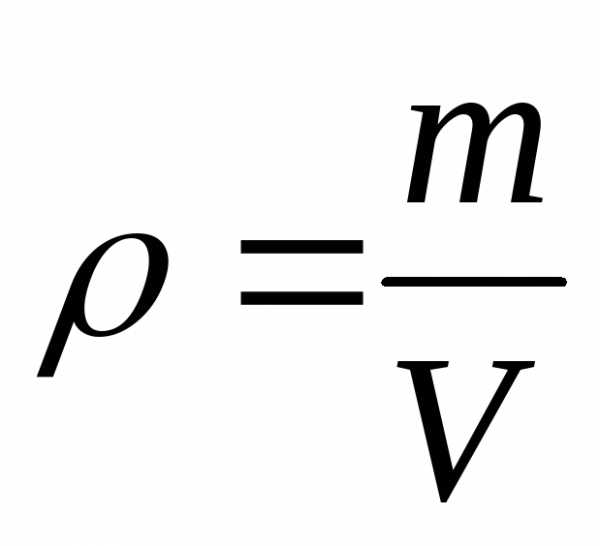 ,
то
,
то
.
Это выражение используется в аэродинамике.
6. Основное уравнение кинетической теории газов (уравнение Клаузиуса).
Основное уравнение молекулярно кинетической теории связывает параметры состояния газа с характеристиками движения молекул.
Для вывода уравнения используется
статистический метод, то есть зная
характеристики отдельных молекул газа
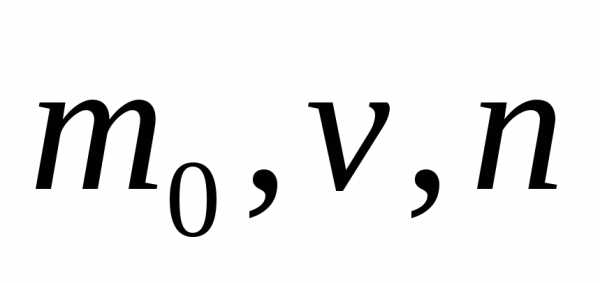 (концентрация)
можно найти
(концентрация)
можно найти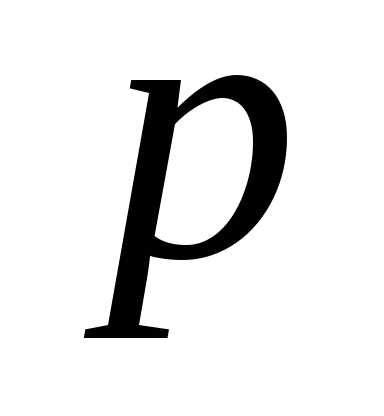 — давление газа, характеристику всего
газа.
— давление газа, характеристику всего
газа.
Для вывода уравнения рассмотрим
одноатомный идеальный газ. Молекулы
движутся хаотически. Скорости молекул
разные. Предположим, что число взаимных
столкновений между молекулами газа
пренебрежимо мало по сравнению с числом
ударов о стенки сосуда, соударения
молекул со стенками сосуда абсолютно
упруги. Найдем давление на стенки
сосуда, предположив, что газ находится
в сосуде кубической формы с ребром
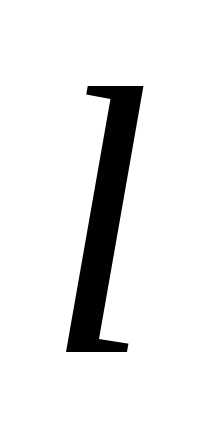 .
Давление ищем как усредненный результат
ударов молекул газа о стенки сосуда.
.
Давление ищем как усредненный результат
ударов молекул газа о стенки сосуда.
|
|
Изменение импульса молекулы за счет столкновения со стенкой равно . |
1). По третьему закону Ньютона стенка
получает импульс от каждой молекулы
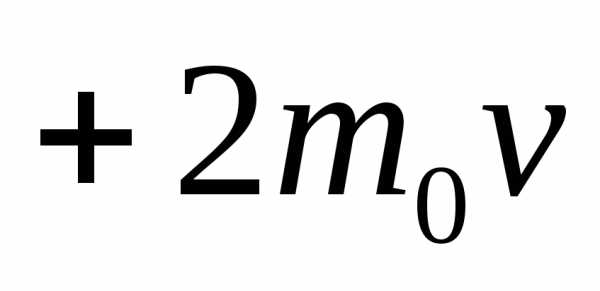
2). За время
 площадки
площадки достигают
только те молекулы, которые заключены
в объеме
достигают
только те молекулы, которые заключены
в объеме
3). Число этих молекул в объеме
 равно
равно
.
4). Число ударов о площадку равно
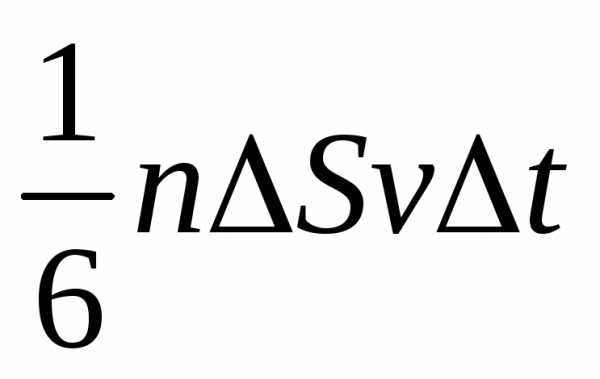 .
.
5). При столкновении молекулы передают площадке импульс
Учитывая, что — сила, а
— сила, а — давление,
— давление,
имеем для давления
(1)
Если в объеме газ содержит
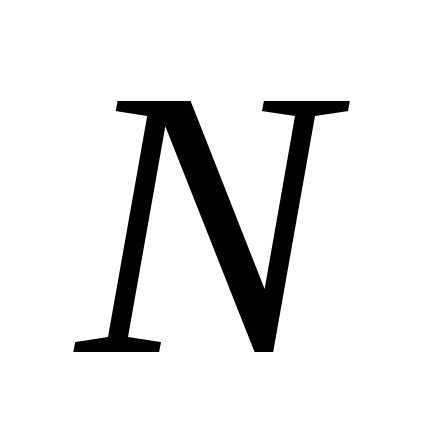 молекул, которые движутся со скоростями,
то надо ввести понятие о среднеквадратичной
скорости по формуле
молекул, которые движутся со скоростями,
то надо ввести понятие о среднеквадратичной
скорости по формуле
. (2)
Тогда выражение (1) примет вид
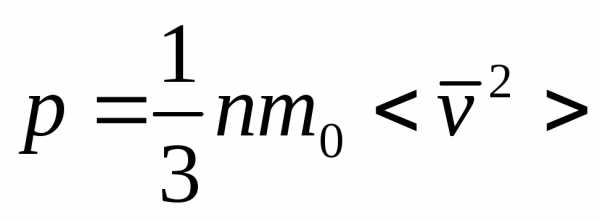 =
=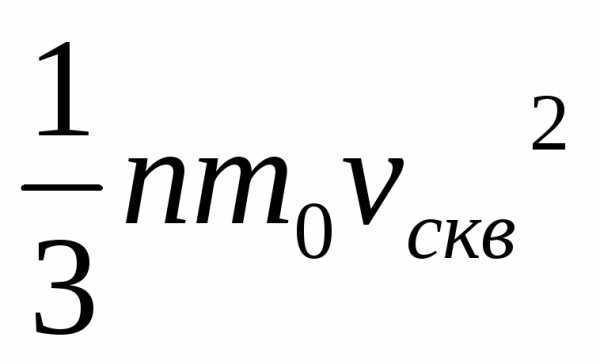
— Основное уравнение кинетической теории газов.
Это уравнение можно преобразовать, замечая, что
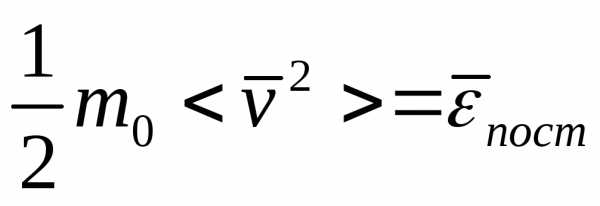 .
.
Тогда
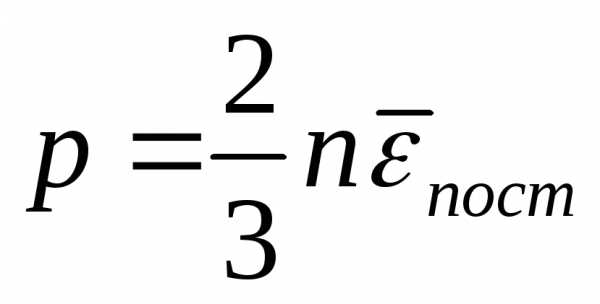 .
.
С другой стороны
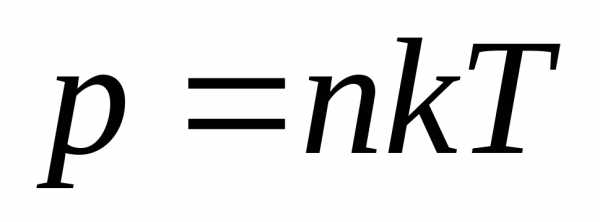 .
.
Поэтому
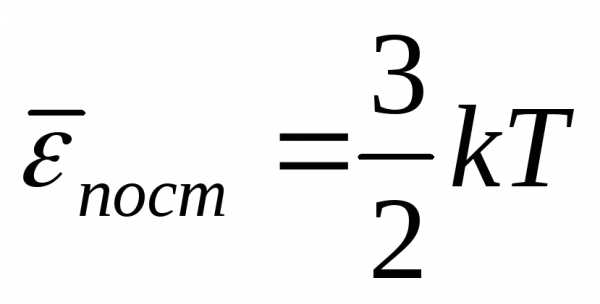 .
.
Средняя кинетическая энергия хаотического
движения молекул прямо пропорциональна
температуре и не зависит от массы. При
Т=0
 = 0, движение молекул газа прекращается
и давление равно нулю.
= 0, движение молекул газа прекращается
и давление равно нулю.
Абсолютная температура, Т – это мера средней кинетической энергии поступательного движения молекул идеального газа. Но это верно лишь при умеренных температурах, пока нет распада или ионизации молекул и атомов. Если число частиц в системе мало, то это тоже неверно, так как нельзя ввести понятие средней квадратичной скорости.
Из
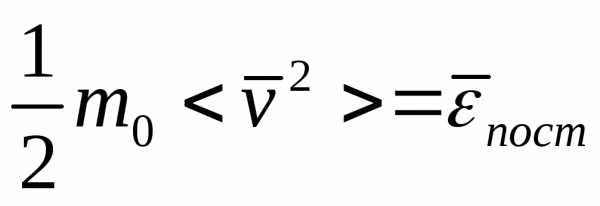 и
и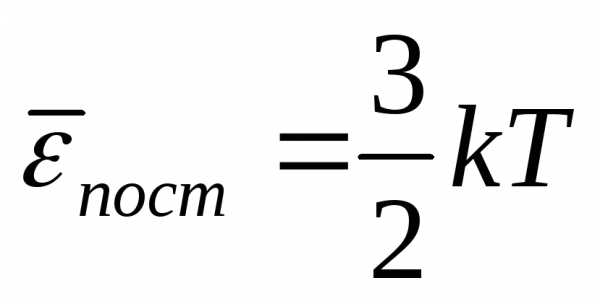 следует
следует
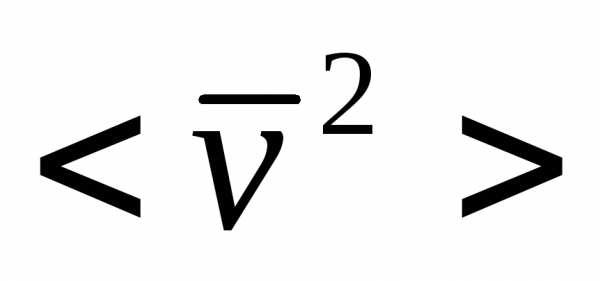 =
=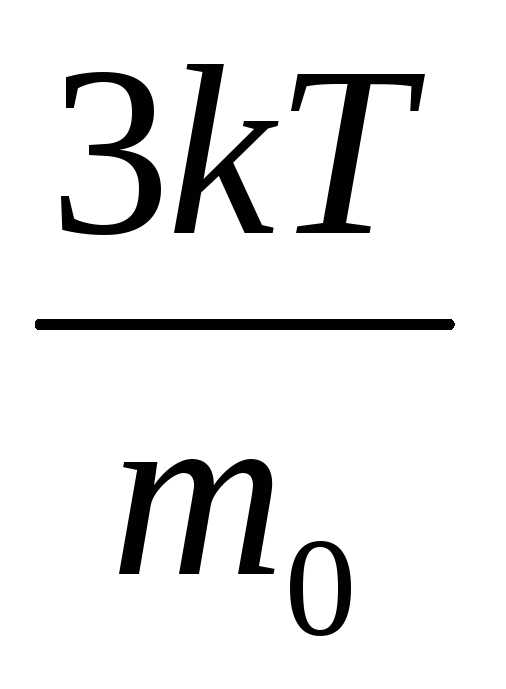 .
.
studfiles.net
Уравнение состояния идеального газа | Наука
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
- $ p\cdot V_M=R\cdot T, $
где
Так как $ V_M=\frac{V}{\nu} $, где $ \,\nu $ — количество вещества, а $ \,\nu=\frac{m}{M} $, где $ \,m $ — масса, $ \,M $ — молярная масса, уравнение состояния можно записать:
- $ p\cdot V=\frac{m}{M}R\cdot T. $
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
В случае постоянной массы газа уравнение можно записать в виде:
- $ \frac{p\cdot V}{T}=\nu\cdot R, $
- $ \frac{p\cdot V}{T}=\mathrm{const}. $
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
- $ T=\mathrm{const}\Rightarrow P\cdot V=\mathrm{const} $ — закон Бойля — Мариотта.
- $ p=\mathrm{const}\Rightarrow\frac{V}{T}=\mathrm{const} $ — Закон Гей-Люссака.
- $ V=\mathrm{const}\Rightarrow\frac{P}{T}=\mathrm{const} $ — закон Шарля (второй закон Гей-Люссака, 1808 г.)
С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
- $ \,\mathrm{H}_2+\mathrm{Cl}_2=2\mathrm{HCl}. $
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
- $ \,\mathrm{N}_2+3\mathrm{H}_2=2\mathrm{NH}_3. $
- $ T=\mathrm{const}\Rightarrow p\cdot V=\mathrm{const} $ — закон Бойля — Мариотта.
Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
- $ p=(\gamma-1)\rho\varepsilon, $
где $ \,\gamma $ — показатель адиабаты, $ \,\varepsilon $ — внутренняя энергия единицы массы вещества.
Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях. более существенным является второе обстоятельство и произведение $ \,P\cdot V $ немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение $ \,P\cdot V $ увеличивается.
Реальный газ
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Уравнение состояния идеального газа. Список первоначальных авторов статьи можно посмотреть в истории правок. Так же, как и в этом проекте, тексты, размещённые в Википедии, доступны на условиях GNU FDL.
ru.science.wikia.com
Идеальный одноатомный газ, теория и примеры
Определение идеального одноатомного газа
Количество атомов в молекуле оказывает влияние на то, как распределяется энергия по степеням свободы. Так для одноатомного газа молекула имеет три степени свободы (). Формулу для расчета внутренней энергии идеального одноатомного газа очень просто получить.
Внутренняя энергия одноатомного идеального газа
Учтем, что молекулы идеального газа представлены как материальные точки, которые не взаимодействуют на расстоянии. Отсутствие сил взаимодействия между молекулами обозначает, что потенциальная энергия взаимодействия молекул постоянна. Суммарная энергия покоя самих молекул также неизменна, так как молекулы при тепловых процессах не изменяются. Следовательно, внутренняя энергия идеального одноатомного газа является суммой кинетических энергий поступательного движения молекул и еще некоторая постоянная.
Обозначим внутреннюю энергию газа как U, тогда сказанное выше запишем как:
где – сумма кинетических энергий поступательного движения молекул; N – число молекул в газе. Примем во внимание то, что средняя кинетическая энергия молекулы () равна:
По закону о равномерном распределении энергии по степеням свободы имеем:
для одноатомного газа:
– постоянная Больцмана; T – температура по шкале Кельвина.
Внутреннюю энергию одноатомного идеального газа можно записать как:
Обычно постоянную величину в выражении (5) опускают, так как в расчётах она роли не играет.
Выражение (5) говорит о том, что внутренняя энергия идеального газа определена его температурой. Она является функцией состояния и не зависит от процесса который провели для того чтобы газ пришел в состояние с этой температурой. При этом изменение внутренней энергии идеального газа определено только его начальным и конечным состояниями, и не связано с характером процесса.
Выражение (5) часто используют в виде:
где m – масса газа; – молярная масса газа; – универсальная газовая постоянная; – количество вещества.
Теплоемкость одноатомного идеального газа
Для изохорного процесса, проводимого в идеальном газе работа равна нулю (A), поэтому первое начало термодинамики:
запишем как:
где – теплоемкость газа при постоянном объеме. Используя выражения (8) и (6) получим:
Используя формулу (10) можно вычислить молярную теплоемкость любого одноатомного газа при постоянном объеме:
Молярная теплоемкость одноатомного газа при изобарном процессе () связана с соотношением Майера:
Примеры решения задач
ru.solverbook.com
Реальный газ, основные понятия и формулы
Что такое реальный газ
Уравнение Менделеева-Клапейрона описывает параметры состояния разреженных газов (находящихся при не слишком больших давлениях и при достаточно высоких температурах). При обычных условиях (т.е. при комнатной температуре и атмосферном давлении) это уравнение применимо ко многим газам (например, таким как азот и кислород). Наиболее близки по своим свойствам к идеальному газу гелий и водород. При низких температурах и высоких давлениях поведение газа начинает существенно отличаться от поведения идеального газа. С повышением плотности газа процессы столкновений играют все большую роль, поэтому размерами молекул и их взаимодействием пренебрегать уже нельзя.
Взаимодействие между молекулами реального газа носит сложный характер, поэтому получить уравнение состояния, которое бы количественно правильно описывало поведение реального газа во всей области возможных изменений его температуры и плотности, не представляется возможным. Можно, однако, записать приближенное уравнение, которое учитывает основные качественные особенности взаимодействия молекул.
Уравнение Ван-дер-Ваальса
Поправка учитывает быстро возрастающие на малых расстояниях силы отталкивания: молекулы как бы занимают определенный объем, меньше которого газ не может быть сжат. Таким образом, поправка к объему характеризует ту часть объема, которая недоступна для движения молекул и равна нескольким суммарным объемам всех молекул, содержащихся в газе.
Поправку
называют внутренним молекулярным давлением. Эта поправка учитывает притяжение молекул, следствием которого является уменьшение давления газа. Молекулы идеального газа, сталкиваясь со стенками сосуда, оказывают на него давление. При учете притяжения на каждую подлетевшую к стенке молекулу действует сила, «отталкивающая» ее от стенки обратно в объем – сила притяжения молекул объема. Это притяжение молекул со стороны объема ослабляет силу удара молекул о стенку, при этом давление на стенку уменьшается на величину .
Значенияпостоянных Ван-дер-Ваальса a и b зависят от природы газа, но не зависят от температуры, Константа (параметр) a характеризует взаимодействие между молекулами на больших расстояниях – дальнодействие сил, параметр b характеризует взаимодействии на малых расстояниях – близкодействие сил взаимодействия.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Идеальный газ. Основное уравнение МКТ. Молекулярная физика
Идеальный газ. Основное уравнение МКТ. Молекулярная физика
Идеальный газ — это просто!
Идеальный газ
Идеальный газ — это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.Понятие «идеальный газ» вводится для математического описания поведения газов.
Реальные разреженные газы ведут себя как идеальный газ!
Свойства идеального газа:
— взаимодействие между молекулами пренебрежительно мало
— расстояние между молекулами много больше размеров молекул
— молекулы — это упругие шары
— отталкивание молекул возможно только при соударении
— движение молекул — по законам Ньютона
— давление газа на стенки сосуда — за счет ударов молекул газа
Скорость молекул газа
В теории газов скорость молекул принято определять через среднее значение квадрата скорости молекул.
Хотя скорости различных молекул сильно отличаются друг от друга, но среднее значение квадрата скорости молекул есть величина постоянная.
Формула для расчета среднего значения квадрата скорости молекул газа:
где
n — число молекул в газе
v — модули скоростей отдельных молекул в газе
В теории газов часто используется понятие кинетической энергии молекул.
Используя среднее значение квадрата скорости молекул, получаем формулу для определения средней кинетической энергии молекул:
Основное уравнение МКТ газа
Основное уравнение МКТ связывает микропараметры частиц (массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р — давление, V — объем, Т — температура).
Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Ниже приведены различные выражения для основного уравнения МКТ:
где
р — давление газа на стенки сосуда(Па)
n — концентрация молекул, т.е. число молекул в единице объема ( 1/м3)
— масса молекулы (кг)
— средний квадрат скорости молекул (м2/с2)
ρ — плотность газа (кг/м3)
— средняя кинетическая энергия молекул (Дж)
Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.
Дополнительные расчетные формулы по теме
Формула для расчета концентрации молекул:
где
N — число молекул газа
V — объем газа (м3)
Формула для расчета плотности газа:
где
mo — масса молекулы (кг)
n — концентрация молекул (1/м3)
Молекулярная физика. Термодинамика — Класс!ная физика
Основные положения МКТ. Масса и размер молекул. Количество вещества. — Взаимодействие молекул. Строение твердых тел, жидкостей и газов. — Идеальный газ. Основное уравнение МКТ. — Температура. Тепловое равновесие. Абсолютная шкала температур. — Уравнение состояния идеального газа. — Изопроцессы. Газовые законы. — Взаимные превращения жидкостей и газов. Влажность воздуха. — Твердые тела. Кристаллические тела. Аморфные тела.
class-fizika.ru