Геометрические свойства
К ним относят длину ткани, ее ширину, толщину и массу.
Длину ткани определяют ее измерением в направлении нитей основы. При настилании ткани перед раскроем длина куска может увеличиваться в результате растяжения. Поэтому ткани с большой растяжимостью должны укладываться в настил с использованием специального настилочного оборудования без растяжения.
Ширина ткани — расстояние между краями ткани. Ее определяют измерением в направлении, перпендикулярном нитям основы. Ширину измеряют с кромками или без кромок. Ширины выпускаемых тканей разнообразны: бельевых 60—100 см; платьевых 90—110 см; пальтовых 130—150 см. Однако при раскрое изделий на ткани не любой ширины удается разложить лекала с минимальными межлекальными потерями, т. е. не все ширины тканей являются рациональными с точки зрения швейного производства. Качество сырья, а также нарушение технологических режимов производства тканей приводит к тому, что кусок ткани на разных участках имеет разную ширину. Это неблагоприятно сказывается на процессах раскроя тканей в швейном производстве: усложняется процесс настилания и увеличиваются отходы тканей.
Толщина тканей колеблется в широких пределах: от 0,14 мм у очень тонких платьевых до 3,5 мм у очень толстых пальтовых. Под толщиной материала принято понимать расстояние между наиболее выступающими участками поверхности нитей на лицевой и изнаночной сторонах. Толщина ткани зависит от линейной плотности нитей (пряжи), переплетения, плотности, фаз строения и отделки тканей. Применение нитей высокой линейной плотности, увеличение абсолютной плотности ткани, применение Многослойных переплетений и такие операции отделки, как аппретирование, валка, ворсование, увеличивают толщину тканей, а опаливание, стрижка, прессование и каландрирование уменьшают ее. Толстые ткани труднее окрашивать, подвергать влажно-тепловой обработке.
Измерение толщины ткани производят на специальном приборе — толщиномере. Ткань помещают между двумя полированными пластинами прибора. Нижняя пластина неподвижная, а верхняя подвижная и соединена со стрелкой, показывающей на шкале толщину испытуемого материала в долях миллиметра. В зависимости от конструкции толщиномера давление верхней пластины на мате риал может быть постоянным или регулируемым. Рекомендуют измерять толщину тканей при давлении 0,1—0,2 кПа.
Толщина ткани и прямо связанная с ней поверхностная плотность влияют на конструкцию изделия, на величину припусков, ширину и конструкцию швов, обусловливают выбор прокладочных материалов. Чем толще ткань, тем большие припуски необходимо предусматривать при конструировании изделия. Если материалы толстые, нужно увеличивать ширину швов, при этом использовать швы с минимальным числом слоев ткани (стачные вразутюжку, накладные с открытым срезом, расстрочные). Для изделий из толстых тканей выбирают более толстые и жесткие прокладки.
От толщины материала зависит число полотен в настиле при раскрое. Чем толще ткань, тем меньше полотен в настиле. При увеличении толщины материала увеличивается и расход ниток. В зависимости от толщины ткани выбирают тип швейного оборудования, регулируют высоту подъема зубчатой рейки и давление лапки на материал.
Масса ткани выражается характеристикой, которую называют поверхностной плотностью. Поверхностная плотность изменяется для различных тканей от 12 до 760 г/м. Наиболее легкими тканями являются газ и шифон, наиболее тяжелыми — шинельные сукно и драпы. Поверхностная плотность каждой ткани — показатель регламентированный. Отклонение фактической поверхностной плотности от установленной в нормативной технической документации является пороком, влекущим за собой изменения структуры ткани. Поверхностная плотность является показателем материалоемкости ткани и ее добротности.
Определение поверхностной плотности ткани может производиться экспериментальным и расчетным методами. При экспериментальном определении прямоугольный образец ткани выдерживают в течение 10—24 ч в нормальных лабораторных условиях, измеряют его длину и ширину нескладной линейкой и затем взвешивают с точностью до 0,01 г. Расчет поверхностной плотности б, г/м производится по формуле
G= 10m\(Lb)
где m — масса образца, г; L— длина образца, мм; b ширина образца, мм.
Массу вычисляют с точностью до 0,01 г, а результат округляют до 0,1 г.
Масса одежных тканей оказывает влияние на процессы швейного производства. Так, больших затрат усилий и времени требуют настилание тяжелых тканей, а также монтажно-переместительные операции на швейном потоке. Носка одежды из тяжелых тканей приводит к утомляемости и дискомфорту человека. Поэтому снижение поверхностной плотности является одной из главных задач при создании новых тканей и других текстильных материалов для одежды.
Похожие статьи:
poznayka.org
Геометрические свойства тканей
К ним относят длину ткани, ее ширину, толщину и массу (поверхностную плотность).
- Длинуткани определяют ее измерением в направлении нитей основы. Она колеблется от 10 до 150 м. При настилании ткани перед раскроем длина куска может увеличиваться в результате растяжения. Поэтому ткани с большой растяжимостью должны укладываться в настил с использованием специального настилочного оборудования без растяжения.
- Ширина ткани — расстояние между краями ткани. Она колеблется от 40 до 250 см. Ее определяют измерением в направлении, перпендикулярном нитям основы. Ширину измеряют с кромками или без кромок. Ширины выпускаемых тканей разнообразны: бельевых 60-100 см; платьевых 90-110 см; пальтовых 130-150 см. Однако при раскрое изделий на ткани не любой ширины удается разложить лекала с минимальными межлекальными потерями, т.е. не все ширины тканей являются рациональными с точки зрения швейного производства. Качество сырья, а также нарушение технологических режимов производства тканей приводит к тому, что кусок ткани на разных участках имеет разную ширину. Это неблагоприятно сказывается на процессах раскроя тканей в швейном производстве: усложняется процесс настилания и увеличиваются отходы тканей.
- Толщинатканей колеблется в широких пределах: от 0,14 мм у очень тонких платьевых до 3,5 мм у очень толстых пальтовых. Под толщиной материала принято понимать расстояние между наиболее выступающими участками поверхности нитей на лицевой и изнаночной сторонах. Толщина ткани зависит от линейной плотности нитей (пряжи), переплетения, плотности, фаз строения и отделки тканей. Применение нитей высокой линейной плотности, увеличение абсолютной плотности ткани, применение многослойных переплетений и такие операции отделки, как аппретирование, валка, ворсование, увеличивают толщину тканей, а опаливание, стрижка, прессование и каландрирование уменьшают ее. Толстые ткани труднее окрашивать, подвергать влажно-тепловой обработке.
- Масса ткани выражаетсяхарактеристикой, которую называют поверхностной плотностью. Поверхностная плотность – это масса 1 м 2 материала. Поверхностная плотность изменяется для различных тканей от 12 до 760 г/м
2. Наиболее легкими тканями являются газ и шифон, наиболее тяжелыми — шинельные сукна и драпы. Поверхностная плотность каждой ткани — показатель регламентированный. Отклонение фактической поверхностной плотности от установленной в нормативной технической документации является пороком, влекущим за собой изменения структуры ткани. Поверхностная плотность является показателем материалоемкости ткани и ее добротности.
Определение поверхностной плотности ткани может производиться экспериментальным и расчетным методами. При экспериментальном определении прямоугольный образец ткани выдерживают в течение 10-24 ч в нормальных лабораторных условиях, измеряют его длину и ширину и затем взвешивают с точностью до 0,01 г.
Масса одежных тканей оказывает влияние на процессы швейного производства. Так, больших затрат усилий и времени требуют настилание тяжелых тканей, а также монтажно-переместительные операции на швейном потоке. Носка одежды из тяжелых тканей приводит к утомляемости и дискомфорту человека. Поэтому снижение поверхностной плотности является одной из главных задач при создании новых тканей и других текстильных материалов для одежды.
Похожие статьи:
poznayka.org
Геометрическое свойство — Большая Энциклопедия Нефти и Газа, статья, страница 1
Геометрическое свойство
Cтраница 1
Геометрическое свойство, соответствующее этой интегрируемости, хорошо известно: два следующих друг за другом отрезка суть всегда касательные к одному и тому же коническому сечению, имеющему тс же фокусы, что и данный эллипс. Поэтому все движения делятся па аналитические семейства по соответствующим коническим сечениям. [1]
Геометрические свойства галактического динамо отличаются от геометрии как планетных ядер, так и звездных конвективных зон. Диск имеет большой радиус и тонок, крупномасштабная скорость Уф меняется в нем вдоль радиуса, а динамо-коэффициент имеет разные знаки по разные стороны центральной плоскости диска. Протяженность диска по радиусу более чем в пятьдесят раз превышает его толщину. Следовательно, удаленные края могут оказывать только слабое влияние и в качестве первого шага достаточно рассмотреть задачу в бесконечном слое. Ось х направлена по радиусу наружу, а ось z перпендикулярна слою так, что xyz составляют правую систему коордй нат. [2]Геометрические свойства голограмм описываются голографическими уравнениями оптических лучей. Эти уравнения позволяют определять траекторию прохождения лучей через голограмму. [3]
Геометрические свойства MG
Геометрические свойства пологих поверхностей используются в технических теориях оболочек. [5]
Геометрические свойства скалярных произведений, отличающихся друг от друга лишь множителем, практически одни и те же. Напротив, ортогональная геометрия во многом отличается от симп-лектической: редукция соотношений g — — g и g — g друг к другу таким простым способом невозможна. [6]
Часто геометрические свойства тел определяются словесно с помощью соответствующих терминов. В этом случае параметрические критерии, необходимые для определения конфигурации тела, в уравнения не вводят. [7]
Микроскопические геометрические свойства образцов, так же как распределение размера и формы зерен, можно измерить в результате экспериментов, для интерпретации которых может быть использована рассмотренная модель. [8]
Геометрические свойства поверхности постоянной кривизны существенно зависят от знака кривизны, поэтому следует отдельно рассматривать поверхности положительной, нулевой и отрицательной кривизны. [9]
Геометрические свойства рассмотренной структуры материала 4D, определенные единым углом пересечения волокон разных семейств 9 и необходимостью касания волокна с тремя другими волокнами из разных семейств, еще не достаточны для однозначного расчета коэффициента армирования. Существенное влияние на значение последнего оказывает плотность распределения волокон каждого направления. В изложенном подходе неявно принималось условие одинаковой плотности распределения волокон всех четырех направлений. [10]
Геометрические свойства решений гиперболических систем были изучены давно, и соответствующая теория достаточно полна. С другой стороны, аналитическое исследование проблемы встретило серьезные трудности и еще находится в стадии развития. Главный источник этих трудностей связан со следующим специфическим свойством нелинейных гиперболических систем: в общем случае задача с начальными условиями не имеет решения, даже если эти условия достаточно гладкие. [11]
Геометрические свойства реального физического пространства и времени соответствуют не геометрии Евклида, а геометрии Римана. [12]
Установленные геометрические свойства области D являются необходимыми условиями разрешимости задачи профилирования крыла в указанном классе решений. [13]
Геометрические свойства изотерм двойных систем с несколькими химическими соединениями отличаются большой сложностью. На их основе не представляется возможным предложить для определения состава образующихся соединений простые методы, аналогичные методу изомолярных серий. Однако вид уравнений свойства с несколькими химическими соединениями зависит от их состава. Уравнения изотерм свойства могут быть использованы для установления состава химических соединений методом проб. [14]
Геометрические свойства рассмотренной структуры материала 4D, определенные единым углом пересечения волокон разных семейств 9 и необходимостью касания волокна с тремя другими волокнами из разных семейств, еще не достаточны для однозначного расчета коэффициента армирования. Существенное влияние на значение последнего оказывает плотность распределения волокон каждого направления. В изложенном подходе неявно принималось условие одинаковой плотности распределения волокон всех четырех направлений. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Геометрические характеристики сечений | ПроСопромат.ру
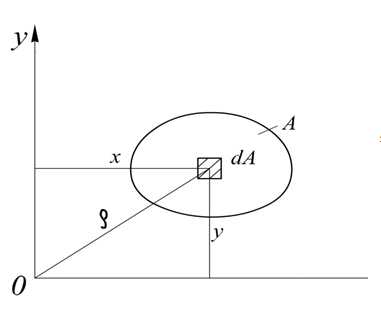
При решении задач сопротивления материалов разрушению и деформированию, сохранения или потери начальной формы равновесия стержней, как правило, используются следующие геометрические характеристики поперечных сечений, описываемые интегралами
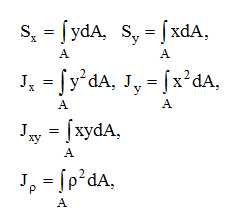
где Sx, Sy – статические моменты площади поперечного сечения (могут быть положительными, отрицательными или равными нулю), Jx, Jy– осевые моменты инерции сечения (положительны, не могут равняться нулю), Jxy – центробежный момент инерции сечения (может быть положительным, отрицательным или равным нулю), Jρ– полярный момент инерции сечения (положителен), не равен нулю), dA – элемент площади сечения, х, у – координаты элемента площади.
Размерность статических моментов площади- длина в третьей степени, моментов инерции — длина в четвертой степени.
Для сечения, состоящего из отдельных частей или разделенного на отдельные части (фигуры)
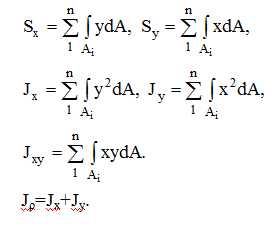
Оси, относительно которых статические моменты площади равны нулю, называются центральными осями. Согласно сути теоремы о моменте равнодействующей (теоретическая механика)
Sx=Ayc, Sy=Axc,
где хс, ус – координаты центра тяжести сечения.
Таким образом, применительно к составному сечению
Это формулы для определения координат центра тяжести составного сечения.
Зависимости между геометрическими характеристиками относительно параллельных осей (ОХ||О′Х′, ОУ||О′У′)
где a, b –расстояния между, соответственно, осями Х и Х/ и осями Y и Y/
Если оси Х и У являются центральными, то формулы «перехода» от центральных осей
В случае поворота координатных осей Х и У на угол α зависимости между моментами инерции формулы «перехода» от центральных осей
Из этих формул вытекает замечательное следствие, которое часто используется в качестве контроля, проверки:
Сумма осевых моментов инерции относительно любых двух взаимно перпендикулярных осей не меняется при повороте осей.
Главные оси и главные моменты инерции
В любой точке плоскости существуют такие две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции имеют экстремальные значения (максимальное и минимальное). Такие оси называются главными, а осевые моменты инерции относительно этих осей –главными моментами инерции.
Если главные оси проходят к тому же и через центр тяжести сечения, то они называются главными центральными осями, а осевые моменты инерции – главными центральными моментами инерции.
Практическое значение имеют именно эти главные центральные оси (обозначим их U и V) и главные центральные моменты инерции относительно их, поскольку они входят во все расчетные формулы сопротивления материалов.
Положение главных осей находится из выражения
где — угол между главными и исходными осями.
Этому условию удовлетворяют сразу два значения угла, отличающихся на 90˚, значит формула определяет положение сразу обеих главных центральных осей. Найденное из этого условия значение угла α0 откладывается между максимальной главной осью и той из центральных осей, относительно которой момент инерции больше.
Главные моменты инерции определяются следующим образом:
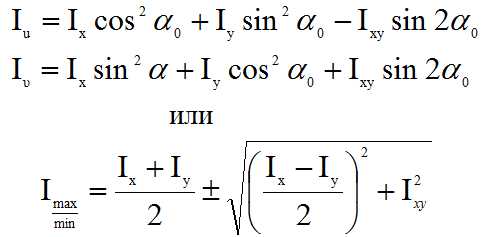
Геометрическими характеристиками сечения также являются:
— Радиус инерции
Радиусом инерции называют корень квадратный из отношения момента инерции к площади сечения, эта величина характеризует разброс площади по периферии сечения:
— Осевые моменты сопротивления
Осевой момент сопротивления (W) представляет собой отношение осевого момента инерции относительно оси к расстоянию от этой оси до наиболее удаленной точки сечения:
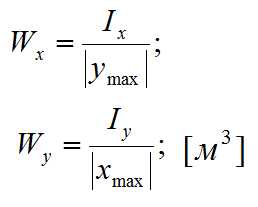
Все геометрические характеристики для простых фигур можно найти в рубрике
« Таблицы»- см. здесь, а для профилей проката — здесь.
prosopromat.ru
Геометрические характеристики
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНЫХ СЕЧЕНИЙ
ГЕОМЕТРИЯ СЕЧЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ
Площадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
Рассмотрим поперечное сечение произвольной формы. Назначим декартову систему координат. Выделим элементарную площадку dA. Обозначим расстояние от центра тяжести элементарной площадки до оси z через y, до оси y через z, до начала координат через ρ. Тогда геометрические характеристики поперечного сечения можно представить в виде момента площади
Площадь (А)
– момент нулевого порядка
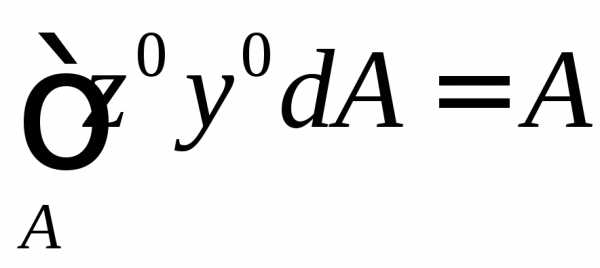 .
.
Статический момент площади (S) – момент первого порядка , могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
Момент инерции (I) — момент второго порядка. Различают осевые (Iz, Iy), центробежный (Izy) и полярный (Iρ) моменты инерции:
. Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ ФИГУР
ПРЯМОУГОЛЬНИК ПОЛУКРУГ РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
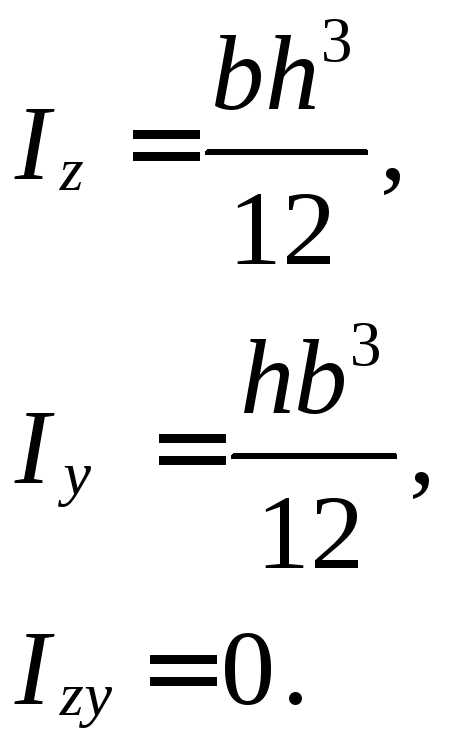
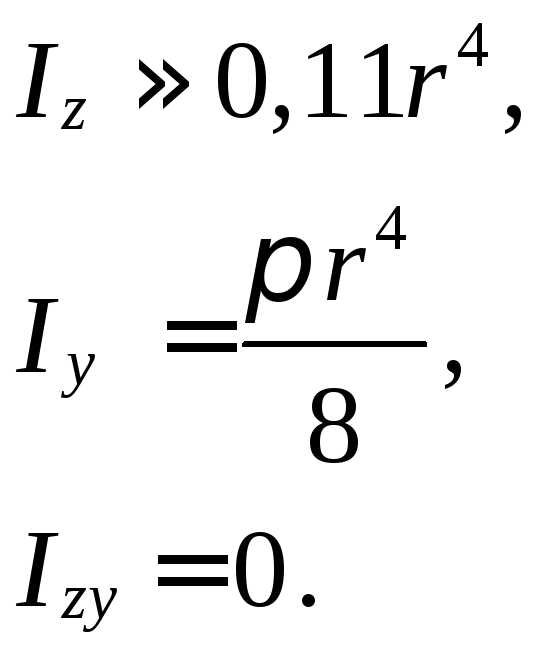
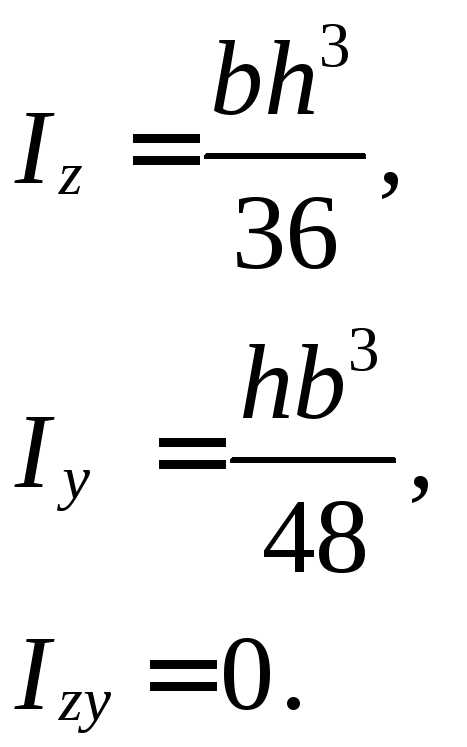
КРУГ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
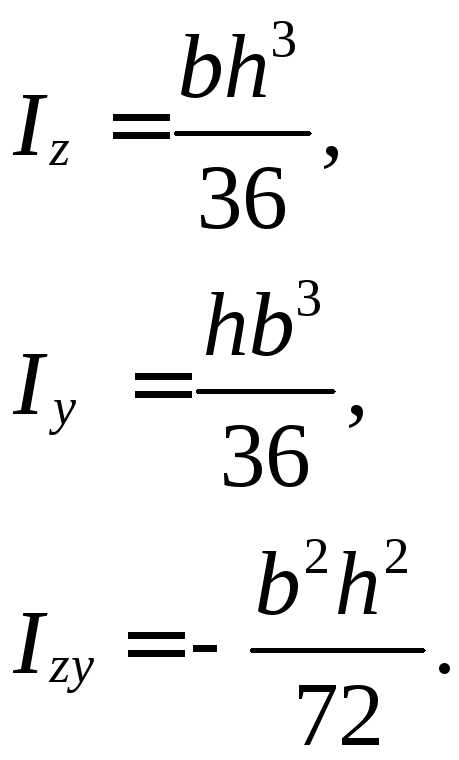
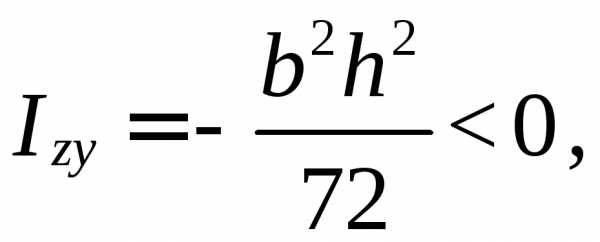
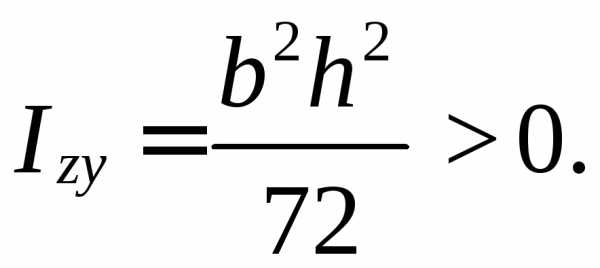
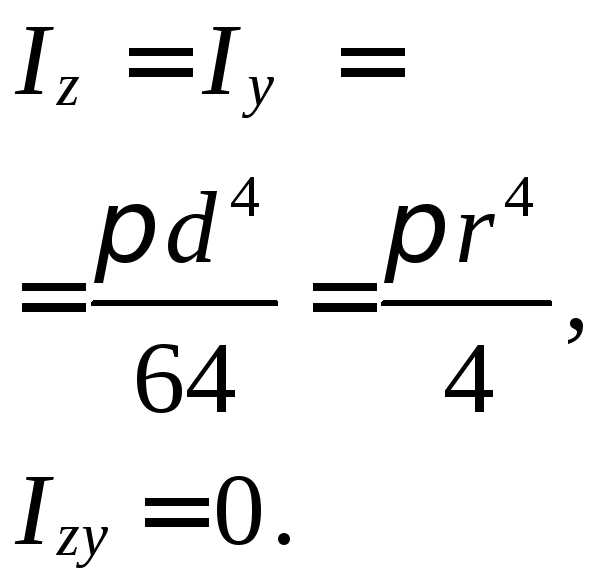
МОМЕНТЫ ИНЕРЦИИ СОСТАВНЫХ СЕЧЕНИЙ
Для определения геометрических характеристик составных сечений используется следующий подход. Сечение разбивают на несколько простых фигур, моменты инерции которых известны. В центре тяжести каждой фигуры назначают локальную систему координат. Выбирают систему координат относительно которой будет производится расчет. Затем все геометрические характеристики отдельных частей суммируются, а геометрические характеристики отверстий вычитаются. Пример приведен ниже.
Сечение сложной формы разбиваем на три прямоугольника,
назначаем локальные системы координат с началом в
центре тяжести каждого прямоугольника. Расчет
будем производить в системе координат yz.
Ось y — проходит через левую, а ось z —
через нижнюю грань составного сечения.
При вычислении геометрических характеристик
необходимо помнить, что статический момент
площади фигуры относительно центральных
осей всегда равен нулю, также, как и центробежный момент инерции симметричного сечения.
ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
Аналогично формулам изменения нормальных и касательных напряжений при ПНС получены зависимости
Моменты инерции относительно центральных осей, т.е. осей, проходящих через центр тяжести сечения, называют центральными. Оси, относительно которых центробежный момент инерции обращается в ноль, называют главными и относительно этих осей моменты инерции принимают экстремальное значение. Если главные оси проходят через центр тяжести сечения, то эти оси называют главными центральными, а моменты инерции относительно их – главными центральными моментами инерции.
Главные моменты
инерции определяют, как
Положение главных осей инерции можно
найти с помощью формулы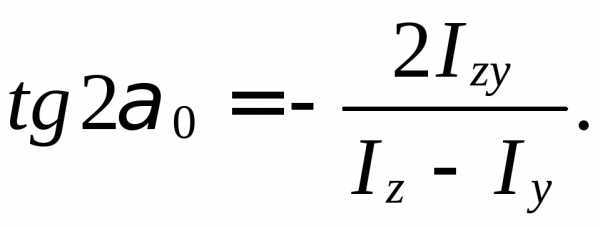
Используя приведенный выше материал, вычислим геометрические характеристики сечений, не имеющих осей симметрии и симметричных сечений.
ПРИМЕР 1
Определить положение главных центральных осей инерции и вычислить моменты инерции относительно них. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
Решение
По сортаменту определим необходимые для расчета характеристики прокатного профиля. Необходимо обратить внимание на систему координат, принятую в сортаменте.
Двутавр №20: А=26,8см2, b=10см, Уголок 10/6,3: А=15,5см,
Ix=1840см4, Iy=115см4, номер Ix=153см4, Iy=47,2см4, x0=1,58см,
двутавра соответствует его. y0=3,4см, Ixy=48,6см4.
высоте в см. В нашей Высота уголка составляет
системе координат 10см, а ширина полки 6,3см.
Iz1=Ix=1840см4, Iy1=Iy=115см4 Iy2=Ix=153см4, Iz2=Iy=47,2см4.
Пусть площадь двутавра будет А1, а площадь уголка А2, присвоим эти же индексы и остальным геометрическим характеристикам.
Назначим локальные системы координат, проходящие через центры тяжести двутавра и уголка. В строительстве принято направлять ось абсцисс вдоль стержня, тогда в поперечном сечении располагаются оси y и z.
Определим положение центра тяжести сечения (zс, yс)
Выберем за начало отсчета систему координат y1 и z1.
После нахождения координат нанесем с учетом знака на чертеж центр тяжести сечения. Если координаты были найдены верно, то центр тяжести должен находиться на прямой между центром тяжести двутавра и уголка. В данном случае эта проверка выполняется, поэтому можно приступить к следующим действиям. Проведем через центр тяжести центральные оси. Выставим расстояния от центральных осей сечения до осей, проходящих через центры тяжести уголка и двутавра. Все дальнейшие расчеты будут выполнены относительно центральных осей всего сечения.
2. Вычислим моменты инерции сечения
Т.к. центробежный момент инерции не равен нулю, значит, оси y и z не являются главными осями инерции.
4. Определим положение главных осей инерции
Нанесем главные оси инерции на чертеж, учитывая, что угол α0 получился отрицательный, поэтому поворот осей осуществляется по ходу часовой стрелки. Ближе к исходной оси, относительно которой момент инерции был больше (Iz), располагается ось umax, следовательно, рядом с осью, относительно которой момент инерции был меньше (Iy), будет находиться ось vmin.
5. Вычислим значения главных центральных моментов инерции сечения
38
studfiles.net
Персональный сайт — Геометрические фигуры и их свойства
Геометрические фигуры и их свойства
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
1. Противоположные стороны прямоугольника равны и параллельны.
2. Все углы прямоугольника прямые. Сумма углов прямоугольника равна 360°.
3. Диагонали прямоугольника равны.
4. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.
5. Диагонали прямоугольника делят его на два равные треугольника.
6. В прямоугольнике сумма углов, прилегающих к одной стороне, равна 180 °.
Р = 2 (a + b), S = ab, где a и b — соседние (смежные) стороны прямоугольника.
Если в прямоугольнике проведена биссектриса, которая пересекает одну из сторон, то она отсекает от прямоугольника равнобедренный треугольник.
Прямоугольник имеет две оси симметрии: прямые, проходящие через точку пересечения диагоналей перпендикулярно противоположным сторонам.
Квадрат — это прямоугольник, у которого все стороны равны.
Формула площади квадрата: S=a ²=½ d ², где а — сторона квадрата, d — диагональ квадрата.
Свойства квадрата:
1. Противоположные стороны равны и параллельны.
2. Все углы прямые.
3. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
4. Точка пересечения диагоналей квадрата является центром симметрии квадрата, центром вписанной и описанной окружностей.
5. Квадрат имеет четыре оси симметрии.
ychitelll.ucoz.ru
Сортамент фасонных профилей: Геометрические характеристики фигур
Геометрические характеристики фигур / Геометрические характеристики простых фигур: прямоугольника, квадрата, треугольника, круга, полукруга
Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.
Геометрические характеристики прямоугольника и квадрата
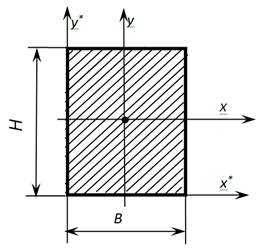
Осевые моменты инерции прямоугольника (квадрата)
Геометрические характеристики прямоугольного треугольника
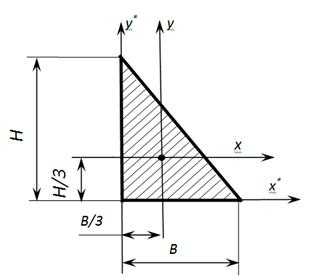
Осевые моменты инерции прямоугольного треугольника
Геометрические характеристики равнобедренного треугольника
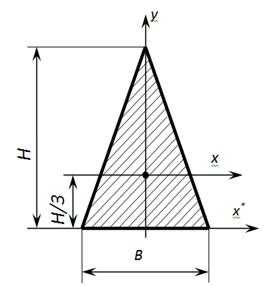
Осевые моменты инерции равнобедренного треугольника
Геометрические характеристики круга
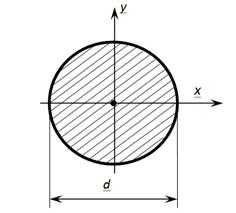
Осевые моменты инерции круга
Геометрические характеристики полукруга
Осевые моменты инерции полукруга
sopromato.ru
