Итоговая контрольная работа по математике для 10-х классов
Пояснительная записка.
Промежуточная аттестация по математике (алгебра и начала математического анализа, и геометрия) в 10 классах проводится в форме теста, состоящего из двух частей (модели экзаменационной работы по математике в 11 классах в 2014 году).
Тест составлен с использованием заданий из открытого банка тестовых заданий единого государственного экзамена (ЕГЭ) за курс математики средней (полной) общей школы с учетом программного материала, изученного десятиклассниками за 2013-2014 учебный год.
Назначение экзаменационной работы:
оценить уровень предметных компетенций учащихся 10 классов по математике (алгебра и начала математического анализа).
Характеристика структуры и содержание итоговой контрольной работы.
Работа состоит из двух частей.
Задания с кратким ответом части 1 итоговой контрольной работы предназначены для определения математических компетентностей учащихся 10 классов. Ответом на задания части 1 является целое число или промежуток.
Часть 2 направлена на проверку владения материалом на высоком и повышенном уровнях. Ее назначение – дифференцировать хорошо успевающих школьников по уровню подготовки, выявить наиболее подготовленную часть учащихся 10 классов. Эта часть содержит 3 заданий повышенного и высокого уровней сложностей по курсу алгебры и начал анализа, и геометрии 10 класса, требующих полной записи решений и ответа.
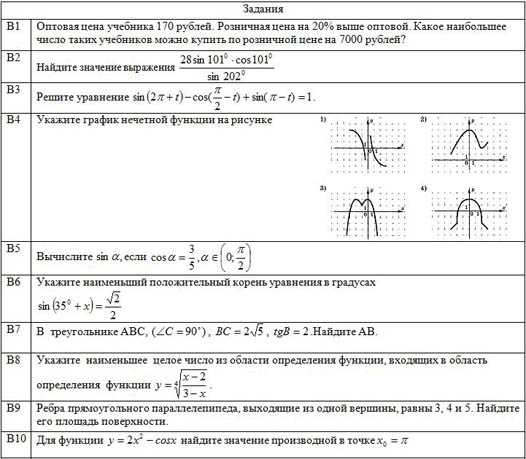
Часть 1 В первой части итоговой контрольной работы по алгебре содержатся задания по ключевым разделам курса алгебры и начал анализа, и геометрии 10 класса.
Время выполнения итоговой контрольной работы
На выполнение итоговой контрольной работы отводится 120 минут (2часа).
Система оценивания выполнения отдельных заданий и итоговой работы в целом.
За выполнение каждого задания ученик получает определенное число баллов. Правильно выполненная вся работа оценивается 2 балла. В таблице 5 приводится система формирования общего балла.
В случае правильного выполнения задания части 1(№1-14) учащемуся засчитывается 1 балл, если ответ неверный или отсутствует – 0 баллов. Задание части 1 считается выполненным правильно, если вписан верный ответ.
Задание части 2 (№15, 16, 17) считается выполненным правильно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл (2, 3), соответствующий данному заданию.
Исправления и зачеркивания, если они сделаны аккуратно, в каждой части итоговой контрольной работы, не являются основанием для снижения отметки.
При выполнении заданий части 2 можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.
С учетом числа заданий базового уровня, разработана шкала перевода первичных баллов в отметки по пятибалльной системе.
Таблица перевода суммарного балла в 5-балльную шкалу.
Весь материал — в документе.
videouroki.net
| I | II | III | IV | V | VI | VII | |
| А1 | 3 | 4 | 2 | 2 | 3 | 4 | 1 |
| А2 | 1 | 2 | 1 | 3 | 1 | 2 | 4 |
| А3 | 2 | 2 | 2 | 1 | 2 | 3 | 1 |
| А4 | 3 | 2 | 4 | 1 | 4 | 4 | 3 |
| А5 | 2 | 4 | 2 | 1 | 2 | 4 | 2 |
| А6 | 2 | 3 | 4 | 4 | 1 | 2 | 2 |
| А7 | 3 | 2 | 1 | 4 | 3 | 1 | 3 |
| В1 | 3 | 7 | 4 | 0 | 3 | 3 | 7 |
| В2 | 10 | 12 | 2 | 4 | 3 | 10 | 1 |
| С1 | (-∞; -5)U(5; ∞) | (-∞; 0)U(1; ∞) | (-∞; -3)U(5; ∞) | (-∞; -3)U(4; ∞) | (-∞; -4)U(9; ∞) | (-∞; -3)U(5; ∞) | (-∞; -5)U(11; ∞) |
doc4web.ru
Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)
Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)
Просмотр содержимого документа
«Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)»
Пояснительная записка
к тексту годовой контрольной работы
по алгебре за курс 10 класса (уч. Мордкович А.Г.).
Базовый уровень
Годовая контрольная работа составлена в соответствии с программным материалом курса «Алгебра и начала анализа» и требованиями федеральных государственных образовательных стандартов. Задания данной работы отражают следующие основные темы курса алгебры: «Тригонометрические выражения», «Тригонометрические уравнения», «Производная», «Применение производной».
Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре текстов в формате ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. Использованы задания из открытого банка задач ЕГЭ по математике. На выполнение работы отводится 40 минут.
Элементы анализа:
Нахождение значения тригонометрического выражения.
Решение тригонометрического уравнения и нахождение наименьшего положительного корня.
Нахождение значения тригонометрического выражения. Применение формулы косинуса двойного угла.
Нахождение значения тригонометрической функции по известной кофункции
Нахождение значения производной рациональной функции в точке.
Нахождение значения производной тригонометрической функции в точке.
Применение производной. Нахождение точек экстремума.
а) Решение тригонометрического уравнения методом замены и сведением к квадратному
б) Нахождение корней уравнения, принадлежащих данному отрезку.
Применение производной.Нахождение наибольшего и наименьшего значения дробной функции на отрезке.
Несмотря на то, что всего в работе 9 заданий, элементов анализа всего 10. Поэтому критерии оценивания следующие:
«3» — верно выполнено 4-6 заданий
«4» — верно выполнено 7-8 заданий
«5» — верно выполнено 9-10 заданий
Итоговая контрольная работа
10 класс.
I вариант
Найдите значение выражения: 24.
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения:
Найдите и
Найдите значение производной функцииу = х2 – 6х + 1 в точке х0=-1.
Найдите значение производной функции в точке:
у = -3 + 2, х0 = .
Найдите точки экстремума и определите их характер:
у = х3 + 3х2 – 9х – 2.
а) Решите уравнение:
2
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Итоговая контрольная работа
10 класс.
II вариант
Найдите значение выражения: 46.
Решить уравнение: — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции в точке у = х2 – 5х + 2 в точке х0=-2.
Найдите значение производной функции в точке:
у = 3 -, х0 = .
Найдите точки экстремума и определите их характер: у = 2х3 — 10х2 + 6х.
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = 2х + на отрезке .
Итоговая контрольная работа
10 класс.
III вариант
Найдите значение выражения: 37
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции у = х3 + 4х2 – 1 в точке х0=-1.
Найдите значение производной функции в точке: у = — 2, х0 = .
Найдите точки экстремума и определите их характер: у = х3 + х2 – 5х – 3.
а)Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Итоговая контрольная работа
10 класс.
IV вариант
Найдите значение выражения: 34.
Решить уравнение и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции у = х4 – 2х — 1 в точке х0=-2.
Найдите значение производной функции в точке: у = — 2, х0= .
Найдите точки экстремума и определите их характер: у = х3— х2 – х +3.
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
kopilkaurokov.ru
Итоговая (годовая) контрольная работа по математике для 10 класса — Алгебра — Сдаем зачеты дистанционно — Каталог материалов
Цель работы:
проверить уровень математической подготовки учащихся 10 класса с позиций Единого Государственного экзамена.
Содержание работы:
итоговая (годовая) контрольная работа по алгебре в 10 классе рассчитана на два астрономических часа. Она составлена по материалам ЕГЭ 2010 года. Работа состоит из двух частей. Первая часть содержит одиннадцать заданий ( В1- В11 ) базового уровня, требующих краткого ответа, вторая – два задания ( С1- С2 ) повышенного уровня, для которых следует привести полное решение.
Оценивание работы:
каждое задание первой части оценивается одним баллом. Во второй части первое задание – два балла, второе – три балла. Вся работа оценивается шестнадцатью баллами.
ПЕРЕВОД БАЛЛОВ В ОТМЕТКУ:
БАЛЛ | 0 — 4 | 5 — 10 | 11 — 12 | 13 – 16 |
ОТМЕТКА | 2 | 3 | 4 | 5 |
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ( 10 КЛАСС) ВАРИАНТ 1
В1
В2

В3
В4
В5
В6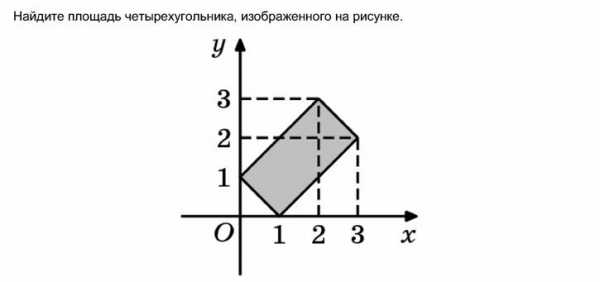 В7
В7
В8
В9
В10
В11
C1 Решите систему уравнений:
C2 Решите неравенство:
log √1/6 ( 5 x+1 — 25x ) ≤ -2
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ( 10 КЛАСС) ВАРИАНТ 2
В1
В2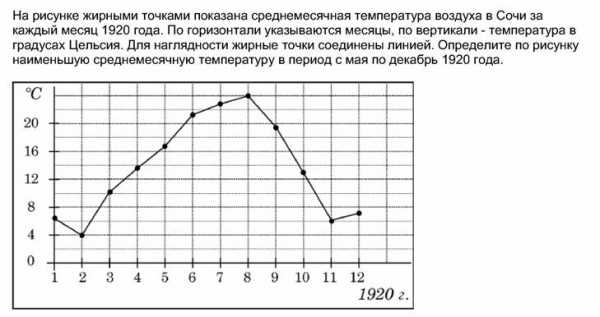
В3В4
В5В6
В7
В8
В9
В10
В11
C1 Решите систему уравнений:
C2 Решите неравенство:
log√1/2 ( 3 x+2 — 9 x ) ≥ -6
О Т В Е Т Ы
| Вариант 1 | Вариант 2
|
В1 | 10080 | 23 |
В2 | 10 | 6 |
В3 | — 0,75 | 2,75 |
В4 | 0,1 | 12 |
В5 | 178200 | 17050 |
В6 | 4 | 12 |
В7 | 4 | 512 |
В8 | -40 | — 24,32 |
В9 | — 10,5 | 3,5 |
В10 | 30 | 7 |
В11 | 20 | 8 |
С 1 | ( 0,5; 1,5) | ( 5; 1 ) |
С 2 | [log 5 2; log 5 3] | (-∞; 0] U [ log 3 8; 2) |
school1gorodec.ucoz.ru
Итоговая контрольная работа в 10 классе
Итоговая контрольная работа по математике – 10 кл.
Контрольная работа по математике для учащихся 10 класса содержит задания алгебраического и геометрического материала. На выполнение работы отводится 4 часа. Работа состоит из 12 заданий. Задания В1-В9 базового уровня сложности по материалу курса математики. Задания С1-С3 повышенной сложности. При выполнении контрольной работы необходимо записать полное решение и ответ. Работа предлагается учащимся в конце учебного года. Она позволяет проверить знания учащихся по темам: «Преобразование рациональных выражений», «Тригонометрические уравнения», «Логарифмические уравнения», «Показательные уравнения», «Иррациональные уравнения», «Решение уравнений с параметром», «Вычисление объема и площади поверхности куба», «Нахождение угла между плоскостями».
Урок соответствует ФГОС.
Цели:
Образовательная: проверить усвоение учащимися изученного материала.
Развивающая: способствовать совершенствованию практических навыков учащихся.
Воспитательная: психологический настрой на сдачу ЕГЭ учащимися.
27-33 балла – «5»;
16- 26 баллов – «4»;
10-15 баллов – «3»
Просмотр содержимого документа
«Итоговая контрольная работа в 10 классе »
Итоговая контрольная работа по математике – 10 кл.
Контрольная работа по математике для учащихся 10 класса содержит задания алгебраического и геометрического материала. На выполнение работы отводится 4 часа. Работа состоит из 12 заданий. Задания В1-В9 базового уровня сложности по материалу курса математики. Задания С1-С3 повышенной сложности. При выполнении контрольной работы необходимо записать полное решение и ответ. Работа предлагается учащимся в конце учебного года. Она позволяет проверить знания учащихся по темам: «Преобразование рациональных выражений», «Тригонометрические уравнения», «Логарифмические уравнения», «Показательные уравнения», «Иррациональные уравнения», «Решение уравнений с параметром», «Вычисление объема и площади поверхности куба», «Нахождение угла между плоскостями».
Урок соответствует ФГОС.
Цели:
Образовательная: проверить усвоение учащимися изученного материала.
Развивающая: способствовать совершенствованию практических навыков учащихся.
Воспитательная: психологический настрой на сдачу ЕГЭ учащимися.
Контрольная работа 10 класс
В1. Вычисли:
а) (1б.)
б) (1б.)
в) (1б.)
В2. Реши уравнения:
а) (1б.)
б) (1б.)
в) (1б.)
г) 1. (1б.) 2. Найди корни на (1б.)
В3. Реши графически:
а) 2х = 6-х (1б.)
б) (1б.)
B4. В правильной 4-х угольной пирамиде сторона основания а = 6см, боковое ребро b = 5см. Найти:
а) h, H (1б.)
б) Sпир (дм2) (1б.)
в) (бок. ребром; основанием) (1б.)
г) (бок. гр; основанием) (1б.)
В5. y = -2cosx.
а) Построить график при х (1б.)
б) Описать свойства функции у на (1б.)
В6. Дано: cosα=0,6; α Найти:
а) sinα (1б.)
б) (1б.)
в) cos2α (1б.)
В7. Реши неравенство (2б.)
В8. Реши неравенство (2б.)
В9. Vкуба=8л. Найти:
а) Площадь поверхности куба(см2) . (1б.)
б) Vкуба , ребро которого в 5 раз больше ребра данного куба. (1б.)
в) S поверхности куба ребро которого в 5 раз больше ребра данного куба (дм2). (1б.)
С1. В кубе найти угол между плоскостями (А1ВD)и(ABC). (2б.)
С2 Реши неравенство: (2б.)
С3 Найди все значения параметра Р, при которых уравнение х2 = Р(х-3) имеет хотя бы
один корень. (3б.)
27-33 балла – «5»;
16- 26 баллов – «4»;
10-15 баллов – «3»
kopilkaurokov.ru
Итоговая контрольная работа по математике 10 класс.
Итоговая контрольная работа по математике 10класс.
Базовый уровень
В – 1 В — 2
1. Вычислить: 1. Вычислить:
2. Упростить выражение при 2. Упростить выражение при
3. Решить уравнение: 3. Решить уравнение:
2) 2) .
4. Решите уравнение 4. Решите уравнение
5. Решите неравенство: 5. Решите неравенство: 5.
6. Доказать тождество: 6. Доказать тождество:
7. Решить уравнение 7. Решить уравнение
8. В прямоугольном параллелепипеде 8. В прямоугольном параллелепипеде
ABCDA1B1C1D1 . ABCDA1B1C1D1 . Найдите площади Найдите площади
боковой и полной поверхности боковой и полной поверхности параллелепипеда. параллелепипеда.
multiurok.ru
Итоговая контрольная работа по математике (для учащихся 10 класса)
Математика, 10 класс
Урок
Тема: Итоговая контрольная работа за 10 класс (тест)
Цель: проверить усвоение программных знаний учащихся за 10 класс; способствовать развитию внимания при выполнении задания; развивать логическое мышление.
Тип урока: проверка и коррекция знаний, умений и навыков.
Наглядность и оборудование: текст итоговой контрольной работы.
Ход урока:
Организационный момент.
Сообщение темы и постановка цели урока.
Текст контрольной работы.
1 вариант
1 уровень: каждое задание оценивается в 1 бал
Найдите значение выражения
а) – 6 б) в) 6 г) 11,25
Упростите выражение
а) – 4 б) 4 в) г) 0
Упростите выражение
а) б) в) 0 г)
Найдите значение выражения , если ,
а) б) в) г)
Через любые три точки, не лежащие на одной прямой, проходит …
а) бесконечно много плоскостей б) две плоскости в) единственная плоскость
Прямая с, параллельная прямой а, пересекает плоскость β. Прямая b параллельна прямой а, тогда:
а) прямые b и с пересекаются; б) прямая b лежит в плоскости β;
в) прямые b и с скрещиваются; г) прямые b и с параллельны;
Выберите верное утверждение.
а) если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая также параллельна данной плоскости;
б) если две прямые параллельны третьей прямой, то они пересекаются;
в) если прямая и плоскость не имеют общих точек, то прямая лежит в плоскости;
г) прямая и плоскость называются скрещивающимися, если они не имеют общих точек.
Какая градусная мера угла между перпендикулярными плоскостями?
а) 180° б) 0° в) 90° г) 60°.
Плоскость γ, перпендикулярна прямой пересечения плоскостей α и β таких, что α┴β, и пересекает их по прямым a и b. Каково взаимное расположение прямых a и b?
а) Параллельные б) пересекаются в) скрещивающиеся г) перпендикулярны.
2 уровень: задание оценивается в 3 бала
Решите уравнение:
2 вариант
1 уровень: каждое задание оценивается в 1 бал
Найдите значение выражения
а) – 14 б) -30 в) 34 г)
Упростите выражение
а) 0 б) 2 в) г)
Упростите выражение
а) 0 б) в) г)
Найдите значение выражения , если
а) б) в) – 0,5 г) 0,5
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой…
а) лежит одна точка б) лежат все общие точки в) лежит две точки
Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
а) Скрещиваются или пересекаются; б) пересекаются или параллельны;
в) скрещиваются или параллельны; г) только параллельны;
Выберите верное утверждение.
а) если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости;
б) если плоскость проходит через данную прямую, параллельную другой плоскости, то эта плоскость параллельна другой плоскости;
в) если две прямые параллельны третьей прямой, то они скрещивающиеся;
г) если две прямые пересекают плоскость, то они параллельны;
Прямая а перпендикулярна плоскости α и лежит в плоскости β. Какое взаимное расположение плоскостей α и β?
а) Параллельные б) перпендикулярны в) совпадают
Сколько наклонных можно провести из точки к плоскости?
а) Одну б) две в) ни одной г) множество
2 уровень: задание оценивается в 3 бала
Решите уравнение: .
Подведение итогов урока.
Учащиеся рассматривают задания, с которыми не справились на контрольной работе.
Домашнее задание.
kopilkaurokov.ru



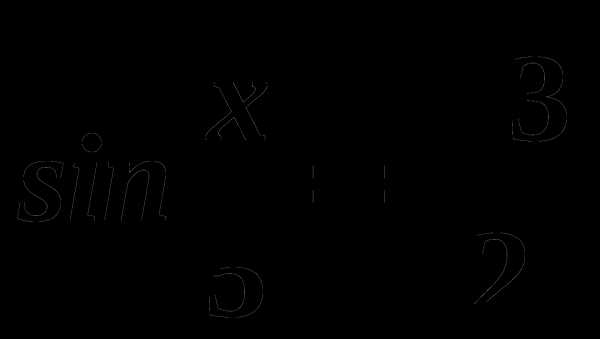
 , n € Z 3)
, n € Z 3) 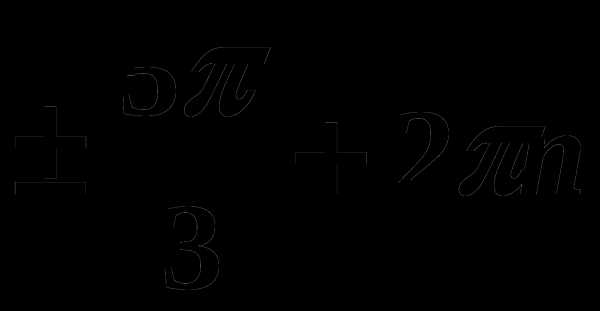 , n € Z
, n € Z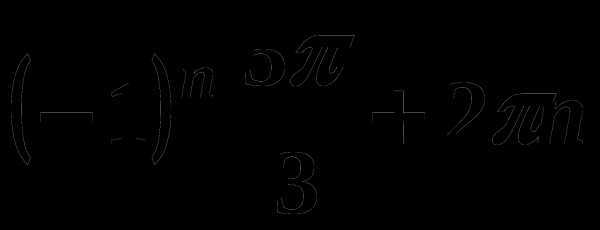 , n €Z 4)
, n €Z 4) 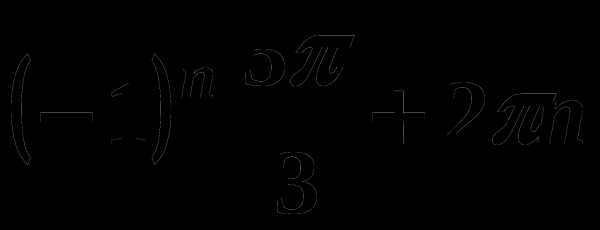 , n € Z
, n € Z
 2) [-3; 7] 4) [0; +∞)
2) [-3; 7] 4) [0; +∞)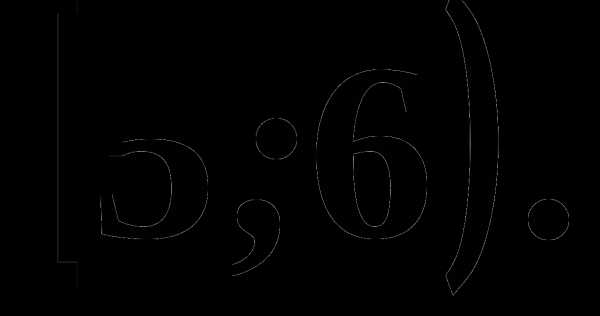
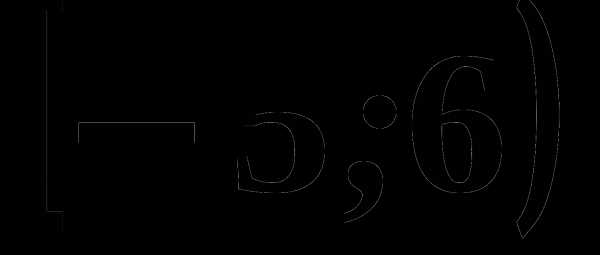
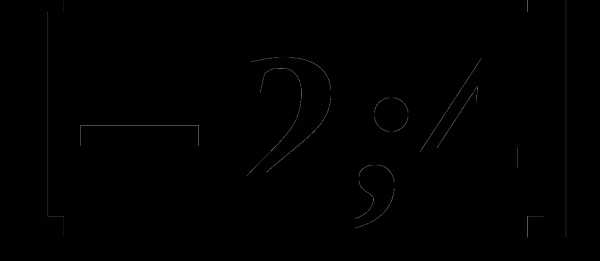

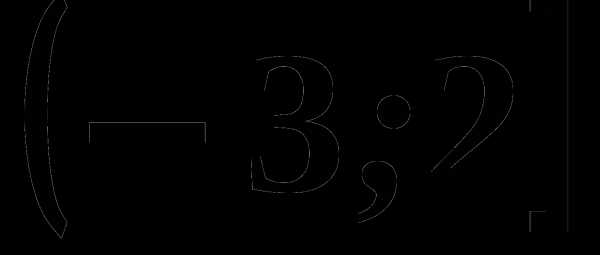
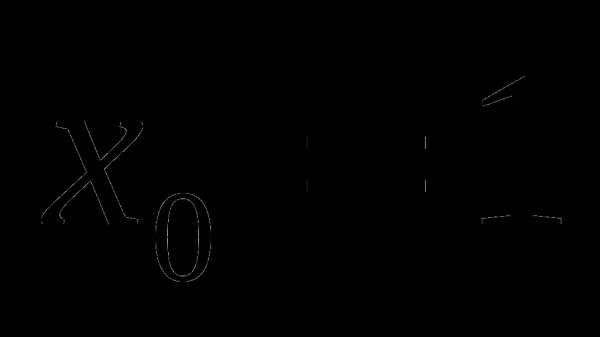
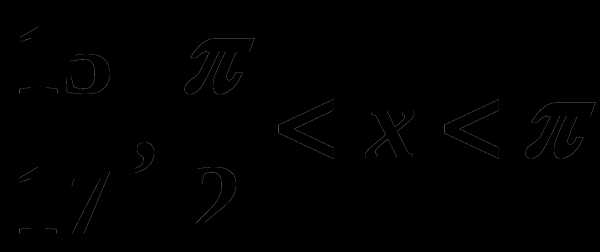

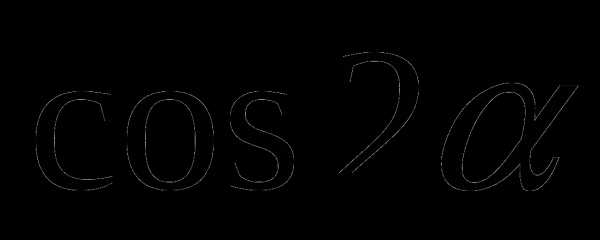 ; 3)
; 3)  ;
;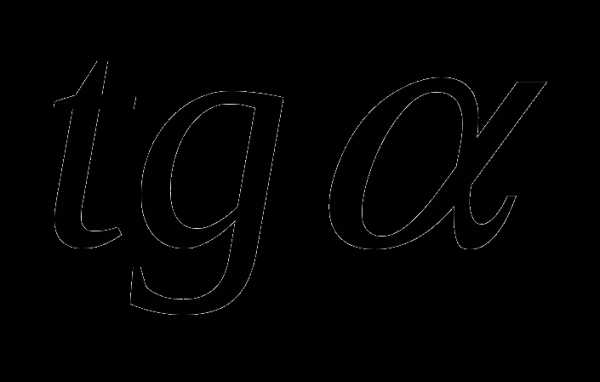 ; 4) .
; 4) .
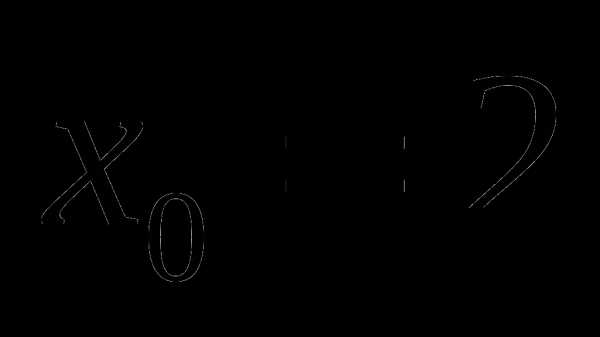 .
.
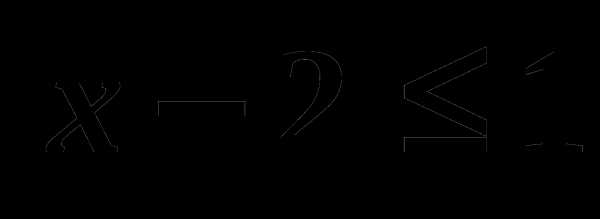
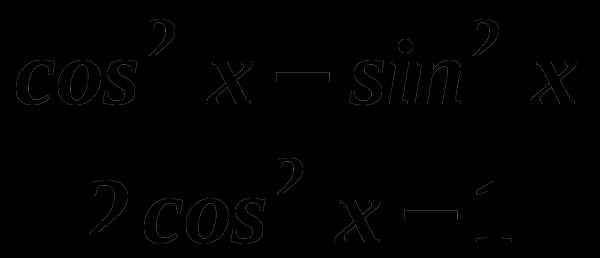
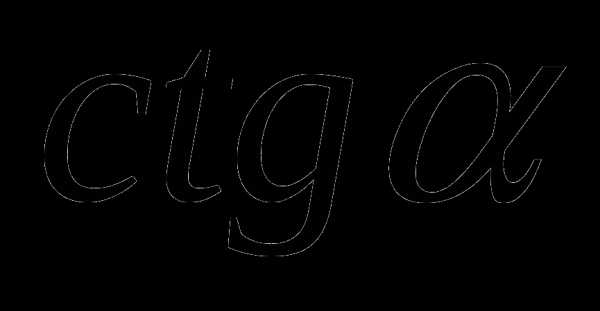 ;
;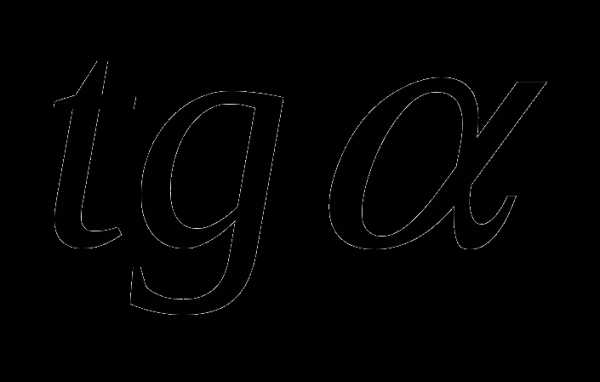 ; 4)
; 4) 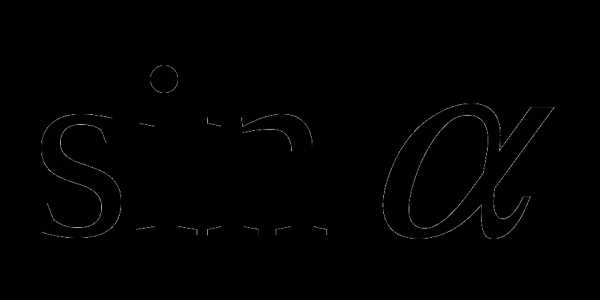 .
.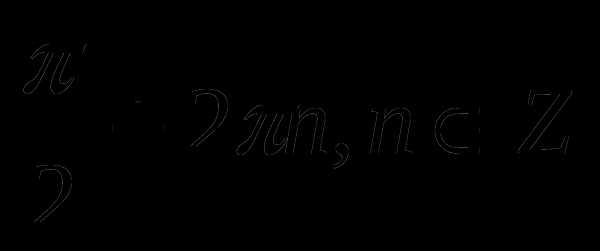 ; 3)
; 3) 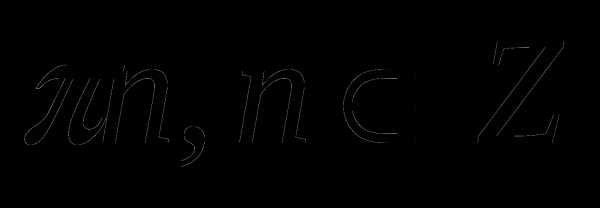 ;
; ; 4) .
; 4) . 
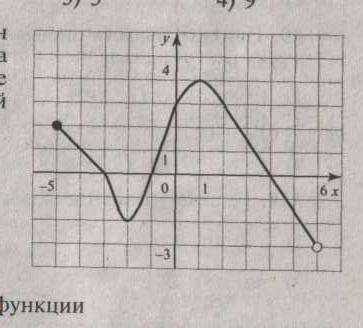
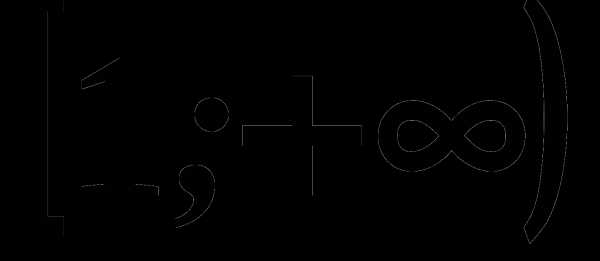
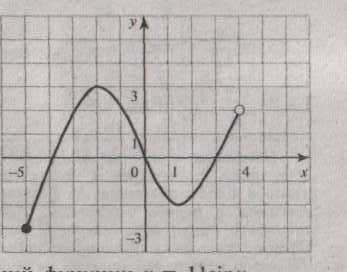 4. На рисунке изображен график функции, заданной на промежутке
4. На рисунке изображен график функции, заданной на промежутке 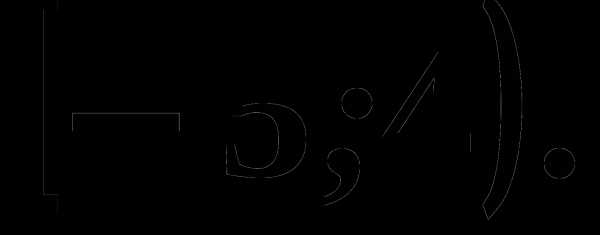 Укажите множество значений этой функции.
Укажите множество значений этой функции.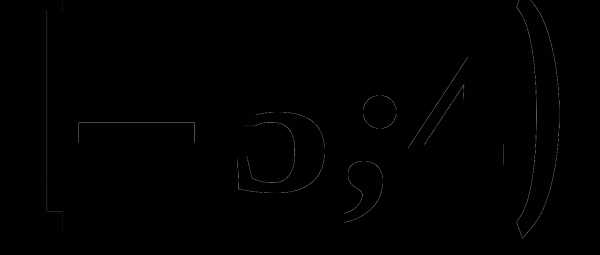
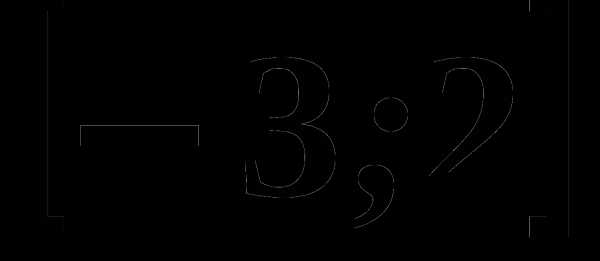
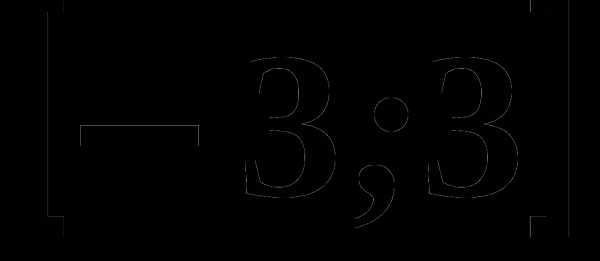
 .
.
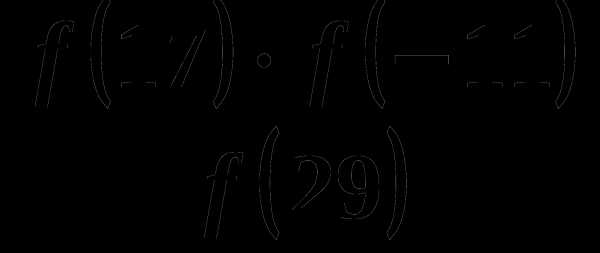 , если f(5)=3.
, если f(5)=3.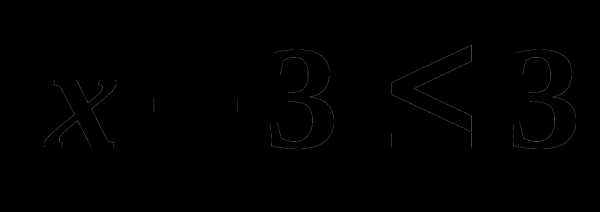

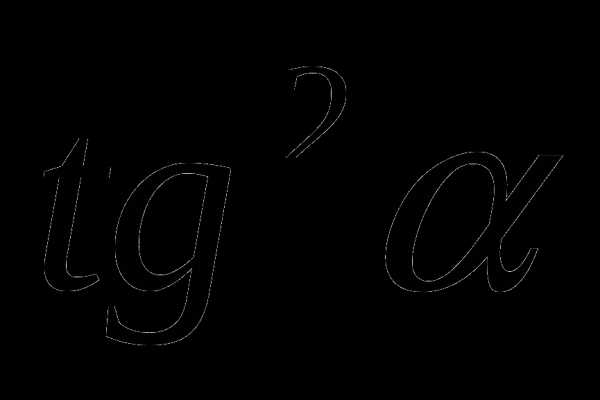 ; 3)
; 3) 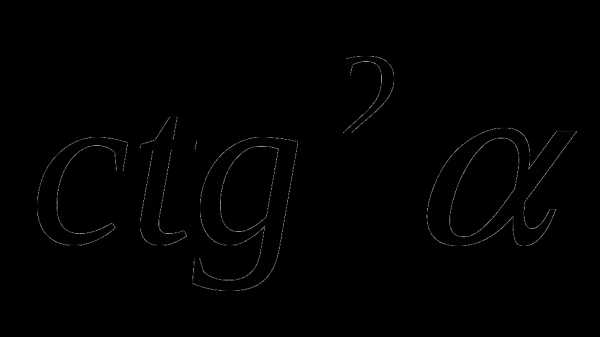 ;
;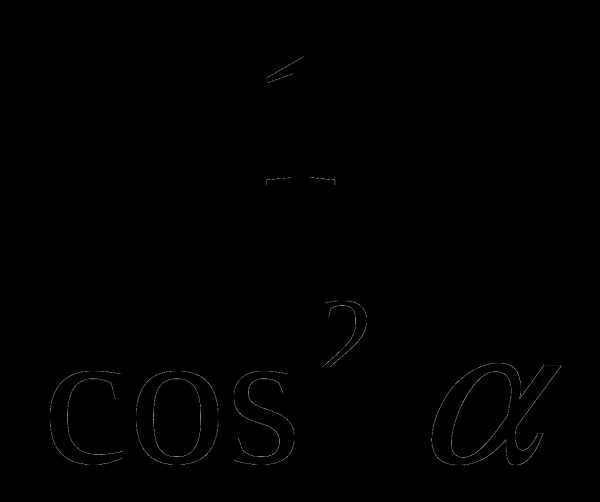 ; 4) 4.
; 4) 4.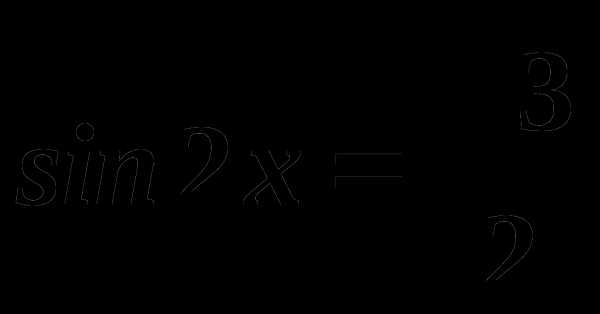
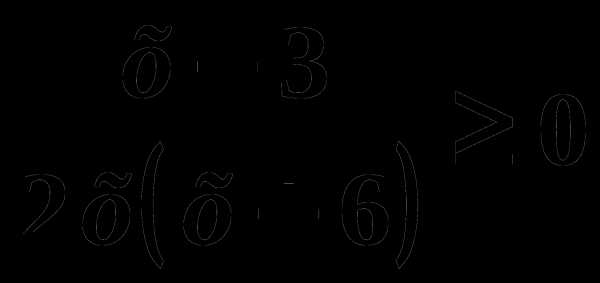
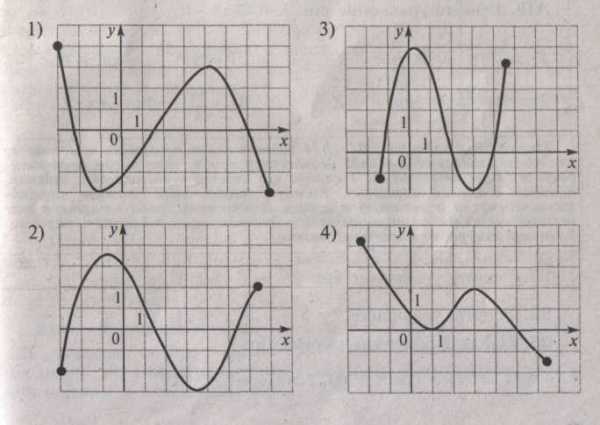
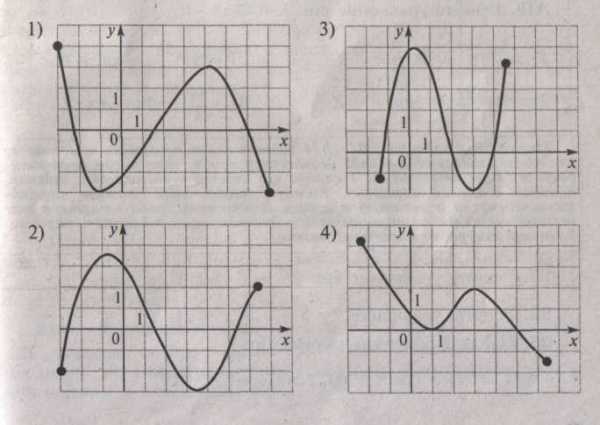
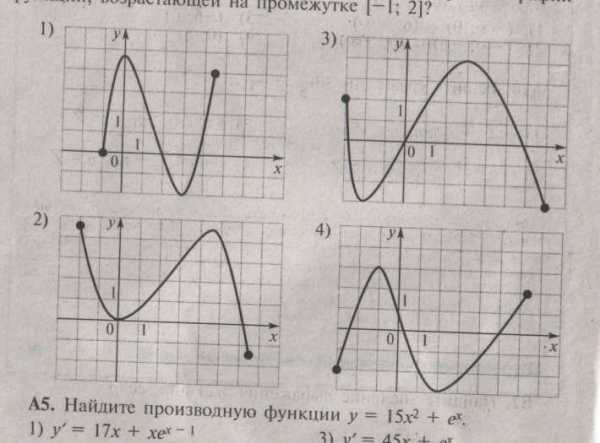 А4. На каком из следующих рисунков изображен график функции, возрастающей на промежутке
А4. На каком из следующих рисунков изображен график функции, возрастающей на промежутке 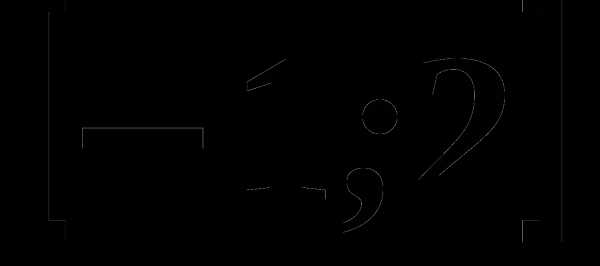
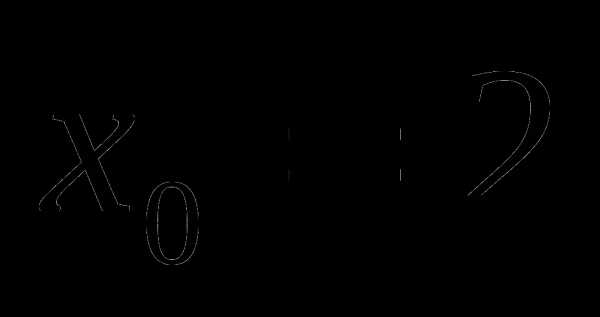 .
.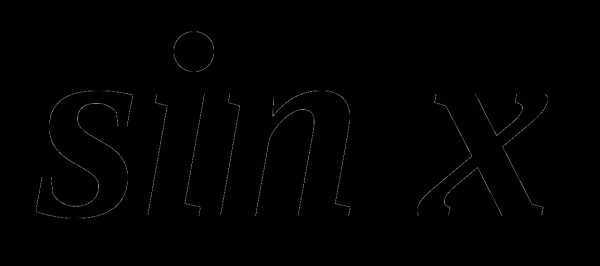 , если cosx=
, если cosx=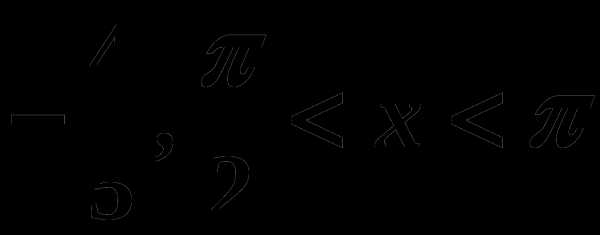
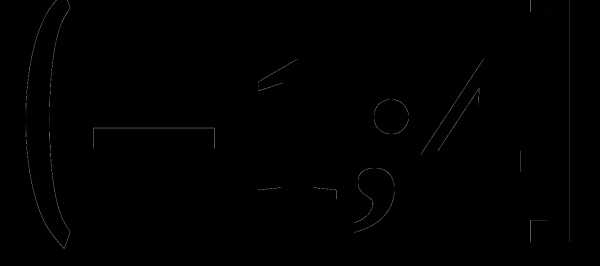 она задается формулой f(x)=1+2x-x2. Найдите значение выражения 2f(-15)+3f(18).
она задается формулой f(x)=1+2x-x2. Найдите значение выражения 2f(-15)+3f(18).
 ; 3)
; 3)  ;
;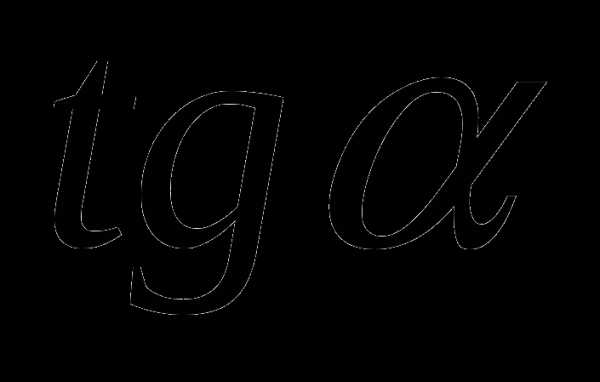 .
.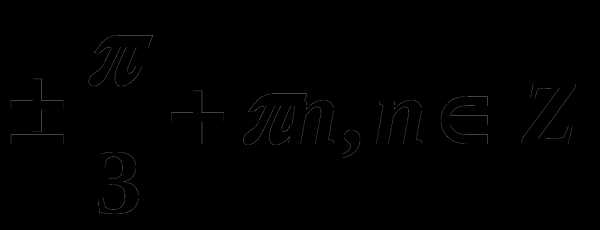 ; 3)
; 3) 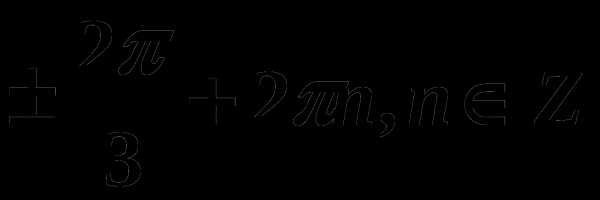
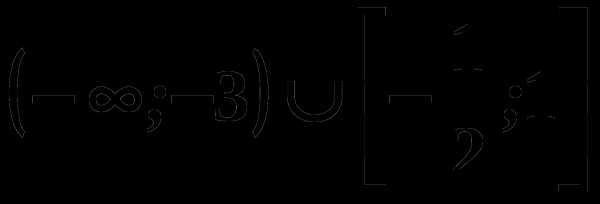 ; 3)
; 3)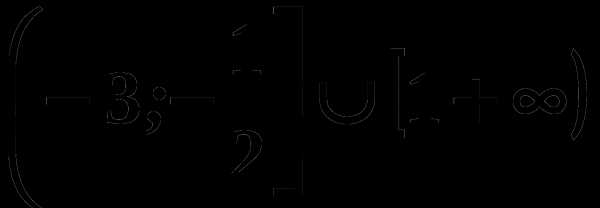 ;
; .
.
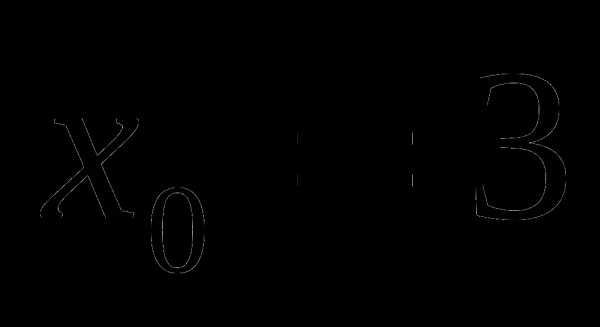 .
.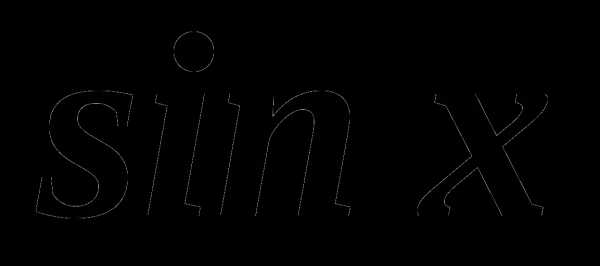 , если cosx=
, если cosx=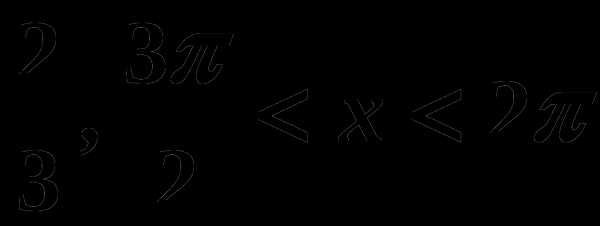
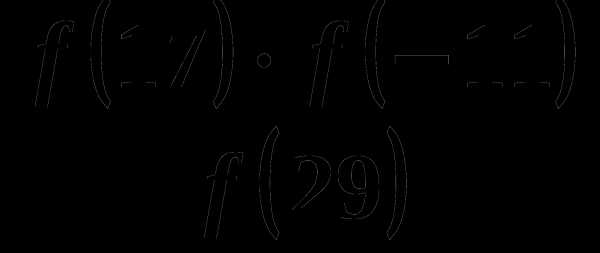 , если f(5)=3.
, если f(5)=3.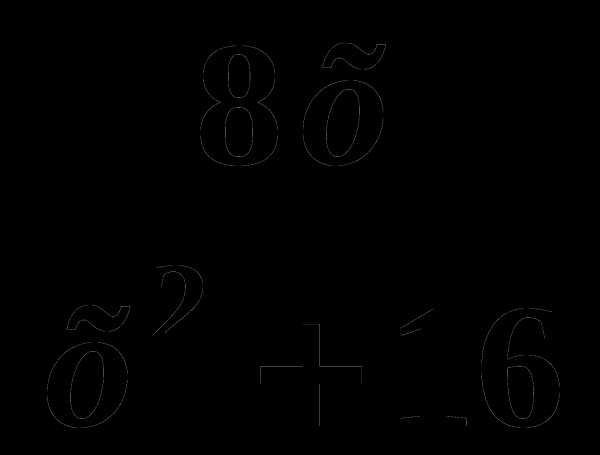 при
при 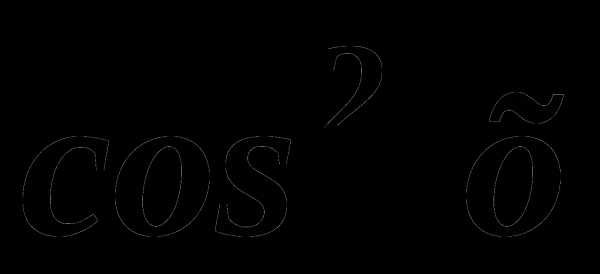 ; 4)sin2x.
; 4)sin2x.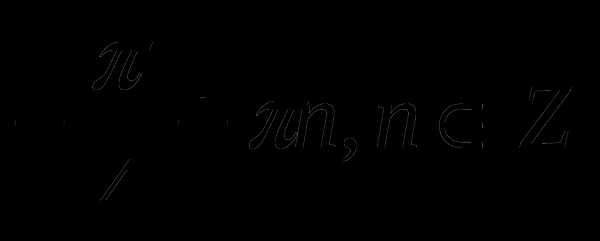 ; 3)
; 3)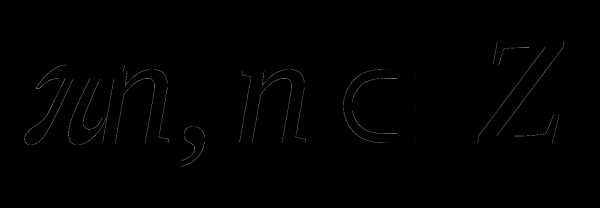
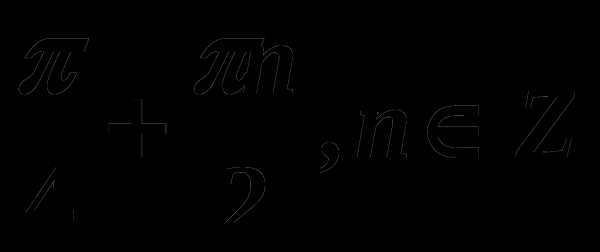 ; 4) .
; 4) .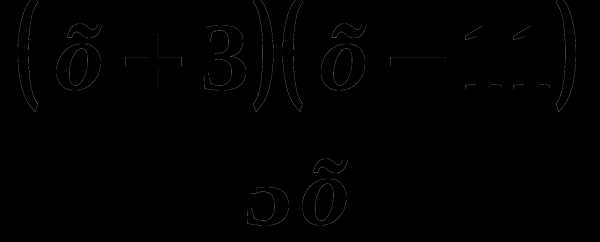
 А5. Найдите множество значений функции
А5. Найдите множество значений функции  .
.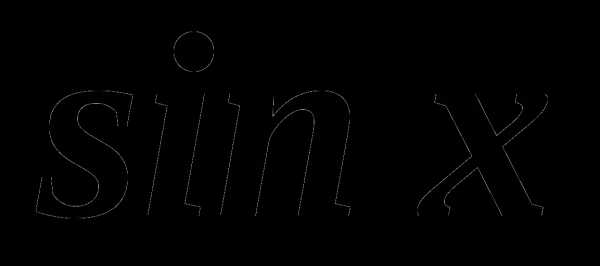 , если cosx=
, если cosx=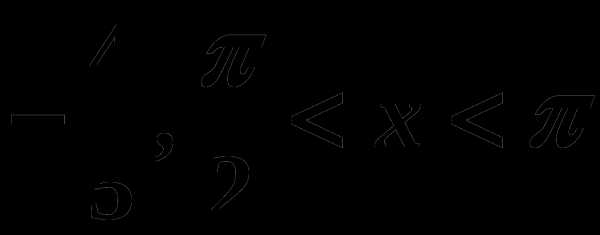
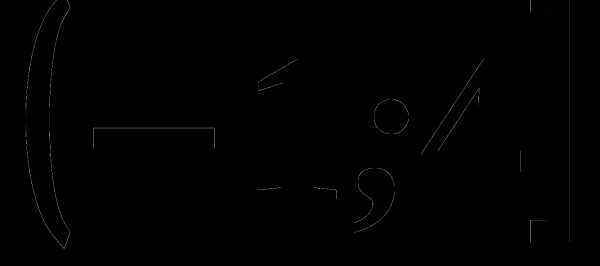 она задается формулой f(x)=1+2x-x2. Найдите значение выражения 2f(-15)+3f(18).
она задается формулой f(x)=1+2x-x2. Найдите значение выражения 2f(-15)+3f(18).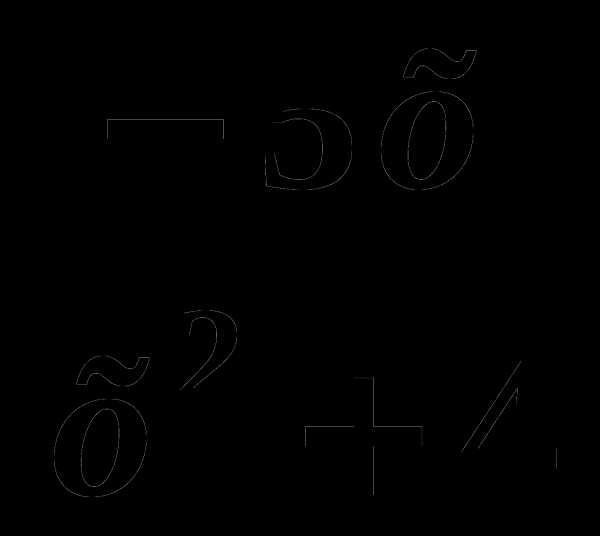 при .
при .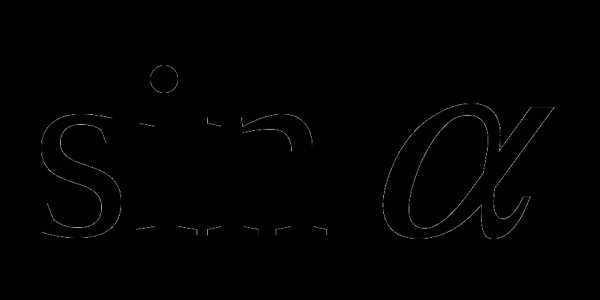 3)
3)
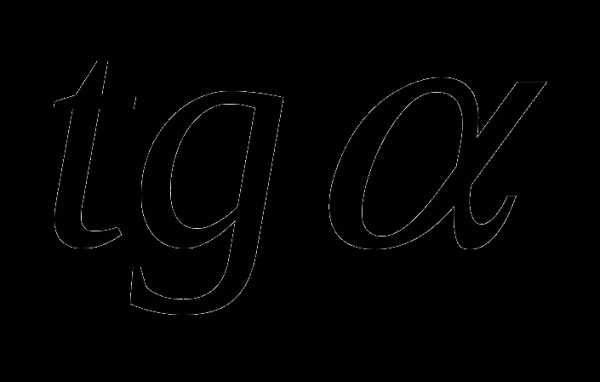 4) 1.
4) 1.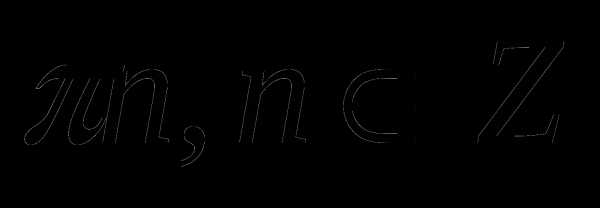 3)
3) 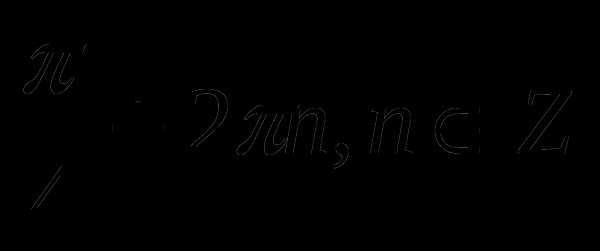
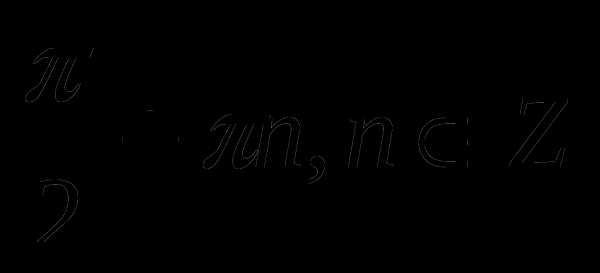 4)
4) 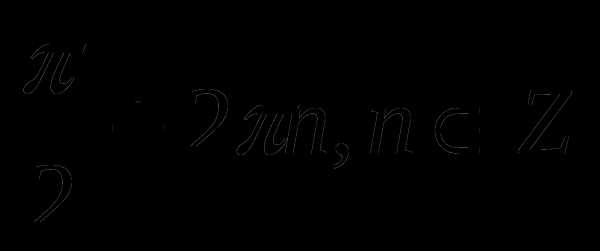
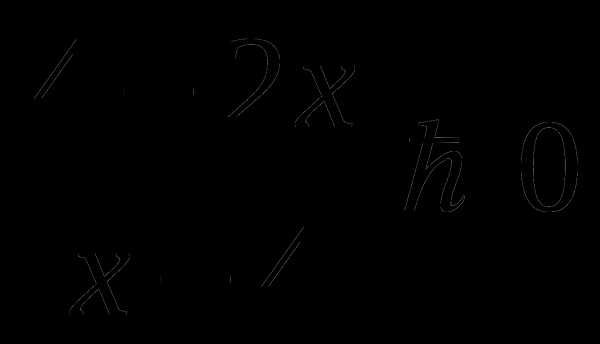
 ) [-1; 2]
) [-1; 2] .
. ;
;  ].
].