Формулы кинематики по физике 10 класс – Разработка урока по физике «Основные понятия и уравнения кинематики. Формулы кинематики»

Основные понятия кинематики | ЭТО ФИЗИКА

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.

Механическое движение относительно (см 1.2) Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.

Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.

В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.

В системе СГС (Сантиметр, грамм, секунда) приняты соответственно

сантиметр и секунда.

Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела.

Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.

Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.

Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.

Понятие материальной точки играет важную роль в механике.

Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.

Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени

радиус-вектора     (векторный способ), проведенного из

начала координат до данной точки (рис. 1.1.1).

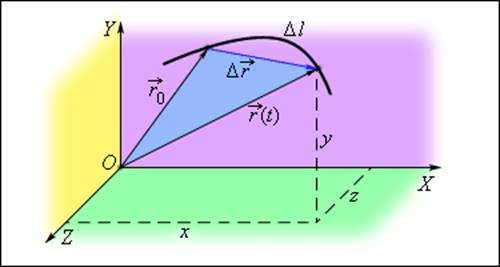
Рисунок 1.1.1.

Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t)

 и радиус-вектора

 – радиус-вектор положения точки в начальный момент времени

 

Перемещением тела

     

называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

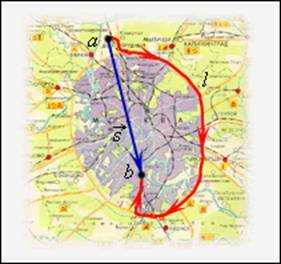
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения  При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

Рисунок 1.1.2. Пройденный путь l и вектор перемещения  при криволинейном движении тела. a и b – начальная и конечная точки пути

Для характеристики движения вводится понятие средней скорости:

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt,

В математике такой предел называют производной и обозначают

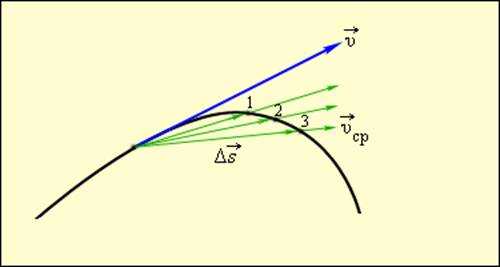
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

Рисунок 1.1.3. Средняя и мгновенная скорости.  – перемещения за времена  соответственно.   При t→0

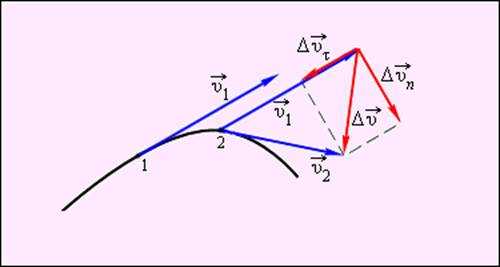
При движении тела по криволинейной траектории его скорость  изменяется по модулю и направлению. Изменение вектора скорости   за некоторый малый промежуток времени Δt можно задать с помощью вектора  (рис. 1.1.4).

Вектор изменения скорости  за малое время Δt можно разложить на две составляющие:  направленную вдоль вектора  (касательная составляющая), и  направленную перпендикулярно вектору  (нормальная составляющая).

Рисунок 1.1.4. Изменение вектора скорости по величине и направлению.  – изменение вектора скорости за время Δt

Мгновенным ускорением (или просто ускорением)  тела называют предел отношения малого изменения скорости  к малому промежутку времени Δt, в течение которого происходило изменение скорости:

Направление вектора ускорения  в случае криволинейного движения не совпадает с направле нием вектора  скорости  Составляющие вектора ускорения  называют касательным (тангенциальным)   и нормальным   ускорениями (рис. 1.1.5).

Рисунок 1.1.5. Касательное и нормальное ускорения

Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

Вектор   направлен по касательной к траектории.

Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.

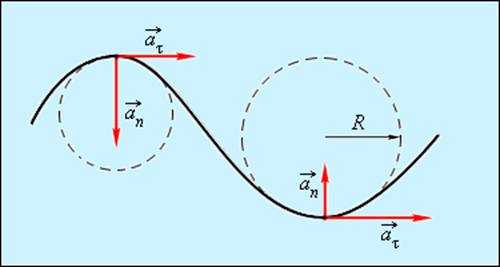
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

Рисунок 1.1.6. Движение по дугам окружностей

Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:  

(Эта формула сделана в Mathtype

)

Вектор      всегда направлен к центру окружности.

Из рис. 1.1.5 видно, что модуль полного ускорения равен

Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , скорость   и ускорение . Путь l является скалярной величиной. Перемещение  , скорость   и ускорение  – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.

www.its-physics.org

Основные понятия кинематики и формулы :: SYL.ru

Для того чтобы понять, что изучает механика, необходимо рассмотреть, что означает движение в самом общем смысле. Значение этого слова подразумевает под собой изменение чего-либо. Например, политическое движение выступает за равноправие разных слоев населения вне зависимости от их расовой принадлежности. Раньше его не было, затем что-то изменилось и теперь каждый человек имеет равные права. Это движение цивилизации вперед. Еще пример — экологическое. В прошлом, выбравшись на природу, никто не задумывался о том, что оставляет после себя мусор. Сегодня же любой цивилизованный человек соберет его за собой и отвезет в специально отведенное место для дальнейшей утилизации.

Что-то подобное можно наблюдать и в механике. При механическом движении изменяется положение тела в пространстве относительно других предметов с течением времени. Основная задача механики — указать, где находится объект в любой момент, учитывая даже тот, который еще не наступил. То есть, предсказать положение тела в заданное время, а не только узнать, где именно в пространстве оно находилось в прошлом.

Кинематика — это раздел механики, который изучает движение тела, не анализируя его причины. Это значит, что она учит не объяснять, а описывать. То есть, придумать способ, с помощью которого можно было бы задать положение тела в любой момент времени. Основные понятия кинематики включают в себя скорость, ускорение, расстояние, время и перемещение.

Сложность в описании движения

Первая проблема, с которой сталкивается кинематика — это то, что у каждого тела есть определенный размер. Допустим, необходимо описать движение какого-нибудь предмета. Это значит научиться обозначать его положение в любой момент времени. Но каждый предмет занимает в пространстве какое-то место. То есть, что все части этого объекта в один и тот же момент времени занимают разное положение.

Какую точку в таком случае необходимо взять для описания нахождения всего предмета? Если учитывать каждую, то расчеты окажутся слишком сложными. Поэтому решение ответа на этот вопрос можно максимально упростить. Если все точки одного тела движутся в одинаковом направлении, то для описания движения достаточно одной такой, которую содержит это тело.

Виды движения в кинематике

Существует три типа:

1. Поступательным называется движение, при котором любая прямая проведенная в теле остается параллельной самой себе. Например, автомобиль, который движется по шоссе, совершает такой вид движения.
2. Вращательным называется такое движение тела при котором все его точки движутся по окружностям с центрами, лежащими на одной прямой, называемой осью вращения. Например, вращение Земли относительно своей оси.
3. Колебательным называется движение, при котором тело повторяет свою траекторию через определенный отрезок времени. Например, движение маятника.

Основные понятия кинематики — материальная точка

Любое сложное движение можно описать как комбинацию двух простейших видов — поступательного и вращательного. Например колесо автомобиля или юла, стоящая на движущейся прямо платформе, участвуют одновременно в этих двух типах перемещения.

Но что делать, если движение тела нельзя представить в виде комбинации? Например, если автомобиль едет по ухабистой дороге, его положение будет меняться очень сложным образом. Если рассчитывать только то, что этот транспорт перемещается из одного города в другой, то в такой ситуации становится не важно какого размера тело движется из точки А в точку Б и им можно пренебречь. В данном случае важно только за какое время автомобиль прошел определенное расстояние и с какой скоростью двигался.

Однако следует учитывать, что пренебрежение размером допускается не в каждой задаче. Например, если рассчитывать движение при парковке автомобиля, то игнорирование величины данного тела, приведет к пагубным последствием. Поэтому, только в тех ситуациях, когда в рамках конкретной задачи, размерами движущегося объекта можно пренебречь, то такое тело принято называть материальной точкой.

Формулы кинематики

Числа, с помощью которых задается положение точки в пространстве, называются координатами. Чтобы определить его на прямой, достаточно одного числа, когда речь идет о поверхности, то двух, о пространстве — трех. Большего количества чисел в трехмерном мире (для описывания положения материальной точки) не требуется.

Существует три основных уравнения для понятия кинематики, как раздела о движении тел:

1. v = u + at.
2. S = ut + 1/2at².
3. v² = u² + 2as.

Где:

v = конечная скорость,

u = Начальная скорость,

a = ускорение,

s = расстояние, пройденное телом,

t = время.

Формулы кинематики в одномерном пространстве:

V = V_o + at

X — X_o = V_o t + 1/2a t2

V² = V_o¹ + 2a (X — X_o)

X — X_o = 1\2 (V_o + V) t
Где,

V — конечная скорость (м / с),

V_o — начальная скорость (м / с),

a — ускорение (м / с²),

t — время (с),

X — конечное положение (м),

X₀ — начальное положение (м).

Формулы кинематики в двумерном пространстве

Поскольку следующие уравнения используются для описания материальной точки на плоскости, стоит рассматривать ось X и Y.

Учитывая направление Х:

a_x = constant

V_fx = V_ix + a_x Δt

X_f = X_i + V_ix Δt +1/2a_x Δt²

Δt = V_fx-V_ix /a_x

V_fx² = V_ix² + 2ax Δx

X_f = X_i + 1/2 (V_fx + V_ix) Δ t .
И учитывая направление y:

a_y = constant

V_fy = V_iy + a_y Δt

y_f = y_i + V_iy Δt + 1/2 a_x Δt²

Δt = V_fy — V_iy/a_y

V_fy² = V_iy² + 2_ay Δ_y

y_f = y_i +1/2 (V_fy + V_iy) Δt.

Где,

V_f — конечная скорость (м / с),

V_i — начальная скорость (м / с),

a — ускорение (m / с²),

t — время (с),

X — конечное положение (м),

X₀ — начальное положение (м).

Перемещение брошенного снаряда — лучший пример для описания движения объекта в двух измерениях. Здесь тело перемещается, как в вертикальном положении У, так и в горизонтальном положении Х, поэтому можно сказать, что предмет имеет две скорости.

Примеры задач по кинематике

Задача 1: Начальная скорость грузовика равна нулю. Изначально этот объект находится в состоянии покоя. На него начинает действовать равномерное ускорение в течение временного интервала 5,21 секунды. Расстояние, пройденное грузовиком, составляет 110 м. Найти ускорение.

Решение:
Пройденное расстояние s = 110 м,
начальная скорость v_i = 0,
время t = 5,21 с,
ускорение a =?
Используя основные понятие и формулы кинематики, можно заключить, что,
s = v_it + 1/2 a t²,
110 м = (0) × (5.21) + 1/2 × a (5.21)²,
a = 8,10 м / с².

Задача 2: Точка движется вдоль оси х (в см), после t секунд путешествия, ее можно представить, используя ​​уравнение x = 14t² — t + 10. Необходимо найти среднюю скорость точки, при условии, что t = 3s?

Решение:
Положение точки при t = 0, равно x = 10 см.
При t = 3s, x = 133 см.
Средняя скорость, V_av = Δx/Δt = 133-10/3-0 = 41 см / с.

Что такое тело отсчета

О движении можно говорить только если существует что-то, относительно чего рассматривается изменение положения изучаемого объекта. Такой предмет называется телом отсчета и оно условно всегда принимается за неподвижное.

Если в задаче не указано в какой системе отчета движется материальная точка, то телом отсчета считается земля по умолчанию. Однако, это не означает, что за неподвижный в заданный момент времени объект, относительно которого совершается движение, нельзя принять любой другой удобный для расчета. Например, за тело отсчета можно взять движущийся поезд, поворачивающий автомобиль и так далее.

Система отсчета и ее значение в кинематике

Для описания движения необходимы три составляющие:

1. Система координат.
2. Тело отсчета.
3. Прибор для измерения времени.

Тело отсчета, система координат, связанная с ним и прибор для измерения времени образуют систему отсчета. Бессмысленно говорить о движении, если ее не указывать. Правильно подобранная система отсчета, позволяет упростить описание перемещения и, наоборот, усложнить, если она выбрана неудачно.

Именно по этой причине, человечество долго считало, что Солнце движется вокруг Земли и что она находится в центре вселенной. Такое сложное движение светил, связанное с тем, что земные наблюдатели находятся в системе отсчета, которая очень замысловато движется. Земля вращается вокруг свое оси и одновременно вокруг Солнца. На самом деле, если сменить систему отсчета, то все движения небесных тел легко описываются. Это в свое время было сделано Коперником. Он предложил собственное описание мироустройства, в котором Солнце неподвижно. Относительно него описать движение планет гораздо проще, чем если телом отсчета будет являться Земля.

Основные понятия кинематики — путь и траектория

Пусть некоторая точка первое время находилась в положении А, спустя некоторое время она оказалась в положении В. Между ними можно провести одну линию. Но для того, чтобы эта прямая несла больше информации о движении, то есть было понятно откуда и куда двигалось тело, это должен быть не просто отрезок, а направленный, обычно обозначающийся буквой S. Перемещением тела, называется вектор, проведенный из начального положения предмета в конечное.

Если тело изначально находилось в точке А, а затем оказалось в точке В, это не означает, что оно двигалось только по прямой. Из одного положения в другое можно попасть бесконечным количеством способов. Линия, вдоль которой движется тело, является еще одним основным понятием кинематики — траекторией. А ее длина называется путь, который обычно обозначается буквами L или l.

www.syl.ru

Перечень формул по курсу физики 10 класса – Документ 1 – УчМет

Муниципальное автономное общеобразовательное учреждение

МАОУ СОШ №11 г. Североуральск Свердловской области

Учебник: Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский. Физика, 10 класс. Классический курс. М.: Просвещение, 2010

МЕХАНИКА
Кинематика
Уравнения равномерного движения x = x0 +t s =	x – координата тела ,м x0 – начальная координата тела ,м — начальная скорость тела, м/с — скорость тела, м/с t –время, с a – ускорение, м/с2 s – перемещение, м cp – средняя скорость, м/с
Уравнения равноускоренного прямолинейного движения x = x0 +t + s = s = ; s = a = = cp =
Криволинейное и вращательное движение ω = ; ω = ; ω = ω R ; T= ; T= aц = ; aц = ω2 R	— угловое перемещение, рад (радиан) ω – угловая скорость ,рад/с T – период, с ν – частота вращения, с-1 aц –центростремительное ускорение , м/с2 -линейная скорость, м/с R –радиус ,м t –время, с — число оборотов ( безразмерное)
Динамика. Законы сохранения
= m второй закон Ньютона	m – масса, кг F- сила, Н (ньютон) a — ускорение, м/с2 k – жесткость деформируемого тела, Н/м x –деформация тела, м r — расстояние, м (метр) G – гравитационная постоянная G = 6,67 ∙10-11 Н∙ м2 /кг2 μ – коэффициент трения (безразмерный) N — сила нормального давления, Н P – вес тела, Н g — ускорение свободного падения, м/с2 A – работа, Дж N – мощность, Вт (ватт) t – время, с – скорость, м/с p – импульс тела, кг∙м/с E – энергия, Дж h – высота , м α – угол, град — масса планеты, кг
Fупр = kx закон Гука
Fтр = μ N сила трения (N — сила нормального давления, Н )
F=G закон всемирного тяготения
g = G ускорение свободного падения
P =mg вес тела в покое или движущегося равномерно прямолинейно
P = m (g +a) вес тела движущегося с ускорением направленным вверх
P = m (g -a) вес тела движущегося с ускорением направленным вниз
A = F s cos α механическая работа
N = ; N = F cos α мощность
Ek = кинетическая энергия
Ep =m g h потенциальная энергия
E = Ek + Ep полная механическая энергия
E = Ek + Ep = const закон сохранения полной механической энергии
A = Ek2 — Ek1 теорема о кинетической энергии
A = -(Ep2 – Ep1) теорема об изменении потенциальной энергии
= m импульс тела
=
01 + 02 = 1 + 2 закон сохранения импульса тела
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Молекулярная физика
плотность вещества	—давление, Па (паскаль) V—объём, м3 Т—термодинамическая температура, К (кельвин) —масса, кг М— молярная масса, кг/моль N—число атомов или молекул (безразмерная) n— концентрация, м-3 Мr—относительная атомная ( молекулярная) масса 0— масса атома, кг — средняя кинетическая энергия, Дж (джоуль) — среднее значение квадрата скорости, м2/с2 ρ—плотность, кг/м3 ν—количество вещества, моль NА— постоянная Авогадро , NА=6,02 ∙1023 моль-1 k— постоянная Больцмана, k=1,38 ∙ 10-23 Дж/К R—универсальная газовая постоянная, R= 8,31 Дж/(моль ∙К) -давление насыщенного пара при данной температуре, Па — относительная влажность воздуха, %
концентрация
; количество вещества
N= ; N= число атомов или молекул
0 N масса вещества
M= 0 молярная масса
= определение давления
= ; основное уравнение молекулярно –кинетической теории
=
связь между давлением идеального газа, его концентрацией и температурой
физический смысл абсолютной температуры
средняя кинетическая энергия
= ; = средняя квадратичная скорость молекул
RT уравнение Менделеева — Клапейрона
уравнение состояния идеального газа, объединенный газовый закон
T=t +273 связь между шкалами Цельсия и Кельвина
100% относительная влажность воздуха
Термодинамика
; ; внутренняя энергия идеального газа	U — внутренняя энергия, Дж — число степеней свободы (безразмерная) А — работа внешних сил , Дж (джоуль) A/— работа газа , Дж (джоуль) Q — количество теплоты, Дж c — удельная теплоёмкость , Дж/(кг К) L (r) — удельная теплота парообразования, Дж/кг λ — удельная теплота плавления, Дж/кг q- удельная теплота сгорания топлива, Дж/кг η -коэффициент полезного действия (безразмерная или %) R—универсальная газовая постоянная, R= 8,31 Дж/(моль ∙К) —давление, Па (паскаль) V—объём, м3 Т—термодинамическая температура, К (кельвин) —масса, кг М— молярная масса, кг/моль
A/=p (V2 – V1) = p ∆V работа газа
Формулы количества теплоты
Q = c (T2 –T1) ; Q= c (t2 — t1) при нагревании и охлаждении Q= r ; ( Q=L ) Q= — r при парообразовании и конденсации Q=λ ; Q = -λ при плавлении и кристаллизации Q=q при сгорании топлива
∆U=A + Q ; Q= ∆U +A/ первый закон термодинамики A =- A/
100% КПД теплового двигателя — количество теплоты, полученное от нагревателя, Дж — количество теплоты, отданное холодильнику, Дж
=100% КПД идеального теплового двигателя Т1 –температура нагревателя, К Т2–температура холодильника, К
ЭЛЕКТРОСТАТИКА
F=k закон Кулона	q—электрический заряд, Кл (кулон) r—расстояние, м (метр) d—расстояние, м k—коэффициент пропорциональности F—сила, Н (ньютон) Е—напряженность электрического поля, В/м, Н/Кл S—площадь, м2 R—радиус, м А—работа, Дж (джоуль) U—напряжение, В (вольт) С—электроёмкость, Ф (фарад) е— элементарный заряд, Кл W—потенциальная энергия, Дж ε—диэлектрическая проницаемость (безразмерная) σ—поверхностная плотность заряда, Кл/м2 —электрическая постоянная Ф/м —потенциал, В (вольт) — объёмная плотность энергии электрического поля Дж/ м3 Физические константы: =8,85 ∙10-12 Ф/м k =9 ∙109 Н м2/Кл2 е =1,6 ∙10-19 Кл
= напряженность электрического поля
E=k напряженность поля точечного заряда
E= напряженность поля бесконечной равномерно заряженной плоскости
E= напряженность поля плоского конденсатора
σ = поверхностная плотность зарядов
ε= диэлектрическая проницаемость
работа перемещения заряда в поле
потенциальная энергия заряда в однородном электростатическом поле
= потенциал
= k потенциал поля точечного заряда
U= напряжение
U=— =∆ напряжение, разность потенциалов
E = связь напряженности с разностью потенциалов в однородном электрическом поле
C= электроёмкость конденсатора
C= электроёмкость плоского конденсатора
C=4 εR электроёмкость сферического проводника
= + + + … при последовательном соединении конденсаторов
C =++ … при параллельном соединении конденсаторов
= ; = энергия электрического поля конденсатора
= =∙ объёмная плотность энергии электрического поля
ЗАКОНЫ ПОСТОЯННОГО ТОКА
I= ; I =n qS сила тока	q—электрический заряд, Кл (кулон) r—внутреннее сопротивление источника тока, Ом —длина проводника, м — удельное электрическое сопротивление , Ом∙м α—температурный коэффициент сопротивления, К-1 T- термодинамическая температура, К I —сила тока, А (ампер) —напряжение, В (вольт) S—площадь, м2 R—сопротивление проводника, Ом А—работа, Дж (джоуль) электродвижущая сила, В (вольт) —работа сторонних сил, Дж Iкор.зам – сила тока короткого замыкания, А -количество проводников (безразмерное) t –время, с P – мощность, Вт Q –количество теплоты, Дж —масса, кг М— молярная масса, кг/моль k –электрохимический эквивалент вещества, кг/Кл валентность вещества (безразмерная) -число Фарадея = 9,6 ∙ 104 Кл/моль
R= сопротивление проводника
R = R0 (1+αt) = R0 (1+α∆T) зависимость сопротивления металлического проводника от температуры
I= закон Ома для участка цепи
электродвижущая сила I= закон Ома для полной цепи
Iкор.зам .= сила тока короткого замыкания
При последовательном соединении проводников Uобщ = U1 + U2 + U3 + … I общ = I 1 = I 2 = I 3 + … R общ = R 1 + R 2 + R 3 + …
При параллельном соединении проводников Uобщ = U 1 =U 2 = U 3 + … I общ = I 1 + I 2 + I 3 + … = + + + … R

www.uchmet.ru

Шпоры по физике.

Кинематика	Модуль 1. Формулы и определения по кинематике Размер архива 14.8 Кb
Динамика	Модуль 2. Формулы и определения по динамике Размер архива 6.59 Кb
Законы сохранения	Модуль 3. Формулы и определения по законам сохранения импульса и энергии Размер архива 7.48 Кb
Динамика сред	Модуль 5. Формулы и определения по динамике сред Размер архива 4.27 Кb
МКТ	Модуль 6. Формулы и определения по молекулярно-кинетической теории Размер архива 3.68 Кb
Термодинамика	Модуль 7. Формулы и определения по термодинамике Размер архива 5.56 Кb
Тепловое расширение	Модуль 8. Формулы и определения по тепловому расширению тел Размер архива 4.03 Кb
Электростатика	Модуль 9. Формулы и определения по электростатике Размер архива 4.06 Кb
Электрический ток	Модуль 1. Формулы и определения по теме электрический ток Размер архива 7.98 Кb
Электромагнетизм	Модуль 2. Формулы и определения по теме электромагнетизм Размер архива 6.88 Кb
Колебания	Модуль 3. Формулы и определения по теме механические и электрические колебания Размер архива 7.10 Кb
Волны	Модуль 4. Формулы и определения по теме волны Размер архива 3.49 Кb
Оптика	Модуль 5. Формулы и определения по теме оптика Размер архива 5.06 Кb. &nbsp
Квантовая физика	Модуль 7. Формулы и определения по теме квантовая физика Размер архива 3.37 Кb. &nbsp

glavsoft.narod.ru

формулы по физике кинематика 10 класс Видео

…

3 лет назад

Основные формулы по кинематике, для лучшего запоминания под музыку.

…

2 лет назад

все уроки по ФИЗИКЕ — https://www.youtube.com/watch?v=bs2TZzrCWBk&list=PLBnDGoKqP7baNZXcs0—6oU24hi1qU0Yq&index=6&t=344s ЕГЭ по физике …

…

2 лет назад

Если Вы решили научиться решать задачи по физике с нуля, то Вы попали туда куда надо. На своем канале я буду…

…

6 лет назад

Записывайтесь на бесплатное вводное занятие — https://foxford.ru/I/NG На сайте школьники могут подготовиться к ЕГЭ,…

…

3 лет назад

Подпишись на группу в ВК, когда будет больше людей — будет много интересного: https://vk.com/scimfiz.

…

2 лет назад

Как за 3 дня выучить 200 формул по физике. Подробная инструкция www.repetitorfizik.ru.

…

4 лет назад

Урок физики в Ришельевском лицее.

…

3 лет назад

ОГЭ по физике — https://www.youtube.com/playlist?list=PLBnDGoKqP7bbt-TdXajsHFh5iJ4pJ4ZOD все уроки по ФИЗИКЕ …

…

4 лет назад

Видеоурок ориентирован на учащихся 9-11 классов школы. Он будет особенно полезен для тех, кто готовится сдава…

…

3 лет назад

JOIN VSP GROUP PARTNER PROGRAM: https://youpartnerwsp.com/ru/join?92473.

…

2 лет назад

все уроки по ФИЗИКЕ — https://www.youtube.com/watch?v=v8CVc-vRY60&list=PLBnDGoKqP7baNZXcs0—6oU24hi1qU0Yq&index=8&t=9s ЕГЭ по физике …

…

3 лет назад

Для наилучшего запоминания формулы и определения физики под классическую музыку. Вторая часть https://youtu.be/7momV…

…

5 лет назад

Лекция базового школьного уровня. Конструктивная критика приветствуется. группа вконтакте: http://vk.com/skillupeducat…

…

2 лет назад

все уроки по ФИЗИКЕ — https://www.youtube.com/watch?v=j2wcifERB1k&list=PLBnDGoKqP7baNZXcs0—6oU24hi1qU0Yq&index=7&t=110s ЕГЭ по физике …

…

3 лет назад

JOIN VSP GROUP PARTNER PROGRAM: https://youpartnerwsp.com/ru/join?92473.

…

4 лет назад

Урок физики в Ришельевском лицее.

…

1 лет назад

Решение задач по курсу школьной физики. Основные формулы.

…

4 лет назад

Движение по окружности. Лекция базового школьного уровня. группа вконтакте http://vk.com/skillupeducation канал на youtube…

…

2 лет назад

все уроки по ФИЗИКЕ — https://www.youtube.com/watch?v=AEmr5ejq-Bs&list=PLBnDGoKqP7baNZXcs0—6oU24hi1qU0Yq&index=5&t=2s ЕГЭ по физике …

…

5 лет назад

«Физика для семиклассников» от преподавателя Лицея №1557. Курс видеолекций читает Черников Алексей Владимир…

…

6 лет назад

I created this video with the YouTube Video Editor (http://www.youtube.com/editor)

inlove.kz

это… Кинематика: определение, формулы, задачи

Что такое кинематика? Это подраздел механики, который изучает математические и геометрические методы описания движения идеализированных объектов. Они относятся к нескольким категориям. Темой сегодняшней статьи станут аспекты, которые так или иначе связаны с понятием «кинематика точки». Мы разберем многие вопросы, но начнем с самых что ни на есть фундаментальных понятий и объяснений их применения в данной области.

Какие объекты рассматриваются?

Если кинематика — это раздел физики, который изучает способы описания движения тел в разноразмерных пространствах, значит, нужно оперировать и самими телами, верно? Чтобы быстрее понять, о чем идет речь, вы можете найти предназначенный для школьников мультимедийный урок. Кинематика для понимания вообще проста, если разобраться в ее основах. При ознакомлении с ними вы заметите, что в теории присутствует информация о том, что данный раздел физики изучает закономерности движения материальных точек. Заметьте, как обобщенно дано определение объектов. С другой стороны, материальные точки не являются единственными рассматриваемыми кинематикой объектами. Этот раздел физики изучает принципы движения также и абсолютно твердых тел, и идеальных жидкостей. Очень часто все эти три понятия объединяют в одно, говоря просто «идеализированные объекты». Идеализация в данном случае нужна для условностей расчетов и отхода от возможных систематических погрешностей. Если вы посмотрите определение материальной точки, то заметите, что о ней написано следующее: это тело, размерами которого в соответствующей ситуации можно пренебречь. Это можно понимать так: по сравнению с пройденным расстоянием линейные размеры объекта ничтожно малы.

Что используется для описания?

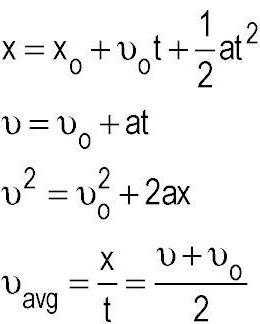
Как было сказано ранее, кинематика – это подраздел механики, который изучает способы описания движения точки. Но если это так, значит для совершения подобных операций нужны какие-то фундаментальные понятия и принципы, наподобие аксиоматических? Да. И в нашем случае это они имеются. Во-первых, в кинематике заведено за правило разрешать задачи, не оглядываясь на силы, действующие на материальную точку. Все мы прекрасно знаем, что тело будет ускоряться или замедляться в том случае, если на него действует определенная сила. И кинематика – это тот подраздел, который позволяет оперировать ускорением. Однако природа возникающих сил здесь не рассматривается. Для описания движения применяются методы математического анализа, линейной и пространственной геометрии, а также алгебры. Также определенную роль играют координатные сетки и сами координаты. Но об этом мы поговорим чуть позднее.

История создания

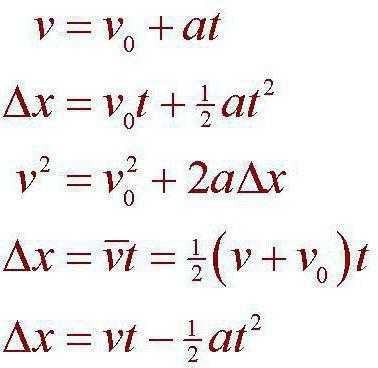
Первые работы по кинематике были составлены великим ученным Аристотелем. Именно он сформировал некоторые фундаментальные принципы этой отрасли. И даже несмотря на то, что в его работах и выводах содержалось некоторое количество ошибочных мнений и размышлений, его труды все равно представляют огромную ценность для современной физики. Работы Аристотеля впоследствии изучал Галилео Галилей. Он проводил знаменитые опыты с Пизанской башней, когда исследовал закономерности процесса свободного падения тела. Изучив все вдоль и поперек, Галилей подверг размышления и выводы Аристотеля жесткой критике. Например, если последний писал о том, что сила – это причина движения, Галилей доказал, что сила есть причина ускорения, но никак не того, что тело возьмет и придет в движение и будет перемещаться. По мнению Аристотеля, тело могло приобретать скорость только при воздействии определенной силы. Но ведь мы знаем, что это мнение ошибочно, поскольку существует равномерное поступательное движение. Это в лишний раз доказывают формулы кинематики. А мы перейдем к следующему вопросу.

Кинематика. Физика. Основные понятия

В этом разделе имеется некоторое количество фундаментальных принципов и определений. Начнем, пожалуй, с главного из них.

Механическое движение

Наверное, со школьной скамьи нам пытаются заложить мысль о том, что можно считать механическим движением. Мы с ним сталкиваемся ежедневно, ежечасно, ежесекундно. Механическим движением мы будем считать процесс, который происходит в пространстве с течением времени, а именно изменение положения того или иного тела. При этом очень часто к процессу применяют относительность, то есть говорят о том, что положение, скажем, первого тела изменилось по отношению к положению второго. Давайте представим, что на стартовой черте у нас стоят два автомобиля. Отмашка оператора или загорелись огни – и машины срываются с места. В самом начале уже происходит изменение положения. Причем говорить можно об этом долго и нудно: относительно конкурента, относительно линии старта, относительно зафиксированного зрителя. Но, наверное, идея понятна. То же самое можно сказать и про двух людей, которые идут либо в одну сторону, либо в разные. Положение каждого из них относительно другого изменяется в каждый момент времени.

Система отсчета

Кинематика, физика – все эти науки используют такое фундаментальное понятие, как системы отсчета. На самом деле оно имеет очень важную роль и применяется в практических задачах едва ли не повсеместно. С системой отсчета могут быть связаны еще две важные составляющие.

Координатная сетка и координаты

Последние представляют собой не что иное, как набор цифр и букв. Пользуясь определенным логическими установками, мы можем составить свою одномерную или двухмерную координатную сетку, которая позволит нам решать простейшие задачи по изменению положения материальной точки за тот или иной отрезок времени. Обычно на практике применяется двухмерная координатная сетка с осями Х («икс») и У («игрек»). В трехмерном пространстве добавляет ось Z («зэт») а в одномерном присутствует только Х. Часто с координатами работают артиллеристы и разведчики. А впервые мы с ними сталкиваемся еще в начальной школе, когда начинаем чертить отрезки определенной длины. Ведь градуировка есть не что иное, как использование координат для обозначения начала и конца.

Кинематика 10 класс. Величины

Основные величины, которые используются при решении задач по кинематике материальной точки, – это расстояние, время, скорость и ускорение. Давайте поговорим о двух последних подробнее. Обе эти величины – векторные. Иными словами, они имеют не только численный показатель, но и определенное заданное направление. Движение тела будет происходить в ту сторону, в которую направлен вектор скорости. При этом нельзя забывать и о векторе ускорения, если мы имеем случай неравномерного движения. Ускорение может быть направлено в ту же сторону, либо в противоположную. Если они сонаправлены, то тело начнет двигаться все быстрее и быстрее. Если разнонаправлены, то будет происходить замедление объекта до тех пор, пока он не остановится. После этого при наличии ускорения тело обретет противоположную скорость, то есть тронется в обратном направлении. Все это на практике весьма и весьма четко показывает кинематика. 10 класс – это как раз тот период, когда данный раздел физики раскрывается в достаточной мере.

Формулы

Формулы кинематики достаточно просты как для вывода, так и для запоминания. Например, формула пройденного за то или иное время объектом расстояния имеет следующий вид: S = VoT + aT^2/2. Как мы видим, в левой части у нас стоит как раз-таки расстояние. В правой части можно обнаружить начальную скорость, время и ускорение. Знак «плюс» стоит исключительно условно, поскольку ускорение может принимать отрицательное скалярное значение при процессе торможения объекта. Вообще, кинематика движения подразумевает существование одного вида скорости, мы постоянно говорим «начальная», «конечная», «мгновенная». Мгновенная скорость появляется в определенный момент времени. Но ведь если так подумать, то конечная или начальная составляющие есть не что иное, как ее частные проявления, верно? Тема «Кинематика» является, наверное, излюбленной у школьников, поскольку она проста и интересна.

Примеры задач

В простейшей кинематике существуют целые категории самых разных задач. Все они так или иначе связаны с движением материальной точки. Например, в некоторых требуется определить расстояние, пройденное телом за определенное время. При этом могут быть известны такие параметры, как начальная скорость и ускорение. А может быть, перед учеником поставят задачу, которая как раз-таки будет заключаться в необходимости выразить и посчитать ускорение тела. Разберем пример. Автомобиль стартует из статичного положения. Какой путь он успеет пройти за 5 секунд, если его ускорение равно трем метрам, деленным на секунду в квадрате?

Для решения этой задачи нам потребуется формула S = VoT + at^2/2. В нее мы просто подставляем имеющиеся данные. Это ускорение и время. Следует обратить внимание на то, что слагаемое Vot уйдет на нуль, поскольку начальная скорость равна нулю. Таким образом, мы получаем численный ответ 75 метров. Вот и все, задача решена.

Итоги

Таким образом, мы разобрались с фундаментальными принципами и определениями, привели пример формулы и поговорили об истории создания данного подраздела. Кинематика, понятие которой вводится в седьмом классе на уроках физики, продолжает постоянно совершенствоваться в рамках релятивистского (неклассического) раздела.

fb.ru

Формулы кинематики — Кинематика — Механика — Каталог файлов

КИНЕМАТИКА (ФОРМУЛЫ)  Координата и перемещение при равномерном движении по прямой x = xo + vxt, Sx = x − xo = vxt, где xo − начальная координата.  Закон сложения скоростей (для поступательного движения системы отсчета) v1 = v12 + v2, где v1 − скорость первого тела (например, относительно земли), v12 − скорость первого тела относительно второго тела (подвижной системы отсчета), v2 − скорость второго тела (относительно земли). Аналогичный вид имеют закон сложения перемещений S1 = S12 + S2 и закон сложения ускорений a1 = a12 + a2. Эту формулу в виде v12 = v1 − v2 называют формулой для относительной скорости двух тел.  Средняя скорость при неравномерном движении по прямой vcp = S/t.  Два последовательных этапа с разными скоростями: vcp = (S1 + S2)/(t1 + t2), где S1 = v1t1, S2 = v2t2.  Скорость и перемещение при равноускоренном движении по прямой vx = vox + axt Sx = voxt + axt2/2, где vox − начальная скорость.  Связь между скоростями и перемещением: vx2 − vox2 = 2axSx.  Средняя скорость при равноускоренном движении: Sx = (vox + vx)t/2.  Свободное падение (vo = 0). Скорость и перемещение (ось y направлена вниз, ay = g) vy = gt, Sy = gt2/2.  Высота в момент времени t h(t) = H − gt2/2, где H − начальная высота.  Время падения и конечная скорость: t = √{2H/g}, v = √{2gH}.  Бросок вертикально вверх с начальной скоростью vo. Скорость и перемещение (ось y направлена вверх, voy = vo, ay = −g): vy = vo − gt, Sy = vot − gt2/2.  Время подъема до высшей точки (где vy = 0) и высота подъема t1 = vo/g, hmax = vo2/(2g).  Полное время полета (до возврата в точку броска) t2 = 2t1 = 2vo/g.  Горизонтальный бросок со скоростью vo. Проекции скорости и перемещения (ось x направлена горизонтальна, ось y − вертикально вниз): 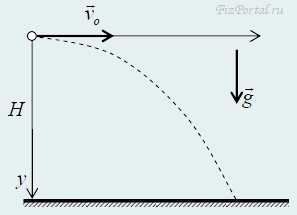vx = vo, Sx = vot, vy = gt, Sy = gt2/2, (по горизонтали − равномерное движение со скоростью vo, по вертикали − свободное падение). Модули скорости и угол наклона скорости к горизонту: v = √{vx2 + vy2} = √{vo2 + (gt)2} tgβ = vy/vx = gt/vo.  Время до падения на землю (начальная высота H) и дальность полета: t = √{2H/g} S = vo√{2H/g}.  Бросок под углом к горизонту с начальной скоростью vo. Проекция скорости и перемещения (ось x направлена горизонтально, ось y − вертикально вверх): vx = vocosα, Sx = votcosα, vy = vosinα − gt, Sy = votsinα − gt2/2, (по горизонтали − равномерное движение со скоростью vocosα, по вертикали − бросок вертикально вверх с начальной скоростью voy = vosinα).  Время подъема до высшей точки (vy = 0) и максимальная высота t1 = vosinα/g, hmax = (vosinα)2/(2g).  Полное время и дальность полета t2 = 2t1 = 2vosinα/g, S = vxt2 = vo2sin(2α)/g.  Равномерное вращение с угловой скоростью ω. Угол поворота (в рад) и число оборотов: φ = ωt, N = φ/(2π) = νt, где ν − частота вращения (ν = ω/(2π)).  Период вращения: T = 1/ν = 2π/ω.  Связь между угловыми и линейными перемещениями l = φR, v = ωR, где l − длина дуги.  Центростремительное ускорение: aц = v2/R = ω2R.  Объем и масса (жидкости, газа), проходящие через сечение S струи за время Δt (уравнение расхода): ΔV = SvΔt, Δm = ρΔV = ρSvΔt, где v − скорость струи, ρ − плотность (жидкости, газа).

abpbrf.ucoz.ru