Формулы 8 класс – Презентация к уроку по физике (8 класс) по теме: Тренажер по физике. Формулы.8 класс | скачать бесплатно - Управленческое образование

Содержание

Химия 8 класс. Все формулы и определения. Кратко, таблицы, схемы.

«Химия 8 класс. Все формулы и определения»

Ключевые слова: Химия 8 класс. Все формулы и определения, условные обозначения физических величин, единицы измерения, приставки для обозначения единиц измерения, соотношения между единицами, химические формулы, основные определения, кратко, таблицы, схемы.

1. Условные обозначения, названия и единицы измерения
некоторых физических величин, используемых в химии

Физическая величина	Обозначение	Единица измерения
Время	t	с
Давление	p	Па, кПа
Количество вещества	ν	моль
Масса вещества	m	кг, г
Массовая доля	ω	Безразмерная
Молярная масса	М	кг/моль, г/моль
Молярный объем	V_n	м³/моль, л/моль
Объем вещества	V	м³, л
Объемная доля		Безразмерная
Относительная атомная масса	A_r	Безразмерная
Относительная молекулярная масса	M_r	Безразмерная
Относительная плотность газа А по газу Б	D_Б(А)	Безразмерная
Плотность вещества	р	кг/м³, г/см³, г/мл
Постоянная Авогадро	N_A	1/моль
Температура абсолютная	Т	К (Кельвин)
Температура по шкале Цельсия	t	°С (градус Цельсия)
Тепловой эффект химической реакции	Q	кДж/моль

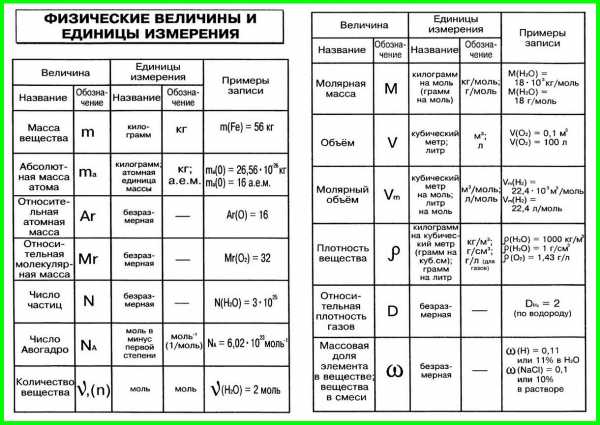
2. Соотношения между единицами физических величин

3. Химические формулы в 8 классе

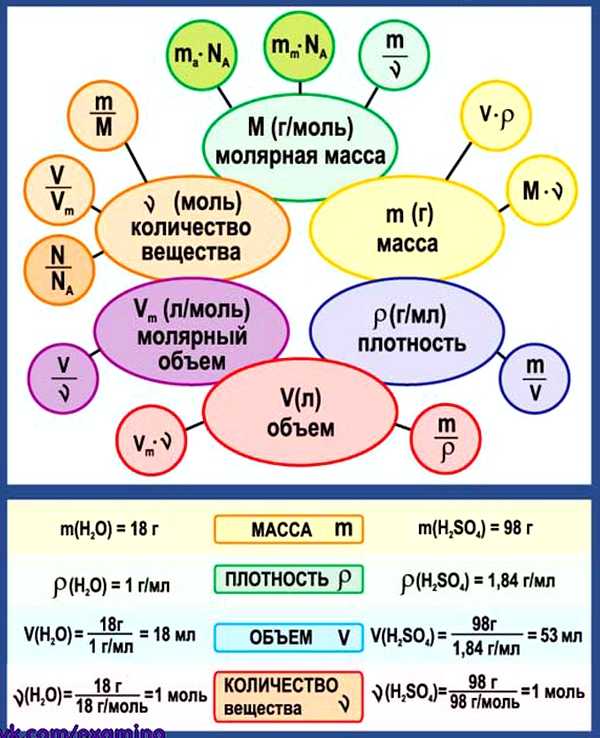
Схема. Химические формулы в 8 классе

4. Основные определения в 8 классе

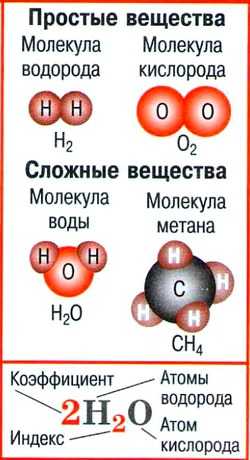
Атом — мельчайшая химически неделимая частица вещества.
Химический элемент — определённый вид атомов.
Молекула — мельчайшая частица вещества, сохраняющая его состав и химические свойства и состоящая из атомов.
Простые вещества — вещества, молекулы которых состоят из атомов одного вида.

Сложные вещества — вещества, молекулы которых состоят из атомов разного вида.
Качественный состав вещества показывает, из атомов каких элементов оно состоит.
Количественный состав вещества показывает число атомов каждого элемента в его составе.
Химическая формула — условная запись качественного и количественного состава вещества посредством химических символов и индексов.
Атомная единица массы (а.е.м.) — единица измерения массы атома, равная массы 1/12 атома углерода ¹²С.
Моль — количество вещества, в котором содержится число частиц, равное числу атомов в 0,012 кг углерода ¹²С.
Постоянная Авогадро (Na = 6*10²³ моль^-1) — число частиц, содержащихся в одном моле.
Молярная масса вещества (
М) — масса вещества, взятого в количестве 1 моль.
Относительная атомная масса элемента Аr — отношение массы атома данного элемента m₀ к 1/12 массы атома углерода ¹²С.
Относительная молекулярная масса вещества Мr — отношение массы молекулы данного вещества к 1/12 массы атома углерода ¹²С. Относительная молекулярная масса равна сумме относительных атомных масс химических элементов, образующих соединение, с учётом числа атомов данного элемента.
Массовая доля химического элемента ω(Х) показывает, какая часть относительной молекулярной массы вещества X приходится на данный элемент.

АТОМНО-МОЛЕКУЛЯРНОЕ УЧЕНИЕ
1. Существуют вещества с молекулярным и немолекулярным строением.
2. Между молекулами имеются промежутки, размеры которых зависят от агрегатного состояния вещества и температуры.

3. Молекулы находятся в непрерывном движении.
4. Молекулы состоят из атомов.
6. Атомы характеризуются определённой массой и размерами.
При физических явлениях молекулы сохраняются, при химических, как правило, разрушаются. Атомы при химических явлениях перегруппировываются, образуя молекулы новых веществ.

ЗАКОН ПОСТОЯНСТВА СОСТАВА ВЕЩЕСТВА
Каждое химически чистое вещество молекулярного строения независимо от способа получения имеет постоянный качественный и количественный состав.

ВАЛЕНТНОСТЬ
Валентность — свойство атома химического элемента присоединять или замещать определённое число атомов другого элемента.

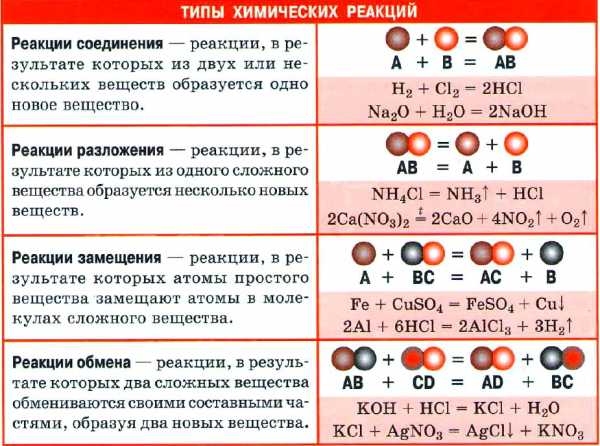
ХИМИЧЕСКАЯ РЕАКЦИЯ
Химическая реакция — явление, в результате которого из одних веществ образуются другие. Реагенты — вещества, вступающие в химическую реакцию. Продукты реакции — вещества, образующиеся в результате реакции.

Признаки химических реакций:
1. Выделение теплоты (света).
2. Изменение окраски.
3. Появление запаха.
4. Образование осадка.
5. Выделение газа.

Химическое уравнение — запись химической реакции с помощью химических формул. Показывает, какие вещества и в каком количестве вступают в реакцию и получаются в результате реакции.

ЗАКОН СОХРАНЕНИЯ МАССЫ ВЕЩЕСТВ
Масса веществ, вступивших в химическую реакцию, равна массе веществ, образовавшихся в результате реакции. В результате химических реакций атомы не исчезают и не возникают, а происходит их перегруппировка.

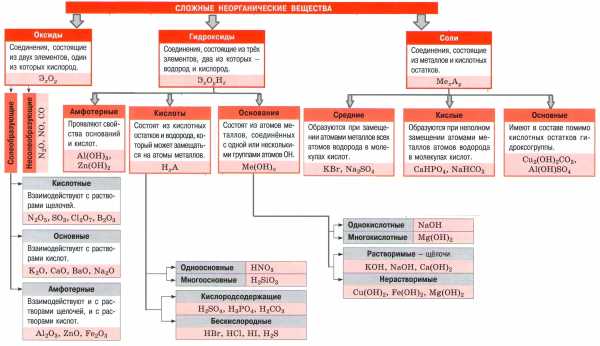
Важнейшие классы неорганических веществ

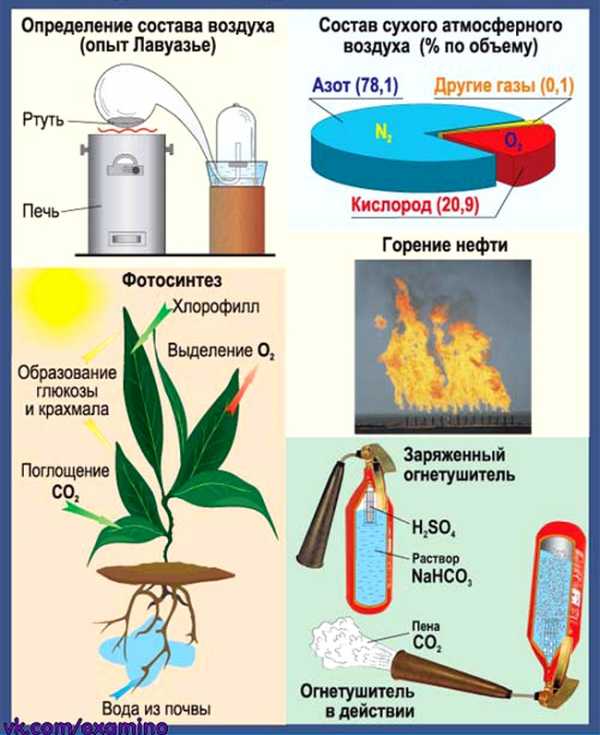
Воздух. Кислород. Горение

Конспект урока «Химия 8 класс. Все формулы и определения».

Следующая тема: «».

Химия 8 класс. Все формулы и определения

4.8 (95.56%) 18 votes

uchitel.pro

Основные формулы, изучаемые в 7-8 классах в помощь учащимся.

Формулы, изучаемые в 7-8 классах.

величина

Основная формула

Физ.величины, которые можно рассчитать зная основную формулу.

площадь

S=a∙b

Площадь круга

S=π∙r²; S=π∙d²

⁴

Объём

V=a∙b∙c; V=S∙h

Скорость

V = S

Путь S=V

∙t

Время t = S/V

плотность

ρ = m

Масса m =ρ ∙V

Объём V = m/ρ

Сила тяжести

F_тяж=m∙g

F_тяж

Масса m = F_тяж

Вес тела

P=m∙g

Масса m = P

Сила упругости

F_упр = k∙ΔL

к-жесткость,

ΔL-деформация

к = F_упр_{F_упр}

^ΔL

ΔL= F_упр

^{^kΔL}

^{0 x}

Сила трения

F_тр=μ∙N

μ – коэффициент трения

N-сила реакции опоры

N F_тр

F_тр

Давление

р = F

Сила давления F=p∙S

Площадь S = F/p

Гидростатическое давление

р=ρ∙g∙h

Плотность жидкости ρ = р

^g^∙^h

высота столба жидкости h = p

^ρ∙g

Сила Архимеда

F_арх = ρ_ж∙V_т∙∙g

V_т – объём F_арх

погруженной

части тела

Плотность жидкости ρ_ж= F_арх

^V^т∙∙^g

Объём V_т = F_арх

^ρ^ж^∙^g

Условие равновесия рычага

F₁∙L₁ = F₂∙L₂

F₁= L₂; L_1,L₂ – плечи сил

^F²^L¹

L₁L₂

F₁F₂

Момент силы

M = F ∙ L

Неподвижный блок

Не дает выигрыша в силе, но меняет её направления действия

F =P

P F

Подвижный блок

Дает выигрыш в силе в 2 раза

F = P

Механическая работа

A = F ∙S∙cosα F

^α S

Сила F = A

^S∙cosα

^{Перемещение S = A__}

^F∙cosα

Мощность

N = A/t

N = F ∙V

Сила F = N/V

Скорость V=N/F

Потенциальная энергия

Е_потенц = mgh (поднятое над землей тело)

Е_потенц = k ΔL²

^{²(упруго деформированное тело)}

Масса тела m= Е_потенц

^gh

^{Жесткость k= 2 ∙Е_потенц}

ΔL²

Деформация ΔL = 2 ∙Е_потенц

Кинетическая энергия

Е_кин = m V²

Масса m=2∙ Е_кин

V²

Скорость тела V= 2∙ Е_кин

Полная мех.энерг.

E_пол = Е_{потенц.} + Е_кин

КПД

η= А_{полезная}_{_∙100%}

^А^{затраченная}

Количество теплоты

Q_{нагревание} = с∙m∙(t₂-t₁)

Q_плавл = λ∙m

Q_{парообр} = L∙m

Q_{горение} = q ∙m

с – удельная теплоемкость

λ – удельная теплота плавления

L- удельная теплота парообразования

q – удельная теплота горения

Сила тока

I = q/t

Эл.заряд q = I∙t

Время t = q/I

Напряжение

U = A/q

Работа тока А = U∙q

Эл.заряд q = A/U

Закон Ома для участка цепи

I = U/R

Напряжение U = I∙R

Сопротивление R = U/I

Сопротивление проводника

R = ρ∙L

Удельное сопротивление ρ=RS

^{Длина проводника L = RS}

^ρ

Площадь поперечн.сечения S = ρ∙L

Последовательное

соединение

проводников

I_общ = I₁ = I₂

R_общ = R₁ + R₂

U_общ = U₁ + U₂

R₁R₂

Параллельное соединение проводников

U_общ = U₁ = U₂

I_общ = I₁ + I₂

R_общ = R₁ ∙ R₂

_{^{R₁ + R₂}}

R₁

R₂

Работа электрического тока

А = U ∙q

A = U ∙I ∙t

A = P∙ t

Мощность эл.тока

P = A/t

P= U ∙ I

P= I²∙R (для послед.соед.)

P= U²/R(для парал.соед.)

Закон Джоуля – Ленца

Q = I²R t(для послед.соед)

Q = U² t(для паралл.соед.)

Q = A = U ∙I ∙t

Оптическая сила линзы

D = 1/F

Фокусное расстояние F = 1/D

2F F F 2F

infourok.ru

8 класс формулы единицы — Мои файлы — Каталог файлов

команда
	Задание
	1	2	3	4	итог
«….»
«….»
«….»
«….»
«….»
Максимальное число баллов за задание	15	10	20	15	60

Учащиеся делают самооценку знаний по предложенным критериям:

Критерии самооценки команд:

Число набранных командой баллов

Оценка по 5-балльной шкале

55 — 60

5 (пять)

45 — 54

4 (четыре)

25 — 44

3 (три)

0 — 24

2 (два)

Оборудование:

Раздаточный материал (тексты заданий), ПК, проектор.

Задание 1. «Физические величины»

Соотнесите физическую величину и её буквенное обозначение:

Физическая величина	Её буквенное обозначение (символ)
Сила тока	t
Электрический заряд	Q
Электрическое напряжение	P
Электрическое сопротивление	q
Температура	A
Оптическая сила линзы	F
Удельная теплоёмкость вещества	U
Удельная теплота парообразования	I
Удельная теплота плавлении	R
Количество теплоты	ρ
Коэффициент полезного действия	D
Работа электрического тока	c
Мощность электрического тока	λ
Удельное электрическое сопротивление	L
Фокусное расстояние линзы	η

Задание 2 «Физические приборы»

Соотнесите физические величины и физические приборы для их измерения:

Физический прибор	Физическая величина
Амперметр	Температура
Вольтметр	Масса
Электроскоп	Электрическая мощность
Термометр	Объём
Часы	Сила тока
Весы	Работа электрического тока
Мензурка	Электрический заряд
Ваттметр	Электрическое напряжение
Электросчётчик	Время
Линейка	Длина, расстояние

Задание №3 «Единицы физических величин»

Назовите единицы измерения физических величин в Системе Интернациональной

Физическая величина	Единица величины
Сила тока
Электрический заряд
Электрическое напряжение
Электрическое сопротивление
Температура
Масса
Удельная теплоёмкость вещества
Удельная теплота парообразования
Удельная теплота плавления
Количество теплоты
Коэффициент полезного действия
Работа электрического тока
Мощность электрического тока
Удельное электрическое сопротивление
Энергия
Площадь поперечного сечения
Фокусное расстояние линзы
Оптическая сила линзы
Удельная теплота сгорания
Элементарный заряд

Задание 4 «Физические формулы»

Соотнесите название физической величины и формулу для её расчёта:

Физическая величина	Формула
Количество теплоты, необходимое для плавления тела	η = A_п / A
Количество теплоты, необходимое для превращения жидкости в пар	I = q / t
Количество теплоты, выделяемое при сгорании топлива	P = I^.U
Коэффициент полезного действия	Q=cm(t₂ – t₁)
Количество теплоты, необходимое для нагревания тела	U = A / q
Сила тока	D = 1 / F
Напряжение	Q = λm
Сопротивление проводника	A = Pt
Работа электрического тока	Q = Lm
Мощность электрического тока	R = ρℓ /S
Оптическая сила линзы	Q = qm
Зависимость силы тока на участке цепи от его сопротивления и напряжения на его концах (Закон Ома для участка цепи)	U = U₁ + U₂
Количество теплоты, выделяемое проводником с током	I = U / R
Сопротивление участка цепи, состоящей из двух последовательно соединённых проводников	Q = I²Rt
Напряжение на участке цепи, состоящем из двух последовательно соединённых проводников	R = R₁+ R₂

Ответы

Задание №1«Физические величины»

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
8	4	7	9	1	11	12	14	13	2	15	5	3	10	6

Задание №2 «Физические приборы»

1	2	3	4	5	6	7	8	9	10
5	8	7	1	9	2	4	3	6	10

Задание №3 «Единицы физических величин»

Физическая величина	Единица величины
Сила тока	А
Электрический заряд	Кл
Электрическое напряжение	В
Электрическое сопротивление	Ом
Температура	^оС
Масса	кг
Удельная теплоёмкость вещества	Дж /кг^.град
Удельная теплота парообразования	Дж /кг
Удельная теплота плавлении	Дж /кг
Количество теплоты	Дж
Коэффициент полезного действия	%
Работа электрического тока	Дж
Мощность электрического тока	Вт
Удельное электрическое сопротивление	Ом /мм² м
Энергия	Дж
Площадь поперечного сечения проводника	мм²
Фокусное расстояние линзы	м
Оптическая сила линзы	дптр
Удельная теплота сгорания	Дж/кг
Элементарный заряд	Кл

Задание №4 «Физические формулы»

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
7	9	11	1	4	2	5	10	8	3	6	13	14	15	12

olegovna11.ucoz.ru

Математика 8 класс все правила и формулы по алгебре и геометрии

Графическое решение линейного уравнения с двуям переменными, способы решения линейного уровнения с двумя переменными.

Математика 8 класс все правила и формулы по алгебре и геометрии

Задача 1. Диагональ прямоугольника равна 16 и составляет со стороной угол 30°. Найти площадь прямоугольника.

Катет AD можно было найти иначе – через косинус ∠САD. Так как косинусом острого угла прямоугольного треугольника называется отношение прилежащего углу катета к гипотенузе, то отсюда следует: катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла.

Подставим найденные значения в формулу площади прямоугольника.

Задача 2. Диагональ прямоугольника составляет с его стороной, равной 10 см, угол 60°. Найти периметр и площадь прямоугольника.

8.2.3. Прямоугольник. Решение задач

Задача 1. Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти периметр прямоугольника.

AB 2 +AD 2 =BD 2 . Получаем: х 2 +(х+7) 2 =17 2 ⇒ х 2 +х 2 +14х+49=289;

2х 2 +14х-240=0; х 2 +7х-120=0, отсюда по теореме Виета х1=-15; х2=8.

Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника:

Задача 2. Периметр прямоугольника 94 см, а диагональ 37 см. Найти площадь прямоугольника.

AB 2 +AD 2 =BD 2 . Получаем: х 2 +(47-х) 2 =37 2 ⇒ х 2 +47 2 -94х+ х 2 =1369;

2х 2 -94х+2209—1369=0; 2х 2 -94х+840=0. Делим обе части равенства на 2. Получаем:

Х 2 -47х+420=0. Найдем дискриминант.

D=b 2 -4ac=47 2 -4∙1∙420=2209—1680=529=23 2 >0; 2 д. к.

Так как АВ=х, то либо АВ=12, тогда AD=47-12=35; либо АВ=35, тогда AD=47-35=12. Таким образом, стороны прямоугольника равны 12 см и 35 см. Площадь прямоугольника S□ = AB∙AD=12∙35=420 (см 2 ). Ответ: 420 см 2 .

Задача 3. Стороны прямоугольника относятся как 3:4, а площадь прямоугольника равна 108 см 2 . Найти диагональ прямоугольника.

Так как S□ = AB∙AD и по условию равна 108 см 2 , то можно составить уравнение:

3х∙4х=108. Тогда 12х 2 =108, а разделив обе части равенства на 12, получаем:

Х 2 =9. Отсюда х=3, так как х – положительное число. Стороны прямоугольника

Тогда АВ=3х=3∙3=9 и AD=4х=4∙3=12. Из прямоугольного треугольника BAD по теореме Пифагора найдем BD – искомую диагональ прямоугольника.

BD 2 =AB 2 +AD 2 =9 2 +12 2 =81+144=225, отсюда BD=15 см. Ответ: 15 см.

Задача 4. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите диагональ прямоугольника, если его меньшая сторона равна 15 см.

АС 2 =AB 2 +ВС 2 =15 2 +30 2 =225+900=1125, отсюда получаем:

Задача 5. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 7 см дальше, чем от большей стороны. Диагональ прямоугольника равна 26 см. Найдите стороны прямоугольника.

ОМ 2 +МА 2 =АО 2 или х 2 +(х+7) 2 =13 2 . Упрощаем равенство:

Х 2 +х 2 +14х+49=169; 2х 2 +14х-120=0; х 2 +7х-60=0. Корни этого приведенного квадратного уравнения удобно найти по теореме Виета.

Х1=-12, х2=5. Так как сторона выражается положительным числом, то ОМ=х=5 см. тогда ОК=5+7=12 (см). АК=ОМ=5 см и АМ=ОК=12 см – это половинки сторон прямоугольника. Тогда АВ=2∙АК=10 см и AD=2∙МА=24 см. Ответ: 10 см и 24 см.

8.2.5. Основные тригонометрические тождества. Часть 2

Основные тригонометрические тождества.

Пример 1. Вычислить значения cosα, tgα, ctgα, если sinα = 5/13 и угол α – острый.

Решение. Найдем cosα по формуле 1б), учитывая, что угол α – острый.

Тангенс α найдем по формуле 2). Подставим значения синуса и косинуса.

Так как по формуле 6) tgα ∙ ctgα = 1, то ctgα = 1 : tgα. Говорят, что котангенс – это «перевернутый» тангенс, следовательно,

Пример 2. Вычислить значения sinα, tgα, ctgα, если cosα = 0,6 и угол α – острый.

Тангенс α найдем по формуле 2). Подставим значения синуса и косинуса.

Пример 3. Вычислить значения sinα, cosα, ctgα, если tgα = 15/8 и угол α – острый.

Котангенс – это «перевернутый» тангенс, поэтому, ctgα = 8/15. Далее находим cosα.

Применим формулу 7), подставив в эту формулу данное значение тангенса Α.

Пример 4. Вычислить значения sinα, cosα, tgα, если ctgα = 9/40 и угол α – острый.

Тангенс – это «перевернутый» котангенс, поэтому, tgα = 40/9. Далее находим cosα,

Применяя ту же формулу 7). Подставим в эту формулу полученное значение тангенса Α.

8.2.4. Основные тригонометрические тождества. Часть 1

Основные тригонометрические тождества.

Secα читают: «секанс альфа». Это число, обратное косинусу альфа.

Соsecα читают: «косеканс альфа». Это число, обратное синусу альфа.

Примеры. Упростить выражение:

Е) sin 4 α+2sin 2 αcos 2 α+cos 4 α; Ж) tg 2 α – sin 2 αtg 2 α; З) ctg 2 αcos 2 α – ctg 2 α; И) cos 2 α+tg 2 αcos 2 α.

Б) cos 2 α – 1 =- (1 – cos 2 α) = — sin 2 α также применили формулу 1);

В) (1 – cosα)(1+cosα) = 1 – cos 2 α = sin 2 α. Вначале мы применили формулу разности квадратов двух выражений: (a – b)(a+b) = a 2 – b 2 , а затем формулу 1);

Г) sin 2 αcosα – cosα. Вынесем общий множитель за скобки.

Sin 2 αcosα – cosα = cosα(sin 2 α – 1) = — cosα(1 – sin 2 α) = — cosα ∙ cos 2 α = — cos 3 α. Вы, конечно, уже заметили, что так как 1 – sin 2 α = cos 2 α, то sin 2 α – 1 = — cos 2 α. Точно так же, если 1 – cos 2 α = sin 2 α, то cos 2 α – 1 = — sin 2 α.

Е) sin 4 α+2sin 2 αcos 2 α+cos 4 α. Имеем: квадрат выражения sin 2 α плюс удвоенное произведение sin 2 α на cos 2 α и плюс квадрат второго выражения cos 2 α. Применим формулу квадрата суммы двух выражений: a 2 +2ab+b 2 =(a+b) 2 . Далее применим формулу 1). Получим: sin 4 α+2sin 2 αcos 2 α+cos 4 α = (sin 2 α+cos 2 α) 2 = 1 2 = 1;

Ж) tg 2 α – sin 2 αtg 2 α = tg 2 α(1 – sin 2 α) = tg 2 α ∙ cos 2 α = sin 2 α. Применили формулу 1), а затем формулу 2).

З) ctg 2 αcos 2 α – ctg 2 α = ctg 2 α(cos 2 α – 1) = ctg 2 α ∙ (-sin 2 α) = — cos 2 α.

И) cos 2 α+tg 2 αcos 2 α = cos 2 α(1+tg 2 α) = 1. Мы вначале вынесли общий множитель за скобки, а содержимое скобок упростили по формуле 7).

Мы применили формулу 7) и получили произведение суммы двух выражений на неполный квадрат разности этих выражений – формулу суммы кубов двух выражений:

8.1.4. Признаки параллелограмма

I. Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.

Задача 1. Из вершин В и D параллелограмма АBCD, у которого АВ≠ ВС и угол А — острый, проведены перпендикуляры BK и DM к прямой АС. Докажите, что четырехугольник BMDK — параллелограмм.

Так как ВК и DM перпендикулярны одной и той же прямой АС, то ВК II DM. Кроме того, ВК и DM являются высотами, проведенными в равных треугольниках Δ АВС и Δ CDA из вершин равных углов ∠B и ∠D к одной и той же стороне АС, следовательно, ВК = DM. Имеем: две стороны ВК и DM четырехугольника BMDK параллельны и равны, значит, BMDK – параллелограмм, что и требовалось доказать.

II. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.

Задача 2. На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственно точки M, N, P и Q так, что AM=CP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD и MNPQ — параллелограммы.

1. По условию в четырехугольнике ABCD противоположные стороны состоят из равных отрезков, поэтому равны, т. е. AD=BC, AB=CD. Следовательно, ABCD – параллелограмм.

2. Рассмотрим Δ MBN и Δ PDQ. BM=DP и BN=DQ по условию. ∠B =∠D как противолежащие углы параллелограмма ABCD. Значит, Δ MBN = Δ PDQ по двум сторонам и углу между ними (1-й признак равенства треугольников). А в равных треугольниках против равных углов лежат равные стороны. Отсюда MN=PQ. Мы доказали, что противоположные стороны MN и PQ четырехугольника MNPQ равны. Аналогично, из равенства треугольников Δ MAQ и Δ PCN следует равенство сторон MQ и PN, которые являются противоположными сторонами четырехугольника MNPQ. Имеем: противоположные стороны четырехугольника MNPQ попарно равны. Следовательно, четырехугольник MNPQ – параллелограмм. Задача решена.

III. Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Задача 3. Диагонали параллелограмма ABCD пересекаются в точке O, Докажите, что четырехугольник MNPQ, вершинами которого являются середины отрезков OA, OB, OC и OD, — параллелограмм.

По свойству диагоналей параллелограмма ABCD его диагонали AC и BD точкой пересечения делятся пополам, т. е. ОА=ОС и ОВ=OD. Диагонали четырехугольника MNPQ так же пересекаются в точке О, которая будет серединой каждой их них. Действительно, так как вершины четырехугольника MNPQ по условию являются серединами отрезков ОА, ОС, ОВ и OD, то BN=ON=OQ=DQ и AM=OM=OP=CP. Следовательно, диагонали MP и NQ четырехугольника MNPQ в точке пересечения делятся пополам, следовательно, четырехугольник MNPQ – параллелограмм, что и требовалось доказать.

8.1.3. Свойство углов и сторон параллелограмма

Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

8.2.2. Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Египетский треугольник — это прямоугольный треугольник со сторонами 3, 4 и 5.

3²+4²=5². На рисунке (выше) показан египетский треугольник.

Задача. Две стороны прямоугольного треугольника равны 6 см и 8 см. Найти третью сторону. (Рассмотреть два случая).

1 случай. Пусть две данные стороны — катеты прямоугольного треугольника.

Решение. По теореме Пифагора:

2 случай. Пусть две данные стороны — катет и гипотенуза прямоугольного треугольника.