Задачи на проценты, сплавы и смеси Подготовка к ОГЭ по математике №22
ОГЭ 9 класс
№22 Задачи на проценты, сплавы и смеси
1. Задание 22
Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Решение.
Пусть кг и кг — массы первого и второго растворов, взятые при смешивании. Тогда кг — масса полученного раствора, содержащего кг кислоты. Концентрация кислоты в полученном растворе 20 %, откуда
Решим систему двух полученных уравнений:
Замечание. Решение можно сделать несколько проще, если заметить, что из полученных уравнений следует: , откуда .
Ответ: 2 кг.
2. Задание 22
Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Решение.
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение:
Выразим x через y:
Следовательно, отношение, в котором нужно взять сплавы: Ответ:
3. Задание 22
При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
В каком отношении были взяты первый и второй растворы?
Решение.
Пусть первый раствор взят в количестве грамм, тогда он содержит 0,2 грамм чистой кислоты, а второй раствор взят в количестве грамм, тогда он содержит 0,5 грамм чистой кислоты. При смешивании двух этих растворов получится раствор массой + грамм, по условию задачи, он содержит 0,3( + ) чистой кислоты. Следовательно, можно составить уравнение:
Выразим через : Следовательно, отношение, в котором были взяты растворы: Ответ:
4. Задание 22
На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
Решение.
Заметим, что победителем на выборах окажется Зайцев. Пусть количество голосов, отданных за Зайцева равно . Тогда за Журавлёва и Иванова вместе отдали . Процент голосов, отданных за Зайцева Ответ: 75%.
Пусть количество голосов, отданных за Зайцева равно . Тогда за Журавлёва и Иванова вместе отдали . Процент голосов, отданных за Зайцева Ответ: 75%.
5. Задание 22
Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Решение.
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение:Откуда
Масса третьего сплава равна 16 кг.
Ответ:16 кг.
6. Задание 22
Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
Сколько сухих фруктов получится из 288 кг свежих фруктов?
Решение.
Свежие фрукты содержат 20% питательного вещества, а высушенные — 72%. В 288 кг свежих фруктов содержится 0,2 · 288 = 57,6 кг питательного вещества. Такое количество питательного вещества будет содержаться в кг высушенных фруктов. Ответ: 80.
7. Задание 22
Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли г 10-процентного раствора, тогда взяли и г 12-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 11%. Ответ: 11%.
8. Задание 22
Задание 22
Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
Решение.
Заметим, что сухая часть свежих фруктов составляет 14%, а высушенных — 77%. Значит, для приготовления 72 кг высушенных фруктов требуется кг свежих. Ответ: 396 кг.
9. Задание 22
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, в первом растворе содержится килограмма кислоты.
Ответ: 8,7.
10. Задание 22
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, в первом растворе содержится кг кислоты Ответ: 2,6
11. Задание 22
Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты.
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во втором растворе содержится кг кислоты. Ответ: 19,5
12. Задание 22
Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во первом растворе содержится кг кислоты. Ответ: 2.
Ответ: 2.
13. Задание 22
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во втором растворе содержится кг кислоты. Ответ: 2,8
14. Задание 22
Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, в первом растворе содержится кг кислоты. Ответ: 15,6.
15. Задание 22
Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во втором растворе содержится кг кислоты. Ответ: 18,6
Ответ: 18,6
16. Задание 22
Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, в первом растворе содержится кг кислоты. Ответ: 11.
17. Задание 22
Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во втором растворе содержится кг кислоты Ответ: 23,1
18. Задание 22
Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение.
Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи:
Таким образом, во втором растворе содержится килограмма кислоты
Ответ: 4,2
19. Задание 22
Задание 22
Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Решение.
Заметим, что сухая часть свежих фруктов составляет 12%, а высушенных — 70%. Значит, для приготовления 6 кг высушенных фруктов требуется кг свежих.
Ответ: 35 кг.
20. Задание 22
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.
Ответ: 58.
21. Задание 22
Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
Решение.
Свежие фрукты содержат 7% питательного вещества, а высушенные — 84%. В 252 кг свежих фруктов содержится 0,07 · 252 = 17,64 кг питательного вещества. Такое количество питательного вещества будет содержаться в кг высушенных фруктов.
Ответ: 21.
Задачи на сплавы и смеси с решениями.
Задача №1.
Сплав меди и цинка весом 20кг содержит 30% меди. Добавили 22кг цинка. Сколько нужно добавить меди, чтобы в сплаве стало 60% цинка.
Решение:
I способ:
30% 70%
20кг = 6кг + 36кг
Добавили цинка — +22кг
42кг = 6кг + 36кг
100% = 40% + 60%
36кг составляет 60%.
36:0.6=60кг – новый сплав.
60(кг) = 6(кг) + 36(кг) + x(кг)
x=18 (кг).
II способ:
Очень удобно в задачах на сплавы, смеси, концентрации составлять таблицу по условию задачи (жирным шрифтом), а затем заполнять пустые клетки, руководствуясь законом сохранения массы(объема) и формулами расчета «Процент от числа»
Для начала нужно определить количество объектов, которые участвуют в условии задачи ( в нашем случае их 4), затем занести в таблицу все, что говорится о каждом объекте. По вопросу задачу вводится переменная ( в нашем случае это x кг меди)
|
Объекты |
I |
добавили цинка |
добавили меди |
получили сплав |
|
масса (кг) |
20 |
22 |
x |
20+22+x |
|
% меди |
30 |
100 |
||
|
% цинка |
|
100 |
|
|
|
масса меди (кг) |
|
|
|
60 |
|
масса цинка (кг) |
|
|
|
|
Теперь начинаем заполнение пустых клеток:
|
Объекты |
I |
добавили цинка |
добавили меди |
получили сплав |
|
масса (кг) |
20 |
22 |
x |
20+22+x=42+x |
|
% меди |
30 |
0 |
100 |
100-60=40 |
|
% цинка |
100-30=70 |
100 |
0 |
60 |
|
масса меди (кг) |
(20*30)/100 |
0 |
x |
(42+x)*40/100=(20*30)/100+0+x |
|
масса цинка (кг) |
(20*70)/100 |
100 |
0 |
|
Нам, в принципе, достаточно заполнения четырех строк, чтобы составить уравнение.
Обратим внимание на «желтую» клетку- эта клетка является ключом составления уравнения задачи, т.к. мы ее можем заполнить по формуле «40 % от числа 42+x», а также по закону сохранения массы: (20*30)/100+0+x.
Следовательно, имеем уравнение:
Ответ: 18.
Задача №2.
Имеется сплав серебра с медью. Вычислите массу сплава и процентное содержание серебра в нем, зная, что сплавив его с 3кг чистого серебра, получается сплав, содержащий 90% серебра, а сплавив его с 2кг чистого серебра, получается сплав, содержащий 86% серебра.
Решение:
Xкг – масса исходного сплава
(X+3)кг – масса первого сплава
(X+2)кг – масса второго сплава
(X+3)*0.9(кг) – содержание серебра в первом сплаве
(X+2)*0.86(кг) – масса серебра во втором сплаве
(X+3)*0.9-(X+2)*0.86=1
X=0.5
Табличный способ:
По первому предложению составляем таблицу
|
Объект |
I |
II |
Смесь |
|
m кг |
x |
3 |
3+x |
|
% серебра |
p |
100 |
90 |
|
mсеребра кг |
x*p/100 |
3*100/100 |
(3+x)*90/100=x*p/100+3*100/100 |
По второму предложению составляем таблицу
|
Объект |
I |
II |
Смесь |
|
m кг |
x |
2 |
2+x |
|
% серебра |
p |
100 |
86 |
|
mсеребра кг |
x*p/100 |
2*100/100 |
(2+x)*86/100=x*p/100+2*100/100 |
В результате в «желтых» клетках имеем уравнения для системы:
Тогда 0,5p=15, p=30
Ответ: 0,5 кг; 30 % серебра.
Задача №3.
Из 50т руды получают 20т металла, который содержит 12% примесей. Сколько процентов примесей содержит руда?
Решение:
1) Сколько примесей содержится в металле?
20*0.12=2.4(т)
2) 50т = 20т + 3т = (17.6 + 2.4) +30= 17.6+ (2.4 + 30)
металл примеси примеси чистый примеси
металл
3) 50т – 100%
32.4т – x%
50/32,4=100/x ; x=64.8
Табличный способ:
|
Объект |
I |
II |
Получили |
|
m тн |
50 |
50-20=30 |
20 |
|
% примесей |
p |
100 |
12 |
|
mпримесей тн |
50*p/100 |
30 |
20*12/100=50*p/100-30 |
12*20=50p-3000
50p=3240
p=64. 8
8
Ответ: 64.8%.
Задача №4.
Сплав меди и цинка весом 60 кг содержит 40% меди. Сколько нужно добавить цинка, чтобы в сплаве его концентрация достигла 80%.
Решение:
Табличный способ:
|
Объект |
I |
II |
Получили |
|
m кг |
60 |
x |
60+x |
|
% цинка |
100-40=60 |
100 |
80 |
|
mцинка кг |
60*60/100 |
x |
(60+x)*80/100=60*60/100+x |
Имеем:
(60+x)*0. 8=36+x
8=36+x
48+0.8x=36+x
x=60 кг цинка нужно добавить.
Задача №5.
К 15 литрам 10%-ого раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение:
1) Пусть добавили Xл 5%-ного раствора соли.
(15+X)л – столько стало нового раствора
(15+X)*0.08л – столько в нем содержится соли
2) В 15 литрах 10%-ного раствора содержится
15*0.1=1.5(л) соли
3) В Xл 5%-ного раствора содержится 0.05Xл соли
X=10.
Добавили 10л 5%-ного раствора соли.
Табличный способ:
|
Объект |
I |
II |
Получили |
|
m л |
15 |
x |
15+x |
|
% соли |
10 |
5 |
8 |
|
mсоли л |
15*10/100 |
x*5/100 |
(15+x)*8/100=15*10/100+5x/100 |
Имеем:
8(15+x)=150+5x
3x=30
x=10
Ответ: 10л
Задача №6.
В лаборатории есть раствор соли 4-х различных концентраций. Если смешать I, II, III растворы в весовом отношении 3:2:1, то получится 15%-ный раствор. II, III, IV растворы в равной пропорции дают при смешивании 24%-ный раствор, и , наконец, раствор составленный из равных частей I и III растворов, имеет концентрацию 10%. Какая концентрация будет при смешении II и IV растворов в пропорции 2:1?
Решение:
1) Пусть в 1кг I р-ра – Xкг соли
II р-ра – Yкг соли
III р-ра – Zкг соли
IV р-ра – tкг соли
2) В условии говорится, что если мы смешаем 3кг I раствора, 2кг II раствора и 1кг III раствора, то в получившихся 6кг р-ра будет 6*0.15=0.9кг соли. Но в 3-х кг I р-ра имеется (3X)кг соли, в 2кг II р-ра ее (2Y)кг и в одном кг III р-ра – Zкг. Отсюда получается первое уравнение 3x+2y+Z=0.9
3) Рассуждая аналогично, получим, что
Y + Z + t = 0.72
X + Z = 0.2,
Т.е. получим систему:
Из этой системы нам нужно вычленить 2y + t.
2y+t=0,5(3x+2y+Z)+(y+Z+t)-1,5(x+Z)=0,5.0,9+0,72-1,5.0,2=0,87
Значит, если смешать 2кг второго раствора и 1кг четвертого, то в получившихся 3кг смеси будет 0.87кг соли, что составляет 29%, что и требовалось найти.
3кг – 100%
0.87кг – x%
3/0,87=100/x;
x = 29%.
Ответ: 29%
Задача №7.
Даны два сплава. Первый весит 4кг и содержит 70% серебра. Второй весит 3кг и содержит 90% серебра. Сколько кг второго сплава надо сплавить со всем первым сплавом, чтобы получить r%-ный сплав серебра? При каких r задача имеет решение?
Решение:
В первом сплаве – 2.8кг серебра. Пусть надо взять x(кг) второго сплава, чтобы сплавив его со всем первым сплавом, получить такой сплав, как требуется. Весь сплав будет весить (x+4)кг. Серебра в нем будет (2.8+0.9x)кг.
По условию ( 2,8+0,9x)/(x+4)=r/100
(x+4)кг – 100%
2.8+0.9x – r%, откуда x=(4r-280)/(90-r). Задача имеет решение тогда и только тогда, когда 0?x?3 (только в таких пределах можно что-либо взять из куска весом в 3кг), т.е. 0?(4r-280)/(90-r)?3 , откуда 70?r?80 .
Задача имеет решение тогда и только тогда, когда 0?x?3 (только в таких пределах можно что-либо взять из куска весом в 3кг), т.е. 0?(4r-280)/(90-r)?3 , откуда 70?r?80 .
Ответ: x=(4r-280)/(90-r), задача имеет решение при 70?r?80.
|
Этап урока |
Деятельность учителя |
Деятельность учащихся |
||||||||||||||||
|
1.Организационный этап |
Эмоциональный настрой учащихся на урок. Проводит диалог с учащимися Слайд 1. Добрый день ребята, садитесь! Как у вас настроение? Сегодня мы с
вами продолжим подготовку к ОГЭ по математике и разберем некоторые задачи из
КИМ, а именно №22. Эпиграфом нашего урока будет античный афоризм «Незнающие
пусть научатся, знающие — вспомнят еще раз».
|
Просмотр слайда и диалог с учителем. |
||||||||||||||||
|
2. Постановка цели и задач урока. |
Слайд 2. Посмотрите пожалуйста на экран и сформулируйте тему урока и цель. |
Просмотр слайда. Формулирование темы урока «Решение задач на сплавы, смеси и растворы» и цели: Научиться решать задачи на смеси, сплавы и растворы/ Вспомнить алгоритм решения задач на смеси, сплавы и растворы.
|
||||||||||||||||
|
3. Актуализация знаний. Мотивация учебной деятельности учащихся. |
Слайд 3. Тему определили, цель поставили. Будем решать? Прежде, чем мы начнем говорить о решении задач, давайте проведем
небольшой тест: скрестите руки на груди. А теперь поднимите руку те, у кого
левая рука оказалась сверху. Но раз мы с вами такие разные, то и подход к решению одной и той же задачи у каждого будет свой. Сегодня мы с вами разберем различные способы решения одних и тех же задач, которые встречаются на экзаменах как по математике, так и по химии, чтобы каждый из вас имел возможность выбрать тот путь, который будет для него наиболее понятным. Слайд 4. Сегодня мы с вами рассмотрим 3 метода решения задач: Табличный, метод стаканчиков, метод рыбки. |
Участвуют в тесте, в диалоге.
|
||||||||||||||||
|
4. |
Слайд 5. Не бывает практики без теории. Давайте с вами вспомним теоретические аспекты решения задач на сплавы, смести и растворы. Что нам необходимо помнить при решении задач: |
Записывают в тетрадь теоретические аспекты решения задач. |
||||||||||||||||
|
5. Опыт |
При решении задач нам необходимо учитывать один Закон. Давайте попробуем его сформулировать в ходе проведения химического опыта. Я прошу выйти 1 ученика для проведения опыта. ОПЫТ: в стакан раствора марганцовки розового цвета объёмом 150 мл вливаем перекись водорода прозрачную объёмом 50 мл и получаем раствор светло коричневого цвета объёмом 200 мл. Слайд 6. «Закон сохранения объёма или массы». Если два сплава (раствора) соединяются в один «новый» сплав
(раствор), то V+ –
сохраняется объём; m = —
сохраняется масса.
|
Ученик проводит химический опыт, все учащиеся комментируют химический опыт, тем самым выдвигают варианты формулировки закона. |
||||||||||||||||
|
6. Объяснение нового материала |
Слайд 7. На экране Задача: Смешали 4л 18%-го водного раствора некоторого вещества с 6 л 8%-го раствора этого же вещества. Найдите концентрацию получившегося раствора. Слайд 8. Давайте вместе с вами решим ее 1 способом – табличным методом. |
Решение. Заполним таблицу по условию задачи:
1) 4×0,18+6×0,08=0,72+0,48=1,2(л) – масса раствора в смеси; 2) 4+6=10(л) – масса смеси; 3)
— концентрация получившегося
раствора. :12%.
|
||||||||||||||||
|
Слайд 9. Простой метод решения таких задач «метод стаканчиков»:
4кг 6кг (4+6)
|
Записывают решение задачи методом стаканчиков
0,72+0,48=10х х=0,12=12% Ответ: 12%.
|
|||||||||||||||||
|
Слайд 10. Старинный способ решения задач на смеси, сплавы и растворы –метод рыбки.
|
Записывают решение
6(х-8)=4(18-х) 6х-48=72-4х 6х+4х=72+48 10х=120 х=12 Ответ: 12% |
|||||||||||||||||
|
7. |
Ребята, устали решать? Раздаю капсулы от киндер-сюрпризов. Что в руках? А что содержит капсула? Ваши капсулы тоже содержат инструкцию, которую вам сейчас необходимо выполнить.
|
Отвечают: да/нет Капсула киндер-сюрприза Игрушку, инструкцию по сборке игрушки. Выполняют инструкци. |
||||||||||||||||
|
8. Закрепление изученного материала |
Продолжим работу. Сейчас вам будет предложен тест, который размещен на рабочем столе ваших ноутбуков, под названием «Решение задач на сплавы, смеси и растворы». Тест включает в себя задачи, которые вы решаете любым из трех рассмотренных сегодня на уроке методов. После выполнения теста обязательно завершите его и ознакомьтесь с результатом и оценкой, которую вы получите за решение теста. Кто справится раньше, на столах у вас расположены листы с дополнительными задачами. |
Выполняют тест. |
||||||||||||||||
|
9. Информация о домашнем задании,
инструктаж по его выполнению. |
Домашнее задание: задача №8,9 с листов на столе. Решите в тетради любым методом. Или можете решить задачи на сплавы, смеси и проценты с Образовательного портала подготовки к экзаменам «РЕШУ ОГЭ» Дмитрия Гущина №22. |
Записывают домашнее задание |
||||||||||||||||
|
10. Рефлексия (Подведение итогов занятия) |
Справились с тестом? Согласны с результатом? Полезным ли для вас оказался сегодняшний урок? Смогли ли вы выбрать наиболее подходящий для вас способ решения? Будете ли вы использовать эти методы в дальнейшем и при решении заданий ОГЭ? Притча: Шёл
мудрец, а навстречу ему три человека, которые везли под горячим солнцем
тележки с камнями для строительства. Мудрец остановился и задал каждому по
вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой
ответил, что целый день возил проклятые камни. — Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок. — Кто работал так, как первый человек? ( поднимают руки) — Кто работал добросовестно? ( поднимают руки) -Кто принимал участие в строительстве храма науки? ( поднимают руки) Спасибо за урок! Мне было приятно с вами работать! Удачного дня.
|
Диалог с учителем. |
Авторская программа элективного курса «Решение задач на смеси и сплавы»
Авторская программа элективного курса
для учащихся 10 -11 классов
«Решение задач на смеси и сплавы
учителя математики
высшей квалификационной категории
МБОУ «СОШ № 6» Дорофеевой Л. И.
И.
Пояснительная записка
Умение решать текстовые задачи является высшим этапом в познании математики. С помощью текстовой задачи формируются важные умения, связанные с анализом текста, выделением главного в условии, составлением плана решения, проверкой полученного результата и, наконец, развитием речи обучающегося. В ходе решения текстовой задачи формируется умение переводить её условие на математический язык уравнений, неравенств, их систем, графических образов, т.е. составлять математическую модель. Решение задач способствует развитию логического и образного мышления, повышает эффективность обучения математики и смежным дисциплинам.
Среди различных текстовых задач, встречающихся в школе и предлагаемых на выпускных экзаменах за курс основной и средней школы, задачи на смеси, сплавы и растворы не пользуются популярностью, но в последнее время встречаются все чаще и чаще. Этот тип задач направлен на расширение, углубление и систематизацию знаний обучающихся по решению текстовых задач и позволяет реализовать межпредметные связи математики и химии.
Этот тип задач направлен на расширение, углубление и систематизацию знаний обучающихся по решению текстовых задач и позволяет реализовать межпредметные связи математики и химии.
За время обучения в школе решается огромное число задач. При этом решаются одни и те же задачи. И в итоге большая часть учеников овладевает общим умением решения задач, а встретившись с задачей незнакомого или малознакомого вида, теряются и не знают, как к ней подступиться.
Программа курса «Решение задач на смеси, сплавы, концентрацию» адресована обучающимся 10 -11 классов, и рассчитана на 17 часов. Данный курс предназначен, в первую очередь, обучающимся, желающих расширить и углубить свои знания по математике, сделать правильный выбор профиля обучения в старших классах и качественно подготовиться к государственной (итоговой) аттестации.
Разработка программы элективного курса обусловлена тем, что задачи с использованием таких понятий как концентрация, процентное содержание вещества в смеси, растворе, сплаве в школьном курсе математики практически отсутствуют. В школьном курсе математики рассматриваются простейшие задачи по данной теме, задачам же на сложные проценты, на смеси и сплавы не уделяется должного внимания. В предлагаемых заданиях на экзаменах в 9 и 11 классах присутствует целый блок задач данной тематики. Особенностью данного курса является его межпредметная связь с химией, так как большая часть задач, которые рассматриваются в данном курсе, напрямую связаны с химическими процессами.
В школьном курсе математики рассматриваются простейшие задачи по данной теме, задачам же на сложные проценты, на смеси и сплавы не уделяется должного внимания. В предлагаемых заданиях на экзаменах в 9 и 11 классах присутствует целый блок задач данной тематики. Особенностью данного курса является его межпредметная связь с химией, так как большая часть задач, которые рассматриваются в данном курсе, напрямую связаны с химическими процессами.
Цель курса:
освоение и систематизация знаний, относящихся к понятию процента и его широкому практическому примен
Задача B14: смеси и сплавы
Многие ученики ненавидят эту задачу и даже не пытаются ее решать. И совершенно зря, потому что смеси и сплавы — одни из самых легких задач B14.
Для решения требуется выполнить три простых шага:
- Составляем таблицу, в которой указываем общую массу и массу «чистого» вещества для каждой смеси или сплава.
 Все данные берутся прямо из условия задачи. Например, 50 литров кислоты с концентрацией 15% — это m
0 = 50 литров общей массы и m
1 = 0,15 · 50 = 7,5 литров «чистого» вещества;
Все данные берутся прямо из условия задачи. Например, 50 литров кислоты с концентрацией 15% — это m
0 = 50 литров общей массы и m
1 = 0,15 · 50 = 7,5 литров «чистого» вещества; - Если какие-то ячейки таблицы остались не заполненными, обозначаем их переменными x, y и т.д. Чаще всего в качестве неизвестной величины выступает масса, реже — концентрация;
- Составить уравнения по правилу: при объединении двух смесей/сплавов их массы складываются. Другими словами, масса полученной смеси равна сумме масс исходных смесей. Аналогично, складываются массы «чистых» веществ.
Если все сделать правильно, то получится одно-два линейных уравнения. Решаем их — получаем ответ. А вот фиг! После того, как решите уравнение, никогда (слышите, никогда!) не записывайте ответ. Запомните:
Прежде чем записать ответ, вернитесь к задаче и еще раз прочитайте, что требуется найти. Потому что решить уравнение — это еще не значит решить текстовую задачу.

Это правило работает для всех текстовых задач, а не только для B14. Многие ученики сосредотачиваются на решении уравнения, но совершенно забывают, что, собственно, требовалось найти. Получается, что по существу задача решена верно, а ответ — неправильный.
Задача. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Итак, у нас есть три вещества:
- 4 литра 15-процентного раствора;
- 6 литров 25-процентного раствора;
- Третий раствор с неизвестной концентрацией.
Составим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (15%) | 4 | 0,15 · 4 = 0,6 |
| Раствор 2 (25%) | 6 | 0,25 · 6 = 1,5 |
| Раствор 3 | x | y |
По условию, нам не дана ни масса нового раствора, ни масса чистого вещества в нем. Поэтому обозначим общую массу x, а массу основного вещества y.
Поэтому обозначим общую массу x, а массу основного вещества y.
Поскольку при смешивании все массы складываются, получаем уравнения:
4 + 6 = x ⇒ x = 10;
0,6 + 1,5 = y ⇒ y = 2,1.
Уравнения получились настолько простыми, что даже не пришлось составлять систему. Но это еще не ответ! В задаче требуется найти концентрацию нового раствора. Чтобы найти ее, разделим массу чистого вещества на общую массу раствора:
y : x = 2,1 : 10 = 0,21
Итак, доля чистого вещества равна 0,21. Чтобы перевести долю в проценты, умножим на сто:
0,21 · 100 = 21
Задача. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Обозначим массу 30-процентного раствора x, а массу 60-процентного раствора y. Получим таблицу:
Получим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (30%) | x | 0,3x |
| Раствор 2 (60%) | y | 0,6y |
| Чистая вода | 10 | 0 |
| Раствор 3 (50%) | 10 | 0,5 · 10 = 5 |
| Смесь «30% + 60% + вода» | x + y + 10 | 0,3x + 0,6y + 0 |
| Смесь «30% + 60% + 50%» | x + y + 10 | 0,3x + 0,6y + 5 |
По условию, концентрация смеси «30% + 60% + вода» равна 36%. Получаем уравнение:
0,3x + 0,6y + 0 = 0,36 · (x + y + 10)
Аналогично, концентрация смеси «30% + 60% + 50%» равна 41%. Отсюда получаем еще одно уравнение:
0,3x + 0,6y + 5 = 0,41 · (x + y + 10)
Решаем полученную систему, вычитая первое уравнение из второго:
Теперь вспомним, что надо найти. А нужна масса 30-процентного раствора. Та самая, которую мы обозначили за x. Следовательно, x = 60 — это и есть ответ.
А нужна масса 30-процентного раствора. Та самая, которую мы обозначили за x. Следовательно, x = 60 — это и есть ответ.
В заключение — два слова об уравнениях. Взгляните на задачи, приведенные выше: все уравнения — линейные. Никаких квадратов, никаких дискриминантов и тем более дробно-рациональных выражений. Вот почему задачи на смеси и сплавы считаются очень легкими.
Смотрите также:
- Простая задача B14 на смеси и сплавы
- Сложная задача B14 на смеси и сплавы
- Сложные выражения с дробями. Порядок действий
- Типичные задачи B12 с функциями
- Наибольшее и наименьшее значение
- Задача B4: Скачать файл на разной скорости
Задачи на смеси и сплавы
Вопросы занятия:
· решить типичные задачи на смеси и сплавы;
· повторить основные методы решения таких задач.
Материал урока
И прежде чем приступить к решению задач, давайте повторим немного теории. Для всех веществ выполняется закон сохранения объёма или массы.
Для всех веществ выполняется закон сохранения объёма или массы.
Другими словами, если два сплава или раствора соединяют в один сплав или раствор, то объём полученного раствора или сплава равен сумме объёмов исходных растворов или сплавов.
То есть, если мы смешаем пять литров яблочного сока и семь литров персикового сока, то получится двенадцать литров яблочно-персикового сока.
Масса растворенного вещества при смешивании двух растворов суммируется.
Задачи на смеси и сплавы бывают двух основных видов:
Первый вид. Две смеси определённой массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
Второй тип. В некоторый раствор с некоторой концентрацией вещества добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Рассмотрим задачу.
Пример.
Решим ещё одну задачу.
Пример.
Рассмотрим задачу.
Пример.
Решим ещё одну задачу.
Пример.
Рассмотрим ещё одну задачу.
Пример.
Рассмотрим ещё одну задачу.
Пример.
Рассмотрим ещё одну задачу.
Пример.
Рассмотрим ещё одну задачу.
Пример.
Решим ещё одну задачу.
Пример.
Итоги урока
Подведем итоги урока. Сегодня на уроке мы вспомнили, как решаются задачи на смеси или сплавы.
Задачи на смеси и сплавы
Задачи на смеси и сплавы легко решить, если правильно оформить условие. Такие задачи проще решать с помощью системы уравнений. Рассмотрим решение задач на смеси и сплавы на примерах.
Начнем с задачи на смеси.
1) Сколько граммов 4-процентного и сколько граммов 10-процентного растворов соли нужно взять, чтобы получить 180 граммов 6-процентного раствора?
Решение:
Пусть x граммов 4-процентного и y граммов 10-процентногорастворов соли нужно взять.
|
4% |
10% |
6% |
|
|
Раствор |
x |
y |
180 |
|
Соль |
0,04x |
0,1y |
0,06·180=10,8 |
Составим и решим систему уравнений:
Для удобства умножим почленно второе уравнение на 100
Первое уравнение умножим почленно на -10:
Сложив почленно первое и второе уравнение, получим
Отсюда x=120. Подставив в уравнение x+y=180 найденное значение x=120, находим y=60.
Значит, 120 граммов 4-процентного и 60 граммов 10-процентного растворов нужно взять.
Ответ: 120 г, 60 г.
Следующая — задача на сплавы.
2) Сколько килограммов 25-процентного и сколько килограммов 50-процентного сплавов меди нужно взять, чтобы получить 20 килограммов 40-процентного сплава?
Решение:
Пусть x килограммов 25-процентного и y килограммов 50-процентного сплавов меди нужно взять.
|
25% |
50% |
40% |
|
|
Сплав |
x |
y |
20 |
|
Медь |
0,25x |
0,5y |
0,4·20=8 |
Составим и решим систему уравнений:
Умножим второе уравнение на -4:
Сложив почленно первое и второе уравнение, имеем:
Подставив в первое уравнение найденное значение y=12, находим
Значит, 8 кг 25-процентного и 12 кг 50-процентного сплавов надо взять.
Ответ: 8 кг и 12 кг.
И еще одна задача на смеси и сплавы.
3) В первом бидоне — молоко, жирность которого составляет 3%, во втором — сливки жирностью 18%. Сколько надо взять молока и сколько сливок, чтобы получить 10 литров молока жирностью 6%?
Решение:
Пусть x литров молока жирностью 3% и y литров сливок жирностью 18% надо взять.
|
3% |
18% |
6% |
|
|
Молоко или сливки |
x |
y |
10 |
|
Жир |
0,03x |
0,18y |
0,06·10=0,6 |
Составим и решим систему уравнений:
Умножим второе уравнение системы на 100:
Затем второе уравнение разделим почленно на -3:
Сложим почленно первое и второе уравнение:
Подставим в первое уравнение системы:
Значит, 8 литров молока жирностью 3% и 2 литра сливок жирностью 18% надо взять.
Ответ: 2 л и 8 л.
Соотношение и пропорция – Задачи смеси на сплаве – MATH MADE EASY
Что такое сплав? Сплавы — это не что иное, как смесь двух или более металлов вместе в разных пропорциях в химии. Например, Сталь — это название, данное сплаву железа с углеродом, обычно с другими элементами, такими как никель и кобальт. Латунь представляет собой смесь меди с цинком и иногда другими элементами.
Пока все хорошо, но эта тема становится неинтересной, когда математика касается сплавов.Для решения вопросов, связанных со сплавами, необходимо хорошее знание концепции Ratio & Proportion. На первый взгляд отношение и пропорция кажутся простыми, но они становятся немного сложными, если их применять в темах, связанных со сплавами. Почему? Потому что это требует обратного распространения в мыслительном процессе. Поясню это вопросом:
Вопрос – Два металла X и Y используются для изготовления двух сплавов. Если весовое соотношение X : Y в первом сплаве 6 : 5, а во втором 7 : 13, то сколько кг металла X необходимо выплавить вместе с 11 кг первого сплава и 20 кг второго сплава, чтобы произвести новый сплав, содержащий 40% металла Y?
Если весовое соотношение X : Y в первом сплаве 6 : 5, а во втором 7 : 13, то сколько кг металла X необходимо выплавить вместе с 11 кг первого сплава и 20 кг второго сплава, чтобы произвести новый сплав, содержащий 40% металла Y?
Решение : Лучший способ решить такие проблемы — следовать принципу обращения.Это означает, что вместо того, чтобы решать проблему сверху вниз, давайте попробуем решить ее снизу вверх. Что такое нижний подход? Позвольте мне объяснить вам ниже:
Шаг 1 : Давайте назовем новый сплав как Alloy3, так что у нас есть следующее уравнение
Alloy3 = 11 кг сплава 1 + 20 кг сплава 2 ————- Уравнение 1
Шаг 2 : Теперь возникает вопрос, сколько металла X нужно добавить в сплав 3, чтобы % Y стал 40%? Таким образом, если Y составляет 40% в сплаве3, то X должен составлять 60%.Это означает, что мы должны сначала узнать первоначальный состав сплава 3, т.е. сколько в нем металла X и металла Y в кг? Можем ли мы это узнать? Можно, вернемся к вопросу, состав сплава 3 уже указан в уравнении 1 выше. Теперь давайте разобьем уравнение 1 дальше, как показано ниже:
Теперь давайте разобьем уравнение 1 дальше, как показано ниже:
Сплав 3 = [a кг металла X + b кг металла Y] (Сплав 1) + [c кг металла X + d кг металла Y] (Сплав 2)
Сплав 3 = (a+c) кг металла X + (b+d) кг металла Y ————- Уравнение 2
Шаг 3: На этом шаге мы пытаемся найти a,b,c и d уравнения 2.Для этого мы дали дополнительную информацию в вопросе, например, сплав 1 имеет металл X и Y в соотношении 6: 5, а сплав 3 использует 11 кг сплава 1, что означает
.Металл X в сплаве1, т. е. «a» = 11 x 6/(6+5) = 6 кг, поэтому металл Y, представляющий собой «b», будет равен 11-6 = 5 кг.
Аналогично
Металл X в сплаве2, т. е. «c» = 20 x 7/(7+13) = 7 кг, поэтому металл Y, обозначающий «d», будет равен 20-7 = 13 кг. Аналогично
Итак, мы вычислили a, b, c и d уравнения 2! Теперь у нас есть уравнение 2, переписанное как:
.Сплав 3 = (6+7) кг металла X + (5+13) кг металла Y
Шаг 3: Теперь вернемся к основному вопросу, сколько металла X нужно добавить в сплав 3, чтобы металл Y стал 40% сплава 3? Допустим, нам нужно добавить z кг металла X в сплав3, чтобы получить следующее уравнение
.
Металл Y в кг / (масса сплава3 + z кг металла X) = 40%
18 / (31 + z) = 40 % = 40/100
=> 18 = .4 (31 + z) дает
z = 14 кг металла X
Нравится:
Нравится Загрузка…
Родственные
Опубликовано MathsMadeEasy
По профессии я инженер и работаю в ИТ-компании в Индии в лаборатории передовых исследований и разработок. Я люблю математику, и цель этого блога — использовать мой академический и деловой опыт, чтобы помочь миллионам людей во всем мире открыть для себя этот предмет и решить сложные вопросы.Просмотреть все сообщения пользователя MathsMadeEasy
металлургия | Определение и история
Современное использование металлов является кульминацией долгого пути развития, растянувшегося примерно на 6500 лет. Принято считать, что первыми известными металлами были золото, серебро и медь, находившиеся в самородном или металлическом состоянии, из которых самыми ранними, по всей вероятности, были самородки золота, найденные в песках и гравии в руслах рек. Такие самородные металлы стали известны и ценились за их декоративную и утилитарную ценность во второй половине каменного века.
Такие самородные металлы стали известны и ценились за их декоративную и утилитарную ценность во второй половине каменного века.
Самая ранняя разработка
Золото можно агломерировать в более крупные куски путем холодной ковки, но самородная медь не может, и важным шагом на пути к Веку металлов стало открытие того, что такие металлы, как медь, могут быть преобразованы в формы путем плавления и отливки в формы; среди самых ранних известных изделий этого типа — медные топоры, отлитые на Балканах в 4-м тысячелетии до н. э. Еще одним шагом стало открытие того, что металлы можно извлекать из металлосодержащих минералов. Они были собраны, и их можно было отличить по цвету, текстуре, весу, цвету пламени и запаху при нагревании.Заметно больший выход, полученный при нагревании самородной меди с сопутствующими оксидными минералами, мог привести к процессу плавки, поскольку эти оксиды легко восстанавливаются до металла в слое древесного угля при температурах выше 700 ° C (1300 ° F) в качестве восстановителя. , угарный газ, становится все более стабильным. Чтобы осуществить агломерацию и отделение расплавленной или выплавленной меди от сопутствующих минералов, необходимо было ввести оксид железа в качестве флюса. Этот дальнейший шаг вперед можно объяснить наличием минералов оксида железа госсан в выветрелых верхних зонах месторождений сульфидов меди.
, угарный газ, становится все более стабильным. Чтобы осуществить агломерацию и отделение расплавленной или выплавленной меди от сопутствующих минералов, необходимо было ввести оксид железа в качестве флюса. Этот дальнейший шаг вперед можно объяснить наличием минералов оксида железа госсан в выветрелых верхних зонах месторождений сульфидов меди.
Во многих регионах в последующий период производились медно-мышьяковые сплавы, обладающие превосходными свойствами по сравнению с медью как в литом, так и в деформируемом виде. Сначала это могло быть случайным из-за сходства по цвету и цвету пламени между ярко-зеленым медно-карбонатным минералом малахитом и продуктами выветривания таких медно-мышьяковых сульфидных минералов, как энаргит, а позже за этим мог последовать целенаправленный отбор соединений мышьяка на основе их чесночного запаха при нагревании.
Содержание мышьяка варьировалось от 1 до 7 процентов, олова до 3 процентов. Практически не содержащие мышьяка медные сплавы с более высоким содержанием олова — другими словами, настоящая бронза — по-видимому, появились между 3000 и 2500 годами до нашей эры, начиная с дельты Тигра и Евфрата. Открытие значения олова могло произойти благодаря использованию станнита, смешанного сульфида меди, железа и олова, хотя этот минерал не так широко доступен, как основной минерал олова, касситерит, который, должно быть, был конечным источником. металла.Касситерит поразительно плотный и встречается в виде гальки в аллювиальных отложениях вместе с арсенопиритом и золотом; это также происходит в определенной степени в госсанах оксида железа, упомянутых выше.
Открытие значения олова могло произойти благодаря использованию станнита, смешанного сульфида меди, железа и олова, хотя этот минерал не так широко доступен, как основной минерал олова, касситерит, который, должно быть, был конечным источником. металла.Касситерит поразительно плотный и встречается в виде гальки в аллювиальных отложениях вместе с арсенопиритом и золотом; это также происходит в определенной степени в госсанах оксида железа, упомянутых выше.
Хотя бронза могла развиваться независимо в разных местах, наиболее вероятно, что культура бронзы распространилась через торговлю и миграцию народов с Ближнего Востока в Египет, Европу и, возможно, Китай. Во многих цивилизациях производство меди, мышьяковой меди и оловянной бронзы какое-то время продолжалось одновременно.Возможное исчезновение медно-мышьяковых сплавов трудно объяснить. Производство могло быть основано на полезных ископаемых, которые не были широко доступны и стали дефицитными, но относительная нехватка минералов олова не мешала значительной торговле этим металлом на значительных расстояниях. Возможно, оловянные бронзы в конечном итоге стали предпочитаться из-за возможности отравления мышьяком от паров, образующихся при окислении мышьякосодержащих минералов.
Возможно, оловянные бронзы в конечном итоге стали предпочитаться из-за возможности отравления мышьяком от паров, образующихся при окислении мышьякосодержащих минералов.
По мере разработки выветрелых медных руд в данных местах добывались и плавились более твердые сульфидные руды под ними.Используемые минералы, такие как халькопирит, сульфид меди и железа, нуждались в окислительном обжиге для удаления серы в виде диоксида серы и получения оксида меди. Это не только требовало больших металлургических навыков, но также окисляло тесно связанное железо, что в сочетании с использованием флюсов из оксида железа и более сильными восстановительными условиями, создаваемыми усовершенствованными плавильными печами, приводило к более высокому содержанию железа в бронзе.
Невозможно провести четкую границу между бронзовым веком и железным веком.Небольшие куски железа должны были производиться в медеплавильных печах, поскольку использовались флюсы оксида железа и железосодержащие сульфидные руды меди. Кроме того, более высокие температуры печи создали бы условия для более сильного восстановления (то есть более высокое содержание монооксида углерода в газах печи). Ранний кусок железа с дороги в провинции Дренте, Нидерланды, был датирован 1350 годом до нашей эры, датой, которую обычно принимают за средний бронзовый век для этой области. С другой стороны, в Анатолии железо использовалось уже в 2000 г. до н. э.Есть также случайные ссылки на железо и в более ранние периоды, но этот материал имел метеоритное происхождение.
Кроме того, более высокие температуры печи создали бы условия для более сильного восстановления (то есть более высокое содержание монооксида углерода в газах печи). Ранний кусок железа с дороги в провинции Дренте, Нидерланды, был датирован 1350 годом до нашей эры, датой, которую обычно принимают за средний бронзовый век для этой области. С другой стороны, в Анатолии железо использовалось уже в 2000 г. до н. э.Есть также случайные ссылки на железо и в более ранние периоды, но этот материал имел метеоритное происхождение.
Как только была установлена взаимосвязь между новым металлом, обнаруженным в медных плавках, и рудой, добавленной в качестве флюса, естественным образом последовала работа печей для производства только железа. Несомненно, к 1400 г. до н. э. в Анатолии большое значение приобрело железо, а к 1200–1000 гг. до н. э. из него в больших масштабах изготавливали оружие, первоначально лезвия кинжалов.По этой причине 1200 г. до н.э. был принят за начало железного века. Данные раскопок указывают на то, что искусство изготовления железа зародилось в гористой местности к югу от Черного моря, где доминировали хетты. Позже это искусство, по-видимому, распространилось среди филистимлян, поскольку в Гераре были обнаружены грубые печи, датируемые 1200 г. до н. э., вместе с рядом железных предметов.
Позже это искусство, по-видимому, распространилось среди филистимлян, поскольку в Гераре были обнаружены грубые печи, датируемые 1200 г. до н. э., вместе с рядом железных предметов.
Плавка оксида железа с древесным углем требовала высокой температуры, и, поскольку температура плавления железа 1540 °C (2800 °F) тогда была недостижима, продукт представлял собой просто губчатую массу пастообразных глобул металла, смешанных с полужидкий шлак.Этот продукт, позже известный как блюм, вряд ли можно было использовать в том виде, в каком он был, но повторный нагрев и горячая ковка устранили большую часть шлака, создав кованое железо, продукт гораздо лучшего качества.
На свойства железа сильно влияет присутствие небольшого количества углерода, при этом значительное увеличение прочности связано с содержанием менее 0,5 процента. При достижимых тогда температурах — около 1200 ° C (2200 ° F) — восстановление древесным углем давало почти чистое железо, которое было мягким и имело ограниченное применение для оружия и инструментов. с изобретением лучших мехов железо поглощало больше углерода.Это привело к цветению и продуктам из железа с различным содержанием углерода, что затрудняло определение периода, в течение которого железо могло быть преднамеренно упрочнено путем науглероживания или повторного нагревания металла в контакте с избытком древесного угля.
с изобретением лучших мехов железо поглощало больше углерода.Это привело к цветению и продуктам из железа с различным содержанием углерода, что затрудняло определение периода, в течение которого железо могло быть преднамеренно упрочнено путем науглероживания или повторного нагревания металла в контакте с избытком древесного угля.
Углеродосодержащее железо имело еще одно большое преимущество, заключавшееся в том, что, в отличие от бронзы и безуглеродистого железа, его можно было сделать еще более твердым путем закалки, т. е. быстрого охлаждения путем погружения в воду. Нет никаких свидетельств использования этого процесса закалки в раннем железном веке, так что он должен был быть либо неизвестен тогда, либо не считался выгодным, поскольку закалка делает железо очень хрупким и за ним должен следовать отпуск или повторный нагрев при более низкая температура, чтобы восстановить ударную вязкость.То, что, по-видимому, было установлено на раннем этапе, было практикой многократной холодной ковки и отжига при 600–700 ° C (1100–1300 ° F), температура, естественно достигаемая при простом огне. Эта практика распространена в некоторых частях Африки даже сегодня.
Эта практика распространена в некоторых частях Африки даже сегодня.
К 1000 г. до н. э. железо стало известно в Центральной Европе. Его использование медленно распространялось на запад. Производство железа было широко распространено в Великобритании во время римского вторжения в 55 г. до н. э. В Азии железо также было известно в древности, в Китае около 700 г. до н.э.
Преимущества сплавов по сравнению с чистым металлом
Сплавы
решают многие проблемы, связанные с использованием чистых металлов для различных проектов. Чистые металлы мягче, подвержены коррозии и дороже, чем сплавы. Таким образом, свойства сплавов допускают больше вариантов и применений, чем чистые металлы. Чтобы оценить эти преимущества, узнайте, чем эти материалы отличаются по своим свойствам и применению. Выбирая сплавы, вы получаете лучшие возможности для литья и других металлических проектов, чем при использовании чистых металлов.
Что такое сплав?
Сплавы объединяют два или более вещества для создания продукта с лучшими свойствами, чем любая из его частей. Как правило, сплавы представляют собой продукт смешивания металлов, хотя существуют и другие сплавы, в которых используются металлы и неметаллы. Например, углерод является неметаллическим компонентом стали.
Как правило, сплавы представляют собой продукт смешивания металлов, хотя существуют и другие сплавы, в которых используются металлы и неметаллы. Например, углерод является неметаллическим компонентом стали.
Большинство сплавов начинаются с плавления и объединения двух или более металлов. Во время этого процесса смешивания металлы также могут подвергаться очистке для удаления загрязняющих примесей, которые могут негативно повлиять на продукт.Различные методы производства сплавов направлены на защиту расплавленной смеси от окисления. При плавлении на воздухе шлак, образующийся сверху, не позволяет кислороду загрязнять сплав под ним. Плавление сплавов в вакууме также предотвращает окисление. Дуговая плавка и индукционная плавка — это два варианта создания сплавов, использующих электричество для облегчения процессов плавления и смешивания.
Сплавы настолько важны для производства и промышленности, что названия эпох человеческой истории связаны с конкретными материалами.Например, бронзовый век ознаменовал эпоху, когда люди открыли, как сделать этот сплав, соединив медь и олово. Латунь смешивает цинк и медь. Хотя эти сплавы были жизненно важны для древнего мира и до сих пор находят множество применений, стальные сплавы являются наиболее часто используемыми типами в промышленности. Алюминиевые сплавы также ценны в производстве, особенно для автомобильных компонентов. Латунь и бронза — другие сплавы, часто используемые для фитингов, компонентов сантехники и подшипников.
Латунь смешивает цинк и медь. Хотя эти сплавы были жизненно важны для древнего мира и до сих пор находят множество применений, стальные сплавы являются наиболее часто используемыми типами в промышленности. Алюминиевые сплавы также ценны в производстве, особенно для автомобильных компонентов. Латунь и бронза — другие сплавы, часто используемые для фитингов, компонентов сантехники и подшипников.
Свойства сплавов
Особые свойства сплавовзависят от металлов, из которых они изготовлены.Например, когда золото плавится с цинком, полученный сплав имеет блеск золота, но с дополнительной прочностью, обеспечиваемой добавлением цинка. Металлурги выбирают типы металлов для объединения в сплавы на основе желаемых характеристик конечного продукта.
По сравнению с чистыми металлами сплавы имеют лучшую коррозионную стойкость, более низкую стоимость, более высокую прочность и лучшую обрабатываемость. Производство и состав сплавов определяют такие особенности, как обрабатываемость, пластичность и хрупкость.
Преимущество сплавов
Сплавы
предлагают множество преимуществ, которых нет у чистых металлов. Используя сплавы, вы получаете преимущество индивидуальной смеси металлов, которая сочетает в себе положительные свойства материалов. В зависимости от компонентов сплава изделия, в которых они используются, могут иметь следующие преимущества по сравнению с предметами, изготовленными из чистых металлов:
- Коррозионная стойкость
- Лучшая способность к пайке
- Прочные детали
- Легкий вес для прочности
- Теплопроводность
- Электропроводность
Специалисты по выбору сплавов и комбинированию металлов для получения идеальных пропорций могут оптимизировать их свойства для используемого продукта.
Примеры сплавов
Сплавы включают несколько типов комбинаций металлов. Вот несколько примеров сплавов и их применения.
- Состав латуни: Этот универсальный сплав, когда-то называемый красной латунью, лучше всего подходит для отливок, требующих умеренной обрабатываемости и прочности, таких как сантехника или трубная арматура.

- Композитная латунь для клапана: Имеет аналогичный состав и используется как композиционная латунь.
- Марганцевая бронза: Высокопрочный сплав для тяжелых условий эксплуатации, за исключением сред, требующих коррозионной стойкости.
- Оловянная бронза: Используется в различных втулках, деталях клапанов, шестернях, насосах, поршневых кольцах и подшипниках.
- Алюминиевая бронза: По прочности равна марганцевой бронзе. Кроме того, он обладает отличной коррозионной стойкостью.
- 713.0 алюминиевый сплав: Не требует термической обработки для придания прочности и может работать в приложениях, предъявляющих высокие требования к сплаву.
- Алюминиевый сплав A356.0: Стойкий к горячему растрескиванию, легко поддающийся сварке и средней механической обработке, этот алюминиевый сплав подходит для автомобильных компонентов, таких как картеры трансмиссии, картеры заднего моста и масляные поддоны.

- Титановые сплавы: Устойчивость титана к коррозии делает эти сплавы особенно подходящими для морского использования, например, компонентов подводных лодок.
- Прочие сплавы цветных металлов
- Другие сплавы латуни и бронзы
- Прочие алюминиевые сплавы
Что такое чистый металл?
Чистые металлы не содержат других примесей. Эти металлы проявляют только свои природные свойства. Однако многие металлы обладают нежелательными свойствами, которые делают их использование в чистом виде неприемлемым для промышленного применения.Например, многие чистые металлы, такие как золото, по своей природе мягкие из-за их однородной атомной структуры. Однако, смешивая их с разными металлами, в сплавы вводятся новые атомы, укрепляющие материал.
Свойства чистых металлов
Чистые металлы обладают различными свойствами. Однако многие из них подвержены коррозии или ржавчине, например, железо. Смешивание железа с другими металлами позволяет получить устойчивую к ржавчине нержавеющую сталь.
Смешивание железа с другими металлами позволяет получить устойчивую к ржавчине нержавеющую сталь.
Вес – еще одно свойство чистых металлов, скорректированное легированием.Некоторые металлы, такие как золото или железо, обладают естественной плотностью. Однако их сочетание с алюминием или титаном повышает прочность при одновременном снижении веса. Многие аэрокосмические проекты используют титановые сплавы для дополнительной прочности и легкого веса, что было бы невозможно с чистыми металлами.
Примеры чистых металлов
В природе появляются чистые металлы. Рассмотрим эти примеры чистых металлов и то, как они улучшают сплавы.
- Золото: Может служить основным металлом в сплаве для придания красоты ювелирным изделиям или проводимости в электронике.
- Титан: Увеличивает прочность без увеличения веса сплавов.
- Медь: Этот металл обладает коррозионной стойкостью, тепло- и электропроводностью и пластичностью по сравнению с легированными металлами.

- Алюминий: Как и титан, алюминий является основным металлом, добавляемым в сплавы для улучшения обрабатываемости, коррозионной стойкости и снижения веса.
- Цинк: Цинк чаще всего используется при цинковании стали для защиты ее от коррозии.
- Олово: Олово хорошо подходит для многих операций холодной обработки, включая прядение, прокатку и экструзию. Кроме того, он обеспечивает защиту от коррозии других металлов при их легировании.
Вышеупомянутые чистые металлы также можно комбинировать друг с другом или с другими металлами для получения сплавов.
Чем сплав отличается от чистого металла?
Комбинация металлов дает сплавы с более желательными свойствами, чем у чистых металлов.Физические и химические свойства делают сплавы предпочтительными для многих промышленных применений в различных секторах. Отличия сплавов и чистых металлов заключаются в следующем.
Сплавы и чистые металлы: физические свойства
Сплавы имеют отличные от чистых металлов физические свойства. Эти изменения включают изменения массы, проводимости, удобоукладываемости и термостойкости.
Эти изменения включают изменения массы, проводимости, удобоукладываемости и термостойкости.
По массе легированные металлы могут быть менее плотными, чем чистые металлы, при сохранении такой же прочности.В автомобильной и аэрокосмической промышленности алюминиевые и титановые сплавы ценятся за их легкость и прочность.
Проводимость определяет, насколько хорошо металлы или сплавы могут передавать электроны для передачи тепла или электричества. Интеграция различных металлов может увеличить или уменьшить передачу тепла или электричества в зависимости от конечного использования продукта. Например, медные сплавы обладают высокой проводимостью благодаря врожденной способности меди хорошо переносить электроны.
Удобообрабатываемость показывает, насколько хорошо материалы могут выдерживать изменение своей формы при использовании холодных или горячих методов.Некоторые чистые металлы настолько мягки, что обладают хорошей обрабатываемостью, но низкой прочностью. Легирование этих материалов обеспечивает прочность и работоспособность. Например, холодная обработка и включение в сплавы быстро придают чистому олову дополнительную прочность.
Например, холодная обработка и включение в сплавы быстро придают чистому олову дополнительную прочность.
Наконец, термостойкость или температура плавления чистых металлов изменяются при их сплавлении с другими материалами. Чистые металлы имеют одну температуру плавления, температуру, при которой их твердая форма превращается в жидкость. Однако сплавы имеют диапазон температур, который может вызвать изменения в структуре материала.Часто этот диапазон выше, чем для отдельных металлов. Таким образом, сплавы в большинстве случаев обладают превосходной стойкостью к термическому напряжению по сравнению с чистыми металлами.
Легирование чистого металла изменяет физические свойства, чтобы улучшить их для увеличения числа возможных применений сплавов.
Сплавы и чистые металлы: химические свойства
Наиболее существенное различие между сплавами и чистыми металлами происходит на молекулярном уровне. У них нет одинаковой химии.Чистые металлы содержат атомы только этого элемента — например, все железо или золото. Эти чистые металлы обычно подвергаются обработке для удаления примесей других материалов. Сплавы имеют атомарные компоненты нескольких элементов. Поэтому они имеют химическую структуру, отличную от чистых металлов.
Эти чистые металлы обычно подвергаются обработке для удаления примесей других материалов. Сплавы имеют атомарные компоненты нескольких элементов. Поэтому они имеют химическую структуру, отличную от чистых металлов.
Физические свойства изменяются из-за изменений на атомарном уровне. Эти изменения происходят потому, что химический состав металлов становится другим при сплавлении. Например, чистые металлы часто легко реагируют с другими химическими веществами в окружающей среде, что приводит к ржавчине.Смешивание этих металлов с другими для предотвращения коррозии увеличивает их долговечность.
Другим типом химических изменений, происходящих при смешивании металлов, является повышенная молекулярная стабильность материала. Движение атомов внутри структуры металла может повлиять на прочность материала. Атомы легко проходят через чистые металлы, потому что все они одинаковы. Однако смешивание одного металла с другим приводит к появлению атомов разного размера, которые препятствуют движению, делая сплавы прочнее.
Преимущества сплавов в отливках — почему сплавы более полезны, чем чистые металлы?
Различия между чистыми металлами и сплавами делают сплавы гораздо более полезными для нескольких применений.Выбирая смесь металлов в сплаве, можно подобрать материал, отвечающий требованиям его конечного использования. Например, выбирая нержавеющую сталь вместо железа, вы получаете более долговечный, устойчивый к коррозии металл, который лучше противостоит погодным условиям.
Сплавы обладают коррозионной стойкостью, которую не могут обеспечить чистые металлы. Поэтому они полезны в ситуациях, когда они могут подвергаться воздействию химикатов, воды, морской соли или пара. Эти условия быстро изнашивают многие чистые металлы, такие как железо.
Еще одним преимуществом сплавов перед чистыми металлами является их дополнительная прочность. Комбинирование металлов повышает структурную целостность готового изделия. Это качество делает сплавы пригодными для применения в тяжелых условиях или при высоких нагрузках, например, внутри двигателей.
Наконец, выбор сплавов вместо чистых металлов дает вам больший контроль над весом готовой детали. Сплавы могут обеспечить прочность, не утяжеляя автомобили, самолеты или другие транспортные средства, в конструкции которых используются легкие и прочные металлы.
Почему мы должны использовать сплавы вместо чистых металлов для отливок?
Хотя преимущества сплавов по сравнению с чистыми металлами очевидны, многие люди до сих пор задаются вопросом: «Почему в отливках сплавы предпочтительнее чистых металлов?» Этот распространенный вопрос требует решения, чтобы клиенты могли выбрать правильный металл для своего продукта.
Из-за структуры чистых металлов в готовой продукции могут возникать некоторые проблемы. Металлы могут легко подвергаться коррозии или не соответствовать требованиям прочности.Кроме того, использование чистых металлов может сделать детали слишком дорогими или слишком тяжелыми для массового производства. Сплавы преодолевают эти проблемы из чистых металлов, создавая прочные компоненты, детали с большей коррозионной стойкостью, меньшим весом, большей термостойкостью или меньшими затратами. Поэтому при выборе отливок лучшим вариантом являются сплавы.
Поэтому при выборе отливок лучшим вариантом являются сплавы.
превосходят чистые металлы для отливок по многим параметрам. Следующим выбором является определение типа используемых сплавов. Комбинация металлов, их пропорции и процесс литья будут влиять на свойства создаваемых компонентов.Поэтому тщательно выбирайте сплавы, исходя из того, что вам от них нужно. Например, для некоторых деталей может потребоваться дополнительная прочность, меньший вес, большая термостойкость, лучшая защита от коррозии или улучшенное функционирование в условиях нагрузки.
Как контроль качества в процессе литья имеет значение
Конкретный процесс литья также влияет на качество почти так же, как выбор между использованием сплава и чистого металла. Чистые металлы имеют присущие им проблемы, которые решает объединение их в сплавы.Однако при литье из сплавов необходимо соблюдать тщательные методы, чтобы обеспечить качество готовой детали.
Во-первых, размер и форма зерен в материале определяют качество отливки. В процессе должны использоваться более низкие температуры сплава, заливаемого в отливку, и более высокие скорости охлаждения для оптимизации конечного продукта. При литье под давлением охлаждение формы ускоряет охлаждение металла по сравнению с литьем в песчаные формы, что приводит к образованию более мелких зерен. В некоторых случаях добавление измельчителей зерна также может помочь уменьшить размер частиц в сплавах.
В процессе должны использоваться более низкие температуры сплава, заливаемого в отливку, и более высокие скорости охлаждения для оптимизации конечного продукта. При литье под давлением охлаждение формы ускоряет охлаждение металла по сравнению с литьем в песчаные формы, что приводит к образованию более мелких зерен. В некоторых случаях добавление измельчителей зерна также может помочь уменьшить размер частиц в сплавах.
Во-вторых, изменение состояния сплавов также влияет на конечное качество. Фазовые изменения, такие как замерзание, заставляют включения проникать в промежутки между ветвями дендритов. Большее расстояние между этими плечами отрицательно влияет на качество заброса.
В-третьих, сведение к минимуму проникновения воздуха в отливку снижает пористость. Быстрое охлаждение отливки может уменьшить проникновение воздуха в металл. Однако при литье под давлением воздух все равно попадет в деталь. Однако есть способы свести к минимуму загрязнение воздуха.Варианты сделать это включают использование методов, отличных от литья под давлением. Гравитационное литье или литье под низким давлением может решить проблему пористости и связанной с этим хрупкости.
Гравитационное литье или литье под низким давлением может решить проблему пористости и связанной с этим хрупкости.
Отливки из литейного сплава Warner Brothers
Раскройте свой источник высококачественных отливок из сплавов, доставленных в кратчайшие сроки. Узнайте больше о наших предложениях по цветному литью и их преимуществах. Мы используем уникальный процесс, известный только нашей компании по литью металлов. Поэтому никто другой не может обеспечить такое качество, как мы.Интегрируя первоклассные материалы в наш запатентованный процесс, мы можем добиться непревзойденных результатов в литье из сплавов и многом другом. После того, как вы определились с параметрами своего проекта, свяжитесь с нами в Warner Brothers Foundry, чтобы получить предложение.
сплав | решение |
В качестве существительных разница между сплавоми раствором заключается в том, что сплав представляет собой металл, представляющий собой комбинацию двух или более элементов, по крайней мере один из которых является металлом, в то время как раствор представляет собой гомогенную смесь, которая может быть жидким, газообразным или твердым, образованным при растворении одного или нескольких веществ. В качестве глаголасплав означает смешивать или комбинировать; часто используется из металлов.
|
6.7A: Сплавы замещения — Химия LibreTexts
Когда расплавленный металл смешивается с другим веществом, существует два механизма, которые могут вызвать образование сплава: (1) атомный обмен или (2) междоузельный механизм .Относительный размер каждого элемента в смеси играет основную роль в определении того, какой механизм будет реализован.
Когда атомы относительно близки по размеру, обычно применяется метод обмена атомами, при котором некоторые из атомов, составляющих металлические кристаллы, замещаются атомами другой составляющей. Это называется замещающим сплавом . Примеры сплавов замещения включают бронзу и латунь, в которых некоторые атомы меди замещены либо атомами олова, либо атомами цинка.
Почему возникают сплавы замещения: склеивание
Связь между двумя металлами лучше всего описывается как комбинация металлического «обмена электронами» и ковалентной связи, одна не может возникнуть без другой, и соотношение одного к другому меняется в зависимости от вовлеченных компонентов. Металлы разделяют свои электроны по всей своей структуре, этот поток электронов является причиной многих характеристик, связанных с металлами, включая их способность действовать как проводники.Различное количество и сила ковалентных связей могут меняться в зависимости от различных конкретных металлов и того, как они смешиваются. Ковалентная связь отвечает за кристаллическую структуру, а также за температуру плавления и различные другие физические свойства.
Рисунок \(\PageIndex{2}\): Примеры металлических сплавов замещения. В зависимости от конкретного типа сплава замещения они могут иметь несколько кристаллических структур. Две из возможных структур включают Face Center Cubic (слева) и Cubic Center Cubic (справа).Структура металлического сплава не ограничивается этими двумя структурами, но вместе они составляют большую часть обычных сплавов.
В зависимости от конкретного типа сплава замещения они могут иметь несколько кристаллических структур. Две из возможных структур включают Face Center Cubic (слева) и Cubic Center Cubic (справа).Структура металлического сплава не ограничивается этими двумя структурами, но вместе они составляют большую часть обычных сплавов. По мере увеличения сходства электронной структуры металлов, входящих в состав сплава, снижаются металлические характеристики сплава. Чистые металлы полезны, но их применение часто ограничивается свойствами каждого отдельного металла. Сплавы допускают смеси металлов, обладающие повышенной стойкостью к окислению, повышенной прочностью, электропроводностью и температурой плавления; Практически любым свойством можно управлять, регулируя концентрацию сплава.Примером может служить латунная дверная фурнитура, она прочная и устойчива к коррозии лучше, чем чистый цинк или медь, два основных металла, из которых состоит латунный сплав. Комбинация также имеет низкую температуру плавления, что позволяет легко отливать ее во множество различных форм и размеров. (1) Есть много других аспектов сплавов замещения, которые можно было бы изучить более подробно, но основная концепция заключается в том, что каждый отдельный металл в сплаве придают конечному продукту его химические и физические свойства.
(1) Есть много других аспектов сплавов замещения, которые можно было бы изучить более подробно, но основная концепция заключается в том, что каждый отдельный металл в сплаве придают конечному продукту его химические и физические свойства.
Сплавы замещения сыграли важную роль в развитии человеческого общества и культуры, какими мы их знаем сегодня.Сам бронзовый век назван в честь сплава замещения, состоящего из олова в металлическом растворе меди. Древние бронзы очень загрязнены или даже неправильно маркированы, содержат большое количество цинка и мышьяка, а также множество примесей. Эти многочисленные замещающие сплавы позволили создать более прочные инструменты и оружие, они позволили повысить производительность как в мастерской, так и на поле боя. Потребность в сырье, таком как олово и медь, для производства бронзы также стимулировала рост торговли, поскольку их руды редко встречаются вместе.Нынешнее химическое понимание сплавов замещения не было бы таким глубоким, если бы не полезность сплавов для человека.
Резюме
Сплав представляет собой смесь металлов, объемно-металлические свойства которой отличаются от свойств составляющих ее элементов. Сплавы могут быть образованы путем замены одного атома металла на другой атом того же размера в решетке (сплавы замещения), путем вставки меньших атомов в отверстия в решетке металла (сплавы внедрения) или комбинацией того и другого.Хотя элементный состав большинства сплавов может варьироваться в широких пределах, некоторые металлы соединяются только в фиксированных пропорциях, образуя интерметаллическое соединение
.Каталожные номера
- Смоллман, Р. Э., Нган, А. Х. В., и Смоллман, Р. Э. (2007). Металлургия и современные материалы . Амстердам: Баттерворт Хайнеманн.
- Ван, Ф.Э.. (2005). Теория соединения металлов и сплавов . Амстердам: Эльзевир.
- Дикинсон, О.ТПК (1994). Эгейский бронзовый век . Кембриджская мировая археология. Кембридж: Издательство Кембриджского университета.

Проблемы
- Встречаются ли сплавы замещающих металлов в природе на поверхности земли?
- Какие две характеристики металла необходимы для образования сплава замещения?
- Могут ли кислород или азот быть частью кристаллической структуры сплава замещения?
Решения
- Нет, окислительная природа земной атмосферы, а также потребность в специфических и концентрированных металлах не позволяют им встречаться в природе.
- Похожие радиусы и аналогичная электроотрицательность.
- Только металлические элементы могут образовывать необходимые металлические связи, позволяющие образовывать сплавы.
гранецентрированный куб и объемноцентрированный куб. От чистого никеля (0 мол. % хрома) до примерно 40-50 мол. % хрома структура является гранецентрированной кубической. В этой структуре атомы Cr замещают атомы Ni в гранецентрированной кубической структуре никеля.
 Однако при добавлении количества хрома, превышающего определенный процент (который зависит от температуры), эта структура перестает быть стабильной.На другом конце диаграммы, от чистого хрома до примерно 75% хрома (в зависимости от температуры), структура представляет собой объемно-центрированную кубическую структуру с никелем, замещающим объемно-центрированную кубическую структуру хрома. Область между двумя фазами называется двухфазной областью. При этих составах две фазы (богатая никелем гранецентрированная кубическая и богатая хромом объемноцентрированная кубическая) существуют вместе (раствор в этой области не является гомогенным). Используя фазовую диаграмму, ответьте на следующие вопросы.а. Каков относительный состав смеси в точке А? При какой температуре плавится твердая смесь такого состава? б. Возможна ли однородная твердая смесь, состоящая из 50 % Ni и 50 % Cr? Если да, то какую кристаллическую структуру он будет иметь? в. Каков относительный состав в точке B? Какова кристаллическая структура в точке B? д.
Однако при добавлении количества хрома, превышающего определенный процент (который зависит от температуры), эта структура перестает быть стабильной.На другом конце диаграммы, от чистого хрома до примерно 75% хрома (в зависимости от температуры), структура представляет собой объемно-центрированную кубическую структуру с никелем, замещающим объемно-центрированную кубическую структуру хрома. Область между двумя фазами называется двухфазной областью. При этих составах две фазы (богатая никелем гранецентрированная кубическая и богатая хромом объемноцентрированная кубическая) существуют вместе (раствор в этой области не является гомогенным). Используя фазовую диаграмму, ответьте на следующие вопросы.а. Каков относительный состав смеси в точке А? При какой температуре плавится твердая смесь такого состава? б. Возможна ли однородная твердая смесь, состоящая из 50 % Ni и 50 % Cr? Если да, то какую кристаллическую структуру он будет иметь? в. Каков относительный состав в точке B? Какова кристаллическая структура в точке B? д. При какой температуре твердое тело, находящееся в точке В, начинает плавиться?
При какой температуре твердое тело, находящееся в точке В, начинает плавиться?
Задача 105 Тяжелая Сложность
Сплав представляет собой смесь металлов, состоящую из двух или более элементов.Как и во всех смесях, относительное количество элементов в сплаве может варьироваться. В некоторых случаях компоненты сплава могут иметь различную кристаллическую структуру. Например, никель-хромовый сплав состоит из никеля, имеющего гранецентрированную кубическую структуру, и хрома, имеющего объемно-центрированную кубическую структуру. Какую структуру принимает сплав? Это зависит от относительных составов. Фазовые диаграммы для таких сплавов показывают структуру в зависимости от состава сплава.Например, здесь показана фазовая диаграмма никеля и хрома от 700°С до 1900°С:
Обратите внимание, что на диаграмме есть две разные твердые фазы: гранецентрированная кубическая и объемноцентрированная кубическая. От чистого никеля (0 мол. % хрома) до примерно 40-50 мол. % хрома структура является гранецентрированной кубической. В этой структуре атомы Cr замещают атомы Ni в гранецентрированной кубической структуре никеля. Однако при добавлении количества хрома, превышающего определенный процент (который зависит от температуры), эта структура перестает быть стабильной.На другом конце диаграммы, от чистого хрома до примерно 75% хрома (в зависимости от температуры), структура представляет собой объемно-центрированную кубическую структуру с никелем, замещающим объемно-центрированную кубическую структуру хрома. Область между двумя фазами называется двухфазной областью. При этих составах две фазы (богатая никелем гранецентрированная кубическая и богатая хромом объемноцентрированная кубическая) существуют вместе (раствор в этой области не является гомогенным). Используя фазовую диаграмму, ответьте на следующие вопросы.
От чистого никеля (0 мол. % хрома) до примерно 40-50 мол. % хрома структура является гранецентрированной кубической. В этой структуре атомы Cr замещают атомы Ni в гранецентрированной кубической структуре никеля. Однако при добавлении количества хрома, превышающего определенный процент (который зависит от температуры), эта структура перестает быть стабильной.На другом конце диаграммы, от чистого хрома до примерно 75% хрома (в зависимости от температуры), структура представляет собой объемно-центрированную кубическую структуру с никелем, замещающим объемно-центрированную кубическую структуру хрома. Область между двумя фазами называется двухфазной областью. При этих составах две фазы (богатая никелем гранецентрированная кубическая и богатая хромом объемноцентрированная кубическая) существуют вместе (раствор в этой области не является гомогенным). Используя фазовую диаграмму, ответьте на следующие вопросы.
а. Каков относительный состав смеси в точке А? При какой температуре плавится твердая смесь такого состава?
б. Возможна ли однородная твердая смесь, состоящая из 50 % Ni и 50 % Cr? Если да, то какую кристаллическую структуру он будет иметь?
Возможна ли однородная твердая смесь, состоящая из 50 % Ni и 50 % Cr? Если да, то какую кристаллическую структуру он будет иметь?
с. Каков относительный состав в точке B? Какова кристаллическая структура в точке B?
д. При какой температуре твердое тело, находящееся в точке В, начинает плавиться?
РЕШЕНО:Решение задач на смешение значений Ювелир объединил сплав, который стоит \ 4.30 за унцию со сплавом, который стоит \ 1,80 за унцию. Сколько унций каждого из них было использовано для приготовления смеси из 200 унций стоимостью \ 2,50 за унцию?
Стенограмма видео
, который решит эту проблему, состоит в том, чтобы сделать таблицу с этими столбцами суммы, стоимости и стоимости, которая равна восьмикратному значению. Итак, есть два типа союзников, которые называют его юристом. А мне нравится так два типа союзников теперь первая л. I. Мы не знаем, сколько у нас будет в месяц, но мы знаем, что себестоимость равна 4. 30 за пачку и таким же образом поднять ее дом таким же образом для Элли, чтобы вы знали, что это стоит одно очко. Это, знаете ли, доллары за взлеты. Но когда он делает их вместе, тогда мы знаем, что на сборку уйдет 200 фунтов стерлингов. Конечно, и стоимость дома составит 2,50 доллара. Таким образом, мы можем рассчитать значение, которое будет 200 умножить на 2,5 года. А это равно 500. Теперь мы можем вернуться и заполнить здесь черные. Итак, поскольку мы не знаем, сколько от L я выиграл, нам нужно, мы будем обозначать это буквой X, и тогда количество L I тоже будет 200 минус шесть, потому что в уме будет 200, теперь мы можем умножать.Так что это будет четыре балла в эти старые времена X, а это будет один балл. Это ваше умножение на 200 минус X. Итак, теперь мы готовы написать наше уравнение. Итак, эти две здесь объединили стрельбу на 500. Итак, четыре точки для нуля х плюс 1,8 умножить на 200 минус х равно 500. И это линейное уравнение, которое не может быть решено. Итак, для начала мы привыкли распределять собственность.
30 за пачку и таким же образом поднять ее дом таким же образом для Элли, чтобы вы знали, что это стоит одно очко. Это, знаете ли, доллары за взлеты. Но когда он делает их вместе, тогда мы знаем, что на сборку уйдет 200 фунтов стерлингов. Конечно, и стоимость дома составит 2,50 доллара. Таким образом, мы можем рассчитать значение, которое будет 200 умножить на 2,5 года. А это равно 500. Теперь мы можем вернуться и заполнить здесь черные. Итак, поскольку мы не знаем, сколько от L я выиграл, нам нужно, мы будем обозначать это буквой X, и тогда количество L I тоже будет 200 минус шесть, потому что в уме будет 200, теперь мы можем умножать.Так что это будет четыре балла в эти старые времена X, а это будет один балл. Это ваше умножение на 200 минус X. Итак, теперь мы готовы написать наше уравнение. Итак, эти две здесь объединили стрельбу на 500. Итак, четыре точки для нуля х плюс 1,8 умножить на 200 минус х равно 500. И это линейное уравнение, которое не может быть решено. Итак, для начала мы привыкли распределять собственность. 1,80 умножается на 200, а затем умножается на минус X. Таким образом, 4,30 X плюс 3 60 минус одно очко — ваш X равен 500.Затем мы можем вычесть 3·60 с обеих сторон, вычитая 3·60 с обеих сторон на 3·60 минус 3·16 дня после того, как он стал нулем. Теперь у нас есть четыре точки VI ноль х минус 1,80 х равно 100 полностью и так как четыре точки х и 1,80 х. Они как термины. Мы можем объединить их. Сложение дает 2,5 х, равно 1 40 и тогда начинают отбиваться оба от них по 2,5. Итак, делим боевой фут на пять, и теперь мы получаем, что X равно 56 дому, поэтому мы вернемся к таблице, и теперь X равно 56. Таким образом, 200 минус X будет 200 минус 56, что будет 144.Значит, нам нужно 56 домов от Ally One и 144 дома от Ally to. Итак, давайте запишем это. В смеси должно быть 56 унций с одного и 144 дома с юриста.
1,80 умножается на 200, а затем умножается на минус X. Таким образом, 4,30 X плюс 3 60 минус одно очко — ваш X равен 500.Затем мы можем вычесть 3·60 с обеих сторон, вычитая 3·60 с обеих сторон на 3·60 минус 3·16 дня после того, как он стал нулем. Теперь у нас есть четыре точки VI ноль х минус 1,80 х равно 100 полностью и так как четыре точки х и 1,80 х. Они как термины. Мы можем объединить их. Сложение дает 2,5 х, равно 1 40 и тогда начинают отбиваться оба от них по 2,5. Итак, делим боевой фут на пять, и теперь мы получаем, что X равно 56 дому, поэтому мы вернемся к таблице, и теперь X равно 56. Таким образом, 200 минус X будет 200 минус 56, что будет 144.Значит, нам нужно 56 домов от Ally One и 144 дома от Ally to. Итак, давайте запишем это. В смеси должно быть 56 унций с одного и 144 дома с юриста.


 #Смеси и сплавы
#Смеси и сплавы А — у кого сверху оказалась правая рука. У тех
из нас, у кого левая рука оказалась сверху, в большей степени работает правое
полушарие. Такие люди имеют образное мышление. Они должны ясно представить
себе каждый процесс, а левополушарные (те, у кого сверху оказалась правая
рука) имеют математический склад ума. Для таких людей более простым путем при
решении задач является применение формул, и не играют большой роли образы.
А — у кого сверху оказалась правая рука. У тех
из нас, у кого левая рука оказалась сверху, в большей степени работает правое
полушарие. Такие люди имеют образное мышление. Они должны ясно представить
себе каждый процесс, а левополушарные (те, у кого сверху оказалась правая
рука) имеют математический склад ума. Для таких людей более простым путем при
решении задач является применение формул, и не играют большой роли образы. 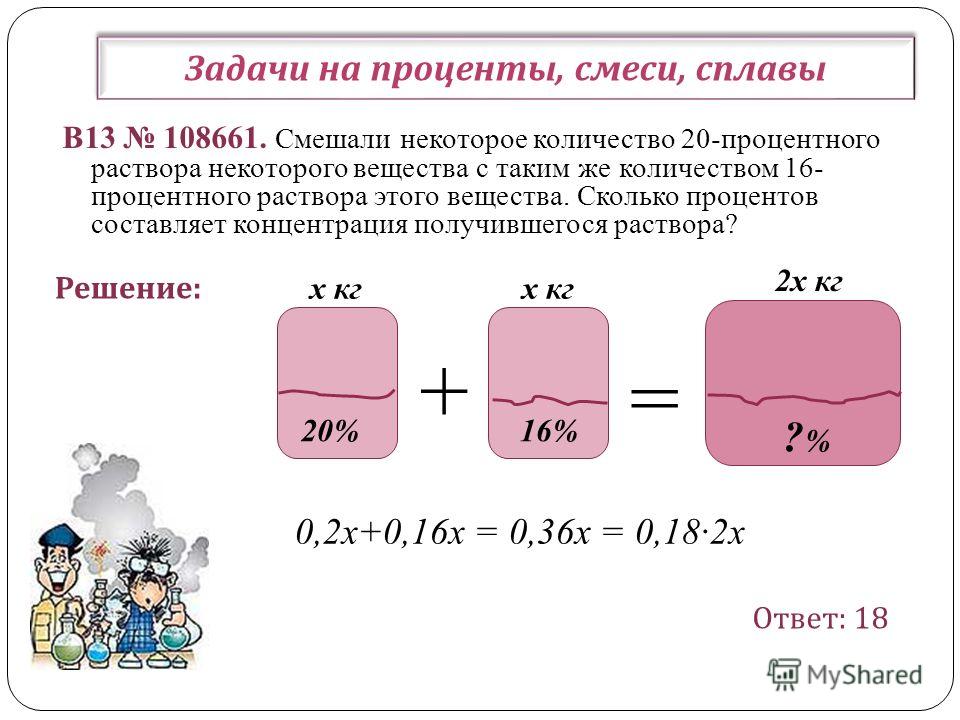 Первичное
усвоение новых знаний
Первичное
усвоение новых знаний

 Физкультминутка
Физкультминутка И подними руки вверх, опусти
И подними руки вверх, опусти 
 У второго спросил мудрец: «А
что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою
работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием:
«А я принимал участие в строительстве храма!».
У второго спросил мудрец: «А
что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою
работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием:
«А я принимал участие в строительстве храма!».
 }}
}}