Работа, мощность, энергия
1
Двое ухватились за веревку и тянут ее в разные стороны. Один из них перетянул. Означает ли это, что он прилагает к веревке большую силу, нежели другой? Сравните работы, совершаемые силами, приложенными к веревке.
Ответ
Силы одинаковы по величине; работы тоже одинаковы по величине, но противоположны по знаку, так как в одном случае направления силы, действующей на веревку и ее перемещения совпадают, а в другом случае — противоположны.
2
Чему равна работа А по подъему цепи, взятой за один конец и лежащей на плоскости, на высоту, равную ее длине? Длина цепи l = 2 м, масса m = 5 кг.
Ответ
3
Оконная шторка массой М = 1 кг и длиной l = 2 м свертывается на тонкий валик наверху окна.
Ответ
4
Гибкий резиновый шланг длиной l висит так, что один из его концов находится на 1/3 l ниже другого. В шланг налито максимально возможное количество воды; ее плотность равна ρ. Какую минимальную работу нужно совершить, чтобы вылить воду из шланга, поднимая его за нижний конец и удерживая верхний конец на неизменной высоте? Внутренний диаметр шланга d. Массой шланга пренебречь. Радиус закругления шланга в изгибе много меньше l.
Ответ
5
Цепь массой М и длиной l лежит у границы двух соприкасающихся полуплоскостей из разных материалов.
Какую работу надо совершить, чтобы передвинуть цепь на вторую полуплоскость? Коэффициенты трения полуплоскостей с цепью соответственно равны k1 и k2. Решить задачу также графически.
Ответ
A = ½ (k1 + k2) Mgl.
6
Мотор с полезной мощностью 15 кВт, установленный на автомобиле, может сообщить ему при движении по горизонтальному участку дороги скорость 90 км/ч. Тот же мотор, установленный на моторной лодке, обеспечивает ей скорость не выше 15 км/ч. Определить силу сопротивления Fc движению автомобиля и моторной лодки при заданных скоростях.
Ответ
Fс1 = 600 Н; Fс2 = 3600 Н.
Трамвай массой М проходит по улице, поднимающейся вверх под углом α к горизонту с определенной скоростью. На горизонтальном участке пути он может с той же скоростью идти с прицепным вагоном массой М1.
Как велика масса М1, если коэффициент трения качения колес равен k? Мощность двигателя постоянна.
Ответ
.
8
Локомотив, работая с постоянной мощностью, может вести поезд массой М = 2000 т вверх по уклону α1 = 0,005 со скоростью v1 = 30 км/ч или по уклону α2 = 0,0025 со скоростью v2 = 40 км/ч. Определить величину силы сопротивления Fc, считая ее постоянной.
Ответ
9
Пуля, летящая с определенной скоростью, углубляется в стенку на расстояние l1 = 10 см. На какое расстояние l2 углубляется в ту же стенку пуля, которая будет иметь скорость вдвое большую?
Ответ
10
Пуля, летящая со скоростью v0, пробивает несколько одинаковых досок, расположенных на некотором расстоянии друг от друга.
В какой по счету доске застрянет пуля, если ее скорость после прохождения первой доски равна v1 = 0,83 v0?
Ответ
Пуля застрянет в 4-й доске.
11
Какую работу надо совершить, чтобы заставить поезд массой
Ответ
а) A1 = 5·104 кДж;
б) A2 = 1,6·105 кДж.
12
Поезд массой М = 2000 т, двигаясь с места с ускорением a = 0,2 м/с2, достигает нужной скорости через минуту, после чего движется равномерно.
Определить мощность тепловоза при установившемся движении, если коэффициент сопротивления k = 0,005.
Ответ
13
Автомобиль массой М = 2000 кг трогается с места и идет в гору, наклон которой α = 0,02. Пройдя расстояние s = 100 м, он развивает скорость v = 32,4 км/ч. Коэффициент сопротивления к = 0,05. Определить среднюю мощность, развиваемую двигателем автомобиля.
Ответ
14
Ракета массой М с работающим двигателем неподвижно «зависла» над Землей. Скорость вытекающих из ракеты газов u. Определить мощность двигателя.
Ответ
15
В каком случае двигатель автомобиля должен совершить большую работу: для разгона с места до скорости 27 км/ч или на увеличение скорости от 27 до 54 км/ч? Силу сопротивления и время разгона в обоих случаях считать одинаковыми.
Ответ
Во втором случае, причем
16
Камень массой m = 200 г брошен с горизонтальной поверхности под углом к горизонту и упал на нее обратно на расстоянии s = 5 м через t = 1,2 с. Найти работу бросания. Сопротивлением воздуха пренебречь.
Ответ
17
Определить работу, которую нужно произвести для того, чтобы сжать пружину на х = 10 см, если для сжатия ее на х0 = 1 см необходима сила F0 = 100 Н.
Ответ
18
Вагон массой М = 2*104 кг, двигаясь со скоростью v = 0,5 м/с, ударяется в два неподвижных пружинных буфера. Найти наибольшее сжатие буферов х, если буфер сжимается на 1 см при действии силы 5*104 Н.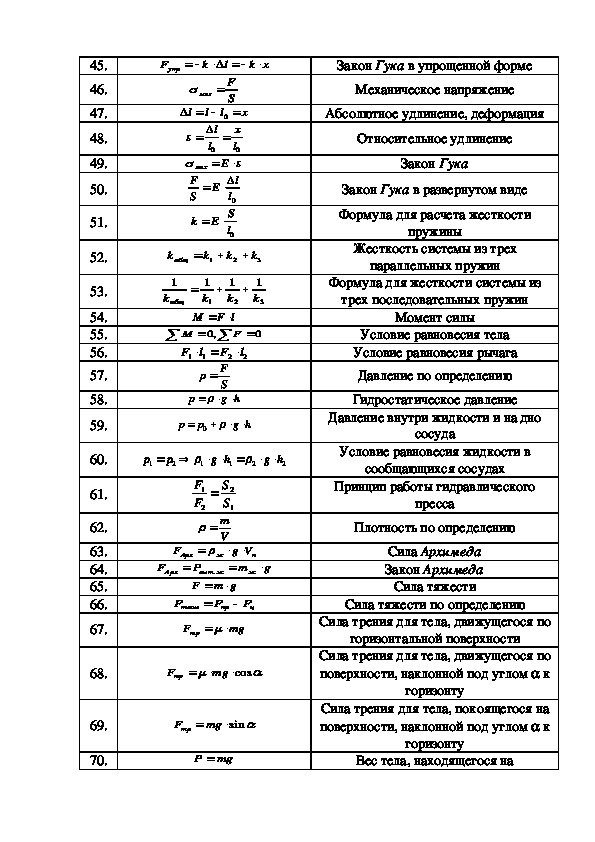
Ответ
19
Действуя постоянной силой F = 200 Н, поднимают груз массой М = 10 кг на высоту h = 10 м. Какую работу А совершает сила F? Какой потенциальной энергией U будет обладать поднятый груз?
Ответ
A = 2·103 Дж, U = 103 Дж.
20
Лифт массой М = 1000 кг равноускоренно поднимался лебедкой. На некотором отрезке пути длиной l = 1 м лифт двигался со средней скоростью vср = 5 м/с и его скорость возросла на Δv = 0,5 м/с. Какую работу совершила сила, перемещающая лифт на указанном отрезке его пути?
Ответ
21
Какую работу совершит сила
Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.Ответ
22
Некоторая сила толкает тело массой m = 16 кг вверх по наклонной плоскости длиной l = 3,1 м и с наклоном α = 30° к горизонту.
1. Скорость тела у основания наклонной плоскости была v0 = 0,6 м/с, а у ее верхнего края v1 = 3,1 м/с. Чему равна работа, произведенная силой? Трения нет.
2. Чему равна работа той же силы и какова будет кинетическая энергия тела в верхней точке наклонной плоскости, если есть трение и коэффициент трения k
= 0,1?Сила направлена вдоль наклонной плоскости.
Ответ
1. A = 317 Дж;
2. A = 317 Дж; Eк = 34,4 Дж.
23
Грузовой автомобиль массой М = 6*103 кг въезжает на паром, привязанный к берегу двумя канатами, со скоростью v = 18 км/ч.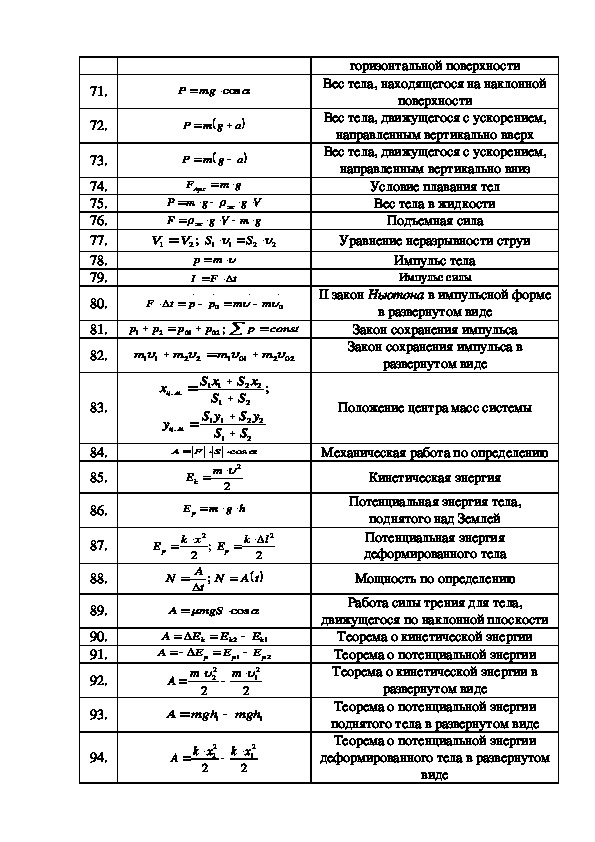
Въехав на паром, автомобиль остановился, пройдя при торможении путь s = 10 м. Определить суммарную силу натяжения канатов.
Ответ
24
Автомобиль, шедший со скоростью v = 54 км/ч, при резком торможении стал двигаться «юзом» (заторможенные колеса не вращаются, скользят по дороге). Определить ускорение a и путь s, который пройдет автомобиль, если коэффициент трения скольжения колес об асфальт: а) в сырую погоду
Ответ
а) a1 ≈ 2,94 м/с2; s1 ≈ 38,3 м;
б) a2 ≈ 6,86 м/с2; s2 ≈ 16,4 м.
25
Автомобиль с полностью включенными тормозами (колеса не вращаются) может удержаться на склоне горы с уклоном до 23°.
Каков тормозной путь автомобиля s при торможении на горизонтальной дороге при скорости движения 10 м/с? Коэффициент сцепления колес с грунтом на склоне горы и на дороге одинаков.
Ответ
26
Сани с грузом массой М = 120 кг скатываются по уклону горы под углом к горизонту α = 14°. Длина спуска l = 60 м. Коэффициент трения скольжения саней k = 0,14. Определить: а) ускорение a1 саней при движении с горы; б) скорость v в конце спуска; в) время спуска t1; г) кинетическую энергию Т1; д) какое расстояние s прокатятся сани после спуска по горизонтали; е) сколько времени t2 продолжается движение по горизонтали; ж) ускорение a2 при движении по горизонтальному участку пути.
Ответ
а) a1 = 1,04 м/с2;
б) v ≈ 11,2 м/с;
в) t1 = 10,7 с;
г) Т1 ≈ 7620 Дж;
д) s = 45,3 м;
е) t2 ≈ 8 с;
ж) a2 = 0,14g.
27
Тело скользит вниз по наклонной плоскости. Угол наклона плоскости к горизонту α = 20°, длина ее l = 4 м, коэффициент трения тела о плоскость k = 0,2. С какой скоростью v будет двигаться тело в момент перехода с наклонной плоскости на горизонтальную поверхность?
Ответ
28
Бассейн площадью S = 100 м2, заполненный водой до уровня h = 1 м, разделен пополам вертикальной перегородкой. Перегородку медленно передвигают в горизонтальном направлении так, что она делит бассейн в отношении 1:3. Какую для этого надо совершить работу, если вода не проникает через перегородку?
Ответ
29
Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность двигателя первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.
Ответ
30
Самолет для взлета должен иметь скорость v = 25 м/с. Длина пробега перед взлетом s = 100 м. Какова мощность моторов, если масса самолета m = 1000 кг и коэффициент сопротивления k = 0,02? Считать движение самолета при взлете равноускоренным.
Ответ
31
Поезд массой М = 5*105 кг поднимается со скоростью 30 км/ч в гору с уклоном 10 м на километр. Коэффициент сопротивления k = 0,002. Определить мощность, развиваемую тепловозом.
Ответ
32
Разогнавшись, конькобежец некоторое время движется по горизонтальной ледяной дорожке равномерно. Затем, перестав отталкиваться, он, двигаясь равнозамедленно, проезжает до остановки путь s = 60 м в течение t = 25 с. Масса конькобежца m = 50 кг. Определить: а) коэффициент трения; б) мощность, затрачиваемую конькобежцем при равномерном движении.
Ответ
а) k ≈ 0,02;
б) N ≈ 46 Вт.
33
Тепловоз тянет поезд, общая масса которого m равна 2000 т. Принимая, что мощность тепловоза N постоянна и равна 1800 кВт и что коэффициент сопротивления k = 0,005, определить: а) ускорения поезда a в те моменты, когда скорость поезда v1 = 4 м/с и когда скорость поезда v2 = 12 м/с; б) максимальную скорость vмакс поезда.
Ответ
а) a1 = 0,176 м/с2, a2 = 0,026 м/с2;
б) vмакс ≈ 66 км/ч.
34
Шкив радиусом R делает n оборотов в секунду, передавая ремнем мощность N.
Найти силу натяжения Т ремня, идущего без скольжения.
Ответ
35
Найти мощность воздушного потока, имеющего поперечное сечение в виде круга диаметром d = 18 м и текущего со скоростью v = 12 м/с. Плотность воздуха (при нормальных условиях) ρ = 1,3 кг/м3.
Ответ
36
Горный ручей с сечением потока S образует водопад высотой h. Скорость течения воды в ручье v. Найти мощность водопада.
Ответ
.
37
Уклон участка шоссе равен 0,05. Спускаясь под уклон при выключенном двигателе, автомобиль движется равномерно со скоростью v = 60 км/ч. Какова должна быть мощность двигателя автомобиля, чтобы он мог подниматься на такой же подъем с той же скоростью? Масса автомобиля m = 1,5 т.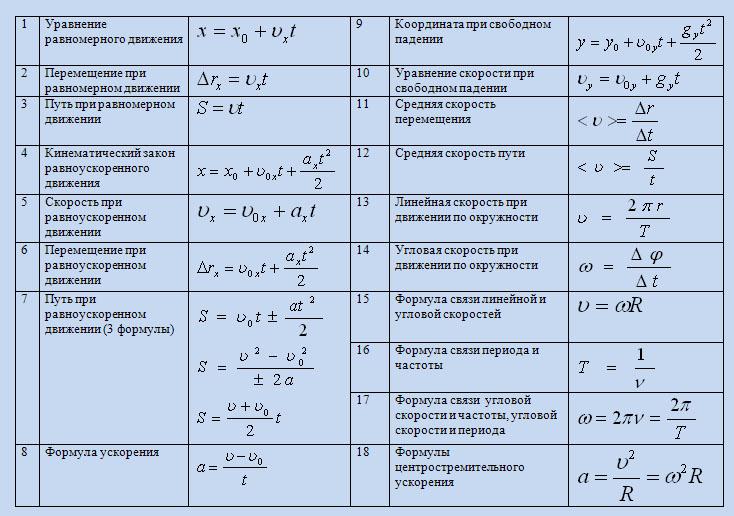
Ответ
38
Грузовики, снабженные двигателями мощностью N1 и N2, развивают скорости соответственно v1 и v2. Какова будет скорость грузовиков, если их соединить тросом?
Ответ
.
39
Аэросани движутся вверх по слабому подъему с установившейся скоростью v1 = 20 м/с; если они движутся в обратном направлении, т. е. под уклон, то при той же мощности двигателя устанавливается скорость v2 = 30 м/с. Какая скорость v установится при той же мощности двигателя во время движения по горизонтальному пути?
Ответ
40
Поезд массой m = 500 т шел равномерно по горизонтальному пути. От поезда оторвался задний вагон массой m1 = 20 т.
Проехав после этого s = 240 м, машинист прекратил доступ пара в машину. На каком расстоянии l друг от друга остановятся оторвавшийся вагон и остальной состав поезда? Предполагается, что сила тяги при работе машины постоянна, а сопротивление движению поезда и вагона пропорционально их массам.
Ответ
41
Найти работу, которую необходимо совершить, чтобы втащить тело массой m = 50 кг на горку произвольного профиля по плоской траектории из точки А в точку В, расстояние между которыми по горизонтали l = 10 м, а по вертикали h = 10 м. Коэффициент трения между телом и горкой всюду одинаков и равен k = 0,1. Профиль горки такой,что касательная к нему в любой точке составляет острый угол с горизонтом. Сила, приложенная к телу, всюду действует по касательной к траектории его перемещения.
Ответ
Гидростатика
1
В полый куб с ребром a налита доверху жидкость плотностью ρ.
Определить силы, действующие на грани куба.
Ответ
На дно действует сила ρga3, на боковую грань 1/2ρga3.
2
Сосуд, имеющий форму усеченного конуса с приставным дном, опущен в воду. Если в сосуд налить 200 г воды, то дно оторвется. Отпадет ли дно, если на него поставить гирю 200 г? налить 200 г масла? налить 200 г ртути?
Ответ
Если сосуд сужается кверху, то гиря и ртуть не оторвут дно, а масло оторвет. Если сосуд сужается книзу, то наоборот.
3
В сосуд с водой вставлена трубка сечением S = 2 см2. В трубку налили 72 г масла (ρм = 900 кг/м3). Найти разность уровней масла и воды.
Ответ и решение
Ответ: Δh = 4 см.
Согласно условию равновесия неоднородных жидкостей в сообщающихся сосудах:
.
Или:
.
Откуда
.(1)
Чтобы найти H, запишем выражение для массы масла в трубке:
,
откуда
.(2)
Окончательно, подставив (2) в (1), получим:
.
4
При подъеме груза массой m = 2 т с помощью гидравлического пресса была затрачена работа A = 40 Дж. При этом малый поршень сделал n = 10 ходов, перемещаясь за один ход на h = 10 см. Во сколько раз площадь большого поршня больше площади малого, если к. п. д. пресса равен 1.
Ответ
5
В сообщающиеся сосуды диаметрами D1, и D2 налита вода. На сколько изменится уровень воды в сосудах, если положить кусок дерева массой m в первый сосуд? во второй? Плотность воды ρ0.
Ответ
В обоих случаях уровень воды увеличивается на
.
6
В колена U-образной трубки налиты вода и спирт, разделенные ртутью. Уровень ртути в обоих коленах одинаков. На высоте 24 см от уровня ртути колена соединены горизонтальной трубкой с краном.
Вначале кран закрыт. Определить высоту столба спирта h2 (ρс = 800 кг/м3), если высота столба воды h1 = 32 см. Что будет, если открыть кран? При каком расположении трубки при открывании крана будет сохраняться равновесие?
Ответ
7
Льдина площадью поперечного сечения S = 1 м2 и высотой H = 0,4 м плавает в воде. Какую работу надо совершить, чтобы полностью погрузить льдину в воду?
Ответ
≈ 7,84 Дж.
8
В стакане плавает кусок льда. Изменится ли уровень воды, когда лед растает? Рассмотреть дополнительно случаи: 1) когда во льду находился пузырек воздуха; 2) когда во льду находилась свинцовая пластинка.
Ответ
Лед вытесняет воду, вес которой равен весу льда. Когда лед растает, образуется такое же количество воды, поэтому уровень не изменится.
1) Тоже не изменится, т. к. массой воздуха можно пренебречь.
2) Понизится, т. к. объем воды, которая образуется, когда лед растает, вместе с объемом свинца будет меньше, чем в случае куска чистого льда того же веса.
9
Одна из бутылок наполнена водой, другая — ртутью. Потонет ли бутылка с водой, если ее опустить в воду? Потонет ли бутылка с ртутью, если ее опустить в ртуть?
Ответ
Бутылка с водой потонет, а с ртутью — нет.
10
Прямоугольная коробочка из жести массой m = 76 г с площадью дна S = 38 см2 и высотой H = 6 см плавает в воде. Определить высоту h надводной части коробочки.
Ответ
11
Кастрюля емкостью 2 л доверху наполнена водой. В нее ставят тело объемом 0,5 л и массой 0,6 кг. Сколько воды вытечет из кастрюли?
Ответ
12
Жестяная банка с грузом плавает на поверхности воды, налитой в сосуд. При этом уровень воды в сосуде равен H1. Больше или меньше H1 будет уровень H2, если груз из банки переложить на дно сосуда? Плотность груза больше плотности воды.
Решение
H2 станет меньше H1, поскольку груз будет вытеснять объем воды, равный своему объему, а находясь в жестяной банке, груз вытесняет объем воды, масса которого равна массе груза.
13
В сосуд с вертикальными стенками и площадью дна S налита жидкость с плотностью ρ. На сколько изменится уровень жидкости в сосуде, если в него опустить тело произвольной формы массой m, которое не тонет?
Ответ
14
В U-образной трубке сечением S налита жидкость с плотностью ρ. На сколько поднимется уровень жидкости в правом колене трубки по отношению к первоначальному уровню, если в левое колено опустили тело массой m и плотностью ρ1 < ρ?
Ответ
15
На дне водоема установлена бетонная конструкция грибовидной формы, размеры которой указаны на рисунке.
Глубина реки H. С какой силой F давит конструкция на дно реки? Плотность бетона ρ, воды ρ0.
Решение
Сила давления бетонной конструкции на дно складывается из веса конструкции и разности сил, возникающих в результате гидростатического давления на верхнюю и нижнюю поверхности конструкции:
.
Вес конструкции равен:
.
Сила, возникающая в результате гидростатического давления на верхнюю поверхность конструкции, равна:
.
Сила, возникающая в результате гидростатического давления на нижнюю поверхность конструкции, равна:
.
Таким образом, искомая сила F равна:
.
16
Деревянный кубик лежит на дне сосуда. Всплывет ли он, если в сосуд налить воду (вода не проникает под кубик)?
Решение
Не всплывет, т. к. выталкивающая сила не возникает из-за отсутствия воды под нижней гранью кубика.
17
Круглая дырка площадью S1 в дне сосуда прикрыта без усилия конической пробкой с площадью основания S2. При каком наибольшем значении плотности материала пробки ρ можно добиться ее всплытия, доливая воду в сосуд? Плотность воды ρ0.
Решение
Архимедова сила, действующая на пробку, достигает максимума, когда уровень воды достигнет верха пробки. Пробка всплывет, когда подъемная сила превысит вес пробки. Подъемная сила равна весу воды, объем которой равен объему заштрихованной области пробки на рисунке:
.
Найдем подъемную силу:
.
Найдем вес пробки:
.
Тогда ρ найдем из уравнения:
,
откуда
.
Поскольку малый и большой конус подобны:
,
тогда
.
18
Пустую открытую бутылку погрузили в воду горлышком вниз на некоторую глубину h и опустили. При этом бутылка не всплывала, не опускалась, а находилась в положении равновесия. Почему? Будет ли это равновесие устойчивым? Определить глубину погружения, если емкость бутылки V0 = 0,5 л, масса m = 0,4 кг.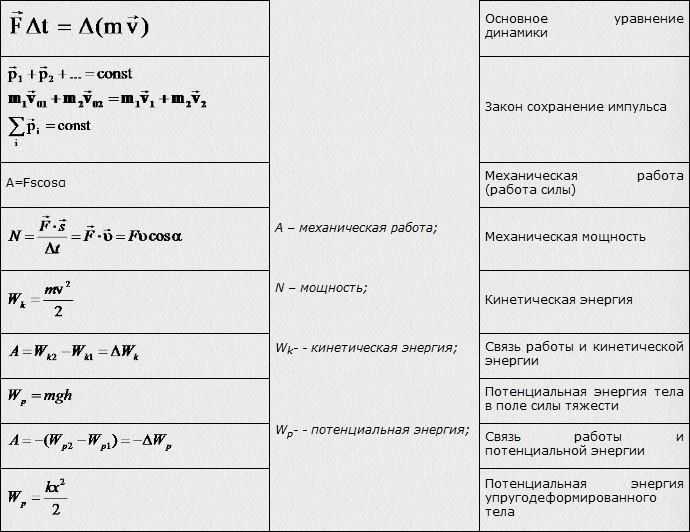
Давление атмосферы p0 = 101 кПа, температура постоянная. Объемом стенок бутылки пренебречь.
Решение
Давление воды на глубине h: p1 = p0 + ρgh. Для воздуха в бутылке, сжимающегося по мере погружения бутылки, можно записать закон Бойля-Мариотта: p0V0 = p1V1, где V0 и V1 — объем воздуха в бутылке соответственно до и после погружения. Поскольку бутылка находится в равновесии, то ее вес равен архимедовой силе: mg = ρV1g. Таким образом, получаем систему уравнений:
Решив ее, получим:
.
Равновесие будет неустойчивым.
19
Полый шар (внешний радиус R1, внутренний R2), сделанный из материала с плотностью ρ1 плавает на поверхности жидкости с плотностью ρ2.
Какова должна быть плотность ρ вещества, которым следует заполнить внутреннюю полость шара, чтобы он находился в безразличном равновесии внутри жидкости?
Решение
Чтобы шар находился в состоянии безразличного равновесия, вес вытесняемой шаром жидкости должен быть равен весу шара:
.
Отсюда находим ρ:
.
20
Полый шар, отлитый из чугуна, плавает в воде, погрузившись ровно наполовину. Найти объем V внутренней полости шара, если масса шара m = 5000 г, а плотность чугуна ρ = 7,8 г/см3.
Решение
Поскольку шар наполовину погружается в воду, то архимедова сила, действующая на шар, равна весу воды, объем которой равен половине объема шара. Объем шара складывается из искомого объема V и объема чугунной части шара, равного m/ρ.
Таким образом, можно составить уравнение:
,
где ρ0 плотность воды, откуда:
≈ 9360 см3.
21
На весах уравновешен сосуд с водой. Как изменится равновесие, если в воду целиком опустить подвешенный на нитке брусок размером 5x3x3 см3 так, чтобы он не касался дна? Какой груз и на какую чашку надо положить, чтобы сохранить равновесие?
Решение
В соответствии с 3-м законом Ньютона, на чашку весов с сосудом с водой будет действовать сила, равная по модулю выталкивающей силе, действующей на брусок, но направленной в противоположную сторону. Таким образом, чтобы уравновесить весы, необходимо в противоположную чашку весов положить груз массой m = ρV = 45 г.
22
Алюминиевый и железный сплошные шары уравновешены на рычаге.
Нарушится ли равновесие, если шары погрузить в воду? Рассмотреть два случая: а) шары одинаковой массы; б) шары одинакового объема.
Решение
Ответ: а) железный шар перевесит, поскольку на алюминиевый шар действует большая выталкивающая сила, чем на железный, так как объем алюминиевого шара больше объема железного шара такой же массы. б) железный шар перевесит, поскольку момент выталкивающей силы, действующей на алюминиевый шар, больше момента выталкивающей силы, действующей на железный шар, так как плечи рычага в этом случае не равны.
23
Вес куска железа в воде P = 1,67 H. Найти его объем Vж. Плотность железа ρж = 7,8 г/см3.
Решение
Вес куска железа в воде равен разности веса куска железа вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
= 25,1 см3.
24
Вес тела в воде в три раза меньше, чем в воздухе. Какова плотность материала тела?
Решение
Вес тела в воде равен разности веса тела вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
,
или:
,
откуда:
= 1500 кг/м3.
25
Брусок дерева плавает в воде. Как изменится глубина погружения бруска в воде, если поверх воды налить масло?
Ответ
Уменьшится, поскольку увеличится давление на нижнюю грань бруска дерева.
26
Некоторое тело плавает на поверхности воды в закрытом сосуде. Как изменится глубина погружения тела, если накачать воздух в сосуд?
Ответ
Ответ: не изменится, если сжимаемость тела такая же, как и у воды.
Если сжимаемость тела больше, чем у воды, то глубина увеличится. Если сжимаемость тела меньше, чем у воды, то глубина погружения тела уменьшится.
27
Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 0,75 всего объема поплавка погружено в воду. Определить силу натяжения нити F, если масса поплавка равна 2 кг и плотность пробки 0,25 г/см3. Массой нити пренебречь.
Решение
Сила натяжения нити равна разности архимедовой силы и веса пробки:
,
где ρ0 плотность воды.
Вынесем mg за скобки:
.
Подставив числовые значения, получим F ≈ 40 H.
28
На крюке динамометра висит ведерко. Изменится ли показание динамометра, если ведерко наполнить водой и погрузить в воду?
Ответ
Уменьшится на величину веса воды, вытесняемой стенками и дном ведра.
29
Сосуд, предельно наполненный водой, висит на динамометре. Изменится ли показание динамометра, если в воду опустить гирю, подвешенную на нити, не касаясь дна?
Ответ
Не изменится, поскольку вес воды, которая выльется, равен силе, противодействующей архимедовой силе, действующей на гирю.
30
На рычажных весах уравновешены сосуд с водой и штатив с медной гирей массой m = 100 г (рисунок). Затем гиря, подвешенная на нити, опускается в воду. Как восстановить равновесие весов? Плотность меди ρм = 8,9 г/см3.
31
Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду, причем равновесие достигается тогда, когда палочка расположена наклонно к поверхности воды и в воде находится половина палочки.
Какова плотность материала, из которого сделана палочка?
32
Два шарика радиусами r1 и r2, сделанные из материалов с плотностями ρ1 и ρ2, соединены невесомым стержнем длиной l. Затем вся система помещена в жидкость с плотностью ρ, причем ρ < ρ1 и ρ < ρ2. В какой точке стержня нужно его повесить, для того чтобы система находилась в равновесии при горизонтальном положении стержня?
33
Из сосуда, заполненного водой, выходит труба радиусом r и высотой h (рисунок). Труба закрыта круглой пластиной радиусом R и массой М, которую прижимает к трубе давление воды. С какой силой F нужно подействовать на пластину в точке А, для того чтобы она повернулась, открыв трубу? Сосуд заполнен водой до высоты H. Толщина пластины пренебрежимо мала.
34
На весах уравновешено тело, погруженное в жидкость.
Изменится ли показание весов при нагревании жидкости вместе с погруженным в нее телом?
35
Сплошное однородное тело объемом V, плотность материала которого ρ, плавает на границе между тяжелой жидкостью с плотностью ρ1 и более легкой жидкостью с плотностью ρ2. Какая часть объема тела V1 будет находиться в тяжелой жидкости?
36
Кубик из дерева, имеющий сторону 10 см, плавает между маслом и водой, находясь ниже уровня масла на 2,5 см. Нижняя поверхность кубика на 2,5 см ниже поверхности раздела. Какова масса m кубика, если плотность масла 0,8 г/см3? Определить силы давления F1, и F2 на верхнюю и нижнюю грани кубика. Изменится ли глубина погружения кубика в воду при доливании масла?
37
Стальной кубик плотностью 7,8 г/см3 плавает в ртути (плотность 13,6 г/см3).
Поверх ртути наливается вода так, что она покрывает кубик тонким слоем. Какова высота H слоя воды? Длина ребра кубика а = 10 см. Определить давление р на нижнюю грань кубика.
38
Кусок пробки весит в воздухе 0,147 Н, кусок свинца 1,1074 Н. Если эти куски связать, а затем подвесить к чашке весов и опустить в керосин, то показания весов будет 0,588 Н. Определить плотность пробки, учитывая, что плотность керосина 0,8 г/см3, а свинца 11,3 г/см3.
39
В сосуд с водой погружается открытый цилиндрический стакан: один раз дном вверх, а другой — дном вниз, на одну и ту же глубину. В каком из этих случаев работа, которую нужно совершить, чтобы погрузить стакан в воду, будет больше? Вода из сосуда не выливается и в стакан, погруженный дном вниз, не попадает.
40
Две одинаковые по массе оболочки шара — одна из эластичной резины, а вторая из прорезиненной ткани — наполнены одним и тем же количеством водорода и у Земли занимают равный объем.
Который из шаров поднимется выше и почему, если водород из них выходить не может?
41
Во сколько раз изменится подъемная сила газа, наполняющего аэростат (дирижабль), если будет применяться гелий вместо водорода?
42
К динамометру подвешена тонкостенная трубка ртутного барометра. Что показывает динамометр? Будут ли изменяться его показания при изменении атмосферного давления?
43
Определить приближенно массу газовой оболочки, окружающей земной шар.
44
Г-образная трубка, длинное колено которой открыто, наполнена водородом. Куда будет выгнута резиновая пленка, закрывающая короткое колено трубки?
45
В трубе с сужением течет вода. В трубу пущен эластичный резиновый мячик. Как изменится его диаметр при прохождении узкой части трубы?
46
Тело, имеющее массу m = 2 кг и объем V = 1000 см3, находится в озере на глубине h = 5 м.
Какая работа должна быть совершена при его подъеме на высоту H = 5 м над поверхностью воды?
Равна ли совершенная при этом работа изменению потенциальной энергии тела? Объясните результат.
47
В водоеме укреплена вертикальная труба с поршнем таким образом, что нижний ее конец погружен в воду. Поршень, лежавший вначале на поверхности воды, медленно поднимают на высоту H = 15 м. Какую работу пришлось при этом совершить? Площадь поршня S = 1 дм2, атмосферное давление р = 101 кПа. Весом поршня пренебречь.
48
Подводная лодка находится на глубине h = 100 м. С какой скоростью через отверстие в корпусе лодки будет врываться струя воды? Сколько воды проникает за один час, если диаметр отверстия равен d = 2 см? Давление воздуха в лодке равно атмосферному давлению. Изменением давления внутри лодки пренебречь.
49
Из брандспойта бьет струя воды.
Расход воды Q = 60 л/мин. Какова площадь поперечного сечения струи S1 на высоте h = 2 м над концом брандспойта, если вблизи него сечение равно S0 = 1,5 см2?
50
Почему быстролетящая пуля пробивает в пустом пластмассовом стакане лишь два маленьких отверстия, а стакан, наполненный водой, разбивается при попадании пули вдребезги?
Основные формулы и методические рекомендации по решению задач на законы сохранения в механике
«Лучше знать, даже если знание очень
скоро повлечет за собой гибель, чем
обрести вечную жизнь ценой тусклого
скотского непонимания вселенной, которая
невидимо для нас бурлит во всем своем волшебстве»
Айзек Азимов
В данной теме речь пойдёт о законах сохранения в механике,
вспомним некоторые важные формулы, относящиеся к данному разделу, а также дадим
несколько советов по решению задач.
Механическая система — это совокупность тел или частей одного и того же тела, взаимодействующих между собой.
Основные вопросы, которые будут затрагиваться при рассмотрении законов сохранения — это импульс и закон сохранения импульса; механическая работа и мощность; а также механическая энергия и закон ее сохранения.
Импульс тела — это векторная физическая величина, равная произведению массы тела на его скорость, а ее направление совпадает с направлением вектора скорости тела. Импульс тела еще очень часто называют количеством движения.
На основании определения импульса тела, можно сформулировать и записать второй закон Ньютона в следующем виде: импульс равнодействующей сил, действующих на данное тело, равен изменению импульса тела.
Из такой записи второго закона Ньютона легко заметить, что
импульс тела изменяется под действием данной силы одинаково у тел любой массы,
если только время действия сил одинаково.
Импульс системы тел равен геометрической сумме импульсов тел системы. Таким образом, импульс системы тел могут изменить только внешние силы.
При этом для системы тел справедлив закон сохранения импульса, согласно которому в замкнутой системе импульс системы тел сохраняется при любых взаимодействиях этих тел. Система считается замкнутой, если тела системы взаимодействуют только между собой.
Реактивное движение – это движение, возникающее при отделении от тела его части с некоторой относительно тела скоростью.
Механической работе – это скалярная физическая величина, характеризующая процесс перемещения тела под действием силы, и численно равная произведению модуля силы на модуль перемещения и на косинус угла между направлением вектора силы и вектора перемещения.
Далее будет рассматривать работу трех сил: силы тяжести,
силы упругости и силы трения.
Если тело перемещается под действием силы тяжести из положения 1 в положение 2, определяемые соответственно высотами h1 и h2, то работа этой силы будет определяться произведением массы перемещаемого тела на ускорение свободного падения и на разницу высот между начальным и конечным положением тела. При этом следует помнить, что сила тяжести является консервативной силой, поэтому ее работа не зависит от формы траектории, по которой перемещается тело, и на замкнутой траектории равна нулю.
Если движение тела происходит под действием сил упругости, то работа такой силы будет рассчитываться по формуле
где k — это коэффициент жесткости
пружины, x1 и x2
— ее абсолютное удлинение в положениях один и два соответственно. Так как сила
упругости, так же как и сила трения, является консервативной силой, то
ее работа тоже не зависит от формы траектории и на замкнутой траектории равна
нулю.
При рассмотрении работы силы трения следует учитывать то, что ее вектор направлен противоположно вектору перемещения. Поэтому значение работы будет отрицательным и будет определяться произведением модуля силы трения и модуля перемещения. При этом следует помнить, что, в отличие от силы упругости и силы тяжести, сила трения не является консервативной силой. Поэтому ее работа будет зависеть от формы траектории, по которой перемещается тело, и на замкнутой траектории она отлична от нуля.
Механическая энергия – это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу.
Механическую энергию делят на два вида — на кинетическую энергию и потенциальную энергию тела.
Кинетическая энергия — это энергия, которой обладает
тело вследствие своего движения. Ее величина зависит от массы тела и его
скорости.
При этом следует помнить о том, что изменение кинетической энергии
тела равно работе равнодействующей всех сил, действующих на тело. Это
утверждение называют теоремой о кинетической энергии. Она справедлива
независимо от того, какие силы действуют на тело: упругости, трения или
тяжести.
Потенциальная энергия — это энергия системы, определяемая взаимным расположением тел (или частей тела друг относительно друга) и характером сил взаимодействия между ними.
Потенциальную энергию разделяют на два вида:
– Потенциальную энергию тела при гравитационном взаимодействии. Потенциальная энергия в поле тяготения определяется как произведение массы тела на ускорение свободного падения и на высоту тела, относительного выбранного нулевого уровня. А ее изменение, взятое с обратным знаком, равно работе силы тяжести.
– Потенциальную энергию упруго деформированного тела.
Что касается потенциальной энергии упруго деформированного тела, то это
энергия, которая обусловлена взаимодействием частей тела между собой. При этом
она равна работе, которую совершает сила упругости, чтобы деформированную
пружину вернуть в первоначальное состояние, взятой с обратным знаком. Или
говорят, что она равна работе, которую совершают внешние силы, чтобы
недеформированную пружину сжать или растянуть.
Следует помнить о том, что тела могут одновременно обладать и кинетической и потенциальной энергией. Поэтому полная механическая энергия тела или системы тел определяется суммой кинетической и потенциальной энергии. Для нее выполняется закон сохранения энергии, согласно которому в замкнутой системе тел, взаимодействующих силами тяготения или силами упругости, полная механическая энергия остается неизменной.
Известно, что для облегчения совершения механической работы
издавна используются различные приспособления — простые механизмы.
Это
устройства, в которых работа совершается только за счет механической энергии.
Все простые механизмы служат для преобразования силы.
Наиболее часто встречающимися простыми механизмами являются рычаги и блоки.
Рычаг — это твердое тело, имеющее неподвижную ось вращения, на которое действуют силы, стремящиеся его повернуть вокруг этой оси.
Различают два рода рычага.
К рычагу первого рода относят рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону.
А рычаг второго рода — это рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу.
Блок представляет собой колесо с желобом, укрепленным в обойме. Различают два вида блоков — неподвижный блок и подвижный.
У неподвижного блока ось вращения закреплена и при
подъеме грузов она не опускается и не поднимается.
Такой блок никакого
выигрыша в силе не дает, но позволяет менять ее направление.
В отличие от неподвижного блока, подвижный позволяет получить выигрыш в силе в два раза, а его ось вращения поднимается и опускается вместе с грузом.
Следует упомянуть и об условии равновесия рычага, согласно которому рычаг будет находиться в равновесии, если алгебраическая сумма моментов всех сил, действующих на него, равна нулю. При этом принято считать момент сил, вращающих тело по часовой стрелке, положительным, а против часовой стрелки — отрицательным.
Сведем в таблицу основные формулы законов сохранения энергии.
|
Формула |
Описание формулы |
|
Импульс тела (количество движения), где m — масса тела, – скорость тела. |
|
|
Второй
закон Ньютона, где –
импульс силы ,
–
время её действия, –изменение
импульса тела. |
|
|
Закон сохранения импульса, где – импульсы тел до взаимодействия, – импульсы тел после взаимодействия |
|
|
Работа постоянной силы, sx – модуль перемещения, α — угол между вектором силы и вектором перемещения. |
|
|
Работа силы тяжести, где h1 и h2 — начальная и конечная высота тела относительного нулевого уровня. |
|
|
Работа силы упругости, где k — жесткость пружины, х1 и х2 — начальное и конечное значение линейной деформации. |
|
|
Работа
силы трения. |
|
|
Мощность, где Δt — промежуток времени, за который совершается работа А, Fυ— проекция силы на направление движения, υ — мгновенная скорость. |
|
|
КПД механизма, где Ап – полезная работа, Аз – вся затраченная (совершённая) работа. |
|
|
Кинетическая энергия тела. |
|
|
Теорема о кинетической энергии, где ∆Ек — изменение кинетической энергии, А — работа равнодействующей сил. |
|
|
Потенциальная
энергия тела, поднятого над Землей, где h — высота
тела относительно нулевого уровня. |
|
|
Потенциальная энергия деформированного тела, где x — линейная деформация. |
|
|
Полная механическая энергия системы тел. |
|
|
Закон сохранения механической энергии. |
|
|
Изменение полной механической энергии системы тел, где A1 — работа внешних сил, А2 — работа силы трения. |
|
|
Момент силы, где l — плечо силы. |
|
|
Условие равновесия рычага. |
Методические рекомендации по решению задач на закон сохранения
импульса.
1) Внимательно проанализировав условие задачи, сделать чертеж с указанием на нем для каждого тела векторы импульсов в начале и в конце процесса взаимодействия.
2) Установить, является ли рассматриваемая система замкнутой или нет.
3) Если система замкнута или выполняется одно из следующих условий: а) внешние силы уравновешиваются, б) время взаимодействия мало, в) проекция равнодействующих внешних сил на какое-то направление равна нулю, то следует записать закон сохранения импульса в векторном виде.
4) Если же система незамкнута и не выполняется ни одно из прошлых условий, то записать второй закон Ньютона в импульсной форме, рассматривая движение всех тел системы в одной и той же инерциальной системе отсчета.
5) Спроецировать записанные уравнения на выбранные оси
координат. Их выбирают так, что бы легко было определить геометрические, а по
ним и алгебраические проекции импульсов на соответствующие направления.
6) Если есть необходимость, то следует дополнить систему полученных уравнений кинематическими и динамическими уравнениями движения, ирешить полученную систему относительно искомой величины.
Методические рекомендации по решению задач на закон сохранения и превращения энергии.
1) Делаем чертеж, отметив на нем положения тела, оговоренные в условии задачи (включая начальное).
2) Выбрать нулевой уровень отсчета потенциальной энергии и связываем с ним одну из координатных осей, а другую ось располагаем в плоскости движения тела. Если тело движется под действием силы тяжести, то за нулевой уровень принимаем самое нижнее положение движущегося тела, и записываем формулу для расчета полной механической энергии.
3) Необходимо выяснить, какие силы в рассматриваемой системе являются внешними, внутренними, консервативными и неконсервативными.
5) Для замкнутой системы, в которой действуют только
консервативные силы, записываем закон сохранения энергии.
Если в замкнутой
системе действуют силы трения, то необходимо записать закон сохранения и
превращения энергии. А если система незамкнута и внешние силы совершают работу,
то надозаписать формулу для определения изменения механической энергии.
6) Составить по необходимости дополнительные уравнения из динамики или кинематики, или дополнить систему законом сохранения импульса.
7) Решить полученную систему уравнений относительно неизвестной величины, проверить размерность и проанализировать полученный результат.
Формулы по физике 10-11 класс
Уравнение скорости при равноускоренном движении υ=υ0+a∙t
Ускорение a=(υ—υ 0)/t
Скорость при движении по окружности υ=2πR/Т
Центростремительное ускорение a=υ2/R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R2
Вес тела, движущегося с ускорением а↑ Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx2/2
Кинетическая энергия тела Ek=mυ2/2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υТ
Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр.
кин. энергия молекул одноатомного газа Ek=3/2∙kT
Основное уравнение МКТ P=nkT=1/3nm0υ2
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P0∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты при нагревании Q=Cm(T2-T1)
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q1 — Q2)/ Q1
КПД идеал. двигателей (цикл Карно) η= (Т1 — Т2)/ Т1
Закон Кулона F=k∙q1∙q2/R2
Напряженность электрического поля E=F/q
Напряженность эл.
поля точечного заряда E=k∙q/R2
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E0/E
Потенциальная энергия взаимод. зарядов W= k∙q1q2/R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε∙ε0/d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед. соединения I1=I2=I, U1+U2=U, R1+R2=R
Законы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I2Rt
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυsinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI2/2
Период колебаний кол.
контура T=2π ∙√LC
Индуктивное сопротивление XL=ωL=2πLν
Емкостное сопротивление Xc=1/ωC
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-XL)2+R2
ART’s PAGES — Учеба — ФОИСТ КиПОП ИТМО — 1 Курс — 1 Семестр
Физика
(1-й Курс, 1-й Семестр)
(2004 год) Преподаватели:
Практика — Сологуб Валерий Васильевич
Лекции — Федоров Борис Александрович
Все решения к «Сборнику задач по общему курсу физики» В. С. Волькенштейн. Часть 1 (1999 г.) (4 975
Kb) — Механика, молекулярная физика и
термодинамика.
Все решения к «Сборнику задач по общему курсу физики» В. С. Волькенштейн. Часть
2 (1999 г.) (4 420 Kb) — Электричество и
магнетизм, колебания и волны, оптика,
физика атома и атомного ядра.
В этой книге можно найти некоторые задачи, заданные для самостоятельного выполнения.
Или использовать данные задачи, как
образец для решения своих задач.
Для просмотра учебника нужна специальная
программа, которую можно скачать из раздела
программы (DJVU Reader или DjVuSolo).
Руководство к лабораторному
практикуму по механике и молекулярной физике
(1 768 Kb) — методичка для выполнения
лабораторных работ в первом семестре (1999
год).
Формат DJVU. (качество сканирования не очень
хорошее).
Для просмотра учебника нужна специальная
программа, которую можно скачать из раздела
программы (DJVU Reader или DjVuSolo).
Лабораторные работы 1 семестр
(1 410 Kb) — Лабораторные работы по физике за
первый семестр. В архив я засунул все работы,
какие смог найти, поэтому и размер такой
большой. Работы есть с 1-й по 11-ю, в основном,
скачанные с других сайтов.
Теоретический минимум по физике (18 Kb) — список понятий, определений и законов теоретического минимума по физике, которые нужно знать, от 1998 года.
Теоретический минимум по физике (8 Kb) — программа аттестационного тестирования по курсу общей физики за 1-й семестр первого курса для студентов всех технических факультетов. Официально предоставлена преподавателем в 2004 году.
Теоретический минимум по физике тест (36 Kb) — примеры вопросов из тестов по теоретическому минимуму, проходивших раньше (механика и молекулярка). Также в архиве лежит материал, который обязательно нужно знать на тесте (только для механики).
Билеты на экзамен по физике (21 Kb) — билеты, которые были на экзамене по физике в 1998 году.
Лекции по механике (49 Kb) — конспект по механике.
Основные формулы по физике
(41 Kb) — шпаргалки — «основные формулы по
механике и молекулярной физике».
Задачи по механике (443 Kb) — Решение первого типовика (механика — 9 задач) по физике. 10-й вариант.
Задачи по молекулярной физике (42,6 Kb) — Решение второго типовика (молекулярная физика — 8 задач). 10-й вариант.
формул Mechanics-I для быстрого пересмотра | Инженерное дело
Получите важные формулы из подразделения Механика-I для быстрого пересмотра. Эти формулы очень полезны во время конкурсных экзаменов. Этот модуль включает в себя главы – Измерение и измерение, Кинематика, Законы движения и работы, Мощность и энергия
Когда экзамены не за горами, невозможно пересмотреть полные книги, поэтому мы придумали формулы для единиц измерения и важные термины. После того, как вы тщательно изучили главы и хорошо поняли их, нет необходимости изучать их снова и снова.Вы можете пересматривать только важные формулы и термины, что сэкономит ваше драгоценное время.
В связи с этим найдите важные формулы электростатики и электрического тока для быстрого повторения.
Эти формулы будут полезны на различных инженерных вступительных экзаменах, таких как IIT JEE, UPSEE, WBJEE и т. д.
В программах UPSEE и WBJEE, где большинство вопросов задается непосредственно по формулам, это краткое примечание очень важно.
Механика-I
Базовые величины и единицы СИ
Базовое количество | Единицы СИ | |
Имя | Символ | |
Длина | счетчик | м |
Масса | килограмм | кг |
Время | секунда | с |
Электрический ток | Ампер | А |
Термодинамическая температура | Кельвин | К |
Количество вещества | Крот | моль |
Сила света | Кандела | CD |
Точность, прецизионность приборов и погрешности измерений
- Результат каждого измерения любым измерительным прибором содержит некоторую неопределенность.
Эта неопределенность называется ошибкой. - Точность измерения — это мера того, насколько близко измеренное значение к истинному значению величины.
- Точность сообщает нам, с каким разрешением или пределом измеряется величина.
- Наименьшее значение, которое может быть измерено измерительным прибором, называется его наименьшим значением.
Эта неопределенность называется ошибкой.UPSEE 2017 Solved Sample Paper Set-1
Комбинация ошибок
- Если Z = A + B, то ± ΔZ = ± ΔA ± ΔB, где A и B — две физические величины, ΔA и ΔB — их абсолютные погрешности, а ΔZ — погрешность их суммы или разности
- Если Z = AB, то ΔZ/ Z = (ΔA/A) + (ΔB/B)
- , если Z = A p B q /C r , то ΔZ/Z = p (ΔA/A) + q (ΔB/B) + r (ΔC/C)
Размерные формулы и размерные уравнения
- Выражение, показывающее, как и какие из основных величин представляют размерности физической величины, называется размерной формулой данной физической величины.
- Уравнение, полученное приравниванием физической величины к ее размерной формуле, называется размерным уравнением физической величины.
- Размерные уравнения объема [V], скорости [v], силы [F] и плотности массы [ρ] могут быть выражены как
[V] = [M 0 L 3 T 0 ]
[v] = [M 0 LT −1 ]
[F] = [MLT −2 ]
[ρ] = [ML −3 T 0 ]
JEE Main Mathematics Solved Sample Paper Set-VII
Размерный анализ и его приложения
- Проверка размерной согласованности уравнений
- Вывод отношений между физическими величинами
- Расстояние — это скалярная величина, которая относится к тому, «сколько объект прошел» во время своего движения.
- Перемещение — это векторная величина, которая относится к «кратчайшему пути, пройденному объектом» во время его движения.
- Средняя скорость определяется как изменение положения или перемещения (Δx), деленное на интервалы времени (Δt ), в которых происходит перемещение
- Средняя скорость определяется как общая длина пройденного пути, деленная на общий интервал времени, в течение которого происходило движение
- Среднее ускорение a за интервал времени определяется как изменение скорости, деленное на интервал времени
JEE Main Physics Solved Sample Paper Set-VII
КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ
где, Δx = перемещение (конечное положение – начальное положение),
v = скорость или скорость в любое время, v o = начальная скорость или скорость, t = время, a = ускорение
Графики:
- Когда движение равномерное, скорость объекта постоянна или его ускорение равно 0.
- Когда тело имеет равномерное ускорение или замедленное движение, то ускорение постоянно.
- Графики для равномерно ускоренного или запаздывающего объекта показаны ниже:
Закон инерции
- Каждый продолжает находиться в состоянии покоя или равномерного прямолинейного движения, если какая-либо внешняя сила не заставляет его действовать иначе.
Первый закон движения Ньютона
- Если суммарная внешняя сила, действующая на тело, равна нулю, его ускорение равно нулю.Ускорение может быть отличным от нуля, только если на тело действует внешняя сила.
Второй закон движения Ньютона
- Скорость изменения количества движения тела прямо пропорциональна приложенной силе и происходит в направлении действия силы.
где p = импульс, a = ускорение
Третий закон движения Ньютона
- На каждое действие всегда есть равное и противоположное противодействие.
F AB = −F BA
(сила, действующая на A, на B) = −(сила на B, на A)
Сохранение импульса
- Полный импульс изолированной системы взаимодействующих частиц сохраняется.
Трение
- Трение представляет собой тангенциальную составляющую чистой контактной силы между двумя соприкасающимися твердыми телами.
- Трение между двумя или более твердыми телами, которые не движутся относительно друг друга, называется трением покоя.
- Подобно другим силам, эта сила также образует пару равных и противоположных сил, действующих на два разных тела.
- Направление силы трения на тело противоположно относительному движению (или его стремлению) этого тела относительно другого тела.
Круговое движение
Как решать задачи по механике
- Нарисуйте схему, схематично показывающую различные части узла кузова, звенья, опоры и т. д.
- Выберите удобную часть сборки как одну систему.
- Нарисуйте диаграмму свободной части этой детали.
- В диаграмму свободного тела включите информацию о силах (их величинах и направлениях), которые либо известны, либо в которых вы уверены (например, направление натяжения струны по ее длине). Остальные следует рассматривать как неизвестные, определяемые по законам движения.
- Применяйте третий закон Ньютона везде, где это необходимо.
д.Работа
- Изменение кинетической энергии частицы равно работе, совершаемой над ней результирующей силой.
Математически K f − K i = W
- Работа силы определяется как произведение составляющей силы в направлении смещения и величины этого смещения.
Математически,
W = (F cos θ )d = F.d
Работа, совершаемая переменной силой
- Пусть f(x) — переменная сила, тогда площадь между графиком F(x) и x представляет собой работу, проделанную за перемещение
Сохранение механической энергии
- Согласно закону сохранения полной механической энергии полная механическая энергия системы сохраняется, если силы, совершающие над ней работу, консервативны.
Обратите внимание
Потенциальная энергия струны
где, F = усилие пружины, x = смещение от положения равновесия, k = жесткость пружины
Мощность
Единицы мощности
- Единицей мощности в системе СИ является ватт.
- Существует еще одна единица мощности, а именно лошадиная сила (л.с.) 1 л.с. = 746 Вт
Столкновения
- При всех столкновениях полный импульс сохраняется, т.е.е. начальный импульс системы равен конечному импульсу системы.
- Закон сохранения кинетической энергии (даже при упругом столкновении) применяется после того, как столкновение закончилось, а не в каждый момент столкновения.
JEE Main Chemistry Solved Sample Paper Set-VII
Следующая страница
Предыдущая страница
Физика — Классическая механика
Классическая механика (последнее обновление: 8 февраля 2021 г.
)Глава 1.Центры Mass
| 1.1 | Введение и некоторые определения | ||||||
| Районы на самолете | |||||||
| Самолет на самолете | |||||||
| Резюме Формулы для плоских пластин и кривых | |||||||
| 1.6 | Теоремы Паппа | ||||||
| 1.7 | Однородный твердый тетраэдр, пирамида и конус | 3||||||
| Полый конус | |||||||
Глава 2. Момент инерции
4
Тензор инерции.Глава 3. Системы Частицы
| 3.1 | 3.1 | Введение |
| Момент силы | ||
| 3.3 | Момент импульса | |
| 3.4 | Обозначения | |
| Линейный импульс | ||
| Сравнение | ||
| 3.10 | Кинетическая энергия | |
3. 11 | Крутящий момент и скорость изменения углового момента | крутящий момент, угловой импульс и точка движения |
| вириал теорема | 9
Глава 4. Жесткое вращение тела
| 4.1 | Введение||
| Угловая скорость и Эльрериан Углы | ||
| Кинетическая энергия | ||
| 4,5 | Уравнения Эйлера движения||
| Бесплатное движение жесткого асимметричного топ | ||
4. 10 | 4.10 | TOP |
Глава 5. Коллезии
| 5.1 | |
| Отпрыгивая шарики | |
| 5.3 | головной столкновение движущейся сферы с изначально стационарной сферой |
| Два стол Прямоугольные блоки |
Глава 6. Движение в сопротивлении среде
| 6.1 | Введение |
| 6.2 | Универсано ускоренное движение |
| 6.3 | Движение, при котором сопротивление пропорционально скорости |
| 6.4 | Движение, при котором сопротивление пропорционально квадрату скорости. |
Глава 7. Проектирование
| Нет сопротивления воздуха |
Глава 8.Импульсивные силы
| 8.1 | Введение | |
| 80026 |
Глава 9.
| 9.1 | |
| 9.3 | Примеры |
| 9.4 | Виртуальная работа |
Глава 10. Rocket Motion
| ВВЕДЕНИЕ |
3Глава 11. Простое и демпфированное колебательное движение
| 11.1 | Простое гармоническое движение | |
| 11,2 | Масса, прикрепленная к упругой пружине | |
| 11,3 | Торсионный маятник | |
| 11,3 | 4 | Обычные однородные дифференциальные уравнения второго порядка |
Глава 12. Принудительные колебания
| 12.1 | Подробнее о дифференцированных уравнениях |
| 12.2 | Принудительное колебательное движение |
| 12.3 | Электрический аналог |
Глава 13.Lagrangian Mechanics
13. 1 | Введение | ||||
| Компоненты ускорения | |||||
| 13,6 | Скользящее мыло в конической ванне | ||||
| 13,7 | Скользящее мыло в полусферической ванне | 19203Больше примеров | |||
| 13.9 | Гамильтонский вариационный принцип |
| 14.1 | 9 Введение|
| Гамильтон Уравнения движения | |
| 14.4 | Примеры |
| 14.5 | Скобки Пуассона |
Глава 15.Специальная относительность
15. 1 | ВВЕДЕНИЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Скорость света | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Скорость является родственником. Фундаментальный постулат специальной теории относительности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.59 | Преобразования Лоренца | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Но это выступает в здравый смысл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Преобразование Лоренца в качестве вращения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Timelike и Spacelike 4-Vectors | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.9 | 9||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Twins Paradox | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A, B и C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.13 | Одновременность | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.14 | Порядок событий, причинно-следственная связь и передача информации | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Добавление скоростей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ускорение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.21 | Масса | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.22 | Импульс | Некоторые математические результаты | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| кинетическая энергия | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Единицы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.29 | Сила | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.30 | Электромагнетизм |
16
28| 16.1 | Введение | |||||||||||||||||||||||||||||||||||
| 16.3 | Давление | |||||||||||||||||||||||||||||||||||
| Давление на горизонтальной поверхности. Давление на глубине z | ||||||||||||||||||||||||||||||||||||
| 16.5 | Давление на вертикальной поверхности | |||||||||||||||||||||||||||||||||||
| Принцип архимеда | ||||||||||||||||||||||||||||||||||||
| Некоторые простые примеры | ||||||||||||||||||||||||||||||||||||
| 17.1 | 9 Введение||||||||||||||||||||||||||||||||||||
| Массы, две пружины и кирпичная стена | ||||||||||||||||||||||||||||||||||||
| 17,4 | Двойной маятник кручения | |||||||||||||||||||||||||||||||||||
| 17,5 | Двойной маятник | |||||||||||||||||||||||||||||||||||
| Линейная триатамная молекула | ||||||||||||||||||||||||||||||||||||
| Две массы, три пружины, два кирпичных стены | ||||||||||||||||||||||||||||||||||||
| Вода | ||||||||||||||||||||||||||||||||||||
| 17.11 | A Общая вибрационная система | |||||||||||||||||||||||||||||||||||
| 17.12 | A Приводная система 7.1026 | |||||||||||||||||||||||||||||||||||
| Омкрашенная управляемая система | Глава 18. 30161 | |||||||||||||||||||||||||||||||||||
3| Уравнение теста в прямоугольника Координаты и другие простые отношения | |
18. 4 | Площадь катеноида |
Глава 19. Циклоида
| 19.1 | Введение | ||||||
| Тангенс на циклоид | |||||||
| Движение на циклоидах, CUSPS | |||||||
| 19.6 | Движение по циклоиде вершинами вниз | ||||||
| 19.7 | Брахистохронное свойство циклоиды | Контрактные и расширенные циклоиды | |||||
| Примеры циклоидального движения в физике |
Глава 20. Miscellanea
| 20.1 | 9 Введение|||||||||||
| Поверхностное натяжение | |||||||||||
|
2.1Глава 21. Центральные силы и эквивалентный потенциал
| 21.1 | Введение | |
| 21.2 | Движение под центральной силой | |
Размеры| 22.1 | масса, длина и времени | |
| безразмерных величин | ||
| 22,6 | Различные основные величины |
Приложение A. Разные задачи
Приложение B.Решения различных задач
Wolfram|Alpha Примеры: Механика
Другие примеры
ДинамикаРасчет движения объектов под действием крутящих моментов и сил.
Выполните вычисление второго закона Ньютона:
Вычислите движение бруска по наклонной плоскости:
Еще примеры
Другие примеры
Кинематика Расчет движения свободно движущихся объектов и небесных тел.
Найдите уравнения, связанные с задачей двух тел:
Проанализируйте упругое столкновение в одном измерении:
Еще примеры
Эластомеханика
Расчет эффектов деформации, напряжения и других форм деформации.
Рассчитать инженерную деформацию:
Найдите напряжение в цилиндре:
Определить значение коэффициента Пуассона для деформации:
Выполните расчет потери устойчивости столбца Эйлера:
Рассчитаем прогиб балки под нагрузкой:
Еще примеры
Механические системы
Исследуйте уравнения движения для множества механических систем.
Найдите уравнения, связанные с механической системой:
Еще примеры
Классическая механика
Вычислите лагранжианы и гамильтонианы для физической системы.
Вычислите уравнения Эйлера–Лагранжа:
Вычислите уравнения движения из гамильтониана:
Еще примеры
Уравнения для уравнения физики CERT
V = U + AT AT — V = U + AT AT — VELOCITY
MA —
FD — TOURE
MV — Momentum (P)
½MV² — кинетическая энергия
MGH — Потенциальная энергия
FS — работа
W / T — Power
1 KX — Сила весной1 / f — Период (F = частота)
GMM / r² – Сила притяжения между двумя массами
E/q – Сила заряда электрическим полем
F/q – Электрическое поле
W/Q – Разность потенциалов
3 90 – емкости (C)
RA / L —
RA / L — Удельное сопротивление
IR — Разница потенциалов (V)
IV — мощность (Условия напряжения)
I²R — Power (Условия сопротивления)
Робщ=Р₁+Р₂+Р₃….
– Полное сопротивление (серия)
(1/R₁)+(1/R₂)+(1/R₃)+…=(1/Rtotal) – Полное сопротивление параллельно
Bev – Сила B Поле на заряженной частицы
bi l — силу B поля на проволоке
BA —
BA — магнитный поток
þgh — давление в жидкости
F / A — давление
HF — Энергия (волна)
HF-работа Функция — кинетическая энергия
V / λ — длина волны MC² — Energy (с Ref в C) Fλ — скорость волны sin i /sin r – показатель преломления (n) 1/n – sin критического угла C (1/u)+(1/v)=1/f – Зеркала и линзы s = ut + ½at² – расстояние в единицах u, t и a v² = u² + 2as – скорость в единицах u, s и a M₁U₁ + M₂U₂ = M₁V₁ + M₂V₂ — Сохранение импульса S / R — Угол в радианах θ θ / t —1 угловая скорость
v = rω — отношения между линейной скоростью и угловой Velocity
RΩ² = V² / R — Centripetal Acceleration
MROM² = (MV²) / R — Centrippetal Force
мг — Вес
GM₁M₂ / d² — Закон о гравитации Ньютона
GM / R² — г с точки зрения M и R
4π²R³ / GM — T²
1 м / V — ПлотностьPV = Constance — Boyle Закон
FS — моменту
FD – Пара
.
