Как вычислять в системах счисления
Число может быть записано в любой из существующих позиционных систем счисления, где значение каждого числового знака (цифры или буквы) зависит от его позиции (разряда). Помимо десятичной, наиболее известны двоичная, шестнадцатеричная и восьмеричная системы. В позиционной системе счисления можно производить над числами арифметические операции. Вычитание и сложение определяются правилами сложения однозначных чисел и порядком основания. Для умножения и деления достаточно применять таблицу умножения в соответствующей системе счисления.Все арифметические действия с числами в системах выполняются, начиная с младшего разряда (справа налево). При любой операции числа записываются так, чтобы крайние знаки справа были точно друг под другом. Действия с одноразрядными числами, то есть, состоящими из одного знака, производятся с учетом основания системы счисления. При разрядности системы N, ее числа имеют значения от 0 до N-1. Если получаемые значения свыше N-1, то из результата вычитается N-1, остаток записывается в текущие единицы и к числу добавляется следующий разряд.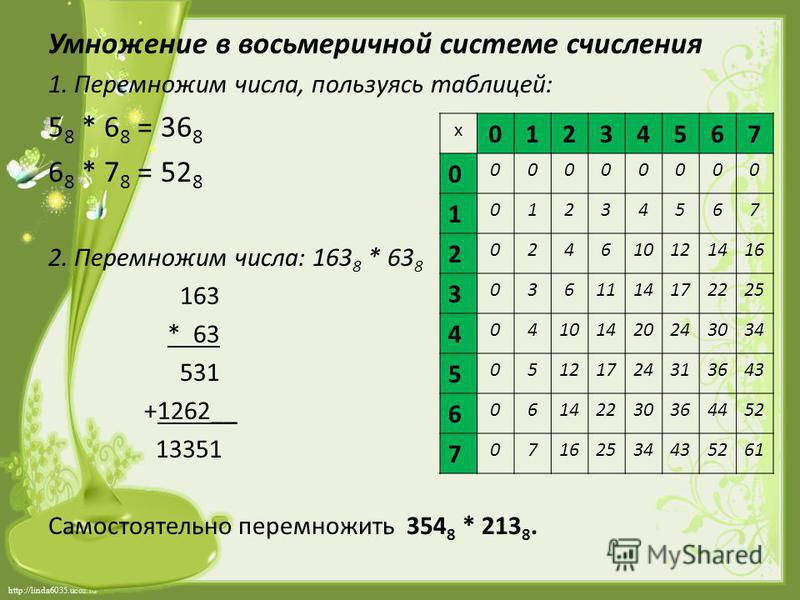
При сложении многоразрядных чисел (содержащих в записи несколько числовых или буквенных знаков) нужно дополнительно производить перенос при переполнении разряда и учитывать его при сложении последующих цифр или знаков числа. В двоичной системе с основанием 2 имеется всего две цифры: 0 и 1. Переполнение здесь происходит при сложении единиц, при этом в младший разряд записывается 0 и добавляется 1 в старший. Аналогично в любой другой позиционной системе счисления, только учитывается соответствующее основание.
Вычитание производится по уже известным правилам займа единицы из старшего разряда. Вычитая два числа в восьмеричной системе, например, числа 2743 и 1371, запишите ихдруг под другом – сверху уменьшаемое, снизу вычитаемое, еще ниже проведите горизонтальную черту. Справа налево отнимайте единицы сначала младшего разряда, затем последующего и т.д. При вычитании из 3 числа 1 – в результате будет 2, далее из 4 вычитается 7 и здесь потребуется провести займ из старшего разряда.
Для этого к 4 прибавьте основание данной системы счисления – число 8, из получившегося значения (8+4=12) вычитайте число 7 – останется 5, запишите этот результат под чертой.
В последующем, старшем разряде из 7 вычтите занятую единицу, останется число 6. Из него уже отнимите число, стоящее ниже – 3. В результате останется 3, запишите результат под чертой. Проведите вычитание над последними числами – 2-1=1 – окончательный результат операции в восьмеричной системе выглядит так: 1352.
Умножение многоразрядных двоичных чисел производится в соответствии со специальной таблицей по обычной схеме, применяемой и в десятичной системе. Произведение чисел выполняется с помощью попеременного умножения одноразрядных чисел, соответствующей записи результатов и их дальнейшего сложения столбиком со сдвигом.
Арифметические действия в восьмеричной системе счисления
библиотека
материалов
Содержание слайдов
Номер слайда 1
* Арифметические операции в восьмиричной системе 8 класс Автор: Чиркова И.
А
* Рассмотрим «Сложение» 2 6 68 + 6 6 18 1 1 6 + 2 = 7 6 + 6 + 1 = 13 = 8 + 5 2 + 6 + 1 = 9 = 8 + 1 1 1 в перенос 1 78 1 5 1 в перенос
Номер слайда 3
* Решим примеры: 6 5 48 + 3 1 68 1 2 7 38 + 7 3 28
Номер слайда 4* Рассмотрим «Вычитание» 5 5 18 – 3 6 78 (1 + 8) – 7 = 2 (5 – 1 + 8) – 6 = 6 (5 – 1) – 3 = 1 заем 28 1 6 заем
Номер слайда 5
Сложение, вычитание, умножение в двоичной системе счисления
1.
Проверка домашнего задания 1. Выполните сложение, вычитание,умножение в двоичной системе
счисления
12)
1111000
10111
10001111
2
2
2
1111000
10111
1100001
2
2
2
1111000
10111
2
2
101011001000
2
13)
11000
1101
100101
2
2
2
11000
1101
1011
2
2
2
1101
11000
100111000
2
2
2
15)
1100100
100011
10000111
2
2
2
1100100
100011
1000001
2
2
2
100011
1100100
110110101100
2
2
2
13. Сколько учеников в классе?
Количество рядов – 3 8
В ряду – 616 парт
За одной партой – 102 учеников
Не заняты – 4 8 парты
Ответ: 28 учеников
15. Сколько компьютеров в 3 классе?
1000002по 1011 2
?
1 класс
2 класс
3 класс
Ответ: 10
«Ум заключается не только в знании, но и
в умении прилагать знание в дело».
Аристотель
18. Арифметические операции в позиционных системах счисления
9991087610
187510
9+6=15=10+5
9+7+1=18=10+7
9+8+1=18=10+8
20. Сложение в позиционных системах счисления
Цифры суммируются по разрядам, и если при этом возникает избыток, тоон переносится влево
двоичная
система
1 1
восьмеричная
система
шестнадцатеричная
система
1 11
1
10101
1101
+
+
2154
736
3 1 12
1 00 0 10
4+6=10=8+2
1+1=2=2+0
1+0+0=1
1+1=2=2+0
1+1+0=2=2+0
5+3+1=9=8+1
1+7+1=9=8+1
1
+
1
8 D8
3 BC
C 94
8+12=20=16+4
13+11+1=25=16+9
8+3+1=12=C16
1+2=3
1+1=2=2+0
Ответ: 1000102
Ответ: 31128
21. Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого меньше цифрывычитаемого, то из старшего разряда занимается единица основания
двоичная
система
1
восьмеричная
система
1
1
-1 0 1 0 1
1011
—
01 0 10
1
1
43506
5042
2-1=1
0-0=0
2-1=1
Ответ: 10102
1
— С 9 4
3 В С
36 4 44
1-1=0
шестнадцатеричная
система
8 4 8
6-2=4
8-4=4
4-0=4
16+4-12=20-12=8
16+8-11=24-11=13=D16
11-3=8
8+3-5=11-5=6
Ответ: 364448
Ответ: 84816
22.
Умножение в позиционных системах счисления При умножении многозначных чисел в различных позиционных системахприменяется алгоритм перемножения чисел в столбик, но при этом
результаты умножения и сложения записываются с учетом основания
системы счисления
двоичная
система
восьмеричная
система
2 2
4
1
х1
1011
1101
1
11011
1 1 1 0 1 1
11011
101011111
11
х
163
63
531
1262
13351
1
1+1+1=3=2+1
1+1+1=3=2+1
1+1=2=2+0
Ответ: 1010111112
Ответ: 133518
23. Деление в позиционных системах счисления
Деление в любой позиционной системе производится по тем же правилам,как и деление углом в десятичной системе. При этом необходимо
учитывать основание системы счисления.
двоичная
система
восьмеричная
система
100011
1110
1110
1 0 ,1
1 11 0
1110
0
Ответ: 10,12
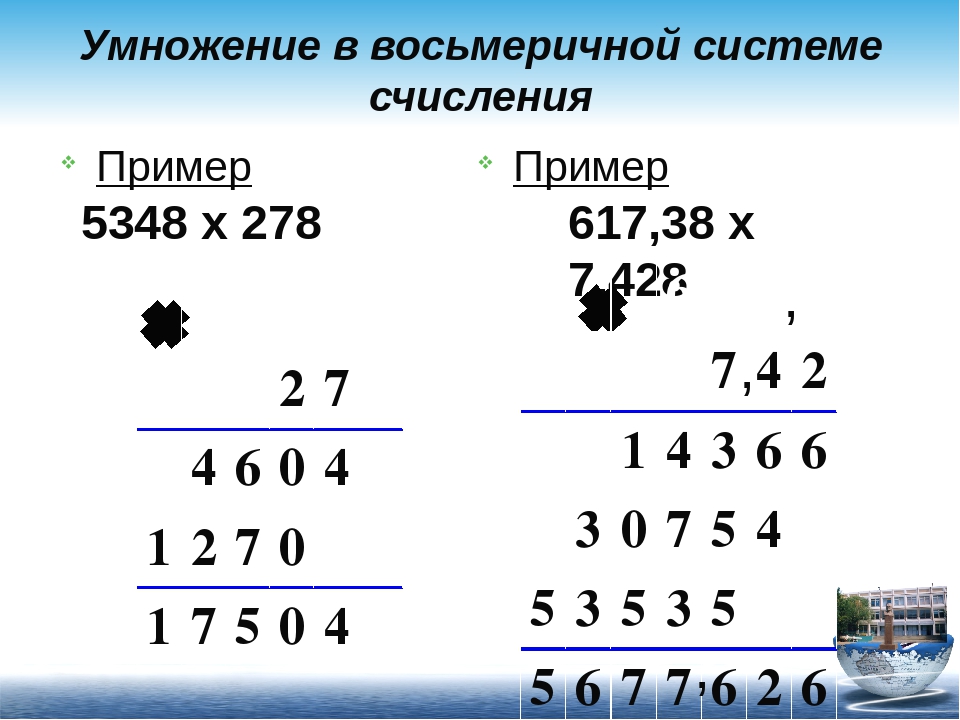
Примеры
3 5 38
+ 7 3 68
1311
1 3 5 38
+ 7 7 78
2352
Пример:
С В А16
+ A 5 916
1713
Примеры:
1011012
– 111112
1110
1100112
– 101012
11110
Примеры
–
6 6 28
1 5 68
504
1 1 5 68
– 6 6 28
274
Пример:
А 5 916
– 1 В А16
89F
Примеры:
11012
1112
1011011
Выполни действия, заданные в таблице
1 уровень: найди координаты 5,6,7 точки.
2 уровень: найди координаты 1,2,3,4 точки.
3 уровень: найди координаты 1,2,3,4,5,6,7,8 точки.
Переведи полученные значения в десятичную
систему счисления.
Результат занеси в таблицу
Отметь в системе координат найденные точки. Не
забудь проставить их порядковые номера.
Точки соедини последовательно по правилу:
1 уровень: 5-6-7-5
2 уровень: 1-2-3-4-1
3 уровень: 1-2-3-4, 5-6-7, 6-8.
32. Домашнее задание
1. Уровень знания:Знать алгоритмы выполнения арифметических
действий в позиционных системах счисления
2.Уровень понимания:
Выполните действия:
А) Выполнить вычитание:
а) 1100000011,011(2) — 101010111,1(2) = 110101011,111(2).
б) 1510,2(8) — 1230,54(8) = 257,44(8).
в) 27D,D8(16) — 191,2(16) = EC,B8(16).
Б) 3. Сложить числа:
а) 10000000100(2) + 111000010(2) = 10111000110(2).
б) 223,2(8) + 427,54(8) = 652,74(8).
в) 3B3,6(16) + 38B,4(16) = 73E,A(16).
В) Выполнить умножение:
а) 100111(2) ´ 1000111(2) = 101011010001(2).
б) 1170,64(8) ´ 46,3(8) = 57334,134(8).
в) 61,A(16) ´ 40,D(16) = 18B7,52(16).
3.Творческий уровень: Восстановите двоичные
цифры:
**0*0*1**1+10111*1011=100*1*00010;
1*01+1**=10100.
Спасибо за внимание!
Задания к зачётной работе «Система счисления. Перевод чисел. Арифметические операции в разных системах счисления»
Ход занятияВариант 11. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
а) 948;
б) 763;
в) 994,125;
г) 523,25;
д) 203,82.
2. Переведите числа в десятичную систему счисления.
а) 1110001112;
б) 1000110112;
в) 1001100101,10012;
г) 1001001,0112;д) 335,78;
е) 14C,A16.
3. Выполните сложение чисел.
а) 11101010102+101110012;
б) 101110102+100101002;
в) 111101110,10112+1111011110,12;
г) 1153,28+1147,328;
д) 40F,416+160,416.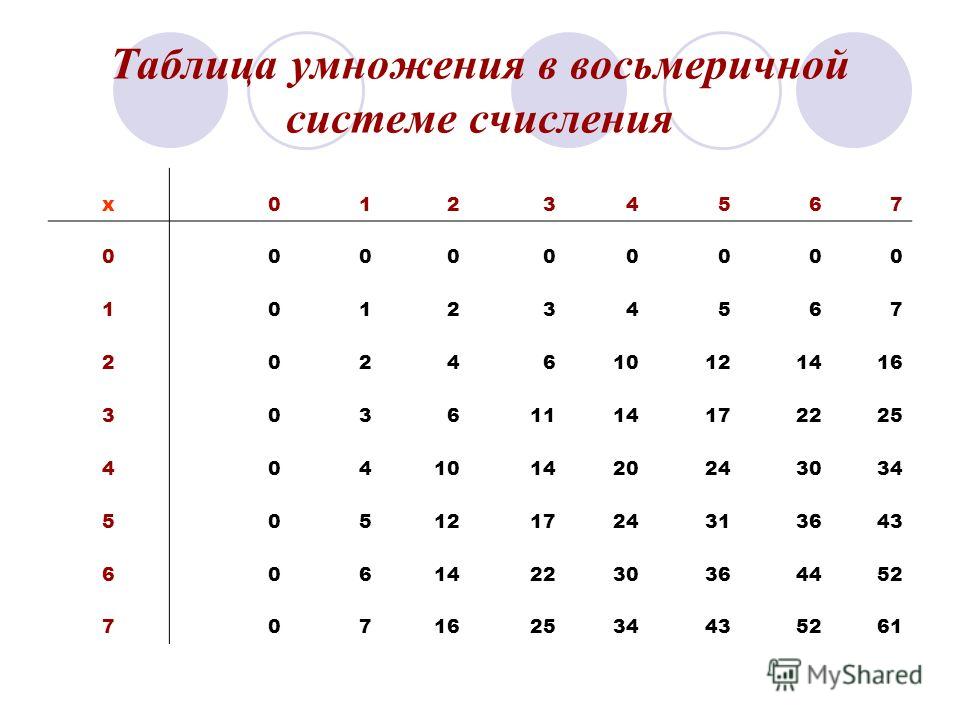
4. Выполните вычитание чисел.
а) 10000001002-1010100012;
б) 10101111012-1110000102;
в) 1101000000,012-1001011010,0112;
г) 2023,58-527,48;
д) 25E,616-1B1,516.
5. Выполните умножение чисел.
а) 10010112*10101102;
б) 1650,28*120,28;
в) 19,416*2F,816.
Вариант 2
1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
а) 563;
б) 264;
в) 234,25;
г) 53,125;
д) 286,16.
2. Переведите числа в десятичную систему счисления.
а) 11000100102;
б) 100110112;
в) 1111000001,012;
г) 10110111,012;
д) 416,18;
е) 215,716.
3. Выполните сложение чисел.
а) 101111112+1100100002;
б) 1100101002+10111000012;
в) 1000000101,01012+1010000110,012;
г) 1512,48+1015,28;
д) 274,516+DD,416.
4. Выполните вычитание чисел.
а) 1000001001
2-1111101002;
б) 11110001012-11001101012;
в) 1100110101,12-1011100011,012;
г) 1501,348-1374,58;
д) 12D,316-39,616.
5. Выполните умножение чисел.
а) 1111012*10101112;
б) 1252,148*76,048;
в) 66,6816*1E,316.
Вариант 3
1. Переведите числа из десятичной системы
счисления в двоичную, восьмеричную и
шестнадцатеричную системы счисления.
а) 279;
б) 281;
в) 841,375;
г) 800,3125;
д) 208,92.
2. Переведите числа в десятичную систему счисления.
а) 11001110012;
б) 100111012;
в) 1111011,0012;
г) 110000101,012;
д) 1601,568;
е) 16E,B416.
3. Выполните сложение чисел.
а) 10001000012+10111001102;
б) 11011100112+1110001012;
в) 1011011,012+1000101110,10012;
г) 665,18+1217,28;
д) 30C,716+2А1,816.
4. Выполните вычитание чисел.
а) 111100102-101010012;
б) 11101000012-10110010012;
в) 1101001010,12-1011101001,110112;
г) 166,148-143,28;
д) 287,А16-62,816.
5. Выполните умножение чисел.
а) 10010012*1000102;
б) 324,28*122,128;
в) F,416*38,616.
Вариант 4
1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
а) 737;
б) 92;
в) 934,25;
г) 413,5625;
д) 100,94.
2. Переведите числа в десятичную систему счисления.
а) 11100000102;
б) 10001002;
в) 110000100,0012;
г) 1001011111,000112;
д) 665,428;
е) 246,1816.
3. Выполните сложение чисел.
а) 111101002+1101000012;
б) 11011102+1010010002;
в) 1100110011,12+111000011,1012;
г) 1455,048+203,38;
д) 14Е,816+184,316.
4. Выполните вычитание чисел.
а) 10000101012-1001010002;
б) 10010110112-1010011102;
в) 111111011,1012-100000010,012;
г) 341,28-275,28;
д) 249,516-ЕЕ,А16.
5. Выполните умножение чисел.
а) 10010002*10100112;
б) 412,58*13,18;
в) 3B,A16*10,416.
Ответы
Вариант 1
| Задание 1 | Задание 2 | Задание 3 |
| а) 94810=11101101002=16648=3B416; б) 76310=10111110112=13738=2FB16; в) 994,12510=1111100010,0012=1742,18=3Е2,216; г) 523,2510=1000001011,012=1013,28=20В,416; д)203,8210=11001011,11012=313,64368=СВ,D1EB16. 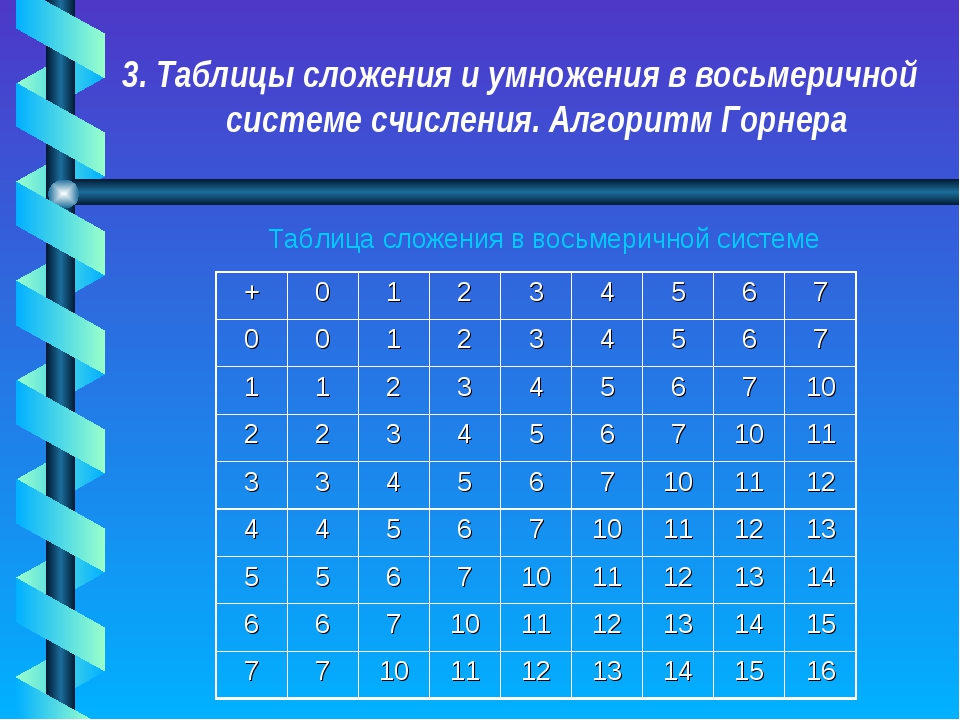 | а) 44510; б) 28310; в) 613,562510; г) 73,37510; д) 221,87510; е) 332,62510. | а) 100011000112; б) 1010011102; в) 10111001101,00112; г) 2322,528; д) 56F,816. |
| Задание 4 | Задание 5 | |
| а) 101100112; б) 111110112; в)11100101,1112; г) 1274,18; д) AD,116. | а) 11001001100102; б) 222576,048; в) 4AF,616. |
Вариант 2
| Задание 1 | Задание 2 | Задание 3 |
| а) 56310=10001100112=10638=23316; б) 26410=1000010002=4108=10816; в) 234,2510=11101010,012=352,28=EA,416; г) 53,12510=110101,0012=65,18=35,216; д) 286,1610=100011110,001012=436,12178=11E,28F5C16.  | а) 78610; б) 15510; в) 961,2510; г) 183,2510; д) 270,12510; е) 533,437510. | а) 10010011112; б) 100011101012; в)10010001011,10012; г) 2527,68; д) 351,916. |
| Задание 4 | Задание 5 | |
| а) 101012; б) 100100002; в) 010010,012; г) 104,648; д) F3,D16. | а) 10100101110112; б) 122542,2068; в) С13,63816. |
Вариант 3
| Задание 1 | Задание 2 | Задание 3 |
| а) 27910=1000101112=4278=11716; б) 28110=1000110012=4318=11916; в) 841,37510=1101001001,0112=1511,38=349,616; г) 800,312510=1100100000,01012=1440,248=320,516; д)208,9210=11010000,111012=320,7278=D0,EB85116.  | а) 82510; б) 15710; в) 123,12510; г) 389,2510; д) 897,7187510; е) 366,70312510. | а) 101000001112; б) 101001110002; в)1010001001,11012; г) 2104,38; д) 5AD,F16. |
| Задание 4 | Задание 5 | |
| а) 10010012; б) 110110002; в) 1100000,101012 г) 22,748; д) 225,216. | а) 1001101100102; б) 42035,5248; в) 35B,B816. |
Вариант 4
| Задание 1 | Задание 2 | Задание 3 |
| а) 73710=10111000012=13418=2E116; б) 9210=10111002=1348=5С16; в) 934,2510=1110100110,012=1646,28=3А6,416; г) 413,562510=110011101,10012=635,448=19D,916; д) 100,9410=1100100,11112=144,74128=64,F0A3D16. 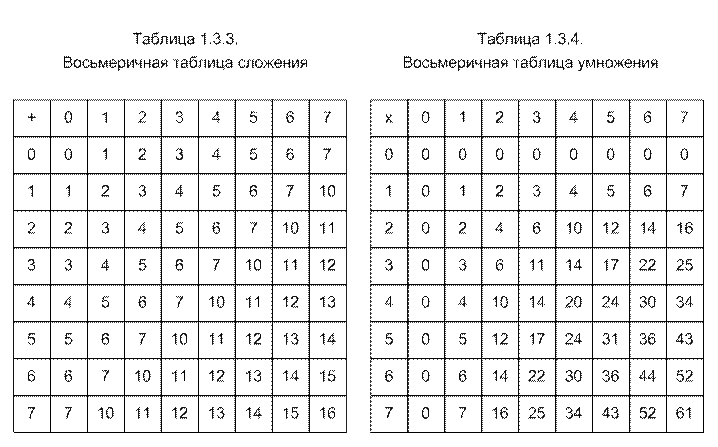 | а) 89810; б) 6810; в) 388,12510; г) 607,0937510; д) 437,5312510; е) 582,0937510. | а) 10100101012; б) 1101101102; в) 1001111011,0012; г) 1660,348; д) 2D2,B16. |
| Задание 4 | Задание 5 | |
| а) 111011012; б) 1000011012; в) 11111001,0112; г) 448; д) 15А,B16. | а) 10111010110002; б) 5626,158; в) 3С8,Е816. |
Решенные примеры восьмеричного умножения
Это моя третья статья по восьмеричной арифметике. В этой статье я собираюсь объяснить умножение восьмеричных чисел. Я также расскажу об умножении с использованием восьмеричной таблицы умножения. Есть мои сообщения о восьмеричном сложении и восьмеричном вычитании.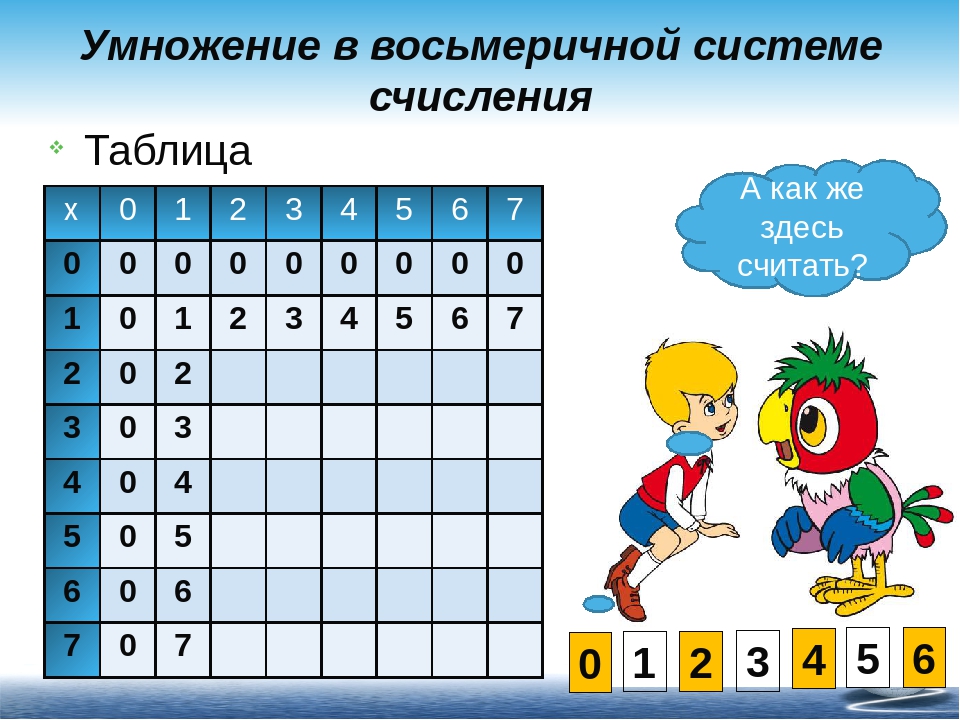
Ключевые вопросы:
Как выполнить восьмеричное умножение?
Как произвести дробное умножение восьмеричных чисел?
Обсудить восьмеричную таблицу умножения
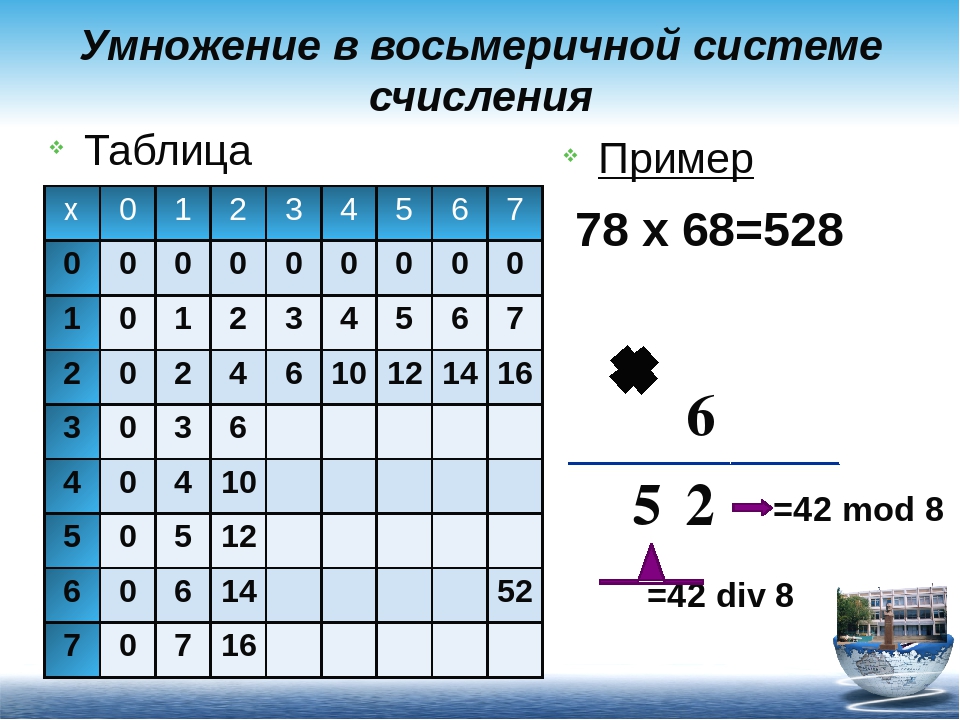
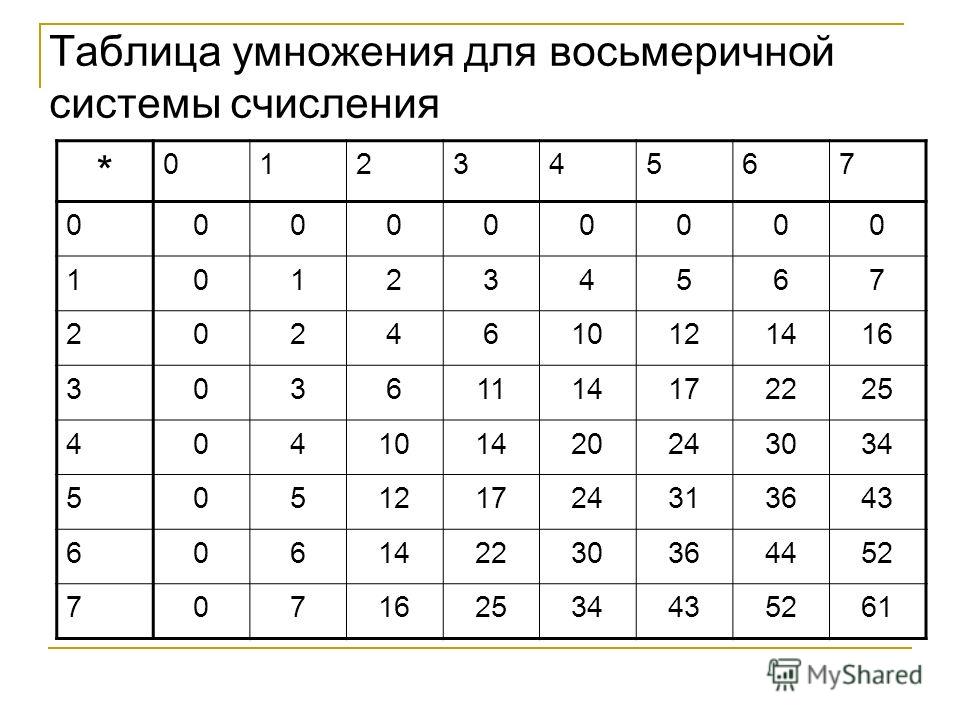
Восьмеричная таблица умножения:
| х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Примеры восьмеричного умножения:
Процесс умножения восьмеричных чисел такой же, как и в других системах счисления.
Вы можете проверить свой результат с помощью этого онлайн-конвертера. О чем следует помнить при умножении восьмеричных чисел:Если сумма превышает 7 (0,1,2,3,4,5,6,7), вам необходимо вычислить эквивалентное восьмеричное значение.
Разделите число на 8 и найдите эквивалентное восьмеричное значение. Частное будет перенесено, а остаток будет принят как сумма
.
Например 5) 8 * 6) 8 = 30) 10
5
* 6
36) 8
3 ← частное
8⟌30
24
6 ← остаток в виде суммы
Пример # 01: 777) 8 * 33) 8
2 2 ← нести
7 7 7
* 33
1 1 1 ← нести
2 7 7 5
2 7 7 5 Х
3 2 7 4 5
| | Десятичный | Восьмеричный эквивалент | Сумма / остаток | Перенос / частное |
7 * 3 | 21 | 21 ÷ 8 = 25 | 5 | 2 |
7 * 3 | 21 + 2 | 23 ÷ 8 = 27 | 7 | 2 |
7 * 3 | 21 + 2 | 23 ÷ 8 = 27 | 7 | 2 |
7 + 5 | 12 | 12 ÷ 8 = 14 | 4 | 1 |
7 + 7 + 1 | 15 | 15 ÷ 8 = 17 | 7 | 1 |
2 + 7 + 1 | 10 | 10 ÷ 8 = 12 | 2 | 1 |
Ответ: 32745) 8
Пример № 02: 466.
4) 8 * 2,7) 8
1 1 1
5 5 3
4 6 6. 4
* 2. 7
1
4 1 7 5 4
1 1 5 5 0 Х
1 5 7 4. 5 4
| | Десятичный | Восьмеричный эквивалент | Сумма / остаток | Перенос / частное |
7 * 4 | 28 | 28 ÷ 8 = 24 | 4 | 2 |
7 * 6 | 42 + 3 | 45 ÷ 8 = 5 | 5 | 5 |
7 * 6 | 42 + 5 | 47 ÷ 8 = 47 | 7 | 4 |
7 * 4 | 28 + 5 | 33 ÷ 8 = 41 | 1 | 4 |
2 * 4 | 8 | 8 ÷ 8 = 10 | 0 | 1 |
2 * 6 | 12 + 1 | 13 ÷ 8 = 15 | 5 | 1 |
2 * 6 | 12 + 1 | 13 ÷ 8 = 15 | 5 | 1 |
2 * 4 | 8 + 1 | 9 ÷ 8 = 11 | 1 | 1 |
7 + 5 | 12 | 12 ÷ 8 = 14 | 6 | 1 |
Ответ: 1574.
54) 8
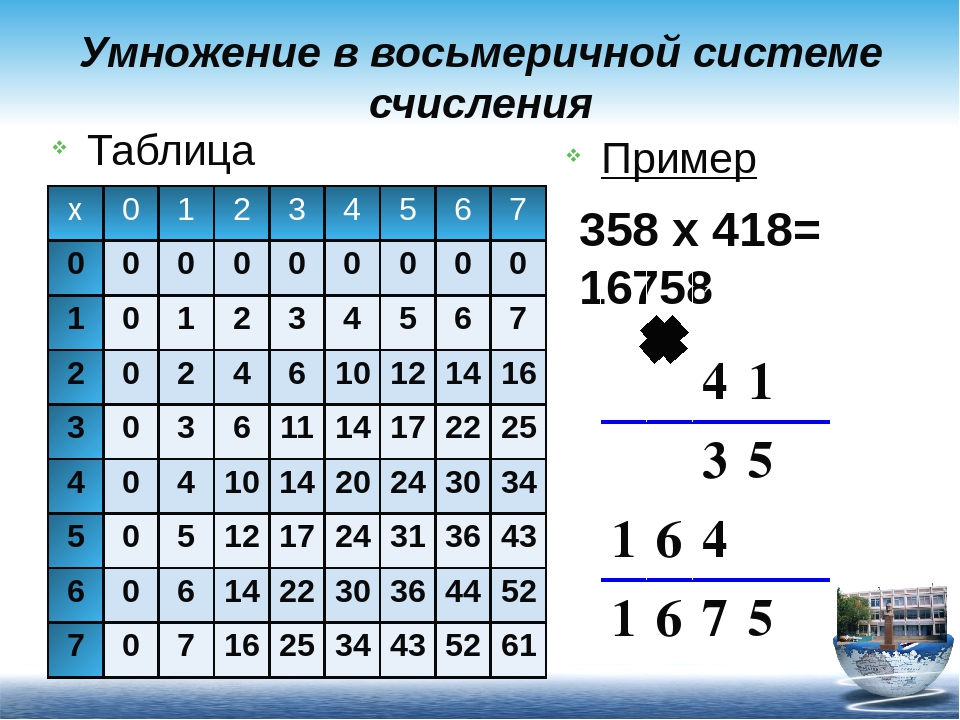
Пример # 03: 3636) 8 * 741) 8
Попробуем решить пример с использованием восьмеричной таблицы умножения.
Х = 3636
Y = 741
1 * 6 найдите пересечение 3 и 6. То есть 6. Аналогичным образом для всех продуктов обратитесь к таблице.
5 3 5
3 1 3
3 6 3 6
* 7 4 1
1 1
3 6 3 6
1 7 1 7 0 Х
3 2 5 2 2 Х Х
3 4 4 7 7 3 6
Ответ: 3447736) 8
Вывод:
Это все об умножении восьмеричных чисел.Я проверил и проверил все ответы и решения. Если вы все же обнаружите логическую или типографскую ошибку, пожалуйста, сообщите мне. Если вы сочтете этот пост полезным, пожалуйста, оцените его.
Рекомендуемые книги
Умножение восьмеричных чисел (база 8) (A)
Добро пожаловать в Рабочий лист по умножению восьмеричных чисел (основание 8) (A) со страницы «Рабочие листы умножения» на Math-Drills.
com. Этот математический лист был создан 18.02.2016 и был просмотрен 1 раз на этой неделе и 100 раз в этом месяце.Его можно распечатать, загрузить или сохранить и использовать в вашем классе, домашней школе или другой образовательной среде, чтобы помочь кому-то выучить математику.
Учителя могут использовать рабочие листы по математике в качестве тестов, практических заданий или учебных пособий (например, в групповой работе, на строительных лесах или в учебном центре). Родители могут работать со своими детьми, чтобы дать им дополнительную практику, помочь им освоить новые математические навыки или сохранить свои навыки свежими во время школьных каникул. Учащиеся могут использовать рабочие листы по математике для овладения математическими навыками на практике, в учебной группе или для взаимного обучения.
Используйте кнопки ниже, чтобы распечатать, открыть или загрузить PDF-версию таблицы по математике «Умножение восьмеричных чисел» (основание 8) (A).
Размер файла PDF составляет 50982 байта. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. Если существует больше версий этого рабочего листа, другие версии будут доступны под изображениями для предварительного просмотра. Для более того, используйте строку поиска для поиска некоторых или всех этих ключевых слов: математика, число, системы, восьмеричное, умножение .
Кнопка Печать запускает диалоговое окно печати вашего браузера. Кнопка Открыть открывает весь PDF-файл в новой вкладке браузера. Кнопка Загрузить инициирует загрузку математической таблицы в формате PDF. Версии для учителей включают как страницу вопроса, так и ключ ответа. Версии для учащихся, если они есть, включают только страницу с вопросами.
Умножение восьмеричных чисел (основание 8) (A) Рабочий лист по математике, страница 1Умножение восьмеричных чисел (основание 8) (A) Рабочий лист по математике, страница 2Другие версии:
Другие рабочие листы умножения
Восьмеричная система счисления— значение, преобразование, решаемые примеры, практические вопросы
Восьмеричная система счисления — это тип системы счисления с основанием из восьми и цифрами от 0 до 7.
Система счисления — это система именования, представления или выражения чисел в различных типах форм. Основные способы представления чисел выполняются четырьмя способами: восьмеричная система счисления, двоичная система счисления, десятичная система счисления и шестнадцатеричная система счисления.
Определение восьмеричной системы счисления
Система счисления, основанная на восьми и использующая цифры от 0 до 7, называется восьмеричной системой счисления. Слово восьмеричное используется для обозначения чисел, в основе которых лежит восемь.Восьмеричные числа имеют много применений и важности, например, они используются в компьютерах и цифровых системах счисления. В системе счисления восьмеричные числа можно преобразовать в двоичные числа, двоичные числа в восьмеричные числа, сначала преобразовав двоичное число в десятичное число, а затем десятичное число в восьмеричное число.
Подобно восьмеричной системе счисления, двоичная система счисления представлена основанием 2, десятичная система счисления представлена основанием 10, а шестнадцатеричная система счисления представлена основанием 16.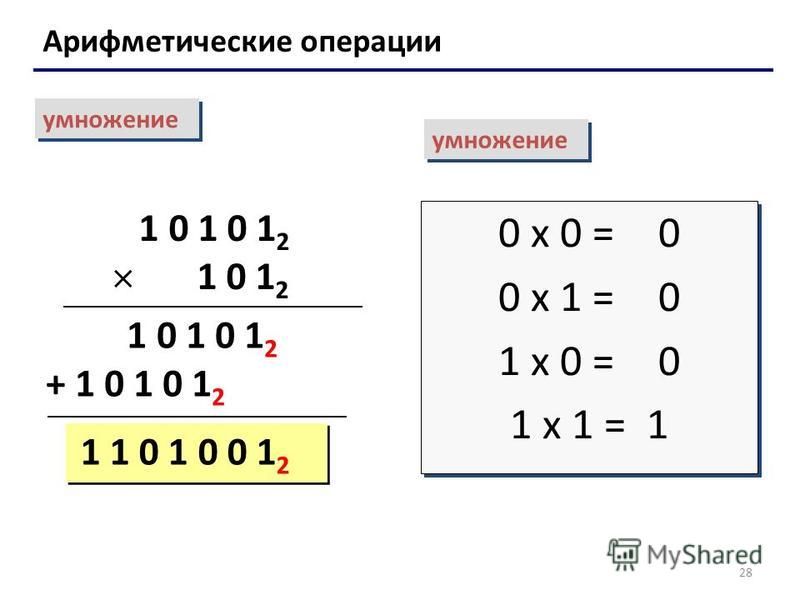
Вот несколько примеров этих систем счисления:
- \ ((10) _ {2} \) — двоичное число
- \ ((119) _ {10} \) — десятичное число
- \ ((51) _ {6} \) — шестнадцатеричное число
При решении восьмеричного числа каждое место представляет собой степень восьми. Например: \ ((347) _ {8} \) = 3 x 8 2 + 4 x 8 1 + 7 x 8 0
Преобразование восьмеричных в двоичные числа
Для процесса преобразования нам нужно преобразовать каждое число из восьмеричного числа в двоичное.Каждую цифру необходимо преобразовать в 3-битное двоичное число и, следовательно, получить двоичный эквивалент восьмеричного числа. Ниже приведено табличное представление двоичных чисел в восьмеричные числа и наоборот.
Пример 1 — Преобразование \ ((14) _ {8} \) в двоичное число
Решение — Учитывая \ ((14) _ {8} \) восьмеричное число, с помощью приведенной выше таблицы мы можем написать \ ((14) _ {8} \) = \ ((001 100 ) _ {2} \).
Нули слева не имеют значения.Следовательно, \ ((14) _ {8} \) = \ ((001 100) _ {2} \).
Пример 2 — Преобразование \ ((11100101) _ {2} \) в восьмеричное число.
Решение — Учитывая, что \ ((11100101) _ {2} \) является двоичным числом, с помощью приведенной выше таблицы мы сначала записываем число в его 3-битное двоичное число, поскольку перед цифрами необходимо добавить ноль. для формирования 3-битного двоичного числа. Итак, число можно записать как \ ((011100101) _ {2} \). Следовательно, 3-битное двоичное число — это 011, 100, 101. Глядя на ту же таблицу выше, мы можем преобразовать эти двоичные числа в их восьмеричные числа, чтобы получить окончательное число.Отсюда числа 3, 4, 5
Следовательно, \ ((11100101) _ {2} \) = \ ((345) _ {8} \)
Преобразование восьмеричного числа в десятичное
Преобразование восьмеричных чисел в десятичные выполняется очень просто. Число расширяется с основанием восемь, где каждое число умножается с уменьшающей степенью 8.
В десятичной системе счисления после преобразования используется основание 10.
Например, — Преобразует восьмеричное число \ ((121) _ {8} \) в его десятичную форму.
Решение — \ ((121) _ {8} \) = 1 x 8 2 + 2 x 8 1 + 1 x 8 0
= 1 х 64 + 2 х 8 + 1 х 1
= 64 + 16 + 1
Следовательно, \ ((121) _ {8} \) = \ ((81) _ {10} \)
Преобразование десятичного числа в восьмеричное
Для преобразования десятичного числа в восьмеричное используется другой метод. В этом методе десятичное число делится на 8 каждый раз, когда получается напоминание из предыдущей цифры.Первый полученный остаток — это младшая значащая цифра (LSD), а последний остаток — самая старшая цифра (MSD). Разберемся с преобразованием на примере.
Например, — Преобразуйте десятичное число 321 в восьмеричную форму.
Решение — Нам нужно начать делить число 321 на 8
321/8 дает частное 40, а остаток равен 1
40/8 дает частное 5, а остаток равен 0
Итак, здесь частное равно 5, а остаток равен 0.
Восьмеричное число начинается от MSD до LSD, то есть 501
Следовательно, \ ((321) _ {10} \) = \ ((501) _ {8} \)
Преобразование восьмеричных в шестнадцатеричные числа
Шестнадцатеричный формат представлен с основанием 16 и состоит как из чисел, так и из букв. Цифры от 0 до 9 представлены в обычном виде, но от 10 до 15 он обозначается как A, B, C, D, E, F. Преобразование восьмеричного в шестнадцатеричное осуществляется в два этапа, т.е. сначала выполняется преобразование восьмеричного. число в десятичное число, а затем преобразовать его в шестнадцатеричное число.Давайте посмотрим на пример, чтобы лучше понять этот метод.
Например, — \ ((121) _ {8} \) = \ ((81) _ {10} \)
Решение — У нас уже есть десятичное число 81 10 , поэтому нам нужно только преобразовать его в шестнадцатеричное число. Чтобы определить шестнадцатеричное число, нам нужно разделить число 81 на 16, пока остаток не станет меньше 16.
Оно полностью делится с ответом 5 и остатком 1.
Следовательно, \ ((121) _ {8} \) = \ ((51) _ {16} \)
Восьмеричная система счисления Связанные темы
Прочтите эти интересные статьи, чтобы узнать больше о восьмеричной системе счисления и связанных с ней темах.
Важные моменты
- Преобразование восьмеричных чисел в двоичные и наоборот очень просто.
- Для преобразования восьмеричных чисел в шестнадцатеричные числа необходимо преобразовать восьмеричное число в десятичное, а затем в шестнадцатеричное.
- Основание каждой из четырех систем счисления очень важно.
Часто задаваемые вопросы о восьмеричной системе счисления
Что такое восьмеричная система счисления?
Система счисления, основанная на восьми и использующая цифры от 0 до 7, называется восьмеричной системой счисления.Слово восьмеричное используется для обозначения чисел, в основе которых лежит восемь.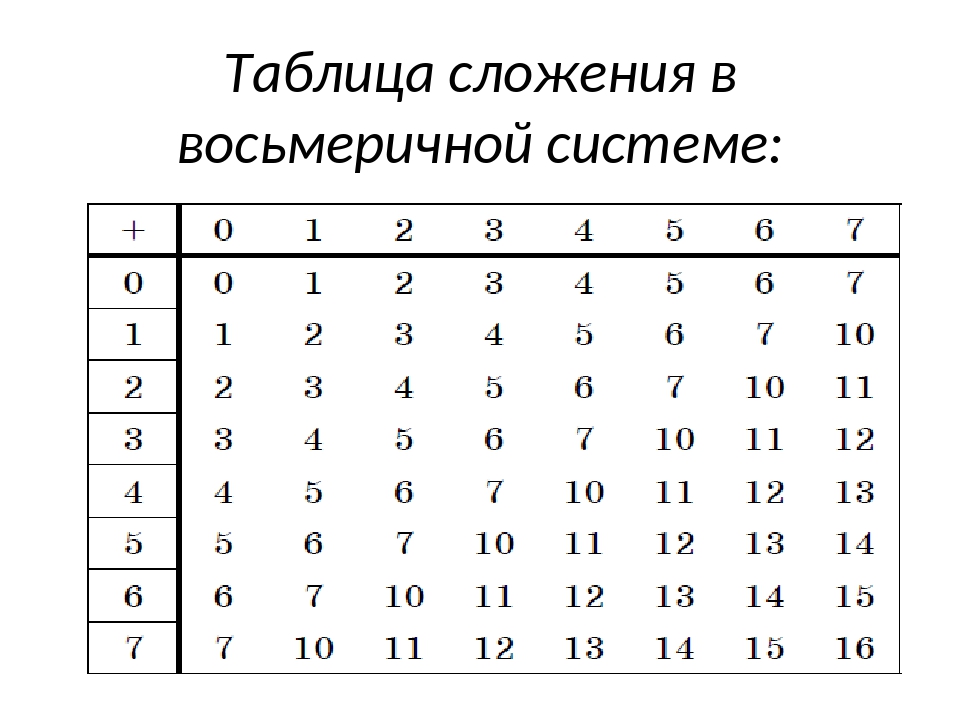
Восьмеричные числа имеют много применений и важности, например, они используются в компьютерах и цифровых системах счисления. Слово Octal — это краткая форма латинского слова Oct, что означает короткий.
Как используются восьмеричные числа?
Система восьмеричных чисел широко используется в компьютерных приложениях и цифровых системах счисления. Вычислительные системы используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова.Восьмеричное число также используется в авиационном секторе в виде кода.
В чем важность восьмеричной системы счисления?
В восьмеричной системе счисления используются цифры от 0 до 7, которые могут быть образованы из двоичных чисел путем группировки двоичных цифр в его 3-битном представлении. В восьмеричных числах используется меньшее количество цифр по сравнению с десятичными и шестнадцатеричными, что упрощает вычисление за меньшее количество шагов.
Какие четыре типа системы счисления?
Четыре основных типа системы счисления:
Какие символы используются в восьмеричной системе счисления?
Восьмеричная система счисления — это система счисления с основанием 8, что означает, что для представления любого числа в восьмеричной системе необходимо 8 различных символов.
Это символы 0, 1, 2, 3, 4, 5, 6 и 7. Наименьшее двузначное число в этой системе — \ ((10) _ {8} \), что эквивалентно десятичному числу 8.
Каковы преимущества и недостатки восьмеричной системы счисления?
Преимущества восьмеричной системы счисления заключаются в том, что она составляет одну треть от двоичной системы счисления, процесс преобразования восьмеричной системы счисления в двоичную и наоборот очень прост, а в восьмеричной форме легко обрабатывать ввод и вывод. Недостатки восьмеричной системы счисления состоят в том, что существует дополнительное требование к системе внутри компьютера, которая обеспечивает более легкое преобразование восьмеричных чисел в двоичные числа до того, как она будет фактически применена к цифровой платформе.
Как преобразовать восьмеричное число в десятичное?
Чтобы преобразовать восьмеричную систему в десятичную, нам нужно расширить число с основанием восемь, где каждое число умножается с уменьшающей степенью 8.
После получения произведения мы складываем числа, чтобы получить десятичное число. В десятичной системе счисления после преобразования используется основание 10.
Как преобразовать десятичное число в восьмеричное?
Чтобы преобразовать десятичное число в восьмеричное, десятичное число делится на 8 каждый раз, когда получается напоминание из предыдущей цифры.Первый полученный остаток — это младшая значащая цифра (LSD), а последний остаток — самая старшая цифра (MSD).
Как преобразовать восьмеричное число в шестнадцатеричное?
Шестнадцатеричный формат представлен с основанием 16 и состоит как из чисел, так и из букв. Цифры от 0 до 9 представлены в обычном виде, но от 10 до 15 он обозначается как A, B, C, D, E, F. Преобразование восьмеричного в шестнадцатеричное осуществляется в два этапа, т.е. сначала выполняется преобразование восьмеричного. число в десятичное число, а затем преобразовать его в шестнадцатеричное число.
Восьмеричная система счисления— Карьера сегодня
Восьмеричная система счисления имеет основание восемь и использует числа от 0 до 7.
Это классификация системы счисления, кроме двоичных, десятичных и шестнадцатеричных чисел. Восьмеричный символ используется для представления чисел с основанием 8 .
Восьмеричное число имеет различные применения и важность. Он обычно используется в компьютерных основах. В этой статье мы узнаем, как преобразовать восьмеричное число в десятичное.Преобразование двоичного числа в восьмеричное также является простым методом, при котором мы сначала преобразуем двоичное в десятичное, а десятичное — в восьмеричное.
| Восьмеричная система счисления |
| База — 8 |
| Восьмеричный символ — 0, 1, 2, 3, 4, 5, 6 и 7 |
Определение системы восьмеричных чисел
Система счисления, в основе которой лежит «восемь», называется восьмеричной системой счисления. В нем используются числа от 0 до 7. Давайте рассмотрим пример, чтобы понять концепцию.
Как мы уже говорили, любое число с основанием 8 является восьмеричным числом, например 24 8 , 109 8 , 55 8 и т. Д.
Как восьмеричное число представлено основанием 8, таким же образом двоичное число представлено основанием 2, десятичное число — основанием 10, а шестнадцатеричное число представлено основанием 16. Примеры для этих систем счисления:
- 22 2 — двоичное число
- 100 10 десятичное число
- 40 16 шестнадцатеричное число
Если мы решаем восьмеричное число, каждое место представляет собой степень восьми.
- 124 8 = 1 × 8 2 + 2 × 8 1 + 4 × 8 0
Таблица восьмеричных чисел
Мы используем только 3 бита для представления восьмеричных чисел. Каждая группа будет иметь различное значение от 000 до 111.
Восьмеричное цифровое значение | Двоичный эквивалент |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Преобразование десятичной системы счисления в восьмеричную
Для преобразования десятичного числа в восьмеричное используется восьмеричный метод.
В этом методе десятичное число каждый раз делится на 8, получается остаток. Первый остаток, который мы получаем, — это младшая значащая цифра (LSD), а последний остаток — самая старшая цифра (MSD). Давайте разберемся с преобразованием на справочном примере;
Проблема : Предположим, 560 — десятичное число. Преобразуйте его в восьмеричное число.
Решение : Если 560 — десятичное число, то
560/8 = 70, а остаток 0
70/8 = 8, а остаток 6
8/8 = 1, а остаток 0
И 8/0 = 0, а остаток равен 1
Итак, восьмеричное число начинается от MSD до LSD, т.е.е. 1060
Следовательно, 560 10 = 1060 8
Задача: Преобразовать 0,52 в восьмеричное число.
Решение: Дробную часть десятичного числа необходимо умножить на 8.
0,52 × 8 = 0,16 с переносом 4
0,16 × 8 = 0,28 с переносом 1
0,28 × 8 = 0,24 с переносом 2
0,24 × 8 = 0,92 с переносом 1
Итак, для дробного восьмеричного числа мы читаем сгенерированный перенос сверху вниз.
Следовательно, 4121 — восьмеричное число.
Преобразование восьмеричной системы счисления в десятичную
Давайте узнаем здесь, преобразование восьмеричного числа в десятичное число или основания 8 в основание 10.
Пример: Предположим, 215 8 — восьмеричное число, тогда его десятичная форма будет иметь вид
.215 8 = 2 × 8 2 + 1 × 8 1 + 5 × 8 0
= 2 × 16 + 1 × 8 + 5 × 1
= 45 10
Пример: Пусть 125 — восьмеричное число, обозначенное 125 8 .Найдите десятичное число.
125 8 = 1 × 8 2 + 2 × 8 1 + 5 × 8 0
= 1 × 16 + 2 × 8 + 5 × 1
= 37 10
Преобразование двоичной системы счисления в восьмеричную
Двоичное число можно преобразовать в восьмеричное с помощью приведенной ниже таблицы.
Восьмеричное число | Эквивалентное двоичное число |
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Пример: Преобразование (100010) 2 в восьмеричное число.
Решение: С помощью таблицы запишем,
100 → 4
и 010 → 2
Следовательно, (100010) 2 = 42
Точно так же мы можем преобразовать восьмеричное число в двоичное с помощью таблицы.
Восьмеричная система счисления в шестнадцатеричную
Шестнадцатеричное число состоит из цифр и букв. Он представлен с основанием 16. Цифры от 0 до 9 представлены в обычном виде, но от 10 до 15 он обозначается как A, B, C, D, E, F.Преобразование восьмеричного числа в шестнадцатеричное требует двух шагов.
- Сначала преобразуйте восьмеричное число в десятичное.
- Затем преобразуйте десятичное число в шестнадцатеричное.
Разберемся на примере. Мы возьмем тот же пример, где мы преобразовали восьмеричное число в десятичное, например;
(215) 8 = (45) 10
Теперь преобразуйте (45) 10 в шестнадцатеричное число, разделив 45 на 16, пока не получите остаток меньше 16.
Следовательно, мы можем написать: (45) 10 = (2D) 16
Или (215) 8 = (2D) 16
Восьмеричная таблица умножения| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Приложения восьмеричной системы счисления
Система восьмеричного числа широко используется в компьютерных приложениях, а также в авиационном секторе для использования числа в форме кода.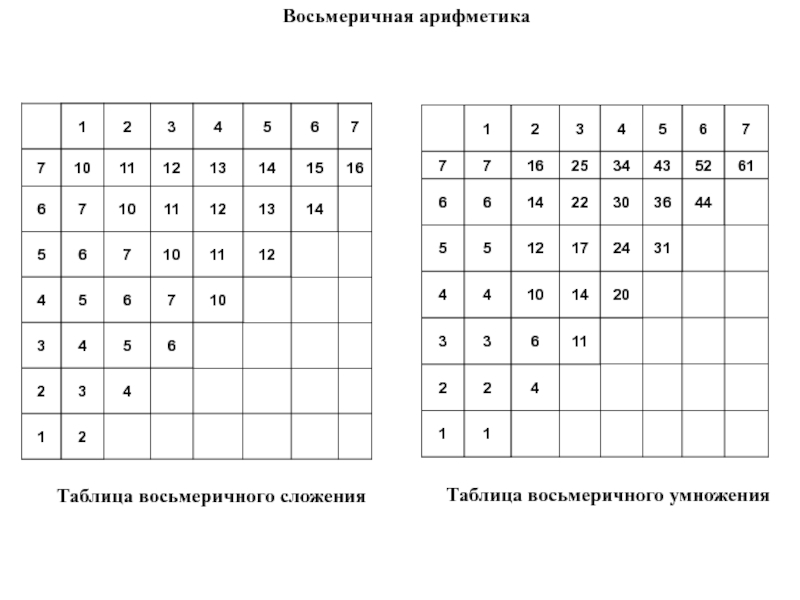
На основе приложений восьмеричной системы счисления разработано несколько вычислительных систем. Все вычислительные системы современного поколения используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова. Точно так же для различных языков программирования восьмеричные числа используются для кодирования или записи зашифрованного языка, который понимается только вычислительной машиной.
Также в авиационном секторе или области или, скажем, в авиационной промышленности, транспондеры, используемые в самолетах, передают код, который выражается четырех восьмеричным числом.Эти коды опрашиваются наземным радаром.
№ 2535: Таблицы умножения
Компьютеры считают, что проще всего работать с двумя цифрами — ноль и единица. Эти двоичные цифры называются битами. Чтобы записать возраст Вселенной, нужно тридцать четыре бита. Это больше, чем одиннадцать в нашей десятичной системе, но в компьютере есть гораздо более простые таблицы умножения: ноль умножить на ноль, ноль умножить на единицу и один умножить на единицу.
Вот и все!
Широко распространено мнение, что мы используем десять цифр, потому что именно столько у нас пальцев.Это более чем необходимо для хорошей работоспособной системы счисления. Я бы предпочел восемь. Но я просто рад, что мы не родились с двадцатью пальцами. Я бы никогда не просмотрел свои таблицы умножения.
Я Энди Бойд из Хьюстонского университета, где интересовался тем, как работают изобретательные умы.
[аудио: тройка — магическое число]
(Музыкальная тема)Для связанных эпизодов см. БОЛЬШИЕ ЧИСЛА и НОЛЬ, среди многих других.
Системы счисления, обсуждаемые в этом эпизоде, известны как позиционные системы . Позиционные системы счисления работают, выбирая основание , которое равно количеству цифр в системе. Положение цифры в цепочке цифр соответствует степени основания.
Например, в нашей стандартной десятичной системе счисления мы имеем
52,907 (базовая десятка) =
5 x 10 4 + 2 x 10 3 + 9 x 10 2 + 0 x 10 1 + 7 x 10 0 .
В восьмерке у нас есть
147,253 (базовая восьмерка) =
1 x 8 5 + 4 x 8 4 + 7 x 8 3 + 2 x 8 2 + 5 x 8 1 + 3 x 8 0 .
Обратите внимание, что оба этих числа, 52 907 (десять по основанию) и 147 253 (восемь по основанию), представляют собой одно и то же количество; они просто выражаются в двух разных системах счисления.
Таблицы умножениядля двоичной (основание два), четвертичной (основание четыре), восьмеричной (основание восемь) и десятичной (основание десять) систем счисления показаны ниже. Обратите внимание, что необходимо запомнить лишь немногим более половины значений в этих таблицах, поскольку изменение порядка умножения на противоположное не меняет результата (например, 6 x 8 = 8 x 6).
Следует отметить, что однозначные таблицы сложения , подобные таблицам умножения, также необходимы для освоения базовой арифметики, но не обсуждаются в этом выпуске.
Большинство людей осваивают эти таблицы без особых проблем.
Дополнительную информацию о позиционных системах счисления см., Например, на http://en.wikipedia.org/wiki/Positional_notation.
Изображения таблиц умножения были вырезаны с веб-сайта http://www.cut-the-knot.org/blue/SysTable.shtml.
Двигатели нашей изобретательности Авторские права © 1988-2009, Джон Х.Линхард.
Как сложить два восьмеричных числа? — AnswersToAll
Как сложить два восьмеричных числа?
Восьмеричное сложение Чтобы использовать эту таблицу, просто следуйте инструкциям, использованным в этом примере: сложите 68 и 58. Найдите 6 в столбце A, затем найдите 5 в столбце B. Точка в области «сумма», где пересекаются эти два столбца, представляет собой «сумму» двух чисел.
68 + 58 = 138.
Как решить восьмеричные числа с основанием 8?
Восьмеричная система счисления
- Восьмеричная система счисления имеет основание восемь и использует числа от 0 до 7.
- Система счисления, в основе которой лежит «восемь», называется восьмеричной системой счисления.
- Следовательно, 56010 = 10608
- 1258 = 1 × 82 + 2 × 81 + 5 × 80
Какое дополнение двоичного числа 10000000 до 2?
Если вы запишете 128 в 8-битном двоичном формате, вы получите 10 000 000. Обратите внимание, что добавление двойного дополнения дает то же самое число 10000000.
Почему мы используем восьмеричную и шестнадцатеричную систему счисления?
Восьмеричный и шестнадцатеричный числа используют человеческое преимущество, заключающееся в том, что они могут работать с большим количеством символов, при этом его можно легко конвертировать между двоичными числами, потому что каждая шестнадцатеричная цифра представляет 4 двоичных цифры (16 = 24), а каждая восьмеричная цифра представляет 3 (8 = 23).
Как компьютер умножает два числа?
Двоичный умножитель — это электронная схема, используемая в цифровой электронике, такой как компьютер, для умножения двух двоичных чисел. Большинство методов включают вычисление набора частичных произведений, которые затем суммируются с помощью двоичных сумматоров.
Что произойдет, если вы умножите двоичное число на 2?
4 ответа. Это тривиально с точки зрения битовых операций. Умножение на 2 эквивалентно сдвигу влево на 1 бит, деление — сдвигу вправо.точно так же тривиально умножить и разделить на любую степень 2.
Как вычислить двоичное деление?
Правила двоичного деления: 1 ÷ 1 = 1. 1 ÷ 0 = Бессмысленно. 0 ÷ 1 = 0… .Каковы правила бинарного деления?
| Ссылки по теме MATHS | |
|---|---|
| Пара линейных уравнений с двумя переменными | Свойства Медианы |
Как сделать восьмеричное умножение по основанию 8?
Воспользуйтесь этим онлайн-калькулятором восьмеричного умножения для умножения.
Введите два восьмеричных числа в калькулятор умножения по основанию 8, чтобы получить результат. Восьмеричная система счисления или система счисления с основанием 8 с использованием цифр от 0 до 7. Это похоже на умножение двоичных чисел, но двузначные или трехзначные произведения все равно останутся в одном столбце.
Как сложить восьмеричное число в Excel?
Восьмеричное сложение. Следующая таблица восьмеричного сложения поможет вам справиться с восьмеричным сложением. Чтобы использовать эту таблицу, просто следуйте инструкциям, использованным в этом примере: сложите 6 8 и 5 8. Найдите 6 в столбце A, затем найдите 5 в столбце B.
Как определяется переход для восьмеричного умножения?
Перенос определяется как произведение 8. Воспользуйтесь этим онлайн-калькулятором восьмеричного умножения для выполнения умножения. Введите два восьмеричных числа в калькулятор умножения по основанию 8, чтобы получить результат. Восьмеричная или базовая 8 система счисления с использованием цифр от 0 до 7.
Каковы правила вычитания восьмеричных чисел?
6 8 + 5 8 = 13 8. Вычитание восьмеричных чисел происходит по тем же правилам, что и вычитание чисел в любой другой системе счисления.Единственная вариация — заимствованное количество. В десятичной системе вы заимствуете группу из 10 10.
Восьмеричный калькулятор
— сложение, вычитание, умножение и деление
Восьмеричный калькулятор
Восьмеричный формат значений не используется так часто, как двоичный или десятичный формат. Он также известен как формат с основанием 8. Это потому, что он имеет всего 8 значений (0,1,2,3,4,5,6,7). С точки зрения математических операций, не так просто складывать или вычитать восьмеричные числа.
Во-первых, это длительный вариант, а во-вторых, он требует высоких математических навыков, чтобы выполнять эти операции без ошибок.
Этот калькулятор представляет собой комбинацию из следующих
- Калькулятор восьмеричного сложения
- Восьмеричный калькулятор вычитания
- Восьмеричный калькулятор умножения
- Восьмеричный калькулятор деления
стресс выполнения преобразования вручную.Вам нужно выполнить несколько шагов, и каждый из них должен быть на 100% правильным. В остальном фактор времени имеет решающее значение. Если необходимо выполнить несколько сравнений одновременно, вам понадобится надежный инструмент для этой цели. Пройдя процесс использования, мы можем получить более подробную информацию о калькуляторе с основанием 8.
Этапы удобного использования
Для большинства пользователей вопрос, просты ли этапы использования инструмента или нет.
Никто не любит проходить сложные этапы.Этот восьмеричный калькулятор очень прост. Пройдя через шаги, можно достичь лучшего понимания.
- Входные параметры
Есть три входных параметра, которые пользователь должен ввести. Первое текстовое поле предназначено для ввода первого восьмеричного значения, необходимого для расчета. После этого вам необходимо выбрать операцию, которую необходимо выполнить. Возможные варианты: сложение, вычитание, умножение и деление. Последнее поле ввода предназначено для второго восьмеричного значения.После ввода данных необходимо нажать кнопку «Рассчитать».
- Результаты
Результаты будут показаны в текстовой строке, представленной ниже. Например, рассмотрим пример. Возьмите первое восьмеричное значение как 7, а второе как 122. В этом примере математическая операция является сложением. После того, как вы ввели эти значения, вам будет показан результат «131».
Простой интерфейс восьмеричного калькулятора для пользователей
Инструмент должен быть максимально простым, чтобы пользователи не волновались.
Сложные инструменты обычно отвергаются, и пользователи не очень их ценят. Этот восьмеричный калькулятор очень прост, что делает его лучшим вариантом по сравнению с другими альтернативами в Интернете. Вам нужно ввести только три входа, и после этого будет рассчитан результат.
Каждый ученик спрашивает, как складывать восьмеричные числа? Сложить или умножить восьмеричные числа не так просто, как десятичные числа. Вам нужно выполнить несколько промежуточных шагов, и тогда результат будет сгенерирован.С помощью этого инструмента вам не нужно выполнять какие-либо вычисления, и инструмент сделает все. С точки зрения пользователя, калькулятор восьмеричного сложения — хороший вариант. Это экономит много времени для пользователей, и они могут выполнить несколько восьмеричных вычислений за несколько минут.
Бесплатное использование без ограничений Получить 100% бесплатный технологический инструмент не так-то просто.
