Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:
Мы же здесь будем все подробно разбирать шаг за шагом + показать
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове.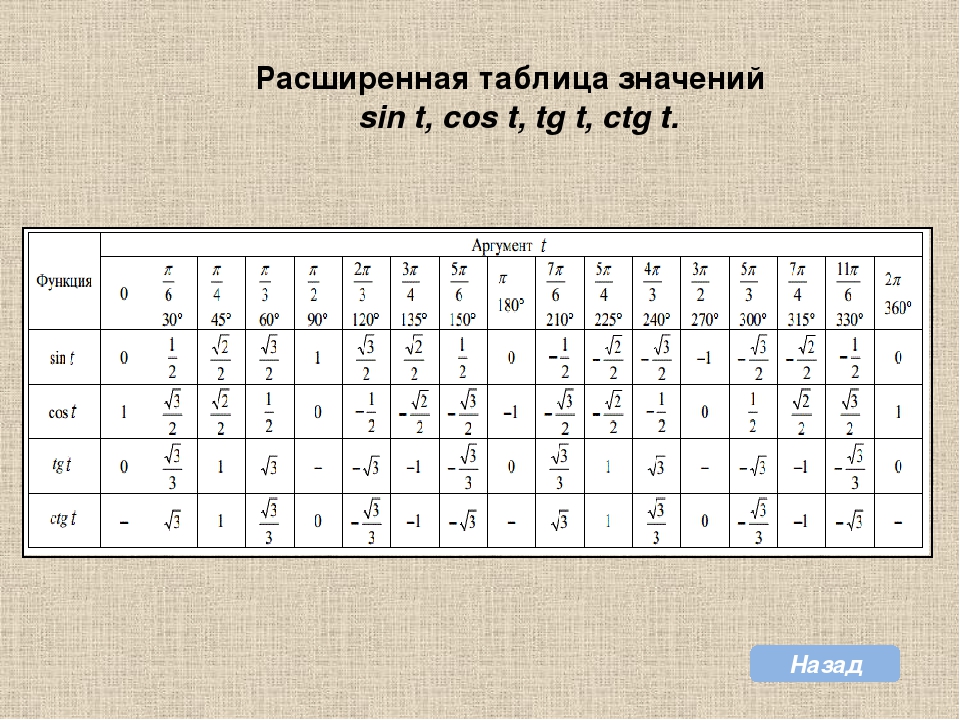
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, градусов, или .
Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
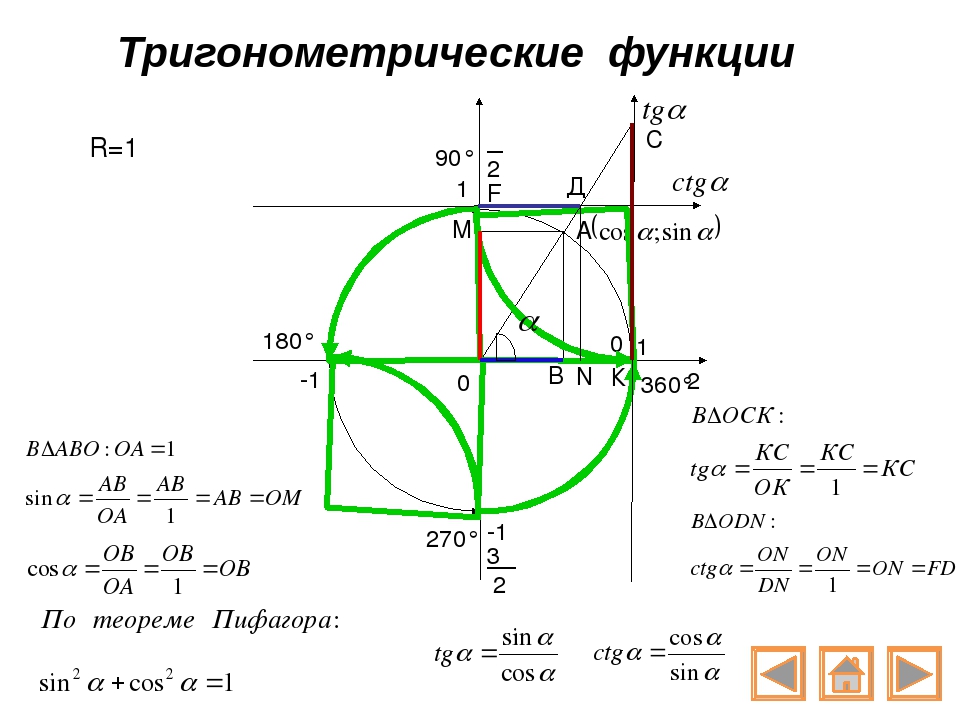
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
Разработка урока по теме «Тригонометрические функции. Формулы тригонометрии». 10-й класс
Цели урока:
- Проверка знания свойств тригонометрических функций, умения применять их при выполнении упражнений.
- Проверка знания тригонометрических формул, умения применять их при преобразовании тригонометрических выражений.
- Проверка знания формул приведения, уровня владения этими формулами.
- Развитие логического мышления, внимания,
познавательного интереса, интуиции, способности
к творчеству.
- Воспитания серьезного отношения к учебному труду.
Формы работы: фронтальная, индивидуальная.
Оснащение урока:
- Мультимедийный проектор;
- Экран;
- Маркерная доска;
- Индивидуальные карточки с заданиями для каждого ученика с заданиями повышенного уровня сложности.
Предварительная подготовка к уроку:
- Создание презентации
- Изготовление индивидуальных карточек с заданиями повышенного уровня сложности.
Ход урока
Ребята, сегодня у нас итоговый, зачетный урок по
теме “Тригонометрические функции и их свойства.
Основные тригонометрические формулы”. Мы с вами
хорошо поработали над данной темой, изучили
много нового и интересного.
Я уверена, что
сегодня покажите хорошие и отличные знания.
(Слайд 1)
Цели урока: (Слайд 2)
- Закрепление материала по теме “Тригонометрические функции. Формулы тригонометрии”.
- Проверка знаний в форме смотра знаний.
Девиз урока: (Слайд 3)
“Не бойтесь формул!
Учитесь владеть этим инструментом
Человеческого гения!
В формулах заключено величие
и могущество
Человеческого разума….”
Марков А.А
Слово “тригонометрия” известно с давних времен, оно было известно еще до нашей эры. (Слайд 4)
Зарождение тригонометрии относится к глубокой древности. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”.
Одним из основоположников тригонометрии
считается древнегреческий астроном Гиппарх,
живший во 2 веке до нашей эры.
Гиппарх (Hipparchos)
(около 180—190 до н. э., Никея, — 125 до н. э., Родос),
древнегреческий учёный
Гиппарх является автором первых тригонометрических таблиц и одним из основоположников астрономии.
Учет ваших устных ответов будут вести мои помощники- консультанты: учащиеся 11 класса. В конце урока мы оценим устную работу каждого ученика. Этот результат повлияет на общий итог работы каждого ученика.
Итак, начинаем. Я желаю вам успеха и удачи.
Первая часть урока1.
- Дайте определение синуса
- Определение косинуса
- Какая функция называется тангенсом?
- Определение котангенса
- Какой угол поворота называют положительным?
- Какой угол поворота называют отрицательным?
Значения синуса и косинуса
Значения тангенса и котангенса
Значения тригонометрических функций.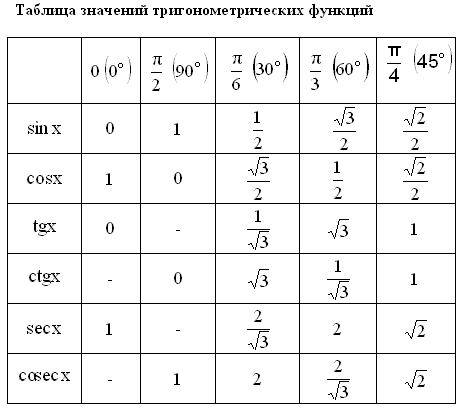
(Слайд 4)
Какой четверти принадлежит угол: (Слайд 5)
Найти ошибки: (Слайд 6)
Определите четверть, если: (Слайд 7)
Индивидуальное задание №1. Определите знак выражения. На выполнение задания отводится 3 минуты. За каждое верно выполненное задание вы можете получить 1 балл. (Слайд 8)
2.
Еще с 8 класса вы знаете значения синуса, косинуса, тангенса углов 30°, 45° и 60°. Сейчас ваши знания значительно расширились. Как таблицу умножения, вы должны знать значения тригонометрических функций углов: 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°. Сейчас мы и проверим знание тригонометрической таблицы.
Знание табличных значений: (Слайд 9)
Индивидуальное задание №2. Найдите значение выражения. (Слайд 10). На выполнение задания 3 минуты. За каждое верно выполненное задание – 1 балл.
Учитель проверяет выполнения задания№1. Все
решено заранее.
Результаты проверки выносятся на
маркерную доску. Учащиеся сразу узнают свои
результаты.
3.
- Какие тригонометрические функции являются четными?
- Какие тригонометрические функции являются нечетными?
Четность функций. (Слайд 11)
- Что называется радианом?
- Чему равен один радиан?
- Как радианы перевести в градусы?
- Как градусы перевести в радианы?
Индивидуальное задание №3. Перевести градусы в радианы, а радианы в градусы.
(Слайд 12).
На выполнения задания отводится 3 минуты. За каждое верно выполненное задание – 0,5 балла.
Учитель проверяет задание №2. Результаты – на маркерной доске.
4.
- Я вам называю углы в градусах, вы их переводите в
радианы: 90°, 180°, 30°, 270°,45°, 360°, 60°.
- А сейчас обратная работа: надо перевести углы в градусы: /2, , /4, 2, /6, 3/2, /3
Индивидуальное задание № 4. Вычислите. (Слайд 13)
Учитель проверяет выполнения задания №3, выставляет результаты на маркерной доске.
5.
- Ребята, назовите основные тригонометрические формулы.
- Назовите основное тригонометрическое тождество.
- Как вы считаете, почему это тождество называется основным? Убедите меня в этом!
Индивидуальное задание №5.
На выполнение задания отводится 5 минут. За каждое верно выполненное задание вы можете заработать 2 балла.
Учитель проверяет выполнение предыдущего задания. Результаты выполнения заносятся в таблицу на маркерной доске.
6.
Тригонометрические тождества позволяют нам
легко и быстро упрощать тригонометрические
выражения.
Предлагаю вам следующее устное
задание:
- Упростите выражение: (Слайд 15)
Индивидуальное задание №6. Упростите выражения: (Слайд 16)
Учитель проверяет выполнения задания №5. Результаты- на маркерной доске.
7.
- Какие формулы позволяют нам переходить от больших углом к острым углам первой четверти?
- Для каких углов название исходной функции не изменяется?
- Для каких углов название исходной функции изменяется?
- По какой функции мы определяем знак функции в правой части равенства?
- Замените функцией угла ?. (Слайд 17)
Индивидуальное задание №7. Формулы приведения. (Слайд 18). На выполнение задания отводится 4 минуты. За каждое верно выполненное задание вы получите 1 балл.
На маркерной доске выставляются результаты
выполнения предыдущего задания.
К доске приглашаю двоих учеников: записать формулы двойного угла, другой формулы сложения.
Пока ребята записывают формулы, остальные отвечают на мои вопросы: Вычислите, использую формулы тригонометрии. (Слайд 19)
Индивидуальное задание №8: В виде тестов. На листе указано, сколько получите баллов за каждое задание. В вашем распоряжении 5 минут.
Вторая часть урока
Учащимся предлагаются задания повышенного уровня сложности. Каждый ученик получает карточку, на которой задания трех уровней сложности: на 3, 4 и 5 баллов. Какие задания выполнять и в каком порядке решает каждый индивидуально. Ученики стремятся набрать как можно больше баллов.
Учитель сразу проверяет выполнение заданий, которые решены заранее. Все баллы заносятся в таблицу на маркерной доске. Одновременно заносятся результаты выполнения индивидуального задания №8.
Консультанты подводят итоги подсчета устных
ответов учащихся.
Результаты заносятся в
специальную графу в таблице учета работы каждого
ученика.
Таблица учета работы каждого ученика
| Фамилия, имя | Устные ответы | № 1 | № 2 | № 3 | № 4 | № 5 | №6 | №7 | Задания повышенного уровня сложности. | Итог |
Содержание карточки с заданиями повышенного уровня сложности:
- Докажите тождество: ctg2a — cos2a = ctg2acos2a (3 балла)
- sina + cos?a= Найти: sinacosa (4 балла)
- sinacosa = Найти: sina + cosa (4 балла)
- sina = — , ctga>0 Найти: (5 баллов)
- cosa = — , ctga<0 Найти: (5 баллов)
- tga = Найти: (4 балла)
- сtga = Найти: (4 балла)
- Вычислите: tg1°tg3°tg5°. …….tg85°tg87°tg89° (5 баллов)
- Вычислите: ctg2°ctg4°ctg6°…….ctg84°ctg86°ctg88° (5 баллов)
- ctga = Найти: sina, cosa (3 балла)
- Упростите: + tga (3 балла)
- Вычислите: ctgsintgcos(3 балла)
…….tg85°tg87°tg89° (5 баллов)Учитель подводит результаты работы на уроке каждого ученика, анализирует, делает выводы.
Спасибо за урок! (Слайд 20)
Формулы по тригонометрии от репетитора по математике — Колпаков Александр Николаевич
Справочные материалы по тригонометрии. Формулы. Определения и свойства.
Комплект предназначен для слабых и средних по уровню учащихся, для репетиторов по математике и школьных преподавателей. Он специально адаптирован мной для слабых и средних по уровню учеников. В материалах применяются, на мой взгляд, лучшие приемы уменьшения нагрузки на память и упрощения работы с большими объемами информации. Их содержание дает репетитору по математике возможность преподнести тригонометрию в удобной для работы и для запоминания форме.
В помощь репетитору по математике, работающему со слабыми учащимися, я специально исключил из списка формул те, которые не входят в основную программу, а также сложные формулы и различные формулы-следствия.
Определение тригонометрических функций:
Определение: синусом угла поворота на называется ордината точки, изображающей данный угол.
Определение: косинусом угла поворота называется абсцисса точки, изображающей данный угол.
Определение: тангенсом угла поворота называется отношение ординаты точки, изображающей угол, к ее абсциссе.
Определение: котангенсом угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате.
Основные тригонометрические свойства:
(основное тригонометрическое тождество)
Четность и нечетность тригонометрических функций:
нечетная
четная
нечетная
нечетная
примечание репетитора по математике:
функция незывается нечетной, если противоположным значениям аргумента соответствуют противоположные значения функции.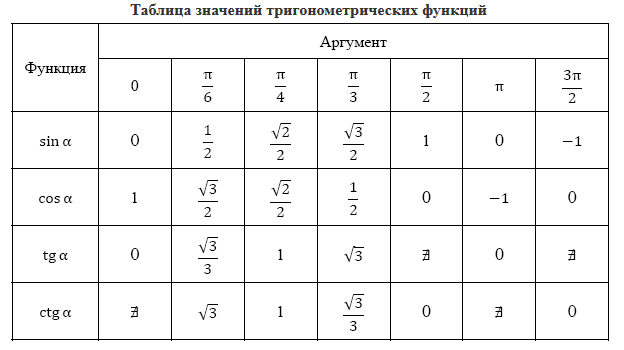
Функция называется четной, если противоположным значениям аргумента соответствуют равные значения функции.
Знаки тригонометрических функций
Таблица значений тригонометрических функций
Щелкните на таблице для ее увеличения.
Прочтите о том, как репетитору по математике заучить с учеником таблицу значений.
Формулы приведения:
Чтобы написать правую часть формул приведения нужно:
1) найти четверть в которой лежит угол в скобках, считая X острым углом.
2) поставить знак данной функции в данной четверти.
3) сменить или сохранить функцию.
При или функция меняется (, )
При или функция не меняется.
Формулы сложения углов:
Формулы двойного угла:
Формулы сложения тригонометрических функций:
Простейшие тригонометрические уравнения:
1) Уравнения вида
Уравнения вида ,
Частные формулы:
где
Общая формула:
,
где
Удобные случаи
2) Уравнения вида
Уравнения вида ,
Частные формулы:
где
Общая формула:
,
где
Удобные случаи
1) Уравнения вида
Уравнения вида
,
Частные формулы:
где
Общая формула:
,
где
Решение на круге.
1) Уравнения вида
Уравнения вида
,
Частные формулы:
где
Общая формула:
,
где
Решение на круге.
Предлагаю репетиторам по математике использовать на своих занятиях материалы сайта в реальном времени. Часто во время занатия дети не выключают компьютер. Загрузите страничку с формулами и начинайте урок.
Вместо распечатывания формул на листочке дайте ученику ссылку на страницу или попросите сделать ее стартовой при входе в интернет. Это увеличит частоту появления формул перед глазами ученика и они быстрее запомнятся.
С уважением, Колпаков Александр Николаевич.
Репетитор по математике Москва.
Метки: Алгебра, Ученикам
Таблица тригонометрии — Изучите CBSE
Тригонометрия Таблица : Тригонометрия — это раздел математики, который занимается изучением длины, углов и их взаимосвязей в треугольнике.
Тригонометрические соотношения применимы только для прямоугольных треугольников, при этом один из углов равен 90 o
Тригонометрический стол
Тригонометрическая таблица состоит из следующих взаимосвязанных тригонометрических соотношений: sin, cos, tan, cos, sec, cot.
- sin (величина, обратная косекансу) = противоположная гипотенуза
- cos (величина, обратная секущей) = смежная по гипотенузе
- тангенс (величина, обратная котангенсу) = противоположна соседнему
- Детская кроватка (обратная касательной) = смежная по противоположной
- косекунд (обратно синусу) = гипотенуза относительно противоположного
- сек (обратно косинусу) = гипотенуза над соседним
Расчеты можно легко выполнить, запомнив таблицу функций, наиболее известную как Тригонометрическая таблица .Это находит применение в нескольких сферах. Некоторые из них включают навигационные видеоигры, авиацию, науку, географию, инженерию, геометрию и т.
Д. Тригонометрическая таблица помогла во многих разработках и в области машиностроения для первых инноваций.
Таблица тригонометрических соотношений дает нам значения стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °. Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти отношения. Поэтому очень важно знать и помнить отношения этих стандартных углов.
Уловки для запоминания таблицы тригонометрии
Тригонометрическая таблицаЗапоминание таблицы тригонометрии будет полезно, поскольку она находит множество приложений, и есть много способов запомнить таблицу. Знание формул, соотношений и идентичностей тригонометрии автоматически приведет к выяснению таблицы и значений. Таблица тригонометрических соотношений зависит от формул тригонометрии таким же образом, как все функции тригонометрии взаимосвязаны друг с другом.
Прежде чем начинать, лучше попытаться запомнить эти значения и знать следующие тригонометрические соотношения дополнительных углов.
- sin x = cos (90∘ − x)
- cos x = sin (90∘ − x)
- tan x = детская кроватка (90∘ − x)
- детская кроватка x = загар (90∘ − x)
- сек x = детская кроватка (90∘ − x)
- детская кроватка x = сек (90∘ − x)
Взаимосвязи тригонометрических соотношений
- 1 / sin x = cosec x
- 1 / cos x = сек x
- 1 / сек x = cos x
- 1 / коричневый x = детская кроватка x
- 1 / детская кроватка x = желто-коричневый x
- 1 / мкс x = sin x
Этапы создания тригонометрической таблицы:
Шаг 1 : Нарисуйте табличный столбец с необходимыми углами, такими как 0, 30 o , 45 o , 60 o , 90 o , 180 o , 270 o , 360 o в верхнем ряду и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце.
Шаг 2 :
Шаг 3 :
Шаг 4 :
Шаг 5 :
Шаг 6 :
Шаг 7 :
Тригонометрический стол | Шаги по созданию таблицы
Нажмите, чтобы оценить этот пост!
[Всего: 3 Среднее: 3,7] Тригонометрия — это наука об измерении треугольников.
Учитывая некоторые стороны и углы треугольника, тригонометрия помогает нам вычислить оставшиеся стороны и углы.Тригонометрические соотношения помогают нам найти значения стандартных углов, таких как 0 °, 30 °, 45 °, 60 ° и т. Д.
Тригонометрические отношения Если мы рассмотрим ∆ ABC, расположенный под прямым углом к B, то сторона, противоположная ∠ B, то есть AC, является гипотенузой, и если AB выбрана в качестве начальной линии, то AB называется базой, а BC будет перпендикулярной.
Итак, тригонометрические отношения можно представить как
Таблица тригонометрических соотношений
| θ | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° | ||||||||||
| 90π140 | π / 4 | π / 3 | π / 2 | π | 3π / 2 | 2π | ||||||||||||
| sin θ | 0 | 1/2 | 1 / √2 / 2 | 1 | 0 | -1 | 0 | |||||||||||
| cos θ | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 | 0 | 1 | |||||||||||
| tan θ | 0 | 1 / √3 | 1 | √3 | N. D. | 0 | ND | 0 | ||||||||||
| детская кроватка θ | ND | √3 | 1 | 1 / √3 | 0 | ND | 0 | ND | 0 θ | ND | 2 | √2 | 2 / √3 | 1 | ND | -1 | ND | |
| сек θ | 1 | √2 | 2 | ND | -1 | N.Д. | 1 |
Здесь мы предоставим вам уловки для запоминания таблицы тригонометрических соотношений, чтобы вы могли напрямую использовать ее для решения задач.
Перед тем, как перейти к тригонометрической таблице, вы должны знать тригонометрические формулы, которые вам очень помогут легко запомнить ее.
Во-первых, вспомним и запомним следующие формулы тригонометрии:
Sin x = cos (90 ° -x)
Cos x = sin (90 ° -x)
Желто-коричневый x = детская кроватка (90 ° -x)
Детская кроватка x = желто-коричневый (90 ° -x)
Сек x = cosec (90 ° -x)
Cosec x = sec (90 ° -x)
1 / sin x = cosec x
1 / cos x = сек x
1 / tan x = детская кроватка x
ШАГ 1: — Нарисуйте таблицу из 6 строк и 6 столбцов.
В строке перечислите углы, такие как 0 °, 30 °, 45 °, 60 °, 90 °, и запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс) в первом столбце.
ШАГ 2: — Определите значение синуса
- Чтобы определить значения sin, разделите 0, 1, 2, 3, 4 на 4 под корнем соответственно. См. Пример ниже. Чтобы определить значение sin 0 ° √0 / 4 = 0
Углы (в градусах) 0 ° 30 ° 45 ° 60 ° 90 ° 180 ° 270 ° 360 ° sin 0 1/2 1 / √2 √3 / 2 1 0-1 0
ШАГ 3: — Определите значение косинуса
Значение cos — это угол, противоположный углу sin.Чтобы определить значение cos, разделите на 4 в обратной последовательности sin. Например, разделите 4 на 4 под корнем, чтобы получить значение cos 0 °. См. Пример ниже.
Для определения значения cos 0 °
√4 / 4 = 1
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| √3 / 2 | 1 / √2 | 1/2 | 0 | -1 | 0 | 1 |
ШАГ4: — Определить значение тангенса
Загар равен sin, деленному на cos.
tan = sin / cos. Чтобы определить значение tan при 0 °, разделите значение sin при 0 ° на значение cos при 0 ° См. Пример ниже.
загар 0 ° = 0/1 = 0
Точно так и таблица была бы.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| tan | 1 / √3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
ШАГ 5: — Определите значение котангенса
Стоимость детской кроватки равна величине, обратной загар.Значение cot при 0 ° будет получено путем деления 1 на значение tan при 0 °. Таким образом, значение будет:
детская кроватка 0 ° = 1/0 = бесконечно или не определено
Так же, таблица для детской кроватки приведена ниже.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| 90 | √3 | 1 | 1 / √3 | 0 | ∞ | 0 | ∞ |
ШАГ 6: — Определите значение косеканса
Значение cosec при 0 ° является обратной величиной sin при 0 °.
cosec 0 ° = 1/0 = бесконечно или не определено
Таким же образом, таблица для cosec приведена ниже.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| co | 2 | √2 | 2 / √3 | 1 | ∞ | -1 | ∞ |
ШАГ 7: — Определите значение секанса
Значение sec может быть определено всеми обратными значениями cos.Значение sec на 0∘ противоположно cos на 0∘. Таким образом, значение будет:
сек 0∘ = 11 = 1
Таким же образом ниже приведена таблица для сек.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| сек | 2 / √3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Часто задаваемые вопросы
Что такое тригонометрия?
Тригонометрия — это раздел математики, который занимается соотношением сторон треугольника (прямоугольного треугольника) и его углов.
Как найти значение тригонометрических функций?
Все тригонометрические функции связаны со сторонами треугольника, и их значения можно легко найти с помощью следующих соотношений:
- Sin = Противоположный / Гипотенуза
- Cos = Соседний / Гипотенуза
- Tan = Противоположный / Соседний
- Cot = 1 / Tan = Соседний / Противоположный
- Cosec = 1 / Sin = Гипотенуза / Противоположный
- Sec = 1 / Cos = Гипотенуза / Смежная
Что такое тригонометрические функции и их типы?
Тригонометрические функции или круговые функции определяются как функции угла прямоугольного треугольника.Существует 6 основных типов тригонометрических функций:
- Функция Sin
- Функция Cos
- Функция Tan
- Функция Cot
- Функция Cosec
- Функция Sec
Таблица тригонометрии: формулы, приемы, примеры
Тригонометрическая таблица по сути представляет собой табличную компиляцию тригонометрических соотношений значения для различных обычных углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °, а также необычных углов, таких как 180 °, 270 ° и 360 °.
{\ circ} \). Существуют различные тригонометрические отношения, такие как синус, косинус, тангенс, косеканс, секанс и котангенс. Согласно математическим стандартам, \ (\ sin, \ cos, \ tan, \ operatorname {cosec}, \ mathrm {sec} \) и \ (\ mathrm {cot} \) являются сокращенными формами этих соотношений. Студенты должны запомнить эти значения, чтобы решать тригонометрические задачи. Прокрутите вниз, чтобы узнать больше о таблице значений тригонометрии!
Пройдите бесплатные пробные тесты CBSE Class 10 прямо сейчас!
Последнее обновление:
👉 18 октября : Центральный совет среднего образования (CBSE) выпустил 10-й и 12-й листы данных CBSE по основным предметам.
👉 21 октября : CBSE выпустила 10 и 12 даты для второстепенных предметов.
Practice Embibe’s Эксклюзивные образцы документов CBSE Term 1 на основе новых рекомендаций:
Здесь, в Embibe, вы можете получить бесплатный пробный тест CBSE Revised MCQ 2021 по всем темам.
Тест MCQ, предлагаемый Embibe, основан на пересмотренных учебниках, бумажных шаблонах и учебной программе CBSE на 2021 год. Эта серия пробных тестов включает в себя исчерпывающий выбор соответствующих вопросов и их решений.Кандидаты в CBSE Board могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены.
Изучите концепции экзамена на Embibe
Таблица тригонометрии — Введение в тригонометрию
Что такое тригонометрический стол?
Проще говоря, тригонометрическая таблица представляет собой набор значений тригонометрических соотношений для обычно используемых стандартных углов, включая 0 °, 30 °, 45 °, 60 °, 90 °.Иногда его также используют для нахождения значений для других углов, таких как 180 °, 270 ° и 360 °, в виде таблицы. В пределах тригонометрических соотношений и между соответствующими углами существуют различные шаблоны. Следовательно, легко предсказать значения таблицы тригонометрии, а также использовать таблицу в качестве справочной информации для расчета тригонометрических значений для других нестандартных углов.
Различные тригонометрические функции в математике — это синусоидальная функция, косинусная функция, функция загара, функция кроватки, функция секунд и функция косинуса.{\ circ} -x \ right) \)
Тригонометрические значения
Тригонометрия — это исследование взаимосвязи между сторонами треугольника (прямоугольного треугольника) и его углами. Термин тригонометрическое значение используется для коллективного определения значений различных соотношений, таких как синус, косинус, тангенс, секанс, котангенс и косеканс в тригонометрической таблице.Каждое тригонометрическое соотношение связано со сторонами прямоугольного треугольника, и тригонометрические значения находятся с использованием этих соотношений.
Таблицы стандартной угловой тригонометрии
Таблица тригонометрических соотношений — это, по сути, табличный набор значений для тригонометрических функций с различными обычными углами, такими как 0 °, 30 °, 45 °, 60 ° и 90 °, а также необычными углами, такими как 180 °, 270 °, и 360 °.
{ \ circ} \) в верхнем ряду и все тригонометрические функции \ (\ sin, \ cos, \ tan, \ operatorname {cosec}, \ mathrm {sec} \) и cot в первом столбце.{\ circ} = \ frac {1} {1} = 1 \).
Аналогично, таблица для сек показана ниже.
Следовательно, необходимая тригонометрическая таблица для всех тригонометрических соотношений выглядит следующим образом:
Попытка пробного теста
Уловки для запоминания Таблица тригонометрии
Таблица тригонометрии может быть полезна в различных ситуациях, и ее легко запомнить. Запомнить тригонометрическую таблицу просто, если вы знаете формулу тригонометрии и трюк с тригонометрической таблицей.В качестве тригонометрических формул используются для создания таблицы тригонометрических соотношений.
Давайте научимся вспоминать тригонометрическую таблицу одной рукой! Как показано на изображении, дайте каждому пальцу стандартный угол. Мы будем считать пальцы при заполнении таблицы синусов, но мы просто заполним данные в обратном порядке для таблицы cos.
1-й шаг: Чтобы вычислить стандартный угол для таблицы синусов, посчитайте пальцы на левой стороне.
2-й шаг: Разделите количество пальцев на четыре.{\ circ} = \ frac {1} {2} \).
Проверьте наши математические решения NCERT для классов 10, 11 и 12:
Сводка тригонометрической таблицыВ этой статье мы обсудили таблицу тригонометрических значений в градусах и радианах. Мы изучили шаги по созданию таблицы, приемы запоминания значений в ней и таблицу тригонометрических значений для единичной окружности, а также решили несколько примеров. Также мы решили несколько важных вопросов по таблице тригонометрии Class 10.
ПРАКТИЧЕСКИЕ ВОПРОСЫ ПО ТРИГНОМЕТРИЧЕСКОЙ ТАБЛИЦЕ
Часто задаваемые вопросы по таблице тригонометрических значений
Здесь мы перечислили некоторые из наиболее важных часто задаваемых вопросов, связанных с таблицей тригонометрических значений.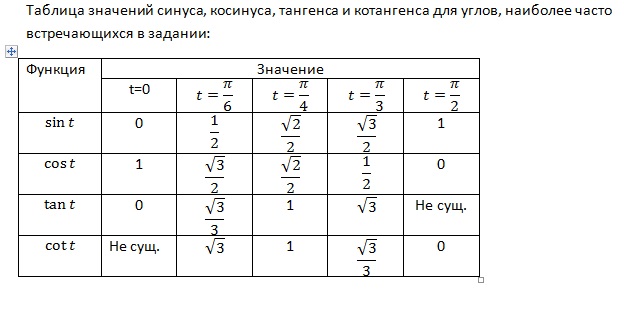
Кандидаты должны прочитать эти вопросы и ответы, чтобы развеять свои сомнения по той же теме.
1 кв. Что такое тригонометрия?
Ответ . Тригонометрия — это раздел математики, который занимается соотношением сторон треугольника (прямоугольного треугольника) и его углов.
Q.2. Как создать таблицу тригонометрических соотношений?
Ответ: Шаги по созданию и запоминанию тригонометрической таблицы описаны ниже.{\ circ} \) в верхнем ряду и все тригонометрические функции \ (\ sin, \ cos, \ tan, \ operatorname {cosec}, \ sec \) и cot в первом столбце.
2-й шаг: Определите значение \ (\ sin \).
3-й шаг: Измените порядок значений \ (\ sin \), чтобы получить значения \ (\ cos \).
4-й шаг: Значения \ (\ sin \), деленные на значения \ (\ cos \), дают значение \ (\ tan \).
5-й шаг: Обратное значение \ (\ tan \) равно значению \ (\ cot \).
{\ circ} \ ) находятся в этой таблице.
Q.4. Как узнать ценности в тригонометрии?
Ответ: Вам просто нужно запомнить значение синуса, тогда значение косинуса можно определить, поместив данные синуса в обратном порядке. Значение тангенса можно определить, разделив синус на косинус. Значение секанса можно определить, взяв обратную величину косинуса, а значение косеканса можно определить обратной величиной синуса.
В.5. Какое отношение к синусу?
Ответ: Синусоидальные отношения — это пропорции длины противоположной стороны угла, который они представляют относительно гипотенузы.
\ (\ sin \ theta = \ frac {\ text {Противоположная сторона}} {\ text {Гипотенуза}} \)
Q.6. Каковы три основных тригонометрических соотношения?
Ответ: Существует три основных тригонометрических отношения: синус, косинус и тангенс.
Используя их, мы можем определить значения трех других тригонометрических соотношений, используя соотношение
\ (\ frac {1} {\ sin x} = \ operatorname {cosec} x \)
\ (\ frac {1} {\ cos x} = \ sec x \)
\ (\ frac {1} {\ tan x} = \ cot x \)
Прочтите эту статью и запомните необходимые формулы тригонометрии.Затем самостоятельно создайте таблицу тригонометрии.
Мы надеемся, что эта подробная статья о таблице тригонометрии вам поможет. Если у вас есть какие-либо вопросы, не стесняйтесь спрашивать в разделе комментариев ниже. Мы свяжемся с вами в ближайшее время. Удачного обучения!
174 Просмотры
Таблица тригонометрии | Таблица тригонометрических соотношений и углов
Сомнения в математике
Тригонометрия
Слово «тригонометрия» происходит от греческих слов «Trigonometria», что означает «измерение треугольника». Фактически, тригонометрия — это изучение взаимосвязи между сторонами и углами треугольника.
В этой главе мы изучим некоторое соотношение сторон прямоугольного треугольника относительно его острых углов, называемое тригонометрическими отношениями угла. Мы ограничимся нашим обсуждением только острым углом. Однако эти отношения могут быть расширены и на другие углы. Мы также определим тригонометрические соотношения для углов измерения 0 o и 90 o . Мы рассчитаем тригонометрические отношения для некоторых конкретных углов и установим некоторые тождества, включающие эти соотношения, называемые тригонометрическими тождествами.
Тригонометрия — это вспомогательный раздел математики. В основном он включает изучение углов, длины и взаимосвязи с другими углами. Часто студенты сталкиваются с серьезными проблемами при понимании всех этих аспектов. Команда Entrancei подготовила для студентов исчерпывающую таблицу тригонометрии. Эта таблица в основном состоит из прямых углов и других вспомогательных углов.
Значение таблицы тригонометрии восходит к древним временам и имеет решающее значение даже сегодня.
Эта таблица имеет большое значение как для научных, так и для математических расчетов. Этот расчет можно легко вычислить, изучив эту таблицу.
Почему важна тригонометрия?
Эти приложения к этой таблице относятся не только к 12-му классу, но и к профессиональным курсам, таким как инженерное дело. Студенты должны знать, что на основе этих таблиц были заложены основы первых механических устройств.
Тригонометрические значения могут быть очень полезны при выполнении сложных вычислений.Даже сегодня высокотехнологичные расчеты спутников и ракет выполняются на основе тригонометрических значений. Легкость определения значений для разных углов сделала эту таблицу самой популярной. Запоминание этих таблиц тригонометрии является важным аспектом для поступления студентов на экзамены. Эта таблица не только точна для вашего ответа, но и делает ваши вычисления достаточно быстрыми. Через него можно узнать, насколько взаимосвязаны тригонометрические значения и формулы.
С помощью таблицы тригонометрии можно легко найти значения 0 °, 30 °, 45 °, 60 ° и 90 °.
Эти таблицы были очень эффективны, когда не было электронных калькуляторов. Эти формулы очень легко запомнить, и студенты держат все значения на кончиках языка. Основные функции, такие как Cos, Sine, Tan, Cot, Cosec, Sec, можно легко определить с помощью этой таблицы. Команда Entrancei состоит из экспертов с огромным опытом в предоставлении качественной помощи студентам. Решите Тригонометрических вопроса подготовленных экспертами.
Как эффективно изучить тригонометрическую таблицу?
Эта таблица тригонометрии полезна не только для школ или экзаменов, но и для конкурсных экзаменов.Студенты с полным знанием таблицы тригонометрии могут получить более высокие оценки по сравнению со своими сверстниками. Команда Entrancei состоит из экспертов, успешно сдавших экзамены на национальном уровне. С помощью этой таблицы учащиеся могут существенно повлиять на свои Всеиндийские ранги.
Команда не только предоставила учащимся полную таблицу тригонометрии, но и предложила уловки для ее запоминания.
Большинство студентов не могут вспомнить значения таблицы и в конечном итоге теряют легкие отметки.
Почему Энтранси лучше всего подходит для тригонометрических трюков?
Студенты могут напрямую загрузить полную и точную таблицу с веб-сайта Entrancei. Чтобы студенты могли с комфортом изучить каждый аспект. Команда также предоставила секретные подсказки и уловки для решения критических проблем с тригонометрическими значениями.
Сама идеология сделать образование доступным для всех. Команда Entrancei проверила, есть ли все значения в таблице тригонометрии на предмет каких-либо расхождений.Мы бесплатно предоставили полную таблицу. Студенты могут загрузить полную таблицу одним щелчком мыши. Все, что нужно сделать студентам, — это зарегистрироваться у нас. Поднимитесь по лестнице к успеху с Entrancei.
Тригонометрические отношения 0 o и 90 o Давайте посмотрим, что происходит с тригонометрическими отношениями угла A, если If становится все меньше и меньше в прямоугольном треугольнике ABC.
Точка c приближается к точке B, и, наконец, когда ÐA становится очень близким к 0 o , AC становится почти таким же, как AB.
О тригонометрическом столе
Тригонометрия — один из древнейших предметов, изучаемых учеными всего мира. Астрономы использовали тригонометрию для расчета расстояния от Земли до планет и звезд. Тригонометрия также используется в географии для построения карт, определения положения острова относительно друг друга. по долготе и широте и т. д.
Темы для обсуждения
Тригонометрические отношения
Идентификаторы тригонометрии
Углы тригонометрии
Взаимоотношения
Прочие тригонометрические соотношения
Высота и расстояние
ВЫСОТА И РАССТОЯНИЕ
Пусть A будет вершиной башни, а C — глазом человека, с которого он наблюдает за вершиной башни, тогда AC называется линией обзора.
Угол, образованный линией взгляда с горизонтальным уровнем, называется углом подъема вершины башни от глаза человека. Прочтите учебник NCERT и решите вопросы, чтобы получить помощь от входных решений NCERT для класса 10 по математике.
Следовательно, линия взгляда — это линия, проведенная от глаза наблюдателя к точке в объекте, рассматриваемом наблюдателем, т. Е. Угол возвышения наблюдаемой точки — это угол, образованный линией взгляда с горизонтом, когда просматриваемая точка находится выше горизонтального уровня.Пусть C — объект, а A — глаз человека, с которого он наблюдает за объектом C, тогда AC называется линией взгляда. Угол, образованный линией взгляда с горизонтальным уровнем, называется углом обзора Угол обзора — это линия, проведенная от глаза стороннего наблюдателя к точке объекта, рассматриваемого наблюдателем, т. е. угол, образованный линией взгляда с горизонтальный уровень называется углом депрессии. Угол наклона точки на наблюдаемом объекте — это угол, образованный линией взгляда с горизонтальным уровнем, когда точка находится ниже горизонтального уровня, т.
е.е., случай, когда мы опускаем голову, чтобы посмотреть на просматриваемую точку.
Список тригонометрических таблиц
Найдите ниже список всех формул и таблицы тригонометрии, используемых в математике.
Использование тригонометрического столаАкадемическая группа вводит в курс дела использование таблицы тригонометрии в следующем PDF-файле. как решить численное, используя правильное использование таблицы тригонометрии.Настоятельно рекомендуется, чтобы учащиеся запомнили таблицу тригонометрии для использования в будущем. Таблица тригонометрии используется почти во всех главах тригонометрии во всех классах, поэтому прочтите теорию тригонометрии подробно. См. Таблицу тригонометрии и вопросы по тригонометрии, подготовленные entryi.
ТРИГОНОМЕТРИЧЕСКИЕ ИДЕНТИЧНОСТИ Слово тригонометрия означает «измерение трех углов». Оно образовано от греческих слов три, гония, метрон, три означает три, гония означает угол, а метрон означает меру.
УГОЛ
Угол — это угол поворота вращающейся линии относительно фиксированной линии.
Примечание: Если вращение происходит по часовой стрелке, измеренный угол отрицательный, а при вращении против часовой стрелки он положительный.
РАЗЛИЧНЫЕ УГЛЫ ИЗМЕРЕНИЯШестидесятеричная система (или) Британская система
В шестидесятеричной системе прямой угол делится на 90 равных частей, называемых градусами.Кроме того, каждый градус делится на шестьдесят равных частей, называемых минутами, и каждая минута делится на шестьдесят равных частей, называемых секундами.
Таким образом, 1 прямой угол = 90 градусов (90 °)
1 ° = 60 минут (60 ¢)
1 ¢ = 60 секунд (60 ¢¢)
Десятичная система или французская система
1 прямой угол делится на 100 равных частей. Каждая часть называется оценкой.
1 прямой угол = 100 градусов (100 г )
1 класс = 100 минут (100 ¢)
1 минута = 100 секунд (100 ¢¢)
Радианная мера
Угол, образованный дугой, длина которой равна радиусу данной окружности в ее центре, называется одним радианом.
Связь между градусом и радианом.
Если D — это градусная мера угла, а R — его мера в радианах, тогда.
Важные формулы тригонометрии
‘; } иначе, если (json.file_format == ‘indexed’) { если (totalPage == 0) { displayHtml = displayHtml + ‘
Тригонометрических таблиц
Тригонометрических таблиц PI = 3.141592 … (примерно 22/7
= 3,1428)
радиан = градус x PI / 180 (преобразование градуса в рад)
градус = радианы x 180 / PI (преобразование рад в градус)
| Рад | град | Грех | Cos | Тан | Csc | сек | Детская кроватка | ||
|---|---|---|---|---|---|---|---|---|---|
| .0000 | 00 | . 0000 | 1,0000 | .0000 | —— | 1,0000 | —— | 90 | 1,5707 |
| .0175 | 01 | .0175 | .9998 | .0175 | 57.2987 | 1.0002 | 57.2900 | 89 | 1,5533 |
| .0349 | 02 | .0349 | .9994 | .0349 | 28,6537 | 1.0006 | 28,6363 | 88 | 1.5359 |
| .0524 | 03 | .0523 | .9986 | .0524 | 19.1073 | 1,0014 | 19.0811 | 87 | 1,5184 |
. 0698 | 04 | .0698 | .9976 | .0699 | 14,3356 | 1,0024 | 14.3007 | 86 | 1,5010 |
| .0873 | 05 | .0872 | .9962 | .0875 | 11,4737 | 1.0038 | 11.4301 | 85 | 1.4835 |
| . 1047 | 06 | . 1045 | .9945 | . 1051 | 9,5668 | 1,0055 | 9,5144 | 84 | 1,4661 |
| .1222 | 07 | . 1219 | .9925 | . 1228 | 8.2055 | 1,0075 | 8,1443 | 83 | 1,4486 |
. 1396 | 08 | . 1392 | . 9903 | .1405 | 7,1853 | 1,0098 | 7.1154 | 82 | 1.4312 |
| . 1571 | 09 | . 1564 | . 9877 | . 1584 | 6.3925 | 1.0125 | 6.3138 | 81 | 1.4137 |
| . 1745 | 10 | . 1736 | . 9848 | . 1763 | 5,7588 | 1.0154 | 5,6713 | 80 | 1,3953 |
| .1920 | 11 | .1908 | . 9816 | . 1944 | 5.2408 | 1.0187 | 5.1446 | 79 | 1,3788 |
. 2094 | 12 | . 2079 | .9781 | . 2126 | 4,8097 | 1.0223 | 4,7046 | 78 | 1,3614 |
| . 2269 | 13 | . 2250 | . 9744 | . 2309 | 4,4454 | 1.0263 | 4,3315 | 77 | 1,3439 |
| .2443 | 14 | . 2419 | . 9703 | . 2493 | 4,1336 | 1.0306 | 4.0108 | 76 | 1,3265 |
| . 2618 | 15 | . 2588 | . 9659 | .2679 | 3,8637 | 1.0353 | 3,7321 | 75 | 1,3090 |
. 2793 | 16 | ,2756 | .9613 | . 2867 | 3.6280 | 1.0403 | 3,4874 | 74 | 1.2915 |
| . 2967 | 17 | . 2924 | . 9563 | . 3057 | 3,4203 | 1.0457 | 3,2709 | 73 | 1,2741 |
| .3142 | 18 | .3090 | . 9511 | . 3249 | 3,2361 | 1.0515 | 3,0777 | 72 | 1,2566 |
| .3316 | 19 | . 3256 | . 9455 | . 3443 | 3,0716 | 1.0576 | 2,9042 | 71 | 1,2392 |
. 3491 | 20 | . 3420 | . 9397 | . 3640 | 2,9238 | 1.0642 | 2,7475 | 70 | 1,2217 |
| .3665 | 21 | .3584 | . 9336 | . 3839 | 2,7904 | 1.0711 | 2,6051 | 69 | 1,2043 |
| .3840 | 22 | .3746 | . 9272 | .4040 | 2,6695 | 1.0785 | 2,4751 | 68 | 1,1868 |
| .4014 | 23 | .3907 | . 9205 | .4245 | 2,5593 | 1.0864 | 2,3559 | 67 | 1. 1694 |
| . 4189 | 24 | .4067 | . 9135 | .4452 | 2.4586 | 1.0946 | 2,2460 | 66 | 1,1519 |
| .4363 | 25 | .4226 | . 9063 | .4663 | 2.3662 | 1,1034 | 2,1445 | 65 | 1,1345 |
| . 4538 | 26 | .4384 | .8988 | . 4877 | 2,2812 | 1.1126 | 2,0503 | 64 | 1.1170 |
| .4712 | 27 | . 4540 | .8910 | . 5095 | 2.2027 | 1,1223 | 1,9626 | 63 | 1. 0996 |
| .4887 | 28 | . 4695 | . 8829 | . 5317 | 2,1301 | 1,1326 | 1,8807 | 62 | 1.0821 |
| . 5061 | 29 | . 4848 | . 8746 | .5543 | 2,0627 | 1,1434 | 1,8040 | 61 | 1.0647 |
| . 5236 | 30 | .5000 | . 8660 | . 5774 | 2,0000 | 1,1547 | 1,7321 | 60 | 1.0472 |
| . 5411 | 31 | .5150 | . 8572 | . 6009 | 1,9416 | 1,1666 | 1,6643 | 59 | 1. 0297 |
| .5585 | 32 | .5299 | .8480 | . 6249 | 1.8871 | 1,1792 | 1,6003 | 58 | 1.0123 |
| . 5760 | 33 | . 5446 | . 8387 | .6494 | 1,8361 | 1.1924 | 1,5399 | 57 | .9948 |
| .5934 | 34 | . 5592 | .8290 | .6745 | 1,7883 | 1,2062 | 1.4826 | 56 | . 9774 |
| .6109 | 35 | . 5736 | . 8192 | .7002 | 1.7434 | 1,2208 | 1,4281 | 55 | . 9599 |
| . 6283 | 36 | . 5878 | .8090 | .7265 | 1,7013 | 1,2361 | 1,3764 | 54 | .9425 |
| .6458 | 37 | .6018 | .7986 | . 7536 | 1,6616 | 1,2521 | 1,3270 | 53 | .9250 |
| .6632 | 38 | . 6157 | .7880 | . 7813 | 1,6243 | 1,2690 | 1,2799 | 52 | .9076 |
| . 6807 | 39 | .6293 | . 7771 | .8098 | 1,5890 | 1,2868 | 1,2349 | 51 | . 8901 |
| .6981 | 40 | .6428 | .7660 | . 8391 | 1,5557 | 1.3054 | 1,1918 | 50 | . 8727 |
| .7156 | 41 | . 6561 | . 7547 | . 8693 | 1,5243 | 1,3250 | 1,1504 | 49 | . 8552 |
| .7330 | 42 | .6691 | . 7431 | .9004 | 1.4945 | 1,3456 | 1,1106 | 48 | . 8378 |
| . 7505 | 43 | . 6820 | . 7314 | .9325 | 1,4663 | 1,3673 | 1. 0724 | 47 | . 8203 |
| . 7679 | 44 | . 6947 | . 7193 | . 9657 | 1,4396 | 1,3902 | 1.0355 | 46 | .8029 |
| 0,7854 | 45 | . 7071 | . 7071 | 1,0000 | 1,4142 | 1,4142 | 1,0000 | 45 | . 7854 |
| Cos | Грех | Детская кроватка | сек | Csc | Тан | град | Рад |
Тригонометрический стол | Таблица тригонометрии класс 10 — Электрический дневник
Тригонометрия — одна из самых важных и сложных глав математики.
В индийской школьной системе он начался в 10-м классе CBSE, ICSE и других государственных советов.
Таблица тригонометрии от 0 до 90 для класса 10
В большинстве приложений тригонометрии мы используем углы от 0 до 90 для нахождения его числового значения с различными тригонометрическими тождествами. здесь мы начинаем находить числовое значение тригонометрического отношения для углов 0,30,45,60 и 90 градусов. Эта таблица числовых значений также используется учащимися 10-х классов As таблица тригонометрии класс 10. Числовые значения для различных углов приведены ниже: —
1/2 | 1 / √2 | ||||
2 | |||||
Cosecθ | 2 / √3 |
Из приведенной выше таблицы любой может легко найти числовое значение любых углов любых тригонометрических тождеств
Пример
Sin0 = 0
Sin45 = 1 / √2
Трюк с тригонометрическим столом для воспоминаний на вечность
Студенты всегда ищут уловку, чтобы запомнить числовое значение тригонометрических тождеств.
Но с воспоминаниями нет никакого трюка, но здесь я предложу некоторую идею, которая действительно поможет вам вспомнить числовое значение любых тригонометрических тождеств. Для этого вам нужно запомнить хотя бы формулу и все числовые значения Sinθ. если вы положите x = 0, а затем решите для Cosx, вы получите
Cosx = 1
Положите x = 30 и решите для Cosx, тогда вы получите
.если вы запомните все значение Sinx, то, используя приведенную выше формулу, вы можете легко вычислить оставшееся значение Cosx.
Чтобы вычислить значение tanx, для различных значений угла используйте эту формулу
tanx = Sinx / Cosx
Для расчета Tan0 положите X = 0 в приведенной выше формуле
Tan0 = Sin0 / Cos0
Tan0 = 0/1
tan0 = 0
Для расчета Tan30 положите X = 30 в приведенной выше формуле
tan30 = Sin30 / Cos30
tan30 = (1/2) / (√3 / 2)
тан30 = 1 / √3
используя эту технику, вы можете легко вычислить все оставшееся значение tanx.
Представленная здесь таблица предоставит числовое значение всех значений тригонометрического значения для углов от более 90 до 360.
√3 / 2 | 1/2 | 0 | — (1/2) | — (√3 / 2) | |
— (1/2) | — (√3 / 2) | — 1 | — (√3 / 2) | — (1/2) | |
— (√3) | 0 | 1 / √3 | √3 | ||
1 / √3 | |||||
— (2 / √3) | — ∞ | 2 | |||
Cosecθ | 2 / √3 | ∞ | -2 | — (2 / √3) |
Формулы тригонометрии для класса 10
Формулы тригонометрии для класса 10 Тригонометрия — самая важная глава для студентов, учатся ли они на досках CBSE / ICSE или готовятся к соревнованиям, таким как IIT или SSC.
В CBSE / NCERT тригонометрия представлена в , 10-м классе (Глава 8), а в ICSE — в 9-м классе. В большинстве случаев студенты находят главу «Тригонометрия» очень сложной для понимания и усвоения всех формул Тригонометрии . В этой статье вы найдете все тригонометрических формул для класса 10 .
Прочитав эту статью, что вы поймете: —
- В этой статье мы постараемся помочь студентам облегчить им понимание тригонометрии.
- Мы сделаем несколько коротких трюков , чтобы формулы тригонометрии для 10-го класса было легко усвоить.
- Кроме того, вам не нужно заучивать их все наизусть. Вместо этого вы разработаете методику, позволяющую извлекать из некоторых формул вместо их запоминания.
Тригонометрические формулы class10 скачать pdf
Что такое тригонометрия?
Это слово «тригонометрия» произошло от объединения двух греческих слов «trigōnon», что означает «треугольник», и «metron», что означает «мера».
Таким образом, используется для измерения Треугольников .
Проще говоря, Тригонометрия — это раздел математики, в котором мы изучаем отношения между длинами сторон и углами треугольников.
А теперь позвольте мне сделать это проще!
- ВОПРОС (i): — если нам даны две стороны прямоугольного треугольника и попросят найти третью сторону, какую математическую концепцию мы будем использовать, чтобы найти третью сторону?
ОТВЕТ: — Очевидно, это очень просто! Мы будем использовать теорему Пифагора .
- ВОПРОС (ii): — Если нам даны одна сторона и один угол (отличный от 90 °) прямоугольного треугольника и вас попросят найти остальные стороны этого треугольника, как вы его найдете? ?
ОТВЕТ: — Для этого вам необходимо понять новую концепцию, известную как «Тригонометрия».
Реальные приложения тригонометрии и формул!
Большую часть времени мы задаемся вопросом , какая польза от тригонометрии в нашей жизни ?.
Возможно, вы не применяли тригонометрию напрямую для решения своих повседневных жизненных проблем, но косвенно она используется в различных вещах, которые мы видим вокруг себя.
- Как вы думаете, мы узнали, что высота горы Эверест составляет 8848 метров. Очевидно, с помощью тригонометрии.
- Как мы узнали, что расстояние между «Землей» и «Солнцем»? когда мы ни разу не были на «Солнце». вы можете измерить расстояние до ближайших объектов в космосе, используя метод тригонометрии, называемый Тригонометрический параллакс или Звездный параллакс.
- Функции синуса и косинуса (которые вы изучите позже) являются фундаментальными для теории периодических функций, описывающих звуковые и световые волны.
- Тригонометрия также используется в строительстве, видеоиграх, летной технике, морской инженерии, археологии, криминологии, навигации, океанографии, картографии (создание карт), спутниковых системах.
- К вашему удивлению, почти каждое научное открытие, связанное с расстоянием, доказывается только благодаря тригонометрии.
ПРИМЕЧАНИЕ. — Мы подробно обсудили эти реальных приложений тригонометрии в этой статье, просмотрите их.
Тригонометрические отношения: —
Прежде всего, обсудим, что такое Тригонометрические отношения . Тригонометрические отношения — это, по сути, отношение между измерением углов и длинами сторон прямоугольного треугольника.
Теперь давайте обсудим, сколько типов тригонометрических соотношений возможно.
В прямоугольном треугольнике у нас есть три стороны, названные (H) Гипотенуза (самая длинная сторона), (P) Перпендикуляр (сторона, противоположная углу) и (B) База . Если нас попросят взять любые две стороны из этих трех сторон и сформировать соотношение, мы обнаружим, что возможны шесть соотношений (P / H, B / H, P / B, H / P, H / B, B / P ).
Мы присвоили каждому соотношению свое имя.
Тригонометрические отношения: —
- sinθ = (Перпендикуляр (P)) / (Гипотенуза (H)).
- cosθ = (База (B)) / (Гипотенуза (H)).
- tanθ = (Перпендикуляр (P)) / (Основание (B)).
- cosecθ = (Гипотенуза (H)) / (Перпендикуляр (P)).
- сек θ = (Гипотенуза (H)) / (База (B)).
- cotθ = (Основание (B)) / (Перпендикуляр (P)).
Взаимные тригонометрические отношения: —
- sin θ = 1 / (косек θ)
- косекунд θ = 1 / (sin θ)
- cos θ = 1 / (сек θ)
- сек θ = 1 / (cos θ)
- тангенс угла наклона θ = 1 / (детская кроватка θ)
- детская кроватка θ = 1 / (тангенс угла θ)
Важные взаимосвязи между тригонометрическими отношениями: —
tanθ = (sin θ) / (cos θ)
cot θ = (cos θ) / (sin θ)
Тригонометрический стол: —
Эта таблица тригонометрических отношений помогает нам найти значения стандартных тригонометрических углов , таких как 0 °, 30 °, 45 °, 60 ° и 90 °.
| Тригонометрические отношения | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° |
| sin A | 0 | 1/2 | 1 / √2 | √3 / 2 | 1 |
| cos A | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 |
| желто-коричневый A | 0 | 1 / √3 | 1 | √3 | Не определено |
| детская кроватка A | Не определено | √3 | 1 | 1 / √3 | 0 |
| код A | Не определено | 2 | √2 | (2√3) / 3 | 1 |
| сек A | 1 | (2√3) / 3 | √2 | 2 | Не определено |
youtube.com/embed/xgrUnjou2UA» frameborder=»0″ allowfullscreen=»allowfullscreen»>
Тригонометрические формулы и тождества: —
Теперь есть формул тригонометрии и тождества , которые вы должны выучить.Эти соотношения и тождества очень полезны при решении тригонометрических задач.
Формулы тригонометрии для 10 класса: —
Тригонометрические формулы в 10-м классе основаны на тригонометрических отношениях. Существуют три основные тригонометрические формулы для 10-го класса, и с их помощью вы можете сделать другие отождествления.
1) cos 2 A + sin 2 A = 1.
- a) cos 2 A = 1 — sin 2 A.
- б) sin 2 A = 1 — cos 2 A.
2) 1 + tan 2 A = сек 2 A.
- a) сек 2 A — загар 2 A = 1.
- б) загар 2 A = сек 2 A — 1.
3) детская кроватка 2 A + 1 = cosec 2 A.
- a) cosec 2 A — детская кроватка 2 A = 1.
- б) детская кроватка 2 A = cosec 2 A — 1.
Есть еще две Тригонометрические формулы для 10 класса : —
(i) сек A — загар A = 1 / (сек A + загар A)
(ii) cosec A — детская кроватка A = 1 / (cosec A + кроватка A)
Получить все формулы тригонометрии для класса 10 pdf: —
.
