Таблицы DPVA.ru — Инженерный Справочник |
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Механические колебания. Свободные и вынужденные колебания. Гармонические колебания. Упругие колебания. Математический маятник. Превращения энергии при гармонических колебаниях
Поделиться:
| |||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. |
||||||
|
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления.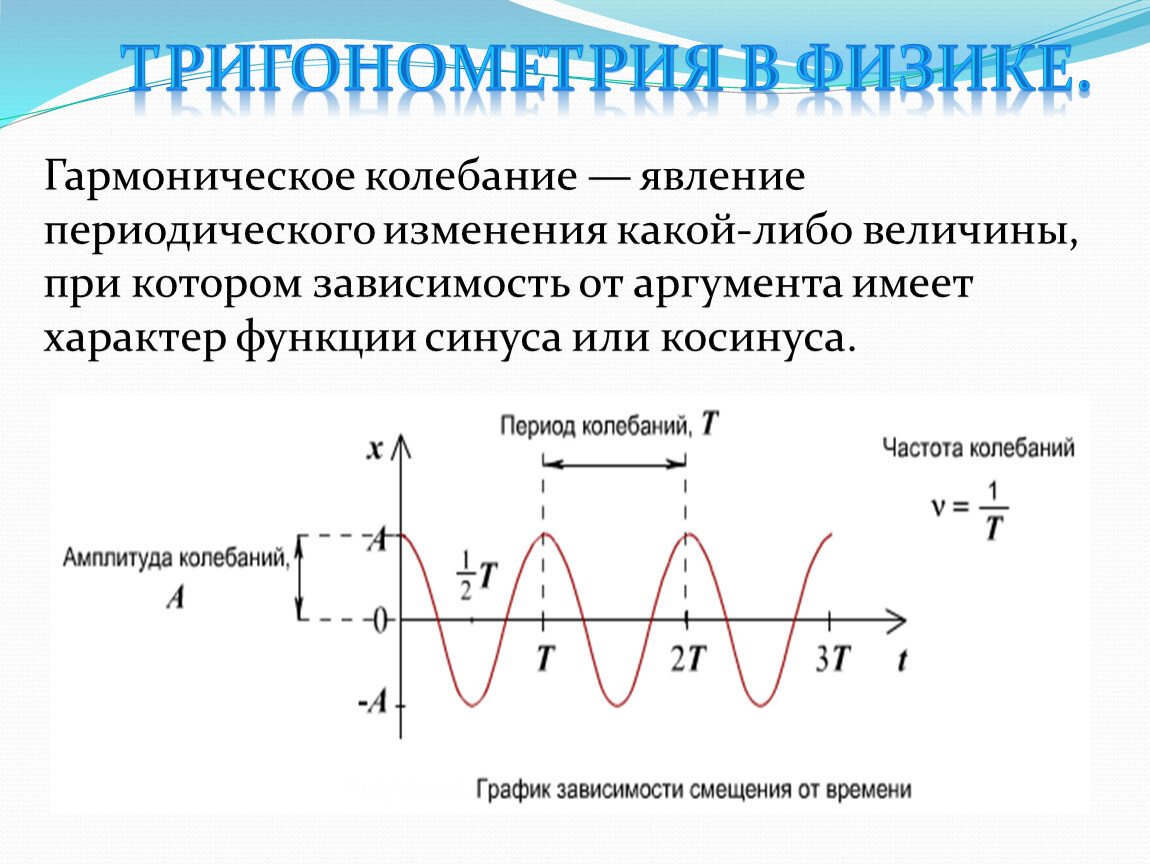 Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator
Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator
|
|||||
Оптика и волны
Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.
Уравнение затухающих колебаний
Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости
где r
 Поэтому уравнение движения примет вид:
Поэтому уравнение движения примет вид:
|
|
(1.62) |
или
|
|
(1.63) |
Здесь новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если .
Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:
Поэтому уравнения (1.15) примут теперь вид:
|
|
(1.64) |
Подставляем первое уравнение во второе:
|
|
(1.65) |
или
|
|
(1. |
Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.
Анализ решений
Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:
|
(1.67) |
 Сведем новую задачу к предыдущей. Для этого вместо переменной x определим новую переменную X, связанную с x соотношением:
Сведем новую задачу к предыдущей. Для этого вместо переменной x определим новую переменную X, связанную с x соотношением:
|
|
(1.68) |
Дифференцируя функцию x(t), получаем:
|
|
(1.69) |
Подставляем эти выражения в (1.67):
|
|
(1. |
Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной . Получаем в итоге дифференциальное уравнение для функции X(t):
|
|
(1.71) |
Здесь возможны два случая. Пусть сначала . Тогда можно ввести параметр
так что уравнение (1.71) примет вид:
Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:
Значит, мы нашли общее решение уравнения затухающих колебаний (1.
|
|
(1.72) |
Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний: . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой и с амплитудой, изменяющейся по закону (рис. 1.22)
Рис. 1.22. Свободные затухающие колебания
Видео 1.17 Механические (маятник) затухающие колебания — запись песком
Видео 1.18 Затухание колебаний камертона — осциллограф и собственные уши
Коэффициент затухания определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
Период затухающих колебаний равен:
|
|
(1.73) |
Пусть первое наибольшее положительное отклонение достигается в момент времени . Последующие наибольшие отклонения того же знака (A’, A», A»’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:
|
|
(1.74) |
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:
|
|
(1. |
Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:
|
|
(1.76) |
Определим количество колебаний, которое совершит система за время . За это время амплитуда уменьшается в е раз, а число колебаний равно:
|
|
(1. |
Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется величина, называемая добротностью:
|
|
(1.78) |
которая пропорциональна числу колебаний Nе, совершаемых системой за то время , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при находим:
|
|
(1. |
Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании () имеем:
|
|
(1.80) |
где E0— значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:
|
|
(1.81) |
Следовательно,
|
|
(1. |
то есть при слабом затухании добротность, с точностью до множителя , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
При увеличении затухания частота колебаний
стремится к нулю, а период колебаний растет. В предельном случае
период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
Видео 1.19 Электрические затухающие колебания в LCR-контуре
Видео 1.20 Фазовые кривые затухающих колебаний в LCR-контуре. Критическое сопротивление.
Гармонические колебания.
 Амплитуда, период и частота колебательного движения
Амплитуда, период и частота колебательного движения
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В
рамках данной темы будет рассмотрен простейший вид колебательного движения —
гармонические колебания.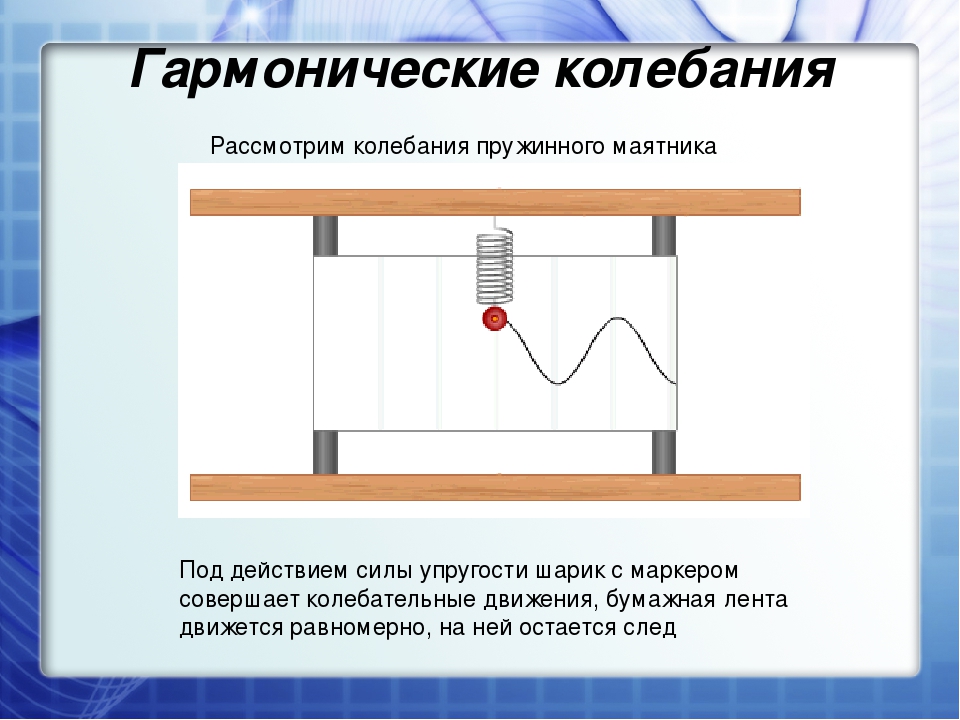
Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если
ленту перемещать с постоянной скоростью в направлении, перпендикулярном
плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая
точка которой соответствует положению колеблющегося груза в тот момент, когда
он проходил над ней. Из опыта видно, что след, который оставляет песок на листе
бумаги, есть некая кривая.
Из опыта видно, что след, который оставляет песок на листе
бумаги, есть некая кривая.
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда
колебаний — максимальное смещение тела от положения равновесия.
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т. е.
частота — это величина обратная периоду и равная числу полных колебаний, совершаемых
за 1 секунду.
е.
частота — это величина обратная периоду и равная числу полных колебаний, совершаемых
за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это
следует из известных вам законов и формул, в которых указанные величины попарно
связаны прямо пропорциональной зависимостью, например законом Гука или вторым
законом Ньютона. Из этих формул видно, что сила и ускорение достигают
наибольших значений, когда колеблющееся тело находится в крайних положениях,
где смещение наиболее велико, и равны нулю, когда тело проходит через положение
равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
Основные выводы:
– Гармонические колебания
— это колебания, при которых смещение колеблющейся точки от положения
равновесия изменяется с течением времени по закону синуса или косинуса.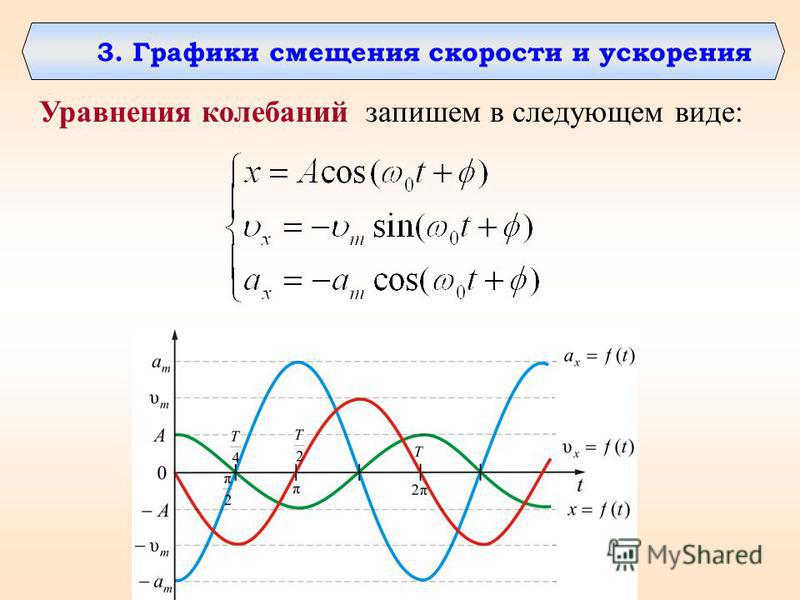
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник
— это система, состоящая из материальной точки массой m
и пружины, которая совершает колебания в вертикальной плоскости.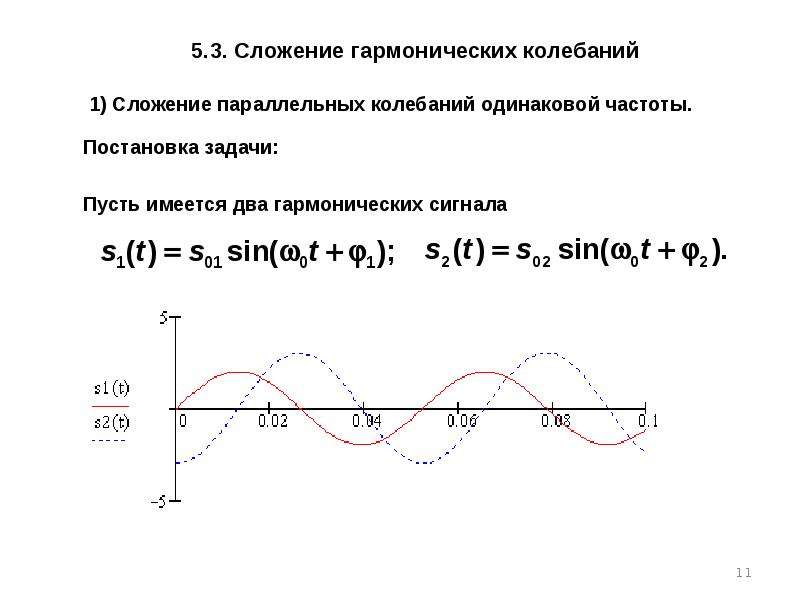
Механические колебания. Свободные и вынужденные колебания. Амплитуда, период, частота, фаза колебаний. Уравнение гармонических колебаний. Математический маятник.
Муниципальное бюджетное общеобразовательное учреждение
«Гвардейская школа № 1» Симферопольского района Республики Крым
ул. Карла Маркса, дом 97, сп Гвардейское, Симферопольский район,
Республика Крым, Российская Федерация, 297513
тел. (3652) 32-30-45, e-mail: [email protected] ОГРН 1159102031329, ИНН 9109010395
«Механические колебания. Свободные и вынужденные колебания. Амплитуда, период, частота, фаза колебаний.
Уравнение гармонических колебаний.
Математический маятник»
(разработка урока)
учитель физики и химии
высшей категории, учитель-методист
Стулень Виктор Иванович
сп Гвардейское. 2016 год
2016 год
10 класс. Урок № 45.
Тема. «Механические колебания. Свободные и вынужденные колебания. Амплитуда, период, частота, фаза колебаний. Уравнение гармонических колебаний. Математический маятник»
Цели урока:
1) учебные: формировать умение наблюдать и анализировать физические явления;
ознакомить обучающихся с наиболее распространённым видом движения в природе и технике — колебательным движением на примере математического маятника;
ввести понятия характеристик колебательного движения;
выяснить условия существования свободных колебаний.
2) воспитательные: формировать навыки коллективной и групповой (парной) работы в сочетании с самостоятельностью обучающихся;
способствовать развитию умений вести диалог и занимать активную позицию на уроке;
приучать детей к доброжелательному общению, взаимопомощи, взаимопроверке, самооценке, умению слушать других.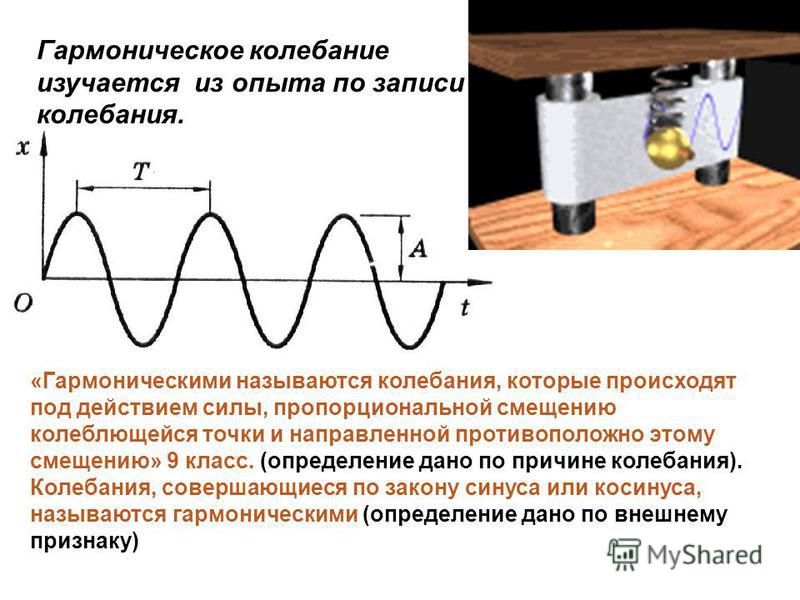
3) развивающие: продолжить развивать внимание и умение логически мыслить;
развивать монологическую речь с применением физических терминов;
совершенствовать навыки решения расчётных задач.
Тип урока: урок изучения и первичного закрепления новых знаний.
Формы работы: решение задач, беседа по вопросам, рассказ учителя, работа обучающихся в группах (парах), индивидуальная работа обучающихся.
Оборудование и дидактический материал: карточки с заданиями; шарик на нити, метроном, штатив с 2 лапками и муфтами, пружина с петлёй, набор стандартных грузов, мячик; ЦОР физика 10 №1, №2, №3, №4 «Механические колебания и волны»; таблица №7 (комплект 2) «Свободные колебания. Величины, характеризующие колебательное движение», таблица №8 (комплект 2) «Гармонические колебания. Затухающие колебания», таблица №9 (комплект 2) «Вынужденные колебания. Резонанс», презентация по теме «Механические колебания», ноутбук с мультимедиа доской.
Затухающие колебания», таблица №9 (комплект 2) «Вынужденные колебания. Резонанс», презентация по теме «Механические колебания», ноутбук с мультимедиа доской.
Ход урока.
«Я всегда хочу учиться, но не всегда
хочу, чтобы меня учили» (У. Черчилль)
1. Организация начала урока.
Приветствие обучающихся и фиксация отсутствующих на уроке.
— Эпиграфом к уроку я предлагаю слова Уинстона Черчилля: «Я всегда хочу учиться, но не всегда хочу, чтобы меня учили». Эти слова должны стать девизом вашей учебной деятельности. Знайте, что самостоятельно находить ответы на вопросы, пытаться решить проблемные ситуации, наблюдать за явлениями природы и анализировать, самостоятельно проводить опыты — это очень увлекательно и полезно для развития личности. Не бойтесь ошибиться при ответе на вопросы, так как не ошибается только тот, кто не работает.
— Хочется надеяться, что сегодняшний урок разбудит у вас жажду новых познаний и стремление использовать открытые эффекты и закономерности на практике.
2. Актуализация опорных знаний обучающихся. Подготовка к усвоению нового материала.
2.1. Анализ выполнения контрольной работы №4 по теме «Законы сохранения в механике», оглашение оценок.
2.2. Две пары работают на месте (задания распечатаны, на столах, Приложение 1):
1) Решение задачи. Тело свободно падает с высоты 160 метров. Вычислите его скорость в момент касания к земле.
2) Решение задачи. Тело массой 60 кг движется со скоростью 2,5 , его догоняет тело массой 80 кг, которое движется со скоростью 4 . Вычислите скорость тел после неупругого удара.
2.3. Решение задач у доски (на «+», «-» в тетрадях) (задачи распечатаны, зачитываются, пока отвечающий выходит к доске, и вручаются ему, Приложение 2):
Задача 1. Тело массой 25 кг движется со скоростью 8 , навстречу ему движется тело массой 15 кг со скоростью 6 . Вычислите скорость тел после неупругого удара.
Тело массой 25 кг движется со скоростью 8 , навстречу ему движется тело массой 15 кг со скоростью 6 . Вычислите скорость тел после неупругого удара.
— ответы решения задачи:
Дано:m1 = 25 кг
1= 8
m2 = 15 кг
2= — 6
СИ
= ?
m1 * 1 + m2 * 2 = * (m1 + m2) = =
= = = 2,75
Ответ: = 2,75
Задача 2. Вычислите кинетическую энергию тела массой 8 кг на высоте 3 метра от земли, если оно свободно падало с высоты 15,5 метров.
— ответы решения задачи:
Дано:m = 8 кг
h = 15,5 м
h1 = 3,0 м
g = 9,8
СИ
Ек = ?
Ек = Еп – Еп1 Ек = 8 кг * 9,8 * (15,5 м – 3,0 м) =
Ек = m * g * h – m * g * h1 980 Дж
Ек = m * g * (h – h1)
Ответ: Ек = 980 Дж
2. 4. Актуализация субъективного опыта обучающихся.
4. Актуализация субъективного опыта обучающихся.
— Посмотрите внимательно на движение тел.
Демонстрация: по столу катится мячик, метроном отсчитывает время. В чём различия этих движений?
— Движение мяча — прямолинейное движение, а движение стрелки метронома — повторяющееся периодически движение.
— Подобное стрелке метронома движение осуществляют также ветки деревьев под действием ветра, провода линий ЛЭП под действием ветра, маятник часов, сердце человека, струны музыкальных инструментов, качающиеся качели, голосовые связки.
— Колебательное движение происходит и в жизни нашей планеты: землетрясения, приливы и отливы.
— Это всё примеры колебательного движения или механических колебаний.
— Надеюсь, что такое распространение колебательных движений в природе и жизни человека вас серьёзно заинтересовало. С этим движением мы сегодня на уроке и ознакомимся.
3. Формулирование темы урока при участии обучающихся.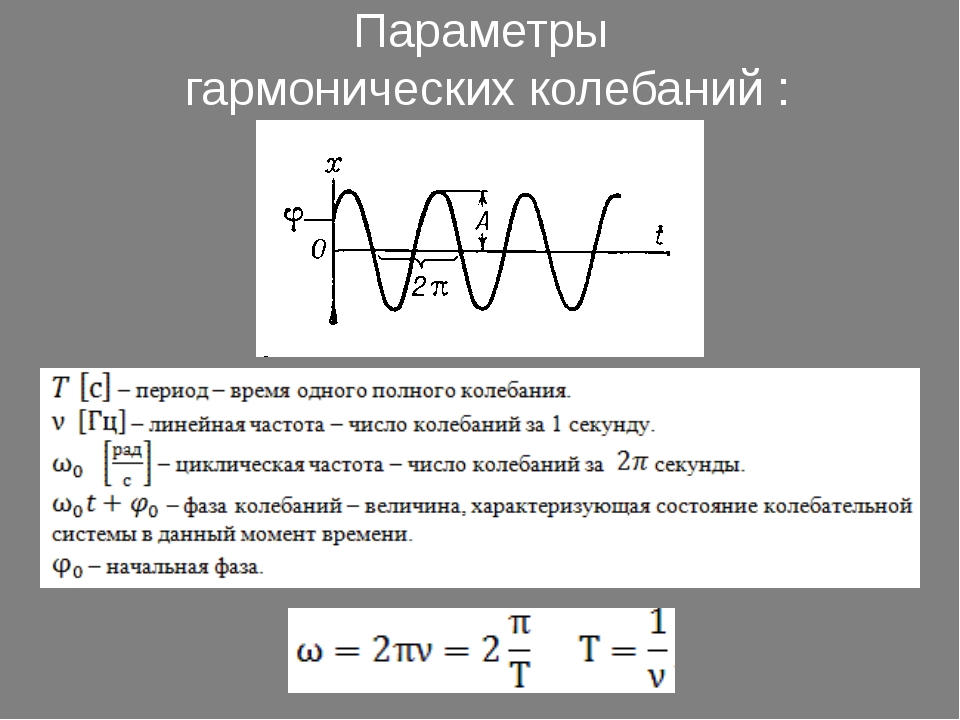
Проблемный вопрос: Как вы думаете, какие характеристики описывают механические колебания?
— Сегодня мы изучим механические колебания, а также их характеристики.
— Все записывают число (прописью), «Классная работа» и тему урока:
Механические колебания. Свободные и вынужденные колебания.
Амплитуда, период, частота, фаза колебаний. Уравнение
гармонических колебаний. Математический маятник.
4. Обучающиеся предлагают формулировки целей и задач урока. Мотивация учебной деятельности.
— изучить наиболее распространённый в природе и технике вид движения — колебательное движение;
— выяснить условия существования свободных колебаний;
— узнать формулы, которые описывают основные характеристики колебательного движения;
— изучить уравнения, описывающие гармонические колебания;
— изучить колебания математического маятника;
— научиться решать задачи на вычисление основных характеристик колебательного движения;
— быть уверенным в своих силах, уметь самостоятельно решать задачи и выполнять другие учебные задания.
Это тема, с которой начинается новый раздел физики «Колебания и волны», который мы будем изучать на протяжении 9 часов, в конце темы вы напишите контрольную работу.
5. Изучение нового материала.
При изучении нового материала возможно использование ресурсов: 1) ЦОР физика 10 №1, №2, №3, №4 «Механические колебания и волны»; 2) презентация по теме «Механические колебания»; 3) таблица №7 (комплект 2) «Свободные колебания. Величины, характеризующие колебательное движение», таблица №8 (комплект 2) «Гармонические колебания. Затухающие колебания», таблица №9 (комплект 2) «Вынужденные колебания. Резонанс».
5.1. Механические колебания.
— Колебания — один из самых распространённых видов движения в природе и технике.
— Сначала давайте запишем определение механических колебаний.
Механические колебания – это физические процессы,
точно или приблизительно повторяющиеся через
одинаковые интервалы времени.
— Механические колебания осуществляют ветки деревьев под действием ветра, провода линий ЛЭП под действием ветра, маятники часов, сердце человека, струны музыкальных инструментов, качающиеся качели, голосовые связки.
— Колебательное движение происходит и в жизни нашей планеты: землетрясения, приливы и отливы.
— Также примерами колебательного движения являются: колебания тела на пружине и шарика, закреплённого на нити.
— Эти примеры легко представить, тем более, что при выполнении лабораторных работ мы часто сталкивались с этими опытами.
Демонстрация: колебания шарика, закреплённого на нити, и тела на пружине.
— Скажите, пожалуйста, в чём их особенность?
1. Во время колебаний тело периодически отклоняется от положения равновесия.
2. Для того, чтобы получить колебательное движение, на тело воздействуют извне силой.
— Вторая особенность, на которую вы указали, даёт возможность разделить колебательное движение на два вида: свободные и вынужденные.
5.2. Свободные и вынужденные колебания.
— Рассмотрим виды колебаний по таблице №7 (комплект 2) «Свободные колебания. Величины, характеризующие колебательное движение» и таблице №9 (комплект 2) «Вынужденные колебания. Резонанс».
— Свободные колебания – это колебания, происходящие в механической системе под действием внутренних сил системы после кратковременного воздействия внешней силы.
— К свободным колебаниям мы отнесём колебания тел на пружине и на нити, чашки весов.
Условия возникновения свободных механических колебаний:
— запишите из учебника (стр. 91).
1) В одном определённом положении тела в пространстве, называемом положением равновесия, равнодействующая сил, приложенных к телу, должна быть равна нулю. При выведении тела из положения равновесия равнодействующая всех сил должна быть отличной от нуля и направлена к положению равновесия.
При выведении тела из положения равновесия равнодействующая всех сил должна быть отличной от нуля и направлена к положению равновесия.
2) Для начала свободных колебаний система должна быть выведена из положения равновесия внешним воздействием.
3) Силы трения в системе должны быть малы по сравнению с силами, зависящими от координат.
— Вынужденные колебания — это колебания, происходящие под постоянным воздействием внешних сил.
— А к вынужденным, например, качели, которые мы периодически подталкиваем; колебания веток деревьев под действием ветра; колебания проводов линий ЛЭП под действием ветра, колебание маятника часов под действием пружины или груза; струны гитары.
5.3. Период, частота, амплитуда, фаза колебаний.
— Важнейшими характеристиками колебательного движения тел являются период, частота, амплитуда и фаза колебаний.
5.3.1. Период колебаний тела.
— Запишите определение периода колебаний из учебника (с. 92):
92):
Минимальный интервал времени, через который тело оказывается
в той же точке пространства и движется с той же скоростью и с тем
же ускорением, называется периодом колебаний (Т).
— Другими словами: период колебаний (Т) — это время, за которое совершается одно полное колебание.
— Если тело совершило N колебаний за время t, то период колебаний определяется по формуле: T =
— Единица измерения периода колебаний тела в системе СИ – 1 секунда = 1с. Также период колебаний может измеряться во внесистемных единицах времени — минутах, часах и так далее.
— На рисунке ниже период колебаний — это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия O в крайнюю левую точку и обратно через точку O снова в крайнюю правую.
— За полный период колебаний тело проходит путь, равный четырем амплитудам.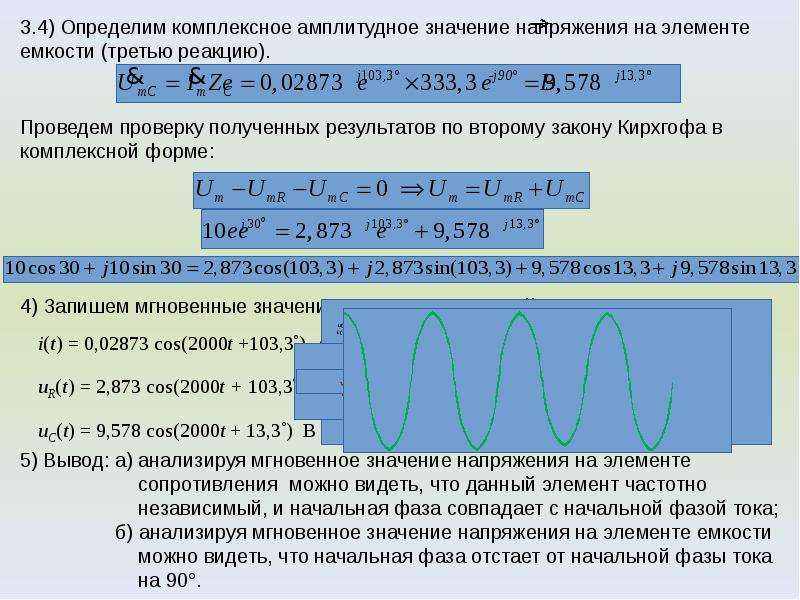 Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
— Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, то есть для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
5.3.2. Частота колебаний тела.
— Запишите определение частоты колебаний из учебника (с. 92):
Физическая величина, равная числу колебаний, совершаемых
за одну секунду, называется частотой колебаний ().
— Единица измерения частоты колебаний в системе СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894) (приложение 3), 1 герц = 1 Гц.
— Если частота колебаний равна 1 Гц, то это значит, что за каждую секунду тело совершает одно колебание.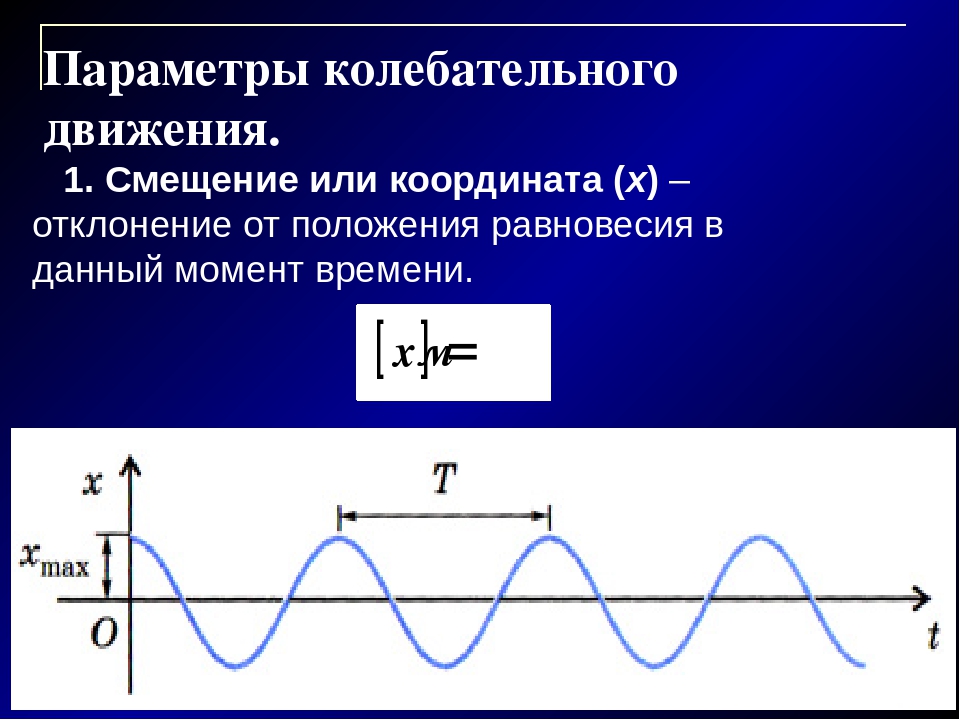
— Если тело совершило N колебаний за время t, то частота колебаний определяется по формуле: = .
— Частота и период колебаний связаны соотношениями: T = или = .
— Механические колебания груза на пружине и шарика на нити — это движение, при котором смещение зависит от времени по закону синуса или косинуса. А такие колебания называют гармоническими.
— Период функции косинус равен 2.
— Число полных колебаний, совершённых за 2 секунд, называют циклической, или круговой, частотой ().
— Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
— Единица измерения циклической частоты колебаний в системе СИ 1
— Кроме периода и частоты одной из основных характеристик колебаний является амплитуда колебаний.
5.3.3. Амплитуда колебаний тела.
— Запишите определение амплитуды колебаний из учебника (с. 92):
92):
Амплитудой (лат. amplitude — величина) механических колебаний тела называется наибольшее смещение тела от положения равновесия.
— Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже).
— Амплитуда колебаний измеряется в единицах длины — метрах (сантиметрах и так далее). На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
5.3.4. Фаза колебаний тела. Гармонические колебания.
— Рассмотрим гармонические колебания по таблице №8 (комплект 2) «Гармонические колебания. Затухающие колебания».
— Запишите определение гармонических колебаний из учебника (с. 92):
Если координата х тела, совершающего колебания вдоль оси
ОХ, изменяется со временем t по формуле синуса или косинуса
x = x0 * sin 2 * * t или x = x0 * cos 2 * * t, то такие
колебания называются гармоническими колебаниями.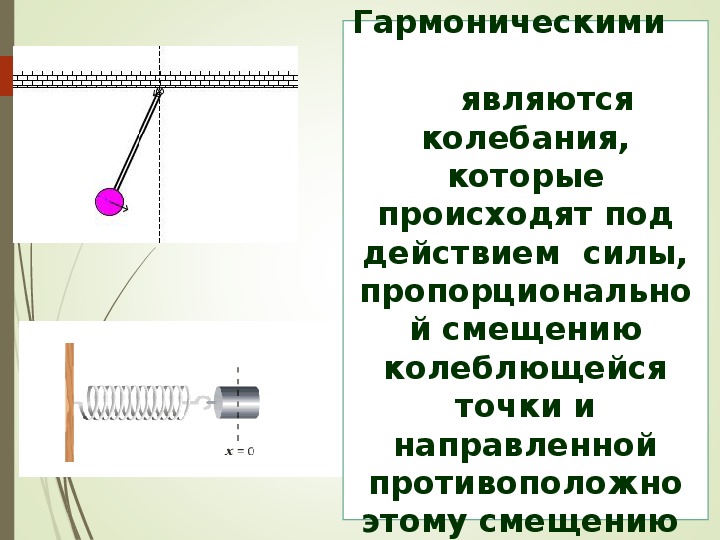
— В этих уравнениях х0 — амплитуда колебаний, — частота колебаний.
— Вместо частоты в уравнении гармонических колебаний тела может быть использована циклическая частота : = 2 * ,
х = x0 * cos * t.
— Если использовать период колебаний, получим такую формулу:
х = x0 * cos * t.
— Запишите определение фазы колебаний из учебника (с. 92):
Величина, стоящая под знаком косинуса или синуса,
называется фазой () гармонических колебаний.
= 2 * * t = * t = * t
5.4. Уравнение гармонических колебаний.
— Все гармонические колебания имеют математическое выражение. Их свойства характеризует совокупность тригонометрических уравнений, сложность которых определяется сложностью самого колебательного процесса, свойствами системы и средой, в которой они происходят, то есть, внешними факторами, воздействующими на колебательный процесс.
— Например, в механике гармоническое колебание представляет собой движение, которому свойственны: — прямолинейный характер; — неравномерность; — перемещение физического тела, которое происходит по синусоидальной или косинусоидальной траектории, а зависимости от времени.
— Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону: x = х0 * cos (ω * t + α).
— Выясним смысл входящих в эту формулу величин.
— Положительная величина х0 является наибольшим по модулю значением координаты (модуль косинуса равен единице), то есть наибольшим отклонением от положения равновесия. Следовательно, х0 — амплитуда колебаний.
— Аргумент косинуса ωt+α называется фазой колебаний и он определяет место (положение) колеблющейся материальной точки в данный конкретный момент времени при заданной амплитуде.
— Величина α, равная значению фазы при t = 0, называется начальной фазой.
— Начальная фаза отвечает начальной координате тела: α = x0 * cos α.
— Многообразие колебательных процессов естественным образом приводит к тому, что существует большое количество осцилляторов.
— Перечислим их основные типы:
а) пружинный осциллятор — обычный груз, обладающий некой массой m, который подвешен на упругой пружине.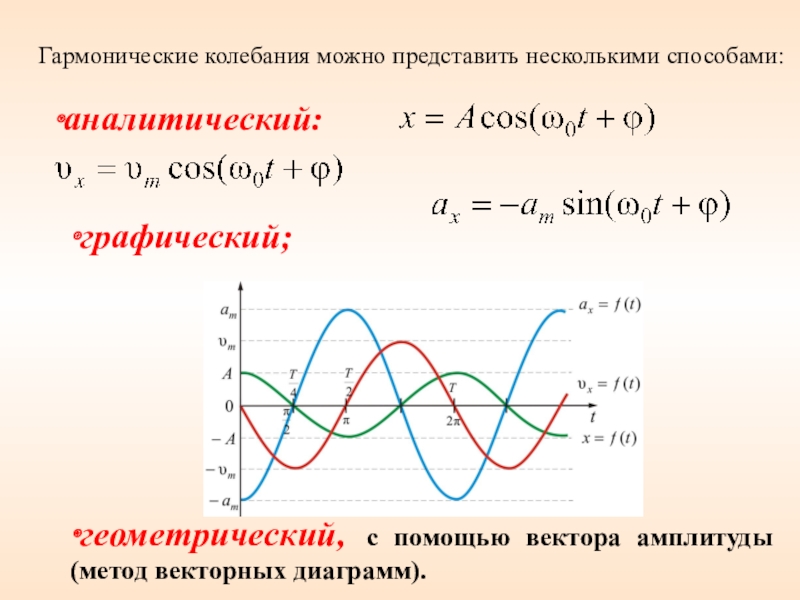
— Он совершает колебательные движения гармонического типа, которые описываются формулой F = — kx.
б) физический осциллятор (маятник) — твердое тело, совершающее колебательные движения вокруг статичной оси под воздействием определенной силы;
в) математический маятник (в природе практически не встречается).
— Он представляет собой идеальную модель системы, включающей колеблющееся физическое тело, обладающее определенной массой, которое подвешено на жесткой невесомой нити.
Ф И З К У Л Ь Т М И Н У Т К А
5.5. Математический маятник.
— Теперь ещё раз обратимся к модели тела, подвешенного к нити. Её можно назвать математическим маятником.
— Запишите определение математического маятника из учебника (с. 92):
Тело массой m столь малых размеров, что его можно считать
материальной точкой, подвешенное на невесомой и нерастяжимой
нити длиной l, называется математическим маятником.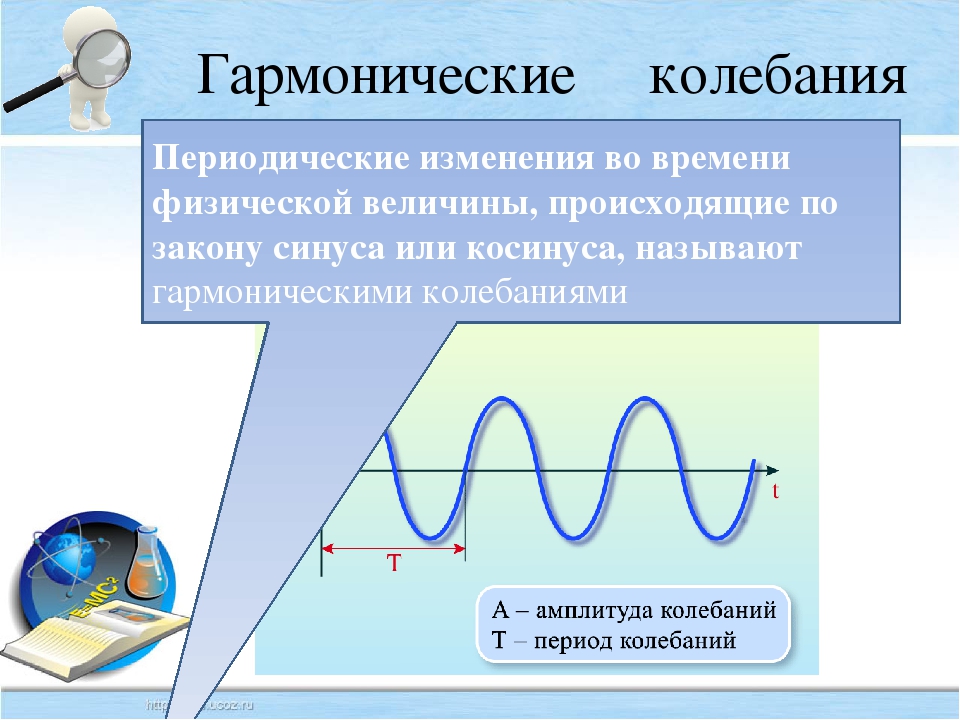
— Математический маятник — это система, состоящая из материальной точки, подвешенной на тонкой нерастяжимой нити.
— Почему в нашем случае тело — шарик — мы считаем материальной точкой?
— Диаметр шара намного меньше длины нити.
— Какая физическая величина заставляет маятник совершать движения?
— Сила. Давайте с вами вспомним, какие силы действуют на тело, подвешенное к нити, при выведении его из положения равновесия?
— Выполните в своих тетрадях рисунок тела, подвешенного на нити, выведенного из положения равновесия, и сил, действующих на него.
— На шарик действует сила упругости или сила натяжения нити, направленная вдоль нити вверх, и сила тяжести, направленная перпендикулярно вниз.
— А приводит в движение систему их равнодействующая, которая направлена в сторону возвращения тела в положение равновесия.
— Формула для вычисления периода математического маятника:
T = 2 *
— Мы видим, что период математического маятника зависит от длины нити маятника l и от величины g. Что же это за величина?
Что же это за величина?
— Это ускорение свободного падения, которое равно 9,8 м/с.
— Скорость движения шарика максимальна в точке положения равновесия и равна нулю в точках амплитуды колебаний.
— Высота поднятия шарика над определённым нулевым уровнем максимальна в точках амплитуды колебаний и равна нулю в точке положения равновесия.
6. Первичное закрепление изученного материала.
6.1. Первичная проверка понимания изученного.
Вопросы:
1. Какой процесс называют «механические колебания»?
2. Какой процесс называют «свободные колебания»?
3. Какой процесс называют «вынужденные колебания»?
4. Какую характеристику колебаний называют «периодом колебаний»?
5. Какую характеристику колебаний называют «частотой колебаний»?
6. Какую характеристику колебаний называют «амплитудой колебаний»?
Какую характеристику колебаний называют «амплитудой колебаний»?
7. Какую характеристику колебаний называют «фазой колебаний»?
8. Какие колебания называют гармоническими колебаниями?
9. Какую систему называют математическим маятником?
6.2. Первичное закрепление изученного материала.
1) Две группы (пары) обучающихся получают задание для выполнения на месте (распечатано приложение 4, выдано на пару), с отчётом у доски.
Задача 1. Из приведенных выше примеров выберите примеры свободных и вынужденных колебаний: движение пилы при распиливании дров; колебание игрушки-неваляшки; движение гитарных струны; движение ветки под действием ветра; движение иголки в швейной машинке.
Задача 2. Длина подвеса шарика математического маятника равна 2 метра 45 сантиметров. Вычислите период колебаний математического маятника.
Вычислите период колебаний математического маятника.
2) У доски или устно с пояснениями работает один обучающийся, остальные работают на месте (на «+», «-» в тетрадях) (работающему распечатано приложение 5).
Задача. Математический маятник длиной 99,5 см за одну минуту совершил 30 полных колебаний. Определите период колебаний маятника и ускорение свободного падения в том месте, где находится маятник.
— ответы решения задачи:
Дано:l = 99,5 см
t = 1 мин
N = 30
СИ
0,995 м
60 с
U = ?
Решение:
T = T = = 2 с
T = 2 * g = =
T2 = 4* = 9,81
g =
Ответ: g = 9,81
7. Закрепление, обсуждение и коррекция изученного материала.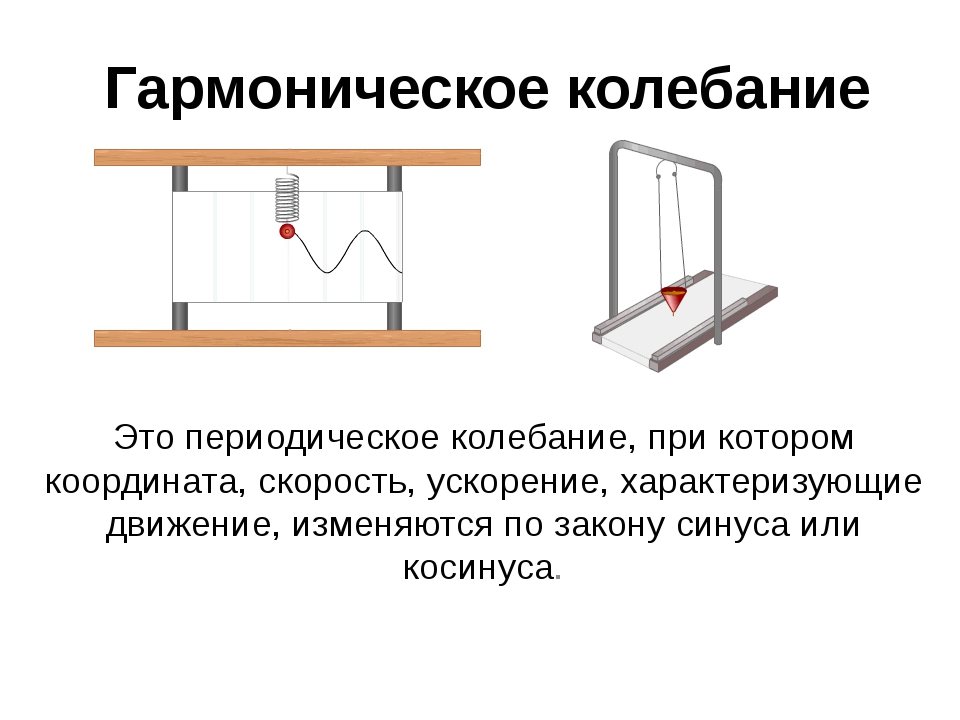
Отчет групп, представитель пары (группы) записывает ход решения задачи на доске:
— ответы решения задачи 1:
— Свободные колебания: колебание игрушки-неваляшки;
— Вынужденные колебания: движение пилы при распиливании дров; движение гитарных струны; движение ветки под действием ветра; движение иголки в швейной машинке.
— ответы решения задачи 2:
Дано:l = 2 м 45 см
g = 9,8
СИ
2,5 м
Т = ?
T = 2 * T = 2 * 3,14 * = 3,14 с
Ответ: Т = 3,14 с
8. Подведение итогов занятия. Рефлексия.
Подведение итогов занятия, учитель:
— Сегодня на уроке мы изучили механические колебания; свободные и вынужденные колебания; амплитуду, период, частоту и фазу колебаний; уравнение гармонических колебаний, математический маятник.
— Давайте ещё раз повторим формулы для вычисления периода и частоты колебаний, положения тела-осциллятора, периода колебаний математического маятника.
1-2 обучающихся вслух повторяют формулу.
Рефлексия (раздать распечатку таблички, Приложение 6)
— Проведите стрелочки к тем утверждениям, которые соответствуют вашему состоянию в конце урока.
9. Задаётся и объясняется домашнее задание
— Ребята! Сегодня вы плодотворно работали и благодаря этому стали ещё на ступеньку умнее.
— Запишите, пожалуйста, домашнее задание к следующему уроку (задание появляется на мультимедиа доске или записано на обороте обычной доски):
Учить §17 (с.91 — 94) (механические колебания),
решить задачу №17.2 (с. 97)
— До свидания, ребята! Спасибо вам за сотрудничество и активную работу на уроке.
Приложение 1.
Решение задачи 1. Тело свободно падает с высоты 160 метров. Вычислите его скорость в момент касания к земле.
Решение задачи 2. Тело массой 60 кг движется со скоростью 2,5 , его догоняет тело массой 80 кг, которое движется со скоростью 4 . Вычислите скорость тел после неупругого удара.
Приложение 2.
Задача 1. Тело массой 25 кг движется со скоростью 8 , навстречу ему движется тело массой 15 кг со скоростью 6 . Вычислите скорость тел после неупругого удара.
Задача 2. Вычислите кинетическую энергию тела массой 8 кг на высоте 3 метра от земли, если оно свободно падало с высоты 15,5 метров.
Приложение 3.
Приложение 4.
Задача 1. Из приведенных выше примеров выберите примеры свободных и вынужденных колебаний: движение пилы при распиливании дров; колебание игрушки-неваляшки; движение гитарных струны; движение ветки под действием ветра; движение иголки в швейной машинке.
Задача 2. Длина подвеса шарика математического маятника равна 2 метра 45 сантиметров. Вычислите период колебаний математического маятника.
Приложение 5.
Задача. Математический маятник длиной 99,5 см за одну минуту совершил 30 полных колебаний. Определите период колебаний маятника и ускорение свободного падения в том месте, где находится маятник.
Приложение 6.
Физика — 10
Гармоническое колебание и его график. Самым простым колебательным движением является гармоническое колебание.
● Гармонические колебания — это колебания, при которых величины, характеризующие движение, изменяются со временем по закону синуса или косинуса.
Изменения положения тела, совершающего свободные гармонические колебания, описываются кривой, которая является синусоидой или косинусоидой.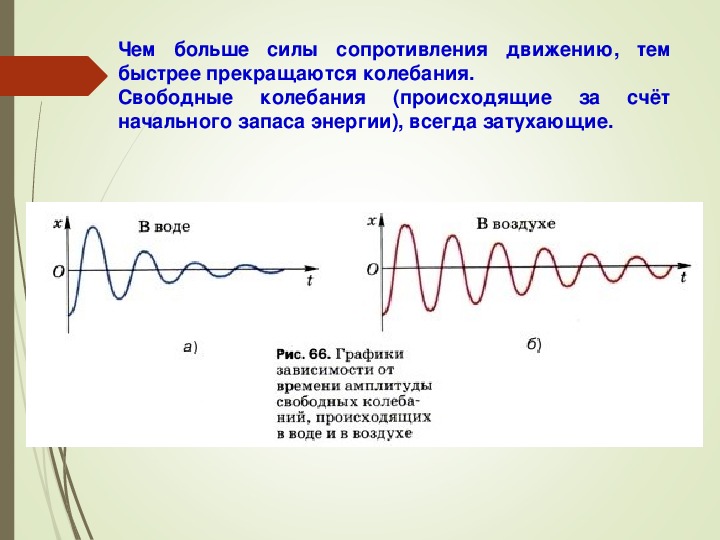
Кривую синусоиды (или косинусоиды) с легкостью можно наблюдать во время проведения опыта как с пружинным, так и с нитевым маятником, представляющим собой наполненную песком воронку с небольшим отверстием внизу (b).
Эта кривая соответствует графику изменения перемещения маятника х от времени t по закону синуса или косинуса (c):
x = xmsinωt(4.6)
или
x = xmcosωt (4.7)
Из графика видно, что за время, равное периоду колебания (t = T ), маятник совершает одно полное колебание (см: c).
● Затухающие колебания — это колебания в замкнутой колебательной системе, в которой в результате действия сил трения происходит постепенное уменьшение полной механической энергии системы и уменьшение амплитуды колебаний.
Исследование-2. Применение
Применение Определение характеристик маятника
Задача 2. Материальная точка, совершая колебания вдоль прямой линии с частотой 2 Гц, проходит за 2 секунды путь в 4 см. Чему равна амплитуда колебаний этой материальной точки?
Обсуждение результатов:
- Что общего и чем отличаются амплитуда и перемещение маятника?
- Чему равен путь, пройденный маятником, колеблющимся вдоль прямой линии, за промежуток времени t при определенной частоте колебаний?
Механические колебания — СтудИзба
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
План
1. Колебания. Характеристики гармонических колебаний.
Колебания. Характеристики гармонических колебаний.
2. Свободные (собственные) колебания. Дифференциальное уравнение гармонических колебаний и его решение. Гармонический осциллятор.
3. Энергия гармонических колебаний.
4. Сложение одинаково направленных гармонических колебаний. Биение. Метод векторной диаграммы.
5. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
6. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Частота затухающих колебаний. Изохронность колебаний. Коэффициент, декремент, логарифмический декремент затухания. Добротность колебательной системы.
Рекомендуемые файлы
7. Вынужденные механические колебания. Амплитуда и фаза вынужденных механических колебаний.
8. Механический резонанс. Соотношение между фазами вынуждающей силы и скорости при механическом резонансе.
9. понятие об автоколебаниях.
1. Колебания. Характеристики гармонических колебаний.
Колебания – движение или процессы, обладающие той или иной степенью повторности во времени.
Гармонические (или синусоидальные) колебания – разновидность периодических колебаний, которые могут быть заменены в виде
(1)
где a – амплитуда, — фаза, — начальная фаза, — циклическая частота, t – время (т.е. применяются со временем по закону синуса или косинуса).
Амплитуда (а) – наибольшее отклонение от среднего значения величины, совершающей колебания.
Фаза колебаний ( ) – изменяющийся аргумент функции, описывающей колебательный процесс (величина t+, стоящая под знаком синуса в выражении (1) ).
Фаза характеризует значение изменяющейся величины в данный момент времени. Значение в момент времени t=0 называется начальной фазой ().
В качестве примера на рисунке 27.1 представлены математические маятники в крайних положениях с разностью фаз колебаний =0 (27. 1.а) и = (27.1б)
1.а) и = (27.1б)
Разность фаз колебаний маятников проявляется отличием в положении колеблющихся маятников.
Циклической или круговой частотой называется количество колебаний, совершаемое за 2 секунд.
Частотой колебаний (или линейной частотой) называется число колебаний в единицу времени. За единицу частоты принимается частота таких колебаний, период которых равен 1с. Эту единицу называют Герц (Гц).
Промежуток времени, за который совершается одно полное колебание, а фаза колебания получает приращение, равное 2, называется периодом колебания (рис. 27.2).
2. Свободные колебания. Свободными или собственными называются такие колебания, которые происходят в системе, выведенной из положения равновесия и предоставленной самой себе.
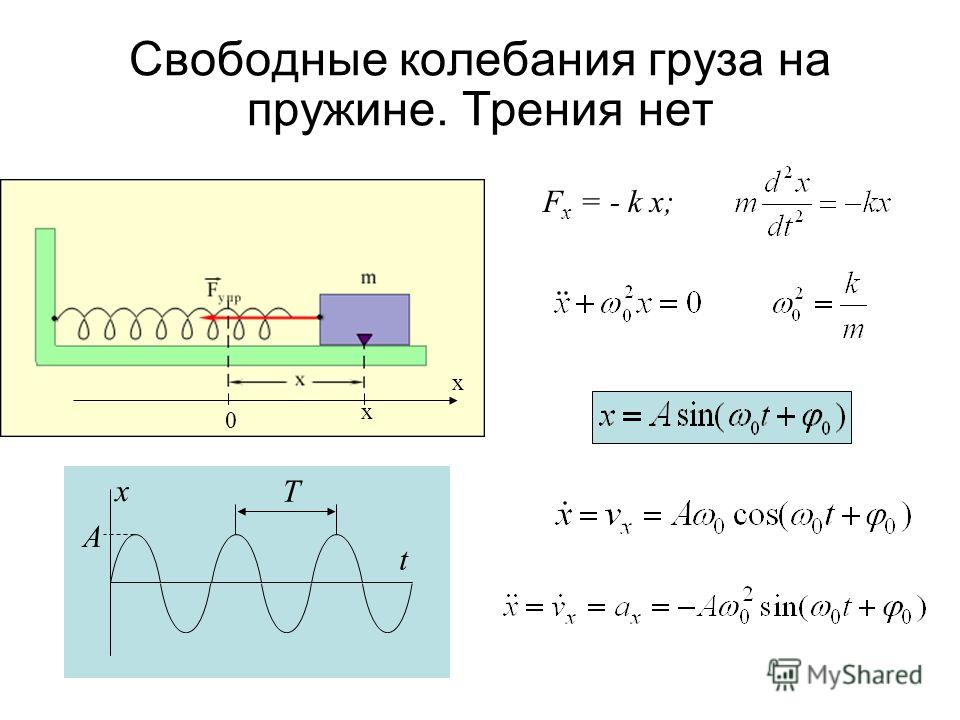
Рассмотрим колебания груза на пружине, совершаемые на гладкой горизонтальной поверхности (рис. 27.3). Если растянуть пружину на некоторое расстояние х, и затем отпустить, то на груз будет действовать упругая сила = — кх, где к — коэффициент пропорциональности, называемый жесткостью пружины. Знак «-» указывает на то, что сила направлена в сторону, противоположную направлению оси Х (направлению растяжения). В проекции на ось Х второй закон Ньютона на уравнение движения запишется
Знак «-» указывает на то, что сила направлена в сторону, противоположную направлению оси Х (направлению растяжения). В проекции на ось Х второй закон Ньютона на уравнение движения запишется
.
Поделив обе части уравнений на m
и перенеся в левую часть
.
Обозначив , получим линейное дифференциальное однородное уравнение второго порядка
(2)
(линейное – т.е. и сама величина х, и ее производная в первой степени; однородное – т.к. нет свободного члена, не содержащего х ; второго порядка – т.к. вторая производная х).
Уравнение (2) решается (*) подстановкой х = . Подставляя в (2) и проводя дифференцирование
.
Получаем характеристическое уравнение
.
Это уравнение имеет мнимые корни: ( -мнимая единица).
Общее решение имеет вид
где и — комплексные постоянные.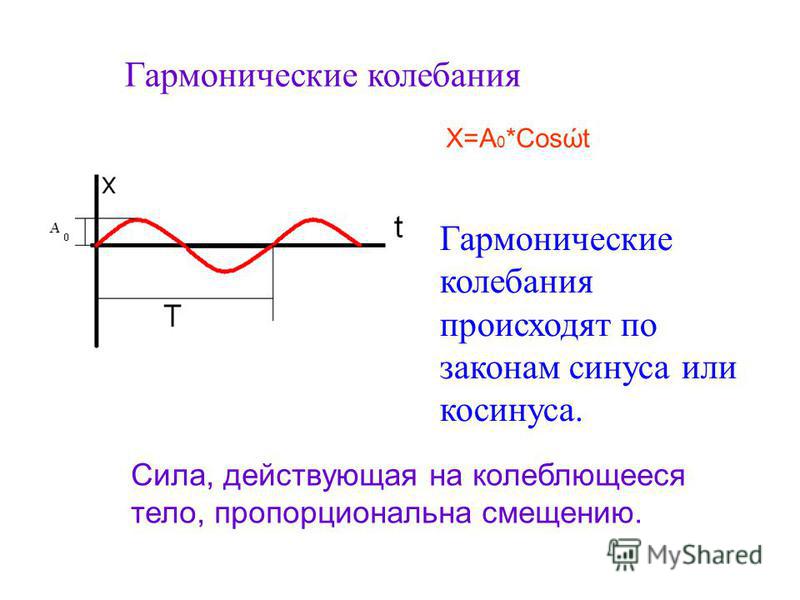
Подставляя корни, получим
(3)
(Замечание: комплексным числом z называется число вида z = x + iy, где x,y – вещественные числа, i – мнимая единица (= -1). Число х называется вещественной частью комплексного числа z.. Число у называется мнимой частью z).
(*) В сокращенном варианте решение можно опустить
Выражение вида можно представить в виде комплексного числа с помощью формулы Эйлера
аналогично
(т.к. .
Положим и в виде комплексных постоянных = А, а = А, где А и произвольные постоянные. Из (3) получим
Обозначив получим
Используя формулу Эйлера
Т.е. получим решение дифференциального уравнения для свободных колебаний
(4)
где — собственная круговая частота колебаний, А – амплитуда.
Смещение х применяется со временем по закону косинуса, т.е. движение системы под действием упругой силы f = -кх представляет собой гармоническое колебание.
Если величины, описывающие колебания некоторой системы периодически изменяются со временем, то для такой системы пользуются термином «осциллятор».
Линейным гармоническим осциллятором называется такой, движение которого описывается линейным уравнением .
3. Энергия гармонических колебаний. Полная механическая энергия системы, изображенной на рис. 27.2 равна сумме механической и потенциальной энергий.
Продифференцируем по времени выражение (, получим
= = -asin(t + ).
Кинетическая энергия груза (массой пружины пренебрегаем) равна
E = .
Потенциальная энергия выражается известной формулой подставляя х из (4), получим
т.к. .
Полная энергия
величина постоянная.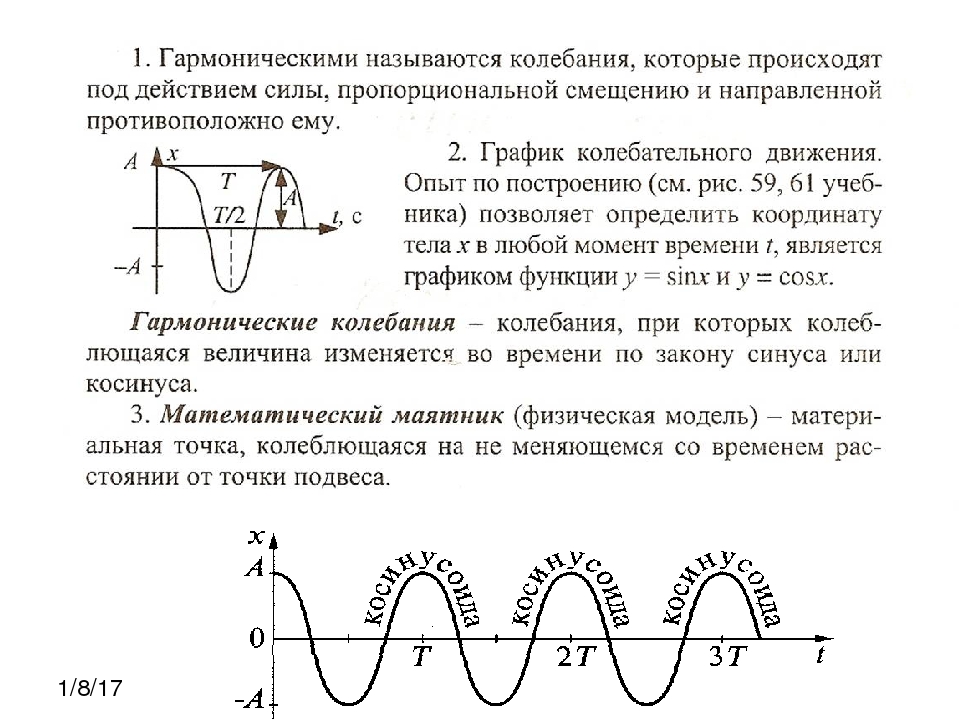 В процессе колебаний потенциальная энергия переходит в кинетическую и наоборот, но каждая энергия остается неизменной.
В процессе колебаний потенциальная энергия переходит в кинетическую и наоборот, но каждая энергия остается неизменной.
4. Сложение одинаково направленных колебаний.. Обычно одно и то же тело участвует в нескольких колебаниях. Так, например, звуковые колебания, воспринимаемые нами при слушании оркестра представляют собой сумму колебаний воздуха, вызываемых каждым из музыкальных инструментов в отдельности.
Рассмотрим сложение двух гармонических колебаний одинакового направления. Смещение х колеблющегося тела будет суммой смещений и . Положим равными, для простоты, амплитуды и начальные фазы Тогда
.
Воспользовавшись формулой суммы косинусов, получим
(5)
Биения. Пусть два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Обозначим частоту одного из колебаний , частоту второго . При этом Амплитуды обоих колебаний будем полагать одинаковыми и равными а.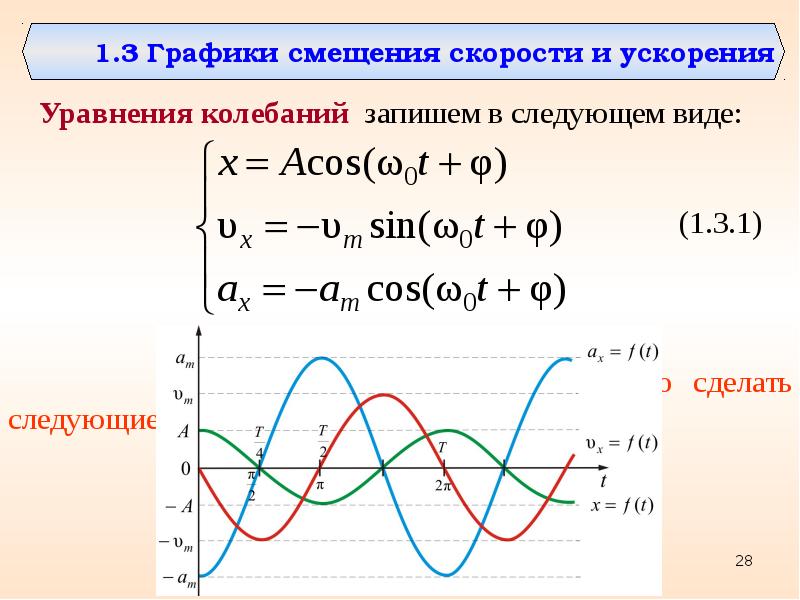 Начальные фазы для упрощения задачи положим равными нулю. Тогда
Начальные фазы для упрощения задачи положим равными нулю. Тогда
Сложим эти колебания, воспользовавшись формулой (5), получим
(6)
Во втором сомножителе (6) пренебрегли по сравнению с . Множитель меняется гораздо медленнее, чем (т.к. ). Результирующее колебание х можно рассматривать как гармоническое с частотой , амплитуда которого меняется по закону от -2а до +2а (амплитуда – величина положительная). Такие колебания называются биениями. Они представлены на рис.27.4.
Частота пульсаций амплитуды называется частотой биений. Промежуток времени между соседними моментами времени, когда амплитуда максимальна, называется периодом биений Тб. За это время разность фаз изменяется на , т.е.
Таким образом период биений
Метод векторной диаграммы.
Колебания изображаются графически в виде векторов на плоскости (рис. 27.5). Вектор-амплитуда вращается с угловой скоростью против часовой стрелки. Если в момент t = 0 вектор образует с осью Х угол , то проекцию вектора на ось Х можно записать в виде гармонического закона .
27.5). Вектор-амплитуда вращается с угловой скоростью против часовой стрелки. Если в момент t = 0 вектор образует с осью Х угол , то проекцию вектора на ось Х можно записать в виде гармонического закона .
Следовательно, проекция вектора на ось Х будет совершать гармонические колебания с амплитудой, равной длине вектора, круговой частотой, равной угловой скорости вращения вектора, и начальной фазой, равной углу образуемому вектором с осью в начальный момент времени.
Такой способ удобно использовать при сложении колебаний одного направления. Рассмотрим случай, когда частоты складываемых колебаний одинаковы.
Каждое из складываемых колебаний можно представить с помощью векто
ров и , сумма проекций которых на ось Х равна проекции суммы векторов
Так как векторы и вращаются с одной и той же угловой скоростью , с той же угловой скоростью вращается и вектор . Значит, результирующее колебание тоже является гармоническим и имеет вид
,
где и находим на рис. 27.6
27.6
5. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
Фигуры Лиссажу – это замкнутые траектории точки, совершающей два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским ученым Ж.Лиссажу.
Вид фигур Лиссажу зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. Рассмотрим случай, когда частоты складываемых колебаний одинаковы, а координаты точки х и у изменяются по законам
(7)
где — разность фаз обоих колебаний. Уравнения (7) представляют уравнение траектории в параметрической форме, где параметр t – время. Решая совместно оба уравнения с целью исключения параметра t, получим (без вывода) уравнение
(8)
Рассмотрим некоторые частные случаи.
1) При = 0 уравнение (8) принимает вид
откуда получается уравнение прямой
Колеблющаяся точка перемещается по этой прямой (рис.27.7).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид достаточно сложных кривых.
6. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение.
В любой реальный колебательной системе есть силы сопротивления (трения), действия которых приводит к уменьшению амплитуды и энергии колебаний. Такие колебания называют затухающими.
В этом случае, уравнение движения для системы на рис.27.3 будет иметь вид
.
Учитывая, что а силу сопротивления, которая обычно пропорциональна скорости, можно записать как где r – коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления, уравнение движения приобретает вид
.
Перенося члены из правой части в левую, поделив уравнение на m и обозначив, получим уравнение в виде
(9)
где — частота, с которой совершались бы свободные колебания системы в отсутствии сопротивления среды (собственная частота системы).
Коэффициент , характеризующий скорость затухания
колебаний, называется коэффициентом затухания.
Решение уравнения (9) имеет вид
(10)
где и — постоянные, определяемые начальными условиями — частота затухающих колебаний
График функции (10) показан на рис.27.10.
Множитель в уравнении (10) называют амплитудой затухающих колебаний. Такие колебания можно рассматривать как гармонические с частотой и уменьшающейся со временем амплитудой . Заметим, что независимость частоты (периода) собственных колебаний от амплитуды называется
изохронностью. Изохронность характерна для линейных систем.
Изохронность характерна для линейных систем.
В линейных системах изохронность практически соблюдается только в области достаточно малых амплитуд.
Другое замечание. Если то процесс называется апериодическим (непериодическим). Выведенная из положения равновесия система, возвращается в положение равновесия, не совершая колебаний (рис.27.11, кривая 1). Кривая 2 получается в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия.
Кроме коэффициента затухание характеризуют и другими величинами. Найдем отношение амплитуд, соответствующих моментам времени, отличающимся на период
.
Это отношение называется декрементом затухания, а его натуральный логарифм – логарифмическим декрементом затухания
(11)
где Т – период затухающих колебаний. Для выяснения физического смысла возьмем некоторое время за которое амплитуда уменьшается в е раз (время релаксации). Тогда т.к. (из (11) ), то . Обозначим количество колебаний за время , тогда и , т.е. логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Тогда т.к. (из (11) ), то . Обозначим количество колебаний за время , тогда и , т.е. логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Кроме того, для характеристики колебательной системы часто употребляется такая величина
(12)
называемая добротностью колебательной системы (добротностью осциллятора). Добротность пропорциональна числу колебаний NB, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в е раз.
7. Вынужденные механические колебания. Свободные колебания реальной колебательной системы являются затухающими. Чтобы колебания были незатухающими, необходимо компенсировать потери энергии, обусловленные силами сопротивления. Это можно сделать, воздействуя на систему (рис.27.3) внешней силой, изменяющейся по гармоническому закону где — частота вынуждающей силы. Уравнение движения запишется с учетом всех сил () запишется в виде
Уравнение движения запишется с учетом всех сил () запишется в виде
Поделив обе части на m и перенося первые два члена из правой части в левую, получим
Обозначив, как и в п.6 , получим дифференциальное уравнение вынужденных колебаний
(13)
Уравнение является неоднородным. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения
.
Общее решение однородного уравнения (правая часть (13) равна нулю) нам уже известно
.
Слагаемое играет заметную роль только в начальной стадии процесса (рис.27.12).
С течением времени из-за экспоненциального множителя роль уменьшается и по прошествии некоторого времени им можно пренебречь и остается только частные решения неоднородного уравнения (без вывода)
(14)
Функция (14) описывает установившиеся вынужденные гармонические колебания с частотой, равной частоте вынужденной силы.
Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных и) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.
8. Механический резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.
Чтобы найти резонансную частоту , нужно найти максимум амплитуды функции (14), т.е. максимум функции
(15)
Или, что-то же самое, найти минимум выражения, стоящего под корнем в знаменателе (15).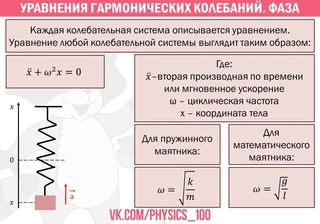 Продифференцировав выражение
Продифференцировав выражение
по и приравняв к нулю, получим
.
Проведя дальнейшие простые преобразования, получим
,
а т.к. частота по своему смыслу не может быть отрицательной, то выбираем решение со знаком «+». Итак, резонансная частота
(16)
График зависимости амплитуды вынужденных колебаний от частоты изменения вынуждающей силы в соответствии с выражением (15) представлен на рис.27.13. При →0 все кривые приходят к одному и тому же значению , . При , . Чем меньше , тем острее максимум.
Происхождение резонансного усиления колебаний можно уяснить себе, обратив внимание на соотношение между фазами вынуждающей силы и скорости. Если , то между вынуждающей силой и скоростью существует определенная разность фаз, поэтому в течение некоторой доли каждого периода сила направлена противоположно , т.е. стремится замедлить движение. При резонансе же фазы силы и скорости совпадают, так что сила «подталкивает» движение.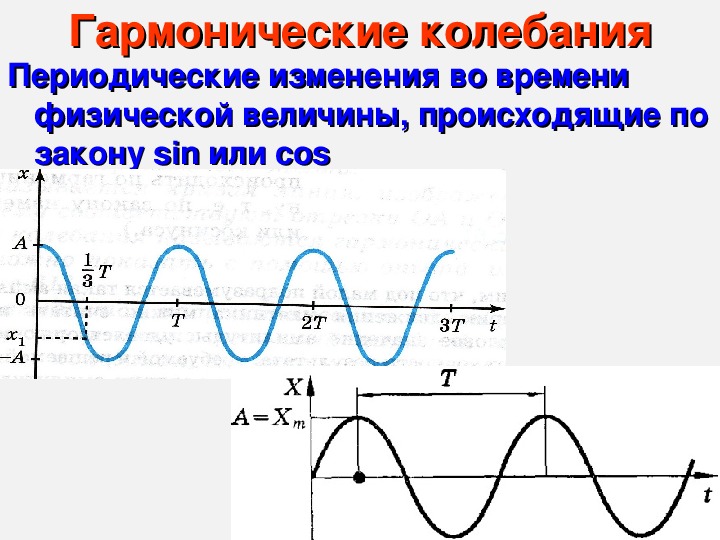
9. Понятие об автоколебаниях. Автоколебания – незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, не обладающего колебательными свойствами. Свойства колебаний определяются самой системой.
Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в такт с ее колебаниями.
Форма, амплитуда и частота колебаний задаются самой системой.
Примером автоколебательной системы могут служить часы. Энергия берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза, но ни пружина, ни груз не являются вынуждающей силой, формулирующей колебания(внешняя сила не обладает колебательными свойствами). Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струей. Другие примеры – электрический звонок, скрипка и т.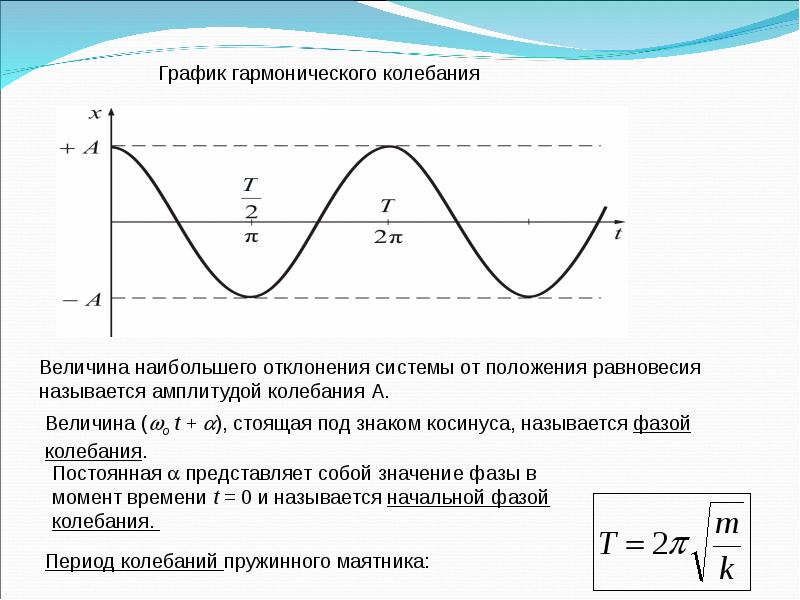 п.
п.
Вопросы для самоконтроля.
1. Какие колебания называются гармоническими? Приведите примеры гармонических колебаний.
2. Дайте определение следующих характеристик гармонического колебания: амплитуды, фазы, начальной фазы, периода, частоты, циклической частоты.
3. Выведите дифференциальное уравнение гармонических колебаний и напишите его решение.
Вам также может быть полезна лекция «Характеристика типов темперамента».
4. Как изменяются со временем кинетическая и потенциальная энергии гармонического колебания? Почему полная энергия гармонического колебания остается постоянной?
5. Выведите дифференциальное уравнение, описывающее затухающие колебания и напишите его решение.
6. Что такое логарифмический декремент затухания и добротность колебательной системы?
7. Выведите дифференциальное уравнение вынужденных колебаний и проанализируйте решение.
8. Что такое резонанс? Нарисуйте график зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы, когда эта сила является простой гармонической функцией времени.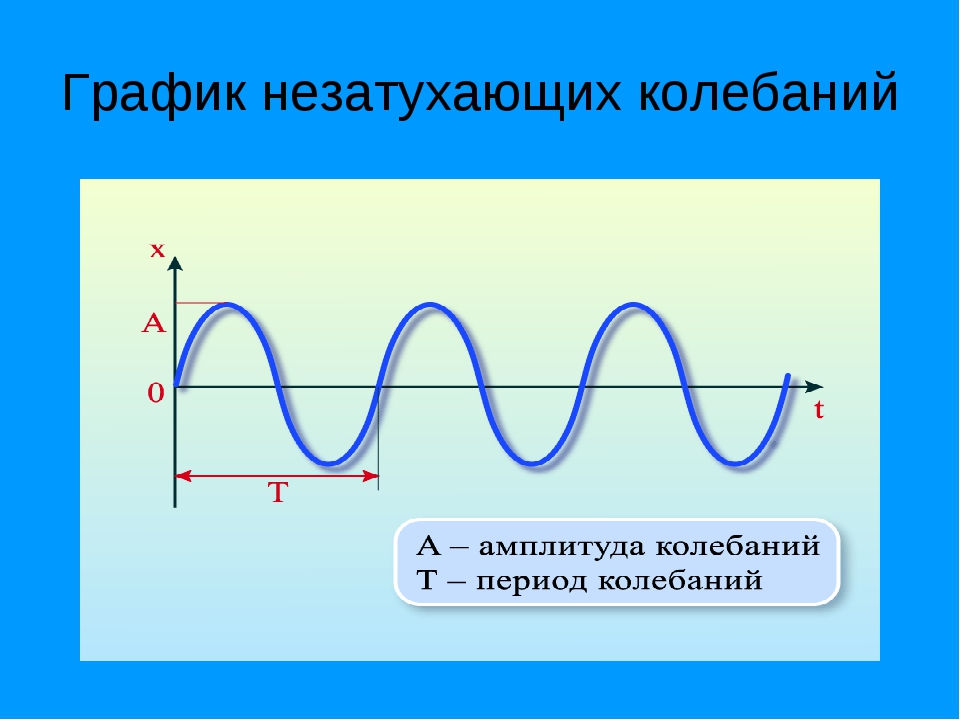
9. Что такое автоколебания? Приведите примеры автоколебаний.
Свободная вибрация – обзор
8.3.3 Свободная вибрация анизотропной прямоугольной пластины
Свободная вибрация тонкой анизотропной прямоугольной пластины или многослойной композитной пластины исследуется с помощью модифицированного DQM. Для сравнений вводятся безразмерные частотные параметры, определяемые формулой , E 11 — модуль упругости в главном направлении 1, а μ 12 и μ 21 — соответственно большой и меньший коэффициенты Пуассона.
Свойства материала пластины: E11/E22=2,45, G12=0,48E22, µ12=0,23. Геометрические параметры h/a=0,006, a/b=1,0.
Для трехслойных угловых слоев θ,−θ,θ симметричных многослойных прямоугольных пластин жесткость пластины при изгибе в уравнении (8.2) определяется как
(8.29)Dij=13∑k=13(Q¯ij)k(zk3−z3) i,j=1,2,6
, где z k и zk−1 — координаты верхней и нижней поверхности слоя k — th , а Q¯ij (i,j=1,2,6) вычисляются по формуле
(8. 30) q¯11 = q11cos4θ + 2q12 + 2q66cos2θsin2θ + q22sin4θq¯22 = q11sin4θ + 2q12 + 2q66cos2θsin2θ + q22cos4θq¯12 = q¯21 = q12 + q22-4q66cos2θsin2θ + q12cos4θ + sin4θq¯66 = q12 + q22-2q12-2q66cos2θsin2θ + Q66cos4θ + sin4θq¯16 = q11-q22-2q66cos3θsinθ + q12-q22 + 2q66cosθsin3θq¯26 = q11-q22-2q6coSθsin3θ + q12q66cosθsin3θ + q12-q22 + 2q66cos3θsinθ
30) q¯11 = q11cos4θ + 2q12 + 2q66cos2θsin2θ + q22sin4θq¯22 = q11sin4θ + 2q12 + 2q66cos2θsin2θ + q22cos4θq¯12 = q¯21 = q12 + q22-4q66cos2θsin2θ + q12cos4θ + sin4θq¯66 = q12 + q22-2q12-2q66cos2θsin2θ + Q66cos4θ + sin4θq¯16 = q11-q22-2q66cos3θsinθ + q12-q22 + 2q66cosθsin3θq¯26 = q11-q22-2q6coSθsin3θ + q12q66cosθsin3θ + q12-q22 + 2q66cos3θsinθ
, где положительный угол θ измеряется против часовой стрелки от x -axis в направлении волокна, то есть от оси x к оси основного материала 1, показанной на рис.7.4.
С некоторыми изменениями можно использовать программу 2 для получения частот. В таблице 8.9 перечислены первые восемь частотных параметров для трехслойных угловых θ,−θ,θ симметричных ламинированных прямоугольных пластин со всеми свободно опертыми краями (SSSS). Толщина каждого слоя одинакова, а общая толщина ламинированной плиты составляет ч . Результаты, перечисленные в таблице 8.9, получены с помощью модифицированного DQM с сеткой III и номером сетки N , равным 21. MMWC-3 используется для применения множественных граничных условий.Данные Лейссы [9] также включены для сравнения. Видно, что результаты, полученные с помощью модифицированного DQM, очень близки и постоянно меньше, чем решения Лейссы с верхней границей. При θ=0o результаты DQ точно такие же, как и точные решения.
MMWC-3 используется для применения множественных граничных условий.Данные Лейссы [9] также включены для сравнения. Видно, что результаты, полученные с помощью модифицированного DQM, очень близки и постоянно меньше, чем решения Лейссы с верхней границей. При θ=0o результаты DQ точно такие же, как и точные решения.
Таблица 8.9. Частотные параметры λ¯ для трехслойного угла θ, -θ, θ симметричные ламинированные квадратные пластины (SSSS)
| PLY-угол | Метод | Номер | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||
| 0° | DQM | 1 90.171 | 33,248 | 44,387 | 60,682 | 64,457 | 90,145 | 93,631 | 108,46 | |||
| CLPT [9] | 15,19 | 33,30 | 44,42 | 60,78 | 64,53 | 90,29 | — | — | ||||
| Точная 15,171 | 33,248 44,387 | 60. 682 64.457 682 64.457 | 90,145 — | — | ||||||||
| 15 | ° DQM | 15.396 | 34,030 | 43,820 | 60,733 | 66,560 | 91,340 | 91,377 | 108,78 | |||
| CLPT [9] | 15,43 | 34,09 | 43,80 | 60,85 | 66,67 | 91,40 | — | — | — | |||
| DQM | 15.853 | 35.768 | 42.768 | 42.524 | 61.275 | 71.275 | 71.546 | 85.589 | 93.489 | 108,65 | ||
| CLPT [9] | 15,90 | 35,86 | 42,62 | 61,45 | 71,71 | 85,72 | — | — | ||||
| 45 ° | DQM | 16,084 | 36.832 | 41.688 | 41.688 | 61.643 | 76.862 | 79.814 | 94.814 | 94.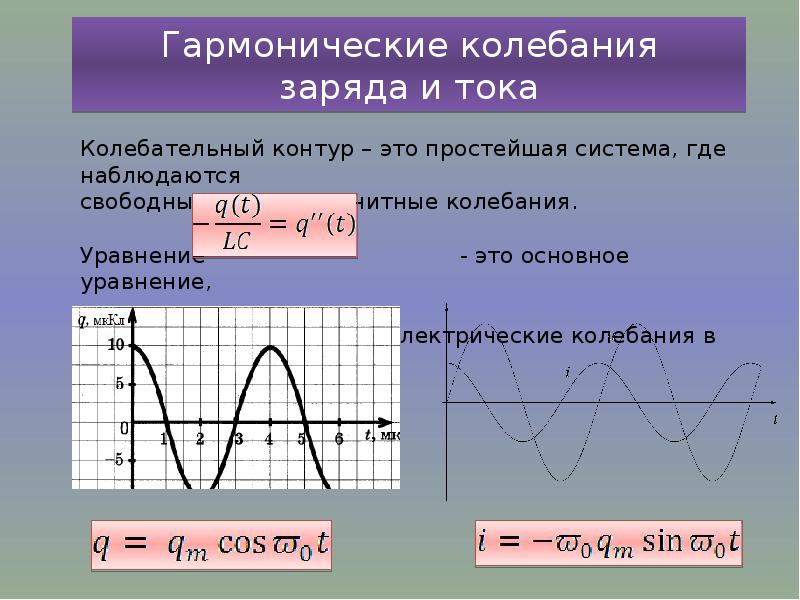 388 388 | 94.388 | |
| CLPT [9] | 16.14 | 36.93 | 41.81 | 61.85 | 77.04 | 80.00 | – | – | ||||
Далее считается свободное колебание всех трехслойных плит с угловыми кромками. Первые восемь ненулевых параметров частоты моды перечислены в таблице 8.10. Поскольку решения с верхней границей недоступны, результаты конечных элементов, полученные NASTRAN с мелкой сеткой, включены для сравнения.
Таблица 8.10. Частотные параметры λ¯ для трехслойных уголковых слоев θ, -θ, θ симметричные ламинированные квадратные пластины (FFFF)
| PLY-угол | Метод | Mode Mode | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 0° | DQM | 2 90.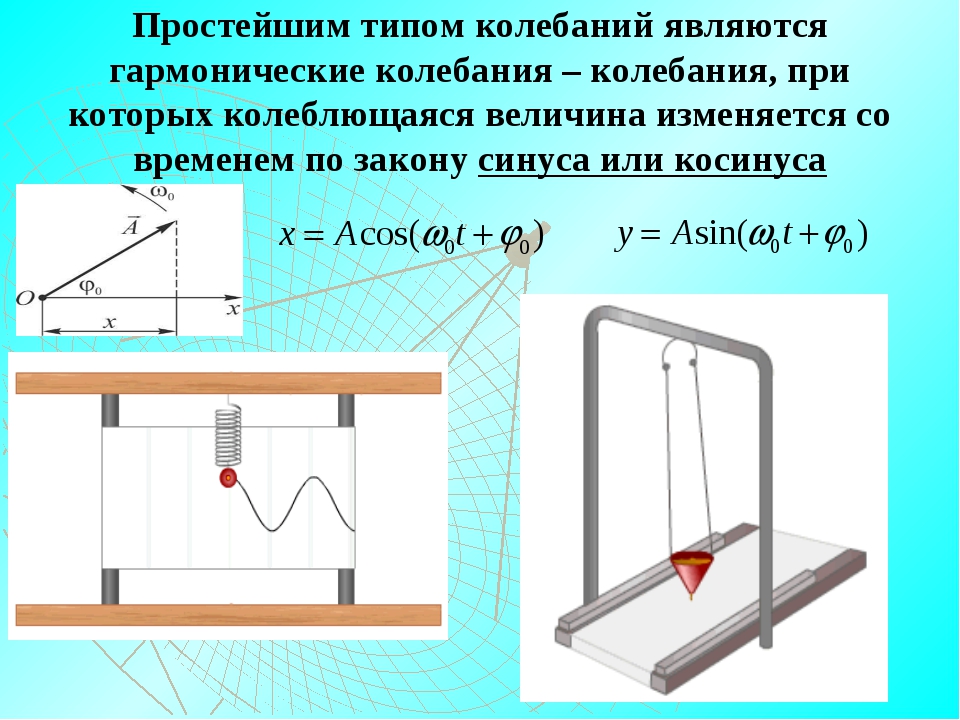 9836 9836 | 14,119 | 22,379 | 24,671 | 29,862 | 39,387 | 48,556 | 49,301 | ||
| ПЭМ | 9,9820 | 14,121 | 22,381 | 24,669 | 29,860 | 39,402 | 48,549 | 49.310 | |||
| 15 ° | DQM | 10.250 | 14.160 | 14.160 | 21.731 | 21.731 | 24.851 | 30.210 | 39.930 | 47.865 | +51,398 |
| ПЭМ | 10,248 | 14,161 | 21,733 | 24,849 | 30,206 | 39,945 | 47,862 | 51,400 | |||
| 30 ° | DQM | 10,793 | 14,350 | 20.299 | 25.287 | 30.604 | 42.287 | 42.287 | 48.047 | 53.550 | 53.550 |
| FEM | 10.791 | 14. 352 352 | 20.301 | 25,284 | 30,599 | 42,303 | 48,044 | 53,551 | |||
| 45 ° | DQM | 11,067 | 14,550 | 19,465 | 25,547 | 30,643 | 46,116 | 48,293 | 48,368 | ||
| 11.063 | 14.545 | 19.460 | 19.460 | 25.531 | 30.621 | 30.621 | 46.091 | 48.251 | 48.251 | 9.343 | |
Результаты перечислены в таблице 8.10 получены с помощью модифицированного DQM с сеткой V, а номер сетки N равен 21. MMWC-3 используется для применения множественных граничных условий. В конечно-элементном анализе используется сетка 100×100 (30 603 степеней свободы) для обеспечения точности решения. Результаты, приведенные в таблице 8.10, относятся к случаям, когда основное направление материала θ изменяется от 0° до 45° с шагом 15°.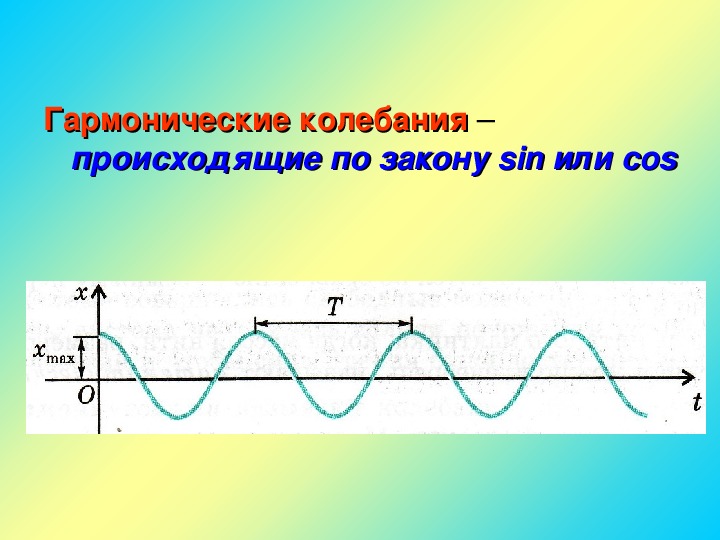 Если используется Grid III, результаты остаются прежними. Другими словами, DQM как с Grid III, так и с Grid V может дать аналогичные точные результаты.Это сильно отличается от случаев изотропных косых пластин со свободными углами. Сильная сингулярность напряжений на тупых углах пластины существует при большом угле перекоса.
Если используется Grid III, результаты остаются прежними. Другими словами, DQM как с Grid III, так и с Grid V может дать аналогичные точные результаты.Это сильно отличается от случаев изотропных косых пластин со свободными углами. Сильная сингулярность напряжений на тупых углах пластины существует при большом угле перекоса.
Из Таблицы 8.10 видно, что результаты, полученные с помощью модифицированного DQM, очень близки к данным конечных элементов и фактически должны быть более точными, чем результаты конечных элементов. Поскольку данные конечных элементов не являются ни решениями с верхней границей, ни решениями с нижней границей, поэтому данные DQ либо немного меньше, либо больше, чем данные конечных элементов.
Внеплоскостная свободная вибрация и вынужденная гармоническая реакция изогнутой балки бумага. Во-первых, даются решения гармонических волн для исследования соотношения дисперсии между частотой и волновым числом, частотой среза, смещением, отношением амплитуд и фазовой диаграммой.
 Получены результаты частотного спектра для проверки работы Канга и Ли.Кроме того, собственные частоты одиночной и составной криволинейной балки рассчитываются путем решения характеристического уравнения в случае свободно-свободной, защемленно-зажатой и свободнозащемленной границ. Наконец, передаточные матрицы изогнутой вне плоскости балки получаются путем объединения непрерывности между различными интерфейсами. Кривые пропускаемости одиночной и составной изогнутой балки сравниваются, чтобы найти зону внимания вибрации. Эта работа будет полезна для расширения изучения внеплоскостных колебаний изогнутых балок.
Получены результаты частотного спектра для проверки работы Канга и Ли.Кроме того, собственные частоты одиночной и составной криволинейной балки рассчитываются путем решения характеристического уравнения в случае свободно-свободной, защемленно-зажатой и свободнозащемленной границ. Наконец, передаточные матрицы изогнутой вне плоскости балки получаются путем объединения непрерывности между различными интерфейсами. Кривые пропускаемости одиночной и составной изогнутой балки сравниваются, чтобы найти зону внимания вибрации. Эта работа будет полезна для расширения изучения внеплоскостных колебаний изогнутых балок. 1. Введение
Изогнутые балки широко используются во многих застроенных и арочных конструкциях из-за их ценного инженерного применения. По сравнению с прямыми балками, пластинами и валами изогнутые балки чрезвычайно сложны, и проблемы с вибрацией этих изогнутых балочных конструкций по-прежнему серьезны, особенно внеплоскостная вибрация.
Свободная вибрация и реакция передачи изогнутых элементов были тщательно исследованы. Мейс провел подробное исследование вибрационного поведения балочных систем, разделив волны на положительные и отрицательные волны, используя волновой подход.Он также вывел матрицу отражения в случае свободно опертой, защемленной и свободной границ. Из волновой точки теоретически получено характеристическое уравнение балки для анализа свободных колебаний [1]. Хуанг исследовал свободные колебания вращающихся тонких колец, используя волновой подход. Решения гармонических волн, частотные спектры, отношение амплитуд смещения и частоты отсечки также анализируются теоретически [2].
Мейс провел подробное исследование вибрационного поведения балочных систем, разделив волны на положительные и отрицательные волны, используя волновой подход.Он также вывел матрицу отражения в случае свободно опертой, защемленной и свободной границ. Из волновой точки теоретически получено характеристическое уравнение балки для анализа свободных колебаний [1]. Хуанг исследовал свободные колебания вращающихся тонких колец, используя волновой подход. Решения гармонических волн, частотные спектры, отношение амплитуд смещения и частоты отсечки также анализируются теоретически [2].
Используя основное уравнение, Канг проанализировал свободные колебания плоской круглой криволинейной балочной системы, принимая во внимание множество точечных разрывов, таких как упругая опора, присоединенная масса и изменения кривизны.Определены дисперсионные уравнения и частоты отсечки [3]. Основываясь на теории Флюгге, Ли рассмотрел волновое движение изогнутых в плоскости балок с постоянной кривизной. Матрица отражения матрицы распространения смещения выводится численно.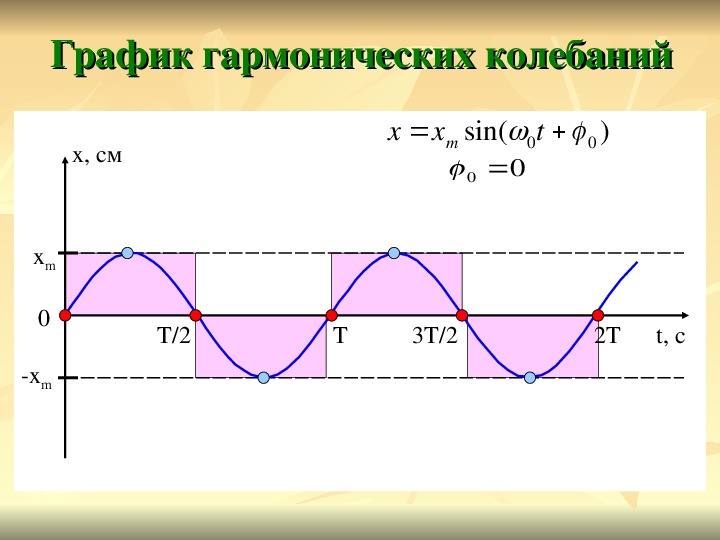 Свободные колебания и потоки энергии, связанные с волнами в искривленной балке, также подробно обсуждаются [4, 5]. Хаусон представил точные внеплоскостные собственные частоты составных изогнутых балок Тимошенко. Собственные частоты непрерывной криволинейной балки рассчитываются при учете эффектов сдвигового прогиба и вращательной инерции [6].Лю представил радиальные колебания круглой пластины, используя подход распространения волн и классический метод, содержащий решение Бесселя и решение Ханкеля для теоретического расчета собственной частоты [7]. Основываясь на управляющем уравнении криволинейной балки в плоскости и вне плоскости, Лю проанализировал передаточную характеристику периодических изогнутых балок, используя метод передаточной матрицы и теорему Блоха. Их теоретические расчеты также моделируются методом МКЭ [8]. Ли разделил основные характеристические дифференциальные уравнения для внеплоскостных колебаний изогнутых неоднородных балок постоянного радиуса и проиллюстрировал влияние коэффициента конусности, центрального угла и длины дуги на собственные частоты изогнутых балок [9].
Свободные колебания и потоки энергии, связанные с волнами в искривленной балке, также подробно обсуждаются [4, 5]. Хаусон представил точные внеплоскостные собственные частоты составных изогнутых балок Тимошенко. Собственные частоты непрерывной криволинейной балки рассчитываются при учете эффектов сдвигового прогиба и вращательной инерции [6].Лю представил радиальные колебания круглой пластины, используя подход распространения волн и классический метод, содержащий решение Бесселя и решение Ханкеля для теоретического расчета собственной частоты [7]. Основываясь на управляющем уравнении криволинейной балки в плоскости и вне плоскости, Лю проанализировал передаточную характеристику периодических изогнутых балок, используя метод передаточной матрицы и теорему Блоха. Их теоретические расчеты также моделируются методом МКЭ [8]. Ли разделил основные характеристические дифференциальные уравнения для внеплоскостных колебаний изогнутых неоднородных балок постоянного радиуса и проиллюстрировал влияние коэффициента конусности, центрального угла и длины дуги на собственные частоты изогнутых балок [9]. Туфекчи исследовал внеплоскостную свободную вибрацию круглой арки с однородным поперечным сечением, принимая во внимание эффекты поперечного сдвига и инерции вращения. Результаты показали, что инерция вращения при изгибе и кручении, а также деформация сдвига оказывают существенное влияние на резонансную частоту, даже если рассматриваются тонкие неглубокие арки [10]. Ву предложил новый подход к анализу свободных колебаний арок с учетом эффектов деформации сдвига и инерции вращения. Он рассчитал собственные частоты для зажато-зажатой и свободно-свободной границ [11].Чтобы получить собственные частоты и формы колебаний изогнутых балок с шарнирно-шарнирными, шарнирно-зажимными и защемленно-зажимными границами, Ли вывел дифференциальные уравнения, описывающие внеплоскостные свободные колебания упругих криволинейных балок с переменной кривизной. Их экспериментальные измерения показывают, что собственные частоты хорошо согласуются с теоретическими результатами [12]. Приняв классическую теорию тонкой пластины Кирхгофа, Заде суммирует влияние кривых дисперсионного соотношения на распространение неплоских волн в плоских упругих пластинах с постоянной кривизной [13].
Туфекчи исследовал внеплоскостную свободную вибрацию круглой арки с однородным поперечным сечением, принимая во внимание эффекты поперечного сдвига и инерции вращения. Результаты показали, что инерция вращения при изгибе и кручении, а также деформация сдвига оказывают существенное влияние на резонансную частоту, даже если рассматриваются тонкие неглубокие арки [10]. Ву предложил новый подход к анализу свободных колебаний арок с учетом эффектов деформации сдвига и инерции вращения. Он рассчитал собственные частоты для зажато-зажатой и свободно-свободной границ [11].Чтобы получить собственные частоты и формы колебаний изогнутых балок с шарнирно-шарнирными, шарнирно-зажимными и защемленно-зажимными границами, Ли вывел дифференциальные уравнения, описывающие внеплоскостные свободные колебания упругих криволинейных балок с переменной кривизной. Их экспериментальные измерения показывают, что собственные частоты хорошо согласуются с теоретическими результатами [12]. Приняв классическую теорию тонкой пластины Кирхгофа, Заде суммирует влияние кривых дисперсионного соотношения на распространение неплоских волн в плоских упругих пластинах с постоянной кривизной [13]. Уолш исследовал передачу мощности вибрации в криволинейных балках с учетом момента инерции и деформации сдвига [14]. Чидамбарам обобщил обширную опубликованную литературу о колебаниях изогнутых стержней, балок, колец и арок произвольной формы. Он теоретически вывел характеристические дифференциальные уравнения плоскостных, внеплоскостных и связанных колебаний. Его исследования в основном сосредоточены на собственных частотах для расширенных мод и неэкстенсивных мод с различными граничными условиями [15].Ван исследовал колебания изогнутой балки в плоскости, рассматривая момент инерции и эффект сдвига. Он получил дисперсионное соотношение волнового числа и частоты и проанализировал радиальную и тангенциальную связанные запрещенные зоны периодического искривленного луча [16].
Уолш исследовал передачу мощности вибрации в криволинейных балках с учетом момента инерции и деформации сдвига [14]. Чидамбарам обобщил обширную опубликованную литературу о колебаниях изогнутых стержней, балок, колец и арок произвольной формы. Он теоретически вывел характеристические дифференциальные уравнения плоскостных, внеплоскостных и связанных колебаний. Его исследования в основном сосредоточены на собственных частотах для расширенных мод и неэкстенсивных мод с различными граничными условиями [15].Ван исследовал колебания изогнутой балки в плоскости, рассматривая момент инерции и эффект сдвига. Он получил дисперсионное соотношение волнового числа и частоты и проанализировал радиальную и тангенциальную связанные запрещенные зоны периодического искривленного луча [16].
Вышеупомянутая литература в основном посвящена анализу вибрации в плоскости изогнутых балок, в то время как анализ вибрации вне плоскости изогнутых балок встречается редко. Кроме того, насколько известно авторам, исследуется множество внеплоскостных свободных колебаний и характеристик передачи изогнутых элементов в случае, если не учитываются момент инерции и сила сдвига. Чтобы точно показать динамическое поведение, в этой статье делается попытка провести подробное исследование изогнутых балок, включая два фактора для анализа соотношения дисперсии, свободных колебаний и отклика передачи.
Чтобы точно показать динамическое поведение, в этой статье делается попытка провести подробное исследование изогнутых балок, включая два фактора для анализа соотношения дисперсии, свободных колебаний и отклика передачи.
Документ состоит из пяти разделов. Раздел 1 представляет собой краткое введение. В разделе 2 характеристическое уравнение внеплоскостной вибрации для изогнутой балки рассчитано теоретически с учетом момента инерции и эффекта сдвига. В разделе 3 классическим методом вычисляются собственные частоты одиночных и составных криволинейных моделей с зажато-зажатыми, свободно-свободными и зажато-свободными границами.В разделе 4 получена передаточная характеристика модели одиночного и периодического искривленного луча. Раздел 5 является заключением.
2. Теоретический анализ
2.1. Управляющие уравнения
Рассмотрим небольшой сегмент неплоскостной модели искривленной балки, показанной на рисунке 1, где – поперечное смещение, – наклон изгиба, – угол поворота, – крутящий момент, – изгибающий момент о радиальная ось, и представляет собой поперечную силу. После учета поперечной силы и момента инерции связанное определяющее уравнение неплоскостной криволинейной балки можно записать следующим образом [6]: где – плотность, площадь поперечного сечения, второй момент площади, полярная секунда момент и радиус центра.
После учета поперечной силы и момента инерции связанное определяющее уравнение неплоскостной криволинейной балки можно записать следующим образом [6]: где – плотность, площадь поперечного сечения, второй момент площади, полярная секунда момент и радиус центра.
2.2. Harmonic Wave Solution
Для решения уравнений (1)–(3) , , и задаются гармонической формой: где – частота окружности, – мнимая единица, , , – амплитуда поперечного смещения, изгибный уклон и угол поворота соответственно. Подставляя уравнения (4)–(6) в уравнения (1)–(3), можно иметь
Уравнения (7)–(9) можно представить в следующем матричном виде:
Составляя определитель коэффициента нулевая матрица, ее можно упростить до
Здесь конкретное выражение параметров дает следующее:
Согласно определению гармонического движения можно получить следующие соотношения, , , , , и :
тогда можно определить как корень характеристических уравнений (2)–(19), и .Таким образом, удовлетворяет следующему соотношению: где , , и – корни уравнения (20).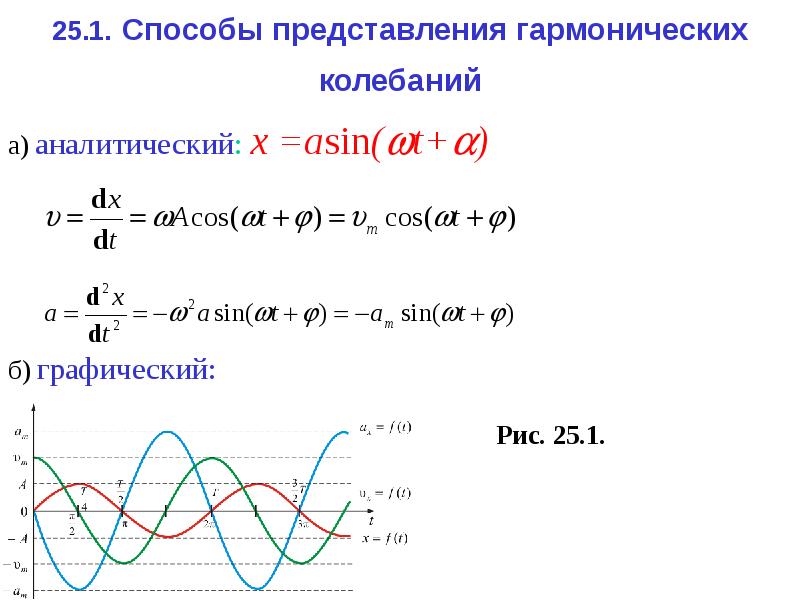 Поэтому можно переписать так:
Поэтому можно переписать так:
Для удобства упрощения здесь можно получить следующие соотношения:
2.2.1. Частота отсечки
Уравнение (11) описывает соотношение спектра частот дисперсии для распространения волны в искривленном луче. Частота среза, обозначенная , определяет этот дополнительный частотный спектр для изогнутого луча. Когда предел стремится к нулю, уравнение (11) может быть дополнительно упрощено как
Решая уравнение (27), три корня для дают
Из уравнения (13d) можно получить
Здесь, дает следующих трех корней: (i) Учитывая первый корень , а именно , из уравнений (29) и (30), получить , , и .Вышеупомянутые характеристики показывают, что есть только вращательное движение, но нет изгибающего и крутильного движения. (ii) Учитывая второй корень , а именно, из уравнений (29) и (30), получить , , и . Это показывает, что криволинейная балка имеет только изгибающее и крутильное движение, но не вращательное движение. (iii) Рассмотрим третий корень , а именно . Согласно уравнениям (29) и (30), это указывает , , и , что приводит только к изгибающему и вращательному движению, но не к крутильному движению.
Согласно уравнениям (29) и (30), это указывает , , и , что приводит только к изгибающему и вращательному движению, но не к крутильному движению.
2.2.2. Частотный спектр
Волны можно разделить на положительные и отрицательные волны, в то время как волна распространяется в криволинейном луче. Такое поведение волнового движения имеет важное значение для характеристик изогнутой балки. Здесь параметр материала приведен в таблице 1, а параметр конструкции выбран следующим образом.
| |||||||||||||||||
Структурный параметр: Радиус, длина, ширина, толщина и фактор формы.
Путем вычисления корней характеристического уравнения (20) можно теоретически получить дисперсионные соотношения криволинейной балки. На рисунке 2 показаны реальные и мнимые волновые числа движения частотного спектра для модели изогнутой балки.
На рис. 2 видно, что эти волны делят частотный спектр на четыре области при распространении волны в данной модели, а именно область I, область II, область III и область IV. Есть три точки бифуркации: , и . Затем можно заметить, что эти точки бифуркации играют важную роль в определении поведения волнового движения. Здесь значение частоты отсечки можно рассчитать как , изображенное на рисунке 2. На этой частоте окружность изогнутого луча имеет радиальную длину волны, и она называется кольцевой частотой [4].
Уравнение (20) можно рассматривать как кубическое уравнение, содержащее переменный параметр . В силу , уравнение (20) имеет шесть корней, а именно три волны прямого распространения и три волны отрицательного распространения. Как показано на рис. 2, частотные спектры симметричны для модели протяженной изогнутой балки [2]. В области I все волновые моды являются чисто реальными, так что общая волна может распространяться вдоль искривленного луча без затухания. В области II из-за сложной волны существуют реальные и воображаемые связанные волновые моды, которые указывают на то, что волны имеют положительное и отрицательное направление.В области III в аналогичных случаях волны бывают как положительными, так и отрицательными. В области IV чисто реальной является только одна волновая мода, соответствующая распространяющейся волне, а другая волна будет постепенно рассеиваться.
Как показано на рис. 2, частотные спектры симметричны для модели протяженной изогнутой балки [2]. В области I все волновые моды являются чисто реальными, так что общая волна может распространяться вдоль искривленного луча без затухания. В области II из-за сложной волны существуют реальные и воображаемые связанные волновые моды, которые указывают на то, что волны имеют положительное и отрицательное направление.В области III в аналогичных случаях волны бывают как положительными, так и отрицательными. В области IV чисто реальной является только одна волновая мода, соответствующая распространяющейся волне, а другая волна будет постепенно рассеиваться.
Основываясь на теории Лава, Канг вывел плоскостное уравнение искривленного луча и проанализировал дисперсионные соотношения частотного спектра, показанные на рис. 3. Аналогичным образом, на основе теории Флюгге, Ли также получил дисперсионные соотношения, показанные на рис. 4. и 5, и настоящие результаты подтверждают правильность работы Канга.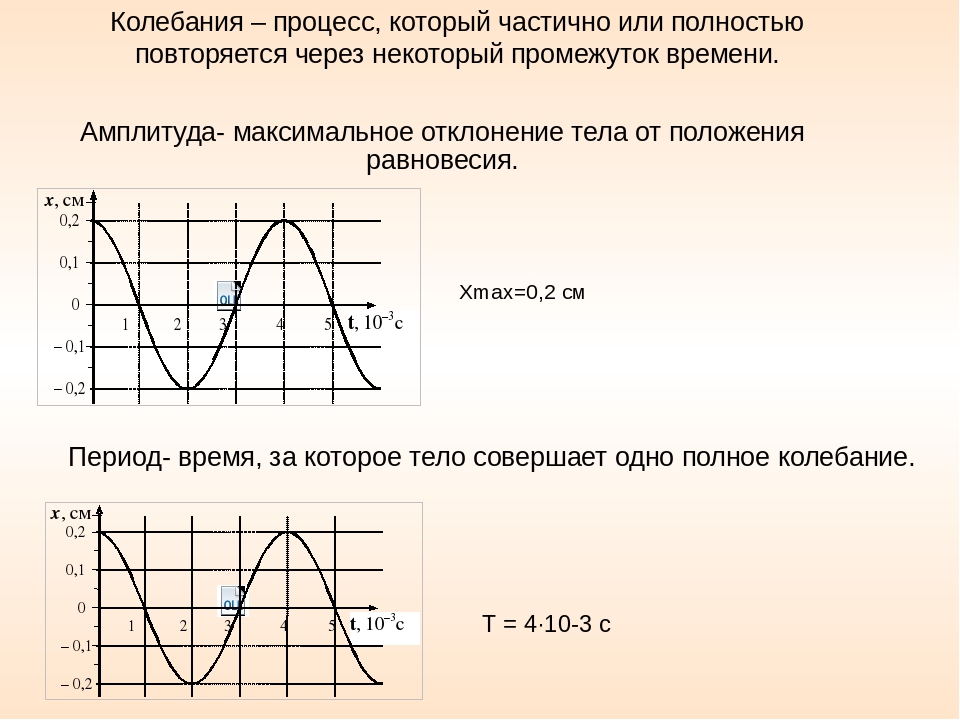 Эти работы очень важны для анализа моделей криволинейных балок, поскольку это упрощенная модель с пренебрежением эффектами вращательной инерционной сдвиговой деформации. На самом деле, эти факторы являются существенными и не могут быть проигнорированы. В настоящее время исследования вне плоскости проводятся редко. Чтобы провести дальнейшее исследование, в этой статье не только подчеркиваются дисперсионные соотношения, но также основное внимание уделяется свободным колебаниям и принудительному отклику.
Эти работы очень важны для анализа моделей криволинейных балок, поскольку это упрощенная модель с пренебрежением эффектами вращательной инерционной сдвиговой деформации. На самом деле, эти факторы являются существенными и не могут быть проигнорированы. В настоящее время исследования вне плоскости проводятся редко. Чтобы провести дальнейшее исследование, в этой статье не только подчеркиваются дисперсионные соотношения, но также основное внимание уделяется свободным колебаниям и принудительному отклику.
2.2.3. Коэффициент амплитуды смещения
Поперечное смещение, наклон изгиба и угол поворота внеплоскостной вибрации изогнутой балки не являются независимыми друг от друга.То есть, они связаны друг с другом. Из уравнений (22) и (23) можно теоретически получить отношение амплитуд и фазу поперечного смещения и наклона изгиба для трех положительных волн, приняв .
На рис. 6 показано отношение амплитуды и фазы поперечного смещения к углу поворота для трех положительных волн для изогнутой балки. Аналогично, на рисунке 7 показано отношение амплитуды и фазы наклона изгиба к углу поворота для трех положительных волн для изогнутой балки.Из рисунков 6 и 7 видно, что четыре области, показанные на рисунке 2, явно не отмечены, но отмечена частота среза. Кроме того, можно заметить, что фазы поперечного смещения и наклона изгиба находятся между и .
Аналогично, на рисунке 7 показано отношение амплитуды и фазы наклона изгиба к углу поворота для трех положительных волн для изогнутой балки.Из рисунков 6 и 7 видно, что четыре области, показанные на рисунке 2, явно не отмечены, но отмечена частота среза. Кроме того, можно заметить, что фазы поперечного смещения и наклона изгиба находятся между и .
3. Свободные колебания криволинейной балки
В этом разделе теоретически рассчитаны свободные колебания внеплоскостных колебаний одинарной криволинейной балки с использованием классического метода. Согласно классическому граничному условию можно получить характеристическое уравнение криволинейной балки.
3.1. Для одинарной модели
Собственные частоты внеплоскостной вибрации для одинарной изогнутой балки, показанной на рис. 8, получены теоретически с использованием классического метода. Согласно классическому граничному условию можно получить характеристическое уравнение криволинейной балки.
Для искривленной балки с защемленно-защемленными границами можно получить
Для свободно-свободных границ имеем следующие соотношения:
Для защемленно-свободных границ получим
В этом случае уравнение (26) можно дополнительно сократить до
Уравнение (33) является характеристическим уравнением внеплоскостных колебаний для криволинейной балки с защемленными свободными границами.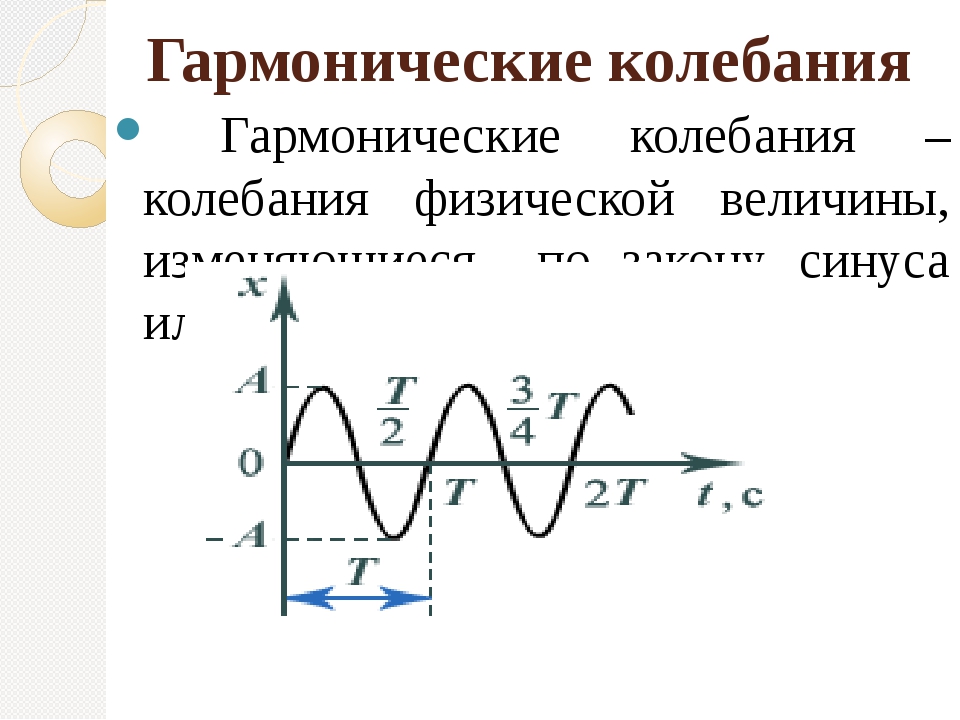 Аналогично, теоретически может быть получено и характеристическое уравнение с зажато-зажатой и свободно-свободной границами. На рис. 9 представлена характеристическая кривая собственной частоты криволинейного луча в случае защемленно-зажатой, свободно-свободной и защемленно-свободной границ. Решив характеристическое уравнение, можно получить собственную частоту изогнутой балки. Можно найти, что точка пересечения характеристической кривой на оси X является собственной частотой. В табл. 2 приведены собственные частоты, рассчитанные на зажато-зажатой и свободно-свободной границах.На рис. 10 показана реакция передачи внеплоскостной вибрации для модели изогнутой балки. Можно обнаружить, что значения собственной частоты на рис. 10 равны значениям для свободного случая в табл. 2, что иллюстрирует правильность численных результатов.
Аналогично, теоретически может быть получено и характеристическое уравнение с зажато-зажатой и свободно-свободной границами. На рис. 9 представлена характеристическая кривая собственной частоты криволинейного луча в случае защемленно-зажатой, свободно-свободной и защемленно-свободной границ. Решив характеристическое уравнение, можно получить собственную частоту изогнутой балки. Можно найти, что точка пересечения характеристической кривой на оси X является собственной частотой. В табл. 2 приведены собственные частоты, рассчитанные на зажато-зажатой и свободно-свободной границах.На рис. 10 показана реакция передачи внеплоскостной вибрации для модели изогнутой балки. Можно обнаружить, что значения собственной частоты на рис. 10 равны значениям для свободного случая в табл. 2, что иллюстрирует правильность численных результатов.
| |||||||||||||||||||||||||||||
3.
 2. Для составной модели
2. Для составной модели Аналогично, собственные частоты внеплоскостных колебаний для составной изогнутой балки также рассчитываются численно с использованием классического метода. Согласно классическому граничному условию можно получить характеристическое уравнение криволинейной балки.
Процесс решения зажато-зажатых и свободно-свободных границ для составной модели криволинейной балки, показанной на рисунке 11, аналогичен случаю без защемления. Здесь представлен свободный от зажимов случай для расчета собственных частот.Для свободно защемленных границ имеем
В этом случае, комбинируя уравнения (32) и (33), можно установить следующий набор соотношений:
Решив корень в уравнении (35), можно получить собственные частоты внеплоскостных колебаний составной криволинейной балки. На рис. 12 приведены характеристические кривые собственной частоты внеплоскостных колебаний составной криволинейной балки в случае трех классических границ. Можно найти, что точка пересечения характеристической кривой на оси X является собственной частотой. Значения собственной частоты, полученные для этих трех случаев, приведены в таблице 3. На рисунке 13 показана характеристика передачи внеплоскостной вибрации для композитной изогнутой балки, а собственные частоты, описанные на рисунке 13, такие же, как и в таблице 3. Другими словами, точки резонанса на кривых передачи, полученных с помощью импульсной характеристики, являются собственными частотами.
Значения собственной частоты, полученные для этих трех случаев, приведены в таблице 3. На рисунке 13 показана характеристика передачи внеплоскостной вибрации для композитной изогнутой балки, а собственные частоты, описанные на рисунке 13, такие же, как и в таблице 3. Другими словами, точки резонанса на кривых передачи, полученных с помощью импульсной характеристики, являются собственными частотами.
| |||||||||||||||||||||||||||||||||||
4.
 Отклик передачи для периодического искривленного луча
Отклик передачи для периодического искривленного луча 4.1. Базовая модель
В этом разделе для дальнейшего изучения характеристик передачи в качестве численного примера для анализа передаваемости путем применения метода матрицы переноса взяты периодические модели криволинейных балок для внеплоскостной вибрации. Здесь на Рисунке 14 представлена базовая модель, состоящая из восьми периодов, состоящих из смолы материала I и стали материала II. Углы из смолы и стали равны и соответственно.В таблице 4 приведены параметры материала. Модуль сдвига, плотность и коэффициент Пуассона смолы равны , и , соответственно. Модуль сдвига, плотность и коэффициент Пуассона стали равны , , и .
На приведенных выше рисунках показаны два отклика на разных частотах. Напомним, что значение ω n исходит из физических характеристик системы (m, k), а ω 0 исходит из силы, приложенной к системе. Эти отклики суммируются для получения синего отклика (общее решение) на третьем рисунке. Установившийся отклик На самом деле эта наложенная реакция длится недолго. Амплитуда вынужденной вибрацииАмплитуда установившейся вынужденной вибрации зависит от отношения вынужденной частоты к собственной частоте. Когда ω 0 приближается к ω n (отношение приближается к 1), величина D становится очень большой.2} \] |
|||||||||||||||||||||||||||||||||||||||||
На рисунке выше мы можем обсудить различные случаи:
- ω 0 = ω n : резонанс .
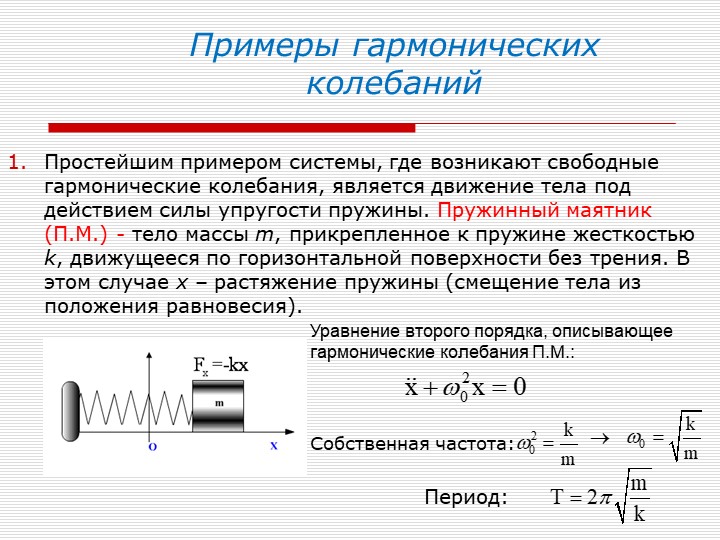 Это приводит к колебаниям очень большой амплитуды и связано с высокой нагрузкой и выходом из строя системы.
Это приводит к колебаниям очень большой амплитуды и связано с высокой нагрузкой и выходом из строя системы. - ω 0 ~ 0, MF ~ 1 : Вынуждающая функция является почти статической, оставляя по существу статическое отклонение и ограниченную естественную вибрацию.
- ω 0 < ω n : Увеличение положительно и больше 1, что означает, что колебания находятся в фазе (когда сила действует влево, система смещается влево) и амплитуда вибрации больше, чем статическое отклонение.
- ω 0 > ω n : Увеличение отрицательное, а абсолютное значение обычно меньше 1, что означает, что вибрация не совпадает по фазе с движением вынуждающей функции (когда сила действует на влево система смещается вправо) и амплитуда вибрации меньше статического прогиба.
- ω 0 >> ω n : Сила меняет направление слишком быстро, чтобы блок мог реагировать на движение.

Вращающийся дисбаланс
Одной из частых причин вынужденной гармонической вибрации в механических системах является дисбаланс вращения. Это происходит, когда ось вращения не проходит через центр масс. В этой ситуации центр масс вместо того, чтобы оставаться неподвижным, испытывает некоторое ускорение. Это вызывает силу на оси, которая меняет направление при вращении центра масс. Мы можем представить это как небольшую массу м , вращающуюся вокруг оси вращения на некотором расстоянии, называемом эксцентриситетом, e .Вынужденная угловая частота, ω 0 , в данном случае является угловой частотой вращающейся системы.
МЭК3403
(Эти примечания были изменены по сравнению с версией, созданной Крис Снук)
Преамбула
Простое определение механического вибрация движение частицы или твердого тела, которое совершает колебания о положении равновесия. Колебательное движение
проходит цикл:
Колебательное движение
проходит цикл: - начальное возмущение (перемещение или скорость)
- восстановление
- перерегулирование
- восстановление
- перерегулирование
- ….
Результирующее движение является синусоидальным, с «угловым частота сущ. (n равно 2 пи, умноженным на количество циклов в во-вторых.)
Теперь восстанавливающая сила может проявляться во многих формах. В
маятник возникает в момент
гравитационная сила, действующая на «боб», пропорциональна
отклонение в сторону от оси.Во многих из
систем, которые мы будем здесь рассматривать, может привести
от растяжения или сжатия пружины, так что
ускорение зависит от жесткости пружины и массы
быть перемещенным. Он мог бы даже описать
Кресло-качалка!
В
маятник возникает в момент
гравитационная сила, действующая на «боб», пропорциональна
отклонение в сторону от оси.Во многих из
систем, которые мы будем здесь рассматривать, может привести
от растяжения или сжатия пружины, так что
ускорение зависит от жесткости пружины и массы
быть перемещенным. Он мог бы даже описать
Кресло-качалка!
В механической системе вибрация обычно нежелательна
потому что это увеличивает напряжения в механических компонентах,
связаны с потерями энергии и циклическими
стрессы могут способствовать проблемам с усталостью.Тем не мение,
могут быть случаи, когда мы хотим, чтобы возникла вибрация
например, вибрационные смесители или системы обработки материалов.
В любом случае нам нужно хорошее понимание
глубинные явления и способность моделировать такие
поведение, так что мы можем предсказать поведение
колебательная система при заданных условиях эксплуатации.
Мы начнем, я надеюсь, с пересмотра материала из курса MEC2401 Динамика 1.
Начнем с рассмотрения небольшой массы m, сидящей на горизонтальная поверхность без трения, прикрепленная к левой стенки линейной упругой пружиной. Это классическая пружинно-массовая система многих студентов текстовые книги. Изначально система находится в своем положение равновесия (то есть пружина не растягивается и не сжимается).
Масса затем перемещается на расстояние x o к правильно, и система выходит из состояния покоя.
В этот момент пружина растянута и поэтому обеспечивая возвращающую силу влево. Эта сила вызывает ускорение массы влево пропорционально к приложенной силе.
Когда масса проходит положение равновесия, сила
весной равна нулю, но масса теперь имеет кинетическую
энергии (импульса) и продолжает двигаться влево. В настоящее время
масса должна совершить работу, чтобы сжать пружину, поэтому ее
кинетическая энергия уменьшается по мере накопления упругой энергии в
пружина увеличивается.
В настоящее время
масса должна совершить работу, чтобы сжать пружину, поэтому ее
кинетическая энергия уменьшается по мере накопления упругой энергии в
пружина увеличивается.
Этот переход кинетической энергии в потенциальную энергию и обратно является центральным элементом колебательной системы.
Нажмите на изображение выше, чтобы увидеть анимацию.
Некоторые определения
Во-первых, мы должны получить нашу основную терминологию правильно. [Непрерывная система]
Это имеет два значения. В одной непрерывной системе
это тот, который состоит из компонентов реальной формы.В
в нашем примере выше пружина представляет собой спирально закрученную проволоку.
известного диаметра, с большим диаметром витка и реальным
конечная геометрия. Если вернуться к своим заметкам из MEC2301
Дизайн элементов машин можно разработать как спиральный
пружины на самом деле работают и соотношение между усилием
и сжатие пружины (смещение), вызванное
сочетание катушки, диаметра проволоки и количества
активные катушки. Второе значение заключается в том, что время
непрерывное, а не «ступенчатое» время цифрового
моделирование.
Второе значение заключается в том, что время
непрерывное, а не «ступенчатое» время цифрового
моделирование.
[Дискретный или сосредоточенный Модели параметров] Если мы объединим все вышеперечисленное поведения мы обнаруживаем, что можем свалить в одну кучу все физические вести себя вместе и наблюдать за общими отношениями что сила пружины F и смещение пружины при любой момент х связаны между собой, и мы называем этот термин жесткостью k система.Подход с сосредоточенными параметрами позволяет нам разработать стандартные методы анализа того, что в противном случае быть сложными системами. Альтернатива система «распределенный параметр» относится к другому классу полностью, что мы не будем здесь рассматривать. Ан например «Slinky», где вся динамика находится в распределенная масса пружины!
[Степень свободы]
Это количество независимых измерений, необходимых
для описания положения системы в любой момент времени. В нашей системе пружинных масс нам нужно использовать только x, положение
массу, потому что это также дает нам расширение или
сжатие пружины.
В нашей системе пружинных масс нам нужно использовать только x, положение
массу, потому что это также дает нам расширение или
сжатие пружины.
[Переменные состояния] В приведенной выше простой системе пружины-массы нам нужно знать как водоизмещение x и скорость v определить будущее поведение. Это особенно важно, когда мы рассматриваем системы с демпфированием.
[Свободная вибрация] Свободная вибрация – это движение, возникающее при движении системы. выведен из положения равновесия и в результате движение свободно от какого-либо дополнительного воздействия/силы.
[Недемпфированный свободный
вибрация] — это свободное колебание системы, которая
не имеет включенного демпфирования. Такая система будет
теоретически вибрировать вечно. Однако в реальной жизни мы
знайте, что всегда есть некоторая потеря энергии и, таким образом, все
свободные колебания со временем затухнут.
[Затухание свободных колебаний] свободная вибрация, когда есть какая-то форма демпфирования поведение. Наиболее распространенным, который мы рассматриваем, является вязкостное демпфирование (сила демпфирования пропорциональна скорость).
[Принудительно (бесплатно или демпфированная) вибрация] — это вибрация, которая постоянно управляется какой-то внешней вынуждающей функцией. Это может быть электродвигатель, который может иметь небольшой неуравновешенная масса, сотрясающая вибрирующую система.Эта вынужденная вибрация будет продолжаться еще долго после любая свободная вибрация затихла.
[Собственная частота]
обратно времени, необходимому для одного полного
цикл движения колебательной системы. Это обычно
обозначается как f
хотя иногда f n тоже есть
использовал. Единицы: герц
(Гц) = 1 цикл в секунду.
Единицы: герц
(Гц) = 1 цикл в секунду.
[натуральный круговой (или угловая) частота] измеряется в радианах в секунду (чтобы упростить математику дифференцирования) и имеет символ , где = 2 pi f n
1.Уравнения движения
Прямое применение 2-го закона Ньютона
Нашей первой задачей является разработка уравнений движения для наша пружинно-массовая система. Рассмотрим массу и измерить его смещение от положения равновесия как х и его скорость как v.
В любой позиции x, мы можем нарисовать диаграмму свободного тела массы и рассмотреть силы, действующие на него.
Масса находится справа от положения покоя, поэтому x положителен, и
поэтому пружина прикладывает силу к массе слева
пропорциональна жесткости и x, поэтому F = kx. собственный вес
(мг), действующая вниз, и нормальная сила,
ролики противодействуют этому включены для
полнота. Если бы масса сместилась влево, x был бы отрицательным.
а возвращающая сила F будет действовать в другом направлении.
собственный вес
(мг), действующая вниз, и нормальная сила,
ролики противодействуют этому включены для
полнота. Если бы масса сместилась влево, x был бы отрицательным.
а возвращающая сила F будет действовать в другом направлении.
Применение второго закона Ньютона в форме приводит нас к уравнению движения для этой пружинно-массовой системы:
Еще одна манипуляция с уравнением движения: необходимо, чтобы он принял форму второго порядка обыкновенное дифференциальное уравнение:
Но вместо этого мы можем записать это как два первого порядка уравнения
где «точка» представляет d/dt и Это значительно упрощает работу при наличии демпфирования или когда мы хотим смоделировать что-либо.
| |
Упражнение 1.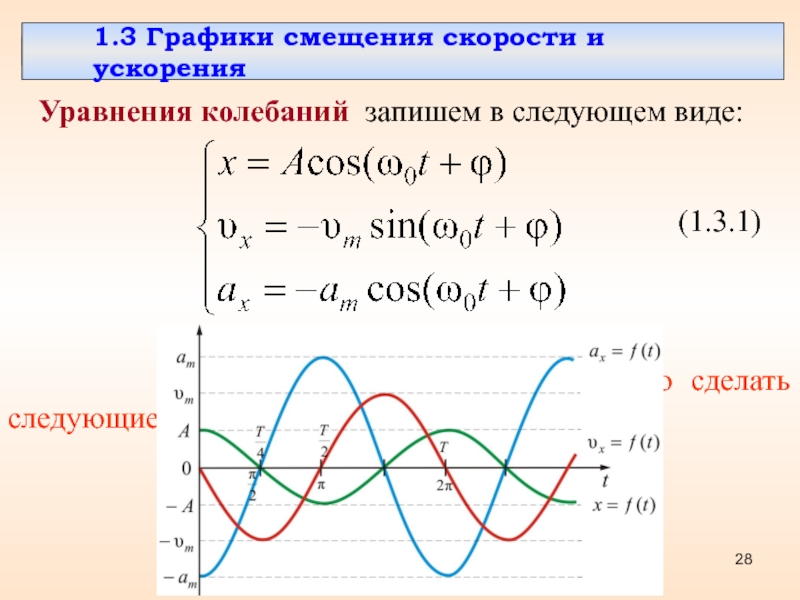 1 1 Мы можем изменить это уравнение движения так, чтобы можно найти ускорение как функцию жесткость и настоящее положение: или разбить его на уравнения первого порядка как и Теперь мы можем интегрировать v, чтобы получить x, в то же время время интегрирования (-kx/m), чтобы получить в.Но мы сначала смотрим на программное обеспечение а не алгебра. Когда время движется на небольшой шаг dt вперед, x изменяется на новое значение x + v*dt Точно так же новое значение v равно v — (k/m)*x*dt Итак, когда мы превратим их в две строки компьютера code у нас есть способ смоделировать систему.  Сначала мы задаем x и v их начальные условия,
выбрать подходящее малое значение для dt, тогда мы
запустить цикл, содержащий
Сначала мы задаем x и v их начальные условия,
выбрать подходящее малое значение для dt, тогда мы
запустить цикл, содержащий x = x + v*dt; и постройте график x и v в зависимости от t по мере продвижения. Теперь вы должны применить эти знания, пытаясь решить следующую задачу: Для пружинно-массовой системы с
m=1 кг и k=15 Н/м Еще лучше, вы попробуете несколько подходов и сравните результаты. В разделе 3.1
вы найдете простое решение, которое использует
JavaScript. |
Использование методов работы-энергии (гамильтониан)
Это метод
анализировать системы, когда гораздо проще
Метод «законов Ньютона» не очевиден. Всегда сначала пробуйте Newton!
Всегда сначала пробуйте Newton! |
В качестве примера мы сейчас попробуем ту же задачу используя метод работы-энергии.Отметим, что нет внешние силы, действующие на систему (т.е. массу) и поэтому полная энергия системы постоянна (не меняется во времени). Итак,
T = кинетическая энергия
V г = гравитационная потенциальная энергия (ноль в этом примере)
V e = упругая потенциальная энергия (энергия хранится весной) Замена этих терминов:
Дальнейшее упрощение приводит к:
| По отзыву
что синус 2 + cos 2 =1, вы
видно, что решение может быть выражено в виде
синусоидальная волна со сдвигом по фазе, такая как Теперь скорость будет пропорциональна косинус вместо синуса, и Пифагор будет приравняем сумму квадратов к 1.  Нажмите на эту ссылку, чтобы увидеть пример «кругового движения». |
Если это выражение постоянно, то скорость его изменения по времени равен нулю:
Очевидным и тривиальным решением является dx/dt=0, так что другое решение представляет больший интерес. Когда мы делим по dx/dt получаем:
Это, конечно, то самое уравнение движения, которое мы получается прямым применением второго закона Ньютона.Этот энергетический подход, кажется, требует много работы, но это может принести плоды, когда мы перейдем к более сложным системы и системы с более чем одной степенью Свобода.
В целом, однако, этот метод больше подходит для эрудированные статьи, а не для нападок на прям проблема.
Возможно, вы захотите проработать раздел о гамильтониане и
лагранжевы подходы, которые будут
более подробно рассмотрены позже.
2. Общее решение
Общий вид линейной незатухающей однородной дифференциальное уравнение второго порядка часто записывают в по следующей форме:Но берегись! Вибрация не только в пружинах и массы. Вы должны уметь анализировать простые маятник длины L, чтобы получить аналогичное уравнение, где
Уравнение движения для более сложной системы, которая имеет демпфирование, будет иметь «средний срок», включающий дх/дт.
Во всех последующих анализах
всегда используется для представления квадратного корня термина в
фронт x, угловая частота, на которой система
будет колебаться без затухания.
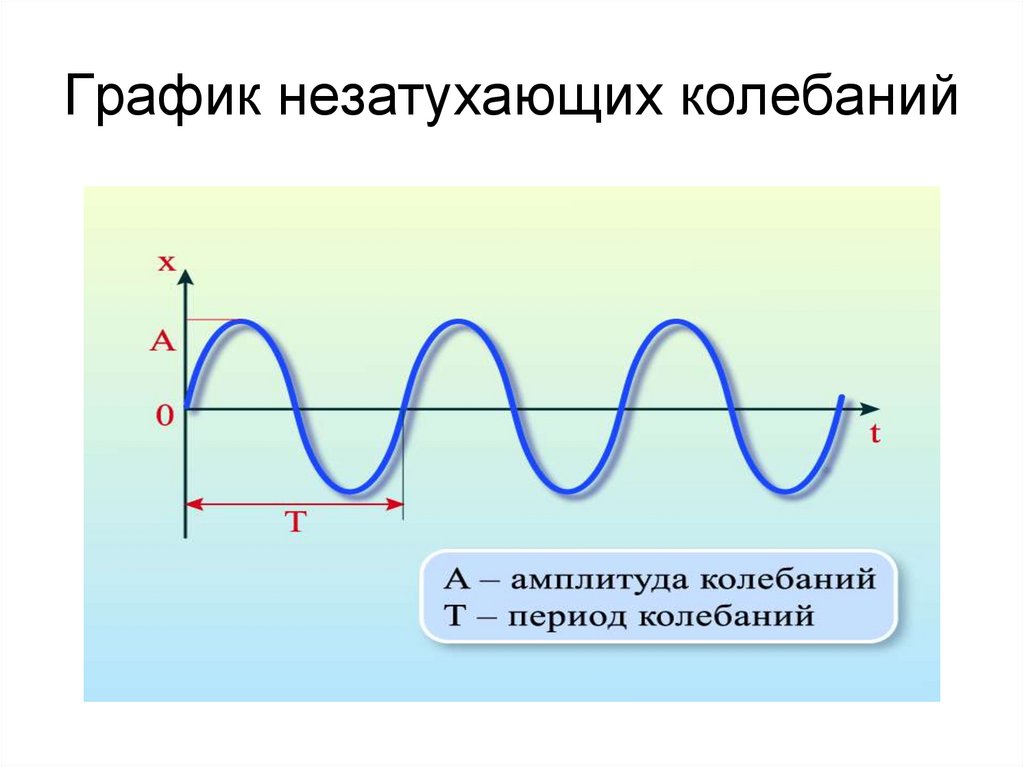 Логичный выбор:
Логичный выбор: или альтернативно
, где А и В (или С и
psi) являются константами, которые определяются из
начальные условия (перемещение и скорость)
система.
На приведенной ниже диаграмме показано, что оба эти решения описывают ту же самую историю зависимости x от времени. Этот сюжет представляет собой мало отличается от нормы, поскольку система имеет начальное перемещение x 0 и начальное скорость v 0 .
| |
Упражнение 2.1По общему виду решения определить константы A и B, если начальное положение x 0 и начальная скорость v 0 . 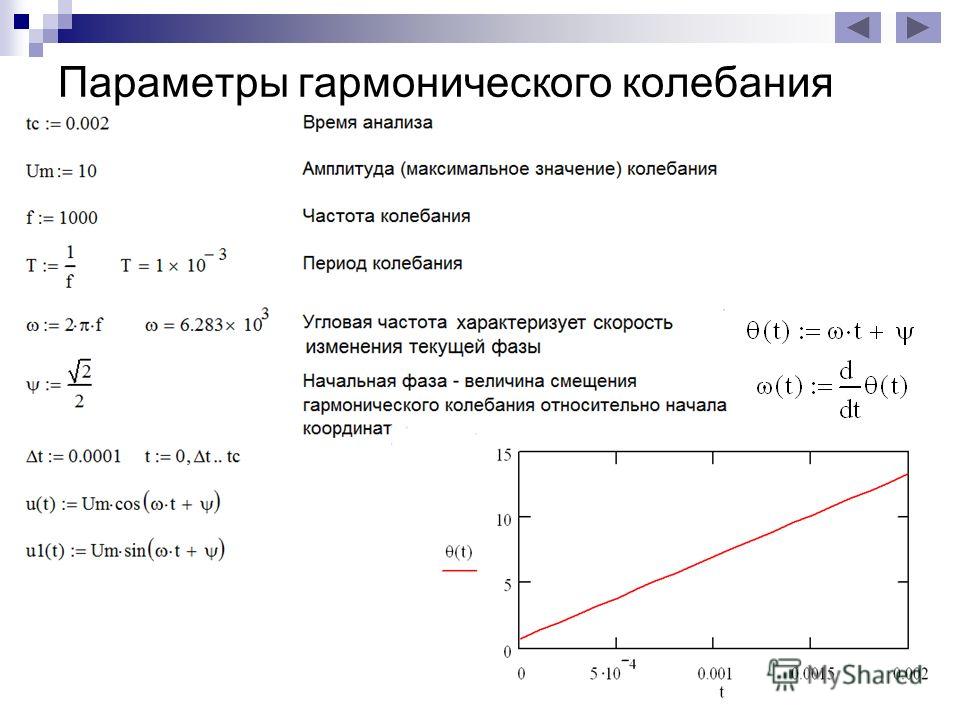 Напишите выражения для x, v и a для систему пружинно-массовой, замените их в уравнение движения и убедитесь, что это, действительно, решение системы. |
Все можно сделать намного проще, если вы представляете синусоида как действительная часть комплекса экспоненциальный. Вы должны помнить, что
e jt = cos(t)
+ j sin(t)
(в школе вы, вероятно, использовали i вместо j и называли это ‘cis(t)’.)
, поэтому х, который колеблется с угловой частотой омега, может быть записано как действительная часть
или
где C является сложным, а «забавный R» означает «настоящий часть».
3. Затухание свободной вибрации
Ваша причина для анализа системы, вероятно, потому что вы хотите добавить «демпфирование», способ впитать свою энергию, чтобы он не продолжал вибрировать в течение Когда-либо.Каждая механическая система подвержена трению, которое действует как потребитель энергии (передавая часть энергии из системы и в окружающую среду). Трение не пропорциональна положению или скорости и, таким образом, наша уравнение движения становится нелинейным, и любое замкнутое Анализ формы сложен.Но симуляция легко, если вы можете записать некоторые «уравнения состояния».
Здесь очень простая симуляция автомобиля столкновение с лежачим полицейским, чтобы смягчить его только трением.
Достаточно подробный код, который вы можете увидеть (и отредактировать!) в
окно использует логику, чтобы определить, является ли трение
сила направлена вверх или вниз:
если(скорость>=0) {трение=-.5};
если(скорость<0) {трение=
.5};
ускорение =
springcoeff*(земля-высота тела) + трение;
скорость = скорость +
ускорение*dt;
рост = рост +
скорость*dt;
В коде немного больше «хозяйственных операций» для переместить дисплей.
Когда симуляция не запущена, измените «+ трение» в линии ускорения на «- трение» на увидеть, как колебания зашкаливают.
Но когда вы собираетесь демпфировать систему, вы, вероятно, добавить приборную панель или вязкостной демпфер к нему, чтобы ограничить или замедлить любую вибрацию.
Наиболее распространенный демпфер представляет собой заполненный жидкостью цилиндр с поршень с отверстиями или другими масляными путями. поршень должен сделать работать (прилагать силу) к рабочей жидкости для привода его через демпферные отверстия. для большинства условий сила F равна пропорциональна скорости поршня v, а постоянная пропорциональности называется вязким демпфированием коэффициент, обозначаемый c.Это измеряется с точки зрения «Ньютонов на (метр в секунду)», и поэтому его ед. Нс/м.
(Не путайте с коэффициентом демпфирования «дзета», см. далее ниже.)
Развитие уравнения движения следует тому же подход, как и раньше, сначала диаграмма свободного тела масса в каком-то месте x считается, а силы, действующие на массу, равны включены.Чтобы наш кинематический анализ был непротиворечивым, скорость v +ve в том же направлении, что и x. Прямое применение секунды Ньютона закон ведет нас к
Мы можем видеть выгоду от моделирования взлома уравнение в два выражения первого порядка, потому что эти просто
и
и изменить код легко.
Но для алгебраического решения мы должны рассмотреть некоторые более сложные функции, чем кос и синус.
Мы можем использовать то же удобное обозначение, что и раньше, в качестве «незатухающей собственной частоты», но это уже не фактическая частота резонанс. Его квадрат просто представляет коэффициент x в уравнении. Конечно, это коэффициент должен быть положительным, иначе мы получим положительную обратную связь и решение будет иметь экспоненциальное решение, которое убегает.
Для среднего срока амортизации ввести величину дзета, где .
Это полезно, когда осмысление журнальных статей и материалов учебников, но, вероятно, будет отвлекать, когда вы имеете дело с практическим примером или экзаменационным вопросом.
Зета — безразмерная величина, называемая коэффициентом демпфирования или коэффициентом демпфирования, и является мерой серьезности демпфирования.С этими замены дифференциальное уравнение становится:
Наша чистая синусоидальная форма решения не применима в этой ситуации. Он мог бы принять форму амплитуда вибрации, которая затухает из-за демпфирования или это может быть простой экспоненциальный спад. Итак, давайте рассмотрим экспоненциальное решение:
Когда мы дифференцируем x, чтобы получить v, мы просто имеем выражение для x, теперь умноженное на лямбда.
Снова дифференцируйте, чтобы получить ускорение, и теперь это выражение умножается на лямбда в квадрате.
Итак, когда мы подставляем их обратно в дифференциал уравнение мы получаем
и мы можем убрать множитель (представляющий x), чтобы оставить характеристика уравнение:
Корни этого квадратного уравнения:
Функция для x может быть смесью экспонент эти значения,
которую вы могли бы вспомнить как «дополнительную функцию».
Таким образом, это решение можно записать как
.
Квадратный корень требует особого внимания, так как возможность его содержания (называемого «подкоренной») быть нулевым или отрицательным. Ведь до сих пор мы рассматривали незатухающие системы, где дзета нуль. Квадратный корень тогда просто содержит -1, давая нам j, который превращает экспоненту в синус волна.
Существует три класса решений:
Если >1 система передемпфирован
Если дзета больше 1, то подкоренное число положительное и решение будет иметь два действительных корня. Движение затухает с ростом t, не имея колебательной составляющей.
Если =1, система «критически демпфированный»
Если дзета равна 1, то подкоренное число равно нулю.Тогда оба корня равны отрицательные действительные числа (равные — ) и форма решения:В системе с критическим демпфированием движение затухает при приближении x к нулю. по мере увеличения t. Опять же, колебаний нет, но система с критическим демпфированием быстрее приближается к равновесию что передемпфированная система. Такое поведение показано на следующем графике зависимости x от t.
Если
<1, система недодемпфированныйЕсли дзета меньше 1, то подкоренное число равно -ve, а квадратный корень числа -ve дает нам комплексное решение:
В скобках стоит знакомое выражение представляет собой синусоиду, но в несколько ином круговая частота, затухающая собственная частота: 90 514
Метод нахождения этого члена состоит в том, чтобы сначала найти незатухающая собственная частота (как если бы демпфер был удалены), чтобы затем найти коэффициент демпфирования, а затем решить для омега д .
Но, конечно, проще всего просто
решить квадратное уравнение численно!
Но недодемпфированный ответ представляет собой синусоиду, т.е.
умножается на экспоненциальный член, который представляет собой
распадаться со временем. Учитывая уравнение системы в
форма
реальная часть корней будет просто -a, так что это экспонента просто e -a t , это означает, что колебание затухает с постоянной времени от 1/а.
Это можно проиллюстрировать:
Когда уравнение неизвестно, коэффициент демпфирования обычно определяется экспериментально. на существующей системе или испытательном оборудовании, изучив амплитуды последовательных колебаний, начиная с
где время между последовательные вершины.
Логарифмический декремент может быть использован и переставлен для решения для Зета.
| |
Практический вопрос 3.1 на незатухающей свободной вибрацияНайдите максимальное ускорение пружины как показано, если m=100 кг, каждый k=200 кН/м и начальные условия задачи таковы смещение 0.1 м ниже равновесия положение со скоростью спуска 0,3 м/с при то мгновение. (Предположим, что масса не качается и не «закручивается».) Подсказки: 1. Нарисуйте свободную диаграмму массы и работы. составить уравнение движения на основе две пружины. 2. Убедитесь, что вы работаете последовательно и правильные единицы. 3. Проверьте вывод уравнения движение с помощью гамильтониана. 4. Проверьте геометрию задачи, чтобы убедиться, что пружины ослабевают во время колебаний (если они делают, проблема стала нелинейной!!). |
|
|
Практический вопрос 3.2 на недемпфированном свободном вибрацияВычислите собственную частоту пружинно-массовая система показана ниже. Каждая масса равна m=5 кг, а линейная упругая пружина имеет постоянную k=325 Н/м. Подсказки: 1. Внимательно изучите геометрию. Вам следует обратите внимание, что требуется только одно измерение (степень свободы) для описания движения системы.Хороший выбор — смещение вверх по склону, при котором случае вам понадобится некоторая тригонометрия, чтобы связать движение вертикальной массы к наклонной один. Помните, что строка, соединяющая они не меняют длину. 2. Нарисуйте диаграмму свободного тела каждой массы и составить уравнение движения на основе весна. 2. Убедитесь, что вы работаете последовательно и правильные единицы. 3. Проверьте вывод уравнения движение с помощью гамильтониана. 4. Вы можете принять угол наклона, если вы нужно. |
| |
Практический вопрос 3.3 на демпфированном свободном вибрацияПоказанная ниже система пружинно-массового демпфера имеет условия: m1 = m2 = 5 кг k = 150 Н/м В конструкции указан коэффициент демпфирования 0,5. методические рекомендации. Наклонная масса смещена на 25 мм вниз от положение равновесия и вышел из состояния покоя. (a) Определить требуемое значение вязкости
коэффициент демпфирования. |
| |
Практический вопрос 3.4 о свободном демпфировании вибрацияКлассическая система пружинно-массового демпфера, лежащая в горизонтальная плоскость имеет условия: м = 1 кг k = 36 Н/м с = 1 Нс/м Масса смещена на 30 мм от точки равновесия. положение и выпущено от отдыха. (a) Является ли система недостаточной, чрезмерной или критической?
демпфированный? (ниже представлено решение для моделирования) |
3.1 Упрощенное моделирование.
В практическом вопросе 1.1 вы, вероятно, использовали Matlab, чтобы найти решение.Существует очень простой способ моделирования системы с помощью JavaScript (его код очень похож на C), и вы можете запустить его в любом браузере. Вы можете увидеть ряд примеров на www.jollies.com (хотя некоторые из них уже довольно старые).
Если вы не знакомы с C, вот несколько указателей:
Каждое «присваивание», где значение переменной измененное должно заканчиваться точкой с запятой.
«Переменные состояния» (вещи, которые изменяются со временем, рассказывая нам, что именно происходит) — это позиция и скорость массы, x и v.
«Уравнения состояния» говорят нам о скорости их изменения, поэтому
что мы можем определить их следующее значение. В этом случае
dx/dt = v;и
dv/dt = сила/м;где сила — это выражение, которое будет включать настоящее x и v и любую входную функцию.
Мы можем обновить позицию, добавив (скорость * временной шаг) к этому. Это приближение будет более достаточно, если шаг по времени мал достаточно. На таком языке, как Basic, мы могли бы написать
x = x + v*dt;
Кроме того, C имеет альтернативную «умную» нотацию записать это как
x += v*dt;
‘Jollies’ дает нам два способа отображения вывода. Первый заключается в перемещении изображений на экране по мере того, как вы увидите в примере ниже.Второй — по с помощью графического объекта, на котором можно рисовать графики. В более старые браузеры мы должны использовать ‘апплет’ graph.class, если симуляция должна работать. Теперь этот Интернет Explorer 9 распознает объект «холст», с которого мы можем начать изменить на это. (Он уже работает в FireFox.)
Простое решение Jollies к Вопросу 1.1 связана здесь.
| |
Моделирование вопроса 3.4С небольшим шагом по времени мы можем использовать простой алгоритм Эйлера. интеграции, где мы говорим, что новый смещение x изменяется добавлением скорости v умножить на временной шаг dt. х += v*dt;Точно так же скорость изменяется добавлением время разгона dt. Для системы, где м = 1 кг имеем ускорение = -36*x — 1*v, поэтому v += (-36*x -v)*dt;и, конечно же, мы обновляем время с помощью t += dt; если мы хотим построить что-нибудь.Теперь мы просто нужно двигать картинку и ходить по кругу снова. Мы можем инициализировать перемещение и скорость до запуска модели. Нажмите здесь, чтобы увидеть модель в действии. |
4. Принудительная вибрация
Во многих ситуациях система может подвергаться внешнее флуктуационное возмущение (сила или перемещение).Это может быть вызвано несбалансированными вращающимися частями в машина, или может быть из-за движения системы фундамент (например, землетрясение).
Существуют различные формы функции принуждения F=F(t) и смещения фундамента х В = х В (т). Некоторые возможности показаны ниже:
Из всех этих форм вынуждающей функции гармоническая для меня.е. синусоида) является наиболее распространенным и будет рассмотрено далее здесь.
4.1 Принудительное возбуждение
Рассмотрим простую систему пружина-масса-демпфер. ниже, где разбалансированный двигатель вызывает дополнительная (вынуждающая) сила F и x-компонента этой сила изменяется гармонически. Теперь заметим, что мы должны учитывайте частоту возбуждения или принуждения (), а также незатухающую естественную частоты () и затухающего естественного частота ().Уравнение движения для этой системы:
Перестановка и выражение в знакомой форме дает:
… и если бы мы хотели, чтобы уравнение имело «классический орнаментальная форма», производя те же замены, что и раньше выходы:
|
|
Практический вопрос 4.1Чтобы увидеть это в более простом свете, рассмотрим системаКогда вы пытались решить его с помощью фазы углы, щелкните ссылку HowTo, чтобы увидеть простой способ! |
4.2 Базовое возбуждение
Во многих случаях возбуждение не связано с непосредственным приложенная сила, вместо этого это может быть вызвано нарушением основание (что приводит к изменению длины пружины). Примеры из них землетрясения, которые сотрясают структуру, структуру переносимая вибрация от соседнего оборудования, сотрясающая машину сидя на пьедестале или подвеске автомобиля ударяясь о лежачий полицейский. Следующий рисунок иллюстрирует это явление: Уравнение движения этой системы: Перестановка и выражение в знакомой форме дает:где F 0 =b, поэтому мы могли бы выразить это как
Ясно, что это выражение имеет тот же вид, что и для гармонической силы,
разница только в том, что на этот раз F = kb.
Таким образом, метод анализа для приложенной силы и для приложенное базовое возбуждение идентично, за исключением этого срок.
| |
Пример 4.2 Моделирование вынужденной вибрацииКак и раньше, с небольшим шагом по времени мы можем использовать простую интеграцию Эйлера, где мы говорим, что новое смещение x изменяется путем добавления скорость v, умноженная на временной шаг dt. х += v*dt;Точно так же скорость изменяется добавлением время разгона dt. Для системы, где м = 1 кг и где пружина смещается на ввод , мы имеем ускорение = 25*(ввод -x) — 2*v Но мы можем добавить элементы управления в симуляцию так что мы можем варьировать параметры. Нажмите здесь, чтобы увидеть
модель в действии — вас попросят сделать
больше с этим позже. |
4.3 Незатухающая вынужденная вибрация
Начнем с простого случая, когда затухание незначительно. и, таким образом, =0. Уравнение движения затем становится: Полное решение этого выражения состоит из двух частей:(а) Реакция на ступенчатое изменение аналогична случаю где нет принудительного возбуждения.Во многих текстах это называется дополнительным функция (x c ) или переходная характеристика.
(b) Текущая реакция на возбуждение, называемая частным решением (x p ) или стационарное состояние решение.
Итак, решение есть сумма этих двух,
x(t) = x c + x p
Как и следовало ожидать, конкретное решение должно быть та же самая функция, что и принудительная функция:
где Х — это величина смещения.
Отсюда следует, что и подстановка этих терминов в уравнение движения, затем разделив на все на 2 и, наконец, заменив 2 на урожайность к/м:
Амплитуда смещения в любой момент времени может то выразить как: собственная частота системы и зависит от массы и жесткости.— частота возбуждения, которая зависит по характеру возмущения.Если нарушение вызванный разбалансировкой вращающегося вала, затем изменится по мере увеличения скорости двигателя.
Есть несколько особых случаев, которые следует учитывать:
(a) Если =0, то машина
стационарный, и X = F 0 /k, который является статическим
отклонение стационарной системы.
(б) Если <
затем по мере увеличения X увеличивается.
в) Если = то
математически мы подходим к ситуации, когда X = (F 0 /k)/0
и теоретически, если бы мы могли управлять системой на этом
скорости, то амплитуда колебаний приближалась бы
бесконечность.
Если вы посмотрите на решение чуть выше, вы увидите, что один из членов синуса умножается на время т. Верно, что теоретически амплитуда может стать бесконечным, но потребовалась бы бесконечная длина время добраться туда.
В реальной жизни всегда есть некоторое демпфирование для поглощения энергии поэтому амплитуда ограничена. Кроме того, если амплитуда становится слишком высоким, тогда части системы могут выйти из строя.Там имели место многочисленные катастрофические сбои, когда система вышел из строя, потому что он работал в резонансе (также называемом критическая частота).
(г) Если > то по мере увеличения X становится отрицательна и постепенно снижается. Отрицательный X означает, что смещение происходит в направлении, противоположном движущая сила, другими словами водоизмещение 180 градусов в фазе с движущей силой.
Дальнейшее упрощение может быть сделано для конкретного решение, деленное на статический прогиб. Это приводит нас к отношению М которая называется амплитудой отношение или увеличение фактор.
Обычно строится зависимость величины M от отношения частоты возбуждения к собственной частоте вибрационная система.
Затухание вынужденной вибрации
Добавление демпфирования к уравнениям движения приводит к синусоидальное частное решение требует фазы сдвиг. Требуется более сложное выражение:Используя вторую форму этого выражения в уравнении движения приводит к: и Использование «декоративных» символов начинает проявляться стоит, когда мы рассматриваем возбуждение системы в ее незатухающем состоянии. собственная частота.
Теперь выражение для тангенса фазового угла станет бесконечным, т.е. фазовый угол будет равен девяноста градусов.
«Коэффициент увеличения» теперь составляет всего 1/(2 дзета) (см. ниже).
Итак, если вы тестируете неизвестную систему, применяя принудительной функции, вы можете сначала изменить частоту, пока фазовый сдвиг на девяносто градусов, затем прочтите амплитуда для расчета коэффициента демпфирования.
Для системы с недостаточным демпфированием дополнительные и отдельные решения теперь можно комбинировать:
Переходный первый член (с экспоненциальной функцией) уменьшается с увеличением времени, а второй член будет продолжаться за счет вынуждающей функции или базового возбуждения.Снова сравнение со статическим перемещением приводит к коэффициент амплитуды или коэффициент увеличения:
Коэффициент увеличения зависит от отношения частот и коэффициент демпфирования и проиллюстрирован как:Итак, каковы коэффициенты затухания красных кривых? проиллюстрировано выше?
| |
ДеятельностьБыла смоделирована система пружинно-массового демпфера. доступен [здесь].Модель анимирует диаграмму, чтобы указать амплитуда вибрации для данной комбинации жесткость и демпфирование.
|
5. Жесткие кузова
Теперь перенесем наше внимание на твердое тело, положение которого можно описать одной степенью свободы. Учитывать вращательные колебания однородного тонкого стержня, обычно сидит горизонтально и возбуждается гармоническим усилие на его правом конце.Бар достаточно такой прочности, что он не прогибается во время вибрации, поэтому мы можем рассматривать его как твердое тело. То амплитуда колебаний настолько мала, что направление сил меняется не слишком сильно.Теперь разработаем диаграмму свободного тела стержня, смещенного на некоторый малый угол, тэта, путем удаления пружины и демпфера и заменив их эквивалентными силами.То силы, необходимые для статического равновесия, были удалены и мы рассматриваем только изменяющиеся силы на стержне.
Штанга свободно вращается вокруг точки вращения «О» и бар вращается вокруг этой точки, а также имеет угловой скорость и угловое ускорение относительно этой точки. То определение стержня как тонкого позволяет нам использовать табличные данные для нахождения момента инерции массы около точки «О».Используя вращательное уравнение движения (и с моменты против часовой стрелки) :
Знакомые приближения теперь можно использовать для упрощения это выражение и представить его в привычной форме:
Теперь заметим, что уравнение движения имеет тот же вид. общий вид, как прежде, и все предыдущие способы решение применить.
|
|
Практический вопрос 5.5 на вибрации твердого телаЭкспериментальный двигатель массой 220 кг установлен на испытаниях подставка под пружинные крепления в точках A и B, каждая из которых имеют жесткость k=100кН/м, а внешний диаметр 50мм. Массовый момент инерции двигатель относительно его центра G составляет 2,95 кг.м 2 .
|
Вся работа на данный момент (кроме практических вопросов) 5.5) включает одноосное движение и может быть описано по одной степени свободы. Теперь эта работа будет распространяется на системы с более чем одной степенью свободы.
Aero 16 — Вибрация самолета
Флаттер — это неустойчивое состояние, при котором нестационарная аэродинамика возбуждает естественную частоты конструкции, по которой течет воздух.Результирующий вибрации могут возрасти до такой величины, что конструкция потерпеть поражение.
Шум это вибрация, которая возбуждает воздух и может быть услышана. Когда вибрация является случайным, шум немузыкальный или беспорядочный. Когда вибрация является гармоническим, в результате получается тон, подобный тому, который воспроизводится музыкальным инструмент. Это может звучать как свист слива или легкое течь в двери.
2. ПРИЧИНЫ ВИБРАЦИИ САМОЛЕТА
Нормальные и ненормальные вибрации происходят по нескольким причинам. Аэродинамика, механические неисправности, а внешние факторы, такие как атмосферная турбулентность, могут вызвать вибрация. Все вибрации имеют связанные частоты и величины которые могут быть легко обнаружены или едва заметны для полета экипаж и пассажиры.Для некоторых вибраций, например связанных при работающем двигателе у летного экипажа есть специальные приборы для измерения величины. Другие вибрации обнаруживаются визуально, по звуку, или чувствовать, и анализ может зависеть от опыта летного экипажа.
Обычный
вибрация.
Каждый самолет имеет уникальную характеристику нормальной вибрации. Это
следствием распределения массы и структурной жесткости, которые
приводят к колебательным режимам на определенных частотах.Когда внешний
силы, действующие на самолет, такие как нормальный поток воздуха над поверхностями,
возникают вибрации очень низкого уровня. Как правило, это воспринимается как
фоновый шум. Более заметной, но также нормальной является реакция
самолета к турбулентному воздуху, в котором величина
вибрация может быть больше и, таким образом, ясно видна и ощущается. Двигатель
работа на некоторых скоростях шпули может привести к усилению вибрации
потому что дисбаланс золотника возбуждает двигатель и передает эту вибрацию
по всему планеру.Наконец, работа некоторых механических
компоненты, такие как насосы, могут быть связаны с нормальным шумом и
вибрация.
Большинство летных экипажей признают эти обычные события, которые становятся базой опыта, из которого летные экипажи обнаруживают аномальные вибрации.
Вибрация Термины и определения | Инженеры Край
Термины и определения вибрации
Сопротивление и механика материалов | Акселерометры
Ниже приведены термины и определения, связанные с вибрацией.
Ускорение
Векторная величина, определяющая скорость изменения скорости.
Акселерометр
Датчик, электрический выход которого пропорционален ускорению.
Усилитель заряда
Усилитель, выходное напряжение которого пропорционально выходному заряду пьезоэлектрического преобразователя. Имеет преимущество
что выходное напряжение не зависит от длины соединительного кабеля от преобразователя.
Податливость
Легкость, с которой система может быть смещена или сжата при заданной силе. Обратное значение жесткости.
Критическое демпфирование
Минимальное вязкое демпфирование, которое позволит смещенной системе вернуться в исходное положение без колебаний
Перемещение
Векторная величина, определяющая изменение положения тела. Обычно измеряется от исходного положения.
Демпфирование
Любые средства рассеивания энергии вибрации в вибрирующей системе.
Коэффициент демпфирования
Отношение фактического демпфирования к критическому демпфированию на резонансной частоте.
Степень свободы
В механической системе равен минимальному количеству независимых координат, необходимых для полного определения положения
всех частей системы в любой момент времени.
Динамическая масса
Отношение приложенной силы к результирующему ускорению при простом гармоническом движении.
Динамический модуль
Отношение напряжения к деформации в условиях вибрации.
Возбуждение
Внешняя сила или движение, приложенное к системе, которое заставляет систему реагировать таким же образом.
Сила
Замедление Действие, придающее массе ускорение.
Удар
Возбуждение конструкции силовым импульсом, например. с помощью ударного молотка.
Импульс
Четко определенный пульс. Периодический импульс – это повторяющиеся импульсы.
Интегратор
Электрический частотный фильтр, используемый для преобразования сигнала виброускорения в сигнал, амплитуда которого пропорциональна
скорость или перемещение.
Рывок
Векторная величина, определяющая скорость изменения ускорения во времени.
Механический импеданс
Отношение приложенной силы к результирующей скорости при простом гармоническом возбуждении. Называется импедансом движущей точки, если
сила и скорость измеряются в одной и той же точке, иначе называемой передаточным сопротивлением.
Мобильность
Механический вход. Инверсия механического импеданса.
Модальный анализ
Процесс определения форм колебаний и связанных с ними параметров, собственной частоты и затухания.
Собственная частота
Частота, с которой будет вибрировать упруго закрепленная масса, когда она находится в свободном состоянии
вибрация.
Периодическая вибрация
Колебательное движение, амплитуда которого повторяется через фиксированные промежутки времени.
Случайная вибрация
Вибрация, мгновенная амплитуда которой не указана ни в какой момент времени. Мгновенная амплитуда может быть только
определяется статистически с помощью функции распределения вероятностей, которая дает долю общего времени, в течение которого амплитуда находится в пределах заданных интервалов амплитуды.Псевдо,
или Periodic и Burst random являются специальными формами.
Резонанс
Условия пикового вибрационного отклика, при которых небольшое изменение частоты возбуждения вызывает снижение отклика системы.
Ответ
Движение или другой результат, возникающий в результате возбуждения при определенных условиях.
Удар
Быстрая кратковременная передача механической энергии.
Простое гармоническое движение
Периодическое движение, смещение которого изменяется как синусоидальная функция времени.
Жесткость
Отношение изменения силы к соответствующему изменению смещения упругого элемента.
Передаваемость
Отношение амплитудной характеристики системы в установившемся режиме вибрации к амплитуде возбуждения.
Скорость
Векторная величина, определяющая скорость изменения смещения во времени.
Виброизолятор
Эластичная опора, уменьшающая передачу.
Измеритель вибрации
Прибор для измерения колебательного перемещения, скорости или ускорения.
Интенсивность вибрации
Критерий прогнозирования опасности, связанной с определенными уровнями вибрации машины.
Предусилитель напряжения
Предусилитель, вырабатывающий выходное напряжение, пропорциональное входному напряжению пьезоэлектрического акселерометра.
Входное напряжение зависит от емкости кабеля.
Стоячие волны – Гиперучебник по физике
Обсуждение
введение
Может быть, вы заметили, а может быть, и нет. Иногда, когда вы вибрируете струну, или шнур, или цепь, или кабель, можно заставить их вибрировать таким образом, что вы генерируете волну, но волна не распространяется. Он просто сидит там, вибрируя вверх и вниз на месте.Такая волна называется стоячей волной , и ее нужно увидеть, чтобы оценить.
Бегущая волна в действии Стоячая волна в действии
Я впервые обнаружил стоячие волны (или я впервые помню, что видел их), играя с телефонным кабелем. Если вы встряхнете телефонный шнур правильным образом, можно создать волну, которая, кажется, стоит на месте. Если вы потрясете телефонный шнур любым другим способом, вы получите волну, которая ведет себя так же, как и все другие волны, описанные в этой главе; волны, которые распространяются — бегущие волны .Бегущие волны имеют высокие точки, называемые гребнями, и низкие точки, называемые впадинами (в поперечном случае), или точки сжатия, называемые сжатиями, и точки растяжения, называемые разрежениями (в продольном случае), которые проходят через среду. Стоячие волны никуда не уходят, но у них есть области, где возмущение волны очень мало, почти нулевое. Эти местоположения называются узлами . Есть также области, где возмущение довольно интенсивное, большее, чем где-либо еще в среде, называемые пучностями .
Стоячие волны могут образовываться при различных условиях, но их легко продемонстрировать в среде, которая является конечной или ограниченной. Телефонный шнур начинается на базе и заканчивается на трубке. (Или наоборот?) Другими простыми примерами конечных сред являются гитарная струна (она идет от лада к подставке), пластик (ограничивается ободом), воздух в комнате (ограничивается стены), вода в озере Мичиган (оно ограничено берегами) или поверхность Земли (хотя и не ограничена, поверхность Земли конечна).В общем, стоячие волны могут быть созданы любыми двумя одинаковыми волнами, распространяющимися в противоположных направлениях и имеющими правильную длину волны. В ограниченной среде стоячие волны возникают, когда волна с правильной длиной волны встречает свое отражение. Интерференция этих двух волн дает результирующую волну, которая кажется неподвижной.
Стоячие волны не образуются ни при каких обстоятельствах. Они требуют, чтобы энергия подавалась в систему с соответствующей частотой. То есть, когда частота возбуждения , применяемая к системе, равна ее собственной частоте .Это состояние известно как резонанс . Стоячие волны всегда связаны с резонансом. Резонанс можно определить по резкому увеличению амплитуды результирующих колебаний. По сравнению с бегущими волнами с той же амплитудой, создание стоячих волн относительно легко. В случае с телефонным шнуром небольшие движения руки приведут к гораздо большим движениям телефонного шнура.
Любая система, в которой могут образовываться стоячие волны, имеет многочисленные собственные частоты.Набор всех возможных стоячих волн известен как гармоника системы. Простейшая из гармоник называется основной или первой гармоникой. Последующие стоячие волны называются второй гармоникой, третьей гармоникой и т. д. Гармоники выше основной, особенно в теории музыки, иногда также называют обертонами . Какие длины волн будут образовывать стоячие волны в простой одномерной системе? Есть три простых случая.
один размер: два фиксированных конца
Если среда ограничена так, что ее противоположные концы можно считать неподвижными, то на концах будут найдены узлы.Простейшая стоячая волна, которая может образоваться в этих условиях, имеет одну пучность посередине. Это половина длины волны. Чтобы сделать следующую возможную стоячую волну, поместите узел в центр. Теперь у нас есть одна целая длина волны. Чтобы сделать третью возможную стоячую волну, разделите длину на трети, добавив еще один узел. Это дает нам полторы длины волны. Должно стать очевидным, что для продолжения все, что нужно, — это продолжать добавлять узлы, разделяя среду на четверти, затем на пятые, шестые и т. д.Для этой системы существует бесконечное число гармоник, но сколько бы мы ни делили среду, мы всегда получаем целое число полудлин волн ( 1 2 λ, 2 2 λ, 3 2 λ, …, n 2 λ).
В этой последовательности существуют важные соотношения между самими гармониками. Длины волн гармоник представляют собой простые доли длины основной волны. Если бы основная длина волны равнялась 1 м, длина волны второй гармоники была бы 1 2 м, третьей гармоники была бы 1 3 м, четвертой гармоники 1 4 м и так далее.Поскольку частота обратно пропорциональна длине волны, частоты также связаны между собой. Частоты гармоник кратны основной частоте. Если бы основная частота равнялась 1 Гц, частота второй гармоники была бы 2 Гц, третьей гармоники – 3 Гц, четвертой – 4 Гц и так далее.
одно измерение: два свободных конца
Если среда ограничена так, что ее противоположные концы можно считать свободными, то на концах будут находиться пучности.Простейшая стоячая волна, которая может образоваться в этих условиях, имеет один узел посередине. Это половина длины волны. Чтобы сделать следующую возможную стоячую волну, поместите в центр еще одну пучность. Теперь у нас есть одна целая длина волны. Чтобы сделать третью возможную стоячую волну, разделите длину на трети, добавив еще одну пучность. Это дает нам полторы длины волны. Должно стать очевидным, что мы получим те же соотношения для стоячих волн, образованных между двумя свободными концами, что и для двух закрепленных концов.Разница лишь в том, что узлы были заменены пучностями и наоборот. Таким образом, при образовании стоячих волн в линейной среде с двумя свободными концами внутри среды помещается целое число полудлин волн, а обертоны кратны основной частоте
.один размер: один фиксированный конец — один свободный конец
Когда среда имеет один фиксированный конец и один свободный конец, ситуация меняется интересным образом. Узел всегда будет образовываться на фиксированном конце, а пучность всегда будет образовываться на свободном конце.Простейшая стоячая волна, которая может образоваться в этих условиях, имеет длину в четверть длины волны. Чтобы сделать следующую возможную стоячую волну, добавьте узел и пучность, разделив рисунок на трети. Теперь у нас есть три четверти длины волны. Повторяя эту процедуру, мы получаем пять четвертей длины волны, затем семь четвертей и т. д. В таком расположении всегда присутствует нечетное число четвертей длины волны. Таким образом, длины волн гармоник всегда кратны основной длине волны с нечетным числом в знаменателе.Точно так же частоты гармоник всегда кратны основной частоте.
Приведенные выше три случая показывают, что, хотя не все частоты приводят к стоячим волнам, простая одномерная система обладает бесконечным числом собственных частот, которые будут возникать. Это также показывает, что эти частоты являются простыми кратными некоторой основной частоте. Однако для любой реальной системы трудно, если вообще возможно, создать высокочастотные стоячие волны.Камертоны, например, сильно вибрируют на основной частоте, очень мало на второй гармонике и фактически совсем не вибрируют на более высоких гармониках.
фильтрация
Самое лучшее в стоячей волне не то, что она кажется неподвижной, а то, что амплитуда стоячей волны намного больше, чем амплитуда возмущения, вызывающего ее. Это похоже на получение чего-то ни за что. Вложите немного энергии с правильной скоростью и наблюдайте, как она накапливается во что-то с большим количеством энергии.Эта способность усиливать волну одной конкретной частоты по сравнению с волной любой другой частоты имеет множество применений.
- В основном все нецифровые музыкальные инструменты работают непосредственно по этому принципу. То, что вкладывается в музыкальный инструмент, — это вибрации или волны, охватывающие диапазон частот (для духовых — это жужжание губ, для трости — хриплый писк трости, для перкуссии — относительно беспорядочные удары, для струн — это выщипывание или царапание; для флейт и органных труб это турбулентность, вызванная выдуванием).Что усиливается, так это основная частота плюс ее кратные. Эти частоты громче остальных и слышны. Все остальные частоты сохраняют свои первоначальные амплитуды, а некоторые даже деусиливаются. Эти другие частоты тише по сравнению с ними и не слышны.
- Вам не нужен музыкальный инструмент, чтобы проиллюстрировать этот принцип. Неплотно сложите руки вместе и держите их рядом с ухом, образуя маленькую камеру. Вы заметите, что одна частота усиливается из фонового шума в пространстве вокруг вас.Варьируйте размер и форму этой камеры. Усиленная высота звука изменяется в ответ. Это то, что люди слышат, когда подносят к ушам ракушку. Это не «океан», а несколько избранных частот, усиленных шумом, который всегда нас окружает.
- Во время речи человеческие голосовые связки колеблются в гораздо меньшем диапазоне, чем во время пения. Как же тогда можно отличить звук одной гласной от другой? Английский не является тональным языком (в отличие от китайского и многих африканских языков).Существует небольшая разница в основной частоте голосовых связок для носителей английского языка во время повествовательного предложения. (Вопросительные предложения становятся ближе к концу. Не так ли?) Голосовые связки вибрируют не на одной частоте, а на всех частотах гармоник. Различное расположение частей рта (зубы, губы, передняя и задняя часть языка и т. д.) сложным образом способствует разным гармоникам. Это усиливает одни частоты и ослабляет другие. Это заставляет «EE» звучать как «EE», а «OO» — как «OO».
- Фильтрующий эффект резонанса не всегда полезен или выгоден. Люди, работающие рядом с механизмами, подвергаются воздействию различных частот. (Это то, что представляет собой шум .) Из-за резонанса в ушном канале звуки с частотой около 4000 Гц усиливаются и, таким образом, становятся громче других звуков, поступающих в ухо. Каждый должен знать, что громкие звуки могут повредить слух. Чего, возможно, не знают все, так это того, что воздействие громких звуков только одной частоты может повредить слух на этой частоте.Люди, подвергающиеся воздействию шума, часто теряют слух на частоте 4000 Гц. Страдающие этим заболеванием не слышат звуки вблизи этой частоты с той же остротой, что и здоровые люди. Это часто является предшественником более серьезных форм потери слуха.
двухмерный
Тип рассуждений, использованный до сих пор в обсуждении, также может быть применен к двумерным и трехмерным системам. Как и следовало ожидать, описания немного сложнее. Стоячие волны в двух измерениях имеют множество приложений в музыке.Круглая барабанная головка представляет собой довольно простую систему, на которой можно изучать стоячие волны. Вместо узлов на противоположных концах, как это было у гитарных и фортепианных струн, весь ободок барабана представляет собой узел. Другие узлы представляют собой прямые линии и окружности. Частоты гармоник не являются простыми кратными основной частоты.
На приведенной выше диаграмме показаны шесть простых режимов вибрации круглой головки барабана. Знаки плюс и минус показывают фазу пучностей в конкретный момент времени.Числа соответствуют схеме наименования (D, C), где D – это количество узловых диаметров, а C – количество узловых окружностей.
Стоячие волны в двух измерениях широко применялись для изучения корпусов скрипок. Скрипки, изготовленные итальянским скрипичным мастером Антонио Страдивари (1644–1737), славятся чистотой звучания в широком динамическом диапазоне. Физики-акустики уже довольно давно работают над воспроизведением скрипок, не уступающих по качеству скрипкам Страдивари.Один из методов, разработанный немецким физиком Эрнстом Хладни (1756–1794), включает рассыпание песчинок на пластину из разобранной скрипки, которую затем зажимают и заставляют вибрировать смычком. Песчинки отскакивают от оживленных пучностей и скапливаются в тихих узлах. Полученные в результате образец Хладни для разных скрипок можно было затем сравнить. Предположительно, образцы от более звучащих скрипок будут в чем-то похожи. Методом проб и ошибок скрипичный дизайнер должен уметь создавать компоненты, поведение которых имитирует поведение легендарного мастера.Это, конечно, только один фактор в дизайне скрипки.
три измерения
В одномерном случае узлы были точками (нульмерными). В двумерном случае узлы были кривыми (одномерными). Размерность узлов всегда на единицу меньше размерности системы. Таким образом, в трехмерной системе узлы будут двумерными поверхностями. Наиболее важным примером стоячих волн в трех измерениях являются орбитали электрона в атоме.В атомном масштабе обычно более уместно описывать электрон как волну, чем как частицу. Квадрат волнового уравнения электрона дает функцию вероятности нахождения электрона в любой конкретной области. Орбитали, используемые химиками, описывают форму области, где высока вероятность нахождения того или иного электрона. Электроны ограничены пространством, окружающим ядро, примерно так же, как волны в гитарной струне ограничены струной.Ограничение струны в гитаре заставляет струну вибрировать с определенной частотой. Точно так же электрон может вибрировать только с определенной частотой. В случае электрона эти частоты называются собственными частотами , а состояния, связанные с этими частотами, называются собственными состояниями или собственными функциями . Набор всех собственных функций электрона образует математический набор, называемый сферическими гармониками . Этих сферических гармоник бесконечное множество, но они специфичны и дискретны .То есть промежуточных состояний нет. Таким образом, атомный электрон может поглощать и излучать энергию только определенными небольшими пакетами, называемыми квантами . Он делает это, совершая квантовый скачок из одного собственного состояния в другое. Этот термин был извращен в популярной культуре, чтобы обозначать любые внезапные, большие изменения. В физике все наоборот. Квантовый скачок — это наименьшее возможное изменение системы, а не самое большое.
| |1,0,0⟩ | |||||
| |2,0,0⟩ | |2,1,0⟩ | |2,1,1⟩ | |||
| |3,0,0⟩ | |3,1,0⟩ | |3,1,1⟩ | |3,2,0⟩ | |3,2,1⟩ | |3,2,2⟩ |
математика
в математике, бесконечная последовательность фракций 1 4 1 , 1 , 1 , 1 4 3 , 1 4 , … называется гармонической последовательностью .Удивительно, но количество гармоник, описываемых гармонической последовательностью, точно такое же, как и гармоник, описываемых последовательностью «только шансы»: 1 7 , …. «Что? Очевидно, что в гармонической последовательности больше чисел, чем в последовательности «только шансы». Неа. Там точно такое же количество. Вот доказательство. Я могу установить однозначное соответствие между целыми и нечетными числами.Наблюдать. (Однако мне придется поиграть с форматом чисел, чтобы они правильно выстроились на экране компьютера.)
01, 02, 03, 04, 05, 06, 07, 08, 09, …
01, 03, 05, 07, 09, 11, 13, 15, 17, …
Это может продолжаться вечно. Это означает, что нечетных чисел ровно столько же, сколько целых чисел. И целые числа, и нечетные числа являются примерами исчисляемых бесконечных множеств.
Существует бесконечное число возможных длин волн, которые могут образовывать стоячие волны при всех обстоятельствах, описанных выше, но существует еще большее количество длин волн, которые не могут образовывать стоячие волны.«Что? Как вы можете иметь больше, чем бесконечное количество чего-то?» Ну, я не хочу доказывать это прямо сейчас, поэтому вам придется мне поверить, но существует больше действительных чисел между 0 и 1, чем целых чисел между нулем и бесконечностью. У нас не только у нас все рациональные числа менее одного ( 1 2 , 3 5 , 733 , 733 2741 и т. Д.) У нас также есть все возможные алгебраические номера ( √2, 7 − √13 и т. д.) и целый сонм причудливых трансцендентных чисел (π, e, e π , число Фейгенбаума и т.д.). Все эти числа вместе образуют неисчисляемое бесконечное множество , называемое действительным числом . Количество целых чисел — это бесконечность, называемая алеф нуль (ℵ 0 ), количество действительных чисел — это бесконечность, называемая c (для континуума ). Изучение бесконечно больших чисел известно как трансфинитная математика .

 Свободные и вынужденные колебания. Гармонические колебания.
Свободные и вынужденные колебания. Гармонические колебания.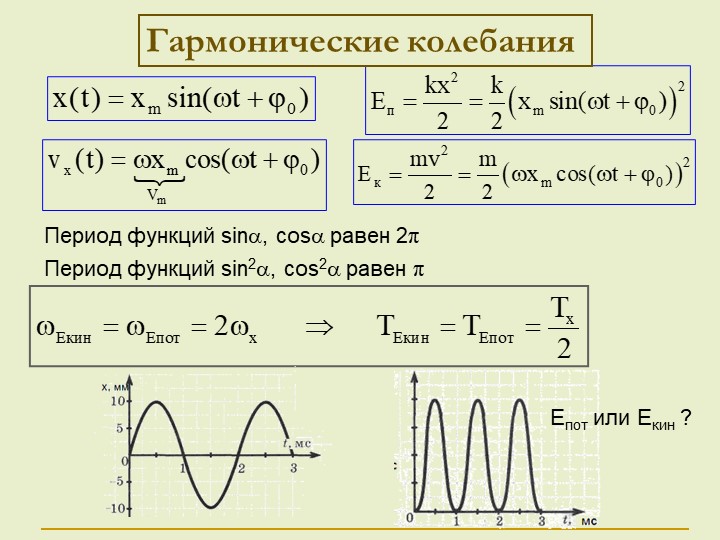 66)
66)
 75)
75) 77)
77) 79)
79) 82)
82) 32 × 10 10
32 × 10 10 



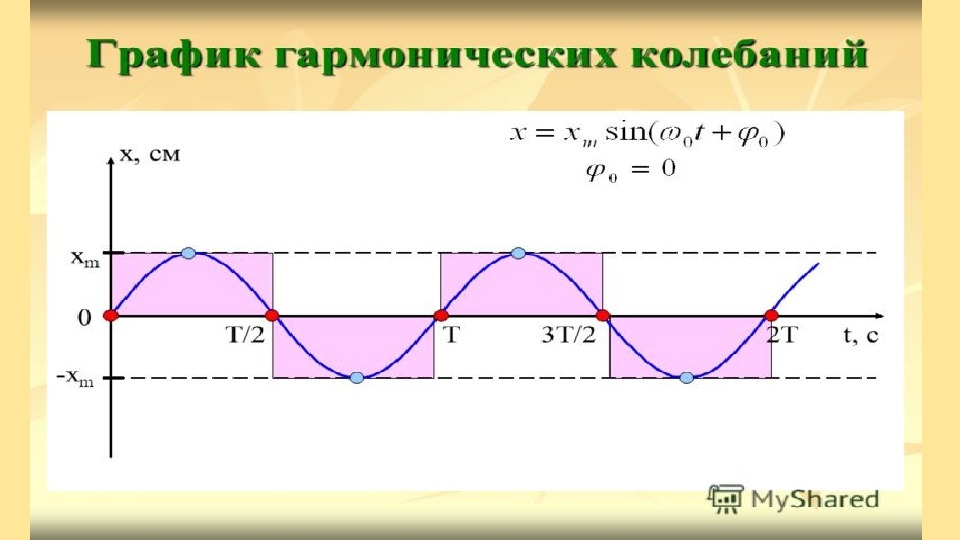 Видно, что область снижения вибрации смещается в сторону низких частот с увеличением радиуса кривизны, но амплитуда вибрационного внимания практически не меняется.
Видно, что область снижения вибрации смещается в сторону низких частот с увеличением радиуса кривизны, но амплитуда вибрационного внимания практически не меняется.  Исследование финансировалось Национальным проектом ключевых исследований и разработок Китая (грант № 2019YFB2006400) и крупными научно-техническими проектами провинции Хэйлунцзян (грант №2019ZX03A02).
Исследование финансировалось Национальным проектом ключевых исследований и разработок Китая (грант № 2019YFB2006400) и крупными научно-техническими проектами провинции Хэйлунцзян (грант №2019ZX03A02). 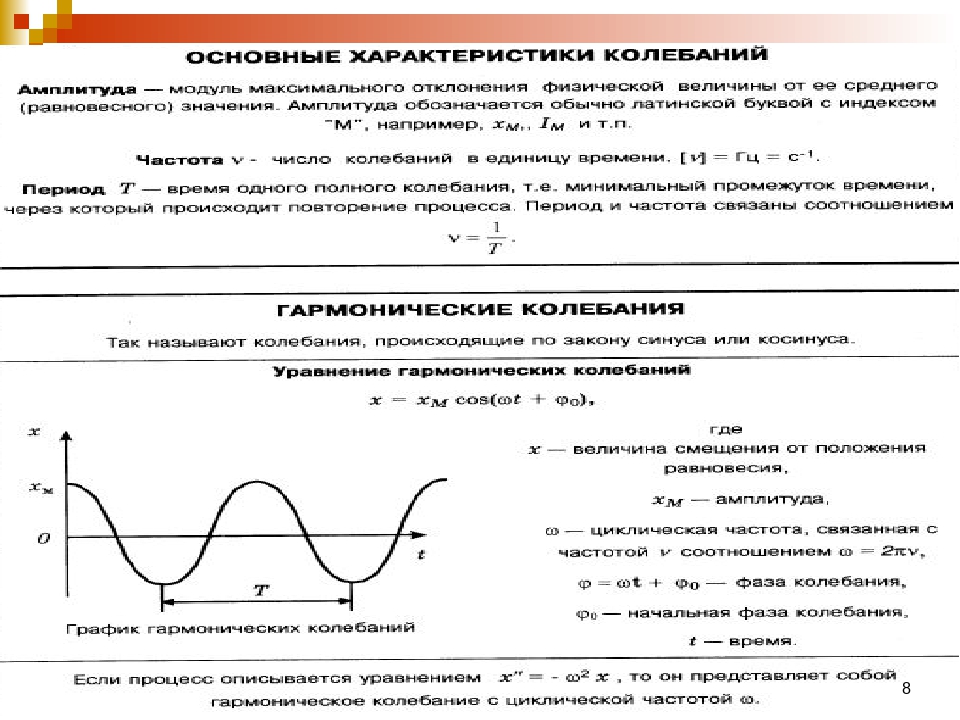 2} \ sin (\omega_0 t) + C \sin (\omega_n t + \phi) \]
2} \ sin (\omega_0 t) + C \sin (\omega_n t + \phi) \] 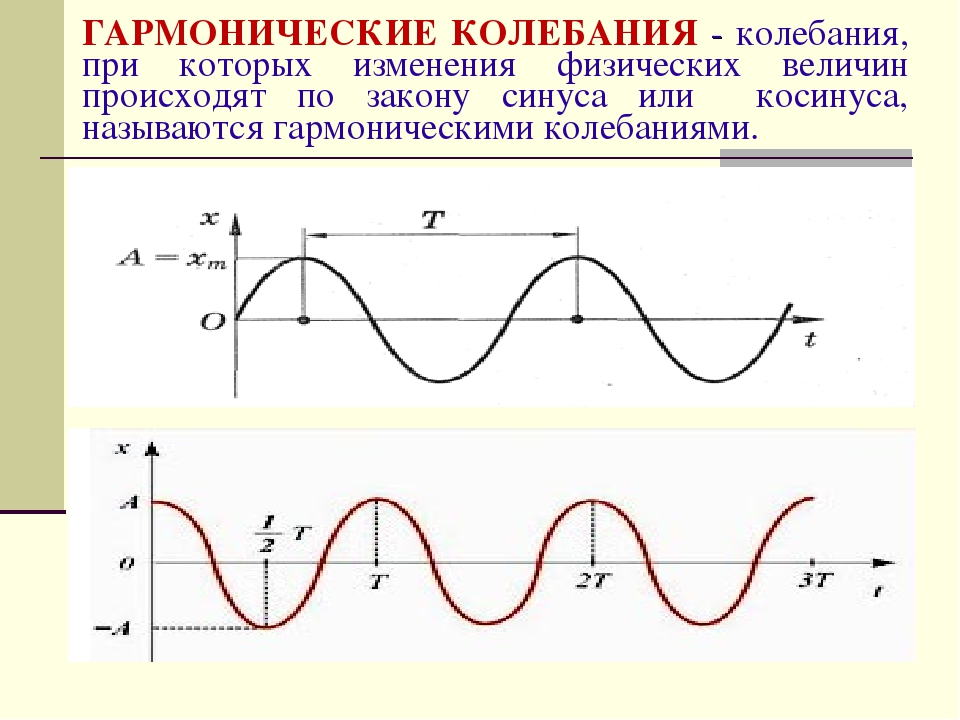 Каждая реальная система имеет некоторое демпфирование, и естественная реакция системы будет демпфирована.Однако до тех пор, пока действует внешняя гармоническая сила, отклик на нее останется. При оценке отклика системы на гармоническую воздействующую функцию мы обычно рассматриваем стационарный отклик, когда естественная реакция затухает, а отклик на воздействующую функцию остается.
Каждая реальная система имеет некоторое демпфирование, и естественная реакция системы будет демпфирована.Однако до тех пор, пока действует внешняя гармоническая сила, отклик на нее останется. При оценке отклика системы на гармоническую воздействующую функцию мы обычно рассматриваем стационарный отклик, когда естественная реакция затухает, а отклик на воздействующую функцию остается.