Приложение для решения задач геометрии ▷ ➡️ Creative Stop ▷ ➡️
Приложение для решения геометрических задач. Геометрия — не ваша сильная сторона, и вам нужна дополнительная помощь. Это нормально. Вот почему я сегодня здесь.
В сегодняшнем уроке я расскажу вам, какие из лучших применения решать геометрические задачи которые можно загрузить на любое устройство, и большинство из них бесплатны и очень просты в использовании.
Разрешить геометрию (Android / iOS)
Один из лучших приложение для решения геометрических задач Это называется Разрешить геометрию, имя, которое не оставляет сомнений в том, какова его «миссия».
Resolve Geometry — особенно полезный ресурс для учеников начальной и средней школы. Его интерфейс очень «чистый» и интуитивно понятный, что облегчает использование пользователем, который может найти решение проблемы в несколько нажатий.
После установки Resolve Geometry на ваше устройство Android o Ios, запустите приложение, нажав кнопку открытый или щелкнув его значок, расположенный на главной странице вашего устройства.
И как только приложение запустится, вы должны увидеть главный экран, содержащий различные геометрические фигуры:
Чтобы решить математическую задачу, нажмите на интересующую вас геометрическую фигуру и на открывшемся экране обведите пальцем каждую сторону фигуры.
После прорисовки стороны укажите ее длину: впишите в поле номер длина, нажмите на cm выбрать единицы измерения для стороны и подтвердить операцию, нажав команду добавлять.
Если вы не знаете, какой длины одна сторона фигуры, не вводите ничего в это поле. число, нажмите оранжевый значок увеличительного стекла
.Указав характеристики каждой стороны выбранной геометрической фигуры, прикоснитесь к значок двойного листа (вверху справа) и на открывшемся экране нажмите оранжевую кнопку Решить чтобы решить вашу проблему и увидеть различные шаги, предпринятые алгоритмом.
Вы также можете использовать Solve Geometry на своем ПК, просто зайдите на официальный сайт этого сервиса с помощью любого браузер веб.
Калькулятор геометрии (Android / iOS)
Калькулятор геометрии — еще одно приложение, которое вам следует серьезно рассмотреть, если вы хотите быстро и легко решать геометрические задачи.
Его интерфейс очень похож на предыдущий, поэтому, если вы уже пробовали приложение, которое я показал вам в предыдущем абзаце, у вас не будет проблем с использованием этого другого бесплатного решения.
Прежде чем описывать использование Калькулятора геометрии, я хотел бы уточнить, что для доступа ко всем функциям, включенным в приложение, необходимо совершить покупку некоторых элементов внутри приложения (2,95 евро).
После завершения загрузки калькулятора геометрии на свой Android-устройство или iOS, откройте приложение и на главном экране коснитесь одной из доступных геометрических фигур: треугольник, Cuadrado, прямоугольник, Paralelogramo, и так далее
На открывшемся экране вы можете нажать кнопку значок книги чтобы прочитать соответствующую статью, опубликованную в Википедии, или вы можете нажать на значок треугольника с шестеренкой для выбора параметра для расчета.
Чтобы начать расчет площади, периметра и других параметров, введите в соответствующие поля (напр. a: es h: ) правильные значения и нажмите опцию Сделанный чтобы увидеть окончательный результат операции.
a: es h: ) правильные значения и нажмите опцию Сделанный чтобы увидеть окончательный результат операции.
Если вы заметили, что введенные данные неверны, нажмите значок X (вверху), чтобы удалить введенные данные и ввести новые. Однако, чтобы вернуться в начальное меню, нажмите кнопку. < и выберите новую геометрическую фигуру для решения других задач.
Геометрикс (Android)
Еще одно полезное приложение решать геометрические задачи es Геометрикс, 100% бесплатный, который, помимо того, что он полный, также очень прост в использовании.

Как только вы завершите загрузку Geometryx на свой мобильный телефон или планшет, откройте приложение и на главном экране нажмите одну из доступных геометрических фигур: Cuadrado, прямоугольник, Правильный многоугольник, эллипс и так далее
На открывшемся экране введите данные, относящиеся к выбранной геометрической фигуре, в формы, расположенные под разделом Введите ваши входные данные и используйте легенду в правом верхнем углу, чтобы «двигаться» правильным образом.
Как только вы закончите ввод входных данных, приложение автоматически рассчитает площадь, периметр и т. Д. Вы можете увидеть все результаты, прокрутив экран вниз.
Как видите, Geometryx имеет красивую анимацию, которая делает работу с пользователем более увлекательной.
Однако, если рассматриваемые анимации вам не нравятся, вы можете удалить их, нажав на символ (+) и в меню, которое открывается слева, удалив галочка находится рядом со статьей анимации.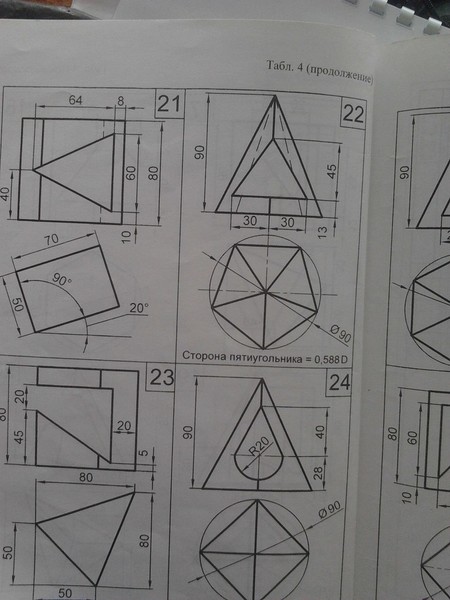
Геометрия GeoGebra (Android / iOS)
Еще одно приложение, которое я хочу посоветовать вам попробовать, это Геогебра Геометрия. Это бесплатное приложение, доступное как для Android-устройства как и iOS, он является одним из самых полных, которые вы можете загрузить на свое устройство.
По сравнению с приложениями, которые я упоминал в предыдущих абзацах, он позволяет пользователю создавать геометрические конструкции с чрезвычайной простотой для решения наиболее распространенных геометрических задач.
После установки GeoGebra Geometry на ваше устройство откройте его и используйте инструменты, расположенные вверху, для рисовать желаемые геометрические фигуры.
Для этого щелкните один из доступных вариантов (например, Точка, Право o Многоугольник ) и вставьте выбранный геометрический элемент в плоскость, коснувшись белой области и нажав стрелка внизу справа, чтобы увидеть его характеристики.
После прикосновения к стрелка расположен в правом нижнем углу, нажмите на символ (?) находится слева, выберите пункт Геометрия и в открывшемся меню коснитесь одной из доступных функций.
При выборе одного из вариантов, упомянутых выше, внимательно следуйте инструкциям, которые вы видите на экране, чтобы точно знать, какой «синтаксис» использовать для запись команды правильно, что позволит вам решить проблему.
Напоминаю, что вы также можете получить доступ к услугам, которые предлагает GeoGebra, на вашем компьютере. Для этого подключитесь к официальному сайту GeoGebra или загрузите приложение на Окна 10 и используйте инструменты, которые последний предоставляет в ваше распоряжение.
Другие приложения для решения геометрических задач
Не убедили ли вас решения, о которых я говорил до сих пор? Попробуйте эти:
- Геометрия — калькулятор (Android) — Если вы ищете геометрический калькулятор, который имеет множество функций, но при этом прост в использовании, это приложение для вас.
 Он имеет интуитивно понятный интерфейс, который позволяет не только легко искать геометрические фигуры, но, прежде всего, решать различные задачи.
Он имеет интуитивно понятный интерфейс, который позволяет не только легко искать геометрические фигуры, но, прежде всего, решать различные задачи.
- Простая геометрия (Android) — Если вы никогда не помните правильные формулы для решения геометрических задач, это приложение поможет вам исправить эту ситуацию. Фактически, простая геометрия — это форма с богатым содержанием, с которой можно легко справиться даже niños. Видеть значит верить!
- Геометрия для всех (Android) — Если вы ищете форму, предлагающую дополнительную информацию, вам обязательно стоит попробовать это приложение. Геометрия для всех, по сути, включает в себя не только информацию о формулах, которые следует применять к задачам, связанным с плоскими фигурами, но и твердыми. Это идеальный помощник для общего обзора геометрических формул перед экзаменом в классе.
- 3D магометрия (iOS) — это приложение — не простая форма для проверки при необходимости, а многое другое.
 Mageometry 3D, помимо того, что делает основные геометрические формулы легкодоступными, позволяет вам в несколько касаний решить самые сложные геометрические задачи, в которых пирамиды, параллелепипеды, конусы, сферы и многие другие фигуры являются объектами. Его можно приобрести в App Store по цене 3,49 евро.
Mageometry 3D, помимо того, что делает основные геометрические формулы легкодоступными, позволяет вам в несколько касаний решить самые сложные геометрические задачи, в которых пирамиды, параллелепипеды, конусы, сферы и многие другие фигуры являются объектами. Его можно приобрести в App Store по цене 3,49 евро.
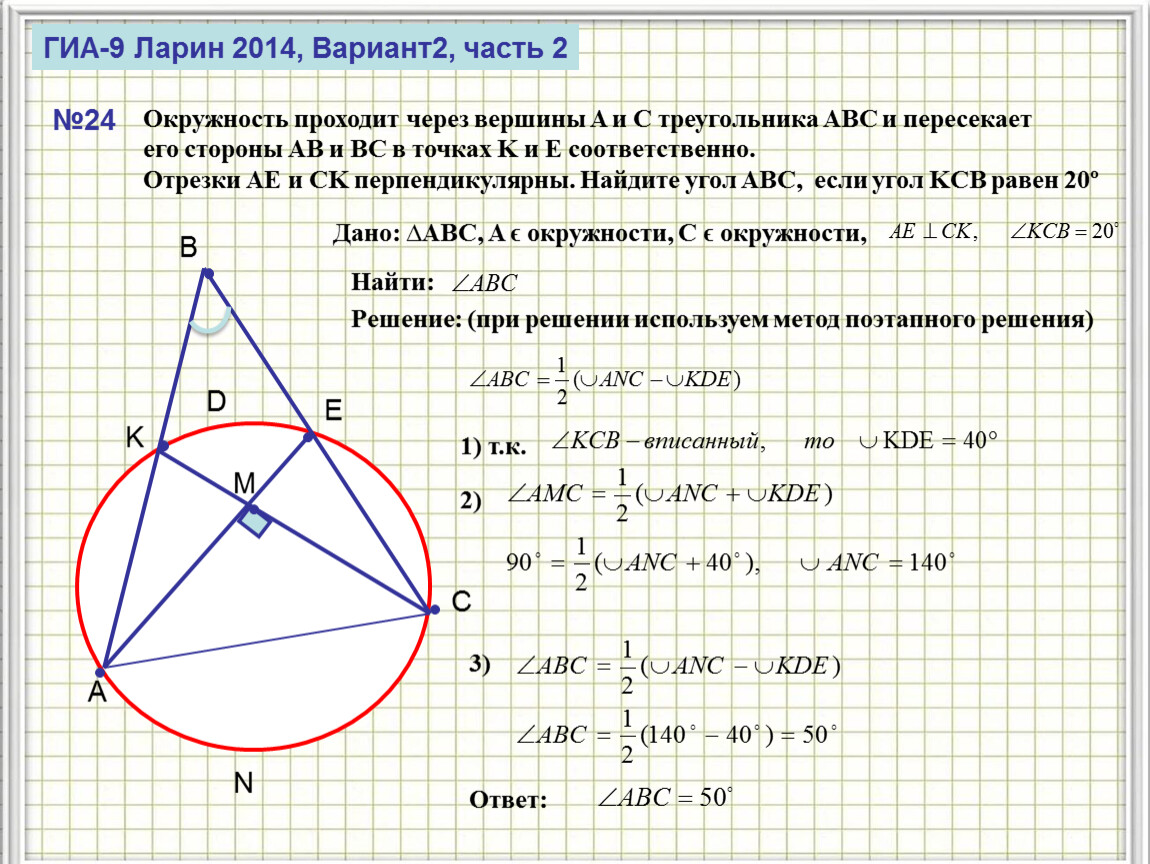
Алгоритм решения задач на доказательство равенства треугольников
Проблемы преподавания геометрии в 7 классе общеизвестны. Учителю необходимо добиться, что бы ученики осознали необходимость доказательства различного рода положений; выработать у них навык решения таких задач.
Единство теории и практики — один из основных принципов преподавания геометрии. Решению задач отводится большая роль. Задачи по геометрии следует решать не от случая к случаю, а повседневно, на каждом уроке, в тесной связи с изучаемой теорией. На уроках геометрии надо чаще решать задачи на доказательство и построение. Очень важно научить ученика понимать чертеж, выделять на чертеже необходимые детали. Часто ученик не понимает содержание теоремы или решение задачи из-за того, что не видит отчетливо на чертеже те фигуры, о которых идет речь и рассмотрение которых дает решение вопроса.
Часто ученик не понимает содержание теоремы или решение задачи из-за того, что не видит отчетливо на чертеже те фигуры, о которых идет речь и рассмотрение которых дает решение вопроса.
Я предлагаю для обучения учащихся решению задач на доказательство равенства треугольников воспользоваться следующим алгоритмом, который содержит некоторые подсказки, помогает отыскать на чертеже необходимые для доказательства фигуры.
Алгоритм решения задач на доказательство равенства треугольников
1. РАССУЖДАЕМ
Чтобы доказать, что два треугольника равны, необходимо найти три пары соответственно равных элементов:
- две стороны и угол между ними (1 признак)
- сторону и два прилежащих к ней угла (2 признак)
- три стороны (3 признак)
Равные элементы (стороны или углы) могут быть указаны в условии задачи, либо анализируем чертёж (вертикальные углы, общая сторона, биссектриса угла, медиана в треугольнике или середина отрезка).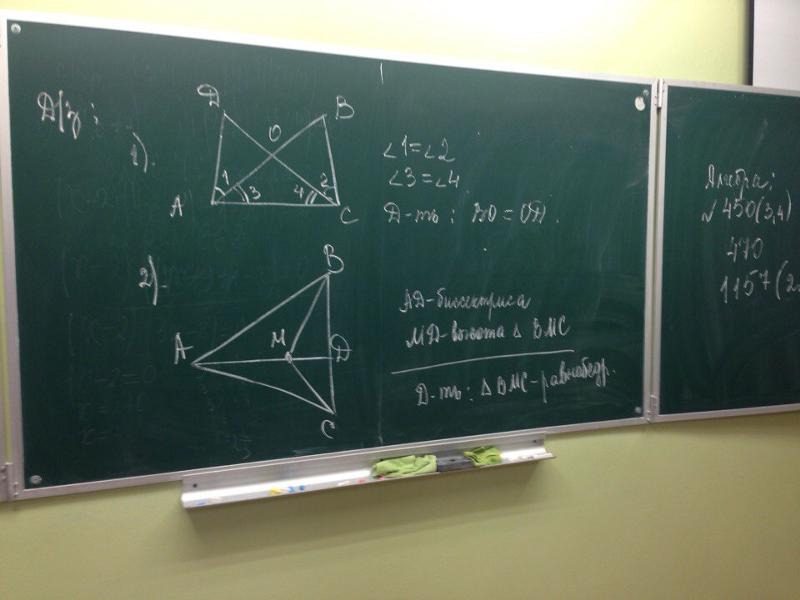 Равные элементы необходимо отметить на чертеже – это облегчит рассуждения.
Равные элементы необходимо отметить на чертеже – это облегчит рассуждения.
2. ЗАПИСЫВАЕМ РЕШЕНИЕ
Рассмотрим треугольник… и треугольник….
- … =… (по условию)
- … =… (по условию)
- …=… (почему данные элементы равны?)
Значит треугольник… равен треугольнику… по (указать признак равенства треугольников)
Итак, как выписать равные элементы.
1. Выписываем те элементы, равенство которых дано в условии.
2. Недостающие равные углы можно получить из следующих условий:
|
1 |
|
(по св-ву вертикальных углов) |
|
2 |
|
DC – биссектриса. (т. к. DC – биссектриса) |
|
3 |
|
RO – высота. Это означает равенство углов: (т. к. RO – высота)
|
|
4 |
|
RO QP. Это означает равенство углов: (т. к. RO QP)
|
|
5 |
|
Для треугольников ВСЕ и АСD угол С общий: — общий |
|
6 |
|
Углы, смежные с равными – равны. (как смежные с равными) |
Недостающие равные стороны можно получить из следующих условий:
|
1 |
|
Общая сторона DC (общая) |
|
2 |
|
RO – медиана. Это означает равенство отрезков, сторон: QO=OP (т. к. RO – медиана) |
|
3 |
|
O – середина отрезка QP. QO=OP (т. к. O – середина QP) |
Кроме того, равенство сторон или углов треугольников может следовать из равенства других треугольников.
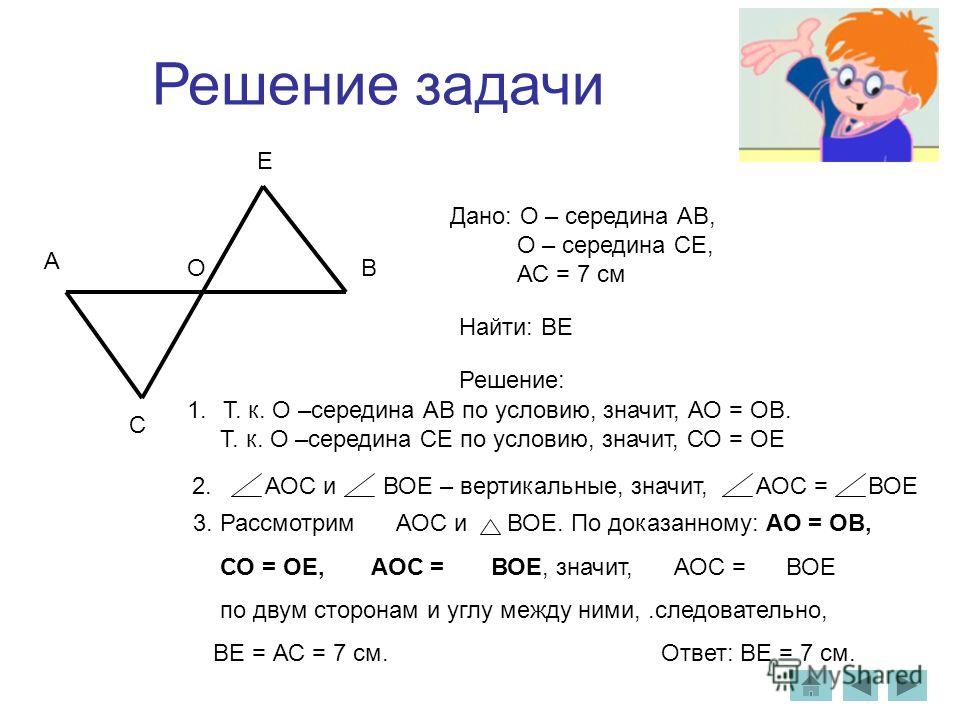
Пример оформления задачи.
В
Дано: ВО=OD, АО=СО С
Док-ть: О
А D
Доказательство:
АО= СО (по усл. )
)
ВО= DO (по усл.) по 1 признаку
(верт.)
Ч.т.д.
|
В данном курсе приведены условия и решение задач по геометрии. Есть также некоторое количество задач из курса алгебры, если их содержание предполагало знания по геометрии. Задачи структурированы по темам: Планиметрия, Треугольники, Четырехугольники, Многоугольники, Стереометрия и т.д. Все задачи по геометрии — с решением. Если Вы не нашли решение задачи по геометрии интересующего Вас типа, напишите об этом в форуме — практически наверняка курс будет дополнен Вашей задачей. Обратите внимание на то, что задача (тип задачи) решение которой Вас интересует, может находиться несколько в ином разделе, чем Вы рассчитываете. Например, в разделе «теорема синусов», если ее решение предполагает использование данной теоремы. Для решающего это не всегда очевидно.
Для ознакомления со справочной информацией, которая часто необходима для решения, например, относительно формул площади треугольника, площади параллелограмма, признаков подобия треугольников и т.д. перейдите к соответствующему разделу. Как правило, каждая глава содержит необходимую справочную информацию. Идея курса — решение конкретных задач на примерах для получения навыков в их решении. |
У даному курсі приведені умови і рішення задач з геометрії. Є також деяка кількість завдань з курсу алгебри, якщо їх вміст передбачав знання по геометрії. Завдання структуровані по темах: Планіметрія, Трикутники, Чотирикутники, Багатокутники, Стереометрія і так далі. Всі завдання по геометрії — з рішенням. Якщо Ви не знайшли рішення задачі по геометрії того типу, що цікавить Вас, напишіть про це на форумі — курс буде доповнений Вашим завданням. Звернiть увагу на те, що завдання (тип завдання) вирішення якого Вас цікавить, може знаходитися декілька в іншому розділі, чим Ви розраховуєте. Наприклад, в розділі «теорема синусів», якщо її рішення передбачає використання даної теореми. Для учня це не завжди очевидно. Для ознайомлення з довідковою інформацією, яка часто необхідна для вирішення, наприклад, відносно формул площі трикутника, площі паралелограма, ознак подібності трикутників і так далі — перейдіть до відповідного розділу. Як правило, кожна глава містить необхідну довідкову інформацію. Ідея курсу — вирішення конкретних завдань на прикладах для здобуття навиків в їх рішенні. |
Дар или навык? Что такое математические способности и как их развить
Успехи других людей – это всегда немного загадка. Почему у одних получается решать сложные математические задачи, а другие, как бы ни старались, не могут выйти на новый уровень? Неужели математика и правда подвластна не всем? На эти вопросы ответил Назар Агаханов, председатель Центральной предметно-методической комиссии по математике Всероссийской олимпиады школьников. С 1995 года руководил национальной командой России на международных математических олимпиадах.
В 2010 году Назар Хангельдыевич стал лауреатом премии Правительства РФ в области образования за научно-практическую разработку «Система развития всероссийских предметных олимпиад школьников, отбора и подготовки национальных сборных команд России на международные олимпиады по физике и математике». Когда проявляются математические способности, как их развивать и кому не стоит идти в олимпиадное движение – рассказал эксперт.
Фото: https://mipt.ru/
Математические способности – это умение построить новые модели, не повторяющие стандартные алгоритмы, которым научили в школе. На базе таких маленьких открытий и строятся наука и технологии. Именно поэтому математика позволяет находить способных детей.
Некоторые ученые считают, что порядка 10% людей обладают высокими математическими способностями. И это нормально. Если нет математических способностей, значит, есть что-то другое. Важно помогать детям открывать интересные сферы, но не навязывать.
«Каждый родитель хочет, чтобы его ребенок вырос успешным человеком, и сейчас очень популярна позиция, что развивать нужно с пеленок. Может быть, так и есть, но в любом случае лучше отталкиваться от искреннего интереса ребенка. Талант погибнет, если заставлять его делать несвойственное. Часто родители хотят использовать любые возможности, в частности, например, отправляют заниматься ментальной арифметикой, ложно полагая, что это шаг в математику, но это бессмысленная трата времени, ведь математика – это творчество. Не зря же задачи и решения называют красивыми», – говорит Назар Агаханов.
Не зря же задачи и решения называют красивыми», – говорит Назар Агаханов.
Чаще всего склонность к математике начинает проявляться в начальной школе, но это не значит, что сразу нужно вести ребенка на несколько кружков и интенсивно развивать эти способности. Достаточно одного урока занимательной математики в неделю.
Более серьезные кружки начинают работу с учениками 5-6 классов. На этом этапе изучения математики обогнать сверстников очень легко. Круг задач еще достаточно узок и владение приемами их решения позволяет обойти даже, возможно, потенциально более сильных сверстников именно за счет знаний, а вот дальше, в 7-8 классах, для высоких результатов нужно чувствовать математику, здесь и проявляются математические способности. В это время преподаватели работают со школьником на развитие математического аппарата, укрепляется который уже в старших классах.
Поэтому нередко бывает, что ярко проявляющие себя в 5-7 классах школьники начинают терять свои позиции в старших классах и выгорают от непонимания, почему теперь не получается быть сильнее других. Хотя выгорание возможно и по другой причине – слишком долгие занятия олимпиадными задачами. Интерес все-таки нужно поддерживать, переключаясь на другую деятельность.
Хотя выгорание возможно и по другой причине – слишком долгие занятия олимпиадными задачами. Интерес все-таки нужно поддерживать, переключаясь на другую деятельность.
Характер и воля: что помогает добиваться успехов в олимпиадах
Трудолюбие и готовность много работать – наверное, самые очевидные качества, которые нужны в любой сфере для достижения высоких результатов.
«Способности – это фундамент. Чтобы подняться на несколько ступенек вверх, нужно работать. При наличии этих двух пунктов и еще хорошего педагога, все остальное уходит на второй план. Даже атмосфера в семье и материальное благополучие. В сборную часто попадают дети, у которых не очень устроено семейное положение. Можно даже сделать частный вывод, что чем больше благоустроен быт, тем меньше ребенок настроен трудиться», – рассказывает Назар Агаханов.
Еще один важный пункт, над которым нужно работать каждому олимпиаднику, – психологическая устойчивость. На олимпиаде ребенок от волнения может показать результат хуже, чем его потенциал. Более ярко это проявляется в спорте, когда ребенок, приезжая на международные соревнования, проваливается. Нужно уметь воспринимать состязания не как конкурс, где тебе придется преодолевать невероятные сложности, а как удовольствие от того, что ты встретишься с интересными задачами и попробуешь их решить. Самостоятельно психологическую устойчивость развивать сложно. Для этого важна среда.
На олимпиаде ребенок от волнения может показать результат хуже, чем его потенциал. Более ярко это проявляется в спорте, когда ребенок, приезжая на международные соревнования, проваливается. Нужно уметь воспринимать состязания не как конкурс, где тебе придется преодолевать невероятные сложности, а как удовольствие от того, что ты встретишься с интересными задачами и попробуешь их решить. Самостоятельно психологическую устойчивость развивать сложно. Для этого важна среда.
«Задумайтесь, почему в хороших математических школах так много детей, показывающих высокие результаты? Во-первых, конечно, в лучших школах собираются лучшие учителя. Во-вторых, в конкурентной борьбе с равными тебе сверстниками ты привыкаешь – нужно доказывать, что ты лучший. Несколько раз сначала ты можешь сорваться из-за волнения, а дальше уже будешь спокоен», – говорит Назар Агаханов.
Интересуйтесь всем: советы по эффективному олимпиадному тренингу
Если юный математик идет в олимпиадное движение только ради поступления в университет, лучше оставить эту затею. По словам эксперта, количество бюджетных мест по России определенно превосходит количество способных ребят, заканчивающих школы. Проблемы с тем, чтобы ребенок был талантлив в математике, а его не хотели брать на учебу в вуз, нет. Такие ребята с легкостью сдают экзамены. Повторимся, этот фактор абсолютно для математики не работает.
По словам эксперта, количество бюджетных мест по России определенно превосходит количество способных ребят, заканчивающих школы. Проблемы с тем, чтобы ребенок был талантлив в математике, а его не хотели брать на учебу в вуз, нет. Такие ребята с легкостью сдают экзамены. Повторимся, этот фактор абсолютно для математики не работает.
Пожалуй, нужно искренне любить соревноваться, чтобы спокойнее переживать возможный стресс. А педагог поможет раскрыть способности и стать лучше. Заниматься с преподавателями можно и онлайн, и оффлайн. Но эксперт уверен, что онлайн-формы не заменят личного общения.
«Важен не объем пройденного материала, а то, как преподаватель послушал решение и рассуждения ребенка. Именно поэтому подготовка к международным олимпиадам во всех странах проходит примерно одинаково – учитель помогает разобрать ошибки, а не начитывает лекции. Школьник может увидеть решения тысяч задач и от этого не продвинуться, но, если он сам углубился в вопрос, попробовал решить, увидел трудные места, ему приоткроется новое знание. Дистанционные формы, к сожалению, в этом не столь эффективны, потому что важен живой диалог и прямая беседа. При этом место проживания – не крест для успехов. Хорошие преподаватели есть в регионах и это факт», – утверждает Назар Агаханов.
Дистанционные формы, к сожалению, в этом не столь эффективны, потому что важен живой диалог и прямая беседа. При этом место проживания – не крест для успехов. Хорошие преподаватели есть в регионах и это факт», – утверждает Назар Агаханов.
Еще одна возможность прокачаться – различные турниры и летние школы, которые есть практически в каждом регионе. Можно подобрать для себя наиболее подходящие. Такие площадки собирают большое количество ребят из разных городов в одном месте, дают возможность и пообщаться, и вместе решать задачи, и познакомиться с педагогами, которые входят в жюри.
Еще один важный пункт на пути к эффективным занятиям – вовремя отдыхать. Спорт, прогулки, активный отдых – хороший инструмент для качественной перезагрузки между занятиями. Но не единственный.
«Большое количество открытий в математике происходит на стыке дисциплин, когда ты можешь переключиться, перенести свои способности на другое направление, в котором не являешься специалистом самого высокого уровня. Поэтому при стремлении добиться чего-то серьезного в математике, стоит интересоваться всеми предметами в школе и вообще разносторонне развиваться», – говорит Назар Агаханов.
Поэтому при стремлении добиться чего-то серьезного в математике, стоит интересоваться всеми предметами в школе и вообще разносторонне развиваться», – говорит Назар Агаханов.
Отсюда возникает вопрос, если тратить время на другие интересы, то сколько тогда нужно заниматься именно математикой? Конкретного ответа здесь нет, все очень индивидуально. Формулу поможет выработать внутреннее ощущение – заниматься нужно ровно столько, чтобы чувствовать, что ты находишься в форме. А вот перед олимпиадными турами важно не перегружать мозг слишком интенсивными занятиями, чтобы не устать.
Обрати внимание: самые распространенные ошибки начинающих олимпиадников
Многие начинающие олимпиадники делают ошибки из-за того, что не продумывают решение глубоко. Чаще всего это происходит из-за невнимательности и игнорирования части условий. Поэтому Назар Агаханов рекомендует, как банально бы это ни было, детально читать условия задач и использовать в решении все обозначенные параметры.
В решении геометрических задач чаще всего встречаются логические ошибки, когда то, что надо доказать, каким-то образом встраивается в логику решения. Пример: нужно доказать равенство углов. Школьник отталкивается от фразы «так как эти углы равны», решает задачу и попадает в логическую ловушку, делая некорректные выводы.
Распространенная ошибка в алгебре и комбинаторике – длинное решение с перебором вместо короткого. Решение методом перебора – нормальный подход, но, если пропускается какой-то случай, решение может не засчитаться, потому что именно в этом случае и было верное решение.
Обычные объявленияНайдено 22 865 объявлений Найдено 22 865 объявленийХотите продавать быстрее? Узнать как |
|||||
|
|||||
Решение задач по теме «Смежные и вертикальные углы»
Тип урока: урок закрепления нового материала
Цели урока:
- Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
- Развивающие: развивать умение анализировать условие задачи;
- Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).

Структура урока:
- I этап. Организационный момент
- II этап. Актуализация опорных знаний
- III этап. Закрепление изученного материала
- IV этап. Зарядка для глаз
- V этап. Самостоятельная работа
- VI этап. Домашнее задание
- VII этап. Итог урока
(Слайд 1-2)
Приветствие, сообщение темы, целей и задач.
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.
(Слайд 3)
Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)
Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)
Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)
(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?
Ответ.
- Сумма смежных углов равна 180° (теорема)
∠1 + ∠2 = 180°
- Если два угла равны, то и смежные с ними углы равны.
- Если угол не развернутый, то его градусная мера меньше 180°.
- Угол, смежный с прямым, есть прямой угол.
(Слайд 5)
Вопросы. Могут ли два смежных угла быть равными:
а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ: (да, т.к. 83° + 97°= 180°)
(Слайд 6)
Устно.
| Дано:
∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4 |
Доказательство.
1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, |
Доказать ∠1 = ∠2 |
(Слайд 7)
Вопрос. Какие углы называются вертикальными?
(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).
∠ 1 и ∠ 3 – вертикальные углы
∠ 2 и ∠ 4 – вертикальные углы
(Слайд 8)
Вопрос. Каким свойством обладают смежные углы?
Ответ. Вертикальные углы равны. (теорема)
∠ 1 = ∠ 3
∠ 2 = ∠ 4
III этап. Закрепление изученного материала. Решение задач.(Слайд 9)
№3 (учебник)
Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза |
Решение. 1. Пусть ∠2 = х, тогда ∠1=2х 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Ответ: ∠1= 120°, ∠2= 60°, |
| Найти ∠1 и ∠2 |
(Слайд 10)
№6(2)
Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7 |
Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. |
| Найти ∠1 и ∠2 |
(Слайд 11)
Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1 |
Решение 1. 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° |
| Найти ∠1 и ∠2 |
(Слайд 12)
Дано: а ∩ b ∠2 меньше ∠1 в 4 раза |
Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), Ответ: 144°, 36°, 144°, 36°. |
| Найти ∠1, ∠2, ∠3 и ∠4 |
(Слайд 13)
Дано: AС ∩ ВD = O ∠ВОС = 23° |
Решение 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, 3. Ответ: 157°, 157°, 23°. |
Найти: ∠СОD, ∠АОВ, ∠АОD. |
(Слайд 14)
Устно. Вопрос. Назовите смежные и вертикальные углы.
Ответ.
Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .
Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ.
IV этап. Зарядка для глаз(Слайд 15)
V этап. Самостоятельная работа (на листочках).
Самостоятельная работа (на листочках).
| Вариант 1 | Вариант 2 |
| №1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы. | №1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы. |
| №2. Разность смежных углов равна 50°. Найдите меньший угол. | №2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол. |
Ответы
| Вариант 1 | Вариант 2 |
№1. 93°, 87°, 93°. 93°, 87°, 93°. |
№1. 62°, 118°, 62° |
| №2. 75°. | №2. 36°. |
- §2. Пункты 14-15.
- Задачи на стр. 26. № 6(4), № 12.
- Повторили понятия смежных и вертикальных углов
- Научились решать задачи, используя знания о смежных и вертикальных углах.
- Стали еще на одну ступеньку выше в изучении геометрии.
Математика влияет на развитие мозга — Российская газета
Лобачевскими и Гауссами рождаются или становятся? Ответ ученые пытаются найти уже ни одно десятилетие. Изучают мозг выдающихся ученых, ищут ген математики. Безрезультатно.
Французские ученые решали более простой вопрос: откуда вообще появляется способность к математике. Существуют две гипотезы. По одной, есть люди, которые интуитивно чувствуют пространство и числа. Попросту говоря, человек математиком рождается. По другой, склонность к этой науке — побочный эффект появления языка и речи.
Существуют две гипотезы. По одной, есть люди, которые интуитивно чувствуют пространство и числа. Попросту говоря, человек математиком рождается. По другой, склонность к этой науке — побочный эффект появления языка и речи.
В эксперименте участвовали профессиональные математики и обычные люди примерно с одинаковым образованием. Всем предложили ответить на сложные математические тесты по алгебре, геометрии, топологии, а также тесты на общий кругозор — по истории, географии и т.д. На томографе ученые смотрели, что происходит в мозге добровольцев.
Математики успешно выступили в обоих заданиях. «Гуманитарии» хороший результат показали в тестах на кругозор, но провалили математические. А что же происходило в головах? Математические тесты активировали у математиков определенные зоны в коре мозга. Но «молчали» у добровольцев из общей группы. Интересно, что они все же включались, когда требовалось сделать простые арифметические действия, например на сложение или умножение.
Вывод? Математическое мышление высокого уровня работает в зонах, которые отвечают за восприятие чисел, пространства и времени и отличаются от зон, связанных с языком. То есть, по мнению французских ученых, склонность к математике должна проявляться уже в детстве. И это родители могут увидеть, наблюдая, насколько их чадо ориентируется в пространстве и в мире чисел.
То есть, по мнению французских ученых, склонность к математике должна проявляться уже в детстве. И это родители могут увидеть, наблюдая, насколько их чадо ориентируется в пространстве и в мире чисел.
— На самом деле, с зонами, которые видны во время тестов на МРТ, все не так однозначно, — сказал корреспонденту «РГ» член-корреспондент РАН Алексей Иваницкий. — Нет зон, которые «кричат» или «молчат». Некоторые во время решения задач немного активней, чем другие. Почему «гуманитарии» не справляются с математическими задачами? Скорей всего, определенные зоны у них менее развиты. Но, думаю, что они заложены в мозге подавляющего числа людей, но у одних они развивались при обучении, а у других так и остались в зачаточном состоянии, так как их не тренировали.
В свое время ученые из Стэнфордского университета отобрали группу обычных восьмилетних школьников и шесть лет на МРТ изучали их мозг. У тех, кто занимался математикой и достиг определенных успехов, структуры мозга значительно отличались: больше развита внутритеменная борозда коры, которая помогает выполнять сравнительный анализ и работать с числами, а также затылочная и префронтальная доли, которые отвечают за прогнозирование. Чем выше были успехи в математике, тем сильнее оказалась активность в гиппокампе, который отвечает за память. Словом, на часто звучащий вопрос, а зачем нам синусы и тангенсы, биномы и логарифмы, ответ однозначный — они мозги развивают. Кстати, в китайских балетных училищах за математику спрашивают так же строго, как за танец.
Чем выше были успехи в математике, тем сильнее оказалась активность в гиппокампе, который отвечает за память. Словом, на часто звучащий вопрос, а зачем нам синусы и тангенсы, биномы и логарифмы, ответ однозначный — они мозги развивают. Кстати, в китайских балетных училищах за математику спрашивают так же строго, как за танец.
App Store: Photomath
Изучайте математику, проверяйте домашние задания и готовьтесь к предстоящим тестам и экзаменам ACT/SAT с помощью самого популярного приложения для изучения математики в мире! Получили сложную домашнюю работу или классные задания? Избавьтесь от тупика как можно скорее с помощью наших пошаговых объяснений и анимаций.
Мы предоставим вам все необходимое, от базовой арифметики до продвинутого исчисления и геометрии. Вы МОЖЕТЕ заниматься математикой!
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
• Объяснение словесных задач!
• Бесплатное использование
• Пошаговые объяснения для каждого решения
• Эксклюзивная анимация с практическими рекомендациями
• Прокрутка нескольких методов решения для каждой задачи
• Многофункциональный научный калькулятор
• Интерактивные графики
МАТЕМАТИЧЕСКИЕ ТЕМЫ
• Базовая математика/предварительная алгебра: арифметика, целые числа, дроби, десятичные числа, степени, корни, множители
• Алгебра: линейные уравнения/неравенства, квадратные уравнения, системы уравнений, логарифмы, функции, матрицы, графики, многочлены
• Геометрия ( только специальные учебники)
• Тригонометрия/Предварительное исчисление: тождества, конические сечения, векторы, последовательности и ряды, логарифмические функции
• Исчисление: пределы, производные, интегралы, построение кривых
• Статистика: комбинации, факториалы
«Ответ не все, что вы получите от этого бесплатного приложения. Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post
Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post
«Пошаговое руководство полезно для учащихся, которые не имеют доступа к репетитору и испытывают трудности с решением математических задач». — Forbes
«Вирусное видео о новом приложении выглядит как воплощение мечты для всех, у кого проблемы с математикой». — Время
___________________________________________
Хотите повысить свой опыт обучения? С Photomath Plus вы получаете:
ЭКСПЕРТНЫЕ ОБЪЯСНЕНИЯ
Высококачественные одобренные учителем объяснения для каждой задачи в избранных учебниках, включая задачи со словами и геометрией! Изучайте или повторяйте математические понятия в своем собственном темпе.
АНИМАЦИЯ
Подробная анимация, которая поможет вам визуализировать и понять каждый математический шаг.
СОВЕТЫ И ПОДСКАЗКИ
Повысьте уровень своего обучения, поняв, «как» и «почему» решаются математические задачи, или вспомните забытые термины и понятия с помощью нашего встроенного глоссария.
• Оплата будет снята с вашей учетной записи Apple ID при подтверждении покупки.
• Подписка продлевается автоматически, если она не будет отменена по крайней мере за 24 часа до окончания текущего расчетного периода.
• С вашего аккаунта будет взиматься плата за продление в течение 24 часов до окончания текущего периода.
• Управляйте подпиской или отмените ее в настройках своей учетной записи в App Store после покупки.
• Предложения и цены могут быть изменены без предварительного уведомления.
Предложения или вопросы? Напишите нам по адресу [email protected]
Веб-сайт: www.photomath.com
Facebook: @Photomathapp
Twitter: @Photomath
Условия использования: https://photomath.com/en/termsofuse
Политика конфиденциальности: https: //фотоматематика.com/en/privacypolicy
| Применимые группы | Для личного пользования | Группа запуска | Микропредприятие | Среднее предприятие |
| Срок авторизации | Постоянный | Постоянный | Постоянный | Постоянный |
| Портрет Авторизация | Постоянный | Постоянный | Постоянный | |
| Авторизованное соглашение | Персональная авторизация | Авторизация предприятия | Авторизация предприятия | Авторизация предприятия |
| Онлайн-счет | ||||
|
Маркетинг в социальных сетях (Facebook, Twitter, Instagram и т. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Маркетинг цифровых медиа (SMS, электронная почта, интернет-реклама, электронные книги и т. д.) |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Интернет, мобильные устройства, дизайн страницы программного обеспечения Веб-дизайн и дизайн приложений, программное обеспечение и игровой скин, H5, электронная коммерция и продукты и т. Д. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Физическая печатная продукция Упаковка продукции, книги и журналы, газеты, открытки, плакаты, брошюры, купоны и т. |
Личное Коммерческое использование (лимит печати 200 копий) |
Ограничение 5000 Копий Печать | Ограничение 20000 Копий Печать | Не ограничено Копий Печать |
|
Отчет о маркетинге продукции и бизнес-плане Предложение по сетевому дизайну, дизайну VI, маркетинговому планированию, PPT (без перепродажи) и т. д. |
Личное Коммерческое использование |
|||
|
Маркетинг и показ наружной рекламы Наружные рекламные щиты, автобусная реклама, витрины, офисные здания, гостиницы, магазины, другие общественные места и т. д. |
Личное Коммерческое использование (лимит печати 200 копий) |
|||
|
Массовые цифровые СМИ
(CD, DVD, фильм, ТВ, видео и т. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Перепродажа физической продукции текстиль, чехлы для мобильных телефонов, открытки, календари, чашки, футболки |
||||
|
Перепродажа через Интернет Мобильные обои, шаблоны дизайна, элементы дизайна, шаблоны PPT и используйте наши дизайны в основном элементе для перепродажи. |
||||
| Портрет Коммерческое использование |
(Только для обучения и общения) |
|||
|
Использование портретной чувствительности (табачная, медицинская, фармацевтическая, косметическая и другие отрасли промышленности) |
(Только для обучения и общения) |
(Свяжитесь со службой поддержки для настройки) |
(Свяжитесь со службой поддержки для настройки) |
(Свяжитесь со службой поддержки для настройки) |
| Применимые группы | Для личного пользования | Группа запуска | Микропредприятие | Среднее предприятие |
| Срок авторизации | Постоянный | Постоянный | Постоянный | Постоянный |
| Портрет Авторизация | Постоянный | Постоянный | Постоянный | |
| Авторизованное соглашение | Персональная авторизация | Авторизация предприятия | Авторизация предприятия | Авторизация предприятия |
| Онлайн-счет | ||||
|
Маркетинг в социальных сетях (Facebook, Twitter, Instagram и т. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Маркетинг цифровых медиа (SMS, электронная почта, интернет-реклама, электронные книги и т. д.) |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Интернет, мобильные устройства, дизайн страницы программного обеспечения Веб-дизайн и дизайн приложений, программное обеспечение и игровой скин, H5, электронная коммерция и продукты и т. Д. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Физическая печатная продукция Упаковка продукции, книги и журналы, газеты, открытки, плакаты, брошюры, купоны и т. |
Личное Коммерческое использование (лимит печати 200 копий) |
Ограничение 5000 Копий Печать | Ограничение 20000 Копий Печать | Не ограничено Копий Печать |
|
Отчет о маркетинге продукции и бизнес-плане Предложение по сетевому дизайну, дизайну VI, маркетинговому планированию, PPT (без перепродажи) и т. д. |
Личное Коммерческое использование |
|||
|
Маркетинг и показ наружной рекламы Наружные рекламные щиты, автобусная реклама, витрины, офисные здания, гостиницы, магазины, другие общественные места и т. д. |
Личное Коммерческое использование (лимит печати 200 копий) |
|||
|
Массовые цифровые СМИ
(CD, DVD, фильм, ТВ, видео и т. |
Личное Коммерческое использование (Ограничение 20 000 показов) |
|||
|
Перепродажа физической продукции текстиль, чехлы для мобильных телефонов, открытки, календари, чашки, футболки |
||||
|
Перепродажа через Интернет Мобильные обои, шаблоны дизайна, элементы дизайна, шаблоны PPT и используйте наши дизайны в основном элементе для перепродажи. |
||||
| Портрет Коммерческое использование |
(Только для обучения и общения) |
|||
|
Использование портретной чувствительности (табачная, медицинская, фармацевтическая, косметическая и другие отрасли промышленности) |
(Только для обучения и общения) |
(Свяжитесь со службой поддержки для настройки) |
(Свяжитесь со службой поддержки для настройки) |
(Свяжитесь со службой поддержки для настройки) |
Геометрия аэрофотосъемки
Одиночная вертикальная аэрофотосъемка
Геометрия аэрофотоснимка основана на простом фундаментальном условии коллинеарности . По определению, три или более точек, лежащих на одной прямой, называются коллинеарными . В фотограмметрии единственный луч света — это прямая линия; на эту прямую всегда должны приходиться три основные точки: отображаемая точка на земле, точка фокусировки объектива камеры и изображение точки на пленке или массиве изображений цифровой камеры, как показано на рисунке ниже.
По определению, три или более точек, лежащих на одной прямой, называются коллинеарными . В фотограмметрии единственный луч света — это прямая линия; на эту прямую всегда должны приходиться три основные точки: отображаемая точка на земле, точка фокусировки объектива камеры и изображение точки на пленке или массиве изображений цифровой камеры, как показано на рисунке ниже.
Линия аэрофотосъемки
Авторы и права: Дистанционное зондирование окружающей среды: взгляд на земные ресурсы Джона Р.Дженсен © 2007. Используется с разрешения.
Представьте себе пучок бесчисленных лучей света, составляющих один аэрофотоснимок или цифровой кадр в момент экспонирования. Длина каждого луча от фокуса камеры до отображаемой точки на земле определяется высотой объектива камеры над землей и высотой этой точки над землей. Длина каждого луча от фокальной точки до фотографического изображения определяется фокусным расстоянием объектива.
Теперь представьте, что фокальная плоскость камеры наклонена относительно земли из-за крена, тангажа и рыскания самолета. Это повлияет на длину каждого светового луча в пучке, а также повлияет на положение точки изображения на двумерной фотографии. Если мы хотим сделать точные измерения по фотографии и связать эти измерения с расстояниями в реальном мире, мы должны знать точное положение и угловую ориентацию фотографии по отношению к земле.Сегодня мы можем измерять положение и угловую ориентацию камеры относительно земли с помощью технологии прямой геопривязки GPS/IMU. Но у пионеров фотограмметрии этого преимущества не было. Вместо этого они разработали математический процесс, основанный на условии коллинеарности, который позволил им вычислить положение и ориентацию фотографии на основе известных точек на земле. Эта геометрическая взаимосвязь между изображением и фоном называется внешней ориентацией .Он состоит из шести математических элементов: координат x, y и z точки фокусировки камеры и трех углов поворота: омега (крен), фи (тангаж) и каппа (рыскание) по отношению к земле. Математический процесс вычисления элементов внешнего ориентирования по известным точкам на земле называется фотограмметрическим термином пространственной резекции .
Это повлияет на длину каждого светового луча в пучке, а также повлияет на положение точки изображения на двумерной фотографии. Если мы хотим сделать точные измерения по фотографии и связать эти измерения с расстояниями в реальном мире, мы должны знать точное положение и угловую ориентацию фотографии по отношению к земле.Сегодня мы можем измерять положение и угловую ориентацию камеры относительно земли с помощью технологии прямой геопривязки GPS/IMU. Но у пионеров фотограмметрии этого преимущества не было. Вместо этого они разработали математический процесс, основанный на условии коллинеарности, который позволил им вычислить положение и ориентацию фотографии на основе известных точек на земле. Эта геометрическая взаимосвязь между изображением и фоном называется внешней ориентацией .Он состоит из шести математических элементов: координат x, y и z точки фокусировки камеры и трех углов поворота: омега (крен), фи (тангаж) и каппа (рыскание) по отношению к земле. Математический процесс вычисления элементов внешнего ориентирования по известным точкам на земле называется фотограмметрическим термином пространственной резекции .
Снова обратитесь к рисунку выше. Если бы мы были вместе в классе, я мог бы продемонстрировать концепцию резекции пространства, используя свой рабочий стол и фотографию своего рабочего стола, сделанную сверху.Я мог бы использовать кусочки нити для представления отдельных лучей света; каждая строка имеет фиксированную длину в зависимости от расстояния от рабочего стола до камеры, когда была сделана фотография. Теперь вам нужно попытаться представить эту демонстрацию так, как я описываю ее словами. Если вы чувствуете разочарование, представьте себя Лаусседа, пытающимся разобраться в этом самостоятельно в 1800-х годах.
Я прикрепляю один конец веревки к определенной точке на рабочем столе, другой конец веревки прикрепляю к изображению этой точки на фотографии и туго натягиваю веревку.С помощью этого единственного куска веревки я не могу точно определить или зафиксировать положение фокальной точки камеры или ориентацию фокальной плоскости камеры, как это было, когда была сделана фотография. Теперь я выбираю вторую точку, добавляю второй кусок веревки и туго натягиваю обе нити. Я не могу перемещать фотографию так же сильно, как мог бы, если бы был прикреплен только один кусок веревки, но фотография все еще может катиться и скручиваться относительно рабочего стола. Если я укажу еще третью точку (которая не лежит на одной прямой с первыми двумя) и прикреплю третий кусок веревки, то теперь у меня будет жесткое решение; геометрическое соотношение между рабочим столом и фотографией фиксировано, и я могу определить точку фокусировки камеры на моей настольной модели.Добавление большего количества точек повышает надежность геометрического решения и сводит к минимуму последствия любых небольших ошибок, которые я мог допустить, либо обрезав нить до нужной длины, либо прикрепив нити точно к указанным точкам. Когда мы переопределяем решение, добавляя дополнительные избыточные измерения, мы можем выполнять статистические расчеты для количественной оценки точности нашего геометрического решения.
Теперь я выбираю вторую точку, добавляю второй кусок веревки и туго натягиваю обе нити. Я не могу перемещать фотографию так же сильно, как мог бы, если бы был прикреплен только один кусок веревки, но фотография все еще может катиться и скручиваться относительно рабочего стола. Если я укажу еще третью точку (которая не лежит на одной прямой с первыми двумя) и прикреплю третий кусок веревки, то теперь у меня будет жесткое решение; геометрическое соотношение между рабочим столом и фотографией фиксировано, и я могу определить точку фокусировки камеры на моей настольной модели.Добавление большего количества точек повышает надежность геометрического решения и сводит к минимуму последствия любых небольших ошибок, которые я мог допустить, либо обрезав нить до нужной длины, либо прикрепив нити точно к указанным точкам. Когда мы переопределяем решение, добавляя дополнительные избыточные измерения, мы можем выполнять статистические расчеты для количественной оценки точности нашего геометрического решения.
В этом курсе у нас нет времени вдаваться в математику аналитической фотограмметрии, но мы надеемся, что вы сможете понять ее как настоящую науку об измерениях.На самом деле, фотограмметрию традиционно преподавали как субдисциплину гражданского строительства и геодезии, а не как географию. Фотограмметрия — это не только создание аккуратных и полезных карт; Ключевая функция фотограмметриста как геопространственного профессионала состоит в том, чтобы делать авторитетные заявления о пространственной точности и правильности фотограмметрических измерений и продуктов картирования. Как вы увидите в этом и последующих уроках, вы можете легко научиться нажимать кнопки в программном обеспечении, чтобы создавать аккуратные и интересные продукты дистанционного зондирования для использования в ГИС.Требуется более строгое образование, чтобы делать количественные заявления о пространственной точности этих продуктов. По моему мнению, обязанность фотограмметриста или специалиста по ГИС состоит в том, чтобы информировать конечных пользователей об ошибке, содержащейся в продукте данных, и в первую очередь предоставлять им продукт. Понимание ошибок и потенциальных последствий ошибок является очень важной частью процесса принятия решений. Существует также особый язык, используемый для формулирования утверждений об ошибках и точности.Вы немного изучите этот язык в Уроке 6.
Понимание ошибок и потенциальных последствий ошибок является очень важной частью процесса принятия решений. Существует также особый язык, используемый для формулирования утверждений об ошибках и точности.Вы немного изучите этот язык в Уроке 6.
Стереопара
После того, как внешняя ориентация одного вертикального аэрофотоснимка решена, другие точки, идентифицированные на фотографическом изображении, могут быть спроецированы как дополнительные лучи света, дополнительные отрезки нити, проходящие через фокус камеры и пересекающие поверхность цели ( земля или мой рабочий стол). Если целевая поверхность идеально плоская, то высоты трех известных точек определяют математическую плоскость, представляющую всю поверхность.Тогда можно точно определить местонахождение любой другой точки, которую мы можем идентифицировать на изображении на целевой поверхности, просто спроецировав одну прямую линию. В действительности поверхность цели никогда не бывает идеально плоской. Мы можем спроецировать луч света от изображения через фокальную плоскость, но мы не можем определить точку, в которой он пересекает целевую поверхность, если мы не знаем форму поверхности и высоту этой точки. В контексте нашей демонстрации выше нам нужно знать точную длину нового куска нити, чтобы установить местоположение интересующей точки на целевой поверхности.Здесь в игру вступает концепция стереоскопического измерения. Я поручил вам просмотреть ту часть главы Дженсена, в которой описываются методы стереоскопического просмотра. Вы не будете нести ответственность за детали, но я надеюсь, что вы уйдете несколько пораженным тем фактом, что само наше собственное видение работает в соответствии с этими принципами. Мы смогли построить целую науку измерения вокруг чего-то, что является естественной, встроенной характеристикой физического человеческого существа.
В контексте нашей демонстрации выше нам нужно знать точную длину нового куска нити, чтобы установить местоположение интересующей точки на целевой поверхности.Здесь в игру вступает концепция стереоскопического измерения. Я поручил вам просмотреть ту часть главы Дженсена, в которой описываются методы стереоскопического просмотра. Вы не будете нести ответственность за детали, но я надеюсь, что вы уйдете несколько пораженным тем фактом, что само наше собственное видение работает в соответствии с этими принципами. Мы смогли построить целую науку измерения вокруг чего-то, что является естественной, встроенной характеристикой физического человеческого существа.
Преимущество стереофотографии в том, что мы можем извлекать из нее трехмерную информацию. Вернемся к примеру, который я описал выше. На этот раз представьте, что у меня есть две фотографии моего рабочего стола, сделанные с двух разных точек зрения, и что отдельные изображения на самом деле перекрываются. Одно изображение взято с левой стороны моего стола, а другое — с правой стороны моего стола.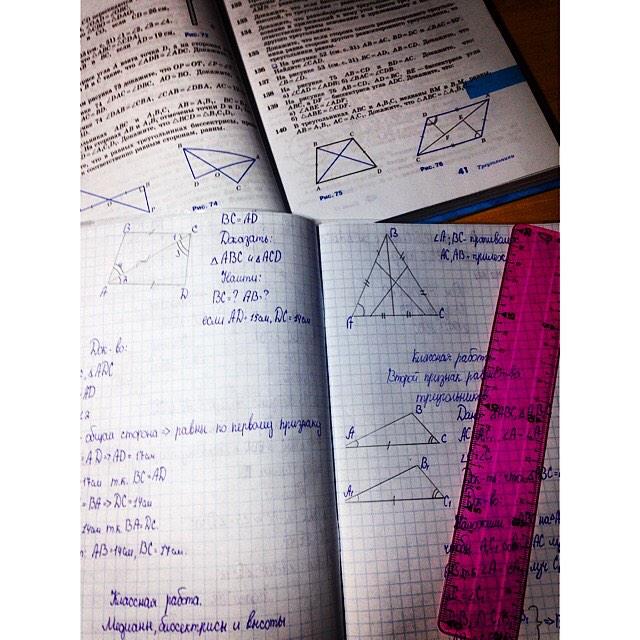 Середина моего рабочего стола видна на обеих фотографиях. Теперь предположим, что мы установили параметры внешнего ориентирования для каждой из двух фотографий; Итак, мы точно знаем, где они оба находились в момент воздействия относительно рабочего стола.Теперь у нас есть два пучка световых лучей, некоторые из которых пересекаются в середине моего рабочего стола. Фундаментальный постулат геометрии гласит, что если две прямые пересекаются, то их пересечение составляет ровно одну точку. Вуаля! Теперь мы можем точно локализовать любую точку на поверхности рабочего стола, независимо от ее формы, в трехмерном пространстве. Для любой данной точки, общей для обеих фотографий, мы теперь знаем точную длину каждого из двух кусков веревки (по одному от каждой фотографии), которые соединяются с изображенной точкой на земле.В фотограмметрии мы называем это пересечением пространств . Если у нас есть две фотографии, точно ориентированные в пространстве относительно друг друга, мы всегда можем пересечь две линии, чтобы найти трехмерную наземную координату любой точки, общей для обеих фотографий.
Середина моего рабочего стола видна на обеих фотографиях. Теперь предположим, что мы установили параметры внешнего ориентирования для каждой из двух фотографий; Итак, мы точно знаем, где они оба находились в момент воздействия относительно рабочего стола.Теперь у нас есть два пучка световых лучей, некоторые из которых пересекаются в середине моего рабочего стола. Фундаментальный постулат геометрии гласит, что если две прямые пересекаются, то их пересечение составляет ровно одну точку. Вуаля! Теперь мы можем точно локализовать любую точку на поверхности рабочего стола, независимо от ее формы, в трехмерном пространстве. Для любой данной точки, общей для обеих фотографий, мы теперь знаем точную длину каждого из двух кусков веревки (по одному от каждой фотографии), которые соединяются с изображенной точкой на земле.В фотограмметрии мы называем это пересечением пространств . Если у нас есть две фотографии, точно ориентированные в пространстве относительно друг друга, мы всегда можем пересечь две линии, чтобы найти трехмерную наземную координату любой точки, общей для обеих фотографий. Две фотографии, ориентированные относительно друг друга, называются стереомоделью .
Две фотографии, ориентированные относительно друг друга, называются стереомоделью .
Кроме того, у нас может быть большой блок аэрофотоснимков, перекрывающихся в направлении полета, а также между соседними линиями полета, ориентированных относительно друг друга.Этот построенный блок представляет собой все пересекающиеся пучки световых лучей со всех перекрывающихся фотографий. Вы можете себе представить, что многие точки будут видны на нескольких фотографиях. Фактически, при прямом перекрытии 60% каждая точка на одной линии полета видна 3 раза. Если точка попадает в область бокового перекрытия 30% между двумя линиями полета, она будет видна 6 раз; шесть лучей пересекутся в одной точке. На самом деле, поскольку некоторая степень ошибки измерения неизбежна, пересечение будет происходить внутри какой-то сферы, которая представляет собой неопределенность проекции координат рассматриваемой точки.Как я упоминал ранее, математические уравнения фотограмметрии позволяют нам количественно определить эту неопределенность в статистических терминах.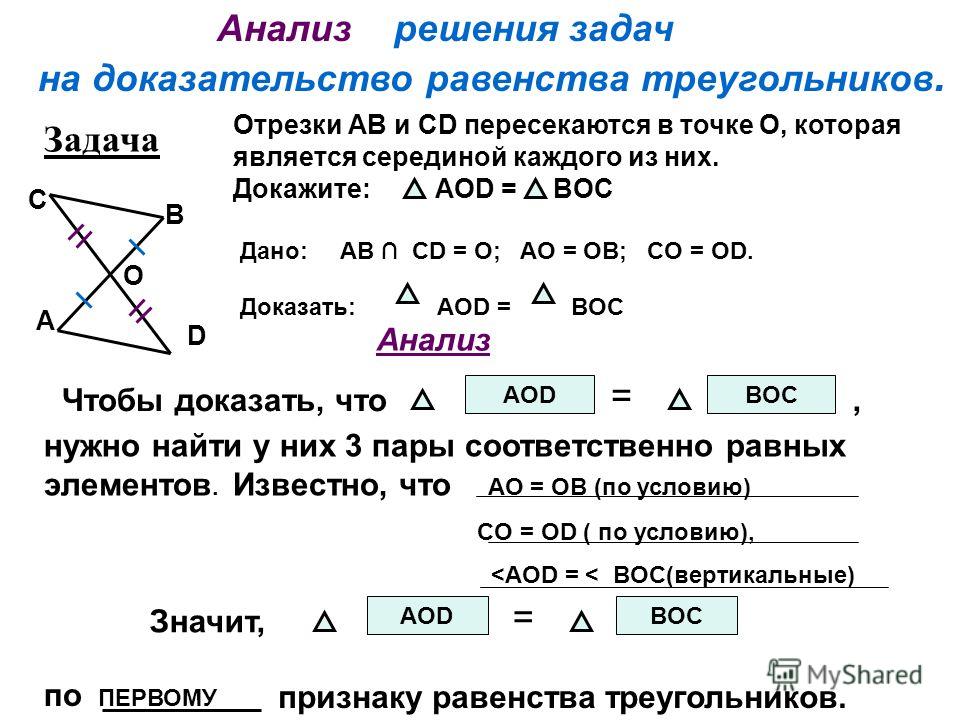 Ваши показания приведут вас к большей глубине и деталям, но я надеюсь, что мое объяснение поможет вам создать в уме трехмерную картину, облегчив понимание показаний.
Ваши показания приведут вас к большей глубине и деталям, но я надеюсь, что мое объяснение поможет вам создать в уме трехмерную картину, облегчив понимание показаний.
Сферическое решение — Сиднейский оперный театр
Форма здания постепенно отличалась от конкурсных рисунков Утцона. Его новые кривые были подробно описаны в Красной книге, полном наборе планов, разрезов и фасадов, отправленном правительству Нового Южного Уэльса в марте 1958 года, который расширил схематические рисунки из его заявки на участие в конкурсе.Коньковые профили крыши стали выше и заострённее; форма концевой оболочки больше не консольная, как утес над морем. Эти более высокие профили также позволили увеличить объем сценических башен и зрительных залов.
Однако чертежи, внесенные в Красную книгу, были конструктивно несостоятельными, со сложными изгибами у основания крыши. Каждая оболочка была разной. Отсутствие определяющей геометрии сделало бы невозможным повторное использование опалубки строителями и увеличило бы стоимость здания.
Поскольку годы и итерации продолжались без удовлетворительного решения, решение проблемы превратилось из неотложного в критическое. К концу 1961 года прошло три года с тех пор, как Утзон согнул свою пластиковую линейку на столе, а решение для сборки оболочек все еще не было найдено.
Правительство Нового Южного Уэльса даже спросило Утзона, не следует ли ему подумать о другой инженерной фирме, но архитектор отказался искать что-то еще, убежденный, что его сотрудничество с Arup даст решение.В конце концов, решение придет от самого Утцона.
Различные мифы окружают открытие так называемого Сферического решения, универсального решения проблем сборных оболочек. Культовая скульптурная форма Сиднейского оперного театра в значительной степени зависит от формы этих оболочек, поэтому нельзя недооценивать важность поиска наилучшего решения для крыши.
Как гласит один из самых популярных мифов, Утзон испытал озарение, когда чистил апельсин. Хотя верно то, что решение может быть продемонстрировано таким образом, на самом деле это был архитектор Ээро Сааринен, который однажды утром за завтраком разрезал грейпфрут, чтобы описать тонкую структуру оболочки крыши своего здания TWA, а позже использовал апельсин, чтобы объяснить другим форму раковин.
По его собственному признанию, однажды вечером Утзон был один в своем офисе в Хеллебеке, и его мысли тяготили ряд самых неразрешимых проблем Сиднейского оперного театра.
Утзон складывал корпуса большой модели, чтобы освободить место, когда заметил, насколько похожими оказались формы. Раньше каждая оболочка казалась отличной от других. Но теперь ему пришло в голову, что, поскольку они были так похожи, каждый из них, возможно, мог быть получен из одной постоянной формы, такой как плоскость сферы.
Простота и легкость повторения сразу привлекли внимание.
Это означает, что форма здания может быть изготовлена из повторяющейся геометрии. Не только это, но и однородный рисунок можно было также получить для облицовки внешней поверхности. Это стало бы единственным объединяющим открытием, которое позволило окончательно воплотить отличительные черты Сиднейского оперного театра, от сводчатых арок и вневременного, похожего на парус силуэта оперного театра до исключительно красивой отделки плитки.
Приложение для решения задач по геометрии ▷ ➡️ Творческая остановка ▷ ➡️
Приложение для решения задач по геометрии. Геометрия не ваша сильная сторона, и вам нужна дополнительная помощь. Это нормально. И именно поэтому я здесь сегодня.
В сегодняшнем уроке я расскажу вам, какие приложения являются одними из лучших для решения геометрических задач , которые можно загрузить на любое устройство, и большинство из них бесплатны и очень просты в использовании.
Решить геометрию (Android/iOS)
Одно из лучших приложений для решения геометрических задач называется Решить геометрию , и это имя не оставляет сомнений в том, в чем заключается его «миссия».
Resolve Geometry — особенно полезный ресурс для учащихся начальной и средней школы. Его интерфейс очень «чистый» и интуитивно понятный, что облегчает использование пользователем, который может найти решение проблемы в несколько нажатий.
После установки Resolve Geometry на ваше устройство Android или iOS запустите приложение, нажав кнопку Открыть или щелкнув ее значок, расположенный на главной странице вашего устройства.
И, как только приложение запустится, вы должны увидеть главный экран, содержащий различные геометрические фигуры: Разносторонние треугольники , Равнобедренные треугольники , Равнобедренные треугольники , Прямоугольный треугольник , Куадрадо , Прямоугольник Параллелограмм и т.д.
Чтобы решить математическую задачу, нажмите на интересующую вас геометрическую фигуру и на открывшемся экране обведите пальцем каждую сторону фигуры.
После рисования стороны укажите ее длину: напишите в поле число длину, тапните на см для выбора единицы измерения стороны и подтвердите операцию нажатием команды Добавить .
Если вы не знаете, какой длины одна сторона фигуры, ничего не вводите в поле числа, нажмите на оранжевый значок увеличительного стекла .
Указав характеристики каждой стороны выбранной геометрической фигуры, коснитесь значка двойного листа (вверху справа) и на открывшемся экране нажмите оранжевую кнопку Решите , чтобы решить вашу задачу, и просмотрите различные шаги, алгоритм принял.
Вы также можете использовать Solve Geometry на своем ПК, просто зайдите на официальный сайт этого сервиса с помощью любого веб-сайта-навигатора.
Калькулятор геометрии (Android/iOS)
Калькулятор геометрии — еще одно приложение, которое следует серьезно рассмотреть, если вы хотите быстро и легко решать геометрические задачи.
Его интерфейс очень похож на предыдущий, поэтому, если вы уже пробовали приложение, которое я показал вам в предыдущем абзаце, у вас не возникнет проблем с использованием этого другого бесплатного решения.
Прежде чем описывать использование калькулятора геометрии, я хотел бы уточнить, что для доступа ко всем функциям, включенным в приложение, необходимо совершить покупку некоторых элементов в приложении (2,95 евро).
После завершения загрузки Калькулятора геометрии на устройстве Android или iOS откройте приложение и на главном экране коснитесь одной из доступных геометрических фигур: Треугольник , Куадрадо , Прямоугольник , Параллелограмм , и Т. Д.
На открывшемся экране можно нажать значок книги , чтобы прочитать соответствующую статью, опубликованную в Википедии, или можно щелкнуть значок треугольника с шестеренкой , чтобы выбрать параметр для расчета.
Чтобы начать расчет площади, периметра и других параметров, введите в соответствующие поля (напр. a: es es h: ) правильные значения и нажмите опцию Готово чтобы увидеть окончательный результат операции .
a: es es h: ) правильные значения и нажмите опцию Готово чтобы увидеть окончательный результат операции .
Если вы заметили, что введенные данные неверны, нажмите значок X (выше), чтобы удалить введенные данные и ввести новые. Однако, чтобы вернуться в начальное меню, коснитесь кнопки. < и выбрать новую геометрическую фигуру для решения других задач.
Geometryx (Android)
Еще одно полезное приложение для решения задач по геометрии es Geometrix , 100% бесплатное, которое, помимо того, что оно полное, еще и очень простое в использовании.
С помощью Geometrix можно рассчитать значения и параметры фигур и геометрических тел: площадь, периметр, объем, координаты центра тяжести, высоту, длину стороны, диагонали, площадь основания, площадь поперечного сечения, общую площадь твердые и многое другое.
Как только вы завершите загрузку Geometryx на свой мобильный телефон или планшет, откройте приложение и на главном экране нажмите одну из доступных геометрических фигур: Куадрадо , Прямоугольник , Правильный многоугольник , Эллипс и др.
В открывшемся экране введите данные, относящиеся к выбранной геометрической фигуре, в формы, расположенные под разделом Введите свои входные данные и используйте легенду в правом верхнем углу, чтобы «двигаться» в правильном направлении.
Как только вы закончите вводить данные, приложение автоматически рассчитает площадь, периметр и т. д. Все результаты вы можете увидеть, пролистав экран вниз.
Как видите, в Geometryx есть несколько приятных анимаций, которые делают работу пользователя более увлекательной.
Однако, если рассматриваемые анимации вам не по душе, вы можете удалить их, нажав на символ положительный (+) вывод конденсатора и, в открывшемся слева меню, сняв расположенную рядом галочку к статье Анимации .
Геометрия GeoGebra (Android/iOS)
Еще одно приложение, которое я хочу вам посоветовать, это GeoGebra Geometry . Это бесплатное приложение, доступное как для устройств Android, так и для iOS, является одним из наиболее полных, которые вы можете загрузить на свое устройство.
По сравнению с приложениями, о которых я упоминал в предыдущих абзацах, это позволяет пользователю чрезвычайно просто создавать геометрические построения для решения наиболее распространенных геометрических задач.
После установки GeoGebra Geometry на свое устройство откройте его и используйте инструменты, расположенные вверху, чтобы нарисовать нужные геометрические фигуры.
Для этого нажмите на один из доступных вариантов (напр. Свитера, трикотажные изделия и кардиганы , Закон или Многоугольник ) и вставьте выбранный геометрический элемент в плоскость, коснувшись белой области и нажав стрелку в правом нижнем углу, чтобы увидеть его характеристики.
Коснувшись стрелки , расположенной справа внизу, нажмите символ (?) , расположенный слева, выберите пункт Геометрия и в открывшемся меню коснитесь одной из доступных функций.
При выборе одного из вариантов, упомянутых выше, внимательно следуйте инструкциям, которые вы видите на экране, чтобы точно знать, какой «синтаксис» использовать для правильных команд записи, что позволит вам решить проблему.
Напоминаю, что вы также можете получить доступ к услугам, которые предлагает GeoGebra, на своем компьютере.Для этого подключитесь к официальному сайту GeoGebra или загрузите приложение для Windows 10 и используйте инструменты, которые последняя предоставляет в ваше распоряжение.
Другие приложения для решения геометрических задач
Разве решения, о которых я говорил до сих пор, не особенно убедили вас? Попробуйте это:
- Геометрия — калькулятор (Android) — Если вы ищете геометрический калькулятор с множеством функций, но при этом простой в использовании, это приложение для вас.
 Он имеет интуитивно понятный интерфейс, который позволяет не только легко искать геометрические фигуры, но прежде всего решать различные задачи.
Он имеет интуитивно понятный интерфейс, который позволяет не только легко искать геометрические фигуры, но прежде всего решать различные задачи.
- Простая геометрия (Android): Если вы никогда не помните правильные формулы для решения геометрических задач, это приложение поможет вам исправить эту ситуацию. Простая геометрия, по сути, представляет собой содержательную форму, с которой легко могут справиться даже дети. Пока не увижу, не поверю!
- Геометрия для всех (Android) — Если вы ищете форму, которая предлагает больше информации, вам обязательно стоит попробовать это приложение.На самом деле «Геометрия для всех» включает в себя не только информацию о формулах, которые следует применять к задачам, касающимся плоских фигур, но и объемных. Это идеальный компаньон для общего ознакомления с геометрическими формулами перед классным тестом.
- 3D Mageometry (iOS) — это приложение не просто форма для проверки при необходимости, а гораздо больше. Магеометрия 3D, помимо того, что делает основные геометрические формулы легкодоступными, позволяет в несколько нажатий решать сложнейшие геометрические задачи, в которых объектами являются пирамиды, параллелепипеды, конусы, сферы и многие другие фигуры.Его можно приобрести в App Store по цене 3,49 евро.
Класс 5 Геометрия – основы, задачи и решенные примеры
- Геометрия – это раздел математики, который фокусируется на измерении и соотношении линий, углов, поверхностей, тел и точек.
Угол – это соединение двух лучей с общим концом.
- Угол измеряется в градусах. Степень обозначается °.
Типы угла: острый угол, тупой угол, прямой угол, полный угол, нулевой угол, угол отражения и прямой угол.
Острый угол: Угол, градусная мера которого меньше 90 градусов, но больше 0 градусов.
Тупой угол: Угол, градусная мера которого меньше 180 градусов, но больше 90 градусов.
Прямой угол: Угол, градусная мера которого равна 90 градусов, называется прямым углом.
Полный угол: угол, градусная мера которого равна 360 градусам, называется полным углом.
Нулевой угол: если мера угла равна нулю, его называют нулевым углом.
Угол рефлекса: угол, величина которого больше 180 градусов, но меньше 360 градусов, называется углом рефлекса.
Прямой угол: Угол, градусная мера которого равна 180 градусам, называется прямым углом.
Примечание. Угол 360 градусов и угол 0 градусов различны. На 360 градусов приходится один полный оборот одного луча по отношению к другому. В то время как в нулевом угле такого поворота нет. Оба луча под углом 0 градусов лежат в одной плоскости.
Построение угла 20 градусов с помощью линейки и циркуля.
строк
РЕШЕНИЕ: Углы = ABC, BCA, BAC, CDE, DEC, ECD, AEF, EFA, FAE
Линии = AB, BC, CD, DE, EF, FA, AC, CE
- Круг — это фигура, все точки которой находятся на одинаковом расстоянии от центра.
 Площадь круга= X R 2
Площадь круга= X R 2
Треугольники
- Треугольник — плоская фигура с тремя прямыми сторонами и тремя углами.
- По признаку сторон треугольники делятся на: Разносторонние (все стороны разные), Равнобедренные (две стороны равны), Равнобедренные (Все стороны равны)
- По признаку угла треугольники делятся на: остроугольные (все углы острые), прямоугольные (один угол равен 90 градусов), тупоугольные (один угол тупой), равноугольные (все углы равны).
Куб
- В геометрии куб представляет собой трехмерный твердотельный объект, ограниченный шестью квадратными гранями, сторонами, по три сходятся в каждой вершине.
ПРИМЕР 1: Радиус окружности 3 см. Найдите его диаметр, длину окружности и площадь.
РЕШЕНИЕ: Диаметр = 2 X Радиус = 2 X 3 = 6 см
Окружность = 2 X X R = 2 X X 3 = 18,84 см Площадь = X R 2 = X (3) 2 = 28,27 см 2
ПРИМЕР 2: Найдите количество треугольников на следующем рисунке и назовите их.
РЕШЕНИЕ:Количество треугольников= 3
Это = треугольник ABC, треугольник CDE, треугольник AEF
треугольник ABC = прямоугольный треугольник
треугольник CDE = равнобедренный треугольник
треугольник AEF = прямоугольный треугольник
- Площадь — это величина, выражающая протяженность двумерной поверхности или формы на плоскости.
Площадь прямоугольной поверхности = длина X ширина единиц 2
Площадь квадратной поверхности = a X a = a 2 единиц 2
ПРИМЕР 1: Найдите площадь и периметр прямоугольника длиной 1 см и шириной 2 см
РЕШЕНИЕ: Периметр = 2 X (Длина + Ширина) = 2 X (1+2) = 6 см
Площадь = Длина X Ширина = 1 см X 2 см = 2 см 2
ПРИМЕР 2: Найдите площадь и периметр квадрата со стороной 3см.
РЕШЕНИЕ: Периметр = 4 X 3 см = 12 см
Площадь = 3 см X 3 см = 9 см 2
Q1) Назовите углы.

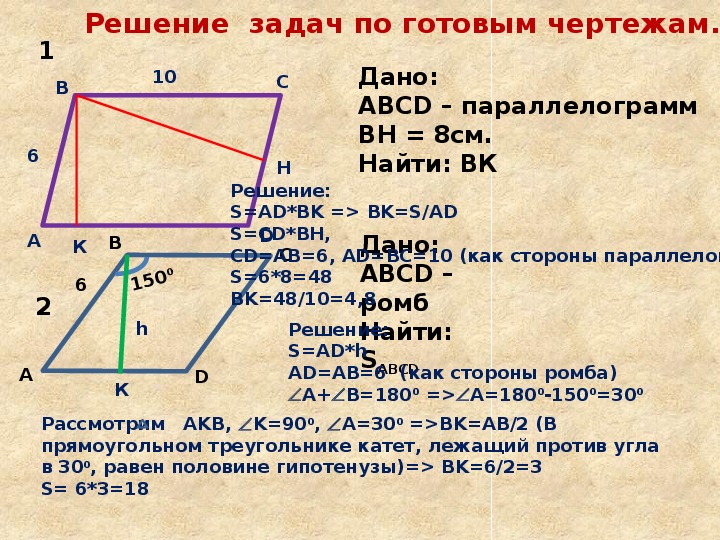 Это означает равенство углов:
Это означает равенство углов:

 Это означает равенство отрезков, сторон:
Это означает равенство отрезков, сторон:

 Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120°
Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120°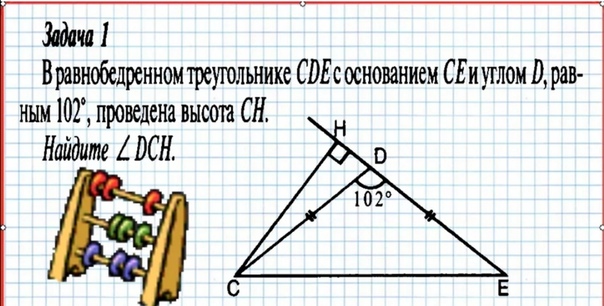 Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию).
Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию).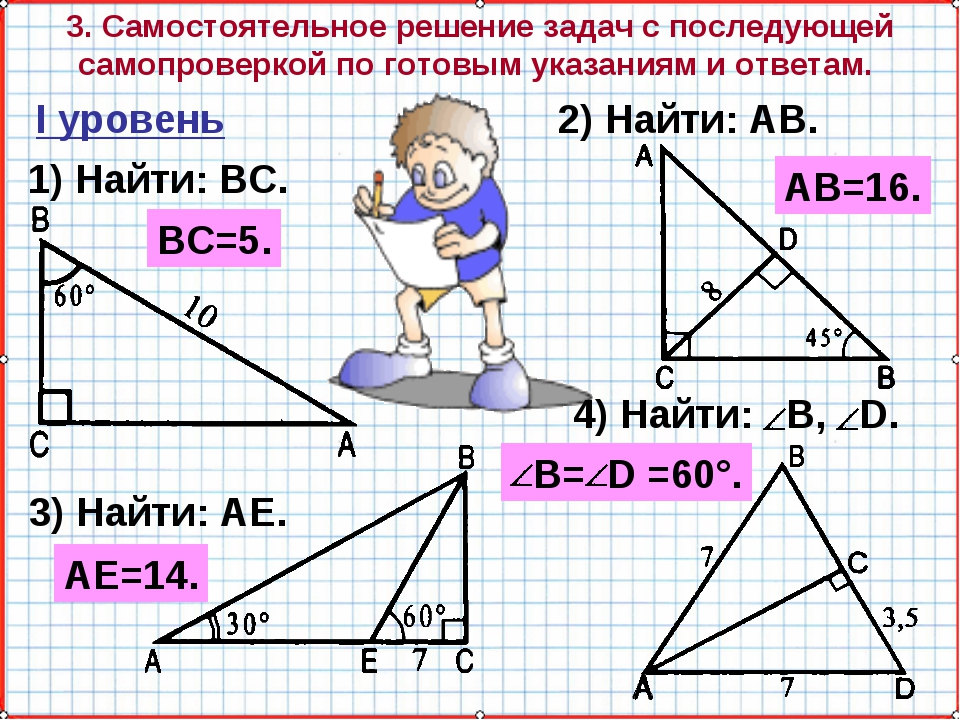
 ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах).
∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). д.)
д.)  д.
д.  д.)
д.)
 д.)
д.)  д.
д.  д.)
д.)