Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра: где V — объем цилиндра,So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.
 141592.
141592.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Калькулятор вычисления объема и площади геометрических фигур
Весь осязаемый мир представляет собой объемные геометрические фигуры и их сочетания. Определение объемов и площадей поверхностей тел может понадобиться не только при решении школьных задач, но также в быту или профессиональной деятельности. Простые объемные тела разделяются на две категории.
Тела вращения
Первая категория — это тела вращения. Такие объемные фигуры образуются путем вращения плоской фигуры вокруг одной из сторон или путем движения образующей кривой вдоль направляющей. Наш каталог предлагает калькуляторы, при помощи которых можно рассчитать параметры следующих тел вращения.
Конус
Конус — фигура, которая создается путем вращения прямоугольного треугольника вокруг одного из катетов. Также конус формируется путем движения образующего луча вдоль направляющей окружности, при этом начало луча остается неподвижным. Для определения площади поверхности конуса используется простая формула:
S = pi × R × (R + l),
где R — радиус основания, l — образующая конуса.
Для подсчета объема конической фигуры используется следующее соотношение:
V = (pi × R2 × h)/3,
где h — высота конуса.
Конусы широко встречаются в быту, производстве или науке. Например, коническую форму имеют вафельные рожки для мороженного, абажуры для светильников, пожарные ведра или воронки. В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
Цилиндр
Цилиндр — тело вращения, которое образуется путем вращения прямоугольника вокруг одной из сторон. Также цилиндр формируется путем движения образующей прямой по направляющей кривой, которая в случае цилиндра может быть окружностью, эллипсом, параболой или гиперболой. Такие «экзотические» цилиндры носят соответствующие названия эллиптических, параболических и гиперболических фигур, однако в реальной жизни наибольшее распространение получил прямой круговой цилиндр. Для определения площади поверхности такого цилиндра используется формула:
S = 2 pi × R × (R + h),
где R — радиус основания, h — высота цилиндра.
Для вычисления объема цилиндра геометры применяют следующее соотношение:
V = pi × R2 × h.
Цилиндр легко встретить в реальной жизни: это и цистерны, и поршни двигателей, и колонны, и трубы газопроводов. Цилиндры широко используются в производстве, поэтому многим инженерам приходится вычислять площади поверхностей или объемы цилиндрических объектов.
Шар
Шар — тело вращения, созданное путем вращения круга около своей оси. Сфера — это поверхность, сформированная путем вращения окружности или полуокружности вокруг своей оси. Таким образом, шар — это пространство, ограниченное сферой. Площадь сферы вычисляется по формуле:
S = 4 pi × R2,
где R — радиус сферы.
Для подсчета объема шара используется следующее выражение:
V = 4/3 pi × R3.
Шар — идеальная фигура, поэтому в природе она встречается довольно часто. К примеру, сферическую форму принимают капли дождя, снежные комья, планеты, звезды, а также ягоды или кроны деревьев. В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
Многогранники
Вторя категория — многогранники. Многогранник или полиэдр — это объемное тело, каждая грань которого является многоугольником. Существует огромное множество многогранников: к ним относятся призмы, пирамиды, параллелепипеды, а также платоновы тела — полиэдры, гранями которых являются правильные многоугольники. В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
Призма
Призма — это полиэдр, который состоит из двух n-угольных оснований, параллельных друг другу и n боковых граней, формирующих боковую поверхность призмы. Грань призмы — это всегда параллелограмм. Простыми словами, если в основании фигуры лежит квадрат, то призма считается четырехугольной, но при этом шестигранной: четыре грани составляют боковую поверхность, а две — поверхность оснований. Если в основании лежит пентагон — то призма пятиугольная и семигранная, а если додекагон — то фигура 12-угольная и 14-гранная. Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
Sb = n × a × h,
где a — сторона параллелограмма, n — количество граней, h — его высота.
Площадь поверхности основания призмы зависит от многоугольника и в общем виде для правильных полигонов рассчитывается как:
So = n/4 × a2 × ctg(pi/n),
где n — количество сторон фигуры, a — длина стороны.
Полная же площадь поверхности определяется как:
S = 2 So + Sb.
Объем призмы вычисляется по следующей формуле:
V = So х h.
Призма — наиболее распространенный в человеческой повседневности полиэдр. Форму призмы имеет огромное число предметов вокруг вас: это системный блок компьютера, сабвуфер, стол, шкаф, комната и здание. Если выйти на улицу, то вы увидите царство призм. Именно поэтому инструмент для определения объемов и площадей поверхности призматических фигур всегда актуален.
Пирамида
Пирамида — это полиэдр, который составлен из n-угольного основания и n боковых граней, формирующих боковую поверхность пирамидальной фигуры. Грань пирамиды — это всегда треугольник. Вид полиэдра определяется в зависимости от того, какой полигон выступает в роли фундамента пирамиды. Следовательно, пирамиды бывают треугольные, четырехугольные, пятиугольные или n-угольные. Площадь боковой порвехности пирамиды рассчитывается согласно выражению:
Sb = 0,5 P х h,
где h — высота пирамиды, P — периметр полигона, лежащего в основании.
Площадь фундамента рассчитывается по общей формуле для любого правильного полигона:
So = n/4 × a2 × ctg(pi/n),
где a — длина стороны, n — количество сторон.
Полная площадь поверхности пирамиды определяется как:
S = So + Sb.
Для определения объема пирамиды используется формула:
V = (So х h)/3,
где h — высота фигуры.
Пирамида — довольно распространенная фигура и широко используется в архитектуре. Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Параллелепипед
Параллелепипед — это гексаэдр с попарно параллельными гранями. Если ребра такого шестигранника равны, то параллелепипед превращается в куб. Параллелепипед — это частный случай прямой четырехугольной призмы, поэтому формулы для расчета площади и объема фигуры выводятся из соотношений для призмы с n = 4. Таким образом, для расчета площади поверхности гексаэдра используется формула:
Таким образом, для расчета площади поверхности гексаэдра используется формула:
S = 4 (a × h) + 2 (a × b),
где a, b — стороны основания параллелепипеда, h — высота фигуры.
Объем полиэдра определяется как:
V = a × b × h.
Параллелепипед, так же как и призма, постоянно встречается в реальности. Форму такого гексаэдра имеет множество вещей вокруг нас: шлакоблоки, бетонные плиты, грузовые контейнеры или картонные коробки. Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Примеры использования
Наш калькулятор позволяет рассчитать объем или площадь поверхности любого из заданных геометрических тел. Рассмотрим пару примеров.
Заливка бетона
К примеру, вы решили построить летний коттедж, а для каждого дома необходим фундамент. Вы выбрали плитный фундамент — монолитную плиту, которую заливают под всей площадью будущего жилища. Вам требуется узнать, сколько бетона понадобится для обустройства такого фундамента. Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
V = 8,1
Таким образом, нам потребуется заказать 8,1 кубометров бетонной смеси.
Пошив мячей
Допустим, вы открыли производство по производству волейбольных мячей, и вам требуется узнать, сколько материала уходит на пошив одного мяча. Согласно данным из Википедии, стандартный волейбольный мяч имеет длину окружности l = 67 см, следовательно, радиус такого мячика составит 10,6 см. Зная радиус, вы без проблем можете определить, сколько синтетической кожи понадобится для создания одного изделия
S = 0,141
Это означает, что для обшивки одного мяча вам понадобится 0,141 квадратных метров кожи.
Заключение
Объемные фигуры постоянно вращаются вокруг нас, поэтому задача определения площадей поверхностей и объемов многогранников остается актуальной задачей. Используйте наш каталог онлайн-калькуляторов и выполняйте необходимые расчеты для решения бытовых или производственных задач.
Формула расчета объема цилиндра: пример решения задачи
Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.
Объем тел
Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.
Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.
На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.
Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.
Понятие о цилиндре
Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.
Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.
Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.
Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.
Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.
Формула объема цилиндра
Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:
V = pi*R2*H, здесь pi = 3,1416
Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.
Вычисление объема бочки
Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.
Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:
V = pi*R2*H = 3,1416*252*100 = 196350 см3
Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:
V = 196350/1000 = 196,35 литра.
То есть в бочку можно налить почти 200 литров воды.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings. DRAG_TEXT_HELP}}
DRAG_TEXT_HELP}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.
|
Один из важнейших инженерных приемов. Отношение объема к площади поверхности любого физического тела = Отношение массы (веса) или запасенного тепла к поверхности опоры, излучения или теплообмена = Отношение инерции тела к площади поперечного сечения или площади сопротивления и т.д.Суть вопроса в том, что V (r3), а S(r2) (объем пропорционален кубу линейного размера, а площадь поверхности — квадрату линейного размера, т.е. объем растет быстрее чем площадь поверхности с ростом линейного размера подобных тел) Представьте себе куб с длиной грани (ребра) 1 метр (1 сантиметр, 1 фут, 1 дюйм или 1 «чего Вам угодно»), далее единицей пусть будет метр — для простоты. Объем этого куба равен 1 м3.
Таблица. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера.
При росте линейного размера объем возрастает намного быстрее, чем площадь поверхности тела, поскольку объем пропорционален кубу линейного размера, а площадь — квадрату. Рисунок. Сравнение динамик площади поверхности и объема физического тела с ростом линейного размера. Минимальным отношением объема к площади поверхности, очевидно, обладает сфера 🙂 Некоторые житейские примеры важности рассматриваемого факта.
|
Рассчитать объем коробки в м3 и литрах онлайн
07.10.2019Сколько будет стоить отправка вашего груза до места назначения? Чтобы ответить на это вопрос, нужно знать его объем в кубических метрах, т. к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.
Картонные коробки — наиболее выгодный и удобный вид упаковки для большинства товаров. Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.
Если в результате расчета оказалось, что вам требуется гофротара индивидуальных размеров, наша компания «МС-ПАК» изготовит нужный тираж на заказ. Рассмотрим, как правильно рассчитать объем картонной коробки.
Рассмотрим, как правильно рассчитать объем картонной коробки.
Поэтапный расчет объема картонной коробки
Для расчета нужно:
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b;
- Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
Формула для вычисления объема V в м3 коробки с прямоугольным или квадратным основанием:V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Рассчитать объем коробки в м
3 и литрах онлайнДля обычных коробок в форме куба или параллелепипеда (со сторонами в виде квадратов или прямоугольников) на нашем сайте есть онлайн-калькулятор, который ускорит расчет.
Пример расчета
После измерения получены значения: а=600 мм, b=400 мм, h= 400 мм.
Переводим их в метры: а=600/1000=0,6 м, b=400/1000=0,4 м, h=400/1000=0,4 м.
Подставляя полученные результаты в формулу для расчета объема, получим значение: V=a*b*h=0,6*0,4*0,4=0,096 м3.
Если в коробки фасуются сыпучие или жидкие грузы, то для расчета необходимого объема используем соотношение 1 м3 = 1000 л и, умножив полученное значение объема в м3 на 1000, получим объем в литрах.
Для нашего примера объем коробки (внутренний) в литрах равен 0,096*1000=96 литров.
Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Укажите любые два значения ниже для расчета.
Калькулятор объема усеченного конуса
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом. Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, математически представляющий собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r .Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:
EX: Клэр хочет наполнить идеально сферический шарик с водой радиусом 0.15 футов с уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание).На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание).На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
где r радиус и h высота конуса
EX: Беа полна решимости выйти из магазина мороженого с хорошо потраченными с трудом заработанными 5 долларами. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее.Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим смежным граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
У Боба есть кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси.Однако в обычном употреблении термин «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 128 h 90 131 и радиусом 90 128 r 90 131. . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r радиус и h высота бака
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником переработки отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 футов 3
Он успешно строит замок из песка в своем доме, и в качестве дополнительного бонуса ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам.Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r — радиус, а h — высота цилиндрической части
EX: Учитывая капсулу радиусом 1,5 фута и высотой 3 фута, определите объем m&m’s из расплавленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет закопать для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1. 5 2 × 3 + 4/3 ×π ×1,5 3 = 35,343 фута 3
5 2 × 3 + 4/3 ×π ×1,5 3 = 35,343 фута 3
Сферическая крышка
Сферический колпак представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпака выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, показанной в калькуляторе:
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Даны r и R : h = R ± √R 2 — r 2
где r — радиус основания, R — радиус сферы, а h — высота сферического колпачка
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса. Он отрезает идеальный сферический колпачок от мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
Он отрезает идеальный сферический колпачок от мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, Джеймс получил новую партию мячей за день до игры, и все усилия Джека оказались напрасными.
Усеченный конус
Коническая усеченная часть — это часть твердого тела, остающаяся после разрезания конуса двумя параллельными плоскостями. Этот калькулятор вычисляет объем для прямого круглого конуса специально. Типичные усеченные конусы, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правой конической усеченной части рассчитывается по следующему уравнению:
| объем = | πh(r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Беа успешно добыла немного мороженого в сахарном рожке и только что съела его таким образом, что мороженое осталось упакованным внутри рожка, а поверхность мороженого параллельна плоскости отверстия рожка. Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3
Эллипсоид
Эллипсоид — это трехмерный аналог эллипса и поверхность, которую можно описать как деформацию сферы путем масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
где a , b и c длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и разрешает ему есть столько мяса, сколько он может поместиться в булочке в форме эллипсоида. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом прямых отрезков. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:
Обобщенный объем пирамиды:
где b площадь основания и h высота
Объем квадратной пирамиды:
где а длина ребра основания
EX: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов.Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы
EX: Beulah занимается защитой окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые плотины были бы хорошей точкой для прокладки трубы через ручей. Объем запатентованного ударопрочного бетона, необходимый для строительства трубы наружным диаметром 3 фута, внутренним диаметром 2.5 футов и длину 10 футов можно рассчитать следующим образом:
| объем = π × | × l0 = 21,6 фута 3 |
Общие единицы объема
| Unit | кубометров | миллилитров | |||||||
| Milliliter (кубический сантиметр) | 0,000001 | 1 | 1 | 0,00001639 | 0,00001639 | 16. 39 39 | |||
| PINT | 0.000473 | 473 | |||||||
| кварта | 0,000946 | 946 | |||||||
| л | 0,001 | 1 000 | |||||||
| галлонов | 0,003785 | 3785 | |||||||
| кубический фут | 0,028317 | 28317 | |||||||
| 0.764555 | 0.764555 | 764 555 | 764 555 | ||||||
| 1 000 000 | 21 000 000 000 | 10 15 |
Объем и площадь поверхности правой круговой Цилиндр [Видео и практика]
Привет и добро пожаловать на это видео о цилиндрах! В этом видео мы рассмотрим, как найти объем и площадь поверхности любого цилиндра.Давайте узнаем о цилиндрах!
Цилиндры — одна из самых распространенных трехмерных фигур, которые мы видим вокруг себя.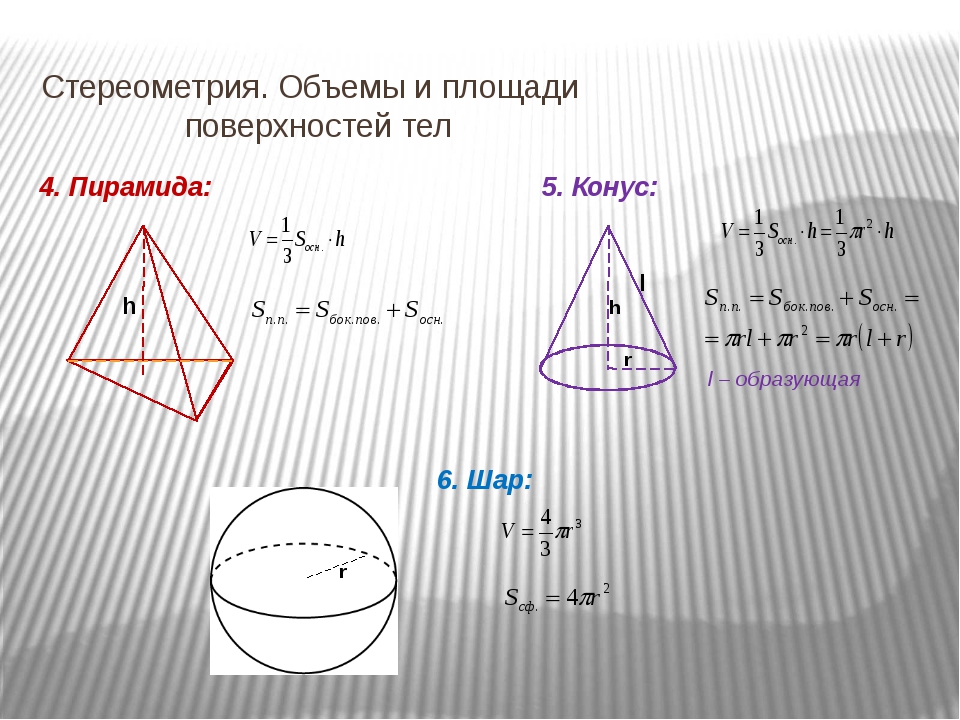 Большинство банок для еды и напитков имеют форму цилиндра. Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы?
Большинство банок для еды и напитков имеют форму цилиндра. Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы?
Как видите, все эти объекты имеют круглые верх и низ и изогнутую поверхность. Цилиндр — это трехмерная фигура с двумя круглыми основаниями, параллельными друг другу и соединенными криволинейной поверхностью.Перпендикулярное расстояние, соединяющее основания цилиндра, составляет высоты , а ось — это линия, проходящая через центры круглых оснований.
Цилиндр, ось которого перпендикулярна основаниям, называется правильным цилиндром . Цилиндр, ось которого не перпендикулярна основаниям, называется косым цилиндром .
Вспомним, что такое объем и площадь поверхности трехмерных фигур и как мы их находим.
Объем трехмерной фигуры — это количество жидкости, которое она может вместить, и измеряется в кубических единицах.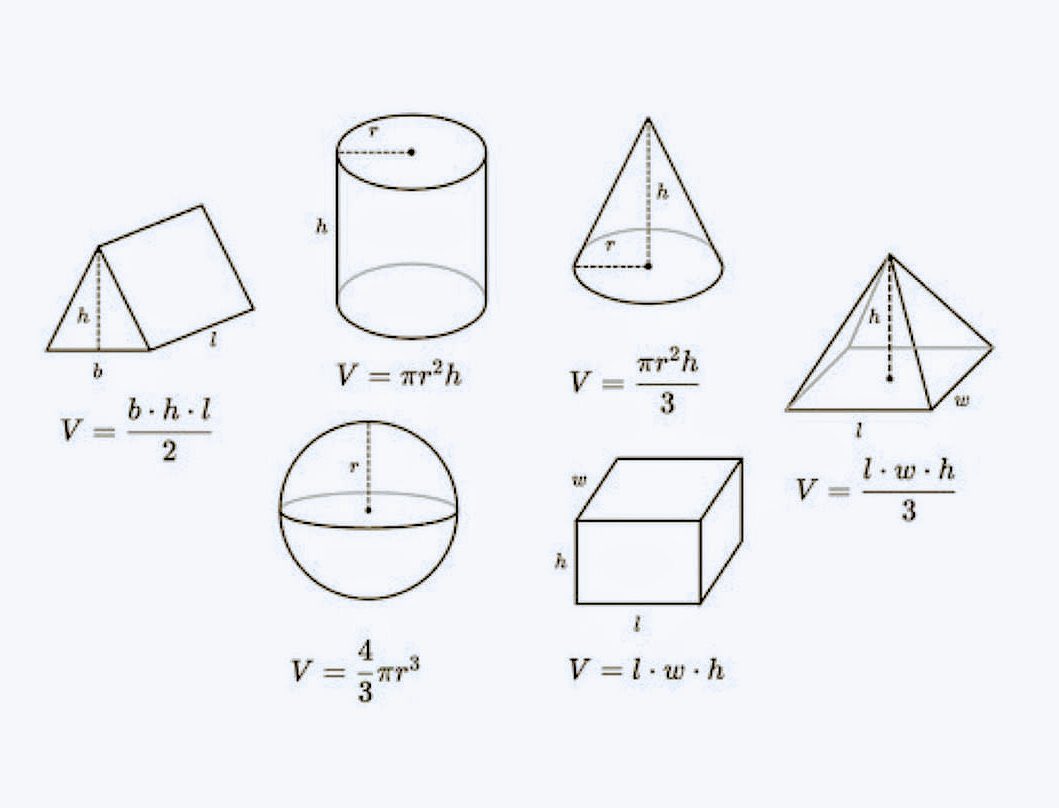
Площадь поверхности трехмерной фигуры представляет собой общую площадь, которую покрывает поверхность фигуры, и измеряется в квадратных единицах.
Показаны формулы для объема (V) и площади поверхности (SA) цилиндра. Чтобы вычислить объем и площадь поверхности любого цилиндра, нам нужны радиус и высота цилиндра.{2}\) часть формулы площади поверхности. Как только цилиндр открыт, мы можем видеть, что изогнутая часть цилиндра на самом деле представляет собой прямоугольник, а длины сторон прямоугольника определяются длиной окружности круглого основания \(2\pi r\) и высотой цилиндра \ (час\).
Рассмотрим пример:
Каковы объем и площадь поверхности цилиндра, если диаметр основания 18 мм, а высота цилиндра 20 мм? (Ответ оставьте в виде \(\pi \))
Итак, чтобы найти объем и площадь поверхности, нам нужны радиус и высота цилиндра.{2}\)
Давайте рассмотрим другой пример.
Площадь поверхности цилиндра составляет 502,4 фута², а радиус основания равен 5 футам.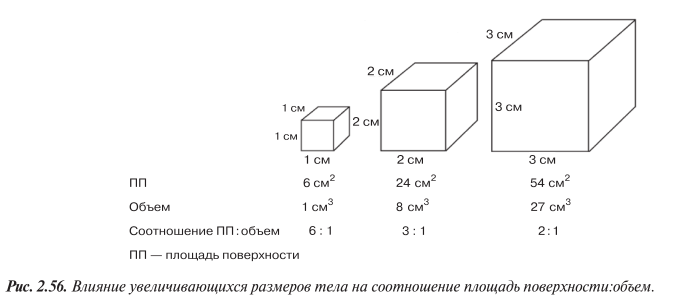 {2}\)
{2}\)
изолировать член с помощью переменной
\(502.4=31.4h+157\)
объединить подобные члены
\(502.4-157=31.4h+157-157\)
вычислить h
\(3145.4 3145.4)разделите обе стороны на коэффициент, чтобы изолировать переменную
\(\frac{345.4}{31.4}=\frac{31.4}{31.4}h\)
Следовательно, высота цилиндра равна 11 футам.
\(11=h\)
У Джоан в магазине есть резервуар для воды высотой 34,8 дюйма и диаметром круглого основания 20.6 дюймов. Она хочет сделать этикетку с логотипом своей компании для боковой стороны резервуара и должна рассчитать площадь поперечного сечения , которая представляет собой площадь поверхности без площади оснований. Какова площадь этикетки? (Используйте 3.14 для \(\pi\))
Поскольку нам нужна только боковая площадь, мы можем удалить площадь кругов из нашей формулы.
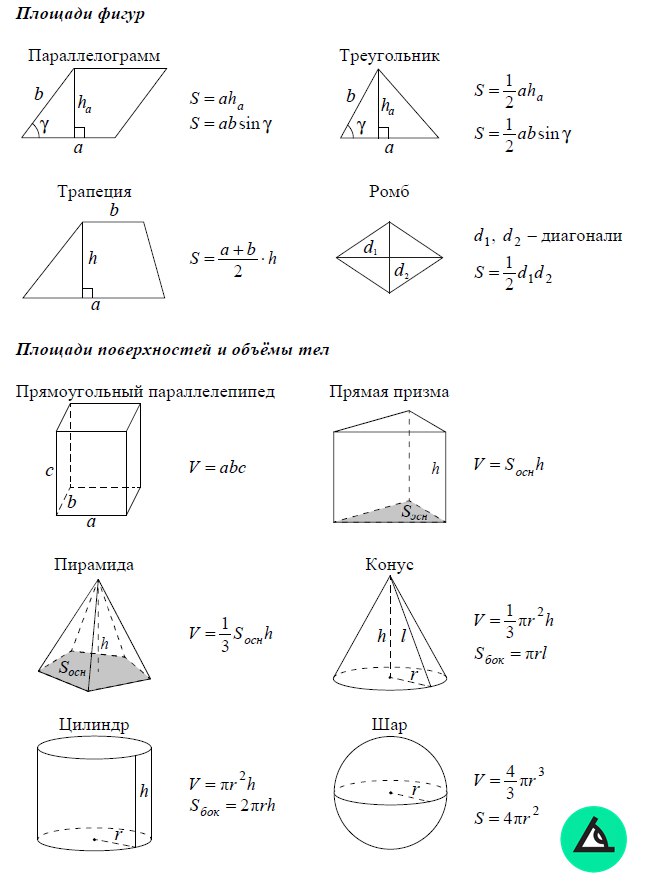
\(\text{боковая площадь }(LA)=2\pi rh\)
Помните, в формуле запрашивается радиус основания, поэтому мы разделим 20.{2}\).
Надеюсь, это видео про объем и площадь поверхности цилиндра было полезным! Спасибо за просмотр и удачной учебы!
Исчисление I — Формулы площади и объема
Показать мобильное уведомление Показать все примечания Скрыть все примечанияПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
*\), и затем мы можем использовать прямоугольники на каждом интервале следующим образом.{{\,b}}{{f\влево(x\вправо) — g\влево(x\вправо)\,dx}}\]
Приведенная выше формула будет работать при условии, что две функции имеют вид \(y = f\left( x \right)\) и \(y = g\left( x \right)\). Однако не все функции имеют такую форму.
Иногда нам придется работать с функциями в виде между \(x = f\left( y \right)\) и \(x = g\left( y \right)\) на интервале \(\left [ {c,d} \right]\) (интервал значений \(y\)…). Когда это происходит, вывод идентичен.{{\,d}}{{f\влево(y\вправо) — g\влево(y\вправо)\,dy}}\]
Таким образом, независимо от формы, в которой находятся функции, мы используем в основном одну и ту же формулу.
Тома для Solid of Revolution
Прежде чем вывести формулу для этого, мы, вероятно, должны сначала определить, что такое тело вращения. Чтобы получить тело вращения, мы начинаем с функции \(y = f\left( x \right)\) на интервале \(\left[ {a,b} \right]\).
*\).{{\,b}}{{A\влево( x \вправо)\,dx}}\end{align*}\]
Значит, в этом случае объем будет интегралом площади поперечного сечения при любых \(x\), \(A\left( x \right)\). Также обратите внимание, что в этом случае площадь поперечного сечения представляет собой круг, и мы могли бы пойти дальше и получить формулу и для этого. Однако приведенная выше формула является более общей и будет работать для любого способа получения поперечного сечения, поэтому мы оставим ее как есть.
В разделах, где мы на самом деле используем эту формулу, мы также увидим, что существуют способы создания поперечного сечения, которые фактически дают площадь поперечного сечения, являющуюся функцией \(y\), а не \(x\).{{\,d}}{{A\влево(y\вправо)\,dy}}\]
Обзор группы инструментов Площадь и объем — ArcGIS Pro
Расчет площади поверхности и объем пространств, содержащихся между трехмерными данными, является неотъемлемой частью многих пространственных операций.
Набор инструментов «Площадь и объем» содержит инструменты, которые предоставляют решения для анализа изменений между поверхностями и создания объемных представлений трехмерных данных.
Инструмент Описание Cut Fill
Вычисляет изменение объема между двумя поверхностями.Это обычно используется для операций вырезания и заполнения.
Difference 3D
Удаляет части объектов-мультипатчей в целевом классе объектов, которые перекрываются с включенными объемами объектов-мультипатчей в классе объектов вычитания.
Вытягивание между
Создает трехмерные объекты путем выдавливания каждого входного объекта между двумя наборами данных триангулированной нерегулярной сети (TIN).
Минимальный ограничивающий объем
Создает объекты-мультипатчи, представляющие объем пространства, занимаемый набором 3D-объектов.
Объем многоугольника
Вычисляет объем и площадь поверхности между многоугольником постоянной высоты и поверхностью.
Surface Difference
Вычислите смещение между двумя поверхностями, чтобы определить, где одна из них находится выше, ниже или совпадает с другой поверхностью.
Объем поверхности
Вычисляет площадь и объем области между поверхностью и базовой плоскостью.

Инструменты группы инструментов Площадь и объем Связанные темы
Отзыв по этой теме?
РАЗ МОДУЛЬ М11 — Площадь, объем и площадь поверхности
Проект улучшения математического образования в школах (TIMES)
вернуться к индексу
Площадь, объем и площадь поверхности
Измерение и геометрия: Модуль 11Year: 8-10
июнь 2011 г.
PDF-версия модуля
Предполагаемые знания
- Знание площадей прямоугольников, треугольников, кругов и составных фигур.
- Определения параллелограмма и ромба.
- Знакомство с основными свойствами параллельных прямых.
- Знакомство с объемом прямоугольной призмы.
- Базовые знания о конгруэнтности и подобиях.
- Поскольку будут задействованы некоторые формулы, учащимся потребуется некоторый опыт работы с подстановкой, а также с дистрибутивным законом.

Мотивация
Площадь плоской фигуры — это мера пространства внутри нее.Вычисление площадей — важный навык, используемый многими людьми в повседневной работе. Строителям и торговцам часто необходимо продумать площади и размеры возводимых ими сооружений, а также архитекторам, дизайнерам и инженерам.
В то время как прямоугольники, квадраты и треугольники обычно встречаются в окружающем нас мире, также встречаются и другие формы, такие как параллелограмм, ромб и трапеция. Рассмотрим, например, этот вид крыши с высоты птичьего полета.
Вид состоит из двух трапеций и двух треугольников.
Точно так же часто встречаются твердые тела, отличные от прямоугольной призмы. Пакет Toblerone ©
(с основанием на конце) представляет собой пример треугольной призмы, а масляная бочка
имеет форму цилиндра. Важно уметь находить объемы таких твердых тел.Медицинские специалисты измеряют такие параметры, как скорость кровотока (что делается с использованием скорости жидкости и площади поперечного сечения потока), а также размер опухолей и новообразований.
В физике площадь под графиком зависимости скорости от времени показывает пройденное расстояние.
В этом модуле мы будем использовать простые идеи для получения ряда фундаментальных формул
для площадей и объемов. Учащиеся должны понять, почему формулы верны, и запомнить их.Содержание
Площадь параллелограмма
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.
Мы можем легко найти площадь параллелограмма, зная его основание b и высоту h.
.
На приведенной ниже диаграмме мы проводим диагональ BD и делим фигуру на два треугольника, каждый с длиной основания b и высотой h. Поскольку площадь каждого треугольника равна bh, общая площадь A равнаА= ч.ч.
Обратите внимание, что два треугольника на диаграмме не только имеют одинаковую площадь, но и являются конгруэнтными треугольниками.
Некоторые учителя могут предпочесть установить формулу площади параллелограмма, не используя формулу площади треугольника, чтобы вычислить площадь треугольника, используя формулу площади параллелограмма.

Это можно сделать, показав, что треугольник справа на левой диаграмме ниже можно расположить слева, чтобы сформировать прямоугольник, основание и высота которого такие же, как у параллелограмма, так что снова площадь равна к бх.
Площадь трапеции
Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна. (Название происходит от греческого слова «стол».)
Мы можем найти площадь трапеции, если знаем длины двух параллельных сторон и перпендикулярное расстояние между этими двумя сторонами.
Как и в случае с параллелограммом, проводим одну из диагоналей. У нас тогда есть два треугольника, оба с высотой h, и один с основанием a, и один с основанием b.
Таким образом, площадь трапеции А равна
Таким образом, формула площади трапеции с параллельными сторонами a и b и перпендикулярным расстоянием h между ними равна
А = h(а+b).
Это можно представить как «высоту, умноженную на среднее значение параллельных сторон».

Упражнение 1
Вот еще один вывод формулы площади трапеции. Предположим, что ABCD
— трапеция.
Возьмем F за середину CD и проведем через нее прямую EG, параллельную AB.
а Объясните, почему треугольники CFG и DFE равны.
b Что это говорит нам о CG и ED?
cОбъясните, почему AE = (BC +AD).
d Используйте формулу площади параллелограмма, чтобы вывести формулу площади трапеции.
Упражнение 2
(В этом упражнении используются подобные треугольники).
На рисунке ABCD представляет собой трапецию, в которой AB параллельна DC, а расстояние между ними h. Точки E и F являются серединами AD и BC соответственно. AG перпендикулярна DC в G и пересекает EF в H. Пусть a = AB, b = DC и = EF.
a Покажите, что EF параллелен DC.
b Рассматривая треугольники AEH и ADG, покажите, что AH = HG = .

c Сравнивая площади трех образованных таким образом или иначе
трапеций, покажите, что площадь трапеции ABCD равна h.Площадь ромба и воздушного змея
Ромб – это четырехугольник, у которого все стороны равны. В модуле Ромбы, Воздушные змеи и Трапеции с помощью простых геометрических рассуждений мы показали
- противоположные стороны параллельны
- диагонали делят друг друга пополам под прямым углом
Таким образом, ромб является параллелограммом, и мы можем вычислить площадь ромба, используя формулу площади параллелограмма.
Возьмем теперь ромб с диагоналями длины x и y.
Поставив ромб на один угол, мы видим, что две диагонали разрезают ромб на четыре прямоугольных треугольника, из которых можно составить четыре прямоугольника внутри
большего прямоугольника.
Поскольку площадь восьми треугольников одинакова (действительно, все они конгруэнтны), площадь ромба равна половине площади большого прямоугольника, т.
е. xy.
Следовательно, если x и y — длины диагоналей ромба, то
Площадь ромба = xy.
Площадь ромба равна половине произведения длин его диагоналей.
Упражнение 3
Предположим, что ABCD представляет собой ромб с одной диагональю 8 см и одной стороной 5 см, как показано на рисунке.
a Используйте теорему Пифагора, чтобы найти
длины другой диагонали.bОтсюда найдите площадь ромба.
Упражнение 4
Воздушный змей – это четырехугольник, у которого две пары смежных сторон равны.
a Используйте конгруэнтность и два равнобедренных треугольника, чтобы показать, что диагонали воздушного змея перпендикулярны.
b Ясно, что мы можем достроить воздушного змея, чтобы сформировать
прямоугольник, площадь которого в два раза больше площади воздушного змея,
, поэтомуПлощадь воздушного змея = xy,
, где x и y — длины диагоналей воздушного змея.

Площадь полигонов
Любой многоугольник можно разрезать на треугольники.Следовательно, площадь любого многоугольника определена и может быть рассчитана путем вычисления площади каждого треугольника.
Объем призмы
Многогранник – это тело, ограниченное многоугольниками. Прямая призма — это многогранник, у которого две конгруэнтные и параллельные грани (называемые основанием и вершиной), а все остальные грани — прямоугольники. Это означает, что когда на основание поставлена прямая призма, все стенки представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «правильную призму».Призма имеет однородное поперечное сечение. Это означает, что когда вы делаете срезы твердого тела параллельно основанию, вы получаете многоугольники, конгруэнтные основанию. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольник.

В модуле Введение в измерения мы видели, что объем прямоугольной призмы определяется произведением площади основания на высоту, или
.Объем = lwh, где l и w — длина и ширина призмы, а h — высота.
Треугольные призмы
В треугольной призме каждое поперечное сечение, параллельное треугольному основанию, представляет собой треугольник, конгруэнтный основанию.
Предположим, у нас есть треугольная призма длиной 4 см, как показано на рисунке.
Мы можем разрезать призму на слои, каждый из которых имеет длину 1 см.
Ранее мы видели, что из остроугольного треугольника можно составить прямоугольник с удвоенной площадью.
Точно так же мы можем собрать треугольную призму, чтобы сформировать прямоугольную призму. Объем каждого из 1 см слоев равен половине объема соответствующей прямоугольной призмы, т.е.
Объем каждого слоя = × 3 × 2 см3.

Отсюда объем треугольной призмы
= × 3 × 2 × 4
Таким образом, объем треугольной призмы равен
Объем = площадь треугольного поперечного сечения × перпендикулярная высота = Ah.
Поскольку любой многоугольник можно разрезать на треугольники, объем любой призмы с многоугольным основанием равен площади A многоугольного основания, умноженной на высоту h, то есть
.Объем = Ач
, где A — площадь основания многоугольника, а h — высота, когда призма стоит на своем основании.
Пример
Найдите объем призмы, изображенной на рисунке.
Решение
Поперечное сечение представляет собой переднюю грань призмы и состоит из треугольника и прямоугольника.
А
= × 8 × 4 + (8 × 6)
= 64 см2.
Том
= Ач
= 64 × 5
= 320 см3.
Упражнение 5
Большой пьедестал в форме призмы, лицевая грань которой представляет собой трапецию.
а Найдите площадь передней грани.
b Найдите объем пьедестала.
Объем цилиндра
Цилиндры повсеместно используются в повседневной жизни. Например, консервы обычно поставляются в банках цилиндрической формы.
Если мы разрежем цилиндр параллельно его основанию, то каждое поперечное сечение будет окружностью того же размера, что и основание.
Таким образом, цилиндр обладает тем же основным свойством, что и призма, и мы возьмем формулу объема цилиндра как произведение площади круглого основания на высоту.
Мы не можем строго доказать эту формулу на данном этапе, потому что доказательство включает в себя построение цилиндра как предела призм.
Если окружность основания цилиндра имеет радиус r, то мы знаем, что площадь окружности равна
A =π r2.Если высота цилиндра h, то его объем равенОбъем = π r2 × h = π r2h.
Пример
Для цилиндра радиусом 7 см и высотой 3 см найти:
а точный объем, выраженный в π .
b приблизительное значение объема с использованием π .
Решение
и
В
= π r2h
б
В
= π r2h
= π × 49 × 3
≈ × 49 × 3
= 147π см3
= 462 см3.

Упражнение 6
Термос высотой 30 см имеет форму двух цилиндров, один внутри другого. Он имеет внутренний радиус 8 см и внешний радиус 10 см. Какой объем между двумя цилиндрами?
Площадь поверхности призмы
Предположим, мы берем прямоугольную призму размером 3 см на 4 см на 5 см и раскрываем ее, как показано ниже.
Мы можем найти площадь сплющенной прямоугольной призмы, сложив площади шести прямоугольников.Есть три пары равных прямоугольников, поэтому их общая площадь равна
.А = 2 х (3 х 4 + 3 х 5 + 4 х 5) = 94 см2.
Это называется площадью поверхности призмы.
Таким образом, площадь поверхности призмы равна сумме площадей ее граней. Действительно, площадь поверхности многогранника также равна сумме площадей всех его граней.
Пример
Найдите площадь поверхности треугольной призмы
, изображенной напротив.
Решение
Площадь лицевой стороны = × 12 × 16 = 96 см2.

Площадь спинки= 96 см2.
Площадь трех прямоугольных граней
= (9 × 20) + (9 × 12) + (9 × 16)
= 432 см2.
Общая площадь поверхности
= 96 + 96 + 432
= 624 см2.
Длина края
Длина ребра призмы равна сумме длин всех его ребер.
Упражнение 7
Найдите общую длину ребра призмы в приведенном выше примере.
Упражнение 8
Палатка из ситца, включая матовый лист
, имеет форму треугольной призмы с размерами, как показано на рисунке.Сколько бязи нужно для изготовления палатки?
Ссылки вперед
Области
Теперь мы можем найти площади основных геометрических фигур.
Мы также видели в модуле по кругам, что площадь круга определяется выражением A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружности, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу.
Мы можем использовать тригонометрию, чтобы найти площади различных фигур, имея достаточно информации об их сторонах и углах.
Тома: пирамиды и призмы
Можно показать, что объем квадратной пирамиды составляет одну треть объема соответствующей прямой призмы с той же высотой и основанием.
Объем пирамиды = Ah,
, где A — площадь основания
, а h — перпендикулярная высота
, измеренная от основания.
Эта формула справедлива для пирамид с многоугольным основанием площадью А.
Поперечные сечения конуса (или сферы) представляют собой окружности, но радиусы сечений различаются.
Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.
Объем конуса = π r2h,
, где r — радиус основания
, а h — высота.Наконец, объем сферы равен
.Объем сферы = π r3,
, где r — радиус сферы.
Это завершает формулу объема для основных твердых тел. Тела с неправильными границами можно рассматривать с помощью интегрального исчисления. Все они рассматриваются в модуле Конусы, пирамиды и сферы .
Площадь поверхности
Точно так же, как мы «разрезали» призму, чтобы найти площадь поверхности, мы можем «разрезать» цилиндр радиусом r и высотой h, чтобы показать, что площадь искривленной поверхности равна 2π rh. Добавляя два круглых конца, мы получаем формулу A = 2π rh + 2π r2 для общей площади поверхности цилиндра.Формула площади поверхности конуса: A = π r2 + π rl, где r — радиус, а l — наклонная высота. Наконец, площадь поверхности сферы определяется выражением A = 4π r2, где r — радиус сферы.

История и приложения
Многие названия фигур и тел, площадь и объем которых мы нашли, происходят от греч. Например, слово «трапеция» (несмотря на латинское окончание) происходит от греческого слова «стол», а «призма» происходит от греческого слова, означающего «пилить» (поскольку поперечные сечения или разрезы конгруэнтны), а слово «цилиндр» происходит от слова «стол». Греческое слово, означающее катиться.Древние греки первыми систематически исследовали площади и объемы плоских фигур и тел.
В эллинистический период великий математик Архимед (ок. 287–212 г. до н. э.) аппроксимировал площадь круга, используя вписанные многоугольники, и нашел очень хорошие приближения к π . Он также вывел формулы объема и площади поверхности шара. Архимед разработал метод нахождения площадей и объемов, названный «методом исчерпывания», который был близок к идеям, используемым в современном исчислении.
До разработки интегрального исчисления, которое подняло площади и объемы на новый уровень абстракции, итальянский математик Бонавентура Франческо Кавальери (1598-1647) разработал результат, известный как принцип Кавальери, который утверждает, что два объекта имеют одинаковый объем, если площади их соответствующих сечений во всех случаях равны.
(Тот же принцип был ранее открыт Цзу Гэнчжи (480–525 гг.) в Китае.) Умное использование этого метода показывает, что объем полушария радиусом r равен объему твердого тела, полученного путем удаления конуса из радиуса r и высоты r из цилиндра той же высоты и радиуса, таким образом показывая, что объем полушария равен π r3.
Принцип Кавальери можно использовать для нахождения объема наклонных тел (в отличие от прямых тел). Таким образом, косая призма имеет параллельные горизонтальные основание и вершину, но стороны не вертикальны. Такое твердое тело называется параллелепипедом (другое греческое слово, означающее параллельные плоскости).
Используя принцип Кавальери, можно показать, что формула объема такая же, как и формула
для призмы, а именно:Объем = площадь основания × перпендикулярная высота.
Следующим большим достижением стало интегральное исчисление, когда можно было придать смысл понятию площади под кривой, используя идеи предела.
Хотя Ферма и Декарт добились в этом значительного прогресса, именно (независимая) работа Ньютона и Лейбница привела к современной теории интеграции.
Существуют приближенные методы нахождения площади фигуры с неровной границей. Одно из них, довольно точное, называется правилом Симпсона, которое было известно Кавальери, переоткрыто Грегори (1638-1675) и приписано Томасу Симпсону (1710-1761).Это правило позволяет найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня он используется кардиологами для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце.
Ответы на упражнения
Упражнение 1
и
КФ = ДФ
(F — середина CD)
КФГ = DFE
(вертикально противоположные углы)
GCF = EDF
(переменные углы)
Треугольник CFG конгруэнтен треугольнику DFE (SAS)
b CG = ED (соответствие сторон конгруэнтных треугольников)
с
2АЭ = АЭ + БГ
= AD — ED + CG + BG
= AD + БГ AE = ( AD + BG )
d Площадь трапеции = площадь параллелограмма
= AE × ч
= ( AD + BG ) × ч
Упражнение 2
a Соедините треугольники ADG и BCK , чтобы получился треугольник ACD ( B и A совпадают).
E и F являются средними точками AC и AD соответственно. Треугольник AFE подобен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
b Треугольник AEH аналогичен треугольнику ADG (AAA)
АХ = ХГ =
с
Район
= (АВ + CD)
= (2(ГД + ЭГ + ДФ))
= гл
Упражнение 3
и 6 см
b 24 см2
Упражнение 4
и Треугольник CBA конгруэнтен CDA (SSS) Треугольник BCE конгруэнтен треугольнику DCE (SAS) CEB = CED = 90° б
Площадь прямоугольника = xy .

Упражнение 5
a 31,5 м2 b 94,5 м3
Упражнение 6
1080π см3
Упражнение 7
123 см
Упражнение 8
60 м2
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области математического образования (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.
0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie.
Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
9.5: Площадь и объем геометрических фигур и объектов
- Последнее обновление
- Сохранить как PDF
- Значение и обозначение для площади
- Формулы площади
- 4
- Поиск областей некоторых общих геометрических фигур
- Значение и обозначение для объема
- Объемные формулы объема
- Найти тома некоторых общих геометрических объектов
- Упражнения
- Упражнения для Обзор
Цели обучения
- знать значение и обозначение области
- знать формулы площади некоторых распространенных геометрических фигур
- уметь находить площади некоторых обычных геометрических фигур
- знать значение и обозначения тома
- знать формулы объема некоторых обычных геометрических объектов
- уметь находить объем некоторых обычных геометрических объектов
Довольно часто бывает необходимо умножить одно число номинала на другое.
2\), или квадратная единица длины (кв. единица длины), может быть физически интерпретирована как площадь поверхности.
Площадь
Площадь поверхности представляет собой количество квадратных единиц длины, содержащихся на поверхности.Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на некоторой поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)
Исследуем площади следующих геометрических фигур.
Формулы площади
Мы можем определить площади этих геометрических фигур, используя следующие формулы.
Нахождение площадей некоторых общих геометрических фигур
Набор образцов A
Найдите площадь треугольника.
Раствор
\(\ begin{array} {rcl} {A_T} & = & {\dfrac{1}{2} \cdot b \cdot h} \\ {} & = & {\dfrac{1}{2} \ cdot 20 \cdot 5 \text{ кв.
2\).
Набор образцов A
Найдите площадь прямоугольника.
Раствор
Давайте сначала переведем 4 фута 2 дюйма в дюймы. Поскольку мы хотим преобразовать в дюймы, мы будем использовать дробную единицу \(\dfrac{\text{12 дюймов}}{\text{1 фут}}\), поскольку в числителе дюймы. Тогда
\(\begin{массив} {rcl} {\text{4 фута}} & = & {\dfrac{\text{4 фута}}}{1} \cdot \dfrac{\text{12 дюймов}}{ \text{1 фут}}} \\ {} & = & {\dfrac{4 \cancel{\text{фут}}}{1} \cdot \dfrac{\text{12 дюймов}}{1 \cancel{\text{ft}}}} \\ {} & = & {\text{48 дюймов}} \end{массив}\)
Таким образом, \(\text{4 фута 2 дюйма = 48 дюймов + 2 дюйма = 50 дюймов}\)
\(\begin{array} {rcl} {A_R} & = & {l \cdot w} \\ {} & = & {\text{50 дюймов} \cdot \text{8 дюймов}} \\ {} & = & {400 \text{кв. дюйм}} \end{массив}\)
Площадь этого прямоугольника 400 квадратных дюймов.
Набор образцов A
Найдите площадь параллелограмма.
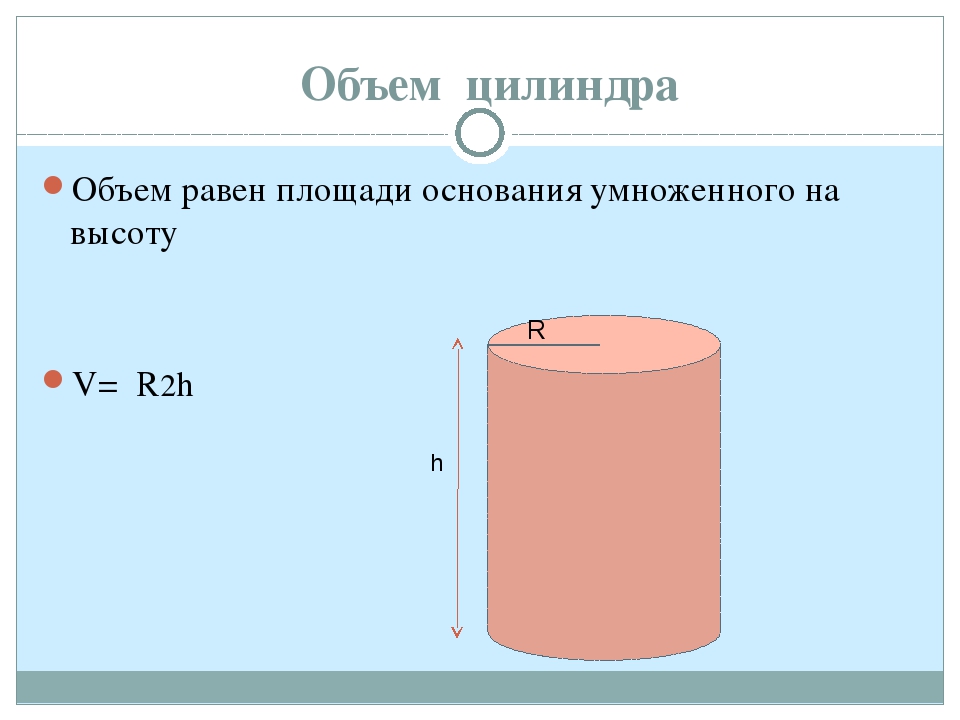
Раствор
\(\begin{array} {rcl} {A_P} & = & {b \cdot h} \\ {} & = & {\text{10.3 см} \cdot \text{6,2 см}} \\ {} & = & {63,86 \text{кв см}} \end{массив}\)
Площадь этого параллелограмма равна 63,86 кв.см.
Набор образцов A
Найдите площадь трапеции.
Раствор
\(\ begin{array} {rcl} {A_ {Trap}} & = & {\dfrac{1}{2} \cdot (b_1 + b_2) \cdot h} \\ {} & = & {\dfrac {1}{2} \cdot (\text{14,5 мм + 20,4 мм}) \cdot (4,1 \text{мм})} \\ {} & = & {\dfrac{1}{2} \cdot (\ текст{34.2} \\ {} & \приблизительно & {(3.14) \cdot (\text{282,24 кв. футов})} \\ {} & \приблизительно & {888,23 \text{кв. футов}} \end{массив}\)
Площадь этого круга составляет приблизительно 886,23 кв. футов.
Тренировочный набор A
Найдите площадь каждой из следующих геометрических фигур.
- Ответить
36 кв см
Тренировочный набор A
- Ответить
37.
503 кв. мм
Тренировочный набор A
- Ответить
13,26 кв. дюйма
Тренировочный набор A
- Ответить
367,5 квадратных миль
Тренировочный набор A
- Ответить
452,16 кв. футов
Тренировочный набор A
- Ответить
44.3\), или единица кубической длины (единица длины cu), может быть физически интерпретирована как объем трехмерного объекта.
Объем
Объем объекта — это количество кубических единиц длины, содержащихся в объекте.Например, 4 куб. мм означает, что 4 куба со стороной 1 мм точно заполнили бы некоторый трехмерный объект.
(Возможно, кубики придется разрезать и переставить, чтобы они соответствовали форме объекта.)
Объемные формулы
Рисунок Формула объема ЗаявлениеПрямоугольный сплошной \(\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота )}} \end{массив}\) Объем прямоугольного тела равен произведению длины на ширину и на высоту.2 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\) Объем конуса равен \(\dfrac{1}{3}\), умноженному на \(\pi\), умноженному на квадрат радиуса, умноженный на высоту. Нахождение объемов некоторых общих геометрических объектов
Набор образцов B
Найдите объем прямоугольного тела.
2 \cdot h} \\ {} & \приблизительно & {(\dfrac{1}{3}) \cdot (3.2 \cdot \text{(5 мм)}} \\ {} & \приблизительно & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{4 кв. мм}) \cdot \ text{(5 мм)}} \\ {} & \ приблизительно & {(\dfrac{1}{3}) \cdot (3.14) \cdot \text{(20 мм3)}} \\ {} & \ приблизительно & {20,9\overline{3} \text{куб.мм}} \\ {} & \ приблизительно & {\text{20,93 куб.мм}} \end{массив}\)
Объем этого конуса примерно 20,93 куб. мм. Объем приблизительный, потому что мы приблизили \(\pi\) к 3,14.
Практический набор B
Найдите объем каждого геометрического объекта.Если требуется \(\pi\), аппроксимируйте его с помощью 3,14 и найдите приблизительный объем.
- Ответить
21 куб. дюйм
Практический набор B
Сфера
- Ответить
904,32 куб. футов
Практический набор B
- Ответить
157 м3
Практический набор B
- Ответить
0.
00942 у.е.
Упражнения
Найти каждое указанное измерение.
Упражнение \(\PageIndex{1}\)
Зона
- Ответить
16 м2
Упражнение \(\PageIndex{2}\)
Зона
Упражнение \(\PageIndex{3}\)
Зона
- Ответить
1.21 кв. мм
Упражнение \(\PageIndex{4}\)
Зона
Упражнение \(\PageIndex{5}\)
Зона
- Ответить
18 кв. дюймов
Упражнение \(\PageIndex{6}\)
Зона
Упражнение \(\PageIndex{7}\)
Точная площадь
- Ответить
\((60.5 \pi + 132) \text{кв. фут}\)
Упражнение \(\PageIndex{8}\)
Приблизительная площадь
Упражнение \(\PageIndex{9}\)
Зона
- Ответить
40,8 кв.
дюйма
Упражнение \(\PageIndex{10}\)
Зона
Упражнение \(\PageIndex{11}\)
Приблизительная площадь
- Ответить
31.0132 кв. д.
Упражнение \(\PageIndex{12}\)
Точная площадь
Упражнение \(\PageIndex{13}\)
Приблизительная площадь
- Ответить
158,2874 кв. мм
Упражнение \(\PageIndex{14}\)
Точная площадь
Упражнение \(\PageIndex{15}\)
Приблизительная площадь
- Ответить
64.2668 кв. дюймов
Упражнение \(\PageIndex{16}\)
Зона
Упражнение \(\PageIndex{17}\)
Приблизительная площадь
- Ответить
43,96 кв.
футов
Упражнение \(\PageIndex{18}\)
Том
Упражнение \(\PageIndex{19}\)
Том
- Ответить
512 см3
Упражнение \(\PageIndex{20}\)
Точный объем
Упражнение \(\PageIndex{21}\)
Приблизительный объем
- Ответить
11.49 куб см
Упражнение \(\PageIndex{22}\)
Приблизительный объем
Упражнение \(\PageIndex{23}\)
Точный объем
- Ответить
\(\dfrac{1024}{3} \pi \text{ куб футов}\)
Упражнение \(\PageIndex{24}\)
Приблизительный объем
Упражнение \(\PageIndex{25}\)
Приблизительный объем
- Ответить
22.
08 куб. дюймов
Упражнение \(\PageIndex{26}\)
Приблизительный объем
Упражнения для повторения
Упражнение \(\PageIndex{27}\)
Сколько сотен в числе 23 426?
- Ответить
4
Упражнение \(\PageIndex{28}\)
Перечислите все делители числа 32.
Упражнение \(\PageIndex{29}\)
Найдите значение \(4 \dfrac{3}{4} — 3 \dfrac{5}{6} + 1 \dfrac{2}{3}\).
- Ответить
\(\dfrac{31}{12} = 2 \dfrac{7}{12} = 2,58\)
Упражнение \(\PageIndex{30}\)
Найдите значение \(\dfrac{5 + \dfrac{1}{3}}{2 + \dfrac{2}{15}}\).
Упражнение \(\PageIndex{31}\)
Найдите периметр.
.
- Ответить
27,9 м



 Отношение объема к площади поверхности любого физического тела = Отношение массы (веса) или запасенного тепла к поверхности опоры, излучения или теплообмена = Отношение инерции тела к площади поперечного сечения…
Отношение объема к площади поверхности любого физического тела = Отношение массы (веса) или запасенного тепла к поверхности опоры, излучения или теплообмена = Отношение инерции тела к площади поперечного сечения…  Каждая сторона имеет площадь1 м
Каждая сторона имеет площадь1 м Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).
Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).