Урок 34. решение задач. часть 1 — Математика — 2 класс
Математика, 2 класс
Урок № 34. Решение задач.
Перечень вопросов, рассматриваемых в теме:
— Как составить план решения задачи?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Схема — своеобразный чертёж, в котором составные части — его элементы и связи между ними изображены условно, без соблюдения масштаба.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –5-е изд. – М.: Просвещение, 2014. – с.10, 11.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.

- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.18.
Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.41.
Теоретический материал для самостоятельного изучения
Посмотрите на эти изображения. Знакомы ли нам они? Да, это схемы задач.
Мы умеем составлять схемы к задачам и по схемам находить задачу.
Определим, какая схема подходит к задаче.
В этой задаче мы находим целое.
Подходит такая схема.
Выберем схему ко второй задаче.
В этой задаче мы находим часть
от целого. Подходит данная схема.
И к последней схеме мы составим такую задачу:
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Сколько всего рыб поймал папа?
Рассмотрите такую схему.
Знакома ли она вам? С такими схемами мы ещё не встречались. Это схемы рассуждения при поиске решения задачи. Составим схему рассуждения при решении уже известной нам задачи. «Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?». Для решения задачи начнём рассуждать от вопроса, составляя при этом схему. Что нужно найти в задаче? «Сколько всего рыб поймал папа?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать, сколько и каких рыб поймал папа.
Это окуни и лещи. Ставим числа 8 и 6,
рисуем стрелки к вопросу.
Можем ли мы ответить на вопрос задачи?
Да.
8 + 6 = 14 (р.) поймал папа
Попробуем составить схему рассуждения к более сложной задаче.
«Папа поймал на рыбалке 8 окуней, а сын на 2 рыбы меньше. Сколько всего рыб поймали папа и сын?».
Что нужно узнать в задаче? «Сколько всего рыб поймали папа и сын?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать сколько рыб поймал папа
и сколько рыб поймал сын. Рисуем два круга и стрелки к вопросу.
Что из этого мы знаем, а что нужно найти?Правильно, мы знаем сколько рыб поймал папа. Ставим число восемь в схему.
Но мы не знаем, сколько рыб поймал сын.
Ставим знак вопроса.
Что нужно знать, чтобы сосчитать рыб, которых поймал сын?
Нужно знать количество рыб у папы и
на сколько меньше поймал рыб сын.
Рисуем два круга и стрелки к вопросу.
Ставим в схему числа восемь и два.
Каким будет первое действие? Узнаем, сколько рыб поймал сын.
1) 8 – 2 = 6 (р.) поймал сын.
Ответили мы на вопрос задачи? Нет. Каким будет второе действие?
Узнаем, сколько всего рыб поймали папа и сын.
2) 8 + 6 = 14 (р.) поймали всего.
Вывод: Для выбора способа решения задачи, мы выстраиваем цепочку рассуждения. Её можно представить в виде схемы. Составляя схему рассуждения «от вопроса к данным», мы отвечаем на такие вопросы: «Что достаточно знать, чтобы ответить на вопрос задачи? Что мы знаем уже? Как найти то, что ещё неизвестно?». Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Тренировочные задания.
1.Выберите схему рассуждения, подходящую к задаче «Юра съел 9 конфет, а Коля на 4 конфеты меньше. Сколько конфет съели мальчики?»
Правильные ответы:
2. Дополните диаграмму данными из текста.
Сел Миша на пенёк, съел пирожок… А ещё две баранки, пять пончиков и девять яблок.
Правильные ответы:
Задачи в 2 действия. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 164 — 191
наверхЗадание 164.
Мама порвала с одного куста 5 помидоров с другого 4. Детям она отдала 6 помидоров. Сколько помидоров осталось?
Решение:
- 5 + 4 = 9 всего собрала
- 9 — 6 = 3 осталось
- Ответ: 3 помидора осталось
Задание 165.

На тарелке было 6 жёлтых яблок и 4 красных. Съели 7 яблок. Сколько яблок осталось на тарелке?
Решение:
- 6 + 4 = 10
- 10 — 7 = 3
- Ответ: 3 яблока осталось на тарелке.
Задание 166.
Решение:
| 8 + 8 + 1= 17 | 7 + 7 — 1= 13 | 13 — 8 — 5 = 0 | 12 — 7 — 5 = 0 |
| 9 + 8 — 10 = 7 | 8 + 3 — 5 = 6 | 11 — 8 — 0 = 3 | 16 — 7 + 6 = 15 |
Задание 167.
К числу 5 прибавили 2, а потом ещё 6.На сколько увеличилось число 5?
Решение:
- 5 + 2 = 7
- 7 + 6 = 13
- 13 — 5 = 8
- Ответ:число 5 увеличелось на 8.
Задание 168.
Марина написала неизвестное число. Если к нему прибавить 8, то получится 10. Какое число написала Марина?
Решение:
- 10 — 8 = 2
- Ответ:Марина написала число 2.

Задание 169.
Найди разность 14 — а, если а = 8, а = 5.
Решение:
- Если а = 8, то 14 — а = 6
- Если а = 5, то 14 — а = 9
Задание 170.
Составь задачу по таблице. Реши её.
| Было | Осталось | |
| ? | 8 грн. | 9 грн. |
Решение:
Петя в магазине потратил на игрушки 8 гривен и у него осталось 9 гривен. Сколько денег было у Пети до покупки игрушек?
- 1) 8 + 9 = 17
- Ответ: 17 гривен.
Задание 171.
Задание 172.
Сумма длин всех сторон многоугольника
периметр многоугольника.
- 2 + 5 + 2 + 4 = 13 (см)
- Ответ: 13 см.
- Проверь, правильно ли найден периметр четырёхугольника. Найди самостоятельно периметр треугольника.
Решение:
- 1) Периметр четырехугольника найден верно.

- 2) P = 3 + 4 + 5 = 12
- Ответ: Периметр треугольника равен 12 см.
Задание 173.
Реши примеры.
Решение:
| 2 + 9 — 7 = 4 | 16 — 8 + 5 = 13 | 14 — 9 + 6 = 11 | 8 + 8 — 9 = 7 |
| 13 — 9 + 8 = 12 | 9 + 9 — 8 = 10 | 15 — 8 — 6 = 1 | 9 — 9 + 5 = 5 |
Задание 174.
На урок труда принесли 7 листов зелёной бумаги и 5 жёлтой. На изготовление коробки израсходовали 4 листа. Сколько листов бумаги осталось?
| Было | Израсходовали | Осталось |
| 7 зеленых 5 желтых |
4 | ? |
Решение
- 1) 7 + 5 = 12 (л.)
- 2) 12 — 4 = 8 (л.)
- Ответ: 8 листов.
Как решить задачу другим способом?
Решение:
- 1) 5 — 4 = 1
- 2) 7 + 1 = 8
Задание 175.

Реши примеры.
Решение:
| 8 — 2 + 7 = 13 | 10 + 5 — 9 = 6 | 14 — 7 + 2 = 9 |
| 9 — 4 + 7 = 12 | 13 — 4 + 5 = 9 | 12 — 9 + 8 = 11 |
Задание 176.
В ящике было 12 кг картофеля. На приготовление завтрака использовали 2 кг картофеля, а на приготовление обеда — 3 кг. Сколько килограммов картофеля осталось в ящике?
- 1) Сколько всего килограмм картофеля использовали на приготовление завтрака и обеда?
- 2) Сколько килограммов картофеля осталось в ящике?
Решение:
- 1) 2 + 3 = 5
- 2) 12 — 5 = 7
- Ответ: 7 кг.
Задание 177.
Реши примеры.
Решение:
| 13 — 7 = 6 | 12 — 5 = 7 | 7 + 4 — 5 = 6 | 12 — 6 + 7 = 13 |
Задание 178.

Решение:
|
|
Задание 179.
Составь задачу по рисунку и реши её устно.
Решение:
У мамы было 10 метров ткани. На пошивку платья она израсходовала 2 м. ткани, а на пошивку юбки 1 м. Сколько ткани осталось у мамы?
- 1) 2 + 1 = 3
- 2) 10 — 3 = 7
- Ответ: 7 метров.
Задание 180.
У Максима было 12 наклеек. В один конверт он положил 4 наклейки, а в другой 3. Сколько наклеек осталось положить в конверт?
- 1) Сколько всего наклеек Максим уже положил в конверт?
- 2) Сколько наклеек осталось положить в конверт?
Решение:
- 1) 4 + 3 = 7
- 2) 12 — 7 = 5
- Ответ: 5 наклеек.
Задание 181.
На прогулку вывели 7 девочек, а мальчиков на 3 меньше. Сколько мальчиков вышло на прогулку? Сколько всего детей вышло на прогулку?
Решение:
- 1) 7 — 3 = 4
- 2) 7 + 4 = 11
- Ответ: 4 мальчика вышло на прогулку, 11 детей всего вышло на прогулку.
Задание 182.
Рассмотри таблицу сложения и вычитания чисел. Объясни, как находить ответы при сложении и вычитании.
Найди по таблице сумму 7 + 9 и разность 15 — 6.
Решение:
Для того что бы выполнить сложение при помощи таблицы, нужно провести воображаемые линии от цифр, которые мы собираемся складывать(вниз от верхнего числа и вправо от цифры, которая расположена в крайней левой колонке). Результатом пересечения этих воображаемых линий будет сумма, выбранных нами цифр.
При вычитании, выбираем вычитаемое из нижнего ряда (выделено синим), уменьшаемое находим в той же колонке, что и вычитаемое. Разность в крайней левой колонке, в том же ряду что и уменьшаемое.
Разность в крайней левой колонке, в том же ряду что и уменьшаемое.
- 1) 7 + 9 = 16
- 2) 15 — 6 = 9
Задание 183.
Числа 13, 16, 18 разложи на два слагаемых так, чтобы одним из слагаемых было число 9. Образец. 14 = 9 + 5.
Решение:
- 1) 13 = 9 + 4
- 2) 16 = 9 + 7
- 3) 18 = 9 + 9
Задание 184.
Решение:
| 1) Дополни до 12. |
2) Увеличь на 7 |
Задание 185.
Из каждой пары выражений выпиши выражение с меньшим значением:
| 17 — 9 и 12 — 3 | 16 — 7 и 12 — 9 |
| 3 + 9 и 4 + 8 | 9 + 4 и 9 + 7 |
Решение:
| 17 — 9 | 12 — 9 |
| 3 + 9 = 4 + 8 | 9 + 4 |
Задание 186.
Найди периметры треугольников.
Периметр какого треугольника больше и на сколько?
Задание 187.
У Толи было 8 тетрадей в клетку и 7 тетрадей в линейку. 5 тетрадей в линейку он отдал другу. Сколько тетрадей осталось у Толи? Реши задачу двумя способами.
Решение:
- 1 способ: 1) 8 + 7 = 15 (тетрадей) всего было у Толи; 2) 15 — 5 = 10 (тетрадей).
- 2 способ: 1) 7 — 5 = 2 (тетради) в линейку осталось у Толи; 2) 2 + 8 = 10 (тетрадей).
- Ответ: у Толи осталось 10 тетрадей.
Задание 188.
На аэродроме было 12 самолётов. Сначала взлетело 2 самолёта, а потом ещё 3. Сколько самолётов осталось на аэродроме?
Решение:
- 1) Способ: сначала вычисляем сколько всего взлетело самолетов, то что получилось, отнимает от количества самолетов, которое стояло сначала на аэродроме.
- 2) Способ: отнимаем количество самолетов, которое сначала взлетело, затем отнимаем самолеты, которые взлетели после них.
Задание 189.
Решение:
| 17 — 9 = 8 | 4 + 8 — 9 = 12 — 9 = 3 | 16 — 9 = 7 | 5 + 9 — 6 = 14 — 6 = 8 |
| 13 — 8 = 5 | 4 + 8 — 9 = 12 — 9 = 4 | 13 — 7 = 6 | 12 — 5 + 8 = 7 + 8 = 15 |
Задание 190.
В ящике было 12 кг лука. В первый день продали 4 кг лука, а во второй 5 кг. Сколько килограммов лука осталось в ящике?
- 1) 12 — 4 = 8 (кг) осталось лука после продажи в первый день;
- 2) 8 — 5 = 3 (кг) осталось лука после продажи во второй день.
- Ответ: осталось 3 кг лука.
Решение:
Сначала узнаем сколько лука осталось в первый день, затем от полученного результата отнимаем лук, проданный во второй день.
- Второй способ:
- 1) 4 + 5 = 9 (кг) лука продали за 2 дня;
- 2) 12 — 9 = 3 (кг).
Задание 191.
Решение:
- 1) На странице было изображено 2 треугольника, а кругов на 8 больше.
 Сколько кругов было на странице?
Сколько кругов было на странице?
- 1) 2 + 8 = 10 (кругов).
- Ответ: на странице было изображено 10 кругов.
- 2)
- 14 — 10 + 4 = 4 + 4 = 8
- 17 — 10 + 4 = 7 + 4 = 11
- 19 — 10 + 3 = 9 + 3 = 12
- 20 — 10 + 3 = 10 + 3 = 13
Задание: —>> 164 — 191
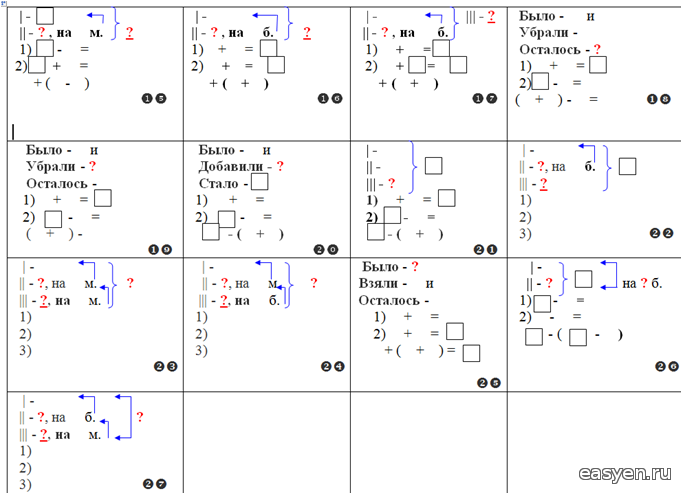
Памятка по оформлению краткой записи к задачам. (1-2 класс)
1. Памятка по оформлению краткой записи к задачам 1-2 класс
Непочатковская Наталия Васильевнаучитель начальных классов МОУ №67
г. Донецка
2. Содержание
СодержаниеПростые задачи
Нахождение суммы 1 2 3
Увеличение числа на
несколько единиц 4
Уменьшение числа на
несколько единиц 5
Нахождение неизвестного
слагаемого 6 7
Нахождение остатка 8
Нахождение неизвестного
вычитаемого 9
Нахождение неизвестного
уменьшаемого 10
Разностное сравнение 11 12
Составные задачи
Нахождение суммы 13 14 15
16
Нахождение остатка 17 18
Нахождение неизвестного
слагаемого 19 20
Нахождение неизвестного
вычитаемого 21 22 23
Нахождение третьего
слагаемого 24
Нахождение неизвестного
уменьшаемого 25 26
Разностное сравнение 27 28
29
3.
 Задача 1 Нахождение суммы Ася вымыла 5 тарелок, а Маша вымыла 4
Задача 1 Нахождение суммы Ася вымыла 5 тарелок, а Маша вымыла 4тарелки. Сколько всего тарелок вымыли дети?
Ася – 5 т.
? Т.
Маша – 4 т.
Решение
5 + 4 = 9 (т.)
Ответ: 9 тарелок вымыли дети.
4. Задача 2 Нахождение суммы
На стоянке было 2 машины. Вечером приехалоещё 5 машин. Сколько всего машин на стоянке?
Было – 2 м.
Приехало – 5 м.
Стало – ? м.
Решение
2 + 5 = 7 (м.)
Ответ: 7 машин всего на стоянке.
5. Задача 3 Нахождение суммы
На опушке леса росло 5 клёнов и 4 тополя, асосен росло столько, сколько клёнов и тополей
вместе. Сколько сосен росло на опушке леса?
Клёнов – 5 д.
Тополей – 4 д.
Сосен – ? д., К. + Т.
Решение
5 + 4 = 9 (д.)
Ответ: 9 сосен росло на опушке леса.
6. Задача 4 Увеличение числа на несколько единиц
У Васи 7 марок, а у Егора на 3 маркибольше. Сколько марок у Егора?
Вася – 7 м.
Егор – ? м., на 3 м. б.
Решение
7 + 3 = 10 (м.
 )
)Ответ: 10 марок у Егора.
7. Задача 5 Уменьшение числа на несколько единиц
В первой группе 10 учеников, а во второйна 3 ученика меньше. Сколько учеников во
второй группе?
В I г. – 10 уч.
Во II г. – ? уч., на 3 уч. м.
Решение
10 – 3 = 7 (уч.)
Ответ: 7 учеников во второй группе.
8. Задача 6 Нахождение неизвестного слагаемого
У Дины было 9 роз. 5 розовых, остальныебелые. Сколько белых роз было у Дины?
Розовые – 5 р.
9 р.
Белые – ? р.
Решение
9 – 5 = 4 (р.)
Ответ: 4 белые розы были у Дины.
9. Задача 7 Нахождение неизвестного слагаемого
Дед Мазай вёз на своей лодке 5 зайцев. Онподобрал ещё несколько зайцев, и их стало 8.
Сколько зайцев подобрал дед Мазай?
Было – 5 з.
Подобрал – ? з.
Стало – 8 з.
Решение
8 – 5 = 3 (з.)
Ответ: 3 зайца подобрал дед Мазай.
10. Задача 8 Нахождение остатка
На проводах сидели 9 ворон. 5 ворон улетели.
Сколько ворон осталось?
Было – 9 в.
Улетели – 5 в.
Осталось – ? в.
Решение
9 – 5 = 4 (в.)
Ответ: 4 вороны осталось.
11. Задача 9 Нахождение неизвестного вычитаемого
На кустике висело 7 ягод клубники. Когданесколько ягод созрело и упало, осталось 5
ягод. Сколько ягод созрело и упало?
Было – 7 яг.
Упало – ? яг.
Осталось – 5 яг.
Решение
7 – 5 = 2 (яг.)
Ответ: 2 ягоды созрело и упало.
12. Задача 10 Нахождение неизвестного уменьшаемого
В зоопарке несколько медведей. Когда трёхмедведей перевезли в другой зоопарк, осталось 6
медведей. Сколько медведей было в зоопарке
первоначально?
Было – ? м.
Перевезли – 3 м.
Осталось – 6 м.
Решение
3 + 6 = 9 (м.)
Ответ: 9 медведей было в зоопарке первоначально.
13. Задача 11 Разностное сравнение
Один мальчик поймал 8 крабов, а другой 3краба. На сколько крабов первый мальчик
поймал больше второго?
I м.
 – 8 к.
– 8 к. на ? б.
II м. – 3 к.
Решение
8 – 3 = 5 (к.)
Ответ: на 5 крабов первый мальчик поймал
больше, чем второй.
14. Задача 12 Разностное сравнение
Один арбуз весит 5 кг, а другой 8 кг. На сколькокилограммов один арбуз легче другого?
I ар. – 5 кг
на ? м.
II ар. – 8 кг
Решение
8 – 5 = 3 (кг)
Ответ: на 3 килограмма один арбуз легче
другого.
15. Задача 13 Нахождение суммы
На пришкольном участке 6 берёз, а лип на 4меньше. Сколько всего деревьев на пришкольном
участке?
Берёз – 6 д.
? д.
Лип – ?д., на 4 д. м.
Решение
1) 6 – 4 = 2 (д.) – лип.
2) 6 + 2 = 8 (д.)
Ответ: 8 деревьев всего на пришкольном участке.
16. Задача 14 Нахождение суммы
В шкафу стоят 2 кастрюли, сковородок на 3 больше,а ваз столько, сколько кастрюль и сковородок
вместе. Сколько ваз стоит в шкафу?
Кастрюли – 2 шт.
Сковородки – ? шт., на 3 шт. б.
Вазы – ? шт.
 , К. + С.
, К. + С.Решение
1) 2 + 3 = 5 (шт.) – сковородок.
2) 2 + 5 = 7 (шт.)
Ответ: 7 ваз стоит в шкафу.
17. Задача 15 Нахождение суммы
У Тани 3 яблока, груш на 2 больше, чем яблок, аперсиков на 4 меньше, чем груш. Сколько всего фруктов
у Тани?
Яблоки – 3 шт.
Груши – ? шт., на 2 шт. б.
? шт.
Персики – ? шт., на 4 шт. м.
Решение
1) 3 + 2 = 5 (шт.) – груш.
2) 5 – 4 = 1 (шт.) – персиков.
3) 3 + 5 = 7 (шт.) – яблок и груш вместе.
4) 7 + 1 = 8 (шт.)
Ответ: 8 фруктов всего у Тани.
18. Задача 16 Нахождение суммы
В коробке 17 жёлтых кубиков, зелёных на 6 меньше, чемжёлтых, а красных на 12 больше, чем зелёных и жёлтых кубиков
вместе. Сколько всего кубиков в коробке?
Жёлтых – 17 к.
? К.
Зелёных – ? к., на 6 к. м.
? К.
Красных — ? к., на 12 к. б.
Решение
1) 17 – 6 = 11 (к.) – зелёных.
2) 17 + 11 = 28 (к.) – жёлтых и зелёных вместе.
3) 28 + 12 = 40 (к.
 ) – красных.
) – красных.4) 28 + 40 = 68 (к.)
Ответ: 68 кубиков всего в коробке.
19. Задача 17 Нахождение остатка
Нашли 4 белых гриба и 6 подосиновиков.8 грибов пошло на суп. Сколько грибов
осталось?
Было – 4 г. и 6 г.
Израсходовали – 8 г.
Осталось – ? г.
Решение
1) 4 + 6 = 10 (г.) – было.
2) 10 – 8 = 2 (г.)
Ответ: 2 гриба осталось.
20. Задача 18 Нахождение остатка
У Феди в аквариуме плавали 23 рыбки. Мальчикподарил 6 рыбок Ване и 4 рыбки Максиму. Сколько
рыбок осталось в аквариуме у Феди?
Было – 23 р.
Подарил – 6 р. и 4 р.
Осталось – ? р.
Решение
1) 6 + 4 = 10 (р.) – подарил.
2) 23 – 10 = 13 (р.)
Ответ: 13 рыбок осталось в аквариуме у Феди.
21. Задача 19 Нахождение неизвестного слагаемого
На поле сидело 22 воробья и 13 синичек. Когдаприлетело ещё несколько птиц, их стало 49.
Сколько птиц прилетело?
Было – 22 п. и 13 п.
Прилетело – ? п.
Стало – 49 п.

Решение
1) 22 + 13 = 35 (п.) – было.
2) 49 – 35 = 14 (п.)
Ответ: 14 птиц прилетело.
22. Задача 20 Нахождение неизвестного слагаемого
У причала стояло 6 катеров. Утром причалило 3катера и несколько катеров причалило вечером, и
после этого у причала стало 19 катеров. Сколько
катеров причалило вечером?
Было – 6 к.
Причалило – 3 к. и ? к.
Стало – 19 к.
Решение
1) 19 – 6 = 13 (к.) – причалило всего .
2) 13 – 3 = 10 (к.)
Ответ: 10 катеров причалило вечером.
23. Задача 21 Нахождение неизвестного вычитаемого
Маша увидела 7 белых и 3 пёстрых бабочек.Когда несколько бабочек улетело, их осталось
5. Сколько бабочек улетело?
Было – 7 б. и 3 б.
Улетело –? б.
Осталось – 5 б.
Решение
1) 7 + 3 = 10 (б.) – было.
2) 10 – 5 = 5 (б.)
Ответ: 5 бабочек улетело.
24. Задача 22 Нахождение неизвестного вычитаемого
На аэродроме было 20 вертолётов. Утромулетело 10 вертолётов.
 Сколько вертолётов
Сколько вертолётовулетело днём, если к вечеру их осталось 6?
Было – 20 в.
Улетели – 10 в. и ? в.
Осталось – 6 в.
Решение
1) 20 – 6 = 14 (в.) – улетели всего.
2) 14 – 10 = 4 (в.)
Ответ: 4 вертолёта улетело днём.
25. Задача 23 Нахождение неизвестного вычитаемого
В букете было 9 гвоздик. Когда несколько гвоздикзавяли, остались 2 красные и 3 розовые гвоздики.
Сколько гвоздик завяло?
Было – 9 г.
Завяли – ? г.
Осталось – 2 г. и 3 г.
Решение
1) 2 + 3 = 5 (г.) – осталось.
2) 9 – 5 = 4 (г.)
Ответ: 4 гвоздики завяло.
26. Задача 24 Нахождение третьего слагаемого
В трёх классах на окнах стоят 35 горшков с цветками.В первом классе 11 горшков, во втором 13. Сколько
горшков с цветками стоит в третьем классе?
I к. – 11 г.
II к. – 13 г.
35 г.
III к. – ? г.
Решение
1)11 + 13 = 24(г.) – в I и II классах.
2)35 – 24 = 11(г.)
Ответ: 11 горшков с цветками стоят в третьем классе.

27. Задача 25 Нахождение неизвестного уменьшаемого
Бабушка испекла блины. Папа съел 15 блинов,мама 10. Сколько всего блинов испекла
бабушка, если осталось 22 блина?
Было – ? б.
Съели – 15 б. и 10 б.
Осталось – 22 б.
Решение
1)15 + 10 = 25(б.) – съели.
2)25 + 22 = 47 (б.)
Ответ: 47 блинов всего испекла бабушка.
28. Задача 26 Нахождение неизвестного уменьшаемого
В пенале лежали карандаши. Когда туда положилиещё 3 простых и 7 цветных карандашей, их стало 22.
Сколько карандашей лежало в пенале сначала?
Было – ? к.
Положили – 3 к. и 7 к.
Стало – 22 к.
Решение
1)3 + 7 = 10 (к.) – положили.
2)22 – 10 = 12 (к.)
Ответ: 12 карандашей лежало в пенале сначала.
29. Задача 27 Разностное сравнение
В зале музея 18 картин. Из них 6 пейзажей, аостальные портреты. На сколько больше
портретов, чем пейзажей?
Пейзажи – 6 к.
18 к.
на ? б.
Портреты – ? к.

Решение
1) 18 – 6 = 12 (к.) – портреты.
2) 12 – 6 = 6 (к.)
Ответ: на 6 портретов больше, чем пейзажей.
30. Задача 28 Разностное сравнение
В саду 15 кустов малины, кустов крыжовника на 3 меньше, чеммалины, а кустов смородины на 11 больше, чем малины. На
сколько меньше кустов смородины, чем крыжовника и малины
вместе?
Малина – 15 к.
Крыжовник – ? к., на 3 к. м.
на ? М.
Смородина – ? к., на 11 к. б.
Решение
1) 15 – 3 = 12 (к.) – крыжовника.
2) 15 + 11 = 26 (к.) – смородины.
3) 15 + 12 = 27 (к.) – малины и крыжовника вместе.
4) 27 – 26 = 1 (к.)
Ответ: на 1 куст меньше смородины, чем крыжовника и малины
вместе.
31. Задача 29 Разностное сравнение
Над полянкой кружились 8 пчёл и 11 стрекоз. 15 из них сели нацветы. На сколько больше насекомых село на цветы, чем
продолжало кружиться?
Было – 8 н. и 11 н.
Сели – 15 н.
на ? б.
Осталось – ? н.

Решение
1) 8 + 11 = 19 (н.) – было.
2) 19 – 15 = 4 (н.) – осталось.
3) 15 – 4 = 11 (н.)
Ответ: на 11 насекомых больше село на цветы, чем продолжало
кружиться.
Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Открытый урок по математике «Путешествие в сказку» (2 класс)
Открытый урок по математике «Путешествие в сказку» (2 класс)
ноябрь
Тема: Закрепление изученного. Решение задач.
ЦЕЛИ УРОКА:
* учить решать задачи на нахождение суммы, совершенствовать вычислительные навыки и умение сравнивать;:
* развивать познавательный интерес к предмету, логическое мышление, внимание; устную речь учащихся;
* воспитывать аккуратность, усидчивость.
ОБОРУДОВАНИЕ: презентация, карточки с заданиями, учебник, рабочая тетрадь.
ХОД УРОКА:
I Организационный момент: (цель: дать положительный настрой на урок)
— Ребята, к нам на урок пришли гости, давайте с ними поздороваемся.
Всем, всем добрый день!
Прочь с дороги наша лень!
Не мешай трудиться,
Не мешай учиться!
— Садитесь, ребята. Проверьте, всё ли у вас готово? Начинаем наш урок.
— Я тетрадь свою открою
И наклонно положу.
Я друзья от вас не скрою –
Ручку я вот так держу.
Сяду прямо, не согнусь.
За работу я возьмусь.
Открываем тетради, записываем число, классная работа.
Прочитайте девиз нашего урока:
С мастерством готовым люди не родятся, а добытым мастерством гордятся.
-Как вы понимаете эти слова?
-Готовы ли вы добывать новые знания, чтобы потом можно было гордиться своим мастерством? Тогда начнём.
II Минутка чистописания.
Повторение нумерации
На доске ряд чисел: 10 21 32 43 54 67 76 87 98
-Прочитайте числа. По какому принципу построен данный ряд?
-Найди «лишнее» число. (67) Докажи. Чем можно заменить?
(67) Докажи. Чем можно заменить?
-Дайте характеристику. Пропишите всю строку данное число, правильно записывая в клетке каждую цифру.
III Актуализация знаний
- Устный счёт.
-Сегодня мы продолжаем увлекательное путешествие по загадочной и великой стране «Математика». Вам предстоит думать, вычислять, соревноваться.
-Начнём урок с разминки, но не физической, а математической.
-А куда мы отправимся, вы определите сами. (решают, записывают ответ в тетради, вывешивают карточки на доске)
- Составление слова
—Если это число уменьшить на 50, то получится 27. (77)
—Вычислите сумму 68 и 30. (98)
—К какому числу прибавили 10 и получили 25. (15)
—Найдите разность 52 и 40. (12)
—К разности 45 и 5 прибавить 8. (48)
—Из суммы 8 и 2 вычти 6. (4)
-Расположите в порядке уменьшения и переверните карточки.
98 77 48 15 12 4
С к а з к а
-Мы отправляемся в сказку.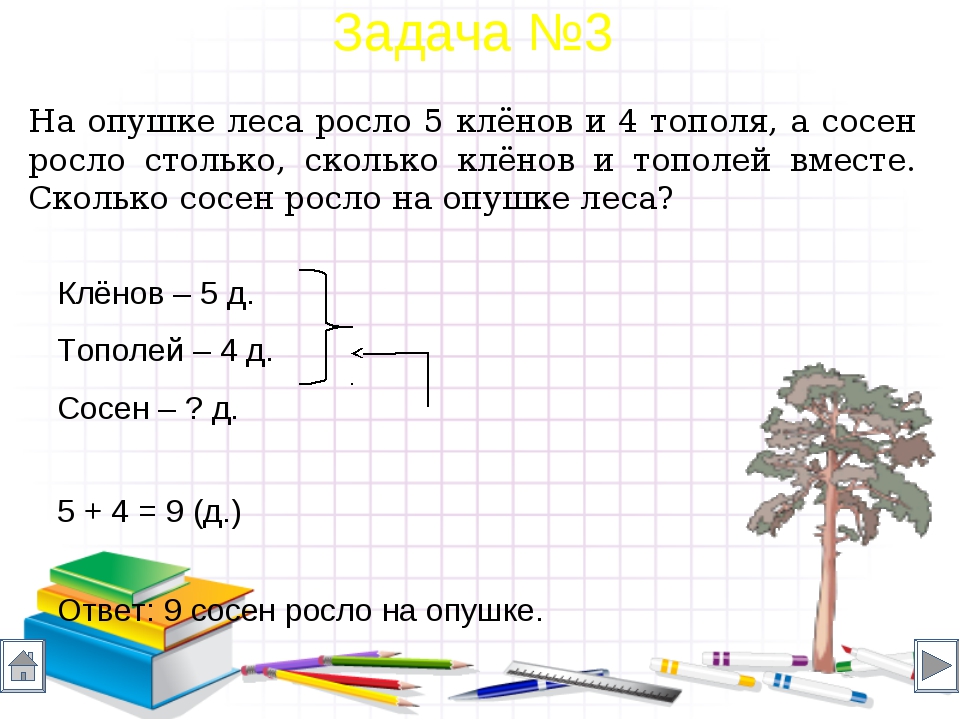 А в какую мы попадём, вы узнаете, если отгадаете загадку.
А в какую мы попадём, вы узнаете, если отгадаете загадку.
Уплетая калачи,
Ехал парень на печи.
Прокатился по деревне
И женился на царевне. (Картинка Емеля и печка)
-Да, мы попали в сказку «По щучьему велению».
-На чём путешествовал Емеля?
-Мы тоже будем путешествовать на печке. Чтобы она задымилась, загорелся в ней огонь, что нужно сделать? Правильно, давайте затопим печь, а для этого нарубим дрова и сложим их в поленницу.
- Игра «Круговые примеры» (поленья с примерами)
46+30 76-6 70-10 60+24 84+6 90-40 50-4
-На каждом полене примеры и их нужно решить. (Поленья висят на доске, ученик выходит, решает пример и складывает в поленницу в нужном порядке.)
-Молодцы, мы растопили печь, теперь отправляемся в путь, в царство царевны Несмеяны.
(Картинка Царевны Несмеяны)
-Ой, кто это? (Баба Яга)
-Баба Яга махнула метлой,
Кочки вдруг появились кругом.
-Она не даёт нам проехать, повсюду сделала большие кочки, а на них вопросы.
-Как называются числа при сложении?
-Как найти 1 слагаемое?
-Из 1 рубля вычти 20 копеек.
-Назови самое большое двузначное число.
-Сколько см в 1 дм?
-Как называются числа при вычитании?
-Что больше 50 см или 5 дм?
-Чтобы проехать дальше, нам нужно продолжить нашу математическую разминку и выполнить некоторые задания.
-Путь открыт. Оцените себя на полях за работу в устном счёте.
Вы, наверное, устали?
Ну, тогда, все дружно встали!
Наш Емеля потянулся, раз нагнулся, два нагнулся.
Руки в стороны развёл, щуку, видно, не нашёл.
Чтобы щуку нам достать, надо на носочки встать.
IV Самоопределение к деятельности.
-Вот наша печка к речке подходит.
Где же здесь плот? Его не находим.
Чтобы на речку плот опустить,
Надо задание скорее решить.
-На перевёрнутых плотах данные для задачи.
-Царевна Несмеяна любит фрукты. В вазе у неё 4 яблока и 3 груши. Сколько слив в вазе? (Задачу решить нельзя, не хватает данных)
-А если я изменю вопрос? В вазе у неё 4 яблока и 3 груши. Сколько яблок в вазе? (Ответ есть в условии задачи, решать не надо)
-Поставьте вопросы, чтобы задача решалась так: 4+3, 4-3.
-Что сегодня мы будем делать на уроке? (Решать задачи)
V Работа по теме урока.
-Какая из записей 4-3 или 4+3 — будет решением следующей задачи?
В вазе 4 яблока и 3 груши, а слив столько, сколько яблок и груш вместе. Сколько слив в вазе?
-О чём говорится в задаче?
-Что говорится о яблоках? О грушах? О сливах? Что это значит? (надо узнать сколько всего яблок и груш)
-Сколько слив? Как получили 7?
- Работа по учебнику.
С. 63, № 1 (у доски с объяснением)
Оцените себя на полях, поняли ли вы как решаются такие задачи.
VI Физминутка для глаз.
Рисуй восьмёрку вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям веди
И на бочок её клади.
Теперь следи горизонтально
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец,
Зарядка окончена. Ты молодец!
VII Закрепление изученного материала.
- Решение примеров.
-Вот мы и к царству уже подошли,
Но Несмеяну никак не нашли.
Наплакала речку, наплакала море
Давайте поможем царскому горю.
-Чтобы Несмеяна не плакала, выполним задание, написанное на слезинках.
1) Из числа 80 вычесть сумму чисел 53 и 7
Из числа 90 вычесть разность чисел 84 и 4
К числу 50 прибавить сумму чисел 20 и 14
К числу 27 прибавить разность чисел 48 и 8
2) 80 – (53 + 7) 50 + (20 + 14)
90 – (84 – 4) 27 + (48 – 8)
-Выполним самопроверку.
-Прочитайте пример, ответ которого самое маленькое двузначное число. 10, 2 пр.
-Прочитайте пример, ответ которого на 1 больше, чем 83. 84, 3 пр.
-Прочитайте пример, в ответе которого десятков на 2 больше, чем единиц. 20, 1 пр.
-Прочитайте пример, ответ которого является предыдущим числом для числа 68. 67, 4 пр.
Сделайте самопроверку и оцените свою работу на полях.
- Конструирование. Работа в парах.
-Емеля подарил Царевне Несмеяне подарок. Он был упакован в красивую коробку. Какой длины нужно взять ленту, чтобы украсить по краям крышку это коробки.
-А в коробке головоломка «Танграм», чтобы Царевна не скучала.
VIII Подведение итогов.
-Что узнали на уроке?
-Чему научились? За что можешь похвалить себя?
-Какие задания были трудными? Над чем надо поработать?
-И в конце возвращаемся к нашему девизу.
С мастерством готовым люди не родятся, а добытым мастерством гордятся.
-Можем мы гордиться собой?
-Чему научились на уроке, чтобы попасть в замок Царевны Несмеяны.
IX Домашнее задание.
-Царевна Несмеяна и Емеля были рады встретиться с вами. Большое спасибо всем вам, ребята.
Все так решали, все отвечали
Сколько препятствий смогли вы пройти.
На этом сказке конец, а кто слушал молодец.
с. 63, № 2, 4
X Рефлексия
-Оцените себя по нашей лестнице достижений, Всё ли у вас получилось, к чему надо стремиться?
Довольны ли вы своей работой?
Резерв с. 63 на полях
1) Из числа 80 вычесть сумму чисел 53 и 7
Из числа 90 вычесть разность чисел 84 и 4
К числу 50 прибавить сумму чисел 20 и 14
К числу 27 прибавить разность чисел 48 и 8
2) 80 – (53 + 7) 50 + (20 + 14)
90 – (84 – 4) 27 + (48 – 8)
Сальникова Юлия
ГДЗ по Математике 2 класс Моро, Бантова учебник Решебник
Здесь представлен учебник по математике для самых маленьких школьников (2 класс) с готовыми ответами и правильными алгоритмами решения. Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Почему решебник по математике Моро нужен каждому второкласснику?
ГДЗ помогают ребенку мотивировать себя, чтобы заниматься самостоятельно, а также постоянно контролировать достигнутый уровень личного прогресса посредством решения проверочных упражнений. Со сборником по математике Моро, Бантовой, Бельтюковой, который полностью соответствуют ФГОС и повсеместно используются в рабочих программах педагогов, легко и удобно заниматься. Верные ответы онлайн имеют следующие преимущества перед иными видами пособий:
- наличие независимых вариантов выполнения многих примеров;
- примеры снабжены ценными методическими указаниями;
- сайт работает с персонального компьютера, ноутбука, планшета и смартфона;
- таблица номерных указателей позволяет быстро находить нужное задание.

С онлайн-решебником можно успешно готовиться к контрольным, проверочным, самостоятельным, и диагностическим работам, выполнять тесты и проходить внешнее независимое тестирование в конце учебного года.
Чем ГДЗ Моро, Бантовой превосходит другие учебники для 2 класса?
Чтобы хорошо успевать по математике и приносить домой исключительно отличные отметки, нужно приучить себя к систематической и тщательной работе. Это касается как отработки устного счета, так и формирования четкого понимания способов решения задач на одно и два действия. Во втором классе общеобразовательной школы ученики знакомятся лишь с самыми простыми понятия, но именно они станут залогом будущих успехов при изучении точных дисциплин. Ни в коем случае нельзя запускать предмет, а возникающие пробелы в знаниях, умениях и навыках необходимо ликвидировать в кратчайшие сроки. Сборник способен оказать значительную помощь в достижении следующих целей:
- повышение текущей успеваемости и степени уверенности в собственных силах на уроках;
- отработка практических навыков в области арифметики;
- формирование самостоятельности при подготовке к урокам;
- расширение кругозора и формирования навыков логического мышления.

Математика относится к тем предметам, которые непременно пригодятся будущему взрослому члену общества. Уметь произвести те или иные практически важные и полезные вычисления необходимо повсеместно. Поэтому пособие Моро для 2 класса рекомендовано наиболее широким массам учащихся, а также их неравнодушным родителям, которые хотели бы держать под контролем учебный прогресс своего сына или дочери.
Конспект урока математики во 2 классе «Решение примеров и задач на сложение и вычитание в пределах 10»
Конспект урока математики во 2 классе «Решение примеров и задач на сложение и вычитание в пределах 10»
Разработан учителем начальных
классов ГБОУ СО «Школа АОП № 6 г. Саратова
Аверьяновой Надеждой Анатольевной
Предмет: математика
Класс: 2
Тема: Решение примеров и задач на сложение и вычитание в пределах 10.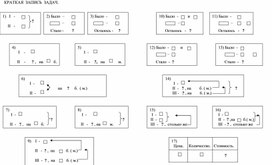
Тип урока. Закрепление
Цель: закрепление вычислительных навыков в пределах 10.
Задачи:
-повторить состав чисел , закрепить приемы сложения и вычитания чисел в пределах 10,
решения задач;
развитие познавательных психических процессов, кругозора, самостоятельности,
самоконтроля, речи;
— воспитание аккуратности, любви к животным, ответственности за животных, взаимопомощи, взаимовыручки, эмпатии.
Оборудование: счеты, счетный материал, картинка с изображением белки, ежа, фигурка зайца из геометрических фигур, линейка, карандаш, ручка, тетрадь по математике.
Ход урока.
№ | Деятельность учителя | Деятельность учащихся | Примечание |
1. | Организационный момент. 1.Введение в урок. Сообщение темы урока. — Сегодня на уроке мы будем решать задачи и примеры на сложение и вычитание в пределах 10. | Учащиеся приветствуют учителя. | Учитель проверяет готовность к уроку. |
3. | Проверка домашнего задания Сейчас откройте все свои тетради, я проверю кто как выполнил домашнее задание. | Учащиеся показывают домашнее задание | |
2. | Устный счет. — Я предлагаю вам заглянуть в осенний лес и посмотреть, как звери готовятся к зиме. Но сначала немного разомнемся. 1) — Назовите числа от 6 до 10, от 7 до 12, от 11 до 5, от 13 до 8. 2) — Назовите соседей числа 10 (11, 12). 3) -За каким числом стоит число 10? — Какое число стоит перед числом 13? -Какое число идет после 10? В лес осенний мы попали Суета вокруг, везде. Урожай все собирают И готовятся к зиме. — Кого мы повстречали в осеннем лесу? Вы это узнаете, отгадав загадку: Словно ёлка, Весь в иголках. Пальчиковая гимнастика «ЕЖ» Маленький колючий ёж До чего же ты хорош. — Что любит собирать ёж? — Давайте поможем ежу собрать яблоки. 4) Состав числа 10. 10 это – 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5. — | Учащиеся отвечают на вопросы (фронтальная работа) Ответы учащихся. Учащиеся соединяют половинки яблок так, чтобы в сумме получилось 10. | Работа с опорой на числовой ряд. Открываю плакат с изображением осени. Учитель просит давать полные ответы. Учащиеся по одному выходят к доске. Работа у доски. |
4. | Закрепление изученного. 1) Работа над задачей. — Отгадайте кто ещё хлопочет в осеннем лесу? Загадка: Кто по ёлкам ловко скачет И взлетает на дубы? Кто в дупле орехи прячет, Сушит на зиму грибы. — Как белочка готовится к зиме? — Что она запасает? — Куда она всё прячет? — Составьте задачу по краткому условию. ( В одну кладовку белочка спрятала 10 орехов, а в другую на 2 ореха меньше. — Запишем условие задачи. — Повторите вопрос задачи. — Запишем решение. — Мы ответили на вопрос задачи? — Запишем ответ. — Как же белочка находит запасы? — У белочки очень хорошая зрительная память. Она помнит куда прячет запасы. 3) Решение примеров. Работа с учебником. — Продолжим считать запасы белки. Решим примеры. Откройте учебник на странице….41 № 119. — Вспомним названия компонентов при сложении (вычитании). Молодцы. | Белка. Делает запасы В кладовой (в дубпе) На веточках развешивает. Учащиеся составляют условие задачи по краткой записи. Учащиеся по одному выходят к доске и решают примеры. | Учитель вывешивает картинку с белкой. Использует таблицу – схему к задаче. . Учащиеся, работающие у доски проговаривают названия компонентов сложения и вычитания. |
5. | Физминутка. А теперь, ребята встали. Быстро руки вверх подняли, В стороны, вперед. Назад Повернулись вправо, влево. Тихо сели, вновь за дело. | ||
6. | Самостоятельная работа. Решите примеры и запишите правильный ответ. Зрительная и дыхательная гимнастика. а) гимнастика для глаз: влево-вправо вверх-вниз по кругу глазами. Закрыли ладошкой глаза(глаза открыты). Смотрим темноту. Зажмурили сильно, сильно, сильно и открыли. б) дыхательная: Вдох носом, выдох через рот. Вдох – 1, 2, 3 носом, выдох длинный через рот. в) Ладошка на уровне рта. Вдохнуть воздух носом глубоко. Задержать дыхание. И сильно ртом выдохнуть. (это четырехфазное дыхание) | Работа по карточкам. Учитель использует индивидуальный и дифференцированный подход. Учитель помогает слабым учащимся. | |
6. | Работа с геометрическим материалом. — Кто из зверей не делает запасы? — Кто спрятался здесь в листве среди травы уши больше головы? Пальчиковая гимнастика «ЗАЙЦЫ» — Кто там скачет на лужайке? Это длинноухий зайка. Посмотрите на картинку из каких геометрических фигур составлена фигура зайца. Туловище – 2 треугольника Голова – прямоугольник Лапки – треугольники Ухо — ромб | Учащиеся отвечают на вопросы. | Учитель вывешивает картинку с фигуркой зайца |
7. | Подведение итога урока. — Наше путешествие по осеннему лесу закончилось. Вам понравилось? — На уроке хорошо работали… | Ответы детей | |
8. | Домашнее задание. С. 31…, № 85 1 группа – ( 1-3 ст. ) стр 37 № 103 (1 ст) 2 группа (1-3 ст/) 3 группа – (1-2 ст.) Урок окончен. Всем спасибо. |
Литература и источники.
1. Программы специальных (коррекционных) образовательных учреждений VIII вида. Подготовительный класс. 1—4 классы. Под редакцией доктора педагогических наук В. В. Воронковой. Допущено Министерством образования и науки Российской Федерации.
4-е издание
2.Журнал «Воспитание и обучение детей с нарушениями развития» №1 2008г
3. Учебник для вузов «Методика преподавания математики в коррекционной школе» М.Н. Перова
Учебник для вузов «Методика преподавания математики в коррекционной школе» М.Н. Перова
4. А.А. Хилько Математика. Учебник для 2 класса вспомогательной школы. Москва «Просвещение» 1993 г.
5. http://tobemum.ru/deti/kak-nauchit/generator-propisi /
Тест: Тест по математике «Решение задач»
Тест по математике «Решение задач»
Тест составлен для контроля и отработки умения решать текстовые задачи. Тест состоит из 18 вопросов. Выполняя тестовые задания, ученик должен выбрать один верный ответ из предложенных.
Математика 2 класс | Автор: Исаева Анжелика Владимировна | ID: 801 | Дата: 2.1.2014
«;} else {document.getElementById(«torf1″).innerHTML=»»;}; if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;}; if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;}; if (answ.charAt(3)==»1″) {document.getElementById(«torf4″). innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
if (answ.charAt(10)==»1″) {document.getElementById(«torf11″).innerHTML=»»;} else {document.getElementById(«torf11″).innerHTML=»»;};
if (answ.charAt(11)==»1″) {document.
innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
if (answ.charAt(10)==»1″) {document.getElementById(«torf11″).innerHTML=»»;} else {document.getElementById(«torf11″).innerHTML=»»;};
if (answ.charAt(11)==»1″) {document. getElementById(«torf12″).innerHTML=»»;} else {document.getElementById(«torf12″).innerHTML=»»;};
if (answ.charAt(12)==»1″) {document.getElementById(«torf13″).innerHTML=»»;} else {document.getElementById(«torf13″).innerHTML=»»;};
if (answ.charAt(13)==»1″) {document.getElementById(«torf14″).innerHTML=»»;} else {document.getElementById(«torf14″).innerHTML=»»;};
if (answ.charAt(14)==»1″) {document.getElementById(«torf15″).innerHTML=»»;} else {document.getElementById(«torf15″).innerHTML=»»;};
if (answ.charAt(15)==»1″) {document.getElementById(«torf16″).innerHTML=»»;} else {document.getElementById(«torf16″).innerHTML=»»;};
if (answ.charAt(16)==»1″) {document.getElementById(«torf17″).innerHTML=»»;} else {document.getElementById(«torf17″).innerHTML=»»;};
if (answ.charAt(17)==»1″) {document.getElementById(«torf18″).innerHTML=»»;} else {document.getElementById(«torf18″).innerHTML=»»;};
}
}
Получение сертификата
getElementById(«torf12″).innerHTML=»»;} else {document.getElementById(«torf12″).innerHTML=»»;};
if (answ.charAt(12)==»1″) {document.getElementById(«torf13″).innerHTML=»»;} else {document.getElementById(«torf13″).innerHTML=»»;};
if (answ.charAt(13)==»1″) {document.getElementById(«torf14″).innerHTML=»»;} else {document.getElementById(«torf14″).innerHTML=»»;};
if (answ.charAt(14)==»1″) {document.getElementById(«torf15″).innerHTML=»»;} else {document.getElementById(«torf15″).innerHTML=»»;};
if (answ.charAt(15)==»1″) {document.getElementById(«torf16″).innerHTML=»»;} else {document.getElementById(«torf16″).innerHTML=»»;};
if (answ.charAt(16)==»1″) {document.getElementById(«torf17″).innerHTML=»»;} else {document.getElementById(«torf17″).innerHTML=»»;};
if (answ.charAt(17)==»1″) {document.getElementById(«torf18″).innerHTML=»»;} else {document.getElementById(«torf18″).innerHTML=»»;};
}
}
Получение сертификатао прохождении теста
ГДЗ по Математике 2 класс
ГДЗ по математике для 2 класса Моро – это сборник готовых домашних заданий по задачам и примерам из учебника по арифметике, составленного известными российскими авторами – М. И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Он используется в большинстве общеобразовательных школ России.
И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Он используется в большинстве общеобразовательных школ России.
Структура ГДЗ по учебнику математики второго класса от Моро
Во втором классе школьники знакомятся с базовыми понятиями арифметики, которые помогут им постигнуть алгебру и геометрию в старших классах, сформировать общее представление о предмете и науке. Они изучают числовой ряд от 1 до 100, порядок действий в сложных примерах, уравнения первого порядка с одной переменной. Они учатся рассчитывать периметр прямоугольника и проводить устные вычисления.
ГДЗ по математике 2 класса Моро, составленные на основе учебника 2015 года в его 6-м издании, включают в себя примеры и задачи на такие темы:
- числа от 1 до 100;
- проведение измерений, миллиметры и метры;
- денежная система исчислений: рубли и копейки;
- сложение и вычитание, скобки и порядок действий;
- измерение времени: часы и минуты;
- периметр многоугольника и длина ломаной линии;
- решение уравнений с одной переменной;
- угол и виды углов;
- прямоугольник и квадрат, их площадь и периметр;
- умножение, деление и их свойства.

Глубокое понимание представленных выше тем – гарантия успешного изучения алгебры и геометрии в старших классах. Ученики должны не просто списать примеры и задачки из решебника, но вникнуть в алгоритм решения.
Готовое домашнее задание для 2 класса на сайте ГДЗ Путина – замена репетиторов, помощь родителям, основа высокой успеваемости младших школьников.
Правильные решения от ГДЗ Путина по математике 2 класса к Моро
В интернете немало сайтов с готовыми домашними заданиями. В чем же преимущества портала ГДЗ от Путина для учеников младших классов и их родителей?
- наличие нескольких вариантов решения одной и той же задачи;
- ответы по самым свежим изданиям учебников российских школ;
- оформление готовых домашних заданий в соответствии с требованиями Министерства образования РФ;
- бесплатный доступ с любого устройства – смартфона, планшета, компьютера.
Эти критерии делают ГДЗ по математике 2 класса к учебнику Моро незаменимым помощником родителей. Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Ответы на задачки, примеры и уравнения в нескольких вариантах упростят постижение арифметики второклассниками – откроют им путь к постижению новых горизонтов в математике.
|
|
А | 9+9-1 | Р | 6+5+0 | Е | |
12-6+2 | Д | 16-10 +8 | О | 9+5-7 | Г | 11 | 17 | 8 | 12 |
Область задачи умножения слов 2-й класс
Добро пожаловать на нашу страницу задач на умножение слов для второго класса.
Здесь вы найдете нашу подборку печатных задач умножения. которые помогут вашему ребенку применять и практиковать свои навыки умножения и умножения для решения ряда «реальных» проблем.
Здесь вы найдете ряд рабочих листов для решения задач, связанных с умножением.
Каждый лист включает в себя решение ряда письменных задач на умножение.
Для каждого рабочего листа ниже есть 3 уровня сложности: A, B и C.
Рабочий лист A — самый простой уровень, подходящий для детей в начале их класса.
Рабочий лист B — это рабочий лист среднего уровня для детей, которые работают на ожидаемом уровне в своем классе.
Рабочий лист C задан на более сложном уровне, подходящем для более способных математиков.
Задачи на каждом листе похожи по формулировке, но их числа усложняются по мере того, как уровень становится сложнее.
Чтобы способствовать развитию навыков тщательной проверки и мышления, на каждом листе есть один «хитрый» вопрос, который не является проблемой умножения. Детям нужно определить эту словесную проблему и решить, какая операция им нужна для ее решения.
Использование этих листов поможет вашему ребенку:
- применять свои навыки умножения и умножения;
- применять свои знания таблицы умножения для выяснения связанных фактов;
- распознает проблемы умножения и пытается обнаружить проблемы с подвохом;
- решить ряд проблем «реальной жизни».
Некоторые листы имеют версию для Великобритании с набором орфографии для Великобритании.
В нашей области задач на умножение слов для 3-го класса вы найдете ряд задач на умножение слов, предназначенных для учеников 3-го класса.
Охватываются следующие области:
- основные информационные бюллетени по умножению;
- фактов умножения до 10х10;
- задач, для решения которых требуются письменные методы умножения (TU x U)
Взгляните на еще несколько наших рабочих листов, похожих на эти.
У нас есть ряд реальных проблем, связанных с различными измерениями, типа самых быстрых насекомых, или длины разных динозавров!
Есть целый ряд различных навыков, от округления и разложения до использования сложения, вычитания и умножения.
Здесь вы найдете подборку таблиц времени умножения. до 10×10 или 12×12, чтобы помочь вашему ребенку в изучении Факты умножения.
Существует широкий выбор таблиц умножения, в том числе цветные и черно-белые, диаграммы меньшего размера, диаграммы с заливкой и пустые диаграммы.
Использование этих таблиц поможет вашему ребенку:
- Узнайте их факты умножения на 10х10 или 12х12;
- Попрактикуйтесь в их таблице умножения.

Все бесплатные распечатываемые математические таблицы в этом разделе основаны на тестах Elementary Math Benchmarks.
Здесь вы найдете ряд бесплатных печатных игр на умножение.
Следующие игры развивают математические навыки умножения в увлекательной и мотивирующей форме.
Использование этих листов поможет вашему ребенку:
- узнать их факты умножения;
- попрактиковаться и улучшить отзыв своей таблицы умножения;
- развивают навыки стратегического мышления.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
|
МАТЕМАТИЧЕСКИЕ ТЕМЫ ДЛЯ ВТОРОГО КЛАССА / МАТЕМАТИЧЕСКИЕ ТЕМЫ 2-ГО КЛАССА
Поддержка семьи / сообщества 2 класс
2 nd Классы по математике
Квартал 1: авг.-Сент.
Считайте по единицам, двойкам и десяткам до 200.
Считайте и запишите числа до 200.
Показывайте числа в различных формах (используя модели, числовые предложения и т. Д.).
Сложить и вычесть до 20.
Решить задачи сложения и вычитания на реальных примерах.
Поймите, что «подростковые» числа состоят из десяти и нескольких единиц (разряды).
Определите и опишите четные и нечетные числа.
Родительские сайты:
Как заставить ребенка полюбить математику: статья с простыми и забавными советами http: // www.businessinsider.com/how-to-make-your-child-love-math-2013-5?op=1
Помощь вашему ребенку в изучении математики : Математика дома …. Математика в продуктовом магазине … http://www2.ed.gov/parents/academic/help/math/index.html
; • Бесплатные Math листы и Printables http://www.education.com/worksheets/math/?cid=55000.0130341&s_kwcid=TC|8363|math%20 для% 20children || S | б | 25173811495 & GCLID = Cj0KEQjw0POdBRCq3arGgYD05pMBEiQAmiUeTvnidI2 o_0x6Z857Gl0yQCpdI_pKjgK3V3K0JQnosrQaAsB88P8HAQ
Веб-сайты студентов:
Лопание воздушного шара: считайте по 5 и 10 секунд http: // www. sheppardsoftware.com/mathgames/earlymath/BalloonPopSkip.htm
sheppardsoftware.com/mathgames/earlymath/BalloonPopSkip.htm
Разместите блоки значений: подсчитайте и введите десятки и единицы http://www.softschools.com/math/place_value/games/tens_and_ones/
Дополнительная игра «Рыбалка» http://www.softschools.com/math/games/fishing_add.jsp
Блоки мышления: моделирование и решение проблем со словами http://www.mathplayground.com/tb_addition/thinking_blocks_addition_subtraction.html
Monkey Drive: четное и нечетное http: // www.sheppardsoftware.com/mathgames/monkeydrive/numbers/MDOddEven.htm
Математика — второй класс — 5012040
Общие примечания
Во 2-м классе учебное время должно быть сосредоточено на четырех важнейших областях: (1) расширение понимания системы десятичной системы обозначений; (2) развитие беглости с помощью сложения и вычитания; (3) использование стандартных единиц измерения; и (4) описание и анализ форм.
1. Учащиеся расширяют свое понимание десятичной системы. Сюда входят идеи счета пятью, десятками и числами, кратными сотням, десяткам и единицам, а также числовые отношения, включающие эти единицы, включая сравнение. Учащиеся понимают многозначные числа (до 1000), записанные в десятичной системе счисления, понимая, что цифры в каждом месте представляют собой количество тысяч, сотен, десятков или единиц (например, 853 — это 8 сотен + 5 десятков + 3 единицы) .
Учащиеся понимают многозначные числа (до 1000), записанные в десятичной системе счисления, понимая, что цифры в каждом месте представляют собой количество тысяч, сотен, десятков или единиц (например, 853 — это 8 сотен + 5 десятков + 3 единицы) .
2. Учащиеся используют свое понимание сложения, чтобы развить беглость при сложении и вычитании в пределах 100.Они решают задачи в пределах 1000, применяя свое понимание моделей сложения и вычитания, и они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые методы для вычисления сумм и разностей целых чисел в десятичной системе счисления, используя свое понимание места. стоимость и свойства операций. Они выбирают и точно применяют методы, соответствующие контексту и задействованным числам, чтобы мысленно вычислить суммы и разности для чисел, состоящих только из десятков или сотен.
3. Учащиеся осознают необходимость стандартных единиц измерения (сантиметр и дюйм), и они используют линейки и другие инструменты измерения, понимая, что линейное измерение включает в себя итерацию единиц. Они понимают, что чем меньше блок, тем больше итераций им нужно для покрытия заданной длины.
Они понимают, что чем меньше блок, тем больше итераций им нужно для покрытия заданной длины.
4. Учащиеся описывают и анализируют формы, исследуя их стороны и углы. Учащиеся исследуют, описывают и рассуждают о разложении и объединении форм для создания других фигур.Строя, рисуя и анализируя двух- и трехмерные формы, учащиеся развивают основу для понимания площади, объема, конгруэнтности, сходства и симметрии в более поздних классах.
Развитие английского языка Специальные примечания к стандартам ELD Раздел:
Учителя обязаны проводить обучение аудированию, устной речи, чтению и письму, которое позволяет изучающим английский язык (ELL) обмениваться информацией, идеями и концепциями для академического успеха в предметной области математики .Для заданного уровня владения английским языком и с визуальной, графической или интерактивной поддержкой учащиеся будут взаимодействовать со словами, выражениями, предложениями и речью на уровне своего класса для обработки или выработки языка, необходимого для академического успеха. Стандарт ELD должен указывать соответствующую концепцию области содержания или тему обучения, выбранную разработчиками учебных программ и учителями, которая максимизирует потребность ELL в коммуникативных и социальных навыках. Чтобы получить доступ к вспомогательному документу ELL, в котором описаны определения и дескрипторы производительности, щелкните следующую ссылку:
https: // cpalmsmediaprod.blob.core.windows.net/uploads/docs/standards/eld/ma.pdf
Руководство по внедрению стандартов Флориды Основной раздел:
Руководство по внедрению стандартов Mathematics Florida было создано для поддержки преподавания и изучения стандартов Mathematics Florida. Руководство разделено на три компонента: сфокусированность, согласованность и строгость. Концентрация означает сужение объема содержания в каждом классе или курсе, чтобы учащиеся достигли более высокого уровня понимания и более глубоко усвоили математические концепции.Стандарты математики позволяют преподавать и изучать математические концепции, сосредоточенные вокруг основных кластеров на каждом уровне обучения, усиленные за счет поддержки и дополнительных кластеров. Определяются основные, вспомогательные и дополнительные кластеры применительно к каждому классу или курсу. Обозначения кластеров для этого курса приведены ниже.
Основные кластеры
MAFS.2.OA.1 Представляйте и решайте задачи, связанные с сложением и вычитанием.
MAFS.2.OA.2 Сложить и вычесть в пределах 20.
MAFS.2.NBT.1 Понятие разряда.
MAFS.2.NBT.2 Используйте представление о числовых значениях и свойствах операций для сложения и вычитания.
MAFS.2.MD.1 Измерьте и оцените длину в стандартных единицах.
MAFS.2.MD.2 Связать сложение и вычитание с длиной.
Поддерживающие кластеры
MAFS.2.OA.3 Работайте с равными группами предметов, чтобы получить основу для умножения.
MAFS.2.MD.3 Работа со временем и деньгами.
MAFS.2.MD.4 Представление и интерпретация данных.
Дополнительные кластеры
MAFS.2.G.1 Разум с формами и их атрибутами.
Примечание. Кластеры не следует сортировать от основных к вспомогательным, а затем обучать в этом порядке. Это нарушит последовательность математических идей и упустит возможность улучшить основную работу класса с помощью вспомогательных и дополнительных кластеров.
самых неправильно понятых математических стандартов в 2-х классах
Когда меня попросили расширить серию «Самые непонятые стандарты» до классов K, 1 и 2, я ухватился за эту возможность.У меня дома четверо моих собственных мальчиков, которые часто говорят, что я никогда не упускаю возможности поговорить о математике и преподавании! Я также заядлый читатель и пользователь предыдущих публикаций из 3-8 классов этой серии, поэтому я был рад внести свой вклад в нее!
В моей роли тренера по математике и когда я путешествую по стране, работая с педагогами по согласованному обучению математике, я заметил некоторые общие темы в обучении в классе K-2, возникающие из-за неправильного понимания математических стандартов. Преподавание математики в начальных классах совсем не обязательно! Это сложная работа, которая требует обучения и пристального внимания к обучению, особенно когда учителя углубляются в развитие концептуального понимания основ математики учащимися в начальных классах.Я надеюсь, что этот пост поможет вам задуматься и научиться поддерживать своих молодых математиков!
Стандартный | Общая инструкция несовпадения |
| 2.OA.A.1 Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия, сложения, разделения и сравнения с неизвестными в целом позиции, например, используя рисунки и уравнения с символом неизвестного, чтобы представить проблему. | Инструкция ориентирована на определение ключевых слов для решения проблемы. Инструкция делает упор на приемах получения ответов, а не на поощрении математического мышления и осмысления. В инструкции не рассматриваются все 15 типов задач на сложение и вычитание или не учитываются типы задач, которые ученики должны освоить к концу второго класса. Мы хотим, чтобы студенты:
* Общие ситуации сложения и вычитания можно найти здесь . |
| 2.OA.C.4 Используйте сложение, чтобы найти общее количество объектов, упорядоченных в прямоугольные массивы до 5 строк и до 5 столбцов; напишите уравнение, чтобы выразить общую сумму как сумму равных слагаемых. | Инструкция выходит за рамки стандартов уровня класса и вводит умножение до 3 rd класса. |
| 2.NBT.A.4 Сравните два трехзначных числа на основе значений сотен, десятков и единиц, используя символы>, = и | Инструкция сфокусирована на процедуре, не опираясь на понимание значения места.
В инструкции упор делается на порядковые номера с использованием процедурных стратегий, а не на сравнении, основанном на более глубоком понимании трехзначных чисел. Instruction рассматривает это обучение как новый навык, а не намеренно основывается на обучении, полученном с первого класса, путем сравнения двузначных чисел. Мы хотим, чтобы студенты:
|
| 2.NBT.B.7 Сложение и вычитание в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на числовом значении, свойствах операций и / или взаимосвязи между сложением и вычитанием; связать стратегию с письменным методом.Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда необходимо составить или разложить десятки или сотни. | Инструкция фокусируется только на процедурных методах для стандартного алгоритма * без построения концептуального понимания. Инструкция ориентирована на выполнение шагов процедуры и не помогает учащимся понять, как складывать или вычитать подобные единицы или составлять и разлагать единицы десятков и сотен. Мы хотим, чтобы студенты:
* Язык «с использованием стандартного алгоритма» не включен в стандарты до 4 класса. |
| 2.MD.B.6 Представляйте целые числа как длины от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2,…, и представляйте суммы целых чисел и разности в пределах 100 на числовой линейной диаграмме. | Инструкция сосредоточена на процедуре или шагах в процессе, а не на понимании того, как сложение и вычитание длины могут быть представлены в числовой строке. Инструкция ориентирована на использование числовой линии в качестве стратегии для сложения и вычитания. Мы хотим, чтобы студенты:
|
Я хотел бы поближе познакомиться с двумя моими любимыми стандартами, оба из которых требуют согласованного обучения для построения концептуального понимания учащимися основных математических идей: 2.NBT.B.7 и 2.MD.B .6. Давайте копаться!
2.NBT.B.7
Сложить и вычесть в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием; связать стратегию с письменным методом.Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда необходимо составить или разложить десятки или сотни.
Сколько себя помню как учителя начальных классов и тренера по математике, стандартный алгоритм сложения и вычитания был проблематичным. Учащиеся могут изучить это как процедуру, без понимания, у учителей или родителей, которые действуют из лучших побуждений. Даже меня так учили в детстве! Теперь мы знаем, насколько важно для студентов понять «почему», стоящее за процедурой.Это лучше подготовит их к будущей математике и углубит их понимание разряда и операций сложения и вычитания, которые позже будут применены для более успешного понимания операций с дробями, десятичных знаков и работы алгебры.
Когда я вижу задачу типа 600 — 432, я знаю, что есть много разных способов поддержать учащихся в решении этого выражения. Студенты, скорее всего, разложат одну из 6 сотен на 10 десятков, а затем разложат десять на 10 единиц.После того, как 600 написано, нарисовано или представлено конкретными объектами, такими как базовые десять блоков или дисками с цифрами 5 сотен, 9 десятков и 10 единиц, студенты могут вычитать. Это нормально показать эту работу, используя письменный метод, который напоминает стандартный алгоритм, если между различными представлениями (моделями или чертежами) и письменным методом установлены явные связи. См. Пример ниже.
Другой способ решения 600–432 для учащихся может заключаться в использовании сложения, суммируя от 432, тем самым подчеркивая связь между сложением и вычитанием.
Важным следствием для обучения при работе в 2.NBT.B.7 является не переходить к процедурному обучению до того, как учащиеся разберутся с системой разностных значений при сложении и вычитании в пределах 1000. Дайте учащимся возможность разработать свои собственные методы решения, помогите им установить связи между представлениями и методами и продвигаться к эффективности с помощью процедуры после того, как концептуальное понимание будет развито.
2.MD.B.6
Представляйте целые числа как длины от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2,…, и представляйте целые числа и разности в пределах 100 на числовой линейной диаграмме.
Я помню, как в начале моей педагогической карьеры, 20 лет назад (я встречаюсь здесь!), И много лет спустя я учил числовую линию как стратегию или метод для моих учеников начальной школы, чтобы складывать и вычитать. Была задействована милая лягушка и много разговоров о «прыжках» по числовой прямой. Студенты «использовали» эту стратегию и большую часть времени приходили к правильному ответу, но понятия не имели, что они делают. Они определенно не связывали числовую линию с единицами длины и не считали эти единицы.Я мог бы все еще делать это сегодня, если бы я не учился у некоторых замечательных основных защитников и лидеров учителей!
В стандартах есть три места, где числовая линия обозначена специально: здесь, во 2 классе, в классе 3, относящемся к дробям как числам, и снова в классе 6, когда учащиеся углубляются в рациональные числа. Умышленно, что числовая линия не используется до 2-го класса. Также намеренно она вводится со счетом «длина». Важно отметить, что заголовок кластера 2.MD.B.6 — это Связать сложение и вычитание с длиной.
Числовые линейные диаграммы могут быть непростыми для учащихся, поскольку в них используются единицы длины, которые труднее увидеть и сосчитать, чем конкретные объекты или изображения. Числовые линейные диаграммы вводятся во 2 классе, когда учащиеся имеют опыт подсчета единиц длины на измерительных инструментах, которые, по сути, являются специальными числовыми линейными диаграммами. Важно помочь учащимся «увидеть» единицы длины, которые подсчитываются между конечными точками, а также числа, обозначающие конечные точки длины от 0.
Давайте посмотрим на это задание из учебной программы Engage NY:
Вы увидите, что ученики используют числовую линию для обозначения длины в сантиметрах. Они добавляют «больше» к заданному числу, а затем пишут уравнение, которое соответствует. Эта задача иллюстрирует сложность и цель 2.MD.B.6 без акцента на процедурах или ответе.
Я надеюсь, что это помогло вам изучить и осмыслить мощные, согласованные инструкции по математике.
Краткая запись задачи и её схематический чертёж
- Охо-хо-хо-хо… И куда этот Плюс подевался? Я один с этим заданием не справлюсь. Ну, царица! Каждый раз какое-нибудь новенькое задание подкинет.
- Добрый день, Минус! Прости, я задержался — на природу загляделся. Уж такой сегодня день красивый! Я набрал целую охапку листьев — здесь листья клёна и каштана.
- А что ты с ними делать собираешься?
- Как что — составлю осенний букет. А еще, они помогут нам разобраться в том задании, которое дала нам царица-Математика — научиться выполнять краткую запись задачи и её схематический чертёж.
- Давай скорее начнём, а то ты и так опоздал.
- Ну что же, приступим. Вот смотри — у меня несколько листьев клёна. 5 из них я поставлю в вазу и осталось ещё 4 листа.
- Да-да, я знаю. Если задать вопрос, то получится вот такая задача:
Плюс собрал несколько листьев клёна. 5 из них он поставил в вазу. После этого осталось ещё 4 листа. Сколько всего листьев собрал Плюс?
Ну, и что дальше?
- А дальше составляем краткую запись.
- И как мы это сделаем?
- Выбираем главные, опорные слова. Что происходило в задаче?
- Сначала ты собрал листья, а потом 5 из них поставил в вазу. И у тебя остались 4 листа.
- Вот именно — собрал, поставил, осталось. Вот они, опорные слова. Запишем их:
- Да, но, сколько собрал, в задаче неизвестно. В ней сказано, что собрал несколько листьев.
- Ну, раз неизвестно, мы поставили вопросительный знак. Ведь именно это и надо узнать в задаче. Её вопрос звучит так: «Сколько всего листьев собрал Плюс?» А, чтобы не писать полностью слово листьев, мы поставим только первую букву л. Ведь, если вместо слова ставится одна или, допустим, две буквы, то говорят, что слово сократили, и подсказывает нам это маленькая точка.
Ну, вот. У нас получилась краткая запись задачи. Глядя на неё мы можем вспомнить всё условие задачи.
- Но ведь нам еще надо сделать и схематический чертёж!
- Ну что же. В этом нам помогут отрезки. Мы ведь их уже отлично рисовать научились. Итак, вот первый отрезок.
Он показывает, сколько листьев я поставил в вазу. Второй отрезок мы начнем рисовать от той точки, которая является концом первого отрезка.
Этот отрезок показывает, сколько листьев у меня осталось. То есть, нам известна та часть листьев, которую я поставил в вазу и та часть листьев, которая осталась. А вот, если объединить все листья вместе, то получится уже не часть, а все листья, то есть целое.
Когда мы объединяем, то есть собираем что-то вместе, находим целое, то, конечно, используем действие сложения. И без меня, Плюса, здесь не обойтись!
Записываю ответ задачи: Плюс собрал 9 листьев клёна.
- Так, отлично, с этой задачей мы справились. Но ведь есть и ещё одна задача.
- Что еще за задача?
- А вот она: На лесной поляне росло 7 мухоморов. Несколько мухоморов съел лось. После этого на поляне осталось 2 мухомора. Сколько мухоморов съел лось?
Теперь моя очередь составлять краткое условие и схематический чертёж. Итак, выделяю числа и опорные слова. Что в задаче происходило? Росло 7 мухоморов. Несколько мухоморов съел лось. Раз несколько, значит, мы не знаем сколько. Дальше написано, что осталось 2 мухомора.
Ну вот, с кратким условием я справился. Так ведь, Плюсик?
- Да, молодец!
- Теперь надо выполнить схематический чертёж.
Росло 7 мухоморов. Рисуем отрезок:
Лось съел, это неизвестно. Пока рисовать не буду, осталось 2 мухомора. Как мне их нарисовать? Откуда начинать? С конца первого отрезка?
Не-е-ет. Ведь семь — это все мухоморы, то есть целое, а два — это часть этих семи. Поэтому откладываем отрезок, обозначающий эти два мухомора от начала первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот отрезок, который является второй частью целого отрезка и будет съеденными мухоморами.
Как известно, часть чего-то целого находим действием вычитания. Так что, теперь моя очередь встать в действие:
Ответ: 5 мухоморов съел лось.
- Это у тебя отлично получилось, Минус. Лихо ты справился с такой трудной задачей.
- И ничего трудного тут нет. Чтобы решить любую задачу, надо сначала представить себе все, что в ней происходит. Затем составить краткое условие, выделив опорные слова, которые нам подскажут, что именно происходит в задаче. А потом нарисовать схематический чертёж. Только надо очень внимательно разобраться, что в задаче целое, а что части.
- Если мы находим наибольшее число, то есть целое, из известных частей, то отрезки рисуем так: сначала первый отрезок, затем второй. При этом, конец первого отрезка одновременно является началом второго отрезка. И такую задачу решаем действием сложения. То есть используем знак плюс.
- А если в задаче надо узнать часть чего либо, то сначала рисуем отрезок, обозначающий самое большое число, то есть целое. Затем от начала первого отрезка рисуем второй отрезок, обозначающий меньшее известное число. Мы как бы разрезаем больший отрезок на части, одна из которых известна, а вторую нужно узнать. И, конечно, если надо узнать часть, то задачу решаем действием вычитания. То есть используем знак минус.
- Ну что, пойдем к царице сдавать задание?
- Ну да! Побежали! Урра!
Советы учителя — Требования к оформлению письменных работ по математике в начальной школе, учитель начальных классов в Москве
Все записи в тетрадях следует оформлять аккуратным каллиграфическим почерком.В 1 классе в период обучения грамоте запись даты ведется учителем или учащимися по центру рабочей строки в виде числа и первых букв названия месяца (1 с.). По окончании периода обучения грамоте дата записывается полностью (1 марта.). Со 2 класса допускается запись даты выполнения работы на полях, с указанием числа и месяца (01.09.).
Запись названия работы производится на следующей рабочей строке по центру с пропуском 1 клетки от числа и оформляется как предложение (Классная работа. Домашняя работа. Самостоятельная работа. Работа над ошибками.).Во всех остальных случаях рекомендуется пропускать 2 клетки. При необходимости вариативность работы фиксируется на следующей строке по центру (Вариант I.).
После выполнения работы (классной или домашней) следует отступать 4 клетки, начиная выполнять очередную работу на пятой клетке. В ходе выполнения работы не допускается необоснованный пропуск строк или наличие пустых мест на строке. Использование правил переноса, принятых в математике, обязательно.
При выполнении работы на странице требуется соблюдать внешние и внутренние поля. Между столбиками выражений, уравнений, неравенств и другими видами заданий отступаются три клетки вправо. Запись нового столбика начинается с четвертой клетки.
При оформлении письменных заданий по математике рекомендуется указывать его номер (No 5) без уточнения вида (Задача, Неравенства, Выражения) Краткая запись условия задачи оформляется в соответствии с их видом (краткая запись, схема, чертеж, таблица, диаграмма, рисунок). Ключевые слова в краткой записи пишутся с большой буквы.
В 1 классе допускается их сокращение по первым буквам: М. – 7 м. Б. – 3 м.
Начиная с 2 класса по усмотрению учителя ключевые слова в краткой записи могут быть зафиксированы полностью: Маленькие – 7 м. Большие – 3 м.
При записи решения задачи по действиям с письменными пояснениями (с записью вопроса) или выражением после каждого действия ставится наименование в круглых скобках с использованием правил сокращения слов. Слово «Ответ» пишется под решением с заглавной буквы с отступлением 1 клетки вниз.
В первом классе ответ задачи может быть записан в краткой форме (От. 10 ябл.).
Со 2 класса слово «Ответ» записывается полностью (Ответ: 10 яблок.).
Оформление условия задачи при помощи схемы, чертежа, таблицы, диаграммы или рисунка осуществляется с использованием линейки и простого карандаша. Краткую запись не следует делать громоздкой, она должна быть удобной, отображать все числовые данные задачи и взаимоотношения между величинами.
При оформлении записи задач геометрического характера необходимо соблюдение следующих норм:- чертежи выполнять простым карандашом по линейке;
- геометрическую фигуру чертить в тех случаях, когда этого требует условие задачи;
- результаты измерений подписывать ручкой;
- обозначения выполнять прописными буквами латинского алфавита.
При оформлении математического диктанта следует записывать только ответы в строчку, отступая одну клетку.
Презентация » Решение задач. Путешествие в космос» 2 класс
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
Номер слайда 3
Учитель начальных классов Хромова Светлана Николаевна Урок математики во 2 классе по УМК «Перспектива»
Номер слайда 4
В 1960 году Юрий Гагарин начал готовиться к полету в космос. Работал упорно, с полной отдачей сил.
Номер слайда 5
. Чтоб сегодня наш урок, Всем пошёл ребятам впрок, Постарайтесь всё понять, Слушать, думать и вникать!
Номер слайда 6
БОРТОВОЙ ЖУРНАЛ Маршрутный лист 12 22 32 ……
Номер слайда 7
12 апреля 1961 года на старте прозвучало его знаменитое «Поехали»!
Номер слайда 8
КЛЮЧЕВОЕ СЛОВО УРОКА 29 — 19 = 4 + 3х6 = (80-70)+6= 26 + 14 = 40 – 35 = 90 : 10 =
Номер слайда 9
КЛЮЧЕВОЕ СЛОВО УРОКА 40-а 22-ч 16-а 10-д 9-а 5-з
Номер слайда 10
КЛЮЧЕВОЕ СЛОВО УРОКА ЗАДАЧА
Номер слайда 11
Номер слайда 12
Номер слайда 13
КЛАСТЕР ЗАДАЧА условие вопрос решение ответ
Номер слайда 14
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 15
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 16
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 17
И так! Внимание ! Взлёт! Наша ракета помчалась вперёд! Прощально мигнут и растают вдали Огни золотые любимой Земли!
Номер слайда 18
Номер слайда 19
Номер слайда 20
Номер слайда 21
. М.кратер- 15 ч. Б.кратер-? ч. на 65 > } ?Ч..
Номер слайда 22
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» Маленький кратер возьмёт в себя 15 человек. А большой кратер на 65 человек больше. Сколько человек возьмут в себя оба кратера?
Номер слайда 23
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» 15+65=80(ч.)-возьмёт большой кратер. 2) 15+80=95(ч.) Ответ: 95 человек возьмут оба кратера.
Номер слайда 24
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 25
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 26
К космическому полёту долго и упорно готовились 12 космонавтов. Они работали над собой, не покладая сил. Наконец, настал торжественный день отбора самых достойных космонавтов. Когда все построились, то выбрали самых сильных, ловких и умелых. А на Земле осталось 7 космонавтов. Сколько космонавтов были удостоены чести полететь в космос ?
Номер слайда 27
К полёту готовились 12 космонавтов. Когда несколько космонавтов полетели , то на Земле осталось 7 . Сколько полетело в космос ?
Номер слайда 28
1) Осталось – 7 косм. Полетело — ? косм. 2) 12 косм. 3) ? косм. 7 ? 12
Номер слайда 29
Решение: 12 –7= 5(косм.) Ответ: 5 космонавтов полетело в космос.
Номер слайда 30
Космонавт взял в космос 18 тюбиков картофельного пюре и 12 тюбиков мясного пюре. Съел он 20 тюбиков с космической пищей. Сколько тюбиков осталось?
Номер слайда 31
1) 18 – 12 + 20 = 2) 20 – ( 18 – 12) = 3) 18 + 12 – 20 =
Номер слайда 32
18 + 12 – 20 = 20 (тюб.) Ответ: 20 тюбиков осталось
Номер слайда 33
1) У Димы 27 марок на тему «Космос», а у Серёжи 10. Сколько марок у Димы? 2) Собаки Белка и Стрелка пробыли в космосе одни сутки. А собаки Ветерок и Уголёк 23 дня. Кто был в космосе больше и на сколько?
Номер слайда 34
108 минут длился первый полет в космос Космический корабль « ВОСТОК»
Номер слайда 35
1 вариант: стр.62 №3,6 2 вариант :стр.64 №3,4
Номер слайда 36
РЕФЛЕКСИЯ Из полета возвратились Мы на землю приземлились. Как слетал ты? Расскажи! И звезду всем покажи!
Номер слайда 37
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 38
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 39
МОЛОДЦЫ!
Дизайн задач в математическом образовании
‘) вар корзинаStepActive = истина var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].slice.call(buybox.querySelectorAll(«.вариант-покупки»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) { var toggle = подписка.querySelector(«.Цена-варианта-покупки») подписка.classList.remove(«расширенный») var form = подписка.querySelector(«.форма-варианта-покупки») если (форма && cartStepActive) { вар formAction = form.getAttribute(«действие») form.setAttribute(«действие», formAction.replace(«/checkout», «/cart»)) document.querySelector(«#ecommerce-scripts»).addEventListener(«load», bindModal(form, formAction, timestamp, index), false) } var priceInfo = подписка.querySelector(«.Информация о цене») var PurchaseOption = toggle.parentElement если (переключить && форма && priceInfo) { toggle.setAttribute(«роль», «кнопка») toggle.setAttribute(«tabindex», «0») переключать.addEventListener(«щелчок», функция (событие) { var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный toggle.setAttribute(«aria-expanded», !expanded) form.hidden = расширенный если (! расширено) { покупкаOption.classList.add(«расширенный») } еще { покупкаOption.classList.удалить («расширить») } priceInfo.hidden = расширенный }, ложный) } } функция bindModal (форма, formAction, метка времени, индекс) { var weHasBrowserSupport = window.fetch && Array.from функция возврата () { var Buybox = EcommScripts ? EcommScripts.Buybox : ноль var Modal = EcommScripts ? EcommScripts.Модальный: ноль if (weHasBrowserSupport && Buybox && Modal) { var modalID = «ecomm-modal_» + метка времени + «_» + индекс var modal = новый модальный (modalID) modal.domEl.addEventListener («закрыть», закрыть) функция закрыть () { form.querySelector («кнопка [тип = отправить]»).фокус() } форма.setAttribute( «действие», formAction.replace(«/checkout», «/cart?messageOnly=1») ) form.addEventListener( «Отправить», Buybox.interceptFormSubmit( Буйбокс.fetchFormAction(окно.fetch), Buybox.triggerModalAfterAddToCartSuccess(модальный), консоль.лог, ), ложный ) document.body.appendChild(modal.domEl) } } } функция initKeyControls() { документ.addEventListener(«keydown», функция (событие) { if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) { если (document.activeElement) { событие.preventDefault() документ.activeElement.click() } } }, ложный) } функция InitialStateOpen() { var buyboxWidth = buybox.смещениеШирина ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = option.querySelector(«.цена-варианта-покупки») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option.querySelector(«.Информация о цене») если (buyboxWidth > 480) { переключить.щелчок() } еще { если (индекс === 0) { переключать.щелчок() } еще { toggle.setAttribute («ария-расширенная», «ложь») form.hidden = «скрытый» priceInfo.hidden = «скрытый» } } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() })()Иллюстративная математика
Задача
Студенты в Mr.Художественный класс Риверы проектирует витраж, чтобы повесить его на входе в школу. Окно будет 2 фута в высоту и 5 футов в ширину. Они нарисовали дизайн ниже:
Они собрали 100 долларов на материалы для проекта. Цветное стекло стоит 5 долларов за квадратный фут, а прозрачное стекло — 3 доллара за квадратный фут. Материалы, необходимые для соединения кусков стекла вместе, стоят 10 центов за фут, а рама стоит 4 доллара за фут.
Достаточно ли у них денег, чтобы покрыть расходы на материалы, которые потребуются для изготовления окна?
Комментарий IM
Целью этого задания является нахождение учащимися площади и периметра геометрических фигур, границами которых являются сегменты и части окружностей, и объединение этой информации для расчета стоимости проекта.Форма областей в витраже намеренно оставлена неуказанной, поскольку один из компонентов навыка моделирования с помощью математики (MP4) заключается в том, чтобы учащиеся сами делали упрощающие предположения. Учитывая точность, необходимую для этих оценок, предположение о том, что кривые в схеме являются дугами окружности, не только разумно, но и наиболее целесообразно. Важно то, что учащиеся осознают, что они делают это предположение, и прямо говорят об этом.
Вопрос о том, должны ли студенты платить за осколки стекла, оставшиеся после вырезания фигур, можно решить по-разному.На самом деле, если бы им пришлось покупать стекло в магазине, стекло, скорее всего, было бы в виде квадратных или прямоугольных листов, и им пришлось бы покупать больше, чем они собирались использовать. Но сколько именно дополнительного материала им придется купить, зависит от того, как продается сырье, поэтому без дополнительной информации было бы трудно определить это, не проведя некоторых исследований того, как продаются витражи. В качестве альтернативы, учитель рисования может уже иметь материалы и просто хочет, чтобы его ученики оставались в рамках определенного бюджета на материалы, которые они используют, зная, что записки могут быть использованы для будущих студенческих проектов.В любом случае это задание может послужить трамплином для хорошего обсуждения в классе вопросов, о которых учащиеся должны подумать при моделировании с помощью математики.
Решение
Есть много способов сделать это. Вот один:
Предположим, что студенты должны платить только за стекло, которое они используют, а не за обрезки. Это означает, что нам нужно вычислить площадь цветного стекла и площадь прозрачного стекла, а также общую длину швов между стеклянными панелями.
Сначала нам нужно найти площадь прозрачного стекла и площадь цветного стекла.
Весь прямоугольник имеет размеры 2 на 5 футов. Предполагая, что все кривые являются частями круга диаметром 1 фут, имеется пять прямоугольников размером 1 на 2 фута либо с 4 полукружиями, либо с 2 полукружиями и 4 четвертями круга из прозрачного стекла. Это означает, что в каждом прямоугольнике размером 1 на 2 фута есть 2 полных круга из прозрачного стекла. Таким образом, имеется 10 полных кругов из прозрачного стекла, каждый диаметром 1 фут (или радиусом $\frac12$ фута).2= \frac52\pi$$
или приблизительно 7,9 квадратных футов. Это означает, что площадь цветного стекла составляет примерно 10 — 7,9 = 2,1 квадратных фута.
Теперь нам нужно найти общую длину «швов» между кусочками стекла.
Опять 10 кругов. Их общая окружность равна
.$$10\раз\пи\раз1$$
, что составляет около 31,4 фута. Есть также четыре 2-футовых прямых «шва». Таким образом, всего получается около 39,4 фута «швов».
Рама 2+2+5+5 = 14 футов.
Стоимость прозрачного стекла: 7,9$ х 3 = 23,70$ долларов.
Стоимость цветного стекла 2,1$ \х5 = 10,50$ долларов.
Стоимость материалов для швов 39,4$\умножить на 0,10 = 3,94$ долларов.
Стоимость рамки $14\times4=56$ долларов.
Общая стоимость материалов $23.70+10.50+3.94+56\около 94$ долларов. Так что, если эти предположения верны, у них достаточно денег, чтобы купить материалы. Если им нужно платить за обрезки или если они ломают куски по ходу дела, у них не так много места для маневра.
(PDF) Разработка математических задач: роль инструментов
223
Chevallar, Y. (1994). Ostensifs и non-otensifs в математической деятельности. Intervention au
Séminaire de l’Associazione Mathesis (Турин, 3 февраля 1994 г.). Actes du Séminaire pour l’année
1993–1994 (стр. 190–200).
Кларк-Уилсон, А., и Тимотеус, Дж. (2013). Проектирование задач в мультирепрезентативной технологической
логической среде: новая рубрика.В К. Марголинас (ред.), Дизайн задач по математике
образование: Труды ICMI Study 22 (стр. 45–52), Оксфорд, Великобритания. Доступно по телефону
http://hal.
archives-ouvertes.fr/hal-00834054
Confrey, J., Hoyles, C., Jones, D., Kahn, K., Maloney, A., Nguyen, K., et al. (2010). Разработка программного обеспечения
для математического взаимодействия посредством моделирования. В C. Hoyles & J.-B. Лагранж
(ред.), Математическое образование и технологии: переосмысление местности – 17-е исследование ICMI
(стр.19–46). Нью-Йорк: Спрингер.
ДиСесса, А., Хаммер, Д., и Шерин, Б. (1991). Изобретая графику: метарепрезентативная экспертиза у детей. Журнал математического поведения, 10, 117–160.
Драйверс, П., Бун, П., Швейцар, М., Бохове, К., и Такома, С. (2013). Цифровой дизайн: RME
принципы проектирования онлайн-задач. В C. Margolinas (Ed.), Дизайн задач в математическом образовании,
, Proceedings of ICMI Study 22 (pp.53–60), Оксфорд, Великобритания. Доступно по телефону
http://hal.
archives-ouvertes.fr/hal-00834054
Энгестрём, Ю. (1987). Обучение путем расширения: теоретико-деятельностный подход к исследованиям в области развития
. Доступно в Интернете по адресу
http://lchc.ucsd.edu/MCA/Paper/Engestrom/expanding/toc.htm.
По состоянию на 18 августа 2014 г.
Фоконье Г. и Тернер М. (1998). Концептуальные интеграционные сети. Когнитивная наука, 22 (2),
133–187.
Фоконье Г. и Тернер М. (2002). То, как мы думаем: концептуальное смешение и скрытые сложности
ума. Нью-Йорк: Основные книги.
Фройденталь, Х. (1973). Математика как учебная задача. Дордрехт: Издательство Рейдель.
Фройденталь, Х. (1991). Возвращаясь к математическому образованию. Дордрехт: Kluwer Academic.
Гейгер, В., и Редмонд, Т. (2013). Разработка задач по математическому моделированию в технологическом контексте
средней школы.В C. Margolinas (Ed.), Дизайн задач в математическом образовании:
Proceedings of ICMI Study 22 (стр. 119–128), Оксфорд, Великобритания. Доступно по адресу
http://hal.archives-
ouvertes.fr/hal-00834054
Геуде Г. и Труш Л. (2009). К новым системам документации для учителей математики.
Образовательные исследования по математике, 71 (3), 199–218.
Хили, Л. (2000). Выявление и объяснение геометрических взаимосвязей: Взаимодействие с прочными и
мягкими конструкциями Cabri.В Т. Накахара и М. Кояма (ред.), Материалы 24-й конференции
Международной группы психологии математического образования (том 1,
, стр. 103–117). Хиросима, Япония: PME.
Хили, Л., Фернандес, С.Х.А.А., и Болит-Франт, Дж. Б. (2013). Разработка заданий для более инклюзивной школы. В К. Марголинас (ред.), Дизайн задач в математическом образовании: Труды
ICMI Study 22 (стр. 61–68), Оксфорд, Великобритания.Доступно по адресу
http://hal.archives-ouvertes.fr/
hal-00834054
Joubert, M. (2013). Использование компьютеров на уроках математики: Повторение теории к
разработка рекомендаций по оформлению задач. В C. Margolinas (Ed.), Дизайн задач в математическом образовании
: Proceedings of ICMI Study 22 (стр. 69–78), Оксфорд, Великобритания. Доступно по телефону
http://hal.archives-ouvertes.fr/hal-00834054
Kaput, J.(1986). Информационные технологии и математика: открытие новых представительских окон
окон. Журнал математического поведения, 5 (2), 187–207.
Киран, К., Драйверс, П., Буало, А., Хитт, Ф., Тангуай, Д., Салданья, Л., и другие. (2006). Со-
появление машинных методов, методов бумаги и карандаша и теоретических размышлений:
Изучение использования CAS в алгебре средней школы. Международный журнал компьютеров для
Mathematical Learning, 11, 205–263.
Кинигос, К., и Лагранж, Ж.-Б. (2014). Перекрестный анализ как инструмент установления связей между теоретическими
ретикальными фреймами при использовании цифровых технологий в математическом обучении. Образовательные исследования по
Математика, 85, 321–327.
6 Разработка математических задач: роль инструментов
Последние исследовательские публикации – математика
Преподаватели математического факультета очень активно публикуют свои оригинальные исследования в научных журналах, книгах и материалах конференций.Ниже приведены некоторые примеры цитат из последних публикаций отдела (с 2017 года). Это не исчерпывающий список. Пожалуйста, посетите страницу профиля преподавателя для получения более подробного списка их публикаций и доступа к их биографическим данным.
- Бал Д. , П. Беннетт, С. Инглиш, К. Макрури, П. Пралат. 2021. Обращение к нулю в случайных регулярных графах. Журнал комбинаторики, том 12 (1), стр. 85–116.
- Бал Д. , Дж. Де Гаэтани .2021. Заметка об игре с обменом конфет. Искусство дискретной и прикладной математики, том 4.
- Сатьям В.Р., А. Симпсон, Дж. ДиНаполи , X. Яо. 2021. Создание робота: сделать математику видимой в неформальной среде обучения STEM. PME-NA 42 Материалы.
- ДиНаполи Дж. , Э. Мюррей , Д. О’Рорк, Дж. Рассел. 2021. Анализ обучения учителей в практикующем сообществе, основанный на видеослучаях преподавания математики. Сообщество для продвижения научных исследований в сфере образования. Веб-семинар.
- Динаполи Дж. , Н. Делсон, Л. Ван Ден Эйнде, Л. Коуэн. 2021. Внедрение иерархии обратной связи для поддержки математической настойчивости в приложении для создания цифровых эскизов. Материалы INTED2021.
- Леонард Х. , В.Д. Бонаккорсо , Дж. ДиНаполи , Э. Мюррей . 2021. Методологические достижения для анализа обучения учителей в практическом сообществе. Труды Американской ассоциации исследований в области образования за 2021 год.
- ДиНаполи Дж. , М. Аменя , Л.В. Д. Эйнде, Н. Делсон, Э. Коуэн. 2021. Моделирование удаленной поддержки математической настойчивости с помощью приложения для создания цифровых эскизов. Журнал теории и практики высшего образования.
- Гринштейн С. , Д. Жаннотт, Э. Фернандес , Дж. Дэвидсон , Э. Помпонио , Д. Акуом . 2021. Изучение переплетенных дискурсов, связанных с обучением преподаванию математики в контексте создания. PME-NA 42 Материалы.
- Мохамед М.М. , Т. Паолетти , М. Вишнубхотла , С. Гринштейн , С.С. Лим . 2021. Поддержка значения студентов для квадратичных вычислений: интеграция RME, количественных рассуждений и проектирования для абстракции. PME-NA 42 Материалы.
- Помпонио Э. , С. Гринштейн , Д. Акуом . 2021. Гармония и диссонанс: энактивистский анализ борьбы за осмысление решения проблем. ПМЕНА 2021.
- Акуом Д.О. , С. Гринштейн . 2021. Манипуляторы, разработанные потенциальными учителями математики в качестве якорей для своих педагогических и концептуальных знаний. ПМЕНА 2021.
- Мунаката М. , А. Вайдья , К. Монахан , Э. Крупа . 2021. Содействие творчеству в общеобразовательных курсах математики. ПРИМУС, Том 31.
- Голнаби А.Х. , Э. Мюррей , Х. Су . 2021.Как координация курса Precalculus может повлиять на академическую успеваемость студентов. Журнал теории и практики высшего образования, том 21 (5).
- Чиоффи Д., С.О. Нита, В.Н. Нита, Б.Г. Нита . 2021. Математика и музыка: нахождение и характеристика одинаково темперированных гамм с использованием приближений непрерывных дробей. Парабола, Том 57 (2).
- Басу Д. , Н. Паноркоу . 2021. Использование математики для изучения повышения уровня моря как экологической и социальной проблемы.PME-NA 42 Материалы.
- Паноркоу Н. , Т. Йорк . 2021. Разработка интегрированного опыта Stem+C. PME-NA 42 Материалы.
- Паноркоу Н. , Э. Гермия . 2021. Изучение рассуждений учащихся о нескольких величинах. PME-NA 42 Материалы.
- Панорков Н. . 2021. Изучение рассуждений студентов о динамических измерениях правильных призм и цилиндров. Познание и обучение.
- О’Мира Дж., А.Вайдья . 2021. Теоретико-сетевой подход к разработке учебных программ. Энтропия, том 23 (10), стр. 1346.
- Вайдья А. . 2021. Связывание энтропии: общая семантика защиты окружающей среды. ETC: Обзор общей семантики, том 77 (3-4).
- Фицджеральд К., М. Массуди, А. Вайдья . 2021. Об модифицированном принципе наименьшего действия с рассеянием. Европейский журнал механики B (жидкости), том 89, стр. 301-311.
- Вайдья А. . 2021. Вклад в преподавание и изучение механики жидкости.Жидкости, том 6 (8), стр. 296.
- Бал Д. , Э. Шудрих . 2020. О размере числа Рамсея всех циклов в зависимости от пути. arXiv Математика.
- Анастос М., Д. Бал . 2020. Свойство Рамсея случайных регулярных и k-out графов. Журнал теории графов, том 93 (3), стр. 363–371.
- Бал Д. , П. Беннетт. 2020. Двудольный процесс без K₂,₂ и двудольное число Рамсея b(2,t). Электронный журнал комбинаторики, том 27 (4).
- Бал Д. , Р. Берковиц, П. Девлин, М. Шахт. 2020. Гамильтоновы циклы Бержа в случайных гиперграфах. Комбинаторика, вероятность и вычисления, том 30 (2).
- Чанг Б.Дж. , А. Вайдья . 2020. Самоорганизация в физических и биологических системах: комментарий к «Морфогенезу как байесовский вывод: вариационный подход к формированию паттернов и контролю в сложных биологических системах» Франца Кучлинга и др.. Обзоры физики жизни, том 33, стр.115-118.
- Катлер Дж. , Н. Касс. 2020. Гомоморфизмы в петле-пороговые графы. Электронный журнал комбинаторики, том 27 (2).
- Suppa S., J. DiNapoli , E. Thanheiser, J. Tobias, Y. Sheunghyun. 2020. Поддержка начинающих учителей математики, впервые преподающих курсы по элементарной математике. Энтузиаст математики, том 17 (3), стр. 493–536.
- ДиНаполи Дж. , Э. Миллер. 2020. Признание и поддержка настойчивости в решении математических задач с помощью каркасов концептуального мышления.Международное общество обучающих наук.
- Марзокки А.С., Дж. Динаполи . 2020. Внедрение педагогики в курсы по математике для будущих учителей начальной школы. IUMPST: Журнал. Том 2 (Педагогика).
- Динаполи Дж. , М. Амениа , Л. Ван Ден Эйнде, Н. Делсон, Э. Коуэн. 2020. Дистанционная поддержка математической настойчивости с помощью приложения для создания цифровых эскизов. Международная конференция по образованию, исследованиям и инновациям.
- Динаполи Дж. , Х. Моралес. 2020. Перевод на упорный: поддержка и признание процесса осмысления для латиноамериканских двуязычных студентов-математиков. Преподавание передового опыта и справедливости в математике, том 11 (2), стр. 26-34.
- Голнаби А.Х. , Э. Мюррей , Х. Су . 2020. Влияние координации курса и поддержки инструктора по предварительному исчислению на неполный рабочий день на успеваемость студентов. Конгресс Политехнического университета Валенсии, Шестая международная конференция по достижениям в области высшего образования.
- Чжан Д., А. Индик, С. Гринштейн . 2020. Влияние разбиения схем на повышение успеваемости по геометрии у учащихся с математическими трудностями и учащихся, которым грозит математическая неудача. Ежеквартальный отчет по неспособности к обучению.
- Ли А , Р. Миллер , Р. П. Туччи . 2020. Заметка об уникальности графов с делителями нуля и петлями (исследование). Успехи математических наук. Ассоциация женщин-математиков, том 21, стр. 173–179.
- Монахан К. , М. Мунаката , А. Вайдья . 2020. Участие в вероятностном мышлении через игру. Учитель математики: Обучение и преподавание ПК-12, Том 113 (9).
- Монахан, К. , М. Мунаката , А. Вайдья , С. Гандини. 2020. Вдохновляя математическое творчество с помощью жонглирования. Журнал гуманистической математики, том 10 (2), стр. 291–314.
- Карлсон М. , Б.Г. Нита , А.Вайдья . 2020. Численные расчеты длины вихреобразования при обтекании эллиптического цилиндра. Жидкости, том 5 (3), стр. 157.
- Гермия Э. , Н. Паноркоу . 2020. Изучение углов в среде программирования. Когнитивные и эмоциональные исследования STME, стр. 121-129.
- Гермия Э. , Н. Паноркоу . 2020. Использование программирования на нулях для исследования координат. Учитель математики: Обучение и преподавание ПК-12 Том 113 (4) стр. 293-300.
- Паноркоу Н. , Э. Гермия . 2020. Изучение количественного мышления учащихся в моделировании круговорота воды в виртуальной экосистеме. Материалы ICLS 2020.
- Панорков Н. . 2020. Динамические рассуждения о площади прямоугольника: случай Лоры и Исаака. Цифровой опыт в математическом образовании.
- Паноркоу Н. , Е.Ф. Гермия . 2020. Интеграция содержания математики и естественных наук посредством ковариационных рассуждений: случай гравитации.Математическое мышление и обучение.
- Басу Д. , Н. Паноркоу , М. Чжу , П. Лал , Б.К. Самантула . 2020. Изучение математики гравитации. Учитель математики: Обучение и преподавание ПК-12, Том 113 (1).
- Панорков Н. . 2020. Обоснование динамических измерений площади и объема. Для изучения математики, том 40 (3), стр. 9–13.
- Мур К.С., Б. Лян, И.Е. Стивенс, Х. Тасова, Т.Паолетти , Ю. Ин. 2020. Количественное обоснование построения концепции. Конференция: Материалы двадцать третьей ежегодной конференции по исследованиям в области математического образования для студентов.
- Самантула Б.К. , М. Мехран , М. Чжу , Н. Паноркоу , П. Лал . 2020. Опыт создания интерактивной облачной системы обучения для STEM-образования. Труды IEEE Integrated STEM Education Conference (ISEC).
- Рана П., П. Бозе, А. Вайдья , В. Рангачари, П. Гош. 2020. Глобальная подгонка и идентификация параметров агрегации амилоида-β с конкурирующими путями. 2020 20-я Международная конференция IEEE по биоинформатике и биоинженерии (BIBE).
- Гош П., П. Рана, В. Рангачари, Дж. Саха, Э. Стин , А. Вайдья . 2020. Теоретико-игровой подход к расшифровке динамики агрегации амилоида-β по конкурирующим путям. Открытая наука Королевского общества, том 7 (4).
- Гош П., Дж. Патерас , В. Рангачари , А. Вайдья . 2020. Сетевой термодинамический анализ агрегации амилоида по конкурирующим путям. Прикладная математика и вычисления, том 393.
- Бал Д. , Л. ДеБиасио. 2019. Новые нижние границы размера-числа Рамси пути. arxiv.org.
- Аранео Дж. , Б.Дж. Чанг , М. Кристальди , Дж. Патерас , А. Вайдья , Р.Вуландана. 2019. Экспериментальное управление авторотацией, вызванной следом, с приложениями к сбору энергии. Международный журнал зеленой энергии, том 16 (15).
- ДиНаполи Дж. . 2019. «Стремление лучше справляться с этим»: изучение улучшения настойчивости у учащихся средней школы по математике. PME-NA 41 Материалы.
- Моралес Х., Дж. ДиНаполи , К. Уилли. 2019. Переводя на упорство: изучение коллективного решения проблем латиноамериканских двуязычных студентов.PME-NA 41 Материалы.
- Фернандес Э. , Э. Лещински . 2019. Математическое взаимодействие с синхронными платформами: примеры и выводы. Справочник по исследованиям онлайн-педагогических моделей для подготовки учителей математики.
- Гринштейн С. , Э. Фернандес , Дж. Дэвидсон . 2019. Раскрытие знаний учителя через создание: пример двух будущих учителей математики. PME-NA 41 Материалы.
- Гринштейн С., М. Руссо. 2019. Преподавание социальной справедливости посредством критического математического исследования. Серия периодических статей, том 41.
- Басу Д. , Гринштейн С. . 2019. Развитие пространства для критических математических исследований с помощью математической деятельности по извлечению знаний. Серия периодических статей, том 41.
- Монахан К. , М. Мунаката , А. Вайдья . 2019. Креативность как эмерджентное свойство сложной образовательной системы.Северо-восточный журнал сложных систем.
- Трабона К., М. Тейлор, Э.Дж. Кляйн, М. Мунаката , З. Рахман . 2019. Совместное профессиональное обучение: воспитание лидеров учителей естественных наук через вертикальные практические сообщества. Профессиональное развитие в образовании, том 45 (3).
- Крупа Е.Е. , М. Мунаката , К.Ю . 2019. День математического поля: встраивайте контент с помощью Play. Преподавание математики в средней школе, том 24 (5), стр.296-299.
- Нита Б. , С. Раманатан. 2019. Жидкости в музыке: математика флейт Пана. Жидкости, том 4 (4), стр. 181.
- Басу Д. , Н. Паноркоу . 2019. Интеграция ковариационных рассуждений и технологий в преподавание и изучение парникового эффекта. Журнал математического образования, том 12 (1), стр. 6–23.
- Басу Д. , Н. Паноркоу . 2019. Расширение контекстуального окружения учащихся с помощью динамических измерений.Материалы 40-й ежегодной конференции Североамериканского отделения Международной группы психологии математического образования.
- Панорков Н. . 2019. Изучение обоснования динамических измерений площади и объема. PME-NA 41 Материалы.
- Панорков Н. . 2019. Изучение динамического измерения объема. PME 43 Конференция Международной группы Труды.
- Басу Д. , Н. Паноркоу , М. Чжу .2019. Изучение социального аспекта изменения климата с помощью математики. Материалы IEEE Integrated STEM Education Conference (ISEC) 2019.
- Паолетти Т. , М. Вишнубхотла , М. Мохамед . 2019. Ковариационные рассуждения для разработки продуктивных значений систем отношений и неравенств. 43-е ежегодное собрание Международной группы психологии математического образования, том 4.
- Паолетти, Т. , С.Гринштейн , М. Вишнубхотла , М. Мохамед . 2019. Разработка задач и трехмерных физических манипуляций для развития ковариационного мышления учащихся. PME 43 Конференция Международной группы Труды.
- Катлер Дж. , А.Дж. Рэдклифф. 2018. Минимизация числа независимых множеств в регулярных графах без треугольников. Дискретная математика, том 341 (3).
- ДиНаполи Дж. . 2018. Использование совместных соревнований на уроках математики.Австралийский учитель математики, том 74 (2), стр. 10–18.
- ДиНаполи Дж. . 2018. Поддержка усидчивости школьников в решении сложных задач по математике. PME-NA 40 Материалы.
- Моралес Х., Дж. ДиНаполи . 2018. Упорство двуязычных латиноамериканцев в решении математической задачи. PME-NA 40 Материалы.
- Моралес Х., Дж. ДиНаполи . 2018. Настойчивость студентов-билингвов Latinx в решении математической задачи: регуманизирующая перспектива.Журнал исследований в области математического образования, том (3).
- Суппа С., Дж. ДиНаполи , Р. Микселл. 2018. Подготовка учителей «имеет ли значение»: взаимосвязь между курсами элементарной математики и анализом преподавания выпускниками. Обучение и развитие учителей математики, том 20 (2), стр. 25-57.
- Гринштейн С. . 2018. Проектирование микромира для топологической эквивалентности. Цифровой опыт в математическом образовании, 4(1), 1-19.
- Гринштейн С., С. Багьери. 2018. Воображение математического мышления для инклюзивной учебной программы: разговор. Исследования в области обучения математике, 10 (3), 1–12.
- Гринштейн С. , Ю. Севентко . 2018. Гонка до 20 лет. Обучение детей математике, том 24 (5), стр. 336.
- Гринштейн С. , Дж. Олмансон. 2018. Реконцептуализация развития педагогических и учебных знаний посредством создания. Журнал Emerging Learning Design.
- Кейси С., К.Lesseig, E. Krupa , D. Monson. 2018. Изучение ответов учителей математики средней школы на работу учащихся по решению линейных уравнений. Обучение и развитие учителей математики.
- Монахан К. , М. Мунаката , А. Вайдья . 2018. Математическое творчество через игру: пример урока вероятности. принято к публикации в журнале «Учитель математики».
- Вишнубхотла М. , М. Мунаката . 2018. Математика петлевых рамок для картин.Национальный совет учителей математики, том 23, выпуск 4, стр. 231–235.
- Тейлор М., Э.Дж. Кляйн, М. Мунаката , К. Трабона, З. Рахман , Дж. Макманус . 2018. Профессиональное развитие учителей-лидеров: использование теории деятельности для понимания сложностей устойчивых изменений. Международный журнал лидерства в образовании, том 22 (6).
- Кляйн Э.Дж., М. Тейлор, М. Мунаката , К. Трабона, З. Рахман , Дж.Макманус . 2018. Навигация по сложным отношениям учителей-лидеров с использованием структуры распределенного лидерства. Педагогическое образование Ежеквартально, том 45 (2), стр. 89-112.
- Рахман З.Г., М. Мунаката , Э. Кляйн, М. Тейлор, К. Трабона. 2018. Выращивание собственных: содействие лидерству учителей среди учителей естественных наук K-12 посредством партнерства между школой и университетом. Дж. Ханцикер (ред.), Лидерство учителей в школах профессионального развития, стр. 235-253.
- Мюррей Э. , К.Дуркин, Т. Чао, Дж. Р. Стар, Р. Виг. 2018. Изучение связей между знанием содержания, знанием педагогического содержания и возможностями изучения математики: выводы из набора данных TEDS-M. Обучение и развитие учителей математики.
- Басу Д. , Н. Паноркоу . 2018. Изучение социальных аспектов парникового эффекта с помощью математического моделирования. PME-NA 40 Материалы.
- Басу Д. , Н. Паноркоу . 2018. Расширение контекстуальных областей измерения учащихся с помощью динамических измерений.PME-NA 40 Материалы.
- Паноркоу Н. , Д. Басу , М. Вишнубхотла . 2018. Исследование объема как основания, умноженного на высоту, с помощью динамического проектирования задач. PME-NA 40 Материалы.
- Панорков Н. . 2018. Переосмысление преподавания и изучения измерения площади. Материалы ICLS 2018.
- Паолетти Т. , И.Е. Стивенс, Н.Л.Ф. Хобсон, К.С. Мур, К.Р. Лафорест. 2018. Обратная функция: методы и значения учителей до начала работы.Образовательные исследования по математике, 97 (1), 93-109.
- Паолетти Т. , В. Крупник, Д. Пападопулос, Дж. Олсен, Т. Фукава-Коннелли, К. Вебер. 2018. Опрос учителей и приглашение принять участие в лекциях по высшей математике. Образовательные исследования по математике, 98 (1), 1-17.
- Рана П., Д. Н. Дин, А. Вайдья , В. Рангачари, П. Гош. 2018. Обзор экспериментов и моделирование взаимодействий Aβ-липид/сурфактант. Биофизика Бихимика Акта-Биомембраны, том 1860 стр.1652-1662 гг.
- Массуди М., А. Вайдья . 2018. Простота и устойчивость: указатели по этике и науке. принято к публикации в журнале «Устойчивое развитие» (специальный выпуск «Устойчивое развитие и этика: размышления о целях ООН в области устойчивого развития»), том 10, выпуск 4, стр. 1303.
- Бал Д. , Л. ДеБиасио. 2017. Разбиение случайных графов на одноцветные компоненты. Электрон. Дж. Комбин. 24, выпуск 1, документ № P1.18.
- Бал Д. , П.Беннетт, Т. Бохман, А. Фриз. 2017. Жадный алгоритм поиска большого 2-паросочетания на случайном кубическом графе. Журнал теории графов, том 88 (3), стр. 449–481.
- Катлер Дж. , Л. Пибоди. 2017. Максимальные кликовые разбиения и гипотеза американских горок. Журнал комбинаторной теории, серия A, 145 стр. 25–35.
- Катлер Дж. , А.Дж. Рэдклифф. 2017. Максимальное количество полных подграфов фиксированного размера в графе с заданной максимальной степенью. Журнал теории графов 84 стр.134-145.
- Гринштейн С. , Э. Лещински , Э. Фернандес . 2017. 3D-проектирование для математического обучения. Преподавание математики в средней школе, 23(1), 51-52.
- Гринштейн С. , К. Экичи. 2017. На стыке преподавания и культурного разнообразия: моделирование педагогики математики с учетом культурных особенностей для Виргинских островов США. Журнал математики и культуры.
- Крупа Э. , М. Хьюи, К. Лессиг, С.Кейси, Д. Монсон. 2017. Изучение того, замечает ли учитель средней школы математическое мышление учащихся. Э. О. Шак, Дж. Вильгельм и М. Х. Фишер (ред.). Исследования в области математического образования (том 6): Springer.
- Крупа Э. , М. Хьюи, К. Лессиг, С. Кейси, Д. Монсон. 2017. Изучение того, замечает ли учитель средней школы математическое мышление учащихся. В EO Schack, J. Wilhelm, & MH Fisher (Eds.). Исследования в области математического образования (том 6): Springer.
- Лещински Э. , Э. Мюррей, М. Петроу . 2017. Распаковка делением фракций. Онкоре.
- Лещински Э. , К. Монахан , М. Мунаката , А. Вайдья . 2017. Проект «Танцующий с ветром»: открытый подход к обучению физике. Журнал преподавания естественных наук в колледже (Национальная ассоциация преподавателей естественных наук), том 46, выпуск 6, стр. 27–33.
- Мюррей Э. , Э. Балдингер, Н. Вассерман, С.Бродерик, Д. Уайт. 2017. Соединение высшей и средней математики. Бакалавриат по математической подготовке школьных учителей: Журнал.
- Нита Б. , П. Нолан, А. Вайдья . 2017. Численное исследование формы тела и гибкости крыла при взаимодействии структуры жидкости. принято к публикации в Computational and AMSTematics, Volume 36 Issue 4 pp. 1733-1746.
- Паноркоу Н. , Я. Кобрин. 2017. Совершенствование практики формирующей оценки учителей посредством профессионального развития на основе траектории обучения.Педагог-педагог по математике. Педагог-педагог по математике.
- Паолетти Т. , М. Вишнубхотла , З. Рахман , Дж. Севентко , Д. Басу . 2017. Сравнение использования диаграмм в учебниках STEM и практических журналах. В книгах А. Вайнберга, К. Расмуссена, Дж. Рабина, М. Вавро и С. Брауна (ред.). Труды двадцатой ежегодной конференции по исследованиям в области математического образования для студентов (стр. 1386–1392). Сан-Диего, Калифорния.
- Паолетти Т. , К. Монахан , М. Вишнубхотла . 2017. Разработка апплетов GeoGebra для максимального вовлечения учащихся. Учитель математики, 110(8), 628-630.
- Паолетти Т. , Дж. Сильверман, К. Монахан , З. Рахман , М. Вишнубхотла , Э. Ф. Гермия. 2017. Правила построения графиков или понимание? Понимание учителей. . В Э. Галиндо и Дж. Ньютон (ред.). Материалы 39-го ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр.536). Индианаполис, Айова: Ассоциация преподавателей математики Hoosier.
- Стивенс И.Е., Т. Паолетти , К.С. Мур, Б. Лян, Х. Х. Хардисон. 2017. Принципы разработки задач, способствующих ковариационному мышлению. В книгах А. Вайнберга, К. Расмуссена, Дж. Рабина, М. Вавро и С. Брауна (ред.). Материалы 20-й ежегодной конференции по исследованиям в области математического образования для студентов (стр. 928–936). Сан-Диего, Калифорния.
- Паолетти Т. . 2017. Количественное рассуждение и обратная функция: несоответствие.В Э. Галиндо и Дж. Ньютон (ред.). Материалы 39-го ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 973–976). Индианаполис, Айова: Ассоциация преподавателей математики Hoosier.
- Паолетти Т. , К.С. Мур, Мур. 2017. Параметрический характер ковариационных рассуждений двух студентов. Журнал математического поведения, 48, 137-151.
- Паолетти Т. , Стивенс, К.С.Мур. 2017. Трюки могут препятствовать рассуждению учащихся. Учитель математики, 110 (6), стр. 446-453.
- Чанг Б.Дж. , Б. Ортега, А. Вайдья . 2017. Производство энтропии в системе жидкость-твердое тело вдали от термодинамического равновесия. Европейский физический журнал E: Мягкая материя и биологическая физика, том 40, стр. 105.
- Рана П., Д. Н. Дин, Э. Стин, А. Вайдья , В. Рангачари, П. Гош. 2017. Концентрация жирных кислот и фазовые переходы модулируют пути агрегации Aβ.Научные отчеты (Nature) Том 7 Статья 10370 стр. 1-16.
- Кастильо Д., Б. Дж. Чанг , К. Шнитцер, К. Сориано, А. Вайдья . 2017. Метастабильные состояния при ориентации шарнирно-симметричных тел в потоке. Международный журнал технических наук, том 111, стр. 19–27.
Создание третьего пространства для обучения разработке математических задач на основе технологий на JSTOR
АбстрактныйВ этой статье мы исследуем способы, с помощью которых создание третьего пространства может преодолеть разрыв между курсовой работой и практикой для будущих учителей математики средней школы (PST), изучающих технологии, педагогику и предметный курс.Преподаватель из университета в партнерстве с двумя учителями средней школы создал пространство, в котором PST опираются и используют как академические, так и практические знания, создавая технологические задачи для старшеклассников. Наши результаты показали повышенное внимание к педагогическим решениям в таких областях, как проектирование технологических задач и методы опроса. Данные также показывают, что успех этого сотрудничества был связан со справедливым распределением работы, чувством собственной значимости, личной выгодой и трудностями, сосредоточенными на поддержании отказа от иерархии.
Информация о журналеПреподаватель математики способствует созданию профессиональной базы знаний для преподавателей математики, которая основывается на практических знаниях, развивает и укрепляет их. Журнал предоставляет средства для того, чтобы практические знания, связанные с подготовкой и поддержкой учителей математики, были не только общедоступными, общими и хранимыми, но также проверенными и улучшенными с течением времени (Hiebert, Gallimore, and Stigler, 2002).
Информация об издателеНациональный совет учителей математики является общественным голосом математического образования, обеспечивающим видение, лидерство и профессиональное развитие для поддержки учителей в обеспечении обучения математике самого высокого качества для всех учащихся. NCTM, насчитывающая почти 90 000 членов и 250 филиалов, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12 класса.«Принципы и стандарты школьной математики» Совета представляют собой руководство по совершенствованию математического образования и призывают всех учащихся заниматься более сложной математикой. NCTM стремится к постоянному диалогу и конструктивному обсуждению со всеми заинтересованными сторонами того, что лучше всего подходит для учащихся нашей страны.
Цифровые технологии в разработке учебных заданий по математике
В этой книге рассказывается о преимуществах и недостатках использования цифровых технологий при разработке уроков и занятий на уроках математики.За последние несколько десятилетий было создано множество идей и методов обучения, включающих новые технологии, в надежде на более эффективное преподавание математических понятий нашим ученикам. Один из ключевых вопросов, рассматриваемых в этой книге, заключается в том, как технологии могут или не могут играть эпистемологическую и педагогическую роль в классе. Как указано во введении, в сборнике исследовательских работ рассматриваются три основных вопроса:
- Какие особенности используемой технологии можно использовать для разработки задач, преобразующих эмпирические знания учащихся, полученные при использовании технологии, в концептуальные математические знания?
- Когда цифровая среда действительно привносит существенное (с точки зрения образования) новое измерение в занятия в классе?
- Каковы некоторые прагматические и семиотические ценности используемой технологии?
Это основные вопросы, которыми задаются различные ученые и ведущие исследователи в области цифрового дизайна.
Книга разделена на четыре раздела: теоретические соображения, разработка задач в средах с динамической геометрией, разработка задач на интерактивных цифровых платформах и вопросы разработки цифровых задач. На протяжении всей книги теории и практики разработки математических учебных заданий, известных как Динамических и интерактивных математических учебных сред (DIMLE), представленных Karadag et al. в 2011 году используются.
В статье «Планиметр как реальный и виртуальный инструмент, опосредующий бесконечно малый подход к площади» понятие дидактического цикла используется для понимания учащимися последовательностей.Представленные действия являются сенсомоторными и символическими. На странице 125 изображен планиметр Амслера 1856 года, который был профессиональным инструментом для измерения площадей плоских фигур. Он состоит из двух соединенных плеч, ограничения которых допускают только взаимное вращение, фиксированного ограничения (фиксированной точки), к которому прикреплено одно из плеч и которое допускает только вращение, линзы, называемой трассером, которая повторяет контур фигуры, площадь которой равна для измерения, колесо, физически вынужденное вращаться только перпендикулярно второму плечу, и счетчик, который отслеживает расстояние, пройденное колесом.С помощью цифровых технологий инструкторы могут использовать планиметр с помощью GeoGebra. Рисунок 3 на странице 127 дает нам изображение планиметра GeoGebra, который является виртуальной моделью планиметра Амслера.
В статье «Разработка инновационных учебных мероприятий для преодоления трудностей в алгебре у учащихся-дискалькуликов: использование функций AlNuSet » Элизабетта Роботти обсуждает учащихся, страдающих дискалькулией развития (DD). В статье алгебра обсуждается не только в ее синтаксическом, но и в семантическом аспектах. AlNuSet означает «Алгебра числовых множеств», и исследование показывает, как студенты DD могут понимать алгебраические обозначения. На страницах 195–197 дается описание AlNuSet , состоящего из трех тесно интегрированных компонентов: алгебраических строк, символического манипулятора и компонента функций. В работе используется только Алгебраическая линия, представляющая алгебраическую переменную как подвижную точку на линии, а именно точку, которую можно перетаскивать по линии с помощью мыши.2-1>x+1\).
Некоторыми другими примерами дизайна цифровых задач являются документы «Поддержка вариаций в разработке задач с помощью использования технологий» Кристиана Бохова и «Напряжения в дизайне математических технологических сред: инструменты и задачи для обучения линейным функциям, » Элисон Кларк-Уилсон. В статье Бохова представлена онлайн-интервенция, разработанная в Утрехтском университете под названием «Algebra met Inzicht» [Алгебра с пониманием] и выполненная с использованием цифровой математической среды (DME).В DME учащиеся могут в любое время работать и получать отзывы о выбранных для них модулях. В статье Кларк-Уилсон исследуется лонгитюдное исследование с участием 15 учителей математики средней школы английского языка и 75 уроков. Исследование прямых линий представлено на страницах 334–335, где студенты сначала не знали, что делать, и нуждались в подсказках. Большинство студентов смогли установить связь, что чем больше коэффициент x , тем круче будет линия.Однако вряд ли кому-то из студентов удалось обобщить на случай дробных или отрицательных коэффициентов.
Эта книга полна исследований постоянно растущего использования цифровых технологий в классе. С увеличением разнообразия программного обеспечения у инструкторов есть множество вариантов на выбор. От демонстраций в классе до работы учащихся в группах и выполнения домашних заданий с помощью этих технологий возможности безграничны. Сосредоточив внимание на разработке задач в рамках DMILE, что расширяет и расширяет обсуждение темы разработки задач Tools and Representations в ICMI Study 22, книга предлагает читателю очень разнообразное и актуальное исследование этих технологий.Я настоятельно рекомендую эту книгу тем преподавателям, которым нужны свежие идеи или которые ищут ценные подходы к разработке задач на основе цифровых инструментов, чтобы студенты могли получить содержательный математический опыт.
Питер Ольшевски — преподаватель математики в Пенн Стейт Эри, Колледж Беренд, редактор Larson Texts, Inc. в Эри, Пенсильвания, а также советник 362-го пенсильванского альфа-бета-отделения Pi Mu Epsilon. С ним можно связаться по адресу [email protected]. Помимо преподавания и редактирования учебников, ему нравится играть в гольф, играть на гитаре, читать, заниматься садоводством, путешествовать и рисовать пейзажи.
Европейский журнал науки и математического образования
- Дом
- Архив
- Том 9, выпуск 3, июль 2021 г.
- Исследование на основе дизайна: характеристики дифференцированных задач для математически одаренных учащихся
Подробнее
1
1 Департамент математики Образование, Стамбул Айдин Университет, Стамбул, Турция
2 Департамент математического образования, Среднего Восточного Технического университета , Анкара, ТУРЦИЯ
* Автор, ответственный за переписку
ОТКРЫТЫЙ ДОСТУП 743 Просмотров 487 Загрузок
РЕЗЮМЕ
В настоящее время необходимость разработки правильных дифференцированных заданий для математически одаренных учащихся является важной темой в зарубежной литературе и практике. В данном дизайн-исследовании ставилась цель проанализировать и построить характеристики для проектирования дифференцированных заданий математически одаренных учащихся.В рамках этого процесса проектирования этапы предварительной подготовки и прототипирования использовались в качестве общей основы для выявления этих характеристик в качестве принципов дизайна исследования. На этапе предварительного исследования были проведены обзоры литературы, опыт практиков и анализ потребностей в отношении предложений и ключевых моментов, отражающих характеристики дифференцированных задач. После этого этапа исходная форма дифференцированных заданий с эскизными принципами построения применялась на уроках в пробных и полевых испытаниях с 12 математически одаренными учениками и 4 учителями математики этих классов.Данные, полученные с помощью качественных методов, делятся на три категории; начальные принципы проектирования как характеристики, полученные на этапе предварительного проектирования, модификации для задач и окончательные принципы проектирования как характеристики, полученные на этапе прототипирования.
ЦИТАТА
Оздемир, Д., и Исиксал Бостан, М. (2021). Исследование на основе дизайна: характеристики дифференцированных задач для математически одаренных учащихся. Европейский журнал науки и математического образования, 9 (3), 125-144. https://doi.org/10.30935/scimath/10995ССЫЛКИ
- Андерсон, Л. В., Кратволь, Д. Р., и Блум, Б. С. (2001). Таксономия обучения, преподавания и оценивания: пересмотр таксономии образовательных целей Блума . Лонгман.
- Арслан, Ч., и Алтун, М. (2007). Обучение решению нестандартных математических задач. İlköğretim Online, 6 (1), 35-49.
- Айдемир, Д., и Чакироглу, Э. (2013). Üstün Yetenekli ilköğretim öğrencilerinin matematik derslerine ilişkin algıları [Одаренные учащиеся начальной школы воспринимают уроки математики]. Материалы 12-го семинара MATDER , (стр. 266-268), Анкара, Турция.
- Айдемир Д. и Тексоз Г. (2014 г., сентябрь). Çevre eğitiminin matematik derslerine entegre edilmesine ilişkin öğrenci görüşleri [Çevre eğitiminin matematik derslerine entegre edilmesine ilişkin öğrenci görüşleri] презентация].XI. Ulusal Fen Bilimleri ve Matematik Eğitimi Kongresi 2014, Адана, Турция.
- Байкоч, Н. (2014). Üstün yesenek gelişimleri ve eğitimleri [Развитие и обучение одаренных людей] . Визе Яинджилык.
- Бин, Дж. (1997). Интеграция учебных программ . Издательство Педагогического колледжа.
- Бергер, С.Л. (1991). Дифференцирующий учебный план для одаренных учащихся. ERIC Центр обмена информацией о детях-инвалидах и одаренных детях.
- Берри, Дж. (2002). Развитие навыков математического моделирования: роль CAS. Zentralblatt für Didaktik der Mathematik 34 (5), 212-220. https://doi.org/10.1007/BF02655824
- Блум, Б. С. (1956). Таксономия образовательных целей: Классификация образовательных целей: когнитивная область . Маккей.
- Блюм, В. (2002). Исследование ICMI 14: Приложения и моделирование в математическом образовании – дискуссионный документ. Образовательные исследования по математике, 51 (1-2), 149-171.https://doi.org/10.1023/A:1022435827400
- Бочкарева Т., Ахметшин Э., Осадчий Э., Романов П. и Коновалова Э. (2018). Подготовка будущего учителя к работе с одаренными детьми. Journal of Social Studies Education Research, 9 (2), 251-265. https://doi.org/10.17499/jsser.76113
- Бриганди, CB, CM Gilson и M. Miller. (2019). Профессиональное развитие и дифференцированное обучение в программе начальной школы: пример обучения для одаренных. Журнал для образования одаренных, 42 (4), 362-395. https://doi.org/10.1177/0162353219874418
- Чемберлин, М.Т., и Чемберлин, С.А. (2010). Улучшение подготовки учителей дослужебной подготовки: полевой опыт работы с одаренными учащимися. Журнал для образования одаренных, 33 (3), 381-416. https://doi.org/10.1177/016235321003300305
- Коллинз, А. (1992). К проектной науке образования. В Э. Скэнлон и Т. О’Ши (ред.), Новые направления в образовательных технологиях (стр.15-22). Спрингер-Верлаг. https://doi.org/10.1007/978-3-642-77750-9_2
- Кресуэлл, Дж. В. (2009). Качественный запрос и дизайн исследования: выбор из пяти традиций . Мудрец.
- Дензин, Н. (1989). Закон об исследованиях: теоретическое введение в социологические методы . Прентис Холл.
- Дерингёль Ю. и Даваслигил Ю. (2020). Влияние дифференцированных математических программ на отношение к математике одаренных детей. Малазийский онлайн-журнал образовательных наук, 8 (1), 27–37.
- Диезманн, К.М., и Уоттерс, Дж. (2001). Совместная работа математически одаренных учащихся над сложными задачами. Журнал для образования одаренных, 25 , 7-31. https://doi.org/10.1177/016235320102500102
- Димитриадис К. (2011). Предоставление математически одаренных детей в начальных школах: исследование четырех различных методов организационного обеспечения, Educational Review, 64 (2 ), 241-260. https://doi.орг/10.1080/00131911.2011.598920
- Инглиш, Л. Д., и Уоттерс, Дж. (2005). Математическое моделирование с 9-летними. В HL Chick и JL Vincent (Eds.), Proceedings of 29th Conference of the Int. Группа психологии математического образования (стр. 297-304). Австралия: Мельбурнский университет.
- Фичичи, А., и Сигле, Д. (2008). Мнение международных учителей о характеристиках одаренных учеников по математике. Journal of Gifted Talented International, 23 (1), 22–37. https://doi.org/10.1080/15332276.2008.11673510
- Фрейман, В. (2006). Задачи для выявления и развития математических способностей в младших классах: подход к сложным ситуациям. Энтузиаст математики, 3 (1), 51-75. https://scholarworks.umt.edu/tme/vol3/iss1/3
- Гэвин, М.К., Каса, Т.М., Фирмендер, Дж.М., и Кэрролл, С.Р. (2013). Влияние дополнительных модулей геометрии и измерений на успеваемость первоклассников по математике. Ежеквартальный журнал для одаренных детей, 57 (2), 71–84. https://doi.org/10.1177/0016986213479564
- Глейзер, Б., и Штраус, А. (1967). Открытие теории заземления. Стратегии качественных исследований . Социологическая пресса. https://doi.org/10.1097/00006199-196807000-00014
- Гравемейер, К. (2006). Исследования развития как метод исследования. В J. Van den Akker, K. Gravemeijer, S. McKenney & N. Nieveer (Eds). Исследования в области образовательного дизайна (стр.115-131). Рутледж.
- Гринс, К. (1997). Оттачивание способностей математически перспективных. Учитель математики, 90 (7), 582. https://doi.org/10.5951/MT.90.7.0582
- Херрингтон, Дж., Маккенни, С., Ривз, Т., и Оливер, Р. (2007). Дизайнерские исследования и докторанты: Методические рекомендации по подготовке диссертационного предложения.
- Хейманн, Х.В. (2003). Зачем учить математику? Направленность на общеобразовательную . Клювер. https://дои.орг/10.1007/978-94-017-3682-4
- Джен, Э., Мун, С., и Самарапунгаван, А. (2015). Использование дизайн-исследований в обучении одаренных. Ежеквартальный журнал для одаренных детей, 59 (3), 190–200. https://doi.org/10.1177/0016986215583871
- Цзянго, М. (2004). Обучение экологическому сознанию в математике . Китайское образование и общество, 37 ( 4), 53–56. https://doi.org/10.1080/10611932.2004.11031651
- Джонсон, Д. Т. (2000). Преподавание математики одаренным ученикам в классе смешанных способностей .Эрик Клирингхаус.
- Джолли, Дж. Л. и Джарвис, Дж. М. (ред.). (2018). Изучение образования для одаренных: перспективы Австралии и Новой Зеландии . Рутледж. https://doi.org/10.4324/9781351227704
- Каневский, Л. (2011). Дифференциально дифференцированный: Какие типы дифференциации нужны учащимся? Ежеквартальный журнал для одаренных детей, 55 (4), 279-299. https://doi.org/10.1177/0016986211422098
- Капут, Дж. (1992). Технологическое и математическое образование.В D. Grouws (Ed.), Справочник по исследованиям в области преподавания и обучения математике (стр. 515-556). Макмиллан.
- Карадуман, Великобритания (2010). Üstün Yetenekli öğrenciler için uygulanan farklılaştırılmış matematik eğitim programları [Программы дифференцированного обучения математике для одаренных учащихся]. Хасан Али Юджел Эгитим Факюльтеси Дергиси, 13 (1), 1-12.
- Карнес, М.Б. и Джонсон, Л.Дж. (1991). Дошкольный/начально одаренный ребенок. Журнал для образования одаренных, 14 (3), 267-283.https://doi.org/10.1177/0162353200307
- Кеннеди-Кларк, С. (2013). Исследование по замыслу: исследование на основе дизайна и студент-исследователь высшей степени . Журнал Learning Design, 6 (2), 26-32. https://doi.org/10.5204/jld.v6i2.128
- Ктистис, С. (2014). Развитие критического мышления у одаренных учащихся в неоднородном классе: общие представления педагогов (Докторская диссертация). Северный центральный университет, Сан-Диего, Калифорния.
- Леш, Р.и Дорр, HM (2003). Модельный взгляд на развитие учителя. В Р. А. Леш и Х. Дорр (редакторы), За гранью конструктивизма: модели и перспективы моделирования решения математических задач, обучения и преподавания (стр. 3-33). Лоуренс Эрлбаум. https://doi.org/10.4324/9781410607713
- Мафумико, ФСМ (2006). Микромасштабные эксперименты как катализатор улучшения учебной программы по химии в Танзании. Tijdschrift voor Didactiek der β-wetenschappen, 1 (2), 69–74.
- Мануэль, Д., и Фрейман, В. (2017). Дифференциация обучения с использованием виртуальной среды: исследование постановки математических задач среди одаренных и талантливых учащихся. Global Education Review , 4 (1).
- Мартин, Р. М. (2002). Отношение одаренных учащихся к математике: внимание к одаренным девочкам в начальных классах (докторская диссертация, Государственный университет Нью-Йорка). Доступен в базе данных ProQuest Dissertations и Theses.
- Масоле, Т. М. (2011). Повышение качества оценки успеваемости в сельском хозяйстве в школах Ботсваны (докторская диссертация), Университет Претории.
- Маккенни, С., Ниевин, Н., и Ван ден Аккер, Дж. (2006). Дизайн исследования с точки зрения учебной программы. В JVD. Akker, K. Gravemeijer, S. McKenney и N. Nieven (Eds.), Educational Design Research (стр. 67-90). Рутледж. https://doi.org/10.4324/9780203088364
- Мерриам, С.Б. (1998). Применение качественных исследований и тематических исследований в образовании . Издательство Джосси-Басс.
- Мхлоло, М.К., и Марумо, Дж.М. (2017). Предварительные результаты исследования, основанного на 10 заповедях Ганя для обучения математически одаренных учащихся. Ассоциация математического образования Южной Африки, 41.
- Майлз, М.Б., и Хуберман, А.М. (1994). Качественный анализ данных: расширенный справочник . Беверли-Хиллз: Sage Publications.
- Мофилд, Э. Л. (2020). Преимущества и препятствия для сотрудничества и совместного обучения: изучение перспектив одаренных учителей образования и учителей общего образования. Одаренный ребенок сегодня, 43 (1), 20-33. https://doi.org/10.1177/1076217519880588
- Ниевин, Н., и Фолмер, Э. (2013). Формирующая оценка в исследованиях образовательного дизайна. В Van den Akker, J., Gravemeijer, K. McKenney, S. & Nieven, N. (Eds). Образовательные дизайнерские исследования , (стр.152-169). Рутледж.
- Озчакыр, Б. (2013). Влияние обучения математике в сочетании с динамической геометрией на успеваемость учащихся седьмого класса в области четырехугольников (неопубликованная магистерская диссертация). Ближневосточный технический университет, Анкара.
- Оздемир, Д. (2016). Проектирование и разработка дифференцированных заданий для математически одаренных учащихся 5-6 классов (Неопубликованная докторская диссертация). Ближневосточный технический университет.
- Оздемир, Д. (2018). Matematikte Üstün Yetenekli İlköğretim Öğrencilerinin Okullarındaki Matematik Derslerine İlişkin Algıları [Восприятие одаренных учащихся начальной школы по математике об уроках математики в их школах]. Кастамону Эгитим Дергиси, 26 (1), 153-160. https://doi.org/10.24106/kefdergi.375695
- Оздемир, Д. А., и Ишиксал Бостан, М. (2021). Дифференцированные потребности математически одаренных учащихся: в какой поддержке они нуждаются? Международный журнал математического образования в области науки и техники, 52 (1), 65-83. https://doi.org/10.1080/0020739X.2019.1658817
- Парк, С. (2005). Сравнение научно одаренных детей и обычных детей в отношениях со сверстниками и самоэффективности. Неопубликованная магистерская диссертация, Чханвонский национальный университет, Кённам.
- Периатирувади, С., и Ринн, А. Н. (2012). Технологии в обучении одаренных: обзор передового опыта и эмпирические исследования .Журнал исследований технологий в образовании, 45 (2), 153–169. https://doi.org/10.1080/15391523.2012.10782601
- Пфайффер, С.И., и Петшер, Ю. (2008). Выявление одаренных детей раннего возраста по шкале оценки одаренности – дошкольная/детсадовская форма. Одаренный ребенок Ежеквартальный, 52 (1), 19-29. https://doi.org/10.1177/0016986207311055
- Пирс Р.Л., Кэссиди Дж.К., Адамс С.М., Ноймайстер К.Л.С., Диксон Ф.А. и Кросс Т.Л. (2011). Влияние кластеризации и учебной программы на развитие математических достижений одаренных учащихся. Журнал для образования одаренных, 34 (4), 569-594. https://doi.org/10.1177/016235321103400403
- Пломп, Т., и Нивен, Н. (ред.) (2013). Введение в исследования в области образовательного дизайна . СЛО.
- Раков, С. (2012). Помощь одаренным учащимся SOAR. Управление образования, 69 (5), 34-40.
- Renzulli, JS (1986) Концепция одаренности с тремя кольцами: модель развития творческой продуктивности. В Р. Дж.Штернберг
- и Дж. Э. Дэвидсон (редакторы) Концепции одаренности (стр. 53–92). Издательство Кембриджского университета.
- Ротигель, Дж. В., и Фелло, С. (2004). Математически одаренные ученики: как мы можем удовлетворить их потребности? Одаренный ребенок Сегодня, 27 (4), 46-
- 51. https://doi.org/10.4219/gct-2004-150
- Райзер, Г.Р., и Джонсен, С.К. (1998). Тест математических способностей для одаренных учащихся . Про-ред.
- Санкар-ДеЛеу, Н.(1999). Одаренные дошкольники: взгляды родителей и учителей на выявление, раннее зачисление и программирование.
- Roeper Review, 21 (3), 174-179. https://doi.org/10.1080/027831993957
- Зигле, Д. (2004). Выявление учащихся с дарами и талантами в области технологий. Одаренный ребенок сегодня , 27 (4), 30-33. https://doi.org/10.4219/gct-2004-146
- Сингер, Ф. М., Шеффилд, Л. Дж., Фрейман, В., и Брандл, М. (2016). Исследования и мероприятия для математически одаренных учащихся.В Исследования и мероприятия для математически одаренных учащихся (стр. 1-41). Спрингер, Чам. https://doi.org/10.1007/978-3-319-39450-3_1
- Шрираман, Б. (2003). Математическая одаренность, решение проблем и способность формулировать обобщения: опыт решения проблем четырех одаренных учеников. Prufrock Journal, 14 (3), 151–165. https://doi.org/10.4219/jsge-2003-425
- Шрираман, Б., и Сондергаард, Б.Д. (2009). О привнесении междисциплинарных идей в образование одаренных.В Л. В. Шавининой (ред.) Международный справочник по одаренности (стр. 1235-1256). Спрингер. https://doi.org/10.1007/978-1-4020-6162-2_64
- Шрираман, Б., Хааволд П. и Ли К. (2013). Математическое творчество и одаренность: комментарий и обзор теории, новые оперативные взгляды и пути вперед. Математическое образование, 45 (1), 215-225. https://doi.org/10.1007/s11858-013-0494-6
- Tieso, CL (2002). Влияние группировки и учебных практик на математические достижения учащихся среднего уровня.Национальный исследовательский центр одаренных и талантливых.
- Ван де Валле, Дж., Карп, К.С., и Бэй-Уильямс, Дж.М. (2013). Методы математики в начальной и средней школе: обучение с развитием . Аллин и Бэкон.
- Ван ден Аккер, Дж., Гравемейер, К., МакКенни, С., и Нивен, Н. (ред.). (2006). Образовательные дизайнерские исследования . Рутледж. https://doi.org/10.4324/9780203088364
- Ван Тассель-Баска, Дж., Хаббард, Г. Ф., и Роббинс, Дж.И. (2021). Дифференциация обучения одаренных учащихся: сопоставление оценочных исследований практики учителя в классе. Справочник по развитию одаренности и талантов в Азиатско-Тихоокеанском регионе, 945-979. https://doi.org/10.1080/02783193.2020.1765919
- Уилкинс, М.М., Уилкинс, Дж.Л.М., и Оливер, Т. (2006). Дифференциация учебной программы для учащихся начальных классов по математике. Обучение детей математике , 13 (1), 6-13. https://doi.org/10.5951/ТКМ.13.1.0006
- Вайнбреннер, С. (2001). Обучение одаренных детей в обычном классе: стратегии и методы, которые каждый учитель может использовать для удовлетворения академических потребностей одаренных и талантливых . Издательство «Свободный дух».
- Евдокимов О. (2007). Использование истории математики для наставничества одаренных учащихся: Заметки для учителей.




 Сколько орехов спрятала белка во вторую кладовку?)
Сколько орехов спрятала белка во вторую кладовку?)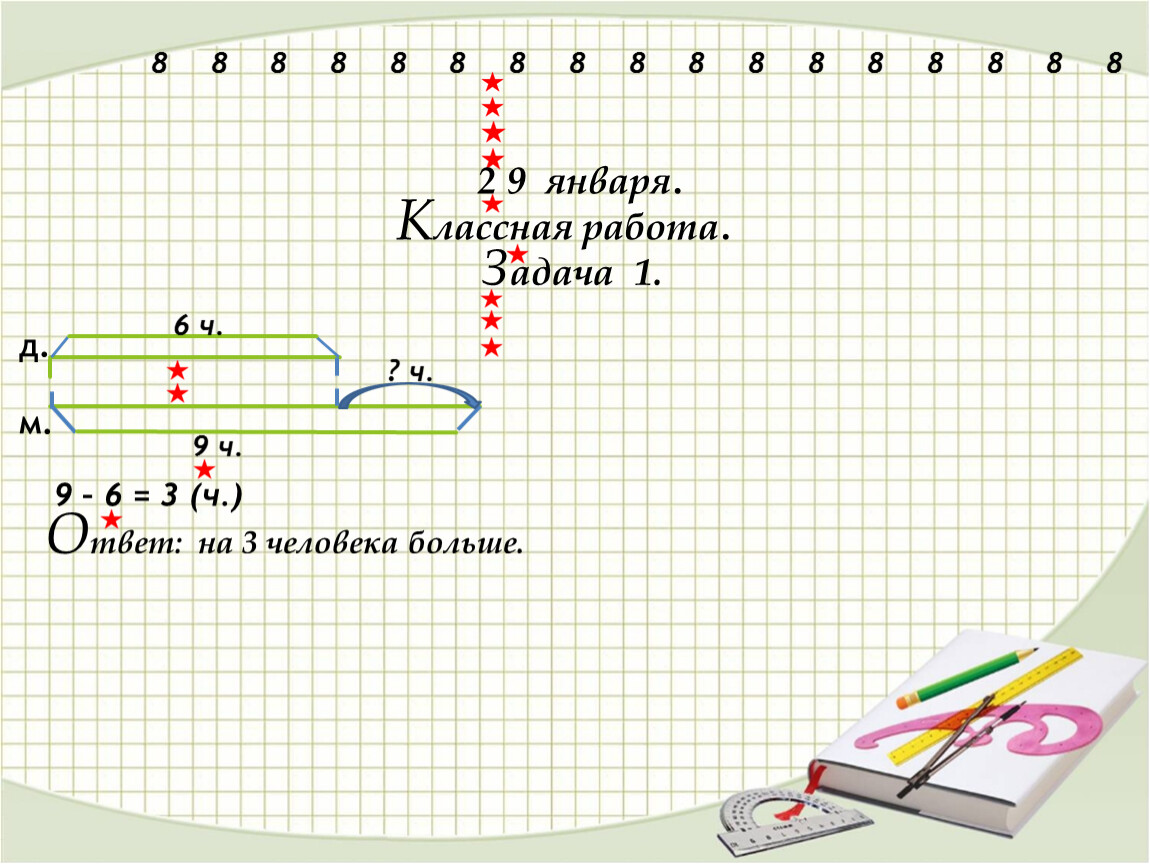



 Вместе с Гердой, вы пойдете на помощь Каю, который оказался в плену у Снежной Королевы. Нужно быть трудными и находчивыми, т.к. в пути вам встретятся много преград.
Вместе с Гердой, вы пойдете на помощь Каю, который оказался в плену у Снежной Королевы. Нужно быть трудными и находчивыми, т.к. в пути вам встретятся много преград. Чем особен этот пример?
Чем особен этот пример?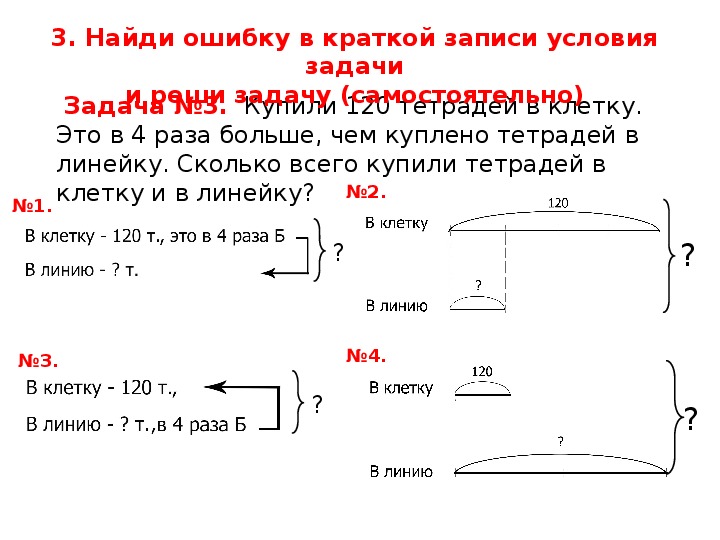 Стоит он неприступной крепостью. Чтобы в него попасть, надо решить задачу.
Стоит он неприступной крепостью. Чтобы в него попасть, надо решить задачу.
 Бегло
сложение вычитания в пределах 20, используя умственные стратегии. Работа с равными группами объектов для
получить основы для умножения.
Бегло
сложение вычитания в пределах 20, используя умственные стратегии. Работа с равными группами объектов для
получить основы для умножения.

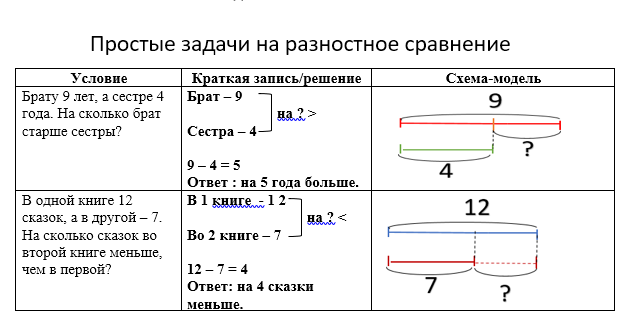
 Относительно
сложение и вычитание до длины.
Работаем со временем с шагом 5 минут. Решение словесных задач, связанных с деньгами,
с использованием символов долларов и центов. Создание и использование измерений
данные.
Относительно
сложение и вычитание до длины.
Работаем со временем с шагом 5 минут. Решение словесных задач, связанных с деньгами,
с использованием символов долларов и центов. Создание и использование измерений
данные.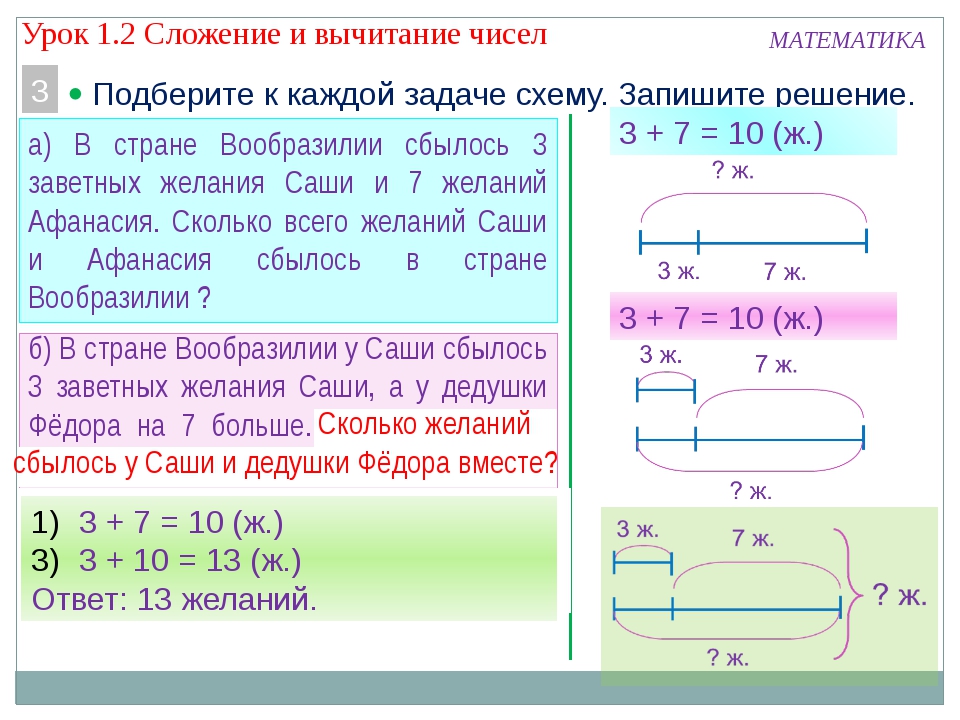
 Раздел
прямоугольники и круги.
Раздел
прямоугольники и круги. .
.