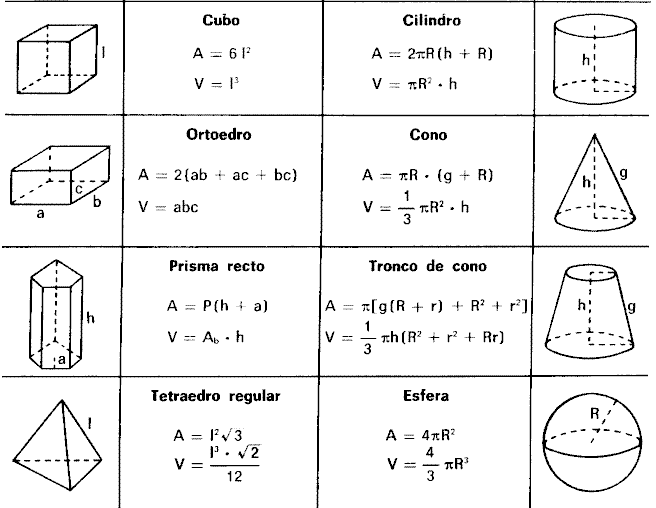
Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
|
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
|
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
|
a |
длина параллелепипеда |
|
b |
ширина параллелепипеда |
|
h |
высота параллелепипеда |
|
P (осн) |
периметр основания |
|
S (осн) |
площадь основания |
|
S (бок) |
площадь боковой поверхности |
|
S (п. |
площадь полной поверхности |
|
V |
объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
|
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см 2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.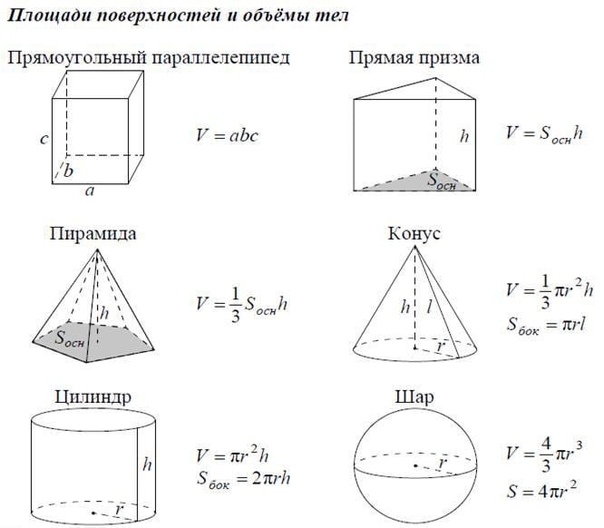
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
|
V параллелепипеда |
V = a × b × h |
|
|
V = Sосн × h |
|
S боковой поверхности |
Sб. |
|
S полной поверхности |
Sп. п. = 2 (ab + ac + bc) |
В чем разница между объемом и площадью поверхности?
Объем и площадь поверхности — это две взаимосвязанные концепции в изучении математики. Они оба важны для понимания, но одинаково важно понимать, чем они отличаются и что они значат. Это особенно актуально для расчета объема и площади поверхности призмы или цилиндра.
Если вы думаете об упаковке подарка в коробку, вы можете получить хорошее представление о том, как различаются объем и площадь поверхности. Во-первых, вы должны учитывать размер коробки, когда вы учитываете размер подарка. Сколько места в салоне нужно иметь для того, чтобы уместился подарок? Измерение емкости коробки, сколько она будет держать, это ее объем. Далее вы должны обернуть подарок. Количество оберточной бумаги, которая покрывает внешнюю часть коробки, очень сильно отличается от емкости коробки. Вам понадобится отдельное измерение или некоторое хорошее предположение, чтобы выяснить сумму сторон всех поверхностей или площади поверхности.
Вам понадобится отдельное измерение или некоторое хорошее предположение, чтобы выяснить сумму сторон всех поверхностей или площади поверхности.
Объем квадратной или прямоугольной коробки довольно легко вычислить. Просто умножьте высоту на длину и ширину, чтобы получить измерение. С квадратом это еще проще, вы просто кубизируете длину одной стороны, поскольку все они имеют одинаковый размер. Если длина стороны
Работа по объему и площади поверхности немного отличается, когда вы пытаетесь рассчитать площадь цилиндра. Формула для объема цилиндра — это площадь одной круглой грани, умноженная на высоту цилиндра. Он гласит: πr 2 xh, или pi умноженный на квадрат радиуса, умноженный на высоту. Получение площади поверхности цилиндра немного сложнее, поскольку круглая часть по существу представляет собой одну непрерывную поверхность. Вычисление площади поверхности цилиндра означает вычисление
боковой площади этой грани.
Формула для объема цилиндра — это площадь одной круглой грани, умноженная на высоту цилиндра. Он гласит: πr 2 xh, или pi умноженный на квадрат радиуса, умноженный на высоту. Получение площади поверхности цилиндра немного сложнее, поскольку круглая часть по существу представляет собой одну непрерывную поверхность. Вычисление площади поверхности цилиндра означает вычисление
боковой площади этой грани.
Формула боковой площади представляет собой следующие значения πr2r или πd (число раз, умноженное на радиус, удвоенный или число раз, умноженное на диаметр), умноженное на высоту, πr2r x h. По сути, это окружность одного круга, умноженная на высоту цилиндра. Чтобы вычислить всю формулу, вам также нужно добавить области верхней и нижней круговых граней. Поскольку в цилиндре они равны, формула 2 πr 2 . Этот расчет затем добавляется к боковой области, чтобы вычислить всю площадь поверхности в следующем выражении:
πr2r xh + 2πr 2 = боковая площадь.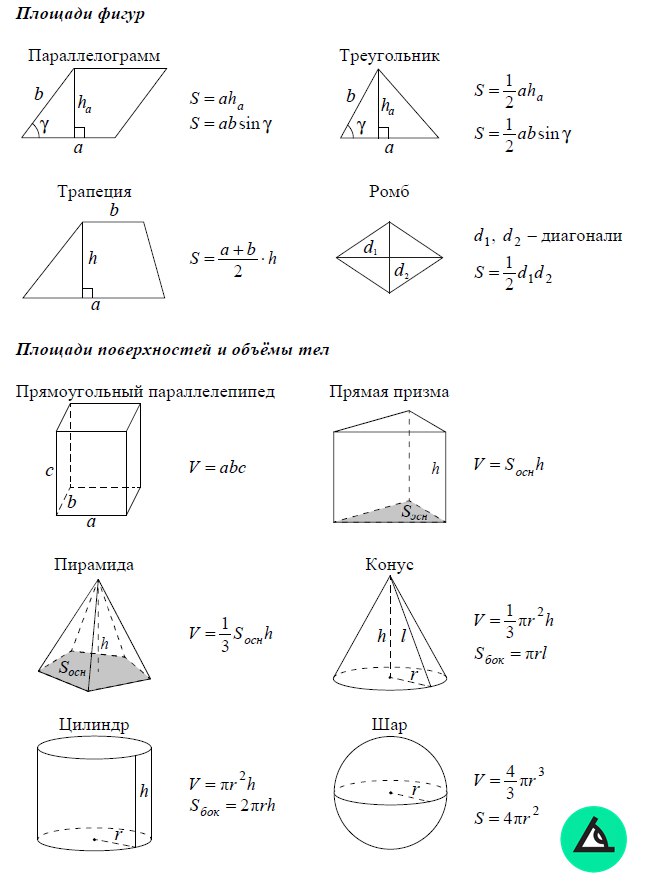
Вы также можете рассматривать разницу между объемом и цилиндром как разницу между тем, что находится внутри и может содержаться, и внешним видом трехмерного объекта. Это ценные отличия, которые нужно понимать во многих приложениях, таких как конструирование, проектирование или даже текущая упаковка. Когда дети жалуются на то, что математика бесполезна вне класса математики, вы можете указать им, что знание разницы между объемом и площадью поверхности означает, что они получили очень красиво упакованный подарок на свой день рождения.
ДРУГИЕ ЯЗЫКИ
Обзор группы инструментов Площадь и объем—ArcGIS Pro
Расчет площади поверхности и объема пространств между трехмерными данными является неотъемлемой частью большого числа пространственных операций. Группа инструментов Площадь и объем содержит инструменты, обеспечивающие решения для анализа разницы между поверхностями и создания объемных представлений трехмерных данных.
| Инструмент | Описание |
|---|---|
Насыпи/Выемки | Вычисляет разницу в объеме между двумя поверхностями. Обычно используется для операций вырезания и заполнения. |
Разница 3D | Исключает участки объектов-мультипатч в целевом классе объектов, которые перекрываются значениями объектов-мультипатч в классе вычитаемых пространственных объектов. |
Блок-диаграмма | Создает 3D объекты путем вытягивания каждого входного объекта между двумя наборами данных TIN. |
Минимальный ограничивающий объем | Создает объекты-мультипатч, представляющие объем пространства, занятый набором 3D объектов. |
Объем полигона | Вычисляет объем и площадь поверхности между полигоном одинаковой высоты и поверхностью. |
Разность поверхностей | Вычисляет смещение между двумя поверхностями и идентифицирует поверхность, лежащую выше, ниже или совпадающую с базовой поверхностью. |
Объем поверхности | Вычисляет площадь и объем области между поверхностью и базовой плоскостью. |
Связанные разделы
Отзыв по этому разделу?
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями.Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.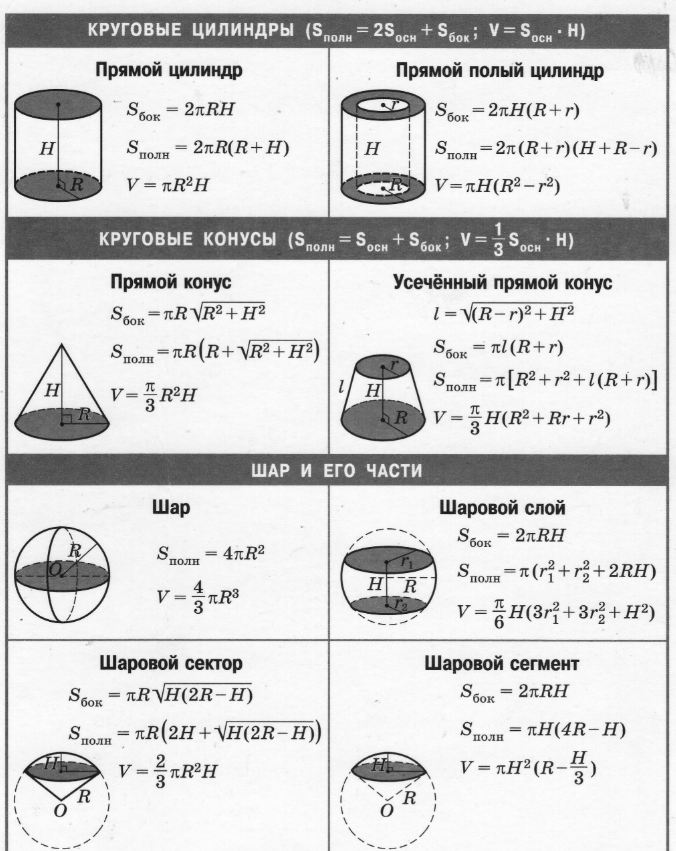
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате.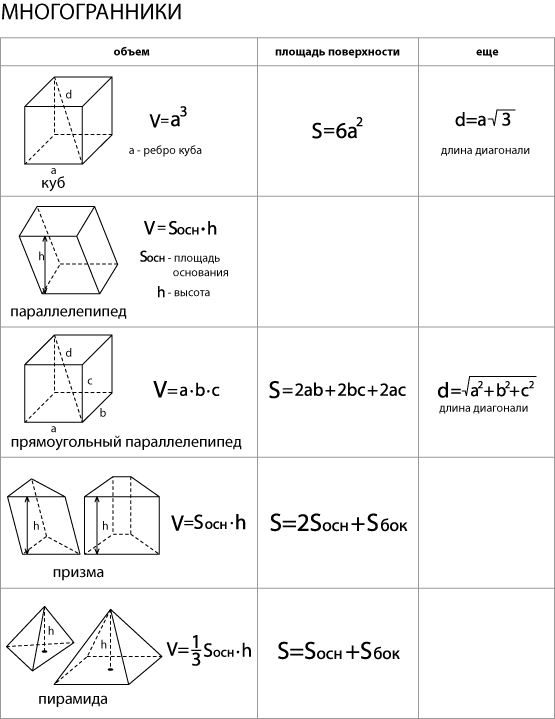 В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings. COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings. AUTHOR}}
AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Вычисление длин, площадей и объемов
В этом разделе будут представлены формулы расчета площади, поверхности, окружности и объема для простых двух- и трехмерных форм.
Площадь и периметр квадрата
Площадь квадрата рассчитывается как квадрат длины одной из его сторон. Следующая формула вычисляет площадь квадрата, сторона которого находится в ячейке с именем сторона:
=сторона^2
Чтобы вычислить периметр квадрата, умножьте длину одной из его сторон на 4. 2)
2)
Радиус окружности равен половине ее диаметра.
Чтобы вычислить длину окружности, необходимо умножить диаметр окружности на величину π. Следующая формула рассчитывает длину окружности, используя ячейку с именем диаметр.
=диаметр*ПИ()
Диаметр окружности равен радиусу окружности, умноженному на 2.
Площадь трапеции
Для вычисления площади трапеции необходимо сложить две параллельные стороны, умножить их сумму на высоту и разделить на 2. Следующая формула вычисляет площадь трапеции, используя ячейки с именами сторона1, сторона2 и высота:
=((сторона1+сторона2)*высота)/2
Площадь треугольника
Площадь треугольника представляет собой сумму основания и высоты треугольника, деленную на два. Следующая формула рассчитывает площадь треугольника, используя ячейки с именами основание и высота:
=(основание*высота)/2
Площадь поверхности и объем шара
Чтобы вычислить площадь поверхности шара, нужно умножить квадрат радиуса на число π, а затем полученное произведение умножить на 4. 2)*высота)
2)*высота)
Объем пирамиды
Чтобы вычислить объем пирамиды, необходимо определить площадь ее основания, а затем умножить ее на высоту и разделить на 3. Представленная ниже формула вычисляет объем пирамиды, используя для расчетов ячейки с именами ширина (ширина основания), длина (длина основания) и высота (высота пирамиды).
=(ширина*длина*высота)/3
В начало
Полезное
| Формула объема параллелепипеда |
Площадь полной поверхности параллелепипеда. а,b,c – ребра параллелепипеда |
| 1) Начертите прямоугольный параллелепипед и найдите его объём, площадь основания, площадь боковых граней, а также площадь полной поверхности, если длина 12см, ширина 7см, высота 16см. 2) Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185,37 и 37. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда? |
5) Сколько кубиков войдет в коробку? |
| 3) Дан прямоугольный параллелепипед, стороны основания которого равны 4 и 5, а боковое ребро равно 3. Найдите наибольшую площадь его грани. | 6) Сколько понадобится краски, чтобы покрасить поверхность бруса, длина которого 40 см, ширина 30 см, а высота 20 см, если для покраски 1 дм2 поверхности нужно 2 г краски? |
| 4) Сколько ленты потребуется, чтобы перевязать коробку так, как это изображено на рисунке? На бантик необходимо оставить 2 дм. Ответ дайте в дм. | 7) Деревянный куб покрасили со всех сторон, потом распилили его на 27 одинаковых кубиков. 8) Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см? |
| Формула объема параллелепипеда |
Площадь полной поверхности параллелепипеда. а,b,c – ребра параллелепипеда |
| 1) Начертите прямоугольный параллелепипед и найдите его объём, площадь основания, площадь боковых граней, а также площадь полной поверхности, если длина 12см, ширина 7см, высота 16см. 2) Даны два прямоугольных параллелепипеда: ребра одного равны 185, 185 и 37; а ребра другого равны 185,37 и 37. Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда? |
5) Сколько кубиков войдет в коробку? |
| 3) Дан прямоугольный параллелепипед, стороны основания которого равны 4 и 5, а боковое ребро равно 3. | 6) Сколько понадобится краски, чтобы покрасить поверхность бруса, длина которого 40 см, ширина 30 см, а высота 20 см, если для покраски 1 дм2 поверхности нужно 2 г краски? |
| 4) Сколько ленты потребуется, чтобы перевязать коробку так, как это изображено на рисунке? На бантик необходимо оставить 2 дм. Ответ дайте в дм. | 7) Деревянный куб покрасили со всех сторон, потом распилили его на 27 одинаковых кубиков. Сколько кубиков не окрашено? 8) Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см? |
Разница между площадью и объемом
Площадь и объем
Как мы знаем, геометрия — это изучение форм. Он имеет дело с плоскими формами и твердыми формами. Мы вычисляем различные термины, связанные с формами, такие как длина, ширина, высота, площадь, периметр, объем и т. Д. Площадь и объем — два важных понятия, используемых в нашей повседневной жизни. Мы видим множество форм, таких как квадраты, прямоугольники, круги, многоугольники и т. Д. Каждая форма имеет свои уникальные свойства и размеры. Следовательно, каждая форма имеет разную площадь и объем в зависимости от их размеров.Итак, здесь, на этой странице, мы изучим разницу между площадью и объемом в математике и формулами, связанными с различными формами.
Мы вычисляем различные термины, связанные с формами, такие как длина, ширина, высота, площадь, периметр, объем и т. Д. Площадь и объем — два важных понятия, используемых в нашей повседневной жизни. Мы видим множество форм, таких как квадраты, прямоугольники, круги, многоугольники и т. Д. Каждая форма имеет свои уникальные свойства и размеры. Следовательно, каждая форма имеет разную площадь и объем в зависимости от их размеров.Итак, здесь, на этой странице, мы изучим разницу между площадью и объемом в математике и формулами, связанными с различными формами.
Площадь
Площадь — это размер области, покрытой любыми двухмерными геометрическими фигурами. Площадь любой формы зависит от ее размеров. У разных форм разные области. Например, площадь квадрата отличается от площади прямоугольника. Площадь фигуры рассчитывается в квадратных единицах (квадратных единицах).
Предположим, что если вы хотите покрасить прямоугольную стену своего дома, вам необходимо знать площадь стены, чтобы рассчитать количество краски, необходимое для покраски стены, и стоимость покраски.
Если две фигуры имеют одинаковую форму, не обязательно, чтобы они имели одинаковую площадь, если и до тех пор, пока их размеры не станут равными. Предположим, два квадрата имеют стороны s и s1, поэтому площади двух квадратов будут равны, если s = s1
Объем
Пространство, занимаемое трехмерным объектом, измеряется в единицах объема этого объекта. Объем твердой формы является произведением трех измерений, поэтому объем выражается в кубических единицах. Предположим, что объем куба измеряется произведением его длины, ширины и высоты.
Внутренняя часть полого объекта может быть заполнена воздухом или жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренняя часть объекта, называется емкостью полого объекта. Таким образом, мы можем сказать, что объем объекта — это мера пространства, которое он занимает, а емкость объекта — это объем вещества, которое может вместить его внутреннее пространство.
Определение площади и объема
Площадь относится к области, покрываемой объектом.А объем относится к количеству или вместимости объекта. Область — это двухмерный объект, тогда как объем — трехмерный объект. Площадь представляет собой простую фигуру, а объем — твердую фигуру. Область охватывает внешнее пространство, а объем — внутреннюю емкость. Площадь измеряется в квадратных единицах, а объем измеряется в кубических единицах.
Обычно площадь рассчитывается для двухмерных объектов, а объем рассчитывается для трехмерных объектов.
Вот графическое изображение площади и объема, которое показывает соотношение между площадью и объемом.
[Изображение будет загружено в ближайшее время]
Давайте попробуем подробно разобраться в отношении между площадью и объемом и разницей между площадью и объемом.
Диаграмма формулы площади для 2D-форм
| Название геометрических фигур | Формула площади | Переменные |
| Прямоугольник | Площадь | l = длина w = ширина |
| Квадрат | Площадь = a2 | a = стороны квадрата |
| Треугольник | Площадь = ½ xbxh | b = основание h = высота |
| Трапеция | Площадь = 1/2 (a + b) h | a = основание 1 b = основание 2 h = высота по вертикали |
| Параллелограмм | Площадь = b × h | a = сторона b = основание h = вертикальная высота |
| Ромб | Площадь = axh | a = сторона ромба h = высота |
| Окружность Площадь = πr2 | r = радиус окружности = 22/7 или 3. | |
| Полукруг | Площадь = ½ πr2 | r = радиус окружности |
Диаграмма формулы объема для трехмерных фигур (сплошные формы)
| Название геометрических фигур | Формула объема | Используемые сокращения | |
| Кубоид | L * b * h | h = высота, l = длина = ширина | |
| Куб | a3 | a = длина сторон | |
| Правая призма | Площадь основания × высота | .. | |
| Правый круговой цилиндр | πr2h | r = радиус h = высота | |
| Правая пирамида | ⅓ (Площадь основания) × | (Площадь основания) × | . |
| Правый круговой конус | ⅓ (πr2h) | r = радиус l = длина | |
| Сфера |
4 / 3πr453 r = радиус | ||
| Полусфера | ⅔ (πr3) | r = радиус |
Разница между площадью и объемом
Некоторые ключевые различия между площадью и объемом в математике заключаются в следующем. :
Площадь по сравнению с объемом
| Площадь является мерой площади покрытия d любыми двухмерными геометрическими фигурами. | Объем — это пространство, занимаемое трехмерным объектом. |
| Площадь измеряется для простых фигур | Объем измеряется для трехмерных (сплошных) фигур. |
| Площадь измеряется в двух измерениях, а именно в длине и ширине. | Объем измеряется в трех измерениях: длина, ширина и высота. |
| Площадь измеряется в квадратных единицах | Объем измеряется в кубических единицах. |
| Площадь охватывает внешнее пространство объекта | Объем — это вместимость объекта |
| Пример: квадрат, прямоугольник, круг и т. Д. | Пример: куб, кубоид, сфера и т. д. |
Эти различия показывают соотношение между площадью и объемом. Поскольку теперь разница между площадью и объемом в математике очевидна, давайте решим несколько примеров.
Решенные примеры
Пример 1:
Стороны квадратного участка равны 9 м.Найдите площадь квадратного участка.
Решение:
Дано, Сторона = a = 9м
По формуле площади квадрата мы знаем, что
Площадь = a2
A = 9 x 9
A = 81 кв.м или 81м2
Пример 2: сторона кубической коробки 9 м. Найдите объем кубической коробки.
Решение:
Дано, Сторона = a = 9м
По формуле объема куба мы знаем, что
V = a3
V = 9 x 9 x 9
V = 729 кв.м или 729м2
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько места для упаковки у вас есть при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание к агрегатам
Площадь выражается в квадратных единицах ( 2 ), потому что она измеряется в двух измерениях (например, длина × ширина).
Объем выражается в кубических единицах ( 3 ), потому что он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см. 3 . 1 литр = 1000 мл = 1000 см 3 .
Британская / Британская система
В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Для получения дополнительной информации см. Нашу страницу «Системы измерения».
Основные формулы для расчета объема
Объем прямоугольных тел
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты».Важно то, что три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу, посвященную умножению на ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эту базовую формулу можно расширить, чтобы охватить объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Остерегайтесь несовместимых единиц!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1.7м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного и тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2 см, поэтому радиус 1 см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .
Длина трубы 1,7 м, поэтому нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых единиц! Площадь в сантиметрах, а длина в метрах. Сначала переведите длину в см. 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литрам или 0,0053 м 3 .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет только долю от общего количества, которое было бы, если бы они продолжались. такой же формы (сечения) насквозь.
такой же формы (сечения) насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь формы основания или конца × высота конуса / пирамиды × 1 / 3
Вернитесь к нашей странице Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как 2 x π x радиус.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала проработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3. 14 x 2,5 x 2,5 = 19,63 см 2
14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы составляет 4/3 × π × радиус 3 .
Таким образом, объем сферы составляет:
.4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20. 83 см 3
83 см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двухмерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите многогранники, с которыми вы сможете легко работать.
Рабочий пример
Вычислите объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью (половина сферы).
Сначала вы делите фигуру на две части: цилиндр и полусферу.
Объем сферы составляет 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть имеет полусферическую форму, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.
0,5 × 4/3 × π × 20 3 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дополнительные материалы по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел. Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Различие между площадью и объемом
Площадь
Чтобы узнать, сколько ковра вам нужно, вам нужно найти площадь пола в вашей спальне, а не объем. Площадь — это двумерное измерение поверхности объекта. В нашем случае мы измеряем поверхность пола вашей спальни. Поскольку он двумерный, мы будем использовать только два измерения, чтобы найти площадь.
Допустим, ваша спальня имеет форму прямоугольника. Чтобы найти площадь спальни, вам просто нужно умножить длину комнаты на измерение ширины комнаты. Если ваша комната 25 футов в длину и 18 футов в ширину, просто умножьте 25 футов на 18 футов, чтобы получить площадь 450 футов в квадрате. Это означает, что вашему мужу нужно купить 450 квадратных футов ковра, чтобы покрыть пол в вашей новой спальне.
Это означает, что вашему мужу нужно купить 450 квадратных футов ковра, чтобы покрыть пол в вашей новой спальне.
Что касается площади, то следует отметить, что единицы будут возведены в квадрат. Это потому, что вы всегда будете умножать два измерения вместе. Точно так же, как x , умноженное на x , даст вам x 2, футы, умноженные на футы, дадут вам ft2. Чтобы убедиться, что вы делаете это правильно, убедитесь, что ваши начальные измерения в тех же единицах!
Объем
Ваш глупый муж сначала попросил вас найти объем спальни. Объем — это трехмерное измерение того, сколько места занимает объект. Если бы мы измерили объем вашей спальни, нам потребовалось бы три разных измерения. Мы уже знаем, что длина 25 футов и ширина 18 футов, но нам также нужна высота. Если высота 20 футов, мы можем умножить все три измерения вместе, чтобы получить объем в 9000 футов в кубе. Это означает, что ваша спальня занимает 9000 кубических футов! Бесполезен для коврового покрытия пола.
Это означает, что ваша спальня занимает 9000 кубических футов! Бесполезен для коврового покрытия пола.
Обратите внимание, что единицы измерения объема всегда будут кубическими.Точно так же, как x , умноженное на себя три раза, даст x 3, так и футы, умноженные сами на себя три раза, дадут фут3.
Зависимость площади от объема в кругах и сферах
Давайте посмотрим на некоторые другие формы: круги и сферы. Одно только название подскажет, следует ли рассчитывать объем или площадь объекта. В то время как оба являются круглыми объектами, круг — это двухмерная фигура, а сфера — трехмерная фигура. Если вы держите бейсбольный мяч в реальной жизни, вы держите сферу.Если вы рисуете бейсбольный мяч на листе бумаги, вы рисуете круг.
Поскольку круг двумерный, мы можем вычислить только его площадь. Допустим, у нас есть круг радиусом 4 дюйма. Чтобы найти его площадь, умножим число пи (3,14) на квадрат радиуса. Другими словами, мы умножим 3,14 на 4 дюйма на 4 дюйма. Это даст нам площадь 50,24 дюйма в квадрате.
Чтобы найти его площадь, умножим число пи (3,14) на квадрат радиуса. Другими словами, мы умножим 3,14 на 4 дюйма на 4 дюйма. Это даст нам площадь 50,24 дюйма в квадрате.
Теперь посмотрим на сферу.Скажем, у нас есть сфера с таким же радиусом 4 дюйма. На этот раз мы хотим найти объем, потому что он трехмерный. Для этого умножим 4/3 на число пи (3.14) на радиус в кубе. Другими словами, у нас есть 4/3 x 3,14 x 4 дюйма x 4 дюйма x 4 дюйма. Это дает нам объем 267,95 дюйма в кубе (округленный до ближайшей десятой).
Краткое содержание урока
Площадь и объем НЕ взаимозаменяемы. Область относится к двумерному измерению поверхности объекта, а объем относится к трехмерному пространственному измерению объекта.Единицы всегда будут возведены в квадрат для площади, а единицы всегда будут в кубе для объема.
Как найти объем и площадь поверхности для 6 общих форм
Наш мир наполнен трехмерными объектами. Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей базовой, верхней и боковых поверхностей (сторон) объекта.Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей базовой, верхней и боковых поверхностей (сторон) объекта.Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Объем — это объем пространства, который занимает трехмерный объект. Также существуют разные формулы для разных трехмерных форм. Общий объем объекта измеряется в кубических единицах.
Общие формулы для объема и площади поверхности
У нас есть для вас шпаргалка — формулы объема и площади поверхности для обычных форм. Использовать его с умом!
Формулы площади поверхности
Площадь поверхности куба составляет 6s² , где s — длина стороны.
Площадь поверхности прямоугольной призмы составляет 2 (wl + hl + hw) , где w — ширина, h — высота, l — длина.
Площадь поверхности сферы составляет 4πr² , где r — радиус сферы.
Площадь поверхности цилиндра составляет 2πrh + 2πr² , где r — радиус цилиндра, а высота — высота.
Площадь поверхности конуса составляет πrs + πr² , где r — радиус конуса, а s — наклон.
Формулы объема
Объем куба s³ , где s — длина стороны.
Объем прямоугольной призмы равен wlh , где w — ширина, h — высота, l — длина.
Объем сферы равен ( 4πr³ ) /3 , где r — радиус сферы.
Объем цилиндра составляет πr²h , где r — радиус цилиндра, а высота — высота.
Объем конуса равен (πr²h) / 3 , где r — радиус конуса, а s — наклон.
Пример расчета объема и площади поверхности
Чтобы найти участки поверхности объектов с криволинейной поверхностью, таких как сфера, нет другого выбора, кроме как запомнить формулы объема и площади поверхности. Но что касается других объектов, мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, с пирамидой вы просто вычисляете площадь основания и добавляете ее к площади каждой стороны треугольника.
Но что касается других объектов, мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, с пирамидой вы просто вычисляете площадь основания и добавляете ее к площади каждой стороны треугольника.
Давайте найдем площадь поверхности и объем квадратной пирамиды с длиной основания 6 дюймов и наклонной высотой 5 дюймов.
Площадь квадратной пирамиды
- Чтобы найти общую площадь поверхности, сначала исследуем площадь основания, которая представляет собой просто квадрат. Мы знаем, что площадь квадрата составляет b² , где b — длина стороны. В данном случае площадь поверхности составляет 6² или 36 квадратных дюймов.
- Затем мы смотрим на четыре стороны, которые представляют собой просто треугольники.Мы знаем, что площадь треугольника составляет всего (bh) / 2 , где b — основание, а h — высота. В этом случае основание треугольника совпадает с основанием пирамиды b.
 Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна:
Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна:
- Когда мы сложим четыре из этих треугольников с площадью квадратного основания, мы получим общую площадь поверхности b² + 4 (bs) / 2, или b² + 2bs для квадратной пирамиды.Подсчитывая числа, мы получаем:
Объем квадратной пирамиды
Объем пирамиды соответствует этой формуле объема:
Мы можем подставить наши значения для высоты и основания, чтобы получить:
Распознавание объема и площади поверхности
Опять же, площадь поверхности измеряет общую площадь внешних поверхностей объекта, а объем измеряет внутреннее пространство, которое занимает объект.
Вы найдете много реальных случаев, когда расчет площади поверхности или объема будет полезен, например, количество воды, необходимое для наполнения бассейна (прямоугольная призма), или количество оберточной бумаги, необходимое для обертывания. свеча (цилиндр) или баскетбольный мяч (шар).Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
свеча (цилиндр) или баскетбольный мяч (шар).Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Дополнительные домашние задания по математике
В чем разница между периметром, площадью и объемом?
Чем объем отличается от периметра и площади?
Периметр формы представляет собой расстояние вокруг нее, область формы — это поверхность или плоское пространство, которое охватывает форма (в 2D), а объем формы — это пространство, которое она занимает в реальном жизнь (в 3D).
Чтобы понять разницу между периметром, площадью и объемом, давайте подробно определим каждый из них:
Определение периметра
Периметр фигуры — это общая длина фигуры, также известная как сумма длин всех ее сторон. Периметр измеряется путем сложения длин его многочисленных сторон. Например, если мы хотим вычислить периметр прямоугольника, мы должны начать с сложения длин его четырех сторон. Поскольку параллельные стороны прямоугольника всегда равны, вам нужно найти только длину двух сторон.
Например, если мы хотим вычислить периметр прямоугольника, мы должны начать с сложения длин его четырех сторон. Поскольку параллельные стороны прямоугольника всегда равны, вам нужно найти только длину двух сторон.
Определение площади
Область формы — это объем пространства внутри ее сторон или краев (т. Е. Размер плоской замкнутой поверхности, которую покрывает форма). Площадь измеряется в квадратных единицах и обычно рассчитывается путем умножения длины фигуры на ее ширину. Однако в зависимости от разных многоугольников он может иметь разные формулы.
Например, если мы хотим вычислить площадь квадрата, нам нужно умножить его длину на ширину.Поскольку стороны квадрата равны, нам нужно умножить размер одной стороны на себя.
Определение объема
Объем фигуры — это объем трехмерного пространства, которое занимает фигура. Объем измеряется в кубических единицах, так как он рассчитывается путем умножения площади фигуры на ее высоту. Поскольку высота всегда измеряется в обычных единицах (метры, сантиметры…), а площадь — в квадратных единицах (квадратные метры, квадратные сантиметры…), объем указывается в кубических единицах (кубических метрах, кубических сантиметрах…).
Поскольку высота всегда измеряется в обычных единицах (метры, сантиметры…), а площадь — в квадратных единицах (квадратные метры, квадратные сантиметры…), объем указывается в кубических единицах (кубических метрах, кубических сантиметрах…).
Например, если мы хотим рассчитать объем цилиндра, мы должны умножить площадь основания (в данном случае площадь одного из кругов) на высоту цилиндра. Высота цилиндра — это расстояние между двумя окружностями, а площадь либо задана, либо должна быть рассчитана.
Как найти периметр геометрической формы?
Чтобы вычислить периметр геометрической фигуры, вам нужно сложить длину всех ее сторон.Если у нас есть прямоугольник длиной a и шириной b , формула для периметра P будет:
P = a + a + b + b
А поскольку у прямоугольника две параллельные стороны, формула принимает вид
P = 2a + 2b
Р = 2 (а + б)
Пример 1
Длина и ширина прямоугольника 8 см и 3 см соответственно.
Периметр этого прямоугольника равен P = 8 + 8 + 3 + 3 = 2 x (8 + 3) = 22 см
Теперь предположим, что у нас есть квадрат.Формула для периметра P этого квадрата:
P = а + а + а + а
P = 4a
Пример 2
Стороны квадрата равны 7 см.
Периметр этого квадрата равен P = 7 + 7 + 7 + 7 = 4 x 7 = 28 см
Как найти площадь геометрической фигуры?
Чтобы вычислить площадь геометрической фигуры, нужно умножить ее длину на ширину. Во избежание путаницы возьмем те же цифры:
Если у нас есть прямоугольник длиной a и шириной b , формула для площади A этого прямоугольника будет:
A = a x b
Пример 1
Высота прямоугольника 12 см, ширина 5 см.
Площадь прямоугольника A = 12 x 5 = 60 см 2
P.S: Не забудьте добавить квадрат ( 2 ) при вычислении площади.
Теперь предположим, что мы хотим вычислить площадь квадрата, формула для площади A :
A = a x a
A = 2
Пример 2
Стороны квадрата, которые мы хотим изучить, равны 9 см каждая.
Следовательно, площадь квадрата A = 9 x 9 = 92 = 81 см 2
Как найти объем геометрической фигуры?
Переходим к объему. Чтобы рассчитать объем геометрической фигуры, вам нужно умножить площадь фигуры на ее высоту.
Чтобы проиллюстрировать это, мы будем придерживаться тех же цифр и вычислить объем правой прямоугольной призмы и куба. Мы также собираемся рассчитать объем цилиндра, чтобы еще больше уточнить формулу:
— Для правого прямоугольного твердого тела, где задана площадь A и высота h , формула для вычисления объема V :
V = A x h
Пример 1
Площадь и высота правой прямоугольной призмы 38 см2 и 6 см соответственно.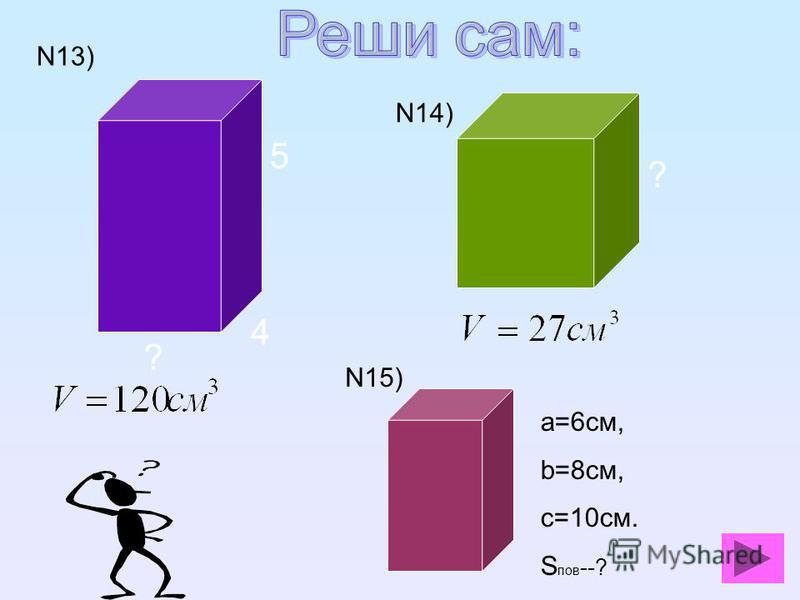
Объем этого прямоугольного тела составляет V = 38 x 6 = 228 см 3
P.S: Не забудьте добавить кубические единицы ( 3 ) при расчете объема.
Для куба это немного особенное. Если площадь равна A и высота h , формула для объема куба V будет:
V = A x h
Но поскольку это куб, стороны равны его высоте, поэтому площадь равна b 2 .Таким образом, формула для объема куба V может быть выражена следующим образом:
V = b 2 x b
V = b 3
Пример 2
У куба есть стороны по 12 см каждая.
Объем этого куба V = 123 = 1728 см 3
Для цилиндра, предположим, что дана площадь A круга, а также его высота h .Формула объема V цилиндра:
V = A x h
Если площадь не указана, мы должны сначала рассчитать ее.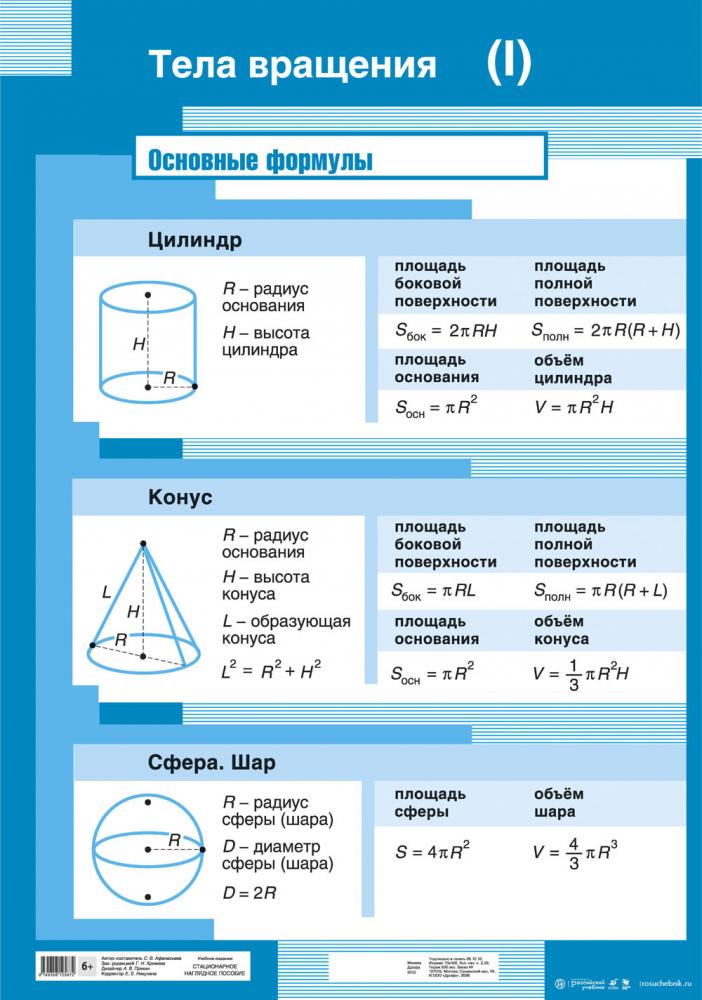 Таким образом, формула принимает следующий вид:
Таким образом, формула принимает следующий вид:
V = A x h
V = π x r² x h
… где r — радиус окружности.
Пример 3
Наш цилиндр имеет высоту 9 см и радиус окружности 4 см.
Чтобы найти объем этого цилиндра, мы должны сначала найти площадь, которая в этом примере равна:
A = π x r² = 3,14 x 4² = 50,24 см2
Теперь мы можем рассчитать объем цилиндра:
V = A x h = 50,24 x 9 = 452,16 см 3
P.S: Имейте в виду, что числа, указанные во всех этих примерах, были в одних и тех же единицах, поэтому, если бы они не были другими, было бы важно их преобразовать.
Площадь и объем
Периметр
Периметр = расстояние по краю.
Можно было пройтись по периметру.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте cm с m.
Периметр состоит из простых блоков.
Пример
П = 5 + 2 + 2 + 3 + 9 + 3 + 2 + 2 см
P = 28 см
Площадь
Площадь = покрытая площадь
Вы можете закрасить область.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивать см, 2 с м 2
1 м 2 = 100 см x 100 см
= 10000 см 2
Площадь насчитывает
2 единиц.
Площадь квадрата
Пример
Посчитаем площадь квадрата
Площадь прямоугольника
Примеры
Вычислить площадь прямоугольников
Площадь треугольника
Площадь треугольника = ½ x основание x высота перпендикуляра
Примеры
Найдите площадь треугольника ниже:
Какая длина основания треугольник, если он имеет площадь 45 см 2 ?
Площадь круга
Площадь воздушного змея
Пример
Рассчитайте площадь следующего воздушного змея:
Площадь трапеции
Площадь трапеции = ½ x среднее значение основания x высота перпендикуляра
Пример
Какова площадь этой трапеции?
(Каждый квадрат соответствует 1 см 2 )
Площадь параллелограмма
Пример
Вычислить площадь параллелограмма:
Площадь ромба
Пример
Посчитаем площадь ромба:
(Размеры указаны по полной диагонали)
Объем
Объем = вместимость
Вы можете заполнить том
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте cm с m.
Объем в единицах
3Обратите внимание, что для кубоида
Пример
Рассчитайте объем кубоида ниже:
Пример
Преобразование 1 м 3 в
литров
Сначала преобразуйте единицы
Но 1 см 3 = 1 мл и 1000 мл = 1 литр
Для литров разделите 3 на 1000.
Так 1000000 см 3 = 1000 литров
1 м 3 = 1000 литров
Объем сферы
Сфера имеет объем
Где r — радиус сферы.
Примеры
Вычислите объем следующей сферы.
Дайте правильный ответ на 1 dp, а также на 2 sig.
Вычислите объем следующей сферы.
Дайте правильный ответ на 1 сигн. Рис.
Вычислите диаметр сферы объемом 700 см 3 .
Дайте правильный ответ с точностью до 1 дп.
Объем конуса
Конус имеет объем
Где r — радиус круговой части конуса, а h — высота перпендикуляра конуса.
Пример
Вычислите объем рожка мороженого диаметром 4 см и высотой 6 см. Дайте правильный ответ с точностью до 1 дп.
Сколько таких рожков можно налить из 1 литра мороженого?
1000 см 3 = 1 л
1000 ÷ 25,1 = 39,84
Таким образом, из одного литра мороженого можно наполнить 39 рожков.
Пример
Вычислите высоту рожка мороженого диаметром 4 см и объемом 35 мл.Дайте правильный ответ с точностью до 1 дп.
Высота конуса 8,4 см.
Пример
Рассчитайте диаметр рожка мороженого высотой 8 см и объемом 90 мл. Дайте правильный ответ с точностью до 1 дп.
Объем призмы
Для призмы V = Ah
Таким образом, объем = площадь x высота (или площадь x длина в положении лежа)
Пример
Каков объем призмы? площадью 37 см 2 а высотой 4 см?
Объем цилиндра
Цилиндр представляет собой круговую призму,
Пример
Вычислите объем консервной банки высотой 0. 8м и диаметром 10 см. Дайте свой правильный ответ на 1 сигфиг.
8м и диаметром 10 см. Дайте свой правильный ответ на 1 сигфиг.
Пример
Вычислите диаметр консервной банки высотой 8 см и объемом 90 мл. Дайте правильный ответ с точностью до 1 дп.
Объем пирамиды
Объем любой пирамиды равен
.
где A — площадь основания пирамиды, а h — ее высота.
Примеры
Каков объем этой квадратной пирамиды?
Каков объем этой прямоугольной пирамиды?
Каков объем этой треугольной пирамиды?
Площадь
Площадь — это общая внешняя площадь
формы.
Пример
Найдите площадь поверхности кубоида:
У этой формы 6 граней
2 грани размером 6 см x 4 см
2 лица имеют площадь 6 см x 2 см
2 лица имеют площадь 2 см x 4 см
2 x 6 см x 4 см = 48 см 2
2 x 6 см x 2 см = 24 см 2
2 x 2 см x 4 см = 16 см 2
Площадь поверхности = 88 см 2
Площадь ≠ Объем
Составная область
Нарезайте удобные формы
Найти недостающие размеры
Рассчитать отдельные площади
Подсчитать итого
Помните
все размеры должны иметь одинаковые единицы измерения!
Пример
Форма = A 1 + A 2
A 1 = 5×2 = 10 см 2
A 2 = 3×9 = 27 см 2
Форма = 37 см 2
Составной том
Нарезайте удобные формы
Найти недостающие размеры
Рассчитать отдельные площади
Подсчитать итого
Пример
© Александр Форрест
Узнайте об объеме и площади поверхности
Из этого видео вы узнаете, как рассчитать объем и площадь поверхности выбранных твердых фигур, таких как призма, сфера, конус, цилиндр и пирамида.
Объем трехмерной фигуры — это объем места, который она занимает.
Боковая область трехмерной фигуры — это сумма самых внешних слоев фигуры, за исключением оснований.
Площадь поверхности трехмерной фигуры — это сумма самых внешних слоев фигуры.
Призма
Объем:
Боковая площадь:
Площадь поверхности:
Пирамида
Объем:
Боковая площадь:
Площадь поверхности:
Цилиндр
Объем:
Боковая площадь:
Площадь поверхности:
Правый круговой конус
Объем:
Боковая площадь:
Площадь поверхности:
Сфера
Объем:
Боковая площадь:
Площадь поверхности:
Стенограмма видеоурока
В этом уроке мы рассмотрим формулы для вычисления объема и площади поверхности.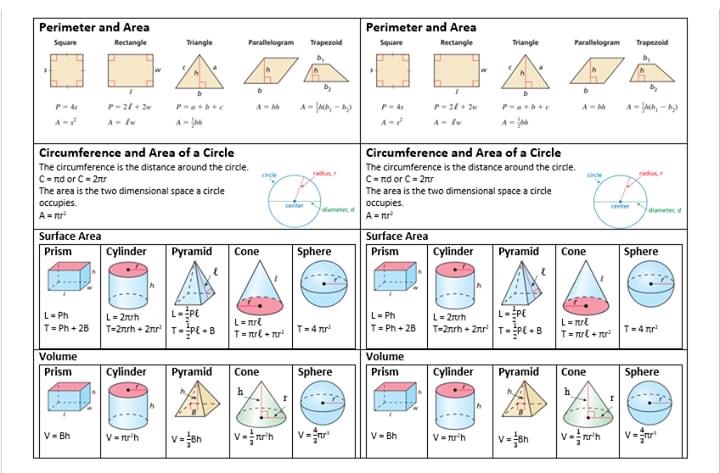
У нас есть сплошная фигура, формула для объема и формула для площади поверхности или площади
Начнем с призмы.
Призма может быть, например, прямоугольной. Где верх и низ одинаковы и вытянуты по вертикали. Нижняя часть представляет собой прямоугольник, а верхняя часть также является прямоугольником. Куб — это тоже призма. У нас есть квадрат со всех шести сторон. У нас также может быть треугольная призма. Верх и низ представляют собой треугольник, а вертикальные линии продолжаются вверх.
Объем
где площадь основания, нам просто нужно узнать, какова площадь основания, а затем умножить ее на высоту.
Для куба мы должны узнать, какова площадь основного квадрата, умноженная на его высоту.
И для этого треугольника мы должны найти площадь основного треугольника, умноженную на его высоту.
Это определение объема призмы.
Что такое боковая область?
Боковая часть — это площадь сторон.
Область передней, задней, левой и правой сторон. Мы должны найти всю боковую область.
Мы должны найти всю боковую область.
Чтобы найти боковую площадь вокруг него, вам просто нужно умножить высоту на периметр.
Надо узнать периметр базы. Для этого нам просто нужно сложить длину, умноженную на ее высоту.
Нам нужно найти общую площадь поверхности, мы должны найти площадь верхней и нижней части и прибавить ее к общей боковой площади.
Теперь давайте посмотрим на объем и площадь поверхности пирамиды.
Пирамида имеет квадратное основание и простирается до точки над ним. Выглядит это примерно так.
У нас квадрат или прямоугольник с основанием, а все стороны — треугольники.
Формула объема пирамиды
где — площадь основания, в данном случае основание — квадрат.
Итак, мы должны вычислить площадь квадрата, умножив ее на его высоту.
Высота от низа до наивысшей точки; если вы внутри, то она идет прямо вниз и будет под прямым углом к основанию.
Для расчета боковой площади пирамиды:
P — периметр основания.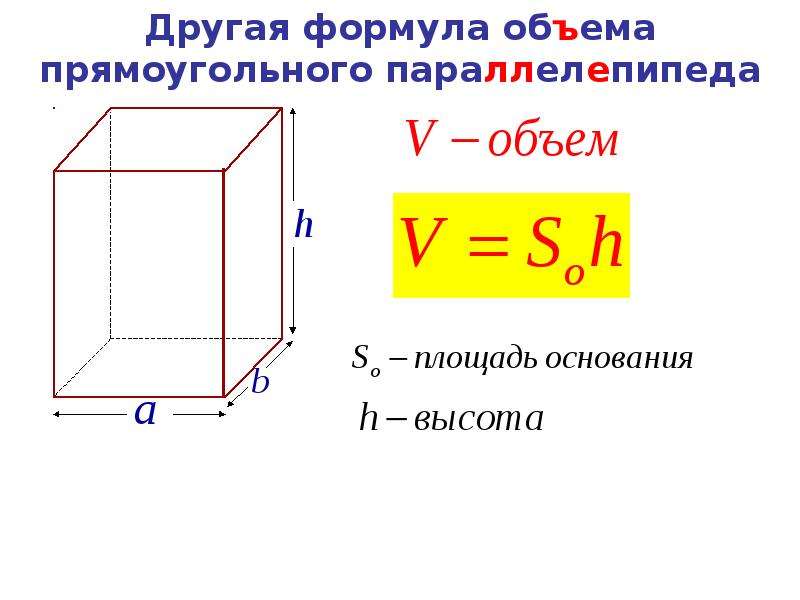
В данном случае это квадрат. Просто сложите все стороны, умножьте его на высоту, и вы получите боковую площадь.
Боковая площадь — это площадь сторон. Исключает площадь основания. Вот почему нам нужно найти площадь квадратного основания и добавить ее.
Теперь посмотрим на цилиндр.
Цилиндр имеет круглую верхнюю и нижнюю части, как у банки, и имеет высоту.
Объем
очень похож на призму.
Здесь основание — круг.
Мы должны найти площадь круга, который есть.
Наша формула сейчас
Боковая зона
Вот формула длины окружности.
У нас есть расстояние от основания круга, умноженное на его высоту.
По сравнению с формулой призмы, где высота умножается на периметр, здесь высота умножается на длину окружности.
Боковое пространство — это область вокруг цилиндра.Но здесь нет верха и низа. Если бы нам нужно было найти общую площадь поверхности цилиндра, нам нужно было бы вычислить площадь верха и низа, а затем добавить их.
Итак, общая площадь поверхности в данном случае составляет
., включая верх и низ.
Общая боковая площадь идет только по бокам.
Теперь пройдемся по правому круговому конусу.
Основание правильного кругового конуса — круг. Затем он поднимается до точки или до вершины.
Объем
где — площадь основания, а — высота, рассчитанная от самого верха до низа.
Основание — круг, поэтому
Наша формула объема теперь
Теперь посмотрим на боковую часть.
Боковая площадь
где — длина стороны конуса.
Это правильный круговой конус, поэтому, если мы проведем высоту посередине и продлим радиус до этой точки, мы получим прямой угол.
Итак, у нас получился прямоугольный треугольник с высотой и радиусом.
Теперь, когда у нас есть прямоугольный треугольник, мы можем найти длину, если она не задана с помощью теоремы Пифагора.
Мы делаем.
Боковая область даст нам область вокруг конуса, но не будет включать нижнюю часть конуса.
Если нам нужна общая площадь поверхности, включая базовый круг, мы должны сделать боковую площадь плюс площадь базового круга.
Обсудим объем и площадь поверхности сферы.
Сфера похожа на шар или мрамор. Это круглая трехмерная фигура.
Объем шара
, а площадь —
Радиус идет от центра к краю.
Если вы делаете кожаный баскетбольный мяч, то можете подумать о площади поверхности. Вы можете использовать площадь поверхности, чтобы определить, сколько кожи вам понадобится для изготовления мяча. Какой площади вам понадобится, чтобы сделать мяч.
Хорошая особенность ближневосточных любительских регионов заключается в том, что вам даются формулы.От вас не требуется запоминать каждую формулу из этого списка.
Они фактически дают вам формулу объема пирамиды, но не формулу поперечной площади.
Кроме того, они дают вам формулу для объема и поперечной площади цилиндра.
Они дают вам формулу для объема и поперечной площади правильного кругового конуса.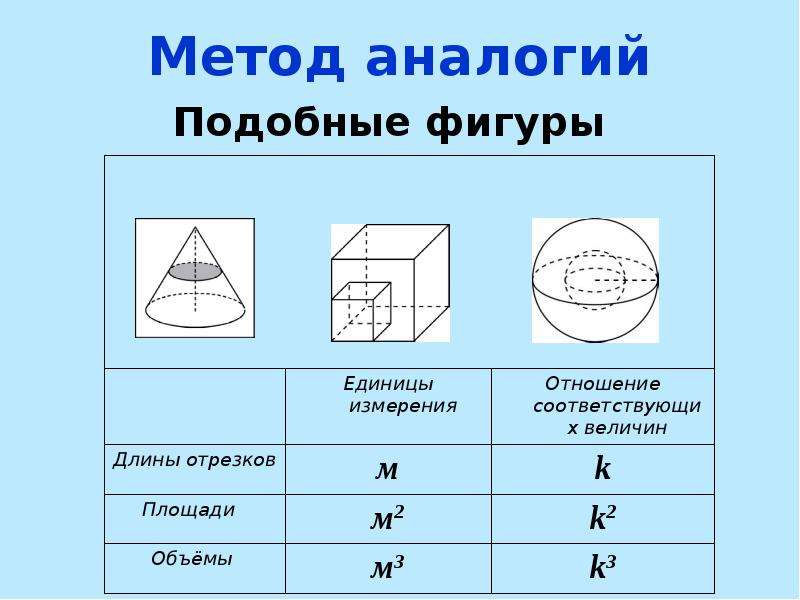

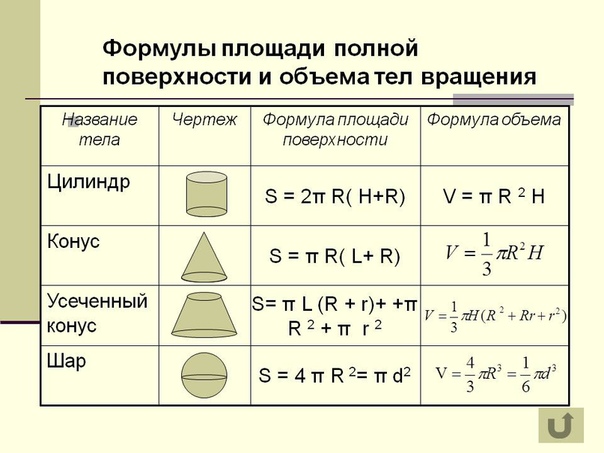
 п.)
п.)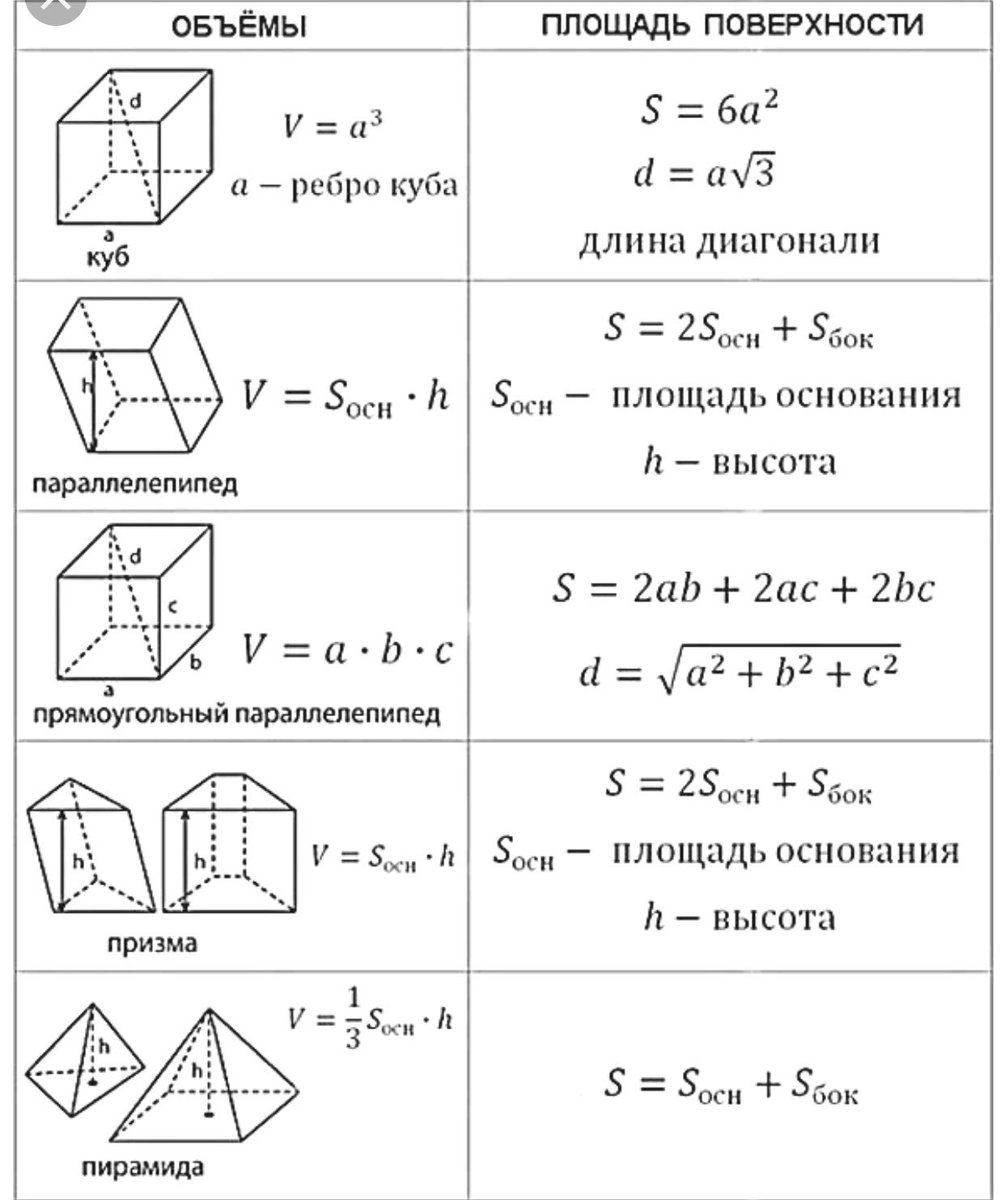 п. = 2 (ac + bc)
п. = 2 (ac + bc)
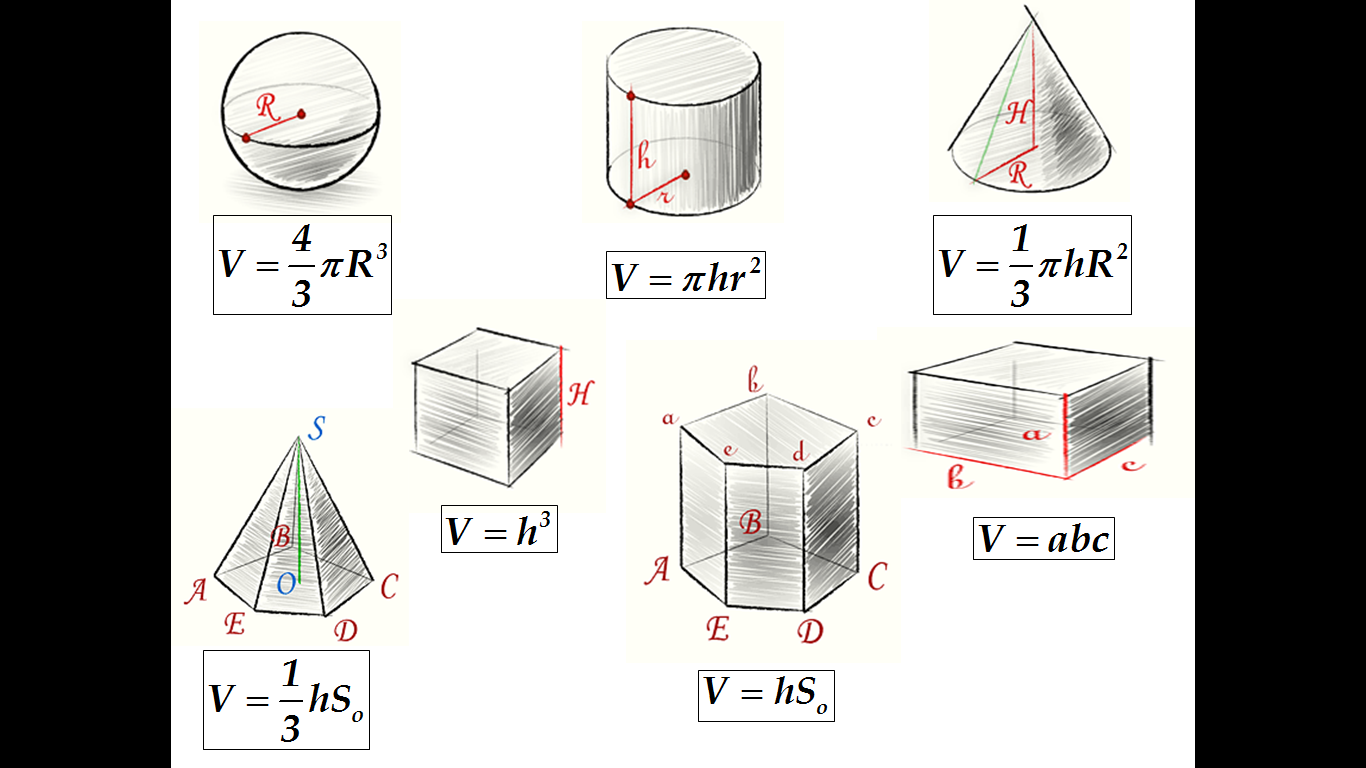
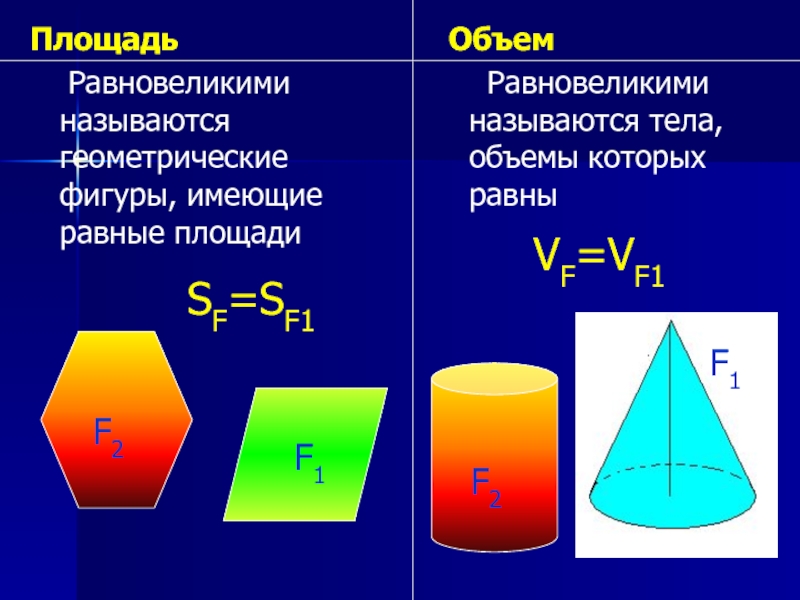 Сколько кубиков не окрашено?
Сколько кубиков не окрашено?  Найдите наибольшую площадь его грани.
Найдите наибольшую площадь его грани. 1416
1416 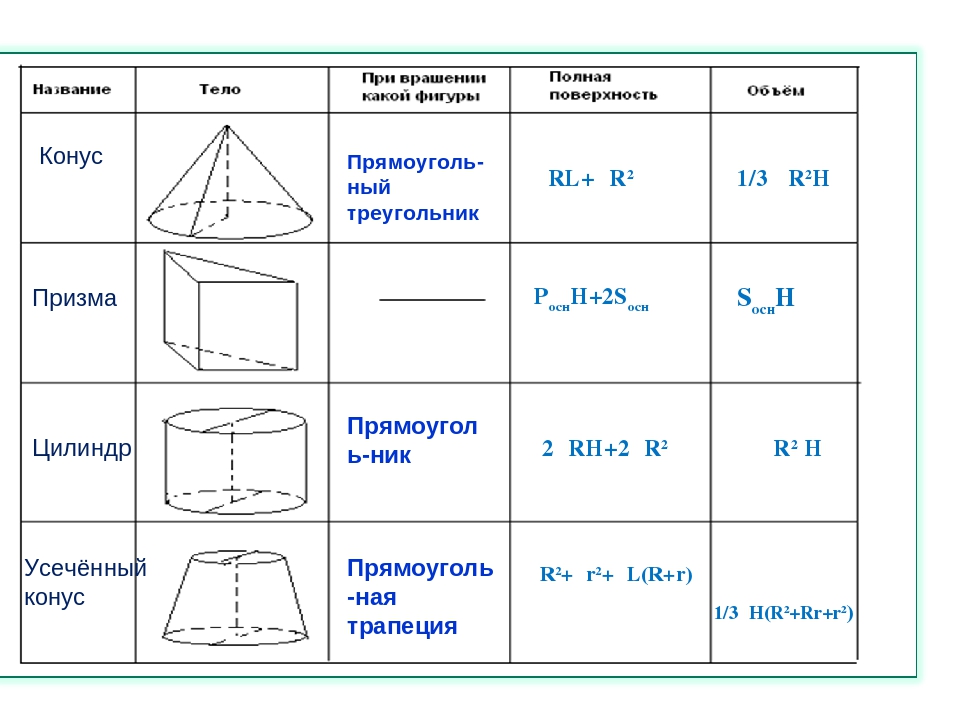 .
.