Конспект по физике механика: Механика. Конспекты по физике 10-11 класс. Гравитация - Управленческое образование

Содержание

Механика. Конспекты по физике 10-11 класс. Гравитация

Подробности: Просмотров: 447

Здесь представлены конспекты по теме «Механика» для 10-11 классов.
!!! Конспекты с одинаковыми названиями различаются по степени сложности.

1. Гидростатика ( повторение 7-8 класса) …….. смотреть

2. Гидростатика и гидродинамика ……… смотреть

3. Законы Ньютона — Механика ……… смотреть

4. Законы сохранения в механике — Механика ……… смотреть

5. Законы сохранения в механике — Механика ……… смотреть

6. Кинематика материальной точки — Механика ……… смотреть

7. Кинематика материальной точки — Механика ……… смотреть

8. Механические колебания ……… смотреть

9. Механические колебания ……… смотреть

10.

Основные понятия кинематики (повторение 8-9 класса) ……… смотреть

11. Основные понятия кинематики ……… смотреть

12. Работа и энергия ……… смотреть

13. Работа и энергия ……… смотреть

14. Силы в механике ……… смотреть

15. Силы в механике ……… смотреть

16. Статика …….. смотреть

Дополнительные конспекты по физике 10-11 класс — Класс!ная физика

Механика — Электродинамика — Термодинамика — Оптика — Квантовая механика
— Астрономия

Знаете ли вы?

Знаете ли Вы, что Кеплер задолго до Ньютона склонялся к мысли о «тяжести», действующей между небесными телами, и именно ею объяснил приливы, приписывая их притяжению вод океана Луной.

… до сих пор существуют сомнения в реальности опытов Галилея по бросанию тел с вершины Пизанской падающей башни. Однако известно, что еще при его жизни эту башню использовал один из сторонников Аристотеля для демонстрации различия в падении тел.

Как бы то ни было, Галилею удалось установить независимость ускорения свободного падения от природы падающих тел.

… по Аристотелю, сила тяготения по мере приближения к центру Земли сохраняет численное значение, но при его прохождении скачком изменяет направление на противоположное. Именно так описывал Данте свое путешествие через самое глубокое место ада (центр Земли). По теории же Ньютона, сила притяжения должна там обратиться в ноль, поскольку им было показано, что помещенное в тонкую сферическую оболочку тело не испытывает на себе действия сил.

… почти 200 лет назад, в 1801 году, немецкий астроном И.Зольднер рассчитал, опираясь на теорию Ньютона, как должны отклоняться световые лучи в поле тяготения Солнца. Более чем через 100 лет английский астроном О.Лодж ввел термин «гравитационная линза», предсказав, что протяженные космические тела, например галактики, отклоняя лучи от далеких объектов, могут создавать несколько их изображений. В 1979 году такая «линза» была впервые обнаружена.

… на поверхности внутренних спутников Юпитера кратеров намного меньше, чем на поверхности внешних. Объясняется это тем, что из-за приливного влияния и магнитного поля гигантской планеты у ближайших спутников выше тектоническая активность, поэтому их поверхность активно «перерабатывается» и старые кратеры исчезают.

… несмотря на то, что на Землю ежесуточно выпадает примерно десять тысяч тонн космического вещества в виде метеоритов и пыли, такой прирост массы за все время эволюции нашей планеты практически не отразился на периоде ее оборота вокруг своей оси.

… под действием приливного «трения» Земля замедляет свое суточное вращение и через миллиарды лет будет смотреть на Луну все время одной стороной, как смотрит Плутон на свой спутник Харон. Луна к тому времени уйдет, по расчетам, на 553 тысячи километров от Земли, а новый месяц станет равным 47,2 суток.

Источник: журнал «Квант»

ГДЗ конспекты по физике 7 класс Задание: Механическое движение Равномерное и неравномерное движение

Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)

Вид УМК: конспекты

Серия: Краткое содержание параграфов учебника для устного ответа

На данной странице представлено детальное решение задания Механическое движение. Равномерное и неравномерное движение по физике для учеников 7 классa автор(ы)

Механическое движение. Равномерное и неравномерное движение

Механика – это раздел физики, который изучает движение и взаимодействие тел.

Тело отсчёта – это тело, относительно которого рассматривается движение.

Материальная точка – это тело, размерами которого можно пренебречь в условиях данной задачи.

Механическое движение – это изменение положения тела относительно других тел с течением времени.

Траектория – это линия, вдоль которой движется тело.

Путь – это длина траектории.

S – путь

[S] = м

1 мм = 0,001 м

1 см = 0,01 м

1 дм = 0,1 м

1 км = 1000 м

Равномерное движение – тело за любые равные промежутки времени проходит равные пути.

Неравномерное движение – если тело за равные промежутки времени проходит разные пути.

Скорость тела при равномерном движении

– это величина, равная отношению пути ко времени, за которое этот путь пройден.

V – скорость

S – путь, м

t – время, с

Скорость = $\frac{Путь}{Время}$

[V] = $\frac{м}{с}$

Например:

54 $\frac{км}{ч}$ = $\frac{54\ \bullet 1000\ м}{3600\ с}$ = 15 $\frac{м}{с}$

Чтобы перевести скорость из $\frac{км}{ч}$ в $\frac{м}{с}$ , необходимо её умножить на 1000 и разделить на 3600.

Чтобы перевести скорость из $\frac{м}{с}$ в $\frac{км}{ч}$ , нужно её умножить на 3600 и разделить на 1000. Или умножить на 3,6.

20 $\frac{м}{с}$ = $\frac{20\ \bullet 3600}{1000}$ = 72 $\frac{км}{ч}$

3 м/с = 3 • 3,6 = 10,8 км/ч

Рис. 1. ГДЗ конспекты по физике 7 класс Задание: Механическое движение Равномерное и неравномерное движение

Add

Новыe решебники

План-конспект урока по физике по теме: Кинематика материальной точки ❤️

Положение точки в пространстве

Цель урока: объяснить, что такое кинематика, какая задача является основной для кинематики, как находить в пространстве координаты материальной точки, повторить действия над векторами.

Ход урока

1. Повторение домашнего задания

А) Что изучает физика?

Б) В чем заключается научный метод познания?

В) Зачем нужна физическая величина? Назовите известные физические величины. В каких единицах измеряются эти величины?

Г) Какие существуют

физические теории?

Д) Какова роль физики в научно – техническом прогрессе?

Е) Что изучает механика?

Ж) Что понимают под относительностью движения?

З) Приведите примеры относительности механического движения.

И) Какие движения подчиняются законам Ньютона?

2. Изучение нового материала

А) Основные понятия кинематики.

Кинематика – это часть механики, которая изучает способы описания движений без учета сил, вызывающих эти движения.

Существуют два способа описания движения тела : 1. движение некоторой точки движущегося тела; 2. движение тела с помощью модели материальной

точки.

Обсуждение вопросов

— Что называется материальной точкой?

— При каких условиях реальное тело можно заменить (мысленно) материальной точкой?

— Является ли материальной точкой снаряд;

А) при определении пройденного снарядом пути?

Б) при расчете формы снаряда, когда его обрабатывают на станке, чтобы он имел наименьшее сопротивление при движении в воздухе.

3. Самостоятельная работа

Укажите, в каких из приведенных ниже случаев, исследуемое тело считается материальной точкой?

А) Определяют давление автомобиля на грунт.

Б) Вычисляют высоту полета искусственного спутника Земли.

В) Измеряют работу, совершенную при поднятии, подъемным краном, поддона с кирпичами определенной массы на высоту 5 этажа.

Г) Пользуясь мензуркой, определяют объем стеклянного шарика.

Д) Рассчитывают путь, пройденный железнодорожным составом длиной 1км за несколько секунд.

Е) Определяют скорость движения Земли по орбите вокруг Солнца.

4. Определение положения точки в пространстве

Беседа с учащимися по вопросам:

— Почему для описания движения тела необходимо выделить особую точку — тело отсчета?

— Можно ли тело отсчета выбрать произвольно?

— Изменится ли положение тела в пространстве, если заменить одно тело отсчета на другое?

— Какие системы координат вам знакомы?

— Что называется системой отсчета?

5, Решение упражнений

А) Изобразите положение точки а и b на плоскости, если координаты точки А равны: х1=2м; у1=4м, координаты точки В равны х2= — 3м; у2= — 2м. ¯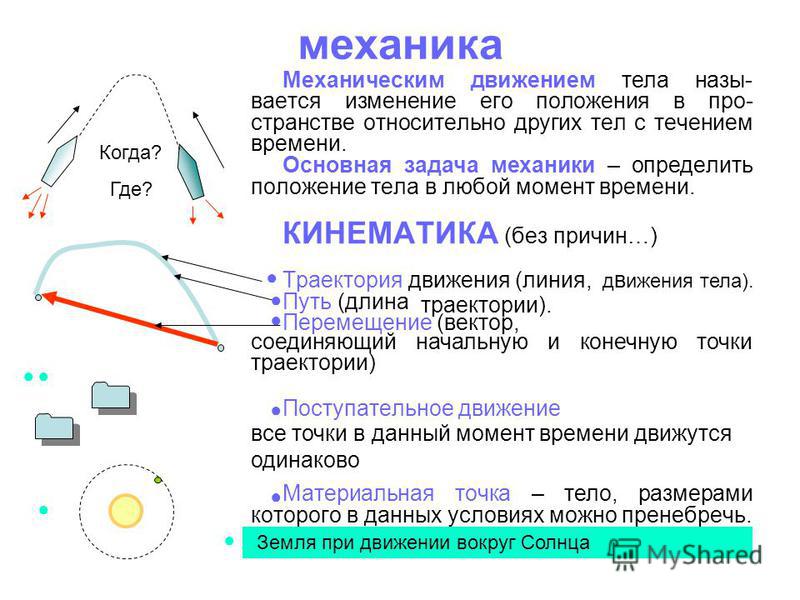

Б) Изобразите положение точки а в пространстве, если её координаты равны: х1=2м, у1=3м, z1=4м. X

Y 6. Итоги урока Y

7. Домашнее задание: § 3 — 6 Z

Механическое движение и его виды. Основная задача механики и способы ее решения в кинематике. Физическое тело и материальная точка. Система отсчета — КИНЕМАТИКА — Уроки физики в 10 классе — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике

КИНЕМАТИКА

Урок № 1

Тема. Механическое движение и его виды. Основная задача механики и способы ее решения в кинематике. Физическое тело и материальная точка. Система отсчета

Цель: охарактеризовать задачи изучения раздела «Кинематика», ознакомить со структурой учебника; дать представление о механическое движение, основную задачу механики и способы ее решения в кинематике; сформировать понятие поступательного движения тел, материальной точки, системы отсчета; показать роль знаний по механике в других науках, в технике; показать, что механическое движение — одна из форм существования материи, один из многочисленных видов изменений в природе, а материальная точка — модель, идеальный объект классической механики.

Тип урока: урок изучения нового учебного материала.

Наглядный: демонстрация поступательного движения тела, случаев, когда тело можно (и не можно) считать материальной точкой, ППС «Физика-9» от «Квазар-Микро».

Ожидаемые результаты. После урока учащиеся:

— различат физическое тело и материальную точку, прямолинейное и криволинейное движение материальной точки;

— смогут обосновать содержание основной (прямой) задачи механики;

— научатся объяснять суть физических идеализаций — материальной точки и системы отсчета.

ХОД УРОКА

И. Организационный момент

Краткая информация о содержании и основные задачи раздела «Кинематика».

II. Объявление темы и цели урока

Формирование новых понятий. Во время беседы с применением демонстрационного эксперимента и ППС «Физика-9» от «Квазар-Микро» рассмотреть следующие вопросы:

• механическое движение и его виды;

• основная задача механики и способы ее решения в кинематике;

• что изучает кинематика;

• физическое тело и материальная точка, система отсчета.

1. Механическое движение

Мы часто называем одни тела подвижными, другие неподвижными.

Деревья, различные здания, мосты, берега рек — неподвижные. Вода в реке, самолеты в небе, автомобили, едущие по дороге, — подвижные.

Что дает нам основание разделять тела на подвижные и неподвижные? Чем они отличаются друг от друга?

Когда мы говорим об автомобиле, который движется, то имеем в виду, что в определенный момент времени он был рядом с нами, а в другие моменты расстояние между нами и автомобилем менялась. Неподвижные тела в течение всего наблюдения не меняют своего положения относительно наблюдателя.

Опыт. Разместим вертикальные вешки на столе на некотором расстоянии друг от друга по одной прямой. Поставим возле первой из них тележка с ниткой и начнем его тянуть. Сначала он перемещается от первой вешки ко второй, затем к третьей и т. д. То есть тележка будет менять свое положение относительно вышек.

Механическое движение — это изменение положения тела относительно других тел или одних его частей относительно других. Примеры механического движения: движение звезд и планет, самолетов и автомобилей, артиллерийских снарядов и ракет, человек идет относительно Земли, движение рук относительно туловища.

Другие примеры механического движения показано на рис. 1.

Рис. 1

Механические движения окружающих тел разделяют на: поступательное, вращательное и колебательное (система периодически возвращается в положение равновесия, например колебания листьев на дереве под действием ветра) движения (рис. 2).

Рис. 2

Особенности поступательного движения (движение пассажиров вместе с эскалатором, движение резца токарного станка и т.п.):

• произвольная прямая в теле, остается параллельной к себе;

• все точки имеют одинаковые траектории, скорости, ускорения.

Эти условия не выполняются для вращательного движения тела (движение колеса автомобиля, колеса обозрения, Земли вокруг Солнца и своей оси и т.д.).

Механическое движение нередко являются частью более сложных немеханических процессов, например тепловых. Изучением механического движения занимается раздел физики, который называется механикой.

2. Основная задача механики и способы ее решения в кинематике

Механическую форму движения материи изучает раздел физики «Механика». Основная задача механики — найти положение тела в пространстве в любой момент времени. Механическое движение происходит в пространстве и времени. Понятия пространства и времени — фундаментальные понятия, которые невозможно определить через какие-то более простые. Для изучения механического движения, что происходит в пространстве и времени, нужно прежде всего уметь измерять промежутки времени и расстояния. Частным случаем движения является покой, поэтому механика рассматривает также условия, при которых тела находятся в покое (эти условия называются условиями равновесия).

3. Что изучает кинематика

Чтобы сформулировать законы механики и научиться их применять, нужно сначала научиться описывать положение тела и его движение. Описание движения составляет содержание раздела механики, называется кинематикой.

4. Физическое тело и материальная точка, система отсчета

Для описания механического движения, как и других физических процессов, происходящих в пространстве и времени, используют систему отсчета. Система отсчета — это совокупность тела отсчета, связанной с ним системы координат (декартовой или другой) и прибора для отсчета времени (рис. 3).

Рис. 3

Систему отсчета в кинематике выбирают, руководствуясь лишь соображениями насчет того, как удобнее всего математически описать движение. Никаких преимуществ одной системы над другой в кинематике не существует. Из-за сложности физического мира реальное явление, которое изучается, всегда приходится упрощать и вместо собственно явления рассматривать идеализированную модель. Так, для упрощения в условиях определенных задач размерами тел можно пренебречь. Абстрактное понятие, которое заменяет реальное тело, которое движется поступательно и размерами которого можно пренебречь в условиях реальной задачи, называется материальной точкой. В кинематике, когда решают задачу, вопрос о том, что именно движется, где движется, почему именно так движется, в основном не рассматривают. Главное одно: как тело движется.

III. Закрепление изученного. Решение задач

1. Самостоятельная работа над материалом ППС «Физика-9» от «Квазар-Микро», в ходе которой учащиеся составляют опорный конспект.

2. Фронтальное опрос

• Что такое механическое движение?

• В чем состоит основная задача механики?

• Движение называют поступательным? Приведите примеры.

• Что называют материальной точкой?

• Что такое система отсчета? Какая разница между телом отсчета и системой отсчета?

• Что называют телом отсчета? Зависит ли описание движения от выбора тела отсчета?

• Приведите пример задачи, в которой планету, например на Землю, нельзя рассматривать как материальную точку.

• В какой системе отсчета проще описывать: а) движение поезда; б) движение предметов внутри вагона; в) движение планет?

IV. Домашнее задание

1. Выучить конспект урока; соответствующий параграф учебника.

2. Решить задачи:

• Маленькому ребенку кажется, что секундная стрелка часов движется, а минутная и часовая стрелки неподвижны. Как доказать ребенку, что она ошибается?

• Приведите примеры задач, в которых Луну: а) можно считать материальной точкой; б) нельзя считать материальной точкой.

3. Дополнительное задание: подготовить презентации.

Методическое пособие. Конспект лекций по физике для под-готовки иностранных студентов подготовительного отделения. Часть 1. Механика. Молекулярная физика и термодинамика. Электричество.

eaDonNTU, Donetsk >
Физико-металлургический факультет (до 23.11. 2018 года) >
Кафедра физики >
Учебно-методические материалы кафедры физики >

Please use this identifier to cite or link to this item: http://ea.donntu.org/handle/123456789/16925

Title:	Методическое пособие. Конспект лекций по физике для под-готовки иностранных студентов подготовительного отделения. Часть 1. Механика. Молекулярная физика и термодинамика. Электричество.
Authors:	Васильев, Анатолий Георгиевич Vasiliev, A. G.
Keywords:	физика твердого тела электромагнетизм механика молекулярная физика термодинамика электричество
Issue Date:	2012
Publisher:	ДонНТУ
Citation:	Методическое пособие. Конспект лекций по физике для подготовки иностранных студентов подготовительного отделения. Ч.1: Механика. Молекулярная физика и термодинамика. Электричество / сост.А.Г. Васильев.- Донецк: ДонНТУ, 2012.- 50 с.
Abstract:	Методическое пособие «Конспект лекций по физике для подготовки иностранных студентов подготовительного отделения. Часть 1. Механика. Молекулярная физика и термодинамика. Электричество» является составной частью комплекта учебно-методических пособий по курсу физики для подготовки иностранных студентов подготовительного отделения. В данном методическом пособии приведены определения основных физических понятий и величин, сформулированы физические законы, кратко разъяснена сущность описываемых ими явлений, изучаемых в разделах: механика; молекулярная физика и термодинамика; электричество. В конце каждой лекции приведен словарь физических терминов изучаемой темы в переводе на английский и арабский языки.
Description:	Данное методическое пособие может быть использовано студентами для самостоятельной подготовки к практическим занятиям, лабораторным работам, решению задач по индивидуальным заданиям, а также при подготовке к сдаче экзамена и зачета.
URI:	http://ea.donntu.edu.ua/handle/123456789/16925
Other Identifiers:	УДК 53(071)
Appears in Collections:	Учебно-методические материалы кафедры физики

Краткий конспект подготовки к ЗНО по физике №12 Элементы механики жидкостей и газов

Конспект 12. Элементы механики жидкостей и газов.

Тема: Элементы механики жидкостей и газов

1. Гидростатика

Определение. Гидростатика – раздел физики, изучающий равновесие жидкостей в гравитационном поле.
Определение. Давление (Па) – величина, характеризующая действие силы , на площадь поверхности , перпендикулярно к этой поверхности.
– давление, Па
Замечание. Формула, указанная выше, верна для всех видов давления: и твердых тел, и в жидкостях, и в газах.
– гидростатическое давление жидкости или газа на определенной глубине под поверхностью, Па
Где ρ – плотность жидкости или газа, кг/м3
h – глубина рассматриваемой точки жидкости или газа под поверхностью, м
Замечание. На одном уровне в однородной жидкости или газе давление одинаково.
Замечание. Следствием действия гидростатического давления является возникновение силы Архимеда.
Закон Паскаля для жидкостей и газов – давление, производимое внешними силами на жидкость или газ, передается без изменения в каждую точку жидкости или газа.
Сообщающиеся сосуды – сосуды, соединенные протоками (примеры: артезианский колодец, шлюзы, чайник, водопроводная система и др.).

Замечание. Поверхности однородной жидкости в сообщающихся сосудах любой формы и сечения устанавливаются на одном уровне. А высоты столбов над уровнем раздела двух разнородных жидкостей обратно пропорциональны плотностям жидкостей.

Гидравлический пресс – машина, действие которой основано, на законе Паскаля, предназначенная для создания больших сжимающих усилий, основная часть – это сообщающиеся цилиндры разного диаметра, снабженные поршнями.

Замечание. Цилиндр заполняется водой, маслом или другой подходящей жидкостью. По закону Паскаля давление покоящейся жидкости передается одинаково по всем направлениям и во все стороны передается без изменений: .
– закон гидравлического пресса
Замечание. Выигрыш в силе получают, воздействуя на малый поршень малым усилием, при этом на большой поршень действует сила во столько раз большая, во сколько площадь большого поршня больше площади малого поршня.
Определение. Атмосферное давление (Па) – давление атмосферы на земную поверхность и все тела, находящиеся на ней.
Нормальное атмосферное давление (при t = 0 ℃) =760 мм.рт.ст.≈ Па.
Замечание. Впервые атмосферное давление измерил Эванджелиста Торричелли.
Устройства для измерения давления газов: ртутный барометр, барометр-анероид («безжидкостный»), манометр металлический.

2. Гидродинамика

Определение. Гидродинамика – раздел физики, изучающий движение жидкостей и газов.
Определение. Идеальная жидкость – модель реальной жидкости, в которой не учитывается внутреннее трение, вязкость и температурные изменения объема.
Закон неразрывности потока жидкости (уравнение неразрывности) – при установившемся движении произведение скорости движения жидкости υ в данном сечении на площадь сечения S является величиной постоянной.
– уравнение неразрывности потока жидкости
– уравнение неразрывности потока жидкости для использования при решении задач

Замечание. Из уравнения неразрывности следует, что скорость жидкости в более узком сечении больше.
– уравнение Бернулли (закон сохранения энергии потока жидкости)
– уравнение Бернулли для использования при решении задач

Где р – внешнее давление в данной точке потока жидкости, Па
ρ – плотность жидкости, кг/м3
υ – скорость потока в данном месте, м/с
h – высота, на которой находится рассматриваемый объем жидкости над нижним уровнем потока, м
Замечание. Полное давление потока жидкости складывается из весового (ρgh), статического (р) и динамического () и остается неизменным.

Примеры проявления законов гидродинамики:

1) Притяжение между телами, находящимися вблизи потоков движущихся жидкостей (газов)

2) Теннисный шарик в потоке воздуха

3) Подъемная сила крыла самолета

Лекции и демонстрации по механике — Кафедра общей физики

КУРС ЛЕКЦИЙ

ПО МЕХАНИКЕ:

Лекция №1 «Кинематика материальной точки»

Содержание лекции: кинематика материальной точки, cистемы отсчёта и системы координат, число степеней свободы, радиус-вектор, линейные и угловые скорости и ускорения, нормальное, тангенциальное и полное ускорения, теорема Банаха-Тарского, движение по окружности, движение точки по произвольной кривой, динамика.

Лекция №2 «Динамика»

Содержание лекции: динамика (продолжение), закон Аристотеля, закон инерции (Галилей), инерциальные системы отсчета, законы Ньютона, закон сохранения импульса, движение тел с переменной массой, уравнение Мещерского, Уравнение Циолковского

Лекция №3 «Работа и энергия»

Содержание лекции: закон сохранения импульса (продолжение), движение центра масс системы, работа сил, теорема о кинетической энергии материальной точки, работа по замкнутому контуру, консервативные (потенциальные) силы, потенциальная энергия, центральное поле.

Лекция №4 «Закон сохранения энергии. Импульс»

Содержание лекции: закон сохранения энергии в механике, общефизический закон сохранения энергии, центр инерции (центр масс), преобразование энергии при смене системы отсчёта. Теорема Кёнига, анализ столкновения двух частиц для абсолютно упругого удара, закон сохранения импульса, построение и использование векторных диаграмм, момент силы.

Лекция №5 «Уравнение моментов»

Содержание лекции: момент силы, момент импульса, уравнение моментов, закон сохранения момента импульса, законы Кеплера.

Лекция №6 «Движение тел в гравитационном поле»

Содержание лекции: движение тел в гравитационном поле, первая космическая скорость, вторая космическая скорость, третий Закон Кеплера, понятие потока вектора, теорема Гаусса, телесный угол.

Лекция №7 «Частная (специальная) теория относительности»

Содержание лекции: частная (специальная) теория относительности.

Лекция №8 «Специальная теория относительности. Вращение тела вокруг неподвижной оси»

Содержание лекции:Специальная теория относительности. Врщение тела вокруг неподвижной оси

Лекция №9 «Вращение твердого тела (продолжение)»

Содержание лекции: Вращение твердого тела (продолжение)

Лекция №10 «Гироскопы»

Содержание лекции: Гироскопы

Лекция №11 «Колебания»

Содержание лекции: Колебания

Лекция №12 «Колебания (продолжение)»

Содержание лекции: Колебания (продолжение)

Лекция №13 «Движение в неинерциальных системах отсчета. Теория упругости»

Содержание лекции: Движение в неинерциальных системах отсчета. Теория упругости

Лекция №14 «Теория упругости (продолжение). Волны»

Содержание лекции: Теория упругости (продолжение). Волны

Консультация перед устным экзаменом по механике

Содержание лекции: Консультация перед устным экзаменом по механике

Реконструкция абстрактной квантовой теории

Кастелл, Л. (1975). Квантовая теория простых альтернатив, в Quantum Theory and the Structures of Time and Space I , L. Castell, M. Drieschner, and CF v. Weizsäcker, eds., Hanser, Munich.

Google Scholar

Крамер, Дж. Г. (1986). Обзоры современной физики , 58 , 647.

Google Scholar

Дришнер, М.(1970). Квантовая механика как общая теория объективного предсказания, Диссертация, Гамбург.

Дришнер, М. (1979). Voraussage, Wahrscheinlichkeit, Objekt , Springer Lecture Notes in Physics, № 99, Берлин.

Эренфест, П. (1932). Zeitschrift für Physik , 78 , 555.

Google Scholar

Герниц, Т. (1986). Международный журнал теоретической физики , 25 , 897.

Google Scholar

Герниц, Т. (1987). О связях между абстрактной квантовой теорией и структурой пространства-времени, International Journal of Theoretical Physics , 27 (5).

Гёрниц, Т. и Вайцзекер, К. Ф. против (1987a). Замечания об интерпретациях квантовой механики С. Коченом, в Proceedings of the Symposium on the Foundations of Modern Physics, Joensuu, 1987 , P.Лахти и П. Миттельштадт, ред. World Scientific, Сингапур.

Google Scholar

Гёрниц, Т. и Вайцзекер, К. Ф. против (1987b). Квантовые интерпретации, International Journal of Theoretical Physics , 26 , 921.

Google Scholar

Гёрниц, Т. и Вайцзекер, К.Ф. против (1988). Копенгаген и транзакционные интерпретации, International Journal of Theoretical Physics , 27 , 237.

Google Scholar

Гейзенберг, В. (1969). Die Quantenmechanik und ein Gespräch mit Einstein, in Der Teil und das Ganze , Chapter 5, Piper, Мюнхен.

Google Scholar

Jauch, JM (1968). Основы квантовой механики , Аддисон-Уэсли, Рединг, Массачусетс.

Google Scholar

Мейер-Абич, А.(1948). Naturphilosophie auf neuen Wegen , Гиппократ, Штутгарт.

Google Scholar

Паули, В. (1932). Einige die Quantenmechanik betreffende Erkundigungsfragen, Zeitschrift für Physik , 80 , 573.

Google Scholar

Шайбе, Э., Зюссманн, Г. и Вайцзекер, К.Ф. против (1958). Zeitschrift für Naturforschung , 13 , 705.

Google Scholar

Смэтс, Дж.Ч. (1927). Холизм и эволюция , Макмиллан, Лондон.

Google Scholar

Weizsäcker, CF v. (1939). Annalen der Physik , 36 , 275.

Google Scholar

Weizsäcker, C. F. v. (1955), Naturwissenschaften , 42 , 521–529, 545–555.

Google Scholar

Weizsäcker, C.F. v. (1971). Die Einheit der Natur , Hanser, Мюнхен ( The Unity of Nature , Farrar, Straus, Giroux, New York (1980a)).

Google Scholar

Weizsäcker, C. F. v. (1985a). Aufbau der Physik , Hanser, Мюнхен.

Google Scholar

Вайцзеккер, К.Ф. в. (1985b). Квантовая теория и пространство-время, симпозиум по основам современной физики, Йоэнсуу, 1987 , П. Лати и П. Миттельштадт, редакторы, World Scientific, Сингапур.

Google Scholar

Weizsäcker, C.F. v. (1986). Реконструкция квантовой теории , в Квантовая теория и структуры времени и пространства VI , Л. Кастелл и К.Ф. против Вайцзеккера, ред., Hanser, Мюнхен.

Google Scholar

Вы когда-нибудь чувствовали, что физика стала слишком абстрактной? : Physics

По иронии судьбы, ваш вопрос сам по себе довольно абстрактен: вы не предлагаете много конкретного материала для обсуждения другими, поэтому нам приходится самим заполнять пробелы.

Есть несколько исторических примеров более высоких уровней абстракции, которые определенно оправдываются задним числом. Мы можем думать об общей формулировке законов классической механики, от законов Ньютона до современной симплектической геометрии через Гамильтона и Лагранжа. Когда Гамильтон и Лагранж придумали свои собственные формулировки, хотя люди могли представить себе, что они более широко применимы к произвольной системе, они не могли представить себе центральную роль, которую они будут играть в современной физике, а именно в квантовой физике и физике частиц высоких энергий.Например, лагранжев формализм необходим для теорий, в которых пространство и время равны. Сам Лагранж не мог этого предвидеть. Точка зрения симплектической геометрии ведет к большому количеству красивой математики, вероятно, еще предстоит увидеть, насколько глубоко это может зайти.

Точно так же первоначальная формулировка электромагнетизма Максвеллом была общеизвестно запутанной. В своей знаменитой книге «Трактат об электричестве и магнетизме » он приводит одиннадцать законов и сложные рисунки «молекулярных вихрей».Современная формулировка, которая во многом опирается на специальную теорию относительности, гораздо более симметрична и в некотором смысле ее гораздо легче понять, но она требует более высокого уровня абстракции.

Некоторые из текущих исследований, направленных на предложение новых абстрактных конструкций, сегодня имеют отношение к расчету амплитуд в физике частиц высоких энергий. Стандартный набор инструментов для этой цели был создан Фейнманом и его диаграммами. До вклада Фейнмана было чрезвычайно сложно выполнять пертурбативные вычисления в квантовой теории поля, это было, по сути, самое передовое исследование того времени в этой области. После вклада Фейнмана это стало обычным делом для студентов бакалавриата. Поэтому трудно подчеркнуть, насколько важным был этот вклад Фейнмана. Тем не менее у нас также есть веские основания полагать, что эти расчеты все еще слишком сильно зависят от нашей повседневной интуиции о пространстве и времени, и что это делает их излишне сложными. Если вы, например, захотите применить метод диаграмм Фейнмана и рассчитать амплитуды N-петлей для рассеяния M-глюонов, вы обнаружите, что сложность этих вычислений растет настолько быстро, что даже компьютеры ограничены низкими значениями N и M.Теперь оказывается, что существует очень простая однострочная формула для таких амплитуд и что более высокие значения N можно получить с помощью некоторых рекуррентных соотношений. Лежащая в основе геометрия была показана Виттеном в 2003 году как теория струн в твисторном пространстве. С тех пор это вызвало значительный интерес как потому, что эти методы обеспечивают конкретные расчеты, которые используются для моделирования событий, измеряемых на коллайдерах высоких энергий, так и потому, что они предполагают, что наше обычное пространство-время возникает из лежащей в основе абстрактной геометрии.

Во всех этих случаях, как вы видите, единственная причина, по которой люди используют более абстрактный уровень, заключается в том, что там все концептуально проще или даже возможно только там, хотя набор математических инструментов может быть сложнее приобрести.

Теория измерений в классической механике | Успехи теоретической и экспериментальной физики

Аннотация

Мы исследуем теорию измерения в классической механике в формулировке классической механики Купмана и фон Неймана (КвН), которая использует гильбертово пространство.Показано различие между классической и квантовой механикой в «относительной интерпретации» состояния объекта измерения и состояния измерительного устройства. Мы также выводим соотношение неопределенностей в классической механике.

1. Введение

Чтобы обсудить принципиальное различие между квантовой и классической механикой, важно сравнить их, используя один и тот же формализм. Бом описал квантовую систему в терминах классической механики [1] и обнаружил, что наличие или отсутствие квантового потенциала характеризует различие между квантовой системой и классической системой.¹

Однако между сравнением в квантовой системе и сравнением в классической системе есть явное различие. Отличие заключается в некоммутативности оператора. В отличие от классической механики квантовая механика описывается в терминах q-чисел, т. е. некоммутативных физических величин. Это различие очевидно в теориях измерения, таких как принцип неопределенности Гейзенберга [2].

Другими словами, квантовая механика — это мир q-чисел.С другой стороны, классическая механика — это мир с-чисел, т. е. коммутативный мир. Такой аргумент, однако, затемняется тем фактом, что они находятся в разных формализмах.

Чтобы прояснить это, важно переписать классическую механику в квантовую механику и сравнить их.

Купман и фон Нейман [3,4] на ранних этапах развития квантовой механики переписали классическую систему в виде квантовой механики с использованием уравнений КвН. Позже Гоцци и Мауро подробно изучили этот формализм [5,6,7].Здесь мы будем называть квантово-теоретическое описание классической механики уравнениями КвН формализмом КвН. Сударшан обсуждал формализм КвН как модель квантово-классического взаимодействия [8].

В формализме КвН классическая механика описывается с помощью некоммутативных операторов, как в квантовой механике. Там классическая механика задается новыми переменными, некоммутативными по отношению к положению и импульсу, а эволюция во времени осуществляется унитарными операторами, состоящими из положения и импульса и этих новых переменных.

Если введенная новая переменная не входит в гамильтониан, то этот формализм эквивалентен классической механике. При таком операторном формализме отличие классической механики от квантовой механики заключается не в некоммутативности операторов, а в виде коммутационных соотношений.

Подводя итог, нормальный случай можно проиллюстрировать

$\begin{align} \begin{массив}{cc} \mathrm{QM} и \mathrm{CM}\\ \mathtt{q-числа} и \mathtt{c-числа} \конец{массив} \end{align}$

(1.

1), но в аргументе Бома это

$\begin{align} \begin{массив}{cc} \mathrm{QM(Бом)} и \mathrm{CM}\\ \mathtt{c-числа} и \mathtt{c-числа} \конец{массив} \end{align}$

(1.2) и это

$\begin{align} \begin{массив}{cc} \mathrm{QM} и \mathrm{CM}(\mathrm{KvN})\\ \mathtt{q-числа} и \mathtt{q-числа} \конец{массив} \end{align}$

(1.3) в формализме КвН.

В этой статье мы применяем теорию квантовых измерений, которая изначально была сформулирована для квантовых систем, к классическим системам и исследуем, как мы описываем измерения классических систем.Показано различие между классической и квантовой механикой в «относительной интерпретации» состояния объекта измерения и состояния измерительного устройства.

Далее мы выводим соотношение неопределенностей в классической механике. До сих пор измерение в классической механике не рассматривалось в достаточной мере. ² Йенс, Уилкенс и Левенштейн обнаружили, что формализм квантовой механики полезен не только для квантовой механики [9]. Это заставляет ожидать, что формализм КвН обретет новый смысл и применение в классической механике.

Структура этой статьи следующая. Во-первых, мы рассмотрим формализм KvN в разд. 2. Затем мы распространяем формализм КвН на квантовую механику и показываем, что это эквивалентно квантовой теории. После рассмотрения проблемы наблюдения с использованием модели фон Неймана в разд. 4, мы обсуждаем в разд. 5 теория измерения в классической механике. В разд. 6 мы строим классическую механическую версию соотношения неопределенностей. В последней главе будет подведение итогов и обсуждение.

Приложения включают следующее.В Приложении А мы комментируем, что формализм КвН для свободных частиц можно рассматривать как модель фон Неймана. Далее, в Приложении B, мы обсуждаем модель фон Неймана в формализме, расширяющем формализм KvN до квантовой механики, который обсуждается в разд. 3. В Приложении C мы вводим оператор Крауса. В Приложении D мы обсуждаем случай, когда начальным условием является единственная известная вероятность.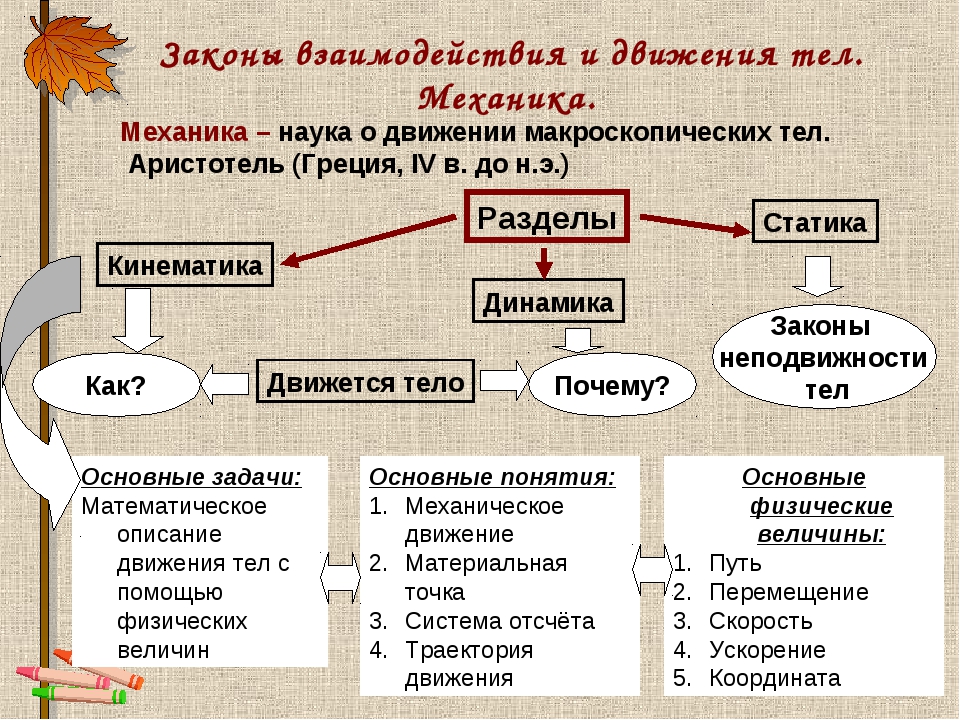 В Приложении E мы комментируем оператор Планка. В Приложении F мы подробно описываем эволюцию времени в модели фон Неймана.

2. Формализм КвН

В этом разделе кратко представлен формализм KvN. В квантовой механике коммутационное соотношение между оператором положения и импульса частицы определяется выражением

$\begin{equation} [\шляпа{х},\шляпа{р}]=i\hbar. \end{equation}$

(2.1)Состояние можно записать в виде |$|\psi\rangle$| как расширение с использованием собственных значений позиции и импульса,

$\begin{equation} |\psi\rangle=\int dx|x\rangle\langle x|\psi\rangle=\int dp|p\rangle\langle p|\psi\rangle.\end{equation}$

(2.2)Эволюция состояния во времени описывается с помощью оператора Гамильтона |$H(\hat{x},\hat{p})$| как

$\begin{уравнение} i{{\hbar}}\frac{\partial}{\partial t}|\psi\rangle={{\hat{H}}}|\psi\rangle. \end{equation}$

(2.3)

Суть формализма КвН заключается во введении операторов |$\hat{\pi}_{x},\hat{\pi}_{p}$| в дополнение к |$\шляпа{х},\шляпа{р}$| и требуют некоммутативности между |$\hat{x},\hat{p}$| и |$\шляпа{\pi}_{x},\шляпа{\pi}_{p}$| в то время как |$\шляпа{х}$| и |$\шляпа{р}$| делаются коммутативными.

$\begin{уравнение} [\ шляпа {х}, \ шляпа {р}] = [\ шляпа {\ пи} _ {х}, \ шляпа {\ пи} _ {р}] = 0, [\ шляпа {х}, \ шляпа { \pi}_{x}]=[\шляпа{p},\шляпа{\pi}_{p}]=i. \end{equation}$

(2.4)Поскольку положение и импульс коммутативны, состояние |$|\psi\rangle$| может быть расширен одновременными собственными состояниями положения и импульса как

$\begin{equation} |\psi\rangle=\int dxdp|x,p\rangle\langle x,p|\psi\rangle. \end{equation}$

(2.5)

То есть в формализме КвН волновая функция (амплитуда вероятности) |$\psi(x,p)=\langle x,p|\psi\rangle$| является сложной функцией в фазовом пространстве.

Следует отметить, что |$\psi(x,p)$| является не псевдовероятностью, как функция Вигнера [15] или функция Хусими [16], а амплитудой вероятности.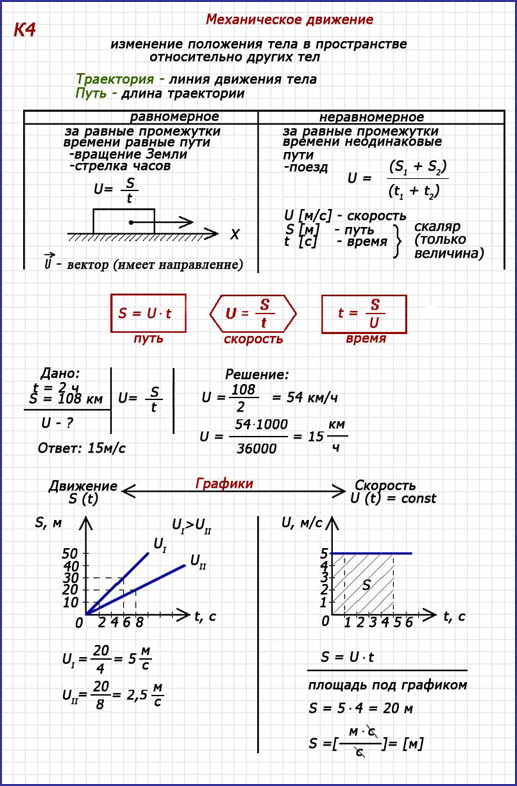

По преобразованию Фурье |$|\psi\rangle$| можно описать как

$\begin{align} |\psi\rangle & =\int dxd\pi_{p}|x,\pi_{p}\rangle\langle x,\pi_{p}|\psi\rangle\\ \end{align}$

(2.6)

$\begin{align} & =\int d\pi_{x}dp|\pi_{x},p\rangle\langle\pi_{x},p|\psi\rangle=\int d\pi_{x}d\pi_{p} |\pi_{x}.\pi_{p}\rangle\langle\pi_{x},\pi_{p}|\psi\rangle.\end{align}$

(2.7)Кроме того, лиувиллиан будет введен в соответствии с гамильтонианом ³

$\begin{equation} \ шляпа {L} = \ гидроразрыва {\ парциальное Н} {\ парциальное \ шляпа {р}} \ шляпа {\ пи} _ {х} — \ гидроразрыва {\ парциальное Н} {\ парциальное \ шляпа {х}} \ шляпа {\ пи} _ {р}. \end{equation}$

(2.8)Уравнение КвН, соответствующее уравнению Шредингера, вводится как

$\begin{equation} я \ гидроразрыв {\ парциальное} {\ парциальное т} | \ psi \ rangle = \ шляпа {L} | \ psi \ rangle. \end{equation}$

(2.9)Применяя |$\langle x,p|$| слева,

$\begin{equation} я \ гидроразрыва {\ парциальное} {\ парциальное т} \ фунтов на квадратный дюйм (х, р, т) = я \ гидроразрыва {\ парциальное Н} {\ парциальное р} \ гидроразрыва {\ парциальное \ фунтов на квадратный дюйм (х, р, т)} {\ парциальное х} -я \ гидроразрыва {\ парциальное Н} {\ парциальное х} \ гидроразрыва {\ парциальное \ фунтов на квадратный дюйм (х, р, т)} {\ парциальное р} \end{equation}$

(2.

{2}}/({2м})$| [5]. Используя уравнение Лиувилля

$\begin{equation} \ шляпа {L} = \ гидроразрыва {\ шляпа {р}} {м} \ шляпа {\ пи} _ {х}, \end{equation}$

(2.11) уравнение КвН дает

$\begin{equation} я \ гидроразрыва {\ парциальное} {\ парциальное t} | \ psi \ rangle = \ frac {\ hat {p}} {m} \ hat {\ pi} _ {x} | \ psi \ rangle. \end{equation}$

(2.12) Теперь применим |$\langle\pi_{x},p|$| слева получаем

$\begin{equation} я \ гидроразрыва {\ парциальное} {\ парциальное t} \ langle \ pi_ {x}, p | \ psi \ rangle = \ frac {p} {m} \ pi_ {x} \ langle \ pi_ {x}, p | \psi\угол.{i\hat{L}t}|x_{0},p_{0}\rangle=\delta\left(x-\frac{p}{m}t\right). \end{equation}$

(2.16)

Это решение воспроизводит линейную орбиту свободной частицы в классической механике.

Поскольку KvN представляет собой переписывание классической механики в формализм квантовой механики, естественно, что гамильтониан |$H$| включает только |$x$| и |$p$|⁠. Однако это не означает, что они представляют собой две независимые свободные частицы.

Это можно понять из формы Лувиля |$\шляпа{L}$|⁠:

|$\шляпа{L}=\frac{\partial H}{\partial\шляпа{p}}\шляпа{\pi } _ {х} — \ гидроразрыва {\ парциальное Н} {\ парциальное \ шляпа {х}} \ шляпа {\ пи} _ {р}.{2}$|⁠. Это представляет флуктуации, как это часто бывает с операторными формами в термодинамике [17].

В квантовой механике это колебание эквивалентно добавлению квантового эффекта. Наш аргумент состоит в том, чтобы обсуждать классическую механику в форме квантовой механики и не включать такой термин.

Однако, выражая квантовый эффект добавлением |$\pi_{x},\pi_{p}$| представляет интерес как способ обсуждения пограничной области между классической механикой и квантовой механикой и изучается как обобщенная классическая механика [7].

3. Связь с квантовой механикой

Теперь рассмотрим связь между формализмом КвН и квантовой механикой.

В квантовой механике позиция |$\hat{x}_{q}$| и импульс |$\hat{p}_{q}$| удовлетворяют каноническому коммутационному соотношению,

$\begin{align} [\шляпа{x}_{q},\шляпа{p}_{q}]=i\hbar. \end{align}$

(3.1)Та же алгебра может быть построена с помощью |$\hat{x},\hat{\pi}_{x},\hat{p},\hat{\pi}_{ р}$|⁠. Если мы определим операторы |$\hat{x}_{\hbar}$| и |$\шляпа{р}_{\hbar}$| как

$\begin{align} \ шляпа {х} _ {\ hbar} & = \ шляпа {х} — \ гидроразрыва {1} {2} \ hbar \ шляпа {\ пи} _ {р}, \\ \end{align}$

(3.2)

$\begin{align} \ шляпа {p} _ {\ hbar} & = \ шляпа {p} + \ frac {1} {2} \ hbar \ шляпа {\ pi} _ {x}, \end{align}$

(3.3) тогда получаем

$\begin{align} [\ шляпа {x} _ {\ hbar}, \ шляпа {p} _ {\ hbar}] = i \ hbar. \end{align}$

(3.4)

Подобная алгебра обсуждается в [1]. [18]. ⁴ ⁵

Тогда мы получим квантовые волновые функции в фазовом пространстве,

$\begin{equation} я \ hbar \ frac {\ partial {\ partial t} | \ psi \ rangle = H \ left (\ hat {x} + \ hbar \ frac {1} {2} \ hat {\ pi} _ {p} ,\шляпа{p}+\hbar\frac{1}{2}\шляпа{\pi}_{x}\right)|\psi\rangle.\label{eq:quantumKvn} \end{equation}$

(3.5)Чтобы восстановить исходный формализм КвН, мы расширяем правую часть уравнения.

{2} H (\ шляпа {x}, \ шляпа {p})} { \partial\hat{x}\partial\hat{p}}\hat{\pi}_{x}\hat{\pi}_{p}\right)+{{\dotsb}}.\end{align}$

(3.7)

Тогда в пределе |$\hbar\to0$| это уравнение возвращается к формализму КвН.

Комментируем, что состояние |$|x_{q}\rangle$| в квантовой механике соответствует |$|x,\pi_{p}\rangle$|⁠, а не |$|x,p\rangle$|⁠. Следовательно, |$|x,\pi_{p}\rangle$| и |$|p,\pi_{x}\rangle$| в формализме КвН имеют связь с квантовой теорией вопреки классической механике.

4. Модель фон Неймана как измерительная теория квантовой механики

4.1. Модель фон Неймана

В этом разделе мы вводим модель фон Неймана как простой пример модели измерений [19].

Система состоит из объекта измерения и измерительного устройства, а также соответствующих физических величин |$\{\шляпа{х},\шляпа{р}\},\{\шляпа{Х},\шляпа{Р}\ }$| удовлетворяют каноническим коммутационным соотношениям

$\begin{align} &[\шляпа{х},\шляпа{р}]=i\hbar,\\ \end{align}$

(4.

{-ix\hat{P}}|\eta\rangle.\end{equation}$

(4.10)Уравнение (4.6) тогда переписывается как

$\begin{equation} |\psi_{\mathrm{после}}\rangle=\int dx\langle x|\phi\rangle|x\rangle\otimes|\eta[x]\rangle. \end{equation}$

(4.11)

С другой стороны, |$|\psi_{\mathrm{after}}\rangle$| можно расширить следующим образом:

$\begin{equation} |\psi_{\mathrm{после}}\rangle=\int dP\langle P|\eta\rangle|\phi[P]\rangle\otimes|P\rangle.\end{equation}$

(4.12)

Это отличается от предыдущего, и его можно интерпретировать так, что цель измерения наблюдала импульс измерительного устройства как |$P$|⁠.

Обратите внимание, что эти два предложения не имеют места в относительном состоянии одновременно.

Напротив, эти два предложения будут иметь место в относительном состоянии в одно и то же время в теории измерения в классической механике.

5. Теория измерений в классической механике

В этом разделе мы обсуждаем теорию измерения в классической механике с использованием формализма КвН и модели фон Неймана.

Как и в предыдущем разделе, система состоит из объекта измерения и измерительного устройства, а также соответствующих физических величин |$\{\hat{x},\hat{p},\hat{\pi}_{x} , \ шляпа {\ pi} _ {p} \} $ | ⁠, | $ \ {\ шляпа {X}, \ шляпа {P}, \ шляпа {\ pi} _ {X}, \ шляпа {\ pi} _{P}\}$| удовлетворяют каноническим коммутационным соотношениям

$\begin{align} [\ шляпа {x}, \ шляпа {p}] & = 0, [\ шляпа {x}, \ шляпа {\ pi} _ {x}] = i, [\ шляпа {p}, \ шляпа {\ pi }_{p}]=i,\\ \end{align}$

(5.1)

$\begin{align} [\ шляпа {X}, \ шляпа {P}] & = 0, [\ шляпа {X}, \ шляпа {\ pi} _ {X}] = я, [\ шляпа {P}, \ шляпа {\ pi }_{P}]=i.{-1}]$|⁠.

Из гамильтониана модели фон Неймана |$\hat{H}=\hat{x}\hat{P}$|⁠ мы получаем лиувиллиан

$\begin{align} \ шляпа {L} & = \ гидроразрыва {\ парциальное \ шляпа {Н}} {\ парциальное \ шляпа {р}} \ шляпа {\ пи} _ {х} — \ гидроразрыва {\ парциальное \ шляпа {Н}} { \ парциальное \ шляпа {х}} \ шляпа {\ пи} _ {р} + \ гидроразрыва {\ парциальное \ шляпа {Н}} {\ парциальное \ шляпа {Р}} \ шляпа {\ пи} _ {Х} — \ гидроразрыва {\ парциальное \ шляпа {H}} {\ парциальное \ шляпа {X}} \ шляпа {\ pi} _ {P} \\ \end{align}$

(5.

{-i \ влево (\ шляпа {P} \ шляпа {\ pi} _ {p} — \ шляпа {x} \ шляпа {\ pi} _ {X} \ справа)}.{-i\left(\шляпа{P}\шляпа{\pi}_{p}-\шляпа{x}\шляпа{\pi}_{X}\справа)}|\phi\rangle\otimes|\ эта\угол\\ \end{align}$

(5.6)

$\begin{align} & =\int dx\:dP|\phi(p\to p-P)\rangle\otimes|\eta(X\to X+x)\rangle\\ \end{align}$

(5.7)

$\begin{align} & =\int dp\:dx\:dX\:dP\phi(x,p)\eta(X,P)|x,p[-P]\rangle\otimes|X[x],P\rangle , \end{align}$

(5.8), где

$\begin{align} |\phi(p\to p-P)\rangle&\equiv\int dp\phi(x,p)|x,p[-P]\rangle,\\ \end{align}$

(5.9)

$\begin{align} |\eta(X\to X+x)\rangle&\equiv\int dX\eta(X,P)|X[x],P\rangle. \end{align}$

(5.10)

Важным отличием от квантовой механики является то, что при интерпретации относительного состояния два утверждения удерживать в относительном состоянии одновременно. ⁹ ¹⁰

(1) измерительное устройство наблюдало положение измерительного устройства как |$x$|⁠,
(2) измерительное устройство наблюдало импульс измерительного устройства как | $P$|⁠,

6.

Соотношения неопределенностей в классической механике

6.1. Соотношение неопределенностей в классической механике с |$\hat{x}$| и |$\шляпа{р}$|

Здесь мы исследуем взаимосвязь между ошибкой и возмущением. Неравенство Одзавы представляет собой относительное выражение для ошибки и возмущения [23]. Мы обсудим, как можно получить неравенство Одзавы в классической механике.

Введем оператор ошибки |$\hat{N}(t)=\hat{X}(t)-{{\hat{x}}}$| и оператор возмущения |$\hat{D}(t)=\hat{p}(t)-\hat{p}$|⁠.{2}$|⁠. Используя соотношения неопределенностей Кеннарда–Робертсона [24,25]

$\begin{equation} \sigma(\шляпа{N})\sigma(\шляпа{D})\geq\frac{1}{2}\langle[\шляпа{N},\шляпа{D}]\rangle, \end{equation}$

(6.3) получаем

$\begin{equation} \epsilon\eta\geq\frac{1}{2}\langle[\hat{N},\hat{D}]\rangle. \end{equation}$

(6.4)Далее, |$[\hat{N}(t),\hat{D}(t)]$| рассчитывается как

$\begin{equation} [\шляпа{N}(t),\шляпа{D}(t)]=[\шляпа{X}(t),\шляпа{p}(t)]-[\шляпа{X}(t), \шляпа{р}]-[\шляпа{х},\шляпа{р}(т)]+[\шляпа{х},\шляпа{р}]. \end{equation}$

(6.5)При разумном предположении |$[\hat{X}(t),\hat{p}(t)]=0$|⁠ это уравнение дает

$\begin{equation } \langle[\шляпа{N},\шляпа{D}]\rangle+\langle[\шляпа{X}(t),\шляпа{p}]+[\шляпа{x},\шляпа{p}(t )]\rangle=\langle[\шляпа{x},\шляпа{p}]\rangle. \end{equation}$

(6.6)Поскольку |$\hat{x}$| и |$\шляпа{р}$| коммутируют в классической механике, получаем

$\begin{equation} \langle[\шляпа{N},\шляпа{D}]\rangle+\langle[\шляпа{X}(t),\шляпа{p}]\rangle+\langle[\шляпа{x},\шляпа{p }(т)]\rangle=0 \end{equation}$

(6.7) и его дифференцирование по времени

$\begin{equation} \frac{d}{dt}\langle[\шляпа{N},\шляпа{D}]\rangle+\langle[\dot{X}(t),\шляпа{p}]\rangle+\langle[\шляпа {x},\dot{\шляпа{p}}(t)]\rangle=0. \end{equation}$

(6.8)Поскольку лиувиллиан задается выражением

$\begin{align} \ шляпа {L} & = \ гидроразрыва {\ парциальное \ шляпа {Н}} {\ парциальное \ шляпа {р}} \ шляпа {\ пи} _ {х} — \ гидроразрыва {\ парциальное \ шляпа {Н}} { \ парциальное \ шляпа {х}} \ шляпа {\ пи} _ {р} + \ гидроразрыва {\ парциальное \ шляпа {Н}} {\ парциальное \ шляпа {Р}} \ шляпа {\ пи} _ {Х} — \ гидроразрыв {\ парциальное \ шляпа {H}} {\ парциальное \ шляпа {X}} \ шляпа {\ pi} _ {P}, \end{align}$

(6.

9) получаем

$\begin{equation} \langle[\dot{\шляпа{X}}(t),\шляпа{p}]\rangle+\langle[\шляпа{x},\dot{\шляпа{p}}(t)]\rangle=0 . \end{equation}$

(6.10)В итоге мы получаем

$\begin{eqnarray} &\langle[\шляпа{N},\шляпа{p}]\rangle+\langle[\шляпа{x},\шляпа{D}]\rangle=-C,&\\ \end{eqnarray}$

(6.11)

$\begin{eqnarray} &\langle[\шляпа{N},\шляпа{D}]\rangle=C& \end{eqnarray}$

(6.12) где |$C$| — некоторая стационарная константа. Тогда для |$t=0$|⁠

$\begin{equation} \langle[\шляпа{N}(0),\шляпа{D}(0)]\rangle=0=C.\end{equation}$

(6.13)Тогда получаем

$\begin{equation} \langle[\шляпа{N},\шляпа{p}]\rangle=\langle[\шляпа{D},\шляпа{x}]\rangle,\langle[\шляпа{N},\шляпа{D} ]\rangle=0.\label{eq:classical} \end{equation}$

(6.14)Обратите внимание, что

$\begin{equation} \epsilon\eta\geq0,\epsilon\sigma(\hat{p})+\eta\sigma(\hat{x})\geq0\label{eq:cl_ozawa} \end{equation}$

(6.15) являются тривиальными неравенствами. Теперь обсудим условие знака равенства. Из уравнения Гейзенберга для |$\hat{L}=\hat{P}\hat{\pi}_{p}-\hat{x}\hat{\pi }_{X}$|⁠ получаем

$\begin{align} \frac{d\hat{x}}{dt}&=0,\frac{d\hat{p}}{dt}=-\hat{P},\\ \end{align}$

(6.

16)

$\begin{align} \frac{d\hat{X}}{dt}&=\hat{x},\frac{d\hat{P}}{dt}=0,\\ \end{align}$

(6.17)

$\begin{align} \ frac {d \ hat {\ pi} _ {x}} {dt} & = \ hat {\ pi} _ {X}, \ frac {d \ hat {\ pi} _ {p}} {dt} = 0,\\ \end{align}$

(6.18)

$\begin{align} \ frac {d \ hat {\ pi} _ {X}} {dt} & = 0, \ frac {d \ hat {\ pi} _ {P}} {dt} = — \ hat {\ pi} _ { п}. \end{align}$

(6.19)Поэтому при начальных условиях |$\hat{x}(0)=\hat{x}_{0},\,\hat{p}(0)=\ шляпа {p} _ {0}, \, \ шляпа {\ pi} _ {x} (0) = \ шляпа {\ pi} _ {x0}, \, \ шляпа {\ pi} _ {p} (0 ) = \ шляпа {\ pi} _ {p0} $ | ⁠, | $ \ шляпа {X} (0) = \ шляпа {X} _ {0}, \, \ шляпа {P} (0) = \ шляпа {P} _ {0}, \, \ шляпа {\ pi} _ {X} (0) = \ шляпа {\ pi} _ {X0} $ | и |$\hat{\pi}_{P}(0)=\hat{\pi}_{P0}$|⁠, получаем

$\begin{align} \шляпа{х}(т)&=\шляпа{х}_{0},\шляпа{р}(т)=\шляпа{р}_{0}-т\шляпа{Р}_{0}, \\ \end{align}$

(6.20)

$\begin{align} \шляпа{X}(t)&=\шляпа{X}_{0}+t\шляпа{x}_{0},\шляпа{P}(t)=\шляпа{P}_{0}, \\ \end{align}$

(6.

21)

$\begin{align} \ шляпа {\ pi} _ {x} (t) & = \ шляпа {\ pi} _ {x0} + t \ шляпа {\ pi} _ {X0}, \ шляпа {\ pi} _ {p} (t )=\шляпа{\pi}_{p0},\\ \end{align}$

(6.22)

$\begin{align} \ шляпа {\ pi} _ {X} (t) & = \ шляпа {\ pi} _ {X0}, \ шляпа {\ pi} _ {P} (t) = \ шляпа {\ pi} _ {P0} -t\шляпа{\pi}_{p0}. \end{align}$

(6.23)Используя эти результаты, |$\hat{N}$| и |$\шляпа{D}$| выражаются как

$\begin{eqnarray} &\шляпа{N}(t)=\шляпа{X}_{0}+(t-1)\шляпа{x}_{0},&\\ \end{eqnarray}$

(6.24)

$\begin{eqnarray} &\шляпа{D}(t)=-t\шляпа{P}_{0}.& \end{eqnarray}$

(6.25)

Эти уравнения совпадают с результатом, полученным в рамках модели квантовой механики фон Неймана.

Затем

$\begin{eqnarray} &\langle x,p,X,P|\шляпа{N}(t)|x,p,X,P\rangle=X+(t-1)x,&\\ \end{eqnarray}$

(6.26)

$\begin{eqnarray} &\langle x,p,X,P|\шляпа{D}(t)|x,p,X,P\rangle=-tP.& \end{eqnarray}$

(6.27)Поэтому несмещенное условие задается

$\begin{equation} Х=(1-т)х, Р=0.{2}=0. & \end{eqnarray}$

(6.30)Тогда в этом условии получаем

$\begin{align} \эпсилон&=\эта=0,\\ \end{align}$

(6.31)

$\begin{align} \сигма(р)&=\сигма(х)=0. \end{align}$

(6.32)Если условие несмещенности не выполняется, то при |$t=1$| мы получаем

$\begin{equation} \epsilon=X,\eta=P. \end{equation}$

(6.33)

Это представляет начальную калибровку устройства. В таком случае |$X=0$| или |$P=0$| является условием знака равенства уравнения(6.15). Случай, когда начальное условие является единственной известной вероятностью, обсуждается в Приложении D.

6.2. Соотношения неопределенностей в классической механике с |$\hat{\pi}_{x}$| и |$\шляпа{\pi}_{p}$|}

Уточняем роль |$\hat{\pi}_{x}$| и |$\шляпа{\pi}_{p}$| в классической механике. Хотя |$\шляпа{\pi}_{x}$| и |$\шляпа{\pi}_{p}$| являются скрытыми переменными в классической механике, их можно выразить в виде физических величин, объединив квантовую механику и классическую механику.

Как указано в разд. 3, |$\шляпа{\pi}_{x}$| и |$\шляпа{\pi}_{p}$| описываются

$\begin{align} \шляпа{\pi}_{x}&=-\frac{2}{\hbar}(\шляпа{p}_{\hbar}-\шляпа{p}),\\ \end{align}$

(6.34)

$\begin{align} \ шляпа {\ pi} _ {p} & = \ frac {2} {\ hbar} (\ шляпа {x} _ {\ hbar} — \ шляпа {x}). \end{align}$

(6.35)

В этих относительных выражениях мы можем определить |$\hat{\pi}_{x}$| и |$\шляпа{\pi}_{p}$| используя как классические, так и квантовые наблюдаемые. ¹¹

Следовательно, в дополнение к обычному возмущению |$\hat{D}$|⁠ следует рассмотреть другое возмущение,

$\begin{equation} \ шляпа {D} _ {\ pi_ {x}} (t) = \ шляпа {\ pi} _ {x} (t) — \ шляпа {\ pi} _ {x}.\end{equation}$

(6.36)По аналогии с

$\begin{equation} [\шляпа{N}(t),\шляпа{D}_{\pi_{x}}(t)]=[\шляпа{X}(t),\шляпа{\pi}_{x}(t )]-[\шляпа{X}(t),\шляпа{\pi}_{x}]-[\шляпа{x},\шляпа{\pi}_{x}(t)]+[\шляпа {х},\шляпа{\пи}_{х}], \end{equation}$

(6.37) с использованием соотношений неопределенностей Кеннарда-Робертсона, некоммутативность |$\hat{x}$| и |$\шляпа{\pi}_{x}$| дает неравенство типа Одзавы:

$\begin{equation} \epsilon\eta_{\pi_{x}}+\epsilon\sigma(\шляпа {\pi}_{x})+{\sigma}({\шляпа{x}}){{\eta}}_{ \pi_{x}}\geq\frac{1}{2}, \end{equation}$

(6.

38) где |$\eta_{\pi_{x}}=\sqrt{\langle\hat{D}_{\pi_{x}}\rangle}$|⁠. Поскольку в этом неравенстве не фигурирует постоянная Планка, оно выполняется даже в классическом механическом пределе.

7. Обсуждение

Мы построили теорию измерения классической механики.

В отличие от квантовой механики, мы обнаружили, что в относительном состоянии одновременно выполняются два предложения.

Это различие в одновременности соответствует результату обсуждения соотношений неопределенностей, и неравенство Одзавы становится тривиальным в классической механике.Если начальное состояние неизвестно, мы можем получить относительное выражение для ошибки и возмущения в модели фон Неймана.

Мы распространили формализм КвН на квантовую теорию и определили |$\hat{\pi}_{x}$| и |$\шляпа{\pi}_{p}$| используя как классические, так и квантовые наблюдаемые. Затем мы также ввели еще одно возмущение на |$\hat{\pi}_{x}$| и получили соотношение неопределенностей типа Одзавы. Поскольку это соотношение не зависит от постоянной Планка, оно выполняется в классической механике.Лечение |$\шляпа{\pi}_x$| и |$\шляпа{\pi}_p$| как наблюдаемые известны как обобщенная классическая механика [7]. В этом случае лувиллиан становится наблюдаемой, а его собственные значения тесно связаны в условиях эргодической теории [26]. Как уже упоминалось, |$\hat{\pi}_x$| и |$\шляпа{\pi}_p$| тесно связаны с эффектом квантовой флуктуации. Это соотношение неопределенностей может быть существенным в теории промежуточного масштаба между классической теорией и квантовой теорией.

Применение этих реляционных выражений к поведенческой экономике в последние годы просто поразительно.Благодаря этим приложениям можно по-новому понять роль фазы в классической механике.

В качестве приложения теории измерений в классической механике можно аналитически сформулировать мысленные эксперименты в классической механике, такие как демон Максвелла и оптические часы Эйнштейна [27]. Хотя многие обсуждали их в прошлом, наше исследование может внести свой вклад в концептуальное обсуждение науки. Дальнейшие исследования покажут это.

Благодарности

Автор благодарит Такахиро Цучиду за прочтение статьи и приглашение на встречу.Он глубоко благодарен Цукасе Юмибаяси за ранний отзыв. Он в долгу перед Akio Sugamoto и Shiro Komata за прочтение этой статьи и полезные комментарии. Он искренне благодарит Изуми Цуцуи, Ли Джеха и Юитиро Мори, Юки Иноуэ за полезные комментарии. Он благодарит Фумио Хиросиму за указание на теорему единственности фон Неймана.

Приложение А

Интерпретация измерений классической механики

Отметим, что формализм КвН для свободной частицы можно рассматривать как модель фон Неймана.{-i\frac{\шляпа{p}}{m}\шляпа{\pi}_{x}t}|p\rangle|x\rangle=|p\rangle|x+\frac{p}{m} т \ угол \end{equation}$

(A.2) можно рассматривать как наблюдение положения |$x$| по импульсу |$p$|⁠.

Обратите внимание, что возмущение в этом случае равно |$\hat{D}_{\hat{\pi}_{p}}=\hat{\pi}_{p}(t)-\hat{\pi} _{p}$|⁠. |$\шляпа{D}_{\шляпа{\pi}_{p}}$| определяется в разд. 6.

Приложение Б. Теория измерений в расширенном формализме КвН

Мы обсуждаем модель фон Неймана в формализме, распространяющем формализм КвН на квантовую механику, который обсуждается в разд.{ix_{\hbar}Pt}|x,\pi_{p}\rangle\otimes|X+\frac{1}{2}x_{\hbar}t,\pi_{P}+x_{\hbar}/\ бар\угол. \end{align}$

(9.7)Обратите внимание, что |$|X+\frac{1}{2}x_{\hbar}t,\pi_{P}+x_{\hbar}/\hbar\rangle$| является собственным состоянием |$\hat{X}_{\hbar}$|⁠:

$\begin{align} \шляпа{X}_{\hbar}|X+\frac{1}{2}x_{\hbar}t,\pi_{P}+x_{\hbar}/\hbar\rangle & =\left(\шляпа {X}+\frac{\hbar}{2}\hat{\pi}_{P}\right)|X+\frac{1}{2}x_{\hbar}t,\pi_{P}+x_ {\hbar}/\hbar\rangle.\\ \end{align}$

(9.8)

$\begin{align} & = x _ {\ hbar} | X + \ frac {1} {2} x _ {\ hbar} t, \ pi_ {P} + x _ {\ hbar}/\ hbar \ rangle \end{align}$

(9.

Как описано выше, квантовое измерение также влияет на |$\hat{\pi}_{P}$| боковая сторона.

Приложение C. Оператор Крауса

Мы обсуждаем оператор Крауса в классической механике, который используется в более современной теории измерения. ¹²

В формализме КвН до сих пор не обсуждалось.

Оператор Крауса получается путем интеграции измерительного устройства.

В квантовой механике состояние |$|\psi(t)\rangle$| задается как

$\begin{equation} |\psi(t)\rangle=\int dX|X\rangle\langle X|\hat{U}(t)|\phi\rangle|\eta\rangle=\int dX\hat{M}(X, t)|\phi\rangle|X\rangle, \end{equation}$

(С.{\ кинжал} (Х, т) \ шляпа {М} (Х, т). \end{align}$

(C.3)Вероятность проективного измерения измерительного устройства равна

$\begin{equation} \mathrm{Pr}(X)=\langle\psi(t)|X\rangle\langle X|\psi(t)\rangle=\langle\psi(t)|\hat{E}(X,t) |\пси(т)\угл. \end{equation}$

(C.4)Состояние после измерения равно

$\begin{align} \шляпа{M}(X,t)|\phi\rangle|X\rangle. {-i\hat{x}P}\langle P|\eta\rangle \end{equation}$

(С.6) В классической механике состояние |$|\psi(t)\rangle$| задается как

$\begin{equation} |\psi(t)\rangle=\int dXdP|X,P\rangle\langle X|\hat{U}(t)|\phi\rangle|\eta\rangle=\int dXdP\hat{M}( X,P,t)|\phi\rangle|X,P\rangle, \end{equation}$

(C.7), где

$\begin{align} \hat{M}(X,P,t) & \equiv\langle X,P|\hat{U}(t)|\eta\rangle=\int dxdp\langle Xx,P|\eta\rangle|x ,p\rangle\langle x,pP|. \end{align}$

(C.8)Точно так же

$\begin{align} \hat{M}(X, \pi_{P},t)&=\int dxd\pi_{p}\langle X+x,\pi_{P}-\pi_{p}|\eta\rangle|x ,\pi_{p}\rangle\langle x,\pi_{p}|,\\ \end{align}$

(С.{iP\шляпа{\pi}_{p}-i\шляпа{x}\pi_{X}}\langle\pi_{X},P|\eta\rangle,\\ \end{align}$

(C.10)

$\begin{align} \hat{M}(\pi_{X},\pi_{P},t)&=\int dxd\pi_{p}\langle\pi_{X},\pi_{P}-\pi_{p}| \eta\rangle|x,\pi_{p}\rangle\langle x+\pi_{X}.\pi_{p}|. \end{align}$

(C.11)

Из формы этих выражений |$\hat{M}(X,t)$| в квантовой механике соответствует |$\hat{M}(X,\pi_{P},t)$| в классической механике и |$\hat{M}(P,t)$| в квантовой механике соответствует |$\hat{M}(\pi_{X},P,t)$|⁠. {2}=t\langle P\rangle_{\eta}.& \end{align}$

(D.4)Тогда несмещенное условие равно

$\begin{equation} \langle X\rangle_{\eta}=(1-t)\langle x\rangle_{\phi},\langle P\rangle_{\eta}=0. \end{equation}$

(D.5)При этом условии

$\begin{align} \эпсилон&=\эта=0,\\ \end{align}$

(D.6)

$\begin{align} \сигма(р)&=\сигма(х)=0. \end{align}$

(D.7)Если условие несмещенности не выполняется, то при |$t=1$| мы получаем

$\begin{eqnarray} &\epsilon=\langle X\rangle_{\eta},\eta=\langle P\rangle_{\eta},&\\ \end{eqnarray}$

(Д.8)

$\begin{eqnarray} &\langle X\rangle_{\eta}\sigma(p)+\langle P\rangle_{\eta}\sigma(x)=0.& \end{eqnarray}$

(D.9)

Приложение E. Планковский оператор

В квантовой механике |$\шляпа{x}_{q}$| и |$\шляпа{p}_{q}$| связаны коммутативно;

$\begin{уравнение} [\шляпа{x}_{q},\шляпа{p}_{q}]=i\hbar, \end{equation}$

(E.1) и время развития состояния

$\begin{equation} i\hbar\frac{d}{dt}|\psi\rangle=\hat{H}|\psi\rangle, \end{equation}$

(Э.

2) где |$\шляпа{Н}$| является гамильтоновым. Обычно постоянная Планка |$\hbar$| постоянно. Мы предлагаем новую квантовую алгебру

$\begin{equation} [\шляпа{х}_{д},\шляпа{р}_{д}]=я\шляпа{ч}, \end{equation}$

(E.3), где |$\hat{h}$| является оператором. Мы называем |$\шляпа{\hbar}$| оператор Планка. Мы вводим сопряженный оператор |$\hat{\hbar}$| |$\hat{I}$|⁠, затем

$\begin{equation} [\ шляпа {\ hbar}, \ шляпа {I}] = я. \end{equation}$

(E.4)

Мы рассматриваем постоянную Планка как оператор, поскольку она естественным образом вводит связь между квантовой механикой и классической механикой.

Введем операторы классической механики |$\hat{x},\hat{p},\hat{\pi}_{x},\hat{\pi}_{p}$|⁠ и коммутативные соотношения

$ \начать{выравнивать} [\шляпа{х},\шляпа{р}]&=0,\\ \end{align}$

(E.5)

$\begin{align} [\шляпа{х},\шляпа{\pi}_{х}]&=я,\\ \end{align}$

(E.6)

$\begin{align} [\шляпа{р},\шляпа{\pi}_{р}]&=i. \end{align}$

(E.7)

Они составляют формализм КвН классической механики.

В классической механике время развития состояния равно

$\begin{equation} i\frac{d}{dt}|\psi_{c}\rangle=\hat{L}|\psi_{c}\rangle, \end{equation}$

(Э.8) где |$\шляпа{L}$| является лиувиллевым. Теперь введем коммутативные соотношения |$\hat{I}$| и |$\шляпа{x}_{q}$| например

$\begin{eqnarray} &[\ шляпа {I}, \ шляпа {x} _ {q}] = \ шляпа {\ pi} _ {p}, & \\ \end{eqnarray}$

(E.9)

$\begin{eqnarray} &[\шляпа{I},\шляпа{p}_{q}]=-\шляпа{\pi}_{x},&\\ \end{eqnarray}$

(E.10)

$\begin{eqnarray} &[\шляпа{I},\шляпа{x}]=[\шляпа{I},\шляпа{p}]=[\шляпа{I},\шляпа{\pi}_{x}]=[\ шляпа {I}, \ шляпа {\ pi} _ {p}] = 0. & \end{eqnarray}$

(E.11) Получаем

$\begin{align} \ шляпа {x} _ {q} & = \ шляпа {x} + \ шляпа {\ hbar} \ шляпа {\ pi} _ {p} \\ \end{align}$

(Е.{-\ шляпа {\ hbar} \ шляпа {\ pi} _ {p} \ шляпа {\ pi} _ {x}} \\ \end{align}$

(E.18)

$\begin{align} & = \ гидроразрыва {\ парциальное \ шляпа {H} (\ шляпа {х}, \ шляпа {р})} {\ парциальное х} \ шляпа {\ пи} _ {р} — \ гидроразрыва {\ парциальное \ шляпа { Н} (\ шляпа {х}, \ шляпа {р})} {\ парциальное р} \ шляпа {\ пи} _ {х} = \ шляпа {L}. \end{align}$

(E.19)

Можно также ввести тепловые флуктуации. Мы можем описать одновременно и тепловую флуктуацию, и квантовую флуктуацию.

Приложение F. Эволюция во времени модели фон Неймана

Здесь мы обсуждаем временную зависимость модели фон Неймана, явно следуя [1].[28].

$\begin{уравнение} V = \эпсилон g(t)xP, \end{equation}$

(F.1) и если взаимодействие происходит только при |$t=t_{1}$|⁠, |$g(t)$| можно приблизительно представить как

$\begin{equation} г (т) = \ дельта (т-т_ {1}). \end{equation}$

(F.2)Поэтому в квантовой теории, используя

$\begin{equation} \шляпа{V}(t)=\эпсилон г(т)\шляпа{х}\шляпа{P}, \end{equation}$

(F.3) мы получаем гамильтониан как

$\begin{equation} \ шляпа {H} = \ шляпа {H} + \ шляпа {V} (т), \end{equation}$

(Ф.4) и эволюцию во времени как

$\begin{equation} i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle=\hat{H}|\psi(t)\rangle. {\ кинжал} (т) \ шляпа {U} (т), \\ \end{align}$

(Ф.{-\frac{i}{\hbar}\epsilon\hat{x}\hat{P}}\hat{U}_{0}(t_{1}). \end{equation}$

(F.13)

Мы можем понять |$\hat{U}_f$| что свободное движение до |$t=t_{1}$|⁠, то взаимодействие |$t=t_1$| и, наконец, выполняется свободное движение.

Это обсуждение можно повторить в классической механике формализма КвН.

В этом случае лиувиллиан |$\hat{L}$|

$\begin{align} \шляпа{L}&=\шляпа{L}_{0}+\шляпа{L}_{1},\\ \end{align}$

(F.14)

$\begin{align} \ шляпа {L} _ {0} & = \ frac {\ partial H_ {0}} {\ partial \ hat {p}} \ hat {\ pi} _ {x} — \ frac {\ partial H_ {0} {\ partial \ hat {x}} \ hat {\ pi} _ {p} + \ frac {\ partial H_ {0}} {\ partial \ hat {P}} \ hat {\ pi} _ {X} -\frac{\partial H_{0}}{\partial\шляпа{X}}\шляпа{\pi}_{P},\\ \end{align}$

(Ф.{-\frac{i}{\hbar}\epsilon\left(\шляпа{P}\шляпа{\pi}_{p}-\шляпа{\pi}_{X}\шляпа{x}\right) }\шляпа{U}_{0}(t_{1}). \end{equation}$

(F.17)

Это показывает, что, подобно квантовой механике, мы можем рассматривать |$U_f$| выполняя свободное движение до |$t=t_{1}$|⁠, взаимодействуя при |$t=t_{1}$|⁠, и после этого выполняя свободное движение.

Каталожные номера

[1]

Bohm

Физ.

166

(

1952

).().

478

.[3]

Купман

Б. О.

Proc. Нац. акад. науч. США,

315

(

1931

). ()[4]

фон Неймана

Дж.

Энн. Мат.

587

(

1932

). ()[5]

Мауро

Д.

Междунар. Дж. Мод. физ. А

1301

(

2002

). ()[6]

Гоцци

Э.

и Д. Мауро. Междунар. Дж. Мод. физ. А

1475

(

2004

). ()[7]

Мауро

Д.

2002

Темы теории Купмана-фон Неймана.Кандидатская диссертация, Università degli Studi di Trieste

. arXiv:quantph/0301172 [квант-ph].

[8]

Sudarshan

E. C. G.

Pramana

117

(

1976 9 ()[9]

Eisert

Wilkens

Lewenstein

Phys. Преподобный Летт.

3077

(

1999

). ()[10]

Холево

А.С.

Пробл. перед. Инф.

(

1973

). ()

[11]

Hausladen

и др.

Физ. Ред. А

1869

(

1996

). ()[12]

Holevo

A. S.

IEEE Trans. Инф. Теория

269

(

1998

). ()[13]

Шумахер

Б.

Уэстморленд

М.D.

Физ. Ред. А

131

(

1997

). ()[14]

Macchiavello

Sacchi

M. F.

Phys. Преподобный Летт.

123

(

2019

). ()[15]

Вигнер

Физ. Рев.

749

(

1932

). ()[16]

Хусими

К.

Proc. Physico-Mathematical Soc. Japan

264

(

1940

[17]

Aibara

Fujimoto

Katagiri

Saitou

Sugamoto

Yamamoto

Yumibayashi

[OUJ Tokyo Bunkyo Field Theory Collaboration],

Prog. Theor. Exp. Phys.

2019

073A02

(

2019

).()[18]

Бондарь

Д. И.

и др. ,

Физ. Преподобный Летт.

109

(

2012

). ()[19]

фон Неймана

Mathematical Foundations of Quantum Mechanics

(

Princeton University Press

Princeton, NJ

1955

)

Родился

Z. Phys.

803

(

1926

).()[21]

Everett

, III,

Rev. Mod. физ.

454

(

1957

()[22]

Zurek

W. H.

Paz

J. P.

Phys. Преподобный Летт.

2508

(

1994

). ()[23]

Одзава

М.

Физ. Ред. А

042105

(

2003

). ()[24]

Кеннард

Э.H.

Z. Phys.

326

(

1927

). ()[25]

Robertson

H. P.

Phys. Рев.

163

(

1929

). () [26] [26]

ARNOLD

V. I.

AVEZ

Эргодические проблемы классической механики

(

Benjamin

New York

1968

). [27]

Эйнштейн

А.

Энн. физ.

322

891

(

1905

). ()[28]

Мелло

P. A.

Модель измерений фон Неймана в квантовой механике

. В:

Материалы конференции AIP

Американский институт физики

2014

стр.

136

–

165

Это статья в открытом доступе, распространяемая в соответствии с лицензией Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии, что оригинал работа цитируется правильно.

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка браузера на прием файлов cookie

Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:

В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.

2020 Международная конференция по ФЕНМА 2020

Цели конференции

Данная конференция продолжает тематику

2012 Первый тайваньско-российский симпозиум «Физика и механика новых материалов и их приложения» (4-6 июня 2012 г. , Ростов-на-Дону, Россия), избранные отчеты, из которых были опубликованы в виде отредактированной книги «Физика и механика новых материалов и их приложения» издательством Nova Science Publishers, Нью-Йорк;
2013 г. Международный симпозиум «Физика и механика новых материалов и их подводное применение» (5-8 июня 2013 г., Гаосюн, Тайвань) , отдельные отчеты о которых были опубликованы как Springer Proceedings «Передовые материалы — физика, механика и приложения» Спрингер, Гейдельберг, Нью-Йорк, Дордрехт, Лондон;
2014 Международный симпозиум «Физика и механика новых материалов и их подводное применение» (27-29 марта 2014 г., Кхонкэн, Тайланд) , избранные отчеты которых были опубликованы в виде отредактированной книги «Расширенные материалы — исследования и приложения» издательством Nova Science Publishers, Нью-Йорк;
2015 Международная конференция «Физика и механика новых материалов и их приложения» (19-22 мая 2015 г., Азов, Россия) , отдельные отчеты о которых были опубликованы как Springer Proceedings «Передовые материалы — производство, физика, механика и применение» Спрингер, Гейдельберг, Нью-Йорк, Дордрехт, Лондон и как Материалы Международной конференции «Физика, механика новых материалов и их приложения», посвященной 100-летию Южного федерального университета, 2015 г. издательством Nova Science Publishers, Нью-Йорк;
2016 г. Международная конференция «Физика и механика новых материалов и их приложения» (19-22 июля 2016 г., Сурабая, Индонезия), избранные отчеты, из которых были опубликованы как Springer Proceedings «Передовые материалы – методы, физика, механика и приложения» Springer, Гейдельберг, Нью-Йорк, Дордрехт, Лондон, а также в материалах Международной конференции по «Физика, механика новых материалов и их приложения» издательством Nova Science Publishers, Нью-Йорк;
2017 г. Международная конференция «Физика и механика новых материалов и их приложения» (14-16 октября 2017 г., Джабалпур, Индия), избранные отчеты, которые будут опубликованы как Springer Proceedings «Advanced Materials – Материалы международной конференции «Физика и механика новых материалов и их применения», PHENMA 2017» Спрингер, Гейдельберг, Нью-Йорк, Дордрехт, Лондон, как Материалы Международной конференции «Физика, механика новых материалов и их приложения» 2017 г. 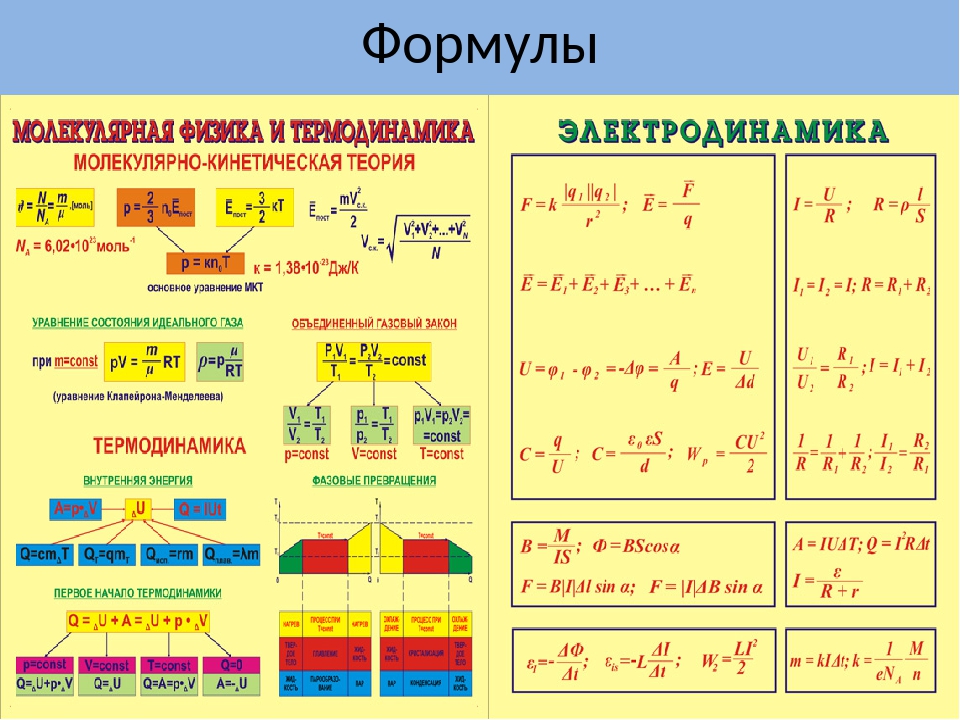издательством Nova Science Publishers, Нью-Йорк, и в двух специальных выпусках Международный журнал «Материальная физика и механика»,(Т.37, № 1) (Том 37, № 2) , Санкт-Петербург, Россия.
2018 г. Международная конференция «Физика и механика новых материалов и их приложения» (9-11 августа 2018 г., г. Пусан, Южная Корея) , отдельные отчеты которого будут опубликованы как Springer Материалы «Advanced Materials — Материалы международной конференции «Физика и механика новых материалов и их приложений», PHENMA 2018» Спрингер, Гейдельберг, Нью-Йорк, Дордрехт, Лондон, как Материалы Международной конференции «Физика, механика новых материалов и их приложения» 2018 г. издательством Nova Science Publishers, Нью-Йорк, и в международных журналах: «Материальная физика и механика» (Санкт-Петербург, Россия), «Прикладные науки» (МДПИ) и «Modern Physics Letters B» (World Scientific Publishing) .
2019 Международная конференция «Физика и механика новых материалов и их применения» (7-10 НОЯБРЯ 2019, ХАНОЙ, ВЬЕТНАМ) , отдельные отчеты которых будут опубликованы как SPRINGER, NOVA, «Журнал передовых диэлектриков» (World Scientific Publishing), «Материаловедение и механика» (Санкт-Петербург, Россия) , «Прикладные науки» и «Modern Physics Letters B» (World Scientific Publishing)

Темы Генеральной конференции включают, помимо прочего, передовые материалы, их синтез и обработку, характеристику, методы исследования и приложения.

В частности, доклады будут посвящены новым пьезоэлектрикам, наноматериалам, другим перспективным материалам и композитам с особыми свойствами, полученным на основе разработанных технологий обработки и современных подходов химии, физики, механики и материаловедения, а также широким применениям материалы, включая промышленность и управление. В публикациях будут представлены соответствующие математические модели, физические эксперименты, компьютерное моделирование, нано- и пьезоэлектрические приложения и др.

Еще одной целью конференции является привлечение исследователей из стран Азии и Азиатско-Тихоокеанского региона, других стран к проведению совместных исследований и научного сотрудничества.

Тезисы

Тезисы объемом до одной страницы в формате WORD (*.docx) необходимо направить по электронной почте до 01 ноября 2020 г. по адресу: [email protected] . До принятия: 01 ноября 2020 г. авторы будут уведомлены о том, был ли вклад принят.

Используемый формат – текст на одной стандартной странице формата А4.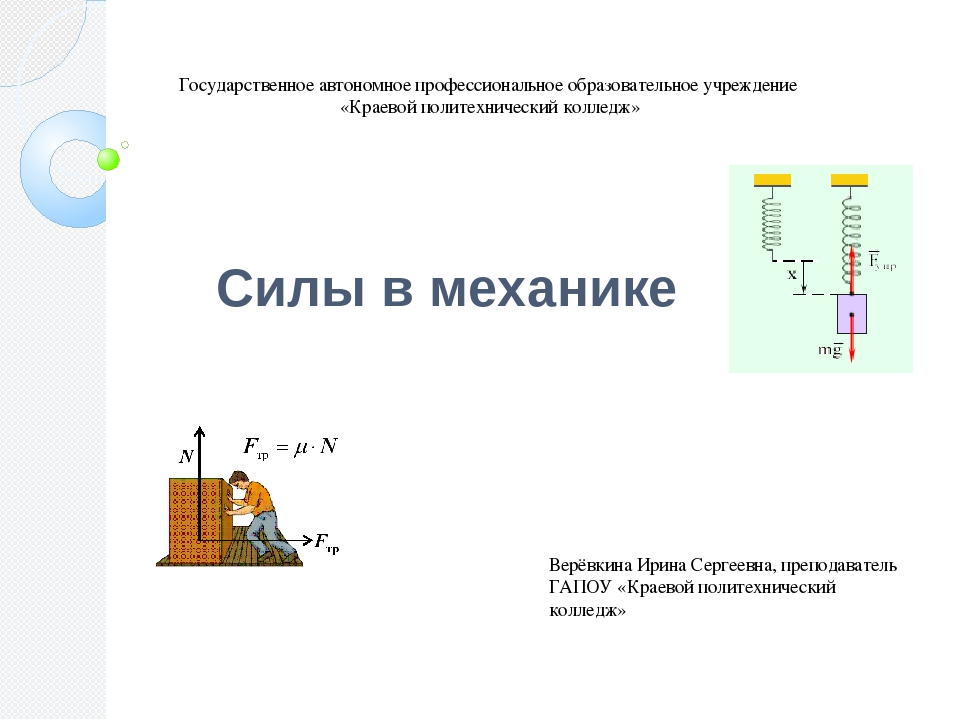 Следует использовать шрифт размером 12 пунктов. Заголовок отображается по центру. Отделяется пустой строкой от имени автора, также по центру. Имя автора, представляющего вклад, должно быть подчеркнуто. Пустая строка отделяет имя от принадлежности, также по центру. Сборник тезисов будет издан до начала конференции.

Труды

Материалы будут опубликованы в виде двух отредактированных книг: «Расширенные материалы» от Springer Nature, Чам, Швейцария и Материалы Международной конференции «Физика, механика новых материалов и их приложения» 2020 г. издательством Nova Science Publishers, Нью-Йорк, а также в международных журналах (журналах SCI): «Журнал передовых диэлектриков» (Всемирное научное издательство), «Прикладные науки» (МДПИ) и «Международный журнал современной физики B (IJMPB)» Всемирное научное издательство).Все журнальные статьи будут опубликованы после рецензирования (взимается плата за публикацию). два журнала). Крайний срок для вкладов в материалы, представленные авторами в электронном виде, 15 декабря 2020 г. . Предполагается, что объем рукописей Springer составит до 15 страниц. Рукописи Nova будут объемом до 6 страниц, а журнальные статьи — до 10 страниц. Инструкции по подготовке рукописей будут разосланы всем представляющим авторам после принятия тезисов.

Официальным языком конференции будет английский .

Регистрация и сборы

Предварительная регистрация будет доступна по электронной почте. Соответствующая регистрационная форма будет представлена в информационные рассылки Секретариата ФЕНМА-2020 и должны быть отправлены для всех тезисов по электронной почте на [email protected] до 1 ноября 2020 г. .

Все полноправных участников должны оплатить регистрационный взнос до 01 декабря 2020 г. , который будет составлять 400 долларов США (450 долларов США после 01 декабря 2020 г.) и включает социальную и техническую программы, кофе-брейк, книгу конференции Тезисы и электронная версия материалов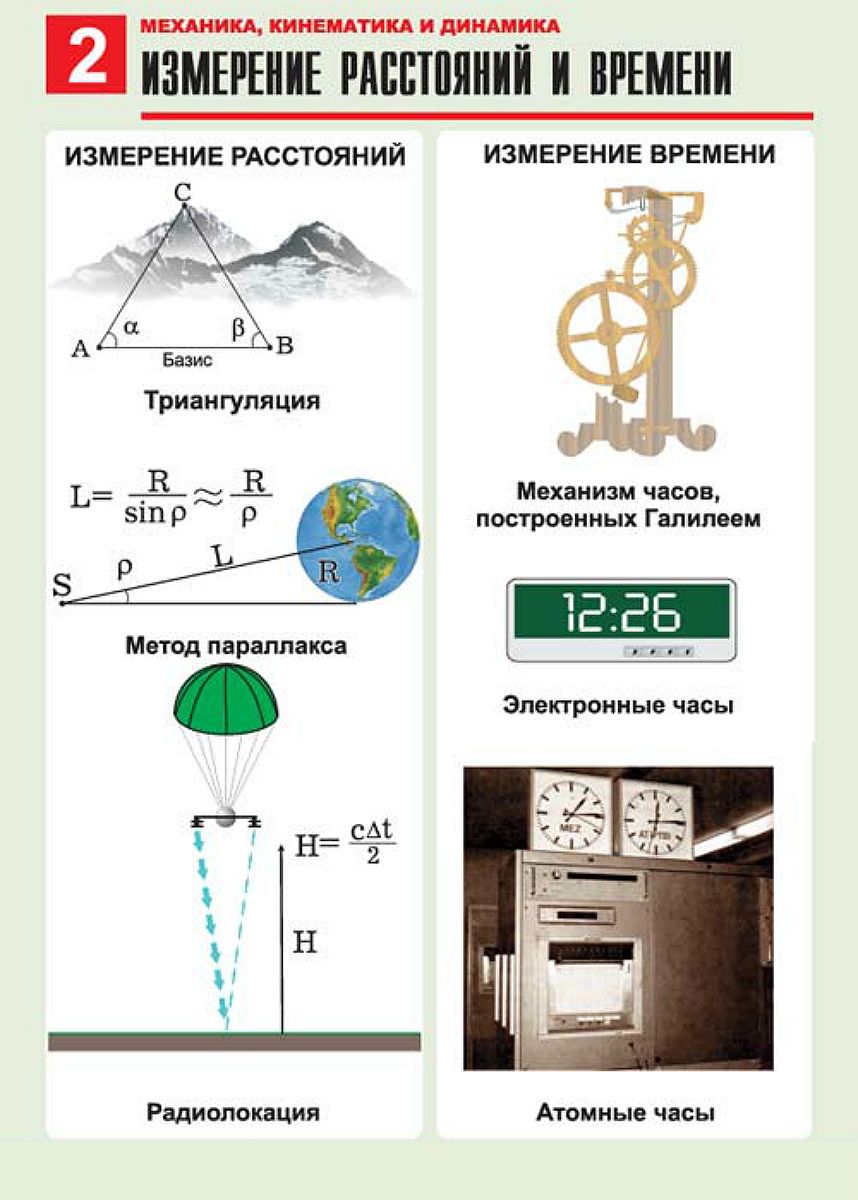 конференции. Электронные версии материалов конференции опубликованные после конференции, будут отправлены по электронной почте соответствующим авторам (1 книга на статью) Секретариатом конференции.

Для молодых ученых (до 35 лет, необходимо удостоверение личности) установлен специальный регистрационный взнос, который будет 100 долларов США (120 долларов США после 1 декабря 2020 г.) . Этот регистрационный взнос не включает материалы конференции.

За конференц-банкет будет внесена специальная оплата.

Регистратура

Книга тезисов с расписанием конференции, билетами на светские мероприятия и другими материалами конференции будет доступна на стойке регистрации конференции.

Дополнительная информация будет доступна на сайте конференции и в Facebook.

Карта местности

Местный Секретариат Конференции

Адрес: Ясуси Такасэ (доктор), Технологический институт Кюсю, 1-1, Sensui-cho, Tobata, Kitakyushu–city, Fukuoka 804-8550, Japan

Факс: Ясуси Такасэ (д-р), +81-93-871-8591 (отдел машиностроения)

Телефон: Нао-Аки Нода, +81-93-871-3124

Электронная почта

: takase. [email protected]

Генеральный секретариат Конференции

электронная почта: [email protected];

Сайт: http://phenma2020.sfedu.ru/

Facebook: https://www.facebook.com/PHENMA2020/

От аэропорта Фукуока до автобусной остановки Kokuraekimae на экспресс-автобусе Nishitetsu Limited до Кокуры (1 час 40 мин.)

От станции Кокура до станции Кюсюкодаймаэ на поезде (6 мин.)

От станции Кюсюкодаймаэ до Кютеча пешком (6 мин.)

От станции Токио до станции Кокура на поезде Синкансэн (4 часа 40 минут)

От станции Кокура до станции Кюсюкодаймаэ на поезде (6 мин.)

От станции Кюсюкодаймаэ до Кютеча пешком (6 мин.)

От аэропорта Кансай до станции Син-Осака экспрессом (50 мин.)

От станции Син-Осака до станции Кокура на синкансэне (2 ч 20 мин.)

От станции Кокура до станции Кюсюкодаймаэ на поезде (6 мин.)

От станции Кюсюкодаймаэ до Кютеча пешком (6 мин. )

Китакюсю

Китакюсю расположен на северной оконечности острова Кюсю и является вторым по численности населения городом на этом острове. С видом на Японское море и Внутреннее море Сето, а также с тем, что сорок процентов площади города составляют густые леса, это город, благословленный изобилием природы.Здесь есть много известных достопримечательностей, включая замок Кокура, портовый город Модзико-Ретро, известняковое плато Хираодай (одно из трех основных карстовых плато Японии) и множество мест для отдыха. В городе Китакюсю также есть обширное меню аппетитных блюд, таких как говядина кокура и яки-удон, а также многие другие деликатесы, собранные в горах и на море.

Гидромеханика – обзор

5.1 Введение

Гидромеханика в целом и пограничные слои в частности математически сложны.Такая сложность иногда не только продвигает вперед изучение и понимание жидкостей, но и продвигает дисциплину прикладной математики. Математика по-прежнему позволяет делать столь необходимые выводы из нескольких дисциплин. С этой целью многие математики продолжают вносить значительный вклад в гидродинамику.

Задачи пограничного слоя связаны с быстрым изменением значения физической переменной в ограниченной области пространства и составляют особый класс задач с сингулярными возмущениями.В связи с этим почти все задачи пограничного слоя связаны с дифференциальными уравнениями, в которых старший член производной умножается на малый параметр. Кроме того, пограничный слой всегда рассматривается как полубесконечный, основной причиной которого является отсутствие необходимости учитывать конечные граничные эффекты там, где можно ожидать всего невообразимого и вообразимого. Рассмотрение бесконечной поверхности может оказаться настолько трудным, что в первую очередь отвлечет внимание от основного интереса исследования. Тем не менее, ничто не мешает молодому поколению исследователей столкнуться с этой проблемой, учитывая их преимущество в том, что они имеют доступ к относительно большему объему знаний, чем предыдущие поколения.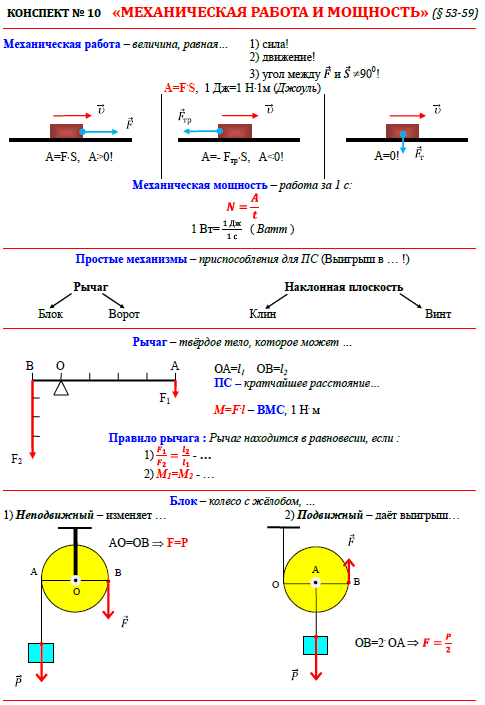

Гидро- или гидродинамика определяется нелинейными дифференциальными уравнениями в частных производных (УЧП), которые очень трудно решить аналитически. Насколько нам известно, общего решения этих уравнений в замкнутой форме не существует. Определяющие уравнения пограничного слоя в первую очередь основаны на упрощении системы нелинейных дифференциальных уравнений в частных производных (УЧП) второго порядка, известных как уравнения движения Навье-Стокса (НС) для вязких течений. Упрощение, предложенное Прандтлем в 1908 году, обычно называют уравнениями пограничного слоя Прандтля (PBL).В отличие от уравнений НС, которые имеют эллиптическую форму, уравнения пограничного слоя имеют параболический характер, и методы их решения основаны на законах подобия течений в пограничном слое.

Для решения задач пограничного слоя можно использовать три основных метода: метод подобия или дифференциальный метод (наиболее распространенный подход), интегральный метод и метод полного численного решения [1]. Многие частные случаи нелинейных УЧП привели к соответствующим изменениям переменных или растягивающих преобразований, в зависимости от задачи, для решения которой они предназначены.Одни преобразования линеаризуют рассматриваемую систему уравнений, другие переводят систему в такую, для которой существует решение. Преобразования, которые сводят систему УЧП к системе обыкновенных дифференциальных уравнений (ОДУ) за счет использования внутренней симметрии задачи, часто называют «преобразованиями подобия». Метод подобия — это оригинальный метод Блазиуса, который был разработан для аналитического решения задач пограничного слоя. Блазиус ввел и использовал независимую переменную, называемую переменной подобия, в уравнениях пограничного слоя Прандтля [2,3].Это было основано на предпосылке, что скорость геометрически подобна вдоль направления потока, где УЧП сохранения преобразуются в ОДУ. Преобразование подобия фиксирует рост пограничного слоя и значительно упрощает анализ и решение основных уравнений. Нахождение переменной сходства, подходящей для проведения трансформации, — это скорее искусство, чем наука, и для этого требуется хорошее понимание проблемы. Количество независимых переменных в УЧП тщательно преобразуется в одну независимую переменную (известную как переменная сходства).Исходные начальные граничные условия также в равной степени преобразуются в соответствующие граничные условия в новой комбинированной переменной.

Метод преобразования подобия является незаменимым инструментом для анализа механического поведения жидкости в целом и особенно процессов в пограничном слое. Асимптотические методы позволяют упростить сложную систему, которая затем обеспечивает просвещенную форму эмпиризма, которую мы называем подобием. Для нахождения переменных подобия было разработано несколько методов и подходов, например, теорема Пи Васи–Бэкингема [4–6].Наиболее строгий и систематический подход к нахождению переменных подобия основан на группе преобразований Ли [7–14]. Предпосылка подхода группы Ли состоит в том, что каждая переменная в исходном уравнении подвергается бесконечно малому преобразованию. Требование инвариантности уравнения относительно этих преобразований приводит к определению потенциальных или возможных симметрий. Этот подход обычно применялся к уравнениям пограничного слоя. Что касается теории пограничного слоя, авторы [15] представили всестороннее описание классических методов, включая несколько возможных результатов в зависимости от перспективы решаемой задачи.В [16] к нестационарным уравнениям пограничного слоя был применен прямой метод Кларксона–Крустала, который используется для нахождения редукций подобия. Важно отметить, что найденная переменная подобия не является уникальной или свойственной только одной задаче; его можно применить к другим подобным проблемам, где это уместно. Кроме того, Хансен [17] обсудил метод «растягивания переменной», используемый для поиска преобразований подобия. В целом, проблемы подобия приводят исходные уравнения PBL к форме, инвариантной по отношению к аффинным преобразованиям.Затем локальное поле течения разрешается с помощью аналитических/численных решений УЧП, управляющих пограничным слоем. Характерно, что профили скоростей течений в пограничном слое представляют собой набор гомотетичных кривых и графиков. Почему они обычно гомотетичны? Что касается профиля скорости, например, мы нормируем на uU∞, и это стремится или приближается к единице. Точно так же, что касается профиля температуры, мы нормируем температуру набегающего потока, или T−T∞, и она стремится к нулю или приближается к ней.Интегральные методы, с другой стороны, дают решения в замкнутой форме, предполагая профиль скорости, температуры и массопереноса концентрации. Он включает в себя интегрирование уравнений от стенки до набегающего потока, что дает общую производительность, включающую рост пограничного слоя. Наконец, полный численный метод использует хорошо зарекомендовавшие себя численные схемы и практические коды моделирования с высокоскоростными компьютерами для решения нескольких задач пограничного слоя.

Следует отметить, что некоторые исследования в литературе обсуждают свои результаты как точные решения . В этом отношении важна осторожность. Как правило, когда мы говорим о « точных решениях » фундаментальных уравнений, таких как уравнения НС, а это могут быть полные уравнения НС или любая из их аппроксимированных форм, при условии, что решения, полученные любым методом, действительно точь-в-точь как они приходят, то есть лучшего решения не найдено. Точность относится к решению самого уравнения. Если рассматриваемое уравнение было приближением более надежного уравнения, то претензия на точность решения должна относиться только к приближенному решению.

9-я Евроконференция по физике горных пород и геомеханике — прием тезисов

9-я ^-я-я Евроконференция по физике горных пород и геомеханике пройдет в Тронхейме, Норвегия, 17-21 октября 2011 г. Основной заголовок конференции:

Лаборатория связи, вычислительный и полевой опыт

Темы
Организаторы приглашают к активному участию представителей научных кругов и представителей промышленности.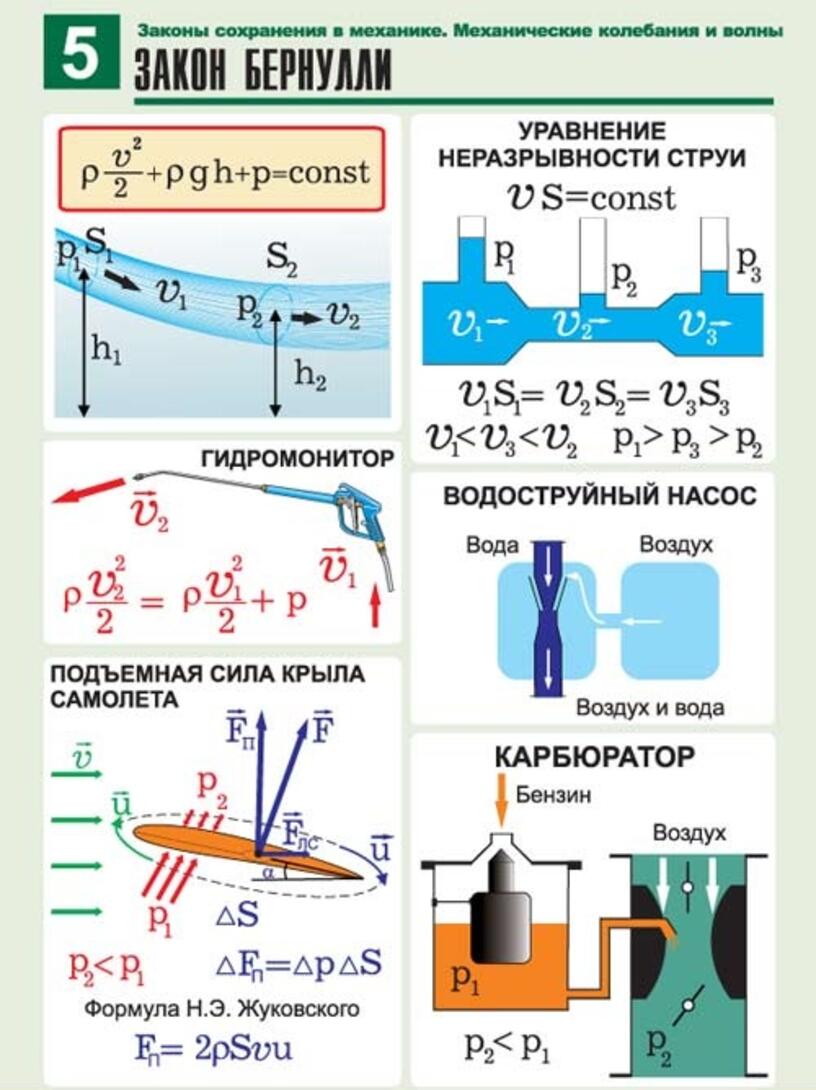 Особое внимание будет уделено промышленному применению физики горных пород и геомеханики для разведки и добычи полезных ископаемых и энергетических ресурсов Земли, включая нефть и геотермальную энергию. Подземное хранение твердых и жидких отходов, включая ядерные отходы и климатический газ, такой как CO ₂ , является еще одной областью, где в будущем потребуются знания в области геомеханики и физики горных пород. Мы приглашаем тезисы, охватывающие как фундаментальные, так и прикладные исследования в области физики горных пород и геомеханики. Особо актуальные темы:

Вычислительная физика горных пород и геомеханика от порового до полевого масштаба
Лабораторные измерения механических и физических свойств горных пород в условиях in situ
Геомеханические и петрофизические аспекты мониторинга подземных процессов
Физика и механика приповерхностных горных пород и грунтов
Физика и механика горных пород на глубине
Поведение сланца и глины
Зарождение, активация и распространение трещин и разломов
Сейсмичность, вызванная горным ударом, добычей полезных ископаемых и стимуляцией

Объем тезисов должен составлять 1-2 страницы, желательно с одним рисунком.

Механика. Конспекты по физике 10-11 класс. Гравитация

Механика. Конспекты по физике 10-11 класс. Гравитация

Знаете ли вы?

ГДЗ конспекты по физике 7 класс Задание: Механическое движение Равномерное и неравномерное движение

План-конспект урока по физике по теме: Кинематика материальной точки ❤️

Краткий конспект подготовки к ЗНО по физике №12 Элементы механики жидкостей и газов

Лекции и демонстрации по механике — Кафедра общей физики

Реконструкция абстрактной квантовой теории

Вы когда-нибудь чувствовали, что физика стала слишком абстрактной? : Physics

Теория измерений в классической механике | Успехи теоретической и экспериментальной физики

Аннотация

1. Введение

2. Формализм КвН

3. Связь с квантовой механикой

4. Модель фон Неймана как измерительная теория квантовой механики

4.1. Модель фон Неймана

5. Теория измерений в классической механике

6.

6.1. Соотношение неопределенностей в классической механике с |$\hat{x}$| и |$\шляпа{р}$|

6.2. Соотношения неопределенностей в классической механике с |$\hat{\pi}_{x}$| и |$\шляпа{\pi}_{p}$|}

7. Обсуждение

Благодарности

Приложение А

Интерпретация измерений классической механики

Приложение Б. Теория измерений в расширенном формализме КвН

Приложение C. Оператор Крауса

Приложение E. Планковский оператор

Приложение F. Эволюция во времени модели фон Неймана

Каталожные номера

Произошла ошибка при настройке пользовательского файла cookie

Настройка браузера на прием файлов cookie

Почему этому сайту требуются файлы cookie?

Что сохраняется в файле cookie?

2020 Международная конференция по ФЕНМА 2020

Местный Секретариат Конференции

Генеральный секретариат Конференции

Гидромеханика – обзор

5.1 Введение

9-я Евроконференция по физике горных пород и геомеханике — прием тезисов

Author: alexxlab

Добавить комментарий Отменить ответ

Рубрики