Числовые и алгебраические выражения — урок. Алгебра, 7 класс.
Числовое выражение состоит из чисел и знаков арифметических действий между ними, также может содержать скобки для указания порядка действий. Числовое выражение должно иметь смысл.
Пример:
6⋅8−2:23+7.
:−2+⋅+77(((8 — не числовое выражение.
Если в выражении вместо чисел используются буквы, тогда имеем алгебраическое выражение.
Алгебраическое выражение состоит из букв и чисел, между которыми стоят знаки арифметических действий, также может содержать скобки. Алгебраическое выражение должно иметь смысл.
Пример:
x3−14y−a.
Буквы в алгебраическом выражении называются переменными, так как они могут принимать разные числовые значения.
Алгебраические выражения можно преобразовывать и упрощать, используя законы сложения и умножения.
Законы сложения
1) От перемены мест слагаемых сумма не изменяется, т. е.
a+b=b+a — переместительный закон сложения.
2) Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых, т. е.
a+b+c=a+b+c — сочетательный закон сложения.
Законы умножения1) От перемены мест множителей произведение не меняется, т. е.
a⋅b=b⋅a — переместительный закон умножения.
2) Произведение не зависит от группировки его сомножителей, т. е.
a⋅b⋅c=a⋅b⋅c — сочетательный закон умножения.
3) Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число, т. е.
a+b⋅c=ac+bc — распределительный закон умножения относительно сложения.
Значение числового выражения — число, полученное в результате выполнения всех действий по порядку в числовом выражении.
Выполнив указанные действия в первом примере, получим
3+5⋅7−4=18.
Число \(18\) — значение выражения.
Значение алгебраического выражения можно найти, если известны значения его переменных.
Если \(x=2\), \(y=-2\), \(a=30\), то выражение x3−14y−a имеет значение \(6\), т. к.
x3−14y−a=23−14⋅−2−30=8+28−30=6.
Если \(z=30\), то выражение z2z−6 имеет значение \(37,5\),
т. к. z2z−6=30224=90024=37.5.
Если \(z=6\), то выражение z2z−6 не имеет смысла, т. к. знаменатель обращается в нуль.
Обрати внимание!
На ноль делить нельзя!
Вывод:в случае если алгебраическое выражение имеет определённое числовое значение при заданном наборе значений переменных, тогда такие значения переменных являются допустимыми;
в случае если алгебраическое выражение не имеет смысла при заданном наборе значений переменных, тогда такие значения переменных являются недопустимыми.
Так, в примере z2z−6 значение \(z=-6\) — допустимое, азначение \(z=6\) — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!
| 1. | Определение суммы и разности чисел | 1 вид — рецептивный | лёгкое | 1 Б. | Определяются сумма и разность чисел с разными и одинаковыми знаками. |
| 2. | Прочитай выражение | лёгкое |
2 Б.
|
Нужно прочитать выражение и найти его значение. | |
| 3. | Использование свойств действий | 1 вид — рецептивный | лёгкое | 1 Б. | Используя свойства действий, делаем вывод о верности равенств. |
4.
|
Найди значение выражения (десятичные дроби) | 1 вид — рецептивный | лёгкое | 2 Б. | Задание на нахождение значения числового выражения с десятичными дробями. |
| 5. | Выполни действия (десятичные дроби) | 1 вид — рецептивный | лёгкое |
1 Б.
|
Задание на вычисление значения числового выражения. |
| 6. | Найди значение выражения (с десятичными дробями) | 1 вид — рецептивный | лёгкое | 1 Б. | Числовые выражения с десятичными дробями. |
7.
|
Выполни действия (обыкновенные дроби) | 1 вид — рецептивный | лёгкое | 1 Б. | Числовые выражения с обыкновенными дробями. |
| 8. | Выполни действие (разные знаки) | 1 вид — рецептивный | лёгкое |
1 Б.
|
Числовые выражения с десятичными дробями разных знаков. |
| 9. | Значение числового выражения | 2 вид — интерпретация | среднее | 2 Б. | Определяется значение числового выражения, выполняя по порядку все действия, указанные в выражении. Действия выполняются со смешанными числами. |
10.
|
Вычисли рациональным способом | 2 вид — интерпретация | среднее | 2 Б. | В упражнении нужно найти значение выражения наиболее рациональным способом, применяя распределительный закон умножения относительно вычитания. |
| 11. | Значение алгебраического выражения | 2 вид — интерпретация | среднее |
2 Б.
|
Находится значение алгебраического выражения при конкретном значении входящих в него переменных. |
| 12. | Определение допустимых значений переменных | 3 вид — анализ | сложное | 2 Б. | Определяются значения переменных, при которых выражение имеет смысл. |
13.
|
Имеет ли смысл выражение | 3 вид — анализ | сложное | 4 Б. | В упражнении определяется, имеет ли смысл выражение, а затем находится его значение, если есть смысл. |
| 14. | Расставить скобки в выражении | 4 вид — творческий | сложное |
3 Б. |
Нужно расставить скобки в выражении, чтобы его значение было бы наибольшим или наименьшим. |
Как находить допустимые значения переменной в выражении. Область допустимых значений
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
48. Виды алгебраических выражений.
Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок составляются алгебраические выражения.
Примеры алгебраических выражений:
Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (в частности, возведения в степень с дробным показателем), то оно называется целым. Из написанных выше целыми являются выражения 1, 2 и 6.
Если алгебраическое выражение составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления, причем используется деление на выражения с переменными, то оно называется дробным. Так, из написанных выше дробными являются выражения 3 и 4.
Так, из написанных выше дробными являются выражения 3 и 4.
Целые и дробные выражения называют рациональными выражениями. Так, из написанных выше рациональными выражениями являются выражения 1, 2, 3, 4 и 6.
Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то такое алгебраическое выражение называется иррациональным. Так, из написанных выше иррациональными являются выражения 5 и 7.
Итак, алгебраические выражения могут быть рациональными и иррациональными. Рациональные выражения, в свою очередь, разделяются на целые и дробные.
49. Допустимые значения переменных. Область определения алгебраического выражения.
Значения переменных, при которых алгебраическое выражение имеет смысл, называют допустимыми значениями переменных. Множество всех допустимых значений переменных называют областью определения алгебраического выражения.
Целое выражение имеет смысл при любых значениях входящих в него переменных. Так, при любых значениях переменных имеют смысл целые выражения 1, 2, 6 из п. 48.
Так, при любых значениях переменных имеют смысл целые выражения 1, 2, 6 из п. 48.
Дробные выражения не имеют смысла при тех значениях переменных, которые обращают знаменатель в нуль. Так, дробное выражение 3 из п. 48 имеет смысл при всех о, кроме , а дробное выражение 4 имеет смысл при всех а, b, с, кроме значений а
Иррациональное выражение не имеет смысла при тех значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени или под знаком возведения в дробную степень. Так, иррациональное выражение 5 имеет смысл только при тех а, b, при которых а иррациональное выражение 7 имеет смысл только при и (см. п. 48).
Если в алгебраическом выражении переменным придать допустимые значения, то получится числовое выражение; его значение называется значением алгебраического выражения при выбранных значениях переменных.
Пример. Найти значение выражения при
Решение. Имеем
50. Понятие тождественного преобразования выражения.
 Тождество.
Тождество.
Рассмотрим два выражения При имеем . Числа 0 и 3 называются соответственными значениями. выражений при Найдем соответственные значения тех же выражений при
Соответственные значения двух выражений могут быть равными друг другу (так, в рассмотренном примере выполняется равенство ), а могут и отличаться друг от друга (так, в рассмотренном примере ).
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Yandex.RTB R-A-339285-1
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1: а, если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Определение 1
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Определение 2
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Определение 3
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Пример 1
Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид (0 , 1 , 2) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что (1 , 1 , 2) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Определение 4
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Пример 2
Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид (− ∞ , 3) ∪ (3 , + ∞) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f (x) .
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.
Пример 3
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Пример 4
Найти ОДЗ выражения 1 3 — x + 1 0 .
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅ .
Пример 5
Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.
То есть это и есть искомая область допустимых значений.
Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .
Пример 6
Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 (x 2 + 3) .
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:
x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0) ∪ (0 , + ∞) .
Ответ: [ − 1 , 0) ∪ (0 , + ∞)
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Тождественные преобразования:
- могут не влиять на ОДЗ;
- могут привести в расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Пример 7
Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Пример 8
Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (− ∞ , 0) ∪ (0 , + ∞) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Пример 9
Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства (x − 1) · (x − 3) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (− ∞ , 1 ] ∪ [ 3 , + ∞) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞) . Значит, ОДЗ полностью записывается так: (− ∞ , 1 ] ∪ [ 3 , + ∞) .
Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (− ∞ , 1 ] ∪ [ 3 , + ∞) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞) . Значит, ОДЗ полностью записывается так: (− ∞ , 1 ] ∪ [ 3 , + ∞) .
Нужно избегать преобразований, которые сужают ОДЗ.
Пример 10
Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Пример 11
Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится (− ∞ 0) ∪ (0 , + ∞) . Причем при вычислении уже работаем со второй упрощенной дробью.
Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится (− ∞ 0) ∪ (0 , + ∞) . Причем при вычислении уже работаем со второй упрощенной дробью.
При наличии логарифмов дело обстоит немного иначе.
Пример 12
Если имеется выражение вида ln x + ln (x + 3) , его заменяют на ln (x · (x + 3)) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с (0 , + ∞) до (− ∞ , − 3) ∪ (0 , + ∞) . Поэтому для определения ОДЗ ln (x · (x + 3)) необходимо производить вычисления на ОДЗ, то есть (0 , + ∞) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Рациональные выражения делятся на целые и дробные выражения .
Определение. Рациональная дробь — дробное выражение вида , где — многочлены. — числитель, — знаменатель.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя — .
Значение алгебраической дроби
, как и любого алгебраического выражения
, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби при а) , б) , в)
Решение. Подставим значения переменных в указанную дробь: а) , б) , в) — не существует (т. к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения .
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2.
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных — знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .
Решение.
..bmp)
Встречаются и другие формулировки данной задачи — найти область определения или область допустимых значений выражения (ОДЗ) . Это означает — найти все допустимые значения переменных. В нашем примере — это все значения, кроме . Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку , как это указано на рисунке:
Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ. .
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. .
Изобразим полученное решение на числовой оси:
Рис. 2
Ответ. .
Пример 6.
Решение. . Мы получили равенство двух переменных, приведем числовые примеры: или и т. д.
Изобразим это решение на графике в декартовой системе координат:
Рис. 3. График функции
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .
Решение. .
Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить в исходное выражение, то получим — не имеет смысла.
Ответ. .
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях указанная дробь равна нулю?
Какие дроби не имеют смысла. Когда алгебраическая дробь имеет смысл
Алгебраическая дробь имеет смысл только в случае неравенства своего знаменателя нулю. Ведь делить на ноль, как известно, нельзя.
При необходимости определить для дроби те значения, когда она смысл имеет, надо записать значение числового ряда за исключеним тех чисел, которы получаются при решении уравнения при приравнивании знаменателя нулю.
По моему дробь имеет смысл всегда, за исключением случая, когда в знаменателе стоит ноль, так как мы помним, что на ноль делить нельзя. Другое дело в высшей математике, там и но ноль делят, получая математические пределы и т.д.
Также мне кажется, что алгебраическая дробь, или написание числа в виде дроби, не имеет смысла, если числитель равен знаменателю. В таком случае можно написать выражение гораздо проще. К примеру, вместо quot;1/1quot; лучше написать просто quot;1quot;.
Ну, а по правилам, главное чтобы снизу дроби не был quot;0quot;.
Проще было бы ответить на вопрос: когда она не имеет смысла? Тогда бы мы ответили, что тогда, когда знаменатель в дроби равен нулю.
 Ведь на ноль делить нельзя, как мы помним еще со школы, ибо он все обращает в ноль.
Ведь на ноль делить нельзя, как мы помним еще со школы, ибо он все обращает в ноль.На ваш же вопрос можно ответить таким образом: когда в знаменателе не ноль (будь-то положительные числа, будь-то отрицательные), дробь существует и несет при этом определенный смысл.
При любом значении числа дробь имеет смысл,кроме одного случая, если только знаменатель не равен нулю, так как на ноль делить нельзя.
Дробь не имеет смысла если знаменатель равен нулю.
Как то так помню со школы.
Алгебраическая дробь имеет смысл только тогда, когда е знаменатель не равен нулю. В противном случае, когда знаменатель равен нулю, алгебраическая дробь не имеет смысла, так как делить на ноль нельзя.
Говоря о дробях важно понимать, что используя знак дроби (то есть черту), мы подразумеваем процесс деления. А так как нам всем известно, что деление на ноль проводить нельзя согласно правил, то можно точно сказать, что алгебраическая дробь имеет смысл в том случае, когда значение е знаменателя отлично от нуля.

Дробь имеет смысл при условии, что ее знаменатель отличен от нуля. В школьной математике важно, чтобы и числитель был строго больше минус бесконечности и строго меньше плюс бесконечности, иначе даже при ненулевом знаменателе дробь все так же quot;скатитсяquot; в бесконечность.
Одним из основных свойств алгебраических дробей, знакомых еще математикам античности, является запрет деления на 0. Когда в знаменатели дроби возникает это quot;пустоеquot; числоquot; дробь теряет смысл. В школьной программе часто можно встретить разнообразные задания, в которых спрашивается когда выражение или дробь не имеет смысла, при каком значении переменной Х. При этом знаменатель дроби представлен неким выражением, например 8х-4 или х+5. Для нахождения ответа таких заданий знаменатель приравнивается к нули и решается как уравнение. Удовлетворяющие этому уравнению значения Х делают дробь не имеющей смысла. В данных примерах дробь с любым числителем не имеет смысла если в первом примере Х= 0.5, а во втором Х=-5.

Насколько мне известно, алгебраическая дробь не имеет смысла, когда е знаменатель равняется нулю, поскольку на него делить нельзя. Таким образом, во всех остальных случаях алгебраическая дробь имеет смысл, и е можно смело использовать для различных расчтов.
Напомню некоторые сведения, касающиеся алгебраических дробей, а также их допустимых значений.
Так как речь идет об алгебраических дробях, можно добавить: знаменатель не равен нулю при каждом допустимом значении переменных.
Одинаковый смысл имеют типы заданий:
Чтобы выполнить любое из данных заданий, нужно найти множество допустимых значений переменных, для этого исключить недопустимые.
Мы приравниваем к 0 знаменатель дроби (знак равенства часто перечеркивают), решаем полученное уравнение (обычно со знаком перечеркнутого равенства), корни его исключаем из множества значений переменных (перечеркнутые значения переменных — это и есть исключенные корни из множества значений переменных).
Таким образом, в ответе запишутся все значения переменных, за исключением найденных.
Пример:
В представленной картинке даны алгебраические дроби.
Если в знаменателе дан многочлен, который ни при каких значениях переменных не обращается в нуль, то дробь будет иметь смысл на всей числовой прямой, т.е. на множестве действительных чисел (см. 2-й пример на картинке ниже), если в задаче дополнительно не указывается другое конкретное множество значений переменных, на котором задана дробь, например, рациональных чисел.

Пример.
Основные понятия
Алгебраические дроби. Арифметические операции над алгебраическими дробями
На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Рациональные выражения делятся на целые и дробные выражения .
Определение. Рациональная дробь — дробное выражение вида , где — многочлены. — числитель, — знаменатель.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя — .
Значение алгебраической дроби , как и любого алгебраического выражения , зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби при а) , б) , в)
Решение.
Подставим значения переменных в указанную дробь: а) , б) , в) — не существует (т. к. на ноль делить нельзя).
к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения .
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2.
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных — знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. .
Встречаются и другие формулировки данной задачи — найти область определения или область допустимых значений выражения (ОДЗ) . Это означает — найти все допустимые значения переменных. В нашем примере — это все значения, кроме . Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку , как это указано на рисунке:
Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ. .
.
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. .
Изобразим полученное решение на числовой оси:
Рис. 2
Ответ. .
Пример 6.
Решение. . Мы получили равенство двух переменных, приведем числовые примеры: или и т. д.
Изобразим это решение на графике в декартовой системе координат:
Рис. 3. График функции
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .
Решение. .
Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить в исходное выражение, то получим — не имеет смысла.
Однако, если подставить в исходное выражение, то получим — не имеет смысла.
Ответ. .
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях указанная дробь равна нулю?
На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется почасти торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В таком случае возникает понятие дробного выражения. С целыми выражениями (не содержащими деление на выражения с переменными) и их свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие рациональной дроби, а также допустимых значений переменных.
Рациональные выражения делятся на целые и дробные выражения
.
Определение. Рациональная дробь — дробное выражение вида , где — многочлены. — числитель, — знаменатель.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя — .
Значение алгебраической дроби , как и любого алгебраического выражения , зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби при а) , б) , в)
Решение. Подставим значения переменных в указанную дробь: а) , б) , в) — не существует (т. к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений
буквенных переменных.
Определение. Допустимые значения переменных — значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения .
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2.
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных — знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. .
Встречаются и другие формулировки данной задачи — найти область определения или область допустимых значений выражения (ОДЗ) . Это означает — найти все допустимые значения переменных. В нашем примере — это все значения, кроме . Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку , как это указано на рисунке:
Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ. .
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. .
Изобразим полученное решение на числовой оси:
Рис. 2
2
Ответ. .
Пример 6.
Решение. . Мы получили равенство двух переменных, приведем числовые примеры: или и т. д.
Изобразим это решение на графике в декартовой системе координат:
Рис. 3. График функции
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .
Решение. .
Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить в исходное выражение, то получим — не имеет смысла.
Ответ. .
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях указанная дробь равна нулю?
Алгебраические выражения и формулы
Алгебраические выражения и распределительное свойство
В алгебре буквы, называемые переменными, используются для обозначения чисел. Комбинации переменных и чисел вместе с математическими операциями образуют алгебраические выражения Комбинации переменных и чисел вместе с математическими операциями, используемыми для обобщения определенных арифметических операций., Или просто выражений . Ниже приведены несколько примеров выражений с одной переменной x:
. Термины Компоненты алгебраического выражения, разделенные операторами сложения.в алгебраическом выражении разделяются операторами сложения и множителями. Компоненты терма разделяются операторами умножения. разделены операторами умножения. Числовой множитель терма называется коэффициентом. Числовой множитель терма. Например, алгебраическое выражение x2y2 + 6xy − 3 можно представить как x2y2 + 6xy + (- 3) и состоит из трех членов. Первый член, x2y2, представляет величину 1x2y2 = 1⋅x⋅x⋅y⋅y, где 1 — коэффициент, а x и y — переменные.Все переменные факторы с их показателями образуют переменную часть терма Все переменные факторы с их показателями .. Если терм написан без переменного множителя, то он называется постоянным термом. Термин, записанный без переменного множителя. компоненты x2y2 + 6xy − 3,
Числовой множитель терма. Например, алгебраическое выражение x2y2 + 6xy − 3 можно представить как x2y2 + 6xy + (- 3) и состоит из трех членов. Первый член, x2y2, представляет величину 1x2y2 = 1⋅x⋅x⋅y⋅y, где 1 — коэффициент, а x и y — переменные.Все переменные факторы с их показателями образуют переменную часть терма Все переменные факторы с их показателями .. Если терм написан без переменного множителя, то он называется постоянным термом. Термин, записанный без переменного множителя. компоненты x2y2 + 6xy − 3,
| Условия |
Коэффициент |
Переменная часть |
|---|---|---|
| x2y2 |
1 |
x2y2 |
| 6xy |
6 |
xy |
| −3 |
−3 |
|
Третий член в этом выражении, −3, называется постоянным членом, потому что он написан без переменного множителя. Хотя переменная представляет собой неизвестную величину и может изменяться, постоянный член не изменяется.
Хотя переменная представляет собой неизвестную величину и может изменяться, постоянный член не изменяется.
Пример 1
Перечислите все коэффициенты и переменные части каждого члена: 10a2−5ab − b2.
Решение:
Мы хотим думать о третьем члене в этом примере −b2 как −1b2.
| Условия |
Коэффициент |
Переменная часть |
|---|---|---|
| 10a2 |
10 |
A2 |
| −5ab |
−5 |
ab |
| −b2 |
-1 |
b2 |
Ответ: Коэффициенты: {−5, −1, 10}; Переменные части: {a2, ab, b2}
При изучении алгебры мы встретим большое количество алгебраических выражений. Обычно в выражениях используются две наиболее распространенные переменные: x и y . Однако выражения могут использовать любую букву (или символ) для переменной, даже греческие буквы, такие как альфа (α) и бета (β). Некоторые буквы и символы зарезервированы для констант, например π≈3,14159 и e≈2,71828. Поскольку количество букв ограничено, вы также будете использовать индексы x1, x2, x3, x4,… для обозначения различных переменных.
Обычно в выражениях используются две наиболее распространенные переменные: x и y . Однако выражения могут использовать любую букву (или символ) для переменной, даже греческие буквы, такие как альфа (α) и бета (β). Некоторые буквы и символы зарезервированы для констант, например π≈3,14159 и e≈2,71828. Поскольку количество букв ограничено, вы также будете использовать индексы x1, x2, x3, x4,… для обозначения различных переменных.
Свойства действительных чисел важны в нашем изучении алгебры, потому что переменная — это просто буква, представляющая действительное число.В частности, распределительное свойство дает любые действительные числа a , b и c , a (b + c) = ab + ac или (b + c) a = ba + ca. заявляет, что если заданы какие-либо действительные числа a , b и c , то
а (b + c) = ab + ac
Это свойство мы часто применяем при упрощении алгебраических выражений. Чтобы продемонстрировать, как это будет использоваться, мы упростим 2 (5−3) двумя способами и получим тот же правильный результат.
Чтобы продемонстрировать, как это будет использоваться, мы упростим 2 (5−3) двумя способами и получим тот же правильный результат.
| Первая рабочая скобка. |
Использование распределительной собственности. |
|---|---|
| 2 (5−3) = 2 (2) = 4 |
2 (5−3) = 2⋅5−2⋅3 = 10−6 = 4 |
Конечно, если содержание круглых скобок можно упростить, мы должны сделать это в первую очередь. С другой стороны, когда содержание круглых скобок не может быть упрощено дальше, мы умножаем каждый член в нем на множитель вне его, используя свойство распределения.Применение дистрибутивного свойства позволяет нам умножать и убирать круглые скобки.
Пример 2
Упростить: 5 (−2a + 5b) −2c.
Решение:
Умножайте только термины, сгруппированные в круглых скобках, для которых мы применяем свойство распределения.
= 5⋅ (−2a) + 5⋅5b − 2c = −10a + 25b − 2c
Ответ: −10a + 25b − 2c
Напомним, что умножение коммутативно, и поэтому мы можем записать свойство распределения следующим образом: (b + c) a = ba + ca.
Пример 3
Упростить: (3x − 4y + 1) ⋅3.
Решение:
Умножить все члены в скобках на 3.
(3x − 4y + 1) ⋅3 = 3x⋅3−4y⋅3 + 1⋅3 = 9x − 12y + 3
Ответ: 9x − 12y + 3
Термины, переменные части которых имеют одинаковые переменные с одинаковыми показателями степени, называются как термины Постоянные термины или термины, переменные части которых имеют одинаковые переменные с одинаковыми показателями степени. , или аналогичные термины. Используются при ссылке на похожие термины. Более того, постоянные термины считаются аналогичными терминами. Если алгебраическое выражение содержит похожие термины, примените свойство распределения следующим образом:
, или аналогичные термины. Используются при ссылке на похожие термины. Более того, постоянные термины считаются аналогичными терминами. Если алгебраическое выражение содержит похожие термины, примените свойство распределения следующим образом:
5x + 7x = (5 + 7) x = 12x4x2 + 5×2−7×2 = (4 + 5−7) x2 = 2×2
Другими словами, если переменных частей термов в точности совпадают с , то мы можем складывать или вычитать коэффициенты, чтобы получить коэффициент одного члена с той же переменной частью. Этот процесс называется объединением одинаковых терминов. Добавление или вычитание одинаковых терминов в алгебраическом выражении для получения одного члена с той же переменной частью.. Например,
12x2y3 + 3x2y3 = 15x2y3
Обратите внимание, что переменные множители и их показатели не меняются. Комбинирование похожих терминов таким образом, чтобы выражение не содержало других похожих терминов, называется упрощением выражения. Процесс объединения похожих терминов до тех пор, пока в выражении не перестанут быть похожие термины. Используйте эту идею для упрощения алгебраических выражений с помощью нескольких похожих терминов.
Процесс объединения похожих терминов до тех пор, пока в выражении не перестанут быть похожие термины. Используйте эту идею для упрощения алгебраических выражений с помощью нескольких похожих терминов.
Пример 4
Упростить: x2−10x + 8 + 5×2−6x − 1.
Решение:
Найдите похожие термины и сложите соответствующие коэффициенты.
1×2–− 10x –– + 8 ––– + 5×2–− 6x ––– 1 ––– Объедините похожие термины. = 6×2−16x + 7
Ответ: 6×2−16x + 7
Пример 5
Упростить: a2b2 − ab − 2 (2a2b2−5ab + 1).
Решение:
Распределите −2, а затем объедините одинаковые термины.
a2b2 − ab − 2 (2a2b2−5ab + 1) = a2b2 − ab − 4a2b2 + 10ab − 2 = −3a2b2 + 9ab − 2
Ответ: −3a2b2 + 9ab − 2
Вычисление алгебраических выражений
Алгебраическое выражение можно рассматривать как обобщение определенных арифметических операций. Выполнение этих операций после замены заданных значений на переменные называется вычислением. Процесс выполнения операций алгебраического выражения для заданных значений переменных. В алгебре переменная представляет собой неизвестное значение. Однако, если проблема специально присваивает значение переменной, вы можете заменить эту букву заданным числом и оценить, используя порядок операций.
Выполнение этих операций после замены заданных значений на переменные называется вычислением. Процесс выполнения операций алгебраического выражения для заданных значений переменных. В алгебре переменная представляет собой неизвестное значение. Однако, если проблема специально присваивает значение переменной, вы можете заменить эту букву заданным числом и оценить, используя порядок операций.
Пример 6
Оценить:
- 5x − 2, где x = 23
- y2 − y − 6, где y = −4
Решение:
Чтобы избежать распространенных ошибок, рекомендуется сначала заменить все переменные круглыми скобками, а затем заменить или заменить Акт замены переменной эквивалентной величиной., соответствующее заданное значение.
а.
5x − 2 = 5 () −2 = 5 (23) −2 = 103−21⋅33 = 10−63 = 43
г.
y2 − y − 6 = () 2− () −6 = (- 4) 2 — (- 4) −6 = 16 + 4−6 = 14
Ответ:
- 43
- 14
Часто алгебраические выражения включают более одной переменной.
Пример 7
Вычислите a3−8b3, где a = −1 и b = 12.
Решение:
После подстановки соответствующих значений мы должны позаботиться об упрощении, используя правильный порядок операций.
a3−8b3 = () 3−8 () 3 Заменить переменные скобками. = (- 1) 3−8 (12) 3 Подставить соответствующие значения. = — 1−8 (18) Упростить. = — 1−1 = −2
Ответ: −2
Пример 8
Вычислить x2 − y22x − 1, где x = −32 и y = −3.
Решение:
x2 − y22x − 1 = () 2− () 22 () −1 = (- 32) 2 — (- 3) 22 (−32) −1 = 94−9−3−1
На данный момент у нас есть сложная дробь.Упростите числитель, а затем умножьте на обратную величину знаменателя.
= 94−91⋅44 −4 = −274 −41 = −274 (−14) = 2716
Ответ: 2716
Ответ на предыдущий пример можно записать как смешанное число, 2716 = 11116. Если исходная задача не содержит смешанных чисел или не является ответом на решение реального приложения, решения будут выражены в виде уменьшенных неправильных дробей.
Если исходная задача не содержит смешанных чисел или не является ответом на решение реального приложения, решения будут выражены в виде уменьшенных неправильных дробей.
Пример 9
Вычислить b2−4ac, где a = −1, b = −7 и c = 14.
Решение:
Подставьте соответствующие значения, а затем упростите.
b2−4ac = () 2−4 () () = (- 7) 2−4 (−1) (14) = 49 + 4 (14) = 49 + 1 = 50 = 25⋅2 = 52
Ответ: 52
Попробуй! Вычислить 3πVhπh, где V = 25π и h = 3.
Ответ: 5
Использование формул
Основное различие между алгеброй и арифметикой — это организованное использование переменных.Эта идея приводит к многоразовым формулам, математической модели многократного использования, использующей алгебраические выражения для описания общего приложения, которые представляют собой математические модели, использующие алгебраические выражения для описания общих приложений. Например, объем правого кругового конуса зависит от его радиуса r и высоты h и моделируется формулой:
Например, объем правого кругового конуса зависит от его радиуса r и высоты h и моделируется формулой:
В = 13πr2h
В этом уравнении переменные и константы используются для описания взаимосвязи между объемом, длиной основания и высотой.Если радиус основания 3 метра, а высота 5 метров, то объем можно рассчитать по следующей формуле: V = 13πr2h = 13π (3 м) 2 (5 м) = 13π⋅93⋅5 м3 = 15π м3 Используя π≈3,14, мы можем приблизительно оценить объем: V≈15 (3,14) = 47,1 кубометра.
Ниже приводится список формул, описывающих площадь и периметр обычных плоских фигур. Буква P обозначает периметр и измеряется в линейных единицах. Буква A обозначает площадь и измеряется в квадратных единицах.
Ниже приводится список формул, описывающих площадь поверхности и объем обычных фигур. Здесь SA представляет собой площадь поверхности и измеряется в квадратных единицах. Буква V обозначает объем и измеряется в кубических единицах.
Буква V обозначает объем и измеряется в кубических единицах.
Пример 10
Диаметр сферического шара 10 дюймов. Определите объем с округлением до сотых.
Решение:
Формула объема шара
В = 43πr3
Эта формула дает объем через радиус, r . Поэтому разделите диаметр на 2 и подставьте в формулу. Здесь r = 102 = 5 дюймов, и у нас
V = 43πr3 = 43π (5 дюймов) 3 = 43π⋅125 дюймов3 = 500π3 дюймов3≈523,60 дюймов3
Ответ: Объем воздушного шара примерно 523.60 кубических дюймов.
Формулы можно найти по множеству предметов. Например, равномерное движение Расстояние D после проезда со средней скоростью r в течение некоторого времени t можно рассчитать по формуле D = rt. моделируется формулой D = rt, которая выражает расстояние D в терминах средней скорости или скорости r и времени, пройденного с этой скоростью, t . Эта формула, D = rt, используется часто и читается как «расстояние равно скорости, умноженной на время. ”
Эта формула, D = rt, используется часто и читается как «расстояние равно скорости, умноженной на время. ”
Пример 11
Поездка Джима заняла 212 часов при средней скорости 66 миль в час. Как далеко он проехал?
Решение:
Подставьте соответствующие значения в формулу, а затем упростите.
D = r⋅t = (66 миль) ⋅ (212 часов) = 661⋅52 миль = 33⋅5 миль = 165 миль
Ответ: Джим проехал 165 миль.
Простой процент Моделируется по формуле I = prt, где p представляет собой основную сумму, инвестированную с годовой процентной ставкой r на t лет.I определяется по формуле I = prt, где p представляет собой основную сумму, инвестированную с годовой процентной ставкой r на t лет.
Пример 12
Рассчитайте простой процент, полученный от двухлетних инвестиций в размере 1250 долларов США при годовой процентной ставке 334%.
Решение:
Преобразуйте 334% в десятичное число, прежде чем использовать его в формуле.
г = 334% = 3.75% = 0,0375
Используйте это, а также тот факт, что p = 1250 долларов и t = 2 года для расчета простых процентов.
I = prt = (1250) (0,0375) (2) = 93,75
Ответ: Простые проценты составляют 93,75 доллара.
Основные выводы
- Думайте об алгебраических выражениях как об обобщении общих арифметических операций, которые формируются путем объединения чисел, переменных и математических операций.
- Дистрибутивное свойство a (b + c) = ab + ac, используется при умножении сгруппированных алгебраических выражений. Применение свойства дистрибутива позволяет нам убрать скобки.
- Объедините одинаковые термины или термины, у которых переменные части имеют одинаковые переменные с одинаковыми показателями степени, путем сложения или вычитания коэффициентов, чтобы получить коэффициент одного члена с той же переменной частью.
 Помните, что переменные множители и их показатели не меняются.
Помните, что переменные множители и их показатели не меняются. - Чтобы избежать распространенных ошибок при оценке, рекомендуется заменить все переменные круглыми скобками, а затем подставить соответствующие значения.
- Использование алгебраических выражений позволяет нам создавать полезные и многократно используемые формулы, моделирующие общие приложения.
Тематические упражнения
-
23 (9y2 + 12y − 3)
-
−34 (8y2 + 20y + 4)
-
12 (13a2−56a + 712)
-
−9 (19a2−53a + 1)
-
35a2−12 + 13a2 + 45
-
16a2 + 23−43a2−19
-
12y2 + 23y − 3 + 35y2 + 13y − 73
-
56×2 + 18x − 1−12×2 + 34x − 45
-
a2b2 + 5ab − 2 + 7a2b2−6ab + 12
-
a2−12ab + 4b2−6a2 + 10ab − 5b2
-
3x2y + 12xy − 5xy2 + 5xy − 8x2y + 2xy2
-
10x2y + 2xy − 4xy2 + 2x2y − 8xy + 5xy2
-
7m2n − 9mn + mn2−6m2n + mn − 2mn2
-
m2n − 5mn + 5mn2−3m2n + 5mn + 2mn2
-
x2n − 3xn + 5 + 2x2n − 4xn − 3
-
5y2n − 3yn + 1−3y2n − 2yn − 1
-
4m2−3mn− (m2−3mn + n2)
-
−3 (y2n − 2yn + 1) + 4y2n − 5
Часть A: Алгебраические выражения и свойство распределения
Перечислите все коэффициенты и переменные части каждого члена.
Умножить.
Объедините похожие термины.
Упростить.
-
−2x + 3, где x = −2
-
8x − 5, где x = −1
-
x2 − x + 5, где x = −5
-
2×2−8x + 1, где x = 3
-
x2 − x + 22x − 1, где x = −12
-
9×2 + x − 23x − 4, где x = −23
-
(3y − 2) (y + 5), где y = 23
-
(3x + 2) (5x + 1), где x = −15
-
(3x − 1) (x − 8), где x = −1
-
(7y + 5) (y + 1), где y = −2
-
y6 − y3 + 2, где y = −1
-
y5 + y3−3, где y = −2
-
a2−5b2, где a = −2 и b = −1
-
a3−2b3, где a = −3 и b = 2
-
(x − 2y) (x + 2y), где x = 2 и y = −5
-
(4x − 3y) (x − y), где x = −4 и y = −3
-
a2 − ab + b2, где a = −1 и b = −2
-
x2y2 − xy + 2, где x = −3 и y = −2
-
a4 − b4, где a = −2 и b = −3
-
a6−2a3b3 − b6, где a = 2 и b = −1
-
a = 34, b = −2 и c = −4
-
a = 12, b = −2 и c = −30
-
a = 1, b = −4 и c = −50
-
a = 1, b = −1 и c = −116
-
a = −2, b = −13 и c = 1
Часть B: Вычисление алгебраических выражений
Оценить.
Оцените b2−4ac с учетом следующих значений.
-
Вычислите периметр и площадь прямоугольника размером 12 футов на 5 футов.
-
Вычислить периметр и площадь прямоугольника размером 5 на 1 метр.
-
Вычислить площадь поверхности и объем шара радиусом 6 сантиметров.
-
Радиус основания правого кругового цилиндра составляет 4 дюйма, а высота — 10 дюймов.
 Рассчитайте площадь поверхности и объем.
Рассчитайте площадь поверхности и объем. -
Рассчитайте объем шара диаметром 18 сантиметров.
-
Диаметр основания правого кругового конуса составляет 6 дюймов. Если высота 112 футов, то рассчитайте ее объем.
-
Учитывая, что высота правого кругового цилиндра равна радиусу основания, выведите формулу для площади поверхности через радиус основания.
-
Учитывая, что площадь основания правого кругового цилиндра составляет 25π квадратных дюймов, найдите объем, если высота равна 1 футу.

-
Хосе смог проехать из Тусона в Феникс за 2 часа со средней скоростью 58 миль в час. Как далеко Финикс от Тусон?
-
Если сверхскоростной пассажирский экспресс развивает в среднем 152 мили в час, то как далеко он может проехать за 34 часа?
-
Маргарет проехала 134 часа со средней скоростью 68 миль в час.Как далеко она ушла?
-
Поездка из Флагстаффа, штат Аризона, в национальный парк Гранд-Каньон заняла 112 часов при средней скорости 54 миль в час.
 Как далеко от Флагстаффа национальный парк Гранд-Каньон?
Как далеко от Флагстаффа национальный парк Гранд-Каньон? -
Рассчитайте простой процент, полученный на 3-летнюю инвестицию в размере 2500 долларов США при годовой процентной ставке 514%.
-
Рассчитайте простой процент, полученный по годовой инвестиции в размере 5 750 долларов США при годовой процентной ставке 258%.
-
Каков простой процент, полученный на 5-летнюю инвестицию в размере 20 000 долларов США при годовой процентной ставке 6%?
-
Каков простой процент, полученный от годовой инвестиции в размере 50 000 долларов США по годовой процентной ставке 4?5%?
-
Время t в секундах, в течение которого объект находится в свободном падении, определяется формулой t = s4, где s представляет собой расстояние в футах, на которое объект упал.
 Сколько времени нужно, чтобы объект упал с высоты 32 фута? (Дайте точный ответ и примерный ответ с точностью до сотых.)
Сколько времени нужно, чтобы объект упал с высоты 32 фута? (Дайте точный ответ и примерный ответ с точностью до сотых.) -
Ток I , измеренный в амперах, определяется формулой I = PR, где P — потребляемая мощность, измеренная в ваттах, а R — сопротивление, измеренное в омах.Если лампочка потребляет 60 Вт мощности и имеет сопротивление 240 Ом, то сколько ампер тока требуется?
Часть C: Использование формул
Преобразуйте следующие температуры в градусы Цельсия, если C = 59 (F − 32), , где F представляет собой градусы Фаренгейта.
-
Найдите и опубликуйте полезную математическую модель. Продемонстрируйте его использование с некоторыми ценностями.
-
Изучите и обсудите историю переменной.
 Что мы можем использовать, если у нас закончились письма?
Что мы можем использовать, если у нас закончились письма? -
Найдите и опубликуйте ссылку на полезный ресурс с описанием греческого алфавита.
-
Учитывая алгебраическое выражение 5−3 (9x − 1), объясните, почему мы не вычитаем сначала 5 и 3.
-
Нужна ли отдельная распределительная собственность более чем на два срока? Например, a (b + c + d) = ab + ac + ad.Объяснять.
-
Как мы можем проверить, правильно ли мы упростили выражение?
Часть D: Обсуждение
ответы
-
Коэффициенты: {−5,1, −1}; переменные части: {x2, x}
-
Коэффициенты: {5, −3,1}; переменные части: {x2, xy, y2}
-
Коэффициенты: {1, −3,9}; переменные части: {x2y, xy2, xy}
-
1415a2 + 310
-
1110y2 + y − 163
-
P = 34 фута; A = 60 квадратных футов
-
SA = 144π квадратных сантиметра; V = 288π кубических сантиметров
переменных и алгебраических выражений
Переменные и алгебраические выражения
Прежде чем приступить к решению уравнений, вы должны иметь общее представление о переменных, а также о переводе и оценке алгебраических выражений.
Переменные
Переменная — это буква, обозначающая число. Буквы x , y , z , a , b , c , m и n , вероятно, являются наиболее часто используемыми переменными. Буквы e и i имеют специальные значения в алгебре и обычно не используются в качестве переменных. Буква o обычно не используется, поскольку ее можно принять за 0 (ноль).
Алгебраические выражения
Переменные используются для преобразования словесных выражений в алгебраические, то есть выражения, состоящие из букв, обозначающих числа. Ключевые слова, которые могут помочь вам переводить слова в буквы и цифры, включают:
- Для сложения: сумма, больше, больше, прибавка
- Для вычитания: минус, меньше, меньше, уменьшить
- Для умножения: раз, произведение, умноженное на, из
- Для деления: делить пополам на, соотношение.

Пример 1
Приведите алгебраические выражения для каждого из следующих утверждений.
1. сумма числа и 5
2. число минус 4
3. шесть умноженное на число
4 . x разделить на 7
5. на три больше, чем произведение 2 и x
1. сумма числа и 5: x + 5 или 5 + x
2. число минус 4: x — 4
3.шестикратное число: 6 x
4. x разделить на 7: или
5. на три больше, чем произведение 2 и x : 2 x + 3
Вычисление выражений
Чтобы оценить выражение, просто замените переменные символами группировки, вставьте значения, заданные для переменных, и выполните арифметические действия. Не забудьте соблюдать порядок операций: скобки, показатели степени, умножение / деление, сложение / вычитание.
Пример 2
Оцените каждое из следующих действий.
1. x + 2 y , если x = 2 и y = 5
2. a + bc — 3, если a = 4, b = 5 и c = 6
3. м 2 + 4 n + 1, если м = 3 и n = 2
4. если a = 2, b = 3 и c = 4
5.–5 xy + z , если x = 6, y = 7 и z = 1
1.
2.
3.
4.
5.
Алгебраические выражения — объяснения и примеры
Алгебра — интересный и увлекательный раздел математики, в котором числа, фигуры и буквы используются для выражения задач. Независимо от того, изучаете ли вы алгебру в школе или сдаете какой-то тест, вы заметите, что почти все математические задачи представлены словами.
Следовательно, необходимость переводить письменные текстовые задачи в алгебраические выражения возникает тогда, когда нам нужно их решить.
Большинство алгебраических задач со словами состоят из рассказов или примеров из реальной жизни. Другие — простые фразы, например, описание математической задачи. Из этой статьи вы узнаете, как написать алгебраических выражений из простых задач со словами, а затем перейти к легко сложным задачам со словами.
Что такое алгебраическое выражение?
Многие люди попеременно используют алгебраические выражения и алгебраические уравнения, не подозревая, что это совершенно разные термины.
Алгебраика — это математическая фраза, в которой две стороны фразы соединены знаком равенства (=). Например, 3x + 5 = 20 — это алгебраическое уравнение, где 20 представляет собой правую часть (RHS), а 3x +5 представляет собой левую часть (LHS) уравнения.
С другой стороны, алгебраическое выражение — это математическая фраза, в которой переменные и константы объединяются с помощью операционных символов (+, -, × & ÷). В алгебраическом символе отсутствует знак равенства (=). Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
Давайте рассмотрим терминологию, используемую в алгебраическом выражении:
- Переменная — это буква, значение которой нам неизвестно. Например, x — это наша переменная в выражении: 10x + 63.
- Коэффициент — это числовое значение, используемое вместе с переменной. Например, 10 — это переменная в выражении 10x + 63.
- Константа — это термин, который имеет определенное значение. В данном случае 63 — это константа в алгебраическом выражении 10x + 63.
Существует несколько типов алгебраических выражений, но основной тип включает:
- Мономиальное алгебраическое выражение
Этот тип выражения имеет только один член, например, 2x, 5x 2 , 3xy и т. Д. .
Алгебраическое выражение, содержащее два, в отличие от термов, например, 5y + 8, y + 5, 6y 3 + 4 и т. Д.
Это алгебраическое выражение с более чем одним членом и с ненулевыми показателями. переменных.Пример полиномиального выражения: ab + bc + ca и т. Д.
переменных.Пример полиномиального выражения: ab + bc + ca и т. Д.
Другие типы алгебраических выражений:
Числовое выражение состоит только из чисел и операторов. В числовое выражение переменная не добавляется. Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
Это выражение содержит переменные вместе с числами, например, 6x + y, 7xy + 6 и т. Д.
Как решить алгебраическое выражение?
Цель решения алгебраического выражения в уравнении — найти неизвестную переменную.Когда два выражения приравниваются, они образуют уравнение, и поэтому становится легче найти неизвестные члены.
Чтобы решить уравнение, поместите переменные с одной стороны, а константы — с другой. Вы можете изолировать переменные, применяя арифметические операции, такие как сложение, вычитание, умножение, деление, квадратный корень, кубический корень и т. Д.
Алгебраические выражения всегда взаимозаменяемы. Это означает, что вы можете переписать уравнение, поменяв местами LHS и RHS.
Пример 1
Вычислите значение x в следующем уравнении.
5x + 10 = 50
Решение
Данное уравнение имеет вид 5x + 10 = 50.
- Выделите переменные и константы;
- Вы можете сохранить переменную на левой стороне, а константы на правой.
5x = 50-10
5x = 40
Разделим обе части на коэффициент переменной;
x = 40/5 = 8
Следовательно, значение x равно 8.
Пример 2
Найдите значение y, когда 5y + 45 = 100.
Решение
Изолировать переменные от констант;
5y = 100-45
5y = 55
Разделим обе части на коэффициент;
y = 55/5
y = 11
Пример 3
Определите значение переменной в следующем уравнении:
2x + 40 = 30
Решение
Разделите переменные из констант;
2x = 30-40
2x = -10
Разделим обе стороны на 2;
x = -5
Пример 4
Найдите t, когда 6t + 5 = 3.
Решение
Отделите константы от переменной,
6t = 5-3
6t = -2
Разделите обе части на коэффициент,
t = -2/6
Упростите дробь,
t = -1/3
Предыдущий урок | Главная страница | Следующий урок
Как решать алгебру
y = 24 — 4x
Пояснение:
Как показано в приведенном выше примере, мы вычисляем значение переменной из одного уравнения и подставляем его в другое.
Нам дано, что
у = 24 — 4x —— (1)
2x + y / 2 = 12 —— (2)
Здесь мы выбираем уравнение (1) для вычисления значения x. Поскольку уравнение (1) уже находится в
самая упрощенная форма:
Поскольку уравнение (1) уже находится в
самая упрощенная форма:
(Подставляя это значение y в уравнение (2), а затем решая для x дает)
2x + (24-4x) / 2 = 12 —— (2) (∵ y = 24 — 4x)
2x + 24 / 2- 4x / 2 = 12
2x + 12 — 2x = 12
12 = 12
Вы можете подумать, что это тот же сценарий, что обсуждался выше (24 = 24).Но
ждать! Вы слишком рано пытаетесь сделать вывод. В предыдущем сценарии
результат 24 = 24 был получен потому, что мы поместили значение переменной в то же уравнение, что и
используется для его вычисления. Здесь мы этого не сделали.
Здесь мы этого не сделали.
Результат 12 = 12 имеет какое-то отношение к природе системы уравнений, которую мы даны.Независимо от того, какой метод решения вы можете использовать, решение системы линейных уравнения лежат в единственной точке, где их линии пересекаются. В этом сценарии две строки в основном одинаковы (одна линия над другой. На следующем рисунке показан этот сценарий.
Такая система называется зависимой системой уравнения.И решение такой системы — это вся линия (каждая точка на линии — это точка пересечения двух линий)
Следовательно, решением данной системы уравнений является вся строка: y = 24 — 4x
Другой возможный сценарий:
Подобно этому примеру, существует другой сценарий, в котором замена одной переменной в уравнение 2 nd приводит к результату, аналогичному показанному ниже:
23 = –46
или
5 = 34
Такой сценарий возникает, когда не существует решения данной системы уравнений. Т.е.,
когда две линии вообще не пересекаются.
Т.е.,
когда две линии вообще не пересекаются.
Следовательно, в случае такого результата, когда кажется, что ваши основные математические правила не работают, простой вывод заключается в том, что решения данной системы не существует. Такая система уравнений называется Несогласованная система .
Вычисление алгебраических выражений, … Пошаговое решение математических задач
3.1 Вычисление алгебраических выражений
Тот же набор правил для порядка операций для целых чисел, который описан в разделе 1.2
, также используется с целыми числами. Правила изложены здесь для удобства обращения в службу
.
Правила порядка работы
1.2 = 8 ÷ 4-9 степеней
= 2-9 делений
= -7 вычитание
2. (7 + 8) ÷ 5 * 4-20
(7 + 8) ÷ 5 * 4-20
(7 + 8) ÷ 5 * 4-20 = 15 ÷ 5 * 4-20 скобок
= 3 * 4-20 дел
= 12-20 умножение
= -8 вычитание
3. 4 * 5- (6 * 2-3) + 4 ÷ 2
4 * 5- (6 * 2-3) + 4 ÷ 2 = 4 * 5- (9) + 4 ÷ 2 круглые скобки
= 20-9 + 2 умножения и деления
= 13 вычитания и сложения
4.(-5-6) / 11 + 3 (-5)
(-5-6) / 11 + 3 (-5) = — 11/11 + 3 (-5) дробная черта является символом включения
= -1 + (- 15) деление и умножение
= -16 сложение
Контрольная работа
| Вопросы | Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найдите значение каждого выражения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. 7 * 5 + 3 * 8 | 1.2 не равны степени x.
Числовая часть термина называется коэффициентом переменной или переменных в термине. Таким образом, в члене 8x, 8 — это коэффициент при x. Выражения с одинаковыми членами можно упростить, применив свойство распределенности, описанное в разделе 1. а (b + c) = ab + ac или ab + ac = a (b + c) или ba + ca = (b + c) a Эта последняя форма особенно полезна, когда b и c — числовые коэффициенты.Например, 3x + 5x = (3 + 5) x Коэффициенты складываются = 8x Мы говорим, что 3x и 5x были объединены или что мы объединили одинаковые термины. Подобные термины можно комбинировать, добавляя (или вычитая) коэффициенты. Примеры По возможности комбинируйте похожие термины 1. 3x-5x = (3-5) x = -2x 2. 6x-2x = (6-2) x = 4x 3. 4 (x-7) +5 (x + 1) = 4x-28 + 5x + 5 Используйте свойство распределения дважды. = 4x + 5x-28 + 5 = 9x-23 Объедините похожие термины.2 + 2а 5. (x + 3x) / 2 + x = (4x) / 2 + x Дробная черта в скобках обозначает включение. = 2х + х = 3х Давайте посмотрим, как наш математический решатель решает эту и подобные задачи.
3.3 Написание алгебраических выражений Алгебра — это язык математиков, и чтобы понимать математику, вы должны понимать язык. Мы хотим иметь возможность превращать английские фразы в их «алгебраические» эквиваленты и наоборот. Итак, если проблема сформулирована на английском языке, мы можем перевести фразы в алгебраические символы и приступить к решению проблемы в соответствии с правилами, разработанными для алгебры. Следующие примеры иллюстрируют, как определенные ключевые слова могут быть переведены в алгебраические символы. Примеры
Определенные слова, например, выделенные жирным шрифтом в предыдущих примерах, являются ключами к операциям.
Особо следует упомянуть слова «частное» и «разница». Как показано в задачах 3 и 6 практического теста, деление и вычитание выполняются со значениями в том порядке, в котором они указаны в задаче.Например, разница между 3 и 5 составляет 3-5 = -2, а разница между 5 и 3 составляет 5-3 = 2. 3.4 Решение уравнения Если уравнение содержит переменную, мы хотим найти значение (или значения) для переменной, которая даст истинное уравнение при замене переменной. Предположим, нам дано уравнение 2х-1 = х + 3 Если подставить x = 4, то 2 * 4-1 = 7 и 4 + 3 = 7 так 2 * 4-1 = 4 + 3 и x = 4 — решение Если подставить x = 5, то 2 * 5-1 = 9 и 5 + 3 = 8 но 9! = 8, так 2 * 5-1! = 5 + 3 и x = 5 не является решением. Два уравнения эквивалентны, если они имеют точно такие же решения. Например, 2x-1 = x + 3 и x + 1 = 5 эквивалентны, поскольку x = 4 является решением для каждого уравнения. Нам нужны некоторые процедуры, которые позволят нам шаг за шагом находить решения уравнений, содержащих переменные. Следующие две идеи являются основными. 1. Все, что делается с одной стороной уравнения, должно делаться с другой. (Это не включает упрощение выражений и объединение похожих терминов.) 2. Задача состоит в том, чтобы найти простое уравнение, такое как x = 4, которое эквивалентно исходному уравнению. В следующих примерах каждое уравнение решается пошаговым образом с объяснением каждого шага. Внимательно изучите каждый пример. Обратите внимание, что эквивалентные уравнения написаны одно под другим. Не записывайте несколько уравнений в одной строке и не ставьте одно уравнение равным другому. Примеры 1. x + 7 = 12 Напишите уравнение. x + 7-7 = 12-7 Прибавить -7 к обеим сторонам x = 5 Упростить. 2. 2x-3 = 13 Напишите уравнение. 2x-3 + 3 = 13 + 3 Прибавьте 3 к обеим сторонам. 2x = 16 Упростить. (2x) / 2 = 16/2 Разделим обе части на 2, коэффициент при x. x = 8 Упростить. 3. 5x-1 = -11 Запишите уравнение. 5x-1 + 1 = -11 + 1 Добавьте +1 к обеим сторонам. 5x = -10 Упростить; теперь одна сторона имеет все термины с переменными и только термины с переменными. (5x) / 5 = -10 / 5 Разделите обе части на 5, коэффициент при x. x = -2 Упростить 4. 3x + 1 = 13 + x Упростить 3x + 1-1 = 13 + x-1 Прибавьте -1 к обеим сторонам. 3x = 12 + x Упростить 3x-x = 12 + x-x Добавьте -x к обеим сторонам. 2x = 12 Упростить; теперь одна сторона имеет все термины с переменными и только термины с переменными. (2x) / 2 = 12/2 Разделим обе части на 2, коэффициент при x. x = 6 Упростить 5. (2x) / 5 + 2 = 6 Напишите уравнение. (2x) / 5 + 2-2 = 6-2 Прибавьте -2 к обеим сторонам. (2x) / 5 = 4 Упростить 5 * (2x) / 5 = 4 * 5 Умножить обе стороны на 5. 2x = 20 Упростить (2x) / 2 = 20/2 Разделим обе стороны на 2 x = 10 Упростить Давайте посмотрим, как наш решатель уравнений решает эту и подобные проблемы. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров. Каждое решение можно проверить, подставив его в исходное уравнение.Истинное утверждение будет результатом, если нет ошибок. Если выражение, представляющее ненулевое число, (а) добавляется, (б) делится на, или (в) умножается на обе части уравнения, новое уравнение будет эквивалентно исходному уравнению. 3,5 Формулы Формулы — это общие правила или принципы, изложенные математически. Например, в бизнесе простой процент — это произведение основной суммы долга, процентной ставки и времени в годах.2 Площадь (A) круга равна произведению числа PI и квадрата радиуса (r). p = 4s Периметр (p) квадрата в 4 раза больше длины одной стороны (сторон). A = 1 / 2bh Площадь (A) треугольника равна половине произведения основания (b) на высоту (h). d = rt Пройденное расстояние равно произведению скорости (r) и времени (t). C = 5/9 (F-32) Температура в градусах Цельсия (C) равна 5/9 разницы между температурой по Фаренгейту (F) и 32. В последней формуле предположим, что F = 212 °, температура кипения воды на уровне моря. Какое значение будет в градусах Цельсия? Замена 212 ° на F дает .
C = 5/9 (212-32) = 5/9 (180) = 100 Предположим, что вопрос обратный. Если C = 20 °, каково будет соответствующее значение F? Подставив 20 вместо C и решив F, получим .20 = 5/9 (Ф-32) 20 * 9/5 = 9/5 * 5/9 (F-32) Умножьте обе стороны на 9/5, обратное значение 5/9. 36 = Ф-32 68 = F Решение для F в терминах C может быть выполнено следующим образом: С = 5/9 (Ф-32) 9/5 * C = 9/5 * 5/9 (F-32) 9 / 5C = F-32 9 / 5C + 32 = F Формула, решенная для C: С = 5/9 (Ф-32) и решено для F равно F = 9 / 5C + 32 Цель здесь состоит в том, чтобы решить формулы для одной из переменных в терминах других переменных.То есть, используя методы решения уравнений, которые имеют только одну переменную, обрабатывайте другие переменные как константы и решайте для желаемой переменной. Примеры 1. Дано P = a + b + c Формула для периметра треугольника Решите для b. Решение: P = a + b + c P-a-c = a + b + c-a-c P-a-c = b 2. Дано P = 2l + 2w Формула для периметра прямоугольника Решите для л Решение: P = 2l + 2w P-2w = 2l + 2w-2w P-2w = 2l (П-ш) / 2 = (2л) / 2 (P-2w) / 2 = l или P = 2l + w P / 2 = (2l + 2w) / 2 P / 2 = (2l) / 2 + (2w) / 2 P / 2 = l + w P / 2-w = l Оба ответа верны, поскольку P / 2-w = P / 2- (2w) / 2 = (P-2w) / 2 3.Дано 3y-4x + 9 = 0, найти y. Решение: 3y-4x + 9 = 0 3г-4x + 9 + 4x-9 = 0 + 4x-9 3y = 4x-9 y = (4x-9) / 3 или y = (4x) / 3-9 / 3 = 4 / 3x-3 Любая из этих форм верна. Если у вас есть один ответ, а другой находится в Ключе ответа, вы должны признать свой ответ правильным, но в другой форме. Давайте посмотрим, как наш решатель уравнений решает эту и подобные проблемы. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров. Решение: В = Т / (Р-5) V (P-5) = T / (P-5) (P-5) Умножьте обе стороны на P-5. В (P-5) = T (В (П-5)) / В = Т / В P-5 = T / V P = T / V + 5 3.6 Задачи со словами (числа и последовательные целые числа) В Разделе 3.3 мы обсуждали перевод английских фраз в алгебраические выражения «Фраза« 8, добавленная к двойному числу »алгебраически переводится как 2x + 8.Как перевести «4 больше, чем число?» Если вы сказали x + 4, вы правы. Теперь цель состоит в том, чтобы преобразовать все предложение в уравнение, а затем решить уравнение. Две приведенные выше фразы могут быть включены в предложение, например следующее: Алгебраически, 2x + 8 = x + 4 «результат» переводится как = Solving, 2х + 8 = х + 4 2х + 8-х = х + 4-х х + 8 = 4 х + 8-8 = 4-8 х = -4 В этом разделе задачи со словами будут просто упражнениями по переводу предложений в уравнения и решению этих уравнений.Более сложные «прикладные» проблемы будут обсуждаться в следующих главах. Такие задачи будут включать геометрические формулы, расстояние, проценты, работу, неравенства и смесь. Примеры 1. Трехкратная сумма числа и 5 равна удвоенному числу плюс 5. Найдите число. Решение Пусть x: неизвестное число.
Число -10. 2. Если число уменьшилось на 36 и в результате получилось, что 76 меньше, чем удвоенное число, какое число? Решение Пусть n = неизвестное число.
Число 40. Целые числа подряд — это два целых числа, которые отличаются на 1, или второе целое число на 1 больше, чем первое целое число. Например, 21 и 22 — последовательные целые числа. -14 и -13 — последовательные целые числа. В общем, если n — одно целое число, то n + 1 — следующее последовательное целое число. Примеры: последовательные целые числа 1. Найдите три последовательных целых числа так, чтобы сумма первого и третьего числа была на 76 меньше трехкратной второй. п + (п + 2) = 3 (п + 1) -76 2n + 2 = 3n + 3-76 2n + 2 = 3n-73 2n + 2 + 73-2n = 3n-73 + 73-2n 75 = п 76 = п + 1 77 = п + 2 Три последовательных целых числа: 75,76 и 77. 2. Три последовательных нечетных целых числа таковы, что их сумма равна -3. Какие целые числа? Пусть n = первое нечетное целое п + (п + 2) + (п + 4) = — 3 3n + 6 = -3 3n = -9 п = -3 п + 2 = -1 п + 4 = + 1 Три последовательных нечетных целых числа: -3, -1 и +1. Math 1010 on-line — Что такое алгебра Уравнение — это утверждение, что два
алгебраические выражения равны.
а + Ь = Ь + адля всех номеров a и b . Это называется коммутативным законом сложения . Менее известный идентичность первая биномиальная формула : (a + b) 2 = a 2 + 2ab + b 2Уравнение верно для некоторых значений переменных.В в этом случае задача часто состоит в том, чтобы выяснить значения переменных для которого уравнение верно. Это называется решением уравнения . Мы потратим много времени на изучение способов решения уравнений. Пример уравнения является 3x + 1 = 4в этом случае очевидно x = 1это решение. Это пример линейного уравнения . Пример квадратного уравнения : х 2 — х — 2 = 0. Менее очевидно, что это уравнение имеет два решения x = -1 или x = 2. В этом классе мы изучим, как управлять алгебраическими выражения, часто с целью решения определенных уравнений. Вычисление алгебраического выраженияОценить алгебраическое выражение означает подставить определенные значения для его переменных. Рассмотрим, например, (очень простой) алгебраический выражениеE = 2x + 1Мы даем ему имя E , чтобы иметь возможность ссылаться на него легко. Оценка E , например, на x = 3 , дает E = 2 * 3 + 1 = 7 .Мы говорим, что значение из E при x = 3 равно 7 . Мы действительно могли оценить E в другом выражении. Например, оценка E при x = 2y + 1 , где y — другая переменная, дает E = 2 * (2y + 1) +1 = 4y + 2 + 1 = 4y + 3 Эквивалентные выраженияДва выражения эквивалентны, если их значения равны для всех возможные оценки двух выражений. Другими словами, листинг их со знаком равенства между ними дает идентичность. Объяснитель урока: Вычисление алгебраических выраженийВ этом объяснителе мы узнаем, как вычислять простые алгебраические выражения. с одной или несколькими переменными и как применить это в реальных задачах. Сначала напомним, что мы можем представить неизвестные значения как переменные и что мы может представлять отношения, включающие одну или несколько переменных, в виде алгебраических выражений. Поскольку эти алгебраические выражения представляют отношения, включающие числа, мы можем оценить эти выражения для конкретных значений переменных.Один из методов, который мы можем использовать для выполнения этой оценки, известен как подстановка. Например, представьте, что нам говорят, что температура,
𝑇, измеряется в градусах Цельсия
может быть приблизительно в градусах кельвина
выражением 𝑇 + 273. Мы можем определить значение, скажем, 35∘C.
в кельвинах
установив значение 𝑇
до 35∘C в
выражение. Получаем 𝑇 + 273 = 35 + 273 = 308.K Есть много других применений этого типа оценки.Например, мы знаем, что площадь квадрата определяется квадратом его длины, а площадь квадрата прямоугольный треугольник равен половине произведения длин его ног. Мы можем использовать это, чтобы определить выражение для области следующей формы. Площадь квадрата равна 𝑎, а прямоугольный треугольник равен половине квадрата, поэтому его площадь равна 12𝑎. Следовательно, площадь всей формы составляет + 12𝑎. Затем мы можем использовать это, чтобы определить площадь этой формы для заданного значения 𝑎.Например, если нам дано, что значение равно 4, тогда мы подставим 𝑎 = 4 в это выражение и оценим, чтобы получить 𝑎 + 12𝑎 = 4 + 124 = 16 + 12 × 16 = 16 + 8 = 24. квадратные единицы Мы используем квадратные единицы, поскольку они представляют собой площадь. Давайте теперь посмотрим на пример, в котором мы будем оценивать алгебраическое выражение с заданным значением одной переменной. Пример 1: Вычисление алгебраического выражения с одной переменнойВычислить 14 + 𝑦, если 𝑦 = 6. ОтветПодставляем значение 𝑦 = 6 в выражение, чтобы получить 14 + 6.Мы знаем это 6 = 6 × 6 = 36, поэтому имеем 14 + 6 = 14 + 36 = 50. В нашем следующем примере, мы будем использовать данное выражение и значение для преобразования температура от градусов Цельсия до градусов Фаренгейта. Пример 2: Связь алгебраического выражения с одной переменной с реальной задачейВыражение 9𝐶 + 1605 можно использовать для преобразования температуры в градусов Цельсия, 𝐶, в градусы Фаренгейта.Если термометр показывает температуру 60∘C, определить температуру в градусах Фаренгейта. Ответ Поскольку данное выражение преобразует температуру,
𝐶 в градусах Цельсия
в градусы Фаренгейта,
нам нужно подставить 𝐶 = 60
в данное выражение. Чтобы оценить это, сначала отметим, что 9 × 60 = 540, давая = 540 + 1605. Затем мы вычисляем, что 540 + 160 = 700, чтобы получить = 7005. Наконец, оцените деление, чтобы получить = 140.∘F Отметим, что важно включать градусы Фаренгейта, поскольку это температура. В нашем следующем примере мы оценим алгебраическое выражение, которое имеет две переменные, каждая с заданным значением. Пример 3: Вычисление алгебраического выражения с двумя переменнымиВычислить 𝑎 −, если 𝑎 = 17 и 𝑏 = −57. ОтветНам нужно подставить значение 𝑎 как 17 и 𝑏 как −57 в выражение.Мы можем заменить 𝑎 = 17, чтобы получить 𝑎 − 𝑏 = 17 − 𝑏. Затем подставляем 𝑏 = −57, что дает нам 𝑎 − 𝑏 = 17 − − 57. Мы знаем, что вычитание отрицательного числа равносильно сложению положительного числа, поэтому
= 17 + 57. Наконец, поскольку знаменатели равны, имеем = 1 + 57 = 67. В нашем следующем примере мы будем использовать данное алгебраическое выражение и значения двух переменных для определения средней валовой прибыли семьи в месяц. Пример 4: Связь алгебраического выражения с двумя переменными с реальной задачейВ прошлом году общий доход семьи составил 46 000 долларов, а их общие расходы составили 48 100 долларов. Используйте выражение 𝐼 − 𝐸12, где 𝐼 представляет собой общий доход, а 𝐸 представляет собой общие расходы, чтобы найти среднюю разницу между ежемесячным доходом и расходами семьи. ОтветНам нужно подставить значения 𝐼 = 46000 и 𝐸 = 48100 в выражение, а затем оцените.У нас есть 𝐼 − 𝐸12 = 46000−4810012. Мы можем вычислить числитель, чтобы получить = −210012. Наконец, мы оцениваем деление на 12, что дает нам = — 175 долларов. Поскольку это сумма в долларах,
мы добавляем к этому значению знак доллара. Следовательно, средняя валовая прибыль семьи в месяц — 175 долларов. В нашем следующем примере мы оценим выражение, включающее подстановку значений двух переменных. Пример 5: Вычисление алгебраического выражения с двумя переменнымиВычислить 7𝑞𝑞 + 2 (𝑝 + 5) для 𝑝 = 3 и 𝑞 = 12. ОтветНам нужно подставить значения 𝑝 = 3 и 𝑞 = 12 в выражение, а затем вычислить. Подставляя эти значения в выражение, мы получаем = 7𝑞𝑞 + 2 (𝑝 + 5) = 7 (12) 12 + 2 (3 + 5). В числителе 7 × 12 = 84. В знаменателе 12 + 2 × (3 + 5) = 28. Следовательно, = 8428. Это частное можно упростить, чтобы получить окончательный ответ: 3. В нашем последнем примере мы будем оценивать алгебраическое выражение, подставляя значения трех переменных. Пример 6: Вычисление алгебраического выражения с тремя переменнымиВычислить + 11 для = 4, 𝑝 = 5 и 𝑡 = 5. Ответ Нам нужно подставить значения 𝑛 = 4,
𝑝 = 5 и 𝑡 = 5 в выражение, а затем вычислить. Мы можем вычислить числитель как 5 × 4 = 5 × 16 = 80, а знаменатель — как 5 + 11 = 16. Следовательно, = 8016 = 8 × 108 × 2 = 102 = 5. В заключение напомним некоторые важные моменты этого объяснителя. Ключевые моменты

|

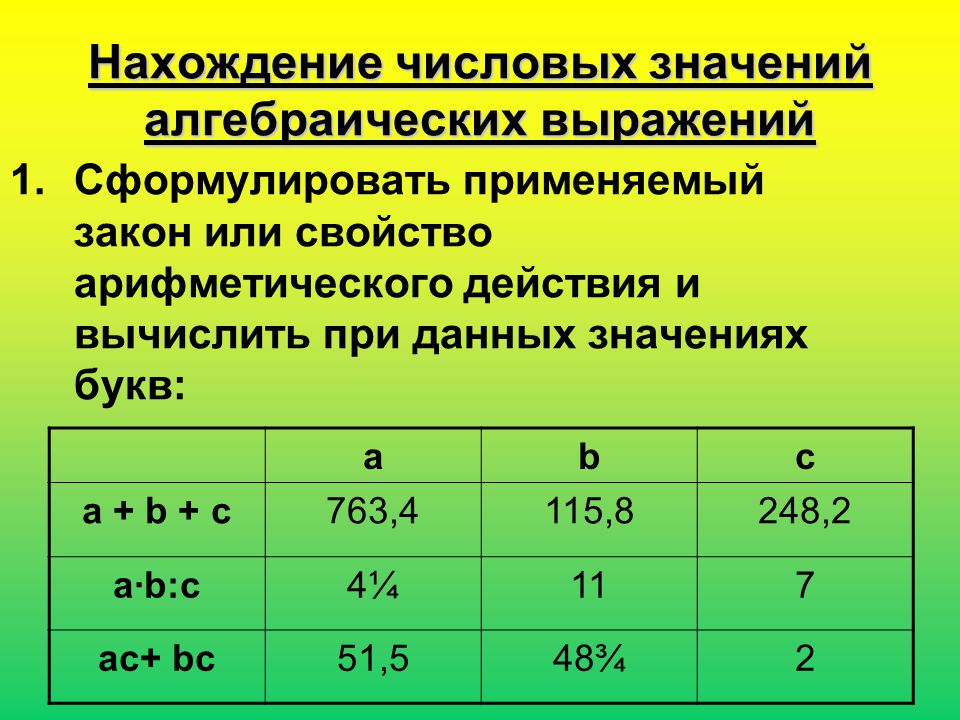 Алгебра, 7 класс.
Алгебра, 7 класс.  1, к целым числам. В распределительной собственности указано, что
1, к целым числам. В распределительной собственности указано, что  Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.  3, умноженное на число, представленное x
3, умноженное на число, представленное x  Научитесь искать эти слова и слова из следующего списка.
Научитесь искать эти слова и слова из следующего списка.  удвоенное произведение двух неизвестных чисел
удвоенное произведение двух неизвестных чисел  Это значение (или значения) называется решением уравнения, и мы решили уравнение.
Это значение (или значения) называется решением уравнения, и мы решили уравнение. 
 4x + 1-x = 13 + x Напишите уравнение.
4x + 1-x = 13 + x Напишите уравнение. 






 Это может быть два разных
значения:
Это может быть два разных
значения:

 Мы называем это подстановкой этого значения в выражение.
Мы называем это подстановкой этого значения в выражение. 
 Это дает нам
9 (60) +1605.
Это дает нам
9 (60) +1605. 

 Подставляя эти значения в выражение, мы получаем
𝑝𝑛𝑡 + 11 = 545 + 11.
Подставляя эти значения в выражение, мы получаем
𝑝𝑛𝑡 + 11 = 545 + 11.