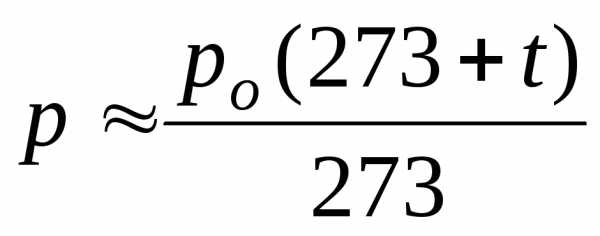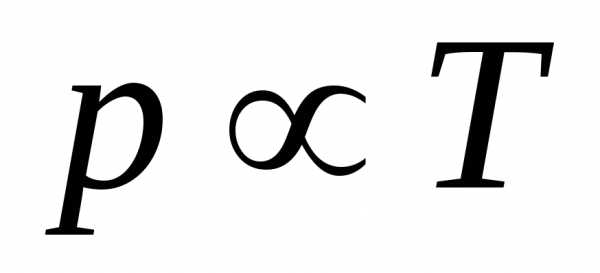Как называется график зависимости давления газа при постоянном объеме – материалы для подготовки к ЕГЭ по Физике

материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.

На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:

• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;

• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).

Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.

Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом

и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.

Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .

Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.

Изотермический процесс

Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.

Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:

Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.

Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:

(1)

Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:

(2)

Данное утверждение называется законом Бойля — Мариотта.

Записав закон Бойля — Мариотта в виде

(3)

можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму

. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.

Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.

Графики изотермического процесса

Вообще, графики термодинамических процессов принято изображать в следующих системах координат:

• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .

График изотермического процесса называется

изотермой.

Изотерма на -диаграмме — это график обратно пропорциональной зависимости .

Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1.

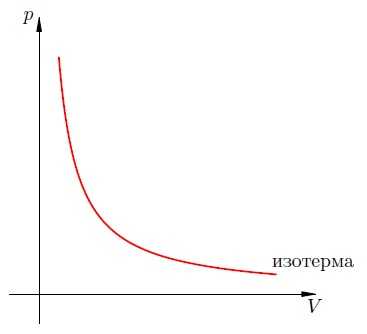
Рис. 1. Изотерма на -диаграмме

Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.

В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре , второй — при температуре .

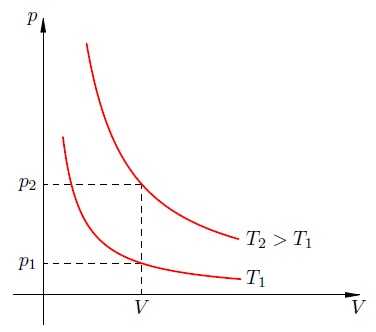
Рис. 2. Чем выше температура, тем выше изотерма

Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .

В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):

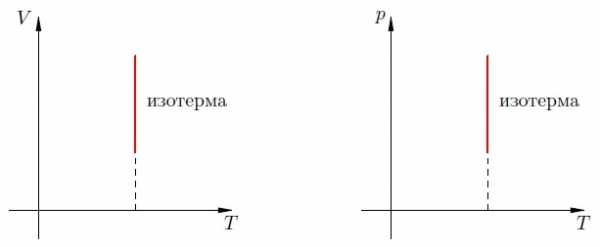
Рис. 3. Изотермы на и -диаграммах

Изобарный процесс

Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.

Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно

где — атмосферное давление.

Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .

Выпишем уравнения состояния:

Поделив их друг на друга, получим:

В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):

(4)

А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:

(5)

Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:

(6)

Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.

Графики изобарного процесса

График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):

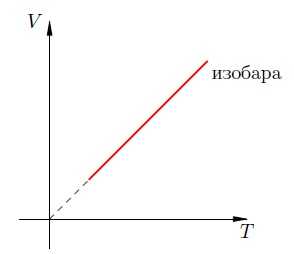
Рис. 4. Изобара на -диаграмме

Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.

Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что

чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5):

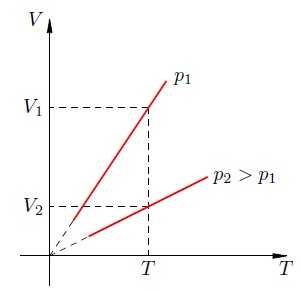
Рис. 5. Чем ниже изобара, тем больше давление

Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).

Стало быть, .

В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):

Рис. 6. Изобары на и -диаграммах

Изохорный процесс

Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.

Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).

Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:

Делим эти уравнения друг на друга:

Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:

(7)

Ввиду произвольности выбора состояний мы приходим к закону Шарля:

(8)

Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:

(9)

Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.

Графики изохорного процесса

График изохорного процесса называется изохорой

. На -диаграмме изохора является прямой линией (рис. 7):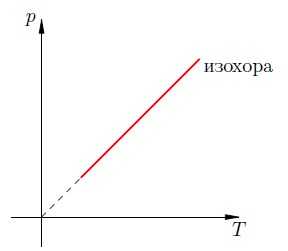

Рис. 7. Изохора на -диаграмме

Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.

Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8):

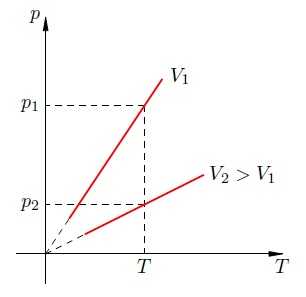
Рис. 8. Чем ниже изохора, тем больше объём

Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .

В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):

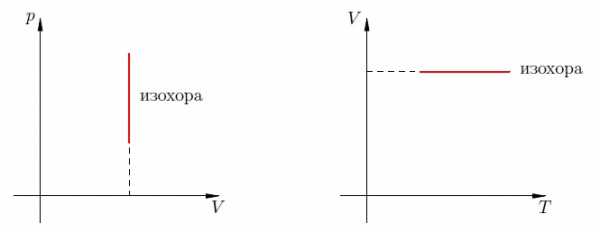
Рис. 9. Изохоры на и -диаграммах

Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.

Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Законы идеальных газов

       В XVII – XIX веках были сформулированы опытные законы идеальных газов. Кратко напомним их.

       Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.

       1. Изохорический процесс. Закон Шарля. V = const.

       Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:

       При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.

       График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ— и VT-диаграммах (рис. 1.6).       Уравнение изохоры:

(1.4.1)

Рис. 1.6        Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде

(1.4.2)

где Р₀ – давление при 0 °С, α — температурный коэффициент давления газа равный 1/273 град^-1. График такой зависимости на Рt-диаграмме имеет вид, показанный на рисунке 1.7.
Рис. 1.7        2. Изобарический процесс. Закон Гей-Люссака. Р = const.

       Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:

       При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

       График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV— и РT-диаграммах (рис. 1.8).

Рис. 1.8        Уравнение изобары:

.

(1.4.3)

       Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде

(1.4.4)

где α =1/273 град ^-1— температурный коэффициент объёмного расширения. График такой зависимости на Vt диаграмме имеет вид, показанный на рисунке 1.9.
Рис. 1.9        3. Изотермический процесс. Закон Бойля – Мариотта. T = const.

       Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.

       Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:

       При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

       График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT— и РT-диаграммах (рис. 1.10).

Рис. 1.10       Уравнение изотермы:

(1.4.5)

       4. Адиабатический процесс (изоэнтропийный):

       Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.

       5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.

       6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится N_A=6,02·10²³молекул (число Авогадро).

       7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:

(1.4.6)

       Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.

       При , давление смеси газов:

(1.4.7)

       8. Объединённый газовый закон (Закон Клапейрона).

       В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа

(1.4.8)

Клапейрон Бенуа Поль Эмиль (1799–1864) – французский физик и инженер. Физические исследования посвящены теплоте, пластичности и равновесию твердых тел. Придал математическую форму идеям Н. Карно, первым оценил большое научное значение его труда. Вывел уравнения состояния идеального газа. Впервые ввел в термодинамику графический метод.

---

ens.tpu.ru

Газовые законы, все формулы и примеры решений

Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.

Рассмотрим каждый из них.

Закон Бойля-Мариотта (изотермический процесс)

Изотермическим процессомназывают изменение состояния газа, при котором его температура остаётся постоянной.

Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:

   

Этот же закон можно переписать в другом виде (для двух состояний идеального газа):

   

Этот закон следует из уравнения Менделеева – Клапейрона:

   

Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.

Графики зависимости параметров газа при постоянной температуре называются изотермами.

Обозначив константу буквой , запишем функциональную зависимость давления от объема при изотермическом процессе:

   

Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах и соответственно.

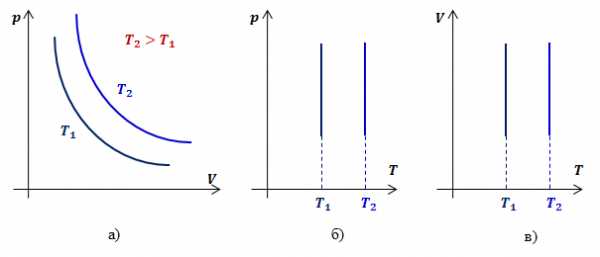
Рис.1. Графики изотермических процессов в различных координатах

Закон Гей-Люссака (изобарный процесс)

Изобарным процессомназывают изменение состояния газа, при котором его давление остаётся постоянным.

Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:

   

Для двух состояний газа этот закон запишется в виде:

   

Этот закон также следует из уравнения Менделеева – Клапейрона:

   

Графики зависимости параметров газа при постоянном давлении называются изобарами.

Рассмотрим два изобарных процесса с давлениями и . В координатах и изобары будут иметь вид прямых линий, перпендикулярных оси (рис.2 а,б).

Определим вид графика в координатах .Обозначив константу буквой , запишем функциональную зависимость объема от температуры при изобарном процессе:

   

Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.

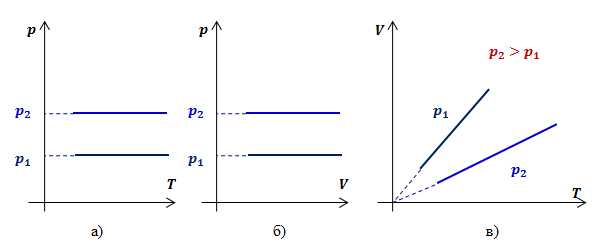
Рис.2. Графики изобарных процессов в различных координатах

Закон Шарля (изохорный процесс)

Изохорным процессомназывают изменение состояния газа, при котором его объем остаётся постоянным.

Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:

   

Для двух состояний газа этот закон запишется в виде:

   

Этот закон также можно получить из уравнения Менделеева – Клапейрона:

   

Графики зависимости параметров газа при постоянном давлении называются изохорами.

Рассмотрим два изохорных процесса с объемами и . В координатах и графиками изохор будут прямые, перпендикулярные оси (рис.3 а, б).

Для определения вида графика изохорного процесса в координатах обозначим константу в законе Шарля буквой , получим:

   

Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).

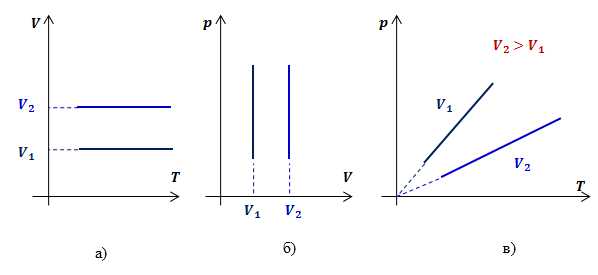
Рис.3. Графики изохорных процессов в различных координатах

Примеры решения задач

ru.solverbook.com

Изопроцессы — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2015; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 сентября 2015; проверки требуют 10 правок.

Изопроце́ссы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

Эта статья или раздел описывает ситуацию лишь применительно к частным случаям (идеальные газы). Необходимо переработать изложение или добавить информацию, чтобы статья описывала более общий случай.

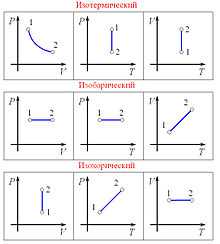Графики изопроцессов в различных системах координат

Изобарный процесс[

ru.wikipedia.org

Закон Шарля — Википедия

Материал из Википедии — свободной энциклопедии

Зако́н Ша́рля или второй закон Гей-Люссака — один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. Экспериментальным путём зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Шарлем и уточнена Гей-Люссаком в 1802 году.

В русско- и англоязычной научной литературе существуют некоторые различия в наименовании законов, связанных с именем Гей-Люссака. Эти различия представлены в следующей таблице:

Русскоязычное название	Англоязычное название	Формула
Закон Гей-Люссака	Закон Шарля (en:Charles’s law) Закон Гей-Люссака Закон объёмов (Volumes Law)	V/T=const{\displaystyle V/T=\mathrm {const} }
Закон Шарля	Закон Гей-Люссака (en:Gay-Lussac’s law) Второй закон Гей-Люссака	P/T=const{\displaystyle P/T=\mathrm {const} }
Закон объёмных отношений	Закон Гей-Люссака (en:Gay-Lussac’s law)

Формулировка закона Шарля следующая:

Давление газа фиксированной массы и фиксированного объёма прямо пропорционально абсолютной температуре газа.

Проще говоря, если температура газа увеличивается, то и его давление тоже увеличивается, если при этом масса и объём газа остаются неизменными.Закон имеет особенно простой математический вид, если температура измеряется по абсолютной шкале, например, в кельвинах. Математически закон записывают так:

P∼T{\displaystyle \qquad P\sim {T}}

или

PT

ru.wikipedia.org

Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 18

Поскольку при изобарическом процессе P постоянно, то после сокращения на P формула принимает вид  

V₁/T₁=V₂/T₂,

или

V₁/V₂=T₁/T_2.

Формула является математическим выражением закона  Гей-Люссака: при постоянной массе газа и неизменном давлении объём газа прямо пропорционален его абсолютной температуре.

Изотермический процесс

Процесс в газе, происходящий при постоянной температуре, называется изотермическим. Изотермический процесс в газе был изучен английским ученым Р.Бойлем и французским ученым Э. Мариотом. Установленная ими опытным путем связь получается непосредственно из формулы путем сокращения на T:

p₁V₁=p₂V₂,

или

p₁/p₂=V₁/V_2.

Формула является математическим выражением закона Бойля — Мариота: при постоянной массе газа и неизменной температуре давление газа обратно пропорционально его объему. Иначе говоря, в этих условиях произведение объёма газа на соответствующее давление есть величина постоянная:

PV=const

График зависимости p от V при изотермическом процессе в газе представляет собой гиперболу и называется изотермой. На рисунке 3 изображены изотермы для одной и той же массы газа, но при разных температурах Т. При изотермическом процессе плотность газа изменяется прямо пропорционально давлению:

ρ₁/ρ₂₌p₁/p₂

Зависимость давления газа от температуры при постоянном объеме

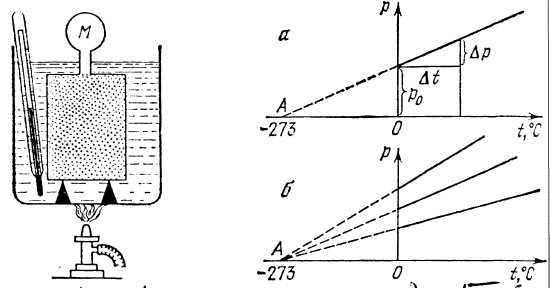
Рассмотрим, как зависит давление газа от температуры, когда его масса и объем остаются постоянными. Возьмем закрытый сосуд с газом и, будем нагревать его (рисунок 4). Температуру газа t будем определять с помощью термометра, а давление манометром М.

Сначала поместим сосуд в тающий снег и давление газа при 0⁰С обозначим р₀ , а затем будем постепенно нагревать наружный сосуд и записывать значения р и t для газа.

Оказывается, что график зависимости р и t, построенный на основании такого опыта, имеет вид прямой линии (рисунок 5).

Если продолжить этот график влево, то он пересечется с осью абсцисс в точке А, соответствующей нулевому давлению газа. Из подобия треугольников на рисунке 5, а можно записать:

P₀/OA=Δp/Δt,

Или

 l/OA=Δp/(p₀Δt).

Если обозначить постоянною l/ОА через α, то получим

α = Δp//(p₀Δt),

Δp= α p₀Δt.

По смыслу коэффициент пропорциональности α в описанных опытах должен выражать зависимость изменения давления газа от его рода.

Величина γ, характеризующая зависимость изменения давления газа от его рода в процессе изменения температуры при постоянном объёме и неизменной массе газа, называется температурным коэффициентом  давления. Температурный коэффициент давления показывает, на какую часть давления газа, взятого при 0⁰С, изменяется при нагревании на 1⁰С. Выведем единицу температурного коэффициента α в СИ:

α =l ΠA/(l ΠA*l⁰C)=l⁰C^-1

При этом длина отрезка ОА получается равной 273⁰С. Таким образом, для всех случаев температура, при которой давление газа должно обращаться в нуль, одинакова и равна – 273⁰С, а температурный коэффициент давления α =1/ОА=(1/273)⁰С^-1.

 
 

При решении задач обычно пользуются приближенным значением α равным α =1/ОА=(1/273)⁰С^-1. Из опытов значение α впервые было определено французским физиком Ж. Шарлем, который в 1787г. установил следующий закон: температурный коэффициент давления не зависит от рода газа и равен (1/273,15)⁰С^-1.  Заметим, что это верно только для газов, имеющих небольшую плотность, и при небольших изменениях температуры; при больших давлениях или низких температурах α зависит от рода газа. Точно подчиняется закону Шарля лишь идеальный газ.          Выясним, как можно определить давление любого газа р, при произвольной температуре t.

Δp=p₁-p₀,

Δt=t-0=t.

Подставив эти значения Δр и Δt в формулу, получим

p₁-p₀=αp₀t,

или

p₁=p₀(1+αt).

Поскольку α~273⁰С, при решении задач формулу можно использовать в следующем виде:

p₁=p₀[1+(273⁰С)t]

К любому изопроцессу применим объединенный газовый закон с учетом того, что один из параметров остается постоянным. При изохорическом процессе постоянным остается объём V, формула после сокращения на V принимает вид

p₁/T₁=p₂/T₂,

vunivere.ru

2132. Зависимость давления газа от объема при постоянной температуре (закон бойля-мариотта)

Введение

Состояние идеального газа полностью описывается измеряемыми величинами: давлением, температурой, объемом. Отношение между этими тремя величинами определяется основным газовым законом:

,

(1)

где р – давление; V- объем; Т – температура;- количество идеального газа в молях;R- универсальная газовая постоянная (8,31 Дж/(Кмоль).

Если одна из величин давление, объем или температура остается постоянной, то другие две величины не могут быть изменены независимо друг от друга. Например, при постоянной температуре выполняется закон Бойля-Мариотта в виде:

(2)

Цель работы

Проверка закона Бойля-Мариотта.

Решаемые задачи

Экспериментальная установка

Приборы и принадлежности

Рис 1. Общий вид установки по изучению закона Бойля – Мариотта. (1) шприц, (2) манометр (отсчет производить по черной шкале), (3) ручной вакуумный насос

В данном эксперименте закон Бойля – Мариотта подтверждается с помощью установки показанной на рисунке 1. Объем воздуха в шприце определяется следующим образом:

(3),

где rрадиус шприца, аh– расстояние от носика до поршня шприца.

Давление в системе нужно находить как:

(4),

где p₀атмосферное давление, аp– давление, измеренное при помощи манометра.

Порядок выполнения работы

1. Установите поршень шприца на отметке 50 мл.

2. Плотно надеть свободный конец соединительного шланга ручного вакуумного насоса на выходной патрубок шприца.

3. Выдвигая поршень, увеличивайте объем с шагом 5 мл, фиксируйте показания маномета по черной шкале.

4. Чтобы определить давление под поршнем, надо из атмосферного давления вычесть показания монометра, выраженного в паскалях. Атмосферное давление равно приблизительно 1 бар, что соответствует 100 000 Па.

5. Для обработки результатов измерений следует учитывать наличие воздуха в соединительном шланге. Для этого измерьте расчитайте объем соединительного шланга, измерив длину шланга рулеткой, а диаметр шланга штангенциркулем, учитывая, что толщина стенок составляет 1,5 мм.

6. Постройте график измеренной зависимости объема воздуха от давления.

7. Рассчитайте зависимость объема от давления при постоянной температуре по закону Бойля-Мариотта и постройте график.

8. Сравните теоретические и экспериментальные зависимости.

2133. Зависимость давления газа от температуры при постоянном объеме (закон шарля)

Введение

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в 1787 г. Жаком Александром Сезаром Шарлем (1746—1823). Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру Т, а соответствующее давлениер— по манометру. Наполнив сосуд тающим льдом, определяли давлениер_о, и соответствующую температуруТ_о. Было установлено, что если при 0^С давлениер_о, то при нагревании на 1^С приращение давления будет вр_о. Величинаимеет одно и то же значение (точнее, почти одно и тоже) для всех газов, а именно 1/273^C^-1. Величинуназывают температурным коэффициентом давления.

Закон Шарля позволяет рассчитать давление газа при любой температуре, если известно его давление при температуре 0^C. Пусть давление данной массы газа при 0^Cв данном объемеp_o, а давление того же газа при температуреtp. Температура меняется наt, а давления изменяется нар_оt, тогда давлениерравно:

(1).

При очень низких температурах, когда газ приближается к состоянию сжижения, а также в случае сильно сжатых газов закон Шарля неприменим. Совпадение коэффициентов и, входящих в закон Шарля и закон Гей-Люссака, не случайно. Так как газы подчиняются закону Бойля — Мариотта при постоянной температуре, тоидолжны быть равны между собой.

Подставим значение температурного коэффициента давления в формулу температурной зависимости давления:

(2).

Величину (273+t) можно рассматривать как значение температуры, отсчитанное по новой температурной шкале, единица которой такая же, как и у шкалы Цельсия, а за нуль принята точка, лежащая на 273^ниже точки, принятой за нуль шкалы Цельсия, т. е. точки таяния льда. Нуль этой новой шкалы называют абсолютным нулем. Эту новую шкалу называют термодинамической шкалой температур, гдеTt+273^.

Тогда, при постоянном объеме справедлив закон Шарля:

(3)

Цель работы

Проверка закона Шарля

Решаемые задачи

• Определение зависимости давления газа от температуры при постоянном объеме

• Определение абсолютной шкалы температур путем экстраполяции в сторону низких температур

Техника безопасности

• Внимание: в работе используется стекло.

• Будьте предельно аккуратны при работе с газовым термометром; стеклянным сосудом и мерным стаканом.

• Будьте предельно внимательны при работе с горячей водой.

Экспериментальная установка

Приборы и принадлежности

• Газовый термометр

• Мобильный CASSY Lab

• Термопара

• Электрическая нагревательная плитка

• Стеклянный мерный стакан

• Стеклянный сосуд

• Ручной вакуумный насос

При откачке воздуха при комнатной температуре с помощью ручного насоса, создается давление на столб воздуха р0+р, где р₀ – внешние давление. Капля ртути также оказывает давление на столб воздуха:

(3),

где _Hg=13,6 г/см³ – плотность ртути;g=9,81 м/c² – ускорение свободного падения; h_Hg – высота капли ртути.

Общее давление на столб воздухав газовом термометре определяется выражением:

(4)

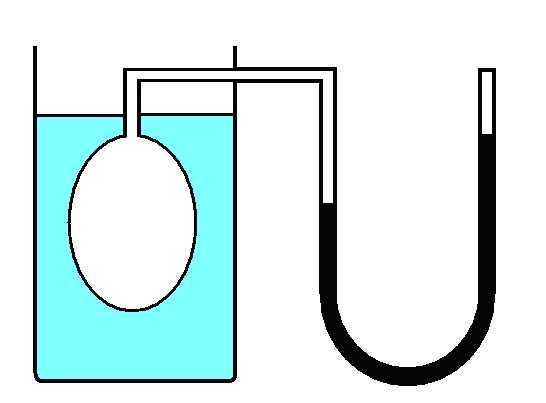
В данном эксперименте этот закон подтверждается с помощью газового термометра. Термометр помещают в воду с температурой около 90°С и эта система постепенно охлаждается. Откачивая воздух из газового термометра с помощью ручного вакуумного насоса, поддерживают постоянный объём воздуха во время охлаждения.

Рис.2.

Порядок выполнения работы

1. Откройте заглушку газового термометра, подключите к термометру ручной вакуумный насос.

2. Поверните осторожно термометр как показано слева на рис. 2 и откачайте воздух из него с помощью насоса так, чтобы капелька ртути оказалась в точке a) (см. рис.2).

3. После того как капелька ртути собралась в точке a)поверните термометр отверстием наверх и спустите нагнетенный воздух ручкойb) на насосе (см. рис.2) осторожно, чтобы ртуть не разделилась на несколько капелек.

4. Нагреть воду в стеклянном сосуде на плитке до 90°С.

5. Налить горячую воду в стеклянный сосуд.

6. Поместить в сосуд газовый термометр, закрепив его на штативе.

7. Поместить термопару в воду, постепенно эта система охлаждается. Откачивая воздух из газового термометра с помощью ручного вакуумного наноса, поддерживаете постоянный объём столба воздуха в течении всего процесса охлаждения.

8. Фиксируйте показание манометра ри температуруТ.

9. Постройте зависимость полного давления газаp₀+p+p_Hgот температуры в^оС.

10. Продолжите график до пересечения с осью абсцисс. Определите температуру пересечения, объясните полученные результаты.

11. По тангенсу угла наклона определите температурный коэффициент давления.

12. Рассчитайте зависимость давления от температуры при постоянном объеме по закону Шарля и постройте график. Сравните теоретические и экспериментальные зависимости.

studfiles.net