|
Урок Принцип относительности Галилея.
 Относительные и инвариантные величины в механике
Относительные и инвариантные величины в механике
Урок№ 6 10 класс Дата____________
Принцип относительности Галилея.
Относительные и инвариантные величины в механике
Цель урока: учащиеся должны знать принцип инерции, относительность движения и покоя, инерциальные системы отсчета.
Тип урока: комбинированный.
План изучения нового материала.
1. Принцип инерции.
2. Инерциальные системы отсчета.
3.Преобразования Галилея.
4.Принцип относительности Галилея.
Ход урока.
l.Проверка домашнего задания. Решение задачи на доске №5 упр№5
II.Изучение нового материала.
1. Принцип инерции. Кинематика описывает механическое движение математически, не объясняя физических причин его существования и изменения, отвечая лишь на вопрос, как движется тело. Динамика объясняет причины, определяющие характер механического движения, т. е. дает ответ на вопрос , почему движется тело. Определение. Динамика – раздел механики, в основе которого лежит количественное описание взаимодействия тел, определяющего характер их движения.
е. дает ответ на вопрос , почему движется тело. Определение. Динамика – раздел механики, в основе которого лежит количественное описание взаимодействия тел, определяющего характер их движения.
Согласно современным физическим представлениям, характер движения тела определяет его взаимодействие с другими телами. Инерция – явление сохранения состояния движения или покоя при отсутствии внешних воздействий. Обобщив результаты изучения движения тел при максимальном уменьшении сил трения, Галилей сформулировал принцип относительности. Если на тело не действуют внешние силы, то оно сохраняет состояние покоя или равномерного прямолинейного движения.
2. Инерциальные системы отсчета. Понятия «движение» и «покой» относительны и зависят от выбора системы отсчета, связанной с телом отсчета. Эквивалентность и взаимозаменяемость состояния покоя и равномерного прямолинейного движения возможны лишь в инерциальных системах отсчета (ИСО), покоящихся или движущихся равномерно и прямолинейно относительно друг друга. Определение. Инерциальная система отсчета — система отсчета, в которой тело, не взаимодействующее с другими телами, сохраняет состояние покоя или равномерного прямолинейного движения.
Определение. Инерциальная система отсчета — система отсчета, в которой тело, не взаимодействующее с другими телами, сохраняет состояние покоя или равномерного прямолинейного движения.
Системы отсчета, в которых принцип относительности не выполняется, называют неинерциальными.
Рассмотреть примеры возможных инерциальных систем отсчета по рис.63 стр.77 учебника. 3. Преобразования Галилея. Преобразования Галилея:
Х – неподвижная система отсчета; Х’ – движущаяся система отсчета.
Координаты тела в различных инерциальных системах отсчета Х и Х’связывают преобразования Галилея.
Х = Х’+υt.
Движение инерциальной системы отсчета не оказывает влияния на прямолинейное равномерное движение тела или его состояние покоя в этой системе.
4.Принцип относительности Галилея
Галилей первым обратил внимание на то, что равномерное прямолинейное движение по отношению к Земле совершенно не сказывается на течении всех механических явлений.
Допустим, вы находитесь в каюте корабля или в вагоне поезда, движущегося плавно, без толчков. Вы можете спокойно играть в бадминтон или пинг-понг, как и на земле. Мяч или волан будет по отношению к стенам и полу перемещаться точно так же, как и по отношению к земле при игре в обычных условиях. Если не посмотреть в окно, то с уверенностью нельзя сказать, что же происходит с поездом: движется он или стоит.
Если в движущемся с постоянной скоростью вагоне изучать падение тел, колебания маятника и другие явления, то результаты будут точно такими же, как и при исследовании этих явлений на Земле.
Лишь при резком торможении поезда нужно прилагать дополнительные усилия, чтобы устоять на ногах. При большой болтанке самолёта или качке парохода на большой волне об игре с мячом не может быть и речи. Все предметы приходится закреплять, чтобы они оставались на своих местах.
Принцип относительности. На основании подобных наблюдений можно сформулировать один из самых фундаментальных законов природы — принцип относительности.
Все механические процессы протекают одинаково во всех инерциальных системах отсчёта.
Это утверждение известно как принцип относительности в механике. Его ещё называют принципом относительности Галилея.
Не нужно думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно различных инерциальных систем отсчёта. Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными скоростями и начальными координатами тел. А начальные величины для данного тела относительно разных систем отсчёта различны.
— Во всех инерциальных системах отсчета законы классической динамики имеют один и тот же вид. Все инерциальные системы отсчета равноправны. Принцип относительности Галилея характеризует симметрию законов физики по отношению к переходу от одной ИСО к другой.
Инвариантные и относительные величины. Инвариантность означает неизменность физической величины или закона при определённых преобразованиях или изменениях условий. Например, сила, с которой мяч ударяется о землю, не зависит от того, кто наблюдал этот удар: человек, стоящий рядом, или пассажир равномерно движущегося автобуса. Или, например, масса космонавта одинакова на Земле и на Луне. Отметим, какие из рассмотренных величин остаются инвариантными при движении тела относительно разных систем отсчёта.
Инвариантность означает неизменность физической величины или закона при определённых преобразованиях или изменениях условий. Например, сила, с которой мяч ударяется о землю, не зависит от того, кто наблюдал этот удар: человек, стоящий рядом, или пассажир равномерно движущегося автобуса. Или, например, масса космонавта одинакова на Земле и на Луне. Отметим, какие из рассмотренных величин остаются инвариантными при движении тела относительно разных систем отсчёта.
Инвариантными при переходе от одной инерциальной системы отсчёта к другой являются ускорение, масса и сила. Также инвариантными будут законы Ньютона, о чём говорит принцип относительности Галилея.
В то же время уравнения движения тел в разных инерциальных системах отсчёта будут выглядеть по-разному.
ВажноВеличины, изменяющиеся при переходе от одной инерциальной системы отсчёта к другой, являются относительными (неинвариантными). Кинематические величины, такие, как скорость, перемещение, траектория движения — примеры относительных величин.

Например, в равномерно движущемся поезде камень будет падать отвесно относительно стен вагона, если начальная скорость камня по отношению к поезду равна нулю (рис. 2.30). Но, с точки зрения наблюдателя на Земле этот камень будет двигаться по параболе (рис. 2.31). Дело в том, что начальная скорость камня по отношению к системе отсчёта, связанной с Землёй, отлична от нуля и равна скорости поезда.
Открытие принципа относительности — одно из величайших достижений человеческого разума. Оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни Солнце не является центром Вселенной.
III.Закрепление изученного материала.
Беседа по вопросам.1).Что изучает динамика? Динамика – раздел механики, в основе которого лежит количественное описание взаимодействия тел, определяющего характер их движения.
2).Какое движение называется движением по инерции? Сформулируйте принцип относительности Галилея. Движение по инерции – это движение без внешних воздействий или со скомпенсированными воздействиями. Принцип относительности Галилея — Во всех инерциальных системах отсчета законы классической динамики имеют один и тот же вид.
Движение по инерции – это движение без внешних воздействий или со скомпенсированными воздействиями. Принцип относительности Галилея — Во всех инерциальных системах отсчета законы классической динамики имеют один и тот же вид.
3).Какую систему отсчета называют инерциальной? Почему прямолинейное равномерное движение тела и состояние покоя физически эквивалентны и взаимозаменяемы лишь в инерциальных системах отсчета? Инерциальная система отсчета – это система отсчета, в которой выполняются законы Ньютона. В частности, это та система, в которой материальная точка , не взаимодействующая с другими телами, или действие на которую других тел скомпенсировано, сохраняет состояние покоя или равномерного прямолинейного движения.
4).Сформулируйте принцип относительности Галилея. Разъясните его смысл. Во всех инерциальных системах отсчета законы классической динамики имеют один и тот же вид. Это значит, что все инерциальные системы отсчета равноправны.
IV.Итог урока. Сегодня на уроке мы выяснили, что понятия « движение» и «покой» относительны и зависят от выбора системы отсчета, связанной с телом отсчета. Эквивалентность и взаимозаменяемость состояния покоя и равномерного прямолинейного движения возможны лишь в инерциальных системах отсчета.
V. Домашнее задание.§6, подготовиться к лабораторной работе.
Конспект по физике на тему «Принцип относительности в классической механике» (11класс)
Принцип относительности в классической механике
Положение о классической механике, той самой механике, которая, как казалось на конец XIX века, полностью описывает окружающий нас мир, сформулировал еще Исаак Ньютон. Основные положения классической механики:
— Движение не оказывает никакого влияния на течение времени. Физики говорят: время абсолютно. Исходя из этого предположения, мы получили классические законы сложения скоростей и перемещений при переходе из одной системы отсчета в другую.
Преобразование Галилея:
где: – радиус-вектор точки в первой СО;
– радиус-вектор точки во второй СО;
– скорость второй СО относительно первой;
– время в первой СО;
– время во второй СО;
В классической механике перемещение и скорость относительны, а время абсолютно. Эти факты связаны с принципом относительности Галилея, который формулируется так: всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчета.
Говорят, что законы классической механики инвариантны относительно преобразований Галилея, то есть при переходе из одной инерциальной системы отсчета в другую инерциальную систему отсчета. Так обстоит дело только в рамках классической механики. Проверим, будут ли эти преобразования инварианты и для других разделов физики.
Противоречия
Перейдем к другим областям физики, может, в других ее разделах найдутся такие явления, ход которых будет существенно разным при переходе из неподвижной системы отсчета в движущуюся равномерно и прямолинейно. Тогда, сопоставив ход явлений в неподвижной и подвижной системах отсчета, мы сможем определить скорость этих систем отсчета друг относительно друга. С развитием электродинамики казалось, что так оно и есть, дело в том, что уравнения Максвелла, которые лежат в основе всей электродинамики, в отличие от законов Ньютона, как оказалось, не инвариантны при переходе из одной системы отсчета в другую. Из уравнений Максвелла следует один важный факт: свет распространяется во всех направлениях с одной и той же скоростью 300 000 км/с, причем эта скорость не зависит от того, движется источник света или покоится. Физиков того времени этот факт не удивлял, им казалось, что свет представляет собой колебания некой всепроникающей среды, которая находится во всех точках Вселенной и называется эфиром. Это распространение света в эфире и обуславливают его постоянство.
Тогда, сопоставив ход явлений в неподвижной и подвижной системах отсчета, мы сможем определить скорость этих систем отсчета друг относительно друга. С развитием электродинамики казалось, что так оно и есть, дело в том, что уравнения Максвелла, которые лежат в основе всей электродинамики, в отличие от законов Ньютона, как оказалось, не инвариантны при переходе из одной системы отсчета в другую. Из уравнений Максвелла следует один важный факт: свет распространяется во всех направлениях с одной и той же скоростью 300 000 км/с, причем эта скорость не зависит от того, движется источник света или покоится. Физиков того времени этот факт не удивлял, им казалось, что свет представляет собой колебания некой всепроникающей среды, которая находится во всех точках Вселенной и называется эфиром. Это распространение света в эфире и обуславливают его постоянство.
Представим себе, что вы находитесь в звездолете, который мчится в космическом вакууме со скоростью относительно далеких звезд (рис. 1).
1).
Вы сидите лицом по ходу движению звездолета и смотрите на лампочку, которая находится в его носовой части. Свет от лампочки, не обращая внимания на ее движение, перемещается относительно звезд со скоростью С = 300 000 км/с. Вы движетесь навстречу свету со скоростью , стало быть, относительно вас свет должен иметь скорость
Вы измеряете эту скорость, сопоставляете ее с известным значением С и приходите к выводу, что двигаетесь со скоростью 50 000 км/с, таким образом, электромагнитные явления вроде бы позволяют отличить покой от равномерного прямолинейного движения. То есть получается парадокс: с одной стороны скорость света 300 000 км/с не должна зависеть от того, движется или покоится источник света, с другой стороны, согласно классическому закону сложения скоростей, она должна зависеть от выбора системы отсчета.
Выходы предлагались разные, одно из мнений, сторонником, которого был Лоренц, гласило: инерциальные системы отсчета, равноправные в механических явлениях, не являются равноправными в законах электродинамики.
То есть в электродинамике существует некая привилегированная, главная, абсолютная система отсчета, которую ученые связывали с так называемым эфиром.
Проверить справедливость наличия системы отсчета, связанной с эфиром, и наличие собственно этого эфира попытались американские ученые Майкельсон и Морли. Они проверяли, существует ли так называемая абсолютная система отсчета, связанная с эфиром, и движущиеся относительно нее все остальные системы отсчета, то есть так называемый эфирный ветер, которые могли влиять на величину скорости света. И, как вы только что убедились, никакого эфирного ветра не существует. Физика того времени столкнулась с неразрешимым парадоксом: что же справедливо – классическая механика, электродинамика Максвелла или что-то другое.
Постулаты СТО
На момент публикации своей работы Альберт Эйнштейн не был признанным мировым ученым, идеи, которые он высказал, казались настолько революционными, что в первое время у них практически не было сторонников. Тем не менее огромное количество экспериментов и измерений, которые были проведены после этого, показали справедливость точки зрения Альберта Эйнштейна.
Тем не менее огромное количество экспериментов и измерений, которые были проведены после этого, показали справедливость точки зрения Альберта Эйнштейна.
Сформулируем еще раз проблемы, с которыми столкнулась физика того времени и поговорим о тех решениях, которые предложил Эйнштейн.
— Не удается обнаружить привилегированную систему отсчета, связанную с неподвижным мировым эфиром.
Значит, ее нет вовсе, нет этой привилегированной абсолютной системы отсчета? Альберт Эйнштейн расширил действие принципа Галилея в механике на всю физику, и так получился принцип относительности от Эйнштейна: всякое физическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчета.
То есть не всякое механическое явление, а любое физическое явление.
Следующая трудность: электродинамика противоречит механике в том, что уравнения Максвелла не инвариантны относительно преобразований Галилея, то есть это как раз та трудность, связанная со скоростью света.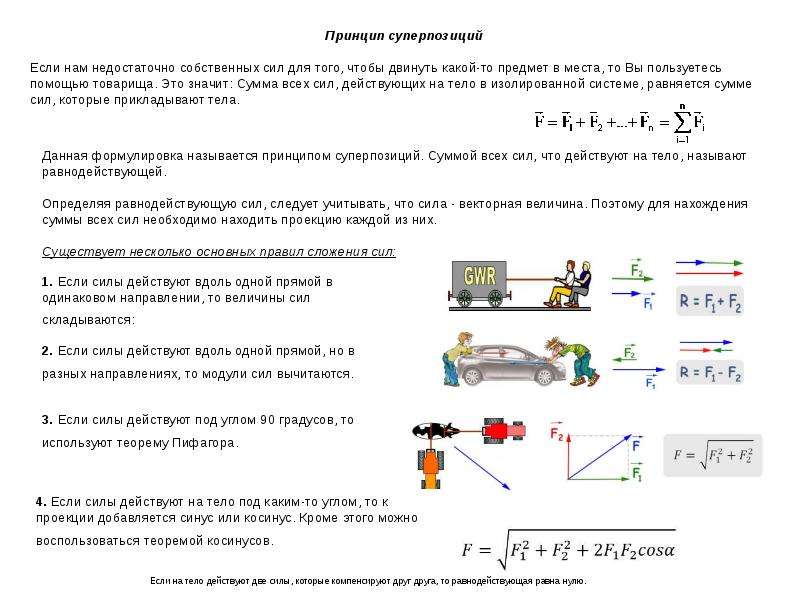
Может, Максвелл неправ? Ничего подобного, электродинамика Максвелла вполне справедлива. Значит, все остальные области физики несправедливы, неверны преобразования Галилея, которые связывают эти части физики? Ведь из них вытекает классический закон сложения скоростей, который мы используем при решении задач, таких как: поезд едет со скоростью 40 км/ч, а пассажир идет по вагону со скоростью 5 км/ч и относительно наблюдателя на земле, этот пассажир будет двигаться со скоростью 45 км/ч (рис. 2).
Эйнштейн фактически заявляет: раз преобразования Галилея несправедливы, то и этот закон сложения скоростей несправедлив. Полный слом устоев, абсолютно очевидный жизненный пример, абсолютно очевидный жизненный закон оказывается несправедливым, в чем же здесь проблема? Проблема глубоко внутри тех основ классической механики, которые закладывались еще Ньютоном. Оказывается, что главная проблема классической механики состоит в том, что предполагается, что все взаимодействия в рамках механики распространяются мгновенно. Рассмотрим, например, гравитационное притяжение тел.
Рассмотрим, например, гравитационное притяжение тел.
Если сместить одно из тел в сторону, то, согласно закону всемирного тяготения, второе тело почувствует этот факт мгновенно, как только изменится расстояние от него до первого тела, то есть взаимодействие передается с бесконечной скоростью. В реальности механизм взаимодействия состоит в следующем: изменение положения первого тела меняет гравитационное поле вокруг него. Это изменение поля начинает бежать с какой-то скоростью во все точки пространства, и, когда достигает точки, в которой находится второе тело, соответствующим образом изменяется и взаимодействие первого и второго тел. То есть скорость распространения взаимодействия обладает какой-то конечной величиной. Но если взаимодействия передаются с какой-то конечной скоростью, значит, в природе должна существовать какая-то предельно допустимая скорость распространения этих взаимодействий, максимальная скорость, с которой взаимодействие может передаваться. Об этом гласит второй постулат, который отводит исключительную роль скорости света, принцип инвариантности скорости света: в каждой инерциальной системе отсчета свет движется в вакууме с одной и той же скоростью. Величина этой скорости не зависит от того, покоится или движется источник света.
Величина этой скорости не зависит от того, покоится или движется источник света.
Таким образом, описанный выше пример с лампочкой в звездолете в реальности нам провести не удастся, это будет противоречить этому постулату теории Эйнштейна. Скорость света относительно наблюдателя в звездолете будет равна С, а не С +V, как мы говорили до этого, и наблюдатель не сможет заметить факт движения звездолета. Классический закон сложения скоростей применительно скорости света не работает, как это ни странно для нас, но скорость света для наблюдателя на Земле и для космонавта будет совершенно одинаковой и равной 300 000 км/с. Именно это положение лежит в основе теории относительности и было вполне успешно доказано огромным количеством экспериментов.
Итоги
Механика, которая была построена на основании этих двух постулатов, носит название релятивистской механики (от английского relativity – «относительность»). Может показаться, что релятивистская механика отменяет классическую механику Ньютона, поскольку в ее основе лежат другие постулаты, но дело в том, что классическая механика Ньютона – это частный случай релятивистской механики Эйнштейна, который проявляется при скоростях, значительно меньших, чем скорость света. В окружающем нас мире мы и живем в таких скоростях, скорости, с которыми мы сталкиваемся, гораздо меньше скорости света. Поэтому для описания нашей жизни достаточно классической механики Ньютона.
В окружающем нас мире мы и живем в таких скоростях, скорости, с которыми мы сталкиваемся, гораздо меньше скорости света. Поэтому для описания нашей жизни достаточно классической механики Ньютона.
Для небольших скоростей, значительно меньших скорости света, мы вполне успешно пользуемся классической механикой, если же мы работаем со скоростями, близкими к скорости света, или хотим большой точности в описании явлений – мы должны пользоваться специальной теорией относительности, то есть релятивистской механикой.
Третий закон Ньютона. Инерциальные системы отсчёта
На прошлых уроках мы с вами выяснили, что любое действие тел друг на друга носит характер ВЗАИМОДЕЙСТВИЯ. Проще говоря, не бывает одностороннего действия одного тела на другое.
Давайте вспомним, что количественной мерой воздействия одного
тела на другое является сила. Именно она является причиной возникновения
ускорения тела или его деформации.
Примеров взаимодействия тел и сообщения ими друг другу ускорений можно привести очень много. Например, если вы, находясь в одной лодке, будете притягивать к себе за канат другую лодку, то и ваша лодка обязательно придёт в движение.
Но действия тел друг на друга обнаруживаются не только при их непосредственном контакте. Для примера установим на одну лёгкую и подвижную тележку магнит, а на вторую — металлический брусок. Если тележку с бруском удерживать на одном месте, а с магнитом отпустить, то мы заметим, как последняя начнёт двигаться в сторону металлического бруска.
Вернём тележку в исходное состояние и повторим опыт, но в этот раз будем удерживать тележку с магнитом. Как видим, теперь тележка с бруском пришла в движение.
Теперь подумаем, а одинаковы ли модули сил, с которыми магнит
и брусок притягиваются друг к другу? Для ответа на этот вопрос немного
видоизменим опыт, прикрепив к концам тележек две одинаковые пружины, вторые
концы которых жёстко закреплены.
Нетрудно заметить, что после остановки тележек пружины, удерживающие их, растянуты совершенно одинаково. Это свидетельствует о том, что на оба тела со стороны пружин действуют одинаковые по модулю силы, но направлены они противоположно друг другу. А так как магнит и брусок покоятся, то силы, с которыми они действуют друг на друга, также равны по модулю и противоположны по направлению.
Результаты наших опытов не случайны. Они ещё раз доказывают, что механическое действие тел друг на друга всегда взаимно — это либо взаимное притяжение, либо взаимное отталкивание. Одностороннего действия не бывает: существует лишь ВЗАИМОДЕЙСТВИЕ.
Ньютон в своём великом труде «Математические начала
натуральной философии» так сформулировал свой третий закон: «Действию
всегда есть равное и противоположное противодействие, иначе взаимодействия двух
тел друг на друга между собой равны и направлены в противоположные стороны».
Если учесть, что под словами «действие» и «противодействие» Ньютон понимал силы, с которыми взаимодействуют тела, то третий закон Ньютона может быть переформулирован так: силы, с которыми взаимодействующие тела действуют друг на друга, направлены по одной прямой, равны по модулю и противоположны по направлению.
Третий закон Ньютона справедлив для тел любых масс, размеров,
форм и состава вещества. В связи с этим может возникнуть логичный вопрос:
«Почему, например, тогда во время прыжка мы движемся вверх, а земля при этом
вниз не движется?» Всё очень просто. Вот у нас есть Земля, с её огромной
массой, а вот мы — крохотное существо на её поверхности. Во время прыжка мы
отталкиваемся с силой, которая действует и на нас, и на Землю. Тогда, согласно
второму закону Ньютона, наша маленькая масса во время взаимодействия должна
получить большое ускорение. В то время как Земля, с её огромной массой, получит
очень крошечное ускорение, которое мы даже не замечаем. Давайте дадим этому
ускорению приближённую оценку. Для этого предположим, что во время прыжка мы
поднялись на высоту 20 см за 1 с. Тогда, согласно формулам кинематики,
приобретённое нами ускорение составило 0,4 м/с2.
Давайте дадим этому
ускорению приближённую оценку. Для этого предположим, что во время прыжка мы
поднялись на высоту 20 см за 1 с. Тогда, согласно формулам кинематики,
приобретённое нами ускорение составило 0,4 м/с2.
Теперь предположим, что наша масса равна 50 кг, а значение массы Земли мы возьмём из таблицы. Тогда найдём, что ускорение, которое приобретает Земля, примерно равно 0,3 ∙ 10–25 м/с2!
Таким образом, видим, что равенство сил не означает равенства результатов их действия.
Теперь обратим внимание ещё на некоторые важные моменты,
вытекающие из третьего закона Ньютона. Во-первых, силы, которые возникают
при взаимодействии тел, приложены к разным телам, и поэтому они не могут
уравновешивать друг друга. А во-вторых, силы, с которыми тела действуют друг
на друга, одной физической природы. Например, планета и её спутник
взаимодействуют друг с другом силами всемирного тяготения. А магнит и
металлический брусок — посредством сил электромагнитного взаимодействия.
А магнит и
металлический брусок — посредством сил электромагнитного взаимодействия.
При изучении первого закона Ньютона мы с вами отмечали, что все законы движения и взаимодействия тел, которые мы уже знаем и будем изучать в дальнейшем, сформулированы для инерциальных систем отсчёта, так как в них они имеют самый простой вид.
Давайте с вами вспомним, что инерциальными называются системы отсчёта, в которых тело, при компенсации внешних воздействий, покоится или движется равномерно и прямолинейно. Их существование постулируется в первом законе Ньютона — законе инерции. Из его формулировки следует, что если известна из опыта хотя бы одна инерциальная система отсчёта, то инерциальными будут любые другие системы отсчёта, движущиеся относительно избранной равномерно и прямолинейно. В этом заключается их принцип равноправности.
И напротив, любая система отсчёта, движущаяся с ускорением
относительно инерциальной, считается неинерциальной системой отсчёта.
При решении большинства задач мы условились инерциальную
систему отсчёта связывать с Землёй. Это так называемая геоцентрическая
система отсчёта. Однако вам известно, что Земля не только вращается вокруг
своей оси, но и обращается вокруг Солнца почти по круговой орбите. Значит, она
движется с ускорением. Поэтому, строго говоря, система отсчёта, связанная с
нашей планетой, не является инерциальной. Но отличие этой системы от инерциальной
будет очень небольшим, так как за те небольшие интервалы времени, за которые мы
проводим эксперименты, дугу орбиты, по которой движется Земля, можно с большой
точностью считать отрезком прямой линии. Ускорение, возникающее из-за вращения
Земли, тоже очень мало́ (оно составляет всего около 0,35 % от ускорения
свободного падения). Поэтому с точностью, необходимой для проведения наших
экспериментов, мы можем считать систему отсчёта, связанную с Землёй,
инерциальной. Как правило, в ней в качестве начала координат выбирается центр
Земли в соответствии с принятой её моделью. Ось z совпадает с осью вращения
земли. А оси x и y находятся в экваториальной плоскости.
Ось z совпадает с осью вращения
земли. А оси x и y находятся в экваториальной плоскости.
Однако, если требуется большая точность (например, при расчётах движений космических аппаратов), то инерциальной можно считать гелиоцентрическую систему отсчёта. В ней точка отсчёта совмещается с центром Солнца, а координатные оси направляются на удалённые звезды.
Как выбор системы отсчёта сказывается на характере движения
тела, посмотрим на примере колебания маятника. Для простоты поместим его на
полюс Земли. Пусть маятник у нас будет идеальным и на него действуют только две
силы — сила притяжения к Земле и сила упругости нити маятника. Согласно второму
закону Ньютона, ускорение маятника совпадает с направлением равнодействующей
силой и поэтому лежит в той же вертикальной плоскости. Следовательно, в
инерциальной системе отсчёта плоскость колебаний должна оставаться неизменной.
Так и будет происходит в гелиоцентрической системе.
А вот в геоцентрической системе отсчёта, являющейся в данном случае неинерциальной, колебания маятника будут выглядеть совершенно иначе. Дело в том, что из-за вращения Земли плоскость колебаний маятника будет поворачиваться. И это смещение становится заметным уже спустя несколько минут наблюдения
Впервые этот опыт был продемонстрирован французским физиком Жаном Фуко во время публичной демонстрации под куполом Пантеона в Париже в 1851 году. Поэтому такой маятник принято называть маятником Фуко. Его часто используют для демонстрации суточного вращения Земли.
Теперь познакомимся с ещё одним важным положением механики — принципом относительности Галилея. Галилей впервые обратил внимание на то, что равномерное и прямолинейное движение по отношению к Земле не сказывается на протекание механических процессов.
Проведём мысленный эксперимент, подобный эксперименту
Галилея. Представьте, что вы находитесь на земле и играете в мяч, подбрасывая
его вверх. Движение мяча достаточно простое: сначала он замедленно летит вверх,
а после — ускоренно падает вниз. Траектория — прямая линия. Переместимся в
каюту корабля или вагон поезда, или в кузов грузовика, движущихся равномерно и
прямолинейно, и повторим опыт. С мячом ничего сверхъестественного не
происходит: он также сначала он замедленно летит вверх, а после — ускоренно
падает вниз. Траекторией является всё та же прямая линия. Другими словами, во
всех инерциальных системах отсчета механические явления при одинаковых условиях
происходят одинаково.
Движение мяча достаточно простое: сначала он замедленно летит вверх,
а после — ускоренно падает вниз. Траектория — прямая линия. Переместимся в
каюту корабля или вагон поезда, или в кузов грузовика, движущихся равномерно и
прямолинейно, и повторим опыт. С мячом ничего сверхъестественного не
происходит: он также сначала он замедленно летит вверх, а после — ускоренно
падает вниз. Траекторией является всё та же прямая линия. Другими словами, во
всех инерциальных системах отсчета механические явления при одинаковых условиях
происходят одинаково.
Галилей первым обратил внимание на эту закономерность и заключил, что «для предметов, захваченных равномерным движением, это движение как бы не существует».
Так был сформулирован принцип относительности Галилея.
В настоящее время он звучит так: во всех инерциальных системах отсчёта все
механические явления при одинаковых начальных условиях происходят одинаковым
образом.
Это утверждение выражает равноправие всех инерциальных систем в механике: никакой механический эксперимент не в состоянии выделить и сделать главной какую-то одну инерциальную систему отсчёта по сравнению с остальными.
Однако не следует думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела в разных инерциальных системах отсчёта. Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными условиями. А они могут отличаться. Вспомните хотя бы мысленный опыт Галилея по сбрасыванию ядра с вершины мачты корабля, который движется равномерно по реке. Для наблюдателя, находящегося на палубе, траекторией движения ядра является прямая линия. А путь и модуль перемещения ядра будут равны.
Но с точки зрения наблюдателя, находящегося на берегу, ядро
будет двигаться по параболе, так как оно имеет некоторую начальную горизонтальную
скорость, равную скорости корабля. А модуль его перемещения не будет равен
пройденному пути.
А модуль его перемещения не будет равен
пройденному пути.
Физические величины, которые будут изменяться при переходе из одной инерциальной системы отсчёта в другую, мы будем называть относительными.
Если же физические величины не изменяются при переходе из одной инерциальной системы отсчёта в другую (например, масса и сила), то их называют инвариантными.
И действительно, сила, с которой мяч ударяется о землю, не зависит от того, кто наблюдал за этим ударом: человек, стоящий возле мяча или который в это время проезжал рядом с постоянной скоростью.
Или вот масса космонавта будет одинакова и на Земле, и на Луне, и на Сатурне с Ураном
Открытие принципа относительности — одно из величайших достижений человечества. Но оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни даже Солнце не являются центром Вселенной.
В заключение отметим, что три закона Ньютона, лежащие в
основе классической механики, выполняются для тел, скорость которых намного
меньше скорости света в вакууме. В процессе развития физики, изучая движение
микроскопических объектов при скоростях, сравнимых со скоростью света,
обнаружили, что в этом случае законы Ньютона не выполняются. Теорией,
описывающей не только медленные, но и быстрые движения частиц, является
специальная теория относительности, основы которой разработаны Эйнштейном в
1905 году. Однако о ней мы с вами будем говорить значительно позднее.
В процессе развития физики, изучая движение
микроскопических объектов при скоростях, сравнимых со скоростью света,
обнаружили, что в этом случае законы Ньютона не выполняются. Теорией,
описывающей не только медленные, но и быстрые движения частиц, является
специальная теория относительности, основы которой разработаны Эйнштейном в
1905 году. Однако о ней мы с вами будем говорить значительно позднее.
Законы электродинамики и принцип относительности краткое. Принцип относительности. Постулаты теории относительности. Рабочая программа учебного предмета муниципального образовательного учреждения средней общеобразовательной школы с. Березняк
Изменились представления о пространстве и времени. Согласно классическим представлениям о пространстве и времени, считавшимся на протяжении веков незыблемыми, движение не оказывает никакого влияния на течение времени (время абсолютно), а линейные размеры любого тела не.зависят от того, покоится тело или движется (длина абсолютна).
Специальная теория относительности Эйнштейна — это новое учение о простраш-гво и времени, пришедшее на смену старым (классичснчсим) представлениям.
§ 75 ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
Принцип относительности в механике и электродинамике. После того как во второй половине XIX в. Максвеллом были сформулированы основные законы электродинамики, возник вопрос: распространяется ли принцип относительности, справедливый для механических явлений, и на электромагнитные явления? Иными словами, протекают ли электромагнитные процессы (взаимодействие зарядов и токов, распространение электромагнитных волн и т. д.) одинаково во всех инерциальных системах отсчета? Или, быть может, равномерное прямолинейное движение, не влияя на механические явления, оказывает некоторое воздействие на электромагнитные процессы?
Чтобы ответить на эти вопросы, нужно было выяснить, меняются ли основные законы электродинамики при переходе от одной инерциальной системы отсчета к другой, или же, подобно законам Ньютона, они остаются неизменными. Только в последнем случае можно отбросить сомнения в справедливости принципа относительности применительно к электромагнитным процессам и рассматривать этот принцип как общий закон природы.
Только в последнем случае можно отбросить сомнения в справедливости принципа относительности применительно к электромагнитным процессам и рассматривать этот принцип как общий закон природы.
Законы электродинамики сложны, и строгое решение этой задачи — нелегкое дело. Однако уже простые соображения, казалось бы, позволяют найти правильный ответ. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и равна с = 3 10 8 м/с. Но в соответствии с законом сложения скоростей механики Ньютона скорость может быть равна скорости света только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся по отношению к этой избранной системе отсчета со скоростью , скорость света должна уже быть равна-. Это означает, что если справедлив обычный закон сложения скоростей, то при переходе от одной инерциальной системы отсчета к другой законы электродинамики должны меняться так, чтобы в этой новой системе отсчета скорость света уже была равна не , а — .
Таким образом, обнаружились определенные противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности. Возникшие трудности пытались преодолеть тремя различными способами.
Первый способ: объявить несостоятельным принцип относительности в применении к электромагнитным явлениям. Эту точку зрения разделял великий голландский физик, основатель электронной теории X. . Электромагнитные явления еще со времен Фарадея рассматривались как процессы, происходящие в особой, всепроникающей среде, заполняющей все пространство, — мировом эфире. Инерциальная система отсчета, покоящаяся относительно эфира, — это согласно Лоренцу особая, преимущественная система отсчета. В ней законы электродинамики Максвелла справедливы и наиболее просты по форме. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
Второй способ:
считать неправильными уравнения Максвелла и пытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы отсчета к другой (в соответствии с обычными, классическими представлениями о пространстве и времени) не менялись. Такая попытка, в частности, была предпринята Г. Герцем. По Герцу, эфир полностью увлекается движущимися телами и поэтому электромагнитные явления протекают одинаково независимо от того, покоится тело или движется. Принцип относительности остается справедливым.
Такая попытка, в частности, была предпринята Г. Герцем. По Герцу, эфир полностью увлекается движущимися телами и поэтому электромагнитные явления протекают одинаково независимо от того, покоится тело или движется. Принцип относительности остается справедливым.
Наконец, третий способ: отказаться от классических представлений о пространстве и времени, с тем чтобы сохранить как принцип относительности, так и законы Максвелла. Это наиболее революционный путь, ибо он означает пересмотр в физике самых глубоких, основных представлений. С данной точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Изменять нужно законы механики, а не законы электродинамики Максвелла.
Единственно правильным оказался именно третий способ. Последовательно развивая его, А. Эйнштейн пришел к новым представлениям о пространстве и времени. Первые два пути, как оказалось, опровергаются экспериментом.
Точка зрения Лоренца, согласно которой должна существовать избранная система отсчета, связанная с мировым эфиром, пребывающим в абсолютном покое, была опровергнута прямыми опытами.
Если бы скорость света была равна 300 000 к м/с только в системе отсчета, связанной с эфиром, то, измеряя скорость света в произвольной инерциальной системе отсчета, можно было бы обнаружить движение этой системы отсчета по отношению к эфиру и определить скорость этого движения.
Эйнштейн Альберт (1879-1955) — великий физик XX в. Создал новое учение о пространстве и времени — специальную теорию относительности. Обобщая эту теорию для неинер-циальных систем отсчета, разработал общую теорию относительности, представляющую собой современную теорию тяготения . Впервые ввел представление о частицах света — фотонах. Его работа по теории броуновского движения привела к окончательной победе молекулярно-кинетической теории строения вещества.
Подобно тому как в системе отсчета, движущейся относительно воздуха, возникает ветер, при движении по отношению к эфиру (если, конечно, эфир существует) должен быть обнаружен «эфирный ветер». Опыт по обнаружению «эфирного ветра» был поставлен в 1881 г. американскими учеными А. Майкельсоном и Э. Морли по идее, высказанной за 12 лет до этого Максвеллом.
Опыт по обнаружению «эфирного ветра» был поставлен в 1881 г. американскими учеными А. Майкельсоном и Э. Морли по идее, высказанной за 12 лет до этого Максвеллом.
В этом опыте сравнивалась скорость света в направлении движения Земли и в перпендикулярном направлении. Измерения проводились очень точно с помощью специального прибора — интерферометра Майкельсона. Эксперименты ставились в разное время суток и различные времена года. Но всегда получался отрицательный результат: движения Земли по отношению к эфиру обнаружить не удалось.
Таким образом, идея о существовании преимущественной системы отсчета не выдержала опытной проверки. В свою очередь, это означало, что никакой особой среды — «светоносного эфира», с которой можно было бы связать такую преимущественную систему отсчета, не существует.
При попытках Герца изменить законы электродинамики Максвелла выяснилось, что новые уравнения неспособны объяснить ряд наблюдаемых фактов. Так, согласно теории Герца движущаяся вода должна полностью увлекать за собой распространяющийся в ней свет , так как она увлекает эфир, в котором свет распространяется. Опыт же показал, что в действительности это не так.
Опыт же показал, что в действительности это не так.
Согласовать принцип относительности с электродинамикой Максвелла оказалось возможным, только отказав-И1ись от классических представлений о пространстве и времени, согласно которым расстояния и течение времени не зависят от системы отсчета.
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Календарно-тематическое планирование, задачи школьнику 11 класса по физике скачать , Физика и астрономия онлайн
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиВо второй половине XIX века Д. Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.
Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны)
; в этом состоит суть механического принципа относительности или принципа относительности Галилея.
Для доказательства этого принципа рассмотрим две системы отсчета: инерциальную систему К
(с координатами x, y, z
), которую условно будем считать неподвижной и подвижную систему K»
(с координатами x», y», z»
), движущуюся относительно К
равномерно и прямолинейно со скоростью u
= const. Примем, что в начальный момент времени t
= 0 начала O
и O»
обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t
имеет вид, изображенный на рис. 5.1. Скорость u
направлена вдоль прямой OO»
, а радиус-вектор, проведенный из точки O
в точку O»
, равен r 0 =ut
.
Расположение систем координат в произвольный момент времени t
имеет вид, изображенный на рис. 5.1. Скорость u
направлена вдоль прямой OO»
, а радиус-вектор, проведенный из точки O
в точку O»
, равен r 0 =ut
.
Координаты произвольной материальной точки A
в неподвижной и подвижной системах отсчета определяются радиусами-векторами r
и r»
, причем
В проекциях на оси координат векторное уравнение (5.1) записывается в виде, называемом преобразованиями Галилея :
(5.2)
В частном случае, когда система K» движется со скоростью v вдоль положительного направления оси x системы K , преобразования координат Галилея имеют следующий вид:
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета. Поэтому система уравнений (5.2) дополняется еще одним соотношением:
(5.3)
Соотношения (5.2) – (5.3) справедливы лишь в случае u . При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
Продифференцируем уравнение (5.1) по времени и учитывая, что u
= const, найдем соотношения между скоростями и ускорениями точки А
относительно обеих систем отсчета:
откуда
(5.4)
А также
(5.5)
Если на точку А
другие тела не действуют, то a
= 0 и согласно (5.5) a»
= 0, т.е. подвижная система K»
является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
Из выражения (5.5) следует, что
т.е. уравнения Ньютона (уравнения динамики) для материальной точки одинаковы во всех инерциальных системах отсчета или инвариантны по отношению к преобразованиям Галилея. Этот результат часто формулируют следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов
.
Классическая механика Ньютона достоверно описывает движение макроскопических тел, движущихся со скоростями, намного меньшими скорости света. В конце XIX в. было установлено, что выводы классической механики противоречат некоторым опытным данным. В частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам Ньютона. Далее возникли затруднения при попытках применить классическую механику для объяснения распространения света. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и приблизительно равна с
= 3*10 8 м/с. Но в соответствии с законами классической физики скорость света может равняться с
только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся относительно избранной системы со скоростью v
, она должна уже равняться с
—v
, или с
+v
. Это означает, что если справедлив закон сложения скоростей классической механики (формула (5. 4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея. Для преодоления возникших трудностей предлагались различные способы:
4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея. Для преодоления возникших трудностей предлагались различные способы:
- Принять несостоятельность принципа относительности применительно к электромагнитным явлениям. Еще со времен Фарадея электромагнитные явления рассматривались как процессы в особой, всепроникающей среде, заполняющей все пространство, — эфире . Согласно Х. Лоренцу инерциальная система отсчета, покоящаяся относительно эфира, — это особая система, в которой законы электродинамики Максвелла справедливы. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
- Считать ошибочными уравнения электродинамики Максвелла и попытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы к другой (в соответствии с классическими представлениями о пространстве и времени) не менялись.
 Такая попытка, в частности, была предпринята Г. Герцем, который считал, что эфир полностью увлекается движущимися телами, поэтому электромагнитные явления протекают одинаково, независимо от того, покоится тело или движется. Принцип относительности справедлив.
Такая попытка, в частности, была предпринята Г. Герцем, который считал, что эфир полностью увлекается движущимися телами, поэтому электромагнитные явления протекают одинаково, независимо от того, покоится тело или движется. Принцип относительности справедлив. - Отказаться от классических представлений о пространстве и времени, с тем, чтобы сохранить и принцип относительности, и законы Максвелла. С этой точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Таким образом, изменять нужно законы классической механики, а не законы электродинамики Максвелла.

Развитие естествознания опровергло эти представления. Никакого абсолютного пространства и времени не существует. Вселенная заполнена материей в форме вещества и поля, а пространство выступает как всеобщее свойство материи. Время всегда связано с движением и развитием материи. Таким образом, пространство – это форма бытия материи, которая выражает ее протяженность и структурность; время – это форма бытия материи, характеризующая длительность существования всех объектов, полей и последовательность смены событий.
Основными свойствами пространства и времени являются: а) единство и неразрывная связь материи, пространства и времени; б) абсолютная непрерывность и относительная прерывность пространства и времени. Непрерывность проявляется в распространении материальных полей в пространстве всех тел и систем, в бесконечном следовании элементов длины при движении тела между двумя точками. Прерывность пространства относительна и проявляется в раздельном существовании материальных объектов и систем, каждая из которых имеет определенные размеры и границы.
 Прерывность времени характеризуется лишь временем существования качественных состояний материи, каждое из которых возникает и исчезает, переходя в другие формы; в) время обладает длительностью, однонаправленностью, необратимостью.
Прерывность времени характеризуется лишь временем существования качественных состояний материи, каждое из которых возникает и исчезает, переходя в другие формы; в) время обладает длительностью, однонаправленностью, необратимостью.Последовательно развивая новые, отличные от классических, представления о пространстве и времени, А. Эйнштейн в начале XX в. создал специальную теорию относительности (СТО). В рамках этой теории удалось согласовать принцип относительности с электродинамикой Максвелла. При этом новая теория не отменяла старую (ньютоновскую механику), а включала ее в себя как частный, предельный случай.
Цель урока: формировать представление учащихся, о том, как изменились понятия о пространстве и времени под воздействием положений специальной теории относительности Эйнштейна.
Ход урока
1. Анализ контрольной работы.
2. Изучение нового материала .
В конце 19 века были сформулированы основные положения электродинамики. Возник вопрос в справедливости принципа относительности Галилея применительно к электромагнитным явлениям. В разных инерциальных системах одинаково ли протекают электромагнитные явления: как распространяются электромагнитные волны, взаимодействуют заряды и токи при переходе от одной инерциальной системы к другой?
Возник вопрос в справедливости принципа относительности Галилея применительно к электромагнитным явлениям. В разных инерциальных системах одинаково ли протекают электромагнитные явления: как распространяются электромагнитные волны, взаимодействуют заряды и токи при переходе от одной инерциальной системы к другой?
Инерциальная – это такая система отсчета, относительно которой свободные тела движутся с постоянной скоростью. Оказывает ли равномерное прямолинейное движение действие на электромагнитные процессы (на механические явления оно не влияет)?
При переходе от одной инерциальной системы к другой законы электродинамики изменяются или как законы Ньютона остаются постоянными?
Например, по законам сложения скоростей в механике скорость может равняться с=3·108м/с только в одной системе отсчета. В другой системе отсчета, которая сама движется со скоростью Ѵ, скорость света должна равняться с̄-Ѵ̄. Но согласно законам электродинамики скорость электромагнитных волн в вакууме по разным направлениям равна с=3·108м/с
Между электродинамикой и механикой Ньютона возникли противоречия.
Чтобы разрешить возникшие противоречия были высказаны три разных способа.
Первый способ Заключался в том, чтобы отказаться от принципа относительности в применении к электромагнитным явлениям. Эту возможность поддерживал основатель электронной теории Х. Л о р е н ц (голл.). Тогда считалось, что электромагнитные явления протекают в «мировом эфире» – это всепроникающая среда, заполняющая все мировое пространство. Инерциальная система отсчета, рассматривалась Лоренцем, как система покоящаяся относительно эфира. В этой системе законы электродинамики строго выполняются и в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
Второй способ заключался в том, чтобы объявить уравнения Максвелла неправильными.
Г. Герц пытался их переписать, таким образом, чтобы они не менялись при переходе от одной инерциальной системы к другой, т. е. как законы механики. Герц полагал, что эфир движется вместе с движущимися телами и поэтому электромагнитные процессы происходят одинаково независимо от движения или покоя тел.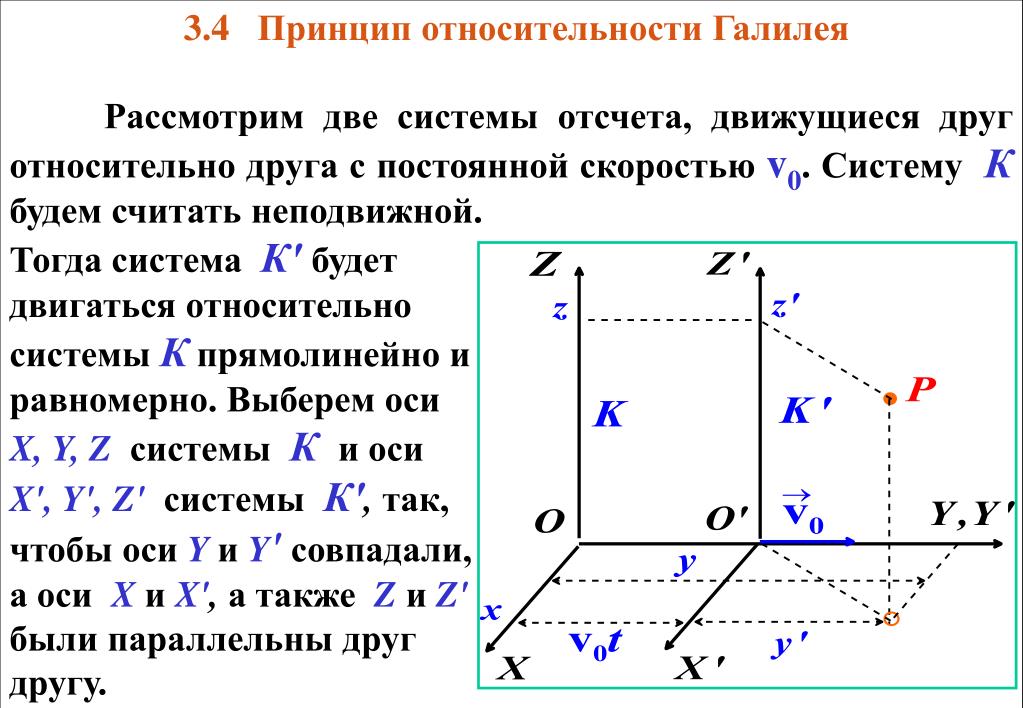 То есть Г. Герц принцип относительности сохранил.
То есть Г. Герц принцип относительности сохранил.
Третий способ состоял в отказе от традиционных представлений о пространстве и времени. Сохранялись уравнения Максвелла и принцип относительности, но пришлось отказаться от самых очевидных, самых основных представлений классической механики.
Этот способ разрешения противоречий оказался в итоге правильным.
Эксперимент опроверг как первую, так и вторую попытку исправления, возникших противоречий между электродинамикой и механикой, оставив принцип относительности без изменений.
Развивая третий способ решения проблемы А. Эйнштейн доказал, что представления о пространстве и времени устарели и заменил их новыми.
Уравнения Максвелла, исправленные Герцем, не могли объяснить наблюдаемые явления. Опыт показал, что среда не может увлекать за собой свет, так как она будет увлекать эфир, в котором свет распространяется.
Опыты американских ученых А. Майкельсона и Э. Морли доказали, что никакой среды типа «светоносного эфира» не существует
Объединить электродинамику Максвелла и принцип относительности оказалось возможным при отказе от традиционных представлений о пространстве и времени, т. е. не зависят от системы отсчета ни расстояние, ни течение времени.
е. не зависят от системы отсчета ни расстояние, ни течение времени.
В конце 19 века
были получены опытные данные, которые
не могли быть объяснены с позиций физики
Ньютона. В частности, если источник и
приемник света движутся навстречу друг
другу равномерно и прямолинейно, то
скорости их по Ньютону должны складываться.
Однако, американский физик Майкельсон
и другие, проводя опыты с помощью
чувствительного интерферометра,
показали, что скорости света в вакууме
не зависят от скорости движения источника
и приемника и одинаковы во всех
инерциальных системах отсчета. Эйнштейн
пришел к выводу, что постоянство
скорости света
– фундаментальный
закон природы. Этот вывод был положен
Эйнштейном в основу разработанной им
специальная теории относительности
(см. раздел 2.5). Была также доказана
инвариантность уравнений Максвелла
(см. раздел 3.5) относительно преобразований
Лоренца, тогда как они не инвариантны
относительно преобразований Галилея
(см. 2.4). Из теории Эйнштейна следовало,
что электромагнитные взаимодействия
(например, зарядов) передаются в вакууме
со скоростью, ограниченной скоростью
света, через поле (концепция близкодействия)
во всех системах отсчета.
Разделение электромагнитного поля на электрическое и магнитное поля относительно – в природе существует единое электромагнитное поле. Свет также имеет электромагнитную природу (рис.3.27).
На основе специальной теории относительности были объяснены закономерности эффекта Доплера для электромагнитных волн. При удалении источника света от наблюдателя со скоростьюVпроисходит изменение частоты (или длины волны на величину Δλ) в спектре излучения источника с длиной волны излучения λ (красное смещение ):
Эффект Доплера нашел применение в радиолокации для измерения скорости Vи расстояния до движущегося объекта, в астрофизике — для измерения скоростей удаления галактик и т.д.
Обусловленное конечностью скорости света изменение видимого положения звезд на небесной сфере получило название аберрации света .
3.7. Квазистационарное магнитное поле
Ток смещения
принципиально отличается от тока
проводимости – он не связан с движением
зарядов. Он обусловлен только изменением
во времени электрического поля (см. 3.5).
Даже в вакууме изменение электрического
поля приводит к возникновению в
окружающем пространстве магнитного
поля
. Именно по этому признаку ток
смещения тождественен току проводимости
и это дает возможность условно называть
его «током».
3.5).
Даже в вакууме изменение электрического
поля приводит к возникновению в
окружающем пространстве магнитного
поля
. Именно по этому признаку ток
смещения тождественен току проводимости
и это дает возможность условно называть
его «током».
Ток смещения j см возникает не только в вакууме или диэлектриках, но и в проводниках при прохождении по ним переменного тока проводимостиj пр. Однако он мал по сравнению сj пр (ввиду этого им пренебрегают).
В массивных проводниках, помещенных в переменное магнитное поле, могут в соответствии с законом (3.70) наводиться индукционные токи. Эти токи являются вихревыми в объеме проводников и известны как токи Фуко .
Токи Фуко создают
собственное магнитное поле, которое в
соответствии с правилом Ленца (см.3.73)
препятствуют изменению вызвавшему их
магнитного потока. Высокочастотные
токи Фуко приводят к нагреванию
проводников, что позволяет их применять
для плавки металлов в индукционных
печах, в микроволновых печах для
нагревания проводящих токи продуктов,
в физиотерапии (тело человека – проводник)
и т. д. В других случаях для уменьшения
потерь на тепло в электрических машинах
и трансформаторах увеличивают
сопротивление токам Фуко, делая их
сердечники не сплошными, а из изолированных
друг от друга тонких пластин.
д. В других случаях для уменьшения
потерь на тепло в электрических машинах
и трансформаторах увеличивают
сопротивление токам Фуко, делая их
сердечники не сплошными, а из изолированных
друг от друга тонких пластин.
В цепях с переменным электрическим током электросопротивление проводников возрастает с увеличением частоты тока. Это объясняется тем, что распределение плотности тока по сечению проводника становится неоднородным с учетом токов Фуко: плотность тока возрастает у поверхности (так называемый скин – эффект ). Это же позволяет делать проводники пустотелами (трубчатыми). На скин – эффекте основаны методики высокочастотной закалки поверхности деталей.
Сила переменного
тока оказывается в один и тот же момент
времени неодинаковой в разных участках
проводника. Это обусловлено конечной
скоростью распространения вдоль
проводника меняющегося электромагнитного
поля. Однако, если учесть малую скорость
движения носителей зарядов по сравнению
со скоростью распространения поля, то
токи можно считать квазистационарными
также как и возбуждаемые ими магнитные
поля.
Переменные токи получают с помощью генераторов. При вращении контура в однородном магнитном поле с угловой скоростью через площадь, ограниченную контуром, периодически изменяется магнитный поток (см. 3.67).
где Ф 0 — максимальное значение потока через площадьSконтура.
Электродвижущая
сила, возникающая при этом (см.3.70), будет
изменяться по синусоидальному закону.
ε 0 =ωФ 0 -амплитуда ЭДС. Если
цепь замкнута, то в ней потечет переменный
ток:
.
Вообще любой проводник помимо омического сопротивления Rобладает индуктивностьюLи емкостью С. Они оказывают току дополнительное сопротивление в виду появления ЭДС самоиндукции (см.3.73) и инертности перезарядки емкости. Тогда амплитудное значение силы переменного тока:
(3.90)
Величина
имеет
характер полного сопротивления
(импеданс
). Она зависит от значенийR,L,Cи частоты. При,
удовлетворяющем условию:
,
полное сопротивление имеет минимальное значение равное R, а амплитуда силы переменного тока достигает максимального значения:
Частота
—
называется резонансной. R L =Lи
R L =Lи
— называют индуктивным и емкостным
сопротивлениями в цепи переменного
тока.
Переменный электрический ток имеет большое практическое применение. Его можно передавать с малыми потерями на большие расстояния и с помощью трансформаторов в широких пределах изменять его силу и напряжение.
Чтобы характеризовать действие переменного тока в сравнении его с постоянным вводится понятиедействующих значений силы тока и напряжения . Действующим значением силы тока называют величинуI, связанную с амплитудойI 0 следующим образом:
аналогично и напряжение
.
Именно они определяют мощность переменного
тока. Можно также дать и другое определениеI Д: действующее
значение силы переменного тока равно
такой силе постоянного тока, который
выделяет в цепи то же количество теплоты,
что и переменный ток.
«Физика — 11 класс»
Законы электродинамики и принцип относительности
Согласно классическим представлениям о пространстве и времени, считавшимся на протяжении веков незыблемыми, движение не оказывает никакого влияния на течение времени (время абсолютно), а линейные размеры любого тела не зависят от того, покоится тело или движется (длина абсолютна).
Специальная теория относительности Эйнштейна — это новое учение о пространстве и времени, пришедшее на смену старым (классическим) представлениям.
Принцип относительности в механике и электродинамике
После того как во второй половине XIX в. Максвеллом были сформулированы основные законы электродинамики, возник вопрос: распространяется ли принцип относительности, справедливый для механических явлений, и на электромагнитные явления? Иными словами, протекают ли электромагнитные процессы (взаимодействие зарядов и токов, распространение электромагнитных волн и т. д.) одинаково во всех инерциальных системах отсчета? Или, быть может, равномерное прямолинейное движение, не влияя на механические явления, оказывает некоторое воздействие на электромагнитные процессы?
Чтобы ответить на эти вопросы, нужно было выяснить, меняются ли основные законы электродинамики при переходе от одной инерциальной системы отсчета к другой, или же, подобно законам Ньютона, они остаются неизменными. Только в последнем случае можно отбросить сомнения в справедливости принципа относительности применительно к электромагнитным процессам и рассматривать этот принцип как общий закон природы.
Только в последнем случае можно отбросить сомнения в справедливости принципа относительности применительно к электромагнитным процессам и рассматривать этот принцип как общий закон природы.
Законы электродинамики сложны, и строгое решение этой задачи — нелегкое дело. Однако уже простые соображения, казалось бы, позволяют найти правильный ответ. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и равна с = 3 10 8 м/с
. Но в соответствии с законом сложения скоростей механики Ньютона скорость может быть равна скорости света только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся по отношению к этой избранной системе отсчета со скоростью , скорость света должна уже быть равна — . Это означает, что если справедлив обычный закон сложения скоростей, то при переходе от одной инерциальной системы отсчета к другой законы электродинамики должны меняться так чтобы в этой новой системе отсчета скорость света уже была равна не , а — .
Таким образом, обнаружились определенные противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности. Возникшие трудности пытались преодолеть тремя различными способами.
Первый способ:
объявить несостоятельным принцип относительности в применении к электромагнитным явлениям. Эту точку зрения разделял великий голландский физик, основатель электронной теории X. Лоренц. Электромагнитные явления еще со времен Фарадея рассматривались как процессы, происходящие в особой, всепроникающей среде, заполняющей все пространство, — мировом эфире. Инерциальная система отсчета, покоящаяся относительно эфира, — это согласно Лоренцу особая, преимущественная система отсчета. В ней законы электродинамики Максвелла справедливы и наиболее просты по форме. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
Второй способ:
считать неправильными уравнения Максвелла и пытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы отсчета к другой (в соответствии с обычными, классическими представлениями о пространстве и времени) не менялись. Такая попытка, в частности, была предпринята Г. Герцем. По Герцу, эфир полностью увлекается движущимися телами и поэтому электромагнитные явления протекают одинаково независимо от того, покоится тело или движется. Принцип относительности остается справедливым.
Такая попытка, в частности, была предпринята Г. Герцем. По Герцу, эфир полностью увлекается движущимися телами и поэтому электромагнитные явления протекают одинаково независимо от того, покоится тело или движется. Принцип относительности остается справедливым.
Третий способ:
отказаться от классических представлений о пространстве и времени, с тем чтобы сохранить как принцип относительности, так и законы Максвелла. Это наиболее революционный путь, ибо он означает пересмотр в физике самых глубоких, основных представлений. С данной точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Изменять нужно законы механики, а не законы электродинамики Максвелла.
равильным оказался именно третий способ. Последовательно развивая его, А. Эйнштейн пришел к новым представлениям о пространстве и времени. Первые два пути, как оказалось, опровергаются экспериментом.
Точка зрения Лоренца, согласно которой должна существовать избранная система отсчета, связанная с мировым эфиром, пребывающим в абсолютном покое, была опровергнута прямыми опытами.
Если бы скорость света была равна 300 000 км/с только в системе отсчета, связанной с эфиром, то, измеряя скорость света в произвольной инерциальной системе отсчета, можно было бы обнаружить движение этой системы отсчета по отношению к эфиру и определить скорость этого движения. Подобно тому как в системе отсчета, движущейся относительно воздуха, возникает ветер, при движении по отношению к эфиру (если, конечно, эфир существует) должен быть обнаружен «эфирный ветер». Опыт по обнаружению «эфирного ветра» был поставлен в 1881 г. американскими учеными А. Майкельсоном и Э. Мор л и по идее, высказанной за 12 лет до этого Максвеллом.
В этом опыте сравнивалась скорость света в направлении движения Земли и в перпендикулярном направлении. Измерения проводились очень точно с помощью специального прибора — интерферометра Майкельсона. Эксперименты ставились в разное время суток и различные времена года. Но всегда получался отрицательный результат: движения Земли по отношению к эфиру обнаружить не удалось.
Таким образом, идея о существовании преимущественной системы отсчета не выдержала опытной проверки. В свою очередь, это означало, что никакой особой среды — «светоносного эфира», с которой можно было бы связать такую преимущественную систему отсчета, не существует.
При попытках Герца изменить законы электродинамики Максвелла выяснилось, что новые уравнения неспособны объяснить ряд наблюдаемых фактов. Так, согласно теории Герца движущаяся вода должна полностью увлекать за собой распространяющийся в ней свет, так как она увлекает эфир, в котором свет распространяется. Опыт же показал, что в действительности это не так
Итак,
согласовать принцип относительности с электродинамикой Максвелла оказалось возможным, только отказавшись от классических представлений о пространстве и времени, согласно которым расстояния и течение времени не зависят от системы отсчета.
Постулаты теории относительности
В основе теории относительности лежат два постулата.
А что такое постулат?
Постулат в физической теории выполняет ту же роль, что и аксиома в математике.
Это — основное положение, которое не может быть логически доказано.
В физике постулат есть результат обобщения опытных фактов.
1.
Все процессы в природе протекают одинаково во всех инерциальных системах отсчета.
Это означает, что во всех инерциальных системах отсчета физические законы имеют одинаковую форму.
Таким образом, принцип относительности классической механики распространяется на все процессы в природе, в том числе и на электромагнитные.
2.
Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит ни от скорости источника, ни от скорости приемника светового сигнала.
Скорость света занимает, таким образом, особое положение.
Более того, как вытекает из постулатов теории относительности, скорость света в вакууме является максимально возможной скоростью передачи взаимодействий в природе.
Для того чтобы сформулировать постулаты теории относительности, нужна была большая научная смелость, так как они противоречили классическим представлениям о пространстве и времени.
В самом деле, допустим, что в момент времени, когда начала координат инерциальных систем отсчета К
и К 1
, движущихся относительно друг друга со скоростью , совпадают, в начале координат происходит кратковременная вспышка света.
За время t
системы отсчета сместятся относительно друг друга на расстояние υt
, а сферическая волновая поверхность будет иметь радиус υt
.
Системы отсчета К
и К 1
равноправны, и скорость света одинакова в той и другой системе отсчета.
Следовательно, с точки зрения наблюдателя, связанного с системой отсчета К , центр сферы будет находиться в точке О , а с точки зрения наблюдателя, связанного с системой отсчета К 1 , — в точке О 1 .
Но ведь не может одна и та же сферическая поверхность иметь центры в точках О и O 1 .
Это явное противоречие вытекает из рассуждений, основанных на постулатах теории относительности.
Итак,
имеется противоречие с классическими представлениями о пространстве и времени, которые при больших скоростях движения несправедливы.
Однако сама теория относительности не содержит противоречий и является абсолютно логичной.
Классный урок на «Радио России – Тамбов», эфир 25 мая 2020 года
Автор ГТРК «ТАМБОВ» На чтение 18 мин. Просмотров 81 Опубликовано
Урок физики для выпускников на канале «Радио России» ведет педагог МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина», учитель физики высшей категории, заведующий кафедрой физики, Денисов Евгений Константинович. Денисов Евгений Константинович говорит об относительности движения.
Описание движения в механике Классическая механика Ньютона хорошо описывает движение макроскопических тел с небольшими скоростями. Когда скорость движения приближается к скорости света, механика перестаёт работать и уступает место специальной теории относительности (СТО 1905г).
Давайте вспомним для начала, как описывается движение в классической механике. Обсуждаемые понятия понадобятся нам в дальнейшем при изложении основ СТО.
Механическое движение
И в классической механике, и в специальной теории относительности мы интересуемся описанием так называемого механического движения.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело А меняет своё положение относительно тела В, то и тело В меняет своё положение относительно тела А. Иначе говоря, если тело А движется относительно тела В, то и тело В движется относительно тела А. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т.
Когда скорость движения приближается к скорости света, механика перестаёт работать и уступает место специальной теории относительности (СТО 1905г).
Давайте вспомним для начала, как описывается движение в классической механике. Обсуждаемые понятия понадобятся нам в дальнейшем при изложении основ СТО.
Механическое движение
И в классической механике, и в специальной теории относительности мы интересуемся описанием так называемого механического движения.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело А меняет своё положение относительно тела В, то и тело В меняет своё положение относительно тела А. Иначе говоря, если тело А движется относительно тела В, то и тело В движется относительно тела А. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Система отсчёта
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним системой координат и часами.
Имеется бесконечное множество систем отсчёта, связанных с различными телами отсчёта. Какую систему отчёта лучше выбрать? Общего ответа на этот вопрос дать нельзя — выбор всегда диктуется конкретной задачей.
д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Система отсчёта
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним системой координат и часами.
Имеется бесконечное множество систем отсчёта, связанных с различными телами отсчёта. Какую систему отчёта лучше выбрать? Общего ответа на этот вопрос дать нельзя — выбор всегда диктуется конкретной задачей. Существует класс систем отсчёта, которые называются инерциальными. Именно в этих системах справедливы основные законы механики: второй и третий законы Ньютона.
Закон сложения скоростей
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта О. Эту систему отсчёта обозначим К и будем называть неподвижной.
Вторая система отсчёта, обозначаемая К’, связана с телом отсчёта О’, которое движется относительно тела со скоростью и. Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы K’ перемещаются параллельно самим себе, так что вектор u можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта K обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью u, то система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта K’.
Заметим, что скорость любой точки вагона равна u.
Существует класс систем отсчёта, которые называются инерциальными. Именно в этих системах справедливы основные законы механики: второй и третий законы Ньютона.
Закон сложения скоростей
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта О. Эту систему отсчёта обозначим К и будем называть неподвижной.
Вторая система отсчёта, обозначаемая К’, связана с телом отсчёта О’, которое движется относительно тела со скоростью и. Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы K’ перемещаются параллельно самим себе, так что вектор u можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта K обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью u, то система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта K’.
Заметим, что скорость любой точки вагона равна u.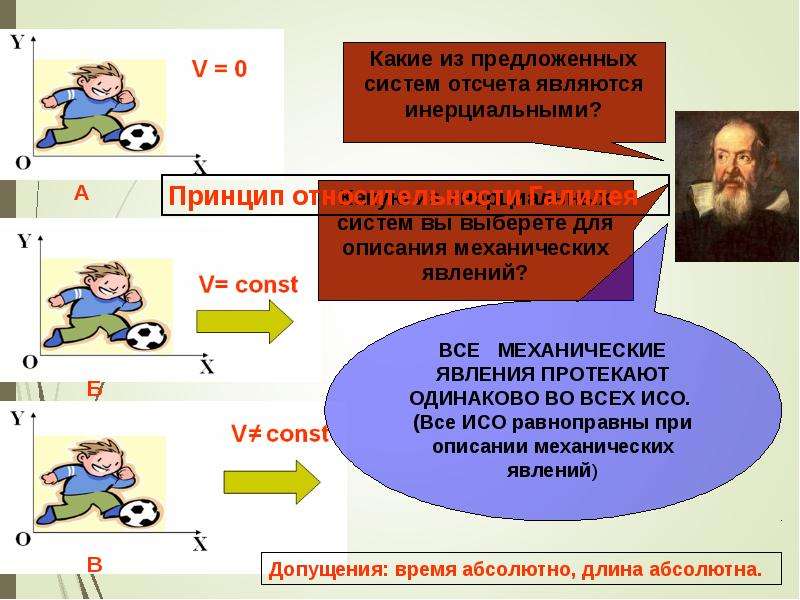 Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью u. Муха переносится вагоном, и потому скорость u движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Тогда появляются ещё две скорости, которые нужно рассмотреть.
Скорость мухи относительно вагона (то есть в движущейся системе K’) обозначается v‘ и называется относительной скоростью.
Скорость мухи относительно земли (то есть в неподвижной системе K) обозначается v и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.
Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью u. Муха переносится вагоном, и потому скорость u движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Тогда появляются ещё две скорости, которые нужно рассмотреть.
Скорость мухи относительно вагона (то есть в движущейся системе K’) обозначается v‘ и называется относительной скоростью.
Скорость мухи относительно земли (то есть в неподвижной системе K) обозначается v и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей. v=u+v‘
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона.
Инерциальные системы отсчёта
Все тела в природе взаимодействуют друг с другом. Однако в некоторых ситуациях воздействия на данное тело со стороны других тел можно не принимать во внимание.
Во всех подобных случаях будем называть тело свободным. Тело называется свободным, если действия на него со стороны других тел или пренебрежимо малы, или компенсируют друг друга.
Повседневный опыт говорит о том, что свободные тела покоятся. Поэтому долгое время считалось, что для поддержания какого бы то ни было движения необходимо осуществлять нескомпенсированное внешнее воздействие со стороны других тел. Но это оказалось неверным.
Как установил Галилей, свободное тело может не только находиться в покое, но и двигаться равномерно и прямолинейно.
v=u+v‘
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона.
Инерциальные системы отсчёта
Все тела в природе взаимодействуют друг с другом. Однако в некоторых ситуациях воздействия на данное тело со стороны других тел можно не принимать во внимание.
Во всех подобных случаях будем называть тело свободным. Тело называется свободным, если действия на него со стороны других тел или пренебрежимо малы, или компенсируют друг друга.
Повседневный опыт говорит о том, что свободные тела покоятся. Поэтому долгое время считалось, что для поддержания какого бы то ни было движения необходимо осуществлять нескомпенсированное внешнее воздействие со стороны других тел. Но это оказалось неверным.
Как установил Галилей, свободное тело может не только находиться в покое, но и двигаться равномерно и прямолинейно. Следует учесть, что движение относительно: оно рассматривается не само по себе, а в определённой системе отсчёта. В различных же системах отсчёта движение данного тела будет выглядеть по-разному.
Утверждение Галилея верно не во всякой системе отсчёта Но всё же такие системы отсчёта существуют, и в этом состоит первый закон Ньютона: существуют такие системы отсчёта, относительно которых свободное тело движется равномерно и прямолинейно.
Явление сохранения скорости тела при отсутствии взаимодействия с другими телами называется инерцией. Поэтому первый закон Ньютона называют ещё законом инерции. Равномерное прямолинейное движение свободного тела называется движением по инерции.
Инерциальная система отсчёта — это система отсчёта, относительно которой свободное тело движется равномерно и прямолинейно.
Таким образом, первый закон Ньютона — это утверждение о существовании инерциальных систем отсчёта.
Система отсчёта, которая движется относительно инерциальной системы отсчёта с изменяющейся скоростью, является неинерциальной.
Следует учесть, что движение относительно: оно рассматривается не само по себе, а в определённой системе отсчёта. В различных же системах отсчёта движение данного тела будет выглядеть по-разному.
Утверждение Галилея верно не во всякой системе отсчёта Но всё же такие системы отсчёта существуют, и в этом состоит первый закон Ньютона: существуют такие системы отсчёта, относительно которых свободное тело движется равномерно и прямолинейно.
Явление сохранения скорости тела при отсутствии взаимодействия с другими телами называется инерцией. Поэтому первый закон Ньютона называют ещё законом инерции. Равномерное прямолинейное движение свободного тела называется движением по инерции.
Инерциальная система отсчёта — это система отсчёта, относительно которой свободное тело движется равномерно и прямолинейно.
Таким образом, первый закон Ньютона — это утверждение о существовании инерциальных систем отсчёта.
Система отсчёта, которая движется относительно инерциальной системы отсчёта с изменяющейся скоростью, является неинерциальной. Галилей заметил, что, находясь в трюме корабля, никакими механическими опытами невозможно установить, покоится ли корабль или движется равномерно и прямолинейно. Стало быть, инерциальные системы отсчёта совершенно неотличимы друг от друга с точки зрения законов механики — в этом состоит принцип относительности Галилея.
Впоследствии Эйнштейн распространил этот принцип с механических опытов на любые физические эксперименты.
Принцип относительности Галилея
Равномерное прямолинейное движение корабля никак не сказывается на протекании механических явлений на этом корабле. Поэтому никакой опыт из механики, проведённый в лаборатории корабля, не в состоянии определить, покоится ли корабль или движется равномерно и прямолинейно.
Принцип относительности Галилея. Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.
Принцип относительности Галилея означает, что законы механики одинаковы во всех инерциальных системах отсчёта.
Галилей заметил, что, находясь в трюме корабля, никакими механическими опытами невозможно установить, покоится ли корабль или движется равномерно и прямолинейно. Стало быть, инерциальные системы отсчёта совершенно неотличимы друг от друга с точки зрения законов механики — в этом состоит принцип относительности Галилея.
Впоследствии Эйнштейн распространил этот принцип с механических опытов на любые физические эксперименты.
Принцип относительности Галилея
Равномерное прямолинейное движение корабля никак не сказывается на протекании механических явлений на этом корабле. Поэтому никакой опыт из механики, проведённый в лаборатории корабля, не в состоянии определить, покоится ли корабль или движется равномерно и прямолинейно.
Принцип относительности Галилея. Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.
Принцип относительности Галилея означает, что законы механики одинаковы во всех инерциальных системах отсчёта. А именно, математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой. Существуют преобразования Галилея которые служат математическим описанием перехода от одной инерциальной системы отсчёта к другой.
Рассмотрим некоторые следствия, вытекающие из преобразований Галилея:
А именно, математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой. Существуют преобразования Галилея которые служат математическим описанием перехода от одной инерциальной системы отсчёта к другой.
Рассмотрим некоторые следствия, вытекающие из преобразований Галилея:
- закон сложения скоростей в механике является следствием преобразований Галилея;
- ускорение частицы одинаково во всех инерциальных системах отсчёта;
- масса частицы одинакова во всех инерциальных системах отсчёта.
 Величины и соотношения, не меняющиеся при определённых условиях, часто называются инвариантными. Так, ускорение, масса и сила инвариантны относительно выбора инерциальной системы отсчёта. Поэтому второй и третий законы Ньютона во всех системах отсчёта имеют одинаковый вид, т. е. инвариантны относительно преобразований Галилея.
Законы механики инвариантны относительно преобразований Галилея — такова альтернативная формулировка принципа относительности Галилея.
Принципы СТО
Теперь перейдем к рассмотрению тел, которые движутся со скоростями близкими к скорости света.
Лоренц (нидерландский физик-теоретик, лауреат Нобелевской премии по физике) заметил, что результаты опыта Майкельсона полностью объясняются, если сделать невероятное предположение: размеры движущегося предмета сокращаются в направлении движения!
Эта гипотеза, названная лоренцевым сокращением, не вытекала на тот момент из каких-либо физических принципов и стояла особняком, будучи призвана лишь справиться с отрицательным результатом опыта.
Величины и соотношения, не меняющиеся при определённых условиях, часто называются инвариантными. Так, ускорение, масса и сила инвариантны относительно выбора инерциальной системы отсчёта. Поэтому второй и третий законы Ньютона во всех системах отсчёта имеют одинаковый вид, т. е. инвариантны относительно преобразований Галилея.
Законы механики инвариантны относительно преобразований Галилея — такова альтернативная формулировка принципа относительности Галилея.
Принципы СТО
Теперь перейдем к рассмотрению тел, которые движутся со скоростями близкими к скорости света.
Лоренц (нидерландский физик-теоретик, лауреат Нобелевской премии по физике) заметил, что результаты опыта Майкельсона полностью объясняются, если сделать невероятное предположение: размеры движущегося предмета сокращаются в направлении движения!
Эта гипотеза, названная лоренцевым сокращением, не вытекала на тот момент из каких-либо физических принципов и стояла особняком, будучи призвана лишь справиться с отрицательным результатом опыта. Но тем не менее оказалась верна. Её объяснение пришло позже, уже в рамках теории относительности Эйнштейна.
Постулаты Эйнштейна
Сформулируем проблемы, с которыми столкнулась физика.
Проблема 1
Но тем не менее оказалась верна. Её объяснение пришло позже, уже в рамках теории относительности Эйнштейна.
Постулаты Эйнштейна
Сформулируем проблемы, с которыми столкнулась физика.
Проблема 1
- Не удаётся обнаружить привилегированную систему отсчёта, связанную с неподвижным мировым эфиром.
- Электродинамика противоречит механике в том, что уравнения Максвелла не инвариантны относительно преобразований Галилея.
 В природе существует предельная, максимальная скорость распространения взаимодействий.
Второй постулат Эйнштейна гласит: в каждой инерциальной системе отсчёта свет движется в вакууме с одной и той же скоростью; величина этой скорости не зависит от того, покоится или движется источник света.
Причина кажущегося парадокса 2 постулата кроется в понятии одновременности. На место нашего интуитивного понимания одновременности приходит чёткое определение этого термина, даваемое в СТО.
Одновременность событий
Сопоставление координат тела и показаний часов — ключевой момент. Здесь мы подходим к важнейшему понятию одновременности событий.
События являются одновременными, если они происходят в один и тот же момент времени по часам наблюдателя.
Отметим здесь два существенных момента:
— Неважно, происходят ли данные события в одной точке пространства или в различных точках. В классической механике мы спокойно говорим об одновременности пространственно разделённых событий.
В природе существует предельная, максимальная скорость распространения взаимодействий.
Второй постулат Эйнштейна гласит: в каждой инерциальной системе отсчёта свет движется в вакууме с одной и той же скоростью; величина этой скорости не зависит от того, покоится или движется источник света.
Причина кажущегося парадокса 2 постулата кроется в понятии одновременности. На место нашего интуитивного понимания одновременности приходит чёткое определение этого термина, даваемое в СТО.
Одновременность событий
Сопоставление координат тела и показаний часов — ключевой момент. Здесь мы подходим к важнейшему понятию одновременности событий.
События являются одновременными, если они происходят в один и тот же момент времени по часам наблюдателя.
Отметим здесь два существенных момента:
— Неважно, происходят ли данные события в одной точке пространства или в различных точках. В классической механике мы спокойно говорим об одновременности пространственно разделённых событий. — Понятие одновременности имеет абсолютный смысл: два события, одновременные в одной системе отсчёта, будут одновременными и в любой другой системе отсчёта. Во всех инерциальных системах отсчёта время течёт одинаково.
Такое понимание одновременности, однако, носит интуитивный характер. И, что совсем плохо, оно базируется на предположении о мгновенности передачи взаимодействий.
В действительности скорость сигнала является конечной и не может превышать скорость света в вакууме. Тем самым наше интуитивное понимание одновременности пространственно разделённых событий оказывается некорректным. Ведь если мы, держа в руках секундомер, фиксируем по нему время наступления окружающих событий и пытаемся судить об их одновременности, то нам придётся считаться с задержками прихода сигналов из различных точек пространства. Более того, эти задержки могут оказываться разными в зависимости от того, находимся ли мы в покоящейся системе отсчёта или в движущейся.
Эйнштейн предложил чёткую программу преодоления указанных трудностей.
— Понятие одновременности имеет абсолютный смысл: два события, одновременные в одной системе отсчёта, будут одновременными и в любой другой системе отсчёта. Во всех инерциальных системах отсчёта время течёт одинаково.
Такое понимание одновременности, однако, носит интуитивный характер. И, что совсем плохо, оно базируется на предположении о мгновенности передачи взаимодействий.
В действительности скорость сигнала является конечной и не может превышать скорость света в вакууме. Тем самым наше интуитивное понимание одновременности пространственно разделённых событий оказывается некорректным. Ведь если мы, держа в руках секундомер, фиксируем по нему время наступления окружающих событий и пытаемся судить об их одновременности, то нам придётся считаться с задержками прихода сигналов из различных точек пространства. Более того, эти задержки могут оказываться разными в зависимости от того, находимся ли мы в покоящейся системе отсчёта или в движущейся.
Эйнштейн предложил чёткую программу преодоления указанных трудностей. Суть её состоит в следующем: раз уж всё оказывается так плохо при измерении времени по одним-единственным часам наблюдателя, то давайте использовать много синхронно идущих часов, расставленных в разных точках пространства. Два события будут считаться одновременными, если совпадают показания часов, расположенных в тех точках, где произошли события.
— Пусть в некоторой точке пространства имеются часы. Если в этой точке происходит событие, то наши часы показывают время данного события. Таким образом, если в этой самой точке происходят два события, то мы всегда можем сказать, одновременны они или нет — просто сравнив показания наших часов в моменты наступления событий.
Итак, с определением одновременности событий, происходящих в одной точке пространства, проблем нет.
— Для определения понятия одновременности пространственно разделённых событий нам понадобится много одинаковых часов, расставленных в пространстве достаточно часто. Каждые часы показывают время событий, происходящих в той точке, где эти часы расположены.
Суть её состоит в следующем: раз уж всё оказывается так плохо при измерении времени по одним-единственным часам наблюдателя, то давайте использовать много синхронно идущих часов, расставленных в разных точках пространства. Два события будут считаться одновременными, если совпадают показания часов, расположенных в тех точках, где произошли события.
— Пусть в некоторой точке пространства имеются часы. Если в этой точке происходит событие, то наши часы показывают время данного события. Таким образом, если в этой самой точке происходят два события, то мы всегда можем сказать, одновременны они или нет — просто сравнив показания наших часов в моменты наступления событий.
Итак, с определением одновременности событий, происходящих в одной точке пространства, проблем нет.
— Для определения понятия одновременности пространственно разделённых событий нам понадобится много одинаковых часов, расставленных в пространстве достаточно часто. Каждые часы показывают время событий, происходящих в той точке, где эти часы расположены. Чтобы была возможность судить об одновременности событий, происходящих в различных точках пространства, все эти часы должны идти синхронно, т. е. показывать одно и то же время.
— Чтобы синхронизировать часы, расположенные в различных точках пространства, Эйнштейн предложил использовать световые сигналы.
Пусть в точках A и B имеются часы. Предположим, что из точки A в точку B посылается световой сигнал, который отражается в точке B и возвращается назад в A.
Пусть в момент отправления сигнала часы A показывали t1, а в момент возвращения сигнала показания тех же часов A равны t2.
Правило Эйнштейна. По определению, часы A и B идут синхронно, если в момент прихода сигнала в точку B показания часов B равны (t1+t2)/2.
Иными словами, часы B должны показывать ровно середину промежутка между t1 и t2.
Чтобы была возможность судить об одновременности событий, происходящих в различных точках пространства, все эти часы должны идти синхронно, т. е. показывать одно и то же время.
— Чтобы синхронизировать часы, расположенные в различных точках пространства, Эйнштейн предложил использовать световые сигналы.
Пусть в точках A и B имеются часы. Предположим, что из точки A в точку B посылается световой сигнал, который отражается в точке B и возвращается назад в A.
Пусть в момент отправления сигнала часы A показывали t1, а в момент возвращения сигнала показания тех же часов A равны t2.
Правило Эйнштейна. По определению, часы A и B идут синхронно, если в момент прихода сигнала в точку B показания часов B равны (t1+t2)/2.
Иными словами, часы B должны показывать ровно середину промежутка между t1 и t2.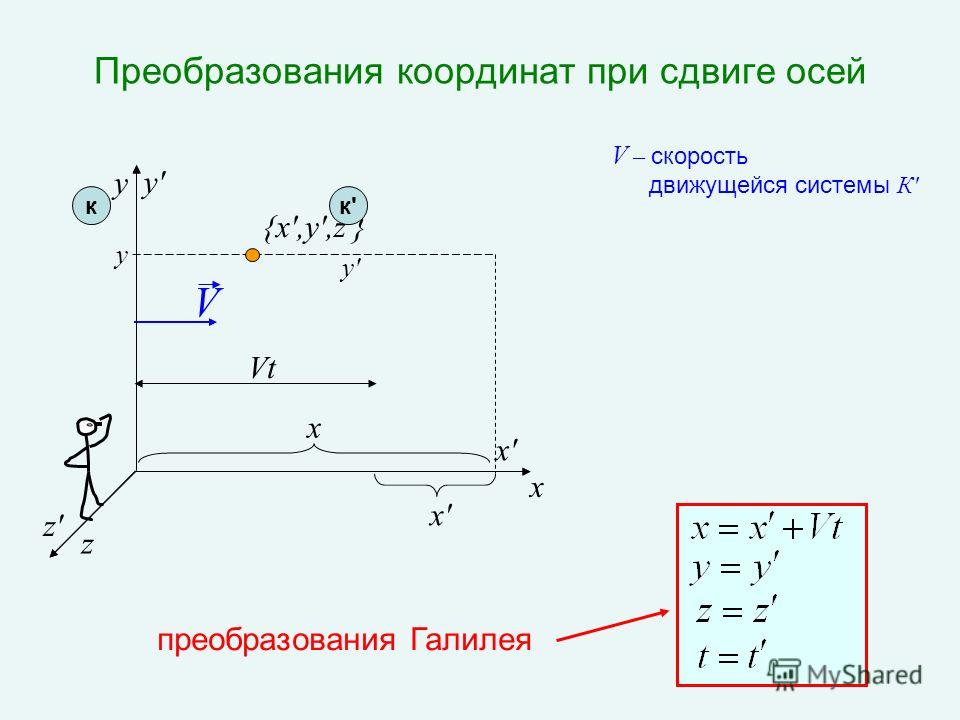 Cветовой сигнал идёт с одной и той же скоростью в обоих направлениях: как от A к В, так и обратно от В к A.
Одинаковость скорости света по всем направлениям — это факт, подтверждаемый многочисленными опытами.
Такой способ не согласуется с правилом Эйнштейна. Если в точке В уже имеются часы, синхронизированные по правилу Эйнштейна с часами A, то перенесённые из A часы покажут в точке В время меньшее, чем первые. При этом перенесённые часы будут отставать тем больше, чем с большей скоростью они двигались. Об этом свидетельствует опыт.
Итак, мы получили релятивистскую систему отсчёта с большим количеством часов. Все часы идут согласованно, они синхронизированы по правилу Эйнштейна. Время каждого события (местное время) измеряется по часам, расположенным в том месте, где событие совершилось.
Теперь можно дать определение одновременности событий.
Два пространственно разделённых события в данной системе отсчёта считаются одновременными, если при наступлении этих событий совпадают показания часов, расположенных в тех точках, где события произошли.
Cветовой сигнал идёт с одной и той же скоростью в обоих направлениях: как от A к В, так и обратно от В к A.
Одинаковость скорости света по всем направлениям — это факт, подтверждаемый многочисленными опытами.
Такой способ не согласуется с правилом Эйнштейна. Если в точке В уже имеются часы, синхронизированные по правилу Эйнштейна с часами A, то перенесённые из A часы покажут в точке В время меньшее, чем первые. При этом перенесённые часы будут отставать тем больше, чем с большей скоростью они двигались. Об этом свидетельствует опыт.
Итак, мы получили релятивистскую систему отсчёта с большим количеством часов. Все часы идут согласованно, они синхронизированы по правилу Эйнштейна. Время каждого события (местное время) измеряется по часам, расположенным в том месте, где событие совершилось.
Теперь можно дать определение одновременности событий.
Два пространственно разделённых события в данной системе отсчёта считаются одновременными, если при наступлении этих событий совпадают показания часов, расположенных в тех точках, где события произошли. Можно запомнить более короткую формулировку: события одновременны, если их местные времена совпадают.
Относительность одновременности
Понятие одновременности пространственно разделённых событий оказывается «привязанным» к данной системе отсчёта. Два события, одновременные в одной системе отсчёта, могут оказаться не одновременными в другой системе отсчёта. В этом нетрудно убедиться на следующем простом примере.
Рассмотрим вагон, который движется вправо со скоростью v. В точке S, находящейся в центре вагона, происходит световая вспышка.
В системе отсчёта, связанной с вагоном, всё происходит точно так же, как в неподвижной лаборатории. По вагонным часам свет придёт в точки A и В одновременно.
Но в системе отсчёта, связанной с землёй, картина окажется иной. Точка A движется навстречу сигналу, а точка В удаляется от него; поэтому для достижения точки A свету потребуется пройти меньшее расстояние, чем для достижения точки В.
Можно запомнить более короткую формулировку: события одновременны, если их местные времена совпадают.
Относительность одновременности
Понятие одновременности пространственно разделённых событий оказывается «привязанным» к данной системе отсчёта. Два события, одновременные в одной системе отсчёта, могут оказаться не одновременными в другой системе отсчёта. В этом нетрудно убедиться на следующем простом примере.
Рассмотрим вагон, который движется вправо со скоростью v. В точке S, находящейся в центре вагона, происходит световая вспышка.
В системе отсчёта, связанной с вагоном, всё происходит точно так же, как в неподвижной лаборатории. По вагонным часам свет придёт в точки A и В одновременно.
Но в системе отсчёта, связанной с землёй, картина окажется иной. Точка A движется навстречу сигналу, а точка В удаляется от него; поэтому для достижения точки A свету потребуется пройти меньшее расстояние, чем для достижения точки В. Но в земной системе отсчёта скорость света будет одинакова в обоих направлениях — ведь согласно второму постулату СТО скорость света не зависит от факта движения источника. Стало быть, по земным часам свет придёт в точку A раньше, чем в точку В.
Таким образом, два события — приход сигнала от источника S в точки A и В — являются одновременными в системе отсчёта вагона и не одновременными в системе отсчёта земли.
Относительность промежутков времени
Снова рассмотрим вагон, который движется со скоростью v. Предположим, что пассажир вагона подбрасывает яблоко; оно летит вертикально вверх, возвращается, и пассажир ловит его.
В системе отсчёта вагона события «яблоко брошено» и «яблоко поймано» происходят в одной точке. Промежуток времени между этими событиями, т. е. время полёта яблока в системе отсчёта вагона, измеряется по одним и тем же часам, расположенным в точке броска-ловли.
Но в системе отсчёта земли наши события происходят в различных пространственных точках.
Но в земной системе отсчёта скорость света будет одинакова в обоих направлениях — ведь согласно второму постулату СТО скорость света не зависит от факта движения источника. Стало быть, по земным часам свет придёт в точку A раньше, чем в точку В.
Таким образом, два события — приход сигнала от источника S в точки A и В — являются одновременными в системе отсчёта вагона и не одновременными в системе отсчёта земли.
Относительность промежутков времени
Снова рассмотрим вагон, который движется со скоростью v. Предположим, что пассажир вагона подбрасывает яблоко; оно летит вертикально вверх, возвращается, и пассажир ловит его.
В системе отсчёта вагона события «яблоко брошено» и «яблоко поймано» происходят в одной точке. Промежуток времени между этими событиями, т. е. время полёта яблока в системе отсчёта вагона, измеряется по одним и тем же часам, расположенным в точке броска-ловли.
Но в системе отсчёта земли наши события происходят в различных пространственных точках. Момент броска яблока фиксируется по часам, расположенным в исходной точке, а момент ловли — по другим часам, расположенным в той точке, куда переместится вагон за время полёта яблока. Эти двое часов синхронизированы по правилу Эйнштейна. Время полёта яблока в системе отсчёта земли — это разность показаний вторых часов в момент ловли и первых часов в момент броска.
И вот оказывается, что время полёта яблока, измеренное по вагонным часам, будет меньше времени полёта, измеренного по часам на земле!
Заменим яблоко на световой сигнал, который бегает между горизонтальными зеркалами, расположенными внутри вагона.
Сначала рассмотрим ход сигнала в системе отсчёта вагона. Сигнал выходит и, идёт вертикально вверх, отражается от зеркала и возвращается.
Время распространения сигнала от нижнего зеркала к верхнему и обратно, измеренное по часам, обозначим τ0.
Теперь перейдём в систему отсчёта земли. Здесь сигнал будет двигаться между зеркалами по ломаной.
Момент броска яблока фиксируется по часам, расположенным в исходной точке, а момент ловли — по другим часам, расположенным в той точке, куда переместится вагон за время полёта яблока. Эти двое часов синхронизированы по правилу Эйнштейна. Время полёта яблока в системе отсчёта земли — это разность показаний вторых часов в момент ловли и первых часов в момент броска.
И вот оказывается, что время полёта яблока, измеренное по вагонным часам, будет меньше времени полёта, измеренного по часам на земле!
Заменим яблоко на световой сигнал, который бегает между горизонтальными зеркалами, расположенными внутри вагона.
Сначала рассмотрим ход сигнала в системе отсчёта вагона. Сигнал выходит и, идёт вертикально вверх, отражается от зеркала и возвращается.
Время распространения сигнала от нижнего зеркала к верхнему и обратно, измеренное по часам, обозначим τ0.
Теперь перейдём в систему отсчёта земли. Здесь сигнал будет двигаться между зеркалами по ломаной. Время распространения сигнала от нижнего зеркала к верхнему и обратно есть разность показаний синхронизированных часов которые находятся уже в другой точке, вагон движется. Обозначим это время через τ.
Полученная формула носит совершенно общий характер. Пусть имеются две системы отсчёта K и K’, причём система K’ движется относительно K со скоростью v. Рассмотрим два события, которые в системе K’ происходят в одной точке пространства. Время τ0 между этими событиями в системе K’ называется собственным временем. По часам системы K между этими событиями проходит время τ, которое связано с собственным временем формулой. В ней собственное время τ0 делится на величину, меньшую единицы; поэтому всегда выполнено неравенство τ > τ0. При этом время τ оказывается тем больше, чем с большей скоростью система K’ движется относительно K.
Время распространения сигнала от нижнего зеркала к верхнему и обратно есть разность показаний синхронизированных часов которые находятся уже в другой точке, вагон движется. Обозначим это время через τ.
Полученная формула носит совершенно общий характер. Пусть имеются две системы отсчёта K и K’, причём система K’ движется относительно K со скоростью v. Рассмотрим два события, которые в системе K’ происходят в одной точке пространства. Время τ0 между этими событиями в системе K’ называется собственным временем. По часам системы K между этими событиями проходит время τ, которое связано с собственным временем формулой. В ней собственное время τ0 делится на величину, меньшую единицы; поэтому всегда выполнено неравенство τ > τ0. При этом время τ оказывается тем больше, чем с большей скоростью система K’ движется относительно K. Данный эффект — так называемое релятивистское замедление времени — оказывается весьма существенным при скоростях, близких к скорости света.
Относительность расстояний
При выводе формулы мы неявно предполагали, что расстояние между зеркалами одинаково как в вагоне, так и на земле.
Вертикальные размеры предметов являются одними и те же как в вагонной, так и в земной системе отсчёта.
Поперечные размеры предметов одинаковы как в покоящейся, так и в движущейся системе отсчёта. Иначе обстоит дело с продольными размерами.
Вновь вернёмся к нашему вагону и рассмотрим стержень AB, расположенный вдоль вектора скорости вагона. Стержень, таким образом, двигается со скоростью v.
Пусть l0 — длина неподвижного стержня, измеренная в вагоне. Она называется собственной длиной стержня. Через l обозначим длину движущегося стержня, измеренную на земле.
В земной системе отсчёта наши события происходят в одной точке.
Данный эффект — так называемое релятивистское замедление времени — оказывается весьма существенным при скоростях, близких к скорости света.
Относительность расстояний
При выводе формулы мы неявно предполагали, что расстояние между зеркалами одинаково как в вагоне, так и на земле.
Вертикальные размеры предметов являются одними и те же как в вагонной, так и в земной системе отсчёта.
Поперечные размеры предметов одинаковы как в покоящейся, так и в движущейся системе отсчёта. Иначе обстоит дело с продольными размерами.
Вновь вернёмся к нашему вагону и рассмотрим стержень AB, расположенный вдоль вектора скорости вагона. Стержень, таким образом, двигается со скоростью v.
Пусть l0 — длина неподвижного стержня, измеренная в вагоне. Она называется собственной длиной стержня. Через l обозначим длину движущегося стержня, измеренную на земле.
В земной системе отсчёта наши события происходят в одной точке. В системе отсчёта вагона указанные события происходят в двух различных точках.
Как видим, собственная длина l0 умножается на величину, меньшую единицы; стало быть, длина движущегося стержня будет меньше длины покоящегося стержня. Это так называемое лоренцево сокращение — все тела сокращают размеры в направлении своего движения.
Подчеркнём ещё раз: длина стержня в системе отсчёта, относительно которой стержень движется, меньше длины этого же стержня в системе отсчёта, относительно которой он покоится. Данный эффект связан лишь с особенностями измерительных процедур, свойственных теории относительности.
Релятивистский закон сложения скоростей
Опять рассмотрим наши системы отсчёта K и K’. Пусть точка А движется вдоль общего направления осей X и X‘.
Пусть u — скорость точки А в системе K; в системе K’ скорость этой точки пусть будет u’.
В системе отсчёта вагона указанные события происходят в двух различных точках.
Как видим, собственная длина l0 умножается на величину, меньшую единицы; стало быть, длина движущегося стержня будет меньше длины покоящегося стержня. Это так называемое лоренцево сокращение — все тела сокращают размеры в направлении своего движения.
Подчеркнём ещё раз: длина стержня в системе отсчёта, относительно которой стержень движется, меньше длины этого же стержня в системе отсчёта, относительно которой он покоится. Данный эффект связан лишь с особенностями измерительных процедур, свойственных теории относительности.
Релятивистский закон сложения скоростей
Опять рассмотрим наши системы отсчёта K и K’. Пусть точка А движется вдоль общего направления осей X и X‘.
Пусть u — скорость точки А в системе K; в системе K’ скорость этой точки пусть будет u’. Как связаны друг с другом u и u’?
Классический закон сложения скоростей, дает следующий результат
Однако данный закон не может быть верным в теории относительности. В самом деле, рассмотрим вместо точки А световой сигнал в вакууме, мчащийся в системе K’ со скоростью u’ = c. Согласно ему получится, что скорость нашего сигнала в системе K будет равна u = c + v. Но это противоречит принципу относительности, в силу которого скорость света в вакууме имеет одно и то же значение во всех инерциальных системах отсчёта.
Возникновение данного противоречия не удивительно: ведь вывод формулы базируется на преобразованиях Галилея, которые в теории относительности уступают место преобразованиям Лоренца. Поэтому правильный закон сложения скоростей нужно выводить теперь из преобразований Лоренца.
Это и есть релятивистский закон сложения скоростей, который приходит на смену классическому.
Теперь уже никакого противоречия не возникает: если скорость сигнала u’ = c в системе K’, то в системе K его скорость равна:
как того и требует принцип относительности.
Как связаны друг с другом u и u’?
Классический закон сложения скоростей, дает следующий результат
Однако данный закон не может быть верным в теории относительности. В самом деле, рассмотрим вместо точки А световой сигнал в вакууме, мчащийся в системе K’ со скоростью u’ = c. Согласно ему получится, что скорость нашего сигнала в системе K будет равна u = c + v. Но это противоречит принципу относительности, в силу которого скорость света в вакууме имеет одно и то же значение во всех инерциальных системах отсчёта.
Возникновение данного противоречия не удивительно: ведь вывод формулы базируется на преобразованиях Галилея, которые в теории относительности уступают место преобразованиям Лоренца. Поэтому правильный закон сложения скоростей нужно выводить теперь из преобразований Лоренца.
Это и есть релятивистский закон сложения скоростей, который приходит на смену классическому.
Теперь уже никакого противоречия не возникает: если скорость сигнала u’ = c в системе K’, то в системе K его скорость равна:
как того и требует принцип относительности. При т.е., при малых скоростях движения релятивистский закон сложения скоростей переходит в классический закон.
Домашнее задание: выполнить тест.
При т.е., при малых скоростях движения релятивистский закон сложения скоростей переходит в классический закон.
Домашнее задание: выполнить тест.
- Эфирный ветер обнаружили …
- Сформулируйте постулаты теории относительности.
- Одновременность пространственно разделенных событий относительна.
- Линейные размеры тела вдоль его скорости…
- Интервалы времени между событиями…
- Возможно ли разогнать космический корабль до скорости выше скорости света?
- СТО используется…
- По реке плывут рядом с одной и той же скоростью плот и лодка. Что потребует от гребца лодки меньших усилий: отстать от плота на 15 метров или обогнать его на 15 метров?
- Самолет летит по замкнутому маршруту Москва — Тамбов — Москва на побитие рекорда скорости. В течение всего полета дует постоянный ветер по направлению Москва — Тамбов. Улучшится или ухудшится рекорд из-за ветра?
- Трофимова Т.И., учеб. пособие для вузов. —7-е изд., перераб. и доп. М.: Высш. шк., 2001. —542 с.
- Бирюков В.В., Денисов Е.К., Тесты по физике для 11 классов, ТОИПКРО, Тамбов 2006
- http://femto.com.ua/index1.html
- http://mathus.ru
Евгений Константинович Денисов
e-mail: [email protected]
План-конспект урока «Третий закон Ньютона. Принцип относительности Галилея» 9 класс
Планконспект урока «Третий закон Ньютона. Принцип
относительности Галилея» 9 класс
Планконспект урока по физике в 9м классе
Цели урока:
Образовательная: Изучить III закон Ньютона, его особенности и значение,
сформировать умение у учащихся применять III закон Ньютона для решения
практических, логических, качественных задач. Изучить принцип
относительности Галилея
Развивающая: развивать умение наблюдать, анализировать. Делать выводы,
формировать учебнокоммуникативные навыки и умения учащихся:
– отвечать на вопросы в соответствии с их характером;
– уметь вести диалог с целью уточнения, получения, систематизации
информации, с целью закрепления данной темы;
– строить рассказ о физическом законе на основе плана;
– умение пользоваться физическими приборами.
Воспитательная: воспитывать культуру учебного труда, уверенность,
самостоятельность, умение слушать своих товарищей.
Здоровьесберегающая: Обеспечить школьникам возможность сохранения
здоровья во время обучения физике.
Тип урока:
Изучение нового материала
Вид урока:
Комбинированный
ТСО: мультимедийная доска, мультимедео и видео сопровождение
Структура урока:
1.
Принцип
относительности Галилея» 9 класс
Планконспект урока по физике в 9м классе
Цели урока:
Образовательная: Изучить III закон Ньютона, его особенности и значение,
сформировать умение у учащихся применять III закон Ньютона для решения
практических, логических, качественных задач. Изучить принцип
относительности Галилея
Развивающая: развивать умение наблюдать, анализировать. Делать выводы,
формировать учебнокоммуникативные навыки и умения учащихся:
– отвечать на вопросы в соответствии с их характером;
– уметь вести диалог с целью уточнения, получения, систематизации
информации, с целью закрепления данной темы;
– строить рассказ о физическом законе на основе плана;
– умение пользоваться физическими приборами.
Воспитательная: воспитывать культуру учебного труда, уверенность,
самостоятельность, умение слушать своих товарищей.
Здоровьесберегающая: Обеспечить школьникам возможность сохранения
здоровья во время обучения физике.
Тип урока:
Изучение нового материала
Вид урока:
Комбинированный
ТСО: мультимедийная доска, мультимедео и видео сопровождение
Структура урока:
1. Организационный этап 2 мин
2. Актуализация опорных знаний 10 мин
3. Изучение новой темы 20 мин
4. Закрепление 5мин
1 5. Рефлексия,д/з. 8 мин
Ход урока.
Организационный этап
Эпиграф: Сделал, что мог, пусть другие сделают лучше.
Йсаак Ньютон(16431727)
Ребята! Я рада Вас приветствовать, и приглашаю совершить на автобусе
увлекательное путешествие по стране «Динамика». И мы знаем, что
основными в динамике являются законы Ньютона, которые мы продолжим
изучать в ходе этого путешествия. А Исаак Ньютон незадолго перед
смертью, словно оглядывая свою жизнь, такую спокойную внешне и такую
неистово бурную внутренне, писал:
«Не знаю, чем я могу казаться миру, но самому себе я кажусь мальчиком,
играющим у моря, которому удалось найти более красивый камешек, чем
другим, в то время как великий океан истины расстилается передо мной
неисследованным»
Актуализация опорных знаний
Но для того что бы отправиться в путь, необходимо
проверить состояние всех деталей автобуса.
Организационный этап 2 мин
2. Актуализация опорных знаний 10 мин
3. Изучение новой темы 20 мин
4. Закрепление 5мин
1 5. Рефлексия,д/з. 8 мин
Ход урока.
Организационный этап
Эпиграф: Сделал, что мог, пусть другие сделают лучше.
Йсаак Ньютон(16431727)
Ребята! Я рада Вас приветствовать, и приглашаю совершить на автобусе
увлекательное путешествие по стране «Динамика». И мы знаем, что
основными в динамике являются законы Ньютона, которые мы продолжим
изучать в ходе этого путешествия. А Исаак Ньютон незадолго перед
смертью, словно оглядывая свою жизнь, такую спокойную внешне и такую
неистово бурную внутренне, писал:
«Не знаю, чем я могу казаться миру, но самому себе я кажусь мальчиком,
играющим у моря, которому удалось найти более красивый камешек, чем
другим, в то время как великий океан истины расстилается передо мной
неисследованным»
Актуализация опорных знаний
Но для того что бы отправиться в путь, необходимо
проверить состояние всех деталей автобуса. Обнаружены неисправности спущены шины, нужно
накачать воздух в колеса, наполнить их знаниями. Для
этого ответим на вопросы по пройденным темам:
1.Что такое сила?
2.Первый закон Ньютона
3.Второй закон Ньютона
4. На автобус действуют сила тяги 6кН и сила трения
3кН. Автобус движется с ускорением 1м\с2. Чему равна
масса автобуса?
Получаем билет в наш автобус – это и есть тема нашего
урока.
Записываем тему в рабочий конспект: Третий закон Ньютона. Принцип
относительности Галилея.
Проложим маршрут для нашей экскурсии. Глядя на тему урока,
сформулируйте задачи, которые хотелось бы решить
Формулируют учащиеся:
2 Изучить третий закон Ньютона;
Познакомиться с принципом относительности Галилея
Изучение новой темы
Мотивация:
Итак, ребята, Вы изучили I и II закон Ньютона, узнали, при каком условии
тело сохраняет свою скорость постоянной в ИСО, о том, что в результате
взаимодействия тело приобретает ускорение, которое прямо
пропорционально силе и обратно пропорционально его массе.
Обнаружены неисправности спущены шины, нужно
накачать воздух в колеса, наполнить их знаниями. Для
этого ответим на вопросы по пройденным темам:
1.Что такое сила?
2.Первый закон Ньютона
3.Второй закон Ньютона
4. На автобус действуют сила тяги 6кН и сила трения
3кН. Автобус движется с ускорением 1м\с2. Чему равна
масса автобуса?
Получаем билет в наш автобус – это и есть тема нашего
урока.
Записываем тему в рабочий конспект: Третий закон Ньютона. Принцип
относительности Галилея.
Проложим маршрут для нашей экскурсии. Глядя на тему урока,
сформулируйте задачи, которые хотелось бы решить
Формулируют учащиеся:
2 Изучить третий закон Ньютона;
Познакомиться с принципом относительности Галилея
Изучение новой темы
Мотивация:
Итак, ребята, Вы изучили I и II закон Ньютона, узнали, при каком условии
тело сохраняет свою скорость постоянной в ИСО, о том, что в результате
взаимодействия тело приобретает ускорение, которое прямо
пропорционально силе и обратно пропорционально его массе. Но ни I, ни II
закон Ньютона не говорит нам о том, что же будет происходить со вторым
взаимодействующим телом. Речь пойдет об этом в III законе Ньютона.
Ударьте рукой по столу. Что вы испытали?
– Боль.
– Почему? Ведь это вы бьете стол, а не он вас.
Ответы на эти вопросы мы узнаем, если изучим III закон Ньютона.
III закон Ньютона объясняет явление отдачи при выстреле. Откат пушки и
есть результат отдачи при выстреле. III закон Ньютона лежит в основе
реактивного движения, движения кальмара и т.д.
Посмотрим кинофильм “III закон Ньютона”.
После просмотра кинофильма мы ответим на вопросы:
– Как формулируется III закон Ньютона?
– Могут ли эти силы возникать по одной?
– Какова природа этих сил?
– Можно ли эти силы складывать?
Откройте учебник на стр. 103, найдите запись третьего зна и коротко
запишите в конспект.
Мы изучили законы Ньютона. Познакомимся еще с одним важным
положением в механике – принципом относительности Галилея.
Какую систему отсчета называют инерциальной?
Будет ли инерциальной система отсчета, которая движется с постоянной
скоростью относительно инерциальной системы отсчета.
Но ни I, ни II
закон Ньютона не говорит нам о том, что же будет происходить со вторым
взаимодействующим телом. Речь пойдет об этом в III законе Ньютона.
Ударьте рукой по столу. Что вы испытали?
– Боль.
– Почему? Ведь это вы бьете стол, а не он вас.
Ответы на эти вопросы мы узнаем, если изучим III закон Ньютона.
III закон Ньютона объясняет явление отдачи при выстреле. Откат пушки и
есть результат отдачи при выстреле. III закон Ньютона лежит в основе
реактивного движения, движения кальмара и т.д.
Посмотрим кинофильм “III закон Ньютона”.
После просмотра кинофильма мы ответим на вопросы:
– Как формулируется III закон Ньютона?
– Могут ли эти силы возникать по одной?
– Какова природа этих сил?
– Можно ли эти силы складывать?
Откройте учебник на стр. 103, найдите запись третьего зна и коротко
запишите в конспект.
Мы изучили законы Ньютона. Познакомимся еще с одним важным
положением в механике – принципом относительности Галилея.
Какую систему отсчета называют инерциальной?
Будет ли инерциальной система отсчета, которая движется с постоянной
скоростью относительно инерциальной системы отсчета. 3 Будут ли выполняться в неинерциальных системах отсчета законы
Ньютона?
Является ли геоцентрическая система строго инерциальной?
Теоретическое обоснование принципа относительности.
Галилео Галилей писал: « Заключите себя с какимнибудь приятелем в зале
под палубой какогонибудь большого корабля и заставьте привести в
движение корабль с какой угодно быстротой и вот ( если только движение
будет равномерным) вы не заметите ни малейшей перемены во всех явлениях
и ни по одному из них не в состоянии будете судить – движется ли корабль
или стоит на месте…»
Вопросы учащимся:
если вы совершаете путешествие в самолете, ощущается ли скорость, с
которой движется самолет?
Необходимо обратить внимание учащихся, что в инерциальных системах
отсчета тождественны законы динамики, а не кинематические величины.
какова форма траектории падения мяча в равномерно и прямолинейно
движущемся автобусе?
( вертикальная линия)
Какую траекторию опишет падающий мяч относительно Земли? ( Часть
параболы)
Почему траектории движения одного и того же тела различны? ( В
движущемся поезде, начальная скорость тела, равна нулю.
3 Будут ли выполняться в неинерциальных системах отсчета законы
Ньютона?
Является ли геоцентрическая система строго инерциальной?
Теоретическое обоснование принципа относительности.
Галилео Галилей писал: « Заключите себя с какимнибудь приятелем в зале
под палубой какогонибудь большого корабля и заставьте привести в
движение корабль с какой угодно быстротой и вот ( если только движение
будет равномерным) вы не заметите ни малейшей перемены во всех явлениях
и ни по одному из них не в состоянии будете судить – движется ли корабль
или стоит на месте…»
Вопросы учащимся:
если вы совершаете путешествие в самолете, ощущается ли скорость, с
которой движется самолет?
Необходимо обратить внимание учащихся, что в инерциальных системах
отсчета тождественны законы динамики, а не кинематические величины.
какова форма траектории падения мяча в равномерно и прямолинейно
движущемся автобусе?
( вертикальная линия)
Какую траекторию опишет падающий мяч относительно Земли? ( Часть
параболы)
Почему траектории движения одного и того же тела различны? ( В
движущемся поезде, начальная скорость тела, равна нулю. А для
наблюдателя на Земле, начальная скорость тела равна скорости автобуса,
относительно Земли.)
Какие явления начнут происходить в автобусе, если он будет двигаться с
ускорением?
( Вода будет выплескиваться из стакана, предметы, находившиеся в покое на
столе, начнут приходить в движение без видимой причины.)
В данном случае автобус считается неинерциальной системой отсчета и
законы Ньютона в ней не выполняются.
4 Закрепление
Физкультминутка. «Поездка в автобусе»
Внимание. Ребята, впереди знак «Извилистая дорога». Вы – пассажиры
автобуса и должны показать, как меняется положение тела пассажира
относительно сиденья кресла, т.е. относительно Земли в разных ситуациях.
Автобус плавно отъезжает от остановки.
Автобус резко тормозит.
Поворот влево на большой скорости.
Поворот вправо на большой скорости.
Автобус плавно отъезжает от остановки.
Автобус резко тормозит.
Поворот влево на большой скорости.
Поворот вправо на большой скорости.
Автобус движется равномерно и прямолинейно.
А для
наблюдателя на Земле, начальная скорость тела равна скорости автобуса,
относительно Земли.)
Какие явления начнут происходить в автобусе, если он будет двигаться с
ускорением?
( Вода будет выплескиваться из стакана, предметы, находившиеся в покое на
столе, начнут приходить в движение без видимой причины.)
В данном случае автобус считается неинерциальной системой отсчета и
законы Ньютона в ней не выполняются.
4 Закрепление
Физкультминутка. «Поездка в автобусе»
Внимание. Ребята, впереди знак «Извилистая дорога». Вы – пассажиры
автобуса и должны показать, как меняется положение тела пассажира
относительно сиденья кресла, т.е. относительно Земли в разных ситуациях.
Автобус плавно отъезжает от остановки.
Автобус резко тормозит.
Поворот влево на большой скорости.
Поворот вправо на большой скорости.
Автобус плавно отъезжает от остановки.
Автобус резко тормозит.
Поворот влево на большой скорости.
Поворот вправо на большой скорости.
Автобус движется равномерно и прямолинейно. Нас остановил контролер. Ответьте на ваши вопросы, которые Вы получили
в билетах.
Отвечаем на вопросы вместе, проводим взаимопроверку.
Котролер убедился в ваших знаниях физики и предлагает веселую задачу .
Белку, прижимающую к себе орехи, посадили на очень гладкий стол и слегка
толкнули по направлению к краю. Приближаясь к краю стола, белка
почувствовала опасность. Она знает законы физики и предотвращает падение
со скользкого стола. Каким образом?
Ответ: Белка должна бросать орехи по направлению движения. Тогда по
закону сохранения импульса скорость белки уменьшается и может стать
равной нулю.
Рефлексия,д/з.
5 Наш урок подходит к завершению. Давайте оценим нашу деятельность на
уроке. Получилось ли у нас решить поставленные задачи к уроку? Вспомним
их.
Изучить третий закон Ньютона;
Познакомиться с принципом относительности Галилея Дамашняе заданне К
следующему уроку
§ 12, упр. 12 №1, 2
— Большое спасибо за приятное путешествие, хочу
надеяться, что сегодняшний урок разбудит у вас жажду
новых знаний.
Нас остановил контролер. Ответьте на ваши вопросы, которые Вы получили
в билетах.
Отвечаем на вопросы вместе, проводим взаимопроверку.
Котролер убедился в ваших знаниях физики и предлагает веселую задачу .
Белку, прижимающую к себе орехи, посадили на очень гладкий стол и слегка
толкнули по направлению к краю. Приближаясь к краю стола, белка
почувствовала опасность. Она знает законы физики и предотвращает падение
со скользкого стола. Каким образом?
Ответ: Белка должна бросать орехи по направлению движения. Тогда по
закону сохранения импульса скорость белки уменьшается и может стать
равной нулю.
Рефлексия,д/з.
5 Наш урок подходит к завершению. Давайте оценим нашу деятельность на
уроке. Получилось ли у нас решить поставленные задачи к уроку? Вспомним
их.
Изучить третий закон Ньютона;
Познакомиться с принципом относительности Галилея Дамашняе заданне К
следующему уроку
§ 12, упр. 12 №1, 2
— Большое спасибо за приятное путешествие, хочу
надеяться, что сегодняшний урок разбудит у вас жажду
новых знаний. Великий океан по-прежнему расстилается
перед вами и не исследован до конца. Оцените свою
работу на уроке. Вам достался орешек от белочки, если
вы все усвоили на уроке то положим его обратно в
красную корзину к белочке, если остались некоторые
вопросы по теме, вы не до конца поняли все на уроке, то
кладем в синюю корзинку белочки. Приложение2
* Если время останется отвечаем на вопросы
1. Вы отталкиваетесь от Земли с силой 50Н. С какой силой Земля отталкивает Вас?
2. 20 человек разделилось на две команды по перетягиванию каната. Какой будет сила
натяжения каната, если каждый прикладывает силу 200Н.
Ожидаемый ответ: 10∙200Н=2000Н
3. Яблоко падает на Землю, потому что его притягивает Земля. Но с такой же силой и
яблоко притягивает земной шар. Можно ли сказать: «Яблоко и земля падают друг на
друга»?
Ожидаемый ответ: Да можно. Равные силы притяжения сообщают яблоку
ускорение
2, а земному шару во столько же раз меньше, во сколько раз масса
Земли превышает массу яблока.
Великий океан по-прежнему расстилается
перед вами и не исследован до конца. Оцените свою
работу на уроке. Вам достался орешек от белочки, если
вы все усвоили на уроке то положим его обратно в
красную корзину к белочке, если остались некоторые
вопросы по теме, вы не до конца поняли все на уроке, то
кладем в синюю корзинку белочки. Приложение2
* Если время останется отвечаем на вопросы
1. Вы отталкиваетесь от Земли с силой 50Н. С какой силой Земля отталкивает Вас?
2. 20 человек разделилось на две команды по перетягиванию каната. Какой будет сила
натяжения каната, если каждый прикладывает силу 200Н.
Ожидаемый ответ: 10∙200Н=2000Н
3. Яблоко падает на Землю, потому что его притягивает Земля. Но с такой же силой и
яблоко притягивает земной шар. Можно ли сказать: «Яблоко и земля падают друг на
друга»?
Ожидаемый ответ: Да можно. Равные силы притяжения сообщают яблоку
ускорение
2, а земному шару во столько же раз меньше, во сколько раз масса
Земли превышает массу яблока. 10м/с
≈
4. Человек стоит на стуле. Когда человек спрыгивает со стула, то мы видим, как он
падает на Землю. Почему же земля не падает на Человека?
5. О каких законах идет речь?
Здоровый человек передвигается по льду или скользкой дороге, делая частые
мелкие шаги.
Получив в боксерском поединке, удар в челюсть, можете смело говорить
после нокдауна «Ох, и ударил я его сегодня».
Проанализируйте и скажите, что объединяет все эти на первый взгляд разные
примеры?
6 Факты из
повседневной
жизни
Пословицы
«Если он не погасит свои фары, то я не погашу свои»,
так рассуждают некоторые водители.
Как аукнется, так и откликнется.
Долг платежом красит.
Что посеешь, то и пожнешь.
Ожидаемый ответ: все эти примеры показывают, что в природе не бывает так,
чтобы только одно тело действовало на другое тело, а это другое тело на первое не
действовало бы. Тела взаимно действуют друг на друга.
7 Приложение 1
1. Лошадь тянет телегу. Сравните модули
силы F1 действия лошади на телегу и F2
действия телеги на лошадь при равномерном
движении телеги
А.
10м/с
≈
4. Человек стоит на стуле. Когда человек спрыгивает со стула, то мы видим, как он
падает на Землю. Почему же земля не падает на Человека?
5. О каких законах идет речь?
Здоровый человек передвигается по льду или скользкой дороге, делая частые
мелкие шаги.
Получив в боксерском поединке, удар в челюсть, можете смело говорить
после нокдауна «Ох, и ударил я его сегодня».
Проанализируйте и скажите, что объединяет все эти на первый взгляд разные
примеры?
6 Факты из
повседневной
жизни
Пословицы
«Если он не погасит свои фары, то я не погашу свои»,
так рассуждают некоторые водители.
Как аукнется, так и откликнется.
Долг платежом красит.
Что посеешь, то и пожнешь.
Ожидаемый ответ: все эти примеры показывают, что в природе не бывает так,
чтобы только одно тело действовало на другое тело, а это другое тело на первое не
действовало бы. Тела взаимно действуют друг на друга.
7 Приложение 1
1. Лошадь тянет телегу. Сравните модули
силы F1 действия лошади на телегу и F2
действия телеги на лошадь при равномерном
движении телеги
А. F1=F2. Б. F1>F2. В. F1>F2
2. Два ученика растягивают динамометра в
противоположные стороны с силами 50 Н
каждый. Каково показание динамометра в
этом случае?
А. 0. Б. 50Н. В. 100Н. Г. Среди
приведенных ответов нет правильного.
3. Зависит ли направление и численное
значение скорости тела от выбора системы
отсчета?
А. Да, зависит модуль и направление.
Б. Зависит только модуль, направление не
изменяется.
В. Модуль скорости не зависит, а
направление изменяется.
Г. Нет, т.к. вид механического движения
не изменяется при переходе из одной
системы отсчета в другую.
4. Система отсчета связанная с телом
инерциальная при условии, что
А. тело покоится
Б. тело движется равномерно и
прямолинейно
8 В. если тело покоится или движется
равномерно и прямолинейно.
Г. нет правильного ответа.
Приложение 2
9 >
F1=F2. Б. F1>F2. В. F1>F2
2. Два ученика растягивают динамометра в
противоположные стороны с силами 50 Н
каждый. Каково показание динамометра в
этом случае?
А. 0. Б. 50Н. В. 100Н. Г. Среди
приведенных ответов нет правильного.
3. Зависит ли направление и численное
значение скорости тела от выбора системы
отсчета?
А. Да, зависит модуль и направление.
Б. Зависит только модуль, направление не
изменяется.
В. Модуль скорости не зависит, а
направление изменяется.
Г. Нет, т.к. вид механического движения
не изменяется при переходе из одной
системы отсчета в другую.
4. Система отсчета связанная с телом
инерциальная при условии, что
А. тело покоится
Б. тело движется равномерно и
прямолинейно
8 В. если тело покоится или движется
равномерно и прямолинейно.
Г. нет правильного ответа.
Приложение 2
9 >
Относительность
Первый закон кажется разумным; второй закон противоречит здравому смыслу.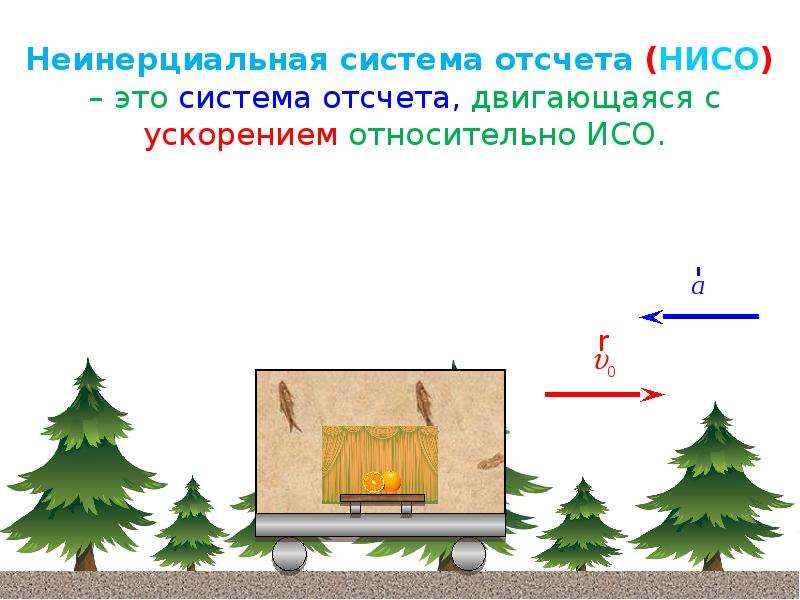 По нашему опыту, скорости просто складываются. Например, если человек бросает в вас мяч со скоростью 10 м/с, когда он едет к вам на велосипеде со скоростью 10 м/с, кажется, что мяч летит к вам со скоростью 20 м/с. Выражение будет таким: u = u ′ v , где u — скорость относительно земли, u ′ — скорость мяча относительно велосипеда, а v — скорость мяча относительно земли. скорость велосипеда.
По нашему опыту, скорости просто складываются. Например, если человек бросает в вас мяч со скоростью 10 м/с, когда он едет к вам на велосипеде со скоростью 10 м/с, кажется, что мяч летит к вам со скоростью 20 м/с. Выражение будет таким: u = u ′ v , где u — скорость относительно земли, u ′ — скорость мяча относительно велосипеда, а v — скорость мяча относительно земли. скорость велосипеда.
Второй закон специальной теории относительности приводит к другому сценарию для света. Если человек едет к вам со скоростью 90 % скорости света и включает фонарик, вы обнаружите, что свет движется к вам со скоростью c , со скоростью света. Более того, это та же самая скорость, наблюдаемая, если бы велосипед был неподвижен относительно вашего положения.
Разные результаты сложения скоростей из опыта и из экспериментов со световыми лучами можно было бы объяснить, только если предположить, что сложение малых скоростей есть частный случай более общего закона сложения скоростей. Физо экспериментально определил правильное уравнение для сложения скоростей, равное
Физо экспериментально определил правильное уравнение для сложения скоростей, равное
Это уравнение дает следующее уравнение для скорости светового луча от всадника, идущего к вам со скоростью v :
Это уравнение для сложения скоростей дает правильные результаты, как и предсказывает второй постулат специальной теории относительности. Попробуйте другие значения, чтобы увидеть, что комбинация скоростей меньше C и даже равная C не может дать комбинированное значение больше C .Обратите внимание, что если u и v относительно малы, знаменатель становится равным 1; тогда выражение сводится к известному уравнению сложения скоростей.
Следствием постулатов Эйнштейна является то, что измерения времени и расстояния являются , а не постоянными при сравнении одной инерциальной системы отсчета с другой, так что скорость света может оставаться постоянной. Другими словами, абсолютного времени и абсолютного расстояния не существует. Все часы во вселенной , а не , отсчитывают время вместе. Замедление времени — это эффект, при котором движущиеся часы идут медленнее, чем такие же неподвижные часы. Выражение
Все часы во вселенной , а не , отсчитывают время вместе. Замедление времени — это эффект, при котором движущиеся часы идут медленнее, чем такие же неподвижные часы. Выражение
Кроме того, не только часы идут медленнее, но и любой физический процесс, на который влияет течение времени, например, химические и биологические процессы. Следовательно, для человека в движущейся системе отсчета изменение временного интервала не может быть обнаружено, поскольку все методы измерения времени замедляются на один и тот же коэффициент.Все относительно.
Замедление времени было измерено в ряде экспериментов. Один эксперимент включал изменение времени распада радиоактивных частиц (мюонов), летящих к поверхности Земли почти со скоростью света. Количество мюонов подсчитывалось на вершине и у подножия горы. На дне было обнаружено больше мюонов, чем можно было бы ожидать по классической теории. Время распада было больше, а значение соответствовало специальной теории относительности. Точные атомные часы, установленные на самолетах и на орбитальных спутниках, подтвердили эту теорию.
Точные атомные часы, установленные на самолетах и на орбитальных спутниках, подтвердили эту теорию.
Сокращение Лоренца — это эффект, заключающийся в том, что наблюдатель, движущийся с объектом заданной длины, обнаружит, что объект укорачивается по сравнению с наблюдателем, находящимся в покое относительно этого движения. (Обратите внимание, что это сокращение происходит только в направлении движения.) Опять же, все относительно. Поскольку все расстояния в направлении движения сокращаются для движущегося наблюдателя, у движущегося наблюдателя нет сравнительной длины, которую он мог бы использовать для обнаружения изменения.Уравнение
Чтобы связать концепцию сокращения длины с замедлением времени, представьте, что вы находитесь на мюоне, приближающемся к Земле почти со скоростью света. Наблюдатель на Земле мог бы сказать, что пришло время распаду частицы, но вы могли бы ответить, что по вашим часам время еще не пришло. В качестве альтернативы, если вы подсчитаете высоту горы, вы обнаружите, что она укорочена в вашей системе отсчета. В некотором смысле и время, и расстояние подтасованы так, что скорость света всегда одинакова.
В некотором смысле и время, и расстояние подтасованы так, что скорость света всегда одинакова.
Представьте себе одного близнеца на ракетном корабле, летящем к звезде и возвращающемся почти со скоростью света. Другой близнец остается дома. Близнец-домохозяйка настаивает на том, чтобы она отдыхала, а другой близнец двигался. Близнец в ракетном корабле настаивает на том, что она отдыхала, пока земля удалялась от нее, а затем возвращалась.
Противоречие в том, что каждый может утверждать, что другой переехал и, следовательно, был тем, кто меньше старел. Кто постарел больше всех? (Невозможно иметь относительную седину.)
Чтобы разрешить парадокс, поймите, что проблема несимметрична. Когда ракетный корабль-близнец покидал Землю, замедлялся до остановки в открытом космосе, разворачивался, чтобы вернуться домой, и замедлялся до остановки на поверхности земли, он ускорялся и замедлялся; следовательно, ее система отсчета не была инерциальной системой отсчета. Путешествующий близнец постарел меньше.
Определение количества движения и энергии должно быть обобщено, чтобы соответствовать специальной теории относительности. Правильное выражение для релятивистского импульса:
.
Обратите внимание, что когда v мало, знаменатель почти равен 1, поэтому импульс приближается к знакомому уравнению: P = mv .Это уравнение можно интерпретировать как означающее, что масса зависит от скорости:
Когда v равно нулю, масса равна m 0 . Член m 0 называется массой покоя .
Эйнштейн предложил знаменитое уравнение эквивалентности массы-энергии : E = mc 2 . Эта энергия представляет собой сумму кинетической энергии и энергии покоя. Соотношение показывает, что масса является формой энергии; поэтому утверждение о сохранении энергии должно включать понятие массы.Поскольку c — такое большое значение, небольшая масса эквивалентна огромной энергии.
Кинетическая энергия массы равна
Используя биномиальную теорему для расширения выражения, можно показать, что для малых v это выражение упрощается до знакомого
Общая теория относительности — это теоретическая основа, применимая к любой системе отсчета — инерциальной или ускоряющейся.Разрабатывая эту теорию, Эйнштейн хотел создать теорию гравитации, включающую в себя специальную теорию относительности и принцип эквивалентности.
Чтобы понять принцип эквивалентности, представьте, что вы находитесь в космическом корабле, летящем в открытом космосе, и не можете видеть за пределами корабля. После свободного плавания внутри корабля вы начинаете дрейфовать к одному концу. Вскоре вы сможете стоять на одной стене. Может иметь место одно из двух условий: (1) космический корабль ускоряется так, что вы прижимаетесь к стене, противоположной направлению ускорения, или (2) корабль приблизился к большой массе с гравитационным полем. Принцип эквивалентности заключается в том, что эксперименты, проводимые либо в равномерно ускоряющейся системе отсчета, либо в инерциальной системе отсчета с гравитационным полем, дают одинаковые результаты.
Принцип эквивалентности заключается в том, что эксперименты, проводимые либо в равномерно ускоряющейся системе отсчета, либо в инерциальной системе отсчета с гравитационным полем, дают одинаковые результаты.
Эйнштейн решил, что концепции пространства следует пересмотреть. Законы Ньютона предполагают евклидово пространство, простирающееся во всех направлениях, как три взаимно перпендикулярные прямые оси. Эйнштейн предложил искривленное пространство-время . Движение объекта можно описать с точки зрения геометрии пространства, а не как реакцию на приложенные силы.
Например, свет распространяется прямолинейно в евклидовом пространстве; однако общая теория относительности рассматривает пространство как искаженное массой. Следовательно, свет может двигаться по криволинейному пути вблизи массивного объекта, что является кратчайшим путем между двумя точками в этом пространстве. Это аналогично изогнутому пути на земной поверхности, который является более коротким расстоянием между двумя городами, чем прямая линия между ними.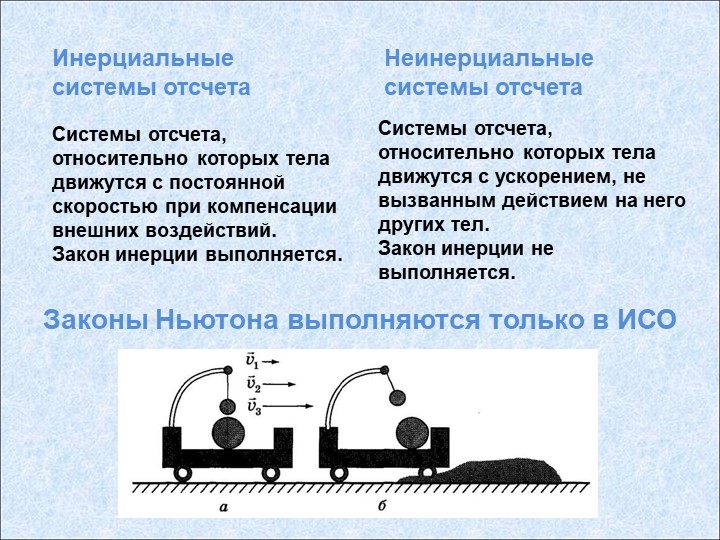
Для проверки своих теорий Эйнштейн предложил три явления, которые можно было бы объяснить с помощью математических формулировок общей теории относительности:
- Точка наибольшего сближения — перигелий — эллиптической орбиты Меркурия движется вокруг Солнца.(На рисунке показано увеличенное изображение этого движения.)
- Отклонение звездного света, проходящего вблизи Солнца, происходит из-за искривления пространства вблизи солнечной массы.
- Гравитационное красное смещение света — это сдвиг частоты между двумя идентичными часами на разной высоте в гравитационном поле.
|
||
Когда Эйнштейн предложил эти тесты, наблюдалось только первое явление. Впоследствии ученые обнаружили и измерили другие эффекты. Все экспериментальные данные согласуются с общей теорией относительности.
Впоследствии ученые обнаружили и измерили другие эффекты. Все экспериментальные данные согласуются с общей теорией относительности.
Концепции специальной теории относительности — глава книги
Специальная теория относительности — увлекательный и важный предмет.Его основные понятия вспоминается здесь в той мере, в какой это необходимо для формулировки общей теории относительности в последующих главах. Рассматриваемые темы включают относительность Галилея, инерциальную рамок, вывод преобразований Лоренца из физических постулатов, собственно временной интервал и пространственно-временные диаграммы, а также приложения к сложению скоростей, сокращение длины, замедление времени и топологический парадокс близнецов.
Специальная теория относительности — увлекательный и важный предмет.Напоминаются его основные понятия
в этой книге только в той мере, в какой это необходимо для формулирования и понимания основных элементов
общая теория относительности. Тем не менее, существует множество учебников, в которых более подробно рассматривается
специальная теория относительности, из которых одна Риндлера особенно рекомендуется для дальнейшего изучения.
чтение [1].
Тем не менее, существует множество учебников, в которых более подробно рассматривается
специальная теория относительности, из которых одна Риндлера особенно рекомендуется для дальнейшего изучения.
чтение [1].
В 1632 году блестящий итальянский физик Галилео Галилей опубликовал книгу, которая должна была в конечном итоге доставить ему массу неприятностей.Он назывался « Диалог о Две главные мировые системы [2] и привели веские аргументы в пользу непротиворечивость коперниканской (солнцецентричной) модели солнечной системы. Аргументы также поддержал превосходство этой модели над моделью Птолемея (землецентричной), что и вызвало последующие проблемы.
В то время одним из аргументов против модели Коперника было то, что если Земля
вращается на восток, то брошенные или брошенные предметы будут стремиться упасть
сзади, на запад.Например, камень, упавший с мачты стоящего корабля. должен приземлиться к западу от мачты. Галилей уже довольствовался экспериментом
что это было не так, — но и то, вопреки самому основанию рассуждения, что
даже если корабль плыл, неважно в каком направлении , камень
всегда приземлялся у подножия мачты. Движение (плавно) движущегося корабля не может
быть обнаружен таким образом! В своей книге он развил эту идею [2]:
должен приземлиться к западу от мачты. Галилей уже довольствовался экспериментом
что это было не так, — но и то, вопреки самому основанию рассуждения, что
даже если корабль плыл, неважно в каком направлении , камень
всегда приземлялся у подножия мачты. Движение (плавно) движущегося корабля не может
быть обнаружен таким образом! В своей книге он развил эту идею [2]:
Закройтесь с другом в главной каюте под палубой на каком-нибудь большом корабле. и возьмите с собой мух, бабочек и других мелких летающих животных.Возьмите большую миску с водой и положите в нее рыбу; повесить пустую бутылку капля в узкий сосуд под ним. Когда корабль стоит на месте, наблюдайте внимательно, как зверушки летят с одинаковой скоростью во все стороны салона. То рыбы равнодушно плавают во все стороны; капли падают в сосуд внизу; и, бросая что-то своему другу, вам нужно бросать это не сильнее в один направление, чем другое, расстояния равны; прыгать ногами вместе, вы проходите равные пространства во всех направлениях.

Когда вы внимательно наблюдали за всем этим (хотя нет сомнения, что когда корабль стоит на месте, все должно происходить именно так), пусть корабль двигайтесь с любой скоростью, которая вам нравится, лишь бы движение было равномерным и не колеблется так и эдак. Вы обнаружите не малейшее изменение во всем названных эффектов, и ни по одному из них нельзя было сказать, двигался ли корабль или стоя на месте [выделено мной].
В прыжках вы будете проходить по полу те же места, что и раньше, и не будете делать большие прыжки к корме, чем к носу, даже если корабль движется довольно быстро, несмотря на то, что за время нахождения в воздухе пол под вами будет двигаться в направлении, противоположном вашему прыжку. В метании что-то своему спутнику, вам не потребуется больше силы, чтобы передать это ему, даже если он находится в направлении носа или кормы, а вы находитесь напротив.
То капли будут по-прежнему падать в сосуд под ним, не падая к корма, хотя пока капли в воздухе корабль пробегает много пролетов. Рыба в их вода будет плыть к передней части чаши с таким же усилием, как и к спине, и с одинаковой легкостью пойдет на приманку, размещенную в любом месте по краям Чаша. Наконец-то бабочки и мухи продолжат свой полет безразлично ко всем сторонам, и никогда не случится, чтобы они сосредоточились к корме, словно утомившись от того, что не поспевал за курсом корабля, от которые они будут разлучать в течение долгих промежутков времени, удерживая себя в воздух.
Идея в среднем абзаце выше (выделено курсивом), показанном на рис. 1.1, заключается в том, что законы
физика одинакова в системах отсчета, движущихся с постоянными скоростями относительно
для другого. Теперь это называется относительности Галилея . Это может быть
заостренные в ньютоновской механике на неизменность законов движения при любых
преобразование координат вида
Теперь это называется относительности Галилея . Это может быть
заостренные в ньютоновской механике на неизменность законов движения при любых
преобразование координат вида
для любого вращения R , ускорение скорости и переводы и б .Например, универсальный закон Ньютона. гравитация,
принимает точно такую же форму в преобразованном координаты:
, что легко проверить.
Приблизить Уменьшить Сбросить размер изображения
Рисунок 1.1. Мысленный эксперимент Галилея: наблюдатель под палубой не может определить по местным опытов, то ли корабль неподвижен на воде, то ли плавно плывет в какой-то направление.
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением Вышеупомянутые преобразования «Галилея» образуют группу из десяти параметров. Обратите внимание, что они
раздельно сохранять пространственные и временные расстояния, т.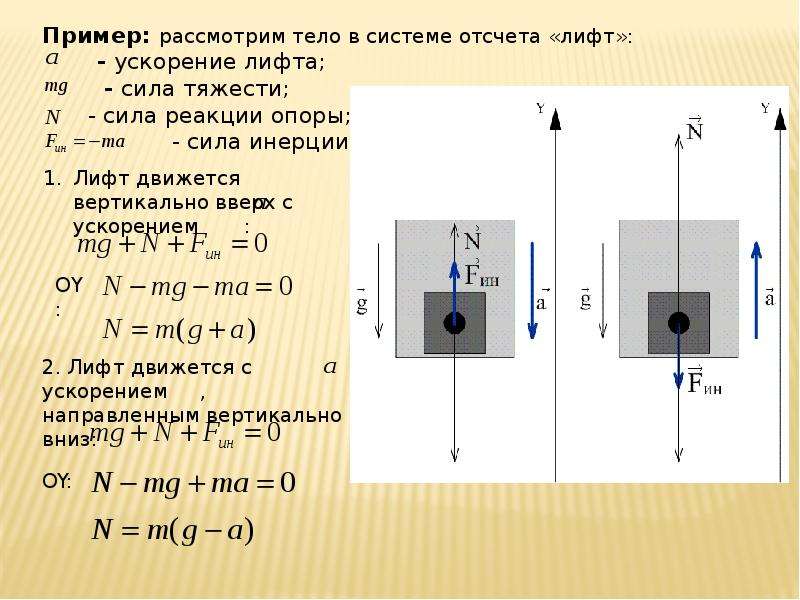 е. писать и ,
е. писать и ,
Чтобы принцип относительности Галилея можно было применить к ньютоновской механике, нужно начать с системой координат, в которой справедлива сама ньютоновская механика. Особенно, Первый закон Ньютона о том, что свободные частицы остаются в покое или движутся прямолинейно. линия, должны держать.То есть траектория свободной частицы должна удовлетворять
. Это было бы , а не , например, если система координат была зафиксирована относительно вращающейся карусели (попробуйте катить мяч на друг во время одного из них).
Первый закон движения Ньютона часто называют законом инерции, и, следовательно, координаты
системы, которые его соблюдают, называются «инерциальными системами отсчета», или, проще говоря,
инерциальные системы отсчета .Таким образом, в любой инерциальной системе отсчета свободные частицы движутся в
прямые линии. Галилееву относительность можно в общих чертах сформулировать в такой форме, что
законы физики имеют одинаковую форму во всех инерциальных системах отсчета.
Галилееву относительность можно в общих чертах сформулировать в такой форме, что
законы физики имеют одинаковую форму во всех инерциальных системах отсчета.
Обратите внимание, что Ньютон не считал инерциальные системы отсчета фундаментальными. Он считал, что пространство и время являются «абсолютными», при этом каждая точка пространства и времени имеет значимую фиксированную значения координат. Он рассматривал использование относительных координат, определенных относительно к некоторому произвольному пространственному и временному происхождению, чтобы быть простым удобством.галилейский теория относительности не противоречит этому убеждению, но подразумевает, что ни один эксперимент может отличить такую «абсолютную» систему отсчета от любой другой инерциальной системы отсчета.
По этой причине принцип относительности Галилея был поставлен под сомнение ранними
интерпретации уравнений Джеймса Клерка Максвелла для электромагнитного поля, которые
постулировал «эфир», через который распространяются электромагнитные волны, аналогично
Распространение звуковых волн в воздухе. Считалось, что эфир покоится относительно
к абсолютному пространству. Удивительно, однако, что все эксперименты, направленные на обнаружение
движение Земли через этот эфир, в первую очередь Майкельсона-Морли.
эксперимент — неудачный, в соответствии с теорией относительности Галилея.
Считалось, что эфир покоится относительно
к абсолютному пространству. Удивительно, однако, что все эксперименты, направленные на обнаружение
движение Земли через этот эфир, в первую очередь Майкельсона-Морли.
эксперимент — неудачный, в соответствии с теорией относительности Галилея.
Тем не менее, уравнения Максвелла по-прежнему создавали трудности для теории относительности Галилея, т.е.
по крайней мере, когда он встроен в ньютоновскую механику. Например, уравнения предсказывали
(в соответствии с экспериментом Майкельсона-Морли), что скорость света в свободном
пространство является фиксированной константой во всех инерциальных системах отсчета, независимо от источника света (т.г., а
лампа), имеющие разные скорости по отношению к разным кадрам. Это не может быть
согласуется с видом преобразований Галилея в уравнении (1.1), при которых
Ньютоновская механика инвариантна. Именно эта несовместимость привела Альберта Эйнштейна
к его «Специальной теории относительности», опубликованной в 1905 г. [3, 4].
[3, 4].
Постулаты
Основные элементы специальной теории относительности Эйнштейна можно сформулировать следующим образом.
Во-первых, инерциальные системы отсчета определяются движением свободных частиц:
Постулат 1: Свободные частицы движутся прямолинейно в инерциальных системах отсчета.
Таким образом, инерциальная система отсчета представляет собой пространственно-временную систему координат, в которой Выполняется первый закон Ньютона (остальные законы должны быть немного изменены). изменен).
Во-вторых, исходя из предсказания уравнений Максвелла в предыдущем разделе, далее предполагается, что:
Постулат 2: Скорость света в вакууме постоянна, c, во всех инерциальных системах отсчета, при измерении с использованием стандартного набора часов и линеек, покоящихся в каждом Рамка.

Требуются стандартные стандарты времени и длины, поскольку в противном случае скорость света может быть численно разной в разных направлениях, даже в та же инерциальная система отсчета — e.г., если координаты измерялись в x -направление и y -направление с использованием линеек, имеющих разные единицы. Постулат 2 подразумевает, что только соглашение о стандартных часах является на самом деле необходимо, как пространственное расстояние между двумя точками, находящимися в состоянии покоя в заданном инерциальная система отсчета может быть определена через время для света, чтобы распространяться между ними.
Первый и второй постулаты по-прежнему допускают возможность того, что стандартная длина и
шкалы времени могут быть определены только с точностью до общего масштабного коэффициента, поскольку прямолинейные
движение и скорость света инвариантны при таком масштабировании. Если бы это было так,
то было бы физически бессмысленно, например, сравнивать скорости
покоящиеся часы в разных инерциальных системах отсчета, так как не было бы «абсолютной» скорости даже
для часов в состоянии покоя. Существуют различные варианты устранения этой возможности,
подходящее существо:
Если бы это было так,
то было бы физически бессмысленно, например, сравнивать скорости
покоящиеся часы в разных инерциальных системах отсчета, так как не было бы «абсолютной» скорости даже
для часов в состоянии покоя. Существуют различные варианты устранения этой возможности,
подходящее существо:
Постулат 3: Если стандартные часы в состоянии покоя в первой инерциальной системе отсчета перемещаются на скорость относительно второй инерциальной системы отсчета, затем стандартные часы в состоянии покоя в второй кадр движется со скоростью по отношению к первому кадру, и движущиеся часы в каждом кадре тикают по тому же курсу.

В качестве альтернативы может потребоваться, чтобы объем данного пространства-времени область одинакова для всех наблюдателей, или что законы физики не масштабно-инвариантный (подразумевающий существование стандартной шкалы времени для каждого инерциального кадра), как обсуждается в приложении A.
Наконец, мы не можем фактически полностью принять широкое понятие относительности Галилея в секция 1.2, что законы физики имеют одинаковую форму в всех инерциальных системах отсчета. А постулат необходим, чтобы исключить инвариантность физических законов между инерциальными системами отсчета связаны с такими преобразованиями, как пространственные отражения и изменение направления время (при котором законы физики, как известно, не являются инвариантными, от частицы эксперименты с распадом), или связанные заменой временной координаты на пространственную координата (которая преобразует досветовое движение в сверхсветовое движение и наоборот):
Постулат 4: Законы физики инвариантны в инерциальных системах отсчета, связанных непрерывная последовательность промежуточных преобразований координат.

На языке теории групп это означает, что физически соответствующая группа преобразований между инерциальными системами непрерывно связана с личность. Это делает правдоподобной идею о том, что системы и наблюдатели могут, непрерывные операции, переход от состояния покоя в первой инерциальной системе отсчета к состоянию отдых во второй инерциальной системе отсчета без изменения законов физики.
Инвариантный пространственно-временной интервал
Приведенных выше четырех постулатов достаточно, чтобы вывести группу пространственно-временных координат
преобразования, связывающие инерциальные системы отсчета (см. приложение А). Они называются (собственно ортохронными)
Преобразования Лоренца, после их первого первооткрывателя, Хендрика Лоренца [4], и имеют некоторые
существенные отличия от преобразований Галилея в (1. 1).
1).
Вывод в приложении А показывает, в частности, что преобразования между инерциальными системами отсчета сохранить величину
, связывающую любые две точки и в пространстве-времени, где c — инвариантная скорость
свет в вакууме.Это можно непосредственно сравнить с (1.4) для преобразований Галилея при
в котором пространственные и временные расстояния сохраняются раздельно. В особенности
относительностью является только указанная выше комбинация пространственного и временного расстояний.
инвариантным и называется инвариантным пространственно-временным интервалом. Говорят, что две точки
быть времяподобными разделенными , светоподобными разделенными , и
разделены пробелом для значений, которые соответственно являются положительными, нулевыми и отрицательными (см. рис.
1.2). Обратите внимание, что имеет единицы времени.
Приблизить Уменьшить Сбросить размер изображения
Рисунок 1.2. Диаграммы пространства-времени и причинно-следственная структура. Каждая точка пространства-времени имеет инвариант
прошлый и будущий световой конус, определяемый областями, из которых световые сигналы могут быть
непосредственно принимаются и передаются. Внутренности световых конусов определяют
абсолютное прошлое и абсолютное будущее каждой точки.Траектории частиц
времяподобны, и, следовательно, двигаться от абсолютного прошлого к абсолютному будущему любого
данная точка. Все события вне световых конусов точки разделены пространством
от точки, и поэтому никакой (субсветовой) сигнал или частица не могут быть отправлены или получены
от них. В пределе Галилея c → ∞ прошлое и будущее
световые конусы данной точки ( t ,x, y, z ) сглаживаются и сливаются в
единая гиперплоскость, соответствующая набору пространственных положений в фиксированное время
т .
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемЛюбая частица, движущаяся со скоростью света в некоторой инерциальной системе отсчета, имеет из (1.5) и, следовательно, должна двигаться со скоростью света во всех инерциальных системах отсчета. Таким образом, световые конусы на рисунке 1.2 инвариантны.
Далее, если и относятся к последовательным положениям свободной частицы в пространстве-времени, то в система покоя частицы имеет , и поэтому
Таким образом, свободная частица движется по времениподобной траектории, и
продолжительность
равно времени, затраченному частицей на перемещение между
два местоположения в пространстве-времени относительно его собственной системы отсчета.С
имеет одно и то же значение во всех инерциальных системах отсчета, имеет одинаковую физическую
значение во всех инерциальных системах отсчета и называется инвариантом или собственно
время. Обратите внимание, из этого также следует, что любая частица, имеющая систему покоя, не может двигаться быстрее.
чем скорость света, поскольку это потребовало бы изменения от положительного значения до отрицательного значения.
Обратите внимание, из этого также следует, что любая частица, имеющая систему покоя, не может двигаться быстрее.
чем скорость света, поскольку это потребовало бы изменения от положительного значения до отрицательного значения.
Наконец, если и относятся к двум конечным точкам тела, такого как линейка, то в структура покоя тела, которую человек имеет в любой момент времени.Отсюда из (1.5) (имеется в виду мнимость). Следовательно, концы покоящегося тела пространственноподобны. разделены, а инвариантный интервал
определяет расстояние D между этими конечными точками в его рама покоя, называемая правильным расстоянием или остатком длина .
Преобразования Лоренца
Общие преобразования Лоренца – это преобразования координат между инерциальными
фреймы, сохраняющие инвариантный интервал в (1.5). Они имеют линейную форму (см. приложение A)
приложение A)
для некоторых 4 × 4 матриц L и пространственно-временной перенос вектор a , где G обозначает матрицу 4 × 4 . Второе уравнение гарантирует, что имеет одинаковое значение во всех инерциальных системах отсчета. Постулат 4 выше далее требует, чтобы и , соответствующие подгруппе собственно ортохронные преобразования Лоренца (см. приложение А).
Собственные ортохронные преобразования Лоренца образуют группу из десяти параметров, аналогично преобразованиям Галилея в уравнении (1.1). Шесть из этих параметров соответствуют пространственные повороты и переводы, а также переводы во времени, как и для Группа Галилея. Однако преобразования между двумя кадрами, имеющими ненулевое относительная скорость в обоих случаях различна (как и должно быть, поскольку скорость свет инвариантен).В частности, ускорение скорости против в x -направление соответствует преобразованию Лоренца
где
Таким образом, координаты x и t преобразовать как
, что сводится к соответствующему ускорению Галилея, в пределе. Следовательно, специальная теория относительности хорошо аппроксимируется Галилеем.
относительность для систем отсчета, имеющих малые относительные скорости. Легко проверить, что, как того требует (1.6). Обобщение на произвольный
повышение скорости рассматривается в вопросе 1.3 в конце этой главы.
Следовательно, специальная теория относительности хорошо аппроксимируется Галилеем.
относительность для систем отсчета, имеющих малые относительные скорости. Легко проверить, что, как того требует (1.6). Обобщение на произвольный
повышение скорости рассматривается в вопросе 1.3 в конце этой главы.
Добавление скорости
Чтобы проверить, что усиление в (1.9) действительно соответствует двум кадрам с относительной скоростью v в направлении x , рассмотрим бесконечно малую часть пространственно-временной траектории между ξ и , где ξ обозначает вектор пространства-времени.Теперь, взяв обратное преобразование в (1.9) (эквивалентное заменив v на ), имеем
Отсюда, если траекторную скорость в двух системах отсчета обозначить соответственно через и , то
Следовательно, частица, покоящаяся в штрихованных координатах, т. е. при , имеет скорость u = v в
незаштрихованные координаты. То есть загрунтованная система движется со скоростью v .
относительно незагрунтованной рамы.Отметим также, что частица, покоящаяся в незаштрихованном
координат, т. е. при u = 0, имеет скорость в штрихованных координатах, как того требует постулат 3 в разделе
1.3.
е. при , имеет скорость u = v в
незаштрихованные координаты. То есть загрунтованная система движется со скоростью v .
относительно незагрунтованной рамы.Отметим также, что частица, покоящаяся в незаштрихованном
координат, т. е. при u = 0, имеет скорость в штрихованных координатах, как того требует постулат 3 в разделе
1.3.
Формула сложения скоростей в (1.10) может быть дополнительно использована для проверки неизменность скорости света, как того требует постулат 2. В частности, взятие сразу дает u = c также, независимо от относительной скорости v .
Сокращение длины
Если и обозначают концы линейки в системе покоя, то расстояние
между ними дается . Как отмечалось ранее, это называется «правильной дистанцией» или «отдыхом».
длина’. Далее, в кадре, где линейка движется со скоростью в в
x -направление, пусть x 1 и x 2 будут положениями конечных точек в равные моменты времени. Уравнение (1.9) тогда дает
Уравнение (1.9) тогда дает
Следовательно, определение «длины» D линейки в данном кадра, чтобы быть расстоянием между его конечными точками в равные моменты времени, каждый имеет
Поскольку для , это называется сокращением длины .
Обратите внимание, что сокращение длины не следует путать с кажущейся длиной подвижный стержень. Это потому, что на самом деле нельзя «видеть» конечные точки одновременно. в общем, поскольку свету потребуется разное время, чтобы достичь глаза от каждой конечной точки, если они расположены на разном расстоянии.Можно показать, например, что контур движущейся сферы является круглым для любого инерциального наблюдателя, а не сжимается в направлении относительного движения [1]. В относительности то, что вы получаете, не обязательно то, что вы видите! Релятивистская оптика здесь далее рассматриваться не будет.
Замедление времени
Если и обозначить время последовательных ударов часов в системе покоя,
тогда его период покоя определяется как . В кадре, где часы движутся со скоростью в в
в направлении x галочки будут разделены на , и на пространственное расстояние .Отсюда, используя (1.9), имеем
В кадре, где часы движутся со скоростью в в
в направлении x галочки будут разделены на , и на пространственное расстояние .Отсюда, используя (1.9), имеем
Таким образом, период относительно подвижной системы отсчета равен by
Поскольку для , это называется замедлением времени . Это, движущиеся часы тикают медленно.
Подобно сокращению длины, замедление времени не следует путать с кажущимся период движущихся часов. В частности, так как часы будут в разное расстояния между последовательными тиками, эти тики будут занимать разное время для приходят к наблюдателю в состоянии покоя.Это приводит к релятивистскому эффекту Доплера, обсуждалось в главе 2.
Читателям предлагается попытаться ответить на вопросы, отмеченные звездочкой (*), как для
развивать понимание и потому, что они, как правило, имеют отношение к последующим главам. Другой
вопросы предназначены для тех, кто хочет исследовать более глубоко.
Другой
вопросы предназначены для тех, кто хочет исследовать более глубоко.
Вопрос 1.1* Берт и Эрни начали с точки пространства-времени в некоторой инерциальной системе отсчета.Берт двинулся по прямой к , а Эрни сначала двинулся к , а затем к . Кто постарел больше всего, когда они снова встретились? (единицы выбираются такое, что c = 1).
Подсказка : рассчитайте прошедшее собственное время с помощью (1.5).
Вопрос 1.2* Показать, что определяющее свойство преобразований Лоренца в (1.6), т. е. при , обеспечивает одно и то же значение интервала в (1.5) во всех инерциальных системах отсчета.
Вопрос 1.3 (Общая форма усиления Лоренца)
Убедитесь, что преобразование Лоренца в (1. 7), соответствующее увеличению скорости в направлении x , можно обобщить на
блочно-матричная форма
7), соответствующее увеличению скорости в направлении x , можно обобщить на
блочно-матричная форма
, где I — единичная матрица 3 × 3 .Показать для общий 3-вектор , причем , что частица, покоящаяся в нештрихованной системе отсчета (т.е. с ) имеет скорость в штриховой системе отсчета. Проверь это . Как эти свойства связаны с постулатом 3 в разделе 1.3?
Вопрос 1.4 (Топологический парадокс близнецов)
Обратите внимание, что в вопросе 1 нет парадокса.1 выше: Берт ведет себя как свободная частица,
двигаясь по одной прямой (относительно любой инерциальной системы отсчета), тогда как Эрни
меняет направление и скорость (относительно любой инерциальной системы отсчета). Таким образом, существует
фундаментальная физическая асимметрия в их движениях, которая лежит в основе различных количеств
которым они стареют.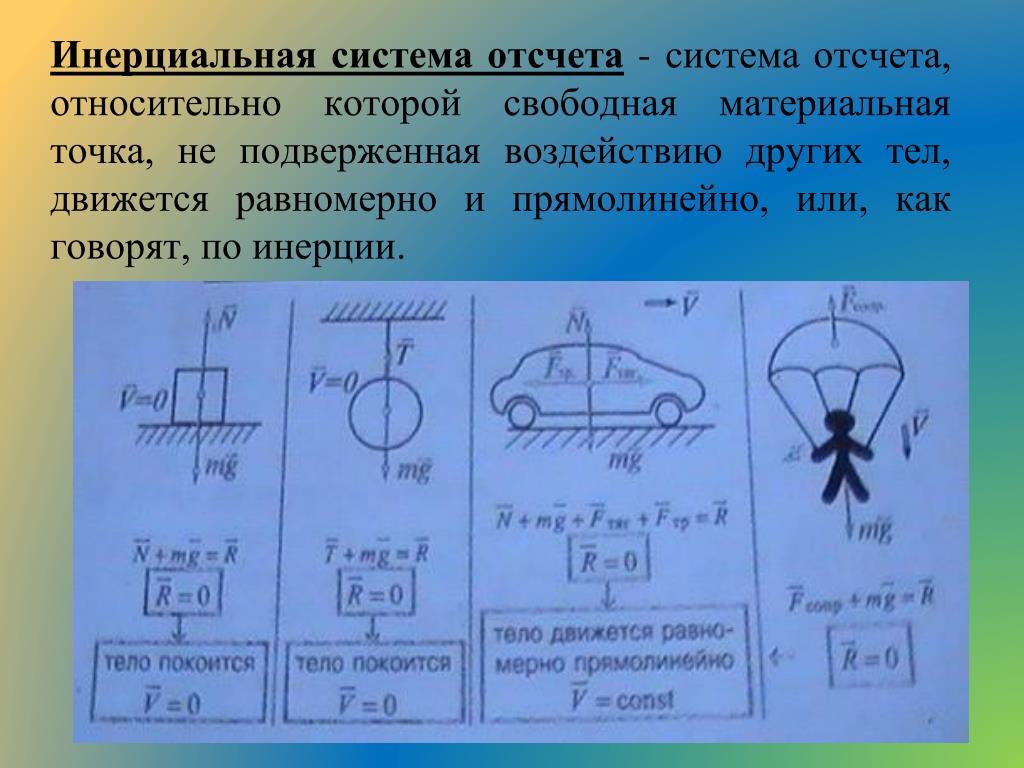
Рассмотрим, однако, случай цилиндрического пространства-времени с одним пространственным измерением которое является периодическим в некоторой инерциальной системе отсчета, так что x отождествляется с х + л .Предположим, что Берт и Эрни снова начинают с точка пространства-времени, но Берт в этом кадре остается в покое, а Эрни движется в x — направление на скорости v . Таким образом, оба движутся в прямая линия, и физическая асимметрия вопроса 1.1 выше больше не присутствует. Действительно, из с точки зрения Эрни, он находится в покое, а Берт движется в x — направление со скоростью. Убедитесь, что все же Берт состарится больше всего, когда они встретимся снова в свое время.Это настоящий парадокс близнецов?
[Разрешение в рамках специальной теории относительности обсуждается Дреем [5]].
Вопрос 1.5 Стрела с длиной покоя A 0 пущена горизонтально и летит с постоянной скоростью в открытый конец стрелы. цилиндр с длиной покоя .
-
(i)
Когда кончик стрелки достигает другого конца цилиндра, стрелка полностью внутри цилиндра относительно: Парадоксально ли это? -
(ii)
Если дальний конец цилиндра закрыт неподвижной сплошной стенкой, то препятствует дальнейшему движению стрелы, с какой минимальной скоростью должна двигаться стрела ход в , чтобы гарантировать, что он закрыт цилиндром относительно обоих остальных кадры? Подсказка : оперенный конец стрелы не может быть затронут наличие стены перед каким-либо физическим сигналом или ударной волной, генерируемой наконечник, ударяющийся о стену, передается со скоростью света или меньше вдоль длина стрелы.

Специальная теория относительности (физика) | Encyclopedia.com
Специальная теория относительности описывает то, как взаимосвязаны ощущения наблюдателем времени и пространства, в то время как общая теория относительности рассматривает взаимосвязь между массой, пространством, гравитацией и движением. Альберт Эйнштейн (1879–1955), движимый озабоченностью проблемными особенностями электромагнетизма, особенно взаимосвязью между электрическими и магнитными полями, предложил специальную теорию относительности в 1905 году.Однако, поскольку большую часть характера и следствий специальной теории относительности легче развить в области кинематики (описания движения), в этой статье основное внимание будет уделено тому, как движение влияет на результаты измерений пространства и времени.
Инерциальные системы отсчета
Термин система отсчета обычно относится к системе координат (подобной декартовой системе с тремя взаимно перпендикулярными осями, обозначенными x, y, и z ), в можно удобно описать объект вместе с набором синхронизированных часов, с помощью которых можно определить время в любом месте в этой системе координат. Имея такую систему отсчета, можно указать координаты любого события E , указав его местоположение ( x, y, z ) и время ( t ) его возникновения в обозначениях: E ( х, у, г, т ).
Имея такую систему отсчета, можно указать координаты любого события E , указав его местоположение ( x, y, z ) и время ( t ) его возникновения в обозначениях: E ( х, у, г, т ).
Из всех возможных систем отсчета Специальная теория относительности занимается только инерциальными системами отсчета — системами отсчета, в которых выполняется первый закон Ньютона (иногда называемый законом инерции). Можно показать, что любая система отсчета, которая движется с постоянной скоростью (постоянной скоростью и направлением) относительно инерциальной системы отсчета, также является инерциальной системой отсчета.
Постулаты
Специальная теория относительности Эйнштейна исходит из двух фундаментальных постулатов относительно результатов сравнения наблюдений физических явлений (наборов событий) наблюдателями в двух или более инерциальных системах отсчета. Эти два постулата можно сформулировать следующим образом: (1) скорость света одинакова во всех инерциальных системах отсчета, независимо от движения источника; и (2) форма всех физических законов (не только относящихся к механике) одинакова во всех инерциальных системах отсчета. Первый постулат представляет собой отход от общепринятого представления о том, что скорость света относительно его источника будет фиксированной, как в случае пули, выпущенной из ружья. Второй постулат представляет собой значительное расширение классического принципа относительности, применимое только к законам механики.
Первый постулат представляет собой отход от общепринятого представления о том, что скорость света относительно его источника будет фиксированной, как в случае пули, выпущенной из ружья. Второй постулат представляет собой значительное расширение классического принципа относительности, применимое только к законам механики.
Предсказания
Из этих двух постулатов можно вывести ряд интересных предсказаний.
Относительность одновременности. Преобразование Лоренца , , названное в честь голландского физика Хендрика Антона Лоренца (1853–1928), представляет собой набор уравнений, который позволяет вычислять координаты события в одной системе отсчета по координатам того же события в другой системе отсчета.Предположим, что в системе отсчета S наблюдатель отмечает два события, которые происходят в разных местах, но в одно и то же время. Наблюдатель S говорит, что эти два события произошли одновременно. Затем рассмотрим другую систему отсчета Ś, которая движется с постоянной скоростью относительно S . Применение преобразования Лоренца к координатам событий в S для получения координат тех же двух событий в S ́ приводит к замечательному результату. Наблюдатели в S ́ сказали бы, что эти два события произошли в разное время.То есть события, которые кажутся одновременными в одной инерциальной системе отсчета, не будут наблюдаться как одновременные в любой другой инерциальной системе отсчета. Величина временного разделения будет зависеть от относительной скорости двух кадров. Одновременность не является абсолютной, но зависит от системы отсчета наблюдателя. Другими словами, не существует универсального времени, с которым могли бы согласиться все наблюдатели.
Уменьшение длины. Рассмотрим измерительную линейку, ориентированную параллельно оси x системы отсчета S , которая движется со скоростью v вдоль той же оси x .Пусть S ́, рассмотрим часы, покоящиеся в S ́. По отношению к любому наблюдателю, находящемуся в состоянии покоя в 90 559 S, 90 560 часы S ́ движутся со скоростью 90 559 против 90 560. По мере движения они проходят многочисленные 90 559 S 90 560 часов, которые распределены по всей системе отсчета 90 559 S. 90 560 Предположим, что часы S ′ был синхронизирован, чтобы отображать точно то же время, что и одни конкретные часы S в тот момент, когда часы S ́ проходили мимо них. Теперь предположим, что в какой-то более поздний момент отображение часов S ́ сравнивается со вторыми часами S , когда они проходят мимо них.И снова применение преобразования Лоренца для предсказания координат этого второго события, проходящего через часы, приводит к неожиданному результату: часы S ́ будут отставать от вторых часов S . Движущиеся часы (часы S ́ движутся относительно системы отсчета S ) записывают меньше прошедшего времени, чем стационарные часы S . Это явление называется замедлением времени . Многочисленные эмпирические тесты подтвердили этот своеобразный эффект.
Существует симметрия, которую необходимо признать в отношении явления замедления времени.Сравнивая эквивалентные наблюдения наблюдателей в двух разных системах отсчета, каждый сказал бы (с полным основанием), что часы другого идут медленно. Эта симметрия заставила некоторых людей подвергнуть сомнению идею о том, что близнецы с разной историей движений на самом деле достигают разного возраста. Стандартный сценарий так называемого парадокса близнецов предполагает, что пара близнецов очень заинтересована в проверке теории относительности. В то время как один из близнецов остается дома, другой взлетает на ракете и летит со скоростью, составляющей значительную часть скорости света, в течение нескольких лет, как измеряется его собственными часами с календарем, а затем разворачивается, чтобы повернуть вспять.После воссоединения со своим близнецом, насколько возраст путешественника будет сопоставим с возрастом сидящего дома брата или сестры? С точки зрения домоседа, часы путешественника шли медленно на протяжении большей части пути, как туда, так и обратно (направление путешествия не имеет значения). Так что, казалось бы, на воссоединении путешественник будет моложе своего родного близнеца. Однако как насчет того, чтобы посмотреть на вещи с точки зрения путешественника? Не будет ли так, что часы домоседа идут медленно, так что домосед будет младшим братом или сестрой при воссоединении? Это обычное представление парадокса близнецов — противоречивые выводы, вытекающие из симметрии явления замедления времени.
Оказывается, однако, что настоящего парадокса, противоречивых предсказаний нет. Путешественник действительно моложе на воссоединении. В историях движения близнецов не было эффективной симметрии. Один все время оставался в одной системе отсчета; другой несколько раз ускорялся от одного кадра к другому. Количество времени, прошедшее между разлукой и воссоединением близнецов, будет разным для каждого из них из-за разной истории движения. Странно, может быть, но похоже на правду.
Связь массы и энергии. . Если существует одно математическое соотношение, которое лучше всего характеризует популярную концепцию специальной теории относительности, то оно должно быть уравнением E = mc 2 ;, , где E представляет энергию, m представляет массу, а c — скорость света. Но что на самом деле означает это знакомое уравнение? В самых общих чертах это означает, что масса — это особая форма энергии и что при соответствующих обстоятельствах она может быть преобразована в другие формы энергии.Ядерные реакторы, например, обеспечивают условия для контролируемого преобразования части массы-энергии отдельных радиоактивных ядер в тепло, которое затем используется для приведения в действие обычных генераторов электроэнергии. Аналогичным образом электростанция, работающая на угле, осуществляет такое же преобразование массы-энергии в тепло посредством химических, а не ядерных реакций.
Однако в знакомом E = mc 2 есть нечто большее. Масса m, , фигурирующая в этом уравнении, представляет собой релятивистскую массу , , значение которой зависит от скорости рассматриваемого объекта.В самом деле, когда скорость объекта v, приближается к скорости света, значение его релятивистской массы приближается к бесконечности. Фактически это означает, что для ускорения объекта до скорости света потребуется бесконечное количество энергии. Имея только ограниченное количество доступной энергии, скорость небольших объектов (таких как атомные составляющие) может быть увеличена (в устройстве ускорителя частиц) до значения, приближающегося к скорости света, но никогда не равного или превышающего его. Ничему, имеющему массу, нельзя придать относительно локального наблюдателя скорость, равную или превышающую скорость света.Это ограничение скорости навязывается не законом, а самой природой Вселенной, а именно отношениями между пространством, временем, движением и энергией.
Это ограничение скорости применяется только в локализованной области космоса. Если кто-то рассматривает движение чрезвычайно удаленных объектов, скажем, в миллиардах световых лет, то должен быть включен еще один фактор — расширение самого пространства. На языке общей теории относительности пространство — это не просто ничто, в которое могут быть помещены вещи, а конкретное нечто, обладающее свойствами и способное действовать и подвергаться воздействию.Одна из вещей, которую делает космическое пространство, по-видимому, расширяется. Наблюдается, что далекие галактики удаляются от Земли, потому что пространство между ними и Землей расширяется. Движение далеких галактик, которое можно приписать этому явлению пространственного расширения, не ограничивается только что обсуждавшимся ограничением скорости света.
Значение для религиозной мысли
Теорию относительности следует четко отличать от того, что обычно обозначается словом релятивизм. Моральный релятивизм, например, предполагает, что не существует универсальных стандартов правильного и неправильного поведения. Точно так же эпистемический релятивизм предполагает, что не существует независимых от наблюдателя стандартов объективного знания. Однако, как отмечалось выше, специальная теория относительности не влечет за собой отказа от стандартов для сравнения наблюдений различных наблюдателей. Напротив, теория относительности очень четко определяет эти стандарты. Релятивистская механика отличается от классической механики не отказом от стандартов, а тем, что предлагает особый и новый набор стандартов, которые приводят предсказания и наблюдения в соответствие.
Еще одна особенность специальной теории относительности, которая предполагает применение к религиозной мысли, — это демонстрация того факта, что здравый смысл иногда нуждается в корректировке. У большинства людей есть здравые представления о пространстве и времени, которые прекрасно функционируют в их повседневной жизни. Люди используют эти понятия, когда планируют свои путешествия с места на место и в течение дня. Эти понятия здравого смысла включают следующее:
- Все беспристрастные наблюдатели должны договориться о временном интервале между двумя событиями.
- Все беспристрастные наблюдатели должны согласовать расстояние между двумя точками.
- Всегда можно ускорить работу.
- Близнецы остаются одного возраста, что бы они ни делали.
Однако каждое из этих ожиданий оказывается неверным, и представления о пространстве и времени необходимо модифицировать, чтобы понять, что открыли тщательные наблюдения и измерения.
Происхождение таких недостатков представлений о пространстве и времени здравого смысла легко определить: эти представления основаны на ограниченном опыте.Пока физики не провели наблюдения и измерения частиц, движущихся со скоростями, приближающимися к скорости света, недостатки человеческих представлений о пространстве и времени не могли быть обнаружены. Расширение человеческого опыта с пространством, временем и движением в новые скоростные режимы выявило эти недостатки и вдохновило на модификации, подобные предложенным Лоренцем и Эйнштейном. Урок очевиден: эпистемический догматизм (у меня есть полное и окончательное понимание X ) часто должен заменяться эпистемическим смирением (то, что я теперь думаю, что знаю, может когда-нибудь нуждаться в модификации в ответ на расширение опыта).Это не значит отчаиваться и требовать никаких знаний. Это скорее означает оставаться открытым для исправления, даже прославляя знание дня. По этим вопросам богословие и наука полностью согласны друг с другом.
См. также Эйнштейн, Альберт; Относительность, Общая теория; Пространство и время
Библиография
Адамс, Стив. относительность: введение в физику пространства-времени. Лондон: Тейлор и Фрэнсис, 1997.
Эйнштейн, Альберт.смысл относительности (1921). Принстон, Нью-Джерси: Princeton University Press, 1966.
Харрисон, Эдвард Р. Космология: наука о Вселенной, 2-е изд. Нью-Йорк: Издательство Кембриджского университета, 2000.
Макфарланд, Эрни. Специальная теория относительности Эйнштейна: откройте ее для себя. Торонто: trifolium, 1998.
мермин, н. Дэйвид. пространство и время в специальной теории относительности. проспект Хайтс, илл.: Waveland Press, 1989.
Мур, Томас А. путеводитель по пространству-времени.Нью-Йорк: Макгроу Хилл, 1995.
Риндлер, Вольфганг. Введение в специальную теорию относительности, 2-е издание. Оксфорд: Clarendon Press, 1991.
Тейлор, Эдвин Ф., и Уилер, Джон А. Физика пространства-времени: введение в специальную теорию относительности, 2-е издание. Сан-Франциско: w. час Фримен, 1992.
Ховард Дж. фургон до
Энциклопедия науки и религии ВАН ТИЛЛ, ХОВАРД Дж.
Значение Общая теория относительности
Значение Общая теория относительности| HPS 0410 | Эйнштейн для всех | |
Назад на страницу основного курса
Онтология пространства и времени:
Относительность ускоренного движения
Джон
Д.Нортон
Кафедра истории и философии науки
Университет Питтсбурга
Связанный документ: Технический Приложение
Онтология — это изучение того, что существует. Самый распространенный Проблема в том, чтобы решить, что реально, а что нет. Ваше отражение в зеркало настоящее? Существуют ли миражи в пустыне? Являются радуга настоящая? Все это случаи, в которых, кажется, существует реальная вещь в мире.Однако при ближайшем рассмотрении мы обнаруживаем, что ни один из них не реальная вещь или, по крайней мере, ни одна из них не имеет независимого существования. Миражи а радуги возникают из-за аномалий в атмосфере, перенаправляющих свет на наши глаза вводящими в заблуждение способами. Ваше зеркальное отражение существует и перестает существовать существует именно тогда, когда вы делаете.
https://en.wikipedia.org/wiki/File:Full_featured_double_rainbow_at_Savonlinna_1000px.jpg
Онтология пространства и времени задает аналогичные вопросы о реальности некоторых пространственно-временных аспектов мира.Там есть популярное мнение о том, что «относительность» каким-то образом установила нереальность вещи, связанные с пространством и временем, которые мы раньше считали реальными. это справедливо для специальной теории относительности. Мы наивно думаем, что имеет смысл говорить движется что-то или нет; и ньютоновская физика закрепила идею в его основаниях. Устанавливая относительность движения по инерции, Эйнштейн исключил абсолютный покой из физика.
Однако специальная теория относительности не оправдала лозунг «Все движение относительно.«Ибо ускорение остается абсолютным в особых относительность. Как мы видели ранее глава, проект Эйнштейна по поиску общей теории относительность должна была продолжить эту релятивизацию. Если бы он мог распространить принцип относительности на все движения, он бы устранить этот остаток абсолютности движения.
Эйнштейн неоднократно заявлял об успехе в этом проекте. Однако, удалось ли ему это, остается в лучшем случае оспаривается.На мой взгляд, он не преуспел в этой конкретной цели. Это, конечно, не противоречит теории Эйнштейна. Он остается и сегодня нашим лучшая теория пространства, времени и гравитации. Однако Эйнштейну удалось родственная онтологическая цель: он установил, что его пространственно-временная координата системы не имеют независимой реальности. Сначала это может показаться очевидным. Однако было не так легко осознать всю значимость этого отсутствия независимая реальность. Мы увидим, что это было с трудом завоеванным пониманием Эйнштейн.Прозрение живет. В современной переформулировке Эйнштейна анализ есть опровержение конкретной формы пространства-времени субстантивализм: представление о том, что пространство является субстанцией.
Эта глава объяснит и разовьет эти идеи. Взгляды Эйнштейна легко просмотреть, и при первом беглом чтении они выглядят вполне убедительно. Однако при ближайшем рассмотрении становится ясно, что уместить все части вместе таким образом, который соответствует утверждениям Эйнштейна.Как В результате утверждения Эйнштейна стали предметом многочисленных споров. я буду не пытаться исследовать широкий спектр различных точки зрения. Это потребовало бы громоздкого повествования. Скорее я буду лежать то, что я считаю самым ясным путем в этом эпизоде.
Читатели, заинтересованные в обзоре различных точек зрения найдете в моем «Общем Ковариация и основы общей теории относительности: восемь десятилетий Диспут», Отчеты о прогрессе в физике , 56 (1993), стр.791-858.
Абсолютное против относительного Пространство и время
Основополагающие дебаты в современной литературе восходят к Мастерски написанный Ньютоном Principia Mathematica . Современные дебаты обрамлены его идеями и реакцией 17-го века. им мыслители века. Ньютон ввел идею абсолютности пространства и времени, когда он заявил в своих Principia (Книга 1 Схолия к Определениям)
| «И.Абсолютное, истинное и математическое время, само по себе и из своего
природа течет равномерно, не обращая внимания ни на что внешнее, и
другое название называется длительностью: относительная, кажущаяся и общая
время, является неким осмысленным и внешним (будь то точным или
неравномерная) мера длительности посредством движения, которое
обычно используется вместо истинного времени; например, час, день,
месяц, год. II. Абсолютное пространство, по своей природе, безотносительно ни к чему внешнее, остается всегда одинаковым и неподвижным. Относительное пространство некоторое подвижное измерение или мера абсолютных пространств; который наши чувства определяют его положение к телам; и что такое вульгарно принято за недвижимое пространство; такова размерность подземное, воздушное или небесное пространство, определяемое его положение относительно земли.» |
Основная идея состоит в том, что абсолютное пространство и время существуют независимо от какой-либо вещи или любого явления в мире. Более того, абсолютное пространство остается в покое: оно обеспечивает наше физическое теории с абсолютным понятием движения или его отсутствия.
Лейбниц лихо оспаривал Ньютона при его жизни, в переписке с представителем Ньютона Сэмюэлем Кларком. Лейбниц сформулировал реляционистскую концепцию пространства и время, которое остается традиционным контрапунктом ньютоновской абсолютность.Он утверждал:
«Как
по моему собственному мнению, я не раз говорил, что считаю пространство
что-то просто относительное, как время, что я считаю это порядком
сосуществования, поскольку время — это порядок следования».
(Третье письмо Кларку)
Говоря более современным языком, Лейбниц утверждает, что
вещи связаны пространственно, но пространства нет;
и есть события, связанные во времени, но времени нет.За
пример — мой пример — солнце и планеты не обитают в космосе. Скорее
это тела, находящиеся в пространственных отношениях: земля так далеко
от солнца; и это далеко от луны; и это далеко от Венеры; и так
на. Этот список исчерпывает все пространственные факты в планетной системе.
Там нет никакой дополнительной вещи, «пространства». Точно так же планеты не движутся
примерно вовремя. Скорее, это одна конкретная конфигурация пространственных отношений.
за ним последовал другой, а затем еще один.Эта последовательность исчерпывает все
временные факты планетарной системы. Нет ничего лишнего,
«время.»
«Солнечная система Митчелс (около 1846 г.)»
http://www.tablespace.net/maps2/index.html
Эта реляционная концепция пространства и времени была позднее применен Эрнстом Махом в его критике Представления Ньютона о пространстве и времени. Он написал:
| «Когда
мы говорим, что тело K изменяет свое направление и скорость исключительно
влиянием другого тела К’, мы утверждали
представление о том, что к нему невозможно прийти, кроме как к другим телам А,
ДО НАШЕЙ ЭРЫ.. . . присутствуют относительно которых движение
тело K было оценено. Таким образом, на самом деле мы просто
осознавая отношение тела К к А, В, С… . . Если теперь мы
внезапно пренебрегать А, В, С. . . . и попытка говорить о
поведение тела К в абсолютном пространстве, мы вовлекаем себя
в двукратной ошибке. Во-первых, мы не можем знать, как К.
действуют в отсутствие А, В, С.. . . ; а во втором
месте, все средства были бы недостаточными для формирования суждения о
поведение К и проверить то, что у нас было
предиката, — который, таким образом, был бы лишен всех
научное значение». Эрнст Мах, Наука механики. 4-е изд. Чикаго: Открытый суд, 1919, стр. 229-30. |
Цель Эйнштейна: общая теория относительности Движение
В 1905 году Эйнштейн все еще был патентным клерком.Промытый с успех его специальной теории относительности, он стремился продолжить. В 1907 г., как мы видели ранее главу, он был готов продвигаться к цели действительно всеобщего теория относительности. Эйнштейн ясно дал понять в своих первых спекулятивных шагах для достижения этой цели он стремился расширить принцип относительности от движения по инерции ко всякому движению. Он изложил свою цель во вступительных словах своей первой публикации в 1907 г. исследовательские идеи, которые привели бы к завершенной общей теории относительность восемь лет спустя:
| «Так
мы применили принцип относительности, т.
постулирование независимости законов природы от государства
движения системы отсчета, только до без ускорения
справочные системы.Возможно ли, что принцип относительности
справедливо также для систем, которые ускоряются относительно друг друга?»
А. Эйнштейн, «Über das Relativätprinzip und die aus demselben gezogenen Folgerungen», Jahrbuch der Radioaktivität und Elektronik 4 (1907): 411-462, на с. 454.» |
Эйнштейна имела явные реляционистские симпатии.В 1913 году, в середине разработки общей теории относительности, он провозглашено:
«К
говорить о движении, а следовательно, и об ускорении тела А самого по себе.
не имеет значения. Можно говорить только о движении или ускорении тела
A относительно других тел B, C и т. д. Что выполняется в кинематической связи для
ускорение должно иметь место и для инерционного сопротивления, с которым
тела сопротивляются ускорению.. .»
А. Эйнштейн, «Zum gegenwärtigen Stand des
Проблемы гравитации». Physikalische Zeitschrift 14
(1913): 1249-1262, на с. 1260.
Здесь формулировка Эйнштейна удивительно близка к реляционистской концепции, которую мы видели выше у Эрнста Маха. Эйнштейн был заядлым читателем сочинений Маха и хвалил его за Критика ньютоновской концепции абсолютного пространства и времени.
К 1916 году общая теория относительности была завершена и Эйнштейн был уверен, что ему удалось расширить теорию относительности движения к ускорению.Однако его формулировка только то, что это означало, было косвенным. Вот его компактная версия из его популярная статья 1919 года «Что такое теория относительности», написанная для Times Лондона (29 ноября 1919 г.):
«Если независимость от физических законов состояния движения координаты система ограничивается равномерным поступательным движением координаты системы по отношению друг к другу? Какое отношение природа имеет к нашему системы координат и их состояние движения? Если это необходимо для цель описания природы, использование системы координат введены нами произвольно, то выбор состояния ее движения должен не подвергаться никаким ограничениям; законы должны быть полностью независимыми этого выбора (общий принцип относительности).»
Здесь общий принцип относительности стал утверждение, включающее «произвольные системы координат». Оглядываясь назад, сейчас кажется очевидным, что Эйнштейн переопределил то, что было бы для теории удовлетворять обобщенному принципу относительность. Исходной идеей в случае специальной теории было подробно в самом начале глава здесь. В том, что никакой эксперимент не может выявить нашу униформу движение.Все равномерные движения экспериментально неразличимы. Если это особый принцип должен распространяться на ускорение, мы ожидаем, что теория уверяют нас, что никакой эксперимент не может выявить наше ускорение. Все движения — равномерные и ускоренные — были бы экспериментально неразличимы.
Однако система координат — это всего лишь способ задания чисел к событиям в пространстве и времени. (Подробнее об этом ниже.) Это кажется трюизмом что мы можем использовать любую такую систему, которая нам нравится.Мы всегда могли это сделать, даже в ньютоновской теории, пока мы тщательно отслеживаем, какие система, которую мы используем для присвоения номеров. Как нам подключить наблюдательная неразличимость исходного специального принципа с это свобода выбора систем координат?
Для Эйнштейна связь между ними было с самого начала. Чтобы его увидеть, нам нужно обратить особое внимание на то, как он сформулировал первоначальный принцип относительность специальной теории.Это было продолжением того конкретного способ сформулировать принцип, который привел Эйнштейна к его более поздней версии общий принцип относительности. Ключевым фактом, который необходимо отметить, является то, что Эйнштейн использовал системы координат в качестве заменителей состояний движения. С использованием их суррогатное материнство, он выразил принцип относительности в терминах форме, которую законы физики принимают, когда они записаны в этих координатах системы.
Вот как это работало.
Системы координат и инерциальные системы отсчета ссылки в специальной теории относительности
Мы изначально сформулировал принцип относительности специальной теории относительности в точки зрения инерциальных систем отсчета. Эти состоят из физических систем связанных стержней, находящихся в состоянии однородных движение по инерции, к которому подобно устроены синхронизированные часы. прикрепил.
Использовать такую рамку из ссылка для присвоения пространственных и временных координат событиям.В случае, если сетка стержней укладывается в квадратную решетку, как показано, затем мы выбираем один узел как началу присваиваются нулевые пространственные координаты. Затем мы выбираем три направления перпендикулярны друг другу и совмещены со стержнями. Эти стать осями x, y и z. Значения координат назначаются с помощью расстояний, измеренных стержнями. Пункты один, два и трем длинам стержней вдоль оси x присваиваются координаты x 1, 2 и 3. Система повторяется для осей y и z.Вот как это выглядит:
Аналогичная стратегия позволяет назначить время координировать t с событиями. Координата времени для события просто время, показанное часами, совпадает с событием.
Что получается система координат для пространства и времени чаще всего используется в специальной теории относительности. При применении в пространстве-времени система координат выглядит так:
Эти системы координат стали для Эйнштейна суррогатными для систем отсчета.Суррогатное материнство не вызывает проблем, т.к. пока мы помним, что это специально выбранные координаты. То пространственные координаты x, y, z соответствуют результатам измерений с стержни, покоящиеся в инерциальной системе отсчета. Координата времени t соответствует измерениям времени, сделанным синхронизированными часами в состоянии покоя в система отсчета. Простое сокращение для описания этого специального характер состоит в том, что эти координаты имеют «метрическое значение» — они возникают непосредственно в результате измерений.
Ковариация Лоренца
Чтобы увидеть относительность движения по инерции, нам нужно
ввести инерциальные системы отсчета в относительном движении. Каждый кадр будет
имеют свои метрически значимые системы координат. Мы можем преобразовать
между ними, как мы можем перевести текст на одном языке
в другой. Если мы знаем координаты какого-то события, в одной координате
системы, Эйнштейн продемонстрировал, что мы можем найти координаты этой
то же событие в другой системе отсчета с помощью правил
мы теперь знаем как «преобразование Лоренца».»
Давайте посмотрим, как появились уравнения в книге Эйнштейна. оригинальная бумага 1905 года. Ниже я покажу уравнения, но без необходимости для читателя понять их полное содержание. Все это имеет особое значение в преобразовании Эйнштейна. описывает.
| Начните с некоторой системы координат, x, y, z и t
адаптированы к одной инерциальной системе отсчета. Теперь рассмотрим другую инерциальную систему отсчета, которая движется со скоростью v в направлении x этого кадра.Лоренц уравнения преобразования говорят нам, как координаты эта новая инерциальная система отсчета — τ для времени, ξ, η и ζ для пространства — должны быть отнесены к событиям в пространстве и времени, учитывая некоторые конкретные t, x, y и z. Вот как трансформация впервые появилась в оригинале Эйнштейна Бумага 1905 года. (В оригинальной работе Эйнштейна 1905 года он использовал «V» для обозначения скорости свет вместо привычного теперь «ц.») |
После этого преобразования Эйнштейн обратился к давая формальное выражение для удовлетворения принципа относительность. Его неофициальное заявление состоит в том, что законы природы одинаковы во всех инерциальных системах отсчета. Это тождество будет выражаться как формальное условие на пути законов природы написаны. Под «формальным» я подразумеваю, что условие относится непосредственно к как выглядят уравнения, выражающие законы, записанные символами на страница.
Возьмите законы электродинамики Максвелла. В его
в оригинальной статье Эйнштейн пишет два основных уравнения
электродинамики Максвелла в системе координат t, x, y, z,
следующее. Опять же, содержание уравнений не будет проблемой. Все
важно то, что вы просматриваете уравнения и видите, что они имеют
координаты x, y, z, t в них и электрическое и магнитное поля
количества X, Y, Z, L, M, N.
Эйнштейн применил закон Лоренца преобразование, чтобы найти, как уравнения теории Максвелла будут выражается в новой системе координат τ, ξ, η и ζ. Он нашел:
Существенным моментом является то, что преобразованный набор уравнения так же, как оригинал. Все, что изменилось, это то, что есть происходила систематическая замена «старые» величины t, x, y, z, X, Y, Z, L, M, N по их «новым» коррелятам, τ, ξ, η, ζ, X’, Y’, Z’, L’, M’, N’.Эта анимация показывает, что форма уравнения не изменились:
Когда законы теории сохраняют свою форму, когда величины преобразуются преобразованием Лоренца, теория имеет свойство «лоренцевой ковариантности».
Симметрия и принцип Относительность движения по инерции
Это свойство ковариации Лоренца дает Эйнштейну относительность движения по инерции.Ибо представьте, что есть какой-то конфигурация электрических и магнитных полей X, Y, Z, L, M, N в старом t, x, y, z система координат. Электродинамика Максвелла допускает, что конфигурации просто потому, что конфигурация удовлетворяет Максвеллу уравнения. Теперь мы можем видеть, что идеальный клон такая конфигурация возможна в новой инерциальной системе отсчета ссылка. Мы просто повторно выражаем исходную конфигурацию в терминах τ, ξ, η, ζ, X’, Y’, Z’, L’, M’, N’ и мы уверены, что это новое конфигурация также допускается уравнениями Максвелла.
То есть ковариация Лоренца гарантирует, что все, что может произойти в первой инерциальной системе отсчета, может также произойти в второй. Это гарантирует нам, что любой эксперимент, который мы можем провести в электродинамике, в одной инерциальной системе отсчета могут быть точно воспроизведены в любой другая инерциальная система отсчета. А это как раз и означает, что принцип относительности движения по инерции выполняется.
| в t, x, y, z, X, Y, Z, L, M, N |
в τ, ξ, η, ζ, X’, Y’, Z’, L’, M’, N’ |
Изображение: https://commons.wikimedia.org/wiki/Файл:Induction_experiment.png
Вот краткое заявление Эйнштейна этого состава с 1940 года:
»
содержание ограниченной теории относительности может быть, соответственно,
в одном предложении: все законы природы должны быть так обусловлены, чтобы
они ковариантны по отношению к преобразованиям Лоренца».
Из «Основ теоретической физики»
в идей и мнений.
Пока все хорошо.Эта связь между формальным условие лоренцевой ковариантности и физический принцип относительность движения по инерции работает. Однако его успех зависит от ограничение на вполне определенный набор систем координат. Те, что связаны преобразованием Лоренца имеют специальные свойство, что пространство и время проявляются совершенно одинаково в каждый. Говоря более неформально, пространство и время выглядят точно так же, всего . их аспекты, при описании любой из этих специальных координат системы.
В более поздних работах этот факт о преобразовании Лоренца выражается описанием преобразования как «симметрии трансформация» или, точнее, «симметрия пространства и времени». То есть это отображение, которое оставляет пространство и время неизменными.
Чтобы помочь закрепить идею, более простой и знакомый пример являются симметриями обычного евклидова космос. Это переводы и повороты. То есть евклидово пространство то же самое, если мы переезжаем на новое место; и то же самое, если повернуть наш вид.Мы может повторно выразить это в терминах координат. Выложите некоторую систему координат в Евклидово пространство. Все свойства пространства, описанные в этом система координат снова появляется одинаково, если мы перемещаем («переносим») всю систему координат в другую часть пространства; также, если мы вращаем системе координат под любым углом.
Эта идея симметрии ОСНОВНОЕ ПОНЯТИЕ для реализации принципа относительности.это присутствует в специальной теории относительности. Однако мы увидим, что он отсутствует когда мы перейдем к общей теории относительности.
От ковариации Лоренца к общему Ковариация
Схвачен принцип относительности движения по инерции формально лоренцевской ковариантностью физических законов: законы сохраняют свою форма, когда мы преобразуем Лоренца между различными системами координат. Что если мы перейдем к большей группе преобразований среди большего набора систем координат? Их условно называют «генералами». преобразования.«Эти преобразования будут включать те, которые связать системы координат, адаптированные к инерциальным системам отсчета, к системы координат, адаптированные к ускоряющим системам отсчета. Если законы физики остаются неизменными по форме, когда мы применяем эти общие преобразования мы расширили ковариантность Лоренца до общей ковариантности. Тогда, утверждал Эйнштейн, мы обобщили принцип относительности к ускоренному движению.
|
Вот как Эйнштейн сформулировал идею в своей основной обзорной статье 1916 года, написанной сразу после завершение общей теории относительности.Эйнштейн указывает, что его соображения приводят к тому, что координаты теряют свою прямое метрическое значение. Он продолжает «The метод, применявшийся до сих пор для закладки координат в Таким образом, пространственно-временной континуум определенным образом разрушается, и кажется, нет другого пути, который позволил бы нам приспособиться системы координат в четырехмерную вселенную, чтобы мы могли бы ожидать от их применения особенно простого Формулировка законов природы.Так что нет ничего для этого но рассматривать все мыслимые системы координат, на принцип, как в равной степени пригодный для описания природы. Это сводится к требованию, чтобы: Общие законы природы выражались уравнениями которые справедливы для всех систем координат. то есть являются ковариант по отношению к любым заменам (обычно ковариантный). Ясно, что физическая теория, удовлетворяющая этому
постулат будет также подходящим для общего постулата
относительность. Для суммы всех подстановок в любом случае
включает те, которые соответствуют всем относительным движениям
трехмерные системы координат». |
Простая идея в том, что
общая теория относительности движения = общая ковариация
Маскируется за технической
квалификация. «Все мыслимые» системы координат ведет
нам гораздо больше преобразований, чем нужно для выражения общего
относительность движения. В то время как некоторые преобразования будут суррогатами для
переключится с неускоренной системы отсчета на ускоряющуюся, другие
нет. Простейшим из этих других случаев являются преобразования, которые просто
переключать пространственные координаты, но не затрагивая время
координировать вообще. Рассмотрим, например, преобразование координат, которое
просто меняет местами пространственные координаты x и y событий.Нет смысла
изменение состояния движения, но мы ввели новую координату
система.
Принцип эквивалентности
Не сразу понятно, как это задумал Эйнштейн простая идея для воплощения. Однако его принцип эквивалентности представил вполне конкретную иллюстрацию этого.
| В более раннем главе мы уже видели этот принцип как центральный для Эвристика Эйнштейна в его открытии общей теории относительности. Если мы начнем в свободном от гравитации пространстве и будем равномерно ускоряться в фиксированном направлении, то свободные тела в нашем районе будут падать с равномерным ускорением. Они падают так же, как если они находятся в гравитационном поле. принцип Эйнштейна эквивалентности удалил «как если бы». Они, утверждает он, действительно в гравитационном поле, пусть и особого характера. Этот принцип предоставил Эйнштейну единственный пример релятивистски хорошо себя ведет гравитационное поле.Ранние годы работы Эйнштейна по общей теории относительности, начиная с 1907 г. сосредоточился на этом частном случае гравитационного поля. Он исследовал его свойства в деталях и искали более общую теорию просто путем обобщающие эти свойства. |
Эта эвристическая ценность принципа затмила то, что было для Эйнштейна основополагающее значение принципа. Это было Первый шаг Эйнштейна к обобщенному принцип относительности.
Вот наиболее тщательное и полное изложение
Принцип, который я нашел. Он появился в относительно неизвестной газете
Эйнштейн с 1916 года.
«Убер Фридрих Котлерс Абхандлунг Убер Эйнштейн».
Aquivalenzhypothese und die Gravitation.» Annalen der Physik 51
(19и6), стр. 639-642. («О статье Фридриха Коттлера «Об Эйнштейне
гипотеза эквивалентности и гравитации».) Перевод с «Что
был принцип эквивалентности Эйнштейна?» Исследования по истории
и Философия науки , 16 (1985), стр.203-246; перепечатано в
Д. Ховард и Дж. Стачел (ред.), Эйнштейн и история
Общая теория относительности: исследования Эйнштейна Vol. Я, Бостон: Биркхаузер,
1989, стр. 5-47.
» Принцип эквивалентности . Начиная с этого предельного случая специального теории относительности, можно задаться вопросом, является ли наблюдатель, равномерно ускорено относительно [инерциальной системы координат] K в области считается, должен понимать свое состояние как ускоренное, или нет ли остается для него точкой зрения, согласно (приблизительно) известному законы природы, по которым он может интерпретировать свое состояние как «отдых».
Выражаясь точнее: действуют ли законы природы, известные определенному приближении, позволяют считать систему отсчета K’ покоящейся, если равноускорено относительно K?
Или в более общем плане: можно ли расширить принцип относительности также к системам отсчета, которые (равномерно) ускорены относительно друг друга?
Ответ звучит так: насколько мы действительно знаем законы природы, ничего мешает нам рассматривать систему К’ как покоящуюся, если мы предположим, что наличие гравитационного поля (однородного в первом приближении) относительно К’; все тела падают с одинаковым ускорением независимо их физической природы в однородном гравитационном поле, а также относительно нашей системы К’.
Предположение, что можно со всей строгостью рассматривать К’ как покоящееся без любые законы природы, не выполняющиеся по отношению к К’, я называю «принцип эквивалентности». »
Принцип расширяет множество рассматриваемых систем координат от адаптированных к инерциальные системы отсчета в специальной теории относительности, чтобы включить те адаптированы к равномерно ускоряющимся системам отсчета. Преобразования рассматриваемые теперь включают те, которые связаны с этими инерционными системы координат в равномерно ускоряющиеся системы координат.То расширение ковариантности формулировок Эйнштейна, чтобы включить эти последние превращения рассматривались Эйнштейном как промежуточные на путь к полной общей ковариантности. Он заметил в той же статье 1916 г. выделенный текст:
» Требование общей ковариантности уравнений охватывает принцип эквивалентность как частный случай. »
Эта расширенная ковариация означала для Эйнштейна, что «один может рассматривать [равномерно ускоряющуюся систему координат] K ‘как покоящуюся в вся строгость.«То есть принцип расширил относительность движения по инерции
Принцип эквивалентности Принцип ковариации…
| Некоторые цифры помогут нам яснее увидеть, что Эйнштейн утверждает. Рассмотрим две его системы координат K и K’. Первая система К адаптирована к инерциальной системе отсчета и имеет координаты T, X, Y и Z. Система координат K’ адаптирована к равномерно ускоряющейся системе отсчета эталон, который ускорялся с постоянным ускорением g в +x направление К.Для простоты будем рассматривать только малые расширения пространства-времени и малых ускорений, так что соотношения между двумя системами координат являются ньютоновскими, достаточно близкими. Этот это упрощение, которое Эйнштейн использовал сам в своем изложении 1911 года принцип эквивалентности, «О влиянии гравитации на Распространение Света». |
| Вот инерциальная
система координат К.Оси координат Y и Z не
показаны, так как они не играют роли в анализе. Свободное тело в нем остается в покое, на что указывает вертикальный жирный шрифт линия. |
| Вот как равномерно ускоряющая система координат K’ относится к K. |
| Мы можем перерисовать
фигуре так, чтобы ось t равномерно ускоряющейся координаты
система вертикальная.Это дает нам представление о том, как кто-то движется с
равномерно ускоряющаяся система отсчета. Свободное тело ускоряется в направлении -x с ускорением г. |
| На основании принципа эквивалентности,
Эйнштейн уверяет нас, что наблюдатель движется вместе с ускоряющей системой отсчета.
ссылки не нужно понимать -x, направленный
ускорение как следствие ускорения наблюдателя.То
наблюдатель может рассматривать состояние наблюдателя как «покоящееся» и
движение свободного тела как за счет наличия однородного
гравитационное поле, действующее в направлении -х. |
Для реализации утверждения Эйнштейна о том, что принцип эквивалентность является принципом ковариации, мы нужно посмотреть, как его можно использовать для обеспечения одинаковости формы физического законы. Применимым законом является тот, который управляет движением по инерции в специальная теория относительности свободного тела, показанная на рисунках.
В инерциальной системе координат К применимый закон просто пишет, что тело не разогнано:
Ускорение = 0
То есть, если вы хотите
формулы:
d 2 x/dt 2 = 0 d 2 y/dt 2
= 0 d 2 y/dt 2 = 0
В равномерно ускоряющейся системе координат соответствующий закон гласит, что тело имеет постоянное, ненулевое ускорение:
Ускорение = постоянное ≠ 0
То есть, если вы хотите
формулы:
d 2 x/dt 2 = -g d 2 y/dt 2
= 0 d 2 y/dt 2 = 0
Эти два выражения можно объединить в одно, если мы позволим что константа может быть равна нулю, а может и не равняться нулю.Закон управляющие движением тела по обеим координатам системы К и К’ это:
Ускорение = постоянное
Мы получили результат, к которому стремился Эйнштейн. Принцип эквивалентности привело нас к расширению используемых нами систем координат до описать движение тел в специальной теории относительности. Он делает это в некотором роде что оставляет форму применимого закона неизменной. То есть мы расширили ковариантность теории, чтобы включить равномерное ускорение.Для Эйнштейна это распространяет принцип относительности на ускорение.
… Но не Принцип Относительность движения
Принцип эквивалентности в формулировке Эйнштейна как обрисованный выше, является принципом ковариации. Однако это не принцип относительности. То есть это не так, если термин «принцип относительности» должен иметь то же значение, что и в специальных относительность. Там ключевой идеей был принцип относительности движение по инерции устранило абсолютный покой, поскольку принцип абсолютный покой, ненаблюдаемый и недоступный для всех экспериментальных определение.
В более раннем глава, принцип относительности движения по инерции и некоторые его важные последствия были резюмированы следующим образом:
Принцип теории относительности: законы физики одинаковы во всех инерциальных системах отсчета. ссылки.
Отсюда следует, что:
Абсолютное движение не может появиться ни в одном законе физики.
Все эксперименты проводятся одинаково во всех инерциальных системах отсчета.
Никакой эксперимент не может выявить абсолютное движение наблюдателя.
Принцип эквивалентности, согласно Эйнштейну, таков: Теперь предполагается устранить отличительный статус движения по инерции. За предполагается, что это расширяет относительность движения от движения по инерции к ускоренному движению. Однако инерционный и ускоренные движения остаются абсолютно различимыми. То есть, если мы в инерциальной системе отсчета мы найдем свободные тела для движения равномерно по прямым линиям.Если же мы находимся в равномерно ускоренной системе отсчета, мы найдем свободные тела для ускорения в соответствии с движениями, производимыми однородным гравитационным полем.
Эти последние замечания описывают эксперимент, который мы можем провести, чтобы определить, является ли наша система отсчета инерционным или равноускоренным: достаточно наблюдать за движением свободных тел. Эйнштейн сказал, что мы можем рассматривать ускоренную систему отсчета как «в отдых.«Что бы он ни имел в виду под этим, этого недостаточно, чтобы дать нам наблюдательная эквивалентность движения по инерции и ускоренного движения.
| Более абстрактный способ сделать то же самое это. Принципы относительности реализуются симметрией преобразования, как описано выше. Преобразование Лоренца – это Симметрия пространства-времени Минковского. Преобразование из инерционного к ускоренным системам координат не является Симметрия пространства-времени Минковского.Чтобы быть симметрией, пространство и время должны были бы проявляться точно так же в системы координат, связанные преобразованием симметрии. То переход от инерциальных систем координат к равномерно ускоренные системы координат не в состоянии достичь этого. Структура пространства и времени определяется движением свободных тел. Эти движения в обоих случаях различны. |
Здесь я сосредоточился на том, что принцип эквивалентности не является.Однако что-то дает. В более раннем главе я описал, как Эйнштейн неоднократно использовал его для создания результаты о гравитации, которые приблизили его к окончательной общей теории. Пожалуй, самая важная идея была представлена вот в чем. Пространство-время Минковского специальной теории относительности не следует рассматривать как свободное от гравитации кейс. Скорее, это частный случай гравитационное поле. Чтобы увидеть это, мы ничего не делаем с пространством-временем.Мы просто ускоряемся и обнаруживаем, что однородное гравитационное поле проявляется вокруг нас. Этот факт в конечном итоге приведет к мысли о том, что геометрические структуры, составляющие пространство-время Минковского, — это все, что необходимо для теории гравитации. Идея реализована в целом. относительности, сделав специальную теорию относительности частным случаем плоской пространство-время. Общая теория относительности охватывает случаи, когда пространство-время перестают быть плоскими и появляются более разнообразные гравитационные явления.
Как обеспечить общую ковариацию
Принцип эквивалентности описывает одно расширение ковариация специальной теории относительности. Интерес Эйнштейна заключался во многом большее расширение. Он искал теорию, ковариантность которой преобразования связывают все мыслимые системы координат (если использовать его выражение). К этим преобразованиям относятся те, которые связаны с все разные виды ускоренного движения, такое неравномерное ускорение в одном направлении или вращательные движения.
Однако разложение ковариации не решает только что набросал проблему. Это же возражение применимо к другому преобразованию. Если у нас есть преобразования, которые устанавливают нашу структуру отсчета и его системы координат во вращение, то абсолютный факт вращения проявится в эффектах, возникающих из-за центробежных и кориолисовых сил.
Чтобы увидеть, что эта проблема не решена дальнейшим расширение ковариантности теории, мы должны смотреть более подробно о том, что нужно для введения произвольной координаты системы в теорию.
В специальной теории относительности стандартная инерциальная координата системы имеют особый статус. Они не только позволяют нам обозначать события четырьмя числами. Они «метрически значительными.» Их различия также позволяют нам определить измеримые расстояния между точками пространственных гиперповерхностей; и время прошло по времениподобным мировым линиям. Они также позволяют нам выделить инерционные движения. Они описываются просто как те траектории, для которых пространственные координаты x, y и z точки линейно зависят от времени.(Например, точка, движущаяся по времениподобной геодезической с половиной скорости свет в направлении x описывается как x = c/2 t, y = z = 0.)
При переходе к произвольным системам координат мы теряем это метрическое значение. Чтобы сохранить эту часть физического содержание теории, нам нужно восстановить эту метрическую информацию. Это делается путем создания математической структуры, связанной с этим метрическая информация явная.
Вот простой пример того, как эти структуры сделаны явными. Пример одномерный. Рассмотрим времена в будущем. Мы можем измерить эти раз обычным способом, используя хорошо сконструированные часы. Тогда мы можем поговорить что будет через год, через десять лет, через сто лет сейчас и так далее. В ближайшем будущем ожидается смена всего на один год. значительный. Если мы рассматриваем время на миллионы лет вперед, тогда разница всего в один год незначительна.Так что нам может понравиться использовать временную координату, которая сжимает время в более отдаленных будущее. Простой способ сделать это — использовать логарифм по основанию 10. обычное время.
То есть, если T = время, считанное часами, то логарифмическое время t
т = журнал Т
Легко переключаться между двумя временными интервалами. координаты какого-то события. t = log T переводит нас из часового времени в логарифмическое время.T = 10 t возвращает нас от логарифмического к часы время.
| Логарифмический время т | Часы время Т |
| 0 | 1 |
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
| 4 | 10 000 |
| 5 | 100 000 |
| 6 | 1 000 000 |
| … | … |
| Различия часового времени T говорят нам, как
прошло много времени, измеряемого физическими часами.
Различия логарифмического времени t не говорят нам об этом, или, по крайней мере,
они не делают это напрямую. В каждую эпоху времени будет
коэффициент преобразования, применяемый к небольшим разностям логарифмических
времени t, чтобы восстановить количество времени часов T, которое прошло, когда они
представлять. При небольших различиях часового времени ΔT и логарифмического времени Δt коэффициент преобразования: |
ΔT = 2,3025 Тл Δt
Величина 2,3025 T функционирует как «временная метрика.» То есть с его помощью мы можем брать небольшие разности логарифмическое время Δt и преобразовать их во время, прошедшее по показаниям часов. Например, мы можем спросить
, сколько часов проходит, когда мы переходим от логарифмического времени t = 2.000 до т = 2,001?
Разница Δt = 0,001. Применяя приведенную выше формулу, находим, что истекшее время часов составляет
ΔT = 2,3025 T Δt = 2,3025 x 100 x 0,001 = 0,23
Это соответствует прямому переводу логарифмического времени в часы. т = 2 соответствует T = 100. t = 2,001 соответствует T = 100,23.
Эта временная метрика является частным случаем временная метрика. Для любой новой временной координаты t, которую мы вводим, мы можем найти соответствующую темпоральную метрику.( формула приведена на боковой панели выше. Это (dT/dt).
Метрический тензор
| В последнем разделе показано, как одномерной теории времени и сделать ее общековариантной. Тот же метод работает для четырехмерной теории пространства-времени. В специальной теории относительности, координаты T, X, Y и Z адаптированы к инерциальные системы отсчета имеют метрическое значение.Если мы сейчас замените их некоторым произвольным набором из четырех координат, x 0 , х 1 , х 2 , х 3 , теряем это метрическое значение. Мы должны вернуть физическое содержимое исходной системы координат T, X, Y и Z. |
Как и в случае с одномерной теорией времени, мы делаем это с помощью введение поправочных коэффициентов, позволяющих восстановить утраченные метрические факты.Однако единый номер больше не достаточно. Для работы нам нужна целая таблица из 16 чисел. За по формальным причинам эти 16 чисел представлены в виде двухиндексной таблицы: g first index, второй индекс , где индексы идут от 0 до 3. Следующие Эйнштейн, гиковские буквы мю «μ» и ню «ν» часто выбирают в качестве ярлыков для первый и второй индексы.
| г мкν
= |
|
Эта таблица является метрикой пространства-времени.Будем писать как g μν или просто г , по необходимости. Если у нас есть события, чьи координаты отличаются лишь небольшим приращением, мы можем использовать эту таблицу, чтобы определить собственная разница во времени между событиями (если они времяподобные отношения) или правильное расстояние между ними (если они космические отношения). Эти пространственные и временные различия в совокупности дают нам понятие «интервал», описанное ранее глава.Этой информации достаточно, чтобы определить, какие инерционные движения. Ибо, как мы видели ранее главу, движения по инерции — это те времениподобные кривые, которые имеют истекло максимальное собственное время.
Эта таблица значений также фиксирует структуру светового конуса (описано в предыдущей главе) пространства-времени. Поскольку существует нулевой интервал между событиями, которые светлый, разделенный. Итак, когда в этой таблице указано, какие события разделенные нулевым интервалом, он автоматически указывает структура светового конуса.
Чтобы указать всю метрическую информацию в пространстве-времени, мы
нужно присвоить одну из этих таблиц каждому
событие в пространстве-времени, то есть каждой четверке пространства-времени
координаты. В особых случаях каждому событию назначается одна и та же таблица.
Как правило, каждому событию назначается отдельная таблица.
Если мы знаем таблицу в одной системе координат в какой-то событие, мы можем определить, что оно есть в другом, по стандартному набору правила.Конкретный набор правил, используемых для этого преобразования определяют математический характер этого метрика пространства-времени. Детали не должны задерживать нас на этом, кроме упомянуть имя. Эта таблица величин преобразуется «тензорно» так, что эта величина известна как «метрический тензор».
Дополнительные сведения, если они вам нужны, см. в разделе Технические Приложение.
Нарушение симметрии
Если мы начнем с метрического тензора, введенного выше, он является механическим вопросом, чтобы заполнить оставшиеся части теории, поэтому что он в целом является ковариантным.Однако такая теория не реализует автоматически обобщенный принцип относительности. Самый быстрый способ убедиться в этом — заметить, что все описанное выше относится к к пространству-времени Минковского специальной теории относительности. То же методы, используемые в общей теории относительности для обеспечения общего ковариация. Однако они также работают для специальной теории относительности. Специальный относительность имеет относительность только движения по инерции. Переписывая теорию в общековариантной форме этого факта не меняет.
Мы можем использовать метрический тензор, чтобы уточнить, как работает преобразование симметрии. Что значит пространство-время «смотреть то же самое», когда мы переходим из одной системы координат в другую? это так, если мы восстановим точно такую же таблицу чисел в метрическом тензоре г мкν .
Чтобы увидеть, как это работает, возьмите стандартный системы координат, адаптированные к инерциальной системе отсчета в специальная теория относительности.Во всех таких системах координат метрический тензор принимает особенно простую форму на каждом мероприятии:
| -1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Здесь единицы измерения
пространство и время выбраны так, чтобы скорость света равнялась единице;
то есть с=1.
Когда мы используем преобразование Лоренца для преобразования в стандартной координаты некоторой другой инерциальной системы отсчета, мы восстанавливаем точно такая же таблица для значений метрического тензора. В этом смысле, все метрические отношения пространства-времени одинаковы, если судить из любой инерциальной системы координат. Преобразование Лоренца представляет собой Симметрия пространства-времени Минковского.
Теперь рассмотрим преобразование из инерциальной системы отсчета ссылка на равномерно ускоряющуюся систему отсчета ссылки, используемой в принципе эквивалентности.В координате система адаптирована к ускоряющейся системе отсчета с ускорением a, восстанавливаем таблицу значений метрического тензора:
| -а 2 x 2 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Наличие координаты x в первой ячейке table означает, что мы назначаем другую таблицу для события в соответствии со значением координаты x события.
Как и прежде, c = 1. Ускорение a находится в направлении X стандартной системы координат, адаптированной к инерциальная система отсчета. Ускоряющая система координат имеет координаты t, x, y, z, где оси x, y и z параллельны X, Y оси Z инерциальной системы координат. Это преобразование дается в своей простейшей форме Эйнштейном в гораздо более поздней статье: А. Эйнштейн и Н. Розен, «Проблема частиц в общей теории относительности», Physical Обзор , 48 (1935), стр.73 — 77, на с. 74.
Подробнее о расчете см. в Техническом Приложение.
Наличие непостоянной g 00 = -а 2 х 2 следует, что преобразование не является симметрией. Для соответствующего члена в метрике в инерциальной системе координат просто константа, -1. Этот непостоянный член в преобразованной метрике отвечает за ускорение движения свободных точек, судя по ускоряющая система отсчета.
Распространение принципов
Эйнштейн ошибался, утверждая, что его общая теория теория относительности распространила принцип относительности на ускорение. Это было ясно в начале с завершением теории, по крайней мере, для некоторых. Однако было легко не платить много внимание на этот пробел. Ибо теория Эйнштейна была явно экстраординарная теория этого типа. Можно было просто обратиться непосредственно к применение теории.Или можно было бы повторить какую-нибудь версию Эйнштейна. претензии, не слишком размышляя над ними, а затем перейти к приложения теории.
Некоторые пытались исправить Эйнштейна. Наиболее подробно из них усилий была статья 1917 года Эриха Кречмана. Длительный и подробный анализ показал, что общая ковариация не достаточно, чтобы распространить принцип относительности на ускорение, но что то, что мы теперь называем расширением группы симметрии теории, есть то, что будет необходимо.
Статья была хорошо аргументирована и требовала ответа. Эйнштейн дал его в статье 1918 года. В ней Эйнштейн теперь признал, что он не сделал различия, которые он должен был сделать. Теперь он дал более сложный объяснение того, что он считал основополагающими принципами своей теории. Они заключался в трех принципах.
» (а) Принцип относительности. Законы природы являются лишь утверждениями пространственно-временные совпадения; поэтому они находят свою уникальную, естественную выражение в общековариантных уравнениях.
(b) Принцип эквивалентности. Инерция и вес идентичны в сущность. Отсюда и из результатов специальной теории относительности, обязательно следует, что симметричный «фундаментальный тензор» (g µν ) определяет метрические свойства пространства, инерциальную отношения тел в нем, а также гравитационные эффекты. мы позвоним состояние пространства, описываемое фундаментальным тензором, «G-поле.’
(в) Принцип Маха. G-поле определяется без остаток по массе тел. Так как масса и энергия эквивалентно по результатам специальной теории относительности и поскольку энергия формально описывается симметричным тензором энергии (T µν ), это означает, что G-поле обусловлено и определяется энергией тензор.»
А. Эйнштейн, «Prinzipielles zur allgemeinen Relativitaetstheorie», Annalen der Physik , 55 (1918), стр.240-44.
Этот ответ закодировал фрагментацию рассказа Эйнштейна об основах его общей теории относительность. Если это еще не было ясно, то теперь стало ясно, что Эйнштейн теория не была просто основана на единственном принципе, обобщенном принцип относительности. Скорее Эйнштейн опирался на коллекцию идеи с самого начала. За годы построения им теории, вопрос о том, идеально ли подогнаны все детали, не вызывал особого беспокойства.Важно было то, что этот набор идей привел Эйнштейна к к необычной новой теории. Как только теория была завершена, Стандартное повествование Эйнштейна об основаниях теории заключалось в том, чтобы рассказать о идеях, которыми он руководствовался.
Принимая во внимание три принципа Эйнштейна очередь:
(а) Принцип относительности. Что бросается в глаза эта формулировка состоит в том, что принцип больше не утверждает прямо относительность всех движений.Его импорт мигрировал таким образом, чтобы его можно было изучить ниже.
(b) Принцип эквивалентности. акцент Эйнштейна больше не относится к идее рассматривать ускоренное движение как покой. Скорее непосредственный смысл этого принципа состоит в том, что структуры в пространстве-времени которые учитывают движение по инерции так же, как и гравитация.
(c) Принцип Маха. Это последняя
развитие идей мы уже видели
ранее как «относительность инерции».«Эйнштейн вселял надежду
что эта общая теория относительности реализует некую версию
относительность инерции или принцип Маха. Однако эти надежды угасли и
в конце концов Эйнштейн полностью отказался от этого принципа.
Вместо принципа Маха Эйнштейн отступил к опасения, которые должен был устранить принцип Маха. Есть, он утверждал, причинный дефект в классическом физики и специальной теории относительности.Вот как Эйнштейн описал проблему в его 1921 г. Значение теории относительности (Лекция III):
«Все предыдущие рассуждения были основаны на предположении, что все инерциальные системы эквивалентны для описания физических явлений, но что они предпочтительнее для формулировки законов природе, к пространствам отсчета в другом состоянии движения. Мы можем не придумай никакой причины для этого предпочтения определенных состояний движения всем другие, согласно нашим предыдущим рассмотрениям, либо в воспринимаемых тел или в понятии движения; наоборот, надо рассматривать как независимое свойство пространственно-временного континуума.То принцип инерции, в частности, по-видимому, заставляет нас приписать физически объективные свойства пространственно-временного континуума. Так же, как это было необходимо с ньютоновской точки зрения, чтобы сделать оба утверждения: tempus est absolutum , spatium est absolutum , поэтому из точки зрения специальной теории относительности мы должны сказать, континуума spatii et temporis est absolutum . В этом последнем утверждении absolutum означает не только «физически реальный», но и «независимый в своем физическом свойства, имеющие физический эффект, но сами не подверженные влиянию физические условия.»
Отступление Эйнштейна к достоинству классической латыни, насколько я понимаю, блеф. Соответствуют ли пространство и время классическая физика или специальная теория относительности — это эмпирический вопрос. Здесь нет более глубокий закон природы с латинской родословной, который запрещает вещи которые действуют, не подвергаясь действию. Философ Мориц Шлик возражал уже в 1920 году к причинным размышлениям Эйнштейна. Он написал:
«.. . мы можем . . . считать выражение «абсолютное пространство» перефразируя тот факт, что эти [центробежные] силы существуют. Они были бы тогда просто непосредственными данными; и вопрос, почему они возникают в в одних телах и отсутствуют в других, были бы на одном уровне с вопрос, почему тело находится в одном месте в мире, а не в Другая. …Я полагаю, что динамика Ньютона вполне в порядке в том, что касается принцип причинности.»
Мориц Шлик, Космос и Время в современной физике. Trans HL Brose (Нью-Йорк Оксфорд Университетское издательство, 1920), с. 40.
Тем не менее, идея причинного дефекта в пространстве-времени теории, предшествующие общей теории относительности, сохранились в более поздней традиции который осуждает такие теории как укрывательство нежелательных «абсолютные объекты».
Более полный рассказ о фрагментации эйнштейновского фундаментальное объяснение выходит за рамки того, что здесь возможно, за пределы нескольких замечания выше.Для получения более подробной информации, включая сведения о Статью Кречмана 1917 года и ответ Эйнштейна 1918 года см. Ковариация и основы общей теории относительности: восемь десятилетий Диспут», Отчеты о прогрессе в физике , 56 (1993), стр. 791-858.
Проблемы с принципами
Мы видели в более раннем глава, в которой Эйнштейн сделал известное теперь различие между конструктивной и принципиальной теориями.Различие оказался решающим в последние недели многолетнего исследования Эйнштейна. в электродинамику, которая привела к специальной теории относительности. В В конце этих исследований он решил сформулировать теорию как логические следствия всего двух принципов. Это решение позволило Эйнштейна, чтобы убрать многие отвлекающие детали в электродинамике и показать что его теория на самом деле была просто теорией пространства и времени.
Эта награда теперь высоко ценится.Переход к принципиальное обоснование теории — ценный прогресс. Eсть опасность однако. Что, если теория не допускает формулировки с точки зрения простых принципов того типа, который предпочитал Эйнштейн? Усилия по упорство в их поиске погрузит теорию в болото фундаментальных путаницы.
Такова, я думаю, судьба общей теории относительности в Руки Эйнштейна. Поскольку мутирующий набор принципов Эйнштейна обеспечивает плохой фундамент.Почти любая теория пространство и время могут быть заданы в общековариантной формулировке, если достаточно настойчив и изобретателен. Отсюда следует, что очень мало можно выводится из принципа общей ковариантности.
На его месте основы общей теории относительность можно дать, просто повторяя знакомые факты в общей теории относительности. Пространство-время Минковского является работоспособным теории пространства и времени в малых областях пространства-времени, удаленных от больших массы.Чтобы охватить весь спектр гравитационных процессов, достаточно постулирует, что эти дальнейшие процессы проявляются в искривлении пространство-время. Остаются детали согласования масштабов кривизна к величинам напряжения-энергии-импульса в пространстве-времени. Этот как теория была представлена в более раннем глава.
Системы координат теряют свою независимость Реальность
Цель Эйнштейна в поиске расширения принципа относительности ускорения, должен был лишить инерциальные системы отсчета привилегированный статус, которым они пользовались в специальной теории относительности.В начале эти усилия, он использовал системы координат пространства-времени в качестве суррогатов для системы отсчета и их состояния движения. Как у Эйнштейна исследования развивались, его концепции мигрировали и мутировал. К моменту завершения своей общей теории относительности в 1916 году, его целью больше не были системы координат которые представляют собой инерционные движения. Скорее это были системы координат в их владеть правом.
Адекватная теория, настаивал теперь Эйнштейн, должна позволять Системы координат пространства-времени не имеют независимого существования.Это, как он теперь увидел, было реальным значением общей ковариации. Ибо, как мы видели выше, процедура превращения теории в обычно ковариантная форма требует извлечения физического содержания, неявно удерживаемого в предпочтительных системах координат и повторного захвата этого контента как явные структуры в пространстве-времени.
Мне кажется, нет проблем с использованием предпочтительного системы координат, несущие физическое содержание теории.Так что я нахожу это трудно согласиться с утверждением Эйнштейна о том, что мы должны лишить системы координат этого физического содержания. Как аналитическая геометрия евклидова пространства дефектна, если мы ограничимся Декартовы системы координат?
Однако выяснилось, что общая ковариация общая теория относительности лишила системы координат пространства-времени их независимое существование. Полный масштаб этой потери не сразу признал Эйнштейн.Это было с трудом завоеванное понимание это привело его к примечательному эпизоду в истории теории относительности: «Аргумент дыры» Эйнштейна против общей ковариантности и его последующие отказ в аргументе «точка-совпадение».
Об этом, как мы увидим, сообщил Эйнштейн в первом из его трех принципов 1918 года (переформулированный) принцип относительность.
Работа Эйнштейна над его дырочным аргументом и его опровержение
является предметом следующего
глава, содержание которой непосредственно вытекает из содержания этой главы.
Авторское право Джон Д. Нортон. 12 ноября 2019 г.
Специальная теория относительности, введение — Энциклопедия Нового Света
- Эта статья задумана как общедоступное введение в предмет.
Специальная теория относительности — фундаментальная физическая теория пространства и времени, разработанная Альбертом Эйнштейном в 1905 году [1] как модификация ньютоновской физики.Он был создан для решения некоторых насущных теоретических и экспериментальных вопросов физики того времени, связанных со светом и электродинамикой. Предсказания специальной теории относительности близко соответствуют предсказаниям ньютоновской физики для скоростей, которые малы по сравнению со скоростью света, но быстро расходятся для скоростей, составляющих значительную часть скорости света. С момента своего появления специальная теория относительности неоднократно проверялась экспериментально, и ее предсказания подтверждались этими проверками.
Эйнштейн постулировал, что скорость света одинакова для всех наблюдателей, независимо от их движения относительно источника света. Это полностью противоречило классической механике, которая была принята веками. Подход Эйнштейна был основан на мысленных экспериментах и расчетах. В 1908 году Герман Минковский переформулировал теорию на основе различных постулатов более геометрического характера. [2] Его подход основывался на существовании определенных взаимосвязей между пространством и временем, которые в классической физике считались совершенно отдельными.Эта переформулировка заложила основу для дальнейшего развития физики.
Специальная теория относительности делает многочисленные предсказания, которые несовместимы с ньютоновской физикой (и повседневной интуицией). Первое такое предсказание, описанное Эйнштейном, называется относительностью одновременности, согласно которой наблюдатели, находящиеся в движении относительно друг друга, могут расходиться во мнениях относительно того, произошли ли два события одновременно или одно произошло раньше другого. Другими важными предсказаниями специальной теории относительности являются замедление времени (при котором движущиеся часы тикают медленнее, чем когда они находятся в состоянии покоя по отношению к наблюдателю), сокращение длины (при котором движущийся стержень может оказаться короче, чем когда он находится в состоянии покоя). покоя относительно наблюдателя) и эквивалентность массы и энергии (записывается как E = mc 2 ).Специальная теория относительности предсказывает нелинейную формулу сложения скоростей, которая не позволяет наблюдать скорости, превышающие скорость света. Специальная теория относительности также объясняет, почему уравнения электромагнетизма Максвелла верны в любой системе отсчета и почему электрическое поле и магнитное поле являются двумя аспектами одного и того же.
Специальная теория относительности получила экспериментальную поддержку во многих отношениях, [3] [4] , и было доказано, что она намного точнее ньютоновской механики.Самым известным экспериментальным подтверждением является эксперимент Майкельсона-Морли, результаты которого (показывающие, что скорость света постоянна) были одним из факторов, побудивших сформулировать специальную теорию относительности. Другими важными тестами являются эксперимент Физо (который был впервые проведен за несколько десятилетий до того, как была предложена специальная теория относительности), обнаружение поперечного эффекта Доплера и эксперимент Хефеле-Китинга. Сегодня ученые настолько довольны идеей, что скорость света всегда одна и та же, что метр теперь определяется как расстояние, пройденное светом за 1/299 792 458 th секунды.Это означает, что скорость света теперь определяется как 299 792 458 м/с.
Системы отсчета и теория относительности Галилея: классическая прелюдия
Система отсчета — это просто набор неподвижных объектов. Как только скорость определенного объекта произвольно определена равной нулю, скорость всего остального во Вселенной может быть измерена относительно него. Когда поезд движется с постоянной скоростью мимо платформы, можно сказать, что платформа покоится, а поезд движется, или что поезд покоится, а платформа движется мимо него.Эти два описания соответствуют двум разным системам отсчета. Их соответственно называют опорной рамой платформы и опорной рамой поезда (иногда просто рамой платформы и рамой поезда).
Естественно возникает вопрос, можно ли физически различать разные системы отсчета? Другими словами, можно ли провести какие-то эксперименты, чтобы заявить, что «сейчас мы находимся в абсолютно стационарной системе отсчета»? Аристотель считал, что все объекты стремятся перестать двигаться и прийти в состояние покоя, если на них не действуют никакие силы.Галилей оспаривал эту идею и утверждал, что концепция абсолютного движения нереальна. Все движения были относительными. Наблюдатель, который не мог сослаться на какой-то изолированный объект (если, скажем, он был заключен внутри закрытого космического корабля), никогда не смог бы различить, по мнению какого-то внешнего наблюдателя, он покоится или движется с постоянной скоростью. Любой эксперимент, который он мог бы провести, дал бы один и тот же результат в обоих случаях. Однако ускоренные системы отсчета экспериментально различимы. Например, если космонавт, летящий в открытом космосе, увидит, что чай в его чашке стоит под наклоном, а не горизонтально, он сможет сделать вывод, что его космический корабль движется с ускорением.Таким образом, не все системы отсчета эквивалентны, но у людей есть класс систем отсчета, все движущиеся с одинаковой скоростью по отношению друг к другу, во всех из которых выполняется первый закон Ньютона. Они называются инерциальными системами отсчета и являются фундаментальными как для классической механики, так и для СТО. Таким образом, теория относительности Галилея утверждает, что законы физики не могут зависеть от абсолютной скорости, они должны оставаться неизменными в любой инерциальной системе отсчета. Таким образом, относительность Галилея является фундаментальным принципом классической физики.
Математически это говорит о том, что если перевести все скорости в другую систему отсчета, законы физики не изменятся. Что это за преобразование, которое нужно применить к скоростям? Галилей дал общепринятую «формулу» для сложения скоростей: если
- Частица P движется со скоростью v относительно системы отсчета A и
- Система отсчета A движется со скоростью u относительно системы отсчета B, затем
- Скорость P относительно B равна v + u.
Формула преобразования координат между различными системами отсчета называется преобразованием Галилея. Тогда принцип относительности Галилея требует, чтобы законы физики оставались неизменными, если к ним применяется преобразование Галилея. Законы классической механики, такие как второй закон Ньютона, подчиняются этому принципу, потому что они имеют тот же вид после применения преобразования. Поскольку закон Ньютона включает производную скорости, любая постоянная скорость, добавленная в преобразовании Галилея к другой системе отсчета, ничего не дает (производная постоянной равна нулю).Однако добавление изменяющейся во времени скорости (соответствующей ускоренной системе отсчета) изменит формулу (см. Псевдосилу), поскольку теория относительности Галилея применима только к неускоренным инерциальным системам отсчета.
Время одинаково во всех системах отсчета, потому что в классической механике оно абсолютно. Все наблюдатели измеряют точно такие же промежутки времени, и существует такая вещь, как абсолютно правильные часы.
Инвариантность длины: евклидова картина
Длина объекта постоянна на плоскости при вращении на плоскости, но не при вращении вне плоскости.В специальной теории относительности пространство и время объединены в единый четырехмерный континуум, называемый пространством-временем. Чтобы получить представление о том, на что похоже пространство-время, мы должны сначала взглянуть на евклидово пространство ньютоновской физики.
Этот подход к специальной теории относительности начинается с понятия «длина». В повседневном опыте кажется, что длина предметов остается неизменной независимо от того, как их вращают или перемещают с места на место; в результате простая длина объекта не меняется или является «неизменной».{2}.\,}
Одна из основных теорем векторной алгебры состоит в том, что длина вектора не меняется при его вращении. Однако при ближайшем рассмотрении мы узнаем, что это верно только в том случае, если мы рассматриваем вращения, ограниченные плоскостью. Если мы введем вращение в третьем измерении, то мы сможем отклонить линию от плоскости. В этом случае проекция линии на плоскость станет короче. Означает ли это, что длина не является инвариантной? Очевидно нет. Мир трехмерен, и в трехмерной декартовой системе координат длина определяется трехмерной версией теоремы Пифагора:
- k2=x2+y2+z2.{2}}. Длина объекта постоянна независимо от того, вращается ли он или перемещается из одного места в другое в трехмерной системе координат.
Неизменен при любом вращении. Очевидное нарушение инвариантности длины произошло только потому, что мы «пропустили» измерение. Кажется, что при условии, что все направления, в которых объект может быть наклонен или расположен, представлены в системе координат, длина объекта не изменяется при вращении. В классической механике достаточно трехмерной системы координат, потому что в этом контексте время считается абсолютным и независимым от пространства.Можно рассмотреть отдельно.
Обратите внимание, что неизменность длины обычно не считается динамическим принципом и даже не является теоремой. Это просто утверждение о фундаментальной природе самого пространства. Пространство, как мы его обычно понимаем, называется трехмерным евклидовым пространством, потому что его геометрическая структура описывается принципами евклидовой геометрии. Формула расстояния между двумя точками является фундаментальным свойством евклидова пространства, она называется евклидовым метрическим тензором (или просто евклидовой метрикой).В общем случае формулы расстояния называются метрическими тензорами.
Обратите внимание, что повороты в основном связаны с концепцией длины. На самом деле можно определить длину или расстояние как то, что остается неизменным (неизменно) при вращении, или определить вращение как то, что сохраняет неизменной длину. Имея одно, можно найти другое. Зная формулу расстояния, мы можем узнать формулу преобразования координат во вращение. Если, с другой стороны, у нас есть формула вращения, то мы можем найти формулу расстояния.
Постулаты специальной теории относительности
Эйнштейн разработал специальную теорию относительности на основе двух постулатов:
- Первый постулат — Специальный принцип относительности — Законы физики одинаковы во всех инерциальных системах отсчета. Другими словами, не существует привилегированных инерциальных систем отсчета.
- Второй постулат — Инвариантность c — Скорость света в вакууме не зависит от движения источника света.
Специальная теория относительности может быть выведена из этих постулатов, как это сделал Эйнштейн в 1905 году. Постулаты Эйнштейна по-прежнему применимы в современной теории, но происхождение постулатов более очевидно. Выше было показано, что существование универсально постоянной скорости (скорости света) является следствием моделирования Вселенной как частного четырехмерного пространства, обладающего некоторыми специфическими свойствами. Принцип относительности является результатом сохранения структуры Минковского при преобразованиях Лоренца, которые постулируются как физические преобразования инерциальных систем отсчета.
Формулировка Минковского: введение пространства-времени
После того, как Эйнштейн формально вывел специальную теорию относительности из контринтуитивного утверждения, что скорость света одинакова для всех наблюдателей, возникла потребность в более удовлетворительной формулировке. Минковский, опираясь на математические подходы, использованные в неевклидовой геометрии [5] , и математические работы Лоренца и Пуанкаре, понял, что геометрический подход является ключевым. Минковский показал в 1908 году, что новая теория Эйнштейна может быть объяснена естественным образом, если понятие отдельного пространства и времени заменить одним четырехмерным континуумом, называемым пространством-временем.Это была новаторская концепция, и Роджер Пенроуз сказал, что теория относительности не была по-настоящему полной, пока Минковский не переформулировал работу Эйнштейна.
Концепцию четырехмерного пространства трудно представить себе. В начале может помочь простое мышление в терминах координат. В трехмерном пространстве для обозначения точки нужны три действительных числа. В пространстве Минковского нужно четыре действительных числа (три пространственные координаты и одна временная координата) для обозначения точки в конкретный момент времени.Эта точка в конкретный момент времени, заданная четырьмя координатами, называется событием. Расстояние между двумя разными событиями называется пространственно-временным интервалом.
Траектория в четырехмерном пространстве-времени, обычно называемом пространством Минковского, называется мировой линией. Поскольку она определяет и положение, и время, частица, имеющая известную мировую линию, имеет полностью определенную траекторию и скорость. Это похоже на построение графика смещения частицы, движущейся по прямой линии, в зависимости от прошедшего времени.Кривая содержит полную информацию о движении частицы.
Точно так же, как для измерения расстояния в трехмерном пространстве необходимы все три координаты, мы должны включать время, а также три пространственные координаты при расчете расстояния в пространстве Минковского (далее называемом М). В некотором смысле пространственно-временной интервал дает комбинированную оценку того, как далеко происходят два события в пространстве, а также время, прошедшее между их возникновением.
Но есть проблема.Время связано с пространственными координатами, но они не эквивалентны. Теорема Пифагора рассматривает все координаты на равных (подробнее см. Евклидово пространство). Мы можем поменять местами две пространственные координаты, не меняя длины, но мы не можем просто поменять местами пространственную координату со временем, они принципиально разные. Совсем другое дело, когда два события разделены в пространстве и разделены во времени. Минковский предположил, что формула для расстояния нуждается в изменении.{2}.\,}
Следует отметить два основных момента. Во-первых, время измеряется в тех же единицах, что и длина, путем умножения ее на постоянный коэффициент преобразования. Во-вторых, и это более важно, временная координата имеет другой знак, чем пространственная координата. Это означает, что в четырехмерном пространстве-времени одна координата отличается от других и по-разному влияет на расстояние. Это новое «расстояние» может быть нулевым или даже отрицательным. Эта новая формула расстояния, называемая метрикой пространства-времени, лежит в основе теории относительности.Эта формула расстояния называется метрическим тензором M. Этот знак минус означает, что большая часть наших интуитивных представлений о расстояниях не может быть непосредственно перенесена в пространственно-временные интервалы. Например, пространственно-временной интервал между двумя событиями, разделенными как во времени, так и в пространстве, может быть равен нулю (см. ниже). Отныне термины «формула расстояния» и «метрический тензор» будут использоваться взаимозаменяемо, как и термины «метрика Минковского» и «пространственно-временной интервал».
В пространстве-времени Минковского пространственно-временной интервал является инвариантной длиной, обычная трехмерная длина не обязана быть инвариантной.Пространственно-временной интервал должен оставаться неизменным при вращении, но обычные длины могут меняться. Как и раньше, нам не хватало измерения. Обратите внимание, что все, что до сих пор является просто определениями. Мы определяем четырехмерную математическую конструкцию, которая имеет специальную формулу для расстояния, где расстояние означает то, что остается неизменным при вращении (в качестве альтернативы можно определить вращение как такое, при котором расстояние остается неизменным).
Теперь физическая часть. Вращения в пространстве Минковского имеют иную интерпретацию, чем обычные вращения.Эти вращения соответствуют преобразованиям систем отсчета. Переход из одной системы отсчета в другую соответствует вращению пространства Минковского. Интуитивное обоснование этого дается ниже, но математически это динамический постулат, точно так же, как предположение, что физические законы должны оставаться неизменными при преобразованиях Галилея (что кажется настолько интуитивным, что мы обычно не признаем его постулатом).
Поскольку по определению вращение должно сохранять расстояние одинаковым, переход к другой системе отсчета должен сохранять неизменным пространственно-временной интервал между двумя событиями.Это требование можно использовать для получения явной математической формы преобразования, которое необходимо применять к законам физики (сравните с применением преобразований Галилея к классическим законам) при смещении системы отсчета. Эти преобразования называются преобразованиями Лоренца. Точно так же, как преобразования Галилея являются математической формулировкой принципа относительности Галилея в классической механике, преобразования Лоренца являются математической формой принципа относительности Эйнштейна.Законы физики должны оставаться неизменными при преобразованиях Лоренца. Уравнения Максвелла и уравнение Дирака удовлетворяют этому свойству, и, следовательно, они являются релятивистски правильными законами (но классически неверными, поскольку они не преобразуются правильно при преобразованиях Галилея).
С утверждением метрики Минковского, общего названия формулы расстояния, приведенной выше, теоретическая основа специальной теории относительности завершена. Всю основу специальной теории относительности можно резюмировать геометрическим утверждением: «изменения системы отсчета соответствуют вращениям в четырехмерном пространстве-времени Минковского, которое определяется формулой расстояния, приведенной выше.Уникальные динамические предсказания СТО проистекают из этого геометрического свойства пространства-времени. Можно сказать, что специальная теория относительности является физикой пространства-времени Минковского. В случае пространства-времени необходимо рассмотреть шесть независимых вращений. Три из них являются стандартными вращениями на плоскости в двух направлениях пространства. Остальные три являются вращениями в плоскости как пространства, так и времени: эти вращения соответствуют изменению скорости и описываются традиционными преобразованиями Лоренца.
Как упоминалось ранее, формулы расстояний можно заменить формулами вращения. Вместо того, чтобы исходить из инвариантности метрики Минковского как фундаментального свойства пространства-времени, можно сформулировать (как это было сделано в классической физике с галилеевой относительностью) математическую форму преобразований Лоренца и потребовать инвариантности физических законов относительно этих преобразований. Это не относится к геометрии пространства-времени, но даст тот же результат. На самом деле это был традиционный подход к СТО, первоначально использовавшийся самим Эйнштейном.Однако часто считается, что этот подход дает меньше информации и является более громоздким, чем более естественный формализм Минковского.
Системы отсчета и преобразования Лоренца: новый взгляд на теорию относительности
Мы уже обсуждали, что в классической механике изменения системы координат соответствуют преобразованиям Галилея координат. Адекватно ли это в релятивистской картине Минковского?
Предположим, есть два человека, Билл и Джон, на разных планетах, удаляющихся друг от друга.Билл и Джон находятся на разных планетах, поэтому они оба думают, что они неподвижны. Джон рисует график движения Билла в пространстве и времени, как показано на рисунке ниже:
Мнение Джона о Билле и мнение Билла о себе
Джон видит, что Билл движется не только во времени, но и в пространстве, но Билл думает, что движется во времени один. Билл сделал бы такой же вывод о ходатайстве Джона. На самом деле эти два вида, которые классически считались бы разницей в системах отсчета, связаны просто преобразованием координат в М.Представление Билла о его собственной мировой линии и представление Джона о мировой линии Билла связаны друг с другом просто вращением координат. Одно может быть преобразовано в другое вращением оси времени. Геометрия Минковского обрабатывает преобразования систем отсчета очень естественным образом.
Изменения в системе отсчета, представленные преобразованиями скоростей в классической механике, представлены вращениями в пространстве Минковского. Эти вращения называются преобразованиями Лоренца. Они отличаются от преобразований Галилея уникальной формой метрики Минковского.Преобразования Лоренца являются релятивистским эквивалентом преобразований Галилея. Законы физики, чтобы быть релятивистски правильными, должны оставаться неизменными при преобразованиях Лоренца. Физическое утверждение о том, что они должны быть одинаковыми во всех инерциальных системах отсчета, остается неизменным, но изменяется математическое преобразование между различными системами отсчета. Законы движения Ньютона инвариантны относительно преобразований Галилея, а не Лоренца, поэтому они сразу же распознаются как нерелятивистские законы и должны быть отброшены в релятивистской физике.Уравнение Шрёдингера также нерелятивистское.
Уравнения Максвелла сложнее. Они записываются с использованием векторов и, на первый взгляд, правильно преобразуются при преобразованиях Галилея. Но при ближайшем рассмотрении становится очевидным несколько вопросов, которые не могут быть удовлетворительно решены в рамках классической механики (см. Историю специальной теории относительности). Они действительно инвариантны относительно преобразований Лоренца и являются релятивистскими, хотя и были сформулированы до открытия специальной теории относительности.Классическую электродинамику можно назвать первой релятивистской теорией в физике. Чтобы сделать очевидным релятивистский характер уравнений, они записываются с использованием 4-компонентных векторных величин, называемых 4-векторами. 4-векторы корректно преобразуются при преобразованиях Лоренца. Уравнения, записанные с использованием 4-векторов, автоматически являются релятивистскими. Это называется явно ковариантной формой уравнений. 4-векторы составляют очень важную часть формализма специальной теории относительности.
Постулат Эйнштейна: постоянство скорости света
Постулат Эйнштейна о том, что скорость света постоянна, является естественным следствием формулы Минковского [6]
Утверждение 1:
- Когда объект движется со скоростью c в определенной системе отсчета, пространственно-временной интервал равен нулю.{2}=0\,}
Предложение 2:
- Объект, движущийся со скоростью 90 559 c 90 560 в одной системе отсчета, движется со скоростью 90 559 c 90 560 во всех системах отсчета.
Доказательство:
- Пусть объект движется со скоростью v при наблюдении из другой системы отсчета. Изменение системы отсчета соответствует повороту в M. Поскольку пространственно-временной интервал должен сохраняться при вращении, пространственно-временной интервал должен быть одинаковым во всех системах отсчета.{2}=0\,}
- |v|=c.{\displaystyle |v|=c.\,}
Пути световых лучей имеют нулевой пространственно-временной интервал, и, следовательно, все наблюдатели получат одно и то же значение скорости света . Следовательно, если предположить, что Вселенная имеет четыре измерения, которые связаны формулой Минковского, скорость света представляется постоянной, и ее не нужно предполагать (постулировать) постоянной, как в исходном подходе Эйнштейна к специальной теории относительности.
Задержка часов и сокращения стержня: Подробнее о преобразованиях Лоренца
Другим следствием неизменности пространственно-временного интервала является то, что часы будут идти медленнее на объектах, которые движутся относительно вас. Это очень похоже на то, как 2D-проекция линии, повернутой в третье измерение, становится короче. Длина не сохраняется просто потому, что мы игнорируем одно из измерений. Вернемся к примеру Джона и Билла.{2}\,}
Пространственно-временной интервал, с 2 , является инвариантным.{2}}}}}}\,}.
Итак, если Джон увидит часы, которые покоятся в кадре Билла на одну секунду, Джон обнаружит, что его собственные часы измеряют между этими же тактами интервал t, , называемый координатным временем, , который больше единицы. второй. Говорят, что часы в движении замедляются по сравнению с часами покоящихся наблюдателей. Это известно как «релятивистское замедление времени движущихся часов». Время, которое измеряется в остальной системе отсчета часов (в системе отсчета Билла), называется собственным временем часов.
Таким образом, в специальной теории относительности изменения в системе отсчета также влияют на время. Время больше не является абсолютным. Не существует универсально правильных часов, время течет с разной скоростью для разных наблюдателей.
Точно так же можно показать, что Джон также заметит, что измерительные стержни, покоящиеся на планете Билла, короче в направлении движения, чем его собственные измерительные стержни. Это предсказание известно как «релятивистское сокращение длины движущегося стержня». Если длина стержня, покоящегося на планете Билла, равна X {\ displaystyle X}, то мы называем эту величину собственной длиной стержня.{2}}}}}
Приведенные выше формулы для задержки часов и сокращения длины являются частными случаями общего преобразования.
Альтернативно, эти уравнения для замедления времени и сокращения длины (здесь полученные из инвариантности пространственно-временного интервала) могут быть получены непосредственно из преобразования Лоренца, установив X = 0 для замедления времени, что означает, что часы в состоянии покоя в системе отсчета Билла или установив t = 0 для сокращения длины, что означает, что Джон должен одновременно измерить расстояния до конечных точек движущегося стержня.
Следствием преобразований Лоренца является модифицированная формула сложения скоростей:
- s = v + u1 + (v / c) (u / c). {\ displaystyle s = {v + u \ over 1 + (v / c) (u / c)}.}
Одновременность и часы рассинхронизация
Как это ни парадоксально, специальная теория относительности предполагает, что в состоянии покоя мы на самом деле движемся во времени со скоростью света. Ускоряясь в пространстве, мы замедляемся во времени. При скорости света в космосе время замедляется до нуля. Это поворот оси времени относительно оси пространства.Мы наблюдаем, что объект ускоряется релятивистски, так как его ось времени не находится под прямым углом.
Следствием этого в пространстве-времени Минковского является то, что часы будут выглядеть не в фазе друг с другом по всей длине движущегося объекта. Это означает, что если один наблюдатель установит линию синхронизированных часов, чтобы все они показывали одинаковое время, то другой наблюдатель, который движется вдоль линии с высокой скоростью, увидит, что все часы показывают разное время. Это означает, что наблюдатели, движущиеся относительно друг друга, воспринимают разные события как одновременные.Этот эффект известен как «релятивистская фаза» или «относительность одновременности». Релятивистская фаза часто упускается из виду изучающими специальную теорию относительности, но если ее понять, то легче понять такие явления, как парадокс близнецов.
«Плоскость одновременности» или «поверхность одновременности» содержит все те события, которые происходят в один и тот же момент для данного наблюдателя. События, одновременные для одного наблюдателя, не одновременны для другого наблюдателя в относительном движении.Наблюдатели имеют вокруг себя набор одновременных событий, которые они считают составляющими настоящий момент. Относительность одновременности приводит к тому, что наблюдатели, которые движутся относительно друг друга, имеют разные наборы событий в настоящий момент.
Чистый эффект четырехмерной вселенной заключается в том, что наблюдатели, движущиеся относительно вас, как будто имеют временные координаты, наклоняющиеся в направлении движения, и считают одновременными вещи, которые не являются одновременными для вас.Пространственные длины в направлении движения сокращаются, потому что они наклоняются вверх и вниз по отношению к оси времени в направлении движения, подобно вращению из трехмерного пространства.
При интерпретации пространственно-временных диаграмм требуется большая осторожность. Диаграммы представляют данные в двух измерениях и не могут точно показать, как, например, появляется пространственно-временной интервал нулевой длины.
Соотношение массовых скоростей
E = mc 2 , где m означает массу покоя (инвариантная масса), проще всего применимо к одиночным частицам без чистого импульса.Но это также применимо к обычным объектам, состоящим из многих частиц, пока частицы движутся в разных направлениях, так что общий импульс равен нулю. Масса объекта включает вклад тепла и звука, энергий химической связи и захваченного излучения. Знакомые примеры — бак с бензином или тарелка горячего супа. Кинетическая энергия их частиц, тепловое движение и излучение вносят вклад в их вес по шкале согласно формуле E = mc 2 .{2}} из выражения для E{\displaystyle E}, и это тоже допустимая сохраняемая величина, хотя и некрасивая.{2}} имеет физический смысл, Эйнштейн рассматривал процессы излучения и поглощения. Ему нужно было установить, что объект теряет массу, когда излучает энергию. Он сделал это, проанализировав излучение двух фотонов в двух разных кадрах.
После того, как Эйнштейн впервые сделал свое предложение, стало ясно, что слово масса может иметь два разных значения. Масса покоя — это то, что Эйнштейн назвал m, но другие определили релятивистскую массу как:
-
- mотн=m01−v2c2.{2}}, когда объект движется.
Оригинальные статьи Эйнштейна [10] рассматривали m как то, что теперь можно было бы назвать массой покоя , и некоторые утверждают, что ему не нравилась идея «релятивистской массы». [11] Когда современные физики говорят «масса», они обычно имеют в виду массу покоя, поскольку, если бы они имели в виду «релятивистскую массу», они просто сказали бы «энергия».
Мы можем переписать выражение для энергии в виде ряда Тейлора:
-
- E=m0c2[1+12(vc)2+38(vc)4+516(vc)6+…].Часть {2}} не имеет значения, так как она постоянна. По той же причине в теории относительности можно вычесть энергию покоя из полной энергии. Чтобы увидеть, имеет ли энергия покоя какой-либо физический смысл, необходимо рассмотреть испускание и поглощение энергии в разных системах отсчета.
Члены более высокого порядка являются дополнительной поправкой к ньютоновской механике, которая становится важной при более высоких скоростях. Уравнение Ньютона — это всего лишь низкоскоростное приближение, но чрезвычайно хорошее.Например, все расчеты, использованные при отправке астронавтов на Луну, могли быть выполнены с использованием уравнений Ньютона без каких-либо поправок более высокого порядка.
Эквивалентность массы и энергии: солнечный свет и атомные бомбы
Эйнштейн показал, что масса — это просто еще одна форма энергии. Энергетический эквивалент массы покоя m равен E = mc 2 . Эта эквивалентность подразумевает, что масса должна быть взаимопреобразуема с другими формами энергии. Это основной принцип атомных бомб и производства энергии в ядерных реакторах и звездах (таких как Солнце).
Стандартная модель строения материи гласит, что большая часть «массы» атома находится в атомном ядре, и что большая часть этой ядерной массы находится в интенсивном поле светоподобных глюонов, окутывающих кварки. Таким образом, большая часть того, что называется массой объекта, уже находится в форме энергии, энергии квантового цветового поля, удерживающего кварки.
Солнце, например, подпитывает свою огромную выработку энергии, превращая каждую секунду 600 миллиардов килограммов водорода-1 (один протон) в 595.2 миллиарда килограммов гелия-4 (2 протона в сочетании с 2 нейтронами) — разница в 4,2 миллиарда килограммов — это энергия, которую Солнце излучает в космос каждую секунду. По оценкам, Солнце будет продолжать превращать 4,2 миллиарда килограммов массы в энергию в течение следующих 5 миллиардов лет или около того, прежде чем покинуть главную последовательность.
Атомные бомбы, положившие конец Второй мировой войне, для сравнения, преобразовали около тридцатой унции массы в энергию.
Энергия, связанная с химическими реакциями, настолько мала, что закон сохранения массы является отличным приближением.
Общая теория относительности: взгляд вперед
В отличие от законов движения Ньютона, теория относительности не основана на динамических постулатах. Он ничего не предполагает о движении или силах. Скорее, он имеет дело с фундаментальной природой пространства-времени. Он связан с описанием геометрии фона, на котором происходят все динамические явления. Таким образом, в некотором смысле это метатеория, теория, излагающая структуру, которой должны следовать все другие теории. По правде говоря, специальная теория относительности — это всего лишь частный случай.Предполагается, что пространство-время плоское. То есть предполагается, что структура пространства Минковского и метрический тензор Минковского постоянны повсюду. В ОТО Эйнштейн показал, что это не так. Структура пространства-времени модифицируется присутствием материи. В частности, формула расстояния, приведенная выше, больше не действует в целом, кроме как в пространстве, свободном от массы. Однако точно так же, как искривленная поверхность может считаться плоской в бесконечно малом пределе исчисления, искривленное пространство-время можно считать плоским в малом масштабе.{2}\,}
Говорят, что метрика Минковского действительна локально, , но она не может дать меру расстояния на больших расстояниях. Это недействительно глобально. Фактически, в общей теории относительности сама глобальная метрика становится зависимой от распределения массы и изменяется в пространстве. Центральная проблема общей теории относительности состоит в том, чтобы решить известные уравнения поля Эйнштейна для заданного распределения массы и найти формулу расстояния, применимую в данном конкретном случае.Формулировка пространства-времени Минковского была концептуальной ступенькой к общей теории относительности. Его принципиально новое мировоззрение позволило развить не только общую теорию относительности, но и в некоторой степени квантовые теории поля.
См. также
Примечания
- ↑ Эйнштейн, Альберт, Об электродинамике движущихся тел, Annalen der Physik 17: 891-921. Проверено 18 декабря 2007 г.
- ↑ Герман Минковски, Raum und Zeit, 80. Versammlung Deutscher Naturforscher, Physikalische Zeitschrift 10: 104-111.
- ↑ UCR, Что является экспериментальной основой специальной теории относительности? Проверено 22 декабря 2007 г.
- ↑ Core Power, Какова экспериментальная основа специальной теории относительности? Проверено 22 декабря 2007 г.
- ↑ С. Уолтер и Дж. Грей (ред.), «Неевклидов стиль теории относительности Минковского». Символическая вселенная (Оксфорд, Великобритания: Oxford University Press, 1999, ISBN 0198500882).
- ↑ 6.0 6.1 Альберт Эйнштейн, Р. В. Лоусон (пер.), Относительность. Специальная и общая теория (Лондон, Великобритания: классика Routledge, 2003).
- ↑ Ричард Фейман, Шесть не очень простых произведений (Рединг, Массачусетс: Addison-Wesley Pub, ISBN 0201150255).
- ↑ Герман Вейль, Пространство, Время, Материя (Нью-Йорк, Нью-Йорк: Dover Books, 1952).
- ↑ Кип Торн и Роджер Блэндфорд, Заметки по физике Калифорнийского технологического института, Калифорнийский технологический институт. Проверено 18 декабря 2007 г.
- ↑ FourmiLab, Специальная теория относительности. Проверено 19 декабря 2007 г.
- ↑ UCR, Часто задаваемые вопросы по физике Usenet. Проверено 19 декабря 2007 г.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Баис, Сандер. 2007. Очень специальная теория относительности: иллюстрированное руководство . Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN 067402611X.
- Робинсон, Ф.Н.Х. 1996. Введение в специальную теорию относительности и ее приложения . Ривер Эдж, Нью-Джерси: World Scientific Publishing Company. ISBN 9810224990.
- Стефани, Ганс. 2004. Теория относительности: введение в специальную и общую теорию относительности . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 0521010691.
Внешние ссылки
Все ссылки получены 22 декабря 2019 г.
Специальная теория относительности для широкой аудитории (знания математики не требуются)
- Эйнштейн Онлайн Введение в теорию относительности от Института гравитационной физики им. Макса Планка.
Объяснение специальной теории относительности (с использованием простой или более сложной математики)
Кредиты
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в New World Encyclopedia :
Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
Инерциальные системы отсчета — Исследование Вселенной
Ранее в этом году я отправился в непростое путешествие, чтобы изучить специальную теорию относительности Эйнштейна. Я просмотрел всего одну или две страницы Роберта Резника Введение в специальную теорию относительности , и тут всплыло слово «Инерциальные системы отсчета». Книга просто списала его « как фреймворк, не находящийся под ускорением ».
Это показалось мне вполне справедливым, и я не придал этому большого значения.Но через пять страниц в книге это слово стало повторяться так часто, что я начал задаваться вопросом, понимаю ли я вообще, что это значит.
Концепция инерциальных систем отсчета очень фундаментальна для физики, но обманчиво интуитивна. Например, когда вы в последний раз просыпались утром и задавались вопросом: «Я действительно стою или двигаюсь?» Это настолько нелепый вопрос, что, если только вы не под кайфом (под наркотиками), никто на самом деле не задает его себе, но, возможно, им следует.
Чтобы действительно понять инерциальные системы отсчета, рассмотрим следующий гипотетический сценарий.
«Поднимите шторы!»
Вспомните одно из тех ленивых воскресных утра, когда вам совсем не хочется ничего делать. Вы бодрствуете 15 минут, но слишком ленивы, чтобы встать с кровати. Ты просто лежишь, чешешь живот и пялишься в потолок.
Сцена, напоминающая хит Бруно Марса «Сегодня мне не хочется ничего делать, я просто хочу полежать в своей постели…»
Вы не помните, как вернулись домой после вчерашней вечеринки с друзьями.
С усилием вы встаете с кровати, потягиваетесь, приседаете и даже подпрыгиваете, пытаясь стряхнуть с себя головокружение.
Вы идете в ванную, чтобы умыться, когда у вас звонит телефон: это ваша подруга Эми.
Частично Эми ответственна за похмелье, которое вы чувствуете этим утром. Она была той, кто поощрял вас пить накануне вечером — всегда подсказывал, чтобы вы снова наполнили свой стакан.
Вы отвечаете на телефонные звонки.
Она говорит, что стоит прямо возле твоего дома и призывает тебя посмотреть в окно, так как у нее есть для тебя сюрприз.
Прижав трубку к уху и надеясь, что она не держит в руках еще одну бутылку шампанского, ты быстро подходишь к окну. Задергиваешь шторы и… ты в движущемся поезде!
<Что!>
Судя по всему, вы каким-то образом находитесь в купе, которое выглядит точно так же, как ваша спальня.
В то время как минуту назад вы были на 100% уверены, что ваша спальня неподвижна, закреплена на Земле, все это было разорвано.
Думайте об этом как о чрезмерной шутке ваших сумасшедших друзей, которые только что проделали с этим много дополнительных миль.Судя по всему, после того, как вы устроили вечеринку всю субботу, они припарковали ваше нокаутированное тело в заранее подготовленной копии вашей комнаты в кабине поезда и ждали, пока вы сойдете с ума — и это сработало!
Теперь вся эта история кажется маловероятной, особенно та ее часть, где вы не заметили, что все это время находились в движущемся поезде. Удивительно, но это, пожалуй, единственная доля правды в этой истории. Когда все было на своих местах, даже хладнокровный трезвый человек не мог знать, что он или она находится в движущемся поезде.Ваши друзья знали принцип инерциальных систем отсчета и рассчитывали на это.
Загадочно, но факт.
Идеализация этой истории
Для ясности давайте продолжим эту странную историю. Если мы стремимся понять парадоксальную природу инерциальных систем отсчета, мы должны добавить к уже выдуманному сценарию еще три столь же маловероятных предположения. По сути, мы собираемся провести здесь полноценный мысленный эксперимент!
- Во-первых, предположим, что поезд все время двигался с постоянной скоростью по прямой линии.Путь был прямым; за все время не было ни углов, ни возвышений.
- Во-вторых, мы предполагаем, что рельсы были очень гладкими. Не было ни стука, ни малейшей вибрации.
- В-третьих, мы предполагаем, что вы были лишены всех внешних улик. Окна были наглухо закрыты, шторы опущены — снаружи не было ни света, ни воздуха, ни звука все это время.
Итак, , почему вы не заметили, что находитесь в движущемся поезде ?
В этой статье.
Ответ на этот вопрос и понятие инерциальных систем отсчета в целом и составляет задачу данной статьи. Это для обычного читателя. Тем, кто хочет разобраться в инерционных системах отсчета в случайном, основанном на статьях формате текста. Таким образом, некоторые концепции могут показаться опытным людям слишком упрощенными, но это только для ясности. Я просто собираю вещи таким образом, чтобы (надеюсь) это имело смысл.
Хотя введение этой статьи намекает на специальную теорию относительности, а заключение намекает на специальную теорию относительности, эта статья в целом не посвящена специальной теории относительности.Специальная теория относительности используется здесь только для того, чтобы показать, как различные концепции в физике интегрируются друг с другом.
Закон инерции
С инерциальными системами отсчета тесно связано другое понятие, называемое инерцией. Это свойство, присущее всей материи, вынуждает тело поддерживать свое состояние либо в состоянии покоя, либо в движении с постоянной скоростью по прямой линии.
Проще говоря, покоящееся тело остается в покое, а движущееся тело продолжает двигаться с неизменной скоростью по прямой, если на него не действует неуравновешенная внешняя сила .
Это утверждение является первым законом движения Ньютона, также называемым законом инерции; это также формальное определение инерции.Это может показаться простым и, возможно, самым интуитивным законом во всей физике, но не будьте так уверены. А пока запомните это утверждение, мы вернемся к нему позже.
Что мы подразумеваем под системами отсчета
Не будучи слишком формальным, вы можете думать о системе отсчета как о части пространства, в котором происходит физическое событие, которое можно наблюдать.Таким образом, у нас есть все формы системы отсчета, такие как лабораторная система отсчета, система отсчета в классе или система отсчета в спальне, и если мы хотим быть более общими, мы можем иметь манхэттенскую систему отсчета. или даже система отсчета Земли.
Буквально, когда вы просыпаетесь утром, вы находитесь в своей системе отсчета спальни , вы идете в душ и находитесь в своей ванной системе отсчета . Вы прыгаете в свою машину, вы находитесь в своей системе отсчета автомобиля , вы добираетесь до своего офиса, и вы находитесь в своей системе отсчета офиса и так далее.
В нашем предыдущем сценарии поезда мы могли бы сказать, что вы находитесь в системе отсчета поезда , а ваша подруга Эми, которая стоит на Земле, находится в системе отсчета Земли (имеет смысл?).
Несмотря на то, что существует бесчисленное множество систем отсчета, все они могут быть сгруппированы только в две категории: инерциальные и неинерциальные системы отсчета.
Системы отсчета и закон инерции.
Физики используют закон инерции для определения «инерциальной системы отсчета» из целого набора систем отсчета.
Подумайте о ситуации «проснуться в поезде» во вступлении к этой статье.
Предположим, вы еще не знаете, что находитесь в движущемся поезде и просто лежите в постели, пытаясь вспомнить, что произошло прошлой ночью.
Внезапно вы оглядываетесь и видите, как ваш телефон соскальзывает с прикроватной тумбочки и падает на пол.
(Предположим, что машинист немного сбавил скорость — но вы этого не знаете)
Вы не знаете, что (или кто) заставило телефон соскользнуть и упасть.
С вашей точки зрения, это движение вашего телефона прямо противоречило бы закону инерции, который требует, чтобы покоящихся тела оставались в покое, если на них не действует сила . Но вы не можете придумать никакой силы, которая действовала на телефон.
Возможно, произошло одно из следующих событий:
- Вы все еще в похмелье, дезориентированы и воображаете вещи.
- Ты спишь.
- Это волшебство
- Закон инерции может быть ошибочным
Давайте остановимся на четвертом варианте, так как он наиболее важен для нашего обсуждения.Если закон инерции неверен, то объекты, первоначально покоящиеся, могут начать двигаться сами по себе без каких-либо сил, принуждающих их. Это объяснило бы загадку.
Ограничение закона инерции.
Что ж, оказывается, закон инерции не так универсален, как мы сначала предполагали. Это не универсально; закон действует только в особых ситуациях – инерциальных системах отсчета!
На самом деле, по определению, инерциальная система отсчета — это та, в которой выполняется закон инерции.Если закон инерции каким-либо образом нарушается, то какой бы ни была эта система отсчета, она не является инерциальной системой отсчета.
Хорошим примером инерциальной системы отсчета является Земля. Если вы оставите объект в покое, он останется в покое навсегда, а движущийся будет продолжать двигаться с равномерным движением, если на объект не действует результирующая внешняя сила. В земной системе отсчета закон инерции выполняется для большинства практических целей.
Примером неинерционной рамы является автомобиль, движущийся по каменистой дороге или поворачивающий за угол.Если бы вы положили книгу на приборную доску, она бы как-то соскользнула или сдвинулась, даже если к книге не применялась сила. Это связано с тем, что система отсчета, в данном случае система отсчета автомобиля, ускоряется, поэтому закон инерции здесь не действует.
В этой системе координат мы имеем то, что физики называют фиктивными силами или псевдосилами для объяснения закона инерции. Проще говоря, физика становится намного сложнее в этих системах отсчета, потому что мы должны учитывать эти воображаемые силы.
Например, когда в нашей истории поезд замедляет ход, книги могут падать с полки, телефон соскальзывает с прикроватной тумбочки, и вас толкает к краю кровати. Вы не можете объяснить эти силы со своей точки зрения; закон инерции не соблюдается. Чтобы объяснить закон инерции в такой сцене, вы должны ввести мнимые силы.
Система отсчета поезда против системы отсчета Земли.
Так как инерция реализуется для тел, покоящихся и тел, движущихся с равномерным движением, то закон инерции справедлив и в системе отсчета, покоящейся или в системе отсчета, движущейся с равномерным движением относительно другой системы отсчета ссылки.
Учитывая наш сценарий в поезде, ваша комната в поезде и ваша комната обратно на «неподвижной» Земле содержат инерциальные системы отсчета. Один из них неподвижен, а другой движется с равномерным движением относительно другого.
Тела (такие как ваша кровать, телефон и все в вашей комнате, включая вас самих), содержащиеся в этих двух разных сценах, проявляют одну и ту же инерцию — одно и то же сопротивление изменениям в движении. Что касается тел, то оба сценария совершенно аналогичны благодаря инерции, развиваемой телами в двух средах.
У вас было преимущество перед всеми остальными в вашей комнате в том, что вы воспринимали окружающую среду с помощью своих пяти чувств. Вот почему нам пришлось пойти на многое, чтобы лишить вас всех улик, указывающих на то, что вы находитесь в движущемся поезде, ваше тело, как и все остальное в комнате, вело себя таким образом, что было бы неотличимо от того, что оно вело бы в неподвижном состоянии . Настройка .
Инерциальные системы отсчета и законы физики.
Одним из интересных свойств инерциальных систем отсчета является то, что законы механики выполняются во всех инерциальных системах отсчета совершенно одинаково.
Это имеет решающее значение для причины, по которой вы не заметили движения поезда. Законы механики, которые работают на земле, также будут работать в любой системе отсчета, движущейся с постоянной скоростью по отношению к земле, например, в вашем поезде.Таким образом, вы не могли заметить ничего особенного, когда растягивались или прыгали со скакалкой, потому что те же самые законы, которые управляют упругостью и свободным падением объектов на земле, работают точно так же в вашей системе отсчета поезда.
Если бы твоя подруга Эми позвонила тебе и сразу сказала, что ты в движущемся поезде, ты бы ей не поверил.Пока поезд продолжал двигаться прямолинейно по гладкому рельсу с постоянной скоростью, у вас не было возможности узнать, что вы движетесь.
На самом деле, единственный способ понять, что вы находитесь в движущемся поезде, это поднять шторы и увидеть пейзаж, проносящийся мимо вас.
Нет никакого эксперимента, который вы могли бы провести в поезде и который позволил бы вам узнать, что вы движетесь относительно земли.
Это вводит важный факт: наблюдатели в разных инерциальных системах отсчета, как правило, не согласятся, кто движется, а кто неподвижен.
Все эксперименты, которые они проводят, приведут к одинаковым результатам. Не существует эксперимента, который мог бы установить, кто движется, а кто стоит на месте.
На самом деле законы физики одинаковы во всех инерциальных системах отсчета .
Это принцип специальной теории относительности, предложенный Альбертом Эйнштейном в 1905 году.
Альберту Эйнштейну приписывают специальную теорию относительности. Теория, которая вращается вокруг наблюдений, сделанных наблюдателями в разных системах отсчета.Кто тогда движется?
Поскольку законы физики одинаковы во всех инерциальных системах отсчета, то наблюдатели в разных инерциальных системах отсчета не договорятся о том, кто движется, а кто неподвижен. Все, что они могут сказать, это то, что «Наблюдатель X» движется с определенной скоростью относительно меня.
Фраза «Я стою на месте» имеет смысл только тогда, когда вы указываете, с какой точки отсчета вы стоите на месте. Это может быть Земля, автобус или поезд.
Следовательно, согласно физике, вопрос: «Действительно ли я стою на месте?» на самом деле ничего не значит, если мы не укажем систему отсчета.Вы вполне можете стоять неподвижно в одной системе отсчета и двигаться в другой. Подробнее об этом читайте в статье, что такое движение.
Заключение
Нельзя переоценить важность систем отсчета. Физика была бы очень запутанной, если бы мы не проводили полезного различия между инерциальной и неинерциальной системами отсчета. Например, законы физики в своей простейшей форме формулируются в инерциальной системе отсчета. В неинерциальной системе отсчета мы должны учитывать другие фиктивные силы, действующие на объект, потому что закон инерции в этих системах отсчета недействителен.
Это, конечно, неформальное введение в инерциальные системы отсчета. Если вы ищете более формальный анализ этих концепций, включая принцип относительности и фиктивные силы, перейдите по этим ссылкам в Википедии. Что касается книги для начинающих, ознакомьтесь с «Специальной теорией относительности » Дэвида Морина для энтузиастов-новичков . В качестве электронной книги вы можете прочитать первую главу книги Брайана Грина «Элегантная вселенная ». Или вы можете втиснуть все это (включая эту статью), посмотрев это чудесно сделанное видео на YouTube (это около 30 минут, но оно того стоит!)
Системы отсчетаТеоретики квантовой информации создают новое «понимание» квантовой механики
Рисунок 1.Измерение вращения Штерна-Герлаха (SG). Кредит: Тимоти МакдевиттРичард Фейнман однажды сказал: «Думаю, я могу с уверенностью сказать, что никто не понимает квантовую механику». Поскольку Фейнман получил Нобелевскую премию по физике за свою работу в области квантовой теории, он определенно понял, как ее использовать. Действительно, квантовая механика (КМ) «выдержала все испытания» и «мы все знаем, как ее использовать и применять к задачам», однако Мюррей Гелл-Манн (который также получил Нобелевскую премию за свою работу в области квантовой теории) согласился с этим. Фейнман, говоря: «Мы научились жить с тем фактом, что никто не может этого понять.»
Они имели в виду, что фундаментальные принципы, на которых строится QM, являются математически абстрактными, поэтому они не «имеют смысла» сами по себе. Поскольку физика является редуктивной объяснительной дисциплиной, фундаментальные принципы или аксиомы теории сами по себе не могут быть объяснены с помощью этой теории. Поэтому, если теорию нужно «понять», эти фундаментальные принципы или аксиомы должны «иметь смысл» сами по себе. В ответ на такое положение вещей теоретики квантовой информации реорганизовали математическую структуру КМ в попытке открыть теоретико-информационные аксиомы, лежащие в основе КМ, которые «имеют смысл», чтобы КМ можно было «понять».» То, что они обнаружили, может вас удивить.
Требования к реконструкции QM
Люсьену Харди обычно приписывают создание первой из этих «аксиоматических реконструкций КМ, основанных на принципах теории информации» в его статье 2001 года «Квантовая теория из пяти разумных аксиом». С тех пор было произведено гораздо больше таких реконструкций, и в сообществе квантовой информации есть волнение по поводу этих теоретико-информационных реконструкций КМ.Например, Маркус Мюллер сказал:
.Можно ли вывести квантовую теорию из простых принципов, подобно тому как преобразования Лоренца можно вывести из принципа относительности и постоянства скорости света? Захватывающий ответ — «да», и наша группа внесла существенный вклад в достижение этой исследовательской цели.
Рис. 2. Последовательные измерения спина SG. Кредит: Энтропия 2022, 24(1), 12Как видно из его заявления, цель состоит в том, чтобы найти аксиомы для КМ, которые «имеют смысл», подобно постулатам специальной теории относительности (СТО) Эйнштейна.
Напоминаю, что первым из постулатов СТО Эйнштейна является принцип относительности: «Законы физики должны быть одинаковыми во всех инерциальных системах отсчета», также известный как «нет предпочтительной системы отсчета» (NPRF). Второй постулат (также известный как «постулат света») заключается в том, что «все измеряют одинаковую скорость света, 90 559 c 90 560, независимо от их движения относительно источника», и он, возможно, следует из NPRF. То есть уравнения электромагнетизма Максвелла, которые являются законами физики, предсказывают значение для 90 559 c 90 560 , поэтому NPRF подразумевает, что все должны измерять одно и то же значение.Сочетание принципа относительности и постулата света (кратко «NPRF + c «) приводит к кинематической структуре, лежащей в основе СТО, называемой пространством Минковского с его преобразованиями Лоренца между инерциальными системами отсчета. Таким образом, Крис Фукс говорит, что было бы «полезно попытаться свести математическую структуру квантовой механики к некоторым четким физическим утверждениям», подобным утверждениям СТО.
Что открыли теоретики квантовой информации
В оригинальной статье Харди 2001 года он отметил, что, удалив единственное слово «непрерывный» из его пятой аксиомы, «существуют непрерывные обратимые преобразования между чистыми состояниями», его пять «разумных» аксиом производят классическую теорию вероятностей вместо квантовой теории вероятностей.С тех пор многие теоретики квантовой информации признали важность «непрерывной обратимости» в своих аксиоматических реконструкциях КМ. Например, Адам Кобернински и Маркус Мюллер сказали: «Мы предполагаем, что (непрерывная) обратимость может быть постулатом, наиболее близким к тому, чтобы быть кандидатом на проблеск подлинно физического ядра «квантовой реальности»».
Рис. 3. Классически ожидаемый результат последовательных измерений спина SG. Кредит: Энтропия 2022, 24(1), 12Каслав Брукнер и Антон Цайлингер прекрасно подхватили это в своем фундаментальном информационно-теоретическом принципе информационной неизменности и непрерывности:
Суммарная информация одного бита инвариантна при непрерывном изменении между различными комплектами взаимодополняющих измерений.
Как видите, принципы квантовой теории информации — очень общие утверждения. Это сделано намеренно, поскольку теоретики квантовой информации ищут принципы, которые можно применить к максимально широкому набору физических реализаций. Хотя эта общность делает их очень мощными объяснительными принципами, неудачным следствием этого является то, что принципы теории информации не столь прозрачны, как постулаты СТО Эйнштейна. Таким образом, некоторые из нас, работающие над основами квантовой механики, но не над квантовой теорией информации как таковой, не полностью оценили основополагающие последствия таких принципов, как информационная неизменность и непрерывность.Следовательно, не все в основах квантовой механики находят принципы теории информации полезными для «понимания» КМ.
Выделение важных выводов
Чтобы помочь другим людям, таким как мы (физику В. М. Стаки, математику Тимоти Макдевитту и философу Майклу Зильберштейну), оценить объяснительную силу этих реконструкций КМ, мы опубликовали «Нет предпочтительной системы отсчета в Фонде квантовой механики». В этой статье мы объясняем, как фундаментальный принцип информационной инвариантности и непрерывности на самом деле влечет за собой принцип относительности, примененный к инвариантному измерению постоянной Планка ч , в точной аналогии с NPRF + c для SR.Мы сделали это, выбрав соответствующую физическую реализацию, т. е. измерение спина Штерном-Герлахом (SG).
Рис. 4. Два полных набора взаимодополняющих измерений спина, связанных пространственным вращением. Кредит: Энтропия 2022, 24(1), 12Рисунок 1 представляет собой схему, показывающую измерение спина SG пучка электронов, например, через валентный электрон атома серебра в исходном эксперименте. Магниты СГ выравниваются по оси z и получают два результата измерения спина, т.е.т. е. вверх (+1) и вниз (-1) относительно z-шляпы. Думая о каждом электроне как о обладающем магнитным моментом, случайно ориентированным в пространстве, мы классически ожидали бы, что такое измерение вызовет все возможные отклонения электронного луча. [Примечание: магнитное поле SG вблизи северного полюса сильнее, чем у южного полюса, поэтому преобладает его влияние на электроны.]
Поскольку, как показано на рис. 1, измерение дает только два отклонения, вверх и вниз, мы можем предположить, что по какой-то странной причине источник производит только электроны с магнитными моментами, выровненными или противоположными вдоль z-шляпы.В этом случае, если мы проведем последующее измерение вращения луча со спином вверх (S = +1 z-hat) вдоль нового направления b-hat, повернутого на тета относительно z-hat (рис. 2), мы просто ожидаем уменьшенное отклонение луча cos(theta) вдоль b-шляпы (рис. 3). Но загадочным образом мы продолжаем видеть только отклонения вверх и вниз по направлению b-hat, точно так же, как мы видели по z-hat (рис. 2).
Как указывает Стивен Вайнберг, эти измерения вращения SG представляют собой измерение (плюс-минус) «универсальной постоянной природы, постоянной Планка ч » ( ч , разделенной на 4 пи, если быть точным).Таким образом, кто-то мог бы использовать открытие Планком этой универсальной постоянной природы через его уравнение излучения черного тела (закон физики) вместе с принципом относительности, чтобы предсказать это загадочное свойство спина электрона до эксперимента Штерна-Герлаха. В случае измерений c разные инерциальные системы отсчета связаны разными относительными скоростями. В случае измерений СГ ч разные инерциальные системы отсчета связаны разной взаимной ориентацией в пространстве (рис. 4).«Ускорения» и «пространственные вращения» являются действительными преобразованиями между инерциальными системами отсчета как в преобразованиях Галилея, так и в преобразованиях Лоренца.
Все это следует как частный пример принципа информационной неизменности и непрерывности. Бит информации (результат измерения плюс-минус ч , рис. 1) сохраняется (должен быть одинаковым, рис. 2) при непрерывном изменении между разными комплектами взаимодополняющих [спиновых] измерений (между разными инерциальными системами отсчета). связаны пространственными вращениями, рис. 4).И требование, чтобы распределение результатов 90 559 усредняло 90 560 по cos(theta) (рис. 3), дает распределение результатов измерения спина в соответствии со структурой кубитового гильбертова пространства, лежащей в основе аксиоматических реконструкций КМ.
Таким образом, теоретики квантовой информации показали, что NPRF + h приводит к кинематической структуре в основе КМ, называемой гильбертовым пространством, в точной аналогии с NPRF + c , ведущей к кинематической структуре в основе СТО, называемой пространством Минковского. (Рисунок 5).
Рис. 5. Принцип относительности в основе КМ и СТО. Кредит: В.М. СтакиУдивительный результат?
Если соединить принцип относительности с теорией относительности, то покажется невозможным, чтобы принцип относительности лежал в основе нерелятивистской квантовой механики. Но принцип относительности не ограничивается законами классической физики, он относится ко всем физикам.И то, что в основе теории лежит принцип относительности, не означает, что теория является «релятивистской». Ньютоновская механика с ее преобразованиями Галилея между инерциальными системами отсчета соответствует принципу относительности, и ньютоновская механика, безусловно, «нерелятивистская». Таким образом, нет оснований априори отвергать этот результат как невозможный.
Заключение
Практически все вводные учебники по физике вводят SR через NPRF + c , потому что NPRF + c «имеет смысл» для большинства физиков.Таким образом, никто не слышит, чтобы лауреаты Нобелевской премии по физике говорили: «Никто не понимает специальную теорию относительности». Будем надеяться, что NPRF + h поможет физикам «разобраться» в информационной инвариантности и непрерывности в основе аксиоматических реконструкций квантовой механики, и нобелевские лауреаты по физике больше не будут говорить: «Никто не понимает квантовую механику».
Эта история является частью диалога Science X Dialog, где исследователи могут сообщать о результатах своих опубликованных научных статей. Посетите эту страницу для получения информации о ScienceX Dialog и о том, как принять в нем участие.
Дополнительная информация: Уильям Стаки и др., Нет предпочтительной системы отсчета в Фонде квантовой механики, 90 559, энтропия 90 560 (2022). DOI: 10.3390/e24010012
Биография: Уильям Стаки получил докторскую степень по физике в 1987 году, защитив диссертацию по общей теории относительности (руководитель диссертации Луи Виттен), и начал преподавать физику в Элизабеттаунском колледже в 1988 году.
- E=m0c2[1+12(vc)2+38(vc)4+516(vc)6+…].Часть {2}} не имеет значения, так как она постоянна. По той же причине в теории относительности можно вычесть энергию покоя из полной энергии. Чтобы увидеть, имеет ли энергия покоя какой-либо физический смысл, необходимо рассмотреть испускание и поглощение энергии в разных системах отсчета.
-
- mотн=m01−v2c2.{2}}, когда объект движется.


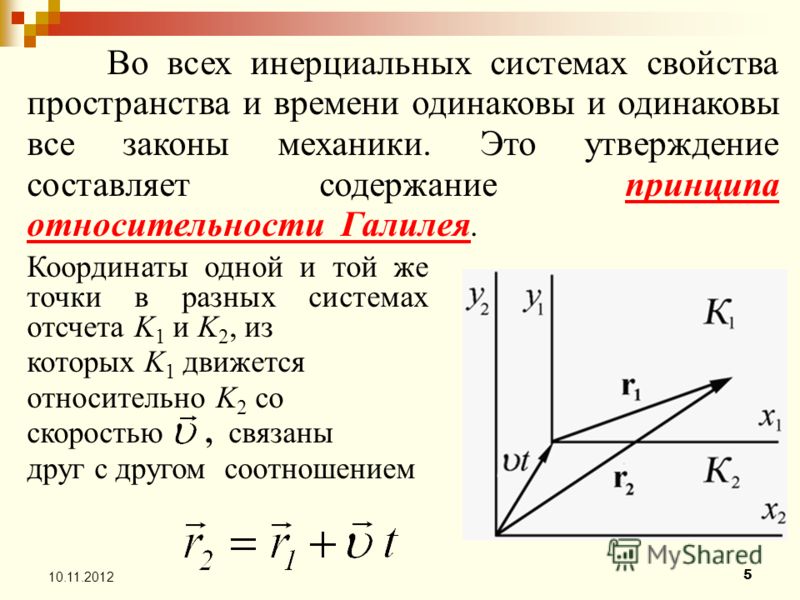 Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными скоростями и начальными координатами тел. А начальные скорости и начальные координаты данного тела относительно разных систем отсчета различны.
Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными скоростями и начальными координатами тел. А начальные скорости и начальные координаты данного тела относительно разных систем отсчета различны.