ГДЗ Алгебра 10 класс Александрова
Алгебра 10 класс
Самостоятельные работы (Базовый уровень)
Александрова
Мнемозина
Вроде бы в десятом классе школьники уже много знают и многое умеют, но это не избавляет их от проблем в учебе. Наоборот, порой кажется, что все, изучаемое ранее напрочь стерлось из их памяти, и они начинают допускать элементарные ошибки. Такая несуразица может негативно сказаться на результатах контрольных и прочих проверок, поэтому подросткам стоит собраться с мыслями и приложить побольше усилий к освоению новых тем. Поможет им справиться с трудностями и лучше усвоить материал решебник к учебнику «Алгебра и начала математического анализа. Самостоятельные работы 10 класс (базовый уровень)» Александрова.
Параметры учебного пособия
Сборник содержит сорок восемь самостоятельных работ, которые охватывают всю тематику этого учебного курса. Задания распределены по четырем вариантам, поэтому подготовка будет носить всесторонний и более полноценный характер.
Реальна ли его поддержка
Надобность контрольных работ неоспорима, но вот готовиться к ним порой сущее мучение. Пытаясь успеть за школьной программой подростки порой упускают некоторые нюансы. И хотя в начале это не особо заметно, так как учителя материал не спрашивают, а с д/з можно справиться довольно легко, ведь не проблема найти широкую поддержку в интернете. Но вот при первых же испытаниях сразу можно провалиться, если задание будет касаться тех аспектов, которые были упущены ранее. Подготовиться ко всякого рода неожиданностям можно при помощи решебника к учебнику «Алгебра и начала математического анализа. Самостоятельные работы 10 класс (базовый уровень)» Александрова. «Мнемозина», 2017 г.
Похожие ГДЗ Алгебра 10 класс
Название
Условие
Решение
Математика.
 10 класс. Уровень стандарта: тетрадь для оценивания результатов обучения. В 2 частях. Ч1. Алгебра, цена 25 грн
10 класс. Уровень стандарта: тетрадь для оценивания результатов обучения. В 2 частях. Ч1. Алгебра, цена 25 грн Математика. 10 класс. Уровень стандарта: тетрадь для оценивания результатов обучения. В 2 частях. ЧАСТЬ 1. Алгебра и начала анализа
Корниенко Т.Л., Фиготина В.И.
Код:123-Т949023Р
Количество страниц:64
Формат, мм:170х260
Вес:0.0900 кг
Обложка:Мягкая
Язык издания:Рус.
АННОТАЦИЯ
Тетрадь соответствует требованиям новой учебной программы по математике (уровень стандарта) для учащихся 10–11 классов общеобразовательных учебных заведений и предназначена для текущего и итогового оценивания учебных достижений учащихся по алгебре и началам анализа.
В пособии представлены два вида проверочных работ — самостоятельные и контрольные работы, которые приведены в двух равноценных вариантах. Содержание работ позволяет оценить уровень усвоения учащимися учебного материала каждой темы или ее части.
Кроме классических, в пособии предложены работы компетентностного характера — одна самостоятельная по каждой теме и одна контрольная в конце пособия.
 Степенные функции, их свойства и графики
Самостоятельная работа № 5. Функции, их свойства и графики
Контрольная работа № 1. Функции, их свойства и графики
Самостоятельная работа № 6. Синус, косинус, тангенс угла. Радианное измерение углов. Тригонометрические функции числового аргумента
Самостоятельная работа № 7. Основные соотношения между тригонометрическими функциями одного аргумента
Самостоятельная работа № 8. Формулы приведения
Самостоятельная работа № 9. Периодичность функций. Свойства и графики тригонометрических функций
Самостоятельная работа № 10. Формулы сложения и следствия из них
Самостоятельная работа № 11. Применение формул сложения и следствий из них
Самостоятельная работа № 12. Простейшие тригонометрические уравнения
Самостоятельная работа № 13. Тригонометрические функции
Контрольная работа № 2. Тригонометрические функции
Самостоятельная работа № 14. Производная функции, ее геометрический и физический смысл
Самостоятельная работа № 15. Правила вычисления производных
Самостоятельная работа № 16.
Степенные функции, их свойства и графики
Самостоятельная работа № 5. Функции, их свойства и графики
Контрольная работа № 1. Функции, их свойства и графики
Самостоятельная работа № 6. Синус, косинус, тангенс угла. Радианное измерение углов. Тригонометрические функции числового аргумента
Самостоятельная работа № 7. Основные соотношения между тригонометрическими функциями одного аргумента
Самостоятельная работа № 8. Формулы приведения
Самостоятельная работа № 9. Периодичность функций. Свойства и графики тригонометрических функций
Самостоятельная работа № 10. Формулы сложения и следствия из них
Самостоятельная работа № 11. Применение формул сложения и следствий из них
Самостоятельная работа № 12. Простейшие тригонометрические уравнения
Самостоятельная работа № 13. Тригонометрические функции
Контрольная работа № 2. Тригонометрические функции
Самостоятельная работа № 14. Производная функции, ее геометрический и физический смысл
Самостоятельная работа № 15. Правила вычисления производных
Самостоятельная работа № 16.
Контрольная работа по теме Формулы приведения и сложения для 10 класса
Автор публикации: Стогова Н.Л.
Краткое описание:
…Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ I
Вычислите:
а) sin150º;
б) cos29ºcos16º — sin29ºsin16º;
в) sin240º + cos [pic] ;
г) [pic] ;
д) ctg1ºctg2ºctg3º [pic] … [pic] ctg88◦ [pic] ctg89º
Найдите значение трех других тригонометрических функций угла [pic] :
cosα= [pic] и [pic]
Упростите выражение:
а) [pic] ;
б) [pic] ;
в) [pic]
Найдите наибольшее значение выражения [pic]
Вычислите при данных условиях [pic] , если tg [pic] =2
_________________________________________________________________________
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ II
Вычислите:
а) cos240º;
б) sin29ºcos16º +sin16ºcos29º;
в) cos150º + sin [pic] ;
г) [pic] ;
д) tg1ºtg3ºtg5º [pic] … [pic] tg89º
Найдите значение четырех основных тригонометрических функций угла [pic] :
sinα= [pic] и [pic]
Упростите выражение:
а) [pic] ;
б) [pic] ;
в) [pic]
Найдите наибольшее значение выражения [pic]
Вычислите при данных условиях [pic] , если tg [pic] =3
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ III
Вычислите:
а) sin390º;
б) cos76ºcos31º + sin76ºsin31º;
в) sin530º — cos [pic] ;
г) [pic] ;
д) tg88ºtg86ºtg84º [pic] … [pic] tg2º
Найдите значение четырех основных тригонометрических функций угла [pic] :
25sin² [pic] + 5sin [pic] — 12 = 0 и [pic]
Упростите выражение:
а) [pic] ;
б) [pic] ;
в) [pic]
Найдите наибольшее значение выражения [pic]
Вычислите при данных условиях [pic] , если сtg [pic] = [pic]
_____________________________________________________________________________
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ IV
Вычислите:
а) cos420º;
б) sin76ºcos31º — sin31ºcos76º;
в) cos770º — sin [pic] ;
г) [pic] ;
д) ctg2ºctg4ºctg6º…ctg88º
Найдите значение четырех основных тригонометрических функций угла [pic] :
25cos² [pic] — 5cos [pic] — 12 = 0 и [pic]
Упростите выражение:
а) [pic] ;
б) [pic] ;
в) [pic]
Найдите наибольшее значение выражения [pic]
Вычислите при данных условиях [pic] , если tg [pic] = [pic]
Что такое коэффициент масштабирования? — Определение, формула и примеры — Видео и стенограмма урока
Использование масштабного коэффициента
Если две цифры похожи, то вы можете связать разные характеристики фигуры с помощью масштабного коэффициента. В качестве примера представьте себе два одинаковых квадрата. У одного длина стороны 2 дюйма, а у другого — 4 дюйма. Это дает масштабный коэффициент 1: 2 от маленького квадрата к большому квадрату.
В качестве примера представьте себе два одинаковых квадрата. У одного длина стороны 2 дюйма, а у другого — 4 дюйма. Это дает масштабный коэффициент 1: 2 от маленького квадрата к большому квадрату.
Чтобы получить длину стороны одного квадрата с учетом длины стороны другого, вы можете умножить или разделить на коэффициент масштабирования. Давайте посмотрим на квадраты, показанные выше.
Предположим, вам сказали, что меньший квадрат имеет длину стороны 2 дюйма, а масштабный коэффициент от меньшего к большему составляет 1: 2. Помните, это означает, что 1 дюйм в меньшем квадрате равен 2 дюймам в большем квадрате. . Если мы умножим на коэффициент масштабирования 1/2, мы получим меньшее число.Поэтому мы должны «разделить» на коэффициент масштабирования, чтобы получить большее число.
Мы видим, что этот результат соответствует картинке.
Чтобы получить периметр одного квадрата по периметру другого, вы можете умножить или разделить его на масштабный коэффициент. Меньший квадрат имеет периметр 8 дюймов. Мы хотим найти периметр большего квадрата. Нам снова нужно будет разделить на коэффициент масштабирования 1: 2.
У большего квадрата будет периметр 16 дюймов.Имеет ли это смысл? Спросите себя: «Я перехожу от меньшей фигуры к большей или от большей к меньшей?» В этом случае мы перешли от меньшего числа к большему, поэтому мы ожидаем, что наш ответ будет больше, чем исходный периметр. Следовательно, наш ответ имеет смысл!
Чтобы получить площадь одного квадрата по площади другого, вы можете умножить или разделить на квадрат масштабного коэффициента. В нашем примере меньший квадрат имеет площадь 4 квадратных дюйма. Так же, как мы разделили на коэффициент масштабирования, чтобы определить периметр большего квадрата, мы теперь разделим на квадрат коэффициента масштабирования.
Так же, как мы разделили на коэффициент масштабирования, чтобы определить периметр большего квадрата, мы теперь разделим на квадрат коэффициента масштабирования.
Чтобы получить объем одного куба с учетом объема другого, вы можете умножить или разделить на куб масштабный коэффициент. Чтобы решить, следует ли вам умножать или делить, вы должны учитывать значение коэффициента масштабирования и переходить от большего к меньшему значению или от меньшего к большему.
Представьте, что вместо квадратов у нас есть два куба, похожие на большие игральные кости. У меньшего куба длина стороны 2 дюйма, а у другого — 6 дюймов.Объем первого куба составляет 8 кубических дюймов, а масштабный коэффициент от большего куба к меньшему равен 3: 1. Чтобы найти объем большего куба, мы можем умножить на куб масштабный коэффициент (обратите внимание, как наш масштабный коэффициент больше единицы; мы знаем, что хотим получить больший ответ, поэтому мы умножаем, а не делим).
Таким образом, объем второго куба составляет 216 кубических дюймов. Проверяя нашу работу, мы видим, что:
Мы можем использовать эти примеры определения длины стороны, периметра, площади и объема для любой пары похожих фигур.Это делает знание масштабного коэффициента невероятно полезным.
Пример задач из математического класса
Вы можете показать, что две фигуры похожи, найдя масштабный коэффициент для каждой пары соответствующих сторон. На картинке красная и черная фигуры слева похожи, а цифры справа — нет.
Мы можем записать отношения соответствующих сторон — обратите внимание, что цифры обращены в противоположные стороны, поэтому мы должны быть осторожны, чтобы сопоставить самую короткую сторону с самой короткой стороной, самую длинную сторону с самой длинной стороной и так далее. Начиная с диагональной стороны каждой фигуры, получаем:
Начиная с диагональной стороны каждой фигуры, получаем:
| BD: JK | AB: IK | переменного тока: HI | CD: HJ |
|---|---|---|---|
| 2,82: 1,41 | 4: 2 | 2: 1 | 2: 1 |
Все эти отношения равны, поэтому цифры аналогичны.
Во второй паре цифр мы получаем следующие соотношения, переходя от красного к черному:
| BD: JK | AB: IK | переменного тока: HI | CD: HJ |
|---|---|---|---|
| 2.82: 4.47 | 4: 4 | 2: 4 | 2: 2 |
Легко видеть, что эти соотношения не равны. Поэтому цифры не похожи.
Если вам сказали, что две цифры похожи, то вы можете использовать масштабный коэффициент, чтобы найти недостающую длину стороны. Например, треугольники на этой картинке похожи. Нам говорят, что масштабный коэффициент от зеленого треугольника к черному равен 1: 2, а длина сторон зеленого треугольника составляет 3, 4 и 5 единиц. Какова длина сторон черного треугольника?
Какова длина сторон черного треугольника?
Поскольку коэффициент масштабирования от зеленого к черному равен 1: 2, это означает, что на каждую единицу длины зеленого треугольника приходится 2 единицы длины черного треугольника. Итак, длины сторон черного треугольника вдвое больше, чем соответствующие стороны зеленого треугольника. Следовательно, черный треугольник имеет длину стороны 6, 8 и 10 единиц.
Чтение чертежей
Масштабный коэффициент критически важен для чертежей. Если здание или его часть должны быть построены должным образом, необходимо точно следовать плану. Некоторые распространенные масштабы чертежей — 1:20, или 1:50, и 1: 4, или 1: 8. Если чертеж имеет масштаб 1: 4, это означает, что один дюйм на чертеже равен 4 дюймам на готовом. часть. Окно шириной 28 дюймов в готовом здании, следовательно, будет 7 дюймов на чертеже в масштабе 1: 4.
Фигурки моделей
Конструирование моделей — популярное хобби.Модели автомобилей, поездов и фигурок созданы в масштабе, чтобы выглядеть более реалистично. Некоторые общие модели автомобилей имеют масштаб 1:18, 1:24 и 1:25. Это означает, что размер модели составляет 1/18, 1/24 или 1/25 от фактического размера автомобиля. Когда второе число в масштабном коэффициенте становится больше, размер модели становится меньше по сравнению с реальным объектом. На изображении, представленном здесь, модель автомобиля выполнена в масштабе 1:36. Один дюйм на модели равен 36 дюймам на реальной машине.
Краткое содержание урока
Масштабный коэффициент используется во многих приложениях, в которых используются аналогичные фигуры, включая чертежи и модели. Масштабный коэффициент представляет собой сравнение размера одной геометрической фигуры и размера аналогичной геометрической фигуры. Чтобы найти коэффициент масштабирования между двумя похожими фигурами, найдите две соответствующие стороны и запишите соотношение этих двух сторон.
Масштабный коэффициент представляет собой сравнение размера одной геометрической фигуры и размера аналогичной геометрической фигуры. Чтобы найти коэффициент масштабирования между двумя похожими фигурами, найдите две соответствующие стороны и запишите соотношение этих двух сторон.
Если вы начнете с меньшего числа, ваш масштабный коэффициент будет меньше единицы. Если вы начнете с большей цифры, ваш масштабный коэффициент будет больше единицы. Отношение площади одной фигуры к площади другой аналогичной фигуры равно квадрату масштабного коэффициента между двумя фигурами.Отношение объема одной фигуры к объему другой подобной фигуры равно кубу масштабного коэффициента между двумя фигурами.
Результаты обучения
Когда вы закончите, вы сможете:
- Объяснить, что такое коэффициент масштабирования
- Найдите коэффициент масштабирования между двумя похожими фигурами
- Перечислите некоторые варианты использования масштабных коэффициентов в реальной жизни
Работа, энергия и сила
Кинетическая энергия — это энергия движения. Объект, который движется — будь то вертикальное или горизонтальное движение — обладает кинетической энергией. Существует много форм кинетической энергии — колебательная (энергия, обусловленная колебательным движением), вращательная (энергия, обусловленная вращательным движением) и поступательная (энергия, обусловленная движением из одного места в другое). Чтобы не усложнять задачу, мы сосредоточимся на поступательной кинетической энергии. Количество поступательной кинетической энергии (далее фраза кинетическая энергия будет относиться к поступательной кинетической энергии), которую имеет объект, зависит от двух переменных: массы (m) объекта и скорости (v) объекта.Следующее уравнение используется для представления кинетической энергии (KE) объекта.
Объект, который движется — будь то вертикальное или горизонтальное движение — обладает кинетической энергией. Существует много форм кинетической энергии — колебательная (энергия, обусловленная колебательным движением), вращательная (энергия, обусловленная вращательным движением) и поступательная (энергия, обусловленная движением из одного места в другое). Чтобы не усложнять задачу, мы сосредоточимся на поступательной кинетической энергии. Количество поступательной кинетической энергии (далее фраза кинетическая энергия будет относиться к поступательной кинетической энергии), которую имеет объект, зависит от двух переменных: массы (m) объекта и скорости (v) объекта.Следующее уравнение используется для представления кинетической энергии (KE) объекта.
KE = 0,5 • м • v 2
где м = масса объекта
v = скорость объекта
Это уравнение показывает, что кинетическая энергия объекта прямо пропорциональна квадрату его скорости. Это означает, что при двукратном увеличении скорости кинетическая энергия увеличится в четыре раза.При трехкратном увеличении скорости кинетическая энергия увеличится в девять раз. А при четырехкратном увеличении скорости кинетическая энергия увеличится в шестнадцать раз. Кинетическая энергия зависит от квадрата скорости. Как часто говорят, уравнение — это не просто рецепт решения алгебраических задач, но и руководство к размышлениям о взаимосвязи между величинами.
Это означает, что при двукратном увеличении скорости кинетическая энергия увеличится в четыре раза.При трехкратном увеличении скорости кинетическая энергия увеличится в девять раз. А при четырехкратном увеличении скорости кинетическая энергия увеличится в шестнадцать раз. Кинетическая энергия зависит от квадрата скорости. Как часто говорят, уравнение — это не просто рецепт решения алгебраических задач, но и руководство к размышлениям о взаимосвязи между величинами.
Кинетическая энергия — скалярная величина; у него нет направления. В отличие от скорости, ускорения, силы и количества движения, кинетическая энергия объекта полностью описывается только величиной.2.
1 Джоуль = 1 кг • м 2 / с 2
Мы хотели бы предложить … Как скорость автомобиля (и, следовательно, его кинетическая энергия) влияет на расстояние, которое потребуется для его торможения до остановки? Взаимодействуйте, исследуйте и узнавайте ответ на этот вопрос с помощью нашей интерактивной программы «Тормозное расстояние».
 Вы можете найти его в разделе Physics Interactives на нашем сайте.Интерактивное средство «Тормозное расстояние» позволяет учащемуся исследовать влияние скорости на тормозной путь игрушечной машины.
Вы можете найти его в разделе Physics Interactives на нашем сайте.Интерактивное средство «Тормозное расстояние» позволяет учащемуся исследовать влияние скорости на тормозной путь игрушечной машины.
Проверьте свое понимание
Используйте свое понимание кинетической энергии, чтобы ответить на следующие вопросы. Затем нажмите кнопку, чтобы просмотреть ответы.
1. Определите кинетическую энергию автомобиля американских горок массой 625 кг, движущегося со скоростью 18.3 м / с.
2. Если бы американские горки в описанной выше задаче двигались с удвоенной скоростью, то какова была бы его новая кинетическая энергия?
3. Мисси Дьюотер, бывшая ныряльщица с платформы цирка братьев Ринглинг, имела кинетическую энергию 12 000 Дж незадолго до того, как попала в ведро с водой. Если масса Мисси 40 кг, то какова ее скорость?
4. 900-килограммовый компактный автомобиль, движущийся со скоростью 60 миль / час, имеет около 320 000 Джоулей кинетической энергии. Оцените его новую кинетическую энергию, если он движется со скоростью 30 миль / час. (ПОДСКАЗКА: используйте уравнение кинетической энергии как «руководство к размышлению».)
900-килограммовый компактный автомобиль, движущийся со скоростью 60 миль / час, имеет около 320 000 Джоулей кинетической энергии. Оцените его новую кинетическую энергию, если он движется со скоростью 30 миль / час. (ПОДСКАЗКА: используйте уравнение кинетической энергии как «руководство к размышлению».)
Формула восстановления — Что такое формула уменьшения? Примеры
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка.Работа с выражениями более высокой степени утомительна и утомительна, и здесь формулы редукции даны как простые выражения со степенью n для решения этих выражений более высокой степени. Эти формулы сокращения были получены из базовых формул интегрирования и работают с теми же правилами интегрирования.
Какова формула сокращения?
Следующие ниже формулы редукции полезны при работе с выражениями более высокой степени, включающими алгебраические переменные, функции тригонометрии, логарифмические функции. {2} (2 x) +1 / 2 \ ln \ sec (2 x) + C \)
{2} (2 x) +1 / 2 \ ln \ sec (2 x) + C \)
Часто задаваемые вопросы по формуле редукции
Что такое формула приведения?
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка. Работа с выражениями более высокой степени утомительна и утомительна, и здесь формулы редукции даны как простые выражения со степенью n для решения этих выражений более высокой степени. Следующие ниже формулы редукции полезны при работе с выражениями более высокой степени, включающими алгебраические переменные, тригонометрические функции, логарифмические функции.Формулы редукции представлены здесь в виде набора из четырех формул.
Какова цель формулы сокращения?
Формула приведения используется, когда данный интеграл нельзя вычислить иначе. Многократное применение формулы редукции помогает нам вычислить данный интеграл.
Что такое формула приведения в тригонометрии?
Следующие ниже формулы редукции полезны при работе с выражениями более высокой степени, включающими алгебраические переменные, функции тригонометрии, логарифмические функции.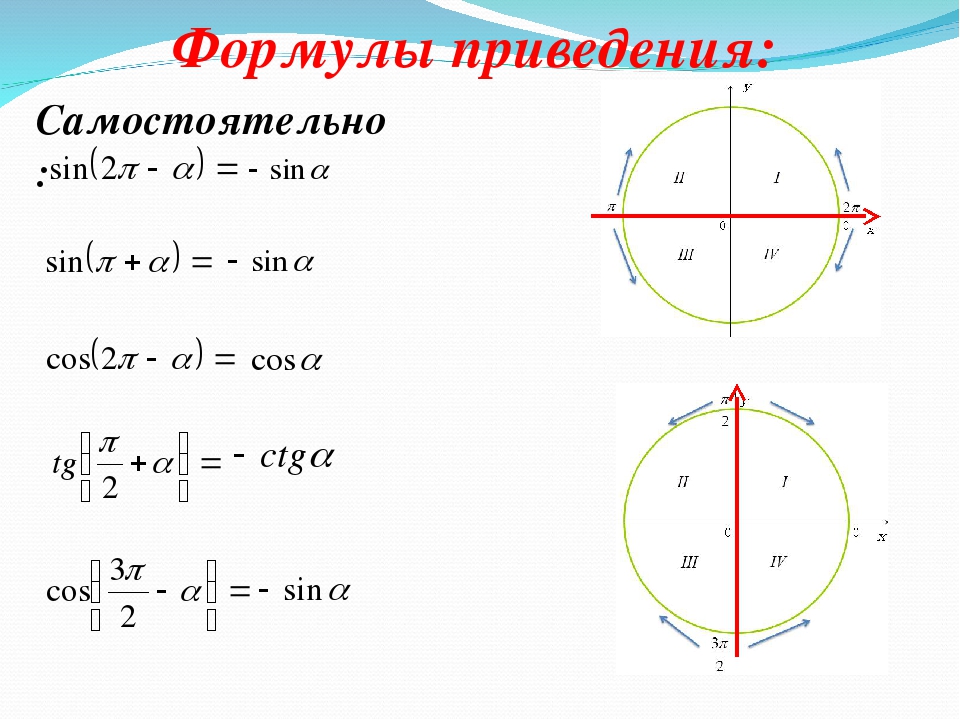 {n — 2} x.dx \)
{n — 2} x.dx \)
Какое количество домашних заданий правильное?
Многие учителя и родители считают, что домашнее задание помогает учащимся развить учебные навыки и пересмотреть концепции, изученные в классе. Другие считают домашнюю работу разрушительной и ненужной, ведущей к выгоранию и отвлекающим детей от школы. Десятилетия исследований показывают, что проблема более тонкая и сложная, чем думает большинство людей: домашнее задание полезно, но лишь в определенной степени. Учащиеся старших классов получают больше, а младшие — гораздо меньше.
Национальный PTA и Национальная ассоциация образования поддерживают «10-минутное домашнее задание» — 10 минут домашнего задания каждую ночь на каждый класс. Но многие учителя и родители сразу же отмечают, что важно качество домашнего задания и то, насколько оно соответствует потребностям учащихся, а не количество времени, потраченного на него.
Руководство не учитывает студентов, которым, возможно, потребуется тратить больше или меньше времени на выполнение заданий. В классе учителя могут вносить коррективы, чтобы поддержать испытывающих трудности учеников, но дома задание, на выполнение которого у одного ученика уходит 30 минут, может занять у другого в два раза больше времени — часто по независящим от них причинам.А домашние задания могут увеличить разрыв в успеваемости, ставя учащихся из малообеспеченных семей и учащихся с ограниченными возможностями обучения в невыгодное положение.
В классе учителя могут вносить коррективы, чтобы поддержать испытывающих трудности учеников, но дома задание, на выполнение которого у одного ученика уходит 30 минут, может занять у другого в два раза больше времени — часто по независящим от них причинам.А домашние задания могут увеличить разрыв в успеваемости, ставя учащихся из малообеспеченных семей и учащихся с ограниченными возможностями обучения в невыгодное положение.
Однако 10-минутное руководство полезно для установления предела: когда дети тратят слишком много времени на домашнее задание, есть реальные последствия, которые следует учитывать.
видеоНебольшие пособия для учеников начальной школы
Когда маленькие дети идут в школу, основное внимание следует уделять воспитанию любви к учебе, а слишком много домашних заданий может подорвать эту цель.А молодые студенты часто не обладают учебными навыками, чтобы в полной мере использовать домашнее задание, поэтому это может означать неэффективное использование времени (Купер, 1989; Купер и др. , 2006; Марцано и Пикеринг, 2007). Более эффективным занятием может быть вечернее чтение, особенно если в этом участвуют родители. Преимущества чтения очевидны: если к концу третьего класса учащиеся не умеют хорошо читать, они с меньшей вероятностью преуспеют в учебе и закончат среднюю школу (Fiester, 2013).
, 2006; Марцано и Пикеринг, 2007). Более эффективным занятием может быть вечернее чтение, особенно если в этом участвуют родители. Преимущества чтения очевидны: если к концу третьего класса учащиеся не умеют хорошо читать, они с меньшей вероятностью преуспеют в учебе и закончат среднюю школу (Fiester, 2013).
Для учительницы второго класса Жаклин Фиорентино незначительные преимущества домашнего задания не перевешивали потенциальный недостаток, заключающийся в том, что в раннем возрасте дети обращаются к школе против школы, поэтому она экспериментировала с отказом от обязательных домашних заданий.«Произошло нечто удивительное: они стали больше работать дома», — пишет Фиорентино. «Эта вдохновляющая группа 8-летних детей использовала свое только что обретенное свободное время для изучения тем и тем, которые им интересны». Она побуждала своих учеников читать дома и предлагала дополнительное домашнее задание, чтобы продлить уроки в классе и помочь им просмотреть материал.
Умеренные пособия для учащихся средней школы
По мере того, как учащиеся созревают и развивают учебные навыки, необходимые для более глубокого изучения темы — и сохранения того, чему они учатся, — они также получают больше пользы от домашних заданий. Еженедельные задания могут помочь им подготовиться к учебе, и исследования показывают, что домашнее задание может приносить умеренную пользу учащимся средней школы (Cooper et al., 2006). Недавние исследования также показывают, что домашнее задание по математике в Интернете, которое можно адаптировать к уровню понимания учащихся, может значительно повысить результаты тестов (Roschelle et al., 2016).
Еженедельные задания могут помочь им подготовиться к учебе, и исследования показывают, что домашнее задание может приносить умеренную пользу учащимся средней школы (Cooper et al., 2006). Недавние исследования также показывают, что домашнее задание по математике в Интернете, которое можно адаптировать к уровню понимания учащихся, может значительно повысить результаты тестов (Roschelle et al., 2016).
Однако есть риски, если назначать слишком много: исследование 2015 года показало, что, когда ученикам средней школы давалось более 90-100 минут ежедневного домашнего задания, их результаты на тестах по математике и естествознанию начали снижаться (Фернандес-Алонсо, Суарес-Альварес, И Муньис, 2015).Преодоление этого верхнего предела может истощить мотивацию и сосредоточенность учащихся. Исследователи рекомендуют, чтобы «домашнее задание представляло определенный уровень сложности или затруднений, но не было настолько сложным, чтобы препятствовать усилиям». Учителя должны избегать повторяющихся заданий, не требующих больших усилий, и назначать домашние задания «с целью привить рабочие привычки и способствовать автономному, самостоятельному обучению».
Другими словами, важно качество домашнего задания, а не количество. Брайан Штабник, опытный учитель английского языка в средних и старших классах, предлагает учителям сделать шаг назад и задать себе следующие пять вопросов:
- Сколько времени потребуется на выполнение?
- Все ли учащиеся учтены?
- Приведет ли задание к успеху в будущем?
- Поместит ли задание материал в контекст, недоступный для классной комнаты?
- Предлагает ли задание поддержку, когда учителя нет?
Больше преимуществ для старшеклассников, но и риски
К тому времени, когда они дойдут до старшей школы, ученики должны быть на пути к тому, чтобы стать самостоятельными учениками, поэтому домашнее задание действительно дает толчок к обучению в этом возрасте, если оно не является подавляющим (Купер и др., 2006; Марцано и Пикеринг, 2007). Когда учащиеся тратят слишком много времени на домашнее задание — более двух часов каждую ночь, — это отнимает драгоценное время, чтобы отдохнуть и провести время с семьей и друзьями. Исследование, проведенное в 2013 году, показало, что старшеклассники могут испытывать серьезные проблемы с психическим и физическим здоровьем, от повышенного уровня стресса до недосыпания, когда им задают слишком много домашних заданий (Galloway, Conner, & Pope, 2013).
Домашнее задание в старшей школе всегда должно относиться к уроку и выполняться без посторонней помощи, а обратная связь должна быть четкой и ясной.
Учителям также следует иметь в виду, что не все учащиеся имеют равные возможности выполнять домашнее задание дома, поэтому неполное домашнее задание может не быть истинным отражением их обучения — это может быть больше результатом проблем, с которыми они сталкиваются за пределами школы. Им могут мешать такие проблемы, как отсутствие тихого места в доме, такие ресурсы, как компьютер или широкополосное соединение, или поддержка родителей (OECD, 2014). В таких случаях низкая оценка домашнего задания может быть несправедливой.
Поскольку количество времени, обсуждаемое здесь, является общим, учителя средней и старшей школы должны знать, сколько домашнего задания задают другие учителя. Может показаться разумным назначать ежедневное домашнее задание 30 минут, но по шести предметам это три часа — намного больше разумного количества даже для старшеклассника. Психолог Морис Элиас считает это распространенной ошибкой: отдельные учителя создают правила выполнения домашних заданий, которые в совокупности могут ошеломить учеников. Он предлагает учителям вместе разработать общешкольную политику выполнения домашних заданий и сделать ее ключевой темой вечернего школьного вечера и первых родительско-педагогических встреч в учебном году.
Может показаться разумным назначать ежедневное домашнее задание 30 минут, но по шести предметам это три часа — намного больше разумного количества даже для старшеклассника. Психолог Морис Элиас считает это распространенной ошибкой: отдельные учителя создают правила выполнения домашних заданий, которые в совокупности могут ошеломить учеников. Он предлагает учителям вместе разработать общешкольную политику выполнения домашних заданий и сделать ее ключевой темой вечернего школьного вечера и первых родительско-педагогических встреч в учебном году.
Родители играют ключевую роль
Домашнее задание может быть мощным инструментом, помогающим родителям более активно участвовать в обучении своего ребенка (Walker et al., 2004). Он может дать представление о сильных сторонах и интересах ребенка, а также побудить к разговору о его жизни в школе. Если родители положительно относятся к домашнему заданию, их дети с большей вероятностью будут разделять те же ценности, что способствует успеху в учебе.
Но также возможно, что родители будут властными, придавая слишком большое значение результатам тестов или оценкам, что может негативно сказаться на детях (Madjar, Shklar, & Moshe, 2015).Родители должны избегать излишнего вмешательства или контроля — учащиеся сообщают, что чувствуют себя менее мотивированными к обучению, когда им не хватает места и автономии для выполнения домашней работы (Orkin, May, & Wolf, 2017; Patall, Cooper, & Robinson, 2008; Silinskas И Кикас, 2017). Таким образом, хотя домашнее задание может побудить родителей более активно заниматься своими детьми, важно не превращать его в источник конфликта.
тестов с двумя независимыми образцами, непрерывный результат
Есть много приложений, в которых интересно сравнить две независимые группы относительно их средних баллов по непрерывному результату.Здесь мы сравниваем средние значения между группами, но вместо того, чтобы производить оценку разницы, мы проверим, является ли наблюдаемая разница (увеличение, уменьшение или разница) статистически значимой или нет. Помните, что проверка гипотез дает оценку статистической значимости, тогда как оценка дает оценку эффекта, и оба важны.
Помните, что проверка гипотез дает оценку статистической значимости, тогда как оценка дает оценку эффекта, и оба важны.
Здесь мы обсуждаем сравнение средних значений, когда две группы сравнения независимы или физически разделены. Две группы могут определяться конкретным атрибутом (например,g., пол, диагноз сердечно-сосудистых заболеваний) или могут быть установлены исследователем (например, участники, которым назначено экспериментальное лечение или плацебо). Первый шаг в анализе включает вычисление описательной статистики по каждой из двух выборок. В частности, мы вычисляем размер выборки, среднее значение и стандартное отклонение в каждой выборке и обозначаем эту сводную статистику следующим образом:
для образца 1:
- n1
- s1
для образца 2:
- n2
- с2
Обозначение образца 1 и образца 2 произвольное.В условиях клинических испытаний принято называть группу лечения 1 и контрольную группу 2. Однако при сравнении, например, мужчин и женщин, любая группа может быть 1 или 2.
Однако при сравнении, например, мужчин и женщин, любая группа может быть 1 или 2.
В приложении двух независимых выборок с непрерывным результатом интересующим параметром при проверке гипотез является разница в средних значениях генеральной совокупности, μ 1 -μ 2 . Нулевая гипотеза всегда заключается в том, что между группами нет разницы в отношении средних значений, то есть
Нулевая гипотеза также может быть записана следующим образом: H 0 : μ 1 = μ 2 .Согласно исследовательской гипотезе исследователь может выдвинуть гипотезу о том, что первое среднее значение больше второго (H 1 : μ 1 > μ 2 ), что первое среднее меньше второго (H 1 : μ 1 <μ 2 ), или что средства различны (H 1 : μ 1 ≠ μ 2 ). Три различных альтернативы представляют собой верхний, нижний и двусторонний тесты соответственно. Следующая тестовая статистика используется для проверки этих гипотез.
Следующая тестовая статистика используется для проверки этих гипотез.
Статистика для тестирования H 0 : μ 1 = μ 2
, где df = n 1 + n 2 -2.
ПРИМЕЧАНИЕ: Формулы выше предполагают одинаковую изменчивость в двух популяциях (т.е. дисперсии генеральной совокупности равны, или s 1 2 = s 2 2 ). Это означает, что результат одинаково варьируется в каждой из сравниваемых популяций. Для анализа у нас есть образцы из каждой из сравниваемых популяций.Если дисперсии выборки аналогичны, то предположение об изменчивости популяций, вероятно, является разумным. В качестве ориентира, если отношение дисперсий выборки s 1 2 / s 2 2 находится между 0,5 и 2 (т. Е. Если одно отклонение не более чем вдвое превышает другое), то формулы выше уместны. Если отношение дисперсий выборки больше 2 или меньше 0,5, тогда необходимо использовать альтернативные формулы для учета неоднородности дисперсий.
Статистика теста включает Sp, которая представляет собой объединенную оценку общего стандартного отклонения (снова предполагая, что дисперсии в популяциях схожи), вычисленного как средневзвешенное значение стандартных отклонений в выборках, как показано ниже:
Поскольку мы предполагаем равные дисперсии между группами, мы объединяем информацию об изменчивости (выборочные дисперсии), чтобы произвести оценку изменчивости в генеральной совокупности. Примечание. Поскольку Sp является средневзвешенным значением стандартных отклонений в выборке, Sp всегда будет находиться между s 1 и s 2 .)
Пример:
Данные измерения n = 3 539 участников, посетивших седьмое обследование потомства в рамках Фрамингемского исследования сердца, показаны ниже.
|
|
Мужчины |
Женщины |
||||
|
Характеристика |
п |
|
S |
п |
|
с |
|
Систолическое артериальное давление |
1,623 |
128. |
17,5 |
1 911 |
126,5 |
20,1 |
|
Диастолическое артериальное давление |
1,622 |
75,6 |
9,8 |
1,910 |
72.6 |
9,7 |
|
Общий холестерин сыворотки |
1,544 |
192,4 |
35,2 |
1,766 |
207,1 |
36,7 |
|
Масса |
1,612 |
194.0 |
33,8 |
1,894 |
157,7 |
34,6 |
|
Высота |
1,545 |
68,9 |
2,7 |
1,781 |
63. |
2,5 |
|
Индекс массы тела |
1,545 |
28,8 |
4,6 |
1,781 |
27,6 |
5,9 |
Предположим, теперь мы хотим оценить, существует ли статистически значимая разница в средних систолических АД между мужчинами и женщинами, используя 5% уровень значимости.
- Шаг 1. Установите гипотезы и определите уровень значимости
H 0 : μ 1 = μ 2
H 1 : μ 1 ≠ μ 2 α = 0,05
- Шаг 2. Выберите соответствующую статистику теста.
Поскольку обе выборки большие (> 30), мы можем использовать статистику Z-теста вместо t. Обратите внимание, что пакеты статистических вычислений используют t повсюду.Перед применением формулы мы сначала проверяем, обосновано ли предположение о равенстве дисперсий генеральной совокупности. В руководстве предлагается изучить соотношение дисперсий выборки, s 1 2 / s 2 2 . Предположим, мы называем мужчин группой 1, а женщин группой 2. Опять же, это произвольно; это нужно только отметить при интерпретации результатов. Отношение дисперсий выборки составляет 17,5 2 / 20,1 2 = 0,76, что находится между 0.5 и 2, предполагая, что предположение о равенстве дисперсий населения является разумным. Соответствующая статистика теста —
В руководстве предлагается изучить соотношение дисперсий выборки, s 1 2 / s 2 2 . Предположим, мы называем мужчин группой 1, а женщин группой 2. Опять же, это произвольно; это нужно только отметить при интерпретации результатов. Отношение дисперсий выборки составляет 17,5 2 / 20,1 2 = 0,76, что находится между 0.5 и 2, предполагая, что предположение о равенстве дисперсий населения является разумным. Соответствующая статистика теста —
.
- Шаг 3. Настройте правило принятия решения.
Это двусторонний тест, использующий статистику Z и 5% уровень значимости. Отклонить H 0 , если Z < -1,960 или Z > 1,960.
- Шаг 4. Вычислите статистику теста.
Теперь мы подставляем данные выборки в формулу для статистики теста, определенную на шаге 2.Перед заменой мы сначала вычислим Sp, объединенную оценку общего стандартного отклонения.
Обратите внимание, что объединенная оценка общего стандартного отклонения Sp находится между стандартными отклонениями в группах сравнения (т. Е. 17,5 и 20,1). Sp немного ближе по величине к стандартному отклонению у женщин (20,1), поскольку в выборке было немного больше женщин. Напомним, Sp — это средневзвешенное значение стандартных отклонений в группах сравнения, взвешенное по соответствующим размерам выборки.
Сейчас тестовая статистика:
Мы отклоняем H 0 , потому что 2,66 > 1,960. У нас есть статистически значимые доказательства при α = 0,05, чтобы показать, что существует разница в среднем систолическом артериальном давлении между мужчинами и женщинами. Значение p равно p <0,010.
Здесь мы снова обнаруживаем статистически значимую разницу в средних систолических АД между мужчинами и женщинами при p <0,010. Обратите внимание, что разница в средних значениях выборки (128.2-126,5 = 1,7 единиц), но эта разница превышает ожидаемую случайно.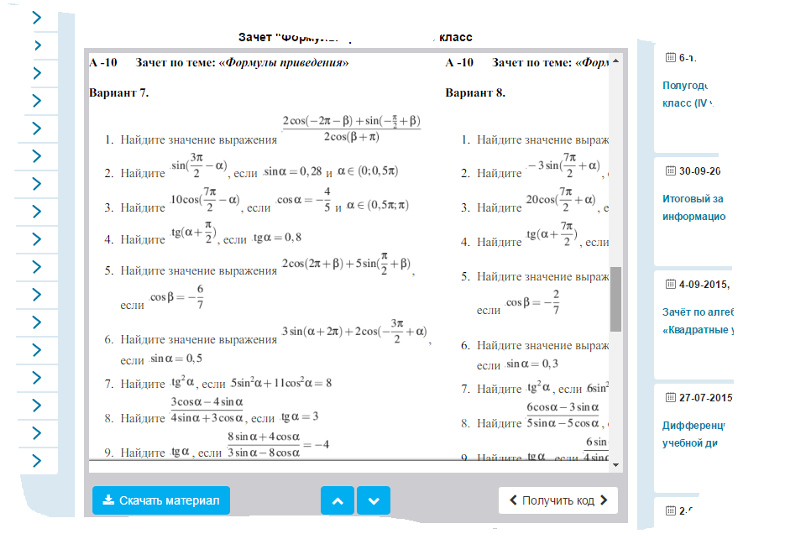 Это клинически значимая разница? Большой размер выборки в этом примере определяет статистическую значимость. 95% доверительный интервал для разницы средних систолических артериальных давлений: 1,7 + 1,26 или (0,44, 2,96). Доверительный интервал обеспечивает оценку величины разницы между средними значениями, тогда как проверка гипотезы и p-значение обеспечивают оценку статистической значимости разницы.
Это клинически значимая разница? Большой размер выборки в этом примере определяет статистическую значимость. 95% доверительный интервал для разницы средних систолических артериальных давлений: 1,7 + 1,26 или (0,44, 2,96). Доверительный интервал обеспечивает оценку величины разницы между средними значениями, тогда как проверка гипотезы и p-значение обеспечивают оценку статистической значимости разницы.
Выше мы провели исследование по оценке нового препарата, предназначенного для снижения общего холестерина. В исследовании участвовала одна выборка пациентов, каждый из которых принимал новое лекарство в течение 6 недель и измерял уровень холестерина. В качестве средства оценки эффективности нового препарата средний уровень общего холестерина после 6 недель лечения сравнивался со средним уровнем общего холестерина, сообщенным NCHS в 2002 году для всех 203 взрослых взрослых. В конце примера мы обсудили уместность фиксированного препарата сравнения, а также альтернативный дизайн исследования для оценки эффекта нового препарата с участием двух групп лечения, где одна группа получает новое лекарство, а другая — нет. Здесь мы вернемся к примеру с параллельной или параллельной контрольной группой, что очень типично для рандомизированных контролируемых исследований или клинических испытаний (см. Модуль EP713 о клинических испытаниях).
Здесь мы вернемся к примеру с параллельной или параллельной контрольной группой, что очень типично для рандомизированных контролируемых исследований или клинических испытаний (см. Модуль EP713 о клинических испытаниях).
Пример:
Предлагается новый препарат для снижения общего холестерина. Рандомизированное контролируемое исследование предназначено для оценки эффективности лекарства в снижении холестерина. В испытании участвуют тридцать участников, которых случайным образом распределяют для приема нового препарата или плацебо.Участники не знают, какое лечение им назначено. Каждого участника просят пройти назначенное лечение в течение 6 недель. По истечении 6 недель у каждого пациента измеряется общий уровень холестерина, и статистика выборки выглядит следующим образом.
|
Лечение |
Размер выборки |
Среднее значение |
Стандартное отклонение |
|---|---|---|---|
|
Новый препарат |
15 |
195. |
28,7 |
|
Плацебо |
15 |
227,4 |
30,3 |
Есть ли статистические доказательства снижения среднего общего холестерина у пациентов, принимающих новый препарат в течение 6 недель, по сравнению с участниками, принимающими плацебо? Мы запустим тест, используя пятиэтапный подход.
- Шаг 1. Установите гипотезы и определите уровень значимости
H 0 : μ 1 = μ 2 H 1 : μ 1 <μ 2 α = 0,05
- Шаг 2. Выберите соответствующую статистику теста.
Поскольку обе выборки маленькие (<30), мы используем статистику t-критерия. Перед применением формулы мы сначала проверяем, обосновано ли предположение о равенстве дисперсий генеральной совокупности.Отношение дисперсий выборки, s 1 2 / s 2 2 = 28,7 2 / 30,3 2 = 0,90, которое находится между 0,5 и 2, что предполагает, что предположение о равенстве совокупности отклонения разумные. Соответствующая статистика теста:
Соответствующая статистика теста:
.
- Шаг 3. Настройте правило принятия решения.
Это тест с нижним хвостом, использующий t-статистику и 5% уровень значимости. Соответствующее критическое значение можно найти в таблице t (в дополнительных ресурсах справа).Для определения критического значения t нам нужны степени свободы df, определяемые как df = n 1 + n 2 -2 = 15 + 15-2 = 28. Критическое значение для теста с нижним хвостом с df = 28 и α = 0,05 составляет -1,701, а правило принятия решения: отклонить H 0 , если t < -1,701.
- Шаг 4. Вычислите статистику теста.
Теперь мы подставляем данные выборки в формулу для статистики теста, определенную на шаге 2. Перед заменой мы сначала вычислим Sp, объединенную оценку общего стандартного отклонения.
Теперь тестовая статистика,
Мы отклоняем H 0 , потому что -2,92 < -1,701. У нас есть статистически значимые доказательства при α = 0,05, чтобы показать, что средний уровень общего холестерина ниже у пациентов, принимающих новый препарат в течение 6 недель, по сравнению с пациентами, принимающими плацебо, p <0,005.
У нас есть статистически значимые доказательства при α = 0,05, чтобы показать, что средний уровень общего холестерина ниже у пациентов, принимающих новый препарат в течение 6 недель, по сравнению с пациентами, принимающими плацебо, p <0,005.
Клиническое испытание в этом примере обнаруживает статистически значимое снижение общего холестерина, тогда как в предыдущем примере, где у нас был исторический контроль (в отличие от параллельной контрольной группы), мы не продемонстрировали эффективность нового препарата.Обратите внимание, что средний уровень общего холестерина у пациентов, принимающих плацебо, составляет 217,4, что сильно отличается от среднего уровня холестерина, зарегистрированного среди всех американцев в 2002 году из 203 и использованного в качестве средства сравнения в предыдущем примере. Историческое контрольное значение могло быть не самым подходящим компаратором, поскольку уровни холестерина со временем увеличивались. В следующем разделе мы представляем еще один дизайн, который можно использовать для оценки эффективности нового препарата.
Видео — Сравнение двух независимых образцов с непрерывным результатом (8:02)
Ссылка на расшифровку видео
вернуться наверх | предыдущая страница | следующая страница
Средневзвешенное значение: Формула: как найти средневзвешенное значение
Что такое средневзвешенное значение?
Средневзвешенное значение является своего рода средним.Вместо того, чтобы каждая точка данных вносила равный вклад в окончательное среднее значение, некоторые точки данных вносят больший «вес», чем другие. Если все веса равны, то средневзвешенное значение равно среднему арифметическому (обычному «среднему», к которому вы привыкли). Средневзвешенные значения очень распространены в статистике, особенно при изучении популяций.
Посмотрите это видео, в котором показано, как найти средневзвешенное значение:
Не можете посмотреть видео? Кликните сюда.
Когда вы находите «обычное» среднее значение для набора чисел, все числа имеют одинаковый вес.Например, если вы хотите найти среднее арифметическое 1, 3, 5, 7 и 10:
- Сложите ваши точки данных: 1 + 3 + 5 + 7 + 10 = 26.
- Разделим на количество предметов в наборе: 26/5 = 5,2.
Что мы подразумеваем под «равным весом»? Первое предложение в некоторых тестах (например, этом) иногда звучит так: «Все вопросы имеют одинаковый вес»). Это означает, что все вопросы на экзамене приносят одинаковое количество баллов. Если у вас есть экзамен на 100 баллов и 10 вопросов, каждый вопрос оценивается в 1/10 балла.В приведенном выше вопросе у вас есть набор из пяти чисел. Вы можете представить себе каждое число, составляющее 1/5 от общего среднего (поскольку в наборе 5 чисел).
Среднее взвешенное.
В некоторых случаях может потребоваться, чтобы число было более весомым. В этом случае вам нужно будет найти средневзвешенное значение . Чтобы найти средневзвешенное значение:
В этом случае вам нужно будет найти средневзвешенное значение . Чтобы найти средневзвешенное значение:
- Умножьте числа в наборе данных на веса.
- Сложите результаты.
Для указанного выше набора чисел с равными весами (1/5 для каждого числа) математическое вычисление для нахождения взвешенного среднего будет следующим:
1 (* 1/5) + 3 (* 1/5) + 5 (* 1/5) + 7 (* 1/5) + 10 (* 1/5) = 5.2.
Пример задачи : вы сдаете три экзамена по 100 баллов в своем классе статистики и набираете 80, 80 и 95. Последний экзамен намного легче, чем первые два, , поэтому ваш профессор придал ему меньшее значение. Веса для трех экзаменов:
- Экзамен 1: 40% вашей оценки. (Примечание: 40% в виде десятичной дроби — 0,4.)
- Экзамен 2: 40% вашей оценки.
- Экзамен 3: 20% вашей оценки.
Каково ваше окончательное средневзвешенное значение для класса?
- Умножьте числа в наборе данных на веса:
. 4 (80) = 32
4 (80) = 32
,4 (80) = 32
,2 (95) = 19 - Сложите числа. 32 + 32 + 19 = 83.
Процент веса, присвоенный каждому экзамену, называется весовым коэффициентом.
нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Формула взвешенного среднего
Средневзвешенное значение найти относительно легко. Но в в некоторых случаях веса могут в сумме не равняться 1. В таких случаях вам нужно будет использовать формулу взвешенного среднего.Единственная разница между формулой и приведенными выше шагами состоит в том, что вы делите на сумму всех весов.
На изображении выше представлена техническая формула для взвешенного среднего. Проще говоря, формулу можно записать как:
Средневзвешенное значение = Σwx / Σw
- Σ = суммирование (другими словами… сложите их!).
- w = вес.
- x = значение.
Чтобы использовать формулу:
- Умножьте числа в наборе данных на веса.

- Сложите числа на шаге 1 вверх. Отложите это число на мгновение.
- Сложите все веса.
- Разделите числа, найденные на шаге 2, на число, которое вы нашли на шаге 3.
В приведенном выше примере задачи оценок все веса в сумме дают 1 (0,4 + 0,4 + 0,2), поэтому вы должны разделить свой ответ (83) на 1:
83/1 = 83.
Однако предположим, что ваши средневзвешенные значения в сумме составили 1,2 вместо 1. Вы разделите 83 на 1,2, чтобы получить:
83/1.2 = 69,17.
Предупреждение: На средневзвешенное значение могут легко повлиять выбросы в ваших данных. Если у вас есть очень высокие или очень низкие значения в вашем наборе данных, средневзвешенное значение не может быть хорошей статистикой, на которую можно полагаться.
Список литературы
Everitt, B. S .; Скрондал, А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.
МУДРЕЦ.
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
39 Поведенческие цели для IEP | Версия для печати | Выполнение работ / заданий
Поведение Цели IEP
Не могу поверить, что раньше не поднимал эту тему.Ну ладно, могу. Это чрезвычайно сложная предметная область IEP. Это также тот, который больше всего влияет на наших детей изо дня в день, и, на мой взгляд, с ним обычно обращаются хуже всего. Я вижу ужасные FBA, выполненные благонамеренными сотрудниками, у которых нет дела, и результаты показывают это.
Но цели могут быть отправной точкой. Если вы не можете определить, с чем борется ваш ребенок, иногда перечитывание целей, описывающих желаемое поведение, может помочь вам в этом.
Если вы не можете определить, с чем борется ваш ребенок, иногда перечитывание целей, описывающих желаемое поведение, может помочь вам в этом.
Обратите внимание: когда речь идет о различных нуждах ребенка, существует много общего. Если вы ищете Социально-эмоциональные цели , у меня тоже есть их список. Если вы не нашли здесь то, что вам нужно, вы сделали это там.
В этом посте много списков. Так что возьмите чашку чего-нибудь и покопайтесь. Поведение — сложная тема, и вы не можете говорить о целях поведения, не говоря также о FBA s, дисциплине, слушаниях проявлений и так далее.Как я уже сказал, «база знаний, которую я бы не хотел иметь», но я имею.
Но не будем ставить телегу впереди лошади.
Прикрепите его, чтобы он у вас был! Вы должны начать с FBA. Друг и специалист по поведению написал этот отличный пост о поведении и FBA . Это определенно должно стать вашей отправной точкой, если у вашего ребенка не было FBA.
Можете ли вы достичь целей в отношении поведения без FBA?
Короткий ответ — да. Однако лучше всего сначала выполнить FBA.И как вы узнаете, что вам нужны поведенческие цели, если вы не проводили никаких оценок поведения? Вам понадобится FBA для реализации плана поведения в рамках IEP.
При этом, если бы поведение моего ребенка было минимальным и адекватно учитывалось в IEP без FBA, я не уверен, что я бы стал бороться с этим. Все ситуации разные.
Главное, что нужно запомнить: Любое поведение вам что-то говорит. Что ваш ребенок пытается сказать?
Можно ли составить план поведения без IEP?
Опять же, краткий ответ — да.Я видел, как это было сделано (хотя я не сомневался в правомерности этого, поскольку это не был мой клиент). Для некоторых детей единственной областью потребности может быть поведение. Поэтому в некотором роде логично, что им нужен только план поведения, а не полноценная IEP.
Однако я считаю, что это ужасная практика. Если у ребенка поведение, достаточное для обоснования плана поведения, ему следует иметь индивидуальную программу обучения (IEP). И поэтому он предлагает процессуальную защиту в отношении дисциплинарных слушаний и слушаний по делу.Вы также можете прочитать об этом ниже. Опять же, это сложная тема с множеством касательных.
Обучай навыку или восполняй недостаток.
В поведении много говорят о том, чтобы «делать правильный выбор». Просто убедитесь, что у ребенка есть набор навыков, прежде чем будет установлено ожидание . Очень легко понять, чего вы хотите от ребенка. Целей поведения в классе никогда не достичь, если не будет фундамента.
Если ребенку не хватает навыков, этого никогда не произойдет.Это восходит к вашему FBA. Убедитесь, что поведение, указанное в списке, определяется как «воля ребенка» или «отсутствие набора навыков».
Есть огромная разница, но оба могут закончиться исключением из школы.
Два моих любимых эксперта по поведению — Росс Грин, и Питер Герхард.
Поведенческие цели для IEP
Мне не нужно было изобретать велосипед. Есть много отличных сайтов, с которых можно почерпнуть.Я включил несколько целей, от которых я не был так без ума. Многие из них были в списке с другими достойными целями.
У некоторых была формулировка вроде «правильно будут вести себя с ума». Вы ведь знаете, что с этим не так? Кто сказал, как правильно злиться? Знает ли об этом ребенок? А как это сделать? Так что, хотя я считаю, что большинство из них хороши, есть отправные точки.
Для чисел используйте цифру из исходных линий ребенка и двигайтесь вверх оттуда. Я убрал такие слова, как «спокойное тело» и «тихие руки».«Если ребенку нужно стимулировать, писать сценарий, хлопать или раскачивать во время выполнения задания, какой в этом вред?
Список целей поведения
Это лишь часть огромного списка.-(Formuly-privedenija)-reshenie-9.7.jpg) Мне нравится, что некоторые из этих поведенческих целей включают цели завершения работы.
Мне нравится, что некоторые из этих поведенческих целей включают цели завершения работы.
- К моменту истечения срока действия этой IEP _______ будет управлять конфликтами, независимо от поддержки учителя, в 4 из 5 наблюдаемых событий в течение двухмесячного периода, согласно результатам наблюдений и оценок успеваемости.
- К моменту истечения срока действия этой IEP, учитывая контрольный список самоконтроля, _______ будет демонстрировать саморегуляцию в течение 90% еженедельных сессий, что измеряется наблюдениями в течение 2 месяцев.
- По истечении этого IEP, получив письменное задание, _______ начнет свою работу, о чем свидетельствует начало написания писем на своей бумаге в течение 1 минуты после того, как задание будет представлено в 80% из минимум 20 записанных возможностей за период 2 месяца, согласно результатам наблюдения и оценки работы.
- На протяжении всей школьной среды, используя пятикомпонентную доску для жетонов с наглядным изображением его правил (следуйте указаниям и имейте безопасное тело), перечисленных вверху, _______ будет следовать обоим своим правилам (следовать указаниям и иметь безопасное тело) заработать все пять своих жетонов за каждый получасовой период, в группах и 1: 1 академических сессиях, в 80% испытаний, проверенных в рамках 4/5 наблюдений в течение как минимум 2-месячного периода до истечения этого IEP, как измерено по наблюдениям и оценкам производительности.

- _______ запросит (используя его / ее метод общения) и сделает перерыв, когда он понадобится, и вернется к задаче после перерыва независимо в 8 из 10 возможностей в течение как минимум двух месяцев, согласно наблюдениям и результатам оценка до истечения срока действия настоящего IEP.
Цели поведения IEP по категориям
Спасибо читательнице за то, что прислали мне по электронной почте этот список, которым ей поделились в школе. Некоторые из них, как написано, на самом деле не поддаются измерению.Помните, что вы всегда можете вставить желаемое поведение в формулу цели IEP, чтобы сделать его конкретным и измеримым.
Цели выполнения / выполнения работ
- Получив задание или указание, ______ начнет выполнение задания в течение 1 минуты и будет выполнять задание не менее 10 минут независимо с не более чем двумя подсказками на 8 из 10 независимых заданий, согласно данным персонала.
- Получив максимум одну словесную реплику, _______ будет заниматься нежелательной деятельностью в небольшой группе и / или независимым заданием без протеста и останется на задаче, не уклоняясь от нее (ванная комната, получение куртки, завязывание обуви, заточка карандаш и др.
 ) в течение 20 минут в 3 из 4 испытаний, согласно наблюдениям и документации персонала.
) в течение 20 минут в 3 из 4 испытаний, согласно наблюдениям и документации персонала. - _______ продемонстрирует поведение при выполнении задания в общеобразовательной обстановке в 75% интервалов в течение 10-минутного периода с использованием подходящего фиджера и одного напоминания для взрослых в 4/5 испытаниях, как измерено наблюдениями и данными.
- ________ будет заниматься заданием во время обучения в больших и малых группах в разных условиях в течение 10 минут с не более чем 1 подсказкой учителя в 4 из 5 испытаний, согласно данным, нанесенным на карту учителем.
- С перерывами на движения и использованием стратегий саморегуляции _____ продемонстрирует способность уделять внимание задаче в среднем в 75% интервалов в течение 20-минутного урока.
- Используя обученные стратегии саморегулирования и контрольные списки самоконтроля, ______ самостоятельно приступит к выполнению задачи (включая нежелательные задачи) в течение 2 минут после направления в среднем для 80% возможностей в разных средах.

- С использованием обученных стратегий саморегуляции и контрольных списков самоконтроля, как только ______ приступит к самостоятельной задаче, он будет сосредоточен на ней в течение не менее 10 (используйте исходное число) минут, без подсказок взрослых, в течение в среднем 80% возможностей в разных средах.
- Получив задание, ____ самостоятельно выполнит задание / задание и попросит о помощи, если необходимо, с точностью 80% в 5 из 5 последовательных испытаний в небольшой группе, согласно наблюдениям, проводимым учителем. .
- Когда ему дается нежелательная задача в сочетании с использованием стратегий саморегулирования и системы вознаграждений, ______ начнет задачу в течение 1 минуты и завершит соответствующим образом измененную версию задачи в течение заранее назначенного соответствующего количества времени (с использованием таймера) по 8 из 10 возможностей, согласно данным персонала.
Цели участия в классе
- _______ будет демонстрировать поднятие руки для участия в обучении всего класса и / или малых групп, 80% времени в 5 из 5 интервалов, согласно наблюдениям учителя.

Навыки совладания / эмоциональная регуляция / саморегуляция Цели программы IEP
- В классе ______ будет использовать позитивный разговор с самим собой и стратегии выживания, чтобы справиться со стрессовыми ситуациями или рабочими требованиями, в которых он / она проявляет тревожное или замкнутое поведение (т.е. опускать голову, говоря, что он / она не может что-то сделать), демонстрируемая посредством участия в 30-минутном занятии или ситуации в спокойной и позитивной манере с одной подсказкой в 2/3 случаях.
- На консультациях _______ будет точно определять чувства и подходящие стратегии выживания при представлении реальных или воображаемых ситуаций с точностью 80% в 4 из 5 испытаний.
- Когда _____ расстроен, расстроен или зол, он будет использовать стратегию саморегуляции / преодоления (перерыв в движении, глубокое дыхание, тихий перерыв, глубокое давление / тяжелая работа и т. Д.)), чтобы избежать неожиданного поведения, с одним напоминанием, при использовании 4 из 5 возможностей, измеренных с помощью наблюдений и документации.

- __________ улучшит свои навыки саморегуляции, что продемонстрировано путем использования инструмента (например, внутреннего тренера, сенсорной поддержки, успокаивающего перерыва), чтобы помочь в адаптации к ожидаемому эмоциональному состоянию (например, зеленой зоне — когда мы чувствуем себя спокойными, счастливыми, содержание, и сфокусировано) с одним напоминанием для взрослых в 8 из 10 случаев в небольшой группе, по результатам измерения за двухнедельный период
- ______ улучшит понимание регулирования, что продемонстрировано путем выявления случаев, в которых он / она могли бы извлечь пользу из использования инструмент для помощи в регулировании и определения того, какой инструмент был бы полезен для каждого случая с точностью 80%.
- При представлении проблемы (нежелательная задача, неприятная ситуация, критика / исправление) ______ точно определит размер проблемы (большая проблема, маленькая проблема) и определит соответствующий эмоциональный ответ (сделайте перерыв, поговорите с Учитель, сделайте глубокий вдох, замените разочарование хорошими мыслями и т.
 д.) и вернитесь к текущему заданию в 4 из 5 испытаний, как измерено данными, нанесенными учителем.
д.) и вернитесь к текущему заданию в 4 из 5 испытаний, как измерено данными, нанесенными учителем. - При возникновении неприятной ситуации (например, нежелательная задача, требование и / или нежелательное поведение сверстников) с одной подсказкой ________ будет использовать стратегии выживания (т.е. сделайте перерыв, сделайте глубокий вдох и т. д.), а затем вернитесь к задаче и продолжайте выполнять ее не менее 10 (используйте исходное число + улучшение) минут со средним значением 95% за 8 последовательных школьных недель во всех классах.
- Когда ______ сталкивается с ситуацией, которая вызывает у него беспокойство или разочарование (т. Е. Нежелательная задача, неожиданное препятствие, такое как ______, задачи, воспринимаемые как слишком сложные, незнакомый взрослый и нежелательный взрослый), он будет самостоятельно продемонстрировать соответствующую эмоциональную реакцию, найдя решение своей проблемы или используя стратегию восстановления ожидаемого эмоционального состояния (сделайте перерыв, поговорите с учителем и т.
 д.)) и вернуться к текущей задаче в течение 2 минут в среднем для 80% экземпляров как во всех средах, так и в каждой среде.
д.)) и вернуться к текущей задаче в течение 2 минут в среднем для 80% экземпляров как во всех средах, так и в каждой среде.
Самоконтроль IEP Goals
- _______ будет демонстрировать самообладание своего тела и голоса (хорошее личное пространство, держать руки / руки / ноги близко к телу и соответствующий уровень голоса) по отношению к ожидаемым уровням в классе и сверстникам вокруг него на 80% 20-минутного периода.
- ________ будет демонстрировать самоконтроль в классе, поднимая руку и ожидая ответа от учителя, когда он / она задает вопрос в классе, с точностью 80% в 5 из 5 испытаний, согласно оценке наблюдение учителя и сбор данных.
Цели IEP с самоконтролем
- _______ продемонстрирует способность распознавать ожидаемое и неожиданное поведение, а также оценивать свое поведение в рамках своей системы самоконтроля с точностью 80% по сравнению с оценками поведения учителем.
- ______ продемонстрирует способность точно распознавать свой уровень тревожности с помощью визуальной системы самооценки (например, термометра чувств) с точностью 80% по сравнению с наблюдениями и данными учителя.
Цели IEP по борьбе с агрессией
- _________ будет воздерживаться от физической агрессии (т. Е. Пинков, ударов, толчков, споткнуться) во всех средах в школе в течение 4 недель подряд со всеми взрослыми и детьми, как измерено по данным событий.
- _________ будет воздерживаться от агрессии (т. Е. Ударов, пинков, толканий) 100% дня, в любой среде, со всеми взрослыми и детьми, согласно данным специальных образовательных мероприятий, в течение 8 недель подряд.
Anxiety IEP Goals
- На консультациях _____ будет точно определять ситуации, которые могут вызывать тревогу, и подходящие стратегии преодоления или расслабления при представлении реальных или воображаемых ситуаций с точностью 80% в 4 из 5 испытаний.
- ______ продемонстрирует способность точно распознавать свой уровень тревожности с помощью визуальной системы самооценки (например, термометра чувств) с точностью 80% по сравнению с наблюдениями и данными учителя.

Отрицательные комментарии и жесты-цели
Благодаря использованию когнитивно-поведенческого вмешательства (стратегия обучения регулированию мыслей и убеждений при консультировании в сочетании с ежедневным подкреплением по мере использования инструментов) _____ сократит количество негативных комментариев и жестов в среднем до 1 раз в час во всем классе. настройки, измеренные в течение 6 дней пробного использования.
Несоответствие / следование инструкциям
- Когда дается неприятная ситуация (т.е. нежелательная задача, невозможность выбрать предпочтительный вид деятельности, например, компьютеры и т. д.) _______ будет участвовать в несоблюдении требований не более чем на 20 минут в течение недели, как измерено с помощью данных выборки времени.
- Получив трехступенчатое функциональное указание от взрослого, _____ выполнит все три шага с максимум одной дополнительной подсказкой в 4 из 5 испытаний, согласно наблюдениям учителя и данным.

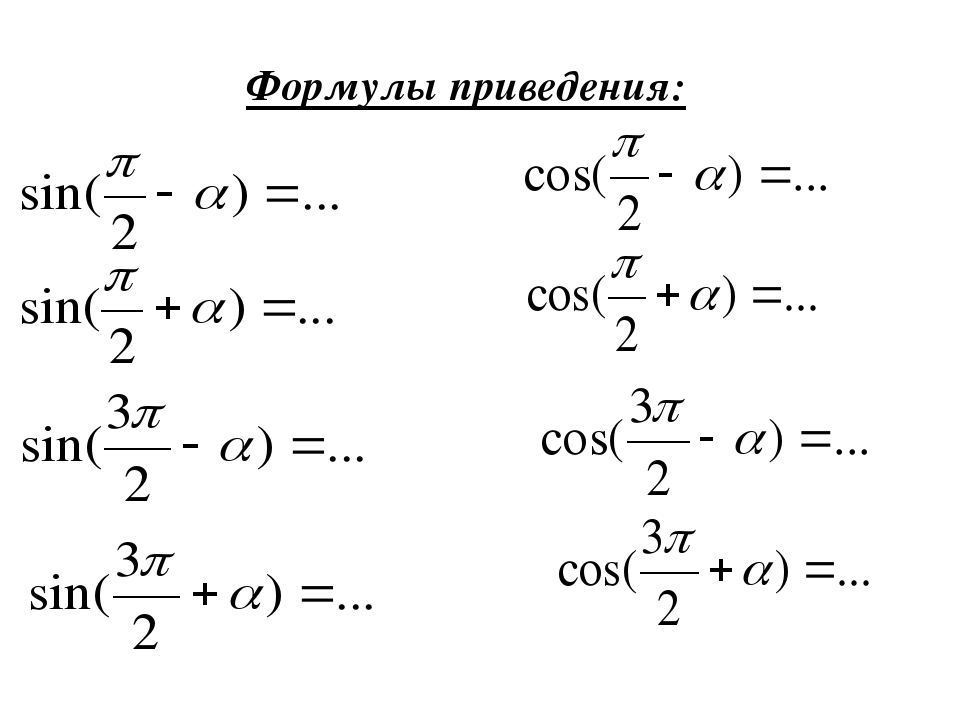 2
2 -(Formuly-privedenija)-reshenie-9.9.jpg) 4
4  9
9