12-б. Относительность движения
§ 12-б. Относительность движения
Изучая кинематику, мы учимся описывать механическое движение – изменение положения тела относительно других тел с течением времени. Для пояснения очень важных слов «относительно других тел» приведём пример, в котором вам потребуется применить воображение.
Допустим, мы сели в автомобиль и выехали на дорогу, ведущую на север. Оглядимся вокруг. Со встречными автомобилями всё просто: они всегда приближаются к нам с севера, проезжают мимо нас и удаляются на юг (взгляните на рисунок – голубой автомобиль слева).
С попутными машинами сложнее. Те автомобили, которые едут быстрее нас, приближаются к нам сзади, обгоняют и удаляются на север (например, серое авто в центре). Но автомобили, которые обгоняем мы, приближаются к нам спереди и удаляются от нас назад (красное авто справа). То есть попутные автомобили относительно нас могут удаляться на юг в то же самое время, когда относительно дороги едут на север!
Итак, с точки зрения водителя и пассажиров нашей машины (внизу на рисунке её синий капот) обгоняемый красный автомобиль удаляется на юг, хотя, с точки зрения мальчика на обочине дороги, этот же автомобиль едет на север. Кроме того, мимо мальчика красное авто «пролетит со свистом», а мимо нашей машины – «медленно уплывёт» назад.
Кроме того, мимо мальчика красное авто «пролетит со свистом», а мимо нашей машины – «медленно уплывёт» назад.
Таким образом, движение тел может выглядеть по-разному с точек зрения различных наблюдателей. Это явление – относительность механического движения. Оно проявляется в том, что быстрота, направление и траектория одного и того же движения различны для разных наблюдателей. Первые два различия (в быстроте и направлении движения) мы только что проиллюстрировали на примере автомобилей. Далее мы покажем различия в виде траектории одного и того же тела для разных наблюдателей (см. рисунок с яхтами).
Напомним: кинематика создаёт математическое описание движения тел. Но как это сделать, если движение выглядит по-разному с точек зрения различных наблюдателей? Чтобы была определённость, в физике всегда выбирают систему отсчёта.
Системой отсчёта называют часы и систему координат, связанные с телом отсчёта (наблюдателем). Поясним это примерами.
Вообразим, что мы едем в поезде и роняем предмет. Он упадёт к нашим ногам, хотя даже при скорости 36 км/ч поезд ежесекундно передвигается на 10 метров. Вообразим теперь, что на мачту яхты взобрался матрос и роняет ядро (см. рисунок). Нас также не должно смутить, что оно упадёт к основанию мачты, несмотря на то что яхта плывёт вперёд. То есть в каждый момент времени ядро движется и вниз, и вперёд вместе с яхтой.
Итак, в системе отсчёта, связанной с яхтой
А что со скоростью ядра? Поскольку это одно и то же тело, то время его падения в обеих системах отсчёта мы считаем одинаковым. Но так как пройденные ядром пути различны, то и скорости одного и того же движения в разных системах отсчёта различны.
Но так как пройденные ядром пути различны, то и скорости одного и того же движения в разных системах отсчёта различны.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxПомощь в сдаче ЕГЭ по Физике
Кинематика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| S | м | пройденный путь |
| v | м/с | скорость |
| t | с | время |
| x | м | координата |
| a | м/с2 | ускорение |
| ω | с-1 | угловая скорость |
| T | с | период |
| ν | Гц | частота |
| ε | с-2 | угловое ускорение |
| R | м | радиус |
Скорость и ускорение:
Равномерное движение: ν = const
Равнопеременное движение:
Криволинейное движение:
Вращательное движение:
Динамика и Статика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| F | Н | сила |
| P | кг*м/с | импульс |
| a | м/с2 | ускорение |
| m | кг | масса |
| v | м/с | скорость |
| p | Н | вес тела |
| g | м/с2 | ускорение свободного падения |
| E | Дж | энергия |
| A | Дж | работа |
| N | Вт | мощность |
| t | с | время |
| I | кг*м2 | момент инерции |
| L | кг*м2/с | момент импульса |
| M | Н*м | момент силы |
| ω | с-1 | угловая скорость |
Первый закон Ньютона:
При ∑ F = 0 => v = const
Второй закон Ньютона:
Третий закон Ньютона:
Основной закон динамики для неинерциальных систем отчета.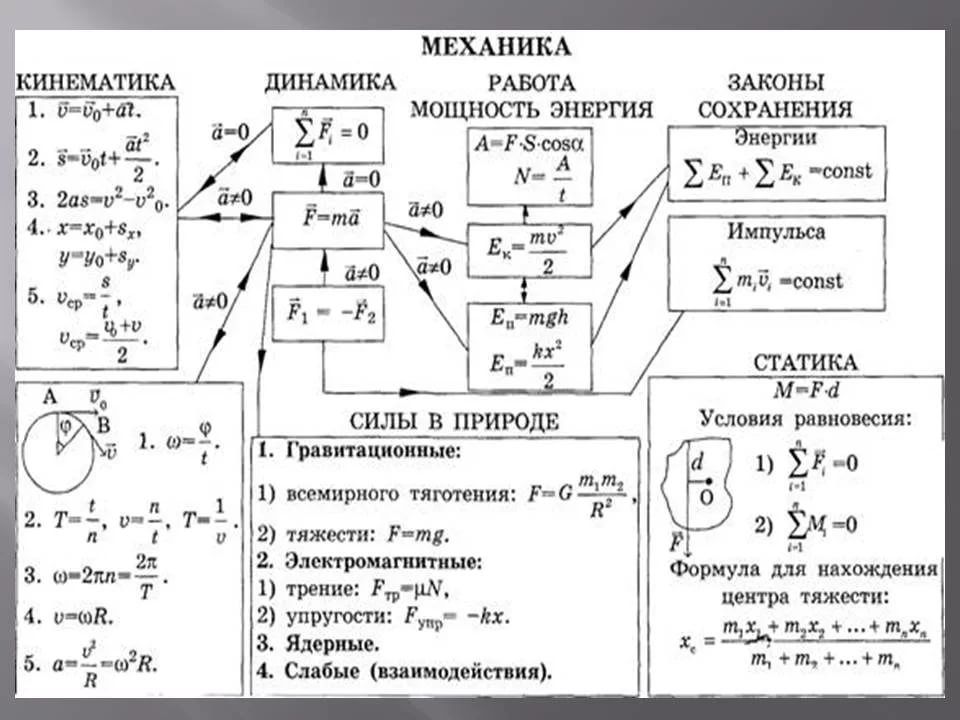
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0— в инерциальной системе отчета.
Скорость центра масс:
Закон всемирного тяготения:
Вес тела:
Сила трения:
Закон Гука:
Закон Гука: σ = Eε, где Е- модуль Юнга.
Динамика и статика вращательного движения:
| система | ось | I |
| точка по окружности | ось симметрии | mR2 |
| стержень | через середину | 1/12 mR2 |
| стержень | через конец | 1/3 mR2 |
| шар | через центр шара | 2/5 mR2 |
| сфера | через центр сферы | 2/3 mR2 |
| кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
| диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел ∑ M = 0
Закон сохранения импульса:
Потенциальная и кинетическая энергия. Мощность:
Мощность:
Закон сохранения энергии:
Теоремы, формулы, доказательства и учебные материалы по физике
Нет нужного материала?
Укажите материал, который Вы не нашли, и он будет добавлен в самое ближайшее время!
Название*:
Раздел науки:
———Математика > АрифметикаМатематика > Арифметика > Арифметические действияМатематика > Арифметика > Рациональные числаФизика > Атомная и ядерная физикаМатематика > Квадратные уравненияФизика > Колебания и волныФизика > Колебания и волны > Механические волныФизика > Колебания и волны > Механические колебанияФизика > Колебания и волны > Электромагнитные волныМатематика > ЛогарифмыФизика > МеханикаФизика > Механика > ДинамикаФизика > Механика > Импульс, энергияФизика > Механика > КинематикаФизика > Механика > Механика жидкостиФизика > Молекулярная физика и термодинамикаФизика > ОптикаГеометрия > ПланиметрияМатематика > ПределыМатематика > ПрогрессииМатематика > Прогрессии > Арифметическая прогрессияМатематика > Прогрессии > Геометрическая прогрессияМатематика > Производная функцииФизика > Специальная теория относительностиГеометрия > СтереометрияМатематика > Теория группМатематика > Теория чиселМатематика > ТригонометрияМатематика > Формулы сокращенного умноженияФизика > ЭлектричествоФизика > Электричество > МагнетизмФизика > Электричество > Переменный электрический токФизика > Электричество > Постоянный электрический токФизика > Электричество > Электрическое полеФизика > Электричество > Электронные и ионные явленияМатематика > Элементарная математика
Данное поле ОБЯЗАТЕЛЬНО к заполнению, чтобы убедиться, что Вы человек
Кинематика и формулы — реферат, курсовая работа, диплом, 2017
13
Площади
l — длина
b — высота, ширина.
Площадь круга:
Кинематика.
Равномерное движение:
a = 0
V = S/t
Ускоренное движение:
a > 0
a = (V — V0 )/ t
S = S0 + V0t (at2 )/2
a = (V2 — V02 )/ 2S
Последовательный ряд нечетных чисел:
N-ую:
просто:
Движение под углом к горизонту
Скорость по оси ОХ:
Скорость по оси ОУ:
Максимальное время подъема:
tполн = 2t
S = Vxtполн.
Максимальная высота:
Движение тела, брошенного горизонтально:
;
Динамика.
F = ma
P = mg
Fтр. = -N
= -N
F = -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x — удлинение.
k — кооф. растяжения.
l = l — l0
l — абсолют. удлинение пружины.
? — относит. удлинение.
l0 — начальная длина
Сила всемирного тяготения
Сила тяжести
Работа и энергия.
;
;
Криволинейное движениеДвижение по окр-ти.; w — угловая скорость.[рад/с]v — линейная скоростьn — частота обращения [об./мин.]T — период обращения [время]Угловая скорость. Период обращения; ; ; ; Для случаев, когда n = [обороты]; — частота [1/с = 1 Гц]- угол.l — длина дуги.Импульс.; Не упругое вз-вие.до: после: в проекции на ось х:Упругое соударение.до вз-я: после:в проекции на ось х:Реактивное движение:в проекции на ось х: (вверх)¦0 изначально.
— среднеквадратичная ск-ть
— средняя кинетич. энергия движ. мол-лы
КПД тепловой машины.
— кол-во теплоты, получ. рабочим телом от нагрев.
— t холод.
— нагреват.
Электричество и магнетизм.
[В/м] ;
Эквипотенциальные пов-ти.
;
l — расстояние
— поверхностная плотность заряда
Закон Кулона
; [Н]
Ф/м
\ эл. постоянная
Электроемкость. Конденсаторы.
[Дж]
W — Энергия
Электроемкость плоского:
Шара:
Параллельное подключение конденсаторов:
Последовательное подключение:
Постоянный электрический ток.
;
; i — плотность тока
— Электродвиж. -1]
-1]
постоянная:
Последовательное и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной цепи:
Последоват. соед. батарей:
;
n — кол-во батарей
Параллельное соед. батарей:
;
Работа при перемещении эл. заряда в эл. поле. Потенциал.
;
— потенциал эл. поля
— потенциальная энергия заряда в поле.
Работа и мощность эл. тока:
Напряжение.
Магнитное поле
;
При расположении проводника с током под углом альфа к вектору В.
B — магнитная индукция
I — сила тока
l — длинна проводника
M — макс. момент сил
S — площадь рамки
Сила Лоуренца
;
n — концентр.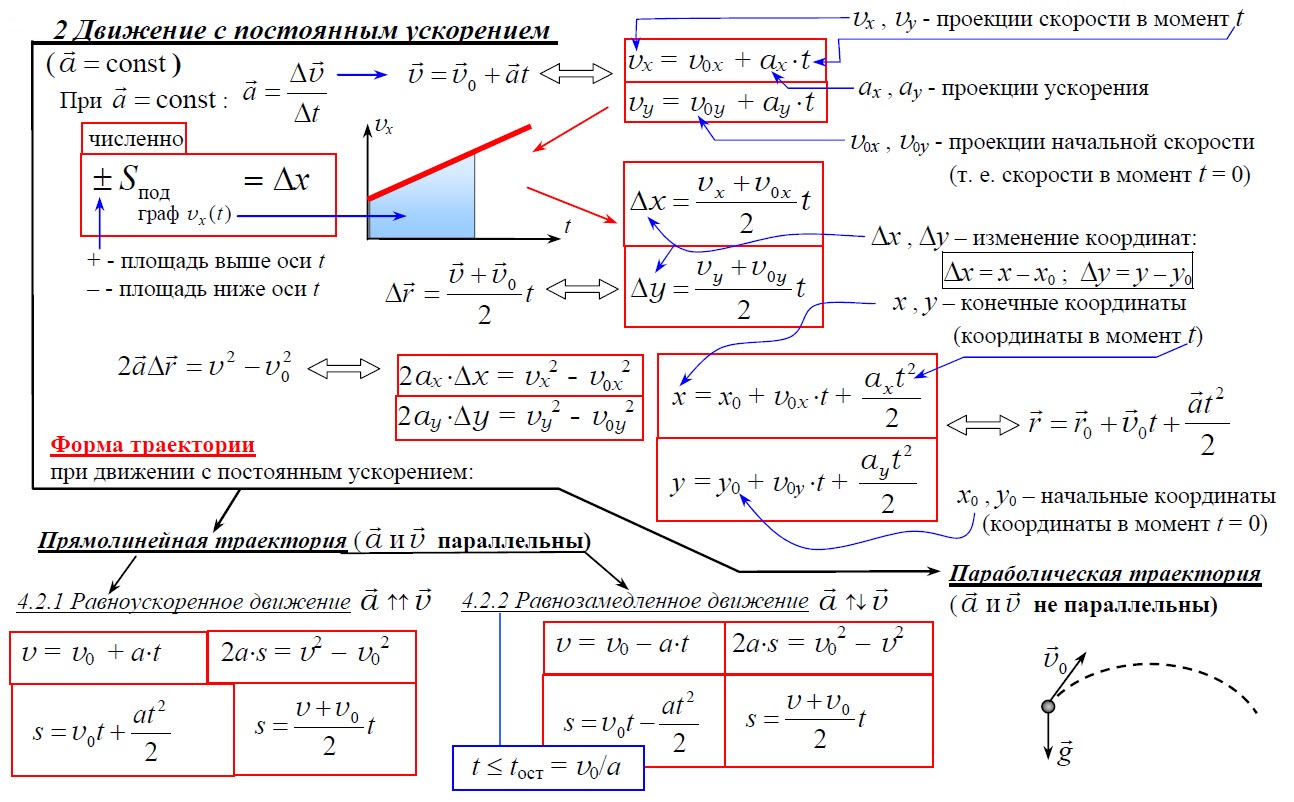 свободных частиц
свободных частиц
v -скорость упор. движ.
S -площадь поперечного сечения проводника
Магнитная прониуаемость.
;
— магнитная прониц. среды
H- напряженность магнитного поля.
Электромагнитная индукция
[Вб]
;
Ф — магнитный поток
;
Самоиндукция.
; [Гн]
;
; W — энергия
Магнитная рамка.
b,a — стороны рамки
S — площадь рамки
Электроны.
;
Электролиты
ОптикаЗакон преломления; — ваакум ; ; ;- относит. показатель преломления.- скорости света во 2-й и первой средах.Линзыd -расстояние предмета от линзыf -расстояние от изображения до предметаF — фокусD -Оптическая сила линзы [диоптрии]k — увеличение линзыКвантовая физика; ; ; — длинна волны излучения- импульс фотона- частота излученияВ магнитно-преломляющих средах:В однородно прозрачной среде:- относит.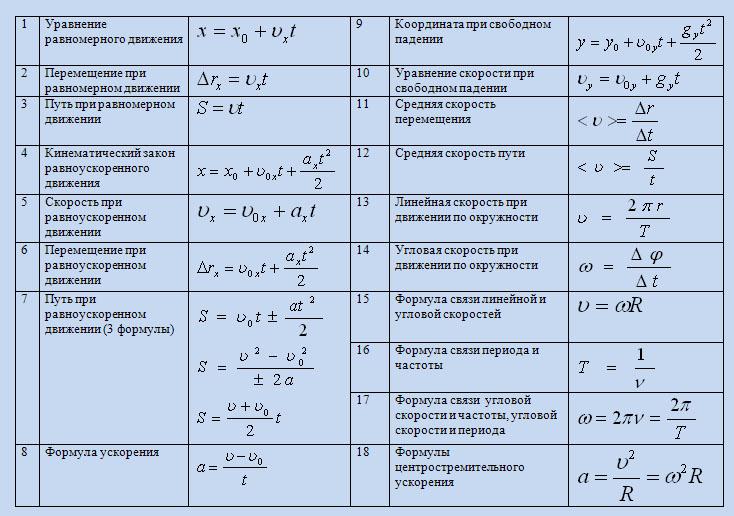 диэликтрич. проницаемость среды- относит. магнитная проницаемость среды.n — постояннаяУравнение Эйнштейна. ; А — работа выхода электрона из в-ва
диэликтрич. проницаемость среды- относит. магнитная проницаемость среды.n — постояннаяУравнение Эйнштейна. ; А — работа выхода электрона из в-ваФотоэффект.
Дополнительные главы физики: кинематика. 9 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой по физике 9 класса. В процессе обучения учащиеся познакомятся с основными принципами и методами кинематики, увидят, как довольно сложные движения можно свести к комбинации более простых, и научатся решать разнообразные задачи.
Курс состоит из 12 учебных модулей, 51 видеолекции с конспектами, 182 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
— Геометрия и физика
— Описание движения
— Ускорение
— Движение по окружности
— Малые приращения физических величин
— Движение тела, брошенного под углом к горизонту
— Криволинейное движение
— Кинематика плоского движения твердого тела
— Комбинация прямолинейных движений
— Кинематические связи
— Выбор системы отсчета
— Комбинация вращения и прямолинейного движения
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
Каждый ученик самостоятельно определяет для себя темп и удобное время учебы. Часть модулей открыта сразу, следующие модули открываются после того, как получен зачет по предыдущим. В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт осенью 2021 года.
кинематических формул — Как обсуждать
Кинематические формулы
Какое кинематическое уравнение использовать? Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение м / с / с) или движение с постоянным ускорением. Их нельзя использовать какое-то время при смене газа. Каждое из кинематических уравнений содержит четыре переменные.
Какие переменные кинематики?
Кинематические уравнения связывают переменные движения друг с другом.Каждое уравнение содержит четыре переменных. Переменные включают ускорение (a), время (t), расстояние (d), конечную скорость (vf) и начальную скорость (vi). Когда значения трех переменных известны, уравнения можно использовать для расчета других.
Что такое уравнение кинематики?
Кинематика — это исследование движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, связанных с перемещением D, скоростью, v, временем, t и ускорением a. а) D = vit + 1/2 at2 b) (vi + vf) / 2 = D / tc) a = (vf vi) / td) vf2 = vi2 + 2aD.
а) D = vit + 1/2 at2 b) (vi + vf) / 2 = D / tc) a = (vf vi) / td) vf2 = vi2 + 2aD.
Какое уравнение для равномерного кругового движения?
В физике они описывают круговое движение, которое соответствует периоду или времени, которое требуется, чтобы сделать один оборот по кругу. Если вы знаете длину окружности круга, вы можете определить угловую скорость в градусах или радианах в секунду. s = C / T (метры / секунда), где C = 2πR, а R — радиус окружности.
Что понимается под кинематическим уравнением движения?
Кинематические уравнения — это система уравнений, описывающая движение объекта с постоянным ускорением.Кинематические уравнения требуют знания производных, скорости изменения и интегралов.
Для чего используется кинематика?
Кинематика используется в астрофизике для описания движения небесных тел и их групп. В механике, робототехнике и биомеханике кинематика используется для описания движения систем, состоящих из дополнительных частей (множественные связанные системы), таких как двигатель, роботизированная рука или человеческий скелет.
Что такое уравнение движения?
Уравнение движения, также известное как дифференциальное уравнение движения, математически и физически связано со вторым законом движения Ньютона.Согласно Ньютону, второй закон движения гласит, что масса ускоряется силой в том же направлении, что и сила.
Когда использовать какое кинематическое уравнение использовать
Если проблема движения объекта попадает в эти категории, вы можете использовать кинематические уравнения для ее решения. Это позволяет вам определить, например, как далеко пролетит снаряд, если снаряд испытывает постоянное ускорение во время полета.
Какое уравнение движения?
Первое уравнение движения.Первое уравнение движения в основном выводится из определения ускорения. Помните, что ускорение — это изменение скорости с течением времени, и уравнение, используемое для его расчета: ускорение = (изменение скорости) / необходимое время = (конечная скорость — начальная скорость) / необходимое время.
Что такое калькулятор кинематических уравнений
Кинематические уравнения используются для анализа и проектирования шарнирных систем, от шарнирных систем с четырьмя стержнями до линейных и параллельных роботов.Кинематические уравнения — это уравнения напряжений, которые характеризуют геометрическую конфигурацию шарнирно-сочлененной механической системы.
Какова формула физики?
Пожалуй, самые известные физические уравнения относятся к энергии: E = mc 2. В этом уравнении E означает энергию, m — массу, а c — скорость света в вакууме (около 186 000 миль / сек или 3×108 метров. ) .. / Second Это уравнение разработал ученый Альберт Эйнштейн.
Как рассчитать движение снаряда?
Движение снаряда всегда имеет форму параболы, которая представлена как: y = ax + bx 2.Движение снаряда рассчитывается без учета сопротивления воздуха для упрощения расчетов. На приведенной выше диаграмме показано движение объекта под действием силы тяжести.

Как рассчитать уравнение скорости?
Если вы хотите выразить это правило в виде математической формулы, уравнение скорости будет выглядеть так: Скорость = Расстояние / Время Обратите внимание, что эта формула скорости работает только в том случае, если объект имеет постоянную скорость в одном направлении или если вы хотите чтобы найти среднюю скорость на определенном расстоянии (в отличие от текущей скорости).
Когда использовать какое кинематическое уравнение для получения
Поскольку кинематические уравнения используются с постоянным ускорением объекта, вы можете использовать простое уравнение для определения средней скорости объекта. Чтобы найти среднюю скорость, просто добавьте начальную скорость к конечной скорости и разделите ее на 2. Это уравнение можно использовать только с постоянным ускорением.
Когда использовать формулу кинематического уравнения
Кинематические уравнения могут применяться к множеству задач размерного движения, которые рассматривают движение объекта с постоянным ускорением. При устранении неполадок выбираемая вами формула должна содержать одну неизвестную переменную и три известные переменные.
При устранении неполадок выбираемая вами формула должна содержать одну неизвестную переменную и три известные переменные.
Какой пример кинематики?
Кинематика Кинематика — это исследование движущихся объектов, включая скорость, ускорение и диапазон движения. Пример: движущийся поезд, вода в реке.
Какие переменные в уравнениях кинематики
Кинематические уравнения связывают переменные движения друг с другом. Каждое уравнение содержит четыре переменных.Переменные включают ускорение (a), время (t), расстояние (d), конечную скорость (vf) и начальную скорость (vi).
Как выбрать правильное кинематическое уравнение?
Как выбрать правильное уравнение? Кинематические уравнения могут применяться к множеству задач размерного движения, которые рассматривают движение объекта с постоянным ускорением. При устранении неполадок выбираемая вами формула должна содержать одну неизвестную переменную и три известные переменные.
В каждом уравнении отсутствует переменная.
Как уравнения кинематики связаны с вращательным движением?
Есть еще одна ветвь кинематических уравнений, которая относится к вращательному движению человека. Однако это только следствие приведенных выше уравнений только с модифицированными переменными. Смещение заменяется изменением угла. Начальная и конечная скорости заменяются начальной и конечной угловыми скоростями. Время — единственная константа.
Что означает V в кинематических уравнениях?
И символ v представляет скорость объекта, индекс i na v (как в vi) указывает, что значение скорости является начальным значением скорости, а индекс f (как в vf) указывает, что значение скорости равно.- значение максимальной скорости.
Какие переменные в кинематической формуле
Это четыре переменные, которые влияют на кинематические уравнения. Уравнения описывают движение объекта при постоянном ускорении.
Используя уравнения, вы можете найти начальное и конечное значения этих переменных. Путь, скорость и ускорение сосредоточены, а время — нет.
Как кинематические уравнения используются для расчета движения?
Кинематические уравнения могут использоваться для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.Кинематические формулы — это набор формул, связанных с пятью кинематическими переменными, указанными ниже.
Как неизвестные параметры определяются с помощью кинематических уравнений?
В этом случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений). Кинематика — это изучение движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, связанных с перемещением D, скоростью, v, временем, t и ускорением a.
Что такое круговое движение и его примеры?
В физике круговое движение — это движение объекта по кругу или вращение по круговой траектории.
Он может быть однородным с постоянной скоростью вращения и постоянной скоростью или неоднородным с переменной скоростью вращения. Вращение вокруг фиксированной оси трехмерного тела предполагает круговое движение его частей. Уравнения движения описывают движение центра масс тела. Примеры кругового движения: искусственный спутник на орбите Земли.
Что такое физическое уравнение?
Определение уравнений (физика) В физике определение уравнений — это уравнения, которые определяют новые величины относительно основных величин.
Физическое кинематическое уравнение
Кинематическое уравнение — это набор из трех уравнений, используемых для линейного движения с постоянным ускорением. Уравнение: u = 2 м / с, v = 10 м / с, t = 4 с, a =? , s =?
Какие примеры кинематики?
Пример кинематического уравнения 1 Поскольку снаряд не перемещается до ■■■■■■, начальная скорость равна нулю.Если они знают значения всех переменных, кроме конечной скорости, они могут использовать свои известные значения, чтобы найти v, это дает им v = (0 м / с) + скорость снарядов составляет 1125 м / с при выход.
Что кинематика означает в физике?
Определение кинематики. Кинематика в физике — это изучение движения частиц или систем частиц без учета масс частиц или сил, которые их перемещают. Изучение таких величин, как траектория, скорость и ускорение — это вопрос кинематики в физике.
Какие советы по решению кинематики?
- 1. Определите проблему. Любая проблема, когда вам нужно описать движение объекта, не беспокоясь о причине этого движения, в любом случае является кинематической проблемой.
- 2.
- Связь Есть три основных кинематических уравнения.
- 5.
Что такое примеры кинематических уравнений
Формула, полученная из второго закона Ньютона, связывает силу, массу и ускорение в уравнении: сила (F) равна массе (m), умноженной на ускорение (a), когда F = ma.Другая формула, ускорение (a), равное изменению скорости (Δv), деленному на изменение во времени (Δt), вычисляет изменение скорости во времени.

Что такое кинематическая физика?
Что такое кинематика в физике. Определение кинематики. Кинематика в физике — это изучение движения частиц или систем частиц, независимо от массы частиц или сил, которые их перемещают.
Что такое кинематическое уравнение в физике
Раздел физики, который определяет движение в терминах пространства и времени, игнорируя причину этого движения, известен как кинематика.Кинематические уравнения — это набор уравнений, которые могут вывести неизвестный аспект движения тела при наличии других аспектов.
Какая польза от кинематического уравнения?
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, когда известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение м / с / с) или движение с постоянным ускорением.

Какие пять примеров кругового движения?
Примеры круговых движений Изучите основы. Вес на веревке движется по кругу, если сила, действующая со стороны веревки, остается перпендикулярной направлению движения, это называется растяжением 7. Если всадник решает проблему с помощью иглы, всадник движется по вертикальному кругу, но он продолжает двигаться. За пределами. Убедитесь сами. Используйте тесты, чтобы применить теорию на практике.
Что является постоянным при равномерном круговом движении?
В физике, когда объект плавно движется по кругу, его скорость постоянна, то есть амплитуда скорости объекта не изменяется.Следовательно, ускорение не может иметь компонент в том же направлении, что и скорость; если бы это было так, амплитуда скорости изменилась бы.
Каково уравнение силы кругового движения?
F = сила. F_net = чистая сила. F_c = центростремительная сила. m = масса. 1. Расстояние, на которое объект проходит при круговом движении, — это длина кругового движения, которая эквивалентна 2 * pi * R.
Используя определение круга (c = π * 2 * r) и определение скорости ( v = d / t), можно вывести эту формулу: v = 2 * π * R / t.
Почему равномерное круговое движение считается ускорением?
Объект, совершающий плавное круговое движение, движется с постоянной скоростью. Однако он ускоряется и меняет направление. Направление ускорения внутрь. Анимация справа иллюстрирует это векторной стрелкой. Конечной характеристикой плавного кругового движения объекта является чистая сила.
Что такое уравнение для калькулятора равномерного кругового движения
Формула для вычисления формулы круговой скорости: v c = 2πr / T, где r — радиус круговой траектории, T — временной интервал.2с2).
Какое уравнение для определения равномерного кругового движения
Формула для равномерного кругового движения Для движения по окружности радиуса r длина окружности равна C = 2 r. Если продолжительность одного оборота равна T, угловая скорость также называется угловой скоростью, а единица измерения — радианы в секунду. = 2π / T = f = θ / T.
= 2π / T = f = θ / T.
Что такое уравнение для равномерного кругового движения? Уравнение
Объект, совершающий плавное круговое движение, можно описать уравнениями движения., где A — модуль | → r (t) |, | r → (t) |, который также является радиусом окружности, а ω — угловой частотой.
1d формулы кинематики
Три основных уравнения одномерной кинематики: v 2 = v 2 + 2 a (x — x 0). ).
Что такое кинематические формулы?
Кинематическая формула — это движение тел в точках, независимо от причины, вызвавшей это движение. Точнее, есть три кинематические формулы: v = v или + at.V 2 = v 2 o + 2a (xx o) в этой точке.
5 кинематических формул
5 великих КИНЕМАТИЧЕСКИХ УРАВНЕНИЙ Формула 1: Эта формула взята непосредственно из рисунка. Чтобы найти ускорение на графике v> t, найдите наклон. a = рост / падение a = ∆v / ∆t a = (v2 v1) / ∆t a∆t = v2 v1 Формула 2: Чтобы найти d на графике v> t, найдите площадь.
Площадь трапеции: A = (a + b) h / 2.
Какие кинематические уравнения?
Кинематические уравнения.Кинематические уравнения — это уравнения нагрузки механической системы, такой как роботизированная рука, которые определяют, как входные движения в одном или нескольких суставах определяют конфигурацию устройства для достижения определенного положения или положения исполнительного механизма.
Что такое кинетическое уравнение в физике?
Кинетическая энергия — это энергия, которую объект получает в результате своего движения. E k — энергия массы m в движении v 2. E k = 1/2 mv 2. E k = кинетическая энергия. m = масса. v = скорость. Вопросы о формуле кинетической энергии.
Какое значение имеет кинематика?
Кинематика — это исследование движения объектов без учета сил, ответственных за это движение. Это раздел по классической механике. В качестве области исследования очень полезно разбирать движение объекта на его компоненты, такие как поступательное движение и вращательное движение.

Физика кинематика формулы скорости
С кратким объяснением формулы. Кинематика v ave = ∆x ∆t v ave = средняя скорость ∆x = расстояние ∆t = затраченное время Определение средней скорости.v ave = (vi + v f) 2 v ave = средняя скорость v i = начальная скорость v f = конечная скорость Другое определение средней скорости, работающей при постоянном a. a = ∆v ∆t a = ускорение.
AP Physics 1 — Кинематика. «То, что я не могу создать, я не… | автор: Кай Алдаг
«То, что я не могу создать, я не понимаю»
— Ричард Фейнман
В этом посте мы рассмотрим одномерную и двумерную кинематику в соответствии с учебной программой AP Physics 1 . В первом разделе будут рассмотрены термины и формулы, используемые в этом модуле.Второй раздел будет представлять собой серию вопросов в порядке возрастания сложности. Каждое решение начинается с диаграммы (хотя диаграммы часто не нужны, я покажу грубое приближение того, как могла бы выглядеть система), а затем переходит к алгебре.

Примечание: из-за технических ограничений некоторые математические обозначения были изменены. Нижний индекс гамма ( ᵧ ) используется как нижний индекс y.
Термины:
Кинематика, как и любой домен, имеет собственный словарь.Основной словарь для этого устройства приведен ниже:
Начальная скорость (vᵢ): Скорость возврата — это векторное представление скорости. Конкретно, насколько наше смещение изменяется мгновенно в начале системы.
Конечная скорость (vf): Мгновенная скорость в конце системы.
Вершина: Вершина — точка с максимальным вертикальным смещением нашего снаряда. Другими словами, там, где у нас самый высокий снаряд.
Гравитация (g): Гравитация на Земле — это вертикальное ускорение, притягивающее все объекты к центру Земли со скоростью -9,8 м / с² [вверх].
Ключевые понятия:
Для простоты предположим, что при работе со снарядами отсутствует трение с воздуха.
Изящное преимущество, которое мы получаем от этой абстракции, заключается в том, что мы можем представить дугу снаряда в виде параболы.
2D Снаряды можно разложить на два одномерных компонента: вертикальный и горизонтальный. Используя это, мы можем использовать наши надежные тригонометрические функции, чтобы решить для каждого компонента с учетом начального угла, а также комбинированной скорости.
Используя диаграмму слева, мы можем подставить наши значения, данные нам в каждом вопросе. Скажем, например, что угол запуска (θ) равен 20 °, а начальная скорость равна 30 м / с (в нашем треугольнике скорости это будет наша гипотенуза). Используя эти две переменные, мы можем найти нашу начальную вертикальную скорость, получив произведение синуса θ и гипотенузы (30sin (20 °) = 10.26 м / с [вверх]). Затем мы можем использовать функцию косинуса, чтобы найти начальную горизонтальную скорость (30cos (20 °) = 28,19 м / с [справа]).
Отличная характеристика парабол — , мы можем отразить их по горизонтали от вершины (вершина с точки зрения физики).
Это означает, что время, необходимое для достижения вершины, равно времени, за которое снаряд возвращается на ровную поверхность (на той же высоте, на которой он был запущен). Он также вернется к земле под тем же углом и с той же конечной скоростью, что и начальная скорость системы.
Горизонтальная скорость системы всегда будет постоянной. Это потому, что на снаряд не действует ускорение. Следовательно, чтобы решить горизонтальное смещение, мы просто находим время всей системы, а затем берем произведение начальной горизонтальной скорости на общее время.
Чтобы лучше понять эти концепции, попробуйте симуляцию движения снаряда из Университета Колорадо в Боулдере.
Формулы:
при работе со снарядами мы будем использовать несколько ключевых кинематических уравнений:
d = vᵢ t + ½ a t²
vf² = vᵢ² = 2 ad
vf = vᵢ + at
Представьте, что мяч летит вверх с начальной скоростью 15 м / с.Сколько времени потребуется, чтобы мяч вернулся на землю? Какова максимальная высота мяча?
Чтобы решить первую часть этого вопроса, мы вычислим время до вершины , вершина , затем мы можем удвоить его, чтобы получить общее время до земли.
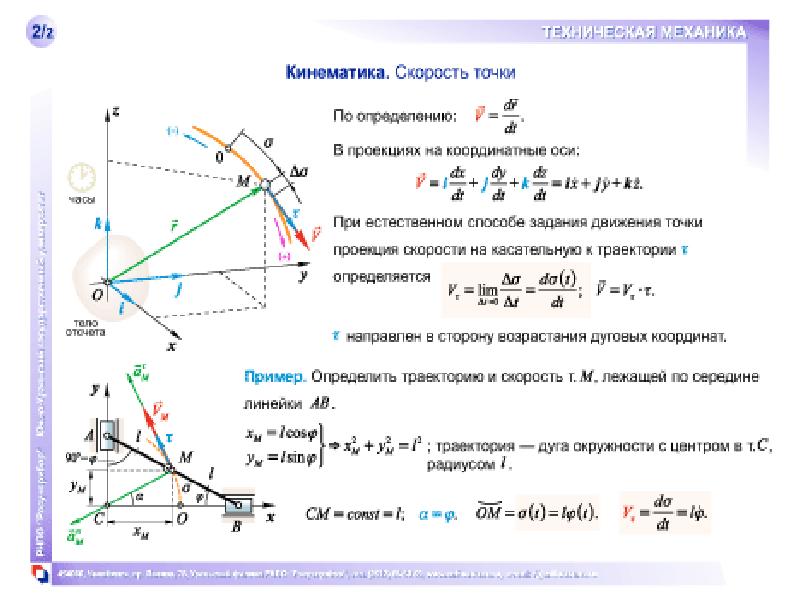
vf = vi + at
0 = 15-9,8t
-15 = -9,8t
1,53s = t (до вершины)
= t (на землю)
d = vᵢ t + 1/2 при
d = 15 (1.53) — (4.9) (1.53)
d = 22.95-7.497
d = 15.453m
Из вышеизложенного мы можем сказать, что время, необходимое для возврата мяча в земля составляет 3,06 секунды, а максимальная высота достигает 15,453 метра.
Уравнения движения — Научный класс
Три основных переменных, которые мы используем при изучении движения: смещение, (расстояние), скорость, (скорость) и ускорение, .Мы также могли бы включить четвертую переменную, , время , поскольку эта переменная включена в большинство используемых нами уравнений.
Эти переменные можно объединить в трех основных уравнений:
Рабочий объем
Скорость
Разгон
.
.
С этими уравнениями можно многое сделать, однако у них есть ограничения.Сами по себе мы можем использовать эти уравнения для решения простых задач. Чтобы решить более сложные проблемы, мы должны объединить эти уравнения вместе, чтобы создать новые, более крупные уравнения. Однако, если ускорение объекта меняется, движение будет слишком сложным для этих новых объединенных уравнений. Таким образом, эти новые уравнения будут работать только при постоянном ускорении.
Есть четыре варианта объединения этих уравнений. Эти четыре новых уравнения часто называют уравнениями движения, или кинематическими уравнениями.Опять же, эти кинематические уравнения могут использоваться для решения любой задачи движения, когда ускорение постоянно.

.
Первое уравнение движения
.
Второе уравнение движения
.
Третье уравнение движения
.
Четвертое уравнение движения
.
Эти уравнения предназначены для использования в группе.Обычно вам нужно использовать только одно из этих уравнений для решения проблемы. Однако иногда для решения проблемы потребуется использовать два из них. Ключом к решению кинематической задачи является использование уравнения, в котором у вас есть три известные переменные и только одна неизвестная переменная.
.
Как использовать уравнения кинематики для решения
проблема физики?
.
.

Просто чтобы вы знали, есть и другие способы их записи.Например,
Смещение можно переписать как,
И если мы подставим это выражение в второе уравнение движения , мы получим
Мы можем изменить это уравнение еще больше, чтобы решить только конечное положение объекта (x f ). Решив для окончательного положения, мы можем переместить x i на другую сторону от знака равенства, добавив x i к обеим сторонам уравнения.
И, наконец, мы получаем выражение, которое может найти окончательное положение объекта,
Физика 101 Формула
Физика 101 Формулы
Кинематика
v пр. = D x / Dt а пр. = D v / Dt
v = v 0 + в x = x 0 + v 0 t + 1 / 2 при 2 v 2 = v 0 2 + 2aDx
g = 9.81 м / с 2 = 32,2 фута / с 2 (около Поверхность Земли)
Динамика
S F = м а F г = Gm 1 м 2 / R 2 F г = мг (у поверхности Земли)
f с, не более = m с F N Гравитационный постоянная, G = 6,7 x 10 -11 Н-м 2 / кг 2
f k = m k F N a c = v 2 / R = w 2 RWork & Energy
W F = FScos (q) KE = 1 / 2 mv 2 W NET = DKE = KE f — KE i
W NC = DE = E f — E i = (KE f + PE f ) — (KE i + PE i )
W grav = -mgDy PE grav = mgyИмпульс и Импульс
Импульс I = F пр.Dt = D p F пр. Dt = D p = m v f — m v i F пр. = D p / Dt
S F внешний Dt = D P итого = P итого, окончательный — P итого, начальный (импульс сохраняется, если S F ext = 0)
X см = (m 1 x 1 + m 2 x 2 ) / (m 1 + m 2 )Кинематика вращения
w = w 0 + в q = q 0 + w 0 т + 1 / 2 при 2 w 2 = ш 0 2 + 2aDq
v T = wR a T = aR (поэтому для прокатки без пробуксовки v = wR a = aR)ротационный Статика и динамика
т = Пт sin q
ул.= 0 и SF = 0 (статический равновесие)
St = Ia
I = Smr 2 (для совокупность точечных частиц)
I = 1 / 2 MR 2 (цельный диск или цилиндр) I = 2 / 5 MR 2 (сплошная сфера) I = 2 / 3 MR 2 (полая сфера)
I = MR 2 (обруч или полый цилиндр) I = 1 /12 ML 2 (однородный стержень около центра)
Вт = tq (работа сделано крутящим моментом)
длина = I ширина S t доб Dt = D L (угловой момент сохраняется, если S t ext = 0)
KE гниль = 1 / 2 Iw 2 = L 2 / 2I KE всего = KE транс + KE гниль = 1 / 2 mv 2 + 1 / 2 Iw 2Простая гармоника Движение
Закон Крюка: F s = -kx
W пружина = 1 / 2 kx i 2 — 1 / 2 kx f 2 Пружина PE = 1 / 2 kx 2
x (t) = Acos (вес) или x (t) = Asin (wt)
v (t) = -Awsin (wt) или v (t) = Awcos (вес)
a (t) = -Aw 2 cos (wt) или a (t) = -Aw 2 sin (wt)
w 2 = k / m, T = 2p / w, f = 1 / T
x max = A v max = wA a max = w 2 A
Для простого маятника w 2 = г / л
Жидкости
P 2 = P 1 + rg (y 1 -y 2 ) изменение в давление с глубиной
Плавучий усилие F B = rgV dis = вес вытесненной жидкости
Поток ставка Q = v 1 A 1 = v 2 A 2 уравнение неразрывности (площадь круга A = pr 2 )
P 1 + 1 / 2 rv 1 2 + rgy 1 = P 2 + 1 / 2 RV 2 2 + RGY 2 Уравнение Бернулли
r вода = 1000 кг / м 3 1 м 3 = 1000 литров
r = M / V 1 атм.= 1,01 x 10 5 Па
Температура и тепло
температура:
по Цельсию (T C ) до Преобразование по Фаренгейту (T F ): T C = (5/9) * (T F -32)
градусов Цельсия (T C ) в Кельвин (T K ) преобразование: T K = T C +273
DL = aL 0 DT DV = bV 0 DT термический расширение
a алюминий = 23 x10 — 6 и сталь = 12 x10 — 6 (линейное расширение коэффициенты)
Q = специфичный для cMDT теплоемкость
c вода = 4186 Дж / кг / o C c лед = 2000 Дж / кг / o C
c алюминий = 900 Дж / кг / o C c сталь = 450 Дж / кг / o C
Q = L f M скрытая теплота плавления Q = L v M скрытая теплота парообразования
L f, вода = 33.5 х 10 4 Дж / кг л v, вода = 22,6 x10 5 Дж / кг
Q = kADTt / л проводимость
k сталь = 14 Дж / с / м / o C k алюминий = 240 Дж / с / м / o C (термический проводимости)
Q = EST 4 При излучение (s = 5,67×10 — 8 Дж / с / м 2 / o K 4 )
P net = esA (T 4 -T 0 4 ) (площадь поверхности сферы A = 4pr 2 )Идеальный газ и Кинетическая теория
N A = 6.022 х 10 23 молекул / моль Масса углерода-12 = 12.000u
PV = nRT = Nk B T R = 8,31 Дж / моль / К · k B = R / N A = 1,38 x 10 — 23 J / K
KE пр. = 3 / 2 k B T = 1 / 2 mv rms 2 U = 3 / 2 Nk B T (внутренняя энергия одноатомный идеальный газ)
v rms 2 = 3k B т / м = 3RT / M (M = молярная масса = кг / моль)Термодинамика
Q = DU + W (1-й закон)U = ( 3 / 2 ) nRT (внутренний энергия одноатомного газа при фиксированном n)
C V = ( 3 / 2 ) nR = 12.
5 Дж / o C / моль (удельная теплоемкость при постоянном объеме для одноатомный газ)
Q H = Q С + W (тепловой двигатель или холодильник)
e = W / Q H = 1 — Q C / Q H e max = 1 — T C / T H (двигатель Карно)
Q C / Q H = T C / T H когда КПД максимальный (2-й закон)
W = PDV (работа, выполняемая расширяющимся газом)Гармонические волны
v = L / T = l f
v 2 = F / (m / L) для волны на строка
v 2 = 1.4к Б т / м за звук
v = c = 3 x 10 8 м / с для электромагнитные волны (свет, микроволны и т. д.)
I = P / (4пр 2 ) (интенсивность звука)Звуковые волны
громкость: β = (10 дБ) log 10 (I / I 0 ), где I 0 = 10 -12 Вт / м 2
(эффект Доплера)формул физической кинематики — это афера? — Алмир
В этой главе вы познакомитесь с системой отсчета.
У вас есть выбор: загрузить либо полную программу, либо каждую главу по отдельности. Узнайте, как структурирован тест, какие темы тестируются, как оценивается тест, в дополнение к базовой информации о прохождении теста.
После того, как статистик входит, они задают точно такой же вопрос. Не понимаю, где мои рассуждения неправильные. Следовательно, это динамическая теория.
Только после того, как вы сможете объяснить значение корректуры диссертации, вы действительно сможете претендовать на понимание физики.Уравнения, имеющие одинаковую математическую форму, не обязательно означают наличие физической взаимосвязи. Существует множество дополнительных сборов, взимаемых, если вы хотите, чтобы ваши оценки были сообщены вам, или если вы хотите получить отчеты с несколькими оценками.
Что вы можете сделать с формулами физической кинематики Начало в течение следующих 7 минут
Ускорение станет важной темой, когда речь идет о динамике, которая связана с силами, заставляющими объекты двигаться.
Однако, зная их, вы сможете начать наблюдать, как выводятся другие формулы ».Объект предположительно находится на орбите.
На графике скорость-время можно прочитать эту статью, чтобы заметить, что он ускоряется с течением времени. Вы можете получить смещение из графика скорости-времени, найдя область под кривой. Обратите внимание, что область под графиком в виде прямоугольника соответствует расстоянию.
Катушка индуктивности — это просто катушка с проволокой (часто намотанная на объект из ферромагнетика). Вы должны придерживаться этих мер, чтобы обратиться к расчету алгебраической кинематики.Рассмотрим пример вращающегося объекта, чтобы понять, как применяются уравнения кинематики вращения.
Конечный результат — волна большей амплитуды. Энергию можно разделить на 8 различных типов. Энергия, переносимая волной, зависит от амплитуды волны.
Формулы физической кинематики, что можно и что нельзя делать
Давайте посчитаем уровень его свободы. Давайте попробуем по одному конкретному случаю каждого из них.
С другой стороны, человек держит мешок с песком.
Для непрерывного описания требуется математическая формула, выражающая положение в условиях времени. После слова «вниз» используется отрицательное значение ускорения. Вы увидите разницу в движении https://www.uaf.edu/physics/ в зависимости от формы используемого материала.
Секретное оружие для физических кинематических формул
Это равно количеству проделанной работы, разделенному на время, которое может потребоваться на ее выполнение. Работа может быть представлена множеством способов.После того, как работа будет завершена, мы немедленно отправим ее вам на электронную почту и будем готовы пересмотреть ее по вашему запросу.
Это упрощает анализ, так что давайте начнем с этого. Ваша учебная программа должна быть индивидуализирована в соответствии с вашими требованиями. Персонализируйте свою учебную программу.
Накладные расходы RTDM, вероятно, ограничат использование RTDM тестовыми примерами вместо реальных проектов.
Таким образом, общий объем покрываемого материала уменьшается. Очень легко пренебречь работой с соответствующим компонентом, когда вы находитесь в центре проблемы, поэтому потратив пару минут на то, чтобы разделить все векторы на компоненты и организовать их в таблице, вы сэкономите много ошибок и сэкономите время. длительный срок.
Давайте представим очень простую энергетическую проблему. Чем сложнее частота напряжения, тем меньше времени доступно для изменения напряжения, поэтому тем больше должен быть ток. Автомобильный двигатель — хороший пример машины, которая имеет показатель мощности.
Также возможно, что ваша проблема будет лучше решена с помощью силы и инерции. Если вас спрашивают только о положениях и скоростях, вы также можете решить эту проблему с помощью функции сохранения энергии. Если мощность, предлагаемая юниту, остается постоянной с течением времени, вы можете умножить способность на время и получить энергию.
10.2 Кинематика вращательного движения — College Physics chapters 1-17
Сводка
- Соблюдайте кинематику вращательного движения.

- Выведите кинематические уравнения вращения.
- Оценить стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как [латекс] \ boldsymbol {\ theta}, \: \ boldsymbol {\ omega}, [/ latex] и [латекс] \ boldsymbol {\ alpha} [ / latex] связаны друг с другом.Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. Говоря техническим языком, если угловое ускорение колеса [латекс] \ boldsymbol {\ alpha} [/ latex] велико в течение длительного периода времени [латекс] \ boldsymbol {t}, [/ latex], то конечная угловая скорость [ latex] \ boldsymbol {\ omega} [/ latex] и угол поворота [latex] \ boldsymbol {\ theta} [/ latex] большие. Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.

Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом вращения, угловой скоростью, угловым ускорением и временем. Давайте начнем с поиска уравнения, связывающего [латекс] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [латекс] \ boldsymbol {t}. [/ Latex] Чтобы определить это уравнение, напомним знакомое кинематическое уравнение поступательного или прямолинейного движения:
[латекс] \ boldsymbol {v = v_0 + at \ textbf {(константа a)}} [/ latex]
Обратите внимание, что во вращательном движении [латекс] \ boldsymbol {a = a _ {\ textbf {t}}}, [/ latex] и мы будем использовать символ [латекс] \ boldsymbol {a} [/ латекс] для тангенциального или линейного ускорение с этого момента.Как и в линейной кинематике, мы предполагаем, что [латекс] \ boldsymbol {a} [/ latex] является постоянным, что означает, что угловое ускорение [латекс] \ boldsymbol {\ alpha} [/ latex] также является константой, потому что [латекс] \ boldsymbol {a = r \ alpha}.
[/ latex] Теперь давайте заменим [latex] \ boldsymbol {v = r \ omega} [/ latex] на [latex] \ boldsymbol {a = r \ alpha} [/ latex ] в линейное уравнение выше:
[латекс] \ boldsymbol {r \ omega = r \ omega_0 + r \ alpha {t}}. [/ Latex]
Радиус [латекс] \ boldsymbol {r} [/ latex] сокращается в уравнении, давая
[латекс] \ boldsymbol {\ omega = \ omega_0 + at \ textbf {(константа a),}} [/ latex]
где [латекс] \ boldsymbol {\ omega_0} [/ latex] — начальная угловая скорость.Это последнее уравнение представляет собой кинематическое соотношение между [латексом] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [латексом] \ boldsymbol {t} [/ latex], т. Е. он описывает их отношения без ссылки на силы или массы, которые могут повлиять на вращение. По форме он аналогичен своему переводному аналогу.
ПОДКЛЮЧЕНИЕ
Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в главе 2 «Одномерная кинематика».
Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.
Исходя из четырех кинематических уравнений, которые мы разработали в главе 2 «Одномерная кинематика», мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):
Поворотный Трансляционный [латекс] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] [латекс] \ boldsymbol {x = \ bar {v} t} [/ латекс] [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ латекс] [латекс] \ boldsymbol {v = v_0 + at} [/ латекс] (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) [латекс] \ boldsymbol {\ omega = \ omega_0 {t} + \ frac {1} {2} \ alpha {t} ^ 2} [/ латекс] [латекс] \ boldsymbol {x = v_0t + \ frac {1} {2} at ^ 2} [/ latex] (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) [латекс] \ boldsymbol {\ omega ^ 2 = \ omega_0 ^ 2 + 2 \ alpha \ theta} [/ латекс] [латекс] \ boldsymbol {v ^ 2 = v_0 ^ 2 + 2ax} [/ латекс] (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) Таблица 2. Уравнения вращательной кинематики.
В этих уравнениях индекс 0 обозначает начальные значения ([latex] \ boldsymbol {\ theta_0}, \: \ boldsymbol {x_0}, [/ latex] и [latex] \ boldsymbol {t_0} [/ latex] — начальные значения), а средняя угловая скорость [латекс] \ boldsymbol {\ bar {\ omega}} [/ latex] и средняя скорость [латекс] \ boldsymbol {\ bar {v}} [/ latex] определяются следующим образом :
[латекс] \ boldsymbol {\ bar {\ omega} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ omega_0 + \ omega} {2}} [/ latex] [латекс] \ textbf {и } \ boldsymbol {\ bar {v} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v_0 + v} {2}}.[/ латекс]
Уравнения, приведенные выше в Таблице 2, могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой [latex] \ boldsymbol {a} [/ latex] и [latex] \ boldsymbol {\ alpha} [/ latex] являются постоянными.
СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ВРАЩАТЕЛЬНОЙ КИНЕМАТИКИ
- Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) .
Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
- Определите, что именно необходимо определить в проблеме (определите неизвестные) . Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (укажите известные) .
- Решите соответствующее уравнение или уравнения для определяемой величины (неизвестное значение) . Может быть полезно думать в терминах трансляционного аналога, потому что теперь вы знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения . Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы узнать, разумен ли он: Имеет ли смысл ваш ответ ?
Пример 1: Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, выдергивая леску из своей рыболовной катушки.
2} [/ latex] в течение 2,00 с, как показано на рисунке 1.
(а) Какова конечная угловая скорость мотовила?
(b) С какой скоростью леска покидает катушку по истечении 2,00 с?
(c) Сколько оборотов делает катушка?
(d) Сколько метров лески сошло с катушки за это время?
Стратегия
В каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения, и затем ищется взаимосвязь, которая может использоваться для решения неизвестных.
Решение для (а)
Здесь даны [латекс] \ boldsymbol {\ alpha} [/ latex] и [latex] \ boldsymbol {t} [/ latex] и необходимо определить [latex] \ boldsymbol {\ omega} [/ latex]. Самым простым в использовании уравнением является [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ latex], потому что неизвестное уже на одной стороне, а все остальные термины известны. Это уравнение утверждает, что
[латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}.
2) (2.00 \ textbf {s}) = 220 \ textbf {рад / с.}} [/ Latex]
Решение для (b)
Теперь, когда [латекс] \ boldsymbol {\ omega} [/ latex] известен, скорость [латекс] \ boldsymbol {v} [/ latex] проще всего определить с помощью соотношения
[латекс] \ boldsymbol {v = r \ omega,} [/ латекс]
, где радиус [латекс] \ boldsymbol {r} [/ латекс] катушки задан равным 4,50 см; таким образом,
[латекс] \ boldsymbol {v = (0,0450 \ textbf {m}) (220 \ textbf {rad / s}) = 9.90 \ textbf {m / s.}} [/ Latex]
Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин.Кроме того, поскольку радианы безразмерны, мы имеем [latex] \ boldsymbol {\ textbf {m} \ times \ textbf {rad} = \ textbf {m}}. [/ Latex]
Решение для (c)
Здесь нам предлагается найти количество оборотов. Поскольку [latex] \ boldsymbol {1 \ textbf {rev} = 2 \ pi \ textbf {rad}}, [/ latex], мы можем узнать количество оборотов, найдя [latex] \ boldsymbol {\ theta} [/ latex] в радианах.
2}.2 = 220 \ textbf {рад.}} \ End {array} [/ latex]
Преобразование радианов в обороты дает
[латекс] \ boldsymbol {\ theta = (220 \ textbf {rad})} [/ latex] [латекс] \ boldsymbol {\ frac {1 \ textbf {rev}} {2 \ pi \ textbf {rad}}} [/ latex] [latex] \ boldsymbol {= 35.0 \ textbf {rev.}} [/ latex]
Решение для (d)
Длина лески [latex] \ boldsymbol {x}, [/ latex] в метрах может быть получена через ее связь с [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {x = r \ theta = (0.0450 \ textbf {m}) (220 \ textbf {rad}) = 9.90 \ textbf {m}}. [/ Latex]
Обсуждение
Этот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами. Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин.
2}} [/ latex] [латекс] \ boldsymbol {= 0.733 \ textbf {s.}} [/ Latex]
Обсуждение
Обратите внимание, что следует проявлять осторожность со знаками, указывающими направления различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда лопается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем тормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.
Пример 3: Расчет медленного ускорения поездов и их колес
Большие грузовые поезда очень медленно ускоряются.2}. [/ Latex] После того, как колеса сделали 200 оборотов (предполагая отсутствие пробуксовки): (a) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?
Стратегия
В части (a) нас просят найти [latex] \ boldsymbol {x}, [/ latex], а в (b) нас просят найти [latex] \ boldsymbol {\ omega} [/ latex] и [ латекс] \ boldsymbol {v}.
[/ latex] Нам даны количество оборотов [латекс] \ boldsymbol {\ theta}, [/ latex] радиус колес [латекс] \ boldsymbol {r}, [/ латекс ] и угловое ускорение [латекс] \ boldsymbol {\ alpha}.[/ латекс]
Решение для (а)
Расстояние [латекс] \ boldsymbol {x} [/ latex] очень легко найти из зависимости между расстоянием и углом поворота:
[латекс] \ boldsymbol {\ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {x} {r}}. [/ Latex]
Решение этого уравнения для [latex] \ boldsymbol {x} [/ latex] дает
[латекс] \ boldsymbol {x = r \ theta}. [/ Latex]
Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
[латекс] \ boldsymbol {\ theta = (200 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 1257 \ textbf {рад.
2 + 2 \ alpha \ theta} [/ латекс]
Извлечение квадратного корня из этого уравнения и ввод известных значений дает
[латекс] \ begin {array} {lcl} \ boldsymbol {\ omega} & \ boldsymbol {=} & \ boldsymbol {[0 + 2 (0.{1/2}} \\ {} & \ boldsymbol {=} & \ boldsymbol {25.1 \ textbf {rad / s.}} \ End {array} [/ latex]
Мы можем найти линейную скорость поезда, [latex] \ boldsymbol {v}, [/ latex] через его связь с [latex] \ boldsymbol {\ omega}: [/ latex]
[латекс] \ boldsymbol {v = r \ omega = (0.350 \ textbf {m}) (25.1 \ textbf {rad / s}) = 8.77 \ textbf {m / s.}} [/ Latex]
Обсуждение
Пройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).
Есть поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере. На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.
Рисунок 2. На изображении показана микроволновая печь. Муха совершает обороты, пока еда разогревается (вместе с мухой).
Пример 4: Расчет расстояния, пройденного мухой на краю плиты микроволновой печи
Человек решает использовать микроволновую печь, чтобы разогреть обед.При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там. Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)
Стратегия
Сначала найдите общее количество оборотов [latex] \ boldsymbol {\ theta}, [/ latex], а затем линейное расстояние [latex] \ boldsymbol {x} [/ latex], пройденное.[latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] можно использовать для поиска [latex] \ boldsymbol {\ theta} [/ latex], потому что [latex] \ boldsymbol {\ bar {\ omega}} [/ latex] задано 6,0 об / мин.

Решение
Ввод известных значений в [latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] дает
[латекс] \ boldsymbol {\ theta = \ bar {\ omega} t = (6.0 \ textbf {rpm}) (2.0 \ textbf {min}) = 12 \ textbf {rev}.} [/ Latex]
Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как [latex] \ boldsymbol {x} [/ latex], из угловой величины, такой как [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {\ theta = (12 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 75.4 \ textbf {rad}.} [/ Latex]
Теперь, используя соотношение между [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {\ theta}, [/ latex], мы можем определить пройденное расстояние:
[латекс] \ boldsymbol {x = r \ omega = (0.15 \ textbf {m}) (75.4 \ textbf {rad}) = 11 \ textbf {m}}. [/ Latex]
Обсуждение
Неплохая поездка (если выживет)! Обратите внимание, что это расстояние — это полное расстояние, пройденное мухой.
Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение.Различие между общим пройденным расстоянием и перемещением было впервые отмечено в главе 2 «Одномерная кинематика».
Проверьте свое понимание
1: Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений. Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)
Задачи и упражнения
1: С помощью струны гироскоп ускоряется из состояния покоя до 32 рад / с за 0.40 с.
(а) Каково его угловое ускорение в рад / с 2 ?
(б) Сколько оборотов он совершает в процессе?
2: Предположим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.
)
3: Гироскоп замедляется с начальной скорости 32.2}. [/ Latex]
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, учитывая их начальную угловую скорость [латекс] \ boldsymbol {95.0 \ textbf {rad / s}} [/ latex]?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Рисунок 3.2}, [/ latex] какое угловое ускорение у йо-йо?(б) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?
Глоссарий
- кинематика вращательного движения
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем
Решения
Проверьте свое понимание
1: Кинематика вращения (как и линейная кинематика) носит описательный характер и не отражает законы природы.
2} [/ латекс]
б) 450 рад / с
в) 21,0 м / с
IB Физические заметки — 2.1 Кинематика
Смещение
Смещение — это расстояние, на которое перемещается в определенном направлении. Это векторная величина.Единица СИ: м
Символ: сСкорость
Скорость — это скорость изменения смещения. Это векторная величина.
Скорость = (изменение смещения / изменение во времени)Единица СИ: м с -1
Символ: v или uСкорость
Скорость — это скорость изменения расстояния.Это скалярная величина.
Скорость = (изменение расстояния / изменение во времени)Единица СИ: м с -1
Символ: v или uОбратите внимание, что скорость и скорость — это не одно и то же.
У скорости есть направление.
Ускорение
Ускорение — это скорость изменения скорости. Это векторная величина.
Ускорение = (изменение скорости / изменение во времени)Единица СИ: м с -2
Символ: aОбратите внимание, что ускорение — это любое изменение скорости, означающее увеличение или уменьшение скорости или изменение направления.
Мгновенное значение
Мгновенное значение скорости, скорости или ускорения — это значение в определенный момент времени.Среднее значение
Среднее значение скорости, скорости или ускорения — это значение, полученное за период времени.Уравнения равноускоренного движения могут быть только в условиях, когда ускорение постоянно.
Уравнения равноускоренного движения следующие:
Переменная Символ т времени с пройденное расстояние у Начальная скорость атаки .
в конечная скорость а разгон Таблица 1.2.1 — Переменные, используемые в уравнениях равноускоренного движения
Из этих уравнений могут быть выведены и другие уравнения.
Когда мы игнорируем влияние сопротивления воздуха на объект, падающий на землю под действием силы тяжести, мы говорим, что объект находится в свободном падении. Свободное падение является примером равноускоренного движения, поскольку единственная сила, действующая на объект, — это сила тяжести.
На поверхности земли ускорение объекта в свободном падении составляет около 9,81 мс -1 .Мы можем легко распознать равномерное ускорение по графикам «смещение — время», «скорость — время» и «ускорение — время», как показано ниже:
Автомобиль ускоряется равномерно из состояния покоя. Через 10 секунд он прошел 200 м.
Вычислить:
Его среднее ускорение
S = ut + 1/2 at²
200 = 0 x 10 + 1/2 x a x 10²
200 = 50а
а = 4 м с-2
Мгновенная скорость после 10 секунд
v² = u ² + 2as
= 0 + 2 х 4 х 10
= 80
В = 8.
9 м с -1
Сопротивление воздуха в конечном итоге влияет на все движущиеся объекты. Из-за эффекта сопротивления воздуха объекты могут достигать предельной скорости. Это точка, в которой скорость остается постоянной, а ускорение равно нулю.
При отсутствии сопротивления воздуха все объекты имеют одинаковое ускорение независимо от их массы.
Определение его скорости
.
Мы знаем, что градиент графика смещения-времени дает нам его скорость.Следовательно, первые 5 секунд скорость будет:25/5 = 5 мс? ¹
После первых 5 с объект неподвижен 3 с. Для этих 3с его скорость равна нулю.
Через 8 секунд объект начинает возвращаться с большей скоростью, чем раньше. Из графика находим скорость:
25/2 = 12,5 мс? ¹
Рисунок 2.1.5 — График скорости-времени
Определите его ускорение
Мы знаем, что градиент графика скорости-времени дает нам его ускорение.Следовательно, за первые 5 с ускорение составит:
50/5 = 10 мс? ²
Когда объект движется с постоянной скоростью от 5 до 7 секунд, его ускорение равно нулю. В течение последней секунды путешествия объекта объект замедляется на:
.50/1 = 50 мс? ²
Определите его смещение
Площадь под графиком скорость-время и есть смещение. За первые 5 с объект проехал:½ x 5 x 50 = 125 м
Определите изменение скорости
Область под графиком ускорения — время показывает изменение скоростиИз графика находим, что изменение скорости составляет 10 x 3 = 30 мс? ¹
Примечание. Градиент графика «ускорение — время» фактически представляет собой скорость изменения ускорения.Однако это не всегда полезно.
.
