Формулы по динамике: Ошибка: 404 Материал не найден

Более 40 основных формул по физике с объяснением

Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы  неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.

Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика, термодинамика и молекулярная физика, электричество. Их и возьмем!

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Основные формулы по физике динамика, кинематика, статика

Начнем с самого простого.

Старое-доброе любимое  прямолинейное и равномерное движение.

Формулы кинематики:

 

Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.

 

После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

 

Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!

 

Основные формулы молекулярной физики и термодинамики

Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.

 

Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Формулы, термодинамика

Основные формулы по физике: электричество

Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.

 

Далее берем постоянный и переменный ток.

 

И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.

 

На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса. Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».

Автор: Иван

Иван Колобков, известный также как Джони.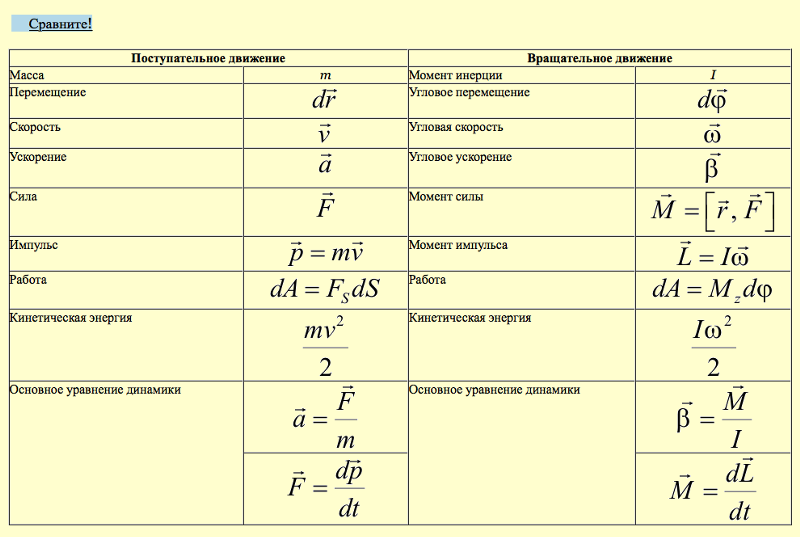 Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

+50 формул по физике за 7-11 класс с пояснением

Мы собрали основные формулы по физике с пояснениями в картинках. Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!

Основные формулы по физике: кинематика, динамика, статика

Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:

Также давайте вспомним движение по кругу:

 

Медленно, но уверенно мы перешли более сложной теме – к динамике:

Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:

После статики можно рассмотреть и гидростатику:

Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:

Нужна работа? Есть решение!

Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.

Подробнее Гарантии Отзывы

Основные формулы термодинамики и молекулярной физики

Последняя тема в механике – это “Колебания и волны”:

Теперь можно смело переходить к молекулярной физике:

Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:

Основные формулы электричества

Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

Переходим к постоянному электрическому току:

Далее добавляем формулы по теме: “Магнитное поле электрического тока”

Электромагнитная индукция тоже важная тема для знания и понимания физики.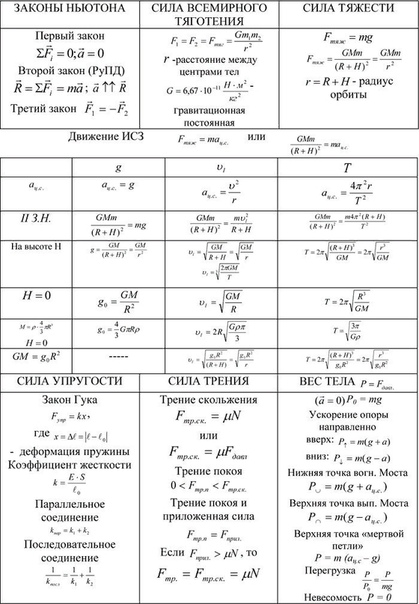 Конечно, формулы по этой теме необходимы:

Ну и, конечно, куда же без электромагнитных колебаний:

 

Основные формулы оптической физики

Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:

Основные формулы элементов теории относительности

И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:

Основные формулы световых квантов

Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:

На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.

Это были основные формулы физики

В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.

Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.

Надеемся, что подборка формул вам понравилась!

P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.

Более 50 основных формул по физике с пояснением обновлено: 22 ноября, 2019 автором: Научные Статьи.Ру

Динамические массивы в Excel

Что такое динамические массивы

В сентябре 2018 года Microsoft выпустила обновление, которое добавляет в Microsoft Excel совершенно новый инструменты: динамические массивы (Dynamic Arrays) и 7 новых функций для работы с ними. Эти вещи, без преувеличения, совершенно кардинальным образом меняет всю привычную технику работы с формулами и функциями и касаются, буквально, каждого пользователя.

Рассмотрим простой пример, чтобы объяснить суть.

Предположим, что у нас есть простая табличка с данными по городам-месяцам. Что будет если мы выделим любую пустую ячейку справа на листе и введем в нее формулу-ссылку не на одну ячейку, а сразу на диапазон?

Во всех прошлых версиях Excel после нажатия на Enter мы бы получили содержимое только одной первой ячейки B2. А как иначе?

Ну, или можно было бы завернуть этот диапазон в какую-нибудь аггрегирующую функцию типа =СУММ(B2:C4) и получить по нему общий итог.

Если бы нам потребовались операции посложнее примитивной суммы, например, извлечение уникальных значений или Топ-3, то пришлось бы вводить нашу формулу как формулу массива, используя сочетание клавиш Ctrl+Shift+Enter.

Теперь всё по-другому.

Теперь после ввода такой формулы мы можем просто нажать на Enter — и получить в результате сразу все значения, на которые мы ссылались:

Это не магия, а новые динамические массивы, которые теперь есть в Microsoft Excel. Добро пожаловать в новый мир :)

Особенности работы с динамическими массивами

Технически, весь наш динамический массив хранится в первой ячейке G4, заполняя своими данными необходимое количество ячеек вправо и вниз. Если выделить любую другую ячейку массива, то в строке формул ссылка будет неактивной, показывая, что мы находимся в одной из «дочерних» ячеек:

Попытка удалить одну или несколько «дочерних» ячеек ни к чему не приведёт — Excel тут же заново их вычислит и заполнит.

При этом ссылаться на эти «дочерние» ячейки в других формулах мы можем совершенно спокойно:

Если копировать первую ячейку массива (например из G4 в F8), то и и весь массив (его ссылки) сдвинется в том же направлении, как и в обычных формулах:

Если нам нужно переместить массив, то достаточно будет перенести (мышью или сочетанием Ctrl+X, Ctrl+V), опять же, только первую главную ячейку G4 — вслед за ней перенесется на новое место и заново развернётся весь наш массив.

Если вам нужно сослаться где-нибудь еще на листе на созданный динамический массив, то можно использовать спецсимвол # («решётка») после адреса его ведущей ячейки:

Например, теперь можно легко сделать выпадающий список в ячейке, который ссылается на созданный динамический массив:

Ошибки динамических массивов

Но что будет, если для развёртывания массива не будет достаточно пространства или на его пути окажутся ячейки уже занятые другими данными? Знакомьтесь с принципиально новым типом ошибок в Excel — #ПЕРЕНОС! (#SPILL!):

Как всегда, если щелкнуть мышью по значку с желтым ромбом и восклицательным знаком, то мы получим более подробное пояснение по источнику проблемы и сможем быстро найти мешающие ячейки:

Аналогичные ошибки будут возникать, если массив выходит за пределы листа или натыкается на объединенную ячейку. Если удалить препятствие, то всё тут же исправится на лету.

Динамические массивы и «умные» таблицы

Если динамический массив указывает на «умную» таблицу, созданную сочетанием клавиш Ctrl+T или с помощью Главная — Форматировать как таблицу (Home — Format as Table), то он также унаследует её главное качество — автоподстройку размеров.

При добавлении новых данных внизу или справа «умная» таблица и динамический диапазон тоже будут автоматически растягиваться:

При этом, однако, есть одно ограничение: мы не можем использовать ссылку на динамический диапазон в форумулах внутри «умной» таблицы:

Динамические массивы и другие функции Excel

Хорошо, скажете вы. Всё это интересно и забавно. Не нужно, как раньше, вручную протягивать формулу со ссылкой на первую ячейку исходного диапазона вниз и вправо и всё такое. И всё?

Не совсем.

Динамические массивы — это не просто еще один инструмент в Excel. Теперь они внедрены в самое сердце (или мозг) Microsoft Excel — его вычислительный движок. А это значит что и другие, привычные нам формулы и функции Excel теперь тоже поддерживают работу с динамическими массивами. Давайте разберём несколько примеров, чтобы вы осознали всю глубину произошедших изменений.

Транспонирование

Чтобы транспонировать диапазон (обменять местами строки и столбцы) в Microsoft Excel всегда имелась встроенная функция ТРАНСП (TRANSPOSE). Однако, чтобы её использовать, вы должны были сначала правильно выделить диапазон для результатов (например, если на входе был диапазон 5х3, то вы должны были обязательно выделить 3×5), потом ввести функцию и нажать сочетание Ctrl+Shift+Enter, т.к. она умела работать только в режиме формул массива.

Теперь можно просто выделить одну ячейку, ввести в нее эту же формулу и нажать на обычный Enter — динамический массив сделает всё сам:

Таблица умножения

Этот пример я обычно приводил, когда меня просили наглядно показать преимущества формул массива в Excel.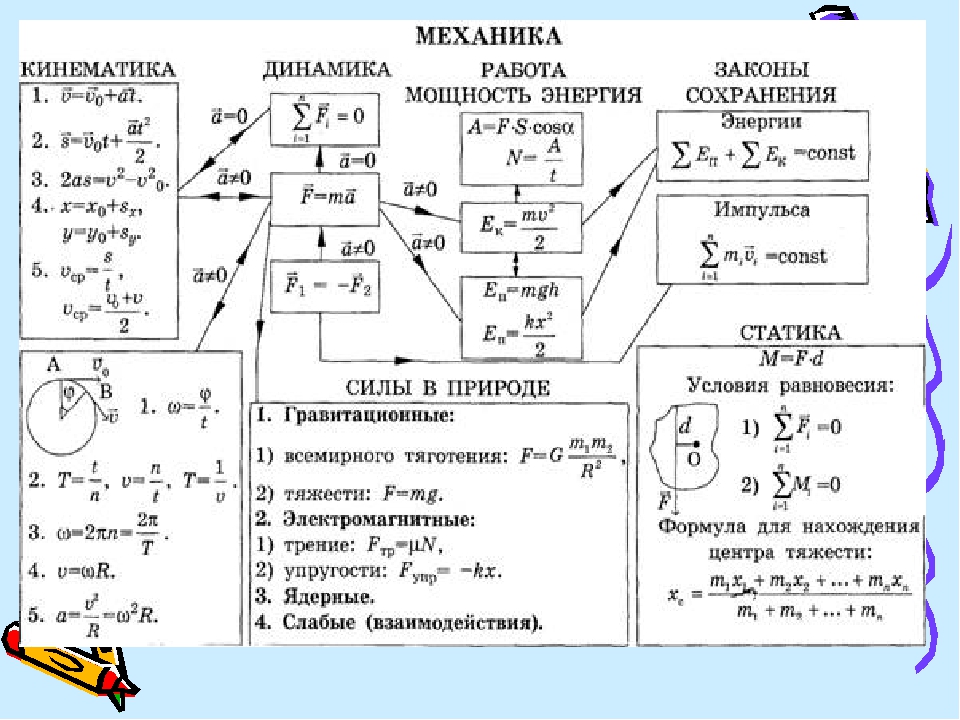 Теперь чтобы посчитать всю таблицу Пифагора достаточно встать в первую ячейку B2, ввести туда формулу перемножающую два массива (вертикальный и горизонтальный набор чисел 1..10) и просто нажать на Enter:

Склейка и преобразование регистра

Массивы можно не только перемножать, но склеивать стандартным оператором & (амперсанд). Предположим, нам нужно сцпеить имя и фамилию из двух столбцов и поправить скачущий регистр в исходных данных. Делаем это одной короткой формулой, которая формирует весь массив, а потом применяем к нему функцию ПРОПНАЧ (PROPER), чтобы привести в порядок регистр:

Вывод Топ-3

Предположим, что у нас есть куча чисел, из которых нужно вывести три лучших результата, расположив их в порядке убывания. Теперь это делается одной формулой и, опять же, без всяких Ctrl+Shift+Enter как раньше:

Если захочется, чтобы результаты располагались не в столбец, а в строку, то достаточно заменить в этой формуле двоеточия (разделитель строк) на точку с запятой (разделитель элементов внутри одной строки). В англоязычной версии Excel роль этих разделителей играют точка с запятой и запятая, соответственно.

ВПР извлекающая сразу несколько столбцов

Функцей ВПР (VLOOKUP) теперь можно вытаскивать значения не из одного, а сразу из нескольких столбцов — достаточно указать их номера (в любом желаемом порядке) в виде массива в третьем аргументе функции:

Функция СМЕЩ (OFFSET) возвращающая динамический массив

Одной из самых интересных и полезных (после ВПР) функций для анализа данных является функция СМЕЩ (OFFSET), которой я посвятил в своё время целую главу в своей книжке и статью здесь. Сложность в понимании и освоении этой функции всегда была в том, что она возвращала в качестве результата массив (диапазон) данных, но увидеть его мы не могли, т.к. Excel до сих пор не умел работать с массивами «из коробки».

Сейчас эта проблема в прошлом. Посмотрите, как теперь с помощью одной формулы и динамического массива, возвращаемого СМЕЩ, можно извлечь все строки по заданному товару из любой отсортированной таблицы:

Давайте разберём её аргументы:

• А1 — стартовая ячейка (точка отсчёта)
• ПОИСКПОЗ(F2;A2:A30;0) — вычисление сдвига от стартовой ячейки вниз — до первой найденной капусты.
• 0 — сдвиг «окна» вправо относительно стартовой ячейки
  
• СЧЁТЕСЛИ(A2:A30;F2) — вычисление высоты возвращаемого «окна» — количества строк, где есть капуста.
• 4 — размер «окна» по горизонтали, т.е. выводим 4 столбца

Новые функции для динамических массивов

Помимо поддержки механизма динамических массивов в старых функциях, в Microsoft Excel были добавлены несколько совершенно новых функций, заточенных именно под работу с динамическими массивами. В частности, это:

• СОРТ (SORT) — сортирует входной диапазон и выдает динамический массив на выходе
  
• СОРТПО (SORTBY) — умеет сортировать один диапазон по значениям из другого
  
• ФИЛЬТР (FILTER) — извлекает из исходного диапазона строки, удовлетворяющие заданным условиям
• УНИК (UNIQUE) — извлекает из диапазона уникальные значения или убирает повторы
  
• СЛМАССИВ (RANDARRAY) — генерит массив случайных чисел заданного размера
• ПОСЛЕД (SEQUENCE) — формирует массив из последовательности чисел с заданным шагом
  

Подробнее про них — чуть позже. Они стоят отдельной статьи (и не одной) для вдумчивого изучения 🙂

Выводы

Если вы прочитали всё написанное выше, то, думаю, уже осознаёте масштаб изменений, которые произошли. Очень многие вещи в Excel теперь можно будет делать проще, легче и логичнее. Я, признаться, немного в шоке от того, сколько статей теперь придется корректировать здесь, на этом сайте и в моих книгах, но готов это сделать с легким сердцем.

Подбивая итоги, в плюсы динамических массивов можно записать следующее:

• Можно забыть про сочетание Ctrl+Shift+Enter. Теперь Excel не видит различий между «обычными формулами» и «формулами массива» и обрабатывает их одинаково.
• Про функцию СУММПРОИЗВ (SUMPRODUCT), которую раньше использовали для ввода формул массива без Ctrl+Shift+Enter тоже можно забыть — теперь достаточно просто СУММ и Enter.
• Умные таблицы и привычные функции (СУММ, ЕСЛИ, ВПР, СУММЕСЛИМН и т. д.) теперь тоже полностью или частично поддерживают динамические массивы.
• Есть обратная совместимость: если открыть книгу с динамическими массивами в старой версии Excel, то они превратятся в формулы массива (в фигурных скобках) и продолжат работать в «старом стиле».

Нашлось и некоторое количество минусов:

• Нельзя удалить отдельные строки, столбцы или ячейки из динамического массива, т.е. он живёт как единый объект.
• Нельзя сортировать динамический массив привычным образом через Данные — Сортировка (Data — Sort). Для этого есть теперь специальная функция СОРТ (SORT).
• Динамический диапазон нельзя превратить в умную таблицу (но можно сделать динамический диапазона на основе умной таблицы).
  

Само-собой, это еще не конец и, я уверен, Microsoft продолжит совершенствовать этот механизм в будущем.

Где скачать?

И, наконец, главный вопрос :)

Microsoft впервые анонсировало и показало превью динамических массивов в Excel еще в сентябре 2018 года на конференции Ignite. В последующие несколько месяцев происходило тщательное тестирование и обкатка новых возможностей сначала на кошках сотрудниках самой Microsoft, а потом на добровольцах-тестировщиках из круга Office Insiders. В этом году обновление, добавляющее динамические массивы стали постепенно раскатывать уже по обычным подписчикам Office 365. Я, например, получил его только в августе с моей подпиской Office 365 Pro Plus (Monthly Targeted).

Если в вашем Excel ещё нет динамических массивов, а поработать с ними очень хочется, то есть следующие варианты:

• Если у вас подписка Office 365, то можно просто продождать, пока до вас дойдет это обновление. Как быстро это случится — зависит от настройки частоты доставки обновлений для вашего Office (раз в год, раз в полгода, раз в месяц). Если у вас корпоративный ПК, то можно попросить вашего администратора настроить загрузку обновлений почаще.
  
• Можно записаться в ряды тех самых добровольцев-тестировщиков Office Insiders — тогда вы будете первым получать все новые возможности и функции (но есть шанс повышенной глючности в работе Excel, само-собой).
• Если у вас не подписка, а коробочная standalone-версия Excel, то придется ждать до выхода следующей версии Office и Excel в 2022 году, как минимум. Пользователи таких версий получают только обновления безопасности и исправления ошибок, а все новые «плюшки» теперь достаются только подписчикам Office 365. Sad but true 🙂
  

В любом случае, когда динамические массивы появятся в вашем Excel — после этой статьи вы будете к этому уже готовы 🙂

Ссылки по теме

Урок 7. законы динамики ньютона — Физика — 10 класс

Законы динамики Ньютона

Необходимо запомнить

ВАЖНО!

Масса – одна из основных характеристик материи. Способы измерения массы:

— сравнение с эталоном;

— взвешивание на весах.

В классической механике масса – аддитивная величина; не зависит от рода взаимодействия и скорости движения тела: $m_{сист} = \sum_{i=1}^{n}mi$. {n}Fi$.

Первый закон Ньютона: если на тело не действуют другие тела, то тело движется прямолинейно и равномерно: $\overrightarrow{F} = 0$.

Важно! Если есть ИСО, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.

Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: $\overrightarrow{a} = \frac{\overrightarrow{F}}{m}$.

Другая запись формулы второго закона Ньютона (основное уравнение динамики): $\overrightarrow{F} = m \overrightarrow{a}$ .

Третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению: $\overrightarrow{F}_{12} = -\overrightarrow{F}_{21}$.

Второй закон Ньютона для системы тел: приращение импульса $\Delta \overrightarrow{P}$ системы тел равно по величине и по направлению импульсу внешних сил, действующих на тело, за то же время: $\Delta \overrightarrow{p} = \overrightarrow{F} \Delta t$.

Границы применимости: справедливы для материальных точек или поступательно движущихся тел; для скоростей много меньше скорости света в вакууме; выполняются в ИСО.

Решение задачи на применение второго закона Ньютона

Статические и динамические симуляторы машин Формулы 1

После введения запрета на тесты по ходу сезона команды Формулы 1 вынуждены заменять реальную работу на трассах исследованиями в аэродинамической трубе и компьютерным моделированием.

Мы уже писали о системах вычислительной гидродинамики, позволяющих инженерам проводить виртуальную «продувку» аэродинамических решений, в этом году в чемпионате дебютировала первая машина, полностью разработанная на компьютерах CFD, но сегодня речь пойдёт о другом направлении работы, в котором используются сложные компьютерные системы – виртуальных симуляторах машин.

Команды Формулы 1 используют два типа симуляторов – статический и динамический. В статическом используется реальный или приближенный к нему монокок, жестко закреплённый перед большим сферическим экраном. На экране воспроизводится картинка, имитирующая конкретную трассу и её прохождение с использованием руля, педалей и других органов управления. Рисунок и особенности трассы передаются очень точно, обычно компании-поставщики арендуют автодром на несколько дней, чтобы снять максимально детальную электронную копию, привязанную к координатам GPS.

Динамический симулятор базируется на решениях, используемых в авиации для подготовки пилотов. Первый такой тренажер на примитивной электромеханической платформе появился в США ещё в 1919 году и был предназначен для тренировки запуска двигателя и подготовки к взлёту, спустя десять лет система могла, пусть и с небольшой степенью достоверности, имитировать полёт, контролируя позицию воздушного судна по трём осям. Современные технологии позволяют добиться большего.

Многие команды используют симуляторы небольшой голландской компании Cruden BV, которая известна и на рынке развлечений под брендом Hextech. Базовый симулятор Cruden имеет шесть степеней свободы, его применяют для обучения гонщиков – молодежь отрабатывает навыки управления многочисленными системами машины, а опытные пилоты могут сосредоточиться на прохождении конкретной связки поворотов с использованием виртуальных решений, копирующие реальные новинки, подготовленные командой.

Любопытно, что для неопытных гонщиков часто используют более острые настройки, которые несколько преувеличивают реальные реакции машины – так легче получить необходимые навыки, чем прислушиваясь к небольшим изменениям в поведении машины.

Программное обеспечение обычно базируется на алгоритмах Racer и rFactor, которые доступны рядовым болельщикам, но с множеством доработок, позволяющих учитывать детальные настройки аэродинамики, характеристики покрытия, износ резины. В результате, используя компьютерную модель нового аэродинамического обвеса, инженеры могут оперативно оценить её влияние на баланс машины, услышать комментарии гонщиков, понять направление дальнейшей работы.

Возможен и обратный процесс – у команд есть возможность построить виртуальную машину, соответствующую пожеланиям гонщика, его стилю пилотирования, работе с рулём, настройкам тормозов, выбору точек торможения. Часто разработанные таким образом решения воплощаются в конструкции реальных машин.

Используются и более необычные подходы, к примеру – метод случайного поиска, когда компьютер перебирает различные сочетания аэродинамических элементов, меняя их свойства и размеры, в поиске оптимального времени прохождения конкретной трассы или связки поворотов. Не всегда найденные решения удаётся воплотить в жизнь, но иногда это позволяет взглянуть на ситуацию с другой стороны.

Гонщики активно используют симуляторы для подготовки к Гран При и поддержания формы. Виртуальная машина надёжна, не нуждается в дозаправках и смене шин, а обычную программу трёхдневных тестов в Хересе позволяет отработать за десять часов.

Конечно, в ближайшее время компьютеры не заменят живую работу на трассе, но прогресс очевиден. Вряд ли программисты, разрабатывавшие игры для приставок и первых персональных компьютеров, могли надеяться, что однажды их идеи будут использоваться для подготовки боевых гонщиков Формулы 1.

Динамическое рассеяние света (фотонная корреляционная спектроскопия)

(другие названия данного метода: фотонная корреляционная спектроскопия; квазиупругое рассеяние света)

Для измерения размеров наночастиц используется метод динамического рассеяния света (ДРС). Данный метод позволяет определить коэффициент диффузии дисперсных частиц в жидкости путем анализа корреляционной функции флуктуаций интенсивности рассеянного света. Далее, из коэффициента диффузии рассчитывается радиус наночастиц.

Основные идеи метода динамического рассеяния света

• Броуновское движение дисперсных частиц или макромолекул в жидкости приводит к флуктуациям локальной концентрации частиц. Результатом этого являются локальные неоднородности показателя преломления и соответственно — флуктуации интенсивности рассеянного света при прохождении лазерного луча через такую среду.
• Коэффициент диффузии частиц обратно пропорционален характерному времени релаксации флуктуаций интенсивности рассеянного света. Это характерное время, в свою очередь, есть время затухания экспоненциальной временной корреляционной функции рассеянного света, которая измеряется с помощью цифрового коррелятора.
• Размер частиц (гидродинамический радиус) рассчитывается по формуле Стокса-Эйнштейна, которая связывает размер частиц с их коэффициентом диффузии и вязкостью жидкости.

Метод динамического рассеяния света используется также для измерения скоростей потоков жидкостей и газов. Традиционно, этот вариант метода носит название лазерной доплеровской анемометрии (ЛДА). В частности, данная конфигурация метода ДРС используется для измерения электрофоретической подвижности наночастиц, откуда рассчитывается их дзета-потенциал. 2 $$

Волновой вектор флуктуаций концентрации описывается выражением:

$$ q = \frac{4\pi n}{\lambda} \sin \left(\frac{\theta}{2}\right) $$

В выражениях 4-6: a и b — экспериментальные константы, n- показатель преломления жидкости, в которой взвешены дисперсные частицы,λ — длина волны лазерного света и θ — угол рассеяния.

Схема процесса рассеяния света

 

Автокорреляционная функция рассеянного света

Величины t_c, a и b могут быть найдены путем аппроксимации измеренной корреляционной функции теоретической экспоненциальной функцией. Для сферических невзаимодействующих между собой частиц размер их может быть рассчитан с использованием формулы Стокса-Эйнштейна:

$$ D = \frac{k_bT}{6\pi \eta R} $$

где k_B — константа Больцмана, T — абсолютная температура и η — сдвиговая вязкость среды, в которой взвешены частицы радиуса R.

Из формулы Стокса-Эйнштейна понятно, что с помощью динамического рассеяния света можно решать задачи измерения вязкости жидкости. Для случая рассеяния света на дисперсных частицах известного размера, измеренное характерное время флуктуаций позволяет рассчитать вязкость жидкости. Причем в данном случае можно говорить о микрореологической вязкости, которая, в принципе, может отличаться от вязкости, измеренной на макроскопических масштабах.

Проблема аппроксимации экспериментальных данных проста для рассмотренного случая рассеяния света монодисперсными сферическими частицами. Для полидисперсных образцов интерпретация экспериментальных данных усложняется. Для реально достижимой точности измерений могут быть получены только два-три параметра одномодального полидисперсного распределения: средний размер частиц, ширина и асимметрия распределения. Для многомодальных полидисперсных систем можно говорить о средних размерах частиц каждой компоненты и относительном вкладе каждой компоненты в интенсивность рассеяния. Важно отметить, что два близких размера частиц полидисперсной системы будут разрешаться в виде отдельных компонент только, если их размеры отличаются друг от друга не менее, чем в 2-3 раза.

Билл Джелен. Динамические массивы в Excel

Незаметно для меня Microsoft совершил прорыв, представив в сентябре 2018 новые возможности – динамические массивы. Ниже – перевод книги Bill Jelen. Excel Dynamic Arrays Straight to the Point. Книги серии Straight to the Point предназначены для глубокого освещения одного аспекта Excel.

Билл Джелен – основатель сайта MrExcel.com и автор множества книг о Excel. Сайт бесплатно отвечает на более чем 30 000 вопросов в год. В моем блоге представлены три книги Джелена:

Скачать заметку в формате Word или pdf, примеры в формате Excel

Содержание

1. Начало работы
2. Функция СОРТ
3. Функция СОРТПО
4. Функция ФИЛЬТР
5. Функция УНИК
6. Комбинирование функций
7. Функция ПОСЛЕД
8. Функция СЛМАССИВ
9. Почему формулы массива (Ctrl+Shift+Enter) такие жесткие: неявное пересечение
10. Функция ПРОСМОТРX и динамические массивы
11. Обычные функции, использующие динамические массивы
12. Динамические массивы и функции кубов

Введение

Ранее многие люди пытались изучать формулы массива и потерпели неудачу. Майк Гирвин написал отличную книгу, чтобы объяснить, как работают формулы массива. Целые главы той книги здесь будут сведены к коротким предложениям, благодаря новым функциям.

О динамических массивах было объявлено 24 сентября 2018 года, но даже в MS Excel 2019 они пока не представлены. Динамические массивы доступны только в Office 365. Я думаю, что парадигма покупки бессрочной лицензии на Office каждые три или шесть лет устарела, и рекомендую переходить на подписку.

Как организована эта книга. В главе 1 вы узнаете о концепции формулы, распространяющейся на соседние ячейки. Вы увидите, как непустая ячейка может блокировать разлив массива, и как это исправить. Вы услышите о неявном пересечении и о том, как нотация @ может решить эту проблему. Главы 2–8 посвящены каждой из шести новых функций и их комбинациям. Глава 9 основана на превосходном видео Джо Макдэйда. Из этой главы вы узнаете термины, которые использует команда Excel Calc: Подъем, Трансляция, Попарный подъем, Усечение массива и Неявное пересечение. В главе 10 рассматриваются два способа, с помощью которых динамические массивы делают новую функцию ПРОСМОТРX более мощной. В 11-й – приведены 24 примера объединения динамических массивов с рядом обычных функций Excel. В 12-й главе показано, как динамические массивы могут работать с  функциями кубов.

Оригинальные файлы с примерами можно загрузить с сайта автора. К каждой главе я приложу файл, адаптированный к настоящему переводу.

Глава 1. Начало работы

Формулы теперь могу разливаться

В этой главе рассматривается новая формула =A2:A20, ошибка #ПЕРЕНОС! и новый неявный оператор пересечения @.

Начнем с базовой формулы массива. Перейдите в ячейку Е3. Наберите =A2:C10. В более ранних версиях Excel вам пришлось бы включить этот диапазон в качестве аргумента какой-нибудь функции, или использовать формулу массива, одновременно нажав Ctrl+Shift+Enter.

Рис. 1. Формула указывает на диапазон ячеек

Теперь же достаточно нажать Enter. Excel возвращает значения в 27 ячеек, которые выбираются автоматически вправо и вниз. Посмотрите на формулу в строке формул… здесь нет фигурных скобок, а это значит, что никто не нажимал Ctrl+Shift+Enter.

Рис. 2. Одна формула вернула множество значений

Ячейка E4 содержит текст Central, и, хотя строка формул показывает формулу для этой ячейки, она отображается серым цветом. Давайте проверим с помощью VBA, что содержится в ячейках Е3 и Е4?

Рис. 3. VBA подтверждает, что в ячейке Е4 не формула

VBA показывает, что в ячейке Е3 – формула, а в Е4 – нет. Также в Excel можно ввести формулу =ЕФОРМУЛА(E4). Она вернет ЛОЖЬ. И еще одна проверка. Выберете диапазон D1:h30, и пройдите по меню Главная –> Найти и заменить –> Формулы. Будет выделена только ячейка E3.

Один из первых вопросов на YouTube в ответ на мои первые видео с динамическими массивами был: можно ли вы копировать и вставлять значения? Да! Выберите диапазон E3:G11, нажмите Ctrl+C, кликните правой кнопкой мыши на выбранную новую ячейку и выберите Специальная вставка –> Значения.

Что происходит, если формула не может пролиться?

Что произойдет, если ячейка, куда должен разлиться диапазон, будет занята?

Рис. 4. Как Excel справится с занятой ячейкой?

Excel вернет ошибку #ПЕРЕНОС! Excel сообщает, что не может вернуть массив целиком. Поэтому не вернет ни одного результата. Если выбрать контекстное меню слева от ячейки с ошибкой, можно  выделить мешающие ячейки. Возможно, их получится перенести в другое место листа.

Рис. 5. Ошибка #ПЕРЕНОС! и ее контекстное меню

Как только вы очистите ячейки, мешающие размещению массива, он автоматически разольется.

Существует несколько типов ошибки #ПЕРЕНОС! Та, что выше, называется Диапазон для переноса данных не пустой. Другие ошибки:

• Неопределенный размер. Вы не можете использовать волатильные функции, например, СЛУЧМЕЖДУ(), в качестве аргумента функции ПОСЛЕДОВ().
• Выходит за пределы листа. Вы не можете ввести функцию =СОРТ(C:C) в ячейке E2.
• Табличная формула. Вы не можете использовать функции динамического массива внутри Таблицы.
• Не хватает памяти. Вам следует ссылаться на диапазон меньшего размера.
• Разлив в объединенные ячейки. Динамический массив не может разливаться в объединенную ячейку.
• Неопознанная ошибка. Excel не может распознать ошибку.

Если ваша формула указывает на Таблицу, динамический массив будет расширяться при добавлении новых строк в Таблицу

Рис. 6. Динамический массив «отслеживает» Таблицу

Сравните с рис. 2. Вы преобразовали диапазон А1:С19 в Таблицу (Ctrl+T). Формула в ячейке Е3 изменилась на =Таблица1. Теперь, если вы добавите еще одну строку в Таблицу (А11:С11), формула в ячейке Е3 не изменится, а динамический массив автоматически расширится еще одной строкой (Е12:G12).

Хотя формулы динамического массива могут указывать на Таблицу, в самой Таблице использовать формулы динамического массива нельзя.

Использование нового типа ссылок на массив: E3#

Как вы захотите сослаться на массив E3:G12, но не знаете, какого он размера, добавьте оператор разлитого диапазона (#) после ячейки, содержащей формулу массива.

Например, =E3 вернет East, =E3# вернет весь массив, формула которого хранится в E3. Неофициально это называется ссылочной нотацией массива. Такая нотация поддерживается только при ссылке внутри одной книги.

Что такое неявное пересечение

Если вы введете =@C2:C11 в любой ячейке в строках со 2 по 10, формула вернет значение из столбца С той строки, в которой вы ввели формулу. Знак @ известен как неявный оператор пересечения.

Рис. 7. Используйте нотацию @, когда вам нужно неявное пересечение.

Dynamics | Физика для идиотов

Динамика — это название правил движения. Это то, что, как вы могли подумать, должно было быть выяснено в первую очередь, но не было полностью заблокировано до недавнего времени. При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах. Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: и все остальное можно вывести из этого. Я так и не узнал, правы ли они, я узнал и эти на всякий случай:

Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они взялись и как их использовать.

При работе с измерениями вы можете использовать скалярные или векторные величины.

Скалярные величины:

• Укажите только величину.
• Энергия, длина, масса, скорость, температура и время — все это скалярные величины.

Векторные величины:

• Имеют как величину, так и направление
• Смещение, Сила, Скорость, Ускорение и Импульс — все векторные величины.

Иногда может показаться, что скорость и скорость — одно и то же (часто они равны друг другу), но на самом деле они немного отличаются.Скорость — это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, — это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассматривать скорость — это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до поворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.

Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я, вероятно, должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (помимо случая с яблоком) своими законами движения:

1. Частица останется в покое или продолжит движение, если на нее не будет действовать внешняя сила.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
3. Каждое действие имеет равную и противоположную реакцию.

Все это нормально, но что на самом деле означают эти законы?

1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.

Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся со скоростью 5, продолжалась бы бесконечно.Очевидно, что в реальной жизни этого не происходит из-за сопротивления воздуха и трения, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу. Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.

2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.

Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, которые часто возникают в Dynamics, и его действительно стоит изучить. Понять это тоже не так уж и сложно. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.

3. Каждое действие имеет равную и противоположную реакцию

Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что в противном случае вы бы прошли прямо!

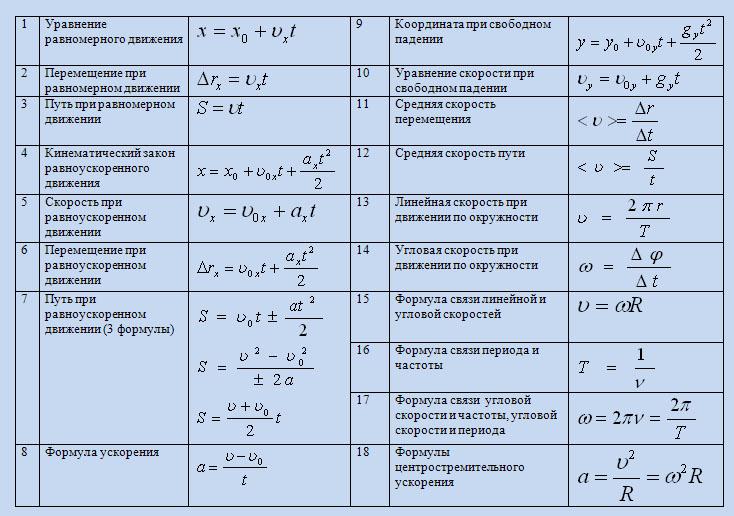
У них так много разных названий, что иногда сложно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще о них не слышали. Прежде всего, давайте взглянем на них:

(1)

(2)

(3)

(4)

(5)

Может показаться, что там есть что вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.

SUVAT Equation 1

Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.

Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:

График, показывающий u против t

Как я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:

SUVAT Equation 2

Ладно, один проиграл, осталось четыре!

Мы знаем, что площадь под графиком равна смещению.Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:

Теперь мы уже знаем это, поэтому мы можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам нашу вторую формулу:

Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!

SUVAT Equation 3

Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.

Если переставить, чтобы сделать тему, то получится:

Теперь вам просто нужно интегрировать этот результат по времени, чтобы получить наше третье уравнение:

SUVAT Equation 4

Мы уже установили, что площадь под графиком (равная смещению) равна:

Если мы умножим скобку, получим:

, что совпадает с:

Наконец, мы просто разложим это на множители, чтобы получить:

SUVAT Equation 5

Можем переставить, сделать тему:

Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:

, который можно упростить до

, а затем

это в конечном итоге дает нам окончательную форму

Вот и все! Эти уравнения определенно стоит изучить, потому что они полезны снова и снова.Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс ^–2 , они в порядке, но если ускорение составляет 12 мс ^–2 , тогда они не будут работать, поскольку ускорение зависит от.

Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и, хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Силу сопротивления любого объекта, движущегося в жидкости, можно рассчитать по формуле:

— плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), — скорость объекта, площадь поперечного сечения объекта и коэффициент сопротивления. Коэффициент аэродинамического сопротивления — это число, которое относится к аэродинамике объекта: куб имеет, а сфера имеет.

Объект, падающий на Землю, в конечном итоге (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:

Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент лобового сопротивления около 0,8 (приблизительное предположение где-то вокруг углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).

Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:

  1. Преподобный ведет свою машину, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс  -1 , а его замедление составляет 2 мс  -2 , сколько времени потребуется машине, чтобы остановиться?  

Хорошо, с такого рода проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс ^-1 .Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t =? с

Отсюда видно, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился объект, давая нам

Наконец, мы помещаем числа в уравнение:

.

 2. Майкл выходит на дорогу, в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не сбить Майкла? 

Еще раз, лучше всего выложить всю имеющуюся у нас информацию:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t = 5 с
s =? м

На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку нам не дали времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Опять же, я собираюсь изменить уравнение, на этот раз чтобы дать в качестве предмета. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор может видеть, что вы сделали.
В любом случае, это дает нам

Подставляя числа в уравнение, получаем:

, чтобы Майкла не ударили! (Уф!)

В приведенном выше примере трение полностью проигнорировано.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). А теперь давайте посмотрим на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (чтобы он не проезжал по дороге). Сила трения равна μ (или μN).

 3. Машина преподобного сломалась на трассе М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может выдвинуть около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине? 

Хорошо, в такой ситуации сначала хорошо нарисовать небольшой набросок того, что происходит.

Диаграмма сил, показывающая, что происходит в примере 3.

Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на равнодействующую силу, мы обнаружим, что сила трения составляет 3000 Н, поэтому Rev не сможет толкнуть автомобиль на обочину дороги.

  4. Бодибилдер случайно проходит мимо и, пытаясь облегчить заторы на постоянно загруженном М1, он решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.  

NB — Принять массу автомобиля 510 кг

Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от очень умного Исаака Ньютона.
Помните, что для определения общей силы необходимо убрать силу трения. Итак, это (3200 + 1800) — 3000. Таким образом, общая сила составляет 2000Н. Снова нам нужно изменить формулу, чтобы на этот раз в качестве испытуемого использовалось и . Это дает нам. Подставляя числа, получаем:

a = 3.9 мс ^-2 (2 s.f.)

Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!

В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «уклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком операций, все будет в порядке.

Итак, давайте начнем с простого простого примера.

Пример наклонной плоскости

На картинке выше мы видим блок, стоящий на склоне. Хорошее место для начала (возможно, единственное место для начала, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом) — это решимость сил.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).

Снаряды

ничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала рассмотрим типичный пример движения снаряда:

.

 Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс  -1 .Найдите максимальную высоту, которую может достичь мяч. 

Ладно, как обычно, рисуем диаграмму:

Пример движения снаряда

Теперь давайте перечислим то, что мы знаем:

• u = 20 sin30 мс ^-1
• v = 0 мс ^-1
• a = -9,81 мс ^-2
• с =? м

Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем, это:, и переставляем ее так, чтобы получился объект:

Затем, наконец, введите числа в уравнение:

и выскакивает ответ:

Смотри, не так ли сложно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для поиска компонентов x и y, вы не ошибетесь.

Иногда вы знаете максимальную высоту, но какой-то другой компонент будет отсутствовать. Например, время, когда мяч находится в воздухе … Опять же, это не проблема, вы просто посмотрите, что вы знаете, , , и воспользуйтесь формулами, чтобы вычислить остальное.

Dynamics — The Physics Hypertextbook

Обсуждение

Почему существует эта страница?

Это не страница о каком-то фундаментальном принципе физики. Это страница о решении конкретной (и распространенной) проблемы механики.

Неформально, динамика — это исследование сил и движения. Говоря более формально, динамика — это раздел механики, изучающий влияние сил на движение объектов. Напротив, статика — это изучение сил без движения; или, более формально, раздел механики, который имеет дело с силами при отсутствии изменений в движении. Динамика предполагает изменение. Статика предполагает неизменность. Важное изменение — это ускорение.

Цель этого раздела книги — служить хранилищем проблем в динамике.Ускорение в каждой задаче будет отличным от нуля в одном направлении. Это верно только для этого раздела. Идея состоит в том, чтобы увидеть, каково решать такие проблемы, чтобы вы могли распознать их, когда они появятся позже.

Увеличить

Аккуратная сила

Возьмите первый закон движения Ньютона и разбейте его на две части. «Покоящийся объект имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию продолжать движение с постоянной скоростью…». В этом длинном главном предложении живет статика.«Если только на это не действует чистая внешняя сила». В этом коротком придаточном предложении мы находим динамику.

Слово «чистая» во фразе « чистая сила» означает общую, комбинированную или общую. Это то, что вы получаете, когда все обдумываете. Слово net связано со словом аккуратный. Поиск чистой стоимости — это что-то вроде уборки математического беспорядка (или, по крайней мере, уменьшения беспорядка). Это может быть записано как ∑ F (с использованием греческой буквы сигма для обозначения суммы и жирным шрифтом, чтобы указать, что силы являются векторами) или как F _net (используя индексированное слово net, чтобы сделать символ более похожим на разговорный язык и курсив, чтобы указать, что знание величины силы часто имеет значение) или другие подобные варианты.

Сила — это векторная величина, что означает, что направление имеет значение. Используйте положительные значения для сил, которые указывают в предпочтительном направлении, и отрицательные значения для сил, которые направлены в противоположном направлении. Если проблема двумерная, выберите два предпочтительных направления под прямым углом — что-то вроде вверх и вправо. Выберите предпочтительные направления, которые сделают вашу жизнь проще. Законы физики не заботятся о том, называете ли вы правое положительное или левое положительным. Пространство в математическом смысле изотропно .Он измеряет одинаково во всех направлениях.

Второй закон движения Ньютона описывает, как связаны чистая сила, масса и ускорение. По сути, чистая сила вызывает ускорение, а масса ему сопротивляется. Лучше всего писать не словами, а символами. Примерно так…

∑ F = м a

или

F нетто = ма

Теперь вы готовы начать следующий этап обучения.

Например

Возьмем беспрецедентный пример обычного велосипеда, который безупречно крутил педали по обычной ровной дороге безупречным образом. Какие силы действуют на велосипед и гонщика (вместе в целом)?

Начните с очевидного. Все имеет вес и вес указывает вниз. Велосипед находится на твердой поверхности, поэтому нормальная сила направлена ​​перпендикулярно этой поверхности. Поверхность ровная, нормальное направление — вверх.Всадник крутит педали. Это означает, что есть какая-то сила, толкающая велосипед вперед. Я не хочу чрезмерно анализировать ситуацию, поэтому давайте просто назовем эту силу push . Даже должным образом накачанные шины сопротивляются качению, ось может нуждаться в смазке, а может и не нуждаться в смазке, и воздух определенно затягивает движущееся тело. Давайте упростим жизнь и назовем все эти силы вместе трением . Гонщик толкает велосипед вперед, а трение толкает назад.

Готовы сделать свободную схему тела.Нарисуйте рамку, изображающую велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра прямоугольника, чтобы обозначить четыре силы, действующие на велосипед и гонщика. Хотя это не всегда необходимо, следует попытаться нарисовать стрелки, длина которых соответствует относительным величинам сил. Длинные стрелки для сильных сил. Короткие для слабых.

Начните с легкой пары — весовой и нормальной. В этом сценарии ничего не происходит в вертикальном направлении. Дорога ровная, и гонщик не выполняет трюков.Вес и нормальный вес уравновешивают друг друга. Нарисуйте одну стрелку вниз, а другую вверх и придайте им одинаковую длину.

Закончите несколько менее легкой парой — толчок и трение. Что-то — это , происходящее в горизонтальном направлении. Движение происходит в горизонтальном направлении. Велосипед куда-то едет. Это должно быть для чего-то полезно. Разве не должно?

Извините, но нет. Движение не имеет значения. Изменение движения — вот что важно. Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной.Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет более сильной из двух.

Если велосипед ускоряется, значит, гонщик толкает велосипед вперед больше, чем трение толкает его назад. Если велосипед движется с постоянной скоростью, то толчок и трение равны. Если велосипед замедляется, сила трения побеждает силу, толкающую велосипед вперед.

Вот несколько рисунков, которые показывают то, что я только что сказал.

Вот набор уравнений, которые показывают то, что я только что сказал. Мне нравится использовать «вверх» и «вправо» в качестве положительных направлений, но это не закон физики. Это просто предпочтение.

	вертикально ∑ F y = 0 N — W = 0 N = Вт
	горизонтально ∑ F x = мА пол. — f = мА
↙	↓	↘
ускорение п > f > 0	постоянная скорость п = f = 0	замедление п < f <0

Идите и решайте проблемы.

Перевернутые (деформированные) координаты

два тела, соединенные струной

Формулы и версии формул — Управление цепочкой поставок | Динамика 365

• 12.09.2017
• 6 минут на чтение

В этой статье

Формула определяет материалы, ингредиенты и результаты конкретного процесса непрерывного производства.Вместе с соответствующим маршрутом формула определяет весь процесс непрерывного производства. Формулы используются для планирования и производства продуктов в непрерывном производстве.

Формула состоит из ингредиентов и количеств, необходимых для производства определенного количества элемента формулы. В зависимости от выполняемой задачи вы можете получить доступ к функциям формулы из управления запасами и складом или из управления информацией о продукте.

Формулы и строки формул

Формула состоит из одной или нескольких строк формулы, которые определяют ингредиенты или элементы, составляющие формулу.Строка формулы может содержать элементы ведомости материалов (BOM), элементы формулы, элементы промежуточного веса, приобретенные элементы, сопутствующие продукты или побочные продукты. Поскольку многие элементы используются в нескольких продуктах, элемент можно использовать в нескольких формулах.

Примером формулы является рецепт печенья с шоколадной крошкой. Ингредиенты для этой формулы состоят из нескольких линий, таких как мука, сахар, яйца, масло и шоколадная стружка. Формула печенья с шоколадной крошкой содержит ингредиенты, которые, вероятно, используются в других формулах.Пока вы готовите печенье с шоколадной крошкой, могут остаться остатки, например, крошки, или некоторые из печенья могут быть пережарены или недоварены. Эти элементы могут быть настроены как побочные продукты или побочные продукты, в зависимости от производственных операций.

При создании строки формулы используется тип строки, чтобы указать, как система должна обрабатывать строку при выполнении сводного планирования и создании пакетных заказов. Каждый тип линии дает разный результат. В следующей таблице описаны типы линий, которые вы можете выбрать.

Тип линии	Описание
Товар	Выберите Предмет , если предмет является сырьем или полуфабрикатом, который выбирается из запасов, или когда предмет является услугой.
Фантом	Выберите Phantom , если вы хотите расчленить любые элементы формул нижнего уровня, содержащиеся в строках формул. Когда вы оцениваете пакетный заказ и элементы формулы разнесены, элементы-компоненты перечисляются в виде строк формулы в пакетном заказе.Дополнительно к производственному маршруту добавляются соответствующие маршруты. Элементы формулы разнесены с использованием текущей конфигурации. При использовании линии Phantom вы можете обрабатывать конфигурации производства и измерения, которые возникают на разных уровнях формулы. Если вы выбираете Phantom для продукта на экспресс-вкладке Engineer страницы Released product details , а затем используете этот продукт в формуле, тип строки строки формулы изменяется на Phantom .Вы не можете выбрать Phantom для номенклатуры промежуточного веса или для номенклатур, у которых тип производства — Сопутствующий продукт , Побочный продукт или Элемент планирования .
Привязанная поставка	Выберите Обособленная поставка , чтобы создать заказ партии, производственный заказ, канбан, заказ на перемещение или заказ на поставку для ингредиента, который содержится в строке формулы. Связанный заказ определяется на основе настроек заказа по умолчанию и типа производства ингредиента и создается при оценке заказа партии.Требуемые количества ингредиентов зарезервированы для заказа партии.
Продавец	Выберите Поставщик , если в производственном процессе используется субподрядчик, и вы хотите создать субпроизводство или заказ на поставку для субподрядчика. Услуга или работа, которую выполняет субподрядчик, должны быть созданы с использованием элемента формулы или элемента услуги. Вы можете прикрепить элемент к родительскому элементу в виде строки формулы. Маршрут должен содержать операцию, назначенную операционному ресурсу субподрядчика.Эта операция добавляется к строке формулы с помощью Oper. № поле.

Формулы-версии

При создании новой формулы необходимо сначала создать версию формулы, прежде чем добавлять элементы строк формулы и их конкретные характеристики. У каждой формулы должна быть хотя бы одна версия. Кнопка Утверждено в версии формулы становится доступной только после успешного сохранения записи версии. Каждая запись версии формулы связана с одним или несколькими сопутствующими и побочными продуктами, которые могут быть произведены при производстве готового продукта.Многие продукты могут быть изготовлены из одних и тех же ингредиентов в разных размерах партий, в нескольких количествах или с использованием разных выходов. Вы можете создать столько версий формулы, сколько вам нужно.

Для управления несколькими активными версиями формулы используйте диапазоны дат действия или поля количества «от». Несколько активных версий формулы могут существовать только в том случае, если диапазон дат и количество «с» не перекрываются.

В отличие от спецификаций, где одна спецификация часто связана со многими версиями спецификаций, для каждой формулы обычно существует только одна версия формулы.Помните, что только одна версия формулы может быть активирована для измерений покрытия и количества для данного продукта. Однако многие версии формул могут существовать по другим причинам, и вы можете выбрать их вручную при создании заказа на партию.

Утверждение и активация формул и версий формул

Формулы и версии формул должны быть утверждены, прежде чем их можно будет использовать для планирования и производства. Формулы обычно активируются перед использованием. Однако во время производства вы можете выбрать версию формулы, которая утверждена, но не активирована.

Чтобы защитить формулу или версию формулы, вы можете установить Блок редактирования и Блокировать удаление параметров утверждения на странице Параметры управления производством .

Если выбрать Редактирование блока и формула утверждена, никакие поля в строках формулы не могут быть удалены или отредактированы. Однако, если вы удалите утверждение формулы, вы можете удалить и изменить строки формулы. Вы также можете создавать новые формулы и новые версии формул.

Если вы выберете Блокировать удаление утверждения , вы не сможете удалить утверждение утвержденной формулы или версии формулы. Однако вы можете создавать новые формулы и новые версии формул, а также удалять активацию версии формулы.

Вы можете добавить больше уровней контроля, используя функцию электронной подписи. Если пользователь настроен так, что во время утверждения формулы требуется электронная подпись, при активации формулы появляется страница Подпись .Пользователь должен быть авторизован для электронной подписи, и сертификат должен быть успешно проверен, прежде чем изменение можно будет зафиксировать. Если подпись не может быть аутентифицирована, утверждение или удаление утверждения отклоняется, а изменение, инициировавшее утверждение или удаление утверждения, возвращается в исходное состояние.

Используйте масштабируемую функцию

Функция масштабирования доступна только в том случае, если для всех компонентов позиции в формуле задано значение Переменное потребление .Эта функция недоступна, если для компонентов элемента установлено значение Фиксированное потребление или Шаговое потребление . При использовании функции «Масштабируемость», если вы изменяете ингредиент в формуле, количество других ингредиентов, которые вы выбираете, корректируется. Размер формулы также корректируется. Аналогичным образом, если вы измените размер формулы, изменится количество всех масштабируемых ингредиентов. Эта функция предназначена специально для создания и обслуживания формул. Он не указывает, будет ли количество ингредиента увеличиваться или уменьшаться в заказе партии.

Использование Шаг потребления

Поэтапное потребление исключает необходимость ввода количества на вкладке Строка формулы для ингредиента. Вместо этого потребление шага настроено так, что оно имеет значение Из серии и значение Количество . Выбирается информация из записи «Шаговое потребление на серию», которая соответствует количеству в заказе партии. Поэтапное потребление полезно, когда скорость потребления не является линейной по отношению к размеру заказа партии и увеличивает требование только при достижении определенного порогового значения количества.Чтобы включить эту функцию для новой формулы, в группе Расчет потребления измените настройку формулы для применимого ингредиента с Стандартный на Шаг . Этот метод потребления указывается на вкладке Настройка страницы Строка формулы .

формул для динамического анализа | Прил. Мех. Ред.

1R6. Формулы для динамического анализа.- RL Huston (Dept of Mech, Indust, and Nucl Eng, Univ of Cincinnati, 598 Rhodes Hall, Cincinnati OH 45221-0072) и CQ Liu (DiamlerChrysler, Auburn Hills MI). Марсель Деккер, Нью-Йорк. 2001. 624 с. ISBN 0-8247-9564-4. 175,00 долларов США.

Проверено Дж. Анхелесом (Департамент механотехники и Центр интеллектуальных машин, McGill Univ, 817 Sherbrooke St W, Montreal, PQ, h4A 2K6, Canada).

Набор формул динамики твердого тела без контекста был бы, мягко говоря, бессмысленным.К счастью, рецензируемая книга выходит за рамки составления такого сборника. Эта книга, по сути, дает исчерпывающий взгляд на предмет, начиная с самых основ. Хотя такая книга обычно предназначена для специализированной аудитории с инженерным или научным образованием, авторы включают такие фундаментальные определения, как время, расстояние, частица и т. Д., Которые, как можно было бы предположить, хорошо известны этой аудитории. Таким образом, материал главы 1 кажется неуместным для такой книги; Более того, несказанный читатель может быть озадачен некоторыми ошибочными определениями, такими как определение частицы , которое авторы основывают на концепции тела , не определенной в этой главе, но не ранее, чем через две главы, и относящейся только к жесткий корпус . частица , которую авторы намерены определить, как ее понимают в инженерных кругах, является механической единицей, не обязательно маленькой , поскольку здесь на карту поставлена ​​неспособность этой сущности изменить свое отношение, и поэтому частица может быть вагоном поезда, если аналитик заинтересован в изучении только его вертикальных колебаний при чистом переводе. Фактически, авторы признают это понятие в главе 3 — читателю нужно пройти на две главы вперед, чтобы получить объяснение определения, которое впервые дается в главе 1.

Глава 2 посвящена элементарной векторной алгебре и векторному исчислению, а глава 3 знакомит с кинематикой частиц. Здесь авторы вводят понятие твердого тела, хотя изучение этого объекта отнесено к главе 6. Рецензенту непонятно, почему основное понятие угловой скорости, собственно твердого тела, вводится в главе 3, хотя авторы возвращаются к этой концепции в главе 6, не связывая эти два обсуждения.Главы 4 и 5 посвящены кинетике и динамике частиц соответственно. Кинетика, как здесь упоминается, относится к независимому изучению активных сил и сил инерции, а динамика — к изучению взаимодействия этих двух видов сил. Обратной стороной посвящения каждой из этих двух частей по одной главе является то, что читателю приходится ждать до главы 6, которую авторы назвали Кинематика тел , чтобы натолкнуться на предмет, который действительно важен для инженеров, а именно на твердые тела. .Кроме того, авторы утверждают в первом абзаце главы 6, что глава «фокусируется» на твердых телах. Дело в том, что в этой главе и на балансе книги авторы не рассматривают ничего, кроме твердых тел.

Твердые тела, с другой стороны, можно рассматривать либо как совокупность материальных точек (частиц), либо как континуумы ​​материи; в любом случае эта материальная сущность вынуждена двигаться таким образом, чтобы сохранялось расстояние между любой парой ее точек (континуум занимает область пространства и, следовательно, он также включает точки).Авторы выбрали традиционный первый подход, который не безупречен. При таком подходе читатель должен поверить в то, что суммирование дискретных членов может привести к интегралу по континууму. С другой стороны, при втором подходе формулировка динамики проста, поскольку доступен весь объем знаний, а именно, относящийся к механике сплошных сред. В этом контексте второй закон Ньютона и уравнение баланса моментов Эйлера становятся естественными выводами законов Эйлера сохранения количества движения и углового момента, соответственно, которые справедливы для любого континуума, будь то жидкость или твердое тело, и, если последнее, то ли деформируемый или жесткий.

Особенностью книги является обширное обсуждение того, как получить матрицы вращения для различных триплетов элементарных поворотов вокруг осей координат. Здесь авторы включают то, что они называют графами конфигурации , мнемоническим средством создания этих матриц с использованием простых правил. Этот рецензент не совсем убежден в полезности этого обширного обсуждения. Авторы пошли еще дальше и включили подраздел с заголовком «Вычислительные алгоритмы.Проблема в том, что в этом подразделе на полстраницы не обнаружено ни одного единственного алгоритма. Затем обсуждение классификации движения имеет некоторые проблемы: обсуждаются смещение и прямолинейное смещение , наряду с движением в плоскости и движением в общей плоскости . Однако авторы упустили из виду рациональный анализ смещений с точки зрения теории групп, доступный в архивной литературе [1] и на английском языке в монографии этого рецензента [2].В той же главе терминология винтового движения содержит ошибки. В самом деле, в наиболее общем случае движения твердого тела ни одна точка тела не остается неподвижной относительно наблюдателя (по сути, системы координат), каким бы наблюдатель ни был. Однако всегда можно найти набор точек тела, точки которых имеют скорость относительно этого наблюдателя минимальной евклидовой нормы, все точки лежат на прямой, которая называется мгновенной винтовой осью движения, все точки на этой линии с одинаковыми скоростями.В пользу этого общего движения авторы ошибочно говорят о существовании центра вращения .

Одним из плюсов книги является отход авторов от обычной практики обращения к так называемым квазикоординатам для учета предполагаемых переменных, из которых, как считается, получаются непроизводные величины, такие как угловая скорость, при дифференцировании по времени. . Здесь, как и во всей книге, авторы неукоснительно следуют подходу Кейна, который является пионером в этом отношении и не зависит от квази-координат и других эзотерических величин, таких как псевдопроизводные , , печально известные тем, что преследуют литературу по этой теме.Подход Кейна, по сути, чрезвычайно полезен при рассмотрении неголономных систем. В главе 10, посвященной этой теме, авторы буквально следуют более ранней работе (Пассерелло и Хьюстон) [3], в которой авторы ввели неголономные связи в уравнения Лагранжа анализируемой системы с целью сокращения числа управляющих уравнений к набору независимых обыкновенных дифференциальных уравнений второго порядка (ОДУ), свободных от сил связи. При этом авторы столкнулись с проблемой решения ряда неизвестных обобщенных скоростей из меньшего числа линейных алгебраических уравнений.Авторы нашли способ обойти это затруднительное положение , добавив тождества в один и тот же набор обобщенных скоростей, тем самым сделав их линейную систему детерминированной, то есть с таким же количеством уравнений, как и неизвестных, и невырожденными. В процессе авторы сделали свои выводы излишне громоздкими. Действительно, как показали в 1998 г. Островская и Анхелес [4], в этом анализе фактически нет необходимости решать какую-либо систему уравнений. Жалко, что авторы не провели литературный обзор — количество библиографических указаний, появившихся за последние 10 лет в этой книге, составляет всего 11.Фактически, восемь из них — либо учебники для студентов, либо монографии; только три являются архивными публикациями, и два из них являются собственными работами первого автора. В главе 7 содержатся дополнительные формулы кинематики твердого тела, а в главе 8 подробно обсуждаются инерционные свойства твердого тела. Главы 9 и 10 посвящены кинетике и динамике твердого тела соответственно. Глава 11, в свою очередь, включает различные типы механических систем, математические модели которых получены с использованием различных формулировок, обсуждаемых в книге: принцип Д’Аламбера; Уравнения Кейна; и уравнения Лагранжа.Последние три главы посвящены механическим системам, состоящим из множества твердых тел. Кстати, набор мог быть намного лучше. Обычная практика требует выделения курсивом букв, встречающихся в математических отношениях; авторы использовали те же римские шрифты текста. В результате чтение становится довольно тяжелым. Не помогает то, что авторы использовали текстовый процессор с довольно ограниченными возможностями набора, а издатель печатал свой документ без набора.

Эта книга не содержит сборника задач в конце главы, по этой причине ее использование в качестве учебника весьма ограничено, но, возможно, авторы никогда не собирались выпускать учебник.В качестве справочного документа для практикующих инженеров и зрелых аспирантов рекомендуется использовать Формулы для динамического анализа .

Динамика — Формулы и задачи — Инженерная механика 3 | Дитмар Гросс

Дитмар Гросс получил диплом инженера по прикладной механике и степень доктора технических наук в Университете Ростока. Он был научным сотрудником Штутгартского университета, а с 1976 года — профессором механики Дармштадтского университета.Его исследовательские интересы в основном сосредоточены на современной механике твердого тела в макро- и микромасштабе, включая современные материалы.

Йорг Шредер изучал гражданское строительство, получил докторскую степень в Ганноверском университете и получил степень бакалавра в Штутгартском университете. Он был профессором механики в Университете Дармштадта и поступил в Университет Дуйсбург-Эссен в 2001 году. Его области исследований — теоретическая и компьютерно-ориентированная механика сплошных сред, моделирование функциональных материалов, а также дальнейшее развитие метода конечных элементов. .

Питер Риггерс был назначен профессором Института механики в ТД Дармштадт в 1990 году. В 1998 году он перешел на работу в Ганноверский университет. С 1990 по 2008 год он занимал кафедру механики гражданского строительства. С 2008 года он является директором Института механики сплошных сред на факультете машиностроения Ганноверского университета имени Лейбница.

Вольфганг Элерс изучал гражданское строительство в Ганноверском университете и получил докторскую степень и докторскую степень в Университете Дуйсбург-Эссен.Он был профессором механики сплошной среды в Университете Дармштадта и поступил в Университет Штутгарта в 1995 году. Его области исследований — компьютерная механика сплошной среды с особым акцентом на связанных проблемах и пористых средах.

Ральф Мюллер получил диплом механика и степень доктора технических наук в Технологическом университете. Он был постдоком в Университете Пьера и Марии Кюри в Париже, Франция, и младшим профессором Дармштадтского университета, где он также получил степень хабилитации.С 2009 года он является профессором прикладной механики Кайзерслаутернского университета. Его научные интересы — механика сплошной среды, микро- и конфигурационная механика, а также численные методы.

границ | Переломные моменты в динамике мнений: универсальная формула в пяти измерениях

1. Введение

Мажоритарные социальные решения традиционно оправдывались теоремой присяжных Кондорсе, которая гласит, что в мажоритарных групповых решениях ошибки в индивидуальном суждении сводятся на нет с произвольной точностью. по мере увеличения числа избирателей.Это подразумевает устойчивое преобладание рационального большинства в демократическом принятии решений. В действительности, однако, демократический мажоритарный подход может вызывать неожиданные, казалось бы, внезапные сдвиги, о чем свидетельствуют такие политические события, как победа в Брексите в 2016 году и выборы Трампа. Существует также вопиющее противоречие в демократии, в которой существуют влиятельные группы интересов, которые обладают непропорциональной властью, несмотря на свой статус меньшинства.

Такие неожиданные и парадоксальные результаты динамики мнений представляют собой сложные головоломки, которые еще предстоит решить.В частности, с учетом того, что общественное мнение в настоящее время является основным ключом к запуску возможных изменений в современных обществах, а также краха политических режимов, понимание механизмов, лежащих в основе формирования общественного мнения, становится важным вопросом, представляющим жизненный интерес.

Так случилось, что с самого начала социофизики [1] изучение динамики мнений было основной темой исследования, которое пролило новый и разрушительный свет на эти парадоксальные особенности, являющиеся результатом решения группы большинства [2–6].Было предложено и еще предстоит предложить множество моделей для описания динамики мнений в социальных системах [7–12]. Большинство из них рассматривают однородные совокупности с локальным правилом обновления и дискретными переменными. Было показано, что серия этих моделей включена в единую объединяющую рамку [13]. Также использовались непрерывные переменные [14, 15]. Тем не менее, несмотря на продолжающееся активное исследование [16–21], проблема динамики общественного мнения все еще не имеет всеобъемлющей и надежной основы, особенно надежного инструмента прогнозирования.

Среди этих моделей стоит основополагающая модель Галама [22–26], которая сочетает в себе обновления правил местного большинства с нарушением локальной симметрии, вызванным бессознательными предрассудками и когнитивными предрассудками в случае равного размера группы в равной степени. Модель выявила некоторую эвристическую способность благодаря успешным предсказаниям нескольких политических событий, таких как победа в Брексите в 2016 году [24, 27], выборы Трампа [28] и отказ Франции от проекта европейской конституции в 2005 году [29]. Впоследствии он был расширен, чтобы включить гетерогенные группы населения с тремя различными психологическими чертами: разнородные предрассудки, негибкость или упрямство [30–37] и противоположность [38–41].Однако исследованы только конкретные комбинации этих признаков [42–44]. Дополнительным ограничением было ограничение групп обновлений размерами 2, 3 и 4.

В этой работе, продолжая исследовать модель Галама в общем пространстве параметров с пятью измерениями, мы получаем одно универсальное уравнение обновления, чтобы следовать временная эволюция распределения мнений среди разнородного населения с любой комбинацией рациональных, упрямых и противоположных агентов для любого среднего уровня скрытых предубеждений и для произвольного размера обсуждаемых групп.

Уравнение обновления позволяет исследовать полную геометрию нижележащего ландшафта. В частности, раскрываются аттракторы и переломные моменты, формирующие веру в возможные динамические потоки. Лежащая в основе динамика общественного мнения, движимая многократным обсуждением среди небольших групп людей во время социальной или политической общественной кампании, становится предсказуемой. Будущее внезапного распространения меньшинства и параллельного коллапса большинства перед их фактическим возникновением обнаруживается, как показано на примере побед Трампа и Брексита в 2016 году.Они стали видимыми в пределах временного горизонта прогноза и, в свою очередь, предсказуемыми.

Кроме того, наличие полного пятимерного ландшафта делает прогнозы более осуществимыми и надежными, поскольку в этом случае не требуется точная оценка значений параметров. Вместо этого важно определить релевантную область притяжения, в которой будет происходить динамика. Однако по границам бассейна необходимы более точные оценки параметров.

Наличие универсальной формулы, которая учитывает общие психологические особенности, делает модель применимой к широкому спектру социальных ситуаций, включая результаты голосования, доли рынка и социальные тенденции.Результаты также позволяют нам представить новые выигрышные стратегии в конкурирующих средах, чтобы выиграть общественные дебаты или получить долю на рынке.

Остальная часть статьи организована следующим образом. В разделе 2 мы описываем вывод универсальной формулы, объединяющей различные компоненты модели Галама. Несколько иллюстраций внезапных и неожиданных вспышек заболеваний меньшинств, полученных с помощью уравнения, представлены в Разделе 3. Раздел 4 содержит некоторые явные выражения для уравнения эволюции для (некоторых) нескольких конкретных значений размера группы r .Мы анализируем математическую структуру универсального уравнения обновления через идентификацию его неподвижных точек в разделе 5. Раздел 6 исследует некоторые аспекты пятимерного пространства параметров модели, указывая на существование критических точек. Результаты проиллюстрированы несколькими численными примерами. Заключительные замечания представлены в последнем разделе.

2. Универсальная формула в пятимерном пространстве параметров

Мы рассматриваем популяцию с N агентами, каждый из которых способен принимать два состояния 1 и 0 соответственно, представляя два исключительных мнения A и B .В данный момент времени t , соответствующие пропорции агентов, владеющих A и B , обозначаются как pt и (1-pt). Чтобы обоснованно использовать пропорции и вероятности, мы сосредоточимся на случаях с N> 100 [26]. Выбирая начальный момент времени t = 0, мы исследуем временную эволюцию p0, вызванную неформальным локальным обсуждением между агентами на последовательных дискретных временных шагах с p0 → p1 → p2 →…

Чтобы учесть этот сложный и неизвестный процесс, мы используем Galam динамическая модель, которая отслеживает динамику мнений по последовательной итерационной схеме.Для реализации одной схемы агенты сначала случайным образом распределяются в небольшие группы размером –. Затем в каждой группе применяется правило большинства для обновления мнений местных агентов. Каждый агент имеет один голос для определения фактического местного большинства. Однако, учитывая неоднородность психологических характеристик агентов, не все из них подчиняются правилу большинства, меняя свое мнение, если они придерживаются выбора местного меньшинства. Рассмотрены три типа агентов: плавающие, негибкие и противоположные.После выполнения локальных обновлений все группы демонтируются, а агенты перетасовываются, тем самым стирая локальные корреляции, которые были созданы путем применения правил локального большинства.

• плавающих голосуют, чтобы определить местное большинство, а после этого те, кто придерживается мнения меньшинства, переходят на сторону большинства. Тем не менее, в случае ничьей в местной группе равного размера, плавающие принимают выбор, созвучный лидирующим предубеждениям среди членов группы [3]. Это вызванное предубеждением разрушение связей активируется агентами бессознательно.Соответственно, при равенстве мнений мнение A выбирается с вероятностью k , а мнение B выбирается с вероятностью (1 − k). Значение k удовлетворяет 0≤k≤1 и является функцией распределения предубеждений в социальной группе.

• негибкие члены также голосуют за определение местного большинства, но, в отличие от плавающих, в случае, если они придерживаются выбора меньшинства, они его придерживаются. Они упрямы и продолжают делать свой предопределенный выбор независимо от местного большинства.Соответственно, негибкий A остается в состоянии 1, а B -негибкий остается в 0. То же самое верно и в случае ничьей. Их соответствующие пропорции, обозначенные как a и b , являются внешними фиксированными параметрами с ограничением 0≤a + b≤1.

• противников — это «плавающие» люди, которые после роспуска групп решают индивидуально изменить свое мнение, чтобы противостоять групповому большинству, в которое они внесли свой вклад. Позиция не зависит от выбора большинства: A, или B. Доля противоположных среди плавающих обозначается как c , удовлетворяющая 0≤c≤ 1. Значение c также является фиксированным внешним параметром со случаем c> 1/2, соответствующим ситуации, когда большинство плавающих объектов систематически перейти к другому мнению, создав продолжающийся альтернативный переход между A и B. Доля плавающих A и B дается выражением (1 − a − b), а доля противников среди всех агентов равна задается формулой c˜ = (1 − a − b) c.

В момент времени t , как только схема завершается с pt → pt + 1, выполняется другая для получения p + 1 → pt + 2 и так далее до тех пор, пока дебаты не завершатся окончательным голосованием в данный момент, что определяет общее количество обновлений, которые необходимо реализовать. Частота обновлений зависит от интенсивности продолжающихся дебатов. Для любой реальной ситуации исходная доля дебатов p0 оценивается с помощью опросов.

Давайте теперь оценим функцию Pa, b, c, k (r), дающую pt + 1 из pt, учитывая следующие значения:

Однако, поскольку противоположное явление математически идентично случайному переворачиванию плавающих элементов с вероятность c среди перетасованных агентов, мы можем отделить эффект c от записи локального обновления как

pt + 1 = (1 − c) [Pa, b, k (r) (pt) −a] + c [ 1 − Pa, b, k (r) (pt) −b], (2)

, что упрощается как

pt + 1 = (1−2c) Pa, b, k (r) (pt) + c (1+ а-б).(3)

Чтобы оценить Pa, b, k (r), отметим, что в данной конфигурации группы размером r с (r − μ) агентами, придерживающимися мнения A и μ агентами, придерживающимися мнения B , вклады в Pa, b, k (r) являются результатом двух разных семейств. Одна семья включает вклады с большинством A и равенством A и B (для равного размера при равенстве с вероятностью k ), в то время как другая семья соответствует взносам с меньшинством A и равенство A и B (для четного размера при равенстве с вероятностью (1 − k)).Эти семейства обозначаются соответственно как Pa, b, c (r, μ) и Qa, b, c (r, μ) при ограничении μ≤ [r / 2], где [x] — целая часть числа . х . Уравнение 1 можно переписать как

Па, b, k (r, μ) (pt) = ∑μ = 0 [r2] {Kk (r, μ) Pa, b (r, μ) (pt) + K1 − k ( r, μ) Qa, b (r, μ) (pt)}, (4)

с

Kk (r, μ) = 1 + (k − 1) δr, 2μ = 1 (r ≠ 2μ) = k ( r = 2μ), (5)

, что позволяет факторизовать зависимость k .

Величина Pa, b (r, μ) (p), которая учитывает вклад в A после одного обновления из конфигураций с (r − μ) агентами с мнением A и μ агентами с мнением B , может быть разложен на сумму вкладов с α A -негибкими и β B -негибкими, где целое число α изменяется от 0 до (r − μ), а β изменяется от 0 до μ, что дает (см. рисунок 1 слева)

Па, b (r, μ) (p) = ∑α = 0r − μ∑β = 0μPa, b, α, β (r, μ) (p).(6)

Поскольку μ≤ [r / 2] ( большинство или равное число), вклады в pt + 1 из уравнения. 6 исходят от всех агентов, кроме B -негибких минус противников после обновления, что дает

Па, b, α, β (r, μ) (p) = (rμ) (μβ) (r − μα) (1 − p −b) μ − β × (p − a) r − μ − αbβaα (r − βr). (7)

Аналогично, величина Qa, b (r, μ) (p), которая составляет вклад в A из конфигураций с μ-агентами с мнением A и (r − μ) агентами с мнением B можно разложить как сумму вкладов с α = 0,…, μ A -негибкими и β = 0 ,…, (R − μ) B -негибкие, дающие (см. Рисунок 1 справа)

Qa, b (r, μ) (p) = ∑α = 0μ∑β = 0r − μQa, b, α, β ( r, μ) (p).(8)

Поскольку μ≤ [r / 2] ( Меньшинство или ничья), вклады в pt + 1 из уравнения. 8 происходят только от A -негибкие после обновления, что дает

Qa, b, α, β (r, μ) (p) = (rμ) (μα) (r − μβ) (1 − p − b) r −μ − β × (p − a) μ − αbβaα (αr). (9)

С использованием формул (x + y) n = ∑ j = 0n (nj) xn − jyj и ny (x + y) n − 1 = ∑ j = 0n (nj) jxn − jyj, суммирование по α и β приводит к

Па, b (r, μ) (p) = (rμ) pr − μ (1 − p ) μ [1 − μr (1 − p) b] (10)

и

Qa, b (r, μ) (p) = (rμ) pμ (1 − p) r − μ [μrpa]. (11)

С использованием тождеств

∑μ = 0 [r2] K1 − k (r, μ) (rμ) pμ (1 − p) r − μ + ∑μ = 0 [r2] Kk (r, μ) (rμ ) pr − μ (1 − p) μ = (p + 1 − p) r = 1 (12)

и

∑μ = 0 [r2] Kk (r, μ) (rμ) μrppμ (1 − p) r −μ + ∑μ = 0 [r2] K1 − k (r, μ) (rμ) r − μrppr − μ (1 − p) μ = 1rp∂η (ηp + 1 − p) r | η = 1 = ( p + 1 − p) r − 1 = 1, (13)

приходим к компактному выражению эволюционной функции Pa, b, k (r) для общего размера группы r в виде

Pa, b, k (r) (p) = Π0 (r) (p, k) + a Π1 (r) (p, k) −b Π2 (r) (p, k), (14)

где

Π0 (r) ( p, k) = ∑μ = 0 [r2] (rμ) Kk (r, μ) pr − μ (1 − p) μ, (15) Π1 (r) (p, k) = ∑μ = 0 [r2 ] (rμ) K1 − k (r, μ) μrppμ (1 − p) r − μ, (16) Π2 (r) (p, k) = ∑μ = 0 [r2] (rμ) Kk (r, μ ) μr (1 − p) pr − μ (1 − p) μ.(17)

Отметим, что соотношение Π2 (r, μ) (p, k) = Π1 (r, μ) (1 − p, 1 − k). Также отметим, что соотношение

Па, b (r, μ) (p) + Qb, a (r, μ) (1 − p) = (rμ) pr − μ (1 − p) μ. (18)

Это гарантирует ковариацию Pa, b, k (r) (p) относительно переименования мнений A и B следующим образом:

Pa, b, k (r) (p) + Pb, a, 1 − k (r) (1 − p) = 1. (19)

На этом этапе, чтобы получить полное уравнение обновления, мы используем уравнение. 3 как

Па, b, c, k (r) (p) = (1−2c) [Π0 (r) (p, k) + a Π1 (r) (p, k) −b Π2 (r) ( p, k)] + c (1 + a − b), (20)

, что позволяет рассчитывать динамику мнений для любого набора параметров (a, b, c, k) при любом размере группы r для любого начального опора p0для заключения A .Таким образом, мы вычислили универсальную формулу для прогнозирования динамики мнений в пространстве параметров пяти измерений.

РИСУНОК 1 . Диаграммы, представляющие группу из r агентов, состоящих из α A -негибких (показано как A), β B -негибких (показано как B), а также rα-β плавающих и противоположных. Агенты разделяются на два мнения, причем μ имеет одно мнение, а (r − μ) — другое, при μ <[r / 2]. Левая диаграмма - это случай, когда мнение A имеет большинство, а правая диаграмма — случай, когда B имеет большинство.

Теперь мы сделаем еще один шаг, чтобы сделать наше уравнение еще более реалистичным, рассмотрев распределение размера с r = 1,2,…, L, где L — самый большой размер обновления. Обычно в большинстве социальных ситуаций L составляет около 4,5 или 6. Размерный вес wr групп размером r должен оцениваться на основе наблюдения при ограничении ∑ r = 1r = Lwr = 1. Включение размера r = 1 позволяет учитывать агентов, которые не участвуют в локальных обсуждениях во время каждого обновления. Затем, используя уравнение.2, соответствующая глобальная доля сторонников A становится

Ga, b, c, k {L} (p) = ∑r = 1r = LwrPa, b, c, k {r} (p) = (1−2c ) R = 1r = Lwr [Π0 (r) (p, k) + a 1 (r) (p, k) −b 2 (r) (p, k)] + c (1 + a − b). (21)

В принципе, уравнение. 21 позволяет внести свой вклад в проблему связи топологии данной сети и динамики, происходящей через сеть [45]. Действительно, набор значений весов wr и L затем может быть извлечен из сети.

3. Несколько иллюстраций внезапных и неожиданных вспышек заболеваний среди меньшинств

Чтобы сделать наше универсальное уравнение обновления более конкретным, мы перечисляем явные выражения для ряда значений r = 3,4,5,6,7,8,9 в Приложение А .Кроме того, чтобы отличить динамические эффекты, возникающие из текущего уравнения обновления, от тех, которые уже присутствовали в предыдущей модели, мы напоминаем, что влияние бессознательных предрассудков было изучено для размера группы r = 4 и эффекта негибкости или упорства. агентов были изучены для групп размером 3. Каждый дает отдельно явление распространения меньшинства, как показано, например, с k = 1 и a = 0,20 и b = 0 на рисунке 2. Соответствующие формулы обновления восстанавливаются из уравнения.2 с P0,0,0,1 (4) (p) = Π0 (4) (p, k) = p2 (3p2−8p + 6) и P0.20,0,0, k (3) (p) = Π0 (3) (p, k) + 0.20Π1 (3) (p, k) = — 2p3 + 3.20p2 + 0.20 (1−2p). Обратите внимание, что P0.20,0,0, k (3) (p) не зависит от k , как и ожидалось для группы нечетного размера. Распространение меньшинства происходит в обоих случаях, но довольно медленно во втором.

РИСУНОК 2 . Слева: изменение на доли опоры A P0,0,0,1 {4} (p) в зависимости от p . Стрелки показывают распространение меньшинства, начиная с начальной поддержки p = 0.25. Справа: изменение на доли опоры A P0.2,0,0, k {3} (p) в зависимости от p . Стрелки показывают миноритарный спред, начиная с начальной поддержки p = 0,25.

В то время как каждый эффект учитывался отдельно, теперь универсальная формула позволяет нам исследовать комбинацию обоих эффектов, либо следуя одной и той же поддержке для A (P0.20,0,0,1 (4) (p)) или соревнуясь за и против A (P0,0.20,0,1 (4) (p)), как показано на рисунке 3 для случая r = 4. Комбинация резко увеличивает распространение меньшинства, но конкуренция показывает, что 20% негибких B действительно преодолевают все преимущества эффекта предубеждения.

РИСУНОК 3 . Слева: изменение на доли опоры A P0.20,0,0,1 {4} (p) в зависимости от p . Стрелки показывают ускорение спрединга меньшинства А, начиная с начальной поддержки p = 0,25. Справа: изменение на доли опоры A P0,0,2,0, k {4} (p) в зависимости от p . Стрелки показывают, что меньшинство А теперь отступает от первоначальной поддержки p = 0,25.

Мы переходим к иллюстрации способности текущего уравнения обновления выявлять внезапные и неожиданные вспышки среди меньшинств, демонстрируя пару поразительных случаев с группами размеров r = 3 и r = 4.

На рисунке 4 каждый график показывает две кривые для эволюции p , доли поддержки для A, как функции количества обновлений с тем же значением r . Два набора значений параметров показаны на каждом рисунке. Только очень небольшие различия различают два набора параметров, в то время как две связанные кривые демонстрируют резкое различие в их соответствующих результатах. График слева является примером случая r = 3 с общим начальным значением p = 0.2. Две линии соответствуют значениям a = 0,170 и a = 0,172 и обычным значениям b = c = 0, показывая резкую разницу, вызванную незначительным изменением параметра a . Точно так же график справа является примером случая r = 4 с общим начальным значением p = 0,2. Две линии — это линии c = 0,04 и c = 0,05 и общие значения a = b = 0,10 и k = 0,6, показывающие эффект, вызванный изменением параметра c на 1%.

РИСУНОК 4 . Эволюция p , доля поддержки A в зависимости от количества обновлений t . Слева: Случай r = 3 с начальным значением p = 0,2. Две линии — это те, у которых a = 0,170 и a = 0,172, и общие значения b = c = 0. Справа: A r = 4 случай с начальным значением p = 0,2. Две линии — это линии c = 0,04 и c = 0,05 и общие значения a = b = 0,10 и k = 0,6.

4. Фиксированные точки динамики

Динамика, реализованная путем многократного применения уравнения. 2 демонстрирует довольно большой спектр различных сценариев в пятимерном пространстве, охватываемом 0≤a≤p≤1, 0≤b≤1 − p≤1, 0≤c≤1, a + b + c≤1, 0 ≤k≤1 и 1≤r≤∞.Пейзаж фазовой диаграммы формируется различными аттракторами и наклонными поверхностями, которые являются решениями уравнения с неподвижной точкой

p⋆ = Pa, b, c, k (r) (p⋆). (22)

Оно имеет вид Интересно упомянуть, что уравнение. 22 является полиномом степени r от p и, таким образом, демонстрирует решения r , из которых не более трех являются действительными и содержатся в диапазоне 0-1. Эта оценка является результатом игры с уравнением и аргументов, размахивающих руками, но математическое доказательство все еще отложено.

В случае трех фиксированных точек p0⋆, ps⋆ и p1⋆ в порядке возрастания наименьшее p0⋆≤1 / 2 является стабильным и представляет B -мажоритарное конечное состояние, а наибольшее p1⋆≥1 / 2 также стабильна, представляя мажоритарное конечное состояние A- . Средневзвешенная ps нестабильна, действует как разделитель областей притяжения к p0⋆ и p1⋆ и является переломным моментом в динамике.

Поскольку создание визуального представления в пяти измерениях невозможно, поскольку интересует эволюция начального значения p0 при фиксированных значениях (a, b, c, k, r), оперативное использование фазовой диаграммы заключается в выборе двух -мерные срезы, показывающие эволюцию p0 как функцию повторных обновлений с p0 → p1 →… → pn, где n — количество итераций.Что касается предсказания реального события, важно определить, если pn> 1/2 (мнение A победа), pn <1/2 (мнение A неудача) или pn≈1 / 2 (зависший результат ).

Альтернативным практическим использованием фазовой диаграммы является извлечение двумерных срезов, которые показывают функцию pt + 1 = Pa, b, c, k (r) (pt) для фиксированного набора значений (a, b , c, k, r). Эти кривые отображают возможные аттракторы и переломные моменты, лежащие в основе динамики, на основе которой можно делать прогнозы.Эти точки расположены на пересечении точек pt + 1 = Pa, b, c, k (r) (pt) и диагонали pt + 1 = pt.

В самом деле, все «срезы» имеют общее свойство иметь по крайней мере один единственный аттрактор для динамики. Кроме того, ряд срезов демонстрирует один дополнительный аттрактор и точку перелома, расположенную между двумя аттракторами. В этих случаях изменение некоторых параметров (a, b, c, k) может привести к слиянию одного аттрактора и точки перелома при критических значениях, в результате чего получается динамика с одним аттрактором.Другая схема состоит в том, что два аттрактора сливаются в переломный момент, чтобы произвести другую динамику с одним аттрактором. Наличие динамики с одним аттрактором подразумевает, что одно определенное мнение обязательно выиграет, независимо от его первоначальной поддержки. Это означает, что обсуждение или продолжительность кампании длится достаточно времени, чтобы пересечь половину, то есть 50% бюллетеней для голосования. На рисунках 5 и 6 показан ряд случаев, иллюстрирующих два вышеупомянутых сценария.

РИСУНОК 5 . Примеры эволюционной функции Pa, b, c, kr (p) вокруг критического значения a = ac для b = c = 0.Размер группы выбран r = 7.

РИСУНОК 6 . Примеры эволюционной функции Pa, b, c, kr (p) вокруг тройного критического значения a = b = at для c = 0. Размер группы выбран r = 7.

5. Исследование фазовой диаграммы

по формуле. 22, когда b = c = 0, увеличение параметра a заставляет p0⋆ и ps⋆ сливаться в одно значение при a = ac, а затем исчезать, чтобы сделать p1⋆ единственным конечным состоянием системы (см. Рисунок 7). Критическое значение a для b = 0, которое мы называем ac (c), получается из

p⋆ − Pac (c), 0, c, k (r) (p⋆) = 0, (23) 1 −∂pPac (c), 0, c, k (r) (p⋆) = 0.(24)

В частности, для c = 0 критическое значение ac (0), которое мы просто называем ac, и связанное с ним pc⋆ получаются из

Π0 (r) (pc⋆, k) Π1 (r) ′ (pc⋆, k) −Π0 (r) ′ (pc⋆, k) Π1 (r) (pc⋆, k) + Π0 (r) (pc⋆, k) −pc⋆Π0 (r) ′ (pc⋆ , k) = 0, (25) ac = pc⋆ − Π0 (r) (pc⋆, k) Π1 (r) (pc⋆, k). (26)

При малом, но ненулевом b Система проходит переход между двумя стабильными фазами с фиксированной точкой и одной фазой с фиксированной точкой, когда a изменяется, при критическом значении выше, чем ac.

РИСУНОК 7 .Пример фазовой диаграммы пространства параметров {a, b}. Размер группы здесь выбран равным r = 9. Области, помеченные как A , B и A / B, представляют значения параметров, с которыми система безоговорочно сходится к большинству A , безусловно к большинству B и к большинству A или B в зависимости от на исходной комплектации соответственно.

Выше определенного значения b , система переходит от B — мажоритарной одиночной фазы с фиксированной точкой к A — мажоритарной одиночной фазы с фиксированной точкой без прохождения через три фазы с фиксированной точкой (см. Рисунок 7).Переход характеризуется тройной критической точкой a = b = at (c):

pt⋆ − Pat (c), at (c), c, k (r) (pt⋆) = 0, (27) 1 − ∂ pPat (c), at (c), c, k (r) (pt⋆) = 0. (28)

Ограничиваясь пока c = 0, тройная точка at = at (0) и связанная с ней pt⋆ получаются как pt⋆ = 1/2 и

at = 1 − −0 (r) ′ (12, k) 2Π1 (r) ′ (12, k). (29)

Поучительно нарисовать фазовую диаграмму на самолет {a, b}. Существует область малых значений a и b , в которой окончательное большинство может пойти в любом направлении в зависимости от его начальной поддержки.Для больших значений a и / или b окончательное большинство предопределено из-за сильного влияния негибких. Когда a или b превышает at, две области с негибким доминированием размещаются рядом друг с другом без промежуточной области, определяемой плавающим элементом. Пример r = 9 показан на рисунке 7.

Зависимость ac и at от r можно увидеть на рисунке 8. Мы перечислим лишь некоторые из них следующим образом: Для r = 3 мы имеем ac = 0,1714 и at = 0,25, а для r = 5, ac = 0.2104 и при = 0,2917. Для r = 7 имеем ac = 0,2358 и at = 0,3167, а для r = 9 ac = 0,2452 и at = 0,3339.

РИСУНОК 8 . Критические параметры ac и at в зависимости от размера группы r .

В целом, приближение к пределу r = ∞, ar = at = 0,5 происходит очень медленно, и для достаточно небольшого размера группы выполняется r≈10, ac≈1 / 4 и at≈1 / 3, что ближе к случаю r = 3, чем r = ∞. Даже при r≈50 мы имеем удивительно малые значения ac≈1 / 3 и при ≈2 / 5.

Снова поучительно посмотреть на фазовую диаграмму на плоскости {a, b} с разными значениями c (рисунок 9).Теперь должно быть очень ясно, что для всех групп размером — влияние контрарианов на формирование окончательного большинства заключается в уменьшении роли плавающих и увеличении силы негибких. Этот факт, который первоначально был обнаружен, например, при r = 3, оказывается характерной чертой модели Галама.

РИСУНОК 9 . Фазовая диаграмма на плоскости {a, b} при r = 9. слева для c = 0,1 и справа для c = 0,2. Области, помеченные как A , B и A / B, представляют значения параметров, с которыми система безоговорочно сходится к большинству A , безусловно к большинству B и к большинству A или B в зависимости от на исходной комплектации соответственно.

6. Резюме

В этом исследовании мы получили универсальную формулу для временной эволюции агентов, следуя динамике мнений Галама в пространстве параметров из пяти измерений, которые являются соответствующими пропорциями негибкости каждой стороны (упрямства), доля противников, среднее значение общих предубеждений и размер группы обновлений.

Сопутствующий ландшафт мнений формируется несколькими аттракторами и поворотными точками, которые приводят к богатому разнообразию нелинейностей и сингулярностей в потоках мнений.Таким образом, внезапные потрясения, такие как распространение меньшинств и крах большинства, получают объяснение, раскрывающее скрытые механизмы возникновения неожиданных и внезапных сдвигов в распределении мнений, таких как победа в Брексите и избрание Трампа. Показана также временная зависимость соответствующих явлений.

Для больших групп, хотя влияние негибких агентов было устранено при соблюдении простого правила большинства, результаты меняются очень медленно, показывая, что более ранние выводы, полученные для групп третьего и четвертого размеров, остаются неизменными.Напротив, для четных размеров, хотя эффект предубеждения ослабевает с увеличением размера, он остается эффективным. Более того, наличие уравнения обновления для любого размера группы — позволяет учитывать комбинации размеров группы, что, в свою очередь, открывает путь для учета базовых сетей.

Изучение одного конкретного случая показало существование критических точек ac и at, в которых угловые и ответвляются линии, разделяющие фазы с негибкостью-доминантой и определяемой плавающей точкой.Примесь и увеличение числа контрарианов эффективно способствует преобладанию негибких элементов и сокращает область параметров, в которой исходный состав плавающих элементов может определять результат формирования мнения большинства. Увеличение размера группы r вызывает умеренное, но явное увеличение как ac, так и at. Соответственно, когда в локальной дискуссии участвует больше агентов, необходимо большее заинтересованное меньшинство, чтобы навязать свою волю большинству, или, что идентично, большее просвещенное меньшинство необходимо для убеждения большинства.

Получение полной фазовой диаграммы динамики мнений дает надежную основу для прогнозирования, для которой прогнозы становятся более надежными, поскольку важно определение области притяжения, в которой имеет место динамика, что обеспечивает некоторую гибкость в точности оценка параметров. Однако вдоль границ бассейна требуется более высокая точность оценки значений параметров. Учитывая конкретную проблему, определение местоположения соответствующего релевантного аттрактора позволяет предвидеть возможное неожиданное изменение тенденции мнения до ее возникновения.

Важно подчеркнуть одну инструментальную особенность модели, заключающуюся в том, что она не полагается на данные, кроме использования нескольких опросов. Действительно, модель не управляется данными, что позволяет построить общий ландшафт динамики, топология которой формируется различными поворотными точками и аттракторами, которые были определены с помощью универсальной формулы.

Однако на данном этапе создание рабочей основы для надежных прогнозов еще предстоит реализовать, поскольку должны быть разработаны специальные инструменты для оценки значений параметров, т.е.е., пропорции негибких сторонников и противников, а также эффективное среднее количество активных предубеждений, связанных с данным вопросом. Эта проблема не может быть решена только с помощью физики. На карту поставлена ​​междисциплинарная структура с участием социологов, чтобы создать новые эффективные сборы для количественной оценки этих параметров.

Тем не менее, было показано, что приблизительных качественных оценок достаточно, чтобы определить, какой бассейн будет определять динамику в некоторых случаях, как это показано на примере Brexit и французского референдума по проекту европейской конституции, в отношении которого действовали наиболее активные предубеждения. пользы от выбора нет.

Соответственно, на данном этапе прогнозы являются качественными в отношении победы или поражения в голосовании, а не в отношении точного значения результата голосования. Согласно прогнозам, поддержка будет увеличиваться до уровня выше пятидесяти процентов, а в конечном итоге — до уровня ниже пятидесяти процентов. Следовательно, для получения надежных количественных прогнозов необходимо приложить междисциплинарные усилия. Тем не менее, наличие универсальной формулы позволяет разработать выигрышные стратегии в конкурирующих средах, расширяя ранее обсуждавшиеся пути [46–50].

В заключение, мы получили потенциально готовую к использованию универсальную формулу, которая, хотя оперативные инструменты для точной настройки параметров все еще отсутствуют, уже дает новую основу для того, чтобы сделать широкий спектр прогнозов выигрышных стратегий в отношении исходов мнений. динамика, включая голосование, рыночные доли и социальные тенденции.

Явные уравнения эволюции для r = 3,4,5,6,7,8,9

Чтобы сделать наше универсальное уравнение обновления более конкретным, мы перечисляем явные выражения для ряда значений r = 3,4,5,6 , 7,8,9 следующим образом:

Π0 (3) (p, k) = p2 (3−2p), Π1 (3) (p, k) = (1 − p) 2, Π2 (3) (p , k) = p2.(30) Π0 (4) (p, k) = p3 (4−3p) + 6kp2 (1 − p) 2, Π1 (4) (p, k) = (1 − p) 2 (1 + 2p) — 3kp (1 − p) 2, Π2 (4) (p, k) = p3 + 3kp2 (1 − p). (31) Π0 (5) (p, k) = p3 (10−15p + 6p2), Π1 (5) (p, k) = (1 − p) 3 (1 + 3p), Π2 (5) (p, k) = p3 (4−3p). (32) Π0 (6) (p, k) = p4 (14−24p + 10p2) + 20kp3 (1 − p) 3, Π1 (6) (p, k) = (1 − p) 3 (1 + 3p + 6p2) −10kp2 (1 − p) 3, Π2 (6) (p, k) = p4 (5−4p) + 10kp3 (1 − p) 2. (33) Π0 (7) (p, k) = p4 (35−84p + 70p2−20p3), Π1 (7) (p, k) = (1 − p) 4 (1 + 4p + 10p2), Π2 (7) (p, k) = p4 (15−24p + 18p2). (34) Π0 (8) ( p, k) = p5 (56−140p + 120p2−35p3) + 70kp4 (1 − p) 4, Π1 (8) (p, k) = (1 − p) 4 (1 + 4p + 10p2 + 20p3) — 35kp3 (1 − p) 4, Π2 (8) (p, k) = p5 (21−35p + 15p2) + 35kp4 (1 − p) 3.(35) Π0 (9) (p, k) = p5 (126−420p + 540p2−315p3 + 70p4), Π1 (9) (p, k) = (1 − p) 5 (1 + 5p + 15p2 + 35p3 ), Π2 (9) (p, k) = p5 (56−140p + 120p2−35p3). (36)

Заявление о доступности данных

Исходные материалы, представленные в исследовании, включены в статью / дополнительный материал и далее Запросы можно направлять соответствующему автору.

Вклад авторов

Все авторы внесли равный вклад в рукопись.

Конфликт интересов

Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Благодарности

Авторы выражают благодарность г-же Миве Оцуки и профессору Шиничиро Инаба за их поддержку во время завершения этой работы. Эта рукопись была выпущена в виде препринта на arXiv [51].

Ссылки

1. Галам, С., Гефен, Й., и Шапир, Ю. Социофизика: новый подход к социологическому коллективному поведению. I. Подлое описание забастовки. J Math Sociol (1982). 9: 1–13. DOI: 10.1080 / 0022250x.1982.9989929. CrossRef Full Text

Google Scholar

2. Бразилия, Р. Физика общественного мнения , Мир физики (2012).

Google Scholar

3. Галам С. Социофизика: моделирование психополитических явлений физиком . Нью-Йорк, штат Нью-Йорк: Springer (2012).

Google Scholar

4. Кастеллано, С., Фортунато, С., и Лорето, В. Статистическая физика социальной динамики. Rev Mod Phys (2009). 81: 591–646. DOI: 10.1103 / revmodphys.81.591. CrossRef Full Text

Google Scholar

6. Нооразар, Х. Последние достижения в динамике распространения общественного мнения: опрос 2020 года. Eur Phys J Plus (2020). 135: 521. DOI: 10.1140 / epjp / s13360-020-00541-2.

CrossRef Полный текст | Google Scholar

7. Снайд-Верон, К. и Снайд, Дж. Эволюция мнений в закрытом сообществе Int J Mod Phys C (2000). 11: 1157–65. DOI: 10,1142 / s012

00000936. CrossRef Full Text

Google Scholar

8.Охромбель Р. Моделирование социофизической модели Шнайд с убедительными единичными мнениями Int J Mod Phys C (2001). 12: 1091. DOI: 10,1142 / s012

01002346. CrossRef Full Text

Google Scholar

9. Коркос, А., Экманн, Дж.П., Маласпинас, А., Малевернь, И., и Сорнетт, Д. Имитация и противоположное поведение: гиперболические пузыри, сбои и хаос. Квант Финанс (2002). 2: 264–81. DOI: 10.1088 / 1469-7688 / 2/4/303. CrossRef Full Text

Google Scholar

10.Бехера, Л., и Швейцер, Ф. О формировании пространственного консенсуса: отличается ли модель Снайд от модели избирателя? Int J Mod Phys C (2003). 14: 1331–54. DOI: 10,1142 / s012

03005467. CrossRef Full Text

Google Scholar

11. Tessone, CJ, Toral, R, Amengual, P, Wio, HS, и San Miguel, M. Модели распространения мнения меньшинств по соседству. Eur Phys J B (2004). 39: 535–44. DOI: 10.1140 / epjb / e2004-00227-5. CrossRef Full Text

Google Scholar

12.Санчес-младший. Модифицированная одномерная модель Снайд . arXiv: cond-mat / 0408518 (2004).

Google Scholar

13. Галам, С. Локальная динамика против социальных механизмов: объединяющая рамка. Europhys Lett (2005 г.). 70: 705–11. DOI: 10.1209 / EPL / i2004-10526-5.

CrossRef Полный текст | Google Scholar

14. Deffuant, G, Neau, D, Amblard, F, and Weisbuch, G. Смешивание убеждений между взаимодействующими агентами. Adv Complex Syst (2000). 03: 87–98. DOI: 10.1142 / s0219525

0078. CrossRef Full Text

Google Scholar

15. Хегсельманн, Р., Краузе, У. Динамика мнений и модели ограниченной уверенности, анализ и моделирование. J Artif Soc Soc Simulat (2002). 5: (3).

Google Scholar

16. Родригес, Н., Боллен, Дж., И Ан, И-Й. Коллективная динамика эволюции убеждений в условиях когнитивной когерентности и социального соответствия. PloS One (2016). 11: e0165910. DOI: 10.1371 / journal.pone.0165910. CrossRef Full Text

Google Scholar

17.Баттистон, Ф., Кайроли, А., Никосия, В., Баул, А., и Латора, В. Взаимодействие между консенсусом и согласованностью в модели взаимодействующих мнений. Phys Нелинейный феномен (2016). 323-324: 12–9. DOI: 10.1016 / j.physd.2015.10.013. CrossRef Full Text

Google Scholar

18. Марсан, Г.А., Белломо, Н., и Гибелли, Л. Стохастические эволюционно-дифференциальные игры на пути к системной теории поведенческой социальной динамики. Math Model Methods Appl Sci (2016). 26: 1051–93. DOI: 10.1142 / s0218202516500251. CrossRef Full Text

Google Scholar

19. Чеон, Т., и Моримото, Дж. Эффекты балансировки в динамике мнений. Phys Lett (2016). 380: 429–34. DOI: 10.1016 / j.physleta.2015.11.012. CrossRef Full Text

Google Scholar

21. Линн, К.В., Пападопулос, Л., Ли, Д.Д. и Бассет, Д.С. Всплески коллективной человеческой активности возникают из-за простых парных корреляций. Phys Rev (2019). 9. DOI: 10.1103% 2FPhysRevX.9.011022.

CrossRef Полный текст | Google Scholar

22.Галам, С. Правило большинства, иерархические структуры и демократический тоталитаризм: статистический подход. J Math Psychol (1986). 30: 426–34. DOI: 10.1016 / 0022-2496 (86) -2. CrossRef Full Text

Google Scholar

23. Галам, С., Чопар, Б., Масселот, А., и Дроз, М. Динамика конкурирующих видов: качественное преимущество по сравнению с географией. Eur Phys J B (1998). 4: 529–31. DOI: 10.1007 / s100510050410. CrossRef Full Text

Google Scholar

24.Галам, С. Динамика мнений меньшинств в демократических дебатах. Phys Stat Mech Appl (2004). 336: 56–62. DOI: 10.1016 / j.physa.2004.01.010. CrossRef Full Text

Google Scholar

25. Галам, С. Гетерогенные убеждения, сегрегация и экстремизм в формировании общественного мнения. Phys Rev E (2005). 71: 046123. DOI: 10.1103 / Physreve.71.046123. CrossRef Full Text

Google Scholar

26. Фазано, Дж., Сорато, А. и Эллеро, А. Модифицированная модель Галама для устного обмена информацией, Physica A (2009).388: 3901–10. doi: 10.1016% 2Fj.physa.2009.06.002

CrossRef Полный текст | Google Scholar

27. Галам, С. Является ли референдум механизмом, позволяющим превратить наши предрассудки в рациональный выбор? Неудачный ответ социофизиков в The Routlrdge Handbook to Referendums and Direct Democracy , Eds. Морел Л. и Квортруп М., Рутледж 19, 334–47 (2018).

Google Scholar

28. Галам, С. Феномен Трампа, объяснение из социофизики. Int J Mod Phys B (2017).31: 1742015. DOI: 10,1142 / s0217979217420152. CrossRef Full Text

Google Scholar

29. Лехир, П. Les mathématiques s’invitent dans le débat européen, (интервью с С. Галамом). Monde (2005 г.). 26/02: 23.

Google Scholar

30. Галам, С., и Московичи, С. К теории коллективных явлений: консенсус и изменение отношения в группах. Eur J Soc Psychol (1991). 21: 49–74. DOI: 10.1002 / ejsp.2420210105. CrossRef Full Text

Google Scholar

31.Галам, С., и Джейкобс, Ф. Роль негибких меньшинств в разрушении демократической динамики общественного мнения. Phys Stat Mech Appl (2007). 381: 366–76. DOI: 10.1016 / j.physa.2007.03.034. CrossRef Full Text

Google Scholar

32. Мартинс, А. и Галам, С. Повышение индивидуальной негибкости в динамике мнений, Phys Rev E (2013). 87, 042807. DOI: 10.1103 / Physreve.87.042807. CrossRef Full Text

Google Scholar

33. Крокидакис Н. и де Оливейра, PMC.Негибкость и независимость: фазовые переходы в модели правила большинства. Phys Rev E (2015). 92: 062122. DOI: 10.1103 / Physreve.92.062122. CrossRef Full Text

Google Scholar

34. Mobilia, M. Нелинейная модель q-избирателя с непреклонными фанатиками. Phys Rev E (2015). 92: 012803. DOI: 10.1103 / Physreve.92.012803. CrossRef Full Text

Google Scholar

35. Пикеринг, В., Шимански, Б.К., и Лим, К. Анализ многомерной игры с именами с заинтересованными меньшинствами. Phys Rev E (2016). 93: 052311. DOI: 10.1103 / Physreve.93.052311. CrossRef Full Text

Google Scholar

36. Бургхардт, К., Рэнд, В. и Гирван, М. Конкурирующие мнения и упорство: соединение моделей с данными. Phys Rev E (2016). 93: 032305. DOI: 10.1103 / Physreve.93.032305. CrossRef Full Text

Google Scholar

37. Юул, Дж. С., и Портер, Массачусетс. Хипстеры в сетях: как меньшинство отдельных лиц может привести к большинству, выступающему против истеблишмента .arXiv: 1707.07187v2 (2018).

Google Scholar

38. Галам, С. Противоположные детерминированные эффекты на динамику общественного мнения: «сценарий зависающих выборов». Phys Stat Mech Appl (2004). 333: 453–60. DOI: 10.1016 / j.physa.2003.10.041. CrossRef Full Text

Google Scholar

40. Ли, Э., Холм, П. и Ли, Ш. Моделирование динамики инакомыслия. Phys Stat Mech Appl (2017). 486: 262–72. DOI: 10.1016 / j.physa.2017.05.047. CrossRef Full Text

Google Scholar

41.Гамбаро, Дж. П., и Крокидакис, Н. Влияние противников на динамику формирования мнения. Phys Stat Mech Appl (2017). 486: 465–72. DOI: 10.1016 / j.physa.2017.05.040. CrossRef Full Text

Google Scholar

42. Джейкобс, Ф. и Галам, С. Динамика двух мнений, порождаемая негибкими, непротиворечивыми и противоположными плавающими точками . arXiv: 0803.3150v1 (2008).

Google Scholar

43. Крокидакис, Н., Бланко, В. Х. и Антенеодо, К. Влияние противников и непримиримых в кинетической модели динамики мнений. Phys Rev E (2014). 89: 013310. DOI: 10.1103 / Physreve.89.013310. CrossRef Full Text

Google Scholar

44. Калил, Н., Мигель, М.С., и Торал, Р. Фанатики в модели избирателей с шумом среднего поля. Phys. Ред. E (2018). 97: 012310.

Google Scholar

45. Баттистон, Ф., Ченчетти, Дж., Якопини, И., Латора, В., Лукас, М., Патания, А. и др. Сети за пределами парных взаимодействий: структура и динамика. Phys Rep (2020). 874: 1–92. DOI: 10.1016 / j.physrep.2020.05.004. CrossRef Full Text

Google Scholar

46. Ван, З., Ся, Ц, Чен, З. и Чен, Г. Распространение эпидемии с положительной и отрицательной профилактической информацией в мультиплексных сетях. IEEE Trans Cybern (2020). [Epub перед печатью]. doi: 10.1109 / TCYB.2019.2960605

Google Scholar

47. Wang, Z, Guo, Q, Sun, S и Xia, C. Влияние распространения осведомленности на эпидемии, подобные SIR, в мультиплексных сетях. Appl Math Comput (2019).349: 134–47. DOI: 10.1016 / j.amc.2018.12.045. CrossRef Full Text

Google Scholar

48. Ли, Дж., Ван, Дж., Сан, С. и Ся, К. Каскадные сбои, вызванные индивидуальной неоднородностью в сложных сетях. Appl Math Comput (2018). 323: 182–92. DOI: 10.1016 / j.amc.2017.11.059. CrossRef Full Text

Google Scholar

49. Javarone, MA. Сетевые стратегии в избирательных кампаниях. J Stat Mech — Theory Exp (2014). 8: P08013. doi: 10.1088% 2F1742-5468% 2F2014% 2F8% 2FP08013

CrossRef Полный текст | Google Scholar

50.Джавароне, М.А., и Сквартини, Т. Фазы формирования мнений в гетерогенных сетях, обусловленные конформизмом: пример модели q-избирателя. J Stat Mech — Theory Exp (2015). P10002. doi: 10.1088% 2F1742-5468% 2F2015% 2F10% 2FP10002

Google Scholar

51. Галам, С. и Чеон, Т. Динамика переломного момента: универсальная формула , arXiv: 1901.09622v1 (2019).

Google Scholar

Формулы для динамики, акустики и вибрации

Предисловие xi

1 Определения, единицы измерения и геометрические свойства 1

1.1 Определения 1

1.2 Символы 8

1.3 Единицы 11

1.4 Движение на поверхности Земли 18

1.5 Геометрические свойства плоских областей 19

1.6 Геометрические свойства твердых тел 30

1.7 Геометрические свойства, определяемые векторами 40

Ссылки 41

2 Динамика частиц и тел 43

2.1 Кинематика и преобразования координат 43

2.2 Закон Ньютона о динамике частиц 50

2.2.1 Системы постоянной массы 50

2.2.2 Системы переменной массы 57

2.2.3 Траектории частиц 58

2.2.4 Работа и энергия 63

2.2.5 Импульс 65

2.2.6 Броня 68

2.2.7 Гравитация и орбиты 71

2.3 Вращение твердого тела 73

2.3.1 Теория вращения твердого тела 73

2.3.2 Вращение одной оси 73

2.3.3 Вращение нескольких осей 84

2.3.4 Гироскопические эффекты 85

Ссылки 87

3 Собственная частота пружинно-массовых систем, маятников, струн и мембран 89

3.1 Гармоническое движение 89

3.2 Константы пружины 91

3.3 Собственные частоты пружинно-массовых систем 99

3.3.1 Одинарная степень свободы 99

3.3.2 Система двух степеней свободы 113

3.4 Моделирование дискретных систем с пружинами и массами 117

3.4.1 Пружины с массой 117

3.4.2 Сильфоны 118

3.5 Собственные частоты маятника 119

3.5.1 Массовые характеристики на основе измерения частоты 120

3.6 Натянутые струны, кабели и собственные частоты цепи 121

3.6.1 Уравнение движения 121

3.6.2 Провисание кабеля 123

3.7 Собственные частоты мембраны 126

3.7.1 Плоские мембраны 126

3.7.2 Изогнутые мембраны 131

Ссылки 132

4 Собственная частота балок 134

4.1 Теория изгиба балки 134

4.1.1 Напряжение, деформация и деформация 134

4.1.2 Многослойные балки 136

4.1.3 Уравнение движения балки 137

4.1.4 Граничные условия и модальное решение 137

4.1.5 Балки на упругом основании 141

4.1.6 Упрощение для труб 141

4.2 Собственные частоты и формы колебаний однопролетных и множественных -Пролетные балки 142

4.2.1 Однопролетные балки 142

4.2.2 Ортогональность, нормализация и максимальные значения 150

4.2.3 Напряжение балок 150

4.2.4 Двухпролетные балки 151

4.2.5 Многопролетные балки 151

4.3 Собственная частота балок с осевой нагрузкой 158

4.3.1 Равномерная осевая нагрузка 158

4.3.2 Линейно изменяющаяся осевая нагрузка 159

4.4 Балки с массами, конические балки, балки с пружинными опорами и поперечные балки 162

4.4.1 Балки с массами 162

4.4.2 Конические и ступенчатые балки 162

4.4.3 Пружинные балки 167

4.4.4 Сдвиговые балки 167

4.4.5 Влияние сдвигающей силы на прогиб Балок 170

4.4.6 Вращательная инерция 170

4.4.7 Многоэтажные здания 174

4.5 Крутильные и продольные собственные частоты балки 176

4.5.1 Продольные колебания балок и пружин 176

4.5.2 Крутильные колебания балок и валов 179

4.5. 3 Круговое поперечное сечение 179

4.5.4 Некруглое поперечное сечение 182

4.6 Распространение волн в пучках 183

4.7 Изогнутые балки, кольца и рамы 184

4.7.1 Кольца в сборе 184

4.7.2 Напряжение и деформация дуг 189

4.7.3 Поддерживаемые кольца и спирали 190

4.7.4 Круговые дуги, дуги и изгибы 190

4.7.5 Самая низкая частота в плоскости Собственная частота дуги 196

4.7.6 Мелкая дуга 197

4.7.7 Рамы портала 198

Ссылки 199

5 Собственная частота пластин и оболочек 203

5.1 Теория изгиба пластин 203

5.1.1 Напряжение и деформация 203

5.1.2 Граничные условия 203

5.1.3 Уравнение движения пластины 205

5.1.4 Прямоугольная пластина с опорой 206

5.1.5 Пластины на упругом основании 207

5.1.6 Сэндвич-пластины 207

5.1.7 Толстые пластины и деформация сдвига 207

5.1.8 Аналогия мембран и нагрузки в плоскости 208

5.1.9 Ортогональность 208

5.2 Собственные частоты пластин и формы мод 209

5.2.1 Собственные частоты пластины 209

5.2.2 Круглые и кольцевые пластины 209

5.2.3 Секторные и круглые ортотропные пластины 214

5.2.4 Прямоугольные пластины 214

5.2.5 Параллелограммные, треугольные и точечные пластины 215

5.2.6 Прямоугольные ортотропные пластины и решетки 215

5.2.7 Жесткие пластины 231

5.2.8 Перфорированные пластины 232

5.3 Цилиндрические оболочки 234

5.3.1 Теория тонкой оболочки Доннелла 235

5.3.2 Собственные частоты цилиндрических оболочек 237

5.3.3 Бесконечно длинные режимы цилиндрической оболочки (j = 0) 241

5.3.4 Цилиндрические оболочки с простой опорой без осевого ограничения 243

5.3.5 Цилиндрические оболочки с другими граничными условиями 246

5.3.6 Свободно-свободная цилиндрическая оболочка 248

5.3.7 Цилиндрически изогнутые панели 249

5.3.8 Влияние средней нагрузки на собственные частоты 250

5.4 Сферические и конические оболочки 250

5.4.1 Сферические оболочки 250

5.4.2 Открытые оболочки и церковные колокола 252

5.4.3 Мелкие сферические оболочки 252

5.4.4 Конические оболочки 254

Ссылки 254

6 Акустика и жидкости 260

6.1 Звуковые волны и децибелы 260

6.1.1 Скорость звука 260

6.1.2 Уравнение акустической волны 264

6.1.3 Децибелы и уровень звуковой мощности 276

6.1.4 Стандарты для измерений 277

6.1.5 Затухание и потери при передаче (TL) 278

6.2 Распространение звука в больших пространствах 285

6.2.1 Распространение акустических волн 285

6.2.2 Звуковое давление на жесткие стены 288

6.2.3 Закон масс для передачи звука 289

6.3 Акустические волны в воздуховодах и помещениях 289

6.3.1 Акустические волны в воздуховодах 289

6.3.2 Глушители и резонаторы 298

6.3.3 Акустика помещения 302

6.4 Собственные акустические частоты и формы колебаний 305

6.4.1 Структурно-акустическая аналогия 306

6.5 Волны на свободной поверхности и плескание жидкости 310

6.6 Суда и плавучие системы 319

6.6.1 Судовые собственные частоты (1 / период) 319

6.7 Добавленная масса структуры в жидкостях 321

6.7.1 Добавленная масса теории потенциального потока 328

6.7.2 Добавленная масса 329

6.7.3 Добавленная масса пластин и оболочек 330

Ссылки 331

Дополнительная литература 335

7 Принудительная вибрация 336

7.7.1.1 Установившаяся вынужденная вибрация 336

7.1.1 Реакция пружины на массу с одной степенью свободы 336

7.1.2 Реакция системы пружина на массу с несколькими степенями свободы 344

7.1.3 Принудительная гармоническая вибрация систем непрерывного действия 347

7.1.4 Общий отклик системы 357

7.2 Переходная вибрация 359

7.2.1 Теория переходной вибрации 359

7.2.2 Непрерывные системы и начальные условия 365

7.2.3 Максимальные переходные характеристики и спектры отклика 371

7.2.4 Стандарты на ударные нагрузки и машины для испытаний на ударную вязкость 374

7.3 Виброизоляция 374

7.3.1 Виброизоляция с одной степенью свободы 374

7.3.2 Виброизоляция с двумя степенями свободы 377

7.4 Случайная вибрационная реакция к спектральным нагрузкам 379

7.4.1 Спектральная плотность мощности и ряд Фурье 380

7.4.2 Комплексное преобразование Фурье и случайный отклик 381

7.5 Решение приближенного отклика 385

7.5.1 Эквивалентные статические нагрузки 389

7.5.2 Масштабирование форм режима для нагрузки 389

Ссылки 391

8 Свойства твердых тел, жидкостей и газов 392

8.1 Твердые вещества 392

8.2 Жидкости 402

8.3 Газы 405

8.3.1 Закон идеального газа 405

Ссылки 409

A Приблизительные методы определения собственной частоты 410

A.1 Взаимосвязь между основной собственной частотой и статическим отклонением 410

A.2 Метод Рэлея 413

A.3 Методы Дункерли и Саутвелла 415

A.4 Приближения Рэлея – Ритца и Шмидта 415

A.5 Процедура Галеркина для непрерывных структур 416

Ссылки 417

B Второе численное интегрирование Ньютона Закон 418

Ссылки 421

C Стандартные октавы и звуковое давление 422

C.