| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Калькуляторы (физика) |
| Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
| Оптика |
| Калькулятор отражения и преломления света |
| Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
| Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Большая энциклопедия школьника
Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний,
необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым
помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию,
в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей,
которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите «Большую энциклопедию
школьника» и найдите нужный ответ вместе с малышом!
Вы подбираете слова и определения для простых вещей,
которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите «Большую энциклопедию
школьника» и найдите нужный ответ вместе с малышом!
Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены
Большая энциклопедия школьника — это твой надёжный путеводитель в мире знаний.
Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной.
С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей,
ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли.
Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься
на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик,
ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!
Отныне никакие вопросы учителей не смогут поставить тебя в тупик,
ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!
|
Ребенок не хочет учить буквы
Ребенок не хочет учить буквы — Понимаете, ведь надо что-то делать! — с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. — Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы … |
Past continuous passive
Страдательный залог образуется с помощью вспомогательного глагола ‘to be’.
Страдательный залог глагола ‘to repair’ в группе ‘continuous’ :
To be repaired = Быть исправленным. |
|
Определение формулы органического вещества по его молярной массе
Задание: Определить формулу углеводорода, если его молярная масса равна 78 г.
№ п/п
Последовательность действий
Выполнение действий
1.
Записать общую формулу углеводорода.
Общая формула углеводорода СхНу
2.
Найти молярную массу углеводорода в общем виде.
М(СхНу)=12х +у
3.
Приравнять найденное в общем виде значение молярной массы к данному в . |
У
У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. — Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру … |
Урок 32. сочетания с повторениями — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №32. Сочетания с повторениями.
Перечень вопросов, рассматриваемых в теме:
- Элементы комбинаторики
- Сочетания с повторениями
Глоссарий по теме
Перестановки
В комбинаторике конечное упорядоченное множество называется перестановкой без повторения, а их число обозначают Рn .
Перестановки элементов одного и того же множества отличаются только порядком расположения элементов друг относительно друга.
Pn=1∙2∙3∙4∙…∙(n-1)∙n
Если элементы множества расставлены по кругу, то это так называемые перестановки n элементов по кругу. Их количество равно (n — 1)!
Если множество содержит одинаковые элементы, то подсчет количества перестановок с повторениями производится следующим образом: элементы первого типа можно переставить между собой (n1 – количество таких элементов) способами, второго типа – способами, k -го типа — способами. Значит, число перестановок с повторениями меньше n! в раз, чем число перестановок без повторения, то есть это число равно
Размещения
В комбинаторике упорядоченные подмножества данного множества называются «размещениями из n элементов на k мест» или, проще: «размещениями из n по k».
Выбор m элементов из множества, содержащего n элементов с повторением и с упорядочиванием выбранных элементов в последовательную цепочку называют размещениями с повторениями из n элементов по m , а общее число обозначают
В комбинаторике подмножества данного множества называются «сочетаниями из n по k элементов» или, проще: «сочетания из n по k».
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Представим себе, что из элементов множества мы составляем всевозможные трехэлементные комбинации, в которых порядок не важен (как в сочетаниях), но выбрав каждый элемент мы возвращаем его обратно в множество и можем выбирать его снова. Сколько же в таком случае мы получим комбинаций
Считаем, что aab, aba или baa одинаковые наборы
aba и abc –разные наборы
Изучение этого случая начнем с простого примера:
В кондитерской имеются пирожные трех видов. Сколькими способами можно заказать набор, состоящий из пяти пирожных?
Поскольку порядок расположения пирожных в коробке не важен, речь идет о сочетаниях. Кроме того, в наборах обязательно будут повторения.
Кроме того, в наборах обязательно будут повторения.
Зашифруем каждый заказ нулями и единицами. Сначала напишем столько единиц, сколько заказали пирожных первого вида. Потом напишем ноль. Дальше напишем столько единиц, сколько заказали пирожных второго вида. Затем опять ноль. Опять напишем столько единиц, сколько заказали пирожных третьего вида.
пирожные | Шифр заказа | ||
Первый вид | Второй вид | Третий вид | |
2 | 2 | 1 | 1101101 |
5 | 1111100 | ||
Каждый «зашифрованный» заказ представляет собой комбинацию из пяти 1 и двух 0. Число выбора заказа равно числу перестановок с повторениями элементов множества {1,1,1,1,1,0,0}. В этом множестве 1 повторяется пять раз и 0 – два раза
Применим формулу для числа перестановок с повторениями
Значит, способов заказать набор пирожных 21.
Выбор m элементов из множества, содержащего n элементов с повторением и без упорядочивания выбранных элементов в последовательную цепочку называют сочетаниями с повторениями из n элементов по m
Пусть множество содержит n элементов, а выборка будет содержать m элементов. Аналогично тому, как мы делали в примере, зашифруем каждую выборку единицами и нулями.
Число единиц равно числу выбираемых элементов, то есть m. Поскольку всего различных элементов в множестве n, то мы должны поставить между единицами (n-1) «перегородку», то есть (n-1) нулей. Число размещений с повторениями равно числу перестановок с повторениями элементов полученного множества из m единиц и (n-1) нулей
Сочетания с повторениями используем тогда, когда порядок расположения элементов в выборке не имеет значения и элементы могут повторяться
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Сколько существует треугольников, длины сторон которых принимают одно из следующих значений: 5, 6, 7, 8, 9?
Решение:
Данные стороны таковы, что любые три из них соответствуют правилу треугольника, т. е. каждая сторона меньше суммы двух других. Значит, любая комбинация из трех сторон образует треугольник. Здесь речь идет о числе сочетаний из 5 элементов по 3 с повторениями:
е. каждая сторона меньше суммы двух других. Значит, любая комбинация из трех сторон образует треугольник. Здесь речь идет о числе сочетаний из 5 элементов по 3 с повторениями:
Ответ: 35
Пример 2.
Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае.
Поскольку , , , , , то существует 5+15+35+70+126=251 чисел, удовлетворяющих условию задачи.
Ответ: 126
основные правила и формулы. Формулы комбинаторики Перестановки и теория вероятностей
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных
комбинаций, подчиненных тем или иным условиям, можно составить из заданных
объектов. Основы комбинаторики очень важны для оценки вероятностей случайных
событий, т. к. именно они позволяют подсчитать принципиально возможное
количество различных вариантов развития событий.
к. именно они позволяют подсчитать принципиально возможное
количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1.
Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5
. Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение:
т. к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой
из n
элементов
называется любой упорядоченный набор
этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их
наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за
определенное направление работы. Тогда при одном и том же списочном составе
комитета, внутри него возможно 5! вариантов перестановок
, которые имеют значение. Количество
разных (и по составу, и по сфере ответственности) вариантов определяется в
этом случае числом размещений
из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т.д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся
комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся
цифр»!!
! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5
— последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т. д.).
д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5.26 | 1.38 | 3. 07 07
|
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0.34 | 1. 42 42
|
— |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3.83 | 4. 52 52
|
— |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P.S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т. е. 25-ю способами.
е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.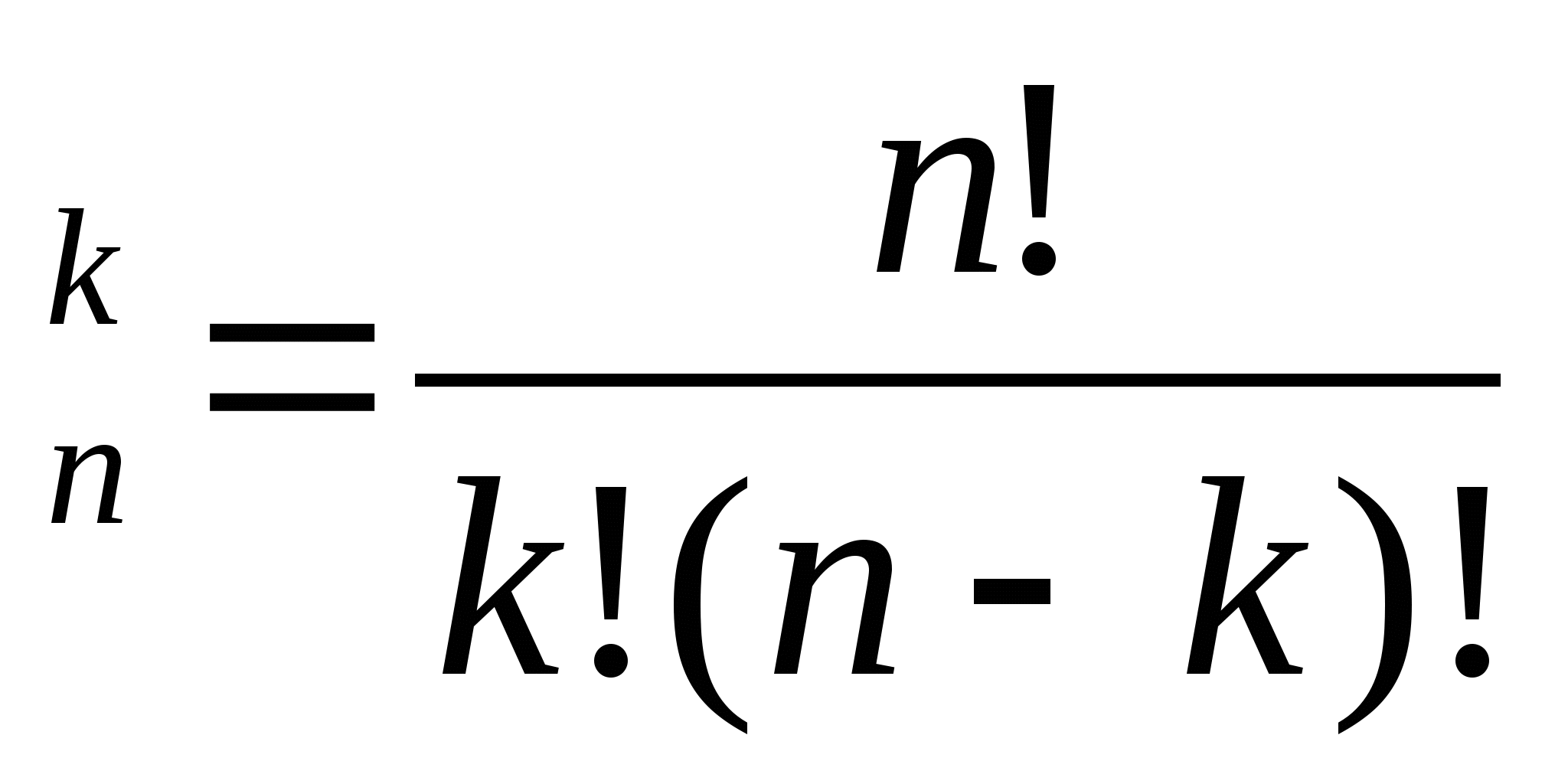
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Как посчитать количество комбинаций из 4. Формулы комбинаторики
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов.
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *. ..*n k .
..*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т. к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1.
Размещением из n
элементов по m
в комбинаторике называется
любой упорядоченный набор
из m
различных
элементов, выбранных из генеральной совокупности в n
элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5
. Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение:
т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6
. Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:
эта задача о числе
перестановок семи разных книг.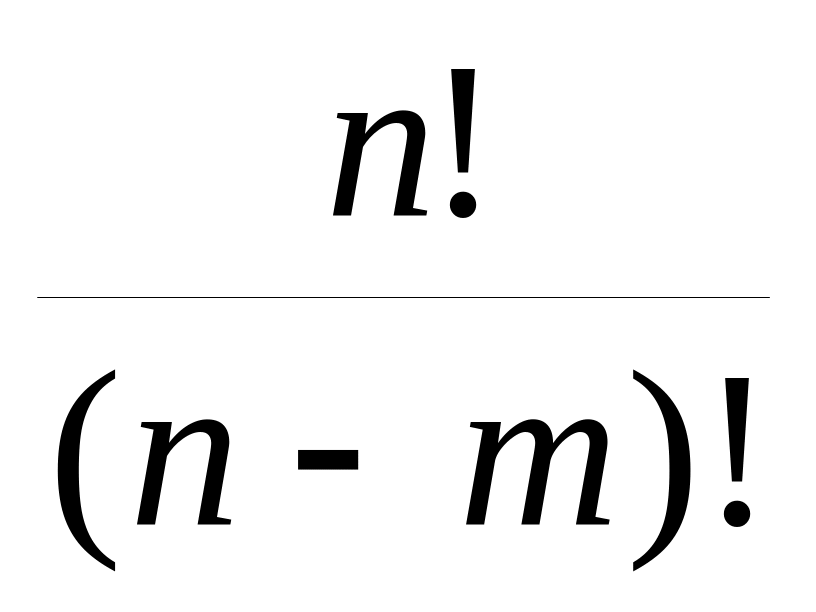 Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке , я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке , я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Может случиться так, что даже супер-число попадает в игру, но это не обязательно. Разница между перестановкой слов или комбинацией состоит в основном в том порядке, в котором мы помещаем элементы, составляющие набор. Если порядок, в котором расположены элементы набора, не имеет значения, то мы скажем, что это комбинация.
Банан — клубника — яблоки или. Если порядок элементов множества имеет значение, то мы говорим, что это перестановка. Например, если мы используем ключ сейфа. Невозможно, чтобы его можно было открыть, если мы используем. Перестановки, в которых разрешено повторять элементы набора.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся
комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся
цифр»!!
! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
В примере безопасности ключ может быть 8 8 8. Если мы хотим знать, сколько перестановок с повторением можно получить, чтобы поместить ключ в сейф, тогда мы должны рассмотреть, сколько элементов можно разместить в каждой из позиций. Это означает, что мы можем разместить любое из 10 чисел в первой позиции, любое из 10 чисел во втором и любом из 10 чисел в третьем, так что у нас есть.
В первой позиции мы можем поместить любое из 10 чисел от 0 до. Для второй позиции мы можем поместить любое число, отличное от того, которое было помещено в первую позицию, то есть любое из 9 оставшихся чисел. Определение способов упорядочения в комбинации.
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999
(вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же!
Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Мы определяем, сколько способов мы можем упорядочить группу г элементов. Наконец, применим следующую формулу. Есть 8 человек, чтобы сформировать комитет из пяти человек. Сколько существует различных возможностей для формирования комитета? Это комбинация, потому что порядок членов комитета не имеет значения.
В позиции 1 может быть любой из 8 членов комитета. Поскольку любой член комитета может находиться только в одной позиции за раз, то во второй позиции может попасть любой из остальных 7 членов. Третья позиция может идти только из одного из оставшихся 6 членов и т.д.
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P. S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»?
В общем-то, даже нечего добавить:)
S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»?
В общем-то, даже нечего добавить:)
Мы указываем, что комитет будет состоять всего из 5 членов, мы определяем, сколько способов мы можем заказать группу 5 элементов. Поскольку комитет сформирован с 5 членами 8, которые могут быть в этом комитете, мы должны. 8-5 = 3, и мы рассчитали, как можно было бы заказать эти 3 оставшихся члена.
Наконец, применим формулу. Вопрос: Сколько разных способов вы можете заказать 16 бильярдных мячей? Помните, что каждый шар может занимать одну позицию, например, если в первой позиции появляется шар 14, этот шар больше не может занимать другую позицию.
Источник отчета не может быть более надежным. В школьном портфолио у нас есть четыре книги разных предметов, уложенных сверху вниз в этом точном порядке. Португальский, математика, история и география. В том числе и в текущем порядке, сколько всего можно собрать в этом кошельке такие книги?
В школьном портфолио у нас есть четыре книги разных предметов, уложенных сверху вниз в этом точном порядке. Португальский, математика, история и география. В том числе и в текущем порядке, сколько всего можно собрать в этом кошельке такие книги?
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5
— последнее сочетание, так как все его элементы равны n — m + i.
Давайте подумаем над этой проблемой. При выборе первой книги, которая будет помещена в портфолио, у нас есть 4 возможности, потому что мы еще не разместили в ней никаких книг, у нас есть четыре книги на выбор: португальский, математика, история и география.
Если мы начнем сбор с португальской книгой, в выборе следующей книги, которая будет размещена на ней, у нас есть 3 возможности: математика, история и география. Если мы выберем книгу истории как вторую книгу кучи, для третьей книги у нас есть только две возможности: математика и география.
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
В разделе на вопрос сколько комбинаций чисел возможно из четырех цифр заданный автором Осознанный лучший ответ это точный ответ 10 в степени 4
Ответ от Uvastorgi
[гуру]
гараж хочешь вскрыть?))
Ответ от Вровень
[гуру]
много-даже и не пытайся-
Ответ от Поросятина
[активный]
эээ. 2=16.
2=16.
4. Длина комбинации 1 > это просто 4 варианта (4 наших случайных не повторяющихся цифры).
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся
комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся
цифр»!!
! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.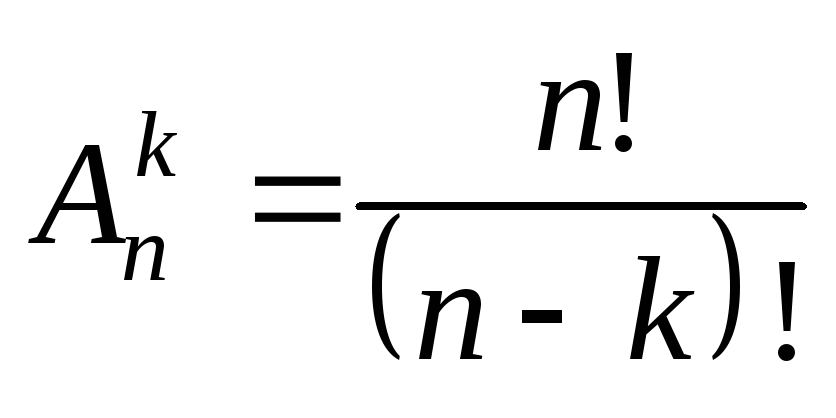
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5
— последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т. д.).
д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5.26 | 1.38 | 3. 07 07
|
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0.34 | 1. 42 42
|
— |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3.83 | 4. 52 52
|
— |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P.S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
основные правила и формулы. Элементы комбинаторики Число размещений из n элементов по m
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999
(вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же!
Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5
— последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5. 26 26
|
1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0. 34 34
|
1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3. 83 83
|
4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P. S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение:
n 1 =6
(т. к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n
элементов по m
в комбинаторике называется
любой упорядоченный набор
из m
различных
элементов, выбранных из генеральной совокупности в n
элементов.
Размещением из n
элементов по m
в комбинаторике называется
любой упорядоченный набор
из m
различных
элементов, выбранных из генеральной совокупности в n
элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5
. Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение:
т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием
из n
элементов по m
в комбинаторике называется любой неупорядоченный набор
из m
различных элементов, выбранных из
генеральной совокупности в n
элементов.
Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:
эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т. д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы.
Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
основные правила и формулы. Сочетания без повторений. Сочетания с повторениями
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент.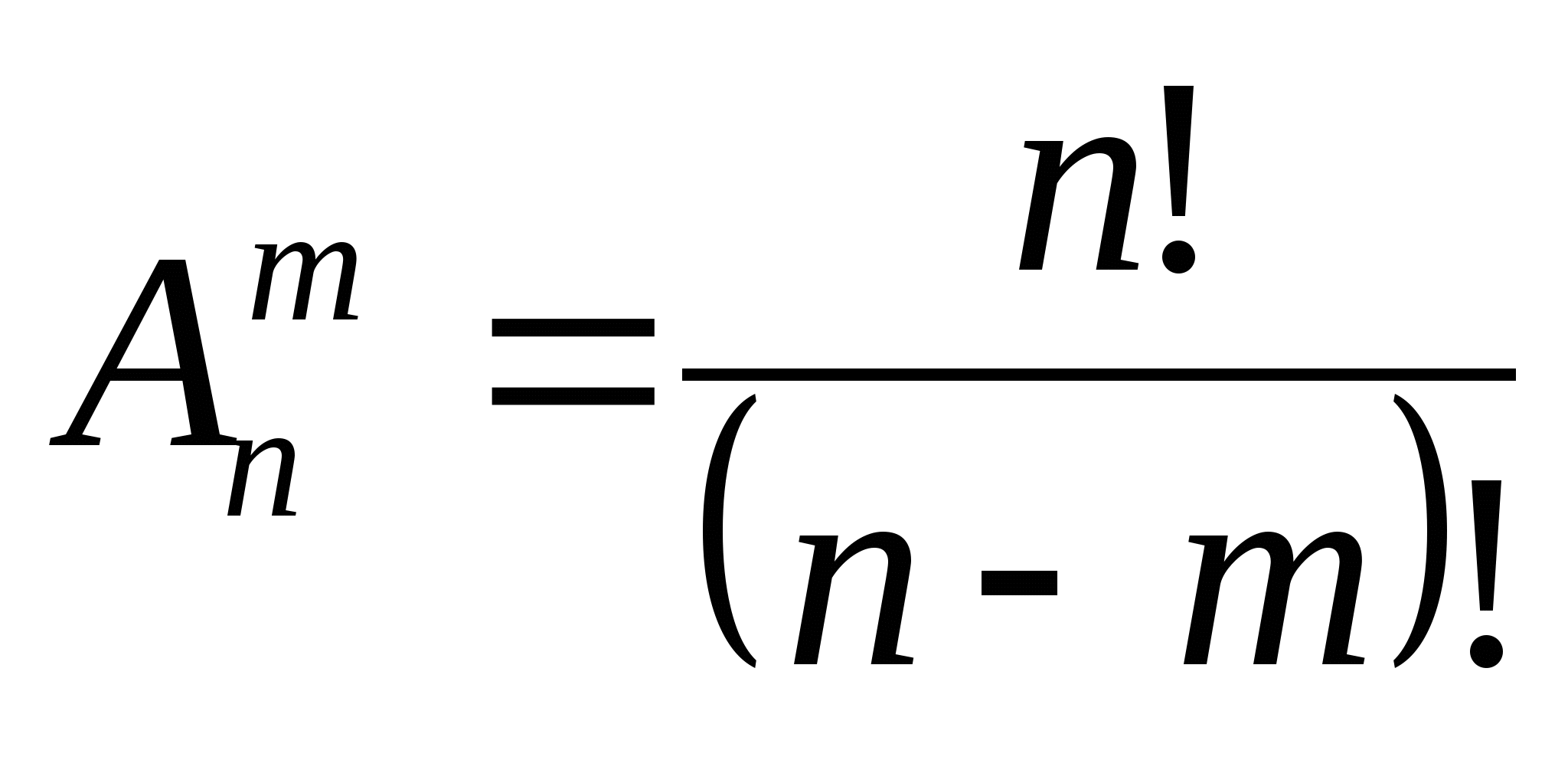 Для предпоследнего — два варианта, и так далее.
Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1.
Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1.
Размещением из n
элементов по m
в комбинаторике называется
любой упорядоченный набор
из m
различных
элементов, выбранных из генеральной совокупности в n
элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5
. Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение:
т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6
.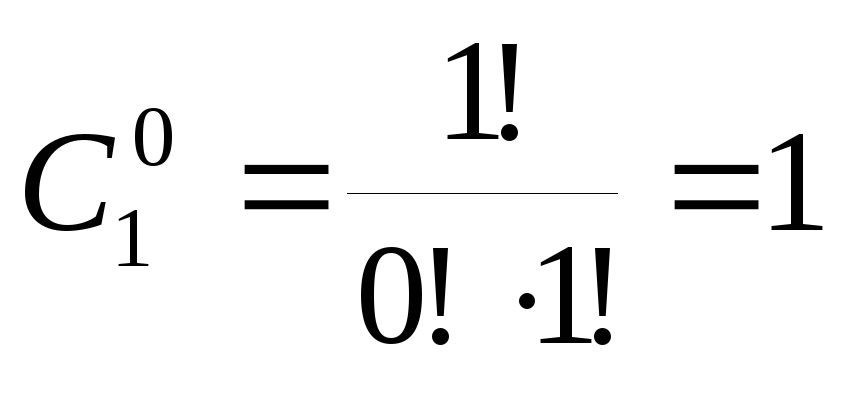 Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:
эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9.
На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение:
В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний
из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т. д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры
, которое содержались в данном четырехзначном числе. Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Ну да, не само число
, а просто его составляющие у
гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов
(наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999
(вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же!
Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007.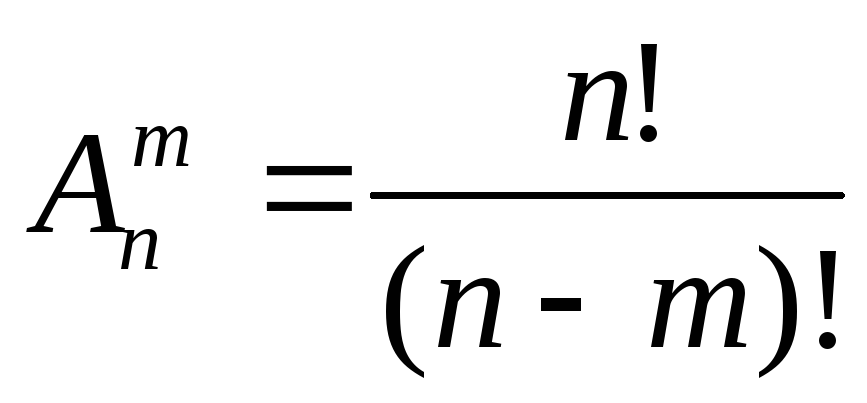 Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5
— последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5. 26 26
|
1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0. 34 34
|
1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3. 83 83
|
4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P. S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
S.
На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Сбои в приеме на воспитание, связанные с проблемным поведением: смягчение порогового эффекта
J Проконсультируйтесь с Clin Psychol. Авторская рукопись; доступно в PMC 2012 1 августа.
Опубликован в окончательной отредактированной форме как:
PMCID: PMC3334279
NIHMSID: NIHMS357799
Philip A. Fisher
Oregon Social Learning Center and University of Oregon
iller
Университет штата Орегон
Энн М. Маннеринг
Государственный университет штата Орегон
Айко Такахаши
Центр социального обучения штата Орегон
Патрисия Чемберлен
Центр социального обучения штата Орегон
Филип А.Фишер, Центр социального обучения штата Орегон и Университет штата Орегон;
Корреспонденция по этой статье должна быть адресована доктору Филиппу А. Фишеру, Центр социального обучения штата Орегон, 10 Shelton McMurphey Boulevard, Eugene, OR 97401. gro.clso@flihp См. Другие статьи в PMC, в которых цитируется опубликованная статья.
Фишеру, Центр социального обучения штата Орегон, 10 Shelton McMurphey Boulevard, Eugene, OR 97401. gro.clso@flihp См. Другие статьи в PMC, в которых цитируется опубликованная статья. Реферат
Цель
Сбои в размещении имеют неблагоприятные последствия для приемных детей. Выявление надежных предикторов сбоев в размещении может помочь в распределении услуг для предотвращения сбоев.Это исследование преследовало две цели: (а) повторить предыдущий вывод о том, что количество ежедневных проблемных поведений ребенка при поступлении в новую приемную семью предсказывает последующие сбои в размещении у приемных дошкольников, и (б) определить, смягчается ли эта связь. путем лечения в приемных семьях.
Метод
Проблемное поведение и сбои в размещении были исследованы у 60 детей, находящихся в обычных приемных семьях (возрастной диапазон = 3,10–5,91 года [ M = 4.34, SD = 0,83], 58,3% мужчин, 93,4% европеоидов) и 57 детей в программе лечения в приемных семьях (возрастной диапазон = 3,01–6,78 лет [ M = 4,54, SD = 0,86], 49,1% мужчина, 82,5% европеоид). Воспользовавшись Контрольным списком ежедневного отчета для родителей, кратким телефонным интервью, воспитатели сообщили о проблемном поведении шесть раз в течение 3 месяцев. Сбои в размещении отслеживались в течение 12 месяцев.
Воспользовавшись Контрольным списком ежедневного отчета для родителей, кратким телефонным интервью, воспитатели сообщили о проблемном поведении шесть раз в течение 3 месяцев. Сбои в размещении отслеживались в течение 12 месяцев.
Результаты
Дети, находящиеся в обычных приемных семьях с 5 или менее проблемным поведением, имели низкий риск нарушения, но их риск увеличивался на 10% для каждого дополнительного поведения ( p =.013). Вмешательство, казалось, смягчило этот «пороговый эффект»; количество проблемного поведения не предсказывало риск прерывания помещения в приемную группу лечения ( p = 0,63).
Выводы
Эти результаты повторяют предыдущие данные, связывающие проблемное поведение детей с нарушениями условий размещения, и дополнительно подчеркивают необходимость ранних профилактических вмешательств.
Ключевые слова: приемная семья, дошкольный период, сбои в размещении, поведенческие проблемы
Примерно 95% приемных детей испытывают по крайней мере одно нарушение в приеме на воспитание, находясь вне дома (Джеймс, 2004), и неблагоприятные последствия эти нарушения психосоциального функционирования хорошо задокументированы (Jonson-Reid & Barth, 2000; Leathers, 2002; Ryan & Testa, 2005). Более того, недавние данные свидетельствуют о том, что такие нарушения также связаны с негативным воздействием на развитие мозга (Fisher, Bruce, Abdullaev, Mannering, & Pears, в печати). Таким образом, определение рентабельных инструментов для прогнозирования и предотвращения нарушений размещения, связанных с проблемным поведением, имеет решающее значение.
Более того, недавние данные свидетельствуют о том, что такие нарушения также связаны с негативным воздействием на развитие мозга (Fisher, Bruce, Abdullaev, Mannering, & Pears, в печати). Таким образом, определение рентабельных инструментов для прогнозирования и предотвращения нарушений размещения, связанных с проблемным поведением, имеет решающее значение.
Проблемное поведение является индикатором риска сбоев в размещении в будущем (Fisher, Burraston, & Pears, 2005; James, 2004; Leathers, 2006; Price et al., 2008). Например, Джеймс обнаружил, что после 6 смен размещения более 60% любых последующих изменений были связаны с поведением.Другие исследователи показали, что исходный уровень экстернализирующего поведения (Newton, Litrownik, & Landsverk, 2000) и количество проблемного поведения (Chamberlain et al., 2006) являются самыми сильными предикторами нарушений трудоустройства в течение 12-месячного периода.
Контрольный список для ежедневного отчета родителей (PDR; Chamberlain & Reid, 1987), краткое телефонное интервью, представляет собой весьма практичный метод оценки проблемного поведения в контексте патронатного воспитания. В предыдущем исследовании с выборкой приемных детей в возрасте от 5 до 12 лет с использованием PDR Чемберлен и др.(2006) обнаружили «пороговый эффект» в связи между проблемным поведением и последующими нарушениями: дети с оценками, равными или ниже выборочного среднего из шести проблемных форм поведения в день, имели низкий риск срыва трудоустройства. Напротив, для детей с показателями PDR, превышающими выборочное среднее, каждое дополнительное проблемное поведение увеличивало вероятность срыва размещения на 25%.
В предыдущем исследовании с выборкой приемных детей в возрасте от 5 до 12 лет с использованием PDR Чемберлен и др.(2006) обнаружили «пороговый эффект» в связи между проблемным поведением и последующими нарушениями: дети с оценками, равными или ниже выборочного среднего из шести проблемных форм поведения в день, имели низкий риск срыва трудоустройства. Напротив, для детей с показателями PDR, превышающими выборочное среднее, каждое дополнительное проблемное поведение увеличивало вероятность срыва размещения на 25%.
В настоящем исследовании мы стремились воспроизвести результаты исследования порогового эффекта Чемберлена и др. (2006) на выборке приемных дошкольников и изучить, можно ли смягчить этот эффект с помощью лечебного вмешательства в приемные семьи.Исследование проводилось в контексте рандомизированного клинического исследования по оценке комплексного лечения в приемных семьях для детей дошкольного возраста (MTFC-P; Fisher, Ellis, & Chamberlain, 1999). В этом комплексном семейном вмешательстве используются принципы социального обучения для уменьшения деструктивного поведения, улучшения просоциального поведения и уменьшения задержек в развитии у приемных дошкольников. Вмешательство включает обучение и постоянную поддержку / консультации для приемных опекунов, индивидуальное и групповое лечение детей, а также услуги по уходу для содействия успешному постоянному трудоустройству.Краткий формат данной статьи исключает подробное описание MTFC-P. Для получения дополнительной информации см. Fisher et al. (1999) или Фишер и Чемберлен (2000).
Вмешательство включает обучение и постоянную поддержку / консультации для приемных опекунов, индивидуальное и групповое лечение детей, а также услуги по уходу для содействия успешному постоянному трудоустройству.Краткий формат данной статьи исключает подробное описание MTFC-P. Для получения дополнительной информации см. Fisher et al. (1999) или Фишер и Чемберлен (2000).
Основываясь на выводах Чемберлена и др. (2006), мы ожидали найти определенное количество проблемных форм поведения, о которых сообщили лица, осуществляющие уход, в PDR, ниже которого будет низкий риск нарушения размещения, а выше которого будет возрастать риск сбои в размещении при каждом дополнительном поведении. Однако, учитывая, что более высокий уровень проблемного поведения является нормой для развития дошкольников (Campbell, 2002), мы выдвинули гипотезу о более высоком пороге количества проблемного поведения, которое было терпимо для воспитателей.Кроме того, мы ожидали, что для детей, получающих вмешательство MTFC-P, более высокие показатели проблемного поведения не будут связаны с повышенным риском нарушения.
Метод
Участники
В этом исследовании участвовало 117 приемных дошкольников: 60 в группе обычного приемного воспитания (RFC) и 57 в группе лечения в приемном доме (TFC). Из 117 участников 19 детей RFC (12 мужчин) и 7 детей TFC (3 мужчины) вышли из исследования в течение периода оценки, а 18 детей RFC (8 мужчин) и 17 детей TFC (6 мужчин) не испытали нарушений при размещении. 1 Эти дети были подвергнуты цензуре при анализе рисков. Показатели удержания для группы RFC составили 81,7% ( n = 49) через 3 месяца, 76,7% ( n = 46) через 6 месяцев, 70,0% ( n = 42) через 9 месяцев и 65,0% ( n = 39) через 12 месяцев после базовой линии. Показатели удержания для группы TFC составили 94,7% ( n = 54) через 3 месяца, 89,5% ( n = 51) через 6 и 9 месяцев и 86,0% ( n = 49) через 12 месяцев после исходного уровня.Показатели удержания, как правило, были выше для группы TFC через 3 месяца, χ 2 (1) = 4,74, p = 0,03, 6 месяцев, χ 2 (1) = 3,38, p =. 07, 9 месяцев, χ 2 (1) = 6,80, p = 0,01) и 12 месяцев, χ 2 (1) = 6,89, p = 0,01. Не было систематических различий в демографических характеристиках или исходных показателях PDR между детьми, которые остались в исследовании или вышли из него. 2 Однако в группе TFC было больше братьев и сестер ( n = 21), чем в группе RFC ( n = 14).
07, 9 месяцев, χ 2 (1) = 6,80, p = 0,01) и 12 месяцев, χ 2 (1) = 6,89, p = 0,01. Не было систематических различий в демографических характеристиках или исходных показателях PDR между детьми, которые остались в исследовании или вышли из него. 2 Однако в группе TFC было больше братьев и сестер ( n = 21), чем в группе RFC ( n = 14).
Поток детей через рандомизированное исследование показан в. Все приемные дети в возрасте от 3 до 6 лет, которые впервые попадали под опеку, повторно поступали на опеку или переходили из одного дома в другую, были приняты на работу через местное окружное отделение государственной системы социальной защиты детей. 3 Отобранные дети ( n = 137) были случайным образом распределены в группу RFC ( n = 73) или TFC ( n = 64) до включения в исследование. 4 Частота отказов после рандомизации существенно не различалась между группами, χ 2 (1) = 0. 01, p = 0,92, что свидетельствует об отсутствии систематической ошибки отбора. Все исследователи, участвовавшие в сборе и кодировании данных, не знали об условиях исследования.
01, p = 0,92, что свидетельствует об отсутствии систематической ошибки отбора. Все исследователи, участвовавшие в сборе и кодировании данных, не знали об условиях исследования.
Диаграмма CONSORT для рандомизированного клинического исследования MTFC-P.
Демографические характеристики выборки на исходном уровне представлены в. Не было различий между группами RFC и TFC по исходному среднему возрасту ребенка, t (115) = 1,24, p = 0,22, пол, χ 2 (1) = 0,99, p =.32, этническая принадлежность, χ 2 (5) = 6,74, p = 0,24, тип размещения, χ 2 (2) = 1,68, p = 0,43, или баллы PDR, t (112 ) = 1,58, p = 0,12. Исследование было одобрено соответствующими внутренними контрольными комиссиями, и было получено информированное согласие от лиц, осуществляющих уход, и социальных работников. Приемные воспитатели могли выйти из исследования в любое время независимо от статуса группы. Семьям была выплачена компенсация за участие.
Семьям была выплачена компенсация за участие.
Таблица 1
Базовая демографическая информация
| Характеристика | RFC ( n = 60) | TFC ( n = 57) | ||||
|---|---|---|---|---|---|---|
| Возраст в годах 6 SD ) | 4.34 (0,83) | 4,54 (0,86) | ||||
| Возрастной диапазон в годах | 3,10–5,91 | 3,01–6,78 | ||||
| Мужчины:% | 58,3 | 49,1 | ||||
| европеоид | 93,4 | 82,5 | ||||
| латиноамериканец | 3,3 | 10,5 | ||||
| коренной американец | 3,3 | 5,3 | ||||
| афроамериканец0 | 1,8 | |||||
| Тип размещения:% | ||||||
| Первый прием в приемную семью | 26,7 | 19,3 | ||||
| Повторный прием в приемную семью | 18,3 | 14 | 14 | home | 55 | 66,7 |
| Оценка PDR: M ( SD ) | 18,41 (12,85) | 22,31 (13,50) | ||||
Процедура лечения
через 3 недели после поступления на лечение (исходный уровень) приемных воспитателей попросили пройти демографическое интервью. Затем их попросили пройти телефонные интервью PDR о проблемном поведении детей в течение предыдущих 24 часов в течение 2 дней подряд, один раз в месяц в течение первых 3 месяцев, пока ребенок находился в их доме. Интервью с PDR проводились одним из сотрудников 2 и 3 дней каждого месяца. Записи о трудоустройстве получали каждые 6 месяцев в местном окружном отделении государственной системы социальной защиты детей. Сотрудники, предоставившие эти записи, не знали об условиях исследования.Если ребенок столкнулся с перебоями в размещении до истечения первых 3 месяцев, рейтинги PDR были получены от следующих приемных воспитателей, когда это было возможно. Любой ребенок TFC, который столкнулся с перебоями в трудоустройстве до окончания исследования, получил услуги MTFC-P в своих новых приемных семьях.
Затем их попросили пройти телефонные интервью PDR о проблемном поведении детей в течение предыдущих 24 часов в течение 2 дней подряд, один раз в месяц в течение первых 3 месяцев, пока ребенок находился в их доме. Интервью с PDR проводились одним из сотрудников 2 и 3 дней каждого месяца. Записи о трудоустройстве получали каждые 6 месяцев в местном окружном отделении государственной системы социальной защиты детей. Сотрудники, предоставившие эти записи, не знали об условиях исследования.Если ребенок столкнулся с перебоями в размещении до истечения первых 3 месяцев, рейтинги PDR были получены от следующих приемных воспитателей, когда это было возможно. Любой ребенок TFC, который столкнулся с перебоями в трудоустройстве до окончания исследования, получил услуги MTFC-P в своих новых приемных семьях.
Невозможно было провести анализ назначенного лечения из-за совпадения истощения со сменой места размещения. Хотя были предприняты все попытки собрать данные из полной выборки, ни один участник, отказавшийся от вмешательства, не согласился участвовать в дальнейшем сборе данных.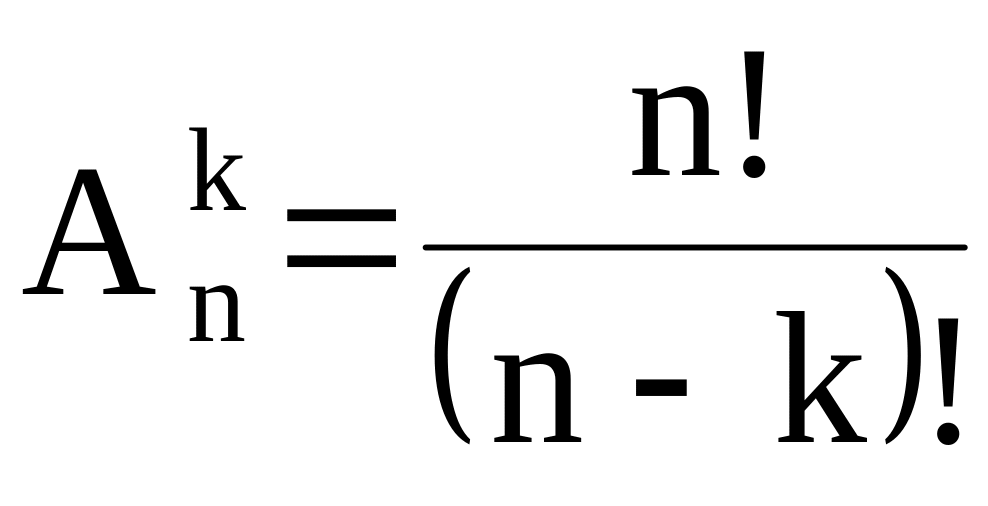
Меры
Сбои в размещении
Между исходным уровнем и 12 месяцами после базового уровня мы зафиксировали сбои в размещении (включая «отсутствие событий») и выбывания из исследования для каждого ребенка. Причины нарушения были указаны в записях о трудоустройстве, полученных из системы социальной защиты детей, и их не нужно было кодировать. Мы определили срыв в размещении как выход из текущего места размещения по отрицательной причине (т. Е. Удаление, которое считается в интересах ребенка или запрошено опекуном).Мы не включали неотрицательные причины сбоев в размещении (т. Е. Меняющиеся обстоятельства в семье, не связанные с поведением ребенка, клинический переход, постоянное размещение в приемных семьях, усыновление и биологическое воссоединение семей). Продолжительность каждого приема на воспитание регистрировалась как зависимая переменная.
Проблемное поведение ребенка
Мы проводили PDR один раз в месяц в 2 дня подряд в течение 3 месяцев (шесть наблюдений), чтобы определить, возникло ли какое-либо из 52 проблемных поведений в течение предыдущих 24 часов.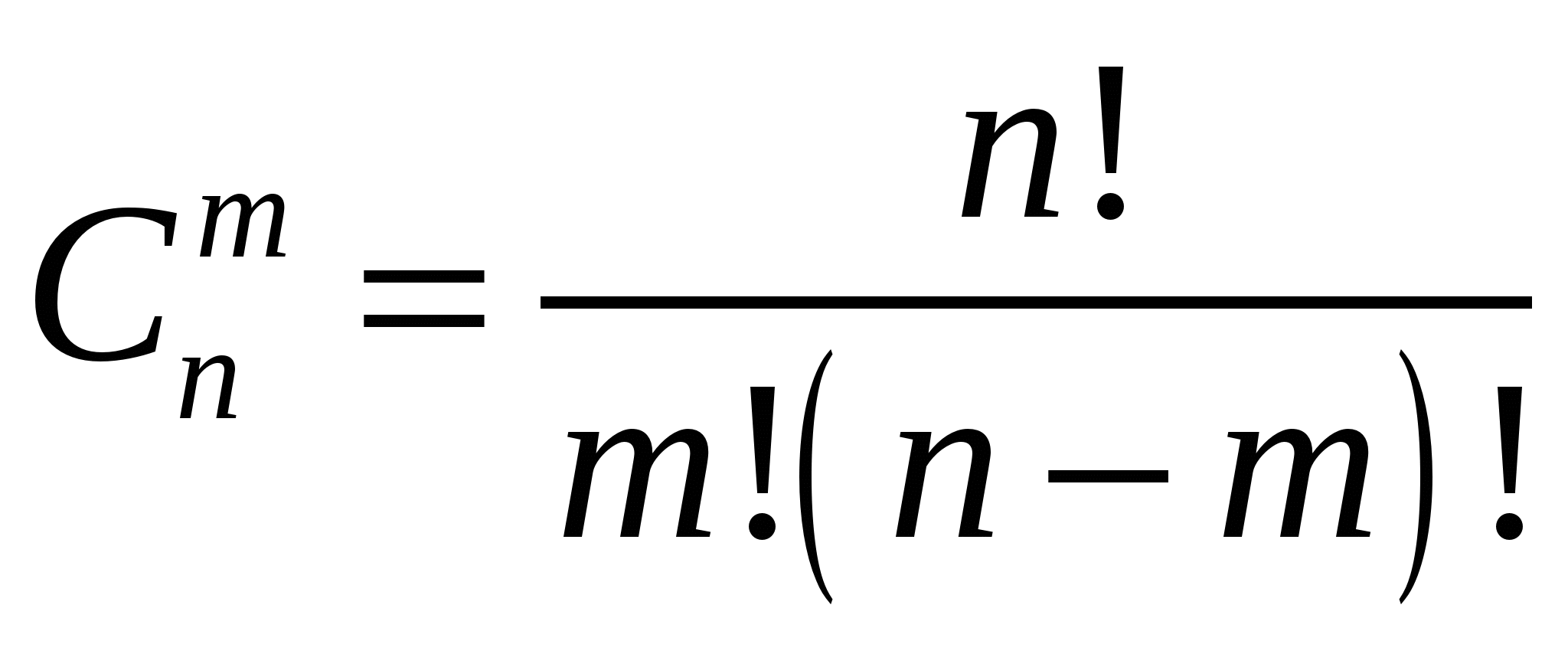 PDR регистрирует возникновение, но не частоту определенного поведения. Надежность и одновременная валидность PDR были продемонстрированы в предыдущих исследованиях (Chamberlain, Moreland, & Reid, 1992; Chamberlain & Reid, 1991). В дополнение к оригинальным 30 предметам PDR, используемым Чемберленом и др. (2006) мы включили 22 пункта для решения проблем поведения, актуальных для дошкольников (см.). Оценка для каждого ребенка представляла собой среднее количество поведений, о которых сообщалось в день, деленное на 6 (т. Е. Количество оценок).
PDR регистрирует возникновение, но не частоту определенного поведения. Надежность и одновременная валидность PDR были продемонстрированы в предыдущих исследованиях (Chamberlain, Moreland, & Reid, 1992; Chamberlain & Reid, 1991). В дополнение к оригинальным 30 предметам PDR, используемым Чемберленом и др. (2006) мы включили 22 пункта для решения проблем поведения, актуальных для дошкольников (см.). Оценка для каждого ребенка представляла собой среднее количество поведений, о которых сообщалось в день, деленное на 6 (т. Е. Количество оценок).
Приложение
Ежедневный отчет родителей Элементы журнала телефонных разговоров
| 1 | Обсуждение | |||||||||
| 2 | Baby talk | |||||||||
| 3 | Обратный разговор | 45 | Прикус | |||||||
| 6 | Шумный / шумный | |||||||||
| 7 | Соревновательный | |||||||||
| 8 | Жалобы | |||||||||
| 9 | 9 | 9 | 9 | |||||||
| 11 | Мечтание | |||||||||
| 12 | Defiance | |||||||||
| 13 | Депрессия / печаль | |||||||||
| 14 | Разрушительность | |||||||||
| 17 | Хитти ng другие | |||||||||
| 18 | Гиперактивность | |||||||||
| 19 | Несоответствующее сексуальное поведение | |||||||||
| 20 | Прерывание | |||||||||
| 21 | Безответственность | Безответственность | Ревность | |||||||
| 24 | Громкость | |||||||||
| 25 | Лежа | |||||||||
| 26 | Негативизм | |||||||||
| 27 | Нервозность||||||||||
| 29 | Не обращая внимания | |||||||||
| 30 | Паутинг | |||||||||
| 31 | Повторяющиеся вопросы | |||||||||
| 32 | Ограничение / удержание | проблемы | ||||||||
| 35 | Саморазрушение | |||||||||
| 36 | Сексуальные разговоры | |||||||||
| 37 | Кратковременный интервал внимания | |||||||||
| 38 | Пропуск приемов пищи | |||||||||
| Загрязнение пола (BM) / другое место | ||||||||||
| 41 | Загрязнение (BM) в штанах / пижаме | |||||||||
| 42 | Кража | |||||||||
| 43 | Клятва / прочие непристойности | Истерики | ||||||||
| 45 | Дразнить / провоцировать | |||||||||
| 46 | Угрожать | |||||||||
| 47 | Мочиться на полу или в другом месте | 48 Смачивающие штаны | ||||||||
| 50 | Whining | |||||||||
| Беспокоиться / тревожиться | ||||||||||
| 52 | Кричать |
Результаты
Описательная статистика сбоев в размещении и баллы PDR для групп RFC и TFC представлены в.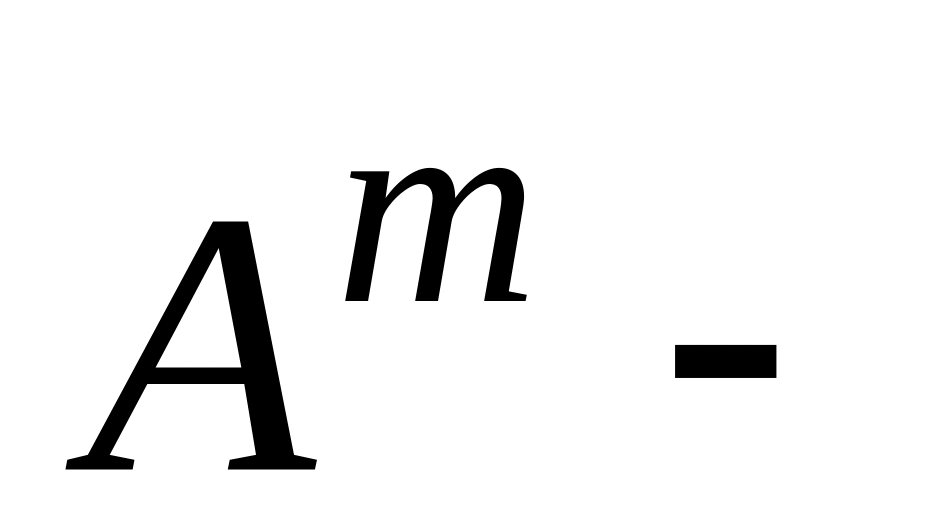 Мы вычислили среднее значение до шести вызовов PDR, чтобы предсказать сбои в размещении. Процент выполненных вызовов PDR не отличался в зависимости от состояния, χ 2 (4) = 4,99, p = 0,29, и большинство приемных воспитателей завершили четыре или более вызовов PDR (RFC = 91,7%; TFC = 100%). 5 Дети, которые испытали нарушение размещения, не различались по группе по среднему баллу PDR, t (17) = 0,20, p = 0,85, среднее время до нарушения, t (17) знак равно42, p = 0,68, или количество нарушений размещения, t (17) = 0,76, p = 0,46.
Мы вычислили среднее значение до шести вызовов PDR, чтобы предсказать сбои в размещении. Процент выполненных вызовов PDR не отличался в зависимости от состояния, χ 2 (4) = 4,99, p = 0,29, и большинство приемных воспитателей завершили четыре или более вызовов PDR (RFC = 91,7%; TFC = 100%). 5 Дети, которые испытали нарушение размещения, не различались по группе по среднему баллу PDR, t (17) = 0,20, p = 0,85, среднее время до нарушения, t (17) знак равно42, p = 0,68, или количество нарушений размещения, t (17) = 0,76, p = 0,46.
Таблица 2
Описательная статистика сбоев при трудоустройстве и баллов PDR
| RFC | TFC | |
|---|---|---|
| Дети, у которых возникли нарушения при трудоустройстве:% ( n 97) 20 n = 12) | 12,3% ( n = 7) | |
| Мужчины, которые испытали нарушение трудоустройства: n | n = 8 | n = 4 |
| Количество сбои в размещении: M ( SD ) | 1. 08 (.29) 08 (.29) | 1,00 (.00) |
| Время до прекращения размещения в месяцах: M ( SD ) | 4,45 (2,64) | 3,82 (3,93) |
| Время до размещения диапазон нарушений в месяцах | 1,38–10,58 | 0,92–10,87 |
| Оценка PDR для детей, переживших нарушение условий размещения: M ( SD ) | 10,73 (5,28) | 10,31 (2,18) |
| Диапазон баллов PDR для детей, которым не удалось разместить ребенка | 0. 50–17,83 50–17,83 | 7,00–13,67 |
Время начиналось на исходном уровне и прекращалось при прерывании размещения, прекращении исследования или окончательной оценке, в зависимости от того, что произошло раньше. Нарушение размещения было интересным событием, а прекращение исследования и ни одно событие не считались цензурированными наблюдениями. Неотрицательные изменения размещения, которые произошли до нарушения или цензуры размещения, игнорировались. Мы использовали модель пропорциональных рисков Кокса, чтобы оценить влияние PDR на время до нарушения размещения.Стандартные ошибки были исправлены для одноуровневых кластеров с использованием надежной сэндвич-оценки (Therneau & Grambsch, 2000).
Мы построили остатки Мартингейла, чтобы проверить функциональную форму отношения PDR – нарушение размещения по группам. В группе RFC наклон PDR был пологим ниже, но линейно увеличивался выше 5 вариантов поведения. В группе TFC такого порогового эффекта не было. Когда мы построили кривые выживаемости Каплана-Мейера по группам, оказалось, что исходные риски различаются по группам. Таким образом, мы стратифицировали модель Кокса и подобрали отдельные базовые риски для каждой группы вместе с кусочно-линейной аппроксимацией без связи, когда PDR составлял 0–5, и с элементом взаимодействия, который позволял линейному наклону для группы RFC отличаться от TFC. группа более 5 моделей поведения.
Опасность нарушения, прогнозируемая на основе базовой PDR для обеих групп, показана в. Для группы RFC кусочно-линейная аппроксимация для PDR выше 5 вариантов поведения была значимой: b = 0,091, exp ( b ) = 1,10, z = 2,48, p = 0,013. Кусочно-линейная аппроксимация предполагает, что опасность срыва размещения одинакова для детей с баллами PDR от 0 до 5 и увеличивается на 10% для каждого дополнительного поведения. Таким образом, ребенок RFC с базовым баллом PDR 16 имеет риск нарушения работы, равный примерно 2.В 7 раз больше, чем у ребенка с базовым баллом PDR 5.
Нарушение размещения соответствовало диаграммам рисков журнала для групп RFC и TFC. Примечание. RFC = обычное патронатное воспитание; TFC = лечение в приемных семьях; PDR = Ежедневный отчет для родителей.
Для группы TFC кусочно-линейная аппроксимация для PDR выше 5 вариантов поведения была незначительной, b = 0,019, exp ( b ) = 1,02, z = 0,476, p = 0,63, что предполагает что опасность нарушения работы у этих детей одинакова, независимо от оценки PDR.Хотя кусочно-линейная аппроксимация была значимой для группы RFC, но не для группы TFC, член взаимодействия не был значимым, b = -0,072, z = -1,34, p = 0,18. Предположение о пропорциональных рисках, основанное на графиках остатков Шенфельда, было разумным.
Обсуждение
Наши результаты дополняют растущий объем доказательств, связывающих проблемное поведение детей с риском нарушения условий размещения, и предоставляют дополнительные доказательства того, что вмешательства снижают этот риск (Чемберлен и др., 2006; Фишер и др., 2005; Джеймс, 2004; Ньютон и др., 2000; Price et al., 2008). Мы обнаружили, что отчеты приемных воспитателей о проблемном поведении ребенка в течение первых 3 месяцев в новом месте размещения предсказывают сбои в размещении в течение 12 месяцев для группы RFC, но не для группы TFC. Параллельно с выводами Чемберлена и др. (2006), риск нарушения в группе RFC был низким для детей с 5 или менее проблемным поведением, но увеличивался линейно на 10% для каждого поведения выше этого порога. Интересно, что вопреки нашей гипотезе этот порог был ниже у дошкольников по сравнению с Чемберленом и соавт.Выборка школьного возраста (2006 г.). Напротив, баллы PDR не предсказывали нарушения размещения в группе TFC. Таким образом, настоящее исследование повторяет предыдущие выводы о том, что обучение воспитателей эффективным методам управления поведением снижает проблемное поведение детей и предотвращает сбои в размещении (Чемберлен и др., 1992; Фишер и др., 2005).
Важно отметить, что наши результаты показывают временную, а не причинную связь между проблемным поведением и нестабильностью размещения; действительно, ассоциация, вероятно, двусторонняя и взаимная.В качестве альтернативы, прогностическая достоверность PDR может быть ограничена контекстами, в которых система защиты детей не предоставляет дополнительную поддержку приемным воспитателям. Определение того, для кого вмешательство будет наиболее эффективным, имеет решающее значение для предоставления услуг приемным семьям. Мы сосредоточились на нарушениях размещения, связанных с проблемным поведением, учитывая предшествующие доказательства того, что проблемное поведение детей предсказывает риск нестабильности размещения (James, 2004), что, в свою очередь, предсказывает отрицательные результаты (Jonson-Reid & Barth, 2000).
При интерпретации и обобщении наших результатов следует учитывать несколько факторов. Во-первых, мы сосредоточились на прогностической полезности проблемного поведения детей и не включали другие факторы, которые могут способствовать риску нарушения условий размещения (James, 2004; Rubin, O’Reilly, Luan, & Localio, 2007). Во-вторых, будет важно воспроизвести эти результаты с детьми, находящимися под опекой родственников, отслеживать сбои в размещении в течение более длительных периодов времени и повторить эти результаты с более разнообразными в этническом отношении группами населения.В-третьих, MTFC-P предлагался детям независимо от того, соответствовали ли они клиническим критериям проблемного поведения; необходимы дальнейшие исследования, чтобы изучить, будет ли снижение риска нарушения размещения реплицироваться в клинических образцах приемных родителей. В-четвертых, нарушения размещения оценивались через 3 месяца после введения PDR; в будущих исследованиях следует выяснить, можно ли надежно снизить риск срыва размещения в более короткие сроки. В-пятых, наблюдались значительные различия в показателях удержания в двух условиях исследования.В-шестых, в выборке было несколько групп братьев и сестер, и их было больше в TFC, чем в условии RFC. В-седьмых, как PDR, так и сбои в размещении связаны с опекунами; как таковые, могут возникнуть проблемы, связанные с общими различиями в этих показателях. Несмотря на эти ограничения, сходные данные из этого исследования и предыдущей работы показывают, что измерение проблемного поведения с помощью PDR представляет собой прагматичный и целесообразный подход к оценке риска сбоев в размещении.
Выявление приемных детей младшего возраста, подверженных риску трудоустройства из-за проблемного поведения, имеет существенные политические последствия.Во-первых, выявление таких детей в дошкольных учреждениях может повысить эффективность профилактических мероприятий и, таким образом, снизить финансовые и психологические издержки, связанные с перебоями в размещении. Несколько исследователей показали, что вмешательства, направленные на управление поведением ребенка и навыки приемных опекунов, уменьшают проблемное поведение и способствуют стабильности размещения (Чемберлен и др., 1992; Фишер и др., 2005; Фишер, Гуннар, Чемберлен и Рейд, 2000; Прайс и др. др., 2008; Смит, Стормшак, Чемберлен и Бриджес Уэйли, 2001).Во-вторых, предотвращение перебоев в размещении может способствовать достижению конечной цели патронатного воспитания: постоянному размещению. PDR представляет собой надежный и экономичный инструмент для выявления детей, подверженных риску предотвратимых проблем с поведением, связанных с трудоустройством. Широкое распространение таких методов в сочетании с мероприятиями, основанными на фактических данных, могло бы улучшить результаты благополучия детей на национальном уровне.
Благодарности
Это исследование и написание данной статьи были поддержаны следующими грантами: MH059780 и MH078105, NIMH, U.S. PHS; DA023920 и DA021424, NIDA, PHS США; и HD045894, NICHD, США PHS. Авторы благодарят участвующие семьи и персонал программ многомерного лечения в приемных семьях, Кристен Гринли за руководство проектом и Мэтью Рабеля за помощь редактора.
Сноски
1 Дети, которые пережили и не испытали нарушения условий размещения, не различались по базовому среднему возрасту, t (115) = 0,87, p = 0,39, этническая принадлежность, χ 2 ( 5) = 3.82, p = 0,58, тип размещения, χ 2 (2) = 0,53, p = 0,77, или оценка PDR, t (112) = 0,71, p = 0,48. Девочки реже, чем мальчики, сталкивались с нарушением трудоустройства, χ 2 (1) = 4,36, p = 0,04, независимо от состояния.
2 Не было никаких исходных различий между детьми, которые остались в исследовании или вышли из исследования по среднему возрасту, t (115) = 0,93, p = 0,36, пол, χ 2 (1) = 0.003, p = 0,95, этническая принадлежность, χ 2 (5) = 2,95, p = 0,71, тип размещения, χ 2 (2) = 0,31, p = 0,94, или PDR балл, t (112) = 1,13, p = 0,26.
3 План рандомизации был разработан в рамках совместного партнерства с руководителями системы социальной защиты детей, чтобы уменьшить неуверенность среди приемлемых приемных воспитателей относительно условий их участия.
4 Чтобы иметь право на участие в исследовании, текущее размещение должно было длиться 3 или более месяцев.
5 Средний процент выполненных вызовов PDR составил 88,3% для группы RFC и 92,7% для группы TFC. В группе RFC 70% ( n = 42) завершили 6 вызовов, 5% ( n = 3) завершили 5 вызовов, 16,7% ( n = 10) завершили 4 вызова, 1,7% ( n = 1) завершили 3 звонка, а 6,7% ( n = 4) завершили 2 звонка. В группе TFC 75,4% ( n = 43) завершили 6 вызовов, 5,3% ( n = 3) завершили 5 вызовов и 19,3% ( n = 11) завершили 4 вызова.
Информация для авторов
Филип А. Фишер, Центр социального обучения штата Орегон и Университет штата Орегон.
Майк Стулмиллер, Орегонский университет.
Энн М. Мэннеринг, Государственный университет Орегона.
Айко Такахаши, Центр социального обучения Орегона.
Патрисия Чемберлен, Центр социального обучения штата Орегон.
Список литературы
- Кэмпбелл С. Поведенческие проблемы у детей дошкольного возраста: проблемы клиники и развития. 2.Нью-Йорк, штат Нью-Йорк: Гилфорд; 2002. [Google Scholar]
- Чемберлен П., Морленд С., Рид К. Расширенные услуги и стипендии для приемных родителей: влияние на показатели удержания и результаты для детей. Защита детей: журнал политики, практики и программ. 1992; 71: 387–401. [PubMed] [Google Scholar]
- Чемберлен П., Прайс Дж. М., Рид Дж. Б., Ландсверк Дж., Фишер П. А., Стулмиллер М. Кто препятствует помещению в приемные семьи и родственников? Жестокое обращение с детьми и безнадзорность. 2006; 30: 409–424. DOI: 10.1016 / j.chiabu.2005.11.004. [PubMed] [CrossRef] [Google Scholar]
- Чемберлен П., Рид Дж. Б.. Наблюдение родителей и отчет о симптомах ребенка. Поведенческая оценка. 1987; 9: 97–109. [Google Scholar]
- Чемберлен П., Рид Дж. Б. Использование специализированной модели лечения по месту жительства для детей и подростков, покидающих государственную психиатрическую больницу. Журнал общественной психологии. 1991; 19: 266–276. DOI: 10.1002 / 1520-6629 (199107) 19: 3 <266 :: AID-JCOP22
310> 3.0.CO; 2–5. [CrossRef] [Google Scholar] - Фишер П.А., Брюс Дж., Абдуллев Ю., Маннеринг А.М., Груш К.С.Влияние ранних неблагоприятных факторов на развитие тормозящего контроля: значение для разработки превентивных вмешательств и потенциального восстановления функций. В: Бардо М.Т., Фишбейн Д.Х., Милич Р., редакторы. Тормозящий контроль и предотвращение злоупотреблений: от исследования к переводу. в прессе. [Google Scholar]
- Фишер PA, Burraston BO, Pears KC. Программа раннего вмешательства в приемные семьи: результаты рандомизированного исследования на постоянное размещение. Жестокое обращение с детьми. 2005; 10: 61–71. DOI: 10.1177/1077559504271561. [PubMed] [CrossRef] [Google Scholar]
- Фишер П.А., Чемберлен П. Многоплановое лечение Приемная семья: программа интенсивного воспитания, поддержки семьи и развития навыков. Журнал эмоциональных и поведенческих расстройств. 2000. 8: 155–164. DOI: 10,1177 / 106342660000800303. [CrossRef] [Google Scholar]
- Фишер П.А., Эллис Б.Х., Чемберлен П. Раннее вмешательство в приемную семью: модель предотвращения риска для маленьких детей, подвергшихся жестокому обращению. Услуги для детей: социальная политика, исследования и практика.1999; 2: 159–182. DOI: 10.1207 / s15326918cs0203_3. [CrossRef] [Google Scholar]
- Фишер PA, Gunnar MR, Chamberlain P, Reid JB. Профилактическое вмешательство для детей дошкольного возраста, подвергшихся жестокому обращению: влияние на поведение детей, нейроэндокринную активность и функционирование приемных родителей. Журнал Американской академии детской и подростковой психиатрии. 2000; 39: 1356–1364. DOI: 10.1097 / 00004583-200011000-00009. [PubMed] [CrossRef] [Google Scholar]
- Джеймс С. Почему сбои при приеме на работу? Исследование причин изменения помещения в приемную семью.Обзор социальных услуг. 2004. 78: 601–627. DOI: 10,1086 / 424546. [CrossRef] [Google Scholar]
- Джонсон-Рид М., Барт Р.П. От помещения в тюрьму: путь к тюремному заключению подростка из приемных семей или групповой опеки под присмотром службы защиты детей. Обзор услуг для детей и молодежи. 2000; 22: 493–516. DOI: 10.1016 / S0190-7409 (00) 00100-6. [CrossRef] [Google Scholar]
- Кожи SJ. Воспитывать поведенческие расстройства и отстраненность приемных детей от опекунов и общественных учреждений. Обзор услуг для детей и молодежи.2002; 24: 239–268. DOI: 10.1016 / S0190-7409 (02) 00175-5. [CrossRef] [Google Scholar]
- Кожи SJ. Сбои в размещении и отрицательные результаты размещения подростков в приемных семьях: роль поведенческих проблем. Жестокое обращение с детьми и безнадзорность. 2006. 30: 307–324. DOI: 10.1016 / j.chiabu.2005.09.003. [PubMed] [CrossRef] [Google Scholar]
- Newton RR, Litrownik AJ, Landsverk JA. Дети и молодежь в приемных семьях: определение взаимосвязи между проблемным поведением и количеством мест.Жестокое обращение с детьми и безнадзорность. 2000; 24: 1363–1374. DOI: 10.1016 / S0145-2134 (00) 00189-7. [PubMed] [CrossRef] [Google Scholar]
- Прайс Дж. М., Чемберлен П., Ландсверк Дж., Рид Дж. Б., Лев Л. Д., Лоран Х. Влияние программы обучения приемных родителей на изменение помещения детей в приемные семьи. Жестокое обращение с детьми. 2008; 13: 64–75. DOI: 10.1177 / 1077559507310612. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
- Рубин Д.М., О’Рейли ALR, Луан X, Локалио Р. Влияние стабильности размещения на поведенческое благополучие детей в приемных семьях.Педиатрия. 2007. 119: 336–344. DOI: 10.1542 / peds.2006–1995. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
- Райан Дж., Testa MF. Жестокое обращение с детьми и преступность среди несовершеннолетних: исследование роли размещения и нестабильности размещения. Обзор услуг для детей и молодежи. 2005. 27: 227–249. DOI: 10.1016 / j.childyouth.2004.05.007. [CrossRef] [Google Scholar]
- Смит Д.К., Стормшак Э.А., Чемберлен П., Бриджес Уэйли Р. Сбои в размещении в приемных семьях. Журнал эмоциональных и поведенческих расстройств.2001; 9: 200–205. DOI: 10.1177 / 106342660100
6. [CrossRef] [Google Scholar]
- Therneau TM, Grambsch PM. Моделирование данных о выживаемости: расширение модели Кокса. Нью-Йорк, штат Нью-Йорк: Спрингер; 2000. [Google Scholar]
(Как) Работают ли стажировки? Изучение количественных данных для теоретически обоснованной программы будущих исследований
https://doi.org/10.1016/j.jvb.2018.09.002 Получение прав и контентаОсновные моменты
- •
-
Условия трудоустройства улучшают перспективы трудоустройства, но есть доказательства по субъективным результатам карьеры неоднозначный.
- •
-
Большинству существующих исследований по трудоустройству недостает теоретической базы и эмпирической строгости.
- •
-
Трудоустройство можно рассматривать как события смены карьеры, которые приводят к построению идентичности в рабочем контексте.
- •
-
Процессы обучения и изменения личности взаимодействуют друг с другом и, таким образом, могут объяснить индивидуальный и карьерный рост при трудоустройстве.
Реферат
Хотя практика стажировки с учителем становится все более популярной в высшем образовании, данные об их влиянии на результаты карьеры остаются немного скудными и атеоретическими.Целью этого систематического обзора литературы является оценка эффективности трудоустройства с точки зрения результатов карьеры, а также определение любых лежащих в основе основных психологических процессов и предложение теоретически обоснованной основы для будущих исследований. Опираясь на теорию перехода (Schlossberg, 1981) и теорию построения карьеры (Savickas, 1997), мы утверждаем, что опыт работы с учителем является центральным опытом перехода, который способствует процессам социального обучения и вызывает изменения в развитии личности как профессионала, тем самым увеличивая возможности карьерного роста. и возможность трудоустройства, что, в свою очередь, положительно повлияет на будущие результаты карьеры.Мы отобрали 2394 систематически отобранных реферата по нескольким базам данных и дисциплинам. Были включены только количественные исследования, которые предлагали либо контрольную группу, либо продольный план, в результате чего был проведен углубленный обзор 40 исследований с применением строгого протокола оценки. Участие в трудоустройстве в целом оказывает положительное (но небольшое) влияние на результаты карьеры: выпускники, прошедшие практику, быстрее находили работу. Стажировки также изменили представление студентов о самоэффективности, их знаниях, навыках и отношении.Мы предполагаем, что эти изменения можно рассматривать как показательные для предлагаемых процессов социального обучения и изменений личности, которые положительно влияют на карьерные ресурсы. Наш обзор указывает на несколько пробелов в литературе, и, основываясь на существующих теориях карьеры, мы разрабатываем теоретическую модель и предлагаем новые возможности для будущих исследований, чтобы интегрировать гетерогенную область исследований трудоустройства и информировать карьерные исследования в других областях.
Ключевые слова
Стажировки
Стажировки
Совместное обучение
Теория карьеры
Теория социального обучения
Теория социальной идентичности
Объективные результаты карьеры
Субъективные результаты карьеры
Статьи о карьерном изменении
CРекомендуемые статьи
© 2018 Авторы.Опубликовано Elsevier Inc.
Рекомендованные статьи
Цитирующие статьи
Медицинский центр для студентов-медсестер Дом
ОБНОВЛЕНИЕ COVID-19
Мы рады сообщить, что Michigan Medicine снимает ограничения в отношении учащихся, не участвующих в программе UM, изучающих медицинские науки, чтобы мы могли в полной мере продолжить наши обязательства по обучению в сфере здравоохранения. Безопасность продолжает оставаться очень важным приоритетом в нашем движении вперед. Пожалуйста, просмотрите информацию о вакцине против COVID-19 и вакцине против гриппа СРОК ДЕЙСТВИЯ МАНДАТА ВАКЦИНЫ .
Отделение клинической помощи в Michigan Medicine координирует размещение всех студентов медсестрой в стационарных и амбулаторных зонах. Мы определяем места размещения всех студентов бакалавриата, в то время как размещение студентов магистратуры определяется отдельными практикующими врачами штата Мичиган. Отделение по размещению в больнице также следит за тем, чтобы все требования были соблюдены до размещения.
К сожалению, w e клинически не размещают запросы о посещении наблюдателя или теневом опыте. Пожалуйста, свяжитесь с отделением / территорией для получения дополнительной информации. Вы и подразделение / территория должны следовать всем руководящим принципам политики.
Копия полиса: Michigan Medicine Политика внешнего наблюдателяСОГЛАШЕНИЕ О СОТРУДНИЧЕСТВЕ
Для обучения студентов в медицинских школах штата Мичиган и школах медсестер, не входящих в UM, требуется соглашение о присоединении. Используется только шаблон соглашения о присоединении, одобренный Michigan Medicine. Школа медсестер (SON) может запросить незначительные изменения для рассмотрения, но серьезные изменения не будут приняты.Кроме того, только определенные лица имеют право вести переговоры и подписывать соглашения о присоединении от имени Michigan Medicine. Таким образом, все соглашения о присоединении будут исходить от нашего контрактного офиса системы здравоохранения Мичиганского университета (UMHS). СТРАНИЦА ПРИСОЕДИНЕНИЯ предоставит вам подробную информацию о заключении соглашения о присоединении между вашей школой и Michigan Medicine. Существуют определенные сроки, которые необходимо соблюдать, поскольку для заключения соглашения обычно требуется время.
КЛИНИЧЕСКИЕ УКАЗАНИЯ ПО РАЗМЕЩЕНИЮ
Все запросы на размещение должны координироваться через Отделение клинического размещения, чтобы обеспечить единообразие процесса. Просим студентов и преподавателей не подходить к персоналу напрямую, чтобы узнать о когортной группе или индивидуальном размещении. Это обеспечит справедливые результаты в высококонкурентном процессе и принесет большее удовлетворение всем.
- Все запросы на размещение должны координироваться через Отделение клинического размещения, чтобы обеспечить единообразный процесс. Инструкторов бакалавриата просят не обращаться к персоналу напрямую с вопросами о когортной группе или местах для наблюдений. . Это обеспечит справедливые результаты в высококонкурентном процессе и принесет большее удовлетворение всем.
- Максимальное количество студентов в любой когортной группе — восемь (8) .
- Все запросы на размещение студентов должны подаваться SON через ACEMAPP , безопасную платформу для клинического образования.
- Все студенты (включая сотрудников) и инструкторы ДОЛЖНЫ зарегистрироваться в ACEMAPP для адаптации.
- В связи с растущим числом потребностей в размещении аспирантов в Michigan Medicine мы больше не можем автоматически размещать аспирантов из внешних школ. Студенты-медсестры будут помещены в клинику Michigan Medicine с приоритетом размещения студентов UM School of Nursing Ann Arbor и Michigan Medicine Employee, которые поступают во внешние школы . Также будет уделено внимание учащимся школы медсестер Флинт UM.Цель Michigan Medicines — разместить как можно больше аспирантов, но в настоящее время мы не в состоянии удовлетворить потребности. Студенты-медсестры будут помещены в клинику Michigan Medicine в соответствии со следующим приоритетом:
- 1 ПРИОРИТЕТ ST Студенты UMSN Ann Arbor и Медицинские работники штата Мичиган, посещающие внешние школы
- 2 ND PRIORITY UM School of Nursing Flint Учащиеся
- 3 ПРИОРИТЕТ РД Неработающие, посещающие внешние школы
СРОКИ РАЗМЕЩЕНИЯ
Все запросы на размещение выполняются в соответствии с Соглашением об аффилировании , ACEMAPP , Secure Portal System, и СЛЕДНИЕ СРОКИ .Вы можете найти эту информацию на нашей КАЛЕНДАРНАЯ СТРАНИЦА .
ОБРАТИТЕ ВНИМАНИЕ: Координатор школы медсестер несет ответственность за то, чтобы все инструкторы и студенты были знакомы с нашим веб-сайтом, чтобы найти информацию и знать, как связаться с нами по вопросам, касающимся адаптации.
Целевая аудитория: студенты, участвующие в клинической практике | Автор / Контактное лицо: Эйприл Стинго
Веб-издатель / дизайнер / разработчик: April Stingo astingo @ med.umich.edu | Отзыв : 03.11.2021Плюсы и минусы приема на работу
Кейтлин Пью
Годы стажировки становятся все более обычным явлением, и все больше и больше курсов бакалавриата предлагают дополнительный год «сэндвича», проведенный в промышленности. Годы стажировки отличаются от традиционных, более коротких стажировок тем, что увеличенная продолжительность позволяет студентам занять место в бизнесе, который несет реальную ответственность.
После второго года обучения физике и астрофизике я проработал год в промышленности в небольшой компании по возобновляемым источникам энергии на северо-востоке Англии. Отказ от учебы на год был обескураживающим, но я думаю, что в долгосрочной перспективе это того стоило. Вот взгляд на плюсы и минусы многолетнего трудоустройства от кого-то, кто там был.
Pro: повысьте шансы на трудоустройство
Безусловно, самое большое преимущество прохождения учебного года — это ваши возможности трудоустройства.Это основная причина, по которой я решил сделать решительный шаг. Большинство студентов заканчивают учебу, практически не имея опыта работы, имеющей отношение к их степени, поэтому наличие полного года опыта гарантированно продвинет вас на много миль впереди конкурентов.
Завершение года работы в отрасли даст вам навыки межличностного общения, необходимые для достижения успеха на рабочем месте, а также дополнительные технические навыки, необходимые для выбранной вами отрасли. Кроме того, тот факт, что вы взяли на себя инициативу завершить дополнительный год, демонстрирует, что вы сосредоточены на карьере и стратегически думаете о своем будущем.Это та приверженность, которую будущие работодатели хотят видеть от кандидатов.
Против: пропустить еще один год с друзьями из универа
FOMO может устанавливаться при рассмотрении года в отрасли. Если ваши друзья остаются в университете, чтобы закончить учебу, вы будете беспокоиться о том, что пропустите весь смех последнего года. Хотя, не бойтесь, третий год вряд ли будет заполнен ночными развлечениями и ленивыми похмельными днями, смотрящими на Netflix на диване с вашими соседями по дому, поскольку диссертации действительно сказываются на вашей социальной жизни.
Хотя это правда, что некоторые из ваших друзей могут не быть там, когда вы вернетесь, другие могут остаться и пройти курсы магистратуры или даже закончить учебный год. Так что маловероятно, что вы станете «Билли не товарищами» в последний год.
Pro: определите направление своей будущей карьеры
К концу второго года учебы в университете я все еще понятия не имел, чем буду заниматься после окончания учебы. Проработав год в солнечной энергетике, я понял, что меня больше интересует работа в другом секторе энергетики.
Год в промышленности — отличный способ испытать карьеру, прежде чем с головой окунуться в постоянную работу выпускника. В лучшем случае вы найдете тот сектор, который вам нравится и который хотите развивать дальше, а в худшем случае вы решите, что этот конкретный путь не для вас. Даже если это произойдет, вы все равно приобретете множество ценных навыков, которые можно передать.
Con: Уравновешивание приложений с вашими исследованиями
Одним из недостатков проведения года размещения является попытка найти его в первую очередь.Процесс подачи заявки для более крупных компаний, как правило, состоит из нескольких этапов и может длиться несколько месяцев. Когда вы дойдете до заключительных этапов, обычно состоящих из личных собеседований и центров оценки, это будет связано с поездками и, возможно, пропуском лекций. Хотя это не идеально, лекторы обычно понимают и отправляют вам контент, который вы пропустите, если объясните свою ситуацию.
Когда вы начнете поступать на работу в аспирантуру, уже пройдя аналогичные процессы подачи заявок на год трудоустройства, у вас будет базовый опыт, из которого можно будет извлечь выгоду, и благодаря этому вы будете лучше работать.
Pro: развивайте свои социальные и профессиональные сети
На рабочем месте вы, вероятно, подружитесь с людьми всех возрастов и жизненных этапов, и, диверсифицируя свои социальные круги, вы получите полезное представление о жизни людей, отличных от вас, что поможет вам стать более здоровым. округлый человек.
Что касается роста вашей профессиональной сети, неизвестно о будущих возможностях, которые могут возникнуть благодаря связям, которые вы устанавливаете в течение года в отрасли.Многие компании предлагают должности выпускников после успешного завершения вашего учебного года, а некоторые даже покроют вашу плату за обучение за последний год обучения.
Con: Некоторые курсы официально не предлагают год в отрасли
Для некоторых существует небольшая проблема, заключающаяся в том, что год размещения не предлагается как часть их курса. Если это относится к вам, не думайте, что это не вариант. Поговорите со своим руководителем курса и спросите, можно ли потратить на год работы в отрасли. В конце концов, руководитель курса заинтересован в том, чтобы их ученики стали более трудоспособными.
Pro: опыт проживания в другой части страны (или мира!)
Для некоторых год размещения дает возможность жить в совершенно другой части страны или даже мира. Есть много возможностей дома и за рубежом, так что продолжайте и сочетайте свой год работы в отрасли с возможностью познакомиться с другой культурой или образом жизни.
Я жил на побережье в течение года обучения, и нет ничего, что я скучаю больше, чем пляжная жизнь.Даже зимой, когда температура опускалась до балтийского уровня, виды оставались прекрасными.
Есть жертвы, которые нужно принести, чтобы прожить год в промышленности, одна из которых — год вашей жизни, но, учитывая огромное количество преимуществ, которые принесет этот год, я думаю, что он на 100% стоит вложенных средств.
Свинец: Сэм Валади (Flickr)
Влияние пандемии COVID-19 на студентов-медиков последнего курса в Соединенном Королевстве: национальное исследование | BMC Medical Education
Целью нашего исследования является определение воздействия вспышки COVID-19 на экзамены, факультативные занятия и стажировку студентов-медиков последнего года обучения и последующее влияние на подготовленность и уверенность студентов в первом финансовом году.Также было изучено текущее отношение студентов к пандемии. Результаты опроса показывают, что респонденты придерживались утилитарного мнения о влиянии COVID-19; почти все респонденты (93,9%) считали, что внесенные изменения были необходимыми мерами во время этой пандемии. 77,3% респондентов отменили факультативные занятия; Хотя это и разочаровало многих, студенты признали необходимость ограничений на поездки по всему миру. Статистический анализ выявляет ключевые вопросы, связанные с обучением, которые следует решать в ближайшее время.Более того, более эффективные способы поддержки студентов в переходе на работу в долгосрочной перспективе являются важным элементом, который требует рассмотрения.
Переход от студента к врачу
Среди респондентов из медицинских школ Великобритании, 16,8% сообщили, что ассистентство студентов было официально отменено, в то время как 43,0% сообщили, что ассистентство было отложено. К счастью, 25,5% не изменили своего помощника, поскольку он был завершен до введения общенациональных ограничений, связанных с COVID-19.Рисунки 4 и 5 демонстрируют, что есть респонденты из медицинских вузов, которые чувствуют себя менее подготовленными или менее уверенными в том, чтобы начать работу в больницах раньше, чем ожидалось. В среднем 59,3% студентов чувствовали себя менее подготовленными, а 22,7% — менее уверенными. Для уверенности асимметричная тенденция на рис. 5 показывает, что большинство респондентов из британских медицинских школ чувствовали себя уверенно, начав в больницах раньше, чем ожидалось, и респонденты только из одной медицинской школы оказались за пределами 95% доверительного интервала.Напротив, при рассмотрении степени готовности было больше респондентов на медицинский вуз, которые чувствовали себя менее подготовленными. Кроме того, большее число пациентов отклонялось от среднего: респонденты из 11 медицинских вузов находились за пределами 95% доверительного интервала, а 6 — за пределами 99% доверительного интервала. Это указывает на значительное отклонение от общей когорты в этом опросе, и в целом большее количество людей в медицинских школах Великобритании чувствовали себя менее подготовленными к оказанию помощи в больницах.Это подчеркивает важность переходного периода для врачей, прибывающих в первый финансовый год.
Цель ассистента для студентов — предоставить студентам расширенные возможности для содействия переходу от студента к врачу и ознакомления с общими задачами, которые они в конечном итоге возьмут на себя в качестве врача на 1 финансовый год [8]. В отличие от традиционной клинической ротации, ассистентские должности интегрированы таким образом, что дает студентам возможность большей интеграции в команду, чтобы помочь развить клинические, практические и административные навыки и взять на себя ответственность в своем профессиональном качестве [14].Анализ показал, что перерыв в ассистентской работе со студентами значительно повлиял как на готовность к первому финансовому году, так и на уверенность в том, что студенты-медики начнут обучение раньше, чем ожидалось ( p = 0,0005 и p = 0,0005 соответственно). Напротив, нарушение факультативов не было значимым ни для подготовленности, ни для уверенности ( p = 0,427 и p = 0,515 соответственно). Это говорит о том, что для студентов-медиков последнего года обучения ассистентство играет ключевую роль в переходе от студента к врачу, в большей степени, чем период по выбору.Учитывая, что 70,9% студентов либо « согласны », либо « полностью согласны » с тем, что помощь в больницах до формального начала работы врачом будет дополнять возможности обучения, утраченные из-за COVID-19, очевидно, что студенчество рассматривает этот переходный период как важная часть их профессионального развития.
Эта пандемия создала возможность для ранней предварительной регистрации для работы в качестве врачей для студентов. Хотя это, вероятно, будет занято рядом студентов-медиков последнего года обучения, стремящихся поддержать передовую рабочую силу, следует признать, что существует противоречие между защитой образования и ответом на требования, предъявляемые к службам здравоохранения [15].
Отрадно видеть, что когорта такая готовая и способная к адаптации, важно учитывать, что студенты потеряли месяцы интенсивной подготовки при переходе от студента к врачу. Совет медицинских школ Великобритании сообщил, что первая обязанность студентов-медиков — продолжить свое образование и «не подвергать опасности свою готовность получить квалификацию в будущем, взяв на себя слишком много дополнительных обязанностей» [16]. Учитывая беспрецедентные перерывы в работе, вызванные пандемией, ясно, что студентов не следует привлекать к работе для повышения квалификации без надлежащих вводных инструкций, четких указаний по работе в рамках их компетенции, пастырской поддержки и соответствующего вознаграждения за их время.Это важно как для ухода за пациентами, так и для благополучия студентов.
Для медицинских школ, направляющих студентов для оказания помощи в больницах во время вспышки COVID-19, это возможность оценить степень вовлеченности, ответственности и ролей, которые им даны. Студентам-медикам могут быть предоставлены целевые возможности волонтерства, которые дополняют их образовательные потребности. Для студентов-медиков, работающих волонтерами в больничных палатах, это возможность сосредоточиться на интеграции в команду и обучении через наставничество, отслеживая врачей, завершающих свою клиническую деятельность [17].На протяжении всего этого студенты не будут «работать» с дополнительным давлением обеспечения достижения конкретных целей обучения и без необходимости подписываться на различные компетенции [18, 19]. Интегрируясь в команду, под длительным клиническим наблюдением и обратной связью, медицинские вузы могут оценить, отражают ли эти возможности волонтерства возможности альтернативных образовательных моделей, таких как Longitudinal Integrated Clerkship (LIC). LIC как образовательная модель приобрела популярность во всем мире и наиболее широко используется в первичной медико-санитарной помощи [20].Модель LIC отличается от студенческого ассистента, поскольку это долгосрочное размещение. Это обеспечивает учащимся длительное участие и непрерывность в уходе за пациентами, что способствует проявлению ответственности и ответственности при адекватном наблюдении [21, 22]. Дополнительными преимуществами LIC являются развитие у студентов сочувствия и ориентации на пациента благодаря их постоянному участию в уходе за пациентом. Медицинская школа Данди первой ввела комплексный LIC, рассчитанный на целый учебный год [20].Другие учреждения, такие как Имперский колледж и Медицинская школа Халл-Йорка, запустили пилотные программы LIC, которые применяются в сфере первичной и вторичной медико-санитарной помощи. В Великобритании еще предстоит увидеть, будут ли LIC более широко включены в учебные программы медицинских школ, но ранние отзывы студентов положительны [23, 24]. Пандемия COVID-19 может дать ценную информацию для оценки того, как можно улучшить клиническую практику в рамках медицинской учебной программы в Великобритании.
Онлайн-тестирование и обучение
Значительная часть студентов последнего курса уже сдавала письменные и клинические экзамены до вспышки COVID-19 или даже до внедрения социального дистанцирования и последующего закрытия университетов.Что касается стран ОБСЕ, чуть менее половины медицинских школ Великобритании уже завершили их, а около трети эти клинические осмотры были отменены. Четыре медицинских школы скорректировали их, используя актеров, а не реальных пациентов.
Точно так же письменные экзамены были сданы до перерыва в более чем половине медицинских школ Великобритании. Анализ влияния сбоев на экзаменах на готовность к экзаменам ОБСЕ и письменным экзаменам показал статистически значимое влияние на готовность ( p = 0.0005). В отличие от этого, нарушения на экзамене не были значительными, когда дело касалось уверенности (письменные экзамены p = 0,369, ОБСЕ p = 0,738). Это может свидетельствовать о том, что студенты воспринимают клинические знания, полученные в результате экзаменов, как важный фактор, способствующий их готовности к работе, в то время как их клиническая уверенность развивается другими способами, кроме академической оценки.
Интересно, что впервые для медицинских школ Великобритании 6 медицинских школ изменили письменный экзамен за последний год, чтобы он проводился удаленно.Если изоляция от COVID-19 продолжится, возможно, что повторная сдача экзаменов также может быть проведена онлайн. В Имперском колледже Лондона онлайн-тестирование состоит из открытого экзамена по книге, состоящего из 150 вопросов, на каждый из которых нужно ответить по 72 секунды. Вопросы были рандомизированы, чтобы не помогать друг другу. Студентам были представлены моделируемые пациенты, и через предоставленный анамнез, результаты обследования и расследования требовалось проработать вопросы [5]. Если психометрический анализ данных этих дистанционных экзаменов окажется сопоставим с анализом закрытых книжных экзаменов, это может ускорить наступающую онлайн-эру оценки студентов-медиков.Формирующие онлайн-оценки уже широко распространены в медицинском образовании; это помогает учащимся и учителям выявлять слабые места и обеспечивать оперативную обратную связь для дальнейшего развития. В отличие от формирующих оценок, итоговые оценки, такие как экзамены на последнем году обучения в медицинской школе, очень важны; с последствиями прохождения или невыполнения студентами с целью определения того, готовы ли студенты перейти к следующему этапу своего обучения или получению гранта [25]. Онлайн-итоговые оценки, введенные в результате пандемии COVID-19 в некоторых медицинских школах, могут предоставить бесценные данные для оценки эффективности онлайн-итоговых оценок в будущем.
Несмотря на закрытие университетских городков, медицинское образование не было полностью приостановлено из-за онлайн-платформ. Виртуальные онлайн-коммуникационные платформы (например, Zoom, Microsoft Teams, Skype) позволили продолжить лекции и обучение в небольших группах, в то время как формирующие оценки позволили продолжить обучение и развитие. Онлайн-программное обеспечение стало важным решением для продолжения медицинского образования, несмотря на сбои из-за COVID-19.
Онлайн-оценка и обучение сопряжены со своими проблемами.Во-первых, для уверенного использования необходимо обеспечить надежность систем онлайн-оценки, особенно возможности подключения к сети. Более того, у некоторых студентов может не быть домашней обстановки, способствующей сдаче экзаменов, у них могут быть тяжелые личные обстоятельства дома или есть препятствия для доступа к адекватным онлайн-ресурсам [5]. В дальнейшем необходимо разработать надежную систему для обеспечения стандартизации настроек удаленного экзамена учащимися и четкое руководство по смягчающим обстоятельствам.Хотя онлайн-оценки и методы обучения стали более заметными в последнее десятилетие, пандемия COVID-19 создала обстоятельства, которые могут ускорить их широкое использование в медицинском образовании.
Ограничения
Наше исследование имеет некоторые ограничения, о которых следует указать. Первое ограничение — это ретроспективный характер дизайна исследования. Несмотря на то, что текущие перспективы студентов-медиков последнего года обучения были установлены, у респондентов не было периода последующего наблюдения.Следовательно, долгосрочное влияние COVID-19 на переходный период от студента к врачу пока невозможно определить.
Еще одним ограничением является разница в количестве участников в разных медицинских вузах (рис. 1). Это различие между медицинскими школами означает, что наши данные не отражают всю когорту студентов-медиков последнего года обучения, которые начнут обучение в первом финансовом году в 2020 году. На основании данных британской фондовой программы 2019 года, общий коэффициент ответов для нашего опроса оценивается всего в 5 человек. .9% от общей национальной когорты студентов-медиков последнего года обучения в первом финансовом году. Признано, что это может означать, что полученные ответы отражают подгруппу студентов, которые чувствуют себя более или менее уверенными и / или подготовленными, и поэтому внешняя валидность этого исследования ограничена.
Кроме того, ответы на поправки к экзаменам для каждой медицинской школы сравнивались между всеми респондентами на предмет единообразия. Учитывая, что расхождения между ответами по медицинским школам практически отсутствовали, процесс проверки с медицинскими вузами не проводился.Мы признаем это ограничением, поскольку остается вероятность неточностей в воспоминаниях респондентов и сообщении об этих изменениях экзамена.
Рекомендации
-
1.
Ускоренный выпуск студентов-медиков не должен идти на компромисс с точки зрения надзора, пастырской поддержки или соответствующего вводного курса для поддержания благополучия как недавно закончивших врачей, так и пациентов.
-
2.
Альтернативные модели клинического образования (которые основываются на преимуществах, предлагаемых ассистентством) на последнем году обучения, такие как продольное интегрированное клеркство, должны быть изучены для более широкого внедрения на национальном уровне, чтобы помочь оптимизировать переход от студента к врачу.
-
3.
Необходимы четкие руководящие принципы по непрерывному развитию образования для студентов-медиков во время кризиса и будущих пандемий.
-
а.
Здоровье и безопасность студентов-медиков не должны подвергаться угрозе для пополнения медицинских кадров.
-
б.
Приоритетом для
студентов-медиков является их непрерывное образование, чтобы обеспечить достижение целей обучения, необходимых для получения диплома врачей, и соответствие стандартам, установленным GMC.
-
а.
-
4.
В медицинских вузах следует оптимизировать использование онлайн-платформ как для обучения, так и для оценивания.
-
а.
Онлайн-платформы предоставляют медицинским школам возможность удаленно предоставлять медицинское образование, чтобы поддерживать профессиональное развитие студентов-медиков в соответствии с требованиями GMC.
-
б.
Для более широкого внедрения дистанционных итоговых оценок в режиме онлайн как части медицинских учебных программ, должны существовать надежные системы, обеспечивающие справедливость этих оценок.
-
c.
В рамках подготовки к будущим пандемиям или другим нарушениям медицинского образования необходимо развивать способность беспрепятственно проводить дистанционные экзамены последнего года обучения.
-
а.
Размещение разрешений на стоянку | Университет Клемсона по делам студентов
Основные правила:
-
Все разрешения должны быть свободны и хорошо видны снаружи транспортного средства.
-
Все преподаватели, сотрудники, студенты, продавцы, подрядчики и посетители должны иметь разрешение на парковку на территории кампуса в любое время. Единственное исключение — это посетители, которые паркуются на местах со счетчиками — разрешение на парковку и оплату парковочных мест для посетителей не требуется.
- Разрешения на парковку бывают в форме виртуальных разрешений, декалей, ярлыков и табличек в зависимости от их классификации.
-
Все правила и положения действуют во время весенних, осенних и летних каникул и праздников.
Ознакомьтесь с таблицей основных параметров парковки, чтобы получить простое руководство по парковке в Университете Клемсона.
Ознакомьтесь с правилами штата, связанными с парковкой в университете Клемсона.
Выберите название разрешения ниже для правил и положений этого разрешения.ВЗАИМОДЕЙСТВИЕ РАЗРЕШЕНИЙ
Разрешение должно быть прикреплено к внутренней части лобового стекла со стороны водителя.
Репозиционированию подлежат следующие разрешения:
РАЗРЕШЕНИЯ, НЕ ВОЗВРАЩАЕМЫЕ ВЗАИМОДЕЙСТВИЕ
Разрешение должно быть прикреплено к внешней стороне заднего лобового стекла со стороны водителя или заднего бампера.
Не подлежат перемещению следующие разрешения:
ВИРТУАЛЬНЫЕ РАЗРЕШЕНИЯ
На транспортном средстве не будет отображаться физическое разрешение. Ваш номерной знак служит вашим разрешением.
Виртуальными являются следующие разрешения:
Разрешение должно быть хорошо видно на левой передней вилке или прилегающей территории.
Разрешение должно быть хорошо видно на крышке заднего колеса.
РАЗРЕШЕНИЯ НА ПОВЕРХНОСТЬ
Разрешениена табличке необходимо повесить на зеркало заднего вида наружу, чтобы номер разрешения был легко виден снаружи автомобиля.
Следующие разрешения имеют бирки:
РАЗРЕШЕНИЯ НА ПЛАТФОРМЫ
Табличка с разрешением должна быть цветной стороной вверх на приборной панели (со стороны водителя) транспортного средства, чтобы номер разрешения был легко виден снаружи транспортного средства.
Следующие разрешения представлены на табличках:
-
Строительство
-
Поставщик — назначен
-
Официальное использование
-
Ведомственный гость
-
Fike Recreation
Если вам необходимо приобрести разрешение, воспользуйтесь одной из следующих ссылок:
— Студенческое разрешение
— Разрешение на работу
— Разрешение на посещение
— Разрешение подрядчика / поставщика
% PDF-1.4 % 309 0 объект > эндобдж xref 309 74 0000000016 00000 н. 0000002424 00000 н. 0000002597 00000 н. 0000002632 00000 н. 0000003825 00000 н. 0000004349 00000 п. 0000004956 00000 н. 0000005377 00000 н. 0000006005 00000 н. 0000006357 00000 н. 0000006789 00000 н. 0000006901 00000 п. 0000007017 00000 п. 0000007131 00000 п. 0000007166 00000 н. 0000007232 00000 н. 0000007331 00000 н. 0000007657 00000 н. 0000008785 00000 н. 0000009778 00000 п. 0000010149 00000 п. 0000010579 00000 п. 0000011016 00000 п. 0000011385 00000 п. 0000011848 00000 п. 0000012306 00000 п. 0000013488 00000 п. 0000013964 00000 п. 0000014477 00000 п. 0000014904 00000 п. 0000015937 00000 п. 0000016114 00000 п. 0000017064 00000 п. 0000017365 00000 н. 0000017676 00000 п. 0000017811 00000 п. 0000017838 00000 п. 0000018197 00000 п. 0000018570 00000 п. 0000019624 00000 п. 0000020416 00000 п. 0000022912 00000 п. 0000023172 00000 п. 0000023967 00000 п. 0000025181 00000 п. 0000025453 00000 п.

 The road is being repaired = Дорогу чинят.
The road is not being repaired = Дорогу не чинят.
Is the road being repaired? = Чинят ли дорогу?
The road was being repaired = Дорогу чинили.
The road was not being repaired = Дорогу не чинили.
Was the road being repaired? = Чинили ли дорогу?
Страдательный …
The road is being repaired = Дорогу чинят.
The road is not being repaired = Дорогу не чинят.
Is the road being repaired? = Чинят ли дорогу?
The road was being repaired = Дорогу чинили.
The road was not being repaired = Дорогу не чинили.
Was the road being repaired? = Чинили ли дорогу?
Страдательный … ..
..