86306 (Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа) — документ, страница 2
Почти также изложен и учебник В. Никитина и П. Суворова.
Вполне научное изложение тригонометрии даёт акад. М. Е. Головин в своём учебнике «Плоская и сферическая тригонометрия с алгебраическими доказательствами», 1789. В этой книге можно найти все важнейшие формулы тригонометрии почти в том виде, в каком принято излагать их в XIX в. (за исключением обратных тригонометрических функций). Автор не нашёл нужным загромождать изложение введением секанса и косеканса, так как эти функции в редких случаях применяются на практике.
В 1804 г. выходит учебник Н. Фусса. Книга предназначена для гимназий. «Плоская тригонометрия,— говорит автор,— есть наука, имеющая предметом из трёх данных и числами изображённых частей прямолинейного треугольника определять три прочие его части». Учебник состоит из 4 равных частей. Общие понятия, решение треугольников, приложение тригонометрии к практической геометрии и геодезии и, наконец, теорема сложения. Учебник Н. Фусса отмежёвывается от сферической тригонометрии.
Учебник Н. Фусса отмежёвывается от сферической тригонометрии.
Шаг вперёд делает академик М. В. Остроградский в 1851 г. В своём конспекте по тригонометрии для руководства в военно-учебных заведениях он выступает как сторонник определения тригонометрических функций, на первом этапе их изучения, как отношений сторон в прямоугольном треугольнике с последующим обобщением их определения и распространением его на углы любой величины. [24]
1.2 Содержание и анализ материала по тригонометрии в различных школьных учебниках
Анализ материала, посвящённого решению тригонометрических уравнений и неравенств, в учебнике «Алгебра и начала анализа» для 10-11 классов под ред. А.Н.Колмогорова и в учебнике «Алгебра и начала анализа» для 10-11 классов авторов Ш.А. Алимова и др. свидетельствует, что различные виды тригонометрических уравнений и неравенств представлены в пособиях по математике для средней школы. Значит, перед учителем стоит задача – формировать у учащихся умения решать уравнения и неравенства каждого вида.
Рассмотрим содержание материала по тригонометрии изложенного в различных учебниках по математике за курс 10 – 11 класс средней школы, с целью его сравнения, анализа и формироваания наиболее приемлемой методики внедрения данной темы в школьном курсе математики.
Башмаков М.И. Алгебра и начала анализа. 10-11
Учебник разбит на 6 глав. Каждая глава открывается списком вопросов и задач. Затем коротко формулируются результаты, которые необходимо достичь после изучения главы. Материал, касающийся темы «Решение тригонометрических уравнений и неравенств» представлен в главе III «Тригонометрические функции» после изучения глав «Функции и графики» и «Производная и её применение».
Четвёртая глава «Показательная и логарифмическая функции» и пятая глава «Интеграл и его применение» не содержат обращений к области тригонометрии вообще, а в шестой главе «Уравнения и неравенства» встречаются и тригонометрические уравнения, и тригонометрические неравенства.
Причём, здесь же вводится основное тригонометрическое тождество.
Здесь же М.И Башмаков рассматривает вопрос решения простейших тригонометрических уравнений по тригонометрической окружности.
Следующие разделы данной темы «Исследование тригонометрических функций» и «Тождественные преобразования». Лишь после этого в разделе «Решение уравнений и неравенств» вводятся различные виды уравнений и некоторые виды неравенств. И соответственно здесь же говорится о способах и методах их решения.
Схема изучения темы «Решение тригонометрические уравнений и неравенств» определяется следующим образом: функция → уравнения → преобразования.[3]
Мордкович А.Г. Алгебра и начала анализа. 10-11
Учебник разбит на 8 глав. В конце изучения каждой главы чётко обозначены основные результаты изучения. Курс изучения математики в 10 классе начинается с изучения главы «Тригонометрические функции». Здесь автор вводит понятия тригонометрической окружности на координатной плоскости, понятия синус и косинус, основные тригонометрические соотношения с ними связанные, решения простейших уравнений по тригонометрической окружности.-(Trigonometricheskie-uravnenija)-reshenie-18.7.jpg) Как таковые формулы приведения вводятся после изучения тригонометрических функций углового аргумента. Далее рассматриваются свойства и графики тригонометрических функций. Во второй главе «Тригонометрические уравнения» подробно рассматривается решение каждого простейшего тригонометрического уравнения, на основе ранее введенных понятий арксинуса, арккосинуса, арктангенса. В этой же главе рассмотрены такие методы решения: разложение на множители и введение новой переменной; метод решения однородных тригонометрических уравнений. Другие методы решения рассматриваются после изучения третьей главы «Преобразование тригонометрических выражений».
Как таковые формулы приведения вводятся после изучения тригонометрических функций углового аргумента. Далее рассматриваются свойства и графики тригонометрических функций. Во второй главе «Тригонометрические уравнения» подробно рассматривается решение каждого простейшего тригонометрического уравнения, на основе ранее введенных понятий арксинуса, арккосинуса, арктангенса. В этой же главе рассмотрены такие методы решения: разложение на множители и введение новой переменной; метод решения однородных тригонометрических уравнений. Другие методы решения рассматриваются после изучения третьей главы «Преобразование тригонометрических выражений».
Здесь схема изучения выглядит следующим образом: функция → уравнения → преобразования.
С точки зрения применения учебник Мордковича удобен для самостоятельного изучения учащимися, т.к. он содержит сильную теоретическую базу. Изложение теоретического материала ведётся очень подробно. В условиях острой нехватки часов для проведения занятий в классе возрастает значение самостоятельной работы учеников с книгой. Опираясь на учебник, учитель прекрасно разберётся в том, что надо рассказать учащимся на уроке, что заставить их запомнить, а что предложить им просто прочесть дома.
Опираясь на учебник, учитель прекрасно разберётся в том, что надо рассказать учащимся на уроке, что заставить их запомнить, а что предложить им просто прочесть дома.
К недостаткам можно отнести не очень большое количество упражнений по этой теме в самом учебнике.[19]
Колмогоров А.Н. Алгебра и начала анализа
Учебник содержит 4 главы. Схема изучения материала по теме «Решение тригонометрических уравнений и неравенств» радикально отличается от предыдущих, т.к. сначала рассматриваются тригонометрические функции числового аргумента и основные формулы тригонометрии. В этой же первой главе, но несколько позже, рассматриваются основные свойства тригонометрических функций, их графики и их исследование. После этого вводятся понятия арксинус, арккосинус, арктангенс, арккотангенс и «параллельно» с этим решение простейших тригонометрических уравнений и неравенств. Автор не называет методов решения тригонометрических уравнений, а описывает алгоритм их решения. Тоже касается и решения тригонометрических неравенств.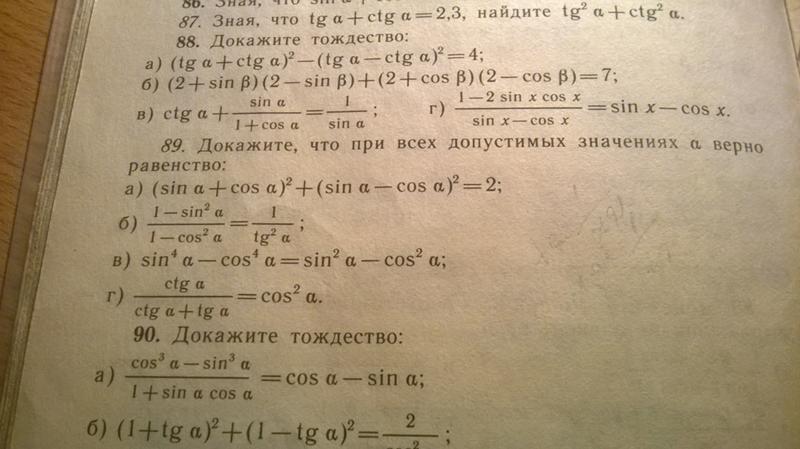
Таким образом, схема изучения выглядит так: преобразования → функции → уравнения.
Стоит отметить, что учебник содержит достаточно много дидактических материалов, как простых так и более сложных. Это естественно обеспечивает учителю возможность варьировать задания для учащихся.
С точки зрения изложения теоретического материала нельзя сказать, что учебник идеально подходит для самостоятельного изучения.[14]
Анализ содержания набора задач в теме «Тригонометрические уравнения» приводит к следующим выводам:
1) преобладающими являются простейшие тригонометрические уравнения, решение которых основано на определениях соответствующих функций в понятиях арксинуса, арккосинуса, арктангенса числа;
2) фактически отсутствуют тригонометрические уравнения, способ решения которых основан на свойстве ограниченности синуса и косинуса;
3) если говорить о связях приемов решения тригонометрических уравнений с приемами тождественных преобразований тригонометрических и алгебраических выражений, то следует отметить, что эти приемы в учебном пособии представлены бедно и однообразно. Рассматриваются приемы тождественных преобразований:
Рассматриваются приемы тождественных преобразований:
а) тригонометрические выражения:
— прием использования основного тригонометрического тождества;
— прием использования формул двойного и половинного аргументы;
— прием преобразования суммы тригонометрических выражений в произведение;
б) алгебраических выражений:
— прием разложения на множители;
— прием преобразования тригонометрического выражения, представляющего собой однородный многочлен относительно синуса и косинуса.
Использование указанных приемов приводит к тригонометрическим уравнениям, которые условно можно разделить на следующие виды:
а) сводящиеся к квадратным относительно тригонометрической функции;
б) сводящиеся к дробно-рациональным относительно тригонометрической функции;
в) сводящиеся к однородным;
г) сводящиеся к виду , где — тригонометрическая функция . [16, c/55]
1.3 Роль и место тригонометрических уравнений и неравенств в ШКМ
Тригонометрия традиционно является одной из важнейших составных частей школьного курса математики.-(Trigonometricheskie-uravnenija)-reshenie-18.15.jpg) И этот курс предполагает задачи, решить которые, как правило, можно, пройдя целенаправленную специальную подготовку.
И этот курс предполагает задачи, решить которые, как правило, можно, пройдя целенаправленную специальную подготовку.
Анализ школьных учебников по математике в полной степени определяет место тригонометрических уравнений и неравенств в линии изучения уравнений и линии изучения неравенств.
Изучению темы «Решение тригонометрических уравнений» часто предшествует изучение таких тем как «Преобразование тригонометрических выражений» и «Основные свойства и графики тригонометрических функций». В разделе «Решение тригонометрических уравнений и неравенств» мы знакомим учащихся с понятиями арксинус, арккосинус, арктангенс.
Опыт преподавания математики показывает, что осознание важности изучаемого материала приходит к ученикам не в процессе его изучения, а в процессе его применения при решении других заданий, т.е. тогда когда он становится средством для решения других задач.
Так, например, решение уравнения , сводится к простейшему уравнению , причём частному виду простейшего, после элементарного преобразования выражения, стоящего в левой части уравнения по формулам сложения косинуса. Аналогичная ситуация может возникнуть и при решении тригонометрических неравенств. Неравенства вида , в принципе становится решаемым только после преобразования выражения стоящего в правой части неравенства. Получим, , а затем с помощью таблицы значений основных тригонометрических функций имеем простое неравенство , решение которого не должно вызвать затруднений у учащихся.
Аналогичная ситуация может возникнуть и при решении тригонометрических неравенств. Неравенства вида , в принципе становится решаемым только после преобразования выражения стоящего в правой части неравенства. Получим, , а затем с помощью таблицы значений основных тригонометрических функций имеем простое неравенство , решение которого не должно вызвать затруднений у учащихся.
Мы видим, что именно здесь школьники могут наблюдать пользу от изучения формул тригонометрии. С их помощью нерешаемое на первый взгляд уравнение или неравенство принимает достаточно простой и, главное знакомый вид. Примерно то же самое происходит и при решении тригонометрических неравенств.
При таком подходе изучения тригонометрии, когда уравнения и неравенства изучаются после формул преобразования тригонометрических выражений, место тригонометрических уравнений и неравенств определяется через систематизацию знаний по темам «Преобразование тригонометрических выражений» и «Основные свойства и графики тригонометрических функций».
Если же тригонометрические уравнения и неравенства изучаются до темы «Преобразование тригонометрических выражений», то здесь место их изучения определяется совершенно противоположным образом. Здесь на изучение тригонометрических уравнений отводится больше времени: как только появляется новая формула, она сразу же используется для решения уравнений или неравенств. То есть в данном случае не формула преобразования является средством для решения тригонометрического уравнения или неравенства, а уравнение выступает как средство закрепления тригонометрических формул.
Таким образом, при любом подходе к изучению тригонометрии, роль изучения уравнений и неравенств неизмеримо велика, не зависимо от места их изучения. Ну и как следствие из этого велико и неизмеримо место изучения методов решения и тригонометрических уравнений и тригонометрических неравенств. Т.к. авторы учебников не уделяют должного внимания обозначению методов решения тригонометрических уравнений и неравенств, попробуем классифицировать уравнения и неравенства, и соответственно методы их решения.
1.4 Виды тригонометрических уравнений и методы их решения
Материал, относящийся к тригонометрии, изучается не единым блоком, учащиеся не представляют себе весь спектр применения тригонометрического материала, дробление на отдельные темы приводит к тому, что тригонометрия изучается в течение нескольких лет.
Алгебра и начала анализа. 8-11классы. Пособие для классов с углубленным изучением математики. Звавич Л.И.
Пособие содержит контрольные работы для 8-11 классов, задания выпускных экзаменов по математике в 9 и 11 классах с углубленным и профильным изучением математики, а также практикум для поступающих в вузы. Ко всем заданиям даны ответы. Книга может использоваться в качестве задачника в классах с сильным составом учащихся, а также для самостоятельных занятий.СОДЕРЖАНИЕ
От авторов 3
I. Контрольные работы
8 класс
усл. отв.
КМ-8-1. Повторение материала 7 класса 5 41
Повторение материала 7 класса 5 41
КМ-8-2. Повторение материала 7 класса 7 41
КМ-8-3. Линейные неравенства. Простейшие системы неравенств , 9 42
КМ-8-4. Доказательство неравенств 12 42
КМ-8-5. Квадратный корень 13 43
КМ-8-6. Преобразование выражений, содержащих квадратный корень 16 43
КМ-8-8. Теоремы Виета 21 45
КМ-8-9. Текстовые задачи, квадратные уравнения с параметром 24 45
КМ-8-10. Квадратичные и кусочно-квадратичные функции 26 46
КМ-8-11. Квадратные неравенства 28 47
КМ-8-12. Простейшие рациональные неравенства 30 47
КМ-8-13. Системы уравнений 32 48
КМ-8-14. Делимость натуральных чисел 34 48
КМ-8-15. Повторение 37 49
КМ-8-16. Повторение 39 49
9 класс
КМ-9-1. Степень с целым показателем 50 85
КМ-9-2. Корни n-й степени 52 85
КМ-9-3. Степень с рациональным показателем 54 86
КМ-9-4.
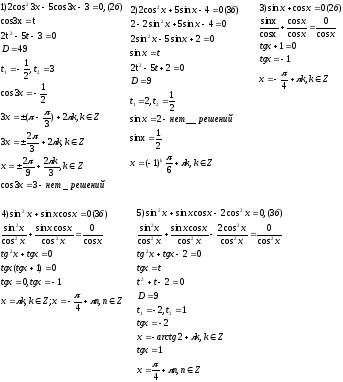 Функции двух переменных. Системы уравнений 56 86
Функции двух переменных. Системы уравнений 56 86КМ-9-5. Тригонометрические функции числового аргумента 57 87
КМ-9-6. Тригонометрические формулы 60 87
КМ-9-7. Преобразование тригонометрических выражений 62 88
КМ-9-8. Числовые последовательности. Арифметическая прогрессия 63 88
КМ-9-9. Геометрическая прогрессия 65 88
КМ-9-10. Метод математической индукции. Суммирование 67 89
КМ-9-11. Повторение (Уравнения. Текстовые задачи) 69 89
КМ-9-12. Повторение (Неравенства. Более сложные текстовые задачи) …. 72 89
КМ-9-13. Повторение (Функции, их свойства и графики) 74 90
КМ-9-14. Повторение (Преобразование выражений. Уравнения и неравенства с параметрами) 77 90
КМ-9-15. Комплексное повторение 79 92
КМ-9-16. Комплексное повторение 82 92
10 класс
КМ-10-1. Тригонометрические функции 93 126
КМ-10-2. Обратные тригонометрические функции 95 126
КМ-10-3.
 Тригонометрические уравнения … . 97 127
Тригонометрические уравнения … . 97 127КМ-10-4. Тригонометрические уравнения … . 99 128
КМ-10-6. Многочлены 102 131
КМ-10-7. Рациональные уравнения и неравенства 105 131
КМ-10-8. Числовые функции 106 132
КМ-10-9. Числовые последовательности. Предел функции на бесконечности . . 110 134
КМ-10-10. Предел и непрерывность 113 135
КМ-10-11. Производная и техника дифференцирования 116 136
КМ-10-12. Производная и ее применение 118 137
КМ-10-13. Производные высших порядков. Полное исследование функции 120 138
КМ-10-14. Повторение 122 139
КМ-10-15. Повторение. Итоговая работа (3—4 ч) 124 140
11 класс
КМ-11-1. Логарифмы и их свойства. Степенная, показательная и логарифмическая функции 141 181
КМ-11-2. Показательные уравнения и неравенства 143 182
КМ-11-3. Логарифмические уравнения и неравенства 146 183
КМ-11-4.
 Иррациональные уравнения и неравенства 149 184
Иррациональные уравнения и неравенства 149 184КМ-11-5. Пределы, связанные с числом е. Техника дифференцирования 151 185
КМ-11-6. Применение производной в задачах, связанных с функциями 154 186
КМ-11-7. Первообразная и интеграл 156 188
КМ-11-8. Определенный интеграл и его приложения 159 189
КМ-11-9. Алгебра комплексных чисел 161 189
КМ-11-10. Геометрическая интерпретация комплексных чисел 163 190
КМ-11-11. Тригонометрическая форма комплексного числа 165 190
КМ-11-12. Многочлены и функции с несколькими переменными 167 192
КМ-11-13. Системы уравнений 170 193
КМ-11-14. Комбинаторика и теория вероятностей 172 194
КМ-11-15. Повторение (Уравнения и неравенства) 175 195
КМ-11-16. Повторение (Производная и первообразная) 177 196
КМ-11-17. Повторение (Комплексные числа — обобщающая контрольная работа) . . 179 196
 11 класс
11 класс1. Вычисление и сравнение иррациональных чисел 197 259
2. Многочлены. Алгебраические уравнения и системы 198 259
3. Тригонометрические уравнения и системы 201 260
4. Тригонометрические неравенства 205 261
5. Показательные уравнения и системы 205 261
6. Показательные неравенства и системы 206 261
7. Логарифмические уравнения и системы 208 262
8. Логарифмические неравенства и системы 211 262
9. Иррациональные уравнения и системы 214 263
10. Иррациональные неравенства и системы 216 263
11. Уравнения, неравенства, системы 217 264
12. Исследование функций. Производные 221 265
13. Построение графиков функций и уравнений. Изображение множеств на плоскости …. 225 265
14. Касательная к графику 226 266
15. Экстремумы, наибольшее и наименьшее значения функции 231 266
16. Первообразная. Неопределенный интеграл 236 267
17.
 Определенный интеграл и вычисление площадей плоских фигур 237 267
Определенный интеграл и вычисление площадей плоских фигур 237 26718. Задачи с параметрами 244 268
19. Комплексные числа 251 269
20. Изображение множеств комплексных чисел на плоскости 255 270
III. Экзаменационные работы
9 класс 272 284
11 класс 277 285
IV. Практикум для поступающих в вузы
1. Задачи на касательную 288
2. Решение уравнений методом замены переменной 304
Тематическое планирование учебного материала 326
Литература 343
Математический диктант по теме «Тригонометрические формулы» 10
Математический диктант по теме «Тригонометрические формулы» 10 — 11 класс.
Учебник «Алгебра и начала математического анализа, геометрия 10 – 11».
Выписать номера правильных формул.
Критерии проверки: все правильно выписанные номера – «5»;
10 – 11 правильно выписанных номеров – «4»;
8 – 9 правильно выписанных номеров – «3»;
|
№ |
Формулы |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
sin2х=2 sinх· cosх |
|
24 |
|
|
25 |
| Деятельность учителя | Деятельность ученика |
| 1. Мотивационно-ориентировочная часть | |
| 1.1. Мотивация | |
| — Начало урока посвятим обзору элементарных функций, изученных в курсе алгебры 7-10 классов. Вспомните, какими формулами они задаются, как называются соответствующие графические образы. — Установите соответствие между графиком функции и формулой. | Слайд 1 (объекты в движении). Ученики перетаскивают формулы на соответствующие им графики, параллельно повторяя, как выглядит график, название соответствующей кривой. Например, — эта формула описывает степенную функцию. Учащиеся повторяют аналитическое задание функций и графические образы. Учитель может добавить следующее: каждому значению аргумента соответствует по определенному закону единственное значение функции, т.е. существует взаимно-однозначное соответствие между x и y. |
| — Какие свойства функции можно исследовать свойства по графику? | Слайд 2 (инструмент «штора»). Свойства:
Учитель, постепенно опуская «штору», повторяет с учениками очередное свойство функции, исследуемое или по графику, или по формуле. |
| — Что такое область определения функции? — Что называется множеством значений функции? — Укажите область определения и множества значений по графическим образам.
| Слайд 3 (выдвижные объекты). Область определения функции – это все значения, которые может принимать ее аргумент. Множество значений – это те значения, которые может принимать переменная y. По графическим образам ответ такой: Например, на фрагменте представлен график квадратичной функции в двух случаях: старший коэффициент положительный – х-любое, значения функции ограничены значением в вершине параболы, не меньше значения в вершине параболы; старший коэффициент отрицательный – х-любое, значения функции не больше значения функции в вершине параболы Учитель вытягивает выдвижные объекты с определениями, на которых приклеены ярлыки «Повторим теорию». Ученики вытягивают фрагменты с графиками и комментируют, как определить область определения и множество значений функций, представленных на графиках. |
| — При каких значениях x имеют смысл выражения? (самостоятельная работа, запись ответов в тетради, один ученик за крыльями доски).
— С какими действиями связаны ограничения по возможным значениям переменной x? Вспомним, когда возможно деление? Когда возможно извлечение корня четной степени? Когда существует степень с дробным показателем? Когда существует степень с нулевым показателем? Когда существует логарифм? Когда существует синус, косинус, тангенс? | Слайд 4 (интерактивное упражнение) Ученики дают комментарии к упражнениям. Например: Не всегда возможно деление. При проверке ученик комментирует ответ, объясняя, когда возможно данное действие. Учитель для обратной связи с целью усиления наглядности использует интерактивное средство СМАРТ доски. При нажатии на домино появляется правильный ответ. Это упражнение является пропедевтическим для изучения области определения функций. По завершении необходимо сделать акцент на прием нахождения допустимых значений x. |
| — Какая функция называется четной (нечетной)? Учитель после ответов учеников вытягивает объект с формулировкой (для наглядного закрепления). — Установите соответствие между графиком и свойством четности (нечетности). | Слайд 5. Выдвижной объект «повтори теорию». — Функция называется четной, если ее область определения симметрична относительно начала координат и значения функции в противоположных точках равны. График обладает симметрией относительно начала координат. — Функция называется нечетной, если ее область определения симметрична относительно начала координат и в противоположных точках значения противоположны. График обладает симметрией относительно начала координат. Повторяются определения, устанавливается соответствие между графиком и названием (четная, нечетная, общего вида). Слайд служит для пропедевтики изучения темы «Четность, нечетность тригонометрических функций». |
| — Как найти область определения и множество значений функций, заданной формулой? | Слайд №6 — Чтобы найти область определения функции, надо определить допустимые значения переменной x, учитывая ограничения, связанные с алгебраическими действиями. — Чтобы найти множество значений, надо определить возможные значения переменной у, учитывая свойства арифметических действий. На слайде заданы эффекты анимации «Появление». Учащиеся имеют возможность наглядно проверить свою версию ответа. |
| — Исследуйте свойства функции, заданной графиком.
На слайде задана анимация «вращение». Ответы указаны на обороте картинки. Проверка осуществляется сразу после предложенного ответа. | Слайд №7 Ученики работают в парах, делают краткие записи в тетрадях. Проверяют правильность друг у друга, вырабатывают одну правильную версию и озвучивают ее при фронтальной проверке. Возможный ответ: «Нуль» функции – это значение аргумента, при котором функция равна нулю. Функция равна нулю в точках пересечения с ось абсцисс. Функция на двух промежутках убывает, на одном – возрастает. Убывает – с увеличением аргумента линия падает вниз. Возрастает – при увеличении аргумента линия поднимается вверх. График простирается не на всей действительной оси, поэтому область определения ограничена отрезком. По оси ординат график тоже ограничен, поэтому область значений тоже ограничена отрезком. На слайде предусмотрены подсказки — выдвижные фрагменты «повтори теорию», эффекты анимации «Поворот»: при наведении на объект он поворачивается и появляется ответ. Эффект хорош для обеспечения обратной связи. |
| — Итак, мы привели знания в систему, повторив основные свойства элементарных функций, которые были изучены в курсе алгебры 7-10 классы. Еще раз акцентируем внимание на том, что свойства можно исследовать как по формуле, так и по графику. — Сегодня на уроке и на последующих уроках мы будем изучать новый вид функций и их свойства. | |
| 1.2 Постановка учебной задачи (цели) урока | |
| — В десятом классе мы изучали логарифмы и связанную с ними логарифмическую функцию и ей обратную показательную функцию, степень и связанную с ней степенную функцию; важный раздел алгебры – тригонометрия. В этом разделе рассмотрели понятия синуса, косинуса, тангенса, основные тригонометрические тождества, тригонометрические уравнения. — По логике вещей, скажите, что еще важно рассмотреть и изучить? Сделайте предположение. | — Мы изучили основные понятия тригонометрии. Возможно, в природе существуют тригонометрические функции. И это нетрудно проверить, если попробовать установить взаимно-однозначное соответствие между действительными числами и значениями их синусов, косинусов, тангенсов. |
| — Как сформулировать цель урока? | — Ввести понятия тригонометрических функций. |
| — Поскольку с каждым видом функции связаны свои свойства, то, наверное, интересно будет познакомиться со свойствами тригонометрических функций. — Какие еще цели можно поставить? | — Изучить свойства тригонометрических функций, заданных формулами. Исследование возможно только по формуле, поскольку не известны графические образы. |
| 1.3 Планирование учебной деятельности | |
| — Мы введем понятия тригонометрических функций и научимся находить их область определения и множество значений в случае их аналитического задания. Далее, на последующих уроках, изучим другие свойства по общей схеме исследования. Запишите тему урока. | Записывают тему урока «Тригонометрические функции. Область определения и множество значений». |
| — Перед вами на партах лежит канва таблицы, такая же заготовка фрагментарно сделана на экране интерактивной доски. В ходе урока мы должны заполнить таблицу полностью. — Все согласны принять правила работы? — Тогда начинаем постепенно заполнять графы таблицы. Как только таблица будет заполнена, мы постараемся связать ее графы и обсудим результаты работы. | Слайд №8 На парте лежит канва таблицы.
Такой образец заполнения, возможно, будет в тетради у ученика, при выполнении следующих указаний учителя. |
| 2. | |
| 2.1 Введение понятий тригонометрических функций. | |
| — Самостоятельная работа с учебником по плану:
| Слайд №9 (для демонстрации для введения понятий тригонометрических функций)
После работы с книгой ученики должны объяснить по данному слайду как вводятся тригонометрические функции. |
| 2.2. Рассмотрение области определения и множества значений. Формирование приемов нахождения области определения и множества значений функций, заданных формулами. | |
| — Как с помощью тригонометрического круга определить, какова область определения и множество значений тригонометрических функций? — Вспомните определение тангенса и котангенса. Выпишите соответствующие соотношения. — Сделайте выводы об области определения и множестве значений. | Слайд №10. (для демонстрации области определения и множества значений)
Параллельно идет заполнение таблицы со свойствами тригонометрических функций. |
| — Итог: ввели понятия тригонометрических функций и рассмотрели их область определения и множество значений. | |
| — Попробуйте выделить типы задач по новой теме. | — Найти область определения функции, заданной формулой; — Найти множество значений функций, заданных формулой. |
| — Проанализируйте решение задач №1, №2 учебника стр. 4. Оформите решения в тетради. — Попробуйте сформулировать приемы решения типичных задач. — Какие необходимы умения и навыки при решении задач данного типа? — Какие способы нахождения области значений? | — Чтобы найти область определения функции, надо определить допустимые значения переменной x, учитывая ограничения, связанные с алгебраическими действиями. При этом сталкиваемся с решением уравнений или неравенства. Необходимо уметь решать уравнения и неравенства известных нам видов. Поэтому хорошо бы повторить приемы решения. — Чтобы найти область значений можно использовать метод оценки, основанный на применении свойств числовых неравенств. Поэтому желательно повторить свойства числовых неравенств. |
| — Вывод: Метод оценки заключается в следующем:
| Слайд №11 (демонстрирует приемы нахождения области значений функции). Учащиеся оформляют метод решения и образец задания на закрепление. |
| — Второй способ: через уравнение с параметром. Учитель объясняет на конкретном примере и дает под запись прием. | Ученики оформляют вместе с учителем решение задания. |
| 2.3. Закрепление. Решение упражнений на отработку навыков. | |
| — Отработка алгоритма. Учитель предлагает выполнить задание самостоятельно. | Ученики, сотрудничая в парах, пытаются решить задание двумя способами, оформляя решение по предложенной схеме в два столбика. По завершению осуществляется проверка по слайду (задана анимация объекта). |
| — Итак, подведем итоги нашей работы.
| — Повторили:
— Ввели понятия тригонометрических функций. — Познакомились со способами исследования на область определения и множество значений. — Взять на заметку, запомнить:
|
| 3. | |
| 3.1. Оценка и самооценка учебной деятельности | |
| Прошу вас на маленьких листочках: поставить себе оценку за работу на уроке; что показалось сложным; какие моменты вызывают трудности. Что понравилось, что не понравилось на уроке? | Ученики выставляют себе оценку за работу на уроке, указывают на сложности восприятия нового материала. |
| 3.2. Подведение итогов урока | |
| — Итак, при постановке цели урока мы использовали оборот «привести знания свойств элементарных функций в систему», ввести понятия тригонометрических функций, исследовать область определения и множество значений и привести эти знания в систему, сформировать приемы исследования данных свойств. — Достигнута ли поставленная нами цель или нет, зависит от того, построена ли система знаний. Как вы считаете? | — Да, действительно, мы привели знания в систему, потому что повторили и систематизировали знания о свойствах функций. — Мы ввели понятия тригонометрических свойств и исследовали область определения и множество значений. Привели и эти знания в систему. Доказательством является заполненная таблица. — На конкретных задачах сформировали приемы нахождения области определения и множества значений (метод оценки, через уравнение с параметром). И эти знания привели в систему, т.к. оформили приемы в виде таблицы. |
| 3.3. Планирование предстоящей учебной деятельности | |
| — На следующем уроке мы научимся исследовать область определения и множество значений функций, имеющих более сложное аналитическое задание. | Ученики записывают домашнее задание. |
▶▷▶ алгебра и начала анализа тригонометрические функции
▶▷▶ алгебра и начала анализа тригонометрические функции| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 26-11-2018 |
алгебра и начала анализа тригонометрические функции — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Алгебра и начала анализа — compendiumsu compendiumsu/mathematics/algebra10/15html Cached Он получается из графика функции у = cos x отражением относительно оси абсцисс и смещением на 1 единицу вверх вдоль оси ординат Алгебра и начала анализа, 10 класс, Задачник, Часть 2 nasholbiz … Экзамены по Алгебре Алгебра и начала анализа , 10 класс, Задачник, Часть 2, Профильный уровень, Мордкович АГ, 2007 Алгебра и начала анализа — shebaspbru shebaspbru/shkola/algebra-09-1987htm Cached А Колмогоров и др — 1987 г Алгебра и начала анализа Функции , производные и тд Скачать бесплатно и по прямой ссылке советский учебник в оригинале, с иллюстрациями Алгебра И Начала Анализа Тригонометрические Функции — Image Results More Алгебра И Начала Анализа Тригонометрические Функции images План-конспект урока по алгебре и началам анализа «Обратные multiurokru/files/plan-konspiekt-uroka-po Cached План-конспект урока Алгебра и начала анализа 11 класс Тема урока: « Обратные ГДЗ Алгебра и начала анализа 10-11 класс Алимов ША 1gdzwork/class-10/gdz-algebra-i-nachala-analiza-10-11-klass Cached Решебник Дидактические материалы по алгебре и началам анализа для 10 класса Решебник Физика 10 класс Решебник Алгебра и начала анализа 10-11 Колмогоров АН Алгебра и начала анализа 10 класс: поурочные планы по tatyanchenkowixsitecom/tatyanchenko/algebra-i-nachala В пособии представлены поурочные планы по курсу « Алгебра н начала анализа » (10 класс), составленные в соответствии с программой по математике Министерства образования РФ (по учебнику А Г Мордковича: Алгебра и начала Алгебра и начала анализа 10 класс Поурочные планы по tatyanchenkowixsitecom/tatyanchenko/algebra-i-nachala В пособии представлены поурочные планы по курсу » Алгебра и начала анализа » (10 класс), составленного в соответствии с программой по математике Министерства образования РФ (по учебнику ША Алимова для 10-11 классов) Алгебра и начала анализа, Задачи и решения, Башмаков МИ nasholcom Экзамены Алгебра и начала анализа , Задачи и решения, Башмаков М И , Беккер БМ, Гольховой ВМ, 2004 Презентация по алгебре для 10 класса «Обратные semenova-klassmoysu/load/uroki/algebra_i_nachala Cached Презентация по алгебре для 10 класса «Обратные тригонометрические функции » Скачать с Алгебра и начала анализа 10-11 класс Учебник Мордкович АГ proreshenoru/uchebniki/algebra/10klass/671-algebra-i Cached Учебник дает цельное и полное представление о школьном курсе алгебры и начал анализа , отвечает требованиям обязательного минимума содержания образования Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 29,200 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- то есть носила чисто Читать ещё Методика преподавания темы: « Тригонометрические функции » в курсе алгебры и начал анализа Выполнила: студентка V курса математического факультета Втюрина Юлия Владимировна В древности тригонометрия возникла в связи с потребностями астрономии
- 10 класс
- Раздел 2 Тригонометрические функции
10 класс (в двух частях) Читать ещё Все они решаются с помощью тригонометрических тождеств и свойств тригонометрических функций
курс математики за 10-11 класс Тригонометрические функции Читать ещё Информация структурирована в виде справочника
- 10 класс
- Задачник
- производные и тд Скачать бесплатно и по прямой ссылке советский учебник в оригинале
алгебра и начала анализа тригонометрические функции — Все результаты Алгебра и начала анализа (10-й класс) Профильный уровень открытыйурокрф/статьи/553726/ Алгебра и начала анализа (10-й класс) Профильный уровень Уроки- презентации по теме «Обратные тригонометрические функции » Мымрина Галина Тригонометрические функции числового аргумента Видеоурок Определения тригонометрических функций : синус, косинус, тангенс и котангенс Алгебра и начала анализа , 10 класс (в двух частях) Учебник для Тригонометрические функции углового аргумента и типовые Видеоурок: Тригонометрические функции углового аргумента и типовые задачи по предмету Алгебра и начала анализа , 10 класс (в двух частях) Тригонометрические функции углового аргумента Видеоурок Изучение тригонометрических функций углового аргумента Алгебра и начала анализа , 10 класс (в двух частях) Учебник для общеобразовательных Видео 10:35 №1 Тригонометрические функции числового аргумента Natalia Prishvitsyna-Merkureva YouTube — 22 июн 2014 г 3:48 Производные тригонометрических функций Начала анализа Учебное видео YouTube — 30 авг 2015 г 3:54 Периодичность тригонометрических функций Урок 4 Учебное видео YouTube — 29 авг 2015 г Все результаты §2 Тригонометрические функции угла и числового аргумента › › 10 класс › Раздел 2 Тригонометрические функции Тригонометрические функции , 10 класс, Алгебра и начала математического анализа Задания составлены профессиональными педагогами ЯКласс §5 Соотношения между тригонометрическими функциями одного › › 10 класс › Раздел 2 Тригонометрические функции Тригонометрические функции , 10 класс, Алгебра и начала математического анализа Задания составлены профессиональными педагогами ЯКласс Картинки по запросу алгебра и начала анализа тригонометрические функции «id»:»cx9hFF5rWyAWQM:»,»ml»:»600″:»bh»:90,»bw»:117,»oh»:716,»ou»:» «,»ow»:945,»pt»:»dist-tutorinfo/filephp/463/Risunki/Formuly_slozh»,»rh»:»dist-tutorinfo»,»rid»:»PyZvwY-nlGpKKM»,»rt»:0,»ru»:» \u003d463\u0026item\u003d4636″,»sc»:1,»st»:»Dist-TutorInfo»,»th»:90,»tu»:» \u003dtbn:ANd9GcRxtygY1eYMdis1q1rzueyIbLtS0qCvrHkD50ujvby-62LQx-w5SC7r5Zw»,»tw»:119 «id»:»yg0JG-35D3MgnM:»,»ml»:»600″:»bh»:90,»bw»:118,»oh»:600,»ou»:» «,»ow»:800,»pt»:»imagesmysharedru/4/204265/slide_1jpg»,»rh»:»mysharedru»,»rid»:»-Y_-O_Zs0HIgqM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»MySharedru»,»th»:90,»tu»:» \u003dtbn:ANd9GcRF_Gjg7rprC5mumXn496xL8ypvYQ_1-h-WUWuq0-TTx62Ltejon1kgzw»,»tw»:120 «id»:»VdIr8mO8Bt8aQM:»,»ml»:»600″:»bh»:90,»bw»:118,»oh»:480,»ou»:» «,»ow»:640,»pt»:»arhivurokovru/kopilka/uploads/user_file_562854fa7″,»rh»:»kopilkaurokovru»,»rid»:»7PFK-CpJ6xpmWM»,»rt»:0,»ru»:» «,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcShbhfAjWnE6eVxE6NJJ8XB1BLgVctkOYcSYMPDfzSqrv6-mVzCm0_MaA»,»tw»:120 «cb»:3,»cl»:3,»cr»:3,»id»:»5yNrdI5lowagNM:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:384,»ou»:» «,»ow»:282,»pt»:»fs00infourokru/images/doc/2/1654/hello_html_m317″,»rh»:»infourokru»,»rid»:»vRfxsroUW2Ws1M»,»rt»:0,»ru»:» \u003d3512″,»sc»:1,»st»:»Инфоурок»,»th»:97,»tu»:» \u003dtbn:ANd9GcR9mZrdUbsGlmFTC2JCZ1NFo1Hpdqu4YOmRfm5_dB2b1v89M8rZKLmlbmo»,»tw»:71 «id»:»TgqIe-azGZ44XM:»,»ml»:»600″:»bh»:90,»bw»:118,»oh»:480,»ou»:» «,»ow»:640,»pt»:»ds04infourokru/uploads/ex/0cec/000d7a6b-a26d2ffe»,»rh»:»infourokru»,»rid»:»hcsTMmE55ScT5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcQVzWEkZX6VR6f0ql_cAeKzbbTIFOFzXReY-DpYdykX-WwlDDGuLUKF5A»,»tw»:120 «cb»:9,»cl»:12,»cr»:12,»ct»:9,»id»:»caz41EeiIRHuyM:»,»ml»:»600″:»bh»:90,»bw»:47,»oh»:1397,»ou»:» «,»ow»:988,»pt»:»cyberleninkaru/viewer_images/14588428/f/1png»,»rh»:»cyberleninkaru»,»rid»:»DEQmz4i162VIWM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»КиберЛенинка»,»th»:99,»tu»:» \u003dtbn:ANd9GcTQ6jkZpW3rOvCBkkVvq6SuSiXLfy2tC3DGC4S4KHuD23GoACKWXI2-EA»,»tw»:70 Другие картинки по запросу «алгебра и начала анализа тригонометрические функции» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты АЛГЕБРА 10: Тригонометрические функции Вариант 1 Похожие АЛГЕБРА И НАЧАЛА АНАЛИЗА 10 /; Градусное и радианное измерение угловых величин Определение тригонометрических функций числового [PDF] Свойства тригонометрических функций — Средняя школа № 1 г «Свойства тригонометрических функций » и карточки для дифференцированной самостоятельной работы по этой Алгебра и начала анализа – 11 [DOC] Методика преподавания темы «Тригонометрические функции» в sovhoznoeedusiteru/DswMedia/trigonometricheskiefunkciidoc Предмет исследования — методика изучения тригонометрических функций в курсе алгебры и начала анализа в 10-11 классе Целью написания данной Пользуясь свойствами тригонометрических функций, Алгебра и Ответы на вопрос – Пользуясь свойствами тригонометрических функций , Алгебра и начала анализа 10 класс Колмогоров АН№100 – читайте на Контрольная работа по алгебре и началам анализа Тема Похожие Контрольная работа по алгебре и началам анализа Тема: Тригонометрические функции (учебник алгебры и начал анализа 10-11, авторов Формулы приведения — Тригонометрические функции — 1-е Формулы приведения — Тригонометрические функции — 1-е полугодие — Алгебра и начала анализа 10 класс Поурочные планы по учебнику Мордковича Повторение Тригонометрические функции и их свойства 10 класс 1 окт 2017 г — Урок повторения, с применением мультимедийной презентации Соответствует УМК Мордкович » Алгебра и начала анализа 10-11 Тест Тригонометрические функции — Математика — 10 класс 13 июл 2016 г — Предмет « Алгебра и начала анализа »10 классТема « Тригонометрические функции » ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ШКОЛЬНОМ 1 УДК 70 ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ШКОЛЬНОМ КУРСЕ АЛГЕБРЫ И НАЧАЛ АНАЛИЗА 0 Камаева СЦ Дагестанский Алгебра и начала анализа N 4 Тригонометрические выражения Тригонометрические функции О произведении Заглавие: Алгебра и начала анализа выражения Тригонометрические функции ; Год издания: 2003 Контрольная работа №1 по теме » Тригонометрические функции» в Контрольная работа №1 по теме » Тригонометрические функции » в 11 классе , алгебра и начала анализа — в разделе Карточки-задания, Свойства и графики тригонометрических функций Урок алгебры и 25 дек 2016 г — План-конспект урока по алгебре (10 класс) на тему: Свойства и графики тригонометрических функций Урок алгебры и начал анализа «Алгебра и начала анализа, 10 класс Графики тригонометрических wwwmysharedru/slide/204265/ Презентация на тему: » Алгебра и начала анализа , 10 класс Графики тригонометрических функций Воробьев Леонид Альбертович, гМинск» Презентация по алгебре и началам анализа «Обратные › Математика 4 февр 2017 г — Обратные тригонометрические функции y=arcsinx y=arccosx дисциплине » Алгебра и начала математического анализа » по теме Тригонометрические функции — Википедия Похожие Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли с центром в начале координат O \displaystyle O O в математическом анализе называется синус угла, радианная мера которого равна Тригонометрические функции | Математика | FANDOM powered by rumathwikiacom/wiki/Тригонометрические_функции Похожие Тригонометрические фу́нкции — математические функции от угла Они безусловно важны при изучении геометрии, а также при исследовании План занятий Дисциплинарного цикла по теме «Тригонометрия wwwstep-into-the-futureru/node/332 Построение углов по заданным значениям тригонометрических функций ( синуса, косинуса, Вейц БЕ, Демидов ИГ Алгебра и начала анализа Презентация для урока алгебры и начала анализа по теме 22 окт 2015 г — Презентация для урока алгебры и начала анализа по теме «Четность, нечетность, периодичность тригонометрических функций » (11 [DOC] федеральное государственное бюджетное образовательное Рабочая программа по дисциплине « Алгебра и начала анализа » разработана на основе Тригонометрические функции числового аргумента §14 Алгебра и начала анализа 10 класс (поурочные планы) 1-е › 5 — 9 классы › Алгебра Алгебра и начала анализа 10 класс (поурочные планы) 1-е полугодие Глава 2 Тригонометрические функции Уроки 27-28 Контрольная работа по Алгебра и начала анализа — Викиверситет Похожие 22 янв 2018 г — 4 Функции 41 Степенная функция ; 42 Показательная функция ; 43 Логарифмическая функция ; 44 Тригонометрические , обратные Методика преподавания темы «Тригонометрические функции» в 8 авг 2007 г — Общие вопросы изучения тригонометрических функций в школе Методика преподавания темы в курсе алгебры и начал анализа Урок 17 Тригонометрические функции и их графики Контроль school-collectioneduru/catalog/rubr/164c80ce-6e8a-48ff-8b3d/112910/ Поурочное планирование к учебнику « Алгебра и начала анализа », 10 класс, Колмогоров АН и др, издательство «Просвещение», 2002 год [PDF] Untitled — МВД России сложения Тригонометрические функции двойного и тройного угла Математика: алгебра и начала математического анализа , геометрии Алгебра и Подготовка к контрольной работе «Тригонометрические функции › › Алгебра › 11 класс 4 мая 2013 г — Предмет, класс Алгебра и начала анализа , 11 класс Авторы учебника Алимов ША, Колягин ЮМ, Сидоров ЮВ, Федорова НЕ, тригонометрические функции irbisbigpibiyskru//cgiirbis_64exe?тригонометрические%20функции Тригонометрические функции [Текст] : пособие для учителей / С В Алгебра и начала анализа [Текст] : 9 — 10 классы : пробный учебник / Н Я Алгебра и начала анализа Функции и их свойства — Варсон wwwvarsonru/analys_funkziihtml Полный комплект цветных таблиц по алгебре и началам анализа Весь курс Алгебра и начала анализа Обратные тригонометрические функции (1) [DOC] алгебра и начала анализа school4kotucozru/docs1/11_klassdocx Данная рабочая программа курса по алгебре и началам анализа разработана Четность, нечетность, периодичность тригонометрических функций [DOC] Пояснительная записка kr-school2edumskoru/uploads/3000/2874/section/197196//Algebra-gumdocx Одной из главных тем в курсе алгебры и начал анализа является тема Сформировать представления понятия тригонометрической функции [DOC] Материалы в помощь учителю для составления рабочей « Алгебра и начала анализа », 10-11 класс, М «Мнемозина», ИМСмирновой Тригонометрические функции углового аргумента, радианная мера угла Шкиль НИ, Слепкань ЗИ, Дубинчук ЕС Алгебра и начала › › Математика › Алгебра 25 мар 2018 г — Тригонометрические функции числового аргумента Шкиль НИ, Слепкань ЗИ, Дубинчук ЕС Алгебра и начала анализа 10-11 « ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Y = SIN X, Y = COS X, ИХ wwwopenclassru/node/49529 Похожие 2 июл 2009 г — Тема » Тригонометрические функции y=sin x и y=cos x и их графики Преобразование графиков» Учебник « Алгебра и начала анализа Предисловие, Алгебра и начала анализа, Тригонометрические Алгебра и начала анализа Тригонометрические функции Проверочный тест 1 Найдите: а) область определения функций, б) множество значений Построение графиков обратных тригонометрических функций в автор: СЦ Камаева — 2012 — Похожие статьи Построение графиков обратных тригонометрических функций в курсе алгебры и начал анализа в общеобразовательной школе Текст научной статьи Тригонометрические функции – наглядное пособие – Дрофа › Алгебра › Наглядные и раздаточные материалы Математика: алгебра и начала математического анализа , геометрия Алгебра и начала математического анализа Углубленный уровень 10 класс тригонометрические функции — БГПУ wwwbgpuru//cgiirbis_64exe?тригонометрические%20функции Алгебра и начала анализа : учебник для 10 -11 кл общеобразоват Математика (геометрия и тригонометрические функции ) : учеб пособие для Тригонометрия: синус, косинус, тангенс, котангенс, свойства fizmatby/math/trigonometry Похожие Математический анализ ; Пределы Закрыть Меню Логин Пароль Математика Математика ->Тригонометрия-> Тригонометрические преобразования, уравнения (часть А) Графики тригонометрических функций Косинусоида [PDF] удк 372851 обратные тригонометрические функции в школьном Ключевые слова: обратные тригонометрические функции , числовая раздел алгебры и начала анализа , посвященный тригонометрическим функциям Алгебра 10 кл (17 таблиц) Тригонометрические функции td-schoolru › › Печатные пособия › Таблицы демонстрационные Похожие Описание Учебный комплект таблиц состоит из 17 таблиц: Тригонометрические функции Синус, косинус, тангенс и котангенс Свойства синуса Теория тригонометрических функций — Реферат , страница 1 Анализ изложения темы « Тригонометрические функции » в различных Учебник Колмогорова « Алгебра и начала анализа » имеет прикладную Построение графиков тригонометрических функций semenova-klassmoysu/load/uroki/algebra_ialgebre/11-1-0-128 Похожие 1 окт 2014 г — Презентация по алгебре для 10 класса «Построение графиков Категория: Алгебра и начала анализа 10-11 классы | Добавил: ELENA [PDF] Федеральное агентство по образованию — Волгоградский wwwvolsuru/Abitur/progexam/data/math_fizpdf АРИФМЕТИКА, АЛГЕБРА И НАЧАЛА АНАЛИЗА (n ∈ N), y = k/x, показательной y = ax (a > 0), логарифмической, тригонометрических функций (y = sin Вместе с алгебра и начала анализа тригонометрические функции часто ищут тригонометрические функции числового аргумента примеры тригонометрические функции числового аргумента 10 класс тригонометрические функции числового аргумента формулы тригонометрические функции углового аргумента тригонометрические функции числового аргумента задачи тригонометрические функции числового аргумента вариант 1 тригонометрические функции числового аргумента знаки их значений тригонометрические функции числового аргумента 10 класс мордкович Навигация по страницам 1 2 3 4 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 » Тригонометрические функции » в курсе алгебры znakka4estvaru › …pedagogika…funkcii…v…i…analiza/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Методика преподавания темы: « Тригонометрические функции » в курсе алгебры и начал анализа В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто Читать ещё Методика преподавания темы: « Тригонометрические функции » в курсе алгебры и начал анализа Выполнила: студентка V курса математического факультета Втюрина Юлия Владимировна В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд» Со временем в нее начали вкрапляться некоторые аналитические моменты В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа Именно в это время тригонометрические зависимости стали рассматриваться как функции Скрыть 2 Предисловие, Алгебра и начала анализа studbooksnet › 2301469/matematika_himiya_fizika… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра и начала анализа Тригонометрические функции Проверочный тест 1 Найдите 2 Функция f(x) называется периодической с периодом Т (Т?0) , если для любого х из области определения функции х ± Т тоже принадлежит области определения функции , и f(х ± Т) = f(x) Свойства: 1 Если Т — период Читать ещё Алгебра и начала анализа Тригонометрические функции Проверочный тест 1 Найдите 2 Функция f(x) называется периодической с периодом Т (Т?0) , если для любого х из области определения функции х ± Т тоже принадлежит области определения функции , и f(х ± Т) = f(x) Свойства: 1 Если Т — период функции f(x), то kT — тоже период f(x), где k — произвольное целое число 2 Если Т — период функции f(x), то период функции f(mx) (m — некоторое действительное число, не равное нулю) равен Т/m Период функций sinx и cosx равен 2р, период функции tgx равен р Примеры Определите период функции : 1 sin2x; 2 tg7x Скрыть 3 Тригонометрические функции числового аргумента interneturokru › …10…trigonometricheskie-funkcii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Все они решаются с помощью тригонометрических тождеств и свойств тригонометрических функций , которые будут использоваться для решения задач и в дальнейшем 1 Алгебра и начала анализа , 10 класс (в двух частях) Читать ещё Все они решаются с помощью тригонометрических тождеств и свойств тригонометрических функций , которые будут использоваться для решения задач и в дальнейшем Список литературы 1 Алгебра и начала анализа , 10 класс (в двух частях) Учебник для общеобразовательных учреждений (профильный уровень) под ред А Г Мордковича –М: Мнемозина, 2009 2 Алгебра и начала анализа , 10 класс (в двух частях) Задачник для общеобразовательных учреждений (профильный уровень) под ред А Г Мордковича –М: Мнемозина, 2007 Скрыть 4 Методика преподавания темы Тригонометрические MirZnaniicom › a…temy-trigonometricheskie…i…analiza Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Методика преподавания темы: « Тригонометрические функции » в курсе алгебры и начал анализа В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто Читать ещё Методика преподавания темы: « Тригонометрические функции » в курсе алгебры и начал анализа Выполнила: студентка V курса математического факультета Втюрина Юлия Владимировна В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд» Со временем в нее начали вкрапляться некоторые аналитические моменты В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа Именно в это время тригонометрические зависимости стали рассматриваться как функции Скрыть 5 §3 Свойства тригонометрических функций Алгебра yaklassru › p/lanit-algebra/10…trigonometricheskie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Теоретические уроки, тесты и задания по предмету §3 Свойства тригонометрических функций , Раздел 2 Тригонометрические функции , 10 класс, Алгебра и начала математического анализа Читать ещё Теоретические уроки, тесты и задания по предмету §3 Свойства тригонометрических функций , Раздел 2 Тригонометрические функции , 10 класс, Алгебра и начала математического анализа Задания составлены профессиональными педагогами ЯКласс — онлайн-школа нового поколения Скрыть 6 школьный курс алгебры , тригонометрия , начала terverru › maththeoryAlgebraphp Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Информация структурирована в виде справочника, разбитого на разделы, соответствующие школьному курсу алгебры и геометрии Алгебра и начала анализа , курс математики за 10-11 класс Тригонометрические функции Читать ещё Информация структурирована в виде справочника, разбитого на разделы, соответствующие школьному курсу алгебры и геометрии Раздел напоминает электронный школьный учебник с ссылками на решенные задачи из пройденной темы в разделах Математика — задачи по Алгебре и Математика — задачи по Геометрии Алгебра и начала анализа , курс математики за 10-11 класс Тригонометрические функции Тригонометрические функции числового аргумента Радианная мера угла Тригонометрические функции различных углов Основные формулы тригонометрии и их свойства Функции синус и косинус Графики функций синус и косинус С Скрыть 7 План-конспект урока по алгебре (10 класс) на тему nsportalru › Школа › Алгебра › …-funktsiy-urok-algebry-i Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Урок алгебры и начал анализа 10 класс Учебное занятие работает на тему: подготовка к итоговой аттестации, обратные тригонометрические функции , тригонометрические уравнения и неравенства Читать ещё Урок алгебры и начал анализа 10 класс Опубликовано 25122016 — 19:20 — Велиханова Марина Александровна Разработка содержит конспект урока, опорный конспект, тест, технологическую карту урока Учебное занятие работает на тему: подготовка к итоговой аттестации, обратные тригонометрические функции , тригонометрические уравнения и неравенства Ресурсы учебного занятия: ИКТ – программа для создания интерактивных графиков функций (Живая геометрия), презентация Скрыть 8 Алгебра и Начала анализа Тригонометрические функции — смотрите картинки ЯндексКартинки › алгебра и начала анализа тригонометрические Пожаловаться Информация о сайте Ещё картинки 9 Алгебра и начала анализа — Викиверситет ruwikiversityorg › wiki/Алгебра_и_начала_анализа Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра и начала анализа Материал из Викиверситета Перейти к навигации Перейти к поиску 43 Логарифмическая функция 44 Тригонометрические , обратные тригонометрические функции Читать ещё Алгебра и начала анализа Материал из Викиверситета Перейти к навигации Перейти к поиску Основная статья: Факультет математики Планируемые курсы: Исследование функций с помощью производной Содержание 1 Действительные (вещественные) числа 11 Целые и рациональные числа 12 Действительные числа 13 Прогрессия 43 Логарифмическая функция 44 Тригонометрические , обратные тригонометрические функции 5 Тригонометрические формулы Действительные (вещественные) числа Целые и рациональные числа целые числа:0, ±1, ±2, ±3 рациональные числа те числа вида m/n Скрыть 10 Реферат по алгебре и началам анализа pandiaru › text/78/294/27018php Показать ещё с сайта Пожаловаться Информация о сайте Тригонометрия изучает важный класс функций – так называемых тригонометрических В курсе алгебры и начала анализа в 10 классе начинается изучение темы «Решение тригонометрических уравнений и неравенств» Читать ещё Тригонометрия изучает важный класс функций – так называемых тригонометрических , а также их применение в геометрии Само название » тригонометрия » греческого происхождения, обозначающие «измерение треугольника»: τρіγωνоν (тригонон) – треугольник, μετρειω (метрейн) – измерение, показывает что этот раздел математики связан с задачами решения треугольников, т е с задачами нахождения одних элементов треугольника по другим его известным элементам В курсе алгебры и начала анализа в 10 классе начинается изучение темы «Решение тригонометрических уравнений и неравенств» Скрыть Дипломная работа: Методика преподавания темы bestreferatru › referat-275981html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Название: Методика преподавания темы Тригонометрические функции в курсе алгебры и начал анализа Раздел: Рефераты по педагогике Тип: дипломная работа Добавлен 18:00:57 11 апреля 2010 Похожие работы Просмотров: 418 Комментариев: 9 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать Читать ещё Название: Методика преподавания темы Тригонометрические функции в курсе алгебры и начал анализа Раздел: Рефераты по педагогике Тип: дипломная работа Добавлен 18:00:57 11 апреля 2010 Похожие работы Просмотров: 418 Комментариев: 9 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Вятский государственный гуманитарный университет Математический факультет Кафедра математического анализа и методики преподавания математики Выпускная квалификационная работа Методика п Скрыть Вместе с « алгебра и начала анализа тригонометрические функции » ищут: алгебра и начала математического анализа алгебра и начала математического анализа 10-11 класс алгебра и начало анализа геометрия алгебра и начала математического анализа 10 класс колягин учебник алгебра и начала математического анализа 10 класс колягин учебник гдз алгебра и начало анализа алимов 10-11 класс учебник арифметика алгебра и начала анализа математический анализ тригонометрия 1 2 3 4 5 дальше Bing Google Mailru Нашлось 93 млн результатов Дать объявление Регистрация Войти 0+ ЯндексБраузер с Алисой, которая готова поболтать Установить Закрыть Попробовать еще раз Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Алиса в ЯндексБраузере Помогает искать в интернете и поддерживает беседы 0+ Скачать
ГДЗ Алгебра 11 класс Никольский, Потапов, Решетникова
Алгебра 11 класс
Учебник
Никольский, Потапов, Решетникова
Просвещение
Тригонометрия, логарифмы, интегралы, комбинаторика, теория вероятности и многое другое — все это предстоит изучить школьникам в последний год своего пребывания в школе. Интенсивная и насыщенная программа порой совершенно не хочет укладываться в голове, но учащимся во что бы то ни стало необходимо овладеть этими знаниями. Поэтому плотная работа с использованием решебника к учебнику «Алгебра и начала математического анализа 11 класс» Никольский, Потапов, Решетникова
Интенсивная и насыщенная программа порой совершенно не хочет укладываться в голове, но учащимся во что бы то ни стало необходимо овладеть этими знаниями. Поэтому плотная работа с использованием решебника к учебнику «Алгебра и начала математического анализа 11 класс» Никольский, Потапов, Решетникова
Параметры данного сборника
Пособие поделено на восемнадцать параграфов и задачи для повторения ранее пройденного материала. Каждый номер в отдельности тщательно разобран авторами и к ним приведены основательные решения, что значительно облегчит учебный процесс. Научившись правильно и периодически работать с ГДЗ по алгебре 11 класс Никольский учащиеся смогут дополнить свои знания и с успехом справляться со всеми заданиями.
Важен ли решебник в учебе
Вот и подходит к концу обучении в школе. Но сначала школьникам необходимо сделать последний рывок, который поможет им получить хороший аттестат. Кроме того, сумев овладеть необходимыми познаниями, ребята могут более спокойно относиться к предстоящим ЕГЭ, ведь появится большая доля вероятности их успешного прохождения. Материал этого года затрагивает разделы, которые раньше изучались только в институте, поэтому ослаблять внимание категорически запрещено. Справляться же с текущим материалом подросткам поможет решебник к учебнику
Но сначала школьникам необходимо сделать последний рывок, который поможет им получить хороший аттестат. Кроме того, сумев овладеть необходимыми познаниями, ребята могут более спокойно относиться к предстоящим ЕГЭ, ведь появится большая доля вероятности их успешного прохождения. Материал этого года затрагивает разделы, которые раньше изучались только в институте, поэтому ослаблять внимание категорически запрещено. Справляться же с текущим материалом подросткам поможет решебник к учебнику
Название
Условие
Решение
Тригонометрические функции (11 класс) — презентация онлайн
МОУ Матвеево – Курганская СОШ №1Школьная информационная служба
Алгебра и начала анализа
в 11 классе.
«Тригонометрический
функции»
Авторы учебника: Ш.А. Алимов, Ю.М.Колягин и
др.
Работу подготовила
методист по информационным
технологиям Зинченко Е.
 В.
В.3. Ход урока:
1. Фронтальный опрос.2. Область определения и множество
значений тригонометрических функций.
3. Чётность и нечётность
тригонометрических функций.
4. Свойства функций y= cos x, y= sin x и
y = tg x.
5. Итог урока.
6. Домашнее задание.
1
4
2
5
3
6
Как можно
получить график
функции у = cos x,
имея график
функции у = sin x?
Какое наибольшее и
наименьшее
значение может
принимать
функция у = cos x?
Каков наименьший
положительный
период функций
y = ctg x и у = tg x?
Как называется
линия, служащая
графиком функции
у = sin x?
Может ли функция
у = tg x принимать
наибольшее
значение?
Каков наименьший
положительный
период функций
y = cos x и
у = sin x?
11. Область определения и множество значений тригонометрических функций.
Найдите область определениякаждой из функций:
1.
 y = 4sin 7x
y = 4sin 7x2. у = 2,5 — cos
5
3. у 9 cos
4x
8
4. y sin
x
х
Найдите множество значений каждой из
функций :
2. y = cos x — 5
1. y = 2sin x
3. y = 2cosx + 3
5. y = 3,5 – 1/2sin x
4. y = sin2 x+ 2
[-6;-4] [-2;2]
й
э
[3;4]
[1;5]
[2;3]
р
л
е
Леонард ЭЙЛЕР
(1707-1783)
Сколько целых значений
имеет функция?
y 1,7 16(cos x sin x) 20
2
2
7
Чётность и
нечётность
тригонометрических
функций.
Выяснить, является ли данная функция
чётной или нечётной:
1) y 2 x sin x
2
x sin x
2) y
2 cos x
4
2
3) y x 5 sin x cos x
2
Свойства функций
y = cos x, y = sin x и
y = tg x.
Сравнить значения выражения, используя
графики тригонометрических функций:
>
а) sin
sin
o
o
б) cos 114
cos 275
в) sin 1 > sin 4
г) sin 6
sin 5
o
o
д) cos 180 cos 194
>
o
74
o
23
Укажите график функции, заданной формулой
A
Б
В
Г
у = 2 cos x
Укажите график функции, заданной формулой
А
Б
В
Г
у = 0,5sin x
Укажите график функции, заданной формулой у = cos 0,5x
A
Б
В
Г
График какой из перечисленных функций
изображён на рисунке?
1) y = 2sin x
2) y = 0,5sin 2x
3) y = -2sin 2x
4) y = -0,5sin 2x
График какой из перечисленных функций
изображён на рисунке?
1) y = 2cos x
2) y = cos 2x
3) y = — cos x
4) y = — sin x
Найдите ошибки в следующих рассуждениях и
исправьте их.

Почему неверно, что:
1.Функция y = x sin2 x – чётная.
2.Множество значений функции y = sin x –
множество всех действительных чисел.
3. Sin 5 не существует.
4.Функция y = cos x – периодическая функция с
наименьшим положительным периодом /2 .
5. у = tg x – убывающая функция для всех х ≠ n,
n Z.
I вариант
№ 7640 (2)
№ 764 (1)
II вариант
Алгебра и тригонометрия
-
Тематический каталог
-
Гуманитарные и социальные науки
- Антропология
- Искусство
-
Каталог связи, кино и театра
- Массовая коммуникация / Связи с общественностью / Кино
- Речевое общение
- Театр
-
английский
- Сочинение
- Развивающий английский
- Литература и творческое письмо
- Техническая связь
- История
-
Междисциплинарные исследования
- Семейные исследования и развитие человека
- Гуманитарные науки
- Расовые и этнические исследования
- Социальная наука
- Женские и гендерные исследования
- Музыка
- Философия
- Политическая наука
- Психология
- Религия
- Социальная работа / семейная терапия / социальные услуги
- Социология
-
Языки мира
- китайский язык
- Французский
- Немецкий
- итальянский
- японский язык
- Языковые методы
- латинский
- португальский
- русский
- испанский язык
-
Математика и наука
- Анатомия и физиология
-
Биология и микробиология
- Специализированная биология / Биология высшего уровня
- микробиология
- Неспециализированная биология
- Химия
- Наука об окружающей среде
- География и атмосферные науки
- Геология и океанография
- Здоровье и кинезиология
-
Математика
- Продвинутая математика
- Исчисление
- Развивающая математика
- Конечная математика и прикладное исчисление
- Гуманитарная математика / Математика для учителей
- Математика для карьеры
- Математика
- Предварительная математика
- Техническая математика
- Питание
- Физика и астрономия
-
Статистика
- Вводная статистика
- Статистика верхнего уровня
-
Профессиональная карьера
-
Бизнес
- Бухгалтерский учет и налогообложение
- Деловые коммуникации
- Предпринимательское право
- Бизнес-математика
- Деловые навыки
- Наука принятия решений
- Финансы
- Страхование
- Введение в бизнес
- МИС
- Управление
- Маркетинг
- Офисные технологии
- Бизнес-статистика
- Коммуникативные науки и расстройства
- Информатика
- Консультирование
- уголовное правосудие
-
Кулинария, Гостиничный бизнес, Путешествия и туризм
- Кулинарное искусство
- Наука о еде
- гостеприимство
- Путешествия и туризм
- Глухие исследования и глухое образование
- экономика
-
Образование
- Учебный план и инструкция
- ЭЛЬ
- Дошкольное образование
- Эд Псих / Тесты и измерения
- Управление образованием и руководство
- Образовательные исследования
- Основы / Введение в преподавание
- Учебная технология
- Подготовка к лицензированию
- Чтение и грамотность
- Специальное образование
-
Скорая помощь и пожарная безопасность (БРЭЙДИ)
- Служба неотложной медицинской помощи (БРЭЙДИ)
- Наука об огне (БРЭДИ)
-
Инжиниринг
- Биоинженерия
- Химическая инженерия
- Гражданская и экологическая инженерия
- Электротехника и вычислительная техника
- Общее машиностроение
- Промышленная инженерия
- Машиностроение и аэрокосмическая техника
- Техническая математика / Техническая физика
-
Мода и дизайн интерьера
- Наука о потреблении
- Мода
- Дизайн интерьера
-
Медицинские профессии
- Базовые курсы здоровья
- Клиническая лаборатория науки
- Стоматологическая помощь
- Гигиена полости рта
- Управление медицинской информацией
- Массажная терапия
- Медицинская помощь
- Кодирование медицинского страхования
- Медицинская терминология
- Медицинская транскрипция
- Помошник медсестры
- Трудотерапия
- Аптечный служащий
- флеботомия
- Физиотерапия
- Хирургическая технология
- Респираторная терапия
-
Информационные технологии
- СНГ: вычислительные концепции
- СНГ: офисные приложения
- Компьютерная графика / Искусство
- Разработка игр
- Безопасность
- Обучение и сертификация
- Юридические исследования и помощник юриста
-
Уход
- ЛПН/ЛВН
- РН
- Успех студентов и развитие карьеры
-
Торговля и технологии
- сельское хозяйство
- Автомобильные технологии
- Строительные и технические профессии
- САПР / Инженерная графика / Чертеж
- Управление строительством и гражданские технологии
- Электроника и электрические технологии
- Инженерные технологии и промышленный менеджмент
- Экологические технологии
- Технические профессии: NCCER / Contren
-
Бизнес
- Изучающие английский язык
-
Войдите, чтобы загрузить ресурсы для преподавателей
- Загрузка и использование ресурсов для преподавателей
-
Гуманитарные и социальные науки
-
Продукты и услуги для обучения
-
Цифровая среда обучения
- Ревель
- Моя лаборатория
- Мастеринг
-
Учебная программа по сестринскому делу
- Преимущества
- Начать
- Отзывы
- Обучение и поддержка
- Редакторы и участники
-
Соседство 3.
 0
0
-
Содержание курса
-
Электронные тексты и Pearson+
-
Pearson eText под руководством инструктора
- Системные Требования
- Доступность
- Мобильное приложение Pearson eText
- Пирсон+
-
Pearson eText под руководством инструктора
- Коллекции Пирсон
-
Электронные тексты и Pearson+
-
Инструменты обучения и взаимодействия
- Репетиторское приложение Aida по исчислению
-
Катализаторы обучения
- Функции
-
Истории пользователей
- Развитие навыков критического мышления
- Вовлечение учащихся в активное обучение
- Использование командного подхода к обучению
- Использование методов взаимного обучения
- Корректировка обучения в режиме реального времени
- Просмотреть все истории
-
Обучение и поддержка
-
Для преподавателей
- Подготовьте своих учеников к работе
- Как я? Видео
-
Для студентов
- Начать
- Купить доступ
- Системные Требования
-
Для преподавателей
- Цены
- Начать
- Официальное уведомление
- Живой ответ
- Медиашаре
- Приложение вне страницы
- Пирсон Преп
-
StatCrunch
- Функции
- Что нового
- Сообщество
- Отзывы пользователей
- Обучение и поддержка
- Запросить дополнительную информацию
- MyDietAnalysis
- MyDietAnalysis2
- Интерактивные лаборатории Пирсон
-
Решения для подготовки к тестированию и тестирования
- Платиновая образовательная группа
- Подготовка к творческому тесту Limmer
- Подготовка к экзамену на получение лицензии учителя
- ТестГен
-
Преподавание английского языка
- Каталог преподавания английского языка
-
Ресурсы по дисциплинам
- Бизнес и экономика
- Инженерия, информатика и программирование
- английский
- Гуманитарные и социальные науки
- Информационные технологии и ИСУ
- Математика и статистика
-
наук
- Биология
- Анатомия и физиология
- Химия
- Физика
- Языки мира
- Профессиональная карьера
- Педагогическое образование и помогающие профессии
- Сестринское дело и здоровье
- Психология
-
Ускорение, редизайн и готовность
-
Ресурсы для начала работы
- Выбор правильных решений для вашего редизайна
-
Решения для математики
- Модульная модель
- Сжатая модель
- Сопутствующая модель
- Модель путей
- Модель исправления, не связанная с курсом
-
Решения для английского языка
- Модульная/лабораторная модель
- Сжатая модель
- Сопутствующая/ускоренная модель обучения
- Интегрированная модель чтения и письма
- Контекстуальная модель обучения
- Модель исправления, не связанная с курсом
- Результаты редизайна
- События и вебинары
- Запросить дополнительную информацию
- Контрольный список готовности к редизайну
-
Ресурсы для начала работы
-
Подготовка к колледжу и профессиональное образование
-
Переход в колледж (K – 12)
-
Решения для математики
- Иллинойс Решения для математики
- Математика Северной Каролины 4
- Решения для чтения и письма
-
Решения для математики
- Программы двойной регистрации
- Результаты и истории успеха
-
Переход в колледж (K – 12)
-
Цифровая среда обучения
-
Продукты и услуги для учреждений
- Аналитические услуги
-
Учебные услуги
- Дизайн учебного плана
- Разработка курса
- Внедрение и управление операциями
- Запросить дополнительную информацию
- Инклюзивный доступ
- Услуги онлайн-обучения Pearson
- Умное мышление онлайн-репетиторство
-
Клиенты
-
Педагоги
- Предварительный просмотр заголовка
-
Институциональные лидеры
- Цифровой ученик
- Удержание и вовлечение
- Ускорение и продвижение
- Справедливость и доступность
- Истории успеха
- Ресурсы
- Запросить дополнительную информацию
-
Ученики
-
Втягиваться
- Как стать блогером
-
Втягиваться
-
Общественные колледжи
- Ресурсы и поддержка
- Образование в частном секторе
- Директора по персоналу
-
Реселлеры колледжей
- Информация для заказа
- Распечатать программу аренды
- Политика возврата
- Обзор и настольные копии
- Увеличение продаж
- Распространение цифровых материалов курса
-
Педагоги
- События
-
Почему выбирают Пирсон?
-
Видеотека: авторы и инновации
- Видеотека по темам
- Видеотека по дисциплинам
- Биографии автора
- О привлечении студентов
- Активное обучение в классе
- Воздействие активного обучения
- Revel Psychology — 1-е издание
- Привлечение учащихся с помощью интерактивных фигур
- Ревельские авторы
- Авторы Ревеля — психология
- Авторы Пирсона — политология
- Авторы Пирсона — программирование
- О цифровых интерактивах
- Цифровые продукты меняют классную комнату
- Привлечение учащихся к цифровым
- Достучаться до сегодняшних студентов
- Обучение на протяжении всей жизни
- Учить учащихся задавать вопросы
- Вдохновляющие студенты
- MyLab IT: подготовка студентов к сертификации
- Написание для цифровой платформы
- Круглый стол авторов Пирсона по цифровому обучению
-
Готовность к карьере и навыки трудоустройства
- Истории трудоустройства
- Решения и партнерство
- Библиотека ресурсов
- Цифровое обучение
-
Стратегии онлайн-обучения и поддержка
- Стратегии онлайн-обучения
- Платформы онлайн-обучения
- Обучение и поддержка платформы
- Связаться с нами
-
Видеотека: авторы и инновации
- Высшее образование >
- Математика и наука >
- Математика >
- Предварительная математика >
- Предварительная математика >
-
Алгебра и тригонометрия
.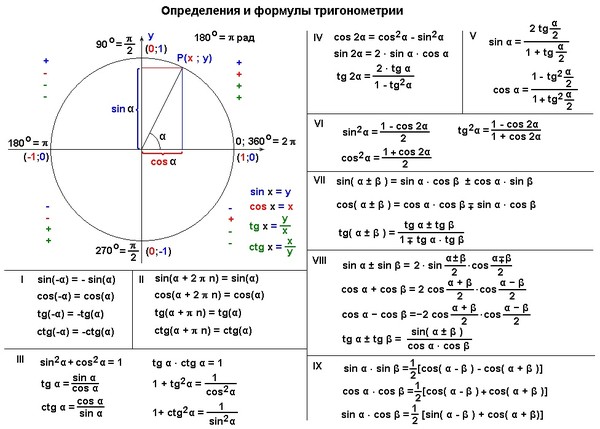
Получите необходимые электронные тексты по цене от 9,99 долл. США в месяц с Pearson+
- PreK–12 Образование
- Высшее образование
- Промышленность и профессиональная деятельность
- Блоги
- О нас
- США
- США
- Соединенное Королевство
- Глобальный
- Войти
- Свяжитесь с нами
- Сумка для книг
Все офисы PearsonСоединенные ШтатыВеликобританияКанадаНидерландыБельгия
Книга NCERT Класс 11 Математика Глава 3 Тригонометрические функции
Книга NCERT для 11 класса по математике Глава 3 Тригонометрические функции доступна для чтения или загрузки на этой странице.Учащиеся 11-го класса или готовящиеся к любому экзамену, основанному на математике 11-го класса, могут обратиться к Книге NCERT для своей подготовки.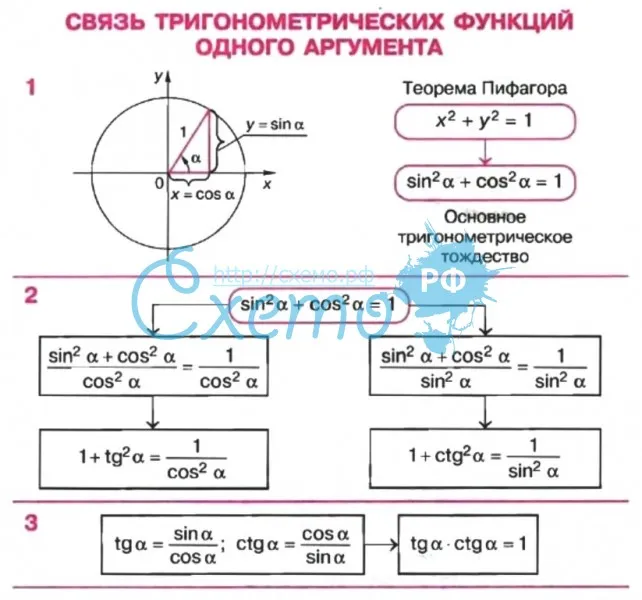 Цифровые книги NCERT Books Class 11 Maths pdf всегда удобны, когда у вас нет доступа к физической копии.
Цифровые книги NCERT Books Class 11 Maths pdf всегда удобны, когда у вас нет доступа к физической копии.
Здесь вы можете прочитать главу 3 книги NCERT по математике для 11 класса. Также после главы вы можете получить ссылки на заметки по математике для класса 11, решения NCERT, важный вопрос, практические документы и т. д. Прокрутите вниз, чтобы найти тригонометрические функции из книги NCERT Book, книга по математике для класса 11 и важные учебные материалы.
Книга NCERT, класс 11, математика, глава 3, тригонометрические функции
Подписаться на последние обновления
Здесь вы можете получить книгу NCERT, класс 11, математика, глава 3, тригонометрические функции
Книга NCERT, класс 11, математика, глава 3, тригонометрические функции СкачатьСкачать книгу NCERT для 11 класса по математике PDF
Книги NCERT Class 11 скачать легко. Просто нажмите на ссылку, откроется новое окно, содержащее все PDF-файлы NCERT Book Class 11 Maths по главам. Выберите главу, которую вы хотите загрузить, и все готово. У вас будет PDF-файл на вашем устройстве для изучения в автономном режиме.
Выберите главу, которую вы хотите загрузить, и все готово. У вас будет PDF-файл на вашем устройстве для изучения в автономном режиме.
- Нажмите здесь, чтобы перейти на страницу, где вы можете скачать книгу NCERT Maths Book Class 11 в формате PDF.
Купить книгу NCERT по математике для 11 класса онлайн
Вы можете купить книгу NCERT по математике для 11 класса на различных онлайн-платформах и получить доставку на дом в кратчайшие сроки. Для вашего удобства мы курировали прямую ссылку на книгу NCERT Book Class 11 Maths, чтобы вам не нужно было искать ее.Вы можете просто перейти по ссылке, чтобы перейти на сайт Amazon и заказать онлайн.
- Щелкните здесь, чтобы перейти на веб-сайт Amazon и купить книгу NCERT для 11-го класса по математике онлайн.
Решения NCERT для математики 11 класса
После прочтения главы вы можете обратиться к нашим решениям NCERT класса 11. Пошаговые ответы на все вопросы упражнений предоставляются экспертами, чтобы помочь вам лучше подготовиться к экзамену.
Учебный материал для класса 11 – примечания, важные вопросы, практические тесты
Для дальнейшей подготовки к предмету «Математика» в 11 классе вы можете получить «Ревизорские заметки, важные вопросы» на сайте aglasem.ком бесплатно. Также вы можете пройти онлайн-тест и проанализировать уровень своей подготовки.
Здесь учащиеся могут получить заметки NCERT по классу и главе 11 класса, которые очень помогают хорошо понять предмет и его главу. С помощью приведенной ниже ссылки. Вы можете получить примечания NCERT класса 11.
Весь учебный материал был подготовлен, чтобы помочь вам понять тему легче и лучше. Если вам нравятся наши ресурсы, поделитесь публикацией!
Книга NCERT по математике для класса 11 Решения NCERT
Книги NCERT для 11 класса по математике Глава 3 Тригонометрические функции PDF Скачать
Тригонометрические функции Класс 11 Книга NCERT: Если вы ищете лучшие книги по математике для 11 класса, то книги NCERT могут стать отличным выбором для начала вашей подготовки. Книги NCERT для 11-го класса по математике Глава 3 Тригонометрические функции могут быть чрезвычайно полезны для учащихся, чтобы понять концепции простым способом. Книги NCERT по математике для 11-го класса в формате PDF помогут вам во время подготовки как к школьным экзаменам, так и к конкурсным экзаменам.
Книги NCERT для 11-го класса по математике Глава 3 Тригонометрические функции могут быть чрезвычайно полезны для учащихся, чтобы понять концепции простым способом. Книги NCERT по математике для 11-го класса в формате PDF помогут вам во время подготовки как к школьным экзаменам, так и к конкурсным экзаменам.
NCERT Class 11th Maths Chapter 3 Books предоставят вам достоверную информацию, и вы можете положиться на них во время подготовки. Попробуйте попрактиковаться в предыдущих работах и примерах вопросов, прикрепленных к учебникам NCERT по математике для 11-го класса, глава 3, «Тригонометрические функции», чтобы легко решать вопросы на экзамене.
Класс 11 Математика Глава 3 Тригонометрические функции Книга NCERT PDF Скачать
Чтобы лучше подготовиться к экзамену, вы можете обратиться к Решениям NCERT 11-го класса, преобладающим в электронной книге NCERT. Книги NCERT для класса 11 по математике и тригонометрическим функциям будут содержать иллюстративные задачи и решения. Учащиеся могут понять концепции, написанные в учебниках по математике NCERT для 11-го класса для главы 3 «Тригонометрические функции», а также все они написаны исчерпывающим образом.
Учащиеся могут понять концепции, написанные в учебниках по математике NCERT для 11-го класса для главы 3 «Тригонометрические функции», а также все они написаны исчерпывающим образом.
NCERT Учебники по математике для 11-го класса Глава 3 Тригонометрические функции бесплатны, и вы можете получить к ним доступ с помощью доступных быстрых ссылок.
Часто задаваемые вопросы о книгах NCERT для 11-го класса по математике и тригонометрическим функциям PDF
1. Почему следует читать книги NCERT для 11-го класса по математике, глава 3?
Учащиеся могут самостоятельно оценить пробелы в знаниях с помощью книг NCERT для 11-го класса по математике, глава 3, а также получить больше знаний о концепциях математики.
2. Где я могу бесплатно скачать книги NCERT для 11 класса по математике, глава 3, тригонометрические функции в формате PDF?
Вы можете бесплатно скачать книги NCERT для 11-го класса по математике, глава 3, тригонометрические функции в формате PDF на нашей странице.
3. Как скачать учебники NCERT по математике и тригонометрическим функциям для 11 класса в формате PDF?
Все, что вам нужно сделать, это нажать на быстрые ссылки, доступные для 11th Class Maths Trigonometric Functions NCERT Textbooks PDF здесь, и вы будете перенаправлены на новую страницу с возможностью загрузки. Нажмите на опцию загрузки и сохраните их для дальнейшего использования и подготовьте их по мере необходимости.
Книги NCERT
15 лучших учебников по тригонометрии в 2021 году
Когда учащиеся слышат названия математических тем, таких как тригонометрия, они сразу же думают, что это сложно.Большинство студентов считают, что решить задачи по тригонометрии невозможно. Тригонометрия сложна, как и любой другой математический предмет. Но изучение этого предмета не составит труда, если вы сможете понять основные принципы тригонометрии и решить некоторые практические задачи из учебников по тригонометрии.
Чтобы помочь вам изучить дополнительные курсы по тригонометрии для средней школы и колледжа, они включают в себя несколько справочных учебников с другими учебными материалами. Некоторые из этих справочных материалов также сложны для понимания некоторыми учащимися.И не только студенты колледжей или старших классов используют эти учебники для изучения тригонометрии.
Некоторые из этих справочных материалов также сложны для понимания некоторыми учащимися.И не только студенты колледжей или старших классов используют эти учебники для изучения тригонометрии.
Есть бесчисленное множество людей, которым необходимо изучать тригонометрию, чтобы лучше выполнять свою работу, например, математики, физики, химики и даже лесорубы, машинисты, котельщики. Или даже люди, желающие вернуться в школу, используют эти учебники для изучения тригонометрии. Итак, мы рассмотрели лучшие учебники по тригонометрии, которые позволят вам учиться. Здесь мы рассмотрели лучшие доступные учебники по тригонометрии, чтобы помочь вам найти наиболее подходящий учебник для освоения тригонометрии.
Лучшие учебники для изучения тригонометрии в 2021
01. Тригонометрия [10-е издание] — RON Larson
автор многих учебников по математике, охватывающих тригонометрию, алгебру, исчисление и статистику. Вы, должно быть, уже знакомы с этой книгой, так как это один из наиболее часто используемых учебников по тригонометрии на курсах тригонометрии в средней школе или колледже.
Вы, должно быть, уже знакомы с этой книгой, так как это один из наиболее часто используемых учебников по тригонометрии на курсах тригонометрии в средней школе или колледже.
В учебнике Рона Ларсона по тригонометрии (10-е издание) объясняются концепции тригонометрии и теоремы с множеством практических задач, чтобы помочь учащимся получить хорошие знания в области тригонометрии, применяя на практике то, что они изучают. Автор также включил хорошо написанные резюме в конце каждой главы, чтобы помочь учащимся повторить то, что они узнали за небольшой период времени. Каждая глава включает более пятидесяти практических задач с ответами в конце книги.
Если вы хотите учиться на практике, это лучший учебник по тригонометрии для вас, даже если вы новичок.Также в учебник включены платные дополнительные материалы.
Pro Prov- 5
-
- Детальные практики Проблемы
- Удобства для начинающих
- Полезные Конечные данные Глава
- Отзывы в тексте
- могут занять много времени, чтобы закончить книгу
02. Тригонометрия, 11-е издание – Лиал, Джон Хорнсби, Дэвид Шнайдер и Калли Дэниелс
Тригонометрия, 11-е издание – Лиал, Джон Хорнсби, Дэвид Шнайдер и Калли Дэниелс В математике иногда легче понять большие понятия, если вы хорошо разбираетесь в фундаментальных математических понятиях.Эта книга написана четырьмя авторами Маргарет Лайал, Джоном Хорнсби, Дэвидом Шнайдером и Кэлли Дэниелс, которые также опубликовали более 30 математических учебников по алгебре, тригонометрии и исчислению, а также по многим математическим дисциплинам. Эта книга из их серии учебников по алгебре для колледжей, созданных с учетом их опыта.
Даже если вы ничего не понимаете в тригонометрии или в том, как она используется в реальной жизни, эта книга объясняет все, начиная с самых основ тригонометрии, в ободряющем тоне.В каждом разделе есть много примеров задач с пошаговыми ответами и множество упражнений, которые могут оказаться сложными для решения. Это также делает этот учебник по тригонометрии идеальным для студентов колледжей, которые хотят самостоятельно решать более сложные задачи по тригонометрии.

Новый учебник по тригонометрии 11-го издания Маргарет Лайал, Джона Хорнсби, Дэвида Шнайдера и Калли Дэниелс все еще может стоить намного дороже, чем некоторые учебники, которые мы рассмотрели. Но вы можете получить подержанный учебник за небольшую часть стоимости нового учебника.Кроме того, это один из лучших учебников по тригонометрии, который можно использовать, если вы изучаете тригонометрию самостоятельно или ищете книгу с трудными практическими вопросами.
pro prof- Идеально подходит для самостоятельного изучения
- пошаговые инструкции
- Краткие определения
- , используемые в курсах колледжа
- Хорошо для начинающих
- Многие легко задачи
03. Тригонометрия для чайников – Мэри Джейн СтерлингНе все пытаются изучать тригонометрию, потому что они записались на курсы тригонометрии в колледже или средней школе.
 Или некоторые могут даже знать тригонометрию, и вам нужен краткий обзор, чтобы сохранить память о тригонометрии. Они ищут только книгу по тригонометрии, удобную для начинающих и простую для прочтения.
Или некоторые могут даже знать тригонометрию, и вам нужен краткий обзор, чтобы сохранить память о тригонометрии. Они ищут только книгу по тригонометрии, удобную для начинающих и простую для прочтения. Тригонометрия для чайников написана Мэри Джейн Стерлинг, преподавателем математики в Университете Пеории, более двадцати лет. Она также опубликовала несколько книг по алгебре, предварительному исчислению и несколько рабочих тетрадей по математике. Как и в любой другой книге для чайников, в этой также объясняется, «как» и «почему» мы используем эти концепции тригонометрии.Все объясняется на простом английском языке, чтобы помочь всем, независимо от их возраста, легко понять тригонометрию. В каждом разделе есть приличное количество практических задач. Но было бы здорово, если бы примеров было больше.
«Тригонометрия для чайников» содержит меньше страниц, чем другие учебники по тригонометрии, которые мы рассматривали, но также подходит для среднего школьного и высшего образования.
prov Студенты говорят, что им стало намного легче понять тригонометрию после обращения к этому учебнику, и они стали лучше сдавать экзамены.
Студенты говорят, что им стало намного легче понять тригонометрию после обращения к этому учебнику, и они стали лучше сдавать экзамены.- 5
- Подходит для каждого возраста
- Достойное количество практики Проблемы
- Меньше страниц, чтобы пройти
- Доступное, чем многие тригонометрические учебники
- , написанные на простом английском
- Не для продвинутых учащихся (например, математиков)
- Меньше примеров в некоторых разделах
-
- Учебник для начинающих
- Учебник
- , используемый в курсах в средней школе и колледжах
- Хорошо объясненные концепции с графиками
- Много практики

- более высокая цена по сравнению с другими учебники
- Несложные задачи по тригонометрии
05. Тригонометрия (издание 2001 г.) – И.М. Гельфанд, Марк СаулТригонометрия используется в таких предметах, как физика, электроника, астрономия и другие математические предметы.Особенно, если вы собираетесь пройти курс математического анализа в колледже или старшей школе, вам обязательно нужно изучить тригонометрию перед началом курса. Этот учебник по тригонометрии был написан известными математиками И. М. Гельфандом и Марком Саулом, которые также опубликовали другие учебники по математике, такие как Алгебра, Геометрия, Функции и графики, Основы математики и др.
Эта книга является уникальным учебником, потому что это 2001-е издание по тригонометрии И. М. Гельфанда и Марка Саула, и вы все еще можете использовать его сегодня для самостоятельного изучения тригонометрии.И этот учебник является наиболее доступным вариантом по сравнению с другими доступными сегодня учебниками по тригонометрии.
 Он до сих пор используется на курсах тригонометрии в колледжах и старших классах в качестве справочного пособия. Авторы объяснили принципы тригонометрии так, чтобы каждый мог их выучить и запомнить без особых проблем.
Он до сих пор используется на курсах тригонометрии в колледжах и старших классах в качестве справочного пособия. Авторы объяснили принципы тригонометрии так, чтобы каждый мог их выучить и запомнить без особых проблем. Книга также включает в себя множество простых и сложных, сложных практических задач. Но в книге нет ответов на них. Хотя это не такая большая проблема, было бы здорово, если бы они включили их в одну книгу.Кроме того, это один из лучших учебников по триггерам, которые вы могли бы использовать для самостоятельного изучения.
Pros- 5
- Легко понять
- Хорошо для самостоятельного изучения
- включает в себя различные практики Проблемы
- Самый доступный Trig TextBook
- Менее количество страниц (не занимает много времени, чтобы закончить книгу)
- Используется в качестве справочника на курсах средней школы и колледжа
- Старее, чем некоторые доступные учебники по триггерам
- Не содержит ответов на практические задачи 9.
 80770
80770
04. Тригонометрия [8-е издание] — Чарльз П.McKeague, Mark D. TurnerЛучший способ изучить тригонометрию — изучить концепции и постоянно применять их к различным типам задач тригонометрии. Тригонометрия Чарльза П. МакКега, Марка Д. Тернера используется в качестве справочного учебника по тригонометрии на многих курсах тригонометрии в колледжах и средних школах.
 Книга состоит из восьми глав, каждая из которых включает область цели обучения и оценку в конце главы.
Книга состоит из восьми глав, каждая из которых включает область цели обучения и оценку в конце главы. Это учебник по тригонометрии для начинающих, предназначенный в основном для учащихся средних школ и колледжей.Все концепции подробно объясняются с помощью приложений тригонометрии, что облегчает понимание принципов тригонометрии. Легкие и средние практические задачи даны с пошаговыми ответами. Было бы здорово, если бы авторы включили гораздо более сложные практические задачи для продвинутых учащихся.
Вы получите компакт-диск с дополнительной помощью и практическими задачами, если купите новый учебник. Но новый может стоить пару сотен баксов. Если вы хотите сэкономить на учебнике, вам следует выбрать подержанный учебник (в некоторых есть компакт-диск, а в некоторых нет) или электронный учебник.
Pro Prov
Когда вы поступаете в колледж из средней школы, даже если вы хороши в тригонометрии, вы все равно можете забыть некоторые понятия. Большинство будет искать другой учебник по тригонометрии, чтобы прочитать и проверить свои знания по тригонометрии, а некоторые могут даже искать другой набор практических задач.
Ричард Н. Ауфманн — автор пользующихся спросом учебников, опубликовавший серию книг по развивающей математике, алгебре и тригонометрии для учащихся колледжей.Автор объясняет концепции тригонометрии, связывая их с реальными ситуациями, что также помогает учащимся быстро понять концепции. Дополнительные материалы, прилагаемые к учебнику, включают учебные пособия, практические задачи и онлайн-репетиторство.
Обзоры в тексте каждой главы даются в новейшем 6-м издании тригонометрии для колледжей Ричарда Н. Ауфманна, чтобы помочь студентам за короткое время повторить основные понятия тригонометрии. Цена по-прежнему высока, если вы хотите купить новый учебник за пару сотен долларов.Но это все еще отличная книга по тригонометрии, к которой можно обратиться, если вы учитесь в колледже.
Цена по-прежнему высока, если вы хотите купить новый учебник за пару сотен долларов.Но это все еще отличная книга по тригонометрии, к которой можно обратиться, если вы учитесь в колледже.
- Легко понять
- Хорошо для студентов колледжа
- Начинающие дружественные
- в тексте тригонометрия концепция отзывы
- включает в себя практические проблемы
- Требуется много времени, чтобы закончить учебник
07.Очерк тригонометрии Шаума [6-е издание] — Роберт Мойер, Фрэнк Эйрес
Изучение математики не всегда связано с чтением понятий. Это больше касается применения изученных концепций в практических задачах. Этот учебник по тригонометрии, написанный Робертом Мойером и Фрэнком Эйресом, входит в серию учебников Шаума Outline. Schaum’s Outline — известная серия учебников, охватывающая такие темы, как алгебра в колледже, физика, дифференциальные уравнения, исчисление, комплексные переменные и другие предметы.
Если вы пропустили лекции по тригонометрии и хотите больше узнать, применяя подход к тригонометрии, «Очерк тригонометрии» Шаума — лучший учебник, который вы можете купить. На данный момент это самый доступный обновленный учебник по тригонометрии, доступный в Интернете. Учебник включает в себя 600 пошаговых решенных практических задач, а также вы получаете бесплатный доступ к более чем 20 онлайн-урокам по тригонометрии.
Даже если вы ответите на все практические задачи внутри, вам не потребуется много времени, чтобы закончить учебник.Хотя это может быть не идеальный учебник по тригонометрии для начинающих, это лучший вариант, если вы уже знакомы с высшей математикой и хотите освежить свои знания по тригонометрии.
Pro Prov- 618 Решенные тригонометрические проблемы
- Доступный Учебник
- Идеально подходит для обновления Trigonometry Знания
- Бесплатные Тригонометрические Учебники
- Отлично подходят для людей, которые хочет Tryigonometry Refresher
- Не очень подходит для начинающих
Лучшие учебники по алгебре и тригонометрии в 2021 году
08.
 Алгебра и тригонометрия [6-е издание] – Боб Блитцер
Алгебра и тригонометрия [6-е издание] – Боб Блитцер
Эта книга написана Робертом Ф. Блитцером, издателем, который является магистром многих книг по математике, включая развивающую математику, алгебру и исчисление. Для тех, кто хочет отточить свои знания по алгебре и тригонометрии или для тех, кто возвращается в школу, но хочет подготовиться, это еще один учебник для изучения алгебры и тригонометрии.
Если вы плохо разбираетесь в алгебре и тригонометрии, а также занимаетесь самообразованием, вам стоит купить этот учебник.Новое издание (6-е издание Алгебры и тригонометрии) включает в себя множество бонусов и краткие обзоры по каждой теме в тексте. Это помогает учащимся просмотреть темы, которые они уже изучили за небольшой период времени.
Автор объяснил математические понятия, просто указав, как они применяются в реальных ситуациях. Алгебра и тригонометрия Блитцера содержат много хорошо объясненных практических задач, что делает эту книгу идеальной для самостоятельного изучения.
-
- Лучший тригонометрический УчебныйБугольник для самостоятельно изучения
- Пошаговая практика Проблемы
- Краткое описание текста для предварительных условий Тем
- Использованные реальные ситуации для объяснения контента 5
09.Колледжская алгебра и тригонометрия: метод единичного круга [5-е издание] – Марк ДугопольскиЧтобы получить хорошие оценки по математическому предмету, необходимо изучить математические концепции и следовать основным стратегиям, а также иметь навыки решения проблем. Марк Дугопольски, автор книги по алгебре и тригонометрии для колледжей, применил поощряющий подход к преподаванию алгебры и тригонометрии, чтобы студенты не отвлекались от поставленных задач.
По сравнению с некоторыми другими учебниками по тригонометрии в этом нет серьезных опечаток.Язык несколько сложнее для понимания новичком. Автор объясняет важные понятия алгебры, которые могут пригодиться, если вы собираетесь выполнять предварительное исчисление.
 На DVD есть более тысячи практических задач с ответами.
На DVD есть более тысячи практических задач с ответами. Не лучший учебник для самостоятельного изучения тригонометрии. Однако, если вы учитесь в колледже и хотите повторить алгебру и тригонометрию или использовать учебник по тригонометрии в классе, это еще один отличный вариант.
Pro Prov- поощряет тона
- 1000+ Проблемы практики с ответами
- Хороший выбор для промежуточного уровня Учащийся
- Держат учащийся сосредоточен на теме
- Не начинание
- Точка максимальной цены
10.Алгебра и тригонометрия [10-е издание] — Майкл СалливанУчебник по математике был написан Майклом Салливаном, профессором математики Чикагского государственного университета, опубликовавшим пятнадцать хорошо известных учебников по математике по таким темам, как алгебра для колледжей, конечная математика, предварительное исчисление.
и Статистика. Большинство курсов колледжей, которые включают тригонометрию или алгебру, используют этот учебник в качестве справочного пособия, поскольку большинству профессоров он нравится, так как он был написан для математических специальностей.
Это один из лучших учебников по тригонометрии для тех, кто хотя бы записался на курс в колледже, включающий алгебру и тригонометрию. Автор написал эту книгу, предполагая, что читатель уже знает основные понятия. Учебник также включает в себя множество практических задач, которые наиболее трудно решить.
Так как это учебник по тригонометрии с более чем тысячей страниц, потребуется некоторое время, чтобы понять концепции и решить практические задачи. В какой-то момент вам также может понадобиться репетиторство по учебнику.Поэтому, если вы не являетесь специалистом по математике или просто занимаетесь самостоятельным изучением тригонометрии и алгебры, вам следует держаться подальше от этой книги, по крайней мере, до тех пор, пока вы не освоите основные понятия.
Pros
-
- Учебник продвижения уровня
- Хорошо для математических массивов
- Много практики Проблемы
- не упрощает понятия
- , а не на новичке
- не для себя -Изучение
- Может потребоваться дополнительное обучение
В двух словахИзучение математических тем сложно, потому что вы должны понимать принципы и применять их к практическим задачам до тех пор, пока не научитесь.Изучение тригонометрии может быть немного трудным, но если бы вы могли использовать хороший учебник по тригонометрии и дополнительные материалы, вы могли бы легко добиться большего успеха. Есть много учебников по тригонометрии, доступных для покупки. Тем не менее, наличие хорошего учебника в соответствии с вашей ситуацией и опытом обучения также может сыграть роль в том, насколько хорошо вы будете изучать и осваивать тригонометрию.
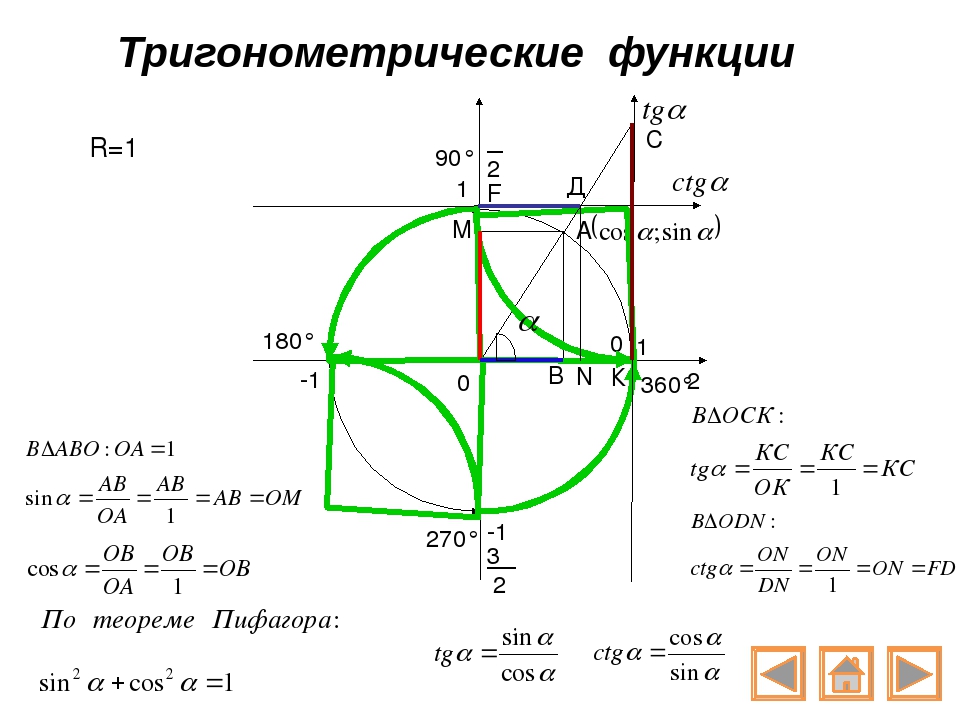
SUNY Orange: Математика — учебники
Курс №
Название курса
Название книги
Автор
Издатель
ISBN
МАТ 010
Основы арифметики
Арифметика для студентов
MITE и Дэвид Липпман
ОЭР
Открытый образовательный ресурс
МАТ 020
Основы алгебры
Начало алгебры с приложениями
8-е издание
Ауфманн/Локвуд
Сенгаж
9781133839118
МАТ 101
Элементарная алгебра
Начало алгебры с приложениями
8-е издание
Ауфманн/Локвуд
Сенгаж
9781133839118
МАТ 102
Алгебра среднего уровня
Алгебра среднего уровня
13-е издание
Биттингер
Пирсон
9780134707365
МАТ 107 Техническая математика 1
Техническая математика
11 издание
Вашингтон/Эванс
Пирсон
0-13-443770-5
МАТ 111 Математика для учителей начальной школы
Подход к решению задач по математике для учителей начальной школы
Бильштейн/Либескинд/Лотт
Пирсон
0-321-98729-2
МАТ 113 Математика для гуманитарных наук Природа математики — 13-е издание
Карл Смит Сенгаж 9781133947257 МАТ 121 Колледж Алгебра
Колледж Алгебра
8-е издание
Блитцер
Пирсон
9780136
8 МАТ 122 Колледж тригонометрии
Аналитическая тригонометрия с приложениями
11 издание
Барнетт/Зиглер/Байлин
Вили
9780470648056
МАТ 120 Введение.
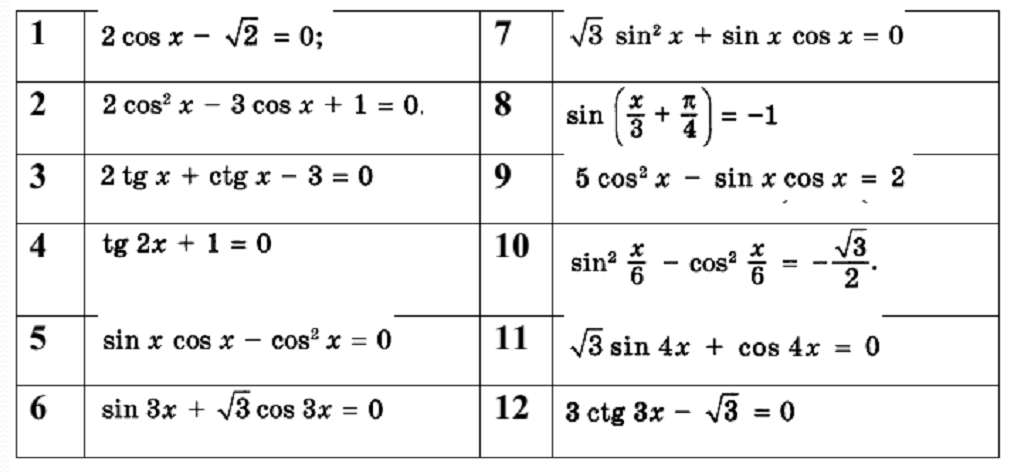 к статистике
к статистике Основы статистики Триолы
6-е издание
Триола
Пирсон
9780134685779
МАТ 131 Предварительное исчисление
Предварительное исчисление
11 издание
Ларсон
Сенгаж
97801357711576
МАТ 136 Дискретная математика
Дискретная математика
4-е издание
ЭПП
Сенгаж
1111775788
Матовый 205 Исчисление I
Исчисление
11 издание
Ларсон/Эдвардс
Сенгаж
978133727534-7
МАТ 206 Исчисление II
Исчисление
11 издание
Ларсон/Эдвардс
Сенгаж
978133727534-7
Матовый 207 Исчисление III
Исчисление
11 издание
Ларсон/Эдвардс
Сенгаж
978133727534-7
МАТ 211 Линейная алгебра
Элементарная линейная алгебра
11 издание
Антон
Вили
9781118677308
МАТ 214 Дифференциальные уравнения
Дифференциальные уравнения
9-е издание
Зилл/Райт
Сенгаж
978-1-305-96579-9
Электронные учебники по математике, осень/весна 2021–2022 гг.

Некоторые курсы по математике оптимизированы для работы в Интернете и требуют доступа к веб-страницам издателей.Учащиеся должны обратиться к расписанию курса, чтобы узнать, зарегистрированы ли они для участия в веб-расширенной курс.
МАТ 020 Основы алгебры
Расширенный WebAssign
EWA и eBook-SMTB-Stand Alone
Cengage Learning WebAssign
9781337763622
МАТ 020 Основы алгебры/АЛЕКС АЛЕКС Доступ на 18 недель
Макгроу Хилл
9781260634020
МАТ 030 Основы математических рассуждений 9781926
- 3
МАТ 101 Элементарная алгебра Расширенный веб-присвоение EWA и eBook-SMTB-Stand Alone
Cengage Learning WebAssign
9781337763622
МАТ 102 Алгебра среднего уровня MyMathLab
Комплект доступа для учащихся MyMathLab — автономный
Пирсон
9780135
- 0
МАТ 121 Колледж Алгебра
MyMathLab
Комплект доступа для учащихся MyMathLab — автономный
Пирсон
9780136970514
МАТ 120 Введение.
 к статистике
к статистике MyMathLab
Комплект доступа для учащихся MyMathLab — автономный
Пирсон
9780135374221
МАТ 205,206,207 Исчисление I, II, III
Расширенный WebAssign
EWA и eBook-SMTB-Stand Alone
Cengage Learning WebAssign
9781337652650
Решения NCERT для класса 11 по математике, глава 3, тригонометрические функции
NCERT Solutions for Class 11 Math Chapter 3 Trigonometric Functions сформулированы для объяснения фундаментального применения тригонометрических формул и графиков их функций.
 Тригонометрия — важная часть математики в 11 классе, которая включает в себя изучение различных отношений между сторонами и углами треугольников. Тригонометрические функции применяются для определения этих отношений и имеют множество приложений в различных других областях, включая науку и технику. Они часто используются для основных геометрических вычислений и для объяснения числовых решений. Знание тригонометрических функций жизненно важно для таких предметов, как астрономия и география. NCERT Solutions Class 11 Maths Chapter 3 предложит учащимся необходимые базовые навыки для изучения тригонометрических отношений и функций, а также их практического применения.
Тригонометрия — важная часть математики в 11 классе, которая включает в себя изучение различных отношений между сторонами и углами треугольников. Тригонометрические функции применяются для определения этих отношений и имеют множество приложений в различных других областях, включая науку и технику. Они часто используются для основных геометрических вычислений и для объяснения числовых решений. Знание тригонометрических функций жизненно важно для таких предметов, как астрономия и география. NCERT Solutions Class 11 Maths Chapter 3 предложит учащимся необходимые базовые навыки для изучения тригонометрических отношений и функций, а также их практического применения.Глава 3 математики для 11 класса позволит учащимся обобщить понятие тригонометрических соотношений на тригонометрические функции. Изучение свойств тригонометрических функций и операций, основанных на них, имеет решающее значение для изучения математики. Благодаря регулярной практике в классе 11 Maths NCERT Solutions Chapter 3 учащиеся быстро освоят решения уравнений с использованием тригонометрических функций.
 Широкий спектр проблем и примеров, представленных в этих решениях, способствует более глубокому пониманию концепций.Чтобы изучить и попрактиковаться с NCERT Solutions Глава 3 Тригонометрические функции, загрузите упражнения, приведенные по ссылкам ниже.
Широкий спектр проблем и примеров, представленных в этих решениях, способствует более глубокому пониманию концепций.Чтобы изучить и попрактиковаться с NCERT Solutions Глава 3 Тригонометрические функции, загрузите упражнения, приведенные по ссылкам ниже. Решения NCERT для класса 11 по математике Глава 3 PDF
В тригонометрии используется множество формул, теорем и шагов для решения сумм, поэтому очень важно, чтобы дети уделяли достаточно времени практике. Решения NCERT для класса 11 по математике Глава 3 умело смоделирована для поддержки обучения математике более высокого уровня. Комплексный формат этих решений очень надежен для улучшения навыков решения проблем увлекательными способами.Чтобы изучить и попрактиковаться в тригонометрических функциях с этими решениями, щелкните ссылки на файл в формате pdf, приведенные ниже.
☛ Загрузить Математика класса 11 Решения NCERT Глава 3 Тригонометрические функцииNCERT Class 11 Math Chapter 3 Загрузить PDF
Решения NCERT для класса 11 по математике, глава 3, тригонометрические функции
Решения NCERT Класс 11 Математика Глава 3 Тригонометрические функции чрезвычайно полезны для развития математических рассуждений у учащихся.
 С помощью этих хорошо структурированных ресурсов студенты получат упрощенный подход к эффективной подготовке к экзаменам. Тщательно размещенных иллюстраций, вопросов и примеров, представленных в этих решениях, достаточно, чтобы улучшить фундаментальные математические знания, чтобы преуспеть на экзаменах. С помощью этих решений дети могут легко планировать свою учебную программу и формат повторения. Чтобы попрактиковаться в математических тригонометрических функциях класса 11 решений NCERT Solutions, попробуйте ссылки, приведенные ниже.
С помощью этих хорошо структурированных ресурсов студенты получат упрощенный подход к эффективной подготовке к экзаменам. Тщательно размещенных иллюстраций, вопросов и примеров, представленных в этих решениях, достаточно, чтобы улучшить фундаментальные математические знания, чтобы преуспеть на экзаменах. С помощью этих решений дети могут легко планировать свою учебную программу и формат повторения. Чтобы попрактиковаться в математических тригонометрических функциях класса 11 решений NCERT Solutions, попробуйте ссылки, приведенные ниже. - Класс 11 Математика Глава 3 Упражнение 3.1 — 7 Вопросы
- Класс 11 Математика Глава 3 Пример 3.2 — 10 вопросов
- Класс 11 Математика Глава 3 Пример 3.3 — 25 вопросов
- Класс 11 Математика Глава 3 Пример 3.4 — 9 вопросов
- Класс 11 Математика Глава 3 Разное Пример — 10 вопросов
☛ Скачать книгу NCERT по математике для 11 класса, глава 3,
Рассматриваемые темы: решений NCERT Математика класса 11 Глава 3 Тригонометрические функции охватывают некоторые важные темы, в том числе введение в тригонометрические отношения и тождества, меру углов, знаки, домен и диапазон тригонометрических функций.
 Другая важная тема, включенная в эти решения, — это тригонометрические решения суммы и разности двух углов с использованием формул.
Другая важная тема, включенная в эти решения, — это тригонометрические решения суммы и разности двух углов с использованием формул. Всего вопросов: Класс 11 Математика Глава 3 Тригонометрические функции содержит 51 вопрос в 4 упражнениях плюс 10 вопросов в одном разнообразном упражнении. Они в первую очередь основаны на представлении тригонометрических функций, их приложений и формул.
Список формул в NCERT Solutions Class 11 Math Chapter 3
Запоминание важных формул и понятий необходимо для четкого понимания терминов и операций, связанных с тригонометрическими функциями.NCERT Solutions Class 11 Maths Глава 3 предоставит подробные сведения обо всем этом вместе с их приложениями с помощью интересных иллюстраций. Каждая концепция в этих решениях хорошо объяснена соответствующими примерами и примерами задач, что способствует более глубокому пониманию этой темы. Формулы являются неотъемлемой частью этого урока, поэтому создание таблицы формул может быть полезно для учащихся, когда им нужно попрактиковаться в этой теме.
 Некоторые из важных терминов, формул и понятий, связанных с тригонометрическими функциями, которые объясняются в этих решениях, перечислены ниже:
Некоторые из важных терминов, формул и понятий, связанных с тригонометрическими функциями, которые объясняются в этих решениях, перечислены ниже: - Тригонометрические функции: Тригонометрические функции — это действительные функции, которые связывают угол прямоугольного треугольника с отношением длин его сторон.Грех, Кос и Тан — три основные функции.
- Тригонометрические уравнения: Тригонометрические уравнения — это уравнения, в которых используются тригонометрические функции. Эти тригонометрические уравнения также известны как тригонометрические тождества, когда значения неизвестных углов, для которых определены функции, выполняются.
- Тригонометрические тождества: Тригонометрическое уравнение, включающее сумму и разность углов, представляет собой тригонометрическое тождество.Например, sin 2 θ + cos 2 θ = 1
- Тождества суммы и разности: Тождества суммы и разности включают следующие формулы.

- sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x+y) = cos(x)cos(y) – sin(x)sin(y)
- тангенс(х+у) = (тангенс х + тангенс у)/(1-тангенс х • тангенс у)
- sin(x–y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x−y) = (tan x–tan y)/(1+tan x • tan y)
Часто задаваемые вопросы о решениях NCERT, класс 11, математика, глава 3
В чем важность решений NCERT для математики класса 11, глава 3, тригонометрические функции?
NCERT Solutions for Class 11 Maths Глава 3 Тригонометрические функции разработаны высококвалифицированными учителями и экспертами по математике для содействия эффективному изучению математики.Каждое упражнение этих решений сформулировано в соответствии с рекомендациями CBSE для поддержки углубленного изучения тригонометрических функций и их взаимосвязей. Эти грамотно структурированные решения подходят для повышения математических знаний учащихся. Регулярная практика этих решений повысит уверенность учащихся в хороших результатах.
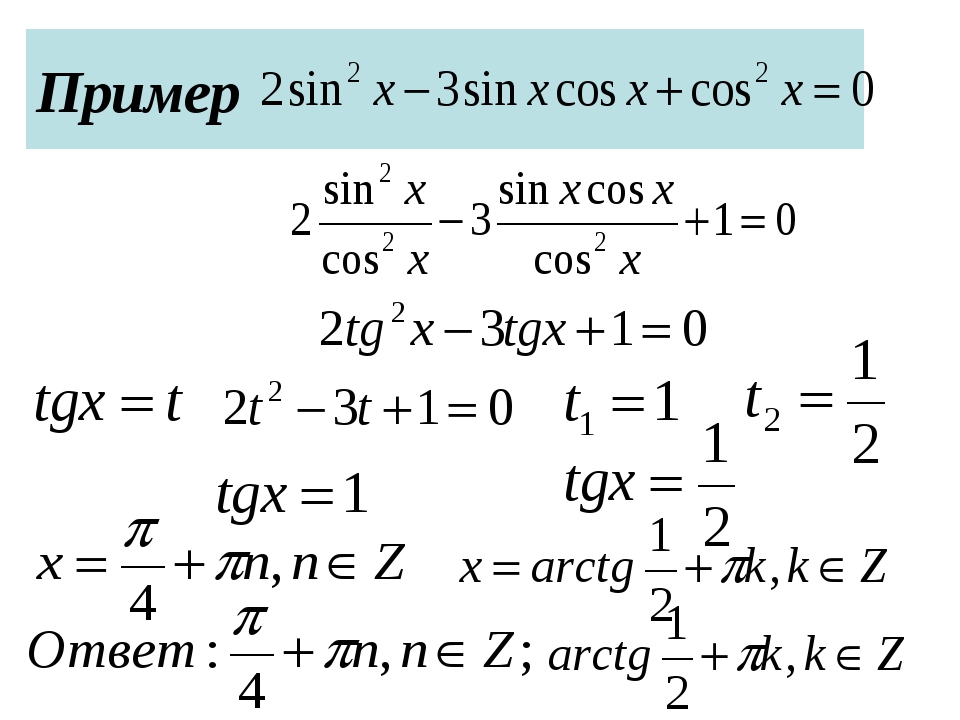
Какие важные темы рассматриваются в NCERT Solutions Class 11 Math Chapter 3?
NCERT Solutions Class 11 Maths Глава 3 кратко знакомит с тригонометрическими отношениями и тождествами, а также с некоторыми основными понятиями, которые ранее изучались в 10 классе.Важными темами, затронутыми в этих решениях, являются угловые меры, тригонометрические функции, их знаки, область определения и диапазон. Сумма и разность двух углов с использованием тригонометрических функций также включены в эту главу.
Нужно ли мне практиковать все вопросы, представленные в классе 11 Math NCERT Solutions Trigonometric Functions?
NCERT Solutions Class 11 Математические тригонометрические функции разработаны таким образом, чтобы облегчить углубленное изучение концепций. Каждый вопрос, включенный в эти решения, направлен на улучшение концептуальной ясности, чтобы учащиеся могли легко их освоить.Фундаментальные знания о тригонометрических функциях и их использовании позволят учащимся применять свои знания в практических ситуациях.
 Эти решения также составляют основу для изучения продвинутых математических тем, включая исчисление. Таким образом, все суммы должны практиковаться с лазерным фокусом.
Эти решения также составляют основу для изучения продвинутых математических тем, включая исчисление. Таким образом, все суммы должны практиковаться с лазерным фокусом. Сколько вопросов в классе 11 Решения NCERT по математике Глава 3 Тригонометрические функции?
NCERT Solutions for Class 11 Math Chapter 3 Trigonometric Functions содержит 61 вопрос в 5 упражнениях.Этих задач достаточно, чтобы обеспечить глубокое понимание всей темы тригонометрических функций, включая важные формулы, тождества, отношения и операции, связанные с тригонометрическими функциями. Свободный от жаргона и понятный математический словарь, используемый в этих решениях, достаточно хорош для того, чтобы легко передать четкое пошаговое понимание каждой темы, а также подтем.
Каковы важные формулы в математике класса 11 NCERT Solutions Chapter 3?
NCERT Solutions Class 11 Maths Chapter 3 объясняет формулы, связанные с суммой и разностью двух углов в тригонометрических функциях.
 Некоторые из важных понятий, связанных с этой темой, основаны на выводе выражений для тригонометрических тождеств суммы и разности углов. Эти жизненно важные концепции подробно описаны с помощью интересных примеров, чтобы учащиеся могли лучше их понять. Кроме того, дети должны также пересмотреть формулы, с которыми они столкнулись на предыдущих занятиях, поскольку они также необходимы для выполнения задач по тригонометрии в 11 классе.
Некоторые из важных понятий, связанных с этой темой, основаны на выводе выражений для тригонометрических тождеств суммы и разности углов. Эти жизненно важные концепции подробно описаны с помощью интересных примеров, чтобы учащиеся могли лучше их понять. Кроме того, дети должны также пересмотреть формулы, с которыми они столкнулись на предыдущих занятиях, поскольку они также необходимы для выполнения задач по тригонометрии в 11 классе. Почему я должен практиковать решения NCERT для класса 11 по математике, глава 3, тригонометрические функции?
NCERT Solutions for Class 11 Maths Глава 3 Тригонометрические функции — это надежный источник обучения, который дает полное руководство для отличной подготовки к экзамену.С помощью этих решений учащиеся могут пройти всю программу CBSE Class 11 Math Chapter 3. Формат этих решений интуитивно понятен, что способствует простому и легкому обучению. Таким образом, чтобы получить наилучшие результаты, дети должны практиковать эти решения.

Школы Лонг-Бич – Учебная программа
Класс/курс Издатель учебника, годМарки ТК-5 Калифорния, займись математикой!
Хоутон Миффлин Харкорт, 2015Классы TK-5 Специальный дневной класс (от умеренного до тяжелого, специализированное медицинское обслуживание и УСПЕХ) Раннее умение считать, 2013, Достижение Математика 6 Курс математики «Большие идеи» 1
Обучение большим идеям, 2015Математика 6 АКК Большие идеи MATH Advanced 1
Обучение большим идеям, 2015Математика 7 Большие идеи Курс математики 2
Обучение большим идеям, 2015Математика 7 АКК Большие идеи MATH Advanced 2
Обучение большим идеям, 2015Математика 8 Большие идеи, курс MATH 3
Обучение большим идеям, 2015Алгебра 1 Большие идеи Алгебра математики 1
Обучение большим идеям, 2015Геометрия Большие идеи МАТЕМАТИКА Геометрия
Обучение большим идеям, 2015Геометрия ACC Открытие геометрии
Кендалл Хант, 2013Алгебра 2 Большие идеи МАТЕМАТИКА Алгебра 2
Обучение большим идеям, 2015Алгебра/тригонометрия среднего уровня Алгебра 2 с тригонометрией
(Основной текст) Прентис Холл, 2006 г.
И
Алгебра и тригонометрия: функции и приложения (дополнительный текст)
Аддисон-Уэсли, 1994 г.6–12 классы Специальный дневной класс (от умеренного до тяжелого) Преподавание по стандартам: математика 2008 г., достижение Карьера Математика Потребительская математика
Издательство АГС, 2003 г.CAHSEE Математика Встреча с Калифорнийским вызовом
(Основной текст) AGS Globe, 2002 или 2008
И
Сдача выпускного экзамена средней школы Калифорнии по математике
(Дополнительный текст) Американская книжная компания, 2001 г.Функции, статистика и тригонометрия Функции, статистика и тригонометрия
Математический проект школы Чикагского университета, 2010 или 2015 год 91 384Конечная математика Конечная математика для управления, жизни и социальных наук, 11-е издание
Cengage Learning, 2015Предварительный расчет Предварительное исчисление
Макгроу Хилл, 2014Статистика точки доступа Практика статистики, 5-е издание
Бедфорд, Фриман и Уорт, 2014 г.

 11 класс
11 класс

 График представляет собой две ветви гиперболы. В зависимости от k, ветви располагаются в 1,3 или 2,4 координатных углах.
График представляет собой две ветви гиперболы. В зависимости от k, ветви располагаются в 1,3 или 2,4 координатных углах.

 Деление возможно на неравное нулю число. Логарифмы существуют только для положительных чисел. Корни четной степени существуют только для неотрицательных чисел. Степень с дробным показателем существует для положительных чисел. Синус, косинус существует для любого действительного числа, т.к. это координаты точки единичной окружности, на которой изображаются действительные числа. Тангенс не существует на концах вертикального диаметра единичной окружности. Котангенс не существует на концах горизонтального диаметра.
Деление возможно на неравное нулю число. Логарифмы существуют только для положительных чисел. Корни четной степени существуют только для неотрицательных чисел. Степень с дробным показателем существует для положительных чисел. Синус, косинус существует для любого действительного числа, т.к. это координаты точки единичной окружности, на которой изображаются действительные числа. Тангенс не существует на концах вертикального диаметра единичной окружности. Котангенс не существует на концах горизонтального диаметра.

 Поэтому нули функции: 0 и 6,5.
Поэтому нули функции: 0 и 6,5.

 Используя свойства, построим графические образы.
Используя свойства, построим графические образы.  Операционно-познавательная часть
Операционно-познавательная часть


 Рефлексивно-оценочная часть
Рефлексивно-оценочная часть
 Возможно, предстоит вспомнить способы решения тригонометрических уравнений и неравенств, некоторые тригонометрические формулы. Поэтому в домашнее задание необходимо включить вопросы для повторения этих важных моментов.
Возможно, предстоит вспомнить способы решения тригонометрических уравнений и неравенств, некоторые тригонометрические формулы. Поэтому в домашнее задание необходимо включить вопросы для повторения этих важных моментов.