Тест для подготовки к ОГЭ 2019 математика 1 вариант
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 16
- 17
- 18
- 19
- 20
Информация
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 20
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
ОГЭ 2018 по математике. Тематические тестовые задания / Ю.А. Глазков и др.
Сборник содержит 14 тестов для текущего и тематического контроля по курсу алгебры 9 класса (Алгебра: Учеб. для 9 кл. общеобразоват. организаций / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, СБ. Суворова; Под. ред. С. А. Теляковского. — М.: Просвещение). В тестах используются задания трех форм: с выбором ответа (задания 1-4), с кратким ответом (5-7), с развернутым ответом (8).
Ответы удобно фиксировать в таблице, а решение задачи 8 записывать ниже таблицы. Тогда бланк ответов может иметь, например, такой вид:
Фамилия, имя учащегося ______________________________________
Класс
|
Задание |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
Задание 8
Бланки ответов ученики готовят дома накануне урока выполнения теста или тиражируются заранее учителем. При использовании таких унифицированных бланков учитель может в течение 15 минут проверить 25 работ учащихся.
Инструкции для учащихся по выполнению работы просты.
Ответы к заданиям 1-4 записываются в таблицу ответов в виде одной цифры — номера правильного ответа.
Для заданий 5-7 ответом является число, которое нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её, если это возможно, в десятичную.
Решение задания 8 запишите ниже таблицы ответов.
Эти инструкции сообщаются и напоминаются учащимся до тех пор, пока они не привыкнут к их выполнению.
На выполнение теста потребуется приблизительно 25-30 минут (более точно можно рассчитать, зная особенности класса). Время выполнения работы сообщается учащимся перед ее началом (записывается на доске). Рекомендуем тщательно соблюдать его, чтобы приучить школьников к дисциплине выполнения работы и выработать у них умение планировать время выполнения работы.
Каждый верный ответ к заданиям 1-7 оценивается в 1 балл, за неверный ответ и отсутствие ответа выставляется 0 баллов. За безошибочное решение задания 8 выставляется 2 балла, решение с недочетами оценивается в 1 балл, за незавершенное решение и отсутствие решения ставится 0 баллов. Рекомендуемая шкала перевода баллов в отметку:
|
Баллы |
0-2 |
3-4 |
5-7 |
8-9 |
|
Отметка |
2 |
3 |
4 |
5 |
В конце книги приведены 2 теста: тест 13 — для контроля результатов обобщающего повторения курса 9 класса, тест 14 — итоговый по курсу алгебры основной школы, представленный в формате ОГЭ.
Авторы
www.egeigia.ru
Тесты по математике. ОГЭ 2018. Геометрия, 1 часть (9 класс)
Задание 15. Две сосны растут на расстоянии 15 м одна от другой. Высота одной сосны 30 м, а другой — 22 м. Найдите расстояние (в метрах) между их верхушками.
Задание 16. В треугольнике ABC известно, что угол BAC = 48°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 69° и OAB = 48°. Найдите угол ВСО. Ответ дайте в градусах.
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 7, AD = 9, АС = 32. Найдите АО.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Задание 20. Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой
Задание 15. Две сосны растут на расстоянии 20 м одна от другой. Высота одной сосны 27 м, а другой — 12 м. Найдите расстояние (в метрах) между их верхушками.
Задание 16. В треугольнике ABC известно, что угол BAC = 84°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 56° и OAB = 15°. Найдите угол ВСО. Ответ дайте в градусах.
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 6, AD = 13, АС = 38. Найдите АО.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Задание 20. Какое из следующих утверждений верно?
1) Все равнобедренные треугольники подобны.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Сумма углов прямоугольного треугольника равна 90 градусам.
Задание 15. Две сосны растут на расстоянии 16 м одна от другой. Высота одной сосны 27 м, а другой — 15 м. Найдите расстояние (в метрах) между их верхушками.
Задание 16. В треугольнике ABC известно, что угол BAC = 28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Задание 17. Точка О — центр окружности, на которой лежат точки А, В и С. Известно, что углы ABC = 54° и OAB = 41°. Найдите угол ВСО. Ответ дайте в градусах.
Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 2, АВ = 5, АС = 28. Найдите АО.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Задание 20. Какое из следующих утверждений верно?
1) Сумма острых углов прямоугольного треугольника равна 90 градусам.
2) Средняя линия трапеции равна сумме её оснований.
3) В любой четырёхугольник можно вписать окружность.
Задание 15. Проектор полностью освещает экран А высотой 70 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 150 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Задание 16. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Задание 17. Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
Задание 18. В ромбе ABCD угол ABC равен 134°. Найдите угол ACD. Ответ дайте в градусах.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
Задание 20. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме её оснований.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Задание 15. Проектор полностью освещает экран А высотой 240 см, расположенный на расстоянии 300 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 80 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Задание 16. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.
Задание 17. Площадь круга равна 72. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
Задание 18. В ромбе ABCD угол ABC равен 40°. Найдите угол ACD. Ответ дайте в градусах.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
Задание 20. Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Задание 15. Проектор полностью освещает экран А высотой 50 см, расположенный на расстоянии 140 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран В высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Задание 16. Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Задание 17. Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
Задание 18. В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне АС.
Задание 20. Какое из следующих утверждений верно?
1) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Внешний угол треугольника равен сумме его внутренних углов.
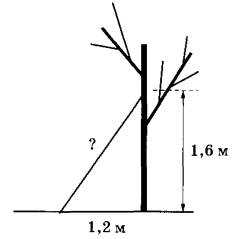
Задание 15. Найдите длину лестницы, которую прислонили к дереву, если её верхний конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м. Ответ дайте в метрах.
Задание 16. В треугольнике ABC известно, что АС = 32, ВМ — медиана, ВМ = 23. Найдите AM.
Задание 17. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.
Задание 18. Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Задание 20. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь квадрата равна произведению его диагоналей.
Задание 15. Две сосны растут на расстоянии 24 м одна от другой. Высота одной сосны 17 м, а другой — 10 м. Найдите расстояние (в метрах) между их вершинами.
Задание 16. В треугольнике ABC известно, что АС = 52, ВМ — медиана, ВМ = 36. Найдите AM.
Задание 17. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA = 32°. Найдите угол NMB. Ответ дайте в градусах.
Задание 18. Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Задание 20. Какие из следующих утверждений верны?
1) Две прямые, перпендикулярные третьей прямой, перпендикулярны.
2) В любой прямоугольной трапеции есть два равных угла.
3) Все диаметры окружности равны между собой.
Задание 15. Пожарную лестницу длиной 10 м приставили к окну третьего этажа дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
Задание 16. Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь этого треугольника.
Задание 17. Окружность с центром в точке О описана около равнобедренного треугольника ABC, в котором АВ =ВС и угол ABC = 88°. Найдите угол ВОС. Ответ дайте в градусах.
Задание 18. Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Задание 20. Какие из следующих утверждений верны?
1) Диагонали ромба равны.
2) Всякий равносторонний треугольник является равнобедренным.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Задание 15. Две сосны растут на расстоянии 36 м одна от другой. Высота одной сосны 25 м, а другой — 10 м. Найдите расстояние (в метрах) между их вершинами.
Задание 16. Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Задание 17. Окружность с центром в точке О описана около равнобедренного треугольника ABC, в котором АВ = ВС и угол ABC = 25°. Найдите угол ВОС. Ответ дайте в градусах.
Задание 18. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Задание 20. Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Все квадраты имеют равные площади.
3) Один из углов треугольника всегда не превышает 60 градусов.
infourok.ru
