Разбор и решение задания №21 ОГЭ по математике
x2 +7x+12.
Составим квадратное уравнение для вычисления оставшихся двух корней:
x2 +7x+12=0
6. Решим его с помощью формул корней и дискриминанта
7. Получили три корня 3; -3; -4.
Ответ: 3;-3;-4.
Третий вариант задания
Решите уравнение
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: — подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. Получаем квадратный трехчлен
x2 +3x+2.
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
7. Получили три корня -2; -1; 1.
Ответ: -2; -1; 1.
Демонстрационный вариант 2017 (сокращение дроби)
Сократите дробь
Решение:
Разложим 18 в числителе на множители 9 и 2:
Далее представим 9 как 3² и раскроем скобки в числителе:
При делении степени вычитаются, поэтому запишем:
Выполнив вычисления, получим:
Ответ: 96
spadilo.ru
Разбор и решение задания №26 ОГЭ по математике
Комплексная геометрическая задача
Разбор типовых вариантов заданий №26 ОГЭ по математике
Первый вариант задания
Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 5 и MB =10. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.
Алгоритм решения:
- Делаем чертеж.
- Определяем равенство угла между касательной и хордой и угла АВС.
- Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
- Показываем, что треугольники DAC и DCB подобны.
- Составляем соотношения сторон подобных треугольников.
- Составляем систему равенств.
- Решаем систему.
- Записываем ответ.
Решение:
1. Выполняем чертеж данной задачи:

2. Рассматриваем АСD. В нем:
Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,
4. Рассмотрим DAC и DCB. У них:
∠ DCA = ∠ DBC по доказанному выше,
∠ D – общий.
Следовательно, DAC DCB по двум углам.
5. Из определения и свойств подобных треугольников имеем:
6. Составим систему равенств:
7. Решим систему:
Ответ: 10.
Второй вариант задания
Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 9 и MB = 12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.
Алгоритм решения:
- Сделаем чертеж.
- Определим равенство углов CDB и АВС.
- Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
- Покажем, что треугольники DAC и DCB подобны.
- Составим соотношения сторон подобных треугольников.
- Составим систему равенств.
- Решим систему.
- Запишем ответ.
Решение:
1. Делаем чертеж.

2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей,
угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла.
⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА.
Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD.
3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,
4. Рассмотрим DAC и DCB. У них:
∠ DCA = ∠ DBC по доказанному выше,
∠ D – общий.
Значит, DAC DCB по двум углам.
5. Из определения и свойств подобных треугольников имеем:
6. Составим систему равенств:
7. Решим систему:
Отсюда
Так как AD = DB-21, имеем:
Таким образом, искомая длина CD=36.
Ответ: 36.
Четвертый вариант задания
Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cos ∠BAC = √11 / 6
Алгоритм решения:
- Сделаем чертеж.
- Установим подобие треугольников AFM и ANF.
- Определим сторону FM.
- Определим ∠FNA.
- Найдем .
- Составим теорему синусов и найдем радиус окружности.
- Запишем ответ.
Решение:
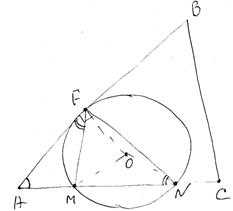
1. Рассмотрим треугольники AFM и ANF. У них:
Угол A является общим, а
по доказанному выше.
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:
3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:
Полученное значение означает, что AFM является равнобедренным. У него основание AF.
4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда
5. Найдем
Значит,
6. Из FMN по теореме синусов:
где R – радиус описанной окружности.
Отсюда получим значение радиуса окружности:
Ответ: 5,4.
Пятый вариант задания
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .
Решение:
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .
Точка касания M окружностей делит AC пополам по условию.
Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:
180°/2 = 90°.
Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:
AM² = MQ•MO
Отсюда:
QM = AM² / MO
QM = 6² / 8 = 4,5
Ответ: 4,5
spadilo.ru
Разбор и решение задания №23 ОГЭ по математике
Анализ графика функции
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
Если .
Если
2. График функции заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:

4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке :
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
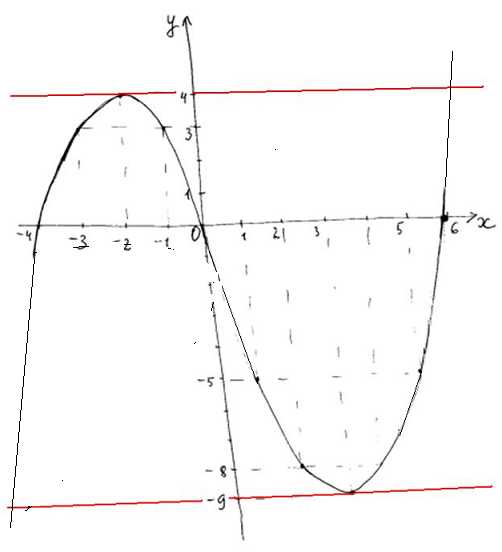
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при — часть парабола, ветви которой направлены вниз. Потому как коэффициент а=-1 – отрицательный.
Определим вершину параболы и .
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если , ветви параболы направлены вверх. Найдем вершину:
, (2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:

Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Если x < 0, то
Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы.
Точки для построения графика:
x | -5 | -4 | -3 | -2 |
y | -1/5 | -1/4 | -1/3 | -1/2 |
2. Если x > 0, то
Функция определена при График представляет собой часть гиперболы.
Точки для построения графика:
3. Построим график заданной функции:
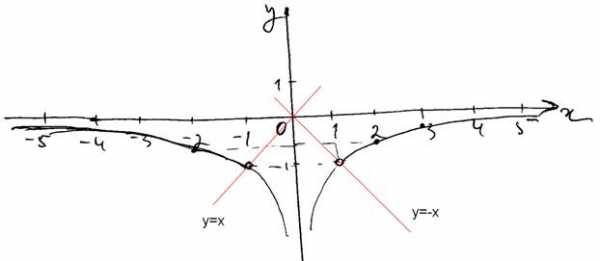
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
При k = 0 прямая совпадает с осью абсцисс и тоже не имеет общих точек с графиком функции.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Раскрываем модуль и для каждого случая.
Если x < 0, то
определена при и представляет собой часть гиперболы. Дополнительные точки для построения:
x | -5 | -4 | -3 | -2 | -1 |
y | -1/5 | -1/4 | -1/3 | -1/2 | -1 |
2. Если x > 0, то
определена при и представляет собой часть гиперболы.
Точки для построения графика:
x | 1 | 2 | 3 | 4 | 5 |
y | -1 | -1/2 | -1/3 | -1/4 | -1/5 |
3. Изображаем график:

Прямая y=kx не имеет общих точек с графиком данной функции, когда k=-16; 0 и 16. Тогда прямые проходят черед точки с абсциссами ¼ и — ¼ . На рисунке эти прямые изображены красным.
При k = 0 прямая совпадает с осью абсцисс. Она тоже не имеет общих точек с графиком.
Ответ: -16; 0; 16.
Шестой вариант задания
Постройте график функции
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.
Разложим числитель дроби на множители:
При x ≠2 и x ≠ 3 функция принимает вид:
её график — парабола, из которой выколоты точки ( -2; -4) и ( 3; 6).
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая.
Вершина параболы имеет координаты ( -0,5; -6,25 ).
Поэтому c = — 6,25, c = — 4 или c = 6.
Ответ: c = — 6,25, c = — 4 или c = 6.
spadilo.ru
Разбор и решение задания №16 ОГЭ по математике
Треугольники, четырёхугольники, многоугольники и их элементы
Перейдем к разбору модуля «Геометрия». В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №16
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:

Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
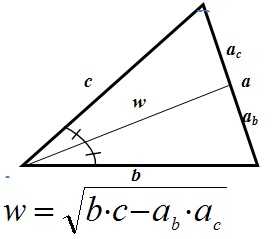
Медиана:
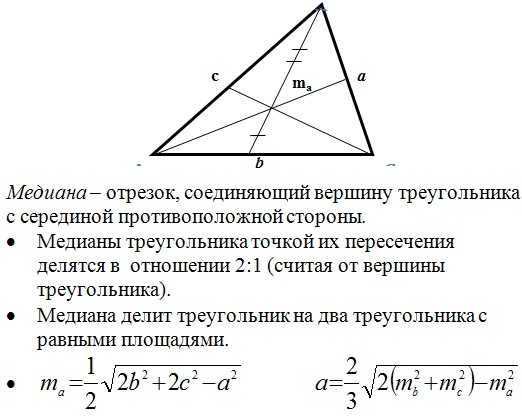
Теперь вспомним основные формулы нахождения площади треугольника:

Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник — треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Прямоугольный треугольник:

Разбор типовых вариантов заданий №16 ОГЭ по математике
Первый вариант задания
В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Ответ: 59°
Второй вариант задания
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Решение:
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
Третий вариант задания
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Решение:
Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 — 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29°
Четвертый вариант задания
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Решение:
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
Пятый вариант задания
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Решение:
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 — 23 = 67°
Ответ: 67°.
Шестой вариант задания
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Решение:
Для решения необходимо вспомнить определение медианы.
Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28.
Седьмой вариант задания
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение:
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30.
Восьмой вариант задания
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Решение:
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18.
Девятый вариант задания
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Решение:
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20.
Десятый вариант задания
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
Решение:
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
Одиннадцатый вариант задания (демонстрационный вариант ОГЭ 2017)
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
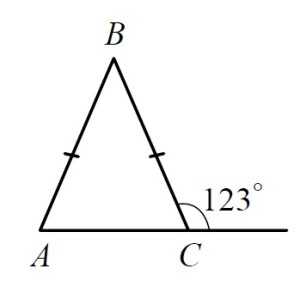
Решение:
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
Ответ: 57°
spadilo.ru
Разбор и решение задания №25 ОГЭ по математике
Четырехугольники
Разбор типовых вариантов заданий №25 ОГЭ по математике
Первый вариант задания
Окружности с центрами в точках I и J пересекаются в точках А и В, причём точки I и J лежат по одну сторону от прямой АВ. Докажите, что прямые АВ и IJ перпендикулярны.
Алгоритм решения:
- Делаем чертеж.
- Определяем место расположения точек I и J.
- Используем свойство серединного перпендикуляра.
- Делаем вывод.
Решение:
1. Делаем чертеж, согласно условия:
2. Определяем место расположения точек I и J:
Точка I равноудалена от точек A и B. Аналогично, точка J равноудалена от концов отрезка AB.
3. По свойству геометрического места точек, равноудаленных от концов отрезка, эти точки расположены на серединном перпендикуляре к отрезку AB.
А если две точки I и J лежат на серединном перпендикуляре, прямая IJ совпадает с ним.
Следовательно, прямые IJ и АВ перпендикулярны.
Второй вариант задания
Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.
Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники CEF и DEF и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника CED.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж по условию задачи:
2. Рассмотрим треугольники CEF и DEF и установим их равенство:
У них CE=DE, как радиусы окружности с центром в точке Е,
Аналогично, CF = DF, как радиусы окружности с центром в точке F.
EF – общая сторона.
Значит, данные треугольники равны.
Тогда по свойству равных фигур .
Рассмотрим треугольник CED. У него CE=DE, поскольку это соответствующие стороны равных фигур. Значит, треугольник равнобедренный.
EF – биссектриса угла E. следовательно, EF – высота по свойству равнобедренного треугольника. Отсюда следует, что .
Утверждение доказано.
Третий вариант задания
Окружности с центрами в точках М и N пересекаются в точках S и Т, причём точки М и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники SMN и TMN и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника SMT.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж согласно условия задачи.
2. Рассмотрим треугольники SMN и TMN. Они равны по трем сторонам:
SM=TM как радиусы окружности с центром в точке М,
SN=TN как радиусы окружности с центром в точке N,
а MN – общая сторона (см. рисунок выше).
3. По свойству равных фигур, , как соответствующие углы в равных треугольниках.
4. Рассмотрим треугольник SMT.
В нем по доказанному выше , а значит MN – биссектриса угла M. Данный треугольник равнобедренный с равными сторонами SM и TM.
Следовательно, MN – высота по свойству биссектрисы равнобедренного треугольника. Следовательно, .
Утверждение доказано.
Четвертый вариант задания
В выпуклом четырёхугольнике ABCD углы ВСА и BDA равны. Докажите, что углы ABD и ACD также равны.
Алгоритм решения:
- Выполняем рисунок по условию задачи.
- Устанавливаем подобие треугольников BOC и AOD.
- Записываем соотношение для сторон.
- Устанавливаем подобие треугольников AOB и DOC.
- Делаем вывод.
Решение:
1. Выполняем чертеж по условию задачи:
2. Рассматриваем треугольники BOC и AOD.У них:
углы ВСА и BDA равны по условию задачи,
углы BOC и AOD равны как вертикальные.
Значит, треугольники BOC и AOD подобны по двум углам.
3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон:
4. Рассматриваем треугольники AOB и DOC. У них:
углы AOB и DOC равны как вертикальные.
Следовательно, данные треугольники подобны.
По свойству подобных фигур соответствующие углы в треугольниках равны. Значит, , а поскольку эти углы совпадают с углами ABD и ACD , то .
Утверждение доказано.
Пятый вариант задания
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC= ED. Докажите, что данный параллелограмм — прямоугольник.
Доказательство:
Рассмотрим треугольники BEC и AED. BE = EA, так как E — середина стороны AB по условию. EC= ED по условию, а BC = AD по свойству параллелограмма (противолежащие стороны равны). Таким образом, BE = EA, EC= ED, BC = AD. Следовательно, треугольники BEC и AED равны по трём сторонам.
В равных треугольниках — равные элементы. Значит, углы CBE и DAE равны. Так как их сумма равна 180° по свойству параллелограмма , то углы равны 90° (180 / 2 = 90 ) .
Следовательно, данный параллелограмм — прямоугольник.
spadilo.ru
Разбор и решение задания №24 ОГЭ по математике
Решение:
1. Выполняем соответствующий чертеж:
2. Трапеция ABCD имеет основаниями стороны ВС и AD, значит, они параллельны. Тогда в ней внутренние односторонние при пересечении прямых, которые содержат эти основания, секущей АВ. Следовательно, они удовлетворяют равенству: .
3. По построению, заданному условием задачи AF и BF являются биссектрисы данных углов. Тогда в треугольнике ABF
Отсюда получаем:
Таким образом, треугольник AFB прямоугольный, а сторона AB – его гипотенуза.
4. Используем теорему Пифагора:
Отсюда АВ=25.
Ответ 25.
Шестой вариант задания
Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 20, BF = 15.
Алгоритм решения:
- Делаем чертеж.
- Рассматриваем углы трапеции и проведенные биссектрисы.
- Определяем вид треугольника AFB.
- Находим длину АВ.
- Записываем ответ.
Решение:
1. Выполняем рисунок, соответствующий данному условию.
2. Рассмотрим трапецию ABCD. В ней как основания. Углы А и В составляют в сумме 1800, как углы при основаниях. Отсюда следует, что как соседние при двух основаниях. По условию лучи AF и BF – биссектрисы этих углов, тогда их сумма
3. Рассматриваем треугольник ABF. В нем угол по свойству углов треугольника, т.е. построенный треугольник AFB – прямоугольный. И гипотенузой в нем является сторона AB.
4. Вычислим сторону по теореме Пифагора: АВ2 = AF2 + BF2
Следовательно, АВ=25.
Ответ: 25.
spadilo.ru
Решение заданий ОГЭ 1 по математике
Раздел сайта ШпаргалкаЕГЭ, посвященный ОГЭ (ГИА) часть 1, освещает одну из наиболее сложных математических тематик. Речь идет о таком подразделе, как Вычисления. Преобразование алгебраических выражений. При этом следует отметить, что специфика ресурса позволяет не просто ознакомиться с текстом задания и найти ответы и решения. В распоряжении пользователей находится целый арсенал приспособлений, позволяющий максимально освоить материал, которому посвящено 1 задание ОГЭ по математике.
Во-первых, к каждой задаче прикреплен качественный видеоролик, в котором подробно разъяснен определенный вариант решения. Во-вторых, на сайте размещены специальные инструменты, позволяющие ускорить проведение подсчетов. Кроме того, каждый учащийся может поработать с тренировочными заданиями, которые позволяют прочно закрепить изученный материал.
Таким образом, если вас интересует любая информация по ОГЭ (ГИА) 2016/2017 – задание No 1, сайт ШпаргалкаЕГЭ станет вашим незаменимым помощником и путеводителем по бескрайним просторам алгебраических выражений.
Отзывы учеников
-
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.
