Как решать задачи по геометрии огэ 9 класс – . , | Pandia.ru

тренинг по геометрии в 9 классе «Решение планиметрических задач из ОГЭ»

Решение планиметрических задач

из ОГЭ

Урок-тренинг по геометрии в 9 классе

Открытый урок-тренинг по геометрии в 9 классе

«Решение планиметрических задач из ОГЭ»

Цели урока:

• отработка умений решать задачи по планиметрии, предлагаемые в тестах ОГЭ;

• развитие внимания, памяти, логического мышления, интереса к предмету,

математически грамотной речи;

• воспитание трудолюбия, усидчивости, чувства ответственности,

познавательной активности.

Тип урока: урок-тренинг.

Оборудование: компьютер, мультимедийный проектор, сборник «Математика.

9 класс. Подготовка к ОГЭ – 2015» под редакцией Ф.Ф.Лысенко,

С.Ю.Кулабухова.

Ход урока

I. Организационный момент.

Сегодня у нас с вами урок по решению геометрических задач из ОГЭ, поскольку на экзамене по математике есть модуль «Геометрия». Занятие будет проходить в виде тренинга. Но сначала давайте еще раз скажем, почему важно изучать геометрию?

Геометрия – это не просто наука о свойствах геометрических

фигур. Геометрия – это целый мир, который окружает нас с

самого рождения. Ведь все, что мы видим вокруг, так или иначе

относится к геометрии, ничто не ускользает от ее внимательного

взгляда. Геометрия помогает человеку идти по миру с широко

открытыми глазами, учит внимательно смотреть вокруг и видеть

красоту обычных вещей, смотреть и думать, думать и делать

выводы.

В качестве эпиграфа нашего урока мы возьмем слова известного математика Пойа:

«Лучше решить одну задачу несколькими способами,

чем несколько задач – одним»

II. Актуализация знаний учащихся.

Задания на экзамене предлагаются каждый год разные. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. Кроме того, в экзаменационной работе есть задание № 13, проверяющее, как ученик ориентируется в теоретическом материале. В каждом варианте в задании №13 предлагается по три вопроса, и надо из них выбрать либо верные утверждения, либо неверные. Иногда из-за одного пропущенного слова меняется смысл сказанного. Поэтому мы начнём наш тренинг с проверки знания теории.

На слайдах вы увидите задания, предлагавшиеся на экзамене в прошлом году, а также задания из сборника для подготовки к экзамену в 2015 году.

Какие из следующих утверждений верны?

1. Через любые три точки на плоскости можно провести окружность.

Неверно.

2. Площадь трапеции равна половине высоты, умноженной на разность

оснований.

Неверно.

3. Существует прямоугольник, диагонали которого взаимно перпендикулярны.

Верно.

4. В любой четырехугольник можно вписать окружность.

Неверно.

5. Отношение площадей подобных треугольников равно коэффициенту подобия.

Неверно.

6. Площадь параллелограмма равна половине произведения его диагоналей.

Неверно.

7. Отношение стороны треугольника к синусу противолежащего угла равно

диаметру описанной окружности.

Верно.

8. Одна из высот прямоугольного треугольника всегда делит его на два

подобных треугольника.

Верно.

9. Биссектрисы любого треугольника точкой пересечения делятся в отношении

2 : 1, считая от вершины.

Неверно.

10. Угол, вписанный в окружность, равен соответствующему центральному углу,

опирающемуся на ту же дугу.

Неверно.

11. Две прямые, перпендикулярные третьей прямой, параллельны друг другу.

Верно.

12. Биссектрисы треугольника пересекаются в центре вписанной в него

окружности.

Верно.

III. Тренинг по решению задач.

Начнем мы с вами с решения задач из первой части экзамена, т.е. с задач, оцениваемых в 1 балл. Вы знаете, что на экзамене при решении этих задач надо только дать правильный ответ, записав его в бланк ответов.

Задача на 1 балл

В треугольнике АВС точка К – середина стороны ВС, точка Р лежит на отрезке АК, АР = 10, РК = 5, ВР = 9. Найдите ВМ.

Решение.

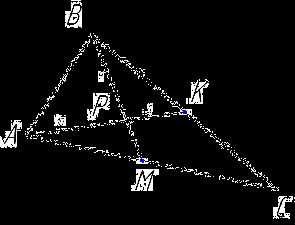
Т. к. точка К – середина стороны ВС, то АК – медиана. Точка Р делит АК в отношении 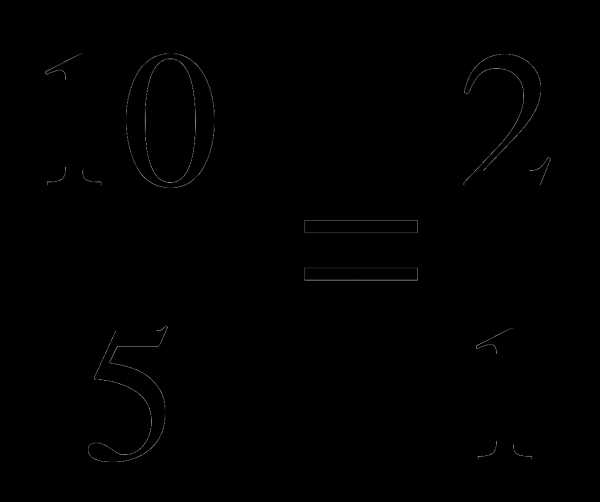. Значит, точка Р – точка пересечения медиан треугольника.

Следовательно, ВМ тоже медиана и 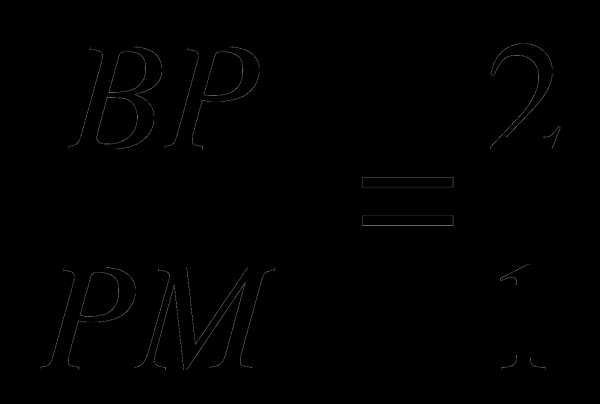РМ = 4,5.

ВМ = ВР + РМ = 9 + 4,5 = 13,5.

Ответ: 13,5.

Задача на 1 балл

Найдите длину отрезка АN, если радиус изображенной на рисунке окружности ОК =3, АК = 2.

Решение.

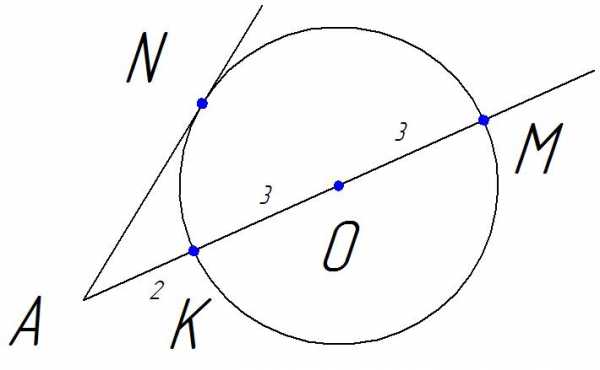
1 способ.

АN – касательная к окружности, АМ – секущая. Если из точки А к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки А до точки касания равен произведению отрезков секущей от точки А до точек пересечения секущей с окружностью. АN² = АК ∙ АМ = 2 ∙ 8 = 16 АN = 4.

2 способ

Проведем радиус ОN. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Значит, ∆АNО – прямоугольный. АО = 5, NО = 3. По теореме Пифагора .

3 способ

. По основному тригонометрическому тождеству .

. .

Ответ: 4.

Во второй части экзаменационной работы есть задачи на 2, 3 и 4 балла.

Задача на 2 балла

В параллелограмме АВСD биссектриса острого угла С пересекает сторону АВ в точке М. Найдите расстояние от В до прямой СМ, если СМ = 30, СВ = 17.

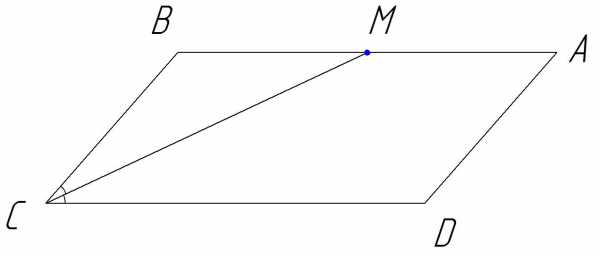
Решение.

Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой. Проведем из точки В к прямой СМ перпендикуляр ВН.

Значит, ρ(В; СМ) = ВН.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Значит, ∆СВМ – равнобедренный. В равнобедренном треугольнике высота, проведенная к основанию, является медианой. Следовательно, ВН – медиана, т.е.

СН = НМ = 15. По теореме Пифагора

ВН = .

Ответ: 8.

Задача на 3 балла

В трапеции АВСD точка К – середина основания АВ. Известно, что СК = КD. Докажите, что трапеция равнобедренная.

Решение.

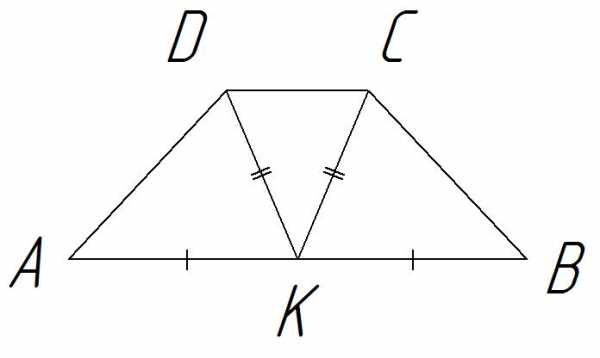
1 способ

Т. к. СК = КD, то ∆СКD – равнобедренный, а в равнобедренном треугольнике углы при основании равны . как накрест лежащие при пересечении параллельных прямых DС и АВ секущей DК, как накрест лежащие при пересечении параллельных прямых DС и АВ секущей СК.

Т. к. , то .

Рассмотрим ∆АКD и ∆ВКС. АК = КВ, DК = СК – по условию, − по доказанному, то ∆

АКD = ∆ВКС по первому признаку равенства треугольников.

Из равенства треугольников следует, что АD= СВ трапеция АВСD – равнобедренная.

2 способ

Проведем высоты DН и СМ. ∆DКН = ∆СКМ по гипотенузе и катету (DН = СМ как расстояния между параллельными прямыми, DК = СК – по условию)

. (Дальше как в первом способе).

3 способ

Из равенства ∆DКН и ∆СКМ следует, что НК = КМ.

.

Значит, прямоугольные треугольники АDН и ВСМ равны по двум катетам

(DН = СМ как расстояния между параллельными прямыми, АН = МВ

по доказанному). Из равенства треугольников следует, что АD= СВ трапеция АВСD – равнобедренная.

Задача на 4 балла

В равнобедренном треугольнике АВС стороны АВ = ВС = 10, соsАВС = 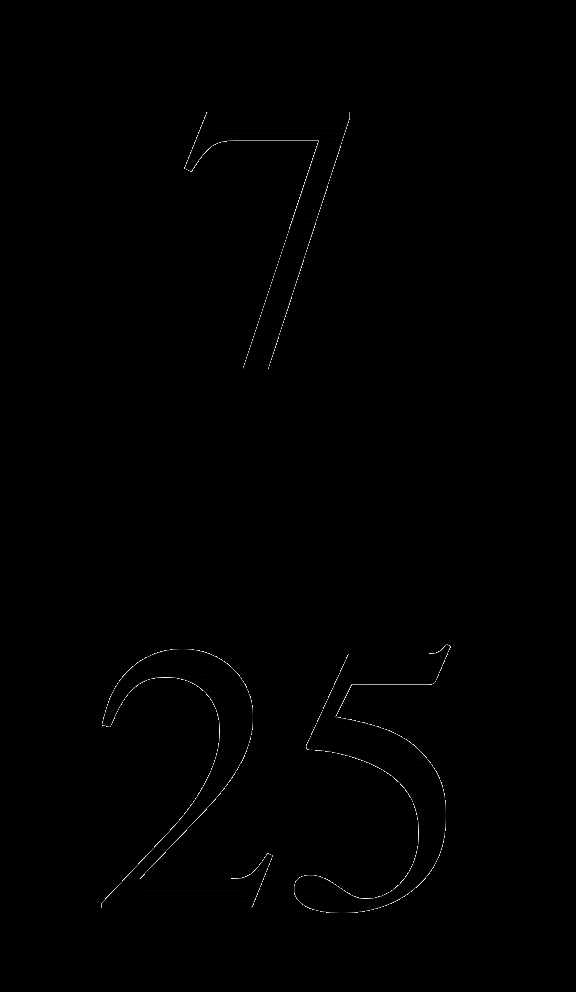. Найдите радиус окружности, вписанной в треугольник.

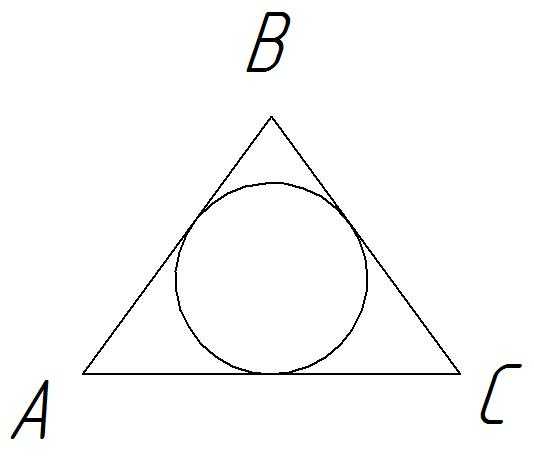
Решение.

По теореме косинусов

1 способ

Радиус окружности, вписанной в треугольник, можно найти с помощью формулы 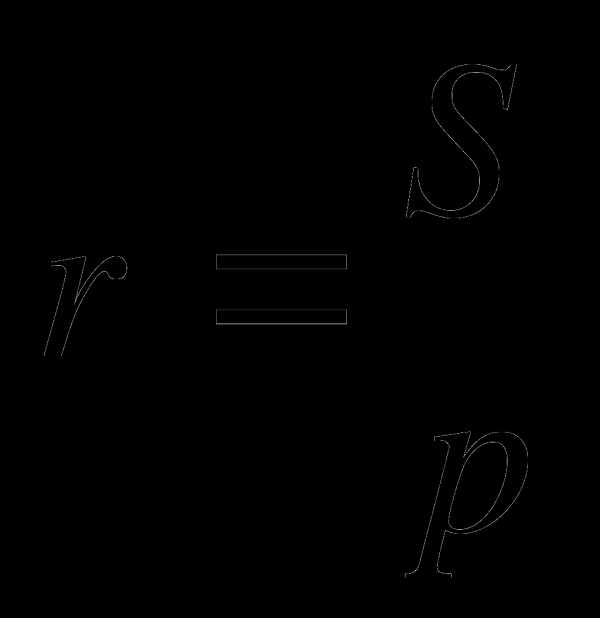. Площадь данного треугольника можно найти следующими способами:

1.

; 2. ; 3. .

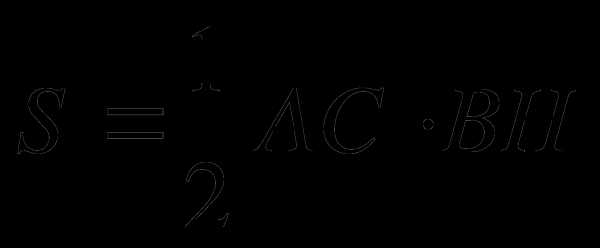
р = . . Значит, .

2 способ.

Мы знаем, что центром окружности, вписанной в треугольник, является точка пересечения его биссектрис. Проведем биссектрису ВН. Т. к. в равнобедренном треугольнике высота, медиана и биссектриса, проведенные к основанию, совпадают, то биссектриса ВН будет и медианой, и высотой.

.

Из ∆АВН по теореме Пифагора .

Проведем радиус ОD в точку касания. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Прямоугольные треугольники АВН и ОВD подобны по двум углам (угол АВН – общий, углы Н и D равны как прямые). В подобных треугольниках сходственные стороны пропорциональны.

Пусть ОН= х, тогда ВО = 8 – х.

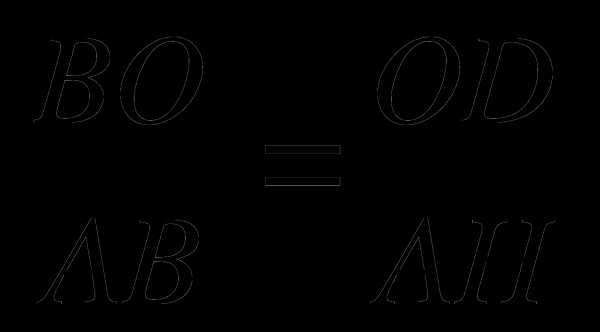
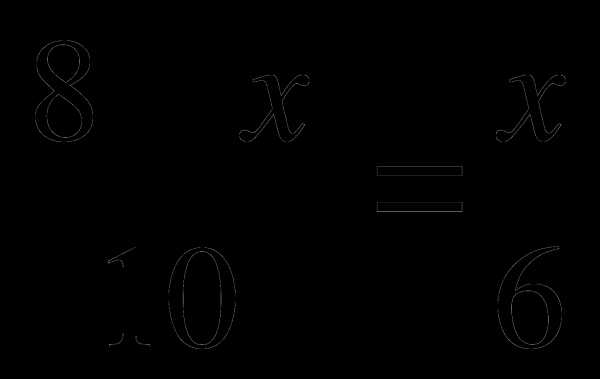
х = 3. Значит, радиус ВО = 3.

3 способ

Начало такое же, как во 2-м способе. Только рассмотрим не подобные треугольники, а прямоугольный треугольник ОВD.

Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.

Пусть ОН = ОD = х, тогда ВО = 8 – х. По теореме Пифагора имеем уравнение:

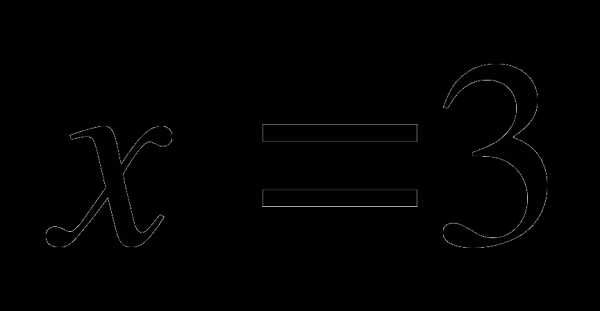
Значит, радиус ВО = 3.

4 способ

Проведем ВН (не будем проводить ОD, но точку касания D обозначим).

Из второго способа .

Из ∆АВН по теореме Пифагора .

Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.

По теореме о касательной и секущей ВD² = ВМ ∙ ВН

16 = ВМ ∙ 8

ВМ = 2

МН = 2r = 8 – 2 = 6 r = 3.

Значит, радиус ВО = 3.

5 способ

Проведем ВН и АО. Т.к. центром окружности, вписанной в треугольник, является точка пересечения биссектрис, то АО – биссектриса угла А, а значит, и биссектриса треугольника АВН. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

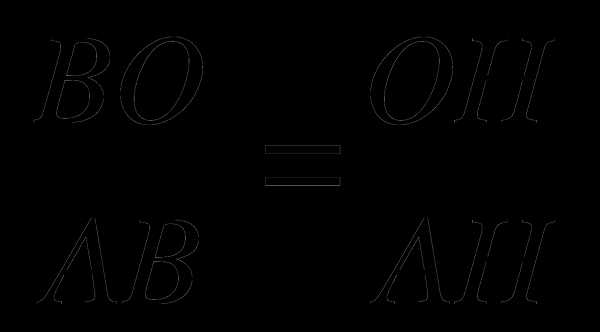. Пусть ОН = х, тогда ВО = 8 – х.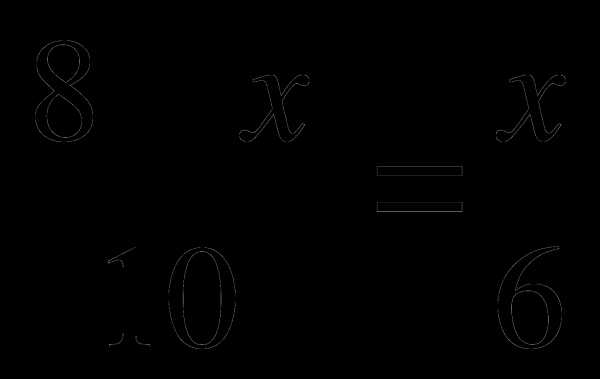 16х = 48 х = 3.

Значит, радиус ВО = 3.

6 способ

Из ∆АВН: ВD = 4.

Из ∆ОВD: ОD = 3.

Значит, радиус ВО = 3.

Ответ: 3.

Домашнее задание.

Задача на 2 балла

Найдите углы вписанного в окружность четырехугольника, если три угла (в последовательном порядке) относятся как 3 : 7 : 5. В ответе укажите больший из них в градусах.

Задача на 4 балла

В равнобедренную трапецию с верхним основанием, равным 2, вписана окружность радиуса 2. Найдите нижнее основание трапеции.

Пожелания и советы учащимся

• Помни и понимай, что подготовка к ОГЭ – это тяжелый труд, где

результат будет прямо пропорционален времени, потраченному на

активную подготовку к экзамену.

• Выполняй как можно больше различных тестов по предмету.

• Тренируйся с секундомером в руках, засекай время выполнения тестов.

• Готовясь к экзаменам, мысленно рисуй себе картину успеха.

Рефлексия

Подведение итогов

Выставление оценок

Литература

1. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов и др. − М. : Просвещение, 2009.

2. Математика. 9 класс. Подготовка к ОГЭ – 2015. Учебно-тренировочные тесты по новой демоверсии / Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова – Ростов-на-Дону: Легион, 2015.

infourok.ru

Открытый урок в 9 классе «Подготовка к ОГЭ по геометрии»

Урок повторения и коррекции знаний

по геометрии в 9 классе

Решение геометрических задач при

подготовке к ГИА

Учитель математики Евдокимова Наталья Ивановна

п. Красноярский 2014 год

Тип урока: Урок повторения и коррекции знаний.

Методы:

— частично-поисковый;

— системные обобщения;

— самооценка.

Цель урока: Повторить знания по теории геометрии, продолжить работу по решению геометрических задач для подготовки к ГИА.

• обучающие – повторить знания по теории геометрии, продолжить работу по подготовке к ГИА. Проверка знаний и их коррекция.

• развивающие – развивать внимание, зрительную память, логическое мышление, интуицию, математическую речь, умение анализировать свои ошибки.

• воспитательные – воспитывать дисциплинированность, высокую работоспособность и организованность, чувство патриотизма, умения проводить оценку и самооценку знаний и умений, уважение друг к другу, развивать коммуникативные компетенции.

Структура урока.

1°. Организационный момент.

2°. Повторение теоретического материала (модуль № 13).

3°. Актуализация опорных знаний. Работа по готовым чертежам (модуль № 9,10, 11)

Индивидуально-дифференцированная работа (карточки № 1-4)

4°. Физкультминутка.

5°. Работа по готовым чертежам (продолжение), (модуль № 12)

6°. Решение задач на доске и в тетради, карточка — задания на урок

7⁰. Итог урока. Задание на дом.

8°. Рефлексия

Формы организации труда:

— индивидуальная;

— фронтальная;

— индивидуально-дифференцированная.

Необходимое оборудование и материалы:

• ноутбук;

• экран;

• проектор;

• слайды;

• карточки

Ход урока

1. Организационный момент.(2 мин.)

В Сочи прошло яркое масштабное событие – XXII Олимпийские зимние игры. Это был праздник для всей страны.

В Сочи побывало более полумиллиона гостей, тысячи спортсменов, множество журналистов и тренеров. Российская Олимпиада произвела ярчайшее впечатление на наших гостей, они надолго запомнят её. Мы представили себя, нашу культуру и нашу страну так, что весь мир будет говорить о нас на протяжении нескольких десятков лет.

Ребята! У нас тоже сегодня гости, и от того как вы себя покажите на уроке, будет зависеть, запомнят ли они нас и захотят ли ещё к нам приехать.

Я надеюсь, что этот урок пройдёт интересно, с большой пользой для всех. Уверена, что на сегодняшнем уроке вы будете активны, внимательны и получите знания, которые пригодятся вам для успешной сдачи ГИА.

Наш урок посвящен Олимпиаде 2014 и зимним видам спорта.

Тема урока: «Решение геометрических задач при подготовке к ГИА» (слайд 1), а девизом урока будут слова Д. Пойа: «Умение решать задачи – такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения» (слайд 2)

ГИА по геометрии включает в себя: 1.Задания тестового характера. 2.Задачи на нахождение нужных элементов. 3. Задачи на доказательство (слайд 3)

Напомню, что в модуле «Геометрия» нужно решить как минимум два задания. Это позволит рассчитывать выпускнику на получение удовлетворительной оценки.

2. Чтобы быть спортсменом нужно не только быть сильным и ловким, но и хорошо знать математику. Начнем с разминки как все спортсмены. Повторим теоретический материал. (слайды 4,5,6) (8мин) Ответы: нет, да, да, да, нет, да, нет, да, нет, да, нет, да, да.

3. Спортсмены в свою очередь тоже готовятся, усиленно тренируются и мечтают о том, чтобы одержать больше побед. А наши с вами победы – это правильно выполненные задания.

Актуализация опорных знаний. Работа по готовым чертежам (слайды 7,8,9,11,12) (13мин) Ответы: №9 – 74; 40; №10 – 4; 117; №11 – 15; 42; №12 – 1,2; .

Четверо учащихся выполняют задания по индивидуально-дифференцированным карточкам. Приложение 1 (Ответы: к1-AC=8; к2— MEF=PEF по трём сторонам, КF –серединный перпендикуляр, по т. каждая точка серединного перпендикуляра к отрезку равноудалена от концов отрезка MK=PK; к3 -32°; к4 -28)

4. Физкультминутка. Какая из картинок лишняя? (конькобежец) (слайд 10) (2мин)

Какую геометрическую фигуру описывает конькобежец, пробегая свою дистанцию? (овал)

Встаньте. Опишите овал глазами, головой, правым плечом, левым плечом, туловищем, правой ногой, левой ногой.

5. Продолжение решения задач по готовым чертежам (слайд 11, 12)

6. Решение задач на доске и в тетради (карточки с заданиями на урок) (15мин) Приложение 2

— Что является важным при решении задач?

— Знание определений, аксиом, теорем и свойств геометрических фигур.

Задача

Задача №25

В параллелограмме ABCD точка К – середина ВС. Известно, что АК=КD, Докажите, что данный параллелограмм – прямоугольник.

Дано: ABCD – параллелограмм

BK=CK

AK=DK

Доказать: ABCD – прямоугольник

Доказательство:

1) треугольник AKD: угол1 равен углу2(как углы при основании равнобедренного треугольника)

2)  угол1 равен углу3, угол2 равен углу4(как накрест лежащие углы при параллельных прямых и секущей)

3) треугольник АКВ равен треугольнику DKC (по двум сторонам и углу между ними)

4) угол В равен углу С(как внутренние односторонние при параллельных прямых и секущей),

5) Сумма односторонних углов равна 180°, следовательно угол В и угол С равны по 90°, то ABCD – прямоугольник.

Молодцы! Все справились правильно с этими заданиями.

Продолжим двигаться к победе.

Дополнительно:

Задача № 24А

Биссектриса тупого угла B параллелограмма ABCD делит сторону AD в отношении 1:2, считая от вершины A. Найдите сторону AB, если полупериметр параллелограмма равен 40. (Ответ: 10)

Задача № 24Б

Найдите угол ACD, если его сторона СА касается окружности, а дуга AD окружности, заключенная внутри этого угла, равна 116°. (Ответ:26)

6. Итог урока. Задание на дом (2мин)

Участие в олимпийских играх это достижения спортсменов, а наши достижения это успешная учеба в школе, получение прочных знаний. Это мы сегодня на уроке доказали. Я очень довольна вашей работой.

Для домашнего задания у нас есть Пьедестал Успеха (слайд 13) Приложение 3

7. Рефлексия. На финишной прямой. (слайд 14) (3мин)

infourok.ru

Конспект урока-тренинга по геометрии «Решение планиметрических задач из ОГЭ» (9 класс)

Урок-тренинг по геометрии в 9 классе

«Решение планиметрических задач из ОГЭ»

Цель и задачи урока:

• отработка умений решать задачи по планиметрии, предлагаемые в тестах ОГЭ;

• развитие внимания, памяти, логического мышления, интереса к предмету,

математически грамотной речи;

• воспитание трудолюбия, усидчивости, чувства ответственности,

познавательной активности.

Тип урока: урок-тренинг.

Оборудование: компьютер, мультимедийный проектор, сборник «Математика.

9 класс. Подготовка к ОГЭ – 2015» под редакцией Ф.Ф.Лысенко,

С.Ю.Кулабухова.

Ход урока

I. Организационный момент.

Сегодня у нас с вами урок по решению геометрических задач из ОГЭ, поскольку на экзамене по математике есть модуль «Геометрия». Занятие будет проходить в виде тренинга. Но сначала давайте еще раз скажем, почему важно изучать геометрию?

Геометрия – это не просто наука о свойствах геометрических

фигур. Геометрия – это целый мир, который окружает нас с

самого рождения. Ведь все, что мы видим вокруг, так или иначе

относится к геометрии, ничто не ускользает от ее внимательного

взгляда. Геометрия помогает человеку идти по миру с широко

открытыми глазами, учит внимательно смотреть вокруг и видеть

красоту обычных вещей, смотреть и думать, думать и делать

выводы.

В качестве эпиграфа нашего урока мы возьмем слова известного математика Пойа:

«Лучше решить одну задачу несколькими способами,

чем несколько задач – одним»

II. Актуализация знаний учащихся.

Задания на экзамене предлагаются каждый год разные. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. Кроме того, в экзаменационной работе есть задание № 13, проверяющее, как ученик ориентируется в теоретическом материале. В каждом варианте в задании №13 предлагается по три вопроса, и надо из них выбрать либо верные утверждения, либо неверные. Иногда из-за одного пропущенного слова меняется смысл сказанного. Поэтому мы начнём наш тренинг с проверки знания теории.

На слайдах вы увидите задания, предлагавшиеся на экзамене в прошлом году, а также задания из сборника для подготовки к экзамену в 2015 году.

Какие из следующих утверждений верны?

1. Через любые три точки на плоскости можно провести окружность.

Неверно.

2. Площадь трапеции равна половине высоты, умноженной на разность

оснований.

Неверно.

3. Существует прямоугольник, диагонали которого взаимно перпендикулярны.

Верно.

4. В любой четырехугольник можно вписать окружность.

Неверно.

5. Отношение площадей подобных треугольников равно коэффициенту подобия.

Неверно.

6. Площадь параллелограмма равна половине произведения его диагоналей.

Неверно.

7. Отношение стороны треугольника к синусу противолежащего угла равно

диаметру описанной окружности.

Верно.

8. Одна из высот прямоугольного треугольника всегда делит его на два

подобных треугольника.

Верно.

9. Биссектрисы любого треугольника точкой пересечения делятся в отношении

2 : 1, считая от вершины.

Неверно.

10. Угол, вписанный в окружность, равен соответствующему центральному углу,

опирающемуся на ту же дугу.

Неверно.

11. Две прямые, перпендикулярные третьей прямой, параллельны друг другу.

Верно.

12. Биссектрисы треугольника пересекаются в центре вписанной в него

окружности.

Верно.

III. Тренинг по решению задач.

Начнем мы с вами с решения задач из первой части экзамена, т.е. с задач, оцениваемых в 1 балл. Вы знаете, что на экзамене при решении этих задач надо только дать правильный ответ, записав его в бланк ответов.

Задача на 1 балл

В треугольнике АВС точка К – середина стороны ВС, точка Р лежит на отрезке АК, АР = 10, РК = 5, ВР = 9. Найдите ВМ.

Решение.

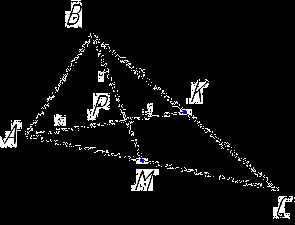
Т. к. точка К – середина стороны ВС, то АК – медиана. Точка Р делит АК в отношении 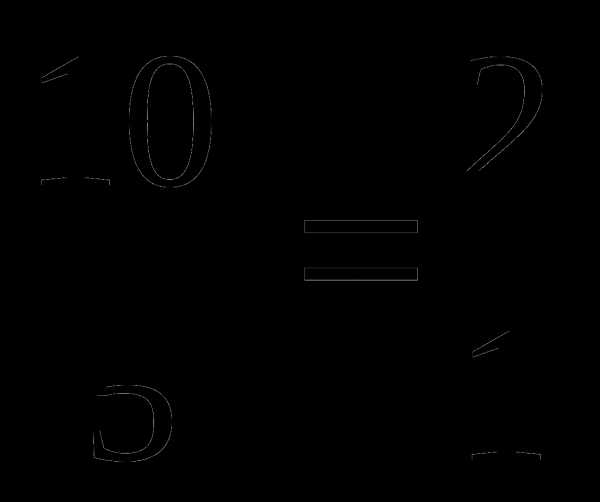. Значит, точка Р – точка пересечения медиан треугольника.

Следовательно, ВМ тоже медиана и 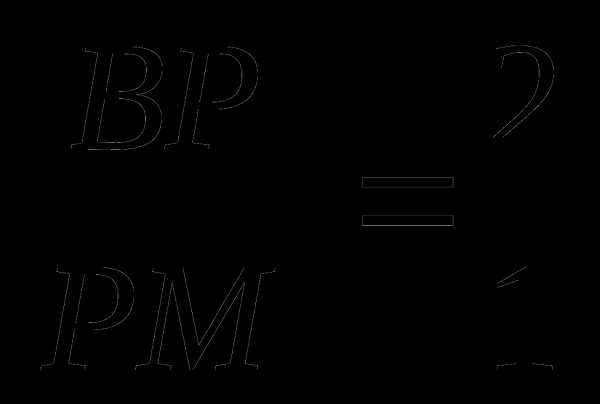РМ = 4,5.

ВМ = ВР + РМ = 9 + 4,5 = 13,5.

Ответ: 13,5.

Задача на 1 балл

Найдите длину отрезка АN, если радиус изображенной на рисунке окружности ОК =3, АК = 2.

Решение.

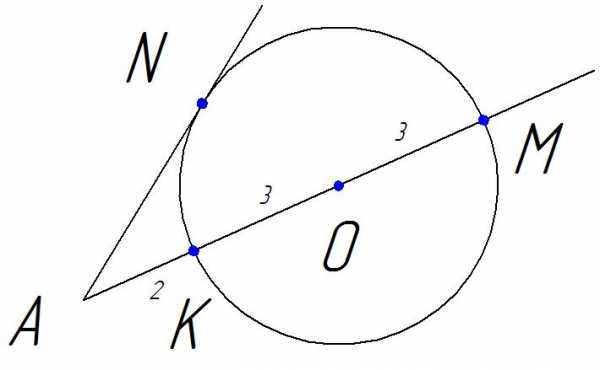
1 способ.

АN – касательная к окружности, АМ – секущая. Если из точки А к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки А до точки касания равен произведению отрезков секущей от точки А до точек пересечения секущей с окружностью. АN² = АК ∙ АМ = 2 ∙ 8 = 16 АN = 4.

2 способ

Проведем радиус ОN. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Значит, ∆АNО – прямоугольный. АО = 5, NО = 3. По теореме Пифагора .

3 способ

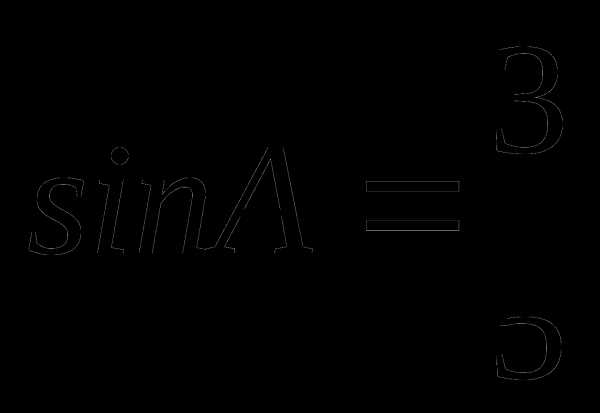. По основному тригонометрическому тождеству .

. .

Ответ: 4.

Во второй части экзаменационной работы есть задачи на 2, 3 и 4 балла.

Задача на 2 балла

В параллелограмме АВСD биссектриса острого угла С пересекает сторону АВ в точке М. Найдите расстояние от В до прямой СМ, если СМ = 30, СВ = 17.

Решение.

Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой. Проведем из точки В к прямой СМ перпендикуляр ВН.

Значит, ρ(В; СМ) = ВН.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Значит, ∆СВМ – равнобедренный. В равнобедренном треугольнике высота, проведенная к основанию, является медианой. Следовательно, ВН – медиана, т.е.

СН = НМ = 15. По теореме Пифагора ВН = .

Ответ: 8.

Задача на 3 балла

В трапеции АВСD точка К – середина основания АВ. Известно, что СК = КD. Докажите, что трапеция равнобедренная.

Решение.

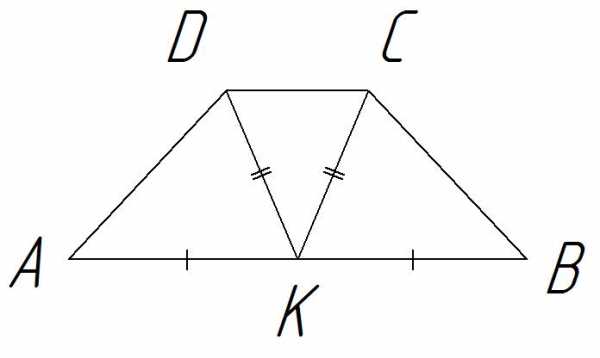
1 способ

Т. к. СК = КD, то ∆СКD – равнобедренный, а в равнобедренном треугольнике углы при основании равны . как накрест лежащие при пересечении параллельных прямых DС и АВ секущей DК, как накрест лежащие при пересечении параллельных прямых DС и АВ секущей СК.

Т. к. , то .

Рассмотрим ∆АКD и ∆ВКС. АК = КВ, DК = СК – по условию, − по доказанному, то ∆АКD = ∆ВКС по первому признаку равенства треугольников.

Из равенства треугольников следует, что АD= СВ трапеция АВСD – равнобедренная.

2 способ

Проведем высоты DН и СМ. ∆DКН = ∆СКМ по гипотенузе и катету (DН = СМ как расстояния между параллельными прямыми, DК = СК – по условию)

. (Дальше как в первом способе).

3 способ

Из равенства ∆DКН и ∆СКМ следует, что НК = КМ.

.

Значит, прямоугольные треугольники АDН и ВСМ равны по двум катетам

(DН = СМ как расстояния между параллельными прямыми, АН = МВ по доказанному). Из равенства треугольников следует, что АD= СВ трапеция АВСD – равнобедренная.

Задача на 4 балла

В равнобедренном треугольнике АВС стороны АВ = ВС = 10, соsАВС = 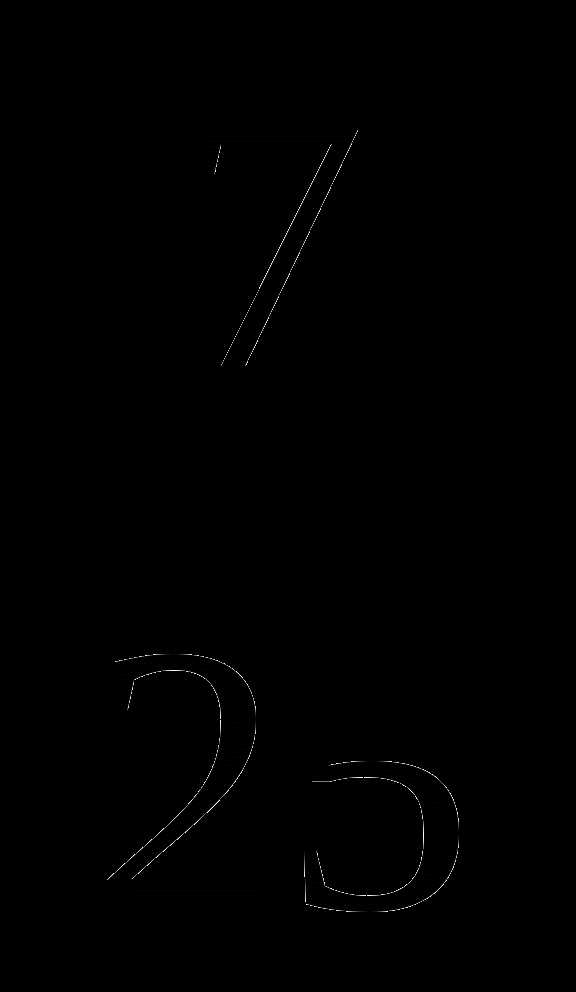. Найдите радиус окружности, вписанной в треугольник.

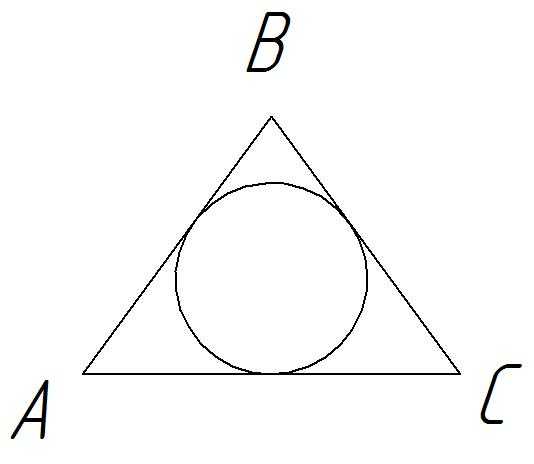
Решение.

По теореме косинусов

1 способ

Радиус окружности, вписанной в треугольник, можно найти с помощью формулы 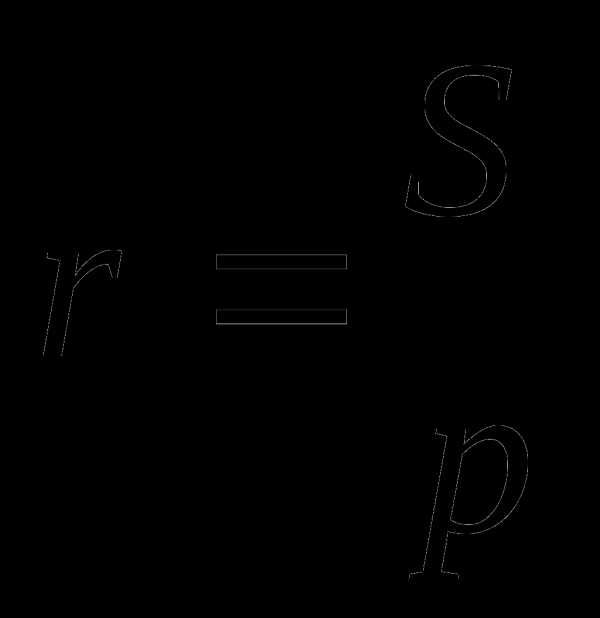. Площадь данного треугольника можно найти следующими способами:

1. ; 2. ; 3. .

р = . . Значит, .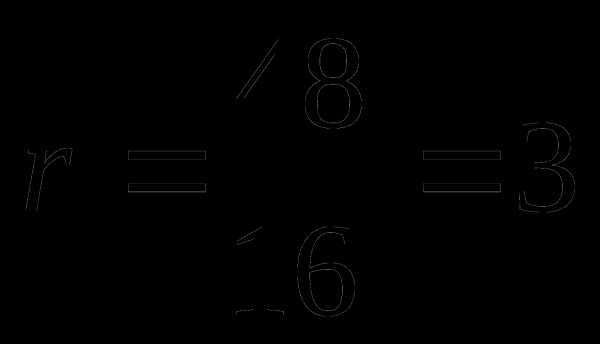

2 способ.

Мы знаем, что центром окружности, вписанной в треугольник, является точка пересечения его биссектрис. Проведем биссектрису ВН. Т. к. в равнобедренном треугольнике высота, медиана и биссектриса, проведенные к основанию, совпадают, то биссектриса ВН будет и медианой, и высотой.

.

Из ∆АВН по теореме Пифагора .

Проведем радиус ОD в точку касания. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Прямоугольные треугольники АВН и ОВD подобны по двум углам (угол АВН – общий, углы Н и D равны как прямые). В подобных треугольниках сходственные стороны пропорциональны.

Пусть ОН= х, тогда ВО = 8 – х.

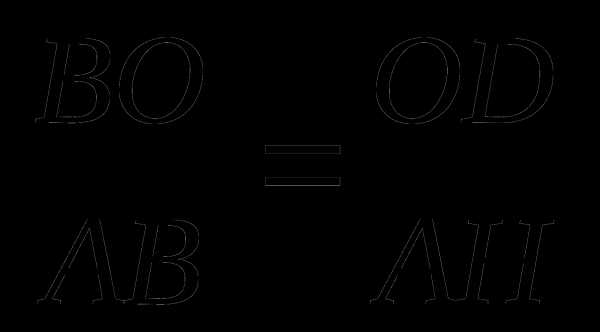
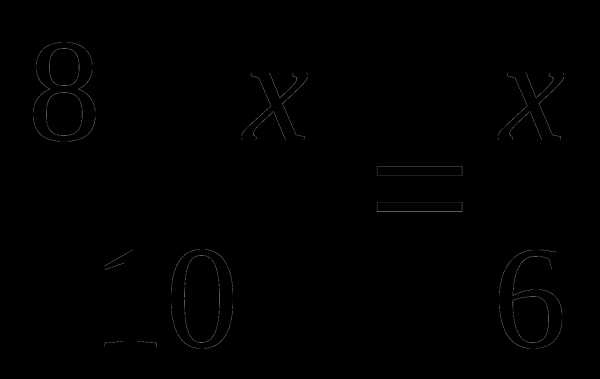
х = 3. Значит, радиус ВО = 3.

3 способ

Начало такое же, как во 2-м способе. Только рассмотрим не подобные треугольники, а прямоугольный треугольник ОВD.

Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.

Пусть ОН = ОD = х, тогда ВО = 8 – х. По теореме Пифагора имеем уравнение:

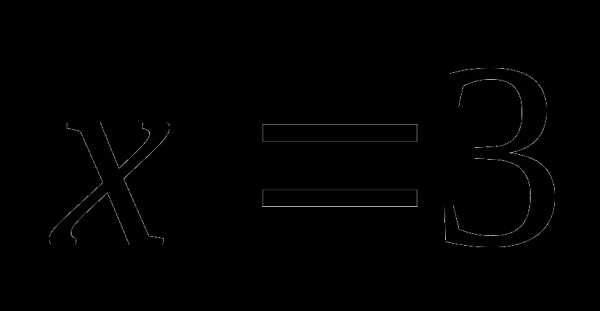
Значит, радиус ВО = 3.

4 способ

Проведем ВН (не будем проводить ОD, но точку касания D обозначим).

Из второго способа .

Из ∆АВН по теореме Пифагора .

Отрезки касательных к окружности, проведенные из одной точки, равны. Значит, АD = АН = 6. ВD = 10 – 6 = 4.

По теореме о касательной и секущей ВD² = ВМ ∙ ВН

16 = ВМ ∙ 8

ВМ = 2

МН = 2r = 8 – 2 = 6 r = 3.

Значит, радиус ВО = 3.

5 способ

Проведем ВН и АО. Т.к. центром окружности, вписанной в треугольник, является точка пересечения биссектрис, то АО – биссектриса угла А, а значит, и биссектриса треугольника АВН. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

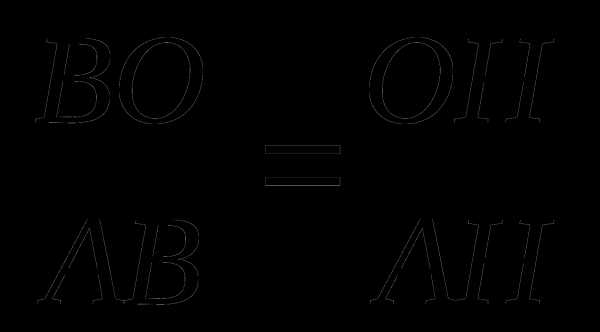. Пусть ОН = х, тогда ВО = 8 – х.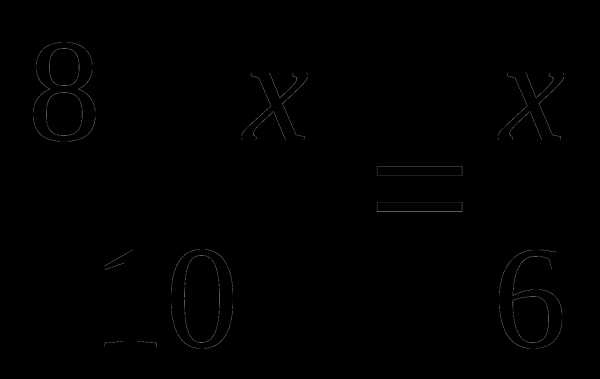 16х = 48 х = 3.

Значит, радиус ВО = 3.

6 способ

Из ∆АВН: ВD = 4.

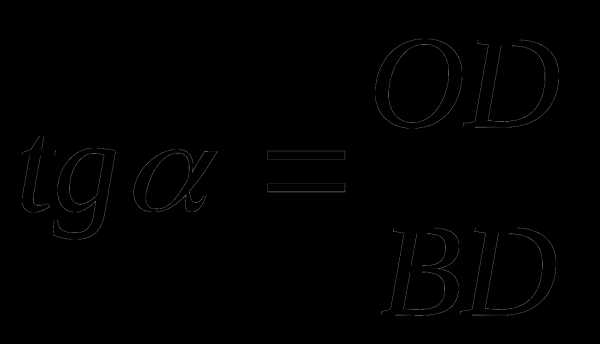
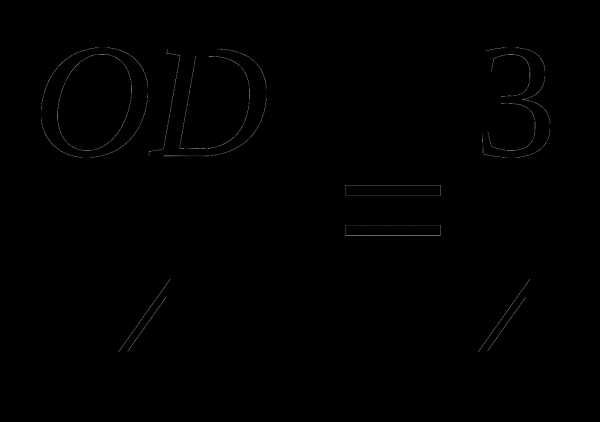
Из ∆ОВD: ОD = 3.

Значит, радиус ВО = 3.

Ответ: 3.

Домашнее задание.

Задача на 2 балла

Найдите углы вписанного в окружность четырехугольника, если три угла (в последовательном порядке) относятся как 3 : 7 : 5. В ответе укажите больший из них в градусах.

Задача на 4 балла

В равнобедренную трапецию с верхним основанием, равным 2, вписана окружность радиуса 2. Найдите нижнее основание трапеции.

Пожелания и советы учащимся

• Помни и понимай, что подготовка к ОГЭ – это тяжелый труд, где

результат будет прямо пропорционален времени, потраченному на

активную подготовку к экзамену.

• Выполняй как можно больше различных тестов по предмету.

• Тренируйся с секундомером в руках, засекай время выполнения тестов.

• Готовясь к экзаменам, мысленно рисуй себе картину успеха.

Рефлексия

Подведение итогов

Выставление оценок

Литература

1. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов и др. − М. : Просвещение, 2009.

2. Математика. 9 класс. Подготовка к ОГЭ – 2015. Учебно-тренировочные тесты по новой демоверсии / Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова – Ростов-на-Дону: Легион, 2015.

infourok.ru

Карточки для подготовки к ОГЭ по геометрии. 9 класс

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике

Подробнее

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший

Подробнее

В 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.

В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,

Подробнее

Геометрия

Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна

Подробнее

Задания В6. . Найдите AB.

Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.

Подробнее

Планиметрия: комбинации фигур.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника

Подробнее

ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)

ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через

Подробнее

Прототипы задания В6-2 (2013)

Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний

Подробнее

AC 6, cos A. Найдите BH.

Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите

Подробнее

Все прототипы заданий В года

1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,

Подробнее

ШКОЛА С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ПРЕДМЕТА

Примерные экзаменационные билеты для проведения устной итоговой аттестации выпускников IX классов общеобразовательных учреждений ГЕОМЕТРИЯ По геометрии предлагается два блока экзаменационных билетов для

Подробнее

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.

Подробнее

ID_7510 1/9 neznaika.pro

1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.

Подробнее

ЗАДАНИЕ 15 Планиметрия Треугольник

ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками

Подробнее

Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.

Подробнее

Все прототипы заданий В3

1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,

Подробнее

В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ

В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ 2011 ВВЕДЕНИЕ Выработка умений находить площади фигур на плоскости относится к основным целям обучения геометрии в школе. Задачи на нахождение площадей входят в содержание

Подробнее

10 класс Повторение планиметрии

Учебное пособие по геометрии 10 класс Повторение планиметрии (задачи в картинках) Для учащихся Лицея 1502 при МЭИ І полугодие Краткое содержание 1. Программа коллоквиума по «Планиметрии». 2. Содержание

Подробнее

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА Вариант 1

^САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами

Подробнее

В.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ

В.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ 2011 ВВЕДЕНИЕ Выработка умений находить длины отрезков и расстояний между точками относится к основным целям обучения геометрии в школе. Задачи на нахождение длин и расстояний

Подробнее

Зачеты по геометрии за курс 7-8 класс

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 28 г.томска Зачеты по геометрии за курс 7-8 класс Составила Смолякова Оксана Геннадьевна учитель математики МАОУ

Подробнее

В.А. Смирнов ГЕОМЕТРИЯ УГЛЫ

В.А. Смирнов ГЕОМЕТРИЯ УГЛЫ 2011 ВВЕДЕНИЕ Выработка умений находить величины углов относится к основным целям обучения геометрии в школе. Задачи на нахождение углов входят в содержание ГИА и ЕГЭ по математике.

Подробнее

Произвольный треугольник

Произвольный треугольник В приведенных ниже формулах используются следующие обозначения: а) с длины сторон АВС лежащие против углов А В и С соответственно б) высоты медианы l l l биссектрисы в) радиус

Подробнее

Метод ключевых задач

Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и

Подробнее

Основные определения, теоремы и формулы планиметрии.

Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне

Подробнее

КИМы по геометрии 7 класс (1) I вариант

КИМы по геометрии 7 класс (1) 1. Периметр треугольника АВС равен 45 см. Сторона АВ равна 11 см, ВС на 8 см больше, чем АВ. Найдите сторону АС. 2. Один из смежных углов в 2 раза больше другого. Найдите

Подробнее

Тема 69 «Комбинированные задачи»

Тема 69 «Комбинированные задачи» Пример 1. В основании прямой призмы лежит прямоугольный треугольник с катетами 7 и 8. Боковые ребра равны 8/π. Найти объем цилиндра, описанного около этой призмы. Ответ

Подробнее

В.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ

В.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ Москва 2011 ВВЕДЕНИЕ Одной из важных целей обучения геометрии в школе является развитие конструктивных умений учащихся, включающих в себя умения изображать различные

Подробнее

Подготовка к ЕГЭ по математике

2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Планиметрия. Комбинации фигур. Александр и Наталья Крутицких

Подробнее

РАБОЧАЯ ПРОГРАММА геометрии 8 класс

РАБОЧАЯ ПРОГРАММА геометрии 8 класс у ч и т е л я Ф и т к о в о й О. А. 2013-2014 учебный год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по геометрии для 8 класса разработана на основе: — Федеральный компонент

Подробнее

ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС

ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС ПРОВЕРОЧНАЯ РАБОТА 1 1) Найти площадь равнобедренного треугольника с углом при основании, если а) боковая сторона равна с; б) основание равно р 2) Стороны параллелограмма

Подробнее

docplayer.ru