Демонстрационный вариант КИМ ГИА — 2018 по математике
ДЕМОНСТРАЦИОННЫЙ ВАРИАНТ КИМ ГИА — 2018 ПО МАТЕМАТИКЕ
Демонстрационные варианты КИМ (контрольных измерительных материалов) ГИА (государственной итоговой аттестации) предназначены для того, чтобы дать возможность будущим участникам экзамена и широкой общественности ознакомиться со структурой экзаменационной работы. Задания, составляющие демоверсию, не входят в реальные варианты ГИА, но являются аналогичными заданиям их составляющим. Демонстрационный вариант КИМ ГИА разрабатывается к началу учебного года «Федеральным институтом педагогических измерений», с целью дать возможность учащимся и преподавателям ознакомиться со структурой заданий, их содержанием, формой, уровнем сложности.
Ознакомление с демонстрационным вариантом ГИА — 2018 по математике необходимо каждому будущему участнику государственного экзамена.
Изменений в КИМ ГИА — 2018 по математике по сравнению с 2017 годом — нет.
Просмотреть или скачать демонстрационный вариант КИМ ГИА — 2018 по математике можно по приведенным ниже ссылкам. С помощью данной демоверсии Вы можете организовать свою подготовку к ГИА. Решение заданий включенных в демонстрационный вариант, позволит качественно подготовиться к экзамену, определить уровень своей подготовки, правильно оценить свои возможности.
ДЕМОНСТРАЦИОНЫЙ ВАРИАНТ КИМ ГИА — 2018 ПО МАТЕМАТИКЕ
Демонстрационный вариант ГИА по математике 2018 года разработан по заданию Федеральной службы по надзору в сфере образования и науки Российской Федерации.
Подготовлен Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений» (ФИПИ).
Инструкция по выполнению работы: Работа состоит из трёх модулей: Алгебра, Геометрия, Реальная математика. Модули выполняются последовательно.
Модули выполняются последовательно.
Общее время экзамена 235 минут.
Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть1), 4 задания повышенного уровня (часть 2) и 2 задания высокого уровня сложности (часть 2).
Модуль «Алгебра» содержит 11 заданий: в части 1 — 8 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 8 заданий: в части 1 — 5 заданий; в части 2 — 3 задания. Модуль «Реальная математика» содержит 7 заданий: все задания — в части 1.
Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и построения выполняйте в черновике. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы.
Если задание содержит рисунок, то на нём непосредственно в тексте работы можно делать все необходимые записи и построения.
Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Для заданий с выбором ответа (2, 3, 8, 14) из четырех предложенных вариантов выберите один верный и обведите номер выбранного ответа в экзаменационной работе. Если Вы обвели не тот номер, то зачеркните обведенный номер крестиком и затем обведите номер верного ответа.
Если варианты ответа к заданию не приводятся, полученный ответ записывается в отведённом для этого месте. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа зачеркните его и запишите рядом новый.
Решения заданий части 2 и ответы к ним запишите на отдельном листе. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.
При выполнении работы Вы можете пользоваться справочными материалами.
Как оценивается работа:
Баллы, полученные Вами за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, из них: не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2, 3 и 4 балла.
При подготовке к государственной итоговой аттестации, рекомендуется тщательно изучить демонстрационный вариант, структуру заданий, их тематику, сложность, а также порядок оценивания работы.
ГИА 2018 — Официальный сайт Администрации Санкт‑Петербурга
Пресс-служба Рособрнадзора:
Заявления на участие в ЕГЭ в сентябрьские сроки принимаются с 6 по 20 августа
Федеральная служба по надзору в сфере образования и науки напоминает о сроках подачи заявлений на участие в едином государственном экзамене в сентябрьские сроки. Прием заявлений осуществляется с 6 по 20 августа включительно. Заявления подаются в места регистрации, определяемые региональными органами управления образованием.
Прием заявлений осуществляется с 6 по 20 августа включительно. Заявления подаются в места регистрации, определяемые региональными органами управления образованием.
Читать полностью
«ВЕСТИ» «Сергей Кравцов: в этом году ЕГЭ прошел максимально спокойно, честно и объективно»
Выпускники лучше справились с первыми ЕГЭ-2018, чем годом ранее
Результаты участников ЕГЭ по географии и математике базового уровня немного выросли по сравнению с прошлым годом, средний балл по информатике в 2018 году незначительно ниже, чем годом ранее.
По предварительным данным, средний балл участников ЕГЭ по математике базового уровня составил в 2018 году 4,29, незначительно улучшившись по сравнению с прошлогодним (4,24). Данный экзамен оценивается по пятибалльной шкале. Базовую математику сдавали 567 тысяч участников, что на 24 тысячи больше, чем годом ранее.
Число участников, которым не удалось набрать минимальные три балла, продолжает сокращаться четвертый год подряд. В 2018 году не преодолели минимальный порог 3,1% участников, что на 0,3% меньше, чем годом ранее.
В 2018 году не преодолели минимальный порог 3,1% участников, что на 0,3% меньше, чем годом ранее.
Читать полностью
Рособрнадзор подвел предварительные итоги апробации итогового собеседования по русскому языку в 9 классах
Предварительные результаты апробация итогового собеседования по русскому языку для выпускников 9 классов, которая проходила во всех регионах России, свидетельствуют, что 95% девятиклассников успешно справились с предложенными заданиями, получив «зачет».
Читать полностью
Глава Рособрнадзора предложил политическим и общественными деятелям присоединиться к «месяцу тишины» в период ЕГЭ-2018
Выступая на XV Всероссийском съезде уполномоченных по правам ребенка в субъектах Российской Федерации, открывшемся сегодня в Москве, руководитель Федеральной службы по надзору в сфере образования и науки Сергей Кравцов предложил политическим и общественным деятелям поддержать традицию «месяца тишины» в период проведения ЕГЭ-2018.
Читать полностью
«ИЗВЕСТИЯ» «Мы видим малейшие искажения в статистике ЕГЭ». Замглавы Рособрнадзора Анзор Музаев — о грядущей экзаменационной кампании и изменениях, ожидающих выпускников
Рособрнадзор напоминает о сроках подачи заявлений на участие в ЕГЭ военнослужащими, поступающими в военные вузы
Федеральная служба по надзору в сфере образования и науки напоминает об особом порядке подачи заявлений на участие в ЕГЭ военнослужащими, проходящими военную службу по призыву и по контракту, которые поступают на обучение в военные образовательные организации высшего образования.
Для участия в ЕГЭ военнослужащие могут подать заявление с указанием учебного предмета или перечня учебных предметов, по которым они планируют сдавать экзамены в текущем году, не позднее, чем за две недели до начала проведения соответствующего экзамена, в места регистрации на сдачу ЕГЭ в субъекте Российской Федерации, где расположена военная образовательная организация высшего образования.
Читать полностью
ЕГЭ-2018: Разработчики КИМ об экзамене по литературе
ЕГЭ по литературе является экзаменом по выбору, результаты которого необходимы для поступления в вузы на такие специальности, как «Филология», «Лингвистика», «Музыкально-театральное искусство», «Журналистика», «Телевидение», «Живопись», «Дизайн», «Музыковедение» и другие.
Минимальный балл по данному предмету, ниже которого вузы не могут устанавливать проходной порог для абитуриентов, составляет 32 тестовых балла.
Читать полностью
Ссылка на лонгрид по литературе
22 мая глава Рособрнадзора в ходе «горячей линии» ответит на вопросы об организации ГИА в 2018 году
«Горячая линия», посвященная проведению государственной итоговой аттестации (ГИА) в 2018 году, пройдет в Ситуационно-информационном центре Федеральной службы по надзору в сфере образования и науки 22 мая в 12:00.
Заместитель министра образования и науки РФ – руководитель Рособрнадзора Сергей Кравцов и специалисты Рособрнадзора ответят на вопросы выпускников, их родителей и педагогов.
Читать полностью
Подготовиться к ЕГЭ помогут видеоролики Рособрнадзора
Серия видеороликов, подготовленная Федеральной службой по надзору в сфере образования и науки, поможет выпускникам и их родителям подготовиться к госэкзаменам как с практической, так и с психологической стороны.
Ролики рассказывают, как лучше говорить об экзаменах взрослому и ребенку, как выбрать предметы для сдачи и построить график подготовки, на что стоит обратить внимание до, во время и после экзамена.
Читать полностью
ЕГЭ-2018: Разработчики КИМ об экзамене по биологии
Единый государственный экзамен по биологии является предметом по выбору. Результаты ЕГЭ по биологии необходимы для поступления в вузы на такие направления подготовки, как «Медицина», «Биология и экология», «Физическая культура», «Психология и педагогика», «Агрономия», «Ветеринария» и отдельные специальности: «Дефектология», «Биоинженерия», «Биоинформатика», «Технологии производства сельскохозяйственной продукции», «Ландшафтная архитектура», «Психология» и другие.
Читать полностью
Ссылка на лонгрид по биологии
Шестиклассники напишут 27 апреля всероссийскую проверочную работу по географии
Всероссийскую проверочную работу (ВПР) по географии напишут 27 апреля учащиеся 6 классов. Данная проверочная работа проводится в 2018 году в режиме апробации, ее проведут 24,7 тысячи школ из всех регионов России.
Читать полностью
Всероссийские проверочные работы по биологии и окружающему миру пройдут 26 апреля
Всероссийская проверочная работа по предмету «Окружающий мир» пройдет 26 апреля для учащихся 4 классов, проверочная работа по биологии – для 5 классов.
ВПР в 4 и 5 классах проводятся в 2018 году в штатном режиме. Проверочную работу по окружающему миру проведут более 39 тысяч школ, по биологии – 37,5 тысяч школ из всех регионов России.
Читать полностью
Шестиклассники напишут 20 апреля всероссийскую проверочную работу по биологии
Всероссийская проверочная работа (ВПР) по биологии проходит 20 апреля для учащихся 6 классов российских школ. Данная проверочная работа проводится в 2018 году впервые, участие школ в ней добровольное. ВПР по биологии проведут более 26 тысяч школ из всех регионов России.
Данная проверочная работа проводится в 2018 году впервые, участие школ в ней добровольное. ВПР по биологии проведут более 26 тысяч школ из всех регионов России.
Читать полностью
Рособрнадзор еще раз напомнил школам о необходимости объективно оценивать результаты ВПР
Федеральная служба по надзору в сфере образования и науки продолжает контролировать объективность проведения школами всероссийских проверочных работ (ВПР), заявил, выступая в рамках ММСО на Форуме руководителей местного самоуправления, осуществляющих управление в сфере образования, заместитель руководителя Рособрнадзора Анзор Музаев.
Он напомнил, что по итогам анализа результатов ВПР, которые проводились весной 2017 года, Рособрнадзором были выявлены признаки необъективности проведения проверочных работ в ряде школ. Перечни таких школ были направлены региональным органам управления образованием.
Читать полностью
Всероссийская проверочная работа по математике для 5 классов и вторая часть работы по русскому языку в 4 классах пройдут 19 апреля
Проведение Всероссийских проверочных работ (ВПР) для российских школьников продолжится 19 апреля: в этот день учащимся 5 классов предстоит написать работу по математике, а 4 классы выполнят вторую часть работы по русскому языку.
ВПР в 4 и 5 классах проводятся в 2018 году в штатном режиме. Проверочная работа по русскому языку пройдет в 39 тысячах школ, по математике – в почти 38 тысячах школ из всех регионов России.
Читать полностью
ЕГЭ-2018: Разработчики КИМ об экзамене по русскому языку
Единый государственный экзамен по русскому языку – один из двух обязательных предметов для всех выпускников, который необходимо сдать для получения аттестата о среднем общем образовании. Минимальное количество баллов для получения аттестата – 24 балла.
Кроме того, результаты ЕГЭ по русскому языку необходимо представить при поступлении в вуз на любое направление подготовки (специальность). Вузы не имеют права устанавливать минимальный проходной порог по этому предмету ниже 36 баллов.
Шестиклассники напишут 18 апреля всероссийскую проверочную работу по математике
Всероссийская проверочная работа (ВПР) по математике пройдет 18 апреля для обучающихся 6 классов. ВПР в 6 классах проводится по решению школы, участие в ней примут 31,7 тысячи школ из всех регионов России.
ВПР в 6 классах проводится по решению школы, участие в ней примут 31,7 тысячи школ из всех регионов России.
На выполнение работы по математике даётся 60 минут. Работа содержит 13 заданий. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости участники могут использовать черновик.
Всероссийские проверочные работы по русскому языку пройдут 17 апреля для учащихся 4 и 5 классов
Первая часть всероссийской проверочной работы (ВПР) по русскому языку пройдет 17 апреля для учащихся 4 классов, им предстоит написать диктант и выполнить два связанных с ним задания. ВПР проводится в штатном режиме, участие в ней примут 39 тысяч школ из всех регионов России.
Читать полностью
Федеральный портал «Российское образование» Расписание ЕГЭ не будет меняться в связи с чемпионатом мира по футболу – Рособрнадзор
80 % российских школ примут участие в апробации итогового собеседования по русскому языку для выпускников 9 классов
Около 80% российских школ примут участие в апробации итогового собеседования по русскому языку для выпускников 9 классов 13 и 16 апреля. Апробация пройдет во всех регионах России.
Апробация пройдет во всех регионах России.
Итоговое собеседование по русскому языку для учащихся 9 классов вводится в рамках реализации Концепции преподавания русского языка и литературы для проверки навыков устной речи у школьников. Планируется, что прохождение итогового собеседования с 2018/2019 учебного года станет для девятиклассников допуском к государственной итоговой аттестации (ГИА-9). Результаты апрельской апробации не будут влиять на допуск учащихся к ГИА-9 в 2018 году.
Читать полностью
Досрочный период ЕГЭ прошел на высоком организационном уровне
Досрочный период ЕГЭ, который в 2018 году проводился с 21 марта по 11 апреля, прошел на высоком организационном уровне, без серьезных нарушений и технологических сбоев.
В досрочный период экзамены сдавали более 23 тысяч человек, в основном это выпускники прошлых лет, желающие улучшить свой результат. Экзамены прошли во всех субъектах РФ, кроме Чукотского автономного округа, в 245 пунктах проведения экзаменов (ППЭ). В их проведении было задействовано более 12 тысяч организаторов и более 2,2 тысяч общественных наблюдателей. Во всех ППЭ в ходе экзаменов велось видеонаблюдение в режиме онлайн.
В их проведении было задействовано более 12 тысяч организаторов и более 2,2 тысяч общественных наблюдателей. Во всех ППЭ в ходе экзаменов велось видеонаблюдение в режиме онлайн.
Читать полностью
ЕГЭ-2018: Разработчики КИМ об экзамене по информатике и ИКТ
ЕГЭ по информатике и информационно-коммуникационным технологиям (ИКТ) – экзамен по выбору, необходимый для поступления в вузы на направления подготовки укрупненных групп специальностей «Математика и механика», «Компьютерные и информационные науки», «Информатика и вычислительная техника», а также другие направления подготовки, связанные с разработкой, развертыванием и эксплуатацией информационных систем.
Читать полностью
Лонгрид «ЕГЭ по информатике»
Рособрнадзор подготовил серию анимированных видеороликов о ЕГЭ-2018
Федеральная служба по надзору в сфере образования и науки подготовила серию анимированных видеороликов о едином государственном экзамене для выпускников 11 классов. Ролики напоминают школьникам об основных особенностях процедуры экзамена, о минимальных баллах для получения аттестата и поступления в вуз, правилах поведения в пункте проведения экзамена, порядке подачи апелляции.
Ролики напоминают школьникам об основных особенностях процедуры экзамена, о минимальных баллах для получения аттестата и поступления в вуз, правилах поведения в пункте проведения экзамена, порядке подачи апелляции.
Читать полностью
Учащиеся 11 классов 20 марта напишут Всероссийскую проверочную работу по иностранному языку
Проведение Всероссийских проверочных работ (ВПР), которые напишут весной текущего года учащиеся 4-х, 5-х, 6-х и 11-х классов, стартует 20 марта с проверочной работы по иностранному языку для 11 классов.
ВПР по иностранному языку проводится впервые, участие в ней школ является добровольным. Проверочные работы пройдут по английскому, французскому и немецкому языкам. Они включают в себя письменную и устную части. В 2018 году школы имеют право выбора – проводить всю работу полностью или только ее письменную часть.
Читать полностью
Глава Рособрнадзора призвал региональных министров лично контролировать проведение досрочного периода ЕГЭ-2018
Региональные министры образования должны взять под личный контроль проведение экзаменов в досрочный период ЕГЭ 2018 года, заявил заместитель министра образования и науки РФ – руководитель Рособрнадзора Сергей Кравцов в ходе селекторного совещания с регионами.
«Наша задача – удержать достигнутый высокий уровень проведения ЕГЭ, и я прошу министров лично курировать досрочный этап: очень детально и тщательно отслеживать проведение всех экзаменов», — сказал Сергей Кравцов.
Читать полностью
ЕГЭ-2018: Разработчики КИМ об экзамене по истории
Рособрнадзор и Федеральный институт педагогических измерений (ФИПИ), разрабатывающий контрольные измерительные материалы (КИМ) для участников ЕГЭ, подготовили новую серию публикаций, рассказывающих выпускникам о том, что их ждет на экзаменах. Что представляет из себя экзаменационная работа по тому или иному предмету? Какие задания могут встретиться участникам ЕГЭ? На что нужно обратить внимание, готовясь к экзамену? Как избежать обидных ошибок и на чем сосредоточиться, выполняя экзаменационную работу? Открывает серию публикаций о ЕГЭ-2018 рассказ о предмете по выбору – истории.
Читать полностью
Лонгрид по истории
Рособрнадзор публикует видеоконсультации разработчиков экзаменационных заданий ЕГЭ-2018
Федеральная служба по надзору в сфере образования и науки начинает публикацию на своем YouTube-канале видеоконсультаций по подготовке к единому государственному экзамену 2018 года.
В создании 12 видеороликов приняли участие руководители федеральных комиссий по разработке контрольных измерительных материалов ЕГЭ-2018, психологи, учителя школ и преподаватели вузов. В видеоматериалах детально разбираются нюансы и особенности каждого предмета, даются советы по подготовке и рекомендации по выполнению отдельных заданий. В первом видео – по обществознанию – речь пойдет об использовании кодификаторов и спецификаций, детальном разборе таких тематических блоков предмета как: «Человек и общество», «Социальные отношения», «Экономика», «Политика» и «Право».
Читать полностью
ФИПИ опубликовал описания и образцы вариантов ВПР 2018 года для учащихся 11 классов
Федеральный институт педагогических измерений (ФИПИ) опубликовал описания и образцы вариантов Всероссийских проверочных работ (ВПР) 2018 года для учащихся 11 классов.
ВПР – это итоговые контрольные работы, проводимые по отдельным учебным предметам для оценки уровня подготовки школьников. В марте-апреле 2018 года учащиеся 11 классов напишут ВПР по шести учебным предметам: истории, географии, биологии, физике, химии и иностранным языкам (английский, немецкий и французский языки). Участие школ в проведении ВПР для 11 классов будет добровольным. ВПР не являются аналогом государственной итоговой аттестации. Они проводятся на региональном или школьном уровне.
В марте-апреле 2018 года учащиеся 11 классов напишут ВПР по шести учебным предметам: истории, географии, биологии, физике, химии и иностранным языкам (английский, немецкий и французский языки). Участие школ в проведении ВПР для 11 классов будет добровольным. ВПР не являются аналогом государственной итоговой аттестации. Они проводятся на региональном или школьном уровне.
На сайте ФИПИ http://www.fipi.ru/vpr можно ознакомиться с образцами проверочных работ по всем предметам, которые дают представление о структуре работы, количестве и форме заданий, уровне их сложности. Для всех образцов работ приведены ответы и критерии оценивания к ним. Также на сайте ФИПИ размещены описания ВПР по каждому из предметов, включающие Кодификатор элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения ВПР. Кодификаторы составлены на основе Федерального компонента государственных стандартов основного общего и среднего (полного) общего образования для изучения предмета на базовом уровне. В описании ВПР содержатся сведения о распределении заданий в работе по блокам содержания и проверяемым способам действий, о системе оценивания отдельных заданий и работы в целом.
В описании ВПР содержатся сведения о распределении заданий в работе по блокам содержания и проверяемым способам действий, о системе оценивания отдельных заданий и работы в целом.
ВПР являются самой массовой оценочной процедурой в системе образования: с момента их введения в 2015 году российские школьники написали около 17 миллионов проверочных работ. Результаты ВПР могут использоваться для формирования программ развития образования на уровне муниципалитетов, регионов и в целом по стране, для совершенствования методики преподавания предметов в конкретных школах, а также для индивидуальной работы с учащимися по устранению имеющихся пробелов в знаниях. Работы выполняются по заданиям, разработанным на федеральном уровне, и проверяются по единым критериям.
Весной 2018 года ВПР также будут проведены для учащихся 4 и 5 классов (в обязательном порядке) и учащихся 6 классов (по выбору). С образцами проверочных работ для этих классов можно ознакомиться на портале ВПР https://vpr.statgrad. org/
org/
Рособрнадзор доработал и ввел в штатную эксплуатацию информационные системы «Карта вузов» и «Мониторинг»
Федеральная служба по надзору в сфере образования и науки доработала и ввела в штатную эксплуатацию информационные системы «Карта вузов» и «Мониторинг».
Портал «Карта вузов» был запущен Рособрнадзором в апреле 2015 года. Он представляет собой путеводитель по высшим учебным заведениям России с подробной информацией о каждом вузе и филиале. Пользователи портала могут, в частности, проверить наличие у вуза лицензии, государственной аккредитации, наличие или отсутствие запрета на прием абитуриентов.
Информация, содержащаяся на портале, была актуализирована. Изменен порядок ее обновления, теперь данные по каждому вузу и филиалу автоматически актуализируются каждые сутки.
Система «Мониторинг» предназначена для удаленного контроля за соблюдения вузами требований к информации, размещаемой на их официальных сайтах. В рамках системы был реализован механизм консультационно-методической поддержки образовательных организаций высшего образования по вопросам размещения информации на их сайтах с учётом требований законодательства.
Для образовательных организаций были созданы личные кабинеты, с помощью которых они могут протестировать свои сайты на предмет соблюдения обязательных требований, чтобы внести необходимые дополнения и исправления. Таким образом, работа системы «Мониторинг» будет способствовать профилактике нарушений.
iREAKTOR Путин рассказал, почему считает ЕГЭ эффективной системой
САНКТ‑ПЕТЕРБУРГСКИЕ ВЕДОМОСТИ Проверить проверяющих. Рособрнадзор грозится опубликовать список школ, которые завышают итоги всероссийских проверочных работ. В Петербурге не испугались.
Итоговое сочинение успешно написали 98% участников
Итоговое сочинение, которое проводилось 6 декабря, успешно написали 98% участников, «незачет» получили около 2%. В основной срок в написании итогового сочинения приняли участие более 645 тысяч человек, из них более 642 тысяч — выпускники текущего года.
Читать полностью
Рособрнадзор продолжит апробацию модели оценки компетенций учителей
Федеральная служба по надзору в сфере образования и науки в следующем году продолжит апробацию модели оценки компетенций учителей, сообщил заместитель руководителя Рособрнадзора Анзор Музаев на заседании Экспертного совета по соблюдению прав и социальной защите педагогических и научных работников при Комитете Государственной Думы по образованию и науки.
В ходе заседания он представил результаты апробации модели уровневой оценки компетенций учителей русского языка и математики, которая была проведена в сентябре 2017 года. Участие в ней приняли около 4,5 тысяч учителей из 13 регионов России. Им было предложено выполнить диагностическую работу, состоящую из предметных, методических и профессиональных задач, а также провести открытый видеоурок.
Утверждено расписание государственной итоговой аттестации 2018 года
Министерство юстиции Российской Федерации зарегистрировало приказы Минобрнауки России, утверждающие расписание проведения единого государственного экзамена (ЕГЭ), государственного выпускного экзамена (ГВЭ) и основного государственного экзамена (ОГЭ) в 2018 году.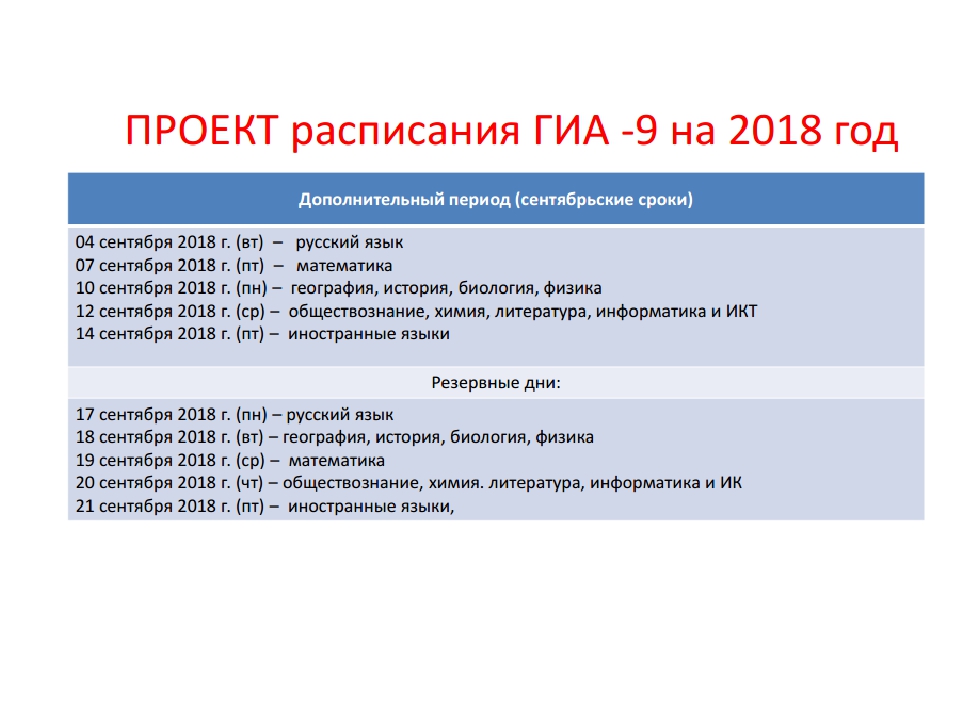
Итоговые экзамены в 2018 году традиционно пройдут в три этапа: досрочный, основной и дополнительный (сентябрьский). Досрочный этап ЕГЭ в 2018 году состоится с 21 марта по 11 апреля, основной – с 28 мая по 2 июля и дополнительный (сентябрьский) – с 4 по 15 сентября.
Досрочный и основной этапы ЕГЭ в 2018 году начнутся с экзаменов по географии и информатике и ИКТ.
Выпускники 2018 года, получившие неудовлетворительные результаты по русскому языку и математике, либо получившие повторно неудовлетворительный результат по одному из этих учебных предметов на ГИА в резервный день, получат возможность участвовать в ГИА по русскому языку и (или) математике базового уровня в дополнительный (сентябрьский) период – с 4 по 15 сентября 2018 года.
Российские школьники заняли первое место в международном исследовании качества образования в начальной школе PIRLS
Российские четвероклассники (выпускники начальной школы) продемонстрировали самые высокие результаты в овладении чтением среди своих сверстников из 50 стран мира по итогам международного исследования PIRLS (Progress in International Reading Literacy Study).
Последний цикл исследования проводился в 2016 году, его результаты были опубликованы 5 декабря 2017 года. В исследовании приняли участие более 340 тысяч учащихся из 50 стран и 11 территорий, в том числе 4577 выпускников начальной школы из 206 школ 42 регионов России.
По данным исследования 2016 года, Россия набрала 581 балл по международной шкале, вернувшись на первое место в рейтинге всех стран-участниц и в очередной раз подтвердив свой статус лидера в области начального школьного образования. Россия уже занимала первое место в исследовании PIRLS в 2006 году, однако в 2011 году уступила его Гонконгу, опустившись на вторую строку. За период с 2011 по 2016 годы российские учащиеся значительно повысили свой результат – на 13 баллов. При этом 70% выпускников начальной школы в России показали высокий уровень читательской грамотности.
Рособрнадзор поставил задачу регионам максимально объективно провести итоговое сочинение
Федеральная служба по надзору в сфере образования и науки провела селекторное совещание с руководителями региональных органов управления образованием о готовности к проведению итогового сочинения.
Основной срок проведения итогового сочинения – 6 декабря, в этот день его напишут более 650 тысяч участников. Никаких принципиальных изменений в процедуре проведения сочинения в этом учебном году нет.
«Это одно из самых масштабных мероприятий наряду с ЕГЭ. Нужно провести сочинение максимально объективно», — заявил в ходе совещания заместитель руководителя Рособрнадзора Анзор Музаев.
Он попросил региональных министров образования обратить особое внимание на школы и муниципалитеты, в отношении которых были вопросы по объективности проведения сочинения в предыдущие годы. В обеспечении объективности проведения сочинения также примут участие общественные наблюдатели.
Итоговое сочинение в выпускных классах введено с 2014/15 учебного года, его успешное написание является допуском к единому государственному экзамену (ЕГЭ).
Советом по вопросам проведения итогового сочинения в выпускных классах были определены следующие направления тем итогового сочинения на 2017/18 учебный год: «Верность и измена», «Равнодушие и отзывчивость», «Цели и средства», «Смелость и трусость», «Человек и общество». В рамках открытых направлений тем итогового сочинения Рособрнадзором разрабатываются конкретные темы итогового сочинения для каждого часового пояса. Сами темы сочинений станут известны выпускникам за 15 минут до начала экзамена.
В рамках открытых направлений тем итогового сочинения Рособрнадзором разрабатываются конкретные темы итогового сочинения для каждого часового пояса. Сами темы сочинений станут известны выпускникам за 15 минут до начала экзамена.
«ИЗВЕСТИЯ»«Мы исключим любое вмешательство в результаты экзамена» . Глава Рособрнадзора Сергей Кравцов — о результатах ЕГЭ-2017 и перспективах на следующий год
Глава Рособрнадзора рассказал родителям школьников о ЕГЭ-2018 и других оценочных процедурах
Руководитель Федеральной службы по надзору в сфере образования и науки Сергей Кравцов в третий раз провел Всероссийскую встречу с родителями, в ходе которой ответил на вопросы о ЕГЭ, итоговой аттестации в 9 классах, всероссийских проверочных работах, исследованиях качества образования, проведении итогового сочинения.
Открывая встречу, Сергей Кравцов рассказал, какие экзамены и проверочные работы ждут школьников в этом учебном году: всероссийские проверочные работы весной пройдут для учащихся 4, 5, 6 и 11 классов, а в октябре будет проведено национальное исследование качества образования по биологии и химии в 10 классах. В проведении ЕГЭ и итогового сочинения в этом году существенных изменений ждать не следует. «В части единого государственного экзамена у нас никаких серьезных изменений нет, для нас важна стабильность», — сказал глава Рособрнадзора.
В проведении ЕГЭ и итогового сочинения в этом году существенных изменений ждать не следует. «В части единого государственного экзамена у нас никаких серьезных изменений нет, для нас важна стабильность», — сказал глава Рособрнадзора.
Вопросы родителей касались изменений системы ЕГЭ, которые могут произойти в будущем. Сергей Кравцов рассказал, что иностранный язык должен стать обязательным предметом на ЕГЭ для выпускников 11 классов с 2022 года. Сейчас разработана дорожная карта мероприятий, реализация которых будет предшествовать данному нововведению, ведется работа с учителями и школьниками. Что касается истории, то вопрос о ее включении в число обязательных предметов еще будет обсуждаться.
Руководитель Рособрнадзора не исключил изменения в дальнейшем сроков подачи заявлений на участие в ЕГЭ. Это может стать возможным в связи с широким распространением технологии печати экзаменационных материалов непосредственно в аудитории проведения ЕГЭ, что позволит сократить время на подготовку к проведению экзаменов. «В этом учебном году срок подачи заявлений останется прежним – до 1 февраля 2018 года», — уточнил он.
«В этом учебном году срок подачи заявлений останется прежним – до 1 февраля 2018 года», — уточнил он.
Интересовались родители также, какими пособиями и ресурсами лучше пользоваться при подготовке к ЕГЭ, как сдать экзамены, проходя службу по призыву в вооруженных силах РФ, особенностями экзаменационных процедур для выпускников с ограниченными возможностями здоровья.
Своим опытом успешной подготовки к экзаменам поделились присутствовавшие на встрече родители двоих трехсотбалльников – выпускников 2017 года, которым удалось набрать 100 баллов на ЕГЭ сразу по трем предметам. По словам Ольги Камзеевой, матери трехсотбалльницы, главное – это настрой на учебу у школьника с 1 по 11 класс, поддержка и понимание со стороны родителей.
Несколько вопросов было задано об итоговом собеседовании по русскому языку, которое должно стать допуском к итоговой аттестации в 9 классах. Сергей Кравцов рассказал, что в текущем учебном году будет продолжена апробация и доработка экзаменационной модели, а в штатный режим, как допуск к ГИА-9, итоговое собеседование, скорее всего, войдет с 2019 года.
Интересовало родителей, будет ли устный экзамен посилен выпускникам школ из национальных республик. Директор Федерального института педагогических измерений (ФИПИ) Оксана Решетникова пояснила, что особых форм проведения собеседования для отдельных регионов вводить не планируется. «Это будет посильная процедура для ваших ребят. Не волнуйтесь, мы все попробуем вместе, внимательно проанализируем все итоги апробаций до введения собеседования в штатный режим», — заверила она.
Также глава Рособрнадзора и руководитель Центра национальных и международных исследований Сергей Станченко ответили на ряд вопросов, связанных с проведением всероссийских проверочных работ и национальных исследований качества образования.
Свои вопросы родители школьников из разных регионов России присылали Сергею Кравцову в течение нескольких недель на специальный почтовый ящик и в социальной сети ВКонтакте. Всего за время подготовки встречи поступило свыше 2 тысяч вопросов и обращений. Некоторые из родителей прислали свои вопросы, записав их на видео.
Помимо родителей из Москвы и Московской области, присутствующих на встрече, свои вопросы руководителю Рособрнадзора в ходе прямых видеоподключений задали жители Республики Крым, Чеченской Республики, Республики Алтай и Ярославской области.
Видеозапись встречи будет опубликована на канале Рособрнадзора в YouTube. Также ответы на поступившие вопросы будут размещены на официальном сайте ведомства.
17 октября руководитель Рособрнадзора проведет Всероссийскую встречу с родителями
17 октября в 11.00 руководитель Федеральной службы по надзору в сфере образования и науки Сергей Кравцов проведет Всероссийскую встречу с родителями.
В ходе встречи руководитель Рособрнадзора и специалисты ведомства ответят на вопросы, касающиеся организации и проведения в 2018 году ЕГЭ и ГИА-9, всероссийских проверочных работ (ВПР), национальных исследований качества образования (НИКО).
Основной площадкой встречи станет Президентский зал Международного мультимедийного пресс-центра МИА «Россия сегодня». В ходе встречи планируются прямые подключения из регионов.
В ходе встречи планируются прямые подключения из регионов.
В настоящее время уже принимаются вопросы:
— по электронной почте [email protected]
— на странице Рособрнадзора в социальной сети https://vk.com/obrnadzorru
Вопросы можно направлять в письменной форме или в формате видеообращения. Ответы на наиболее популярные и интересные из них будут даны в ходе встречи.
Рособрнадзор обсудит итоги апробации модели уровневой оценки компетенций с Ассоциациями учителей-предметников
Федеральная служба по надзору в сфере образования и науки детально обсудить итоги апробации модели уровневой оценки компетенций учителей русского языка и математики, которая является продолжением исследования компетенций учителей, начатого в 2016 году.
Целью методики уровневой оценки компетенций, разработанной специалистами Российского государственного педагогического университета им. А.И. Герцена, является получение достоверной информации об уровне профессиональной компетентности каждого учителя и отдельных групп учителей.
В дальнейшем оценка компетенций учителей должна стать одним из элементов национальной системы профессионального роста учителей, которую сейчас разрабатывает Минобрнауки РФ по поручению Президента Российской Федерации.
О модели, разработанной для оценки компетенций учителей, как будет проходить ее апробация и анализироваться результаты рассказали участники пресс-конференции в Ситуационно-информационном центре Рособрнадзора.
«В течение длительного времени мы проводили подготовительную работу, апробация обсуждалась и с педагогическим сообществом, и с участвующими в ней субъектами РФ. Для нас важна добровольность участия. Результат позволит нам говорить о возможности построения индивидуальной траектории развития профессионализма и компетенций учителя, и здесь потребуется перестройка работы всех институтов, которые работают над повышением квалификации учителей», — заявила заместитель министра образования и науки РФ Татьяна Синюгина.
В апробации разработанной модели примут участие более 4,5 тысяч учителей русского языка и математики из 13 субъектов Российской Федерации, выразивших готовность поучаствовать в ее проведении, рассказал руководитель Рособрнадзора Сергей Кравцов.
«Говоря о качестве образования, нельзя недооценивать роль учителя. Поэтому оценка профессиональных компетенций учителей на разных этапах профессиональной карьеры – это важнейшее направление образовательной политики», — заявил он.
Сергей Кравцов отметил, что результаты выполнения диагностической работы дадут возможность учителям провести самоанализ. «Для нас важно, чтобы в первую очередь сам учитель увидел свои сильные и слабые стороны», — сказал он.
О том, что представляет из себя разработанная модель оценки компетенций учителей, рассказал проректор по научной работе и информатизации РГПУ имени Герцена Михаил Пучков.
Участникам апробации предстоит выполнить диагностическую работу, включающую 20 предметных заданий, три методические задачи и одну профессиональную задачу — проявить свои профессиональные знания и педагогический опыт в предложенной ситуации. Кроме того, участникам апробации предстоит провести открытый видеоурок, который оценят федеральные и региональные эксперты.
В ходе апробации будет также собрана контекстная информация, необходимая для анализа результатов исследования (стаж, квалификационная категория, учебная нагрузка, используемые учебно-методические комплекты и прочее).
Для выполнения работы каждому участнику апробации будет предоставлен электронный личный кабинет. Личные кабинеты созданы и для региональных экспертов, которые будут участвовать в проверке диагностических работ. Система личных кабинетов позволит передавать работы учителей по сети Интернет для проверки экспертами из других регионов.
Персональные результаты участия учителей в апробации не подлежат разглашению. Анализ результатов апробации будет проведен на общем массиве обезличенных данных.
Участие в разработке и экспертизе модели приняли Российская академия образования, ассоциации учителей математики и литературы и русского языка, специалисты Академии повышения квалификации и профессиональной переподготовки работников образования (АПКиППРО).
«Сейчас мы находимся на этапе выбора инструментария для оценки компетенций. Это первый подход к тому, чтобы выработать систему в помощь учителю, который хочет повысить свою квалификацию, с одной стороны, и, с другой стороны, увидеть, чего он стоит сам по себе. Мы в начале большого, долгого и интересного пути», — отметил вице-президент Всероссийской ассоциации учителей математики Максим Пратусевич.
Это первый подход к тому, чтобы выработать систему в помощь учителю, который хочет повысить свою квалификацию, с одной стороны, и, с другой стороны, увидеть, чего он стоит сам по себе. Мы в начале большого, долгого и интересного пути», — отметил вице-президент Всероссийской ассоциации учителей математики Максим Пратусевич.
«Сам подход к выработке инструментария независимой оценки профессионального развития наших педагогов – абсолютно правильный. Учителю, как никому другому, очень важно оценить, насколько он находится на уровне требований, предъявляемых временем. Но здесь не нужно спешить, действовать надо очень осторожно и постепенно. Требуется серьезная проработка методического сопровождения и большая разъяснительная работа», — заявила председатель координационного совета Ассоциации учителей литературы и русского языка Людмила Дудова. Она отметила, что большой интерес педагогов вызвали включенные в исследование профессиональные задачи.
Своими впечатлениями от участия в апробации поделилась учитель математики гимназии № 2 «Квантор» городского округа Коломна Светлана Кузнецова. «Первый этап участия в исследовании, который я прошла – это видеоурок. Я считаю, что это полезно. Любой спортсмен пересматривает свои выступления, любой артист смотрит потом, как он выглядел на сцене, делает замечания самому себе и вносит корректировки. Посмотреть на себя со стороны было очень любопытно, ведь во время урока мы можем чего-то не замечать», — сказала она.
«Первый этап участия в исследовании, который я прошла – это видеоурок. Я считаю, что это полезно. Любой спортсмен пересматривает свои выступления, любой артист смотрит потом, как он выглядел на сцене, делает замечания самому себе и вносит корректировки. Посмотреть на себя со стороны было очень любопытно, ведь во время урока мы можем чего-то не замечать», — сказала она.
Педагог предложила дополнить видеозапись урока возможностью для учителя прокомментировать свои действия на уроке для оценивающих его экспертов и ответить на их вопросы.
Руководитель Рособрнадзора Сергей Кравцов предложил обсудить результаты апробации модели на заседаниях Всероссийской ассоциации учителей математики и Ассоциации учителей литературы и русского языка с участием педагогов, испытавших данную модель оценки на себе.
«Мы готовы к обсуждению, готовы учитывать пожелания и вносить коррективы. Сейчас важно отработать технологию, методологию, обсудить результаты и затем думать о продолжении этой работы», — сказал руководитель Рособрнадзора.
Международные эксперты обсудили вызовы, стоящие перед системой образования в XXI веке
Участники III Международной конференции по оценке качества образования, которая прошла в Москве по инициативе Федеральной службы по надзору в сфере образования и науки, обсудили вызовы, стоящие перед системой образования в XXI веке: чему должна учить современная школа, по каким критериям оценивать образовательные результаты, как сделать качественное образование доступным каждому школьнику.
В области оценки качества образования накоплен значительный опыт, отметили участники конференции, но развитие технологий и средств коммуникации заставляет меняться систему школьного образования и предъявляет новые требования к обучающимся.
Руководители авторитетных международных организаций по оценке качества образования отметили успехи, достигнутые в организации итоговой аттестации школьников в России.
«Я был здесь, когда только начинались разговоры о ЕГЭ. Тогда Россия изучала опыт других стран. И я помню все трудности, которые удалось преодолеть на этом пути. Сегодня коллеги говорят: «Учитесь у России, как можно построить систему экзаменов, которая будет прозрачной, значимой, показательной и объективной», — сказал директор Департамента образования и профессиональной подготовки ОЭСР Андреас Шляйхер. «Мы находимся под большим впечатлением от того, как Россия проводит свою образовательную реформу и формирует свою систему оценки качества образования», — поддержала его президент Международной ассоциации по оценке учебных достижений (IEA) Анне-Берит Кавли.
Тогда Россия изучала опыт других стран. И я помню все трудности, которые удалось преодолеть на этом пути. Сегодня коллеги говорят: «Учитесь у России, как можно построить систему экзаменов, которая будет прозрачной, значимой, показательной и объективной», — сказал директор Департамента образования и профессиональной подготовки ОЭСР Андреас Шляйхер. «Мы находимся под большим впечатлением от того, как Россия проводит свою образовательную реформу и формирует свою систему оценки качества образования», — поддержала его президент Международной ассоциации по оценке учебных достижений (IEA) Анне-Берит Кавли.
Руководитель Рособрнадзора Сергей Кравцов рассказал о задачах, которые стоят перед системой управления качеством образования в России на нынешнем этапе. «Для нас важен опыт, который накоплен по эффективному управлению образованием, достижению высоких образовательных результатов для того, чтобы этот опыт мог реализовываться повсеместно, чтобы каждый школьник получал качественное образование вне зависимости от того, где он проживает, социального положения и достатка родителей. Мы понимаем, к чему нам нужно стремиться, какие вопросы нужно решать, прежде всего, в ряде субъектов Российской Федерации, в сельских школах», — сказал руководитель Рособрнадзора.
Мы понимаем, к чему нам нужно стремиться, какие вопросы нужно решать, прежде всего, в ряде субъектов Российской Федерации, в сельских школах», — сказал руководитель Рособрнадзора.
По его словам, сейчас идет процесс совершенствования и развития инструментов, призванных развивать российское образование и поддерживать высокий уровень его качества. Хорошо работающая система должна быть залогом успешной реализации образовательных возможностей для каждого обучающегося. Составляющие этой системы: объективное оценивание по итогам каждого года обучения по всем предметам, эффективные учебные пособия, современные образовательные стандарты, механизмы развития компетенций учителей, вовлечение экспертного сообщества в обсуждение изменений, происходящих в системе образования. «Все эти элементы очень важны и должны работать в единой системе», — заявил Сергей Кравцов.
Он рассказал, что следующим этапом в деятельности Рособрнадзора станет разработка новых подходов к инспекции школ, механизмов помощи их директорам в улучшении качества образования.
Директор Департамента образования и профессиональной подготовки ОЭСР Андреас Шляйхер уделил основное внимание в своем выступлении изменениям, происходящим в системе школьного образования, которые требуют выработки новых подходов к оценке успешности обучающихся.
По его словам, некоторые вещи, которым традиционно обучали в школах, становятся теперь ненужными. На передний план выходит не знание фактов, а мышление. Простое заучивание материала может быть полезно для решения обычных задач, но неэффективно для решения задач сложных. «В мире завтрашнего дня нужно, чтобы люди разбирались в политической и социальной жизни, в творчестве, в эстетике, дизайне. Обучать нужно немногому, но обучать глубоко и хорошо. На передний план выходит умение конструировать знание. Нужно продвинуть оценивание образования на новые рубежи, и мы в ОЭСР это делаем: оцениваются теперь не только знания и умения, но также подходы и ценности», — заявил Андреас Шляйхер.
Он рассказал, что в рамках исследования PISA в 2015 году оценивались не только знания школьников, но и их социальные навыки, умение работать в команде.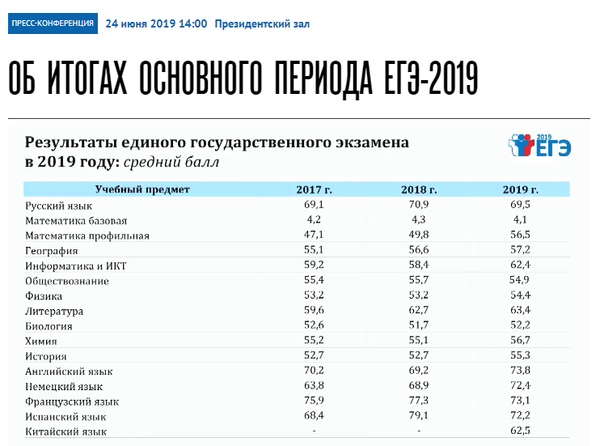 В исследовании 2018 года будет изучаться «глобальная компетентность» — понимание, способность увидеть разные точки зрения. В рамках исследования PISA 2021 года особое внимание будет уделено творчеству, способности к креативному мышлению.
В исследовании 2018 года будет изучаться «глобальная компетентность» — понимание, способность увидеть разные точки зрения. В рамках исследования PISA 2021 года особое внимание будет уделено творчеству, способности к креативному мышлению.
Глава образовательного департамента ОЭСР также отметил, что современная школа не должна отсеивать слабых учеников, необходимо давать возможности для развития каждому. «Сегодня все изменилось – нам нужны все», — сказал он.
Его поддержала президент Международной ассоциации по оценке учебных достижений (IEA) Анне-Берит Кавли. «Страны с наивысшими показателями в исследованиях качества образования смогли улучшить результаты группы наименее успевающих учеников», — констатировала она.
Анне-Берит Кавли отметила, что современный мир сталкивается с быстрыми переменами в технологиях, способах общения людей, с новыми угрозами. Это должно отражаться на школьном образовании и оценивании его результатов. По ее словам, необходимо актуализировать тесты для оценки знаний обучающихся, внедрять в систему оценки знаний современные информационные технологии.
Генеральный секретарь Сингапурского профсоюза учителей Майк Тируман рассказал, какие факторы обеспечивают успешность модели образования Сингапура, который находится в лидерах по данным исследований PISA, TIMSS и PIRLS. По его словам, на передний план в обучении сейчас выходит формирование у школьников навыков и ценностей. «Чего мы хотим добиться от школьников после 10-12 лет обучения? Мы хотим, чтобы наши школьники стали уверенными в себе людьми, людьми с широким кругозором, которые могут мыслить и действовать, понимают сами себя и понимают, чего они хотят. Чтобы они были готовы продолжать учиться всю жизнь, стремились к самосовершенствованию, были активными членами общества и ответственными гражданами», — рассказал Майк Тируман.
Он особо остановился на роли учителей в современной школе и развитии их профессиональных компетенций. По его словам, учитель должен быть не только компетентным профессионалом, знающим свой предмет, но и наставником, способным привить ценности и принципы. Учитель должен уметь сформировать в классе коллектив и быть лидером перемен, привносящим изменения и новации в свою школу. Учителям необходимо иметь возможность постоянно обмениваться опытом со своими коллегами, присутствовать на их уроках и обсуждать эти уроки, чтобы получать обратную связь от других компетентных специалистов.
Учитель должен уметь сформировать в классе коллектив и быть лидером перемен, привносящим изменения и новации в свою школу. Учителям необходимо иметь возможность постоянно обмениваться опытом со своими коллегами, присутствовать на их уроках и обсуждать эти уроки, чтобы получать обратную связь от других компетентных специалистов.
В ходе конференции ее участники также уделили внимание использованию современных технологий в образовательном процессе, новым формам учебных пособий. Представители Франции и Японии рассказали о системах образования своих стран.
В работе III Международной конференции «Образование с высокими возможностями для каждого: международный опыт, оценка, внедрение» приняли участие около 700 педагогов и экспертов в области образования из разных стран.
Глава Рособрнадзора Сергей Кравцов и путешественник Фёдор Конюхов встретились со стобалльниками ЕГЭ-2017 по географии
Руководитель Федеральной службы по надзору в сфере образования и науки Сергей Кравцов и путешественник Фёдор Конюхов встретились с выпускниками, получившими максимальный результат на едином государственном экзамене по географии.
Сергей Кравцов поблагодарил Фёдора Конюхова за поддержку выпускников в сдаче ЕГЭ. В Год экологии путешественник обратился к выпускникам с пожеланиями успехов на государственной итоговой аттестации. Его слова услышали и участники Всероссийской акции «100 баллов для победы», которая началась в Нальчике и в течение апреля и мая прошла в большинстве регионов.
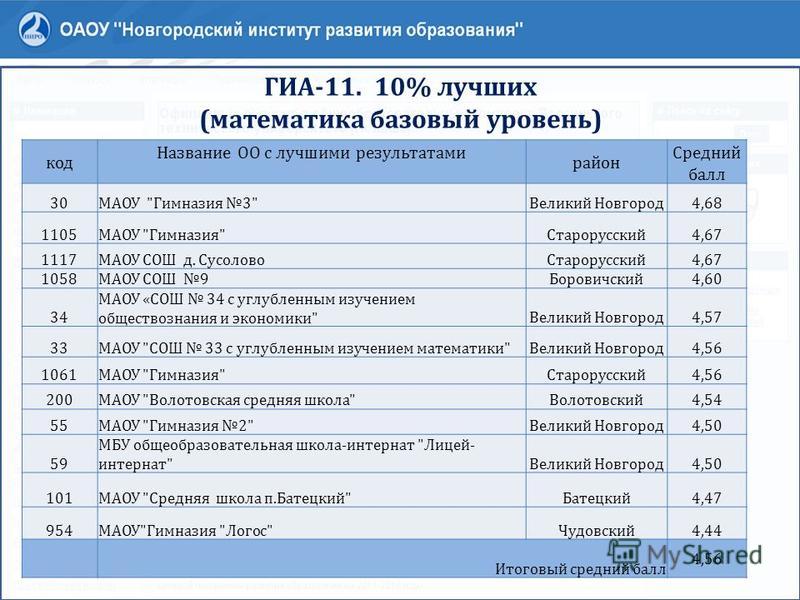
В этом году смогли получить наивысший результат на ЕГЭ по географии – 100 баллов – 18 ребят. Почти все они приехали на встречу с главой Рособрнадзора и известным путешественником. Это выпускники из Томской, Тюменской, Кировской, Пермской, Новгородской, Челябинской, Московской областей, Москвы и Санкт‑Петербурга. Все они уже поступили в ведущие учебные заведения страны: Московский государственный университет имени Ломоносова, Московский государственный институт международных отношений, Московский государственный университет геодезии и картографии, Санкт‑Петербургский горный университет и другие.
«С 2014 года, когда выпускные экзамены стали проходить объективно, у нас появилась идея встречаться со стобалльниками, потому что это уникальные ученики, своим трудом добившиеся максимального результата на ЕГЭ. Мы уже проводили такие встречи с ребятами, набравшими максимальное количество баллов по литературе, химии и физике», — отметил глава Рособрнадзора.
Мы уже проводили такие встречи с ребятами, набравшими максимальное количество баллов по литературе, химии и физике», — отметил глава Рособрнадзора.
Участники встречи задавали вопросы на разные темы: с какими экологическими проблемами сталкивается сегодня наша планета, как привить молодёжи интерес к естественным наукам, с чего начать, если берешься за такое серьёзное дело, как настоящее путешествие.
«Я очень счастлив видеть столько ребят, интересующихся естественными науками. Двадцать первый век остро нуждается в новых исследователях. Сегодня говорят, что мировой океан изучен лишь на три процента. А я уверен, что только на полтора. Я надеюсь, что вы, стобалльники, возьмёте курс на те открытия, которые до вас ещё никто не смог сделать», — сказал Фёдор Конюхов, приветствуя стобалльников.
Сергей Кравцов признался, некогда раздумывал о профессии эколога и много интересовался этой темой. «Каждый человек должен понимать свою значимость в сохранении природы. Если вы разработаете технологию для замены полиэтилена, но сами продолжите загрязнение окружающей среды, ни к чему хорошему это не приведёт. Поэтому, как и в любом другом деле, всегда нужно начинать с себя», — отметил глава Рособрнадзора. Он отметил, что ребята, приехавшие на встречу, выбрали для себя перспективные профессии, за которыми будущее нашей планеты.
Если вы разработаете технологию для замены полиэтилена, но сами продолжите загрязнение окружающей среды, ни к чему хорошему это не приведёт. Поэтому, как и в любом другом деле, всегда нужно начинать с себя», — отметил глава Рособрнадзора. Он отметил, что ребята, приехавшие на встречу, выбрали для себя перспективные профессии, за которыми будущее нашей планеты.
Участниками встречи стали и те выпускники, которые дали старт Всероссийской акции «100 баллов для победы» в Нальчике. В апреле они встречались с выпускниками Северо-Кавказского федерального округа и делились с ними опытом подготовки и сдачи ЕГЭ. Студент Северо-Кавказского федерального университета Даниил Стогний поблагодарил за встречу Фёдора Конюхова и Сергея Кравцова:
«Нам очень важно видеть и разговаривать с такими крупными личностями, которые взяли в руки звезду, может быть, не одну, и указывают нам на то, куда нужно идти, на то, к чему нужно стремиться и где же ещё доставать остальные звёзды, чтобы светить нашей стране, нашей семье, нашей судьбе», — отметил он.
После беседы участники отправились на экскурсию по Дому-музею Фёдора Конюхова и получили памятные подарки – подписанные автором книги знаменитого путешественника.
Рособрнадзор проанализировал предложения граждан по совершенствованию ЕГЭ
Федеральная служба по надзору в сфере образования и науки завершила анализ предложений по совершенствованию единого государственного экзамена (ЕГЭ), поступивших от граждан.
Замечания и пожелания по улучшению ЕГЭ Рособрнадзор ежегодно собирает после завершения основного периода экзаменационной кампании. В этом году предложения принимались до 11 августа. Обращений поступило в два раза меньше чем в прошлом году (около 200) и в десять раз меньше чем в 2014 (около 1000).
Большинство предложений 2017 года носило организационный характер.
Среди наиболее популярных были предложения по корректировке расписания ЕГЭ, совершенствованию процедуры рассмотрения апелляций, поданных участниками ЕГЭ. Также поступили предложения фиксировать время выходов участников ЕГЭ из аудитории, увеличить список дополнительных материалов, которые можно использовать на экзамене, например, добавить в их число циркуль, изменить шрифт контрольных измерительных материалов и ряд других.
Также поступили предложения фиксировать время выходов участников ЕГЭ из аудитории, увеличить список дополнительных материалов, которые можно использовать на экзамене, например, добавить в их число циркуль, изменить шрифт контрольных измерительных материалов и ряд других.
Многие позитивно отметили сокращение сроков проверки экзаменационных работ и выдачи результатов участникам ЕГЭ и высказали пожелания сохранить такой порядок в дальнейшем и еще сократить сроки. Как и в прошлом году, поступили также предложения больше ничего не менять в организации ЕГЭ, сохранив действующий порядок проведения экзаменов.
«Все поступившие предложения внимательно изучены специалистами Рособрнадзора и будут учтены нами в дальнейшей работе. Последние два года предложения граждан по корректировке ЕГЭ не носят революционный характер и касаются в основном незначительных уточнений процедуры. Это говорит о том, что система ЕГЭ устоялась, и в обществе отсутствует запрос на внесение в нее радикальных изменений», – отметил руководитель Рособрнадзора Сергей Кравцов.
Рособрнадзор собирает предложения по совершенствованию ЕГЭ
Предложения по совершенствованию единого государственного экзамена принимаются до 11 августа по электронной почте [email protected]
Изменения ОГЭ 2018 / Содержание блога / Статьи о подготовке к ЕГЭ и ОГЭ на Ege-Merlin.ru
Следующий 2018 год ознаменуется тем, что уже в 10-й раз в Российской Федерации девятиклассники в обязательном порядке пойдут сдавать ГИА ОГЭ. Известно, что эксперименты по внедрению ГИА ЕГЭ И ОГЭ начались еще в 2002 году. Путь, который прошел выпускной экзамен, можно с полным правом назвать тернистым. Сколько было протестов, бойкотов, критики, провалов, разочарования! «Через тернии к звездам» – гласит латинская пословица. И вот наши две звездочки, пусть не гиганты, но уже не карлики – два экзамена ЕГЭ в 11 классе и ОГЭ в 9 классе стали неотъемлемой частью нашей системы непрерывного образования. Постепенно начали внедрять ВПР, и поговаривают, что аналог ГИА введут по окончании 4 класса. Но это все слухи и домыслы.
Постепенно начали внедрять ВПР, и поговаривают, что аналог ГИА введут по окончании 4 класса. Но это все слухи и домыслы.
Как менялся ОГЭ?
Мы подготовили общую таблицу изменений ГИА ОГЭ за последние 10 лет. Методом проб и ошибок, отработки и обкатки ОГЭ стал одним из важных звеньев образовательного процесса.
Как видно из таблицы, самыми изменяемыми предметами являются ОГЭ по русскому языку и математике. Эти два предмета обязательны для сдачи, остальным присвоен статус «по выбору». Если присмотреться к таблице, то сразу становится понятно, что «самыми жаркими» в отношении изменении являлись 2011-2013 гг.
В 2018 году ожидаются кардинальные изменения в ОГЭ по математике и литературе.
Изменения ОГЭ по математике в 2018 году
Как сообщают разработчики КИМ ОГЭ по математики, сильно изменена структура ОГЭ – раздела «Реальная математика» теперь нет, а задания этого раздела распределены по другим разделам – «Алгебра» и «Геометрия».
Действительно, если есть «Реальная математика», то все остальное «Нереальная»? споры по этому поводу велись долго. Теперь в тематическом плане в ОГЭ всего два раздела «Алгебра» и «Геометрия».
Чтобы оценить изменения, приведем сравнительную таблицу.
При этом, несмотря на то, что был расформирован целый раздел, разбалловка и соотношение заданий базовых, повышенной сложности и сложных не меняются.
Как это распределение повлияет на минимальное количество баллов для сдачи ОГЭ пока неизвестно.
Изменения ОГЭ по литературе в 2018 году
ОГЭ и ЕГЭ по литературе являются самыми критикуемыми экзаменами. Вот поэтому изменения по литературе вводятся аккуратно и дозированно. В содержании ОГЭ в этом году значительных изменений нет, а все изменения касаются системы оценивания письменных работ. Благодаря этим изменениям первичный балл увеличен с 23 до 29.
Как распределились баллы?
Как изменится шкала перевода первичных баллов в оценки, станет известно после утверждения в октябре.
Почему мы обратили внимание на увеличение баллов?
Увеличение баллов, как видно из предыдущей таблицы, неравномерно. Задания с относительно небольшим ответом, базового уровня, стали стоить в балловом эквиваленте дороже.
«Разбалловка» в 2017 году
Обратите внимание, что самым главным задание было большое сочинение, которое давало более 50% максимального балла. Естественно, что при подготовке к экзамену девятиклассники в большей степени делали упор на подготовку именно к этому заданию.
«Разбалловка» в 2018 году
В новой версии ОГЭ, кроме сочинения, стоит еще больше внимания обратить на задания базовой сложности. Теперь они оцениваются больше.
Теперь они оцениваются больше.
Анализ результатов государственной(итоговой) аттестации выпускников IX классов 2018-2019 учебный год
Loading…
Анализ государственной (итоговой) аттестации выпускников IX классов
На конец года в параллели 9 классов обучалось 76 чел. Решением педагогического совета (протокол № 6 от 22 мая 2019 года) допущены к государственной итоговой аттестации:
9А класса – в количестве 28 человек
9Б класса – в количестве 24 человека
9В класса – в количестве 23 человек
Деев Даниил Владимирович, обучающийся 9 А класса, не допущен к государственной итоговой аттестации, в связи с тем, что не получил зачет на устном собеседовании.
Государственная итоговая аттестация в 9 классах проходила:
— в форме ОГЭ (русский язык, математика, обществознание, физика, биология, английский язык, химия, география)
Все учащиеся 9-х классов сдавали 2 обязательных экзамена: русский язык, математика. В следующем учебном году будет открыт один профильный класс: социально-экономический (обязательными экзаменами являлись обществознание). Письменные экзамены по русскому языку и математике в форме ОГЭ сдавали 75 обучающихся IX классов.
Письменные экзамены по русскому языку и математике в форме ОГЭ сдавали 75 обучающихся IX классов.
Результаты государственной (итоговой) аттестации
по математике и русскому языку, проводимой в форме ОГЭ
Кол-во, сдававших экзамен | Кол-во выпускников, получивших экзаменационную отметку | Равную годовой | Выше годовой | Ниже годовой |
|
| |||||||||||||||||||
|
| ||||||||||||||||||||||||
«5» | «4» | «3» | «2» | Чел. | % | Чел. | % | Чел | % | ПУ | ПК | ||||||||||||||
Русс. | 42 | 22 | 11 | — | 20 | 27% | 55 | 70% | 2 | 3% | 100% | 85% |
| ||||||||||||
Математика -75 | 10 | 48 | 17 | — | 46 | 61% | 19 | 25% | 13 | 14% | 100% | 77% |
| ||||||||||||
Результаты государственной (итоговой) аттестации
по математике и русскому языку, проводимой в форме ГВЭ
Кол-во, сдававших экзамен | Кол-во выпускников, получивших экзаменационную отметку | Равную годовой | Выше годовой | Ниже годовой |
|
| |||||||||||||||||||
|
| ||||||||||||||||||||||||
«5» | «4» | «3» | «2» | Чел. | % | Чел. | % | Чел | % | ПУ | ПК |
| |||||||||||||
Русс.яз.-0 | — | — | — | — | — | — | — | — | — | — | — | — |
| ||||||||||||
Математика -0 | — | — | — | — | — | — | — | — | — | — | — | — |
| ||||||||||||
Результаты государственной итоговой аттестации
по математике и русскому языку, проводимой в форме ОГЭ
Анализ результатов экзаменов в форме ОГЭ и школьных (годовых) отметок указывает на хорошую работу учителей русского языка и литературы Панферовой В. И. — в 9 Б классе больше 50% обучающихся показали результаты выше годовой, В., Лютовой И. В., Титаревой С. Н., учителя математики Ивашечкина О. В. ( 9 Б класс) по подготовке обучающихся к государственной итоговой аттестации. При сравнении годовых и экзаменационных оценок можно сделать вывод, что 70% обучающихся повысили свои результаты по русскому языку, 33% обучающихся повысили свои результаты по математике. Процент успеваемости по русскому языку составил – 100%, по математике – 96% ( 3 ученика будут пересдавать математику в резервные сроки Журавлева Василиса – 9 А кл, Еремин Вадим – 9 Б, Рынков Арсений – 9 В ), процент качества по математике составил -76%, по сравнению с прошлым годом процент качества снизился на 20 %., по русскому языку процент качества составил- 85%, по сравнению с прошлым годом процент качества понизился на 6 % . По русскому языку повысили свои результаты – 55 чел. ( 70%), получили равную годовой – 20 чел. ( 27 %). Подтвердили свои результаты по математике – 57 % (44 чел), на экзамене получили выше годовых оценок 18 чел.
И. — в 9 Б классе больше 50% обучающихся показали результаты выше годовой, В., Лютовой И. В., Титаревой С. Н., учителя математики Ивашечкина О. В. ( 9 Б класс) по подготовке обучающихся к государственной итоговой аттестации. При сравнении годовых и экзаменационных оценок можно сделать вывод, что 70% обучающихся повысили свои результаты по русскому языку, 33% обучающихся повысили свои результаты по математике. Процент успеваемости по русскому языку составил – 100%, по математике – 96% ( 3 ученика будут пересдавать математику в резервные сроки Журавлева Василиса – 9 А кл, Еремин Вадим – 9 Б, Рынков Арсений – 9 В ), процент качества по математике составил -76%, по сравнению с прошлым годом процент качества снизился на 20 %., по русскому языку процент качества составил- 85%, по сравнению с прошлым годом процент качества понизился на 6 % . По русскому языку повысили свои результаты – 55 чел. ( 70%), получили равную годовой – 20 чел. ( 27 %). Подтвердили свои результаты по математике – 57 % (44 чел), на экзамене получили выше годовых оценок 18 чел. — 33%. Ниже годовых получили – 13 чел. – 23 %.
— 33%. Ниже годовых получили – 13 чел. – 23 %.
Уровень качества знаний обучающихся 9 классов по русскому языку значительно выше уровня на конец года ( 9 А класс на конец года ПК -57%, ГИА – 75%, 9 Б класс на конец года ПК -63%, ГИА – 92%, 9 В класс на конец года ПК – 52% , ГИА – 91 %). Сравнение оценочного уровня результатов экзаменов позволяет сделать вывод, что все учащиеся 9-х классов хорошо усвоили минимум содержания основного образования.
В течение года учащиеся 9-х классов участвовали в проведении диагностических работах системы Статград. У ребят отработан навык заполнения бланков, решением тестов и текстовых задач.
Итоги выполнения заданий базового уровня показывают, что контролируемые на базовом уровне элементы минимума содержания курса русского языка и математики обучающимися усвоены.
Сравнительный анализ итогов экзамена по русскому языку и математике в форме ОГЭ за 3 года.
| 2016-2017 учебный год | 2017-2018 учебный год | 2018-2019 учебный год | ||||||||
% обуч. | кол-во уч-ся | % качества | кол-во уч-ся | % обуч. | % качества | кол-во уч-ся | % качества | % обучен. | |||
русский язык | 100% | 80 | 79% | 80 | 100% | 91% | 75 | 85% | 100% |
| |
алгебра | 100% | 80 | 60% | 80 | 100% | 80% | 75 | 77% | 100% |
| |
учебный год | получили оценки | ||||||||
предмет | «5» | «4» | «3» | «2» | |||||
кол-во
| % от сдававших | кол-во | % от сдававших | кол-во | % от сдававших | кол-во | % от сдававших | ||
2016- 2017 г. | русск.яз | 32 | 40% | 31 | 39% | 17 | 21% | — | — |
алгебра | 18 | 23% | 30 | 38% | 31 | 38% | 1 | 1% | |
2017- 2018 г. | русск.яз | 37 | 46% | 36 | 45% | 7 | 9% | — | — |
алгебра | 17 | 22% | 47 | 59% | 15 | 19% | — | — | |
2018- 2019 г. | русск.яз | 42 | 56% | 22 | 29% | 11 | 15% | — | — |
алгебра | 10 | 13% | 48 | 64% | 17 | 23% | — | — | |
Экзамен в новой форме | Полученный выпускниками ОУ балл в 2017 г. | Полученный выпускниками ОУ балл в 2018 г. | Полученный выпускниками ОУ балл в 2019 г. | ||||||
Мин. | Макс | Сред | Макс | Мин. | Сред | Мин. | Макс | Сред | |
Русс.яз. | 11 | 39 | 32,5 | 39 | 21 | 34 | 23 | 39 | 33,4 |
Математика | 8 | 30 | 17,2 | 30 | 10 | 19 | 8 | 25 | 17,3 |
Из сравнительного анализа итогов экзамена по русскому языку и математике в форме ОГЭ за 3 учебных года можно сделать вывод: уровень обученности по русскому языку остается 100%, по математике в течение 3 лет процент обученности 100 %, уровень качества по прежнему остается высокий по русскому языку, по математике в этом году незначительно понизился. Средний балл по математике понизился на 1,7 балла и составил – 17,3 баллов. Средний балл по русскому языку составил – 33,4 балла.
Средний балл по математике понизился на 1,7 балла и составил – 17,3 баллов. Средний балл по русскому языку составил – 33,4 балла.
Анализ результатов предметов по выбору.
Наиболее популярными предметами по выбору оказались физика, обществознание, география.
ОГЭ по обществознанию не сдали с первого раза 4 человека Бочарников Данила (9А), Мельников Сергей (9 А), Корякин Вадим (9 В), Васильев Вячеслав (9 В). Они будут пересдавать экзамен в резервные сроки.
ОГЭ по физике сдали все 20 чел. (процент успеваемости составил – 100%), процент качества — 42 % (это на 48 % ниже по сравнению с прошлым годом). Самый высокий результат у Мирошничеко Кирилла – 28 баллов (в прошлом году высокий балл был -34). Средний балл по физике составил – 20 баллов (это ниже на 7 баллов по сравнению с прошлым годом). В 9 А классе все обучающиеся сдали экзамен на «4» и «5» — качество составило 33%.
ОГЭ по биологии сдавали 5 учеников, все сдали- процент успеваемости составил 100%, качество – 80 %. (это выше на 9%, чем в прошлом году).
(это выше на 9%, чем в прошлом году).
ОГЭ по английскому языку сдавали 5 человек. Мирошниченко Олеся сдала на 61 балл, процент успеваемости составил – 100%, процент качества составил – 60%., средний составил – 50 баллов. Все участники ОГЭ по английскому языку сдали экзамен хорошо.
Экзамен по химии выбрали 6 учеников. Процент качества составил – 67%, процент успеваемости составил – 100%. Средний балл -26 баллов, это на 3 балла выше, чем в прошлом году. Высокие результаты показали: Шакалова Екатерина – 38 баллов, Нагорная Екатерина – 37 баллов.
Экзамен по географии сдавали 47 учеников, 4 чел. Не сдали 3 чел. Продунова А. -9 а, Корякин В. и Мукина А. из 9 В. Процент успеваемости составил- 92%, а процент качества -64%. Колобаев Андрей набрал 11 баллов по географии, подал на апелляцию. Апелляционная комиссия пересмотрела результаты по географии, повысив результата на 1 балл. В итоге, Колобаев Андрей получил 12 баллов оценка «3». В резервные сроки географию все пересдали.
Экзамен по истории сдавал 1 ученик Андреев Максим. Сдал на 34 балла, оценка «4».
Экзамен по математике в первый поток не сдали -3 человека (Еремин В., Журавлева В., Рынков А. будут пересдавать в резервные сроки – в форме ОГЭ) Экзамен по обществознанию не сдали 4 человека- Бочарников Д., Васильев В., Корякин В., Мельников С. В резрвные сроки ребята обществознание пересдали.
Экзамен по физике не сдали 2 ученика – Скуратова Я., Пархачев И. Для них пересдача будет в резервные сроки – 26 июня. В резервные сроки ребята физику пересдали.
Экзамены по выбору прошли без нарушения инструкций. Экзамены начались во время, опоздавших не было.
Анализируя результаты экзаменов выпускников 9 классов, следует отметить эффективную работу учителей ШМО русского языка, математики (учитель Ивашечкина О. В.) физики, обществознания, английскому языку — по подготовке обучающихся к государственной итоговой аттестации.
Результаты государственной итоговой аттестации позволяют сделать вывод о том, что качество знаний обучающихся 9-х классов соответствует государственным образовательным стандартам, учебный процесс в школе идет удовлетворительно, уровень подготовки по предметам стабилен.
Государственная итоговая аттестация выпускников 9 «_А_» класса осуществлялась по следующим учебным предметам в форме ОГЭ:
№ п/п | Предмет
| Количество сдававших | Отметка | Уровень обучен- ности (в среднем по данному предмету по ОУ) | Качество знаний (в среднем по данному предмету по ОУ) | Баллы | Квалиф. Категория | |||||
2 | 3 | 4 | 5 |
| ||||||||
min | max |
| ||||||||||
1 | Обществознание | 26 | — | 10 | 12 | 4 | 100% | 62% | 13 | 35 | Санкина И. |
|
2 | Химия | 1 | — | — | 1 | — | 100% | 100% | 26 | 26 | Чернышева В. А (высшая) |
|
4. | Математика | 28 | — | 5 | 20 | 3 | 100% | 82% | 11 | 24 | Ивашечкина О. В. (высшая) |
|
5. | Русский язык | 28 | — | 7 | 9 | 12 | 100% | 75% | 23 | 39 | Титарева С. Н. (высшая) |
|
6. | Физика | 6 | — | 4 | 2 | — | 100% | 33% | 11 | 25 | Сигеев С. |
|
7. | География | 19 | — | 6 | 10 | 3 | 100% | 68% | 12 | 32 | Прошкина И. В. (первая) |
|
8. | Английский язык | 4 | — | 2 | — | 2 | 100% | 50% | 35 | 61 | Артеменко И. В. (первая) |
|
Государственная итоговая аттестация выпускников 9 «_Б_» класса осуществлялась по следующим учебным предметам в форме ОГЭ:
№ п/п | Предмет
| Количество сдававших | Отметка | Уровень обучен- ности (в среднем по данному предмету по ОУ) | Качество знаний (в среднем по данному предмету по ОУ) | Баллы | Квалиф. категория | |||||
2 | 3 | 4 | 5 |
| ||||||||
min | max |
| ||||||||||
1 | Обществознание | 20 | — | 5 | 14 | 1 | 100% | 75% | 20 | 36 | Санкина И. Г. (высшая) |
|
2 | Математика | 24 | — | 2 | 17 | 5 | 100% | 90% | 16 | 25 | Ивашечкина О. В. (высшая) |
|
3 | Русский язык | 24 | — | 2 | 5 | 17 | 100% | 92% | 20 | 39 | Панферова В. (высшая) |
|
4 | Биология | 2 | — | — | 2 | — | 100% | 100% | 29 | 36 | Шинкаренко Е.Н. (высшая) |
|
5 | Физика | 14 | — | 7 | 7 | — | 100% | 50% | 18 | 28 | Сигеев С. А. (высшая) |
|
6 | География | 8 | — | 2 | 4 | 2 | 100% | 75% | 18 | 31 | Прошкина И. В. (первая) |
|
7 | Химия | 3 | — | 1 | — | 2 | 100% | 67% | 14 | 38 | Чернышева В. (высшая) |
|
8 | История | 1 | — | — | 1 | — | 100% | 100% | 34 | 34 | Евстратова В. П. (соответствие) |
|
Государственная итоговая аттестация выпускников 9 «_В_» класса осуществлялась по следующим учебным предметам в форме ОГЭ:
№ п/п | Предмет
| Количество сдававших | Отметка | Уровень обучен- ности (в среднем по данному предмету по ОУ) | Качество знаний (в среднем по данному предмету по ОУ) | Баллы | Квалиф. категория | |||||
2 | 3 | 4 | 5 |
| ||||||||
min | max |
| ||||||||||
1 | Обществознание | 20 | — | 6 | 13 | 1 | 100% | 70% | 19 | 36 | Санкина И. |
|
2 | Математика | 23 | — | 9 | 12 | 2 | 100% | 61% | 8 | 23 | Маршавина С. М. (высшая) |
|
3 | Русский язык | 23 | — | 11 | 22 | 42 | 100% | 85% | 23 | 39 | Лютова И. В. (высшая) |
|
4 | География | 20 | — | 8 | 8 | 4 | 100% | 60% | 13 | 31 | Прошкина И. В. (первая) |
|
5 | Английский язык | 1 | — | — | 1 | — | 100% | 100% | 52 | 52 | Литвинова Д. (высшая) |
|
6 | Химия | 2 | — | 1 | — | 1 | 100% | 50% | 9 | 31 | Чернышева В. А. (высшая) |
|
7 | Биология | 3 | — | 1 | 2 | — | 100% | 67% | 19 | 35 | Шинкаренко Е.Н. (высшая) |
|
Сводный анализ
государственной (итоговой) аттестации
выпускников 9-х классов
№ п/п | Предмет
| Количество сдававших | Отметка | Уровень обучен- ности (в среднем по данному предмету по ОУ) | Качество знаний (в среднем по данному предмету по ОУ) | Баллы | Квалиф. категория | |||||
2 | 3 | 4 | 5 |
| ||||||||
min | max | сред-ний |
| |||||||||
1 | Обществознание | 66 | — | 21 | 39 | 6 | 100% | 68% | 18 | 36 | 26 | Санкина И. Г. (высшая) |
2 | Химия | 6 | — | 2 | 1 | 3 | 100% | 67% | 9 | 38 | 26 | Чернышева В. А. (высшая) |
4. | Математика | 75 | — | 17 | 48 | 10 | 100% | 77% | 8 | 25 | 17,3 | Ивашечкина О. (высшая) Маршавина С. М. (высшая) |
5 | Русский язык | 75 | — | 11 | 22 | 42 | 100% | 85% | 23 | 39 | 33,4 | Титарева С. Н. (высшая) Лютова И. В. (высшая) Панферова В. И. (высшая) |
6 | Биология | 5 | — | 1 | 4 | — | 100% | 80% | 19 | 36 | 29,4 | Шинкаренко Е. Н. (высшая)
|
7 | Физика | 20 | — | 11 | 9 | — | 100% | 45% | 18 | 28 | 20 | Сигеев С. А. (высшая) |
8 | География | 47 | — | 16 | 22 | 9 | 100% | 66% | 12 | 32 | 22 | Прошкина И. (первая) |
9 | История | 1 | — | — | 1 | — | 100% | 100% | 34 | 34 | 34 | Евстратова В. П. (соответствие) |
10 | Английский язык | 5 | — | 2 | 1 | 2 | 100% | 60% | 35 | 61 | 50 | Литвинова Д. Ю.(высшая) Артеменко И. В. (первая) |
Решением педагогического совета протокол № 10 от 20 июня 2019 года
- Выдать аттестат об основном общем образовании с отличием, следующим обучающимся:
- Шакаловой Екатерине Алексеевне – 9 Б класс
- Портновой Дарье Викторовне – 9 В класс
- Продлить государственную итоговую аттестацию ученикам 9 В класса Корякину Вадиму (география, общество), Мукиной Анне (география), Рынкову Арсению (математика), Васильеву Вячеславу(обществознание), ученикам 9 А Бочарникову Даниилу (обществознание), Мельникову Сергею (обществознание), Продуновой Анне (география), ученикам 9 Б класса Еремину Вадиму (математика), Скуратовой Яне (физика), Пархачеву Илье (физика).
 В резервные сроки им необходимо пересдать предметы: математику, обществознание, географию и физику.
В резервные сроки им необходимо пересдать предметы: математику, обществознание, географию и физику. - В резервные сроки физику пересдали — Скуратова Яна, Пархачев Илья, обществознание- пересдали Мельников Сергей, Бочарников Данила, Васильев Вячеслав, Корякин Вадим, математику пересдали – Рынков Арсений, Журавлева Василиса, Ерёмин Вадим, географию все пересдали – Корякин Вадим, Продунова Анна, Мукина Анна.
Результаты ГИА
Результаты государственной (итоговой) аттестации выпускников 9 классов
ГИА -2018. В 2018 г. успешно прошли государственную итоговую аттестацию в форме ОГЭ — 87 выпускников (100%) и получили аттестат об основном общем образовании, из них, 11 лицеистов — аттестат особого образца с отличием.
| Предмет |
ОГЭ — СПРАВЛЯЕМОСТЬ (%) — 2017-2018 учебный год |
||
| Лицей №2 | г. Рыбинск Рыбинск |
Ярославская область | |
| Русский язык | 100 | 99,6 | 99,2 |
| Математика | 100 | 98,6 | 98,0 |
| Физика | 100 | 99,4 | 99,5 |
| Информатика | 100 | 99,1 | 97,6 |
| Литература | 100 | 100 | 100 |
| Химия | 100 | 100 | 99,6 |
| Биология | 100 | 98,8 | 98,9 |
| Обществознание | 100 | 98,0 | 97,6 |
| Английский язык | 100 | 100 | 99,8 |
| География | 100 | 96,8 | 97,0 |
По количеству учащихся, показавших отличный результат ОГЭ (на «5»), результаты лицея значительно превышают городской и региональный показатель по русскому языку, математике, физике, информатике, химии.
| Предмет |
Количество учащихся, показавших отличный результат (5) ОГЭ — 2017-2018 учебный год |
|||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Русский язык | 66,7 | 32,7 | 32,9 | |||
| Математика | 50,6 | 15,1 | 16,4 | |||
| Физика | 32,4 | 15,3 | 13,1 | |||
| Информатика | 19,9 | 27,0 | 30,5 | |||
| Литература | 88,6 | 48,4 | 40,3 | |||
| Химия | 25,0 | 31,9 | 38,8 | |||
| Биология | 0 | 1,7 | 4,3 | |||
| Обществознание | 13,8 | 5,8 | 6,4 | |||
| Английский язык | 36,8 | 40,0 | 49,4 | |||
| География | 0 | 15,6 | 18,7 | |||
ГИА -2017. В 2017 г. успешно прошли государственную итоговую аттестацию в форме ОГЭ — 74 выпускника (100%) и получили аттестат об основном общем образовании, из них, 5 лицеистов — аттестат особого образца с отличием.
| Предмет |
ОГЭ — СПРАВЛЯЕМОСТЬ (%) — 2016-2017 учебный год |
||
| Лицей №2 | г. Рыбинск | Яросалвская область | |
| Русский язык | 100 | 99,9 | 99,7 |
| Математика | 100 | 99,3 | 98,3 |
| Физика | 100 | 99,5 | 99,8 |
| Информатика | 100 | 99,8 | 99,6 |
| Литература | 100 | 100 | 99,4 |
| Химия | 100 | 100 | 99,8 |
| Биология | 100 | 99,3 | 98,9 |
| Обществознание | 100 | 99,5 | 98,6 |
| История | 100 | 94,0 | 96,6 |
| Английский язык | 100 | 100 | 99,4 |
| География | 100 | 99,2 | 98,4 |
По среднему баллу ОГЭ результаты лицея превышают городской и региональный показатель по русскому языку, математике, физике, информатике, литературе, химии, биологии, обществознанию, истории и географии.
| Предмет |
ОГЭ — СРЕДНИЙ БАЛЛ — 2016-2017 учебный год |
|||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Русский язык | 34,7 | 30,8 | 31,1 | |||
| Математика | 20,4 | 15,1 | 15,6 | |||
| Физика | 26,8 | 22,3 | 22,7 | |||
| Информатика | 19,9 | 14,9 | 15,0 | |||
| Литература | 21,0 | 17,6 | 17,1 | |||
| Химия | 26,6 | 22,7 | 23,6 | |||
| Биология | 26,7 | 23,3 | 24,4 | |||
| Обществознание | 28,6 | 24,1 | 24,1 | |||
| История | 27,7 | 23,4 | 24,7 | |||
| Английский язык | 55,4 | 57,2 | 57,3 | |||
| География | 26,0 | 20,0 | 20,4 | |||
ГИА -2016. В 2016 г. успешно прошли государственную итоговую аттестацию в форме ОГЭ 81 выпускник, в форме ГВЭ — 1 обучающийся 9-х классов (100%) и получили документ об основном общем образовании, из них, 5 лицеистов — аттестат особого образца с отличием.
| Предмет |
ОГЭ — СПРАВЛЯЕМОСТЬ% — 2015-2016 учебный год |
||
| Лицей №2 | г. Рыбинск | Яросалвская область | |
| Русский язык | 100 | 99,6 | 99,3 |
| Математика | 100 | 98,8 | 98,7 |
| Физика | 100 | 94,0 | 94,5 |
| Информатика | 100 | 97,9 | 96,0 |
| Литература | 100 | 90,7 | 90,1 |
| Химия | 100 | 92,2 | 93,1 |
| Биология | 100 | 92,0 | 91,9 |
| Обществознание | 100 | 88,8 | 89,6 |
| История | 100 | 80,0 | 72,9 |
| Английский язык | 100 | 92,0 | 93,3 |
По среднему баллу ОГЭ результаты лицея превышают городской показатель:
- по математике на 5,5 балла,
- по русскому языку на 4,3 балла,
- по физике на 8 баллов,
- по обществознанию на 7,6 балла,
- по литературе на 7,1 балла,
- по биологии на 6,8 балла,
- по химии на 5,9 балла
- по информатике на 4,9 балла,
- по истории на 3,6 балла.
| Предмет |
ОГЭ — СРЕДНИЙ БАЛЛ — 2015-2016 учебный год |
|||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Русский язык | 34,7 | 30,3 | 30,6 | |||
| Математика | 21,6 | 16,1 | 16,4 | |||
| Физика | 28,8 | 20,8 | 19,9 | |||
| Информатика | 20,3 | 15,4 | 14,2 | |||
| Литература | 23 | 15,1 | 15,0 | |||
| Химия | 26,8 | 20,7 | 20,8 | |||
| Биология | 29 | 22,2 | 22,7 | |||
| Обществознание | 29,6 | 22 | 22,4 | |||
| История | 23,5 | 19,9 | 18,4 | |||
| Английский язык | 44 | 50,4 | 50,9 | |||
ГИА -2015. В 2015 г. успешно прошли государственную (итоговую) аттестацию в форме ОГЭ 75 выпускника 9-х классов (100%) и получили документ об основном общем образовании, из них, 5 лицеистов — аттестат особого образца с отличием. В группе с углублённым изучением математики все выпускники 9-х классов (100%) сдали ГИА на «хорошо» и «отлично».
| Предмет |
СПРАВЛЯЕМОСТЬ% — 2014-2015 учебный год |
||
| Лицей №2 | г. Рыбинск | Яросалвская область | |
| Русский язык | 100 | 99,1 | 99,1 |
| Математика | 100 | 100 | 100 |
По среднему баллу результаты лицея превышают городской показатель по математике на 6,7 баллов, по русскому языку на 21,8 балла.
| Предмет |
СРЕДНИЙ БАЛЛ 2014-2015 учебный год |
|||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Русский язык | 81,1 | 59,3 | 55,1 | |||
| Математика | 23,2 | 16,5 | 16,3 | |||
ГИА -2014. В 2014 г. успешно прошли государственную (итоговую) аттестацию 78 выпускника 9-х классов (100%) и получили документ об основном общем образовании, из них, 9 лицеистов — аттестат особого образца с отличием. В группе с углублённым изучением математики все выпускники 9-х классов (100%) сдали ГИА на «хорошо» и «отлично».
| Предмет | 2013-2014 учебный год | |||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Справляемость % | Качество % | Справляемость % | Качество % | Справляемость % | Качество % | |
| Русский язык | 100 | 92,3 | 99,8 | 66 | 98,9 | 73,7 |
| Математика | 100 | 79,5 | 99,9 | 85 | 98,5 | 59,7 |
По среднему баллу результаты лицея превышают городской и региональный показатель по математике на 7 баллов, по русскому языку на 2,5 балла.
| Предмет | 2013-2014 учебный год | |||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Средний балл | Средний балл | Средний балл | ||||
| Русский язык | 36,1 | 33,4 | 32,6 | |||
| Математика | 21,1 | 14,4 | 14,6 | |||
ГИА -2013. В 2013 г. успешно прошли государственную (итоговую) аттестацию 72 выпускника 9-х классов (100%) и получили документ об основном общем образовании, из них, 7 лицеистов — аттестат особого образца с отличием, 2 ученика награждены Почётной грамотой «За особые успехи в изучении отдельных предметов» по английскому языку. В группе с углублённым изучением математики все выпускники 9-х классов (100%) сдали ГИА на «отлично».
| Предмет | 2012-2013 учебный год | |||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Справляемость % | Качество % | Справляемость % | Качество % | Справляемость % | Качество % | |
| Русский язык | 100 | 85 | 99,6 | 66 | 99,6 | 65,8 |
| Математика | 100 | 100 | 99,7 | 85 | 99,7 | 85,2 |
По среднему баллу результаты лицея превышают городской и региональный показатель по математике на 7 баллов, по русскому языку на 2,5 балла.
| Предмет | 2012-2013 учебный год | |||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Средний балл | Средний балл | Средний балл | ||||
| Русский язык | 34,82 | 32,3 | 32,3 | |||
| Математика | 27,96 | 20,8 | 20,7 | |||
ГИА-2012. В 2012 г. 84 выпускника 9-х классов получили документ об основном общем образовании, из них, 1 лицеист — аттестат особого образца с отличием. Все выпускники 9-х классов (100%) справились с государственной итоговой аттестацией (ГИА) и продемонстрировали лучший в городе результат, высокое качество лицейского образования.
| Предмет | 2011-2012 учебный год | |||||
| Лицей №2 | г. Рыбинск | Яросалвская область | ||||
| Справляемость % | Качество % | Справляемость % | Качество % | Справляемость % | Качество % | |
| Русский язык | 100 | 82,2 | 99,4 | 66,4 | 100 | 78,0 |
| Математика | 100 | 81 | 98,4 | 55,6 | 99,7 | 73,9 |
Государственная итоговая аттестация 2018 — Образовательная программа «Прикладная математика» — Национальный исследовательский университет «Высшая школа экономики»
Здесь мы размещаем информацию для выпускников 2018 года по мере ее поступления и/или актуализации. Следите, пожалуйста, за обновлениями.
Часто задаваемые вопросы.
График выполнения различных этапов подготовки ВКР
Государственная итоговая аттестация (ГИА) включает в себя сдачу междисциплинарного экзамена по направлению подготовки и подготовку и защиту Выпускной квалификационной работы.
К ГИА допускаются студенты, успешно завершившие теоретический курс обучения.
О допуске студента к ГИА выходит соответствующий приказ.
| Суть приказа | Приказ | Приложение к Приказу |
|---|---|---|
| Утврерждение тем и руководителей ВКР | ||
| Изменение тем/руководителей | ||
| О направлении студентов на преддипломную практку | ||
| О составе апелляционной комиссии МИЭМ НИУ ВШЭ | ||
| Состав ГЭК 2017-2018 уч. год | ||
| График проведения ГИА | ||
| О назначении рецензентов | ||
| Приказ о допуске к ГИА 2017-2018 уч. год | Приказ о допуске к ГИА |
Приложение к Приказу о допуске к ГИА |
| Списки студентов, допущенных к ГИА (по группам, подгруппам, датам) | ||
| Выпуск студентов | Приказ об отчислении из НИУ ВШЭ студентов образовательной программы «Прикладная математика» МИЭМ НИУ ВШЭ в связи с получением образования и предоставлении каникул студентам, отчисляемым с момента окончания указанных каникул | |
| Отчисление после каникул |
| |
| ГИА осень 2018 | ||
| График проведения ГИА | ||
| О назначении рецензентов | | |
| Выпуск студентов |
Нормативные документы, регламентирующие процесс ГИА:
Положение о курсовой и выпускной квалификационной работе студентов, обучающихся по программам бакалавриата, специалитета и магистратуры в НИУ ВШЭ (утверждено ученым советом НИУ ВШЭ от 28.11.2014);
Конкретизация на уровне МИЭМ: Правила подготовки и защиты выпускной квалификационной работы для студентов, обучающихся по программам бакалавриата, специалитета и магистратуры МИЭМ НИУ ВШЭ (Одобрен Ученым Советом МИЭМ НИУ ВШЭ 06.10.2015г., Протокол №5, одобрен Методическим центром НИУ ВШЭ).
Конкретизация на уровне образовательной программы: (Утверждено Ученым советом МИЭМ НИУ ВШЭ (Протокол №7 от 02.02.2016, актуализированы на 2017/2018 уч год).
О переносе сроков защиты ВКР
Если Вы не явились на защиту ВКР по уважительной причине, то, для переноса срока защиты ВКР Вам потребуется ознакомиться с алгоритмом и написать соответствующее заявление.
Студент, не прошедший итоговую государственную аттестацию без уважительной причины, в том числе получивший на итоговой государственной аттестации неудовлетворительные результаты, отчисляется из НИУ ВШЭ, и ему выдается академическая справка. Указанный студент, при восстановлении в НИУ ВШЭ, вправе пройти итоговую государственную аттестацию повторно не ранее чем через один год и не позднее чем через два года после прохождения итоговой государственной аттестации впервые. (Положение об итоговой государственной аттестации, п.5.1.)
Шаблоны
Электронные сервисы для подачи заявлений.Архив:ГИА 2017
ОГЭ — Лицей математики и информатики г. Саратов
14 мая 2020 года
ОГЭ 2021
Основные сведения об ОГЭ
https://fipi.ru/oge
Постановление Правительства Российской Федерации от 26.02.2021 № 256 «Об особенностях проведения государственной итоговой аттестации по образовательным программам основного общего и среднего общего образования в 2021 году»
Опубликован обновленный проект расписания ГИА для выпускников 9 классов в 2021 году
Проектом расписания ГИА-9 предусмотрены два периода проведения экзаменов: основной (24 мая – 2 июля) и дополнительный (3-17 сентября). Основной государственный экзамен (ОГЭ) и государственный выпускной экзамен (ГВЭ-9) в 2021 году пройдут только по двум обязательным предметам, русскому языку и математике. ОГЭ и ГВЭ по предметам по выбору для девятиклассников в 2021 году проводиться не будут.
Заявления на участие в ОГЭ принимаются до 1 марта 2021 года.
Проведение основного государственного экзамена (ОГЭ) по предметам по выбору в 2020/21 учебном году отменено, вместо этих экзаменов для девятиклассников будут проведены контрольные работы по одному учебному предмету.
Контрольные работы выпускники смогут выбрать из числа учебных предметов, по которым проводится государственная итоговая аттестация (ГИА-9) по выбору: физика, химия, информатика, биология, история, география, иностранные языки (английский, немецкий, французский, испанский), обществознание, литература. Они будут проведены до начала основного периода ГИА-9 по рекомендованному Рособрнадзором расписанию в период с 17 мая по 21 мая 2021 года.
Учебный предмет, по которому будет проведена контрольная работа, выбирает участник ГИА-9, в том числе исходя из дальнейшей образовательной траектории (например, прием в профильный 10-ый класс).
Варианты контрольной работы по соответствующему учебному предмету будут составляться по спецификации контрольных измерительных материалов (КИМ) ОГЭ 2021 года.
Региональные органы управления образованием вправе самостоятельно ограничить число выполняемых заданий и/или изменить время выполнения контрольной работы.
Органы исполнительной власти субъектов РФ устанавливают минимальные первичные баллы, соответствующие отметкам по пятибалльной шкале, за выполнение контрольной работы на основе рекомендаций Рособрнадзора.
Результаты контрольных работ будут внесены в региональные и федеральную информационные системы ГИА и приема.
______________________________________________________________________________
Формы проведения ГИА 9 – основной государственный экзамен (ОГЭ) и государственный выпускной экзамен (ГВЭ).
ОГЭ – это форма государственной итоговой аттестации по образовательным программам основного общего образования. При проведении ОГЭ используются контрольные измерительные материалы стандартизированной формы.
Для получения аттестата участники сдают обязательные экзамены: русский язык и математика, а также еще 2 экзамена по выбору обучающегося по двум учебным предметам из числа учебных предметов: физика, химия, биология, литература, география, история, обществознание, иностранные языки (английский, французский, немецкий и испанский языки), информатика и информационно-коммуникационные технологии (ИКТ).
Приказ Министерства просвещения Российской Федерации и Федеральной службы по надзору в сфере образования и науки от 07.11.2018 г. № 189/1513 «Об утверждении порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования»
Демоверсии, спецификации, кодификаторы ОГЭ 2021
https://fipi.ru/oge/demoversii-specifikacii-kodifikatory
Пояснение к проектам документов, определяющих структуру и содержание КИМ ОГЭ 2021 г.
Открытый банк заданий ОГЭ
https://fipi.ru/oge/otkrytyy-bank-zadaniy-oge
Областные родительские собрания «Готовимся к экзаменам вместе»
http://minobr.saratov.gov.ru/activities/gia/details.php?ELEMENT_ID=25550
Итоговое собеседование по русскому языку
Итоговое собеседование по русскому языку в 9 классе с 2019 года является условием допуска к государственной итоговой аттестации по образовательным программам основного общего образования (приказ Министерства просвещения Российской Федерации и Федеральной службы по надзору в сфере образования и науки от 7 ноября 2018 года № 189/1513 «Об утверждении порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования»).
На итоговом собеседовании участникам предлагается выполнить четыре задания: чтение текста вслух, его пересказ с привлечением дополнительной информации, монологическое высказывание по одной из выбранных тем и диалог с экзаменатором-собеседником.
В качестве экзаменатора-собеседника может быть назначен учитель по любому предмету, обладающий коммуникативными навыками, грамотной речью, но не преподающий в этом классе.
На выполнение работы каждому участнику отводится в среднем 15-16 минут. Для участников итогового собеседования с ограниченными возможностями здоровья, детей-инвалидов и инвалидов продолжительность процедуры может быть увеличена на 30 минут.
Оценивание итогового собеседования проводится экспертами, в роли которых выступают учителя русского языка и литературы.
Результатом итогового собеседования по русскому языку является «зачет» или «незачет». «Зачет» выставляется от 10 баллов и выше, максимальный результат 20 баллов.
Результаты объявляется участникам не позднее чем через 5 календарных дней после проведения собеседования.
______________________________________________________________________________
http://obrnadzor.gov.ru/ru/press_center/news/index.php?id_4=7329
Основной период ГИА-9 в 2020 году планируется провести с 8 июня по 31 июляФедеральная служба по надзору в сфере образования и науки и Министерство просвещения Российской Федерации подготовили проект нового расписания государственной итоговой аттестации для выпускников 9 классов (ГИА-9).
В соответствии с ним, основной период основного государственного экзамена (ОГЭ) и государственного выпускного экзамена (ГВЭ) для выпускников 9 классов в 2020 году пройдут в сроки с 8 июня по 31 июля. Региональные органы исполнительной власти могут сами определить основные и резервные сроки проведения экзаменов по русскому языку и математике в рамках этого периода. ОГЭ по предметам по выбору в 2020 году проводиться не будет.Участники экзаменов, не прошедшие ОГЭ и ГВЭ или получившие неудовлетворительные результаты по одному или обоим обязательным предметам в резервные сроки, смогут пересдать их в дополнительный период в сентябре. 4 сентября в дополнительный период планируется провести экзамен по русскому языку, 7 сентября – по математике. Резервные дни для проведения экзаменов в дополнительный период: 14 сентября – русский язык, 15 сентября – математика, 18 сентября – русский язык и математика.
http://minobr.saratov.gov.ru/news/23972/
______________________________________________________________________________
ОГЭ 2020
Итоговое собеседование по русскому языку
Итоговое собеседование по русскому языку в 9 классе с 2019 года является условием допуска к государственной итоговой аттестации по образовательным программам основного общего образования (приказ Министерства просвещения Российской Федерации и Федеральной службы по надзору в сфере образования и науки от 7 ноября 2018 года № 189/1513 «Об утверждении порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования»). В 2020 году итоговое собеседование будет проводиться 12 февраля. Для выпускников, получивших «незачет», либо не явившихся на собеседование по уважительной причине, предусмотрены дополнительные сроки: 11 марта и 18 мая.
случайных аттракторов для стохастических уравнений Навье – Стокса на двумерной единичной сфере
Аграчев А., Сарычев А. Управляемость твердого тела в гидродинамике. Неустойчивость в моделях, связанных с потоками жидкости. I. International Mathematical Series (N.Y.), Vol. 6. С. 1–35. Спрингер, Нью-Йорк (2008)
Арнольд, Л .: Случайные динамические системы. Шпрингер, Берлин (1998)
Книга МАТЕМАТИКА Google Scholar
Обен, Т .: Некоторые нелинейные задачи римановой геометрии. Спрингер, Нью-Йорк (1998)
Книга МАТЕМАТИКА Google Scholar
Avez, A., Bamberger, Y .: Mouvements sphériques des fluides visqueux несжимаемые жидкости. J. Méc. 17 (1), 107–145 (1978)
MATH Google Scholar
Бжежняк З .: О регулярности броуновских путей в пространствах Соболева и Бесова.Stoch. Stoch. Отчет 56 , 1–15 (1996)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Бжежняк, З .: Стохастическая свертка в банаховых пространствах. Stoch. Stoch. Отчет 61 , 245–295 (1997)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Brzeźniak, Z., Capiński, M., Flandoli, F .: Пути глобальные аттракторы для стационарных случайных динамических систем.Вероятно. Теория Relat. Поля 95 (1), 87–102 (1993)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Бжежняк, З., Карабалло, Т., Ланга, Дж. А., Ли, Ю., Лукашевич, Г., Реал, Дж .: Случайные аттракторы для стохастических 2-мерных уравнений Навье – Стокса в некоторых неограниченных областях. J. Differ. Equ. 255 (11), 3897–3919 (2013)
ADS MathSciNet Статья МАТЕМАТИКА Google Scholar
Brzeniak, Z., Goldys, B., Le Gia, Q.T .: Случайные динамические системы, порожденные стохастическими уравнениями Навье – Стокса на вращающейся сфере. J. Math. Анальный. Прил. 426 (1), 505–545 (2015)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Бжежняк, З., Ли, Я .: Асимптотическая компактность и поглощающие множества для двумерных стохастических уравнений Навье – Стокса на некоторых неограниченных областях. Пер. Являюсь. Математика. Soc. 358 , 5587–5629 (2006)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Brzeźniak, Z., Peszat, S .: Стохастические двумерные уравнения Эйлера. Аня. Вероятно. 20 , 1796–1832 (2001)
MathSciNet МАТЕМАТИКА Google Scholar
Brzeźniak, Z., van Neerven, J .: Пространственно-временная регулярность для линейных стохастических эволюционных уравнений, управляемая пространственно однородным шумом. J. Math. Kyoto Univ. 43 , 261–303 (2003)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Карабалло Т., Лукашевич Г., Реал Дж .: Аттракторы отката для асимптотически компактных неавтономных динамических систем. Нелинейный анал. 64 (3), 484–498 (2006)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Цао К., Раммаха М.А., Тити Э.С.: Уравнения Навье – Стокса на вращающейся двумерной сфере: регулярность Жевре и асимптотические степени свободы. Zeit. Ang. Математика. Phys. 50 , 341–360 (1999)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Кастен, К., Валадье, М .: Выпуклый анализ и измеримые многофункциональные возможности. Конспект лекций по математике, т. 580. Springer, Berlin (1977)
Крауэл Х., Фландоли Ф .: Аттракторы для случайных динамических систем. Вероятно. Теория Relat. Поля 100 , 365–393 (1994)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Крауэл, Х .: Случайные вероятностные меры на польских пространствах, Монографии по стохастике, т.11. Тейлор и Фрэнсис, Лондон (2002)
MATH Google Scholar
Крауэл, Х .: Глобальные случайные аттракторы однозначно определяются путем притяжения детерминированных компактов. Аня. Математика. Pura Appl., Ser. IV CLXXVI 100 , 57–72 (1999)
Крауэл Х., Дебуш А., Фландоли Ф .: Случайные аттракторы. J. Dyn. Отличаются. Equ. 9 , 307–341 (1995)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Да Прато, Г., Забчик, Дж .: Стохастические уравнения в бесконечных измерениях. Издательство Кембриджского университета, Кембридж (1992)
Книга МАТЕМАТИКА Google Scholar
Да Прато, Г., Забчик, Дж .: Эргодичность для бесконечномерных систем. Издательство Кембриджского университета, Кембридж (1996)
Книга МАТЕМАТИКА Google Scholar
Драйвер, Б.К .: Анализ искривленного винеровского пространства.реальный и стохастический анализ. В: Реальный и стохастический анализ, математика тенденций, стр. 42–198. Birkhäuser Boston, Boston, MA (2004)
Дубровин В.А., Новиков С.П., Фоменко А.Т .: Современная геометрия: теория и приложения. Наука, Москва, 1986. Английский перевод 1-го изд. Части I, II. Спрингер (1984,1985)
Эбин Д., Марсден Дж .: Группы диффеоморфизмов и движение несжимаемой жидкости. Аня. Математика. 92 , 102–163 (1970)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Fengler, M.J., Freeden, W .: нелинейная схема Галеркина, включающая векторные и тензорные сферические гармоники для решения уравнения Навье – Стокса несжимаемой жидкости на сфере. SIAM J. Sci. Comput. 27 , 967–994 (2005)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Фландоли, Ф., Шмальфус, Б .: Случайные аттракторы для трехмерного стохастического уравнения Навье – Стокса с мультипликативным белым шумом. Stoch.Stoch. Отчет 59 , 21–45 (1996)
Статья МАТЕМАТИКА Google Scholar
Ганеш М., Ле Джиа, Q.T., Слоан, И. Х .: Метод псевдоспектральных квадратур для уравнений Навье – Стокса на вращающихся сферах. Математика. Comput. 80 , 1397–1430 (2011)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Григорян А .: Ядро тепла и анализ на многообразиях.AMS, Провиденс (2000)
Google Scholar
Хайрер М., Маттингли Дж .: Теория гипоэллиптичности и уникальной эргодичности полулинейных стохастических уравнений в частных производных. Электрон. J. Probab. 16 (23), 658–738 (2011)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Ильин А.А. Уравнения Навье – Стокса и Эйлера на двумерных многообразиях.Математика. СССР. Сборник 69 , 559–579 (1991)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Ильин А.А. Частично диссипативные полугруппы, порожденные системой Навье – Стокса на двумерных многообразиях, и их аттракторы. Русь. Акад. Sci. Сборник Матем. 78 , 47–76 (1994)
ADS MathSciNet Статья Google Scholar
Ильин А.А., Филатов А.Н .: Об однозначной разрешимости уравнений Навье – Стокса на двумерной сфере. Сов. Математика. Докл. 38 , 9–13 (1989)
MathSciNet МАТЕМАТИКА Google Scholar
Kloeden, P.E., Schmalfuss, B .: Асимптотическое поведение неавтономных разностных включений. Syst. Control Lett. 33 (4), 275–280 (1998)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Норбери Дж., Роулстон И. (ред.): Крупномасштабная динамика атмосферы и океана, т. 1 и 2. Cambridge University Press (2002)
Ондреят, М .: Единственность для стохастических эволюционных уравнений в банаховых пространствах. Диссертация по математике (Раскрытый матем.), Т. 426 (2004)
Schmalfuss, B .: Аттракторы для неавтономных динамических систем. В: Fiedler, B., Gröger, K., Sprekels, J. (eds.) Proceedings of Equadiff 99, pp. 684–689. World Scientific, Берлин (2000)
Глава Google Scholar
Шварц, Г .: Разложение Ходжа: метод решения краевых задач. Конспект лекций по математике, т. 1607. Springer, Berlin (1995)
Книга. Google Scholar
Зейдлер Дж .: Эргодическое поведение стохастических параболических уравнений. Чехослова. Математика. J. 47 (2), 277–316 (1997)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Танабе, Х .: Уравнения эволюции. Питман, Лондон (1979)
MATH Google Scholar
Тейлор М.Э .: Анализ пространств Морри и приложения к Навье – Стоксу и другим эволюционным уравнениям. Commun. Частичная разница. Equ. 17 , 1407–1456 (1992)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Темам, Р .: Уравнения Навье – Стокса.Издательская компания Северной Голландии, Амстердам (1979)
MATH Google Scholar
Temam, R., Wang, S .: Инерционные формы уравнений Навье – Стокса на сфере. J. Funct. Анальный. 117 , 215–242 (1993)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Temam, R., Ziane, M .: Уравнения Навье – Стокса в тонких сферических областях. Contemp.Математика. AMS 209 , 281–314 (1997)
MathSciNet Статья МАТЕМАТИКА Google Scholar
Варшалович Д.А., Москалев А.Н., Херсонский В.К .: Квантовая теория углового момента. World Scientific, Сингапур (1988)
Книга Google Scholar
Валецка Д.Д .: Введение в общую теорию относительности. World Scientific, Сингапур (2007)
Книга МАТЕМАТИКА Google Scholar
Ньюпорт-Меса для сбора информации от родителей о предложениях по математике в средней школе
Объединенный школьный округ Ньюпорт-Меса проведет этим летом родительские собрания для сбора комментариев общественности о планах по изменению того, как классы математики предлагаются ученикам средних школ.
Встреча ориентировочно намечена на 22 августа, еще две — в сентябре. Осенью состоится учебная сессия школьного совета.
Ньюпорт-Меса уведомил родителей в понедельник, что он сохранит текущую программу курсов по математике на 2018-19 учебный год после того, как родители протестовали против возможности отмены курсов с отличием и расширенных курсов для учащихся средней школы.
Во вторник на собрании школьного совета, Supt. Фред Наварро сказал, что окружной комитет, состоящий из учителей, директоров и должностных лиц, продолжит обсуждение того, какие изменения могут быть внесены, чтобы лучше согласовать математические методы с общими основными стандартами штата.
«[Их] беспокоит:« Как уместить два года математики в один? », — сказал Наварро. «Они не хотят, чтобы у наших учеников, которые проходят ускоренное обучение, были какие-либо недостатки».
Наварро объяснил, что потенциальные изменения в образовательных программах округа произошли, когда группа учителей опробовала новые материалы по математике для классов с шестого по восьмой.
Сотрудники округа узнали, что им нужно решать проблемы раньше, добавил Наварро.
Учащиеся, сдавшие вступительный экзамен по математике, по-прежнему будут иметь право на обучение в средней школе или углубленные классы математики.Будет использоваться недавно принятая учебная программа «Иллюстративная математика», но пути обучения останутся прежними.
Родители поблагодарили попечителей за замедление процесса, но критически отнеслись к тому, что они назвали недостаточной прозрачностью в информировании родителей раньше о потенциальных изменениях. Некоторые также просили просмотреть данные и провести исследование, которое комитет использовал, чтобы определить, как исключение продвинутых классов математики было лучшим вариантом.
Джон Гурка, родитель трех мальчиков в округе, сказал, что он рад услышать, что летом будет предложено больше информационных занятий.
Боб Парзик сказал, что он хотел бы услышать прямое мнение комитета на предстоящих родительских собраниях.
Родитель Джиа Гаффани сказала, что Laguna Beach Unified пыталась исключить продвинутые классы, и призвала попечителей обратиться за советом в ближайший округ.
Учитель математики средней школы Бэк-Бэй Деннис Эшендорф высказался против возврата к «несовершенной системе».
Родители впервые получили новости о потенциальных изменениях от окружных властей за несколько дней до учебной сессии 18 июня, на которой директор по учебной программе и инструкциям Джон Дрейк, учителя и эксперт по математике объяснили, почему изменение траектории лучше согласовывает учебную программу с Общими основными государственными стандартами.
В отличие от бывшего государственного экзамена по стандартизированному тестированию и отчетности, который измерял навыки запоминания учащегося, Common Core больше фокусируется на понимании концепций решения задач и реальных математических приложений.
Комитет предложил отменить расширенные или почетные классы математики в средних школах. Вместо этого все учащиеся будут посещать одни и те же курсы математики, пока не достигнут первого года обучения в старшей школе.
Дополнительные уроки математики рассматриваются для учащихся, которые нуждаются в дополнительной помощи или демонстрируют признаки быстрого понимания.
Округ планировал внедрить новую математическую программу во время будущего заседания совета с изменениями, внесенными в 2018-19 учебный год, но попечители поручили персоналу в первую очередь учесть опасения родителей.
Новая система безопасности
В других сферах деятельности школьный совет единогласно утвердил систему управления безопасностью округа стоимостью 46 215 долларов, которая проверяет посетителей по пользовательским базам данных, установленным на школьных сайтах.
Система управления посетителями Raptor поможет обеспечить точный и надежный учет каждого посетителя, входящего в школу, в соответствии с повесткой дня собрания.
Утверждение системы — еще одна недавняя попытка округа усилить меры безопасности в своих 32 кампусах и на рабочих местах.
Twitter: @vegapriscella
Quoc Thong Le Gia
Quoc Thong Le GiaБакалавриат
- Ответственный преподаватель по MATh3301 — Математические вычисления в семестре 1, 2012-2021, (UNSW).
- Ответственный преподаватель по MATh4121 — Математические методы для уравнений с частными производными во 2 семестре 2012-2016 гг. (UNSW).
- Ответственный преподаватель (численные методы) MATh3089 — Численные методы и статистика во 2 семестре 2017—2019 гг. (UNSW).
- Репетитор по высшему исчислению с несколькими переменными (математика 2111) в S1,2010, (UNSW).
- Репетитор по математике IA / B (Math 1131/1231) с 2006 по 2010 год (UNSW).
- Инструктор математики для естественных наук I, осень 2003 г. (Техасский университет A&M).
- Инструктор по инженерной математике I, осень 2003 г., весна 2004 г. (Техасский университет A&M).
- Инструктор по математике для бизнеса, лето 2002 г. (Техасский университет A&M).
Почетные студенты
- Брок Шерлок, 2021 (совместный советник).
- Каллум Скотт. Февраль 2021 г.
- Мишель Цю, февраль 2021 года.
- Крис Ли, Методы машинного обучения, применяемые для кластеризации литературы по COVID-19, UNSW, февраль 2020 г. — ноябрь 2020 г.
- Джеймс Хортл, Обнаружение болезни Альцгеймера с помощью машинного обучения, UNSW, июль 2016 г. — июль 2017 г.
Магистранты
- Юян Ли, Численные методы ценообразования опционов, UNSW, февраль-август 2020 г.
- Ицзя Ма, Численные методы для азиатских опционов, UNSW, февраль-август 2020 г.
- Пэнъюн Чжан, Численные методы для многоактивного уравнения Блэка-Шоулза. UNSW, июнь-декабрь 2019 г.
- Фан Ли, Варианты ценообразования с использованием методов конечных разностей, UNSW, февраль-август 2019 г.
- Юйцзя Лю, Численные решения уравнения Блэка-Шоулза-Мертона, UNSW, февраль-август 2019 г.
- Xiongwen Ke, Обучение на несбалансированных данных, UNSW, март-июнь 2018 г.
к.т.н. студенты
Стринги Quoc Le Gia
Стринги Quoc Le GiaКниги
- Сферические радиальные базисные функции, теория и приложения (совместно с С. Хаббертом и Т. Мортоном) Предзаказ на Amazon.co.uk или же Читать онлайн на Springer
- Фреймы и другие основы в абстрактных и функциональных пространствах: новые методы гармонического анализа. Том 1 (Прикладной и численный гармонический анализ) (редакторы Исаак Песенсон, Куок Тонг Ле Гиа, Азита Майели, Хрушикеш Мхаскар, Дин-Сюань Чжоу)
- Недавние приложения гармонического анализа к функциональным пространствам, дифференциальным уравнениям и науке о данных: новые методы гармонического анализа, Том 2 (Прикладной и численный гармонический анализ) (редакторы Исаак Песенсон, Куок Тонг Ле Гиа, Азита Майели, Хрушикеш Мхаскар, Дин-Сюань Чжоу)
Журнальные статьи
- Новое исследование гауссовости и изотропии для карт CMB (с Дж.Хаманн, И. Х. Слоан, Ю. Г. Ван, Р. С. Уомерсли) появиться в International J. of Modern Physics C , 2021. [arXiv: 1911.11442]
- Аппроксимация зашумленных данных с использованием многомерных сплайнов и методов конечных элементов, (с Lamichhane BP; Harris E) Журнал алгоритмов и вычислительных технологий, вып. 15, 2021. [DOI]
- FaVeST: быстрые векторные сферические гармонические преобразования, (с М. Ли и Ю. Г. Ван), появится в ACM Transactions on Mathematical Software , 2021.[arXiv: 1908.00041]
- Определение параметров объемных дефектов в кремниевых пластинах с помощью машины обучающие модели (с Йоанном Буратти, Йозефом Диком, Яном Чжу, Зивом Хамейри), (Вычислительные материалы 6, 142 (2020). [DOI]
- Стохастические уравнения Навье-Стокса на тонкой сферической области, (совместно с З. Бжезняком, Г. Даривалом), Прикладная математика. и оптимизация, 2020. [DOI], [arXiv: 2002.08873]
- Спектральный метод стохастических уравнений Стокса на сфере, (с Джо Пич), ANZIAM J., т. 60, С52 — С64. [PDF]
- Разреженная изотропная регуляризация сферической гармоники. Представления случайных полей на сфере, (совместно с И. Х. Слоаном, Р. С. Уомерсли, Ю Гуан Ван), Прикладной вычислительный гармонический анализ том 49, выпуск 1, 2020, стр.257—278 [arXiv: 1801.03212] [DOI]
- Квази-Монте-Карло интегрирования более высокого порядка для байсейской оценки, (совместно с Дж. Диком, Р. Н. Гантнером, Ч. Швабом), Computer & Mathematics с приложениями , т.77, выпуск 1, 2019, с.144—172. [arXiv: 1602.07363.] [DOI]
- Неравномерная дискретизация стохастических уравнений теплопроводности с мультипликативным шумом на единичной сфере (совместно с Ёсихито Казаши), Журнал сложности том 50, 2019, стр 43—65. [arXiv: 1706.02838v1] [DOI]
- Мультимасштабная поддержка метода векторной регрессии на сферах со сжатием данных, (совместно с М. Чжун, В. Ван) [PDF], Применимый анализ , том 98, выпуск 8, стр 1496-1519, 2019.[DOI]
- Решение приближенных задач маскировки методами конечных элементов (совместно с Х. Гимперлейн, М. Майщак, Э. П. Стефаном), ANZIAM J. 58 (CTAC2016) pp C162-C174, 2017. [PDF]
- Применение метода Ньютона-Рафсона к пожизненной спектроскопии для определения параметров дефектов (с Янь Чжу, Матиас Клау, Джул, Джанлука Колетти, Зив Хэмери), IEEE Journal of Photovoltaics, 7 (4), 1092—1097, 2017. [DOI]
- Многоуровневая байсейская оценка квази-Монте-Карло высшего порядка, (с Дж.Дик, Р.Н. Гантнер, гл. Шваб), Математические модели и методы в прикладных науках (M3AS) 27 , 953 (2017). [arXiv: 1611.08324.] [DOI]
- Случайные аттракторы для стохастических уравнений Навье — Стокса на двумерной единичной сфере (совместно с З. Бжезняком, Б. Голдисом), Журнал математической механики жидкости. 20 , 227-253 (2018). [PDF] [arXiv: 1402.3097] [DOI]
- Игольчатое приближение для изотропных случайных полей на сфере, (совместно с Юй Гуан Ван, Яном Х.Слоан, Роберт С. Уомерсли), Журнал теории приближений , 216 86—116, 2017. [DOI] [arXiv: 1512.07790.]
- Масштабирование от глобального к локальному: многомасштабный подход RBF, (с И. Х. Слоаном и Х. Вендландом), Успехи в вычислительной математике 43 (3). 581—606, 2017. [DOI] [arXiv: 1406.1333]
- Обратная задача для нелинейного обратного уравнения пространственно-дробной диффузии (совместно с Т. Х. Нгуеном, Х. Д. Нгуеном, Л. Ле), Журнал обратных и некорректно поставленных задач, 25 (4), 2015.[DOI]
- Многоуровневая QMC-дискретизация Галеркина высокого порядка для аффинных параметрических операторных уравнений (совместно с Дж. Диком, Ф. Куо, К. Т. Ле Джиа и Ч. Швабом), SIAM Журнал численного анализа 54 (4) 2541-2568. [arXiv: 1406.4432]
- Многомасштабные методы с радиальными базисными функциями с компактным носителем для задачи Стокса на ограниченные области (совместно с А. Черных), Успехи в вычислительной математике 42 (5): 1187—1208, 2016.[DOI]
- Полностью дискретное игольчатое приближение на сфере (совместно с Я. Г. Ван, И. Слоаном, Р. Уомерсли), Прикладной вычислительный гармонический анализ , 43 (2), 2017, 292-316. DOI: 10.1016 / j.acha.2016.01.003.
- Решение уравнения обратной теплопроводности на единичной сфере (совместно с Х. Т. Нгуеном, Т. Траном), ANZIAM J. (E) 56 (2016), стр. C262 — C278. [URL]
- Квази-Монте-Карло интегрирования высшего порядка для голоморфных параметрических операторных уравнений.(с Дж. Диком и Ч. Швабом) SIAM J. Количественная оценка неопределенности 4, (2016), 48—79. [arXiv: 1409.2180]
- Быстрое умножение матрицы на вектор QMC, (с Дж. Диком, Ф. Куо и Ч. Швабом), SIAM J. Sci. Comput. 37 (2015), A1436 — A1450. [arXiv: 1501.06286]
- Случайные динамические системы, порожденные стохастическим уравнением Навье — Стокса на вращающейся сфере (совместно с З. Бжезняк, Б. Голдис), J. Математический анализ и приложения [DOI] [PDF] [arXiv: 1403.6571]
- QMC-дискретизация Галеркина высокого порядка для параметрических операторных уравнений (совместно с Дж. Диком, Ф. Я. Куо, Д. Нуйенсом, Ч. Швабом), SIAM J. Num. Анализ 52 (2014), с. 2599—2769. DOI [arXiv: 1309.4624]
- Сжатие данных на сфере с использованием многомасштабных радиальных базисных функций (совместно с Х. Вендландом), Успехи в вычислительной математике 40 (2014), с. 923—943 [PDF] [DOI]
- Мультимасштабные методы с компактно поддерживаемыми RBF для Галеркина аппроксимация эллиптических УЧП (с А.Черных), Журнал численного анализа ИМА 34 (2014), стр 569-591. [arXiv: 1211.1431] [DOI]
- Решение параболических уравнений на единичной сфере с помощью преобразований Лапласа и радиального базиса функции (совместно с У. Маклином), Достижения в области вычислительной математики , 20 (2014), стр 353-375. [PDF] [DOI]
- Многомасштабные методы с радиальными базисными функциями с компактным носителем для эллиптических дифференциальных уравнений в частных производных на ограниченных областях (с A.Черных), ANZIAM J. (E) 54 (2012), C137 — C152 [PDF]
- Быстрые итерационные решатели краевых задач на локальном сферическая область (совместно с Т. Траном), ANZIAM J. (E) 54 (2012), C492 — C507 [PDF]
- Мультимасштабное коллокация RBF для решения PDE на сферах (совместно с И. Х. Слоаном и Х. Вендландом), Numerische Mathematik 121 (2012), 99-125. [PDF] | [DOI]
- Аддитивные предобуславливатели Шварца для интерполяции бездивергентного вектора поля на сферах (с Т.Тран), ANZIAM J. (E) 52 (2011), C742 — C758. [PDF]
- Многомасштабная аппроксимация функций из произвольных соболевских пространств масштабированными радиальными базисными функциями на единичной сфере (совместно с И. Х. Слоаном, Х. Вендландом), Прикладной вычислительный гармонический анализ 32 (2012), 401-412. [PDF] | [DOI]
- Псевдоспектральный квадратурный метод для уравнений Навье-Стокса при вращении сферы (совместно с И. Х. Слоаном, М. Ганешем), Математика вычислений, 80 (2011) 1397-1430.[PDF] | [DOI]
- Решение задачи Неймана вне вытянутого сфероида по радиальному базису функции, (совместно с Э. П. Стефаном, Т. Траном), Успехи в вычислительной математике. 34 (2011) (83-103). DOI или [PDF]
- Численное решение параболического уравнения на сфере с использованием преобразований Лапласа и RBF (совместно с У. Маклином), ANZIAM J. (E) 52 (2011 г.), C89-C102. [PDF]
- Радиальный базисный метод Галеркина для уравнений Стокса со сферической поверхностью (совместно с М.Ганеш), ANZIAM J. (E) 52 (2011 г.), C56-C71. [PDF]
- БЭМ без сетки и перекрывающиеся предобуславливатели Шварца для внешних задач на сфероидах (совместно с А. Костя, Э. П. Стефаном, Т. Траном) Студия Геофизика 55 (2011), 465-477. [PDF] | [DOI]
- Устойчивость и предусловие для гибридного приближения на сфере (совместно с И. Х. Слоаном и А. Дж. Уотеном), Numerische Mathematik 118 (2011), 695-711.[PDF] | [DOI]
- Многомасштабный анализ в пространствах Соболева на сфере (совместно с И. Слоаном и Х. Вендландом), SIAM J. по численному анализу 48 (2010) 2065-2090. [PDF]
- Перекрывающийся аддитивный предварительный кондиционер Шварца для интерполяции на единичная сфера сферическими базисными функциями (совместно с Т.Траном), Журнал сложности 26 (2010) 552-573. [PDF]
- Предобуславливатели псевдодифференциальных уравнений на сфере с радиальными базисными функциями, (с I.Х. Слоун, Э. Стефан, Т. Тран), Numerische Mathematik, 115 (1) (2010), 141–163. [PDF] | [DOI]
- Граничные интегральные уравнения на сфере с радиальными базисными функциями: анализ ошибок (совместно с И. Х. Слоаном, Э. Стефаном, Т. Траном), Прикладная вычислительная математика, 59 (11) (2009), 2857-2871. [PDF]
- Перекрывающийся аддитивный метод Шварца для эллиптических УЧП на сферах, (с Т. Траном и И. Х. Слоаном), Математика вычислений, 78 (2009), 79-101.[PDF].
- Постобработка решений несжимаемых уравнений Навье-Стокса на вращающихся сферах (совместно с М. Ганешем), ANZIAM J. (E) 50 (2008 г.), C90-C106. [PDF]
- Численное решение граничного интегрального уравнения со сферическими базисными функциями (совместно с Д. Фамом, Т. Траном), ANZIAM J. (E) 50 (2008 г.), C266-C281. [PDF]
- Интерполяция на сфере: метод быстрого решения (совместно с Т. Траном), АНЗИАМ Дж.(E), 50 (2008), C354-C370. [PDF]
- Квадратурные формулы и локализованные линейные полиномиальные операторы на сфера, (совместно с Х. Маскаром), Численный анализ SIAM, 47 (2008), 440-466. [PDF].
- Аппроксимация локальной радиальной базисной функции на сфере (совместно с К. Гессе), Бюллетень австралийской математики. Общество, 77 (2008), 197-224. [PDF]
- Полиномиальные операторы и локальная аппроксимация решений псевдодифференциальные операторы на сфере (с H.Н. Мхаскар), Numerische Mathematik , 103 (2) (2006), 299-322. [PDF].
- Непрерывные и дискретные оценки ошибок по методу наименьших квадратов на сферах (совместно с Ф. Дж. Нарковичем, Дж. Д. Уордом, Х. Вендландом), J. Прибл. Теория , 143 (1) (2006), 124-133. [PDF].
- Аппроксимация параболических УЧП на сферах методом коллокации, Adv. Comput. Математика. , 22 (2005), 377-397. [PDF].
- Галёркинское приближение эллиптических уравнений в частных производных на сферах, Дж.Прибл. Теория , , 130, (2004), 125-149. [PDF].
- Равномерная норма гиперинтерполяции на единичной сфере в произвольной количество измерений (с Ян Х. Слоан) , Конструктивное приближение 17 : 249-265, 2001. [PDF] [DOI]
Материалы конференции
- Q. T. Le Gia, Численное решение краевой задачи на сфере с использованием радиальные базисные функции, в J. Dick et al. (ред.), Современная вычислительная математика: праздник 80-летия Иэна Слоана , [DOI] [arXiv: 1402.3353]
- Дж. Дик, К. Т. Ле Джиа, гл. Шваб, Квази-Монте-Карло-интегрирование высшего порядка в неопределенности количественная оценка (в трудах ICOSAHOM 2014)
- Q. T. Le Gia, QMC-спектральный метод для эллиптических уравнений в частных производных со случайными коэффициентами на единичная сфера [PDF], Методы Монте-Карло и квази-Монте-Карло 2012, стр 517-534, под ред. Дж. Дика, Ф. Куо, Г. Петерса, И.n) оценки погрешности метода Галеркина для эллиптических УЧП на сферах [PS], Материалы одиннадцатой международной конференции по теории приближений, Гатлинбург, США, 18-22 мая 2004 г.
- Двумерная контурная задача, IMA Workshop для аспирантов, Университет Миннесоты, 19-28 июля 2000 г. [ Слайды]
- Испытательный стенд для изучения распределенных атак типа «отказ в обслуживании», IEEE Системы, человек и кибернетика Обеспечение и безопасность информации Семинар, 6-7 июня 2000 г., Вест-Пойнт, Нью-Йорк.
- FMR: система дополнительных знаний для нечетких областей, европейская Мастерская приобретения знаний. EKAW 1999 г. [PS]
- Компромисс между знанием предметной области и методом решения проблем, Одиннадцатый Семинар по приобретению знаний, моделированию и управлению (KAW’98), Банф, Альберта, Канада, 1998. [HTMLversion]
- От множественной классификации RDR к конфигурации RDR, Труды 3-й AKAW, UNSW, Сидней, 1998 г., стр. 6.1–6.14. [Аннотация]
Представленные статьи
- Б.Lamichhane, E. Harris, Q. T. Le Gia, Аппроксимация зашумленных данных с использованием многомерные сплайны и методы конечных элементов.
- K. Hesse, Q. T. Le Gia, L2 оценки ошибок для полиномиальной дискретной аппроксимации методом наименьших квадратов на сфере из зашумленных данных.
- З. Бжезняк, Гаурав Даривал и К. Т. Ле Джиа, Стохастические уравнения Навье — Стокса в трехмерной тонкой области, [arXiv: 2008.07394]
- А. Костя, К. Т. Ле Джиа, Д. Фам, Э. Стефан, Т. Тран, Решение карты Дирихле-Неймана на сплюснутом сфероиде бессеточным методом [PDF]
Тезисов
Банкноты
- Поведение интерполяционной нормы на сфере.2 = C, где C — бесконечное кардинальное число. [DVI],
- Некоторые решали задачи в реальном анализе. [DVI]
- Условие Стренга-Фикса в методе конечных элементов. [DVI],
- Численное решение для УЧП с использованием вейвлет-приближений. [ GZipped]
- Интерактивный процесс для создания уточняемых функций. [PS]
- Метод конечных элементов для эллиптических УЧП в 2D [PS]
(PDF) Влияние конкретно-графического-абстрактного (CPA) подхода на улучшение математических способностей учащихся начальной школы
Мимбар Секолах Дасар, Том 7, номер 1 апрель 2020 г.
[131]
Хердиан.(2010). Pengaruh Metode Discovery terhadap Kemampuan Analogi dan
Generalisas iMatematis Siswa SMP. (Тезис). Аспирантура, Университет
Пендидикан Индонезия, Бандунг.
Микраянти. (2016). Meningkatkan Kemampuan Penalaran Matematis melalui Pembelajaran
berbasis Masalah. Jurnal Suska Journal of Mathematics Education, 2 (2), 97-98. DOI:
10.24014 / sjme.v2i2.1547
Мирадияни, В. Ф. У.(2012). Penerapan Pendekatan Тип кооперативного обучения Командные игры
Турнир (TGT) Untuk Meningkatkan Kemampuan Penalaran Matematik Peserta
Didik Sekolah Dasar. (Тезис). Специальность PGSD, Пендидиканский университет Индонезии, Пурвакарта.
Путри, Х. Э. (2011). Kemampuan Penalaran Matematik dalam Pembelajaran Matematika di
SD. Журнал Методик Дидактик, 6 (1), 33-38.
Путри, Х. Э. (2017). Pendekatan Concrete-Pictorial-Abstract (CPA), Kemampuan —
Kemampuan Matematis, дан Rancangan Pembelajarannya.Subang: Royyan Press.
Путри, Х. Э., Джулианти, Р., Аджи, Н., Сурьяни, Н. Э. (2017). Pengaruh Pendekatan Concrete-
Иллюстрированный абстрактный (CPA) terhadap Pencapaian Kemampuan Spatial Sense (KSS) Siswa
SD. Методик Дидактик. 13 (1). 42-52. DOI: 10.17509 / md.v13i1.7692
Putri, H. E., Muqodas, I., Wahyudy, M. A., & Nuraeni, F. (2020). Влияние конкретно-графического (
абстрактного CPA) подхода на снижение математической тревожности в начальной школе
.Международная конференция по начальному образованию. 2 (1). 80-93.
Путри, Х. Э., Рахайу, П., Саптини, Р. Д., и Миснарти. (2016). Keterkaitan Penerapan Pendekatan
CPA дан Peningkatan Kemampuan Koneksi Matematis Siswa Sekolah Dasar. Universitas
Pendidikan Indonesia, Purwakarta. [В сети]. Получено с
http://ejournal.upi.edu/index.php/Metodik/Didaktik/article/view3785. [11 октября
2016] http://ejournal.upi.edu/index.php / MetodikDidaktik / article / download / 3785 / 2699.
[27 сентября 2017 г.]
Рахмат, Ф. Р. Ф. (2014). Penerapan Pendekatan Конкретно-репрезентативное-абстрактное (CRA)
untuk Meningkatkan Kemampuan Penalaran Matematis Siswa. (Penelitian Eksperimen
pada Siswa Kelas VIII — MTs. N. Wanayasa). [Тезис]. Математический факультет
Образование, Исламский университет Негери Сунан Гунунг Джати, Бандунг.
Фуади, Р., Джохар, Р., & Мунзир, С. (2016). Peningkatkan Kemampuan Pemahaman dan
Penalaran Matematis melalui Pendekatan Kontekstual, Jurnal Didaktika Matematika,
3 (1). 47-49.
Риккомини, П. Дж., Витцель, Б., и Роббинс, К. (2008). Улучшение преподавания математики для
учащихся с эмоциональными и поведенческими расстройствами: два учебных подхода, основанных на доказательствах
. Помимо поведения, 17 (2), 24-30.
Русеффенди, Э.Т. (2010). Основы Образовательные исследования и области Другие неточные науки.
Бандунг: Бандунг Тарсито.
Ginting, M. S., Prahmana R. C. I., Isa, M., & Murni. (2018). Улучшение способности к рассуждению учащихся начальной школы
через индонезийское реалистичное математическое образование.
Журнал по математическому образованию, 9 (1), 41-54. DOI: 10.22342 / jme.9.1.5049.41-54
Sugiyono. (2012). Метод Пенелитиан Куантитиф, Куалитатиф, дан Комбинаси (Смешанные методы).
Бандунг: Альфабета.
Сугийоно. (2015). Статистика непараметров для пенелитов. Бандунг: Альфабета.
Исследование трехмерной нелинейной динамической системы, описывающей процесс двухуровневой ассимиляции
4open 2020, 3 , 10Исследовательская статья
Исследование трехмерной нелинейной динамической системы, описывающей процесс двухуровневой ассимиляции
Темур Чилачава и Георгий Почхуа *
Сухумский государственный университет, ул. Ана Политковской, д., Тбилиси, Грузия
* Автор для переписки: [email protected]
Поступило:
9
июнь
2020 г.
Принято:
19
июль
2020 г.
Аннотация
В работе предлагается новая общая нелинейная математическая модель, описывающая социальный процесс двухуровневой ассимиляции с учетом квадратичных членов самоограничения прироста населения с трех сторон. В случае постоянных коэффициентов модели найден первый интеграл трехмерной динамической системы, которая в фазовом пространстве решений представляет собой конус.Трехмерная динамическая система сведена к двумерной и с помощью критерия Бендиксона доказана теорема существования в первой четверти фазовой плоскости замкнутой интегральной траектории. Таким образом, найдены условия на параметры модели, которые не полностью усваивают третью сторону.
Ключевые слова: Математическая модель / Двухуровневая ассимиляция / Первый интеграл / Конус / Критерий Бендиксона
© Т. Чилачава и Г. Почхуа, Издательство EDP Sciences, 2020
Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (https: // creativecommons.org / licenses / by / 4.0 /), что разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.
Введение
Одно из самых востребованных направлений прикладной математики — математическое моделирование. Для понимания различных сложных, преимущественно нелинейных процессов, происходящих в природе, в небесных телах, в социальной сфере, необходимо их математическое моделирование. Для более или менее реального описания процессов необходимо учитывать их описывающие основные характеристики и правильно ставить соответствующие математические задачи.Математическое моделирование физических процессов предполагает адекватность модели, которая подтверждается пятью несвязанными законами Ньютона классической механики: законом сохранения массы; закон сохранения импульса; закон сохранения количества движения импульса; первый закон термодинамики — закон сохранения энергии; второй закон термодинамики — закон сохранения энтропии [1–14].
Создание математических моделей более оригинально в социальной сфере, потому что их сложнее обосновать.Мы создали новое направление математического моделирования — «Математическое моделирование информационных войн» [15–17]. В этих моделях пересмотрены две противоборствующие стороны, ведущие друг с другом информационную войну, а также третья миротворческая сторона, пытающаяся погасить информационную войну. Найдены условия по параметрам модели, при которых третья сторона сможет принудить конфликтующие стороны к завершению информационной войны.
Мы также предложили математические модели прогнозирования результатов политических выборов в случае двух или трех партий.Также были рассмотрены модели на случай смены избирательных субъектов перед очередными выборами [18–22].
Мы предложили создать новые нелинейные математические модели экономического сотрудничества между двумя политически (не военными противоборствующими сторонами) взаимно враждующими сторонами (двумя странами или страной и ее правовым регионом), которые рассматривают экономическое или иное сотрудничество между различными группами населения, направленное мирное разрешение конфликтов [23–29].
Принимая во внимание важные тенденции в мире, важно изучать демографию и ассимиляцию социальных процессов с помощью математического моделирования [30–32].
В [33] мы рассмотрели новую нелинейную непрерывную математическую модель лингвистической глобализации. Рассмотрены две категории населения мира: категория, которая мешает, и категория, ведущая к доминирующему положению английского языка. При положительном демографическом факторе населения, препятствующем глобализации, или отрицательном демографическом факторе населения, способствующем глобализации, показано, что динамические системы, описывающие эти процессы, допускают существование двух топологически не эквивалентных фазовых портретов (стабильный узел, предельный цикл).Известно, что в мире скрывается социальный процесс ассимиляции языков. Этот процесс, как правило, предполагает расширение ареала доминирующих языков (государственных языков экономически мощных государств) за счет менее распространенных языков (государственных языков экономически относительно слабых государств). Согласно этой точке зрения, сегодня для менее распространенных языков (в том числе классических) важны условия, при которых не произойдет исчезновение основных языков, т.е.е. не будет полной ассимиляции людей, говорящих на этих языках.
В предыдущей статье [34] была исследована новая нелинейная математическая модель процесса трехуровневой ассимиляции, которая описывается четырехмерными динамическими системами. В случае постоянства коэффициентов особые точки динамической системы не обнаружены. Определены условия на постоянные коэффициенты, при которых можно найти особые точки со всеми четырьмя неотрицательными координатами.Вводя некоторую зависимость между коэффициентами системы, были получены два первых интеграла, и четырехмерная система была сведена к двумерной. Доказана теорема знакопеременной расходимости двумерного векторного поля в некоторой однокогерентной области первого квадранта фазовой плоскости. По критерию Бендиксона было показано, что замкнутая интегральная кривая может полностью лежать в этой области.
Общая математическая модель двухуровневой ассимиляции
Система уравнений
Рассмотрим социальный процесс двухуровневой ассимиляции, когда в одном большом регионе население, говорящее на наиболее распространенном языке, ассимилирует как население, говорящее на втором достаточно распространенном языке, так и население, говорящее на третьем менее распространенном языке (небольшой диапазон распространения языков).В свою очередь, население, говорящее на втором языке, который довольно распространен, ассимилирует население, говорящее на менее распространенном третьем языке. Таким образом, население, говорящее на третьем менее распространенном языке, находится в ситуации двусторонней ассимиляции.
Мы предполагаем, что процесс ассимиляции развивается благодаря многочисленным прямым или дистанционным (электронное общение) взаимным встречам представителей населения, считающих один из этих трех языков своим родным.
Социальный процесс двухуровневой ассимиляции, учитывающий квадратичные члены самоограничивающегося роста населения, описывается следующей нелинейной динамической системой
(1)
с начальными условиями:
(2)
где
-
[0, T ] — период рассмотрения данной модели (для разных случаев период может достигать нескольких десятилетий),
-
u ( t ) — в данный момент времени t количество людей, проживающих в том же регионе (возможно, на континенте), которые считают свой родной язык в этом регионе наиболее распространенным языком (доминирующим языком),
-
v ( t ) — в данный момент времени t количество людей, проживающих в том же регионе, которые считают свой родной язык еще одним распространенным языком в этом регионе,
-
w ( t ) — в данный момент времени t количество людей, проживающих в небольшой части (на небольшой территории) того же региона, которые только в этой части региона считают общий язык своим родной язык,
-
β 1 ( т ), β 3 ( t ) — коэффициент ассимиляции населения, говорящего на втором достаточно разговорном языке, населением, говорящим на наиболее распространенном языке,
-
β 2 ( т ), β 5 ( t ) — коэффициент ассимиляции населения, говорящего на третьем менее распространенном языке, по сравнению с населением, говорящим на наиболее распространенном языке,
-
β 4 ( т ), β 6 ( t ) — коэффициент ассимиляции населения, говорящего на третьем менее распространенном языке, населением, говорящим на втором достаточно разговорном языке,
-
α 1 ( т ), α 2 ( т ), α 3 ( t ) — темпы естественного изменения населения, говорящего на первом, втором и третьем языках соответственно (переменные демографические факторы),
-
δ 1 ( т ), δ 2 ( т ), δ 3 ( t ) — самоограниченные факторы роста населения, говорящего на первом, втором и третьем языках соответственно.
Сценарий развития двухуровневого ассимиляционного процесса представлен на рисунке 1.
|
фигура 1
Развитие двухуровневого ассимиляционного процесса. |
Естественно предположить, что коэффициенты ассимиляции и ограничения роста являются положительными непрерывными функциями на момент рассмотрения модели:
(3)
Нетривиальность двухуровневого процесса ассимиляции (когда результат ассимиляции изначально не прогнозируется) приводит к неравенству:
(4)
Первый интеграл нелинейной системы дифференциальных уравнений
Поверхности второго порядка в фазовом пространстве
Рассмотрим частный случай, когда все коэффициенты модели равны
(5)
С учетом (5) система уравнений (1) принимает вид
(6)
Найдите первый интеграл системы нелинейных дифференциальных уравнений (6) для понижения порядка системы, т.е.е. от трехмерной системы перейти к двумерной.
Динамическая система (6) должна быть записана в следующем виде
(7)
Второе уравнение системы (7) умножаем на (−2) и складываем все три уравнения (первое и третье уравнения не меняются)
(8)
Нам потребуется выполнение следующих условий (система четырех условий) на факторах модели
(9)
или
(10)
Отметим, что система (10) непротиворечива и должна удовлетворять неравенствам (3), (4).
С учетом наложенных условий (9) на коэффициенты модели (8), (5) получаем первый интеграл динамической системы
(11)
Первый интеграл (11) в фазовом пространстве решений ( O , u , v , w ) представляет собой конус.
С учетом (11) трехмерную динамическую систему (6) можно свести к следующей двумерной нелинейной динамической системе
(12)
Найдем ненулевые (нетривиальные) особые точки системы (12)
(13)
или
(14)
Рассмотрим особый случай
(15)
Тогда из (10), (15) получаем
(16)
С учетом (15) решение системы нелинейных алгебраических уравнений (14) примет следующий вид
(17)
где
(18)
Таким образом, в первой четверти фазовой плоскости ( O , u ( t ), v ( t )) особая точка M ( u ) * , в * ) с ненулевыми координатами примет вид
(19)
Положим по определению:
(20)
Тогда система уравнений (12) запишется в векторной форме
(21)
Теорема 1 . Задание (21) в некоторой однокогерентной области D ⊂ ( O, u ( t ), v ( t )) первая четверть фазовой плоскости ( O , u ( t ), v ( t )) имеет решение в виде замкнутой траектории, которая полностью лежит в этой области.
Доказательство . Из (20) с учетом (21) можно получить
(22)
С учетом (22) расхождение векторного поля зарегистрируется в следующем виде
(23)
С учетом (15) уравнение (23) принимает вид
(24)
На фазовой плоскости ( O , u ( t ), v ( t )) рассмотрим кривую, на которой расходимость векторного поля равна нулю.
Согласно (24) эта кривая проверяет уравнение
(25)
или
, решения которого имеют два определения, идентифицирующих две прямые
(26)
Обратите внимание, что вторая прямая не удовлетворяет модельному условию, то есть физическому смыслу функций u ( t ), v ( t ).
Соответственно, согласно (26), в первой четверти фазовой плоскости имеется только одна полупрямая плоскость ( O , u ( t ), v ( t ))
(27)
, где расходимость векторного поля равна нулю.
При этом, если выполняется равенство параметрам модели
(28)
, затем особая точка M ( u * , в * ) (19) лежит на полупрямой (27).
Ясно, что G ( u , v ), расходимость (24) векторного поля, в некоторой однокогерентной области, имеющей физический смысл для первой четверти фазовой плоскости ( O , u ( t ), v ( t )) меняет знак (рис.2). Отметим здесь, что однолинейная область представляет собой полунепрямой участок с нулевой дивергенцией векторного поля и, согласно критерию Бендиксона, в указанной области существует траектория замкнутой системы (21) [35, 36]. Теорема доказана .
|
фигура 2
Качественная картина поведения расходимости векторного поля в первой четверти фазовой плоскости решений. |
Вывод
Таким образом, согласно (24), (27) на фазовой плоскости ( O , u , v ) существует однокогерентная область, где расходимость G ( u ; v ) векторного поля меняет знак и, согласно критерию Бендиксона, в этой области существует замкнутая интегральная кривая, где ( u ( t ) ≠ 0, v ( t ) ≠ 0).
При этом, согласно (11), значения функции w ( t ) никуда не обращаются, что свидетельствует об отсутствии полной ассимиляции третьей стороны в этих условиях.
Список литературы
- Голубятников А., Чилачава Т. (1983), Центральный взрыв вращающегося гравитирующего тела. Репак. СССР, 273, 825–829. [Google Scholar]
- Голубятников А., Чилачава Т. (1984), Оценки движения детонационных волн в гравитирующем газе.Флюид Дин 19, 2, 292–296. [CrossRef] [Google Scholar]
- Чилачава Т. (1985), Проблема сильной детонации в равномерно сжимающемся гравитирующем газе.МГУ, Bull Ser Math Mech 1, 78–83. [Google Scholar]
- Голубятников А., Чилачава Т. (1986), Распространение детонационной волны в гравитирующей сфере с последующим рассеиванием в вакуум. Fluid Dyn 21, 4, 673–677.[CrossRef] [Google Scholar]
- Чилачава Т. (1988), Центральный взрыв в неоднородной сфере, находящейся в равновесии в собственном гравитационном поле.Флюид Дин 23, 3, 472–477. [CrossRef] [Google Scholar]
- Чилачава Т. (1996), Об асимптотическом методе решения одного класса нелинейных задач теории гравитации.Доклады расширенного заседания семинара Института прикладной математики им. И. Векуа 11, 3, 18–26. [Google Scholar]
- Чилачава Т. (1997), О решении одной нелинейной задачи математической физики. Доклады семинара И.Институт прикладной математики им. Векуа 23, 1–9. [Google Scholar]
- Чилачава Т. (1998), Об асимптотическом методе решения одного класса нелинейных смешанных задач математической физики. Бюллетень Грузинской Академии Наук 157, 3, 373–377.[Google Scholar]
- Чилачава Т. (1999), Об асимптотическом методе решения одного класса задач астрофизики. Appl Math Inform 4, 2, 54–66. [Google Scholar]
- Чилачава Т. (2007), Математическое моделирование задач астрофизики.GESJ Comput Sci Telecommunication 13, 2, 93–101. [Google Scholar]
- Чилачава Т., Кереселидзе Н. (2008), Метод интегродифференциальных неравенств для решения модельных задач астрофизики. Труды Сухумского государственного университета, Математика и компьютерные науки IV, 26–56.[Google Scholar]
- Чилачава Т., Циала Д. (2008), Математическое моделирование. Тбилиси, п. 448. [Google Scholar]
- Чилачава Т., Кереселидзе Н. (2009), Метод интегродифференциальных неравенств для решения задач моделирования гравитирующей газовой динамики.GESJ Comput Sci Telecommunication 21, 4, 104–124. [Google Scholar]
- Чилачава Т. (2019), О точных решениях вращающегося трехосного газового эллипсоида Якоби, находящегося в собственном гравитационном поле. Отчеты расширенного заседания семинара И.Институт прикладной математики им. Векуа 33, 11–14. [Google Scholar]
- Чилачава Т., Кереселидзе Н. (2012), Задача оптимизации математической модели превентивной информационной войны, информационных и компьютерных технологий «теория и практика».Материалы Международной научной конференции ICTMC-2010, посвященной 80-летию И.В., Прангишвили, США. Nova, стр. 525–529. [Google Scholar]
- Чилачава Т., Кереселидзе Н. (2011), Математическое моделирование информационных войн.Информационная война 1, 17, 28–35. [Google Scholar]
- Чилачава Т., Чахвадзе А. (2014), Непрерывная нелинейная математическая и компьютерная модель информационной войны с участием авторитетных межгосударственных институтов. GESJ Comput Sci Telecommunication 4 (44), 53–74.[Google Scholar]
- Чилачава Т. (2013), Нелинейная трехпартийная математическая модель выборов, Проблемы управления безопасностью сложных систем. Труды XXI Международной конференции 513–516. [Google Scholar]
- Чилачава Т. (2013), Нелинейная математическая модель динамики избирателей двух политических субъектов.Семинар Института прикладной математики им. И. Векуа, Доклады 39, 13–22. [Google Scholar]
- Чилачава Т. (2016), О некоторых точных решениях нелинейной системы дифференциальных уравнений, описывающих трехпартийные выборы. Appl Math Inf Mech 21, 1, 60–75.[Google Scholar]
- Чилачава Т. (2017), Математическая модель преобразования двухпартийных выборов в трехпартийные. GESJ Comput Sci Telecommunication 2, 52, 21–29. [Google Scholar]
- Чилачава Т., Сулава Л. (2018), Математическое и компьютерное моделирование политических выборов, Одиннадцатой Международной научно-практической конференции Internet-Education Science 2018, Труды, с.113–116. [Google Scholar]
- Чилачава Т., Почхуа Г. (2018), Исследование динамической системы, описывающей математическую модель урегулирования конфликтов посредством экономического сотрудничества. GESJ Comput Sci Telecommunication 3, 55, 18–26.[Google Scholar]
- Чилачава Т., Почхуа Г. (2018), О возможности разрешения конфликта посредством экономического сотрудничества. Проблемы управления безопасностью сложных систем. XXVI Международная конференция, Москва, с.69–74. [Google Scholar]
- Чилачава Т., Почхуа Г. (2019), Исследование нелинейной динамической системы, описывающей математическую модель урегулирования конфликтов посредством экономического сотрудничества. 8-я Международная конференция по прикладному анализу и математическому моделированию, ICAAMM 2019, Сборник трудов, стр.183–187. [Google Scholar]
- Чилачава Т., Почхуа Г., Кекелия Н., Гегечкори З. (2019), Исследование динамических систем, описывающих математические модели разрешения конфликта посредством экономического сотрудничества при двустороннем или одностороннем противодействии.Цхум-Абхазская Академия Наук, Труды, Вып. XVII – XVIII, с. 12–23. [Google Scholar]
- Чилачава Т., Почхуа Г. (2019), Исследование динамических систем, описывающих математические модели разрешения конфликтов посредством экономического сотрудничества.Цхум-Абхазская Академия Наук, Труды, Вып. XVII – XVIII, с. 24–37. [Google Scholar]
- Чилачава Т., Почхуа Г., Кекелия Н., Гегечкори З. (2019), Исследование динамических систем разрешения конфликтов, описываемых математическими моделями.Доклады расширенного заседания семинара Института прикладной математики им. И. Векуа 33, 1–4. [Google Scholar]
- Чилачава Т., Почхуа Г. (2019), Математическое и компьютерное моделирование разрешения политических конфликтов. Проблемы управления безопасностью сложных систем.XXVII Международная конференция, Москва, с. 293–299. [Google Scholar]
- Чилачава Т., Чакаберия М. (2014), Математическое моделирование нелинейного процесса ассимиляции с учетом демографического фактора. GESJ Comput Sci Telecommunication 4, 44, 35–43.[Google Scholar]
- Чилачава Т., Чакаберия М. (2015), Математическое моделирование двусторонней ассимиляции нелинейных процессов. GESJ Comput Sci Telecommunication 2, 46, 79–85. [Google Scholar]
- Чилачава Т., Чакаберия М. (2016), Математическое моделирование нелинейных процессов двухуровневой ассимиляции.GESJ Comput Sci Telecommunication 3, 49, 34–48. [Google Scholar]
- Чилачава Т. (2019), Исследование динамической системы, описывающей процесс глобализации. Springer Proceedings по математике и статистике, математике, информатике и их приложениям в естественных и технических науках 276, 67–78.[Google Scholar]
- Чилачава Т., Пинелас С., Почхуа Г. (2020), Исследование четырехмерных динамических систем, описывающих процессы трехуровневой ассимиляции. Дифференциальные и разностные уравнения с приложениями: Труды Спрингера по математике и статистике (в печати).[Google Scholar]
- Бендиксон И.О. (1901 г.), Sur les Courbes определяет частные дифференциальные уравнения. Acta Math 24, 1, 1–88. [CrossRef] [Google Scholar]
- Клавдий H (1937), Rosarius Dulac Recherche des cycle limites.CR Acad. наук 204, 23, 1703–1706. [Google Scholar]
Цитируйте эту статью как: Chilachava T & Pochkhua G 2020. Исследование трехмерной нелинейной динамической системы, описывающей процесс двухуровневой ассимиляции. 4open, 3 , 10
Все рисунки
|
фигура 2
Качественная картина поведения расходимости векторного поля в первой четверти фазовой плоскости решений. |
|
| По тексту | |
Пи Му Эпсилон — Колледж искусств и наук Сиракузского университета
История и миссия
Пи Му Эпсилон — национальное почетное общество математиков. Основанная в 1914 году в Сиракузском университете, PME в настоящее время имеет более 350 отделений в колледжах и университетах по всей территории Соединенных Штатов. Целью общества является популяризация математической деятельности среди студентов.
Мероприятия
Pi Mu Epsilon проводит математические лекции для студентов и их студентов, дискуссионные панели, посвященные карьере, математические просмотры фильмов и другие общественные мероприятия.Он также проводит консультативные группы и организует занятия по подготовке к соревнованиям Патнэма и экзамену по математике GRE. События объявляются по электронной почте; Чтобы вас добавили в список рассылки, отправьте сообщение Леониду Ковалеву по адресу [email protected]. На этой странице также отображаются недавние и предстоящие события.
Некоторые из недавних презентаций участников Pi Mu Epsilon:
Членство Pi Mu Epsilon
Членство в Pi Mu Epsilon, New York Alpha Chapter открыто для всех студентов с хорошей репутацией в Сиракузском университете, которые соответствуют критериям отбора, перечисленным ниже.
- Специальность в области математики или смежной области, включая, помимо прочего, биологию, химию, экономику, инженерию или физику.
- Завершение двух семестров математического анализа и двух дополнительных курсов математики на уровне математического анализа или выше.
- Средний балл по математике не менее 3,317 и общий средний балл не менее 3,142. Особые случаи с восходящим трендом будут рассмотрены должным образом.
- Заинтересованность ученых в продвижении математики в кампусе и в сообществе Сиракуз.
Исполнительный совет 2021-22
Джейсон Куртачио, Эмма Фентон, Синьюэ Мао, Энтони Маззакан, Айджин Ву
Призывники, весна 2021 года
Дженна Каммерино, Ицзин Чен, Джейсон Куртачио, Эмма Фентон, Лияочен, Уильям Чжаочен, Чжаочен Махани, Энтони Маццакан, Чжуоци (Чи Чи) Тонг, АйЦзин Ву, Гиа Чжао
Призывники весны 2020 года
Ноа Гольдманн, Бин Ляо, Самсон Линь, Цан Луо, Синьюе Мао, Майя Остойн, Коннор Зигуула, Саронифе Варгула
Призывники, весна 2019
Кейси Бринкерхофф, Делонг Чен, Бриттани Райт.
Весна 2018 Призывники
Валери Боктор, Эндрю Каммингс, Мэтью Гонсалес, Эван Льюис, Санли Стечук, Синьсюань Ван, Линь Ян.
Зима 2018 Призывники
Патрик Каммингс, Меган Донато, Эмили Дайкман, Зицзя Лю, Грейс Мехр, Накмон Нагель, Ксинтонг Ван.
Призывники, осень 2016
Брайан Алиса, Руиксин Чен, Алекса Георгакопулос, Ванни Хуанг, Меган Ленц, Томпсон Морган, Тианьи Ван, Юсинь Чжан.
Весна 2016 Призывники
Джордан Барретт, Виктор Каннестро, Макс Энгельхард, Джесси Грин, Мэтью Мелконян, Женьюн Ши, Грант Вебстер.
Весна 2015 Призывники
Вэйи Чен, Тайлер Фернандес, Фейт Хоупек, Вэй-ю Се, Чжаохэн Ли, Маньси Цинь, Мэнгран Чжан.
Весна 2014 Призывники
Мэри-Йоханна Адджети, Кевин Донован, Амин Эльмегни, Фред Гард, Цзя Джин Лей, Хромая Механна, Кейтлин О’Рурк, Ливен Цинь, Тесса Се, Джу Юань, Чжан Чжао.
Весна 2013 Призывники
Крейг Аллен, Грант Гриффитс, Стивен Сороканич III, Синь Тянь, Эшли Валентийн.
Призывники осень 2012 года
Бинцзин Фэн, Синьи (Ширли) Хэ, Стэнли Хоффман, Рэнди Родекер, Шо Чжан.

 яз.-75
яз.-75



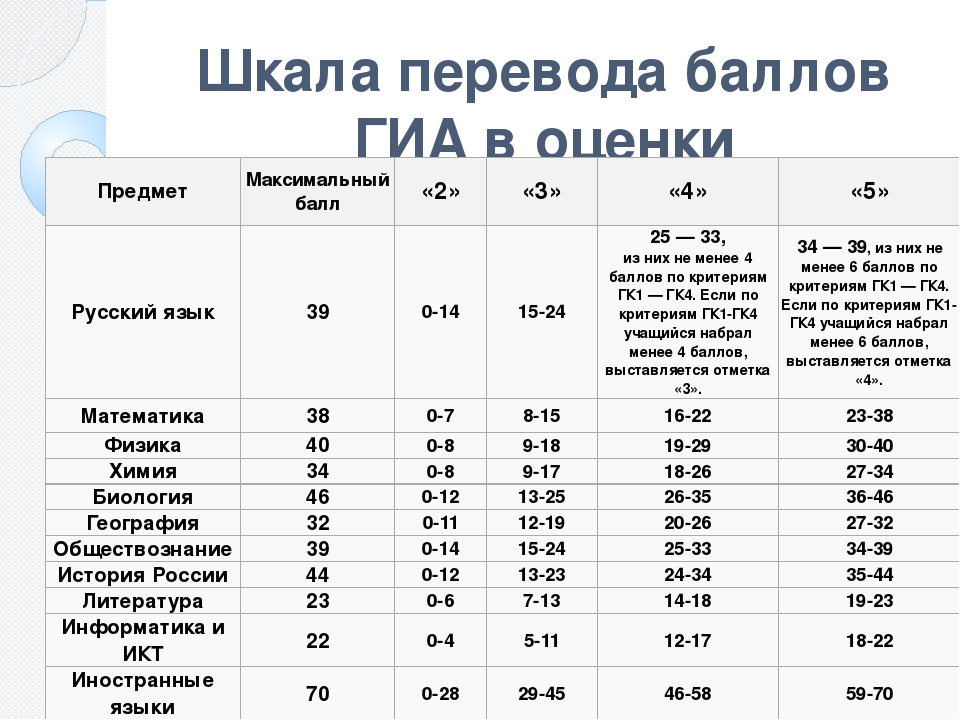 Г. (высшая)
Г. (высшая) А. (высшая)
А. (высшая)
 И.
И. А.
А. Г. (высшая)
Г. (высшая) Ю.
Ю.
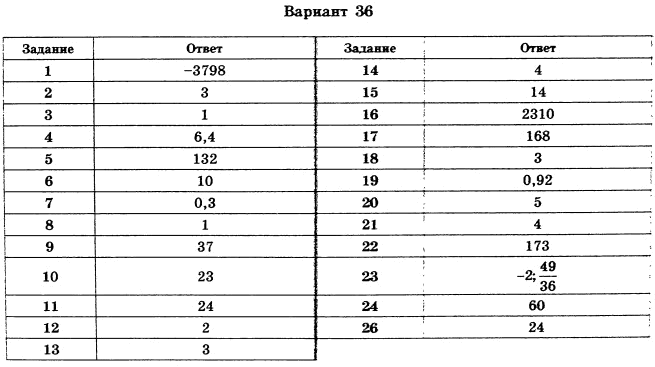 В.
В. В.
В.