Оптические линзы | Физика
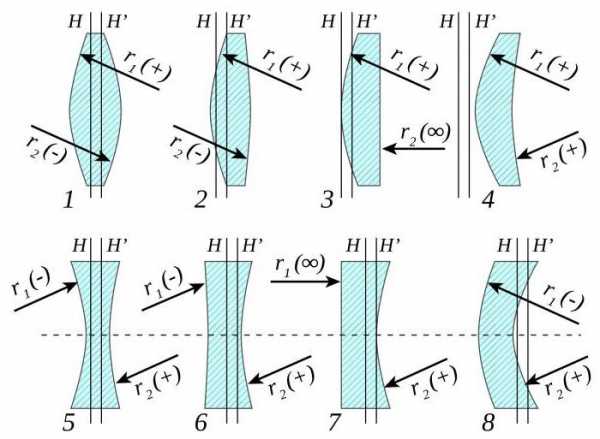
Прозрачные тела, у которых хотя бы одна поверхность искривлена, называются линзами. Чаще всего бывают линзы, симметричные относительно оптической оси. Оптические особенности линзы зависят от радиуса и вида искривления.
Собирающая линза
У выпуклых, или собирающих, линз середина толще, чем края. Параллельный пучок света, например, солнечный луч, падает на выпуклую линзу. Линза собирает пучок света в фокусе F. Расстояние от средней плоскости до фокуса называется фокусным расстоянием линзы f. Чем оно короче, тем больше оптическая сила линзы. Эта сила измеряется в диоптриях.
Возьмем линзу с фокусным расстоянием 0.5 метра. Тогда оптическая сила линзы равна единице, деленной на фокусное расстояние: 1/0.5 м = 2 диоптрии.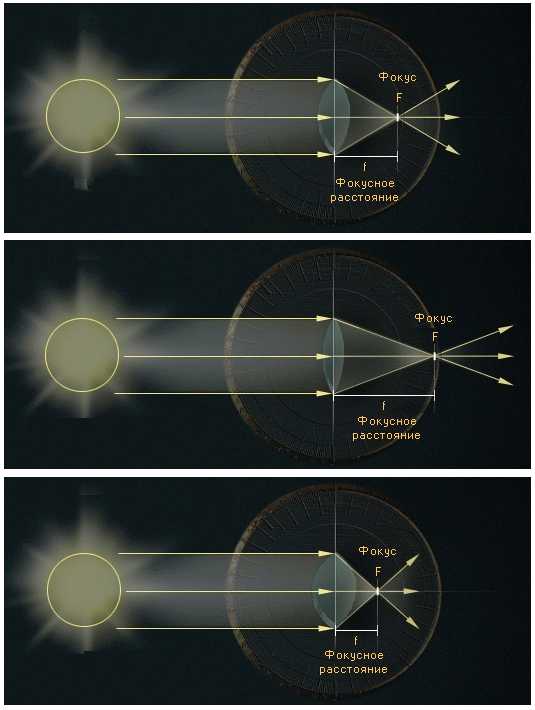
Рассеивающая линза
Вогнутые или рассеивающие линзы — это такие линзы, у которых толщина краев больше, чем толщина посередине.
В этом случае, параллельный пучок света будет рассеиваться. При этом будет казаться, что луч света выходит из одной точки, которая называется мнимым фокусом. Фокусное расстояние в данном случае будет отрицательно и соответственно оптическая сила рассеивающей линзы тоже будет отрицательна.
Возьмем линзу с фокусным расстоянием -0.25 метра. Тогда оптическая сила будет равна: 1/-0.25 = -4 диоптрии.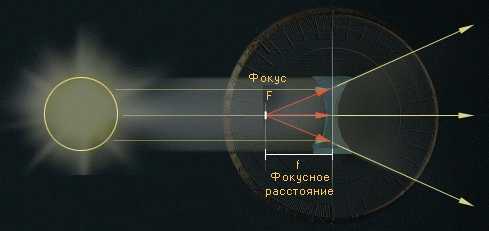
Принцип построения изображения собирающей линзой
Собирающая линза дает действительное изображение. Только оно будет перевернуто вверх ногами.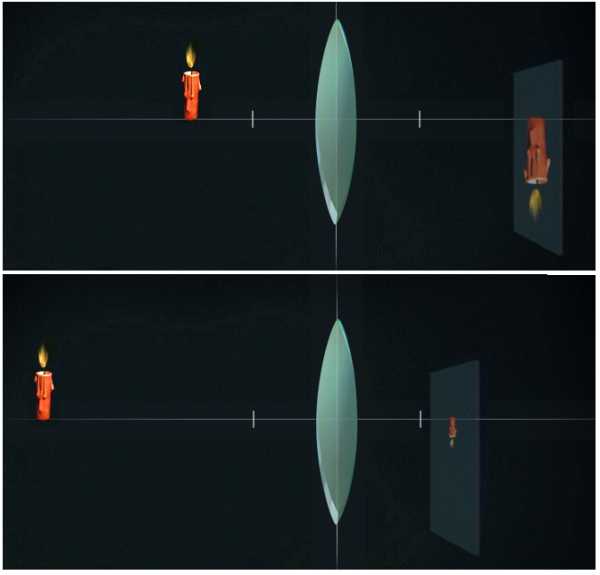
Если мы хотим получить более точное изображение, то, зная длину фокуса, мы можем построить это изображение. Для этого нам необходимы три луча.
Луч, распространяющийся параллельно оптической оси, преломляющийся в линзе и проходящий через фокус, называется параллельным лучом.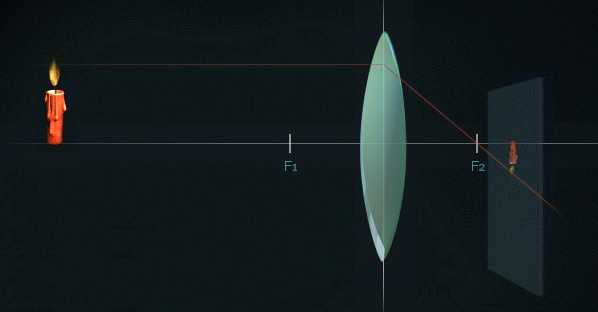
Луч, проходящий через центр линзы, называется основным лучом. Он не преломляется.
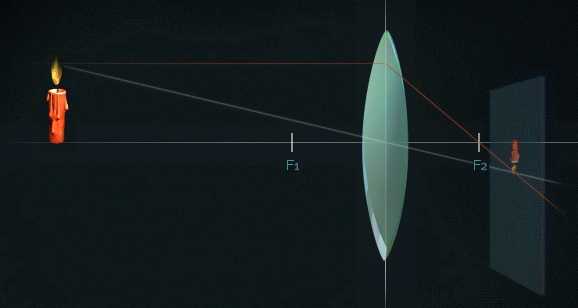
Луч, который проходит перед линзой через фокус и затем распространяется параллельно оптической оси, называется фокусным лучом. В той точке, где пересекаются все три луча, будет наиболее четкое изображение.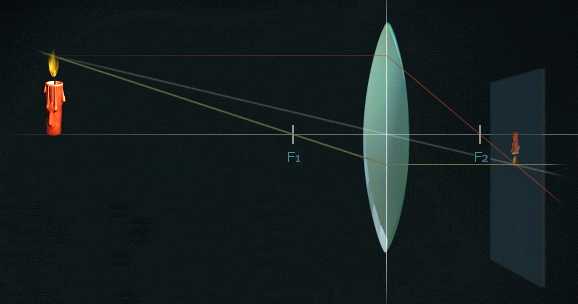
Если расстояние от предмета до линзы очень велико, то расстояние от изображения этого предмета до линзы будет намного меньше, т.е. изображение будет уменьшенным.
Если расстояние от предмета в два раза больше фокусного расстояния, то изображение будет такого же размера, как и сам предмет, и находится оно будет на двойном фокусном расстоянии за линзой.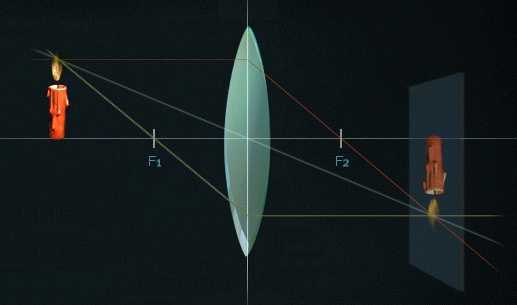
Если приблизить предмет к фокусу, то мы получим увеличенное изображение, находящееся на большом расстоянии по другую сторону линзы.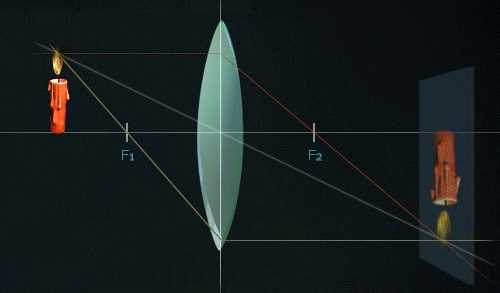
Если предмет находится прямо в фокусе или еще ближе к линзе, то мы получим нечеткое изображение.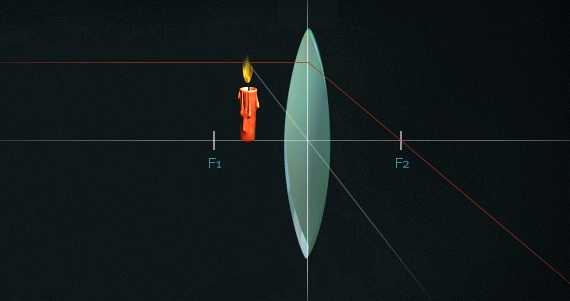
phscs.ru
определение, описание, формула и решение
Существуют объекты, которые способны изменять плотность падающего на них потока электромагнитного излучения, то есть либо увеличивать его, собирая в одну точку, либо уменьшать его путем рассеивания. Эти объекты называются линзами в физике. Рассмотрим подробнее этот вопрос.
Что представляют собой линзы в физике?
Под этим понятием подразумевают абсолютно любой объект, который способен изменять направление распространения электромагнитного излучения. Это общее определение линз в физике, под которое попадают оптические стекла, магнитные и гравитационные линзы.
В данной статье главное внимание будет уделено именно оптическим стеклам, которые представляют собой объекты, изготовленные из прозрачного материала, и ограниченные двумя поверхностями. Одна из этих поверхностей обязательно должна иметь кривизну (то есть являться частью сферы конечного радиуса), в противном случае объект не будет обладать свойством изменения направления распространения световых лучей.
Принцип работы линзы

Суть работы этого незамысловатого оптического объекта заключается в явлении преломления солнечных лучей. В начале XVII века знаменитый голландский физик и астроном Виллеброрд Снелл ван Ройен опубликовал закон преломления, который в настоящее время носит его фамилию. Формулировка этого закона следующая: когда солнечный свет переходит через границу раздела двух оптически прозрачных сред, то произведение синуса угла падения между лучом и нормалью к поверхности на коэффициент преломления среды, в которой он распространяется, является величиной постоянной.

Для пояснения вышесказанного приведем пример: пусть свет падает на поверхность воды, при этом угол между нормалью к поверхности и лучом равен θ1. Затем, световой пучок преломляется и начинает свое распространение в воде уже под углом θ2 к нормали к поверхности. Согласно закону Снелла получим: sin(θ1)*n1 = sin(θ2)*n2, здесь n1 и n2 — коэффициенты преломления для воздуха и воды, соответственно. Что такое коэффициент преломления? Это величина, показывающая, во сколько раз скорость распространения электромагнитных волн в вакууме больше таковой для оптически прозрачной среды, то есть n = c/v, где c и v — скорости света в вакууме и в среде, соответственно.
Физика возникновения преломления заключается в выполнении принципа Ферма, согласно которому свет движется таким образом, чтобы за наименьшее время преодолеть расстояние от одной точки к другой в пространстве.
Виды линз
Вид оптической линзы в физике определяется исключительно формой поверхностей, которые ее образуют. От этой формы зависит направление преломления падающего на них луча. Так, если кривизна поверхности будет положительной (выпуклой), то по выходе из линзы световой пучок будет распространяться ближе к ее оптической оси (см. ниже). Наоборот, если кривизна поверхности является отрицательной (вогнутой), тогда пройдя через оптическое стекло, луч станет удаляться от его центральной оси.
Отметим еще раз, что поверхность любой кривизны преломляет лучи одинаково (согласно закону Стелла), но нормали к ним имеют разный наклон относительно оптической оси, в результате получается разное поведение преломленного луча.
Линза, которая ограничена двумя выпуклыми поверхностями, называется собирающей. В свою очередь, если она образована двумя поверхностями с отрицательной кривизной, тогда она называется рассеивающей. Все остальные виды оптических стекол связаны с комбинацией указанных поверхностей, к которым добавляется еще и плоскость. Каким свойством будет обладать комбинированная линза (рассеивающим или собирающим), зависит от суммарной кривизны радиусов ее поверхностей.
Элементы линзы и свойства лучей

Для построения в линзах в физике изображений необходимо познакомиться с элементами этого объекта. Они приведены ниже:
- Главная оптическая ось и центр. В первом случае имеют в виду прямую, проходящую перпендикулярно линзе через ее оптический центр. Последний, в свою очередь, представляет собой точку внутри линзы, проходя через которую, луч не испытывает преломления.
- Фокусное расстояние и фокус — дистанция между центром и точкой на оптической оси, в которую собираются все падающие на линзу параллельно этой оси лучи. Это определение верно для собирающих оптических стекол. В случае рассеивающих линз собираться в точку будут не сами лучи, а мнимое их продолжение. Эта точка называется главным фокусом.
- Оптическая сила. Так называется величина, обратная фокусному расстоянию, то есть D = 1/f. Измеряется она в диоптриях (дптр.), то есть 1 дптр. = 1 м-1.
Ниже приводятся основные свойства лучей, которые проходят через линзу:
- пучок, проходящий через оптический центр, не изменяет направления своего движения;
- лучи, падающие параллельно главной оптической оси, изменяют свое направление так, что проходят через главный фокус;
- лучи, падающие на оптическое стекло под любым углом, но проходящие через его фокус, изменяют свое направление распространения таким образом, что становятся параллельными главной оптической оси.
Приведенные выше свойства лучей для тонких линз в физике (так их называют, потому что не важно, какими сферами они образованы, и какой толщиной обладают, имеют значение только оптические свойства объекта) используются для построения изображений в них.
Изображения в оптических стеклах: как строить?
Ниже приведен рисунок, где подробно разобраны схемы построения изображений в выпуклой и вогнутой линзах объекта (красной стрелки) в зависимости от его положения.
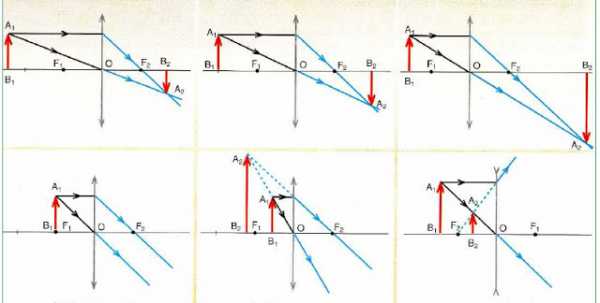
Из анализа схем на рисунке следуют важные выводы:
- Любое изображение строится всего на 2-х лучах (проходящем через центр и параллельном главной оптической оси).
- Собирающие линзы (обозначаются со стрелками на концах, направленными наружу) могут давать как увеличенное, так и уменьшенное изображение, которое в свою очередь может быть реальным (действительным) или мнимым.
- Если предмет расположен в фокусе, то линза не образует его изображения (см. нижнюю схему слева на рисунке).
- Рассеивающие оптические стекла (обозначаются стрелками на их концах, направленными внутрь) дают независимо от положения предмета всегда уменьшенное и мнимое изображение.
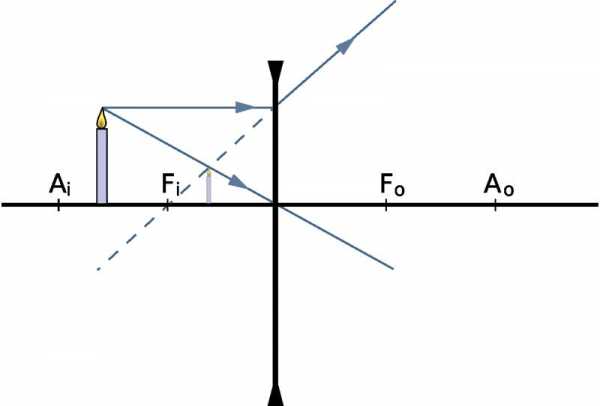
Нахождение расстояния до изображения
Чтобы определять, на каком расстоянии появится изображение, зная положение самого предмета, приведем формулу линзы в физике: 1/f = 1/do + 1/di, где do и di — расстояние до предмета и до его изображения от оптического центра, соответственно, f — главный фокус. Если речь идет о собирающем оптическом стекле, тогда число f будет положительным. Наоборот, для рассеивающей линзы f — отрицательное.
Воспользуемся этой формулой и решим простую задачу: пусть предмет находится на расстоянии do = 2*f от центра собирающего оптического стекла. Где появится его изображение?
Из условия задачи имеем: 1/f = 1/(2*f)+1/di. Откуда: 1/di = 1/f — 1/(2*f) = 1/(2*f), то есть di = 2*f. Таким образом, изображение появится на расстоянии двух фокусов от линзы, но уже с другой стороны, чем сам предмет (об этом говорит положительный знак величины di).
Краткая история
Любопытно привести этимологию слова «линза». Оно ведет происхождение от латинских слов lens и lentis, что означает «чечевица», поскольку оптические объекты по своей форме действительно похожи на плод этого растения.
Преломляющая способность сферических прозрачных тел была известна еще древним римлянам. Для этой цели они применяли круглые стеклянные сосуды, наполненные водой. Сами же стеклянные линзы начали изготавливаться только в XIII веке в Европе. Использовались они в качестве инструмента для чтения (современные очки или лупа).
Активное использование оптических объектов при изготовлении телескопов и микроскопов относится к XVII (в начале этого века Галилей изобрел первый телескоп). Отметим, что математическая формулировка закона преломления Стелла, без знания которой невозможно изготавливать линзы с заданными свойствами, была опубликована голландским ученым в начале того же XVII века.
Другие виды линз
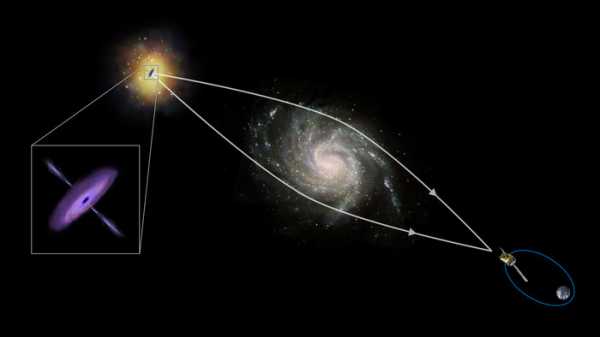
Как было отмечено выше, помимо оптических преломляющих объектов, существуют также магнитные и гравитационные. Примером первых являются магнитные линзы в электронном микроскопе, яркий пример вторых заключается в искажении направления светового потока, когда он проходит вблизи массивных космических тел (звезд, планет).
fb.ru
Тонкие линзы | ЭТО ФИЗИКА
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
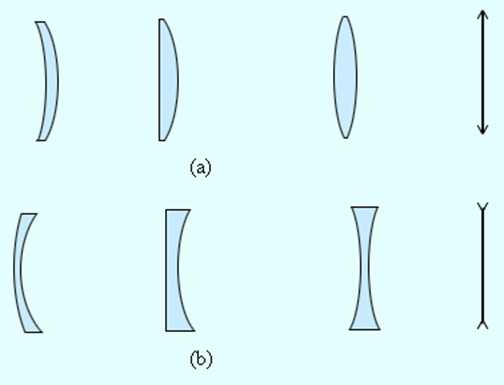
Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).
|
|
|
Рисунок 3.3.1.
Собирающие (a) и рассеивающие (b) линзы и их условные обозначения |
Прямая, проходящая через центры кривизны O1 и O2 сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку
|
|
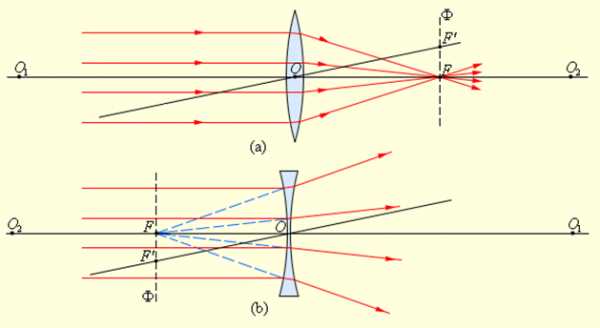
|
Рисунок 3.3.2. Преломление параллельного пучка лучей в собирающей (a) и рассеивающей (b) линзах. Точки O1 и O2 – центры сферических поверхностей, O1O2 – главная оптическая ось, O – оптический центр, F – главный фокус, F’ – побочный фокус, OF’ – побочная оптическая ось, Ф – фокальная плоскость |
Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми, увеличенными и уменьшенными.
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Примеры таких построений представлены на рис. 3.3.3 и 3.3.4.
|
Рисунок 3.3.3. Построение изображения в собирающей линзе |
|
|
|
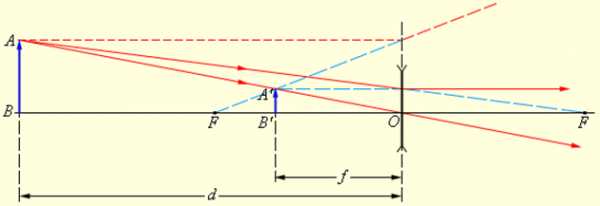
Рисунок 3.3.4. Построение изображения в рассеивающей линзе |
Следует обратить внимание на то, что некоторые из стандартных лучей, использованных на рис. 3.3.3 и 3.3.4 для построения изображений, не проходят через линзу. Эти лучи реально не участвуют в образовании изображения, но они могут быть использованы для построений.
Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м:
Формула тонкой линзы аналогична формуле сферического зеркала. Ее можно получить для параксиальных лучей из подобия треугольников на рис. 3.3.3 или 3.3.4.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.
Величины d и f также подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.
Для случая, изображенного на рис. 3.3.3, имеем: F > 0 (линза собирающая), d = 3F > 0 (действительный предмет).
По формуле тонкой линзы получим: , следовательно, изображение действительное.
В случае, изображенном на рис. 3.3.4, F < 0 (линза рассеивающая), d = 2|F| > 0 (действительный предмет), , то есть изображение мнимое.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h’ и предмета h. Величине h’, как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рис. 3.3.3 и 3.3.4 легко получить формулу для линейного увеличения тонкой линзы:
В рассмотренном примере с собирающей линзой (рис. 3.3.3): d = 3F > 0, , следовательно, – изображение перевернутое и уменьшенное в 2 раза.
В примере с рассеивающей линзой (рис. 3.3.4): d = 2|F| > 0, ; следовательно, – изображение прямое и уменьшенное в 3 раза.
Оптическая сила D линзы зависит как от радиусов кривизны R1 и R2 ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:
Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние
Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея.
Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.
Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.
В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.
Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.
Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом. Специальный затвор позволяет открывать объектив на время экспозиции.
Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных расстояниях.
В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наведение на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкого наведения, получаются размытыми в виде кружков рассеяния. Размер d этих кружков может быть уменьшен путем диафрагмирования объектива, т.е. уменьшения относительного отверстия a / F (рис. 3.3.5). Это приводит к увеличению глубины резкости.
|
Рисунок 3.3.5. Фотоаппарат |
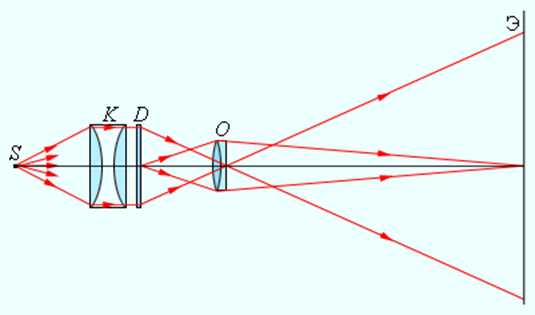
Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D) на удаленном экране Э (рис. 3.3.6). Система линз K, называемая конденсором, предназначена для того, чтобы сконцентрировать свет источника S на диапозитиве. На экране Э создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран Э с одновременным изменением расстояния между диапозитивом D и объективом O.
|
|
|
Рисунок 3.3.6. Проекционный аппарат |
www.its-physics.org
виды линз (физика). Виды собирающих, оптических, рассеивающих линз. Как определить вид линзы?
Линзы, как правило, имеют сферическую или близкую к сферической поверхность. Они могут быть вогнутыми, выпуклыми или плоскими (радиус равен бесконечности). Обладают двумя поверхностями, через которые проходит свет. Они могут сочетаться по-разному, образуя различные виды линз (фото приведено далее в статье):
- Если обе поверхности выпуклые (изогнуты наружу), центральная часть толще, чем по краям.
- Линза с выпуклой и вогнутой сферами называется мениском.
- Линза с одной плоской поверхностью носит название плоско-вогнутой или плоско-выпуклой, в зависимости от характера другой сферы.
Как определить вид линзы? Остановимся на этом подробнее.
Собирающие линзы: виды линз
Независимо от сочетания поверхностей, если их толщина в центральной части больше, чем по краям, они называются собирающими. Имеют положительное фокусное расстояние. Различают следующие виды собирающих линз:
- плоско-выпуклые,
- двояковыпуклые,
- вогнуто-выпуклые (мениск).
Их еще называют «положительными».
Рассеивающие линзы: виды линз
Если их толщина в центре тоньше, чем по краям, то они носят название рассеивающих. Имеют отрицательное фокусное расстояние. Существуют такие виды рассеивающих линз:
- плоско-вогнутые,
- двояковогнутые,
- выпукло-вогнутые (мениск).
Их еще называют «отрицательными».

Базовые понятия
Лучи от точечного источника расходятся из одной точки. Их называют пучком. Когда пучок входит в линзу, каждый луч преломляется, изменяя свое направление. По этой причине пучок может выйти из линзы в большей или меньшей степени расходящимся.
Некоторые виды оптических линз изменяют направление лучей настолько, что они сходятся в одной точке. Если источник света расположен, по меньшей мере, на фокусном расстоянии, то пучок сходится в точке, удаленной, по крайней мере, на ту же дистанцию.
Действительные и мнимые изображения
Точечный источник света называется действительным объектом, а точка сходимости пучка лучей, выходящего из линзы, является его действительным изображением.
Важное значение имеет массив точечных источников, распределенных на, как правило, плоской поверхности. Примером может служить рисунок на матовом стекле, подсвеченный сзади. Другим примером является диафильм, освещенный сзади так, чтобы свет от него проходил через линзу, многократно увеличивающую изображение на плоском экране.
В этих случаях говорят о плоскости. Точки на плоскости изображения 1:1 соответствуют точкам на плоскости объекта. То же относится и к геометрическим фигурам, хотя полученная картинка может быть перевернутой по отношению к объекту сверху вниз или слева направо.
Схождение лучей в одной точке создает действительное изображение, а расхождение – мнимое. Когда оно четко очерчено на экране – оно действительное. Если же изображение можно наблюдать, только посмотрев через линзу в сторону источника света, то оно называется мнимым. Отражение в зеркале – мнимое. Картину, которую можно увидеть через телескоп – тоже. Но проекция объектива камеры на пленку дает действительное изображение.
Фокусное расстояние
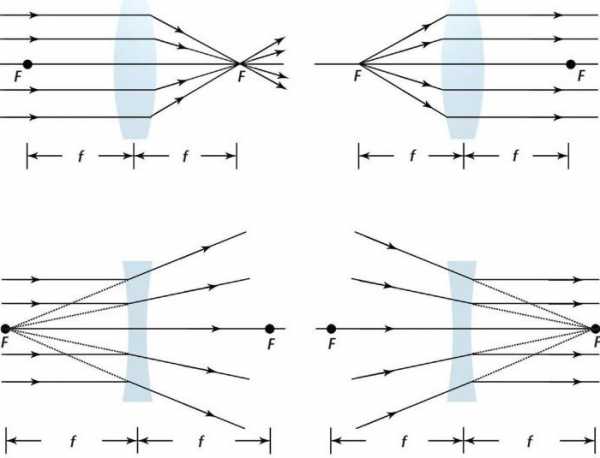
Фокус линзы можно найти, пропустив через нее пучок параллельных лучей. Точка, в которой они сойдутся, и будет ее фокусом F. Расстояние от фокальной точки до объектива называют его фокусным расстоянием f. Параллельные лучи можно пропустить и с другой стороны и таким образом найти F с двух сторон. Каждая линза обладает двумя F и двумя f. Если она относительно тонка по сравнению с ее фокусными расстояниями, то последние приблизительно равны.
Дивергенция и конвергенция
Положительным фокусным расстоянием характеризуются собирающие линзы. Виды линз данного типа (плоско-выпуклые, двояковыпуклые, мениск) сводят лучи, выходящие из них, больше, чем они были сведены до этого. Собирающие объективы могут формировать как действительное, так и мнимое изображение. Первое формируется только в случае, если расстояние от линзы до объекта превышает фокусное.
Отрицательным фокусным расстоянием характеризуются рассеивающие линзы. Виды линз этого типа (плоско-вогнутые, двояковогнутые, мениск) разводят лучи больше, чем они были разведены до попадания на их поверхность. Рассеивающие линзы создают мнимое изображение. И только когда сходимость падающих лучей значительна (они сходятся где-то между линзой и фокальной точкой на противоположной стороне), образованные лучи все еще могут сходиться, образуя действительное изображение.
Важные различия
Следует быть очень внимательными, чтобы отличать схождение или расхождение лучей от конвергенции или дивергенции линзы. Виды линз и пучков света могут не совпадать. Лучи, связанные с объектом или точкой изображения, называются расходящимися, если они «разбегаются», и сходящимся, если они «собираются» вместе. В любой коаксиальной оптической системе оптическая ось представляет собой путь лучей. Луч вдоль этой оси проходит без какого-либо изменения направления движения из-за преломления. Это, по сути, хорошее определение оптической оси.
Луч, который с расстоянием отдаляется от оптической оси, называется расходящимся. А тот, который к ней становится ближе, носит название сходящегося. Лучи, параллельные оптической оси, имеют нулевое схождение или расхождение. Таким образом, когда говорят о схождении или расхождении одного луча, его соотносят с оптической осью.
Некоторые виды линз, физика которых такова, что луч отклоняется в большей степени к оптической оси, являются собирающими. В них сходящиеся лучи сближаются еще больше, а расходящиеся отдаляются меньше. Они даже в состоянии, если их сила достаточна для этого, сделать пучок параллельным или даже сходящимся. Аналогично рассеивающая линза может развести расходящиеся лучи еще больше, а сходящиеся – сделать параллельными или расходящимися.

Увеличительные стекла
Линза с двумя выпуклыми поверхностями толще в центре, чем по краям, и может использоваться в качестве простого увеличительного стекла или лупы. При этом наблюдатель смотрите через нее на мнимое, увеличенное изображение. Объектив камеры, однако, формирует на пленке или сенсоре действительное, как правило, уменьшенное в размерах по сравнению с объектом.
Очки
Способность линзы изменять сходимость света называется ее силой. Выражается она в диоптриях D = 1 / f, где f – фокусное расстояние в метрах.
У линзы с силой 5 диоптрий f = 20 см. Именно диоптрии указывает окулист, выписывая рецепт очков. Скажем, он записал 5,2 диоптрий. В мастерской возьмут готовую заготовку в 5 диоптрий, полученную на заводе-изготовителе, и отшлифуют немного одну поверхность, чтобы добавить 0,2 диоптрии. Принцип состоит в том, что для тонких линз, в которых две сферы расположены близко друг к другу, соблюдается правило, согласно которому общая их сила равна сумме диоптрий каждой: D = D1 + D2.

Труба Галилея
Во времена Галилея (начало XVII века), очки в Европе были широко доступны. Они, как правило, изготавливались в Голландии и распространялись уличными торговцами. Галилео слышал, что кто-то в Нидерландах поместил два вида линз в трубку, чтобы удаленные объекты казались больше. Он использовал длиннофокусный собирающий объектив в одном конце трубки, и короткофокусный рассеивающий окуляр на другом конце. Если фокусное расстояние объектива равно fo и окуляра fe, то дистанция между ними должна быть fo-fe, а сила (угловое увеличение) fo/fe. Такая схема называется трубой Галилея.
Телескоп обладает увеличением 5 или 6 крат, сравнимым с современными ручными биноклями. Этого достаточно для многих захватывающих астрономических наблюдений. Можно без проблем увидеть лунные кратеры, четыре луны Юпитера, кольца Сатурна, фазы Венеры, туманности и звездные скопления, а также слабые звезды в Млечном Пути.

Телескоп Кеплера
Кеплер услышал обо всем этом (он и Галилей вели переписку) и построил еще один вид телескопа с двумя собирающими линзами. Та, у которой большое фокусное расстояние, является объективом, а та, у которой оно меньше – окуляром. Расстояние между ними равно fo + fe, а угловое увеличение составляет fo/fe. Этот кеплеровский (или астрономический) телескоп создает перевернутое изображение, но для звезд или луны это не имеет значения. Данная схема обеспечила более равномерное освещение поля зрения, чем телескоп Галилея, и была более удобна в использовании, так как позволяла держать глаза в фиксированном положении и видеть все поле зрения от края до края. Устройство позволяло достичь более высокого увеличения, чем труба Галилея, без серьезного ухудшения качества.
Оба телескопа страдают от сферической аберрации, в результате чего изображения не полностью сфокусированы, и хроматической аберрации, создающей цветные ореолы. Кеплер (и Ньютон) считал, что эти дефекты невозможно преодолеть. Они не предполагали, что возможны ахроматические виды линз, физика которых станет известна лишь в XIX веке.

Зеркальные телескопы
Грегори предположил, что в качестве объективов телескопов можно использовать зеркала, так как в них отсутствует цветная окантовка. Ньютон воспользовался этой идеей и создал ньютоновскую форму телескопа из вогнутого посеребренного зеркала и положительного окуляра. Он передал образец Королевскому обществу, где тот находится и по сей день.
Однолинзовый телескоп может проецировать изображение на экран или фотопленку. Для должного увеличения требуется положительная линза с большим фокусным расстоянием, скажем, 0,5 м, 1 м или много метров. Такая компоновка часто используется в астрономической фотографии. Людям, незнакомым с оптикой, может показаться парадоксальной ситуация, когда более слабая длиннофокусная линза дает большее увеличение.
Сферы
Высказывались предположения, что древние культуры, возможно, имели телескопы, потому что они делали маленькие стеклянные шарики. Проблема состоит в том, что неизвестно, для чего они использовались, и они, конечно, не могли бы лечь в основу хорошего телескопа. Шарики могли применяться для увеличения мелких объектов, но качество при этом вряд ли было удовлетворительным.
Фокусное расстояние идеальной стеклянной сферы очень короткое и формирует действительное изображение очень близко от сферы. Кроме того, аберрации (геометрические искажения) значительные. Проблема кроется в расстоянии между двумя поверхностями.
Однако если сделать глубокую экваториальную канавку, чтобы блокировать лучи, которые вызывают дефекты изображения, она превращается из очень посредственной лупы в прекрасную. Такое решение приписывается Коддингтону, а увеличитель его имени можно приобрести сегодня в виде небольших ручных луп для изучения очень маленьких объектов. Но доказательств того, что это было сделано до 19-го века, нет.
fb.ru
Линза — Класс!ная физика
Линза
«Физика — 11 класс»
Прозрачное тело, ограниченное сферическими поверхностями, называют линзой.
Виды линз
Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза), выпуклой сферической поверхностью и плоскостью (плосковыпуклая линза), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза).
Эти линзы посредине толще, чем у краев, и все они называются выпуклыми.
Линзы, которые посредине тоньше, чем у краев, называются вогнутыми.
На рисунке изображены три вида вогнутых линз: двояковогнутая, плосковогнутая и выпукло-вогнутая.
Тонкая линза
Мы рассмотрим наиболее простой случай, когда толщина линзы l = АВ пренебрежимо мала по сравнению с радиусами R1 и R2 сферических поверхностей линзы и расстоянием предмета от линзы.
Такую линзу называют тонкой линзой.
В дальнейшем, говоря о линзе, мы всегда будем подразумевать тонкую линзу.
Точки А и В — вершины сферических сегментов — расположены в тонкой линзе столь близко друг от друга, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают буквой О.
Луч света, который проходит через оптический центр линзы, не изменяет своего направления, а только смещается, но, так как линза тонкая, этим смещением можно пренебречь.
Прямую O1O2, проходящую через центры сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью.
Главная оптическая ось тонкой линзы проходит через оптический центр.
Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света.
Это означает, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в одну точку (изображение) независимо от того, через какую часть линзы прошли лучи.
Если по выходе из линзы лучи сходятся, они образуют действительное изображение.
В случае же, когда прошедшие через линзу лучи расходятся, то пересекаются в одной точке не сами эти лучи, а лишь их продолжения.
Изображение в этом случае мнимое.
Его можно наблюдать глазом непосредственно или с помощью оптических приборов.
Лучи или их продолжения будут пересекаться практически в одной точке, если они образуют малые углы с главной оптической осью
Собирающая линза
Обычно линзы изготавливают из стекла.
Выпуклые линзы являются собирающими.
Любую из них схематично можно себе представить как совокупность стеклянных призм.
В воздухе каждая призма отклоняет лучи к основанию.
Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
Точка, в которой пересекаются после преломления в собирающей линзе лучи, падающие на нее параллельно главной оптической оси, называется главным фокусом линзы.
Эту точку обозначают буквой F.
Пучки, параллельные главной оптической оси, можно направить на линзу и с противоположной стороны.
Точка, в которой они сойдутся, пройдя линзу, будет другим главным фокусом.
Таким образом, у линзы два главных фокуса.
В однородной среде они располагаются по обе стороны линзы на одинаковых расстояниях от нее.
Эти расстояния называются фокусным расстоянием линзы; его обозначают буквой F (той же буквой, что и фокус).
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси линзы.
Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке.
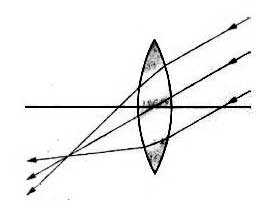
Но примечательно то, что точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус.
Эту плоскость называют фокальной плоскостью.
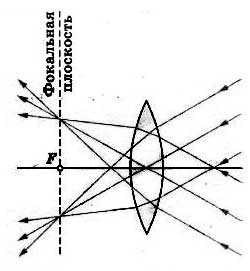
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
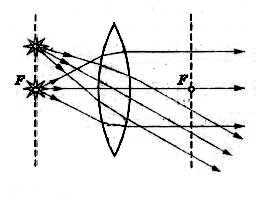
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
Когда же источник находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
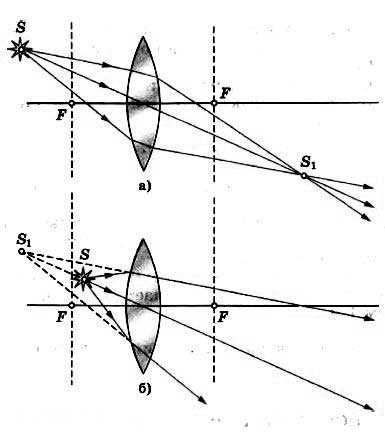
Рассеивающая линза
Вогнутые линзы, находящиеся в оптически менее плотной среде (по сравнению с материалом линзы), являются рассеивающими.
Направив на такую линзу лучи параллельно главной оптической оси, мы получим расходящийся пучок лучей.
Их продолжения пересекаются в главном фокусе рассеивающей линзы.
В этом случае главный фокус является мнимым и расположен на расстоянии F от линзы.
Другой мнимый главный фокус находится по другую сторону линзы на таком же расстоянии, если среда по обе стороны линзы одна и та же.
Оптическая сила линзы
Величину, обратную фокусному расстоянию, называют оптической силой линзы.
Ее обозначают буквой D:
D > 0, если линза собирающая, D < 0, если линза рассеивающая.
Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Оптическую силу D линз выражают в диоптриях (дптр).
Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Световые волны. Физика, учебник для 11 класса — Класс!ная физика
Оптика — Скорость света — Принцип Гюйгенса. Закон отражения света — Закон преломления света — Полное отражение — Линза — Построение изображения в линзе — Формула тонкой линзы. Увеличение линзы — Примеры решения задач. Геометрическая оптика — Дисперсия света — Интерференция механических волн — Интерференция света — Некоторые применения интерференции — Дифракция механических волн — Дифракция света — Дифракционная решетка — Поперечность световых волн. Поляризация света — Поперечность световых волн и электромагнитная теория света — Примеры решения задач. Волновая оптика — Краткие итоги главы
class-fizika.ru
Линзы
Линзы
Линзой называется прозрачное тело, ограниченное двумя криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями. Линзы делятся на выпуклые и вогнутые.
Линзы, у которых середина толще, чем края, называются выпуклыми. Линзы, у которых середина тоньше, чем края, называются вогнутыми.
Если показатель преломления линзы больше, чем показатель преломления окружающей среды, то в выпуклой линзе параллельный пучок лучей после преломления преобразуется в сходящий пучок. Такие линзы называются собирающими (рис. 89, а). Если в линзе параллельный пучок преобразуется в расходящийся пучок, то эти линзы называются рассеивающими (рис. 89, б). Вогнутые линзы, у которых внешней средой служит воздух, являются рассеивающими.
O1, О2 — геометрические центры сферических поверхностей, ограничивающих линзу. Прямая О1О2, соединяющая центры этих сферических поверхностей, называется главной оптической осью. Обычно рассматриваем тонкие линзы, у которых толщина мала по сравнению с радиусами кривизны ее поверхностей, поэтому точки C1 и С2 (вершины сегментов) лежат близко друг к другу, их можно заменить одной точкой О, называемой оптическим центром линзы (см. рис. 89а). Всякая прямая, проведенная через оптический центр линзы под углом к главной оптической оси, называется побочной оптической осью (А1A2 B1B2).
Если на собирающую линзу падает пучок лучей, параллельных главной оптической оси, то после преломления в линзе они собираются в одной точке F, которая называется главным фокусом линзы (рис. 90, а).
В фокусе рассеивающей линзы пересекаются продолжения лучей, которые до преломления были параллельны ее главной оптической оси (рис. 90, б). Фокус рассеивающей линзы мнимый. Главных фокусов — два; они расположены на главной оптической оси на одинаковом расстоянии от оптического центра линзы по разные стороны.
Величина, обратная фокусному расстоянию линзы, называется ее оптической силой. Оптическая сила линзы — D.
За единицу оптической силы линзы в СИ принимают диоптрию. Диоптрия — оптическая сила линзы, фокусное расстояние которой равно 1 м.
Оптическая сила собирающей линзы положительная, рассеивающей — отрицательная.
Плоскость, проходящая через главный фокус линзы перпендикулярно к главной оптической оси, называется фокальной (рис. 91). Пучок лучей, падающих на линзу параллельно какой-либо побочной оптической оси, собирается в точке пересечения этой оси с фокальной плоскостью.
Построение изображения точки и предмета в собирающей линзе.
Для построения изображения в линзе достаточно взять по два луча от каждой точки предмета и найти их точку пересечения после преломления в линзе. Удобно пользоваться лучами, ход которых после преломления в линзе известен. Так, луч, падающий на линзу параллельно главной оптической оси, после преломления в линзе проходит через главный фокус; луч, проходящий через оптический центр линзы, не преломляется; луч, проходящий через главный фокус линзы, после преломления идет параллельно главной оптической оси; луч, падающий на линзу параллельно побочной оптической оси, после преломления в линзе проходит через точку пересечения оси с фокальной плоскостью.
Пусть светящаяся точка S лежит на главной оптической оси.
Выбираем произвольно луч и параллельно ему проводим побочную оптическую ось (рис. 92). Через точку пересечения побочной оптической оси с фокальной плоскостью пройдет выбранный луч после преломления в линзе. Точка пересечения данного луча с главной оптической осью (второй луч) даст действительное изображение точки S — S`.
Рассмотрим построение изображения предмета в выпуклой линзе.
Пусть точка лежит вне главной оптической оси, тогда изображение S` можно построить с помощью любых двух лучей, приведенных на рис. 93.
Если предмет расположен в бесконечности, то лучи пересекутся в фокусе (рис. 94).
Если предмет расположен за точкой двойного фокуса, то изображение получится действительным, обратным, уменьшенным (фотоаппарат, глаз) (рис. 95).
Если предмет расположен в точке двойного фокуса, то изображение получится действительным, обратным, равным предмету (рис. 96).
Если предмет расположен между фокусом и точкой двойного фокуса, то изображение получится действительным, обратным, увеличенным (фотоувеличитель, киноаппарат, фильмоскоп) (рис. 97).
Если предмет расположен в фокусе, то изображение будет в бесконечности (изображения не будет) (рис. 98).
Если предмет расположен между фокусом и оптическим центром линзы, то изображение будет мнимым, прямым, увеличенным (лупа) (рис. 99).
При любом расстоянии от предмета до рассеивающей линзы она дает мнимое, прямое, уменьшенное изображение (рис. 100).
sfiz.ru
Линза: свойства и виды линз
Нам известно, что свет, попадая из одной прозрачной среды в другую, преломляется — это явление преломления света. Причем угол преломления меньше угла падения при попадании света в более плотную оптическую среду. Что это означает, и как это можно использовать?
Если мы возьмем кусок стекла с параллельными гранями, например, оконное стекло, то получим незначительное смещение изображения, видимого сквозь окно. То есть, войдя в стекло, лучи света преломятся, а попадая снова в воздух, вновь преломятся до прежних значений угла падения, только при этом немного сместятся, причем величина смещения будет зависеть от толщины стекла.
Очевидно, что от такого явления практической пользы немного. А вот если мы возьмем стекло, плоскости которого будут расположены друг к другу наклонно, например, призму, то эффект будет совсем иным. Лучи, проходящие сквозь призму, всегда преломляются к ее основанию. Это несложно проверить.
Для этого нарисуем треугольник, источник света и начертим входящий в любую из его боковых сторон луч. Пользуясь законом преломления света, проследим дальнейший путь луча. Проделав эту процедуру несколько раз под разными значениями угла падения, мы выясним, что под каким бы углом не входил луч внутрь призмы, с учетом двойного преломления на выходе он все равно отклонится к основанию призмы.
Линза и ее свойства
Такое свойство призмы использовано в очень простом приборе, позволяющем управлять направлением световых потоков – линзе. Линза – это прозрачное тело, ограниченное с двух сторон изогнутыми поверхностями тела. Рассматривают устройство и принцип действия линз в курсе физики восьмого класса.
По сути, линзу в разрезе можно изобразить в виде двух поставленных друг на друга призм. От того, какими своими частями расположены эти призмы друг к другу, зависит оптическое действие линзы.
Виды линз в физике
Несмотря на огромное разнообразие, видов линз в физике различают всего два: выпуклые и вогнутые, или собирающие и рассеивающие линзы соответственно.
У выпуклой, то есть собирающей линзы края намного тоньше, чем середина. Собирающая линза в разрезе – это две призмы, соединенные основаниями, поэтому все проходящие сквозь нее лучи сходятся к центру линзы.
У вогнутой линзы края, наоборот, всегда толще, чем середина. Рассеивающую линзу можно представить в виде двух соединенных вершинами призм, и, соответственно, лучи, проходящие через такую линзу, будут расходиться от центра.
Люди открыли подобные свойства линз очень давно. Использование линз позволило человеку конструировать самые разнообразные оптические приборы и приспособления, облегчающие жизнь и помогающие в быту и производстве.
Нужна помощь в учебе?
Предыдущая тема: Закон преломления света: как происходит преломление, отношение синусов
Следующая тема:   Оптическая сила линзы: оптическая ось, фокус, фокусное расстояние
Все неприличные комментарии будут удаляться.
www.nado5.ru