движение, скорость, ускорение. Вся теория и формулы
Кинематика: движение, скорость, ускорение.
Теория, формулы, схемы для ОГЭ
Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.
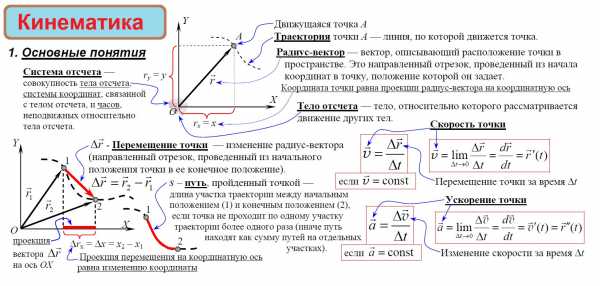
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
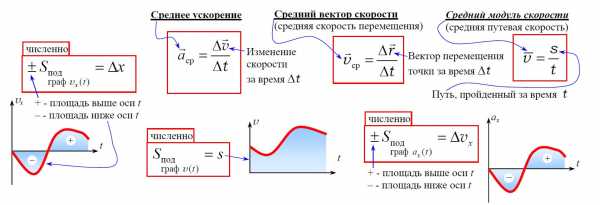
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).

Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Типы движений
1. Равномерное движение
1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

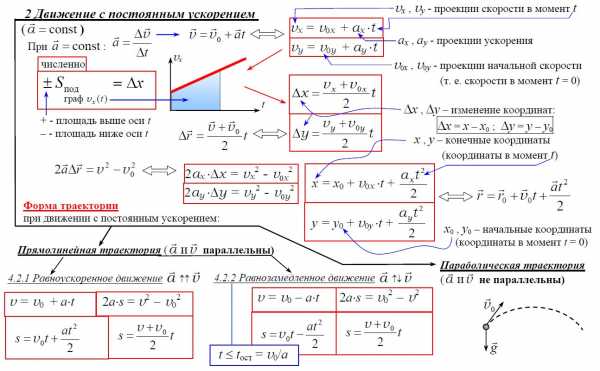
2. Движение с постоянным ускорением
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
3. Гармоническое движение
Виды движений
Прямолинейное движение
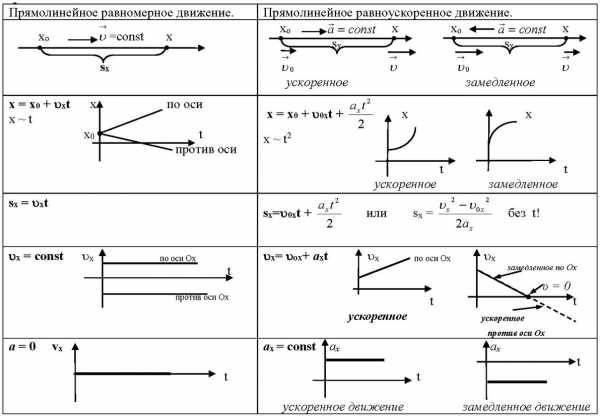
Криволинейное движение

Частные случаи равноускоренного движения под действием силы тяжести

Частные случаи решения задач

Дополнительные материалы по кинематике
Кинематика. Таблица кратко.


Это конспект по теме «Кинематика: движение, скорость, ускорение. Теория, формулы, схемы для ОГЭ». Выберите дальнейшие действия:
Кинематика. Теория, формулы, схемы для ОГЭ
4.9 (97.5%) 8 votesuchitel.pro
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещением может в процессе движение увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
educon.by
Кинематика. Формулы
Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.
| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
scolaire.ru
Формулы. Кинематика | FizPortal
Формулы. Кинематика.Координата и перемещение при равномерном движении по прямой
x = xo + vxt,
Sx = x − xo = vxt,
где xo − начальная координата.
Закон сложения скоростей (для поступательного движения системы отсчета)
где v1 − скорость первого тела (например, относительно земли), v12 − скорость первого тела относительно второго тела (подвижной системы отсчета), v2 − скорость второго тела (относительно земли). Аналогичный вид имеют закон сложения перемещений
S1 = S12 + S2
и закон сложения ускорений
a1 = a12 + a2.
Эту формулу в виде
v12 = v1 − v2
называют формулой для относительной скорости двух тел.
Средняя скорость при неравномерном движении по прямой
Два последовательных этапа с разными скоростями:
vcp = (S1 + S2)/(t1 + t2),
где S1 = v1t1, S2 = v2t2.
Скорость и перемещение при равноускоренном движении по прямой
Sx = voxt + axt2/2,
где vox − начальная скорость.
Связь между скоростями и перемещением:
vx2 − vox2 = 2axSx.
Средняя скорость при равноускоренном движении:
Sx = (vox + vx)t/2.
Свободное падение (vo = 0). Скорость и перемещение (ось y направлена вниз, ay = g)
Высота в момент времени t
h(t) = H − gt2/2,
где H − начальная высота.
Время падения и конечная скорость:
t = √{2H/g}, v = √{2gH}.
Бросок вертикально вверх с начальной скоростью vo. Скорость и перемещение (ось y направлена вверх, voy = vo, ay = −g):
Sy = vot − gt2/2.
Время подъема до высшей точки (где vy = 0) и высота подъема
t1 = vo/g,
hmax = vo2/(2g).
Полное время полета (до возврата в точку броска)
t2 = 2t1 = 2vo/g.
Горизонтальный бросок со скоростью vo. Проекции скорости и перемещения (ось x направлена горизонтальна, ось y − вертикально вниз):
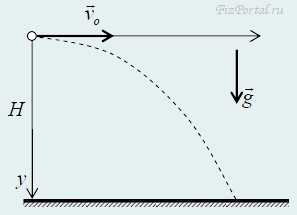
vx = vo, Sx = vot,
vy = gt, Sy = gt2/2,
(по горизонтали − равномерное движение со скоростью vo, по вертикали − свободное падение). Модули скорости и угол наклона скорости к горизонту:
v = √{vx2 + vy2} = √{vo2 + (gt)2}
tgβ = vy/vx = gt/vo.
Время до падения на землю (начальная высота H) и дальность полета:
t = √{2H/g}
S = vo√{2H/g}.
Бросок под углом к горизонту с начальной скоростью vo. Проекция скорости и перемещения (ось x направлена горизонтально, ось y − вертикально вверх):
vy = vosinα − gt, Sy = votsinα − gt2/2,
(по горизонтали − равномерное движение со скоростью vocosα, по вертикали − бросок вертикально вверх с начальной скоростью
voy = vosinα).
Время подъема до высшей точки (vy = 0) и максимальная высота
t1 = vosinα/g, hmax = (vosinα)2/(2g).
Полное время и дальность полета
t2 = 2t1 = 2vosinα/g, S = vxt2 = vo2sin(2α)/g.
Равномерное вращение с угловой скоростью ω. Угол поворота (в рад) и число оборотов:
φ = ωt, N = φ/(2π) = νt,
где ν − частота вращения (ν = ω/(2π)).
Период вращения:
T = 1/ν = 2π/ω.
Связь между угловыми и линейными перемещениями
l = φR, v = ωR,
где l − длина дуги.
Центростремительное ускорение:
aц = v2/R = ω2R.
Объем и масса (жидкости, газа), проходящие через сечение S струи за время Δt (уравнение расхода):
Δm = ρΔV = ρSvΔt,
где v − скорость струи, ρ − плотность (жидкости, газа).
fizportal.ru
Формулы кинематики с пояснениями по физике / Блог :: Бингоскул
- Блог
- →
- Формулы кинематики с пояснениями по физике
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S — путь
- v — скорость
- t — время
Равномерное движение
x=x_0 + v*t
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
Равномерно ускоренное движение: ускорение
a=\frac{v — v_0}{t}
- a — ускорение
- v — скорость
- v0 — начальная скорость
- t — время
Равномерно ускоренное движение: скорость
v=v_0 + at
- v — скорость
- v0 — начальная скорость
- a — ускорение
- t — время
Равномерно ускоренное движение: путь
S=vt + \frac{at^2}{2}
- s — путь
- v — скорость
- t — время
- a — ускорение
Равномерно ускоренное движение: координата
x=x_0 + vt + \frac{at^2}{2}
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
- a — ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_{0}t — \frac{gt^2}{2}
- h — высота
- h0 — начальная высота
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 — gt
- v — скорость
- v0 — начальная скорость
- g — ускорение свободного падения
- t — время
Скорость, ускорение, время
v=at
- v — скорость
- a — ускорение
- t — время
Скорость свободно падающего тела
v=gt
- v — скорость
- g — ускорение свободного падения
- t — время
Центростремительное ускорение
a=\frac{v^2}{R}
- a — центростремительное ускорение
- v — скорость
- R — радиус
Угловая скорость
\omega=\frac{\phi}{t}
- ω — угловая скорость
- φ — угол
- t — время
Равномерное круговое движение
l=R\phi
- l — длина дуги окружности
- R — радиус
- φ — угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v — линейная скорость
- R — радиус
- ω — угловая скорость
Период вращения
T=\frac{t}{N}
- T — период
- t — время
- N — число вращений
T=\frac{2 \pi R}{v}
- T — период
- R — радиус
- v — линейная скорость
T=\frac{2 \pi }{\omega}
- T — период
- ω — угловая скорость
Центростремительное ускорение
a=\frac{4 \pi^{2} R}{T^2}
- a — центростремительное ускорение
- R — радиус
- T — период вращения
a=4 \pi^{2} Rn^2
- a — центростремительное ускорение
- R — радиус
- n — частота вращения
Частота вращения
n=\frac{1}{T}
- n — частота вращения
- T — период вращения
Центростремительное ускорение
a=\omega ^{2}R
- a — центростремительное ускорение
- ω — угловая скорость
- R — радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x — координата (дальность)
- v0 — начальная скорость
- t — время
- α — угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) — \frac{gt^2}{2}
- y — координата (высота подъема )
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
- α — угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) — gt
- vy — вертикальная скорость
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
- t — время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac{v_0^2* \sin (\alpha)^{2}}{2g}
- hмакс — максимальная высота
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac{2v_0 * \sin (\alpha)}{g}
- t — время
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x — координата (дальность)
- x0 — начальная координата
- v — скорость
- t — время
Высота подъема тела, брошенного горизонтально
y=y_0 — \frac{gt^2}{2}
- y — координата (высота подъема)
- y0 — начальная координата (высота)
- g — ускорение свободного падения
- t — время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt{\frac{2h}{g}}
- tмакс — максимальное время
- h — высота
- g — ускорение свободного падения
bingoschool.ru
Все формулы по Кинематике!
Основы кинематики — краткий курс.
Кинематика — это раздел механики, отвечающий на вопрос «Как движутся тела?».
Механическое движение и его виды
Механическое движение — это изменение положение тела в пространстве относительно других тел с течением времени.
Движение тела, при котором все его точки движутся одинаково, называют поступательным движением. Тело, размерами которого в условиях данной задачи можно пренебречь, называют материальной точкой.
Траектория — это линия, вдоль которой движется тело.
Длина траектории — путь, который прошло тело, двигаясь из точки 1 к точке 2. Вектор, соединяющий начало и конец траектории, называют перемещением тела.
Система отсчета
Системой отсчета называют совокупность тела отсчета, связанной с ним системы координат и прибора для исчисления времени. Всякое движение, а также покой является относительным. Координата тела в любой момент времени определяется уравнением:
x = x0 + Sх = x0 + vхΔt
Скорость
Средней скоростью vср материальной точки за промежуток времени Δt называют отношение изменения координаты тела (Δх = х – х0) к промежутку времени (Δt = t – t0), в течение которого это изменение произошло:Мгновенной скоростью материальной точки называют скорость в данный момент времени или в данной точке траектории.
Мгновенная скорость прямолинейного движения материальной точки равна производной от координаты этой точки по времени:
Закон сложения скоростей
Скорость тела в неподвижной системе отсчета вектора v равна векторной сумме скоростей тела относительно подвижной системы вектора v1 и скорости подвижной системы относительно неподвижной:
Закон сложения перемещений
Перемещение тела в неподвижной системе отсчета вектора S равно векторной сумме перемещений тела относительно подвижной системы вектора S1 и перемещения подвижной системы относительно неподвижной:
Прямолинейное равномерное движение
Прямолинейным равномерным движением называется движение, при котором материальная точка (тело) за любые одинаковые промежутки времени совершает одинаковые перемещения. Векторная величина, которая определяется отношением перемещения вектора S тела к промежутку времени Δt, за который данное перемещение было совершено, называется скоростью:
Перемещение тела
При прямолинейном движении перемещение тела Sх вдоль оси Ox : Sх = x – х0.
Координата тела
Координата тела в любой момент времени определяется уравнением: где x0 — начальная координата тела, Sх — перемещение тела вдоль оси Oх, vx — проекция скорости тела на ось Ох:
Графики зависимости кинематических величин от времени
для прямолинейного равномерного движения

График зависимости от времени проекции
перемещения: sх(t) = vх Δt
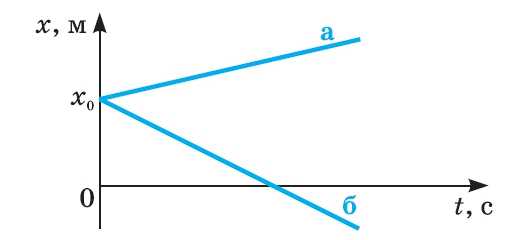
График зависимости от времени координаты:
x(t) = x0 + sх = x0 + vх Δt.
а — движение тела совпадает с направлением
оси Ox;
б — движение тела в противоположном
направлении

График зависимости от времени проекции
скорости: vх = const (константа).
а — движение тела совпадает с направлением
оси Ox;
б — движение тела в противоположном
направлении.
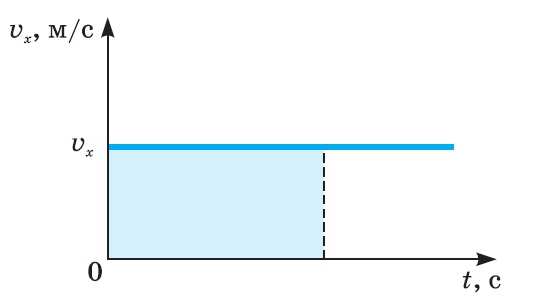
При прямолинейном равномерном движении
на графике зависимости от времени
проекции скорости путь численно равен
площади прямоугольника, ограниченного
сверху линией модуля скорости vх = const,
а снизу — осью времени в промежутках
интервала движения.
Неравномерное движение
Прямолинейное равноускоренное движение
Движение материальной точки, во время которого его скорость за любые одинаковые промежутки времени изменяется на одну и ту же величину, называется равнопеременным (равноускоренным)
xn--80aakeqfhfoqvpv.xn--p1ai
Раздел 1. Физические основы механики Основные формулы Кинематика поступательного движения
1. Скорость при прямолинейном движении в общем случае
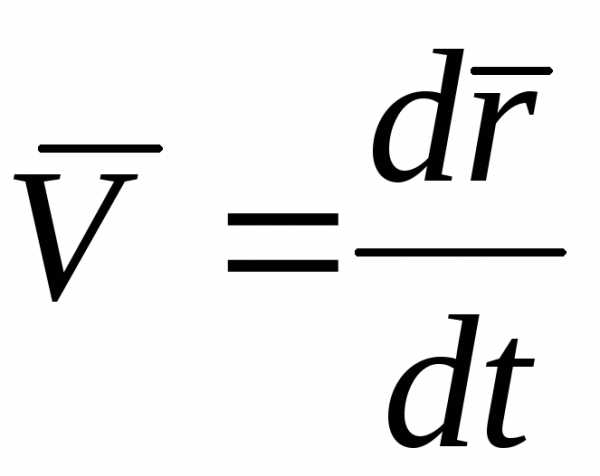 =
Vx
=
Vx
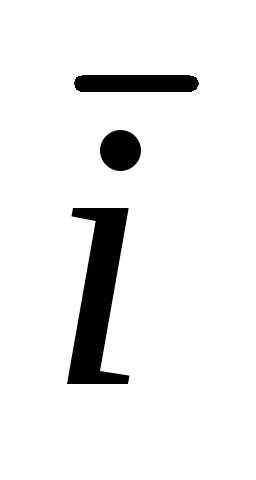 + Vy
+ Vy
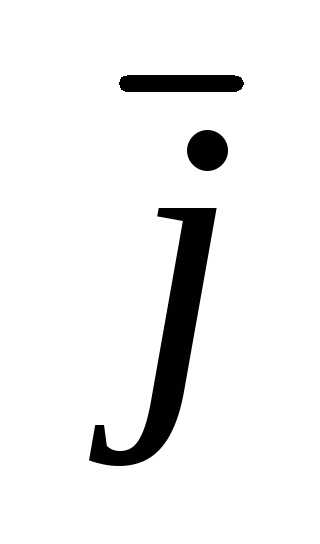 + Vz
+ Vz
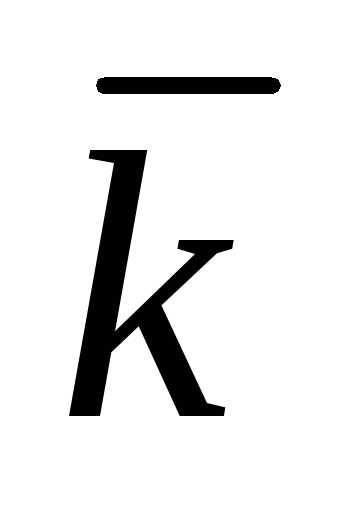 ,
,
V 2 = Vx2+ Vy2+ Vz2.
2. Ускорение
=
ax
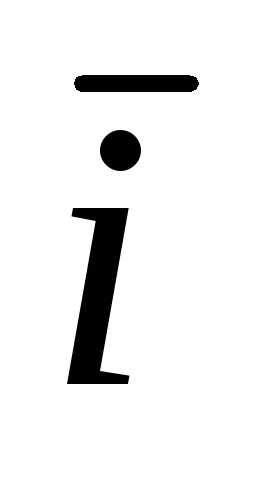 + ay
+ ay
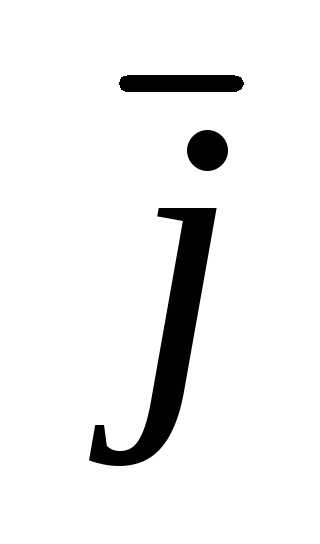 + az
+ az
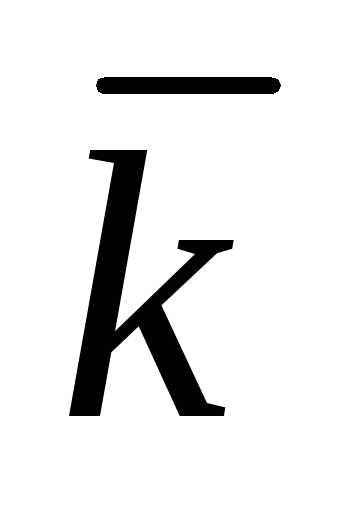 ,
,
a 2 = ax2+ ay2+ az2
3. Уравнения кинематики равноускоренного поступательного движения:
V=V0+at,
S=V0 t+at2/2,
где V – скорость тела в момент времени t; V0 – начальная скорость; a – ускорение движения тела; S – путь, пройденный за время t; t – время движения тела.
4. Полное ускорение при криволинейном движении
a2=a2+an2,
где aτ = dV/dt– тангенциальное ускорение;an = V2/R– нормальное ускорение.
Кинематика вращательного движения
5. Угловая скорость при вращательном движении в общем случае
.
6. Угловое ускорение
.
7. Уравнения кинематики равноускоренного вращательного движения:
ω = ω0+t,
= ω0t+t2/2,
где ω –угловая скорость в момент времениt;ω0– начальная угловая скорость;– угловое ускорение, с которым вращается тело;t– время вращения тела; – угол поворота за времяt.
8. Угловая скорость при равномерном вращательном движении
ω = /t = 2π/T = 2π ν,
где T– период обращения;ν– частота обращения, т. е. число оборотов в единицу времени.
9. Формулы, связывающие угловые и линейные величины при рассмотрении движения вращающегося тела:
S = R, V = ω R,
а = R, an = ω 2 R = V2/R,
где R– радиус траектории, по которой движется тело;a– тангенциальное ускорение;an– нормальное или центростремительное ускорение.
Динамика поступательного движения
10. Основной закон динамики поступательного движения
 dt=d(m
dt=d(m ).
).
11. Второй закон Ньютона
 =
=
 /m,
/m,
где
 – ускорение тела;
– ускорение тела; – сила, действующая на тело; m–
масса тела.
– сила, действующая на тело; m–
масса тела.
12. Закон Гука
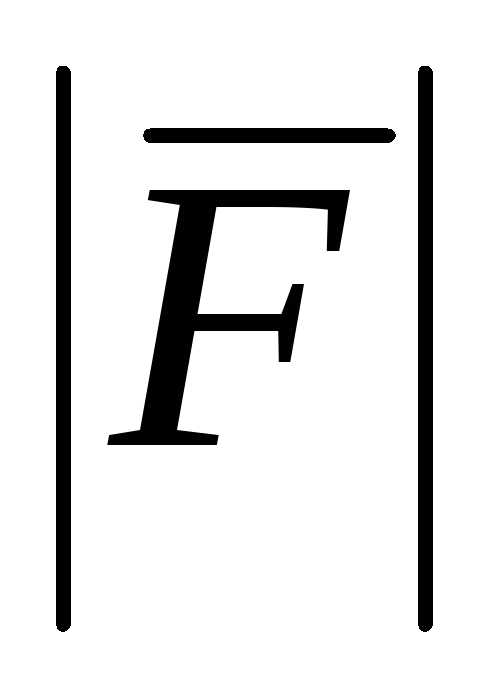 = – kx,
= – kx,
где k– коэффициент упругости;х– величина деформации.
13. Сила трения
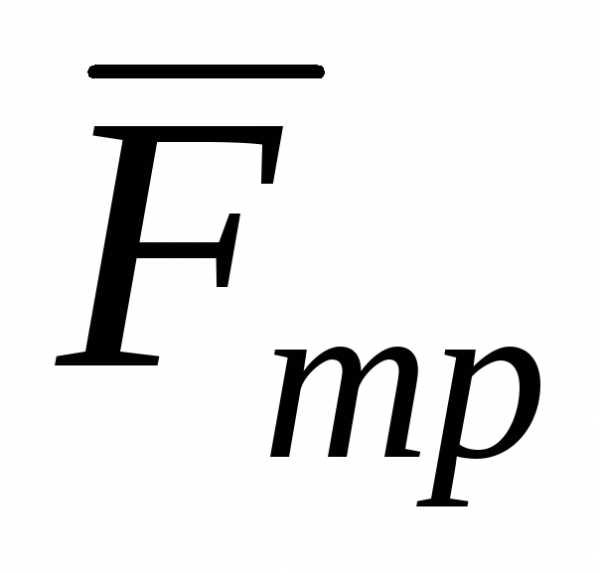 =
=  ,
,
где – коэффициент трения;N– сила нормального давления, прижимающая тело к плоскости при скольжении.
14. Гравитационная сила
F=Gm1m2/r2,
где F– сила гравитационного притяжения между двумя точечными массамиm1иm2;r– расстояние между ними;G– гравитационная постоянная.
15. Закон сохранения импульса
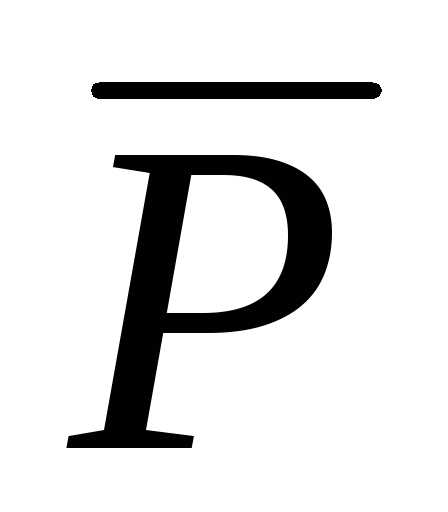 = m1
= m1 1+m2
1+m2 2+ …. +mi
2+ …. +mi i=const.
i=const.
16. Скорость движения тел после неупругого, центрального удара
 = (m1
= (m1 1+m2
1+m2 2)/(m1+m2),
2)/(m1+m2),
где m1–
масса первого тела;m2–
масса второго тела; 1– скорость первого тела до удара;
1– скорость первого тела до удара; 2– скорость второго тела до удара.
2– скорость второго тела до удара.
17. Скорости первого и второго тел после упругого соударения:
 1=[(m1–m2)
1=[(m1–m2)
 1
+ 2m2
1
+ 2m2 2]
/(m1+m2),
2]
/(m1+m2),
 2=[(m2–m1)
2=[(m2–m1)
 2
+ 2m1
2
+ 2m1 1]
/(m1+m2),
1]
/(m1+m2),
18. Механическая работа
A=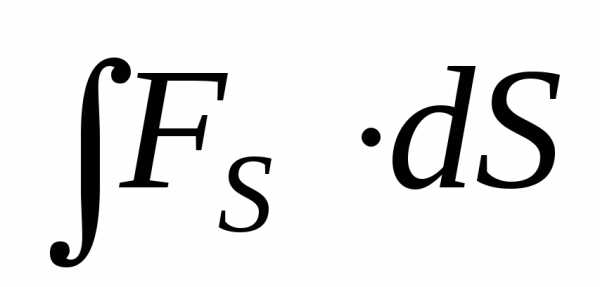 ,
,
где FS– проекция силы на направление пути;S– величина участка пути.
В частном случае постоянной силы, действующей под неизменным углом к перемещению, имеем
A=FScos ,
где F– модуль вектора силы;S– модуль вектора перемещения;– угол между векторами силы и перемещения.
19. Мощность
N=dA/dt.
При постоянной мощности
N = A/t = F V cos α,
где А– работа, произведенная какой-либо силой;t– время, за которое произведена эта работа.
20. Кинетическая энергия
Wк= mV2/2,
где m– масса движущегося тела;V– скорость, с которой это тело движется.
21. Потенциальная энергия тела в поле силы тяжести (вблизи поверхности Земли)
Wп = mgh,
где m– масса тела;g– ускорение свободного падения;h– высота тела над поверхностью Земли.
22. Закон сохранения механической энергии
Wк+Wп=const.
23. Давление в жидкости и газе
P = Fдав/S,
где Fдав– cила давления;S– площадь поверхности.
24. Закон Архимеда
Fa = жgVпогр,
где ж– плотность жидкости;g– уcкорение свободного падения;Vпогр– объем жидкости, вытесненной погруженной частью тела.
studfiles.net
