Оптическая сила линзы — формулы и примеры
Этим сегодня и займемся:
узнаем, что такое линза в физике и какие бывают линзы;
поговорим о том, что такое оптическая сила линзы, на что она влияет и в каких единицах ее измеряют;
свяжем физику с математикой и посмотрим, как с помощью формул можно рассчитать оптическую силу.
А еще мы немного порисуем: даже самые серьезные физики любят иллюстрировать свои объяснения забавными рисунками. 🙂
Что такое линзы
Вспомните, в каких ситуациях вы сталкивались со словом «линза». Верно, есть линзы для зрения, линзы в объективе фотоаппарата. Теперь пришло время разобраться, что такое линза в мире физики.
Ли́нза — прозрачное тело, ограниченное либо двумя сферическими поверхностями, либо одной сферической и одной плоской.
Действие линз основано на законах преломления света. Параллельные пучки световых лучей, проходя через линзу, преломляются и меняют свое направление: они могут сходиться в одной точке или же рассеиваться в разные стороны.
Виды линз
Линзы делятся на две группы: рассеивающие и собирающие, чье назначение понятно из названия. В свою очередь, и рассеивающие, и собирающие линзы бывают различных видов по своему строению. Давайте внимательно рассмотрим рисунок.
Запомните и еще одно отличие: в собирающих линзах середина толще краев, а в рассеивающих — края толще середины.
Хорошая новость: при решении физических задач мы не будем прописывать строение линзы или определять: это вогнуто-выпуклая или выпукло-вогнутая. Мы будем использовать схематичное изображение для собирающей и рассеивающей линзы, где сразу будет понятно, с чем мы имеем дело.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.
Запишитесь и участвуйте в розыгрыше 8 уроков
Что такое оптическая сила линзы
Тема нашей статьи — «Оптическая сила линзы», но чтобы детально разобраться в этом понятии, нам необходимо вспомнить еще несколько моментов, связанных с основными точками и линиями линзы для построения хода лучей. Эти точки будут одинаковыми и для собирающей, и для рассеивающей линз.
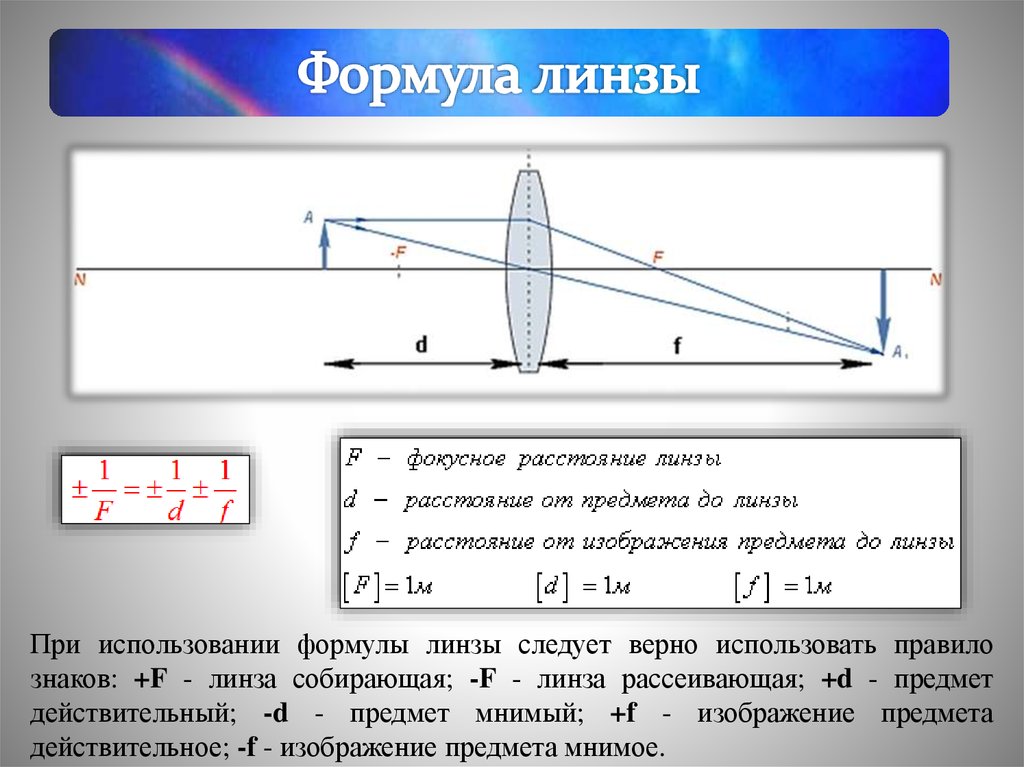
Главная оптическая ось (далее — ГОО) — воображаемая линия, которая проходит через центр линзы и перпендикулярна плоскости линзы. Точка О — оптический центр линзы. Лучи света, которые проходят через эту точку, не будут преломляться.
Фокус линзы
Обратите внимание, что точка фокуса есть и справа, и слева от линзы. Фокус, который располагается левее линзы, называют мнимым фокусом — в нем при определенных условиях могут пересечься не сами лучи, а только их продолжения, и в этой плоскости мы получим только мнимое изображение.
Фокусное расстояние — расстояние от точки F до оптического центра линзы.
На главной оптической оси располагают и точку 2F, но тут все просто — мы ставим ее на двойном фокусном расстоянии. Расстояние от объекта до линзы обозначают буквой d, а от линзы до изображения — буквой f.
В зависимости от того, как близко стоит объект перед линзой, мы будем получать разные по размеру действительные и мнимые изображения объекта. Чтобы характеризовать увеличивающую способность линзы, ввели понятие «оптическая сила».
Оптическая сила линзы — это величина, характеризующая преломляющую способность линзы. Эта величина зависит от радиусов кривизны сферических поверхностей линзы и от показателя преломления материала, из которого она сделана.
Эта физическая величина обозначается латинской буквой D и измеряется в диоптриях. Сокращенное обозначение — дптр.
Как найти оптическую силу линзы с помощью формулы
Оптическая сила — это величина, обратно пропорциональная фокусному расстоянию, следовательно ее можно рассчитать в диоптриях по формуле:
Так как фокусное расстояние измеряется в метрах, можно сделать логичное заключение:
Обратите внимание!
Мы уже знаем, что собирающая и рассеивающая линзы отличаются по своим основным функциям. Это значит, что и оптическая сила этих линз будет отличаться. Для собирающих линз впереди оптической силы ставится знак «+», а для рассеивающих — знак «–».
Разберем еще 3 формулы, которые помогут вам решать задачи по этой теме.
Если необходимо рассчитать оптическую силу системы двух линз, воспользуйтесь формулой:
D = D1 + D2 – dD1D2, где: D — конечная оптическая сила, D1 — оптическая сила первой линзы, D2 — оптическая сила второй линзы, d — расстояние между линзами. Для системы тонких линз оптическая сила рассчитывается как алгебраическая сумма оптических сил каждой линзы:
D = D1 + D2 + D3 + … + Dn. 
Оптическую силу линзы также можно рассчитать через формулу тонкой линзы:
1/F = 1/f + 1/d или D = 1/f + 1/d, так как D = 1/F, где: F — фокусное расстояние, D — оптическая сила линзы, f — расстояние от линзы до изображения, d — расстояние от объекта до линзы.
Проверьте себя
Чтобы закрепить пройденный материал, давайте подведем промежуточные итоги в виде обсуждения в стиле «вопрос-ответ». С помощью этой таблицы вы можете подготовиться к контрольной работе по теме: закройте правую часть рукой и ответьте на вопросы.
Физика Линзы. Оптическая сила линзы
Материалы к уроку
Конспект урока
Явление преломления света лежит в основе действия линз и многих оптических приборов, служащих для управления световыми пучками и получения изображений.
Проведем опыт (1). На оптическом диске закрепим выпуклую линзу и направим горизонтально от осветителя несколько параллельных лучей…. Видим, что лучи после преломления в линзе собираются в одну точку. Вывод: линзы, преобразующие параллельный пучок в сходящийся пучок и собирают его в одну точку, называются собирающими.
Проведем опыт (2). На оптическом диске закрепим вогнутую линзу и направим горизонтально от осветителя несколько параллельных лучей. Видим, что лучи после преломления в линзе расходятся.
Вывод: линзы, которые преобразуют пучок параллельных лучей в расходящийся, называются рассеивающими. Основные параметры и характеристики линзы. Прямая, проходящая через центры окружностей С1 и С2, сферических поверхностей, ограничивающих линзу, называется главной оптической осью линзы. Любая другая прямая, проходящая через оптический центр линзы, называется побочной оптической осью.Проведем опыт (3). На оптическом диске закрепим выпуклую линзу (как в опыте 1) и направляем от осветителя пучок параллельных лучей на линзу. … Видим, что они пересеклись в одной точке, расположенной на главной оптической оси. Изменим угол падения параллельных лучей, перемещая осветитель вверх – вниз. …. Видим, что лучи все равно собираются в одной точке, только эта точка уже находится не на главной оптической оси, а на побочной оси. Вывод: точка, в которой собираются параллельные главной оптической оси лучи, называется главным фокусом линзы. Другие фокусы будут называться побочными фокусами. Они находятся в фокальной плоскости, проходящей перпендикулярно главной оптической оси и проходящей через главный фокус линзы.
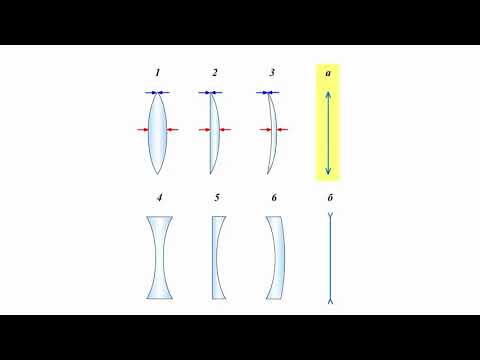
Проведем опыт (4). На оптическом диске закрепим вогнутую линзу и направим горизонтально от осветителя несколько параллельных лучей (как в опыте 2). Лучи из линзы выйдут расходящимся пучком. Если такой расходящийся пучок лучей попадет в глаз, то человеку будет казаться, что лучи выходят из точки F. Такую линзу называют рассеивающей. Вывод: рассеивающая линза имеет мнимый фокус – точка F. Она будет находится на оптической оси с той же стороны, с какой падает свет на линзу. На схемах собирающая линза изображается отрезком прямой с заостренными краями (показывает, что края линзы тоньше середины), а рассеивающая линза изображается отрезком прямой, у которого на краях показаны углы, расходящиеся от отрезка (показывает, что края толще, чем середина). Покажем основные точки и линии, которые нам необходимы для построения изображения предмета в линзах: Это главная оптическая ось, оптический центр линзы О, главные фокусы линзы слева и справа, обозначенные буквами F и двойное фокусное расстояние – 2F (практически равное радиусу линзы R).
Расстояние главного фокуса от линзы называется фокусным расстоянием линзы, обозначается F и измеряется в системе СИ в метрах (м). Собирающая линза имеет положительное фокусное расстояние, а рассеивающая линза имеет отрицательное значение. Например, если указано в задаче, что фокусное расстояние линзы равно «минус 20 см» (F= — 20cм), то это означает, что линза рассеивающая с главным фокусным расстоянием «минус 20 см = 0,2м). В быту говорят, что сильнее та линза, которая сильнее изменяет ход лучей. Линзы с более выпуклыми поверхностями преломляют лучи сильнее, чем линзы с меньшей кривизной. Как же характеризовать более «сильную» линзу? Введем величину, обратную главному фокусному расстоянию линзы и назовем ее – оптическая сила линзы. Оптическая сила линзы обозначается D, рассчитывается по формуле :
Оптическая сила линзы измеряется в диоптриях (дптр).
1 дптр – это оптическая сила линзы, фокусное расстояние которой равно 1 м.
Чем больше оптическая сила линзы, тем сильнее собирает или рассеивает линза падающий на нее параллельный пучок лучей.
Оптическая сила собирающей линзы будет числом положительным, а оптическая сила рассеивающей линзы – числом отрицательным.
Проведем опыт (5). На столе расположим линзу и экран таким образом, чтобы они находились на одной прямой с дальним окном в кабинете. Расположим линзу около экрана и начнем отодвигать линзу в сторону окна. Будем перемещать до тех пор, пока на экране не получится четкое изображение окна. Сделаем вывод: расстояние от линзы до экрана практически равно главному фокусному расстоянию линзы. Измерим это расстояние
Значит, фокусное расстояние F=0,1м и оптическая сила линзы D =1:0,1м =10 дптр.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Преломление и лучевая модель света
Если кусок стекла или другого прозрачного материала принимает соответствующую форму, возможно, что параллельные падающие лучи либо сходятся в точку, либо кажутся расходящимися от точки.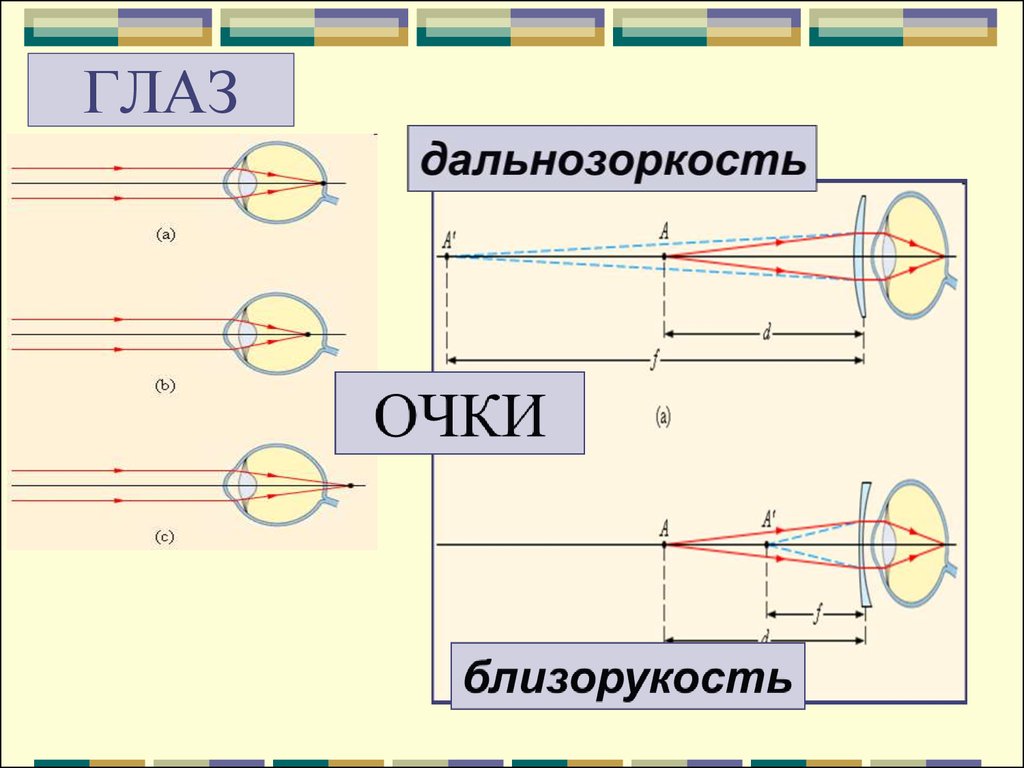
Кусок стекла такой формы называется линзой.
Линза представляет собой просто тщательно отшлифованный или формованный кусок прозрачного материала, который преломляет световые лучи таким образом, чтобы сформировать изображение. Линзы можно представить как набор крошечных преломляющих призм, каждая из которых преломляет свет, создавая собственное изображение. Когда эти призмы действуют вместе, они создают яркое изображение, сфокусированное в точке.
Типы линз
Существует множество типов линз. Линзы отличаются друг от друга формой и материалами, из которых они изготовлены. Наше внимание будет сосредоточено на линзах, которые симметричны относительно их горизонтальной оси, известной как главная ось . В этом разделе мы будем классифицировать линзы как собирающие линзы и рассеивающие линзы. Собирающая линза — это линза, которая собирает лучи света, движущиеся параллельно ее главной оси.
Собирающие линзы можно определить по форме; они относительно толстые посередине и тонкие по верхнему и нижнему краям. А 9Рассеивающая линза 0008 — это линза, которая рассеивает лучи света, идущие параллельно ее главной оси. Рассеивающие линзы также можно определить по форме; они относительно тонкие посередине и толстые по верхнему и нижнему краям.
Двойная выпуклая линза симметрична как по горизонтальной, так и по вертикальной оси. Каждую из двух граней линзы можно рассматривать как изначально часть сферы. Тот факт, что двойная выпуклая линза толще посередине, указывает на то, что она будет сводить лучи света, идущие параллельно ее главной оси. Двойная выпуклая линза является собирающей линзой. А 9Двойная вогнутая линза 0008 также симметрична как по горизонтальной, так и по вертикальной оси. Две грани двояковыпуклой линзы можно рассматривать как изначально являющиеся частью сферы. Тот факт, что двойная вогнутая линза тоньше посередине, указывает на то, что она будет рассеивать лучи света, идущие параллельно ее главной оси.
Двойная вогнутая линза является рассеивающей линзой. Эти два типа линз — двойная выпуклая и двойная вогнутая — будут единственными типами линз, которые будут обсуждаться в этом разделе Учебного пособия по физике.
Язык линз
По мере того, как мы начинаем обсуждать преломление световых лучей и формирование изображений этими двумя типами линз, нам придется использовать различные термины. Многие из этих терминов должны быть вам знакомы, потому что они уже обсуждались в Модуле 13. Если вы не уверены в значении терминов, потратьте некоторое время на их повторение, чтобы их значение прочно усвоилось в вашем уме. Они будут необходимы по мере прохождения Урока 5. Эти термины описывают различные части линзы и включают такие слова, как 9.0003
Если представить симметричную линзу как срез сферы, то через центр сферы проходит линия, которая прикрепляется к зеркалу точно в центре линзы.
Эта воображаемая линия известна как 9.0008 основная ось . Линза также имеет воображаемую вертикальную ось , которая делит симметричную линзу пополам. Как упоминалось выше, световые лучи, падающие на любую сторону линзы и идущие параллельно главной оси, будут либо сходиться, либо расходиться. Если световые лучи сходятся (как в собирающей линзе), то они сойдутся в точку. Эта точка известна как фокальная точка собирающей линзы. Если световые лучи расходятся (как в рассеивающей линзе), то расходящиеся лучи можно проследить в обратном направлении, пока они не пересекутся в точке. Эта точка пересечения известна как фокальная точка рассеивающей линзы. Фокусная точка обозначена буквой F на диаграммах ниже. Обратите внимание, что у каждой линзы есть две точки фокусировки — по одной с каждой стороны линзы. В отличие от зеркал, линзы могут пропускать свет через любую сторону, в зависимости от того, откуда исходят падающие лучи.
Следовательно, каждая линза имеет два возможных фокуса. Расстояние от зеркала до фокальной точки известно как фокусное расстояние (сокращенно f ). Технически линза не имеет центра кривизны (по крайней мере, такого, который имеет какое-либо значение для нашего обсуждения). Однако у линзы есть воображаемая точка, которую мы называем 9.0008 2F точка . Это точка на главной оси, которая в два раза дальше от вертикальной оси, чем фокус.
По мере того, как мы обсуждаем характеристики изображений, создаваемых собирающими и рассеивающими линзами, значение этих словарных терминов будет возрастать. Помните, что эта страница находится здесь, и обращайтесь к ней по мере необходимости.
Мы хотели бы предложить … Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.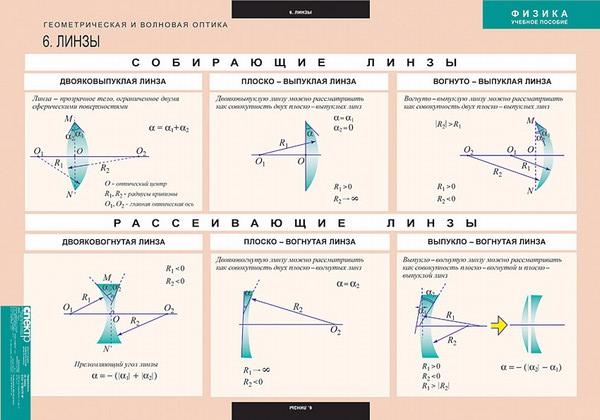
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного стенда Optics Bench. Вы можете найти это в разделе Physics Interactives на нашем сайте. Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений линзами и зеркалами. Это как полный набор оптических инструментов на вашем экране.
Посетите: Optics Bench Interactive
Следующий раздел:
Перейти к следующему уроку:
Analyzing the Universe — Course Wiki: Lenses and Optics
Сходящаяся геометрическая оптика : Выпуклая линза
Для фокусировки изображения в большинстве телескопов, используемых в оптической астрономии, используются выпуклые линзы, работающие за счет преломления, или вогнутые зеркала. которые отражают свет. Вопреки распространенному мнению, основная цель телескопа состоит НЕ в увеличении объектов, а в сборе большего количества света с помощью линз/зеркал, которые имеют гораздо большую площадь, чем человеческий глаз.
Помимо физического размера, фокусное расстояние определяет важное свойство линзы или зеркала. Мы обсудим важность фокусного расстояния чуть позже, но сначала давайте посмотрим на математическое определение, которое напрямую влияет на то, как изготавливаются эти линзы/зеркала. Фокусное расстояние получается:
$$f=\pm\frac{1}{n-1}\times\frac{r}{2}, \:\:\:\left(1\right) $$
где «n» – показатель преломления стекла линзы, f – фокусное расстояние, а r – радиус кривизны линзы, равный положительный в случае выпуклой линзы ( отрицательный в случае вогнутого зеркала, которые мы не будем подробно рассматривать). Этот радиус кривизны можно ясно увидеть ниже для геометрии двояковыпуклой линзы («би» означает, что линзы двусторонние с одинаковой кривизной).
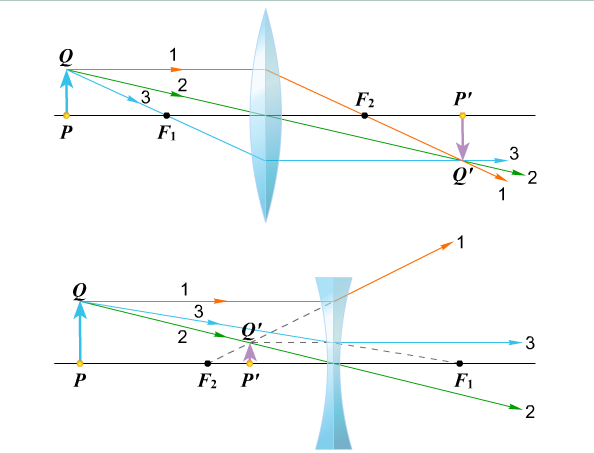
Выпуклая линза : Диаграммы лучей Теперь определим общую номенклатуру, используемую в геометрической оптике.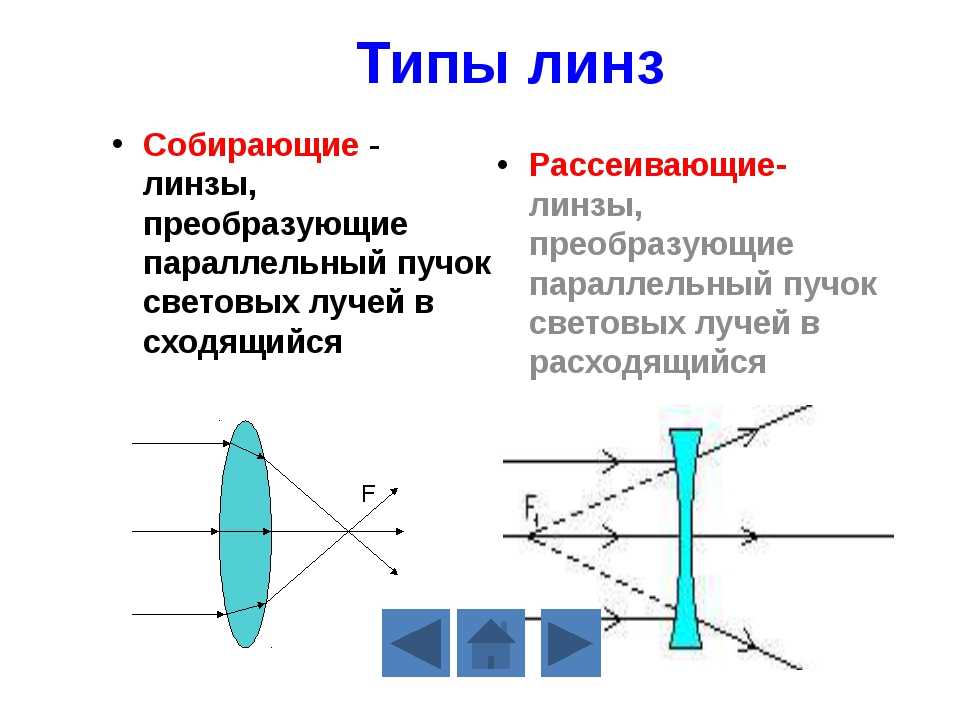
Для выпуклой линзы на изображении ниже мы видим параметры d или , д и , и ф. Все это длины, измеренные относительно объектива/зеркала, где d o — «расстояние до объекта», d i — «расстояние до изображения», а f — фокусное расстояние. Приведенная ниже диаграмма известна как лучевая диаграмма, где объект — это физический объект, на который мы хотим сфокусироваться с помощью линзы/зеркала, а изображение — это место, где свет дает четкую копию реального объекта. Сплошная линия проходит через центр объектива/зеркала и является оптической осью, вдоль которой лежат фокусные точки. Обратите внимание, что изображение кажется перевернутым относительно оптической оси. Также обратите внимание, что эта конкретная лучевая диаграмма верна только тогда, когда объект остается дальше от линзы, чем точка фокуса.
Поскольку мы сейчас рассматриваем диаграммы лучей, давайте поговорим о правилах работы лучей. Мы решили показать все лучи, выходящие из головы объекта (красная стрелка вверху), хотя любое другое положение на объекте будет работать так же хорошо.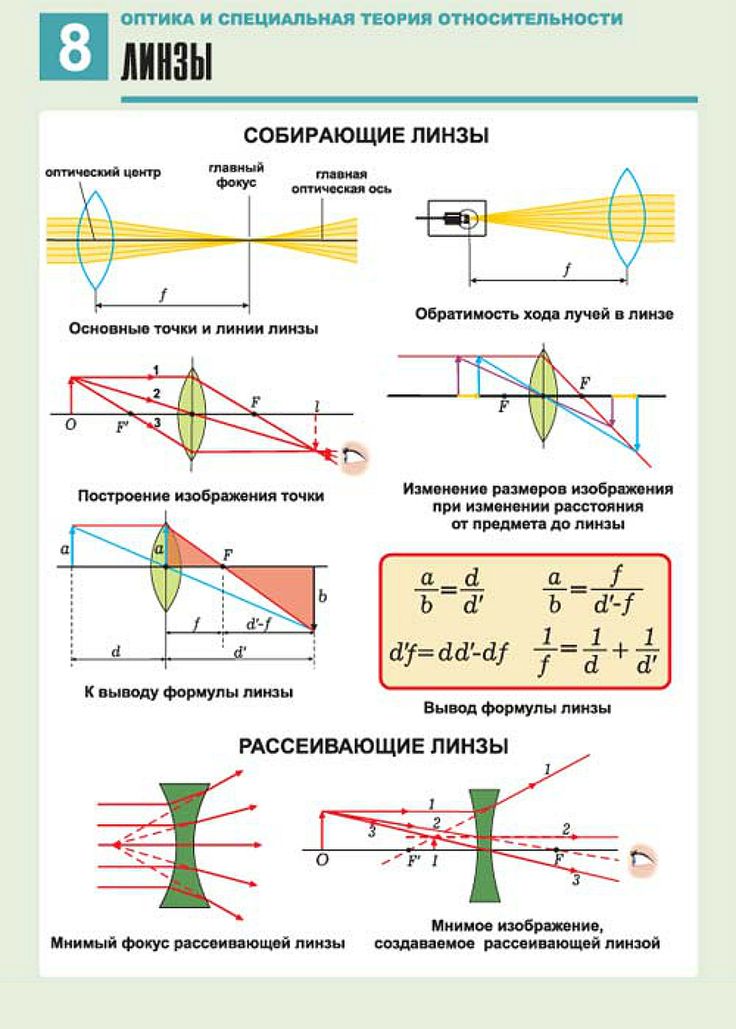
1. Лучи, выходящие из объекта параллельно оптической оси, проходят через фокальную точку линзы со стороны изображения.
2. Луч, проходящий через оптическую ось в центре линзы, не отклоняется от линзы.
3. Луч, идущий от объекта, который считается фокальной точкой линзы со стороны объекта, будет параллелен оптической оси, когда выходит из линзы для формирования изображения.
Математический подход к выпуклой линзе : Уравнение тонкой линзы подобные треугольники мы можем видеть на диаграмме ниже.
Мы видим, что треугольники Δ{ABC} (обозначает треугольник с вершинами в точках A, B и C) и Δ{ADE} должны быть подобны, поскольку они оба прямоугольные, а угол в точке C в Δ{ABC}, совпадает с углом в точке E в Δ{ADE}, поскольку прямые |BC| (которая обозначает линию, идущую от вершины B к вершине C) и |DE| параллельны. Линия |АВ| эквивалентна высоте объекта, а строка |AD| соответствует высоте изображения.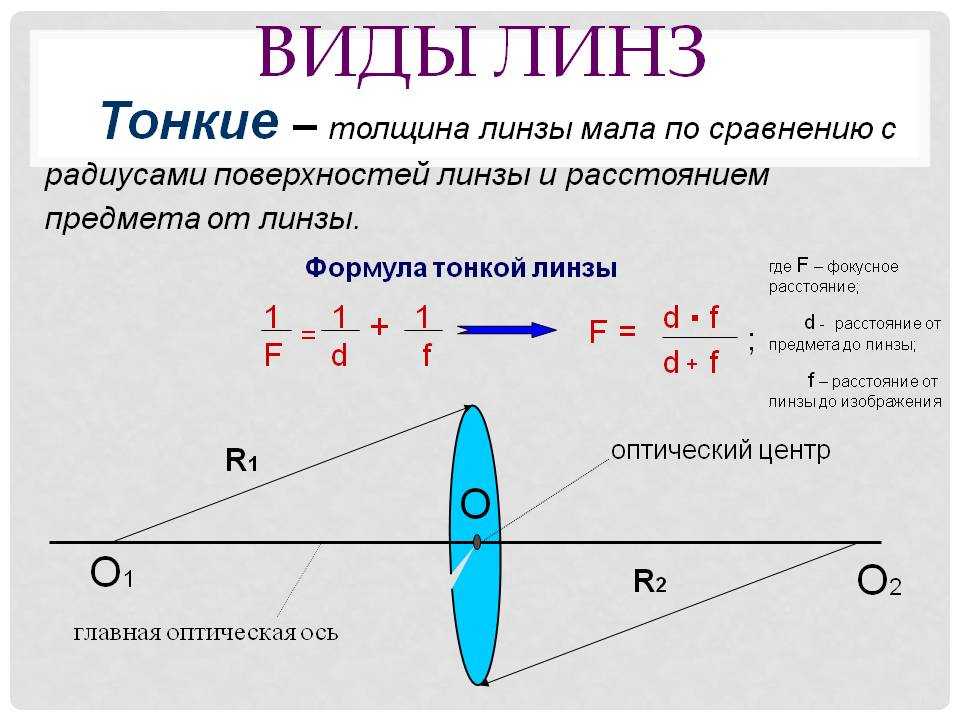
Поскольку мы знаем, что треугольники подобны, отношения соответствующих сторон должны быть равны. Таким образом, мы получаем,
$$\frac{AB}{AD}=\frac{BC}{DE}\equiv\frac{h_o}{h_i}=\frac{d_o}{d_i},\:\:\:\left( 2a\right)$$
, где h o — высота объекта, а h i — высота изображения. Точно так же мы можем манипулировать уравнением (2a), определив увеличение линзы как:
$$\rm{увеличение}\equiv\frac{h_i}{h_o}=\frac{d_i}{d_o}.\:\: \:\left(2b\right)$$
Обратите внимание, что увеличение не свойство объектива само по себе, а вместо этого зависит от того, насколько далеко объект расположен от объектива.
Теперь давайте создадим еще одну пару подобных треугольников на изображении ниже. Мы видим, что треугольники Δ{123} и Δ{425} являются подобными треугольниками, так как угол в точке 2 у обоих треугольников явно одинаков, а линии |13| и |45| снова параллельны.
