|
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой. Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем. ВеличиныПлощадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами. Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три — добавляется еще и высота. Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах. ШиринаКак было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы). Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. ДлинаКак уже было указано, в математике длина, высота, ширина — это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий. В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах. ВысотаНаличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении. На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина — все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.). Радиус и диаметрПомимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными. Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и строчная или заглавная «R»/«r». Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением — диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр. Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение — большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга — «Ø». Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d». ТолщинаБольшинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр — толщина. Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Периметр и площадьВ отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р». Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так — нет информации. Некоторые по незнанию думают, что это связано с английским написанием слова «square». Другие распространенные сокращенияОбозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе. Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее. Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Физика и основные физические величиныБлагодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения — законы Вселенной, конкретнее — то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку. Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого — первого в России учебника по физике. Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд — их всего 7:
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры — Т. Также у всех величин есть своя единица измерения: у силы света — кандела (кд), а у количества вещества единицей измерения является моль. Производные физические величиныПроизводных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным. Итак, площадь является производной от длины, объем — также от длины, скорость — от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила — произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы — все они зависят от массы. Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы — А, а для энергии — Е. Электрический заряд принято обозначать буквой q, а магнитный поток — Ф. СИ: общие сведенияМеждународная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях — греческого. Также возможно в качестве обозначения использование специальных символов. ЗаключениеИтак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных. В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия Список знаковых систем (систем обозначений и т. Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия Ядерная физика … Википедия Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами. Амперметр — это прибор, служащий для измерения силы тока. Что понимают под силой тока? Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время. Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с. Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. I — сила тока. Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время: Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775-1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время: Полученное выражение позволяет определить единицу электрического заряда — кулон (Кл): 1 Кл = 1 А · 1 с = 1 А·с. 1 Кл — это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А. Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА): 1 мА = 0,001 А, 1 мкА = 0,000001 А. Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр. Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется. В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться. Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. 1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока; 2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» — с тем проводом, который идет от отрицательного полюса источника тока. При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение. 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. phscs.ru Основные физические величины, их буквенные обозначения в физике.Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье. Физика и основные физические величиныБлагодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения — законы Вселенной, конкретнее — то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку. Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого — первого в России учебника по физике. Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд — их всего 7:
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры — Т. Также у всех величин есть своя единица измерения: у силы света — кандела (кд), а у количества вещества единицей измерения является моль. Производные физические величиныПроизводных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным. Итак, площадь является производной от длины, объем — также от длины, скорость — от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила — произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы — все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины. Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы — А, а для энергии — Е. Электрический заряд принято обозначать буквой q, а магнитный поток — Ф. СИ: общие сведенияМеждународная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях — греческого. Также возможно в качестве обозначения использование специальных символов. ЗаключениеИтак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных. fb.ru
dik.academic.ru
tutata. Физические величины электрического токаЗдравствуйте, уважаемые читатели нашего сайта! Мы продолжаем цикл статей, посвященных начинающим электрикам. Сегодня мы вкратце рассмотрим физические величины электрического тока, виды соединений и закон Ома. Для начала давайте вспомним, какие существуют виды тока: Переменный ток (буквенное обозначение AC) — вырабатывается благодаря магнитному эффекту. Это тот самый ток, который мы с вами имеем в наших жилищах. Он не имеет никаких полюсов, потому что меняет их много раз за секунду. Это явление (смену полярностей) называют частотой, ее выражают в герцах (Гц). В данный момент у нас в сети используется переменный ток в 50 Гц (то есть перемена направления происходит 50 раз в секунду). Два провода, которые входят в жилище, называются фазным и нулевым, поскольку здесь нет полюсов. Постоянный ток (буквенное обозначение DC) — это тот ток, который получают химическим способом (например батарейки, аккумуляторы). Основные физические величины:
Виды соединений потребителейПроводники при включении в цепь можно соединять друг с другом различными способами:
Последовательным называется соединение, при котором конец предыдущего проводника соединяется с началом следующего. Параллельным называется соединение, при котором все начала проводников соединяются в одной точке, а концы в другой. Смешанное соединение проводников представляет собой совокупность последовательных и параллельных соединений. Все рассказанное нами в данной статье базируется на основном законе электротехники — законе Ома, который гласит, что сила тока в проводнике прямо пропорциональна приложенному напряжению на его концах и обратно пропорциональна сопротивлению проводника. В виде формулы данный закон выражается так: fazaa.ru Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде. Механика
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
Молекулярная физика и термодинамика
Электростатика и электродинамика – формулы по физике
Оптика
Квантовая физика
Физика атомного ядра
| |||
Греческий алфавит
Греческий алфавит |
||||
|---|---|---|---|---|
| A | α | alpha | альфа | |
| B | β | beta | бета | |
| Г | γ | gamma | гамма | |
| Δ | δ | delta | дельта | |
| E | ε | epsilon | эпсилон | |
| Z | ζ | zeta | дзета | |
| H | η | eta | эта | |
| Θ | θ | theta | тета | |
| I | ί | iota | йота | |
| K | κ | kappa | каппа | |
| Λ | λ | lambda | ламбда | |
| M | mu | мю | ||
| N | nu | ню | ||
| Ξ | ξ | xi | кси | |
| O | o | omicron | омикрон | |
| П | π | pi | пи | |
| P | ρ | rho | ро | |
| Σ | σ | sigma | сигма | |
| T | τ | tau | тау | |
| υ | upsilon | ипсилон | ||
| Ф | φ | phi | фи | |
| Х | χ | chi | хи | |
| Ψ | ψ | psi | пси | |
| Ω | ω | omega | омега | |
Формула количества вещества в химии
Определение и формула количества вещества
Моль – количество вещества системы, которое содержит столько определенных структурных звеньев (молекул, атомов, ионов, электронов и т. д.), сколько содержится в 0,012 кг углерода-12.
д.), сколько содержится в 0,012 кг углерода-12.
Масса одного атома 12С равна 12 а.е.м., поэтому число атомов в 12 г изотопа 12С равно:
NA = 12 г / 12 × 1,66057×10-24 г = 1/1,66057×10-24 = 6,0221×10-23.
Таким образом, моль вещества содержит 6,0221×10-23 частиц этого вещества.
Физическую величину NA называют постоянной Авогадро, она имеет размерность [NA] = моль-1. Число 6,0221×10-23 называют числом Авогадро. Таким образом количество вещества будет вычисляться как:
n = N / NA,
где N – число структурных звеньев, а NA — постоянная Авогадро.
Молярная масса (М) – это масса 1 моль вещества. Легко показать, что численные значения молярной массы М и относительной молекулярной массы Mr равны, однако первая величина имеет размерность [M] = г/моль, а вторая безразмерна:
M = NA × m (1 молекулы) = NA × Mr × 1 а. е.м. = (NA ×1 а.е.м.) × Mr = × Mr.
е.м. = (NA ×1 а.е.м.) × Mr = × Mr.
Это означает, что если масса некоторой молекулы равна, например, 44 а.е.м., то масса одного моля молекул равна 44 г.
Постоянная Авогадро является коэффициентом пропорциональности, обеспечивающим переход от молекулярных отношений к молярным. Поэтому другая формула для вычисления количество вещества выглядит следующим образом:
n = m / M,
где m – масса вещества (г), а М – его молярная масса (г/моль).
Количество вещества газа можно рассчитать при помощи закона Авогадро: в равных объемах различных газов при одинаковых условиях (температуре и давлении) содержится одинаковое число молекул. Следовательно, при нормальных условиях 1 моль различных газов занимает объем, равный 22,4 л. Этот объем называется молярным объемом газа:
n= V /Vm,
где V – объем газа (л), а Vm – молярный объем (л/моль).
Примеры решения задач
|
Основные математические символы |
Нет |
Часто используемые математические символы, такие как > и < |
|
Греческие буквы |
Строчные буквы |
Строчные буквы греческого алфавита |
|
Прописные буквы |
Прописные буквы греческого алфавита |
|
|
Буквоподобные символы |
Нет |
Символы, которые напоминают буквы |
|
Операторы |
Обычные бинарные операторы |
Символы, обозначающие действия над двумя числами, например + и ÷ |
|
Обычные реляционные операторы |
Символы, обозначающие отношение между двумя выражениями, такие как = и ~ |
|
|
Основные N-арные операторы |
Операторы, осуществляющие действия над несколькими переменными |
|
|
Сложные бинарные операторы |
Дополнительные символы, обозначающие действия над двумя числами |
|
|
Сложные реляционные операторы |
Дополнительные символы, обозначающие отношение между двумя выражениями |
|
|
Стрелки |
Нет |
Символы, указывающие направление |
|
Отношения с отрицанием |
Нет |
Символы, обозначающие отрицание отношения |
|
Наборы знаков |
Наборы знаков |
Математический шрифт Script |
|
Готические |
Математический шрифт Fraktur |
|
|
В два прохода |
Математический шрифт с двойным зачеркиванием |
|
|
Геометрия |
Нет |
Часто используемые геометрические символы |
Принцип преобразования солнечной энергии в электричество
Солнце и фотоэлектрические модули (СФЭМ — солнечные батареи).

В основе этого способа получения электричества лежит солнечный свет, названный в учебниках как солнечное излучение, солнечная радиация, световой поток или поток элементарных частиц – Фотонов. Для нас он интересен тем, что, так же как и движущийся воздушный поток, световой поток обладает энергией! На расстоянии в одну астрономическую единицу (149 597 870,66 км) от Солнца, на котором и располагается наша Земля, плотность потока солнечного излучения составляет 1360 Вт/м2. А пройдя через земную атмосферу, поток теряет свою интенсивность из-за отражения и поглощения, и у поверхности Земли уже равен ~ 1000 Вт/м2. Здесь и начинается наша работа: использовать энергию светового потока и преобразовать её в необходимую нам в быту энергию – электрическую.
Таинство этого преобразования происходит на небольшом псевдоквадрате со скошенными углами, который вырезан из кремниевого цилиндра (рис. 2), диаметром 125 мм, и имя ему — фотоэлектрический преобразователь (ФЭП). Каким же образом?
Ответ на этот вопрос получили физики, открывшие такое явление как Фотоэффект. Фотоэффект — это явление вырывания электронов из атомов вещества под воздействием света.
В 1900г. немецкий физик Макс Планк высказал гипотезу: свет излучается и поглощается отдельными порциями — квантами (или фотонами). Энергия каждого фотона определяется формулой: Е = h∙ν(аш ню), где h — постоянная Планка, равная 6,626 × 10-34 Дж∙с, ν — частота фотона. Гипотеза Планка объяснила явление фотоэффекта, открытого в 1887 г. немецким ученым Генрихом Герцем и изученного экспериментально русским ученым Александром Григорьевичем Столетовым, который, путем обобщения полученных результатов, установил следующие три закона фотоэффекта:
- При неизменном спектральном составе света сила тока насыщения прямо пропорциональна падающему на катод световому потоку.
- Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.
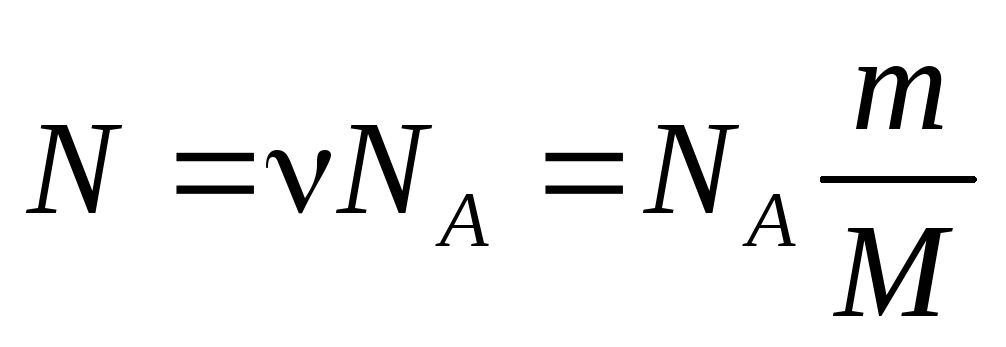
- Фотоэффект не возникает, если частота света меньше некоторой, характерной для каждого вещества, величины, называемой красной границей.
Теорию фотоэффекта, проясняющую таинство, царящее в ФЭПе, развил немецкий ученый Альберт Эйнштейн в 1905г., объяснив законы фотоэффекта с помощью квантовой теории света. Исходя из закона сохранения и превращения энергии, Эйнштейн записал уравнение для энергетического баланса при фотоэффекте:
где: h∙ν – энергия фотона, А – работа выхода – минимальная работа, которую нужно совершить для выхода электрона из атома вещества. Таким образом, получается, что частица света – фотон — поглощается электроном, который приобретает дополнительную кинетическую энергию ½m∙v2 и совершает работу выхода из атома, что дает ему возможность свободно двигаться. А направленное движение электрических зарядов и есть электрический ток, или, правильнее говоря, в веществе возникает Электро Движущая Сила – Э. Д.С.
Д.С.
За уравнение для фотоэффекта в 1921 году Эйнштейну была присуждена Нобелевская премия.
Возвращаясь из прошлого в наши дни, мы видим, что «сердцем» Солнечной батареи является ФЭП (полупроводниковый фотоэлемент), в котором осуществляется удивительное чудо природы – Вентильный фотоэффект (ВФЭ). Он заключается в возникновении электродвижущей силы в p-n переходе под действием света. ВФЭ, или фотоэффект в запирающем слое, — явление, при котором электроны покидают пределы тела, переходя через поверхность раздела в другое твёрдое тело (полупроводник).
Полупроводники — это материалы, которые по своей удельной проводимости занимают промежуточное место между проводниками и диэлектриками и отличаются от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и различных видов излучения. Полупроводниками являются вещества, ширина запрещённой зоны которых составляет порядка нескольких электрон-вольт [эВ]. Ширина запрещенной зоны — это разность энергий электронов в кристалле полупроводника между нижним уровнем зоны проводимости и верхним уровнем валентной зоны полупроводника.
К числу полупроводников относятся многие химические элементы: германий, кремний, селен, теллур, мышьяк и другие, огромное количество сплавов и химических соединений (арсенид галлия и др.) Самым распространённым в природе полупроводником является кремний, составляющий около 30 % земной коры.
Кремнию суждено было стать материалом для солнечной энергетики благодаря его широкому распространению в природе, легкость, подходящая ширина «запрещенной зоны» 1,12 эВ для поглощения энергии солнечного света. Сегодня на рынке коммерческих систем наземного применения наиболее заметны кристаллические кремниевые (около 90% мирового рынка) и тонкопленочные солнечные элементы (около 10% рынка).
Ключевым элементом конструкции кристаллических кремниевых фотоэлектрических преобразователей (ФЭП) является p-n переход. В упрощенном виде ФЭП можно представить в виде «бутерброда»: он состоит из слоев кремния, легированных для получения p-n перехода.
Одним из главных свойств p-n перехода является его способность быть энергетическим барьером для носителей тока, то есть пропускать их только в одном направлении. Именно на этом эффекте и базируется генерация электрического тока в солнечных элементах. Излучение, попадающее на поверхность элемента, генерирует в объеме полупроводника носители заряда с разным знаком — электроны (n) и дырки (p). Благодаря своим свойствам p-n переход «разделяет» их, пропуская каждый тип только на «свою» половину, и хаотически двигающиеся в объеме элемента носители заряда оказываются по разные стороны барьера, после чего могут быть переданы во внешнюю цепь для создания напряжения на нагрузке и электрического тока в замкнутой цепи, подключенной к солнечному элементу.
Именно на этом эффекте и базируется генерация электрического тока в солнечных элементах. Излучение, попадающее на поверхность элемента, генерирует в объеме полупроводника носители заряда с разным знаком — электроны (n) и дырки (p). Благодаря своим свойствам p-n переход «разделяет» их, пропуская каждый тип только на «свою» половину, и хаотически двигающиеся в объеме элемента носители заряда оказываются по разные стороны барьера, после чего могут быть переданы во внешнюю цепь для создания напряжения на нагрузке и электрического тока в замкнутой цепи, подключенной к солнечному элементу.
Так же Вы можете ознакомиться с теорией преобразования энергии Ветра в электрическую энергию используя ветрогенераторы.
Результаты обработки данных эксперимента «Троицк ню-масс» по прямому измерению массы электронного нейтрино
Введение……………………………………………………………………………………………………………………..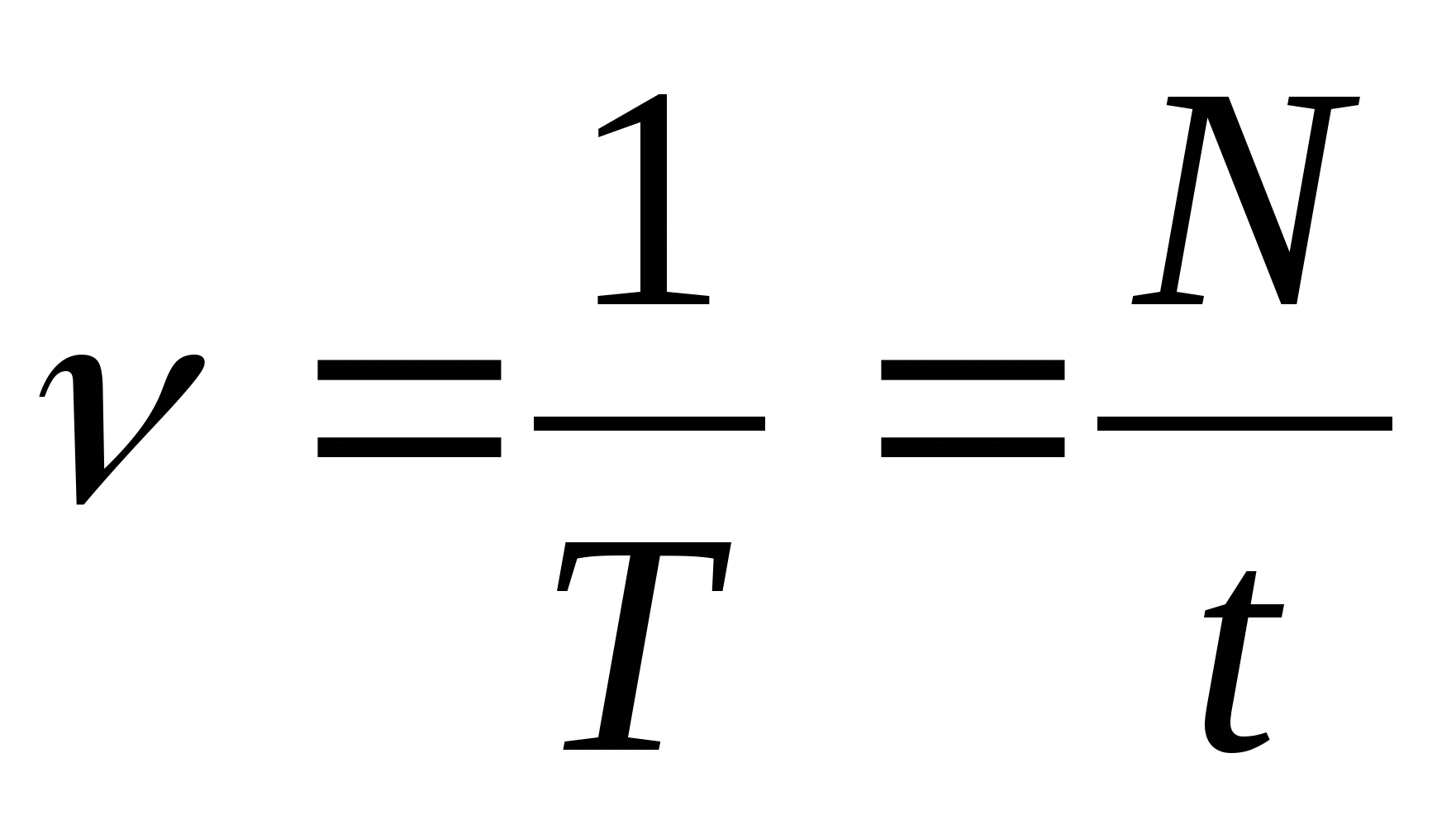 …4
…4
Глава 1. Экспериментальное определение массы нейтрино ……………………………………………..6
1.1. История открытия нейтрино………………………………………………………………………………….6
1.2. Теоретическое описание свойств нейтрино……………………………………………………………8
1.3. Осцилляции нейтрино…………………………………………………………………………………………..9
1.4. История экспериментов по определению массы нейтрино……………………………………11
1.4.1. Двойной бета-распад…………………………………………………………………………………….12
1.4.2. Измерение бета-спектра………………………………………………………………………………..13
1.5. Эксперименты в Троицке и Майнце…………………………………………………………………….16
Глава 2. Установка «Троицк ню-масс». …………………………………………………………………………18
Установка «Троицк ню-масс». …………………………………………………………………………18
2.1. Общий вид установки …………………………………………………………………………………………18
2.2. Тритиевый молекулярный источник электронов ………………………………………………….20
2.3. Адиабатический инвариант и магнитная система транспортировки ……………………..24
2.4. Спектрометр……………………………………………………………………………………………………….26
2.5. Детектор электронов …………………………………………………………………………………………..27
2.6. Криогенная система…………………………………………………………………………………………….29
2.7. Масс-спектрометр…………………………………………………………………………… ………………….29
………………….29
2.8. Фотоэлектронная пушка. …………………………………………………………………………………….31
Глава 3. Описание экспериментального спектра электронов. …………………………………………33
3.1. Спектр электронов в бета-распаде трития. …………………………………………………………..33
3.1.1. Учет отдачи ядра ………………………………………………………………………………………….36
3.1.2. Учет спектра конечных состояний ………………………………………………………………..37
3.1.3. Тепловые эффекты ……………………………………………………………………………………….38
3.1.4. Продолжение спектра в нефизическую область……………………………………………..39
3.2. Потери энергии в газообразном источнике ……………………………………………. ……………42
……………42
3.2.1. Спектр потерь ………………………………………………………………………………………………42
3.2.2. Использование приближенного спектра потерь……………………………………………..45
3.2.3. Вероятность неупругих потерь и эффективная толщина источника ……………….46
3.2.4. Экспериментальное определение эффективной толщины источника ……………..49
3.2.5. Траппинг-эффект………………………………………………………………………………………….55
3.2.6. Полный спектр потерь ………………………………………………………………………………….58
3.3. Функция разрешения спектрометра …………………………………………………………………….58
3.4. Окончательный спектр………………………………………………………………………………………..61
Глава 4. Процедура обработки. ……………………………………………………………………………………..63
……………………………………………………………………………………..63
4.1. Метод квазиоптимальных весов ………………………………………………………………………….63
4.1.1. Суть метода ………………………………………………………………………………………………….64
4.1.2. Проверка эффективности метода…………………………………………………………………..65
4.2. Среда разработки BlackBox…………………………………………………………………………………67
4.2.1. Подсистемы Numass, Numath и Bayesian ……………………………………………………….68
4.3. Предварительная обработка данных ……………………………………………………………………69
4.3.1. Первичный отбор плохих файлов и точек ……………………………………………………..69
4.3.2. Отбор «пачек». ……………………………………………………………………………………………..70
……………………………………………………………………………………………..70
4.4. Процедура отбора данных …………………………………………………………………………………..72
4.4.1. Отброс наборов данных с неточными внешними параметрами ………………………72
4.4.2. Выкидывание точек из спектра……………………………………………………………………..73
4.5. Процедура фитирования ……………………………………………………………………………………..74
4.6. Дополнительные способы контроля…………………………………………………………………….77
4.7. Интерпретация результатов фитирования ……………………………………………………………79
4.8. Независимая проверка результатов ……………………………………………………………………..81
Глава 5. Определение и учет систематических ошибок. …………………………………………………83
…………………………………………………83
5.1. Неопределенность эффективной толщины источника ………………………………………….83
Механические колебания. 9-й класс
Возраст учащихся от 25 лет до 30 лет.
За партами сидят люди, совершившие тяжкие преступления. Поэтому, важной воспитательной задачей каждого учебного предмета, является необходимость осужденного в получении образования. Данный урок способствует развитию интереса учащихся к учению, к изучаемому предмету, к окружающим физическим явлениям. На уроке развиваются познавательные способности учащихся, речь, память, внимание, воображение, восприятие нового материала. На уроке учитель развивает у учащихся навыки самоконтроля и самооценки своей деятельности.
Презентация используется на разных этапах урока дозировано (Слайды работают по щелчку).
(Сл.2)
Тип урока: Урок «открытия новых знаний».
Цель урока: Создать условия для прочного осознанного восприятия темы данного урока. Продолжение формирование целостной картины мира на примере процесса колебаний.
Продолжение формирование целостной картины мира на примере процесса колебаний.
Задачи урока:
- Предметные: Ввести в мир колебательного движения (мотивация). Сформировать у обучающихся представление о колебательном движении, выяснить условия возникновения и существования колебаний, изучить основные характеристики колебаний.
Учить учащихся правильно использовать формулы при решении задач и помочь обучающимся осмыслить практическую значимость данного изучаемого материала. - Метапредметные: Продолжать развивать у обучающихся познавательный интерес к предмету, используя данные о применении изучаемых явлений в окружающей среде, прививать культуру умственного труда, развивать мышление. Учить уметь ставить перед собой цели занятий, слушать, воспринимать, анализировать, сравнивать, наблюдать, обобщать, делать самостоятельно выводы, оценивать полученный результат.
- Личностные: Продолжать развивать у обучающихся коммуникативные компетенции: речь, память, использование физической символики.
 Продолжать развивать креативные способности: мышление, воображение, самоконтроль. Учить извлекать пользу из образовательного процесса для себя.
Продолжать развивать креативные способности: мышление, воображение, самоконтроль. Учить извлекать пользу из образовательного процесса для себя.
Технология: ИКТ.
Оборудование для урока: демонстрационное: шарик на нити, груз на пружине, сосуд (кювета) с растительным маслом (вязкая жидкость), компьютер.
Презентация: «Механические колебания».
Ход урока
- Организационный момент.
- Актуализация опорных знаний. Сообщение темы урока.
- Изучение новых знаний. Мотивация.
- Закрепление изученного материала.
- Рефлексия. Подведение итогов урока.
Ожидаемые результаты:
Обучающиеся должны научиться:
- Формулировать определение механических колебаний, выделять главный признак колебательного движения, распознавать колебательные процессы в окружающем нас мире по его определению, описанию, характерным признакам на основе имеющихся знаний, приводить примеры колебательных движений, грамотно и чётко выражать свои мысли, делать самостоятельно выводы.

- Понимать смысл физических величин, которые характеризуют механические колебания, самостоятельно добывать новые знания об этих физических величинах с помощью эксперимента.
- Решать простейшие задачи с применением формул, которые связывают характеристики колебаний, все результаты выражать в системе СИ.
Конспект урока
1. Орг. момент ( 1 мин.)
Деятельность учителя на уроке: |
Деятельность учеников на уроке: |
Добрый день! Я рада Вас всех сегодня видеть и приветствовать у меня на уроке. У нас с вами хорошее настроение, за окном сияет солнышко, погода прекрасная, улыбка у нас у всех на лице. Все невзгоды и плохое настроение «уходит от нас», мы будем работать на уроке с настроением и желанием получить новые знания. |
Учащиеся приветствуют учителя, желают доброго дня. Открывают тетради, ручки в руках, Слушают учителя. |
2. Актуализация опорных знаний. Сообщение темы урока.
Деятельность учителя на уроке: |
Деятельность учеников на уроке: |
1. Вы узнаете тему нашего урока сегодня, если разгадаете кроссворд, по вертикали которого и прочитаете тему урока. |
1. Учащиеся разгадывают кроссворд. Учащиеся с места дают ответы на вопросы кроссворда, а один ученик у доски записывает ответы в таблицу кроссворда и работает презентация (по щелчку появляется ответ). |
Вопросы для кроссворда:
- Физическая величина, которая характеризует быстроту движения тела?
- Изменение скорости с течением времени – это……
- Физическая величина, характеризующая взаимодействие тел?
- Линия, по которой движется тело.
- Падение тел под действием силы тяжести
- Прибор для измерения длины тела.
- Единица измерения силы.
- Изменение положения тела в пространстве с течением времени – это….
- Что упало на голову Ньютону, и после этого был открыт закон Всемирного тяготения.
 (Сл.4 ).
(Сл.4 ).
3. Изучение новых знаний. Мотивация.
Деятельность учителя на уроке |
Деятельность учеников на уроке |
Учитель объявляет тему урока. И предлагает учащимся самостоятельно сформулировать цель урока. |
Учащиеся слушают учителя, формулируют цель урока, убеждаются в актуальности материала о колебательном движении. Пытаются самостоятельно осмыслить, в чём состоит главное отличие колебательного движения от других видов движения. |
1. Мы живём в мире, где всё находиться в движении. Из всех видов движений особое место для нас сейчас занимают колебательные движения – оно самое распространённое в природе и технике, в окружающем нас мире.
Колеблются деревья, трава на лугу, струны музыкальных инструментов, поршень двигателя внутреннего сгорания, пульсирует Солнце, сердце нашего организма, движение голосовых связок, движение наших внутренних органов, клеточки головного мозга и т.д.
Колебания многогранны. Иногда они выступают как друг и помощник человека, а иногда как коварный враг.
Неучтённые колебания могут привести к разрушению сложных технических сооружений, вызвать серьёзные заболевания человека. Всё это делает необходимым, чтобы их изучили.
Примеров колебаний мы привели много, и, несмотря на это, все колебания имеют общие признаки и описываются одинаковыми математическими уравнениями.
Нам с вами надо выяснить, что такое колебания? По какому признаку мы их можно отличить от других видов движения?
2. Слайд 5
А) колебание шарика на нити
Б) колебание маятника часов
В) колебание груза на пружине
Г) колебания крыльев насекомых и птиц
Д) биение нашего сердца
Е) движение автомобиля на рессорах
Учитель: Вы видите примеры движения тел. Посмотрев внимательно, скажите: Что общего в этих примерах?
Учащиеся: Все движения повторяются.
Учитель: А как они повторяются?
Учащиеся: Через определённое время.
Учитель: А как эти движения можно назвать?
Учащиеся: Колебания.
Учитель: Сделайте вывод из сказанного.
Учащиеся делают вывод.
Учащиеся под диктовку учителя записывают в тетрадь определение колебания и основной признак.
Колебания – это движение, которое периодически повторяется через определённые промежутки времени.
Основной признак колебаний – повторяемость или периодичность. (Сл.6)
3. Проведите эксперимент:
А) груз на нити выведите из состояния покоя
Б) книгу, с помощью вашей руки «заставьте» совершать колебания
Учитель: Эти виды колебаний чем-то отличаются друг от друга?
Учащиеся делают вывод, что шарик на нити после первоначального на него воздействия движется (совершает колебания) сам по себе, а книга совершает движения (колебания) под воздействием внешней силы (под действием силы руки).
Учитель: Верно, эти колебания совершенно разные. Шарик на нити совершает колебания свободно, а книга – под действием руки — т.е. её вынуждают, заставляют совершать колебания – они и называются вынужденными. В зависимости, какие силы действуют на тело, различают свободные и вынужденные колебания. (Сл.7).
Учащиеся делают запись в тетрадь.
1.) Свободные колебания — это колебания, происходящие под действием внутренних сил.
2) Вынужденные колебания = это колебания, происходящие под действием внешних сил, выводящей тело из положения равновесия.
3) Система тел, способная совершать свободные колебания, называется колебательной системой.
Учитель: Приведите примеры различных видов колебаний. (Сл.8)
Учитель: А теперь выясним условия возникновения и существования колебаний.
Демонстрация: шарик на нити, я его отклоняю, но не отпускаю. Чтобы шарик на нити совершал колебания, мы должны подействовать силой. На шарик действует сила, но колебаний нет. Почему?
Учитель: Само по себе тело будет двигаться?
Учащиеся: Нет. Нужна сила, которая будет его возвращать в состояние равновесия, т.е. наличие «возвращающей силы».
Учитель: Правильно. Это первое условие.
Учитель: Как долго тело будет совершать колебания? Почему оно останавливается?
Учащиеся: колебания прекращаются, т. к. трение существует.
к. трение существует.
Учитель: Как вы думаете, как будет вести себя шарик на нити, если его поместить в растительное масло?
Эксперимент: шарик на нити, кювета с растительным маслом.
Учащиеся: делают вывод из эксперимента: Колебания сразу прекращаются, т.к. возникает большое сопротивление движению.
Учитель: Вот вам и второе условие.
Так, какие условия необходимо создать, чтобы возникали и существовали механические колебания?
Учащиеся: Отвечают и делают запись в тетрадях: (Сл.9)
1) Наличие «возвращающей « силы, стремящейся вернуть колебательную систему в положение равновесия
2) В колебательной системе должно быть малое трение.
Учитель: Колебательное движение, как и любое другое движение, характеризуется физическими величинами. Вот сейчас и поговорим о характеристиках колебательного движения.
Эксперимент: У вас на столах шарики на нити разной длины. Приведите их, пожалуйста, в движение.
Приведите их, пожалуйста, в движение.
Ох, «размах» колебаний у вас у всех получился разный.
1. Вот этот «размах» колебаний в физике определяют физической величиной, которую называют – АМПЛИДУДА. (Сл 10).
Хм ( или А) — амплидуда — это максимальное отклонение от положения равновесия (м).
Учитель: Эксперимент: Теперь все вместе получите колебания с амплитудой 15 см, используйте для этого линейку. МОЛОДЦЫ!
2. Внимательно, наблюдайте за колебаниями системы. Что вы заметили?
Учащиеся: положение тела изменяется относительно равновесия.
Учитель: Да, за каждый момент времени колеблющееся тело занимает определённое положение относительно положения равновесия.
Введём новую характеристику – СМЕЩЕНИЕ.
Х – смещение – это отклонение колеблющейся точки от положения равновесия в данный момент времени (м) (это координата тела).
Основными величинами при колебательном движении являются: период, частота.
Период – это время, за которое совершается одно полное колебание – Т (сек). (Сл 11)
Эксперимент №1. Выполните следующее задание. Будьте внимательны:
Отклонив маятник на 15 см от положения равновесия, подсчитайте число n полных колебаний, за время t =20 сек.
Запишите: n =……..
№ 2. Выведите формулу для периода колебаний. Ещё раз внимательно прочитайте определение периода, которое мы записали.
№ 3. Определите период колебаний вашей системы.
Частота колебаний – это число колебаний совершаемых за 1 сек. — n (ню) (Гц)
№ 4. Определите частоту колебаний по своим данным. (Сл.12).
Период и частота колебаний, величины взаимно обратные, т. е. (связаны между собой следующей зависимостью). (Сл.13.).
Учитель: Ребята у вас по результатам эксперимента получились разные результаты. Как вы думаете, почему?
Как вы думаете, почему?
Ученики: Наверное, разные длины маятника.
Учитель: Да, вы правы. Мы этот ответ запомним, и будем работать с ним на следующем уроке.
Учитель: Вот мы и изучили колебательное движение, рассмотрели физические величины, характеризующие колебательное движение.
Теперь проведём закрепление пройденного материала.
4. Закрепление изученного материала.
Деятельность учителя на уроке |
Деятельность учеников на уроке |
Учитель обеспечивает усвоение тех знаний, которые учащиеся приобрели на данном уроке на уровне применения их в изменённой ситуации. Учитель предлагает им исследовать колебания собственного сердца. |
Учащиеся применяют полученные знания для подсчёта пульса своего сердца и вычисляют период и частоту биения своего сердца, соблюдая систему единиц СИ. |
Исследование: проводят учащиеся самостоятельно: (сл. №14).
Подсчитайте частоту и период колебаний собственного сердца, результаты запишите в тетрадь.
Порядок исследования:
1. Положите левую руку удобно на стол и расслабьтесь.
2. Нащупайте пульс пальцами правой руки.
3. Подсчитайте число пульсаций крови за 1 мин.
4. Определите период колебаний вашего сердца – Т
5. Определите частоту колебаний вашего сердца. — n.
6. При вычислении соблюдайте систему СИ.
7. Сравните свой пульс с нормальным пульсом у людей в возрасте от 18 до 30 лет.
Нормальный пульс у людей в возрасте от 20 до 30 лет 72 – 85 частота ударов в минуту.
Это надо знать: Пульс – это количество ударов сердца в минуту (периодические колебания стенок сосудов, вызванные изменениями давления крови в течении одного сердечного цикла.
5. Рефлексия. Подведение итогов урока: (сл.15).
Подведение итогов урока: (сл.15).
| Деятельность учителя на уроке | Деятельность учеников на уроке |
Учитель подводит итоги урока. Оценивает достижения цели урока. |
Учащиеся сами осмысливают свою деятельность на уроке. Дают себе самооценку. |
Учитель: Всюду в нашей жизни мы встречаемся с колебательными движениями: пульсируют сердце и лёгкие, колеблются ветки деревьев при порыве ветра, ноги и руки при ходьбе, пульсируют звёзды, а возможно и вся наша Вселенная, колеблются атомы в узлах кристаллической решётки.
Л.И.Мандельштам говорил, что если посмотреть историю физики, то можно увидеть, что главные открытия были связаны по существу с колебаниями. Предела для знания нет.
Урок наш подошёл к концу, и мы должны подвести итоги нашей работы на уроке.
Вместе подумаем — всё ли нам удалось на уроке, продуктивно ли мы поработали. Думаю, на уроке вы не скучали. Работали все с интересом.
1. А вы как оцениваете свою работу на уроке?
2. Данный материал вам пригодиться в жизни?
3. Где именно, можете мне это сказать?
4. Вспомните наш девиз к уроку:
«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника».
5. Он соответствует нашему уроку?
6. Почему Вы так думаете?
Да, мы свои знания о колебаниях пополнили и использовали разные источники.
На следующих уроках мы продолжим пополнять наши знания о механических колебаниях.
Ваши оценки за урок:… (учитель выставляет оценки за работу на уроке).…
(Д/З в нашей школе учащимся на дом не даётся).
Спасибо за урок! Всего вам доброго! (Сл.16)
Используемая литература для подготовке к уроку.
- «Ф-9», А.
 В.Пёрышкин, Е.М.Гутник, М. «Дрофа». 2007г.
В.Пёрышкин, Е.М.Гутник, М. «Дрофа». 2007г. - Презентация «Механические колебания»
- Интернет-ресурсы.
Постоянная Планка — обзор
Квантовая механика и энергетические диапазоны
Эта область физики, известная как квантовая механика, является сложной, запутанной и в основном математической. В наши цели здесь не входит полный и исчерпывающий обзор предмета. Тем не менее, нам необходимо рассмотреть некоторые из фундаментальных концепций этого предмета, чтобы заложить основу для того, что будет сказано позже о полупроводниках, их свойствах и их работе в качестве солнечных элементов. При рассмотрении объекта, будь то товарный поезд, футбольный мяч, атом аргона или электрон, квантовая механика приписывает этому объекту волновую функцию ψ .
Волновая функция ψ содержит всю информацию об объекте, который является наблюдаемым (т. е. измеримым), но сама по себе не имеет физически наблюдаемых свойств. Однако если мы умножим волновую функцию ψ для некоторого объекта на ее комплексно-сопряженную функцию и проинтегрируем ее по заданному объему пространства V, результирующее значение интеграла будет вероятностью того, что объект существует в объеме Space, V. Таким образом:
Таким образом:
(III.4) ∫ovψψ * dv = вероятность существования в объеме V,
, где ψ * — это комплексное сопряжение ψ .Ясно, что если объемный интеграл распространить на все пространство, то значение интеграла (уравнение III.4) равно единице, ибо поезд, электрон и т. д. должны где-то быть. Волновая функция также является решением волнового уравнения Шрёдингера:
(III.5)ℋΨn=(ℏ/i)(∂[Ψn]/∂t)=En,
, где i — квадратный корень из минус единицы ; ψ n — частный вариант волновой функции, описывающей рассматриваемый объект, известный как собственная функция; и E n представляет собой энергию объекта, когда он описывается этой конкретной собственной функцией и известен как собственная энергия.Количество. ℋ , известен как гамильтониан и определяется как:
(III.6)ℋ=-(ℏ2/2m)∇2+Vp(xj),
, где m — масса объекта, ℏ — Постоянная Планка, деленная на 2π (ℏ=1,054 × 10-34 джоулей-секунд), ∇ 2 — математическая операция * и V p (X j ) — функция потенциальной энергии объекта как местоположения.
Общая форма решения волновой функции уравнения III.5 представлена уравнением III.7:
(III.7)Ψn=AnΨn(x,y,z)exp(-Ent/ℏ).
Для электрона, движущегося в области с постоянной потенциальной энергией, где потенциальная энергия V p меньше полной энергии электрона, E T , решение уравнения Шредингера еще больше упрощается до:
(III.8)Ψ=Aexp(ikxx+ikyy+ikzz)exp(-iωt)
где k x , k y и k z — константы движения (действительные) общего вида 1/ [ℏ√(2m{ET-Vp})],ω=ET/ℏ, а A — нормирующая константа.
После того как волновая функция объекта определена путем решения уравнения Шредингера, можно получить ожидаемое значение различных физических наблюдаемых величин, например импульса объекта P, с помощью простой математической операции:
(III. 9)
=(ℏ/i)∫Ψ*∇ΨdvV,
, где ψ * — комплексно-сопряженное число ψ , V — объем рассматриваемого пространства, а 〈p〉 — ожидаемое значение импульса * . Используя решение бегущей волны для свободного электрона (уравнение III.8), импульс в каждом из направлений x, y и z:
Используя решение бегущей волны для свободного электрона (уравнение III.8), импульс в каждом из направлений x, y и z:
(III.10) Px=ℏkx,Py=ℏky и Pz=ℏkz,
, где ℏk i называется импульсом кристалла в направлении i.
Для больших объектов (таких как карандаш, пуговица или человек) значения различных свойств, которые мы определяем способом, аналогичным уравнению III.9, неотличимы от предсказаний, сделанных классической (ньютоновской) физикой .Однако когда мы входим в мир электрона, движущегося через кристалл, или электронов, движущихся по своим орбитам вокруг атома, тогда решения квантовой механики могут отличаться, и делают это кардинально, от предсказаний классической механики. Например, принцип неопределенности требует, чтобы точность, с которой могут быть одновременно определены положение частицы и импульс этой частицы, была конечной, например:
, где ΔP x и Δx — потенциальная изменчивость (неопределенность) импульс, направленный по оси x, и положение в направлении по оси x. В результате этого факта и допустимой суперпозиции волновых функций частица в общем случае будет описываться волновой функцией ψ T , состоящей из ряда отдельных волновых функций ψ n :
В результате этого факта и допустимой суперпозиции волновых функций частица в общем случае будет описываться волновой функцией ψ T , состоящей из ряда отдельных волновых функций ψ n :
(III.12)ΨT=∫An(E)ψn(x,y,z)exp(-iEnt/ℏ)dE,
где A n (E) — нормирующая функция, зависящая от энергия частиц. Во многих важных ситуациях, например, внутри любого конечного кристалла, существуют граничные условия, которые ограничивают допустимые волновые функции, так что мы можем заменить интеграл уравнения III.12 путем суммирования:
(III.13)Ψn=∑An(E)ψn(x,y,z)exp(-iEnt/ℏ).
В качестве примера рассмотрим частицу, заключенную в ящик с размерами L, M и N. Потенциальная энергия внутри ящика принимается равной нулю, а без ящика считается бесконечной. Решение уравнения Шрёдингера (уравнение III.5) в этом случае имеет вид:
(III.14)ψT=∑A1,m,nsin{k1x}sin{kmy}sin{knz}exp(-iEnt /ℏ),
, где
(III. 15)k1=lπ/L,km=mπ/M,kn=nπ/N,
15)k1=lπ/L,km=mπ/M,kn=nπ/N,
и 1, m, n — ненулевые целые числа.Импульс этой частицы в направлении x (из уравнения III.9) равен ℏπl/L. Таким образом, частица имеет большое количество возможных значений импульса, направленного по оси x, но не бесконечное число значений. Периодический характер волновой функции (индуцированный граничными условиями) требует, чтобы ψ T обращались в нуль при x = 0 и L; при y = 0 и M и при z равно 0 и N (края коробки). Далее можно показать, что допустимые энергии для этой частицы:
(III.16)E=[(ℏk1)2+(ℏkm)2+(ℏkn)2]/2m=[Px2+Py2+Pz2]/2m,
, где m — масса частицы, а P i — импульс частицы в i-м направлении. Обратите внимание, что частица в ящике (которая служит полезным приближением к электрону, ограниченному размерами атома) ограничена определенными определенными энергиями и сопутствующими им волновыми функциями. Когда производится измерение энергии частицы, результатом любого отдельного измерения является одна из возможных энергий (т. г., что для k l = 2, k m = 4 и k n = 5). Если произвести повторное измерение энергий, результатом вполне может быть другое значение энергии. В любой реалистичной системе физических измерений энергия, которую мы получаем, будет представлять собой среднее значение многих отдельных измерений, взвешенных по статистическим вероятностям.
г., что для k l = 2, k m = 4 и k n = 5). Если произвести повторное измерение энергий, результатом вполне может быть другое значение энергии. В любой реалистичной системе физических измерений энергия, которую мы получаем, будет представлять собой среднее значение многих отдельных измерений, взвешенных по статистическим вероятностям.
Большой интерес для нас представляет движение электронов через полупроводниковый кристалл. Потенциальная энергия области, через которую движется электрон, непостоянна (как предполагается уравнением III.8), но является периодической функцией (поскольку кристалл представляет собой упорядоченный периодический массив атомов), что приводит к волновой функции, которая в одном измерении представляет собой сумму ряда членов вида:
(III. 17)ψ(x)=U(x)exp(ikx)exp(-iEt/ℏ),
, где U(x) периодично в x с периодом, равным периоду кристалла.
Когда уравнение Шредингера (уравнение III.5) решается для кристалла с использованием типа волновой функции уравнения III. 17, с учетом периодичности решетки, обнаруживается, что для электронов в кристалле разрешены только определенные энергии [ 19]! На рисунке III.3 мы отображаем разрешенные энергии в зависимости от k, разделенного на пространственный период, a, для одномерного кристалла. Пунктирная линия представляет зависимость энергии от k для свободного электрона, движущегося в постоянном потенциальном поле — очевидно, континуум энергий.
17, с учетом периодичности решетки, обнаруживается, что для электронов в кристалле разрешены только определенные энергии [ 19]! На рисунке III.3 мы отображаем разрешенные энергии в зависимости от k, разделенного на пространственный период, a, для одномерного кристалла. Пунктирная линия представляет зависимость энергии от k для свободного электрона, движущегося в постоянном потенциальном поле — очевидно, континуум энергий.
Рисунок III.3. Разрешенные энергии электронов в одномерном кристалле. Для сравнения пунктирной линией показан разрешенный континуум энергий для свободного электрона.
При переносе рисунка III.3 на трехмерный кристалл наиболее полезным подходом является использование направлений внутри кристалла, определяемых самой кристаллической структурой.На рисунке III.4 зонные структуры полупроводников арсенида галлия, германия и кремния представлены для k в направлениях [100] и [111] [20].
Рисунок III.4. Диаграмма зависимости энергии зоны от импульса для германия, Ge; кремний, Si; и арсенид галлия, GaAS; в направлениях [111] и [100] [20]. E g — энергетическая щель, а x, L и Γ — точки кристалла.
E g — энергетическая щель, а x, L и Γ — точки кристалла.
На рисунках III.3 и III.4 электронам разрешены только значения энергии и k («импульс»), которые помещают их на сплошные линии.На рисунке III.4 разница в энергии между самой высокой точкой в нижнем наборе разрешенных энергетических зон и самой низкой точкой в верхнем наборе разрешенных зон определяется как энергетическая щель (часто называемая запрещенной зоной) и обозначается как E г .
В полупроводнике при температуре ноль Кельвинов электронов ровно столько, чтобы заполнить нижние кривые зависимости энергии от импульса, а на верхних кривых электронов нет (E > E g ). Нижние кривые известны как валентная зона, и электроны в ней ответственны за химические свойства полупроводника.Верхний набор кривых в совокупности известен как зона проводимости. Обратите внимание, что когда валентная зона (или любая другая зона) заполнена электронами, она не может проводить ток. Это так, потому что, когда мы прикладываем электрическое поле к какому-либо объекту для переноса тока, электроны в объекте должны ускоряться в направлении, определяемом полем. Если электрон ускоряется, он должен изменить энергию на какую-то небольшую величину (ΔE ≪ E г ). Если электрон должен изменить энергию, он должен сместиться в другое место на диаграмме энергии-импульса.Однако в полной энергетической зоне это место уже занято другим электроном. Принцип запрета Паули гласит, что в кристалле никакие два электрона не могут занимать одно и то же положение энергии-импульса! Следовательно, электрон не может изменить положение и не может ускориться или изменить энергию. Таким образом, при температуре абсолютного нуля, с полной валентной зоной и пустой зоной проводимости полупроводник не может проводить ток и действует как изолятор.
Если электрон ускоряется, он должен изменить энергию на какую-то небольшую величину (ΔE ≪ E г ). Если электрон должен изменить энергию, он должен сместиться в другое место на диаграмме энергии-импульса.Однако в полной энергетической зоне это место уже занято другим электроном. Принцип запрета Паули гласит, что в кристалле никакие два электрона не могут занимать одно и то же положение энергии-импульса! Следовательно, электрон не может изменить положение и не может ускориться или изменить энергию. Таким образом, при температуре абсолютного нуля, с полной валентной зоной и пустой зоной проводимости полупроводник не может проводить ток и действует как изолятор.
Учебник по физике: свойства периодического движения
Вибрирующий объект колеблется в фиксированном положении.Как и масса на пружине в анимации справа, вибрирующий объект движется по той же траектории с течением времени. Его движение повторяется снова и снова. Если бы не , демпфирующий , колебания продолжались бы вечно (или, по крайней мере, пока кто-нибудь не поймает массу и не остановит ее). Масса на пружине не только повторяет одно и то же движение, но и делает это регулярно. Время, необходимое для завершения одного цикла «туда-сюда», всегда одинаково.Если грузу требуется 3,2 секунды, чтобы совершить первый возвратно-поступательный цикл, то для завершения седьмого возвратно-поступательного цикла потребуется 3,2 секунды. Это как часовой механизм. Это настолько предсказуемо, что по нему можно сверить часы. В физике движение, которое является регулярным и повторяющимся, называется периодическим движением. Большинство объектов, которые вибрируют, делают это регулярно и повторяющимся образом; их колебания периодические. (Отдельное спасибо Олегу Александрову за анимацию массы на пружинке.Это общественное достояние, полученное от WikiMedia Commons. )
Масса на пружине не только повторяет одно и то же движение, но и делает это регулярно. Время, необходимое для завершения одного цикла «туда-сюда», всегда одинаково.Если грузу требуется 3,2 секунды, чтобы совершить первый возвратно-поступательный цикл, то для завершения седьмого возвратно-поступательного цикла потребуется 3,2 секунды. Это как часовой механизм. Это настолько предсказуемо, что по нему можно сверить часы. В физике движение, которое является регулярным и повторяющимся, называется периодическим движением. Большинство объектов, которые вибрируют, делают это регулярно и повторяющимся образом; их колебания периодические. (Отдельное спасибо Олегу Александрову за анимацию массы на пружинке.Это общественное достояние, полученное от WikiMedia Commons. )
Синусоидальный характер вибрации
Предположим, что детектор движения был помещен под вибрирующей массой на пружине для обнаружения изменений положения массы с течением времени. И предположим, что данные от детектора движения могут отображать движение массы на графике зависимости положения от времени. На рисунке ниже изображен такой график. Для обсуждения несколько точек были отмечены на графике, чтобы помочь в последующем обсуждении.
И предположим, что данные от детектора движения могут отображать движение массы на графике зависимости положения от времени. На рисунке ниже изображен такой график. Для обсуждения несколько точек были отмечены на графике, чтобы помочь в последующем обсуждении.
Прежде чем читать дальше, задумайтесь о типе информации, которую передает график. И найдите минутку, чтобы подумать о том, какие величины на графике могут быть важны для понимания математического описания массы на пружине. Если вы нашли время, чтобы обдумать эти вопросы, следующее обсуждение, вероятно, будет более содержательным.
Одной из очевидных характеристик графика является его форма.Многие учащиеся узнают форму этого графика из своего опыта на уроках математики. График имеет форму синусоиды. Если y = sine(x) построить на графическом калькуляторе, будет создан график такой же формы. Вертикальная ось приведенного выше графика представляет положение массы относительно детектора движения.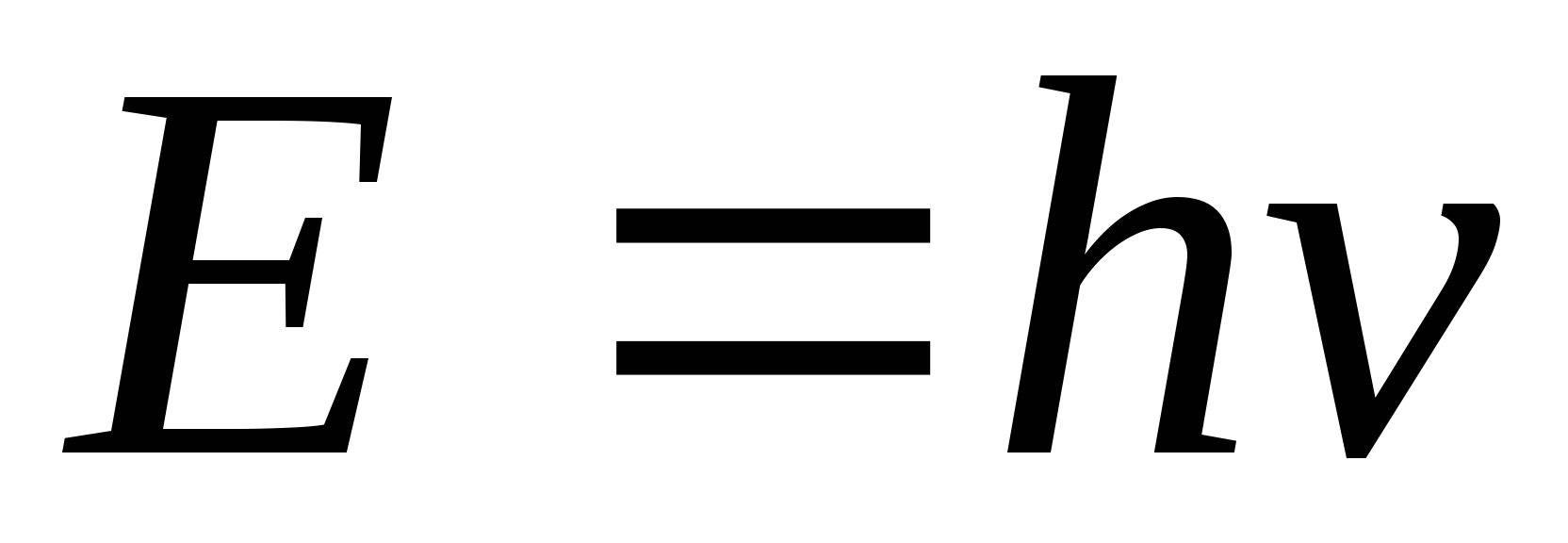 Положение примерно на 0,60 м см выше детектора представляет собой положение покоя массы. Таким образом, масса колеблется взад и вперед относительно этого фиксированного положения покоя с течением времени.Есть что-то синусоидальное о вибрации массы на пружине. И то же самое можно сказать о маятнике, колеблющемся вокруг определенного положения, или о гитарной струне, или о воздухе внутри духового инструмента. Положение массы есть функция синуса времени.
Положение примерно на 0,60 м см выше детектора представляет собой положение покоя массы. Таким образом, масса колеблется взад и вперед относительно этого фиксированного положения покоя с течением времени.Есть что-то синусоидальное о вибрации массы на пружине. И то же самое можно сказать о маятнике, колеблющемся вокруг определенного положения, или о гитарной струне, или о воздухе внутри духового инструмента. Положение массы есть функция синуса времени.
Второй очевидной характеристикой графика может быть его периодическая природа. Движение регулярно повторяется. Время откладывается по горизонтальной оси; поэтому любое измерение, проведенное вдоль этой оси, является измерением времени, в течение которого что-то должно произойти.Полный цикл вибрации можно рассматривать как перемещение массы из положения покоя (А) на максимальную высоту (В), обратно вниз из положения покоя (С) в минимальное положение (D) и затем вернитесь в исходное положение (E). Используя измерения по оси времени, можно определить время одного полного цикла. Масса находится в положении А в момент времени 0,0 секунды и завершает свой цикл, когда она находится в положении Е в момент времени 2,3 секунды. Требуется 2.3 секунды, чтобы завершить первый полный цикл вибрации. Теперь, если движение этой массы является периодическим (т. е. регулярным и повторяющимся), то для совершения любого полного цикла вибрации должно потребоваться то же самое время 2,3 секунды. Такие же измерения по оси времени можно провести для шестого полного цикла вибрации. В шестом полном цикле масса перемещается из положения покоя (U) вверх в положение V, обратно вниз через W в положение X и, наконец, обратно в положение покоя (Y) в интервале времени от 11,6 до 13,9 секунд.Это соответствует времени 2,3 секунды, чтобы завершить шестой полный цикл вибрации. Два времени цикла идентичны. Другие времена цикла указаны в таблице ниже. Изучив таблицу, можно с уверенностью заключить, что движение груза на пружине является правильным и повторяющимся; он явно периодический. Небольшое отклонение от 2,3 с в третьем цикле можно объяснить недостаточной точностью чтения графика.
Масса находится в положении А в момент времени 0,0 секунды и завершает свой цикл, когда она находится в положении Е в момент времени 2,3 секунды. Требуется 2.3 секунды, чтобы завершить первый полный цикл вибрации. Теперь, если движение этой массы является периодическим (т. е. регулярным и повторяющимся), то для совершения любого полного цикла вибрации должно потребоваться то же самое время 2,3 секунды. Такие же измерения по оси времени можно провести для шестого полного цикла вибрации. В шестом полном цикле масса перемещается из положения покоя (U) вверх в положение V, обратно вниз через W в положение X и, наконец, обратно в положение покоя (Y) в интервале времени от 11,6 до 13,9 секунд.Это соответствует времени 2,3 секунды, чтобы завершить шестой полный цикл вибрации. Два времени цикла идентичны. Другие времена цикла указаны в таблице ниже. Изучив таблицу, можно с уверенностью заключить, что движение груза на пружине является правильным и повторяющимся; он явно периодический. Небольшое отклонение от 2,3 с в третьем цикле можно объяснить недостаточной точностью чтения графика.
|
Цикл |
Письма |
раз в начале и |
|
|
1-й |
от А до Е |
0.от 0 до 2,3 с |
2,3 |
|
2-й |
Е тп I |
от 2,3 до 4,6 с |
2,3 |
|
3-й |
от I до М |
4.от 6 с до 7,0 с |
2,4 |
|
4-й |
М до Q |
от 7,0 до 9,3 с |
2,3 |
|
5-й |
от Q до U |
9.от 3 с до 11,6 с |
2,3 |
|
6-й |
U до Y |
от 11,6 до 13,9 с |
2,3 |
Студенты, просматривая приведенный выше график, часто описывают движение массы как «замедление». » Возможно, еще слишком рано подробно говорить о том, что означает , замедляющий . Мы сохраним пространное обсуждение темы для страницы, посвященной движению массы на пружине, позже в этом уроке. А пока давайте просто говорят, что с течением времени масса претерпевает изменения в своей скорости по синусоидальному закону. То есть скорость массы в любой данный момент времени является функцией синуса времени. Таким образом, масса будет как скорость вверх и вниз в течение одного цикла.Поэтому говорить, что масса «тормозится», не совсем точно, так как в каждом цикле есть два коротких интервала, в течение которых она ускоряется. (Подробнее об этом позже.)
» Возможно, еще слишком рано подробно говорить о том, что означает , замедляющий . Мы сохраним пространное обсуждение темы для страницы, посвященной движению массы на пружине, позже в этом уроке. А пока давайте просто говорят, что с течением времени масса претерпевает изменения в своей скорости по синусоидальному закону. То есть скорость массы в любой данный момент времени является функцией синуса времени. Таким образом, масса будет как скорость вверх и вниз в течение одного цикла.Поэтому говорить, что масса «тормозится», не совсем точно, так как в каждом цикле есть два коротких интервала, в течение которых она ускоряется. (Подробнее об этом позже.)
Студенты, которые описывают массу как замедляющуюся (а большинство наблюдательных студентов именно так и описывают это), явно наблюдают что-то в особенностях графика, из-за чего возникает комментарий «замедление». Прежде чем мы обсудим функцию, которая вызывает комментарий «замедление», мы должны повторить вывод из предыдущих абзацев — время завершения одного цикла вибрации НЕ меняется. Потребовалось 2,3 секунды, чтобы завершить первый цикл и 2,3 секунды, чтобы завершить шестой цикл. Что бы ни означало «замедление», мы должны опровергнуть представление о том, что оно означает увеличение продолжительности циклов по мере продолжения движения. Это мнение явно противоречит данным.
Потребовалось 2,3 секунды, чтобы завершить первый цикл и 2,3 секунды, чтобы завершить шестой цикл. Что бы ни означало «замедление», мы должны опровергнуть представление о том, что оно означает увеличение продолжительности циклов по мере продолжения движения. Это мнение явно противоречит данным.
Третьей очевидной характеристикой графика является то, что демпфирование происходит в системе масса-пружина. Некоторая энергия рассеивается с течением времени. Степень, в которой масса перемещается выше (B, F, J, N, R и V) или ниже (D, H, L, P, T и X) положения покоя (C, E, G, I и т. д.).) меняется с течением времени. В первом показанном полном цикле вибрации масса перемещается из положения покоя (А) на высоте 0,60 м над датчиком движения в высокое положение (В) на высоте 0,99 м см над датчиком движения. Это полное смещение вверх 0,29 м. В показанном шестом полном цикле вибрации груз перемещается из положения покоя (U) на высоте 0,60 м над датчиком движения в высокое положение (V) на высоте 0,94 м над датчиком движения. Это полное смещение вверх 0,24 м см.В таблице ниже приведены результаты измерений смещения для нескольких других циклов, отображаемых на графике.
Это полное смещение вверх 0,24 м см.В таблице ниже приведены результаты измерений смещения для нескольких других циклов, отображаемых на графике.
|
Цикл |
Письма |
Максимум вверх |
Максимум вниз |
|
1-й |
от А до Е |
0.от 60 м до 0,99 м |
от 0,60 м до 0,21 м |
|
2-й |
E-I |
от 0,60 м до 0,98 м |
от 0,60 м до 0,22 м |
|
3-й |
от I до М |
0.от 60 м до 0,97 м |
от 0,60 м до 0,23 м |
|
6-й |
U до Y |
от 0,60 м до 0,94 м |
от 0,60 м до 0,26 м |
С течением времени масса продолжает вибрировать, перемещаясь от исходного положения покоя и обратно. Однако величина смещения массы на ее максимальной и минимальной высоте уменьшается от одного цикла к другому. Это показывает, что энергия теряется из системы масса-пружина. Если дать достаточно времени, вибрация массы в конце концов прекратится, поскольку ее энергия рассеется.
Однако величина смещения массы на ее максимальной и минимальной высоте уменьшается от одного цикла к другому. Это показывает, что энергия теряется из системы масса-пружина. Если дать достаточно времени, вибрация массы в конце концов прекратится, поскольку ее энергия рассеется.
Возможно, это наблюдение за рассеянием или потерей энергии является наблюдением, которое вызывает комментарий о «замедлении», обсуждавшийся ранее. В физике (или, по крайней мере, в английском языке) «замедление» означает «становиться медленнее» или «терять скорость».Скорость, физический термин, относится к тому, насколько быстро или медленно движется объект. Сказать, что масса пружины со временем «замедляется», значит сказать, что ее скорость со временем уменьшается. Но, как уже упоминалось (и как будет подробно рассмотрено позже), масса ускоряется в течение двух интервалов каждого цикла. По мере того, как восстанавливающая сила тянет массу обратно к исходному положению (например, из B в C и из D в E), масса ускоряется. По этой причине физик использует другой язык, чтобы передать идею о том, что вибрации «затухают».Мы используем фразу «энергия рассеивается или теряется» вместо того, чтобы говорить «масса замедляется». Язык важен, когда дело доходит до изучения физики. А иногда неправильный язык (в сочетании с поверхностным мышлением) может сбить с толку студента-физика, который искренне пытается усвоить новые идеи.
По этой причине физик использует другой язык, чтобы передать идею о том, что вибрации «затухают».Мы используем фразу «энергия рассеивается или теряется» вместо того, чтобы говорить «масса замедляется». Язык важен, когда дело доходит до изучения физики. А иногда неправильный язык (в сочетании с поверхностным мышлением) может сбить с толку студента-физика, который искренне пытается усвоить новые идеи.
Период и частота
До сих пор в этой части урока мы рассматривали измерения времени и положения груза на пружине.Измерения были основаны на показаниях графика положение-время. Данные на графике были собраны детектором движения, который регистрировал 90 141 историю 90 142 движения с течением времени. Ключевые измерения, которые были сделаны, это измерения:
- время полного цикла массы и
- максимальное смещение массы выше (или ниже) положения покоя.
Эти две измеряемые величины имеют имена.Мы называем эти величины периодом и амплитудой.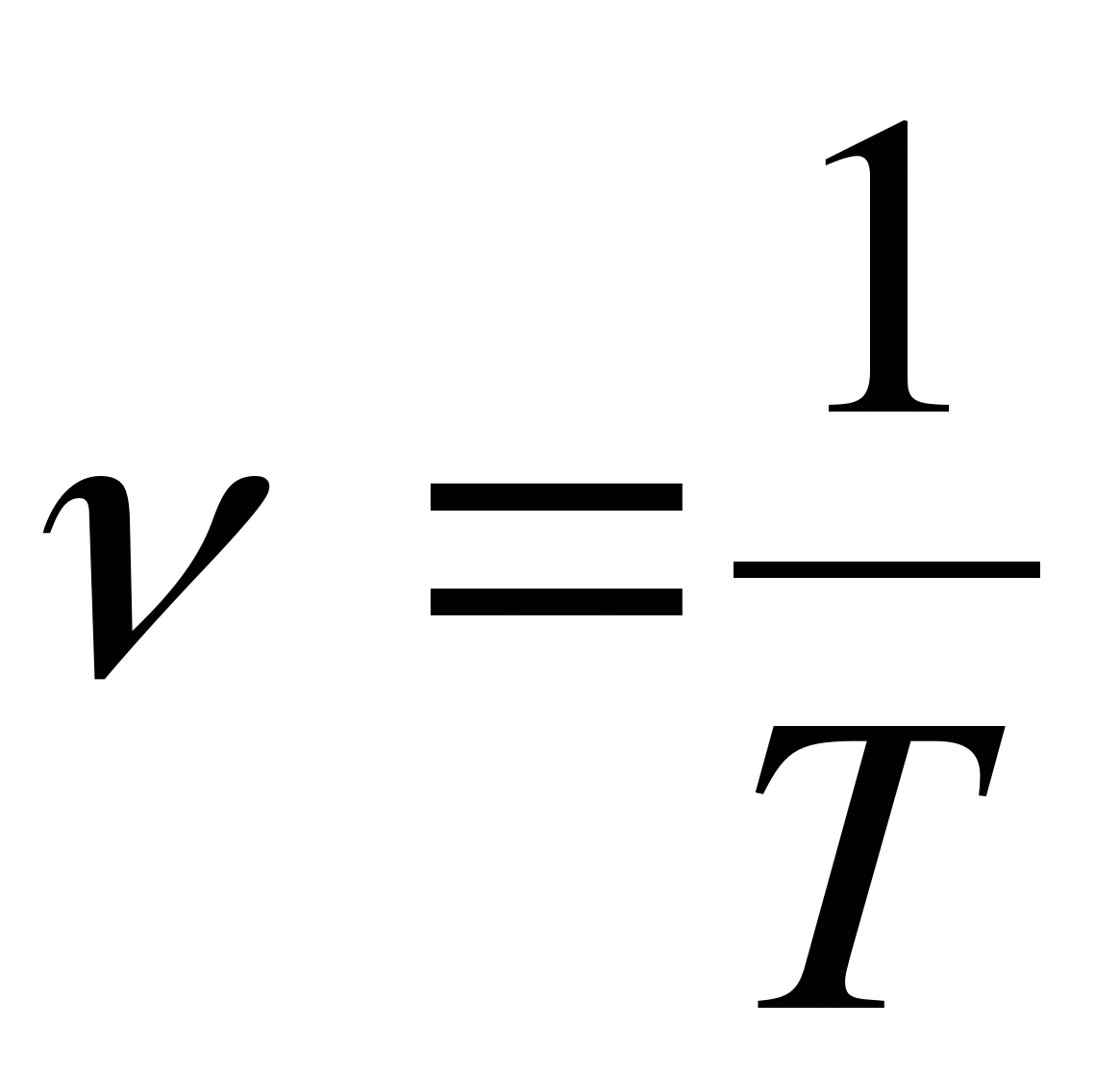
Объект, находящийся в периодическом движении, например, груз на пружине, маятник или кукла-болванчик, будет совершать возвратно-поступательные колебания вокруг фиксированного положения регулярным и повторяющимся образом. Тот факт, что периодическое движение является регулярным и повторяющимся, означает, что его можно математически описать величиной, известной как период. Период движения объекта определяется как время, за которое объект совершает один полный цикл.Будучи временем, период измеряется в таких единицах, как секунды, миллисекунды, дни или даже годы. Стандартной метрической единицей периода является секунда.
Объект в периодическом движении может иметь длинный или короткий период. Например, маятник, привязанный к веревке длиной 1 метр, имеет период около 2,0 секунд. Для сравнения рассмотрим колебания фортепианной струны, играющей среднюю ноту до (ноту до четвертой октавы). Его период примерно равен 0.0038 секунд (3,8 миллисекунды). При сравнении этих двух вибрирующих объектов — маятника длиной 1,0 м и фортепианной струны, играющей среднюю ноту «до» , — мы бы описали струну фортепиано как вибрирующую относительно часто, а маятник — как вибрирующую относительно редко. Обратите внимание, что в описании двух объектов используются термины часто и нечасто . Термины быстрый и медленный не используются, поскольку типы физики резервируют слова быстрый и медленный для обозначения скорости объекта.Здесь в этом описании мы имеем в виду частоту, а не скорость. Объект может находиться в периодическом движении и иметь низкую частоту и высокую скорость. В качестве примера рассмотрим периодическое движение Луны по орбите вокруг Земли. Луна движется очень быстро; его орбита встречается очень редко. Он движется в пространстве со скоростью около 1000 м/с — это быстро. Тем не менее, он совершает полный оборот вокруг Земли один раз за 27,3 дня (период около 2,4×10 5 секунд) — это нечасто.
Обратите внимание, что в описании двух объектов используются термины часто и нечасто . Термины быстрый и медленный не используются, поскольку типы физики резервируют слова быстрый и медленный для обозначения скорости объекта.Здесь в этом описании мы имеем в виду частоту, а не скорость. Объект может находиться в периодическом движении и иметь низкую частоту и высокую скорость. В качестве примера рассмотрим периодическое движение Луны по орбите вокруг Земли. Луна движется очень быстро; его орбита встречается очень редко. Он движется в пространстве со скоростью около 1000 м/с — это быстро. Тем не менее, он совершает полный оборот вокруг Земли один раз за 27,3 дня (период около 2,4×10 5 секунд) — это нечасто.
О таких объектах, как фортепианная струна, которые имеют относительно короткий период (т. е. низкое значение периода), говорят, что они имеют высокую частоту. Частота — это еще одна величина, которую можно использовать для количественного описания движения объекта — периодического движения. Частота определяется как количество полных циклов, происходящих за период времени. Поскольку стандартной метрической единицей времени является секунда, частота измеряется циклами в секунду. Единица цикл/секунда эквивалентна единице Герц (сокращенно Гц).Единица Герц используется в честь Генриха Рудольфа Герца, физика 19-го века, который расширил наше понимание электромагнитной теории световых волн.
Частота определяется как количество полных циклов, происходящих за период времени. Поскольку стандартной метрической единицей времени является секунда, частота измеряется циклами в секунду. Единица цикл/секунда эквивалентна единице Герц (сокращенно Гц).Единица Герц используется в честь Генриха Рудольфа Герца, физика 19-го века, который расширил наше понимание электромагнитной теории световых волн.
Частота понятия и количества лучше всего понятна, если вы привяжете его к повседневному английскому значению этого слова. Частота — это слово, которое мы часто используем, чтобы описать, как часто что-то происходит. Вы можете сказать, что часто проверяете электронную почту, часто разговариваете с другом или часто моете руки при работе с химическими веществами.В этом контексте вы имеете в виду, что вы часто занимаетесь этими видами деятельности. Сказать, что вы часто проверяете электронную почту, означает, что вы делаете это несколько раз в день — вы делаете это часто. В физике частота используется с тем же значением — она указывает, как часто происходит повторяющееся событие. Периодические высокочастотные события происходят часто, с небольшими промежутками времени между каждым событием — подобно колебаниям зубцов камертона вперед и назад. Вибрации настолько часты, что их невозможно увидеть невооруженным глазом.Зубцы камертона с частотой 256 Гц совершают 256 полных колебаний вперед-назад каждую секунду. При такой частоте зубцам требуется около 0,00391 секунды для завершения одного цикла. Камертон на 512 Гц имеет еще более высокую частоту. Его колебания происходят чаще; время завершения полного цикла составляет 0,00195 секунды. При сравнении этих двух камертонов становится очевидным, что камертон с наибольшей частотой имеет наименьший период. Две величины частота и период обратно пропорциональны друг другу.По сути, они являются математическими обратными величинами друг друга. Частота обратно пропорциональна периоду, а период обратно пропорционален частоте.
Периодические высокочастотные события происходят часто, с небольшими промежутками времени между каждым событием — подобно колебаниям зубцов камертона вперед и назад. Вибрации настолько часты, что их невозможно увидеть невооруженным глазом.Зубцы камертона с частотой 256 Гц совершают 256 полных колебаний вперед-назад каждую секунду. При такой частоте зубцам требуется около 0,00391 секунды для завершения одного цикла. Камертон на 512 Гц имеет еще более высокую частоту. Его колебания происходят чаще; время завершения полного цикла составляет 0,00195 секунды. При сравнении этих двух камертонов становится очевидным, что камертон с наибольшей частотой имеет наименьший период. Две величины частота и период обратно пропорциональны друг другу.По сути, они являются математическими обратными величинами друг друга. Частота обратно пропорциональна периоду, а период обратно пропорционален частоте.
Эту взаимосвязь легко понять. В конце концов, две величины концептуально обратны (фраза, которую я придумал). Рассмотрим их определения, приведенные ниже:
Рассмотрим их определения, приведенные ниже:
- период = время завершения одного полного цикла; т.е., секунд/цикл
- частота = количество циклов, которые выполняются за раз; я.е., циклов/сек
Даже определения имеют ответное кольцо к ним. Чтобы понять разницу между периодом и частотой, рассмотрим следующее утверждение:
.Согласно Википедии (и на момент написания этой статьи), Тим Альстром из Окономовок, штат Висконсин, является рекордсменом по аплодисментам. Сообщается, что он хлопнул в ладоши 793 раза за 60,0 секунд.Какова частота и период хлопков г-на Альстрома в ладоши в течение этих 60.0-секундный период?
Амплитуда вибрации
Последней измеримой величиной, описывающей вибрирующий объект, является амплитуда. Амплитуда определяется как максимальное смещение объекта из его положения покоя . Положение покоя — это положение, которое принимает объект, когда он не вибрирует.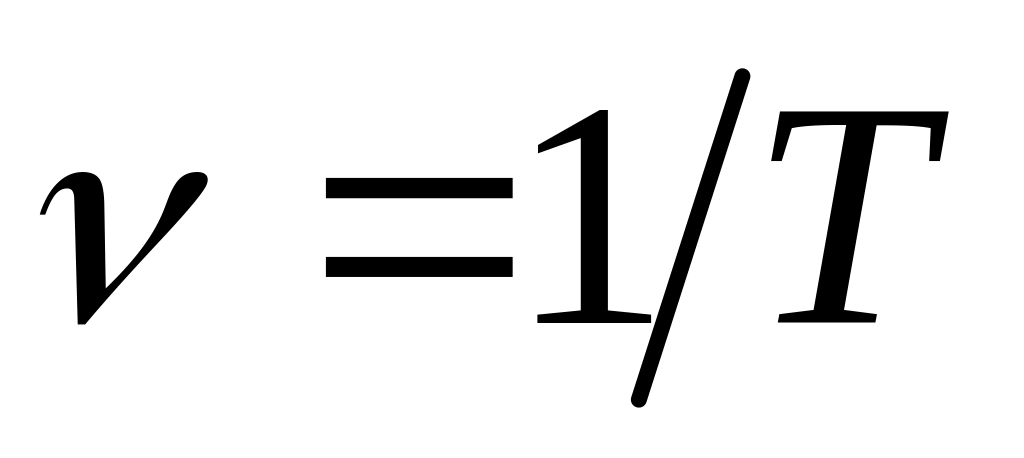 После вибрации объект колеблется вокруг этого фиксированного положения. Если объект представляет собой груз на пружине (как обсуждалось ранее на этой странице), то он может быть смещен максимально на 35 см ниже положения покоя и на 35 см выше положения покоя.При этом амплитуда движения составляет 35 см.
После вибрации объект колеблется вокруг этого фиксированного положения. Если объект представляет собой груз на пружине (как обсуждалось ранее на этой странице), то он может быть смещен максимально на 35 см ниже положения покоя и на 35 см выше положения покоя.При этом амплитуда движения составляет 35 см.
С течением времени амплитуда вибрирующего объекта становится все меньше и меньше. Амплитуда движения является отражением количества энергии, которой обладает вибрирующий объект. Объект, вибрирующий с относительно большой амплитудой, имеет относительно большое количество энергии. Со временем часть этой энергии теряется из-за демпфирования. По мере потери энергии амплитуда уменьшается. Если дать достаточно времени, амплитуда уменьшится до 0, когда объект, наконец, перестанет вибрировать.В этот момент он потерял всю свою энергию.
Мы хотели бы предложить… Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей мессы в Spring Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте.Mass on a Spring Interactive предоставляет учащимся простую среду для изучения свойств периодического движения.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей мессы в Spring Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте.Mass on a Spring Interactive предоставляет учащимся простую среду для изучения свойств периодического движения.
Проверьте свое понимание
1. Наблюдается, что маятник совершает 23 полных оборота за 58 секунд. Определить период и частоту маятника.
2. Масса привязана к пружине и начинает периодически вибрировать.Расстояние между его самым высоким и самым низким положением составляет 38 см. Какова амплитуда колебаний?
18.1 Электрические заряды, сохранение заряда и перенос заряда — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать положительные и отрицательные электрические заряды
- Использование сохранения заряда для расчета количества заряда, переданного между объектами
- Характеристика материалов как проводников или изоляторов на основе их электрических свойств
- Описать электрическую поляризацию и индукционную зарядку
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты
- (5) Учащийся знает природу сил в физическом мире.
 Ожидается, что студент:
Ожидается, что студент:
- (С) описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними; и
- (Э) охарактеризовать материалы как проводники или изоляторы на основе их электрических свойств.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием Электрический заряд, а также следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.Ожидается, что студент:
- (С) описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними; и
- (Э) охарактеризовать материалы как проводники или изоляторы на основе их электрических свойств.
Основные термины раздела
| проводимость | проводник | электрон | индукция |
| изолятор | закон сохранения заряда | поляризация | протон |
Электрический заряд
Вы можете знать кого-то, у кого есть электрическая личность , что обычно означает, что этот человек привлекает других людей. Это высказывание основано на электрическом заряде — свойстве материи, которое заставляет объекты притягиваться или отталкиваться друг от друга. Электрический заряд бывает двух видов, которые мы называем положительными, и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются. Таким образом, два положительных заряда отталкиваются друг от друга, как и два отрицательных заряда. Положительный заряд и отрицательный заряд притягиваются друг к другу.
Это высказывание основано на электрическом заряде — свойстве материи, которое заставляет объекты притягиваться или отталкиваться друг от друга. Электрический заряд бывает двух видов, которые мы называем положительными, и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются. Таким образом, два положительных заряда отталкиваются друг от друга, как и два отрицательных заряда. Положительный заряд и отрицательный заряд притягиваются друг к другу.
Откуда мы знаем, что существует два типа электрического заряда? Когда различные материалы трутся друг о друга контролируемым образом, определенные комбинации материалов всегда приводят к чистому заряду одного типа на одном материале и чистому заряду противоположного типа на другом материале.По соглашению мы называем один тип заряда положительным, а другой — отрицательным. Например, если потереть стекло о шелк, то стекло станет положительно заряженным, а шелк — отрицательно.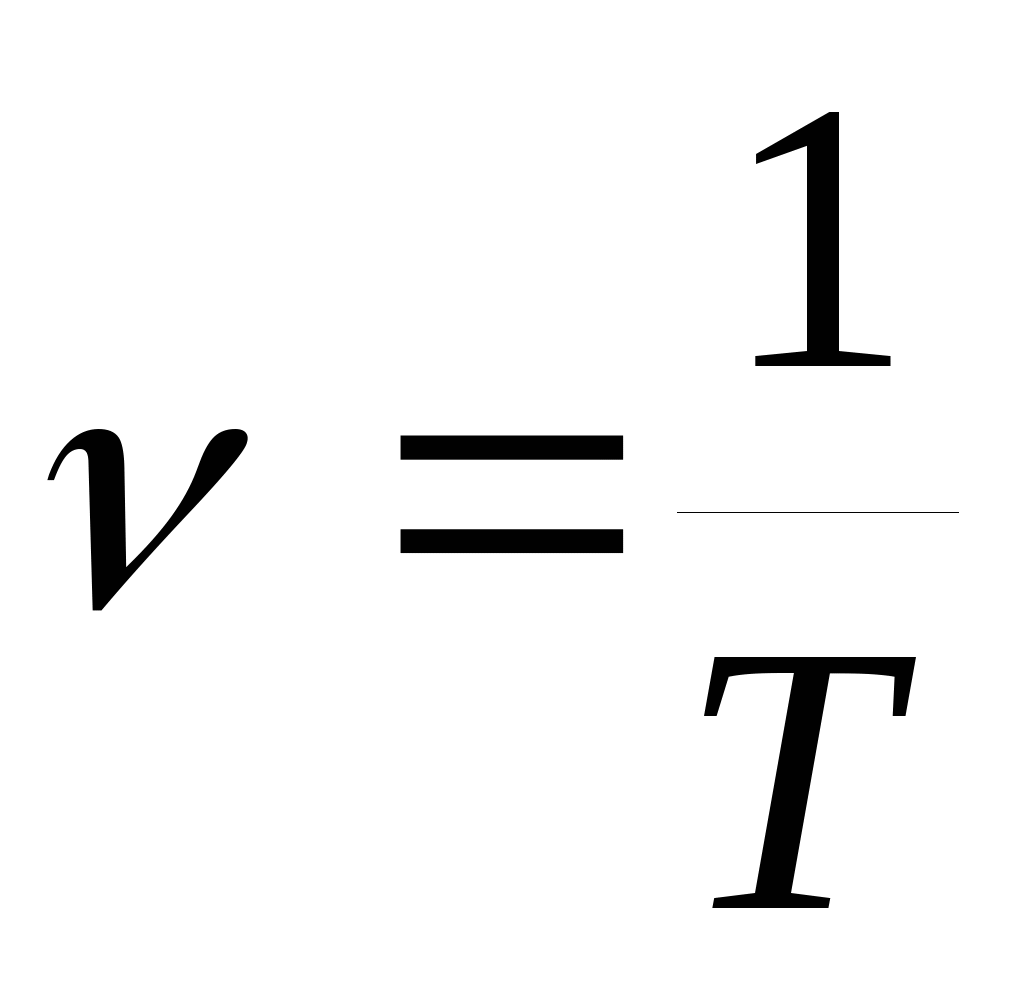 Так как стекло и шелк имеют противоположные заряды, они притягиваются друг к другу, как белье, протертое друг о друга в сушилке. Две стеклянные палочки, натертые таким образом о шелк, будут отталкиваться друг от друга, потому что каждая палочка имеет положительный заряд. Точно так же две шелковые ткани, натертые таким образом, будут отталкивать друг друга, потому что обе ткани имеют отрицательный заряд.На рис. 18.2 показано, как эти простые материалы можно использовать для изучения природы силы между зарядами.
Так как стекло и шелк имеют противоположные заряды, они притягиваются друг к другу, как белье, протертое друг о друга в сушилке. Две стеклянные палочки, натертые таким образом о шелк, будут отталкиваться друг от друга, потому что каждая палочка имеет положительный заряд. Точно так же две шелковые ткани, натертые таким образом, будут отталкивать друг друга, потому что обе ткани имеют отрицательный заряд.На рис. 18.2 показано, как эти простые материалы можно использовать для изучения природы силы между зарядами.
Фигура 18.2 Стеклянная палочка становится положительно заряженной при трении о шелк, тогда как шелк становится отрицательно заряженным. а) Стеклянная палочка притягивается к шелку, потому что их заряды противоположны. б) Две одинаково заряженные стеклянные палочки отталкиваются. в) Две одинаково заряженные шелковые ткани отталкиваются.
Поддержка учителей
Поддержка учителей
Демонстрация учителя
Подготовьте демонстрацию статического электричества. Простая демонстрация может состоять в том, чтобы зарядить стеклянную палочку или расческу, потирая ее о шерсть, шелк или другую ткань, а затем зарядить надутый шарик, потирая его о рубашку или волосы. Поместите воздушный шар на непроводящую электричество поверхность стола и используйте стеклянную палочку или расческу, чтобы оттолкнуть воздушный шар и заставить его катиться по поверхности стола. Развлеките учащихся, толкая воздушный шар сначала в одном направлении, а затем быстро перемещая стеклянную палочку или гребенку к противоположной стороне воздушного шара, чтобы заставить его замедлиться, а затем двигаться в противоположном направлении.Спросите, какая сила действует между шариком и стеклянной палочкой или гребнем (сила отталкивания).
Простая демонстрация может состоять в том, чтобы зарядить стеклянную палочку или расческу, потирая ее о шерсть, шелк или другую ткань, а затем зарядить надутый шарик, потирая его о рубашку или волосы. Поместите воздушный шар на непроводящую электричество поверхность стола и используйте стеклянную палочку или расческу, чтобы оттолкнуть воздушный шар и заставить его катиться по поверхности стола. Развлеките учащихся, толкая воздушный шар сначала в одном направлении, а затем быстро перемещая стеклянную палочку или гребенку к противоположной стороне воздушного шара, чтобы заставить его замедлиться, а затем двигаться в противоположном направлении.Спросите, какая сила действует между шариком и стеклянной палочкой или гребнем (сила отталкивания).
Ученым потребовалось много времени, чтобы выяснить, что скрывается за этими двумя типами зарядов. Само слово электрический происходит от греческого слова elektron для янтаря, потому что древние греки заметили, что янтарь при трении мехом притягивает сухую солому. Почти 2000 лет спустя английский физик Уильям Гилберт предложил модель, объясняющую эффект электрического заряда таинственной электрической жидкостью, которая переходит от одного объекта к другому.Эта модель обсуждалась в течение нескольких сотен лет, но в 1897 г. работа английского физика Дж. Дж. Томсона и французского физика Жана Перрена окончательно положила конец ей. Наряду со многими другими, Томсон и Перрин изучали таинственные катодные лучи , которые, как было известно в то время, состоят из частиц меньше самого маленького атома. Перрин показал, что катодные лучи на самом деле несут отрицательный электрический заряд. Позже работа Томсона привела его к заявлению: «Я не вижу выхода из вывода, что [катодные лучи] представляют собой заряды отрицательного электричества, переносимые частицами материи.
Почти 2000 лет спустя английский физик Уильям Гилберт предложил модель, объясняющую эффект электрического заряда таинственной электрической жидкостью, которая переходит от одного объекта к другому.Эта модель обсуждалась в течение нескольких сотен лет, но в 1897 г. работа английского физика Дж. Дж. Томсона и французского физика Жана Перрена окончательно положила конец ей. Наряду со многими другими, Томсон и Перрин изучали таинственные катодные лучи , которые, как было известно в то время, состоят из частиц меньше самого маленького атома. Перрин показал, что катодные лучи на самом деле несут отрицательный электрический заряд. Позже работа Томсона привела его к заявлению: «Я не вижу выхода из вывода, что [катодные лучи] представляют собой заряды отрицательного электричества, переносимые частицами материи.
Потребовалось несколько лет дальнейших экспериментов, чтобы подтвердить интерпретацию экспериментов Томсона, но наука фактически открыла частицу, которая несет фундаментальную единицу отрицательного электрического заряда. Теперь мы знаем эту частицу как электрон.
Теперь мы знаем эту частицу как электрон.
электрически нейтральны, что означает, что они несут одинаковое количество положительного и отрицательного заряда, поэтому их суммарный заряд равен нулю. Поскольку электроны отрицательны, какая-то другая часть атома должна содержать положительный заряд.Томсон выдвинул так называемую модель сливового пудинга , в которой он описал атомы как состоящие из тысяч электронов, плавающих вокруг в туманной массе положительного заряда, как показано на изображении слева на рис. 18.3. Его ученик, Эрнест Резерфорд, изначально считал эту модель правильной и использовал ее (наряду с другими моделями), чтобы попытаться понять результаты своих экспериментов по бомбардировке золотой фольги альфа- частицами (то есть атомами гелия, лишенными своих электронов).Однако результаты не подтвердили модель Томсона, а скорее разрушили ее! Резерфорд обнаружил, что большая часть пространства, занимаемого атомами золота, на самом деле пуста и что почти вся материя каждого атома сосредоточена в крошечном чрезвычайно плотном ядре, как показано на рисунке справа на рис. 18.3. Позже было обнаружено, что атомное ядро содержит частицы, называемые протонами, каждый из которых несет единицу положительного электрического заряда.
18.3. Позже было обнаружено, что атомное ядро содержит частицы, называемые протонами, каждый из которых несет единицу положительного электрического заряда.
Фигура 18,3 На левом рисунке показана модель сливового пудинга Томпсона, в которой электроны плавают в туманной массе положительного заряда.На правом рисунке показана модель Резерфорда, в которой электроны вращаются вокруг крошечного массивного ядра. Обратите внимание, что размер ядра на этом рисунке сильно преувеличен. Если бы он был нарисован в масштабе относительно размера электронных орбит, ядро не было бы видно на этом рисунке невооруженным глазом. Кроме того, насколько наука может обнаружить в настоящее время, электроны являются точечными частицами, а это означает, что они вообще не имеют размера!
Таким образом, протоны и электроны являются фундаментальными частицами, несущими электрический заряд.Каждый протон несет одну единицу положительного заряда, а каждый электрон несет одну единицу отрицательного заряда. С наибольшей точностью, которую может обеспечить современная технология, заряд, переносимый протоном, равен , в точности , что противоположно заряду электрона. Единицей электрического заряда в СИ является кулон (сокращенно «C»), названная в честь французского физика Шарля Огюстена де Кулона, изучавшего силу между заряженными объектами. Протон переносит +1,602×10-19°С+1.602×10−19С. а электрон переносит -1,602×10-19C, -1,602×10-19C, . Число n протонов, необходимое для получения +1,00 C, равно
С наибольшей точностью, которую может обеспечить современная технология, заряд, переносимый протоном, равен , в точности , что противоположно заряду электрона. Единицей электрического заряда в СИ является кулон (сокращенно «C»), названная в честь французского физика Шарля Огюстена де Кулона, изучавшего силу между заряженными объектами. Протон переносит +1,602×10-19°С+1.602×10−19С. а электрон переносит -1,602×10-19C, -1,602×10-19C, . Число n протонов, необходимое для получения +1,00 C, равно
18.1
Столько же электронов требуется для создания электрического заряда -1,00 Кл. Основная единица заряда часто представляется как e . Таким образом, заряд протона равен 90 616 e 90 142 , а заряд электрона равен −90 616 e 90 142 .Математически e=+1,602×10-19C. e=+1,602×10-19C.
e=+1,602×10-19C.
Ссылки на физику
Измерение основного электрического заряда
Американский физик Роберт Милликен (1868–1953) и его ученик Харви Флетчер (1884–1981) первыми относительно точно измерили основную единицу заряда электрона. Они разработали то, что сейчас является классическим экспериментом, проводимым студентами. Эксперимент Милликена с каплей масла показан на рис. 18.4. Эксперимент включает в себя некоторые концепции, которые будут представлены позже, но основная идея заключается в том, что тонкий масляный туман распыляется между двумя пластинами, которые могут быть заряжены известным количеством противоположного заряда.Некоторые капли масла при распылении накапливают избыточный отрицательный заряд и притягиваются к положительному заряду верхней пластины и отталкиваются от отрицательного заряда нижней пластины. Регулируя заряд на этих пластинах до тех пор, пока вес капли масла не уравновешивается электрическими силами, можно довольно точно определить суммарный заряд капли масла.
Фигура 18,4 Эксперимент с каплями масла включал распыление тонкого тумана масла между двумя металлическими пластинами, заряженными противоположными зарядами.Зная массу капель масла и регулируя электрический заряд пластин, можно точно определить заряд капель масла.
Милликен и Флетчер обнаружили, что капли будут накапливать заряд дискретными единицами порядка -1,59×10-19C, -1,59×10-19C, что находится в пределах 1 процента от современного значения -1,60×10-19C.-1,60× 10-19С. Хотя эта разница может показаться совсем небольшой, на самом деле она в пять раз больше, чем возможная ошибка, о которой сообщил Милликен в своих результатах!
Поскольку заряд электрона является фундаментальной константой природы, определение его точного значения очень важно для всей науки.Это создавало давление на Милликена и его последователей, раскрывающее некоторые не менее важные аспекты человеческой натуры.
Во-первых, Милликен взял на себя исключительную ответственность за эксперимент и был удостоен Нобелевской премии по физике 1923 года за эту работу, хотя его ученик Харви Флетчер, по-видимому, внес значительный вклад в работу.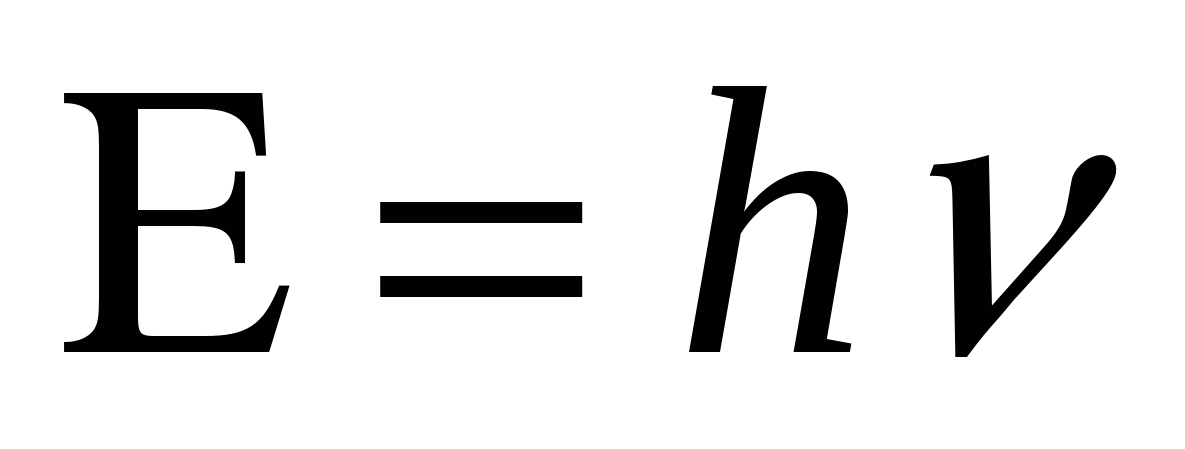 Незадолго до своей смерти в 1981 году Флетчер сообщил, что Милликен вынудил его отдать должное Милликену за работу, в обмен на что Милликен способствовал карьере Флетчера в Bell Labs.
Незадолго до своей смерти в 1981 году Флетчер сообщил, что Милликен вынудил его отдать должное Милликену за работу, в обмен на что Милликен способствовал карьере Флетчера в Bell Labs.
Другой великий ученый, Ричард Фейнман, отмечает, что многие ученые, измерившие фундаментальный заряд после Милликена, не хотели сообщать о значениях, которые сильно отличались от значения Милликена. История показывает, что более поздние измерения медленно ползли вверх от значения Милликена, пока не остановились на современном значении. Почему сразу не нашли ошибку и не исправили значение, спрашивает Фейнман. Очевидно, найдя значение, превышающее пользующееся большим уважением значение, найденное Милликеном, ученые будут искать возможные ошибки, которые могут снизить его значение, чтобы оно лучше согласовывалось со значением Милликена.Это раскрывает важный психологический вес, который несут предвзятые представления, и показывает, как трудно их опровергнуть. Ученые, какими бы преданными логике и данным они ни были, очевидно, так же уязвимы для этого аспекта человеческой природы, как и все остальные. Урок здесь заключается в том, что, хотя хорошо относиться к новым результатам скептически, вы не должны сбрасывать со счетов их только потому, что они не согласуются с общепринятым мнением. Если ваши рассуждения верны и ваши данные надежны, вывод, которого требуют эти данные, необходимо серьезно обдумать, даже если этот вывод не согласуется с общепринятой истиной .
Урок здесь заключается в том, что, хотя хорошо относиться к новым результатам скептически, вы не должны сбрасывать со счетов их только потому, что они не согласуются с общепринятым мнением. Если ваши рассуждения верны и ваши данные надежны, вывод, которого требуют эти данные, необходимо серьезно обдумать, даже если этот вывод не согласуется с общепринятой истиной .
Проверка захвата
Предположим, что Милликен наблюдал каплю масла, несущую три фундаментальные единицы заряда. Каков будет чистый заряд этой капли масла?
- −4,81 × 10 −19 С
- −1,602 × 10 −19 С
- 1,602 × 10 −19 С
- 4,81 × 10 −19 С
Снап Лаборатория
Как и в отличие от обвинений
В этом упражнении исследуется отталкивание и притяжение, вызванное статическим электрическим зарядом.
- Клейкая лента
- Непроводящая поверхность, например пластиковый стол или стул
Инструкции
Процедура для части (a)
- Подготовьте два куска ленты длиной около 4 см. Чтобы сделать ручку, согните один конец примерно на 0,5 см вдвое, чтобы липкая сторона склеилась.
- Прикрепите кусочки ленты бок о бок к неметаллической поверхности, такой как столешница или сиденье стула, как показано на рис. 18.5 (а).
- Отклейте оба куска ленты и повесьте их вниз, держа за ручки, как показано на рис. 18.5(б). Если лента изгибается вверх и прилипает к руке, попробуйте использовать более короткий кусок ленты или просто встряхните ленту, чтобы она больше не прилипала к руке.
- Теперь медленно соедините два куска ленты вместе, как показано на рис. 18.5(c). Что случается?
Фигура 18,5
Процедура для части (b)
- Наклейте один кусок ленты на неметаллическую поверхность и наклейте второй кусок ленты поверх первого, как показано на рис.
 18.6(а).
18.6(а). - Медленно отделите две части, потянув за ручку нижней части.
- Аккуратно проведите пальцем по верхней части второго куска ленты (т. е. по нелипкой стороне), как показано на рис. 18.6(b).
- Разделите два куска ленты, потянув за их ручки, как показано на рис. 18.6(c).
- Медленно соедините два куска ленты. Что случается?
Фигура 18,6
Проверка захвата
Почему на шаге 4 два куска ленты оттолкнулись друг от друга? В шаге 9, почему они привлекли друг друга?
- Одноименные заряды притягиваются, а разноименные отталкиваются.
- Одноименные заряды отталкиваются, а разноименные притягиваются.
- Ленты с положительным зарядом отталкиваются, а ленты с отрицательным зарядом притягиваются друг к другу.
- Ленты с отрицательным зарядом отталкиваются, а ленты с положительным зарядом притягиваются друг к другу.
Сохранение заряда
Поддержка учителей
Поддержка учителей
[BL][OL]Обсудите, что подразумевается под сохранением в физическом смысле.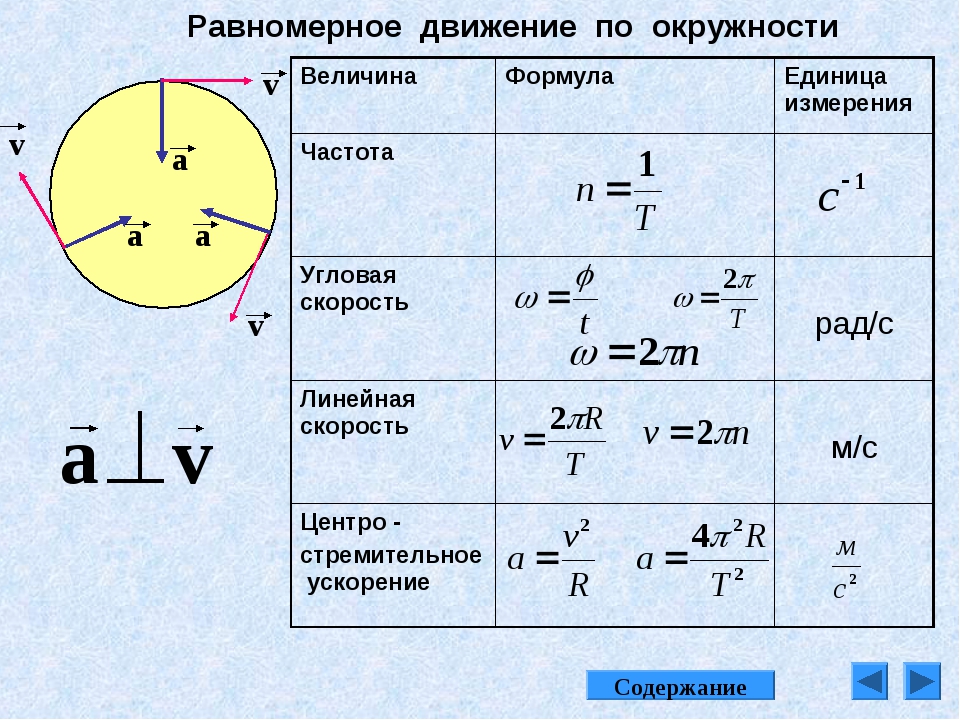 Укажите, как законы сохранения служат правилами учета, которые позволяют нам отслеживать определенные величины.Это похоже на знание того, сколько студентов находится на экскурсии, и использование этой информации, чтобы убедиться, что никто из студентов не пропал без вести. Поскольку ученики не могут раствориться в воздухе, подсчет учеников позволяет учителю узнать, отсутствуют ли какие-либо ученики. Если их нет, то они должны быть где-то еще, и можно начинать поиски.
Укажите, как законы сохранения служат правилами учета, которые позволяют нам отслеживать определенные величины.Это похоже на знание того, сколько студентов находится на экскурсии, и использование этой информации, чтобы убедиться, что никто из студентов не пропал без вести. Поскольку ученики не могут раствориться в воздухе, подсчет учеников позволяет учителю узнать, отсутствуют ли какие-либо ученики. Если их нет, то они должны быть где-то еще, и можно начинать поиски.
[AL]Спросите, с какими еще законами сохранения они встречались в физике, и обсудите, как эти законы используются.
Поскольку основные положительные и отрицательные единицы заряда переносятся протонами и электронами, мы ожидаем, что общий заряд не может измениться ни в одной системе, которую мы определяем.Другими словами, хотя мы можем перемещать заряд, мы не можем создать или разрушить его. Это должно быть верно при условии, что мы не создаем и не уничтожаем протоны или электроны в нашей системе. Однако в двадцатом веке ученые научились создавать и уничтожать электроны и протоны, но обнаружили, что заряд все еще сохраняется. Многие эксперименты и солидные теоретические аргументы возвели эту идею в статус закона. Закон сохранения заряда гласит, что электрический заряд нельзя создать или уничтожить.
Многие эксперименты и солидные теоретические аргументы возвели эту идею в статус закона. Закон сохранения заряда гласит, что электрический заряд нельзя создать или уничтожить.
Закон сохранения заряда очень полезен. Это говорит нам о том, что чистый заряд в системе одинаков до и после любого взаимодействия внутри системы. Конечно, мы должны следить за тем, чтобы в процессе взаимодействия в систему не поступал внешний заряд, а из системы не уходил внутренний заряд. Математически сохранение заряда можно выразить как
qinitial=qfinal.qinitial=qfinal.18.2
, где qinitialqinitial — чистый заряд системы до взаимодействия, а qfinal,qfinal — чистый заряд после взаимодействия.
Рабочий пример
Какой недостающий заряд?
На рис. 18.7 показаны две сферы, изначально имеющие заряд +4 Кл и +8 Кл. После взаимодействия (которое может заключаться в том, что они просто касаются друг друга) синяя сфера имеет заряд +10 Кл, а красная сфера имеет неизвестное количество заряда. Используйте закон сохранения заряда, чтобы найти окончательный заряд на красной сфере.
Используйте закон сохранения заряда, чтобы найти окончательный заряд на красной сфере.
Стратегия
Чистый начальный заряд системы равен qinitial=+4C+8C=+12Cqinitial=+4C+8C=+12C .Итоговый конечный заряд системы равен qfinal=+10C+qredqfinal=+10C+qred, где qredqred — конечный заряд на красной сфере. Сохранение заряда говорит нам, что qinitial=qfinalqinitial=qfinal, поэтому мы можем найти qredqred.
Решение
Приравнивание qinitialqinitial и qfinalqfinal и решение для qredqred дает
qначальный=qконечный+12C=+10C+qкрасный.+2C=qкрасный.qначальный=qконечный+12C=+10C+qкрасный.+2C=qкрасный.18,3
Красная сфера имеет +2 C заряда.
Фигура 18,7 Две сферы, одна синяя и одна красная, изначально имеют заряд +4 C и +8 C соответственно. После взаимодействия двух сфер синяя сфера имеет заряд +10 Кл. Закон сохранения заряда позволяет найти конечный заряд qredqred на красной сфере.Обсуждение
Как и все законы сохранения, закон сохранения заряда представляет собой учетную схему, которая помогает нам отслеживать электрический заряд.
Практические задачи
1 .Какое уравнение описывает сохранение заряда?
- q начальный = q конечный = постоянный
- q начальный = q окончательный = 0
- q начальный − q окончательный = 0
- q начальный / q окончательный = постоянный
В изолированной системе есть два объекта с зарядами q_{1} и q_{2}. Если объект 1 потеряет половину своего заряда, каков будет окончательный заряд объекта 2?
Проводники и изоляторы
Поддержка учителей
Поддержка учителей
[BL]Попросите учащихся определить значение проводника , и изолятора . Объясните, как эти термины используются в физике для обозначения материалов, пропускающих какое-то количество и не пропускающих.
Объясните, как эти термины используются в физике для обозначения материалов, пропускающих какое-то количество и не пропускающих.
[OL]Спросите учащихся, сталкивались ли они с проводниками и изоляторами в своей повседневной жизни. Каковы свойства этих материалов? Будьте готовы обсуждать и различать теплопроводники и изоляторы.
[AL]Спросите, помнят ли учащиеся другие проводники и изоляторы в физике. Обсудите, как теплоизоляторы и проводники функционируют в отношении тепловой энергии.
Материалы можно классифицировать в зависимости от того, позволяют ли они перемещать заряд. Если заряд может легко перемещаться через материал, например металлы, то такие материалы называются проводниками. Это означает, что заряд может быть проведен (т. е. перемещен) через материал довольно легко. Если заряд не может проходить через материал, например резину, то такой материал называется изолятором.
Большинство материалов являются изоляторами. Их атомы и молекулы крепче держатся за свои электроны, поэтому электронам трудно перемещаться между атомами. Однако это возможно. Обладая достаточной энергией, можно заставить электроны двигаться через изолятор. Однако изолятор часто физически разрушается в процессе. В металлах внешние электроны слабо связаны со своими атомами, поэтому не требуется много энергии, чтобы заставить электроны двигаться через металл. Такие металлы, как медь, серебро и алюминий, являются хорошими проводниками. К изоляционным материалам относятся пластик, стекло, керамика и дерево.
Однако это возможно. Обладая достаточной энергией, можно заставить электроны двигаться через изолятор. Однако изолятор часто физически разрушается в процессе. В металлах внешние электроны слабо связаны со своими атомами, поэтому не требуется много энергии, чтобы заставить электроны двигаться через металл. Такие металлы, как медь, серебро и алюминий, являются хорошими проводниками. К изоляционным материалам относятся пластик, стекло, керамика и дерево.
Проводимость некоторых материалов занимает промежуточное положение между проводниками и изоляторами.Они называются полупроводниками . Их можно сделать проводящими при правильных условиях, которые могут включать температуру, чистоту материала и силу, приложенную для проталкивания через них электронов. Поскольку мы можем контролировать, являются ли полупроводники проводниками или изоляторами, эти материалы широко используются в компьютерных микросхемах. Наиболее часто используемым полупроводником является кремний. На рис. 18.8 показаны различные материалы, расположенные в соответствии с их способностью проводить электроны.
На рис. 18.8 показаны различные материалы, расположенные в соответствии с их способностью проводить электроны.
Фигура 18.8 Материалы можно классифицировать по их способности проводить электрический заряд. Косая черта на стрелке означает, что между проводниками, полупроводниками и изоляторами существует очень большой разрыв в проводимости, но рисунок сжат, чтобы поместиться на странице. Цифры под материалами дают их удельное сопротивление в Ом•м (о котором вы узнаете ниже). Удельное сопротивление является мерой того, насколько трудно заставить заряд двигаться через данный материал.
Поддержка учителей
Поддержка учителей
Укажите, что шкала нелинейна, что означает, что проводимость изоляторов намного, намного меньше, чем у проводников.Также отметьте, что полупроводники часто действуют как изоляторы или проводники, но не как материалы с проводимостью, которая находится между изоляторами и проводниками.
Что произойдет, если на проводящий объект поместить избыточный отрицательный заряд? Поскольку одинаковые заряды отталкиваются друг от друга, они будут сталкиваться друг с другом до тех пор, пока не окажутся настолько далеко друг от друга, насколько это возможно. Поскольку заряд может двигаться в проводнике, он движется к внешним поверхностям объекта. На рис. 18.9(а) схематично показано, как избыточный отрицательный заряд равномерно распределяется по внешней поверхности металлического шара.
Что произойдет, если то же самое сделать с изолирующим предметом? Электроны по-прежнему отталкиваются друг от друга, но они не могут двигаться, потому что материал является изолятором. Таким образом, избыточный заряд остается на месте и не распределяется по объекту. На рис. 18.9(b) показана эта ситуация.
Фигура
18,9
(а) Проводящая сфера с избыточным отрицательным зарядом (т. е. электронами). Электроны отталкиваются друг от друга и расходятся, чтобы покрыть внешнюю поверхность сферы. (b) Изолирующая сфера с избыточным отрицательным зарядом. Электроны не могут двигаться, поэтому остаются на своих первоначальных позициях.
(b) Изолирующая сфера с избыточным отрицательным зарядом. Электроны не могут двигаться, поэтому остаются на своих первоначальных позициях.
Поддержка учителей
Поддержка учителей
Обратите внимание, что накопление статического электричества не остается на объекте навсегда. Спросите учащихся, как статический заряд может выйти из объекта. Обратите внимание, что накопление статического электричества рассеивается быстрее во влажные дни, чем в сухие.
Передача и разделение заряда
Поддержка учителей
Поддержка учителей
[BL][OL]Спросите, как концепция статического электричества может быть совместима с переносом заряда.Разве перенос заряда не есть движение заряда, что противоречит статике?
[AL] Попросите учащихся дать определение разделения заряда. Приготовьтесь объяснить, почему это не означает расщепления электронов.
Большинство объектов, с которыми мы имеем дело, электрически нейтральны, что означает, что они имеют одинаковое количество положительных и отрицательных зарядов. Однако перенести отрицательный заряд с одного объекта на другой довольно легко. При переносе отрицательного заряда с одного объекта на другой остается избыток положительного заряда.Откуда мы знаем, что отрицательный заряд является мобильным зарядом? Положительный заряд несет протон, прочно застрявший в ядре атома, а атомы застряли в твердых материалах. Электроны, несущие отрицательный заряд, гораздо легче удалить из своих атомов или молекул, и поэтому их легче перенести.
Электрический заряд может передаваться несколькими способами. Одним из простейших способов передачи заряда является зарядка контактом, при котором поверхности двух предметов, изготовленных из разных материалов, находятся в тесном контакте.Если один из материалов удерживает электроны сильнее, чем другой, то при разделении материалов он уносит с собой некоторое количество электронов. Трение двух поверхностей друг о друга увеличивает передачу электронов, потому что это создает более тесный контакт между материалами. Он также служит для представления свежего материала с полным запасом электронов для другого материала. Таким образом, когда вы идете по ковру в сухой день, ваша обувь трется о ковер, и ваша обувь удаляет с ковра некоторое количество электронов.В результате на вашей обуви появляется избыток отрицательного заряда. Когда вы прикасаетесь к дверной ручке, часть вашего избытка электронов переносится на нейтральную дверную ручку, создавая небольшую искру.
Трение двух поверхностей друг о друга увеличивает передачу электронов, потому что это создает более тесный контакт между материалами. Он также служит для представления свежего материала с полным запасом электронов для другого материала. Таким образом, когда вы идете по ковру в сухой день, ваша обувь трется о ковер, и ваша обувь удаляет с ковра некоторое количество электронов.В результате на вашей обуви появляется избыток отрицательного заряда. Когда вы прикасаетесь к дверной ручке, часть вашего избытка электронов переносится на нейтральную дверную ручку, создавая небольшую искру.
Прикосновение рукой к дверной ручке демонстрирует второй способ передачи электрического заряда — зарядку за счет проводимости. Этот перенос происходит потому, что одноименные заряды отталкиваются, и поэтому лишние электроны, которые вы подобрали с ковра, хотят быть как можно дальше друг от друга. Некоторые из них перемещаются к дверной ручке, где распределяются по внешней поверхности металла.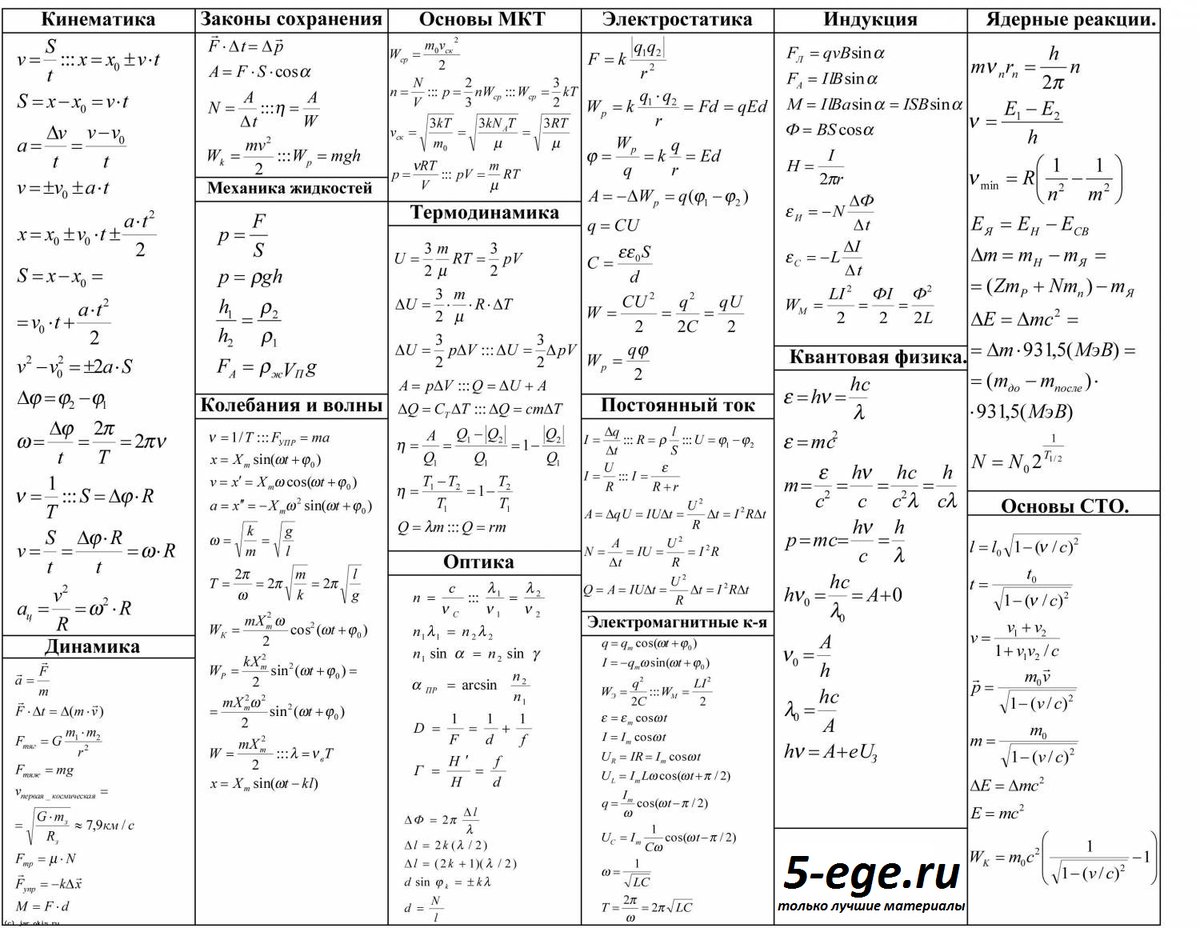 Другой пример зарядки за счет проводимости показан в верхней строке рис. 18.10. Металлический шар со 100 избыточными электронами касается металлического шара с 50 избыточными электронами, поэтому 25 электронов из первого шара переходят во второй шар. Каждая сфера заканчивается 75 избыточными электронами.
Другой пример зарядки за счет проводимости показан в верхней строке рис. 18.10. Металлический шар со 100 избыточными электронами касается металлического шара с 50 избыточными электронами, поэтому 25 электронов из первого шара переходят во второй шар. Каждая сфера заканчивается 75 избыточными электронами.
То же рассуждение применимо к переносу положительного заряда. Однако, поскольку положительный заряд практически не может перемещаться в твердых телах, он передается за счет движения отрицательного заряда в противоположном направлении.Например, рассмотрим нижнюю строку рис. 18.10. Первая металлическая сфера имеет 100 избыточных протонов и касается металлической сферы с 50 избыточными протонами, поэтому вторая сфера передает 25 электронов первой сфере. Эти 25 дополнительных электронов электрически нейтрализуют 25 протонов, так что первая металлическая сфера остается с 75 избыточными протонами. Это показано в нижней строке рисунка 18.10. Вторая металлическая сфера потеряла 25 электронов, поэтому у нее есть еще 25 избыточных протонов, всего 75 избыточных протонов. Конечный результат будет таким же, если мы учтем, что первый шар передал первому шару суммарный положительный заряд, равный заряду 25 протонов.
Конечный результат будет таким же, если мы учтем, что первый шар передал первому шару суммарный положительный заряд, равный заряду 25 протонов.
Фигура 18.10 В верхнем ряду металлическая сфера с 100 избыточными электронами передает 25 электронов металлической сфере с избыточными 50 электронами. После переноса обе сферы имеют по 75 избыточных электронов. В нижнем ряду металлическая сфера с 100 избыточными протонами получает 25 электронов от шара с 50 избыточными протонами. После переноса обе сферы имеют по 75 избыточных протонов.
Поддержка учителей
Поддержка учителей
Укажите, почему общий заряд в каждый момент одинаков.Обсудите, почему перемещение электронов вправо эквивалентно перемещению той же величины положительного заряда влево, но обязательно уточните, что в большинстве случаев в твердых телах движутся только отрицательные заряды.
[BL][OL]Обсудите значение поляризации на повседневном языке.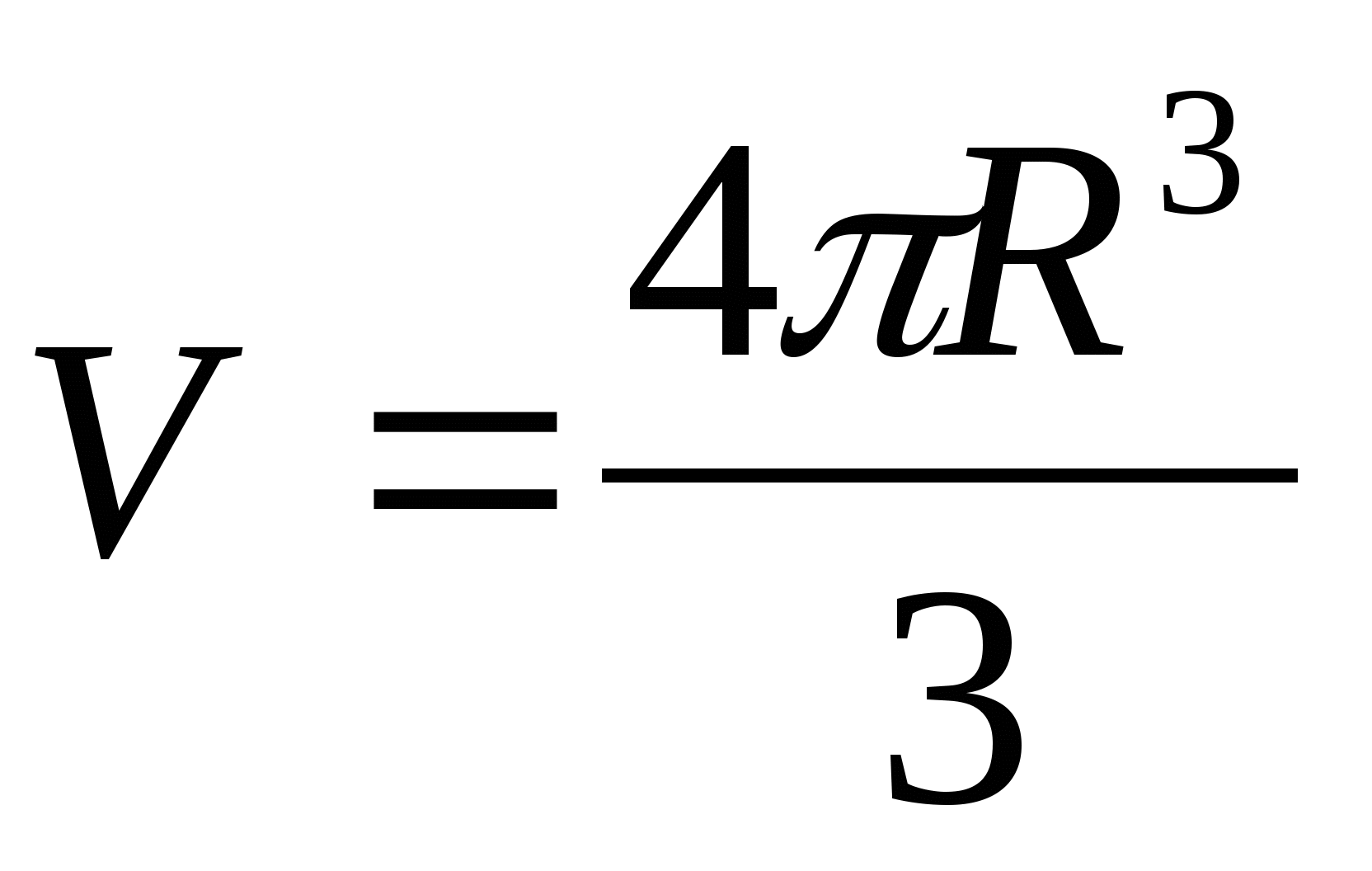 Например, обсудите, что подразумевается под поляризационными дебатами или поляризованным Конгрессом. Сравните и сопоставьте повседневное значение с физическим значением.
Например, обсудите, что подразумевается под поляризационными дебатами или поляризованным Конгрессом. Сравните и сопоставьте повседневное значение с физическим значением.
[AL]Спросите, какие еще примеры поляризации они могут вспомнить из повседневной жизни.
В этом обсуждении вы можете задаться вопросом, как избыточные электроны первоначально попали из вашей обуви в вашу руку, чтобы создать искру, когда вы коснулись дверной ручки. Ответ заключается в том, что 90 616 электронов, а не 90 142, на самом деле переместились с вашей обуви на ваши руки. Вместо этого, поскольку одинаковые заряды отталкиваются друг от друга, избыточные электроны на вашей обуви просто отталкивают часть электронов в ваших ногах. Таким образом, электроны, выбитые из ваших ног, переместились в вашу ногу и, в свою очередь, оттолкнули некоторые электроны в вашей ноге.Этот процесс продолжался во всем вашем теле, пока распределение избыточных электронов не покрыло конечности вашего тела. Таким образом, ваша голова, ваши руки, кончик вашего носа и так далее получили свои дозы избыточных электронов, которые были вытеснены из их нормального положения. Все это было результатом того, что избыток электронов на вашей обуви выталкивал электроны из ваших ног.
Все это было результатом того, что избыток электронов на вашей обуви выталкивал электроны из ваших ног.
Этот тип разделения зарядов называется поляризацией. Как только лишние электроны покидают вашу обувь (путем стирания об пол или уноса во влажном воздухе), распределение электронов в вашем теле возвращается к норме.Каждая часть вашего тела снова электрически нейтральна (то есть с нулевым избыточным зарядом).
Явление поляризации показано на рис. 18.1. Ребенок накопил лишний положительный заряд, скользя по горке. Этот избыточный заряд отталкивается и таким образом распределяется по конечностям тела ребенка, особенно по волосам. В результате волосы встают дыбом, потому что избыточный отрицательный заряд на каждой пряди отталкивает избыточный положительный заряд на соседних пряди.
Поляризация может использоваться для зарядки объектов.Рассмотрим две металлические сферы, показанные на рис. 18.11. Сферы электрически нейтральны, поэтому они несут одинаковое количество положительного и отрицательного заряда. На верхнем рисунке (рис. 18.11(а)) две сферы соприкасаются, и положительный и отрицательный заряды равномерно распределены по двум сферам. Затем мы подходим к стеклянному стержню, несущему избыточный положительный заряд, что можно сделать, потирая стеклянный стержень шелком, как показано на рис. 18.11(b). Поскольку противоположные заряды притягиваются друг к другу, отрицательный заряд притягивается к стеклянной палочке, оставляя избыточный положительный заряд на противоположной стороне правой сферы.Это пример зарядки за счет индукции, при которой заряд создается путем приближения к заряженному объекту второго объекта для создания неуравновешенного заряда во втором объекте. Если мы затем разделим две сферы, как показано на рис. 18.11(c), избыточный заряд останется на каждой сфере. Левая сфера теперь имеет избыточный отрицательный заряд, а правая сфера имеет избыточный положительный заряд. Наконец, на нижнем рисунке стержень убран, и противоположные заряды притягиваются друг к другу, поэтому они движутся как можно ближе друг к другу.
На верхнем рисунке (рис. 18.11(а)) две сферы соприкасаются, и положительный и отрицательный заряды равномерно распределены по двум сферам. Затем мы подходим к стеклянному стержню, несущему избыточный положительный заряд, что можно сделать, потирая стеклянный стержень шелком, как показано на рис. 18.11(b). Поскольку противоположные заряды притягиваются друг к другу, отрицательный заряд притягивается к стеклянной палочке, оставляя избыточный положительный заряд на противоположной стороне правой сферы.Это пример зарядки за счет индукции, при которой заряд создается путем приближения к заряженному объекту второго объекта для создания неуравновешенного заряда во втором объекте. Если мы затем разделим две сферы, как показано на рис. 18.11(c), избыточный заряд останется на каждой сфере. Левая сфера теперь имеет избыточный отрицательный заряд, а правая сфера имеет избыточный положительный заряд. Наконец, на нижнем рисунке стержень убран, и противоположные заряды притягиваются друг к другу, поэтому они движутся как можно ближе друг к другу.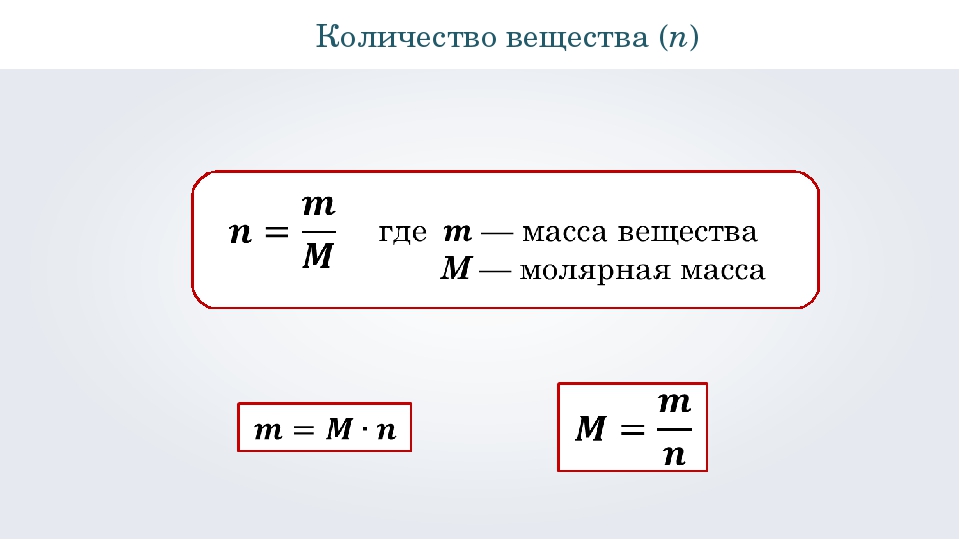
Фигура 18.11 а) Два нейтральных проводящих шара касаются друг друга, поэтому заряд равномерно распределен по обоим шарам. б) Приближается положительно заряженный стержень, который притягивает к себе отрицательные заряды, оставляя на правой сфере избыточный положительный заряд. (c) Сферы разделены. Каждая сфера теперь несет одинаковую величину избыточного заряда. (d) Когда положительно заряженный стержень удаляется, избыточный отрицательный заряд на левой сфере притягивается к избыточному положительному заряду на правой сфере.
Поддержка учителей
Поддержка учителей
Обсудите аналогичную ситуацию с изолирующими сферами. Укажите, как сферы остаются нейтральными, несмотря на то, что они поляризованы на рисунках (b) и (c).
Веселье в физике
Создайте искру на научной ярмарке
Генераторы Ван де Граафа — это устройства, которые используются не только для серьезных физических исследований, но и для демонстрации физики статического электричества на научных ярмарках и в учебных классах. Поскольку они производят относительно небольшой электрический ток, их можно сделать безопасными для использования в таких условиях. Первый такой генератор был построен Робертом Ван де Граафом в 1931 году для использования в исследованиях ядерной физики. На рис. 18.12 показан упрощенный эскиз генератора Ван де Граафа.
Поскольку они производят относительно небольшой электрический ток, их можно сделать безопасными для использования в таких условиях. Первый такой генератор был построен Робертом Ван де Граафом в 1931 году для использования в исследованиях ядерной физики. На рис. 18.12 показан упрощенный эскиз генератора Ван де Граафа.
используются гладкие и заостренные поверхности, а также проводники и изоляторы для создания больших статических зарядов. В варианте, показанном на рис. 18.12, электроны «распыляются» с кончиков нижней гребенки на движущуюся ленту, которая сделана из изоляционного материала, такого как резина.Этот метод зарядки ремня сродни зарядке вашей обуви электронами при ходьбе по ковру. Ремень поднимает заряды до верхнего гребня, откуда они снова передаются, подобно тому, как вы касаетесь дверной ручки и передаете на нее свой заряд. Поскольку подобно зарядам отталкиваются, лишние электроны все устремляются к внешней поверхности шара, который сделан из металла (проводника). Таким образом, сама гребенка никогда не накапливает слишком много заряда, потому что любой полученный ею заряд быстро истощается зарядом, движущимся к внешней поверхности шара.
Таким образом, сама гребенка никогда не накапливает слишком много заряда, потому что любой полученный ею заряд быстро истощается зарядом, движущимся к внешней поверхности шара.
Фигура 18.12 Генераторы Ван де Граафа переносят электроны на металлическую сферу, где электроны равномерно распределяются по внешней поверхности.
Генераторы Ван де Граафа используются для демонстрации многих интересных эффектов, вызываемых статическим электричеством. Прикасаясь к земному шару, человек получает избыточный заряд, поэтому его волосы встают дыбом, как показано на рис. 18.13. Вы также можете создавать мини-молнии, перемещая нейтральный проводник по направлению к земному шару.Другой фаворит — поставить алюминиевые формочки для кексов на незаряженный шар, а затем включить генератор. Будучи изготовлены из проводящего материала, банки накапливают избыточный заряд. Затем они отталкиваются друг от друга и улетают с земного шара один за другим. Быстрый поиск в Интернете покажет множество примеров того, что можно сделать с помощью генератора Ван де Граафа.
Фигура 18.13 Человек, касающийся генератора Ван де Граафа, имеет избыточный заряд, который распространяется по его волосам и отталкивает пряди волос от соседей.(кредит: Джон «ShakataGaNai» Дэвис)
Проверка захвата
Почему электроны не остаются на резиновой ленте, когда достигают верхнего гребня?
- Верхний гребень не имеет избыточных электронов, а избыточные электроны в резиновом ремне передаются гребенке контактным путем.
- В верхней гребенке нет избыточных электронов, а избыточные электроны в резиновой ленте передаются гребенке за счет проводимости.
- В верхней гребенке избыточные электроны, а избыточные электроны в резиновом поясе передаются гребенке за счет проводимости.
- Верхний гребень имеет избыточные электроны, а избыточные электроны в резиновом ремне передаются гребенке при контакте.
Виртуальная физика
Воздушные шары и статическое электричество
Эта симуляция позволяет вам наблюдать накопление отрицательного заряда на воздушном шаре, когда вы третесь им о свитер. Затем вы можете наблюдать, как взаимодействуют два заряженных воздушных шара и как они вызывают поляризацию в стене.
Затем вы можете наблюдать, как взаимодействуют два заряженных воздушных шара и как они вызывают поляризацию в стене.
Проверка захвата
Нажмите кнопку сброса и начните с двух шаров.Зарядите первый шарик, потирая им свитер, а затем переместите его ко второму шарику. Почему второй шарик не двигается?
- Второй шарик имеет одинаковое количество положительных и отрицательных зарядов.
- Второй шар имеет больше положительных зарядов, чем отрицательных.
- Второй шарик имеет больше отрицательных зарядов, чем положительных.
- Второй шар заряжен положительно и имеет поляризацию.
Снап Лаборатория
Поляризующая водопроводная вода
Эта лаборатория продемонстрирует, как легко можно поляризовать молекулы воды.
- Пластмассовый предмет небольших размеров, например, расческа или пластиковая мешалка
- Источник водопроводной воды
Инструкции
Процедура
- Тщательно протрите пластиковый предмет сухой тканью.

- Откройте кран ровно настолько, чтобы из крана потекла гладкая струйка воды.
- Переместите край заряженного пластикового предмета в сторону нити проточной воды.
Что вы наблюдаете? Что происходит, когда пластиковый предмет касается водной нити? Можете ли вы объяснить свои наблюдения?
Почему вода изгибается вокруг заряженного объекта?
-
Заряженный объект индуцирует равномерный положительный заряд на молекулах воды.
-
Заряженный объект индуцирует равномерный отрицательный заряд на молекулах воды.
-
Заряженный объект притягивает поляризованные молекулы воды и ионы, растворенные в воде.

-
Заряженный объект деполяризует молекулы воды и ионы, растворенные в воде.
Рабочий пример
Зарядка капель чернил
Электрически нейтральные капли чернил в струйном принтере проходят через электронный луч, создаваемый электронной пушкой, как показано на рис. 18.14. Некоторые электроны захватываются каплей чернил, так что она становится заряженной. После прохождения электронного луча суммарный заряд капли чернил составляет qinkdrop=-1×10-10Cqinkdrop=-1×10-10C. Сколько электронов захватила капля чернил?
Фигура 18.14 Электроны из электронной пушки заряжают пролетающую каплю чернил.
Стратегия
Один электрон несет заряд qe-=-1,602×10-19Cqe-=-1,602×10-19C . Разделив общий заряд капли чернил на заряд qe-qe- одного электрона, мы получим количество электронов, захваченных каплей чернил.
Разделив общий заряд капли чернил на заряд qe-qe- одного электрона, мы получим количество электронов, захваченных каплей чернил.
Решение
Число n электронов, захваченных каплей чернил, равно
n=qinkdropqe-=-1×10-10C-1.602×10-19C=6×108.n=qinkdropqe-=-1×10-10C-1,602×10-19C=6×108.18,4
Обсуждение
Это почти миллиард электронов! Кажется, что это много, но это совсем немного по сравнению с количеством атомов в капле чернил, которых около 1016,1016. Таким образом, каждый лишний электрон приходится примерно на 1016/(6×108)≈1071016/(6×108)≈107 атомов.
Практические задачи
3 .Сколько протонов необходимо для создания 1 нКл заряда? 1 нКл = 10-9 Кл
- 1.6 × 10 −28
- 1,6 × 10 −10
- 3 × 10 9
- 6 × 10 9
В лаборатории физики вы заряжаете три металлические сферы, две из которых имеют +3\,\text{nC}, а одну — 5\,\text{nC}. Когда вы сведете все три сферы вместе так, что все они соприкоснутся друг с другом, каков будет общий заряд трех сфер?
Когда вы сведете все три сферы вместе так, что все они соприкоснутся друг с другом, каков будет общий заряд трех сфер?
-
+ 1\,\text{nC}
Проверьте свое понимание
5 .Сколько видов электрического заряда существует?
- один тип
- два типа
- три типа
- четыре типа

Какие две основные электрические классификации материалов основаны на том, насколько легко через них могут проходить заряды?
- проводник и изолятор полупроводник
- и изолятор проводник
- и сверхпроводник проводник
- и полупроводник
Правда или ложь — поляризованный материал должен иметь ненулевой суммарный электрический заряд.
- правда
- ложь
Опишите силу взаимодействия двух положительных точечных зарядов.
- Сила притяжения действует вдоль линии, соединяющей два точечных заряда.
- Сила притяжения действует по касательной к линии, соединяющей два точечных заряда.
- Сила отталкивающая и действует вдоль линии, соединяющей два точечных заряда.
- Сила отталкивающая и действует по касательной к линии, соединяющей два точечных заряда.
Чем проводник отличается от изолятора?
- Электрические заряды легко перемещаются в изоляторе, но не в проводящем материале.

- Электрические заряды легко перемещаются в проводнике, но не в изоляторе.
- Проводник имеет большое количество электронов.
- В изоляторе больше зарядов, чем в проводнике.
Правда или ложь — для зарядки объекта с помощью поляризации необходимо коснуться его объектом, имеющим избыточный заряд.
- правда
- ложь
Физика: Ньютоновская физика | Encyclopedia.com
Введение
Ньютоновская физика, также называемая ньютоновской или классической механикой, представляет собой описание механических явлений, связанных с силами, действующими на материю, с использованием законов движения и тяготения, сформулированных в конце семнадцатого века английским физиком Сэром Исаак Ньютон (1642–1727). Несколько идей, разработанных более поздними учеными, особенно понятие энергии (которое не имело научного определения до конца 1700-х годов), также являются частью физики, которую сейчас называют ньютоновской.
Ньютоновская физика может с высокой точностью объяснить структуру большей части видимой Вселенной. Хотя ученым с начала двадцатого века известно, что это менее точное описание физического мира, чем теория относительности и квантовая физика, поправки, необходимые для объектов крупнее атомов, движущихся значительно медленнее света, незначительны. Поскольку ньютоновская физика также математически проста, она остается стандартом для расчета движения почти всех объектов, от деталей машин, жидкостей и пуль до космических кораблей, планет и галактик.
Историческая справка и научные основы
Хотя Ньютон переопределил основные понятия механики и разработал свои законы движения и всемирного тяготения в конце 1600-х годов, он основывал свою работу на важных научных открытиях о материи и движении, которые уже были установлены. Без этих более ранних достижений он не смог бы вывести четыре закона, лежащие в основе ньютоновской физики: его три закона движения и его закон всемирного тяготения.
По крайней мере, с четвертого века до нашей эры и до времен Ньютона европейская научная мысль основывалась в основном на теориях древнегреческих мыслителей, таких как Платон (ок. 428–348 до н. э.) и Аристотель (384–322 до н. э.). На самом деле влияние Аристотеля было настолько велико, что мировоззрение, которого придерживалось большинство европейских ученых до XVII века, называется аристотелевским. Это не исключало исследования событий с помощью эксперимента и математики, которые сейчас составляют основу научного метода, но и не особенно поощряло их.Это потому, что аристотелевцы видели вселенную и все в ней в первую очередь с точки зрения их значения, а не причины и следствия.
Аристотелианцы также унаследовали ошибочные представления о конкретных физических вопросах. Например, если объект находился в движении, они предполагали, что что-то должно поддерживать его в движении, будь то таинственное свойство объекта, называемое импульсом, окружающий воздух или что-то еще. На протяжении многих столетий такое мышление мешало попыткам разгадать физику движения.
Вопреки многим предубеждениям, Средневековье и Ренессанс произвели некоторые важные научные открытия. Работники физического труда, такие как столяры, строители, штурманы и судостроители, накапливали знания о практических методах и материалах. Ученые расширили знания в нескольких областях математики, восстановив давно забытые или плохо скопированные работы греческих математиков Евклида (род. около 300 г. до н.э.) и Архимеда (287–212 гг.) И сделав новые собственные открытия. В 1500-х годах, под влиянием существующих арабских работ, алгебра была разработана итальянскими математиками, такими как Никколо Фонтана Тарталья (1499–1557).Само слово «алгебра» происходит от арабского al-jabr, означает «воссоединение». Прежде чем Галилео Галилей (1564–1642), Ньютон и другие основоположники современной физической науки смогли добиться своего триумфа в шестнадцатом и семнадцатом веках, должно было появиться множество инструментов, физических и интеллектуальных.
Путь был частично подготовлен для нового образа мышления, который французский философ и математик Рене Декарт (1596–1650) назвал Ньютоном и другими «экспериментальной философией» или «механической философией». Декарт полагал, как и большинство более ранних мыслителей, что вселенную можно объяснить нисходящими рассуждениями из общих первых принципов, практически без необходимости в конкретных экспериментах; как известно, он считал, что все знания могут исходить из логического утверждения «я мыслю, следовательно, существую» ( Cogito ergo sum в оригинальной латыни).
Декарт полагал, как и большинство более ранних мыслителей, что вселенную можно объяснить нисходящими рассуждениями из общих первых принципов, практически без необходимости в конкретных экспериментах; как известно, он считал, что все знания могут исходить из логического утверждения «я мыслю, следовательно, существую» ( Cogito ergo sum в оригинальной латыни).
Декарт ошибочно полагал, что ни атомы, ни вакуум не могут существовать. Тем не менее, он предвосхитил современный научный подход, ища всеобъемлющую, механическую, рациональную интерпретацию природы.В частности, он предположил, что движение планет может быть объяснено вихрем или водоворотом «тонкой материи» — материи, не воспринимаемой органами чувств, — перемещаемой по Солнечной системе вращением Солнца вокруг своей оси. Солнце, предположил он, подобно венчику, вращающемуся в центре большой чаши со сливками, заставляет тонкую материю вращаться вокруг себя; поскольку вращение естественным образом уменьшалось бы с расстоянием, это, согласно Декарту, объясняло, почему планеты, более удаленные от Солнца, движутся медленнее, чем те, которые ближе.
Вихревая теория движения планет Декарта была популярна в Европе в то время, когда Ньютон опубликовал свою собственную теорию Солнечной системы в Philosophiae Natu-ralis Principia Mathematica (Математические принципы натуральной философии), обычно называемой просто Principia (1687 г.). Механика Ньютона объяснила как земное, так и планетарное движение, сигнализируя о крахе вихревой теории Декарта и всего его подхода к знаниям. Эксперимент в сочетании с математикой, а не нисходящие философские размышления, определял все серьезные попытки понять физический мир с того времени.
Не случайно движения планет касались и Декарта, и Ньютона. До появления ньютоновской физики наблюдательная астрономия была единственной наукой с математически точными знаниями или предсказательной силой. Химия состояла в основном из разрозненных кусочков практических знаний, накопленных методом проб и ошибок. Современные представления об элементах не начали развиваться до тех пор, пока эксперименты английского ученого Роберта Бойля (1627–1691) не опровергли теорию Платона о том, что вся материя состоит из четырех элементов — земли, воздуха, огня и воды — в 1660 году.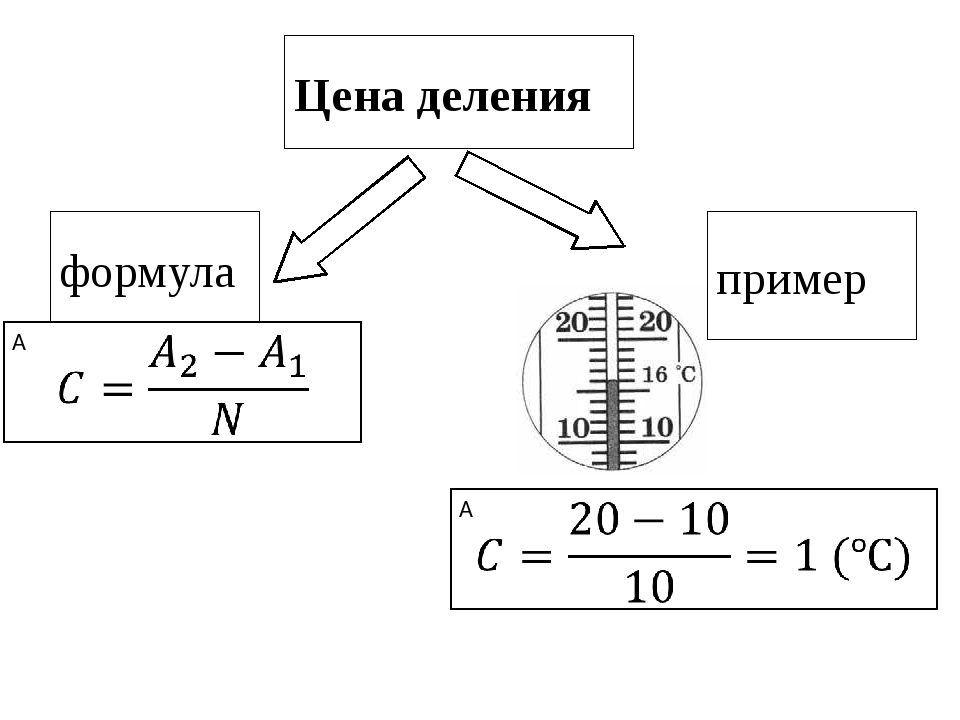
О существовании микроорганизмов не было известно до 1676 года, когда голландец Антони ван Левенгук (1632–1723) построил первый микроскоп. Медицина во времена Ньютона тоже была в зачаточном состоянии; тот факт, например, что сердце перекачивает кровь по телу, получил широкое признание только после 1616 года, когда эта теория была опубликована в трудах английского врача Уильяма Гарвея (1578–1657).
Социальная среда
1600-е годы были временем потрясений во всех аспектах европейского общества, включая религию, науку, политику, торговлю и искусство.Протестантская Реформация, начавшаяся в начале 1500-х годов, расколола многовековой религиозный консенсус Европы примерно по географическому признаку: протестантские страны на севере и римско-католические страны на юге. Реформация поставила под сомнение древние образы мышления и спровоцировала войны, которые десятилетиями терзали континент.
Коммерческая революция, длившаяся с начала 1500-х до 1650-х годов, также помогла разрушить старые стереотипы мышления и побудила к новым открытиям в науке и технике. Требовались методы дальней океанской навигации, стимулирующие новые точные работы в астрономии и часовом деле.
Требовались методы дальней океанской навигации, стимулирующие новые точные работы в астрономии и часовом деле.
Англия, родина Ньютона, переживала особенно жестокие потрясения. С 1642 по 1651 год в ходе кровопролитной гражданской войны
пуритан (протестантов-кальвинистов) противостояли англиканцам (членам английской государственной церкви). После того, как пуритане обезглавили короля Карла I (1600–1649) в 1649 году, Оливер Кромвель (1599–1658) стал сначала председателем Государственного совета, а затем лордом-протектором с 1653 года до своей смерти в 1658 году.Британская монархия была восстановлена при Карле II в 1660 году.
Несколько лет спустя, во время вспышки чумы, юный Исаак Ньютон — пуританин, увлекавшийся не только наукой, но и алхимией, и библейской книгой Откровения — укрылся от мор в загородном доме его матери. Там в течение 18 месяцев (1665–1666) он задумал основные элементы новой физики: три закона движения, закон всемирного тяготения и исчисление. Он также проделал большую работу в области оптики, хотя и не произвел там такого революционного эффекта, как в механике.
Наука
Средневековая астрономия была основана на книге Клавдия Птолемея (ок. 90–168 гг. н. э.) Mathematike Syntaxisis (Математический сборник), более известной на Западе под сокращенной формой арабского названия, Альмагест. Согласно Птолемею, планеты были заключены в огромные кристаллические сферы с центром вокруг Земли и двигались по неизменным совершенным кругам. Их движение было передано сверхъестественными средствами из самой дальней из всех сфер, из сферы неподвижных звезд.Эта модель была оспорена Николаем Коперником (1473–1543) в 1500-х годах. В 1543 году он опубликовал De Revolutionibus orbium coelestium (Шесть книг об обращениях небесных сфер), в которых предположил, что Солнце, а не Земля, находится в центре Вселенной.
Пересмотр Вселенной Коперником вызвал волну новых астрономических работ. Тихо Браге (1546–1601) проводил наблюдения невооруженным глазом за движением солнца, луны и планет, которые были наиболее точными на тот момент. После смерти Браге его помощник Иоганн Кеплер (1571–1630), сторонник системы Коперника, попытался сопоставить точные новые данные наблюдений Браге с уравнениями, описывающими планетарные орбиты, начиная с планеты Марс. Сначала он принял циркуляр
После смерти Браге его помощник Иоганн Кеплер (1571–1630), сторонник системы Коперника, попытался сопоставить точные новые данные наблюдений Браге с уравнениями, описывающими планетарные орбиты, начиная с планеты Марс. Сначала он принял циркуляр
В КОНТЕКСТЕ: ГАЛИЛЕО И ЦЕРКОВЬ
Галилео Галилей (1564–1642) был итальянским физиком, который усовершенствовал современный научный метод. Его работа по ускоренному движению стала важной основой для ньютоновской физики.К сожалению, защита Галилеем коперниканской (или гелиоцентрической) астрономии — представления о том, что Земля вращается вокруг Солнца, а не наоборот, — противоречила установленной религиозной доктрине. Католическая церковь, которая учила, что Земля неподвижна, в 1616 году объявила гелиоцентризм «ложным и полностью противоречащим Писанию».
В 1633 году престарелый Галилей предстал перед инквизицией и был признан виновным в ереси (проповедь неверной веры) и показал орудия пыток, которые применялись бы к нему, если бы он не отказался от своих показаний. Под давлением Галилей публично отказался от своей веры в гелиоцентризм и провел остаток своей жизни под домашним арестом. Слепой и разочарованный, он умер в 1642 году, в том же году, когда родился Исаак Ньютон. Из-за убеждения Галилея ученые в Южной Европе боялись говорить правду в течение десятилетий после этого, и большая часть научной революции после этого была проделана в Англии и Северной Европе.
Под давлением Галилей публично отказался от своей веры в гелиоцентризм и провел остаток своей жизни под домашним арестом. Слепой и разочарованный, он умер в 1642 году, в том же году, когда родился Исаак Ньютон. Из-за убеждения Галилея ученые в Южной Европе боялись говорить правду в течение десятилетий после этого, и большая часть научной революции после этого была проделана в Англии и Северной Европе.
В конце концов церковь признала свою ошибку, но только много лет спустя.В 1822 году церковь сняла запрет на книги, проповедующие точку зрения о том, что Земля вращается вокруг Солнца; в 1981 году Папа Иоанн Павел II (1920–2005) созвал новую комиссию для изучения дела Галилея. В 1992 году комиссия заявила, что дело было отмечено «трагическим взаимопониманием». Некоторым этого было недостаточно, в том числе бывшему директору Ватиканской обсерватории (с 1978 по 2006 год) священнику Джорджу Койну (с 1933 года), который хотел бы более полного признания ответственности за преследование Галилея и настоящих извинений.
орбиты Марса, как это делали все до него, но он не мог подогнать данные наблюдений. В конце концов он обнаружил, что лучше всего подходит не круг, а эллипс (кривая, подобная контуру яйца).
Кеплер первым описал движение планет с помощью математических законов. Он назвал три, два из которых включали время как переменную. Использование времени для математического описания мира было значительным достижением физики; европейская научная традиция, унаследованная от греков, была преимущественно статичной (неподвижной) и геометрической.Его внимание было направлено в первую очередь на форму кривых и редко использовалась математика для описания динамических (зависящих от времени) процессов.
Кеплер опубликовал два своих закона в 1609 г. и третий в 1619 г. Они были чисто описательными, т. е. не предлагали объяснения того, почему планеты ведут себя так, как указано, и не описывали, как какие-либо другие объекты (например, падающие яблоки) могут двигаться.
После Браге и Кеплера Галилей заложил фундамент ньютоновской физики. Он ошибочно отверг доказательство Кеплера о том, что планеты движутся по эллиптическим орбитам, но провел точные эксперименты в лаборатории, чтобы охарактеризовать движение ускоряющихся тел — объектов, меняющих направление или скорость своего движения.Как и Кеплер, он искал математические законы, описывающие, как физические системы изменяются с течением времени.
Он ошибочно отверг доказательство Кеплера о том, что планеты движутся по эллиптическим орбитам, но провел точные эксперименты в лаборатории, чтобы охарактеризовать движение ускоряющихся тел — объектов, меняющих направление или скорость своего движения.Как и Кеплер, он искал математические законы, описывающие, как физические системы изменяются с течением времени.
Галилей пришел к выводу, что расстояние, пройденное постоянно ускоряющимся объектом, пропорционально квадрату времени, в течение которого оно ускоряется. Он также обнаружил, что объекты неуклонно ускоряются под действием гравитации, которую он рассматривал как постоянную силу, не зависящую от расстояния (которое, примерно, находится вблизи поверхности Земли). Он обнаружил, что объекты ускоряются с одинаковой скоростью независимо от их веса, то есть более тяжелый мяч не падает быстрее, чем легкий мяч того же размера.Возможно, самое главное, он обнаружил, что объекты имеют тенденцию сохранять прямолинейное движение, если на них не действует сила.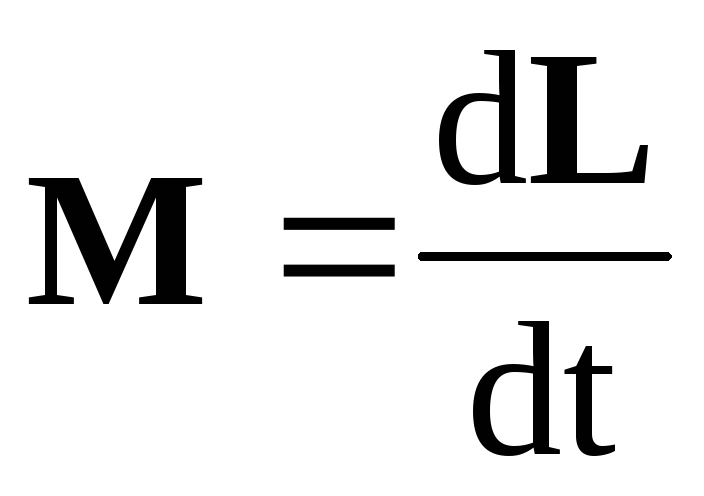 Это опровергло аристотелевскую точку зрения о том, что для поддержания состояния движения объекта необходима сила.
Это опровергло аристотелевскую точку зрения о том, что для поддержания состояния движения объекта необходима сила.
С физикой Галилея и астрономией Кеплера все было готово для триумфа Ньютона.
Физика Ньютона
Влияние Ньютона в основном связано с его основной работой, Philosophiae Naturalis Principia Mathematica, , опубликованной в 1687 году и наиболее известной благодаря сокращенной форме латинского названия, Principia. Эта работа была создана частично по настоянию друга Ньютона, английского астронома Эдмонда Галлея (1656–1742), который также финансировал проект, помогая создать одну из самых важных работ в истории науки.
Из всех ученых, работавших в его время, только Ньютон понимал, что может существовать единая универсальная система механики, то есть физика, описывающая одновременно и земное, и небесное движение. В «Началах » Ньютон установил такую физику своими тремя законами движения и своим законом тяготения.Разработка этих законов и объединение их со строгой идеей «энергии» в конце восемнадцатого века породила систему, ньютоновскую (или механическую) физику, которая до сих пор используется во всем, от инженерного проектирования до анализа галактического движения.
Три закона движения Ньютона таковы:
- Объект остается в покое или движется по прямой линии с постоянной скоростью, если на него не действует ненулевая суммарная сила.
-
Сила, действующая на тело, заставляет его ускоряться (изменять состояние движения) до степени, пропорциональной массе тела.Сформулировав уравнение, записав F для силы, m для массы и a для ускорения, мы получим F = мА. В
другими словами, скорость и импульс объекта изменяются со временем пропорционально силе, действующей на него.
-
Силы возникают парами и направлены в противоположные стороны.
Этот закон чаще всего формулируется так: Каждому действию есть равное и противоположное противодействие. Например, когда ружье стреляет, сила, действующая на пулю, когда она ускоряется в стволе, равна отдаче ружья, действующей на руку или плечо стрелка.
Четвертый основной закон ньютоновской физики — закон всемирного тяготения: F = Gm 1 / r 2 m 2. Здесь F G — это гравитационное притяжение, гравитационная постоянная (фиксированное число, Г = 6,6742 × 10 -11 м 3 кг -1 с -2), 91 210 м 91 211 1 — масса одного объекта, 91 210 м 91 211 2 — масса другого объекта, и r — расстояние между центрами двух объектов.Большие массы означают большую гравитационную силу,
Здесь F G — это гравитационное притяжение, гравитационная постоянная (фиксированное число, Г = 6,6742 × 10 -11 м 3 кг -1 с -2), 91 210 м 91 211 1 — масса одного объекта, 91 210 м 91 211 2 — масса другого объекта, и r — расстояние между центрами двух объектов.Большие массы означают большую гравитационную силу,
В КОНТЕКСТЕ : СЮРПРИЗ: НЬЮТОН БЫЛ ПРАВ!
Несмотря на то, что прошло три столетия с тех пор, как Исаак Ньютон опубликовал свою теорию гравитации в 1687 году, ученые все еще проверяют ее. Закон Ньютона гласит, что гравитационное притяжение между любыми двумя объектами уменьшается пропорционально квадрату расстояния между ними; удвоение расстояния означает одну четвертую силы. Этот тип отношений, называемый законом обратных квадратов, точен в масштабах бейсбольных мячей, планет или галактик, но, согласно квантовой физике, не должен работать, когда объекты находятся близко друг к другу.Массы, разделенные шириной всего в человеческий волос (56 миллионных долей метра или микрометров, мкм), согласно некоторым теориям, должны испытывать заметно меньшее гравитационное притяжение, чем предсказывает закон Ньютона.
В 2006 году группа физиков под руководством Д.Дж. Капнер проверил закон всемирного тяготения Ньютона, измерив гравитационное притяжение между парой маленьких вращающихся металлических дисков на расстоянии всего 56 мкм друг от друга. Они обнаружили, что закон Ньютона остается в силе даже на таком расстоянии.
Этот простой результат, полученный на экспериментальной установке, которая может поместиться в банке с газировкой, может иметь значение для нашего понимания Вселенной в целом.В 1990-х годах астрономы обнаружили, что 70% всей энергии и массы во Вселенной состоит из таинственной «темной энергии» неизвестной до сих пор природы. Некоторые теории, пытающиеся объяснить темную энергию, такие как теория струн, делают предсказания о силе гравитации. По крайней мере, одна такая теория — теория жирного гравитона — была опровергнута недавним экспериментом с вращающимся диском. В ближайшие годы будут проведены еще более точные проверки закона Ньютона, чтобы еще больше ограничить попытки физиков объяснить природу Вселенной.
больше F ; больше расстояние между массами, больше р, значит меньше.
Ньютон показал, что эти четыре закона могут одновременно объяснить лабораторные результаты Галилея — поведение повседневных объектов вблизи поверхности Земли — и движения планет. Единый набор законов, достаточно компактный, чтобы записать его на карточке, мог бы описать движение всех звезд, планет и лун во Вселенной. Более того, чтобы достичь этого поразительного результата, Ньютону пришлось изобрести новый раздел математики, чтобы оперировать величинами, которые меняются со временем нестационарным образом.Он назвал это методом флюксий, но сегодня он известен как исчисление, основной математический язык всех физических наук.
Влияние и проблемы
Большинство отраслей науки находились в беспорядочном состоянии, когда Ньютон опубликовал свой Principia в 1687 году. Ньютонизм Перо и яблоко падают с одинаковой скоростью в вакуумной камере. Этот эксперимент демонстрирует справедливость идей Исаака Ньютона (1642–1727) о гравитации и инерции.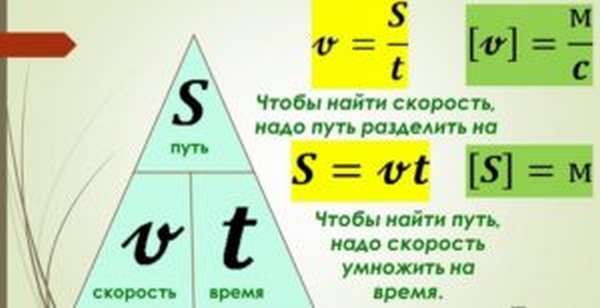 © Джим Шугар/Corbis.Механика была первой научной дисциплиной, достигшей кажущегося совершенства: законы Ньютона прошли все экспериментальные проверки, объяснили приливы и другие сложные проблемы астрономии и победили картезианскую теорию вихрей.
© Джим Шугар/Corbis.Механика была первой научной дисциплиной, достигшей кажущегося совершенства: законы Ньютона прошли все экспериментальные проверки, объяснили приливы и другие сложные проблемы астрономии и победили картезианскую теорию вихрей.
Но это тоже было спорно. Критики, такие как немецкий ученый Готфрид Лейбниц (1646–1716), который изобрел исчисление независимо от Ньютона, нападали на ньютоновскую теорию гравитации как на мистическую или бесполезную: как могла одна масса действовать на другую мгновенно через расстояние, не находясь в прямом или, по крайней мере, в косвенный контакт с ним? Новая теория ничего не объясняла.Эта проблема беспокоила и Ньютона, говоря, что он находит неправдоподобным то, что называется «действием на расстоянии». Тем не менее, он защищал свой метод, написав в 1715 году: «Его [Лейбница] аргументы против меня основаны на метафизических и ненадежных гипотезах и, следовательно, не затрагивают меня: ибо я вмешиваюсь только в экспериментальную философию». Ньютон утверждал, что не имеет значения, объяснил он гравитацию или нет: объяснение было бы желательным, но не могло быть получено до тех пор, пока не было бы доступно точное описание того, что делает гравитация.
Ньютон утверждал, что не имеет значения, объяснил он гравитацию или нет: объяснение было бы желательным, но не могло быть получено до тех пор, пока не было бы доступно точное описание того, что делает гравитация.
Лейбниц также подверг критике предположения Ньютона об абсолютном пространстве, которое, как утверждал последний, если бы существовало, было бы везде плоским (т. е. подчинялось бы законам евклидовой геометрии) и бесконечным во всех направлениях. Философское возражение Лейбница подтвердилось более чем 200 лет спустя, когда немецкий физик Альберт Эйнштейн (1879–1955) показал, что от идеи абсолютного ньютоновского пространства следует отказаться и заменить его искривленным относительным пространством.
Несмотря на недостатки, ньютоновская физика произвела революцию в науке.Математически сформулированные теории, проверенные физическими наблюдениями, стали стандартом почти во всех областях научной мысли. Навсегда была изгнана средневековая опора на авторитетные книги и картезианская опора на разум, не проверенный наблюдениями.
Воздействие на общество
Principia, написанные на латыни и насыщенные математическими формулами, мало читались. Его интеллектуальное влияние на общество было опосредовано авторами, которые поддержали дело «экспериментальной философии» Ньютона и писали для широкой публики.Самым влиятельным из них был французский мыслитель Вольтер, урожденный Франсуа-Мари Аруэ (1694–1778), который точно объяснил науку Ньютона в нетехнических терминах в своей книге Elements de la philosophie de Newton (Элементы философии Ньютона, 1738 г.).
Для Вольтера и ему подобных мыслителей триумф Ньютона в механике доказал, что наука в конце концов объяснит все, включая человеческие действия, в терминах жестких причинно-следственных (детерминистских) законов: «Это было бы очень странно, — писал Вольтер, — что вся природа, все планеты должны подчиняться вечным законам, и что должно быть маленькое животное, пяти футов ростом, которое, пренебрегая этими законами, могло бы действовать, как ему заблагорассудится, исключительно по своему капризу.
Вооруженные железным авторитетом новой науки, эти писатели начали нападать на традиционную религию. Их скептицизм способствовал упадку религиозной веры в индустриальных обществах, который неуклонно продолжается и по сей день, особенно в Европе. В Соединенных Штатах население в целом остается почти повсеместно религиозным, но, согласно опросам ученых, уровень религиозной веры у ученых ниже, причем физики — интеллектуальные наследники Ньютона — являются самой нерелигиозной группой (только около 20% физиков верили в Бога по состоянию на 1998 г.) .Это иронично, учитывая, что сам Ньютон был набожным христианином.
Некоторые современники Ньютона, такие как ирландский философ епископ Беркли (1685–1753), критиковали новый материализм. Однако такие противники вели безнадежную битву, и в восемнадцатом веке интеллектуальный климат в Англии и Северной Европе стал преимущественно пронаучным и детерминистским.
Новая наука также изменила мир в экономической, военной и других областях.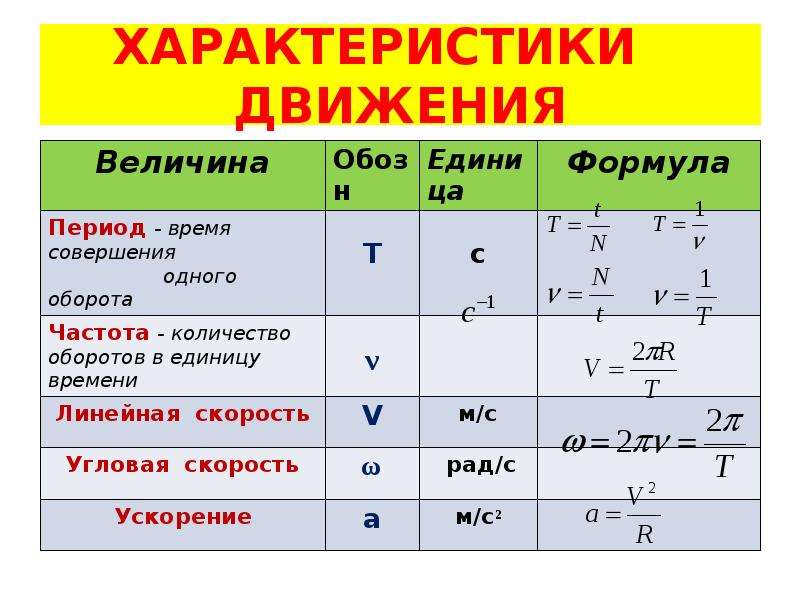 Эти изменения были внесены не только ньютоновской физикой: химия, медицина, математика, электромагнетизм и другие области науки также имели решающее значение.Другие формы науки восприняли галилеевские и ньютоновские методы математической проверки законов. Вместе новая наука высвободила поток новых технологий, которые привели к промышленной революции, начавшейся в конце 1700-х годов и продолжающейся до настоящего времени.
Эти изменения были внесены не только ньютоновской физикой: химия, медицина, математика, электромагнетизм и другие области науки также имели решающее значение.Другие формы науки восприняли галилеевские и ньютоновские методы математической проверки законов. Вместе новая наука высвободила поток новых технологий, которые привели к промышленной революции, начавшейся в конце 1700-х годов и продолжающейся до настоящего времени.
Современные культурные связи
Ньютоновская физика продолжает применяться во всех областях науки и техники, где необходимо учитывать силу, движение и гравитацию. Однако современные физики, в отличие от Ньютона, знают, что его законы работают не при всех обстоятельствах.Поведение объектов, движущихся со скоростью, близкой к скорости света, или взаимодействующих со скоростью субатомных частиц, не описывается точно ньютоновской физикой. Теория относительности и квантовая физика необходимы в таких неньютоновских сферах, и даже у этих теорий есть ограничения.
Несмотря на появление более поздних, более полных теорий, ученые продолжают изучать ньютоновскую физику. Как
В КОНТЕКСТЕ : СОВЕРШЕННАЯ НЬЮТОНОВСКАЯ МАШИНА
Космический корабль является высшей ньютоновской машиной, потому что его движение основано на ракетах, которые являются наиболее простым возможным применением второго закона Ньютона, принципа, согласно которому любая сила, действующая на некоторый объект соединен с равной и противоположной силой, действующей на какой-либо другой объект.Газы, выходящие из ракеты, толкают камеру сгорания ракеты, а камера сгорания с равной и противоположной силой давит на газы. Газы улетают в одну сторону, камера (с присоединенной ракетой) в другую.
Космический корабль, покинувший атмосферу, управляется только силами, создаваемыми его ракетами (второй закон Ньютона), и силой гравитации, описываемой законом всемирного тяготения Ньютона. Таким образом, законы Ньютона объясняют почти все, что влияет на траекторию полета космического корабля. Во время путешествия Аполлона 8, в 1968 году, которое облетело Луну, ребенок на Земле вслух задался вопросом, кто управляет космическим кораблем. Когда вопрос был передан ему по радио, астронавт Билл Андерс ответил: «Я думаю, Исаак Ньютон сейчас большую часть времени за рулем».
Во время путешествия Аполлона 8, в 1968 году, которое облетело Луну, ребенок на Земле вслух задался вопросом, кто управляет космическим кораблем. Когда вопрос был передан ему по радио, астронавт Билл Андерс ответил: «Я думаю, Исаак Ньютон сейчас большую часть времени за рулем».
Космические корабли и ракетная техника оказали глубокое влияние на современное общество. Космические зонды значительно расширили наши знания о планетах и более далеких вселенных, спутники изменили средства связи, а баллистические ракеты, оснащенные неньютоновским изобретением, ядерной бомбой, сделали физически возможным уничтожить большую часть человечества в одно мгновение. несколько минут.
, описанный на врезке, ученые измерили силу гравитации на расстояниях, равных ширине человеческого волоса, чтобы проверить, выполняется ли закон Ньютона для объектов, расположенных так близко друг к другу. Их результаты, опубликованные в 2007 году, показали, что ньютоновская физика сохраняется даже на таких малых расстояниях. Это исключило некоторые из наиболее многообещающих теорий, выдвинутых для объяснения загадочного факта (открытого в конце 1990-х годов), что Вселенная не только расширяется, но и расширяется все быстрее.
Это исключило некоторые из наиболее многообещающих теорий, выдвинутых для объяснения загадочного факта (открытого в конце 1990-х годов), что Вселенная не только расширяется, но и расширяется все быстрее.
В начале 1980-х годов исследования начали фокусироваться на возможности того, что ньютоновская физика может быть неверной даже в неквантовых, нерелятивистских областях — ситуациях, в которых она всегда считалась по существу идеальной. Новый тип физики, называемый модифицированной ньютоновской динамикой (МОНД), впервые предложенный израильским физиком Моти Милгромом в 1983 году, предполагает, что второй закон Ньютона следует модифицировать для малых ускорений. Поскольку небольшие ускорения в астрономических условиях обычны, MOND объясняет ряд наблюдений, которые другие теории описывают как результат неизвестной невидимой формы материи, называемой темной материей.МОНД противоречив; некоторые физики поддерживают это, но большинство убеждено, что эти наблюдения объясняются некой формой темной материи.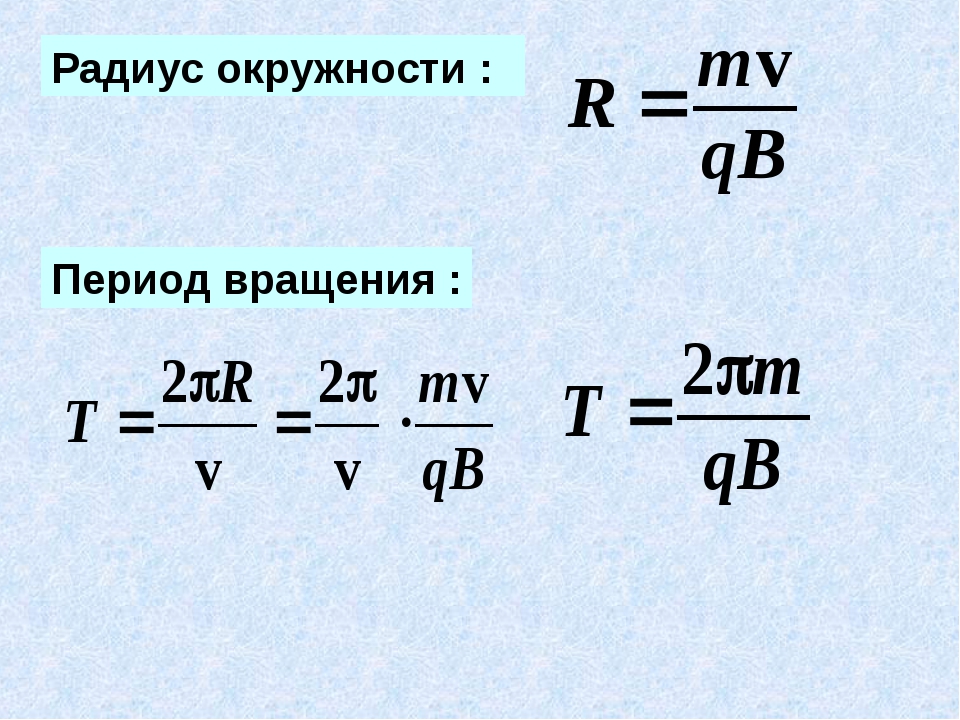 В научном стиле, установленном Ньютоном и Галилеем, вопрос в конечном итоге будет решен путем сравнения предсказаний соперничающих теорий с фактическими наблюдениями.
В научном стиле, установленном Ньютоном и Галилеем, вопрос в конечном итоге будет решен путем сравнения предсказаний соперничающих теорий с фактическими наблюдениями.
См. также Астрономия и космология: механистическая Вселенная; Физика: аристотелевская физика; Физика: формулировка классического физического закона.
библиография
Книги
Белл, Артур. Ньютоновская наука. Лондон: Edward Arnold Publishers, Ltd., 1961.
Коэн, И. Бернар. Ньютоновская революция: с иллюстрациями трансформации научных идей. New York: Cambridge University Press, 1980.
Crombie, AC Medieval and Early Modern Science, Vol. II: Наука в позднем средневековье и раннем Новом времени: XIII–XVII вв. Нью-Йорк: Doubleday, 1959.
Лауэ, Макс фон. История физики. Перевод Ральфа Эспера. Нью-Йорк: Academic Press Inc., 1950.
Периодические издания
Болл, Филип. «Прыжок, который докажет, что Ньютон ошибался». Природа. 446 (2007): 357.
Природа. 446 (2007): 357.
Игнатьев А.Ю. «Возможно ли нарушение второго закона Ньютона?» Письма о физическом обзоре 98 (2007): 101101.
Капнер, Д.Дж., и др. «Проверки гравитационного закона обратных квадратов ниже шкалы длины темной энергии». Physical Review Letters 98, вып.2 (2007).
Говори, Клайв. «Гравитация проходит небольшой тест». Nature 446 (1 марта 2007 г.): 31–32.
Ларри Гилман
Пол Дэвис
К. Ли Лернер
Формула для врачей | Маркен | rossmann.de
Natur trifft auf Wissenschaft
Gemäß dem Firmenmotto «Сначала кожа, потом макияж», составленный PHYSICIANS FORMULA Kosmetik Kollektionen, die auch für empfindliche Haut geeignet sind. Und das bereits seit 1937.Seither setzt die Marke auf «gesunde Schönheit» in höchster Qualität – zu bezahlbaren Preisen. Alle Pflegeprodukte sind dermatologisch getestet und hypoallergen.
Макияж Physicians Formula
Physicians Formula beetet eine umfangreiche Palette и высококачественный косметический продукт. Mit ihren biologischen und hypoallergenen Inhaltsstoffen eignen sich die Produkte von Physicians Formula auch für besonders empfindliche Haut. Dank tierversuchsfreier Herstellung können Sie sich mit gutem Gewissen perfekt stylen.
Mit ihren biologischen und hypoallergenen Inhaltsstoffen eignen sich die Produkte von Physicians Formula auch für besonders empfindliche Haut. Dank tierversuchsfreier Herstellung können Sie sich mit gutem Gewissen perfekt stylen.Für einen gleichmäßigen und perfect Teint sorgt das Physicians Formula Make-up. Gleichen Sie beispielsweise Unregelmäßigkeiten Ihrer Haut mit der Argan Wear Ultra-Nourishing Argan Oil BB Cream SPF 30 aus. Das hochwertige, nicht-komedogene (die Talgdrüsen nicht verstopfende) Arganöl pflegt auf angenehme Weise und macht die Haut geschmeidig und weich. Ideal als Basis für weiteres Make-up oder allein getragen.
Mit dem Physicians Formula Gentle Cover Concealer Stick Decen Sie kleinere Hautpartien ab.Im Nu verschwinden:
- Дункель Эдерхен
- Оженринг
- Unreinheiten
- Кляйне Макель

Фонд «Формула врачей»
Идеальное базовое средство для макияжа с помощью Фонда Physicians Formula Foundation. Passend zu Ihrem Hauttyp finden Sie geeignete Kosmetikprodukte.Besonders beliebt sind diese beiden Foundations von Physicians Formula:- ЗДОРОВЫЙ ФОНД SPF 20
- ФОНД NUDE WEAR TOUCH OF GLOW FOUNDATION
Тональная основа Die Physicians Formula Nude Wear Touch of Glow Foundation — это ультралегкая, струящаяся основа.
 Natürlich, schwerelos und nahezu unsichtbar auf der Haut. Kleine Unreinheiten und Makel verschwinden. Ein angenehm leichter Schimmer schenkt Ihrer Haut Leuchtkraft und Frische.
Natürlich, schwerelos und nahezu unsichtbar auf der Haut. Kleine Unreinheiten und Makel verschwinden. Ein angenehm leichter Schimmer schenkt Ihrer Haut Leuchtkraft und Frische. Бронзер Physicians Formula
Mit einem Physicians Formula Bronzer schenken Sie sich einen strahlenden Teint.Die verschiedenen Bronzer ermöglichen unterschiedlich starke Bräunungsgrade und individuelle Nuancen. Безупречный бронзатор от Physicians Formula с маслом Мурумуру, с бронзатором масла Мурумуру. Er verleiht Ihrer Haut einen angenehm dezenten Glanz. Die Murumuru-масло в комбинации мит Cupuaçu- und Tucuma-масла pflegt und macht Ihre Haut seidig-weich. Einen hellen Teint und einen unvergleichlichen Bronze-Schimmer erzielen die extra-weichen Pigmente. Hochveredelte Perlen glatten zusätzlich Ihre Haut.Формула для врачей ROSSMANN
Eine große Auswahl der Kosmetikprodukte von Physicians Formula erhalten Sie in unserem Интернет-магазин ROSSMANN. Die hochwertigen Produkte mit biologischen und hypoallergenen Inhaltsstoffen sind dermatologisch verträglich und kommen ohne Tierversuche aus. Abgestimmt auf verschiedene Hauttypen, finden Sie hier garantiert die Kosmetikprodukte, die auch für Ihre Haut sehr gut verträglich sind. Dank natürlicher Inhaltsstoffe wie Murumuru-Butter oder Arganöl erhalten Sie mit Physicians Formula einen perfect Look und darüber hinaus eine spezielle Hautpflege.Viele Kosmetikprodukte sind außerdem nicht-komedogen.
Abgestimmt auf verschiedene Hauttypen, finden Sie hier garantiert die Kosmetikprodukte, die auch für Ihre Haut sehr gut verträglich sind. Dank natürlicher Inhaltsstoffe wie Murumuru-Butter oder Arganöl erhalten Sie mit Physicians Formula einen perfect Look und darüber hinaus eine spezielle Hautpflege.Viele Kosmetikprodukte sind außerdem nicht-komedogen. Эксперимент направлен на то, чтобы сделать квантовую физику видимой невооруженным глазом — ScienceDaily
Предсказания квантовой физики были подтверждены бесчисленными экспериментами, но еще никому не удалось обнаружить квантовый физический эффект запутанности непосредственно невооруженным глазом. Теперь это должно стать возможным благодаря эксперименту, предложенному группой, работающей с физиком-теоретиком из Базельского университета. Эксперимент может проложить путь к новым приложениям в квантовой физике.
Квантовой физике более 100 лет, но даже сегодня ее все еще иногда встречают с удивлением. Это относится, например, к запутанности, квантовому физическому явлению, которое можно наблюдать между атомами или фотонами (частицами света): когда две из этих частиц запутаны, физическое состояние двух частиц больше не может быть описано независимо, только полная система, которую обе частицы образуют вместе.
Несмотря на эту особенность, запутанные фотоны являются частью реального мира, что было доказано многими экспериментами.И все же никто не наблюдал запутанных фотонов напрямую. Это связано с тем, что с помощью доступной технологии можно произвести только один или несколько запутанных фотонов, и это число слишком мало для человеческого глаза, чтобы воспринимать эти фотоны как свет.
Запутанные фотоны, усиленные в 100 раз
Николя Сангуард, физик-теоретик из Базельского университета, вместе с двумя квантовыми физиками из Делфта, Нидерланды, и Инсбрука, Австрия, показали в научном журнале Optica , как можно напрямую обнаруживать запутанные фотоны.Основная идея эксперимента заключается в том, что запутанный фотон генерируется, а затем усиливается с помощью специальной техники, не разрушая квантовую физическую запутанность.
В процессе присутствует около 100 запутанных фотонов, что, согласно современным знаниям, является точным числом, необходимым для создания впечатления света у людей. Но хотя сотни фотонов достигают сетчатки, есть и значительные потери: лишь около семи реально достигают одной из 120 миллионов светочувствительных палочек сетчатки.Затем эти фотоны генерируют нервный импульс, который запускает восприятие света в мозгу.
Но хотя сотни фотонов достигают сетчатки, есть и значительные потери: лишь около семи реально достигают одной из 120 миллионов светочувствительных палочек сетчатки.Затем эти фотоны генерируют нервный импульс, который запускает восприятие света в мозгу.
Два запутанных состояния
В эксперименте, предложенном тремя квантовыми физиками, запутанность создается одним фотоном, направленным на полупрозрачное зеркало. Сангуар объясняет, что происходит дальше: «Отдельный фотон не передается и не отражается зеркалом; вместо этого — квантовая физика странна — фотон одновременно передается и отражается.За зеркалом фотон существует в «пропущенном» и «отраженном» состояниях, причем эти два состояния переплетаются с другим».
Детектор фотонов и человек-наблюдатель размещены за зеркалом. Чтобы глаз наблюдателя мог обнаружить запутанные фотоны, они усиливаются в 100 раз с помощью увеличительного стекла, прежде чем они достигнут глаза. Технически это достигается смещением в фазовом пространстве с помощью лазера. Действительно ли человек-наблюдатель и/или детектор обнаруживают запутанные фотоны, выясняется не напрямую, а посредством определения вероятностей.Для этого эксперимент многократно повторяют и полученные данные подвергают статистической обработке.
Действительно ли человек-наблюдатель и/или детектор обнаруживают запутанные фотоны, выясняется не напрямую, а посредством определения вероятностей.Для этого эксперимент многократно повторяют и полученные данные подвергают статистической обработке.
Очень длительный период наблюдения
Пока неизвестно, будет ли эксперимент проводить группа Сангоуара или его реализуют другие квантовые физики. Требуемые технологии — специальные источники фотонов и специальные лазеры — в целом доступны сегодня; однако самым большим препятствием является практическая реализация эксперимента. Человеческий глаз примерно в миллиард раз медленнее считает слабые световые импульсы, чем современные детекторы фотонов.«Согласно первоначальной оценке, потребуется несколько сотен тысяч запусков, пока у нас не будет достаточно данных, чтобы определить, действительно ли мы обнаружили запутанные фотоны. в течение нескольких сотен часов, независимо от того, зафиксировали они только что световой импульс или нет».
Если бы эти препятствия были преодолены, эксперимент показал бы, что человеческий глаз способен напрямую обнаруживать квантовую запутанность и достигать того, что до сих пор требовало сложных и дорогих детекторов.В настоящее время ученые работают над тем, чтобы использовать принцип запутанности для создания защищенных каналов цифровой связи и для квантовых компьютеров. По словам Сангоуарда, эти приложения могут выиграть от нового эксперимента.
Исследовательский проект поддерживается Швейцарским национальным научным фондом в рамках Национального центра компетенций в области исследований в области квантовой науки и технологий (NCCR-QSIT) и Фондом Джона Темплтона в США.
Источник истории:
Материалы предоставлены Университетом Базеля . Примечание. Содержимое можно редактировать по стилю и длине.
RealityCarnival Клиффа Пиковера
(15.09.12) Продолжайте смотреть в глаза этому 3D коту, пока ваша душа и разум не превратятся в субатомную трансцендентную кашу
(14. 09.12) Знаете ли вы, что мамонты жили до 1650 г. до н.э. — после пирамид Египта….
09.12) Знаете ли вы, что мамонты жили до 1650 г. до н.э. — после пирамид Египта….
(13.09.12) 6 небольших математических ошибок, которые привели к огромным бедствиям
(12.09.12) Хотите верьте, хотите нет, но это изображение соли и перца (через topdesignmag.ком)
(11.09.12) Чудо природы и человечества: столкновение капель воды, под мыльным пузырем, в стакане с водой. Высокоскоростная фотография: миры внутри миров
(10.09.12) Фотогалерея фракталов, найденных с помощью Google Earth
(09/09/12) Если вы раньше не слышали о законе Бенфорда, этот пост вас порадует.
(08.09.12) Интересная концепция. Напишите письмо себе в будущее
(07.09.12) Чудесная визуализация загадочных закономерностей простых чисел
(06.09.12) Сможем ли мы с помощью цветных жидкостей повернуть время вспять и найти существ, создавших ткань реальности?
(05.09.12) История физики – это история современной цивилизации.Вселенная в двух словах
(04. 09.12) Красивое видео Джейсона Сильвы о силе благоговения
09.12) Красивое видео Джейсона Сильвы о силе благоговения
(03.09.12) Великолепный стол для печатных плат
(02.09.12) Рецензия на мою последнюю книгу ученого-долгожителя Л. Стивена Коулза, доктора медицины, доктора философии.
(01.09.12) Не знаю, что изображено на этом фото, но любопытно смотреть
(31.08.12) Фрактальная математика порождает поверхности невероятной сложности (от 0Encrypted0)
(30.08.12) Биологический клеточный пирог.Мммм, вкусные митохондрии.
(29.08.12) Было бы здорово пойти на свидание с кем-то, кто носит ожерелье из кишок?
(28.08.12) «Ни одна из клеток, из которых вы состоите, не знает, кто вы, и не заботится о вас.» ~ Дэн Деннет
(27.08.12) Что на самом деле происходит, когда вы вводите Askew в поиске Google?
(26.08.12) Зеленые серьги с бактериофагом T4 — для любителей вирусов
(25.08.12) Фракталы чрезвычайно сложны и требуют изучения множества деталей (от HalTenny)
(24.08.12) Вкусная мысль.26 калорий. Вот как я узнал
(23.08.12) Могут ли пространственно-временные траектории 6-фотонного рассеяния стать великим искусством?
(22.08.12) Синдром Ренфилда: Загадочный случай реального вампиризма
(21.08.12) Класс четвероклассников попросили написать хайку. Это написал один ребенок. Нравится?
(20.08.12) Официантка Hooters думает, что ее призом будет Toyota, но потрясена, увидев, что это «игрушка Йода». Судебный процесс следует
(19.08.12) Напечатанный на 3D-принтере протез руки для девочки.Вызывает слезы на глазах. Технология и превосходство
(18.08.12) Фрактал, который выглядит археологически, но создан с помощью чистой математики (от SuicideBySafetyPin)
(17.08.12) Фрактальный цветок для вашей многомерной возлюбленной
(16.08.12) Мужчина вытатуировал Левит 18:22, запрещающий гомосексуальность, на руке. Но Левит 19:28 запрещает татуировки. (спасибо Мэтту Паркеру)
(15.08.12) Восход солнца, каким его еще не видел ни один человек — на Марсе
(14.08.12) «ЛСД абсолютно помог математикам, художникам и ученым решить их сложные, казалось бы, неразрешимые проблемы»
(13.08.12) Тея Красек, словенская художница, создала видеообзор «Медицинской книги», в котором отметила свои любимые изображения: трепанация, трансплантация сердца, нейротрансмиттеры, причина бубонной чумы, прозопагнозия, стеклянные глаза, вирусы…
(13.08.12) Вымерший головоногий влюбляется в математику и геометрию
(12.08.12) Ого. Моча Эшера
(11.08.12) Празднуем! Наконец-то в наличии, в живом цвете. Околосмертные переживания, лечение пиявками, Карл Юнг, пересадка лица, биологическое оружие, дети из пробирки, позитроны! Если вы заказываете это, пожалуйста, дайте мне знать, что вы думаете и какое изображение вам больше всего нравится!
(10.08.12) Внутри Юпитера может поместиться более 1000 Земель. Классная визуализация для детей всех возрастов
(09.08.12) Крутой учитель математики и крутая математика
(08.08.12) Как нарисовать удивительно реалистичную лошадь за 5 простых шагов
(07.08.12) Смотрите до конца.Выглядит почти как научная фантастика: умопомрачительный фильм, снятый с МКС (космической станции)
(06.08.12) Захватывающий вид на Млечный Путь с поверхности Марса
(05.08.12) Калькулятор Курта был создан узником немецкого концлагеря. Посмотри
(04.08.12) Обширные грибковые сети образуют коллективный разум для общения между деревьями: гигантский ботанический мозг
(03.08.12) Инопланетяне учитывают простые числа в реальности, вызванной ДМТ (научная статья в формате PDF)
(02.08.12) Тигр идет медленно, к горящему кусту апокалипсиса
(01.08.12) «За каждым ныне живущим человеком стоит тридцать призраков, ибо именно в таком соотношении мертвые превосходят числом живых»
(31.07.12) Господи, а как ты это ешь?
(30.07.12) Alien Lights: Illuminated Landscapes by Benoit Paille
(29.07.12) Сфотографированы полупрозрачные муравьи, поедающие цветные жидкости
(28.07.12) Дети Северной Кореи играют на гитаре
(27.07.12) Что произойдет, если вы попытаетесь ударить по бейсбольному мячу, летящему со скоростью 90% скорости света?
(26.07.12) Этот телевизионный прогноз погоды обязательно понравится тем, кто интересуется апокалипсисом.
(25.07.12) Завораживающе.Серия мозгов Чарли Роуза
(24.07.12) Где-то над мозговым луком
(23.07.12) Люди никогда не найдут номер факториона больше 40 585 (pdf)
(22.07.12) Фантомный период в 300 лет был вставлен между 600-м и 900-м годами нашей эры?
(21.07.12) 69 696 — самый большой волнистый квадрат, который когда-либо находили люди (pdf)
(20.07.12) Кричать в экстазе. 727272727272727272727272727 272727272727272727272727272 727272727272727272727272727 272727272727272727 (одно длинное число без пробелов) является простым
(19.07.12) Мозговой синдром Антона: когда слепые отрицают свою слепоту, несмотря на доказательства
(18.07.12) Случайные люди на улицах Бруклина пытаются угадать, что такое бозон Хиггса
(17.07.12) Экзопланеты: все известные планеты в виде вкусных круглых конфет
(16.07.12) Безумие, но правда: на самом деле можно сжать ваши файлы JPEG на 500% без потери качества.
(14.07.12) Мальчик оставляет свой велосипед возле дерева в 1954 году и находит его таким сегодня
(13.07.12) Женщина в мини-юбке: Обращение ко всем Х.Поклонники П. Лавкрафта
(12.07.12) Н.П. Лавкрафт отвечает на ваши вопросы об отношениях
(11.07.12) «Тэтан весит около 1,5 унций [45 грамм]», — говорит врач, взвешивавший людей после их смерти.
(10.07.12) Опрос избирателей спросил, кто из кандидатов в президенты США лучше отражает атаку космических пришельцев
(09.07.12) 5 человек вместе играют на одной гитаре
(08.07.12) Более трети заявлений о разводе в прошлом году содержали слово «Facebook»
(07.07.12) Странные израильские и американские вихревые лучи передают 2.5 терабит в секунду. Эпоха Вихря началась
(06.07.12) Подарите спиральную бутылку Кляйна тому, кого вы любите, в этом или следующем измерении
(05.07.12) Зачем усложнять запоминание паролей, когда этот подход настолько прост и безопасен?
(03.07.12) Ого! Если собрать всю земную воду в одном месте, это будет выглядеть так
(02.07.12) «Чертовски привлекательный.» Книга по физике: от Большого взрыва до квантового возрождения
(01.07.12) Почему «нигерийские» почтовые мошенники на самом деле говорят, что они из Нигерии
(30.06.12) Чистый доход от продаж электронных книг превышает объем продаж книг в твердом переплете, что указывает на исторический момент в издательском деле.
(29.06.12) Почему-то этот полуэротический кавер с голым Тарзаном меня реально смешит
(28.06.12) Фрактальная сущность ДМТ, смотрящая в глубины вашей души
(27.06.12) Представьте, что вы сходите с ума, играя на этой фрактальной шахматной доске.
(26.06.12) Эшер, Эйнштейн, Атомик
(25.06.12) Устройство Терменвокс под названием ВЕЩЬ использовалось Советским Союзом для шпионажа в США.
(24.06.12) Внимательно прислушиваюсь к подземным котятам
(23.06.12) Прохождение Венеры, современная композиция из фужеров
(22.06.12) Мистический портрет: Удивительная красота и разнообразие Нью-Йорка
(21.06.12) Шервин Нуланд о разработке электрошоковой терапии как лекарства от тяжелой депрессии, включая его собственную
(20.06.12) Necrofantasia: фортепианная песня, требующая пианиста-мутанта с 50 пальцами.Также см. Самая сложная песня для фортепиано.
(19.06.12) На сюрреалистическом снимке густонаселенные холмы Мехико выглядят как городской океан
(18.06.12) Сэм Харрис — Смерть и настоящий момент
(17.06.12) Жизнь в странной вселенной, наполненной восстаниями сосисок и хот-догов
(16.06.12) Разве ты не ЛЮБИШЬ эти обои с фрактальной шестеренкой?
(15.06.12) Фрактальные шестеренки разумной вселенной вращаются бесконечно. (Также см. этот.)
(14.06.12) Птицы улетают из моих глаз, в океан реальности
(13.06.12) Исследование «Бог аутизма».Почему аутисты не верят в Бога
(12.06.12) Голова Бенуа Мандельброта, пионера фракталов, представленная в виде фрактала
(11.06.12) Обнаружение утерянного кодекса Архимеда
(10.06.12) Каково это — разбираться в очень сложной математике?
(09.06.12) Вас интересует «Медицинская книга: от знахарей до роботов-хирургов» ? Если у вас есть популярный блог, возможно, я смогу дать вам копию для обзора.
(08.06.12) 11 лучших научных книг 2011 года, Мария Попова
(07.06.12) Дрожь от благоговения.2, в редком оригинальном аудио
(05.06.12) Откусывать фрактальные блины целую вечность
(04.06.12) Отравленные мыши-десантники обрушиваются на человечество
(02.06.12) Список заблуждений Википедии о незаконных наркотиках
(01.06.12) МЕДИЦИНСКАЯ КНИГА: От знахарей до роботов-хирургов! Оформите предзаказ сегодня, чтобы получить 528-страничную цветную книгу в твердом переплете по отличной цене. Темы: околосмертные переживания, лечение пиявками, эксперименты над собой, дети из пробирки, трансплантация лица, биологическое оружие, обрезание и многое другое.
(31.05.12) Дельта реки Лены на севере Сибири (слева) и слепок легкого человека (справа)
(30.05.12) Странное название недели: «Хранитель зоопарка, как сообщается, более часа лижет анус детеныша обезьяны»
(29.05.12) Невероятная физика падений домино. Сможете ли вы разрушить Эмпайр Стейт Билдинг костяшкой в 1 дюйм?
(27.05.12) Кровеносные сосуды головы, одиноко плывущие в море вечности
(26.05.12) В 100 миллиардов раз более вязкая, чем вода
(25.05.12) Hartverdrahtet: аудиовизуальное путешествие в процедурную фрактальную вселенную, сжатое в крохотный программный фрагмент
(24.05.12) Король метамфетамина тратит деньги наркоимперии на 18 753 комикса
(23.05.12) Какое-то странное соревнование между шаромагнитными людьми
(22.05.12) Симуляция Conways Game of Life внутри увеличенной версии Game of Life
(21.05.12) Бойтесь Когтя Архимеда
(20.05.12) Почему люди сходят с ума, думая о 998 001
(19.05.12) Необычный сборник.Последние 10 секунд каждой серии 1-го сезона сериала «Звездный путь: Следующее поколение».
(18.05.12) Таинственные гималайские охотники за медом, рискуя жизнью, собирают самых больших медоносных пчел Земли
(17.05.12) Где сегодня на Земле существуют мусульмане? (картограмма)
(16.05.12) Я почему-то просто обожаю фото сложных, синтезаторов Moog. Ты?
(15.05.12) Клиффорд Столл: 18 минут с живым умом
(14.05.12) Список членов проклятого «Клуба 27»
(13.05.12) Какие книги были в списке бестселлеров Нью-Йорк Таймс в день вашего рождения?
(12.05.12) Обновлено.Головоломка «Исчезающий карандаш» сводит мир с ума. Попробуйте на своих друзьях
(11.05.12) Число такое большое, что ваша голова провалится в черную дыру.
(10.05.12) Круглый штифт лучше входит в квадратное отверстие, чем квадратный в круглое отверстие, вплоть до 9-го размера
(09.05.12) Этот путь имеет бесконечную длину? [анимированный гиф]
(08.05.12) Торт Мебиуса, Бекон Мебиуса, Корабль Мебиуса
(07.05.12) Замечательные математические теоремы, о которых дети должны знать
(06.05.12) Когда Эйнштейн встретил Рабиндраната Тагора — правда и красота, наука и духовность
(05.05.12) Исследование определило, что это самая расслабляющая песня из когда-либо существовавших.
(04.05.12) Тея Красек — словенская художница, увлекающаяся математикой, искусством, музыкой, сюрреализмом и многим другим.Вот ее красочный канал на YouTube
(03.05.12) Ничего себе, древние шумерские пословицы (pdf)
(02.05.12) Интригует. Патент США. Огнеметная музыкальная труба
(01.05.12) Викинги не носили рогатых шлемов, Напоф не был низкорослым и другие исторические мифы развенчаны
(30.04.12) «У материи, как и у людей, мы видим только кожу вещей, мы не можем заглянуть в «машинное отделение»».
(29.04.12) Самые популярные отрывки всех времен на Amazon Kindle!
(28.04.12) Давайте соберемся вместе и насладимся теоремой о пицце
(27.04.12) Беседа с физиками/писателями Брайаном Грином и Лоуренсом Крауссом.(Как шутка еврейского доктора.)
(26.04.12) Причудливый силовой двигатель «моллюск-киборг», создающий сцену для мифопоэтических чудес моллюсков, которые невозможно вообразить.
(25.04.12) Безумный мозг Кубик Рубика шокирует и восхищает
(24.04.12) Странная книга о рыбах чуть не погубила карьеру Исаака Ньютона
(23.04.12) Провокационный. Диетические насыщенные жиры не связаны с повышенным риском сердечных заболеваний?
(21.04.12) Подробное обсуждение самого известного гитарного шнура в истории рока
(20.04.12) Только что опубликованный выпуск «IBM Journal of Research & Development» о Watson/Jeopardy и футуристическом искусственном интеллекте (ИИ)
(19.04.12) Мартин Гарднер, Красота и тайна математики, бесплатное приложение для iPad
(18.04.12) Взгляд в будущее.Шанхай 1990 против 2010. Хорошее сравнение фотографий?
(17.04.12) Интригует. 51% людей, у которых диагностирован рак, умирают от рака. 49% умирают от чего-то другого
(16.04.12) Надуть тонкий баллон. Измените свой размер. Повторение. Безумный фрактал
(15.04.12) «Прости меня, Отец, ибо я согрешил». Работа Клиффа Пиковера
(14.04.12) Ого. Кубик Рубика набор ящиков
(13.04.12) Новое на Pinterest. «Мир Клиффа Пиковера». Наука, научная фантастика, технологии, странная реальность, футуризм, инновации, математика.Следуйте за мной или посещайте каждый день для трансцендентности.
(12.04.12) Чайник с анатомическим сердцем заставляет нас кричать
(11.04.12) 10 советов Нассима Талеба, как изменить свою жизнь. Согласен с любым?
(10.04.12) «Фракталы и Кот в шляпе»
(09.04.12) Возьмите 3 щепотки ДМТ, размешайте грифель Эшера, добавьте математику и фрактальную порцию научной фантастики и хорошо перемешайте.
(08.04.12) После смерти лауреата Нобелевской премии по физике Ричарда Фейнмана эти слова были найдены на его доске.
(07.04.12) Невероятно странно.Сальвадор Дали иллюстрирует «Алису в стране чудес».
(05.04.12) Человек ходит весь день, чтобы создать эффектные фрактальные узоры из снега
(04.04.12) Ого. Доказательство того, что Земля более гладкая, чем бильярдный шар
(03.04.12) Мы живем в математическом объекте? И какое отношение это может иметь к религии?
(02.04.12) Странный заголовок недели: «Умирающая королева муравьёв спарилась с крабовым пауком, поедающим её с головы» (ВИДЕО)
(01.04.12) Невозможный выступ
(31.03.12) Точка Фейнмана — это последовательность из шести девяток, начинающаяся с 762-го десятичного знака числа пи.
(29.03.12) Самый большой суши-ролл в мире
(28.03.12) Трехмерный способ изображения монстров в двухмерном браузере
(27.03.12) Поклонение во фрактальном соборе и, наконец, ощущение присутствия Бога (графика).(Нажмите, чтобы увеличить)
(26.03.12) Ричард Фейнман: Последнее путешествие гения
(25.03.12) Представьте, что вы принимаете ДМТ, смотрите в зеркало и видите в нем свое отражение.
(24.03.12) Реалистичное стеклянное сердце с желудочками для цветочных стеблей. (Нажмите, чтобы увеличить)
(23.03.12) Вот что бывает, когда раздаешь тысячи наклеек тысячам детей
(22.03.12) Радуги, физика, Бог
(21.03.12) 1-минутный фильм о фрактальных космических струнах искривляет наш разум и душу
(20.03.12) Если сатана играет в мини-гольф, то это его любимая лунка
(19.03.12) В детстве у меня была книга «Человеческое тело», которая пробудила мой интерес к науке
(18.03.12) Ого.Книга по математике и книга по физике сегодня заняли 1 и 2 место в журнале Scientific American (посмотрите, пока у них не закончились экземпляры)
(17.03.12) Все достижения человечества — все наши надежды, мечты и страхи — на одном графике
(16.03.12) Мне нравится эта загадочная фотография восхода луны, сделанная Бет Хёкель.
(15.03.12) Необычное временное состояние нейронов заставляет репортера внезапно говорить на языках
(14.03.12) Почему так долго не изобретали колесо
(13.03.12) Мужчина пытается проиллюстрировать странную историю моды и войны
(12.03.12) Фрактальная математика, похожая на карамельную морось
(10.03.12) Откуда математики знают, что 2012 год действительно конец света
(09.03.12) Интригующие и дикие визуализации простых чисел
(08.03.12) Что на самом деле происходит в центре математической сингулярности.Загадочный
(07.03.12) Представьте, что сегодня вечером вы исследуете этот футуристический город с любимым человеком.
(06.03.12) Девушка, инопланетянин, цветок, психоделика, глаза-усики, хорошенькая
(05.03.12) Плач инопланетной рыбы
(04.03.12) Почему математика лучше наркотиков и может стать духовным опытом
(03.03.12) Анатомические поперечные срезы, сделанные из квиллинговой бумаги. Автор Лиза Нильссон
(02.03.12) Безумный фрактальный спирограф (фрактальная рулетка)
(01.03.12) Удивительное открытие, связанное с фотографиями, бутылками Клейна, случайностью, математикой и не только
(29.02.12) Взгляните с трепетом на Прайм Бельфегора: 1000000000000006660000000000000001 — простое палиндромное число, среди нулей которого скрывается 666.915). Что человечество найдет в своих самых глубоких исследованиях?
(23.02.12) Интригующий блог «картинки из математики»
(22.02.12) Увлекательно и познавательно. Физика падения Слинки
(21.02.12) Странный, странный мир, для нас обитаемый…
(20.02.12) Мозги из рук
(19.02.12) Супер-супергений Эд Виттен сидит в кресле и объясняет нам с вами теорию струн. Журнал Time называет Виттена «величайшим физиком-теоретиком в мире».»
(18.02.12) Лего-адронный коллайдер
(17.02.12) Причудливые фрактальные дроби, сокрушающие мозжечок в подчинение
(16.02.12) 10 причин, по которым вам может захотеться выпить кофе
(15.02.12) Таинственная ползучая пена навоза заставляет свинофермы взрываться. Большой взрыв свиньи
(14.02.12) 7 миллиардов человек ходят по точке слева. 12 из них прошли по точке справа
(13.02.12) Мужчина делает предложение любви всей своей жизни в двоичном коде.Это сработало
(12.02.12) Мистическое покадровое видео Млечного Пути, пересекающего небо над Южной Дакотой. Мечтать со мной
(10.02.12) 1344-страничное графическое произведение всей великой западной литературы!
(09.02.12) Любопытным математикам: кофейная чашка, которая топологически НЕ совпадает с пончиком
(08.02.12) Женщины в науке: почему так мало? (видео)
(07.02.12) «Математика — это сексуально! 5IVE лучших популярных книг на эту тему, которые это доказывают
(06.02.12) Симпатичный набор Мандельброта.(Нажмите, чтобы увеличить)
(05.02.12) Индивидуалисты разума: наводящие на размышления интервью Дэвида Джея Брауна о сознании
(04.02.12) Toto’s Africa от Perpetuum Jazzile. Стоит послушать
(03.02.12) Если вы подвергаетесь воздействию красного цвета во время прохождения теста IQ, ваш IQ ниже
(02.02.12) Величайшие книги всех времен по версии 125 известных авторов
(01.02.12) Обрезание мужчин — одна из самых эффективных «прививок» от СПИДа, снижающая вероятность заражения на 60% и более
(31.01.12) Фракталы, научная фантастика, мозг пришельцев
(30.01.12) 10 женщин, оказавших наибольшее влияние на технологии в 2011 г.
(29.01.12) Вскрытие свиньи анатомия оригами
(28.01.12) Патент США.Гигантский мармеладный мишка
(27.01.12) «Физические книги — это знаки нашей идентичности, своего рода преемственность на протяжении всей жизни, носитель памяти.»
(26.01.12) Наслаждайтесь этой расслабляющей гифкой голштинской породы, наслаждающейся приятной чисткой зубов:
(25.01.12) Безумные пазлы для детей всех возрастов!
(24.01.12) Произведите впечатление на своих друзей на следующей вечеринке этой удивительной и причудливой фразой: «Слабые гипер-Вудинские кардиналы». Наслаждаться
(23.01.12) Математические статьи смертоносного «Унабомбера»
(22.01.12) 16 самых умных детей в истории
(21.01.12) Женщина, геометрия, руки, узор
(20.01.12) Новый вид обезьян обнаружен и быстро съеден
(19.01.12) Почему ночью небо темное?
(18.01.12) Огромный субконтрабас-саксофон: «мать всех саксофонов»
(17.01.12) Ваш безумный фрактальный многоквартирный дом далекого будущего.Представьте, что вы живете в этом городе. Нажмите, чтобы увеличить
(16.01.12) Лавкрафт знакомится с трехмерными фракталами
(15.01.12) Хотели бы вы подняться на самую высокую гору во всей Солнечной системе?
(14.01.12) Стивен Хокинг теперь примет ваши вопросы (YouTube)
(13.01.12) Фото. Прежде чем уснуть этой ночью, поразмышляйте о красоте вселенной.
(12.01.12) Коровы, разумные языки и стремление к превосходству
(11.01.12) Загадочный кот, высоко над деревьями, превосходящий пространство и время
(10.01.12) Очень красивые гармонии в необычной песне: «Mumford and Sons — Little Lion Man»
(09.01.12) Для вас математические задроты.Таинственное и чудесное доказательство того, что число пи=4. На каком шаге ошибка?
(08.01.12) Скандальный епископ на пенсии Джон Спонг обсуждает глубочайшие тайны христианства (YouTube)
(07.01.12) Два человека с искусственным интеллектом, с мимикой лица, неожиданно оказываются лицом к лицу. Завязывается разговор. Вот еще один пример того, что происходит, когда вы позволяете двум искусственным интеллектам разговаривать
(06.01.12) Прекрасная математика: почему у твоих друзей больше друзей, чем у тебя (и почему твоя девушка шлюха)
(05.01.12) Алан Мур, реальность, кукольный змеиный бог, Теренс МакКенна, наука
(04.01.12) Я подумал, что, возможно, вам будет интересна эта страница обложек моих книг на разных языках.Сколько языков мы знаем?
(03.01.12) Предсказания Роберта Хайнлайна на 2000 год (от 1952 года)
(02.

 Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width». Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
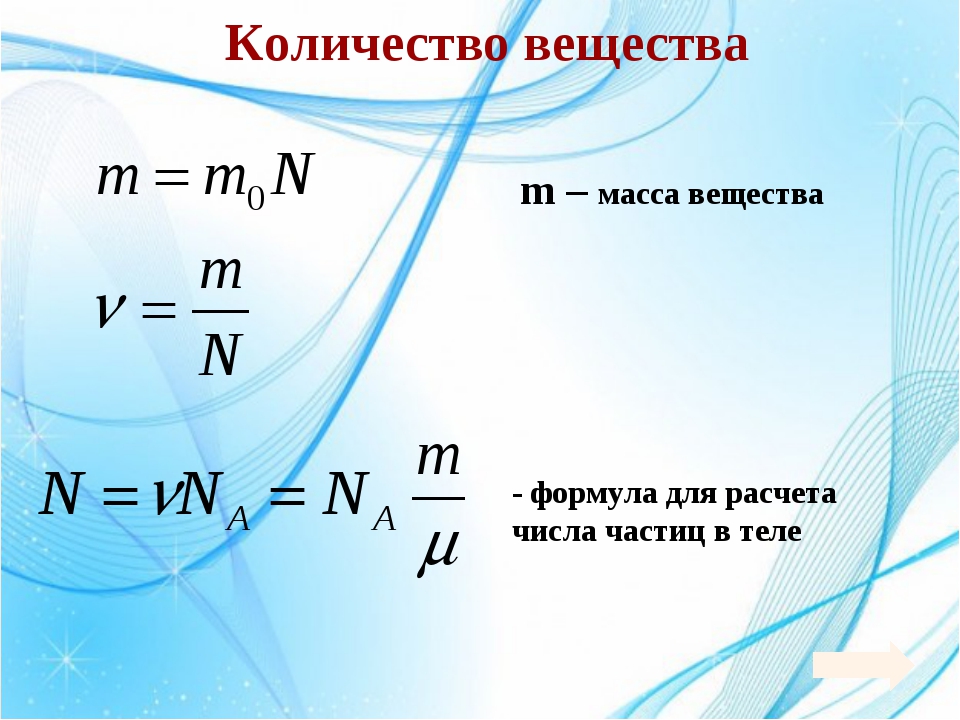
 Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее. Однако в нем математическая площадь — это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Однако в нем математическая площадь — это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»). Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
 Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.

 К альтернативным теориям гравитации часто… … Википедия
К альтернативным теориям гравитации часто… … Википедия
 Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
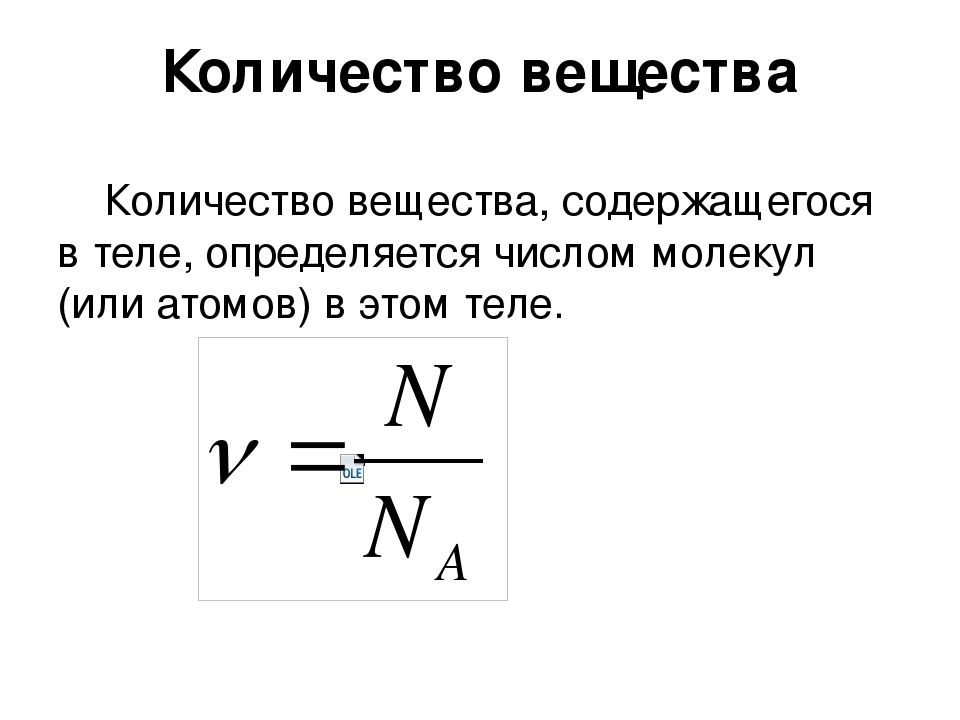 При этом необходимо соблюдать следующие правила:
При этом необходимо соблюдать следующие правила: По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?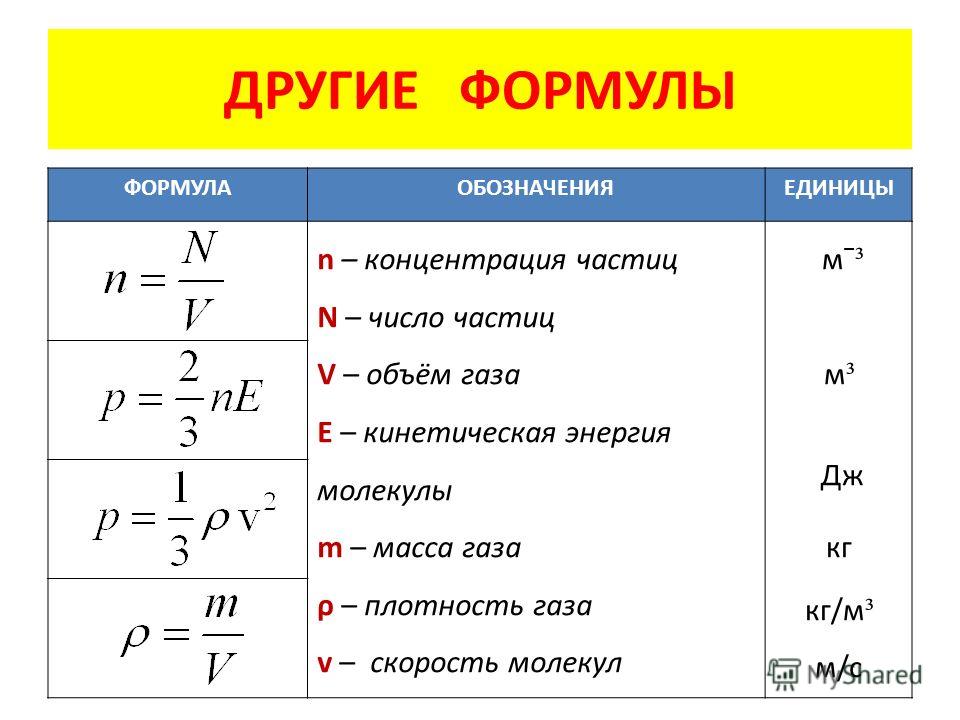



 Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
 electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος)
electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος)
 electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия
electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия
 gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия
gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия
 kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона
kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона
 massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка
massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка
 quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции
quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции
 spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга
spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга
 volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant)
volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant)
 Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект
), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект
 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон
14159…, пи-связь, пи-плюс мезон, пи-ноль мезон
 Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
 ru
ru
 Он поляризован и течет в определенном направлении.
Он поляризован и течет в определенном направлении.
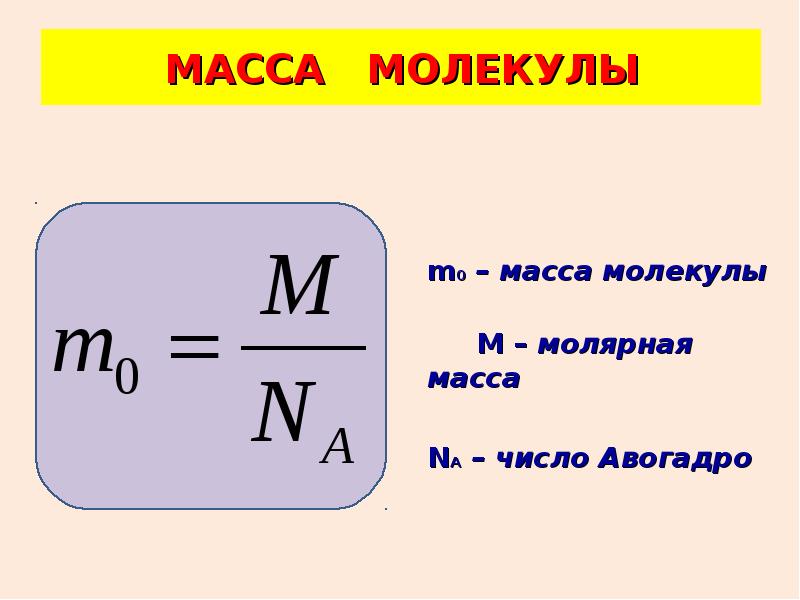
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT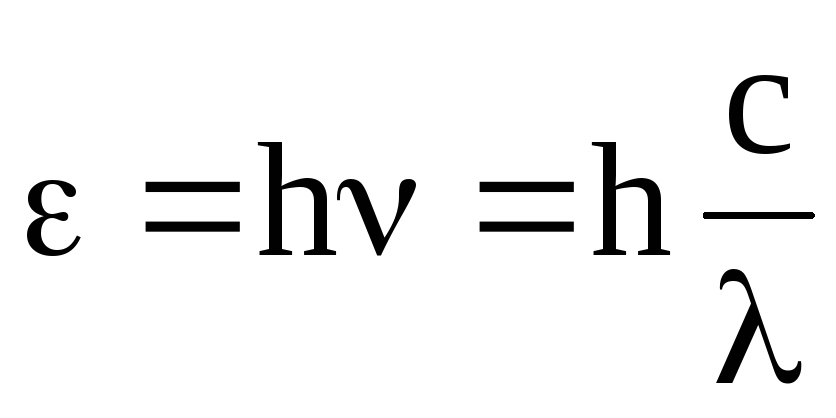 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC

 Активно участвуют в беседе с учителем, формулируют определения, делают выводы по теме, проводят исследования, осмысливают результаты, получают формулы, ведут записи в тетрадях.
Активно участвуют в беседе с учителем, формулируют определения, делают выводы по теме, проводят исследования, осмысливают результаты, получают формулы, ведут записи в тетрадях.