НАЧАЛА ФИЗИКИ
Далее, поскольку закон должен быть симметричным по отношению к взаимодействующим телам, то сила притяжения тела к Земле должна быть пропорциональна и массе Земли. А поскольку естественно предположить, что сила должна убывать с ростом расстояния между телами, то для силы взаимодействия двух тел массами m и M получается такая формула
(13.2)
где r — расстояние между телами; n — показатель степени, который Ньютону предстояло определить; G — коэффициент, названный впоследствии гравитационной постоянной. Из формулы (13.2) и второго закона механики Ньютон следует, что ускорение свободного падения тел на поверхности Земли равно
(13.2)
где m и M — массы тела и Земли; R — радиус Земли. Сделать вычисления по этой формуле с использованием известного ускорения свободного падения (и подобрать таким образом n) Ньютон не мог, поскольку масса Земли и гравитационная постоянная были не известны.
О существовании взаимодействия массивных тел на расстоянии говорили и до Ньютона (Н. Коперник, И. Кеплер и Р. Декарт). По-видимому, первым, кто сказал о центральном характере этой силы и предложил правильную зависимость силы от расстояния был Р. Гук. Публикации Гука, в которых он изложил свой подход к гравитационному взаимодействию, как причине эллиптических траекторий планет, относятся к 1666 и 1674 годам. В трактате «О движении Земли» (1674 г.) он высказал идею тяготения и дал свою систему мироздания. В 1680 г. Гук пришел к выводу, что сила тяготения обратно пропорциональна квадрату расстояния. Тем не менее, соображения Гука о гравитации носили характер догадки, и никак не были обоснованы (в частности, Гук не показал, как из закона обратных квадратов следует эллиптичность траекторий планет).
Подробное изложение закона всемирного тяготения (с выводами законов Кеплера) было дано
Ньютоном в «Математических началах натуральной философии» (1687 г.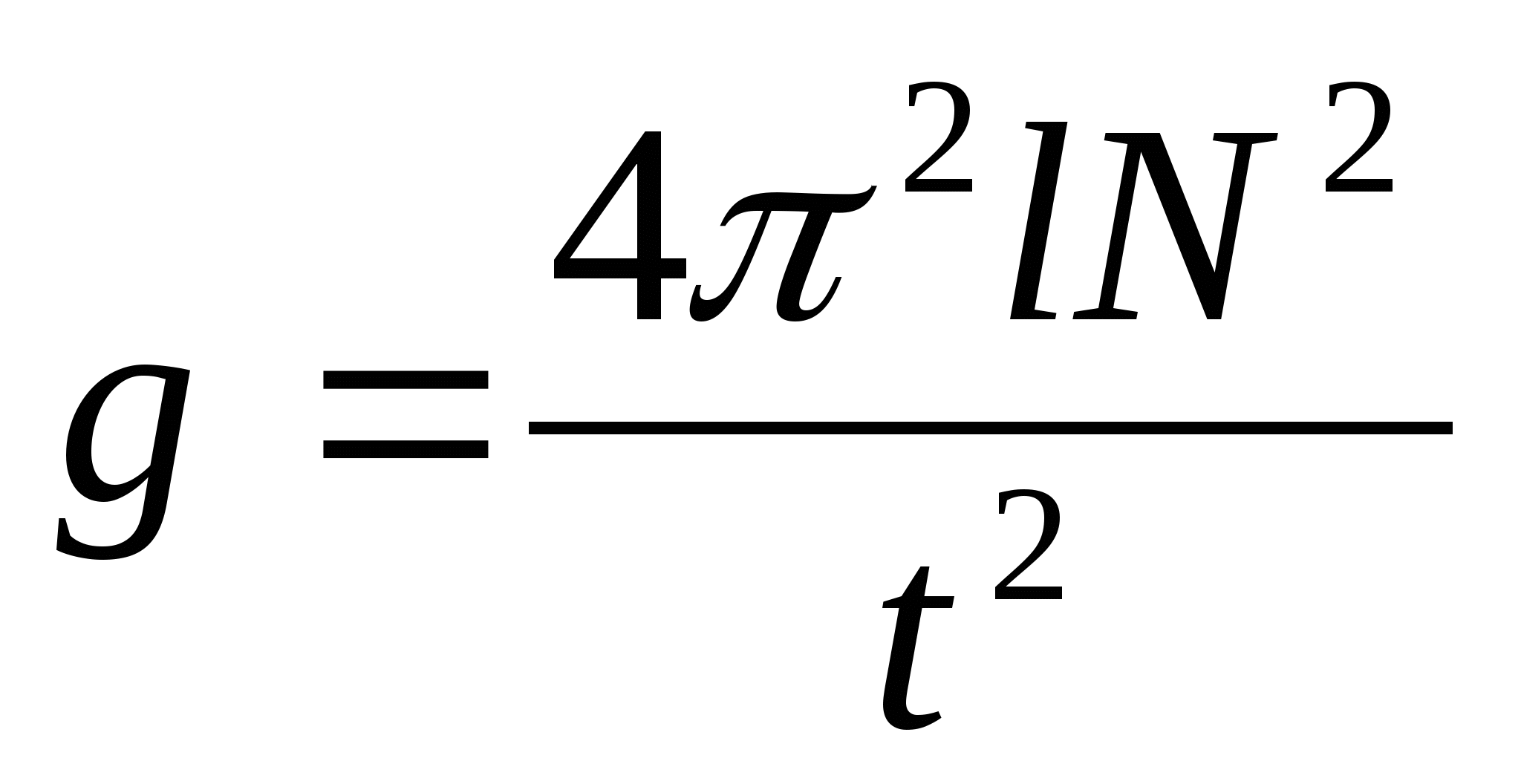 ). Когда известный астроном Э. Галлей (на деньги которого издавались «Начала») прочитал рукопись «Начал» и не увидел ссылки на Гука, он предложил Ньютону такую ссылку сделать. Ньютон не мог отказать своему другу и спонсору и сослался на Гука, но очень своеобразным способом.
). Когда известный астроном Э. Галлей (на деньги которого издавались «Начала») прочитал рукопись «Начал» и не увидел ссылки на Гука, он предложил Ньютону такую ссылку сделать. Ньютон не мог отказать своему другу и спонсору и сослался на Гука, но очень своеобразным способом.
202/597
Сила тяжести: формула, единицы измерения, особенности
Сила тяжести и ее источник: FreepickРазбираетесь с такой физической категорией, как сила тяжести? Формула, ее составляющие и единицы измерения укажут, что сильнее притянет Земля — яблоко или поезд. Отличается ли сила тяжести от силы тяготения? Объясним, как не перепутать эти две величины.
Что такое сила тяжести
Каждый день наблюдаем, как тела вокруг деформируются (меняют форму или размеры), ускоряются или тормозят, падают. В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?
О чем идет речь?
Понятие силы
Силой называют физическую векторную величину, которая оказывает воздействие на тело, а ее источниками становятся другие тела. Что означает понятие векторной величины? Это говорит о том, что сила наделена направлением. В зависимости от того, куда она направлена, можно получить разные результаты.
Это как если стоять на вершине горы на сноуборде, то от направления толчка будет зависеть дальнейшее движение. Таков результат приложения силы в этом случае. Силы, которые изучают ученые-физики, разнообразны и очень важны для нашей повседневной жизни.
Определение и значение силы тяжести
Одна из них носит название сила тяжести. Физика предлагает следующее определение: сила тяжести — это величина, которая показывает, насколько сильно Земля притягивает тело, которое расположено на ее поверхности или рядом с ней. Таким образом, направление этой силы — центр нашей планеты.
Сила тяжести на Земле крайне важна по следующим причинам:
- Наша планета притягивает все, что попадает в сферу действия этой силы, будь то твердое тело, жидкость или газ.

- Благодаря ее существованию стало возможным создание атмосферы (молекулы газов, которые ее составляют, не улетают в космические просторы), появились и остаются на своих местах моря и океаны.
- Любой предмет, который приподнимаем и роняем, обязательно упадет вниз по направлению к Земле.
Кстати, именно из-за воздействия этой силы люди не могут летать. Самостоятельно развить скорость, на которой полет становится возможным (так называемую первую космическую) человек не способен, а потому в обычной жизни всегда твердо стоит ногами на Земле.
Сила тяжести и сила тяготения: отличия
Падение перьев как пример силы тяжести: FreepickСила тяжести, определение которой дали выше, схожа с силой тяготения. Оба варианта связывает сила притяжения.
Однако эти две силы не одно и то же, хоть их и часто путают. Давайте разберемся, в чем тут дело.
Еще в 1682 году Исаак Ньютон открыл закон о всемирном тяготении. Сформулирован он был так: тела притягивают друг друга, а сила этого тяготения — величина, прямо пропорциональная произведению их масс и обратно пропорциональна расстоянию, возведенному в квадрат.
Математически силу тяготения записывают так: F = G×M×m/R², где:
- F — сила тяготения, Н;
- M — масса первого тела (часто планеты), кг;
- m — масса второго тела, кг;
- R — дистанция между ними, м;
- G — постоянная величина (G = 6,67×10⁻¹¹ м³×кг⁻¹×с⁻²).
Продемонстрировать эту силу легко — достаточно встать на весы. Стрелка сразу же отклонится, показывая вес тела. Так происходит из-за очень большой массы Земли, благодаря которой мы придавлены к ней. На Луне, масса которой меньше, вес человека меньше в несколько раз.
Итак, закон о всемирном тяготении и соответствующая сила необходимы для вычисления силы взаимодействий между разнообразными телами. При этом их размеры должны быть меньше, чем расстояние между ними.
Теперь вернемся к нашей теме и рассмотрим подробно, что же такое сила тяжести, обозначение которой дали выше, и как она связана с силой тяготения.
Сила тяжести: формула, единицы измерения
Напомним, что когда говорим о силе тяжести, то имеем в виду силу, с которой осуществляет притяжение наша планета.
Формула силы тяжести такова: F = m×g, где:
- F — сила тяжести, Н;
- m — масса тела, кг;
- g — ускорение свободного падения, м/с².
В этой формуле видим новую величину — ускорение свободного падения. Так называют ускорение, которое приобретает тело рядом с Землей во время свободного и беспрепятственного падения. Рядом с поверхностью Земли значение этой величины примерно равняется 9,81 м/с², а в приблизительных расчетах используют округленное значение 10 м/с².
По этой формуле рассчитывается сила тяжести, единица измерения которой — Ньютоны (в честь Исаака Ньютона).
Капл дождя падают на Землю благодаря силе тяжести: FreepickЧему равна сила тяжести? Глядя на эту формулу, можно сказать, что сила тяжести схожа с весом тела. В покое на Земле эта величина и вес будут идентичны. Но это не одно и то же. Почему? Объяснение не сложное:
- Силой, с которой на тела действует Земля, называют силу тяжести.
- Вес тоже сила, с которой тела действуют на опору.

- То есть у них отличаются точки действия: первая направлена на центр массы тел, а вес направлен на опору.
Кроме того, на величину силы тяжести влияет масса и планета, на которой проводятся измерения. Вес определяется также ускорением, с которым происходит движение тела и опоры.
К примеру, вес тела в лифте определяется тем, в каком направлении и как быстро происходит движение тела. Сила тяжести не учитывает, куда и что движется: эти внешние факторы на нее не влияют.
Итак, с весом разобрались. А что же с силой тяготения, которую упоминали выше? Можем ли две эти силы приравнять? На этот раз ответ будет утвердительным. Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.
Выразим это математически:
- F = m×g.
- F = G×M×m/R².
- m×g = G×M×m/R².
Если обе части полученного уравнения разделить на массу, то получим такую формулу: g = G×M/R².
Величина g (ускорение свободного падения) уникальна для каждой планеты:
- На нашей Земле свободно падающее тело с каждой секундой ускоряется примерно на 9,81 метр (м/с²).
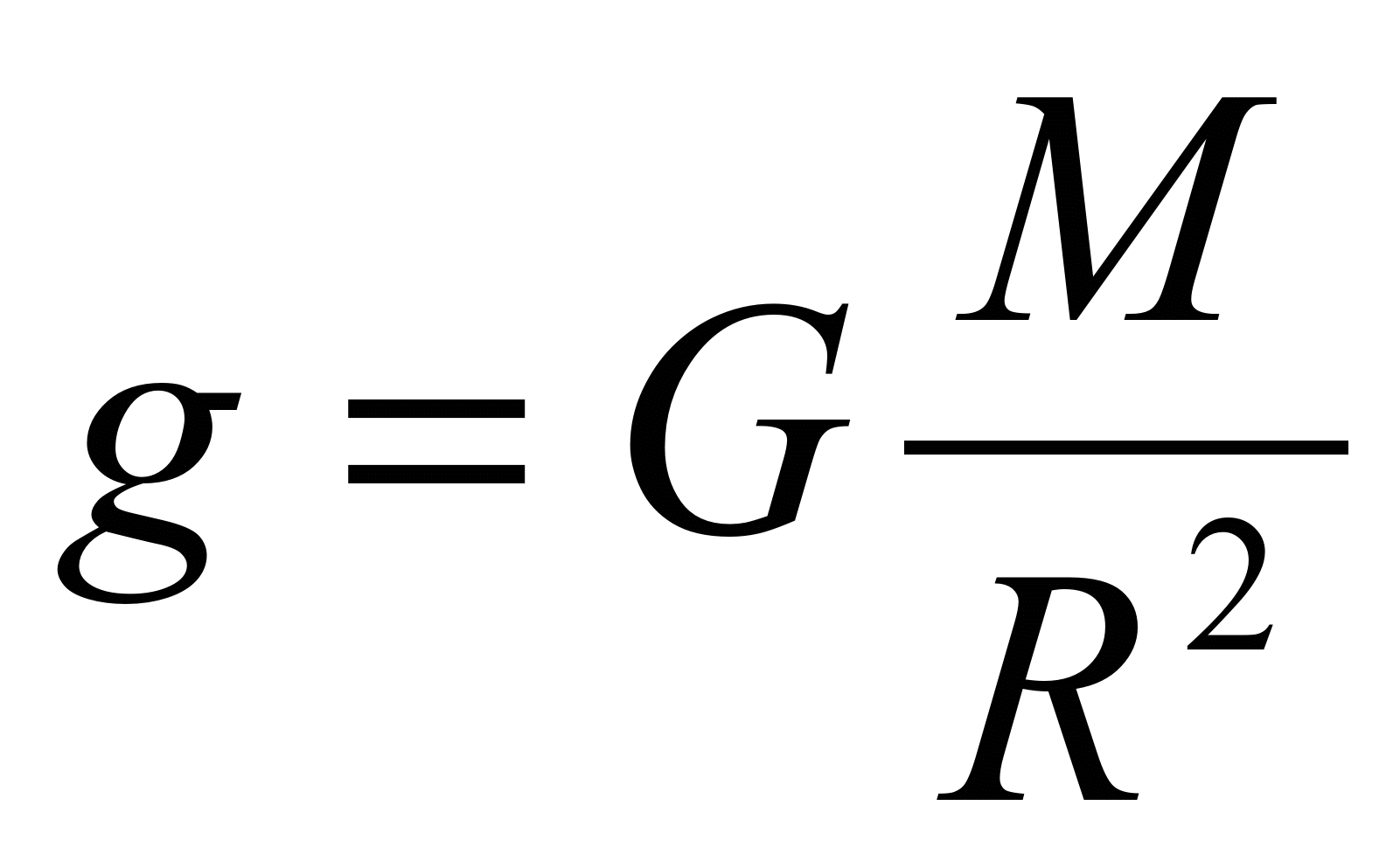
- Ускорение свободного падения рядом с Луной имеет величину всего 1,62 м/с².
- На Юпитере это значение достигает 26,2 м/с². Человек, который весит 60 кг, на этой планете почувствует себя так, будто бы поправился на 100 кг.
Как изменится величина, если тело будет падать 4 секунды? Попробуем подсчитать:
- Скорость падения в начальной точке составит 0 м/с².
- В течение первой секунды она увеличится до 9,81 м/с².
- За вторую секунду величина вырастет вдвое и составит 19,62 м/с².
- Третья секунда добавить еще одну величину ускорения и получится 29,43 м/с².
- В четвертую секунду скорость движения тела достигнет 39,24 м/с², что равняется приблизительно 141 км/ч.
Отметим, что яблоко и кирпич будут падать с равной скоростью. Только очень легкие предметы во время падения замедляет воздух, оказывая им ощутимое сопротивление. Так, птичье перышко будет совершать падение очень медленно и плавно.
Задумываемся об этом или нет, на каждого из нас оказывает воздействие сила тяжести. Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.
Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.
Оригинал статьи: https://www.nur.kz/family/school/1909020-sila-tyazhesti-formula-edinitsy-izmereniya-osobennosti/
Свободное падение тел. Ускорение свободного падения
Свободное падение тел. Ускорение свободного падения
- Подробности
- Просмотров: 1306
Свободное падение — это движение тел только лишь под действием притяжения Земли ( под действием силы тяжести)
В условиях Земли падение тел считается условно свободным, т.к. при падении тела в воздушной среде всегда возникает еще и сила сопротивления воздуха.
Идеальное свободное падение возможно лишь в вакууме, где нет силы сопротивления воздуха, и независимо от массы, плотности и формы все тела падают одинаково быстро, т. е. в любой момент времени тела имеют одинаковые мгновенные скорости и ускорения.
Наблюдать идеальное свободное падение тел можно в трубке Ньютона, если с помощью насоса выкачать из неё воздух.
В дальнейших рассуждениях и при решении задачпренебрегаем силой трения о воздух и считаем падение тел в земных условиях идеально свободным.
УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ
При свободном падении все тела вблизи поверхности Земли независимо от их массы приобретают одинаковое ускорение, называемое ускорением свободного падения.
Условное обозначение ускорения свободного падения — g.
Ускорение свободного падения на Земле приблизительно равно :
g = 9,81м/с2.
Ускорение свободного падения всегда направлено к центру Земли.
Вблизи поверхности Земли величина силы тяжести считается постоянной, поэтому свободное падение тела — это движение тела под действием постоянной силы.
Вектор силы тяжести и создаваемого ею ускорения свободного падения направлены всегда одинаково.
Все формулы для равноускоренного движения применимы для свободного падения тел.
Величина скорости при свободном падении тела в любой момент времени:
перемещение тела:
В этом случае вместо ускорения а, в формулы для равноускоренного движения вводится ускорение свободного падения g =9,8м/с2.
___
В условиях идеального падения падающие с одинаковой высоты тела достигают поверхности Земли, обладая одинаковыми скоростями и затрачивая на падение одинаковое время.
При идеальном свободном падении тело возвращается на Землю со скоростью, величина которой равна модулю начальной скорости.
Время падения тела равно времени движения вверх от момента броска до полной остановки в наивысшей точке полета.
Только на полюсах Земли тела падают строго по вертикали.
ЗНАЕШЬ ЛИ ТЫ
Лишь итальянскому ученому Галилео Галилею удалось установить, что траекторией тела, брошенного под углом к горизонту в безвоздушном пространстве, является парабола.
А итальянец Тарталья (1500 – 1557г.), даже не зная законов движения, пришел к выводу, что наибольшей дальности стрельбы можно достичь, если наклонить орудие к горизонту под углом 45 градусов.
___
Минимальная скорость, которую достаточно сообщить брошенному вертикально вверх телу для того, чтобы оно не вернулось обратно, называют второй космической скоростью.
ЗАГЛЯНИ НА КНИЖНУЮ ПОЛКУ
1. А что ты знаешь о падающих кошках?
2. А помнишь ли ты переход Суворова через Альпы?
3. Галилео Галилей (из книги Я.Голованова «Этюды об ученых»)
4.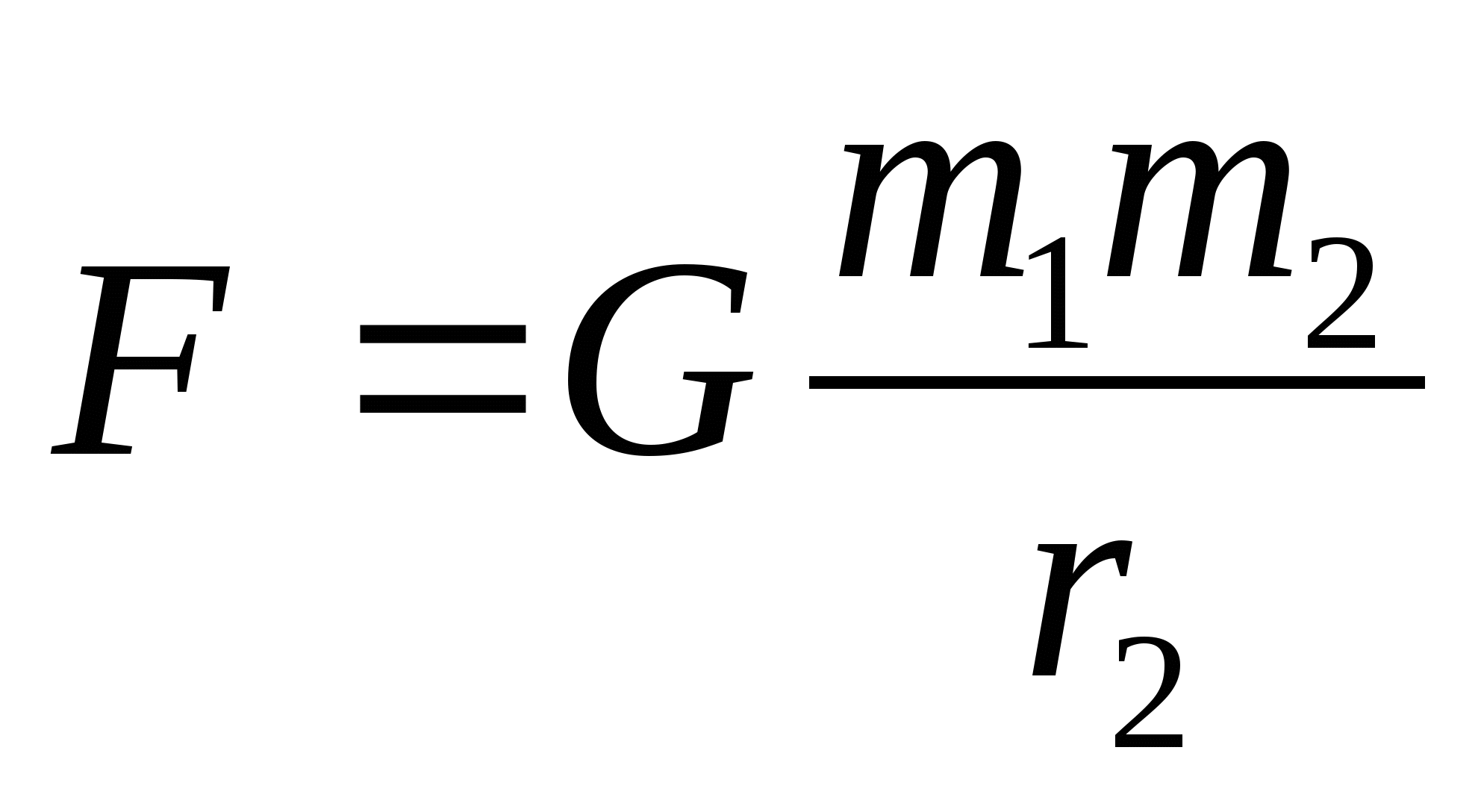 Наш закон бутерброда.
Наш закон бутерброда.
5.Сколько весит тело, когда оно падает?
6.Из пушки на Луну.
7.Сверхдальняя стрельба.
8.Затяжной прыжок парашютиста.
А КАКОВО ПАДЕНИЕ ТЕЛ В РЕАЛЬНЫХ УСЛОВИЯХ?
Если выстрелить из ружья вертикально вверх, то, учитывая силу трения о воздух, свободно падающая с любой высоты пуля приобретет у земли скорость не более 40 м/с.
___
В реальных условиях из-за наличия силы трения о воздух механическая энергия тела частично переходит в тепловую. В результате максимальная высота подъема тела оказывается меньше, чем могла бы быть при движении в безвоздушном пространстве, а в любой точке траектории при спуске скорость оказывается меньшей, чем скорость на подъеме.
___
При наличии трения падающие тела имеют ускорение, равное g, только в начальный момент движения. По мере увеличения скорости ускорение уменьшается, движение тела стремится к равномерному.
ХОЧЕШЬ ПОИГРАТЬ?
— жми здесь.
СДЕЛАЙ САМ
Как ведут себя падающие тела в реальных условиях?
Опыт1
Возьмите небольшой диск из пластмассы, толстого картона или фанеры. Вырежьте из обычной бумаги диск такого же диаметра. Поднимите их, держа в разных руках, на одинаковую высоту и одновременно отпустите. Тяжелый диск упадет быстрее, чем легкий. На каждый диск действует при падении одновременно две силы: сила тяжести и сила сопротивления воздуха. В начале падения равнодействующая силы тяжести и силы сопротивления воздуха будет больше у тела с большей массой и ускорение более тяжелого тела будет больше. По мере увеличения скорости тела сила сопротивления воздуха увеличивается и постепенно сравнивается по величине с силой тяжести, падающие тела начинают двигаться равномерно, но с разной скоростью ( у более тяжелого тела скорость выше).
Аналогично движению падающего диска можно рассматривать движение падающего вниз парашютиста при прыжке с самолета с большой высоты.
Опыт 2
Положите легкий бумажный диск на более тяжелый пластмассовый или фанерный, поднимите их на высоту и одновременно отпустите. В этом случае они будут падать одновременно. Здесь сопротивление воздуха действует только на тяжёлый нижний диск, а сила тяжести сообщает телам равные ускорения в независимости от их масс.
ПОЧТИ АНЕКДОТ
Парижский физик Ленорман, живший в 18 веке, взял обычные дождевые зонты, закрепил концы спиц и прыгнул с крыши дома. Затем ободренный успехом он изготовил уже специальный зонт с плетеным сиденьем и кинулся вниз с башни в Монпелье. Внизу его окружили восторженные зрители. Как называется ваш зонт? Парашют! — ответил Ленорман ( буквальный перевод этого слова с французского — «против падения»).
ИНТЕРЕСНО
Если Землю просверлить насквозь и бросить туда камень, что будет с камнем?
Камень будет падать, набрав посередине пути максимальную скорость, дальше полетит по инерции и достигнет противоположной стороны Земли, причем его конечная скорость будет равна начальной. Ускорение свободного падения внутри Земли пропорционально расстоянию до центра Земли. Камень будет двигаться как груз на пружинке, по закону Гука. Если начальная скорость камня равна нулю, то период колебания камня в шахте равен периоду обращения спутника вблизи поверхности Земли, независимо от того, как прорыта прямая шахта: через центр Земли или по любой хорде.
Ускорение свободного падения внутри Земли пропорционально расстоянию до центра Земли. Камень будет двигаться как груз на пружинке, по закону Гука. Если начальная скорость камня равна нулю, то период колебания камня в шахте равен периоду обращения спутника вблизи поверхности Земли, независимо от того, как прорыта прямая шахта: через центр Земли или по любой хорде.
___
Знаменитая «падающая» башня — это колокольня собора в городе Пизе, часть редкостного по своей красоте архитектурного ансамбля. Благодаря своему конструктивному изъяну она известна во всем мире. Башня достигает в высоту 55 метров, а надпись на ней свидетельствует, что заложена она в 1174 году. В 1564 году в Пизе родился Галилео Галилей, будущий знаменитый ученый. Судя по его собственным рассказам, он использовал Пизанскую башню для своих опытов. С верхнего ее этажа он бросал различные предметы, чтобы доказать, что скорость падения не зависит от веса падающего тела.
Всем отдыхать!
Свободно падаем . .. расслабляемся …
.. расслабляемся …
Динамика — Класс!ная физика
Инерциальные системы отсчета. Первый закон Ньютона — Второй закон Ньютона — Третий закон Ньютона — Свободное падение тел — Закон всемирного тяготения — Ускорение свободного падения на Земле и других небесных телах — Криволинейное движение. Равномерное движение тела по окружности — Искусственные спутники Земли (ИСЗ) — Импульс тела. Закон сохранения импульса — Реактивное движение в природе — Реактивное движение в технике. Реактивные двигатели — Закон Гука
«Определение ускорения свободного падения при помощи маятника».
Лабораторная работа по физике на тему:
«Определение ускорения свободного падения при помощи маятника».
Оборудование:
Часы с секундной стрелкой
Измерительная лента с погрешностью =0,5 см
Шарик с отверстием
Нить
Штатив с муфтой и кольцом
Теоретическая часть:
Для измерения ускорения свободного падения применяются разнообразные гравиметры, в частности маятниковые приборы. С их помощью удается измерить ускорение свободного падения с абсолютной погрешностью порядка 10-5 м/с2.
С их помощью удается измерить ускорение свободного падения с абсолютной погрешностью порядка 10-5 м/с2.
В работе используется простейший маятниковый прибор – шарик на нити. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебания равен
Для увеличения точности измерения периода нужно измерить время t остаточно большого числа N полных колебаний маятника. Тогда период
T=t/N
И ускорение свободного падения может быть вычислено по формуле
Проведение эксперимента:
Установить на краю стола штатив.
У его верхнего конца укрепить с помощью муфты кольцо и повесить к нему шарик на нити. Шарик должен висеть на расстоянии 1-2 см от пола.
Измерить лентой длину l маятника.
Возбудить колебания маятника, отклонив шарик в сторону на 5-8 см и отпустив его.
Измерить в нескольких экспериментах время t 50 колебаний маятника и вычислить tср :
Где .
Вывод: Получается, что ускорение свободного падения, измеренное при помощи маятника, приблизительно равно табличному ускорению свободного падения (g=9,81 м/с2) при длине нити 1 метр.
Связь между силой тяжести и массой тела. Ускорение свободного падения
68 ч, 2 ч в неделю
Продолжительность урока – 45 мин
Пояснительная записка Предлагаемый урок посвящен «созданию» понятия о «новой» физической величине – ускорении свободного падения. На данном уроке «открывается» «новый» физический закон взаимосвязи массы тела с действующей на него силой тяжести. Как следствие, появляется «новая» физическая величина, представляющая собой коэффициент пропорциональности в полученной зависимости. Вводится ее название и единица. Таким образом, урок соответствует этапу конкретизации части опорной схемы-конспекта деятельности по введению новой физической величины[1, с. 86]:
86]:
Как ввести физическую величину? → Через формулу → Коэффициент пропорциональности в законе → Что характеризует → Единица → Определение физической величины.
Образовательная цель урока: подготовка учащихся, усвоивших следующие знания:
- Сила тяжести, действующая на тело, прямо пропорциональна его массе;
- Ускорение свободного падения – физическая величина, численно равная силе тяжести, действующей на тело массой 1 кг.
Цель по развитию учащихся: подготовка учащихся, овладевших следующими видами деятельности:
- Построение графика зависимости одной величины от другой на основе экспериментальных данных;
- «Открытие» закона взаимосвязи силы тяжести, действующей на тело, и его массы;
- Введение через формулу «новой» физической величины.
Содержание учебного материала
Вступительная беседа.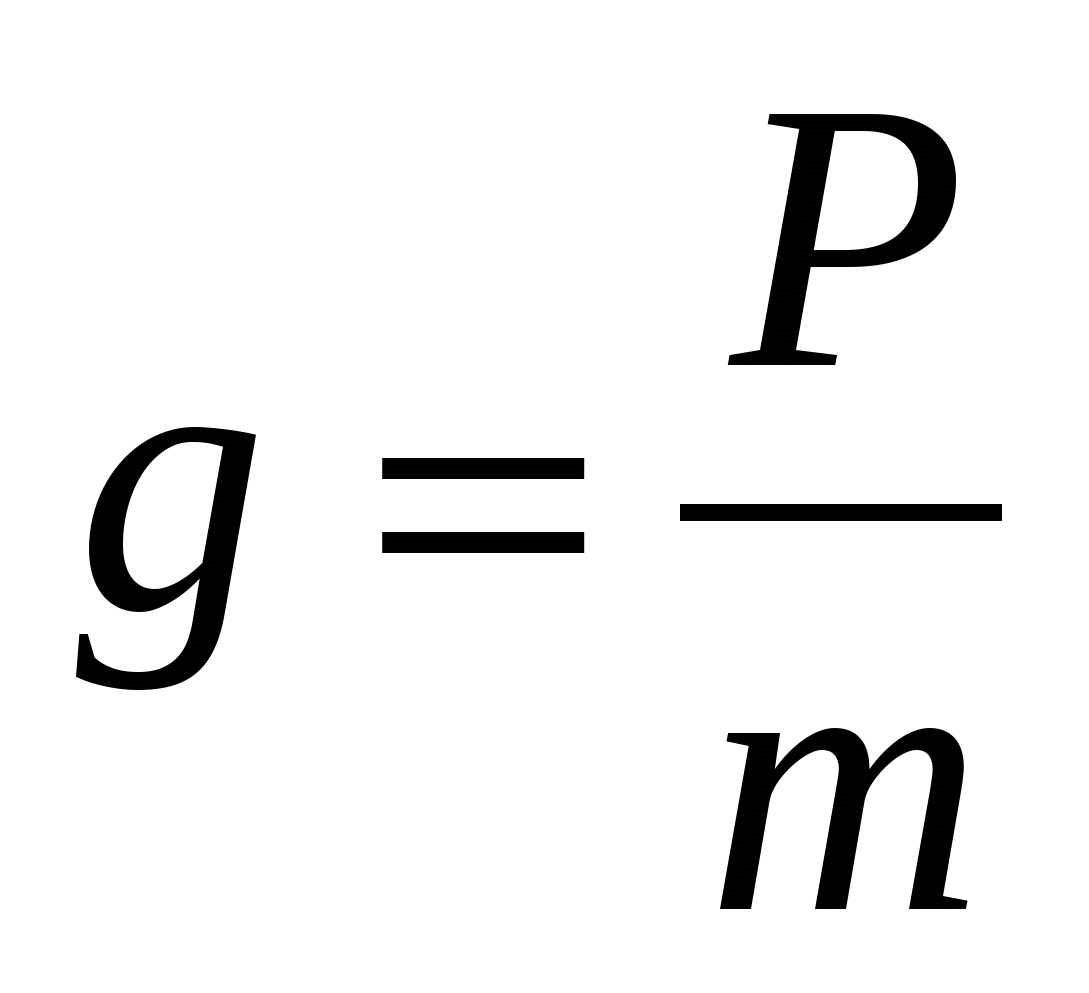 Актуализация опорных знаний
Актуализация опорных знаний
| Вопросы учителя | Ответы учеников |
Что произойдет, если какой-либо предмет выпустить из рук? |
Он упадет на землю. |
Если тело бросить в горизонтальном направлении, полетит ли оно прямолинейно? |
Нет, не полетит, его траекторией будет кривая линия. |
В чем же причина наблюдаемых явлений? |
На тела действует сила-сила притяжения к Земле. Ее называют силой тяжести. |
Сравним два тела с разной массой. Что можно сказать про тело с большей массой? |
Оно тяжелее; тело с меньшей массой будет легче. |
А что значит «тяжелее»? |
Это значит, что на него действует большая сила тяжести. |
Как вы думаете, какой вид у этой зависимости? |
Можно предположить, что чем больше масса тела, тем больше действующая на него сила тяжести. |
А как нам это проверить? |
Провести экспериментальное исследование. |
Цель работы: экспериментально установить вид зависимости силы тяжести, действующей на тело от его массы.
Оборудование: груз наборный; динамометр 0-5 Н; штатив.
Порядок выполнения работы.
1. Подготовьте таблицу для записи результатов измерений.
№ измерения |
Масса груза m, г |
Сила тяжести F, H |
|
|
|
2. Соберите основание штатива, закрепите в нем вертикально длинный стержень. К верхнему концу стержня прикрепите муфту. В муфте зажмите горизонтально короткий стержень.
Соберите основание штатива, закрепите в нем вертикально длинный стержень. К верхнему концу стержня прикрепите муфту. В муфте зажмите горизонтально короткий стержень.
3. Удостоверьтесь, что указатель динамометра находится напротив нулевой отметки его шкалы. При необходимости скорректируйте его положение <…>.
4. Подвесьте динамометр верхним крючком к горизонтальному стержню штатива <…>.
5. Исследуйте состав наборного груза. По цифрам, выбитым на его частях, определите массу каждой части.
6. Скомплектуйте наборный груз так, чтобы суммарная масса его частей составила 50 г.
7. Подвесьте груз к нижнему крючку динамометра и измерьте действующую на него силу тяжести.
8. Измерьте силу тяжести, действующую на груз массой 100 г, 150 г и 200 г.
9. На основе полученных данных постройте график зависимости силы тяжести от массы груза.
Анализ результатов измерений Ученики совместно с учителем анализируют полученный график и приходят к выводу о прямо пропорциональной зависимости силы тяжести, действующей на тело от массы этого тела («Известно, что, во сколько раз масса одного тела больше массы другого тела, во столько же раз сила тяжести, действующая на первое тело, больше силы тяжести, действующей на второе тело» [2, с. 77]).
77]).
Обобщая полученный вывод на результаты измерений, получают в итоге равенства отношений ===.
Последовательно вычисляют полученные отношения и получают, что ≈≈≈≈9,8. Из этих же отношений выходят на единицу величины, Н/кг.
Наконец, приходят к выводу: «Чтобы определить силу тяжести, действующую на тело любой массы, необходимо 9,8 Н/кг умножить на массу этого тела» [Там же, с. 78]. По учебнику находят информацию о том, что «величину 9,8 Н/кг обозначают буквой g, и формула для силы тяжести будет иметь вид: F=gm, где m — масса тела, g — ускорение свободного падения [Там же] ». Полагая в этой формуле m=1 кг, приходят к тому, что: «Ускорение свободного падения – физическая величина, численно равная силе тяжести, действующей на тело массой 1 кг».
Домашнее задание1. Заполните таблицу:
Название физической величины |
Е(е) |
Е(е) |
Формула |
Сила тяжести |
|
|
|
Ускорение свободного падения |
|
|
|
Масса тела |
|
|
|
2. Решите задачу: «Определите силу тяжести, действующую на тело массой 3,5 кг; 400 г; 1,5 т; 60 г» [Там же, с. 10, упр. 10.1]
Решите задачу: «Определите силу тяжести, действующую на тело массой 3,5 кг; 400 г; 1,5 т; 60 г» [Там же, с. 10, упр. 10.1]
- Ивашкина Д.А. Материалы курса «Эксперимент как метапредметная деятельность: реализация ФГОС на примере курса физики»: лекции 1–4. М.: Педагогический университет «Первое сентября», 2014.
- Перышкин А.В. Физика. 7 кл.: учебник. М.: Дрофа, 2014.
- Степанов С.В. Механика. Методические рекомендации по использованию лабораторного набора по механике. М., 2009.
Стоимость г
В Блоке 2 Физического класса было дано уравнение для определения силы тяжести ( F грав ), с которой объект массой м был притянут к Земле
F грав = m * g
Теперь в этом модуле введено второе уравнение для расчета силы тяжести, с которой объект притягивается к Земле.
, где d представляет собой расстояние от центра объекта до центра Земли.
В первом уравнении выше g упоминается как ускорение свободного падения. Его значение 9,8 м / с 2 на Земле. То есть ускорение свободного падения на поверхности земли на уровне моря составляет 9,8 м / с 2 . При обсуждении ускорения свободного падения было упомянуто, что значение g зависит от местоположения. Есть небольшие вариации в значении g относительно поверхности земли. Эти вариации возникают из-за различной плотности геологических структур под каждым конкретным участком поверхности.Они также являются результатом того факта, что Земля не является действительно сферической; земная поверхность находится дальше от центра на экваторе, чем на полюсах. Это приведет к увеличению значений g на полюсах. По мере того, как человек движется дальше от поверхности Земли — скажем, в точку орбиты вокруг Земли — значение g все еще изменяется.
Значение g зависит от местоположения
Чтобы понять, почему значение g так зависит от местоположения, мы воспользуемся двумя приведенными выше уравнениями, чтобы вывести уравнение для значения g.Во-первых, оба выражения силы тяжести приравниваются друг к другу.
Теперь обратите внимание, что масса объекта — м — присутствует по обе стороны от знака равенства. Таким образом, m можно исключить из уравнения. Это оставляет нам уравнение для ускорения свободного падения.
Приведенное выше уравнение демонстрирует, что ускорение свободного падения зависит от массы Земли (приблизительно 5,98×10 24 кг) и расстояния ( d ), на котором объект находится от центра Земли.Если значение 6,38×10 6 м (типичное значение радиуса Земли) используется для расстояния от центра Земли, то будет рассчитано значение g, равное 9,8 м / с 2 . И, конечно же, значение g будет меняться по мере того, как объект перемещается дальше от центра Земли. Например, если объект был перемещен в место, находящееся на расстоянии двух земных радиусов от центра Земли, то есть в два раза умноженными на 6,38×10 6 м, то будет найдено существенно другое значение g. Как показано ниже, на удвоенном расстоянии от центра Земли значение g становится равным 2.45 м / с 2 .
Например, если объект был перемещен в место, находящееся на расстоянии двух земных радиусов от центра Земли, то есть в два раза умноженными на 6,38×10 6 м, то будет найдено существенно другое значение g. Как показано ниже, на удвоенном расстоянии от центра Земли значение g становится равным 2.45 м / с 2 .
В таблице ниже показано значение g в различных точках от центра Земли.
|
Расположение |
Расстояние от центра Земли |
Стоимость, грамм |
|
Поверхность Земли |
6.38 x 10 6 м |
9,8 |
|
1000 км над поверхностью |
7,38 x 10 6 м |
7,33 |
|
2000 км над поверхностью |
8,38 x 10 6 м |
5. |
|
3000 км над поверхностью |
9,38 x 10 6 м |
4,53 |
|
4000 км над поверхностью |
1.04 x 10 7 м |
3,70 |
|
5000 км над поверхностью |
1.14 x 10 7 м |
3,08 |
|
6000 км над поверхностью |
1,24 x 10 7 м |
2,60 |
|
7000 км над поверхностью |
1,34 x 10 7 м |
2.23 |
|
8000 км над поверхностью |
1,44 x 10 7 м |
1,93 |
|
9000 км над поверхностью |
1,54 x 10 7 м |
1,69 |
|
10000 км над поверхностью |
1. |
1,49 |
|
50000 км над поверхностью |
5,64 x 10 7 м |
0,13 |
Как видно из приведенного выше уравнения и таблицы, значение g изменяется обратно пропорционально расстоянию от центра Земли.Фактически, изменение g с расстоянием подчиняется закону обратных квадратов, где g обратно пропорционально расстоянию от центра Земли. Это соотношение обратных квадратов означает, что при удвоении расстояния значение g уменьшается в 4 раза. При увеличении расстояния втрое значение g уменьшается в 9 раз. И так далее. Эта обратная квадратная зависимость изображена на рисунке справа.
Расчет g на других планетах
То же уравнение, используемое для определения значения g на поверхности Земли, можно также использовать для определения ускорения свободного падения на поверхности других планет. Значение g на любой другой планете можно рассчитать, исходя из массы планеты и ее радиуса. Уравнение принимает следующий вид:
Значение g на любой другой планете можно рассчитать, исходя из массы планеты и ее радиуса. Уравнение принимает следующий вид:
Используя это уравнение, можно вычислить следующие значения ускорения свободного падения для различных планет.
|
Планета |
Радиус (м) |
Масса (кг) |
г (м / с 2 ) |
|
Меркурий |
2.43 х 10 6 |
3,2 х 10 23 |
3,61 |
|
Венера |
6.073 x 10 6 |
4,88 x10 24 |
8,83 |
|
Марс |
3. |
6,42 х 10 23 |
3,75 |
|
Юпитер |
6,98 x 10 7 |
1.901 х 10 27 |
26,0 |
|
Сатурн |
5.82 х 10 7 |
5,68 x 10 26 |
11,2 |
|
Уран |
2,35 х 10 7 |
8,68 x 10 25 |
10,5 |
|
Нептун |
2.27 х 10 7 |
1,03 х 10 26 |
13,3 |
|
Плутон |
1,15 х 10 6 |
1,2 х 10 22 |
0,61 |
Ускорение свободного падения объекта — это измеримая величина. Тем не менее, из универсального закона всемирного тяготения Ньютона вытекает предсказание, согласно которому его значение зависит от массы Земли и расстояния, на котором объект находится от центра Земли. Значение g не зависит от массы объекта и зависит только от местоположения — планеты, на которой находится объект, и расстояния от центра этой планеты.
Тем не менее, из универсального закона всемирного тяготения Ньютона вытекает предсказание, согласно которому его значение зависит от массы Земли и расстояния, на котором объект находится от центра Земли. Значение g не зависит от массы объекта и зависит только от местоположения — планеты, на которой находится объект, и расстояния от центра этой планеты.
Даже на поверхности Земли наблюдаются локальные вариации значения g.Эти вариации связаны с широтой (Земля не является идеальной сферой; она выпуклость посередине), высотой и местной геологической структурой региона. Используйте виджет Gravitational Fields ниже, чтобы исследовать, как местоположение влияет на значение g. А для большего визуального восприятия попробуйте соответствующее Value of g Interactive из раздела Physics Interactives на нашем веб-сайте.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно.Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Гравитация» и / или нашего интерактивного приложения «Значение g на других планетах». Вы можете найти их в разделе Physics Interactives на нашем веб-сайте. Оба интерактивных модуля позволяют учащемуся интерактивно исследовать влияние характеристик планеты на гравитационное поле.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Гравитация» и / или нашего интерактивного приложения «Значение g на других планетах». Вы можете найти их в разделе Physics Interactives на нашем веб-сайте. Оба интерактивных модуля позволяют учащемуся интерактивно исследовать влияние характеристик планеты на гравитационное поле.
Расчет ускорения свободного падения: формула и концепция — видео и стенограмма урока
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что объект ускоряется всякий раз, когда на него действует чистая внешняя сила, и чистая сила равна массе объекта, умноженной на его ускорение.Математически это дается формулой F = m * a , где F — чистая сила, действующая на объект, m — масса объекта, а a — ускорение.
Как видно из формулы, масса является мерой сопротивления объекта ускорению. Масса также является мерой количества вещества в объекте. Массу часто путают с весом. Вес — сила тяжести, действующая на объект. Вес объекта зависит от его местоположения во Вселенной.
Масса также является мерой количества вещества в объекте. Массу часто путают с весом. Вес — сила тяжести, действующая на объект. Вес объекта зависит от его местоположения во Вселенной.
Например, если бы вы стояли на поверхности Луны, ваш вес был бы примерно 1/6 вашего веса на поверхности Земли. Это связано с тем, что среднее ускорение свободного падения на поверхности Луны составляет примерно 1/6 среднего ускорения свободного падения на поверхности Земли. Если вы хотите быстро похудеть, отправляйтесь на Луну!
К сожалению, поскольку масса — это количество вещества, содержащегося в вашем теле, ваша масса постоянна во всей Вселенной.Если вы хотите похудеть, правильнее будет сказать, что вы пытаетесь похудеть. Это потому, что на самом деле вы пытаетесь уменьшить размер своего тела, а не просто уменьшить количество чешуек.
Когда ускорение происходит под действием силы тяжести, мы заменяем a на g во втором законе движения Ньютона, где g представляет собой ускорение свободного падения.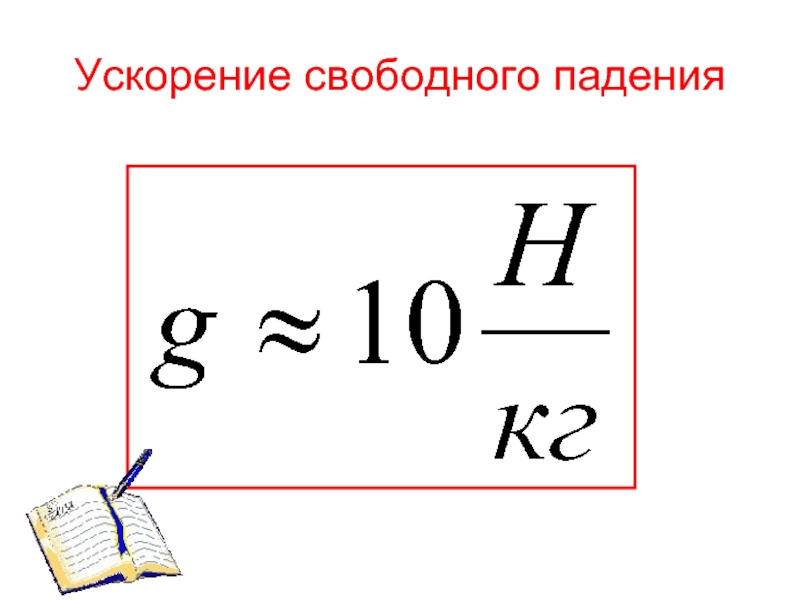 Как мы заявляли ранее, сила тяжести, действующая на вещество, определяется как вес, поэтому мы заменяем F на W .Тогда формула принимает вид W = мг.
Как мы заявляли ранее, сила тяжести, действующая на вещество, определяется как вес, поэтому мы заменяем F на W .Тогда формула принимает вид W = мг.
Мы могли бы решить для г , чтобы получить формулу г = Вт / м , но эта форма уравнения не обеспечивает практического применения для определения ускорения свободного падения. Второй закон Ньютона в форме W = mg наиболее полезен для связи веса и массы, когда ускорение свободного падения уже известно.
Закон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона гласит, что каждый объект оказывает гравитационную силу на любой другой объект.2.
Довольно часто, когда мы используем эту формулу, масса одного объекта намного больше, чем масса другого объекта. Например, когда мы рассматриваем силу гравитации, действующую на наши тела, два вовлеченных объекта — это наши тела и Земля. Другой пример — сила тяжести, действующая на мяч, когда он свободно падает на землю после того, как его бросили прямо вверх.
Другой пример — сила тяжести, действующая на мяч, когда он свободно падает на землю после того, как его бросили прямо вверх.
И масса наших тел, и масса шара ничтожны по сравнению с массой Земли.В этом случае мы можем заменить m1 и m2 в формуле на m для представления гораздо меньшего объекта и M для представления гораздо большего объекта. Как показывает формула, d — это расстояние между центрами двух объектов. Расстояние от центра Земли до центра наших тел или до центра шара по существу такое же, как расстояние от центра Земли до поверхности Земли. Следовательно, мы также можем заменить d на R , что является средним радиусом Земли.2 , который определяет ускорение свободного падения, когда у нас есть массивный объект, оказывающий гравитационную силу на другой объект с относительно незначительной массой. Примером такой ситуации является сила притяжения Земли на наши тела.
Выделенный словарь
- Второй закон движения Ньютона : объект ускоряется всякий раз, когда на него действует чистая внешняя сила, и чистая сила равна массе объекта, умноженной на его ускорение
- Масса : мера сопротивления объекта ускорению; мера количества материи в объекте
- Вес : сила тяжести, действующая на объект
- Закон всемирного тяготения Ньютона : каждый объект оказывает гравитационную силу на любой другой объект; он пропорционален массам обоих объектов и обратно пропорционален квадрату расстояния между их центрами
Результаты обучения
Этот урок направлен на то, чтобы пролить свет на гравитационное ускорение, чтобы помочь вам:
- Обсудить основы формулы, связанные с ускорением свободного падения
- Различия между массой и массой
- Государственные законы Ньютона
- Рассчитайте ускорение по формулам Ньютона
Формула ускорения силы тяжести
Вблизи поверхности Земли ускорение силы тяжести приблизительно постоянно. Однако на больших расстояниях от Земли или вокруг других планет или лун ускорение другое. Ускорение свободного падения зависит от массы тела, расстояния от центра масс и постоянной G, которая называется «универсальной гравитационной постоянной». Его значение = 6,673 x 10 -11 Н · м 2 / кг 2 .
Однако на больших расстояниях от Земли или вокруг других планет или лун ускорение другое. Ускорение свободного падения зависит от массы тела, расстояния от центра масс и постоянной G, которая называется «универсальной гравитационной постоянной». Его значение = 6,673 x 10 -11 Н · м 2 / кг 2 .
g = ускорение свободного падения (единицы м / с 2 )
G = универсальная гравитационная постоянная, G = 6.673 x 10 -11 Н · м 2 кг 2
м = масса большого тела (например, Земли)
r = расстояние от центра масс большого тела
Ускорение от силы тяжести Вопросы по формуле:
1) Радиус Луны 1,74 x 10 6 м. Масса Луны 7,35 х 10 22 кг. Найдите ускорение свободного падения на поверхности Луны.
Ответ: На поверхности Луны расстояние до центра масс такое же, как и радиус: r = 1.74 x 10 6 м = 1740 000 м. Ускорение свободного падения на поверхности Луны можно найти по формуле:
Ускорение свободного падения на поверхности Луны можно найти по формуле:
г = 1,620 м / с 2
Ускорение свободного падения на поверхности Луны составляет 1,620 м / с. 2 .
2) Радиус Земли 6,38 x 10 6 м. Масса Земли 5.98x 10 24 кг. Если спутник вращается вокруг Земли на высоте 250 км над поверхностью, какое ускорение свободного падения он испытывает?
Ответ: Ускорение свободного падения зависит от расстояния от центра масс большого тела до спутника.Это расстояние складывается из радиуса Земли и расстояния от спутника до поверхности:
r = (6,38 x 10 6 м) + (250 км)
r = 6 380 000 + 250 000 м
r = 6 630 000 м
Ускорение свободного падения спутника можно найти по формуле:
г = 9,078 м / с 2
Ускорение свободного падения на высоте спутника, 250 км над поверхностью Земли, равно 9. 078 м / с 2 .
078 м / с 2 .
Обзор силы гравитации Рона Куртуса
SfC Home> Физика> Гравитация>
Рон Куртус
Гравитация — это сила , которая притягивает объекты к Земле. Это приближение силы тяжести , которая притягивает объекты массы друг к другу на больших расстояниях.
( Примечание : Гравитация на Луне — это сила, которая притягивает объекты к поверхности Луны.)
Уравнение силы тяжести: F = mg , где g — ускорение свободного падения. Единицы могут быть обозначены в метрической (СИ) или английской системе. Уравнение также указывает вес объекта ( Вт = мг).
Основной особенностью этой силы является то, что все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и на других планетах имеет разные значения ускорения свободного падения. Однако действие силы схоже.
Вопросы, которые могут у вас возникнуть:
- Что такое уравнение гравитации?
- Какая самая выдающаяся характеристика гравитации?
- Что такое гравитация в другом месте?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Полезный инструмент: Конвертация единиц
Уравнение гравитации
Согласно закону всемирного тяготения Ньютона , гравитация — это сила, притягивающая объекты друг к другу.Для объектов, относительно близких к Земле, эта сила называется гравитацией, и ее уравнение:
F = мг
где
- F — сила, притягивающая объекты к Земле
- м — масса объекта
- g — ускорение свободного падения; это число является постоянным для всех масс материи
- мг — произведение м умноженное на г
Примечание : Для проверки того, что сила тяжести равна силе тяжести для объектов, близких к Земле, см. Постоянные факторы гравитации.
Ускорение свободного падения
Ускорение силы тяжести на Земле обозначено g . Его значение:
г = 9,807 метров на секунду в квадрате (м / с 2 ) в метрической системе измерения или системе СИ
г = 32,2 фута на секунду в квадрате (фут / с 2 ) в английской системе измерения
Примечание : Поскольку в большинстве учебников используется г = 9.
8 м / с 2 и 32 фут / с 2 , в этих уроках мы также будем использовать округленную версию.
В уравнении F = мг вы должны использовать ту же систему измерения для массы, м , что и для г .
Примечание: Некоторые учебники небрежно определяют g как ускорение силы тяжести . Это неверно и вводит в заблуждение, поскольку сила тяжести не ускоряется.Выражение должно быть — ускорение из-за силы тяжести , что является правильным описанием g .
Следует проявлять осторожность при определении научных терминов.
Масса и масса
Вес объекта данной массы — это сила тяжести, действующая на этот объект:
w = мг
где
- w — вес в ньютонах (Н) или фунт-сила (фунт)
- м — масса в килограммах или фунт-масса (фунт-масса)
Примечание : Часто возникает путаница в обозначении веса и массы.
Хотя килограмм считается единицей массы, он часто используется для обозначения веса. Вы должны знать, что вес 1 кг массы равен w = 9,8 ньютона.
Кроме того, фунт должен быть силой, но его часто называют массой. Масса 1 фунт-сила равна 1/32 массы фунта.
Опять же, вы должны быть точными в формулировке научных терминов.
Взвешивание объекта
Вы можете определить вес объекта на откалиброванных весах — обычно с пружиной, сопротивляющейся силе груза.
Массу объекта можно измерить с помощью весов, сравнивая с объектом данной массы.
Объекты падают с одинаковой скоростью
Наиболее выдающейся характеристикой силы тяжести является тот факт, что все объекты падают с одинаковой скоростью — если предположить, что влияние сопротивления воздуха незначительно. Это связано с тем, что ускорение свободного падения g является константой для всех объектов, независимо от их массы.
Это кажется нелогичным, поскольку можно ожидать, что тяжелый предмет упадет быстрее, чем предмет, который весит меньше. Но это факт. Попробуйте уронить два объекта одновременно с одинаковой высоты, убедившись, что они достаточно тяжелые, чтобы на них не влияло сопротивление воздуха. Вы увидите, что они одновременно упали на землю.
Но это факт. Попробуйте уронить два объекта одновременно с одинаковой высоты, убедившись, что они достаточно тяжелые, чтобы на них не влияло сопротивление воздуха. Вы увидите, что они одновременно упали на землю.
( Для получения дополнительной информации см. Принцип эквивалентности силы тяжести. )
Гравитация в другом месте
Когда вы говорите о гравитации, вы имеете в виду гравитацию около Земли. Однако то же самое уравнение гравитации справедливо для объектов около Луны или других планет, за исключением того, что значение г другое.В таких случаях вы обычно указываете, где находится гравитация, например «гравитация на Луне» или «гравитация на Марсе».
Гравитация на Луне
Сила тяжести на Луне составляет примерно 1/6 силы тяжести на Земле для данной массы. Таким образом:
F м = мг м
где
- F м — сила или вес на Луне
- м — масса объекта
- g m — ускорение свободного падения на Луне
Значение для г м равно 1. 6 м / с 2 или 5,3 фут / с 2 .
6 м / с 2 или 5,3 фут / с 2 .
Вес и масса на Луне
Значение для г м составляет примерно 1/6 значения для г на Земле. Таким образом, объект на Луне будет весить около 1/6 своего веса на Земле.
Используя пружинные весы, если вы весите на Земле 60 кг (132 фунта), то на Луне вы будете весить всего 10 кг (22 фунта). Однако, используя шкалу баланса и на Земле, и на Луне, ваша масса будет одинаковой.
Упавшие предметы
Если вы уроните на Луну два объекта разного веса, они упадут на землю с одинаковой скоростью. Вам не придется беспокоиться о влиянии сопротивления воздуха, поскольку на Луне нет воздуха.
Поскольку g m = g /6, объекты будут падать с меньшей скоростью.
( См. Уравнения силы тяжести для падающих предметов, а затем примените g м , чтобы получить другие значения.)
Сводка
Гравитация — это сила, притягивающая объекты к Земле. Это частный случай гравитации. Уравнение силы тяжести: F = мг, в результате чего все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и гравитация на других планетах имеют разные значения ускорения свободного падения, но эффекты силы схожи.
Это частный случай гравитации. Уравнение силы тяжести: F = мг, в результате чего все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и гравитация на других планетах имеют разные значения ускорения свободного падения, но эффекты силы схожи.
Будьте как можно лучше
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Сила гравитации — Журнал «Вселенная сегодня»
Земное притяжение — Википедия
Как работает гравитация? — Как работает материал
Стандартная сила тяжести — Среднее значение по сравнению с вариацией из-за положения на Земле — Википедия
Международная формула силы тяжести — Изменение силы тяжести в зависимости от расстояния от экватора — Отдел геофизики.Университет Оклахомы
Я чувствую себя легче, поднимаясь в гору, но разве я? — Национальная физическая лаборатория FAQ
Книги
(Примечание: Школа для чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом по простой науке о гравитации
Книги по углубленной физике гравитации с самым высоким рейтингом
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.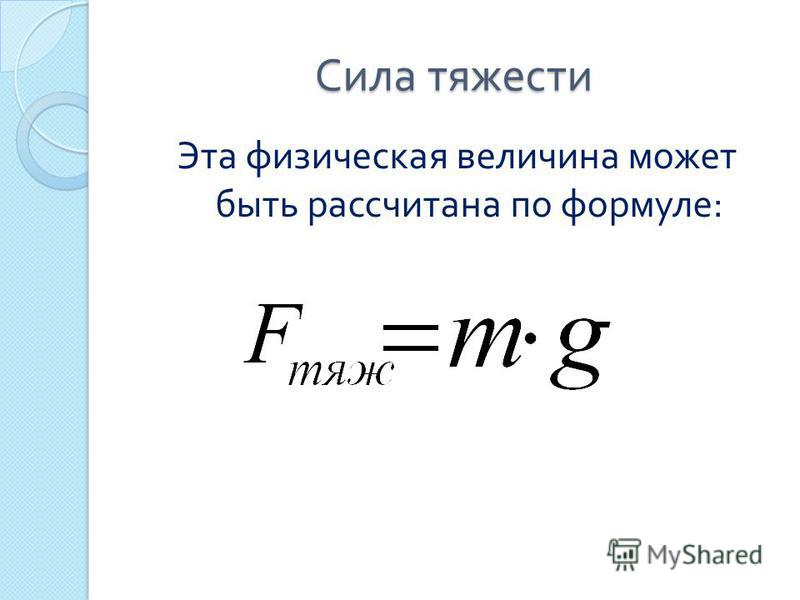 Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_overview.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Обзор силы тяжести
Какое значение имеет G?
NIST принял участие в новом импульсе, направленном на решение постоянной и растущей проблемы в физике: значение G. Ньютоновской постоянной гравитации, используемой для расчета силы притяжения гравитации между объектами, более 300 лет. Но хотя ученые веками пытались измерить его значение, G по-прежнему известен только с 3 значащими цифрами. Напротив, другие константы были измерены с гораздо большей точностью; масса электрона в килограммах, например, известна примерно с 8 цифрами. i
Но хотя ученые веками пытались измерить его значение, G по-прежнему известен только с 3 значащими цифрами. Напротив, другие константы были измерены с гораздо большей точностью; масса электрона в килограммах, например, известна примерно с 8 цифрами. i
Что еще хуже, чем больше экспериментов проводят исследователи для определения гравитационной постоянной, тем больше расходятся их результаты.
9-10 октября 2014 года несколько десятков ученых со всего мира собрались в NIST, чтобы обсудить возможные варианты.
«Мы все здесь, потому что у нас проблема с G — и я имею в виду, мальчик, есть ли у нас проблема с G», — сказал Карл Уильямс, начальник отдела квантовых измерений PML, собравшейся группе в первое утро встреча. «Это стало одной из серьезных проблем, которые необходимо решить физике».
Гравитационная постоянная известна как «большая G», чтобы отличать ее от «маленькой g», ускорения, вызываемого силой тяжести Земли. ii Несмотря на название, большая G крошечная — около 6. 67 x 10 -11 м 3 кг -1 s -2 — и сравнительно слабая, примерно в триллион триллионов триллионов раз слабее, чем электромагнитная сила, ответственная за прикрепление сувенирных магнитов к холодильникам. А его слабость затрудняет измерение.
67 x 10 -11 м 3 кг -1 s -2 — и сравнительно слабая, примерно в триллион триллионов триллионов раз слабее, чем электромагнитная сила, ответственная за прикрепление сувенирных магнитов к холодильникам. А его слабость затрудняет измерение.
Экспериментаторы использовали множество подходов — качающиеся маятники, массы в свободном падении, балансирные балки и крутильные весы, которые измеряют крутящий момент или вращение проводов, поддерживающих массы, которые притягиваются к другим массам.Но график всех результатов за последние 15 лет показывает относительно широкий разброс значений в диапазоне примерно 6,67 x 10 -11 м 3 кг -1 с -2 .
Кроме того, CODATA — Комитет Международного совета по науке по данным для науки и технологий, который анализирует результаты отдельных экспериментов и предоставляет международно принятые наборы значений фундаментальных физических констант — был вынужден увеличить неопределенность в своей последней рекомендации для значение G из-за расхождения экспериментов. iii
iii
На семинаре NIST 53 участника единогласно согласились, что что-то нужно делать. Они рекомендовали одной или нескольким организациям проводить ежегодные или двухгодичные встречи, посвященные конкретно кампании по определению большого значения G с большей точностью, и они поддержали идею сосредоточения внимания на новых подходах к измерению, таких как установка атомной интерферометрии, используемая в недавнем исследовании. эксперимент с лазерным охлаждением атомов рубидия. iv
Предполагается, что основной причиной этих расхождений являются систематические неточности в измерениях, и большая часть обсуждения была сосредоточена на снижении шума.По мнению участников, одним из способов решения этой проблемы является проведение разными командами независимых экспериментов с использованием одного и того же оборудования. Две группы с особенно отклоняющимися результатами предложили свое оборудование во время встречи, ожидая обсуждения с командами, которые будут повторно использовать ресурсы.
Участники семинара проявили умеренный интерес к формированию консорциума, организации, которая централизовала бы процесс достижения консенсуса. Потенциальная выгода от консорциума будет заключаться в предоставлении NIST и другим национальным измерительным институтам (NMI) средств поддержки, например, в виде услуг по прецизионной метрологии длины, для членов.
«Очевидно, что нет правильного ответа, как двигаться вперед», — сказал Уильямс. «Но есть международная поддержка в разрешении спора о большой G, и поэтому сейчас для нас прекрасное время в этом отношении».
Константы, которые они меняют: NIST публикует последние корректировки фундаментальных показателей.
Дополнительная информация: i Масса электрона 9.109 382 91 (40) x 10 -31 кг, где число в скобках указывает на погрешность в двух последних цифрах.

ii Для расчета гравитационного притяжения между двумя объектами необходимо взять произведение двух масс и разделить расстояние между ними на квадрат, а затем умножить это значение на G . Уравнение: F = Gm 1 m 2 / r 2 .
iii Последний набор CODATA, выпущенный в 2010 году, рекомендовал для G значение 6.673 84 (80) x 10 -11 м 3 кг -1 с -2 по сравнению с предыдущим результатом в 2006 г. 6,674 28 (67) x 10 -11 м 3 кг -1 с -2 . Значения в скобках указывают стандартную неопределенность (основанную на стандартном отклонении), в данном случае плюс или минус 0,000 80 x 10 -11 м 3 кг -1 с -2 и плюс-минус 0,000 67 x 10 -11 м 3 кг -1 с -2 соответственно.
iv В этом эксперименте исследователи засунули два облака холодных атомов рубидия в вакуумную камеру с помощью лазерного излучения. Атомы ускорялись по-разному в зависимости от размещения масс с высокой плотностью (вольфрамовые массы всего около 500 кг), расположенных в различных конфигурациях. Различия в ускорении из-за гравитационного притяжения атомов к массам вольфрама можно уловить в интерференционной картине облаков. Дж. Рози, Ф. Соррентино, Л. Каччапуоти, М. Преведелли и Дж.М. Тино. Прецизионное измерение ньютоновской гравитационной постоянной с использованием холодных атомов. Природа . Vol. 510. 518–521. 26 июня 2014 г. DOI: 10.1038 / nature13433
Атомы ускорялись по-разному в зависимости от размещения масс с высокой плотностью (вольфрамовые массы всего около 500 кг), расположенных в различных конфигурациях. Различия в ускорении из-за гравитационного притяжения атомов к массам вольфрама можно уловить в интерференционной картине облаков. Дж. Рози, Ф. Соррентино, Л. Каччапуоти, М. Преведелли и Дж.М. Тино. Прецизионное измерение ньютоновской гравитационной постоянной с использованием холодных атомов. Природа . Vol. 510. 518–521. 26 июня 2014 г. DOI: 10.1038 / nature13433
Ссылка :
Какое значение имеет G? (2014, 28 октября)
получено 30 декабря 2021 г. с https: // физ.org / news / 2014-10-what-is-the-value-of.html
с https: // физ.org / news / 2014-10-what-is-the-value-of.html
Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.
Гравитация
Падающее яблоко
Гравитация повсюду вокруг нас.Он может, например, заставить яблоко упасть на землю:
Гравитация постоянно действует на яблоко, поэтому оно движется все быстрее и быстрее … другими словами, оно ускоряется.
Игнорируя сопротивление воздуха, его скорость увеличивается на 9,8 метра в секунду каждую секунду . То есть два лота «в секунду» и пишется:
То есть два лота «в секунду» и пишется:
9,8 м / с 2
9,8 м / с 2 — ускорение под действием силы тяжести у поверхности Земли.Почти все в нашей жизни происходит вблизи поверхности Земли, поэтому это значение часто используется и записывается как small g :
г = 9,8 м / с 2
Среднее значение г составляет 9,80665 м / с 2 , но значения различаются по всему миру, например, в Калькутте 9,78548, Лондоне 9,81599 и Токио 9,79805.
Таким образом, большинство людей просто используют 9.8 м / с 2
Чтобы удержать яблоко против силы тяжести, нужна сила.
Сила — это масса, умноженная на ускорение ( F = m a ), и в этом случае ускорение составляет g :
F = m г
Пример: сколько силы удерживать яблоко массой 0,1 кг?
F = m г
F = 0. 1 кг × 9,8 м / с 2
1 кг × 9,8 м / с 2
F = 0,98 кг м / с 2
Сила измеряется в Ньютонах ( Н ), что совпадает с кг м / с 2
F = 0,98 N
Итак, чтобы удерживать яблоко, требуется сила около 1 Ньютон .
Мы также говорим, что яблоко имеет вес 0,98 Н.
Чтобы преобразовать массу в кг в силу в Ньютонах, умножьте на 9.8 м / с 2
Другой пример:
Пример: стальная балка весом 100 кг равномерно установлена на двух опорах. Сколько силы приходится на каждую опору?
На балку действует сила тяжести, направленная вниз:
F = m г
F = 100 кг × 9,8 м / с 2 = 980 N
Поскольку каждая опора равномерно расположена на опоре, она несет половину веса (980/2 = 490):
Но что такое гравитация?
Теперь вы знаете, как справиться с гравитацией здесь, на Земле (просто умножьте массу на 9.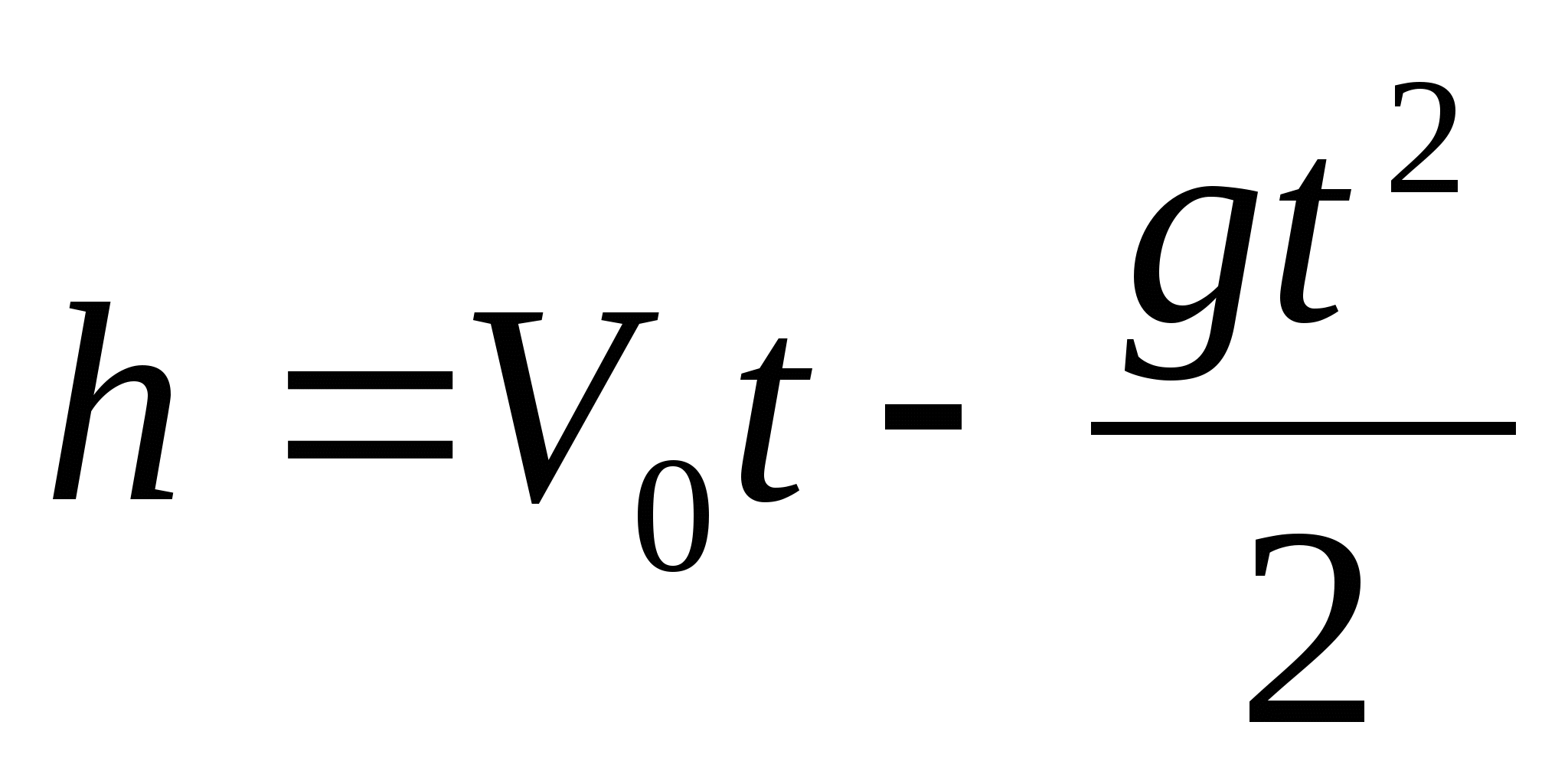 8 м / с 2 , чтобы получить силу), но что такое гравитация на самом деле?
8 м / с 2 , чтобы получить силу), но что такое гравитация на самом деле?
Что ж, масса и энергия делают пространство искривленным (или искаженным), поэтому для объектов естественно следовать по пути друг к другу.
Здесь объект естественным образом следует за пространством-временем в направлении
Земля
Это приводит к тому, что объекты притягиваются друг к другу , что мы называем Гравитацией .
Гравитация : притяжение объектов с массой или энергией друг к другу.
Это притяжение проявляется в виде силы:
На- на
- меньше для более удаленных объектов
- больше для объектов большей массы (например, Солнца)
Представьте себе всего два шара:
Каждый шар состоит из множества кусочков массы и энергии, которые притягиваются друг к другу:
(на самом деле нужно лотов на частиц больше!)
Но мы обычно упрощаем это, представляя, что масса и энергия каждого шара находятся в его центре, называемом Центром тяжести.
(Но помните, что мы просто представляем, что вся масса находится в центре, чтобы упростить вычисления.)
Ньютон разработал формулу силы притяжения:
- F — сила (в Ньютонах), равная, но противоположная в направлении для обоих объектов
- G — гравитационная постоянная, приблизительно 6,674 × 10 -11 Н · м 2 / кг 2
- m 1 и m 2 — две массы (в кг)
- d — расстояние между центрами каждой массы (в метрах)
Пример: две машины массой 800 кг и 1500 кг находятся на расстоянии 3 м друг от друга
Гравитационное притяжение между двумя автомобилями составляет:
F = G м 1 м 2 д 2
Факс = 6.674 × 10 -11 Н м 2 / кг 2 × 800 кг × 1500 кг (3 м) 2
F ≈ 0,000009 N
Они очень слабо (всего 9 миллионных долей Ньютона) притягиваются друг к другу!
Пример: Яблоко и Земля
Яблоко массой 0,1 кг
Земля имеет массу 5,972 × 10 24 кг
От центра яблока до центра Земли составляет 6371 км (6. 371 × 10 6 м)
371 × 10 6 м)
F = G м 1 м 2 д 2
F = 6,674 × 10 -11 Н м 2 / кг 2 × 0,1 кг × 5,972 × 10 24 кг (6,371 × 10 6 м) 2
F = 0,98 N
(Это то же значение, что и в предыдущем расчете, так что это кажется вполне правильным!)
Идет обоими путями
Яблоко тянет и Землю!
Но Земля настолько невероятно массивна, что почти не влияет на нее.
Рассчитаем ускорение для яблока и для Земли:
Пример (продолжение): Зная, что сила равна 0,98 Н, каково ускорение яблока
и Земли?Для яблока :
| F = m a | ||
| Мы знаем, что F составляет 0,98 Н, а m равно 0,1 кг | 0.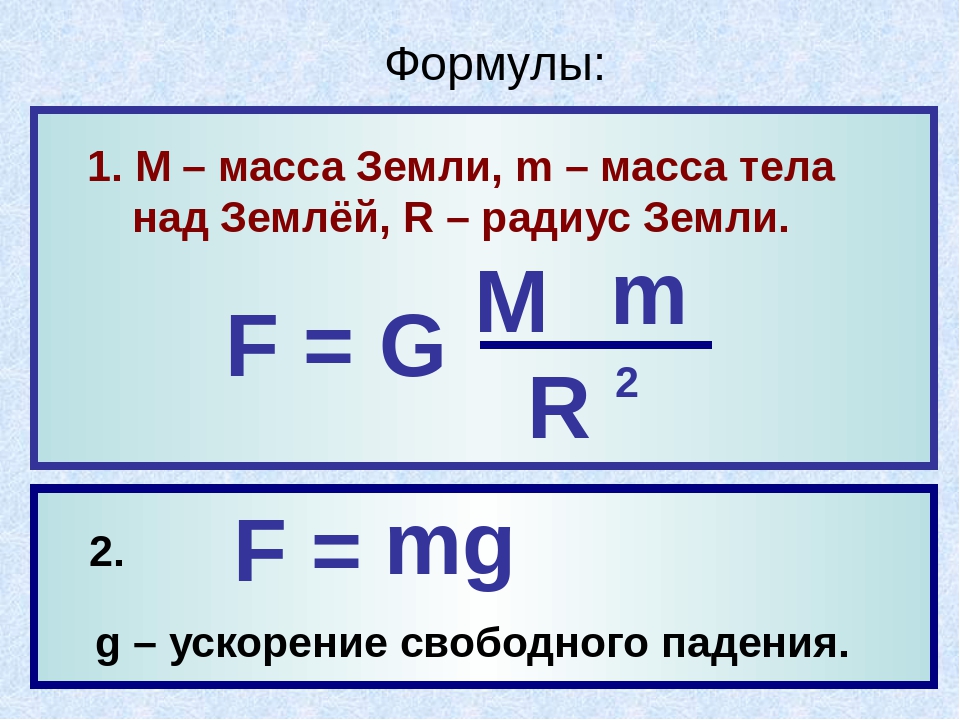 98 Н = 0,1 кг a 98 Н = 0,1 кг a |
|
| Разделите обе стороны на 0,1 кг | 0,98 Н / 0,1 кг = a | |
| Поменять стороны | a = 0,98 Н / 0,1 кг | |
| Ответ: | a = 9,8 м / с 2 |
Это ускорение свободного падения g, которое мы все испытываем каждый день.
А для Земли :
| F = m a | ||
| F составляет 0,98 Н, а m равно 5,972 × 10 24 кг | 0,98 N = 5,972 × 10 24 кг a | |
| Разделите обе стороны на 5,972 × 10 24 кг | 0,98 Н / 5,972 × 10 24 кг = a | |
| Поменять стороны | a = 0. 98 Н / 5.972 × 10 24 кг 98 Н / 5.972 × 10 24 кг |
|
| Ответ: | a = 1,64 × 10 -25 м / с 2 |
Это очень маленькое ускорение , неудивительно, что мы не замечаем, как Земля движется из-за яблока.
Но гораздо более крупный объект, такой как Луна (с массой 7.342 × 10 22 кг ), действительно оказывает заметное влияние на Землю.
Луна вращается вокруг Земли на расстоянии около 384000 км каждые 27,3 дня
И Земля также имеет «орбиту» (больше похожую на колебание) с Луной около 5000 км (что на самом деле меньше радиуса Земли), также каждые 27,3 дня.
Ваша очередь: попробуйте вычислить силу притяжения между Землей и Луной.
Играйте
Поиграйте с гравитацией в Gravity Freeplay.
Сводка
- Пространство кривой массы и энергии, которое естественным образом заставляет объекты двигаться навстречу друг другу
- этот аттракцион мы называем гравитацией
- это постоянное притяжение заставляет объекты ускоряться навстречу друг другу
- ускорение имеет согласующую силу ( F = m a )
- у поверхности Земли ускорение свободного падения составляет 9.
 8 м / с 2
8 м / с 2 - , таким образом, массой 1 кг испытывает гравитационное притяжение 9,8 Ньютона силы
Расчет гравитационных сил | IOPSpark
Закон всемирного тяготения Ньютона
Земля и космос
Расчет гравитационных сил
Повествование о физике за 11–14
Узнайте, как рассчитать гравитационные силы
Предположим, вы хотите рассчитать величину гравитационной силы, действующей между вами и вашим коллегой, когда вы приближаетесь друг к другу (на расстоянии одного метра) в коридоре.Мы можем сделать это довольно просто, используя уравнение Ньютона: сила сила тяжести = G × M × м расстояние 2 .
Предположим: ваша масса м 60 килограмм; масса вашего коллеги M 70 кг; ваше межцентровое расстояние, r , составляет 1 м; и G составляет 6,67 × 10 -11 ньютон квадратный метр килограмм -2 .
Подставляя эти значения в уравнение, получаем 6.67 × 10 -11 ньютон квадратный метр килограмм -2 × 60 килограмм × 70 килограмм1 метр 2 . Вы можете выработать эту силу, и вы получите 2,8 × 10 -7 ньютон.
Другими словами, вы прикладываете к своему коллеге притягивающую силу гравитации в 0,28 миллионных долей ньютона! Сила существует, но она слишком мала, чтобы ее можно было заметить на практике.
Из чисел ясно, что из-за того, что величина G настолько мала, величина гравитационной силы будет очень мала, если только тот или иной объект не имеет очень большую массу.
Вы можете использовать уравнение Ньютона, чтобы проверить эмпирическое наблюдение, что масса в 1 килограмм испытывает гравитационное притяжение около 10 Н на поверхности Земли. Это расчет гравитационного притяжения на поверхности Земли
Это расчет гравитационного притяжения на поверхности Земли
сила сила тяжести = G × M × м отрыв 2
Где: масса, м, , 1 килограмм; масса Земли, M , составляет 6,0 × 10 24 килограмм; радиус Земли (разделение масс), r , равен 6.4 × 10 6 м; и G составляет 6,67 × 10 -11 ньютон на квадратный метр килограмм-2 }.
Вставляем эти значения в уравнение и вычисляем его, чтобы получить силу в 9,8 ньютона.
Как и ожидалось, сила притяжения Земли на массу в 1 килограмм на ее поверхности составляет около 10 Н.
.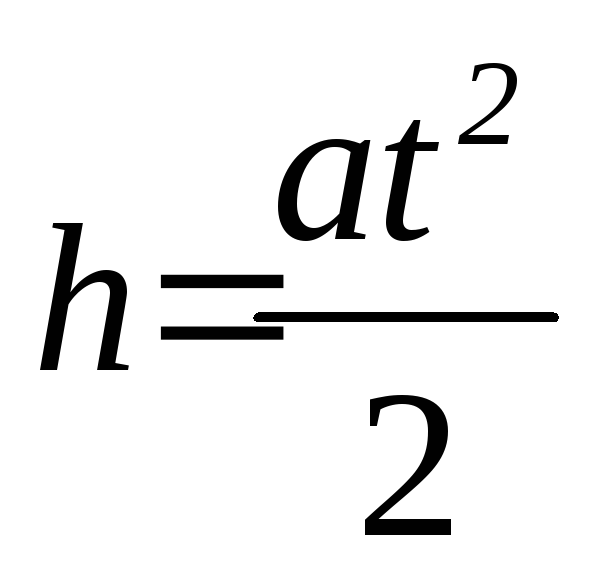

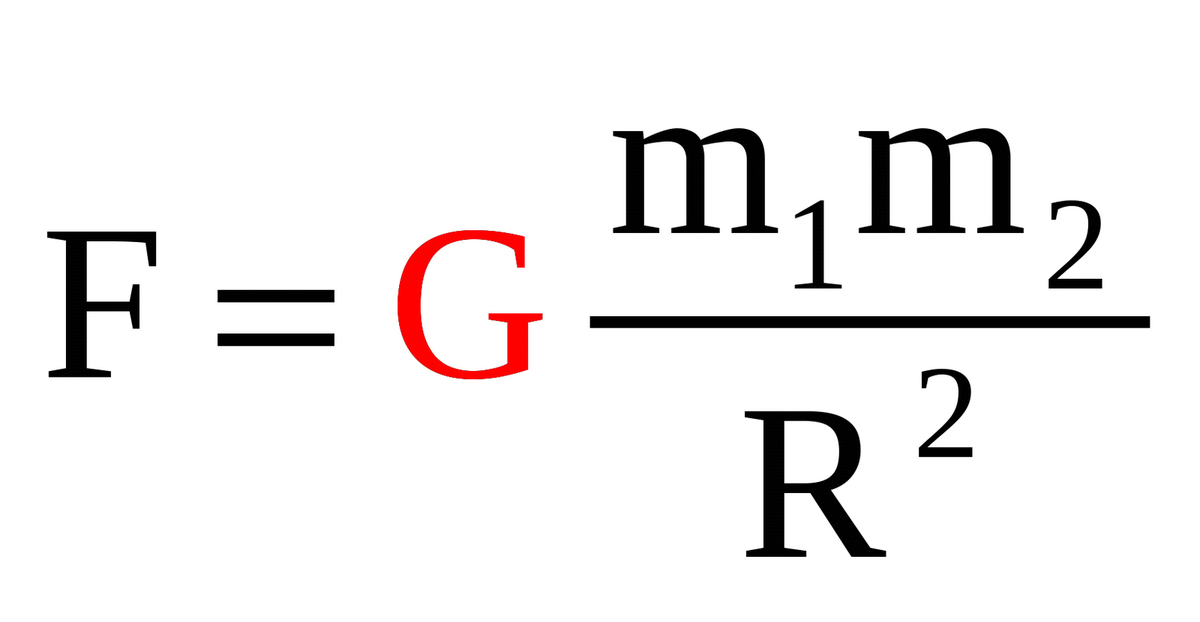
 68
68 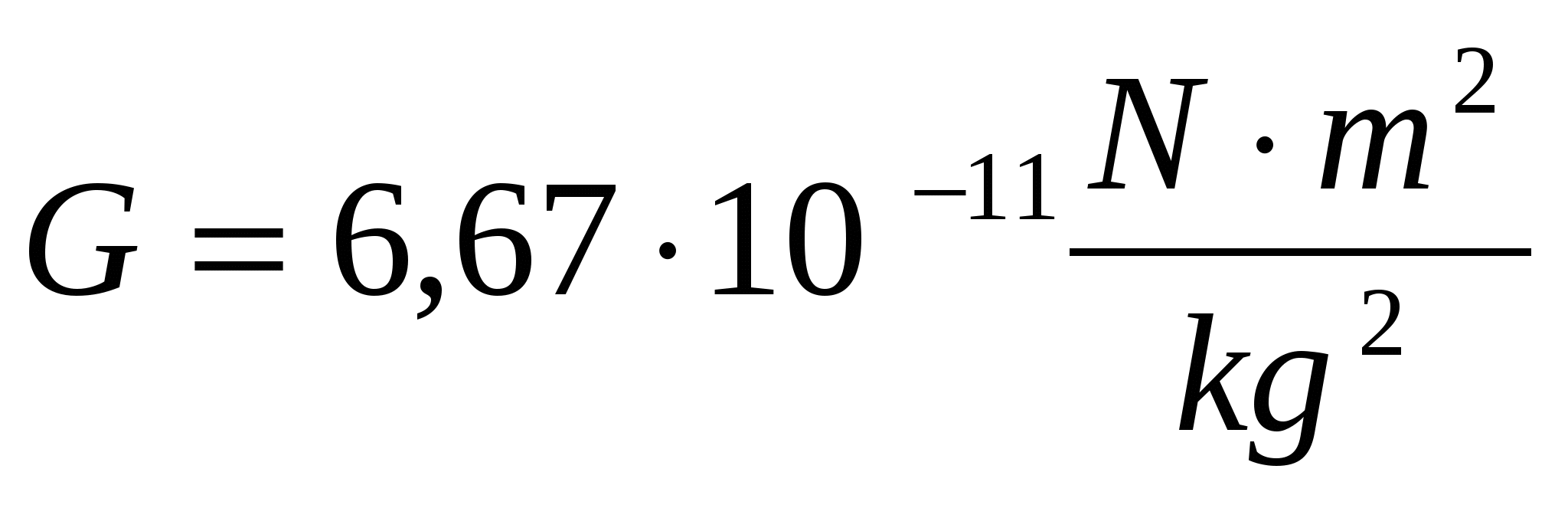 64 x 10 7 м
64 x 10 7 м  38 х 10 6
38 х 10 6