Видео уроки егэ 2018 по математике: Видео уроки ЕГЭ по математике профильного уровня в Москве - Управленческое образование

Содержание

ГДЗ по алгебре 10 класс Колягин, Ткачева Просвещение ответы и решения онлайн

Решившим получить полное среднее образование в школе необходимо уже с 10-го класса сосредоточить максимум внимания на дисциплинах, по которым выпускники сдают обязательные ЕГЭ. В первую очередь — это математика. Здесь следует уделить достаточно времени изучению алгебры, задания по которой составляют основной блок задач в экзамене. Чтобы освоить курс глубоко и полно, рекомендуется заниматься самостоятельно. Помочь в этом смогут гдз по алгебре за 10 класс Колягин, если уделить такой подготовке хотя бы полчаса-час в день. Также следует регулярно контролировать полученные результаты, запоминать правильное оформление работ: порядок записи условия, алгоритма решения и ответов.

Кому будут необходимы справочные материалы по алгебре в 10 классе?

В числе тех, кто регулярно и системно применяет верные решения по алгебре за 10 класс Колягина, Ткачевой в своей практике — такие пользователи:

десятиклассники, серьезно заинтересованные в математических знаниях и их практическом применении. Например те, кто участвует с специализированных научно-конкурсных мероприятиях по алгебре, проводимых на внешкольных и школьных платформах. При помощи предлагаемого источника они дополнят свои знания, особенно если в классе изучают предмет по другим пособиям, УМК;
подростки, часто пропускающие школьные занятия в связи с получением дополнительных знаний на профильных площадках ВУЗов, принимающие участие в конкурсах и спортивных мероприятиях. С помощью платформы эти школьники восполнят образовавшиеся в знаниях пробелы, успешно освоят сложные темы, подготовятся к контрольной, проверочной по дисциплине;
выпускники, повторяющие курс пройденного по алгебре в 10-м классе;
репетиторы, помогающие десятиклассникам осваивать школьный курс алгебры, как базового, так и повышенного уровня. Поскольку сборник подготовлен в соответствии с регламентами ФГОСов последних поколений, по нему можно без проблем составить и внедрить собственную результативную программу подготовки.

Положительные стороны применения сборников готовых решений

Пока не все учителя и родители убеждены в необходимости применения еуроки ГДЗ в процессе подготовки домашних заданий и классной работы. Те же, кто убедился в целесообразности такого подхода, отвечают скептикам следующими аргументами:

решебник доступен постоянно, в любое время и для всех пользователей;
нахождение нужного решения занимает минимум времени, что важно, если ответ необходим в условиях ограниченности сроков, форс-мажора, например, на контрольной;
это выгодно экономически, позволяя сэкономить на посещении дорогих платных курсов, найме репетиторов;
еуроки просты в применении, понятны и логичны.

Используя на практике онлайн решения по алгебре за 10 класс (авторы Колягин, Ткачева), старшеклассники учатся работать самостоятельно и проверять результаты своей деятельности. Этот полезный навык обязательно пригодится им и в будущем.

Профессор предложил вернуть 9-летнюю студентку МГУ в школу — Панорама

Судьба 9-летней студентки факультета психологии МГУ Алисы Тепляковой по-прежнему остается в центре внимания. Останется ли она в университете? Ведь ее учеба забуксовала на первой же сессии. А если уйдет из вуза, то куда подастся? Эксперты в области образования сказали, чтобы они рекомендовали бы Алисе в этой ситуации. Об этом пишет mk.ru.

«Нет таких одаренных детей, которые в 8-9 лет были бы готовы поступить в университет, – считает профессор НИУ ВШЭ в Санкт-Петербурге, заведующий Лабораторией социологии образования и науки Даниил Александров. – В 99% случаев одаренные дети не готовы к этому не только социально, но и интеллектуально, потому что интеллект не сводится к способностям осваивать какой-то материал. Бывает, что некоторые способные к математике дети в 9 лет могут решать сложные математические задачи 11-го класса. Но это не значит, что они в 9 лет способны заниматься математикой в том же самом смысле, в каком готовят студентов на математическом факультете в вузе».

По словам профессора, университет и старшие классы школы – это не только освоение набора знаний. Это освоение социальных навыков, это общение со сверстниками, ребенок учится пользоваться своим интеллектом в реальной жизни. И для всех людей важно пройти определенные моменты этой жизни.

«В случае Алисы родители хотят, чтобы был индивидуальный план и чтобы она занималась дома, но зачем тогда учиться в МГУ – только для «бумажки»? – продолжает Александров. – Это на самом деле большая проблема. Ребенок проходит и школу, и университет дома, не способен ни с кем общаться нормально…

Подкидывание детей на верхние этажи образования в раннем возрасте никуда не ведет, кроме как к неприятностям для детей. Даже дети, поступающие в 15 лет в вуз, оказываются не адаптированными к университетской жизни, а что уж говорить о 9-летних?..»

– Что, если Алиса все-таки окончит психфак МГУ?

– Даже если представить, что человек как бы умудряется закончить МГУ с какими-то оценками, потому что он не в аудитории, не со всей строгостью обычного обучения, а на облегченном варианте индивидуального плана, то все это, на мой взгляд, бессмысленное действие. Мы понимаем, что человек учится для того, чтобы быть либо практическим, либо академическим психологом, но ребенок в 15 лет не может быть ни тем, ни другим по многим причинам.

– Что делать родителям, у которых дети так же ускоренно развиваются, еще в раннем детстве?

– Во-первых, надо сказать, что в большинстве случаев ранние интеллектуальные таланты диагностируются плохо, то есть в 9 лет еще нельзя понять, действительно ли человек талантливый математик или просто бойко решает в уме задачи. Яркие способности к физике, к программированию не проявляются в 9 лет.

Соответственно, мнение большинства специалистов в мире, которым я доверяю, состоит в том, что детям до 8-го класса вообще не нужно специализированное обучение. Дети могут ходить в какие-то кружки и проверять себя. И если к 8-му классу становится очевидно, к чему он склонен, тогда можно заниматься этим направлением серьезно.

Безусловно, талантливым детям рекомендуется сочетание каких-то интеллектуальных занятий, например, со спортом или каким-то видом искусства. Причем желательно в коллективе. Это должны быть внешкольные занятия, чтобы у детей расширялся круг общения. Они учатся работать, общаться с разными взрослыми, у которых разные задачи.

– А какой вариант есть у Алисы – она же не может вернуться в школу?

– Мне кажется, что ей вообще не надо учиться в университете, а университету не нужно ее учить. Я думаю, что она могла бы вернуться в какую-то хорошую школу. И неважно, что она сдала ЕГЭ. В Москве много хороших частных школ, и я бы на их месте сказал бы: давайте девочка у нас поучится, давайте посмотрим. А через несколько лет, может, выяснится, что у нее совсем другие интересы, она и не хочет рано поступать на психологию, а найдет свой интерес. Это возможно, когда у неё появится большая самостоятельность в поведении.

Психолог Елена Мошкова, которая в числе прочего занимается одаренными детьми, считает, что Алиса не сама выбрала психологию:

– Она явно способный человек. Теперь остается вопрос, как «разгрести» эту ситуацию с МГУ. Ведь дело не в том, чтобы найти какие-то другие возможности для ребенка, а чтобы с ними согласился отец. Работа сейчас должна быть не столько с ребенком, сколько с отцом. Он ни на какие предложения не реагирует позитивно.

Новости Стерлитамака :: г. Стерлитамак. Стерлитамакский портал (СТЕРЛИТАМАК.РФ, СТР.РФ, СТЕРЛИТАМАК.РУ, СТР.РУ) :: Стерлитамак город

Раздел новости Стерлитамака. Стерлитамакские новости — это обзор самых интересных событий, происходящих в городе Стерлитамаке. Новости Стерлитамака создаются не только администраторами портала, но и любым жителем, стремящимся к тому, чтобы все в Стерлитамаке были в курсе последних новостей города. Добавляя сообщение в раздел «новости Стерлитамак», каждый из нас вносит свою лепту в то, чтобы все мы были более информированы о событиях города Стерлитамака.

Ведь именно новости г.Стерлитамак интересуют нас в жизни больше всего, ведь мы хотим быть в курсе всех событий, и мы не хотим пропустить важные и интереснейшие мероприятия. Добавь новость Стерлитамака сам и расскажи о ней всем гостям и жителям города Стерлитамака.

Поиск:

Самое популярное на STR.RU

Интересное на STR.RU

Витрина Стерлитамака

31.01  Куплю оптом кабель, провод, дорого, самовывоз
31.01  Куплю кабель и провод по максимальным ценам
30.01  Обучение на гитаре
30.01  Куплю оптом кабель, провод, дорого, самовывоз
30.01  Куплю кабель и провод по максимальным ценам
29.01  Куплю оптом кабель, провод
29.01  Куплю кабель и провод по максимальным ценам
28.01  Куплю оптом кабель, провод, дорого, самовывоз

27.01 Наборщик текстов на дому — работа на пк (копирайтер)
27.

01 ЗАКУПАЕМ КАБЕЛЬНУЮ ПРОДУКЦИЮ С МОНТАЖА ПО РФ

Анализ инструкций по математике с использованием концепции обучения для надежного понимания (AIM-TRU) — Математика

4 октября 2018 г.

Эйлин Мюррей (PI) получила грант от Math for America.

Опубликовано в: Математическое образование PhD

Компоненты AIM-TRU

Это научно-практическое партнерство между тремя университетами (Университет штата Монклер, Университет штата Нью-Йорк в Баффало, Университет ДеПола) и двумя программами лидерства учителей (MƒA, Программа магистратуры штата Нью-Йорк), работающими над созданием видео основанная на модели профессионального развития, которая последовательно интегрирует ключевые элементы учебных систем.

В этом проекте мы неоднократно усовершенствовали подход к профессиональному развитию, который является инновационным, поскольку он основан на практике, включает видео и фокусируется на открытом высококачественном учебном ресурсе

. Наш проект называется «Анализ инструкций по математике с использованием концепции обучения для надежного понимания» (AIM-TRU).

В AIM-TRU учителя совместно анализируют видео-кейсы, показывающие, как другие учителя проводят уроки под названием Classroom Challenges . Classroom Challenges — это 100 бесплатных высококачественных планов уроков по математике, разработанных Центром математического образования Shell для поддержки преподавания в соответствии с концепцией Teaching for Robust Understanding (TRU). Важнейшим элементом этих уроков является то, что они построены так, чтобы стимулировать насыщенные беседы в классе о глубоких математических идеях, что делает их идеальным средством для видеокейсов.

Чтобы создать эти видеокейсы, наша исследовательская группа предлагает учителям-добровольцам из дочерних программ лидерства записывать уроки Classroom Challenge в своих классах на видеопленку.Затем мы определяем эпизоды, показывающие, что учащиеся занимаются насыщенной математической деятельностью, и вырезаем из них видеосюжет с соответствующими материалами кейса, включая план урока, стенограммы и контекст. Эти видеокейсы составляют основу нашей модели PD, где учителя используют эти материалы, а также наборы вопросов для размышления, основанные на структуре TRU. При разработке модели PD члены нашей исследовательской группы организовали семинары на основе видео-кейсов с восемью различными группами учителей в Нью-Йорке, Буффало, Чикаго, Вашингтоне и Лос-Анджелесе.Мы собрали видеоданные и/или полевые заметки для этих сессий, чтобы продолжать совершенствовать видеокейсы и модель PD.

лекций Кемпфа | Математика | Университет Джона Хопкинса

Эта серия специальных лекций посвящена Джорджу Кемпфу.

Весна 2019 г.

Бхаргав Бхатт, Мичиганский университет ( Плакат )

Четверг, 4 апреля, 16:00–17:00, Латроб 120: Интерполяция p-адических теорий когомологий
Пятница, 5 апреля, 15:00-16:00, Кригер 304: Гипотеза о прямом слагаемом

Осень 2018

Михалис Дафермос, Принстонский и Кембриджский университеты ( Poster )

Весна 2018 г.

Обновление

(23 апреля 2018 г.): весенние лекции Kempf 2018 г. отменены.

Осень 2017

Ричард Мелроуз, Массачусетский технологический институт ( Плакат )

Весна 2017 г.

Луис Каффарелли, Техасский университет

Весна 2016 г.

Хоаким Ортега-Серда, Университет Барселоны ( Плакат )

Весна 2015 г.

Элиас Штайн, Принстон

Понедельник, 13 апреля: Что думать о проекции Коши-Сегу
, вторник, 14 апреля: Сингулярные интегралы: теория произведений и ее развитие

Весна 2014 г.

Кристофер Хакон, Университет Юты

Четверг, 13 марта: Бирациональная классификация алгебраических многообразий
Пятница, 14 марта: О гипотезах Шокурова о логканонических порогах

Осень 2013

Пьер Картье, IHES и Университет Париж-Дидро

Четверг, 21 ноября: О космической группе Галуа, рассказ о геометрии, теории чисел и физике
Пятница, 22 ноября: Квантовая группа как группа Галуа для некоторых разностных уравнений: еще один пример некоммутативной геометрии

Весна 2013 г.

Мачей Зворски, Беркли

Скорости распада в квантовой и классической динамике

Весна 2012 г.

Тобиас Колдинг, Массачусетский технологический институт

Средняя кривизна потока
Кривизна Риччи

Осень 2011 г.

Бернд Штурмфельс, Калифорнийский университет в Беркли

Многоракурсная геометрия
Мустафин Сорта

Весна 2011 г.

Федор Богомолов, Институт Куранта

Теорема Куммера и проективная геометрия
Проблема Арфа-Кервера в алгебраической топологии

Осень 2010 г.

Казуя Като, Чикагский университет

Классификация пространств вырождающихся структур Ходжа
Вырождение Ходжа и p-адических структур Ходжа

Весна 2010 г.

Дэн Фрид, Техасский университет

Операторы Дирака и дифференциальная K-теория
Группы петель и скрученная К-теория

Осень 2009 г.

Эрик Бедфорд, Университет Индианы

Динамика сложных поверхностных автоморфизмов
Динамика рациональных поверхностных автоморфизмов

Весна 2009 г.

Кен Оно, Университет Висконсин-Мэдисон

Раскопки видений мастера: гармонические формы Маасса
Делители Хегнера, L-функции и формы Маасса

Виктор Гийемен, Массачусетский технологический институт

Осень 2008 г.

Джеймс МакКернан, Массачусетский технологический институт

Конечное поколение канонического кольца
Новый взгляд на теорему о конусах

Весна 2008 г.

Янош Коллар, Принстон

Какие степени голоморфных функций являются интегрируемыми
Диофантовы подмножества функциональных полей кривых

Осень 2007 г.

Валерий Алексеев, УГА

Канонические пределы разновидностей
Тропическая геометрия против классической геометрии

Д. Х. Фонг, Колумбия

Устойчивость и постоянная скалярная кривизна

Ларс Хессельхольт, Массачусетский технологический институт

Гомеоморфизмы многообразий и алгебраическая K-теория
Абсолютный комплекс де Рама-Витта и основная теорема
Введение в алгебраическую К-теорию

Весна 2007 г.

Казухиро Фудзивара

Подсчет количества решений в конечных полях
Представления Галуа и арифметическая геометрия многообразий Симуры

Рави Вакил

Геометрическое правило Литтлвуда-Ричардсона
Закон Мерфи в алгебраической геометрии: пространства модулей с плохим поведением

Осень 2006 г.

Ив Андре

Теория неоднозначности, старая и новая
Периоды и мотивы

Вильгельм Шлаг

О течении Шредингера на поверхностях вращения
Дисперсионные оценки для волновых уравнений и приложения к устойчивости солитонов

Весна 2006 г.

Роберт Брайант

Поверхности Aufwiedersehen, пересмотренные
Градиентные солитоны Калера-Риччи

Осень 2005 г.

Эзра Гетцлер

Теория Ли для дифференциальных градуированных алгебр Ли
Открытые/закрытые модульные операды
Открытые/замкнутые пространства модулей Делиня-Мамфорда и топологическая теория поля

Юрий Чинкель

Геометрия над конечными полями
Арифметика над функциональными полями

Весна 2005 г.

Майкл Дуглас

Теория струн и геометрия

Матильда Марколли

Квантовая статистическая механика Q-решеток
Перенормировка и мотивная теория Галуа

Архивные материалы по математике 3012: Прикладная комбинаторика

Профессор Уильям Т.Троттер (Заслуженный)

Электронная почта: trotter at math dot gatech dot edu

Руководство по курсу и образец программы (весна 2018 г.

)

Онлайн-учебник — в свободном доступе!

Дополнительные видео и слайды

Несмотря на то, что в первую очередь предназначен для студентов дистанционного обучения, видеоролики, подготовленные в 2015 году и доступные по адресу Веб-сайт Math 3012 Open Resources также должен иметь значение для студентов, проходящих курс в кампусе.Слайды в формате PDF также были подготовлены в 2015, которые коррелируют с этими видео. Однако в осеннем семестре 2017 г. и новые версии перечислены сразу ниже. В любом случае содержание курсов всегда несколько различается из семестра в семестр, отражая как усилия преподавателей по улучшению курс, освещая текущие и разворачивающиеся разработки в области комбинаторики.

2017 Слайды по темам

1 — Введение в комбинаторику
2 — Строки и биномиальные коэффициенты
3 — Индукция и рекурсия
4 — Принцип голубиной норы и сложность
5 — Основы теории графов
6 — Цепи Эйлера и гамильтоновы циклы 90 036
7 — Раскраска графика
8 — Планарные графики
9 — Продвинутые темы по теории графов
10 — Основные понятия Posets
11 — Цепные и антицепные разделы
12 — Графики покрытия и графики сопоставимости
13 — Интервальные заказы и интервальные графики
14 — Подмножество решеток
15 — Включение-исключение
16 — Генерирующие функции
17 — Уравнения оператора продвижения
18 — Алгоритмы связующего дерева
19 — Алгоритмы кратчайших путей
20 — Сетевые потоки
21 — Потоки с единичными мощностями
22 — Решение проблемы Дилуорта
23 — Приложения вероятности к комбинаторике

2015 Слайды по темам

Лекция 1 — 18 августа 2015 г.
Лекция 2 — 20 августа 2015 г.
Лекция 3 — 25 августа 2015 г.
Лекция 4 — 27 августа 2015 г.
Лекция 5 — 1 сентября 2015 г.
Лекция 6 — 3 сентября 2015 г.
Лекция 7 — 8 сентября 2015 г.
Лекция 8 — 10 сентября 2015 г.
Лекция 9 — 15 сентября 2015 г.
Лекция 10 — 22 сентября 2015 г.
Лекция 11 — 24 сентября 2015 г.
Лекция 12 — 29 сентября 2015 г.
Лекция 13 — 1 октября 2015 г.
Лекция 14 — 6 октября 2015 г.
Лекция 15 — 8 октября 2015 г.
Лекция 16 — 15 октября 2015 г.
Лекция 17 — 20 октября 2015 г.
Лекция 18 — 27 октября 2015 г.
Лекция 19 — 29 октября 2015 г.
Лекция 20 — 3 ноября 2015 г.
Лекция 21 — 5 ноября 2015 г.
Лекция 22 — 10 ноября 2015 г.
Лекция 23 — 12 ноября 2015 г.
Лекция 24 — 17 ноября 2015 г.
Лекция 25 — 19 ноября 2015 г.
Лекция 26 — 1 декабря 2015 г.
Лекция 27 — 3 декабря 2015 г.

Решения некоторых проблем с нечетными номерами в тексте

Архив тестов WTT

Осень 2018

Осень 2017

Осень 2015

Осень 2014

Весна 2013 г.

Осень 2011

Осень 2010

Осень 2009 г.

Осень 2007 г.

Осень 2006 г.

Осень 2004 г.

Осень 2003 г.

Презентации

Компьютерные программы, заголовочные файлы и файлы данных

Обновлено 7 января 2018 г.

Изучение эффективности видео-виньеток для развития навыков обратной связи с учителями по математике

АПА

Муньис-Родригес Л., Алонсо П., Родригес-Муньис Л. Дж., Де Конинк К., Вандерлинде Р. и Вальке М. (2018). Изучение эффективности видео-виньеток для развития навыков обратной связи студентов-преподавателей по математике. Eurasia Journal of Mathematics, Science and Technology Education, 14 (11), em1573.https://doi.org/10.29333/ejmste/

Ванкувер

Муньис-Родригес Л., Алонсо П., Родригес-Муньис Л.Дж., Де Конинк К., Вандерлинде Р., Вальке М. Изучение эффективности видео-виньеток для развития компетентности студентов-учителей по математике. ЕВРАЗИЯ J Math Sci Tech Ed. 2018;14(11):em1573. https://doi.org/10.29333/ejmste/

АМА

Муньис-Родригес Л., Алонсо П. , Родригес-Муньис Л.Х., Де Конинк К., Вандерлинде Р., Вальке М.Изучение эффективности видео-виньеток для развития навыков обратной связи студентов-преподавателей по математике. ЕВРАЗИЯ J Math Sci Tech Ed . 2018;14(11), em1573. https://doi.org/10.29333/ejmste/

Чикаго

Муньис-Родригес, Лаура, Педро Алонсо, Луис Х. Родригес-Муньис, Карен Де Конинк, Рубен Вандерлинде и Мартин Вальке. «Изучение эффективности видео-виньеток для развития компетентности учителей математики в обратной связи». Евразийский журнал математики, науки и технологий образования 2018 14 вып. 11 (2018): em1573. https://doi.org/10.29333/ejmste/

Гарвард

Муньис-Родригес Л., Алонсо П., Родригес-Муньис Л. Дж., Де Конинк К., Вандерлинде Р. и Вальке М. (2018). Изучение эффективности видео-виньеток для развития навыков обратной связи студентов-преподавателей по математике. Eurasia Journal of Mathematics, Science and Technology Education , 14(11), em1573.https://doi.org/10.29333/ejmste/

ГНД

Муньис-Родригес, Лаура и др. «Изучение эффективности видео-виньеток для развития компетентности учителей математики в обратной связи». Eurasia Journal of Mathematics, Science and Technology Education , vol. 14, нет. 11, 2018, em1573. https://doi.org/10.29333/ejmste/

Видео | Микроучебники по математике

.........

МРТ Амортизация	Линейные функции ; линейная амортизация; Бизнес-приложения	Общественные науки	Задача 90, страница 33 найдена в R.Ларсон. Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Производитель содовой	Линейные функции ; функция линейной стоимости; Фиксированная цена; предельная стоимость; Бизнес-приложения	Общественные науки	Задача 82, страница 99, найденная в Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Амортизация нового автомобиля	Экспоненциальная модель ; Бизнес-приложения	Общественные науки	Задача 25, страница 257 найдена в «Larson.Исчисление: прикладной подход, 10-е издание, Cengage Learning, Бостон, 2016 г.».
Доход от жилищного строительства	Модели с квадратичной функцией ; функция спроса; Функция доходов; Бизнес-приложения	Общественные науки	Задача 33, страница 143, найденная у Ванера и Костенобля. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Прибыль производства	Кусочно-определенные функции ; Функции спроса, дохода, затрат и прибыли; Бизнес-приложения	Общественные науки	Задача 76, страница 47 найдена в R.Ларсон, Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Генная регуляция	Теорема сжатия; Теорема о сэндвиче ; Ограничения	Биологический; математический	Задача 32, страница 136 найдена в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Результаты SAT по доходам	Численный поиск пределов ; лимиты; Бизнес-приложение	Общественные науки	Задача 55, страница 215 найдена в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Колеблющееся население	Теорема сжатия; Теорема о сэндвиче ; лимиты; Лимит на бесконечности	математический	Задача 12, страница 130 найдена в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, Pearson, 2011».
Непрерывность кусочно заданной функции	Непрерывность и односторонние пределы ; левый непрерывный; правый непрерывный; Кусочно-определенные функции	математический	Задача 49, страница 83 найдена в «J. Рогавски и К. Адамс. Исчисление, 3-е издание, WH Freeman and Company, Нью-Йорк, 2015 г.».
Реклама в кино	Непрерывность и односторонние пределы ; кусочно-определенные функции; Бизнес-приложения	Общественные науки	Задача 91, страница 237 найдена в «Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Гравитационная сила	Непрерывность и односторонние пределы ; лимиты; Кусочно-определенные функции	Физический; математический	Задача 36, страница 148 найдена в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук, Cengage Learning, 2015».
Грибковый рост	Непрерывность и односторонние пределы ; лимиты; График кусочно-определяемых функций	Биологический; математический	Задача 50, стр. 120 найдено у К. Нойхаузера и М. Ропера. Исчисление для биологии и медицины, 4-е издание, Prentice Hall, Pearson, 2018.
Концентрация соли	Пределы в бесконечности ; Проблема со смесью	Физический	Упражнение 34, стр. 110 в «J.Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Падающая капля дождя	Пределы в бесконечности ; Предельная скорость	Физический	Упражнение 37, стр. 111 в «J. Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Модель «Хищник-жертва»	Пределы в бесконечности ; Горизонтальная асимптота	Биологический	Адаптировано из задачи 15, стр. 130, найденной в «C.Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, 2011».
Численность населения	Пределы в бесконечности ;	Биологический; математический	Задача 11, стр. 130 найдено в C. Neuhauser, Calculus for Biology and Medicine, Third edition, Pearson 2011.
Скорости реакций ферментов и субстратов	Пределы в бесконечности ; Оценка пределов	Физический	Задача 33, страница 99 найдена в «J.Рогавски, К. Адамс. Calculus Early Transcendentals, 3-е издание, Macmillin, 2015».
Цены на сырую нефть	Средняя скорость изменения ; Бизнес-приложения	Общественные науки	Задача 43, страница 252, найденная у Ванера и Костенобля. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Метаболизм ацетаминофена	Средняя и мгновенная скорости изменения ; коэффициент разницы; Определение производной	Биологический	Задача 1.2.5, стр. 25 в «G. Ледер. Математика для наук о жизни: исчисление, моделирование, вероятность и динамические системы, 1-е издание, Springer, Нью-Йорк, 2013 г. ».
Бросьте инструмент	Пределы ; Функции положения и скорости; Мгновенная скорость	Физический	Задачи 103 и 104, стр. 69, найденные в “R. Ларсон и Б. Эдвардс. Исчисление, 9-е издание, Брукс/Коул, Cengage Learning, 2010.
Развитие логистики	Скорость изменения ; Грузоподъемность; Рост населения и равновесие	Биологический	Нойхаузер, Исчисление для биологии и медицины, 3-е издание, Pearson Education, 2011 г., задача 49, стр. 145
Биотическое разнообразие	Применение производных ; Скорость изменения; Экосистемное равновесие	Биологический	Задача 50, страница 145 найдена у Клаудии Нойхаузер.Исчисление для биологии и медицины, третье издание, Пирсон, 2011.
Дизайн шоссе	Производная как наклон касательной ; Квадратичная функция	Физический	Упражнение 64, стр. 171 найдено в «R. Ларсон и Б. Эдвардс. Calculus, 9-е издание, Brooks/Cole, Cengage Learning, 2010».
Расход энергии ящерицы	Применение производных ; Правила дифференциации	Биологический; Физический	Задача 47, страница 595 найдена в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015 г.».
Площадь поверхности тела	Скорость изменения ; Интерпретация производной	Биологический	Задача 35, страница 149 найдена в «J. Рогавски, К. Адамс. Calculus Early Transcendentals, 3-е издание, Macmillin, 2015».
Продажа футболок	Скорость изменения ; Производная; Функция доходов; Бизнес-приложения	Общественные науки	Задача 81, стр. 340 найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. ».
Водяные змеи	Производные как курсы изменения ; Интерпретация производной	Биологический	Задача 49, стр. 183 найдено в R.N. Гринвелл, Н.П. Ричи, М.Л. Лиал, Исчисление для наук о жизни, Пирсон, 2-е издание.
Мертвое море	Производная и мгновенная скорость изменения ;	Физический	Задача 72, страница 213 найдена в “R.Н. Гринвелл, Н.П. Ричи, М.Л. Лиал, Исчисление для наук о жизни, 2-е издание, Пирсон, 2015».
Предельная прибыль	Производная и предельная прибыль ; Функции спроса, дохода, затрат и прибыли; Бизнес-приложения	Общественные науки	Задача 40ac, стр. 116 найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Медианные цены на жилье	Средняя и мгновенная скорость изменения ; производные; Бизнес-приложения	Общественные науки	Задача 88, стр. 274 найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Бляшка в артериях	Производная и мгновенная скорость изменения ;	Биологический	Задача 33, стр. 230 найдено в «S. Schreiber, K. Smith, and W. Getz. Calculus for the Life Sciences, 1st Edition, John Wiley & sons, 2014».
Биомасса	Правило продукта ; Производная как скорость изменения; Популяция рыб	Биологический	Задача 56, страница 202 найдена в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Пополнение запасов	Правило частных ; производные; Скорость изменения; Функция стоимости; предельная стоимость; Бизнес-приложения	Общественные науки	Задача 71, стр. 126 найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Передаточное отношение наконечника	Правило частных ; производные; Скорость изменения	Физический	Страница 141 Задача 52 в «J.Рогавски и К. Адамс. Исчисление, 3-е издание, WH Freeman and Company, Нью-Йорк, 2015 г.».
Устойчивость к инсектицидам	Правило частных ; производные; Скорость изменения	Биологический	Задача 54, страница 201 найдена в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Расход газа	Правила произведения и частного ; производные; Скорость изменения	Физический	Задача 59, страница 141 найдена в «D.Хьюз-Халлетт; А. Глисон; В. МакКаллум. Исчисление, одно- и многомерное, 6-е издание, Wiley & Sons, Inc.”
Индекс массы тела	Частное правило; Цепное правило ; Производная как скорость изменения	Биологический	Задача 67 и 68, стр. 223, Исчисление и его приложения Гольдштейна, Лея, Асмара, Шнайдера. Эд 13 Пирсон.
Проблемы школы медсестер	Дифференциация ; пропорциональность; Производная как скорость изменения	Биологический	Нойхаузер, Исчисление для биологии и медицины, 3-е издание, Pearson Education, 2011 Задача 72, стр. 173
Давление в пазухах	Цепная линейка ; Интерпретация производной	Биологический	Упражнение 56, стр. 213 найдено в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Загрязнение	Цепная линейка ; Интерпретация производной	Физический	Гринвелл, Ричи и Лиал, Исчисление для наук о жизни (второе изд.), Задача 56, стр. 228
Нанимать или не брать на работу	Цепная линейка ; Бизнес-приложения	Общественные науки	Задача 81, страница 353 найдена в «Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Волновое движение	Цепная линейка ; Простое гармоническое движение	Физический	Упражнение 114, стр. 139 в «R. Ларсон и Б. Эдвардс. Calculus, 9-е издание, Brooks/Cole, Cengage Learning, 2010».
Суточный рост	Производные тригонометрических функций ; Правило цепи; Граница функции синуса; Решение неравенств	Биологический; математический	Задача 74, страница 188 найдена в C.Нойхаузер и М. Роупер. Исчисление для биологии и медицины, 4-е издание, Prentice Hall, Pearson, 2018.
Крупная рыба	Пределы в бесконечности ; Экспоненциальный рост; Модель роста фон Берталанфи	Биологический	Нойхаузер, Исчисление для биологии и медицины, 3-е издание, Pearson Education, 2011 Задача 65, стр. 182
Сколько лет?	Экспоненциальный рост и спад ; Бизнес-приложения	Общественные науки	Задача 81, страница 283 найдена в «Larson. Исчисление: прикладной подход, 10-е издание, Cengage Learning, Бостон, 2017 г.».
Интенсивность света в воде	Экспоненциальный рост и спад ; Дифференциальные уравнения; Задача с начальным значением	Физический	Модифицированная версия примера 5.5.6, стр. 256, найденная в «Исчислении для наук о жизни: подход к моделированию» Джеймса Л. Корнетта и Ральфа А. Акермана. Электронная версия том 1. https://open.umn.edu/opentextbooks/BookDetail.aspx?bookId=92
Радиоактивный распад	Экспоненциальный рост и спад ; производная экспоненциальной функции; Период полураспада; Дифференциальные уравнения	Физический	Задача 72, страница 183 найдена в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Pearson Education, Inc.
Генетический дрейф	Производные логарифмических функций ; Правило цепи; Применение производных; Фруктовые мушки	Биологический	Задача 30, страница 229 найдена в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015 г.».
Время в пути	Функции положения, скорости и ускорения ; Применение производных; Графические интерпретации производных	Физический	Задача 34, стр. 201 найдено в C. Neuhauser, Calculus for Biology and Medicine, Third edition, Pearson, 2011.
Поездка на велосипеде	Положение, скорость и ускорение ; первая и вторая производные; Графическая интерпретация производной; Графики тригонометрических функций	Физический; математический	Задача 33, страница 201 найдена в C.Нойхаузер, Исчисление для биологии и медицины, третье издание, Pearson 2011.
Популяция хищников	Цепная линейка ; Неявное дифференцирование	Биологический	Задача 56, страница 1.6.2 найдена в «G. Ledder Mathematics for Life Sciences, 1-е издание, Springer, Нью-Йорк, 2010 г. ».
Производственная функция Кобба-Дугласа	Неявное дифференцирование ; Бизнес-приложения	Общественные науки	Задача 47, страница 150 найдена в R.Ларсон, Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Производственная функция	Неявное дифференцирование ; производственная функция Кобба-Дугласа; Бизнес-приложения	Общественные науки	Задача 29, стр. 448 найдено в «Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Распределение ресурсов	Неявное дифференцирование ; Связанные ставки; Бизнес-приложения	Общественные науки	Задача 27, стр. 448, найденная в Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Посмотрите эти книги	Неявное дифференцирование	Математический; Общественные науки	Задача 48, стр. 243, Исчисление и его приложения Гольдштейна, Лея, Асмара, Шнайдера. Эд 13 Пирсон.
Энергопотребление	Неявное дифференцирование	Биологический	Упражнение 47, с.228 Адлер, Ф. Р. (1998). Моделирование динамики жизни: исчисление и вероятность для ученых-биологов (3-е изд.). Пасифик-Гроув, Калифорния: Брукс/Коул.
Кровь течет	Неявное дифференцирование	Биологический	Томас, Исчисление, 11-е издание, Pearson Education, 2005 г., стр. 220, задача 25
Популяция бактерий	Обратные функции	Биологический	Задача 57, страница 67 найдена в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015 г.».
Скорость в сопротивляющейся среде	Правило Лопиталя	Физический	Упражнение 93, стр. 578 найдено в «R. Ларсон и Б. Эдвардс. Calculus, 9-е издание, Brooks/Cole, Cengage Learning, 2010».
Видовое разнообразие	Правило Лопиталя ; лимиты; Преемственность	Биологический	Задача 67, страница 260 найдена в «C.Нойхаузер и М. Роупер. Исчисление для биологии и медицины, 4-е издание, Prentice Hall, Pearson, 2018».
Цены на автобусные маршруты	Оптимизация ; Экстремумы на закрытом интервале; Функция спроса и максимальный доход; Бизнес-приложения	Математический; Общественные науки	Задача 11 стр. 186. «Исчисление и его приложения». Гольдштейн, Лэй, Шнайдер, Асмар. Эд 13 Пирсон.
Борьба за супермаркет	Оптимизация ; относительный экстремум; Бизнес-приложения	Общественные науки	Пример 2 стр. 173.«Исчисление и его приложения». Гольдштейн, Лэй, Шнайдер, Асмар. Эд 13 Пирсон.
Выращивание клубники	Оптимизация ; относительный экстремум; Бизнес-приложения	Общественные науки	Задача 37, стр. 203 найдено в R. Larson, Calculus: An Applied Approach, 10th edition, Cengage Learning, 2017.
Максимизация прибыли от квартиры	Оптимизация ; относительный экстремум; Бизнес-приложения	Общественные науки	Задача 20, страница 213 найдена в R.Ларсон, Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Средняя стоимость iPhone	Оптимизация ; Минимальная стоимость; Функция стоимости; Бизнес-приложения	Общественные науки	Задача 13, страница 409, найденная в Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Оптимальная скорость	Оптимизация ; Минимальная стоимость; Функция стоимости; Бизнес-приложения	Общественные науки	Адаптировано из задачи 46, стр. 234, найденной в «Р.Ларсон, Исчисление: прикладной подход, десятое издание, Cengage Learning, 2017 г.».
Черный рынок подержанных книг	Оптимизация ; Функция доходов; Максимальный доход; Бизнес-приложения	Общественные науки	Задача 34, стр. 411 найдено в «Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Код этого программного обеспечения	Оптимизация ; относительный экстремум; Максимальный доход; Бизнес-приложения	Общественные науки	Задача 59, страница 413 найдена в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Интубационная трубка при кашле	Абсолютный экстремум на закрытом интервале	Биологический	Задача 73 стр. 279. «Раннее трансцендентальное исчисление». Джеймс Стюарт. Эд 6 Брукс/Коул, Cengage Learning.
Служба национальной безопасности	Оптимизация ; Неявное дифференцирование	Физический; математический	Томас, исчисление, 11-е издание, Pearson Education, 2005 г., задача 138, стр. 533
Максимальная площадь	Оптимизация ; Первый производный тест; Экстремум	математический	Задача 17, страница 245 найдена в «J.Рогавски и К. Адамс. Исчисление, 3-е издание, WH Freeman and Company, Нью-Йорк, 2015 г.».
В самый последний момент	Оптимизация ; Первый производный тест; Экстремум	математический	Адаптировано из задачи 20, стр. 245 в Rogawski, Jon and Colin Adams, Calculus: Early Transcendentals; 3-е изд., WH Freeman, Нью-Йорк, 2015.
Фармакокинетика	Правило Лопиталя ; Лимит в бесконечности; Первый производный тест; экстремумы; Максимум; Минимум	Биологический; математический	Задача 54, страница 284 найдена в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Эпидемия	Приложение Extrema ; максимумы и минимумы; Возрастающие и убывающие функции	Биологический	Задача 12, страница 222 найдена в «J. Арья, Р. Ларднер. Математика для биологических наук, Прентис Холл, Нью-Джерси, 1979 г.».
Минимизация затрат энергии	Оптимизация ; Первый производный тест; Экстремум	Биологический	Задача 1.5.3, стр. 47 в «G. Ледер. Математика для наук о жизни: исчисление, моделирование, вероятность и динамические системы, 1-е издание, Springer, Нью-Йорк, 2013 г.».
Модель для впрыска	Производные в моделировании ; критические точки; Экстремум	Биологический	Задача 60, страница 262 найдена в «Hughes-Hallett, Gleason, McCallum, et al. Исчисление, 6-е издание, John Wiley & Sons, Inc. , 2013 г.».
Билет за превышение скорости	Теорема о среднем значении	математический	Упражнение 59, стр. 177 найдено в «R.Ларсон и Б. Эдвардс. Calculus, 9-е издание, Brooks/Cole, Cengage Learning, 2010».
Погода в Монтане	Теорема о среднем значении	математический	Задача 36, страница 182 найдена в «E. Своковски. Исчисление, 5-е издание, Брукс/Коул, Cengage Learning, 1991».
Средняя скорость	Теорема о среднем значении ; Скорость; Средняя скорость	Математический; Физический	Задача 32, страница 322 найдена в «C.Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, Pearson, 2011».
Исчисление в музыке	Функции возрастания и убывания ; Скорость изменения	Физический	Задача 28 стр. 232. «Раннее трансцендентальное исчисление». Джеймс Стюарт. Эд 6 Брукс/Коул, Cengage Learning.
Контроль популяции червей	Функции возрастания и убывания ; Первый производный тест	Биологический	Адаптировано из: Задача 30 стр. 222 в «C.Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Pearson Education, Inc., Бостон, Массачусетс, 2011 г.».
Гамбургер Прибыль	Функции возрастания и убывания ; Первый производный тест; Максимальная прибыль; Бизнес-приложения	Общественные науки	Задача 53, страница 176 найдена у Р. Ларсона. Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Бой с Пова	Оптимизация ; Первый производный тест; Экстремум	Физический	Небольшая модификация задачи 41, стр. 264 из «J.Стюарт. Исчисление, 6-е издание, Томсон Брукс/Коул, 2008 г. ».
Анализ графиков	График производной ; Локальный максимум и минимум; Производная возрастающей и убывающей функций	математический	Адаптировано из упражнения 21, стр. 176, найденного в «F. Адлер. Моделирование динамики жизни: исчисление и вероятность для ученых-биологов, 3-е издание, Brooks/Cole, Cengage Learning, 2013».
Подробнее об инфляции в США	Анализ графиков ; Локальный максимум и минимум; Точка перегиба	Математический; Общественные науки	Задача 35, стр. 439 найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Отслеживание вертолета	Графическое представление функций ; График производной; Функции положения, скорости и ускорения	Математический; Физический	Адаптировано из: Задача 28 стр. 177 в «J. Адлер. Моделирование динамики жизни, 3-е издание, Брукс/Коул, Бостон, Массачусетс, 2013 г.».
Распространение гриппа, часть 1	Глобальный экстремум ; Первый производный тест; График функции; Пределы в бесконечности; Правило Лопиталя	Биологический	Задача 43, стр. 402 найдено в «Hughes-Hallett, Gleason, McCallum, et al.Исчисление: одно и многомерное, 6-е издание, John Wiley and Sons, Inc., Массачусетс, 2013 г.».
Моно Рост	Функции возрастания и убывания ; Пределы бесконечности; Горизонтальные асимптоты	Биологический	Адаптировано из задачи 7, стр. 274, найденной в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, 2011».
Нехватка медсестер	Относительный экстремум ; Возрастающие и убывающие функции; Первый производный тест	Общественные науки	Задача 89, стр. 262, найдено в «Прикладном исчислении Тана для управленческих, жизненных и социальных наук: краткий подход», 9-е издание, Брукс/Коул, Калифорния, 2011.
Сосудистое разветвление	Оптимизация ; критические точки; экстремумы; Возрастающие и убывающие функции; Кровоток; Закон Пуазейля	Биологический	Задача 55, страница 247 найдена в «J. Рогавски, К. Адамс. Calculus Early Transcendentals, 3-е издание, Macmillin, 2015».
Закон Снелла	Оптимизация ; критические точки; экстремумы; Первый производный тест; Скорость света	Физический	Задача 54, страница 247 найдена в «J.Рогавски, К. Адамс. Calculus Early Transcendentals, 3-е издание, Macmillin, 2015».
Реакция на дозу	Точка перегиба ; Как деривативы влияют на графики	Биологический	Упражнение 53, стр. 273 найдено в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Инфляция в США	Вогнутость ; Скорость изменения; интерпретация графика; бизнес-приложения;	Общественные науки	Задача 65, страница 427 найдена в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Зубы аллигатора	Точка перегиба ; вогнутость; Производная экспоненциальной функции экспоненциальной функции; Правило нескольких цепочек	Биологический	Задача 88, страница 297 найдена в «R.N. Гринвелл, Н.П. Ричи, М.Л. Лиал, Исчисление для наук о жизни, 2-е издание, Пирсон, 2015».
Всплеск наркотиков	Точка перегиба ; Экспоненциальные производные;	Биологический	Стюарт, Исчисление, 6-е издание, Томсон Брукс/Коул, 2008.Задача 71, стр. 404
Точка убывающей отдачи	Точка перегиба ; точка убывающей отдачи; вторая производная; вогнутость; Бизнес-приложение	Общественные науки	Адаптировано из задачи 89, стр. 279, найденной в «S. Т. Тан, Прикладной расчет для управленческих, жизненных и социальных наук, восьмое издание, Брукс/Коул, Cengage Learning, 2011 г.».
Потребление кофе	Экстремальные значения ; Интерпретация второй производной	Математический; Общественные науки	Задача 30 стр. 179.«Исчисление и его приложения». Гольдштейн, Лэй, Шнайдер, Асмар. Эд 13 Пирсон.
Гомперц? Гомперц Кто?	Производные и функции роста ; производная экспоненциальных функций; критические точки; вторая производная; Точки перегиба	Биологический	Задача 56, стр. 223 найдено в «Hughes-Hallett, Gleason, McCallum, et al. Исчисление, 6-е издание, John Wiley & Sons, Inc., 2013 г.».
Производство на душу населения	Экстремумы и тест второй производной ; критические точки; Вогнутость	Общественные науки	Задача 16, страница 342 найдена в F.Адлер. Моделирование динамики жизни, 3-е издание, Brooks/Cole, Cengage Learning, Boston, 2013.
Аллометрический рост	Неявное дифференцирование и вогнутость ; второй производный тест; точка перегиба	Биологический	Задача 43, стр. 224 найдено в Nuehauser, C., Calculus for Biology and Medicine, 3rd edition, Pearson, 2013.
Фактоидная машина	Рисование кривой ; критические точки; Первый производный тест; второй производный тест; точки перегиба; Вогнутость	математический	Задача 29, страница 239 найдена в «F.Адлер. Моделирование динамики жизни, 3-е издание, Брукс/Коул, Cengage Learning, Бостон, 2013 г. ».
Связанные курсы на кубе	Связанные курсы ; Геометрическая интерпретация dV/dx на кубе	математический	Задача 11, страница 180 найдена в «J. Стюарт. Исчисление, 6-е издание, Томсон Брукс/Коул, 2008 г.».
Доходы от нефти	Связанные курсы ; Бизнес-приложения	Общественные науки	Задача 25, стр. 447 найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Адиабатическое расширение воздуха	Связанные курсы ; Неявное дифференцирование	Физический	Упражнение 88, стр. 214 найдено в «J. Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Буксировка лодок	Связанные курсы ; Неявное дифференцирование	Физический	Адаптировано из задачи в: Stewart, J. (2003). Исчисление: Ранние трансцендентальные. Бельмонт, Калифорния: Томсон/Брукс/Коул.
Рост рыбы	Связанные курсы ; неявное дифференцирование; Функция роста фон Берталанфи	Биологический	Упражнение 90, стр. 215 найдено в «J. Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Прочистка артерии	Дифференциал ; Относительное изменение	Биологический	Томас, исчисление, 11-е издание, Pearson Education, 2005, стр. 230, пример 8
Измерительные диски	Дифференциал ; непрерывные функции;	математический	Задача 30, страница 167 найдена в «F.Адлер Моделирование динамики жизни: исчисление и вероятность для ученых-биологов. Третье издание. Брукс/Коул, Cengage Learning. 2013.» Предпосылка в исчислении:
Пружинное выживание	Метод Ньютона	Биологический	Упражнение 55, стр. 215 найдено в «R. Смит, Р. Минтон. Исчисление, третье издание, McGraw-Hill, 2008 г.».
Переформулировать и интегрировать	Интегралы показательных функций ; Задача с начальным значением	математический	Решатель задач исчисления от Dr.Х.Вайсбекер и соавт. 1984 г., стр. 461, № 652.
Лечи меня	Экспоненциальный рост и спад ; Период полураспада; Задача с начальным значением	Биологический	Адаптировано из Примера 1, стр. 197, найденного в Greenwell, R., & Ritchey, N. (nd). Исчисление для наук о жизни (второе изд.).
Каменное ускорение	Первичные производные ; Проблема начального значения; Положение, скорость и ускорение	Физический	Упражнение 44, стр. 311 в «J.Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Она ударила корову?	Задача с начальным значением ; Первообразная; неопределенный интеграл; Положение, скорость и ускорение	Физический	Задача 53, стр. 357 найдено в «S. Schreiber, K. Smith, and W. Getz. Calculus for the Life Sciences, 1st Edition, John Wiley & sons, 2014».
Динамика населения	Задача с начальным значением ; Первообразная; неопределенный интеграл; Основная теорема исчисления	Физический	Задача 10, страница 275 найдена на C.Нойхаузер, Исчисление для биологии и медицины, третье издание, Pearson 2011.
Загрузки на YouTube	Задача с начальным значением ; Первообразная; неопределенный интеграл; Бизнес-приложения	Общественные науки	Задача 52, стр. 483, найденная в Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Выручка DirecTV	Задача с начальным значением ; Первообразная; неопределенный интеграл; Бизнес-приложения	Общественные науки	Задача 56, страница 337 найдена в «R. Ларсон. Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017 г.».
Расходы на здравоохранение	Задача с начальным значением ; Неопределенный интеграл; Бизнес-приложения	Общественные науки	Задача 57, стр. 483, найдено в «Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Длина рыбы	Среднее значение функции и задача с начальным значением ; Первообразная; неопределенный интеграл; Основная теорема исчисления	Биологический	Задача 18, страница 400 найдена в «J.Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015 г.».
Выплата ипотечного кредита	Определенный интеграл ; Бизнес-приложения	Общественные науки	Задача 40, стр. 337, Исчисление и его приложения Гольдштейна, Лея, Асмара, Шнайдера. Эд 13 Пирсон.
Прибыль от iPhone	Определенный интеграл ; Бизнес-приложения	Общественные науки	Задача 59, стр. 525, найденная в Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Загрязненное озеро	Определенный интеграл	Физический	Задача 63, страница 408 найдена в «R.N. Гринвелл, Н.П. Ричи, М.Л. Лиал, Исчисление для наук о жизни, 2-е издание, Пирсон, 2015».
Поток форели	Определенный интеграл ; Интеграл функции абсолютного значения	Биологическое	Упражнение 9, стр. 418 найдено в «F.Адлер. Моделирование динамики жизни: исчисление и вероятность для ученых-биологов, 3-е издание, Brooks/Cole, Cengage Learning, 2013».
Общее пройденное расстояние	Определенный интеграл ; Интеграл функции абсолютного значения	Физический	Задача 46, стр. 360, Исчисление и его приложения Гольдштейна, Лея, Асмара, Шнайдера. Эд 13 Пирсон.
Насос для бассейна	Определенный интеграл ; Работа, совершаемая переменной силой	Физический	Задача 20, страница 373 найдена в «J.Стюарт. Исчисление, 6-е издание, Томсон Брукс/Коул, 2008 г.».
Поведение	Сумма Римана	математический	Адаптировано из упражнения 33, стр. 387, из «F. Адлер. Моделирование динамики жизни: исчисление и вероятность для ученых-биологов, 3-е издание, Brooks/Cole, Cengage Learning, 2013».
Формула сердечного выброса	Сумма Римана ; Вывод интегральной формулы	Биологический; математический	Адаптировано со страницы 403 в «J.Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Плотность растений	Применение определенных интегралов ; Сумма Римана; Плотность населения; Интегрирование по кольцу	Биологический; математический	Проблема 1. 7.7, страница 66 найдена в «G. Ледер. Математика для наук о жизни, 1-е издание, Спрингер, Нью-Йорк, 2010 г.».
Интегрировать эти файлы cookie	Определенный интеграл ; Теорема о среднем значении	Физический; математический	р.Ларсон, Р. Хостетлер, Б. Эдвардс, Исчисление: с аналитической геометрией, 6-е издание, Houghton Mifflin Company, 1998 г., проблема 61, стр. 284
Осадки	Теорема о среднем значении ; Теорема о среднем значении; Определенный интеграл	Физический; математический	Задача 21, стр. 350, найдено в «C. Neuhauser and M. Roper. Calculus for Biology and Medicine, 4th Edition, Prentice Hall, Pearson, 2018».
Средний остаток	Среднее значение функции ; Определенный интеграл; кусочно-определенная функция; Бизнес-приложение	Общественные науки	Задача 44, стр. 566, найденная в Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Выживание животных	Определенный интеграл ; Процент выживаемости; Прирост населения	Биологический	Задача 1, страница 404 найдена в «J. Стюарт, Т. Дэй, Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015.
Как эффективно управлять оборудованием	Основная теорема исчисления ; Амортизация и бизнес-приложения	Математический; Общественные науки	Исчисление Стюарта, 6-е издание, Томсон Брукс/Коул, 2008 г.Задача 67, стр. 323
Движение частиц	Основная теорема исчисления ; Определенный интеграл; Границы; Должность; Скорость; Ускорение	Физический; математический	Задача 23, страница 179 найдена в «D. Хьюз-Халлетт; А. Глисон; В. МакКаллум, Исчисление, одно- и многомерное, 6-е издание, Wiley & Sons, Inc.
Ил в озере	Интегрирование скорости изменения ; Определенный интеграл; Единицы	Физический	Задача 19, стр. 295 найдено в «Hughes-Hallett, Gleason, McCallum, et al.Исчисление, 6-е издание, John Wiley & Sons, Inc., 2013 г.».
Прирост населения	Интеграция путем замены ; Экспоненциальные первообразные	Биологическое	Гринвелл, Ричи и Лиал, Исчисление для наук о жизни (второе изд.), Задача 62, стр. 384
Оценка лотерейных выигрышей	Будущая стоимость; Аннуитет ; Определенный интеграл; Интеграция путем замены; интеграл экспоненциальных функций; Бизнес-приложения	Общественные науки	Задача 74, страница 385 найдена в R.Ларсон, Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017.
Высота кустарников	Интеграция путем замены ; Определенный интеграл; Бизнес-приложения	Общественные науки	Задача 57, стр. 330 найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Сбережения для колледжа	Будущая стоимость; Аннуитет ; Непрерывный поток доходов; Определенный интеграл; интеграл экспоненциальных функций; Бизнес-приложения	Общественные науки	Задача 48, страница 578, найденная у Ванера и Костенобля.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г. .
Фондовая биржа	Интеграция путем замены ; Среднее значение	Математический; Общественные науки	Гринвелл, Ричи и Лиал, Исчисление для наук о жизни (второе изд.), Задача 45, стр. 452
Утечка масла	Основная теорема исчисления ; Интеграция заменой	Физический	Задача 64, страница 408, найденная в Greenwell, R., & Ричи, Н. (nd). Исчисление для наук о жизни (второе изд. )
Место преступления	Экспоненциальный рост и спад ; закон охлаждения Ньютона; Задача с начальным значением (17 минут)	Биологический; Физический	Адаптировано из экспоненциального роста и распада. (н.д.). Получено 12 января 2016 г. с http://www.chaoticgolf.com/
Доход от калькуляторов	Интеграция по частям ; Бизнес-приложения	Математический; Общественные науки	Гринвелл, Ричи и Лиал, Исчисление для наук о жизни (второе изд.) Задача 56, стр. 445
Зарплата спортсмена	Интеграция по частям ; Приведенная стоимость; бизнес-приложения;	Общественные науки	Задача 77, страница 385 найдена в “R. Ларсон. Исчисление: прикладной подход, 10-е издание, Cengage Learning, 2017 г.».
Размер города	Интеграция по частям	Общественные науки	Роберт Уиллетт, Калифорнийский университет в Риверсайде.
Микробная экосистема рубца	Интеграция по частям	Биологический	Упражнение 34, стр. 367 найдено в «J. Стюарт и Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, 2015».
Энергия лампочки	Тригонометрический интеграл ; Определенный интеграл; Энергия; Сила; Напряжение; Сопротивление	Физический	Задача 76, страница 386 найдена в «J.Рогавски, К. Адамс. Исчисление: ранние трансцендентальные, 3-е издание, WH Freeman and Company, Macmillan, 2015».
Электрическое поле от заряженной проволоки	Интегрирование с помощью тригонометрической замены	Физический	Адаптировано из задачи 55, стр. 392, найденной в «J. Рогавски, К. Адамс. Calculus Early Transcendentals, 3-е издание, Macmillin, 2015».
Борьба с популяцией комаров	Интегрирование путем разложения на неполные дроби	Биологический	Адаптировано из: Задача 24, страница 371, найденная в «J. Стюарт, Т. Дэй. Биоисчисление: исчисление для наук о жизни, Cengage Learning, Бостон, 2015 г.».
Химические реакции	Интегрирование путем разложения на неполные дроби	Физический	Адаптировано из упражнения 50, стр. 580, найденного в «Исчислении Томаса, 11-е издание, Pearson Addison Wesley, 2004».
Слухи в школе	Интегрирование путем разложения на неполные дроби ; Определенный интеграл	Математический; Общественные науки	Задача 78, страница 386 найдена в «D.Хьюз-Халлетт; А. Глисон; В. МакКаллум. Исчисление, одно- и многомерное, 6-е издание, Wiley & Sons, Inc.”
Телефонная линия	Производная гиперболических функций	Физический	Задача 51, страница 260 найдена в «J. Стюарт. Исчисление: ранние трансцендентальные, 6-е издание, Thomson Learning Inc, 2008 г.».
Подвешивание кабеля	Интеграл гиперболических функций ; Длина дуги контактной сети	Физический	Адаптировано из задачи 64, стр. 323, найденной в «C.Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, 2011».
На орбиту	Неправильный интеграл ; Работа	Физический	Задачи 85, стр. 589 найдены в “R. Ларсон и Б. Эдвардс. Calculus, 9-е издание, Brooks/Cole, Cengage Learning, 2010».
Распространение гриппа, часть 2	Неправильный интеграл ; Интеграция по частям	Биологический	Задача 43, стр. 402 найдено в «Hughes-Hallett, Gleason, McCallum, et al.Исчисление: одно и многомерное, 6-е издание, John Wiley and Sons, Inc., Массачусетс, 2013 г.».
Реакция на наркотики	Неправильный интеграл ; Интеграция по частям	Биологический	Задача 44, стр. 457 найдено в R.N. Гринвелл, Н.П. Ричи, М.Л. Лиал, Исчисление для наук о жизни, Пирсон, 2-е издание.
Емкость конденсатора	Неправильный интеграл ;	Физический	Адаптировано из задачи 83, стр. 423 в Rogawski, Jon and Colin Adams, Calculus: Early Transcendentals; 3-е изд., WH Freeman, Нью-Йорк, 2015. .
Закон излучения Планка	Несобственные интегралы и тест сравнения ; лимиты; Конвергенция; Дивергенция	Физический; математический	Адаптировано из: Задача 30, стр. 407 из «Hughes-Hallett, Gleason, McCallum, et al. Исчисление, 6-е издание, John Wiley & Sons, Inc., 2013 г.».
Сотовый ответ	Несобственные интегралы и тест сравнения ; Конвергенция; Дивергенция	Биологический; математический	Задача 47, страница 398 найдена в «C.Нойхаузер и М. Роупер. Исчисление для биологии и медицины, 4-е издание, Prentice Hall, Pearson, 2018».
Излишки потребителей и производителей	Область между двумя кривыми ; Приложения определенных интегралов; Бизнес-приложения	Общественные науки	Задача 57, стр. 359, найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Сбережения	Область между кривыми ; Предельные затраты и сбережения	Математический; Общественные науки	Задача 37, страница 418, найденная в Greenwell, R., & Ричи, Н. (nd). Исчисление для наук о жизни (второе изд.).
Стоимость топлива	Область между двумя кривыми ; Бизнес-приложения	Математический; Общественные науки	Задача 51, стр. 358 найдено в «Исчислении: прикладной подход», 10-е издание, Ларсон Р. , Cengage Learning, Бостон, 2015.
Y Область между кривыми	Область между кривыми ; Интеграл от x = f(y)	математический	Томас, Исчисление, 11-е издание, Pearson Education, 2005 г., стр. 416, задача 35
Площадь кругового сектора	Область под кривой ; Интегрирование с помощью тригонометрической замены	математический	Задача 35 стр. 509 в «J.Стюарт. Исчисление одной переменной, 6-е издание, Томпсон Брукс/Коул, Белмонт, Калифорния, 2008 г.».
Солнечное затмение	Область между кривыми ; Площадь Луны	Физический; математический	Задача 41, страница 509 найдена в «J. Стюарт. Исчисление одной переменной, 6-е издание, Томпсон Брукс/Коул, Белмонт, 2008 г.».
Озеро Мид	Объем по поперечному сечению ; Объем нарезки; Определенный интеграл	Физический; математический	Задача 36, страница 421 найдена в «D. Хьюз-Халлетт; А. Глисон; В. МакКаллум. Исчисление, одно- и многомерное, 6-е издание, Wiley & Sons, Inc., 2013 г.»
Бейсбольный мяч в чаше для пунша	Объем по площади поперечного сечения	Физический	Задача 68, страница 364 найдена в «J. Стюарт. Исчисление, 6-е издание, Брукс/Коул, Белмонт, Калифорния, 2008 г.».
Чаша с водой	Тома революции ; Дисковый метод; Основная теорема исчисления; Цепное правило	Физический	Задача 59, страница 430 найдена в «D.Хьюз-Халлетт; А. Глисон; В. МакКаллум. Исчисление, одно- и многомерное, 6-е издание, Wiley & Sons, Inc.”
Тост за город	Тома революции ; Метод шайбы	Физический; математический	Джон Симаньи, Калифорнийский университет в Риверсайде.
Опорожнение радиотелескопа	Объем по методу Шелла ; Цилиндры Революции	Физический	Джон Симаньи, Калифорнийский университет в Риверсайде.
Кольца для салфеток	Объем по цилиндрическим оболочкам	Физический	Задача 46, страница 437 найдена в «J. Стюарт. Исчисление: ранние трансцендентальные, 6-е издание, Thomson Learning Inc, 2008 г.».
Площадь спутниковой антенны	Площадь поверхности тела вращения	Математический; Физический	Задача 28 стр. 574 в «J. Стюарт. Исчисление одной переменной, 6-е издание, Томпсон Брукс/Коул, Белмонт, Калифорния, 2008 г.
Самый большой в мире пончик	Площадь поверхности тора ; Интегрирование с помощью тригонометрической замены	Математический; Физический	Роберт Уиллетт, Калифорнийский университет в Риверсайде.
Определение длины рыбы	Разделимое дифференциальное уравнение ; Уравнение фон Берталанфи; асимптотическая длина; Лимит на бесконечности	Биологический	Задача 23, страница 404 найдена в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Pearson Education, Inc.
Популяция рыб	Разделимое дифференциальное уравнение ; Равновесие; Стабильность; Логистический рост; Популяция рыб	Биологический	Задача 9, страница 418 найдена в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Pearson Education, Inc.
Инсулиновая помпа	Разделимое дифференциальное уравнение ; Интеграция путем замены; Начальное состояние; Лимит на бесконечности	Биологический	Задача 26, страница 439 найдена в C.Нойхаузер и М. Роупер. Исчисление для биологии и медицины, 4-е издание, Prentice Hall, Pearson, 2018.
Эффект Allee	Равновесие и стабильность ; метод собственных значений; Графический метод; Дифференциальные уравнения	Биологический	Задача 24, страница 420 найдена в «C. Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Prentice Hall, Pearson, 2011».
Модель с одним отсеком	Однокамерная модель ; Разделимые дифференциальные уравнения; Равновесие; Стабильность; Изменение концентрации	Физический	Задача 13, страница 419 найдена в «C.Нойхаузер. Исчисление для биологии и медицины, 3-е издание, Pearson Education, Inc.
Предельная полезность	Частные производные ; предельная полезность; Бизнес-приложение	Общественные науки	Задача 73, стр. 454 найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Расходы на жилье	Частные производные ; предельная стоимость; Бизнес-приложение	Общественные науки	Задача 66, страница 635 найдена у Ванера и Костенобля.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Стоимость автомобилей	Экстремумы функций двух переменных ; Частные производные; Бизнес-приложение	Общественные науки	Задача 49, стр. 463 найдено в R. Larson, Calculus: An Applied Approach, 10-е издание, Cengage Learning, 2017.
Борьба с загрязнением	Экстремумы функций двух переменных ; Частные производные; Бизнес-приложение	Общественные науки	Задача 43, стр. 644, найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».
Ограждения	Множитель Лагранжа ; Частные производные; Бизнес-приложение	Общественные науки	Задача 21, стр. 653, найденная в Waner and Costenoble. Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.
Увеличение доходов от фильмов	Множитель Лагранжа ; Частные производные; Бизнес-приложение	Общественные науки	Задача 23, стр. 653 найдено в «Waner and Costenoble.Прикладное исчисление, 7-е издание, Cengage Learning, Бостон, 2016 г.».

Самостоятельное обучение: как это делает один учитель

Послушайте мое интервью с Натали Маккатчен (стенограмма)

Могу поспорить, что, за некоторыми исключениями, большинство учителей считают, что они могли бы лучше справляться с дифференцированным обучением. Дело не в том, что мы не хотим, чтобы делал это — мы знаем, что наши ученики учатся с разной скоростью, что некоторым нужна дополнительная помощь, а другие могут двигаться гораздо быстрее, чем мы им позволяем.Проблема многих из нас в том, что мы просто не можем понять, как с этим справиться. Как организовать класс, в котором каждый ученик работает над разными задачами с разной скоростью?

Впервые я увидел по-настоящему самостоятельную учебную среду во время посещения начальной школы Монтессори два года назад. И хотя я был полностью очарован студенческой средой, размер класса был маленьким. Я задавался вопросом, действительно ли этот метод может быть применен к размерам классов в обычной государственной школе.

Так что я был взволнован, когда на недавней встрече TeachMeet я увидел, что будет сессия по самостоятельному обучению. На сессии Франклин, штат Кентукки, учитель математики средней школы Натали Маккатчен показала нам, как она превратила свой урок алгебры в полностью самостоятельную систему, где учащиеся работают над различными навыками в своем собственном темпе, и как она постепенно знакомится с собой. — темп обучения в других ее математических классах, а также. Я обнаружил, что ее система удивительно проста, и я подумал, что многие другие учителя захотят попробовать ее на себе, поэтому я взял у нее интервью для моего последнего выпуска подкаста (см. проигрыватель ниже) и спросил, могу ли я поделиться ее методами здесь.

Натали Маккатчен

Вот краткое описание того, как она это делает: для каждой главы своего учебника по математике учащиеся проходят предварительный тест, чтобы определить, какими навыками они уже овладели, а какие им еще предстоит освоить. Что касается навыков, которые им еще нужно освоить, они работают самостоятельно на уроках (либо читают их в учебнике, либо смотрят на видео) и решают задачи до тех пор, пока не почувствуют, что овладели навыком. Это настоящая часть для самостоятельного изучения: Учащиеся сами решают, сколько уроков им нужно.Они сами решают, сколько практики давать. «Может быть, есть пять видео, которые вы могли бы посмотреть сегодня», — объясняет Натали своим ученикам. «Вы смотрите столько, сколько вам нужно. Если вы посмотрели два видео и поняли это, то переходите к практике. Если вам нужны все пять, используйте все пять». Вместо того, чтобы заставлять учащихся идти по одному и тому же пути в ногу друг с другом, отрабатывая страницу за страницей навыки, которые у них уже есть, эта система дает им возможность нарастить метакогнитивные мышцы, которые им понадобятся, чтобы учиться всю жизнь.

Когда учащийся чувствует, что готов, он проходит мини-тестирование по одной цели обучения, обычно состоящее всего из нескольких вопросов. Если он хорошо справляется с этой небольшой оценкой, он может перейти к другому навыку. После того, как он овладел всеми навыками, описанными в этой главе, он сдает экзамен по всей главе — это тот же тест, который ему давали в качестве предварительной оценки. Если он преуспеет в этом, он готов перейти к следующей главе.

Как учащиеся узнают, над какими уроками и практиками нужно работать и когда?
Натали создает руководство для каждой главы.Он включает в себя каждую цель обучения, вопрос или вопросы предварительного теста, которые соответствуют этой цели, уроки, которые учащиеся должны посмотреть или прочитать, чтобы узнать об этой цели, практические задачи, которые соответствуют этой цели, и вопрос или вопросы для оценивания для этой цели. цель.

Посмотрите на пример ниже. Если этот учащийся пропустил вопрос 2 в предварительном тесте, ему следует выполнить Урок 2.4 на страницах 102–104 и, возможно, потребуется пройти Практические занятия 2.4 на страницах 403–406 в рамках подготовки к оценке этой учебной цели, которая является пунктом 2a на стр. 38.Ей может понадобиться только прочитать урок и решить одну или две практические задачи, чтобы хорошо сдать экзамен, или она может решить выполнить их все. Точно так же, если она правильно ответила на вопрос 6 на предварительном тесте, ей вообще не нужно проводить урок, практику или оценку для этой учебной цели — она просто отметит это как освоенное в таблице.

Получают ли учащиеся ключи ответов?
Студенты имеют доступ к ответам на все практические вопросы, поэтому Натали не нужно их проверять; Ученик должен решать практические задачи, а затем самостоятельно проверять их, чтобы увидеть, снижают ли они навык.Здесь нет реального стимула для списывания, потому что, если учащийся не освоит навык, он отразится в мини-оценке по этой цели: мини-оценка оценивается учителем, а учащиеся не получают ответа. ключ для него.

Как выглядит время занятий?
«Это очень организованный хаос», — говорит Натали. «Они хранят руководство по главам в тетради для сочинения. Приклеиваем туда все их элементы. Таким образом, они каждый день держат это на своем столе, и я могу пройти и сказать Хорошо, что ты сделал? Где вы сегодня? И в конце урока я могу сказать: Как много ты сделал?» Поскольку все учащиеся работают независимо друг от друга, объем работы, выполняемой в любой день, может варьироваться.«Некоторые дети могут сдать две оценки за урок, в зависимости от того, насколько усердно они работали. Некоторые дети могут превратиться в одного. Некоторые дети, возможно, не попали на оценку в тот день». А поскольку Натали поощряет сотрудничество между учениками, комната занята: «Я действительно предпочитаю, чтобы они работали вместе над уроком, особенно с моими учениками, изучающими алгебру, потому что они такие хорошие математические мыслители, они понимают математику и могут говорить, Я хочу, чтобы они работали вместе. Вы знаете, двое или трое в группе смотрят, сможете ли вы понять это самостоятельно, используя видео.

Что делать, если некоторые дети не могут справиться со всей этой независимостью? Что, если они будут просто дурачиться все время?
Решение Натали этой проблемы было тем, что меня действительно впечатлило в ее системе: Не все учащиеся могут самостоятельно выполнять ; некоторым приходится работать с ней в более традиционной обстановке под руководством учителя. Самостоятельное обучение — это привилегия, предназначенная только для детей, которые относятся к этому серьезно и усердно работают. Если вы ошибетесь, вы можете потерять эту привилегию и вернуться в группу, которая работает напрямую с учителем.«Иногда им приходится возвращаться в стаю, — объясняет она. «Я скажу Знаешь что, вчера ты действительно не так много работал. Я даже не уверен, что вы сделали, я ничего не вижу здесь. Просто возвращайся с нами сегодня. ” Для некоторых учеников это шаг назад, но позже у них появляются другие шансы продвинуться вперед. «Им нравится быть впереди. Знаешь, они думают, что это круто. Иногда я позволяю им выйти в коридор, посидеть за столиком. Им это нравится, но я подчеркиваю, что вам все равно придется работать.

Натали Маккатчен разработала свою систему методом проб и ошибок, и она постоянно совершенствует ее, так что ничего из этого не высечено на камне. Но если вы хотите попробовать повторить ее подход к самостоятельному обучению, вот шаги, которые нужно предпринять:

Шаг 1. Выберите единицу содержания
Это может быть глава учебника или группа навыков или содержания, которым вы обычно обучаете как единое целое в течение нескольких недель. Этот блок должен иметь четко определенные цели обучения, которые, вероятно, продиктованы стандартами, которым следует ваша школа.Если вы уже некоторое время преподаете, вы, вероятно, уже позаботились об этом шаге. В классе Натали каждая глава в ее учебнике по математике представляет собой одну единицу.

Шаг 2. Создание оценки
Решите, что учащиеся должны уметь делать к концу модуля, и создайте оценку, которая это измеряет. Самый простой тип — это тест с четко определенными правильными и неправильными ответами, где каждый элемент (или небольшая группа элементов) в этом оценивании соответствует одной цели обучения.Для навыков, требующих дополнительной интерпретации учителем, таких как письмо, оценивание может быть письменным заданием, таким как вопрос с расширенным ответом с подсказкой и критерием оценки. Каждый навык, указанный в рубрике, соответствует определенной цели обучения.

Шаг 3: Создайте руководство по главам
Следуя модели, показанной выше, настройте руководство, которое показывает, какой вопрос оценивания соответствует каждой цели обучения, а затем перечисляет книги или видеоуроки, которым учащиеся могут следовать, чтобы освоить каждый навык, упражнения, которые дадут учащиеся самостоятельно отрабатывают навыки, а учащиеся могут пройти краткую оценку, чтобы проверить свое мастерство.

Шаг 4. Проведите предварительный тест
Используйте оценку, созданную на шаге 2, для предварительного тестирования навыков учащихся по этому разделу. Используйте результаты, чтобы определить, какие цели обучения уже освоил каждый учащийся, а какие им еще предстоит освоить. [Примечание: в школе Натали используются оценки на основе стандартов, но это не является строгим требованием для этой системы. Вы по-прежнему можете фиксировать выполнение целей обучения в стиле, основанном на стандартах, и преобразовывать эти измерения в традиционные оценки. Чтобы узнать, как это сделать, посмотрите видео Мэтта Таунсли о преобразовании индикаторов, основанных на стандартах, в буквенные оценки.]

Шаг 5: Помогите учащимся определить стандарты для освоения
Раздайте каждому учащемуся руководство по главам, попросите его отметить, какие стандарты они уже освоили (на основе результатов предварительного тестирования), а какие им еще предстоит изучить.

Шаг 6: Предоставление времени, материалов и контроля для самостоятельного обучения
С этого момента учащиеся начнут процесс прохождения уроков самостоятельно.Ваша задача — убедиться, что у них есть материалы, необходимые для работы: если вы отправляете учащихся на просмотр видео, убедитесь, что у них есть устройства для доступа к ним (и наушники, чтобы сохранить звук при себе). Убедитесь, что учащиеся знают, где искать ключи для ответов и где они могут получить доступ к мини-тесту, когда будут готовы его выполнить. Регулярно связывайтесь со студентами, чтобы убедиться, что они правильно используют свое время.

Шаг 7: Итерация
Имейте в виду, что эта система, вероятно, не будет работать идеально с первого раза.Вы можете попробовать это только один раз с коротким разделом, а не пытаться перевести весь год на самостоятельное обучение. Возможно, вы захотите предложить его только тем студентам, у которых есть академические навыки и зрелость, чтобы справиться с этим. Возможно, вам придется настроить его, а затем настроить еще немного. Но говоря от имени детей, которые хотели бы увидеть, как быстро они могут учиться и как далеко они могут зайти, я бы сказал, что стоит серьезно попробовать. ♦

Другие ресурсы:

Это еще не все.
Присоединяйтесь к моему списку рассылки и получайте еженедельные советы, инструменты и вдохновение — в быстрых, небольших упаковках — и все это поможет сделать ваше обучение более эффективным и увлекательным. В благодарность я вышлю вам бесплатную копию моего электронного буклета 20 способов сократить время на получение оценок вдвое .

Я с нетерпением жду возможности познакомиться с вами поближе!

Размещено в:

Категории: Классное руководство, Инструкция, Подкаст

Теги: оценка, дифференциация, одаренное образование, 3-5 классы, 6-8 классы, 9-12 классы, математика, обучение с использованием технологий, тайм-менеджмент

Энтропия, сложность и зрелость нейронных реакций детей во время естественного обучения математике

Реферат

Основная цель нейронауки человека состоит в том, чтобы понять, как мозг функционирует в реальном мире, и измерить нейронные процессы в естественных условиях, которые более экологичны. эффективнее, чем традиционные лабораторные задачи.Важным шагом на пути к этой цели является понимание того, как нейронная активность во время реальных натуралистических задач связана с нейронной активностью в более традиционных лабораторных задачах. В настоящем исследовании мы использовали межпредметные корреляции, чтобы обнаружить надежные нейронные процессы, управляемые стимулом, у детей и взрослых в натуралистической и лабораторной версиях математической задачи, которые имели одинаковое содержание. Мы показываем, что по сравнению с контрольным условием с грамматическим содержанием, натуралистические и упрощенные математические задачи вызывали перекрывающуюся активацию в областях мозга, ранее связанных с математической семантикой.Далее мы исследовали временные свойства нейронных реакций детей во время выполнения естественных и лабораторных задач, чтобы определить, изменяются ли временные паттерны нейронной активности в процессе развития или диссоциируют в зависимости от семантики или содержания задачи. Мы вводим довольно новую меру, еще не использовавшуюся в исследованиях детского обучения с помощью фМРТ: нейронную многомасштабную энтропию. В дополнение к демонстрации новых доказательств естественной математической обработки в развивающемся мозге мы показываем, что нейронная зрелость и нейронная энтропия являются двумя независимыми, но дополняющими друг друга маркерами функционального развития мозга.Мы обсуждаем последствия этих результатов для развития нейронной сложности у детей.

Введение

Дети обычно учатся на обучающих рассказах, в которых новая информация строится на основе прошлой информации в течение нескольких секунд или минут. Напротив, в типичных лабораторных задачах изолированные стимулы повторяются с интервалами от миллисекунд до секунд. Повторяющиеся, быстро развивающиеся, контролируемые парадигмы важны для создания чистых противопоставлений проверочным гипотезам, но в них могут упускаться важные аспекты контекста или непрерывности, которые имеют решающее значение для детских вычислений (Cantlon, 2020).Более того, естественный темп обучения часто отсутствует в традиционных парадигмах нейровизуализации. Исследования ЭЭГ и фМРТ обычно анализируют нервные сигналы с интервалами от миллисекунд до нескольких секунд. Медленные колебания нейронных сигналов часто считаются искусственным шумом и нейтрализуются. Этот подход игнорирует нейронные процессы, которые со временем накапливают знания, значения или информацию (Hasson et al., 2015). В этом смысле чрезмерно упрощенные парадигмы нейровизуализации могут нейтрализовать, игнорировать или удалять нейронные процессы, которые имеют решающее значение для человеческого познания и развития. Альтернативный подход заключается в использовании натуралистических задач, в которых информация постепенно раскрывается в образовательных нарративах, и изучении временных колебаний нейронных сигналов во временных масштабах.

В недавних исследованиях нейровизуализации детей тестировали с помощью натуралистичных обучающих видеороликов для измерения сходства между нервными процессами у детей и взрослых (Cantlon and Li, 2013; Emerson and Cantlon, 2015; Kersey et al., 2019; Lerner et al., 2019; Ричардсон и др., 2018). В этих исследованиях используются меры межсубъектной корреляции для количественной оценки сходства нейронных временных ходов между детьми и взрослыми.При межсубъектной корреляции нейронный ход времени в каждом вокселе проверяется на временную корреляцию между субъектами. Значительная корреляция в нейронных реакциях между субъектами указывает на наличие надежного нейронного процесса, управляемого стимулом, в этой области мозга. Эти исследования установили, что натуралистические парадигмы вызывают паттерны нейронной активации, которые связываются или диссоциируют в зависимости от функции и возраста предсказуемым и надежным образом. Например, Кантлон и Ли (2013) показали, что 4-летние дети демонстрировали временную корреляцию в интратеменной коре, когда они смотрели видео «Улицы Сезам», связанные с числами, в то время как видео, связанные с буквами, вызывали коррелированные нейронные реакции в области Брока.Кроме того, нейронное сходство детей со взрослыми в теменной коре предсказывало их результаты в математических тестах, в то время как их нейронное сходство со взрослыми в области Брока предсказывало их результаты в вербальных тестах. Керси и др. (2019) подтвердили функциональную диссоциацию между естественной зрительной активностью, связанной с математикой и чтением, и продемонстрировали, что области, связанные как с математикой, так и с чтением, демонстрируют незрелые нейронные паттерны у детей в возрасте от 4 до 8 лет. Однако в предыдущих натуралистических исследованиях детей было неясно, как нейронная активность во время натуралистических задач похожа или отличается от активности в более традиционных упрощенных задачах, потому что они не сравнивались напрямую. Этот вопрос важен при изучении развития ребенка, потому что, как упоминалось ранее, критические характеристики темпа и контекста обучения могут быть уникальными для натуралистических задач (Cantlon, 2020).

Здесь мы сравниваем натуралистическую и упрощенную версии задачи по математике, которые имеют общее содержание. В натуралистическом задании учитель объясняет формальные арифметические принципы в учебном повествовании, тогда как в упрощенном задании принципы исследуются в традиционном двухальтернативном задании с принудительным выбором.Основной прогноз заключается в том, что натуралистическая и упрощенная версии арифметических задач должны вызывать перекрывающуюся активацию в областях мозга, которые обрабатывают общее семантическое содержание задач, по сравнению с натуралистическим условием контроля, проверяющим нематематическое содержание (урок грамматики). После проверки этой гипотезы мы изучаем новые методы сравнения временных характеристик натуралистических и упрощенных задач и исследуем нейронные различия в этих процессах. Одним из показателей, который не использовался для изучения развития мозга и который мог бы быть полезен при изучении обучения детей, является временная энтропия нейронного сигнала (Vanderwal et al., 2019). Энтропия классически описывает степень организации временного ряда. Другими словами, он обеспечивает меру сложности базовой структуры временного ряда и оценивает степень его непредсказуемости. Например, рассмотрим одну серию с чередующимися 0 и 1 и другую серию со значениями 0 или 1, выбранными случайным образом с вероятностью . Эти два ряда имеют одинаковое среднее значение и дисперсию, но их энтропия сильно различается. В первом каждое значение может быть предсказано только на основе предыдущего, поэтому ряд очень регулярен и имеет низкую энтропию.Наоборот, значения второго ряда непредсказуемы, что приводит к высокой энтропии. Теперь рассмотрим серию, состоящую из повторяющегося шаблона, состоящего из нулей и единиц (например, [0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 1 0 1 …]). Каждое значение в этом примере повторяется после 7 вхождений, поэтому этот ряд имеет определенную степень структуры, которая делает его несколько регулярным. Его энтропия находится между энтропией двух временных рядов выше.

Колмогоровская сложность является точной мерой этой степени организации (Grunwald and Vitányi, 2004).Однако для физиологических данных, которые содержат лишь умеренное количество временных точек, их можно только приблизить. Было разработано несколько приблизительных мер колмогоровской сложности, таких как выборочная энтропия (SampEn) (Richman and Moorman, 2000). В последние десятилетия он был объединен с методом многомасштабной энтропии (MSE) для анализа сложности биологических сигналов (Costa et al., 2005, 2002). Этот метод впервые был применен ко многим типам биологических сигналов, таких как походка человека (М.Costa et al., 2003) или частоты сердечных сокращений (Norris et al., 2008), а также к электрофизиологическим данным (Heisz and McIntosh, 2013). Оценка многомасштабной энтропии сигналов ЭЭГ оказалась особенно полезной для характеристики тяжести болезни Альцгеймера (Azami et al., 2017; Escudero et al., 2006; Nobukawa et al. , 2019; Park et al., 2007; Yang et al., 2013b), или риск расстройства аутистического спектра (Bosl et al., 2011; Catarino et al., 2011), но и как маркер стресса (Ahammed and Ahmed, 2020) или как показатель автоматизации когнитивных процессов (Grundy et al., 2017; Wang et al., 2019)

Несмотря на то, что в литературе имеется множество примеров применения оценки многомасштабной энтропии сигналов ЭЭГ, она лишь недавно была распространена на литературу по фМРТ. В этом методе выборочная энтропия ЖИРНОГО сигнала оценивается в различных временных масштабах в каждом вокселе мозга. По шкале 1 оценивается выборочная энтропия полного ЖИРНОГО сигнала. В данном вокселе, если ЖИРНЫЙ сигнал следует обычному простому образцу, значение энтропии этого вокселя низкое, тогда как оно выше, если ЖИРНЫЙ сигнал следует регулярному, но сложному образцу, и даже выше, если ЖИРНЫЙ сигнал изменяется непредсказуемо во времени. .В других масштабах оценивается выборочная энтропия крупнозернистых сигналов. Например, каждая точка данных «временного ряда масштаба 10» рассчитывается как среднее значение 10 последовательных и неперекрывающихся точек данных исходного ряда, так что длина «временного ряда масштаба 10» составляет одну десятую длины. исходной серии (см. рис. 1). Таким образом, метод многомасштабной энтропии выявляет динамические свойства ЖИРНОГО сигнала в широком диапазоне временных масштабов.

Хотя энтропия считается беспорядком в термодинамике (Boltzmann, 1964), некоторые данные указывают на то, что увеличение энтропии при обработке информации и передаче нейронных сигналов отражает продвинутую обработку.Например, нейронная энтропия положительно коррелирует с результатами тестов интеллекта у взрослых (Saxe et al., 2018; Yang et al., 2013a). Таким образом, с одной стороны, энтропия считается маркером беспорядка и случайности в материальных науках. С другой стороны, энтропия интерпретируется не как беспорядок, а как богатство когнитивных и нейронных процессов. Здесь мы сравниваем энтропию во времени в нейронных сигналах, генерируемых детьми и взрослыми во время естественных и контролируемых задач обучения. Если нейронная энтропия отражает интеграцию информации с течением времени, то энтропия должна быть больше в условиях естественного обучения по сравнению с контролируемой задачей в течение более длительного периода времени. Более того, если энтропия является мерой продвинутой нейронной обработки, то энтропия должна увеличиваться по мере развития.

Рисунок 1: Мультимасштабная энтропия.

Верх : В каждом вокселе мозга определение мультимасштабной энтропии для периодического ЖИРНОГО сигнала (слева) и случайного ЖИРНОГО сигнала (справа). Каждая точка данных сигнала масштаба n создается путем усреднения n последовательных непересекающихся точек данных исходного временного ряда, что приводит к временному ряду длины L/n, для которого рассчитывается энтропия выборки.Значения энтропии в случае случайного сигнала выше, чем в случае периодического сигнала. Внизу : Увеличенная иллюстрация метода расчета выборочной энтропии: сначала оцените количество повторений каждого шаблона длины два во временном ряду в пределах заданного диапазона допустимых значений. В этом примере паттерн «красный-желтый» повторяется 9 раз, паттерн «желто-синий» повторяется 8 раз, паттерн «сине-синий» повторяется 7 раз и паттерн «сине-красный» повторяется 4 раза, для всего 28. Затем оцените количество повторений каждого шаблона длины три во временном ряду в пределах одного и того же диапазона допустимых значений. Здесь шаблон «красный-желтый-синий» повторяется 6 раз, шаблон «желтый-синий-синий» повторяется 7 раз, а шаблон «синий-синий-красный» повторяется 4 раза, всего 17 раз. отрицательное логарифмическое отношение этих двух чисел: −log(17/28) = 0,217.

Результаты

Метод

32 участника (14 взрослых и 18 детей третьего класса) были просканированы во время фМРТ при выполнении двухальтернативного математического задания с принудительным выбором, урока естественной математики и урока естественной грамматики.И контролируемая математическая задача, и видеоурок по натуралистической математике имели одинаковое математическое содержание. Задание с принудительным выбором напрямую проверяло понимание участниками коммутативного принципа умножения. В каждом испытании им давали несколько секунд, чтобы решить, были ли две символические операции или два массива точек, включая коммутативные пары (например, «2 × 3» или «3 × 2», полный список стимулов см. в Таблице S1). численно равны или нет (верхний ряд рис. 2). Математическое видео было уроком, описывающим и объясняющим коммутативный принцип умножения.В то время как контролируемая математическая задача и математическое видео имели общий контент о коммутативном принципе, видео по грамматике и математическое видео, напротив, имели общие поверхностные черты натуралистического образовательного урока. Содержанием урока грамматики был принцип соединения относительных местоимений в словосочетания. Видеоматериалы по математике и грамматике были разработаны так, чтобы максимально соответствовать реальному школьному уроку, представляя формальную информацию в виде повествования о построении. На обоих уроках один и тот же виртуальный учитель объяснял либо математическое, либо грамматическое правило в трех 80-секундных видеопоследовательностях, что позволяло естественным образом переходить на уроке от простого примера к более сложному примеру, к общему определению и применению принципа.

Рисунок 2: Протокол.

Top : Хронология пробной математической задачи с двумя альтернативами и принудительным выбором. Участникам давали 4 секунды, чтобы решить, были ли результаты двух простых операций или количество точек в двух разных наборах одинаковыми или разными. Средняя и нижняя : Хронология презентации обучающих видео по арифметике и грамматике, а также репрезентативные кадры, извлеченные из каждой из трех последовательностей, составляющих видео.

Поведенческие результаты в контролируемом одинаковом/различном математическом задании

Дети правильно ответили 89.0 ±1,84% испытаний. Точность детей существенно не отличалась от точности взрослых (92,4 ± 2,69%, t(30) = 1,11, p = 0,275), хотя в целом они отвечали медленнее, чем взрослые (дети: 1,97 ± 0,077 с; взрослые: 1,08 ± 0,108 с; t(30) = 7,03, p < 0,001). Дети не ответили на 13,7% испытаний, в то время как взрослые пропустили только 1,98% испытаний. При подсчете пропущенных испытаний как ошибок дети достигли общей точности 76,9 ± 2,43%, что значительно ниже, чем у взрослых (90,8 ± 2,43%). 98%, t(30) = 3,58, p < 0,002). Независимо от того, учитывались ли пропущенные испытания или нет, дети показали значительно лучшие результаты, чем случайность, для каждого состояния (символические/несимволические × 3 категории пар; все ps < 0,05), как и взрослые (все ps < 0,001).

Результаты фМРТ

Задания по математике и грамматике вызывают диссоциативные нейронные реакции при естественном обучении

Сначала мы искали мозговую активность, демонстрирующую более высокие межпредметные корреляции (ISC) во время просмотра арифметического видеоурока, чем во время просмотра грамматического.Как для детей, так и для взрослых полученная карта выявила обширную коррелированную активность в теменных областях и в правой нижней лобной извилине (левые панели рисунка 3). У взрослых дополнительная коррелированная активность была обнаружена в двусторонних задних нижних височных извилинах (средняя левая панель рисунка 3). Мы отмечаем, что у детей видео с арифметикой вызывало более коррелированную активность, чем видео с грамматикой, в областях, очень похожих на взрослых, в основном в правой внутритеменной борозде и правой нижней части лобной извилины, оперкулярной мышце (нижняя левая панель рисунка 3).

Рисунок 3: Коррелированная активация во время естественных и контролируемых задач показывает как модальные, так и содержательные предпочтения.

Слева: Сравнение межпредметных корреляций для арифметических (синий) и грамматических (красный) учебных видео (вверху) среди взрослых, (в центре) среди детей и (внизу) между детьми и взрослыми. Справа : Карты, показывающие значимые корреляции нейронного хода времени во время каждой задачи и их соответствующие перекрытия. В частности, красные, темно-синие и темно-зеленые кластеры показывают коррелированную активацию, соответственно связанную с каждой из наших трех задач.Голубые кластеры представляют коррелированную активацию, общую для обеих математических задач, а розовые кластеры представляют коррелированную активацию, общую для просмотра обоих обучающих видео. Наконец, светло-зеленые кластеры определяют области мозга, демонстрирующие значительно коррелированную активацию для всех трех задач вместе. Все карты отображаются при p <0,001 по вокселям и FDR p <0,05 по кластерам.

Противопоставление видеоуроков по грамматике и грамматике привело к межпредметным корреляциям в нижней лобной области как у детей, так и у взрослых (левые панели рис. 3).У взрослых такие скопления в основном располагались слева в нижней лобной извилине, в треугольной и орбитальной частях нижней лобной извилины. Однако дети проявляли более двустороннюю связанную с грамматикой активность в средних лобных извилинах и в височно-теменном соединении (обратите внимание, что эта разница в латерализации между детьми и взрослыми была подтверждена чувствительным анализом области интереса одного субъекта (ROI), подробно описанным в Дополнительные материалы).

Естествознательное математическое обучение и контролируемое математическое задание демонстрируют перекрывающиеся нейронные реакции в теменной коре

Затем мы сравнили межпредметные корреляции нейронных ответов, вызванных контролируемым арифметическим заданием, с таковыми из видеоурока по натуралистической арифметике. Мы наблюдали заметное перекрытие коррелированной активности для обеих математических задач в билатеральной теменной коре и правой нижней лобной извилине (правые панели рисунка 3) как у детей, так и у взрослых, а также в билатеральной задней нижней височной извилине у взрослых. Основные различия в активации между задачами заключались в моторной коре для контролируемой математической задачи (участники отвечали нажатием кнопок) и активности вдоль верхней височной борозды для видеоурока по натуралистической арифметике, заметно перекрывая нейронные реакции во время видеоурока по грамматике, поскольку оба видео включали разговорный язык (см. Дополнительные материалы для полного описания регионов, демонстрирующих совпадение между нашими тремя задачами).

Чтобы количественно оценить пространственное перекрытие нейронных ответов, вызванных как естественными, так и контролируемыми математическими задачами, мы провели чувствительный анализ репрезентативного сходства одного субъекта в пяти основных математических областях интереса (двусторонняя IPS, двусторонняя pITG и правая IFG Oper). . Для каждого субъекта по всем вокселям наших ROI мы рассчитали коэффициенты корреляции между значениями ISC, наблюдаемыми во время каждого педагогического видео, а также во время математической задачи с принудительным выбором. Затем мы сравнили корреляцию значений ISC, соответствующих двум математическим задачам, с корреляцией значений ISC, соответствующих двум видео (парные t-тесты).У детей и взрослых межпредметные корреляции в левом и правом ВПС были более пространственно коррелированы между натуралистическим арифметическим видео и контролируемым арифметическим заданием, чем между натуралистическим арифметическим видео и грамматическим видео (ts(31) > 4,08, ps < 2,10-4; прим. что для достижения значимости после поправки Бонферрони для множественных сравнений в 5 ROI значение p должно быть меньше 0,01; также обратите внимание, что этот результат был верен для детей и взрослых отдельно, все ps < 0,006).Меньшая, но тем не менее значимая разница была также обнаружена в правом pITG (t(31) = 2,78, ps = 0,0047).

Естественные задачи вызывают большую энтропию, чем контролируемые задачи, особенно в более длительных масштабах времени

Затем мы обратились к сравнению динамических признаков нейронной активности во время натуралистических и контролируемых задач. Для этого мы вычислили значения энтропии в каждом вокселе мозга в течение 10 временных масштабов (метод многомасштабной энтропии, см. рис. 1 и подробности в разделе «Методы»).Затем мы усредняли карты энтропии взрослых и детей по коротким временным шкалам (от 1 до 5), с одной стороны, и по длинным временным шкалам (от 6 до 10), с другой стороны, отдельно для видеоуроков по арифметике и грамматике и для контролируемых математическая задача. Чтобы оценить, какие области мозга демонстрировали различия в энтропии между натуралистическими и контролируемыми задачами, мы ввели эти полученные карты средней энтропии в общий ANOVA. В короткие промежутки времени мы не наблюдали существенной разницы между видео и тестом по математике у детей. У взрослых натуралистическая математическая задача вызывала большую энтропию, чем контролируемая задача, в затылочной коре, клиновидной кости и правой веретенообразной извилине. В более длительных временных масштабах несколько участков в затылочной коре, нижней и верхней височных извилинах, теменной коре и нижней лобной извилине отличали натуралистические и контролируемые задачи как для детей, так и для взрослых. Сайты, на которых видеоурок по арифметике вызвал большую энтропию, чем контролируемая математическая задача, представлены на рисунке 4 и перечислены в таблице S2.Мы отмечаем, что эти карты были удивительно похожи у детей и взрослых, за исключением затылочной коры, где взрослые показали большую разницу в энтропии по сравнению с детьми в разных временных масштабах.

Рисунок 4: Динамические различия в модальности и содержании в длительных временных масштабах.

Вверху — Разница в модальности : Карты контраста энтропии в длинных временных масштабах (от 6 до 10) между натуралистическими и контролируемыми математическими задачами у всех участников вместе (слева), взрослых (в центре) и детей (справа). Внизу — Разница в содержании : Карты оставшихся кластеров после маскирования контрастом энтропии длинных временных шкал между грамматическим видео и контролируемой математической задачей. Все карты отображаются после гауссовского сглаживания на полувысоте 2 мм с p <0,001 по вокселям и FDR p <0,05 по кластерам.

Затем мы проверили, модулируется ли длинномасштабная нейронная энтропия конкретно математическим содержанием. Прямое сравнение видеоуроков математики и грамматики всего мозга со строгой поправкой на множественные сравнения вокселей не выявило каких-либо существенных различий в энтропии.Однако более чувствительный априорный анализ ROI показал, что видеоурок по математике вызывал большую энтропию, чем видеоурок по грамматике, особенно при билатеральном IPS, левой pITG и правой IFG Oper (ts(31) > 1,93, ps <0,031). Затем мы подтвердили это предпочтение контента в анализе всего мозга, замаскировав контраст видеоурока по арифметике и контролируемой математической задачи энтропией, соответствующей видеоуроку по грамматике, в отличие от контролируемой математической задачи (нижний ряд на рис. 4).У взрослых эта карта включала двусторонние теменные участки, двусторонние нижние височные участки и двустороннюю нижнюю часть лобной извилины opercularis. У детей участки, где модуляция энтропии была особенно чувствительна к математическому содержанию, в основном наблюдались билатерально в нижней лобной извилине, а также в правой верхней теменной доле (полные списки см. в таблице S3). Взятые вместе, эти результаты позволяют предположить, что в течение длительных периодов времени энтропия нейронного сигнала в теменной коре увеличивалась не только в зависимости от типа задачи (натуралистическая, а не контролируемая), но также и от семантического содержания задачи (математической). больше, чем грамматика).

Функциональная связность теменных областей усиливается при выполнении естественных задач по сравнению с контролируемыми задачами

Более высокая долгосрочная нейронная энтропия в теменной коре для естественных математических задач по сравнению с контролируемыми математическими задачами может быть результатом долгосрочных взаимодействий между теменными областями и другими областями мозга. головного мозга (McIntosh et al., 2014; Wang et al., 2018). Таким образом, мы оценили корреляцию среднего времени активации каждой из наших трех задач как в левой, так и в правой IPS с течением времени каждого вокселя мозга.Мы отмечаем, что сравнение всего мозга между сетью, функционально подключенной к IPS, во время арифметического видео и видео с грамматикой сообщается в дополнительных материалах, в то время как в следующем разделе основное внимание уделяется только двум задачам, которые имеют одинаковое математическое содержание.

Эти анализы ROI-to-voxel сначала показали, что сеть, функционально подключенная к IPS, была больше во время математического видеоурока, чем во время контролируемого математического задания (математическое видео: 91 218 ± 128 вокселей, математическое задание: 81 611 ± 112 вокселей; парное t-тест: t(31) = 2.40, р = 0,023). Более того, при сравнении естественных и контролируемых математических задач в целом мозге IPS показала большую связь с областями левой височной доли и левой нижней лобной извилины, которые классически участвуют в обработке речи (рис. 5). И наоборот, во время контролируемого математического задания IPS оказалась более коррелированной с областью правой нижней лобной извилины. Наконец, мы оценили силу подключения IPS в связанной с математикой сети, усредняя значения корреляции, извлеченные из трех оставшихся областей интереса, связанных с математикой (двусторонняя pITG и правая IFGOper).Совпадая с нашими предыдущими результатами, парный t-тест показал, что подключение к математической сети было выше во время математического видео, чем во время математических контролируемых задач (математическое видео: z = 0,40 ± 0,0069, математическое задание: z = 0,37 ± 0,0079; парное t-критерий: t(31) = 3,72, p <0,001).

Рисунок 5: Области мозга, функционально связанные с IPS во время выполнения натуралистических и контролируемых математических задач. Внизу : Карта областей мозга, демонстрирующих значительную корреляцию с двусторонней IPS, то есть функционально связанную с ней, во время видеоурока по натуралистической математике больше, чем во время контролируемого математического задания (синий).

Обратный контраст отображается зеленым цветом на том же шаблоне мозга. Обе карты отображаются с p <0,001 по вокселям и FDR p <0,05 по кластерам.

Эти результаты предполагают, что связность внутритеменной борозды была усилена типом задачи (для натуралистической задачи больше, чем для контролируемой математической задачи), и сходятся с нашим анализом различий энтропии между задачами.Таким образом, эти результаты совместимы с идеей о том, что крупномасштабная нейронная энтропия может отражать усиление связи между распределенными областями мозга.

Увеличение нейронной энтропии отражает продвинутую нейронную обработку

Наконец мы рассмотрели вопрос о том, увеличивается ли сложность нейронного сигнала по мере развития. На уровне всего мозга мы начали со сравнения энтропии нейронного сигнала, вызванного нашими тремя задачами у взрослых и детей. Объединив все временные шкалы, мы заметили, что нейронные реакции взрослых обычно имели большую энтропию, чем у детей, по всему мозгу для каждой задачи (верхняя часть рисунка S1). Этот результат был подтвержден более точными анализами в наших заранее определенных областях интересов. Рисунок S1 показывает, что, особенно в короткие промежутки времени, нейронная энтропия была выше у взрослых по сравнению с детьми во всех областях интереса и для всех задач (все ps <0,02). Таким образом, большая энтропия является признаком зрелой обработки, в отличие от неупорядоченной или незрелой обработки.

Для дальнейшего изучения этого вопроса мы затем изучили взаимосвязь между детской нервной энтропией и их нервной зрелостью, которая обычно характеризует, насколько «взрослым» является реакция нервной системы ребенка.Нейронная зрелость обычно определяется как сходство между нейронными реакциями ребенка и среднего взрослого человека для каждого воксела мозга и в ходе выполнения данной задачи (полный анализ нервной зрелости см. в дополнительных материалах). Во время видеоурока по математике в короткие промежутки времени и, в меньшей степени, в длительные промежутки времени мы наблюдали, что детская нейронная энтропия и нейронная зрелость значительно коррелировали в крупной затылочно-теменной сети, включая двусторонние IPS и pITG, а также в двусторонней IFG. Опера (рис. 6).Здесь мы отмечаем, что эти области были удивительно похожи на связанные с математикой развивающиеся области, идентифицированные у детей в возрасте от 4 до 8 лет Kersey et al. (2019) (см. перекрытие на рис. 6). В частности, в длительных временных масштабах мы также наблюдали значительные корреляции между нейронной энтропией и нейронной зрелостью во время видео грамматики в левой IFG tri и STS, а также в некоторых затылочно-теменных участках (см. Рисунок S2).

Рисунок 6: Корреляция нейронной энтропии и нейронной зрелости в развивающихся регионах.

Наложение (выделено коричневым цветом) карт мозга, показывающих развивающиеся математические области из исследования Kersey et al. 2019 (светло-бежевый) и корреляция зрелости нейронов и энтропии во время видеоурока по математике (короткие шкалы светло-оранжевого цвета, длинные шкалы темно-оранжевого цвета).

В наших ранее определенных ROI, связанных с математикой, мы, наконец, сравнили корреляцию между средней энтропией и средними значениями нейронной зрелости для каждой из наших трех задач (рис. 7). В короткие промежутки времени, во время видеоурока по математике, корреляция была особенно сильной в правом полушарии (правая ИПС: коэффициент Пирсона r = 0.622, Р ² = 0,387, р = 0,006; правый pITG: r = 0,777, R ² = 0,604, p < 10-4; и правой IFG Oper: r = 0,788, R ² = 0,621, p < 10-4), и несколько ниже, но все еще значимо в левом полушарии (левая IPS: r = 0,487, R ² = 0,237, p = 0,040 и левый pITG: r = 0,565, R ² = 0,319, p = 0,015). Мы отмечаем, что детская нейронная энтропия и нейронная зрелость также значительно коррелировали в правом IPS во время контролируемого математического задания (r = 0.501, R ² = 0,251, р = 0,034). Однако никакие области, связанные с математикой, кроме правых IPS, не демонстрировали корреляцию между нейронной энтропией и нейронной зрелостью во время видеоурока по грамматике (r = 0,525, R ² = 0,275, p = 0,025). Отметим, что на больших временных масштабах такой специфичности не наблюдалось (см. Дополнительные материалы).

Рисунок 7: Нейронная зрелость и нейронная энтропия для математических и грамматических задач.

Оценка корреляции между зрелостью нейронов и нейронной энтропией в коротких временных масштабах (от 1 до 5) во время наших трех задач в 5 областях интереса, связанных с математикой, которые представлены на раздутом мозге.Уровень прозрачности графиков отражает уровень значимости корреляции: темные цвета соответствуют p < 0,01, средние цвета соответствуют p < 0,05, а светлые цвета указывают на то, что значимость не достигнута. Оранжевые квадраты обозначают корреляции, которые все еще были значимыми после коррекции FDR для множественных сравнений.

Эти данные свидетельствуют о том, что нейронная энтропия увеличивалась с ростом нейронной зрелости в областях, связанных с математикой. В короткие сроки это особенно касалось задач по математике, но не видеоурока по грамматике. Вместе с тем фактом, что нейронная энтропия в целом была выше у взрослых, чем у детей, наши результаты согласуются с гипотезой о том, что повышенная энтропия отражает продвинутую нейронную обработку.

Нервная зрелость связана с уменьшением дисперсии нейронного ответа

В то время как нейронная энтропия, которую можно рассматривать как меру временной изменчивости нейронного ответа, по-видимому, увеличивается в ходе развития, это также относится к амплитудная изменчивость (т.е. дисперсия) нейронного ответа? Чтобы ответить на этот вопрос, мы вычислили дисперсию ЖИРНОГО сигнала в каждом вокселе мозга, для каждого участника и во время каждого задания. Общий дисперсионный анализ показал, что дети в целом демонстрируют большую дисперсию, чем взрослые, для сочетания обеих математических задач (рис. 8). Это, по-видимому, указывает на то, что, в отличие от временной сложности, амплитудная изменчивость нейронных ответов имеет тенденцию к уменьшению по мере развития.

Рисунок 8.

Нейронная зрелость и дисперсия для всех задач.

Карты слева показывают области мозга, которые демонстрируют более высокую амплитудную дисперсию для детей по сравнению со взрослыми (вверху) и во время натуралистического математического видео по сравнению с контролируемой математической задачей (внизу). Графики справа показывают обратную корреляцию, обнаруженную между нейронной зрелостью и дисперсией у детей в заранее определенных областях, связанных с математикой. Как и на рисунке 7, уровень прозрачности отражает уровень значимости корреляции: темные цвета соответствуют p < 0,01, средние цвета соответствуют p < 0.05, а светлые цвета указывают на то, что значимость не достигнута. Оранжевые квадраты обозначают корреляции, которые все еще были значимыми после коррекции FDR для множественных сравнений.

Попутно отметим, что тип задачи также влиял на дисперсию нейронного ответа, но в наборе областей, которые сильно отличались от того, что мы наблюдали до сих пор. Фактически, натуралистическая математическая задача вызвала большую дисперсию, чем контролируемая математическая задача, в основном в первичной зрительной и слуховой коре (в частности, вдоль шпорной борозды и двусторонних извилин Хешля) и, в более общем плане, вдоль верхних височных борозд обоих полушарий. в большой вентрально-затылочной области, в задней поясной извилине, а также в предклинье.

Как и ранее, мы оценили корреляцию между средней дисперсией и средними значениями нейронной зрелости для каждой из наших трех задач в наших связанных с математикой ROI (рис. 8). Во время математического видеоурока мы обнаружили достоверную обратную корреляцию в правой ИПС (коэффициент Пирсона r = -0,625, R ² = 0,390, p = 9,69×10-3), левой pITG (r = -0,764 , R ² = 0,584, p = 5,69×10-4), и правый pITG (r = -0,784, R ² = 0.615, р = 3,26×10-4; и правая IFG Oper: r = 0,788, R ² = 0,621, p = 3,26×10-4). Нервная зрелость детей также была значительно антикоррелирована как в левом, так и в правом pITG во время контролируемого математического задания (слева: r = -0,504, R ² = 0,254, p = 0,039; справа: r = -0,511, R). ² = 0,261, р = 0,043). Однако только правые IPS продемонстрировали корреляцию между дисперсией и нейронной зрелостью во время видеоурока по грамматике (r = -0. 508, R ² = 0,258, р = 0,045). Отметим, что корреляции, обнаруженные во время видеоурока по математике, оставались значимыми после коррекции FDR для множественных сравнений. Эти результаты в целом предполагают, что продвинутая нейронная обработка сопровождается снижением дисперсии нейронного ответа.

Обсуждение

Естественное обучение требует интеграции информации с течением времени. Мы сравнили нейронную активность детей в задаче естественного обучения, в которой изучение математики встроено в построение повествования, с нейронной активностью во время более традиционной задачи принудительного выбора с двумя альтернативами.Измерения межпредметной корреляции выявили надежные нейронные сигналы у испытуемых в IPS во время двух типов математических задач, и этот образец отличался от такового в грамматическом задании. Многомасштабная энтропия — это мера, показывающая изменения сложности нейронных сигналов в различных временных масштабах. Наши данные показывают, что энтропия была значительно выше на грубых временных масштабах в IPS во время натуралистической задачи по сравнению с лабораторной задачей. Этот паттерн не наблюдался для задачи по натуралистической грамматике, что позволяет предположить, что задачи по натуралистической математике вызывают нейронную интеграцию математической информации в течение более длительных периодов времени в IPS.Кроме того, нейронная энтропия в теменной коре увеличивалась по мере развития и, таким образом, вероятно, отражала прогресс в нейронной обработке, в отличие от беспорядка или шума.

Области IPS ранее участвовали в семантической обработке математических понятий (например, Amalric and Dehaene, 2019, 2016; Cantlon and Li, 2013; Dehaene et al., 2003; Huth et al., 2016; Vogel et al. , 2015; Чжан и др., 2012). Например, в 2012 г. Zhang et al. показали, что левая ИПС участвует в семантической обработке геометрических слов наряду со словами-числами.Совсем недавно в исследованиях Amalric and Dehaene (2016, 2019) была выявлена сеть, включающая двусторонние IPS и pITG, которая активировалась, когда участники обрабатывали устные математические утверждения и оценивали их истинностное значение систематическим способом, не зависящим от математической области, или трудность высказывания. Более того, в исследовании фМРТ, которое систематически отображало семантическую информацию, содержащуюся в слуховых повествовательных историях, Huth et al. (2016) показали, что билатеральные теменные, нижнелобные и нижневисочные области были особенно избирательны к словам, относящимся к числам, единицам измерения, положениям и расстояниям (см. Рисунок 2 — Amalric and Dehaene, 2018).

Здесь мы подтверждаем и расширяем эти предыдущие выводы, сравнивая два задания, в которых смысловое содержание одинаково, но формат стимулов разный, – естественно-образовательный урок и лабораторное задание с вынужденным выбором на одном и том же арифметическом принципе. Как натуралистические, так и лабораторные математические задачи модулировали нейронную активацию в IPS и отделялись от нематематической грамматической задачи. Ранее было показано, что мозговые сети для обработки высокоуровневых математических утверждений и более простых математических вычислений перекрываются (Amalric and Dehaene, 2016) и отделяются от сетей, участвующих в обработке эквивалентных нематематических задач (Amalric and Dehaene, 2018; Керси и др. , 2019; Монти и др., 2012). Таким образом, натуралистические и лабораторные математические задачи показали сходство в лежащих в их основе нейронных процессах, и это сходство, вероятно, носит семантический характер.

Несмотря на сходство нейронных процессов между естественными и лабораторными задачами по математике, были также различия в их нейронных сигнатурах. Ключевое различие задач между натуралистическими и контролируемыми задачами заключается в том, что в натуралистической задаче предыдущая информация была необходима для обработки поступающей информации в течение более длительного периода времени.В натуралистическом задании виртуальный учитель объяснял математическую концепцию в течение нескольких секунд, тогда как в лабораторном задании в течение нескольких секунд представлялись изолированные стимулы в жестких задачах. В задаче по натуралистической математике нейронная энтропия была больше, чем энтропия в задаче по контролируемой математике на больших временных масштабах. Предыдущие исследования показали, что медленные колебания нейронных сигналов чувствительны к кумулятивному значению. Например, Хассон и др. (2015) показали, что временные паттерны нейронной обработки более высокого порядка во время натуралистического мышления являются иерархическими и функционально связаны с семантическим вводом.Они показали, что медленные колебания нейронных сигналов зависят от кумулятивной обработки информации от секунд до минут и отслеживают построение смысла повествования по словам, предложениям и событиям. Таким образом, наблюдаемые нами различия в нейронной энтропии между натуралистическими и лабораторными задачами в областях ВПС, которые были чувствительны к семантике математики, вероятно, отражают накопление информации с течением времени, которому способствует непрерывный образовательный нарратив в натуралистической задаче, но не в контролируемая задача.Более того, медленные колебания нейронной активности в ВПС были более чувствительны к уроку математики, чем к уроку грамматики. Это указывает на то, что энтропия нейронного сигнала в теменной коре не была тривиальным отражением сложности натуралистических задач, а зависела от содержания стимула. Таким образом, временная энтропия в натуралистической образовательной задаче является кандидатом на маркер семантической обработки детей в IPS.

Временная энтропия также является полезным маркером развития у детей.Как ранее сообщалось в литературе по электрофизиологии, сложность сигналов ЭЭГ увеличивается по мере развития в детстве (Miskovic et al., 2016) и от детства до юношеского возраста (McIntosh et al., 2008). Кроме того, было высказано предположение, что созревание мозга характеризуется более высокой энтропией сигналов ЭЭГ на коротких временных масштабах (Szostakiwskyj et al., 2017) и сопровождается долгосрочным снижением энтропии как потенциальное следствие перехода от глобального к локальной обработке информации (McIntosh et al., 2014; Ван и др., 2016). Здесь, впервые в исследовании фМРТ, мы также обнаружили, что нейронные реакции взрослых имеют большую энтропию, чем нейронные реакции детей, особенно в мелких временных масштабах.

Кроме того, в областях, связанных с математикой, таких как IPS и pITG, которые были похожи на области развития, связанные с математикой, идентифицированные у детей в возрасте от 4 до 8 лет Kersey et al. (2019), мы обнаружили, что нейронная энтропия детей, вызванная математическими, но не грамматическими задачами, предсказывала их нейронную зрелость.Обнаружение такой корреляции далеко не тривиально, поскольку два сигнала с большей энтропией не обязательно становятся более коррелированными (см. Рисунок S3 для примеров сигналов с диссоциированными значениями корреляции и энтропии). Возможно, такая корреляция в мозгу даже противоречит здравому смыслу. Действительно, можно было бы ожидать, что по мере того, как нейронные сигналы одного человека становятся богаче и сложнее, они с меньшей вероятностью коррелируют с нейронными сигналами другого человека. Однако наши результаты показывают, что сложность нейронных сигналов не только увеличивается по мере развития, но и увеличивается систематическим образом, что приводит к увеличению сходства нейронов у взрослых.В правых IPS и pITG повышенная нейронная сложность и сходство также сопровождались снижением дисперсии. Таким образом, нейронная зрелость, нейронная энтропия и дисперсия сигналов кажутся независимыми, но дополняющими друг друга маркерами развития мозга.

Наконец, наши результаты в целом предполагают, что нейронная энтропия отражает продвинутую нейронную обработку. Сходящиеся данные электрофизиологических исследований показывают, что повышенная нейронная энтропия связана с более широким представлением знаний и способностью обрабатывать информацию (Beharelle et al., 2012; Хейз и др., 2012). В настоящее время нейронная энтропия связана с вероятностью возбуждения нейронов внутри и между областями и их взаимосвязью (Vakorin et al., 2011). Наши выводы о том, что IPS была функционально подключена к более крупной сети во время натуралистической математической задачи, чем во время контролируемой математической задачи, совместимы с этой идеей. Предыдущие исследования ЭКоГ, ЭЭГ и фМРТ у взрослых показали, что энтропия нейронной активности в области зависит от того, насколько эта область взаимосвязана с другими областями мозга (Wang et al., 2018). Более крупные и более взаимосвязанные сети производят большее изменение нейронных ответов с течением времени или энтропию. Таким образом, повышенная энтропия может отражать более широкий репертуар состояний мозга внутри или между сетями или большее функциональное распределение этих состояний по сетям (Bassett and Bullmore, 2006; Deco et al., 2011; Freeman, 2000). В свете этих предыдущих результатов корреляция, которую мы наблюдали между детской нейронной энтропией и нейронной зрелостью в математической сети, может отражать растущую широту и разнообразие нейронных процессов, доступных детям для анализа математической информации в процессе развития.

Методы и материалы

Участники

В исследовании приняли участие 38 человек. В этом исследовании приняли участие 24 типично развивающихся ребенка в конце 3-го класса и 14 взрослых. 6 детей были исключены из дальнейшего анализа из-за чрезмерных движений головой или отказов.

Заявление об этике

Все участники дали информированное согласие после прочтения или прочтения информации о согласии. Протокол был одобрен как Университетом Рочестера, так и Институциональным наблюдательным советом Карнеги-Меллона.

Процедура

Каждое испытание одного и того же/другого задания начиналось с двух белых кругов, расположенных горизонтально на сером фоне, и синего фиксирующего креста в центре экрана. Через 500 мс фиксационный крест исчезал, а в первом круге появлялась первая операция или массив точек. В 1500 мс во втором круге появилась вторая операция или массив точек. Через 1 секунду два круга стали красными, указывая на начало 4-секундного периода ответа. Две операции или массивы точек оставались на экране в течение всего периода отклика.Участников просили нажимать кнопку большим пальцем правой руки, если они думали, что две операции дали одинаковый результат или два массива имели одинаковое количество точек, и в противном случае нажимать кнопку большим пальцем левой руки. Каждое испытание заканчивалось периодом отдыха переменной продолжительности (среднее значение = 5 с, стандартное отклонение = 1 с).

Как первая, так и вторая сессия теста включали 3 прогона по 24 попытки в каждом. Чтобы выполнить межсубъектные корреляции, порядок испытаний был фиксированным в рамках серии, но мы рандомизировали порядок серий.

Прогон фильма начинался с простого синего экрана с черным фиксирующим крестом в центре в течение 10 секунд, чтобы измерить базовый уровень активации до начала воспроизведения фильма. Оба фильма состояли из трех видеофрагментов продолжительностью 80 ± 4 секунды, разделенных 10-секундными перерывами. Участникам не давали никаких конкретных инструкций, кроме просмотра фильма. Половина участников сначала посмотрела фильм по математике, а другая половина сначала посмотрела фильм по грамматике.

Стимулы

Педагогические видеоролики

С помощью онлайн-приложения «Powtoon» мы создали два видеоролика.Видео соответственно объяснили коммутативный принцип умножения и относительных местоимений. Оба фильма визуально совпадали (одинаковый синий фон, одинаковые мультипликационные анимации, одинаковое количество информации на экране, одинаковое сочетание символов и картинок).

Числовые пары

В каждом прогоне одни и те же пары были представлены символически и несимволически. Символические пары представляли собой простые математические операции (например, «2×3» и «3×2»). Их несимволическими аналогами были наборы точек, визуально организованные в подгруппы (например,г. «2 группы по 3 точки» и «3 группы по 2 точки»). Подгруппы одинакового размера в наборе располагались по одинаковой схеме. В каждом прогоне 8 пар проверялись на понимание коммутативного принципа (например, «4×2» и «2×4»). Мы сравнили их с 8 парами с одинаковым количеством элементов, но разными математическими операциями (например, «4+2» и «3×2»). Мы также ввели 8 пар, контролирующих количество и гарантирующих, что испытуемые не просто оценивают количество элементов, но вычисляют точные сложения и умножения (половина из них использовала одну и ту же операцию: e.г. «4х3» и «4х2»; а другая половина использовала разные операции: например. «5+2» и «2×3»). См. Таблицу S1 для полного списка стимулов.

ФМРТ-процедуры

Функциональные изображения были получены на сканере Siemens Prisma 3-Tesla в Рочестерском центре визуализации головного мозга с помощью многоканальных последовательностей изображений (многоканальный коэффициент = 4, коэффициент ускорения срезов = 3, 60 чередующихся осевых срезов, толщина 3 мм и Разрешение в плоскости 3 мм, TR = 2000 мс, TE = 30 мс), с 64-канальной головной катушкой.

Анализ данных фМРТ

Предварительная обработка

Данные фМРТ были обработаны с помощью SPM12.Функциональные изображения были сначала скорректированы по времени среза, повторно выровнены, нормализованы к стандартному пространству мозга MNI, передискретизированы до размера вокселя 2 мм и пространственно сглажены с помощью изотропного гауссовского фильтра 4 мм FMWH. 6 параметров кадрового смещения, извлеченных из предыдущей перестройки, были регрессированы, и был применен 100-секундный фильтр верхних частот. Затем соответствующие сегменты данных каждого субъекта были обрезаны (чтобы удалить первые секунды каждой эпохи, фиксирующей начало неспецифического стимула) и оценены по z (стандартизированы до нулевого среднего и единичной дисперсии) для каждого вокселя и сегмента. Наконец, они были объединены в три файла 4D NIfTI: видеоурок по арифметике, видеоурок по грамматике и задание с принудительным выбором по математике. Перед выполнением каких-либо дальнейших анализов накладывали усредненную маску серого вещества.

Межсубъектные корреляции

Техника межсубъектной корреляции (ISC) представляет собой метод анализа, основанный на данных, который заключается в выявлении областей мозга, в которых реакция на стимул носит систематический характер во времени, т. е. коррелируется между участниками (Nastase et al., 2019). Как внутри групп (дети и взрослые), так и между детьми и взрослыми межсубъектная корреляция рассчитывалась методом исключения. В каждом вокселе временные ряды каждого субъекта коррелировали со средними временными рядами всех других субъектов. Этот подход напрямую дал нам одну R-карту для каждого субъекта, которая была преобразована в z-карту с помощью преобразования Фишера. Обратите внимание, что корреляция между каждым ребенком и группой взрослых обычно интерпретируется и называется нервной зрелостью ребенка. Затем на групповом уровне мы выполнили t-тесты и ANOVA на z-картах каждой задачи. Собрав всех участников вместе, мы выполнили t-тесты и ANOVA на картах корреляции взрослых и взрослых и детей и взрослых.

Многомасштабная энтропия сигнала BOLD

Многомасштабная энтропия (MSE) была предложена для оценки динамической сложности временного ряда с учетом различных временных масштабов. СКО сигнала для трех задач рассчитывали для каждого участника в каждом вокселе, включенном в маску серого вещества.Для этого мы использовали набор инструментов WFDB (https://physionet.org/physiotools/mse/), который реализует двухэтапный анализ, описанный Costa et al. (2002). В этом методе несколько «крупнозернистых» временных рядов фиксированной длины L/n сначала формируются путем усреднения n последовательных непересекающихся точек данных исходного временного ряда длины L (см. рисунок 1). Затем вычисляется выборочная энтропия каждого крупнозернистого временного ряда. Выборочная энтропия (SampEn) представляет собой аппроксимацию сложности Колмогорова, которая была предложена для физиологических сигналов. По сути, он состоит в определении того, насколько воспроизводимым является паттерн длины m во всем временном ряду. Сначала он подсчитывает, сколько раз каждый паттерн длиной m и m+1 соответственно повторяется во временном ряду с учетом коэффициента допуска r. Более подробно, два шаблона [x1,x2] и [y1,y2] считаются равными, если max(|xi-yi|) < r (см. рисунок 1, нижняя панель). Во-вторых, SampEn рассчитывается как отрицательный натуральный логарифм отношения между этими двумя значениями.Различные параметры были выбраны в соответствии с оптимальными параметрами, найденными в предыдущем исследовании фМРТ подростков (Easson and McIntosh, 2019): длина паттерна m = 2; коэффициент допуска r = 0,5; масштабный коэффициент крупнозернистости l = 10. Это дало нам 10 электронных карт (по одной на каждый масштаб) для каждой задачи и каждого участника. Затем эти E-карты были усреднены по коротким шкалам (от 1 до 5) и длинным шкалам (от 6 до 10) и введены в повторное измерение ANOVA для оценки карт всего мозга на уровне группы. Обратите внимание, что если не указано иное, карты отображаются при p < 0.001 по воксам и p <0,05 по кластерам, с поправкой на FDR.

Анализ дисперсии нейронного сигнала

Для вычисления дисперсии нейронного сигнала мы использовали предварительно обработанные данные, центрированные по среднему, но не нормализованные к единичной дисперсии. Для каждого вокселя и для каждой задачи (видеоурок по арифметике, видеоурок по грамматике и связанная математическая задача с принудительным выбором) был извлечен временной ряд каждого субъекта и рассчитана его дисперсия. Затем на групповом уровне мы выполнили дисперсионный анализ полученных карт дисперсии.

Анализ ROI

Области, связанные с математикой и языком, были определены в двух полностью независимых исследованиях. Из исследования составной структуры предложений, проведенного Pallier et al. (2011), мы выбрали 4 (из 6) областей интереса левого полушария: переднюю верхнюю височную борозду (aSTS), височно-теменное соединение (TPJ), а также нижнюю лобную извилину pars orbitalis (IFG Orb) и pars triangularis ( ITF Три). Мы отмечаем здесь, что мы предпочли левополушарную аСТС и ТБС височному полюсу (ТП) и задней верхней височной борозде (pSTS), потому что билатеральные АСТС и ТБС также обычно участвуют в семантической обработке (Binder et al., 2009). Области, связанные с математикой, ранее использовались Амальриком и Дехаеном (2016) и были идентифицированы как обрабатывающие даже сложные математические концепции. Более подробно, 5 областей в двусторонних внутритеменных бороздах (IPS), двусторонних задних нижних височных извилинах (pITG) и правой нижней лобной извилине pars opercularis (IFG Oper) были определены на основе контраста вычислений и предложений сканирования локализатора, выполненного в группа из 83 человек (Pinel et al., 2007).

Каждая из 9 вышеперечисленных областей была затем перенесена на другое полушарие, таким образом определив 4 языковых правополушарных симметричных области в aSTS, TPJ, IFG Orb и IFG tri и 1 математическую левополушарную симметричную область в IFG Oper.Наконец, области IPS и pITG были определены как общие воксели между исходной областью и ее перевернутым аналогом. Таким образом, эта конструкция привела к 14 симметрично парным интересующим областям, в которых мы выполнили различные типы анализа.

Внутри каждого региона и для каждой задачи мы сначала извлекали значения межпредметной корреляции для каждого взрослого (относительно других взрослых) и для каждого ребенка (как относительно других детей, так и относительно взрослых). Для каждого взрослого и детского участника мы также извлекли значения энтропии для каждой шкалы.Эти значения либо усреднялись и вводились в традиционные t-критерии, либо непосредственно использовались для дальнейшего анализа.

Для анализа латерализации мы рассмотрели комбинацию как интенсивности, так и степени межсубъектных корреляций путем оценки суммы положительных значений ISC (∑ISC+) по каждому региону и для каждого участника. Затем для каждой пары регионов рассчитывали индексы латерализации ИСК по классической формуле LI = (∑ИСК+lh — ∑ИСК+rh)/(∑ИСК+lh + ∑ISC+rh). значения LI больше 0.1 обычно характеризуют левостороннюю латерализацию, в то время как значения LI менее -0,1 обычно характеризуют правостороннюю латерализацию.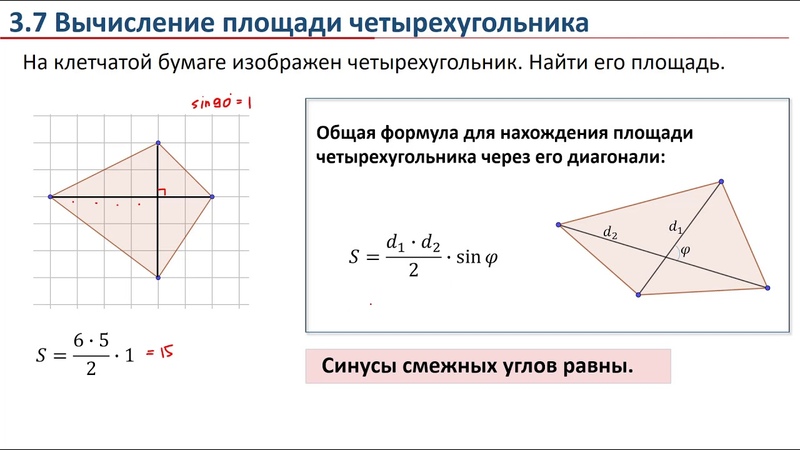 Значения, близкие к 0, характерны для билатерального распределения.

Анализ репрезентативного сходства выполнялся только в областях интереса, связанных с математикой (левая и правая IPS, левая и правая pITG и правая IFG Oper). Этот многовоксельный анализ паттерна обычно позволяет измерить пространственное сходство ЖИРНОГО сигнала, вызванного различными стимулами. Здесь мы применили его, чтобы проверить, насколько пространственно похожа синхронная нейронная активность, вызванная нашими тремя задачами.Для этого мы оценили для каждого участника корреляцию значений ISC во время наших трех задач по всем вокселям каждой ROI, связанной с математикой. Затем мы использовали t-тесты для сравнения значений корреляции обеих математических задач со значениями корреляции обоих видеоуроков.

Чтобы проверить корреляцию между детской нервной зрелостью и нейронной сложностью, мы сначала усреднили средние значения энтропии за короткие промежутки времени (шкалы 1-5) для каждого ребенка и для каждой изначально определенной области интереса (т. е. левый и правый IPS, левый и правый pITG, правый IFG Oper, левый asSTS, левый TPJ, левый IFG Orb и левый IFG tri), к которым мы добавили анатомически определенную левую веретенообразную извилину. Затем мы оценили корреляцию между этими значениями энтропии и средними значениями межсубъектной корреляции для каждого ребенка по отношению к группе взрослых.

Обратите внимание, что ко всем результатам теста применялась поправка Бонферрони или поправка FDR для количества ROI (или пар ROI).

Анализ функциональной связности

Предварительно обработанные данные BOLD были проанализированы с помощью набора инструментов функциональной связности CONN (Whitfield-Gabrieli and Nieto-Castanon, 2012).Как левый, так и правый IPS (определенные выше) использовали в качестве исходного материала при анализе всего мозга. В этом анализе начального числа к вокселу набор инструментов оценивает преобразованные Фишером значения двумерной корреляции между ЖИРНЫМИ временными рядами, усредненными по начальному ROI, и ЖИРНЫМИ временными рядами каждого отдельного вокселя.