Выпускников 2022 года ожидают изменения в ЕГЭ
О том, какие изменения ожидают участников Единого государственного экзамена в 2022 году, рассказали в Комитете по образованию администрации Городского округа Подольск.
В комитете отметили, что с 2022 года ЕГЭ проводится на основе Федерального государственного образовательного стандарта среднего общего образования ФГОС. Изменения коснутся контрольно-измерительных материалов ЕГЭ.
Вот некоторые из них:
- добавлены задания, проверяющие умение выполнять действия с геометрическими фигурами, строить и исследовать простейшие математические модели в ЕГЭ по базовой математике,
- обогащен литературный материал в ЕГЭ по литературе: шире представлена поэзия второй половины XIX – XX веков, отечественная литература XXI века, включена зарубежная литература. Объем сочинения: не менее 200 слов,
- два новых задания будут предложены участникам ЕГЭ по географии.

- увеличено на 10 минут время выполнения письменной части работы по иностранным языкам (за исключением китайского), оно составит 3 часа 10 минут. Время выполнения заданий устной части работы увеличено на 2 минуты и составит 17 минут,
- уменьшено количество заданий в ЕГЭ по профильной математике, физике, химии, географии,
- сокращено время, отведенное на выполнение экзаменационных работ по истории и обществознанию с 235 до 180 минут в связи с исключением сочинения из заданий.
С полным перечнем изменений можно ознакомиться на сайте Федерального института педагогических измерений (ФИПИ):
Источник: Комитет по образованию администрации Городского округа Подольск
Фото из открытых источников
Математические формулы используемые в средних школах.
 Самые красивые физические и математические формулы
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Самые красивые физические и математические формулы
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей.
Голова идёт кругом от множества математических формул, которые необходимо знать. Зубрёжка и шпаргалки — удел слабых. А вот тем, кто хочет стать в математике сильнее, мы подскажем несколько советов, как запоминать формулы по математике так, чтобы они не выветрились из головы до контрольной, экзамена или ЦТ.
Понимай формулу
Если ты будешь заучивать только последовательность переменных, рискуешь «потерять» всю формулу, когда забудешь символ или знак.
Задействуй все виды памяти
Читай формулы вслух, прописывай на листке по нескольку раз, пока не запомнишь. Задействуй все виды памяти, делая упор на ведущую
.
Визуальная и двигательная память вместе дают больший эффект. Конечно, потенциал для запоминания у каждого разный. Есть специальные методики, которые помогают
.
Задействуй все виды памяти, делая упор на ведущую
.
Визуальная и двигательная память вместе дают больший эффект. Конечно, потенциал для запоминания у каждого разный. Есть специальные методики, которые помогают
.
Обязательно делай формулы наглядными: обводи формулу в рамку, пиши её другим цветом. Так будет легче найти в конспекте и запомнить. А лучше выписывай формулы в отдельный блокнот, структурируя их по темам. Помечай, в какого рода задачах та или иная формула пригодится, в чём её особенность. Заведи привычку пополнять список формул. Подобный «дневник наблюдений за формулами» поможет освежить в памяти важную информацию перед контрольной, экзаменом или ЦТ по математике.
Многие школьники ещё вот что делают: когда раздают проштампованные черновики, ты берёшь и сразу же записываешь на них важные формулы, которые тебе тяжело даются. За полчаса до ЦТ ты эти формулы зрительно запомнил, а потом быстренько написал.
Это экономит время. Особенно такой лайфхак хорош в тригонометрии. Чем больше знаешь формул, тем лучше.
Проверяй себя
Нужно постоянно возвращаться к выученному материалу, чтобы не забыть его. Попробуй метод «Две карточки», он подойдёт для запоминания формул приведения, сокращённого умножения, тригонометрических формул. Возьми две стопки карточек разного цвета, на одной напиши левую часть формулы, а на другой — правую. Раздели таким образом все формулы, что тебе нужно запомнить, затем перемешай обе стопки. Тяни по порядку карточку с левой частью формулы и подбирай её продолжение среди «правых» и наоборот.
Карточки хороши и в геометрии
Чтобы запомнить формулы по геометрии, заведи себе карточки по темам («Формулы площади», «Фомулы для треугольника», «Фомулы для квадрата» и т. д.) и записывай в них информацию следующим образом.
Можно фиксировать формулы в отдельном блокноте и всегда был под рукой — как тебе удобно
Будь на позитиве
Если ты учишь что-либо из-под палки, мозг сам желает избавиться от груза знаний. Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения.
И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
Воспринимай заучивание формул как хорошее упражнение для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужную формулу для решения.
И конечно же, решай как можно больше тестов и задач для подготовки к контрольной, экзамену или ЦТ!
ЦТ по математике — это типовые задачи: чем больше тестов решаешь, тем выше шанс встретить что-то похожее на ЦТ. Невозможно подготовиться к ЦТ по одной задаче. Но когда ты прорешал 100 задач, то 101 задача не вызовет затруднений.
Дмитрий Судник, преподаватель математики в
Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях
На данной странице Вы можете посмотреть или бесплатно скачать самые востребованные математические формулы, таблицы
,а также справочные материалы по высшей математике. Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул достаточно много, они давно известны, и нет никакого смысла переписывать справочники. А вот те формулы, которые очень часто используются для решения задач курса высшей математики, собраны воедино, и могут быть очень полезны при выполнении практических заданий. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы, и т.д.) практически всегда фигурирует та или иная формула.
Итак, прямо сейчас у Вас есть бесплатный доступ к ценным справочным материалам, возможен, как онлайн просмотр, так и скачивание. Удобнее всего сразу распечатать математические таблицы и справочные материалы, которые Вас заинтересуют. Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Почти все файлы размещены прямо на сайте, а значит, могут быть получены в максимально короткий срок, ограниченный только скоростью Вашего Интернет-подключения.
! В случае некорректного отображения pdf используйте следующие рекомендации
Рекомендую просмотреть всем. Данные формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул – никуда. С чего начать изучение высшей математики? С повторения этого. Независимо от уровня Вашей математической подготовки на данный момент, крайне желательно СРАЗУ ВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в ходе решения пределов, интегралов, дифференциальных уравнений и т.д.
В справочнике есть краткая информация о модуле, формулы сокращенного умножения, алгоритм решения квадратного уравнения, правила упрощения многоэтажных дробей, а также важнейшие свойства степеней и логарифмов.
Приведены самые «ходовые» тригонометрические формулы, которые применяются в ходе решения задач по высшей математике. На самом деле таких формул НЕМНОГО, и, собирать десятки других по различным математическим справочникам – пустая трата времени.
При выполнении заданий по математике нередко возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) при значениях аргумента от нуля до 360 градусов. Держать в памяти данную информацию нет никакого смысла, но некоторые значения тригонометрических функций хорошо бы знать . Также представлены формулы приведения для вышеуказанных тригонометрических функций, иногда (чаще всего при решении пределов) требуются. По просьбам посетителей сайта в pdf-файл добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.
Методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнее
разобраться в некоторых темах. Также вы сможете узнать, какие значения функций следует знать наизусть
, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Также вы сможете узнать, какие значения функций следует знать наизусть
, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.
В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.
Ваш гид по разделу «Функции и графики». В pdf-ке систематизирована и законспектирована информация об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
В общем-то, почти то же самое, что в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.
Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенной ряд следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведено биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельным заданием, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.
Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный подбор частного решения по виду правой части. Данная методичка, относится, прежде всего, к уроку Как решить неоднородное уравнение второго порядка?
и поможет вам легко разобраться в подборе частного решения. Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Справка незаменима в ходе решения прикладных задач комплексного анализа – нахождения частного решения ДУ операционным методом и нахождения частного решения системы ДУ этим же способом. Таблица отличается от аналогов тем, что «заточена» именно под вышеуказанные задания, данная особенность позволяет легко освоить алгоритмы решения. Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
В справочном материале приведены формулы факториала, количества перестановок, сочетаний, размещений (с повторениями и без повторений), а также содержательные комментарии к каждой формуле, позволяющие понять их суть. + Правила сложения и умножения комбинаций. Кроме того, в pdf-ке есть краткая информация о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.
Кроме того, в pdf-ке есть краткая информация о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.
Файл содержит перечень формул с краткими комментариями по обеим главам тервера – Случайные события и Случайные величины , в том числе приведены формулы и числовые характеристики распространённых дискретных и непрерывных распределений. Справка систематизирует материал и очень удобна для выполнения практических заданий, заглядываем и сразу находим то, что нужно!
Специальные расчётные программы:В данном разделе вы можете найти вспомогательные программы для решения широких и узколокальных математических задач. Они помогут вам быстро выполнить расчёты и оформить решение.
Универсальный калькулятор
реализован в рабочей книге MS Excel, которая содержит три листа. Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки – без проблем! Кроме того, калькулятор в автоматическом режиме выполняет основные действия с матрицами , считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические дополнения матриц. За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера , посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!
Данная полуавтоматическая программа относится к уроку Формула трапеций, формула Симпсона и помогает рассчитать приближенное значение определенного интеграла на 2, 4, 8, 10 и 20 отрезках разбиения. Прилагается видеоурок по работе с калькулятором. Вычислите ваш определенный интеграл в считанные минуты, и даже секунды!
На данный момент пока всё.
Раздел постепенно пополняется дополнительными материалами и полезными программами. Каждое справочное пособие неоднократно редактировалось и улучшалось, в том числе, с учетом ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите !
С уважением, Емелин Александр
Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
П.А.М. Дирак писал: «У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией. Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе».
Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».
2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.
3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.
Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.
4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.
5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.
6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.
7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.
8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.
9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.
10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.
11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.
12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера — которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён — Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией — до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон — антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.
Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон — антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.
13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»
14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.
Образование — то, что остается после того, как забыто все, чему учили в школе.
Игорь Хмелинский, новосибирский учёный, ныне работающий в Португалии, доказывает, что без прямого запоминания текстов и формул развитие абстрактной памяти у детей затруднительно. Приведу выдержки из его статьи » Уроки образовательных реформ в Европе и странах бывшего СССР»
Заучивание наизусть и долговременная памятьНезнание таблицы умножения имеет и более серьезные последствия, чем неспособность обнаружить ошибки в расчетах на калькуляторе. Наша долговременная память работает по принципу ассоциативной базы данных, то есть, одни элементы информации при запоминании оказываются связанными с другими на основе ассоциаций, установленных в момент знакомства с ними. Поэтому, чтобы в голове образовалась база знаний в какой-либо предметной области, например, в арифметике, нужно для начала выучить хоть что-то наизусть. Далее, вновь поступающая информация попадет из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы столкнемся с нею многократно, и, желательно, в разных обстоятельствах (что способствует созданию полезных ассоциаций). Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Формирование математического аппарата, при котором формулы не заучиваются, происходит медленнее, нежели в противном случае. Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его базы знаний и навыков, происходит значительно быстрее, если большая часть используемой информации (свойства и формулы) находиться в голове. И чем прочнее и дольше она там удерживается, тем лучше.
Сборники для подготовки к егэ. Справочник для подготовки к ЕГЭ: какой выбрать
Пять лучших пособий подготовки к ЕГЭ (ГИА) по математике
Единый государственный экзамен в нашем регионе проводится с 2005г. За прошедшее с тех пор время перепробовала много книг при подготовке обучающихся к экзамену. На сегодняшний день могу назвать свою пятерку лучших, по моему мнению, пособий.
За прошедшее с тех пор время перепробовала много книг при подготовке обучающихся к экзамену. На сегодняшний день могу назвать свою пятерку лучших, по моему мнению, пособий.
Семенов А. В. Единый государственный экзамен. Математика. Комплекс материалов для подготовки учащихся. Учебное пособие. 2017г.
Состоит из двух частей. В первой части задания разбиты по темам, вторая часть содержит 24 тренировочных варианта (12 вариантов профильного уровня, 12 вариантов базового уровня). Содержание пособия сформировано с использованием обновленного открытого банка заданий, соответствует современным требованиям ЕГЭ. Пособие разработано при научно-методической поддержке ФИПИ.
Структура и содержание данного пособия дают возможность использовать его и при самоподготовке, и при организации повторения в классе. Задания в основном даются парами, что позволяет одно из них разобрать коллективно, а другое решить самостоятельно.
В пособии предложены задания разного уровня. Шире представлены базовые задания. В разделе «Задачи повышенной сложности» авторы, не претендуя на полноту, дают представление о заданиях повышенного и высокого уровня. В конце сборника указаны ответы ко всем заданиям и вариантам, комментарии отсутствуют. Разобраны задания с развернутым ответом для одного из вариантов. Тесты составлены в соответствии со спецификацией и демоверсией текущего года. Пособие содержит справочный материал, входящий в КИМ базового уровня.
В разделе «Задачи повышенной сложности» авторы, не претендуя на полноту, дают представление о заданиях повышенного и высокого уровня. В конце сборника указаны ответы ко всем заданиям и вариантам, комментарии отсутствуют. Разобраны задания с развернутым ответом для одного из вариантов. Тесты составлены в соответствии со спецификацией и демоверсией текущего года. Пособие содержит справочный материал, входящий в КИМ базового уровня.
По мнению авторов, пособие может быть использовано с 6 класса. Из опыта работы советую начинать работу с 10 класса. Содержание пособия позволит повторить темы основной школы и подготовиться к экзамену на базовом уровне. Тогда в 11 классе можно сосредоточиться на подготовке к профильной математике. Работа с данной книгой позволит отработать 13-15 заданий, что соответствует 70-80 баллам. Книга сравнительно недорогая, работа по ней продуктивная. К сожалению, встречается достаточно много опечаток в тексте заданий и ответах.
Коннова Е.Г. уровень Математика. Базовый ЕГЭ-2014. Пособие для «чайников». 2011г.
Базовый ЕГЭ-2014. Пособие для «чайников». 2011г.
Данная книга входит в учебно-методический комплекс «Математика. Подготовка к ЕГЭ» под редакцией Ф.Ф. Лысенко. Среди заданий с кратким ответом есть задачи, в которых школьники ежегодно допускают ошибки. Пособие позволяет усилить работу по данным направлениям. Книга предназначена для формирования устойчивых навыков в решении заданий базового уровня. Выделены пять наиболее проблемных тем: «Вычисления и преобразования», «Производная и исследование функций», «Прикладные задачи», «Наибольшие и наименьшие значения функций» и «Построение и исследование математических моделей». В каждой теме доступно разобраны типовые задания из открытого банка, предложены задачи для самостоятельного решения. Книга так же содержит 12 тренировочных вариантов.
В начале каждой темы систематизирован теоретический материал. Содержание соответствует кодификатору ЕГЭ. В конце книги ответы ко всем заданиям и вариантам. Комментарии отсутствуют. Тесты сформированы по заявленным пяти темам. Уровень заданий в тестах соответствует разобранным в темах заданиям.
Тесты сформированы по заявленным пяти темам. Уровень заданий в тестах соответствует разобранным в темах заданиям.
С данным пособием можно начинать работу уже в 10 классе. Более подготовленные школьники могут самостоятельно разобрать готовые решения и выполнять задания для самопроверки. Для обучающихся с недостаточным уровнем подготовки следует разобрать готовые решения в классе или с репетитором, а следующие за ними задания предложить для домашней работы.
Цена пособия соответствует его пользе. Нередко обучающиеся, претендующие на высокие баллы, допускают 1-2 ошибки в заданиях базового уровня. Работа с данным пособием позволяет снизить число ошибок за счет совершенствования навыков решения типовых задач.
Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач. 2012г.
Большее число баллов на ЕГЭ профильного уровня обеспечивают задания с развернутым ответом. Данное пособие обеспечивает подготовку к такого рода заданиям. Изложение материала доступно учащимся с высоким уровнем подготовки.
Переплет мягкий, бумага белая, иллюстрации черно-белые.
В пособии представлены разобранные решения заданий, комментарии и критерии оценки, задачи для самостоятельного решения, подготовительные задачи и список литературы для самостоятельной подготовки к экзамену. Подготовительные задания более простые в сравнении с тренировочными, что позволяет организовать работу на элективных занятиях по нарастанию уровня сложности.
Работать с данным пособием лучше в 11 классе. Книга небольшая, но очень полезная. Повышает шансы получить самые высокие баллы.
Колесникова С. И. Математика. Интенсивный курс подготовки к единому государственному экзамену. 2008г.
Переплет мягкий, бумага серая, иллюстрации черно-белые.
В пособии собраны эффективные методы решения сложных уравнений и неравенств. Книга доступна учащимся с хорошим уровнем подготовки, претендующим на высокие результаты. И хотя издана давно, но полезность ее не уменьшилась. Рассматриваемые в пособии подходы в основном отсутствуют в школьных учебниках. Книга содержит два раздела. В разделе «Эффективные методы решения основных типов задач алгебры и анализа» рассмотрены понятие равносильности, метод рационализации и другие методы решения нестандартных уравнений и неравенств. Во втором разделе — 20 вариантов, решение многих заданий, двух полных вариантов.
Книга содержит два раздела. В разделе «Эффективные методы решения основных типов задач алгебры и анализа» рассмотрены понятие равносильности, метод рационализации и другие методы решения нестандартных уравнений и неравенств. Во втором разделе — 20 вариантов, решение многих заданий, двух полных вариантов.
Для каждого типа уравнений систематизирован теоретический материал, правила иллюстрируются готовыми решениями с комментариями автора. Следует отметить глубокую проработку тем.
Тренировочные варианты не соответствуют современной структуре профильного ЕГЭ по математике, но это ни сколько не умаляет их достоинства. Задания с развернутым решением предполагают умение школьников переносить знания в новую нестандартную ситуацию. Книга Колесниковой С. И. дает такую возможность. Рекомендую для работы репетитора с учащимися с высоким уровнем подготовки.
Вольфсон Б. И. Геометрия. Подготовка к ЕГЭ и ГИА-9. Учимся решать задачи и повторяем теорию. 2013г.
Не секрет, что наибольшее затруднение обучающиеся испытывают при решении геометрических задач. Данное пособие в доступной форме предлагает технологию обучения решения задач.
Данное пособие в доступной форме предлагает технологию обучения решения задач.
Переплет мягкий, бумага серая, иллюстрации черно-белые.
Второе, существенно переработанное издание книги соответствует измененной структуре и содержанию ЕГЭ по математике. Каждый технологический шаг иллюстрирован решениями задач из открытого банка заданий ФИПИ. Проведен анализ геометрических заданий ОГЭ И ЕГЭ. Есть справочный материал, задания для самостоятельной работы. В конце книги приведены ответы без комментариев.
Книга полезна не только учащимся, но и педагогам. Предложенную технологию работы с геометрическими задачами можно реализовать на уроках, начиная с 8 класса. Она позволяет снять страх перед задачами из геометрии, сформировать навыки анализа данных и составления плана решения задачи.
Книгу Вольфсон Б. И. открыла для себя только в этом учебном году, но предполагаю, что углубленная работа над ее содержанием позволит повысить школьникам баллы за счет решения задач № 14 и № 16 с развернутым решением.
Единый государственный экзамен в нашем регионе проводится с 2005 г. За прошедшее с тех пор время перепробовала много книг при подготовке обучающихся к экзамену. На сегодняшний день могу назвать свою пятерку лучших, по моему мнению, пособий.
1. Семенов А. В. Единый государственный экзамен. Математика. Комплекс материалов для подготовки учащихся. Учебное пособие. 2017 г.
Состоит из двух частей. В первой части задания разбиты по темам, вторая часть содержит 24 тренировочных варианта (12 вариантов профильного уровня, 12 вариантов базового уровня). Содержание пособия сформировано с использованием обновленного открытого банка заданий, соответствует современным требованиям ЕГЭ. Пособие разработано при научно-методической поддержке ФИПИ.
Структура и содержание данного пособия дают возможность использовать его и при самоподготовке, и при организации повторения в классе. Задания в основном даются парами, что позволяет одно из них разобрать коллективно, а другое решить самостоятельно.
В пособии предложены задания разного уровня. Шире представлены базовые задания. В разделе «Задачи повышенной сложности» авторы, не претендуя на полноту, дают представление о заданиях повышенного и высокого уровня. В конце сборника указаны ответы ко всем заданиям и вариантам, комментарии отсутствуют. Разобраны задания с развернутым ответом для одного из вариантов. Тесты составлены в соответствии со спецификацией и демоверсией текущего года. Пособие содержит справочный материал, входящий в КИМ базового уровня.
По мнению авторов, пособие может быть использовано с 6 класса. Из опыта работы советую начинать работу с 10 класса. Содержание пособия позволит повторить темы основной школы и подготовиться к экзамену на базовом уровне. Тогда в 11 классе можно сосредоточиться на подготовке к профильной математике. Работа с данной книгой позволит отработать 13-15 заданий, что соответствует 70-80 баллам. Книга сравнительно недорогая, работа по ней продуктивная. К сожалению, встречается достаточно много опечаток в тексте заданий и ответах.
Данная книга входит в учебно-методический комплекс «Математика. Подготовка к ЕГЭ» под редакцией Ф.Ф. Лысенко. Среди заданий с кратким ответом есть задачи, в которых школьники ежегодно допускают ошибки. Пособие позволяет усилить работу по данным направлениям. Книга предназначена для формирования устойчивых навыков в решении заданий базового уровня. Выделены пять наиболее проблемных тем: «Вычисления и преобразования», «Производная и исследование функций», «Прикладные задачи», «Наибольшие и наименьшие значения функций» и «Построение и исследование математических моделей». В каждой теме доступно разобраны типовые задания из открытого банка, предложены задачи для самостоятельного решения. Книга так же содержит 12 тренировочных вариантов.
В начале каждой темы систематизирован теоретический материал. Содержание соответствует кодификатору ЕГЭ. В конце книги ответы ко всем заданиям и вариантам. Комментарии отсутствуют. Тесты сформированы по заявленным пяти темам. Уровень заданий в тестах соответствует разобранным в темах заданиям.
Комментарии отсутствуют. Тесты сформированы по заявленным пяти темам. Уровень заданий в тестах соответствует разобранным в темах заданиям.
С данным пособием можно начинать работу уже в 10 классе. Более подготовленные школьники могут самостоятельно разобрать готовые решения и выполнять задания для самопроверки. Для обучающихся с недостаточным уровнем подготовки следует разобрать готовые решения в классе или с репетитором, а следующие за ними задания предложить для домашней работы.
Цена пособия соответствует его пользе. Нередко обучающиеся, претендующие на высокие баллы, допускают 1-2 ошибки в заданиях базового уровня. Работа с данным пособием позволяет снизить число ошибок за счет совершенствования навыков решения типовых задач.
3. Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач. 2012 год.Большее число баллов на ЕГЭ профильного уровня обеспечивают задания с развернутым ответом. Данное пособие обеспечивает подготовку к такого рода заданиям. Изложение материала доступно учащимся с высоким уровнем подготовки.
Изложение материала доступно учащимся с высоким уровнем подготовки.
Переплет мягкий, бумага белая, иллюстрации черно-белые.
В пособии представлены разобранные решения заданий, комментарии и критерии оценки, задачи для самостоятельного решения, подготовительные задачи и список литературы для самостоятельной подготовки к экзамену. Подготовительные задания более простые в сравнении с тренировочными, что позволяет организовать работу на элективных занятиях по нарастанию уровня сложности.
Работать с данным пособием лучше в 11 классе. Книга небольшая, но очень полезная. Повышает шансы получить самые высокие баллы.
4. Колесникова С. И. Математика. Интенсивный курс подготовки к единому государственному экзамену. 2008г.Переплет мягкий, бумага серая, иллюстрации черно-белые.
В пособии собраны эффективные методы решения сложных уравнений и неравенств. Книга доступна учащимся с хорошим уровнем подготовки, претендующим на высокие результаты. И хотя издана давно, но полезность ее не уменьшилась. Рассматриваемые в пособии подходы в основном отсутствуют в школьных учебниках. Книга содержит два раздела. В разделе «Эффективные методы решения основных типов задач алгебры и анализа» рассмотрены понятие равносильности, метод рационализации и другие методы решения нестандартных уравнений и неравенств. Во втором разделе — 20 вариантов, решение многих заданий, двух полных вариантов.
Рассматриваемые в пособии подходы в основном отсутствуют в школьных учебниках. Книга содержит два раздела. В разделе «Эффективные методы решения основных типов задач алгебры и анализа» рассмотрены понятие равносильности, метод рационализации и другие методы решения нестандартных уравнений и неравенств. Во втором разделе — 20 вариантов, решение многих заданий, двух полных вариантов.
Для каждого типа уравнений систематизирован теоретический материал, правила иллюстрируются готовыми решениями с комментариями автора. Следует отметить глубокую проработку тем.
Тренировочные варианты не соответствуют современной структуре профильного ЕГЭ по математике, но это ни сколько не умаляет их достоинства. Задания с развернутым решением предполагают умение школьников переносить знания в новую нестандартную ситуацию. Книга Колесниковой С. И. дает такую возможность. Рекомендую для работы репетитора с учащимися с высоким уровнем подготовки.
5. Вольфсон Б. И. Геометрия. Подготовка к ЕГЭ и ГИА-9. Учимся решать задачи и повторяем теорию. 2013 год.
Учимся решать задачи и повторяем теорию. 2013 год.
Не секрет, что наибольшее затруднение обучающиеся испытывают при решении геометрических задач. Данное пособие в доступной форме предлагает технологию обучения решения задач.
Переплет мягкий, бумага серая, иллюстрации черно-белые.
Второе, существенно переработанное издание книги соответствует измененной структуре и содержанию ЕГЭ по математике. Каждый технологический шаг иллюстрирован решениями задач из открытого банка заданий ФИПИ. Проведен анализ геометрических заданий ОГЭ И ЕГЭ. Есть справочный материал, задания для самостоятельной работы. В конце книги приведены ответы без комментариев.
Книга полезна не только учащимся, но и педагогам. Предложенную технологию работы с геометрическими задачами можно реализовать на уроках, начиная с 8 класса. Она позволяет снять страх перед задачами из геометрии, сформировать навыки анализа данных и составления плана решения задачи.
Книгу Вольфсон Б. И. открыла для себя только в этом учебном году, но предполагаю, что углубленная работа над ее содержанием позволит повысить школьникам баллы за счет решения задач № 14 и № 16 с развернутым решением.
В этой статье мы даем обзор учебных пособий для подготовки к ЕГЭ по математике. Начнем с традиционных “бумажных” учебников, а потом расскажем о полезных сайтах, потому что большинство школьников готовится к ЕГЭ именно в интернете.
Как выбрать учебник для подготовки к ЕГЭ по математике? Ясно, что это не школьный учебник: в большинстве из них нет даже слова “ЕГЭ”. Ясно, что учебник должен охватывать все темы ЕГЭ по математике, должен быть написан простым и понятным языком, и хорошо, когда в нем есть и необходимая теория, и справочник, и задачи.
Например, книга Анны Малковой “Математика. Авторский курс подготовки к ЕГЭ”. Это учебное пособие для подготовки к ЕГЭ по всем темам, начиная от простых задач первой части до самых сложных — задач с параметрами и задач на числа и их свойства. Книга написана так, что понять ее может даже двоечник, и при этом все темы рассказаны на необходимом уровне математической культуры.
Теперь нужны варианты для тренировки. Можно пользоваться сборниками вариантов под редакцией И. В. Ященко. При этом надо знать, что такие сборники бывают плохие, хорошие и нормальные. Плохой: сборник “50 тренировочных вариантов”. Там собрано одно старье, причем одни и те же задачи повторяются с разными числами. Но нам это не нужно.
В. Ященко. При этом надо знать, что такие сборники бывают плохие, хорошие и нормальные. Плохой: сборник “50 тренировочных вариантов”. Там собрано одно старье, причем одни и те же задачи повторяются с разными числами. Но нам это не нужно.
Хороший сборник — “36 тренировочных вариантов”. Как правило, в таких сборниках дают свежие варианты, то, что реально было последние 2-3 года на экзаменах и даже то, что может попасться в этом году. Минус: некоторые темы второй части там пропущены.
Поскольку под редакцией И. В. Ященко выпущено очень много сборников, задачи в них повторяются. У него вот скудность выбора. Одна книжка, там маленький выбор. Чтобы расширить выбор, берем сборники под редакцией Ф. Ф. Лысенко. Заметим, что задания из сборников под редакцией Ф. Ф. Лысенко часто оказываются теми, которые позже дают на ЕГЭ по математике. Мы наблюдаем эту статистику уже два года.
Можем также посоветовать:
Учебные пособия В.В. Кочагина и М. Н. Кочагиной по стереометрии (часть 2),
Сборники Р. К. Гордина по геометрии (часть 2),
К. Гордина по геометрии (часть 2),
Сборники задач А. Г. Корянова и А. А. Прокофьева — по алгебре, решению неравенств, задачам с параметрами.
Теперь — о сайтах для подготовки к ЕГЭ по математике.
Начнем с официального сайта ФИПИ. Все новые задачи, которые собираются включить в программу ЕГЭ, появляются на этом сайте. И это единственный плюс официального сайта. Минусов намного больше: нет ответов, нет навигации, все задания — по разным темам, разной сложности — свалены в кучу, разобраться в которой почти невозможно.
Есть сайт «Решу ЕГЭ», где можно тренироваться и сразу проверять себя. Вы можете в тестовом режиме посмотреть, сколько вы баллов набрали, проверить ответы и посмотреть варианты решений. Это прекрасно. Единственное — не всегда вовремя появляются новые задания.
Безусловно, для подготовки к ЕГЭ мы используем сайт Ларина. С прошлого года Александр Ларин стал разработчиком вариантов ЕГЭ. И поэтому его тренировочные варианты будут очень ценными для тех, кто сдает ЕГЭ по математике на высокие баллы.
Сайт / — на котором вы находитесь — это практически не только сайт, а печатное издание, сайт-библиотека. Здесь можно не просто порешать задачи, но и изучать необходимую теорию, причем в сжатом виде. Есть полный курс подготовки к ЕГЭ по математике и задачи по всем темам ЕГЭ. Есть также полные курсы подготовки по другим предметам.
В этом смысле хорош также сайт Инны Фельдман. Есть сайт Игоря Яковлева для продвинутых ребят, которые хотят сдать ЕГЭ очень хорошо или подготовиться к олимпиадам. На этом сайте собрана база заданий различных олимпиад.
Эти сайты тоже можно считать учебными пособиями для подготовки к ЕГЭ по математике.
3-е изд. — М.: 2017. — 544 с. М.: 2016. — 544 с.
В справочнике, адресованном выпускникам
средней школы и абитуриентам, в полном объёме дан материал курса
«Обществознание», который проверятся на едином государственном
экзамене. Структура книги соответствует современному кодификатору
элементов содержания по предмету, на основе которого составлены
экзаменационные задания — контрольно-измерительные материалы ЕГЭ (КИМы). В справочнике представлены блоки-модули «Человек и общество»,
«Экономика», «Социальные отношения», «Политика», «Право»,
составляющие основу школьного курса «Обществознание». Краткая и
наглядная — в виде схем и таблиц — форма изложения обеспечивает
максимальную эффективность подготовки к экзамену. Образцы заданий и
ответы к ним, завершающие каждую тему, помогут объективно оценить
уровень знаний, умений и навыков.
В справочнике представлены блоки-модули «Человек и общество»,
«Экономика», «Социальные отношения», «Политика», «Право»,
составляющие основу школьного курса «Обществознание». Краткая и
наглядная — в виде схем и таблиц — форма изложения обеспечивает
максимальную эффективность подготовки к экзамену. Образцы заданий и
ответы к ним, завершающие каждую тему, помогут объективно оценить
уровень знаний, умений и навыков.
Формат: pdf ( 2017 , 3-е изд., 544с.)
Размер: 2,6 Мб
Смотреть, скачать: drive.google
Формат: pdf ( 2016 , 544с.; белый)
Размер: 8 Мб
Смотреть, скачать: drive.google
Формат: pdf (2016 , 544с.; синий)
Размер: 8,1 Мб
Смотреть, скачать: drive.google
СОДЕРЖАНИЕ
Предисловие 6
БЛОК-МОДУЛЬ 1. ЧЕЛОВЕК И ОБЩЕСТВО
Тема 1.1. Природное и общественное в человеке. (Человек как результат
биологической и социокультурной эволюции) 12
Тема 1. 2. Мировоззрение, его виды и формы 17
2. Мировоззрение, его виды и формы 17
Тема 1.3. Виды знаний 20
Тема 1.4. Понятие истины, её критерии 26
Тема 1.5. Мышление и деятельность 30
Тема 1.6. Потребности и интересы 41
Тема 1.7. Свобода и необходимость в человеческой деятельности. Свобода и
ответственность 45
Тема 1.8. Системное строение общества: элементы и подсистемы 50
Тема 1.9. Основные институты общества 55
Тема 1.10. Понятие культуры. Формы и разновидности культуры 58
Тема 1.11. Наука. Основные особенности научного мышления. Естественные и
социально-гуманитарные науки 65
Тема 1.12. Образование, его значимость для личности и общества 78
Тема 1.13. Религия 81
Тема 1.14. Искусство 89
Тема 1.15. Мораль 95
Тема 1.16. Понятие общественного прогресса 101
Тема 1.17. Многовариантность общественного развития (типы обществ) 106
Тема 1.18. Угрозы XXI века (глобальные проблемы) 109
БЛОК-МОДУЛЬ 2. ЭКОНОМИКА
Тема 2.1. Экономика и экономическая наука 116
Тема 2.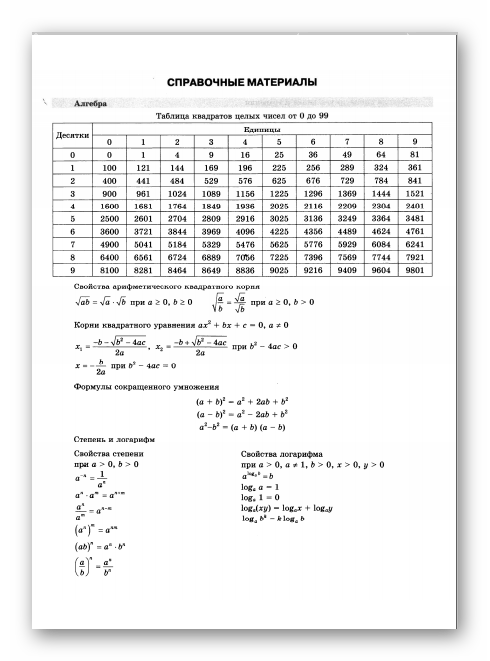 2. Факторы производства и факторные доходы 122
2. Факторы производства и факторные доходы 122
Тема 2.3. Экономические системы 126
Тема 2.4. Рынок и рыночный механизм. Спрос и предложение 134
Тема 2.5. Постоянные и переменные затраты 145
Тема 2.6. Финансовые институты. Банковская система 147
Тема 2.7. Основные источники финансирования бизнеса 154
Тема 2.8. Ценные бумаги 160
Тема 2.9. Рынок труда. Безработица 163
Тема 2.10. Виды, причины и последствия инфляции 173
Тема 2.11. Экономический рост и развитие. Понятие ВВП 177
Тема 2.12. Роль государства в экономике 184
Тема 2.13. Налоги 191
Тема 2.14. Государственный бюджет 195
Тема 2.15. Мировая экономика 202
Тема 2.16. Рациональное экономическое поведение собственника, работника,
потребителя, семьянина, гражданина 210
БЛОК-МОДУЛЬ 3. СОЦИАЛЬНЫЕ ОТНОШЕНИЯ
Тема 3.1. Социальная стратификация и мобильность 216
Тема 3.2. Социальные группы 227
Тема 3.3. Молодёжь как социальная группа 232
Тема 3.4. Этнические общности 235
Тема 3. 5. Межнациональные отношения, этносоциальные конфликты, пути их
разрешения 240
5. Межнациональные отношения, этносоциальные конфликты, пути их
разрешения 240
Тема 3.6. Конституционные принципы (основы) национальной политики в РФ 249
Тема 3.7. Социальный конфликт 252
Тема 3.8. Виды социальных норм 260
Тема 3.9. Социальный контроль 264
Тема 3.10. Семья и брак 267
Тема 3.11. Отклоняющееся поведение и его типы 272
Тема 3.12. Социальная роль 276
Тема 3.13. Социализация индивида 280
БЛОК-МОДУЛЬ 4. ПОЛИТИКА
Тема 4.1. Понятие власти 283
Тема 4.2. Государство, его функции 291
Тема 4.3. Политическая система 304
Тема 4.4. Типология политических режимов 307
Тема 4.5. Демократия, её основные ценности и признаки 310
Тема 4.6. Гражданское общество и государство 314
Тема 4.7. Политическая элита 323
Тема 4.8. Политические партии и движения 327
Тема 4.9. Средства массовой информации в политической системе 336
Тема 4.10. Избирательная кампания в РФ 342
Тема 4.11. Политический процесс 351
Тема 4. 12. Политическое участие 355
12. Политическое участие 355
Тема 4.13. Политическое лидерство 360
Тема 4.14. Органы государственной власти РФ 364
Тема 4.15. Федеративное устройство России 374
БЛОК-МОДУЛЬ 5. ПРАВО
Тема 5.1. Право в системе социальных норм 381
Тема 5.2. Система российского права. Законотворческий процесс в РФ 395
Тема 5.3. Понятие и виды юридической ответственности 401
Тема 5.4. Конституция Российской Федерации. Основы конституционного строя РФ 409
Тема 5.5. Законодательство РФ о выборах 417
Тема 5.6. Субъекты гражданского права 421
Тема 5.7. Организационно-правовые формы и правовой режим предпринимательской
деятельности 428
Тема 5.8. Имущественные и неимущественные права 433
Тема 5.9. Порядок приёма на работу. Порядок заключения и расторжения трудового
договора 440
Тема 5.10. Правовое регулирование отношений супругов. Порядок и условия
заключения и расторжения брака 448
Тема 5.11. Особенности административной юрисдикции 453
Тема 5. 12. Право на благоприятную окружающую среду и способы его защиты 460
12. Право на благоприятную окружающую среду и способы его защиты 460
Тема 5.13. Международное право (международная защита прав человека в условиях
мирного и военного времени) 468
Тема 5.14. Споры, порядок их рассмотрения 473
Тема 5.15. Основные правила и принципы гражданского процесса 476
Тема 5.16. Особенности уголовного процесса 484
Тема 5.17. Гражданство РФ 495
Тема 5.18. Воинская обязанность, альтернативная гражданская служба 501
Тема 5.19. Права и обязанности налогоплательщика 509
Тема 5.20. Правоохранительные органы. Судебная система 513
Тренировочный вариант экзаменационной работы по обществознанию 523
Система оценивания экзаменационной работы по обществознанию 536
Литература 540
Справочник включает материал школьного курса «Обществознание», который
проверяется на едином государственном экзамене (ЕГЭ). Структура книги
соответствует Федеральному государственному стандарту среднего (полного)
образования по предмету, на основе которого разработаны экзаменационные задания
— контрольные измерительные материалы (КИМ), составляющие экзаменационную работу
по обществознанию.
В справочнике представлены следующие содержательные блоки-модули: «Человек и
общество», «Экономика», «Социальные отношения», «Политика», «Право», которые
образуют ядро содержания школьного обществоведческого образования и
соответствуют кодификатору элементов содержания по обществознанию, проверяемых в
рамках ЕГЭ.
Я успела окончить школу еще до той поры, когда вводили ЕГЭ. Конечно, противников подобной системы экзаменов гораздо больше, чем сторонников, но это уже наша с вами реальность, с которой гораздо легче мириться, чем ей противостоять.
ЕГЭ по английскому языку — непростой экзамен. В 2017 году поступить в хороший ВУЗ с базовым уровнем сдачи экзамена по английскому языку вряд ли получится. Чтобы получить высокий балл, нужно начинать подготовку к экзамену как можно раньше.
Как мы знаем, письменная часть состоит из 40 заданий, на которые ученикам выделяется 3 часа, и включает в себя:
- тест-аудирование;
- тест-чтение;
- лексико-грамматические задания, также в форме теста;
- письмо, состоящее из двух этапов.

Стоит сказать, что за первую часть экзамена по английскому языку максимально дают 80 баллов, если ученику необходимо повысить балл, то он обязан прийти на второй день для сдачи устной части.
Если письменную часть можно понатаскать, занимаясь самостоятельно по всевозможным пособиям, то вот для устной части нужен педагог.
Данный пост будет посвящен наиболее удачным учебным пособиям для подготовки к ЕГЭ по английскому языку самостоятельно.
1. Macmillan Exam Skills for Russia
Это единственная на сегодняшний день книга для подготовки к ЕГЭ, которая состоит из 15 полных тестов в новом формате ЕГЭ, включая устную часть. При работе над тестами были учтены все изменения в формате экзамена. Тесты созданы в сотрудничестве с М.В. Вербицкой, председателем предметной комиссии по иностранным языкам ЕГЭ. На сайте Macmillan.ru представлены дополнительные материалы по ЕГЭ для учащихся и учителей: онлайн-тесты, аудиофайлы , видеосоветы и т.д.
2. А.И. Немыкина, А.
 В. Почепаева — ЕГЭ. Устная часть
В. Почепаева — ЕГЭ. Устная часть
Пособие представляет собой сборник тестов для проверки навыков устной речи, а также тренажер для отработки навыков сдачи устной части ЕГЭ по английскому языку на компьютере. Именно с этого учебника стоит начинать подготовку к устной части, если вы занимаетесь самостоятельно. В начале дается полный разбор заданий устной части, а потом 20 тестов с пояснительными материалами.
3. Афанасьева О., Эванс В., Копылова В. — Practice Exam Papers for the Russian National ExamДанное учебное пособие с аудиоприложением содержит 20 вариантов тестов по английскому языку в формате ЕГЭ.
Отличительными чертами учебника являются вариативные задания, соответствующие повышенному и высокому уровням подготовки к ЕГЭ, а также разнообразные по жанрам тексты для аудирования и чтения. Следует отметить и замечательные образцы выполнения заданий по всем видам речевой деятельности.
Скачайте пособие 2010 года по этой ссылке .
Учебники 2007 года вместе с аудио доступны .
4. Музланова Е.С. — Английский язык. ЕГЭ-учебник
Пособие составлено по тематическому принципу и состоит из 16 тематических блоков, которые охватывают весь спектр тем, предусмотренных кодификатором ЕГЭ по английскому языку. Блоки состоят из 5 разделов: чтение, аудирование, говорение, грамматика и лексика, письмо. В каждый раздел включены задания экзаменационного типа, а также полезные советы по их выполнению, что позволит учащимся успешно подготовиться к экзамену. После выполнения всех заданий учащиеся смогут сверить ответы с ключами.
5. Вербицкая М.В. — ЕГЭ. Английский язык. Типовые экзаменационные варианты. 10 (30) вариантовДанный учебник входит в известную всем выпускникам серию «ЕГЭ. ФИПИ — школе», которая подготовлена разработчиками контрольных измерительных материалов единого госэкзамена. Выпускается в 2 видах: 10 вариантов тестов и 30 вариантов. Разница, как вы понимаете, только в количестве тестов. В сборнике из 30 тестов представлены 15 тематических вариантов по всем разделам ЕГЭ, 15 типовых экзаменационных вариантов, задания устной части, инструкции по выполнению, ответы ко всем заданиям и др.
Скачать учебник образца 2015 года с 30 вариантами можно .
6. Юнёва С.А. — Открывая мир с английским языком. 150 эссе для ЕГЭ. Готовимся к ЕГЭПособие адресовано учащимся, самостоятельно готовящимся к ЕГЭ по английскому языку, а так же учителям, которые могут использовать его на занятиях в классе и при подготовке учащихся к зачету, экзамену или олимпиаде. Оно включает в себя 150 эссе, составленных в соответствии со всеми требованиями, предъявляемыми к письменному высказыванию с элементами рассуждения. Основная цель данного пособия состоит в том, чтобы помочь учащимся блестяще справиться с написанием эссе.
|
Итак Вам необходимо пройти вступительный тест…. Много раз студенты (или
будущие студенты) спросили меня, что им нужно делать, чтобы учиться
для предстоящего вступительного теста, потому что они хотят «сдать». Цель размещения тест, чтобы определить, как много вы знаете и насколько хорошо вы это знаете. Там не является «сдачей» или «не сдачей» вступительного теста. Вступительный тест служит только для того, чтобы «поместить» вас в один математический класс. или другой. Он не пытается судить, насколько «умный» или «тупой» Вы; он не пытается сказать, сколько вы можете сделать в будущее; он только судит, основываясь на опыте тех, кто пишет тест, какой урок математики лучше всего соответствует вашим образовательным потребностям прямо сейчас . Тест размещения не работает
не пытайтесь «оценивать» свои знания; вместо этого он пытается определить
каковы ваши текущие знания. Может быть, прошло двадцать лет с тех пор, как вы
окончил среднюю школу. Может быть, вы хорошо разбираетесь в дробях и процентах,
но забыл про «ту штуку с переменными». Нет «прохождения» или «не сдал» вступительный тест; есть только «размещение». В качестве иллюстрации,
Несколько лет назад мне было интересно, на каком уровне читает мой сын, обучающийся на дому.
Я нашел веб-сайт, на котором был тест на чтение, состоящий из длинного
список групп слов. Таким же образом размещение
Тест измеряет не интеллект и не способности, а опыт. И там
в отсутствии опыта нет ничего постыдного, но притворяться, что
опыт, которого у вас на самом деле нет. Если вы попытаетесь «втиснуть»
на вступительный тест и как-то справиться (с помощью удачных догадок на
вопросы с несколькими вариантами ответов, например), чтобы «обмануть» тест
в «оценку» вас, это может привести к тому, что вы будете помещены
на уроке математики, к которому вы должным образом не подготовлены. Я прошел вступительный тест
когда я вернулся в колледж. Прошло несколько лет со школы,
и мое образование было не совсем блестящим, поэтому я решил, что буду
мне нужно возобновить занятия по какому-нибудь более низкоуровневому математическому курсу.Я читаю
описания различных курсов в каталоге. Некоторые из курсов
описал вещи, которые я знал, как делать (поэтому я, вероятно, мог бы пропустить те
курсов), а в описаниях некоторых других курсов использовались слова, которых я даже не знал.
признать (поэтому я, вероятно, не был готов к ним). Но был один курс
в середине, где я вспомнил некоторые вещи из средней школы и
не знал остальных вещей. Когда я занял место test, он состоял из двух частей: исчисления и неисчисления. я даже не пытался ответить на вопросы по расчетной части. я сделал все, что мог, с другой стороны, основываясь на опыте, который у меня был и материал, который я мог вспомнить. И вступительный тест поставил меня правильно в классе, в котором я ожидал начать. В первой половине этого курса Мне было скучно до слез.Затем, примерно на полпути, инструктор подошел к материал, который я никогда раньше не видел, и класс начал становиться интересным. В каком-то смысле можно сказать
что я завалил тест на размещение , , потому что я не мог даже попытаться вычислить половину из него. Но я прошел
размещение обрабатывает с честью,
потому что я честно предоставил информацию, которая нужна тесту в
для того, чтобы правильно поставить меня на лучший курс для моих способностей на тот момент времени . Вы не хотите получать застряли на курсе, который слишком продвинут для вас, и в конечном итоге Ваша голова против стены, провалив один и тот же курс снова и снова и снова снова.Вы хотите начать курс, который подходит именно вам. Так что не постарайтесь «зубрить» или подготовиться к вступительному тесту; не пытайся обмануть тест или «пройти» его. Если вы хотите сделать небольшой обзор освежить то, что вы уже знаете, это здорово. Но самое лучшее вы можете просто расслабиться, сделать все возможное и позволить вступительному тесту сделать его работа. Если вы хотите уделить время изучению материала, включенного в вступительный тест, вы можете попробовать пройти онлайн-курсы, например, предлагаемые MathHelp. Аккумулятор, ACT, ASVAB, CBEST, CHSPE, CLEP, FTCE, GED, GRE, MTEL, NES, PERT, Praxis, TSI, VPT Эти курсы научат вас материалу. Это хороший вариант, если (1) вам просто нужно переподготовку или (2) у вас есть хотя бы несколько недель (или месяцев) для интенсивного обучения перед поступлением в предполагаемое учебное заведение. Верх | Вернуться к индексу
|
|
Этот урок можно распечатать для личного пользования.
|
Бюллетень бакалавриата Stony Brook — весна 2022 г. BulletinMAT
МАТ 118: математическое мышление
Развитие количественного мышления и способности решать проблемы посредством выбора математических тем: логика и рассуждение; числа, функции и моделирование; комбинаторика и вероятность; рост и изменение.Другие темы могут включать геометрию, статистику, теорию игр и теорию графов. Благодаря участию в решении задач учащиеся развивают понимание интеллектуальных возможностей математики и ее связей с другими дисциплинами.
Необходимое условие: C или выше по MAP 103 или уровень 2+ или выше на вступительном экзамене по математике
(Условие должно быть выполнено в течение одного года с начала этого курса.)
DEC: CSBC: число запросов в секунду
3 кредита
MAT 119: основы предварительного исчисления
Этот курс является дополнением к MAT 123: Предварительное исчисление и обеспечивает структурированную среду, в которой учащиеся могут освежить навыки алгебры, необходимые для успеха в предварительном исчислении. Эти темы включают понимание показателей (особенно дробных и отрицательных показателей), манипулирование математическими выражениями, решение уравнений и моделирование/словные задачи.Курс нельзя пройти с CHE 129.
Эти темы включают понимание показателей (особенно дробных и отрицательных показателей), манипулирование математическими выражениями, решение уравнений и моделирование/словные задачи.Курс нельзя пройти с CHE 129.
Необходимое условие: 2+ при размещении или разрешении инструктора МАТ 123
Соответствие: MAT 123
1 кредит, оценка S/U
MAT 122: обзор исчисления с приложениями
Основы математического анализа в автономном односеместровом курсе.Свойства и приложения полиномиальных, экспоненциальных и логарифмических функций. Производные: наклоны, скорость изменения, оптимизация, интегралы, площадь, кумулятивное изменение и среднее значение. Основная теорема исчисления. Акцент на моделировании примеров из экономики. Учащиеся, которые впоследствии захотят поступить на MAT 125 или 131, должны будут набрать 4 балла на вступительном экзамене по математике, прежде чем приступить к любому курсу. Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA).Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA).Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше по MAP 103 или уровень 3 на вступительном экзамене по математике
(Условие должно быть выполнено в течение одного года до начала курса.)
DEC: CSBC: число запросов в секунду
3 кредита
MAT 123: предварительный расчет
Комплексная подготовка к последовательностям регулярного исчисления.Тщательная разработка рациональных, экспоненциальных, логарифмических и тригонометрических функций и их приложений. Асимптотика и построение кривых. Общие примеры моделирования. Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше по MAP 103 или уровень 3 на вступительном экзамене по математике или соответствующему MAT 119 (предварительные требования должны быть выполнены в течение одного года до начала курса.)
DEC: CSBC: число запросов в секунду
3 кредита
MAT 125: Исчисление A
Дифференциальное исчисление, уделяющее особое внимание концептуальному пониманию, вычислениям и приложениям, для учащихся, имеющих необходимую подготовку по математике 12-го класса средней школы. Пределы и непрерывные функции.Дифференцирование элементарных алгебраических, тригонометрических, показательных и логарифмических функций; графическое изображение; моделирование; и максимизация. Правило Лопиталя. Не допускается зачет в дополнение к MAT 131, 141 или AMS 151. Этот курс был обозначен как курс с высоким спросом/контролируемым доступом (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Правило Лопиталя. Не допускается зачет в дополнение к MAT 131, 141 или AMS 151. Этот курс был обозначен как курс с высоким спросом/контролируемым доступом (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше в MAT 123; или уровень 4 на вступительном экзамене по математике; или соответствующий MAT 130
DEC: CSBC: число запросов в секунду
3 кредита
MAT 126: Исчисление B
Продолжение MAT 125, охватывающее интегральное исчисление: суммы Римана, фундаментальная теорема, символические и числовые методы интегрирования, площадь под кривой, объем, приложения, такие как работа и вероятность, несобственные интегралы.Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше по MAT 125, или 131, или 141, или AMS 151, или уровень 6 на вступительном экзамене по математике
DEC: CSBC: число запросов в секунду
3 кредита
MAT 127: Исчисление C
Продолжение MAT 126, охватывающее: последовательности, ряды, ряды Тейлора, дифференциальные уравнения и моделирование.Не может быть зачтено в дополнение к MAT 132, MAT 142, MAT 171 или AMS 161. Этот курс был обозначен как курс с высоким спросом / контролируемым доступом (HD / CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше по MAT 126 или уровень 8 на вступительном экзамене по математике
DEC: CSBC: число запросов в секунду
3 кредита
MAT 130: тригонометрия и логарифмы
Обратные функции, экспоненциальные и логарифмические функции, радианная мера углов и тригонометрические функции. Преподается как компаньон к МАТ 125.
Преподается как компаньон к МАТ 125.
Необходимое условие: MAT 122 с оценкой C или выше, или уровнем 3+ или выше на вступительном экзамене, или разрешением инструктора
Дополнительный реквизит: MAT 125
1 кредит, оценка S/U
МАТ 131: Исчисление I
Дифференциальное и интегральное исчисление с упором на концептуальное понимание, вычисления и приложения для учащихся, имеющих необходимые знания по математике 12-го класса средней школы.Дифференциация элементарной алгебраической; тригонометрические, экспоненциальные и логарифмические функции; графическое изображение; моделирование и максимизация; правило Лопиталя; интеграл Римана; и Основная теорема исчисления. Не допускается зачет в дополнение к MAT 125, 141 или AMS 151. Этот курс был обозначен как курс с высоким спросом/контролируемым доступом (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: B или выше по MAT 123 или уровень 5 на вступительном экзамене по математике
DEC: CSBC: число запросов в секунду
4 кредита
МАТ 132: Исчисление II
Продолжение MAT 131, охватывающее символьные и числовые методы интегрирования; площадь под кривой; объем; приложения, такие как работа и вероятность; последовательности; ряд; ряд Тейлора; дифференциальные уравнения; и моделирование.Не может быть зачтено в дополнение к MAT 127, MAT 142, MAT 171 или AMS 161. Этот курс был обозначен как курс с высоким спросом / контролируемым доступом (HD / CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше по AMS 151 или MAT 131 или 141, или уровень 7 на вступительном экзамене по математике
DEC: CSBC: число запросов в секунду
4 кредита
МАТ 141: Анализ I
Тщательное изучение теории, лежащей в основе исчисления.Развитие системы действительных чисел, пределы и бесконечные последовательности, функции одной действительной переменной, непрерывность, дифференцируемость, интеграл Римана и основная теорема исчисления. Все внимание уделяется доказательствам. Включены все темы MAT131, хотя представление значительно отличается. Не может быть засчитан в дополнение к MAT 125, MAT 131 или AMS 151. Учащийся, успешно завершивший оба MAT 141 и MAT 142, получит эквивалент MAT 320. Этот курс был обозначен как High Demand/Controlled Access (HD). /CA) курс.Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Этот курс был обозначен как High Demand/Controlled Access (HD). /CA) курс.Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: Уровень 5 на вступительном экзамене по математике; приоритет отдается студентам университетских программ с отличием
DEC: CSBC: число запросов в секунду
4 кредита
MAT 142: Анализ II
Продолжение МАТ 141 в том же духе, включая темы МАТ 132, но с акцентом на теорию и включая доказательства основных теорем: методы и приложения интегрирования, бесконечные ряды, ряды Тейлора, моделирование и элементарные дифференциальные уравнения.Учащийся, успешно завершивший как MAT 141, так и MAT 142, получит освобождение от требований к MAT 320. Не может быть засчитан в дополнение к MAT 127, MAT 171 или AMS 161. Этот курс был определен как курс с высоким спросом/контролируемым доступом. (HD/CA) курс. Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Не может быть засчитан в дополнение к MAT 127, MAT 171 или AMS 161. Этот курс был определен как курс с высоким спросом/контролируемым доступом. (HD/CA) курс. Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.
Необходимое условие: C или выше в MAT 141 или разрешение Advanced Track Committee
СБК: число запросов в секунду4 кредита
MAT 171: ускоренное вычисление одной переменной
Один семестр, курс с отличием, который повторяет материал MAT 131 в течение нескольких недель, затем концентрируется на темах, затронутых в MAT 132, с дополнительным вниманием, уделяемым основной теории.В первую очередь предназначен для учащихся, которые изучали исчисление в средней школе. Не может быть засчитан в дополнение к MAT 126, MAT 127, MAT 132, MAT 142 или AMS 161.
Предпосылки: Уровень 5 на экзамене AB Calculus AP, Уровень 3 на экзамене BC Calculus, A или A- в MAT 131 или AMS 151, MAT 141 или уровень 7 на вступительном экзамене по математике. Приоритет отдается студентам в программах с отличием университета.
DEC: CSBC: число запросов в секунду
4 кредита
MAT 200: Логика, язык и доказательство
Базовый курс логики математики, построение доказательств и написание доказательств.Математическое содержание — это прежде всего логика и доказательства, теория множеств, комбинаторика, функции и отношения. Значительное внимание уделяется писательству. Не может быть принято в кредит в дополнение к MAT 250.
Необходимое условие: Уровень 4 на вступительном экзамене по математике или эквивалентном курсе или разрешение преподавателя
СБК: STEM+3 кредита
MAT 203: Исчисление III с приложениями
Векторная алгебра в двух и трех измерениях, многомерное дифференциальное и интегральное исчисление, оптимизация, векторное исчисление, включая теоремы Грина, Гаусса и Стокса. Приложения к экономике, технике и всем наукам с упором на численные и графические решения; использование графических калькуляторов или компьютеров. Не может быть принято в кредит помимо AMS 261.
Приложения к экономике, технике и всем наукам с упором на численные и графические решения; использование графических калькуляторов или компьютеров. Не может быть принято в кредит помимо AMS 261.
Необходимое условие: C или выше по MAT 127, или 132, или 142, или AMS 161, или уровень 9 на вступительном экзамене по математике
СБК: STEM+4 кредита
MAT 211: Введение в линейную алгебру
Введение в теорию линейной алгебры с некоторыми приложениями; векторы, векторные пространства, базисы и размерность, приложения к геометрии, линейные преобразования и ранги, собственные значения и собственные векторы, определители и скалярные произведения.Не могут быть приняты в кредит помимо АМС 210.
Необходимое условие: C или выше в AMS 151 или MAT 131 или 141 или совместная регистрация в MAT 126 или уровень 7 на вступительном экзамене по математике
СБК: STEM+3 кредита
MAT 220: линейная алгебра и геометрия
Векторы и векторная алгебра. Скалярное произведение. Перекрестное произведение и тройное произведение. Аналитическая геометрия. Векторные уравнения прямых и плоскостей. Кривые и поверхности второй степени. Комплексные числа. Линейные пространства и линейные отображения. Матрицы, системы линейных уравнений. Изоморфизмы векторных пространств, базисы и размерность. MAT 220 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 211 и не может приниматься в расчет в дополнение к MAT 211.
Скалярное произведение. Перекрестное произведение и тройное произведение. Аналитическая геометрия. Векторные уравнения прямых и плоскостей. Кривые и поверхности второй степени. Комплексные числа. Линейные пространства и линейные отображения. Матрицы, системы линейных уравнений. Изоморфизмы векторных пространств, базисы и размерность. MAT 220 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 211 и не может приниматься в расчет в дополнение к MAT 211.
Необходимое условие: MAT 131 или эквивалентный курс или уровень 7 или выше на вступительном экзамене по математике или разрешение Advanced Track Committee
Соответствие: MAT 250
СБК: STEM+3 кредита
MAT 250: Введение в продвинутую математику
Введение в программу Advanced Track по математике. Обеспечивает основу основ логики высказываний, кванторов, доказательств, множеств, функций, мощности, отношений, отношений эквивалентности и частных множеств, отношений порядка, комбинаторики. Системы счисления: натуральные числа, целые числа, рациональные, действительные и комплексные числа.
MAT 250 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 200 и не может учитываться в дополнение к MAT 200. Ранее предлагался как MAT 150; не в кредит в дополнение к MAT 150.
Обеспечивает основу основ логики высказываний, кванторов, доказательств, множеств, функций, мощности, отношений, отношений эквивалентности и частных множеств, отношений порядка, комбинаторики. Системы счисления: натуральные числа, целые числа, рациональные, действительные и комплексные числа.
MAT 250 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 200 и не может учитываться в дополнение к MAT 200. Ранее предлагался как MAT 150; не в кредит в дополнение к MAT 150.
Необходимое условие: MAT 131 или эквивалентный курс, или уровень 7 или выше на вступительном экзамене по математике или с разрешения Advanced Track Committee.
СБК: число запросов в секунду4 кредита
MAT 260: Решение задач по математике
Учащиеся активно решают сложные задачи по плоской геометрии, основам теории чисел и математическому анализу и пишут точные аргументы. В ходе курса проводится соответствующая подготовка к решению задач.
В ходе курса проводится соответствующая подготовка к решению задач.
Необходимое условие: Разрешение инструктора
1 кредит
MAT 303: Исчисление IV с приложениями
Однородные и неоднородные линейные дифференциальные уравнения; системы линейных дифференциальных уравнений; серийные решения; преобразования Лапласа; ряд Фурье.Приложения к экономике, технике и всем наукам с упором на численные и графические решения; использование компьютеров. Не может быть использовано для кредита в дополнение к AMS 361 или MAT 308.
Необходимое условие: C или выше по MAT 127, или 132, или 142, или AMS 161, или уровень 9 на вступительном экзамене по математике
СБК: STEM+4 кредита
MAT 307: многомерное исчисление с помощью линейной алгебры
Введение в линейную алгебру: векторы, матрицы, системы линейных уравнений, основания и размерность, скалярное произведение, определители. Многомерное дифференциальное и интегральное исчисление, дивергенция и ротор, линейные и поверхностные интегралы, теоремы Грина, Гаусса и Стокса. Более теоретический и интенсивный, чем MAT 203, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 308 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 203, MAT 211 и MAT 303. Не может быть зачтено в дополнение к MAT 203 или AMS 261.
Многомерное дифференциальное и интегральное исчисление, дивергенция и ротор, линейные и поверхностные интегралы, теоремы Грина, Гаусса и Стокса. Более теоретический и интенсивный, чем MAT 203, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 308 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 203, MAT 211 и MAT 303. Не может быть зачтено в дополнение к MAT 203 или AMS 261.
Необходимое условие: МАТ 127 или МАТ 132
СБК: STEM+4 кредита
MAT 308: дифференциальные уравнения с линейной алгеброй
Линейная алгебра: определители, собственные значения и собственные векторы, диагонализация.Дифференциальные уравнения; существование и единственность решений.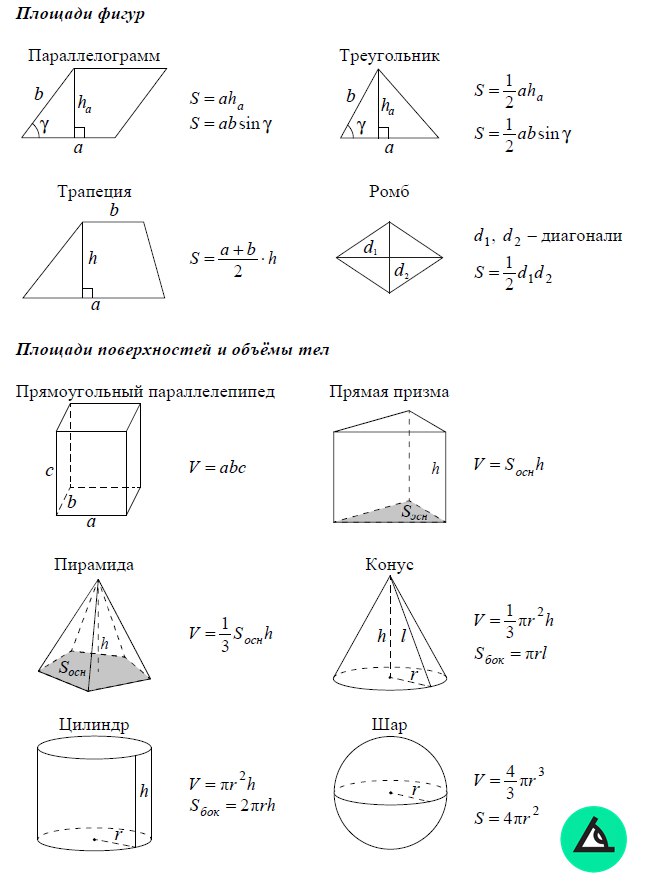 уравнения первого и второго порядка; линейные и нелинейные уравнения. Системы линейных уравнений. Преобразование Лапласа. Приложения к физике. Более теоретический и интенсивный, чем MAT 303, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 307 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 205, MAT 211 и MAT 305. Не может быть зачтено в дополнение к MAT 303 или AMS 361.
уравнения первого и второго порядка; линейные и нелинейные уравнения. Системы линейных уравнений. Преобразование Лапласа. Приложения к физике. Более теоретический и интенсивный, чем MAT 303, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 307 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 205, MAT 211 и MAT 305. Не может быть зачтено в дополнение к MAT 303 или AMS 361.
Необходимое условие: МАТ 307; или МАТ 203 и МАТ 211; или МАТ 132 и МАТ 220; или разрешение инструктора
СБК: STEM+4 кредита
MAT 310: линейная алгебра
Конечномерные векторные пространства, линейные отображения, двойственные пространства, билинейные функции, скалярные произведения. Дополнительные темы, такие как канонические формы, полилинейная алгебра, численная линейная алгебра.
Дополнительные темы, такие как канонические формы, полилинейная алгебра, численная линейная алгебра.
Необходимое условие: C или выше в MAT 211 или 308 или AMS 210 или MAT 220; C или выше по MAT 200 или MAT 250 или разрешение инструктора
4 кредита
МАТ 311: Теория чисел
Сравнения, квадратичные вычеты, квадратичные формы, цепные дроби, диофантовы уравнения, теоретико-числовые функции и свойства простых чисел.
Предпосылки: C или выше в MAT 312 или 313; C или выше по MAT 200 или MAT 250 или разрешение инструктора
3 кредита
MAT 312: Прикладная алгебра
Разделы по алгебре: группы, неформальная теория множеств, отношения, гомоморфизмы. Приложения: коды с исправлением ошибок, теорема Бернсайда, вычислительная сложность, китайская теорема об остатках.Этот курс предлагается как AMS 351, так и MAT 312.
Приложения: коды с исправлением ошибок, теорема Бернсайда, вычислительная сложность, китайская теорема об остатках.Этот курс предлагается как AMS 351, так и MAT 312.
Необходимое условие: C или выше в AMS 210 или MAT 211 или MAT 220
Консультативное требование: MAT 200, или CSE 215, или CSE 150, или эквивалент
3 кредита
MAT 313: Абстрактная алгебра
Группы и кольца вместе с их гомоморфизмами и фактор-структурами.Уникальная факторизация, многочлены и поля.
Необходимое условие: C или выше в MAT 310 или MAT 312 или MAT 315; C или выше по MAT 200 или MAT 250 или разрешение инструктора
3 кредита
MAT 314: Абстрактная алгебра II
Этот курс является продолжением MAT 313, Абстрактная алгебра. Он охватывает модули над кольцами, включая структурную теорему для модулей над PID, теорию полей и расширений полей, а также введение в теорию Галуа.
Он охватывает модули над кольцами, включая структурную теорему для модулей над PID, теорию полей и расширений полей, а также введение в теорию Галуа.
Необходимое условие: МАТ 313 или разрешение инструктора
3 кредита
MAT 315: расширенная линейная алгебра
Конечномерные векторные пространства над полем, линейные отображения, изоморфизмы, двойственные пространства, фактор-векторные пространства, билинейные и квадратичные функции, скалярные произведения, канонические формы линейных операторов, полилинейная алгебра, тензоры.Этот курс служит альтернативой MAT 310. Это интенсивный курс, в первую очередь предназначенный для математических специальностей в программе Advanced Track.
Необходимое условие: B или выше по MAT 200 или MAT 250, и B или выше по MAT 220, или разрешение инструктора
4 кредита
MAT 319: Основы анализа
Тщательное изучение теории, лежащей в основе тем в исчислении с одной переменной, с акцентом на те темы, которые возникают в старшей школе. Реальная система счисления. Пределы функций и последовательностей. Дифференциации, интегрирование и основная теорема. Бесконечная серия.
Реальная система счисления. Пределы функций и последовательностей. Дифференциации, интегрирование и основная теорема. Бесконечная серия.
Необходимое условие: C или выше по MAT 200 или MAT 250 или с разрешения инструктора; C или выше в одном из следующих: MAT 203, 211, 220, 307, AMS 261 или A- или выше в MAT 127, 132, 142 или AMS 161
4 кредита
MAT 320: Введение в анализ
Тщательное изучение теории, лежащей в основе исчисления.Реальная система счисления. Основные свойства функций одной действительной переменной. Дифференцирование, интегрирование и обратная теорема. Бесконечные последовательности функций и равномерная сходимость. Бесконечная серия. Метрические пространства и компактность. Этот курс представляет собой более сложную альтернативу MAT 319, подходящую для студентов, которым удобно работать со строгими доказательствами.
Необходимое условие: B или выше по MAT 200 или MAT 250 или разрешение инструктора; C или выше в одном из следующих: MAT 203, 211, 220, 307, AMS 261 или A- или выше в MAT 127, 132, 142 или AMS 161
4 кредита
MAT 322: анализ в нескольких измерениях
Непрерывность, дифференцирование и интегрирование в евклидовом n-пространстве.Дифференцируемые карты. Теоремы о неявной и обратной функциях. Дифференциальные формы и общая теорема Стокса.
Предпосылки: C или выше в MAT 203, MAT 220, MAT 307 или AMS 261; C или выше в MAT 310 или MAT 315; B или выше в MAT 320
3 кредита
MAT 324: реальный анализ
Введение в меру Лебега и интегрирование. Аспекты рядов Фурье, функциональных пространств, гильбертовых пространств, банаховых пространств.
Аспекты рядов Фурье, функциональных пространств, гильбертовых пространств, банаховых пространств.
Предпосылки: B или выше в MAT 320
3 кредита
MAT 331: Компьютерное решение математических задач
Исследование использования компьютера в качестве инструмента для понимания сложных математических задач посредством проектно-ориентированного подхода.Учащиеся изучают как соответствующие математические концепции, так и способы использования компьютера (а иногда и неправильного использования) для их понимания. Конкретные проблемы могут варьироваться в зависимости от семестра; прошлые темы включали криптографию, фракталы и рекурсию, моделирование полета планера, подгонку кривой, брахистохрону и компьютерную графику. Предыдущий опыт работы с компьютерами не требуется.
Необходимое условие: C или выше в MAT 203 или 205 или 307 или AMS 261
СБК: ТЕХ3 кредита
МАТ 336: История математики
Обзор истории математики с истоков до XIX века с особым вниманием к первоисточникам и взаимодействию между культурой и математикой.Акцент на темы, относящиеся к школьной программе. месопотамская, египетская и греческая математика; неевропейская математика; математика раннего Возрождения; рождение и расцвет исчисления; начало теории вероятностей; и происхождение неевклидовой геометрии и современной концепции числа.
Необходимое условие: MAT 200 или MAT 203 или или MAT 250 или MAT 307 или AMS 261
DEC: HSBC: СПК, СТАС, ВРТД
3 кредита
MAT 341: прикладной реальный анализ
Уравнения в частных производных математической физики: уравнения теплопроводности, волны и уравнения Лапласа. Решения с помощью таких методов, как разделение переменных с использованием ортогональных функций (например, ряды Фурье, функции Бесселя, полиномы Лежандра). Решение Даламбера волнового уравнения.
Решения с помощью таких методов, как разделение переменных с использованием ортогональных функций (например, ряды Фурье, функции Бесселя, полиномы Лежандра). Решение Даламбера волнового уравнения.
Предпосылки: C или выше в следующем: MAT 203 или 220 или 307 или AMS 261; MAT 303 или 305 или 308 или AMS 361
Консультативное условие: MAT 200 или MAT 250
3 кредита
MAT 342: Прикладной комплексный анализ
Комплексные числа, аналитические функции, уравнения Коши-Римана и Лапласа, интегральная формула Коши и приложения.Основная теорема алгебры и принцип максимума. Теорема Коши о вычетах и приложения к вычислению действительных интегралов. Конформные отображения.
Необходимое условие: C или выше в следующем: MAT 203 или MAT 220 или MAT 307 или AMS 261
Консультативное условие: MAT 200 или MAT 250
3 кредита
MAT 351: дифференциальные уравнения: динамика и хаос
Исследование долговременного поведения решений обыкновенных дифференциальных уравнений или повторяющихся отображений, подчеркивающее различие между стабильностью, с одной стороны, и чувствительной зависимостью и хаотическим поведением, с другой. Курс описывает примеры хаотического поведения и фрактальных аттракторов, а также разрабатывает некоторые математические инструменты для их понимания.
Курс описывает примеры хаотического поведения и фрактальных аттракторов, а также разрабатывает некоторые математические инструменты для их понимания.
Предпосылки: C или выше в следующем: MAT 203 или MAT 220 или MAT 307 или AMS 261; МАТ 303 или МАТ 308 или АМС 361; MAT 200 или MAT 250 или разрешение инструктора
3 кредита
MAT 360: геометрические структуры
Формальные геометрии и модели.Темы, выбранные из проективной, аффинной, евклидовой и неевклидовой геометрий.
Предварительное или необходимое: MAT 203, или 220, или 307, или AMS 261; MAT 200 или MAT 250 или разрешение инструктора
3 кредита
MAT 362: дифференциальная геометрия поверхностей
Локальная и глобальная геометрия поверхностей: геодезические, параллельный перенос, кривизна, изометрии, отображение Гаусса, теорема Гаусса-Бонне.
Необходимое условие: C или выше в MAT 319 или MAT 320 или MAT 364; MAT 203 или MAT 307 или MAT 322
3 кредита
MAT 364: топология и геометрия
Обширное введение в топологию и геометрию, математические теории формы, формы и жесткой конструкции.Темы включают интуитивную теорию узлов, решетки и мозаики, неевклидову геометрию, гладкие кривые и поверхности в евклидовом трехмерном пространстве, открытые множества и непрерывность, комбинаторные и алгебраические инварианты пространств, многомерные пространства.
Предпосылки: MAT 203, или 220, или 307, или AMS 261; МАТ 200 или 250
Консультативное условие: MAT 319 или 320
3 кредита
МАТ 371: Логика
Обзор логических основ математики: развитие исчисления высказываний и теории квантификации, понятия доказательства и модели, теорема о полноте, теорема Геделя о неполноте. Этот курс предлагается как CSE 371, так и MAT 371.
Этот курс предлагается как CSE 371, так и MAT 371.
Необходимое условие: CSE 150 или CSE 215 или MAT 200 или MAT 250
3 кредита
MAT 373: анализ алгоритмов
Математический анализ различных компьютерных алгоритмов, включая поиск, сортировку, умножение матриц, быстрое преобразование Фурье и графовые алгоритмы.Сложность времени и пространства. Анализ верхней границы, нижней границы и среднего случая. Введение в полноту NP. Для реализации и сравнения алгоритмов требуются некоторые машинные вычисления. Этот курс предлагается как CSE 373 и MAT 373. Не засчитывается в дополнение к CSE 385.
Предпосылки: C или выше в MAT 211 или AMS 210; CSE 214 или CSE 260
3 кредита
MAT 401: Семинар по математике
Обсуждение конкретной области математики.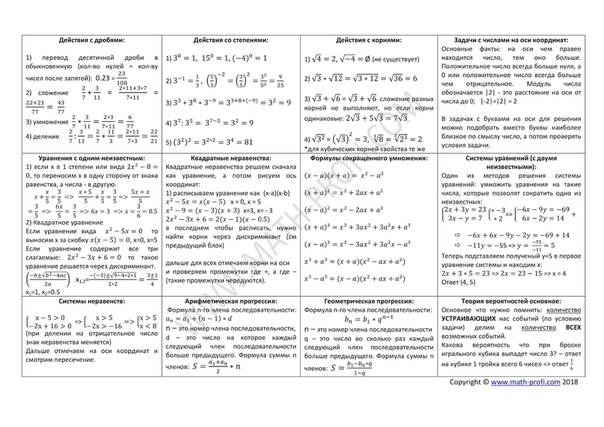 Работа каждого семестра охватывает разные области математики. Можно повторять по мере изменения темы. Предварительные требования будут объявляться вместе с темой каждый раз, когда предлагается курс.
Работа каждого семестра охватывает разные области математики. Можно повторять по мере изменения темы. Предварительные требования будут объявляться вместе с темой каждый раз, когда предлагается курс.
Необходимое условие: У3/У4; разрешение кафедры или преподавателя; дополнительные предварительные условия объявлены с темой
СБК: СПК3 кредита
MAT 402: Семинар по математике
Обсуждение конкретной области математики.Работа каждого семестра охватывает разные области математики. Можно повторять по мере изменения темы. Предварительные требования будут объявляться вместе с темой каждый раз, когда предлагается курс.
Необходимое условие: У3/У4; разрешение кафедры или преподавателя; дополнительные предварительные условия объявлены с темой
СБК: СПК3 кредита
MAT 425: как преподавать коррекционную математику
Предоставляет знания и навыки для преподавания дополнительных занятий по математике в колледже. Он включает анализ трудностей, с которыми сталкиваются студенты на курсах математического колледжа начальных уровней. В нем вновь обращается к довузовской математике, обсуждается ее использование в курсах колледжа, и на основе этого конкретного материала студентов учат, как выявлять и исправлять типичные ошибки и заблуждения, как составлять задачи и тесты, как анализировать и оценивать инициативные работы студентов, и как организовать уроки в среде студентов с
разнообразные задачи и потребности.Студенты узнают, как представлять математику ясно и математически правильно как в устной, так и в письменной форме.
Он включает анализ трудностей, с которыми сталкиваются студенты на курсах математического колледжа начальных уровней. В нем вновь обращается к довузовской математике, обсуждается ее использование в курсах колледжа, и на основе этого конкретного материала студентов учат, как выявлять и исправлять типичные ошибки и заблуждения, как составлять задачи и тесты, как анализировать и оценивать инициативные работы студентов, и как организовать уроки в среде студентов с
разнообразные задачи и потребности.Студенты узнают, как представлять математику ясно и математически правильно как в устной, так и в письменной форме.
Необходимое условие: MAT 200 и степень B или выше в одном из классов исчисления
3 кредита
MAT 444: Экспериментальное обучение
Этот курс предназначен для студентов, которые участвуют в существенной, структурированной экспериментальной учебной деятельности в сочетании с другим классом.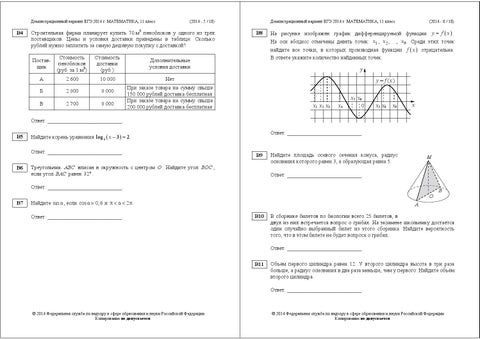 Экспериментальное обучение происходит, когда знания, полученные в результате формального обучения и прошлого опыта, применяются к «реальным» условиям или проблемам для создания новых знаний посредством процесса размышлений, критического анализа, обратной связи и синтеза. Внеклассный опыт, который поддерживает экспериментальное обучение, может включать: сервисное обучение, исследования под руководством наставника, полевые работы или стажировку.
Экспериментальное обучение происходит, когда знания, полученные в результате формального обучения и прошлого опыта, применяются к «реальным» условиям или проблемам для создания новых знаний посредством процесса размышлений, критического анализа, обратной связи и синтеза. Внеклассный опыт, который поддерживает экспериментальное обучение, может включать: сервисное обучение, исследования под руководством наставника, полевые работы или стажировку.
Необходимое условие: WRT 102 или эквивалент; разрешение инструктора и утверждение контракта EXP+ (http://sb.cc.stonybrook.edu/bulletin/current/policiesandregulations/grade_requirements/EXPplus.php)
СБК: опыт+0 баллов, оценка S/U
MAT 458: Эффективно говорите перед аудиторией
Курс с нулевым кредитом, который можно пройти в сочетании с любым курсом MAT, дающим возможность достичь результатов обучения, предусмотренных учебной программой Stony Brook Curriculum SPK.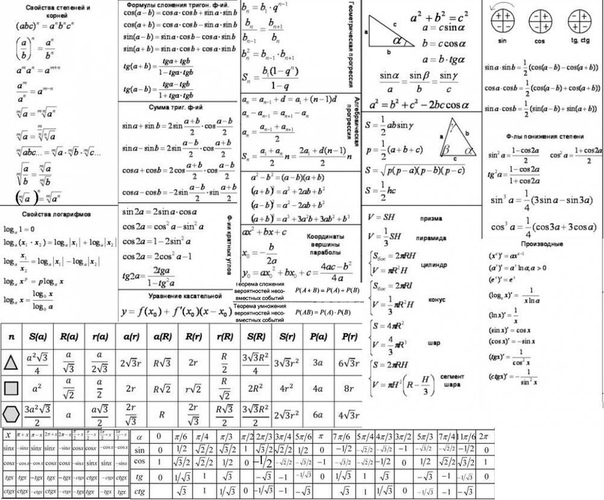
Предварительно или дополнительно: WRT 102 или эквивалент; разрешение инструктора
СБК: СПК0 баллов, оценка S/U
MAT 459: эффективно писать по математике
Курс с нулевым кредитом, который можно пройти вместе с любым курсом MAT 300 или 400 уровней с разрешения инструктора.Курс предоставляет возможность практиковать навыки и приемы эффективного академического письма и удовлетворяет результатам обучения в рамках учебной программы Stony Brook Curriculum WRTD.
Необходимое условие: ВРТ 102; разрешение инструктора
СБК: WRTD0 баллов, оценка S/U
MAT 475: Практикум для студентов бакалавриата
Каждый учащийся помогает преподавать курс математики для младших классов или работает в Центре обучения математике. Работа студента регулярно контролируется преподавателем. Кроме того, еженедельно проводится семинар. В обязанности может входить подготовка материалов для использования и обсуждения учащимися, помощь учащимся в решении проблем и участие в «альтернативных» учебных проектах. Предназначен для студентов старших классов, которые преуспели в последовательности исчисления. Не может быть использован для крупного кредита.
Работа студента регулярно контролируется преподавателем. Кроме того, еженедельно проводится семинар. В обязанности может входить подготовка материалов для использования и обсуждения учащимися, помощь учащимся в решении проблем и участие в «альтернативных» учебных проектах. Предназначен для студентов старших классов, которые преуспели в последовательности исчисления. Не может быть использован для крупного кредита.
Необходимое условие: Разрешение директора бакалавриата
СБК: опыт+3 кредита, оценка S/U
MAT 487: Независимое изучение специальных тем
Курс чтения для детей и взрослых.Темы могут быть выбраны студентом с одобрения курирующего члена факультета, который также берет на себя ответственность за оценку. Тема, которая освещается в курсе, регулярно предлагаемом кафедрой, не подходит для самостоятельного изучения. Может повторяться.
Тема, которая освещается в курсе, регулярно предлагаемом кафедрой, не подходит для самостоятельного изучения. Может повторяться.
Необходимое условие: Разрешение директора бакалавриата
0-6 кредитов
MAT 495: Диссертация с отличием
Студент и курирующий преподаватель вместе выбирают тему по математике, и студент пишет содержательную статью, излагающую тему по-новому.
Необходимое условие: Разрешение директора бакалавриата
СБК: EXP+, WRTD3 кредита
Политика курса для специальности «Экономика»
Обзор политики курса
Курсы по экономике делятся на четыре широкие категории:
- (i) вводные курсы по микроэкономике и макроэкономике
- (ii) основные (промежуточные) курсы по микроэкономике и макроэкономике
- (iii) основные курсы по статистике и эконометрике и
- (iv) дополнительные курсы по экономике.

В этом разделе вы найдете информацию, относящуюся к каждой из этих категорий, а также наши рекомендации по курсам математики, которые дополнят вашу специализацию по экономике.
Intro & Core Micro & Macro
ECON 1110 и 1120: Введение в микроэкономику и макроэкономику
Эти курсы предназначены для широкого введения в область экономики и ознакомления студентов с языком экономики. Эти курсы большие (350-450 студентов).Студенты со всего университета берут их по разным причинам: в качестве подготовки к специальности «Экономика», в качестве подготовки к другим специальностям в Корнелле (AEM, PAM, ILR и ряд других) и просто в качестве курса по выбору. И ECON 1110, и 1120 преподаются во время летних и зимних сессий Корнелла в небольших классах. Учащиеся, заинтересованные в этом варианте, должны проконсультироваться в Корнеллской школе непрерывного образования и летних сессиях.
ECON 3030 и 3040: Микроэкономика и макроэкономика среднего уровня
Эти курсы охватывают основные экономические методологии микроэкономики и макроэкономики, которые будут использоваться на факультативах по углубленной экономике.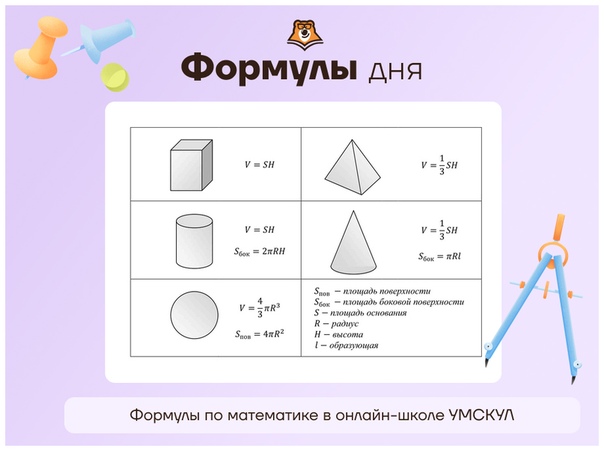 Они требуют и основываются на материалах, преподаваемых в ECON 1110 и ECON 1120, а также требуют MATH 1110. Размер классов обычно составляет 75–90 студентов, и подавляющее большинство из них изучают экономику. ECON 3030 и 3040 иногда (но не всегда) преподаются во время летних сессий Корнелла в небольших классах. Учащиеся, заинтересованные в этом варианте, должны проконсультироваться в Корнеллской школе непрерывного образования и летних сессиях.
Они требуют и основываются на материалах, преподаваемых в ECON 1110 и ECON 1120, а также требуют MATH 1110. Размер классов обычно составляет 75–90 студентов, и подавляющее большинство из них изучают экономику. ECON 3030 и 3040 иногда (но не всегда) преподаются во время летних сессий Корнелла в небольших классах. Учащиеся, заинтересованные в этом варианте, должны проконсультироваться в Корнеллской школе непрерывного образования и летних сессиях.
Примечание: Специалистам по экономике следует пройти вводные и основные курсы по микроэкономике и макроэкономике как можно раньше.Базовая структура специальности «Экономика» заключается в том, что вы сначала изучаете основные методологии на этих курсах, а затем используете эти методологии в своих факультативах по углубленной экономике. Следовательно, чем раньше вы изучите методологии, тем больше гибкости у вас будет при выборе факультативов по углубленной экономике.
Последовательность и необходимые условия
ECON 1110 и ECON 1120 можно брать в любом порядке, и ни один из них не требует предварительных условий.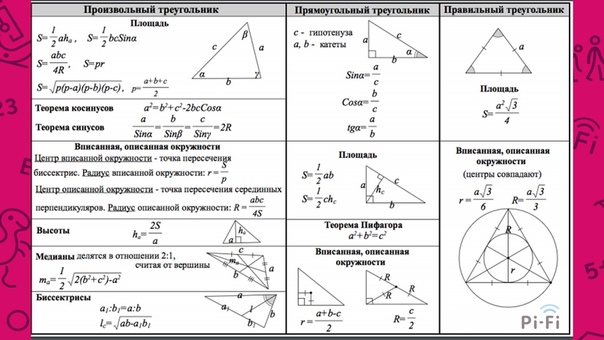 Их даже можно сдавать в одно и то же время, хотя вы можете проверить предварительные расписания, так как они часто приходятся на один и тот же день.Несмотря на то, что многие учащиеся получают зачет или перевод зачета по одному или обоим из этих курсов (см. Политика в отношении зачета вводного курса), студентам, изучающим экономику, настоятельно рекомендуется отказаться от зачетов по крайней мере за один из курсов AP и пройти ECON 1110 или ECON 1120. для оценки подготовки.
Их даже можно сдавать в одно и то же время, хотя вы можете проверить предварительные расписания, так как они часто приходятся на один и тот же день.Несмотря на то, что многие учащиеся получают зачет или перевод зачета по одному или обоим из этих курсов (см. Политика в отношении зачета вводного курса), студентам, изучающим экономику, настоятельно рекомендуется отказаться от зачетов по крайней мере за один из курсов AP и пройти ECON 1110 или ECON 1120. для оценки подготовки.
ECON 3030 и ECON 3040 также можно брать в любом порядке. Их можно выполнять одновременно, но мы рекомендуем проходить их последовательно (в любом порядке), чтобы вы могли уделить достаточно внимания каждому из них.Необходимыми условиями для каждого курса являются ECON 1110, ECON 1120 и MATH 1110. В принципе возможно пройти один из этих курсов без другого вводного курса (т. е. пройти ECON 3030 после изучения только ECON 1110 и MATH 1110, или пройти ECON 3040 после прохождения только ECON 1120 и MATH 1110), но для этого необходимо получить разрешение от инструктора промежуточного курса.
Кредит для ECON 1110 и ECON 1120
Существует множество способов получить зачет по ECON 1110 и ECON 1120, включая зачет за размещение (см. Политика в отношении зачета на начальный курс).Хотя многие студенты прибывают в Корнелл с зачетными баллами по ECON 1110 и/или ECON 1120, студентам, планирующим дальнейшее изучение экономики, настоятельно рекомендуется отказаться от кредитов по крайней мере за один из курсов AP и пройти ECON 1110 или ECON 1120, чтобы оценить свои знания. предварительная подготовка. Кредит за эти курсы должен отображаться в вашей стенограмме Корнелла, если вы намереваетесь стать специалистом по экономике.
Основная статистика и эконометрика
Мы предлагаем две последовательности, охватывающие статистику и эконометрику:
- ЭКОН 3110 и ЭКОН 3120
- ЭКОН 3130 и ЭКОН 3140
Две последовательности охватывают примерно один и тот же набор тем и используют одни и те же пакеты статистических вычислений. Однако ECON 3110-3120 обеспечит более прикладную обработку, в то время как Econ 3130-3140 обеспечит более продвинутую/теоретическую обработку. (Обратите внимание, что для ECON 3130–3140 требуется MATH 1120.) Многим учащимся следует выбрать более прикладное лечение (ECON 3110–3120). Тем не менее, студенты с более сильным математическим образованием, и особенно студенты, которые планируют продолжить обучение в аспирантуре по экономике, должны пройти более продвинутый/теоретический курс (ECON 3130-3140).
Однако ECON 3110-3120 обеспечит более прикладную обработку, в то время как Econ 3130-3140 обеспечит более продвинутую/теоретическую обработку. (Обратите внимание, что для ECON 3130–3140 требуется MATH 1120.) Многим учащимся следует выбрать более прикладное лечение (ECON 3110–3120). Тем не менее, студенты с более сильным математическим образованием, и особенно студенты, которые планируют продолжить обучение в аспирантуре по экономике, должны пройти более продвинутый/теоретический курс (ECON 3130-3140).
Что касается продвинутых факультативов, любая последовательность может служить предварительным условием — т.е.т. е., для любого продвинутого факультатива, требующего статистики, будет достаточно либо ECON 3110, либо ECON 3130, а для любого продвинутого факультатива, требующего эконометрики, будет достаточно ECON 3120 или ECON 3140.
Еще два замечания:
Во-первых, ECON 3130-3140 преподается только как последовательность осень-весна, т. е. ECON 3130 преподается только осенью, а ECON 3140 преподается только весной. В отличие от этого, ECON 3110-3120 можно сдавать осенью-весной или весной-осенью, то есть ECON 3110 преподается как осенью, так и весной, а ECON 3120 также преподается как осенью, так и весной.Также хорошо иметь перерыв между этими курсами — например, вы можете сдать ECON 3110 осенью 2021 года, а затем ECON 3120 осенью 2022 года.
В отличие от этого, ECON 3110-3120 можно сдавать осенью-весной или весной-осенью, то есть ECON 3110 преподается как осенью, так и весной, а ECON 3120 также преподается как осенью, так и весной.Также хорошо иметь перерыв между этими курсами — например, вы можете сдать ECON 3110 осенью 2021 года, а затем ECON 3120 осенью 2022 года.
Во-вторых, можно нормально переключаться с одной последовательности на другую. Если вы начинаете с ECON 3130 для курса статистики, всегда можно переключиться на ECON 3120 для курса эконометрики. Однако, если вы начнете с ECON 3110 для курса статистики, вам не будет разрешено перейти на ECON 3140 для курса эконометрики, потому что материал, изучаемый в ECON 3130, является более продвинутым, чем материал, изучаемый в ECON 3110, а ECON 3140 предполагает знание этого более продвинутого материала.Однако переключения в этом направлении могут производиться в исключительных случаях с разрешения инструктора ЭКОН 3140.
Возьмите статистику и эконометрику на раннем этапе
В идеале, вы должны пройти базовую статистику и эконометрику как можно раньше. Базовая структура специальности «Экономика» заключается в том, что вы сначала изучаете основные методологии, а затем используете эти методологии в своих факультативах по продвинутой экономике. Следовательно, чем раньше вы изучите методологии, тем больше гибкости у вас будет при выборе факультативов по углубленной экономике.Более того, хотя многие факультативы по продвинутой экономике не требуют эконометрики, обсуждаются эмпирические исследования, и вы лучше поймете это исследование, если уже изучали эконометрику.
Базовая структура специальности «Экономика» заключается в том, что вы сначала изучаете основные методологии, а затем используете эти методологии в своих факультативах по продвинутой экономике. Следовательно, чем раньше вы изучите методологии, тем больше гибкости у вас будет при выборе факультативов по углубленной экономике.Более того, хотя многие факультативы по продвинутой экономике не требуют эконометрики, обсуждаются эмпирические исследования, и вы лучше поймете это исследование, если уже изучали эконометрику.
Другие курсы статистики:
В Корнеллском университете преподается много курсов по статистике, и студенты иногда спрашивают, можно ли использовать эти курсы вместо ECON 3110 или ECON 3130. В этом разделе описывается наша текущая политика в отношении альтернативных курсов по статистике.
Мы настоятельно рекомендуем всем специалистам по экономике проходить ECON 3110 или ECON 3130, а не какой-либо другой курс статистики в кампусе.ECON 3110 и ECON 3130 напрямую подготовят вас к нашим курсам по эконометрике, в отличие от других курсов по статистике, и они также гораздо больше ориентированы на экономические примеры. Обычно мы ожидаем, что студенты будут изучать альтернативный курс статистики только в том случае, если они непреднамеренно выбрали этот курс до того, как поняли, что хотят специализироваться на экономике.
Обычно мы ожидаем, что студенты будут изучать альтернативный курс статистики только в том случае, если они непреднамеренно выбрали этот курс до того, как поняли, что хотят специализироваться на экономике.
На самом деле, есть два отдельных вопроса, касающихся курсов альтернативной статистики. Первый вопрос заключается в том, может ли курс альтернативной статистики служить предварительным условием для одного из наших курсов по эконометрике (ECON 3120 или ECON 3140).Второй вопрос: если курс альтернативной статистики может служить предварительным условием для курса эконометрики, может ли он также учитываться при выборе специальности «Экономика».
В общем ответ на второй вопрос будет НЕТ. Хотя темы других курсов по статистике могут быть похожи на темы наших курсов, в наших курсах используется гораздо больше примеров по экономике. Следовательно, мы НЕ позволяем этим курсам засчитываться в счет специальности «Экономика». Единственным исключением является ситуация, когда учащийся сдает и по МАТЕМАТИКЕ 4710, и по МАТЕМАТИКЕ 4720 (см. ниже).
ниже).
Ответ на первый вопрос зависит от уровня математической строгости других курсов по статистике, в частности, исходя из нашей оценки того, насколько хорошо эти курсы подготовят вас к нашим курсам по эконометрике.
Исходя из этого, вот наши правила для определенных курсов:
- МАТЕМАТИКА 4710 и МАТЕМАТИКА 4720: Если учащийся сдает и МАТЕМАТИКА 4710, и МАТЕМАТИКА 4720, эта комбинация курсов может полностью засчитываться вместо ECON 3130.Следовательно, эта комбинация может служить предварительным условием для ECON 3120 или ECON 3140, и эта комбинация может считаться одним курсом по направлению к специальности «Экономика».
- МАТЕМАТИКА 4710: Если учащийся изучает МАТЕМАТИКУ 4710 (а не МАТЕМАТИКУ 4720), этот курс может служить предварительным условием либо для ECON 3120, либо для ECON 3140, но не может засчитываться в счет специальности «Экономика».
- STSCI 3080/BTRY 3080/ILRST 3080 : Этот курс может служить предварительным условием для ECON 3120 или ECON 3140, но не может засчитываться для получения специальности «Экономика».
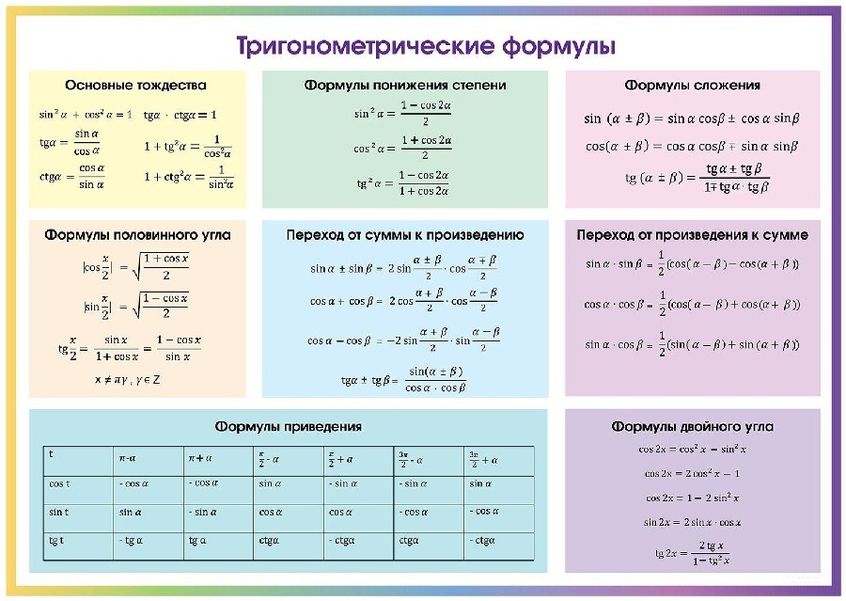
- ORIE 3500: Этот курс может служить предварительным условием для ECON 3120. Он также может служить предварительным условием для ECON 3140, но только при отличном выполнении и с явного специального разрешения инструктора ECON 3140. Этот курс не может быть засчитаны для получения специальности «Экономика».
- PAM 2101 : Этот курс может служить предварительным условием для ECON 3120, если вы получаете оценку B или выше. Этот курс не может служить предварительным условием для ECON 3140, и он не может быть засчитан для получения специальности «Экономика».
- ENGRD 2700: Этот курс может служить предварительным условием для ECON 3120, но он не может быть засчитан для получения специальности «Экономика». Кроме того, не может служить обязательным условием для ECON 3140.
- BRTY 3010/NTRES 3130/STSCI 2200 : Этот курс может служить предварительным условием для ECON 3120, но не может засчитываться для получения специальности «Экономика».
 Кроме того, это не может служить обязательным условием для ECON 3140.
Кроме того, это не может служить обязательным условием для ECON 3140. - Другие курсы: Ни один из курсов в группе ниже не может служить предварительным условием для ECON 3120 или ECON 3140, и, таким образом, ни один из из этих курсов не может быть засчитан для получения специальности «Экономика»: PAM 2100, SOC 3010, AEM 2100, УСТКИ 2100/ИЛРСТ 2100
Дополнительные курсы по выбору
После прохождения вводного и основного курсов оставшиеся курсы экономики будут состоять из ряда дополнительных курсов по экономике.Мы предлагаем широкий спектр факультативов, и, как правило, у студентов есть свобода выбора курсов, которые лучше всего соответствуют их интересам. Однако есть несколько ограничений, которые описаны ниже.
Продвинутые факультативы 3000-го уровня vs. продвинутые факультативы 4000-го уровня:
Факультативы по продвинутой экономике классифицируются как факультативы, для которых требуются основные курсы, и факультативы, для которых не требуются основные курсы. Другими словами, они классифицируются в зависимости от того, требуется ли для них хотя бы один из основных Эконометрика.Номера курсов отражают эти категории: для курсов с номерами 3150–3999 не требуются какие-либо основные курсы, а для курсов с номерами 4000–4989 требуется хотя бы один основной курс.
Другими словами, они классифицируются в зависимости от того, требуется ли для них хотя бы один из основных Эконометрика.Номера курсов отражают эти категории: для курсов с номерами 3150–3999 не требуются какие-либо основные курсы, а для курсов с номерами 4000–4989 требуется хотя бы один основной курс.
Дополнительные курсы по выбору:
Для специальности «Экономика» требуется шесть факультативов по экономике продвинутого уровня. Из них как минимум три должны быть факультативными для уровня 4000.
Курсы с номерами 4900-4989 представляют собой небольшие семинары. Для этих курсов требуется как минимум один из основных курсов методологии по микроэкономике, макроэкономике и эконометрике.Эти курсы рассчитаны на 25 студентов и включают значительный письменный компонент.
Примечание. Учащиеся, завершившие годовую программу с отличием (ECON 4990 и ECON 4991), могут считать ее одним из своих 12 основных курсов. Это НЕ будет считаться факультативом уровня 4000.
Другая информация:
Курсы, преподаваемые другими факультетами, могут быть засчитаны в счет специальности «Экономика» только в том случае, если они включены в перекрестный список с «Экономикой» (это означает, что у них есть номер курса «Экономика»).В частности, обратите внимание, что бизнес-курсы — бухгалтерский учет, маркетинг и т. д. — не могут быть засчитаны в счет специальности «Экономика».
Студенты бакалавриата по экономике могут посещать курсы экономики для выпускников, но только с разрешения преподавателя и вашего консультанта. Курсы магистратуры обычно требуют очень сильной математической подготовки — по крайней мере, в области многомерного исчисления и, в некоторых случаях, реального анализа — и гораздо больше работы, чем курс экономики уровня 3000 или 4000.
Обратите внимание, что курсы независимого обучения (ECON 4999) никогда не могут быть засчитаны для получения специальности «Экономика».
Рекомендации по математике
Требуемая математика для специальности «Экономика»:
Единственным математическим курсом, необходимым для изучения экономики, является МАТЕМАТИКА 1110, который охватывает дифференциальное исчисление. Успешное завершение этого курса (что означает оценку C или выше) требуется для поступления на специальность «Экономика» и является предварительным условием для основных курсов экономики — ECON 3030, ECON 3040, ECON 3110, ECON 3120, ECON 3130, и ECON 3140 (обратите внимание, что ECON 3130 и ECON 3140 также требуют MATH 1120, который охватывает интегральное исчисление).
Успешное завершение этого курса (что означает оценку C или выше) требуется для поступления на специальность «Экономика» и является предварительным условием для основных курсов экономики — ECON 3030, ECON 3040, ECON 3110, ECON 3120, ECON 3130, и ECON 3140 (обратите внимание, что ECON 3130 и ECON 3140 также требуют MATH 1120, который охватывает интегральное исчисление).
Для поступления на специальность «Экономика» зачет по МАТЕМАТИКЕ 1110 должен быть указан в вашей стенограмме Корнелла. Есть много способов получить зачет по МАТЕМАТИКЕ 1110, в том числе зачет за размещение (см. страницу Advanced Placement for Calculus на странице Отдела математики)
Рекомендуемая математика для специальности «Экономика»:
Курсы по экономике часто используют математические методы на уровне, превышающем уровень MATH 1110. На занятиях по статистике и эконометрике используется материал из интегрального исчисления (MATH 1120), а в основной микроэкономике, основной макроэкономике и многих дополнительных факультативах используется материал из многомерного исчисления (MATH 2130 или MATH 2220). ).Эти математические курсы обычно не требуются для курсов экономики, и профессора часто пытаются преподавать любые дополнительные математические методы, которые необходимы. Поэтому, если вам не нравится ходить на математические курсы, вы, вероятно, сможете пережить специализацию по экономике, изучив только MATH 1110. Тем не менее, если вы действительно не любите использовать математику, специальность «Экономика» не является для вас хорошим выбором.
).Эти математические курсы обычно не требуются для курсов экономики, и профессора часто пытаются преподавать любые дополнительные математические методы, которые необходимы. Поэтому, если вам не нравится ходить на математические курсы, вы, вероятно, сможете пережить специализацию по экономике, изучив только MATH 1110. Тем не менее, если вы действительно не любите использовать математику, специальность «Экономика» не является для вас хорошим выбором.
Несмотря на то, что мы не требуем этого, посещение дополнительных математических курсов помимо МАТЕМАТИЧЕСКОЙ 1110 может быть очень полезным как для вашей курсовой работы по экономике в Корнелле (вы лучше поймете материал), так и для вашей жизни после Корнелла (математика является широко применимым навыком) .Мы рекомендуем специалистам по экономике изучать математику, по крайней мере, через курс многомерного исчисления. Для этого требуется еще два или три математических курса помимо MATH 1110, потому что все курсы по многомерному исчислению требуют MATH 1120 (интегральное исчисление).
Есть два пути, по которым наши специалисты обычно выбирают МАТЕМАТИКА 1120:
- МАТЕМАТИКА 2210 и МАТЕМАТИКА 2220: эта последовательность из двух курсов охватывает как линейную алгебру (МАТИКА 2210), так и исчисление с несколькими переменными (МАТИКА 2220). Линейная алгебра — ценный навык, который может быть полезен для курсов по эконометрике и продвинутой теории, а также необходим, если вы хотите рассмотреть возможность работы в аспирантуре по экономике (см. ниже).МАТЕМАТИКА 2210 и МАТЕМАТИКА 2220 — это основная последовательность по линейной алгебре и многомерному исчислению, изучаемая большинством специальностей по математике.
- МАТЕМАТИКА 2130: МАТЕМАТИКА 2130 является «заключительным» курсом в том смысле, что это курс по многомерному исчислению, предназначенный для студентов, которые не намерены углубляться в математику. В принципе, МАТЕМАТИКА 2130 — это курс многомерного исчисления, который наиболее тесно связан с многомерным исчислением, используемым в бакалавриате по экономике (с упором на приложения математики).
 Если вы в первую очередь посещаете математические курсы, чтобы получить максимальную отдачу от специальности «Экономика», этот курс может подойти вам.
Если вы в первую очередь посещаете математические курсы, чтобы получить максимальную отдачу от специальности «Экономика», этот курс может подойти вам.
Еще один вариант для тех учащихся, которые не хотят сдавать МАТЕМАТИКА 2210 и МАТЕМАТИКА 2220, но хотели бы изучить некоторую линейную алгебру наряду с исчислением многих переменных, — сдать и МАТЕМАТИКА 2130, и МАТЕМАТИКА 2310. МАТЕМАТИКА 2310 — это линейная алгебра. курс, который делает упор на практические приложения больше, чем МАТЕМАТИКА 2210. Как и МАТЕМАТИКА 2130, МАТЕМАТИКА 2310 является «конечным» курсом.
Подготовка по математике для программ магистратуры по экономике:
Если вы хотите поступить в аспирантуру по экономике, вам нужно еще больше изучать математику.В экономических исследованиях широко используются математика и докторская степень по экономике. программы предполагают, что студенты входят в программу с сильным математическим образованием. Когда доктор философии программы рассматривают заявления о приеме, одной из самых больших проблем является математическая подготовка студента к дипломной работе по экономике.
При подготовке к дипломной работе по экономике вы должны как минимум пройти (1) МАТЕМАТИКА 1110, (2) МАТЕМАТИКА 1120, (3) курс линейной алгебры, (4) курс многомерного исчисления и (5) курс курс по анализу.Первые четыре курса обсуждаются в разделе выше. Для анализа есть два основных варианта:
- МАТЕМАТИКА 3110: Анализ включает в себя чтение и, в конечном счете, построение формальных математических доказательств. В самом деле, пожалуй, главная польза от анализа состоит в том, чтобы получить опыт построения формальных математических доказательств. MATH 3110 — это курс анализа, разработанный для студентов, которые начинают курс с ограниченным уровнем подготовки/уровня комфорта при чтении формальных доказательств.
- МАТЕМАТИКА 4130: МАТЕМАТИКА 4130 — это версия анализа с отличием, разработанная для студентов, которые начинают курс с опытом и удобством чтения формальных математических доказательств.Преимущество этого курса в том, что он позволяет вам пройти следующий курс анализа — МАТЕМАТИКА 4140.

Помимо анализа, мы рекомендуем вам пройти один или несколько дополнительных математических курсов (и вы станете еще более конкурентоспособными, если будете заниматься математикой дважды). Есть много путей, по которым вы могли бы пойти, в зависимости от ваших интересов:
- Расширенный анализ: МАТЕМАТИКА 4140.
- Дифференциальные уравнения и динамические системы: MATH 3230 и MATH 4200.
- Продвинутая линейная алгебра: МАТЕМАТИКА 4310 (Примечание: в отличие от анализа, расширенная версия линейной алгебры с отличием (MATH 4330) намного сложнее, чем МАТЕМАТИКА 4310.)
- Случайные процессы: МАТЕМАТИКА 4740.
Вы также можете пройти курсы по исследованию операций и информационной инженерии (ORIE) в инженерном колледже. Этот отдел предлагает многочисленные курсы по оптимизации (например, ORIE 3300, ORIE 3310 и ORIE 4320), а также курсы по теории игр (например, ORIE 4350).
Прежде чем приступить к любому курсу продвинутой математики, было бы неплохо получить копию программы и показать ее своему консультанту по экономике или директору бакалавриата, чтобы убедиться, что она содержит материал, полезный для экономики. Даже курс, который в прошлом охватывал полезный материал, может перестать быть полезным, если его ведет другой профессор с другими интересами. Как и в случае с любым другим предметом в Корнелле, содержание математических курсов старшего уровня в значительной степени зависит от интересов и опыта каждого профессора.
Даже курс, который в прошлом охватывал полезный материал, может перестать быть полезным, если его ведет другой профессор с другими интересами. Как и в случае с любым другим предметом в Корнелле, содержание математических курсов старшего уровня в значительной степени зависит от интересов и опыта каждого профессора.
Другие мысли о курсах математики:
Для студентов, которые интересуются специализацией «Экономика», но беспокоятся о своем математическом образовании при поступлении в Корнелл, обратите внимание, что существует значительная академическая поддержка как для МАТЕМАТИЧЕСКОЙ 1110, так и для МАТЕМАТИЧЕСКОЙ 1120.Вы можете записаться на один из курсов академической поддержки, предоставляемых Центром стратегий обучения Корнелла (MATH 1011 для поддержки MATH 1110 и MATH 1012 для поддержки MATH 1120). Кроме того, вы можете пользоваться услугами и ресурсами Центра поддержки математики Корнелла.
Обратите внимание, что факультет математики настоятельно не рекомендует студентам одновременно изучать два курса из группы дифференциального исчисления (дифференциального, интегрального и многомерного) и линейной алгебры, особенно если один курс является обязательным условием для другого. Соблазн удвоить усилия, чтобы быстрее добраться до продвинутых математических курсов, часто может привести к плохим оценкам по одному или обоим предметам и излишне напряженному семестру. Если вы считаете, что должны пройти два из этих курсов одновременно, поговорите с директором по математике бакалавриата, чтобы оценить, возможно ли это каким-либо образом.
Соблазн удвоить усилия, чтобы быстрее добраться до продвинутых математических курсов, часто может привести к плохим оценкам по одному или обоим предметам и излишне напряженному семестру. Если вы считаете, что должны пройти два из этих курсов одновременно, поговорите с директором по математике бакалавриата, чтобы оценить, возможно ли это каким-либо образом.
Некоторые студенты прибывают в Корнелл с зачетом по МАТЕМАТИКЕ 1110, но, тем не менее, опасаются, что им может не хватить уровня знаний по математике, необходимого для основных курсов экономики.Для таких студентов, если вы хотите укрепить свои базовые математические знания, вы можете отказаться от зачетных баллов и сдать МАТЕМАТИКА 1110. В качестве альтернативы вы можете записаться на МАТЕМАТИКА 1120 на первом курсе, и изучение этого нового материала может помочь закрепить материал, который вы выучили. до приезда в Корнелл.
Ресурсы для первокурсников | Факультет математики
Добро пожаловать в математику в Йельском университете!
Мы рады, что вы рассматриваете возможность изучения математики вместе с нами в Йельском университете.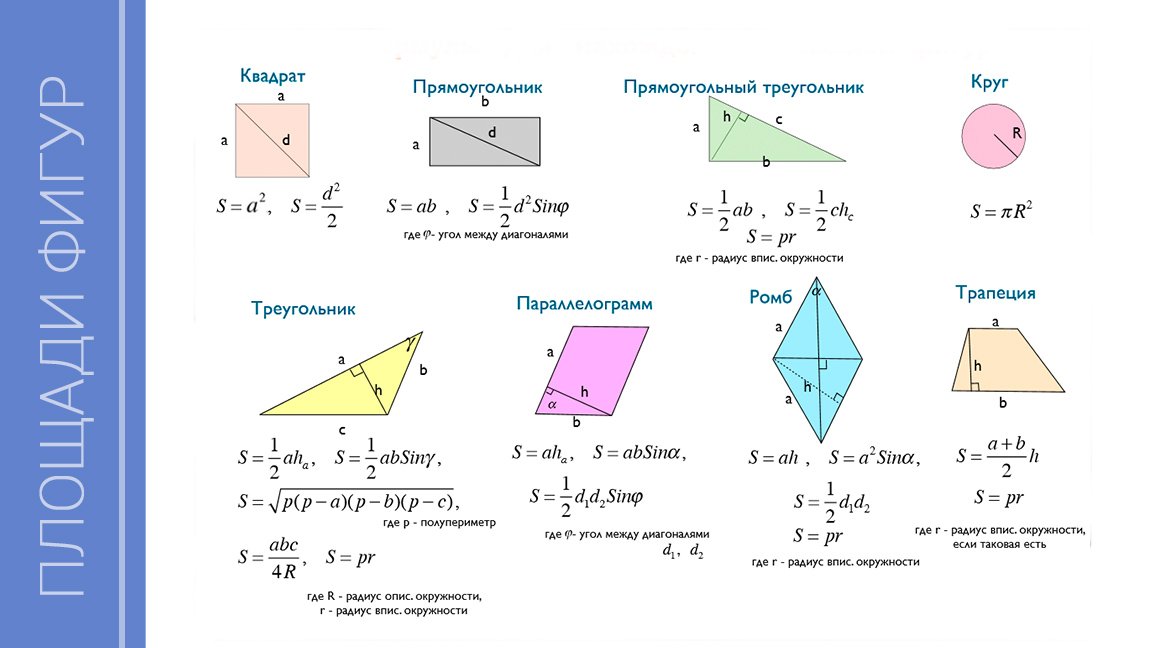 Планируете ли вы пройти один курс, несколько или рассматриваете возможность изучения математики, мы здесь, чтобы поддержать вас.Эта страница поможет вам начать.
Планируете ли вы пройти один курс, несколько или рассматриваете возможность изучения математики, мы здесь, чтобы поддержать вас.Эта страница поможет вам начать.
Вы также можете посмотреть наше ознакомительное видео, в котором представлена основная информация о наших курсах, а в конце есть игра-головоломка!
Новости:
Вступительный экзамен по математике на Canvas будет открыт с 9:00 28 октября до 17:00 3 ноября, в соответствии с датами вступительного экзамена в университет для предварительной регистрации на весну 2022 года. Подробнее об этом тесте см. ниже.
16 и 17 августа 2021 г. состоялосьратуши исчисления и консультирование по размещению.Если вы пропустили ратушу для своего курса, вы можете найти информацию (а иногда и видео с нее) на сайте курса Canvas. Если вам нужна консультация по размещению, обратитесь к таблице внизу этой страницы, чтобы узнать, с кем лучше всего связаться.
Вводные курсы по математике
Math 112 посвящен дифференциальному исчислению, целью которого является измерение мгновенной скорости изменения функции (производной).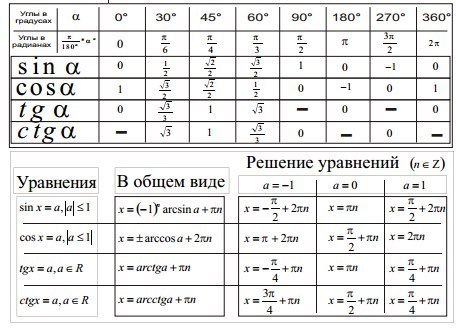 Во-первых, мы определяем пределы, которые позволяют нам строго говорить о мгновенных изменениях.Затем мы определяем производную и находим множество правил, упрощающих ее вычисление. Затем мы применяем производную, чтобы лучше понять поведение функции (что позволяет нам минимизировать затраты или максимизировать прибыль в экономических моделях). Наконец, мы разрабатываем стратегии обращения процесса производной для нахождения первообразных функций. У этих первообразов есть неожиданные применения, например, для вычисления областей и моделирования роста населения.
Во-первых, мы определяем пределы, которые позволяют нам строго говорить о мгновенных изменениях.Затем мы определяем производную и находим множество правил, упрощающих ее вычисление. Затем мы применяем производную, чтобы лучше понять поведение функции (что позволяет нам минимизировать затраты или максимизировать прибыль в экономических моделях). Наконец, мы разрабатываем стратегии обращения процесса производной для нахождения первообразных функций. У этих первообразов есть неожиданные применения, например, для вычисления областей и моделирования роста населения.
Математика 112 требуется вступительный экзамен. Необходимый фон — предварительное исчисление.
Другим вариантом является последовательность Math 110/111 , двухсеместровый курс, в котором объединены темы предварительного исчисления и дифференциального исчисления. Успешное завершение математики 110 и 111 эквивалентно математике 112 в том смысле, что оно удовлетворяет тем же требованиям основной и профессиональной школы (например, домедицинского образования); однако учащийся, завершивший Math 110 и 111, получает два кредита за курс и два кредита QR.
Математика 110 требуется вступительный экзамен. Некоторое предварительное знание предварительного исчисления полезно.
Math 115 исследует математику накопления. В интегральном исчислении мы используем информацию о мгновенных скоростях (например, о скорости движущегося объекта) для вычисления чистых изменений (например, изменения положения). Тесты сходимости рядов и ряды Тейлора помогают нам понять, как работают калькуляторы, а различные другие темы (тела вращения, параметрические уравнения, полярные координаты) позволяют нам применять инструменты исчисления с одной переменной в более широком контексте. На протяжении всего семестра мы рассматриваем как точные, так и приближенные решения задач и исследуем роль ошибки.
Математика 115 и 116 оба охватывают интегральное исчисление, и оба могут использоваться в качестве предварительных условий для любого курса, который требует математики 115. Математика 116 делает акцент на приложениях к биологии и особенно подходит для студентов-биологов и студентов-медиков.
Математика 115 и 116 требуется вступительный экзамен или сдача математики 111 или 112 в Йельском университете. Необходимым фоном является дифференциальное исчисление (эквивалентно Math 112 или AP Calculus AB).
Математика 120 расширяет навыки и знания, которые вы получаете в расчете с одной переменной, на две и три переменные.Мы изучим, как строить графики поверхностей и твердых тел в трех измерениях, дифференцировать и интегрировать функции нескольких переменных, оптимизировать функции нескольких переменных (например, при максимизации прибыли в экономике), мы научимся интегрировать по кривым и поверхностям (например, когда расчет того, сколько энергии будет генерировать солнечная панель, пока на нее светит солнце) и многие другие темы.
Math 120 и 121 оба охватывают многомерное исчисление, и оба могут использоваться в качестве предварительных условий для любого курса, для которого требуется Math 120. Math 121 уделяет особое внимание приложениям к биологии и особенно подходит для студентов-биологов и студентов-медиков.
Math 121 уделяет особое внимание приложениям к биологии и особенно подходит для студентов-биологов и студентов-медиков.
Математика 120 и 121 требуется вступительный экзамен или сдача математики 115 или 116 в Йельском университете. Необходимым фоном является интегральное исчисление (например, Math 115 или AP Calculus BC).
Математика 225 – это курс линейной алгебры, который является частью нашего вводного курса по математике. В линейной алгебре вы изучите ключевой язык и концепции, используемые в чистой математике, а также в самых разных приложениях.Линейная алгебра начинается с изучения систем уравнений со многими переменными и дает детальное понимание того, как работать в абстрактном n-мерном пространстве. Эта версия линейной алгебры фокусируется на концепциях и представляет собой введение в написание математических доказательств.
Мы также предлагаем интенсивную версию этого курса, Math 226 , для учащихся, которым нужны дополнительные задачи.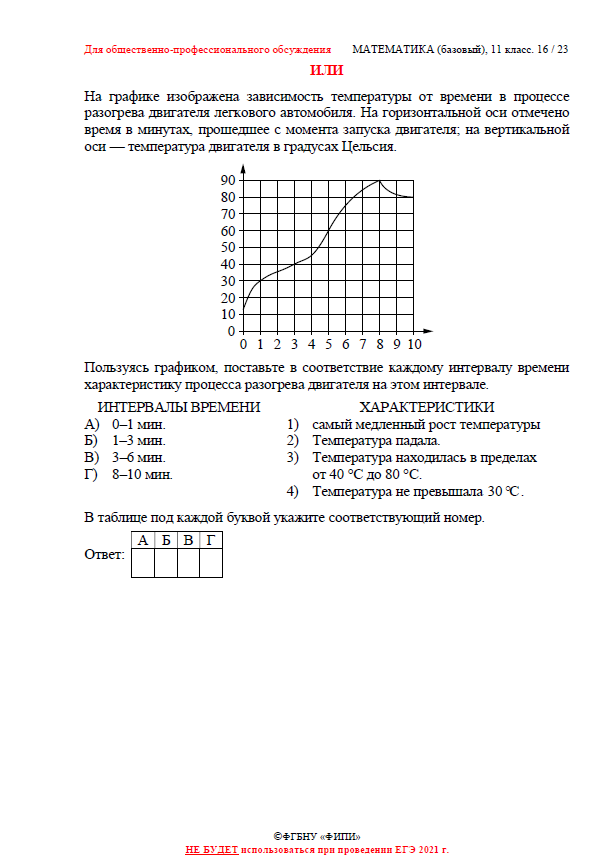 В Math 226 преподаются те же основные темы, что и в Math 225, но он может быть более глубоким, задавать более сложные задачи в домашних заданиях и на экзаменах или охватывать дополнительные дополнительные темы.
В Math 226 преподаются те же основные темы, что и в Math 225, но он может быть более глубоким, задавать более сложные задачи в домашних заданиях и на экзаменах или охватывать дополнительные дополнительные темы.
Если вы начнете с математики 226 и обнаружите, что это отнимает слишком много времени, вы можете перейти к математике 225 до середины семестра. Вы можете узнать больше о том, как работает переход между курсами, в разделе часто задаваемых вопросов по исчислению.
Математика 222 – это курс линейной алгебры, который лучше всего подходит для студентов, которые хотят сосредоточиться на приложениях и практическом решении задач, а не на абстрактной математике и математических доказательствах. Его часто принимают студенты, специализирующиеся в области инженерии, технологий, естественных наук, социальных наук и экономики.Тем, кто занимается математикой, необходимо выполнить задание Math 225 или 226, а не 222.
Математика 222, 225 и 226 не требует вступительного экзамена. Если вы прошли курс интегрального исчисления, вы можете просто зарегистрироваться.
Если вы прошли курс интегрального исчисления, вы можете просто зарегистрироваться.
Математика 255 является введением в настоящий анализ и частью нашего вводного курса по математике. Темы похожи на дифференциальное и интегральное исчисление, но они выполнены строго и сосредоточены на доказательствах и деталях концепций, которые происходят за кулисами в исчислении.Другими словами, наша последовательность вычислений учит вас, как использовать инструменты пределов, производных и интегралов для решения множества задач, тогда как этот курс учит вас, как создавать все эти инструменты с нуля.
Мы также предлагаем интенсивную версию этого курса, Math 256 , для учащихся, которым нужны дополнительные задачи. В Math 256 преподаются те же основные темы, что и в Math 255, но он может быть более глубоким, задавать более сложные задачи в домашних заданиях и на экзаменах или охватывать некоторые дополнительные дополнительные темы.
Мы рекомендуем сначала заняться линейной алгеброй, потому что она более универсальна и является более щадящим введением в доказательства, но вполне нормально сначала заняться анализом.
Math 255 и 256 не используют вступительный экзамен или выбор предпочтения.
Математика 302 – это строгий и увлекательный курс, в котором исследуются некоторые прекрасные связи между линейной алгеброй и реальным анализом. По этой причине его следует сдавать после завершения 225/226 и 255/256.
Этот курс представляет собой введение в многообразия, которые представляют собой низкоразмерные формы, живущие в многомерной вселенной (например, одномерная вешалка для одежды или двумерная яичная скорлупа, каждая из которых живет в трехмерном мире), и он учит, как делать вычисления в этой абстрактной обстановке. Хотя основное внимание в этом курсе будет уделено абстрактным математическим объектам и их свойствам, материал этого курса также применим к широкому кругу тем, включая теоретическую физику и машинное обучение.
Многим учащимся, которые не завершили исчисление с несколькими переменными в старшей школе, было бы полезно пройти курс «Математика 120».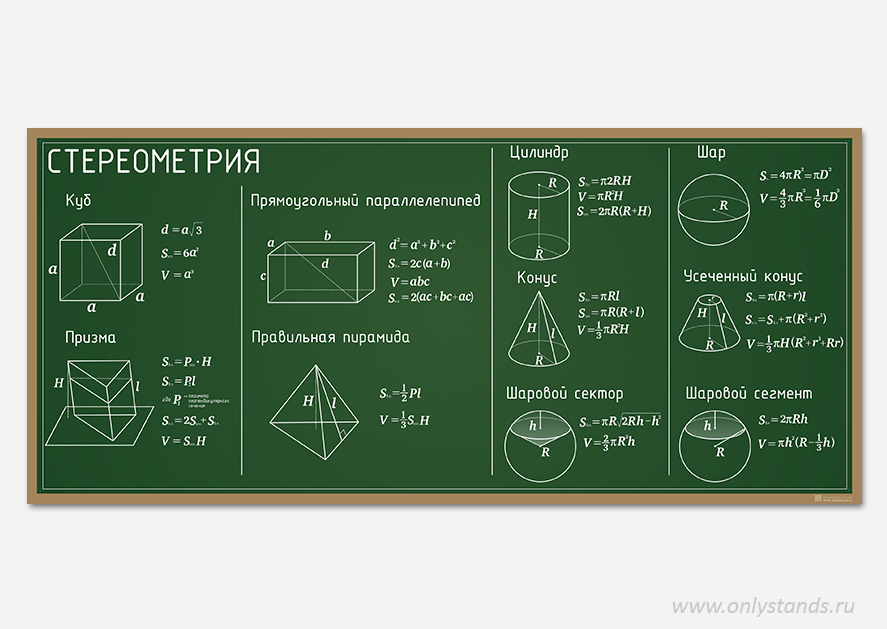 Тем не менее, потенциальные студенты, изучающие математику, и учащиеся, заинтересованные в строгой математике, основанной на доказательствах, должны рассмотреть вместо этого курс «Математика 225/226», «Математика 255/256» и «Математика 302». . Math 302 также подходит для учащихся, которые уже прошли курс Math 120 и хотят узнать больше.
Тем не менее, потенциальные студенты, изучающие математику, и учащиеся, заинтересованные в строгой математике, основанной на доказательствах, должны рассмотреть вместо этого курс «Математика 225/226», «Математика 255/256» и «Математика 302». . Math 302 также подходит для учащихся, которые уже прошли курс Math 120 и хотят узнать больше.
Math 302 не использует вступительный экзамен или выбор предпочтений.
Математика 118 обучает сочетанию многомерного исчисления и линейной алгебры.Он подходит для студентов, специализирующихся в области экономики или социальных наук, которые хотят изучить наиболее актуальную математику за один семестр. Учащиеся, намеревающиеся продолжить изучение математики, должны вместо этого выбрать исчисление с несколькими переменными (математика 120) и линейную алгебру (математика 222, 225 или 226). Необходимым условием для изучения математики 118 является дифференциальное исчисление (например, математика 112 или AP Calculus AB).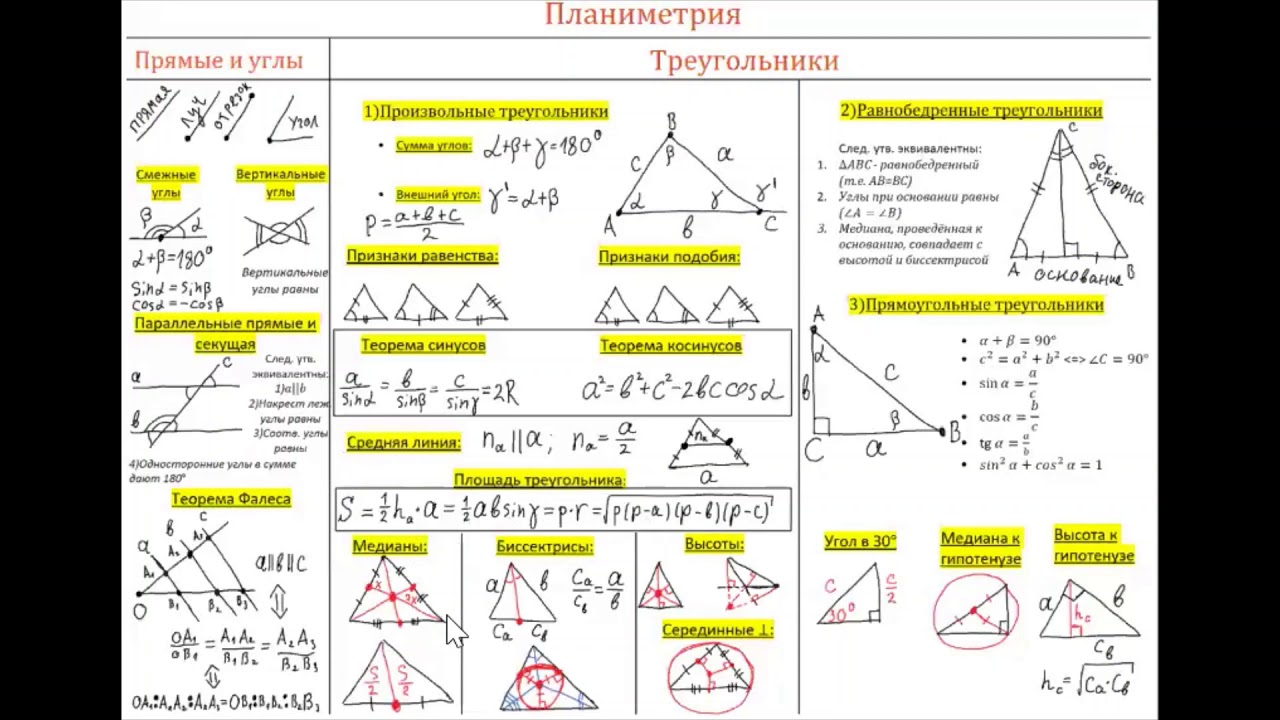 Желательно знание интегрального исчисления.
Желательно знание интегрального исчисления.
Математический факультет предлагает три курса по количественному мышлению (QR), которые предполагают отсутствие опыта вычислений:
Math 106 (Форма пространства) представляет собой введение в математическое мышление с помощью идей геометрии и теории графов.Курс следует историческому повествованию, начиная с античности, и развивает математическую и геометрическую интуицию посредством решения задач и других действий.
В Math 107 (Математика в реальном мире) учащиеся используют математические идеи для решения реальных задач. Темы включают сложные проценты, рост населения, вероятность и ее применение в азартных играх, выплаты по ипотечным кредитам, ложные срабатывания при тестировании на наркотики, компьютерную безопасность и другие вопросы.
Математика 108 (Оценка и ошибка) проводит учащихся через проблемное исследование основных математических принципов и методов, которые помогают понять мир.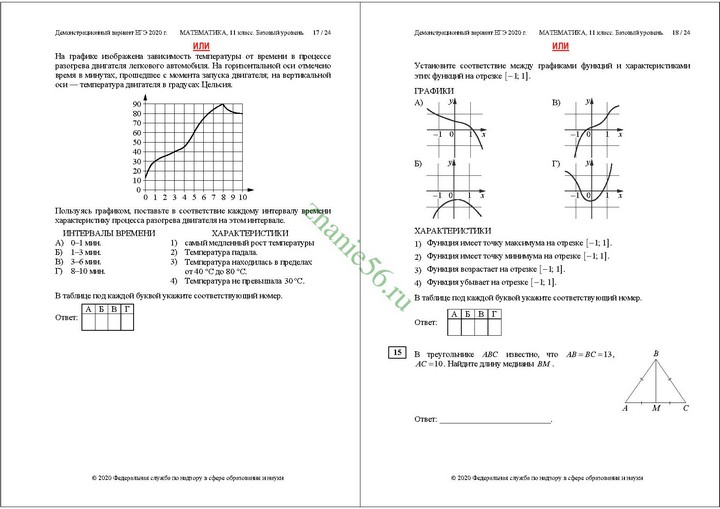 Приложения включают геологию, экологию, финансы и другие области.
Приложения включают геологию, экологию, финансы и другие области.
Математика 241 и 242: вероятность и статистика учат нас собирать, анализировать и интерпретировать данные.
Math 244: дискретная математика включает в себя множество тем, представляющих интерес для информатики.
Math 246: дифференциальных уравнения можно использовать для моделирования сложных систем в биологии, физике, экономике и других областях.
Math 270: Теория множеств лежит в основе математики и часто используется студентами-философами.
.
Выбор первого курса математики в Йельском университете
Многие поступающие студенты записываются на один из наших курсов математики (математика 110, 112, 115, 116, 120 или 121). Если вы рассматриваете этот вариант, вам нужно будет пройти наш вступительный экзамен, чтобы мы могли помочь вам определить, с чего лучше начать.
- Подробную информацию о тесте см.
 в разделе часто задаваемых вопросов об экзамене по математическому анализу и размещению.
в разделе часто задаваемых вопросов об экзамене по математическому анализу и размещению. - Экзамен по математическому анализу открыт с 1 по 31 июля 2021 г.Он снова будет открыт с 9:00 1 ноября до 17:00 4 ноября.
- Все поступающие первокурсники автоматически зачисляются на курс Математика для подготовки к экзамену в конце июня. Второкурсникам, младшим и старшим учащимся следует обращаться по адресу [email protected], чтобы их добавили на сайт.
- Результаты теста доступны сразу после подачи, нажав на вкладку «Результаты размещения». (Если вкладка не загружается, попробуйте другой браузер.)
- Если вы хотите пройти курс, результаты которого отличаются от результатов вашего вступительного экзамена, посетите нашу консультационную сессию по математическому анализу в августе.Консультанты будут рады вам помочь. Учтите, что сначала вы должны пройти тест — без него советники вам не помогут. Подробная информация о сессии будет размещена на этом сайте к середине июля.
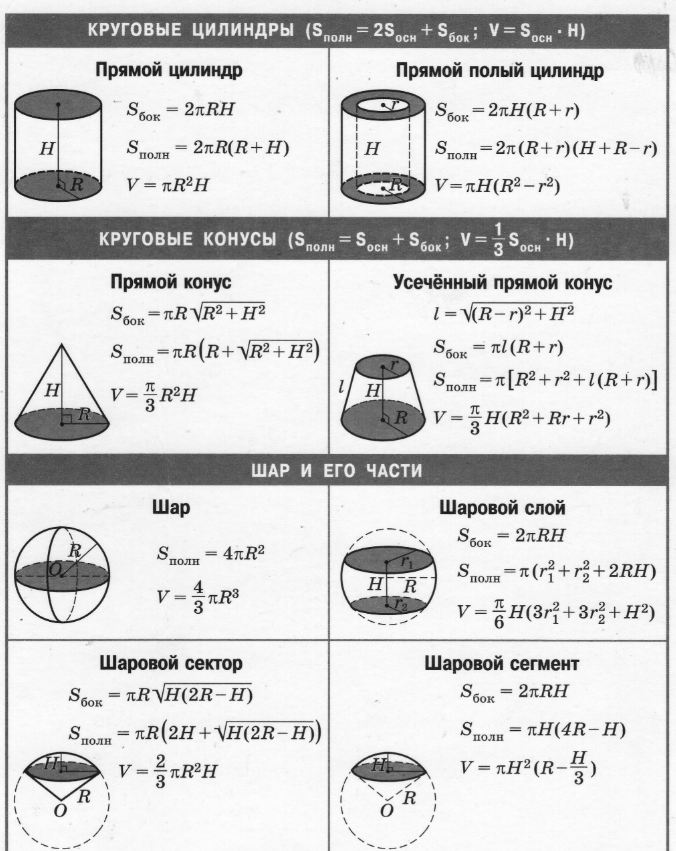
- После того, как вас зачислили на первый курс математического анализа, предварительно зарегистрируйтесь для участия в курсе на веб-сайте выбора предпочтений Йельского университета. Выбор предпочтений обычно открывается в августе (на осенний семестр), в декабре (на весенний семестр) и снова в апреле (на осенний семестр, продолжающие обучение студенты).
-
Вступительный экзамен НЕ требуется для любого курса математики уровня 200 или выше. В частности, он вам не нужен, чтобы записаться на курсы Math 225, 226, 255 или 256.
- Сдать вступительный экзамен на Canvas.
- Если у вас есть вопросы о курсах математического анализа или вступительном экзамене, ознакомьтесь с часто задаваемыми вопросами по математическому анализу и вступительному экзамену.
- Если у вас есть вопросы о вашем размещении, посетите нашу консультационную сессию по математическому анализу в августе. Подробная информация о сессии будет размещена на этом сайте к середине июля.
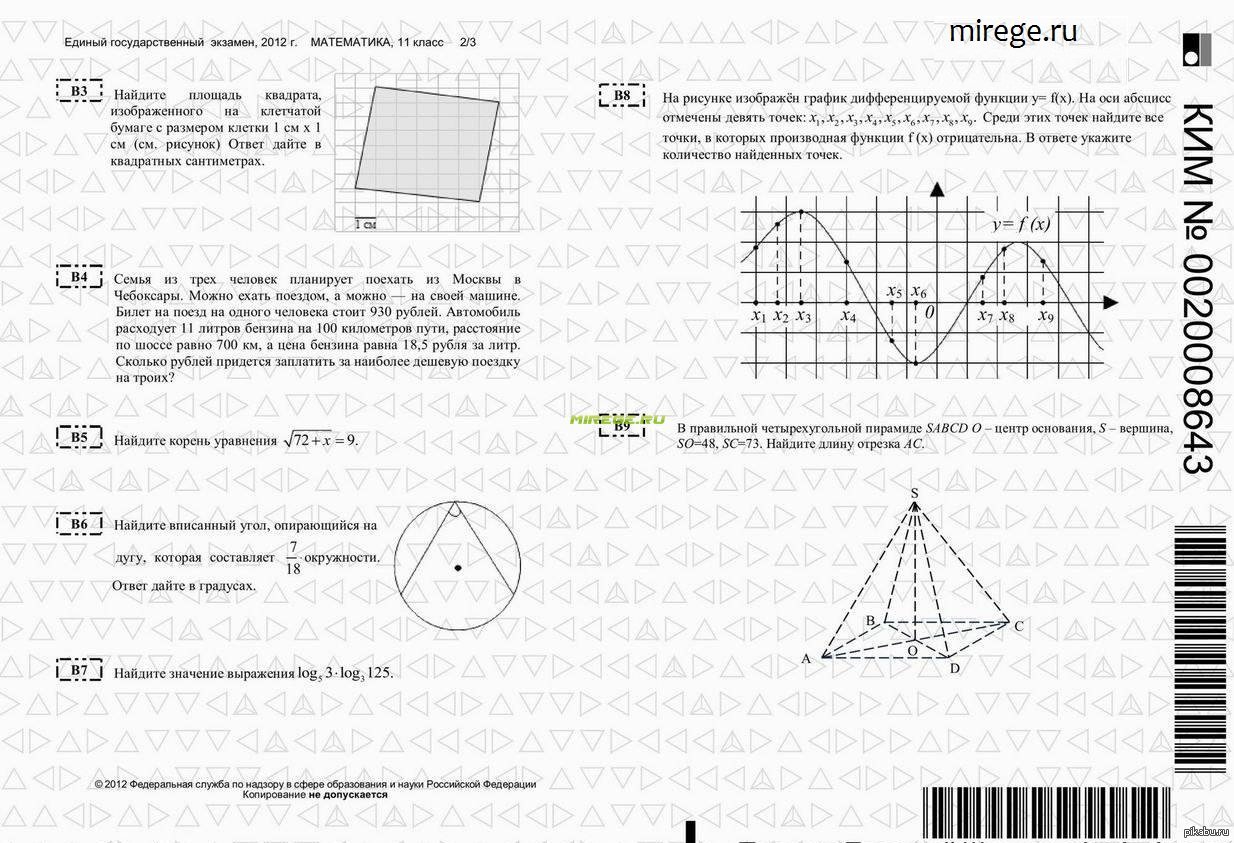
- Предварительно зарегистрируйтесь на свой первый курс математического анализа с помощью Preference selection. Обратите внимание, что вы должны иметь место на курсе, чтобы зарегистрироваться, и вы не можете выбрать предпочтения для более чем одного курса математического анализа одновременно.
- Если вам нужна помощь с размещением и вы пропустили консультационную сессию, напишите преподавателю, указанному ниже в качестве контактного лица курса, на который вы были направлены.
Учащиеся, которые изучали многомерное исчисление в старшей школе, часто начинают учебу в Йельском университете с линейной алгебры: математика 222, 225 или 226.Для получения подробной информации о том, как это можно сделать, см. соответствующий вопрос в нашем FAQ по математике.
Если вы изучали линейную алгебру в старшей школе, ознакомьтесь с вариантами, перечисленными в соответствующем вопросе часто задаваемых вопросов по математике.
Если вы прошли курсы реального анализа, абстрактной алгебры или другие углубленные курсы в старшей школе, обратитесь за консультацией по математическим курсам в отдел математики DUS. Мы будем рады помочь.
Мы будем рады помочь.
Предпосылкой для изучения математики является интегральное исчисление (например, Math 115 или AP Calculus BC).
После предварительных условий вводная последовательность включает:
- Линейная алгебра (математика 225 или 226),
- Реальный анализ (Math 255 или 256) и
- Многомерный анализ или исчисление (Math 302 или 120).
Большинство учащихся проходят курс многомерного исчисления до поступления на курсы математики 225 или 226.
Будущие специалисты по математике и студенты, интересующиеся абстрактной математикой, могут рассмотреть возможность зачисления на курс математики 225 (или 226) сразу после интегрального исчисления (т.г. Math 115 или AP Caclulus BC), а также выполнение требования к векторному анализу/исчислению с несколькими переменными с помощью Math 302. Обратите внимание, что Math 225 не требует вступительного экзамена — если вы прошли курс интегрального исчисления, вы можете просто записаться на Math 225.
Если вы выполнили какую-то часть последовательности в старшей школе, посетите раздел «Часто задаваемые вопросы по математике» для получения информации о вариантах. Затем вам следует проконсультироваться с DUS, который оценит вашу предыдущую курсовую работу, посмотрит, можно ли сделать исключение из требований, и поможет вам выбрать лучший класс для продолжения.
Чтобы получить совет по специальности или курсам математики, посетите наш FAQ по математике, посетите нашу академическую ярмарку в августе или свяжитесь с Math DUS.
Если вы думаете о специальностях по математике, мы рекомендуем вам подписаться на наш список рассылки Math DUS, чтобы получать новости от математического факультета. Вы также можете заглянуть на страницу нашего математического сообщества!
Если вы не изучали математический анализ в старшей школе и хотите изучать математический курс, отличный от математического, вам может понравиться один из наших курсов 100-го уровня без математического анализа, описанных выше.
Если у вас есть дополнительные вопросы, пожалуйста, посетите
Если ваш вопрос там не указан, обратитесь к преподавателю, указанному в следующей таблице. Мы будем рады помочь!
| тип вопроса | электронная почта(за которой следует @yale.edu) |
|---|---|
| Если у вас возникнут вопросы о вашем размещении, пожалуйста, посетите нашу консультационную сессию в августе.* | |
| Другие вопросы вступительного экзамена | Дж.Барнс |
| Математика 110-111 | Роберт Джей Макдональд |
| Математика 112 | Дж. Барнс |
| Математика 115 | Рэйчел.Диторн |
| Математика 120 | Меган Андерсон |
| Математика 121 | джон.холл |
| Математика 225 | Патрик Девлин |
| Основная математика / курсы повышения квалификации / другие вопросы | мики. хавличкова хавличкова |
* Если вы пропустили консультационную сессию, напишите преподавателю, который указан в качестве контактного лица для курса, на который вы были назначены.Обязательно напишите не менее чем за три дня до закрытия выбора предпочтений, иначе преподаватель может не успеть вам помочь.
Yale Peer связи
Служба поддержки учащихся (SAS) работает с учащимися с СДВГ/аутизмом/трудностями в обучении, сенсорными или двигательными нарушениями, проблемами психического здоровья, временными нарушениями, такими как сотрясения мозга и серьезные травмы, и другими. Наша программа взаимодействия со сверстниками разработана таким образом, чтобы первокурсники могли общаться с кем-то, кто имеет непосредственный опыт поиска жилья в Йельском университете.Если вы считаете, что вам могут быть полезны дополнительные ресурсы в отношении академической и общей жизни колледжа, пожалуйста, не стесняйтесь заполнять эту форму, и PL для вашего колледжа свяжется с вами как можно скорее.
Советы по обучению | Кафедра математики
Из кабинета кафедры (с особой благодарностью и признательностью профессору Эду Оксфорду, который собирал эти ценные советы на протяжении 40 лет преподавания):Для большинства из нас математика является трудным, но полезным предметом для изучения.Важность и распространенность математики в нашем все более сложном обществе очевидна и хорошо задокументирована. Обратите внимание, что предсказывает наш Национальный научный фонд: более 80% всех новых рабочих мест, созданных в Соединенных Штатах в течение следующих десяти лет, потребуют глубоких знаний математики.
Очень немногие ученики могут изучать математику с помощью наблюдения. Неизменно требуется много времени, терпения, практики, еще раз практики и еще раз практики, чтобы освоить необходимые навыки и приемы для достижения успеха. Кроме того, успех в этом вопросе требует прочного фундамента . Например, абсолютно необходимым условием является овладение алгеброй и тригонометрией в колледже (ингредиенты курса предварительного исчисления Бейлора), чтобы преуспеть в исчислении.
Чтобы преуспеть в математике — или, если уж на то пошло, в любом другом предмете — необходимо выработать отличные и эффективные привычки к обучению. Время от времени мы слышим следующие причитания от студентов: « Я не знаю, почему я плохо сдал экзамен, потому что я сделал все домашнее задание » или « Я плохо сдал экзамен, хотя Изучал материал более 15 часов ».При ближайшем рассмотрении мы обычно обнаруживаем, что эти студенты просчитались. Мы все подвержены ошибкам такого рода. Ранее этой весной я думал, что провел три часа, работая во дворе; на самом деле я был на улице меньше часа. Но уж точно ощущались как три часа!
Доктор Чарльз Уивер с факультета психологии и неврологии Бэйлора написал отличное руководство, полное очень полезных советов по обучению, которое «обязательны к прочтению» для всех студентов. Его статья «Просто, но непросто: когнитивные принципы, лежащие в основе эффективного обучения» была недавно опубликована в весеннем информационном бюллетене Академии преподавания и обучения Бэйлора за 2012 год. Мы также настоятельно рекомендуем недавнюю книгу (будет опубликована в августе 2012 г. издательством Princeton University Press), написанную доктором Эдвардом Б. Бургером и доктором Майклом Старбердом, под названием «5 элементов эффективного мышления» . Доктор Бургер в 2010 году стал лауреатом престижной премии Бэйлора Роберта Фостера Черри за отличное преподавание.Наконец, еще одна статья, которую мы настоятельно рекомендуем всем студентам, называется «Говорить правду» и написана Стивеном Цукером из Университета Джона Хопкинса. В ней рассматриваются проблемы, с которыми сталкиваются студенты при поступлении в университет. Как он отмечает, Цукер говорит, что « самая большая разница между средней школой и колледжем будет заключаться в ваших курсах математики и естественных наук ».
Его статья «Просто, но непросто: когнитивные принципы, лежащие в основе эффективного обучения» была недавно опубликована в весеннем информационном бюллетене Академии преподавания и обучения Бэйлора за 2012 год. Мы также настоятельно рекомендуем недавнюю книгу (будет опубликована в августе 2012 г. издательством Princeton University Press), написанную доктором Эдвардом Б. Бургером и доктором Майклом Старбердом, под названием «5 элементов эффективного мышления» . Доктор Бургер в 2010 году стал лауреатом престижной премии Бэйлора Роберта Фостера Черри за отличное преподавание.Наконец, еще одна статья, которую мы настоятельно рекомендуем всем студентам, называется «Говорить правду» и написана Стивеном Цукером из Университета Джона Хопкинса. В ней рассматриваются проблемы, с которыми сталкиваются студенты при поступлении в университет. Как он отмечает, Цукер говорит, что « самая большая разница между средней школой и колледжем будет заключаться в ваших курсах математики и естественных наук ».
Пожалуйста, воспользуйтесь тем фактом, что на кафедре математики Университета Бэйлор работают отличные преподаватели, готовые помочь студентам…которые обращаются за помощью. Не ждите, пока не станет слишком поздно. И помните, что мы — отдел, ориентированный на результат. Одного усилия недостаточно, чтобы сдать класс или получить желаемую оценку. Говоря языком математики, усилия необходимы для успеха, но недостаточны.
Комментарии и дополнительные полезные предложения
- Сотовые телефоны/видеоигры/ТВ и концентрация не смешивать! Найдите тихое место для работы, чтобы свести к минимуму перерывы.
- Многие ученики бросают попытки решить задачу, если не могут решить ее за 10 минут.Неправильное отношение! Вполне нормально, что для решения некоторых проблем требуется гораздо больше времени. Важно, чтобы понял проблему. Иногда полезно сначала попытаться решить аналогичную, но более простую задачу.

- Не ожидайте, что все задачи на тестах и экзаменах будут похожи на заданные домашние задания. Для учащихся важно применить то, чему они научились в классе, для решения новых задач. Настоящего отличника следует определять как человека, который может решать такие проблемы и мыслить нестандартно.
- Калькуляторы против мышления: хотя верно то, что « калькуляторы являются мощными инструментами для открытия и понимания концепций », нет никаких сомнений в том, что сегодняшние студенты чрезмерно зависят от калькуляторов. Базовые навыки, такие как сложение, умножение, деление и элементарная тригонометрия, не должны требовать использования калькулятора.
- Вы должны взять на себя ответственность за просмотр справочных материалов, необходимых для изучения предмета. Ваш преподаватель может дать полезные советы относительно справочного материала.
- Большая часть обучения должна происходить вне класса. Как правило, вы должны быть готовы потратить как минимум два продуктивных часа на внеклассные занятия за каждый запланированный час курса.
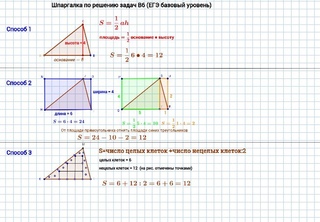
- Не пропускать занятия. Вы несете ответственность за изучение всего материала, который вы пропустили в результате отсутствия. При разумных обстоятельствах инструктор постарается вам помочь.
- Принять участие в уроке. Помогите преподавателю создать здоровую среду обучения. Задавайте конструктивные вопросы, особенно те, которые могут помочь вам и другим лучше понять предмет.
- Все решения проблем должны быть написаны разборчиво и хорошо организованы. Сохраняйте структурированную коллекцию своих решений для дальнейшего использования. Используйте этот сборник при подготовке к экзаменам.
- Выполняйте домашнее задание, когда оно назначено. Если вы не понимаете концепцию или метод, немедленно обратитесь за помощью. Инструктор хочет помочь вам учиться, но вы обязаны немедленно обратиться за помощью, когда это необходимо.
- Внимательно просмотрите все оценочные работы, которые преподаватель возвращает классу.Обратитесь за помощью, если вы не понимаете, как внести необходимые исправления.
 Вдумчивые письменные заметки об исправлениях в оцениваемых работах могут быть очень полезными при подготовке к последующим экзаменам и выполнению домашних заданий.
Вдумчивые письменные заметки об исправлениях в оцениваемых работах могут быть очень полезными при подготовке к последующим экзаменам и выполнению домашних заданий. - Прежде чем приступить к решению домашних заданий, внимательно прочитайте свои конспекты в классе, относящиеся к рассматриваемой теме. Также внимательно прочитайте соответствующие примеры и материал, приведенные в учебнике.
- Не поддавайтесь искушению посмотреть ответ, пока вы не напишете решение.
- Математические рассуждения и четкая коммуникация не менее важны, чем расчеты и числовые ответы. Для полного зачета вы должны показать достаточно организованной работы, чтобы убедить преподавателя в том, что вы понимаете соответствующие концепции.
- Если требуется письменный ответ на проблему, используйте полные предложения с правильной грамматикой.
- Правильно подготовиться ко всем экзаменам. Просмотрите все материалы курса, относящиеся к темам, которые могут быть затронуты на экзамене, включая все домашние задания.
 Попробуйте смоделировать среду тестирования, подготовив списки задач, которые охватывают всю широту материала, который может быть протестирован. Затем сядьте только с карандашом, бумагой и калькулятором (если это разрешено), чтобы определить, сможете ли вы легко справиться с задачами без посторонней помощи. Нереально должным образом просмотреть двух-трехнедельный учебный материал за один-два дня.
Попробуйте смоделировать среду тестирования, подготовив списки задач, которые охватывают всю широту материала, который может быть протестирован. Затем сядьте только с карандашом, бумагой и калькулятором (если это разрешено), чтобы определить, сможете ли вы легко справиться с задачами без посторонней помощи. Нереально должным образом просмотреть двух-трехнедельный учебный материал за один-два дня. - Помогать другим учащимся в обучении. Вербализация предмета другим часто улучшает обучение.Эффективное устное и письменное изложение материала курса является убедительным показателем хорошего знания предмета. Вы можете сформировать учебную группу, чтобы помочь с этим уровнем обучения.
- Приходите на помощь, когда она вам понадобится. Вы можете зайти в кабинет инструктора без предварительной записи в любое время в рабочее время. Вы можете связаться с инструктором по электронной почте, чтобы назначить встречу на время, отличное от рабочего времени.
- В течение осеннего и весеннего семестров с понедельника по пятницу каждую неделю на факультете математики проводится бесплатная «Математическая лаборатория» по курсу SR 326.
 Спросите своего учителя о конкретных часах и деталях. Хотя мы всегда рекомендуем сначала обратиться за помощью к учителю математики, дополнительную помощь можно получить в математической лаборатории.
Спросите своего учителя о конкретных часах и деталях. Хотя мы всегда рекомендуем сначала обратиться за помощью к учителю математики, дополнительную помощь можно получить в математической лаборатории.
Специальности, программы и факультеты | Математика
Математика – универсальная часть человеческой культуры. Это также количественный язык социальных, биологических и физических наук. По этим причинам математика является ценным и важным компонентом гуманитарного образования.Все учащиеся Scripps должны сдать вступительный экзамен, который проводится во время осенней ориентации в Scripps, и им рекомендуется записываться на математические курсы независимо от того, рассматривают ли они возможность получения специальности по математике.
Зачисление на математику
Высшее или неспециальное образование в области математики может привести к карьере в различных областях, включая бизнес, промышленность, правительство, страхование (в качестве актуария) или преподавание. Студенты, которые хотят записаться на курсы математики, отличные от тех, которые предлагаются в Scripps, должны проконсультироваться на факультете математики.В каталоге Курсы математики в Клермонте перечислены все курсы математики, предлагаемые в колледжах Клермонта, и его можно получить в офисе регистратора и на факультете математики.
Математические требования
Каждый студент Скриппса должен выполнить требование по математике, чтобы получить высшее образование. Широкое использование математики в нашей жизни как отдельных людей, так и всего общества указывает на то, что знание математики необходимо для практической жизни и профессионального развития.
Требование по математике может быть выполнено как по теоретической, так и по прикладной математике. Теоретическая математика включает в себя методы исследования, основанные на строгой дедукции и формальных доказательствах, которые отличаются от тех, что используются в других областях. Прикладная математика является фундаментальным инструментом в социальных и естественных науках и во многих других областях. Из-за важности математики для изучения социальных и естественных наук и для работы во многих сферах деятельности учащимся настоятельно рекомендуется продолжать изучение математики выше требуемого уровня.
Требование по математике может быть выполнено одним из следующих способов:
- Пройдя MATH022 SC Великие идеи в современной математике, MATH023 SC Трансцендентные функции; MATH 030 Исчисление I, MATH 031 Исчисление II или MATH 032 Исчисление III.
- Набрав достаточно высокие баллы на вступительном экзамене, чтобы поступить на математический курс Math030 или на математический курс более высокого уровня. (Экзамен по математике проводится во время осенней ориентации.)
- Пройдя один из следующих курсов по статистике: BIOL175 KS Applied Biostatistics, ECON120 SC Statistics или PSYC103 SC Psychological Statistics.
- Прохождение PHIL144 SC Logic and Argumentation.
- Получив 4 или 5 баллов по соответствующему курсу средней школы на экзамене AP Calculus AB или AP Calculus BC.
Широкое использование математики в жизни каждого человека и общества указывает на то, что знание математики необходимо для практической жизни и профессионального развития. Требование по математике может быть выполнено либо по теоретической, либо по прикладной математике. Теоретическая математика включает в себя методы исследования, основанные на строгой дедукции и формальных доказательствах, которые отличаются от тех, что используются в других областях.Прикладная математика является фундаментальным инструментом в социальных и естественных науках и во многих других областях.
Из-за важности математики для изучения социальных и естественных наук и для работы во многих профессиях учащимся настоятельно рекомендуется продолжать изучение математики выше требуемого уровня.
Факультет Скриппса
Курсы бакалавриата — UCLA Mathematics
Описание курса
(То же, что и C&S Bio M32.) Лекция, три часа; обсуждение, один час. Реквизит: Науки о жизни 30A, Науки о жизни 30B. Недоступно для студентов с баллами 31A, 31B, 32A или 32B. Предназначен для студентов, изучающих науки о жизни, которые прошли курс Life Science 30B. Методы и результаты одно- и многомерного исчисления необходимы для количественного обучения биологии. Пределы, дифференцирование (с одной и несколькими переменными), оптимизация, интегрирование и методы интегрирования, полиномы Тейлора и приложения к аппроксимации, ряды Тейлора и другие степенные ряды, вектор-функции, градиенты и множители Лагранжа.P/NP или буквенная градация.
Цели курса
Этот курс развивает принципы и расчеты исчисления, чтобы студенты, изучающие науки о жизни, которые завершили две четверти курса «Математика для ученых-биологов» (Науки о жизни 30A и Науки о жизни 30B), могли продолжить, по мере необходимости, с математикой 33A (линейная алгебра, математика 33B (дифференциальные уравнения) или более поздними курсами старшего уровня. Помимо охвата основных тем одномерного и многомерного исчисления, он направлен на развитие традиционных навыков работы с бумагой и карандашом.Конкретные цели включают: вычисление пределов функций, вычисление производных, использование производных в одной и нескольких переменных для решения (условных) задач оптимизации, а также вычисление и использование определенных и неопределенных интегралов.
Учебник
Нойхаузер, Клаудия и Роупер, Маркус. Расчет для биологии и медицины . 4 -й Эд., Пирсон, 2018.
Обновление наброска: W. Conley 10/20
Общий курс Наброски / График лекций 2
|
| |
| Темы | |
| 1 | Введение в курс.Краткий обзор концепции предела, концепции производной и определения предела производной. Подробнее о лимитах/производных. Обзор триггерных, логарифмических, экспоненциальных функций. & правила произведения и частного. Обзор Цепного правила. Неявное дифференцирование и связанные с ним ставки. Приложения. Другие приложения… |
| 2 | Введение в оптимизацию с одной переменной. Приложения. Оптимизация, критические точки, тест первой производной. Тест второй производной. Приложения. |
| 3 | Обзор основ векторной графики. Скалярное произведение. Ортогональные проекции. Введение в оптимизацию с несколькими переменными. Обзор частных производных. Производные по направлению. Градиент и вычисление производных по направлению. Градиент как векторное поле. |
| 4 | Оптимизация многомерных функций.Тест второй производной. Оптимизация с ограничением через множители Лагранжа. Промежуточный период 1 |
| 5 | Применение многомерной оптимизации. Обзор первообразных, неопределенных интегралов и определенного интеграла. Обзор определенного интеграла, площади под кривой и FTC. |
| 6 | Приложения определенных и неопределенных интегралов. Формулы интегрирования для некоторых простых функций. Введение в интегрирование подстановкой. Интеграция путем замены. |
| 7 | Интеграция по частям. Применение интегрирования по частям с. |
| 8 | Промежуточный период 2 Введение в последовательности и серии. Конвергенция. Примеры. Серия Тейлор. Относительный тест на сходимость. Радиус сходимости. |
| 9 | Ряд Тейлора некоторых известных функций. Полиномы Тейлора как аппроксимации. Применение полиномов Тейлора. |
| 10 | Ряды Фурье для периодических функций. Примеры. Вычисление коэффициентов ряда Фурье. Отношение к линейной алгебре. Приложение к колебательным динамическим системам. Применение рядов Фурье. |
Оценки:
Схема 1:
Обсуждение: 5%
Домашнее задание: 15%
Midterm 1: 20%
MIDETERM 2: 20%
Финальный экзамен на 40%
Схема 2:
Обсуждение: 5%
Домашнее задание: 15 %
Промежуточные экзамены 1 и 2: 30%
Выпускной экзамен 50 %
Основные компетенции
Они смогут распознавать, формулировать и использовать ключевые теоремы исчисления с одной и несколькими переменными.
Результаты обучения:
Тестируемые результаты включают:
- вычисление явных пределов и производных функций с одной и несколькими переменными параметрами для решения задач оптимизации (с ограничениями)
- вычисление и использование определенных и неопределенных интегралов
- вычисление ряда Тейлора и решение задач аппроксимации с использованием полиномов Тейлора
- , вычисление касательных линий и касательных плоскостей
(Поставленные задачи могут включать рациональные, тригонометрические, экспоненциальные и логарифмические функции в любом из вышеперечисленных.


 Но этот вопрос упускает суть.
Но этот вопрос упускает суть.  Идеально,
вступительный тест оценит ваш текущий набор навыков, определит, что
вам не нужны какие-либо коррекционные занятия, и вы поместите вас в предварительную алгебру
или начальный класс алгебры.Или, может быть, вы только что закончили среднюю школу в прошлом
падать. Может быть, вы успешно прошли курс AP по математическому анализу и до сих пор помните все
Это. Затем вступительный тест измерит это, определит, что вы не
нужна алгебра или предварительное исчисление, и оно поместит вас куда-нибудь в исчисление
ряд.
авторское право
© Элизабет Стапель 2002-2011 Все права защищены
Идеально,
вступительный тест оценит ваш текущий набор навыков, определит, что
вам не нужны какие-либо коррекционные занятия, и вы поместите вас в предварительную алгебру
или начальный класс алгебры.Или, может быть, вы только что закончили среднюю школу в прошлом
падать. Может быть, вы успешно прошли курс AP по математическому анализу и до сих пор помните все
Это. Затем вступительный тест измерит это, определит, что вы не
нужна алгебра или предварительное исчисление, и оно поместит вас куда-нибудь в исчисление
ряд.
авторское право
© Элизабет Стапель 2002-2011 Все права защищены
 В инструкции сказано, что ребенок проходит тестирование
должен был читать группы слов, пока, наконец, не смог
прочитать определенное количество слов. С этой остановки ток
можно определить уровень чтения.Смысл этого теста был не в том.
«пройти» или «неудачно» юного читателя или критиковать
его способности или потенциал, а измерить («поместить») его
текущие способности к чтению. Когда мой сын остановился на полпути вниз по
стол, он не «провалился» на тесте; совсем наоборот,
он преуспел для своего возраста; но реальная точка испытания была
что я тогда знал, на каком уровне он мог читать. Какой-то «зачет» был
не суть; измерение было точечным.
В инструкции сказано, что ребенок проходит тестирование
должен был читать группы слов, пока, наконец, не смог
прочитать определенное количество слов. С этой остановки ток
можно определить уровень чтения.Смысл этого теста был не в том.
«пройти» или «неудачно» юного читателя или критиковать
его способности или потенциал, а измерить («поместить») его
текущие способности к чтению. Когда мой сын остановился на полпути вниз по
стол, он не «провалился» на тесте; совсем наоборот,
он преуспел для своего возраста; но реальная точка испытания была
что я тогда знал, на каком уровне он мог читать. Какой-то «зачет» был
не суть; измерение было точечным.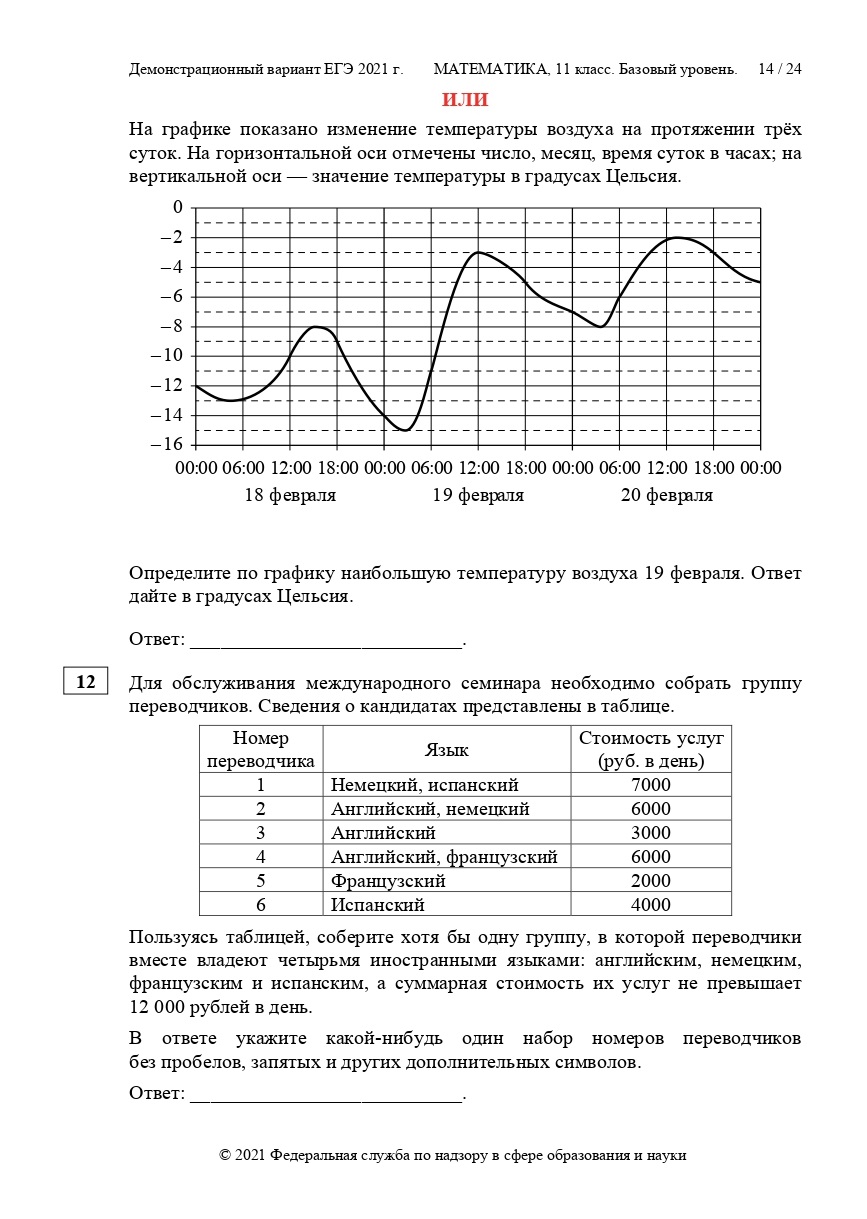 И от грустного
опыт, я могу сказать вам, что это означает, что вы, скорее всего, завалите
ваш первый урок математики, вероятно, во много раз, потому что у вас будет
поступил на курс, не имея необходимой математической подготовки, чтобы понять
материал.
И от грустного
опыт, я могу сказать вам, что это означает, что вы, скорее всего, завалите
ваш первый урок математики, вероятно, во много раз, потому что у вас будет
поступил на курс, не имея необходимой математической подготовки, чтобы понять
материал.
 Я подумал, что этот класс, вероятно,
где мне нужно было бы начать.
Я подумал, что этот класс, вероятно,
где мне нужно было бы начать. С чего я начал? В средней алгебре на больше, чем исчисление.
— но как раз там, где я ожидал, мне, вероятно, нужно будет начать. И вот я,
пишу математический сайт, так что «заваливание» вовсе не означает, что я
«тупой».
С чего я начал? В средней алгебре на больше, чем исчисление.
— но как раз там, где я ожидал, мне, вероятно, нужно будет начать. И вот я,
пишу математический сайт, так что «заваливание» вовсе не означает, что я
«тупой».  ком.
ком. 