Формулы стереометрии для егэ: Основные формулы стереометрии для ЕГЭ по математике 2020-2021.

Готовимся к ЕГЭ. Стереометрия презентация, доклад

Текст слайда:

Угол между прямой и плоскостью — угол между прямой и её проекцией на плоскость

В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁ найдите угол межу
Плоскостью АА₁С и прямой А₁В , если АА₁ = 3, АВ = 4, ВС = 4.

А

В

С

Д

А₁

В₁

С₁

Д₁

4

4

3

Параллелепипед,

в основании

квадрат (по условию).

плоскость АА₁С₁С ,

прямая А₁В.

Угол межу ними —

?

Это угол между

прямой А₁В

и её проекцией

на пл. АА₁С₁С.

АВСД — квадрат (по условию),

диагонали

перпендикулярны.

ВО

АС.

А₁О

ВО

(по т. о 3-х перпендикулярах) →

А₁О проекция А₁В на плоскость АА₁С₁С .

Угол ВА₁О —

искомый

В

А₁

О

∆ ВА₁О

ВА₁О —

определение синуса

1. А₁В

в ∆ ВА₁А

по т. Пифагора,

5

2. ВО

½ ВД

в ∆ АВД

по т. Пифагора,

2√2

3. Sin ВА₁О =

ВО :

А₁В =

2√2 : 5.

5

2√2

5

прямоугольный,

(ВО :

А₁В).

ВА₁О =

arcsin 0,4√2.

ВО

пл. АА₁С₁С

(признак перпендикулярности прямой и плоскости).

В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁ , у которого АА₁ = 4,
А₁Д₁ = 6, С₁Д₁ = 6, найдите тангенс угла между плоскостью АДД₁ и
прямой МК, проходящей через середины рёбер АВ и В₁С₁.

Ответ: 0,6.

Пусть М Є АВ, К Є В₁С₁ .

Искомый угол —

ВК — проекция МК на плоскость ВВ₁С₁С. →

В ∆ ВКМ (прямоугольный),

Tg ВКМ = ВМ : ВК.

12

№ 14.

№ 15.

Ответ

— как и между МК и пл. ВВ₁С₁С. — ?

ВКМ.

Самостоятельно. Ответ.
Затрудняетесь.
Кликнуть план решения.

(ориентир при решении — рис. параллелепипеда к задаче № 14)

Задача 13. Сложная стереометрия

В задаче 13 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:

1. Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются в одной точке и параллельны данным прямым.
2. Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.
3. Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей.

Прямые всегда задаются двумя точками на поверхности или внутри многогранника, а плоскости — тремя. Сами многогранники всегда задаются длинами своих граней.

Традиционный метод решения

В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.

Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.

Именно поэтому задача 14 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.

Преимущества традиционного решения:

1. Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;
2. При правильном подходе значительно сокращается объем вычислений.

Недостатки:

1. Необходимо знать большое количество формул из стереометрии и планиметрии;
2. Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.

Впрочем, если у читателя хорошее стереометрическое воображение, проблем с дополнительными построениями не возникнет. Остальным предлагаю отказаться от традиционного геометрического метода и рассмотреть более эффективный алгебраический подход. Итак, поехали!

Метод координат в задаче 14

1. Метод координат в пространстве — о чем, собственно, идет речь. Работать будем только с векторами. Прямые и плоскости тоже заменяются векторами, поэтому никаких проблем не возникнет.
2. Введение системы координат для многогранников. Дело в том, что в настоящей задаче 14 никаких координат не будет. Их надо вводить самостоятельно.
3. Вычисление угла между двумя прямыми. А это уже решение конкретных задач 14. Мы научимся находить косинус угла между двумя прямыми — где бы эти прямые ни лежали.
4. Вычисление угла между прямой и плоскостью. Во многих задачах 14 встречаются плоскости. Для любой прямой можно рассчитать синус угла между плоскостью и этой прямой. Именно синус — и только затем косинус!
5. Вычисление угла между двумя плоскостями. Тут все просто: заменяем плоскости нормальными векторами и считаем угол между последними. Косинус угла между векторами — это и косинус угла между плоскостями.
6. Дополнительные соображения — как можно упростить вычисления и грамотно их оформить. Все-таки №14 — это не №2, и здесь требуется привести полноценно решение задачи.

Глава 1.

Метод координат в пространстве

§ 1.

Метод координат в пространстве

§ 2.

Введение системы координат

§ 3.

Четырехугольная пирамида в задаче C2

§ 4.

Четырехугольная пирамида: как найти координаты вершин

§ 5.

Координаты вершин правильного тетраэдра

Глава 2.

Уравнение плоскости

§ 1.

Уравнение плоскости в задаче C2. Часть 1: матрицы и определители

§ 2.

Задача C2: уравнение плоскости через определитель

§ 3.

Видеоурок по задачам C2: уравнение плоскости через определитель

Глава 3.

Двугранные углы и расстояния

§ 1.

Угол между двумя прямыми

§ 2.

Задача 14: Угол между плоскостями сечения

§ 3.

Видеоурок по задачам C2: расстояние от точки до плоскости

§ 4.

C2: расстояние между двумя прямыми

§ 5.

Дополнительные соображения

§ 6.

Как найти угол между плоскостями, секущими многогранник?

§ 7.

Задание 14: Площадь сечения многогранника

§ 8.

Задание 14: периметр сечения пирамиды плоскостью

§ 9.

Задача 14 из пробного ЕГЭ 2016 от 3 марта

§ 10.

Сечения многогранников в задаче 14: что нужно знать?

Презентация для подготовки к ЕГЭ по математике

Задания В11

ЕГЭ по математике

Автор: учитель математики

МКОУ «Безголосовская СОШ»

Николайцева Лариса Николаевна

• Тип задания. Стереометрическая задача на нахождение геометрических величин (длин, углов, площадей объёмов).

 

• Характеристика задания. Несложное задание по стереометрии на применение основных формул, связанных с вычислением площадей поверхностей или объёмов многогранников (пирамид и призм) или тел вращения (цилиндров, конусов, шаров), в том числе вписанных или описанных около других многогранников или тел вращения.

• Комментарий . Для решения задачи достаточно знать формулы площадей поверхностей и объёмов пирамиды, призмы, цилиндра, конуса и шара.

Типичные ошибки:

• перепутать площадь поверхности с объемом;
• при изменении радиуса некоторых тел в несколько раз, объем меняем ошибочно в это же количество раз, но надо смотреть на формулу, радиус может быть в квадрате (а значит надо изменять объем дважды в это количество раз) или в кубе (значит надо изменять объем трижды в это количество раз).

В11 2012 год

Прототип задания B11 (№ 245353)

Найдите объем пирамиды, изображенной на рисунке.

Прототип задания B11 (№ 245353)

Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

S

Решение:

Формула объема пирамиды:

3

Рассмотрим основание пирамиды.

6

B

C

3

6

E

A

3

D

F

Отрезок ВЕ разбивает основание на две

равные трапеции.

3

Площадь каждой трапеции равна:

= 13,5

Ответ: 27

Высота пирамиды равна 3 .

S основ = 2 ∙ 13,5 = 27

Теоретические сведения

• Формула площади трапеции:

a

С

В

ABCD — трапеция

ВН — высота

h

D

А

H

b

Задание B11 (№ 269543)

4

Прототип (№ 245353)

Найдите объем пирамиды, изображенной на рисунке.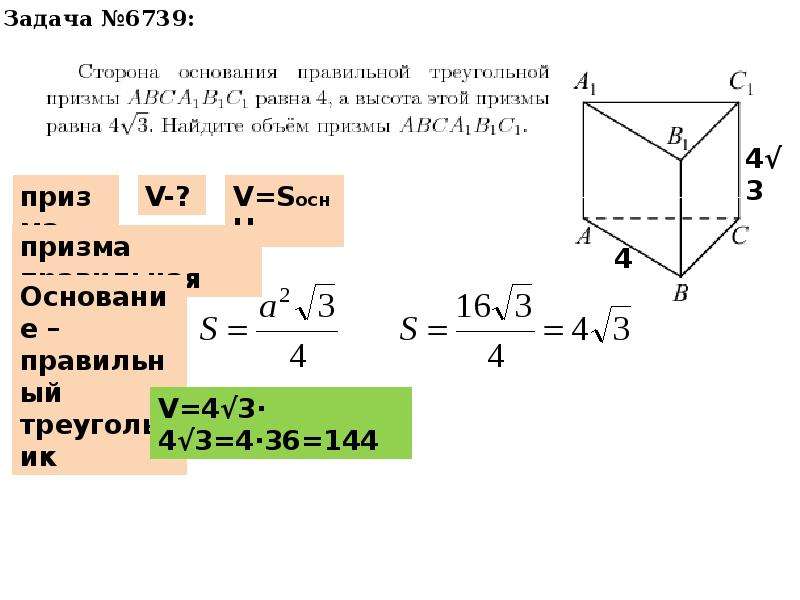 Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 8.

S

Решение:

Формула объема пирамиды:

Рассмотрим основание пирамиды .

8

6

F

4

8

8

6

3

E

A

C

4

3

D

B

Отрезки разбивают основание на три равных прямоугольника, со сторонами 3 и 4

3

S = 3 ∙ 4 =12

Площадь каждого прямоугольника равна:

Ответ: 96

Высота пирамиды равна 8.

S основ = 3 ∙ 12 = 36

Теоретические сведения

• Формула площади прямоугольника:

a – длина прямоугольника

b — ширина прямоугольника

b

S = a ∙ b

a

Задание B11 (№ 270037)

Прототип (№ 245353)

Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 7.

Вынесем отдельно основание пирамиды

6

1

7

Площадь основания

3

состоит из площадей трех

прямоугольников

1

8

5

5

Высота пирамиды равна 7.

Ответ: 119

S основ = 1∙ 3 +6 ∙ 3 + 6 ∙ 5 = 51

Диагн. Раб. 25.01.12

В11 Дана правильная треугольная призма ABCA 1 B 1 C 1 , площадь основания которой равна 6, а боковое ребро равно 8. Найдите объем многогранника, вершинами которого являются точки ABCA 1 C 1 ,

A 1

С 1

В 1

С

A

В

Трен. раб.27.09.11

Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 2, а площадь поверхности равна 104.

B 1

C 1

D 1

А 1

C

B

А

D

Трен. раб. 7. 12. 11

S=2∙5∙4 +2∙5∙5+2∙5∙4=130

Ответ: 130

E 1

D 1

F 1

C 1

B 1

A 1

E

D

F

C

A

B

Он лайн 8.10.11

Ответ: 7

Он лайн 4 тур

2

C 1

B 1

D 1

А 1

C

B

1

А

D

Решу ЕГЭ

Ответ: 4,5

Демо, 2012

Ответ: 9

Ященко

Ответ: 2175

ЕГЭ 2020.

Математика. Профильный уровень. Планиметрия, стереометрия. Ответы — Учебник 2021 — 2022 год

Авторы: Потоскуев Евгений Викторович Издательство: Экзамен ЕГЭ 2020. Математика. Профильный уровень. Планиметрия, стереометрия « Пособие содержит решения опорных задач планиметрии и стереометрии, их использование при решении содержательных геометрических задач на построение, доказательство и вычисление. Нахождение расстояний и углов в пространстве является той важнейшей частью раздела стереометрии, на которой основываются, базируются все ее метрические вопросы, в том числе нахождение площадей и объемов геометрических фигур. В этой связи в данном пособии предлагаются методические рекомендации выработки умения вычислять расстояния, углы между прямыми и плоскостями. Эти умения предлагается вырабатывать посредством выполнения тематических заданий, которые составлены из задач, подобранных по принципу «»от простого — к сложному»» с использованием изображений правильного тетраэдра, куба, правильных пирамиды и призмы. Наряду с геометрическим методом решения стереометрических задач на нахождение расстояний и углов в данном пособии рассматривается векторно-координатный метод их решения. Также предлагаются опорные задачи на геометрические преобразования пространства, комбинации правильных многогранников и сфер. Тематический набор задач каждого задания предваряется решением аналогичных задач. Ко всем задачам указаны ответы. В пособии представлены основные теоремы и формулы планиметрии и стереометрии. Учебное пособие адресовано учащимся и учителям математики школ, лицеев, гимназий, колледжей, а также студентам бакалавриата и магистратуры, аспирантам, преподавателям педвузов. » На этой странице вы можете бесплатно скачать правильные ответы к новому сборнику для 1 полугодия и 2 полугодия обучения в школе. Новый сборник — решебник предназначен для учащихся, учителей школы и родителей, которые хотят помочь своим детям освоить предмет на хорошую оценку! Надеемся, что новые задания из сборника ГДЗ подойдут для следующего 2023 — 2024 учебного года. Полную версию учебника с ответами можно бесплатно скачать в формате ВОРД или PDF и потом распечатать на принтере, а так же читать онлайн. Также здесь можно скачать и распечатать ответы для родителей на домашнее задание, примеры, решения, страница, вопросы, пояснения и объяснения к онлайн заданиям из нового учебника. Купить этот сборник недорого наложенным платежом за наличный или безналичный расчет с доставкой можно в Интернет-магазине или просто нажать кнопку КУПИТЬ Официальный сайт. 2021 — 2022 учебный год. Открытый банк заданий. Полная версия. КДР. РДР. Тренажер. ВПР. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. ФИОКО. ОГЭ. ЕГЭ. ГИА. Школа России. Школа 21 век. ГДЗ. Решебник. Перспектива. КРС. Школа 2100. Таблица. Планета знаний. Страница. Россия. Беларусь. Казахстан. РБ Вид поставки: Электронная книга. Лицензия. Полная версия издательства с картинками Способ доставки: электронная доставка, наложенный платеж Язык книги: Русский Варианты формата книги: Word, PDF, TXT, EPUB, FB2, PDF, MOBI, DOC, RTF, DJVU, LRF Категория: Учебная, методическая литература и словари | Книги для школы | Математика | ЕГЭ по математике   СКАЧАТЬ ОТВЕТЫ  |  КУПИТЬ  |   ЧИТАТЬ ОНЛАЙН  |  ОТЗЫВЫ  |   ОБСУДИТЬ

Боковая область: определение, формула и примеры — видео и расшифровка урока

Боковая поверхность прямого кругового цилиндра

Найдем боковую поверхность прямого кругового цилиндра.

В этом примере нам дан цилиндр высотой 6 см и диаметром 10 см. Помните, что в правильном круговом цилиндре основания — это круги. Чтобы найти площадь боковой поверхности, находим периметр, которым в данном случае является длина окружности (расстояние по окружности), затем умножаем его на высоту цилиндра.

Длина окружности находится по следующей формуле:

C обозначает окружность, d обозначает диаметр, а число «пи» округляется до 3,14. Итак, мы находим длину окружности основания, 3,14 * 10 = 31,4, а затем умножаем ее на высоту, 6.

Причина, по которой мы используем длину окружности при нахождении площади боковой поверхности, заключается в том, что когда мы открываем круглый цилиндр и складываем стороны из квартиры, мы в конечном итоге с прямоугольником.Представьте себе бумажное полотенце. Рулон бумажных полотенец представляет собой цилиндр, но когда вы снимаете бумажное полотенце с рулона, вы получаете прямоугольник. Длина – это окружность, а ширина – это высота рулона.

Чтобы найти площадь сторон этого цилиндра, мы должны умножить длину окружности на высоту. Итак, мы имеем формулу площади боковой поверхности прямого кругового цилиндра:

Площадь боковой поверхности правильного кругового цилиндра = длина окружности

Площадь боковой поверхности прямоугольной призмы

Давайте попробуем другой пример, на этот раз с прямоугольной призмой.

Как видите, длина, ширина и высота указаны. Итак, боковые поверхности — это все поверхности по бокам. Нам нужно найти площадь каждой из четырех сторон… но есть более быстрый способ — вы его видите? Если бы мы нашли периметр основания, а затем умножили его на высоту, то получили бы площадь боковой поверхности.

У нас есть две длины и две ширины. Как и в предыдущем примере, основная формула для площади боковой поверхности:

Как и в случае с круглым цилиндром, если положить прямоугольную призму плоско, это будет выглядеть так:

Итак, сложите длину и ширину и умножьте на высоту, чтобы найти площадь боковой поверхности.Мы можем написать это более кратко:

Площадь боковой поверхности прямого круглого цилиндра и прямоугольной призмы в основном одинакова; найди периметр основания и умножь на высоту фигуры.

Площадь боковой поверхности пирамиды

Далее мы собираемся найти площадь боковой поверхности пирамиды.

Пирамида — это фигура с многоугольным основанием и множеством сторон, называемых гранями, которые соединяются вместе в одной точке, называемой вершиной. Чтобы найти площадь боковой поверхности, найдем половину периметра основания и умножим ее на высоту наклона боковых треугольников. Каждый треугольник имеет наклонную высоту. Наклонная высота — это высота каждого треугольника, а не высота пирамиды. Почему, спросите вы, мы находим половину периметра? Это потому, что каждая из сторон пирамиды представляет собой треугольник, а формула площади треугольника равна половине основания, умноженной на высоту.

Чтобы найти площадь боковой поверхности пирамиды, вы можете найти площадь каждого треугольника, A = 1/2 bh или A = 1/2 lw , затем умножить на количество треугольников , который будет основываться на количестве сторон основания; или можно взять половину периметра и умножить на наклонную высоту.

Давайте попробуем оба способа на этой пирамиде:

Нахождение площади боковой поверхности путем нахождения площади каждого треугольника и умножения на количество треугольников: l обозначает высоту наклона:

Нахождение площади боковой поверхности по формуле: LSA = 1/2 умножить на периметр, умноженный на наклонную высоту:

Площадь боковой поверхности конуса вычисляется так же, как и пирамиды, за исключением того, что основанием является круг, поэтому мы используем половину длины окружности круга, умноженную на наклонную высоту. Итак, допустим, у нас есть конус с наклонной высотой 12.

Резюме урока

Площадь боковой поверхности — это площадь сторон любой трехмерной фигуры. Каждая фигура может иметь разное основание, но площадь боковой поверхности находится одинаково. Найдите периметр основания и умножьте его на высоту любой трехмерной призмы.

При нахождении площади боковой поверхности пирамиды или конуса формула:

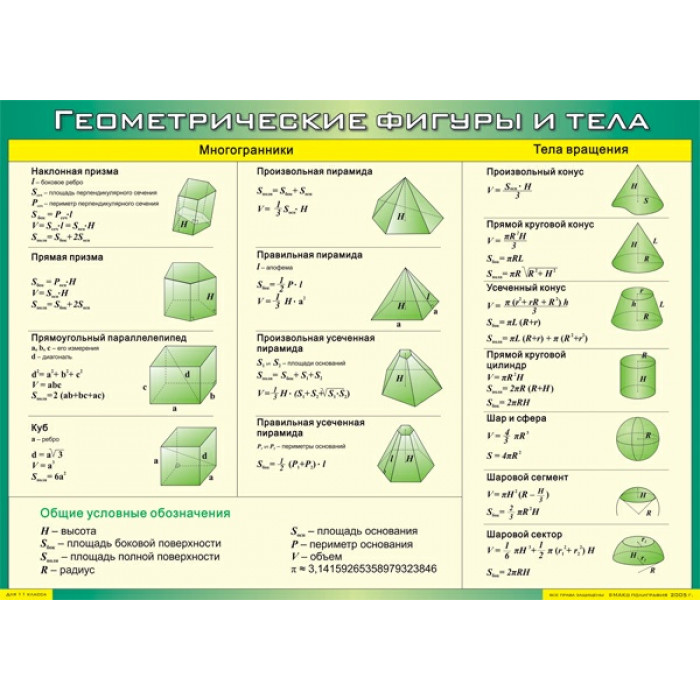
формул. Геометрические фигуры

Видеокурс «Получи пятерку» включает в себя все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задания 1-13 Профильного ЕГЭ по математике. Также подходит для сдачи базового экзамена по математике.Если вы хотите сдать экзамен на 90-100 баллов, вам нужно решить часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 классов, а также для учителей. Все, что нужно для решения части 1 ЕГЭ по математике (первые 12 задач) и задачи 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобаллу, ни гуманитарию.

Вся необходимая теория. Быстрые решения, ловушки и секреты экзамена.Разобрал все актуальные задания части 1 из банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни экзаменационных заданий. Текстовые задачи и теория вероятностей. Простые и легко запоминающиеся алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех видов заданий ЕГЭ. Стереометрия.Хитрые решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля до задачи 13. Понимание вместо зубрежки. Визуальное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. Основа решения сложных задач 2-й части ЕГЭ.

4.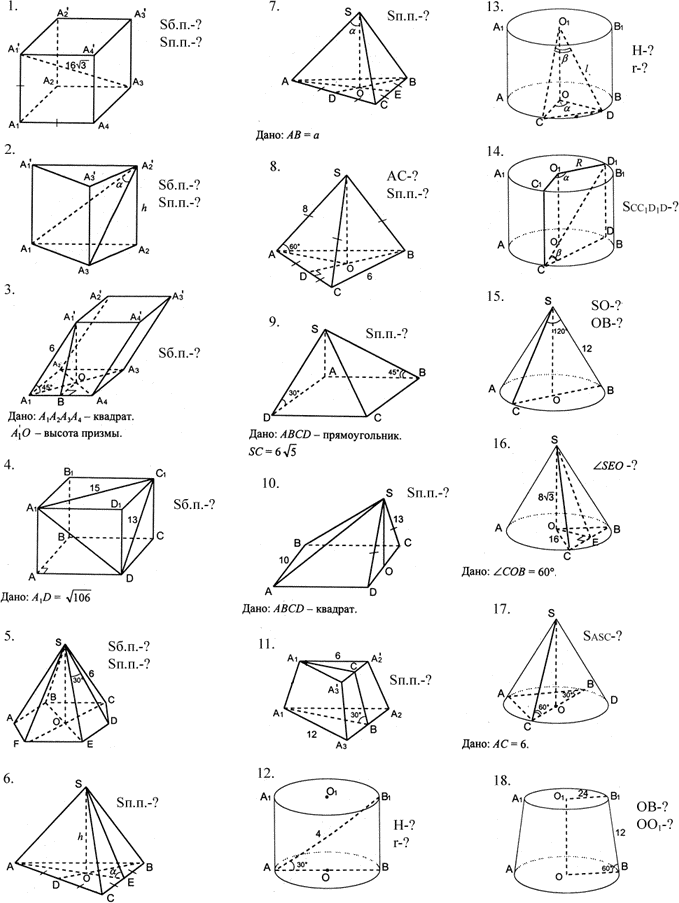 Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата:

5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):

6.Формула радиуса окружности, которая описывается около прямоугольника через синус угла, прилежащего к диагонали, и длину стороны, противоположной этому углу:

7. Формула радиуса окружности, которая описывается около прямоугольника через косинус угла, прилежащего к диагонали, и длины стороны при этом угле:

8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадь прямоугольника:

Угол между стороной и диагональю прямоугольника.

Формулы для определения угла между стороной и диагональю прямоугольника:

1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

Угол между диагоналями прямоугольника.

Формулы для определения угла между диагоналями прямоугольника:

1.Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:

β = 2α

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональю.

Прямоугольник. Так как прямоугольник имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии, т.е. на пересечении диагоналей прямоугольника.

Треугольник. Центр тяжести находится в точке пересечения его медиан. Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в отношении 1:2 от основания.

Круг. Поскольку круг имеет две оси симметрии, его центр тяжести находится на пересечении осей симметрии.

Полукруг. Полуокружность имеет одну ось симметрии, значит центр тяжести лежит на этой оси.Другая координата центра тяжести вычисляется по формуле: .

Многие элементы конструкций изготавливаются из стандартного проката — уголки, двутавры, швеллеры и другие. Все размеры, а также геометрические характеристики прокатных профилей являются табличными данными, с которыми можно ознакомиться в справочной литературе в таблицах нормального сортамента (ГОСТ 8239-89, ГОСТ 8240-89).

Пример 1. Определите положение центра тяжести фигуры, изображенной на рисунке.

Решение:

Оси координат выбираем так, чтобы ось Ох проходила по самому нижнему габариту, а ось Оу — по крайнему левому габариту.

Разбиваем сложную фигуру на минимальное количество простых фигур:

прямоугольник 20×10;

треугольник 15х10;

круг Р = 3 см.

Вычисляем площадь каждой простой фигуры, ее координаты центра тяжести.Заносим результаты расчета в таблицу

Рисунок №.	Площадь рисунка А,	Координаты центра тяжести

Ответ: С (14.5; 4.5)

Пример 2 . Определить координаты центра тяжести составного сечения, состоящего из листового и катаного профилей.

Решение.

Выбираем оси координат, как показано на рисунке.

Обозначим цифры цифрами и выпишем необходимые данные из таблицы:

Рисунок №.	Площадь рисунка А,	Координаты центра тяжести

Рассчитываем координаты центра тяжести фигуры по формулам:

Ответ: С (0; 10)

№ лабораторной работы1 «Определение центра тяжести составных плоских фигур»

Назначение: Определить центр тяжести данной плоской сложной фигуры экспериментальным и аналитическим методами и сравнить их результаты.

Заказ-наряд

Нарисуйте в тетрадях свою плоскую фигуру в размерах с указанием осей координат.

Аналитическое определение центра тяжести.

1. Разбейте фигуру на минимальное количество фигур, центры тяжести которых мы умеем определять.

   Укажите номера площадей и координаты центра тяжести каждой фигуры.

   Рассчитайте координаты центра тяжести каждой фигуры.

   Вычислите площадь каждой фигуры.

   Рассчитать координаты центра тяжести всей фигуры по формулам (нанести положение центра тяжести на чертеж фигуры):

Установка для экспериментального определения координат центра тяжести методом подвеса состоит из вертикальной стойки 1 (см. рис.), к которому прикреплена игла 2 … Плоская фигура 3 из картона, в котором легко проколоть дырку. Отверстия А и В прокалываются в произвольно расположенных точках (желательно на максимально удаленном расстоянии друг от друга). Плоская фигура подвешивается на иглу сначала в точке А и далее в точке В … С помощью отвеса 4 , закрепленной на той же игле, на рисунке карандашом проводится вертикальная линия, соответствующая отвесу.Центр тяжести ОТ фигура будет располагаться на пересечении вертикальных линий, проведенных при подвешивании фигуры в точках НО и В .

Твердотельная геометрия — Математика средней школы

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

‎Формулы +, ваши 4 коллекции в App Store

Четыре формуляра по математике, физике, химии и технике?
Приходится покупать все по отдельности, загружать и открывать? Нет, больше нет!
Formulas + объединяет все важные формуляры в один. Это означает, что вам нужно только купить один, загрузить один — это очень просто.
Приложение охватывает все предметы, которые у вас есть в школьной жизни, и, вероятно, является самым обширным справочником в магазине приложений.

Награды:
Приложение недели: CW40/2012 – Telefon.de

Вы ненавидите долго искать формулы? Благодаря встроенной интеллектуальной функции поиска поиск становится детской игрой, и вы быстро найдете нужные формулы.

Сделано студентами для студентов. Мы знаем, с чем вам приходится бороться в естественно-научных математических предметах, и хотели бы протянуть вам руку помощи с этим приложением.Кому не нужен маленький помощник, которого можно быстро использовать на уроках в школе или дома, когда вы работаете за партой? Даже великий математик/физик/химик/техник бессилен без правильных формул.
Неважно, любите ли вы эти предметы или у вас есть трудности с запоминанием сочетания букв и арифметических операторов, это приложение в любом случае станет вашим лучшим другом.

В дополнение к формулам вы найдете обширные, соответствующие объяснения и графики, которые обеспечивают ясность.
Имеющиеся подсказки к формулам помогут вам и обеспечат хорошие общие знания.

Если вам нужна подсказка, чтобы найти правильный способ расчета, можно использовать инновационную функцию расчета с подробным способом расчета и комментариями (требуется покупка в приложении).

Если у вас есть предложения по улучшению или вы нашли ошибку, мы будем рады их услышать. Чтобы сделать это максимально простым для вас, мы разработали для этого дополнительную процедуру.
Вам нужно будет щелкнуть в правом верхнем углу кнопку «Отправить предложение» на странице конкретной формулы.

Дизайн и графика с http://www.global-art-studios.de

Однако мы настоятельно рекомендуем не использовать это приложение и смартфон во время экзаменов, контрольных, классных или даже выпускных экзаменов и отказываемся от ответственности. за возможное наказание и исключение, а также за сбои в связи с неправильным и неправильным использованием содержимого.

Вступительный экзамен по математике | CTU FCE

Вступительный экзамен по математике | CTU FCE — K-101 Математика

Требования к вступительному экзамену

1. Алгебраические корректировки выражений (операции с дробями, квадратичное трехчленное разложение, специальные множители как ³ + b ³ , степени с рациональными показателями).
2. Уравнения и неравенства (линейные уравнения, квадратные уравнения, уравнения с абсолютными величинами соответственно с двумя абсолютными величинами, уравнения с параметрами, иррациональные уравнения, системы уравнений, линейные неравенства, квадратные неравенства, неравенства с абсолютной величиной).
3. Последовательности (арифметическая последовательность, геометрическая последовательность, рекурсивно введенная последовательность).
4. Функции, их свойства и графики (линейные, квадратичные, рациональные, экспоненциальные и логарифмические функции). 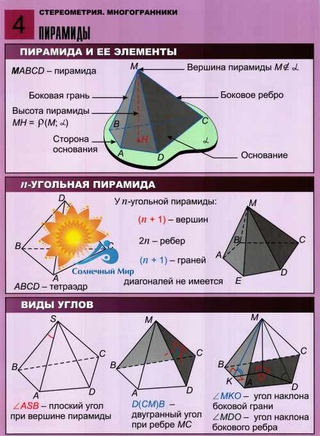Простые показательные и логарифмические уравнения.
5. Комплексные числа (алгебраическая форма, тригонометрическая форма, операции с комплексными числами, модуль комплексных чисел, формула Муавра, квадратные уравнения, биномиальные уравнения).
6. Теорема подобия и сравнения треугольников, теорема Пифагора, теорема Евклида.
7. Основные геометрические фигуры в пространстве (взаимное положение прямых и плоскостей, простых тел, их графическое изображение).
8. Периметры, площади, поверхности и объемы основных геометрических фигур с использованием тригонометрии.
9. Тригонометрия (тригонометрические функции, простые тригонометрические тождества, основные теоремы тригонометрии и их приложения).
10. Аналитическая геометрия линейных и квадратных объектов на плоскости (векторы, пересечение прямых, угол прямых, уравнения конических сечений – стандартный и общий вид).

Конструктивные задачи по стереометрии не включаются во вступительный экзамен в связи с характером теста. Знание стереометрии и основ проекции Монжа проверяется на вступительном испытании (в начале ноября) по предмету «Конструктивная геометрия».

© 2017–2022 FCE CTU в Праге. Пожалуйста, присылайте свои комментарии веб-мастерам.

Сдам экзамен по математике | Сдать экзамен по математике

Контрольный список сдачи теста на стереометрию

Сделай мой стереометрический тест

Если вам нужно подготовиться к стереометрическому тесту, существует множество инструментов, которые вы можете использовать.Тем не менее, если вы хотите узнать больше о методах наставника, есть также множество доступных ресурсов. В этом посте рассматриваются некоторые из этих ресурсов и их полезность.

Одиночный тест обычно является достаточно исчерпывающим показателем того, чего вы достигли в школе. Обычно это может дать вам представление о том, находитесь ли вы на правильном пути или нет. Вот почему так важно понимать, как работает тест по математике. К сожалению, не все учителя владеют такого рода оценкой, поэтому особенно важно гарантировать, что вы получите наилучшую возможную помощь.

Особенно важно готовиться к стереометрическому тесту, если вы знаете структуру конкретных вопросов. Большинство людей считают, что у них есть респектабельное представление о том, чего от них ожидает инструктор, однако конкретную информацию определить довольно сложно. Получение конкретных предложений о том, что вы получили от вас с помощью руководства, поможет вам подготовиться наилучшим образом.

Теория подготовки к тестам, особенно для стереометрии, не является чем-то совершенно новым.Пока на самом деле проводились оценки, люди фактически готовились к ним. Они также часто используются школами и компаниями. Фактически, многие университеты и колледжи теперь требуют, чтобы их студенты сдавали тесты.

Как правило, независимые студенты сдают экзамен непосредственно перед выпуском. Это время, когда они пытаются наверстать упущенное в классе. Если вы собираетесь сдавать экзамен сразу после окончания, убедитесь, что вы готовы заранее.

Прежде чем идти на тест, вам нужно проверить различные источники информации. Начните с Google и найдите предметы теста, которые вас больше всего интересуют. Вам также следует просмотреть журналы и книги по этому вопросу, чтобы получить представление о том, на что похож тест.

Для того, чтобы подготовиться к тестам, рекомендуется прочитать много продуктов по этой теме. Это поможет вам логически мыслить о проблемах, с которыми вы можете столкнуться. Понимание дизайна теста также полезно.Вы должны быть знакомы с дизайном каждой области.

Многих пугают их оценки. К сожалению, это то, что затрагивает большинство стажеров. Даже у тех, кто прекрасно себя чувствует, все же чаще всего возникают сомнения по поводу теста. Если вы чувствуете, что не совсем понимаете вопрос, вы можете обратиться за помощью до начала экзамена.

Выбор идеального времени для чтения вопросов поможет вам лучше понять материал. Примером этого является типичная проблема для стажеров.Они могут понять ответ на вопрос, однако они по-прежнему имеют дело с другими частями теста. По этой причине часто лучше уделить немного времени в начале экзамена и убедиться, что вы полностью понимаете вопрос, прежде чем продолжить.

Чтобы помочь вам с тестами по стереометрии, я включил краткое руководство, которое поможет вам подготовиться. Это основано на чтении книг по этому вопросу. Это очень краткий список ресурсов, которые вы можете использовать, чтобы получить максимальную отдачу от ваших экзаменов.

Многим учащимся не нравятся тесты. Это, скорее всего, потому, что они думают, что это испытания, которые трудно пройти. Наоборот, если вы хорошо подготовились, то вы сможете пройти тест с честью.

И наконец, никогда не позволяйте тесту отвлекать вас. Убедитесь, что вы не торопитесь, чтобы полностью прочитать содержание теста. Это поможет вам получить максимальную отдачу от теста.

Наймите кого-нибудь для проведения теста на стереометрию

Есть много доступных онлайн-выборов, когда речь идет о онлайн-помощи по математике.Вам просто нужно выбрать тот, который наиболее подходит для ваших нужд.

Задания и ответы на тест стереометрии всегда предоставляются в определенном формате. Это отличается от других стандартизированных тестов, таких как физика, английский язык или химия. Формат гарантирует, что проблемы хорошо организованы и не разбросаны по всему тесту.

Если вы пытаетесь найти справку по тесту по математике, вы можете выбрать один из множества веб-сайтов, на которых представлены подробные ответы и примеры задач. Некоторые сайты также дают конкретные инструкции о том, как правильно отвечать на математические вопросы.Эти сайты гораздо более популярны, чем те, которые пользуются базовой помощью.

Отличные веб-сайты также предоставляют подробную информацию о дате, времени и месте проведения теста. Вы можете избежать далеких поездок для учебы, если выберете респектабельный веб-сайт, который предлагает все подробности.

Ваше понимание темы необходимо, если вы хотите хорошо учиться в наши дни и быть в курсе современных моделей. Вот почему важно попытаться найти онлайн-предложения, которые вы можете использовать, чтобы получить максимальную отдачу от вашего теста по математике.

Сначала вам следует убедиться, что вы действительно нашли время для прохождения теста. Таким образом, у вас будет возможность реагировать на проблемы в своем собственном темпе, и вам не нужно будет спешить через весь процесс.

Вам также необходимо предотвратить самостоятельную подготовку к тесту по математике. Вместо этого выберите кого-нибудь, кто сможет присматривать за вами и следить за любой путаницей, которая может возникнуть на тесте. Этот человек также останется в состоянии проверить ваш прогресс, так что у вас будет возможность улучшить свой рейтинг.

Очень важно учитывать количество времени, которое вы можете уделить обучению. Независимо от того, являетесь ли вы стажером или родителем, вы должны четко понимать, сколько у вас времени и сколько помощи вы можете получить. Посмотрите, каково среднее время, прежде чем выбрать лучший вариант для вас.

Хотя вы, возможно, не знакомы с последним дополнением к теме, все же рекомендуется потратить некоторое время, чтобы проверить, какие темы обсуждаются. Это также исключительный способ собрать больше информации по теме перед сдачей теста.

Лица, сдавшие лучшие тесты в прошлом, как правило, понимают основные вопросы, которые нужно задать, и могут хорошо к ним подготовиться. Некоторые даже поймут ответы на эти вопросы.

Чрезвычайно важная вещь, которую нужно сделать, это воспользоваться помощью Интернета и сравнить варианты онлайн-покупки, чтобы найти самое лучшее среди множества доступных. Эти онлайн-альтернативы могут помочь вам сравнить различные используемые тесты, чтобы вы не были поражены результатами, полученными в реальном тесте.

Когда вы думаете, что действительно выбрали сайт, который использует лучшие онлайн-альтернативы для вашего теста по математике, вы можете продолжить и взглянуть на различные типы доступной помощи. Понимание того, какая помощь легко доступна, может дать вам утешение и поможет вам учиться намного лучше и быстрее, чем когда-либо прежде.

Заплатите кому-нибудь за мой тест на стереометрию

Когда вы участвуете в уроке математики, вы обязательно столкнетесь с необходимостью узнать, как лучше всего провести исследование для вашего теста по математике.Необходимо, чтобы вы понимали, что независимо от того, сколько книг по математике у вас есть, всегда будет ситуация, когда вам потребуется выучить пособие по математике. Лучше заранее знать, как подготовиться к тесту по стереометрии, чем нет, и, не зная конкретного сценария, вы можете провалить этот тест или еще хуже.

Сначала вам нужно знать, каким будет ваш тест на стереометрию, прежде чем вы сможете узнать, как подготовиться к нему. Некоторые математические классы имеют особую оценку, которая является одним из требований для проведения теста.Если это так, то вам нужно будет выяснить, будет ли этот тест охватывать то, что вам нужно охватить в вашем реальном тесте. Также будет полезно, если вы точно узнаете, на какие вопросы вам нужно будет ответить в тесте стереометрии, прежде чем идти на тест.

Затем вам нужно будет выяснить, какой вид вспомогательного теста по математике вам потребуется изучить для теста на стереометрию. Есть несколько ресурсов, которые можно использовать для подготовки к любому тесту на стереометрию. Наиболее типичные из них включают онлайн-тесты по математике, а также общие практические тесты.Эти ресурсы полезны, потому что они помогают вам узнать все, что вам нужно, чтобы понять предмет, чтобы пройти настоящий тест.

Чем больше вы будете готовиться к конкретному тесту по математике, тем лучше вы будете к нему подготовлены. Вы также узнаете много нового о самом тесте, и это поможет вам лучше подготовиться к реальной оценке. Лучше всего пройти как можно больше тестов, так как это поможет вам узнать, как устроен тест, а также что вам нужно будет понять.

Взгляните на несколько различных тестов и определите, какие из них вы бы предпочли для тщательной оценки темы. Это чрезвычайно важно, потому что это может помешать вам получить низкую оценку на тесте по стереометрии. Это также может помочь вам лучше подготовиться к реальному тесту.

Также важно решить, где вы собираетесь сдавать Тест. Это важно, потому что он может определить, какой тип продуктов вам потребуется взять с собой.Например, вам могут потребоваться карточки для запоминания или карандаши и бумага, чтобы помочь вам с тестом.

Во многих тестах есть вопросы, требующие исследования соответствующих продуктов на графике, матрице или диаграмме. Если вы не знаете, как это сделать, вам будет полезно взять с собой набор справочных таблиц, чтобы вы могли иметь представление о том, что представляет собой каждый элемент.

Вам также нужно будет выбрать, какой калькулятор подойдет для вашей помощи на экзамене по математике. В большинстве тестов вам будет доступно несколько различных типов калькуляторов, и вам нужно будет понять, какой из них подойдет для вашего конкретного теста по математике.

Некоторые из них будут иметь дополнительные функции, такие как перемещение цифровых клавиш, но они могут вам не понадобиться. Большинство калькуляторов будут иметь небольшое количество предварительно запрограммированных настроек. Важно выяснить, что это такое, прежде чем вы начнете пытаться выяснить остальную часть калькулятора.

Когда вы пытаетесь определить математический принцип, полезно использовать калькулятор, чтобы понять, как это делается. Есть много из них на выбор, и каждый из них будет различаться по тому, насколько просто его использовать.Например, некоторые из них будут ручными, а другие — цифровыми.

Некоторые новички, попавшие в класс, могут не обладать базовыми математическими навыками. Вот почему лучше всего использовать калькулятор на протяжении всего теста. Многие из них будут иметь различные интерактивные альтернативы, которые позволят вам почувствовать концепцию, а затем перейти к практическому использованию настоящего продукта на калькуляторе.

Попрактикуйтесь в использовании различных инструментов и общих правил на калькуляторе, а затем изучите задачу на калькуляторе и формулу, которую он выдает.Это лучший способ получить представление об использовании калькулятора для исправления числа.

Формулы нахождения объема параллелепипеда

Любое геометрическое тело можно охарактеризовать площадью поверхности (S) и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь относительно маленькую букву V и большую букву S, например, так работает человеческий мозг. Рассчитать эти показатели для простых геометрических фигур гораздо проще.

Коробка: определение, типы и свойства

Параллелепипед представляет собой четырехугольную призму с параллелограммом в основании.Зачем может понадобиться формула нахождения объема фигуры? Книги, упаковочные коробки и многие другие предметы быта имеют похожую форму. Помещения в жилых и офисных зданиях обычно представляют собой прямоугольные параллелепипеды.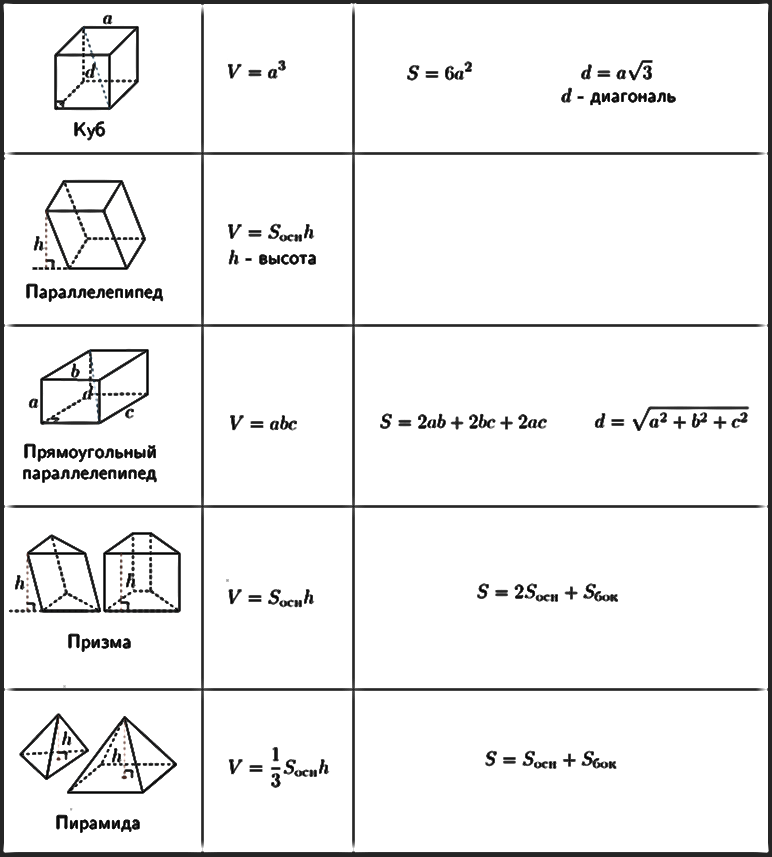 Для установки вентиляции, кондиционеров и определения количества нагревательных элементов в помещении необходимо рассчитать объем помещения.

Фигура имеет 6 граней — параллелограммов и 12 ребер, две произвольно выбранные грани называются основаниями.Параллелепипед может быть нескольких видов. Различия обусловлены углами между соседними ребрами. Формулы для нахождения V разных многоугольников немного отличаются.

Если 6 граней геометрической фигуры являются прямоугольниками, то ее еще называют прямоугольной. Куб — это частный случай параллелепипеда, у которого все 6 граней — равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.

Для решения задач вам понадобятся знания не только готовых формул, но и свойств фигуры.Список основных свойств прямоугольной призмы невелик и очень прост для понимания:

1. Противоположные края фигуры равны и параллельны. Это означает, что противоположные ребра одинаковы по длине и углу.
2. Все боковые грани прямого параллелепипеда — прямоугольники.
3. Четыре главные диагонали геометрической фигуры пересекаются в одной точке и делятся пополам.
4. Квадрат диагонали параллелепипеда равен сумме квадратов измерений фигуры (следует из теоремы Пифагора).

Теорема Пифагора утверждает, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.

Доказательство последнего свойства можно увидеть на изображении ниже. Решение проблемы простое и не требует подробных пояснений.

Формула объема прямоугольного параллелепипеда

Формула нахождения для всех видов геометрических фигур одинакова: V = S*h, где V — искомый объем, S — площадь основания параллелепипеда, h — высота, опущенная из противоположной вершины и перпендикулярно основанию.В прямоугольнике h совпадает с одной из сторон фигуры, поэтому, чтобы найти объем прямоугольной призмы, надо перемножить три измерения.

Объем обычно выражается в см3. Зная все три значения a, b и c, найти объем фигуры совсем не сложно. Самый распространенный тип задач на экзамене — нахождение объема или диагонали параллелепипеда. Без формулы объема прямоугольника решить многие типовые задачи ЕГЭ невозможно.Пример задачи и схема ее решения показаны на рисунке ниже.

Примечание 1 … Площадь поверхности прямоугольной призмы можно найти, умножив на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ак).

Примечание 2 . Площадь поверхности боковых граней легко найти, умножив периметр основания на высоту параллелепипеда.

На основании первого свойства параллелепипедов AB = A1B1 и грани B1D1 = BD.Согласно следствиям теоремы Пифагора, сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла 30°, равен гипотенузе. Применив это знание к треугольнику, мы легко найдем длины сторон AB и AD. Затем полученные значения умножаем и вычисляем объем параллелепипеда.

Формула нахождения объема наклонного параллелепипеда

Чтобы найти объем косого параллелепипеда, нужно площадь основания фигуры умножить на высоту, опущенную на данное основание от противоположного угла.

Таким образом, искомое V можно представить в виде h — количество листов с площадью S основания, поэтому объем колоды равен сумме Vs всех карт.

Примеры решения задач

Задания единого экзамена необходимо выполнить за определенное время. Типовые задачи, как правило, не содержат большого количества вычислений и сложных дробей. Часто ученику предлагают, как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, согласно которому общий объем равен сумме компонентов V.

Как видно из примера на изображении выше, в решении подобных задач нет ничего сложного. Задания из более сложных разделов предполагают знание теоремы Пифагора и ее следствий, а также формулы длины диагонали фигуры. Для успешного решения тестовых заданий достаточно заранее ознакомиться с образцами типовых заданий.

А древние египтяне использовали методы вычисления площадей различной формы, схожие с нашими методами.

В своих книгах «Начала» известный древнегреческий математик Евклид описал довольно большое количество способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, содержащие геометрические сведения, были написаны в XVI$ веке. Они описывают правила нахождения площадей фигур различной формы.

Сегодня с помощью современных методов можно с большой точностью найти площадь любой формы.

Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.2$.

Рисунок 1.

Рисунок 2.

Площадь фигур принято обозначать буквой $S$.

Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.

Если обозначить его длину буквой $a$, а ширину буквой $b$, то формула площади прямоугольника будет выглядеть так:

Определение 1

Цифры называются равными, , если при наложении друг на друга фигуры совпадают.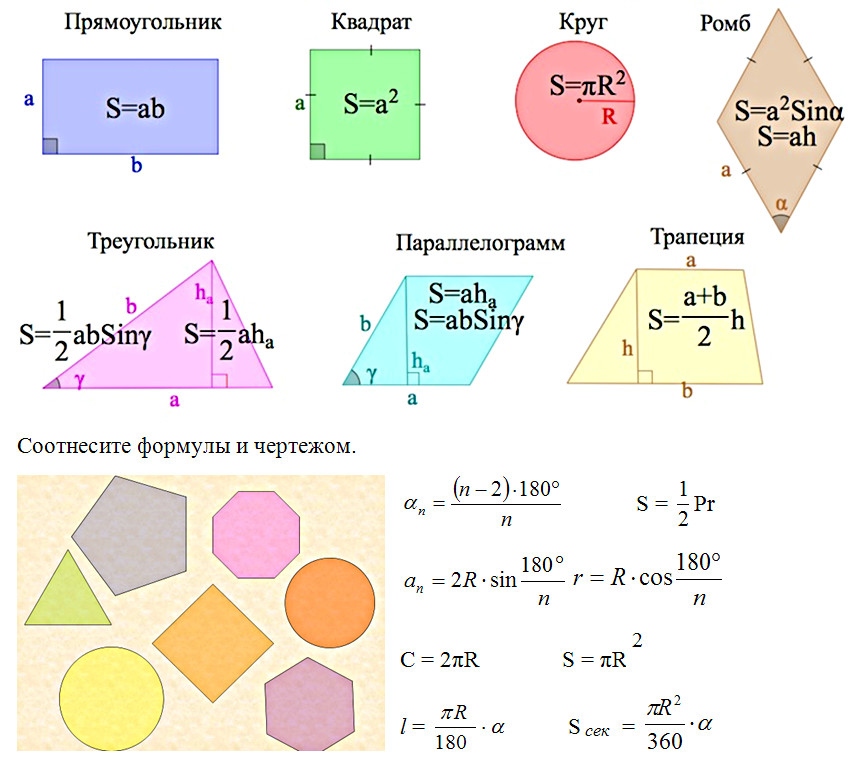 2$. Найдем площадь прямоугольника по формуле:

Как видите, площади, найденные обоими способами, равны.

Рис. 3.

Рис. 4.

Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Это означает, что площадь каждого из треугольников равна половине площади всего прямоугольника.

Определение 2

Прямоугольник с равными сторонами называется квадратом .

Если обозначить сторону квадрата буквой $а$, то площадь квадрата будет найдена по формуле:

Отсюда и название квадрата числа $а$.

Пример 2

Например, если сторона квадрата $5$ см, то его площадь равна:

Объемы

С развитием торговли и строительства во времена древних цивилизаций возникла необходимость найти объемы. В математике есть раздел геометрии, занимающийся изучением пространственных фигур, называемый стереометрией.Упоминания об этой отдельной области математики встречались уже в $IV$ веке до нашей эры.

Древние математики разработали метод вычисления объема простых фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но позже были найдены методы расчета объема фигур более сложной формы.

Объем прямоугольного параллелепипеда

Если заполнить форму влажным песком, а затем перевернуть ее, то получится объемная фигура, которая характеризуется объемом.Если вы сделаете несколько таких фигурок, используя одну и ту же форму, вы получите фигурки, имеющие одинаковый объем. Если заполнить форму водой, то объем воды и объем фигурки из песка тоже будут равны.

Рисунок 5.

Вы можете сравнить объемы двух сосудов, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд полностью заполнен, то сосуды имеют равные объемы. Если при этом в первом остается вода, то объем первого сосуда больше объема второго.3$ — кубический километр.

Общий обзор. Формулы стереометрии!

Здравствуйте, дорогие друзья! В этой статье я решил сделать общий обзор заданий по стереометрии, которые будут на ЕГЭ по математике е. Надо сказать, что задания из этой группы довольно разнообразные, но не сложные. Это задачи на нахождение геометрических величин: длин, углов, площадей, объемов.

Рассматривались: куб, прямоугольный параллелепипед, призма, пирамида, сложный многогранник, цилиндр, конус, шар.Огорчает тот факт, что некоторые выпускники даже не берутся за подобные задачи во время экзамена, хотя более 50% из них решаются элементарно, практически устно.

Остальные требуют небольших усилий, знаний и специальных приемов. В следующих статьях мы рассмотрим эти задачи, не пропустите, подписывайтесь на обновления блога.

Для решения необходимо знать формулы площадей поверхностей и объемов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Здесь нет сложных задач, все они решаются в 2-3 шага, важно «видеть», какую формулу нужно применить.

Все необходимые формулы представлены ниже:

Мяч или сфера. Сферическая или сферическая поверхность (иногда просто сфера) — это геометрическое место точек в пространстве, равноудаленных от одной точки — центра шара.

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота равна радиусу шара

Объем шара в полтора раза меньше объема описываемого вокруг него цилиндра.

Круглый конус можно получить, вращая прямоугольный треугольник вокруг одной из его сторон, поэтому круглый конус также называют конусом вращения. См. также Площадь поверхности круглого конуса

Объем круглого конуса равен трети произведения площади основания S на высоту H:

(H — высота ребра куба)

Параллелепипед – это призма, основанием которой является параллелограмм. У параллелепипеда шесть граней, и все они параллелограммы.Параллелепипед, четыре боковые грани которого являются прямоугольниками, называется прямым. Прямоугольный параллелепипед, все шесть сторон которого равны прямоугольнику, называется прямоугольным.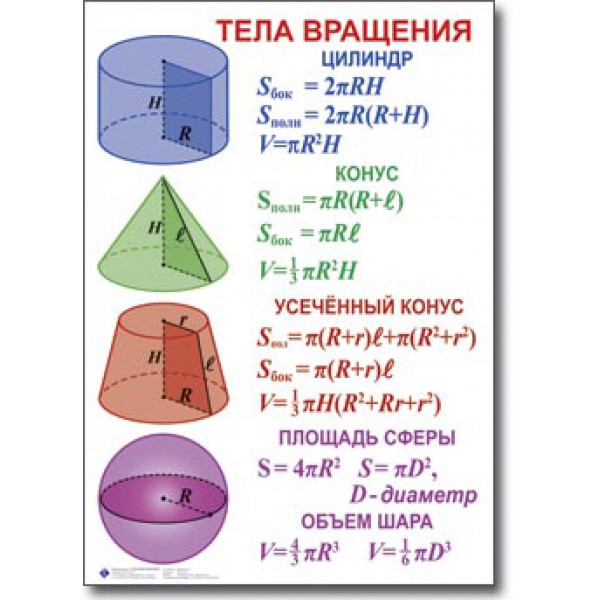

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

(S — площадь основания пирамиды, h — высота пирамиды)

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.

Сечение, параллельное основанию пирамиды, делит пирамиду на две части. Часть пирамиды между ее основанием и этой секцией представляет собой усеченную пирамиду.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde) , нижнего основания усеченной пирамиды S2 (ABCDE ) и среднее пропорциональное между ними.

n — количество сторон правильного многоугольника — основание правильной пирамиды
а — сторона правильного многоугольника — основание правильной пирамиды
h — высота правильной пирамиды

Правильная треугольная пирамида – это многогранник, у которого одна грань – основание пирамиды – правильный треугольник, а остальные – боковые грани – равные треугольники с общей вершиной. Высота падает к центру основания сверху.

Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) , на высоту h (OS)

а — сторона правильного треугольника — основание правильной треугольной пирамиды
h — высота правильной треугольной пирамиды

Вывод формулы объема тетраэдра

Объем тетраэдра вычисляется по классической формуле объема пирамиды.В него необходимо подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Объем тетраэдра — равен дроби, в числителе которой корень квадратный из двух в знаменателе равен двенадцати, умноженный на куб длины ребра тетраэдра

(h длина стороны ромба)

Окружность р составляет примерно три целых и одну седьмую длины диаметра окружности.Точное отношение длины окружности к ее диаметру обозначается греческой буквой π

В результате периметр круга или длина окружности вычисляется по формуле

(r — радиус дуги, n — центральный угол дуги в градусах. )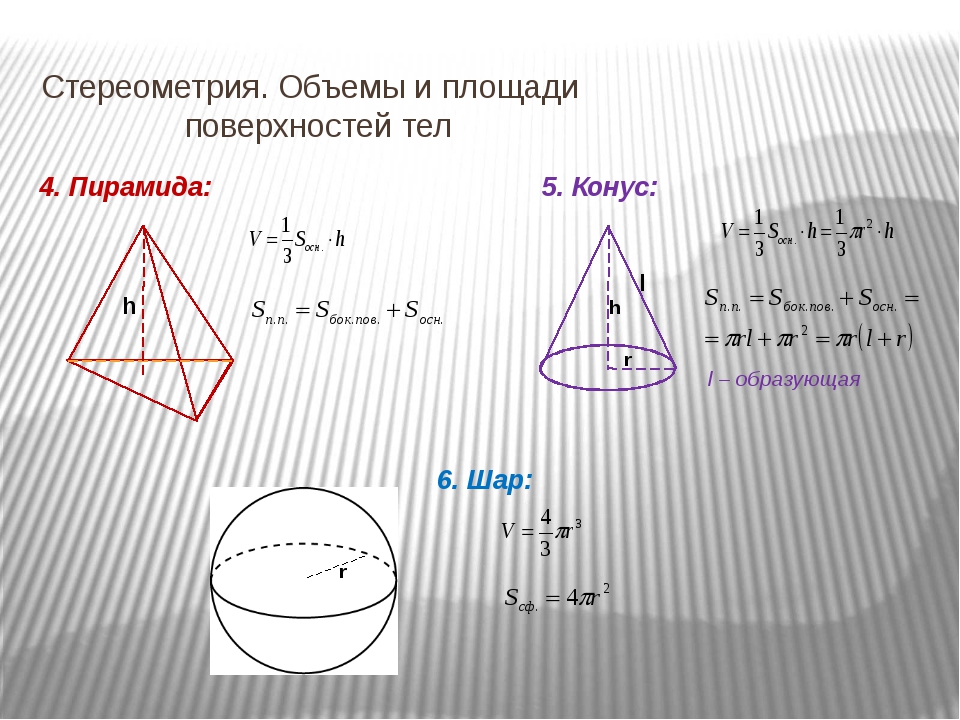

Видеокурс «Получи пятерку» включает в себя все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задания 1-13 Профильного ЕГЭ по математике.Также подходит для сдачи базового экзамена по математике. Если вы хотите сдать экзамен на 90-100 баллов, вам нужно решить часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 классов, а также для учителей. Все, что нужно для решения части 1 ЕГЭ по математике (первые 12 задач) и задачи 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобаллу, ни гуманитарию.

Вся необходимая теория.Быстрые решения, ловушки и секреты экзамена. Разобрал все актуальные задания части 1 из банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни экзаменационных заданий. Текстовые задачи и теория вероятностей. Простые и легко запоминающиеся алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех видов заданий ЕГЭ.Стереометрия. Хитрые решения, полезные шпаргалки, развивающие пространственное воображение. Тригонометрия с нуля до задачи 13. Понимание вместо зубрежки. Визуальное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. Основа решения сложных задач 2-й части ЕГЭ.

Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур можно легко рассчитать с помощью соответствующих формул.Однако все значения, вводимые в формулы, должны быть измерены в метрах. Поэтому, прежде чем подставлять значения в формулу, убедитесь, что все они измерены в метрах, или что вы перевели другие единицы в метры.

• 1 мм = 0,001 м
• 1 см = 0,01 м
• 1 км = 1000 м

Для расчета объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = Д × Ш × В (длина умножить на ширину на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.

• Например, рассчитаем объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножьте длину на ширину и на высоту:
  • 4 × 3 × 2,5
  • = 12 × 2,5
  • = 30. Объем этой комнаты 30 м 3 .
• Куб – это объемная фигура, у которой все стороны равны.Таким образом, формулу расчета объема куба можно записать в виде: объем = L 3 (или W 3 , или H 3 ).

Для расчета объема цилиндрических фигур используют формулу: пи ×R 2×H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндр. Найдите площадь круглого основания, умножив число пи (3.14) на квадрат радиуса окружности (R) (радиус — это расстояние от центра окружности до любой точки этой окружности).Затем умножьте полученный результат на высоту цилиндра (H), чтобы найти объем цилиндра.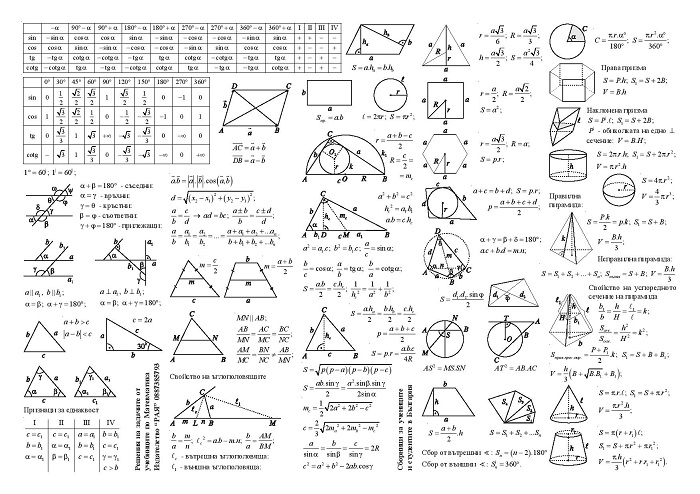 Все значения измеряются в метрах.

• Например, рассчитаем объем колодца диаметром 1,5 м и глубиной 10 м. Разделив диаметр на 2, получим радиус: 1,5/2 = 0,75 м.
  • (3,14) × 0,75 2 × 10
  • = (3,14) × 0,5625 × 10
  • = 17,66. Объем скважины 17,66 м 3 .

Чтобы рассчитать объем шара, используйте формулу: 4/3 x пи × R 3.То есть вам нужно знать только радиус (R) шара.

• Например, рассчитаем объем воздушного шара диаметром 10 м. Разделив диаметр на 2, получим радиус: 10/2 = 5 м.
  • 4/3 x пи × (5) 3
  • = 4/3 х (3,14) х 125
  • = 4,189 × 125
  • = 523,6. Объем баллона 523,6 м 3 .

Для расчета объема конусообразных фигур используйте формулу: 1/3 x pi × R 2 × H.Объем конуса равен 1/3 объема цилиндра такой же высоты и радиуса.

• Например, рассчитаем объем рожка мороженого с радиусом 3 см и высотой 15 см. Переводя в метры, получаем: 0,03 м и 0,15 м соответственно.
  • 1/3 х (3,14) х 0,03 2 х 0,15
  • = 1/3 х (3,14) х 0,0009 х 0,15
  • = 1/3 × 0,0004239
  • = 0,000141. Объем рожка мороженого 0,000141 м 3 .

Используйте несколько формул для расчета объема предметов неправильной формы. Для этого попробуйте разбить фигуру на несколько правильных фигур. Затем найдите объем каждой такой фигуры и сложите результаты.

• Например, рассчитаем объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиусом 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Рассчитав отдельно объем крыши и отдельно объем корпуса, можно найти общий объем зернохранилища:
  • pi × R 2 × H + 1/3 х pi × Р 2 × Н
  • (3.14) х 1,5 2 х 12 + 1/3 х (3,14) х 1,5 2 х 1
  • = (3,14) х 2,25 х 12 + 1/3 х (3,14) х 2,25 х 1
  • = (3,14) х 27 + 1/3 х (3,14) х 2,25
  • = 84 822 + 2 356
  • = 87,178.