Простейшие показательные уравнения, тест | Подготовка к ЕГЭ по математике
В Заданиях №5 ЕГЭ по математике проверяется умение решать простейшие
рациональные,
иррациональные,
показательные,
логарифмические,
тригонометрические уравнения.
Сейчас мы рассмотрим основные типы простейших показательных уравнений, которые могут встретится на экзамене. Если вы плохо помните свойства степеней, то загляните прежде сюда.
Хорошо, если вы помните значения основных натуральных степеней:
Но, согласитесь, можно и не удержать в голове, что, например, 2187 – это седьмая степень тройки. Какие наши действия, если в показательных уравнениях нам попадается, например, 2187?
Во-первых, понимаем, что число делится на 3, так как сумма цифр числа делится на 3. Берем, и делим 2187 на 3. Получим 729. Еще раз делим на 3, если не узнаем по-прежнему, что перед нами шестая степень тройки. Получаем 243… И так далее. В итоге, сообразим, что .
Задание 1.
Найдите корень уравнения .
Решение: + показать
Заметим, . Поэтому, уравнение перепишем так: Равны основания, значит, чтобы выполнялось равенство, необходимо, чтобы Ответ: -1.
Задание 2.
Решить уравнение:
Решение: + показать
Что скрыто от нас в левой части уравнения? Поэтому перепишем уравнение следующим образом: Тогда Ответ: 1.
Задание 3.
Решить уравнение:
Решение: + показать
Задание 4.
Решить уравнение:
Решение: + показать
Задание 5.
Решить уравнение:
Решение: + показать
Поскольку основания – разные, а сами степени при этом равны, то это возможно только в случае, когда показатели степеней нулевые. Ответ: 11.
Задание 6.
Решите уравнение
Решение: + показать
Применяем к свойство степени №2, получаем следующее уравнение: . И разделим обе части равенства на , применяя все то же свойство степени №2: Откуда Ответ: -1,5.
Задание 7.
Решите уравнение
Решение: + показать
Ответ: -1.
Задание 8.
Решите уравнение В ответе укажите наименьший из корней, если их несколько.
Решение: + показать
Вы можете пройти тест №3 по теме «Задачи №5».
egemaximum.ru
Карточки для самостоятельной работы по теме «Показательные уравнения»
Показательные уравнения
Вариант 1
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения:
Найдите решение уравнения:
Решите уравнение .
Решите уравнение .
Решите уравнение .
Показательные уравнения
из открытого банка заданий ЕГЭ
Вариант 2.
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения:
Найдите решение уравнения:
Решите уравнение .
Решите уравнение .
Решите уравнение .
Показательные уравнения
из открытого банка заданий ЕГЭ
Вариант 3.
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения:
Найдите решение уравнения:
Решите уравнение .
Решите уравнение .
Решите уравнение .
Показательные уравнения
Вариант 4.
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения:
Найдите решение уравнения:
Решите уравнение .
Решите уравнение .
Решите уравнение .
Ответы к проверочной работе «Показательные уравнения»
Показательные уравнения
из открытого банка заданий ЕГЭ
вариант5.
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения .
Найдите корень уравнения .
Найдите корень уравнения:
Найдите корень уравнения:
Найдите решение уравнения:
Решите уравнение .
Решите уравнение .
Решите уравнение .
infourok.ru
С1 из тренировочной работы в формате ЕГЭ от 14 ноября 2013
Категория: 13 (С1) УравненияПоказательные выражения, уравнения и неравенства
Елена Репина 2013-11-16 2015-09-04Разбор задания С1 (в новом формате ЕГЭ по математике – «Задание №13») из тренировочной работы №1 от 14 ноября 2013 г. для 11 класса.
Разбор части В этой работы смотрим здесь.
Решите уравнение
а)
б) Найдите все корни этого уравнения, принадлежащие отрезку [-1; 2 ].
Решение:
a) Разделим обе части равенства, например, на .
Заметим, .
Замена: Заметим, что .
Тогда
(посторонний корень) или
Обратная замена:
б) Произведем отбор корней уравнения на отрезке [-1; 2 ].
1) , так как
2) Очевидно, что , так как
;
Ответ: а) б)
Также смотрите С2, С3, С4 тренировочной работы №1 2013 для 11 класса.
Для самостоятельной работы (задание из другого варианта Т/Р №1):
Решите уравнение
а)
б) Найдите все корни этого уравнения, принадлежащие отрезку [-1; 2 ].
Ответ: + показать
a) ; б) .
Автор: egeMax | Нет комментариев
egemaximum.ru
Показательные уравнения
Разделы: Математика
Тема: Показательные уравнения (Приложение 1, слайд 1).
Цель:
1. Познакомить студентов с определением показательного уравнения и основными методами решения показательных уравнений.
2. Сформировать умения и навыки решения несложных показательных уравнений. Развивать навыки самостоятельной работы. Развивать навыки взаимоконтроля.
3. Развивать познавательный интерес к предмету. Развивать творческие способности студентов. (Приложение 1, слайд 2)
Студент должен знать: способы решения простейших показательных уравнений.
Студент должен уметь: решать несложные
уравнения, приводимые к видам: а
Оборудование: плакат с устными упражнениями, раздаточный материал, учебник, жетоны, ПК.
Литература: Яковлев Г.Н. Алгебра и начала анализа, I ч., Богомолов Н.В. Практические занятия по математике.
ХОД ЗАНЯТИЯ
I. Организационный момент.
- Приветствие;
- Перекличка;
II. Проверка д/з.
- У доски на изученную тему, но несколько сложнее домашней, выполнить задание по карточке. (К1)
- На местах выполнить на отдельном листочке задания подобные д/р – 4 человека. (К2, К3, К4, К5)
- Фронтально с группой (за правильный ответ студент получает жетон). (Приложение 1, слайды 3-16)
Какая функция называется показательной?
Какие из функций являются показательными?
у = 2х
у =0,2х
у = (х-2)2
у = х2
у = (П)х
у = 3-х
у = (-3)х
у = 0,5х
Какие характеристики функции вы знаете?
Что такое область определения функции?
Какова область определения показательной функции?
А какова область определения для функции у = (0,3)х?
Что называется областью изменения функции?
Какова область изменения показательной функции?
А какова область изменения для функции у = (0,3)х?
Какими свойствами может обладать показательная функция? Как эти свойства иллюстрируются графиком? (По таблице)
Какие функции называются монотонными?
Дайте определение возрастающей функции?
Дайте определение убывающей функции?
При каком условии показательная функция является возрастающей?
При каком условии показательная функция является убывающей?
Какие из показательных функций являются возрастающими и какие убывающими? (Приложение 1, слайд 17)
у = 5х
у = (0,5)х
у = (0,2)х
у = (2/3)х
у = 7-х
у = (П)х
у = (1/3)х
Сравнить: (Приложение 1, слайд 18)
Вычисляя значения показательной функции, мы постоянно обращаемся к таблице степеней и свойствам степеней. (Приложение 1, слайд 19)
Используя свойство степеней, упростить выражения:
Разложить на множители: (Приложение 1, слайд 20)
Как эту степень представить в виде квадрата, какой-то другой степени? (Приложение 1, слайд 21)
25х, 16х, 81х, 49х, 4х, 36х.
Давайте послушаем и проверим, как на доске выполнено задание по карточке.
Зачитайте задание.
Графики, каких функций вы строили?
Как называется метод, которым вы решали данное уравнение?
Остальные карточки я проверю, и итог подведу в конце урока.
Испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны. На прошлом занятии несколько ребят получили задание подготовить сообщения о применении показательной функции в природе и технике. Этого материала в учебнике нет. Вы должны расширять свой кругозор и в этом помогут их небольшие сообщения. Послушаем их.
Применение в природе и технике.
Нобелевские лауреаты. (Приложение 1, слайд 29)
Итак, показательная функция является основой изучения многих наук, в частности, вы будете изучать явления с помощью показательной функции на уроках физики, электротехники, на уроках механических дисциплин, материаловедении, экономике. Поэтому материал этот очень значимый. И сегодня на уроке мы будем опираться на ваши знания по показательной функции.
III. Мотивация учебной деятельности.
Какие задачи, связанные с понятием показательной функции у = ах, мы можем решать?
- Строить график.
- Читать график.
- Определять принадлежность тоски графику функции.
- Находить область определения и область изменения функции.
А можно ли с помощью графика функции у = 2х найти значение аргумента, при котором значение функции равно 64 или 32?
- С помощью графика это сделать практически невозможно.
Значит, нам нужно найти новый метод решения задач такого типа.
Как называется такой метод?
- Аналитический, алгебраический.
Как будет выглядеть запись поставленной задачи?
2х = 64, 2х = 32.
Что за выражение мы получили?
- Уравнения, в которых переменная стоит в показателе степени.
Таким образом, тема нашего занятия “Показательные уравнения”, а цель: (Приложение 1, слайд 2)
- Из всего многообразия уравнений уметь выделять показательные уравнения.
- Познакомиться с методами решения показательных уравнений.
- Научиться решать простейшие показательные уравнения.
IV. Изучение нового материала.
1. Определение. (Приложение 1, слайд 22)
Уравнения, содержащие переменную только в показателе степени, называются показательными.
2. Являются уравнения из домашней работы показательными? Откройте тетради и посмотрите. Объясните.
3. Рассмотрим методы решения показательных уравнений:
1) Метод уравнивания оснований: (Приложение 1, слайд 23)
кто сможет решить эти уравнения?
а) 2х = 64, в) 3х-2 = , б) 2х = 32,
, , е) 42х-5 = -, ж) 5х = 1
2) Метод вынесения общего множителя за скобки: (Приложение 1, слайд 24)
3) Метод логарифмирования: (Приложение 1, слайд 25)
Какую операцию будем применять к уравнениям в данном методе.
4) Метод замены переменной: (Приложение 1, слайд 26)
V. Закрепление изученного материала.
- Трудная задача – научиться решать показательные уравнения будет упрощена, если уметь классифицировать уравнения по методам их решения.
1) Давайте, вместе определим метод решения данных показательных уравнений:
2х+1 = 32,
7х + 7х+2 = 350,
25х +5х+1 -6 = 0,
9х+4 = 2.
2) Предлагаю самостоятельно выполнить следующее задание.
Сгруппировать уравнения по методам решения. Таблица
Результаты занесите в таблицу: (Приложение 1, слайд 26)
Логарифмирования |
Замена переменного |
Уравнивание |
Вынесение |
А теперь поменяйтесь вариантами и проверьте соседа, как он выполнил задание.
И так, подведем итог. Что получилось в вашей таблице?
Смотрим на экран: “50 лет, юбилей, 1956”. (Приложение 1, слайд 29)
Наш техникум образован в 1956 году и осенью 2006 года отметил свой юбилей – 50 лет.
3) Работаем по учебнику Н.В.Богомолов. Практические занятия по математике: стр.64, № 27 (2), 29 (3), 30 (1) решаем у доски.
4) Выполните самостоятельную работу по решению посмотреть, показательных уравнений.
Задания дифференцированные, по уровню сложности. Уровень сложности вы для себя выберете сами.
Самостоятельная работа
Собираю жетоны, оцениваю работы по карточкам, выставляю оценки.
Собираю работы за 5 мин до звонка.
VI. Домашнее задание: по учебнику Яковлев Г.Н. Алгебра и начала анализа, I ч, §23, п. 1, № 5.29, № 5,30, стр.225.
(Приложение 1, слайд 30)
Выберите каждый по 4 уравнения – степень сложности определите сами. А я буду оценивать д/р с учетом ваших возможностей.
Итог занятия.
VII. Озвучиваю и выставляю оценки.
Сегодня мы с вами познакомились с новым видом уравнений – показательными уравнениями, познакомились с методами их решения и научились решать простейшие уравнения. Мы говорили, что понятие показательной функции было введено в XVII веке. Так вот сейчас ваши знания в этой области находятся на уровне знаний ученых того времени. Сейчас на дворе XXI век. Так что перспектива развития ваших знаний велика. Дерзайте, достигайте уровня ученых наших дней. Информация к размышлению: в этом году Россия не получила ни одной Нобелевской премии.
Приложение 2
Приложение 3
Приложение 4
xn--i1abbnckbmcl9fb.xn--p1ai
Подготовка к ЕГЭ. Прототипы задания 3.» Показательные уравнения»
 В3.
В3.
мирегэ.ру
Иррациональные уравнения
Решение:
Возведём обе части уравнения в квадрат
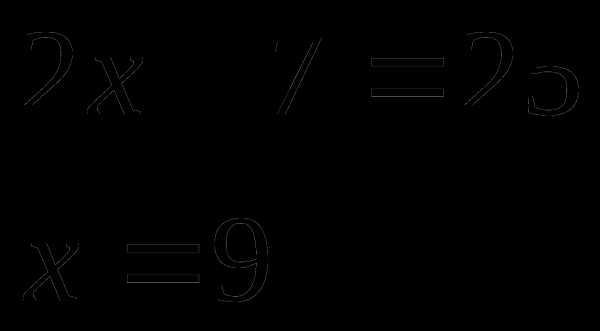
Ответ: х=9.
1. Найдите корень уравнения . Ответ: 6
2. Найдите корень уравнения . Ответ: 11
3. Найдите корень уравнения . Ответ: 4
4. Найдите корень уравнения . Ответ: 2
5. Найдите корень уравнения . Ответ: 60
6. Найдите корень уравнения . Ответ: 2
7. Найдите корень уравнения . Ответ: 24
8. Найдите корень уравнения . Ответ: 3
9. Найдите корень уравнения . Ответ:3
10. Найдите корень уравнения: Ответ: –7
11. Найдите корень уравнения . Ответ: 133
12. Найдите корень уравнения . Ответ: 45
13. Найдите корень уравнения . Ответ: 2
14. Найдите корень уравнения . Ответ: 47
15. Найдите корень уравнения . Ответ: 237
16. Найдите корень уравнения . Ответ: 31
17. Найдите корень уравнения . Ответ: 151
18. Найдите корень уравнения: Если уравнение имеем более одного корня, укажите меньший из них. Ответ: 7
Дробно рациональные уравнения.
1. Найдите корень уравнения: Ответ: – 14
2. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них. Ответ: –3
3. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них. Ответ: – 6
Показательные уравнения.
Решение:
Ответ: x=5,8.
1. Найдите корень уравнения . Ответ: – 1
2. Найдите корень уравнения . Ответ: – 2
3. Найдите корень уравнения: Ответ: 8
4. Найдите корень уравнения . Ответ: 9
5. Найдите корень уравнения . Ответ: 6,5
6. Найдите корень уравнения . Ответ: 3,5
7. Найдите корень уравнения . Ответ: 2
8. Найдите корень уравнения . Ответ: 9,5
9. Найдите корень уравнения . Ответ: 4
10. Найдите корень уравнения . Ответ: 3,5
11. Найдите корень уравнения . Ответ: 1,5
15. Найдите корень уравнения . Ответ: 11
16. Найдите корень уравнения . Ответ: 11
17. Найдите корень уравнения . Ответ: 5,5
18. Найдите корень уравнения . Ответ: 5,75
19. Найдите корень уравнения . Ответ: 8,5
20. Найдите корень уравнения . Ответ: 7,5
21. Найдите корень уравнения . Ответ: 7
22. Найдите решение уравнения: Ответ: – 7,5
23. Найдите корень уравнения . Ответ: 6,5
24. Найдите решение уравнения: Ответ: 3
25. Найдите корень уравнения . Ответ: 0,5
26. Найдите решение уравнения: Ответ: 0,25
Логарифмические уравнения
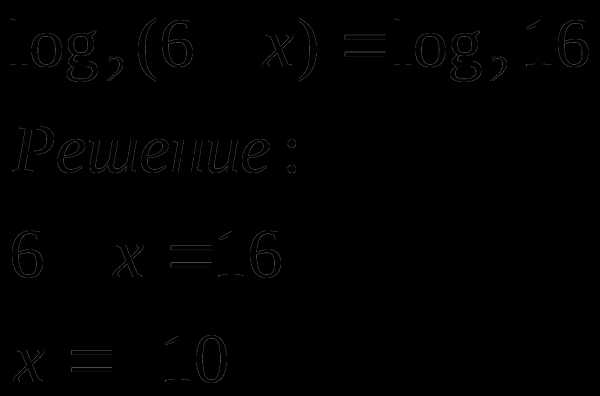 Ответ: х = – 10.
Ответ: х = – 10.
1. Найдите корень уравнения . Ответ: – 11
2. Найдите корень уравнения . Ответ: – 77
3. Найдите корень уравнения . Ответ: 0
4. Найдите корень уравнения . Ответ: 61
5. Найдите корень уравнения: Ответ: – 28
6. Найдите корень уравнения . Ответ: 1
7. Найдите корень уравнения . Ответ: – 6
8. Найдите корень уравнения . Ответ: – 12
9. Найдите корень уравнения . Ответ: – 0,2
10. Найдите корень уравнения . Ответ: – 2
11. Найдите корень уравнения . Ответ: 3,5
12. Найдите корень уравнения . Ответ: 18
13. Найдите корень уравнения . Ответ: 10
14. Найдите корень уравнения . Ответ: 2
15. Найдите корень уравнения . Ответ: 2
16. Найдите корень уравнения . Ответ: 7
Тригонометрические уравнения
1. 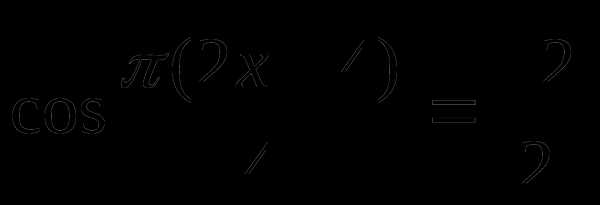 . В ответ запишите наибольший отрицательный корень.
. В ответ запишите наибольший отрицательный корень.
Ответ: − 1,5
2. . В ответ запишите наибольший отрицательный корень.
Ответ: − 3,8
3. 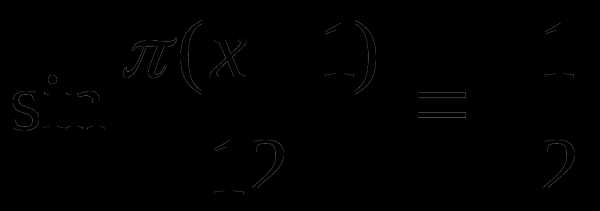 . В ответ запишите наименьший положительный корень.
. В ответ запишите наименьший положительный корень.
Ответ: 13
4.  . В ответ запишите наименьший положительный корень.
. В ответ запишите наименьший положительный корень.
Ответ: 0,6
infourok.ru
| 1. |
Показательное уравнение (дробные показатели)
Сложность: среднее |
2 |
| 2. |
Показательное уравнение(приведение к основанию)
Сложность: среднее |
2 |
| 3. |
Показательное уравнение(приведение к основанию)
Сложность: среднее |
2 |
| 4. |
Показательное уравнение (дробные показатели)
Сложность: среднее |
3 |
| 5. |
Показательное уравнение (корень)
Сложность: среднее |
2 |
| 6. |
Показательное уравнение(приведение к основанию)
Сложность: среднее |
2 |
| 7. |
Показательное уравнение (деление степеней)
Сложность: среднее |
2 |
| 8. |
Показательное уравнение (умножение степеней)
Сложность: среднее |
2 |
| 9. |
Показательное уравнение (умножение степеней)
Сложность: среднее |
2 |
| 10. |
Показательное уравнение (общий множитель)
Сложность: среднее |
2 |
| 11. |
Показательное уравнение (общий множитель)
Сложность: среднее |
2 |
| 12. |
Показательное уравнение (общий множитель)
Сложность: среднее |
3 |
| 13. |
Показательное уравнение (новая переменная)
Сложность: среднее |
4 |
| 14. |
Показательное уравнение (новая переменная)
Сложность: среднее |
3 |
www.yaklass.ru
Показательные уравнения. Подготовка к ЕГЭ
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,3 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока
: урок обобщения и комплексных применений знаний, умений и навыков по теме “Показательные уравнения и способы их решения”.Цели урока.
Оборудование:
компьютер и мультимедийный проектор.На уроке используются информационные технологии: методическое обеспечение к уроку – презентация в программе Microsoft Power Point.
Ход урока
Всякое умение трудом даётся
I. Постановка цели урока (Слайд № 2)
На этом уроке подведём итог и обобщим тему “Показательные уравнения, их решения”. Познакомимся с типовыми заданиями ЕГЭ разных лет по данной теме.
Задачи на решение показательных уравнений могут встречаться в любой части заданий ЕГЭ. В части “В” обычно предлагают решить простейшие показательные уравнения. В части “С” можно встретить более сложные показательные уравнения, решение которых обычно является одним из этапов выполнения задания.
Например (Слайд № 3).
В4 – Найдите наибольшее значение выражения х • у, где (х; у) – решение системы:
В1– Решить уравнения:
а) х • 63х – 36 • 63х = 0;
б) 4х +1 + 8 • 4х= 3.
В4– Найдите значение выражения х + у, где (х; у) – решение системы:
В3
– Решите уравнение: 7х – 2 = 49.С1
– Найдите корни уравнения: 4х2 + 3х – 2 — 0,52х2 + 2х – 1 = 0.С3
– Решите систему уравнений:
II. Актуализация опорных знаний. Повторение
(Слайды № 4 – 6 презентации к уроку)На экран демонстрируется опорный конспект теоретического материала по теме.
Обсуждаются следующие вопросы:
- Какие уравнения называются показательными?
- Назвать основные способы их решения. Привести примеры их видов (Слайд № 4)
- Какую теорему используют при решении простейших показательных уравнений вида: а f(x) = a g(x)?
- Какие ещё методы решения показательных уравнений существуют? (Слайд № 5)
(Самостоятельно решить предлагаемые уравнения к каждому способу и выполнить самопроверку с помощью слайда)
- Метод разложения на множители (основан на свойствах степеней с одинаковыми основаниями, приём: выносится за скобку степень с наименьшим показателем).
- Приём деления (умножения) на показательное выражение, отличное от нуля, при решении однородных показательных уравнений .
-
Решение уравнений двумя последними методами
с последующими комментариями
(Слайд № 6).
Пример
. 4х + 1 – 2 • 4х – 2 = 124, 4х – 2 • (43 — 2) = 124, 4х – 2 • 62 = 124,4 х – 2 = 2, 4 х – 2 = 4 0,5, х – 2 = 0,5, х = 2,5.
Пример.
2 • 22х – 3 • 2х • 5х – 5 • 52х = 0¦: 52х 0,2 • (2/5)2х – 3 • (2/5) х — 5 = 0,
t = (2/5)х, t > 0, 2t2 — 3 t— 5 = 0, t = -1(?…), t = 5/2; 5/2 = (2/5)х , х = ?…
III. Решение заданий ЕГЭ 2010
Учащиеся самостоятельно решают предлагаемые в начале урока на слайде № 3 задания, используя указания к решению, проверяют свой ход решения и ответы к ним с помощью презентации (Слайд № 7). В процессе работы обсуждаются варианты и способы решения, обращается внимание на возможные ошибки при решении.
В3
: а) 7х – 2 = 49, б) (1/6)12 – 7 х = 36. Ответ: а) х = 4, б) х = 2.С1
: 4х2 + 3х – 2 — 0,52х2 + 2х – 1 = 0. (Можно заменить 0,5 = 4– 0,5)Решение. ,
х2 + 3х – 2 = —х2 — 4х + 0,5 …
Ответ: х = -5/2, х = 1/2.
С3
: 5 • 5tgy + 4 = 5-tgy, при сos y < 0.Указание к решению
. 5 • 5tgy + 4 = 5 -tgy ¦•5tgy 0,5 • 52gy + 4 • 5 tgy – 1 = 0. Пусть х = 5 tgy , …
5tgy = -1 (?…), 5tgy =1/5.
Так как tgy = -1 и сos y < 0, то у II координатной четверти
Ответ: у = 3/4 + 2k, k N.
IV. Совместная работа у доски
Рассматривается задание высокого уровня обученности – Слайд № 8. С помощью данного слайда происходит диалог учителя и учащихся, способствующий развитию решения.
С5
– При каком параметре а уравнение 22х – 3 • 2х + а2 – 4а = 0 имеет два корня?Решение.
Пусть t = 2х, где t > 0. Получаем t 2 – 3t + (а2 – 4а) = 0 .
1). Так как уравнение имеет два корня, то D > 0;
2). Так как t1,2 > 0, то t1 • t2 > 0, то есть а2 – 4а > 0 (?…).
Значит,
Ответ: а (– 0,5; 0) или (4; 4,5).
V. Проверочная работа
(Слайд № 9)Учащиеся выполняют проверочную работу на листочках, осуществляя самоконтроль и самооценку выполненной работы с помощью презентации, утверждаясь в теме. Самостоятельно определяют для себя программу регулирования и коррекции знаний по допущенным ошибкам в рабочих тетрадях. Листы с выполненной самостоятельной работой сдаются учителю на проверку.
Подчёркнутые номера – базового уровня, со звёздочкой – повышенной сложности.
Решение и ответы.
3. 2х – 1(5 • 2 4 — 4) = 19, 2х – 1 • 76 = 19, 2х – 1 = 1/4, 2х – 1 = 2 – 2, х – 1 = -2,
х = -1.
4*. 3 • 9х = 2 • 3х • 5х + 5 • 25х | : 25х,
3 • (9/25)х = 2 • (3/5)х + 5,
3 • (9/27)х = 2 • (3/5)х + 5 = 0,
3 • (3/5)2х – 2 • (3/5)х — 5 = 0,…, (3/5) х = -1 (не подходит),
(3/5)х = 5, х = -1.
VI. Задание на дом
(Слайд № 10)- Повторить § 11, 12.
- Из материалов ЕГЭ 2008 – 2010 г. выбрать задания по теме и решить их.
- Домашняя проверочная работа :
xn--i1abbnckbmcl9fb.xn--p1ai
