Малкова решение логарифмических неравенств – Методическое пособие по теме «Логарифмическая функция. Решение логарифмических уравнений, неравенств и систем логарифмических неравенств»

Логарифмические неравенства. Примеры и методы решения

Вам кажется, что до ЕГЭ еще есть время, и вы успеете подготовиться? Быть может, это и так. Но в любом случае, чем раньше школьник начинает подготовку, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, а значит, возможность получить дополнительный балл.

Вы уже знаете, что такое логарифм(log)? Мы очень надеемся, что да. Но даже если у вас нет ответа на этот вопрос, это не проблема. Понять, что такое логарифм очень просто.

Почему именно 4? В такую степень нужно возвести число 3, чтобы получилось 81. Когда вы поняли принцип, можно приступать и к более сложным вычислениям.

Неравенства вы проходили еще несколько лет назад. И с тех пор они постоянно встречаются вам в математике. Если у вас проблемы с решением неравенств, ознакомьтесь с соответствующим разделом.
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в общем.

Логарифмические неравенства (определение)

Самое простое логарифмическое неравенство.

Простейшие логарифмические неравенства не ограничиваются этим примером, есть еще три, только с другими знаками. Зачем это нужно? Чтобы полнее понять, как решать неравенство с логарифмами. Теперь приведем более применимый пример, все еще достаточно простой, сложные логарифмические неравенства оставим на потом.

 

Как это решить? Все начинается с ОДЗ. О нем стоит знать больше, если хочется всегда легко решать любое неравенство.

Что такое ОДЗ? ОДЗ для логарифмических неравенств

Аббревиатура расшифровывается как область допустимых значений. В заданиях для ЕГЭ нередко всплывает данная формулировка. ОДЗ пригодится вам не только в случае логарифмических неравенств.

Посмотрите еще раз на вышеприведенный пример. Мы будем рассматривать ОДЗ, исходя из него, чтобы вы поняли принцип, и решение логарифмических неравенств не вызывало вопросов. Из определения логарифма следует что, 2х+4 должно быть больше нуля. В нашем случае это означает следующее.

Это число по определению должно быть положительным. Решите неравенство, представленное выше. Это можно сделать даже устно, здесь явно, что X не может быть меньше 2. Решение неравенства и будет определением области допустимых значений.
Теперь перейдем к решению простейшего логарифмического неравенства.

Отбрасываем из обеих частей неравенства сами логарифмы. Что в результате у нас остается? Простое неравенство.

Решить его несложно. X должен быть больше -0,5. Теперь совмещаем два полученных значения в систему. Таким образом,

Это и будет область допустимых значений для рассматриваемого логарифмического неравенства.

Зачем вообще нужно ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не входит в область допустимых значений, значит, ответ попросту не имеет смысла. Это стоит запомнить надолго, так как в ЕГЭ часто встречается необходимость поиска ОДЗ, и касается она не только логарифмических неравенств.

Алгоритм решения логарифмического неравенства

Решение состоит из нескольких этапов. Во-первых, необходимо найти область допустимых значений. В ОДЗ будет два значения, это мы рассмотрели выше. Далее нужно решить само неравенство. Методы решения бывают следующими:

• метод замены множителей;
• декомпозиции;
• метод рационализации.

В зависимости от ситуации стоит применять один из вышеперечисленных методов. Перейдем непосредственно к решению. Раскроем наиболее популярный метод, который подходит для решения заданий ЕГЭ практически во всех случаях. Далее мы рассмотрим метод декомпозиции. Он может помочь, если попалось особенно «заковыристое» неравенство. Итак, алгоритм решения логарифмического неравенства.

Примеры решения :

Мы не зря взяли именно такое неравенство! Обратите внимание на основание. Запомните: если оно больше единицы, знак остается прежним при нахождении области допустимых значений; в противном случае нужно изменить знак неравенства.

В результате мы получаем неравенство:

Теперь приводим левую часть к виду уравнения, равному нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Надеемся, что с решением такого простого уравнения у вас не будет проблем. Ответы -4 и -2. Это еще не все. Нужно отобразить эти точки на графике, расставить «+» и «-». Что нужно для этого сделать? Подставить в выражение числа из интервалов. Где значения положительны, там ставим «+».

Ответ: х не может быть больше -4 и меньше -2.

Мы нашли область допустимых значений только для левой части, теперь нужно найти область допустимых значений правой части. Это не в пример легче. Ответ: -2. Пересекаем обе полученные области.

И только теперь начинаем решать само неравенство.

Упростим его, насколько возможно, чтобы решать было легче.

Снова применяем метод интервалов в решении. Опустим выкладки, с ним уже и так все понятно по предыдущему примеру. Ответ.

Но этот метод подходит, если логарифмическое неравенство имеет одинаковые основания.

Решение логарифмических уравнений и неравенств с разными основаниями предполагает изначальное приведение к одному основанию. Далее применяйте вышеописанный метод. Но есть и более сложный случай. Рассмотрим один из самых сложных видов логарифмических неравенств.

Логарифмические неравенства с переменным основанием

Как решать неравенства с такими характеристиками? Да, и такие могут встретиться в ЕГЭ. Решение неравенств нижеследующим способом тоже полезно скажется на вашем образовательном процессе. Разберемся в вопросе подробным образом. Отбросим теорию, перейдем сразу к практике. Чтобы решать логарифмические неравенства, достаточно однажды ознакомиться с примером.

Чтобы решить логарифмическое неравенство представленного вида, необходимо привести правую часть к логарифму с тем же основанием. Принцип напоминает равносильные переходы. В итоге неравенство будет выглядеть следующим образом.

Собственно, остается создать систему неравенств без логарифмов. Используя метод рационализации, переходим к равносильной системе неравенств. Вы поймете и само правило, когда подставите соответствующие значения и проследите их изменения. В системе будут следующие неравенства.

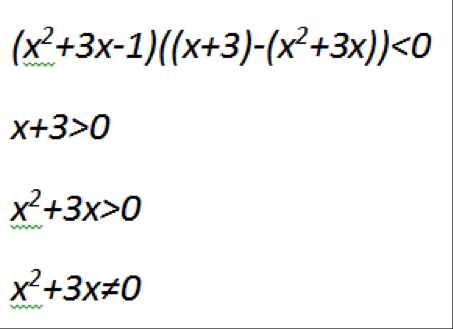
Воспользовавшись методом рационализации при решении неравенств нужно помнить следующее: из основания необходимо вычесть единицу,  х по определению логарифма из обеих частей неравенства вычитается (правое из левого), два выражения перемножаются и выставляются под исходным знаком по отношению к нулю.

Дальнейшее решение осуществляется методом интервалов, здесь все просто. Вам важно понять отличия в методах решения, тогда все начнет легко получаться.

В логарифмических неравенствах много нюансов. Простейшие из них решать достаточно легко. Как сделать так, чтобы решать каждое из них без проблем? Все ответы вы уже получили в этой статье. Теперь впереди вас ждет длительная практика. Постоянно практикуйтесь в решении самых разных задач в рамках экзамена и сможете получить наивысший балл. Успехов вам в вашем непростом деле!

Похожие статьи

Рекомендуем почитать:

karate-ege.ru

Решение логарифмических неравенств

Решение логарифмических неравенств имеет много общего с решением показательных неравенств:

а) При переходе от логарифмов к выражениям, стоящим под знаком логарифма, мы также сравниваем основание логарифма с единицей;

б) Если мы решаем логарифмическое неравенство с помощью замены переменных, то нужно решать относительно замены до получения простейшего неравенства.

Однако, есть одно очень важное отличие: поскольку логарифмическая функция имеет ограниченную область определения, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, необходимо учитывать область допустимых значений.

Если при решении логарифмического уравнения  можно найти корни уравнения, а потом сделать проверку, то при решении  логарифмического неравенства этот номер не проходит: при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать ОДЗ неравенства.

Итак. Простейшее логарифмическое неравенство имеет вид:

V , где V — один из знаков неравенства: <,>, ≤ или ≥.

Если основание логарифма больше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство

равносильно системе:

Если основание логарифма больше нуля и меньше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный

, и неравенство

равносильно системе:

Рассмотрим примеры решения логарифмических неравенств.

1. Решим  неравенство:

Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:

Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.

Решим систему неравенств:

Корни квадратного трехчлена: ,  

Отсюда:

Ответ:

2. Решим неравенство:

Мы видим, что  в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:

Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).

Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:

Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма. Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:

Отсюда:

Ответ: 

 

3. Решим неравенство:

В нашем неравенстве логарифм стоит в квадрате, поэтому это логарифмическое неравенство  мы будем решать с помощью замены переменных.

Сначала приведем логарифмы к одному основанию:

Введем замену переменных:

.

Получим квадратное неравенство:

Значит, .

Запишем это двойное неравенство в виде системы:

Вот только теперь, когда мы получили систему простейших неравенств относительно , мы можем  вернуться к исходной переменной.

Перейдем к выражениям, стоящим под знаком логарифма:

Последнее неравенство системы — это ОДЗ неравенства. Заметим, что оно выполняется, если выполняется второе неравенство системы, поэтому нет необходимости его решать.

Решим систему.

Первое неравенство системы преобразуется к виду

 Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значениях .

Второе неравенства преобразуется к виду , отсюда 

Ответ: 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Решение особых логарифмических неравенств

Отдельной темой при изучении показательных и логарифмических неравенств стоят неравенства, содержащие неизвестное в основании и в показателе степени.

В этой статье мы изучим пошаговый алгоритм решения неравенств, которые назовем «особые логарифмические неравенства», хотя их, с тем же успехом, можно отнести к «особым показательным неравенствам».

Рассмотрим решение неравенств вида:

Как мы знаем, переход в показательном неравенстве от степеней к показателям степеней зависит от основания степени:

если основание степени больше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства сохраняется

если основание степени больше нуля, но меньше единицы, то при переходе к выражениям, стоящим в показателе, знак неравенства меняется на противоположный.

Поскольку наше неравенство не совсем показательное: основание нашей степени зависит от х, рассмотрим отдельно случаи, когда  и . В этих случаях нам надо найти, при каких значениях х выполняются эти условия, а затем проверить, верно ли наше неравенство при этих значениях неизвестного.

Нужно обратить внимание на то, что если в основании степени стоит ноль, то показатель степени должен быть положительным.

В общем виде мы получим совокупность четырех систем неравенств:

              

На практике неравенства c неизвестным в основании и в показателе степени удобно решать по такому алгоритму:

1. Рассматриваем отдельно два случая, когда основания степеней равны 0 или 1. Найдем, при каких значении х  выполняются эти условия и проверим, верно ли наше неравенство при этих значениях х. Следим за тем, чтобы у степени, в основании  которой стоит ноль,  показатель был положительным.

2. Записываем правую часть неравенства в виде степени с тем же основанием, что и в левой части.

3. Рассматриваем  еще два случая, когда основания степеней принимают значения больше ноля или от ноля до единицы.

Давайте рассмотрим пример решения неравенства такого типа.

Решим неравенство:

Запишем системы, которые у нас получатся:

1.

2.

3.

4.

Запишем решения каждой системы:

1) 

2)

3) 

4) (

Объединим все решения: 

Ответ: 

Предлагаю вам посмотреть ВИДЕОУРОК с подробным решением неравенства уровня С3:

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Решение логарифмических неравенств с переменным основанием

Решение логарифмических неравенств с переменным основанием.

В этой статье мы поговорим о том, как решать логарифмические неравенства, которые содержат неизвестную величину в основании логарифма.

Как мы помним, при решении логарифмических неравенств, мы сравниваем основание логарифма с единицей. Если в основании логарифма стоит выражение, зависящее от неизвестного, то нам надо рассмотреть два случая: когда это выражение больше единицы, и когда оно принимает значение от нуля до единицы.

Но есть и более простой способ.

Рассмотрим решение логарифмического неравенства с переменным основанием в общем виде.

Пусть неравенство имеет вид

Мы помним, что

Если основание логарифма больше единицы (p(x)>1), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется.

Если основание логарифма больше нуля и меньше единицы (0<p(x)<1), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный.

Чтобы не рассматривать эти два случае по отдельности, давайте запишем переход от логарифмов к выражениям, стоящим под знаком логарифма в таком виде:

Знак первого множителя в этом произведении определяет знак второго множителя:

если p(x)>1,  то f(x)>g(x) — знак неравенства сохраняется

если 0<p(x)<1, то f(x)<g(x) — знак неравенства меняется на противоположный.

Тогда, с учетом ОДЗ, исходное неравенство

будет равносильно системе:

Последние четыре неравенства системы — ОДЗ исходного неравенства.

Решим, для примера, такое неравенство: 

Представим правую часть неравенства в виде логарифма по основанию 

Получим неравенство:

Перейдем к равносильной системе неравенств:

Решим каждое неравенство системы по отдельности, на своей координатной прямой.

Сначала преобразуем первое неравенство системы к виду

и решим это неравенство методом интервалов.

Корни квадратного трехчлена в первых скобках:

,   

Корни квадратного трехчлена во вторых скобках:

,   .

Нанесем эти корни на координатную прямую и расставим знаки:

 

Решение второго неравенства системы:

Решение третьего неравенства: 

Теперь совместим решение всех неравенств на одной координатной прямой:

 

Нас интересует промежуток, над которым проходит три стрелки.

Ответ:  .

А теперь я предлагаю вам посмотреть ВИДЕОУРОК, в котором я объясняю решение логарифмического неравенства с переменным основанием и с модулем в выражении, стоящем под знаком логарифма:

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Логарифмические неравенства

1.Решить неравенство:

   

ОДЗ:

   

   

Решение:

   

Так как основание логарифма больше 1, то знак неравенства сохраняем:

   

   

   

Ответ:

 

2.Решить неравенство:

   

ОДЗ:

   

   

Решение:

   

Так как основание логарифма меньше 1, то знак неравенства меняем:

   

   

   

Пересекаем решение и ОДЗ, имеем:

 

3.Решить неравенство:

   

ОДЗ:

   

Решим методом интервалов. Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – тоже выколотая точка, так как знак строгий. Таким образом, .

Решение:

   

   

Переходим к сравнению подлогарифмических выражений, знак сохраняем: основание больше 1:

   

   

   

   

Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – точка закрашенная, она войдет в решение, так как знак неравенства не строгий. Таким образом, .

При наложении решения на ОДЗ получим:

Ответ: .

 

4.Решить неравенство:

   

ОДЗ:

   

   

Решение этой системы –

Решение:

   

   

   

   

   

   

Корни:

   

   

Поскольку знак неравенства нестрогий, то точки входят в решение: на рисунке их нужно изобразить закрашенными. Решение неравенства: .

Накладывая решение на область допустимых значений, получаем:

Ответ:

 

5.Решить неравенство:

   

ОДЗ:

   

Решение этой системы –

Решение:

   

   

   

   

   

Точка 1 является выколотой – это корень знаменателя, точка 2 – корень четной кратности, а мы помним, что в таких точках знак интервала не изменяется! Поэтому решение будет выглядеть так:

Решение неравенства

Решение неравенства:

   

Это полностью укладывается в ОДЗ, поэтому ответ таким и будет:

Ответ:

 

6.Решить неравенство:

   

ОДЗ:

   

Допустимые значения :

Решение неравенства проведем методом рационализации:

   

   

   

Упрощаем:

   

   

Раскладываем на множители:

   

Отмечаем полученные точки на координатной прямой:

Решение неравенства

Наложив это решение на ОДЗ, имеем:

Ответ:

 

easy-physic.ru

Как решать С3. Урок 5. ЕГЭ по математике 2014. Логарифмические неравенства с переменным основанием — решения.егэцентр.рф

Решение простейших логарифмических неравенств и неравенств, где основание логарифма фиксировано, мы рассматривали в прошлом уроке.

А что делать, если в основании логарифма стоит переменная?

Тогда нам на помощь придет рационализация неравенств. Чтобы понять, как это работает, давайте рассмотрим, например, неравенство:

$$\log_{2x} x^2 > \log_{2x} x.$$

Как положено, начнем с ОДЗ.

ОДЗ

$$\left[ \begin{array}{l}x>0,\\ 2x ≠ 1. \end{array}\right.$$

Решение неравенства

Давайте рассуждать, как если бы мы решали неравенство с фиксированным основанием. Если основание больше единицы, избавляемся от логарифмов, и знак неравенства не меняется, если меньше единицы — меняется.

Запишем это в виде системы:

$$\left[ \begin{array}{l} \left\{ \begin{array}{l}2x>1,\\ x^2 > x; \end{array}\right. \\ \left\{ \begin{array}{l}2x<1,\\ x^2 < x; \end{array}\right. \end{array} \right.$$

Для дальнейших рассуждений перенесем все правые части неравенств влево.

$$\left[ \begin{array}{l} \left\{ \begin{array}{l}2x-1>0,\\ x^2 -x>0; \end{array}\right. \\ \left\{ \begin{array}{l}2x-1<0,\\ x^2 -x<0; \end{array}\right. \end{array} \right.$$

Что у нас получилось? Получилось, что нам нужно, чтобы выражения `2x-1` и `x^2 — x` были одновременно либо положительными, либо отрицательными. Такой же результат получится, если мы решим неравенство:

$$(2x-1)(x^2 — x) >0.$$

Это неравенство так же как и исходная система верно, если оба множителя либо положительны, либо отрицательны. Получается можно от логарифмического неравенства перейти к рациональному (учтя при этом ОДЗ).

Сформулируем метод рационализации логарифмических неравенств

$$\log_{f(x)} g(x) \vee \log_{f(x)} h(x) \Leftrightarrow (f(x) — 1)(g(x)-h(x)) \vee 0,$$ где `\vee` — это любой знак неравенства. (Для знака `>` мы только что проверили справедливость формулы. Для остальных предлагаю проверить самостоятельно — так запомнится лучше).

Вернемся к решению нашего неравенства. Разложив на скобки (чтобы было лучше видно нули функции), получим

$$(2x-1)x(x — 1) >0.$$

Метод интервалов даст следующую картину:

(Поскольку неравенство строгое и концы интервалов нас не интересуют, они не закрашены.) Как видно, полученные интервалы удовлетворяют ОДЗ. Получили ответ: `(0,\frac{1}{2}) \cup (1,∞)`.

Пример второй. Решение логарифмического неравенства с переменным основанием

$$\log_{2-x} 3 \leqslant \log_{2-x} x.$$

ОДЗ

 $$\left\{\begin{array}{l}2-x > 0,\\ 2-x ≠ 1, \\ x > 0. \end{array}\right.$$

$$\left\{\begin{array}{l}x < 2,\\ x ≠ 1, \\ x > 0. \end{array}\right.$$

Решение неравенства

По только что полученному нами правилу рационализации логарифмических неравенств, получим, что данное неравенство тождественно (с учетом ОДЗ) следующему:

$$(2-x -1 ) (3-x) \leqslant 0.$$

$$(1-x) (3-x) \leqslant 0.$$

Совместив это решение с ОДЗ, получим ответ: `(1,2)`.

Третий пример. Логарифм от дроби

$$\log_x\frac{4x+5}{6-5x} \leqslant -1.$$

Дробь нам добавила чуть больше сложности в нахождении ОДЗ и не более того. `-1` нужно представить как логарифм с основанием `x`.

ОДЗ

$$\left\{\begin{array}{l} \dfrac{4x+5}{6-5x}>0, \\ x>0,\\ x≠ 1.\end{array} \right.$$

Поскольку система относительно сложная, давайте сразу нанесем решение неравенств на числовую ось:

Таки образом, ОДЗ: `(0,1)\cup \left(1,\frac{6}{5}\right)`.

Решение неравенства

Представим `-1` в виде логарифма с основанием `x`.

$$\log_x\frac{4x+5}{6-5x} \leqslant \log_x x^{-1}.$$

С помощью рационализации логарифмического неравенства получим рациональное неравенство:

$$(x-1)\left(\frac{4x+5}{6-5x} -\frac{1}{x}\right)\leqslant0,$$

$$(x-1)\left(\frac{4x^2+5x — 6+5x}{x(6-5x)}\right)\leqslant0,$$

$$(x-1)\left(\frac{2x^2+5x — 3}{x(6-5x)}\right)\leqslant0.$$

Совместив решение с ОДЗ, получим ответ: `\left[\frac{1}{2},1\right)`.

Четвертый пример. Решение логарифмического неравенства

$$\log_{x^2} (x+2) < 1.$$

ОДЗ

$$\left\{\begin{array}{l} x≠ ±1,\\ x≠0, \\ x>-2. \end{array}\right.$$

Решение неравенства

$$\log_{x^2} (x+2) < \log_{x^2} x^2,$$

$$(x^2-1) (x+2 — x^2) <0,$$

$$(x^2 -1) ( x^2 -x -2) >0,$$

$$(x-1)(x+1) ( x-2)(x+1)>0,$$

Совместив с ОДЗ, получим ответ: `(-2,-1)\cup(-1,0)\cup (0,1)\cup (2,∞)`.

Задания для тренировки

Решите неравенства:

• `\log_{x^{-2}}(x+2) > -1`,
• `\log_{\frac{16}{25-x^2}} \left(\dfrac{14}{24 — 2x -x^2} \right)>1`,
• `\log_5 \sqrt{3x+4} — \log_x 5 >1` (на закуску :).

На этом все. Все вопросы в комментарии, и обязательно оставляйте лайки, чтобы ресурс развивался и дальше!

 

xn--e1aajtm3cwc.xn--c1adb6aplz9c.xn--p1ai

Методическое пособие по теме «Логарифмическая функция. Решение логарифмических уравнений, неравенств и систем логарифмических неравенств»

Разделы: Математика

---

Логарифмические уравнения, неравенства и системы логарифмических неравенств входят в число задач, предлагаемых на едином государственном экзамене по математике. Пособие может быть использовано для подготовки к единому государственному экзамену, а также для более глубокого изучения темы “Логарифмическая функция. Решение логарифмических уравнений, неравенств и систем логарифмических неравенств”.

В данном пособии представлены самостоятельные работы для отработки и закрепления навыков решения логарифмических уравнений, неравенств и систем логарифмических неравенств.

Самостоятельные работы рассчитаны на учащихся физико-математических классов, однако, могут быть использованы и для хорошо успевающих учащихся общеобразовательных учреждений. За каждую из проведенных работ выставляется оценка, что послужит достаточной мотивацией для наиболее полной и качественной домашней проработки пройденного накануне материала.

В приложении 1 приведена самостоятельная работа, в которой учащимся предлагается решить логарифмические уравнения, используя при этом определение логарифма, основное логарифмическое тождество и другие преобразования логарифмов. В процессе решения необходимо провести проверку полученных ответов на соответствие с ограничениями, предусмотренными при использовании логарифмической функции. Кроме того, одно из логарифмических уравнений в процессе решения потребует тригонометрических преобразований, а также проверку найденных корней на соответствие с ограничениями, введенными в связи с использованием логарифма, т.е. учащимся придется решать тригонометрическое неравенство и отбирать нужные корни в соответствии с полученным ограничением. Задания 3 и 4 являются наиболее сложными в работе и рассчитаны на более высокий уровень подготовки учащихся. Эту работу полезно использовать и в средней общеобразовательной школе для лучшего запоминания и усвоения основных понятий по данной теме, исключив из нее задания 3 и 4.

В приложении 2 содержится самостоятельная работа на решение логарифмических неравенств. В работу включены различные типы логарифмических неравенств. При этом задания 1, 2 и 3 целесообразно давать учащимся общеобразовательной школы. Для решения неравенства 4 от учащихся потребуются навыки работы с неравенствами, содержащими модуль. Неравенства 4, 5 и 6 предназначены для учащихся физико-математических классов.

В приложении 3 приведены три системы неравенств, каждая из которых содержит логарифмическое неравенство с переменной в основании, а также показательное неравенство, сводящееся к квадратному с помощью замены переменной, либо решаемое при помощи обобщенного метода интервалов. Эта самостоятельная работа рассчитана на учащихся с достаточно высоким уровнем математической подготовки и рекомендуется для проведения в классах с углубленным изучением математики.

Самостоятельные работы составлены в четырех вариантах эквивалентной сложности, которые удобно использовать для промежуточного контроля знаний учащихся, отработки практических навыков решения задач по теме “Логарифмическая функция”.

Представленные в пособии работы позволяют учащимся лучше усвоить пройденный материал по указанной теме, что подтверждено практикой.

Самостоятельные работы содержат ответы, что позволит значительно сократить время проверки работ преподавателем.

Данное пособие также может быть использовано для организации повторения при подготовке учащихся старших классов к успешной сдаче единого государственного экзамена по математике.

Литература

1. Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в ВУЗы – М.: “Издательство Оникс”, 2007.
2. Сергеев И.Н., Панферов В.С. ЕГЭ 2013. Математика. Задача С3. Уравнения и неравенства – Москва: “Издательство МЦНМО”, 2013.
3. Колесникова С.И. Показательные и логарифмические уравнения. ЕГЭ. Математика. – Москва: ООО “Азбука – 2000”, 2012.
4. Колесникова С.И. Показательные и логарифмические неравенства. ЕГЭ. Математика. – Москва: ООО “Азбука – 2000”, 2013.
5. Ященко И. В., Шестаков С.А., Трепалин А. С., Захаров П. И. Подготовка к ЕГЭ по математике. Новая демонстрационная версия 2014.- Москва: “Издательство МЦНМО”, 2014.

Использованные интернет-ресурсы

1. http://reshuege.ru/

Приложение 1

Приложение 2

Приложение 3

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai