Задания по тригонометрии 10 класс с решениями – Методическая разработка по алгебре (10 класс) по теме: методический материал «Система заданий по теме решние тригонометрических уравнений», 10 класс | скачать бесплатно

Тригонометрические уравнения. Задания ЕГЭ по математике (профильный уровень)

а) 1. Согласно формуле приведения, ctg\left( \frac{3\pi }2-x\right) =tgx. Областью определения уравнения будут такие значения x, что \cos x \neq 0 и tg x \neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 \cos ^2 \frac x2=1+\cos x. Получим уравнение: 5(1+\cos x) =\frac{11+5tgx}{1+tgx}.

Заметим, что \frac{11+5tgx}{1+tgx}= \frac{5(1+tgx)+6}{1+tgx}= 5+\frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 \cos x=5 +\frac{6}{1+tgx}. Отсюда \cos x =\frac{\dfrac65}{1+tgx}, \cos x+\sin x =\frac65.

2. Преобразуем \sin x+\cos x по формуле приведения и формуле суммы косинусов: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left( x-\frac\pi 4\right) = \frac65.

Отсюда \cos \left(x-\frac\pi 4\right) =\frac{3\sqrt 2}5. Значит, x-\frac\pi 4= arc\cos \frac{3\sqrt 2}5+2\pi k, k \in \mathbb Z,

или x-\frac\pi 4= -arc\cos \frac{3\sqrt 2}5+2\pi t, t \in \mathbb Z.

Поэтому x=\frac\pi 4+arc\cos \frac{3\sqrt 2}5+2\pi k,k \in \mathbb Z,

или x =\frac\pi 4-arc\cos \frac{3\sqrt 2}5+2\pi t,t \in \mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=\frac\pi 4+arccos \frac{3\sqrt 2}5 и b=\frac\pi 4-arccos \frac{3\sqrt 2}5.

1. Докажем вспомогательное неравенство:

\frac{\sqrt 2}{2}<\frac{3\sqrt 2}2<1.

Действительно, \frac{\sqrt 2}{2}=\frac{5\sqrt 2}{10}<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Заметим также, что \left( \frac{3\sqrt 2}5\right) ^2=\frac{18}{25}<1^2=1, значит \frac{3\sqrt 2}5<1.

2. Из неравенств (1) по свойству арккосинуса получаем:

arccos 1<arc\cos \frac{3\sqrt 2}5<arc\cos \frac{\sqrt 2}2,

0<arccos\frac{3\sqrt2}{5}<\frac{\pi}{4}.

Отсюда \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

0<a<\frac\pi 2.

Аналогично, -\frac\pi 4<arccos\frac{3\sqrt2}{5}<0,

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

0<b<\frac\pi 2.

При k=-1 и t=-1 получаем корни уравнения a-2\pi и b-2\pi.

\Bigg( a-2\pi =-\frac74\pi +arccos \frac{3\sqrt 2}5,\, b-2\pi =-\frac74\pi -arccos \frac{3\sqrt 2}5\Bigg). При этом -2\pi <a-2\pi <-\frac{3\pi }2,

-2\pi <b-2\pi <-\frac{3\pi }2. Значит, эти корни принадлежат заданному промежутку \left( -2\pi , -\frac{3\pi }2\right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если k\geqslant 1 и t\geqslant 1, то корни больше 2\pi. Если k\leqslant -2 и t\leqslant -2, то корни меньше -\frac{7\pi }2.

academyege.ru

Урок повторения и контроля знаний в 10 классе по теме «Формулы тригонометрии»

Нефтеюганское районное муниципальное общеобразовательное бюджетное учреждение «Салымская средняя общеобразовательная школа №1»

Разработка урока алгебры в 10 классе

по теме « ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ «

Урок разработан учителем математики

первой квалификационной категории

Николаевой Ириной Николаевной

2013год

Тема. Тригонометрические формулы.

Класс 10.

Учебник. Алгебра и начала математического анализа. 10 класс в 2 частях. Мордкович А.Г.

Тип урока: урок повторения и контроля знаний.

Цель: повторить изученные формулы тригонометрии, проверить знание учащимися тригонометрических формул и умение их применять при решении примеров.

Задачи:

Обучающие:

• повторить определение синуса, косинуса, тангенса, котангенса числа; повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом; повторить формулы приведения, формулы сложения, формулы двойного угла, формулы понижения степени;

• продолжить формирование умений и навыков по применению тригонометрических формул;

• проконтролировать степень усвоения знаний, умений и навыков по теме.

Развивающие:

• развивать умения и навыки по решению задач на применение тригонометрических формул;

• развивать умения и навыки в работе с тестами мобильного класса

Воспитательные:

• развивать творческую самостоятельность и инициативу;

• стимулировать мотивацию и интерес к изучению тригонометрии.

Методы обучения: диалогический, сравнительный, обобщающий, метод контроля и самоконтроля.

Формы организации познавательной деятельности: индивидуальная, парная, фронтальная.

Средства обучения:

1. Проектор, ноутбук для учителя, мобильный класс (15 ноутбуков, связанных сетью, для учащихся).

2. Программа MyTestX на каждом компьютере мобильного класса.

3. Тест «Формулы тригонометрии» на каждом компьютере мобильного класса.

4. Презентация для проведения урока «»Тригонометрические формулы».

5. Раздаточный материал:

6. Материалы — карточки для создания на доске обобщающей таблицы: название формулы, запись формулы, примеры заданий, формулы одного аргумента, формулы приведения, формулы двойного угла, формулы понижения степени, формулы суммы и разности аргументов.

Место (роль) мультимедийной разработки в учебном занятии:

Презентация «Тригонометрические формулы» проводится в первой половине урока и помогает систематизировать теоретические знания. Компьютерный тест — нестандартная форма проверочной работы по геометрии с помощью мобильного класса, проводится во второй половине урока и позволяет проконтролировать знания учащихся по теме, тут же оценить и увидеть вопросы, на которые каждый конкретный ученик не знает правильного ответа.

Оформление доски.

Упростить выражение:

1)

2)

3)

4)

5)

ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ

Название формул

Запись формул

Примеры заданий

Развернутый конспект урока

Ход урока.

1. Организация начала урока. Приветствие.

2. Постановка цели урока.

вопрос

3. Повторение ранее изученного материала.

Устный счет

1. дописать формулы

учащийся у интерактивной доски

2. математический диктант

учащийся у меловой доски

3. работа в парах

4. Проверка усвоения знаний по теме

Тестирование на компьютере

5. Подведение итогов урока

— Здравствуйте, ребята, садитесь. Сегодня у нас не совсем обычный урок. У нас присутствуют гости, и я надеюсь, что мы их не разочаруем. Тема нашего урока «Тригонометрические формулы». Запишите тему в тетради.

— Как вы думаете, что вас ждет сегодня на уроке?

— Зачем нужно знать формулы тригонометрии?

— для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами;

— разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать.

Актуальность темы вызвана подготовкой к ЕГЭ. Каждый год результаты ЕГЭ по математике показывают, что выпускники хуже всего справляются с заданиями по тригонометрии. Очевидно причина в большом количестве формул, которые необходимо запомнить. Зная формулы можно решить как простые так и более сложные задания ЕГЭ.

— Какие формулы тригонометрии вы мы изучили?

-формулы приведения, формулы двойного аргумента, формулы понижения степени, формулы сложения, основные тригонометрические формулы (формулы одного аргумента)

(учитель прикрепляет карточки с названиями формул в первый столбец таблицы на доске)

— Повторим основные формулы, решим несколько простых примеров.

Следующие виды работ на данном этапе урока происходят одновременно :

1. «Восстанови формулы». Один учащийся у интерактивной доски дописывает формулы:

• tg α =

• sin² α +cos² α = 1

• 1+ tg² α =

• sin(-α) = — sin α

• tg (-α) = — tg α

• ctg α =

• tg α∙ ctg α = 1

• 1+ ctg² α =

• cos (-α) = cos α

• ctg (-α) = — ctg α

• cos² α = 1- sin² α

• sin² α = 1- cos² α

• tg α =

• ctg α =

2. Устный математический диктант

Один учащийся у меловой доски решает устно несколько заданий, записывая только ответы и формулы, которые применял.

Остальные учащиеся работают в парах.

На карточках №1-6 выписаны задания (Приложение 1.) Учащиеся упрощают, записывают решение, ответ, формулы, которыми они пользовались, заполняя таблички.

Проверка

Обратить внимание на решение карточки №1, 4 задания на них одинаковы, но решить надо по формулам указанным в названии карточки. Во время проверки обратить внимание на способы решения.

По ходу завершения работы выходит один человек из пары к доске и прикрепляет в таблицу соответствующего столбца нужную карточку: название формулы, формулу, 1 задание в качестве примера.

Обобщение

— Поднимите руку те, кому достались карточка с заданиями ЕГЭ. Запиши на доске решение своего уравнения.

Учащийся на интерактивной доске оформляет решение уравнения С1 (уравнение из доме версии 2013).

Остальные учащиеся начинают работу над тестом за компьютером. (Приложение 2).

— Кто закончит тест приступаете к решению уравнения.

Проверка решения уравнения, обсуждение решения.

— Ребята назовите формулы, которые использовали для решения данного уравнения?

— косинус двойного угла, формулы приведения

— А какие формулы необходимо применить для решения уравнения?

ответы учащихся

— Я знаю почему вы затрудняетесь с ответом. Для решения данного уравнения нужно применить формулу Преобразования суммы тригонометрических функций в произведение, но данную тему мы начнем изучать на следующем уроке.

Приложение 1. Карточки для работы учащихся.

Задание

Решение

Ответ

Формулы

1

Упростить выражение: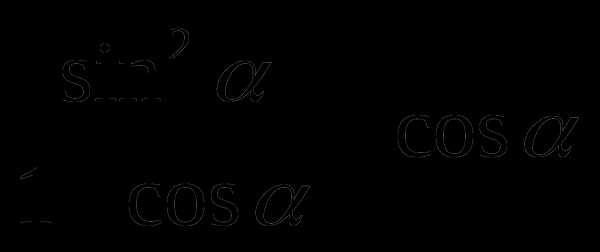

2

Упростить выражение:

3

Упростить выражение: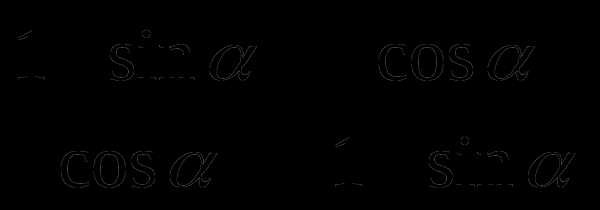

4

Упростить выражение: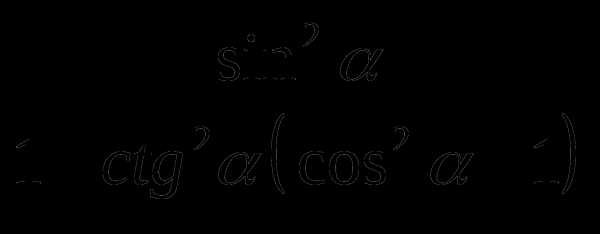

5

Решить уравнение: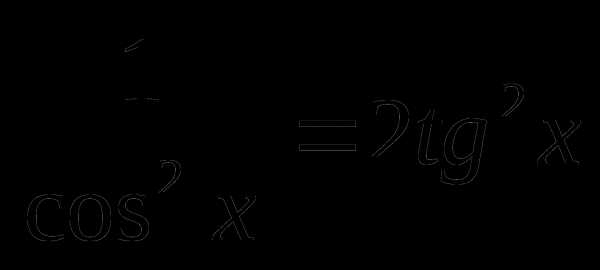

Задание

Решение

Ответ

Формулы

1

Вычислить:

Синус суммы

2

Вычислить:

Косинус суммы

3

Вычислить:

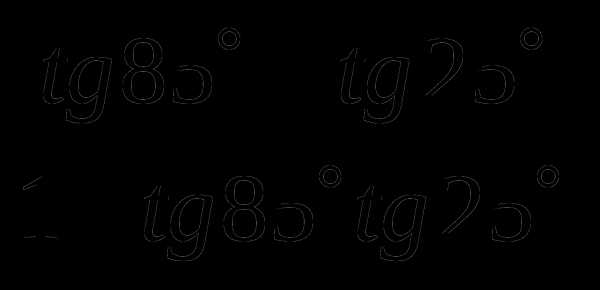
Тангенс разности

4

Вычислить:

Косинус суммы

5

Вычислить: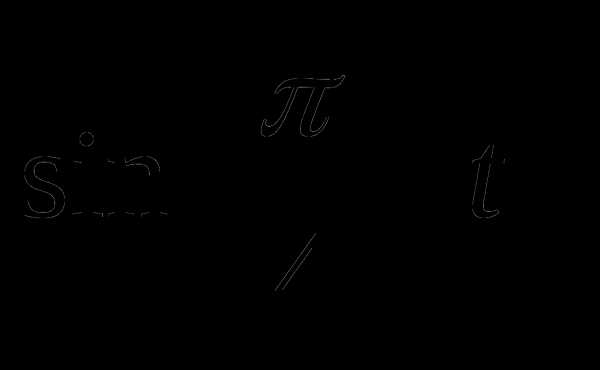

Зная, что , .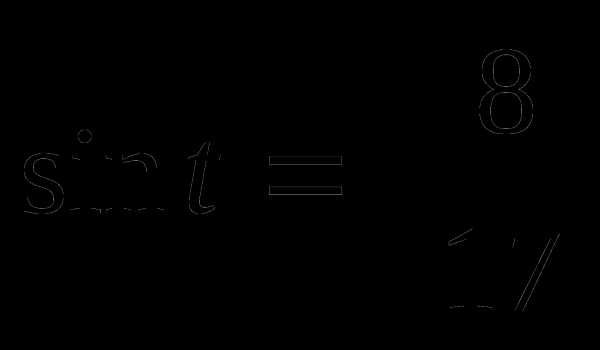

Синус суммы

Задание

Решение

Ответ

Формулы

1

Упростить выражение:

2

Упростить выражение:

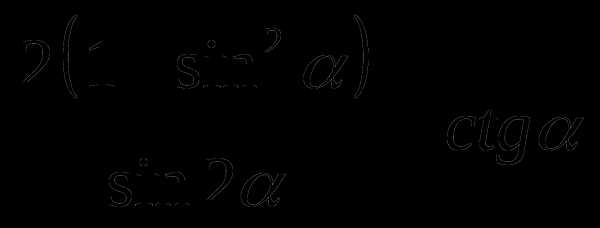
3

Упростить выражение:

4

Найти 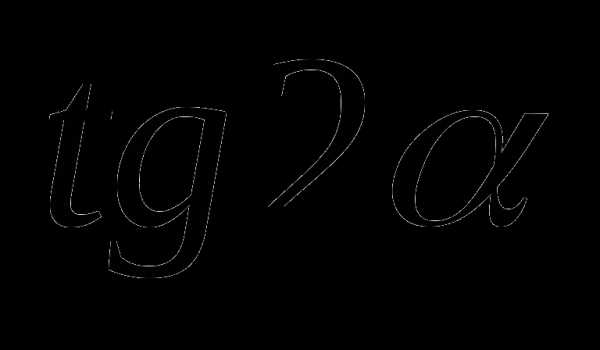, если известно, что , .

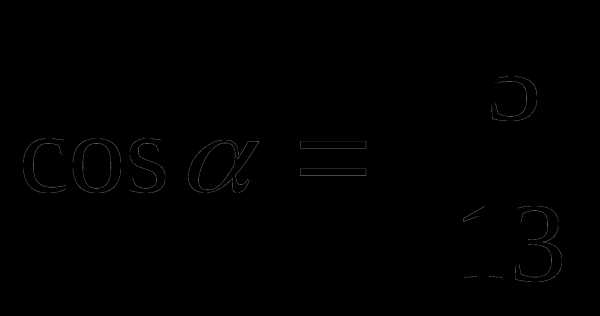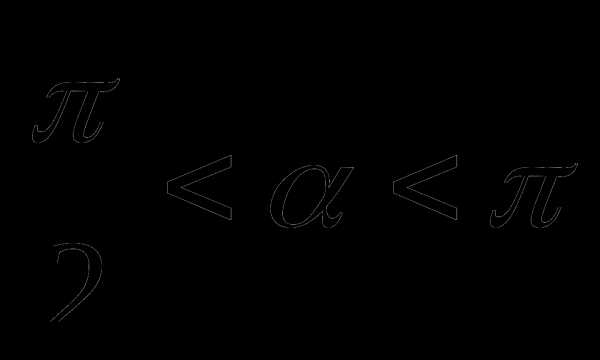5

Решить уравнение:

Упростить выражение: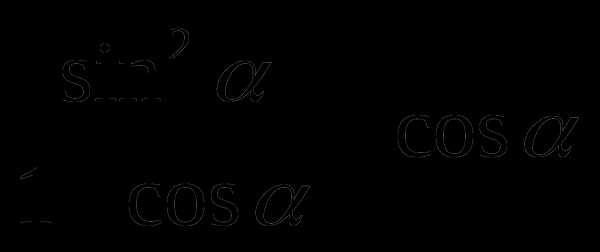

2

Упростить выражение:

3

Упростить выражение:

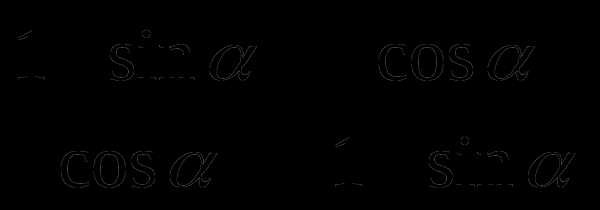
4

Упростить выражение:

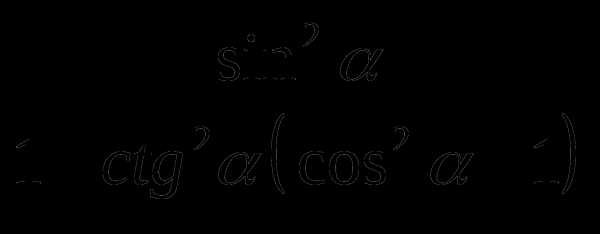
5

Решить уравнение:

Задание

Решение

Ответ

Формулы

1

Упростить выражение:

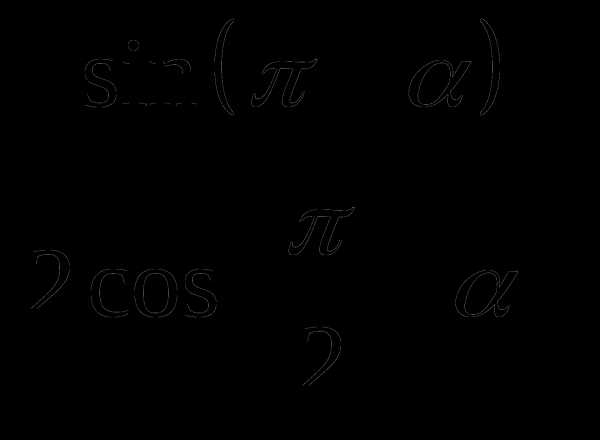
2

Упростить выражение:

3

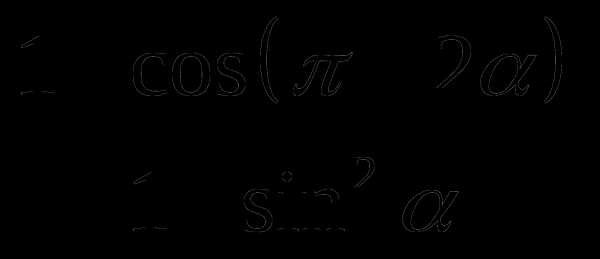
4

Вычислить:

5

Решить уравнение:

Задание

Решение

Ответ

Формулы

1

Вычислить:

2

Найдите 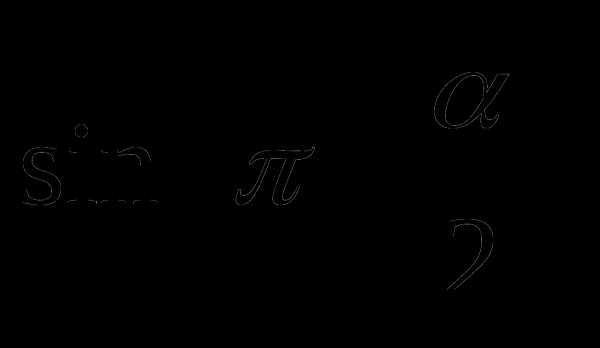, есл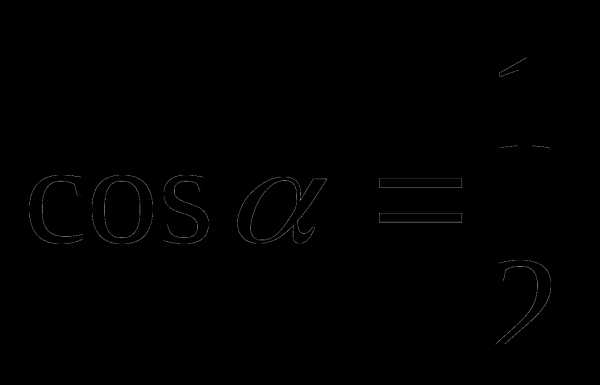и и

3

ПРИЛОЖЕНИЕ 2.

Тест: D:\РАБОТА\МАТЕМАТИКА\ТЕСТЫ\Формулы суммы и разности тригонометрических функций.mtf

Формулы тригонометрии

Автор: Николаева И.Н.

Описание:

Тест предназначен для проверки умений применять формулы синуса косинуса, тангенса и контангенса сумму и разности двух аргументов, а так же формул двойного угла.

Инструкция к тесту:

Внимательно отвечай на вопросы теста. Помни второй раз запустить тест невозможно!

Задание #1

Вопрос:

Вычисли:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #2

Вопрос:

Вычисли:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #3

Вопрос:

Упрости выражение:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #4

Вопрос:

Установи соответствие:

Укажите соответствие для всех 5 вариантов ответа:

1)

2)

3)

4)

5)

__

__

__

__

__

Задание #5

Вопрос:

Упрости выражение:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #6

Вопрос:

Вычисли:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #7

Вопрос:

Упрости выражение

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #8

Вопрос:

Вычисли:

Выберите один из 5 вариантов ответа:

1)

2) 1

3)

4) 1/2

5)

Задание #9

Вопрос:

Упрости выражение:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Задание #10

Вопрос:

Вычисли:

Выберите один из 5 вариантов ответа:

1)

2)

3)

4)

5)

Ответы:

1) (1 б.) Верные ответы: 5;

2) (1 б.) Верные ответы: 5;

3) (1 б.) Верные ответы: 1;

4) (1 б.) Верные ответы:

1;

5;

2;

3;

4;

5) (1 б.) Верные ответы: 5;

6) (1 б.) Верные ответы: 4;

7) (1 б.) Верные ответы: 2;

8) (1 б.) Верные ответы: 2;

9) (1 б.) Верные ответы: 3;

10) (1 б.) Верные ответы: 1;

Конец

infourok.ru

Практикум решения задач по тригонометрии. 10 класс

Найдите корни уравнения:  В ответе запишите наибольший отрицательный корень.

Найдите корни уравнения:  В ответ запишите наибольший отрицательный корень.

Найдите корни уравнения:  В ответ запишите наибольший отрицательный корень.

Решите уравнение . В ответе напишите наибольший отрицательный корень.

Решите уравнение . В ответе напишите наименьший положительный корень.

Решите уравнение . В ответе напишите наименьший положительный корень.

Решите уравнение . В ответе напишите наименьший положительный корень.

Найдите , если  и .

Найдите , если  и .

Найдите , если .

Найдите , если .

Найдите значение выражения , если 

Найдите , если  и .

 Найдите , если 

Найдите , если 

Найдите , если 

Найдите , если 

Найдите значение выражения , если .

Найдите , если .

Найдите значение выражения .

Найдите значение выражения 

Найдите значение выражения .

Найдите значение выражения 

Найдите значение выражения 

Найдите значение выражения 

Найдите значение выражения .

Найдите значение выражения .

Найдите значение выражения .

Найдите значение выражения .

Найдите значение выражения .

Найдите значение выражения 

Найдите значение выражения 

Найдите значение выражения .

Найдите значение выражения 

Найдите значение выражения .

Найдите значение выражения .

Найдите значение выражения: 

Найдите значение выражения .

Найдите значение выражения 

Найдите значение выражения 

infourok.ru

Задачи по тригонометрии — уровень B. Подготовка к ЕГЭ по математике

Для учеников, имеющих средний или слабый уровень знаний по тригонометрии репетитор по математике разбивает подготовку к задачам С1 с ЕГЭ на несколько этапов. Один из них — решение уравнений на замену переменной. Прорешайте размещенный ниже комплект заданий, а затем уже переходите к рассмотрению уравнений с ограничениями. Я собирал номера из разных задачников. Некоторые составлял сам. Главная цель, которая преследовалась — предоставить репетитору по математике достаточное количество номеров на отработку навыков выполнения замены в разных ситуациях. Все уравнения снабжены ответами. Учебный дидактический комплект для качественной подготовки к ЕГЭ по математике с репетитором.

Уравнение на моментальную замену переменной

————————————————————————————
1)

Ответ:

————————————————————————————
2)

Ответ:

————————————————————————————
3)

Ответ:

————————————————————————————
4)

Ответ:

————————————————————————————
5)

Ответ:

————————————————————————————
6)

Ответ:

————————————————————————————
Уравнения на замену переменной после некоторого преобразования

————————————————————————————
7)

Ответ:

————————————————————————————
8)

Ответ:

————————————————————————————
9)

Ответ:

10)

Ответ:

————————————————————————————
11)

Ответ:

————————————————————————————
12)

Ответ:

————————————————————————————
13)

Ответ:

————————————————————————————
14)

Ответ:

————————————————————————————
Уравнения на формулы двойного угла и замену переменной (отобрано репетитором по математике)

————————————————————————————
15)

Ответ:

————————————————————————————
16)

Ответ:

————————————————————————————
17)

Ответ:

————————————————————————————
18)

Ответ:

————————————————————————————
19)

Ответ:

————————————————————————————
20)

Ответ:

————————————————————————————
21)

Ответ:

————————————————————————————
22)

Ответ:

————————————————————————————
23)

Ответ:

————————————————————————————
Уравнения на замену с применением формул приведения

————————————————————————————
24)

Ответ:

————————————————————————————
25)

Ответ:

————————————————————————————
26)

Ответ:

————————————————————————————
Скоро будут доступны другие уравнения, также сортированные по типам.

Указание репетитора по математике: предлагать ученику подобные уравнения можно только после отработки с ним темы «обратные тригонометрические функции» и «простейшие тригонометрические уравнения». Кроме этого нужно повторить с формулы двойного угла и основное тригонометрическое тождество. Каждое решение должно сопровождаться рисунком, даже если школьник справляется c уравнениями и без них. Слабому ученику репетитору желательно подготовить теоретический листочек с необходимыми формулами и примерами рисунков к простейшим типовым уравнениям вида Cosx=a; Sinx=a; tgx=a и ctgx=a.

Колпаков А.Н. Репетитор по математике — составитель комплекта. Москва. Строгино.

Метки: ЕГЭ по математике, Тригонометрия

ankolpakov.ru

Практикум по тригонометрии 10 класс

Практикум по тригонометрии 10 класс

Задание №1. Отметить точки на числовой окружности, соответствующие данному числу:

а) .

б) .

в) .

г) .

Задание №2. Отметить точки на числовой окружности, соответствующие данному числу:

а) .

б) .

в) .

г) .

Задание №3. Найти на числовой окружности точку :

;

а) =

б) =

в) =

г) =

д) =

Задание №4:

Найти на числовой окружности точку, соответствующую заданному числу: а) 1; б) – 1; в) – 3,5; г) 0,5; д) 0,785; е) 2; ж) 5.

Задание №5.

Какой четверти числовой окружности принадлежит точка, соответствующая числу:

;

а) 9; – 9; 17; – 31;

б) 20; 23; 28; — 43;

в) 50; 85; 156; 200.

Задание №6. Заданы точки, написать формулу.

Самостоятельная работа №1.

Вычислить: а) б) в) ; г)

д) е) ; ж) .

Самостоятельная работа №2.

Вычислить:

а)

б)

в)

г)

Самостоятельная работа №3

Найти область определения каждого из выражений:

Самостоятельная работа №4 ( 15 мин.)

Записать все решения уравнения:

Практическая работа №1

Решите уравнения и покажите эти решения на тригонометрической окружности:

x =

x =

x =

x =

x =

x =

7.

8.

Практическая работа №2

Решите уравнения и покажите эти решения на тригонометрической окружности:

1.

x=

2.

x=

3.

x=

4.

x=

5.

x=

6.

x=

7.

x=

8.

x=

Практическая работа №3

Решите уравнения и покажите эти решения на тригонометрической окружности:

1.

x=

2.

x=

3.

x=

4.

x=

5.

x=

6.

x=

7.

x=

8.

x=

9.

x=

Решение тригонометрических уравнений

Вариант 1

Решить уравнения:

1.

2.

3.

4.

5.

6.

Вариант2

Решить уравнения:

1.

2.

3.

4.

5.

6.

infourok.ru

Задания к зачету по теме «Тригонометрические функции» 10 класс

Documents войти Загрузить ×

1. Математика

advertisement advertisement

Related documents

Урок-презентация «Преобразование графиков». 10-й класс Цели: Обобщить знания и умения,

– черный – бирюзовый clBlack

Тестовые задания по аттестации

10 класс Задача 1. Решение. Ответ.

Двойной интеграл в полярных координатах

Приложение 6б

Решения 3

studydoc.ru

Спецкурс «Тригонометрия» — Математика — 10 класс

Программа спецкурса для учащихся 10-11 классов

Программа по математике «Тригонометрия в ЕНТ» составлена на основе учебной программы по алгебре и началам анализа для 10-11 классов в соответствии с требованиями государственного общеобязательного стандарта среднего образования.

Данная программа предназначена для повышения эффективности подготовки учащихся 10-11 классов к итоговой аттестации по алгебре и началам анализа за курс средней школы и предусматривает их подготовку к дальнейшему математическому образованию.

Раздел «Тригонометрия» школьного курса математики наиболее сложный для учащихся. Одной из причин этого является недостаточное количество программных часов, отводимое на изучение этого раздела, а так же поверхностное изложение некоторых важных вопросов, связанных с решением тригонометрических уравнений, отбором и исследованием корней, решением тригонометрических неравенств. Анализ сдачи единого национального тестирования показал, что ученики допускают много ошибок при выполнении заданий именно этого раздела или вообще не приступают к выполнению такого задания. Для устранения данной причины и недостатков в получении тригонометрических знаний разработан данный спецкурс.

Программа спецкурса рассчитана на учащихся 10-11 классов, но может быть использована тем, кому она понадобится при учебе, подготовке различного рода экзаменам, в частности, к ЕНТ. Данный курс рассчитан на 68 часов.

Для реализации данного спецкурса используется различные формы организации занятий, такие как лекция и семинар, групповая, индивидуальная, работа в парах, исследовательская и проектная деятельность учащихся, практикумы и консультации.

№ п/п	Тема	Количество часов		Форма и методы работы	Контроль
Основные понятия тригонометрии. Формулы тригонометрических функций одного и того же аргумента (4 часа)
1	Радианное измерение углов. Синус, косинус, тангенс, котангенс произвольного угла	1		ПР	СР
2	Основные тригонометрические тождества	1		Семинар практикум	СР
3	Формулы приведения	1		Семинар практикум	СР
4	Применение формул приведения и основных тригонометрических тождеств	1		ИР	Тест №1
Формулы тригонометрии (11 часов)
5	Формулы суммы и разности двух углов	1		ГР	СР
6	Формулы преобразования сложения тригонометрических функций	1		ГР	СР
7	Формулы преобразования произведения тригонометрических функций	1		ГР	СР
8	Применение формул суммы и разности, сложения и произведения	1		Практикум	Работа с тестами
9	Формулы тригонометрических функций двойного угла	1		ПР	СР
10	Формулы тригонометрических функций половинного угла	1		ПР	СР
11	Формулы тригонометрических функций тройного угла	1		ПР	СР
12	Применение формул тригонометрических функций двойного, тройного и половинного аргументов	1		Практикум	Работа с тестами
13	Степени синуса и косинуса	1		Семинар практикум	СР
14	Применение формул степени синуса и косинуса	1		Практикум	Работа с тестами
15	Преобразование тригонометрических выражений	1		ИР	Тест №2
Тригонометрические функции (10 часов)
16	Определение тригонометрических функций	1	ПР			СР
17	Свойства и графики тригонометрических функций синус и косинус	1	ГР			СР
18	Преобразование графиков тригонометрических функций синус и косинус	1	Практикум			Работа с тестами
19	Свойства и графики тригонометрических функций тангенс и котангенс	1	ГР			СР
20	Преобразование графиков тригонометрических функций тангенс и котангенс	1	Практикум			Работа с тестами
21	Преобразование графиков тригонометрических функций	1	ИР			Тест №3
22	Определение и свойства обратных тригонометрических функций синус и косинус	1	ГР			СР
23	Определение и свойства обратных тригонометрических функций тангенс и котангенс	1	ГР			СР
24	Вычисление значений тригонометрических функций от аркфункций	1	Практикум			Работа с тестами
25	Вычисление значений тригонометрических функций от аркфункций	1	ИР			Тест №4
Тригонометрические уравнения и их системы (10 часов)
26	Основные тригонометрические уравнения	1		Практикум	СР
27	Тригонометрические уравнения, приводимые к алгебраическим относительно одной тригонометрической функции	1		Практикум	СР
28	Тригонометрические уравнения, решаемые путем преобразования тригонометрическими формулами	1		Практикум	СР
29	Тригонометрические уравнения, решаемые путем понижения степени уравнения	1		Практикум	СР
30	Решение однородных тригонометрических уравнений	1		Практикум	СР
31	Тригонометрические уравнения, решаемые путем ведения дополнительного угла	1		Практикум	СР
32	Решение уравнений с обратными тригонометрическими функциями	1		Практикум	СР
33	Системы тригонометрических уравнений	1		Практикум
34	Решение тригонометрических уравнений и их систем	1		Практикум	Работа с тестами
35	Решение тригонометрических уравнений и их систем	1		ИР	Тест №5
Решение тригонометрических неравенств и их систем (7 часов)
36	Неравенство тригонометрической функции синус	1		Практикум	СР
37	Неравенство тригонометрической функции косинус	1		Практикум	СР
38	Неравенство тригонометрической функции тангенс	1		Практикум	СР
39	Неравенство тригонометрической функции котангенс	1		Практикум	СР
40	Системы тригонометрических неравенств	1		Практикум	Работа с тестами
41	Решение тригонометрических неравенств и их систем	1		Практикум	Работа с тестами
42	Решение тригонометрических неравенств и их систем	1		ИР	Тест №6
Производная тригонометрических функций (6 часов)
43	Правила нахождения производных	1		ГР	СР
44	Производная тригонометрических функций	1		ГР	СР
45	Касательная к графику тригонометрических функций	1		Практикум	Работа с тестами
46	Применение производной	1		Практикум	Работа с тестами
47	Применение производной	1		Практикум	Работа с тестами
48	Производная тригонометрических функций	1		ИР	Тест №7
Первообразная и интеграл (4 часа)
49	Определение, свойство и правила первообразных	1		ГР	СР
50	Первообразная тригонометрических функций	1		Практикум	Работа с тестами
51	Площадь криволинейной трапеции	1		Практикум	Работа с тестами
52	Нахождение первообразной тригонометрических функций	1		ИР	Тест №8
Повторение (часов)
53	Работа над проектом	1	Консультация
54	Работа над проектом	1	Сбор информации
55	Учебный проект	1	Урок презентация			Защита проектов
56	Учебный проект	1	Урок презентация			Защита проектов
57	Зачет	1	Опрос			Билеты
58	Зачет	1	Опрос			Билеты
59	Контрольная работа	1
60	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
61	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
62	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
63	Тригонометрия	1	ИР			Тест №9
64	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
65	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
66	Тригонометрия в ЕНТ	1	Практикум			Работа с тестами
67	Тригонометрия	1	ИР			Тест №10
68	Итоговое занятие	1

multiurok.ru