Задания В11. Логарифмические выражения | Подготовка к ЕГЭ по математике
Часть 4.
Здесь смотрим части 1, 2, 3, 5
При решении задач, что мы сегодня рассматриваем, нам понадобятся свойства логарифмов.
Числовые логарифмические выражения
Задание 1.
Найдите значение выражения .
Решение: + показать
Задание 2.
Найдите значение выражения .
Решение: + показать
Представим как и далее воспользуемся следующим свойством логарифмов: при : А теперь применяем основное логарифмическое тождество: Ответ: 49.
Задание 3.
Найдите значение выражения .
Решение: + показать
Задание 4.
Найдите значение выражения .
Решение: + показать
Задание 5.
Найдите значение выражения .
Решение: + показать
Ответ: 12.
Задание 6.
Найдите значение выражения .
Решение: + показать
Складывать логарифмы не имеем право, у них разные основания.
Тогда
Ответ: 1,5.
Задание 7.
Найдите значение выражения .
Решение: + показать
Задание 8.
Найдите значение выражения .
Решение: + показать
Ответ: 2.
Задание 9.
Найдите значение выражения .
Решение: + показать
Задание 10.
Найдите значение выражения .
Решение: + показать
Ответ: 9.
Задание 11.
Найдите значение выражения .
Решение: + показать
Ответ: 1.
Задание 12.
Найдите значение выражения .
Решение: + показать
Ответ: 9.
Задание 13.
Найдите значение выражения .
Решение: + показать
Ответ: 0.
Задание 14.
Вычислите значение выражения: .
Решение: + показать
В самом конце мы применили основное логарифмическое тождество, а до этого – следствие из свойства 7 логарифмов. Ответ: 2.
Задание 15.
Найдите значение выражения .
Решение: + показать
Обратите внимание, это не произведение логарифмов. У логарифма по основанию подлогарифмным выражением является . Ответ: 0,25.
Буквенные логарифмические выражения
Задание 1.
Найдите , если .
Решение: + показать
При имеем: Ответ: -32.
Задание 2.
Найдите значение выражения , если .
Решение: + показать
🙂 После плодотворной работы не помешало бы и отдохнуть немного… –>+ показать
Жизнь полна неожиданностей, неправда ли?

Вы можете пройти обучающий тест по теме «Преобразование логарифмических выражений».
Тест по теме «Логарифмы и их свойства»
Методическая разработка «Тестовые задания по математике»
Тема «Логарифмы и их свойства»
Тест предназначен для проведения контроля знаний учащихся 10 класса или студентов 1 курса СПО в конце изучения темы «Логарифмы и их свойства». Тест дает возможность быстро и эффективно провести диагностику усвоения материала по теме. Данный вид контроля стимулирует у учащихся стремление к систематической самостоятельной работе по изучению дисциплины.
Структура работы и типы заданий. Контрольно-измерительный материал (тест) представлен двумя эквивалентными по содержанию и сложности вариантам, каждый из которых состоит из двух частей, включающих12 заданий.
Часть I состоит из 10 заданий: 8 заданий с выбором ответа и 2 задания, требующих записи ответа в виде числа.
Часть II состоит из 2 заданий, на которые необходимо представить подробное решение.
К тесту приведены инструкция, «ключи» к тесту, критерии оценивания и бланк ответов.
Общее время на выполнение работы – 40 минут.
Оценка выполнения работы. Работа проверяется в соответствии с «ключами» к тесту.
Каждое верно выполненное задание № 1-8 оценивается в один балл (максимальное число баллов – 8).
Каждое верно выполненное задание № 9-10 оценивается в два балла (максимальное число баллов – 4).
Каждое верно выполненное задание № 11-12 оценивается в три балла (максимальное число баллов – 6). Решение правильное, получен верный ответ — 3 балла. Допущена вычислительная ошибка, но ответ получен верный – 2 балла. Допущена ошибка, которая привела к неправильному ответу – 1 балл. Другие случаи — 0 баллов.
Максимальное число баллов за выполнение всего теста – 18.
Критерии оценивания:
«5» — 16 – 18 баллов
«4» — 13 – 15 баллов
«3» — 10 – 12 баллов
«2» — 0 – 9 баллов.
«Ключи» к тесту:
Вариант 1
Часть I.
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ответ | c | a | d | a | b | a | b | b |
| № вопроса | 9 | 10 |
| ответ | 3,5 | 4 |
Часть II.
| № вопроса | 11 | 12 |
| ответ | 6,8 |
Вариант 2
Часть I.
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ответ | a | b | b | a | c | d | b | c |
| № вопроса | 9 | 10 |
| ответ | 2,5 | 10 |
Часть II.
| № вопроса | 11 | 12 |
| ответ | 49,25 |
Инструкция к заданиям: Работа состоит из 12 заданий различного уровня сложности: базовый уровень (часть I) – 10 заданий и повышенный уровень (часть II) – 2 задания.
Часть I: задания с выбором ответа № 1-8 — в бланке ответов необходимо отметить только одну букву правильного ответа. В заданиях № 9-10 требуется записать ответ в бланк (ответом должно быть некоторое целое число или число, записанное в виде десятичной дроби).
Часть II: в заданиях № 11-12 требуется записать в бланке ответов подробное обоснованное решение.
Все необходимые вычисления и преобразования выполняются на черновике. Записи в черновике не учитываются при оценивании работы.
Рекомендуется выполнять задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его и постарайтесь выполнить те, в ответах на которые вы уверены. К пропущенным заданиям можно будет вернуться в оставшееся время.
Общее время на выполнение работы – 40 минут.
Желаю успеха!
Вариант 1
Часть I
1. Вычислить:
a) 16;
b) 48;
c) 96;
d) 168.
2. Вычислить:
a) 3;
b) 13,5;
c) 36;
d) 4.
3. Даны числа: a = , b = и c = . Расположить числа в порядке возрастания.
a) a, b, c
b) c, b, a
c) a, c, b
d) c, a, b
4. Найти число х:
a) 8;
b) ;
c) 6;
d) .
5. Вычислить:
a) 1;
b) 2;
c) 3;
d) -1.
6. Упростить, применив основное логарифмическое тождество:
a) 54;
b) 81;
c) 29;
d) 48.
7. Вычислить:
a) 1;
b) 2;
c) 3;
d) 4.
8. Найти значение выражения:
a) ;
b) 9;
c) 20;
d) 5.
9. Найти значение выражения: , если
Ответ: _____________
10. Найти x по данному его логарифму:
Ответ: _____________
Часть II
11. Найти х по данному его логарифму (, , ):
.
12. Вычислить: .
Вариант 2
Часть I
1. Вычислить:
a) 70;
b) 35;
c) 10;
d) 205.
2. Вычислить:
a) 16;
b) 3;
c) 4;
d) 34.
3. Даны числа a = , b = и c = . Расположить числа в порядке возрастания.
a) a, b, c
b) b, c, a
c) c, a, b
d) c, b, a
4. Найти число х:
a) ;
b) 216;
c) ;
d) 18.
5. Вычислить:
a) 1;
b) 2;
c) 3;
d) 4.
6. Упростить, применив основное логарифмическое тождество:
a) 75;
b) 15;
c) 25;
d) 18.
7. Вычислить:
a) -1;
b) 1;
c) 2;
d) 3.
8. Найти значение выражения:
a) ;
b) 13;
c) 1;
d) 3.
9. Найти значение выражения: , если
Ответ: _____________
10. Найти x по данному его логарифму:
Ответ: _____________
Часть II
11. Найти х по данному его логарифму (, , ):
.
12. Вычислить: .
Бланк ответов:
| Фамилия Имя ____________________ | Группа ________________ | Дата _____________ | |||||||
| Тест по теме «Логарифмы и их свойства» | |||||||||
| Вариант__________
Часть I | |||||||||
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| ответ |
|
|
|
|
|
|
|
| |
|
| |||||||||
| № вопроса | 9 | 10 |
| ||||||
| ответ |
|
| |||||||
| Часть II | |||||||||
| № 9.
Ответ: _____________________ | |||||||||
| № 10.
Ответ: _____________________ | |||||||||
| Оценка: |
| ||||||||
xn--j1ahfl.xn--p1ai
Логарифмы, примеры решений
Теория про логарифмы
Логарифм по основанию 10 называется десятичным логарифмом и обозначается :
а логарифм по основанию называют натуральным и обозначают :
Примеры
ПРИМЕР 3| Задание | Вычислить значение выражения
|
| Решение | Перейдем в каждом из слагаемых к логарифму по основанию 18, используя формулу перехода . Получим:
Так как сумма логарифмов равна логарифму произведения, последняя сумма перепишется в виде:
Число 324 можно представить как степень 18, получим
далее выносим степень как коэффициент перед знаком логарифма:
Учитывая, что , окончательно будем иметь:
|
| Ответ |
| Задание | Вычислить |
| Решение | Перейдем во всех логарифмах к основанию 2, используя формулу перехода к новому основанию:
получим
Представим 4 и 8 в виде степени двойки и вынесем полученные степени за знак логарифма как коэффициент:
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решебник Примеры для самостоятельного решения Тест Логарифмы Логарифм числа и его преобразование
Все вопросы и замечания просьба направлять по адресу [email protected]Решебник
Примеры для самостоятельного решения
Тест
Логарифмы
Логарифм числа и его преобразование
Определение. Логарифмом числа по основанию называется показатель степени , в которую надо возвести основание a, чтобы получить данное число .
— любое действительное число,
> 0– логарифмируемое число,
— основание логарифма, > 0 , 1
При любом > 0 , 1 и любых > 0, > 0 верны следующие равенства:
1.
2.
3.
4. для любого kR
5. для любого
6.
7.
8. (формула перехода к новому основанию)
9. , b 1
10. , b 1.
Замечание. Отметим важную особенность формул 1, 2, 3, 4, 5. Их правые и левые части, взятые по отдельности, определены на разных множествах значений переменных и . В формуле 1 левая часть определена лишь при > 0, а правая – для всех R. В формулах 2 и 3 левые части определены для всех пар значений и одного знака (то есть при ), а правые – лишь для > 0 и > 0. В формуле 4 при k = 2n, где nN, n 0, левая часть определена для всех 0, правая же – только для > 0. В формуле 5 при k = 2n левая часть определена для всех и , а правая для . Отличие множеств определения следует учитывать при применении этих формул для преобразования уравнений. Оно может привести как к потере решений, так и к появлению посторонних значений неизвестных. При решении примеров на это следует обращать внимание.
Решебник
Теория
Примеры для самостоятельного решения
Тест
|
Пример1. Вычислить: а) ; б) ; в) |
Решение.
|
Пример 2. Вычислить: а) ; б) ; в) ; г) .
|
Решение.
|
Пример 3. Вычислить: а) ; б) ; в) . |
Решение.
|
Пример 4. Вычислить: а) ; б) ; в) . |
Решение:
|
Пример 5. Вычислить: а) ; б) ; в) . |
Решение.
|
Пример 6. Вычислить: а) ; б) ; в) . |
Решение:
|
Пример 7. Вычислить: а) ; б) ;
|
Решение:
|
Пример 8. Вычислить: а) ; б) .
|
Решение.
|
Пример 9. Вычислить: а) ; б) .
|
Решение.
|
Пример 10. Вычислить: .
|
Решение.
|
Пример 11. Вычислить: .
|
Решение:
|
Пример 12. Вычислить: .
|
Решение:
|
Пример 13. Вычислить: .
|
Решение:
|
Пример 14. Вычислить: .
|
Решение.
|
Пример 15. Вычислить: .
|
Решение:
|
Пример 16. Выразить через логарифмы по основанию 2: а) ; б) ; в) . |
Решение.
|
Пример 17. Вычислить: .
|
Решение.
|
. |
для любого kR (формула перехода к новому основанию)
|
|
Пример 18. Вычислить: а) ; б) .
|
Решение:
|
Пример 19. Вычислить: .
|
Решение:
|
Пример 20. Вычислить: .
|
Решение.
|
. |
, b 1 для любого kR |
|
Пример 21. Вычислить: .
|
Решение.
|
Пример 22. Вычислить: .
|
Решение.
|
. |
, b 1 |
|
Пример 23.Вычислить выражение при условии . |
Решение.
Для закрепления пройденного материала рекомендуем пройти следующий тест.
Примеры для самостоятельного решения
Теория
Решебник
Тест
Вычислить:
1. а) ,
б) ,
в) .
Решение.
Ответ.
2. а) ,
б) ,
в) .
Решение.
Ответ.
3. а) ,
б) ,
в) .
Решение.
Ответ.
4. а) ,
б) ,
в) .
Решение.
Ответ.
5. а) ,
б) ,
в) .
Решение.
Ответ.
6. а) ,
б) ,
в) .
Решение.
Ответ.
7. а) ,
б) .
Решение.
Ответ.
8. а) ,
б) .
Решение.
Ответ.
9. а) ,
б) .
Решение.
Ответ.
10. .
Решение.
Ответ.
11. Выразить через логарифмы по основанию 3:
а) ,
б) ,
в) ,
г) .
Решение.
Ответ.
Вычислить:
12. а) ,
б) .
Решение.
Ответ.
13. .
Решение.
Ответ.
14. .
Решение.
Ответ.
15. .
Решение.
Ответ.
16. .
Решение.
Ответ.
17. .
Решение.
Ответ.
18. .
Решение.
Ответ.
19. .
Решение.
Ответ.
20. .
Решение.
Ответ.
21. .
Решение.
Ответ.
Теория
Решебник
Примеры для самостоятельного решения
Тест
Решение
Теория
Решебник
Примеры для самостоятельного решения
Тест
1. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
2. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
3. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
4. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
5. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
6. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
7. а).
б) .
назад к условию задачи для самостоятельного решения
8. а).
б) .
назад к условию задачи для самостоятельного решения
9.а) .
б) .
назад к условию задачи для самостоятельного решения
10. .
назад к условию задачи для самостоятельного решения
11.а) .
б) .
в) .
г) .
назад к условию задачи для самостоятельного решения
12. а) .
б) .
назад к условию задачи для самостоятельного решения
13.
.
назад к условию задачи для самостоятельного решения
14. .
назад к условию задачи для самостоятельного решения
15. .
назад к условию задачи для самостоятельного решения
16. .
назад к условию задачи для самостоятельного решения
17. .
назад к условию задачи для самостоятельного решения
18. .
назад к условию задачи для самостоятельного решения
19. .
.
назад к условию задачи для самостоятельного решения
20. .
.
назад к условию задачи для самостоятельного решения
21. .
назад к условию задачи для самостоятельного решения
Теория
Решебник
Примеры для самостоятельного решения
Тест
Ответы
|
1. а) 6, б) 4, в) –2. назад 2. а) –1, б) –9, в) -4. назад 3. а) 2, б) , в) 1,5. назад 4. а) 9, б)25, в) 9. назад 5. а) 9, б) 49, в) . назад 6. а) , б) 3,5, в). назад 7. а) 1, б) 0. назад 8. а) 1, б) 2. назад 9. а) 2, б) 2. назад 10. 1. назад |
11. а) , б) , в) , г) . назад 12. а) 5, б)2. назад 13. 890. назад 14. 24, назад 15. . назад 16. 2. назад 17. 5. назад 18. . назад 19. 4,5 назад 20. . назад 21. 0. назад |
Теория
Решебник
Примеры для самостоятельного решения
Тест
mognovse.ru
вычисления логарифмов — Колпаков Александр Николаевич
Комплект простейших заданий уровня А на вычисление логарифмов, который репетитор по математике регулярно использует на своих занятиях с большинством учеников. Материал предназначен для учащихся 10-11 классов и преподавателей в помощь при подготовке к ЕГЭ, а также для текущей школьной работы, направленной на отработку вычислительных навыков.
Вычислите:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
Напутствие репетитора по математике:
Вычисляя логарифмы, применяйте следующие формулы:
и
Для решения каждого задания представьте основание логарифма и число под его знаком в виде степени с одним и тем же основанием и вынесите полученные показатели из-под логарифма в его коэффициент. Логарифм с оставшимися равными числами будет равен единице.
Надо сказать, что в 80% задачниках по математике (школьных учебниках и пособиях по подготовке к ЕГЭ) крайне мало вычислительных упражнений на логарифмы, связанных со свойствами степеней. Если репетитор по математике использует стандартные пособия, то в его распоряжении оказывается обычно не более 5 — 6 примеров на логарифмы по каждому алгоритму их вычисления. Я уже давно не пользуюсь никакими задачниками и предлагаю ученикам свои материалы. В заданиях перемешиваю различные виды чисел: десятичные, обыкновенные, корни, дроби, степени с отрицательными показателями.
Вычислите логарифмы с использованием следующих формул:
и
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
Задачи на основное логарифмическое тождество:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
Задачи на формулу перехода к новому основанию
1)
2)
3)
4)
5)
6)
7)
8)
9)
Комментарий репетитора по математике относительно состава задач. Задания на логарифмы составлены по классическим законам методики и дидактики и имеют достаточное количеством однотипных упражнений. На первый взгляд может показаться, что все номера, взятые из одного раздела, как две капли воды похожи друг на друга. Отличие наблюдается только в числах. Но любой опытный репетитор по математике Вам скажет, что достаточно в одном из таких однотипных примеров поменять какое-нибудь целое число, например, на иррациональное или на дробное и перед ученик мгновенно растеряется. Поэтому я постарался обыграть все возможные числовые ситуации разнообразить номера десятичными и обыкновенными дробями, корнями разных степеней, комбинациями действий и коэффициентов, окружающих логарифмы.
В реальности я подаю задания ученику на отдельном листочке А4 с максимально плотным расположением примеров. Все на одном листе! Один из таких планов с представлен ниже:
Ученикам:
Задания можно использовать для самостоятельной подготовки к ЕГЭ по математике с целью научиться решать простейшие задачи на логарифмы из части В. Регулярно повторяйте с репетитором формулы, ибо без их уверенного запоминания Вам будет нелегко соориентироваться в вычислениях, в которых применяются сразу две или даже три формулы сразу.
Преподавателям:
Напишите свое мнение о качестве материалов. Понравилась ли Вам подборка упражнений?
ankolpakov.ru
Задания по теме «Логарифмы»

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Краткое описание документа:
ЛОГАРИФМЫ
Вычисления:
-
lg 15 – lg 3 = lg 5
-
lg 25 – lg 5 = lg 5
-
lg 100 – lg 10 – lg 10 = 1
-
lg10 5 + lg 2 = lg 10 = 1
-
log9 15 + log9 18 – log9 10 = log9 151×08 = log9 21700 = log9 27= log9 (9×3) = log9 9 + log9 3 = 1 +log9√9 = 1 + log9 9 1\2 = 1 + 1\2 = 3\2
-
log812 – log8 15 + log8 20 = log8 121×520 = log8 16 = log24 23 = 3\4
-
log2 log3 81 = log2 log3 34 = log2 4 = 2
-
log3 log2 8 = log3 log2 23 = log3 3 = 1
-
2 log 27 lg10 1000 = 2 log27 3 = lg27 32 = lg33 32 = 2\3
-
1\3 log9 log2 8 = 1\3 log9 3 = 1\3 log32 3 = 1\6
-
3 log2 log4 16 + log1\2 2 = 3 log2 2 + log 1\2 (1\2)-1 = 3 — 1 = 2
Общая информация
Номер материала: 532871

Похожие материалы
Оставьте свой комментарийinfourok.ru
Практический материал по теме: » Логарифмы».

МБОУ Алексеево-Лозовская СОШ
Практический материал
по математике
в 10 классе по теме:
«Логарифмы».
ПОДГОТОВИЛА:
учитель математики
высшей категории
МБОУ Ал.-Лозовская СОШ
Чертковского района
Ростовской области
Шконда Ирина Андреевна
2015 год
Содержание.
Задания для устной работы.
Задания для самостоятельной работы (обязательный уровень).
Вопросы теории. Примеры-алгоритмы.
Контрольная работа по теме: « Логарифмы». ( 4 варианта).
Задания для устной работы.
1
1
2
3
1
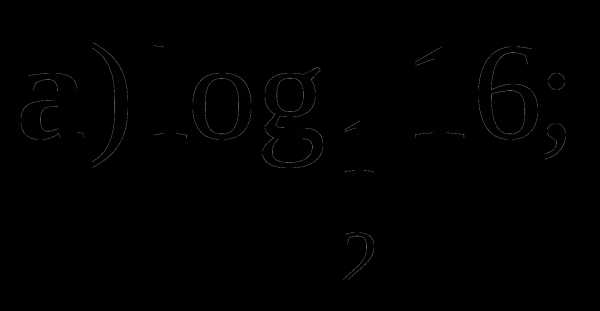
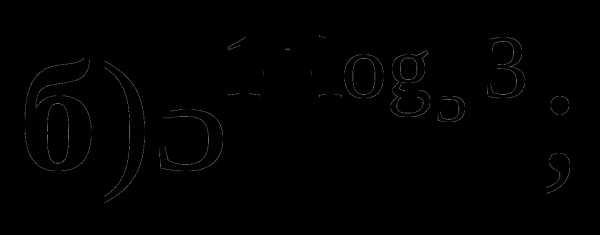
2
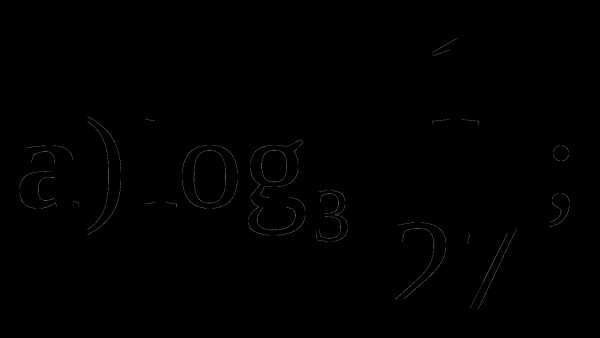
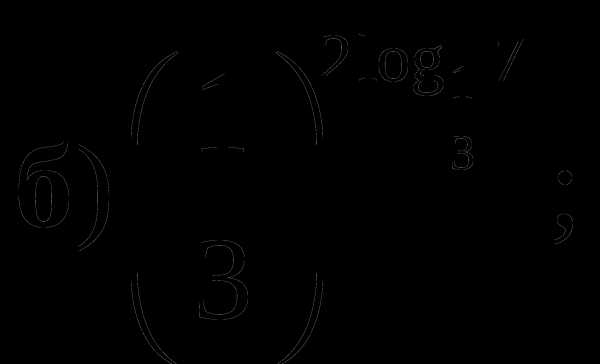
3
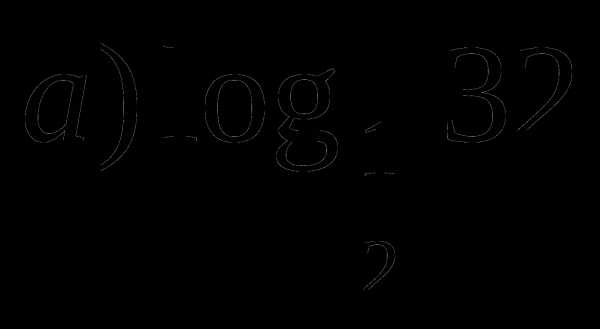
б)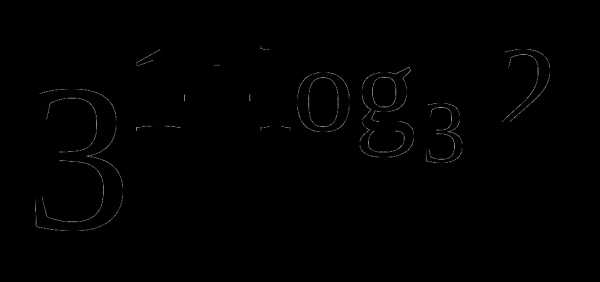
в)
4
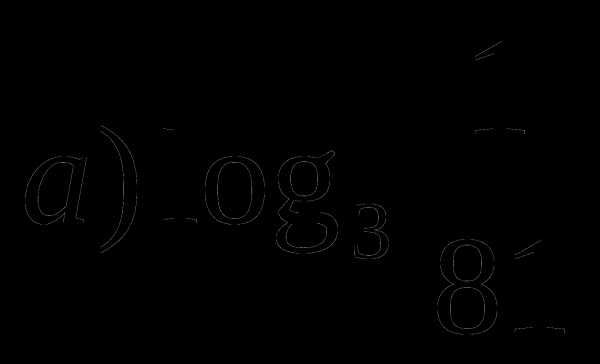
б)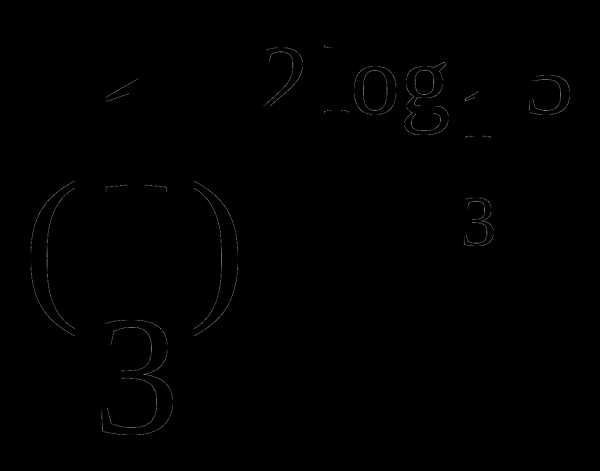
в)
5
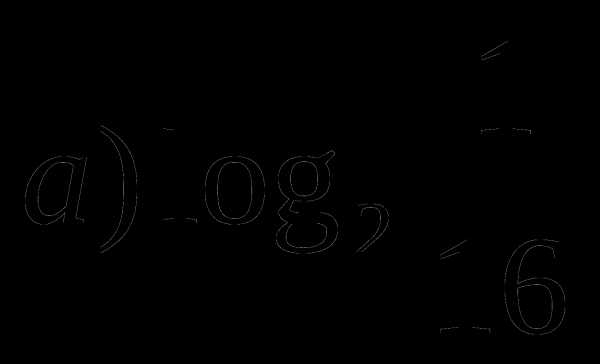
б)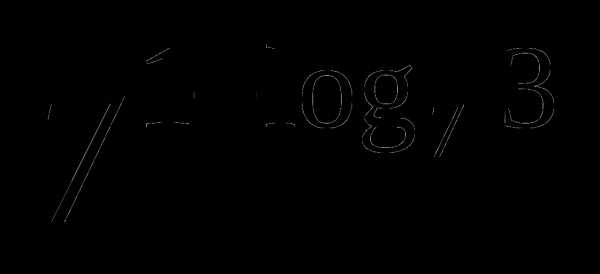
в)
6
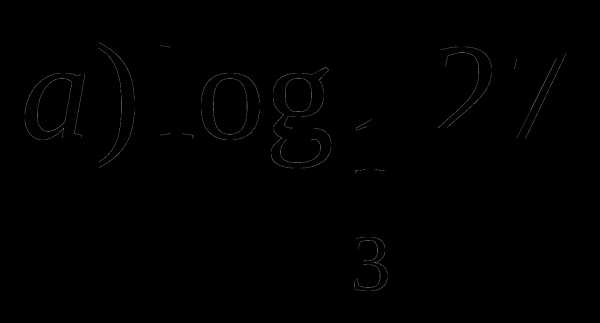
б)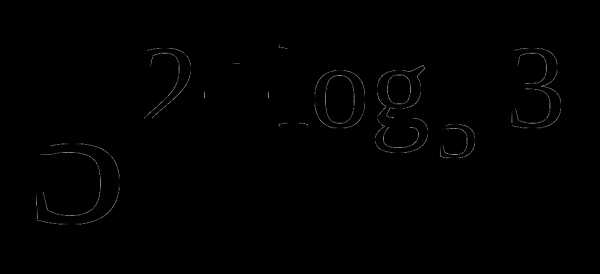
в)
№ варианта
Ответы
1


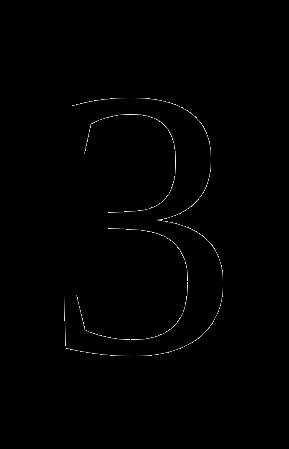
2
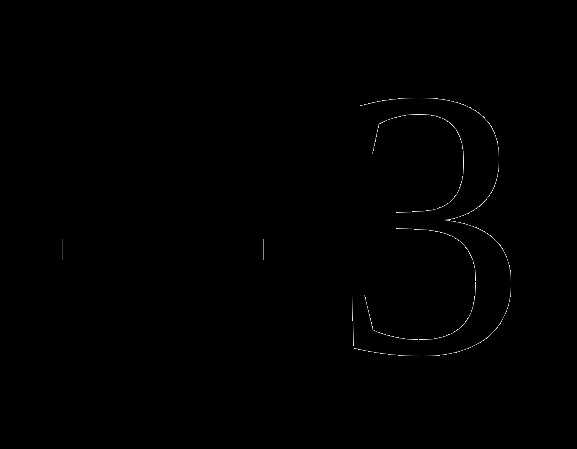
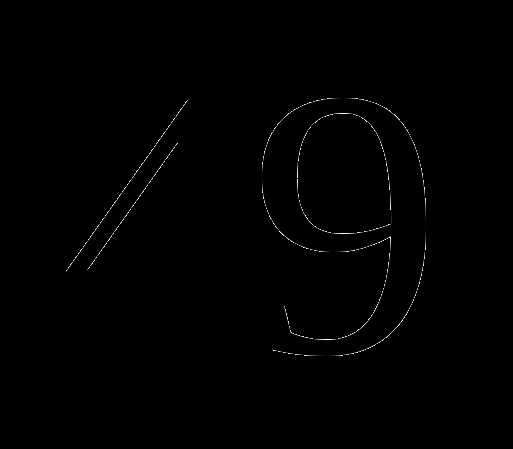

3
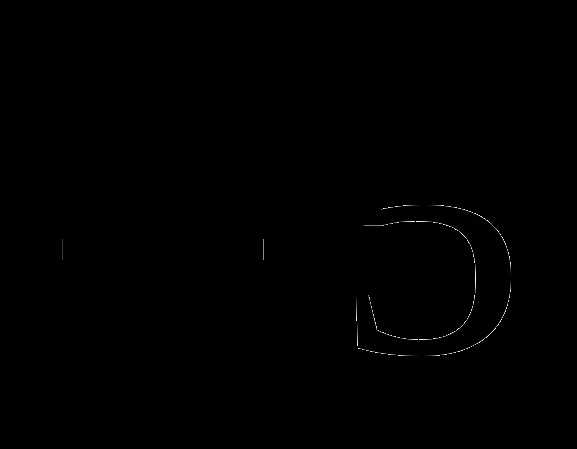
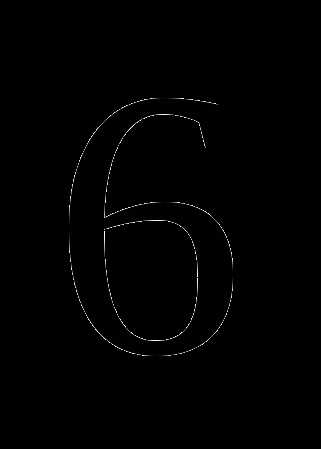

4

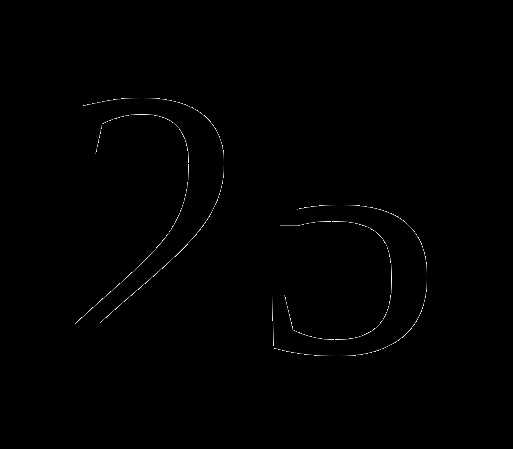
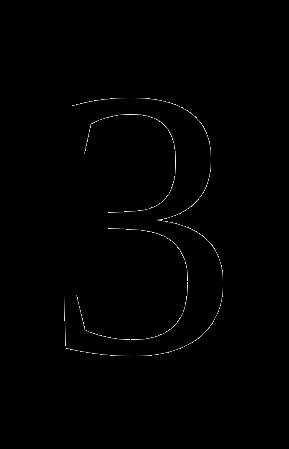
5


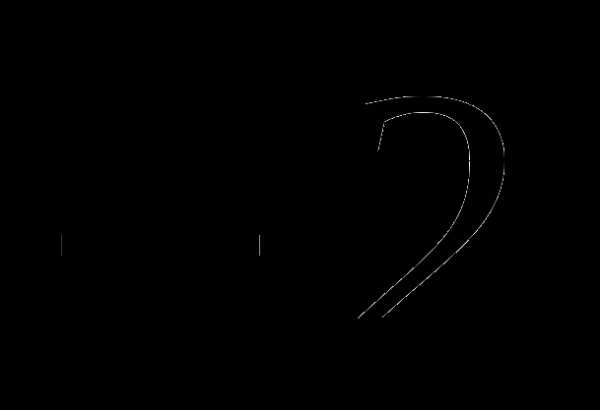
6
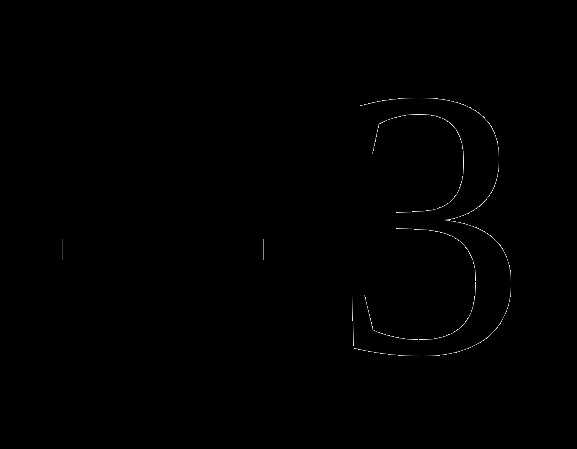
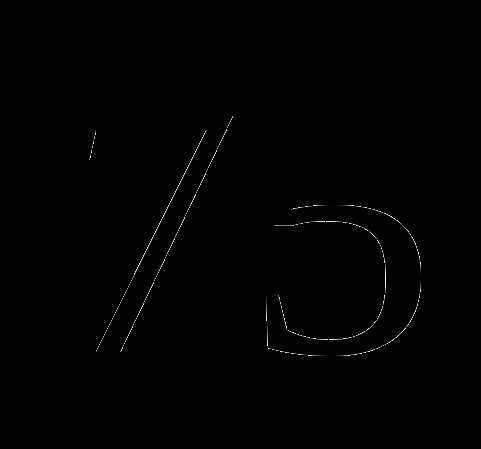
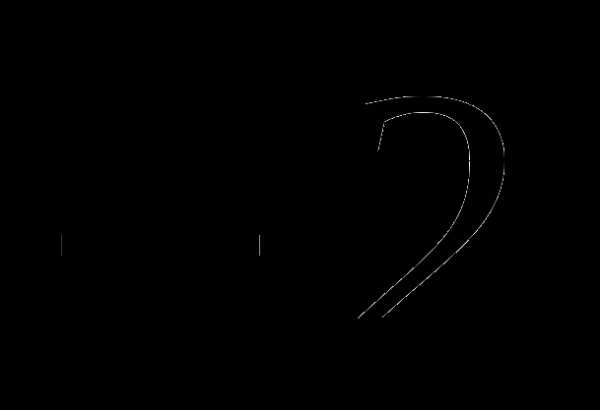
Задания для самостоятельной работы (обязательный уровень).
Вычислить:
Вычислить:
Сравнить.
Решить уравнение
Решить неравенство
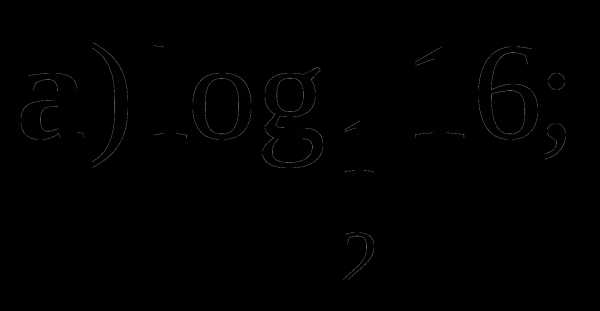
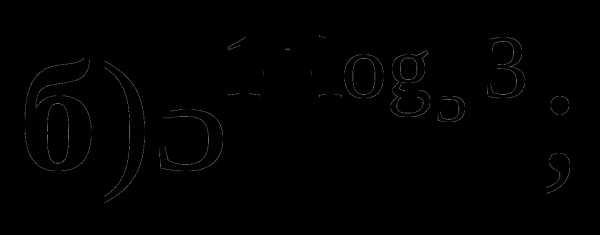
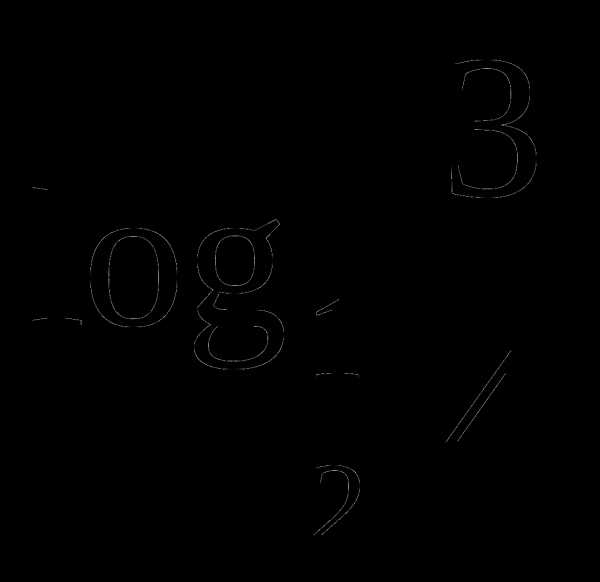 и
и 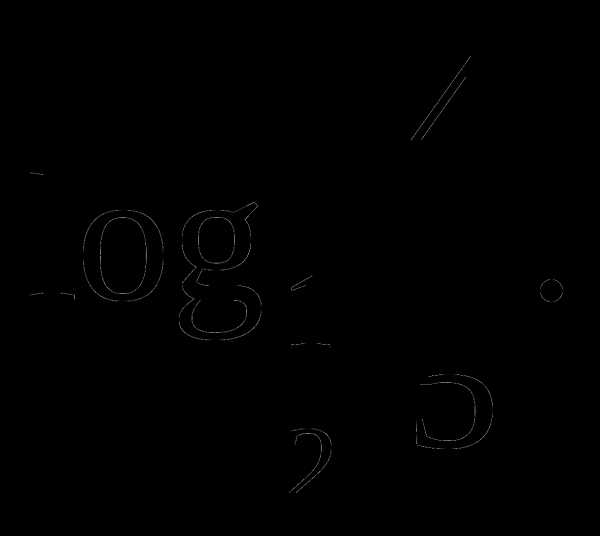
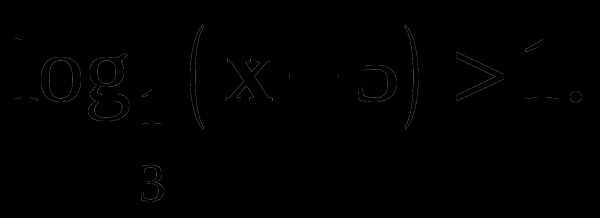
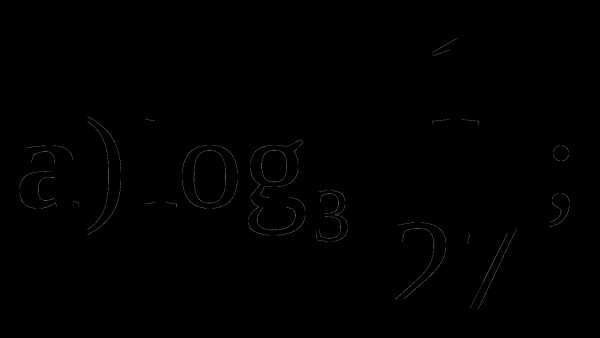
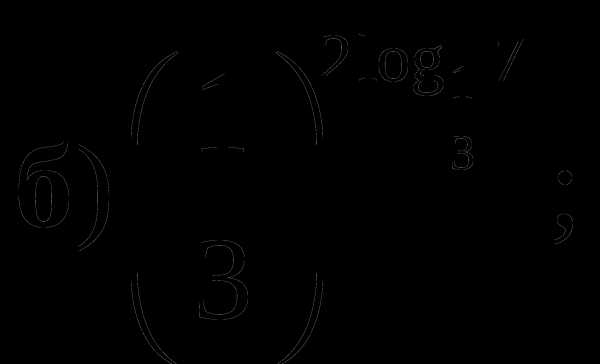
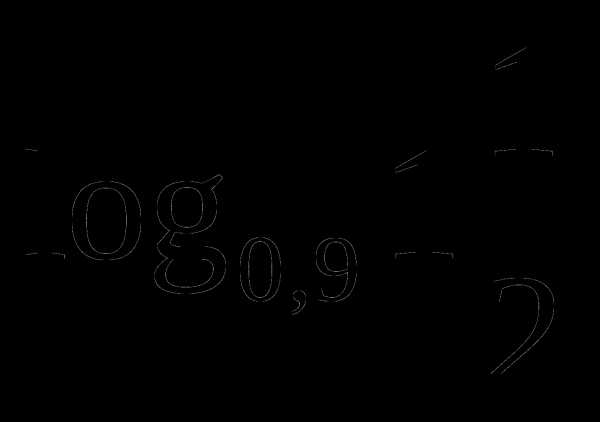
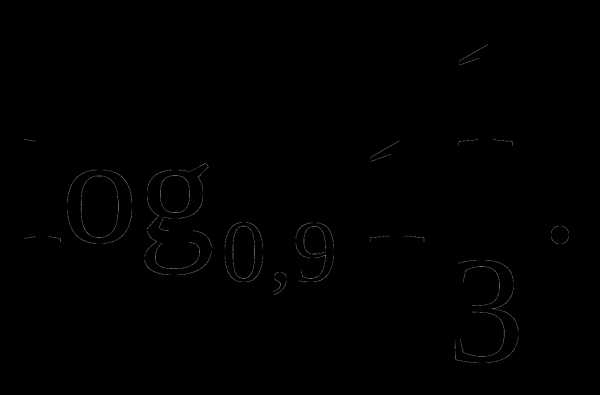
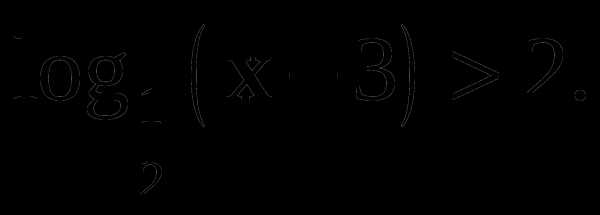
а)
б)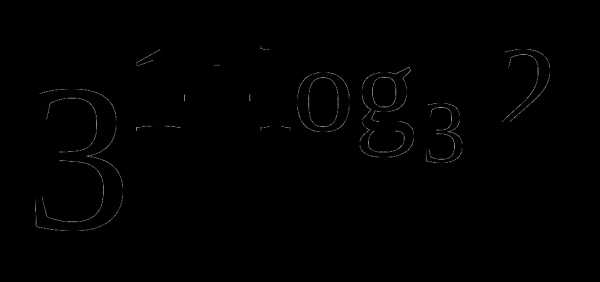
в)
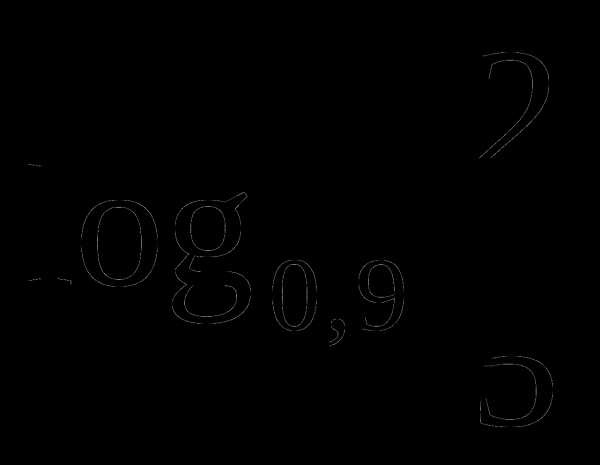

а)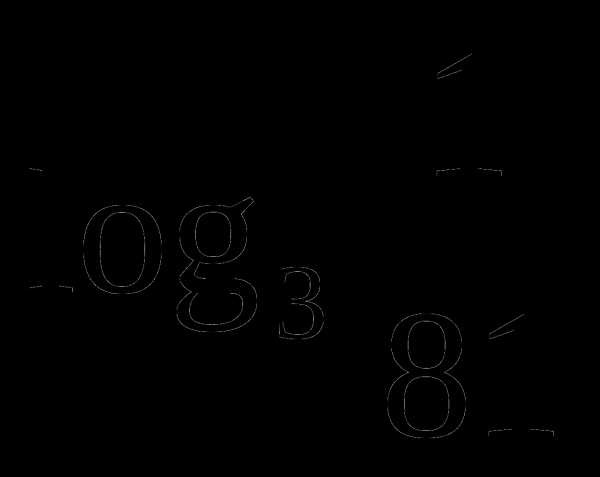
б)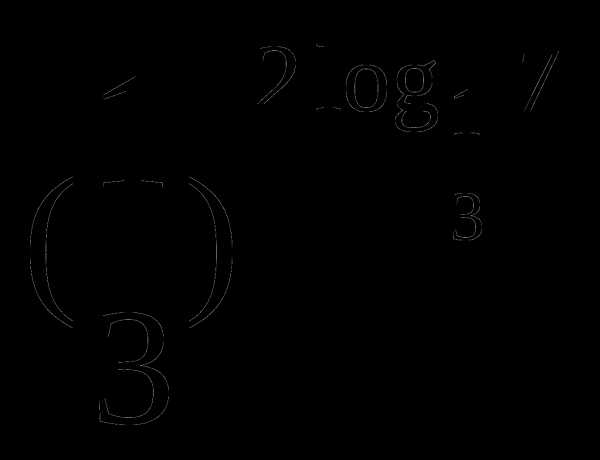
в)
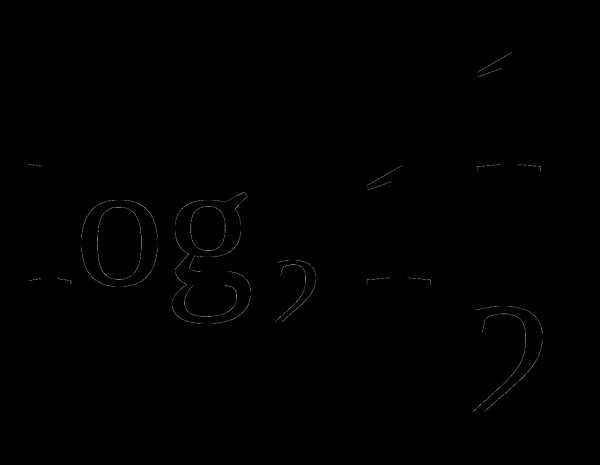

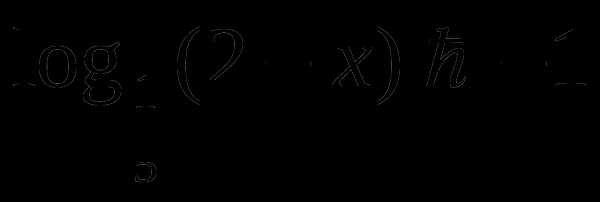
а)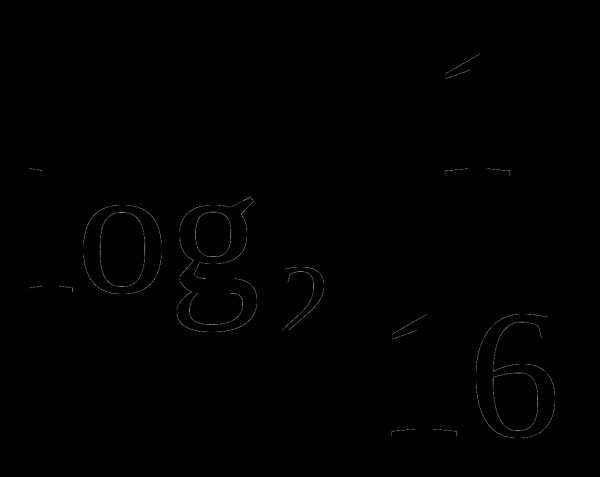
б)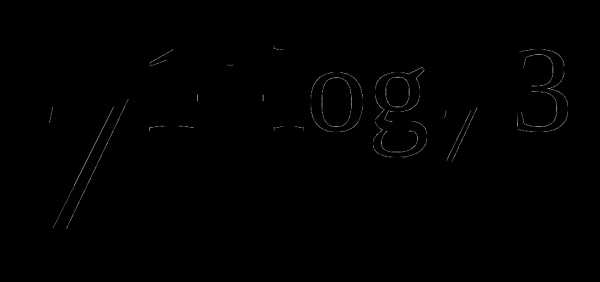
в)
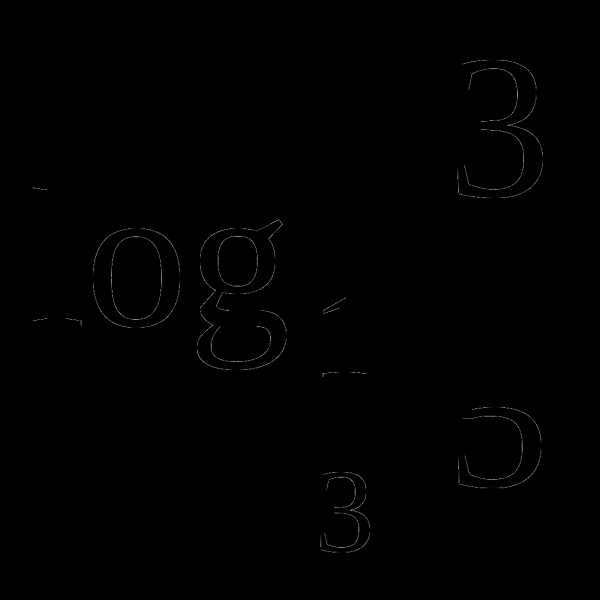
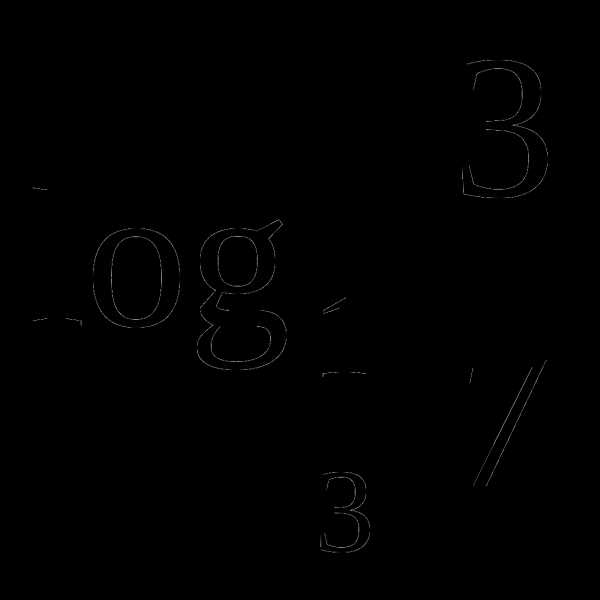
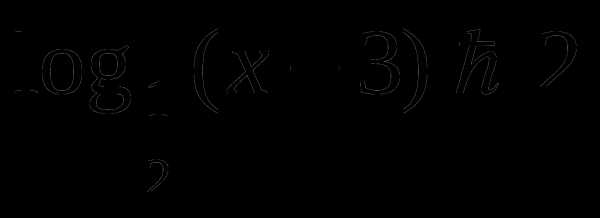
а)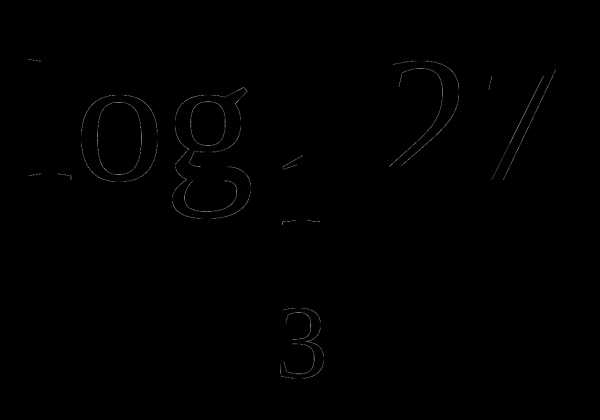
б)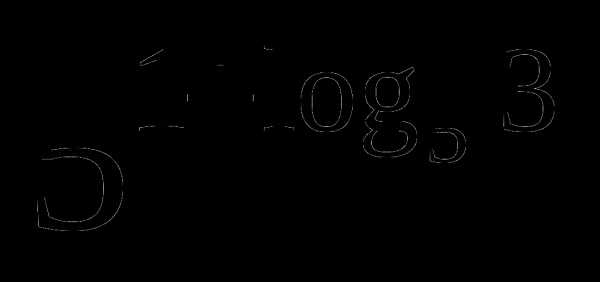
в)
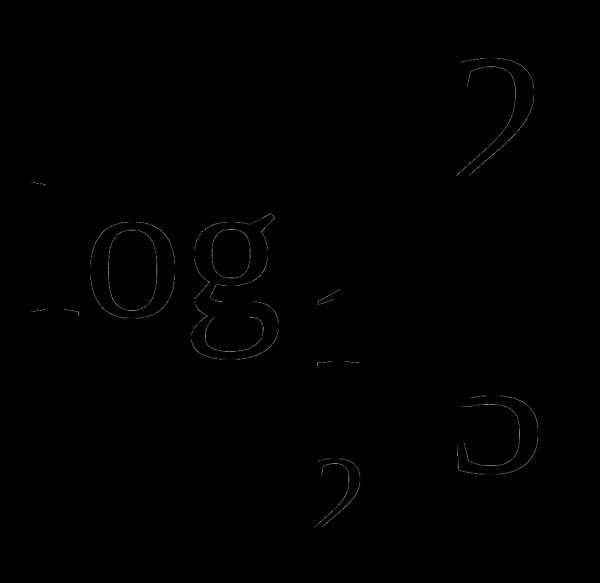
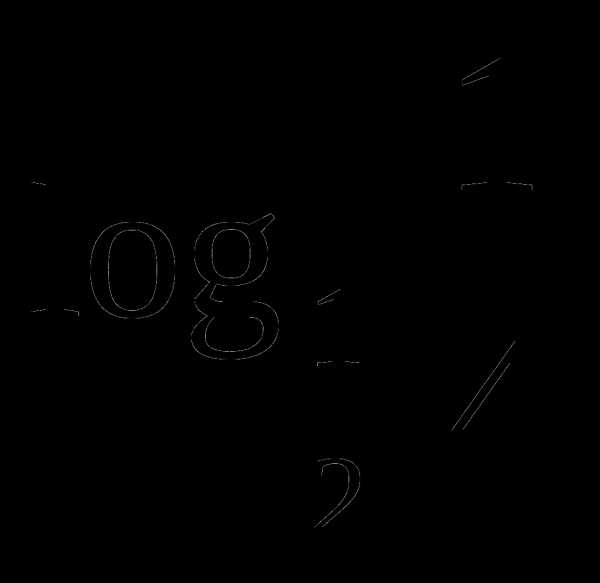
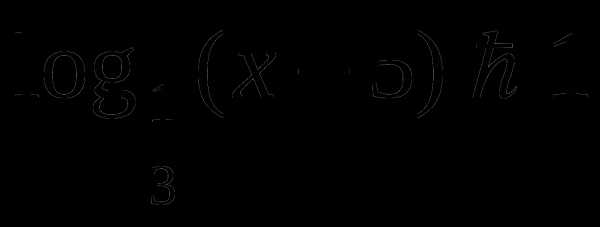
Вопросы теории. Примеры-алгоритмы.
№ п/п
Алгоритмы
1
Логарифмом числа  по основанию
по основанию  , где называется показатель степени, в которую нужно возвести число
, где называется показатель степени, в которую нужно возвести число  , чтобы получить число
, чтобы получить число  , то есть
, то есть
2
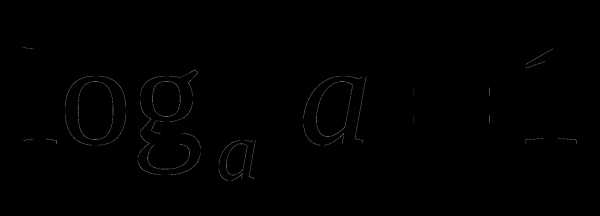 ;
; 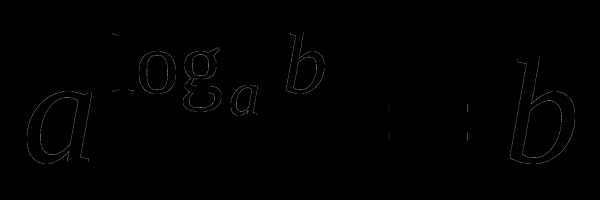 ;
; 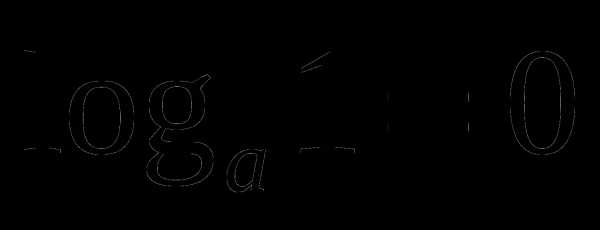
; 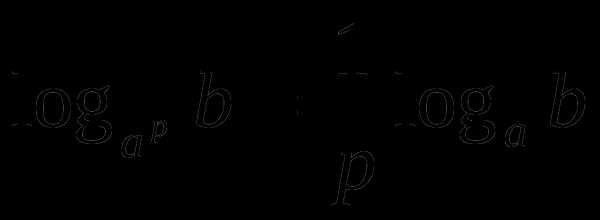
3
;
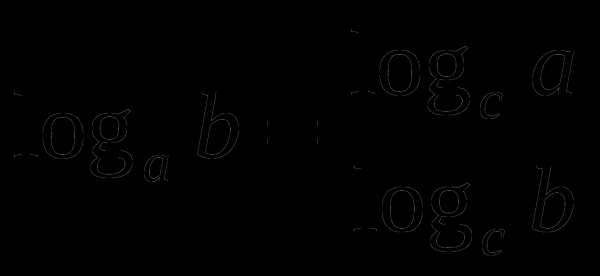 ;
; 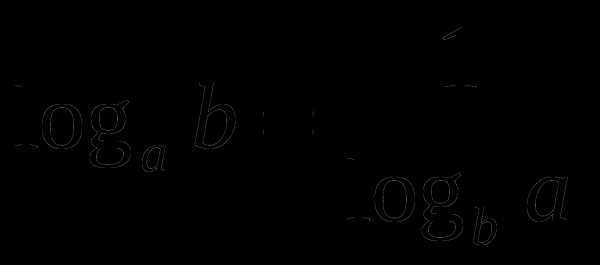
4
5
6
7
8,9
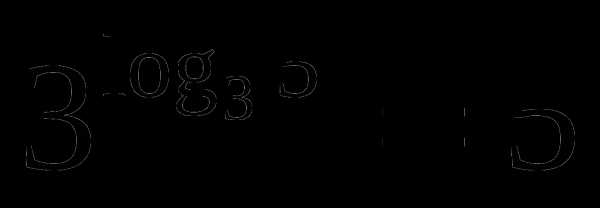 ;
;
10
11
Контрольная работа по теме: « Логарифмы».
Вариант 3
Вариант 4
Вычислить:1)
 ;2)
;2)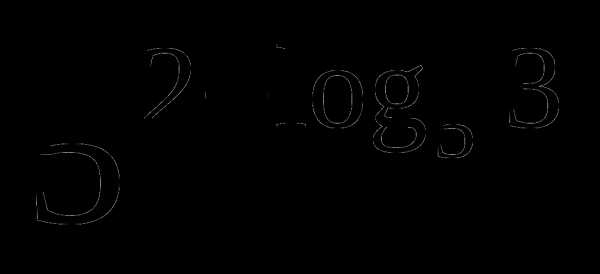 ;3)
;3)Сравнить числа:
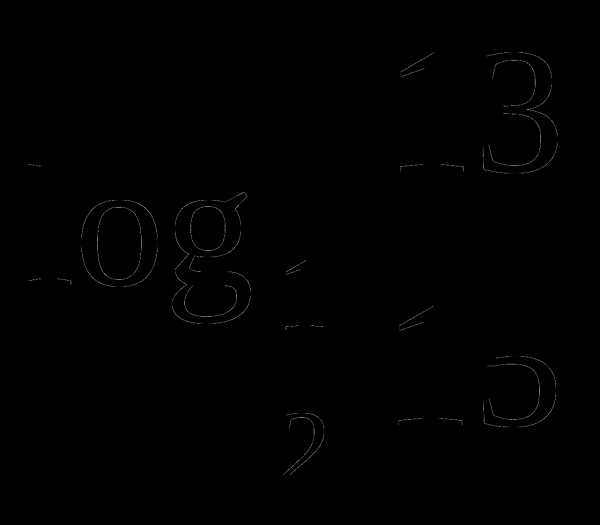 и
и 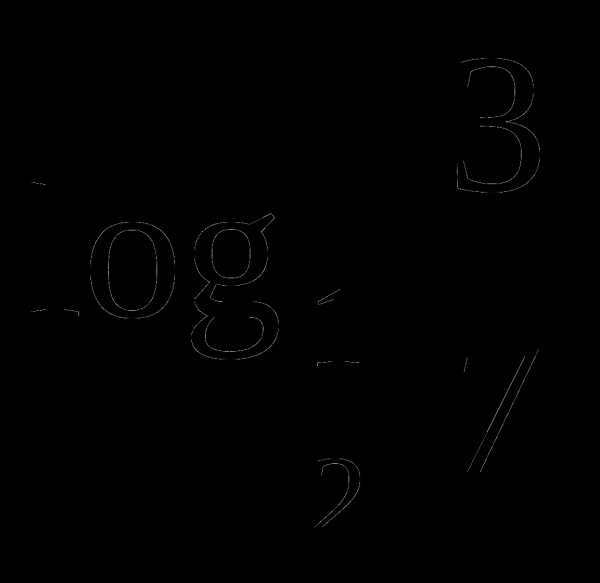 . .
. .Решить уравнение: .
Решите неравенство:
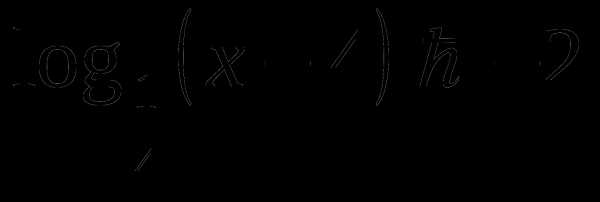 .
.Решить уравнение: .
Решить неравенство: .
(Дополнительно) Решить неравенство: .
Вычислить:1)
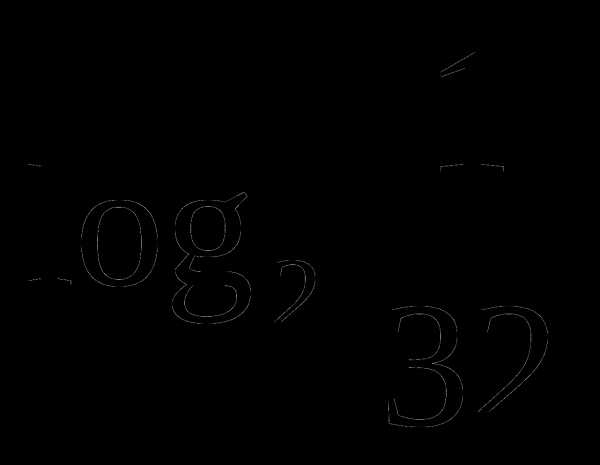 ;2)
;2)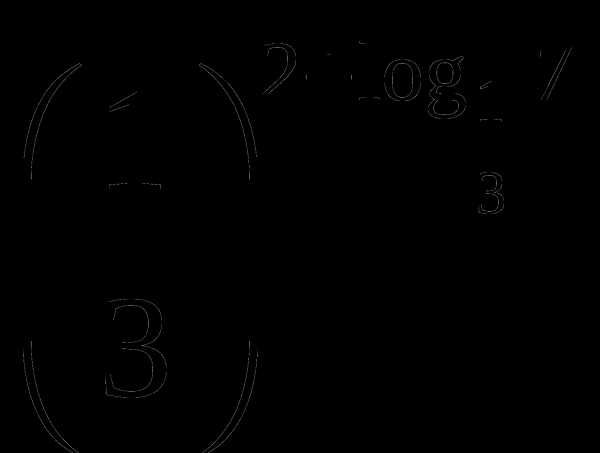 ;3) .
;3) .Сравнить числа:
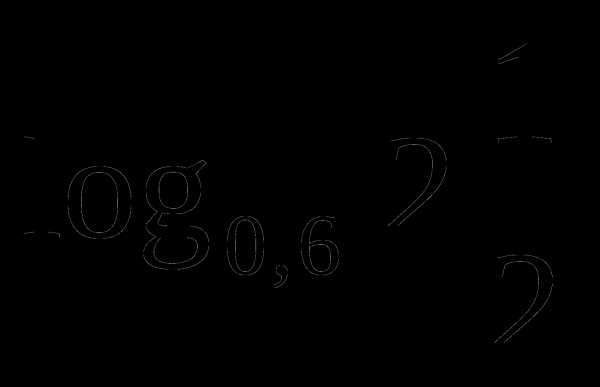 и
и 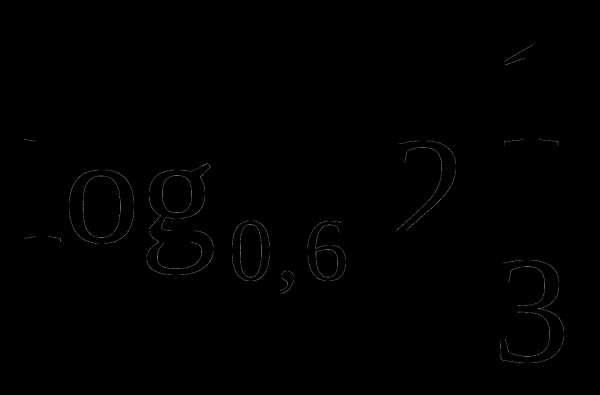 .
.Решить уравнение: .
Решите неравенство:
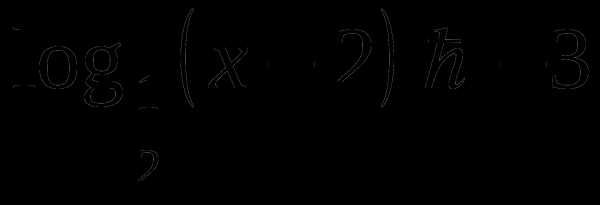 .
.Решить уравнение: .
Решить неравенство: .
(Дополнительно) Решить неравенство: .
infourok.ru
