решение задач с помощью алгебры логики.
Одним из мощных методов решения логических задач является решение с помощью законов алгебры логики.
Алгоритм решения логических задач с помощью алгебры логики: 1) внимательно изучить условие; 2) выделить простые высказывания и обозначить их латинскими буквами; 3) записать условие задачи на языке алгебры логики; 4) составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице; 5) упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых F = 1, проанализировать результаты.

Задача1 » Кто преступник»
Определить участника преступления, исходя из двух
1) «Если Иванов не участвовал или Петров участвовал,
то Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не
участвовал».
Рассмотрим решение этой несложной задачи двумя способами: с помощью таблиц истинности и с помощью алгебраических преобразований.
1 способ
Составим выражения:
I — «Иванов участвовал в преступлении»;
P — «Петров участвовал в преступлении»;
S — «Сидоров участвовал в преступлении»
.
Запишем посылки в виде формул:
¬I˅P→S и ¬I→¬S
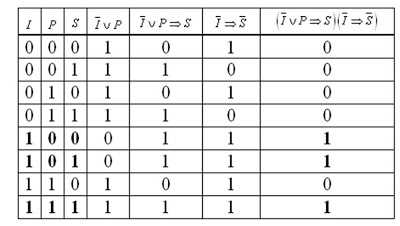
Из таблицы видно, что совершил преступление Иванов
Способ 2
Применим для решения этой же задачи преобразования с
помощью законов алгебры логики:
( ¬I˅P→S) &( ¬I→¬S)=(¬(¬I˅P)˅S) & (I˅¬S) =
= (I & ¬P ˅S) &(I ˅¬S) = I&¬P˅ I & S˅ I &¬P &¬S ˅0=
= I&¬P ˅ I & S =I & (¬P˅S)
Из последнего выражения видно, что выражение верно, если I=1, значит преступник — Иванов.
Задача 2 «Прогноз погоды»
Решим эту задачу средствами алгебры логики.
1. Выделим простые высказывания и запишем их через переменные
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь» 2. Запишем логические функции (сложные высказывания) через введенные переменные:
Если не будет ветра, то будет пасмурная погода без дождя:
A → B & C
Если будет дождь, то будет пасмурно и без ветра:
С → B & A
Если будет пасмурная погода, то будет дождь и не будет ветра
B → C &
в) Запишем произведение указанных функций:
F=(A→ B & C) & (C→B & A) & (B→ C & A)
Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
= (¬A v B & ¬C) & (¬C v B&A) & (¬B v C&A) =
= (¬A v B & ¬C) & (¬B v C&A) & (¬C v B&A) =
= (¬A &¬ B v B&¬C&¬B v ¬A&C&A v B&¬C&C&A) &
= ¬A & ¬B &(C v B&¬A) =A&¬B&C v¬ A&¬B&B&¬A = 3. Приравняем результат единице, т.е. наше выражение должно быть истинным:F = ¬A &¬ B & ¬C = 1 и проанализируем результат: Логическое произведение равно 1, если каждый множитель равен 1. ¬A = 1; ¬B = 1; ¬C = 1.значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Задача 3 «История с амфорой».
Алеша, Боря и Гриша нашли в земле сосуд.
Рассматривая удивительную находку, каждый высказал по два предположения.
Введем следующие обозначения:
«Это сосуд греческий» — G;«Это сосуд финикийский» — F;
«Сосуд изготовлен в III веке» — V3;
«Сосуд изготовлен в IV веке» — V4;
«Сосуд изготовлен в V веке» — V5. Формализуем задачу, записав в данных обозначениях условия задачи. Со слов учителя следует, что Алеша прав только в чем-то одном: или G = 1, или V5 = 1. Таким образом, тождественно истинным будет высказывание: G¬V5 v ¬GV5.=1 Аналогично, из слов Бори и учителя следует: F¬V3 v ¬FV3 = 1, а из слов Гриши и учителя: ¬G¬V4 v GV4 = 1. Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так: V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5 = 1, Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием: 1 = (G¬V5 v ¬GV5) & (F¬V3 v ¬FV3) & (¬G¬V4 v GV4) & (F¬G v ¬FG) & (V3¬V4¬V5 ˅ ¬V3V4¬V5
Задача 4 «Поход в кино».
Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма. Андрей сказал: «Я хочу посмотреть французский боевик». Маша сказала: «Я не хочу смотреть французскую комедию». Аня сказала: «Я хочу посмотреть американскую мелодраму».
в) «Нефранцузская комедия» ¬¬A&C˅¬A&¬C
3. Запишем произведение :(¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=1. Упростим формулу: (¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)= (¬A&B˅A&¬B) & (A&¬B˅¬ А&В)&( A&C˅¬A&¬C)= =(¬A&B& A&¬B˅ A&¬B& A&¬B˅¬A&B &¬А&В˅ A&¬B&¬A&B)&( A&C˅¬A&¬C)= =(A&¬B ˅¬A&B)&( A&C˅¬A&¬C)= A&¬B& A&C˅¬A&B& A&C˅ A&¬B&¬A&¬C˅¬A&B&¬A&¬C= = ¬A&B&¬C˅ A&¬B&C =1 6. Составим таблицу истинности для выражения:
¬A&B&¬C˅ A&¬B&C:
Ответ: ребята выбрали американский боевик.
А
inf61.blogspot.com
«Решение логических задач средствами алгебры логики»
Разделы: Информатика
Цель урока: познакомить учащихся с методом решения логических задач средствами алгебры логики.
Задачи урока:
образовательная – знакомство учащихся с понятием решения логических задач средствами алгебры логики;
развивающие – развитие логического мышления учащихся, памяти, внимания, а также интереса к разделу информатики — алгебре логики;
воспитательные – работа над повышением знаний основных понятий и законов алгебры логики, достижение сознательного усвоения материала учащимися с применением полученных знаний на практике.
Тип урока: проверка знаний и изучение нового материала.
Возраст учащихся: 10-11 класс.
Оборудование урока:
Требования к знаниям и умениям учащихся:
учащиеся должны знать:
- основные понятия и определения алгебры логики;
- основные законы алгебры логики;
учащиеся должны уметь:
- упрощать логические выражения;
- строить таблицы истинности;
- строить логические схемы по логическому выражению и наоборот;
- записывать составные высказывания в виде логических функций.
Системы оценивания: По ходу урока учащиеся решают задачи в индивидуальных карточках, которые будут оценены учителем по пятибалльной шкале.
План урока:
- Организационная часть.
- Повторение пройденных тем.
- Физкультминутка.
- Изучение нового материала.
- Закрепление изученного материала.
- Подведение итогов урока.
- Домашнее задание.
Ход урока
1. Организационная часть
- приветствие;
- проверка отсутствующих;
- постановка целей урока.
Учитель. Нам известны три способа решения логических задач:
1. с помощью рассуждений;
2. с помощью таблиц;
3. средствами алгебры логики.
Первым способом мы умеем решать логические задачи с первого класса. Вторым способом мы научились решать на предыдущих уроках. А вот третьим способом – средствами алгебры логики – научимся решать сегодня.
2. Повторение пройденных тем.
Учитель. Прежде чем перейти к изучению новой темы нам будет необходимо вспомнить некоторые пройденные темы, а именно, упрощение логических выражений с помощью законов алгебры логики и запись составных высказываний в виде логических выражений.
(Все задачи на повторение пройденной темы решаются учениками на доске с объяснением применяемых правил и законов).
Первое задание. Упростить логическое выражение. (Демонстрируется слайд).
_______________
F =
Решение (используются законы де Моргана, закон двойного отрицания, распределительный закон):
_______________ _____
F = = A v B & = (A v B) & (B v C) = B v (A & C)
Дальше ученики самостоятельно решают подобную задачу в своих индивидуальных карточках.
Второе задание. Проверить правильность упрощения построением таблиц истинности. (Демонстрируется слайд).
Учитель. Для проверки правильности упрощения мы строим таблицы истинности для исходного и упрощенного логического выражения. Если данные в последних столбцах таблиц истинности совпадают, значит мы правильно упростили логическое выражение.
Решение:
Таблица истинности для исходного логического выражения
А |
В |
C |
A V B |
B V C |
F |
||
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Таблица истинности для упрощенного логического выражения
А |
В |
C |
A & C |
B V А & C |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Из таблиц истинности видно, что упрощение верное.
Дальше ученики самостоятельно решают подобную задачу в своих индивидуальных карточках.
Третье задание. Построить логическую схему полученного упрощенного логического выражения. (Демонстрируется слайд).
(Продемонстрировать и объяснить работу схемы).
Дальше ученики самостоятельно решают подобную задачу в своих индивидуальных карточках.
Четвертое задание. Записать следующее высказывание в виде логического выражения: «Если я хорошо подготовлюсь по русскому языку, математике и физике, то я получу пятерки или четверки».
Решение: выделим в составном высказывании простые и обозначим их логическими переменными:
А – хорошо подготовлюсь по русскому языку;
В – хорошо подготовлюсь по математике;
С – хорошо подготовлюсь по физике;
D – получу пятерки;
Е – получу четверки.
Тогда составное высказывание будет записано следующим образом:
F = (A & B & C) —> (D V E)
Дальше ученики самостоятельно решают подобную задачу в своих индивидуальных карточках.
Пятое задание. Решить логическую задачу с помощью рассуждений. (Демонстрируется слайд).
Принцу необходимо спасти принцессу от злого колдуна. Принцесса находится в одной из комнат с надписями на дверях:
- В этой комнате сидит тигр.
- Принцесса находится в комнате 1.
- Тигр сидит в комнате 2.
Колдун сообщил принцу, что одно из этих утверждений является истинным. И если принц с первого раза отгадает, где находится принцесса, то колдун освободит ее.
Учитель. Сейчас мы узнаем, есть ли среди нас принцы. Кто поможет принцессе? Если кто-то готов выручить ее, то он должен щелкнуть мышкой по двери и дверь откроется. (Демонстрируется слайд)
III. Физкультминутка. Разгадывание кроссворда за компьютером.
(Учащиеся встают, разминаются, садятся за компьютеры и решают кроссворд, подготовленный в MS Excel. Оценку, выставленную компьютером, ученики заносят в карточку).
IV. Изучение нового материала. (Демонстрируются слайды)
Учитель. Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее:
Если не будет ветра, то будет пасмурная погода без дождя.
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра? (Ответы учеников)
Решим эту задачу средствами алгебры логики.
Решение:
а) Выделим простые высказывания и запишем их через переменные:
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь»
б) Запишем логические функции (сложные высказывания) через введенные переменные:
1. Если не будет ветра, то будет пасмурная погода без дождя:
A —> B & C
2. Если будет дождь, то будет пасмурно и без ветра:
С —> B & A
3. Если будет пасмурная погода, то будет дождь и не будет ветра
B —> C & A
в) Запишем произведение указанных функций:
F=(A —> B & C) & (C —>B & A) & (B —> C & A)
г) Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
F=(A —> B & C) & (C —>B & A) & (B —> C & A)
= (A v B & C) & (C v B&A) & (B v C&A) =
= (A v B & C) & (B v C&A) & (C v B&A) =
= (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)=
= A & B &(C v B&A) =A&B&C v A&B&B&A =
= A&B&C
д) Приравняем результат единице, т.е. наше выражение должно быть истинным:
F = A & B & C = 1
е) Проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1.
Поэтому:
A = 1; B = 1; C = 1;
Значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Учитель. Ребята, вы познакомились с новым методом решения логических задач. Как вам кажется, какой из трех способов решения логических задач является самым точным? (Ответы учеников)
V. Закрепление изученного материала.
Учитель. Запишем условие еще одной интересной задачи из жизни, которую мы начнем решать в классе, а закончим дома самостоятельно.
Задача. Джеку, Питеру и Майку предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Джек показал, что преступники скрылись на синем Мерседесе, Питер сказал, что это был черный Джип, а Майк утверждал, что это был Форд Мустанг и ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо марку машины, либо только ее цвет. Какого цвета и какой марки была машина?
Учитель. Можно ли раскрыть это преступление? Имея в виду, что у нас каждое преступление раскрывается, и, учитывая, что следователи изучали в школе алгебру логики, с уверенностью можно сказать, что преступники будут наказаны. Кто из вас поможет следствию и правильно вычислит цвет и марку машины, узнаем на следующем уроке, а сейчас вместе напишем логическую функцию.(Учитель помогает детям записать правильно логическое выражение.)
Учитель. Какая связь между алгеброй логики и компьютером? Как используются элементы алгебры логики в вычислительной технике? Что такое триггер и сумматор?
(Ответом на это будет выступление ученика с показом слайдов, подготовленных им заранее).
VI.Подведение итогов урока.
Учитель. Сегодня мы научились решать логические задачи средствами алгебры логики. Мы с вами выяснили, что самым точным способом решения логических задач является изученный нами сегодня способ. Но более простым способом вам показался решение логических задач с помощью таблиц. К сожалению, не все логические задачи можно решить с помощью таблиц, поэтому приходится решать их средствами алгебры логики.
(Поставить оценки наиболее активным ученикам. Собрать индивидуальные карточки для проверки.)
VII. Домашнее задание.
Учитель. Попробуйте решить домашнее задание – задачу об ограблении банка всеми тремя известными вам способами и сравнить результаты.
xn--i1abbnckbmcl9fb.xn--p1ai
Логические задачи очень разнообразны. Способов их решения тоже немало. Но наи-большее распространение получили следующие три способа решения логических задач: Обычно используется следующая схема решения: ЗАДАЧА 1.
Решение: Введём логические переменные: ЗАДАЧА 2.
Необходимо рассмотреть четыре возможности. Место штурма Кто пленник Ответ Надо сформулировать вопрос, ответ на который в первых двух случаях будет «да», и «нет» в двух остальных. Пусть вопрос будет таким: «Верно ли, что штурм назначен на юж-ные ворота и ты лжец, или неправда, что штурм назначен на южные ворота и ты рыцарь?» ЗАДАЧА 3.
Решение: Максимальное количество дней и соответствующее расписание можно най-ти прямым перебором. При четырёх переменных надо рассмотреть 16 логических возможно-стей. Однако более рационально построить составное высказывание, истинное для заданных условий, а затем преобразовать соответствующую ему формулу к СДНФ. Введём логические переменные: ЗАДАЧА 4.
Решение: Если выбрать какую – то букву из заданного множества и спросить, являет-ся ли она задуманной, то в общем случае потребуется 7 вопросов для установления искомой буквы. Чтобы была возможность определять любую букву при помощи трёх вопросов, надо разбить множество на три подмножества. Возьмём три такие подмножества: {B, D, F, H}, {E, F, G, H}, {C, D, G, H}. ЗАДАЧА 5.
Решение: Введём обозначения для логических высказываний: ЗАДАЧА 6.
Решение: Рассмотрим простые высказывания:
ЗАДАЧА 7.
Решение: Обозначим через P1, P2, P3, высказывания, состоящие в том, что, соответ-ственно, первый, второй, третий школьник изучали логику. Из условия задачи следует ис-тинность высказывания: ЗАДАЧА 8.
Решение: Рассмотрим простые высказывания: ЗАДАЧА 9.
Решение: Рассмотрим простые высказывания: Задача Эйнштейна. Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по одному человеку отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных.
Решение: ШАГ 1
ШАГ 2
ШАГ 3
ШАГ 4
Тогда шведу, у которого собака (2), остаётся пятый дом. По условию (10), кошка живет в первом или в третьем доме, но в третьем доме — птицы, а значит, кошка в первом доме. Следовательно, рыбку держит немец.
Конечно, это решение предполагает, что недостающие в условиях задачи животное и есть искомая рыбка. Кроме того, предполагается, что первый дом — слева. Тем не менее, прямо в условиях это нигде не указано. Многие поэтому утверждают, что единственный правильный ответ — «в задаче не хватает данных», так как мы не можем быть уверены в том, что рыбки, например, вообще живут хотя бы в одном из этих домов. Однако, этим суждением зачастую «покрывают» свою неудачу в решении задачи.
|
www.openclass.ru
| Задачи по теме «Алгебра логики»
Задача 2. Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предложения:
Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино? Ответ. Т.к. два высказывания должны быть «истина», а одно «ложь», то правильный ответ следующий: Аня и Сергей не пойдут в кино, а пойдет Вика. Задача 2. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения: Задача 3. В нарушении правил обмена валюты подозревают четыре работника банка – А, В, С и D. Известно, что:
Кто из подозреваемых нарушил правила обмена валюты? Задача 4. На вопрос, какая завтра будет погода, синоптик ответил:
Подумав немного, синоптик уточнил, что его три высказывания можно лаконично записать в виде одного составного высказывания. Сформулируйте его, решив задачу с помощью логических операций. Задача 5. Определите, кто из подозреваемых участвовал в преступлении, если известно:
Задача 6. Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:
Известно, что в каждом ответе только одно утверждение истинно. Как распределились места? |
infourok.ru
Методы решения логических задач
Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.
Формальный способ решения логических задач
Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций.
Составить единое логическое выражение для всех требований задачи.
Используя законы алгебры логики, попытаться либо упростить полученное выражение и вычислить все его значения, либо построить таблицу истинности для рассматриваемого выражения, либо доказать истинность (ложность) некоторых утверждений методом рассуждений.
Выбрать решение — набор значений простых высказываний, при котором построенное логическое выражение является истинным.
Проверить, удовлетворяет ли полученное решение условию задачи.
Рассмотрим, как можно использовать эти способы для решения задач.
Решение логических задач средствами алгебры логики
Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Решение. Введём обозначения:
Р1 – первый учащийся изучал логику;
Р2 – второй учащийся изучал логику;
Р3 – третий учащийся изучал логику.
Из условия задачи следует истинность высказывания . Воспользуемся соотношением (20) и упростим исходное высказывание:
.
Высказывание
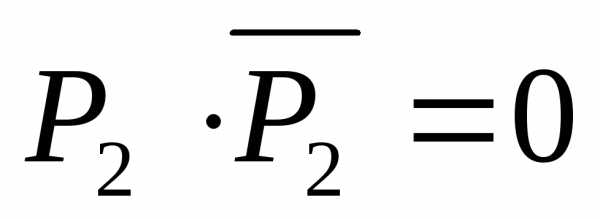 (согласно
(11)), а, следовательно, ложно и высказывание
(согласно
(11)), а, следовательно, ложно и высказывание
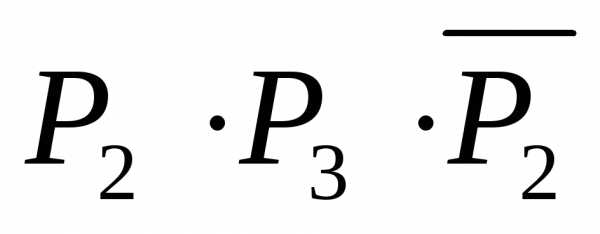 .
Поэтому должно быть истинным высказывание
.
Поэтому должно быть истинным высказывание
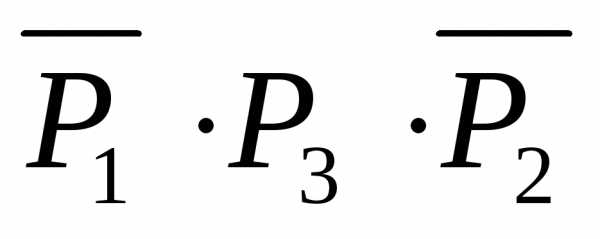 .
.
Ответ. Логику изучал третий учащийся, а первый и второй не изучали.
Задача «Прогноз». Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение. Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Джон:
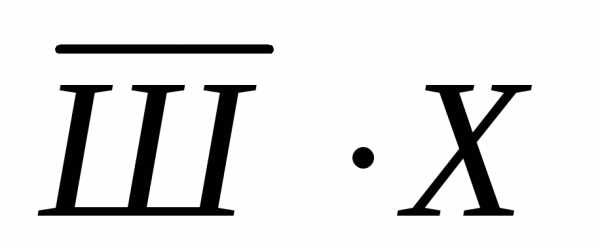 ,Ник:
,Ник:
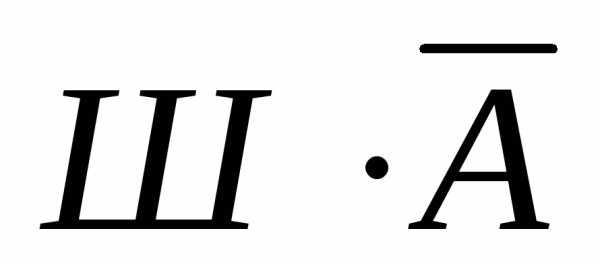 ,
Питер:
,
Питер:
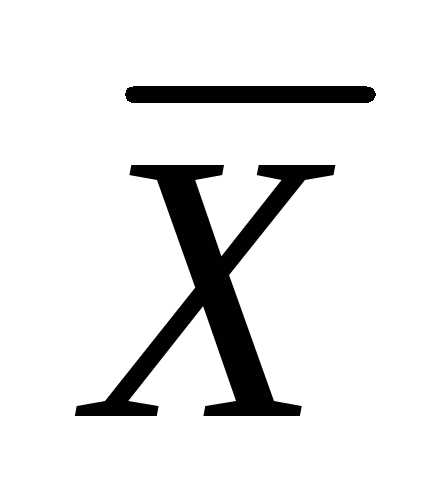 .
.
Учитывая то, что предположения лишь двух друзей подтвердились, а предположения третьего неверны, запишем все возможные комбинации истинности двух из трёх высказываний. Тогда истинное высказывание будет иметь вид:
=1.
Упростим это выражение. Используя (11), установим, что первые два слагаемые тождественно-ложные. Тогда, с учётом формул де Моргана для третьего слагаемого:
Произведение будет истинным только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
studfiles.net
Применение инструмента алгебры логики при решении логических задач
История с амфорой
Антон, Борис и Григорий нашли в земле сосуд, о котором каждый высказал по два предположения:
-
Антон: «Сосуд греческий и изготовлен в V столетии»;
-
Борис: «Сосуд финикийский и изготовлен в III столетии»;
-
Григорий: «Сосуд не греческий и изготовлен в IV столетии».
Специалист сказал ученикам, что каждый из них не ошибся только в одном из двух предположений. Определить место и столетие изготовления сосуда.
Решение:
Введем следующие обозначения:
$G$ — «Сосуд греческий»;
$F$ — «Сосуд финикийский»;
$S_3$ — «Сосуд изготовлен в $III$ столетии»;
$S_4$ — «Сосуд изготовлен в $IV$ столетии»;
$S_5$ — «Сосуд изготовлен в $V$ столетии».
Запишем условие задачи с помощью обозначений:
Антон прав только в одном предположении: $G = 1$ или $S_5 = 1$. Тогда $G\overline{S_5}\vee \overline{G}S_5=1$.
Аналогично для слов Бориса: $F\overline{S_3}\vee \overline{F}S_3=1$.
Для слов Григория: $\overline{G}\overline{S_4}\vee GS_4=1$.
Т.к. сосуд может быть изготовлен только в одном из столетий и только в одной из стран, запишем условия:
\[S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5=1,\] \[F\overline{G}\vee \overline{F}G=1.\]Применим операцию логического умножения к полученным тождественно истинным высказываниям, результат которого также должен быть тождественно истинным:
\[\left(G\overline{S_5}\vee \overline{G}S_5\right)\wedge \left(F\overline{S_3}\vee \overline{F}S_3\right)\wedge \left(\overline{G}\overline{S_4}\vee GS_4\right)\wedge \left(F\overline{G}\vee \overline{F}G\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Перемножим первую на третью скобку и вторую на четвертую:
\[=\left(G\overline{S_5}\overline{G}\overline{S_4}\vee \overline{G}S_5\overline{G}\overline{S_4}\vee G\overline{S_5}GS_4\vee \overline{G}S_5GS_4\right)\wedge \] \[\wedge \left(F\overline{S_3}F\overline{G}\vee \overline{F}S_3F\overline{G}\vee F\overline{S_3}\overline{F}G\vee \overline{F}S_3\overline{F}G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Т.к. $G\overline{G}=0$, $GG=G$, $\overline{G}\overline{G}=\overline{G}$, упростим выражения:
\[=\left(\overline{G}S_5\overline{S_4}\vee G\overline{S_5}S_4\right)\wedge \left(F\overline{S_3}\overline{G}\vee \overline{F}S_3G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Перемножим первые две скобки и упростим выражение:
\[=\left(\overline{G}S_5\overline{S_4}\overline{F}S_3G\vee G\overline{S_5}S_4\overline{F}S_3G\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\overline{G}\vee G\overline{S_5}S_4F\overline{S_3}\overline{G}\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\overline{G}S_5\overline{S_4}F\overline{S_3};\]$\overline{G}S_5\overline{S_4}F\overline{S_3}=1$, что возможно только в случае:
\[\overline{G}=1, S_5=1, \overline{S_4}=1, F=1, \overline{S_3}=1.\]Ответ: сосуд финикийский и изготовлен в $V$ столетии.
spravochnick.ru
Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:- изучается условие задачи;
- вводится система обозначений для логических высказываний;
- конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
- определяются значения истинности этой логической формулы;
- из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Три свидетеля дорожного происшествия сообщили сведения о скрывшемся нарушителе. Боб утверждает, что тот был на красном «Рено», Джон сказал, что нарушитель уехал на синей «Тойоте», а Сэм показал, что машина была точно не красная, и по всей видимости, это был «Форд».
Когда удалось отыскать машину, выяснилось, что каждый из свидетелей точно определил только один из параметров автомобиля. А в другом ошибся, какая и какого цвета была машина у нарушителя?
Ответ записать в виде двух слов, разделенных пробелом: МАРКА, ЦВЕТ.
Решение.
Обозначим высказывания:
A = «машина красного цвета»;Согласно условию:
B = «машина была «Рено»;
C = «машина синего цвета»;
D = «машина была «Тойота»;
E = «машина была «Форд».
из показаний Боба следует, что A \/ B истинно;Следовательно, истинна конъюнкция (A \/ B) /\ (C \/ D) /\ (¬A \/ E) = 1
из показаний Джона следует, что C \/ D истинно;
из показаний Сэма следует, что ¬A \/ E истинно.
Раскрывая скобки, получаем:
(A \/ B) /\ (C \/ D) /\ (¬A \/ E) = (A /\ C \/ A /\ D \/ B /\ C \/ B /\ D) /\ ( ¬A \/ E) =
A /\ C /\ ¬A \/ A /\ D /\ ¬A \/ B /\ C /\ ¬A \/ B /\ D /\ ¬A \/ A /\ C /\ E \/ A /\ D /\ E \/ B /\ C /\ E \/ B /\ D /\ E = 1.
Из полученных восьми слагаемых семь (согласно условию) являются ложными. Остается единственное истинное слагаемое:
B /\ C /\ ¬A = 1.
Значит, нарушитель скрылся на автомобиле «Рено» синего цвета.
Ответ: РЕНО, СИНИЙ.
Пример.
Трое друзей, болельщиков автогонок
«Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об
Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих
друзей подтвердилось, а оба предположения третьего из друзей оказались неверны.
Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:Ш — победит Шумахер;
Х — победит Хилл;
А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание истинно только при Ш=1, А=0, Х=0.
Ответ.
Победителем этапа гонок стал Шумахер.
Задача для самопроверки:
На перемене в кабинете биологии 8 ребят баловались и разбили дорогой микроскоп. Их всех вызвали к директору и выслушали:
Ира: Это Антон разбил.
Наташа: Нет, Антон не бил!
Сергей: А я тоже знаю, что это Наташа разбила!
Антон: Нет, ни Наташа, ни Сергей этого не делали!
Оля: А я видела, что разбил Сергей!
Максим: Это кто-то чужой!
Костя: Это либо Наташа, либо Сергей – больше некому!
Кто разбил микроскоп, если известно, что из этих восьми высказываний истинны только два?
Ответ записать в виде первой буквы имени.
logikinformatik.blogspot.com
