Вводная контрольная работа по алгебре в 10 классе
Предмет: алгебра и начала анализа Класс 10 «Б» Дата __________
Урок № 6
Тема урока: Вводная контрольная работа
Цели урока: 1) проверить знания учащихся на начало учебного года
2) развитие, памяти, внимания, самостоятельности
3) воспитание трудолюбия и аккуратности.
Тип урока: Комплексное применение ЗУН
Оборудование: тетрадь для контрольных работ
Домашнее задание:
Содержание
Учитель
Ученики
Время
I Организационный момент
Психологический настрой
Слушают
1
II Постановка цели урока
Сообщает
Слушают, запоминают
1
III Контрольная работа
Поясняет задания
2
Контролирует
Решают самостоятельно на местах
40
IV Подведение итогов урока
Собирает тетради
Сдают тетради
1
Контрольная работа
Вариант 2.
№1. Упростить выражение:
(2х+1 + ) : (2х — )
№2. Решить неравенство, используя метод интервалов.
> 0
№3. Докажите тождество:
= 2
№4. В арифметической прогрессии d= -0,4, n= 12, = 2,4.
Найти , .
№5. У треугольника со сторонами 16 см и 8 см проведены высоты к этим сторонам. Высота, проведенная к стороне 16 см, равна 6 см. Чему равна высота, проведенная к стороне 8 см?
Вариант 1.
№1. Упростить выражение:
( — ) : (p – q + )
№2. Решить неравенство, используя метод интервалов.
0
№3. Докажите тождество:
=
№4. В арифметической прогрессии d= 5, = -35, = 250.
Найти , n.
№5. Стороны параллелограмма 6 см и 8 см, а его площадь 96 см2 . Чему равна большая сторона параллелограмма?
infourok.ru
| Решение. Во время распродажи шампунь станет стоить 160 − 0,25 160 = 120 рублей. Разделим 1000 на 120:
. Значит, можно будет купить 8 флаконов шампуня.
Ответ: 8. Ответ: 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| Вариант1 | 8 | 10 | 1 | -7 | -2 | Решение 1 неравенства Ответ:3 | 16 | ||||
| Вариант2 | 20 | 7 | -0,5 | -4 | -8 | Решение 2 системы | 14 | ||||
| Вариант3 | 6 | 12 | -3 | 2 | 6 | или | 4 | ||||
| Вариант4 | 34 | 5 | -1 | -6 | 6 | или | 12 | ||||
doc4web.ru
Стартовая контрольная работа в 10 классе
Входная административная контрольная работа по алгебре в 10 классе.
Вариант 1.
- Сократите дробь .
- Решите неравенство 5х – 7 ≥ 7х – 5.
- Решите уравнение х2 – 10х + 25 = 0.
- Сравните 56,78 ? 106 и 5,687 ? 107.
- Решите систему уравнений:
- Постройте график функции у = 7х – 5 и найдите, при каких значениях х значения у не меньше – 40.
- В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
- Сократите дробь .
- Решите неравенство
Вариант 2
- Сократите дробь .
- Решите неравенство 3х – 8 ≥ 8х – 3.
- Решите уравнение х2 – 14х + 49 = 0.
- Сравните 4,567 ? 109 и 45,76 ? 108.
- Решите систему уравнений:
- Постройте график функции у = 6х – 7 и найдите, при каких значениях х значения у не больше – 49.
- В арифметической прогрессии второй член равен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 21 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.
- Сократите дробь .
- Решите неравенство
Просмотр содержимого документа
«Стартовая контрольная работа в 10 классе »
kopilkaurokov.ru
Алгебра «Входной контроль» 10 Класс
Входной контроль, 10 класс
1 вариант
Разложите на множители квадратный трехчлен: .
Постройте график функции . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: .
Решите систему уравнений:
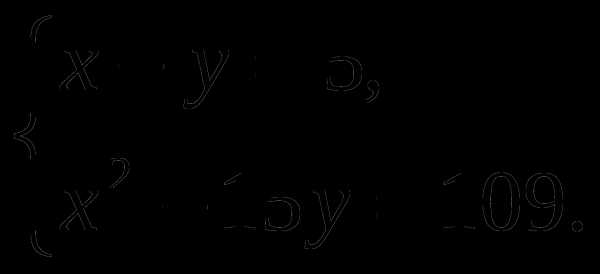
Упростите выражение:.
Решите уравнение:
 .
.
Входной контроль, 10 класс
2 вариант
Разложите на множители квадратный трехчлен: .
Постройте график функции . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: .
Решите систему уравнений:
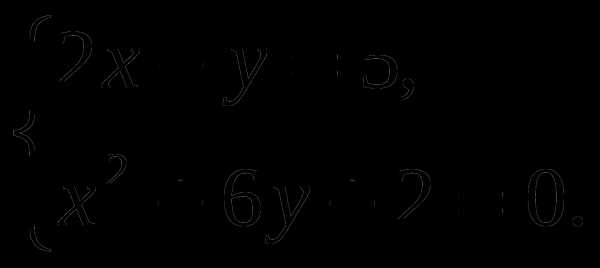
Упростите выражение:.
Решите уравнение: .
Входной контроль, 10 класс
вариант
Разложите на множители квадратный трехчлен: .
Постройте график функции . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: .
Решите систему уравнений:
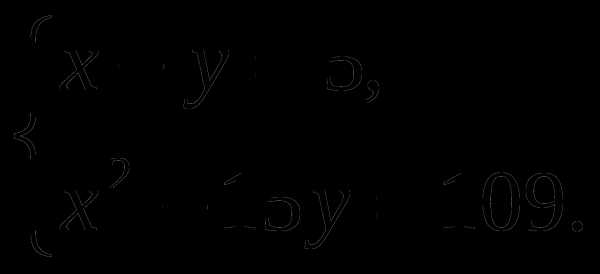
Упростите выражение:.
Решите уравнение:
 .
.
Входной контроль, 10 класс
вариант
Разложите на множители квадратный трехчлен: .
Постройте график функции . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: .
Решите систему уравнений:
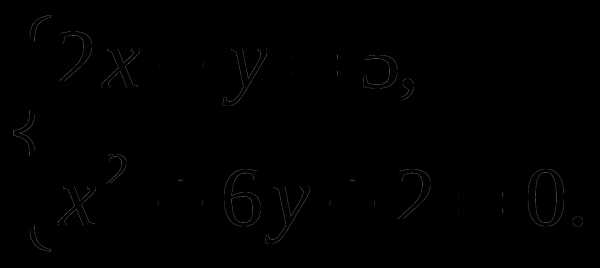
Упростите выражение:.
Решите уравнение: .
doc4web.ru
Контрольная работа по алгебре. 10 класс
4. Решить уравнение:
2 — 9х + 14 = 0
5. Периметр равностороннего треугольника равен 12 см.
Найти радиус описанной окружности.
6. Моторная лодка прошла против течения реки 84 км и вернулась в пункт
отправления, затратив на обратный путь на 8 часов меньше.
Найдите скорость
течения реки,
если скорость лодки в неподвижной воде равна 10 км/ч.
Ответ дайте в км/ч.
3 вариант
1. Чему равно значение выражения при а=1/4
2. Решить неравенство: х(х-3)(2х+7 ) 0
3. Решите систему уравнений
х + у =3
4. Найдите нули функции:
5. Периметр квадрата равен 12 см.
Найти радиус описанной окружности.
6. Моторная лодка прошла против течения реки 143 км и вернулась в пункт
отправления, затратив на обратный путь на 2 часа меньше.
Найдите скорость
лодки в неподвижной воде,
если скорость течения равна 1 км/ч.
Ответ дайте в км/ч.
infourok.ru
вводная контрольная работа по математике 10 класс
Вводная контрольная работа по математике 10 класс
Вариант 1.
В заданиях 1-10 напишите краткое решение и ответ.
Сократите дробь
Найдите наибольшее значение функции у = -х2 + 6х – 4.
Решите неравенство методом интервалов 3+х8-х≤0Найдите сумму сорока первых членов последовательности (bn), заданной формулой bn = 4п – 2
Найдите шестой член геометрической прогрессии (bn), если b1 = 0,81 и q = — 13В окружности с центром О проведена хорда MK. Найдите ∠MOK, если ∠OMK = 51°
Длина окружности равна 13π. Найдите радиус этой окружности.
Сторона ромба АВСD равна 5 см, ∠C = 120°. Найдите скалярное произведение векторов AB и ADИз прямоугольного листа бумаги, длина которого 36 см, а ширина – 29 см, хотят сделать развертку куба. Чему равна площадь поверхности этого куба?
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых
В заданиях 11-12 напишите полное решение и ответ.
Две сенокосилки, работая вместе, могут убрать поле за 7,5 ч, а работая порознь, первая сенокосилка убирает поле на 8 ч быстрее второй. За сколько часов могут убрать поле первая и вторая сенокосилки, работая по отдельности?
Каждое основание АD и BС трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов А и В этой трапеции пересекаются в точке К, биссектрисы внешних углов C и D пересекаются в точке Е. Найдите периметр трапеции ABCD, если длина отрезка КЕ равна 28.
Вариант 2.
В заданиях 1-10 напишите краткое решение и ответ.
Сократите дробь
Найдите наименьшее значение функции у = х2 — 8х + 7.
Решите неравенство методом интервалов 5-хх+7≥0Найдите сумму шестидесяти первых членов последовательности (bn), заданной формулой bn = 3п — 1.
Найдите седьмой член геометрической прогрессии (bn), если b1 = -32 и q = 12.
Точки B,D и N лежат на окружности с центром О. Найдите ∠BOD, если ∠BND =48°
Длина окружности равна 26π. Найдите радиус этой окружности.
Сторона ромба MNPK равна 3 см, ∠Р = 60°. Найдите скалярное произведение векторов MN и MKИз прямоугольного листа бумаги, длина которого 36 см, а ширина – 27 см, хотят
сделать развертку куба. Чему равна площадь поверхности этого куба?
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
В заданиях 11-12 напишите полное решение и ответ.
Две бригады трактористов, работая вместе, могут вспахать поле за 3 ч. Работая порознь, первая бригада вспахивает поле на 4 ч быстрее второй. За сколько часов могут вспахать поле первая и вторая бригады, работая по отдельности?
Каждое основание АD и BС трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов А и В этой трапеции пересекаются в точке F, биссектрисы внешних углов C и D пересекаются в точке M. Найдите периметр трапеции ABCD, если длина отрезка FM равна 26.
Задания 1- 10 оцениваются 1 баллом, задания 11 и 12 от 0 до 3 баллов.
Максимальное количество баллов – 16
«5» — 13-16 баллов
«4» — 9-12 баллов (включая 2 балла по геометрии)
«3» — 6-8 баллов (включая 1 балл по геометрии)
«2» менее 6 баллов
Приложенные файлы
profhelp.net
Входная контрольная работа по алгебре 10 класс, Закатилова Ирина Павловна
1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
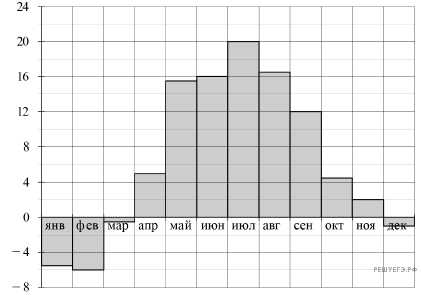
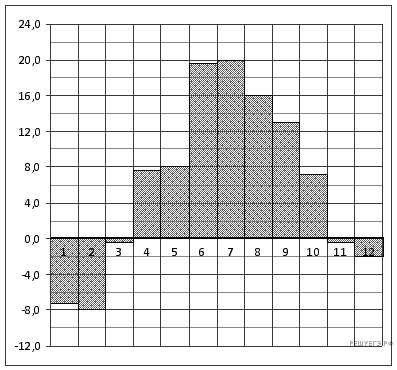
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?
3.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
4. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
5.Найдите значение выражения
6.Решите на выбор одно из неравенств системы:
7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пустькм/ч — скорость моторной лодки, тогда скорость лодки по течению равна км/ч, а скорость лодки против течения равна км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
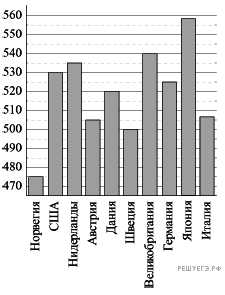
2.На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.
3.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Решите уравнение
5.Найдите значение выражения
6. Решите на выбор одно из неравенств системы:
7.Решение.
Область определения уравнения задается соотношением. На области определения имеем:
Оба найденный решения удовлетворяют условию , меньший из них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
|
www.prodlenka.org