Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению…
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени. Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
educon.by
Основные формулы тригонометрии | umath.ru
1. Определения синуса, косинуса, тангенса и котангенса угла.
Синус угла (обозначается ) – ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинус угла (обозначается ) – абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенс угла (обозначается ) – отношение синуса угла к его косинусу, т.е.
Котангенс угла (обозначается ) – отношение косинуса угла к его синусу, т.е.
2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :
Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом функции:Число является наименьшим положительным периодом синуса и косинуса, а число – наименьшим положительным периодом тангенса и котангенса.
Для любого целого справедливы равенства
5. Формулы сложения:
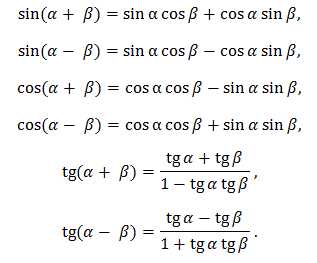
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10. Формулы суммы и разности косинусов:
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:
umath.ru
основные понятия, история :: SYL.ru
Синус, косинус, тангенс – при произнесении этих слов в присутствии учеников старших классов можно быть уверенным, что две трети из них потеряют интерес к дальнейшему разговору. Причина кроется в том, что основы тригонометрии в школе преподаются в полном отрыве от реальности, а потому учащиеся не видят смысла в изучении формул и теорем.
В действительности данная область знаний при ближайшем рассмотрении оказывается весьма интересной, а также прикладной – тригонометрия находит применение в астрономии, строительстве, физике, музыке и многих других областях.
Ознакомимся с основными понятиями и назовем несколько причин изучить этот раздел математической науки.
История
Неизвестно, в какой момент времени человечество начало создавать будущую тригонометрию с нуля. Однако документально зафиксировано, что уже во втором тысячелетии до нашей эры египтяне были знакомы с азами этой науки: археологами найден папирус с задачей, в которой требуется найти угол наклона пирамиды по двум известным сторонам.
Более серьезных успехов достигли ученые Древнего Вавилона. На протяжении веков занимаясь астрономией, они освоили ряд теорем, ввели особые способы измерения углов, которыми, кстати, мы пользуемся сегодня: градусы, минуты и секунды были заимствованы европейской наукой в греко-римской культуре, в которую данные единицы попали от вавилонян.
Предполагается, что знаменитая теорема Пифагора, относящаяся к основам тригонометрии, была известна вавилонянам почти четыре тысячи лет назад.
Название
Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее – взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.
Например, в прошлом человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.
Основные понятия
Для освоения тригонометрии с нуля требуется понять и запомнить несколько основных терминов.
Синус некоторого угла – это отношение противолежащего катета к гипотенузе. Уточним, что противолежащий катет – это сторона, лежащая напротив рассматриваемого нами угла. Таким образом, если угол составляет 30 градусов, синус этого угла всегда, при любом размере треугольника, будет равен ½. Косинус угла – это отношение прилежащего катета к гипотенузе.
Тангенс – это отношение противолежащего катета к прилежащему (либо, что то же самое, отношение синуса к косинусу). Котангенс – это единица, деленная на тангенс.
Стоит упомянуть и знаменитое число Пи (3,14…), которое представляет собой половину длины окружности с радиусом в одну единицу.
Популярные ошибки
Люди, изучающие тригонометрию с нуля, совершают ряд ошибок – в основном по невнимательности.
Во-первых, при решении задач по геометрии необходимо помнить, что использование синусов и косинусов возможно только в прямоугольном треугольнике. Случается, что учащийся «на автомате» принимает за гипотенузу самую длинную сторону треугольника и получает неверные результаты вычислений.
Во-вторых, поначалу легко перепутать значения синуса и косинуса для выбранного угла: напомним, что синус 30 градусов численно равен косинусу 60, и наоборот. При подстановке неверного числа все дальнейшие расчёты окажутся неверными.
В-третьих, пока задача полностью не решена, не стоит округлять какие бы то ни было значения, извлекать корни, записывать обыкновенную дробь в виде десятичной. Часто ученики стремятся получить в задаче по тригонометрии «красивое» число и сразу же извлекают корень из трёх, хотя ровно через одно действие этот корень можно будет сократить.
Этимология слова «синус»
История слова «синус» поистине необычна. Дело в том, что буквальный перевод этого слова с латыни означает «впадина». Всё потому, что верное понимание слова затерялось при переводе с одного языка на другой.
Названия базовых тригонометрических функций произошли из Индии, где понятие синуса обозначалось словом «тетива» на санскрите — дело в том, что отрезок вместе с дугой окружности, на которую он опирался, походил на лук. Во времена расцвета арабской цивилизации индийские достижения в области тригонометрии были заимствованы, и термин перешел в арабский язык в виде транскрипции. Случилось так, что в этом языке уже было похожее слово, обозначающее впадину, и если арабы понимали фонетическую разницу между родным и заимствованным словом, то европейцы, переводящие научные трактаты на латынь, по ошибке буквально перевели арабское слово, никакого отношения к понятию синуса не имеющее. Им мы и пользуемся по сей день.
Таблицы значений
Существуют таблицы, в которые занесены числовые значения для синусов, косинусов и тангенсов всех возможных углов. Ниже представим данные для углов в 0, 30, 45, 60 и 90 градусов, которые необходимо выучить как обязательный раздел тригонометрии для «чайников», благо запомнить их довольно легко.
Если случилось так, что числовое значение синуса или косинуса угла «вылетело из головы», есть способ вывести его самостоятельно.
Геометрическое представление
Начертим круг, через его центр проведем оси абсцисс и ординат. Ось абсцисс располагается горизонтально, ось ординат – вертикально. Обычно они подписываются как «X» и «Y» соответственно. Теперь из центра окружности проведем прямую таким образом, чтобы между ней и осью X получился нужный нам угол. Наконец, из той точки, где прямая пересекает окружность, опустим перпендикуляр на ось X. Длина получившегося отрезка будет равна численному значению синуса нашего угла.
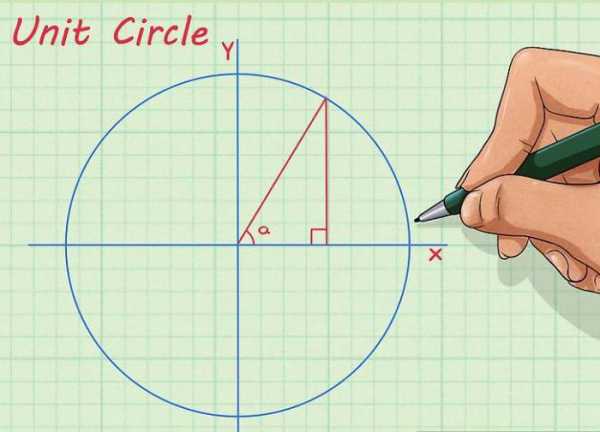Данный способ весьма актуален, если вы забыли нужное значение, например, на экзамене, и учебника по тригонометрии под рукой нет. Точной цифры вы таким образом не получите, но разницу между ½ и 1,73/2 (синус и косинус угла в 30 градусов) вы точно увидите.
Применение
Одними из первых специалистов, использующих тригонометрию, были моряки, не имеющие никакого другого ориентира в открытом море, кроме неба над головой. Сегодня капитаны кораблей (самолётов и других видов транспорта) не ищут кратчайший путь по звёздам, зато активно прибегают к помощи GPS-навигации, которая без использования тригонометрии была бы невозможна.
Практически в каждом разделе физики вас ждут расчёты с использованием синусов и косинусов: будь то приложение силы в механике, расчёты пути объектов в кинематике, колебания, распространение волн, преломление света – без базовой тригонометрии в формулах просто не обойтись.
Ещё одна профессия, которая немыслима без тригонометрии – это геодезист. Используя теодолит и нивелир либо более сложный прибор – тахиометр, эти люди измеряют разницу в высоте между различными точками на земной поверхности.
Повторяемость
Тригонометрия имеет дело не только с углами и сторонами треугольника, хотя именно с этого она начинала своё существование. Во всех областях, где присутствует цикличность (биологии, медицине, физике, музыке и т. д.) вы встретитесь с графиком, название которого наверняка вам знакомо — это синусоида.
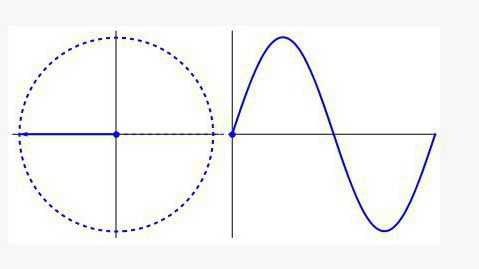Такой график представляет собой развёрнутую вдоль оси времени окружность и внешне похож на волну. Если вы когда-нибудь работали с осциллографом на занятиях по физике, вы понимаете, о чем идет речь. Как музыкальный эквалайзер, так и прибор, отображающий сердечные ритмы, используют формулы тригонометрии в своей работе.
В заключение
Задумываясь о том, как выучить тригонометрию, большинство учащихся средней и старшей школы начинают считать её сложной и непрактичной наукой, поскольку знакомятся лишь со скучной информацией из учебника.
Что касается непрактичности — мы уже увидели, что в той или иной степени умение обращаться с синусами и тангенсами требуется практически в любой сфере деятельности. А что касается сложности… Подумайте: если люди пользовались этими знаниями больше двух тысяч лет назад, когда взрослый человек имел меньше знаний, чем сегодняшний старшеклассник, реально ли изучить данную область науки на базовом уровне лично вам? Несколько часов вдумчивых занятий с решением задач – и вы достигнете своей цели, изучив базовый курс, так называемую тригонометрию для «чайников».
www.syl.ru
Основные виды тригонометрических уравнений
Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.
\(\blacktriangleright\) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^2(x)+bf(x)+c=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к квадратному уравнению.
Часто при решении таких уравнений используются
основные тождества: \[\begin{array}{|ccc|}
\hline \sin^2 \alpha+\cos^2 \alpha =1&& \mathrm{tg}\, \alpha \cdot
\mathrm{ctg}\, \alpha
=1\\ &&\\
\mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos
\alpha}&&\mathrm{ctg}\, \alpha
=\dfrac{\cos \alpha}{\sin \alpha}\\&&\\
1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} && 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&&\\
\hline
\end{array}\]
формулы двойного угла: \[\begin{array}{|lc|cr|}
\hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\
\sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\
& & & \cos{2\alpha}=1-2\sin^2 \alpha\\
\hline &&&\\
\mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\,
\alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha
= \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\
\hline
\end{array}\]
Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)
С помощью формулы \(\cos^2\alpha=1-\sin^2\alpha\) уравнение сводится к виду:
\(6\sin^2x+13\sin x+7=0\). Сделаем замену \(t=\sin x\). Т.к. область значений синуса \(\sin x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(6t^2+13t+7=0\). Корни данного уравнения \(t_1=-\dfrac76, \ t_2=-1\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:
\(\sin x=-1 \Rightarrow x=-\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)
С помощью формулы двойного угла для косинуса \(\cos
2\alpha=1-2\sin^2\alpha\) имеем:
\(\cos4x=1-2\sin^22x\). Сделаем эту подстановку и получим:
\(2\sin^22x+5\sin 2x+2=0\). Сделаем замену \(t=\sin 2x\). Т.к. область значений синуса \(\sin 2x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(2t^2+5t+2=0\). Корни данного уравнения \(t_1=-2, \ t_2=-\dfrac12\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену: \(\sin 2x=-\dfrac12 \Rightarrow x_1=-\dfrac{\pi}{12}+\pi n, \ x_2=-\dfrac{5\pi}{12}+\pi n, n\in\mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\, x+3\mathrm{ctg}\,x+4=0\)
Т.к. \(\mathrm{tg}\,x\cdot \mathrm{ctg}\,x=1\), то \(\mathrm{ctg}\,x=\dfrac1{\mathrm{tg}\,x}\). Сделаем замену \(\mathrm{tg}\,x=t\). Т.к. область значений тангенса \(\mathrm{tg}\,x\in\mathbb{R}\), то \(t\in\mathbb{R}\). Получим уравнение:
\(t+\dfrac3t+4=0 \Rightarrow \dfrac{t^2+4t+3}{t}=0\). Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:
\(\begin{cases} t^2+4t+3=0\\t\ne 0 \end{cases} \Rightarrow \left[\begin{gathered} \begin{aligned} &t_1=-3\\&t_2=-1 \end{aligned}\end{gathered}\right.\)
Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=-3\\ &\mathrm{tg}\,x=-1 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=-\mathrm{arctg}\,3+\pi n\\ &x=-\dfrac{\pi}4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^3(x)+bf^2(x)+cf(x)+d=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к кубическому уравнению.
Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: \[\begin{array}{|lc|cr|}
\hline &&&\\
\sin {3\alpha}=3\sin \alpha -4\sin^3\alpha &&&
\cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline
\end{array}\]
Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)
При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\):
\(12\sin^3x-9\sin x+11\sin x-3+11-22\sin^2 x=0\). Сделаем замену \(\sin x=t, \ t\in[-1;1]\):
\(6t^3-11t^2+t+4=0\). Подбором находим, что один из корней равен \(t_1=1\). Выполнив деление в столбик многочлена \(6t^3-11t^2+t+4\) на \(t-1\), получим:
\((t-1)(2t+1)(3t-4)=0 \Rightarrow\) корнями являются \(t_1=1, \ t_2=-\dfrac12, \ t_3=\dfrac43\).
Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\sin x=1\\&\sin x=-\dfrac12 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}2+2\pi n\\[1ex]&x=-\dfrac{\pi}6+2\pi n\\[1ex] &x=-\dfrac{5\pi}6+2\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=0}}, \quad a\ne 0,c\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin^2 x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos^2 x\) или на \(\sin^2 x\). Разделим, например, на \(\cos^2 x\):
\(a \ \dfrac{\sin^2x}{\cos^2x}+b \ \dfrac{\sin x\cos x}{\cos^2x}+c \ \dfrac{\cos^2x}{\cos^2x}=0 \Leftrightarrow a\mathrm{tg}^2\,x+b\mathrm{tg}\,x+c=0\)
Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm{tg}\,x\) сводится к квадратному уравнению:
\(at^2+bt+c=0\), способ решения которого вам известен.
Уравнения вида \[I’. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=d}}, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]
Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде
\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)
Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)
Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:
\(\sin^2x+3\sin x\cos x-4\cos^2x=0\). Разделим данное уравнение на \(\cos^2x\):
\(\mathrm{tg}^2\,x+3\mathrm{tg}\,x-4=0\) и сделаем замену \(t=\mathrm{tg}\,x, \ t\in\mathbb{R}\). Уравнение примет вид:
\(t^2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\). Разделим, например, на \(\cos x\):
\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac ba\)
Пример 6. Решить уравнение \(\sin x+\cos x=0\)
Разделим правую и левую части уравнения на \(\sin x\):
\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)
\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]
Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:
1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: \({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2 {\dfrac x2}+\cos^2 {\dfrac x2}\Big)}}\) данное уравнение сведется к уравнению \(I\):
Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Распишем \(\sin 2x=2\sin x\cos x, \ \cos 2x=\cos^2x-\sin^2 x, \ -1=-\sin^2 x-\cos^2x\). Тогда уравнение примет вид:
\((1+\sqrt3)\sin^2x+2\sin x\cos x+(1-\sqrt3)\cos^2x=0\). Данное уравнение с помощью деления на \(\cos^2x\) и замены \(\mathrm{tg}\,x=t\) сводится к:
\((1+\sqrt3)t^2+2t+1-\sqrt3=0\). Корнями этого уравнения являются \(t_1=-1, \ t_2=\dfrac{\sqrt3-1}{\sqrt3+1}=2-\sqrt3\). Сделаем обратную замену:
\(\left[ \begin{gathered} \begin{aligned}&\mathrm{tg}\,x=-1\\ &\mathrm{tg}\,x=2-\sqrt3 \end{aligned}\end{gathered}\right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac{\pi}4+\pi n\\[1ex] &x=\mathrm{arctg}\,(2-\sqrt3)+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{\alpha}=\dfrac{2\mathrm{tg}\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2} &&& \cos{\alpha}=\dfrac{1-\mathrm{tg}^2\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2}\\&&&\\ \hline \end{array}\] уравнение сведется к квадратному уравнению относительно \(\mathrm{tg}\, \dfrac x2\)
Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Сделаем подстановку \(\sin 2x=\dfrac{2\mathrm{tg}\,x}{1+\mathrm{tg}^2\,x}, \ \cos2x=\dfrac{1-\mathrm{tg}^2\,x}{1+\mathrm{tg}^2\,x}\) и замену \(\mathrm{tg}\,x=t\):
\(\dfrac{(\sqrt3+1)t^2+2t+1-\sqrt3}{1+t^2}=0 \Rightarrow (\sqrt3+1)t^2+2t+1-\sqrt3=0\) (т.к. \(1+t^2\geqslant 1\) при всех \(t\), то есть всегда \(\ne 0\))
Таким образом, мы получили то же уравнение, что и, решая первым способом.
3 СПОСОБ: при помощи формулы вспомогательного угла.
\[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac
a{\sqrt{a^2+b^2}}\]
Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end{array}\]
Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt{1^2+(-\sqrt3)^2}=2\):
\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)
Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \ \dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:
\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)
Решениями данного уравнения являются:
\(\left[ \begin{gathered} \begin{aligned} &2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex] &2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=\dfrac{\pi}{12}+\pi n\\[1.5ex] &x=-\dfrac{\pi}4+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)
Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.
\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[{\Large{a(\sin x\pm \cos x)+b\sin x\cos x+c=0}}, \text{где } a\ne 0, b\ne 0,\] то с помощью формулы \[{\large{(\sin x\pm\cos x)^2=1\pm2\sin x\cos x}} \ \ (*)\] данное уравнение можно свести к квадратному.
Для этого необходимо сделать замену \(t=\sin x\pm \cos x\), тогда \(\sin x\cos x=\pm \dfrac{t^2-1}2\).
Заметим, что формула \((*)\) есть не что иное, как формула сокращенного умножения \((A\pm B)^2=A^2\pm 2AB+B^2\) при подстановке в нее \(A=\sin x, B=\cos x\).
Пример 10. Решить уравнение \(3\sin 2x+3\cos 2x=16\sin x\cos^3x-8\sin x\cos x\).
Вынесем общий множитель за скобки в правой части: \(3\sin 2x+3\cos
2x=8\sin x\cos x(2\cos^2 x-1)\).
По формулам двойного угла \(2\sin x\cos x=\sin 2x, 2\cos^2x-1=\cos
2x\) имеем: \[3(\sin 2x+\cos 2x)=4\sin 2x\cos 2x\] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену \(t=\sin 2x+\cos 2x\), тогда \(\sin 2x\cos
2x=\dfrac{t^2-1}2\). Тогда уравнение примет вид: \[3t=2t^2-2 \Rightarrow 2t^2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).
По формулам вспомогательного аргумента \(\sin2x+\cos
2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned}
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex]
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned}
\end{gathered} \right. \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex]
&\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned}
\end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex]
&2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n
\end{aligned}
\end{gathered} \right. \Rightarrow \)
\(\Rightarrow \left[ \begin{gathered} \begin{aligned}
&x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex]
&x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n
\end{aligned}
\end{gathered} \right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:
\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\):
\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)
\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\):
\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)
\(\sin^2x-\cos^2x=-\cos2x\)
\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\):
\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)
\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)
\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\):
\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)
shkolkovo.net
Простейшие тригонометрические уравнения и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
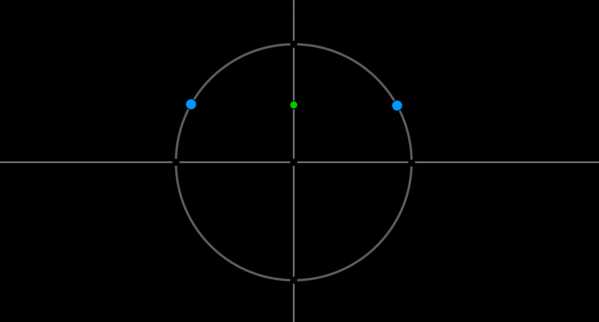
Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.
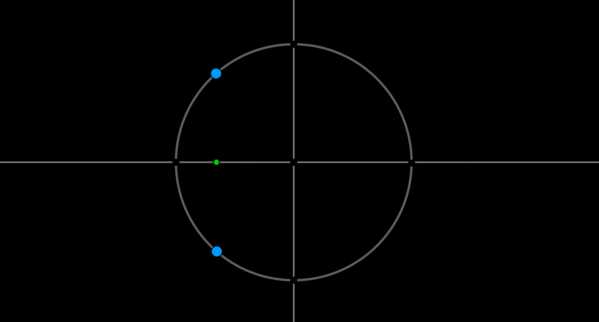
Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).
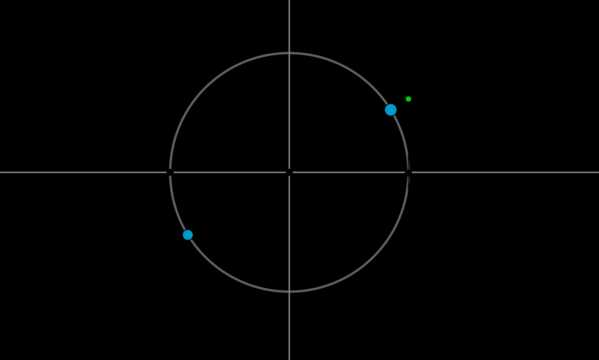
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).
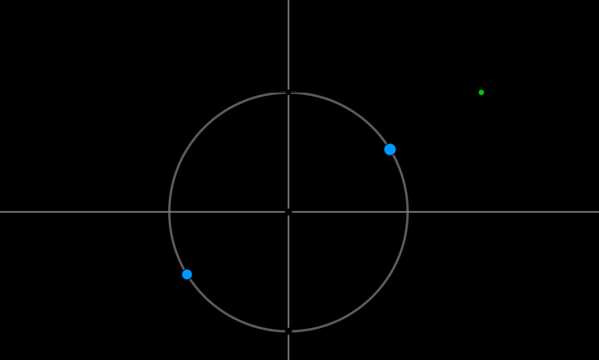
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin{array}{l|c|c}
\hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\
\hline &&\\
\sin x=a & -1\leq a\leq 1 & \left[
\begin{gathered}
\begin{aligned}
&x=\arcsin a+2\pi n\\
&x=\pi -\arcsin a+2\pi n
\end{aligned}
\end{gathered}
\right. \ \ , \ n\in \mathbb{Z}\\&&\\
\hline &&\\
\cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline
\end{array}\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \ n\in\mathbb{Z}\). Отметим эти точки на окружности:
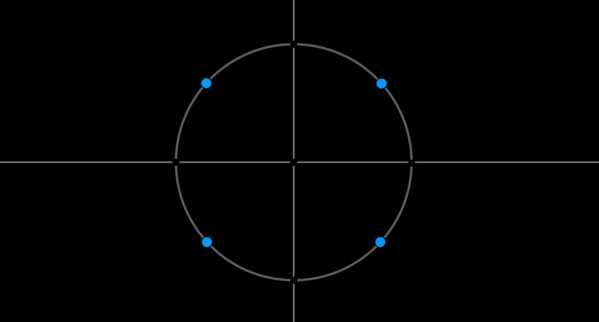
Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
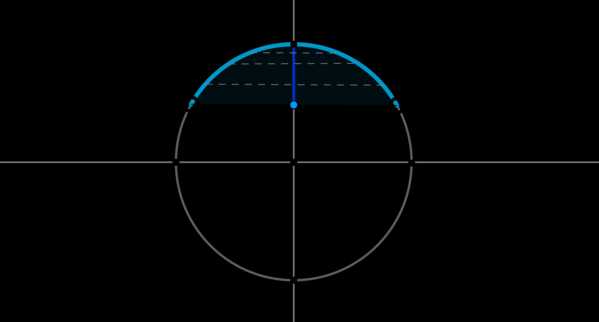
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x <\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
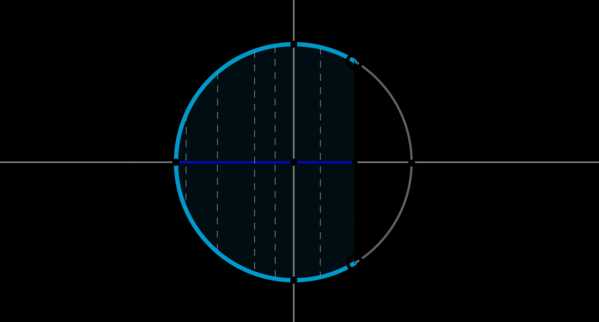
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x \geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x = \dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.
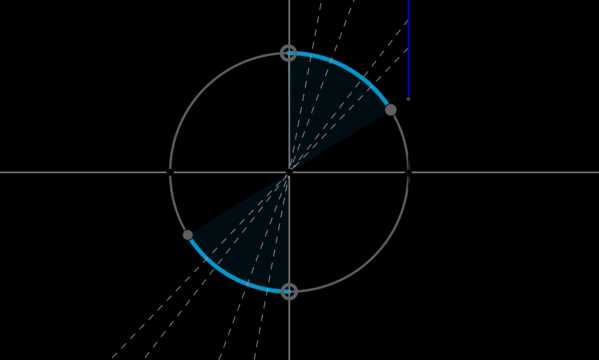
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x \leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x = \sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.
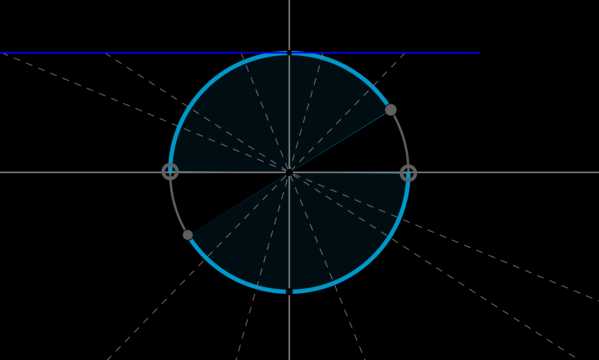
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности: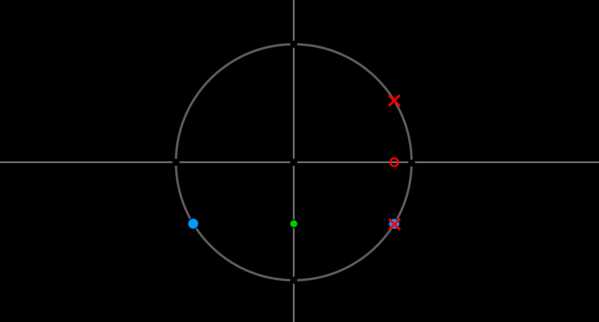
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n —
\text{ четном}\\ -\sin \alpha, \text{при } n — \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n —
\text{ четном}\\ -\cos \alpha, \text{при } n — \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\ x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c — \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases} \sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt] \cos \dfrac x2=1 \end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned} &\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt] &\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb{Z}\).
shkolkovo.net
?Тригонометрические формулы (более 100 шт.)
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).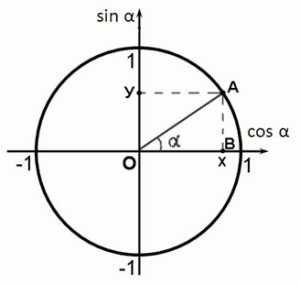
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. Знак функции зависит только от того, в какой из четвертей располагается аргумент.
Содержание статьи:
Тригонометрические функции угла `(-\alpha)`
При изменении знака аргумента с «+» на «-» только функция косинус не меняет своего значения. Она называется четной. Ее график симметричен относительно оси ординат.
Остальные функции (синус, тангенс, котангенс) нечетные. При смене знака аргумента с «+» на «-» их значение также изменяется на отрицательное. Их графики симметричны относительно начала координат.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Основные тригонометрические тождества
Основные тригонометрические тождества – это формулы, устанавливающие связь между тригонометрическими функциями одного угла (`sin \ \alpha, \ cos \ \alpha, \ tg \ \alpha, \ ctg \ \alpha`) и которые позволяют находить значение каждой из этих функций через любую известную другую.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac{\pi n} 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1{cos^2 \alpha}=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1{sin^2 \alpha}=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.
Вывод их можно получить из предыдущей группы (сложения и вычитания аргументов). Например, тождества двойного угла легко получить, заменив `\beta` на `\alpha`.
Формулы понижения степени
Формулы квадратов (кубов и т. д.) тригонометрических функций позволяют перейти от 2,3,… степени к тригонометрическим функциям первой степени, но кратных углов (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).
`sin^2 \alpha=\frac{1-cos \ 2\alpha}2,` ` (sin^2 \frac \alpha 2=\frac{1-cos \ \alpha}2)`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2,` ` (cos^2 \frac \alpha 2=\frac{1+cos \ \alpha}2)`
`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`
`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
`cos \ \alpha+sin \ \alpha=\sqrt{2} \ cos (\frac{\pi}4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt{2} \ sin (\frac{\pi}4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \ cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ ctg \2\alpha`
Следующие формулы преобразовывают сумму и разность единицы и тригонометрической функции в произведение.
`1+cos \ \alpha=2 \ cos^2 \frac{\alpha}2`
`1-cos \ \alpha=2 \ sin^2 \frac{\alpha}2`
`1+sin \ \alpha=2 \ cos^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1-sin \ \alpha=2 \ sin^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла.
`sin \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac{1 — tg^{2}\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 — tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac{\pi}{2}+ \pi n, n \in Z`
`ctg \ \alpha = \frac{1 — tg^{2}\frac{\alpha}{2}}{2tg\frac{\alpha}{2}},` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Формулы приведения
Формулы приведения можно получить, используя такие свойства тригонометрических функций, как периодичность, симметричность, свойство сдвига на данный угол. Они позволяют функции произвольного угла преобразовать в функции, угол которых находится в пределе между 0 и 90 градусами.
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Выражение одних тригонометрических функций через другие
`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
100 формул / Все формулы по тригонометрии
Основные тригонометрические тождества
Формулы, связывающие тригонометрические функции одного и того же аргумента:
\(sin^2x+cos^2x=1\)
\(tgx= \frac{sinx}{cosx}\)
\(ctgx= \frac{cosx}{sinx}\)
\(tgxctgx=1\)
\(tg^2x+1= \frac{1}{cos^2x}\)
\(ctg^2x+1= \frac{1}{sin^2x}\)
Формулы двойного аргумента (угла)
\(sin2x=2cosxsinx\)
\(sin2x= \frac{2tgx}{1+tg^2x}= \frac{2ctgx}{1+ctg^2x} = \frac{2}{tgx+ctgx}\)
\(cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x\)
\(cos2x= \frac{1-tg^2x}{1+tg^2x}= \frac{ctg^2x-1}{ctg^2x+1}= \frac{ctgx-tgx}{ctgx+tgx} \)
\(tg2x= \frac{2tgx}{1-tg^2x}= \frac{2ctgx}{ctg^2x-1}= \frac{2}{ctgx-tgx}\)
\(ctg2x= \frac{ctg^2x-1}{2ctgx}= \frac{ctgx-tgx}{2}\)
Формулы тройного аргумента (угла)
\(sin3x=3sinx-4sin^3x\)
\(cos3x=4cos^3x-3cosx\)
\(tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}\)
\(ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}\)
Формулы половинного аргумента (угла)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
\(tg \frac{x}{2}= \frac{1-cosx}{sinx}= \frac{sinx}{1+cosx}\)
\(ctg \frac{x}{2}= \frac{1+cosx}{sinx}= \frac{sinx}{1-cosx}\)
Формулы квадратов тригонометрических функций
\(sin^2x= \frac{1-cos2x}{2}\)
\(cos^2x= \frac{1+cos2x}{2}\)
\(tg^2x= \frac{1-cos2x}{1+cos2x}\)
\(ctg^2x= \frac{1+cos2x}{1-cos2x}\)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
Формулы кубов тригонометрических функций
\(sin^3x= \frac{3sinx-sin3x}{4}\)
\(cos^3x= \frac{3cosx+cos3x}{4}\)
\(tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}\)
\(ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}\)
Формулы тригонометрических функций в четвертой степени
\(sin^4x= \frac{3-4cos2x+cos4x}{8}\)
\(cos^4x= \frac{3+4cos2x+cos4x}{8}\)
Формулы сложения аргументов
\(sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta\)
\(cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta \)
\(tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}\)
\(ctg(\alpha + \beta)= \frac{-1 + ctg \alpha ctg \beta }{ctg \alpha + ctg \beta}\)
\(sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta\)
\(cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta\)
\(tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}\)
\(ctg(\alpha — \beta)= \frac{-1 — ctg \alpha ctg \beta }{ctg \alpha — ctg \beta}\)
Формулы суммы тригонометрических функций
\(sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}\)
\(cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}\)
\(tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{sin \alpha sin \beta}\)
\((sin\alpha + cos\alpha)^2= 1+sin2\alpha \)
Формулы разности тригонометрических функций
\(sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}\)
\(cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}\)
\(tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}\)
\((sin\alpha — cos\alpha)^2= 1-sin2\alpha \)
Формулы произведения тригонометрических функций
\(sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}\)
\(sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}\)
\(cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}\)
\(tg\alpha \cdot tg\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} = \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta}\)
\(ctg\alpha \cdot ctg\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} = \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta}\)
\(tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}\)
100formul.ru
